Preprint
Article
Motor Imagery Classification Using Trial Extension in Spatial Domain with Rhythmic Components of EEG
Altmetrics
Downloads
122
Views
87
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
27 July 2023
Posted:
28 July 2023
You are already at the latest version
Alerts
Abstract
A single paragraph of about 200 words maximum. Electroencephalography (EEG) accumulates the electrical activities of human brain. It is an easy and cost effective tool to characterize motor imagery (MI) task used in brain computer interface (BCI) implementation. The MI task is represented by short time trial of multichannel EEG. In this paper, the raw EEG is decomposed into a finite set of narrowband signals obtained from individual EEG channels using Fourier transformation based bandpass filter. Each of the subband signals represents narrowband rhythmic components which characterize the brain activities related to motor imagery. The subband signals are arranged to extent the dimension of EEG trial in spatial domain. The spatial features are extracted from the set of extended trials using common spatial pattern (CSP). An optimum number of features are used to classify the motor imagery tasks represented by EEG trials. Artificial neural network is used to classify MI tasks. The performance of the proposed method is evaluated using two publicly available benchmark datasets. The experimental results show that it performs better than the recently developed algorithms.
Keywords:
Subject: Computer Science and Mathematics - Signal Processing
1. Introduction
Brain-computer interface (BCI) is a modern technology that helps people to control external machines or devices without using any muscles or peripheral nerves [1]. It has potential applications in neuroscience and neuro-engineering. The recent application of BCI offers neurorehabilitation to assist stroke patients in restoring their impaired motor functions [2]. The usage of prosthetics, robots, and other electronic devices in neurorehabilitation tasks is fully controlled by motor imagination [3]. The non-invasive electroencephalography (EEG) is a comfortable and relatively easy method for BCI implementation. The BCI user's brain activity is typically measured by EEG [4]. In general, the analysis of EEG signal has been the subject of several studies, because of its ability to yield an objective mode of recording brain stimulation which is widely used in brain-computer interface researches with application in medical diagnosis and rehabilitation engineering.
Motor imagery (MI) is a common mental task that is widely used in BCI implementation [5]. In MI based BCI, a subject is required to perform an imagination in the brain corresponding to specific task. It provides high degree of freedom and it helps motor disabled people to communicate with the device by performing sequence of MI tasks. The recorded EEG signals related to MI are classified to translate into corresponding control command for different imaginary tasks like movement of hand, foot etc. [6]. In terms of neurophysiology, motor imagery accompanies attenuation or enhancement of rhythmical synchrony over the sensorimotor cortex. MI has been used to encourage neuroplasticity in a patient's brain after a stroke [3]. This paper focuses on EEG based classification of two motor imagery tasks.
Feature extraction over EEG signals for MI based BCI system is crucial to the classification performance. It is an important step in the process of electroencephalogram (EEG) signal classification. Any feature represents a distinguishing property, a recognizable measurement, and a functional component obtained from a section of a pattern. Extracted features are meant to minimize the loss of important information embedded in the signal. In addition, they also simplify the amount of resources needed to describe a huge set of data accurately. It is necessary to minimize the complexity of implementation, to reduce the computational cost, and to cancel the potential need to compress the information. Recently, a variety of methods have been widely used to extract the features from EEG signals, among these methods are fast Fourier transform (FFT) [7], time frequency distributions (TFD) [8], eigenvector methods (EM) [9], wavelet transform (WT) [10] and auto regressive method (ARM) [11].
The multivariate EEG signal is collected using a set of sensors spatially distributed over the scalp. The spatial filtering approach is very much effective to extract features from EEG. Spatial features were extracted using Common Spatial Pattern (CSP) filters in the cortical source space. The CSP algorithm has been widely used for feature extraction in EEG-based BCI systems for motor imagery (MI) [12]. As the EEG signals have noise and over-the-fitting issues, various regularized CSP algorithms are introduced to cater to these issues [13]. It is a feature extraction method that uses spatial filters to maximize the discriminability of two classes.
A number of methods including filter bank CSP (FBCSP) [14,15], subband CSP [16], sparse filter-bank CSP [17], and discriminative filter bank CSP [18] have been proposed to extract the features from the narrowband EEG signals for MI classification. The sparse representation of CSP feature is implemented in [19] for two classes of MI discrimination. These works promote the implementation of subband CSP to obtain the discriminative features, thereby yielding a reliable classification of MI tasks. Different subband decomposition approaches are already implemented including empirical mode decomposition (EMD) [20]. Although EMD is fully data adaptive approach, it requires a high computational cost. To resolve the problem of high computational cost, discrete wavelet transform (DWT) is widely used for signal decomposition into a finite set of subbands [21]. The multivariate wavelet transform (mWT) is introduced in [22] to decompose multichannel EEG signal followed by feature extraction. The wavelet transformation decomposes the signal with the nature of dyadic filterbank. It is difficult to obtain a subband with desired cut-off frequencies. The use of Fourier transform based bandpass filter resolves such problem.
The features obtained from narrowband EEG signals become more discriminative for classification [23]. The performance of MI-BCI significantly depends on the selection of effective frequency bands of the EEG signal from which the features are extracted [24]. To determine the changes of motor imagery task in narrowband signals, it is required to include the subband signals in the trials to extract the spatial features. Therefore, the subband approach with CSP method is implemented in this work to extract the effective features from the narrowband EEG. In addition to the narrowband signals, the wideband signal can contain some apparent features to enhance MI classification. Without considering this issue, the narrowband signals are used for feature extraction in the subband CSP-based methods.
The existing methods extract features from individual subband and the features obtained from all the subbands are combined. In that case, the co-variation of different subbands is not considered during feature extraction. It is noted that different frequency components are not independent to represent any motor imagery task and hence it is required to extract features by considering the co-variation of different narrowband signals. In this paper, multivariate EEG is decomposed into a finite set of subbands using Fourier transform based bandpass filter. The obtained narrowband signals are arranged to extend the size of trial. The CSP features are extracted from the extended trial. It includes the narrowband signals as individual row in the trial. Thus, all the narrowband signals as well as the fullband signal are considered together to derive the features used in effective MI classification system. The discrimination of MI tasks is performed by using artificial neural network.
The rest of the paper is organized as follows. Section II provides the description of data used in this study. The methodology is described in Section III. The experimental results are presented in Section IV and discussion is illustrated in section V. Finally, Section VI draws a conclusion about this study.
2. Data Description
The Publicly available two benchmark datasets are used to evaluate the performance of the proposed method. The datasets are described in the following subsections.
Dataset I: BCI Competition III dataset 4a is well known dataset to evaluate the performance of motor imagery classification. The data were recorded from five healthy subjects of age group 24 – 25 years, denoted as ‘aa’, ‘al’, ‘av’, ‘aw’, and ‘ay’ [25]. The subjects are properly instructed in priory about the experimental condition. The EEG data are recorded while they sat on a comfortable chair and their eye movements were avoided. The visual stimulus was presented for 3.5s and during that time duration, the participant was asked to perform three motor imagery tasks, i.e., right hand, left hand and right foot movement. Two motor imagery tasks of right hand and foot were taken into consideration for classification. Total 280 trials of EEG with 118 channels were recorded for each subject while they performed the motor imagery tasks according to the instruction. The trials were divided into training and testing groups in the dataset. The labeled training data are used in this study to evaluate the performance of the proposed method. The recorded signals are filtered using a band-pass filter between 0.05-200 Hz and sampled at 1000 Hz and quantized by 16 bit resolution. The EEG signal is downsampled at 100 Hz for further processing. The detail about the experimental setup is provided in the study [25]. In this study, the EEG trial of 2 s length (0.5 – 2.5 s) is extracted to obtain the meaningful feature to be used classification. It is consider that the first 0.5s (0–0.5 s) and last 0.5 s (3.5 – 4.0 s) are the duration for pre and post imagination.
Each trial of EEG recorded with 118 channels includes some irrelevant signal because all the channels are not required to discriminate two motor imagery tasks. The selection of relevant and minimum number of channels will be effective in terms of computational cost. The relevant zone of motor activity is motor cortex region including primary, supplementary and premotor cortex area [26]. It is required to select the electrodes placed at these areas. Several studies are performed to use a selected number of channels to design the MI-BCI. The 18 channels from the area of sensorimotor cortex are used in, while 30 channels are selected in [27,28] to classify two motor imagery tasks. Considering the previous studies [27,28], 30 channels in sensory-motor cortex area are selected for MI tasks classification as indicated in Figure 1. Throughout this paper, the multichannel EEG refers to the signals recorded from the selected 30 electrodes. These are “C5, C3, C1, C2, C4, C6, CP5, CP3, CP1, CP2, CP4, CP6, P5, P3, P1, P2, P4, and P6”.
Dataset II: Publicly available EEG data obtained from BCI Competition IV dataset I [29] is used to evaluate the performance of the proposed motor imagery classification method. The EEG data was collected from seven healthy subjects (labeled as ‘a’, ‘b’, ‘c’, ‘d’ ‘e’, ‘f’, and ‘g’). The motor imagery was performed without feedback at the time of recording. Each subject performed two motor imagery tasks among three of left hand movement, right hand movement, and foot movement. Every different MI task is treated as a different class. Visual cues were displayed for the duration of 4s during and each subject was required to perform the predefined motor imagery task. The number of total trials is 200 and each trail was randomized so that all subjects imagined two tasks equally. Trails were interleaved with 2s of a blank screen and 2s with a fixation cross shown in the center of the screen with superimposed on the cues. All EEG signal was recorded from 59 electrodes according to the international 10-20 system using BrainAmp MR plus amplifiers and an Ag/AgCl electrode cap. Signals were band-pass filtered between 0.05 and 200Hz and then digitized at 1000Hz with 16-bit resolution. The data used in this study is down-sampled at 100Hz.
It is well known that the center part of the brain is mostly active during the motor imagery. We have selected 23 channels out of 59 to be used in this study. The selected channels are: “FC5”, “FC3”, “FC1”, “FCZ”, “FC2”, “FC4”, “FC6”, “CZ”, “C3”, “C4”, “C1”, “C2”, “C5”, “C6”, “T7”, “T8”, “CCP3”, “CCP4z”, “CP5”, “CP1”, “CPZ”, “CP2”, “CP6” according to the 10-20 system [30]. It is also known that the time segment selection of motor imagery is a critical issue for EEG classification [24]. The EEG of 3.5s (0.5s to 4s) segment is used here. A zero phase Butterworth bandpass (8 – 30Hz) filter is applied to all the trial before any further processing.
3. Methods
A multiband approach to extract features from the EEG signal is implemented in this study to enhance the classification accuracy of motor imagery tasks in BCI paradigm. A block diagram of the proposed method is shown in Figure 2. The multichannel EEG signals are decomposed into a set of subbands corresponding to the rhythmic components. The subband signals are used to extend the EEG trials in spatial dimension. The common spatial pattern (CSP) based features are extracted from the newly generated trials. The artificial neural network (ANN) classifier is trained to create a classification model using the extracted features. The steps to implement the method are mentioned below:
- i.
- The multichannel EEG signal is decomposed into subbands. Each subband represents a rhythmic component.
- i.
- ii. Each trial extended in the spatial dimension by arranging the obtained subband signals.
- i.
- iii. Common spatial pattern (CSP) is applied on the newly generated trials to extract spatial features
- i.
- iv. Separate training and test sets of publicly available datasets are used to train ANN and evaluate the performance of the proposed method respectively.
3.1. Subband Decomposition
The narrowband signals containing the significant information about movement imagination enhances the MI classification performance. A stronger response to the specific motor imagery task is found in a narrowband signal rather than the signal with full bandwidth. Therefore, the optimum selection of subbands is very important for better accuracy of MI classification. The related studies claim that most brain activities exist within the frequency band 4-30 Hz [29]. The frequency band 4-40 Hz EEG signal is used in this study. Besides the traditional rhythmic components the beta is divided into smaller categories as low beta band from 13 to 21Hz, high beta band from 21 to 30Hz [31]. Many hypothetical functions have been suggested for the beta rhythms such as coordination among multiple representations in the cortex, inhibition of movement and motor planning, signaling of decision making, focusing action-selection network functions. Existence of several beta rhythms with different frequencies, topographies and with different functional properties presumes no single neuronal mechanism for their generation [31]. The multichannel EEG is decomposed using forth order Butterworth bandpass filter into four subbands with frequency ranges 7–12Hz, 13–20Hz, 21–30Hz and 31–35Hz which correspond the rhythmic components alpha, low beta, high beta and gamma respectively. The individual rhythmic component has direct effect on different brain activities including motor imagery activities. The selected narrowband rhythmic components are used to enhance the accuracy of MI classification.
3.2. Trial Extension
The traditional spatial filtering based feature extraction method is performed directly from the multichannel EEG signals. The subband signals contain relative more frequency-localized discriminative features for MI classification. The selected ranges of frequencies are suppressed from the EEG signals to enhance the classification performance [32,33], whereas, it is very hard to select such sub-bands after multiband decomposition. Considering the situation, all the usable subbands are kept and arranged to reconstruct the trials. The narrow band signals are used to produce more discriminative feature for EEG classification. The subbands obtained from each channel are spatially arranged to facilitate the feature extraction method using spatial filter. The inclusion of the subbands to regenerate the trial is performed in the spatial dimension.
The bandpass filtering scheme is applied here for the multiband decomposition of EEG data , where x(c) represent cth channel of EEG trial X. The subbands obtained from cth channel is denoted by xs(c), where c=1,2,…,C represents the channels’ index and s=1,2,…,4 is index of subbands. The frequency ranges of the usable four subbands are 7–12Hz, 13–20Hz, 21–30Hz and 31–35Hz. The cth channel x(c) can be represented with 4 subbands as
where each of is the sth subband of cth channel. It is noted that the each channel is added itself as a row in addition to the subbands in the reconstructed trial. The newly generated trial corresponding to EEG data X with C channels can be represented as
In the reconstructed EEG trial X’, the four subbands of any channel is appended as individual rows just after the channel itself as illustrated in Eq. (2). The single row of each channel is extended by 4 in the spatial dimension and hence the spatial dimension is extended to 5 times from the original one. The first subband of each channel illustrates the lowest frequency component filtered from that specific channel. The extended trial including the subbands obtained from individual channels is illustrated in Figure 3. In the newly reformed trial each row represents a narrow band signal in addition to the original channel of EEG signals.
3.3. Feature Extraction
Discriminative features play an important role in the BCI application. It is very challenging to find out potential features in the field of brain-computer interface (BCI). Recent studies have generally investigated how to modify existing methods or develop novel techniques for feature extraction because of features’ direct influence on the performance of the BCI system [34]. One of the most successful and well-known methods in BCI applications to extract features from multichannel EEG is common spatial pattern (CSP) [35]. The spatial filter is designed such that the variance of filtered data from one class is maximized while that of the other class is minimized. The resultant features minimize the intra-class variance while maximizing the inter-class variance. The CSP decomposes a multichannel EEG into several additive components. It increases the separation between two classes in terms of variance [35]. Such property of CSP makes it an effective spatial filter to classify MI tasks using multichannel EEG classification. The first CSP based spatial filter was implemented in [36] to effectively classify the movement-related EEG for BCI implementation.
Let Ei,1 and
denote the ith EEG training trials selected from the two different classes with dimensions C×N, where C represents the number of channels and N is the number of discrete samples. The CSP method derives the features based on the simultaneous diagonalization of the covariance matrices of both classes. It finds a spatial filter to transform the EEG data with a projection matrix, such that the ratio of variance between the two classes becomes maximized.
where
and Kq is the number of trials belonging to class q (q=1,2). The optimal solution of Eq. (3) can be obtained by solving a generalized eigenvalue problem. A matrix
including the spatial filters is formed by the eigenvectors corresponding to the M largest and smallest eigenvalues. For a given EEG sample E, the feature vector is constructed as v=[v1,v2,…,v2M] with entries [30]
where var(.) represents the variance. Log transformation is done in order to normalize the elements of vm. Thus obtained feature vector is used to train the ANN for training and classification.
3.4. Classification by ANN
Artificial neural network (ANN) has been widely used in pattern recognition problems for the last few decades [37]. The feed-forward neural network (FNN) is used in this study for MI classification of EEG signals. Such models are called feed-forward because the information only travels forward in the neural network, through the input neuron, then through hidden layers (single or multiple), and finally through the output neuron. It is represented by a combination of many simpler neurons and the connections among them. It works well for nonlinearly separable data. The neuron is the building block of FNN. When multiple neurons are connected in an effective way, it establishes the required relationship between the neurons to deal with nonlinear data.
A set of selected features derived from the EEG signals is fed into the neural network to perform the classification. The efficient configuration of FNN to address this problem includes one input, one hidden, and one output layer. The output layer contains one neuron to classify two classes of data. The number of neurons in the hidden later is chosen on the basis of maximizing the performance using grid search approach. The number of input neurons is subject-specific and determined by dimension of the feature vector. The target values are set to 1 and 0 to represent hand and foot movement imagery found in EEG signals respectively. The hyperbolic tangent sigmoid (HTS) function is used for the input- and hidden-layer transfer function. The Softmax function is assigned to the output layer. The definition of HTS and the Softmax function are given by Eq. (5) and (6) respectively.
where represents the hypothesis of the neuron and is the total number of neurons in the output layer. Scaled conjugate gradient backpropagation is used as a network training function to update the weight and bias values of FNN.
4. Experimental Results
Publicly available two datasets denoted by Dataset I and Dataset II are used to evaluate the performance of the proposed method. The BCI competition III (IVa) is referred here as Dataset I and BCI competition IV (I) is referred as Dataset II containing five and seven subjects respectively. Different experiments are conducted with these two datasets to illustrate the efficiency of the proposed approach for MI classification. Binary classification is considered in this study to discriminate two motor imagery tasks. After pre-processing, each channel of any EEG trial is decomposed into four subbands signals which are the four rhythmic components alpha, low beta, high beta and gamma. The components reflect different motor activities and hence have a vital role in MI classification. The obtained subbands i.e. rhythmic components are arranged in spatial dimension to implement the proposed trial extension method. The four components obtained from a channel are appended as individual row after the channel itself. Then the dimension of any trial becomes 5C×N, where C is the number of channels and N is the number of temporal samples.
The CSP is applied to the regenerated (extended) EEG trials to extract the spatial features. Thus computed features are applied to train the classifier leading to evaluate the performance of the proposed method by using artificial neural network (ANN). The k-fold (k=5) cross-validation is used to measure the algorithm’s performance in term of classification accuracy. For each subject, the dataset is divided randomly into k equal groups. The (k-1) groups are assigned for training and the rest one is for testing. The process is repetitive for k times. The accuracy is calculated by averaging the results of k repetitions. The performance is evaluated by classification accuracy Acc=100×(TC/TN) where TN and TC is the number of trails in test dataset and number of trials correctly recognized out of TN respectively. The performance of the proposed method including trial extension (iTE) with FfNN is evaluated with Dataset I. In addition to iTE the performance evaluation is also carried out excluding trial extension (eTE) approach. Each of the EEG channel is bandpass filtered using the frequency range 7Hz – 35Hz in eTE. It is implemented by applying CSP on the original trial (without extension) to obtain the spatial features leading to apply FNN for MI classification. The two pairs of CSP features and five neurons are assigned to the hidden layer of FNN are used for both the methods. The performances of iTE and eTE are illustrated in Figure 4.
It is observed that the average classification performance is enhanced by 2.52% with iTE compared to eTE method for Dataset I. The performances of iTE for individual subjects are relatively higher than that of eTE. The standard deviation of the MI classification accuracy with iTE is relatively lower than that with eTE. The similar results are presented in Figure 5 with Dataset II. It is observed that there is an improvement of MI classification performance using iTE compared to eTE, whereas the standard deviation with iTE is lower than with eTE.
The selection of the number of pairs of CSP filters is a vital factor for MI classification. On the other hand the use of the number of neurons in hidden layer is also a crucial factor to fixup the optimal performance of FNN. Both the factors are determined experimentally to maximize the classification accuracy. The scalp EEG is very much subject-sensitive tool to measure the neural response against motor activities. Hence, the number of pairs of CSP features and the number of neurons in hidden layer are selected through grid search approach for a specific subject. The features’ pairs and the number of neurons are gradually increased to observe the performance of FNN. The maximum accuracy is spotted in the grid as illustrated in Figure 6. The numbers of neurons as well as the features’ pairs corresponding to the maximum accuracy are selected as usable factors to train the FNN for the specific subject. The similar method is repeated for each subject of both datasets to obtain the maximal performance of the proposed algorithm. Thus the parameters are tuned to maximize the performance of MI classification with iTE and it is termed as iTE-tP (iTE with tuned parameters). In case of subject ‘aa’ of Dataset I, the maximum classification accuracy is obtained with 3 pairs of CSP features and 6 neurons used in hidden layers of FNN as illustrated in Figure 6.
The performance of iTE-tP is compared with iTE as well as eTE methods for Dataset I as illustrated in Table 1.
It is observed that the proposed method iTE-tP outperforms the other two approaches. The average MI classification accuracy over five subjects with iTE-tP is 93.88% which is higher than both iTE (90.12%) and eTE (87.64%). The performance of the proposed iTE-tP method is enhanced by 3.76% and 5.24% compared to iTE and eTE methods respectively. There is a significant improvement of MI classification performance with respect to iTE and eTE. The statistical significant analysis is also performed to illustrate the superiority of the proposed method iTE-tP. Statistical test is performed to measure the significance of the proposed method. Tukey-Kramer based post-hoc test [38] suggests that the proposed iTE-tP method achieved significantly higher accuracy across 5 subjects for motor imagery classification than the other methods (iTE-tP vs iTE: p<0.05, iTE-tP vs eTE: p<0.002)
The performances of iTE-tP, iTE as well as eTE based methods with Dataset II are illustrated in Table 2.
The proposed tuned parameter based method (iTE-tP) exhibits maximum classification accuracy among the mentioned three methods. Its accuracy is enhanced by about 1.12% and 4.58% with respect to iTE and eTE methods respectively. The 100% MI classification accuracy is achieved using iTE-tP method for the subject ‘e’. Although the maximum classification accuracy for subject ‘b’ is achieved by iTE the average MI classification accuracy (91.55%) is accomplished by the proposed iTE-tP. Tukey-Kramer based post-hoc test [38] suggests that the proposed iTE-tP method achieved significantly higher accuracy across 5 subjects for motor imagery classification than the other methods (iTE-tP vs iTE: p>0.06, iTE-tP vs eTE: p<0.002).
5. Discussion
Publicly available two datasets (Dataset I and Dataset II) are used to evaluate the performance of the method introduced in this study. The Dataset I i.e. BCI Competition III (IVa) is used in several recently reported methods to evaluate the MI classification performance [39,40,41,42]. The comparative performances in terms of classification accuracy of the proposed method with Dataset I are illustrated in Table 5. The average classification accuracy of the proposed approach iTE-tP over all subjects is 93.88%. The performance of this method is compared with the methods implemented using regularized Riemannian features (RRF) [43] and sparse group representation model (SGRM) of the CSP features [19]. The average classification accuracies of RRF and SGRM with dataset III (4a) are 87.21% and 77.70%, respectively. It is noted that the Riemannian manifold-based feature is used in regularized Riemannian features (RRF) [43] method rather than CSP. The attractor metagene-based feature selection is used in [19] with proper parameter optimization of SVM (AM-SVM) to implement the MI classification for BCI application with an average accuracy of 85.00%. There is an improvement in classification accuracy (92.20%) using neighborhood component analysis based feature selection (NCFS) [24]. It is observed that SSCSP method [40] uses sparse CSP to obtain an accuracy of 73.36%. The spatial regularization of CSP is implemented in SRCSP [38] with a classification accuracy of 76.37% using BCI Competition III (4a) dataset. The transfer kernel common spatial pattern (TKCSP) is introduced by Dai et al. [42]. The proposed method outperforms TKCSP by 13.44% in terms of classification accuracy. The accuracy with unsupervised discriminative feature selection (UDFS) based method [34] is 89.86%. The average performance of iTE-tP across all subjects in Dataset I is 93.88% which is at least 1.68% higher than that of all the recently reported works illustrated in Table 3.
Friedman’s ANOVA is performed to study the significance level. The test is performed to detect the differences in the performances of the various methods. According to the result of Friedman’s ANOVA, the methods have a significant main effect on classification accuracy (p<0.05). To test the statistical significance of the methods mentioned in Table 3, the Tukey–Kramer-based post-hoc test is performed. Based on the results of this statistical test, the proposed method iTE-tP achieves more significant improvement of performance for MI-BCI over the subjects than other methods (iTE-tP vs. RRF: p<0.03; iTE-tP vs. SGRM: p<0.02; iTE-tP vs. SSCSP: p<0.01; iTE-tP vs. SRCSP: p<0.03; iTE-tP vs. TKCSP: p<0.03; iTE-tP vs. AM-SVM: p<0.04; iTE-tP vs. UDFS: p<0.04; iTE-tP vs. NCFS: p>0.06; iTE-tP vs. eTE: p<0.002). The EEG trial extension using narrowband signals of individual channels has a significant role in the improvement of classification accuracy. The narrowband features as well as the selection of the number of CSP features improves the classifier performance. It is also observed that the proposed iTE-tP approach outperforms the recently reported algorithms.
The MI classification performance in term of accuracy the proposed method is compared with a number of recently reported methods using Dataset II. There are seven subjects (namely a, b, c, d, e, f, g) in the dataset, whereas, only four (a, b, f, g) of them are used to evaluate the performances in several algorithms [44,45,46,47,48]. The classification accuracies of these four subjects are illustrated in Table 4. The maximum average classification accuracy (89.53%) over the mentioned four subjects is achieved using iTE-tP. It is higher than any other methods reported in Table 4. The average accuracy of the method VaS-SVMlkis 87.72% which is 1.81% lower than that of iTE-tP. The performance of proposed method iTE-tP is compared to noise assisted multivariate EMD (NA-MEMD) [44], correlation-based channel selection with regularized CSP features (CCS-RCSP) [45], channel selection using correlation coefficient with features extraction by filter-bank CSP (CC-FBCSP) [46] and channel selection time domain parameters and correlation coefficient (TDP-CC) [47]. The non-stationary property is considered to calculate CSP (NS-CSP) in [49] and bi-spectrum based channel selection implemented in [50]. The performance of iTE-tP is also compared with [49] and [50]. The MI classification accuracy of iTE-tP is higher than that of all algorithms as mentioned in Table 4.
The 83.30% of classification accuracy is achieved for four subjects by using NA-MEDM based method in [44]. Its accuracy is 6.23% lower than that of the proposed iTE-tP. With NA-MEMD the IMFs effective for MI classification are selected heuristically, whereas, all the subbands within the specified frequency band are used in the proposed method and hence the performance is improved.
The channel selection based MI classification methods recently draw attention of the related research community. The performances of proposed methods are compared with recently developed three algorithms described in [45,46,47] as illustrated in Table 4. The effective EEG channels are selected using correlation based method, correlation coefficient, time domain parameter with correlation coefficient in CCS-RCSP [45], CC-FBCSP [46] and TDP-CC [47] respectively. The CSP based feature has been used in all of the three methods. The average classification accuracy of the proposed iTE-tP method is at least 5.13% higher than any one of the channel selection based approaches [45,46,47]. The proposed methods emphasizes on the extraction of potential features from trials which are regenerated using narrowband signals of each channel. The components representing MI task are localized in frequency scale and hence the performance of MI classification is increased. The channel selection based methods [45,46,47] have only focused on the selection of effective channels rather than the extraction of distinctive features.
Statistical test is performed to measure the significance of the proposed method. Tukey-Kramer based post-hoc test [38] suggests that the proposed iTE-tP achieved significantly higher accuracy across four subjects for motor imagery classification than the other methods (iTE-tP vs VaS-SVMlk: p>0.052, iTE-tP vs NA-MEMD: p<0.05; iTE-tP vs, CCS-RCSP: p<0.04, iTE-tP vs CC-FBCSP: p<0.04, iTE-tP vs TDP-CC: p<0.05, iTE-tP vs NS-CSP: p<0.01, iTE-tP vs BCS-CSP: p<0.04, iTE-tP vs eTE: p<0.001).
The performance of the proposed method iTE-tP is evaluated using all of seven subjects of Dataset II as shown in Table 5. The frequency-optimized spatial region based CSP features are introduced in (LRFCSP) [51]. The effective features are obtained from the selected spatial regions. Feng et al. proposed a novel correlation-based time window selection (CTWS) algorithm to solve the problem of fixed time window of the MI-based BCIs system [52]. The frequency-optimized features perform for MI classification. The few local regions are selected to derive the optimum set of features to improve the classification performance. The subspace optimization based feature has been used to attain optimal performance. The average MI classification accuracies over seven subjects of recently developed algorithms CTWS [52], LRFCSP [51] and VaS-SVMlk [48] are compared with iTE-tP as illustrated in Table III. It is observed that the average classification accuracies of iTE-tP is higher than that of LRFCSP [51], CTWS [52] as well as VaS-SVMlk [48] over the seven subjects. The highest average accuracy (91.55%) is achieved by iTE-tP over all the method mentioned in Table 5.
Table 5.
Comparison of MI classification accuracy (%) of the proposed work with recently developed methods using all subjects of Dataset II.
Table 5.
Comparison of MI classification accuracy (%) of the proposed work with recently developed methods using all subjects of Dataset II.
| Subject | LRFCSP [51] | CTWS [52] | VaS-SVMlk [48] | eTE | Proposed iTE-tP |
| a | 87.40 | 83.00 | 92.50 | 83.45 | 94.14 |
| b | 70.00 | 67.00 | 77.00 | 60.88 | 78.08 |
| c | 67.40 | 85.50 | 82.70 | 76.44 | 84.89 |
| d | 92.90 | 93.00 | 96.40 | 90.43 | 97.78 |
| e | 93.40 | 99.00 | 97.20 | 92.68 | 100.00 |
| f | 88.80 | 85.50 | 88.80 | 79.54 | 91.04 |
| g | 93.20 | 81.00 | 92.60 | 81.88 | 94.86 |
| Mean | 84.70 | 84.86 | 89.60 | 80.76 | 91.55 |
| SD | 5.78 | 10.4 | 7.41 | 10.48 | 7.11 |
The maximum accuracy only for subject ‘c’ (85.50%) is attained by the method CTWS, whereas, the proposed method iTE-tP exhibits maximum accuracy for other six subjects. The maximum average accuracy is achieved by iTE-tP for seven subjects (shown in Table 4). The average classification accuracy (over seven subjects) of iTE-tP is 6.85%, 6.69% and 1.95% higher than that of LRFCSP [51] and CTWS [52] and VaS-SVMlk [48] respectively. The results imply the superiority of the proposed method iTE-tP over the seven subjects of Dataset II. The statistical test is performed to check the significance of the proposed method. Tukey-Kramer based post-hoc test [38] suggests that the proposed iTE-tP achieved significantly higher accuracy across the seven subjects for motor imagery classification than the other methods (iTE-tP vs LRFCSP: p<0.03; iTE-tP vs CTWS: p<0.03; iTE-tP vs VaS-SVMlk: p>0.05; iTE-tP vs eTE: p<0.002). The important reason of performance improvement of the proposed method is the integration of the rhythmic components of EEG signals in trial regeneration. The rhythmic components exhibit better representation of neural activities represented by scalp EEG signals. Hence, the features extracted from the proposed regenerated trials are more discriminative for MI classification.
5. Conclusions
A trial extension based feature extraction method is implemented in this paper for MI classification using EEG signals. The experimental evaluation is performed by publicly available Dataset I and Dataset II. With the first dataset, the 30 channels out of 118 are used to represent a two-class (right hand and right foot movement) MI task for EEG classification in the BCI paradigm. The multichannel EEG is decomposed into four subbands that include mu, low beta, high beta, and gamma within the frequency range of 7–35 Hz. The extracted subbands and the full-band signals of EEG channel are arranged to extend the trial dimension which is termed as trial regeneration. The common spatial pattern (CSP) based features are extracted from the EEG signals of extended trials and then feed-forward neural network is used for classification. CSP produces a high dimensional feature data. It is noted that the selection of the number of usable features and the number of hidden layer neurons are the crucial factors in MI classification. A subject dependent grid search approach is implemented to select number of features as well as the number of hidden neuros in FNN. The trial extension, the selection of features and number of hidden neurons enhance the MI classification accuracy of the proposed method.
A filter bank is designed to separate the narrowband rhythmic components containing the signal components usable for movement-related MI classification. In addition to the components, the EEG channel with full band (8–35 Hz) is also included in the trial. The inclusion of the fullband signal has a vital role in the discrimination of MI tasks. The scenario becomes clear when the performance of the proposed method is evaluated using publicly available EEG dataset. Different experimental evaluations are conducted for the two-class MI-based EEG classification problem. The obtained results are compared with different recently developed algorithms and it is observed that the proposed trial extension enhances the MI classification accuracy. The foregoing therefore establishes the superiority of the proposed method.
Author Contributions
Conceptualization, M. K. I. Molla; methodology, M. K. I. Molla; software, Sakir Ahmed and A. M. M. Almassri; validation, M. K. I. Molla and Sakir Ahmed; formal analysis, M. K. I. Molla; investigation, A. M. M. Almassri; resources, H. Wagatsuma; data curation, Sakir Ahmed; writing—original draft preparation, Sakir Ahmed and M. K. I. Molla; writing—review and editing, H. Wagatsuma; visualization, Sakir Ahmed; supervision, M. K. I. Molla; project administration, H. Wagatsuma; funding acquisition, H. Wagatsuma. All authors have read and agreed to the submission version of the manuscript.
Funding
This work was supported in part by JSPS KAKENHI (16H01616, 17H06383) and JSPS Invitational Fellowships for Research in Japan (FY2019, ID: S19169).
Informed Consent Statement
Not applicable.
Data Availability Statement
All the data used in this study are publicly available.
Conflicts of Interest
The authors declare no conflict of interest.
References
- S. Gao, Y. Wang, X. Gao, and B. Hong, “Visual and auditory brain– computer interfaces,” IEEE Trans. Biomed. Eng., vol. 61, no. 5, pp. 1436–1447, May 2014.
- van Dokkum, L.; Ward, T.; Laffont, I. Brain computer interfaces for neurorehabilitation – its current status as a rehabilitation strategy post-stroke. Ann. Phys. Rehabilitation Med. 2018, 58, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Nuyujukian, P.; Fan, J.M.; Kao, J.C.; Ryu, S.I.; Shenoy, K.V. A High-Performance Keyboard Neural Prosthesis Enabled by Task Optimization. IEEE Trans. Biomed. Eng. 2015, 62, 21–29. [Google Scholar] [CrossRef] [PubMed]
- Lotte, F.; Bougrain, L.; Cichocki, A.; Clerc, M.; Congedo, M.; Rakotomamonjy, A.; Yger, F. A review of classification algorithms for EEG-based brain–computer interfaces: a 10 year update. J. Neural Eng. 2018, 15, 031005. [Google Scholar] [CrossRef] [PubMed]
- G. Pfurtscheller, C. Brunner, A. Schlögl, F. Lopes da Silva, "Mu rhythm (de)synchronization and EEG single-trial classification of different motor imagery tasks," NeuroImage, vol. 31, no. 1, pp: 153-159, May 2006.
- Wu, W.; Gao, X.; Hong, B.; Gao, S. Classifying Single-Trial EEG During Motor Imagery by Iterative Spatio-Spectral Patterns Learning (ISSPL). IEEE Trans. Biomed. Eng. 2008, 55, 1733–1743. [Google Scholar] [CrossRef]
- Faust, O.; Acharya, R.; Allen, A.; Lin, C. Analysis of EEG signals during epileptic and alcoholic states using AR modeling techniques. IRBM 2008, 29, 44–52. [Google Scholar] [CrossRef]
- C. Guerrero-Mosquera and A. N. Vazquez, “New approach in features extraction for EEG signal detection,” in Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC '09), pp. 13–16, September 2009.
- Übeyli, E.D. Analysis of EEG signals by combining eigenvector methods and multiclass support vector machines. Comput. Biol. Med. 2008, 38, 14–22. [Google Scholar] [CrossRef]
- Cvetkovic, D.; Übeyli, E.D.; Cosic, I. Wavelet transform feature extraction from human PPG, ECG, and EEG signal responses to ELF PEMF exposures: A pilot study. Digit. Signal Process. 2008, 18, 861–874. [Google Scholar] [CrossRef]
- Subasi, A.; Kiymik, M.K.; Alkan, A.; Koklukaya, E. Neural Network Classification of EEG Signals by Using AR with MLE Preprocessing for Epileptic Seizure Detection. Math. Comput. Appl. 2005, 10, 57–70. [Google Scholar] [CrossRef]
- Lemm, S.; Blankertz, B.; Curio, G.; Muller, K.-R. Spatio-spectral filters for improving the classification of single trial EEG. IEEE Trans. Biomed. Eng. 2005, 52, 1541–1548. [Google Scholar] [CrossRef]
- Samek, W.; Vidaurre, C.; Müller, K.-R.; Kawanabe, M. Stationary common spatial patterns for brain–computer interfacing. J. Neural Eng. 2012, 9, 026013. [Google Scholar] [CrossRef]
- Ang, K.K.; Chin, Z.Y.; Wang, C.; Guan, C.; Zhang, H. Filter Bank Common Spatial Pattern Algorithm on BCI Competition IV Datasets 2a and 2b. Front. Neurosci. 2012, 6, 39. [Google Scholar] [CrossRef]
- Higashi, H.; Tanaka, T. Simultaneous Design of FIR Filter Banks and Spatial Patterns for EEG Signal Classification. IEEE Trans. Biomed. Eng. 2012, 60, 1100–1110. [Google Scholar] [CrossRef]
- Novi, Q.; Guan, C.; Dat, T.H.; Xue, P. Sub-band common spatial pattern (SBCSP) for brain-computer interface. 3rd Int. IEEE/EMBS Conf. on Neural Engineering 2007, 204–207. [CrossRef]
- Zhang, Y.; Zhou, G.; Jin, J.; Wang, X.; Cichocki, A. Optimizing spatial patterns with sparse filter bands for motor-imagery based brain–computer interface. J. Neurosci. Methods 2015, 255, 85–91. [Google Scholar] [CrossRef]
- Thomas, K.P.; Guan, C.; Lau, C.T.; Vinod, A.P.; Ang, K.K. A New Discriminative Common Spatial Pattern Method for Motor Imagery Brain–Computer Interfaces. IEEE Trans. Biomed. Eng. 2009, 56, 2730–2733. [Google Scholar] [CrossRef]
- Jiao, Y.; Zhang, Y.; Chen, X.; Yin, E.; Jin, J.; Wang, X.Y.; Cichocki, A. Sparse Group Representation Model for Motor Imagery EEG Classification. IEEE J. Biomed. Heal. Informatics 2018, 23, 631–641. [Google Scholar] [CrossRef]
- M. K. I. Molla, M. R. Islam, T. Tanaka, T. Rutkowski, “Artifact suppression from EEG signals using data adaptive time domain filtering,” Neurocomputing, vol. 97, no. 0, pp: 297 – 308, Nov 2012.
- Q. Zhang, A. Benveniste, “Wavelet networks,” IEEE Transactions on Neural Networks, vol. 3, no. 6, pp: 889-898, Nov 1992.
- Oweiss, K.G.; Anderson, D.J. Noise reduction in multichannel neural recordings using a new array wavelet denoising algorithm. Neurocomputing 2001, 38-40, 1687–1693. [Google Scholar] [CrossRef]
- M. R. Islam, T. Tanaka and M. K. I. Molla, “Multiband Tangent Space Mapping and Feature Selection for Classification of EEG during Motor Imagery”, Journal of Neural Engineering, 15(4), May 2018.
- M. K. I. Molla, A. A. Shiam, M. R. Islam and T. Tanaka, "Discriminative Feature Selection Based Motor Imagery Classification Using EEG Signal" IEEE Access, Vol. 8, pp: 98255-98265, May, 2020.
- G. Dornhege, B. Blankertz, G. Curio, and K. R. Müller, Boosting bit rates in non-invasive EEG single-trial classifications by feature combination and multi-class paradigms, IEEE Trans. Biomed. Eng., 51, 993-1002, 2004.
- He, L.; Hu, D.; Wan, M.; Wen, Y.; von Deneen, K.M.; Zhou, M. Common Bayesian Network for Classification of EEG-Based Multiclass Motor Imagery BCI. IEEE Trans. Syst. Man, Cybern. Syst. 2015, 46, 843–854. [Google Scholar] [CrossRef]
- Sreeja, S.R.; Rabha, J.; Samanta, D.; Mitra, P.; Sarma, M. Classification of Motor Imagery Based EEG Signals Using Sparsity Approach. Proc. of International Conference on Intelligent Human Computer Interaction 2017, 47–59. [Google Scholar] [CrossRef]
- J. Rabha, K. Y. Nagarjuna, D. Samanta, P. Mitra and M. Sarma, Motor imagery EEG signal processing and classification using machine learning approach, Proc. of International Conference on New Trends in Computing Sciences (ICTCS), 61-66, 2017.
- Yeh, C.-Y.; Su, W.-P.; Lee, S.-J. An efficient multiple-kernel learning for pattern classification. Expert Syst. Appl. 2013, 40, 3491–3499. [Google Scholar] [CrossRef]
- G. Klem, H. Lüders, H. Jasper HH, C. Elger, “The ten-twenty electrode system of the International Federation,” Electroencephalograph clinical neurophysiology, vol. 52, no. 3, pp: 3-6,1999.
- Juri, D. Kropotov, "Functional Neuromarkers for Psychiatry–Applications for Diagnosis and Treatment", Science Direct Publication, 2016.
- Hsu, K.-C.; Yu, S.-N. Detection of seizures in EEG using subband nonlinear parameters and genetic algorithm. Comput. Biol. Med. 2010, 40, 823–830. [Google Scholar] [CrossRef]
- Molla, K.I.; Tanaka, T.; Osa, T.; Islam, M.R. EEG signal enhancement using multivariate wavelet transform Application to single-trial classification of event-related potentials. IEEE Int. Conference on Digital Signal Processing 2015, 804–808. [Google Scholar] [CrossRef]
- Shiam, A. A.; Islam, M.R.; Tanaka, T.; Molla, M.K.I. Electroencephalography Based Motor Imagery Classification Using Unsupervised Feature Selection,” Proc. of Cyberworld, 2019.
- Zhang, Y.; Wang, Y.; Zhou, G.; Jin, J.; Wang, B.; Wang, X.; Cichocki, A. Multi-kernel extreme learning machine for EEG classification in brain-computer interfaces. Expert Syst. Appl. 2018, 96, 302–310. [Google Scholar] [CrossRef]
- Suefusa, K.; Tanaka, T. Asynchronous Brain–Computer Interfacing Based on Mixed-Coded Visual Stimuli. IEEE Trans. Biomed. Eng. 2017, 65, 2119–2129. [Google Scholar] [CrossRef]
- G. Bebis, M. Georgiopoulos, “Feed-forward neural networks.” IEEE Potentials 1994, 13, 27–31.
- M. K. I. Molla, N. Morikawa, M. R. Islam and T. Tanaka, “Data-adaptive Spatiotemporal ERP Cleaning for Single-trial BCI Implementation,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, Vol. 26, Issue 7, pp:1334 – 1344, June 2018.
- S. Selim, M. M. Tantawi, A. S. Howida, and A. Badr, “A CSP\AM-BA-SVM Approach for Motor Imagery BCI System,” IEEE Access, 6, pp. 49192–49208, 2018.
- Arvaneh, M.; Guan, C.; Ang, K.K.; Quek, H.C. Spatially sparsed common spatial pattern to improve BCI performance,” in Proc. of IEEE International Conference on Acoustics, Speech and Signal Processing 2011, 2412–2415. [CrossRef]
- Lotte, F.; Guan, C. Spatially regularized common spatial patterns for EEG classification,” in Proc. of 20th International Conference on Pattern Recognition 2010, 3712–3715. [Google Scholar] [CrossRef]
- Dai, M.; Zheng, D.; Liu, S.; Zhang, P. Transfer Kernel Common Spatial Patterns for Motor Imagery Brain-Computer Interface Classification. Comput. Math. Methods Med. 2018, 2018, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.; Lal, S.; Guesgen, H.W. Small Sample Motor Imagery Classification Using Regularized Riemannian Features. IEEE Access 2019, 7, 46858–46869. [Google Scholar] [CrossRef]
- Park, C.; Looney, D.; Rehman, N.U.; Ahrabian, A.; Mandic, D.P. Classification of Motor Imagery BCI Using Multivariate Empirical Mode Decomposition. IEEE Trans. Neural Syst. Rehabilitation Eng. 2012, 21, 10–22. [Google Scholar] [CrossRef] [PubMed]
- Jin, J.; Miao, Y.; Daly, I.; Zuo, C.; Hu, D.; Cichocki, A. Correlation-based channel selection and regularized feature optimization for MI-based BCI. Neural Networks 2019, 118, 262–270. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.; Chung, W. Optimal Channel Selection Using Correlation Coefficient for CSP Based EEG Classification. IEEE Access 2020, 8, 111514–111521. [Google Scholar] [CrossRef]
- Park, Y.; Chung, W. Selective Feature Generation Method Based on Time Domain Parameters and Correlation Coefficients for Filter-Bank-CSP BCI Systems. Sensors 2019, 19. [Google Scholar] [CrossRef]
- Wang, H.; Xu, T.; Tang, C.; Yue, H.; Chen, C.; Xu, L.; Pei, Z.; Dong, J.; Bezerianos, A.; Li, J. Diverse Feature Blend Based on Filter-Bank Common Spatial Pattern and Brain Functional Connectivity for Multiple Motor Imagery Detection. IEEE Access 2020, 8, 155590–155601. [Google Scholar] [CrossRef]
- Jin, J.; Liu, C.; Daly, I.; Miao, Y.; Li, S.; Wang, X.; Cichocki, A. Bispectrum-Based Channel Selection for Motor Imagery Based Brain-Computer Interfacing. IEEE Trans. Neural Syst. Rehabilitation Eng. 2020, 28, 2153–2163. [Google Scholar] [CrossRef]
- Park, Y.; Chung, W. Frequency-Optimized Local Region Common Spatial Pattern Approach for Motor Imagery Classification. IEEE Trans. Neural Syst. Rehabilitation Eng. 2019, 27, 1378–1388. [Google Scholar] [CrossRef]
- Feng, J.; Yin, E.; Jin, J.; Saab, R.; Daly, I.; Wang, X.; Hu, D.; Cichocki, A. Towards correlation-based time window selection method for motor imagery BCIs. Neural Networks 2018, 102, 87–95. [Google Scholar] [CrossRef]
- Molla, K.I.; Saha, S.K.; Yasmin, S.; Islam, R.; Shin, J. Trial Regeneration With Subband Signals for Motor Imagery Classification in BCI Paradigm. IEEE Access 2021, 9, 7632–7642. [Google Scholar] [CrossRef]
Figure 1.
Thirty electrodes encircled in green are selected out of 118 and used in this study for experimental evaluation.
Figure 1.
Thirty electrodes encircled in green are selected out of 118 and used in this study for experimental evaluation.
Figure 2.
Block diagram of the proposed MI classification system.
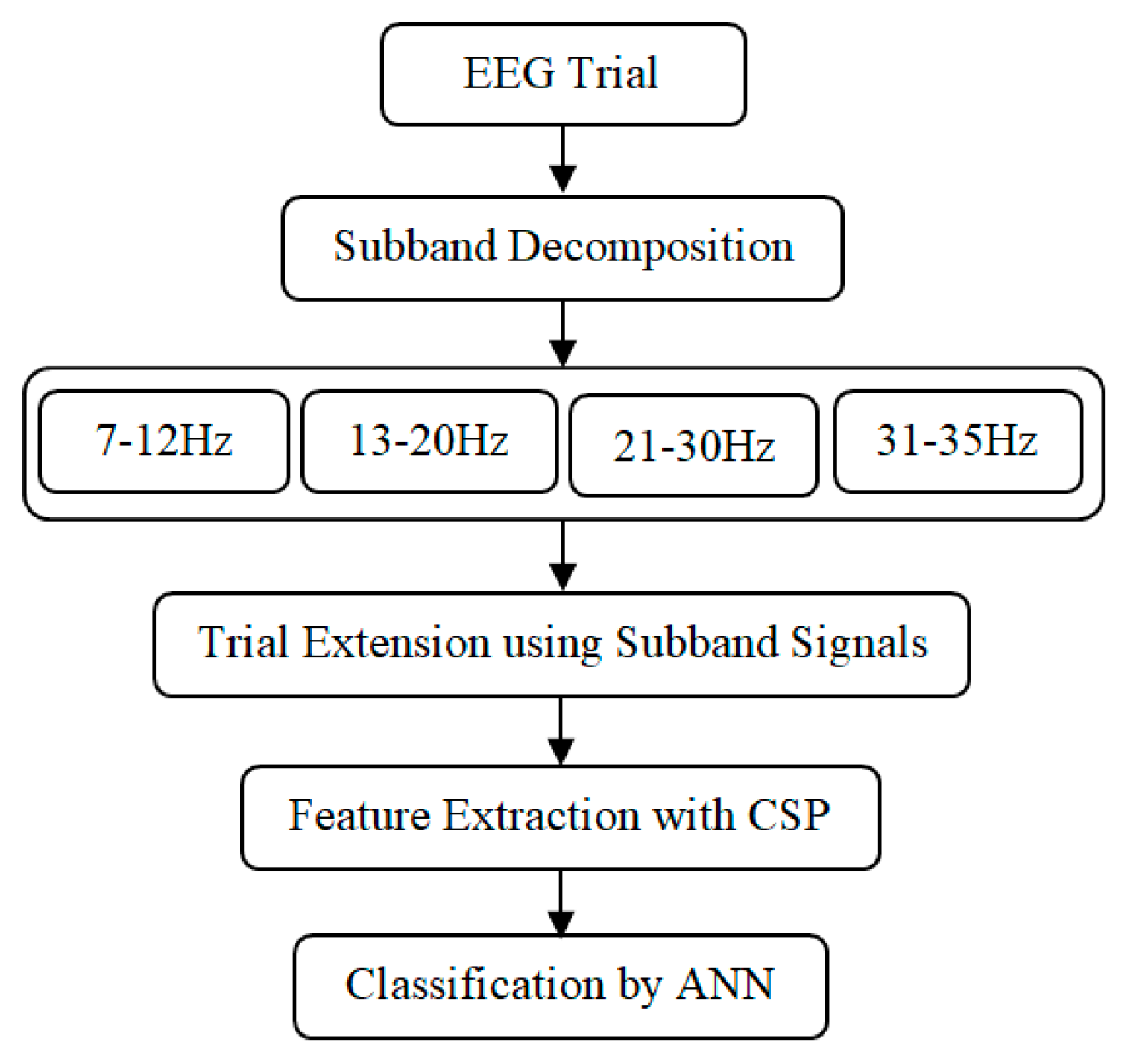
Figure 3.
Arrangement of subband signals used for trial extension in spatial domain.
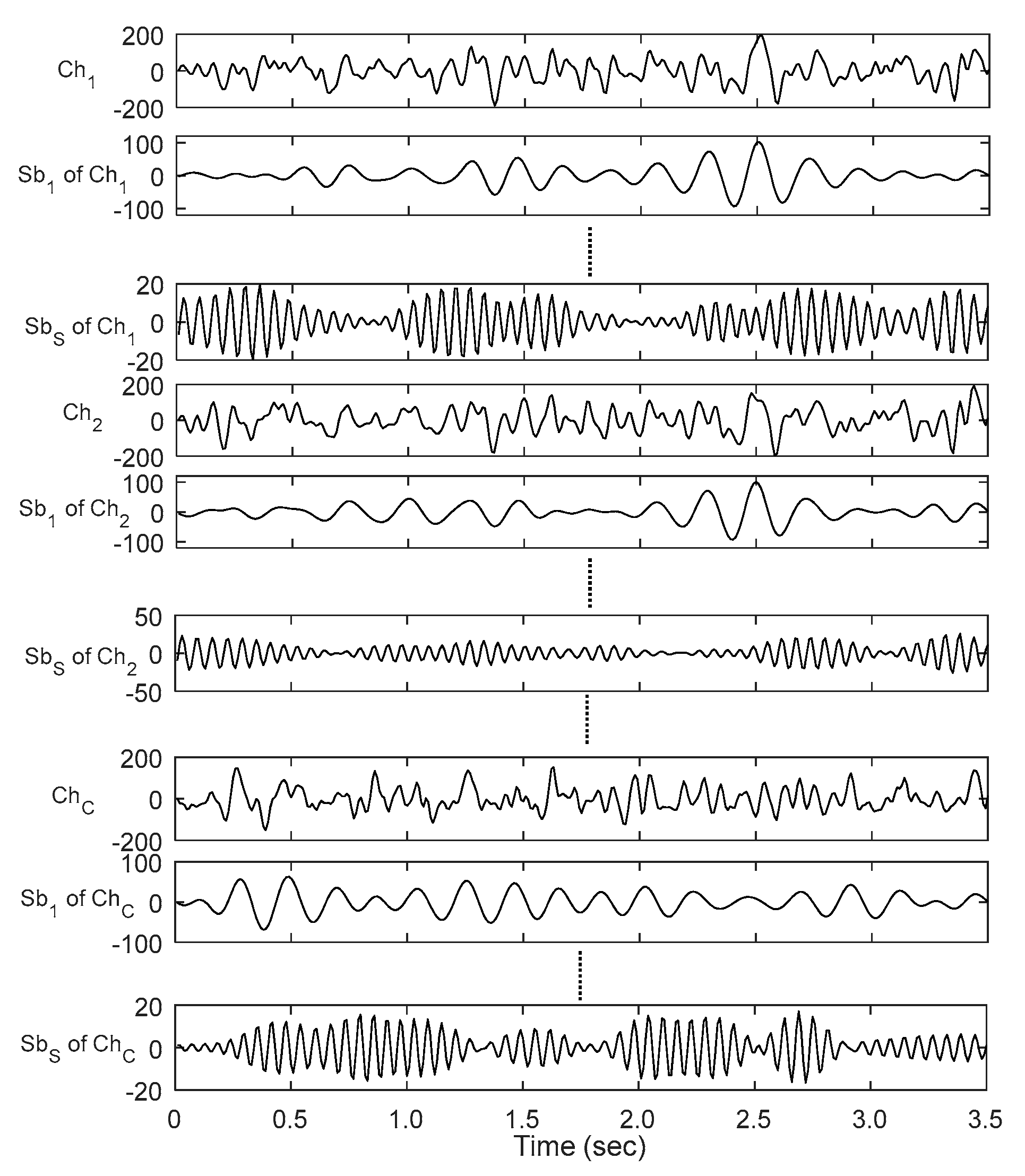
Figure 4.
MI classification performance (in percentage) of iTE with Dataset I. The results are compared with eTE method.
Figure 4.
MI classification performance (in percentage) of iTE with Dataset I. The results are compared with eTE method.
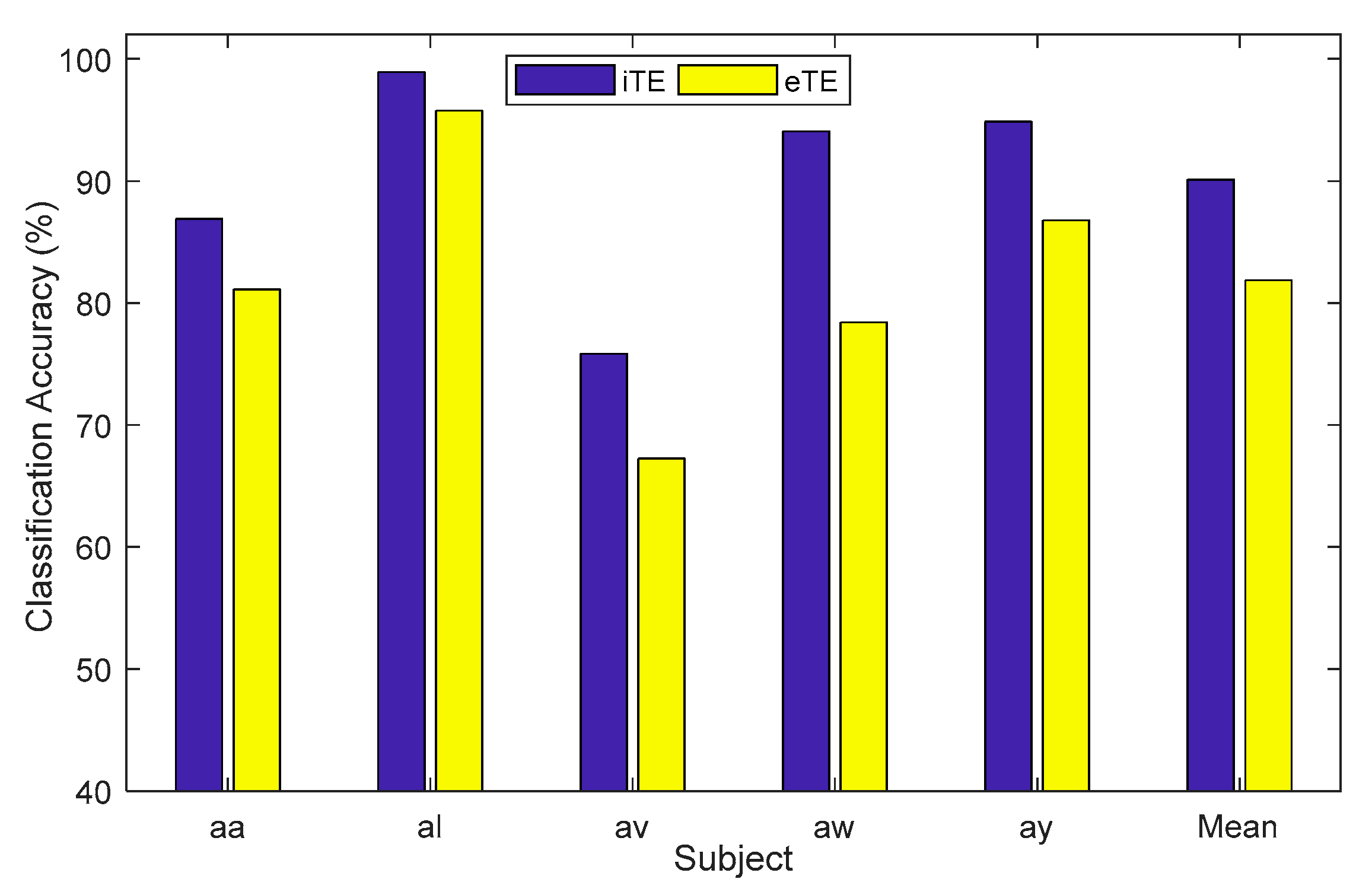
Figure 5.
MI classification performance (in percentage) of iTE with Dataset II. The performance factors are compared with eTE approach.
Figure 5.
MI classification performance (in percentage) of iTE with Dataset II. The performance factors are compared with eTE approach.
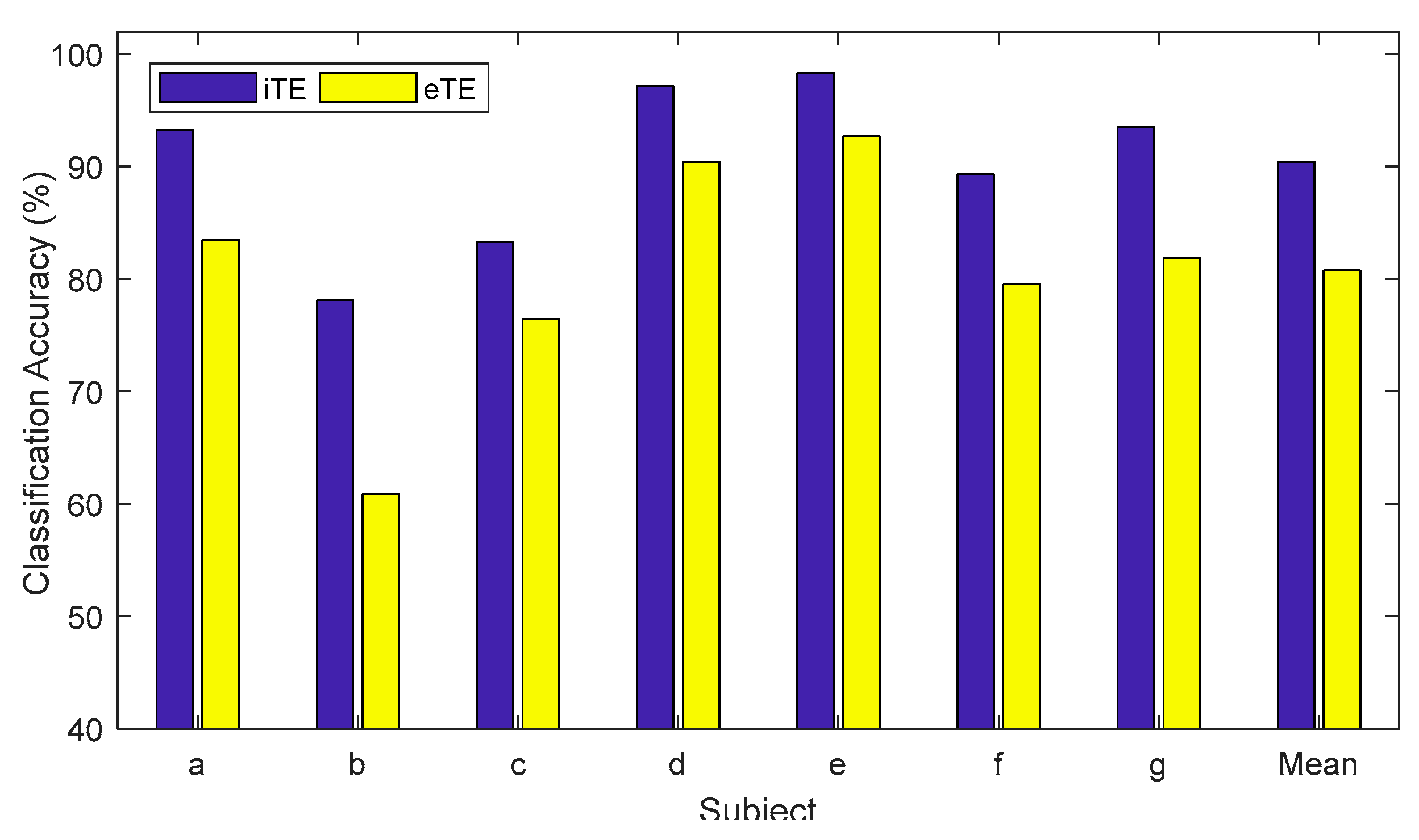
Figure 6.
The grid search approach to determine the number of hidden neurons and the pairs of CSP features of subject ‘aa’ from Dataset I. The pairs of CSP features and the hidden neurons and are selected as 3 and 6 respectively.
Figure 6.
The grid search approach to determine the number of hidden neurons and the pairs of CSP features of subject ‘aa’ from Dataset I. The pairs of CSP features and the hidden neurons and are selected as 3 and 6 respectively.
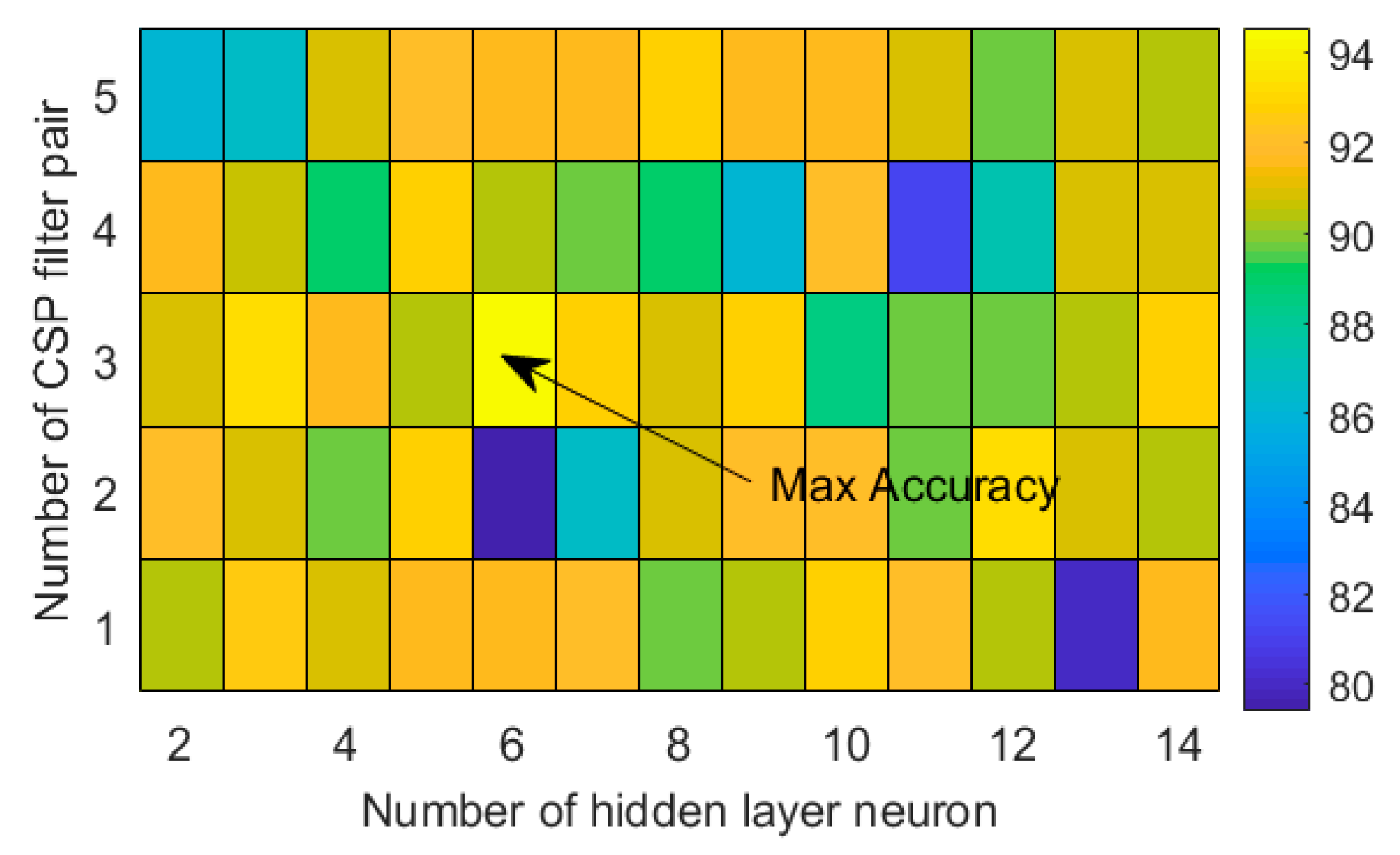
Table 1.
Classification accuracies of iTE-tP, iTE as well as eTE method with Dataset I.
| Subject | iTE | iTE-tP | eTE |
| aa | 86.90 | 94.94 | 81.12 |
| al | 98.92 | 98.18 | 95.76 |
| av | 75.84 | 76.25 | 67.24 |
| aw | 94.06 | 100.00 | 78.42 |
| ay | 94.86 | 100.00 | 86.78 |
| Mean | 90.12 | 93.88 | 81.87 |
| SD | 9.08 | 9.00 | 10.53 |
Table 2.
Classification accuracies of iTE-tP, iTE as well as eTE method with Dataset II.
| Subject | iTE | iTE-tP | eTE |
| a | 93.24 | 94.14 | 83.45 |
| b | 78.15 | 78.08 | 60.88 |
| c | 83.30 | 84.89 | 76.44 |
| d | 97.12 | 97.78 | 90.43 |
| e | 98.33 | 100.00 | 92.68 |
| f | 89.28 | 91.04 | 79.54 |
| g | 93.55 | 94.86 | 81.88 |
| Mean | 90.43 | 91.55 | 80.76 |
| SD | 7.39 | 7.11 | 10.48 |
Table 3.
Comparison of classification accuracy (%) of the proposed iTE-tP method with recently developed algorithms using Dataset I.
Table 3.
Comparison of classification accuracy (%) of the proposed iTE-tP method with recently developed algorithms using Dataset I.
| Methods | Subjects | Mean±STD | ||||
| aa | al | av | aw | ay | ||
| RRF [43] | 81.25 | 100.00 | 76.53 | 87.05 | 91.26 | 87.22±9.08 |
| SGRM [19] | 73.90 | 94.50 | 59.50 | 80.70 | 79.90 | 77.70±12.67 |
| SSCSP [40] | 72.32 | 96.42 | 54.10 | 70.54 | 73.41 | 73.36±13.50 |
| SRCSP [41] | 69.64 | 96.43 | 59.18 | 70.09 | 86.51 | 76.37±13.31 |
| TKCSP [42] | 68.10 | 93.88 | 68.47 | 88.40 | 74.93 | 78.76±10.54 |
| AM-SVM [39] | 86.61 | 100.00 | 66.84 | 90.63 | 80.95 | 85.00±11.00 |
| UDFS [34] | 86.98 | 97.45 | 76.04 | 93.93 | 94.94 | 89.86±8.65 |
| NCFS [24] | 90.00 | 98.93 | 76.71 | 98.21 | 97.14 | 92.20±9.36 |
| eTE | 81.12 | 95.76 | 67.24 | 78.42 | 86.78 | 81.87±10.53 |
| Proposed iTE-tP | 94.94 | 98.18 | 76.25 | 100.00 | 100.00 | 93.88±9.00 |
Table 4.
Comparison of MI classification accuracy (%) of the proposed work with recently developed methods using four subjects (a, b, f, g) of Dataset II.
Table 4.
Comparison of MI classification accuracy (%) of the proposed work with recently developed methods using four subjects (a, b, f, g) of Dataset II.
| Method | Subject | Mean±STD | |||
| a | b | f | g | ||
| VaS-SVMlk [48] | 92.50 | 77.00 | 88.80 | 92.60 | 87.72±7.36 |
| NA-MEMD [44] | 85.90 | 77.60 | 78.80 | 90.90 | 83.30±6.25 |
| CCS-RCSP [45] | 85.50 | 67.00 | 79.50 | 94.50 | 81.60±11.50 |
| CC-FBCSP [46] | 86.50 | 69.50 | 87.50 | 94.00 | 84.40±8.20 |
| TDP-CC [47] | 86.50 | 57.25 | 92.50 | 90.50 | 81.69±16.80 |
| NS-CSP [49] | 82.00 | 67.50 | 65.00 | 87.50 | 75.50±11.00 |
| BCS-CSP [50] | 79.00 | 79.00 | 92.00 | 88.00 | 84.50±5.69 |
| eTE | 83.45 | 60.88 | 79.54 | 81.88 | 76.44±10.50 |
| Proposed iTE-tP | 94.14 | 78.08 | 91.04 | 94.86 | 89.53±6.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated









