This paper Numerically investigates the effectiveness of the turbine rotating blade nozzle position on the vortex and film composite cooling performance. The coolant injecting nozzles arranged near the pressure surface side (PS-side-in) .vs. arranged near the suction surface side (SS-side-in) are compared at the rotating speed range of 0-4000rpm with fluid and thermal conjugate approach. Results show that the nozzle position presents different influences under low and higher rotating speed. In terms of the mainstream flow, rotation makes the stagnation line move from the PS-side pressure surface side to the SS-side suc-tion surface side, which changes the coolant film attachment on the blade leading edge surface. The nozzle position however indicates limited influence on the coolant film flow. In terms of the internal channel vortex flow, the coolant injecting from the nozzles forms a high-velocity region near the target wall which brings about enhancing convective heat transfer. The direction of the near wall vortex flow is opposite and align to the Coriolis force direction in both the PS-side-in and SS-side-in, respectively. Therefore, the Coriolis force augments to the heat transfer of the internal vortex cooling in SS-side-in while weakens the internal heat transfer in PS-side-in. Such effects become more intense with higher rotational speed. The blade surface area-averaged dimensionless temperature that inversely proportional to the actual temperature is 7.8% higher in SS-side-in as compared to that in PS-side-in. The SS-side-in suggests more superior composite cooling perfor-mance under the relatively higher rotating speed.

Keywords:

Subject: Engineering - Aerospace Engineering

1. Introduction

Gas turbines have gained significant popularity in various applications such as aircraft, marine propulsions, and electricity generation, and they continue to undergo advancements. As one of the crucial factors contributing to the enhanced engine power and operating efficiency, the inlet temperature of the turbine part has surpassed to 1644-1700K. Consequently, the working conditions for turbine blades have become increasingly severe[1]. To counteract this challenge while minimizing coolant consumption, effective cooling methods have become imperative. Vortex cooling is a specialized approach for cooling the turbine blade leading-edge part. Vortex cooling combines the advantages of intense convective heat transfer observed in impingement cooling and the uniform heat flux distribution associated with axial flow. In practical scenarios, the blade leading edge cooling (such as vortex cooling) is usually utilized in conjunction with external film cooling (EFC) in the blade leading edge (BLE), and such a cooling method is called as the vortex and film composite cooling (VFCC)[1].

The heat transfer performance of composite film and vortex cooling is influenced by three primary factors. These factors encompass the geometrical parameters, the mass transfer between the internal vortex cooling (IVC) flow and the mainstream flow (MF), the heat transfer brought about by the blade material, and the aerodynamic factors (injection blowing rate ratio, rotational speed, temperature ratio, etc.). Researchers have conducted many studies on the IVC and EFC conception as cited in the following text.

In terms of IVC, earlier research mainly focused on the swirl-flow structure generation and measurement. Kreith et al.[2] combined the twisted tape with a cylinder channel to generate a swirl flow field with the axial inlet flow. They found that the swirl velocity reduced by 80-90% at around 50 times diameter downstream along the cylinder channel axis. Ling et al.[3] utilized the tangential nozzle and measured the target surface temperature using transient liquid crystal technique. Results showed that the Reynolds number of the coolant injecting flow led to distinct heat transfer intensity increment. Besides, the near-wall velocity distribution of the vortex flow field was measured in detail. Most of the recent studies on IVC focused on the influences of geometrical and aerodynamic factors on the IVC performance. Du et al.[6,7] established a IVC structure which consists a semi-cylinder, several tangential placed nozzles with a coolant inlet chamber. They systematically studied the influences of the jet nozzle aspect ratio, jet nozzle angle and jet nozzle amount on the flow and heat transfer characteristics of IVC. Fan et al.[6] experimentally tested the influences of the coolant inlet Reynolds Number on the heat transfer intensity of the IVC structure put forward by Du et al.[4]. Wang et al.[7] found the mechanism of the vortex chamber cross-section area influence on the IVC characteristics.

As for EFC, researchers mainly focused on investigating the geometrical factors influences on the performance of the EFC. They also tried to introduce some special structures to optimize the EFC performance. Zhao et al.[8] utilized film holes to connect the internal axial flow cooling channel with the MF. They numerically compared the adiabatic EFC efficiency of the cylindrical film holes and fan-shaped film holes. Zhu et al.[9] numerically compared the showerhead EFC performance of the cylindrical film hole, fan-shaped film hole and the converging round-to-slot film hole in the BLE. Ye et al.[15,16] introduced the groove structure into the showerhead film hole on the BLE to optimize the EFC effectiveness.

In the previous work, it can be concluded that systematically and detailed investigations have been carried out separately on the IVC and the EFC. Whereas, the IVC and EFC are combined to cool the BLE. Although the internal cooling is involved in the research on the EFC above, the internal cooling in those studies is the axial flow cooling, which is different from the impingement cooling or the IVC in the practical BLE.

Some researchers focused on the IVC characteristics in the practical situations. In those studies, the IVC conception is placed in the BLE. Besides, they merged the film holes with the IVC structure to study the performance of the VFCC. Fan et al.[12] combined a row of film holes with the IVC structure and studied the film hole circumferential angle effect. Du et al.[13] numerically researched the rotation effects on the IVC based on the VFCC established by Fan et al. [12]. Li et al.[14] introduced a rectangular channel as the airfoil cascade into the IVC model put forward by Fan et al. [12] and explored the IVC intensity as well as the adiabatic EFC effectiveness. Zhang et al.[15] experimentally explored the performance of the VFCC influenced by the MF. The IVC chamber was placed in a symmetrical BLE, where the MF flow field near the BLE was different from the practical situation. Wang et al.[16] numerically studied the nozzle position effect on the VFCC performance in a vane of GE E3 (General Electric Energy Efficient Engine). In that case, the MF flow field near the BLE was asymmetrical. And results showed that the position of internal coolant injecting nozzles would impact the heat transfer of the IVC and the coverage level of the EFC. However, the heat conduction of the blade material was not considered in their study.

From the foregoing discussion, most of the studies were linked to the impacting mechanism of aerodynamic and geometrical parameters on IVC performance. Nevertheless, there remains a limited number of investigations on predicting and analyzing the performance of IVC in MF cascades. VFCC, which combines EFC and IVC, is commonly employed to cool the BLE in the practical cases. The characteristics of the VFCC are dominated by the coverage of EFC, heat transfer of IVC, heat transfer through the blade material, and the effects of rotation. Nearly all the studies mentioned above used a semi-cylinder configuration to substitute the profile of the BLE, such as the experiment carried out by Zhang et al.[15]. In those simulations, the MF was symmetrical. However, it should be noted that the MF flow field in blade cascades is inherently asymmetrical. Therefore, those studies on the MF effects of the VFCC are quite different from the practical situation. In addition, the heat conduction through the blade material would connect the hot gas in the MF and the IVC flow. This heat conduction has a simultaneous impact on the heat transfer of the internal cooling and the effectiveness of the EFC. Consequently, it is essential to recognize that the fluid-thermal coupling simulating method is required which does not exist in the previous studies on the VFCC.

To further investigate the characteristics of the VFCC, it is imperative to conduct comprehensive investigations that consider asymmetrical MF effects, influence of the fluid-thermal coupling, and the effects of rotation and this is the strength or contribution of the current paper. A VFCC model is put forward and studied within the asymmetrical MF. Specifically, the structure of the IVC model is referred to the model in Du et al. [6,7] and Fan et al. [6]. The MF cascade structure and the blade profile are put forward based on the base stage1 blade in the test rig[17]. The MF flow field in the cascade will be asymmetrical. In our paper, the conjugate approach is carried out by introducing the blade material solid part to connect the MF flow field and the internal vortex flow field. The VFCC models with different coolant injection nozzle arrangements are established. The temperature distribution of the blade surface, the heat transfer distribution of the IVC, and the coolant film coverage of the EFC are calculated under different rotational speeds. This work might contribute to a more thorough understanding of the complex interactions of the BLE cooling and provide valuable references for the application of IVC in practical scenarios.

2. Materials and Numerical Methods

2.1. Geometrical details

For convenience, the following technical phrases will be substitute to the respective abbreviations: internal vortex cooling (IVC), external film cooling (EFC), dimensionless temperature (delta), vortex and film composite cooling (VFCC), blade leading edge (BLE), mainstream flow (MF), SST k-ω with γ-θ transition model (SST~γ-θ), SST k-ω model (SST), the standard k-ω model (k-ω), and stagnation line (SL).

Figure 1 illustrates the three dimensional computational model. The boundaries are also be pointed out. The calculation model, as depicted in Figure 1 (a) and (b), comprises the cascade with the blade, film hole channels, IVC chambers, and the BLE material part of the blade as one integrated entity. The VFCC system consists of a inlet chamber connecting with a semi-cylinder vortex chamber (the connecting part consists of eight coolant injection nozzles) and twenity-four film holes channels (the coolant inside the vortex chamber could only enter the MF cascade through the film holes). The upstream and downstream segments is set to one and one point five times the length of the blade chord, respectively. For clarity, Figure 1 presents only a partial view of the upstream and downstream segments. The extended upstream segment ensures the formation of the MF boundary layer before impacting the BLE surface.

Figure 2 presents the top view of the structure of the BLE of the blade. Given the IVC structure is asymmetrical compared to the classical symmetrical cooling conception such as impingement cooling, there are mainly two types of nozzle arrangements as indicated in Figure 2. The case in which the nozzles set near the side of pressure surface is called “PS-side-in” case, and the case in which the nozzles set near the side of suction surface is called “SS-side-in” case in the following text. In Figure 2 (b), there are two sections of the BLE: the segment of the pressure surface and the segment of suction surface. Our analysis primarily focuses on the isotherms distribution on the surface of the BLE, specifically on the suction surface leading edge part and the pressure surface leading edge part depicted in Figure 2 (b).

Figure 3 exhibits the sizes of the vortex chamber of the VFCC model. The incline angle of the film holes with the showerhead configuration is set to 25°to blade height direction, with a 30° angle between adjacent rows of film holes (close to the GE E3 stage1 blade configuration[17]) as presented in Figure 2. Here, the inclined angle of 25° relative to the blade height is identical to the VFCC experiment with showerhead film holes[25]. Such an inclined angle setting of film hole configuration in the BLE is commonly applied in gas turbine blades as the coolant will be forced to move towards blade height direction due to the influence of the centrifugal force. The film hole channels at different height are labelled as Row1, Row2…Row8. Furthermore, the film holes located on the segment of the pressure surface, the segment of suction surface, and the position between them (Figure 2), are designated as RowP, RowS, and RowM, respectively. The entire computational model are rotational. The rotational axis is the Z-axis, with a length of 364mm[17] from the rotational axis to the hub wall of the cascade.

As for the coolant flow path, the coolant initially blows into the inlet chamber from the boundary called internal inlet. Next, the coolant flows through the coolant injecting nozzles, and enters the vortex chamber as the tangential jet. Finally, the coolant flows through the film hole channels into the cascade, then becomes the film attached to the blade surface or mixes with the hot gas of the MF. As for the MF, in the stationary case, the MF hot gas flows into the cascade with an angle 30° to the Y-axis in the absolute coordinate. The MF inlet flow angle will gradually increases with the rising angular velocity. Such phenomenon will be discussed in Figure 7.

The profile of the blade, the configuration and sizes of the film holes, and the rotating axis setting in our setup are identical to the test rig used by NASA[17]. Furthermore, the IVC structure replicated and scaled from the experimental rig developed by Fan et al.[6].

2.2. Mesh generating

Figure 4 (a) and (b), displays a whole view and a partial view of the mesh, respectively. To generate the unstructured mesh with requested high-quality, the commercial software ANSYS 12.1 was utilized. The connecting surfaces between the solid domains and the fluid domains are set to the interfaces. In order to achieve low y⁺ values, at least 12 prism layers were implemented in the regions near the boundary of the walls. Figure. 4 (c) presents the y⁺ contour on the pressure surface under one of the calculating conditions. It could be captured that the y⁺ is lower than 1 on the pressure surface of the blade. The y⁺ values on other walls are all check to ensure y⁺ is lower than 1. This approach ensures that the flow field in the regions near the wall is calculated directly rather than relying on empirical wall functions, by which the calcuating results will be much more accurate.

2.3. Solution procedure and boundary conditions

In the study conducted by Du et al.[13], the flow field and heat transfer distribution of IVC influenced by rotation were numerically investigated using the standard k-ω turbulence model coupled with the three-dimensional steady viscous RANS equation (Reynolds averaged Navier-Stokes). Similarly, Zhang et al.[15] and Wang et al.[16] examined the blade surface temperature, heat transfer intensity and flow field of the VFCC under the effect of the MF solving the RANS equation coupled with the realizable k-ε model or SST~γ-θ, respectively. These studies demonstrated that the two-equation turbulence models employed were effective in capturing flow field distribution and accurately simulating the distribution of the heat transfer affected by rotation. Consequently, our research also adopts the 3D steady viscous RANS model together with the turbulence model of two-equation for calculation, which applicable in engineering as the previous studies. If the hot spot in the MF inlet flow is involved, the transient unsteady simulation should be conducted to capture the interaction process between the coolant jet of the EFC flow and the hot spot.

For discretizing the convection term, we applied the high-resolution correction in the second-order format. Initially, the timestep is set to 10^-4 s and is updated during iteration referring to the timescale factor value of 0.05. To ensure convergence, the monitors are set based on those critical variables throughout the iteration step. These variables include Reynolds numbers of the coolant inlet flow as well as the cascade inlet flow, the averaged target wall Nusselt number of the internal cooling chamber, the delta of area-averaged blade leading surface, and the film hole channel massflow rate.

The definition of Nusselt number Nu is identical with the previous studies on the IVC performance. The Nusselt Number Nu is defined as:

Nu = q_wD_c/ (λ(T-T_w))

(1)

where:

q_w is the heat flux of the target wall shown in Figure 2 (W/m2)
D_c means the cross section hydraulic diameter of internal vortex chamber (m)
λ represents the fluid thermal conductivity (W/(m·K))
T_w represents the target wall temperature

The dimensionless temperature θ is:

θ = (T_∞ - T) / (T_∞ - T_c)

(2)

where(the following positions are given in Figure 1)

T_∞ stands for the cascade inlet flow temperature
T_c represents the coolant flow temperature of internal inlet

The higher θ indicates the lower actual temperature of the fluid or the blade wall. Convergence is achieved when the oscillation amplitude of the profiles of these variables' varying with the iteration step is lower than 5% of the average values.

Table 1 presents the boundary conditions set in the simulation. As for the MF cascade boundaries, the total temperature of the cascade inlet, the total pressure of the cascade inlet, and the static pressure of the cascade outlet are 206.431 kPa, 683 K, and 68.81 kPa, respectively. These values are obtained from experimental data in NASA experiment[17]. The turbulent intensity of the cascade inlet is set to a high level of 10%. As for the boundaries of the internal cooling chambers, the inlet total temperature is 352 K, while turbulent intensity of the internal inlet and the total pressure of the internal inlet are medium (5%) and 360 kPa, respectively. All the boundary conditions mentioned above are set based on the stationary coordinate (absolute coordinate). All walls are treated as the adiabatic and non-slip walls. The working medium is assumed to be the air ideal gas. The material of the solid is set as steel whose thermal conductivity is 60.5 W/(m·K) as the formula and property of the alloy of the gas turbine blade cannot be simply defined. The variation of the thermal conductivity versus temperature will be required if the researchers get interested, which is not the focus of the current research.

2.4. Grid independence analysis

To reduce numerical uncertainty and discretization errors, a grid invariant analysis is performed. This test helps determine the appropriate Number of nodes for the simulation. In this analysis, the case with an angular velocity of 3000 rpm is selectedto conduct the grid independence analysis. There are three grids generated with the same growing rate at X-, Y-, and Z- directions, resulting in node numbers of 2.70 million, 7.42 million, and 18.79 million, respectively. All the three grids undergo smoothing, and the mesh quality standard are thoroughly checked prior to calculation.

The area-averaged delta on the suction surface part θ_S and the pressure surface part θ_P of the BLE (see Figure 2 (b)), along with the area-averaged Nusselt number on the target wall (see Figure 2 (b)) of the IVC chamber Nu_a, are calculateded and exhibited in Table 2. Additionally, Figure 5 illustrates the distribution of the coolant flow pressure in the vortex chamber, accompanied by the error bars of the numerical uncertainty. The grid with a node Number of 7.42 million is used for calculating the pressure distribution as shown in Figure. 5. The numerical uncertainty is evaluated using the GCI_fine method put forward by Celik et al.[18]. In their methods, an extrapolation value will be obtained by solving the GCI_fine equation utilizing the computational results calculated from a coarse, a medium and a fine grid. The numerical uncertainty is calculated based on the extrapolation value and with the results from those three grids. As shown in Table 2, the maximum numerical uncertainty not exceeding 5% of the pressure distribution solution.

2.5. Turbulence model verification

To obtain accurate and reliable numerical results, the selection of an appropriate turbulence model is crucial. Wang et al.[16] have demonstrated that the SST~γ-θ exhibits superior simulation accuracy to the SST and the k-ω, as illustrated in Figure 6. Figure 6(a) shows a flat board film cooling experiment carried out by Kohli et al.[19], where the SST~γ-θ demonstrates superior performance in predicting the distribution of the film cooling eeffectiveness. This model accurately captures the laminar-to-turbulent transition at the downstream region of the film hole.

In Figure 6(b) and (c), a comparison is shown between simulation and experimental data from the NASA GE E3 experiment[17]. All the three turbulence models adequately predict the distribution of the vane efficiency. However, discrepancies between the numerical results and experimental data become more pronounced within the blade height range of 5% to 40%. Such a phenomenon may be attributed to non-uniform inlet flow field conditions or fluctuations in inlet flow velocity during the experiment.

3. Results and discussion

In a study by Safi et al.[20], a Numerical investigation was conducted to explore the rotational influences on the impingement cooling performance in the BLE of gas turbines. The simulations covered a rotating speed range of 0-750 rpm, revealing the underlying mechanism of rotational influences on the VFCC performance in the BLE of gas turbine. In the current research, similar simulations are performed within an extended rotating speed range of 0-4000 rpm, which aligns with the range studied by Safi et al.[20].

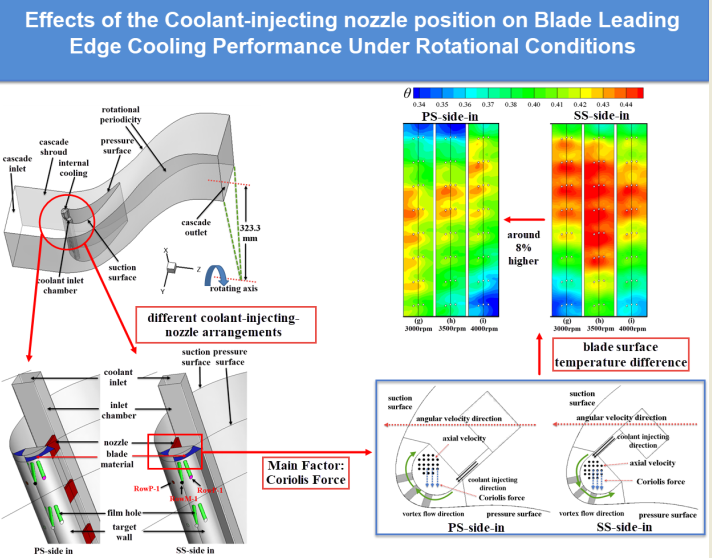
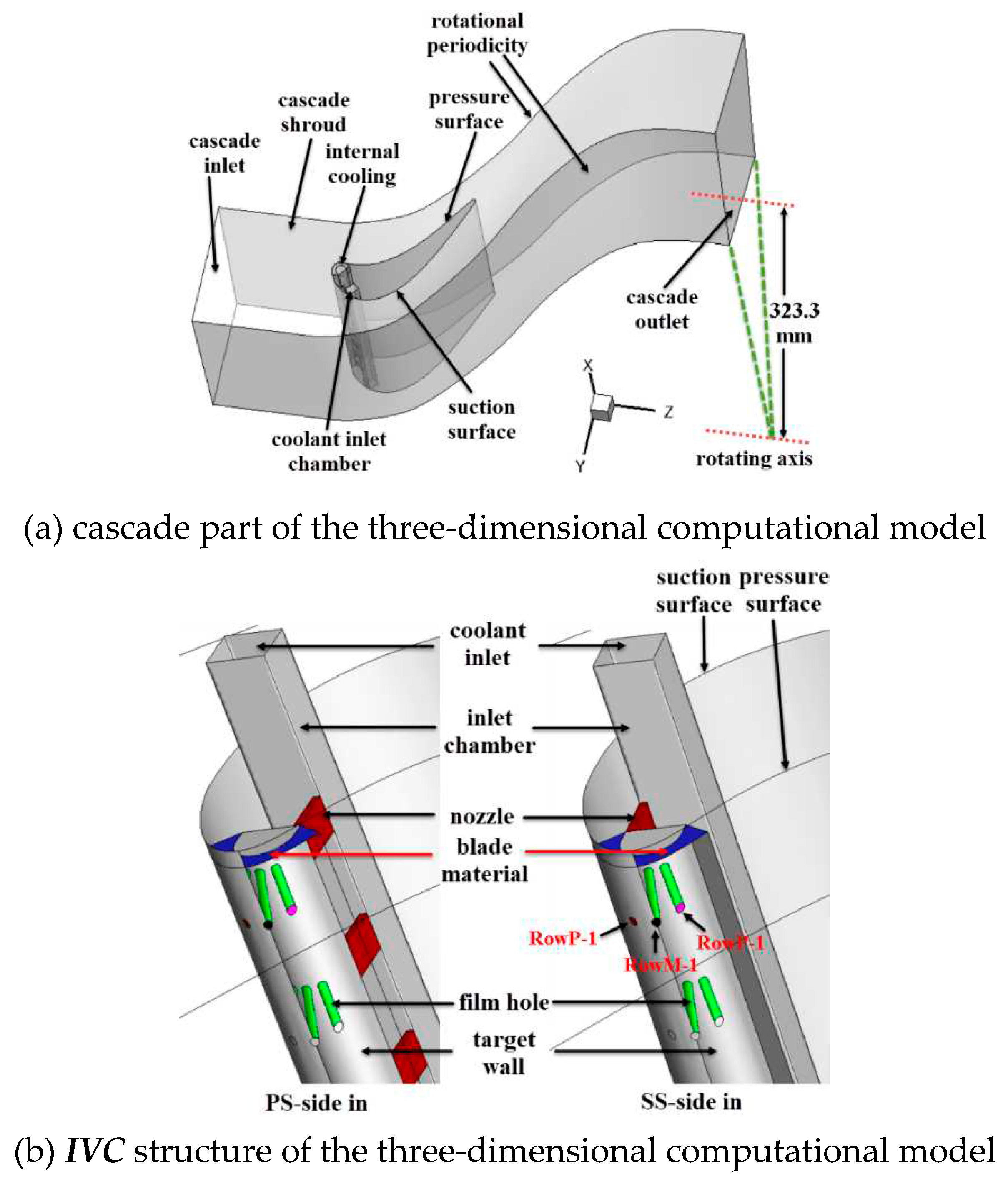
3.1. Rotation influences on the external flow

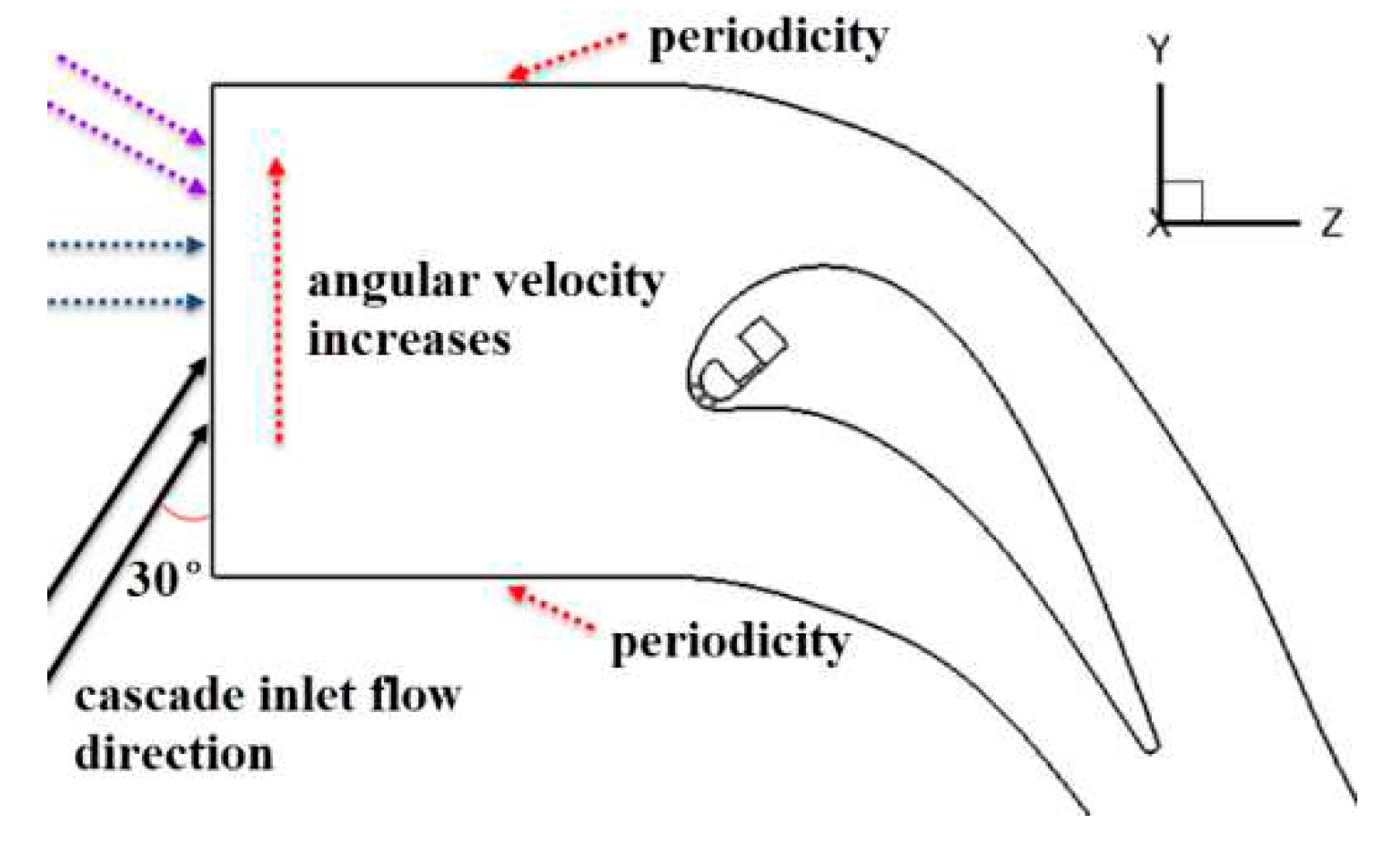
Figure 7 shows the sketmatic figure of the direction of the MF inlet flow versus the angular velocity. There are three types of velocity vector: the MF inlet flow absolute velocity c, the angular velocity u and the MF inlet flow velocity relative to the rotation frame w, in which c= u + w. When the angular velocity u is 0rpm, velocity c and velocity w are identical. The angle between the velocity w and Y- axis is 30°. As the angular velocity u increases under the fixed velocity c, the angle between the velocity w and Y- axis gradually increases. A flow stagnating to the blade will bring about a line-shaped stagnation region on the BLE surface, whose position is related to the flow direction. Given the blade could be regarded as a rotation frame, it can be concluded in Figure 7 that the stagnation region will move from the pressure surface side to the suction surface side on the BLE surface with the increasing angular velocity u. Such a phenomenon can be seen in Figure 8. The line-shaped stagnation region is termed “SL (stagnation line)” in the following text.

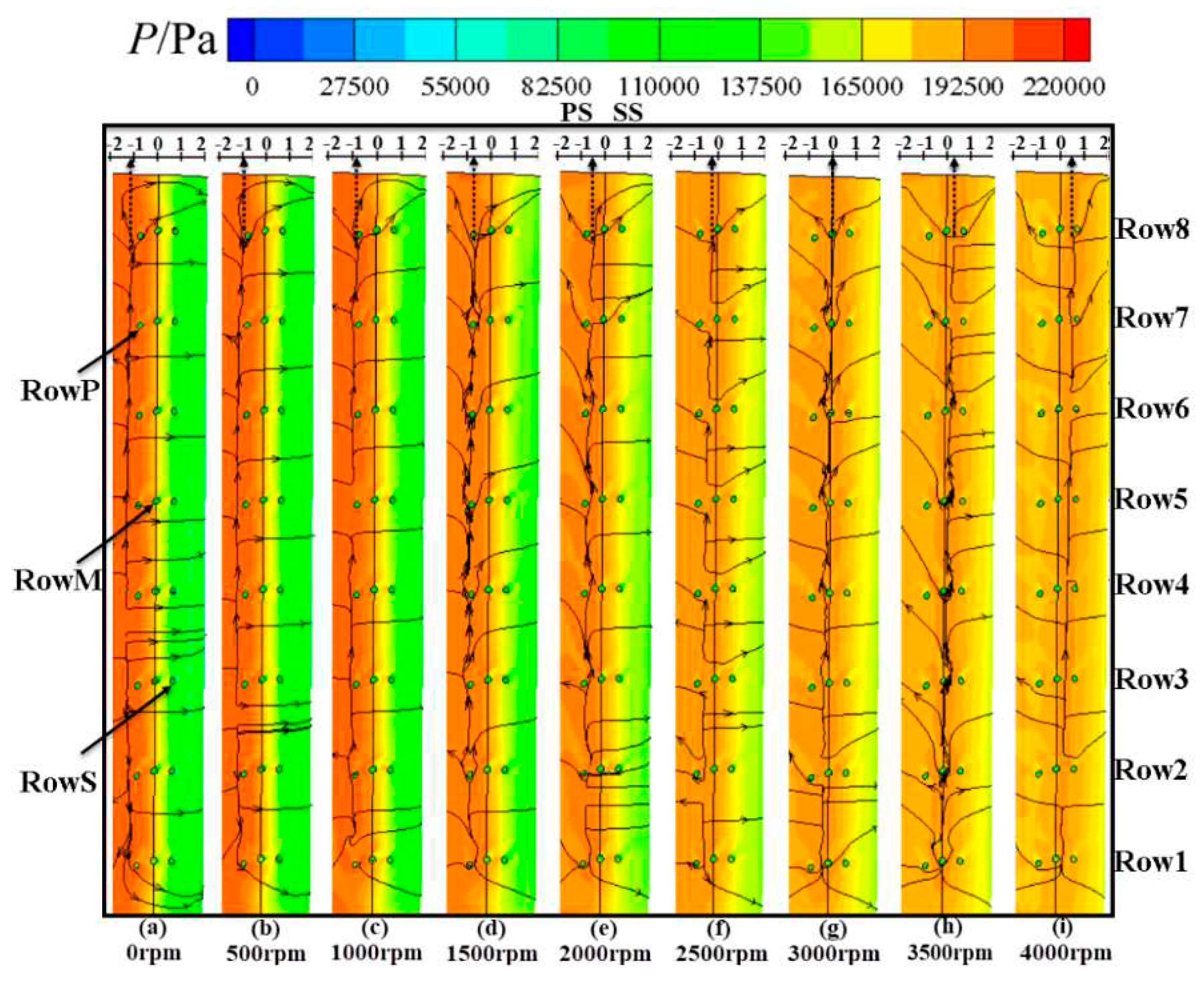
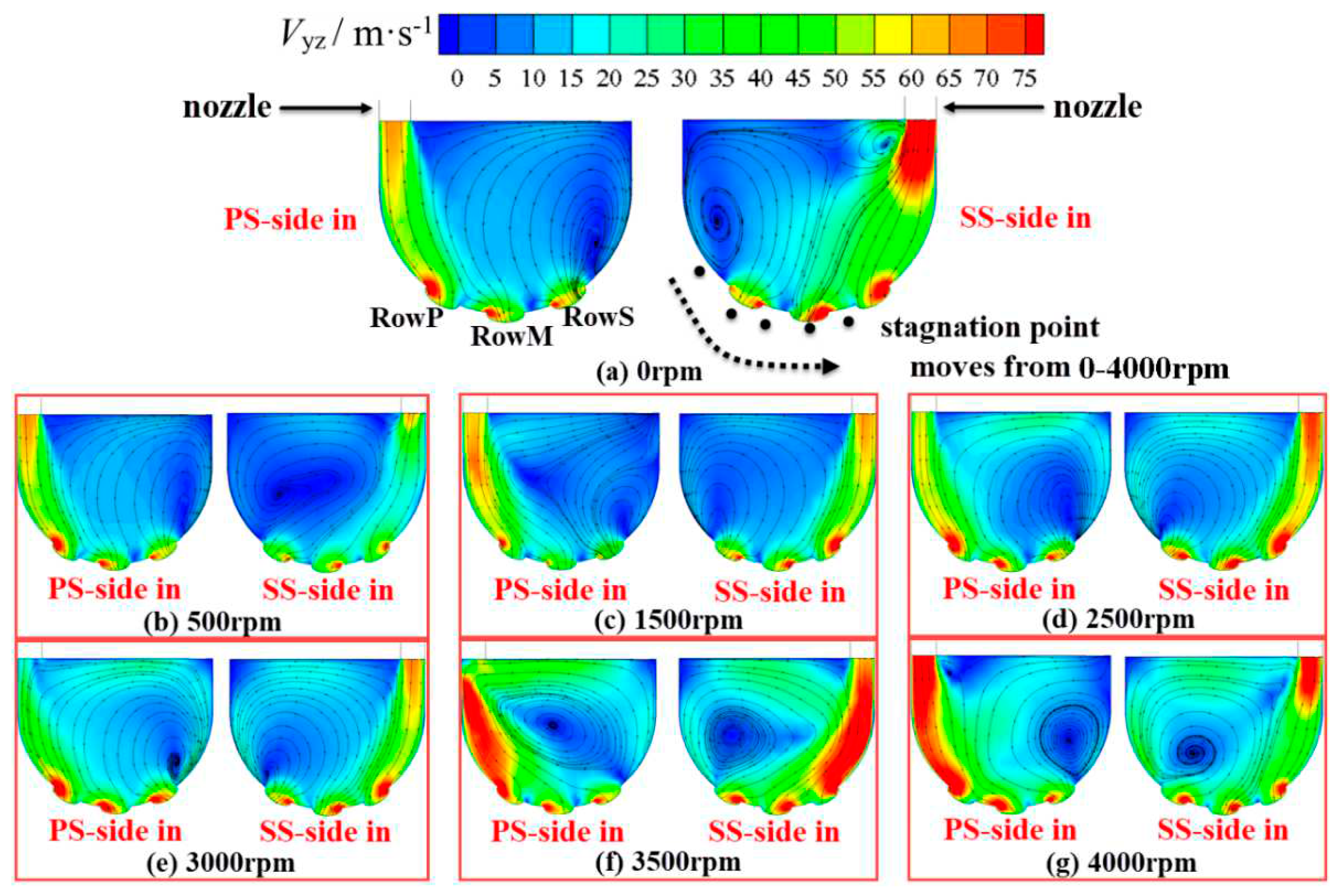
Figure 8 illustrates the pressure contour and surface streamlines on the BLE. The presence of SLs could be observed as characterized by the opposite streamline directions on each side of these lines. At 0 rpm, the SL presents a relatively straight profile from hub to shroud side and is positioned to the left side of RowP. When the rotating speed rises, the SL shifts towards the suction surface of the blade and eventually settles on the left of film hole RowS. This shift is attributed to the keeping growing norm of the circumferential velocity u as presented in the velocity triangle, leading to a direction change in the of w, as explained in Figure 7. Metaphorically, the upper portion of the SL moves "faster" towards the blade suction surface compared to the portion near the hub with increasing rotating speed, primarily due to the higher circumferential velocity near the shroud. This difference becomes more distinct at higher rotating speeds. Additionally, the surface streamlines gradually curve towards the side of the shroud given the effects of the growing centrifugal force associated with the growing rotational speed. It is worth noting that the position of the SL aligns with RowP and RowM positions at 1500 rpm, 3000 rpm and 3500 rpm, respectively. The position of the SL will affect the heat and mass transfer between the coolant film flow and the MF.

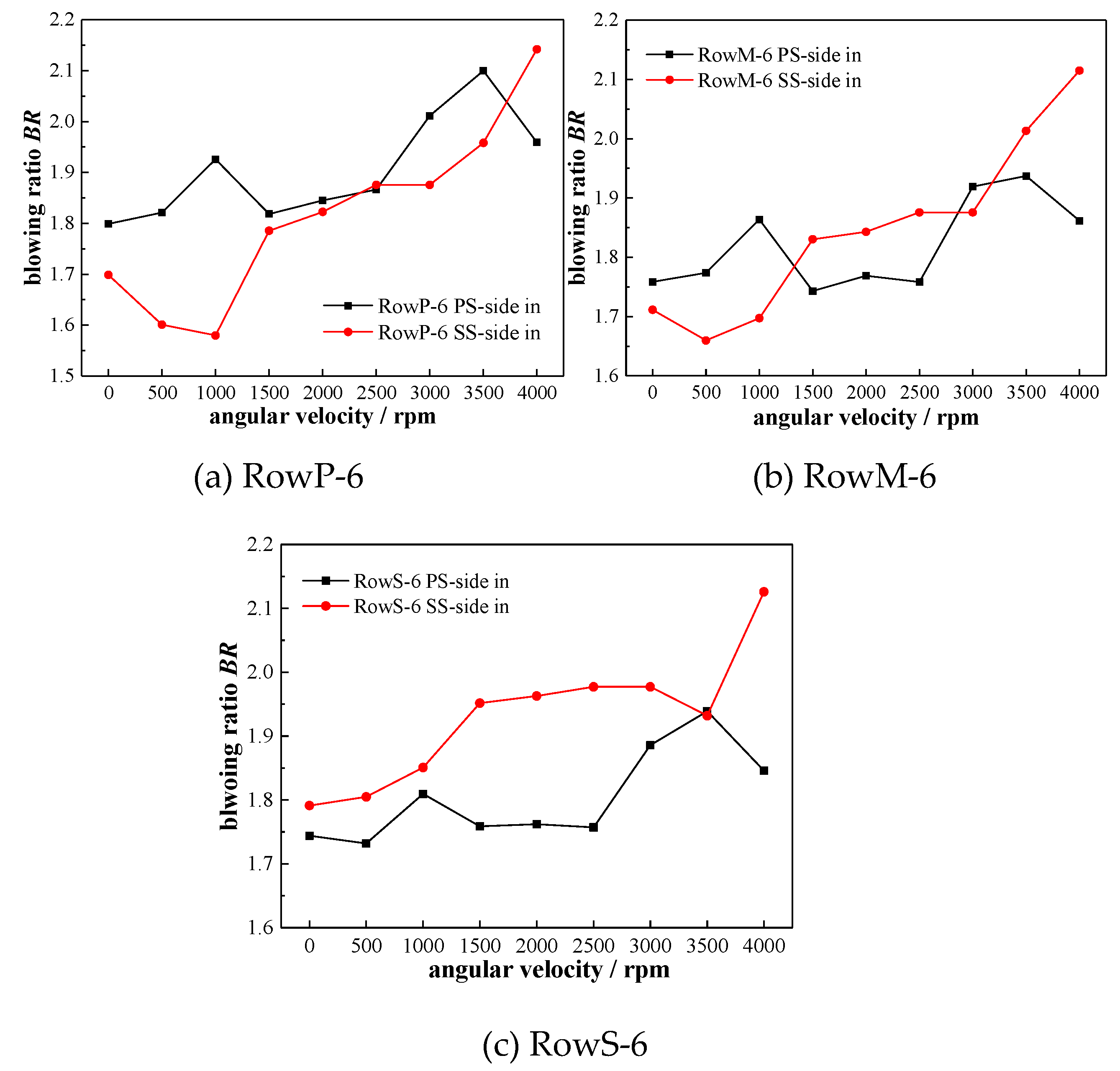
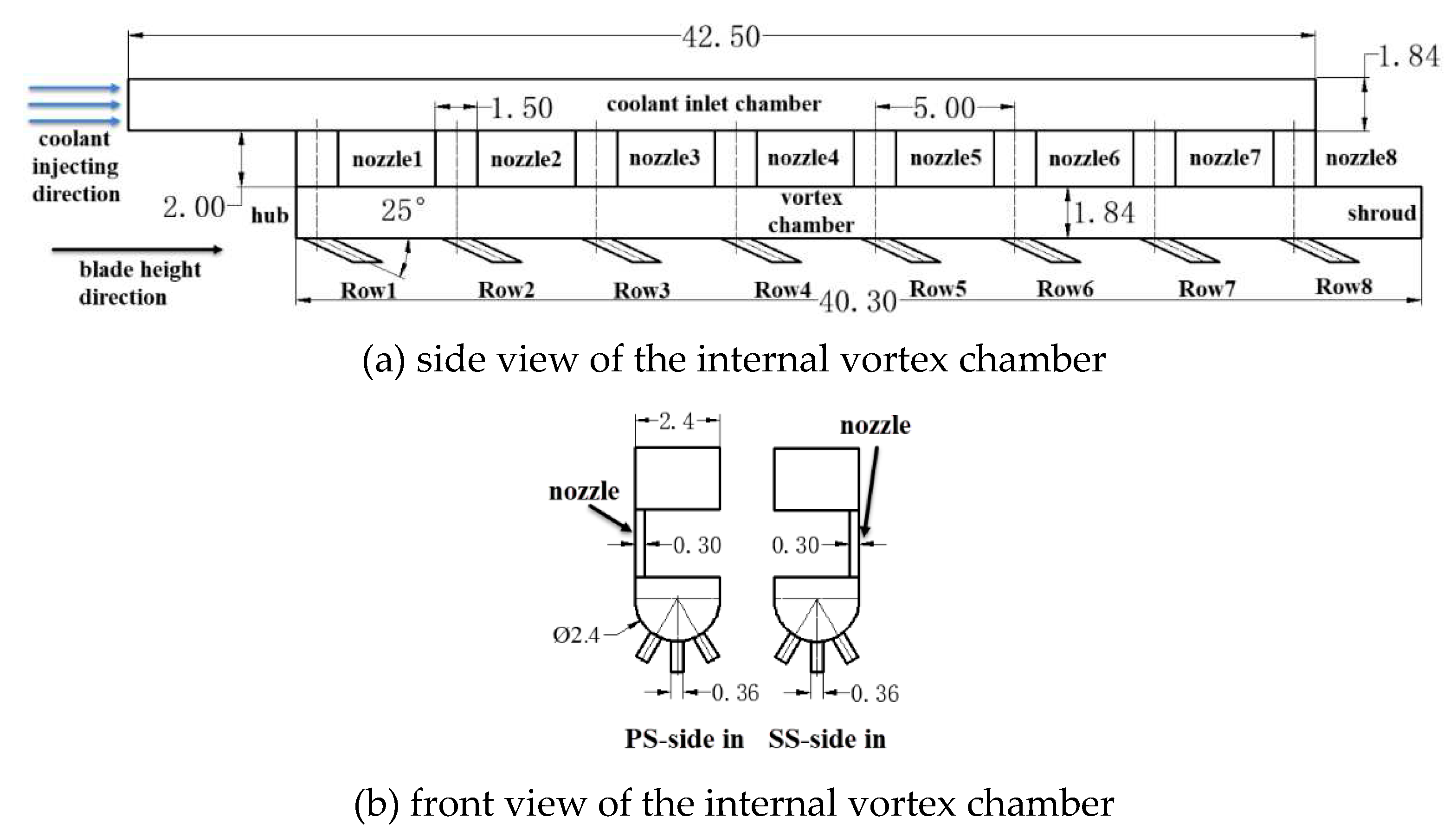
Figure 9 presents the blowing ratio variation versus the rotating speed in PS-side-in and SS-side-in. Referring to Figure 2, RowP-6, RowM-6 and RowS-6 represents the sixth-row of film hole locates at the pressure surface, the suction surface, and the position between the suction surface and pressure surface, respectively. In general, the blowing ratios of those three film holes fluctuant increase with the growing rotational speed. Such a phenomenon is brought about by the enlarging centrifugal force caused by the increasing rotating speed, which as a result, forces the coolant to move along the blade height direction. It is noteworthy that, the blowing ratios of RowP-6 and RowM-6 at 0-1000rpm are lower in PS-side-in than that in SS-side-in. The reasons are explained as following. On the one hand, the coolant injecting nozzles stay closer to RowP in PS-side-in than SS-side-in as can be seen in Figure 2. Hence, more coolant will flow to the MF through RowP in PS-side-in than the SS-side-in. On the other hand, the SL appears near RowP and RowM at 0-1000rpm as indicated in Figure 8, which brings about higher MF pressure near RowP and RowM but lower MF pressure near RowS. In that case, in SS-side-in, higher proportion of the coolant directly flows into the MF through RowS rather than RowP or RowM. This causes a lower blowing ratio of RowP and RowM as well as a higher blowing ratio of RowS in SS-side-in compared to PS-side-in at 0-1000rpm. Such phenomena will bring about the difference for the performance of the VFCC in the following discussion.

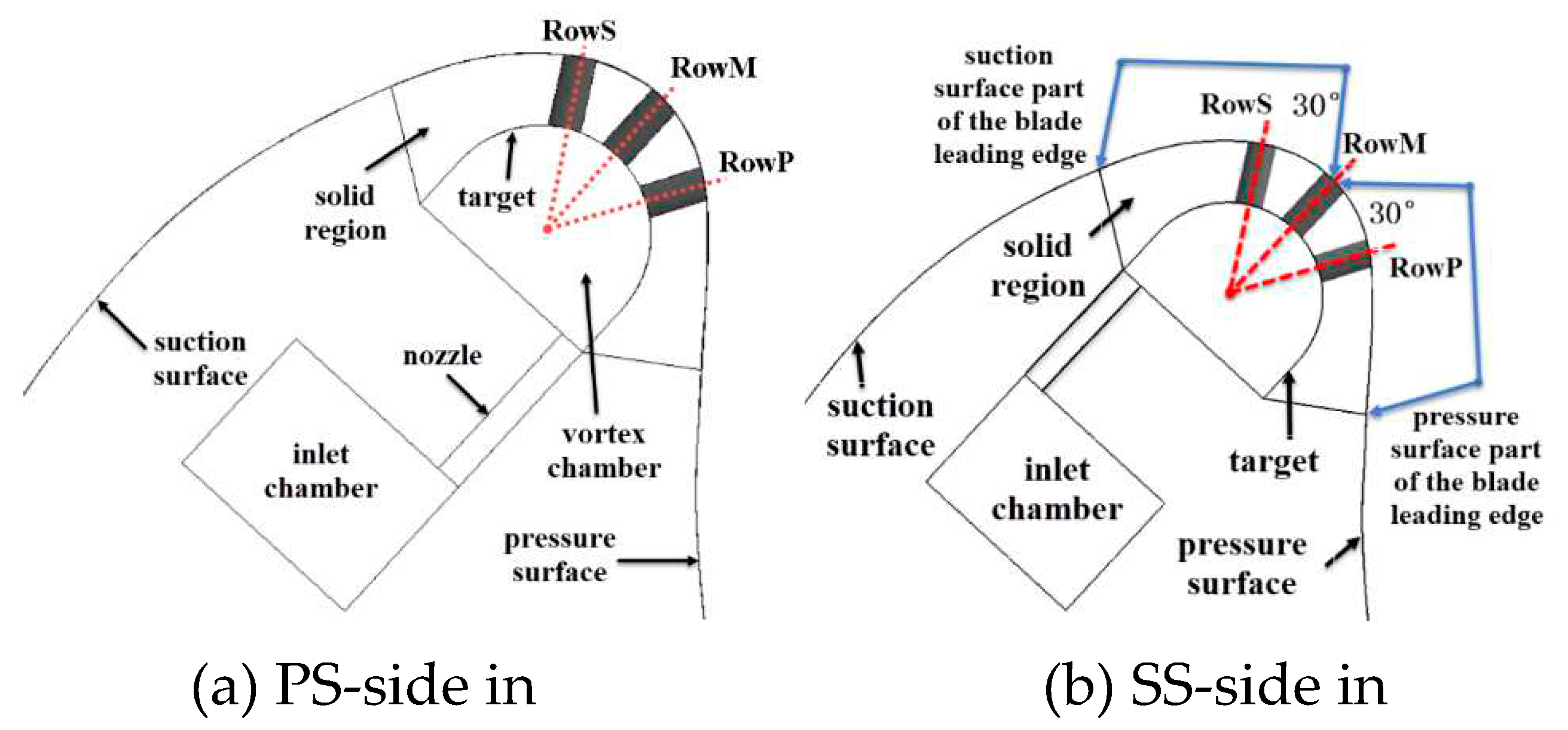
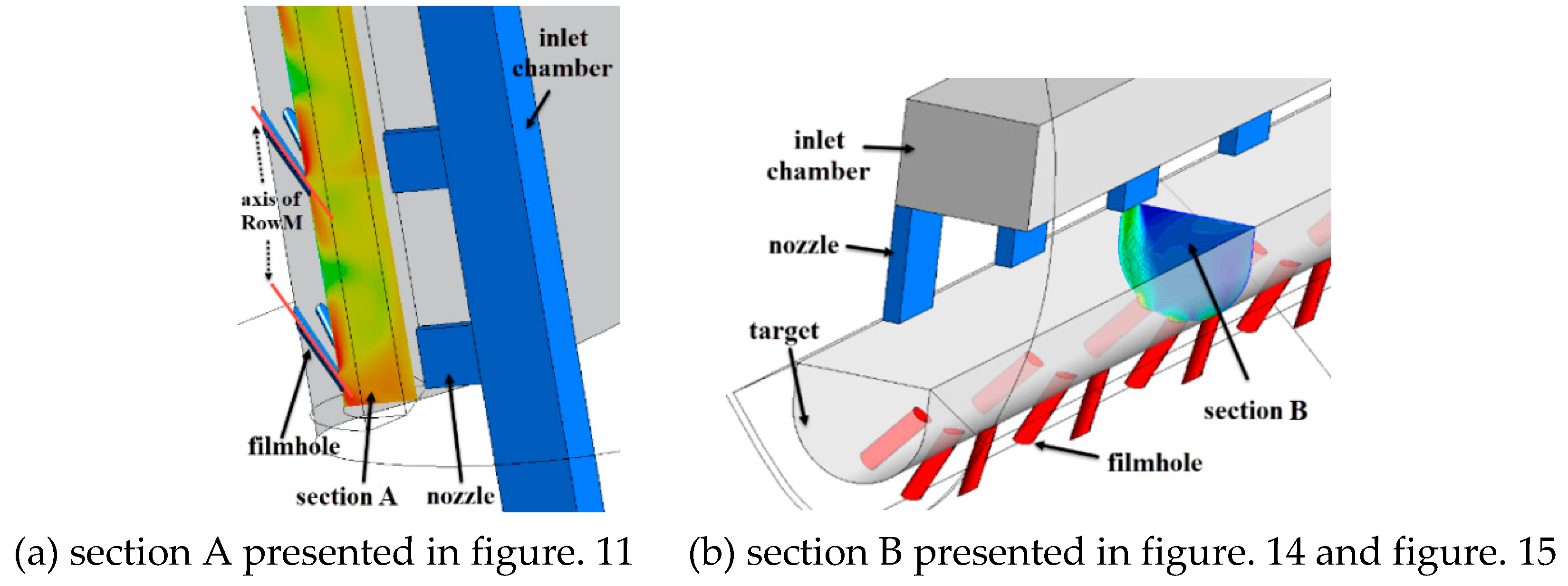
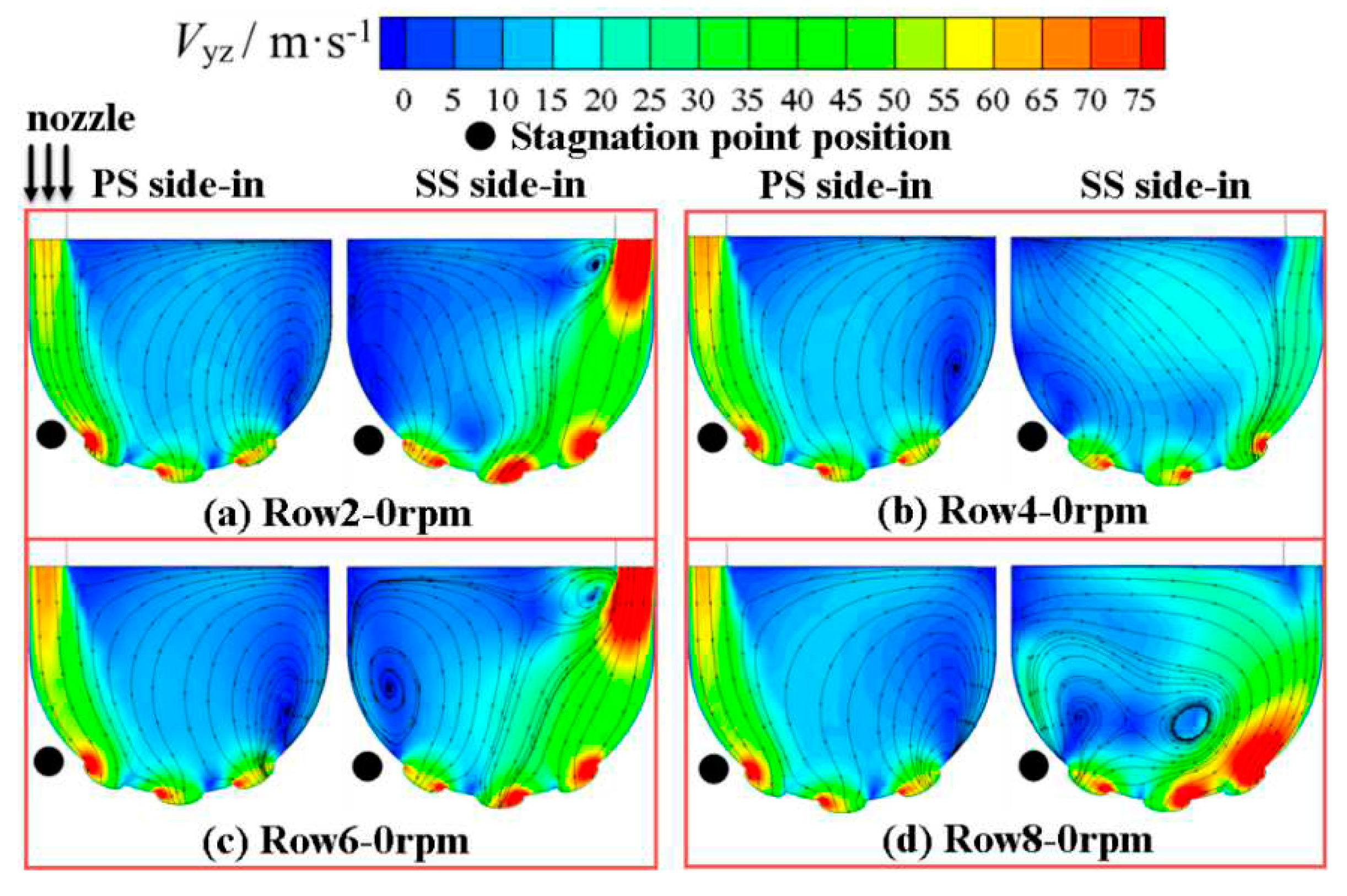
Figure 10 depicts different types of cross-sections for analysis in Figure 11, Figure 14 and Figure 15. Section A presented in Figure 10 (a) locates on the axis of RowM and is parallel to the blade height. There are three types of section A. They locates on the axis of RowP, RowM and RowS, respectively. Section A is created to ‘capture’ the external near wall flow field of the EFC as presented in Figure 11. Section B shown in Figure 10 (b) locates on the blade height of Row6 and is vertical to the blade height to ‘capture’ the flow field of the IVC in Figure 14 and Figure 15.

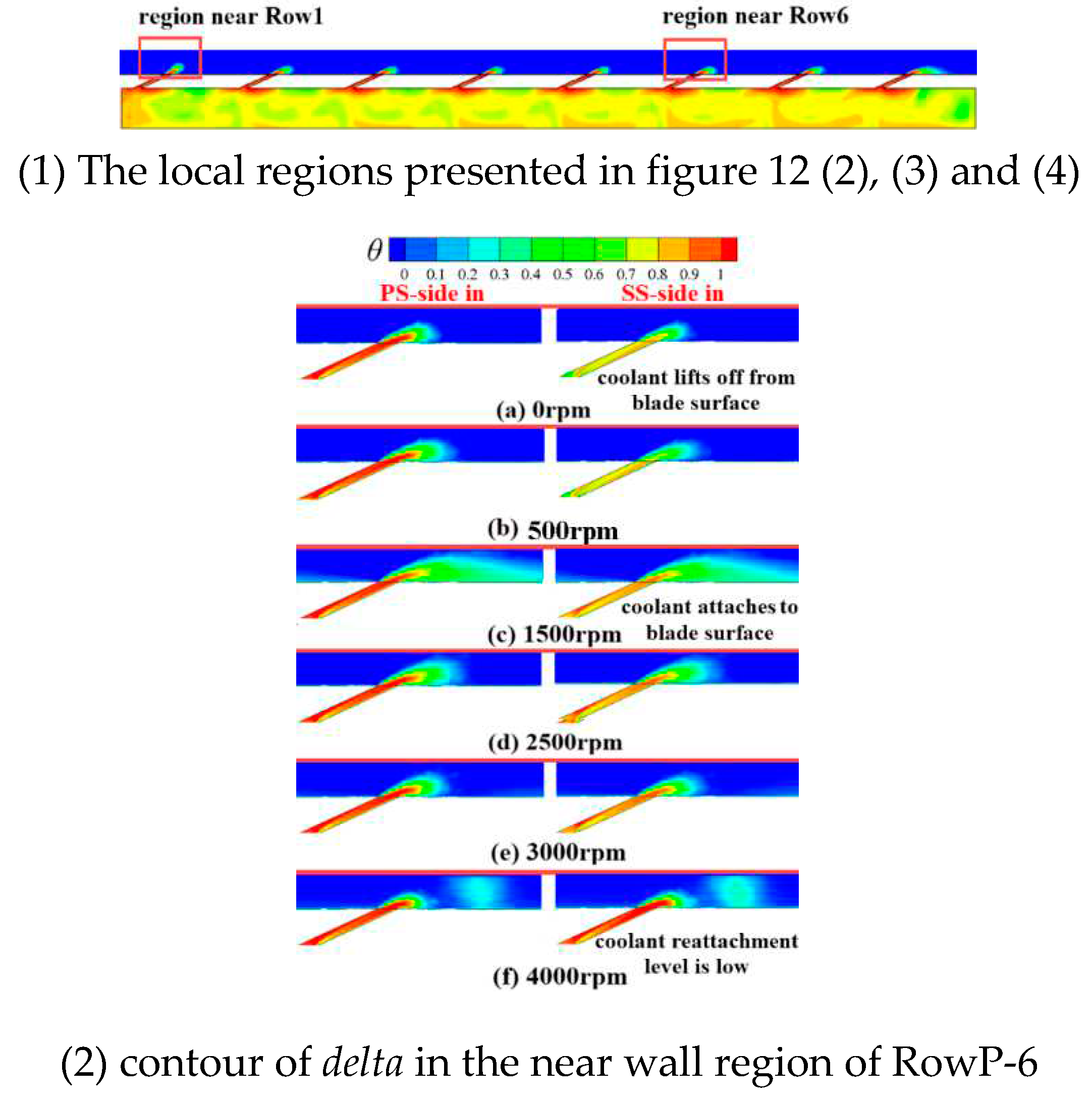
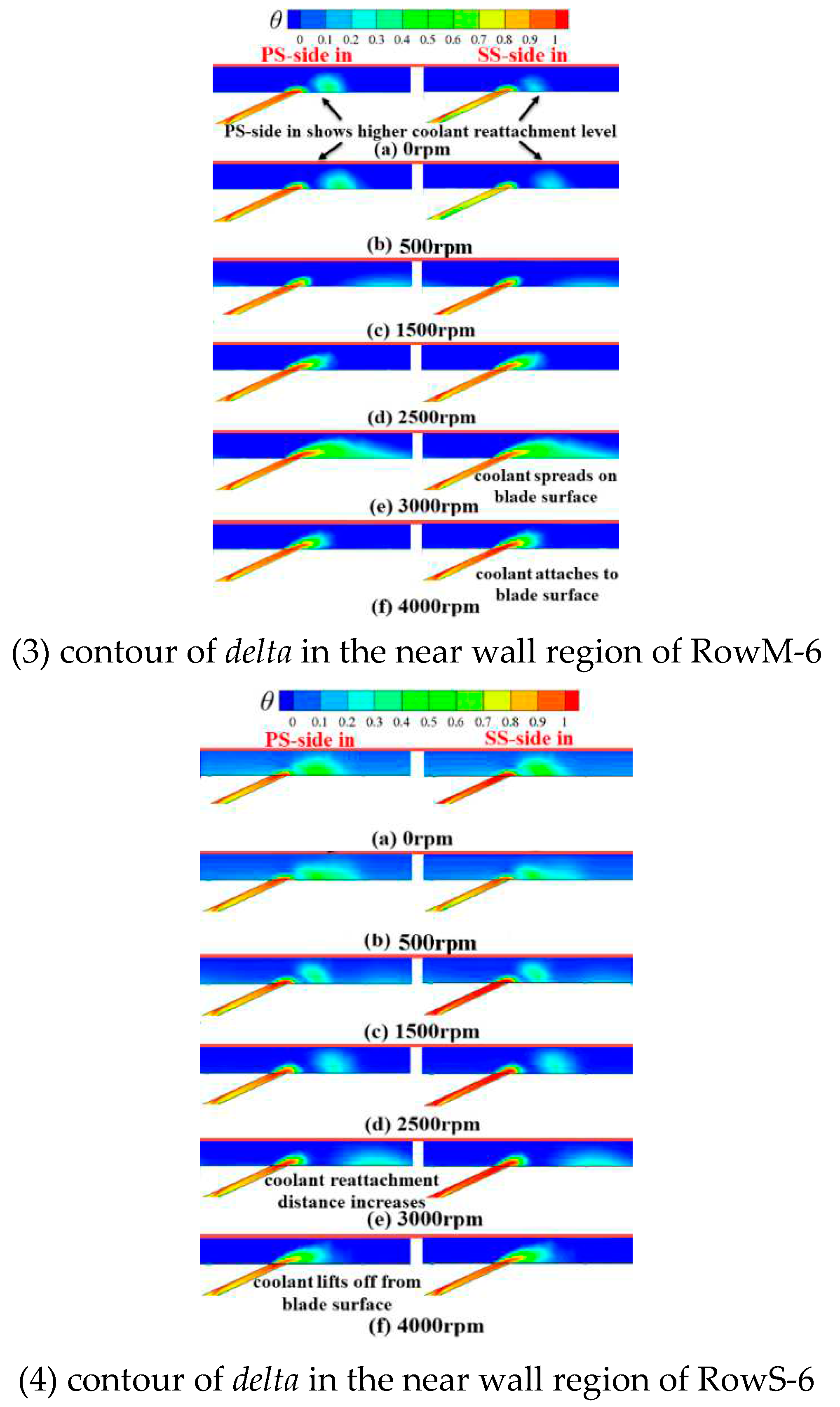
Figure 11 presents the θ contour on section A as presented in Figure 10 (b) to exhibit the spreading level of the coolant film on the blade surface. Figure 11 (1), (2) and (3) illustrate the local-region θ contour near RowP-6, RowM-6 and RowS6 in PS-side-in and SS-side-in, respectively. In general, there are mainly three types of EFC flow regimes under all of the rotating speed scenarios. First, the coolant jet lifts away from the surface of the blade and penetrates into the MF, such as the phenomena revealed in Figure 11(2)(a), 11(3)(d) and 11(4)(f). The coolant jet lifting off is caused by the low MF pressure at the outer side region of the film hole and the higher blowing ratio of the film hole. In that case, the coolant film thus fails to protect the blade surface from the MF hot gas sufficiently. Second, the coolant jet is suppressed by the MF to the surface of the blade and spreads on the blade surface. This phenomenon appears when the position of the SL aligns with the film hole position as presented in Figure 8. At 1500rpm, the SL stays at the position of RowP. Given the pressure and temperature of the MF near the SL position is the highest within the whole fluid domain, the coolant jet from RowP is suppressed onto the blade surface, leading to a large coolant film coverage area on the blade surface as seen in Figure 11(2)(c). Similarly, the coolant film from RowM attaches to the surface of the blade well at 3000rpm as reveled in Figure 11(3)(e). Third, the coolant jet lifts off initially and then reattachment to the surface of the blade as shown in Figure 11(2)(f), 11(3)(a) and 11(4). The reattachment level is affected by both the stagnation position and rotating speed. The increasing centrifugal force as a result of the increasing rotating speed makes the coolant film flow towards the side of the shroud, therefore increasing the reattachment distance as seen in Figure 11(4). Furthermore, the SL gets closer to film hole RowS with an increasing rotating speed. The high-pressure hot gas of the MF flow around the SL then pushes the coolant jet away and increases the reattachment zone.

The coolant film flow distribution in PS-side-in is rather similar to that in SS-side-in, especially at the rotating speed higher or equal to 1000rpm. At 0rpm or 500rpm, the coolant film from RowM shows higher attachment level in PS-side-in compared to SS-side-in. Because the value of blowing ratio of RowM in PS-side-in is higher than that in SS-side-in as presented in Figure 9(b). Higher blowing ratio of RowM indicates that larger amount of coolant reattaches to the surface of the blade. In general, the coolant film attachment levels in PS-side-in and SS-side-in under the identical rotating speed are almost the same. This suggests that there’s little difference of the EFC effectiveness between PS-side-in and SS-side-in.

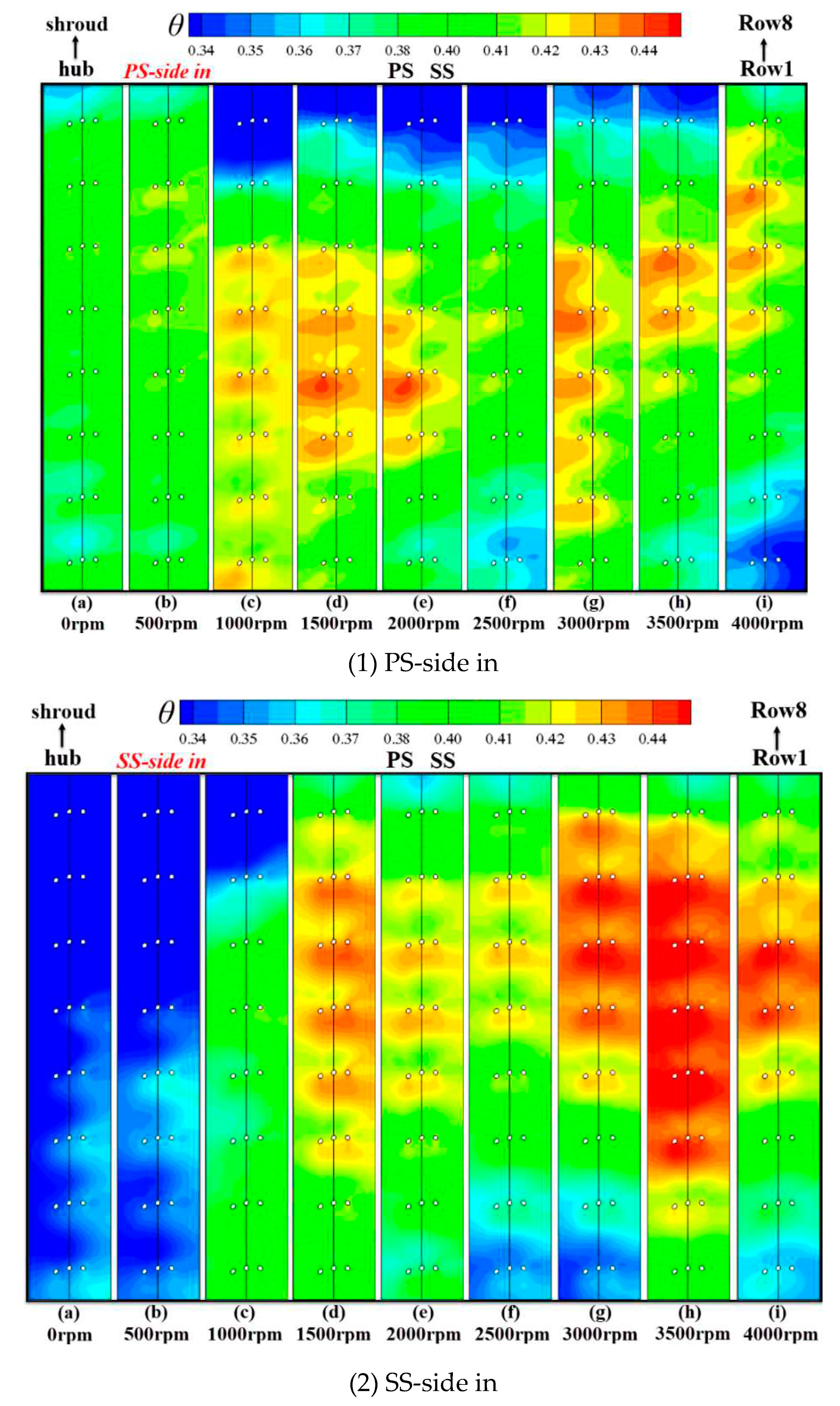
Figure 12 presents delta (defined in eq(2)) contour on the BLE surface of the PS-side-in and SS-side-in under all rotating speed range. In general, there are distinct differences on the temperature distributions on the BLE between the PS-side-in and the SS-side-in. Whereas the coolant film coverage situations on those two cases are quite similar as plotted in Figure 11. This concludes that the dominating factor that brings about such temperature distribution differences is related to the IVC rather than the EFC.

As for the similarities, large-area of the low-temperature regions could be captured at 1500rpm, 3000rpm and 3500rpm, in which the position of the SL aligns with the film hole position. Large-area of coolant film coverage brings about large-area of low temperature regions. When the SL exists at other positions, the coolant film is pushed away by the high-pressure MF near the SL, leading to a higher area-averaged temperature on the BLE surface.

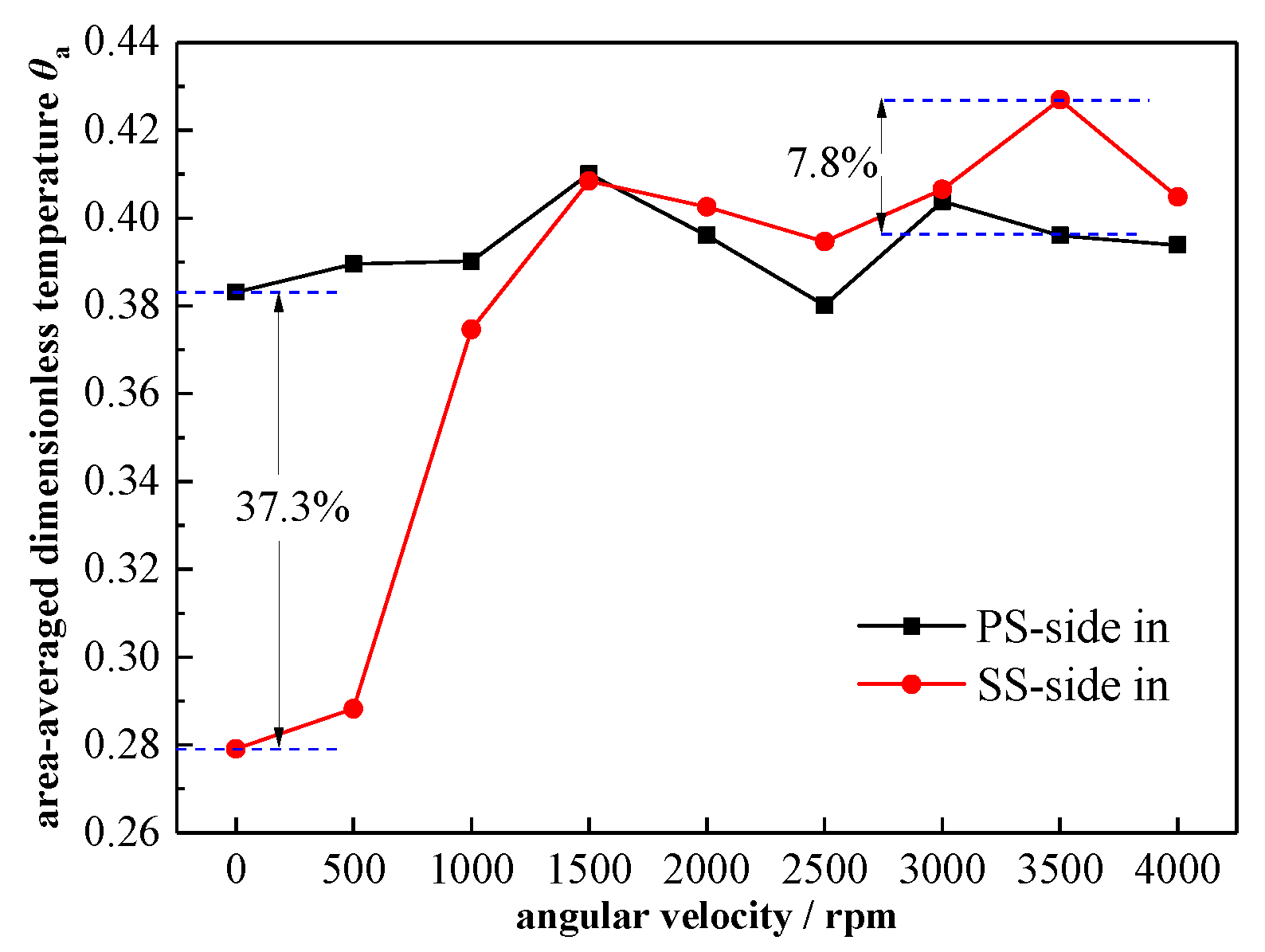
As for the differences, there are mainly three aspects of dissimilarities between the PS-side-in and the SS-side-in. First, the blade surface temperature is much higher in SS-side-in than that of the PS-side-in when the rotating speed is lower or equal to 1000rpm. Second, the blade surface temperature in SS-side-in becomes higher than that in the PS-side-in when the rotating speed is higher than 1500rpm. Such a variation becomes larger with the increasing rotating speed. Those phenomena could also be captured in Figure 13, which shows the area-averaged delta (θ_a) on the BLE surface under all rotating speeds. The highest differences appear at 0rpm and 3500rpm, where θ_a in PS-side-in is 37.3% higher than the SS-sid-in and θ_a in SS-side-in is 7.8% higher than that in PS-side-in, respectively. Third, there are large-area of high-temperature regions appear near the shroud in the PS-side-in at 1000-3500rpm. Nevertheless, those high-temperature regions disappear in the SS-side-in.

In summary, the arrangement of the internal coolant injecting nozzles confirms little influence on the flow field of the EFC. However, the nozzle arrangement presents significant influences on the temperature of the BLE. This indicates that the nozzle configurations will change the IVC performance, and then affects the VFCC performance. The discussion on the IVC is presented next.

3.2. Rotation influences the on IVC flow

The rotation influences on the flow field of the IVC are discussed in Figure 14 and Figure 15. Figure 14 shows contour of velocity V_yz as well as the streamline on the Y-Z section as presented in Figure 8 (c). V_yz is defined as:

V_yz = (V_y²+ V_z²)^0.5

(3)

where

V_y stands for the Y- component of the coolant velocity in the rotational frame

V_z stands for the Z- component of the coolant velocity in the rotational frame

As can be seen in Figure 14, the coolant blows into the vortex chamber tangentially and scours the target surface. The coolant flow ‘crashes’ the target surface and forms large-scale vortices, leading to intense convective heat transfer on the target wall. A high-velocity region near the target wall and a low-velocity region in the core region of the vortex chamber are formed. Position of the target wall is indicated in Figure 2. Then the coolant flows towards the MF through the showerhead film holes drove by the relatively larger pressure difference between the vortex chamber and the cascade, which is pointed out as the ‘suction effect’ by Fan et al.[12]. Such a ‘suction effect’ changes the position and the intensity of the vorticity of the large-scale vortex in the vortex chamber. In addition, the coolant flow will be accelerated by the ‘suction effect’, which will augment the heat transfer intensity around the region near the film holes. As the intensity of the ‘suction effect’ is dominated by the position of the stagnation point as presented in Figure 14.

When the rotating speed is relatively low, particularly at 0-500rpm, the stagnation point stays near RowP, bringing about higher-pressure and lower-pressure at the outer region of RowP and RowS. Therefore, high proportion of the coolant from the nozzle directly flows into the MF through RowS in SS-side-in rather than flows along the target wall. As for PS-side-in, relatively low proportion of the coolant from the nozzle flows into RowP. Some coolant is forced by the suction effect of RowS and flows downstream along the target wall. Such a phenomenon is more distinct as revealed in Figure 15, that presents the velocity contour and streamline on the cross-sections at various blade height at 0rpm. It can be concluded that, the much more intense “suction effect” of RowS in SS-side-in makes the large-scale vortex losing its original shape. The flow field in the vortex chamber in SS-side-in is more chaotic than that in PS-side-in. Therefore, the intensity of the internal heat transfer in SS-side-in will be much lower than that in PS-side-in. This conclusion could be captured in Figure 17, which shows the area-averaged Nusselt Number Nua on the target surface. The value of Nua in PS-side-in is 52.6% higher than the SS-side-in. The low the intensity of the internal heat transfer explains well the reason why the blade surface temperature in SS-side-in is much higher at 0-500rpm than that in PS-side in as seen in Figure 12(a) and (b).

When the rotating speed is higher than 1500rpm, there’s an opposite result in internal heat transfer intensity. The intensity of the internal heat transfer in SS-side-in becomes higher than the PS-side-in. Such a phenomenon could be observed in Figure 14. In Figure 14 (d)~(f), the high-velocity near wall region originating from the nozzle covers a larger area in SS-side-in than that in PS-side-in. There are mainly two reasons. Firstly, as the rotational speed gradually grows to 3500rpm, the stagnation point gradually moves towards the position near RowS, leading to a relatively higher-pressure and lower-pressure at the outer side of RowS and RowP. As for the PS-side-in, high proportion of coolant from the nozzle directly flows into RowP rather than flows downstream along the target wall. For the SS-side-in, relatively low proportion of coolant from the nozzle flows into RowS, and some coolant flows downstream along the target wall. Hence, the high-velocity near wall region in SS-side-in covers a relatively larger proportion of the target wall than that in PS-side-in, allowing a larger intensity of the heat transfer of the IVC in SS-side-in compared to PS-side-in.

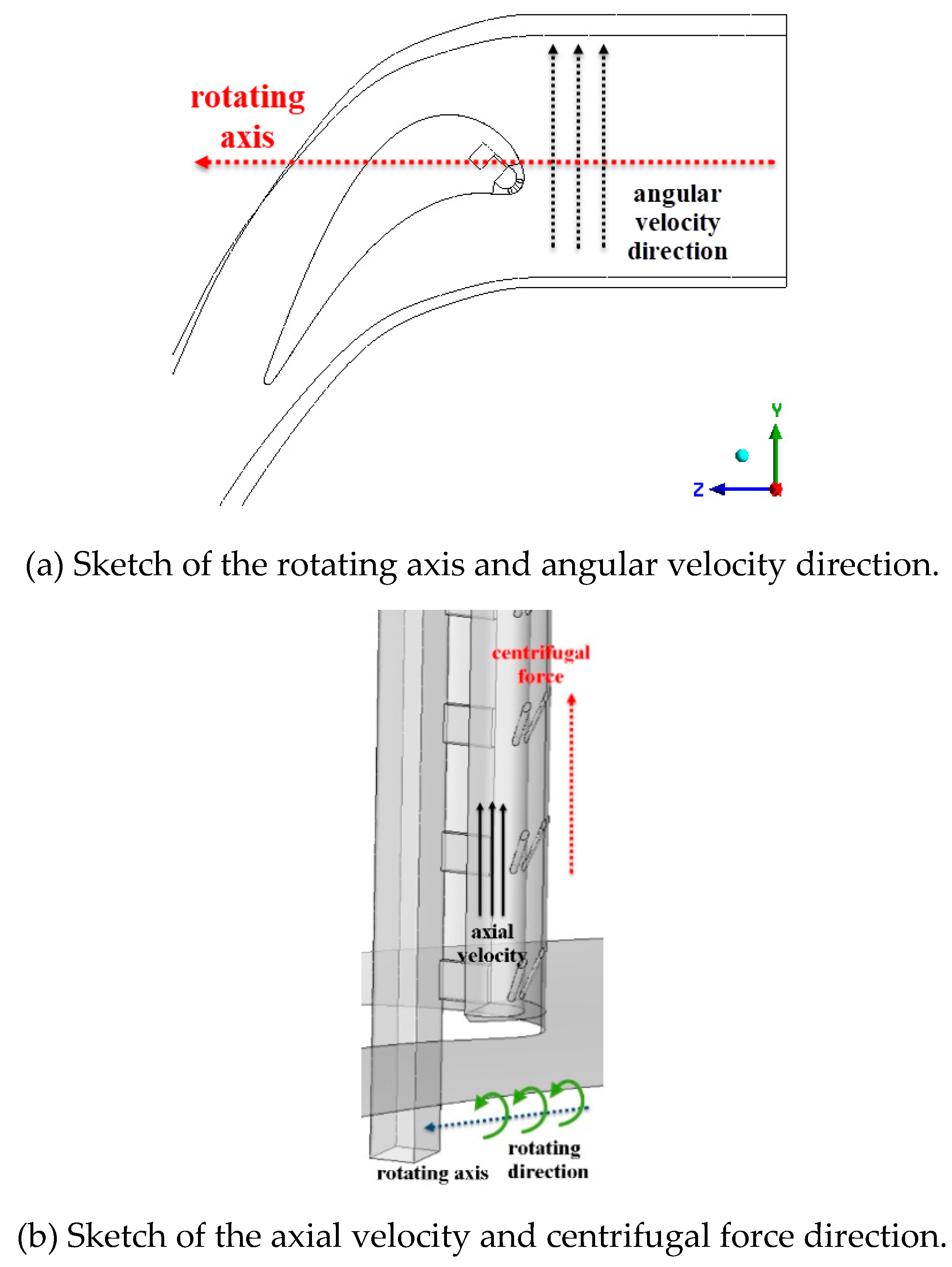
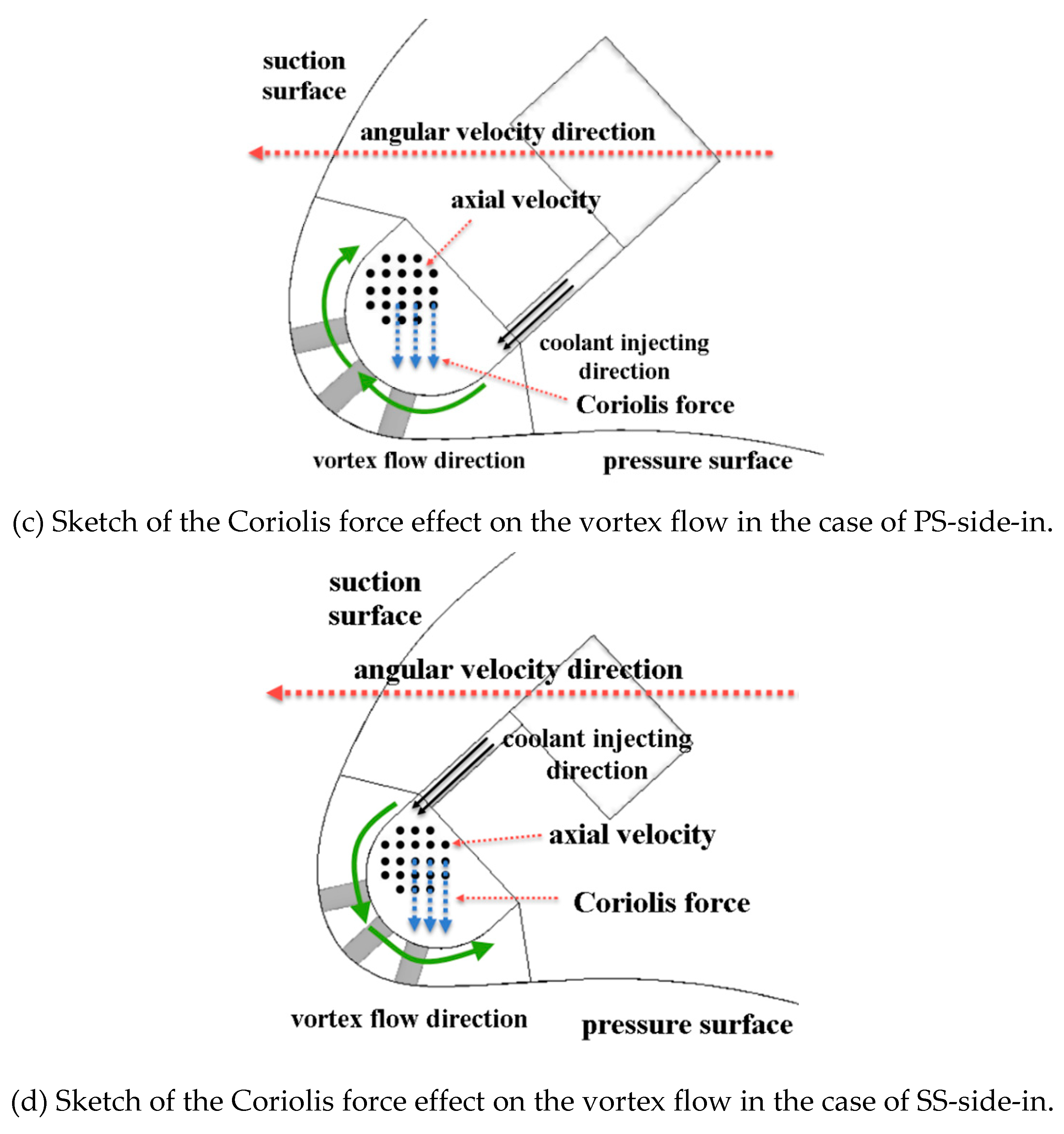
Secondly, the differences of the internal vortex flow field between the PS-side-in and the SS-side-in are related to the centrifugal force and the Coriolis force brought about by the rotation. Figure 16 exhibits the sketch of the Coriolis force effect on the internal vortex flow. Figure 16(b) shows the direction of the centrifugal force and the axial velocity. The rotation brings about the centrifugal force towards the blade height direction, which forces the coolant flows towards shroud and forms the axial velocity V_r. The higher rotating speed leads to the higher axial velocity V_r. As seen in Figure 16(a) and (c), the red dotted line represents the direction of the angular velocity ω. Therefore, based on the equation F_c=-2ω×V_r, the Coriolis force Fc could be represented by the blue dotted line. The higher rotating speed leads to the ω and V_r, which permits higher Coriolis force Fc. In terms of the PS-side-in, the direction of the Coriolis force F_c is nearly opposite to the near wall vortex flow direction, that prevents the high-velocity coolant near the target wall developing downstream. In terms of the SS-side-in, the direction of the Coriolis force F_c is like the near wall vortex flow direction, which promotes the high-velocity coolant near the target wall developing downstream. Therefore, the Coriolis force will provide a more intense of heat transfer of the IVC in SS-side-in than that in PS-side-in, and this effect will be more intensify under higher rotating speed.

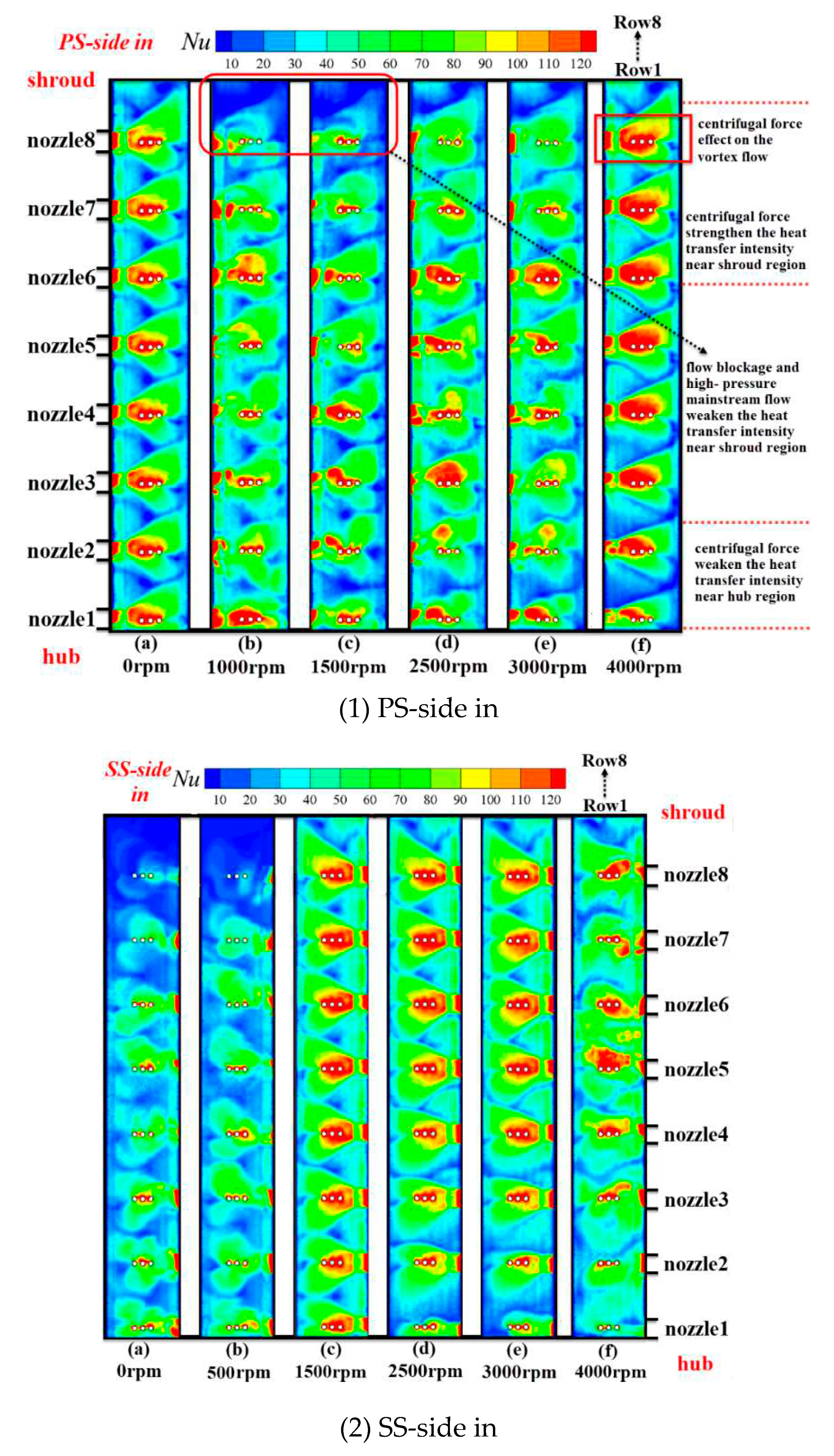
Figure 17 exhibits the Nusselt contour on the target surface in the PS-side-in and SS-side-in. It can be noticed that the high-Nu region originating from the nozzle develops downstream and covers a relatively larger area in the SS-side-in compared to that in the PS-side-in region at 1500-3000rpm. In addition, the angular velocity ω and the axial velocity V_r close to the shroud region are higher than the other regions in the vortex chamber. Thus, the Coriolis force effect on the vortex flow will be more intense close to the shroud region, resulting in higher Nu around the shroud region in the SS-side-in as compared to PS-side-in. Given the coolant flow is unable to flow axially out of the vortex chamber through the shroud wall, there will be flow blockage near the shroud region. Together with the effect of the high-pressure MF outer flow, the intensity of the vortex flow heat transfer close to the shroud region in PS-side-in will be weakened. This explained the phenomenon shown in Figure 12 that large-area of high temperature regions appear near the shroud region in PS-side-in rather than that in SS-side-in. Another noteworthy observation is the high-Nu region close to the film holes. This heat transfer enhancement phenomenon is brought about by the “suction effect” as discussed before.

To sum up, the arrangement of the coolant injecting nozzles makes a difference in the interaction between the Coriolis force and the internal vortex flow. The nozzle position will significantly impact the intensity of the internal heat transfer, and change the overall VFCC performance. The nozzles arranged near the pressure surface side is recommended to the turbines running under relatively low rotating speed range. And the nozzles arranged near the suction surface side is recommend for the relatively high rotating speed conditions. Such conclusion cannot be drawn in the IVC research under the symmetrical MF as in the past work or neglecting the MF effects.

Previous studies, including Li et al. [21] and Wang et al. [16], have evaluated the performance of VFCC in BLE by separately analyzing the effectiveness θ of the EFC as well as the heat transfer intensity (Nu) of the IVC. However, these studies were carried out under the adiabatic conditions, so a higher value for both θ and Nu was considered indicative of superior performance of a specified VFCC. In the present research, we found that the BLE surface temperature is affected by the heat conduction between IVC flow and the external film coolant coverage within conjugate approach. The higher intensity of the internal heat transfer results in the lower actual temperature on the BLE surface. However, a lower intensity of the internal heat transfer does not necessarily mean a higher actual temperature on the BLE surface. This is because better coolant film coverage on the BLE surface and lower internal heat transfer intensity can also lead to relatively better cooling performance. Therefore, when heat conduction brought about by the blade material is taken into consideration, the temperature on the BLE surface will be the more reasonable criterion for evaluation as compared to Nu.

To properly evaluate the cooling concept performance, it's important to consider the flow loss and heat transfer situation simultaneously. Shevchuk et al. [22] have proposed an aerodynamic parameter that takes into account both the heat transfer situation and pressure loss. The defination of this aerodynamic parameter is defined as:

Φ = (Nu_a /Nu₀) / ((f / f₀) ^(1/3))

(4)

Nu_a represents the area-averaged Nusselt number on the target wall of the vortex chamber.

Nu₀ = 0.023Re_D^0.8Pr^0.4 stands for the Dittus-Boelter correlation of the smooth channel axial flow, in Nu₀:

Re_D = ρUD_c/μ (U stands for the average axial velocity of the vortex flow)
Pr stands for the Prandtl Number

f₀ = 0.184Re_D^-0.2 means the Blasius friction

f = 2 (P_in-P_out) D_c/(ρV_j²L) stands for the loss of pressure, in f:

P_out stands for the mean pressure of the film hole channel internal side
P_in stands for the mean pressure of the coolant flow at internal inlet
V_j stands for the velocity of the coolant flow at internal inlet
D_c means the cross-section hydraulic diameter of the vortex chamber
T_w represents the target wall temperature
ρ represents the fluid density
L represents the vortex chamber axial length

The aim of incorporating cooling structures in turbine blades is to lower temperature of the blade and prevent thermal damage while minimizing coolant usage. Thus, in equation (4), we can replace Nusselt number Nu with the delta on the BLE surface. Similarly, friction factor f can be substituted with the mass flow of the coolant at the internal inlet M_c. This approach yields a more appropriate criterion φ for assessing the impact of rotation on the performance of VFCC in engineering application scenarios:

φ = (θ_a / θ₀) / ((M_c / M_c0) ^(1/n))

(5)

where:

θ_a means delta on the BLE surface (area-averaged value)
θ₀ means delta on the BLE surface (area-averaged value) at stationary case (0 rpm)
M_c means the mass flow of the coolant flow at the internal inlet
M_c0 means the mass flow of the coolant flow at the internal inlet at stationary case (0 rpm)
n is the alterable weighting index whose meaning is provided in the following text

A higher delta on the blade surface (namely a lower blade surface temperature) together with a lower consumption of the coolant air means a higher value of VFCC performance parameter φ. By adjusting the value of n, engineers can modify this criteria used to evaluate cooling performance. When n is relatively higher, the temperature of the blade surface becomes the more important criterion, while when n is relatively lower, the coolant consumption takes on greater significance. Table 3 and Table 4 show the value of φ for n = 3 in the case of PS-side-in and SS-side-in, respectively.

It's evident that coolant consumption rises steeply with the growing rotating speed. When the SL is positioned near RowP, coolant consumption is considerably lower at 1500rpm and 3000rpm. The SS-side-in shows superior cooling performance to the PS-side-in under the relatively high rotating speed. These findings hold true for the cooling structure examined in this study.

Our goal is to examine how rotational effects impact the characteristics of the composite conjugate cooling. Given that various sorts of gas turbines have their own designated rotating speeds, it's important to conduct more thorough simulations within specific ranges of rotating speeds while designing the BLE cooling conceptions such as the VFCC structures for various gas turbine applications (air, sea, land).

4. Conclusion

In this study, the impacts of rotation and the coolant injecting nozzle position on the characteristics of the vortex and film composite conjugate cooling are explored under the MF within practical cases. The governing equations solved in the numerical simulations are the three-dimensional steady RANS coupled with SST~γ-θ. Additionally, incorporating blade material solid region into the internal cooling structure brings about the fluid-thermal coupling. By comparing coolant injecting nozzles placed near the pressure surface side (PS-side-in) versus the suction surface side (SS-side-in), we can analyze how EFC flow interacts with IVC flow, and how rotation affects IVC flow. We also define the dimensionless temperature θ for analysis, which varies inversely with temperature.

In terms of the MF, the position of the SL is the main factor brought about by the rotation. When the position of the SL aligns with the film holes, coolant jet that flows from film holes is suppressed effectively onto the blade surface, providing extensive coverage and resulting in a lower temperature distribution on the blade surface. On the other hand, when the SL remains in other positions, the coolant film lifts off from the blade surface, leading to a higher blade surface temperature. However, the impact of nozzle position on coolant film attachment is not easily discernible.

For the IVC the centrifugal force as a result of the rotation makes the coolant move axially. The axial velocity and the angular velocity bring about the Coriolis force. The direction of the Coriolis force is opposite and similar to the near-wall vortex flow direction in the PS-side-in and SS-side-in, respectively. This makes the internal heat transfer intensity in SS-side-in case higher than that in PS-side-in under high rotating speed, leading to a lower temperature of the blade surface in SS-side-in with the heat conduction brought about by the blade material.

Given the comparison of the aerodynamic parameter involving both the BLE surface temperature and the coolant consumption, the nozzles arranged near the pressure surface side is recommended to the turbines running under relatively low rotating speed range. And the nozzles arranged near the suction surface side is suggested to the relatively high rotating speed conditions.

Author Contributions

Jiefeng Wang: Conceived and designed the analysis, Collected the data, Performed the analysis, Wrote the paper; Eddie Yin Kwee NG: Conceived and designed the analysis, Revised the paper; Jianwu Li: Collected the data; Yanhao Cao: Collected the data; Yanan Huang: Collected the data; Liang Li: Conceived and designed the analysis, Revised the paper.

Funding

This work was supported by the [National Science and Technology Major Project] under Grant [2017-I-0009-0010].

Conflicts of Interest

The authors declare no conflict of interest.

References

Han, J.-C.; Dutta, S.; Ekkad, S. Gas Turbine Heat Transfer and Cooling Technology; Taylor & Francis: Boca Raton, FL, USA, 2012. [Google Scholar]
Kreith, F.; Sonju, O. The Decay of a Turbulent Swirl in a Pipe. Journal of Fluid Mechanics 1965, 22, 257–271. [Google Scholar] [CrossRef]
Ling, J.P.; Ireland, P.T.; Harvey, N.W. Measurement of heat transfer coefficient distributions and flow field in a model of a turbine blade cooling passage with tangential injection; proceedings of the ASME Turbo Expo 2006: Power for Land, Sea, and Air, Barcelona, Spain, F, 2006 [C]. American Society of Mechanical Engineers.
Du, C.; Li, L.; Wu, X.; et al. Effect of jet nozzle geometry on flow and heat transfer performance of vortex cooling for gas turbine blade leading edge. Applied Thermal Engineering 2015, 93, 1020–1032. [Google Scholar] [CrossRef]
Du, C.; Li, L.; Chen, X.X.; et al. Numerical Study on Effects of Jet Nozzle Angle and Number on Vortex Cooling Behavior for Gas Turbine Blade Leading Edge; proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, South Korea, F, 2016 [C].
Fan, X.; Li, L.; Zou, J.; et al. Local heat transfer of vortex cooling with multiple tangential nozzles in a gas turbine blade leading edge cooling passage. International Journal of Heat and Mass Transfer 2018, 126, 377–389. [Google Scholar] [CrossRef]
Wang, J.; Du, C.; Wu, F.; et al. Investigation of the vortex cooling flow and heat transfer behavior in variable cross-section vortex chambers for gas turbine blade leading edge. International Communications in Heat and Mass Transfer 2019, 108, 104301. [Google Scholar] [CrossRef]
Zhao, H.-J.; Jiang, Y.-T.; Zheng, Q.; et al. Particle Deposition Characteristics of U-Shaped Rib Channel of Marine Gas Turbine. Tuijin Jishu/Journal of Propulsion Technology 2021, 42, 1906–1914. [Google Scholar]
Zhu, X.D.; Zhang, J.Z.; Tan, X.M. Numerical assessment of round-to-slot film cooling performances on a turbine blade under engine representative conditions. International Communications in Heat and Mass Transfer 2019, 100, 98–110. [Google Scholar] [CrossRef]
Ye, L.; Liu, C.; Du, K.; et al. Influences of groove configuration and density ratio on grooved leading-edge showerhead film cooling using the pressure sensitive paint measurement technique. Int J Heat Mass Tran 2022, 190, 122641. [Google Scholar] [CrossRef]
Ye, L.; Liu, C.; Li, B.; et al. Detailed showerhead cooling effectiveness measurements on the notched leading-edge surface: Effect of freestream turbulence and density ratio. International Communications in Heat and Mass Transfer 2022, 135, 106142. [Google Scholar] [CrossRef]
Fan, X.; Du, C.; Li, L.; et al. Numerical simulation on effects of film hole geometry and mass flow on vortex cooling behavior for gas turbine blade leading edge. Applied Thermal Engineering 2016, 112, 472–483. [Google Scholar] [CrossRef]
Du, C.; Li, L.; Fan, X.; et al. Rotational influences on aerodynamic and heat transfer behavior of gas turbine blade vortex cooling with bleed holes. Applied Thermal Engineering 2017, 121, 302–313. [Google Scholar] [CrossRef]
Li, L.; Du, C.H.; Chen, X.X.; et al. Numerical study on flow and heat transfer behavior of vortex and film composite cooling. Journal of Mechanical Science and Technology 2018, 32, 2905–2917. [Google Scholar] [CrossRef]
Zhang, M.; Wang, N.; Han, J.C. Internal heat transfer of film-cooled leading edge model with normal and tangential impinging jets. Int J Heat Mass Tran 2019, 139, 193–204. [Google Scholar] [CrossRef]
Wang, J.; Li, L.; Li, J.; et al. Numerical investigation on flow and heat transfer characteristics of vortex cooling in an actual film-cooled leading edge. Applied Thermal Engineering 2021, 185, 115942. [Google Scholar] [CrossRef]
Timko, L. Energy efficient engine high pressure turbine component test performance report [R], 1984. NASA-CR-168289, https://ntrs.nasa.gov/citations/19900019237.
Celik, I.B.; Ghia, U.; Roache, P.J.; et al. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. Journal of fluids Engineering-Transactions of the ASME 2008, 130, 078001. [Google Scholar]
Kohli, A.; Bogard, D. Adiabatic effectiveness, thermal fields, and velocity fields for film cooling with large angle injection. J. Turbomach. 1997, 119, 352–358. [Google Scholar] [CrossRef]
Safi, A.; Hamdan, M.O.; Elnajjar, E. Numerical investigation on the effect of rotation on impingement cooling of the gas turbine leading edge. Alexandria Engineering Journal 2020, 59, 3781–3797. [Google Scholar] [CrossRef]
Li, L.; Du, C.; Chen, X.; et al. Numerical study on flow and heat transfer behavior of vortex and film composite cooling. Journal of Mechanical Science and Technology 2018, 32, 2905–2917. [Google Scholar] [CrossRef]
Shevchuk, I.V.; Jenkins, S.C.; Weigand, B.; et al. Validation and analysis of Numerical results for a varying aspect ratio two-pass internal cooling channel. Journal of heat transfer 2011, 133, 1085–1094. [Google Scholar] [CrossRef]

Figure 1. The three dimensional computational model.

Figure 2. Sketch of the two cases with different nozzle position.

Figure 3. IVC structure sizes of the VFCC model.

Figure 4. Schematic of the calculating mesh and y⁺ checking.

Figure 5. Profile of the coolant flow pressure in the vortex chamber along blade height with the numerical uncertainty.

Figure 6. Comparison of the prediction data obtained from the turbulence models to the experiment data [24].

Figure 7. Schema of transfer learning technique with pre-trained models for binary classification.

Figure 8. Pressure contour and surface streamline on the leading-edge region of the blade under all rotating speeds.

Figure 9. Blowing ratios of the film holes Row6 under all rotating speeds.

Figure 10. Schema of transfer learning technique with pre-trained models for binary classification.

Figure 11. Near-wall contour of delta on the cross-section A presented in figure 10(a).

Figure 12. Contours of delta on the BLE surface under all rotating speeds.

Figure 13. Area-averaged delta on the BLE surface under all rotating speeds (PS-side-in .vs. SS-side-in).

Figure 14. Schema of transfer learning technique with pre-trained models for binary classification.

Figure 15. Streamline and contour of velocity on the cross-section B presented in figure 10(b) at various blade heights under 0rpm.

Figure 16. Sketch of the Coriolis force effect on the IVC flow.

Figure 17. Nu contour on the target wall in the case of SS-side-in .vs. PS-side-in.

Table 1. Boundary conditions for simulation.

Region	Parameter	Value
MF cascade (fluid)	total temperature of cascade inlet (stationary)	683 K
	total pressure of cascade inlet (stationary)	206.431 kPa
	static pressure of cascade outlet (stationary)	68.81 kPa
	turbulence intensity of cascade inlet	high (10%)
internal chamber (fluid)	total temperature of internal inlet (stationary)	352 K
	turbulence intensity of internal inlet	medium (5%)
	total pressure of internal inlet (stationary)	360 kPa
blade material (solid)	thermal conductivity of steel	60.5 W/(m·K)
	angular velocity ω	0, 500, 1000, 1500, 2000, 2500, 3000, 3500, 4000rpm

Table 2. Numerical uncertainty (GCI) and extrapolation results calculated from the grid independence method.

Grid number (million)	Nu_a	θ_P	θ_S
2.70	65.76	0.4139	0.4163
7.42	65.26	0.4122	0.4161
18.79	67.20	0.4165	0.4206
Extrapolation	67.78	0.4190	0.4190
GCI	1.09%	0.75%	0.60%

Table 3. Aerodynamic parameters of PS-side-in.

ω/rpm	0	500	1000	1500	2000	2500	3000	3500	4000
θ_a	0.3831	0.3895	0.3901	0.4101	0.3960	0.3802	0.4038	0.3960	0.3938
M_c/M_c0	1.000	1.001	1.394	0.592	0.396	1.620	1.833	2.813	3.010
φ	1.00	1.02	0.91	1.27	1.41	0.84	0.86	0.73	0.71

Table 4. Aerodynamic parameters of SS-side-in.

ω/rpm	0	500	1000	1500	2000	2500	3000	3500	4000
θ_a	0.2791	0.2883	0.3746	0.4082	0.4025	0.3946	0.4066	0.4269	0.4047
M_c/M_c0	1.289	1.988	1.673	1.023	1.024	1.023	1.125	1.954	0.735
φ	0.67	0.60	0.82	1.06	1.04	1.02	1.02	0.89	1.17

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Study on Effects of Modern Turbine Blade Coolant Injecting Nozzle Position on Film Cooling and Vortex Composite Performance under Rotating Conditions

Abstract