A Correction Method for the Motion Measurement of the Ship-Borne Mechanical Platform Based on Multi-Sensor Fusion

Preprint

Article

A Correction Method for the Motion Measurement of the Ship-Borne Mechanical Platform Based on Multi-Sensor Fusion

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

28 July 2023

Posted:

31 July 2023

You are already at the latest version

Alerts

Abstract

In order to perform multi-degree-of-freedom motion measurements of marine machinery such as ship-borne mechanical platform in an absolute environment without a reference, absolute measurement methods using acceleration sensors and tilt gyroscopes are typically employed. However, due to the influence of wave forces on ship-borne mechanical platform, the coupling between different degrees of freedom can cause mutual interference, resulting in significant sensor measurement disturbances that make efficient computation and real-time analysis challenging. Specifically, when ship-borne mechanical platform swings, the proof mass of the acceleration sensor produces an undesirable signal output in the vertical direction, which leads to imprecise acceleration integration, thereby affecting accurate motion collection and posture estimation. To address these challenges, by analyzing the influence of the inclination angle of the ship-borne mechanical platform on the sensor measurement, and using the working principle of the acceleration sensor and angle sensor, a correction method for the motion measurement of the ship-borne mechanical platform based on multi-sensor fusion is proposed. In this article, we first analyze the influence of inclination angle on the integral effect in the heave direction. Then the configuration using four groups of acceleration sensors to correct the integral effect is proposed. Finally, the optimal inclination angle is determined through Kalman filtering based on the measured value of angle sensors and estimated values from the acceleration sensor sets. Experiments have proved that the average error of the corrected heave displacement signal is 25.34 mm, which is better than the integral displacement signal of a single acceleration sensor. At the same time, the acceleration sensor is used to calculate the roll angle and pitch angle of the ship-borne mechanical platform, and combined with the angle sensor signal to perform Kalman filtering, which filters out the errors caused by the shaking and instability of the mechanical platform, and can more accurately estimate the true inclination of the platform. Therefore, this method can enhance the precision and accuracy of the ship-borne mechanical platform motion signal acquisition, providing more valuable experimental data for research in marine engineering and related fields.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

Due to the nature of the motion experienced by ship-borne mechanical platform on the sea, there are three degrees of freedom that need to be considered: heave, roll, and pitch. Typically, the motion signal in the heave direction is acquired through double integration of data from an acceleration sensor. However, ship-borne mechanical platform on the sea also experiences movements in roll and pitch directions, which can cause the acceleration sensor to deviate from the ideal horizontal plane. These inclination angles cause additional horizontal forces exerted on the piezoelectric element of the acceleration sensor, leading to errors in the displacement measurement obtained through integration. As a result, it becomes difficult to accurately calculate the attitude of the ship-borne mechanical platform.

Key concerns in the attitude estimation of ship-borne mechanical platform are mainly about improving accuracy and real-time performance of the sensor system, particularly under the influence of low-frequency motion caused by sea waves. Challenges arise as each type of sensor has its limitations and they cannot solely obtain accurate multidimensional attitude data. Yet, aggressively increasing the number of sensors is not a wise solution, since it brings massive computational burden. To achieve precise estimation of ship-borne mechanical platform attitude while eliminating the information redundancy, efficient multiple sensor fusion method with multilevel information processing abilities is required.

To address the shortcomings of a single sensor in accurately estimating real-time and comprehensive multi-degree-of-freedom information, scholars have conducted extensive research on multi-sensor-fusion techniques. Luo R C developed the general paradigm of a sensor data fusion system in 1988.[1] Durrant-Whyte H F presented a fully decentralized architecture for data fusion problems in 1990.[2] Wen W described an algorithm for implementing a multi-sensor system in a model-based environment with consideration of the constraints in 1992.[3] Harris C J formally introduced the process of data fusion and sensor integration with a variety of implementation architectures, that recognize data fusion as a critical element in overall systems integration in 1998.[4] Llinas J provided a tutorial on data fusion, introducing data fusion applications, process models, and identification of applicable techniques in 1998.[5] Chen S designed a detection system based on multi-sensor data fusion technology in 2003.[6] Herpel T modeled sensor phenomena, road traffic scenarios, data fusion paradigms and signal processing algorithms and investigate the impact of combining sensor data on different levels of abstraction on the performance of the multi-sensor system by means of discrete event simulation in 2008.[7] At the same year, Manjunatha P proposed a multi-sensor data fusion algorithm in WSN using fuzzy logic for event detection application, improved the reliability and accuracy of the sensed information.[8] Dong J presented an overview of recent advances in multi-sensor fusion. Firstly, the most popular existing fusion algorithms are introduced, with emphasis on their recent improvements. Advances in main applications fields in remote sensing, including object identification, classification, change detection and maneuvering targets tracking, are described. Both advantages and limitations of those applications are then discussed.[9] Wolter P T used partial least squares (PLS) regression to integrate different combinations of satellite sensor data to determine the best combination of sensor data in 2010.[10] Medjahed H proposed an automatic in-home healthcare monitoring system with several sensors that can be installed at home and enables to get a full and tightly controlled universe of data sets in 2011.[11] Banerjee T P propose and investigate a hybrid method for fault signal classification based on sensor data fusion by using the Support Vector Machine (SVM) and Short Term Fourier Transform (STFT) techniques in 2012.[12] Frikha A proposed A modified Analytical Hierarchy Process (AHP) that incorporates several criteria to determine the weights of a sensor reading set.[13] Azimirad E present a comprehensive review of data fusion architecture, and exploring its conceptualizations, benefits, and challenging aspects, as well as existing architectures in 2015.[14] G Fortino proposed a system which is based on a multi-sensor data fusion schema to perform automatic detection of handshakes between two individuals and capture of possible heart-rate-based emotion reactions due to the individuals’ meeting.[15] S Rawat used back-propagation neural network to solve an inherent problem of multi-sensor data fusion in wireless sensor network applications in 2016.[16] Duro J A proposed a novel multi-sensor data fusion framework to enable identification of the best sensor locations for monitoring cutting operations in 2016.[17] Maimaitijiang M evaluated the power of high spatial resolution RGB, multispectral and thermal data fusion to estimate soybean (Glycine max) biochemical parameters including chlorophyll content and nitrogen concentration in 2017.[18] Jing L proposed an adaptive multi-sensor data fusion method based on deep convolutional neural networks (DCNN) for fault diagnosis in 2017.[19] Kumar P proposed a novel multi-sensor fusion framework for Sign Language Recognition (SLR) using Coupled Hidden Markov Model (CHMM) in 2017.[20] Bouain M proposed a Multi-Sensor Data Fusion (MSDF)embedded design for vehicle perception tasks using stereo camera and Light Detection and Ranging (LIDAR) sensors in 2018.[21] Xiao F proposed a weighted combination method for conflicting pieces of evidence in multi-sensor data fusion in 2018.[22] Zhang W proposed a mathematical model based on a multi-sensor data fusion algorithm. The safety distance of the line drone is diagnosed in 2019.[23] De Farias C M proposed a MDF technique that divides the monitored interval into a set of intervals (non-overlapped intervals and overlapped intervals) and attributes each interval to an abstract sensor in 2019.[24] Xiao F proposed a novel method for multi-sensor data fusion based on a new belief divergence measure of evidences and the belief entropy in 2019 and then proposed a hybrid MSDF method in 2020.[25,26] Muzammal M proposed a data fusion enabled Ensemble approach in 2020.[27] Li N proposed a RUL prediction method based on a multi-sensor data fusion model in 2021.[28] Kashinath S A reviewed DF methods used for real-time and multi-sensor (heterogeneous) TFA studies in 2021.[29] Fei S used machine learning (ML) methods for fusion of unmanned aerial vehicle (UAV)-based multi-sensor data can improve the prediction accuracy of crop yield in 2023.[30] Han C proposed an absolute displacement measurement method and its application in ship motion measurement.[31] However, in the field of three-degree-of-freedom motion measurement of ship-borne mechanical platforms, the method of multi-sensor fusion has been seldomly used. There are still many technical problems in the application of ship-borne mechanical platform motion measurements. Especially, the inherent interference between the effects of different degree-of-freedom ship movements on sensor outputs cause challenges to traditional sensor-fusion methods.

In this paper, in order to improve the accuracy of the ship-borne mechanical platform motion signal computed by the double integration of the single-degree-of-freedom acceleration sensor, a ship-borne mechanical platform motion measurement correction method based on multi-sensor fusion is proposed with a set of angle sensors and four sets of acceleration sensor sensors. The proposed sensor configuration eliminates the influence of the inclination angle on the integral displacement signal in the heave direction, and utilizes the Kalman filter to estimate the optimal inclination angle and heave displacement. In the proposed Kalman filtering-based algorithm, the calculated angle signal is used as the estimation value, and the angle signal collected by the angle sensor is used as the observation value to iteratively optimize the inclination angles. In order to prove the effectiveness of the method, we verified the proposed algorithm on the laboratory platform by simulating the motion of the ship-borne mechanical platform and computing the multi-sensor fusion heave displacement estimation. Finally, the estimated data was compared with the standard motion signal obtained by a laser sensor. It is verified that the algorithm can restore the actual motion characteristics of the ship-borne mechanical platform with improved accuracy through data fusion of acceleration sensors and tilt angle sensor compared with methods using only one type of motion sensor.

The main contributions of this paper are summarized as follows:

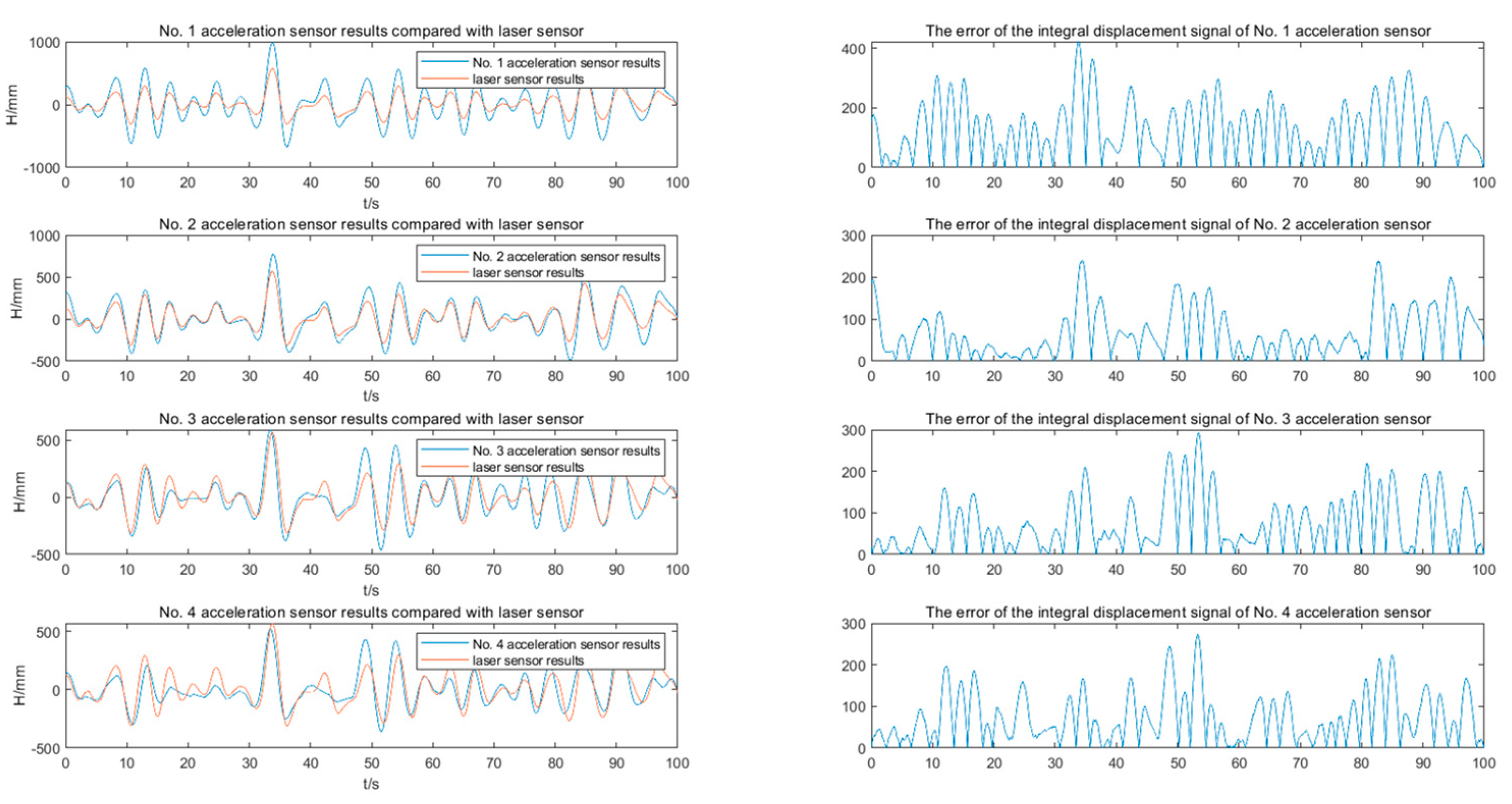
A method for measuring and correcting the heave direction of ship-borne mechanical platform motion based on multi-acceleration-sensor fusion is proposed. The heave displacement signal of the platform under unknown tilt angle is calculated by the outputs of 4 sets of acceleration sensors with improved accuracy.
A method for measuring the change of inclination angle of ship-borne mechanical platform motion based on Kalman filtering technique using sensor fusion of acceleration sensor and angle sensor is proposed. The calculated tilt angle of the platform in roll and pitch direction calculated by 4 sets of acceleration sensors is used as the estimation value, and the inclination angle signal measured by the angle sensor is used as the observation value. Innovation-based adaptive Kalman filtering is used to obtain the inclination angle and the heave displacement of the platform with higher accuracy.

The subsequent sections of this manuscript are organized as follows: Section 2 presents the effect of tilt angle on the integrated displacement signal in the heave direction. Section 3 details the correction principle and the proposed correction method for ship-borne mechanical platform motion measurement based on multi-sensor fusion. Section 4 designs experiments to verify the effectiveness of the ship-borne mechanical platform motion measurement correction method based on multi-sensor fusion. Section 5 presents the conclusion and provides suggestions for future work.

2. Preliminary Work

There are two main types of acceleration sensors at present: piezoelectric sensors and capacitive sensors. Both sensors output acceleration-related signal but with different working mechanisms.

Capacitive acceleration sensors use changes in capacitance to measure acceleration. It usually consists of two parallel metal plates with a central mass. When the sensor is subjected to acceleration, the mass will be displaced relative to the metal plate, thereby changing the capacitance value between the metal plates. By measuring the change of the capacitance value, the acceleration experienced by the sensor can be calculated.

Piezoelectric acceleration sensors use the piezoelectric effect for measurement. It usually consists of one or more piezoelectric crystals, a vibrating proof mass and signal processing circuitry. When the sensor is subjected to acceleration, the vibrating proof mass compresses or stretches the piezoelectric crystal, which creates an electrical charge and generates a voltage signal. The signal processing circuit will amplify, filter and digitize the voltage signal, and finally obtain the measured value of acceleration.

However, in ship-borne mechanical platform motion measurement, capacitive sensors have many disadvantages:

Capacitance is seriously interfered by the marine environment, such as temperature, humidity and other factors. Generally, it needs to be shielded and filtered, otherwise it will affect the measurement accuracy.
Capacitive sensors need to be installed on the hull, which is easily subjected to vibration and shock from the hull.
In marine environments, capacitive sensors are susceptible to seawater corrosion and water pressure, requiring special protection methods.

Therefore, piezoelectric sensors are usually more suitable for the use in ship-borne mechanical platform motion measurements. Piezoelectric sensors are not affected by harsh environments such as high temperature and high pressure, and have better anti-interference ability, which provide more accurate measurement results. We will discuss the acceleration sensor based on piezoelectric effects in the rest of the article.

During the process of measuring acceleration with a piezoelectric sensor, the output results can be directly affected by vertical and horizontal movements, such as pitching and rolling. These movements can alter the orientation of the sensor and therefore affect the accuracy of measurements. Additionally, any tilting movements can also impact the sensor's signal, in addition to any coupling effects on the overall system. Mainly because any movement or tilting of the acceleration sensor can affect the orientation of the mass within the device, and therefore alter the output signal. For example, if the acceleration sensor is tilted to one side, the gravitational force acting on the mass will be shifted, leading to inaccurate measurements. Similarly, if the acceleration sensor is subjected to any pitching or rolling movements, the direction of gravitational force will change and affect the measurements accordingly.

To compensate for these effects, it is important to properly calibrate the acceleration sensor and account for any potential sources of error. This can include adjusting for any tilting or coupling effects, the influence of inclination angle on the integrated displacement signal in the heave direction is shown in Figure 1.

When the ship-borne mechanical platform is at its horizontal position, the relationship between the heave acceleration and the support force

F_{N}

of the ship-borne mechanical platform to the acceleration sensor is given by

F_{N} - G = m a,

(1)

where

m

and

G

are the mass and the gravity force of the proof mass, respectively. As the output voltage of the piezoelectric sensor is approximately linear to the applied stress, we obtain that

C = \frac{V_{o u t}}{a} = \frac{K}{m}

(2)

where

K

is the linearized piezoelectric coefficient. The sensitivity

C

of the acceleration sensor could be expressed as

C = \frac{V_{o u t}}{a} = \frac{K}{m},

(3)

However, in real-world applications, pitch angle

θ_{p}

and roll angle

θ_{r}

tilt the ideal coordinates and the data should be accordingly adjusted in real-time. The transformation matrix from the earth coordinate system to the accelerator platform coordinate system is obtained as follows:

\begin{matrix} R_{x y}^{t} = (\begin{matrix} 1 & 0 & 0 \\ 0 & \cos θ_{p}^{t} & - \sin θ_{p}^{t} \\ 0 & \sin θ_{p}^{t} & \cos θ_{p}^{t} \end{matrix}) (\begin{matrix} \cos θ_{r}^{t} & 0 & \sin θ_{r}^{t} \\ 0 & 1 & 0 \\ - \sin θ_{r}^{t} & 0 & \cos θ_{r}^{t} \end{matrix}) (\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}) \\ = (\begin{matrix} \cos θ_{r}^{t} & \sin θ_{p}^{t} \sin θ_{r}^{t} & \cos θ_{p}^{t} \sin θ_{r}^{t} \\ 0 & \cos θ_{p}^{t} & - \sin θ_{p}^{t} \\ - \sin θ_{r}^{t} & \sin θ_{p}^{t} \cos θ_{r} & \cos θ_{p}^{t} \cos θ_{r}^{t} \end{matrix}) \end{matrix} .

(4)

Since the acceleration sensor only measures normal acceleration in the O-X₁Y₁ plane, the detected acceleration

\bar{a}

could be calculated by

\bar{a} = \frac{F_{N} - G c o s θ_{r} c o s θ_{p}}{m} .

(5)

Therefore, the output voltage of the piezoelectric sensor is

V_{o u t} = \frac{F_{N} - G c o s θ_{r} c o s θ_{p}}{K} = \frac{\bar{a} + \frac{G}{m} (1 - c o s θ_{r} c o s θ_{p})}{C} .

(6)

The actual acceleration

a

of the sensor can be obtained by

a = \frac{\bar{a}}{c o s θ_{r} c o s θ_{p}} = \tilde{C} (θ_{r}, θ_{p}) V_{o u t} + \tilde{D} (θ_{r}, θ_{p}),

(7)

where

\tilde{C} (θ_{r}, θ_{p})

and

\tilde{D} (θ_{r}, θ_{p})

are slope correction factor and intercept correction factor of the acceleration sensor, respectively:

\tilde{C} (θ_{r}, θ_{p}) = \frac{C}{c o s θ_{r} c o s θ_{p}},

(8)

\tilde{D} (θ_{r}, θ_{p}) = g (1 - \frac{1}{c o s θ_{r} c o s θ_{p}}) .

(9)

Now we assume that the accelerator has a displacement of

d H

in the heave direction. In other words, the movement of the sensor can be denoted as:

d T_{G} = (\begin{matrix} 0 \\ 0 \\ d H \end{matrix}) .

(10)

During this small time period,

θ_{p}

and

θ_{r}

can be regarded as constant. Therefore, the displacement of the acceleration sensor under ship-borne mechanical platform coordinate system is computed as follows:

\begin{matrix} d T_{L} = R_{x y}^{t} d T_{G} = (\begin{matrix} \cos θ_{r}^{t} & \sin θ_{p}^{t} \sin θ_{r}^{t} & \cos θ_{p}^{t} \sin θ_{r}^{t} \\ 0 & \cos θ_{p}^{t} & - \sin θ_{p}^{t} \\ - \sin θ_{r}^{t} & \sin θ_{p}^{t} \cos θ_{r} & \cos θ_{p}^{t} \cos θ_{r}^{t} \end{matrix}) ∙ (\begin{matrix} 0 \\ 0 \\ d H \end{matrix}) \\ = (\begin{matrix} \cos θ_{p}^{t} \sin θ_{r}^{t} d H \\ \sin θ_{p}^{t} d H \\ \cos θ_{p}^{t} \cos θ_{r}^{t} d H \end{matrix}) \end{matrix} .

(11)

As shown in Figure 2, the integration result of the sensor output is essentially the track along

d X

(the black arrows), which can be obtained by Equation (11):

d X = d T_{L} (3) = \cos θ_{p}^{t} \cos θ_{r}^{t} d H .

(12)

Based on the relationship of

d X

and

d H

in Equation (12), the displacement correction function is thus established:

Z = \int d H = \int \cos^{- 1} θ_{p}^{t} \cos^{- 1} θ_{r}^{t} d X,

(13)

where

Z

is the actual displacement of the sensor in the heave direction (the blue arrow).

3. Proposed Algorithm

In this work, a multi-sensor fusion ship-borne sensing platform consisting of one gyroscope for angle detection and four piezoelectric acceleration sensors for displacement detection is developed. The proposed sensing system aims to optimize the real-time estimation of the three degrees of freedom ship-borne mechanical platform movement through two novel multi-sensor fusion algorithms, which will be discussed in detail in the following. The sensor configurations are demonstrated in Figure 3. Four uniaxial acceleration sensors S_A, S_B, S_C, and S_D are installed at the corners of the square platform with sides of length L. Besides, a gyroscope for tilt angle detection is fixed at the center of the square platform.

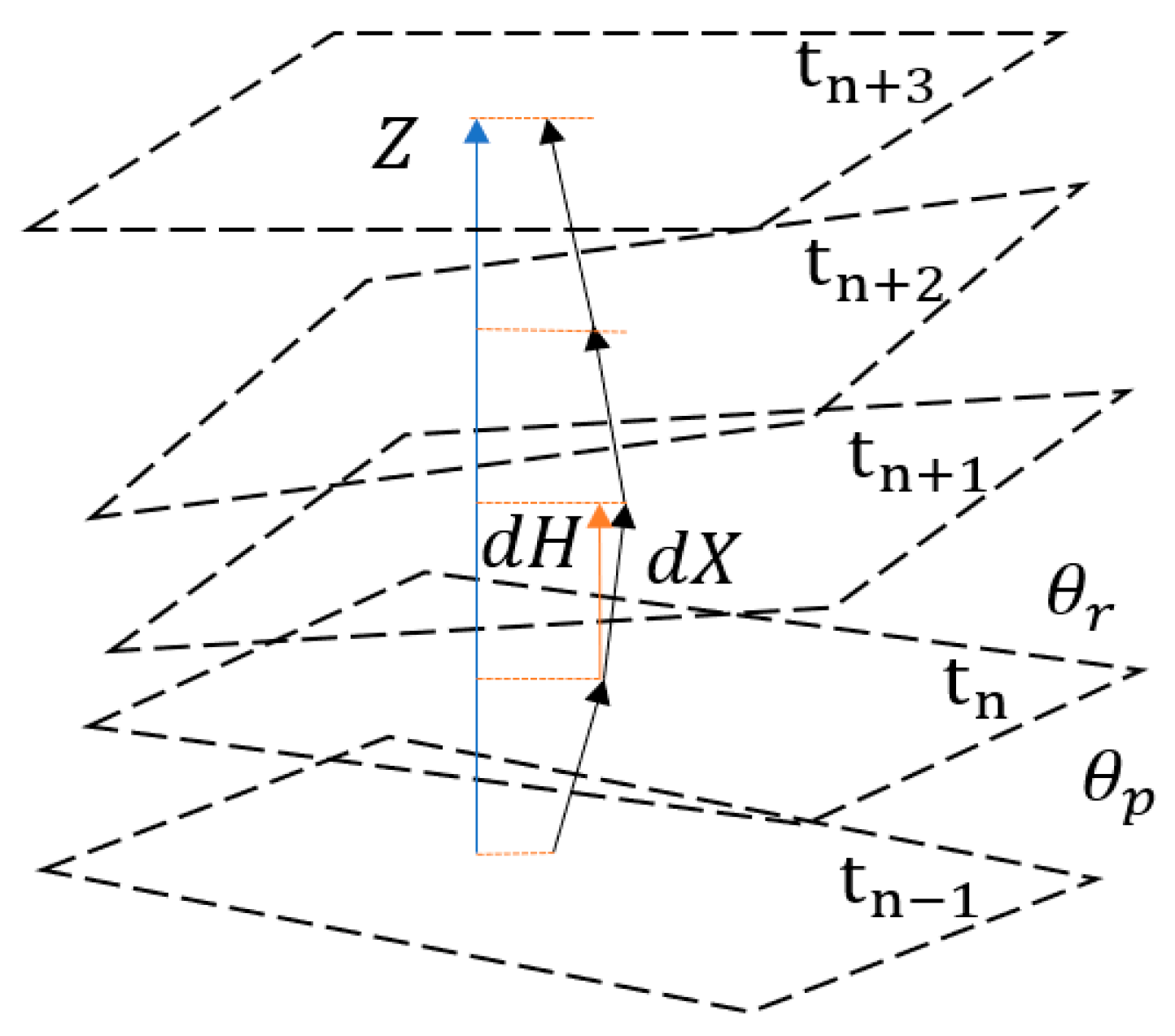
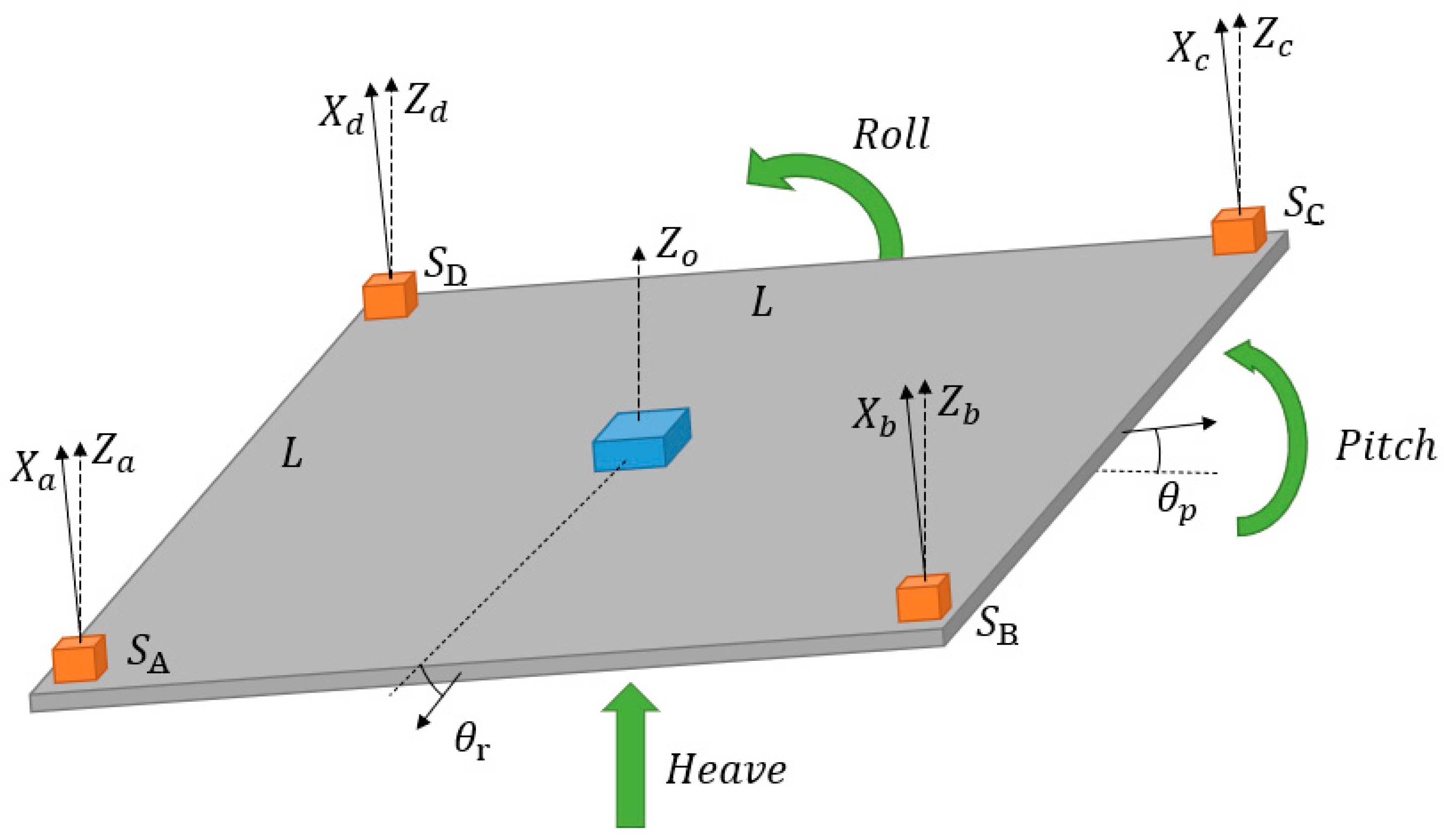
3.1. Multi-Sensor Fusion of Acceleration Sensor Sets

In the actual heave direction, four acceleration sensors have displacements of Z_A, Z_B, Z_C, and Z_D, respectively. These displacement values can be obtained by the double integral over time of the sensor outputs. However, due to the unstable tilting motion of the ship-borne mechanical platform, the measured acceleration data tracks the displacement along direction perpendicular to the mounting base instead. We denote these deflected displacements as X_A, X_B, X_C, and X_D, respectively. As is discussed in Section 2, we can theoretically calculate the actual heave displacement according to the available sensor data and the ship-borne mechanical platform motion status:

\{\begin{matrix} Z_{a} (t) = \int_{0}^{t} d Z_{a} + Z_{a} (0) = \int_{0}^{t} \cos^{- 1} θ_{p} (t) \cos^{- 1} θ_{r} (t) d X_{a} + Z_{a} (0) \\ Z_{b} (t) = \int_{0}^{t} d Z_{b} + Z_{b} (0) = \int_{0}^{t} \cos^{- 1} θ_{p} (t) \cos^{- 1} θ_{r} (t) d X_{b} + Z_{b} (0) \\ Z_{c} (t) = \int_{0}^{t} d Z_{c} + Z_{c} (0) = \int_{0}^{t} \cos^{- 1} θ_{p} (t) \cos^{- 1} θ_{r} (t) d X_{c} + Z_{c} (0) \\ Z_{d} (t) = \int_{0}^{t} d Z_{d} + Z_{d} (0) = \int_{0}^{t} \cos^{- 1} θ_{p} (t) \cos^{- 1} θ_{r} (t) d X_{d} + Z_{d} (0) \end{matrix} .

(14)

Considering the real-time operations in the controlling process, the above equation can also be written in discrete forms:

\{\begin{matrix} Z_{a}^{t} = Z_{a}^{t - 1} + \cos^{- 1} θ_{p} (t) \cos^{- 1} θ_{r} (t) V_{a}^{t} ∆ t \\ Z_{b}^{t} = Z_{b}^{t - 1} + \cos^{- 1} θ_{p} (t) \cos^{- 1} θ_{r} (t) V_{b}^{t} ∆ t \\ Z_{c}^{t} = Z_{c}^{t - 1} + \cos^{- 1} θ_{p} (t) \cos^{- 1} θ_{r} (t) V_{c}^{t} ∆ t \\ Z_{d}^{t} = Z_{d}^{t - 1} + \cos^{- 1} θ_{p} (t) \cos^{- 1} θ_{r} (t) V_{d}^{t} ∆ t \end{matrix},

(15)

where

V_{a}^{t}

V_{b}^{t}

V_{c}^{t}

, and

V_{d}^{t}

are the real-time velocity obtained by the four sensor outputs at time

t

, respectively.

Because of the known spatial arrangement of the sensor sets, the outputs of four acceleration sensors can be synthetically combined to estimate the tilt angles. The kinematic equation for the pitch angle is:

\sin θ_{p}^{t} = \frac{(Z_{d}^{t} + Z_{c}^{t}) - (Z_{a}^{t} + Z_{b}^{t})}{L} = \frac{1}{L} [\sum_{i = 0}^{t} \cos^{- 1} θ_{p}^{t} \cos^{- 1} θ_{r}^{t} V_{d}^{t} Δ t + \sum_{i = 0}^{t} \cos^{- 1} θ_{p}^{t} \cos^{- 1} θ_{r}^{t} V_{c}^{t} Δ t - \sum_{i = 0}^{t} \cos^{- 1} θ_{p}^{t} \cos^{- 1} θ_{r}^{t} V_{a}^{t} Δ t - \sum_{i = 0}^{t} \cos^{- 1} θ_{p}^{t} \cos^{- 1} θ_{r}^{t} V_{b}^{t} Δ t] \begin{matrix} = \frac{1}{L} \sum_{i = 0}^{t} (- V_{a}^{t} - V_{b}^{t} + V_{c}^{t} + V_{d}^{t}) \cos^{- 1} θ_{p}^{t} \cos^{- 1} θ_{r}^{t} Δ t \end{matrix} .

(16)

Similarly, the kinematic equation for the roll angle is:

\sin θ_{r}^{t} = \frac{(Z_{b}^{t} + Z_{c}^{t}) - (Z_{a}^{t} + Z_{d}^{t})}{L} = \frac{1}{L} [\sum_{i = 0}^{t} \cos^{- 1} θ_{p}^{t} \cos^{- 1} θ_{r}^{t} V_{b}^{t} Δ t + \sum_{i = 0}^{t} \cos^{- 1} θ_{p}^{t} \cos^{- 1} θ_{r}^{t} V_{c}^{t} Δ t - \sum_{i = 0}^{t} \cos^{- 1} θ_{p}^{t} \cos^{- 1} θ_{r}^{t} V_{a}^{t} Δ t - \sum_{i = 0}^{t} \cos^{- 1} θ_{p}^{t} \cos^{- 1} θ_{r}^{t} V_{d}^{t} Δ t] \begin{matrix} = \frac{1}{L} \sum_{i = 0}^{t} (- V_{a}^{t} + V_{b}^{t} + V_{c}^{t} - V_{d}^{t}) \cos^{- 1} θ_{p}^{t} \cos^{- 1} θ_{r}^{t} Δ t \end{matrix} .

(17)

By combining Equation (16) and (17), roll angle and pitch angle can be solved. In this way, an estimation of heave displacement is made in real-time utilizing the above solutions in Equation (15).

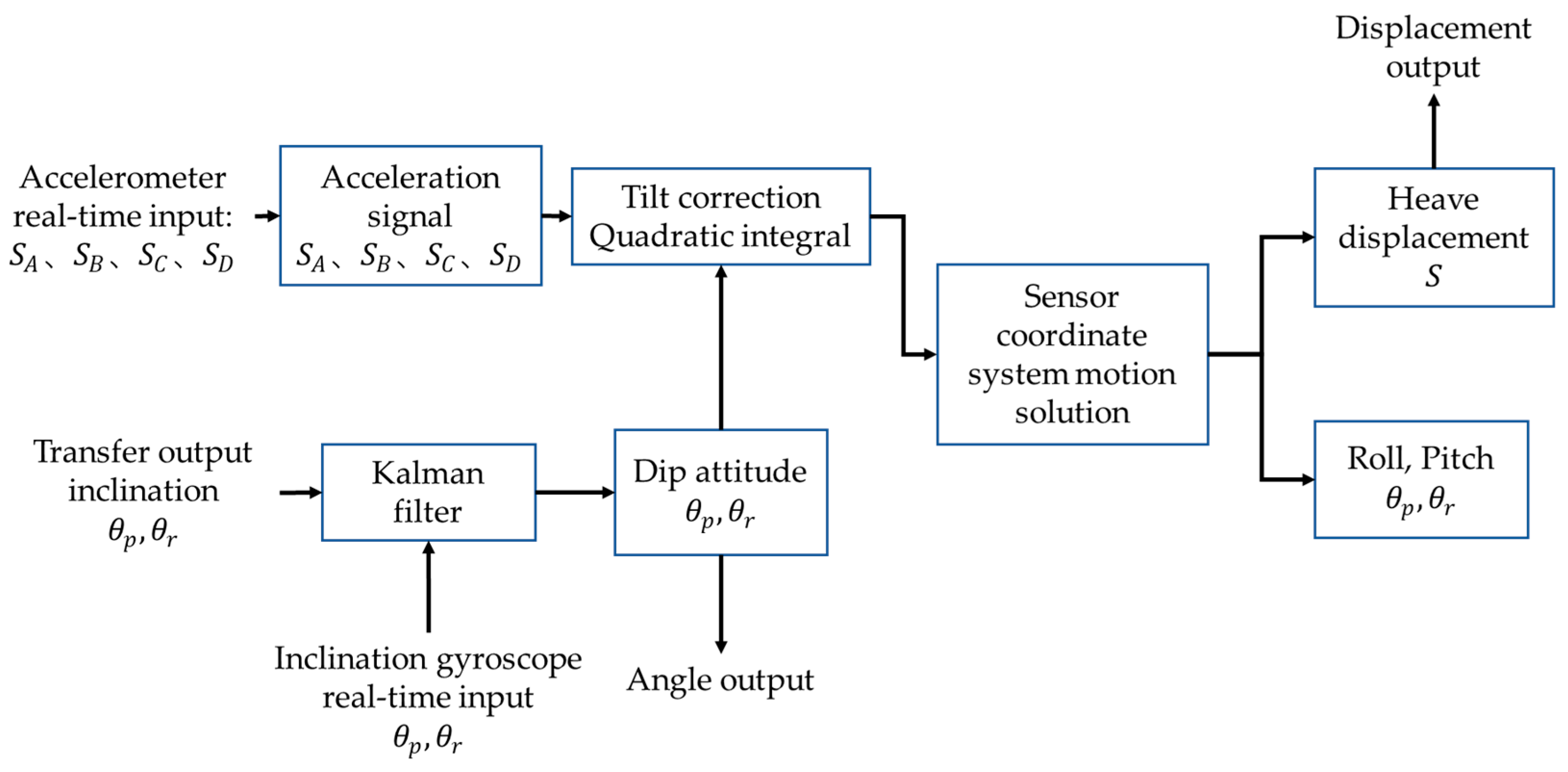
3.2. Motion estimation based on Kalman filtering

In the previous section, a tilt angle estimation method relying on just four acceleration sensor sets is proposed. Another type of commonly used ship-borne sensor is the gyroscope for direct angle detection. Generally, piezoelectric acceleration sensors have superior robustness and accuracy due to their direct electromechanical transduction characteristics. Whereas, angle sensors possess lower drift with the help of gravity. It would greatly improve the precision of motion estimation if these two types of sensor signals are rationally combined. In this work, we adopt Kalman filtering technique, in which the measurement data from the angle sensor

ϑ = {[ϑ_{p} {, ϑ}_{r}]}^{T}

is the observation and the computed data from the acceleration sensor sets

θ = {[θ_{p} {, θ}_{r}]}^{T}

is the estimate. In this case, the system state dynamics in discrete form can be written as:

\{\begin{matrix} θ_{k} = ϕ_{k - 1}^{k} θ_{k - 1} + Γ_{k - 1} W_{k - 1} \\ ϑ_{k} = N_{k} θ_{k} + V_{k} \end{matrix},

(18)

where

θ_{k}

and

θ_{k - 1}

are the computed angle vectors from acceleration sensor sets at time k and time k-1, respectively.

ϕ_{k - 1}^{k}

denotes the state transition matrix.

Γ_{k - 1}

and

W_{k - 1}

represent the noise drive matrix and noise vector, respectively.

ϑ_{k}

N_{k}

, and

V_{k}

are measurement vector from the angle sensor, measurement matrix, and measurement noise vector at time k, respectively. Both

W_{k - 1}

and

V_{k}

are assumed to have zero mean normal distributions with

E (W_{k} W_{k}^{T}) = 0

and

E (V_{k} V_{k}^{T}) = R_{k}

In Kalman filtering process, prior state estimate is first performed:

{\hat{θ}}_{k - 1}^{k} = ϕ_{k - 1}^{k} {\hat{θ}}_{k - 1} .

(19)

The prior estimate covariance is:

P_{k - 1}^{k} = ϕ_{k - 1}^{k} P_{k - 1} {ϕ_{k - 1}^{k}}^{T} + Q_{k - 1} .

(20)

Afterwards, the state estimate is updated based on the observation data and we have posterior state estimate as:

{\hat{θ}}_{k} = {\hat{θ}}_{k - 1}^{k} + K_{k} (ϑ_{k} - N {\hat{θ}}_{k - 1}^{k}),

(21)

where K is the optimal Kalman gain, given by:

K_{k} = \frac{P_{k - 1}^{k} N_{k}^{T}}{N_{k} P_{k - 1}^{k} N_{k}^{T} + R} .

(22)

The posterior estimate covariance is:

P_{k} = (I - K_{k} N_{k}) P_{k - 1}^{k} .

(23)

However, it is hard to accurately evaluate the statistical characteristics of noises in both integral error and angle measurement. Such limitation hinders the implementation of Kalman filtering in estimating ship-borne mechanical platform motion in real-time. A robust adaptive filtering technique is thus needed, in which robust estimation theory is applied to eliminate the measurement outliers and adaptive factor is incorporated to control the influence of dynamic model error. Given these considerations, we further propose an innovation-based adaptive filtering step to verify the angle measurement results. The procedures are shown as follows. First, the innovation

{\tilde{ϑ}}_{k - 1}^{k}

and its covariance

C_{k}

are computed:

\{\begin{matrix} {\tilde{ϑ}}_{k - 1}^{k} = ϑ_{k} - N_{k} {\hat{θ}}_{k - 1}^{k} \\ C_{k} = N_{k} P_{k - 1}^{k} {N_{k}}^{T} + R_{k} \end{matrix} .

(24)

Then, we define a weigh boundary value function as:

β = \sqrt{\frac{{ϑ_{k}}^{T} ϑ_{k}}{t r (C_{k})}} .

(25)

The adaptive factor

α

is thus determined by:

α = \{\begin{matrix} 1, β \leq c \\ \frac{c}{β}, β > c \end{matrix},

(26)

where c is a constant set between 0.9 and 1. Here c = 0.9 is adopted. We can then adjust the Kalman gain accordingly:

K_{k} = \frac{1}{α} ∙ \frac{P_{k - 1}^{k} N_{k}^{T}}{N_{k} P_{k - 1}^{k} N_{k}^{T} + R} .

(27)

By repeating the two processes of predict and update, the motion state estimation can be iteratively optimized until the results are converged. The whole Kalman filtering process are schematically illustrated in Figure 4.

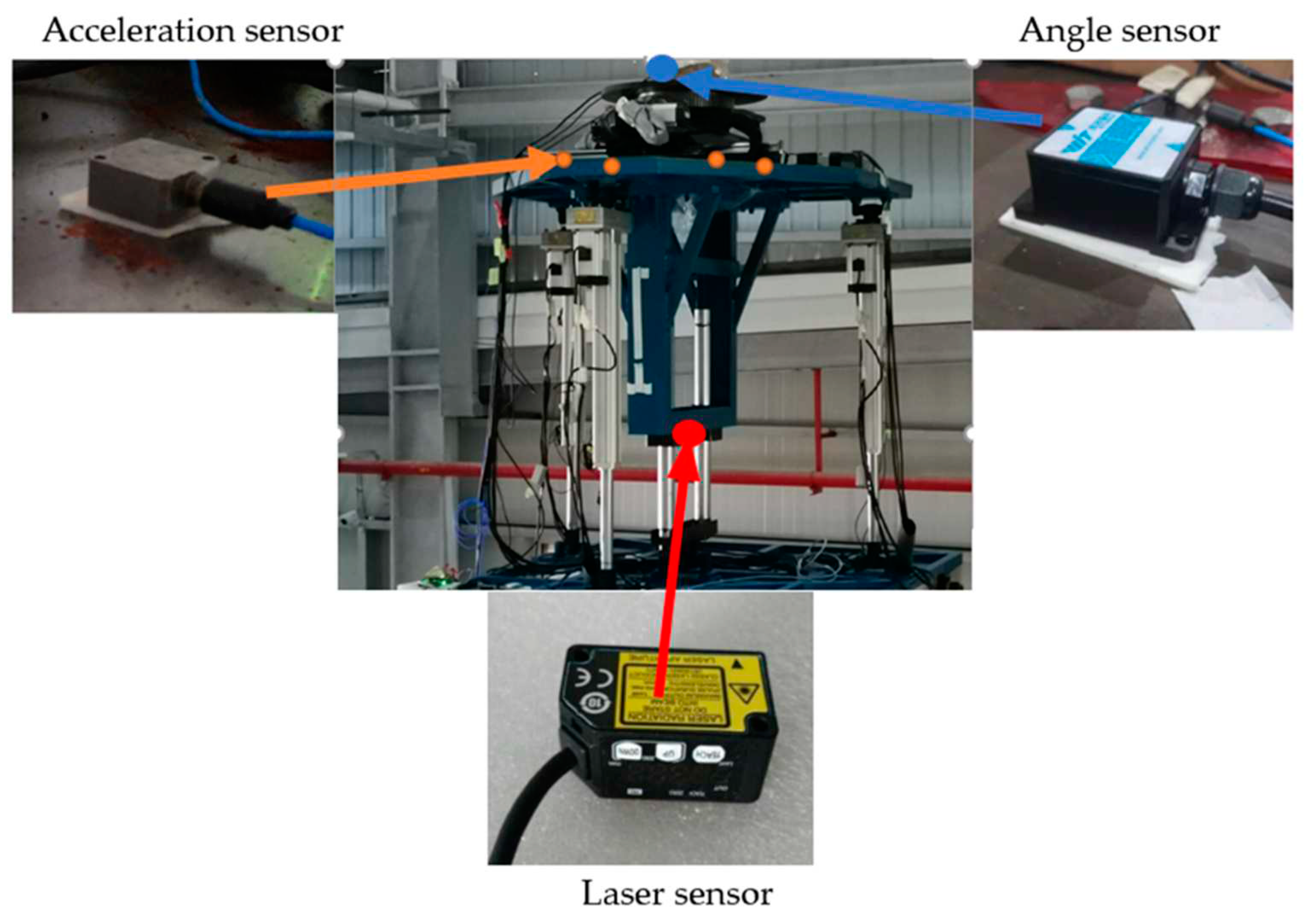
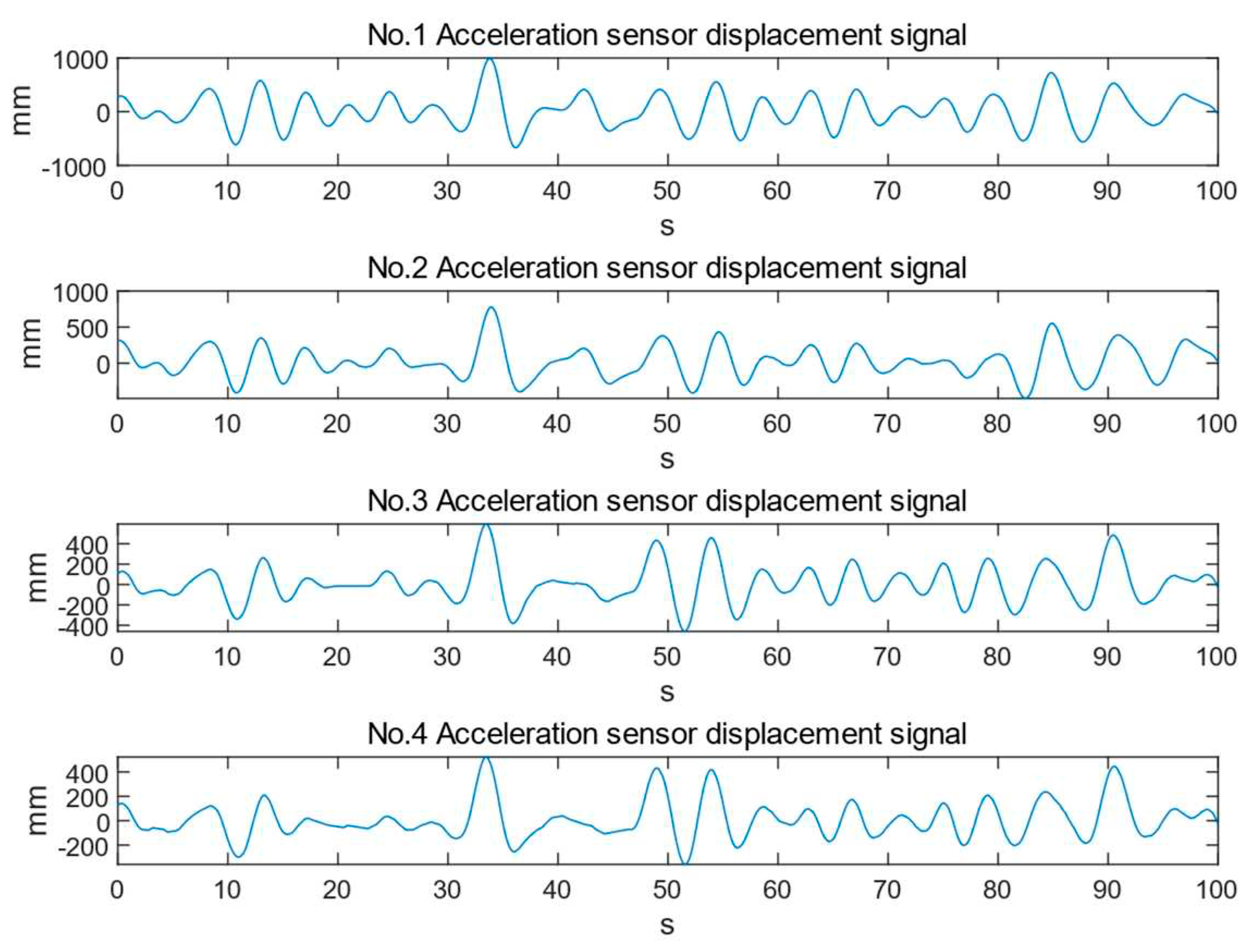
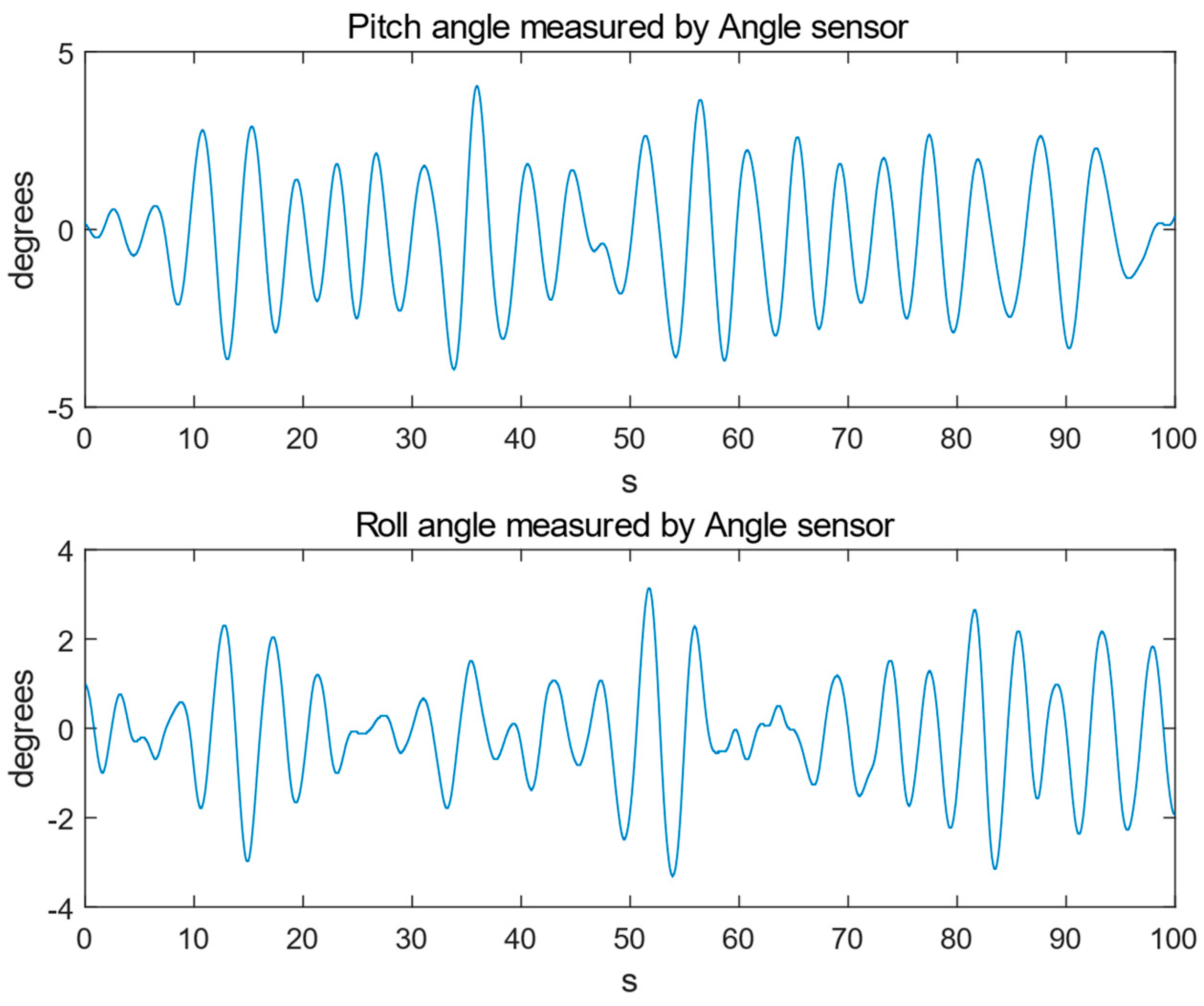
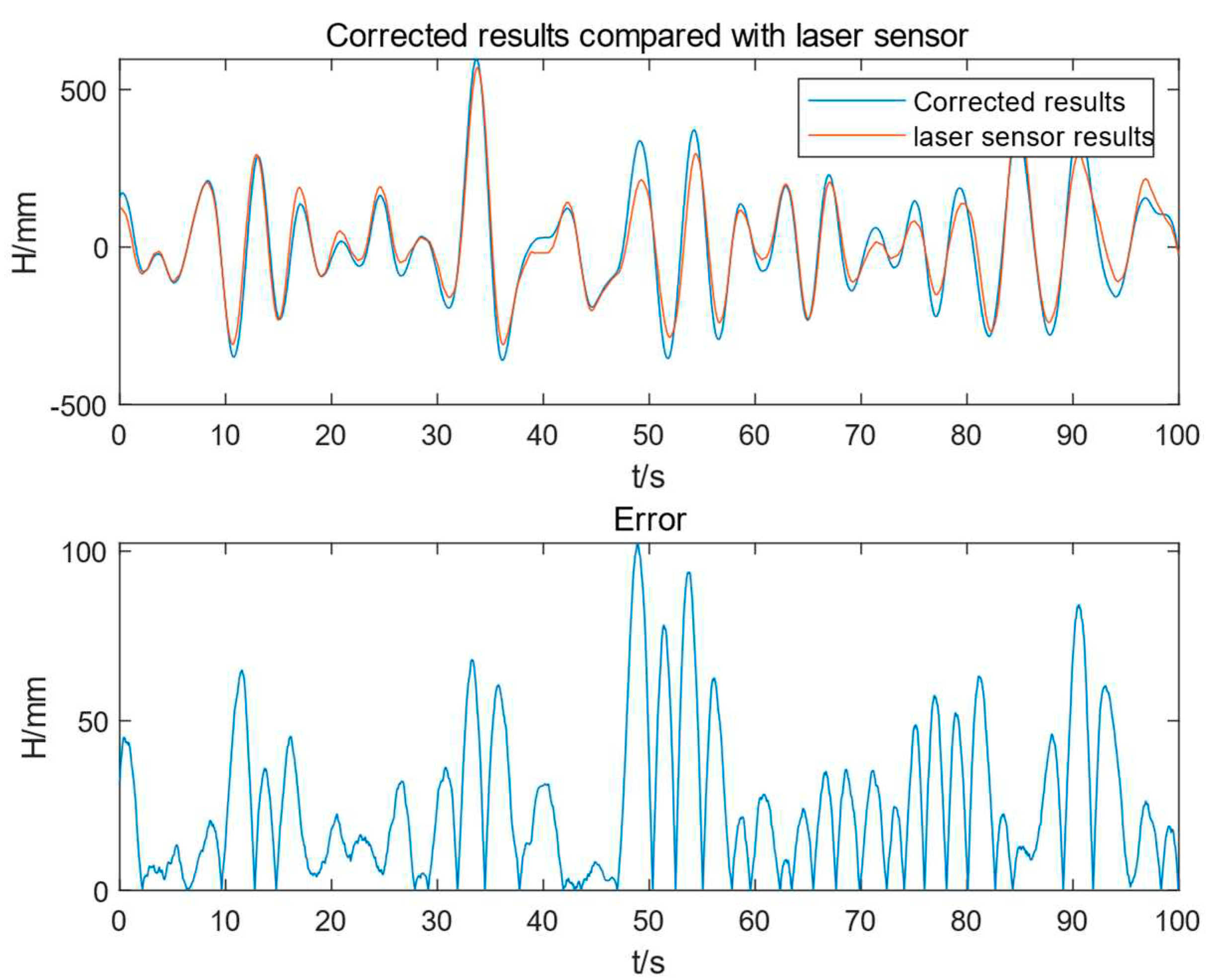
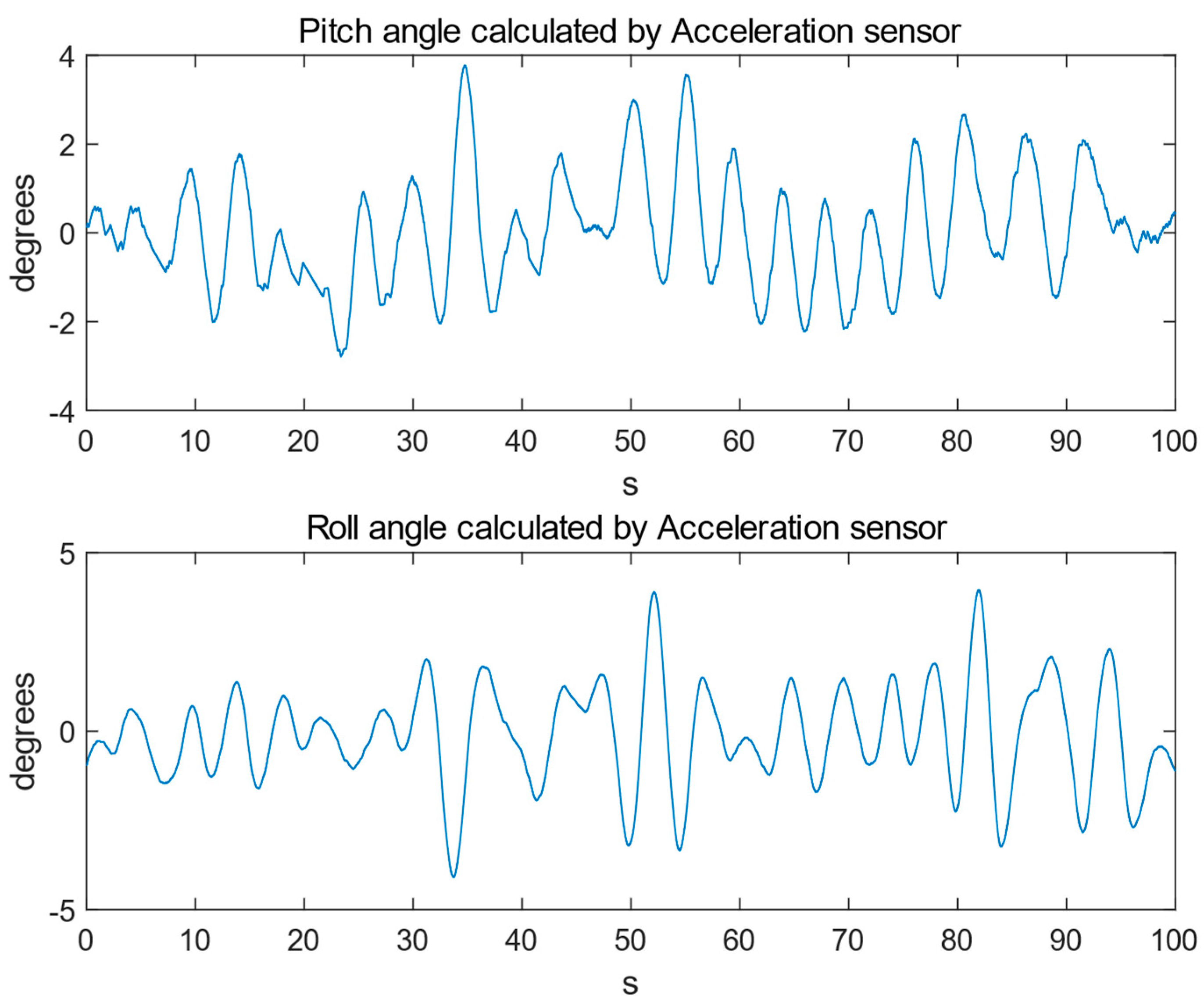
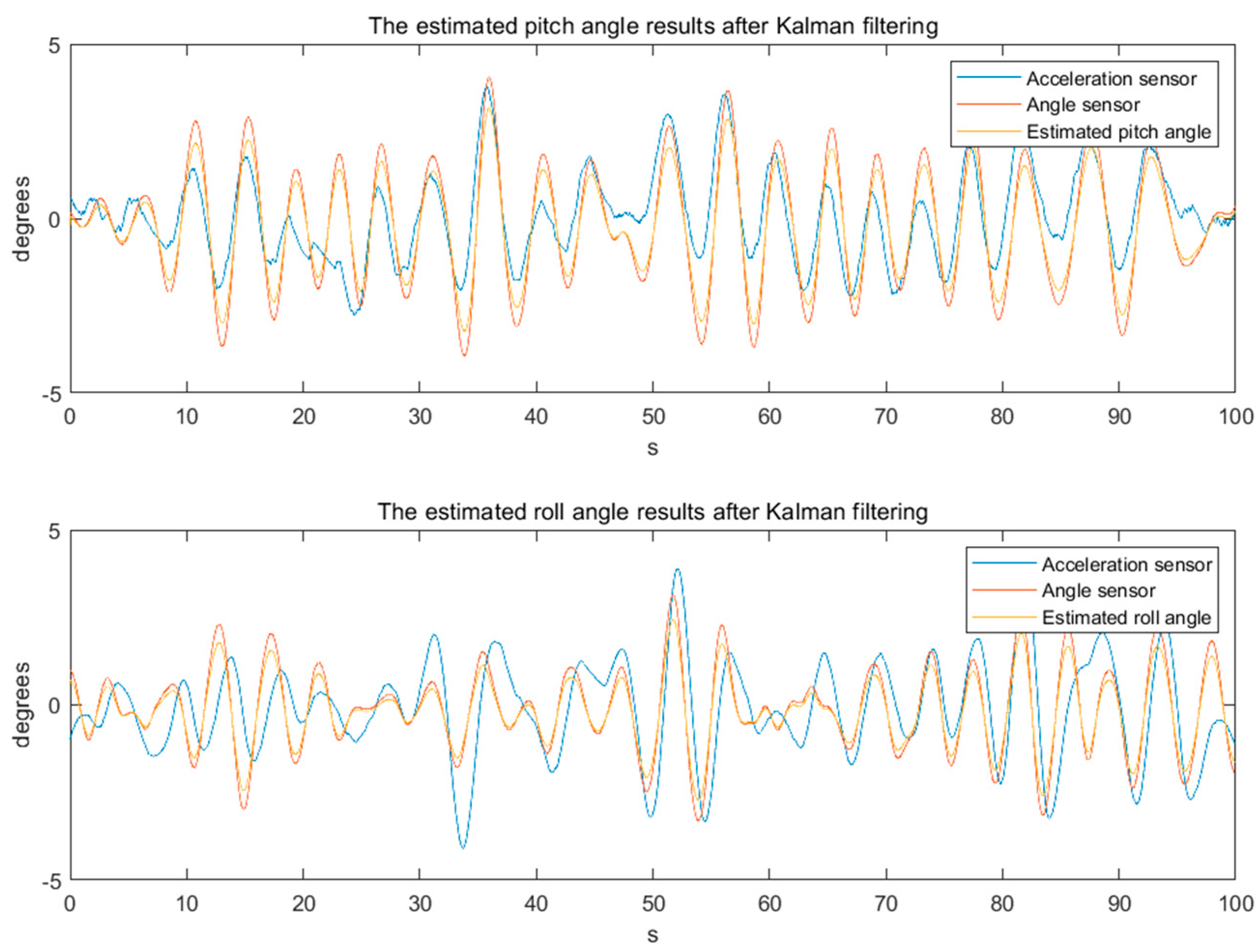
4. Experimental Results

To experimentally verify the feasibility of the proposed algorithm, we set up the ship-borne mechanical platform with one gyroscope and four piezoelectric acceleration sensors in lab. As shown in Figure 5, four acceleration sensors were fixed at the corners of a square on the six-degree-of-freedom wave compensation platform (orange points). One gyroscope for angle measurement was placed at the center of the upper plane (blue point). A laser ranging sensor is installed on the center bracket under the platform (black) to provide the standard heave motion signal of the ship-borne mechanical platform.

By sending instructions to the servo controller, the ship-borne mechanical platform was controlled to simulate the three-degree-of-freedom movement of the ship. We used a data collector to acquire all sensor data with sampling frequency of 200Hz and sampling time of 100 seconds. Figure 6 displays the obtained signal after integrating four acceleration sensors respectively.

Pitch and roll angle values for observation input in filtering process were obtained by the angle sensor. Their outputs are shown in Figure 7.

Using the proposed multi-sensor fusion method, the displacement values integrated by the four acceleration sensors were corrected, and the real displacement signal in the heave direction was finally calculated. The estimated displacement signal was compared with the standard displacement signal collected by the laser sensor. The laser displacement signal is considered to be the real heave displacement value of the ship-borne mechanical platform. The data shows that the heave displacement signal corrected based on multi-sensor fusion can effectively improve the accuracy of displacement signal measurement compared with the integrated displacement signal of a single acceleration sensor. The comparison results of the displacement signal based on multi-sensor fusion correction and displacement signal of the laser sensor are shown in Figure 8. The comparison results of the integrated displacement signal of a single acceleration sensor and the displacement signal of the laser sensor are shown in Figure 9.

After analyzing the above results, we found that the average error between the displacement signal corrected by using multiple sensors and the laser standard heave displacement signal was 25.34 mm. As a comparison, when a single acceleration sensor was used, the error of the heave displacement signal denoted by No. 1-4 is [128.1711 mm, 65.32 mm, 73.63 mm, 71.8513 mm]. The experimental data results showed that the multi-sensor fusion correction method for the ship-borne mechanical platform proposed in this paper could effectively improve the measurement accuracy.

At the same time, based on multi-sensor fusion data, we used the acceleration sensor to calculate the roll angle signal and pitch angle signal of the ship-borne mechanical platform, and perform Kalman filtering on the inclination signal and angle sensor signal to estimate inclination angle with improved accuracy. Here, the value of our process noise Q in Kalman filtering was [4 0; 0 1]; the value of observation noise variance R was 1, which made the estimated value more inclined to the angle sensor signal data. The results of the roll angle signal and pitch signal of the ship-borne mechanical platform calculated using the integrated displacement signal of the acceleration sensor were shown in Figure 10. After Kalman filtering with combination of angle sensor measurement signal and the calculated angle data through acceleration sensors, the comparison of these three sets of angle information are shown in Figure 11.

Combining the roll angle and pitch angle signals collected by the angle sensors in Figure 7, correlation analysis was performed on the angle signals calculated based on multiple acceleration sensors. The results showed that the correlation coefficient of the two groups of signals was 0.87, which proved that the inclination signal of the ship-borne mechanical platform calculated by the acceleration sensor was reliable. It can be seen from the experimental results that the angle signal calculated by the acceleration sensor and the angle signal measured by the angle sensor have the following advantages after Kalman filtering:

Reduce influence of noise and error. The angle signal calculated by the acceleration sensor usually has large noise and error. Meanwhile, the angle signal measured by the angle sensor may also be affected by external interference. Through Kalman filtering, these noises and errors can be filtered out, so as to obtain more accurate angle signals.
Improved response speed. The angle signal calculated by the acceleration sensor has a faster response speed, but there are large noises and errors. On the other hand, the angle signal measured by the angle sensor has a slower response speed, but possess higher precision. Through Kalman filtering, the advantages of the two can be combined, which not only improves the response speed, but also improves the accuracy.
Improve system stability. Since the angle signal calculated by the acceleration sensor has large noise and errors, the system may jitter or become unstable. Through adaptive Kalman filtering, these noises and errors can be filtered out, thereby improving the stability of the system.
Reduced cost: the cost of the angle signal calculated by acceleration sensors is lower than that of the angle signal measured by advanced angle sensors. Through the Kalman filter, the angle signal calculated by the acceleration sensor can be filtered to obtain a result comparable to or even better than the angle signal measured by the angle sensor, thereby reducing the cost of using expensive gyroscopes.

5. Conclusions

This paper proposes a correction method for shipborne platform motion measurements based on multi-sensor fusion. First, by analyzing the principle of the piezoelectric acceleration sensor, a correction method with novel configuration of four acceleration sensors is proposed based on the fusion results, which eliminates the influence of the roll angle and pitch angle on the displacement signal after acceleration integration. Secondly, adaptive Kalman filtering is performed to combine the angle signals collected by the angle sensor and the angle signal calculated by the acceleration sensor sets. The estimated inclination angle of the ship-borne mechanical platform showed improved correlation with the standard motion data obtained by a laser sensor as verified by the experiments.

The advantage of this method is that it can improve the accuracy of measuring the displacement signal of the ship-borne mechanical platform in the heave direction. It can correct the influence of the roll angle and pitch angle on the integral of the heave direction when the ship-borne mechanical platform moves with three degrees of freedom, eliminate the error caused by the inclination angle, and greatly improve the reliability of the motion signal. At the same time, the disadvantage of this method is that multiple sets of acceleration sensors are used, and there is a signal calibration problem, and the sensitivity of the calibration cannot be well controlled, which will also cause errors in the measurement of the displacement signal.

In the present work, the system we built is based on the fusion of four acceleration sensors to correct the displacement signals of the ship-borne mechanical platform in the heave direction, and by combining the angle sensor data, Kalman filtering is performed on the roll angle signal and the pitch angle signal to estimate the true inclination angle. In the future work, we will further study the calibration problem of multiple acceleration sensors. By combining algorithms such as neural networks, the sensors can be calibrated with nonlinear characteristics to overcome the problem of acceleration sensitivity under different sea conditions.

At the same time, in order to reduce costs, we may also look for directions such as the use of inertial mechanical structures for research. By designing a novel inertial mechanical structure instead of multi-sensor fusion to correct the angle effect, the cost of solving the angle effect is further reduced.

Author Contributions

Conceptualization, R.Z.; Data curation, X.H.; Formal analysis, R.Z.; Funding acquisition, X.H.; Methodology, R.Z.; Supervision, X.H.; Writing—original draft, R.Z.; Writing—review and editing, R.Z. and X.H. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China, grant number 31300783.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The original data contributions presented in the study are included in the article; further inquiries can be directed to the corresponding authors.

Conflicts of Interest

The authors declare no conflict of interest.

References

Luo, R.C.; Lin, M.-H.; Scherp, R.S. Dynamic Multi-Sensor Data Fusion System for Intelligent Robots. IEEE Journal on Robotics and Automation 1988, 4, 386–396. [Google Scholar] [CrossRef]
Durrant-Whyte, H.F.; Rao, B.Y.S.; Hu, H. Toward a Fully Decentralized Architecture for Multi-Sensor Data Fusion. In Proceedings of the Proceedings., IEEE International Conference on Robotics and Automation; IEEE; 1990; pp. 1331–1336. [Google Scholar]
Wen, W.; Durrant-Whyte, H.F. Model-Based Multi-Sensor Data Fusion. In Proceedings of the Proceedings 1992 IEEE international conference on robotics and automation; IEEE; 1992; pp. 1720–1726. [Google Scholar]
Harris, C.J.; Bailey, A.; Dodd, T.J. Multi-Sensor Data Fusion in Defence and Aerospace. The Aeronautical Journal 1998, 102, 229–244. [Google Scholar] [CrossRef]
Llinas, J.; Hall, D.L. An Introduction to Multi-Sensor Data Fusion. In Proceedings of the ISCAS’98. Proceedings of the 1998 IEEE International Symposium on Circuits and Systems (Cat. No. 98CH36187); IEEE, 1998; Vol. 6, pp. 537–540.
Chen, S.; Bao, H.; Zeng, X.; Yang, Y. A Fire Detecting Method Based on Multi-Sensor Data Fusion. In Proceedings of the SMC’03 Conference Proceedings. 2003 IEEE International Conference on Systems, Man and Cybernetics. Conference Theme-System Security and Assurance (Cat. No. 03CH37483); IEEE, 2003; Vol. 4, pp. 3775–3780.
Herpel, T.; Lauer, C.; German, R.; Salzberger, J. Multi-Sensor Data Fusion in Automotive Applications. In Proceedings of the 2008 3rd International Conference on Sensing Technology; IEEE; 2008; pp. 206–211. [Google Scholar]
Manjunatha, P.; Verma, A.K.; Srividya, A. Multi-Sensor Data Fusion in Cluster Based Wireless Sensor Networks Using Fuzzy Logic Method. In Proceedings of the 2008 IEEE region 10 and the third international conference on industrial and information systems; IEEE; 2008; pp. 1–6. [Google Scholar]
Dong, J.; Zhuang, D.; Huang, Y.; Fu, J. Advances in Multi-Sensor Data Fusion: Algorithms and Applications. Sensors 2009, 9, 7771–7784. [Google Scholar] [CrossRef] [PubMed]
Wolter, P.T.; Townsend, P.A. Multi-Sensor Data Fusion for Estimating Forest Species Composition and Abundance in Northern Minnesota. Remote Sens Environ 2011, 115, 671–691. [Google Scholar] [CrossRef]
Medjahed, H.; Istrate, D.; Boudy, J.; Baldinger, J.-L.; Dorizzi, B. A Pervasive Multi-Sensor Data Fusion for Smart Home Healthcare Monitoring. In Proceedings of the 2011 IEEE international conference on fuzzy systems (FUZZ-IEEE 2011); IEEE; 2011; pp. 1466–1473. [Google Scholar]
Banerjee, T.P.; Das, S. Multi-Sensor Data Fusion Using Support Vector Machine for Motor Fault Detection. Inf Sci (N Y) 2012, 217, 96–107. [Google Scholar] [CrossRef]
Frikha, A.; Moalla, H. Analytic Hierarchy Process for Multi-Sensor Data Fusion Based on Belief Function Theory. Eur J Oper Res 2015, 241, 133–147. [Google Scholar] [CrossRef]
Azimirad, E.; Haddadnia, J.; Izadipour, A.L.I. A COMPREHENSIVE REVIEW OF THE MULTI-SENSOR DATA FUSION ARCHITECTURES. J Theor Appl Inf Technol 2015, 71. [Google Scholar]
Fortino, G.; Galzarano, S.; Gravina, R.; Li, W. A Framework for Collaborative Computing and Multi-Sensor Data Fusion in Body Sensor Networks. Information Fusion 2015, 22, 50–70. [Google Scholar] [CrossRef]
Rawat, S.; Rawat, S. Multi-Sensor Data Fusion by a Hybrid Methodology–A Comparative Study. Comput Ind 2016, 75, 27–34. [Google Scholar] [CrossRef]
Duro, J.A.; Padget, J.A.; Bowen, C.R.; Kim, H.A.; Nassehi, A. Multi-Sensor Data Fusion Framework for CNC Machining Monitoring. Mech Syst Signal Process 2016, 66, 505–520. [Google Scholar] [CrossRef]
Maimaitijiang, M.; Ghulam, A.; Sidike, P.; Hartling, S.; Maimaitiyiming, M.; Peterson, K.; Shavers, E.; Fishman, J.; Peterson, J.; Kadam, S. Unmanned Aerial System (UAS)-Based Phenotyping of Soybean Using Multi-Sensor Data Fusion and Extreme Learning Machine. ISPRS Journal of Photogrammetry and Remote Sensing 2017, 134, 43–58. [Google Scholar] [CrossRef]
Jing, L.; Wang, T.; Zhao, M.; Wang, P. An Adaptive Multi-Sensor Data Fusion Method Based on Deep Convolutional Neural Networks for Fault Diagnosis of Planetary Gearbox. Sensors 2017, 17, 414. [Google Scholar] [CrossRef] [PubMed]
Kumar, P.; Gauba, H.; Roy, P.P.; Dogra, D.P. Coupled HMM-Based Multi-Sensor Data Fusion for Sign Language Recognition. Pattern Recognit Lett 2017, 86, 1–8. [Google Scholar] [CrossRef]
Bouain, M.; Ali, K.M.A.; Berdjag, D.; Fakhfakh, N.; Atitallah, R. Ben An Embedded Multi-Sensor Data Fusion Design for Vehicle Perception Tasks. J. Commun. 2018, 13, 8–14. [Google Scholar] [CrossRef]
Xiao, F.; Qin, B. A Weighted Combination Method for Conflicting Evidence in Multi-Sensor Data Fusion. Sensors 2018, 18, 1487. [Google Scholar] [CrossRef]
Zhang, W.; Ning, Y.; Suo, C. A Method Based on Multi-Sensor Data Fusion for UAV Safety Distance Diagnosis. Electronics (Basel) 2019, 8, 1467. [Google Scholar] [CrossRef]
De Farias, C.M.; Pirmez, L.; Fortino, G.; Guerrieri, A. A Multi-Sensor Data Fusion Technique Using Data Correlations among Multiple Applications. Future Generation Computer Systems 2019, 92, 109–118. [Google Scholar] [CrossRef]
Xiao, F. Multi-Sensor Data Fusion Based on the Belief Divergence Measure of Evidences and the Belief Entropy. Information Fusion 2019, 46, 23–32. [Google Scholar] [CrossRef]
Xiao, F. Evidence Combination Based on Prospect Theory for Multi-Sensor Data Fusion. ISA Trans 2020, 106, 253–261. [Google Scholar] [CrossRef]
Muzammal, M.; Talat, R.; Sodhro, A.H.; Pirbhulal, S. A Multi-Sensor Data Fusion Enabled Ensemble Approach for Medical Data from Body Sensor Networks. Information Fusion 2020, 53, 155–164. [Google Scholar] [CrossRef]
Li, N.; Gebraeel, N.; Lei, Y.; Fang, X.; Cai, X.; Yan, T. Remaining Useful Life Prediction Based on a Multi-Sensor Data Fusion Model. Reliab Eng Syst Saf 2021, 208, 107249. [Google Scholar] [CrossRef]
Kashinath, S.A.; Mostafa, S.A.; Mustapha, A.; Mahdin, H.; Lim, D.; Mahmoud, M.A.; Mohammed, M.A.; Al-Rimy, B.A.S.; Fudzee, M.F.M.; Yang, T.J. Review of Data Fusion Methods for Real-Time and Multi-Sensor Traffic Flow Analysis. IEEE Access 2021, 9, 51258–51276. [Google Scholar] [CrossRef]
Fei, S.; Hassan, M.A.; Xiao, Y.; Su, X.; Chen, Z.; Cheng, Q.; Duan, F.; Chen, R.; Ma, Y. UAV-Based Multi-Sensor Data Fusion and Machine Learning Algorithm for Yield Prediction in Wheat. Precis Agric 2023, 24, 187–212. [Google Scholar] [CrossRef]
Han, C.; Hu, X. An Absolute Displacement Measurement Method and Its Application in Ship Motion Measurement. J Mar Sci Eng 2023, 11, 931. [Google Scholar] [CrossRef]

Figure 1. Schematic diagram of the influence of inclination angle on the integrated displacement signal in the heave direction.

Figure 2. Schematic diagram of the acceleration data integration for displacement estimation in tilted conditions.

Figure 3. Illustration of the proposed multi-sensor fusion ship-borne sensing platform with one gyroscope and four piezoelectric acceleration sensors.

Figure 4. Procedure of the proposed Kalman filtering-based motion estimation algorithm by combining acceleration sensor data and angle sensor data.

Figure 5. Experimental setup for the proposed sensor platform.

Figure 6. Displacement signal obtained by integral of four acceleration sensors outputs.

Figure 7. Angle signal obtained by angle sensor.

Figure 8. The comparison results of the displacement signal based on multi-sensor fusion correction and displacement signal of the laser sensor.

Figure 9. The comparison results of the integrated displacement signal of a single acceleration sensor and the displacement signal of the laser sensor.

Figure 10. the estimated results of the roll angle and pitch angle.

Figure 11. Results of estimated pitch and roll angles after Kalman filtering.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Correction Method for the Motion Measurement of the Ship-Borne Mechanical Platform Based on Multi-Sensor Fusion

Abstract

1. Introduction

2. Preliminary Work

3. Proposed Algorithm

3.1. Multi-Sensor Fusion of Acceleration Sensor Sets

3.2. Motion estimation based on Kalman filtering

4. Experimental Results

5. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe