Quantum Knowledge in Phase Space

Preprint

Article

Quantum Knowledge in Phase Space

Altmetrics

Downloads

120

Views

Comments

A peer-reviewed article of this preprint also exists.

Davi Geiger^*

This version is not peer-reviewed

Submitted:

25 July 2023

Posted:

28 July 2023

You are already at the latest version

Alerts

Abstract

Quantum physics through the lenses of Bayesian statistics consider probabilities to be degree of believes or knowledge and subjective. A Bayesian derivation of the probability density function in phase space is presented. The entropy proposed by Geiger and Kedem \cite{GeiKed2022a,GeiKed2022b} in phase space is expanded to define quantitatively interference and entanglement. Comparisons between each of these two quantities and the entropy are made. A brief presentation of entanglement in phase space to the spin degree of freedom and to mixed states completes the work.

Keywords:

Subject: Physical Sciences - Theoretical Physics

1. Introduction

This journal issue celebrates Claude Shannon’s 1948 formulation of ”lost information" in phone-line signals [3]. It is curious that when von Neumann asked Shannon how he was getting on with his information theory, Shannon replied (according to [4])

”The theory was in excellent shape, except that he needed a good name for "missing information". "Why don’t you call it entropy", von Neumann suggested. "In the first place, a mathematical development very much like yours already exists in Boltzmann’s statistical mechanics, and in the second place, no one understands entropy very well, so in any discussion you will be in a position of advantage."

The concept of Shannon entropy for pure states in quantum phase spaces can capture key physical properties, interference and entanglement, that precedes von Neumann entropy for mixed states. Interference is a key quantum phenomenon, present in one particle state, that is not conceptualized in classical statistical physics[5,6]. The possibility of a superposition of states that yield a new state where information can be destroyed has no part in classical statistical physics. Going beyond one particle state, entanglement is a phenomenon in quantum physics without a parallel to classical statistical physics. It has been the cornerstone of much advancement in quantum physics (e.g., [7,8,9,10] and references). Despite these well known properties of quantum physics, a quantification of interference and entanglement has been elusive.

A quantification of these concepts in quantum phase space for pure states is proposed through Shannon entropy and related concepts (see Appendix B for a brief review).

A topic that has captivated much of quantum physics discussions since its first days, namely the role of measurement in physics, is revisited. Measurements are associated with events in statistics, since through measurements full knowledge of a physical variable is acquired. The role of knowledge in quantum physics is then discussed.

1.1. Bayesian Knowledge in Quantum Physics

In the field of statistics two views offered by the Bayesian [11] and the frequentist [12,13] divide the experts. Bayesian thinking is based on the idea that probabilities represent a degree of belief or knowledge about the events while the frequentist approach is based on the idea that the probability of an event occurring is equal to the long-run frequency with which that event occurs.

One goal here is to show that starting with a quantum state, and through a Bayesian view, one can arrive to the joint probability density in phase space. This joint probability density has all the knowledge of such variables or all the knowledge associated with such a state. The conditional probability

P (X / Y)

is interpreted as the knowledge we have about the random variable X given the knowledge we have about the random variable Y. The knowledge about Y may exist in the form of a prior

P^{prior} (Y)

and if a deterministic transformation from Y to X is given, we will know

P^{from - Y} (X)

from

P^{prior} (Y)

, i.e., we will have

P (X | Y) = P^{from - Y} (X)

. Then, one can ask for an event probability

P (X = x | Y)

without being given an event in Y. Note that conditional probabilities do not necessarily describe a cause and consequence relation but rather they are knowledge or information relation.

The Bayesian view of quantum physics also says that knowledge associated with a state is subjective to the observer. For example two observers conducting an experiment of quantum teleportation[7,9,14,15] will have different knowledge about the experiment according to when and where a measurement is obtained. According to the special theory of relativity information or knowledge can not be transferred instantaneously and so observers of an entangled pair traveling at long distances will possess different knowledge of the variables at the time one of them is measured and so their predictions about the outcome of the other variable will differ, e.g., see [16,17]. These experiments suggest that quantum physics is best described as a Bayesian theory. It is worth to stress that a theory of knowledge is not necessarily a theory of cause and consequence.

Here knowledge and information are meant to be the same thing, so Shannon’s proposed entropy to quantify loss of information is the same as to quantify loss of knowledge. There is much work in information in quantum physics, e.g., [18,19] and references, but they use von Neumann mixed states entropy as a starting point which attributes zero information content for all pure states. Here our starting point is pure states, the core of quantum physics theory. The emphasis in using the term knowledge is that it is the language used in Bayesian theory and it stresses that it is subjective. Yet, the Bayesian view provides all the predictions quantum theory can make today and perhaps can be expand it as presented in the next discussion.

1.2. Entropy, Interference, and Entanglement

Following the work [1,2] Shannon entropy of a state in phase space is adopted to be the loss of knowledge or the loss of information such a state describes.

That work explores the possibility that knowledge (or information) can not be gained in a closed quantum system. Here the objective is to quantify interference and entanglement in terms of information loss or gained. The Kullback-Liebler divergence (reviewed in B) is employed to define interference as a loss of information if one replaces the state probability density in phase space by a ”classical probability density" in phase space (to be made precise). The Kullback-Liebler divergence is also employed to define entanglement as a loss of information if one replaces a state probability density in phase space by a product of states probability density in phase space (to be made precise). Such quantification of interference and entanglement could help our understanding of physical system evolution, for example by restricting which physical phenomena are allowed according to the gain or loss of interference or entanglement.

Position and spin are degrees of freedom required to specify a quantum state. This paper addresses how knowledge in phase space is quantified for position and spin DOFs.

1.3. Paper Organization

In the next Section 2 the Bayesian formulation of probability density in position-momentum phase space is developed. Section 3 proposes the quantification of interference in phase space and compares it to the entropy in phase space. Section 4 proposes the quantification of entanglement in phase space and compares it to the entropy in phase space. Section 5 expands the concept of phase space to spin systems and proposes the quantification of entanglement for spin systems. Such quantification can also be expanded to Qbit technology. We also briefly show the approach to mixed states and compare it to von Neumann entropy. Section 6 concludes the paper.

2. Quantum Phase Space Probabilities and Entropy

Given a state

| Ψ_{t} 〉

evolving in time, one constructs the density matrix

ρ_{t} = | Ψ_{t} 〉 〈 Ψ_{t} |

. Projecting it simultaneously to the position basis

| x 〉

and momentum basis

| p 〉

(or spatial frequency basis

| k 〉 = \frac{1}{ℏ} | p 〉)

) to obtain

\begin{matrix} ρ_{t}^{x} (x) & = 〈 x | ρ_{t} | x 〉 = {| ψ_{t} (x) |}^{2} \\ ρ_{t}^{k} (k) & = 〈 k | ρ_{t} | k 〉 = {| ϕ_{t} (k) |}^{2}, \end{matrix}

(1)

which is Born’s rule applied to position space and momentum space respectively. For the entire paper the chosen units set

ℏ = 1

. Then the spatial frequency variable k and the quantum momentum variable p will have the same value. The presentation here is with the spatial frequency variable k as it is meaningful in quantum mechanics and quantum field theory[20]. The work presented here is applicable to both disciplines.

Let us first assume, there is a joint distribution in phase space

ρ (x, k, t)

and study properties of such distribution and then derive its expression.

Early attempts to create a quantum state in phase space by Wigner [21] or by Husimi [22] ended up with pseudo-distributions that fail Kolmogorov probability axioms and also have consistency difficulties with special relativity. Thus, the pursue of this new approach.

While a distribution at any time

t_{0}

can be described by

ρ_{t_{0}}^{x} (x) = δ (x - x_{0})

or by

ρ_{t_{0}}^{k} (k) = δ (k - k_{0})

, where

δ (.)

is the Dirac delta distribution, one can not have at any time

t_{0}

the distribution

ρ (x, k) \neq δ (x - x_{0}) δ (k - k_{0})

. This limitation is derived from the fact that

ψ (x, t) = 〈 x | Ψ_{t} 〉

and

ϕ (k, t) = 〈 k | Ψ_{t} 〉

are the Fourier transform of each other. If one acquires full knowledge of one of the variables at time t, expressed by a Dirac delta distribution, then the other phase space variable must be described by a uniform distribution, indicating maximum entropy in this other variable. It is this constraint of our knowledge about the pair of variables x and k at time t that yields the uncertainty principle as clearly formulated by Robertson[23].

In quantum physics

ρ_{t} (x, k)

represents knowledge of the variables and not a probability of an outcome of a measurement, since it is not possible to measure both variables simultaneously. Statistically, it is not feasible the event

(x, k)

at time t. For the Bayesian interpretation, it is not possible to have full knowledge of the two variables simultaneously, but still,

ρ_{t} (x, k)

offers some knowledge of the two variables. Note also that one may acquire empirically the full knowledge of one variable for one particle without directly measuring it, for example via an entanglement scenario where the measurement occurs for the other particle.

Geiger and Kedem [1] proposed a quantification of knowledge of a quantum state through Shannon entropy associated to the phase space distribution, namely

\begin{matrix} S_{t} = - \int d x d k ρ_{t} (x, k) log ρ_{t} (x, k) . \end{matrix}

(2)

The two extreme scenarios of complete lack of knowledge of a state given by uniform distribution on both variables or of complete knowledge of a state given by a Dirac delta function on both variables, where the entropy diverges to ∞ or

- \infty

in Hilbert space, respectively, can not occur in quantum physics. This is due to the Fourier property that links the quantum state projection in position space and the projection in momentum space.

The Bayesian view to derive the expression for the joint distribution

ρ_{t} (x, k)

is now presented.

Theorem 1

(Joint Distribution in Phase Space). Given a state

| Ψ_{t} 〉

, evolving in time according to some Hamiltonian. Then, the joint distribution in phase space is

ρ_{t} (x, k) = | ψ_{t} {(x) |}^{2} {| ϕ_{t} (k) |}^{2}

, where

ψ_{t} (x) = 〈 x | Ψ_{t} 〉

and

ϕ_{t} (k) = 〈 k | Ψ_{t} 〉

are the projection in position basis and spatial frequency basis.

Proof.

From Bayes’ theorem applied to the density

ρ_{t} (x, k)

we have

ρ_{t} (x, k) = ρ_{t}^{cond - x} (k | x) ρ_{t}^{x} (x)

, where

ρ_{t}^{x} (x) = 〈 x | Ψ_{t} 〉 〈 Ψ_{t} | x 〉 = {| ψ_{t} (x) |}^{2}

is thee prior over the variable x. The knowledge gained for the variable k, given the prior knowledge over the variable x, leads to the conditional probability distribution as follows

\begin{matrix} 〈 k | Ψ_{t} 〉 & = \int d x 〈 k | x 〉 〈 x | Ψ_{t} 〉 \\ ⇓ \\ ρ_{t}^{cond - x} (k | x) & = \int d x \int d x^{'} 〈 k | x 〉 〈 x | Ψ_{t} 〉 〈 Ψ_{t} | x^{'} 〉 〈 x^{'} | k 〉 \\ = \frac{1}{\sqrt{2 π}} \int d x 〈 x | Ψ_{t} 〉 e^{- i k x} \frac{1}{\sqrt{2 π}} \int d x^{'} 〈 Ψ_{t} | x^{'} 〉 e^{i k x^{'}} \\ = ϕ_{t} (k) ϕ_{t}^{*} (k) \end{matrix}

(3)

where

〈 k | x 〉 = \frac{1}{\sqrt{2 π}} e^{- i k x}

. The same procedure applies if the starting point of Bayes theorem is

ρ_{t} (x, k) = ρ_{t}^{cond - k} (x | k) ρ_{t}^{k} (k)

with the prior

ρ_{t}^{k} (k) = {| ϕ_{t} (k) |}^{2}

. □

Clearly,

ρ_{t} (x, k) = ρ_{t}^{x} (x) ρ_{t}^{k} (k)

is not the product of two independent random variables due to the Fourier transform constraint between the two density functions.

3. Interference

Given two states

| Ψ^{A} 〉

and

| Ψ^{B} 〉

and a general superposition of these two states as in (A2). The projection of this state superposition to phase space written in polar coordinates is

\begin{matrix} ψ (x) & = 〈 x | Ψ 〉 = \frac{e^{i ν}}{\sqrt{Z_{P}}} (cos θ_{1} | ψ^{A} (x) | e^{i ξ_{A} (x)} + sin θ_{1} | ψ^{B} (x) | e^{i (ξ_{B} (x) - φ_{1})}) \end{matrix}

(4)

\begin{matrix} ϕ (k) & = 〈 k | Ψ 〉 = \frac{e^{i ν}}{\sqrt{Z_{Q}}} (cos θ_{1} | ϕ^{A} (k) | e^{i χ_{A} (k)} + sin θ_{1} | ϕ^{B} (k) | e^{i (χ_{B} (k) + φ_{1})}) \end{matrix}

(5)

where

| . |

is the magnitude value,

ξ_{A, B} (x)

are the complex phases associated to the wave functions

ψ_{A, B} (x)

and similarly

χ_{A, B} (k)

are the complex phases associated to the wave functions

ϕ_{A, B} (k)

The probability densities are written as

\begin{matrix} p (x) & = {| ψ (x) |}^{2} = \frac{1}{Z_{P}} (p^{c} (x) + | ψ^{A} (x) | | ψ^{B} (x) | sin 2 θ_{1} cos (ξ_{A} (x) - ξ_{B} (x) - φ_{1})), \\ q (k) & = {| ϕ (k) |}^{2} = \frac{1}{Z_{Q}} (q^{c} (k) + | ϕ^{A} (k) | | ϕ^{B} (k) | sin 2 θ_{1} cos (χ_{A} (k) - χ_{B} (k) - φ_{1})) \end{matrix}

(6)

where the normalization constants are

Z_{P} = 1 + sin 2 θ_{1} \int d x (| ψ^{A} (x) | | ψ^{B} (x) | cos (ξ_{A} (x) - ξ_{B} (x) - φ_{1}))

and

Z_{Q} = 1 + sin 2 θ_{1} \int d k | ϕ^{A} (k) | | ϕ^{B} (k) | cos (χ_{A} (k) - χ_{B} (k) - φ_{1})

, and

\begin{matrix} p^{c} (x) & = c o s^{2} θ_{1} | ψ^{A} {(x) |}^{2} + {sin}^{2} θ_{1} {| ψ^{B} (x) |}^{2} \\ q^{c} (k) & = {cos}^{2} θ_{1} | ϕ^{A} {(x) |}^{2} + {sin}^{2} θ_{1} {| ϕ^{B} (x) |}^{2} \end{matrix}

(7)

are probability densities without the interference terms. The upper-index c refers to these probability densities also representing classical statistical combination (weighted average) of probability densities associated to the quantum states A and B.

There is no interference when

the functions’ support in phase space do not overlap, i.e.,

$\begin{matrix} | ψ^{A} (x) | | ψ^{B} (x) | & = 0; \forall x, and | ϕ^{A} (k) | | ϕ^{B} (k) | = 0; \forall k, \end{matrix}$

(8)
the complex phases are aligned up to a constant multiple of $\frac{π}{2}$ , i.e.,

$\begin{matrix} ξ_{A} (x) - ξ_{B} (x) - φ_{1} = n \frac{π}{2}; n \in Z^{+}, and χ_{A} (k) - χ_{B} (k) - φ_{1} = m \frac{π}{2}; m \in Z^{+}, \end{matrix}$

(9)
either $θ_{1} = 0, \frac{π}{2}$ , since then there is no superposition of states. This will effectively occur when $ψ^{A} (x) = ψ^{B} (x)$ .

Also, IFF there is no interference,

P (x) = p^{c} (x)

and

Q (x) = q^{c} (x)

. Figure 2 illustrates some scenarios with each state being a coherent state and for some parameters these conditions occur.

Definition 1

(Interference:). Given two states

| Ψ^{A} 〉

| Ψ^{B} 〉

and their linear superposition

| Ψ 〉

given by (A2). Interference,

I

, is the amount of information lost when

ρ^{c} (x, k) = p^{c} (x) q^{c} (k)

is used to approximate

ρ (x, k) = p (x) q (k)

. It is calculated via the Kullback-Liebler divergence between the phase space probability densities

ρ (x, k)

and

ρ^{c} (x, k)

. More formally,

\begin{matrix} I (θ_{1}, φ_{1}, | Ψ^{A} 〉, | Ψ^{B} 〉) & = D_{K L} (p (x) q (k) | | p^{c} (x) q^{c} (k)) \\ = CrossS (p (x), p^{c} (x)) - S (P (x)) + CrossS (q (k), q^{c} (k)) - S (q (k)) \\ = {\int d x | ψ (x) |}^{2} log (1 + \frac{| ψ^{A} (x) | | ψ^{B} (x) | sin 2 θ_{1} cos (ξ_{A} (x) - ξ_{B} (x) - φ_{1})}{{cos}^{2} θ_{1} | ψ^{A} {(x) |}^{2} + {sin}^{2} θ_{1} {| ψ^{B} (x) |}^{2}}) \\ + {\int d k | ϕ (k) |}^{2} log (1 + \frac{| ϕ^{A} (k) | | ϕ^{B} (k) | sin 2 θ_{1} cos (χ_{A} (k) - χ_{B} (k) - φ_{1})}{{cos}^{2} θ_{1} | ϕ^{A} {(k) |}^{2} + {sin}^{2} θ_{1} {| ϕ^{B} (k) |}^{2}}), \end{matrix}

(10)

where

CrossS (p, q)

is the cross entropy between probability distributions p and q (see (A10)). As one vary the combination of the two states the larger is

I

the larger the interference contribution to the distribution

ρ (x, k) = p (x) q (k)

Clearly, one can consider the interference just in position representation or just in spatial frequency representation. However, here, the quantification of the interference in phase space distinguish the case (a) when a projection of superposition of two states in position space does not interfere but the same state projection in spatial frequency does interfere, from the case (b) a superposition of two states that do not interfere neither in position nor in spatial frequency.

One comparison of interest is between the Kullback-Liebler divergence (KLD) (10) and the entropy (2). Figure 2 illustrates some scenarios where these two quantities are evaluated and comparisons are made. The entropy seems to capture better the notion of overlap of the superposition of states. The classical addition of probability densities and the quantum superposition do occur when both states are similar and superposed, then the KLD will be small and the entropy will be small. However, when there is no overlap between the two states, again, the KLD will be small while the entropy will be large, i.e., for scenarios where the classical weighted average distribution is a good approximation but the states do not overlap, the entropy is large.

Both concepts may be helpful to characterize the knowledge one has about the superposition of states. The KLD captures the distinction between classical probability and quantum probability, while the entropy captures a balance between the KLD distinction and the concept of overlap of two states in quantum phase space. For the entropy, the larger the overlap, the less entropy there is. One important advantage of the entropy over the KLD is that one does not need to know the classical distribution to evaluate the entropy. The entropy is only dependent on the probability density of the superposed state and as such, it may play a role in creating predictions for quantum physics as proposed by Geiger and Kedem [1], where they proposed that the time arrow is dictated by the entropy.

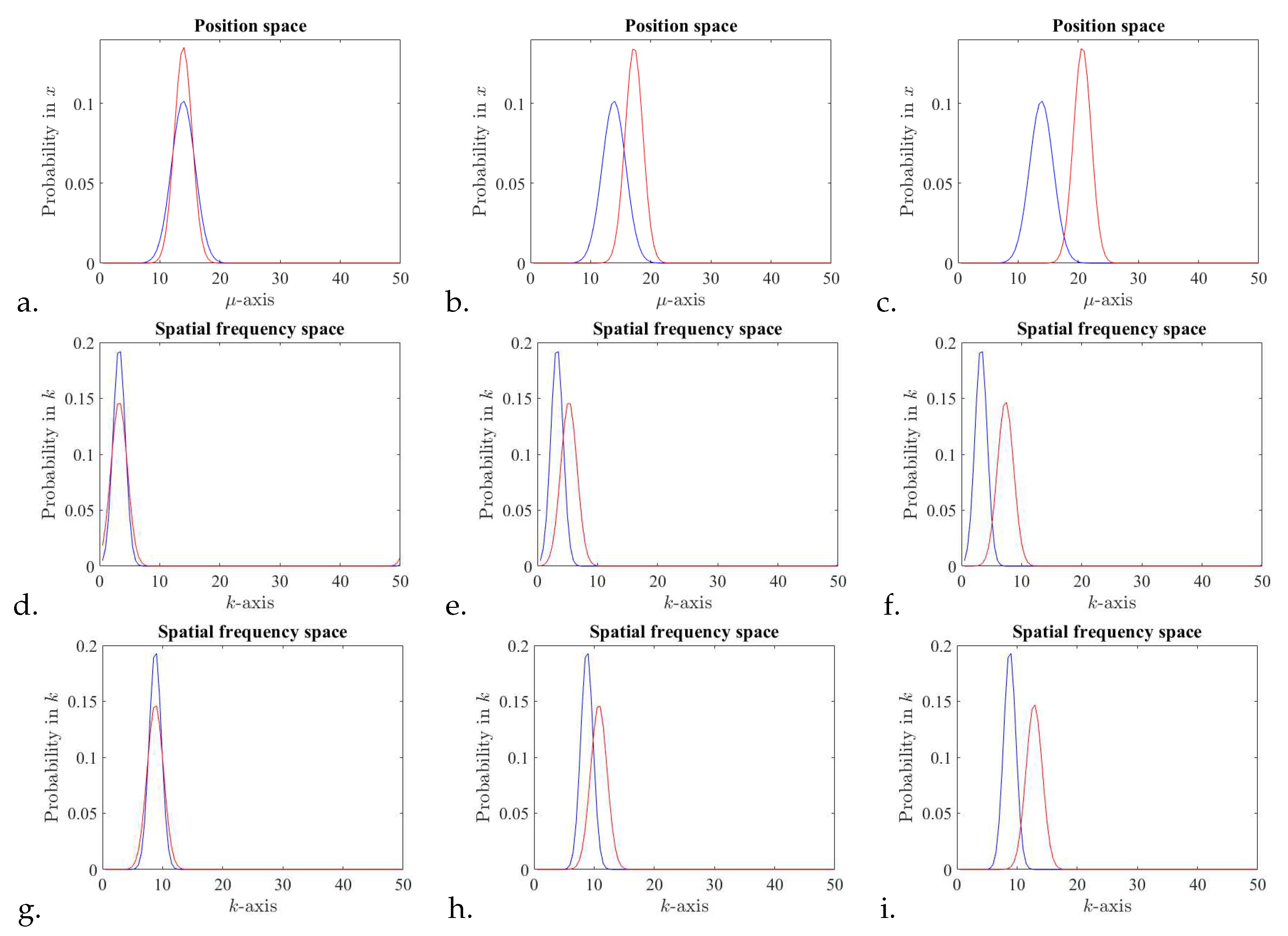
Figure 1. Probability densities in phase space for two coherent states, A and B with centers, variances as follows. For all a., b., c. position space probabilities, with $μ_{A} \approx 27.8$ with $σ_{A} = 5.6$ and for a. $μ_{B} \approx 27.8$ , b. $μ_{B} \approx 34.8$ , c. $μ_{B} \approx 41.7$ , all with $σ_{B} = 4.2$ . Note that for each coherent state, the spatial frequency value is the phase of the coherent state in position space. For d., e., f., Spatial frequency space probabilities, with $k_{A} \approx 0.35$ and d. $k_{B} \approx 0.35$ , e. $k_{B} \approx 0.61$ , f. $k_{B} \approx 0.87$ . For g., h., i., spatial frequency space probabilities, with $k_{A} \approx 1.04$ and g. $k_{B} \approx 1.04$ , h. $k_{B} \approx 1.30$ , i. $k_{B} \approx 1.56$ .

It is noticeable the role of the period associated to the phase differences, in position and in spatial frequency, as per (9). For coherent states, the phase difference in position is the center differences in the spatial frequency domain, and vice-versa, the phase difference in spatial frequency is the center difference in the position domain. The periodic range for

Δ μ

is reduced for Figure 2c,d creating the oscillations in the KLD and entropy.

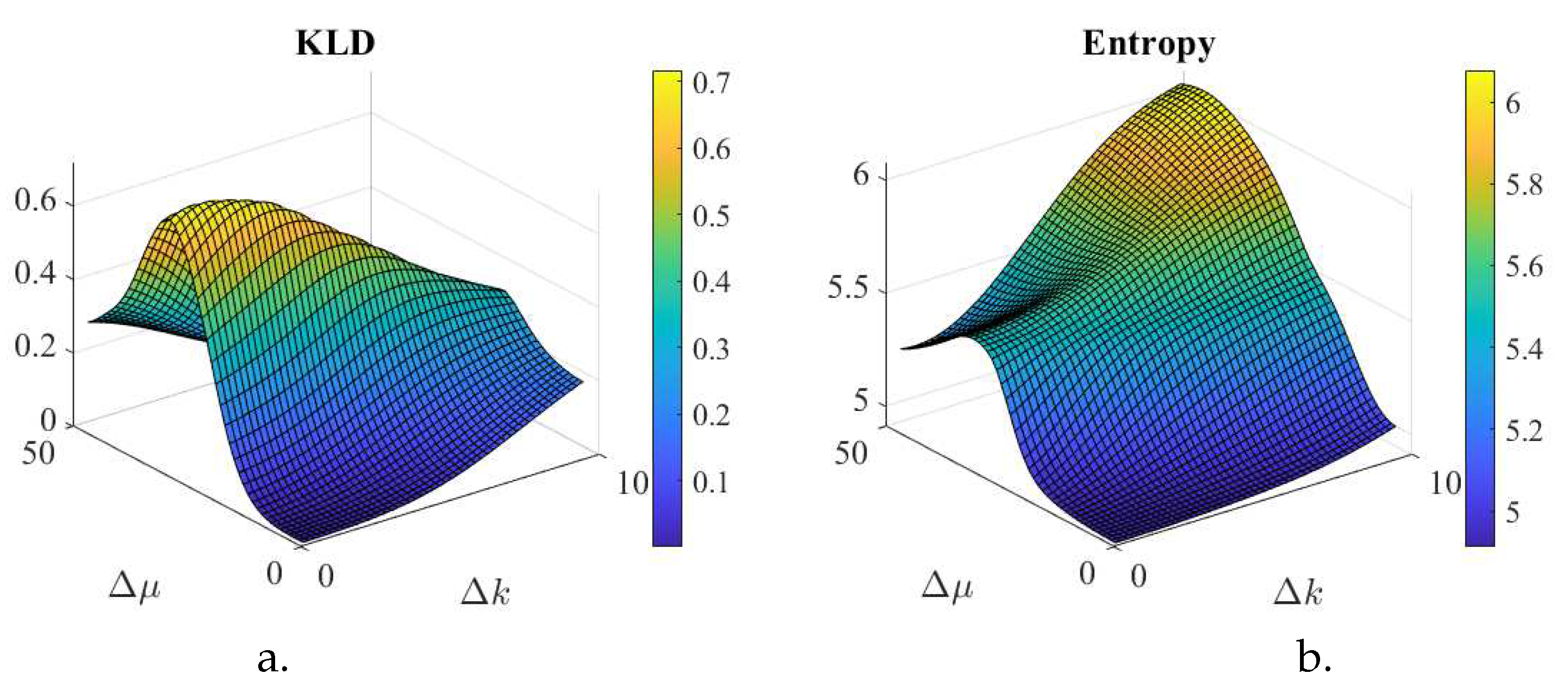
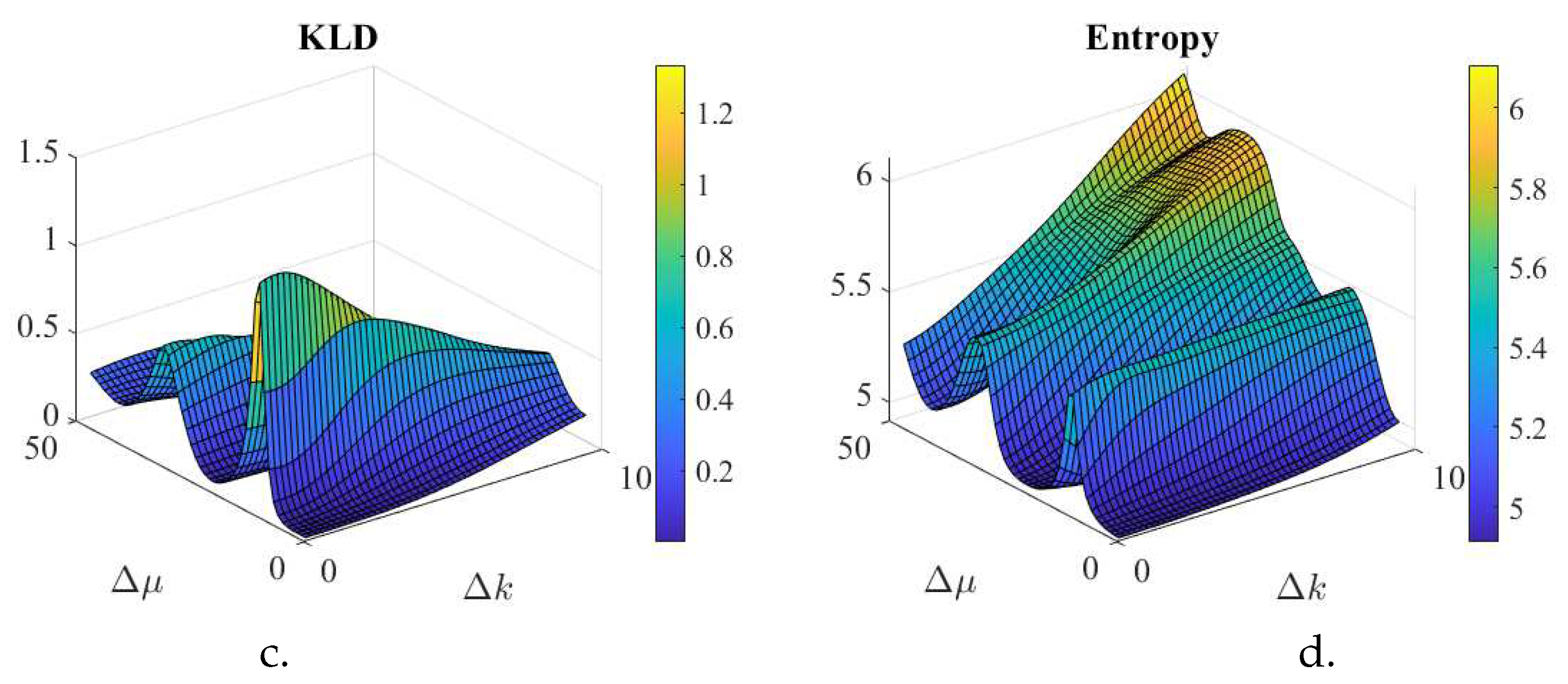
Figure 2. Interference Simulations for a superposition of two coherent states as shown in Figure 1. One coherent state has

μ_{A} = 27.8

σ_{A} = 5.6

, and for a.,b., the phase is

k_{A} = 0.3472

while for c.,d., the phase is

k_{A} = 1.0417

. Varying the other state with fixed

σ_{B} = 4.1667

48 \times 48

increments from

μ_{B} = [μ_{A}, \dots, 41.6667]

, and for a.,b., the phase varies as

k_{B} = [k_{A}, \dots, 0.8681]

, while for c.,d., the phase varies as

k_{B} = [k_{A}, \dots, 1.5625]

. The plots are all with

Δ μ = μ_{B} - μ_{A}

Δ k = k_{B} - k_{A}

. It is noticeable how the KLD and the entropy become small as the two states closely overlap, i.e., where

δ μ \approx δ k \approx 0

. However, the KLD becomes small as the states do not overlap while the entropy gets to be larger. As the phase increases from (a. b.) to (c. d.) oscillation increases for both (KLD and Entropy) as periods reduces.

Figure 2. Interference Simulations for a superposition of two coherent states as shown in Figure 1. One coherent state has

μ_{A} = 27.8

σ_{A} = 5.6

, and for a.,b., the phase is

k_{A} = 0.3472

while for c.,d., the phase is

k_{A} = 1.0417

. Varying the other state with fixed

σ_{B} = 4.1667

48 \times 48

increments from

μ_{B} = [μ_{A}, \dots, 41.6667]

, and for a.,b., the phase varies as

k_{B} = [k_{A}, \dots, 0.8681]

, while for c.,d., the phase varies as

k_{B} = [k_{A}, \dots, 1.5625]

. The plots are all with

Δ μ = μ_{B} - μ_{A}

Δ k = k_{B} - k_{A}

. It is noticeable how the KLD and the entropy become small as the two states closely overlap, i.e., where

δ μ \approx δ k \approx 0

4. Entanglement

Given two states

| Ψ^{A} 〉

and

| Ψ^{B} 〉

and a general two-state composed from these two states as in (). Let the wave function given by () be rewritten in polar coordinates as

\begin{matrix} ψ (x, y) & = 〈 x | 〈 y | {| Ψ 〉}_{2} \\ = \frac{e^{i ν}}{\sqrt{Z_{2, P}}} (cos θ_{2} | Ψ^{A} (x) | | Ψ^{B} (y) | e^{i (ξ_{A} (x) + ξ_{B} (y))} + sin θ_{2} | Ψ^{A} (y) | | Ψ^{B} (x) | e^{i (ξ_{A} (y) + ξ_{B} (x) + φ_{2})}) \\ ϕ (k_{x}, k_{y}) & = 〈 k_{x} | 〈 k_{y} | {| Ψ 〉}_{2} \\ = \frac{e^{i ν}}{\sqrt{Z_{2, Q}}} (cos θ_{2} | Φ^{A} (k_{x}) | | Φ^{B} (k_{y}) | e^{i (χ_{A} (k_{x}) + χ_{B} (k_{y}))} + sin θ_{2} | Φ^{B} (k_{x}) | | Φ^{A} (k_{y}) | e^{i (χ_{A} (k_{y}) + χ_{B} (k_{x}) + φ_{2})}) \end{matrix}

(11)

where

θ_{2} = \frac{π}{4}

and

φ_{2} = 0, π

describe bosons and fermions respectively. When expanding to Qbits, this restriction is lifted.

The probability density in position space is

\begin{matrix} p (x, y) & = {| ψ (x, y) |}^{2} = \frac{1}{Z_{2, P}} ({cos}^{2} θ_{2} | Ψ^{A} {(x) |}^{2} | Ψ^{B} {(y) |}^{2} + {sin}^{2} θ_{2} | Ψ^{B} {(x) |}^{2} {| Ψ^{A} (y) |}^{2} \\ + sin 2 θ_{2} cos (ξ_{A} (x) - ξ_{B} (x) + ξ_{B} (y) - ξ_{A} (y) - φ_{2}) | Ψ^{A} (x) | | Ψ^{B} (y) | | Ψ^{A} (y) | | Ψ^{B} (x) |) \end{matrix}

(12)

Similarly the probability density

q (k_{x}, k_{y})

in spatial frequency space is

\begin{matrix} q (k_{x}, k_{y}) & = | ϕ (k_{x}, k_{y}) |^{2} = \frac{1}{Z_{2, Q}} ({cos}^{2} θ_{2} | Φ^{A} (k_{x}) |^{2} | Φ^{B} (k_{y}) |^{2} + {sin}^{2} θ_{2} | Φ^{B} (k_{x}) |^{2} {| Φ^{A} (k_{y}) |}^{2} \\ + sin 2 θ_{2} cos (χ_{A} (k_{x}) - χ_{B} (k_{x}) + χ_{B} (k_{y}) - χ_{A} (k_{y}) - φ_{2}) | Φ^{A} (k_{x}) | | Φ^{B} (k_{y}) | | Φ^{A} (k_{y}) | | Φ^{B} (k_{x}) |) \end{matrix}

(13)

The product of states, or the disentangled states, are described by the two-state (11) with

θ_{2} = 0, \frac{π}{2}

, i.e.,

\begin{matrix} θ_{2} & = 0 θ_{2} = \frac{π}{2} \\ p^{D 1} (x, y) & = | Ψ^{A} {(x) |}^{2} | Ψ^{B} {(y) |}^{2} p^{D 2} (x, y) = | Ψ^{B} {(x) |}^{2} {| Ψ^{A} (y) |}^{2} \\ q^{D 1} (k_{x}, k_{y}) & = | Φ^{A} (k_{x}) |^{2} | Φ^{B} (k_{y}) |^{2} q^{D 2} (k_{x}, k_{y}) = | Φ^{B} (k_{x}) |^{2} {| Φ^{A} (k_{y}) |}^{2} \end{matrix}

(14)

where the upper index D1 and D2 indicate two different disentangle states.

Lemma 1.

Given two states

| Ψ^{A} 〉

| Ψ^{B} 〉

and the two-state

| Ψ 〉

per (). Refer by

p^{D} (x, y) q^{D} (k_{x}, k_{y})

to any of the disentangled states (14). The Kullback-Liebler divergence

D_{K L} (p (x, y) q (k_{x}, k_{y}) | | p^{D} (x, y) q^{D} (k_{x}, k_{y}))

for bosons or fermions, where

θ_{2} = \frac{π}{4}

and

φ_{2} = 0, π

respectively, is invariant to any choice of disentangled states.

Proof.

The lemma follows from performing the decomposition of the logarithm of products into the sum of logarithms and then using the symmetric properties of fermions and bosons. More precisely,

\begin{matrix} D_{K L}^{D} = - S (p, q) + \int d x d y d k_{x} d k_{y} p (x, y) q (k_{x}, k_{y}) log (p^{D} (x, y) q^{D} (k_{x}, k_{y})) \end{matrix}

(15)

where

D_{K L}^{D} = D_{K L}^{D} (p (x, y) q (k_{x}, k_{y}) | | p^{D} (x, y) q^{D} (k_{x}, k_{y}))

. Then, for D1 we get

\begin{matrix} D_{K L}^{D 1} & = - S (p, q) + \int d x d y p (x, y) log (| Ψ^{A} {(x) |}^{2} {| Ψ^{B} (y) |}^{2}) + \int d k_{x} d k_{y} q (k_{x}, k_{y}) log (| Φ^{A} (k_{x}) |^{2} {| Φ^{B} (k_{y}) |}^{2}) \\ = - S (p, q) + \int d x p (x) log | Ψ^{A} {(x) |}^{2} + \int d y p (y) log {| Ψ^{B} (y) |}^{2} \\ + \int d k_{x} q (k_{x}) log | Φ^{A} (k_{x}) |^{2} + \int d k_{y} q (k_{y}) log {| Φ^{B} (k_{y}) |}^{2} \end{matrix}

(16)

where

p (x) = \int d y p (x, y)

p (y) = \int d x p (x, y)

q (k_{x}) = \int d k_{y} q (k_{x}, k_{y})

q (k_{y}) = \int d k_{x} q (k_{x}, k_{y})

. Note that the integrals yield the same functions

p (.)

and

q (.)

due to the symmetric properties for bosons and fermions.

Similarly, for D2 we get

\begin{matrix} D_{K L}^{D 2} & = - S (p, q) + \int d x p (x) log | Ψ^{B} {(x) |}^{2} + \int d y p (y) log {| Ψ^{A} (y) |}^{2} \\ + \int d k_{x} q (k_{x}) log | Φ^{B} (k_{x}) |^{2} + \int d k_{y} q (k_{y}) log {| Φ^{A} (k_{y}) |}^{2} \end{matrix}

(17)

and clearly every term here has a perfect match in (16), e.g.,

\int d x p (x) log | Ψ^{B} {(x) |}^{2} = \int d y p (y) log {| Ψ^{B} (y) |}^{2}

and so

D_{K L}^{D 2} = D_{K L}^{D 1}

. □

Definition 2

(Entanglement:). Given two states

| Ψ^{A} 〉

| Ψ^{B} 〉

and the two-state

| Ψ 〉

, shown in (), that when projected in phase space yields the probability density distribution

ρ (x, y, k_{x}, k_{y}) = p (x, y) q (k_{x}, k_{y})

. Entanglement,

E

, is the amount of information lost when the product of states is used to approximate

ρ (x, y, k_{x}, k_{y})

. More formally,

\begin{matrix} E (θ_{2}, φ_{2}, | Ψ^{A} 〉, | Ψ^{B} 〉) & = D_{K L} (p (x, y) q (k_{x}, k_{y}) | | p^{D} (x, y) q^{D} (k_{x}, k_{y})) \\ = CrossS (p (x, y) q (k_{x}, k_{y}), p^{D} (x, y) q^{D} (k_{x}, k_{y})) - S (p (x, y) q (k_{x}, k_{y})) \end{matrix}

(18)

The entanglement is reduced to the combination of the first two terms in (12) and (13), i.e., the third term vanishes, when

the functions’ support in phase space do not overlap, i.e.,

$\begin{matrix} | ψ^{A} (x) | | ψ^{B} (x) | & = 0; \forall x, and | ϕ^{A} (k) | | ϕ^{B} (k) | = 0; \forall k, \end{matrix}$

(19)
the complex phases are aligned up to a constant multiple of $\frac{π}{2}$ , i.e.,

$\begin{matrix} ξ_{A} (x) - ξ_{B} (x) + ξ_{B} (y) - ξ_{A} (y) - φ_{2} = n \frac{π}{2}; n \in Z^{+}, \\ and χ_{A} (k_{x}) - χ_{B} (k_{x}) + χ_{B} (k_{y}) - χ_{A} (k_{y}) - φ_{2} = m \frac{π}{2}; m \in Z^{+}, \end{matrix}$

(20)
$θ_{2} = 0, \frac{π}{2}$ . This will effectively occur when $ψ^{A} (x) = ψ^{B} (x)$ , a symmetric combination.

One comparison of interest is between the entanglement (18) and the entropy (2). Figure 3 illustrate some scenarios combining two coherent states where these two quantities are evaluated and a comparisons is made. While the definition of entanglement is through the KLD, the entropy captures a similar behavior and it can be evaluated from the state itself, without having to know what the product of the states would be. For quantum predictions based on entanglement, the entropy may be the best method to use.

The entanglement increases the further a part the two states are from each other, which is suitable for teleportation experiments.

5. Entanglement for Spin or Qbit Phase Space

The degrees of freedom (DoFs) in quantum physics specify the wave function (projection of the state in position space) and the spin. Thus, when quantifying our knowledge of a quantum system one must also quantify our knowledge of a spin state. Qbits are similar to spin in formalism, but with less constraints such as no need to obey Pauli exclusion principle. What follows also applies to Qbits.

Let us consider two spin states

| ξ_{A} 〉

and

| ξ_{B} 〉

, each formed with

N^{A}

and

N^{B}

particles with spin s, respectively. A spin state formed from these two states with well defined spin magnitude

s \in [s_{N}, s_{N} - 1, \dots, \frac{1}{2} mod (2 s_{N}, 2)]

, where

s_{N} = N s

and

N = N^{A} + N^{B}

, is written as

\begin{matrix} | ξ_{s} 〉 = \frac{e^{i ν_{2}}}{\sqrt{Z_{2}}} (cos θ_{2} | ξ^{A} 〉 | ξ^{B} 〉 + e^{i φ_{2}} sin θ_{2} | ξ^{B} 〉 | ξ^{A} 〉) . \end{matrix}

(21)

This state is an eigenstate of the operator

S^{2}

of N particles of spin s with eigenvalue

s

In the case of phase space of position and spatial frequency, the basis functions for a product of N Hilbert spaces is given by

| x_{1} 〉 \dots | x_{N} 〉

and

| k_{1} 〉 \dots | k_{N} 〉

. Note that these are the eigenstates of the operators

X = x_{1} \dots x_{N}

and

K = k_{1} \dots k_{N}

. For the product of spin states, the space structure is more complex and following Geiger and Kedem [2] the basis of the product of spin spaces is the common eigenstates of the operators

S_{z}

and

S^{2}

for the entire space.

The operator

S_{z}

associated to

| ξ_{s} 〉

is given by

\begin{matrix} S_{z} = S_{z}^{A} \otimes I_{2 N^{B}} + I_{2 N^{A}} \otimes S_{z}^{B} \end{matrix}

(22)

where

I_{N}

is the identity of dimension N and ⊗ is the exterior product. Let us refer to the eigenstates of

S_{z}

and

S^{2}

{| ξ_{s, m_{s}} 〉; s = s_{N}, s_{N} - 1, \dots \frac{1}{2} mod (2 * s_{N}, 2), m_{s} = - s, \dots, s}

The phase space for the spin associated to the operators

S_{z}

and

S^{2}

is derived from quantizing the sphere, the surface of the ball with a radius of the spin magnitude

ℏ s_{N}

, as developed by the Geometric Quantization (GQ) method, e.g., see [24,25,26]. Geiger and Kedem [2] have proposed this approach to evaluate the entropy of a quantum state. Let us briefly summarize their work.

Given a spin state

| ξ_{s} 〉

as in (21), with N particles and a well defined spin magnitude s (an eigenvector of the operator

S^{2}

). Projecting in the basis of the eigenstates of

S_{z}

{| ξ_{s, m} 〉; m = - s, \dots, s}

, to obtain

\begin{matrix} | ξ_{s} 〉 = \sum_{m = - s}^{s} α_{s, m} | ξ_{s, m} 〉, \end{matrix}

(23)

where

α_{s, m} = 〈 ξ_{s, m} | | ξ_{s} 〉 \in C

and

1 = \sum_{m = - s}^{s} {| α_{s, m} |}^{2}

. The conjugate basis to

{| ξ_{s, m} 〉}

{| ϕ 〉; [0, 2 π]}

, obtained by identifying the angle

ϕ

, the rotation angle around the z-axis of the operator

e^{- i S_{z} ϕ}

, as the operator that commutes with

S_{z}

In the basis of the conjugate operator

ϕ

, the spin state is

\begin{matrix} | ξ_{s} 〉 & = \int_{0}^{2 π} | ϕ 〉 〈 ϕ | | ξ_{s} 〉 d^{} ϕ = \int_{0}^{2 π} λ_{s} (ϕ) | ϕ 〉 d^{} ϕ, \end{matrix}

(24)

where

\begin{matrix} λ_{s} (ϕ) = 〈 ϕ | | ξ_{s} 〉 = \sum_{m = - s}^{s} α_{s, m} 〈 ϕ | | ξ_{s, m} 〉 = \sum_{m - s}^{s} α_{s, m} ψ_{s, m} (ϕ) . \end{matrix}

(25)

and

\begin{matrix} ψ_{s, m} (ϕ) = \{\begin{matrix} \frac{1}{\sqrt{2 π}} e^{i (s + m) ϕ}, & m \geq 0 & (northern hemisphere), \\ \frac{1}{\sqrt{2 π}} e^{i (- s + m) ϕ}, & m < 0 & (southern hemisphere) . \end{matrix} \end{matrix}

(26)

The two solutions in (26) are periodic in

ϕ

and differ by a phase (gauge) transformation of

e^{- i 2 s ϕ}

Thus, for a state

| ξ_{s} 〉

with density matrix

ρ_{s} = | ξ_{s} 〉 〈 ξ_{s} |

, the probabilities of the phase space are the product of the probabilities

{ρ_{s, m} = 〈 ξ_{s, m} | ρ_{s} | ξ_{s, m} 〉 = | α_{s, m} |^{2}}

with the probability densities

{ρ_{s} (ϕ) = 〈 ϕ | ρ_{s} | ϕ 〉 = | λ_{s} (ϕ) |^{2}}

. Note that given

{α_{s, m}}

one obtains

{λ_{s} (ϕ)}

via the predefined set of functions (26), i.e., one can interpret

ρ_{s} (ϕ)

as a conditional probability density

ρ_{s} (ϕ / {α_{s, m}})

Thus the entropy (2) of a spin state

| ξ_{s} 〉

with spin

s

in spin phase space is

\begin{matrix} S = S^{z} + S^{ϕ} & = - \sum_{m = - s}^{s} ρ_{s, m} ln ρ_{s, m} - \int ρ_{s} (ϕ) ln ρ_{s} (ϕ) d^{} ϕ \end{matrix}

(27)

\begin{matrix} = - \sum_{m = - s}^{s} | α_{s, m} |^{2} ln | α_{s, m} |^{2} - \int | λ_{s} {(ϕ) |}^{2} ln {| λ_{s} (ϕ) |}^{2} d^{} ϕ . \end{matrix}

(28)

The first term is the Shannon entropy capturing the randomness of the spin value along the z-axis. The second term is differential entropy capturing the randomness of the spin value in the plane perpendicular to the z-axis, i.e., the entropy of the polarization angle

ϕ

Extending the work of [2] to also define the Kullback-Liebler divergence between a combination of a state as described by (11) and the product of the states

| ξ^{A} 〉 | ξ^{B} 〉

. The densities in spin phase space associated to the product state

| ξ^{A} 〉 | ξ^{B} 〉

are derived from the projections

\begin{matrix} | ξ^{A} 〉 | ξ^{B} 〉 = \sum_{m = - s}^{s} α_{s, m}^{A, B} | ξ_{s, m} 〉 \Rightarrow α_{s, m}^{A, B} = 〈 ξ_{s, m} | | ξ^{A} 〉 | ξ^{B} 〉 \Rightarrow λ_{s}^{A, B} (ϕ) = \sum_{m - s}^{s} α_{s, m}^{A, B} ψ_{s, m} (ϕ), \end{matrix}

(29)

Definition 3

(Spin Entanglement:). Given two spin states

| ξ^{A} 〉, | ξ^{B} 〉

and the combination

| ξ_{s} 〉

, shown in (30), that when projected in spin phase space yields the probability density distribution

ρ_{s, m} (ϕ) = | α_{s, m} |^{2} {| λ_{s} (ϕ) |}^{2}

. Spin entanglement, s

E

, is the amount of information lost when the product of states is used to approximate

ρ_{s, m} (ϕ)

. More formally,

\begin{matrix} E (θ_{2}, φ_{2}, | ξ^{A} 〉, | ξ^{B} 〉) & = D_{K L} (| α_{s, m} |^{2} | λ_{s} {(ϕ) |}^{2} | | α_{s, m}^{A, B} |^{2} {| λ_{s}^{A, B} (ϕ) |}^{2}) \\ = CrossS (| α_{s, m} |^{2} | λ_{s} {(ϕ) |}^{2}, | α_{s, m}^{A, B} |^{2} {| λ_{s}^{A, B} (ϕ) |}^{2}) - S (| α_{s, m} |^{2} | λ_{s} (ϕ) |^{2}) \end{matrix}

(30)

One comparison of interest to be made in the future is between spin entanglement (30) and spin entropy (27).

5.1. Expansion to Mixed States

One extension of this approach to mixed states starts from the density matrix derived from the general state (21), namely

\begin{matrix} ρ_{s} = | ξ_{s} 〉 〈 ξ_{s} | & = \frac{1}{Z_{2}} ({cos}^{2} θ_{2} | ξ^{A} 〉 | ξ^{B} 〉 〈 ξ^{B} | 〈 ξ^{A} | + {sin}^{2} θ_{2} | ξ^{B} 〉 | ξ^{A} 〉 〈 ξ^{A} | 〈 ξ^{B} | \\ + \frac{1}{2} e^{- i φ_{2}} sin 2 θ_{2} | ξ^{A} 〉 | ξ^{B} 〉 〈 ξ^{A} | 〈 ξ^{B} | + \frac{1}{2} e^{i φ_{2}} sin 2 θ_{2} | ξ^{B} 〉 | ξ^{A} 〉 〈 ξ^{B} | 〈 ξ^{A} |) . \end{matrix}

(31)

Then, tracing out the density matrix (and assuming the states

| ξ^{A} 〉, | ξ^{B} 〉

to be in orthogonal Hilbert spaces to each other)

\begin{matrix} ρ_{s}^{Mixed} = 〈 ξ^{A} | | ξ_{s} 〉 〈 ξ_{s} | | ξ^{A} 〉 + 〈 ξ^{B} | | ξ_{s} 〉 〈 ξ_{s} | | ξ^{B} 〉 = {cos}^{2} θ_{2} | ξ^{B} 〉 〈 ξ^{B} | + {sin}^{2} θ_{2} | ξ^{A} 〉 〈 ξ^{A} | . \end{matrix}

(32)

Then, von Neumann entropy is the Shannon entropy of this mixed state. While this is of interest to much research, it is clear that Shanon entropy of pure states precedes von Neumann entropy. Also, von Neumann entropy obtained by tracing out pure states has some similarity to the the entropy of the superposition of two states (A2), except it is not considering the conjugate variable of the phase space. In the work of [1] they showed invariant properties of the Shannon entropy in phase space that von Neumann entropy would not have.

6. Conclusion

The concept of Shannon entropy and Kullback-Liebler divergence for pure states in quantum phase spaces can capture key physical properties, interference and entanglement, that precedes von Neumann entropy for mixed states.

This work is much influenced by Geiger and Kedem [1,2], and here an introduction to the Bayesian statistic view was made to construct the phase space probability density. The Bayesian approach sees quantum physics as a theory of degree of knowledge or degree of belief that is subjective to the observer. Through the Bayesian theory, and Fourier transform, one can describe the conditional probabilities in phase space and infer the joint distribution in phase space. In this formulation, quantum physics is a theory of information. However, one can not conclude that it is a causal theory.

The objective was to quantify interference and entanglement in terms of information loss or gain, using the Kullback-Liebler divergence (rooted on Shannon entropy). A comparison to the Shannon entropy of the state and some similarities between the two quantities were revealed. One advantage of the entropy is that it can be inferred from the quantum state, without any reference to the two states that were used to compute the divergence. This difference may be important if physical phenomena are allowed or not according to the gain or loss of interference or entanglement. A brief presentation extended to spin phase space the definition of entanglement.

Extrapolating to a philosophical interpretation, and revisiting the Bohr vs Einstein debate, e.g., see [27,28] and references, the view put forward here is similar to the epistemological view of Bohr: quantum theory is today the best model for predictions. The view put forward here also resonates with the ontological concern of Einstein adding the question: "Is quantum theory a causal theory ?" If not, ”is there a causal theory to be discovered ?" After all, probabilistic models are not necessarily causal models and according to the teleportation experiment an observer gaining knowledge from one measurement can immediately infer the value of the other variable. This is a knowledge relation but not a causal relation. Regarding the question ”Is there a causal theory to be discovered ?", it is beyond the scope of this work. However, one must note that the unitary evolution of the quantum state is described by a causal theory. The Hamiltonian does describe a causal relation by evolving the quantum state through time. One may still ask if the knowledge of the state interfere with the state behavior (as suggested by [1] to define the arrow of time) or to note that a complete description of the physical phenomena including the acquisition of knowledge (sometimes in the form of a measurements) cannot be described by a causal theory.

The quest here was for a better understanding of quantum theory as a Bayesian theory and the use of Shannon entropy and related concepts to characterize interference and entanglement. However, by adopting the Bayesian theory view, the question of a complete causal theory was left open.

Acknowledgments

This paper is partially based upon work supported by both the National Science Foundation under Grant No. DMS-1439786 and the Simons Foundation Institute Grant Award ID 507536 while the authors were in residence at the Institute for Computational and Experimental Research in Mathematics in Providence, RI, during the spring 2019 semester “Computer Vision” program.

Appendix A. Combining two states

Consider a quantum state

| Ψ^{A} 〉

in Hilbert space and its representation in phase space

\begin{matrix} ψ^{A} (x) = 〈 x | Ψ^{A} 〉 and ϕ^{A} (k) = 〈 k | Φ^{A} 〉 \end{matrix}

(A1)

Here the time parameter is not shown for simplicity/clarity. Figure 1 show some scenarios of two coherent states projected in one dimension position and spatial frequency.

Given two quantum states in Hilbert space,

| Ψ^{A} 〉

and

| Ψ^{B} 〉

, are one can combine them as follows: (i) a superposition of these two states or (ii) a sum of an exterior product of the two states (product of the two Hilbert spaces). More precisely, a general quantum state formed from these two states can be written as

\begin{matrix} (i) One - State Superposition : & | Ψ 〉 = \frac{e^{i ν_{1}}}{\sqrt{Z}} (cos θ_{1} | Ψ^{A} 〉 + e^{i φ_{1}} sin θ_{1} | Ψ^{B} 〉) \end{matrix}

(A2)

\begin{matrix} (ii) Two - State : & {| Ψ 〉}_{2} = \frac{e^{i ν_{2}}}{\sqrt{Z_{2}}} (cos θ_{2} | Ψ^{A} 〉 | Ψ^{B} 〉 + e^{i φ_{2}} sin θ_{2} | Ψ^{B} 〉 | Ψ^{A} 〉) \end{matrix}

(A3)

where

φ_{1, 2}, ν_{1, 2} \in [0, π]

θ_{1, 2} \in [0, \frac{π}{2}]

and

Z, Z_{2}

are normalization constants. For bosons or fermions there is the constraint

θ_{2} = \frac{π}{4}

and

φ_{2} = 0, π

respectively, so these states will be either symmetric or anti-symmetric. The special case when two boson states occupy the same state is also captured by

θ_{2} = 0, \frac{π}{2}

The projection to the spatial basis leads to the wave functions

\begin{matrix} (i) & ψ (x) = 〈 x | ψ 〉 = \frac{e^{i ν}}{\sqrt{Z}} (cos θ_{1} ψ^{A} (x) + e^{i φ_{1}} sin θ_{1} ψ^{B} (x)) \end{matrix}

(A4)

\begin{matrix} (ii) & ψ (x, y) = 〈 x | 〈 y | {| Ψ 〉}_{2} = \frac{e^{i ν}}{\sqrt{Z_{2}}} (cos θ_{2} ψ^{A} (x) ψ^{B} (y) + e^{i φ_{2}} sin θ_{2} ψ^{B} (x) ψ^{A} (y)) \end{matrix}

(A5)

and similarly for scenario (i)

ϕ (k) = 〈 k | ψ 〉

and for scenario (ii)

ϕ (k_{x}, k_{y}) = 〈 k_{x} | 〈 k_{y} | {| Ψ 〉}_{2}

. The phase space entropy (2) for each of these scenarios is

\begin{matrix} (i) S (| Ψ 〉) & = - \int \int d x d k p (x) q (k) log (p (x) q (k)) \end{matrix}

(A6)

\begin{matrix} (ii) S ({| Ψ 〉}_{2}) & = - \int \int \int \int d x d k_{x} d y d k_{y} p (x, y) q (k_{x}, k_{y}) log (p (x, y), q (k_{x}, k_{y})) \end{matrix}

(A7)

where

p (x) = {| ψ (x) |}^{2}

q (k) = {| ϕ (k) |}^{2}

p (x, y) = {| ψ (x, y) |}^{2}

q (k_{x}, k_{y}) = {| ϕ (k_{x}, k_{y}) |}^{2}

Appendix B. Entropy Concepts

The Rényi entropy of order

α

of a given continuous distribution

P (x)

\begin{matrix} H_{α} (P) = \frac{1}{1 - α} log (\int P^{α} (x) d x) \end{matrix}

(A8)

The work shown in this paper can be extended to Rényi entropy.

Shannon entropy can be derived from Rényi entropy as follows

\begin{matrix} S (P) = lim_{α \to 1} H_{α} (P) = - \int P (x) log P (x) d μ (x) \end{matrix}

(A9)

where

μ

is some reference measure, usually a Lebesgue measure on a Borel

σ

-algebra.

The cross entropy of two probability distributions

p (x)

and

q (x)

on the variable x is given by

\begin{matrix} CrossS (p, q) = - \int p (x) log q (x) d μ (x) . \end{matrix}

(A10)

The Kullback-Liebler divergence between two probability distributions

p (x)

and

q (x)

is given by

\begin{matrix} D_{K L} (p | | q) = - \int p (x) log \frac{q (x)}{p (x)} d μ (x) = CrossS (p, q) - S (p) . \end{matrix}

(A11)

References

Geiger, D.; Kedem, Z.M. On Quantum Entropy. Entropy 2022, 24. [Google Scholar] [CrossRef] [PubMed]
Geiger, D.; Kedem, Z.M. Spin Entropy. Entropy 2022, 24. [Google Scholar] [CrossRef] [PubMed]
Shannon, C.E. A mathematical theory of communication. The Bell system technical journal 1948, 27, 379–423. [Google Scholar] [CrossRef]
Avery, J. Information Theory and Evolution. World Scientific. ISBN 981-238-400-6 2003.
Dirac, P. The Principles of Quantum Mechanics; Comparative Pathobiology - Studies in the Postmodern Theory of Education, Clarendon Press, 1981.
Feynman, R.P.; Weinberg, S., Eds. Elementary particles and the laws of physics: The 1986 Dirac memorial lectures; Cambridge University Press, 1999.
Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality be Considered Complete? Physical Review 1935, 47, 777–780. [Google Scholar] [CrossRef]
Bell, J. On the Einstein Podolsky Rosen Paradox. Physics 1964, 1, 195–290. [Google Scholar] [CrossRef]
Bouwmeester, D.; Mattle, K.; Eibl, M.; Weinfurter, H.; Zeilinger, A. Experimental quantum teleportation. Nature 2006, 390, 575–579. [Google Scholar] [CrossRef]
Popescu, S.; Short, A.; Winter, A. Entanglement and the foundations of statistical mechanics. Nature Phys 2006, 2, 754–758. [Google Scholar] [CrossRef]
Bayes, T. An Essay toward solving a Problem in the Doctrine of Chances. Philosophical Transactions of the Royal Society of London 1764, 53, 370–418. [Google Scholar] [CrossRef]
Cournot, A.A. Exposition de la théorie des chances et des probabilités. L. Hachette, Paris 1843.
Venn, J. The Logic of Chance: An essay on the foundations and province of the theory of probability, with especial reference to its logical bearings and its application to Moral and Social Science, and to Statistics. Macmillan & Co, London.
Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar] [CrossRef] [PubMed]
Boschi, D.; Branca, S.; De Martini, F.; Hardy, L.; Popescu, S. Experimental Realization of Teleporting an Unknown Pure Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels. Phys. Rev. Lett. 1998, 80, 1121–1125. [Google Scholar] [CrossRef]
Boyd, R.W. Slow and fast light: fundamentals and applications. Journal of Modern Optics 2009, 56, 1908–1915. [Google Scholar] [CrossRef]
Ferrie, C. Quantum Entanglement Isn’t All That Spooky After All. Scientific American 2023. [Google Scholar]
Deutsch, D. Quantum theory, the Church–Turing principle and the universal quantum computer. Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences 1985, 400, 97–117. [Google Scholar] [CrossRef]
Nielsen, M.A.; Chuang, I. Quantum Computation and Quantum Information; Cambridge University Press, 2010.
Weinberg, S. The quantum theory of fields: Volume 1, (Foundations); Cambridge University Press, 1995.
Wigner, E.P. On the quantum correction for thermodynamic equilibrium. Phys. Rev. 1932, 40, 749–759. [Google Scholar] [CrossRef]
Husimi, K. Some Formal Properties of the Density Matrix. Proceedings of the Physico-Mathematical Society of Japan. 3rd Series 1940, 22, 264–314. [Google Scholar] [CrossRef]
Robertson, H.P. The Uncertainty Principle. Physical Review 1929, 34, 163–164. [Google Scholar] [CrossRef]
Woodhouse, N.M.J. Geometric quantization; Oxford University Press, 1997.
Blau, M. Symplectic Geometry and Geometric Quantization. Lecture Notes, http://www. ictp. trieste.it/ mblau/lecturesGQ.ps.gz 1992.
Nair, V.P. Elements of geometric quantization and applications to fields and fluids. arXiv preprint arXiv:1606.06407 2016.
Marage, P.; Wallenborn, G. , or How to Interpret Quantum Mechanics. In The Solvay Councils and the Birth of Modern Physics; Marage, P., Wallenborn, G., Eds.; Birkhäuser Basel: Basel, 1999; pp. 161–174. [Google Scholar] [CrossRef]
Becker, A. What Is Real?: The Unfinished Quest for the Meaning of Quantum Physics; Basic Books, 2018.

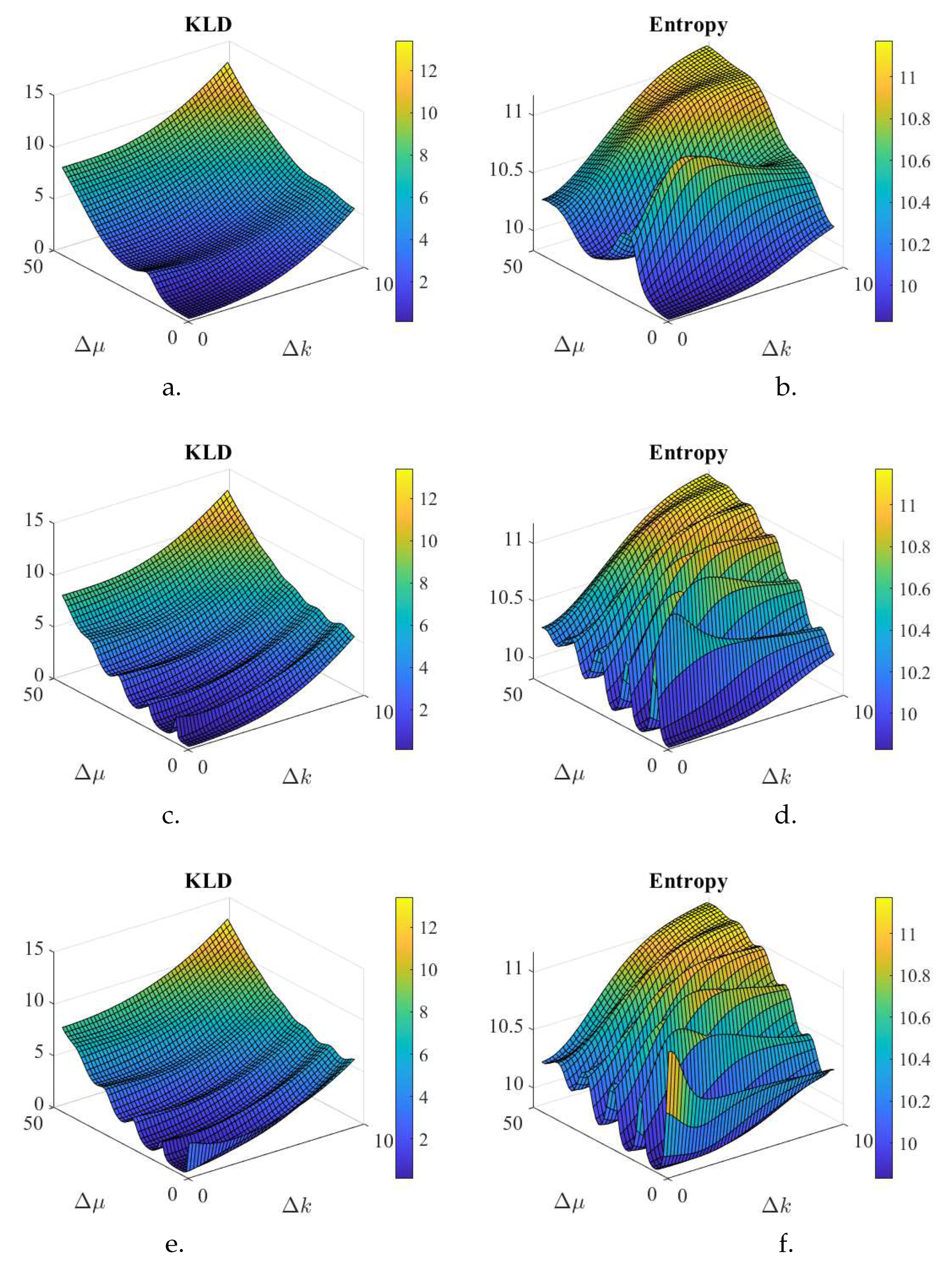
Figure 3. Entanglement simulations from two coherent states shown in Figure 1. Note that the phase of the coherent state projected to position space is the center of the coherent state projected in the spatial frequency space, and vice-versa. Coherent state

| Ψ^{A} 〉

has a fixed set of parameters,

μ_{A} = 27.8

σ_{A} = 5.6

in position space, and for a. & b. the phase is

k_{A} = 0.3

while for c. & d & e. & f. the phase is

k_{A} = 1.0

. Coherent state

| Ψ^{B} 〉

in position has fixed

σ_{B} = 4.1667

but the center and phase vary in 48 increments each, as follows:

μ_{B} \in [μ_{A}, \dots, 41.7]

, and for a. & b.

k_{B} \in [k_{A}, \dots, 0.9]

, while for c. & d & e. & f. the phase varies as

k_{B} \in [k_{A}, \dots, 1.6]

. When combining the two states

θ_{2} = \frac{p i}{4}

is fixed. Cases a. & b. & c. & d. show KLD and Entropy, respectively, for a symmetric entanglement where phase

φ_{2} = 0

. Cases e. & f. show KLD and Entropy, respectively, for an anti-symmetric entanglement where phase

φ_{2} = π

. The effect of the phase

φ_{2}

is only noticeable when the two states are very similar to each other and then both, KLD and entropy, yield large values for the anti-symmetric case (after all anti-symmetric functions must vanish in these cases, while the product of states does not). While the KLD has a more smooth behavior, both of them increase as the separation of the two coherent state parameters increases. The larger values of the phase parameters in c. & d & e. & f. clearly cause a periodic behavior following the prediction from the phase parameter (20) though the entropy is noticeably more sensitive to the oscillation.

| Ψ^{A} 〉

has a fixed set of parameters,

μ_{A} = 27.8

σ_{A} = 5.6

in position space, and for a. & b. the phase is

k_{A} = 0.3

while for c. & d & e. & f. the phase is

k_{A} = 1.0

. Coherent state

| Ψ^{B} 〉

in position has fixed

σ_{B} = 4.1667

but the center and phase vary in 48 increments each, as follows:

μ_{B} \in [μ_{A}, \dots, 41.7]

, and for a. & b.

k_{B} \in [k_{A}, \dots, 0.9]

, while for c. & d & e. & f. the phase varies as

k_{B} \in [k_{A}, \dots, 1.6]

. When combining the two states

θ_{2} = \frac{p i}{4}

is fixed. Cases a. & b. & c. & d. show KLD and Entropy, respectively, for a symmetric entanglement where phase

φ_{2} = 0

. Cases e. & f. show KLD and Entropy, respectively, for an anti-symmetric entanglement where phase

φ_{2} = π

. The effect of the phase

φ_{2}

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Quantum Knowledge in Phase Space

Abstract

1. Introduction

1.1. Bayesian Knowledge in Quantum Physics

1.2. Entropy, Interference, and Entanglement

1.3. Paper Organization

2. Quantum Phase Space Probabilities and Entropy

3. Interference

4. Entanglement

5. Entanglement for Spin or Qbit Phase Space

5.1. Expansion to Mixed States

6. Conclusion

Acknowledgments

Appendix A. Combining two states

Appendix B. Entropy Concepts

References

MDPI Initiatives

Important Links

Subscribe