The Predicate of the Current Mathematical Knowledge Substantially Increases the Constructive and Informal Mathematics and Why It Cannot Be Adapted to Any Empirical Science

Preprint

Article

The Predicate of the Current Mathematical Knowledge Substantially Increases the Constructive and Informal Mathematics and Why It Cannot Be Adapted to Any Empirical Science

Altmetrics

Downloads

657

Views

190

Comments

A peer-reviewed article of this preprint also exists.

Apoloniusz Tyszka^*

This version is not peer-reviewed

Submitted:

05 September 2023

Posted:

07 September 2023

Read the latest preprint version here

Alerts

Abstract

We assume that the current mathematical knowledge K is a finite set of statements which is time-dependent. This set exists only theoretically. Ignoring K and its subsets, sets exist formally in ZFC theory although their properties can be time-dependent (when they depend on K) or informal. In every branch of mathematics, the set of all knowable truths is the set of all theorems. This set exists independently of K. Algorithms always terminate. We explain the distinction between algorithms whose existence is provable in ZFC and constructively defined algorithms which are currently known. By using this distinction, we obtain non-trivial statements on decidable sets X⊆N that belong to constructive and informal mathematics and refer to the current mathematical knowledge on X. This and the next sentence justify the article title. For any empirical science, we can identify the current knowledge with that science because truths from the empirical sciences are not necessary truths but working models of truth from a particular context. For a set X⊆N whose infiniteness is false or unproven, we define which elements of X are classified as known. No known set X⊆N satisfies Conditions (1)-(4) and is widely known in number theory or naturally defined, where this term has only informal meaning. (1) A known algorithm with no input returns an integer n satisfying card(X)<ω ⇒ X⊆(-∞,n]. (2) A known algorithm for every k∈N decides whether or not k∈X. (3) No known algorithm with no input returns the logical value of the statement card(X)=ω. (4) There are many elements of X and it is conjectured, though so far unproven, that X is infinite. (5) X is naturally defined. The infiniteness of X is false or unproven. X has the simplest definition among known sets Y⊆N with the same set of known elements. We prove that the set X={n∈N: the interval [-1,n] contains more than 29.5+(11!/(3n+1))∙sin(n) primes of the form k!+1} satisfies Conditions (1)-(5) except the requirement that X is naturally defined. We have: 501893∈X, Condition (1) holds with n=501893, card(X∩[0,501893])=159827, X∩[501894,∞)={n∈N: the interval [-1,n] contains at least 30 primes of the form k!+1}. We present a table that shows satisfiable conjunctions of the form #(Condition 1)∧(Condition 2)∧#(Condition 3)∧(Condition 4)∧#(Condition 5), where # denotes the negation ¬ or the absence of any symbol. No set X⊆N will satisfy Conditions (1)-(4) forever, if for every algorithm with no input, at some future day, a computer will be able to execute this algorithm in 1 second or less.

Keywords:

Subject: Computer Science and Mathematics - Logic

MSC: 03A05; 03F55

1. Introduction and Why Such Title of the Article

This article is a continuation of [14,15,16]. The main mathematical results of this article were presented at the 25th Conference Applications of Logic in Philosophy and the Foundations of Mathematics, see http://applications-of-logic.uni.wroc.pl/XXV-Konferencja-Zastosowania-Logiki-w-Filozofii-i-Podstawach-Matematyki. We assume that the current mathematical knowledge

K

is a finite set of statements which is time-dependent. This set exists only theoretically. Ignoring

K

and its subsets, sets exist formally in

Z F C

theory although their properties can be time-dependent (when they depend on

K

) or informal. In every branch of mathematics, the set of all knowable truths is the set of all theorems. This set exists independently of

K

. Algorithms always terminate. We explain the distinction between algorithms whose existence is provable in

Z F C

and constructively defined algorithms which are currently known. By using this distinction, we obtain non-trivial statements on decidable sets

X \subseteq N

that belong to constructive and informal mathematics and refer to the current mathematical knowledge on

X

. This and the next sentence justify the article title. For any empirical science, we can identify the current knowledge with that science because truths from the empirical sciences are not necessary truths but working models of truth from a particular context, see [17, p. 610].

2. Summary of the Main Mathematical Results

For a set

X \subseteq N

whose infiniteness is false or unproven, we define which elements of

X

are classified as known. No known set

X \subseteq N

satisfies Conditions (1)-(4) and is widely known in number theory or naturally defined, where this term has only informal meaning.

(1) A known algorithm with no input returns an integer n satisfying $card (X) < ω \Rightarrow$ $X \subseteq (- \infty, n]$ .
(2) A known algorithm for every $k \in N$ decides whether or not $k \in X$ .
(3) No known algorithm with no input returns the logical value of the statement $card (X) = ω$ .
(4) There are many elements of $X$ and it is conjectured, though so far unproven, that $X$ is infinite.
(5) $X$ is naturally defined. The infiniteness of $X$ is false or unproven. $X$ has the simplest definition among known sets $Y \subseteq N$ with the same set of known elements.

We prove that the set

X = {n \in N : t h e i n t e r v a l [- 1, n] c o n t a i n s m o r e t h a n

\frac{11!}{3 n + 1} \cdot sin (n) p r i m e s o f t h e f o r m k! + 1}

satisfies Conditions (1)-(5) except the requirement that

X

is naturally defined. We present a table that shows satisfiable conjunctions of the form

# (Condition 1) \land (Condition 2) \land # (Condition 3) \land (Condition 4) \land # (Condition 5)

where # denotes the negation ¬ or the absence of any symbol.

3. Basic Definitions and Examples

Algorithms always terminate. Semi-algorithms may not terminate. There is the distinction between existing algorithms (i.e. algorithms whose existence is provable in

Z F C

) and known algorithms (i.e. algorithms whose definition is constructive and currently known), see [2], [9], [11, p. 9]. A definition of an integer n is called constructive, if it provides a known algorithm with no input that returns n. Definition 1 applies to sets

X \subseteq N

whose infiniteness is false or unproven.

Definition 1.

We say that a non-negative integer k is a known element of

X

, if

k \in X

and we know an algebraic expression that defines k and consists of the following signs: 1 (one), + (addition), − (subtraction), · (multiplication), ^ (exponentiation with exponent in

N

), ! (factorial of a non-negative integer), ( (left parenthesis), ) (right parenthesis).

The set of known elements of

X

is finite and time-dependent, so cannot be defined in the formal language of classical mathematics. Let t denote the largest twin prime that is smaller than ((((((((9!)!)!)!)!)!)!)!)!. The number t is an unknown element of the set of twin primes.

Definition 2.

Conditions(1)-(5)concern sets

X \subseteq N

(1) A known algorithm with no input returns an integer n satisfying $card (X) < ω \Rightarrow$ $X \subseteq (- \infty, n]$ .
(2) A known algorithm for every $k \in N$ decides whether or not $k \in X$ .
(3) No known algorithm with no input returns the logical value of the statement $card (X) = ω$ . (4)There are many elements of $X$ and it is conjectured, though so far unproven, that $X$ is infinite.
(5) $X$ is naturally defined. The infiniteness of $X$ is false or unproven. $X$ has the simplest definition among known sets $Y \subseteq N$ with the same set of known elements.

Condition (3) implies that no known proof shows the finiteness/infiniteness of

X

. No known set

X \subseteq N

satisfies Conditions (1)-(4) and is widely known in number theory or naturally defined, where this term has only informal meaning.

Example 1.

The set

X = P_{n^{2} + 1}

satisfies Condition (3) .

Let

[\cdot]

denote the integer part function.

Example 2.

The set

X = \{\begin{matrix} N, & if [\frac{((((((((9!)!)!)!)!)!)!)!)!}{π}] i s o d d \\ \emptyset, & o t h e r w i s e \end{matrix}

does not satisfy Condition (3)because we know an algorithm with no input that computes

[\frac{((((((((9!)!)!)!)!)!)!)!)!}{π}]

. The set of known elements of

X

is empty. Hence, Condition(5)fails for

X

Example 3.

([2], [9], [11, p. 9]). The function

N ∋ n \overset{h}{⟶} \{\begin{matrix} 1, & i f t h e d e c i m a l e x p a n s i o n o f π c o n t a i n s n c o n s e c u t i v e z e r o s \\ 0, & o t h e r w i s e \end{matrix}

is computable because

h = N \times {1}

or there exists

k \in N

such that

h = ({0, \dots, k} \times {1}) \cup ({k + 1, k + 2, k + 3, \dots} \times {0})

No known algorithm computes the function h.

Example 4.

The set

X = \{\begin{matrix} N, & i f t h e c o n t i n u u m h y p o t h e s i s h o l d s \\ \emptyset, & o t h e r w i s e \end{matrix}

is decidable. This

X

satisfies Conditions(1)and(3)and does not satisfy Conditions(2),(4), and(5). These facts will hold forever.

4. Number-Theoretic Results

Edmund Landau’s conjecture states that the set

P_{n^{2} + 1}

of primes of the form

n^{2} + 1

is infinite, see [12,13,19].

Statement 1.

Condition (1) remains unproven for

X = P_{n^{2} + 1}

Proof.

For every set

X \subseteq N

, there exists an algorithm

Alg (X)

with no input that returns

n = \{\begin{matrix} 0, & if card (X) \in {0, ω} \\ max (X), & otherwise \end{matrix}

This n satisfies the implication in Condition (1), but the algorithm

Alg (P_{n^{2} + 1})

is unknown because its definition is ineffective. □

Statement 2.

The statement

\exists n \in N (card (P_{n^{2} + 1}) < ω \Rightarrow P_{n^{2} + 1} \subseteq [2, n + 3])

remains unproven in

Z F C

and classical logic without the law of excluded middle.

Let

f (1) = 10^{6}

, and let

f (n + 1) = f {(n)}^{f (n)}

for every positive integer n.

Statement 3.

The set

X = {k \in N : (10^{6} < k) \Rightarrow (f (10^{6}), f (k)) \cap P_{n^{2} + 1} \neq \emptyset}

satisfies Conditions (1)-(4). Condition (5) fails for

X

Proof.

Condition (4) holds as

X \supseteq {0, \dots, 10^{6}}

and the set

P_{n^{2} + 1}

is conjecturally infinite. Due to known physics we are not able to confirm by a direct computation that some element of

P_{n^{2} + 1}

is greater than

f (10^{6})

, see [7]. Thus Condition (3) holds. Condition (2) holds trivially. Since the set

{k \in N : (10^{6} < k) \land (f (10^{6}), f (k)) \cap P_{n^{2} + 1} \neq \emptyset}

is empty or infinite, Condition (1) holds with

n = 10^{6}

. Condition (5) fails as the set of known elements of

X

equals

{0, \dots, 10^{6}}

. □

Statements 4 and 7 provide stronger examples.

Conjecture 1.

([1, p. 443], [4]). The are infinitely many primes of the form

k! + 1

For a non-negative integer n, let

ρ (n)

denote

29.5 + \frac{11!}{3 n + 1} \cdot sin (n)

Statement 4.

The set

X = {n \in N : t h e i n t e r v a l [- 1, n] c o n t a i n s m o r e t h a n ρ (n) p r i m e s o f t h e f o r m k! + 1}

satisfies Conditions (1)-(5) except the requirement that

X

is naturally defined.

501893 \in X

. Condition (1) holds with

n = 501893

card (X \cap [0, 501893]) = 159827

X \cap [501894, \infty) =

{n \in N :

t h e

i n t e r v a l

[- 1, n]

c o n t a i n s

a t

l e a s t

p r i m e s

o f

t h e

f o r m

k! + 1}

Proof.

For every integer

n ⩾ 11!

, 30 is the smallest integer greater than

ρ (n)

. By this, if

n \in X \cap [11!, \infty)

, then

n + 1, n + 2, n + 3, \dots \in X

. Hence, Condition (1) holds with

n = 11! - 1

. We explicitly know 24 positive integers k such that

k! + 1

is prime, see [3]. The inequality

card ({k \in N ∖ {0} : k! + 1 i s p r i m e}) > 24

remains unproven. Since

24 < 30

, Condition (3) holds. The interval

[- 1, 11! - 1]

contains exactly three primes of the form

k! + 1

1! + 1

2! + 1

3! + 1

. For every integer

n > 503000

, the inequality

ρ (n) > 3

holds. Therefore, the execution of the following MuPAD code

m:=0:

for n from 0.0 to 503000.0 do

if n<1!+1 then r:=0 end_if:

if n>=1!+1 and n<2!+1 then r:=1 end_if:

if n>=2!+1 and n<3!+1 then r:=2 end_if:

if n>=3!+1 then r:=3 end_if:

if r>29.5+(11!/(3*n+1))*sin(n) then

m:=m+1:

print([n,m]):

end_if:

end_for:

displays the all known elements of

X

. The output ends with the line

[501893.0, 159827]

, which proves Condition (1) with

n = 501893

and Condition (4) with

card (X) ⩾ 159827

. □

Statement 4 and its proof imply the following corollary.

Corollary 1.

If we add to

X

the set

⋃_{i = 1}^{29} {11! \cdot n : (n \in N) \land (n i s t h e i - t h p r i m e o f t h e f o r m k! + 1)}

then the following statements holds:

$X$ does not satisfy Condition (1),
$card (X) < ω \Rightarrow card (X) ⩽ 159827 + 29$ ,
according to the current knowledge, the above upper bound cannot be decreased,
$X$ satisfies Conditions (2)-(4),
the infiniteness of $X$ is false or unproven.

Definition 3.

Conditions (1a)-(5a)concern sets

X \subseteq N

(1a) A known algorithm with no input returns a positive integer n satisfying $card (X) < ω \Rightarrow$ $X \subseteq (- \infty, n]$ .
(2a) A known algorithm for every $k \in N$ decides whether or not $k \in X$ .
(3a) No known algorithm with no input returns the logical value of the statement $card (X) < ω$ .
(4a)There are many elements of $X$ and it is conjectured, though so far unproven, that $X$ is finite.
(5a) $X$ is naturally defined. The finiteness of $X$ is false or unproven. $X$ has the simplest definition among known sets $Y \subseteq N$ with the same set of known elements.

Statement 5.

The set

X = {n \in N : t h e i n t e r v a l [- 1, n] c o n t a i n s m o r e t h a n

6.5 + \frac{10^{6}}{3 n + 1} \cdot sin (n) s q u a r e s o f t h e f o r m k! + 1}

satisfies Conditions (1a)-(5a) except the requirement that

X

is naturally defined.

95151 \in X

. Condition (1a) holds with

n = 95151

card (X \cap [0, 95151]) = 30311

X \cap [95152, \infty) =

{n \in N :

t h e

i n t e r v a l

[- 1, n]

c o n t a i n s

a t

l e a s t

s q u a r e s

o f

t h e

f o r m

k! + 1}

Proof.

For every integer

n > 10^{6}

, 7 is the smallest integer greater than

6.5 + \frac{10^{6}}{3 n + 1} \cdot sin (n)

. By this, if

n \in X \cap (10^{6}, \infty)

, then

n + 1, n + 2, n + 3, \dots \in X

. Hence, Condition (1a) holds with

n = 10^{6}

. It is conjectured that

k! + 1

is a square only for

k \in {4, 5, 7}

, see [18, p. 297]. Hence, the inequality

card ({k \in N ∖ {0} : k! + 1 i s a s q u a r e}) > 3

remains unproven. Since

3 < 7

, Condition (3a) holds. The interval

[- 1, 10^{6}]

contains exactly three squares of the form

k! + 1

4! + 1

5! + 1

7! + 1

. Therefore, the execution of the following MuPAD code

m:=0:
for n from 0.0 to 1000000.0 do
if n<25 then r:=0 end_if:
if n>=25 and n<121 then r:=1 end_if:
if n>=121 and n<5041 then r:=2 end_if:
if n>=5041 then r:=3 end_if:
if r>6.5+(1000000/(3*n+1))*sin(n) then
m:=m+1:
print([n,m]):
end_if:
end_for:

displays the all known elements of

X

. The output ends with the line

[95151.0, 30311]

, which proves Condition (1a) with

n = 95151

and Condition (4a) with

card (X) ⩾ 30311

. □

Statement 6.

The set

X = {k \in N : card ([- 1, k] \cap P_{n^{2} + 1}) < 10^{10000}}

satisfies the conjunction

\neg (C o n d i t i o n 1 a) \land (C o n d i t i o n 2 a) \land (C o n d i t i o n 3 a) \land (C o n d i t i o n 4 a) \land (C o n d i t i o n 5 a)

To formulate Statement 7 and its proof, we need some lemmas. For a non-negative integer n, let

θ (n)

denote the largest integer divisor of

10^{10^{10}}

smaller than n. For a non-negative integer n, let

θ_{1} (n)

denote the largest integer divisor of

10^{10}

smaller than n.

Lemma 1.

For every integer

j > 10^{10^{10}}

θ (j) = 10^{10^{10}}

. For every integer

j > 10^{10}

θ_{1} (j) = 10^{10}

Lemma 2.

For every integer

j \in (6553600, 7812500]

θ (j) = 6553600

Proof.

6553600 equals

2^{18} \cdot 5^{2}

and divides

10^{10^{10}}

7812500 < 2^{24}

7812500 < 5^{10}

. We need to prove that every integer

j \in (6553600, 7812500)

does not divide

10^{10^{10}}

. It holds as the set

\{2^{u} \cdot 5^{v} : (u \in {0, \dots, 23}) \land (v \in {0, \dots, 9})\}

contains 6553600 and 7812500 as consecutive elements. □

Lemma 3.

The number

6553600^{2} + 1

is prime.

Proof.

The following PARI/GP ([8]) command

isprime(6553600^2+1,{flag=2})

returns 1. This command performs the APRCL primality test, the best deterministic primality test algorithm ([20, p. 226]). It rigorously shows that the number

6553600^{2} + 1

is prime. □

In the next lemmas, the execution of the command isprime(n,{flag=2}) proves the primality of n. Let

κ

denote the function

N ∋ n \overset{κ}{⟶} t h e e x p o n e n t o f 2 i n t h e p r i m e f a c t o r i z a t i o n o f \underset{︸}{n + 1} \in N

Lemma 4.

The set

X_{1} = {n \in N : {(θ_{1} (n) + κ (n))}^{2} + 1 i s p r i m e}

is infinite.

Proof.

Let

i = 142101504

. By the inequality

2^{i} ⩾ 2 + 10^{10}

and Lemma 1, for every non-negative integer m, the number

{(θ_{1} (2^{i} \cdot (2 m + 1) - 1) + κ (2^{i} \cdot (2 m + 1) - 1))}^{2} + 1 = {(10^{10} + i)}^{2} + 1

is prime. □

Before Open Problem 1,

X

denotes the set

{n \in N : {(θ (n) + κ (n))}^{2} + 1 i s p r i m e}

Lemma 5.

For every

n \in X \cap (10^{10^{10}}, \infty)

and for every non-negative integer j,

3^{j} \cdot (n + 1) - 1 \in X \cap (10^{10^{10}}, \infty)

Proof.

By the inequality

3^{j} \cdot (n + 1) - 1 ⩾ n

and Lemma 1,

θ (3^{j} \cdot (n + 1) - 1) + κ (3^{j} \cdot (n + 1) - 1) = 10^{10^{10}} + κ (n) = θ (n) + κ (n)

□

Lemma 6.

card (X) ⩾ 629450

Proof.

By Lemmas 2 and 3, for every even integer

j \in (6553600, 7812500]

, the number

{(θ (j) + κ (j))}^{2} + 1 = {(6553600 + 0)}^{2} + 1

is prime. Hence,

{2 k : k \in N} \cap (6553600, 7812500] \subseteq X

Consequently,

card (X) ⩾ card ({2 k : k \in N} \cap (6553600, 7812500]) = \frac{7812500 - 6553600}{2} = 629450

□

Lemma 7.

10242 \in X

and

10242 \notin X_{1}

Proof.

The number

10240 = 2^{11} \cdot 5

divides

10^{10^{10}}

. Hence,

θ (10242) = 10240

. The number

{(θ (10242) + κ (10242))}^{2} + 1 = {(10240 + 0)}^{2} + 1

is prime. The set

\{2^{u} \cdot 5^{v} : (u \in {0, \dots, 10}) \land (v \in {0, \dots, 10})\}

contains 10000 and 12500 as consecutive elements. Hence,

θ_{1} (10242) = 10000

. The number

{(θ_{1} (10242) + κ (10242))}^{2} + 1 = {(10000 + 0)}^{2} + 1 = 17 \cdot 5882353

is composite. □

Statement 7.

The set

X

satisfies Conditions (1)-(5) except the requirement that

X

is naturally defined.

Proof.

Condition (2) holds trivially. Let

δ

denote

10^{10^{10}}

. By Lemma 5, Condition (1) holds for

n = δ

. Lemma 5 and the unproven statement

P_{n^{2} + 1} \cap [δ^{2} + 1, \infty) \neq \emptyset

show Condition (3). The same argument and Lemma 6 yield Condition (4). By Lemma 4, the set

X_{1}

is infinite. Since Definition 1 applies to sets

X \subseteq N

whose infiniteness is false or unproven, Condition (5) holds except the requirement that

X

is naturally defined. □

The set

X

satisfies Condition (5) except the requirement that

X

is naturally defined. It is true because

X_{1}

is infinite by Lemma 4 and Definition 1 applies only to sets

X \subseteq N

whose infiniteness is false or unproven. Ignoring this restriction,

X

still satisfies the same identical condition due to Lemma 7.

Proposition 1.

No set

X \subseteq N

will satisfy Conditions(1)-(4)forever, if for every algorithm with no input, at some future day, a computer will be able to execute this algorithm in 1 second or less.

Proof.

The proof goes by contradiction. We fix an integer n that satisfies Condition (1). Since Conditions (1)-(3) will hold forever, the semi-algorithm in Figure 1 never terminates and sequentially prints the following sentences:

(T) n + 1 \notin X, n + 2 \notin X, n + 3 \notin X, \dots

(1)

Figure 1. Semi-algorithm that terminates if and only if

X

is infinite.

Figure 1. Semi-algorithm that terminates if and only if

X

is infinite.

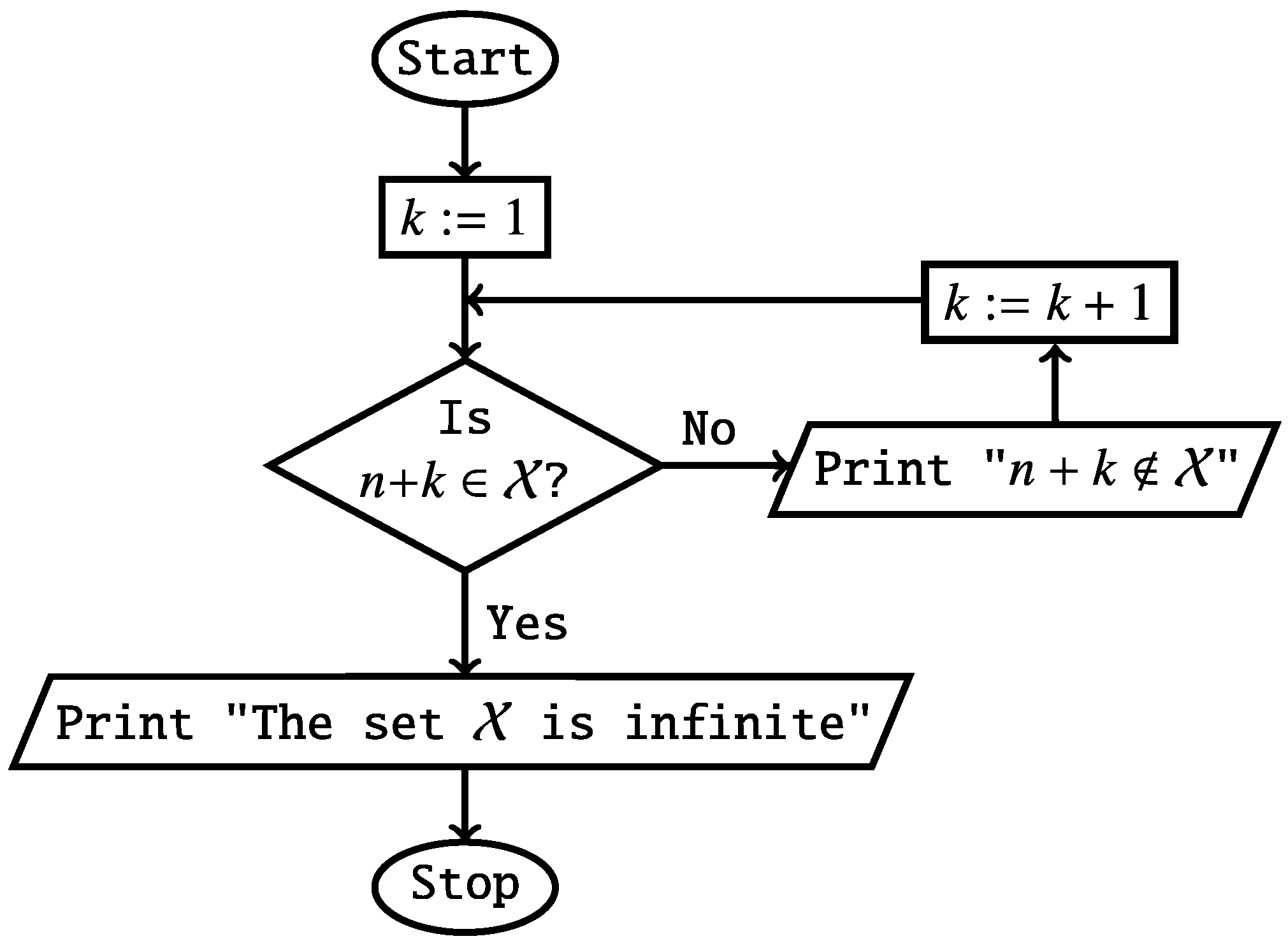The sentences from the sequence (T) and our assumption imply that for every integer

m > n

computed by a known algorithm, at some future day, a computer will be able to confirm in 1 second or less that

(n, m] \cap X = \emptyset

. Thus, at some future day, numerical evidence will support the conjecture that the set

X

is finite, contrary to the conjecture in Condition (4). □

The physical limits of computation ([7]) disprove the assumption of Proposition 1.

Openproblem 1.

Is there a set

X \subseteq N

which satisfies Conditions (1)-(5)?

Open Problem 1 asks about the existence of a year

t ⩾ 2023

in which the conjunction

(C o n d i t i o n 1) \land (C o n d i t i o n 2) \land (C o n d i t i o n 3) \land (C o n d i t i o n 4) \land (C o n d i t i o n 5)

will hold for some

X \subseteq N

. For every year

t ⩾ 2023

and for every

i \in {1, 2, 3}

, a positive solution to Open Problem i in the year t may change in the future. Currently, the answers to Open Problems 1–5 are negative.

5. Satisfiable Conjunctions Which Consist of Conditions `(1)-(5)` and Their Negations

The set

X = P_{n^{2} + 1}

satisfies the conjunction

\neg (C o n d i t i o n 1) \land (C o n d i t i o n 2) \land (C o n d i t i o n 3) \land (C o n d i t i o n 4) \land (C o n d i t i o n 5)

The set

X = {0, \dots, 10^{6}} \cup P_{n^{2} + 1}

satisfies the conjunction

\neg (C o n d i t i o n 1) \land (C o n d i t i o n 2) \land (C o n d i t i o n 3) \land (C o n d i t i o n 4) \land \neg (C o n d i t i o n 5)

The numbers

2^{2^{k}} + 1

are prime for

k \in {0, 1, 2, 3, 4}

. It is open whether or not there are infinitely many primes of the form

2^{2^{k}} + 1

, see [6, p. 158] and [10, p. 74]. It is open whether or not there are infinitely many composite numbers of the form

2^{2^{k}} + 1

, see [6, p. 159] and [10, p. 74]. Most mathematicians believe that

2^{2^{k}} + 1

is composite for every integer

k ⩾ 5

, see [5, p. 23]. The set

X = \{\begin{matrix} N, i f 2^{2^{f (9^{9})}} + 1 i s c o m p o s i t e \\ {0, \dots, 10^{6}}, o t h e r w i s e \end{matrix}

satisfies the conjunction

(C o n d i t i o n 1) \land (C o n d i t i o n 2) \land \neg (C o n d i t i o n 3) \land (C o n d i t i o n 4) \land \neg (C o n d i t i o n 5)

Openproblem 2.

Is there a set

X \subseteq N

that satisfies the conjunction

(C o n d i t i o n 1) \land (C o n d i t i o n 2) \land \neg (C o n d i t i o n 3) \land (C o n d i t i o n 4) \land (C o n d i t i o n 5) ?

The set

X = \{\begin{matrix} N, i f 2^{2^{f (9^{9})}} + 1 i s c o m p o s i t e \\ {0, \dots, 10^{6}} \cup \\ {n \in N : n i s t h e s i x t h p r i m e n u m b e r o f t h e f o r m 2^{2^{k}} + 1}, o t h e r w i s e \end{matrix}

satisfies the conjunction

\neg (C o n d i t i o n 1) \land (C o n d i t i o n 2) \land \neg (C o n d i t i o n 3) \land (C o n d i t i o n 4) \land \neg (C o n d i t i o n 5)

Openproblem 3.

Is there a set

X \subseteq N

that satisfies the conjunction

\neg (C o n d i t i o n 1) \land (C o n d i t i o n 2) \land \neg (C o n d i t i o n 3) \land (C o n d i t i o n 4) \land (C o n d i t i o n 5) ?

It is possible, although very doubtful, that at some future day, the set

X = P_{n^{2} + 1}

will solve Open Problem 2. The same is true for Open Problem 3. It is possible, although very doubtful, that at some future day, the set

X = {k \in N : 2^{2^{k}} + 1 i s c o m p o s i t e}

will solve Open Problem 1. The same is true for Open Problems 2 and 3.

Table 1 shows satisfiable conjunctions of the form

# (Condition 1) \land (Condition 2) \land # (Condition 3) \land (Condition 4) \land # (Condition 5)

where # denotes the negation ¬ or the absence of any symbol.

Table 1. Five satisfiable conjunctions.

Definition 4.

We say that an integer n is a threshold number of a set

X \subseteq N

, if

card (X) < ω \Rightarrow X \subseteq (- \infty, n]

If a set

X \subseteq N

is empty or infinite, then any integer n is a threshold number of

X

. If a set

X \subseteq N

is non-empty and finite, then the all threshold numbers of

X

form the set

[max (X), \infty) \cap N

Openproblem 5.

Is there a known threshold number of

P_{n^{2} + 1}

Open Problem 5 asks about the existence of a year

t ⩾ 2023

in which the implication

card (P_{n^{2} + 1}) < ω \Rightarrow P_{n^{2} + 1} \subseteq (- \infty, n]

will hold for some known integer n.

Let

T

denote the set of twin primes. Is there a known threshold number of

T

Open Problem 4 asks about the existence of a year

t ⩾ 2023

in which the implication

card (T) < ω \Rightarrow T \subseteq (- \infty, n]

will hold for some known integer n.

References

C. K. Caldwell and Y. Gallot, On the primality of n! ±1 and 2 × 3 × 5 × ⋯×p±1, Math. Comp. 71 (2002), no. [CrossRef]
J. Case and M. Ralston, Beyond Rogers’ non-constructively computable function, in: The nature of computation, Lecture Notes in Comput. Sci., 7921, 45–54, Springer, Heidelberg, 2013, http://link.springer.com/chapter/10.1007/978-3-642-39053-1_6.
Factorial prime, http://en.wikipedia.org/wiki/Factorial_prime.
Is n! + 1 often a prime?, http://math.stackexchange.com/questions/853085/is-n-1-often-a-prime.
J.-M. De Koninck and F. Luca, Analytic number theory: Exploring the anatomy of integers, American Mathematical Society, Providence, RI, 2012.
M. Křížek, F. Luca, L. Somer, 17 lectures on Fermat numbers: from number theory to geometry, Springer, New York, 2001.
S. Lloyd, Ultimate physical limits to computation, Nature 406 (2000), 1047–1054, http://doi.org/10.1038/35023282. [CrossRef]
PARI/GPonline documentation, http://pari.math.u-bordeaux.fr/dochtml/html/Arithmetic_functions.html.
R. Reitzig, How can it be decidable whether πhas some sequence o f digits?, http://cs.stackexchange.com/questions/367/how-can-it-be-decidable-whether-pi-has-some-sequence-of-digits.
P. Ribenboim, The little book of bigger primes, 2nd ed., Springer, New York, 2004.
H. Rogers, Jr., Theory of recursive functions and effective computability, 2nd ed., MIT Press, Cambridge, MA, 1987.
N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, A002496, Primes of the form n² + 1, http://oeis.org/A002496.
N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, A083844, Number of primes of the form x² + 1 < 10 n, http://oeis.org/A083844.
A. Tyszka, Statements and open problems on decidable sets X ⊆ N that refer to the current knowledge on X, Journal of Applied Computer Science & Mathematics 16 (2022), no. 2, 31–35, http://www.jacsm.ro/view/?pid=34_5, http://doi.org/10.4316/JACSM.202202005. [CrossRef]
A. Tyszka, Statements and open problems on decidable sets X ⊆ N, Pi Mu Epsilon J. 15 (2023), no. 8, 493–504.
A. Tyszka, Statements and open problems on decidable sets X ⊆ N that contain informal notions and refer to the current knowledge on X, Creat. Math. Inform. 32 (2023), no. 2, 247–253, http://semnul.com/creative-mathematics/wp-content/uploads/2023/07/creative_2023_32_2_247_253.pdf, http://doi.org/10.37193/CMI.2023.02.12. [CrossRef]
B. L. J. Webb, Science, Truth, and Meaning: From Wonder to Understanding, World Scientific, Singapore, 2021.
E. W. Weisstein, CRC Concise Encyclopedia of Mathematics, 2nd ed., Chapman & Hall/CRC, Boca Raton, FL, 2002.
Wolfram MathWorld, Landau’s Problems, http://mathworld.wolfram.com/LandausProblems.html.
S. Y. Yan, Number theory for computing, 2nd ed., Springer, Berlin, 2002.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

The Predicate of the Current Mathematical Knowledge Substantially Increases the Constructive and Informal Mathematics and Why It Cannot Be Adapted to Any Empirical Science

Abstract

1. Introduction and Why Such Title of the Article

2. Summary of the Main Mathematical Results

3. Basic Definitions and Examples

4. Number-Theoretic Results

5. Satisfiable Conjunctions Which Consist of Conditions (1)-(5) and Their Negations

References

MDPI Initiatives

Important Links

Subscribe

5. Satisfiable Conjunctions Which Consist of Conditions `(1)-(5)` and Their Negations