In Mathematics, in Contradistinction to Any Empirical Science, the Predicate of the Current Knowledge Substantially Increases Its Constructive and Informal Part

Preprint

Article

In Mathematics, in Contradistinction to Any Empirical Science, the Predicate of the Current Knowledge Substantially Increases Its Constructive and Informal Part

Altmetrics

Downloads

658

Views

190

Comments

A peer-reviewed article of this preprint also exists.

Apoloniusz Tyszka^*

This version is not peer-reviewed

Submitted:

17 October 2023

Posted:

19 October 2023

Read the latest preprint version here

Alerts

Abstract

We assume that the current mathematical knowledge K is a finite set of statements from both formal and constructive mathematics, which is time-dependent and publicly available. Any theorem of any mathematician from past or present belongs to K. The set K exists only theoretically. Ignoring K and its subsets, sets exist formally in ZFC theory although their properties can be time-dependent (when they depend on K) or informal. In every branch of mathematics, the set of all knowable truths is the set of all theorems. This set exists independently of K. Algorithms always terminate. We explain the distinction between algorithms whose existence is provable in ZFC and constructively defined algorithms which are currently known. By using this distinction, we obtain non-trivial statements on decidable sets X⊆N that belong to constructive and informal mathematics and refer to the current mathematical knowledge on X. This and the next sentence justify the article title. For any empirical science, we can identify the current knowledge with that science because truths from the empirical sciences are not necessary truths but working models of truth from a particular context. The feature of mathematics from the article title is not quite new. Church's thesis, which is known from the beginning of computability theory, is based on the observation that the currently known computable functions are recursive, where the notion of a computable function is informal. It proves that the predicate of the current mathematical knowledge slightly increases the intuitive mathematics. For a set X⊆N whose infiniteness is false or unproven, we define which elements of X are classified as known. No known set X⊆N satisfies Conditions (1)-(4) and is widely known in number theory or naturally defined, where this term has only informal meaning. (1) A known algorithm with no input returns an integer n satisfying card(X)<ω ⇒ X⊆(-∞,n]. (2) A known algorithm for every k∈N decides whether or not k∈X. (3) No known algorithm with no input returns the logical value of the statement card(X)=ω. (4) There are many elements of X and it is conjectured, though so far unproven, that X is infinite. (5) X is naturally defined. The infiniteness of X is false or unproven. X has the simplest definition among known sets Y⊆N with the same set of known elements. We prove that the set X={n∈N: the interval [-1,n] contains more than 29.5+(11!/(3n+1))∙sin(n) primes of the form k!+1} satisfies Conditions (1)-(5) except the requirement that X is naturally defined. 501893∈X. Condition (1) holds with n=501893. card(X∩[0,501893])=159827. X∩[501894,∞)={n∈N: the interval [-1,n] contains at least 30 primes of the form k!+1}. If we add to X some set W satisfying 14≤card(W)≤23, then the following statements hold: X does not satisfy Condition (1), 159827+14≤card(X), the above lower bound is currently the best known, card(X)<ω ⇒ card(X)≤159827+23, the above upper bound is currently the best known, X satisfies Conditions (2)-(5) except the requirement that X is naturally defined. Analogical statements hold, if we add to X the set ⋃_{x∈N, x divides 99!} {k∈N: k-501894 is the x-th element of P(n^2+1)}, where P(n^2+1) denote the set of primes of the form n^2+1. For a non-negative integer n, let θ(n) denote the largest integer divisor of 10^{10^{10}} smaller than n. Let κ:N→N be defined by setting κ(n) to be the exponent of 2 in the prime factorization of n+1. The set X={n∈N: (θ(n)+κ(n))^2+1 is prime} satisfies Conditions (1)-(5) except the requirement that X is naturally defined. Condition (1) holds with n=0^{10^{10}}. We present a table that shows satisfiable conjunctions of the form #(Condition1)∧ (Condition 2)∧#(Condition 3)∧(Condition 4)∧#(Condition 5), where # denotes the negation ¬ or the absence of any symbol. No set X⊆N will satisfy Conditions (1)-(4) forever, if for every algorithm with no input, at some future day, a computer will be able to execute this algorithm in 1 second or less. The physical limits of computation disprove this assumption.

Keywords:

Subject: Computer Science and Mathematics - Logic

MSC: 03A05; 03F65

1. Introduction and why such title of the article

We assume that the current mathematical knowledge

K

is a finite set of statements from both formal and constructive mathematics, which is time-dependent and publicly available. Any theorem of any mathematician from past or present belongs to

K

. The set

K

exists only theoretically. Ignoring

K

and its subsets, sets exist formally in

Z F C

theory although their properties can be time-dependent (when they depend on

K

) or informal. In every branch of mathematics, the set of all knowable truths is the set of all theorems. This set exists independently of

K

Algorithms always terminate. We explain the distinction between algorithms whose existence is provable in

Z F C

and constructively defined algorithms which are currently known. By using this distinction, we obtain non-trivial statements on decidable sets

X \subseteq N

that belong to constructive and informal mathematics and refer to the current mathematical knowledge on

X

. These results, mainly from [15], and the next sentence justify the article title. For any empirical science, we can identify the current knowledge with that science because truths from the empirical sciences are not necessary truths but working models of truth from a particular context, see [16, p. 610].

The feature of mathematics from the article title is not quite new. Observation 1 is known from the beginning of computability theory and shows that the predicate of the current mathematical knowledge slightly increases the intuitive mathematics.

Observation 1.

Church’s thesis is based on the fact that the currently known computable functions are recursive, where the notion of a computable function is informal.

2. Basic definitions and examples

Algorithms always terminate. Semi-algorithms may not terminate. There is the distinction between existing algorithms (i.e. algorithms whose existence is provable in

Z F C

) and known algorithms (i.e. algorithms whose definition is constructive and currently known), see [2], [9], [11, p. 9]. A definition of an integer n is called constructive, if it provides a known algorithm with no input that returns n. Definition 1 applies to sets

X \subseteq N

whose infiniteness is false or unproven.

Definition 1.

We say that a non-negative integer k is a known element of

X

, if

k \in X

and we know an algebraic expression that defines k and consists of the following signs: 1 (one), + (addition), − (subtraction), · (multiplication), ^ (exponentiation with exponent in

N

), ! (factorial of a non-negative integer), ( (left parenthesis), ) (right parenthesis).

The set of known elements of

X

is finite and time-dependent, so cannot be defined in the formal language of classical mathematics. Let t denote the largest twin prime that is smaller than ((((((((9!)!)!)!)!)!)!)!)!. The number t is an unknown element of the set of twin primes.

Definition 2.

Conditions(1)-(5)concern sets

X \subseteq N

(1)A known algorithm with no input returns an integer n satisfying

card (X) < ω \Rightarrow

X \subseteq (- \infty, n]

(2)A known algorithm for every

k \in N

decides whether or not

k \in X

(3)No known algorithm with no input returns the logical value of the statement

card (X) = ω

(4)There are many elements of

X

and it is conjectured, though so far unproven, that

X

is infinite.

(5)

X

is naturally defined. The infiniteness of

X

is false or unproven.

X

has the simplest definition among known sets

Y \subseteq N

with the same set of known elements.

Condition (3) implies that no known proof shows the finiteness/infiniteness of

X

. No known set

X \subseteq N

satisfies Conditions (1)-(4) and is widely known in number theory or naturally defined, where this term has only informal meaning.

Let

[\cdot]

denote the integer part function.

Example 1.

The set

X = \{\begin{matrix} N, & if [\frac{((((((((9!)!)!)!)!)!)!)!)!}{π}] i s o d d \\ \emptyset, & o t h e r w i s e \end{matrix}

does not satisfy Condition (3)because we know an algorithm with no input that computes

[\frac{((((((((9!)!)!)!)!)!)!)!)!}{π}]

. The set of known elements of

X

is empty. Hence, Condition(5)fails for

X

Example 2.

([2], [9], [11, p. 9]). The function

N ∋ n \overset{h}{⟶} \{\begin{matrix} 1, & i f t h e d e c i m a l e x p a n s i o n o f π c o n t a i n s n c o n s e c u t i v e z e r o s \\ 0, & o t h e r w i s e \end{matrix}

is computable because

h = N \times {1}

or there exists

k \in N

such that

h = ({0, \dots, k} \times {1}) \cup ({k + 1, k + 2, k + 3, \dots} \times {0})

No known algorithm computes the function h.

Example 3.

The set

X = \{\begin{matrix} N, & i f t h e c o n t i n u u m h y p o t h e s i s h o l d s \\ \emptyset, & o t h e r w i s e \end{matrix}

is decidable. This

X

satisfies Conditions(1)and(3)and does not satisfy Conditions(2),(4), and(5). These facts will hold forever.

3. Number-theoretic results

Edmund Landau’s conjecture states that the set

P_{n^{2} + 1}

of primes of the form

n^{2} + 1

is infinite, see [13,14,18].

Statement 1.

Condition (1) remains unproven for

X = P_{n^{2} + 1}

Proof.

For every set

X \subseteq N

, there exists an algorithm

Alg (X)

with no input that returns

n = \{\begin{matrix} 0, & if card (X) \in {0, ω} \\ max (X), & otherwise \end{matrix}

This n satisfies the implication in Condition (1), but the algorithm

Alg (P_{n^{2} + 1})

is unknown because its definition is ineffective. □

Statement 2.

The statement

\exists n \in N (card (P_{n^{2} + 1}) < ω \Rightarrow P_{n^{2} + 1} \subseteq [2, n + 3])

remains unproven in

Z F C

and classical logic without the law of excluded middle.

Conjecture 1.

([1, p. 443], [4]). The are infinitely many primes of the form

k! + 1

For a non-negative integer n, let

ρ (n)

denote

29.5 + \frac{11!}{3 n + 1} \cdot sin (n)

Statement 3.

The set

X = {n \in N : t h e i n t e r v a l [- 1, n] c o n t a i n s m o r e t h a n ρ (n) p r i m e s o f t h e f o r m k! + 1}

satisfies Conditions (1)-(5) except the requirement that

X

is naturally defined.

501893 \in X

. Condition (1) holds with

n = 501893

card (X \cap [0, 501893]) = 159827

X \cap [501894, \infty) =

{n \in N :

t h e

i n t e r v a l

[- 1, n]

c o n t a i n s

a t

l e a s t

p r i m e s

o f

t h e

f o r m

k! + 1}

Proof.

For every integer

n ⩾ 11!

, 30 is the smallest integer greater than

ρ (n)

. By this, if

n \in X \cap [11!, \infty)

, then

n + 1, n + 2, n + 3, \dots \in X

. Hence, Condition (1) holds with

n = 11! - 1

. We explicitly know 24 positive integers k such that

k! + 1

is prime, see [3]. The inequality

card ({k \in N ∖ {0} : k! + 1 i s p r i m e}) > 24

remains unproven. Since

24 < 30

, Condition (3) holds. The interval

[- 1, 11! - 1]

contains exactly three primes of the form

k! + 1

1! + 1

2! + 1

3! + 1

. For every integer

n > 503000

, the inequality

ρ (n) > 3

holds. Therefore, the execution of the following MuPAD code

m:=0:

for n from 0.0 to 503000.0 do

if n<1!+1 then r:=0 end_if:

if n>=1!+1 and n<2!+1 then r:=1 end_if:

if n>=2!+1 and n<3!+1 then r:=2 end_if:

if n>=3!+1 then r:=3 end_if:

if r>29.5+(11!/(3*n+1))*sin(n) then

m:=m+1:

print([n,m]):

end_if:

end_for:

displays the all known elements of

X

. The output ends with the line

[501893.0, 159827]

, which proves Condition (1) with

n = 501893

and Condition (4) with

card (X) ⩾ 159827

. □

T. Nagell proved in [8] (cf. [12, p. 104]) that the equation

x^{2} - 17 = y^{3}

has exactly 16 integer solutions, namely

(\pm 3, - 2)

(\pm 4, - 1)

(\pm 5, 2)

(\pm 9, 4)

(\pm 23, 8)

(\pm 282, 43)

(\pm 375, 52)

(\pm 378661, 5234)

. The set

⋃_{\overset{(x, y) \in Z \times Z}{(x^{2} - y^{3} - 17) \cdot (y^{2} - x^{3} - 17) = 0}} {{(x + 8)}^{8}}

has exactly 23 elements. Among them, there are 14 integers from the interval

[1, 2199894223892]

. Let

W

denote the set

⋃_{\overset{(x, y) \in Z \times Z}{(x^{2} - y^{3} - 17) \cdot (y^{2} - x^{3} - 17) = 0}} {k \in N : k i s t h e {(x + 8)}^{8} - t h e l e m e n t o f P_{n^{2} + 1}}

From [14], it is known that

card (P_{n^{2} + 1} \cap [2, 10^{28})) = 2199894223892

. Hence,

card (W \cap [2, 10^{28})) = 14

and 14 elements of

W

can be practically computed. The inequality

card (P (n^{2} + 1)) ⩾ {(378661 + 8)}^{8}

remains unproven. The last two sentences and Statement 3 imply the following corollary.

Corollary 1.

If we add

W

X

, then the following statements hold:

X

does not satisfy Condition (1),

159827 + 14 ⩽ card (X)

the above lower bound is currently the best known,

card (X) < ω \Rightarrow card (X) ⩽ 159827 + 23

the above upper bound is currently the best known,

X

satisfies Conditions (2)-(5)except the requirement that

X

is naturally defined. Analogical statements hold, if we add to

X

the set

⋃_{\overset{x \in N}{x d i v i d e s 99!}} {k \in N : k - 501894 i s t h e x - t h e l e m e n t o f P_{n^{2} + 1}}

Definition 3.

Conditions(1a)-(5a)concern sets

X \subseteq N

(1a)A known algorithm with no input returns a positive integer n satisfying

card (X) < ω \Rightarrow

X \subseteq (- \infty, n]

(2a)A known algorithm for every

k \in N

decides whether or not

k \in X

(3a)No known algorithm with no input returns the logical value of the statement

card (X) < ω

(4a)There are many elements of

X

and it is conjectured, though so far unproven, that

X

is finite.

(5a)

X

is naturally defined. The finiteness of

X

is false or unproven.

X

has the simplest definition among known sets

Y \subseteq N

with the same set of known elements.

Statement 4.

The set

X = {n \in N : t h e i n t e r v a l [- 1, n] c o n t a i n s m o r e t h a n

6.5 + \frac{10^{6}}{3 n + 1} \cdot sin (n) s q u a r e s o f t h e f o r m k! + 1}

satisfies Conditions (1a)-(5a) except the requirement that

X

is naturally defined.

95151 \in X

. Condition (1a) holds with

n = 95151

card (X \cap [0, 95151]) = 30311

X \cap [95152, \infty) =

{n \in N :

t h e

i n t e r v a l

[- 1, n]

c o n t a i n s

a t

l e a s t

s q u a r e s

o f

t h e

f o r m

k! + 1}

Proof.

For every integer

n > 10^{6}

, 7 is the smallest integer greater than

6.5 + \frac{10^{6}}{3 n + 1} \cdot sin (n)

. By this, if

n \in X \cap (10^{6}, \infty)

, then

n + 1, n + 2, n + 3, \dots \in X

. Hence, Condition (1a) holds with

n = 10^{6}

. It is conjectured that

k! + 1

is a square only for

k \in {4, 5, 7}

, see [17, p. 297]. Hence, the inequality

card ({k \in N ∖ {0} : k! + 1 i s a s q u a r e}) > 3

remains unproven. Since

3 < 7

, Condition (3a) holds. The interval

[- 1, 10^{6}]

contains exactly three squares of the form

k! + 1

4! + 1

5! + 1

7! + 1

. Therefore, the execution of the following MuPAD code

m:=0:

for n from 0.0 to 1000000.0 do

if n<25 then r:=0 end_if:

if n>=25 and n<121 then r:=1 end_if:

if n>=121 and n<5041 then r:=2 end_if:

if n>=5041 then r:=3 end_if:

if r>6.5+(1000000/(3*n+1))*sin(n) then

m:=m+1:

print([n,m]):

end_if:

end_for:

displays the all known elements of

X

. The output ends with the line

[95151.0, 30311]

, which proves Condition (1a) with

n = 95151

and Condition (4a) with

card (X) ⩾ 30311

. □

Statement 5.

The set

X = {k \in N : card ([- 1, k] \cap P_{n^{2} + 1}) < 10^{10000}}

satisfies the conjunction

\neg (C o n d i t i o n 1 a) \land (C o n d i t i o n 2 a) \land (C o n d i t i o n 3 a) \land (C o n d i t i o n 4 a) \land (C o n d i t i o n 5 a)

For a non-negative integer n, let

θ (n)

denote the largest integer divisor of

10^{10^{10}}

smaller than n. Let

κ : N \to N

be defined by setting

κ (n)

to be the exponent of 2 in the prime factorization of

n + 1

Statement 6.

([15, p. 250]). The set

X = {n \in N : {(θ (n) + κ (n))}^{2} + 1 i s p r i m e}

satisfies Conditions (1)-(5) except the requirement that

X

is naturally defined. Condition (1) holds with

n = 10^{10^{10}}

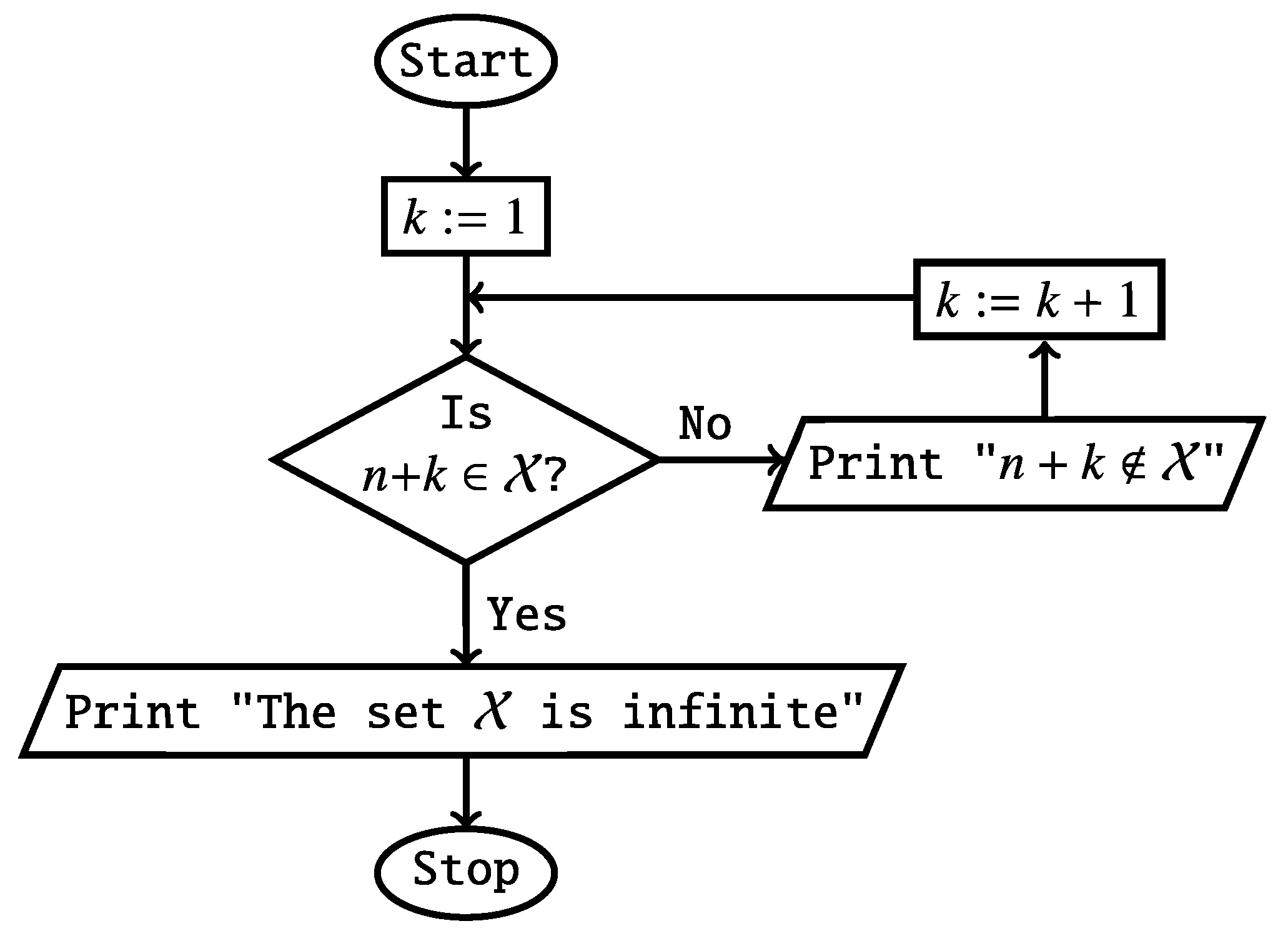
Statement 7.

No set

X \subseteq N

will satisfy Conditions (1)-(4) forever, if for every algorithm with no input, at some future day, a computer will be able to execute this algorithm in 1 second or less.

Proof.

The proof goes by contradiction. We fix an integer n that satisfies Condition (1). Since Conditions (1)-(3) will hold forever, the semi-algorithm in Figure 1 never terminates and sequentially prints the following sentences:

(T) n + 1 \notin X, n + 2 \notin X, n + 3 \notin X, \dots

(1)

The sentences from the sequence (T) and our assumption imply that for every integer

m > n

computed by a known algorithm, at some future day, a computer will be able to confirm in 1 second or less that

(n, m] \cap X = \emptyset

. Thus, at some future day, numerical evidence will support the conjecture that the set

X

is finite, contrary to the conjecture in Condition (4). □

The physical limits of computation ([7]) disprove the assumption of Statement 7.

Open Problem 1.

Is there a set

X \subseteq N

which satisfies Conditions(1)–(5)?

Open Problem 1 asks about the existence of a year

t ⩾ 2023

in which the conjunction

(C o n d i t i o n 1) \land (C o n d i t i o n 2) \land (C o n d i t i o n 3) \land (C o n d i t i o n 4) \land (C o n d i t i o n 5)

will hold for some

X \subseteq N

. For every year

t ⩾ 2023

and for every

i \in {1, 2, 3}

, a positive solution to Open Problem i in the year t may change in the future. Currently, the answers to Open Problems 1–5 are negative.

4. Satisfiable conjunctions which consist of Conditions `(1)-(5)` and their negations

The set

X = P_{n^{2} + 1}

satisfies the conjunction

\neg (C o n d i t i o n 1) \land (C o n d i t i o n 2) \land (C o n d i t i o n 3) \land (C o n d i t i o n 4) \land (C o n d i t i o n 5)

The set

X = {0, \dots, 10^{6}} \cup P_{n^{2} + 1}

satisfies the conjunction

\neg (C o n d i t i o n 1) \land (C o n d i t i o n 2) \land (C o n d i t i o n 3) \land (C o n d i t i o n 4) \land \neg (C o n d i t i o n 5)

Let

f (1) = 10^{6}

, and let

f (n + 1) = f {(n)}^{f (n)}

for every positive integer n. The set

X = \{\begin{matrix} N, i f 2^{2^{f (9^{9})}} + 1 i s c o m p o s i t e \\ {0, \dots, 10^{6}}, o t h e r w i s e \end{matrix}

satisfies the conjunction

(C o n d i t i o n 1) \land (C o n d i t i o n 2) \land \neg (C o n d i t i o n 3) \land (C o n d i t i o n 4) \land \neg (C o n d i t i o n 5)

Open Problem 2.

Is there a set

X \subseteq N

that satisfies the conjunction

(C o n d i t i o n 1) \land (C o n d i t i o n 2) \land \neg (C o n d i t i o n 3) \land (C o n d i t i o n 4) \land (C o n d i t i o n 5) ?

The numbers

2^{2^{k}} + 1

are prime for

k \in {0, 1, 2, 3, 4}

. It is open whether or not there are infinitely many primes of the form

2^{2^{k}} + 1

, see [6, p. 158] and [10, p. 74]. It is open whether or not there are infinitely many composite numbers of the form

2^{2^{k}} + 1

, see [6, p. 159] and [10, p. 74]. Most mathematicians believe that

2^{2^{k}} + 1

is composite for every integer

k ⩾ 5

, see [5, p. 23]. The set

X = \{\begin{matrix} N, i f 2^{2^{f (9^{9})}} + 1 i s c o m p o s i t e \\ {0, \dots, 10^{6}} \cup \\ {n \in N : n i s t h e s i x t h p r i m e n u m b e r o f t h e f o r m 2^{2^{k}} + 1}, o t h e r w i s e \end{matrix}

satisfies the conjunction

\neg (C o n d i t i o n 1) \land (C o n d i t i o n 2) \land \neg (C o n d i t i o n 3) \land (C o n d i t i o n 4) \land \neg (C o n d i t i o n 5)

Open Problem 3.

Is there a set

X \subseteq N

that satisfies the conjunction

\neg (C o n d i t i o n 1) \land (C o n d i t i o n 2) \land \neg (C o n d i t i o n 3) \land (C o n d i t i o n 4) \land (C o n d i t i o n 5) ?

It is possible, although very doubtful, that at some future day, the set

X = P_{n^{2} + 1}

will solve Open Problem 2. The same is true for Open Problem 3. It is possible, although very doubtful, that at some future day, the set

X = {k \in N : 2^{2^{k}} + 1 i s c o m p o s i t e}

will solve Open Problem 1. The same is true for Open Problems 2 and 3.

Table 1 shows satisfiable conjunctions of the form

# (Condition 1) \land (Condition 2) \land # (Condition 3) \land (Condition 4) \land # (Condition 5)

where # denotes the negation ¬ or the absence of any symbol.

Definition 4.

We say that an integer n is a threshold number of a set

X \subseteq N

, if

card (X) < ω \Rightarrow X \subseteq (- \infty, n]

If a set

X \subseteq N

is empty or infinite, then any integer n is a threshold number of

X

. If a set

X \subseteq N

is non-empty and finite, then the all threshold numbers of

X

form the set

[max (X), \infty) \cap N

Open Problem 4.

Is there a known threshold number of

P_{n^{2} + 1}

Open Problem 4 asks about the existence of a year

t ⩾ 2023

in which the implication

card (P_{n^{2} + 1}) < ω \Rightarrow P_{n^{2} + 1} \subseteq (- \infty, n]

will hold for some known integer n.

Let

T

denote the set of twin primes.

Open Problem 5.

Is there a known threshold number of

T

Open Problem 5 asks about the existence of a year

t ⩾ 2023

in which the implication

card (T) < ω \Rightarrow T \subseteq (- \infty, n]

will hold for some known integer n.

References

C. K. Caldwell and Y. Gallot, On the primality of n! ± 1 and 2 × 3 × 5 × ⋯ × p ± 1, Math. Comp. 71 (2002), no. 237, 441–448. [CrossRef]
J. Case and M. Ralston, Beyond Rogers’ non-constructively computable function, in: The nature of computation, Lecture Notes in Comput. Sci., 7921, 45–54, Springer, Heidelberg, 2013, http://link.springer.com/chapter/10.1007/978-3-642-39053-1_6.
Factorial prime, http://en.wikipedia.org/wiki/Factorial_prime.
Is n! + 1 often a prime?,http://math.stackexchange.com/questions/853085/is-n-1-often-a-prime.
J.-M. De Koninck and F. Luca, Analytic number theory: Exploring the anatomy of integers, American Mathematical Society, Providence, RI, 2012.
M. Křížek, F. Luca, L. Somer, 17 lectures on Fermat numbers: from number theory to geometry, Springer, New York, 2001.
S. Lloyd, Ultimate physical limits to computation, Nature 406 (2000), 1047–1054. [CrossRef]
T. Nagell, Einige Gleichungen von der Form ay² + by + c = dx³, Norske Vid. Akad. Skrifter, Oslo I (1930), no. 7.
R. Reitzig, How can it be decidable whether π has some sequence o f digits?, http://cs.stackexchange.com/questions/367/how-can-it-be-decidable-whether-pi-has-some-sequence-of-digits.
P. Ribenboim, The little book of bigger primes, 2nd ed., Springer, New York, 2004.
H. Rogers, Jr., Theory of recursive functions and effective computability, 2nd ed., MIT Press, Cambridge, MA, 1987.
W. Sierpiński, Elementary theory of numbers, 2nd ed. (ed. A. Schinzel), PWN – Polish Scientific Publishers and North-Holland, Warsaw-Amsterdam, 1987.
N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, A002496, Primes of the form n² + 1, http://oeis.org/A002496.
N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, A083844, Number of primes of the form x² + 1 < 10ⁿ, http://oeis.org/A083844.
A. Tyszka, Statements and open problems on decidable sets $𝒳$ ⊆ℕ that contain informal notions and refer to the current knowledge on X, Creat. Math. Inform. 32 (2023), no. 2, 247–253, http://semnul.com/creative-mathematics/wp-content/uploads/2023/07/creative_2023_32_2_247_253.pdf.
B. L. J. Webb, Science, Truth, and Meaning: From Wonder to Understanding, World Scientific, Singapore, 2021.
E. W. Weisstein, CRC Concise Encyclopedia of Mathematics, 2nd ed., Chapman & Hall/CRC, Boca Raton, FL, 2002.
Wolfram MathWorld, Landau’s Problems, http://mathworld.wolfram.com/LandausProblems.html.

Figure 1. Semi-algorithm that terminates if and only if

X

is infinite.

Figure 1. Semi-algorithm that terminates if and only if

X

is infinite.

Table 1. Five satisfiable conjunctions.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

In Mathematics, in Contradistinction to Any Empirical Science, the Predicate of the Current Knowledge Substantially Increases Its Constructive and Informal Part

Abstract

1. Introduction and why such title of the article

2. Basic definitions and examples

3. Number-theoretic results

4. Satisfiable conjunctions which consist of Conditions (1)-(5) and their negations

References

MDPI Initiatives

Important Links

Subscribe

4. Satisfiable conjunctions which consist of Conditions `(1)-(5)` and their negations