Prerpints.org logo
Preprint
Article

Edge Consistency Feature Extraction Method for Multi-source Image Registration

Altmetrics

Downloads

90

Views

26

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

26 July 2023

Posted:

31 July 2023

You are already at the latest version

Alerts
Abstract
Multi-source image registration often suffered from great radiation and geometric differences. Specifically, gray scale and texture from similar landforms in different source images often show significantly different visual features. And these differences disturb the corresponding point extraction in the following image registration process. Considering that edges between heterogeneous images can provide homogeneous information and more consistent features can be extracted based on image edges, an edge consistency radiation-change insensitive feature transform (EC-RIFT) method is proposed in this paper. Firstly, the noise and texture interference are reduced by preprocessing according to the image characteristics. Secondly, image edges are extracted based on phase congruency, and an orthogonal Log-Gabor filter is performed to replace the global algorithm. Finally, the descriptors are built with logarithmic partition of the feature point neighborhood, which improves the robustness of descriptors. Comparative experiments on datasets containing multi-source remote sensing image pairs show that the proposed EC-RIFT method outperforms other registration methods in terms of precision and effectiveness.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Vision and Graphics

1. Introduction

With the continuous breakthrough of remote sensing technology, the ways to obtain information through multi-source satellites, unmanned aerial vehicles, and other sensors have gradually increased, the space-air-ground integrated system based on multi-sensors has gradually improved. Due to the different methods and principles of data acquisition by different sensors, the acquired Earth observation data have their own information advantages, and the edge intelligence greatly improves multi-source data transmission and processing speed [1]. In order to integrate the multi-source remote sensing data to achieve complementary advantages and improve the data availability, information fusion of remote sensing images is usually required. Multi-source image registration refers to the technology of matching images in the same scene obtained by different image sensors and establishing the spatial geometric transformation relationship between them. Its accuracy and efficiency will directly impact the subsequent tasks, such as remote sensing interpretation in land-use surveillance[2].
However, due to the large differences in the operating mechanisms and conditions of imaging sensors, multi-source remote sensing images often show significant variations in the geometric and radiometric features. These obvious differences between multi-source remote sensing images are reflected in the registration process as the same landform or target in the image presents distinct image features, especially internal texture features. Therefore, algorithms such as SIFT proposed for homologous registration often fail [3]. Traditional multi-source image registration methods can be divided into two categories: area-based and feature-based methods. Region-based methods often use similarity measures and optimization methods to accurately estimate transformation parameters. A typical solution is to evaluate similarity with MI [4], which is generally limited by high computational complexity. Another approach is to improve processing efficiency through the domain transfer techniques such as fast Fourier Transform (FFT) [5]. However, facing the large-scale remote sensing images, region-based methods are sensitive to severe noise caused by imaging sensors and atmosphere, making it difficult to be applied widely. Therefore, feature-based methods are more commonly used in remote sensing field. These methods usually detect significant features between images (such as points, lines, and regions) and then identify correspondence by describing the detected features. The PSO-SIFT algorithm optimizes the calculation of image gradients based on SIFT and exploits the intrinsic information of feature points to increase the number of accurate matching points for the problem of multi-source image matching [6]. OS-SIFT is mainly focused on SAR images and optical images matching, and uses the multiscale exponential weighted average ratio and multiscale Sobel operator to calculate the SAR image and optical image gradients to improve the robustness [7]. The multiscale histogram of local main orientation (MS-HLMO) [8] develop a basic feature map for local feature extraction and a matching strategy based on Gaussian scale space. The development of deep learning technology has accelerated the research of computer vision, and more and more learning-based methods have emerged in registration field [9]. A common strategy is to generate deep and advanced image representations, such as using the network to train feature detectors[10], descriptors[11], or similarity measures, instead of traditional registration steps. There are also many methods based on Siamese networks or pseudo-Siamese networks[12], which obtain the deep feature representation by training the network [13], and then calculate the similarity of the output feature map to achieve template matching. However, there are few available multi-source remote sensing datasets and the acquisition cost is high, which greatly limits the development of learning-based methods.
These early feature-based methods are mainly based on gradient information, but the application in multi-source image registration is often limited as the sensitivity to illumination differences, contrast differences, etc. In recent years, as the concept of phase congruency (PC) [14] is introduced into image registration, more and more registration methods based on it show superior performance. The histogram of orientated phase congruency (HOPC) feature descriptor achieves matching between multiple modal images by constructing descriptors from phase congruency intensity and orientation information [15]. Li et al proposed a radiation change insensitive feature transformation (RIFT) algorithm to detect significant corner and edge feature points on the phase congruency map and constructed the max index map (MIM) descriptor based on the Log-Gabor convolution image sequences [16]. Yao et al proposed a histogram of absolute phase consistency gradients (HAPCG) algorithm, which extended the phase consistency model, established absolute phase consistency directional gradients, and built the HAPCG descriptors [17]. Fan et al proposed a 3MRS method based on a 2D phase consistency model to construct a new template feature based on Log-Gabor convolutional image sequences and use 3D phase correlation as a similarity metric [18]. In general, although these phase-congruency-based registration methods demonstrate excellent performance in multi-source image matching, there are still two problems for remote sensing images registration: (1) the interference of noise and texture on feature extraction cannot be avoided; (2) the computation of phase congruency involves Log-Gabor transforms at multiple scales and directions, which is heavy in computation and results in the extension of feature detection time.
The key to automatic registration of multi-source images lies in how to extract and match feature points between heterogeneous images. Since edges are relatively stable features in multi-source images, which can maintain stability when the imaging conditions or mode change [19], feature extraction based on edge contour information can greatly enhance the registration performance. As shown in Figure 1, for the same area, terrain selected by the red box exhibits significant differences in multi-source images, while the edge marked with the green box tends to be more consistent.
Therefore, a multi-source remote sensing image registration method based on homogeneous features is proposed in this paper, namely edge consistency radiation-variation insensitive feature transform (EC-RIFT). Firstly, in order to suppress speckle noise without destroying edge integrity, non-local mean filter is performed on SAR images, and edge enhancement is applied to visible images with abundant texture to help extract coherent features. Secondly, image edge information is extracted based on phase congruency, and orthogonal Log-Gabor filter (OLG) is chosen instead of global filter algorithm for feature dimension reduction, speeding up the feature detection. Finally, the EC-RIFT algorithm constructs descriptors based on the sector neighborhood of edge feature points, which is more sensitive to nearby points and improves the robustness of the descriptors, thus improving the registration accuracy. The main contributions of our paper are as follows.
1.
To capture the similarity of geometric structures and morphological features, phase congruency is used to extract image edges, and the differences between multi-source remote sensing images are suppressed by eliminating noise and weakening texture.
2.
To reduce computing costs, phase congruency models are constructed using Log-Gabor filtering in orthogonal directions.
3.
To increase the dependability of descriptor features with richer description information, sector descriptors are built based on edge consistency features.
The rest of the paper is organized as follows: Section 2 introduces the proposed method in detail. Section 3 evaluates the proposed method by comparing experimental results with other representative methods. Section 4 discusses several important aspects related to the proposed method. Finally, the paper is concluded in Section 5.

2. Materials and Methods

The EC-RIFT algorithm process can be divided into five steps: image preprocessing, feature point detection, descriptor construction, feature matching, and outlier removal. The main process of the proposed framework is shown in Figure 2. The blue boxes indicate the focus of the research in this paper. The following subsections provide a detailed description.

2.1. Multi-source Image Preprocessing

2.1.1. Non-local Mean Filtering

SAR images are always corrupted by speckle noise, leading to the challenge of subsequent tasks such as feature detection, so it is necessary to suppress the speckle noise first. The non-local mean filtering algorithm (NLM) defines similar pixels as the same neighborhood pattern and uses the information within a fixed size window around the pixel to represent it, the loss of image structure information during the noise reduction process can be avoided, and thus performs well in maintaining image edge and structure information [20]. The NLM filtering is calculated as (1):
u ˜ x = ∑ y ∈ I w x , y * v y
Where v is the original image, u ˜ is the denoised image, and the weight w ( x , y ) represents the similarity between points x and y, which is determined by the distance | | V ( x ) − V ( y ) | | between rectangular regions V(x), V(y), as shown in (2) -(4).
w x , y = 1 Z x e x p ( − ∥ V x − V y ∥ 2 h 2 )
∥ V x − V y ∥ 2 = 1 d 2 Σ z ∈ S d ∥ v x + z − v y + z ∥ 2
Z x = Σ y e x p ( − ∥ V x − V y ∥ 2 h 2 )
Where Z is the normalization parameter, h is the smoothing parameter, and S d denotes the search window region that regulates the degree of Gaussian function’s decay.

2.1.2. Co-occurrence Filtering

To take full advantage of the edge information of image, the edges need to be enhanced while weakening the texture. The co-occurrence filter (CoF) is an edge-preserving filter in which pixel values that appear more frequently in the image are weighted higher in the co-occurrence matrix, so the image texture can be smooth without considering the grayscale difference [21]. And pixel values that rarely appear at the same time are weighted lower in the co-occurrence matrix, which can better maintain the boundaries. The CoF is defined according to (5):
J p = ∑ q ∈ N p G σ s p , q · M I p , I q · I q ∑ q ∈ N p G σ s p , q · M I p , I q
Where J p and I q represent the output and input pixel values respectively, p and q are pixel indices, G denotes the Gaussian filter, σ s is the standard deviation of G, and M is calculated from the co-occurrence matrix as (6)
M I p , I q = C I p , I q h I p h I q
Where h ( p ) and h ( q ) are histograms of pixels p and q, indicating the occurrence frequency of p and q. The co-occurrence matrix C is computed as (7).
C I p , I q = ∑ p , q e x p − d p , q 2 2 σ 2
In equation (7), d denotes the Euclidean distance, σ 2 is a fixed value, σ 2 = 2 5 + 1 .
The comparison of images with/without preprocess is shown in Figure 3. There are significant geometric and radiometric differences between the original images, making it more difficult to be matched with high precision. It is clear that the speckle noises in SAR image (a) are filtered in (b), and the textures in optical image (c) are suppressed in (d) with complete edge maintained. The edge information left in the two images has a stronger consistency.

2.2. Edge Feature Detection

Edge information can largely reflect the structural features of objects and is more stable in heterogeneous images, so feature detection based on complete edges can provide a more reliable foundation for registration. The phase congruency model can overcome the effects of contrast and brightness changes and extract more complete feature edges than gradients. The features of phase congruency need to be extracted by Log-Gabor filter, and the high dimension of it brings about the a longer computation time. The number of scales and orientations are set to 4 and 6, respectively. Therefore, in this paper, a 2D orthogonal Log-Gabor filter (OLG) is used instead of the global filter to achieve feature dimension reduction [22].
The geometric structure of images can be well preserved by phase congruency. Oppenheim first identified the ability of phase to extract significant information from images [23], and later Morrone and Owens proposed a model of phase congruency [24]. Since the degree of phase congruency is independent of the overall amplitude of signal, it has better robustness and gives more detailed edge information than the gradient operator when employed for edge detection. Kovesi simplified the calculation of phase congruency with Fourier phase components and extended the model to 2D [14]. Kovesi employed Log-Gabor filters in the computation which were demonstrated to be more natural for human eyesight.
The intensity value of phase congruency is calculated as equation (8):
P C x , y = ∑ s ∑ o ω o x , y A s o x , y Δ Φ s o x , y − T ∑ s ∑ o A s o x , y + ξ
Where s and o separately denote the filter scale and orientation, ω o denotes the weight, and ξ is a minimal constant preventing the denominator from being 0. A s o and ϕ s o denote the amplitude and phase of the PC, respectively, and can be derived from equation (9) and (10):
A s o x , y = E s o x , y 2 + O s o x , y 2
ϕ s o x , y = a r c t a n O s o x , y / E s o x , y
E s o and O s o represent the results of even-symmetric filtering and odd-symmetric filtering convolved with image I respectively. The calculation formula is shown in (11):
E s o x , y , O s o x , y = I x , y * L e v e n x , y , s , o , I x , y * L o d d x , y , s , o
L is a 2D Log-Gabor filtering function, defined as (12):
L ρ , θ , s , o = e x p − ρ − ρ s 2 2 σ ρ 2 e x p − θ − θ s o 2 2 σ θ 2
Where σ represents the bandwidth, ρ s and θ s o are the center frequencies of Log-Gabor filtering.
The edges extracted based on phase congruency are often used for edge detection as the ability to be unaffected by local light variations in the image, and they can contain various information, especially information at low edge contrast.
A 2D OLG is formed with two Log-Gabor filters with mutually orthogonal directions, which can be expressed by (13). The OLG proposed reduces the amount of computation while avoiding the redundancy of features, thus can improve the running speed under the premise of ensuring the integrity of features.
O L ρ , θ , s , o = ∣ L ρ , θ , s , o − L ρ , θ ± π 2 , s , o ∣
To validate the the effect of OLG algorithm on removing redundant features, the FAST algorithm is applied based on the phase congruency representations processed in the two strategies respectively, and the results are shown in Figure 4. (a) - (d) denote features detected based on LG algorithm, and (e) - (h) are based on OLG algorithm. To illustrate the effectiveness of the proposed algorithm, image pairs SAR1/OPT1 and SAR2/OPT2 of different landforms are selected for comparison. It can be observed that the OLG algorithm performs better on depicting the image edges, and some of the isolated points were removed compared with the results of LG. The feature points obtained by the orthogonal method tend to be more recognizable, which makes it more likely to get the correct match in the subsequent processing.

2.3. Sector Descriptor Construction

Referring to the RIFT algorithm, the descriptors construction of EC-RIFT is performed on the maximum index map (MIM). Accumulates the amplitudes A s o x , y in the same direction at N s scales first to obtain A o ( x , y ) , and then the MIM is constituted with the direction index value ω , which represents the maximum values of these pixels.
To enhance the robustness and uniqueness of the descriptors, the GLOH-like approach is chosen to construct the descriptors in this paper [25]. For the obtained features based on edge consistency, the statistical histogram in log-polar coordinates enables the descriptors to be more sensitive to near points than distant points. As shown in Figure 5, the pixels in the neighborhood of keypoints are divided into log-polar coordinate concentric circles with radius set to 0.25r and 0.75r, supposing that the radius of neighborhood is r. If the area of divided sector is too small, the features are not sufficient, while the larger section will increase the descriptor dimension and the burden of computation. The pixels are divided into 8 equal parts in the angular, each equal part being π / 4 , so that 16 sectors and 1 circle are formed, for a total of 17 image sub-blocks. The points on the same ring are close to each other, so the feature points are equally discriminated. Each block computes a histogram of 6 directions, resulting in a descriptor vector of 17 × 6 = 102 dimensions. To simplify the calculation, if some descriptor component exceeds the threshold value, the component is set to the threshold size, and the threshold value is empirically set as 0.2 in this paper. Finally, the descriptor vector is normalized.

2.4. Feature Matching and Outlier Removal

An effective algorithm to match feature points is the Nearest Neighbor Distance Ratio (NNDR) method, which is proposed by Lowe [3]. It screens out local features by comparing the distances of nearest neighbor and second nearest neighbor features, and filters out features with low discrimination. A feature point is more likely to be correctly matched if the point most similar to its descriptor is close, and the point less similar to it is far apart.
After the feature matching, there are still some mismatched point pairs, so the EC-RIFT algorithm chooses the fast sample consensus (FSC) algorithm to remove the outliers [26] and estimate the parameters of the affine transformation model.

3. Experiments and Results

In this section, we first introduced the datasets and evaluation metrics. Subsequently, we investigated the effectiveness of the proposed method in stages. Finally, aiming at proving the superiority of the EC-RIFT, the results were presented and evaluated by comparing them with three representative multi-source image registration methods.

3.1. Datasets

Two types of datasets are used to evaluate the registration performance of the EC-RIFT algorithm in this paper. The first is formed from 7 pairs of SAR images and optical images with various sizes and sources. The image pairs in other modalities are also employed to assess the generalization ability of proposed algorithm. Both datasets are described in detail.
The SAR and optical images are obtained from different sensors, such as Terra SAR-X, Gaofen satellites, Google Earth, Landsat satellites and aerial vehicles, covering the various resolutions and sizes. The multi-source image dataset consists of infrared-optical, day-night, depth-optical pairs, widely employed in remote sensing image registration. All image pairs capture various terrains, including urban areas, fluvial deposits, rivers and farmland. And images exhibit significant geometric and radiometric differences, posing challenges for registration. The data are shown in Figure 6, in which (a) - (f) denote the sar-optical data, and (g) - (i) present multi-source data employed in the experiments.

3.2. Evaluation Criterion

For quantitative evaluation, the repeatability [27], root mean square error (RMSE), and running time are selected to evaluate the performance of the proposed method.
Repeatability [27] is often used as a metric to evaluate the quality of detected features, which is defined to represent the rate of potential corresponding points in all detected points. The repeatability can be calculated as equation (14):
R e p e a t a b i l i t y = N c N 1 + N 2 / 2
Where N c represents the number of potential corresponding points, N 1 and N 2 represent the total number of feature points detected in the reference image and moving image, respectively. If a feature point meets the conditions as formula (15), it is considered as a potential corresponding point. Where i represents the index of keypoint, ( x 1 i , y 1 i ) is the keypoint coordinates of the reference image, and ( x 2 i , y 2 i ) is the keypoint coordinates obtained after affine transformation of the moving image.
x 2 i − x 1 i 2 + y 2 i − y 1 i 2 < 2
The root mean square error (RMSE) is used to evaluate the precision of the registration results. RMSE is defined as (16):
R M S E = ∑ i = 1 n ( x 2 i − x 1 i ) 2 + ( y 2 i − y 1 i ) 2 n
Where n is the number of matching pairs, ( x 1 i , y 1 i ) is the keypoint coordinates of the reference image, and ( x 2 i , y 2 i ) is the keypoint coordinates obtained after affine transformation of the image to be registered. The smaller the value of RMSE, the higher the precision of registration.

3.3. Registration Results and Analysis

To demonstrate the effect of each processing section on the registration results, experiments are designed to evaluate the registration results. And the comparison experiments were conducted with HAPCG, OS-SIFT and RIFT algorithms to prove the proposed method has better performance in registration.

3.3.1. Comparison Experiment of preprocessing algorithms

The preprocessing step can help to realize the registration of multi-source images with large radiometric differences. To demonstrate the effectiveness of algorithm applied in this paper, the pair6 are chosen for the experiment, whose similarity of the original data is too low to be registered by all the four algorithms. The Figure 7 depicts the registration results obtained with/without the denoising and enhancement process. (a) represents the matching result of original data, which is obviously unable to be registered. The SAR and optical images in (b) and (c) are preprocessed respectively. Even if one of the images is processed, the image pairs failed to register. For the denoised SAR image and enhanced optical image, the corresponding points are matched correctly, as shown in (d). It is clear that the noise in the original SAR image and the texture in the optical image have a strong impact on registration, and more correct matching pairs are obtained after preprocessing.
In addition, comparison experiments are conducted on images preprocessed with aforementioned steps. As listed in Table 1, our method performs the best among the four methods in terms of RMSE and running time.
It should be noted that this step is optional for remote sensing image registration. There are serious radiation and geometric distortion in data for this experiment, which bring greater challenges to registration, and the proposed steps contribute to extracting corresponding features.

3.3.2. Comparison Experiment of OLG and LG

Since OLG algorithm can reduce redundancy in feature detection, the repeatability is chosen to evaluate its effectiveness. A higher repeatability indicates a higher probability of extracting the corresponding features. The results are shown in Figure 8.
The OLG algorithm achieves scores higher than or equal to LG on all images, demonstrating the contribution to improving the registration accuracy.
In addition, the feature detection time and registration precision of OLG are tested in this experiment, and the results are listed in Table 2. As can be seen from Table 2, for all image pairs, OLG can reduce the feature detection time by nearly half, and the accuracy are improved on all data.

3.3.3. Comparison Experiment of Square Descriptor and Sector Descriptor

The purpose of this experiment is to compare the performance of square descriptors and the sector descriptors used in this paper. The similarity between the descriptor vectors on paired features determines the success rate of matching. In order to illustrate that the proposed descriptors are capable to extract the common information better, we chose two metrics to measure the similarity of the paired descriptors. Cosine similarity and Pearson correlation coefficient are commonly used methods to measure the similarity between two vectors, both in the range of [-1,1]. A value of 1 means that the vectors are completely similar, and -1 indicates the opposite.
Five pairs of points are selected randomly from Pain1 for this experiment, then the descriptors are bulid in square and sector methods respectively. The similarity of vectors are shown in the Figure 9. The bars in light color represent cosine similarity, and those in dark color represent Pearson correlation coefficient of two methods. The sector descriptor (the orange bars) outperforms than square descriptor (the blue bars) on all points selected. It can be proved that descriptors based on sector neighborhood fit the corresponding points matching better.
Besides, the comparison experiment of registration results is shown in Figure 10. For the reliability of experiment, all parts of the method are kept consistent except for the descriptor construction step. This result demonstrates that our descriptors have a higher robustness, and thus conducive to multi-source image registration.

3.3.4. Comparative results with other methods

To analyze the performance of proposed method, the accuracy and efficiency are compared with three methods: HAPCG, OS-SIFT, and RIFT algorithm. For the fairness of the experiment, all methods use the same matching method, and parameters are set under the recommendations of their authors.
Figure 11 represents the matching results of the EC-RIFT algorithm. It was clear that the sufficient features are matched correctly, confirming the effectiveness of the proposed method for SAR and optical image registration. Table 3 shows the quantitative results of the four methods. The EC-RIFT method is capable of steadily registering image pairs with lower error and time.
The performance of OS-SIFT is the most vulnerable. For pair2-5, the × means that the algorithm fails to register, and the N A N in table represents the number of correct matching is less than five, which we find unconvincing. Other methods can obtain enough matching pairs to achieve registration tasks. In terms of RMSE, the proposed method outperforms other three methods in all image pairs. For pair2, the results obtained by our method are 38.97% and 11.19% better than those obtained by HAPCG and RIFT, achieving significant accuracy improvement. The running times of HAPCG method for pair4 and pair5 are less than our method, but as shown in Figure 12 the average time for all image pairs of our method is 7.31s, which is still the shortest of these methods. It should be noted that the OS-SIFT is annotated as N A N because it obtains valid results only on pair1 and takes longer than our algorithm on it.

3.4. Experiments on multi-source Images

The experimental results on SAR-optical images demonstrated the effectiveness and superiority of our method. As an extension, we focus on the registration performance of other multi-source images in this subsection. The visual results are shown in Figure 13 . The EC-RIFT successfully matched a large number of points on these image pairs.
Table 4 lists the comparative registration results of RIFT and EC-RIFT for multi-source images. Our method obtains robust registration results and generally outperforms RIFT method in terms of RMSE and running time, implying that it has good generalization ability to be transferred to images in other modalities.

4. Discussion

Taking both the quantitative and the qualitative results into account, experimental results in Section 3 illustrate that the proposed method achieves better registration performance for multi-source images. In this section, we first validate the idea that smoothing textures and noises can enhance the edge features, which are more stable between multi-source images. Additionally, the rotation and scale invariances of method are analyzed, leading to the limitations and future work expectations.

4.1. The effect of noises on MIM

Since image descriptors are built based on the histogram statistics of MIM, the distribution in the neighborhood of feature points on MIM determines the probability of corresponding points being matched. Therefore, we compare the MIMs of original images and processed images to research the effect of this step.
As shown in Figure 14, the influence of speckle noises are significant in SAR image, the irregular interference will directly disturb the robustness of descriptors. And the textures which are not present in SAR image also exacerbate the difference between MIMs. The MIMs of processed image pairs are much more similar, leading to higher registration accuracy.
Note that the preprocessing methods in this paper are selected according to the characteristics of the images. For images of other modalities, the idea of eliminating noise and texture differences between image pairs still hold, but the specific algorithms need to be redesigned.

4.2. Fine-registration and Considerable Difference

The imaging spatial resolution difference between satellite and drone is great, and the imaging level is uneven between different satellites. The scale is different depending on the height, the rotation is different depending on the orbit, and the distortion is different depending on the modality. Therefore, the multi-sensor data for situational awareness needs to be fine-registered first in the space-air-ground integrated network.
Our research is based on the assumption that remote sensing images have been registered with geographic information, which means that there are mainly translation differences between the input image pairs. Actually, there is only a tiny scale difference the coarse-registered images calibrated by the location or attitude information, and the rotation angle is subtle, in which case our method works well. The feature matching results of image pairs with scale and rotation differences are shown in Figure 15. The resolution of SAR image in (a) is reduced from 500px × 492px to 400px × 394px, while the resolution of optical image remains the original. The SAR images of two sizes are manually rotated clockwise by 5 degrees in (b) and (c), respectively. For indistinctive differences in scale and rotation, whether one or both exist on the image pairs, the proposed method can obtain enough matching pairs.
However, our method is sensitive to significant scale differences and rotation transformations, so it may fail in these scenes. In terms of rotation-invariance, the solution has been proposed in [29], but it is computationally heavy and time-consuming. In terms of scale-invariance, methods based on image pyramid [30] may help to improve the registration performance. In future work, we will focus on proposing more efficient approach to improve the feature invariance of significant scale and rotation.

5. Conclusions

Aiming at handling the challenge of extracting consistent features from multi-source images with severe geometric and radiometric distortions, this paper proposes a robust registration method based on the edge consistency features. We first design the denoising and enhancing algorithms according to the characteristics of remote sensing images, to reduce the interference of redundant information on registration. Then the orthogonal method is adopted for feature extraction to improve computational efficiency. Finally, the sector-neighborhood descriptor is constructed to obtain a more robust representation. Compared with other representative registration methods, the proposed method obtains higher speed and accuracy, which can effectively realize the registration task of SAR and optical images. Due to the potential of real-time performance, the improved algorithm is expected to be applied in edge intelligence analysis [31] and on-orbit satellite platforms [32]. Besides, the proposed method is proven to have a superior generalization ability to be applied to images in other modalities.

Author Contributions

Conceptualization, Y.Z.; methodology, Y.Z. and Z.H.; validation, Y.Z.; investigation, Z.D. and C.H.; writing-original draft preparation, Z.H. and N.L.; writing-review and editing, N.L. and C.C.; supervision and suggestions, L.C., Z.D. and C.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Key Research and Development Program of China(2020YFB1807500), the National Natural Science Foundation of China (62072360, 62001357, 62172438,61901367), the key research and development plan of Shaanxi province(2021ZDLGY02-09, 2023-GHZD-44, 2023-ZDLGY-54), the Natural Science Foundation of Guangdong Province of China(2022A1515010988), Key Project on Artificial Intelligence of Xi’an Science and Technology Plan(2022JH-RGZN-0003, 2022JH-RGZN-0103, 2022JH-CLCJ-0053), Xi’an Science and Technology Plan(20RGZN0005) and the Xi’an Key Laboratory of Mobile Edge Computing and Security (201805052-ZD3CG36).

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
SAR Synthetic Aperture Radar
EC-RIFT Eedge Consistency Radiation-variation Insensitive Feature Transform
NLM Non-local Mean
CoF Co-occurrence Filter
OLG Orthogonal Log-Gabor
RMSE Root Mean Square Error

References

  1. Chen, C.; Wang, C.; Liu, B.; He, C.; Cong, L.; Wan, S. Edge Intelligence Empowered Vehicle Detection and Image Segmentation for Autonomous Vehicles. IEEE Transactions on Intelligent Transportation Systems 2023, pp. 1–12. [CrossRef]
  2. Lv, N.; Zhang, Z.; Li, C. A hybrid-attention semantic segmentation network for remote sensing interpretation in land-use surveillance. International Journal of Machine Learning and Cybernetics 2023, 14, 395–406. [CrossRef]
  3. Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. International Journal of Computer Vision 2004, 60, 91–110. [CrossRef]
  4. Chen, H.; Sebastian.; Varshney.; Pramod, K.; Arora.; Manoj, K. Performance of Mutual Information Similarity Measure for Registration of Multitemporal Remote Sensing Images. IEEE Transactions on Geoscience and Remote Sensing 2003, 41, 2445 – 2454. [CrossRef]
  5. Ye, Y.; Bruzzone, L.; Shan, J.; Bovolo, F.; Zhu, Q. Fast and Robust Matching for Multimodal Remote Sensing Image Registration. IEEE Transactions on Geoscience and Remote Sensing 2019, PP, 1–12. [CrossRef]
  6. Ma, W.; Wen, Z.; Wu, Y.; Jiao, L.; Gong, M.; Zheng, Y.; Liu, L. Remote Sensing Image Registration With Modified SIFT and Enhanced Feature Matching. IEEE Geoscience and Remote Sensing Letters 2016, 14, 3–7. [CrossRef]
  7. Xiang, Y.; Wang, F.; You, H. OS-SIFT: A Robust SIFT-Like Algorithm for High-Resolution Optical-to-SAR Image Registration in Suburban Areas. IEEE Transactions on Geoscience and Remote Sensing 2018, 56, 3078–3090. [CrossRef]
  8. Gao, C.; Li, W.; Tao, R.; Du, Q. MS-HLMO: Multiscale Histogram of Local Main Orientation for Remote Sensing Image Registration. IEEE Transactions on Geoscience and Remote Sensing 2022, 60, 1–14. [CrossRef]
  9. Ma, W.; Zhang, J.; Wu, Y.; Jiao, L.; Zhu, H.; Zhao, W. A Novel Two-Step Registration Method for Remote Sensing Images Based on Deep and Local Features. IEEE Transactions on Geoscience and Remote Sensing 2019, pp. 1–10. [CrossRef]
  10. Zhou, L.; Ye, Y.; Tang, T.; Nan, K.; Qin, Y. Robust Matching for SAR and Optical Images Using Multiscale Convolutional Gradient Features. IEEE Geoscience and Remote Sensing Letters 2022, 19, 1–5. [CrossRef]
  11. Zhuoqian, Y.; Tingting, D.; Yang, Y. Multi-temporal Remote Sensing Image Registration Using Deep Convolutional Features. IEEE Access 2018, 6, 38544–38555. [CrossRef]
  12. Zhang, H.; Ni, W.; Yan, W.; Xiang, D.; Bian, H. Registration of Multimodal Remote Sensing Image Based on Deep Fully Convolutional Neural Network. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2019, PP, 1–15. [CrossRef]
  13. Hughes, L.; Marcos, D.; Lobry, S.; Tuia, D.; Schmitt, M. A deep learning framework for matching of SAR and optical imagery. ISPRS Journal of Photogrammetry and Remote Sensing 2020, 169, 166–179. [CrossRef]
  14. Kovesi, P. Phase congruency: A low-level image invariant. Psychological Research 2000, 64, 136–148. [CrossRef]
  15. Ye, Y.; Shan, J.; Bruzzone, L.; Shen, L. Robust Registration of Multimodal Remote Sensing Images Based on Structural Similarity. IEEE Transactions on Geoscience and Remote Sensing 2017, 55, 2941–2958. [CrossRef]
  16. Li, J.; Hu, Q.; Ai, M. RIFT: Multi-Modal Image Matching Based on Radiation-Variation Insensitive Feature Transform. IEEE Transactions on Image Processing 2020, 29, 3296–3310. [CrossRef]
  17. Yao, Y.; Zhang, Y.; Wan, Y.; Liu, X.; Guo, H. Heterologous Images Matching Considering Anisotropic Weighted Moment and Absolute Phase Orientation. Geomatics and Information Science of Wuhan University 2021, 46, 1727.
  18. Fan, Z.; Liu, Y.; Liu, Y.; Zhang, L.; Zhang, J.; Sun, Y.; Ai, H. 3MRS: An Effective Coarse-to-Fine Matching Method for Multimodal Remote Sensing Imagery. Remote Sensing 2022, 14, 478. [CrossRef]
  19. Sui, H.; Liu, C.; Gan, Z. Overview of multi-modal remote sensing image matching methods. Journal of Geodesy and Geoinformation Science 2022, 51.
  20. Buades, A.; Coll, B.; Morel, J. A non-local algorithm for image denoising. 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05) 2005, 2, 60–65. [CrossRef]
  21. Jevnisek, R.J.; Avidan, S. Co-occurrence Filter. 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 2017, pp. 3816–3824. [CrossRef]
  22. Yang, H.; Fu, Y.; Zeng, J. Face recognition algorithm based on orthogonal Log-Gabor filter binary mode. Transactions on Intelligent Systems 2019, pp. 330–337.
  23. Oppenheim, A.; Lim, J. The importance of phases in signal. IEEE transaction on Computer Science 1981, 69, 333–382.
  24. Morrone, M.C.; Owens, R.A. Feature detection from local energy. Pattern Recognition Letters 1987, 6, 303–313. [CrossRef]
  25. Mikolajczyk, K.; Schmid, C. A performance evaluation of local descriptors. IEEE Transactions on Pattern Analysis and Machine Intelligence 2005, 1615-1630. [CrossRef]
  26. Wu, Y.; Ma, W.; Gong, M.; Su, L.; Jiao, L. A Novel Point-Matching Algorithm Based on Fast Sample Consensus for Image Registration. IEEE Geoscience and Remote Sensing Letters 2015, 12, 43–47. [CrossRef]
  27. Mikolajczyk, K.; Schmid, C. An Affine Invariant Interest Point Detector. Proc European Conf on Computer Vision, LNCS 2350 2002, 1.
  28. Zhang, Y.; Chen, C.; Liu, L.; Lan, D.; Jiang, H.; Wan, S. Aerial Edge Computing on Orbit: A Task Offloading and Allocation Scheme. IEEE Transactions on Network Science and Engineering 2023, 10, 275–285. [CrossRef]
  29. Li, J.; Shi, P.; Hu, Q.; Zhang, Y., Rift2: Speeding-up rift with a new rotation-invariance technique. ArXiv, vol. abs/2303.00319, 2023. [CrossRef]
  30. Gao, C.; Li, W. Multi-scale PIIFD for Registration of Multi-source Remote Sensing Images. Journal of Beijing Institute of Technology 2021, 30, 12. [CrossRef]
  31. Chen, C.; Yao, G.; Liu, L.; Pei, Q.; Song, H.; Dustdar, S. A Cooperative Vehicle-Infrastructure System for Road Hazards Detection with Edge Intelligence IEEE Transactions on Intelligent Transportation Systems 2023. [CrossRef]
  32. Hnatushenko, V.; Kogut, P.; Uvarov, M. Variational approach for rigid co-registration of optical/SAR satellite images in agricultural areas Journal of Computational and Applied Mathematics 2022, 400, 113742. [CrossRef]
Preprints 80580 g001
Figure 1. Texture and edge differences between multi-source images.
Figure 1. Texture and edge differences between multi-source images.
Preprints 80580 g001
Preprints 80580 g002
Figure 2. Implementation flow chart of EC-RIFT algorithm.
Figure 2. Implementation flow chart of EC-RIFT algorithm.
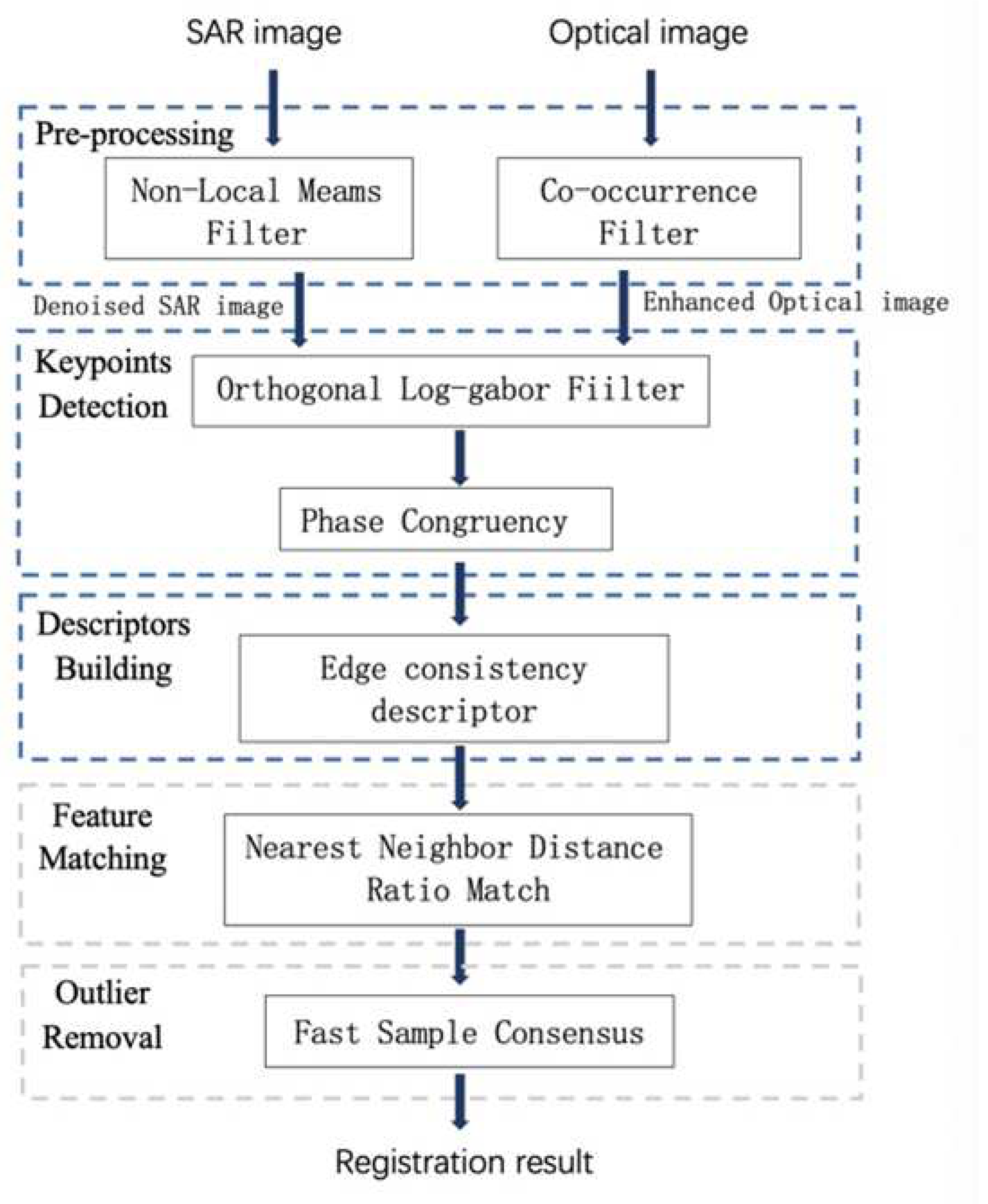
Preprints 80580 g002
Preprints 80580 g003
Figure 3. Results of preprocessing.
Figure 3. Results of preprocessing.
Preprints 80580 g003
Preprints 80580 g004
Figure 4. Features detected with LG/OLG.
Figure 4. Features detected with LG/OLG.
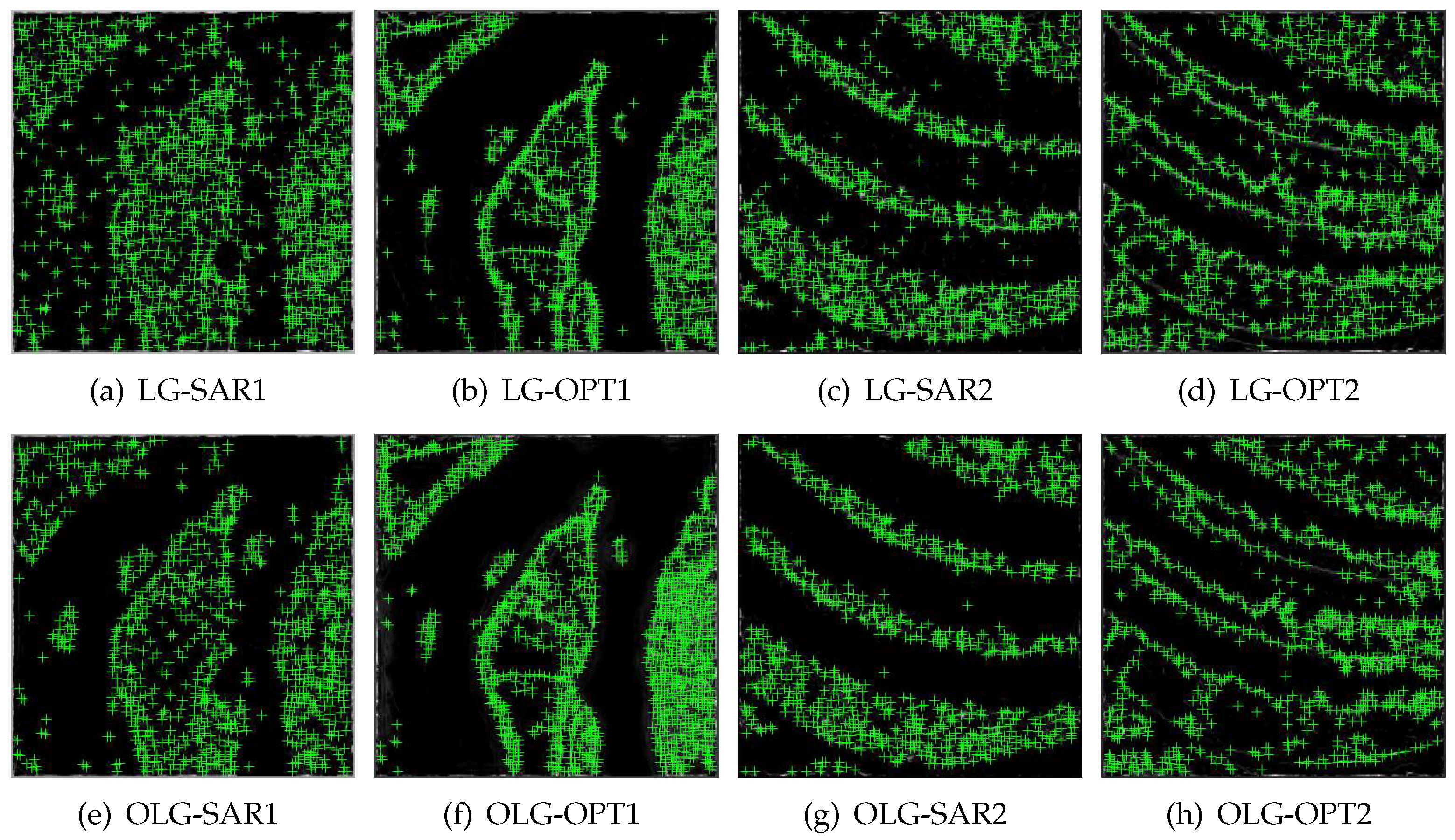
Preprints 80580 g004
Preprints 80580 g005
Figure 5. The descriptors of EC-RIFT method.
Figure 5. The descriptors of EC-RIFT method.
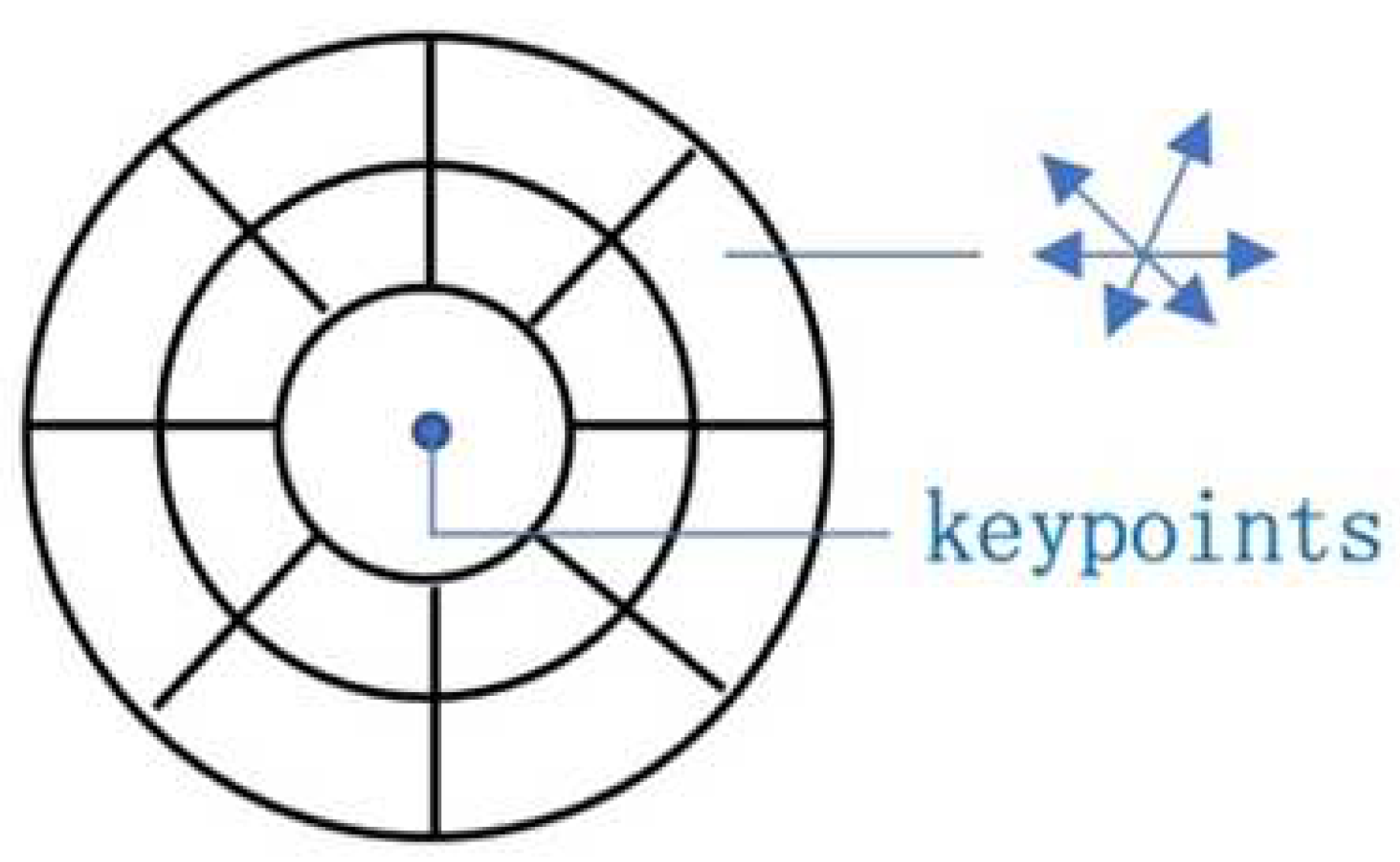
Preprints 80580 g005
Preprints 80580 g006
Figure 6. Dataset presentation.
Figure 6. Dataset presentation.
Preprints 80580 g006
Preprints 80580 g007
Figure 7. Registration results with/without preprocessing.
Figure 7. Registration results with/without preprocessing.
Preprints 80580 g007
Preprints 80580 g008
Figure 8. Repeatability of OLG and LG.
Figure 8. Repeatability of OLG and LG.
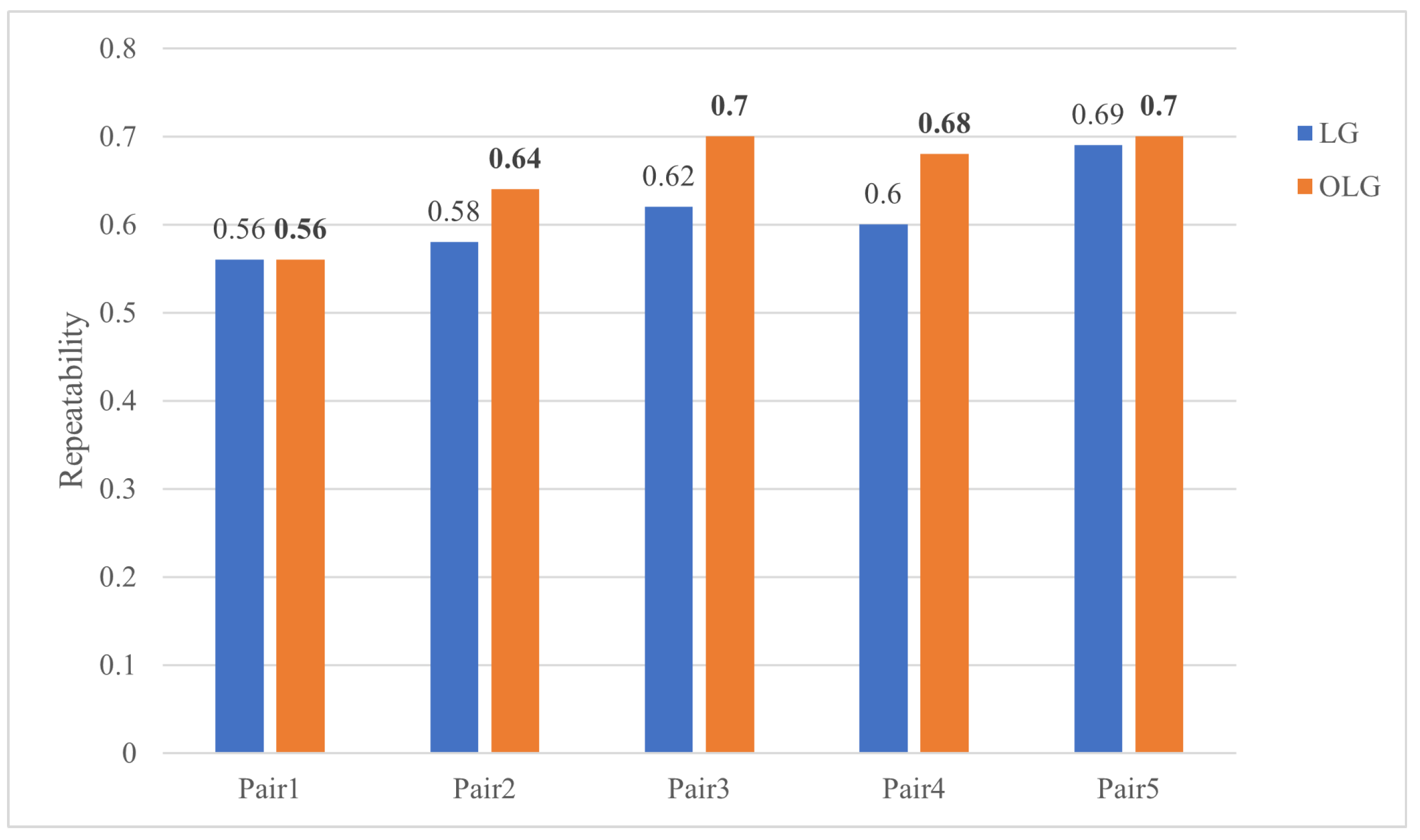
Preprints 80580 g008
Preprints 80580 g009
Figure 9. The similarity of MIM.
Figure 9. The similarity of MIM.
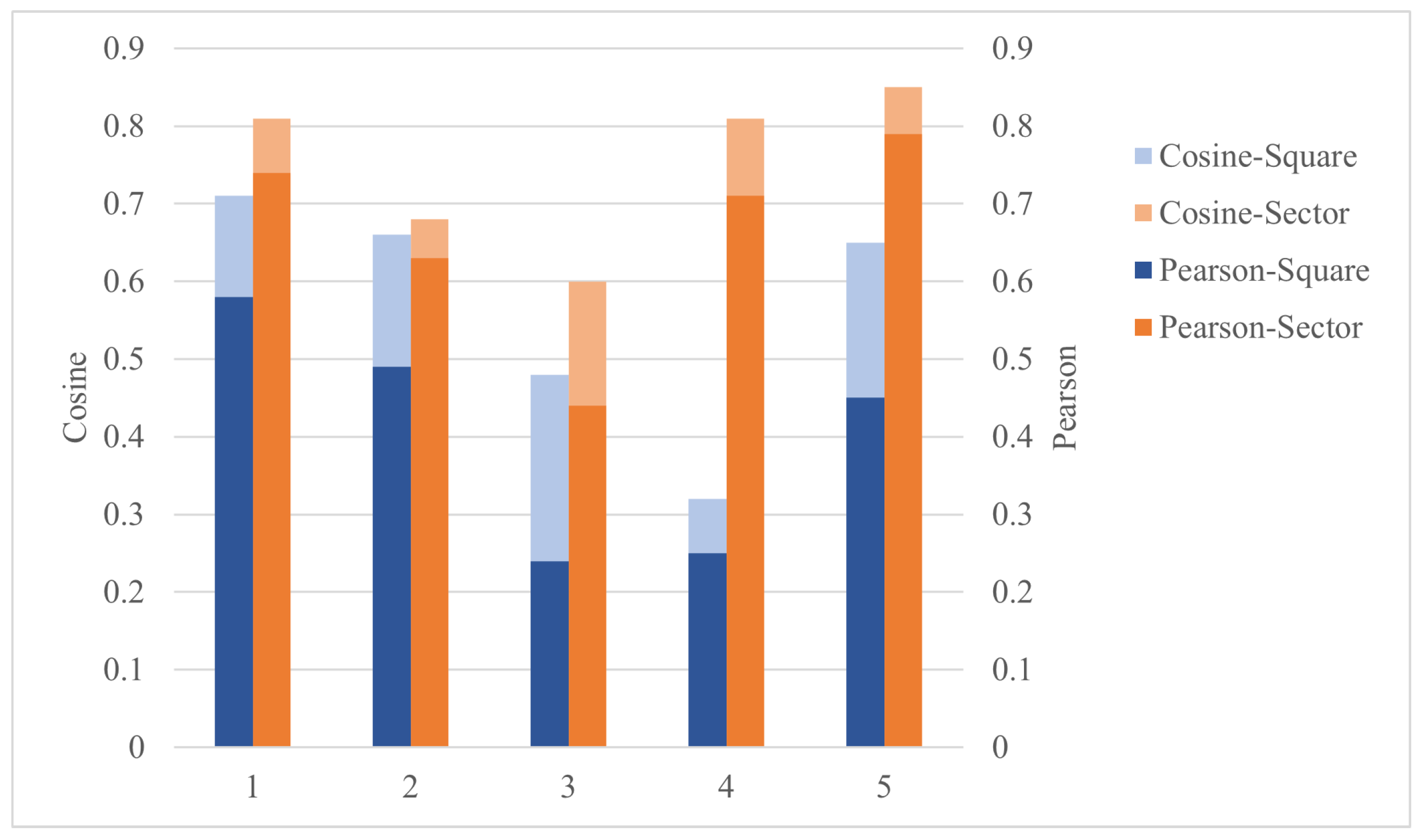
Preprints 80580 g009
Preprints 80580 g010
Figure 10. Comparison of OLG and LG.
Figure 10. Comparison of OLG and LG.
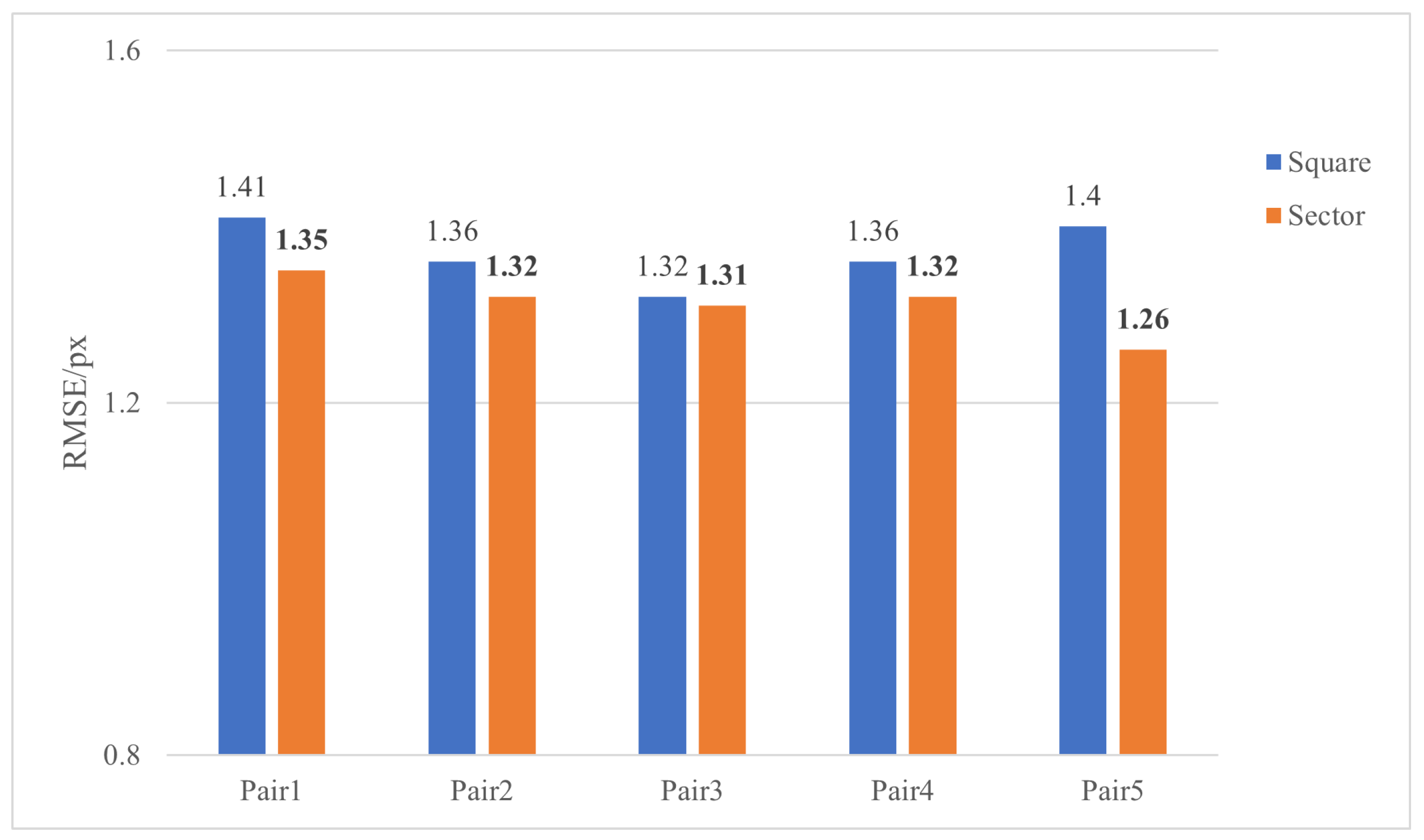
Preprints 80580 g010
Preprints 80580 g011
Figure 11. Matching results for sar-optical images.
Figure 11. Matching results for sar-optical images.
Preprints 80580 g011
Preprints 80580 g012
Figure 12. Average running time of registration methods.
Figure 12. Average running time of registration methods.
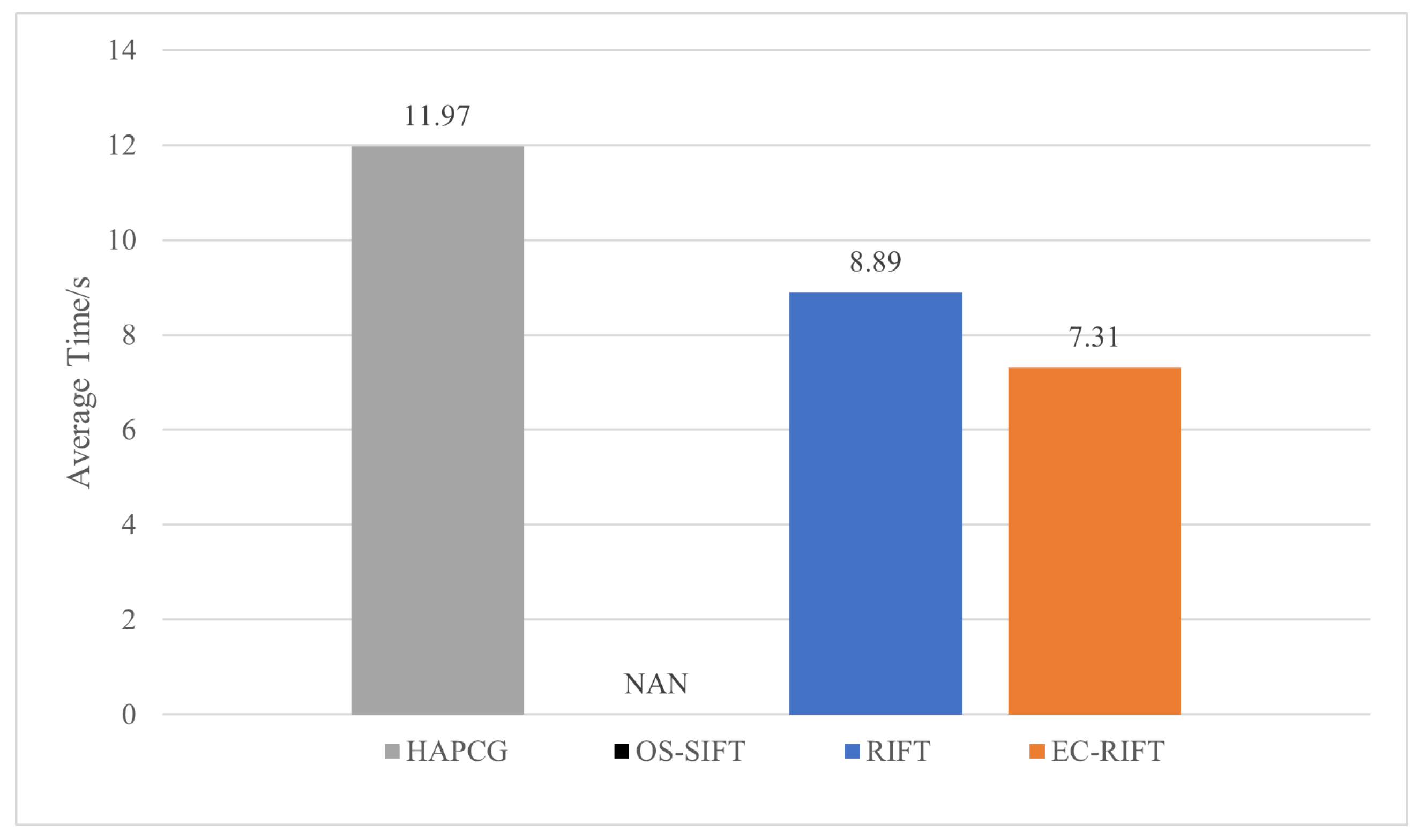
Preprints 80580 g012
Preprints 80580 g013
Figure 13. Matching results for multi-source images.
Figure 13. Matching results for multi-source images.
Preprints 80580 g013
Preprints 80580 g014
Figure 14. MIMs of images.
Figure 14. MIMs of images.
Preprints 80580 g014
Preprints 80580 g015
Figure 15. Matching results with scale and rotation differences.
Figure 15. Matching results with scale and rotation differences.
Preprints 80580 g015
Table 1. Comparison of preprocessed data registration results.
Table 1. Comparison of preprocessed data registration results.
Data Method RMSE/px Running time/s
Pair6 HAPCG 0.88 2.8
OS-SIFT × ×
RIFT 0.99 2.26
EC-RIFT 0.95 1.99
Pair7 HAPCG 1.59 2.56
OS-SIFT × ×
RIFT 1.11 1.79
EC-RIFT 0.92 1.76
Table 2. Registration results of OLG and LG.
Table 2. Registration results of OLG and LG.
Data Filter Detection time/s RMSE/px
Pair1 LG 0.99 1.41
OLG 0.58 1.35
Pair2 LG 3.20 1.36
OLG 1.81 1.32
Pair3 LG 1.50 1.32
OLG 1.04 1.27
Pair4 LG 0.99 1.34
OLG 0.65 1.33
Pair5 LG 0.23 1.40
OLG 0.15 1.29
Table 3. Comparison with other methods
Table 3. Comparison with other methods
Data Method RMSE/px Running time/s
Pair1 HAPCG 1.95 9.98
OS-SIFT 1.38 9.15
RIFT 1.37 10.45
EC-RIFT 1.35 8.81
Pair2 HAPCG 1.95 26.13
OS-SIFT × ×
RIFT 1.34 14.26
EC-RIFT 1.19 11.01
Pair3 HAPCG 1.93 13.64
OS-SIFT NAN NAN
RIFT 1.32 6.41
EC-RIFT 1.28 5.06
Pair4 HAPCG 1.97 7.98
OS-SIFT × ×
RIFT 1.35 9.36
EC-RIFT 1.24 9.27
Pair5 HAPCG 1.76 2.12
OS-SIFT NAN NAN
RIFT 1.36 3.95
EC-RIFT 1.31 2.39
Table 4. Quantitative results for multi-source images
Table 4. Quantitative results for multi-source images
Data Method RMSE/px Running time/s
Infrared-optical RIFT 1.16 14.70
EC-RIFT 1.16 13.13
Day-night RIFT 1.27 12.37
EC-RIFT 1.26 10.68
Depth-optical RIFT 1.36 11.98
EC-RIFT 1.33 11.50
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated