Preprint
Article
Parallel Subgradient-Like Extragradient Approaches for Variational Inequality and Fixed Point Problems with Bregman Relatively Asymptotical Nonexpansivity
Altmetrics
Downloads
83
Views
12
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
24 July 2023
Posted:
02 August 2023
You are already at the latest version
Alerts
Abstract
In a p-uniformly convex and uniformly smooth Banach space, let the pair of variational inequality and fixed point problems (VIFPPs) consist of two variational inequality problems (VIPs) involving two uniformly continuous and pseudomonotone mappings and two fixed point problems implicating two uniformly continuous and Bregman relatively asymptotically nonexpansive mappings. This article designs two parallel subgradient-like extragradient algorithms with inertial effect for solving this pair of VIFPPs, where each algorithm consists of two parts which are of symmetric structure mutually. Under mild registrations, we prove weak and strong convergence of the suggested algorithms to a common solution of this pair of VIFPPs, respectively. Lastly, an illustrative example is furnished to verify the applicability and implementability of our proposed approaches.
Keywords:
Subject: Computer Science and Mathematics - Analysis
MSC: 47H05; 47H10; 65K15; 65Y05; 68W25
1. Introduction
Let and be the metric projection from H onto C with C being convex and closed in a real Hilbert space H. Suppose that the and are the inner product and induced norm in H, respectively. Given a nonlinear operator . We denote by the fixed-point set of S. Also, the and → are used to stand for the real-number set, the weak convergence and the strong convergence, respectively. A self-mapping S on C is known as being of asymptotical nonexpansivity if ∃ (nonnegative real sequence) s.t.
with . In particular, in case , S reduces to a nonexpansive mapping. Let be a mapping. Recall that so-called variational inequality problem (VIP) is to find such that
Here denotes the set of solutions of the VIP. In 1976, under weaker assumptions, Korpelevich [24] put forward the extragradient rule for approximating an element of , i.e., for any starting , is the sequence generated by
with . If , then converges weakly to an element in . To the best of our understanding, the Korpelevich extragradient rule is one of the most effective approaches for solving the VIP till now. The literature on the VIP is vast and the Korpelevich extragradient rule has acquired the extensive attention paid by numerous scholars, who ameliorated it in various ways; see e.g., [1-6, 8-9, 13-16, 19, 21-23, 25-28, 31, 34].
Recently, Thong and Hieu [21] first put forth the inertial subgradient extragradient rule, i.e., for any starting , is the sequence generated by
with constant . Under suitable assumptions, they proved the weak convergence of to an element of . Subsequently, Thong and Hieu [15] introduced two inertial subgradient extragradient algorithms with linear-search process for solving the VIP with Lipschitz continuous monotone mapping A and the fixed-point problem (FPP) of a quasi-nonexpansive mapping S with demiclosedness property in H.
Algorithm 1.1 (see [15, Algorithm 1]). Initialization: Given . Choose any initial .
Iterations: Compute below:
Step 1. Put and calculate , wherein is picked as the largest s.t. .
Step 2. Calculate , where .
Step 3. Calculate . When , one has . Put and return to Step 1.
Algorithm 1.2 (see [15, Algorithm 2]). Initialization: Given . Choose any initial .
Iterative steps: Compute below:
Step 1. Putt and calculate , wherein is picked as the largest s.t. .
Step 2. Calculate , where .
Step 3. Calculate . When , one has . Put and return to Step 1.
With the help of suitable assumptions, it was proved in [15] that the sequences generated by the suggested algorithms converge weakly to a point in . In addition, combining the subgradient extragradient method and the Halpern’s iteration rule, Kraikaew and Saejung [22] proposed the Halpern subgradient extragradient rule for solving the VIP, and showed that the sequence generated by the proposed rule converges strongly to a point in . Recently, Reich et al. [27] put forward two gradient-projection algorithms for solving the VIP for uniformly continuous pseudomonotone mapping. In particular, they used a novel Armijo-type line search to acquire a hyperplane which strictly separates the current iterate from the solutions of the VIP under consideration. They proved that the sequences generated by two algorithms converge weakly and strongly to a point in , respectively.
On the other hand, let where C is convex and closed in a uniformly smooth and p-uniformly convex Banach space E for satisfying . Let be the duality mapping of E, and let be the dual of E with the duality . Suppose that the norm and the duality pairing between E and are denoted by and , respectively. Let , be the Bregman distance with respect to (w.r.t) and be Bregman’s projection w.r.t. from E onto C, and presume that s.t. , and . Assume that is uniformly continuous and pseudomonotone operator and S is Bregman relatively nonexpansive self-mapping on C. Very recently, inspired by the research works in [27], Eskandani et al. [31] proposed the hybrid projection approach with linesearch process for approximating a point in .
Algorithm 1.3 (see [31]). Initialization: Given and choose randomly.
Iterations: Compute below:
Step 1. Calculate and . If and , then stop; . If this case does not occur, then,
Step 2. Calculate , with both and being the smallest s.t. .
Step 3. Calculate and , with and .
Again put and return to Step 1.
With the help of suitable conditions, it was proven in [31] that converges strongly to .
This article designs two parallel subgradient-like extragradient algorithms with inertial effect for resolving a pair of variational inequality and fixed point problems (VIFPPs) in uniformly smooth and p-uniformly convex Banach space E. Here two variational inequality problems (VIPs) involve two uniformly continuous pseudomonotone operators and two fixed point problems implicate two uniformly continuous Bregman relatively asymptotically nonexpansive mappings. Moreover, each algorithm consists of two parts which are of symmetric structure mutually. With the help of appropriate registrations, it is proven that the sequences generated by the suggested algorithms converge weakly and strongly to a solution of this pair of VIFPPs, respectively. Lastly, an illustrative instance is furnished to check the implementability and applicability of the proposed approaches.
The structure of the article is described as follows: Section 2 releases certain terminologies and preliminary results for later applications. Section 3 is focused on discussing the convergence of the suggested algorithms. In Section 4, the major outcomes are utilized to deal with the CFPP and VIPs in an illustrative instance. Our results improve and develop the revelent ones obtained previously in [15, 27, 31].
2. Preliminaries
Let () be a real Banach space, whose dual is denoted by . We use the and to represent the strong and weak convergence of to , respectively. Moreover, the set of weak cluster points of is denoted by , i.e., . Let and with . A Banach space E is referred to as being strictly convex if for each with , one has . E is referred to as being uniformly convex if , s.t. with , one has . It is known that a uniformly convex Banach space is reflexive and strictly convex. The modulus of convexity of E is the function defined by . It is also known that E is uniformly convex if and only if . Moreover, E is referred to as being p-uniformly convex if s.t. for .
The nonnegative function on is called the modulus of smoothness of E if . E is said to be uniformly smooth if , and q-uniformly smooth if s.t. . Recall that E is of p-uniform convexity iff is of q-uniform smoothness; see e.g., [32] for more details. Putting for each , we say that is uniformly convex on bounded sets (see [31]) if , where is specified below
The is known as the gauge function of f with uniform convexity. It is clear that the gauge is nondecreasing.
Let be a convex function. If the limit exists for each , then f is referred to as being Gâteaux differentiable at y. In this case, the gradient of f at y is of linearity, and is formulated as . The f is referred to as being of Gâteaux differentiablility if it is of Gâteaux differentiablility at any . In case is achieved uniformly for any , we say that f is of Fréchet differentiablility at y. Besides, f is referred to as being of uniform Fréchet differentiablility on a subset if is achieved uniformly for . When the norm of E is of Gâteaux differentiablility, E is said to be of smoothness.
Let for . The is specified below
It is known that E is of smoothness iff is of single value from E into . Also, E is of reflexivity iff is of surjectivity, and E is strictly convex iff is of one-to-one property. So it follows that, when the smooth Banach space E is of both strict convexity and reflexivity, is the bijection and in this case, . Also, recall that E is of uniform smoothness iff the function is of uniform Fréchet differentiablility on bounded sets iff is of uniform continuity on bounded sets. Moreover, E is of uniform convexity iff the function is of uniform convexity (see [32]).
Let the function be of both Gâteaux differentiablility and convexity. Bregman’s distance w.r.t. f is specified below
It is worth mentioning that the is not a metric in the common sense of the terminology. Evidently, but can not lead to . Generally, is not of symmetry and fulfill no triangle inequality. However, fulfills the three point equequality
See [20] for many details.
It is remarkable that the on the smooth E is Gâteaux’s derivative of . Thus, Bregman’s distance w.r.t. is specified below
In the p-uniformly convex and smooth Banach space E for , there holds the following relationship between the metric and Bregman distance:
where is some fixed number (see [12]). Via (2.1) it can be easily seen that for each of boundedness, the relation is valid:
Let with C being convex and closed in a strictly convex, smooth and reflexive Banach space E. Bregman’s projection is formulated as minimizers of Bregman’s distance. Bregman’s projection of onto C w.r.t. indicates a unique point s.t. . In the case of Hilbert space, Bregman’s projection w.r.t. reduces to the metric projection. Using [30, Theorem 2.1] and [18, Corollary 4.4], in a uniformly convex Banach space, the characterization of Bregman’s projection is formulated by:
Meantime, (2.2) is equivalent to the descent property
When , reduces to the normalized duality mapping and is written as J. The is formulated below
and .
In terms of [31], the function associated with is specified below
So, . Moreover, by the subdifferential inequality, we obtain
In addition, is convex in the second variable. Hence one has
Lemma 2.1 ([30]). Let E be a uniformly convex Banach space and be two sequences in E such that the first one is bounded. If , then .
Assume that S is a self-mapping on C. Let the indicate the set of fixed points of S, that is, . A point is referred to as an asymptotic fixed point of S if s.t. and . Let the denote the asymptotic fixed point set of S. The terminology of asymptotic fixed points was invented in [11]. A self-mapping S on C is known as being the one of Bregman’s relatively asymptotical nonexpansivity w.r.t. if , and with both and
In particular, if , then S reduces to the one of Bregman’s relatively nonexpansivity w.r.t. , that is, and . In addition, a mapping is known as being
(i) monotone on C if ;
(ii) pseudo-monotone if ;
(iii)ℓ-Lipschitz continuous or ℓ-Lipschitzian if s.t. ;
(iv) of weakly sequential continuity if ,the relation holds: .
Lemma 2.2 ([31]). Let be a constant and suppose that is a uniformly convex function on any bounded subset of a Banach space E. Then
and for , with being the gauge of f with uniform convexity.
Proof. It is easy to show the conclusion.
Lemma 2.3 ([28]). Let be a Banach space for and suppose that is of uniform continuity on any bounded subset of and is of boundedness. Then is of boundedness.
Lemma 2.4 ([10]). Assume with C being convex and closed, and let be of both pseudomonotonicity and continuity. Given . Then .
Lemma 2.5. Suppose that E is a smooth and p-uniformly convex Banach space for , where is of weakly sequential continuity. Assume and . If , and converges for each . Then one has the weak convergence of to an element of .
Proof. First, one has by (2.1). Thus we obtain that is of boundedness. Since E is reflexive, we get . Also, one claims that converges weakly to an element of . Indeed, let with . Then, and s.t. and . Since is weakly sequentially continuous, we obtain both and . Note that . So, utilizing the convergence of the sequences and , we conclude that
which hence yields . From (2.1) we get . This arrives at a contradiction. Thereupon, this means that converges weakly to an element of .
The lemma below was put forth in by [29]. It is easy to verify that the proof of the lemma in Banach spaces is actually the same as in .
Lemma 2.6. Assume with C being convex and closed. Suppose that where is defined on E. If and h is Lipschitz continuous on C with modulus , then , where stands for the distance of x to K.
Lemma 2.7 ([17]). Let be a sequence of real numbers that does not decrease at infinity in the sense that, s.t. for all k. Assume that is defined as , with integer satisfying . Then the following hold:
(i) and ;
(ii) and .
Lemma 2.8 ([7]). Let be a sequence in satisfying , with and being real sequences satisfying the conditions: (i) and ; and (ii) or . Then as .
Lemma 2.9 ([33]). Let and be sequences of nonnegative real numbers satisfying the inequality . If and , then exists.
3. Main Results
In this section, let with C being convex and closed in uniformly smooth and p-uniformly convex Banach space E for . We are now in a position to present and analyze our iterative algorithms for approximating a common solution of a pair of VIFPPs, where each algorithm consists of two parts which are of symmetric structure mutually. Assume always that the following conditions hold:
(C1) are the mappings of both uniform continuity and Bregman’s relatively asymptotical nonexpansivity with sequences and , respectively.
(C2) For , is of both uniform continuity and pseudomonotonicity on C, s.t. with .
(C3) .
Algorithm 3.1. Initialization: Given arbitrarily and let for . Choose and s.t. , and . Moreover, assume , and given the iterates and , choose s.t. , where
Iterations: Compute below:
Step 1. Put and calculate , , and , with and being the smallest s.t.
Step 2. Calculate , with and
Step 3. Calculate , and , with and being the smallest s.t.
Step 4. Calculate and , with , and
Again set and go to Step 1.
The following lemmas are used in the proofs of our main results in the sequel.
Lemma 3.1. Suppose that is the sequence constructed in Algorithm 3.1. Then the following hold: and .
Proof. Note that the former inequality is analogous to the latter. So it suffices to show that the latter holds. Indeed, using the definition of and properties of , one has
Setting in the last inequality, from (2.1) we get
which completes the proof.
Lemma 3.2. Linesearch rules (3.1), (3.3) of Armijo-type and sequence constructed in Algorithm 3.1 are well defined.
Proof. Observe that the rule (3.1) is analogous to the one (3.3). So it suffices to show that the latter is valid. Using the uniform continuity of on C, from one gets . In the case of , it is explicit that . In the case of , we obtain that s.t. (3.3) holds.
It is not hard to check that and are convex and closed for all n. Let us show that . Choose a arbitrarily. Since is Bregman’s relatively asymptotically nonexpansive mapping, by Lemma 2.2 one gets
which hence leads to . Meanwhile, from Lemma 2.4, we get . Thus,
So it follows from (3.3) that
By Lemma 3.1 we have
which together with (3.5), attains
Therefore, . As a result, the sequence is well defined.
Lemma 3.3. Suppose that and are the sequences generated by Algorithm 3.1. If and , then and .
Proof. Note that the former inclusion is analogous to the latter. So it suffices to show that the latter is valid. Indeed, taking a arbitrarily, we know that , s.t. and . So, we have . Noticing the convexity and closedness of C, according to and , one gets . In what follows, ones consider two aspects. If , then (due to for all ). If , by the condition on , one gets . So, we might assume that . From (2.2), we get
and hence
Since is uniformly continuous, using Lemma 2.3 we deduce that is of boundedness. Observe that is also of boundedness. So, using the uniform continuity of on any bounded subset of E, from (3.6) we have
To prove that z lies in , one picks in s.t. . For any k, we choose the smallest s.t. for all ,
Because is decreasing, we get the increasing property of . For the sake of simplicity, is still written as . It is known that for all k (due to ). Then, putting , one gets . Indeed, it is evident that . So, by (3.8) one has . Again from the pseudomonotonicity of one has
Let us show that . Indeed, noticing and , we obtain that
Hence one gets as . Thus, taking the limit as in (3.9), from (C3) one has for all . In terms of Lemma 2.4 we conclude that z lies in .
Lemma 3.4. Suppose that and are the sequences generated by Algorithm 3.1. Then the following hold:
(i) ;
(ii) .
Proof. Note that the claim (i) is analogous to the one (ii). So it suffices to show that the second is valid. To verify the second, we discuss two cases. In case , one may presume that satisfying for all n, which immediately leads to
This together with , arrives at .
In case , we assume that . This ensures that satisfying
We define . Noticing , From (2.1) we get and hence
Because is uniformly continuous on bounded subsets of C, we obtain
From the step size rule (3.3) and the definition of , it follows that
Now, taking the limit as , from (3.12) we have . This, however, yields a contradiction. As a result, as .
In what follows, we show the first main result.
Theorem 3.1. Suppose that E is uniformly smooth and p-uniformly convex, where is of weakly sequential continuity. If under Algorithm 3.1, and , then .
Proof. Note that that the necessity is valid. So we need to only show the statement of sufficiency. Presume . Choose a arbitrarily. Clearly, . Using the definition of , we get . From (2.1), (2.6) and the three point identity of we get
where for some . By Lemma 2.2 we get
Noticing , by (2.1) and (2.3) we get
Because , by (2.1) and (2.3) we have
Combining these inequalities and (3.13), leads to
which hence leads to
Since and , by Lemma 2.9 we deduce that exists. In addition, by the boundedness of , we conclude that , and are also bounded. From (3.14) we obtain
which immediately yields
Since , , and exists, it follows that , , and , which hence yields . From , it is readily known that . Noticing , we obtain from and the definition of that
Hence, using (2.1) and uniform continuity of on bounded subsets of , we conclude that and
Since is of boundedness and E is of reflexivity, we obtain that is nonempty. Next, let us show that . Choose a z in arbitrarily. It is known that satisfying . By (3.15) one gets . Since is of boundedness, one knows that satisfying . So it follows that for all ,
which implies that is -Lipschitz continuous on . Using Lemma 2.6, we get
Since lies in , by (3.14) one has
Since , , and exists, we have and thus . By (3.15) we get
Furthermore, by Lemma 2.2, we have
Therefore,
Taking the limit in the last inequality as , and using uniform continuity of on bounded subsets of E, (3.17) and , we get and hence . Since is uniformly continuous on any bounded subset of , we deduce that
Now let us show . Since is of boundedness, it follows that satisfying . Thus we obtain that for all ,
which guarantees that is -Lipschitz continuous on . By Lemma 2.6, we get
Combining (3.14), (3.16) and (3.19), we have
Thus,
According to Lemma 3.4, we have
In addition, from (3.15) and we infer that and . By Lemma 3.3 we obtain that and . Consequently,
Next we claim that . Indeed, by (3.15) we immediately get
We first claim that and . Actually, using (3.15), (3.18) and uniform continuity of on C for , we obtain that and . Thus, from and (due to the assumptions) we deduce that
and
These together with and , ensure that . Therefore, . This means that . As a result, by Lemma 2.5 one gets the desired conclusion.
In what follows, we prove the second main outcome for finding a solution of a pair of VIFPPs for two operators of both uniform continuity and pseudomonotonicity, and two mappings of both uniform continuity and Bregman’s relatively asymptotical nonexpansivity in E.
Algorithm 3.2. Initialization: Given arbitrarily and let and for . Choose and s.t. , , , and . Moreover, given the iterates and , choose s.t. , where and
Iterations: Compute below:
Step 1. Put , and calculate , , and , where and is the smallest s.t.
.
Step 2. Calculate , with and
.
Step 3. Calculate , and , where and is the smallest s.t.
.
Step 4. Set , and calculate and , where and
.
Again put and return to Step 1.
Theorem 3.2. Suppose that the conditions (C1)-(C3) hold. If under Algorithm 3.2, and , then .
Proof. It is explicit that the necessity of Theorem 3.2 holds. Hence we need to only prove the statement of sufficiency. Assume that . In what follows, we divide our proof into four claims.
Claim 1. One shows that
for some . In fact, put . Noticing and , we obtain from (2.1) and (2.3) that
and
By the similar reasonings to those in the proof of the above theorem, we obtain
where for some . This ensures that is bounded.
Using (2.6) and the last two inequalities, from and we obtain
which immediately arrives at the desired claim. In addition, it is easily known that , and are of boundedness.
Claim 2. One shows that
Indeed, set . By Lemma 2.2 we get
(3.22)
and
Set . From (2.5), we have
Furthermore, from (3.23) one has
This together with (3.24), arrives at
which immediately yields
Claim 3. One shows that
Indeed, by the analogous reasonings to those of (3.20), one gets
Applying (3.26), (3.23) and (3.22), we have
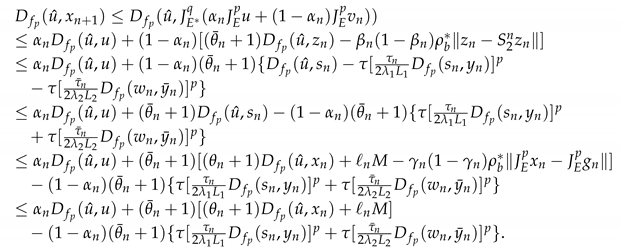
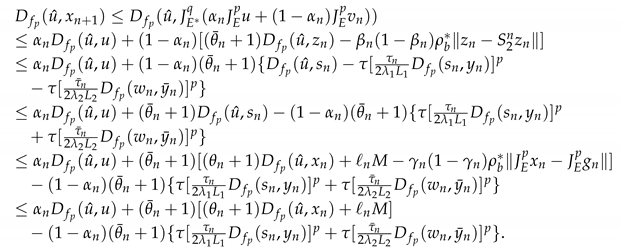
Claim 4. One shows that . Indeed, since E is reflexive and is bounded, one has . Choose a z in arbitrarily. It is known that satisfying . One writes for all n. In what follows, let us prove in the two possible aspects below.
Aspect 1. Assume that s.t. is non-increasing. It is known that and hence . From (3.25) and (3.22) we get
which hence yields
Since and is of boundedness, one obtains , , and , which hence yields . From , it is easily known that . Noticing , we infer from and the definition of that
Hence, using (2.1) and uniform continuity of on any bounded subset of , we conclude that and
Furthermore, from (3.24) and (3.22) we have
By the similar reasonings, we deduce that , which hence leads to (due to ). Using uniform continuity of on bounded subsets of , we get
This together with (3.28) implies that
It is clear that
Let us show that . Indeed, since , it can be readily seen that
In addition, using (2.3), (3.22) and (3.23), we have
which hence yields
So it follows that and hence . Thus, from (3.31) we get
We now claim that and . Indeed, using (3.28), (3.29) and uniform continuity of on C for , we obtain that and . Thus, from and (due to the assumptions) we deduce that
and
These together with and (due to (3.30)), ensure that .
In what follows, we show that . From (3.27), we have
So it follows that , and hence
By Lemma 3.4, we obtain
Applying (3.34) and Lemma 3.3, one gets . Thus one has . Consequently, . Finally, let us prove . One can pick s.t.
Because E is reflexive and is bounded, we might assume . Using (2.2) and we infer that
which along with (3.31), arrives at
From (3.24) and (3.22), we get
Using uniform continuity of on any bounded subset of E, from (3.32) and the boundedness of we get
Noticing and , we deduce that
Thanks to with , utilizing Lemma 2.8 to (3.36) one gets and hence .
Aspect 2. Assume that satisfying for all k, with being the natural-number set. Let be formulated below
Using Lemma 2.7, one has
From (3.25) and (3.22) it follows that
Noticing and , we obtain that and
Also, from (3.24) and (3.22) we have
Noticing and using the similar reasonings to those in Case 1, we get
This together with (3.38) implies that
Noticing , by (3.39) one gets
Applying the same reasonings as in Case 1, one has that ,
and
Using (3.36), we get
which together with (3.37), hence yields
As a result, from (3.42) we deduce that
From (3.42), (3.43) and (3.44), one concludes that
Again using (3.37), one gets . Therefore, . This completes the proof.
Remark 3.1. It can be easily seen from the proof of Theorem 3.2 that if the assumption that , is used in place of the one that and , then Theorem 3.2 is still valid.
Under Algorithm 3.1, setting one obtains the algorithm below for approximating a point in .
Algorithm 3.3. Initialization: Given arbitrarily and let . Choose and s.t. , and . Moreover, assume , and given the iterates and , choose s.t. , where
Iterations: Compute below:
Step 1. Put , and calculate , , and , with and being the smallest s.t.
Step 2. Calculate , with and
Step 3. Calculate and , with .
Again put and return to Step 1.
Corollary 3.1. Let the terms (C1)-(C2) with , be valid, and assume . If under Algorithm 3.3, and , then .
Next, put the identity mapping of E. Then we get . In this case, Algorithm 3.2 can be rewritten as the iterative scheme below for settling a pair of VIPs and the FPP of . By Theorem 3.2 one derives the strong convergence outcome below.
Corollary 3.2. Suppose that the condition (C2) holds, and let . For initial , choose s.t. , where
Suppose that is the sequence constructed by
where and are the smallest nonnegative integers k and j satisfying, respectively,
and the sets , are constructed below
(i) and ;
(ii) and .
Then, provided .
4. Implementability and Applicability
In this section, we provide an illustrative example to demonstrate the applicability and implementability of our suggested approaches. For , we take , and . First, we present an instance involving the mappings of both uniform continuity and pseudomonotonicity, and the mappings of both uniform continuity and Bregman’s relatively asymptotical nonexpansivity satisfying . Put and with the inner product and induced norm being written as and , respectively. The starting are randomly chosen in C. For , let be defined as and for all . Next, let us prove that is the mapping of both Lipschitz continuity and pseudomonotonicity. In fact, for each one has
Thus, is of Lipschitz continuity. Also, one shows that is of pseudomonotonicity. For any , it is easily known that
It is easy to see that is of both Lipschitz continuity and monotonicity. Indeed, we deduce that and
Now, let and be defined as . It is clear that for .
Also, is the mapping of Bregman’s relatively asymptotical nonexpansivity with , and we get . In fact, note that
and
Consequently,
In addition, putting , we obtain
In this case, the conditions (C1)-(C3) are satisfied.
Example 4.1. Let and . Given the iterates and , choose s.t. , where
Algorithm 3.1 is rewritten as follows:
with the sets and the step-sizes being picked as in Algorithm 3.1. By Theorem 3.1, one obtain .
Example 4.2. Let and . Given the iterates and , choose s.t. , where
Algorithm 3.2 is rewritten as follows:
with the sets and the step-sizes being picked as in Algorithm 3.2. By Theorem 3.2, we deduce that .
5. Conclusions
This article designs iterative algorithms for resolving a pair of VIFPPs in uniformly smooth and p-uniformly convex Banach spaces. With the help of parallel subgradient-like extragradient methods with both inertial effect and linesearch process, we fabricate two algorithms for approximating a common solution of the two pseudomonotone VIPs and the CFPP of two mappings of Bregman’s relatively asymptotical nonexpansivity. We are focused on discussing the weak and strong convergence of the proposed algorithms by using standard terms and novel manoeuvres. Besides, an illustrative example is furnished to bear up the applicability and implementability of our proposed approaches. Finally, it is worth mentioning that part of our future research is aimed at achieving the weak and strong convergence results for the modifications of our proposed approaches with Nesterov double inertial extrapolation steps (see [34]) and adaptive stepsizes.
References
- Yao, Y.; Liou, Y.-C.; Kang, S.M. Approach to common elements of variational inequality problems and fixed point problems via a relaxed extragradient method. Comput. Math. Appl. 2010, 59, 3472–3480. [Google Scholar] [CrossRef]
- Jolaoso, L.O.; Shehu, Y.; Yao, J.-C. Inertial extragradient type method for mixed variational inequalities without monotonicity. Math. Comput. Simul. 2022, 192, 353–369. [Google Scholar] [CrossRef]
- Ceng, L.-C.; Petrușel, A.; Yao, J.-C.; Yao, Y. Hybrid viscosity extragradient method for systems of variational inequalities, fixed points of nonexpansive mappings, zero points of accretive operators in Banach spaces. Fixed Point Theory 2018, 19, 487–502. [Google Scholar] [CrossRef]
- Ceng, L.C.; Petruşel, A.; Qin, X.; Yao, J.C. Two inertial subgradient extragradient algorithms for variational inequalities with fixed-point constraints. Optimization 2021, 70, 1337–1358. [Google Scholar] [CrossRef]
- Censor, Y.; Gibali, A.; Reich, S. The Subgradient Extragradient Method for Solving Variational Inequalities in Hilbert Space. J. Optim. Theory Appl. 2011, 148, 318–335. [Google Scholar] [CrossRef]
- Yao, Y.; Shahzad, N.; Yao, J.-C. Convergence of Tseng-type self-adaptive algorithms for variational inequalities and fixed point problems. Carpathian J. Math. 2021, 37, 541–550. [Google Scholar] [CrossRef]
- Xu, H.K.; Kim, T.H. Convergence of Hybrid Steepest-Descent Methods for Variational Inequalities. J. Optim. Theory Appl. 2003, 119, 185–201. [Google Scholar] [CrossRef]
- He, L.; Cui, Y.-L.; Ceng, L.-C.; Zhao, T.-Y.; Wang, D.-Q.; Hu, H.-Y. Strong convergence for monotone bilevel equilibria with constraints of variational inequalities and fixed points using subgradient extragradient implicit rule. J. Inequalities Appl. 2021, 2021, 1–37. [Google Scholar] [CrossRef]
- Zhao, T.-Y.; Wang, D.-Q.; Ceng, L.-C.; He, L.; Wang, C.-Y.; Fan, H.-L. Quasi-Inertial Tseng’s Extragradient Algorithms for Pseudomonotone Variational Inequalities and Fixed Point Problems of Quasi-Nonexpansive Operators. Numer. Funct. Anal. Optim. 2020, 42, 69–90. [Google Scholar] [CrossRef]
- Cottle, R.W.; Yao, J.C. Pseudo-monotone complementarity problems in Hilbert space. J. Optim. Theory Appl. 1992, 75, 281–295. [Google Scholar] [CrossRef]
- Reich, S. A weak convergence theorem for the alternating method with Bregman distances. In Theory and Applications of Nonlinear Operators; Marcel Dekker: New York, 1996; pp. 313–318. [Google Scholar]
- Schöpfer, F.; Schuster, T.; Louis, A.K. An iterative regularization method for the solution of the split feasibility problem in Banach spaces. Inverse Probl. 2008, 24. [Google Scholar] [CrossRef]
- Yang, J.; Liu, H.; Liu, Z. Modified subgradient extragradient algorithms for solving monotone variational inequalities. Optimization 2018, 67, 2247–2258. [Google Scholar] [CrossRef]
- Ceng, L.; Petrușel, A.; Qin, X.; Yao, J. A modified inertial subgradient extragradient method for solving pseudomonotone variational inequalities and common fixed point problems. Fixed Point Theory 2020, 21, 93–108. [Google Scholar] [CrossRef]
- Thong, D.V.; Hieu, D.V. Inertial subgradient extragradient algorithms with line-search process for solving variational inequality problems and fixed point problems, Numer. Algorithms 2019, 80, 1283–1307. [Google Scholar] [CrossRef]
- Shehu, Y.; Iyiola, O.S. Strong convergence result for monotone variational inequalities. Numer. Algorithms 2017, 76, 259–282. [Google Scholar] [CrossRef]
- Maingé, P.-E. Strong Convergence of Projected Subgradient Methods for Nonsmooth and Nonstrictly Convex Minimization. Set-Valued Anal. 2008, 16, 899–912. [Google Scholar] [CrossRef]
- Butnariu, D.; Resmerita, E. Bregman distances, totally convex functions, and a method for solving operator equations in Banach spaces. Abstr. Appl. Anal. 2006, 2006, 84919. [Google Scholar] [CrossRef]
- Vuong, P.T.; Shehu, Y. Convergence of an extragradient-type method for variational inequality with applications to optimal control problems. Numer. Algorithms 2019, 81, 269–291. [Google Scholar] [CrossRef]
- Reem, D.; Reich, S.; De Pierro, A. Re-examination of Bregman functions and new properties of their divergences. Optimization 2019, 68, 279–348. [Google Scholar] [CrossRef]
- Thong, D.V.; Hieu, D.V. Modified subgradient extragradient method for variational inequality problems, Numer. Algorithms 2018, 79, 597–610. [Google Scholar] [CrossRef]
- Kraikaew, R.; Saejung, S. Strong Convergence of the Halpern Subgradient Extragradient Method for Solving Variational Inequalities in Hilbert Spaces. J. Optim. Theory Appl. 2014, 163, 399–412. [Google Scholar] [CrossRef]
- Ceng, L.-C.; Wen, C.-F. Systems of variational inequalities with hierarchical variational inequality constraints for asymptotically nonexpansive and pseudocontractive mappings. Rev. de La Real Acad. de Cienc. Exactas, Fis. Y Nat. Ser. A. Mat. 2019, 113, 2431–2447. [Google Scholar] [CrossRef]
- Korpelevich, G.M. The extragradient method for finding saddle points and other problems. Ekonomikai Matematicheskie Metody 1976, 12, 747–756. [Google Scholar]
- Ceng, L.-C.; Shang, M. Hybrid inertial subgradient extragradient methods for variational inequalities and fixed point problems involving asymptotically nonexpansive mappings. Optimization 2021, 70, 715–740. [Google Scholar] [CrossRef]
- Ceng, L.; Petrușel, A.; Qin, X.; Yao, J. Pseudomonotone variational inequalities and fixed points. Fixed Point Theory 2021, 22, 543–558. [Google Scholar] [CrossRef]
- Reich, S.; Thong, D.V.; Dong, Q.-L.; Li, X.-H.; Dung, V.T. New algorithms and convergence theorems for solving variational inequalities with non-Lipschitz mappings. Numer. Algorithms 2021, 87, 527–549. [Google Scholar] [CrossRef]
- Iusem, A.N.; Nasri, M. Korpelevich’s method for variational inequality problems in Banach spaces. J. Glob. Optim. 2011, 50, 59–76. [Google Scholar] [CrossRef]
- He, Y. A new double projection algorithm for variational inequalities. J. Comput. Appl. Math. 2006, 185, 166–173. [Google Scholar] [CrossRef]
- Butnariu, D.; Iusem, A.N.; Resmerita, E. Total convexity for powers of the norm in uniformly convex Banach spaces. J. Convex Anal. 2000, 7, 319–334. [Google Scholar]
- Eskandani, G.Z.; Lotfikar, R.; Raeisi, M. Hybrid projection methods for solving pseudo-monotone variational inequalities in Banach spaces, to appear in Fixed Point Theory, 2023.
- Takahashi, Y.; Hashimoto, K.; Kato, M. On sharp uniform convexity, smoothness, and strong type, cotype inequalities. J. Nonlinear Convex Anal. 2002, 3, 267–281. [Google Scholar]
- Osilike, M.O.; Aniagbosor, S.C.; Akuchu, B.G. Fixed points of asymptotically demicontractive mappings in arbitrary Banach spaces. PanAm. Math. J. 2002, 12, 77–88. [Google Scholar]
- Yao, Y.; Iyiola, O.S.; Shehu, Y. Subgradient Extragradient Method with Double Inertial Steps for Variational Inequalities. J. Sci. Comput. 2022, 90, 1–29. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





