Prerpints.org logo
Preprint
Article

Non-Cooperative Spectrum Sensing Strategy based on Recurrence Quantification Analysis in the Context of the Cognitive Radio

Altmetrics

Downloads

135

Views

42

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

28 July 2023

Posted:

31 July 2023

You are already at the latest version

Alerts
Abstract
This paper addresses the problem of non-cooperative spectrum sensing in very low signal noise ratio (SNR) conditions. In our approach, detecting an unoccupied bandwidth consists to detect the presence or absence of a communication signal on this bandwidth. Major well known communication signals may contain hidden periodicities, we use the Recurrence Quantification Analysis (RQA) to reveal the hidden periodicities. RQA is very sensitive to a reliable estimation of the phase space dimension m or the time delay τ. In view of the limitations of algorithms proposed in the literature, we have proposed a new algorithm to estimate simultaneously the optimal values of m and τ. The new proposed optimal values allow the states reconstruction of the observed signal and then the estimation of the distance matrix. This distance matrix has particular properties which we have exploited to propose the Recurrence Analysis based Detector (RAD). RAD can detect a communication signal in a very low SNR condition. Using Receiver Operating Characteristic curves, our experimental results corroborate the robustness of our proposed algorithm comparing to classical widely used algorithms.
Keywords: 
Subject: Computer Science and Mathematics  -   Signal Processing

1. Introduction

The need to make better use of the radio spectrum is leading to the development of new spectrum access strategies. Among these strategies, the opportunistic spectrum access based on the Cognitive Radio concepts allows the sharing of a spectral bandwidth between two categories of users: Primary User “PU” and Secondary User “SU”. PU holds the license to exploit the bandwidth and SU is an opportunistic user willing to use the channel when the PU is idle. One of the most crucial challenge for SU is the identification of a free bandwidth by conducting a spectrum sensing [1,2]. Many reliable spectrum sensing methods have been eveloped to help the SU to limit their interference to PU’s transmission [3,4,5,6,7,8,9,10,11]. Among spectrum sensing approaches, we can mention the Waveform Detection (WFD) [12], the Cyclostationary Features based Detection (CFD)[13] and the Energy based Detection (ED) [14,15]. One of the most reliable methods, WFD, requires a prior knowledge on the PU’s signal characteristics. Based on the cyclic spectrum estimation, the CFD requires a relatively high computational cost for a high frequency resolution. The ED is the simplest detection method, but it is unable to distinguish a communication signal from an energetic noise, when the noise is not a weak sense stationary stochastic process or the Signal to Noise Ratio (SNR) is very low. Recently, spectrum sensing algorirthms, based on the promising concept of machine or deep learning, have been proposed [16,17,18,19]. However, these algorithms do not perform well in a non-cooperative context and at a low SNR (SNR ≤ -3 dB) and require a huge database to be optimized. To overcome these issues, we developped a blind strategy based on the Recurrence Quantification Analysis (RQA) of the received signal [20]. The quantification analysis of this recurrence can be used to find out some intrinsic features of a dynamic system, such as: hidden periodicities, stationarity features or linearity properties. Due to modulation standards, transmitted signals may contain hidden periodicities. Using this fact, we use Recurrence Quantification Analysis (RQA) tools to detect if the bandwidth allocated to PU is available or not. The main RQA tool used to quantify the recurrence level is the Recurrence Rate (RR) considered as the probability of having recurring states in a signal. In a recent work, we have proposed the RR based Detector (RRD) [20]. However, RRD is very sensitive to the SNR and depends on the choice of a recurrence threshold. To overcome the RRD limits, we propose in this paper an efficient algorithm called Recurrence Analysis based Detector (RAD). RAD exploits the similitude of distances among various states of the signal in a multidimensional space. This similitude of distances is evaluated by a square symmetrical matrix named the distance matrix. Using symmetrical property, we only exploit the upper triangular part of this matrix in order to reduce considerably the computational cost of the RAD. Then, we show that for a White Gaussian Noise (WGN), the coefficients of the first top diagonal of the distance matrix becomes a representative sample of all other coefficients. This is not the case for a communication signal even with a small SNR. This new approach can detect a communication signal in a very low SNR. We have analytically established the probabilities of detection P d and false alarm P f a . Through Monte Carlo simulations, we studied the Receiver Operating Characteristic (ROC) curves of RAD. The theoretical and experimental results show the ability of RAD to detect the presence of a communication signal as soon as the SNR is greater than − 12 dB with a very low probability of false alarm.
The rest of this paper is organized as follows: Section 2 presents the problem of spectrum sensing and our motivation for RQA. Section 3 deals with the concepts of RQA and the state of the art in the determination of embedding parameters in order to exhibit the hidden recurrences. Section 4 and Section 5 present the Recurrence Analysis based detection model and its theoretical and experimental performance. The last section contains the conclusion and perspectives.

2. Spectrum Sensing Problem

The radio spectrum is a limited natural ressource. Many techniques, such as cooperative communication systems and heterogeneous networks, have been developed to deal with this scarcity of the radio spectrum [21]. However, none of them can meet the strong demand for radio spectrum. The cognitive radio introduced by Mitola [22,23] is a promising solution allowing a dynamic access to the radio spectrum [1]. Dynamic spectrum access (DSA) is defined as a technique by which the operating spectrum of a radio network can be selected dynamically from the available spectrum [21]. The DSA allows the SU to exploit the holes in the spectrum dedicated to PU. The great challenge of DSA for SU remains the spectrum sensing stage during which the SU should detect the presence of PU on a given bandwidth.

2.1. Spectrum Sensing as a Statistical Decision

PU’s signal detection by the SU can be modeled as a binary hypothesis testing problem, given as [21]:
  • Hypothesis H 0 : PU’s signal is absent
  • Hypothesis H 1 : PU’s signal is present
Let y ( n ) be the signal observed by the Secondary User (SU):
y ( n ) = h s ( n ) + b ( n )
with h the channel gain and b ( n ) the channel noise. The noise samples b k are assumed to be independent and identically distributed (i.i.d). The noise b ( n ) is a Complex Circular Gaussian variable E b ( n ) = 0 ; E | b ( n ) | 2 = σ b 2 ; E . denotes the mathematical expectation.
The Test Statistic T, should be compared to a predetermined threshold λ for decision making. In this case, the probability of false alarm P f a and the probability (Pr) of detection P d [24] are defined as follows:
P f a ≜ P r { T ≥ λ | H 0 }
P d ≜ P r { T > λ | H 1 }
where ≜ stands for equal by definition.
For a good performance, P d should be increased as much as possible while keeping P f a under a small preselected value. In the non-cooperative spectrum sensing context, the detection algorithms should be able to find out intrinsic features of the communication signal to enhance a spectrum sensing task. One of the main features can be the recurrence of internal states in the communication signals. Hereinafter, we develop a robust algorithm based on RQA.

2.2. RQA Benefits

The RQA enjoys several specific properties:
1.
RQA is based on the chaos theory and normally used to extract the hidden recurring states of a dynamic system. The various part of a transmission chain such as modulation, filtering, coding, multiplexing, etc, generate hidden recurring states in the communication signals. Therefore, RQA can help detecting the presence of PU’s signal on a desired bandwidth.
2.
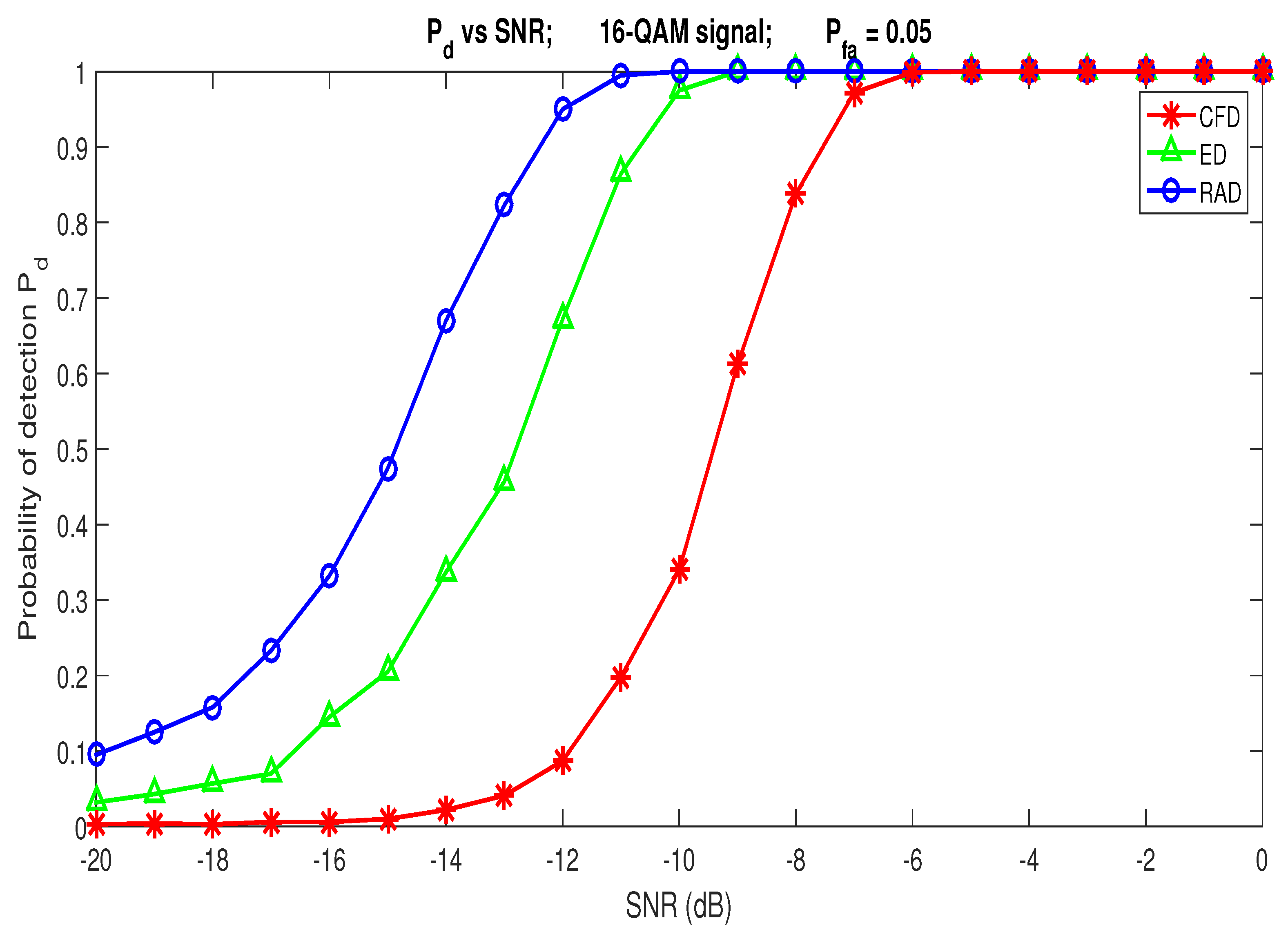
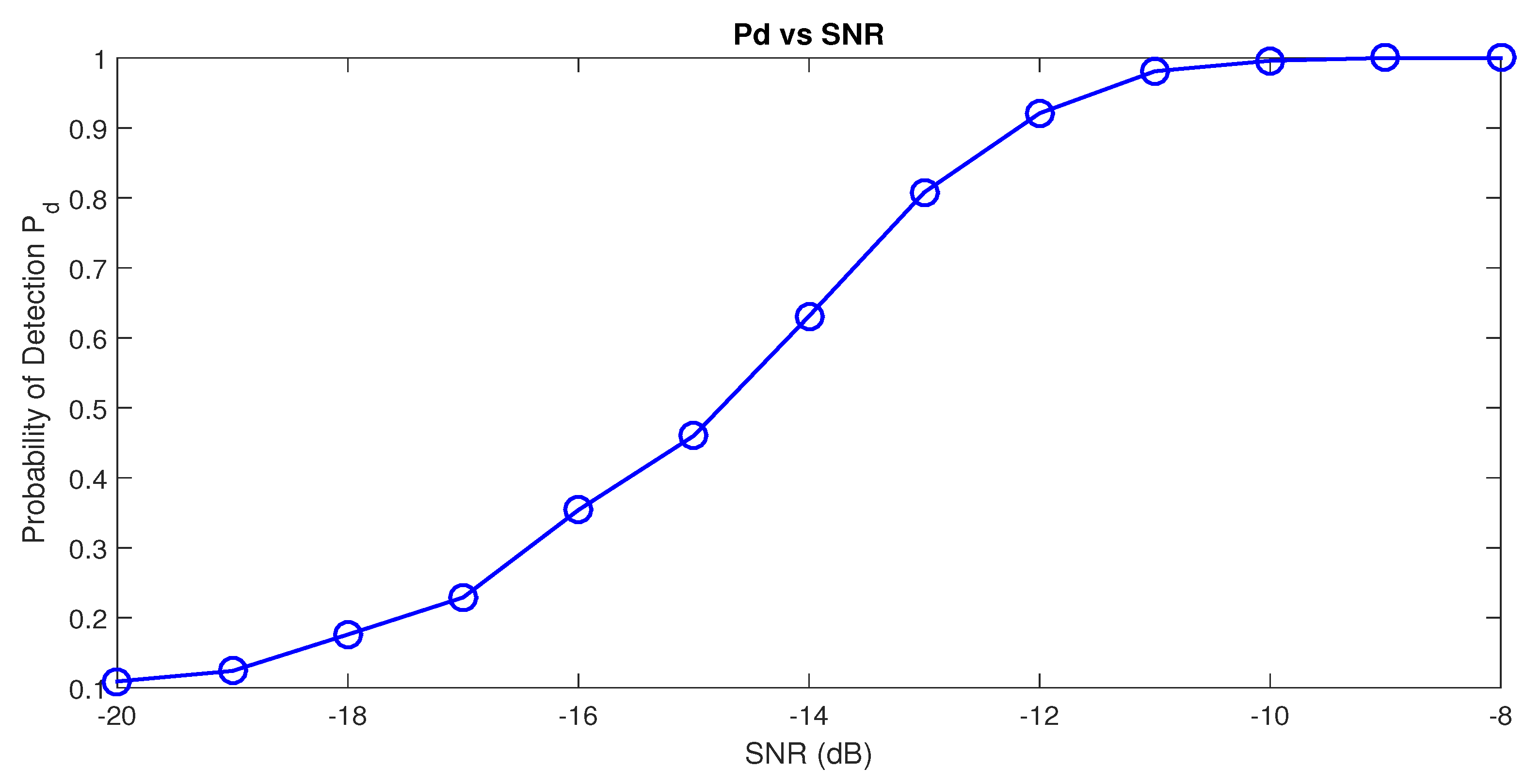
In a previous work [20], we showed that RQA is a promising tool for the spectrum sensing task. Indeed, in a non-cooperative context, we proposed the Recurrence Rate based detection model (RRD) and that previous algorithm was able to detect the presence of PU’s signals with SNR ≥ − 5 dB.
3.
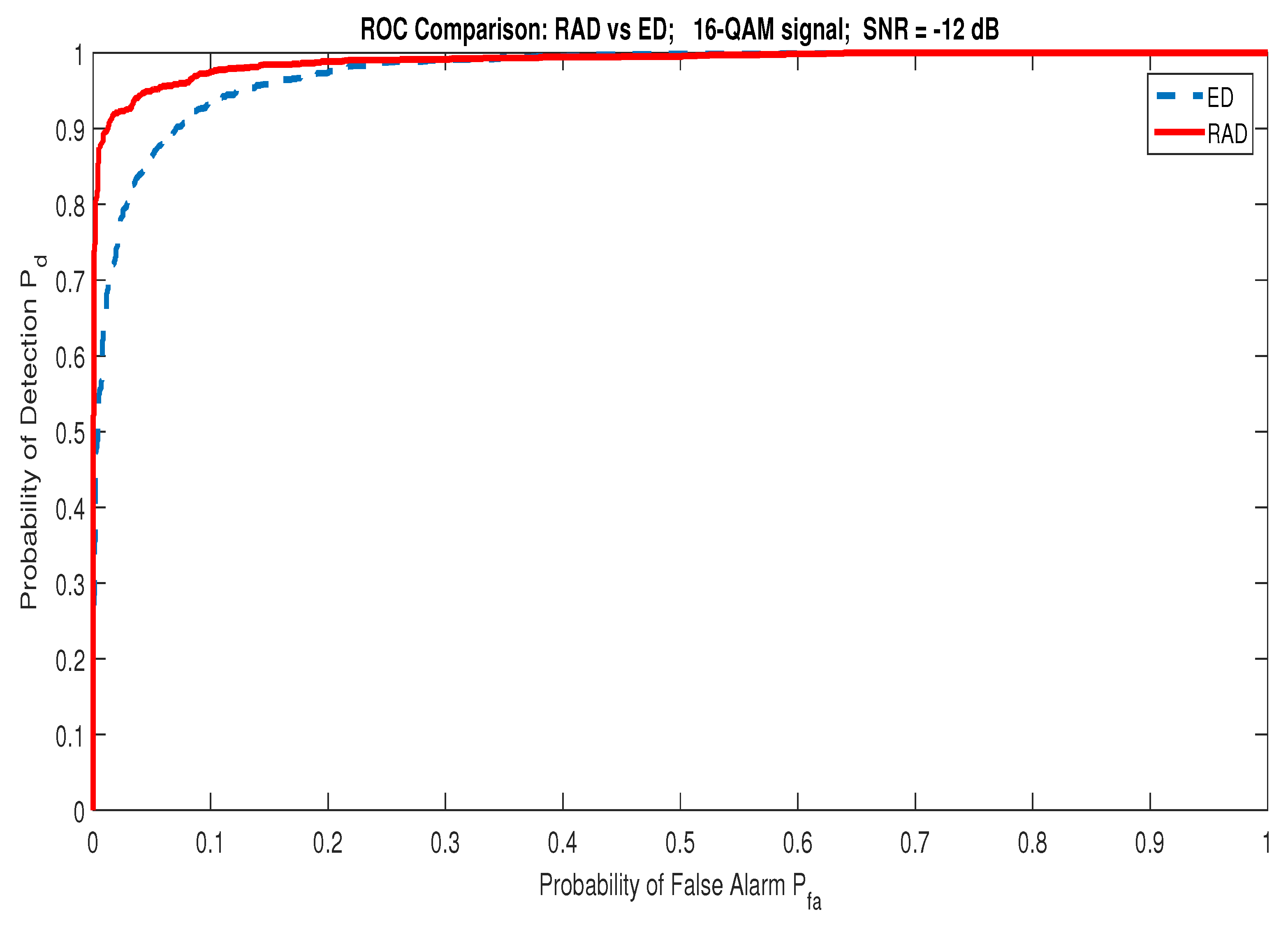
During the detection procedure, a spectrum sensing algorithm based on RQA does not require the estimation of the noise variance as required by some spectrum sensing algorithms such as ED; which is a great advantage.
4.
RQA can help detecting a communication signal in a very low SNR; and contrary to ED, Recurrence Analysis can distinguish a noisy communication signal from a high energy noise.
5.
RQA does not need a high computational cost like CFD. In a non-cooperative spectrum sensing, RQA is more robust compared to widely used ED or CFD.

3. Recurrence Quantification Analysis

Recurrence is a fundamental feature of dynamic systems, which can be exploited to study the behavior of these systems and to discover their intrinsic properties [20,25,26]. To analyze hidden recurrences in dynamic and non-linear systems, an important concept in the chaos theory, RQA can be used [27,28,29,30]. During the evolution of a dynamic system, some internal states can be quasi periodically repeated. In the phase space, the successive states of a dynamic system, form trajectories that characterize the temporal evolution of the system. Knowing the temporal evolution equation, any state of the system can be precisely determined at any time. Unfortunately in real world situations, this equation is unknown; instead, we dispose only a sequence of scalar measurements as time series [31,32]. From these time series, we should reconstruct the phase space. The gold standard method for the phase space reconstruction is the delay-coordinate embedding [31]. The objective of a delay-coordinate embedding method is to use the delayed versions of y ( n ) to form a multi-dimensional observable x k called state vector or state of y ( n ) . The state vector x k at moment k is defined as follows:
x k = [ y k , y k + τ , … , y k + ( m − 1 ) τ ] T
where y k denotes the sample of y at the moment k, τ is the time delay and m, the embedding dimension. The main challenge for the delay-coordinate embedding method is the reliable estimation of τ and m.

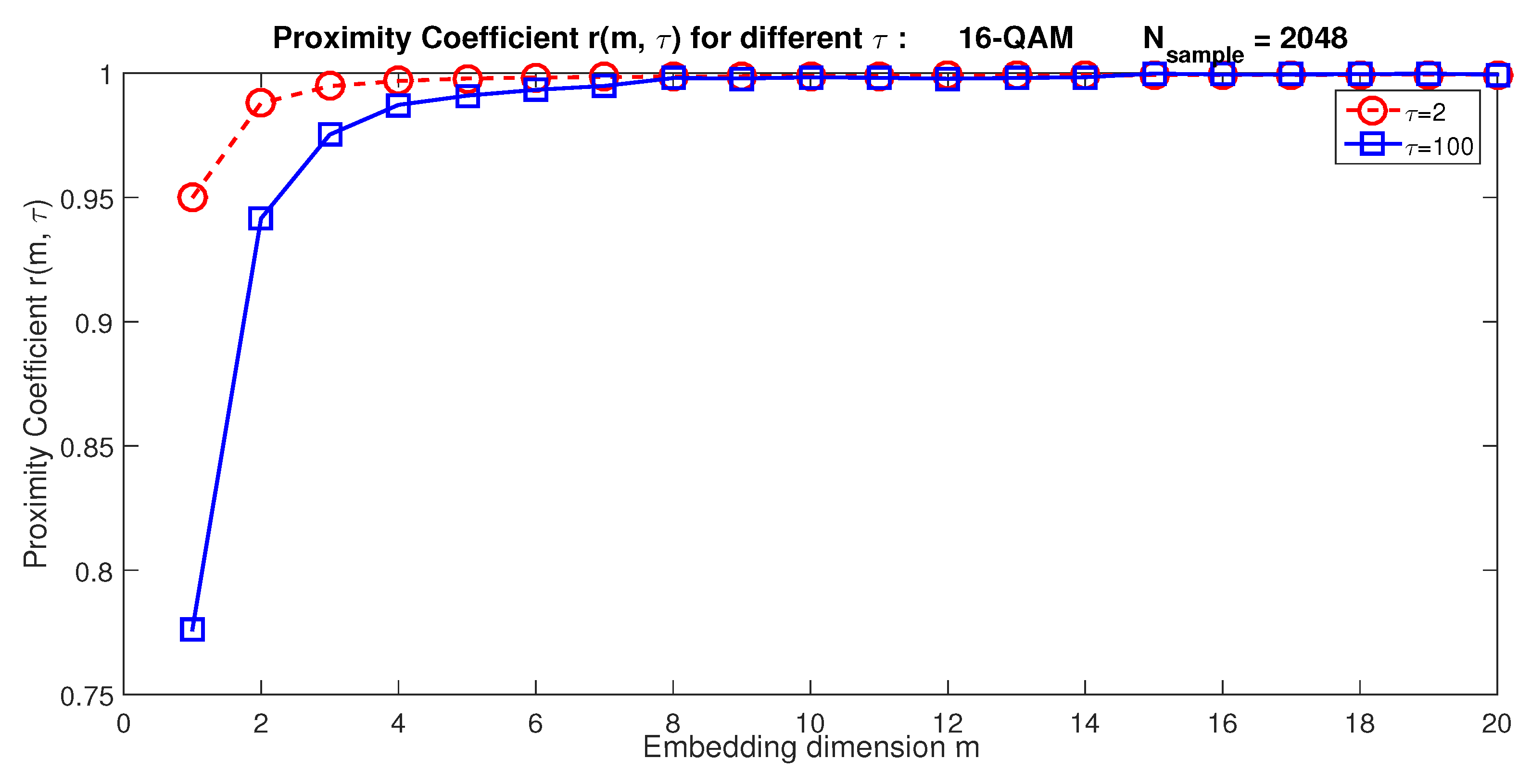
3.1. Estimation of the embedding parameters

3.1.1. Time Delay

Theoretically, the time delay τ can be almost arbitrarily chosen if the observation y ( n ) is noise free with an infinite number of samples. However, these conditions cannot be satisfied in real applications because of noise which can generate statistical dependence among the state vectors x k ; Therefore, the time delay τ has to be wisely chosen in order to reduce this statistical dependence [20,31,33]. To determine the optimal time delay τ 0 , one can use the autocorrelation function, Average Mutual Information (AMI) or phase portrait approach. The most appropriate method is the AMI because it measures the general dependence between two random variables [34]. Therefore, it could provide a better criterion for the optimal time delay τ 0 . The concept of AMI consists, first of all, in estimating the mutual information I ( τ ) between y ( n ) and its delay version y ( n − τ ) by varying the value of τ from 0 to N ; N denotes the number of samples contained in y ( n ) . After that, the optimal τ 0 is chosen as the first τ value that minimizes I ( τ ) [20,35,36]. Based on equation (1), we can conclude that I ( τ ) and indirectly τ 0 , depends on three parameters: the SNR value, the sampling rate and the modulation scheme. Consequently, use AMI method to determine τ 0 is not so suitable in the context of non-cooperative spectrum sensing algorithm.

3.1.2. Embedding Dimension

The optimal embedding dimension m 0 for an observed signal y ( n ) is the minimum dimension for the state vectors x k to give a reliable reconstruction of y ( n ) phase space [30,32]. From the literature, many approaches to estimate m 0 have been developed [33,37,38]. The most used approach is based on the False Nearest Neighbors (FNN) method [38]. According to the principle of FNN, any two true neighboring points in the m − d i m e n s i o n a l reconstructed phase space must remain neighbors in the ( m + 1 ) − d i m e n s i o n a l reconstructed phase space. Otherwise, they are called false neighbors. A perfect embedding means all neighboring points should be true neighbors [20,37,38]. Inspired by the FNN-based algorithm proposed in[37], we identify m 0 by using the distance ratio, a ( i , m ) , defined as follows [37]:
a ( k , m ) = x k ( m + 1 ) − x l ( m + 1 ) ∞ x k ( m ) − x l ( m ) ∞ ;
where k , l = ∈ { 1 , 2 , ⋯ , N − m τ } ; x k ( m ) are the state vectors from the m − d i m e n s i o n a l phase space; and . ∞ is L − i n f i n i t y norm. The major drawback of using the distance ratio a ( k , m ) is its sensitivity to the reference state vector x k . To overcome this drawback, we consider the average value a ¯ ( m , τ ) instead of a ( k , m ) :
a ¯ ( m , τ ) = 1 N − m τ ∑ k = 1 N − m τ a ( k , m )
To investigate the dependence of a ¯ ( m , τ ) on m, the coefficient of proximity r ( m , τ ) is defined as follows:
r ( m , τ ) ≜ a ¯ ( m + 1 , τ ) a ¯ ( m , τ )
When m becomes greater than a limit value m lim , the proximity coefficient r ( m , τ ) converges to one. Hence, m 0 = m lim + 1 becomes the minimum embedding dimension [37]. Based on, equation (7), we can observe that r ( m , τ ) depends of the time delay value τ . This assertion is corroborated by simulation results. Figure 1 illustrates, for example, the evolution of r ( m , τ ) for two extreme values of τ ; for τ = 2 , the optimal value of m 0 = 6 ; whereas τ = 100 , we obtain m 0 = 9 . As m depends on the choice of τ , we propose hereinafter an optimization strategy to find simultaneously the optimal values of m and τ .

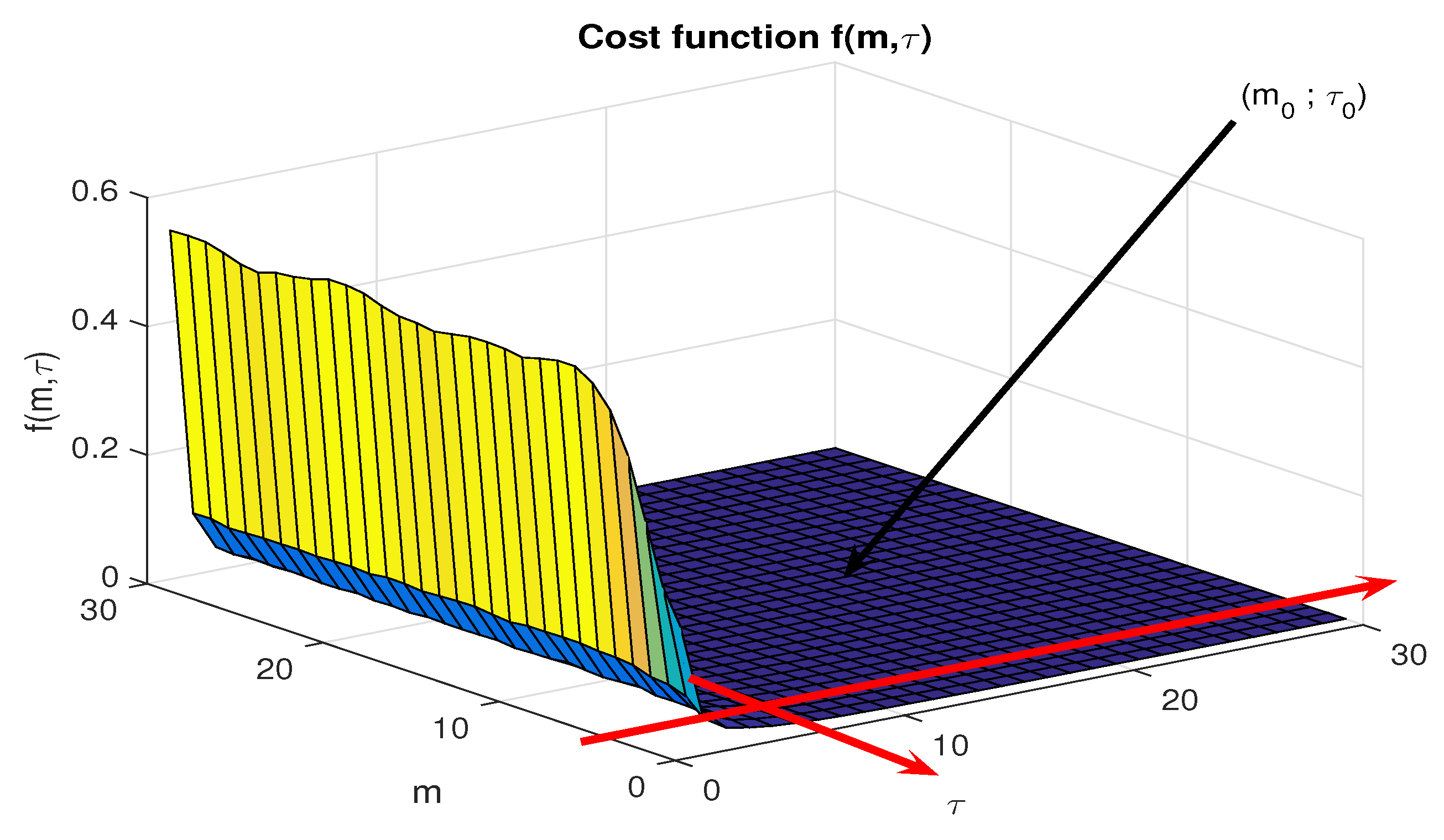
3.1.3. Optimal Values of m and τ

r ( m , τ ) is a bivariate function whose expression leads to
lim ( m , τ ) → ( m 0 , τ 0 ) r ( m , τ ) = 1
So that, we define the cost function f ( m , τ ) :
f ( m , τ ) = a ¯ ( m , τ ) − a ¯ ( m + 1 , τ )
The optimal values m 0 and τ 0 become:
( m 0 , τ 0 ) = a r g m i n ( m , τ ) ∈ N * f ( m , τ )
Numerical results show that values of ( m 0 , τ 0 ) obtained from (10) become independent from modulation schemes, SNR and the number of samples per symbol N s . Figure 2 illustrates the cost function f ( m , τ ) with respect to ( m , τ ) for a noisy 16-QAM signal. We can notice that:
∀ τ ≥ 6 , m ≥ 1 , f ( m , τ ) → 0
The number K of state vectors is given by:
K = N − ( m − 1 ) τ ≥ K m i n
Based on Takens’ theorem1 and the minimum number K m i n of state vectors for reliable detection, we conclude that m 0 and τ 0 should be chosen in the following ranges:
m 0 , τ 0 ∈ 3 ; N − K m i n τ 0 × 6 ; N − K m i n 2
However, we notice that in practice K m i n ≪ N . Consequently, we can:
m 0 , τ 0 ∈ 3 ; N τ 0 × 6 ; N 2
The recurring states in the phase space can be highlighted by the Recurrence Plot.

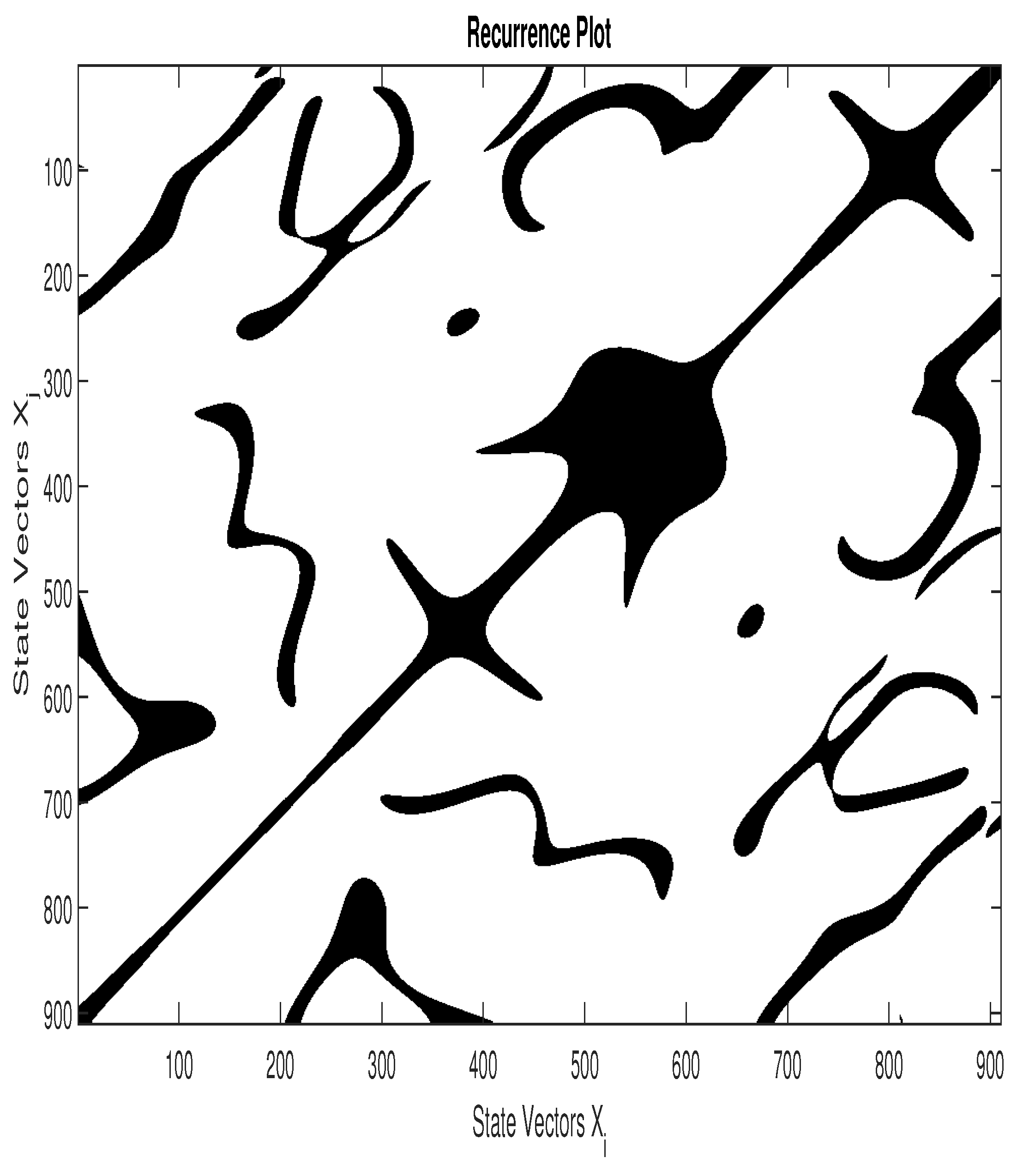
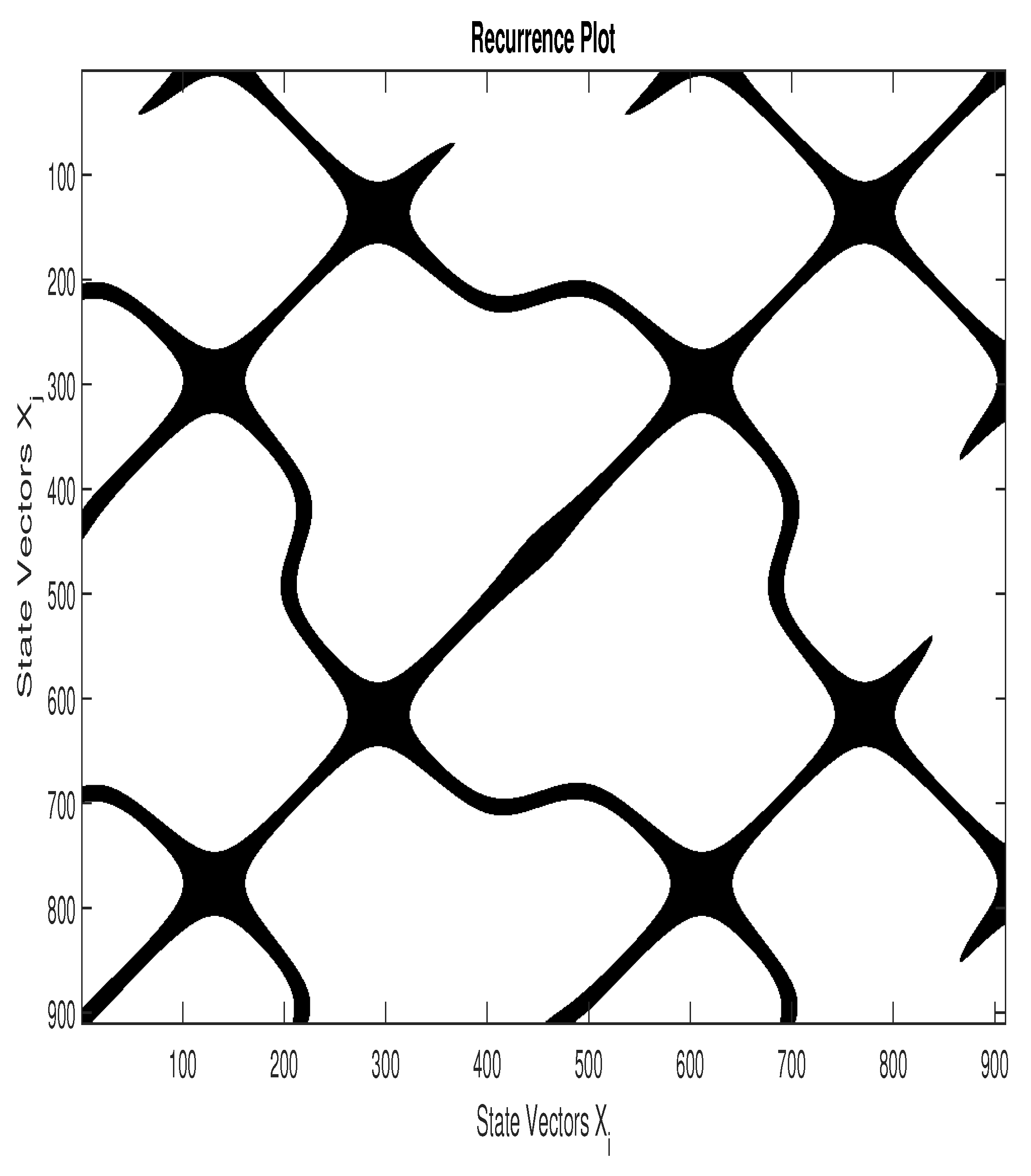
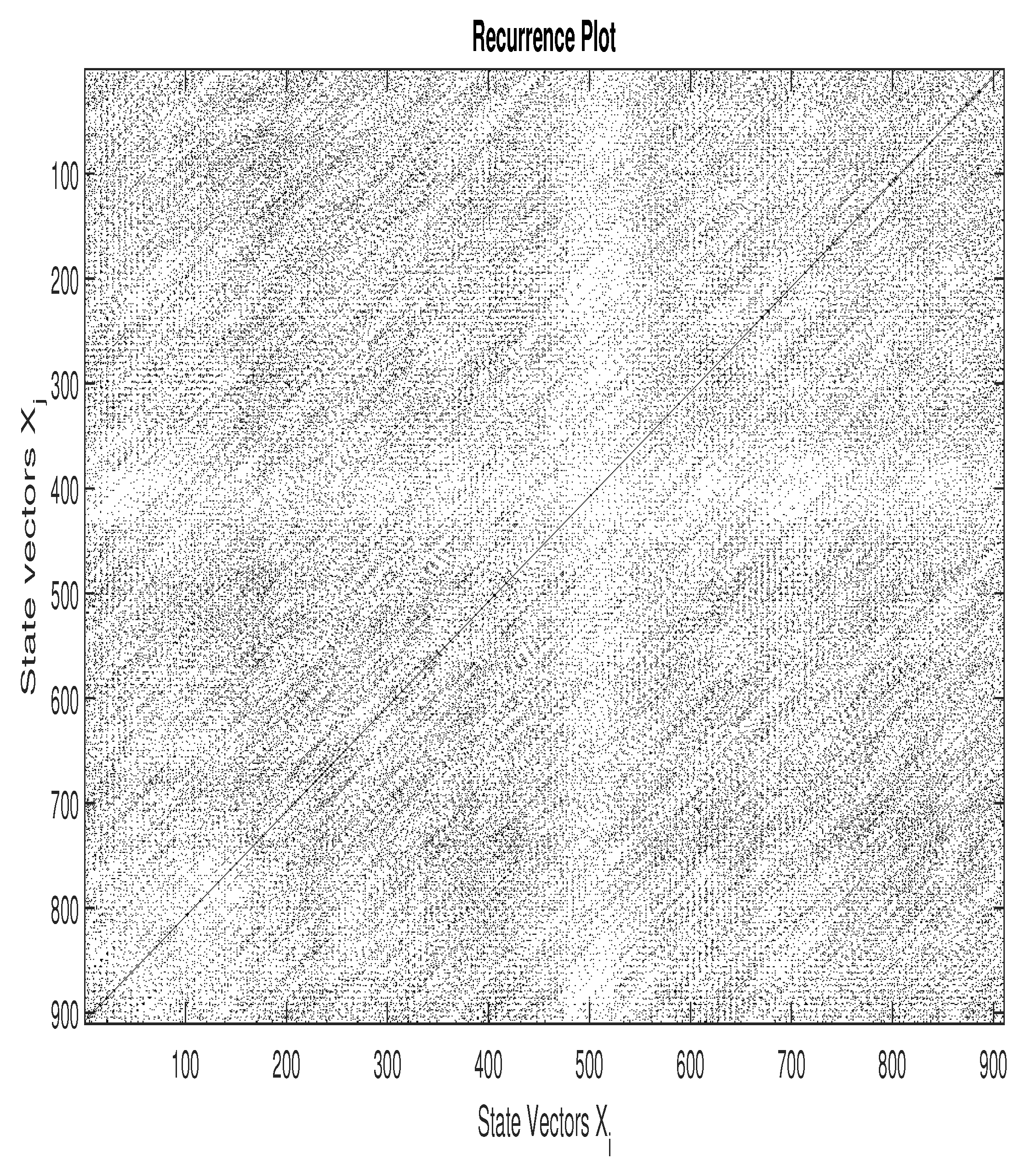
3.2. Recurrence Plot

The Recurrence Plot (RP) illustrates recurrences contained in a signal. RP is based on the recurrence matrix R i , j ( ε , m ) [25,31]:
R i , j ( ε , m ) = Θ ε − x i − x j 2
where i , j ∈ { 1 , ⋯ , K } and K = N − ( m − 1 ) τ denotes the number of reconstructed state vectors x k ; ε is the recurrence threshold, Θ ( . ) represents Heavisides’ step function, and . 2 is the L 2 or Frobenius norm. d i j = x i − x j 2 are the coefficients of the distance matrix M.
According to equation (15), the states x i and x j are recurring states iff x i − x j < ε . In RP, a recurrence is represented by a black dot. If the parameters m, τ and ε are optimal, the RP presents some intrinsic patterns of the system. For example, Figure 3, Figure 4 and Figure 5 represent respectively the RP of 16-QAM signal, GMSK signal and a random zero mean White Gaussian Noise (WGN) with a variance σ b 2 . We can notice that the patterns in the RP of 16-QAM signal are different from those of GMSK signal, whereas the RP of the WGN has no particular pattern. Heuristically, we can set the recurrence threshold is ε = 0.5 σ y where σ y 2 denotes the variance of the observed signal y ( n ) ; the embedding parameters are established to m = 16 and τ = 6 .
As the visual analysis of RP is not objective, Zbilut and Webber introduced a procedure to quantify RP structures [40,41]. In the literature, one have five classical tools to perform the RQA. Some RQA tools are based on the recurrence density, while others use the line structures of the RP [31]. The classical RQA tools are developed and extended in [25,31]. The main challenge with classical or extended RQA tools, is the choice of an optimal recurrence threshold ε of equation (15). A small value of ε does not reveal noticeable occurrences, while a large value of ε may lead to the appearance of neighbors for most of existing points and cause false occurrences [25,42]. The choice of ε is a delicate issue affecting the reliability of the spectrum sensing based on classical or extended RQA tools [20]. To overcome this issue, we propose in the following sections a new algorithm called the Recurrence Analysis based Detector (RAD) which only exploits the distance matrix. This distance matrix does not depend on the recurrence threshold ε ; and nor does proposed detection model RAD.

4. Recurrence Analysis Based Detector

Recurrence Rate (RR) is an essential tool of RQA. Our previous works based on the RQA detection model [20] show that RR-based detection model (RRD) suffers from major shortcomings, such as:
1.
It cannot detect the presence of a communication signal when SNR ≤ − 5 dB.
2.
It is very sensitive to the recurrence threshold ε .
3.
The computational cost is relatively high
4.
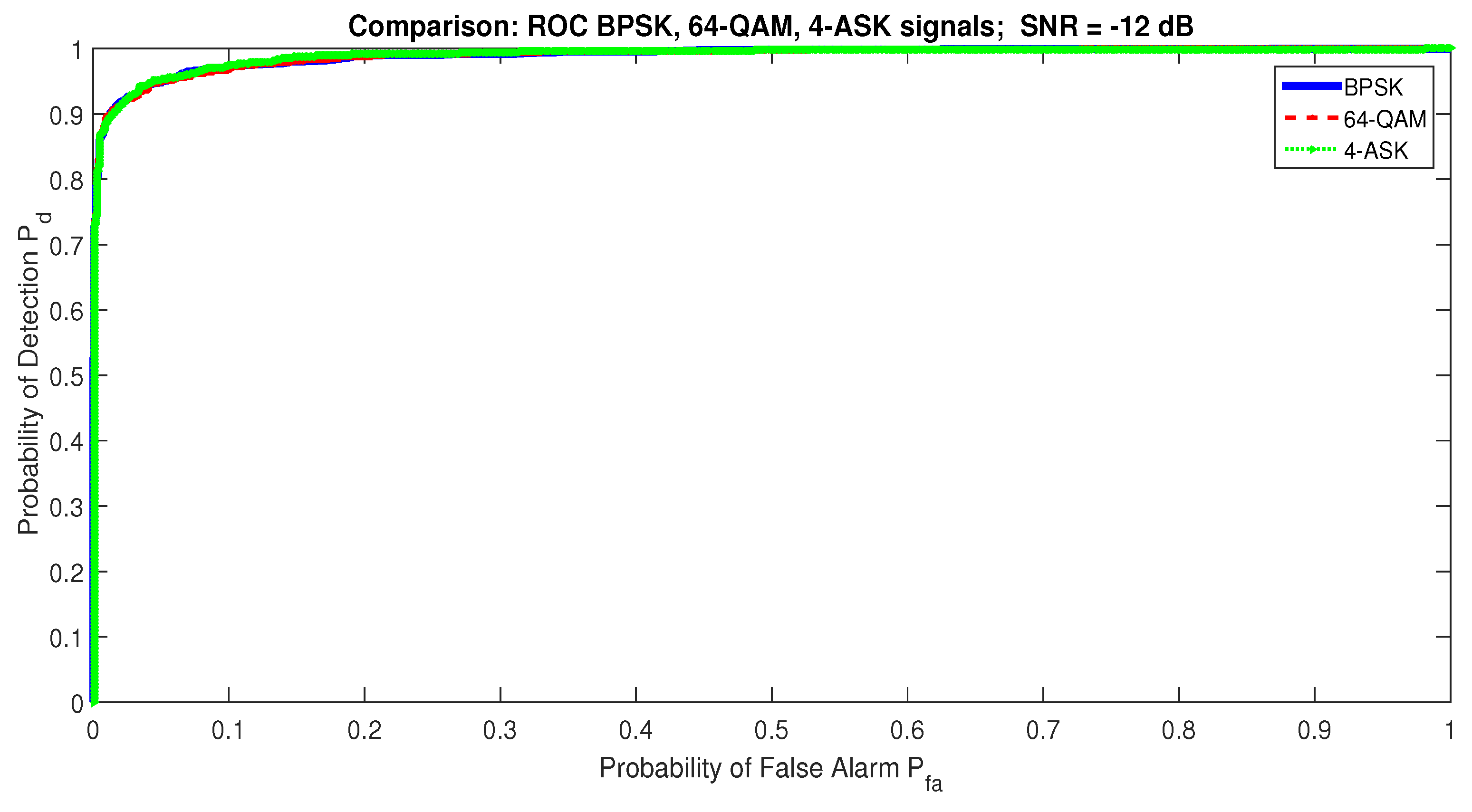
The performance of RRD is sensitive to the type of modulations for a communication signal.
To overcome the above limitations, we develop hereinafter a new detection model, the Recurrence Analysis Detection model (RAD), which is able to operate in very low SNR conditions. In order to reduce drastically the computational cost and avoid the delicate issue of the recurrence threshold ε , the RAD only uses the distances d i j = x i − x j 2 of the upper triangular part of the distance matrix.

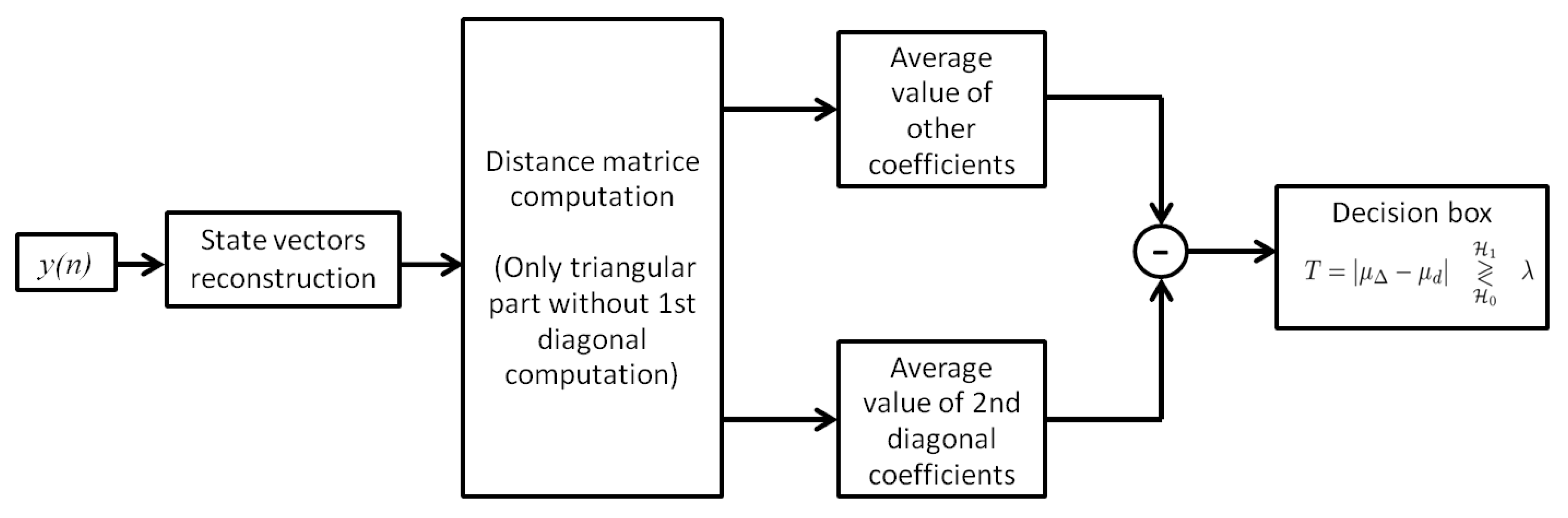
4.1. Detection Model

Usually, the RQA is performed on the entire distance matrix D = ( d i j ) 1 ≤ i , j ≤ K of different state vectors. As D is a symmetrical matrix, in order to reduce the computational cost, we use the upper triangular part of D, without the main diagonal defined by its general coefficients:
D i j = d i j ; ∀ 1 ≤ i < j ≤ K
We denote by u d the coefficients of the first upper diagonal of D and by u Δ , the other coefficients of the upper triangular part of D, without the main diagonal. u d and u Δ verify two great properties:
1.
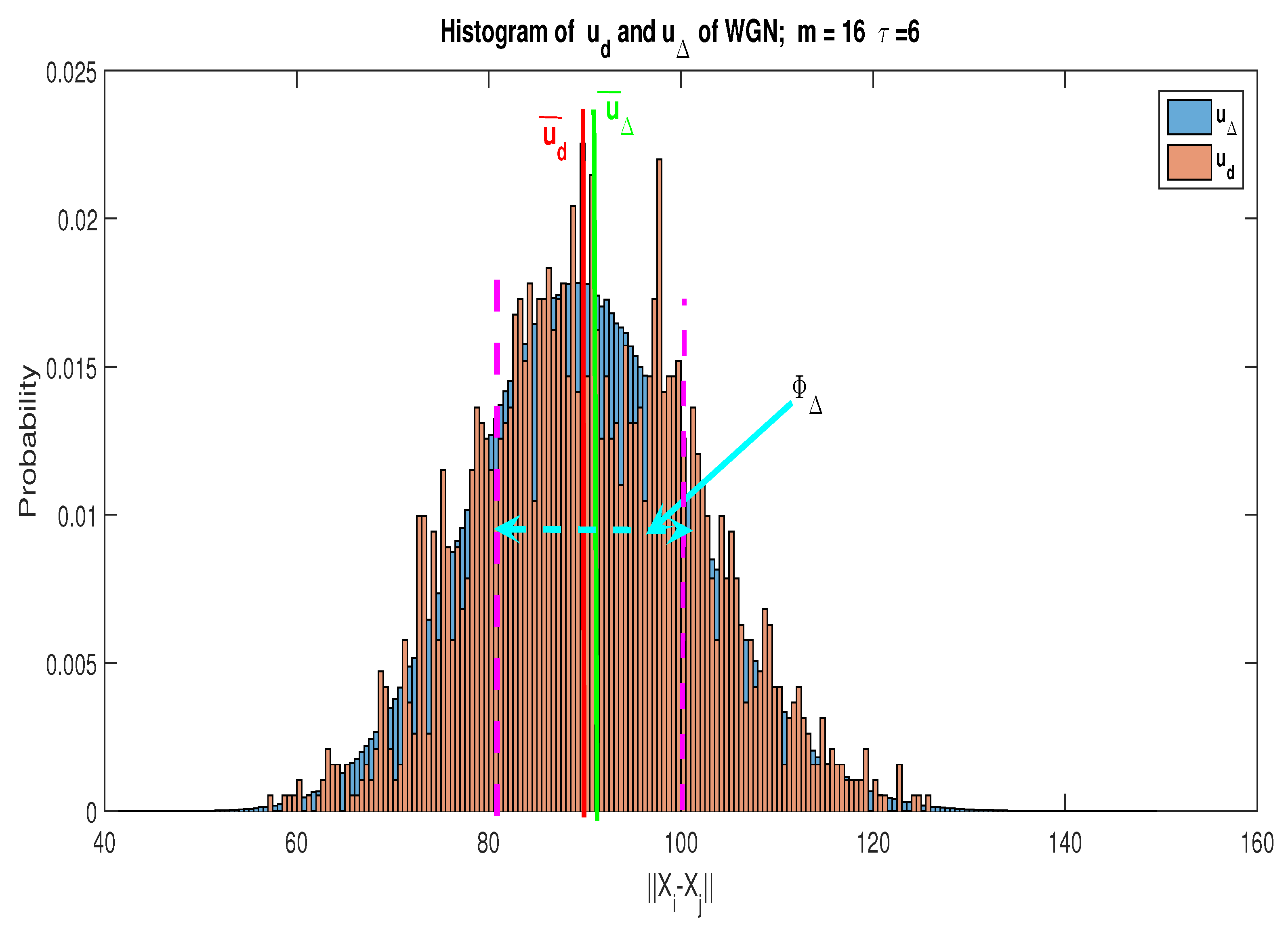
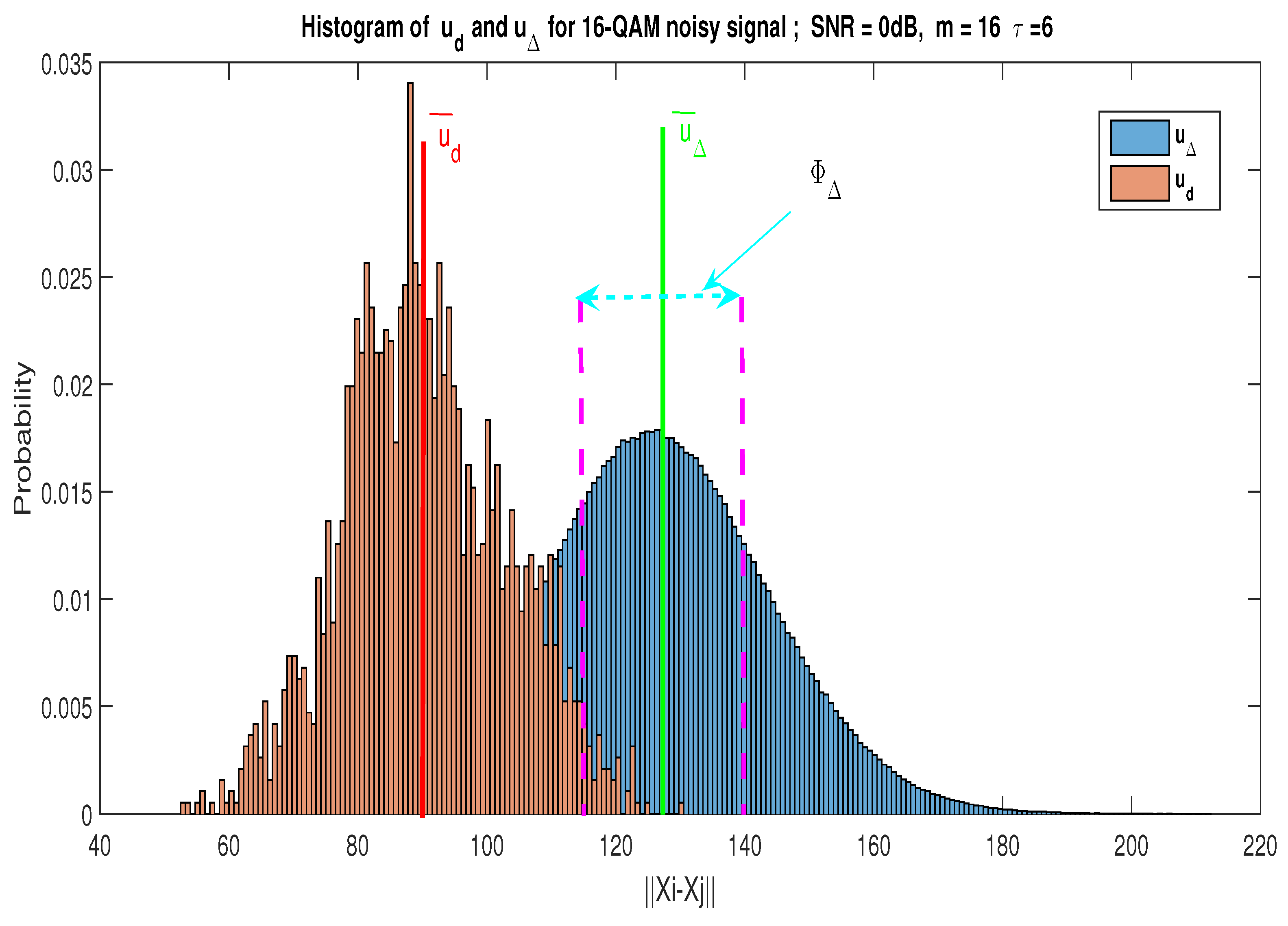
For a WGN, u d and u Δ have the same Probability Density Function (PDF); which is not the case for a noisy communication signal. Hence, to detect the presence of a communication signal, we check if u d is representative of u Δ . To this purpose, we use a statistical test of conformity to evaluate this representativeness [43].
2.
u d of a WGN or a communication signal have the same PDF. This remark allows us to design a detector free of noise variance estimation.
To provide a better understanding of this notion of representativeness, we present the histogram of u d and u Δ of WGN and communication signal respectively in Figure 6 and Figure 7, and we define the confidence interval Φ Δ as follows:
Φ Δ = u ¯ Δ − λ ; u ¯ Δ + λ
where u ¯ Δ is the average value of u Δ and λ is the predetermined detection threshold for RAD. Further details about λ can be founded in subSection 4.2.4.
On the basis of the histogram of distance and by using Kolmogov-Smirnov test [44], for a WGN only, we note that u d and u Δ can be approximated by the same PDF (see Figure 6). Consequently, by using the statistical test of conformity based on the estimation average value, we show that u d is representative of u Δ . Indeed, u ¯ d ∈ Φ Δ ; u ¯ d denotes the average value of u d . Contrariwise in Figure 7, which gives the histogram of distance for a communication signal buried in the WGN with a SNR = 0 dB, we can notice that u ¯ d ∉ Φ Δ ; so u d is not representative of u Δ .
Using the statistical test of conformity, we propose the following test statistic T:
T = | u ¯ Δ − u ¯ d | ≷ H 0 H 1 λ
In the course of our work, we will establish the analytical expressions of the probability of detection P d and the probability of false alarm P f a in order to compare the theoretical and experimental results.

4.2. Analytical Expression of the Probability of False Alarm

The probability of false alarm P f a can be expressed from the PDF of T under H 0 . In order to find this PDF, one should evaluate the PDF of u ¯ Δ and u ¯ d , see equation (18).

4.2.1. The PDF of u ¯ Δ under hypothesis H 0

Under H 0 , the average value u ¯ Δ of u Δ is defined as follows:
u ¯ Δ / H 0 = 1 K Δ ∑ k = 1 K Δ u Δ / H 0 ( k )
where K Δ = ( K − 1 ) ( K / 2 − 1 ) and u Δ / H 0 ( k ) ∈ { d i j ; 1 ≤ i ≤ K − 2 ; i + 2 ≤ j ≤ K } .
Based on the central limit theorem for independent random variables and for a large K, u ¯ Δ / H 0 is asymptotically normally distributed with mean u ¯ Δ / H 0 and variance σ Δ / H 0 2 :
u ¯ Δ / H 0 ↦ N μ Δ / H 0 , σ Δ / H 0 2
where
μ Δ / H 0 = E u ¯ Δ / H 0
σ Δ 2 = v a r u ¯ Δ / H 0
To calculate μ Δ / H 0 and σ Δ / H 0 2 , we can use the PDF f u Δ / H 0 (u) of u Δ / H 0 . An outcome u Δ / H 0 of u Δ / H 0 is given by:
u Δ / H 0 = d i j = ∑ k = 0 m − 1 b i + k τ − b j + k τ 2
As b ( n ) ↦ N 0 , σ b 2 ,then b i + k τ − b j + k τ ↦ N 0 , 2 σ b 2 and v k = b i + k τ − b j + k τ σ b 2 ↦ N 0 , 1 .By setting: Z = ∑ k = 0 m − 1 v k 2 , we can conclude that Z follows a Chi distribution χ ( m ) with m degrees of freedom [45,46]:
Z = u Δ / H 0 σ b 2 ↦ χ ( m )
The expectation value E Z and variance v a r Z of Z are given as follows [45,46]:
E Z = μ Z = 2 Γ m + 1 2 Γ m 2
v a r Z = m − μ Z 2
where Γ ( m ) = ∫ 0 + ∞ x m − 1 e − x d x is the Gamma function.
From equation (24), we show that the PDF f u Δ / H 0 of u Δ / H 0 is defined as follows [47]:
f u Δ / H 0 ( u ) = u m − 1 2 m − 1 σ b m Γ ( m 2 ) exp − u 2 4 σ b 2
The mean μ Δ / H 0 and variance σ Δ / H 0 2 of X ¯ Δ / H 0 can be determined by using equation (24) as follows:
μ Δ / H 0 = σ b 2 E Z
σ Δ / H 0 2 = 2 σ b 2 K Δ v a r Z
Finally, we have u ¯ Δ / H 0 ↦ N μ Δ / H 0 , σ Δ / H 0 2 with :
μ Δ / H 0 = 2 σ b Γ m + 1 2 Γ m 2
σ Δ / H 0 2 = 2 σ b 2 K Δ m − 2 Γ m + 1 2 Γ m 2 2

4.2.2. The PDF of u ¯ d under hypothesis H 0

Under H 0 , the average value u ¯ d of u d is defined as follows:
u ¯ d / H 0 = 1 K d ∑ k = 1 K d u d k / H 0 ( k )
where u d / H 0 ( k ) ∈ { d i , i + 1 } ; 1 ≤ i ≤ K d = K − 1 .
Because of the structure of the upper triangular distance matrix, the coefficients of the first top diagonal u d / H 0 ( k ) are strongly decorrelated. In addition, K d large number. Thus, we can approximate u ¯ d by a Gaussian variable by using the central limit theorem:
u ¯ d / H 0 ↦ N μ d / H 0 , σ d / H 0 2
Using a similar approach to the calculation of the expectation value μ Δ / H 0 and variance σ Δ / H 0 2 of u ¯ Δ / H 0 , we obtain:
μ d / H 0 = 2 σ b Γ m + 1 2 Γ m 2
σ d / H 0 2 = 2 σ b 2 K d m − 2 Γ m + 1 2 Γ m 2 2

4.2.3. The PDF of T under H 0

u ¯ d / H 0 and u ¯ Δ / H 0 are Gaussian random variables. Based on equations (20), (30), (31), (33), (34) and (35) we end up with:
u ¯ Δ / H 0 − u ¯ d / H 0 ↦ N 0 , σ 0 2
where
σ 0 2 = σ Δ / H 0 2 + σ d / H 0 2 − 2 C o v u ¯ d / H 0 , u ¯ Δ / H 0
Applying the random variable transformation theorem [47,48] on T from equation (18), we end up with t ≥ 0 :
f T / H 0 ( t ) = 2 σ 0 2 π exp − t 2 2 σ 0 2

4.2.4. Probability of False Alarm and Detection Threshold

Based on equation (38), the P f a is expressed as follows:
P f a = ∫ λ ∞ f T / H 0 ( t ) d t = e r f c λ σ 0 2
e r f c ( x ) denotes the Complementary Error Function2, and the detection threshold λ is:
λ = σ 0 2 e r f c − 1 P f a

4.3. Analytical Expression of the Probability of Detection

Taking into account the presence of the communication signal s ( n ) and keeping the same approach as under H 0 , we demonstrate that:
u ¯ Δ / H 1 ↦ N μ Δ / H 1 , σ Δ / H 1 2
u ¯ d / H 1 ↦ N μ d / H 1 , σ d / H 1 2
where:
μ Δ / H 1 = 2 σ s 2 + σ b 2 Γ m + 1 2 Γ m 2
σ Δ / H 1 2 = 2 ( σ s 2 + σ b 2 ) K Δ m − 2 Γ m + 1 2 Γ m 2 2
μ d / H 1 = 2 σ b Γ m + 1 2 Γ m 2
σ d / H 1 2 = 2 σ b 2 K d m − 2 Γ m + 1 2 Γ m 2 2
We deduce the PDF of T under the hypothesis H 1 as follows:
f T / H 1 ( t ) = 1 σ 1 2 π e − t − μ 1 σ 1 2 2 + e − t + μ 1 σ 1 2 2
with t ≥ 0 . μ 1 and σ 1 2 are given by:
μ 1 = μ Δ / H 1 − μ d / H 1 ,
σ 1 2 = σ Δ / H 1 2 + σ d / H 1 2 − 2 C o v u ¯ Δ / H 1 , u ¯ d / H 1
Consequently, the Probability of Detection P d becomes:
P d = ∫ λ + ∞ f T / H 1 ( t ) d t = 1 − 1 2 e r f c − λ − μ 1 σ 1 2 − e r f c λ − μ 1 σ 1 2

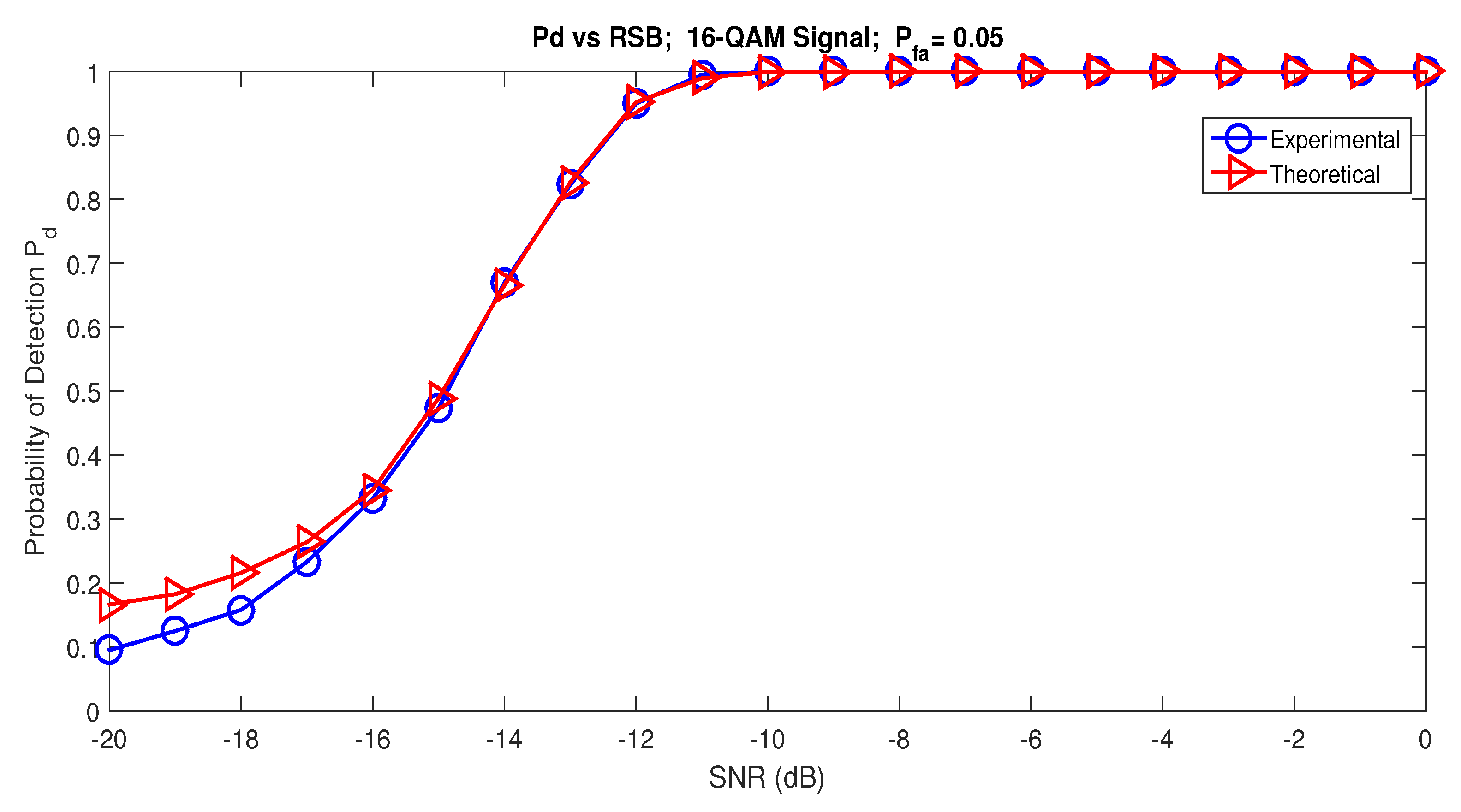
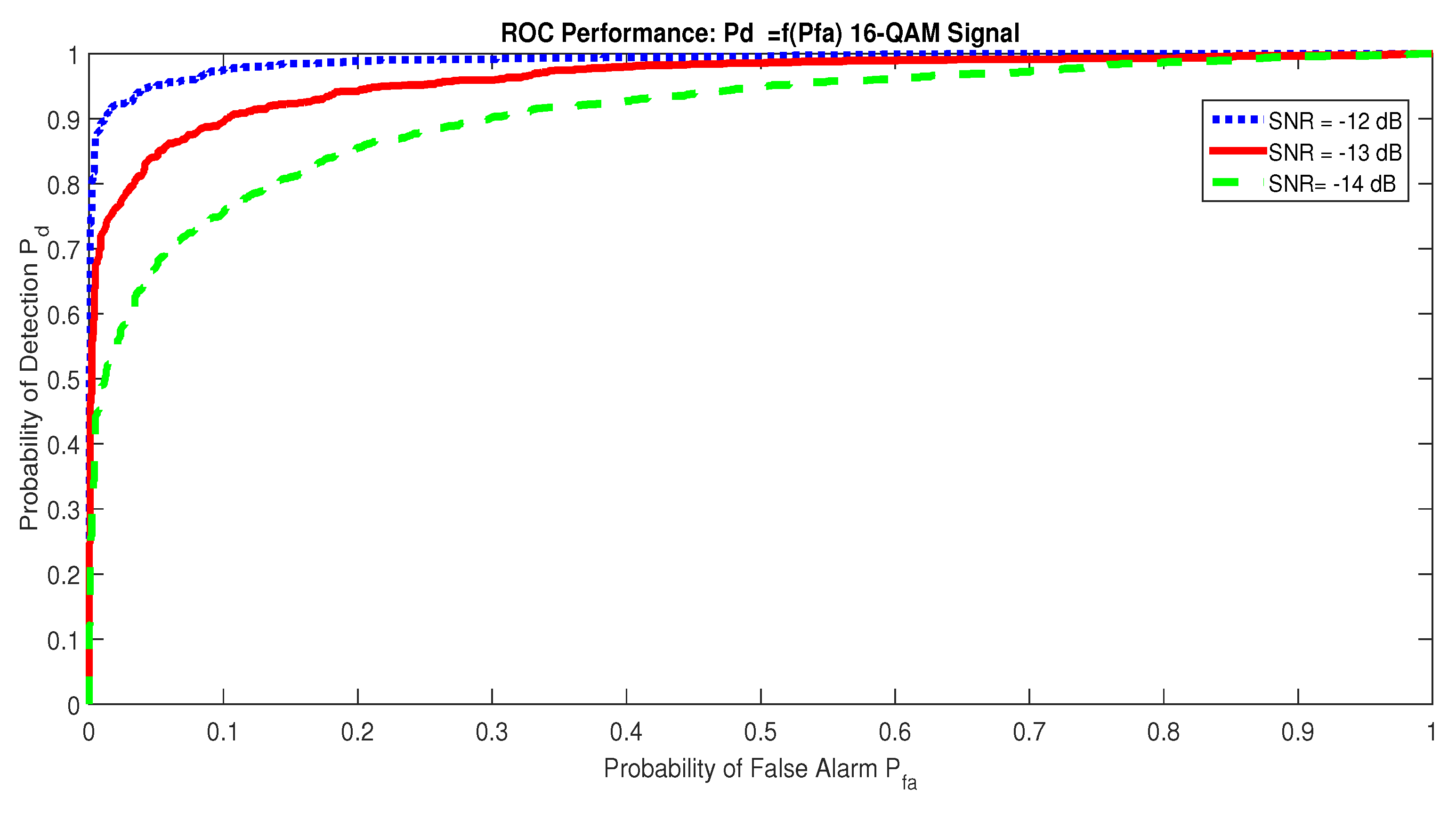
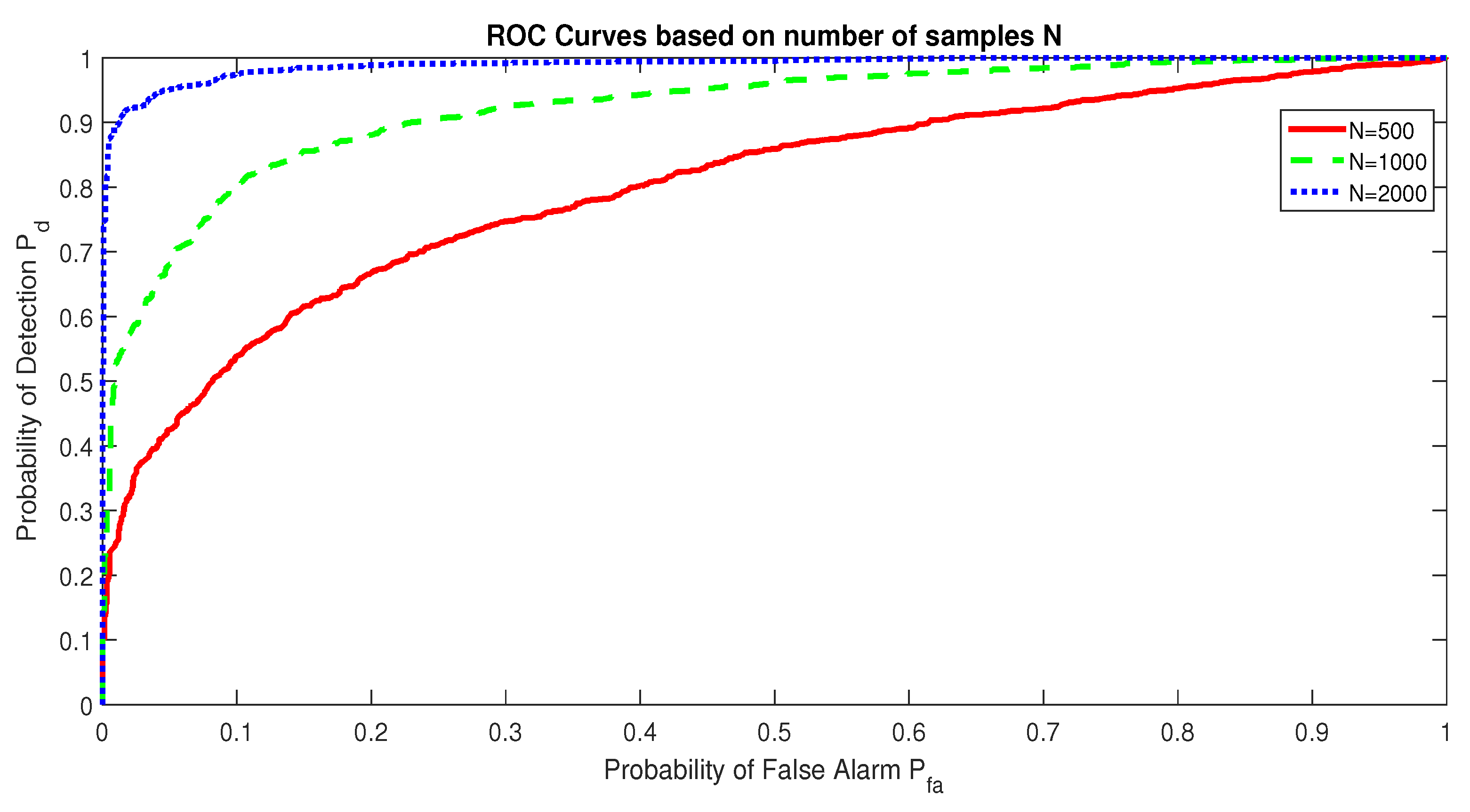
5. Simulations Results

To evaluate the efficiency and the robustness of the proposed detection method, we generate the Receiver Operating Characteristic (ROC) curves using Monte Carlo simulations. The parameters defined in Table 1 are used with different kind of communication signals such as 64-QAM, 16-QAM, BPSK and 4-ASK signals.
In order to compare the theoretical and experimental performance of RAD, we have generated the performance curve P d versus SNR. Figure 8 shows these performance curves. The theoretical curves were generated by equation (50) and the experimental curves according to the Monte Carlo simulations. It can be clearly observed that the theoretical results match with simulated ones. From theoretical and experimental curves, the reliable detection is possible as soon as S N R ≥ − 12 dB with P d ≥ 0.95 and P f a = 0.05 .
The Receiver Operating Characteristic curves for different S N R values can be viewed on Figure 9. Here, the detector RAD is applied on a 16-QAM signal and the observation time is 31.25 ms. For SNR = − 14 dB and P f a = 0.1 , RAD detects the presence of a communication signal with P d = 0.76 ; but for SNR = − 13 dB, P d = 0.9 . The detector proves itself powerful as soon as the SNR ≥ − 12 dB, since the detection probability P d = 0.95 with a very low value of P f a = 0.05 ; see Figure 9.
Another advantage of the proposed detector is its robustness against any type of the classical modulations such as QAM, PSK and ASK; see Figure 10, where the ROC curves for 4-ASK, BPSK and 64-QAM signal are almost identical.
The performance of RAD increases with the number of samples N. Figure 11 depicts this performance evolution based on N in a Gaussian channel where SNR = − 12 dB. We notice that for P f a = 0.1 , the RAD detects the communication signal with P d = 0.5 when N = 500 samples, with P d = 0.8 when N = 1000 samples and with P d = 0.97 when N = 2000 samples.
By comparing RAD to two other blind spectrum sensing algorithms: Energy Detection (ED) [49,50] and Cyclostationary Features Detector (CFD) [51,52] and according to the results presented in Figure 12 and Figure 13, we notice the superiority of RAD to ED and CFD in a Gaussian channel. For example, for the S N R = − 12 dB and P f a = 0.05 , the RAD detects the signal with P d = 0.95 , whereas the probability of detection for the ED is only P d = 0.67 (see Figure 12). Figure 13 shows that the RAD is able to detect the communication signal in very weak low SNR conditions. For − 12 dB ⩽ SNR ⩽ − 10 dB, RAD detects the presence of a communication signal with P d ⩾ 0.95 for P f a = 0.05 . ED achieves RAD performance only when SNR ⩾ − 10 dB and CFD works correctly when SNR ⩾ − 7 dB with P d ⩾ 0.97 .
After testing the performance of the detector in a Gaussian channel, we are now interested in the behaviour of the RAD in the multi-path channel. As a model, we use the model D of Rayleigh channel defined in [53] with the following parameters:
Table 2. Rayleigh Channel Model Features.
Table 2. Rayleigh Channel Model Features.
Model D of Rayleigh Channel
Entity Parameters Value
Features Number of Path 6
Doppler Frequency f d m a x 1,2 kHz
Table 3. Delay and Gain values for 6 paths [53].
Table 3. Delay and Gain values for 6 paths [53].
Path Number 1 2 3 4 5 6
Delay (ns) 0 300 8900 12900 17100 20000
Gain (dB) 0 -2.5 -12.8 -10.0 -25.2 -16.0
Figure 14 summarizes the performance of RAD in a noisy Rayleigh channel. The RAD performance remains almost unchanged. It detects a communication signal with P d ≥ 0.92 with P f a = 0.05 as soon as SNR ≥ − 12 dB.

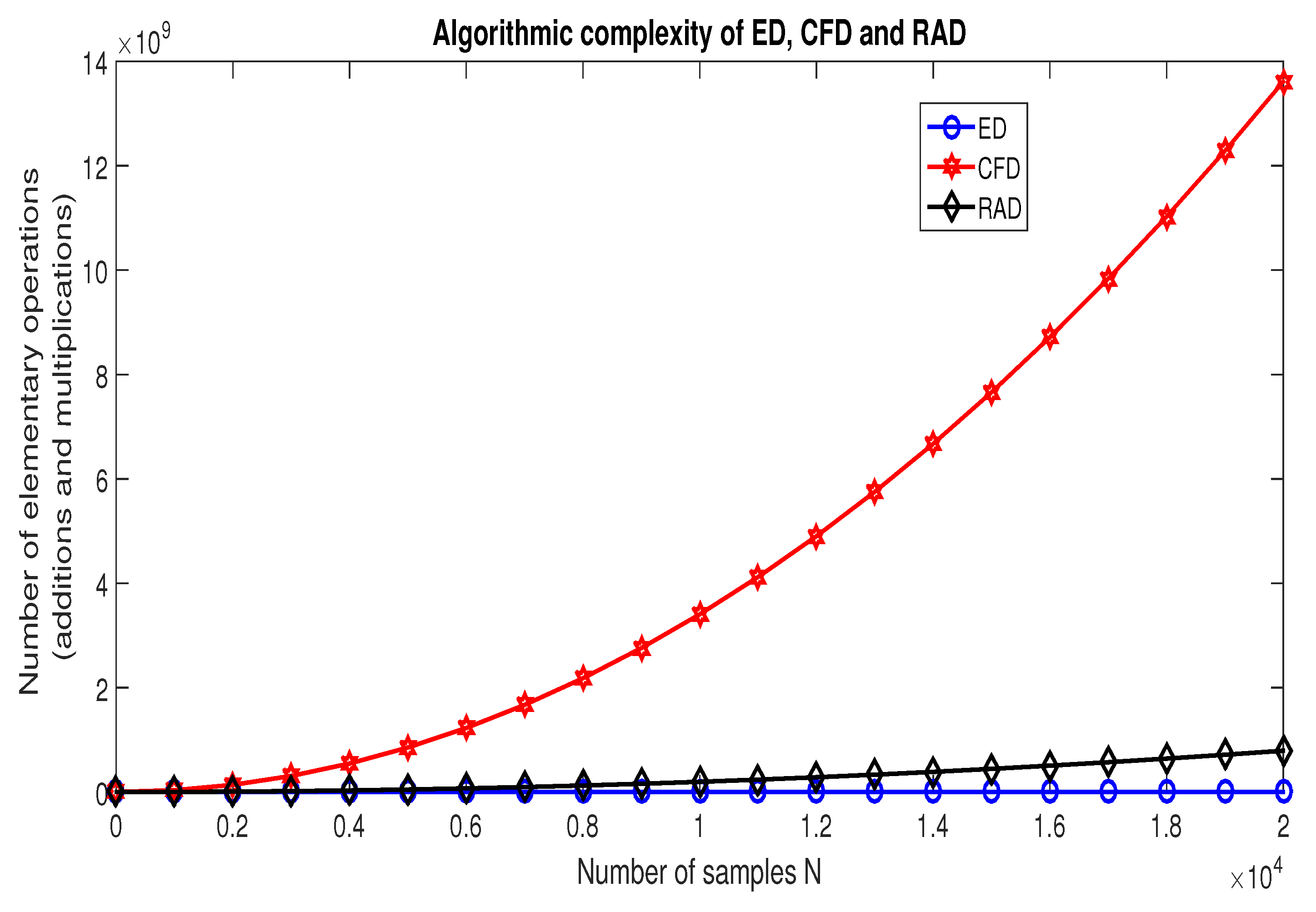
6. Complexity Analysis of Recurrence Analysis Based Detector

Theoretical and experimental analyses show the superiority of RAD compare to Energy based Detector (ED) and Cyclostationary Feature based Detector (CFD) in low SNR scenario detection process. The complexity of the algorithms is measured through the number of complex multiplications that the algorithms has to perform for the calculation of the test statistics [54]. In this section, we provide the complexity analyses of ED, CFD and RAD.

6.1. Complexity Analysis of Energy Based Detector

Let y ( n ) be the observed siganl with N samples y k . The energy E y of y ( n ) is given by:
E y = 1 N ∑ k = 1 N y k 2
The ED detection process can be summarize through the Figure 15.
The complexity computational can be evaluated according to equation (51). N multiplication operations are required to perform y k 2 . Consequently, the computation complexity C E D becomes[54]:
C E D = N

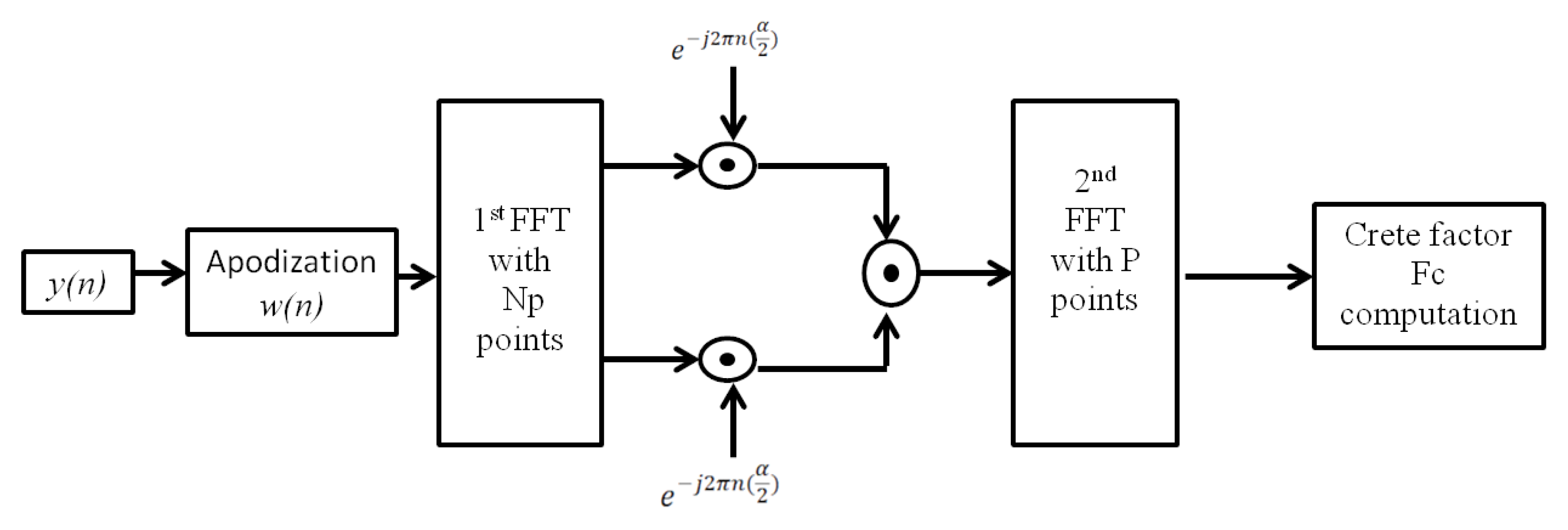
6.2. Complexity Analysis of Cyclostationary Feature Based Detector

In a blind context, the CFD is based on the reliable estimation of the cyclic spectrum [13,55,56]. The crest factor F c of the cyclic spectrum can be used as a decision statistic [13]:
F c ( α ) = max α D ( α ) 1 2 N + 1 ∑ k = 1 2 N + 1 D 2 ( α ) ≷ H 0 H 1 λ C F D
where α stands for the cyclic frequency and D ( α ) denotes the Cyclic Domain Profile (CDP). The computation of F c requires 6 steps [13]. First, a Hamming sliding window w ( n ) is used to apodize the observed signal y ( n ) . Then, we apply a first Fast Fourier Transform (FFT) and calculate the complex demodulates of the apodized signal. After that, we compute the spectral correlation of the different complex demodulates and apply a second FFT. At the end, we obtain the cyclic spectrum and we compute the crest factor F c of the cyclic spectrum.
Let N be the number of samples contained in the observed signal y ( n ) and N p the number of samples contained in each apodized block of y ( n ) . L = N p 4 denotes the decimation factor and P = N L is the number of apodized blocks from y ( n ) . The apodization is carried out with a Hamming window [13,55,57]. Figure 16 summarizes the essential steps of F c computation.
The apodization equation is defined as follows:
r k = w k y k ; k = 1 . . N p
where w k denotes the Hamming window coefficients, y k are the samples of the observed signal y ( n ) and r k becomes the coefficients resulting from the apodization.
The apodization step requires P N p multiplication operations. The second step in CFD detection process is the first FFT applied on apodized blocks. The complexity of FFT computation is known as N p log 2 N p . Consequently, the P apodized blocks require P N p l o g 2 N p multiplication operations. The complex demodulates computation requires P N p 2 multiplication operations and the step of complex demodulates multiplication requires P 2 N p 2 multiplication operations.
The second FFT with P data points to obtain the estimation of cyclic spectrum requires N p 2 P log 2 P multiplication operation and the calculation of crest factor F c alone requires 2 N + 1 multiplication operations.
Finally, the algorithmic complexity of CFD, C C F D , is:
C C F D = 34 N 2 + 64 N L + 10 N + 2

6.3. Algorithmic Complexity of Recurrence Analysis Based Detector

To make decision, RAD uses statistic test defined in equation (18). RAD detection process can be summarized through the Figure 17.
The algorithmic complexity of RAD concern essentially the distance matrix computation and the calculation of average values of distance matrix coefficients. From the observed signal y ( n ) containing N samples, we obtain K = N − ( m − 1 ) τ state vectors. Each state vector contains m coordinates. The distance d i j = x − x j form the state vector x i to other state vectors x j requires m K additions operations. Because we exploit only the upper triangular part of distance matrix with of the main diagonal coefficients, we use m 2 K ( K − 2 ) addition operations. The computation of the average value of the first upper diagonal requires K elementary operations and the average value of other coefficients requires ( K − 2 ) 2 2 elementary operations. The statistic test of RAD requires one addition operation. Consequently, the computation complexity C R A D of RAD becomes:
C R A D = 2 N 2 + 4 N ( τ − m τ − 1 ) + 2 ( m τ ) 2 + 2 τ 2 − 4 m τ 2 − 4 τ + 2 m τ + 6
From the equations (52), (52) and (56), we generated in Figure 18, the curves of evolution of the algorithmic complexity of the detectors ED, CFD and RAD, based on the number of samples contained in the observed signal y ( n ) . These results in Figure 18 show that ED the simplest algorithm, whereas CFD is the most complicated one. We also notice that RAD algorithm is less complicated than CFD algorithm.

7. Conclusions

This paper deals with the problematic of non-cooperative spectrum sensing in very low SNR conditions. Many algorithms have been recently developed to overcome the scarcity of radio spectrum. However, most of them suffer from the noise uncertainty and do not work correctly in a very low SNR conditions. In this paper, we use the promising approach of the Recurrence Quantification Analysis (RQA) to propose a robust detection model, named the Recurrence Analysis based Detection (RAD). RAD benefits from the exploitation of the similitude among the different state vectors. Indeed, our analyzes reveal that for a White Gaussian Noise, the coefficients contained on the first upper diagonal are representative of other coefficients of distance matrix; which is not the case for a communication signal. Thus, by applying a conformity test between the coefficients of the first upper diagonal and other coefficients of the distance matrix, the presence or absence of a communication signal can be revealed. RAD presents five major advantages: It is more robust compared to Energy based Detector (ED) and Cyclostationary Feature Detector (CFD), that are widely used in the non-cooperative spectrum sensing context; it does not suffer from the noise variance estimation because the estimation of the noise variance is not required during the spectrum sensing process; it is able to detect the communication signal in a very low SNR condition; contrary to ED, RAD is able to distinguish a noisy communication signal and a high energy noise; RAD does not need a high computational cost like CFD. Our present work also presents two major contributions. First, we have determined, for Digital communication signals, the optimal values of the time delay τ and embedding dimension m needed for the phase space reconstruction. Second, we have established the analytical expression of detection threshold λ , the probability of detection P d and the probability of false alarm P f a of detection model based on RQA. From ROC curves, we can notice without ambiguity that the RAD is more robust than ED and CFD algorithms. Our current simulations show that RAD is able to detect the communication signal for SNR ≥ -12 dB. In addition to facilitating the blind detection of communication signals, RQA could be used to accurately estimate the characteristic frequencies of the signal of interest. In our future work, we will optimize the performance of the RAD detector based on this reliable estimation of the characteristic frequencies of the signal of interest.

References

  1. Haykin, S. Cognitive radio: brain-empowered wireless communications. IEEE journal on selected areas in communications 2005, 23, 201–220. [Google Scholar] [CrossRef]
  2. Mansour, A.; Mesleh, R.; Abaza, M. New challenges in wireless and free space optical communications. Optics and lasers in engineering 2017, 89, 95–108. [Google Scholar] [CrossRef]
  3. Nasser, A.; Mansour, A.; Yao, K.C.; Chaitou, M.; Charara, H. Spatial and time diversities for canonical correlation significance test in spectrum sensing. Signal Processing Conference (EUSIPCO), 2016 24th European; , 2016; pp. 1232–1236. [CrossRef]
  4. Nasser, A.; Mansour, A.; Yao, K.C.; Charara, H.; Chaitou, M. Spectrum sensing for full-duplex cognitive radio systems. International Conference on Cognitive Radio Oriented Wireless Networks (CROWNCOM); Springer, , 2016; pp. 363–374. [CrossRef]
  5. Nasser, A.; Mansour, A.; Yao, K.; Abdallah, H.; Charara, H. Spectrum sensing based on cumulative power spectral density. EURASIP Journal on Advances in Signal Processing 2017, 1, 38–56. [Google Scholar] [CrossRef]
  6. Moawad, A.; Yao, K.; Mansour, A.; Gautier, R. Autocepstrum Approach for Spectrum Sensing in Cognitive Radio. 2018 15th International Symposium on Wireless Communication Systems (ISWCS); , 2018; pp. 1–6.
  7. Ding, G.; Wang, J.; Wu, Q.; Zhang, L.; Zou, Y.; Yao, Y.; Chen, Y. Robust Spectrum Sensing With Crowd Sensors. IEEE Transactions on Communications 2014, 62, 3129–3143. [Google Scholar] [CrossRef]
  8. Luo, L.; Roy, S. Efficient Spectrum Sensing for Cognitive Radio Networks via Joint Optimization of Sensing Threshold and Duration. IEEE Transactions on Communications 2012, 60, 2851–2860. [Google Scholar] [CrossRef]
  9. Zeng, Y.; Liang, Y. . Eigenvalue-based spectrum sensing algorithms for cognitive radio. IEEE Transactions on Communications 2009, 57, 1784–1793. [Google Scholar] [CrossRef]
  10. Li, B.; Li, S.; Nallanathan, A.; Nan, Y.; Zhao, C.; Zhou, Z. Deep Sensing for Next-Generation Dynamic Spectrum Sharing: More Than Detecting the Occupancy State of Primary Spectrum. IEEE Transactions on Communications 2015, 63, 2442–2457. [Google Scholar] [CrossRef]
  11. Burel, G.; Bouder, C.; Berder, O. Detection of direct sequence spread spectrum transmissions without prior knowledge. GLOBECOM’01. IEEE Global Telecommunications Conference; IEEE, , 2001; Vol. 1, pp. 236–239. [CrossRef]
  12. Zhang, X.; Gao, F.; Chai, R.; Jiang, T. Matched filter based spectrum sensing when primary user has multiple power levels. China Communications 2015, 12, 21–31. [Google Scholar] [CrossRef]
  13. Kadjo, J.M.; Yao, K.C.; Mansour, A. Blind detection of cyclostationary features in the context of Cognitive Radio. IEEE International Symposium on Signal Processing and Information Technology (ISSPIT); , 2016; pp. 150–155.
  14. Sobron, I.; Diniz, P.S.R.; Martins, W.A.; Velez, M. Energy Detection Technique for Adaptive Spectrum Sensing. IEEE Transactions on Communications 2015, 63, 617–627. [Google Scholar] [CrossRef]
  15. Lopez-Benitez, M.; Casadevall, F. Signal Uncertainty in Spectrum Sensing for Cognitive Radio. IEEE Transactions on Communications 2013, 61, 1231–1241. [Google Scholar] [CrossRef]
  16. Yang, K.; Huang, Z.; Wang, X.; Li, X. A Blind Spectrum Sensing Method Based on Deep Learning. Sensors 2019, 19, 2270. [Google Scholar] [CrossRef]
  17. Xue, H.; Gao, F. A machine learning based spectrum-sensing algorithm using sample covariance matrix. 2015 10th International Conference on Communications and Networking in China (ChinaCom). IEEE, 2015, pp. 476–480.
  18. Zhang, K.; Li, J.; Gao, F. Machine learning techniques for spectrum sensing when primary user has multiple transmit powers. 2014 IEEE International Conference on Communication Systems. IEEE, 2014, pp. 137–141. [CrossRef]
  19. Xiao, H.; Zhou, X.; Tian, Y. Research on Wireless Spectrum Sensing Technology Based on Machine Learning. International Conference on Security, Privacy and Anonymity in Computation, Communication and Storage. Springer, 2018, pp. 472–479.
  20. Kadjo, J.M.; Yao, K.C.; Mansour, A. Blind Spectrum Sensing Based on Recurrence Quantification Analysis in the Context of Cognitive Radio. 26th European Signal Processing Conference (EUSIPCO);, 2018; pp. 1835–1839. [CrossRef]
  21. Atapattu, S.; Tellambura, C.; Jiang, H. Energy detection for spectrum sensing in cognitive radio; 2014. [CrossRef]
  22. Mitola, J.; Maguire, G.Q. Cognitive radio: making software radios more personal. IEEE Personal Communications 1999, 6, 13–18. [Google Scholar] [CrossRef]
  23. Mitola, J. Cognitive Radio Architecture Evolution. Proceedings of the IEEE 2009, 97, 626–641. [Google Scholar] [CrossRef]
  24. Naraghi-Pour, M.; Ikuma, T. Autocorrelation-Based Spectrum Sensing for Cognitive Radios. IEEE Transactions on Vehicular Technology 2010, 59, 718–733. [Google Scholar] [CrossRef]
  25. Marwan, N.; Romano, M.C.; Thiel, M.; Kurths, J. Recurrence plots for the analysis of complex systems. Physics Reports 2007, 438, 237–329. [Google Scholar] [CrossRef]
  26. Webber Jr, C.L.; Zbilut, J.P. Recurrence quantification analysis of nonlinear dynamical systems. Tutorials in contemporary nonlinear methods for the behavioral sciences 2005, 94, 26–94. [Google Scholar]
  27. Anishchenko, V.S.; Astakhov, V.; Neiman, A.; Vadivasova, T.; Schimansky-Geier, L. Nonlinear dynamics of chaotic and stochastic systems: tutorial and modern developments; 2007.
  28. Williams, G. Chaos theory tamed; 2014.
  29. Ivancevic, V.G.; Ivancevic, T.T. Complex nonlinearity: chaos, phase transitions, topology change and path integrals; 2008.
  30. Kantz, H.; Schreiber, T. Nonlinear time series analysis; Vol. 7, 2004.
  31. N. Marwan, C.W. Mathematical and Computational Foundations of Recurrence Quantifications. In: Recurrence Quantification Analysis. Understanding Complex Systems. 2015. [CrossRef]
  32. Bradley, E.; Kantz, H. Nonlinear time-series analysis revisited. Chaos: An Interdisciplinary Journal of Nonlinear Science 2015, 25. [Google Scholar] [CrossRef]
  33. Chelidze, D. Reliable Estimation of Minimum Embedding Dimension Through Statistical Analysis of Nearest Neighbors. Journal of Computational and Nonlinear Dynamics 2017, 12. [Google Scholar] [CrossRef]
  34. Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Physical review E 2004, 69. [Google Scholar] [CrossRef]
  35. Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Physical review A 1986, 33. [Google Scholar] [CrossRef]
  36. David, C.; Joseph, P., C. Experimental Nonlinear Dynamics Notes for MCE 567.
  37. Cao, L. Practical method for determining the minimum embedding dimension of a scalar time series. Physica D: Nonlinear Phenomena 1997, 110, 43–50. [Google Scholar] [CrossRef]
  38. Kennel, M.B.; Brown, R.; Abarbanel, H.D.I. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Physics Review A 1992, 45, 3403–3411. [Google Scholar] [CrossRef] [PubMed]
  39. Takens, F. Detecting strange attractors in turbulence. In Dynamical systems and turbulence, Warwick 1980; 1981; pp. 366–381.
  40. Webber Jr, C.L.; Zbilut, J.P. Dynamical assessment of physiological systems and states using recurrence plot strategies. Journal of applied physiology 1994, 76, 965–973. [Google Scholar] [CrossRef] [PubMed]
  41. Zbilut, J.P.; Webber Jr, C.L. Recurrence quantification analysis: Introduction and historical context. International Journal of Bifurcation and Chaos 2007, 17, 3477–3481. [Google Scholar] [CrossRef]
  42. Thiel, M.; Romano, M.C.; Kurths, J.; Meucci, R.; Allaria, E.; Arecchi, F.T. Influence of observational noise on the recurrence quantification analysis. Physica D: Nonlinear Phenomena 2002, 171, 138–152. [Google Scholar] [CrossRef]
  43. Mansour, A. Probabilités et statistiques pour les ingénieurs: cours, exercices et programmation; 2007.
  44. Shorack, G.R.; Wellner, J.A. Empirical processes with applications to statistics; SIAM, 2009.
  45. Gooch, J.W. Encyclopedic dictionary of polymers; 2010.
  46. Abell, M.L.; Braselton, J.P.; Rafter, J.A.; Rafter, J.A. Statistics with mathematica; 1999. [CrossRef]
  47. Papoulis, A.; Pillai, S.U. Probability, random variables, and stochastic processes; 2002.
  48. Miller, S.; Childers, D. Probability and random processes: With applications to signal processing and communications; 2012.
  49. Sobron, I.; Diniz, P.S.; Martins, W.A.; Velez, M. Energy detection technique for adaptive spectrum sensing. IEEE Transactions on Communications 2015, 63, 617–627. [Google Scholar] [CrossRef]
  50. Chin, W.L.; Li, J.M.; Chen, H.H. Low-complexity energy detection for spectrum sensing with random arrivals of primary users. IEEE Transactions on Vehicular Technology 2015, 65, 947–952. [Google Scholar] [CrossRef]
  51. Cohen, D.; Eldar, Y.C. Sub-Nyquist cyclostationary detection for cognitive radio. IEEE Transactions on Signal Processing 2017, 65, 3004–3019. [Google Scholar] [CrossRef]
  52. Tani, A.; Fantacci, R.; Marabissi, D. A low-complexity cyclostationary spectrum sensing for interference avoidance in femtocell LTE-A-based networks. IEEE Transactions on Vehicular Technology 2015, 65, 2747–2753. [Google Scholar] [CrossRef]
  53. Ahmadi, S.; Srinivasan, R.M.; Cho, H.; Park, J.; Cho, J.; Park, D. Channel models for IEEE 802.16 m evaluation methodology document. IEEE 802.16 Broadband Wireless Access Working Group 2007, pp. 03–12.
  54. Zayen, B.; Guibène, W.; Hayar, A. Performance comparison for low complexity blind sensing techniques in cognitive radio systems. 2010 2nd International Workshop on Cognitive Information Processing, 2010, pp. 328–332. [CrossRef]
  55. Gardner, W. Cyclostationarty in communications and signal processing; IEEE PRESS: New York, 1994. [Google Scholar]
  56. Gardner, W. The spectral correlation theory of Cyclostationary time-series. Signal Processing, Elsevier Science Publishers 1986, 11, 13–36. [Google Scholar] [CrossRef]
  57. Gardner, W. Exploitation Of Spectral Redundancy In Cyclostationary Signals. IEEE Signal Processing Magazine 1991, pp. 14–36. [CrossRef]
1
Taken’s theorem, the phase space of a system can be reliably reconstructed if and only iff m ≥ 2 D + 1 , where D ≥ 1 is the dimension of the system attractor[31,39].
2
The Complementary Error Function e r f c ( x ) is defined as follows:
e r f c ( x ) = 2 π ∫ x + ∞ e − θ 2 d θ
Preprints 80867 g001
Figure 1. The proximity coefficient r ( m , τ ) based on the embedding dimension m for a 16-QAM signal.
Figure 1. The proximity coefficient r ( m , τ ) based on the embedding dimension m for a 16-QAM signal.
Preprints 80867 g001
Preprints 80867 g002
Figure 2. The cost function f ( m , τ ) based on ( m , τ ) . The flat area of the curve f ( m , τ ) corresponds to a set of optimal values of m , τ . Consequently, the optimal values m 0 , τ 0 of m , τ should be chosen as follows m 0 , τ 0 ⊂ 3 ; N τ 0 × 6 ; N 2 .
Figure 2. The cost function f ( m , τ ) based on ( m , τ ) . The flat area of the curve f ( m , τ ) corresponds to a set of optimal values of m , τ . Consequently, the optimal values m 0 , τ 0 of m , τ should be chosen as follows m 0 , τ 0 ⊂ 3 ; N τ 0 × 6 ; N 2 .
Preprints 80867 g002
Preprints 80867 g003
Figure 3. RP according to equation (15) of a 16-QAM signal.
Figure 3. RP according to equation (15) of a 16-QAM signal.
Preprints 80867 g003
Preprints 80867 g004
Figure 4. RP of a Gaussian Minimum Shift Keying (GMSK) signal.
Figure 4. RP of a Gaussian Minimum Shift Keying (GMSK) signal.
Preprints 80867 g004
Preprints 80867 g005
Figure 5. RP of White Gaussian Noise.
Figure 5. RP of White Gaussian Noise.
Preprints 80867 g005
Preprints 80867 g006
Figure 6. Histogram of u d and u Δ for a White Gaussian Noise (WGN). We have u ¯ d = 90.6 and u ¯ Δ = 90 . For P f a = 0.01 , the detection threshold of RAD becomes λ = 12.5 . Based on u ¯ Δ value, the confidence interval becomes Φ Δ = 77.5 ; 102.5 . We notice that u ¯ d ∈ Φ Δ . Consequently, using the conformity test, we can conclude that u d is representative of u Δ .
Figure 6. Histogram of u d and u Δ for a White Gaussian Noise (WGN). We have u ¯ d = 90.6 and u ¯ Δ = 90 . For P f a = 0.01 , the detection threshold of RAD becomes λ = 12.5 . Based on u ¯ Δ value, the confidence interval becomes Φ Δ = 77.5 ; 102.5 . We notice that u ¯ d ∈ Φ Δ . Consequently, using the conformity test, we can conclude that u d is representative of u Δ .
Preprints 80867 g006
Preprints 80867 g007
Figure 7. Histogram of u d and u Δ for a noisy 16-QAM signal; SNR=0 dB. In this example, we have u ¯ d = 90 and u ¯ Δ = 127 . With P f a = 0.01 , we obtain λ = 12.5 and Φ Δ = 114.5 ; 139.5 . We notice that u d is not representative of u Δ , because u ¯ d ∉ Φ Δ .
Figure 7. Histogram of u d and u Δ for a noisy 16-QAM signal; SNR=0 dB. In this example, we have u ¯ d = 90 and u ¯ Δ = 127 . With P f a = 0.01 , we obtain λ = 12.5 and Φ Δ = 114.5 ; 139.5 . We notice that u d is not representative of u Δ , because u ¯ d ∉ Φ Δ .
Preprints 80867 g007
Preprints 80867 g008
Figure 8. Theoretical and Experimental Probability of Detection for RAD versus SNR.
Figure 8. Theoretical and Experimental Probability of Detection for RAD versus SNR.
Preprints 80867 g008
Preprints 80867 g009
Figure 9. Receiver Operating Characteristic for 16 − Q A M signal.
Figure 9. Receiver Operating Characteristic for 16 − Q A M signal.
Preprints 80867 g009
Preprints 80867 g010
Figure 10. Robust RQA Detector insensitivity versus classical modulation techniques.
Figure 10. Robust RQA Detector insensitivity versus classical modulation techniques.
Preprints 80867 g010
Preprints 80867 g011
Figure 11. Receiver Operating Characteristic of RAD model based on the number of observed samples in a Gaussian channel with S N R = − 12 dB.
Figure 11. Receiver Operating Characteristic of RAD model based on the number of observed samples in a Gaussian channel with S N R = − 12 dB.
Preprints 80867 g011
Preprints 80867 g012
Figure 12. ROC performance: ED vs RAD. The RAD is superior to ED.
Figure 12. ROC performance: ED vs RAD. The RAD is superior to ED.
Preprints 80867 g012
Preprints 80867 g013
Figure 13. Comparison of Energy Detector (ED), Cyclostationary Features Detector (CFD) and Recurrence Analysis Detector (RAD).
Figure 13. Comparison of Energy Detector (ED), Cyclostationary Features Detector (CFD) and Recurrence Analysis Detector (RAD).
Preprints 80867 g013
Preprints 80867 g014
Figure 14. Performance Curve P d as a function of SNR for 16-QAM signal in a Rayleigh channel
Figure 14. Performance Curve P d as a function of SNR for 16-QAM signal in a Rayleigh channel
Preprints 80867 g014
Preprints 80867 g015
Figure 15. Energy based Detector Process. λ E D denotes the detection threshold of ED.
Figure 15. Energy based Detector Process. λ E D denotes the detection threshold of ED.
Preprints 80867 g015
Preprints 80867 g016
Figure 16. Different steps of CFD detection process.
Figure 16. Different steps of CFD detection process.
Preprints 80867 g016
Preprints 80867 g017
Figure 17. Different steps of RAD detection process.
Figure 17. Different steps of RAD detection process.
Preprints 80867 g017
Preprints 80867 g018
Figure 18. Curves of algorithmic complexity of ED, CFD and RAD.
Figure 18. Curves of algorithmic complexity of ED, CFD and RAD.
Preprints 80867 g018
Table 1. Simulation parameters.
Table 1. Simulation parameters.
Entity Parameters Value
PU’s signal Sampling frequency F e 128 kHz
Symbol frequency 16 kHz
Bandwidth of Interest B 24 kHz
SU’s Detector Observation time 15.6 ms
Samples number N 2000
Embedding parameters dimension m 16
time delay τ 6
Transmission Channel Noise Model WGN
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated