Design and Characterization of a Self-Aligning End-Eﬀector Robot for Single-Joint Arm Movement Rehabilitation

Traditional end-effector robots for arm rehabilitation are usually attached at the hand, primarily focusing on coordinated multi-joint training. Therapy at an individual joint level of the arm for severely impaired stroke survivors is not always possible with existing end-effector robots. The Arm Rehabilitation Robot (AREBO)—an end-effector robot—was designed to provide both single and multi-joint assisted training while retaining the advantages of traditional end-effector robots, such as ease of use and cost-effectiveness (compared to exoskeletons). This work presents the design, optimization, and characterization of AREBO for training single-joint movements of the arm. The AREBO has three actuated and three unactuated degrees of freedom, allowing it to apply forces in any arbitrary direction at its endpoint and self-align to arbitrary orientations within its workspace. The AREBO’s link lengths were optimized to maximize its workspace and manipulability. The AREBO provides single-joint training in both unassisted and adaptive weight support modes using a human arm model to estimate the human arm's kinematics and dynamics without using additional sensors. The characterization of the robot’s controller and the algorithm for estimating the human arm parameters were performed using a two degrees of freedom mechatronic model of the human shoulder joint. The results demonstrate that: (a) the movements of the human arm can be estimated using a model of the human arm and robot’s kinematics, (b) the AREBO has similar transparency to that of existing arm therapy robots in the literature, and (c) the adaptive weight support mode control can adapt to different levels of impairment in the arm. This work demonstrates how an appropriately designed end-effector robot can be used for single-joint training, which can be easily extended to multi-joint training. Future work will focus on the evaluation of the system on patients with any neurological condition requiring arm training.

Keywords:

Subject: Engineering - Bioengineering

1. Introduction

Every year, around 12.2 million people suffer from stroke worldwide (Feigin et al., 2022). It is estimated that 82% of the needs of stroke survivors are unmet due to multiple reasons, including poor access to rehabilitation services and limited healthcare resources (Kamalakannan et al., 2016). Increased focus on mobility soon after a stroke limits the amount of upper limb rehabilitation for recovery during the early sensitive period. 40% of stroke survivors are left with chronic upper limb impairments and activity limitations that impact their quality of life (Hankey et al., 2002).

Rehabilitation robots were introduced to overcome some of these barriers by providing semi-supervised high-intensity training. Rehabilitation robots for the upper limb fall under two categories: 1) Exoskeletons and 2) End-effectors. Exoskeletons, as the name suggests, are exterior skeletons that resemble the human limb segment’s anatomical structure to which they are attached. They are attached at multiple points on the arm to support both single and multi-joint training in a 3D space. Despite these advantages, exoskeletons are generally costly and require longer set-up time than end-effectors due to the strict alignment constraints of the human and robot axes of rotation (Lo and Xie, 2012). Some popular examples of upper limb exoskeletons include Anyexo (Zimmermann et al., 2019), ARMin (Nef and Riener, 2005), Harmony (Kim and Deshpande, 2017), NESM-

γ

(Pan et al., 2022). End-effectors, however, are simpler robots than exoskeletons that are attached only at one point to the arm (usually at the hand) and hence are easy to set up. However, most end-effectors are fully gravity-support planar robots (e.g., MIT Manus (Hogan et al., 1992) and H-man (Campolo et al., 2014)) making them unsuitable for training 3D movements in a non-gravity-eliminated environment. Most end-effectors do not track the kinematics of the human arm, which are useful for tracking compensatory movement patterns (Kitago et al., 2013) and evaluating movement quality. Further, most end-effectors cannot be used for providing assisted training in single-joint movements, which may be relevant for severely impaired patients. Although both types of robots have their pros and cons, the end-effector-based solutions have been more popular than exoskeleton-based ones owing to their simpler structure, reduced cost, and ease of use (Molteni et al., 2018). Developing an end-effector robot capable of adaptive training of single and multi-joint arm movements in 3D with titrated gravity support, while tracking the joint kinematics of the human arm would increase the utility of an end-effector robot for arm therapy. This robot could train: (a) single joint movements of severely impaired patients (e.g., with a weak shoulder joint), and (b) coordinated 3D multi-joint movements of moderately impaired patients with sufficient strength but poor coordination. Such a robot would be a versatile tool for administering a wide range of arm-therapy activities.

Recent work along this line is the EMU robot (Crocher et al., 2018), which has a 6 degrees of freedom (DOF) end-effector kinematic structure with two actuated and four unactuated DOF. EMU was designed for assisted training of 3D arm movements with varying levels of gravity support, and the amount of weight support was estimated using a 4 DOF model of the human arm. It is designed to assist 3D multi-joint arm movements against gravity using its two-actuated DOF, which makes it unsuitable for single-joint movement training. Safe single-joint assisted training requires at least three actuated DOF to apply force in any direction to cause the desired rotary movement of the (arbitrarily oriented) human limb while avoiding undesirable forces that push or pull the limb segment from the joint. We recently proposed the design of a self-aligning 6 DOF end-effector robot, AREBO (Arm Rehabilitation Robot), which has three actuated and three unactuated DOF (Balasubramanian et al., 2021). The three actuated DOF allow the robot to apply safe forces at its endpoint that result in pure rotational movements about a joint. The three unactuated DOF allow it to align to arbitrary orientations within its workspace, which reduces the constraints on the relative position and orientation of the human subject with respect to the robot. This previous work focused on the exposition of the kinematic structure, its optimization, and the algorithm for estimating the human arm parameters for single joint movements.

In the current study, we extend this previous work (Balasubramanian et al., 2021) by: (a) proposing a simplification to the previous kinematic structure, (b) designing, fabricating, and assembling a physical prototype of AREBO (Figure 1), and (c) developing and characterizing the robot controller for human-robot interaction during assisted training of the single-joint movements of the arm.

2. Methods

2.1. Kinematics

2.1.1. AREBO’s Kinematic Chain

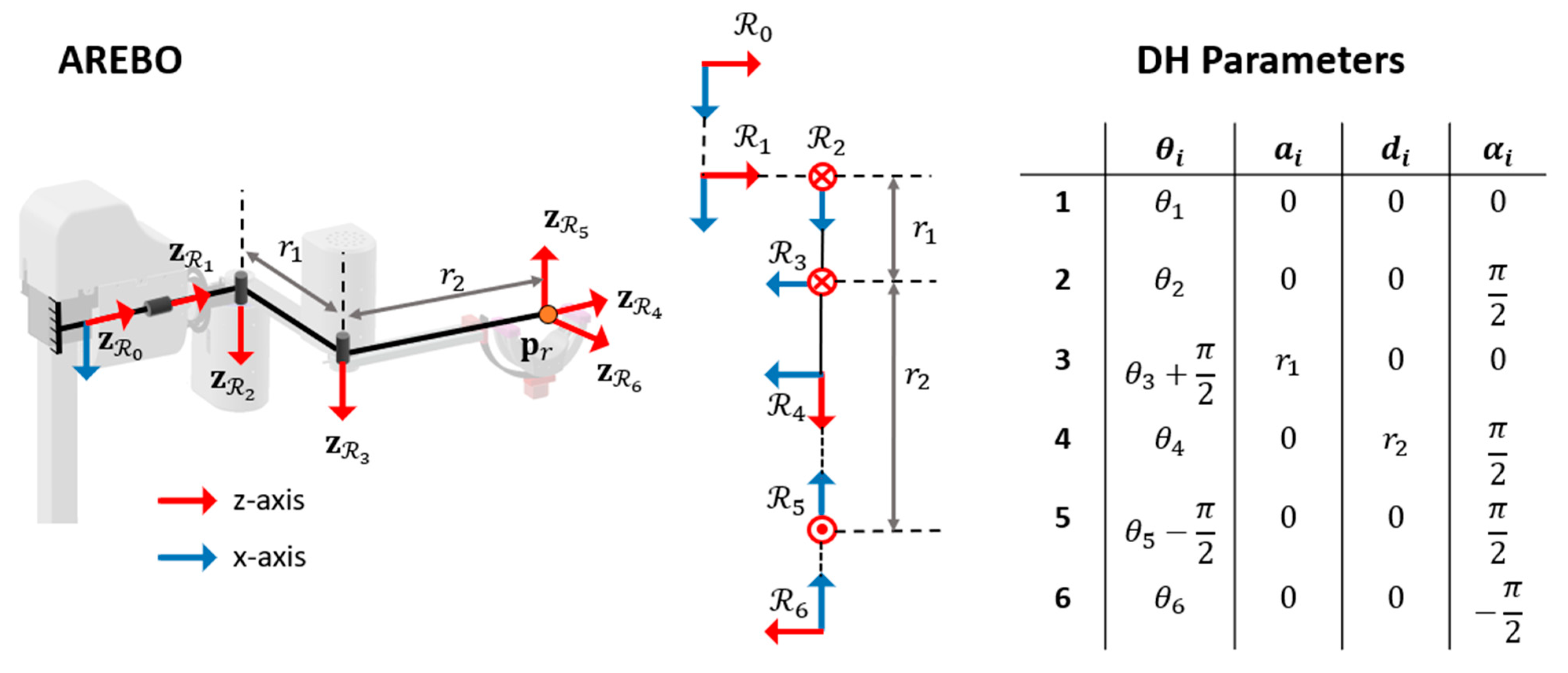
The AREBO was designed to have a 6 DOF kinematic chain (Figure 2) to provide flexibility in attaching the arm to the robot. The three proximal DOF are actuated, which can control the 3D position of the robot’s endpoint; while the three distal DOF of the robot are unactuated forming a spherical joint centered around the robot’s endpoint, which forms the robot’s unactuated segment (Figure 2). Let

R_{0}

be the base frame of the robot that is fixed to the earth and let

R_{1}, R_{2}, \dots, R_{6}

represent the local reference frames attached to each DOF of the robot. The AREBO has six generalized coordinates corresponding to its six DOF,

θ = {[\begin{matrix} θ_{1} & θ_{2} & \dots & θ_{6} \end{matrix}]}^{T} \in {[- π, π)}^{6}

. Figure 2 depicts the AREBO’s kinematic chain along with its Denavit–Hartenberg (DH) parameters for the transformation between subsequent local reference frames. The origin of the

R_{6}

reference frame

(p_{r} \in R^{3})

is referred to as the robot’s endpoint, which is a function of the first three generalized coordinates (

θ_{1}, θ_{2}, θ_{3}

) and the link lengths (

r_{1}, r_{2}

). The

R_{6}

reference frame's orientation

R_{R_{6}}^{R_{0}} \in S O (3)

depends on all six generalized coordinates

θ

. Refer to Supplementary Material for the detailed forward and inverse kinematics of the robot.

The current design has the same kinematic structure as the one proposed by Balasubramanian et al., except for one modification to the unactuated segment of the robot. In Balasubramanian et al., the axes of the three unactuated DOF (

R_{4}, R_{5}, R_{6}

) do not coincide, which led to translations of the arm that cannot be controlled by the robot. Thus, this was modified in the current design to form a spherical joint at the endpoint, as shown in Figure 2, which addresses this issue.

2.1.2. Human-Robot Closed Loop Kinematic Chain

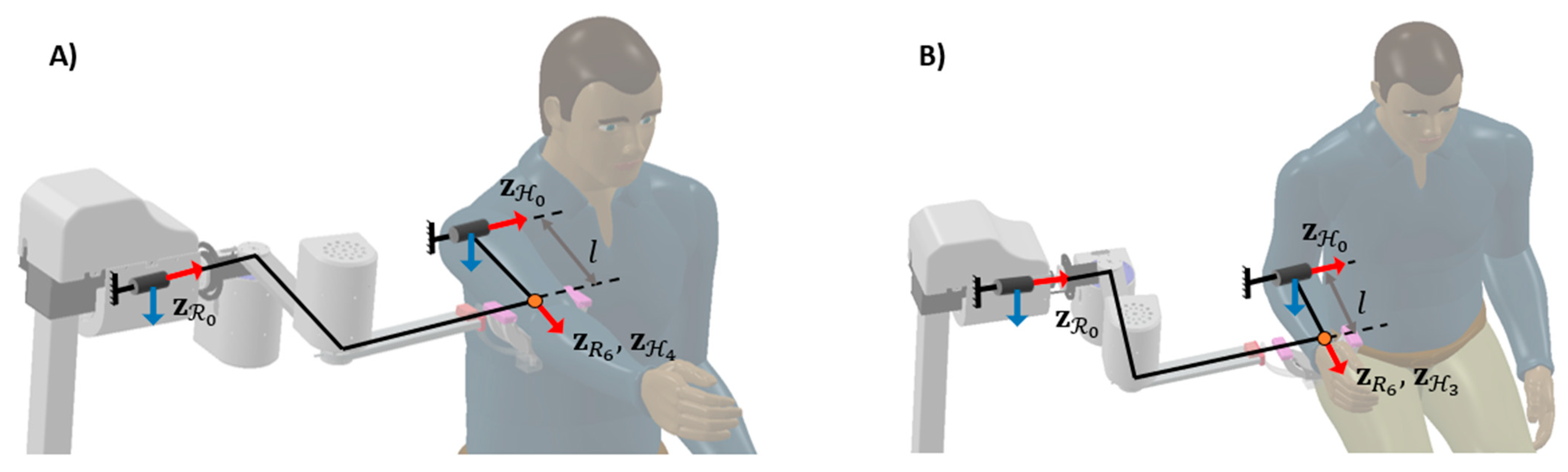
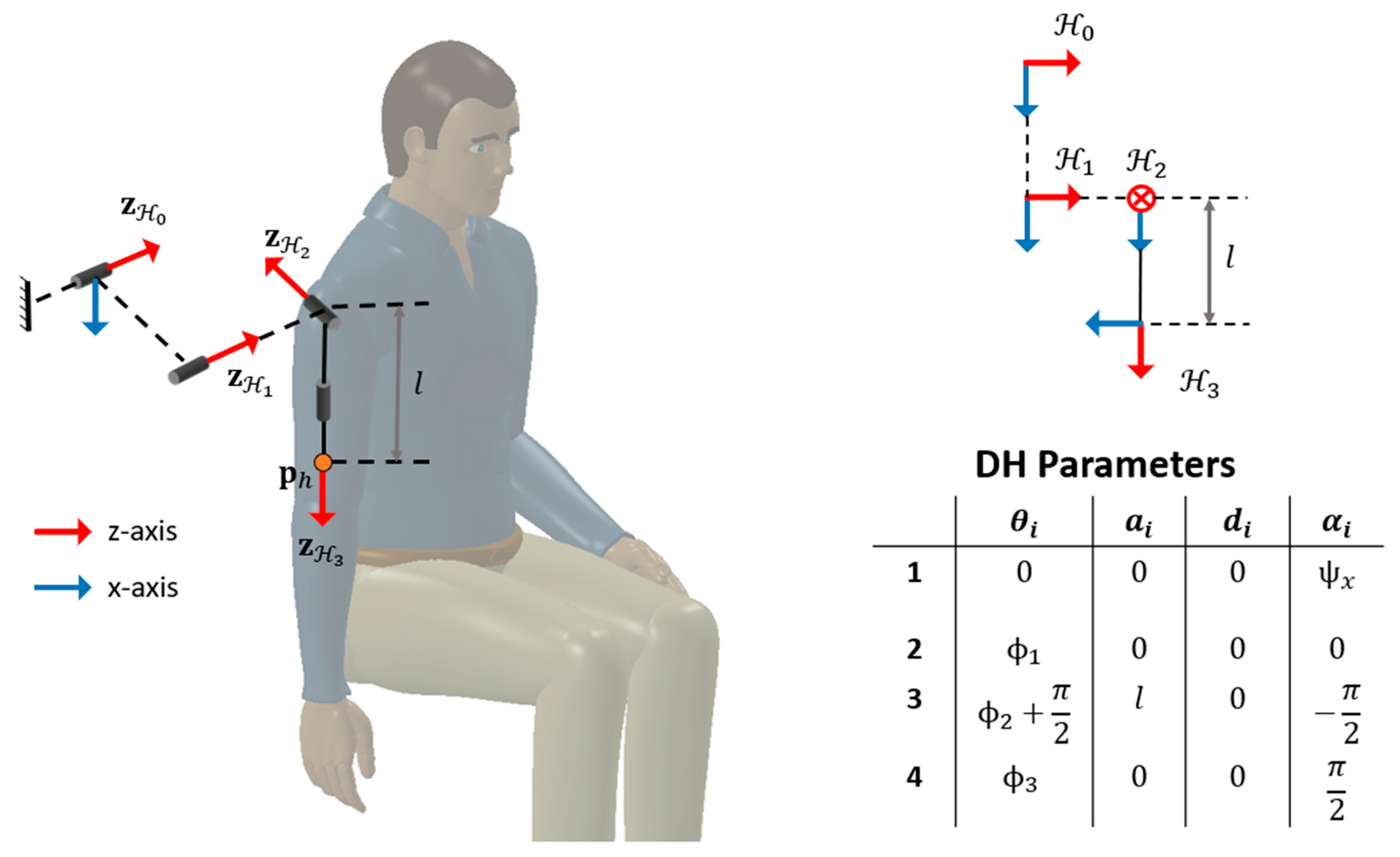
A closed-loop kinematic chain is formed by rigidly attaching the robot to the human arm (upper arm or the forearm as shown in Figure 3). The human arm is assumed to be a 3 DOF joint as shown in Figure 4, along with its DH parameters. The reference frame

H_{0}

is the human base frame (attached to the trunk or the upper arm as shown in Figure 3), while the three reference frames

H_{1}

H_{2}

, and

H_{3}

are the local reference frames corresponding to the three DOF of the human arm. The three generalized coordinates of the human arm are given by

ϕ = {[\begin{matrix} ϕ_{1} & ϕ_{2} & ϕ_{3} \end{matrix}]}^{T} \in {[- π, π)}^{3}

. The origin of the

H_{3}

reference frame is referred to as the endpoint of the arm

(p_{h} \in R^{3}),

and its orientation is given by

R_{H_{3}}^{H_{0}} \in S O (3)

We make the following assumptions on how the robot is connected to the human arm:

The human base frame $H_{0}$ is located close enough to the robot’s base frame $R_{0}$ such that the intersection between the robot and human arm workspaces has a non-zero area.
The endpoint of the arm is attached to the spherical joint at the robot’s endpoint, such that $p_{r}^{R_{0}} = p_{h}^{R_{0}}$ , where $p_{r}^{R_{0}}$ and $p_{h}^{R_{0}}$ are the positions of the robot and arm endpoints with respect to the robot’s base reference frame $R_{0}$ .
The orientation of the human base frame with respect to the robot’s base frame, $R_{H_{0}}^{R_{0}}$ is assumed to be only rotated about the $x_{R_{0}}$ axis.

This type of connection between the arm and AREBO allows the robot to measure and support two DOF movements of the human arm (

ϕ_{1}, ϕ_{2}

) namely: a) shoulder flexion/extension and shoulder abduction/adduction if AREBO is attached to the upper arm, or b) shoulder internal/external rotation and elbow flexion/extension if AREBO is attached to the forearm. In the rest of the paper, we will always assume that the upper arm is connected to the robot while detailing the different features of the system and its evaluation. However, all these can be implemented for the forearm as well, with slight modifications.

2.1.3. Optimization of Link Lengths

The robot link lengths (

r_{1}, r_{2}

) were optimized (like in Balasubramanian et al., 2021) for single joint movements of the arm by maximizing the robot’s workspace and manipulability in a plane orthogonal to the longitudinal axis of the attached arm segment (

z_{H_{3}}

in figure 4). A brute force search was implemented to find the optimal link lengths for the robot for different combinations of the arm parameters, namely the arm lengths, positions, and orientations of the human joint

(H_{0})

with respect to the robot

(R_{0})

. An initial coarse search with link lengths

{(r}_{1}, r_{2})

range between 20 and 50 cm was conducted to locate the region near which the optimum point exists (2 cm increments). After that, a fine search with 1 mm increments in the link lengths revealed the optimum link lengths. Table 1 provides the details of the parameter ranges and step sizes used for the optimization procedure. The objective function for the optimization procedure was defined as the following,

O (r_{1}, r_{2}) = \frac{1}{2} (O_{W} (r_{1}, r_{2}) + O_{M} (r_{1}, r_{2}))

where, the workspace component of the objective function

O_{W} (r_{1}, r_{2})

quantifies the relative intersection between the robot’s and human’s workspaces, averaged across combinations of the human parameters.

O_{M} (r_{1}, r_{2})

is the manipulability of the robot in a plane orthogonal to the arm. The details of these two components are provided in the Supplementary Material.

2.2. Robot Hardware

2.2.1. Mechanical Design

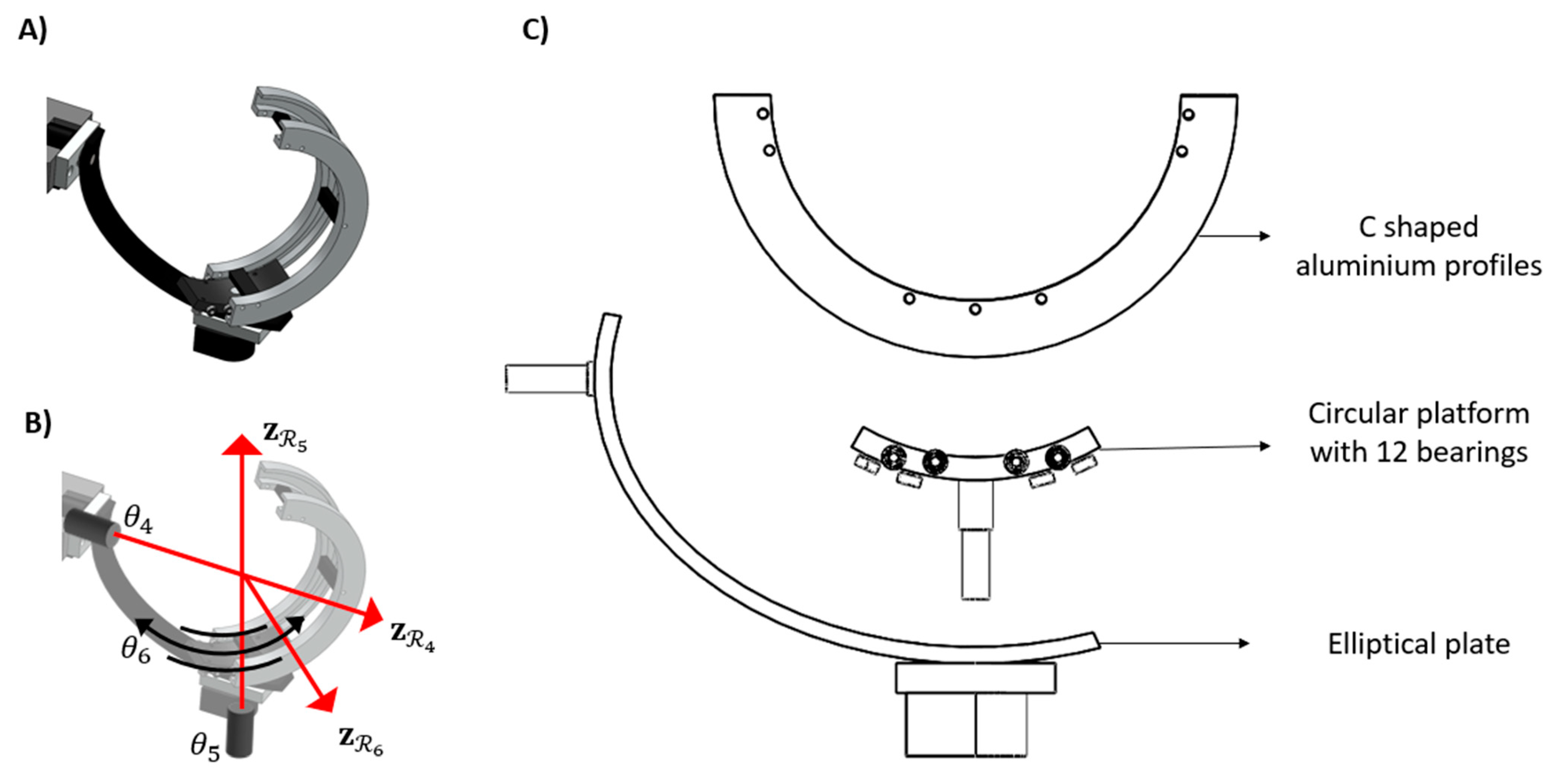
The three proximal joints with the motor and torque sensor assembly were interconnected by two aluminium links and three custom-designed flange couplings with keyways. The tapped hole and key on the motor shaft were utilized to prevent relative motion between the coupling and actuator. The couplings and the links were fabricated with mild steel and aluminium, respectively. The 3D model of the distal spherical joint formed by the robot’s three unactuated DOFs is shown in Figure 5. An elliptical plate with a shaft at one end connects the cuff with the rest of the robot (Figure 5C). The dimensions of the ellipse were calculated to allow a range of motion of 90 degrees for

θ_{5}

. The 5^th joint (

R_{5}

) was formed by a circular segment placed over a shaft. Twelve ball bearings (four on each side and four at the bottom) were strategically placed to clone the behavior of a hinge joint at

R_{6}

. Two C-shaped semi-circular aluminium profiles held together by three spacers formed the 6^th DOF.

The robot’s kinematic chain is mounted on a manually adjustable telescopic mechanism to change the height of

R_{0}

from the ground. This height is varied by rotating the handle that is attached to a bevel gear and lead screw arrangement and has a 260 mm stroke length. This telescopic mechanism is mounted on a plus-shaped chassis constructed from four beams made from

40 m m \times 40 m m

aluminium profile with a mild steel stiffener at its base. The four caster wheels with brakes bestow portability to the entire assembly.

2.2.2. Joint Actuation and Sensing

AREBO’s three actuated DOFs use individual brushless DC motors (details in Table 2) configured through individual controllers to operate in a current control mode. Each actuated joint consists of a reaction-type joint torque sensor that is sandwiched between the actuator’s body and proximal segment of the joint (Figure 6); the torque sensors are used to implement an outer torque control loop about each joint. The rotary encoder on each brushless DC motor senses the joint position of the three actuated DOF

(θ_{1}, θ_{2}, θ_{3})

; two additional rotary encoders were fitted to sense

θ_{4}

and

θ_{5} .

These encoders allow us compute

x_{R_{6}}

and the orientation of

R_{5}

(R_{R_{5}})

since we do not measure

θ_{6}

(Figure 2). The specifications of the actuators and sensors are given in Table 2.

2.2.3. Firmware and Software

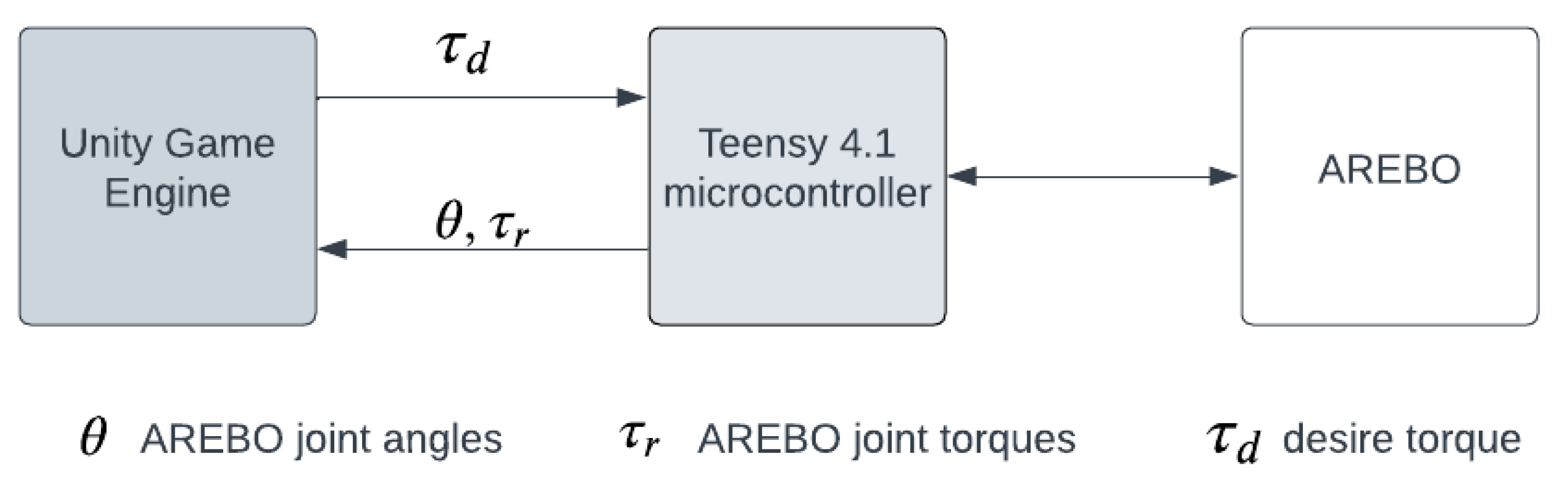
A Teensy 4.1 (PJRC.com, LLC.) microcontroller performs the low-level hardware interfacing to AREBO’s actuators and sensors. The three actuators are controlled through individual pulse width modulation (PWM) lines from the microcontroller to the ESCON 70/10 motor controllers operating in the current control mode. The five encoders are connected to 10 digital lines (channel A, channel B for each encoder). Each torque sensor is connected to an HX711 (dual-channel 24-bit precision A/D weight pressure sensor) load cell amplifier, which connects to the microcontroller through two digital lines (two-wire interface). The firmware on the microcontroller runs at 200 Hz, with each iteration of the firmware code performing sensor reading, control law execution, and data communication with the PC. The different components of the firmware/software system interfacing the robot are depicted in Figure 7.

The software to communicate with the robot was written using the Unity Game Engine (Unity Technologies) to present the graphical user interface to communicate with the robot for reading data and setting control modes and controller parameters. This software reads the sensor data from the firmware via a USB serial link and logs it to the PC at 200 Hz. The software will eventually contain the games used when training arm movements with AREBO.

2.3. AREBO Human-Robot Physical Interaction: Controller Details

As a rehabilitation robot designed for measuring and assisting arm movements, two types of human-robot physical interactions are supported by AREBO, which are defined as two modes of operation of the robot:

(a): Unassisted mode (UAM): This mode allows subjects to perform voluntary active movements with no physical robotic assistance and minimal impedance from the robot’s mechanical structure, which is necessary to actively engage patients during training and to assess their residual ability, and
(b): Adaptive weight support mode (WSM): In this control mode, the robot and user work together to complete a task. While the user voluntarily moves the arm, the robot provides just the amount of weight support needed to compensate for the weakness in the arm. The support from the robot can be fixed or adaptive depending on the training type desired by the user.

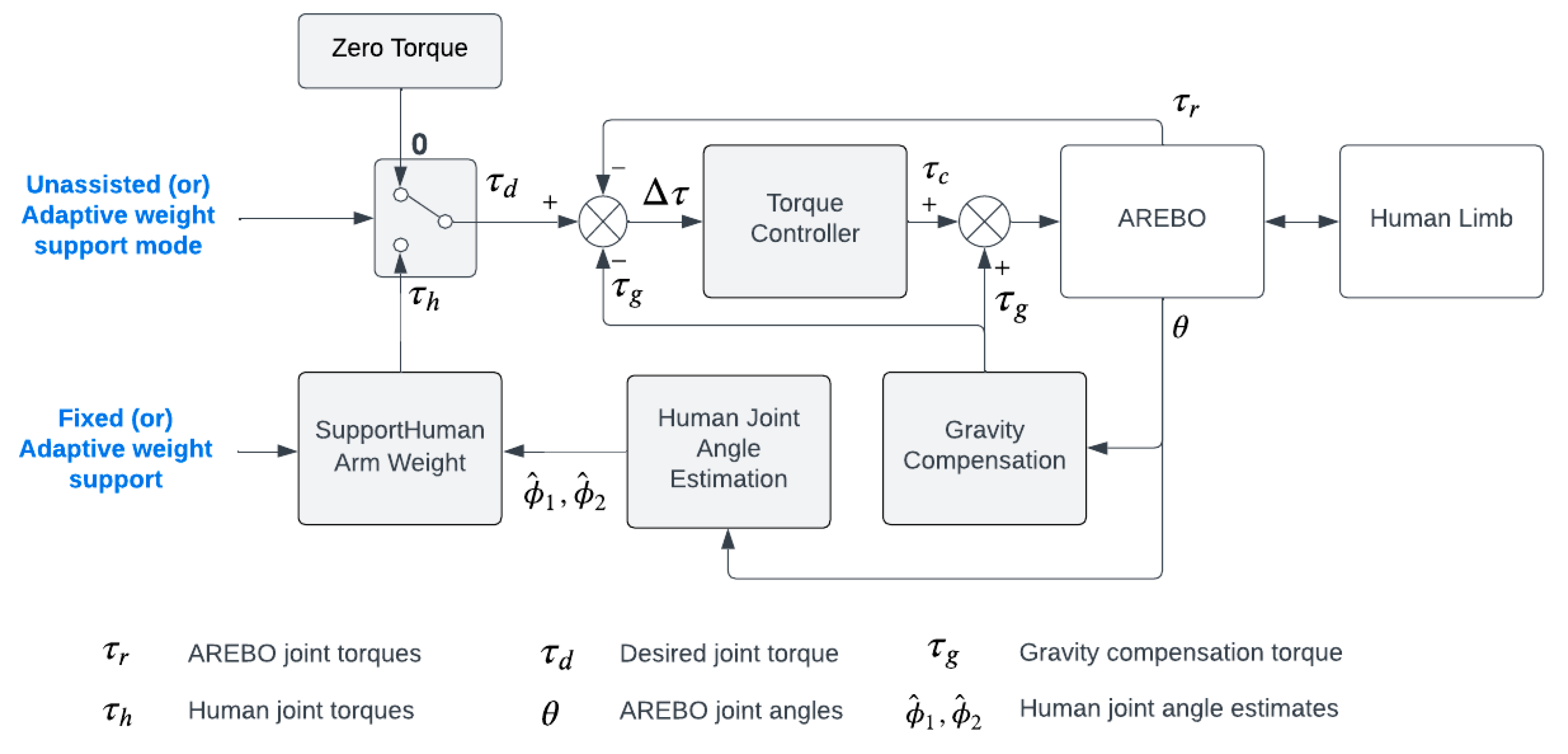
AREBO’s controller architecture that allows the implementation of UAM and WSM is depicted in Figure 8. The controller has the following components:

(a): Low-level current control loop: At the lowest level, a current control loop is implemented by the Maxon motor controllers for each individual motor.
(b): High-level torque control loop: A high-level torque control loop is implemented for each actuated robot using the joint torque sensors, to control the interaction force $(f_{i n t}^{R_{0}} = {[f_{i n t, x}, f_{i n t, y}, f_{i n t, z}]}^{T})$ between the arm and AREBO applied at the robot's endpoint.
(c): Gravity compensation module: A gravity compensation module that computes the torques required at the robot joints to hold the robot in a particular joint configuration against gravity.
(d): Human joint estimation module: This module allows the estimation of the human joint angle from the robot’s joint angles without the need for any additional sensor on the arm.
(e): Human Arm weight support module: This module estimates the torque required to provide a given level of weight support to the arm based on the estimate of the arm’s joint angles.

This controller is used to implement the two modes of training (UAM and WSM) with the robot. The details of each of these modules are provided in the rest of this section.

2.3.1. High-level Torque Control Loop

The purpose of this loop is to control the interaction force

f_{i n t}^{R_{0}} \in R^{3}

between the robot and arm, represented in the robot’s base frame

R_{0}

. This interaction force could be due to the subject applying a force on the robot, i.e., the subject attempting to move voluntarily while connected to the robot, or the robot applying a force on the arm for assisting or resisting movements. The joint torques due to this interaction force

(τ_{i n t} \in R^{6})

is given by,

τ_{i n t} [n] = [\begin{matrix} τ_{i n t, 1} [n] & τ_{i n t, 2} [n] & \dots & τ_{i n t, 6} [n] \end{matrix}] = J^{T} (θ [n]) \cdot f_{i n t}^{R_{0}} [n]

where,

J (\cdot) \in R^{3 \times 6}

is the robot’s Jacobian matrix (details in Supplementary material). AREBO’s kinematic structure will result in zero torques in the last three robot DOF, i.e.,

τ_{i n t, 4} [n] = τ_{i n t, 5} [n] = τ_{i n t, 6} [n] = 0

The torque controller for each of the three actuated joints of AREBO is a PD controller, with the discrete-time control law for the

i^{t h}

DOF is given by the following:

τ_{c, i} [n] = k_{i, 1} ∆ τ_{i} [n] + k_{i, 2} ∆ τ_{i} [n - 1]

{∆ τ}_{i} [n] = τ_{d, i} [n] - τ_{r, i} [n] - τ_{g, i} [n]

where,

$n$ is the current time instant.
The subscript $i$ indicates that these are variables associated with $i^{t h}$ DOF.
$τ_{c, i} [n]$ is the output of the PD controller at the time instant $n$ .
$τ_{g, i} [n]$ is the torque required to fully compensate for the weight of the robot at the current joint configuration $θ [n]$ .
$τ_{d, i} [n]$ is the desired torque, which is manipulated for implementing the unassisted and adaptive weight support control modes.
$τ_{r, i} [n] = τ_{i n t, i} [n] + τ_{g, i} [n]$ , is the torque read by the robot’s joint torque sensor, which contains the torque required to hold the robot in the current configuration $(τ_{g, i} [n])$ , and $τ_{i n t, i} [n]$ the torque due to the interaction force $f_{i n t}^{R_{0}}$ .
$k_{i, 1}$ and $k_{i, 2}$ are the parameters of the PD controllers. The same fixed controller parameters are used for the 2^nd and 3^rd DOF of the robot, while these two parameters are piecewise constant functions of the interaction torque $τ_{i n t, i} [n] = τ_{r, i} [n] - τ_{g, i} [n]$ for the 1^st DOF (details in the Supplementary Material).

2.3.2. Gravity Compensation

The gravity compensation module ensures that the robot’s actuators automatically take care of the robot’s weight for any possible robot joint configuration

θ [n]

. This module uses the current robot joint angles

θ [n]

to compute the torques required to maintain the robot in that configuration against gravity, using the following expression,

R^{3} ∋ g (θ) = [\begin{matrix} τ_{g, 1} (θ) \\ τ_{g, 2} (θ) \\ τ_{g, 3} (θ) \end{matrix}]

where,

τ_{g, i} (θ)

is the torque required at the joint

i

to maintain the robot in the joint configuration

θ

The parameters of the gravity term

g (θ)

were estimated through a calibration procedure where a PD position controller moved and held the robot at joint configurations, while the static joint torques at the first three joints were recorded. The details of the calibration procedure and the parameter estimation procedure are provided in the Supplementary Material.

2.3.3. Human Joint Angle Estimation

The kinematics of the arm can be estimated from AREBO’s joint kinematics if three parameters of the arm are known, namely the length of the human arm

(l)

, the relative orientation

(R_{H_{0}}^{R_{0}})

and the origin

(r_{H_{0}}^{R_{0}})

of the human base frame

(H_{0})

with respect to the robot base frame

(R_{0})

as indicated in Figure 9. The problem of estimating these parameters about the arm can be split into two sub-problems, which can be solved through simple calibration procedures: estimating the (a) orientation

R_{H_{0}}^{R_{0}}

and (b) origin

r_{H_{0}}^{R_{0}}

and the arm length

l

The orientation of the human base joint with respect to the robot’s base joint is assumed to be rotated about the

x_{R_{0}}

axis, i.e.,

R_{H_{0}}^{R_{0}}

is parametrized by a single scalar

ψ_{x}

. This parameter can be estimated from the knowledge of the plane of shoulder flexion/extension movements with zero abduction. The calibration procedure for estimating

ψ_{x}

will require the user to perform flexion/extension movements while attached to the robot, which records its kinematics during the procedure. The endpoint kinematics of the robot can be used to estimate the equation of the plane that contains the flexion/extension plane and, thus the orientation parameter

ψ_{x}

. The algorithm for this estimation process is provided in supplementary material (Algorithm 1).

Once the orientation parameter

ψ_{x}

is estimated, then

R_{H_{0}}^{R_{0}} = [\begin{matrix} 1 & 0 & 0 \\ 0 & \cos ψ_{x} & - \sin ψ_{x} \\ 0 & \sin ψ_{x} & \cos ψ_{x} \end{matrix}]

. With this information, we can estimate the origin

r_{H_{0}}^{R_{0}}

and the arm length

l

parameters through another simple calibration procedure. This is done by having the robot perform small random movements of the arm while recording the robot's kinematics; here, we assume that the human base frame does not undergo any translation or rotation during the calibration procedure. The endpoint kinematics of the robot can be used to estimate $r_{H_{0}}^{R_{0}}$ and

l

. The algorithm for this procedure is provided in the supplementary material (Algorithm 2).

2.3.4. Human Arm Weight Support

AREBO provides adaptive weight support during movements by modulating the amount of de-weighting of the subject’s arm. The de-weighting parameter is a scalar

α \in [0,1]

, where

0

indicates no weight support, and

1

indicates 100% weight support. Arm de-weighting requires an estimate of the torque required for holding the arm against gravity, which is done using a model of the arm. The details of this model and the procedure for estimating the model parameters are discussed in the Supplementary Material.

This arm model provides the torques

τ_{h} (ϕ) = {[\begin{matrix} τ_{h, 1} (ϕ) & τ_{h, 2} (ϕ) & 0 \end{matrix}]}^{T}

required to hold the arm against gravity in the current orientation

ϕ

. Let the interaction force on the arm to generate this moment about the human joints be

f_{h}^{H_{0}} \in R^{3}

, acting at the point of AREBO’s attachment with the arm, which is given by the following expression:

f_{h}^{H_{0}} (ϕ) = J_{h}^{- T} (ϕ) \cdot τ_{h} (ϕ)

where,

J_{h} (ϕ) \in R^{3 \times 3}

is the Jacobian matrix of the arm’s kinematic chain at the arm orientation

ϕ

. Partial de-weighting can be provided by the robot when the human-robot interaction force is set to some fraction of

f_{h}^{H_{0}}

f_{i n t}^{R_{0}} (ϕ) = α R_{H_{0}}^{R_{0}} \cdot f_{h}^{H_{0}} (ϕ)

where, $R_{H_{0}}^{R_{0}}$ is the rotation matrix representing the human base frame

H_{0}

in the robot’s base frame

R_{0} .

The torques at the three joints of the robot to generate this interaction force $f_{i n t}^{R_{0}} (ϕ)$ is given by the following,

τ_{i n t} (θ, ϕ) = J^{T} (θ) \cdot f_{i n t}^{R_{0}} (ϕ)

where,

J (θ) \in R^{3 \times 6}

is the robot’s Jacobian matrix at the robot joint orientation

θ

. This

τ_{i n t} (θ, ϕ)

is set as the desired torque

τ^{d}

to the torque controller (Figure 8).

The level of assistance or de-weighting is decided by the de-weighting parameter

α

which could be either fixed or adaptive. In the case of fixed support,

α

is constant throughout the session and its value is decided by the clinician. In the case of adaptive support, the value of

α

is modulated within a therapy session depending on the success or failure of movements performed by the subject on a trial-by-trial basis.

α [k + 1] = F (S [k], α [k]) α [k] + ∆ (S [k]), k \in Z_{> 0}

where,

$k$ is the trial number (an integer greater than 0).
$S [k]$ is a binary variable indicating the success or failure of trial $k$ .
$F (S [k], α [k]) = \{\begin{matrix} 1, & S [k] = 0 \\ 0.95, & S [k] = 1, α [k] \leq 0.5 \\ 0.98, & S [K] = 1, α [k] > 0.5 \end{matrix}$ is the forgetting factor that reduces the amount of arm support following successful trials.
$∆ (S [k]) = \{\begin{matrix} 0.02, & S [k] = 0 \\ 0 & S [k] = 1 \end{matrix}$ is the learning factor that increases the amount of de-weighting following a failed trial.

2.4. Testing AREBO Controller

The AREBO controller and its different components were tested to evaluate its performance during physical human-robot interaction. To make the development and testing process controlled and repeatable, we developed a mechatronic human shoulder joint simulator, which we refer to as the shoulder joint model (SJM). The SJM was used for carrying out all the experiments to characterize the AREBO controller, which is described in the rest of this section.

2.4.1. Shoulder Joint Model (SJM)

This physical model of the shoulder joint was fabricated to develop, tune, and test the AREBO controller. SJM is a 2DOF setup that has a kinematic structure like that of the human shoulder joint, without the last DOF (

H_{3}

in Figure 3 for internal-external rotations). The two DOF of the SJM are actuated by two brushless DC motors and have individual joint torque sensors (details in the Supplementary Material). Figure 10 depicts the attachment of SJM with AREBO, where the SJM’s link is attached to AREBO’s cuff through a three-axis load cell (Forsentek Ltd., range: 100 N along each axis) sandwiched between them; this load cell measures the interaction force in the local reference frame

H_{2}

, i.e.,

f_{i n t}^{H_{2}}

. The SJM link has multiple threaded holes to attach the robot’s cuff at different distances from the two DOF (i.e., changing

l

). The SJM also has provisions on its link for attaching weights to simulate different arm weights (Figure 10).

The 2 DOF SJM assembly is rigidly mounted on a frame like that of AREBO’s, except for its height adjustment mechanism. The frame contacts the ground through four castor wheels that enable rotation of SJM about

x_{H_{0}}

to set

ψ_{x}

and to translate the origin of the human base frame

H_{0}

with respect to the robot’s base frame,

R_{0}

. The brakes on the wheels are physically engaged each time the setup is brought to its experimental position.

A linear PD position controller with a feedforward gravity compensation term was implemented to control the movements of the SJM; the individual motor controllers were operated in a current control mode. The details of this controller are provided in the Supplementary Material.

The experimental characterization of AREBO described in this section was carried out by connecting the SJM to AREBO as shown in Figure 10 and by fixing different parameters associated with this connection, which is described in Figure 9.

2.4.2. Accuracy of Human Joint Angle Estimation

To evaluate how well the human joint angles can be estimated using AREBO’s joint angles, an experiment was performed with the SJM connected to AREBO. The estimate of human joint angle requires information about the arm parameters, namely the arm length

(l)

and human base fame’s orientation

(R_{R_{0}}^{H_{0}})

. The SJM was first programmed to perform three sinusoidal flexion/extension movements ranging

0 - 90 °

within 15 s while connected to AREBO. The data from this movement was used to estimate the arm parameters. Following this, the SJM was programmed to move in a random polysine trajectory given by the following,

ϕ_{j} (t) = \sum_{i = 1}^{4} A_{j, i} \sin (2 π f_{i} t + ν_{i}) + A_{j, 0}, j = \{1, 2\}

where,

ϕ_{j} (t)

is the human joint angles simulated by the SJM,

f_{i} = {0.1, 0.2, 0.35, 0.3} H z

, and

ν_{i}

is sampled from a uniform distribution between

0

and

2 π

. The values of

{\{A_{j, i}\}}_{1 \leq i \leq 4,1 \leq j \leq 2}

are chosen such that the flexion/extension movements are between

0 a n d 90 °

, and the abduction/adduction movements are between

- 30

and

+ 30 °

. During this polysine movement, the joint angles of AREBO

θ (t)

were recorded, which were then used to estimate the human joint angles

\hat{ϕ} (t)

. This was done by first computing the forward kinematics for AREBO to obtain the endpoint kinematics, which was then used to solve the inverse kinematics for the arm using the arm parameters

l, ψ_{x}

. The estimate of the human joint angles is compared with the ground truth from the SJM’s joint angles

ϕ (t)

obtained from its encoders. The magnitude of the error

\hat{ϕ} (t) - ϕ (t)

provides a measure of the accuracy of the human joint angle estimation procedure, which also includes the procedure for estimating the human arm parameters. The experiment was performed for three different arm parameter combinations. There are several possible sources of error in this estimation procedure, one of which is to evaluate its effect on the joint angle estimation accuracy, which is discussed in the Supplementary Material.

2.4.3. Transparency of the Unassisted Mode (UAM)

The UAM was designed to make the robot transparent to a subject’s voluntary movements when they are connected to the robot. The transparency can be quantified by the magnitude of the interaction force

{‖f_{i n t}^{H_{2}}‖}_{2}

between the robot and arm. The UAM’s transparency in AREBO was tested using the SJM by programming it to re-perform random (polysine) movements under different conditions, while AREBO’s joint angles

(θ)

and SJM’s joint angles

(ϕ)

, along with the interaction force

f_{i n t}^{H_{2}}

from the SJM’s 3-axis load cell were recorded. The three different conditions that were tested include the effect of the (a) different components of the AREBO controller, (b) misalignment between the human and robot joint axes, and (c) different orientations of the human base frame

(ψ_{x})

Effect of the different components of the AREBO controller: In this experiment, the following conditions were tested to evaluate the effects of the different components of the AREBO controller:

Control OFF: The actuators of the robot were switched OFF, which requires the SJM to work against AREBO’s inertia, weight, and friction. This condition provides a measure of the forces required to move AREBO with zero actuation.
Only Gravity Compensation: The gravity compensation module alone is switched on, and the output of the torque controller is set to zero, i.e., $τ^{c} = 0$ . In this condition, the AREBO’s weight is fully compensated, and the SJM only must work against the AREBO’s inertia and friction.
Zero Torque Control: The entire controller is enabled with the weight support parameter set to zero $α = 0$ , i.e., no weight support for the arm is provided. In this mode, the AREBO controller works to keep the interaction force zero. The lower the magnitude of $f_{i n t}^{H_{2}}$ , the better the robot’s transparency.

In this experiment, the SJM was placed such that the origin of the SJM’s base frame coincided with the z-axis of the robot’s base frame

z_{R_{0}}

, and the orientation of the SJM’s base frame with respect to the robot’s base frame was zero, i.e.,

ψ_{x} ≅ 0 °

Effect of misalignment of human and robot joint axes: In this experiment, AREBO’s transparency was evaluated using the zero-torque controller, while the SJM was located at different positions with respect to the robot. The SJM was placed approximately at the corners of a square of side 30 cm, with the centre of the square coinciding with the z-axis of the robot’s base frame (Figure 14A). The SJM was programmed to perform random polysine movements during the experiment for all five positions of the SJM. The orientation of the SJM’s base frame with respect to the robot’s base frame was zero, i.e.,

ψ_{x} ≅ 0 °

Effects of different orientations of the human base frame: To evaluate the effect of different trunk orientations on the robot’s transparency, the SJM was placed at different combinations of three orientations

ψ_{x} ~ (- 15 °, 0 °, 15 °

) and at (0 cm, -15 cm) displacements along the y-axis of the robot’s base frame. The SJM performed the same polysine movement during the 6 takes, while AREBO was set in the zero-torque control mode.

2.4.4. Effect of the Adaptive Weight Support (WSM)

AREBO’s controller can provide either fixed arm weight support or adaptive support by modulating the de-weighting parameter

α

. To test the adaptive capability of the WSM control, the SJM was programmed to simulate arm weakness by limiting the torques produced by the SJM’s motors by an impairment factor

ξ \in [0,1]

, where

ξ = 0

corresponds to a healthy arm, and

ξ = 1

corresponds to a fully flaccid arm. The output of the linear PD position controller and the gravity compensation module is multiplied by

(1 - ξ)

before it is sent to the motors. The details of SJM controller are given in supplementary material.

The first step in this experiment was identifying the human arm model parameters for computing torques required to hold the arm against gravity at different joint positions. Following this, SJM was programmed to perform a series of 300 discrete point-to-point reaching movements consisting of 3 s movement followed by 2 s of rest. The joint trajectory for the

k^{t h}

trial is given by the following,

ϕ_{j} (t; k) = \{\begin{matrix} λ_{j, i} [k] + (λ_{j, f} [k] - λ_{j, i} [k]) \cdot u (t - 5 \cdot \bar{k - 1}) & 5 (k - 1) \leq t < 5 (k - 2) \\ λ_{j, f} [k] & 5 (k - 2) \leq t < 5 k \end{matrix},

k \in \{1,2, \dots 300\}

u (l) = \frac{10 l^{3}}{3^{3}} - \frac{15 l^{4}}{3^{4}} + \frac{6 l^{5}}{3^{5}}, l \in [0,3]

where,

λ_{j, i} [k]

and

λ_{j, f} [k]

are the initial and final positions of the joint

j

of the SJM for the

k^{t h}

trial,

u (\cdot)

is the normalized 3sec long minimum jerk trajectory,

t

is the current time instant of the experiment. Note that the final position of

k^{t h}

trial will be the initial position for the

{(k + 1)}^{t h}

trial, i.e.,

λ_{j, i} [k + 1] = λ_{j, f} [k]

. The initial and final angles for the flexion-extension and abduction-adduction movements were chosen so that these movements are between

0 - 60 °

and

0 - 30 °

, respectively.

The joint angle profile

ϕ_{j} (t; k)

is input as the desired angle to the position controller of the SJM to compute the torque to be commanded from the SJM motor in joint

j

. To simulate impairment of the SJM, the impairment factor was set to the following,

ξ [k] = \{\begin{matrix} 0.6 & 1 \leq k \leq 100 \\ 0.2 & 100 < k \leq 200 \\ 0 & 200 < k \leq 300 \end{matrix}

The different levels of impairment are used to evaluate how the de-weighting parameter adapts to the varying impairment levels. The torque commanded from the SJM for each trial is multiplied by

(1 - ξ [k])

The de-weighting parameter is adapted on a trial-by-trial basis depending on the success or failure of the current trial. A trial was considered successful if the SJM reaches within

\pm 5 °

of the target location. In this experiment, the de-weighting parameter for the first trial is chosen to be 0.3, i.e.,

α [1] = 0.3

3. Results

3.1. Optimum Link Lengths

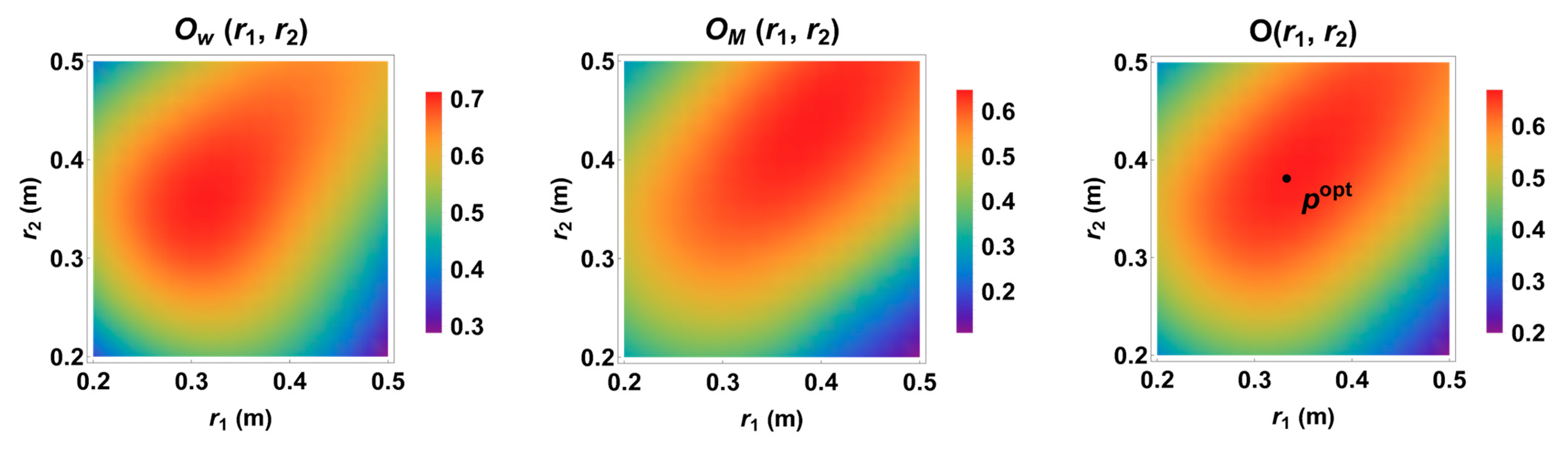
Figure 11 shows the heat map for the distribution of objective function

O (r_{1}, r_{2})

as function of the robot link lengths

r_{1}

and

r_{2}

, along with its workspace

O_{w} (r_{1}, r_{2})

and manipulability

O_{M} (r_{1}, r_{2})

components. All three variables showed a similar distribution trend with a single maximum within the range of values searched for

r_{1}

and

r_{2}

, which occurred at

r_{1} = 333 m m

and

r_{2} = 381 m m

. The physical prototype of the robot was fabricated with these optimal link lengths for the study’s experiments.

3.2. Accuracy of Human Joint Angle Estimation

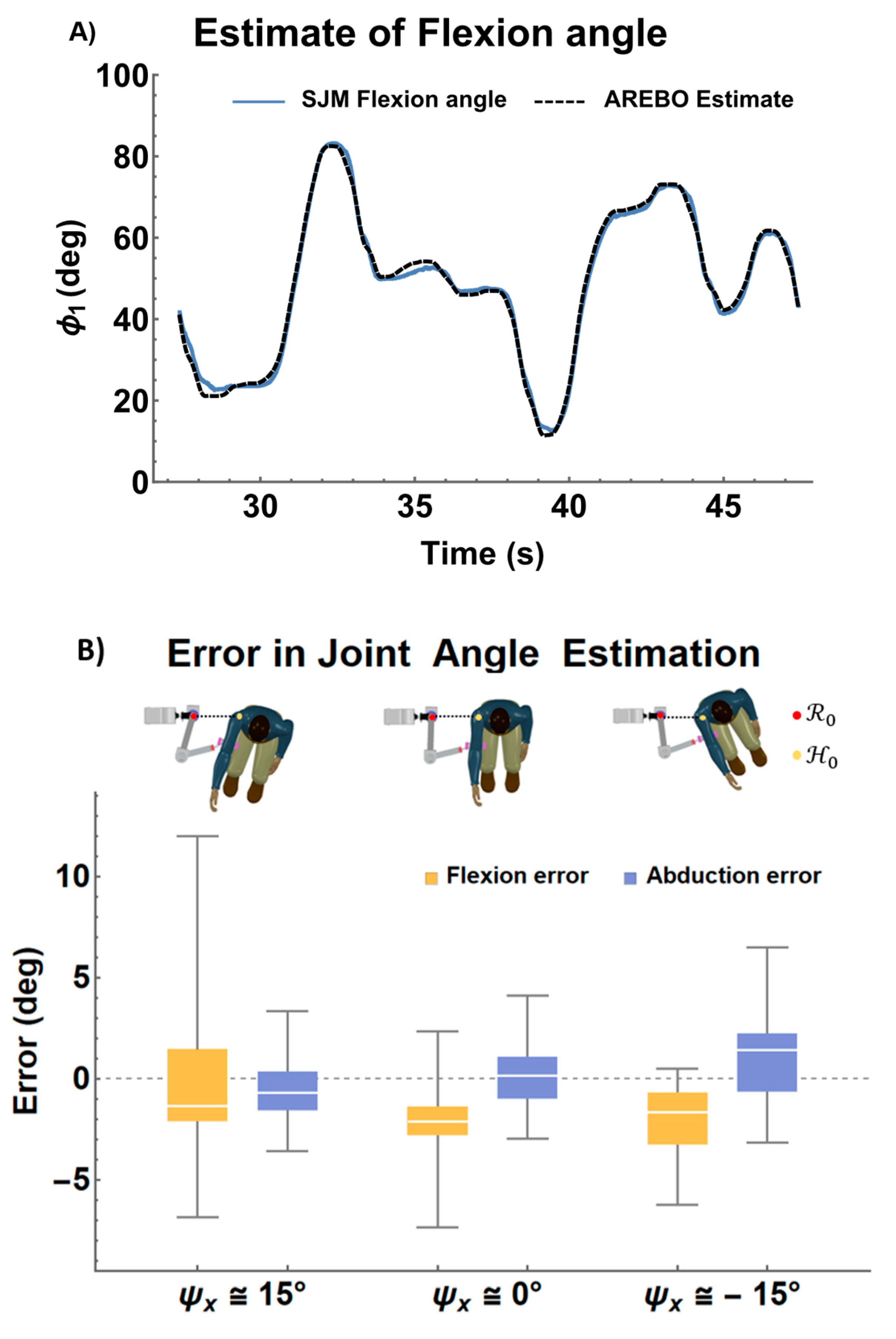
The plot of the actual angle of the SJM

ϕ (t)

and the estimated joint angle

\hat{ϕ} (t)

for the flexion/extension and abduction/adduction joints for a particular trial is shown in Figure 12A. The overall difference between the actual and estimated angles is summarized by the accompanying boxplot (Figure 12B) for the different orientations of the SJM with respect to the robot. The estimation error was similar almost across the different orientation conditions for the flexion/extension and abduction/adduction angles. The only exception was the flexion/extension angle estimation error for the case when the SJM is rotated towards the robot

ψ_{x} ≅ + 15 °

, where the spread of the error was a little wider; the instantaneous error in flexion/extension could be as large at

~ 10 °

. The absolute median error for flexion-extension and abduction-adduction joints were

2.10

and

1.30 °

, respectively.

3.3. Transparency of the Unassisted Mode

The magnitude of the interaction force

{‖ f_{i n t}^{H_{2}} ‖}_{2}

measured using the loadcell sandwiched between the endpoints of AREBO and SJM demonstrating the effect of the different components of the robot’s controller are shown in Figure 13. As expected, the interaction force magnitude reduces significantly with the use of the gravity compensation module and the zero-torque controller. With the zero-torque controller, the magnitude of the interaction force had a median value of 5.88N with an interquartile range (IQR) of 3.52 N, compared to a median of 32.21 N and IQR of 15.76 N when the controller is switched off. The experiment on the effects of the position of the human joint with respect to the robot on transparency revealed that higher interaction forces are encountered when the SJM is behind the robot (points

p_{1}

and

p_{2}

in Figure 14 whose y-coordinates are greater than 0) compared to the points that are inline and front of the robot (points

p_{3}

p_{4}

, and

p_{5}

in Figure 14 whose y-coordinates are less or equal to 0). The interaction forces at all the SJM locations were significantly different (p < 0.05 in one way ANOVA) except

p_{4}, p_{5}

, as revealed by Bonferroni post hoc test.

Figure 14. Effects of the position of human joint on interaction forces. A) The positions of origin of SJM on a square’s center

p_{5}

and vertices

(p_{1}, p_{2}, p_{3}, p_{4})

(marked by yellow circles) with respect to the robot’s origin (marked by black circle), B) The distribution of interaction forces at different locations while SJM performs a random movement (ns – non-significant difference indicated by one way ANOVA)

Figure 14. Effects of the position of human joint on interaction forces. A) The positions of origin of SJM on a square’s center

p_{5}

and vertices

(p_{1}, p_{2}, p_{3}, p_{4})

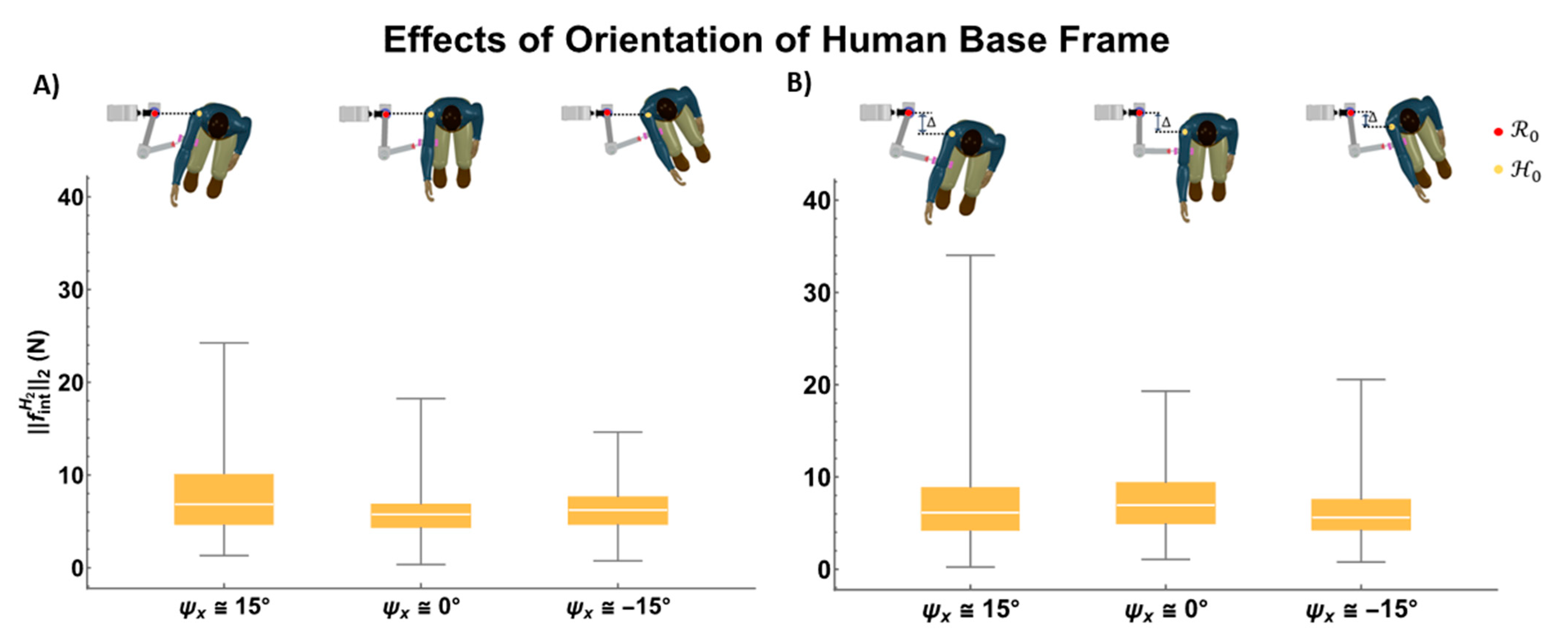
In the experiment on the effects of the orientation of the human base frame (Figure 15), the median value of the interaction force was similar in almost all cases though interaction forces at all the orientations were significantly different (p<0.05 in one way ANOVA). The spread of the interaction force values was slightly higher when the SJM was rotated towards the robot (

ψ_{x} > 0)

, as seen in the two boxplots corresponding to different values of displacement along the y-axis of the robot’s base frame. The interaction force in the six different cases was significantly different (p<0.05 in one way ANOVA).

3.4. Training with the Adaptive Weight Support Mode

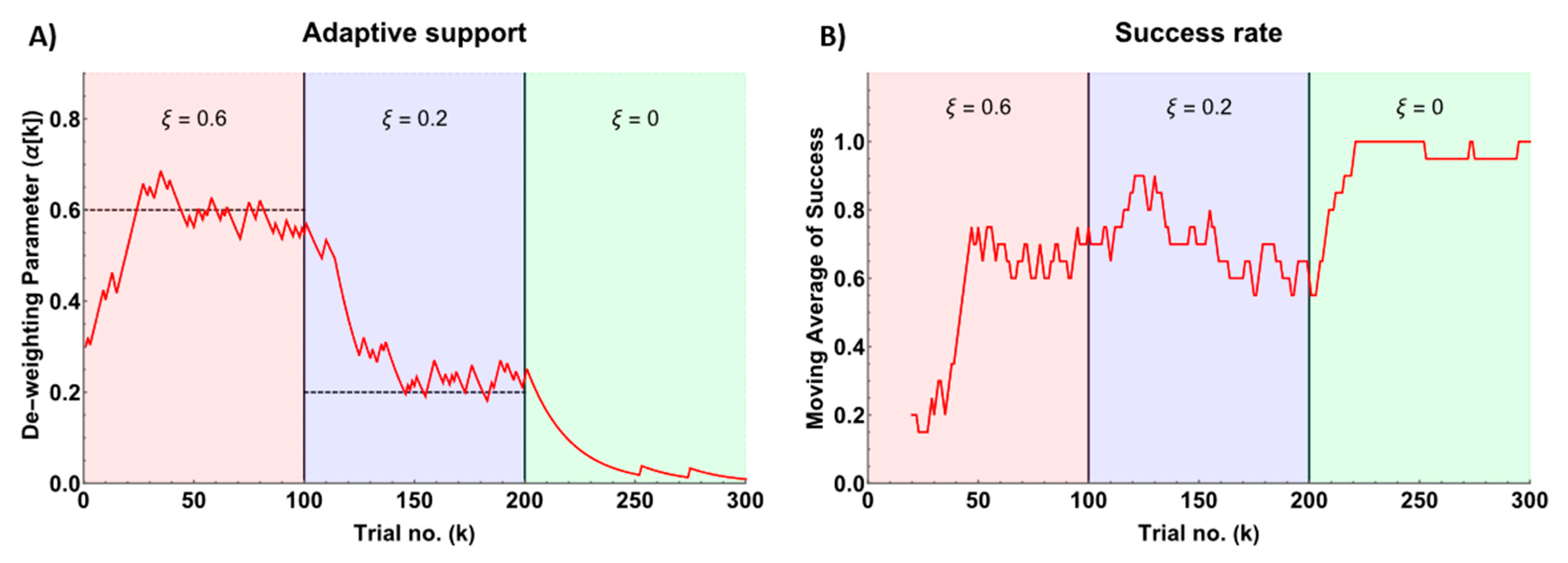
The adaptive de-weighting feature of AREBO was tested by simulating impairments with the SJM at different levels of weakness in the joints. The amount of weakness was held constant for 100 trials to evaluate how AREBO’s controller adapted to the impairment level. The adaptation of the de-weighting parameter

α [k]

as a function of the trial number

k

is shown in Figure 16A. The value of

α [1] = 0.3

, slowly rises to 0.6 within the first 30 trials to compensate for the 60% impairment simulated in the SJM. After the 100^th trial,

α [k]

decays toward 0.2 to account for the 20% simulated impairment. After the 200^th trial, the de-weighting factor slowly decays to 0 as the SJM was simulated to behave like a healthy arm (Figure 16A). This adaptation of the de-weighting parameter helps maintain the trial success rate at around 70% whenever there is some residual impairment in the arm. This is depicted in Figure 16B which shows the success rate in the past 20 trials as a function of the trial number; the success rate is between 60-80% when there is residual weakness in the SJM and its 100% for a healthy arm (Figure 16B).

4. Discussion

This paper presents the physical realization, optimization, and characterization of the end-effector robot – AREBO – introduced in our earlier work (Balasubramanian et al., 2021). The present work’s novelty is the demonstration of using an end-effector robot for sensing and safe training of 3D single joint movements against gravity. AREBO was designed to allow training in both unassisted and adaptive weight support modes. The robot’s capabilities were characterized using a mechatronic shoulder joint model (SJM).

The pre-requisite to providing single-joint training using an end-effector robot is the ability to estimate the movement kinematics of the arm. Although this could be achieved by placing additional sensors on the arm, AREBO uses a model of the human arm to estimate the kinematics of the arm. Knowledge of the estimation error is important in setting safety limits for the arm when using the robot for assisted movement training. AREBO’s human arm kinematics estimation algorithm resulted in an angle error that was mostly between

\pm 5 °

. The

~ 1 °

backlash of the ceramic gearboxes with a three-stage planetary reduction in AREBO’s (and SJM’s) actuators is likely to be a major source of this error. The presence of load-dependent play in AREBO’s unactuated DOF is also a potential contributing factor. This angle estimation error of

\pm 5 °

might be acceptable for training purposes in neurorehabilitation. However, if desired, it could be made much smaller by using harmonic drives and reducing the backlash in the unactuated structures, which will inflate the device cost.

The physical human-robot interaction is implemented through two control modalities: unassisted and adaptive weight support modes. In the unassisted mode, AREBO remains transparent to the movements of the human subject. A robot’s transparency is often quantified through the interaction forces/torques while a subject interacts with the robot performing different movements. The RehabExos (Vertechy et al., 2009) and ABLE (Jarrassé et al., 2010) robots measured the interaction forces at the points of connection between the user and the robot, while the Armin (Just et al., 2018) and ANYexo (Zimmermann et al., 2019) robots measured the peak and mean interaction torque at each joint. In all the above cases, healthy subjects interacted with the robots performing movements with constraints in velocity (angular velocity in the major joint <

30 ° / s

(Just et al., 2018; Zimmermann et al., 2019) and/or the trajectory (e.g. straight or circular path (Just et al., 2018; Zimmermann et al., 2019) or a pointing task (Jarrassé et al., 2010)). In the current study, AREBO’s transparency was quantified by measuring the interaction force and joint torques between the robot and the SJM. AREBO’s mean interaction force was about

~ 6 N

which was lower than that of the ABLE exoskeleton

(~ 10 N)

, but AREBO’s peak interaction force

(~ 15 N)

was higher than the ABLE exoskeleton

(~ 12 N)

(Jarrassé et al., 2010). In terms of joint interaction torques, the peak interaction torque along flexion-extension axis in ARMin and ANYexo was 2.30 Nm and 2.31 Nm, respectively. The peak interaction joint torque for AREBO is 2.67 Nm at the 1^st joint for random movements of range

0 - 90 °

with a 95^th percentile angular speed of

~ 50 ° / s

and an absolute peak speed of

~ 120 ° / s

. These results show that AREBO is on par with existing non-backdriveable robots in terms of transparency. It is possible to further lower the interaction torques by several means, including reducing the inertia of the kinematic chain, opting for lower gear-ratio actuators, and cable-driven transmission for the robot’s third joint by moving the actuator closer to the base. These modifications can be explored for future design revisions of AREBO.

The adaptive weight support training mode compensates for the arm's weight depending on the user's impairment. By reducing the effort to lift the arm against gravity, the arm’s residual capacity can now be allocated to move the arm and experience an increased range of motion. In stroke, there is evidence to show that supporting the shoulder against gravity not only increases the range of motion in the shoulder joint but also facilitates elbow extension (Beer et al., 2007), finger extension and gross hand opening and closing (Lan et al., 2017). Previous studies have also shown that training arm movements with gradual loading of the shoulder can increase the work area of the upper limb by breaking abnormal joint coupling (Ellis et al., 2009). Such training protocols can be easily implemented with AREBO. The adaptive algorithm used in this study adjusts the weight support based on the success/failure of movements performed by the subject. The parameters of this algorithm

(F (S [k], α [k]), ∆ (S [k]))

were tuned empirically to have a success rate of around 70%, which is based on the challenge point hypothesis (Guadagnoll and Lee, 2010) to increase motivation in therapy.

The single-joint training regimes proposed here could easily be extended for assisted coordinated multi-joint training of the arm for less severely affected patients. This can be done by taking an approach like that of the Emu robot (Fong et al., 2017) where a model of the human arm (shoulder and elbow) can be employed, along with an appropriate calibration procedure. One could employ a vision-based pose tracking system to estimate human arm kinematics, which can simplify the calibration procedure for estimating the parameters of the human arm model.

The current study presented the engineering design and characterization of AREBO, which is only the first crucial step towards realizing this system as a useful clinical tool for arm rehabilitation. The following engineering issues need to be addressed before the system will be ready for use by clinicians and patients:

Extension of the algorithms for multi-joint shoulder-elbow arm training, along with exploring the feasibility of using vision-based methods for tracking trunk, shoulder, and elbow kinematics (Dev et al., 2022).
Characterizing the different components of the robot with healthy subjects, including the algorithm for estimating human joint angles, the unassisted mode for evaluating the transparency, and the adaptive weight support mode.
Development of therapy games for unassisted and adaptive weight support training with the robot.
Evaluation of the usability of the robot for arm rehabilitation on different neuromusculoskeletal conditions.

Our current and future work is focused on addressing these issues to get AREBO ready for evaluating its usefulness as a clinical tool for arm rehabilitation.

Author Contributions

SB and SS conceived the idea of AREBO and supervised the entire work presented in the study. SB established the kinematic structure of AREBO with its actuated and unactuated DOF. PK, SE, and MK designed the robot to integrate the actuators and sensors. SB and PK developed the optimization of the link lengths and parameter estimation algorithms. PK implemented the unassisted, adaptive weight support controls and developed the SJM to test and tune the controllers. PK, SB and AN conceived the different experiments in the testing process with regular critical feedback from SS. AN and PK developed the firmware and the graphical user interface in Unity. PK and SB wrote the first draft of the paper. All authors reviewed and approved the final submitted manuscript.

Funding

This work was supported by Portescap CSR funding (Project no. CR1819MEE002PPIPSUJA).

Acknowledgments

The authors would like to thank Mr Sarath Kumar for his help in the assembling of the robot’s electronics and Mr Thiagu, and Mr. Sathish Balaraman for helping with the fabrication and 3d printing.

Conflicts of Interest

The authors declare that there are no conflicts of interest.

References

Balasubramanian, S.; Guguloth, S.; Mohammed, J.S.; Sujatha, S. A self-aligning end-effector robot for individual joint training of the human arm. J. Rehabilitation Assist. Technol. Eng. 2021, 8, 20556683211019866. [Google Scholar] [CrossRef] [PubMed]
Beer, R.F.; Ellis, M.D.; Holubar, B.G.; Dewald, J.P. Impact of gravity loading on post-stroke reaching and its relationship to weakness. Muscle Nerve 2007, 36, 242–250. [Google Scholar] [CrossRef]
Campolo, D.; Tommasino, P.; Gamage, K.; Klein, J.; Hughes, C.M.; Masia, L. H-Man: A planar, H-shape cabled differential robotic manipulandum for experiments on human motor control. J. Neurosci. Methods 2014, 235, 285–297. [Google Scholar] [CrossRef] [PubMed]
Crocher, V.; Fong, J.; Bosch, T.J.; Tan, Y.; Mareels, I.; Oetomo, D. Upper Limb Deweighting Using Underactuated End-Effector-Based Backdrivable Manipulanda. IEEE Robot. Autom. Lett. 2018, 3, 2116–2122. [Google Scholar] [CrossRef]
Dev, T.; Reetajanetsureka; Selvaraj, S.; Magimairaj, H.P.; Balasubramanian, S. Accuracy of Single RGBD Camera-Based Upper-Limb Movement Tracking Using OpenPose. Biosystems and Biorobotics 2022, 28, 251–255. [Google Scholar] [CrossRef]
Ellis, M.D.; Sukal-Moulton, T.; Dewald, J.P.A. Progressive Shoulder Abduction Loading is a Crucial Element of Arm Rehabilitation in Chronic Stroke. Neurorehabilit. Neural Repair 2009, 23, 862–869. [Google Scholar] [CrossRef] [PubMed]
Feigin, V.L.; Brainin, M.; Norrving, B.; Martins, S.; Sacco, R.L.; Hacke, W.; Fisher, M.; Pandian, J.; Lindsay, P. World Stroke Organization (WSO): Global Stroke Fact Sheet 2022. Int. J. Stroke 2022, 17, 18–29. [Google Scholar] [CrossRef] [PubMed]
Fong, J.; Crocher, V.; Tan, Y.; Oetomo, D.; Mareels, I. EMU: A transparent 3D robotic manipulandum for upper-limb rehabilitation. IEEE Int. Conf. Rehabil. Robot. 2017, 2017, 771–776. [Google Scholar] [CrossRef]
Guadagnoli, M.A.; Lee, T.D. Challenge Point: A Framework for Conceptualizing the Effects of Various Practice Conditions in Motor Learning. J. Mot. Behav. 2010, 36, 212–224. [Google Scholar] [CrossRef]
Hankey, G.J.; Jamrozik, K.; Broadhurst, R.J.; Forbes, S.; Anderson, C.S. Long-Term Disability After First-Ever Stroke and Related Prognostic Factors in the Perth Community Stroke Study, 1989–1990. Stroke 2002, 33, 1034–1040. [Google Scholar] [CrossRef] [PubMed]
Hogan, N.; Krebs, H.; Charnnarong, J.; Srikrishna, P.; Sharon, A. MIT - MANUS: A workstation for manual therapy and training I. 1992 Proceedings IEEE International Workshop on Robot and Human Communication, ROMAN 1992, 161–165. [CrossRef]
Jarrasse, N.; Tagliabue, M.; Robertson, J.V.G.; Maiza, A.; Crocher, V.; Roby-Brami, A.; Morel, G. A Methodology to Quantify Alterations in Human Upper Limb Movement During Co-Manipulation With an Exoskeleton. IEEE Trans. Neural Syst. Rehabilitation Eng. 2010, 18, 389–397. [Google Scholar] [CrossRef] [PubMed]
Just, F.; Özen, Ö.; Bösch, P.; Bobrovsky, H.; Klamroth-Marganska, V.; Riener, R.; Rauter, G. Exoskeleton transparency: feed-forward compensation vs. disturbance observer. auto 2018, 66, 1014–1026. [Google Scholar] [CrossRef]
Kamalakannan, S.; Venkata, M.G.; Prost, A.; Natarajan, S.; Pant, H.; Chitalurri, N.; Goenka, S.; Kuper, H. Rehabilitation Needs of Stroke Survivors After Discharge From Hospital in India. Arch. Phys. Med. Rehabilitation 2016, 97, 1526–1532. [Google Scholar] [CrossRef] [PubMed]
Kim, B.; Deshpande, A.D. An upper-body rehabilitation exoskeleton Harmony with an anatomical shoulder mechanism: Design, modeling, control, and performance evaluation. Int. J. Robot. Res. 2017, 36, 414–435. [Google Scholar] [CrossRef]
Kitago, T., Liang, J., Huang, V. S., Hayes, S., Simon, P., Tenteromano, L., et al. (2013). Improvement after constraint-induced movement therapy: Recovery of normal motor control or task-specific compensation? Neurorehabil Neural Repair 27, 99–109. [CrossRef]
Lan, Y.; Yao, J.; Dewald, J.P.A. The Impact of Shoulder Abduction Loading on Volitional Hand Opening and Grasping in Chronic Hemiparetic Stroke. Neurorehabilit. Neural Repair 2017, 31, 521–529. [Google Scholar] [CrossRef] [PubMed]
Lo, H.S.; Xie, S.Q. Exoskeleton robots for upper-limb rehabilitation: State of the art and future prospects. Med. Eng. Phys. 2012, 34, 261–268. [Google Scholar] [CrossRef]
Molteni, F.; Gasperini, G.; Cannaviello, G.; Guanziroli, E. Exoskeleton and End-Effector Robots for Upper and Lower Limbs Rehabilitation: Narrative Review. PM&R 2018, 10, S174–S188. [Google Scholar] [CrossRef]
Nef, T.; Riener, R. ARMin - Design of a Novel Arm Rehabilitation Robot. In Proceedings of the 9th International Conference on Rehabilitation Robotics, Chicago, IL, USA, 28 June–1 July 2005; pp. 57–60. [Google Scholar] [CrossRef]
Pan, J.; Astarita, D.; Baldoni, A.; Dell'Agnello, F.; Crea, S.; Vitiello, N.; Trigili, E. NESM-γ: An Upper-Limb Exoskeleton With Compliant Actuators for Clinical Deployment. IEEE Robot. Autom. Lett. 2022, 7, 7708–7715. [Google Scholar] [CrossRef]
(a)Vertechy, R., Frisoli, A., Dettori, A., Solazzi, M., and Bergamasco, M. (2009). Development of a new exoskeleton for upper limb rehabilitation. 2009 IEEE International Conference on Rehabilitation Robotics, ICORR 2009, 188–193. [CrossRef]
Zimmermann, Y.D.; Forino, A.; Riener, R.; Hutter, M. ANYexo: A Versatile and Dynamic Upper-Limb Rehabilitation Robot. IEEE Robot. Autom. Lett. 2019, 4, 3649–3656. [Google Scholar] [CrossRef]

Figure 1. Picture of AREBO connected to: A) upper arm, and B) forearm. The body segment proximal to the arm segment attached to the robot is constrained from moving.

Figure 2. AREBO’s 6 DOF kinematic chain with its DH parameters. The three proximal DOF

(R_{1}, R_{2}, R_{3})

are actuated and control the 3D position of the robot’s endpoint attached to the arm, and the three distal unactuated DOF

(R_{4}, R_{5}, R_{6})

help the robot to self-align to the orientation of the arm; these three DOF form a spherical joint about the robot’s endpoint

p_{r}

Figure 2. AREBO’s 6 DOF kinematic chain with its DH parameters. The three proximal DOF

(R_{1}, R_{2}, R_{3})

are actuated and control the 3D position of the robot’s endpoint attached to the arm, and the three distal unactuated DOF

(R_{4}, R_{5}, R_{6})

help the robot to self-align to the orientation of the arm; these three DOF form a spherical joint about the robot’s endpoint

p_{r}

Figure 3. Human-robot closed-loop kinematic chain for single joint training of A) shoulder and B) elbow joint.

Figure 4. Details of the three-DOF kinematic chain of the shoulder joint. The endpoint of the arm

p_{h}

is at

H_{3}

at a distance

l

from its origin

H_{0}

. The movements at the shoulder joint associated with the generalized coordinates of the arm are

ϕ_{1}

– flexion/extension,

ϕ_{2}

– abduction/adduction, and

ϕ_{3}

– internal/external rotation.

Figure 4. Details of the three-DOF kinematic chain of the shoulder joint. The endpoint of the arm

p_{h}

is at

H_{3}

at a distance

l

from its origin

H_{0}

. The movements at the shoulder joint associated with the generalized coordinates of the arm are

ϕ_{1}

– flexion/extension,

ϕ_{2}

– abduction/adduction, and

ϕ_{3}

– internal/external rotation.

Figure 5. The realization of the unactuated segment of the robot. A) 3D model of the cuff. B) 3 DOF kinematic diagram of the cuff with all three axes of rotation

(z_{R_{4}}, z_{R_{5}}, z_{R_{6}})

intersecting at the robot’s endpoint. C) Exploded view showing the components of the cuff.

Figure 5. The realization of the unactuated segment of the robot. A) 3D model of the cuff. B) 3 DOF kinematic diagram of the cuff with all three axes of rotation

(z_{R_{4}}, z_{R_{5}}, z_{R_{6}})

intersecting at the robot’s endpoint. C) Exploded view showing the components of the cuff.

Figure 6. Structure of each actuated DOF of AREBO. Each actuated DOF has an electric motor, a gearbox, and a torque sensor in the arrangement shown here. The torque sensor is sandwiched between the actuator body and proximal segment of the link (F). A flange coupling connects the actuator to the adjacent link (D).

Figure 7. Block diagram to show the flow of information between the different components of the system.

Figure 8. Block diagram of the controller implemented in AREBO.

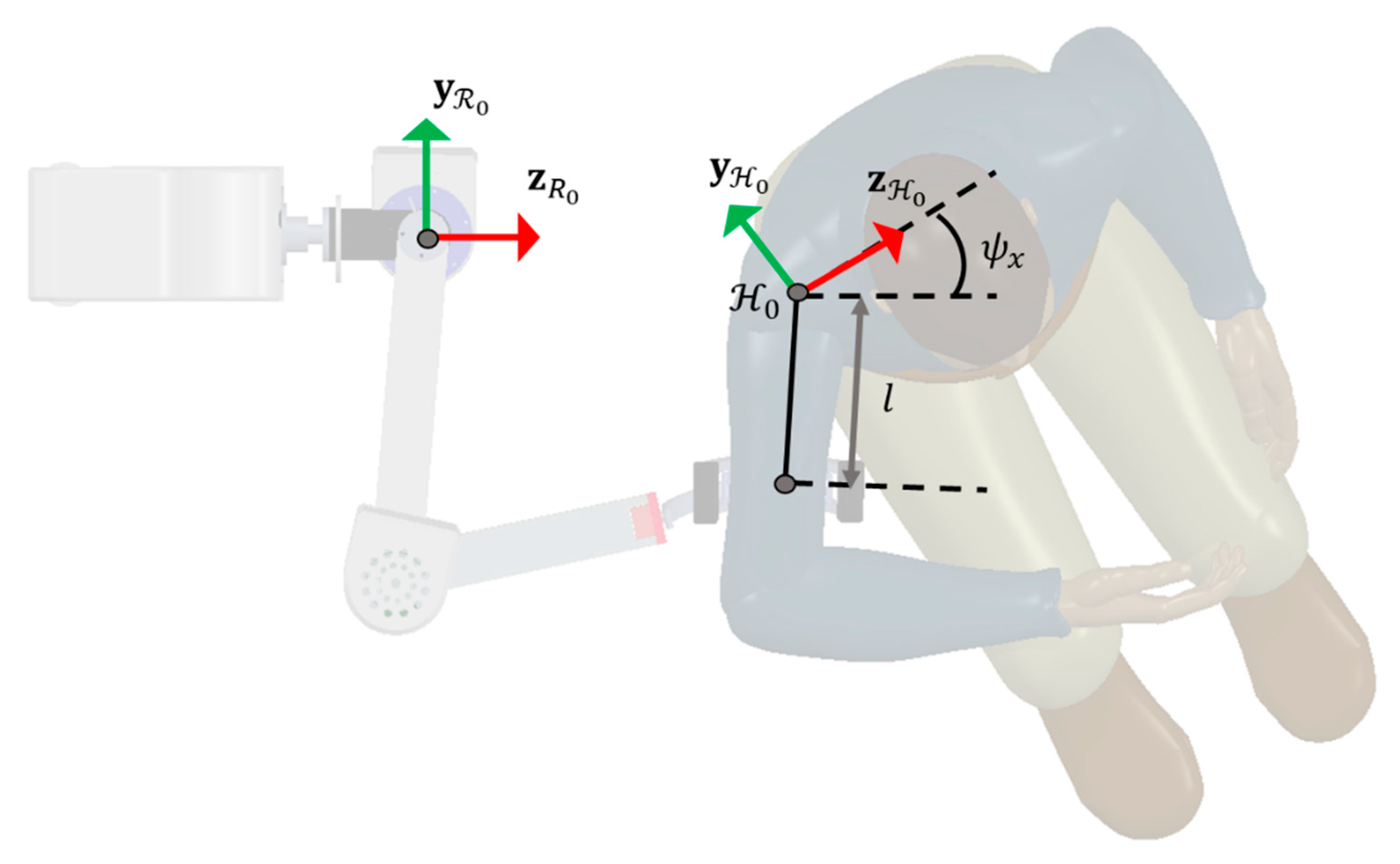
Figure 9. Parameters in the estimation of human joint kinematics. The position and orientation of the human base reference frame

H_{0}

with respect to the robot’s base reference frame

R_{0}

and the distance between the point of attachment of the robot and human joint

l

are given as inputs to the human joint estimation algorithm.

Figure 9. Parameters in the estimation of human joint kinematics. The position and orientation of the human base reference frame

H_{0}

with respect to the robot’s base reference frame

R_{0}

and the distance between the point of attachment of the robot and human joint

l

are given as inputs to the human joint estimation algorithm.

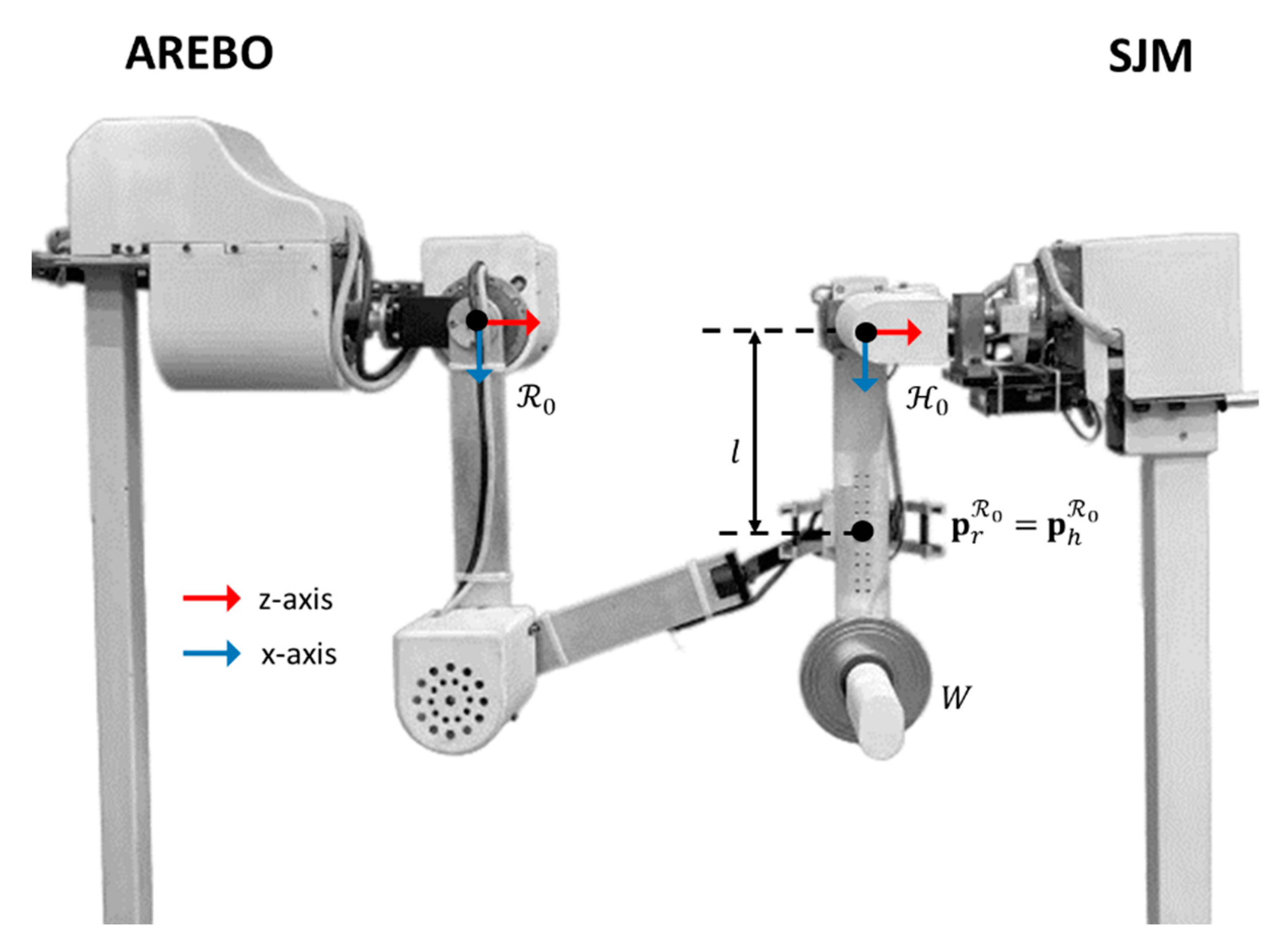
Figure 10. Attachment of SJM with AREBO. The actuated 2 DOF model of the shoulder joint has provisions to add weight

W

, change the distance of attachment with the robot

l

and vary the relative orientation of human

H_{0}

and robot

R_{0}

base reference frames.

Figure 10. Attachment of SJM with AREBO. The actuated 2 DOF model of the shoulder joint has provisions to add weight

W

, change the distance of attachment with the robot

l

and vary the relative orientation of human

H_{0}

and robot

R_{0}

base reference frames.

Figure 11. Heat maps for the variation of objective function

O (r_{1}, r_{2})

and workspace

O_{w} (r_{1}, r_{2})

, manipulability

O_{M} (r_{1}, r_{2})

components as a function of the robot link lengths.

p^{o p t}

is the global maximum of the objective function and the corresponding

r_{1}, r_{2}

are the optimum link lengths.

Figure 11. Heat maps for the variation of objective function

O (r_{1}, r_{2})

and workspace

O_{w} (r_{1}, r_{2})

, manipulability

O_{M} (r_{1}, r_{2})

components as a function of the robot link lengths.

p^{o p t}

is the global maximum of the objective function and the corresponding

r_{1}, r_{2}

are the optimum link lengths.

Figure 12. A) Trajectories of the flexion angle

(ϕ_{1})

recorded in SJM (blue curve) and the estimate by AREBO (dashed black curve) for

ψ_{x} ~ 0

case. B) Boxplots of the errors in flexion and abduction angles estimated by AREBO while SJM was performing random polysine movements.

Figure 12. A) Trajectories of the flexion angle

(ϕ_{1})

recorded in SJM (blue curve) and the estimate by AREBO (dashed black curve) for

ψ_{x} ~ 0

case. B) Boxplots of the errors in flexion and abduction angles estimated by AREBO while SJM was performing random polysine movements.

Figure 15. The interaction forces at three different trunk orientations when SJM is A) inline with the robot

∆ ≅ 0

, B) in front of the robot

, ∆ ≅ - 15 c m

Figure 15. The interaction forces at three different trunk orientations when SJM is A) inline with the robot

∆ ≅ 0

, B) in front of the robot

, ∆ ≅ - 15 c m

Figure 16. A) Adaptation of the de-weighting parameter as a function of the trial number when operating the robot in adaptive weight support mode. Dotted lines are the weakness (

ξ

) set in SJM for the first 200 trails, after which the ‘no weakness’ case was simulated. B) Success rate obtained from AREBO’s adaptive weight support algorithm. The vertical black line segments the plot into three segments to distinguish the 60%, 20% and 0% weakness (

ξ

) simulated in the SJM for trials 0-100, 100-200, and 200-300 respectively.

Figure 16. A) Adaptation of the de-weighting parameter as a function of the trial number when operating the robot in adaptive weight support mode. Dotted lines are the weakness (

ξ

ξ

) simulated in the SJM for trials 0-100, 100-200, and 200-300 respectively.

Table 1. Parameter values and range for the coarse and fine search used in the optimization of the robot link lengths

r_{1}, r_{2}

. CS – coarse search, FS – fine search,

l

– distance between human joint and AREBO’s attachment point,

o_{H_{0}}^{R_{0}} = {[\begin{matrix} o_{x} & o_{y} & o_{z} \end{matrix}]}^{T}

is the origin of the human joint and

ψ_{x}

is the rotation of the human about

x_{H_{0}}

axis.

Table 1. Parameter values and range for the coarse and fine search used in the optimization of the robot link lengths

r_{1}, r_{2}

. CS – coarse search, FS – fine search,

l

– distance between human joint and AREBO’s attachment point,

o_{H_{0}}^{R_{0}} = {[\begin{matrix} o_{x} & o_{y} & o_{z} \end{matrix}]}^{T}

is the origin of the human joint and

ψ_{x}

is the rotation of the human about

x_{H_{0}}

axis.

Parameter		Values (cm)	No of values
$r_{1}$	CS	{20, 22, ...,50}	16
$r_{1}$	FS	{33.1, 33.2, …, 34.9}	19
$r_{2}$	CS	{20, 22, ...,50}	16
$r_{2}$	FS	{37.1, 37.2, …, 38.9}	19
$l$		{15, 17.5, 20}	3
$o_{x}, o_{y}$		{-10, 0, 10}	3
$o_{z}$		{20, 30, 40}	3
$ψ_{x}$ (deg)		{-30, 0, 30}	3

Table 2. Specification of actuators and torque sensors used in SJM. Actuators are from Maxon International Ltd. and torque sensors are from Forsentek Co., Ltd. Three Escon 70/10 ec motor controllers are used along with each actuator.

	Motor	Gearbox	Torque sensor	Encoder
1^st Joint	EC Flat 90, Nominal torque – 0.953 Nm, part no. 607950	GP 52 C, Gear ratio: 53:1, part no. 223090	FTHC, Range – 40 Nm	MILE, 4096 CPT, part no., 651168
2^nd Joint	EC Flat 60, Nominal torque – 0.563 Nm, part no. 614649	GP 52 C, Gear ratio: 43:1, part no. 223089	FTHC, Range – 20 Nm	MILE, 4096 CPT, part no., 651168
3^rd Joint	EC Flat 60, Nominal torque – 0.563 Nm, part no. 614649	GP 52 C, Gear ratio: 43:1, part no. 223089	FTHC, Range - 20 Nm	MILE, 4096 CPT, part no., 651168
4^th Joint	Unactuated joint			Calt, 1000 CPT, Model no. PD30-08G1000BST5
5^th Joint	Unactuated joint			Calt, 1000 CPT, Model no. PD30-08G1000BST5
6^th Joint	Unactuated and not instrumented

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Design and Characterization of a Self-Aligning End-Eﬀector Robot for Single-Joint Arm Movement Rehabilitation

Abstract

1. Introduction

2. Methods

2.1. Kinematics

2.1.1. AREBO’s Kinematic Chain

2.1.2. Human-Robot Closed Loop Kinematic Chain

2.1.3. Optimization of Link Lengths

2.2. Robot Hardware

2.2.1. Mechanical Design

2.2.2. Joint Actuation and Sensing

2.2.3. Firmware and Software

2.3. AREBO Human-Robot Physical Interaction: Controller Details

2.3.1. High-level Torque Control Loop

2.3.2. Gravity Compensation

2.3.3. Human Joint Angle Estimation

2.3.4. Human Arm Weight Support

2.4. Testing AREBO Controller

2.4.1. Shoulder Joint Model (SJM)

2.4.2. Accuracy of Human Joint Angle Estimation

2.4.3. Transparency of the Unassisted Mode (UAM)

2.4.4. Effect of the Adaptive Weight Support (WSM)

3. Results

3.1. Optimum Link Lengths

3.2. Accuracy of Human Joint Angle Estimation

3.3. Transparency of the Unassisted Mode

3.4. Training with the Adaptive Weight Support Mode

4. Discussion

Author Contributions

Funding

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe