Prerpints.org logo
Preprint
Review

Functionalized Chiral Twisted Optical Fibers: A Review

This version is not peer-reviewed.

Submitted:

31 July 2023

Posted:

31 July 2023

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
With the development of the volume of information exchange and perception increases, the demands for intelligent, miniaturized and integrated optical devices for information acquisition are also increasing. As the core component of optical networks for transmitting information, how to further optimize its structural characteristics to generate richer optical characteristics and apply them to information exchange and optical field control has become a key research hotspot. The introduction of chiral twist characteristics has led to new phenomena and applications in optical field transmission and transformation for traditional optical fibers or microstructured optical fibers (MOF). Therefore, this review mainly starts from the principle of chiral optical fibers, introduces their preparation and latest application scenarios, and finally looks forward to their potential future development prospects.
Keywords: 
Subject: 
Physical Sciences  -   Optics and Photonics

1. Introduction

With the rapid development of information technology, optical fibers have become a critical component in communication systems. Optical fibers can transmit a vast amount of information with high speed and low loss. However, the traditional optical fibers have a single structure, limiting their scalability as a carrier of functional optical fibers. To overcome this limitation, various modification methods, such as tapering, splicing, and polishing, have been developed to enrich the functionality of optical fibers.
Recently, a new modification method called "twisting" has attracted much attention in the field of optical fiber modification. Compared with traditional optical fiber modification methods, the twisted optical fiber provides new features and applications [1, 2]. In this review, we provide readers with a comprehensive summary of twisted optical fibers, including traditional optical fibers, photonic crystal fibers, anti-resonant fibers, and multi-core fibers.
To demonstrate the proof-of-concept of the functional twisted optical fibers, several milestone works are investigated, and their application fields are discussed. The results show that the twisted modified optical fibers have enriched the application of functional devices.
However, there are still challenges that need to be addressed to fully exploit the potential of functional twisted optical fibers. In the last section of this review, we present the challenges, prospects, and promising opportunities of the future functional chiral fiber for functionalized devices.
In summary, this paper provides a comprehensive overview of twisted optical fibers and their applications. It is hoped that this review will inspire more research in the field of optical fiber modification and promote the development of functionalized devices.

2. How to Describe the Chiral Twisted fiber

Compared to traditional axially uniform optical fibers, the most obvious change in the chiral twisted optical fiber is its axial refractive index periodic modulation. However, the analysis of axially twisted media is different due to the differences in fiber end faces and torsion conditions.

2.1. Analysis of Twisted Structure Characteristics in Single Core Optical Fiber

Traditional single core fibers usually have a small amount of random core–cladding eccentricity due to fabrication imperfection, thus, core index will form a helical periodic modulation after a melting twist process. Helical long-period fiber grating HLPGs can couple light from the fundamental core mode to cladding modes at particular wavelengths and cause transmission depletions [1], similar to conventional long period fiber gratings [2,3]. The resonant peak wavelengths satisfy the phase matching condition that can be described as [4]:
λ d = ( n e f f c o − n e f f c l , m ) Λ
where n e f f c o and n e f f c l , m are the refractive index of the fundamental core mode and mth cladding mode, respectively. The resonant wavelength λ d changes proportionally as the index difference ( n e f f c o − n e f f c l , m ) or grating period Λ changes. In particular, when the grating period Λ varies due to the temperature or twisting angle variation, the resonant wavelength shift can be clearly observed in the transmission spectrum. In this paper, positive twist is deemed as the direction of applied twist coinciding with HLPG’s torsion direction; otherwise, it is negative. When the twist is positive, the resonant wavelength shifts towards shorter wavelength, corresponding to a decreased grating period, and vice versa. In addition, the amount of shift strongly depends on the angle of applied torsion. Therefore, HLPGs can simultaneously detect the twisting angle and orientation, an apparent advantage over ordinary LPGs.
In addition, when the fiber core is away from the axis of the fiber waveguide, the twisted characteristics will become further complex and cannot be analyzed solely by relying on the theory of long period gratings, as shown in Figure 1(b). When the core mode propagates in the helical core, the cladding WGMs as radiation modes are induced by fiber core bending, that is, due to bending effect of the helical core, the partially guided core mode is converted into cladding WGMs [5].

2.2. Analysis of Twisted Structure Characteristics in Microstructured Optical Fiber

When the torsion structure becomes further complex, such as the torsion of a microstructure optical fiber. At this point, due to the interaction between different structures, the approximation algorithm using single core optical fibers is not very reliable. More rigorous transformation optics model analysis methods are needed.
Transformation optics formalism is based on the fact that in electromagnetism, a change in the coordinate system from {x, y, z} to {x’, y’, z’} is equivalent to a change in material properties [6,7,8]. The permittivity and permeability tensors in the new coordinate system {x’, y’, z’} are given by
ε ' = J − 1 ε J − T det ( J − 1 )   and   μ ' = J − 1 μ J − T det ( J − 1 )
where ε and µ represent the material properties in {x, y, z} (usually Cartesian) coordinates and J − 1 is the inverse of the Jacobian matrix:
J − 1 = [ ∂ x ' ∂ x ∂ x ' ∂ y ∂ x ' ∂ z ∂ y ' ∂ x ∂ y ' ∂ y ∂ y ' ∂ z ∂ z ' ∂ x ∂ z ' ∂ y ∂ z ' ∂ z ]
and J − T is the transposition of J − 1 . Transformation optics can be used in numerical simulations to reduce the dimensionality of some problems by choosing a coordinate system in which the geometry of the waveguide and its material properties become independent of one of the coordinates. In particular, the structure of twisted fibers can be simplified in helicoidal coordinates {x’, y’, z’}, which are related to Cartesian coordinates by [9].
x ' = x cos ( A z ) − y sin ( A z ) y ' = x sin ( A z ) + y cos ( A z ) z ' = z
where A=2π/Λ is the twist rate expressed in [rad/m], which describes the rotation of the x’ and y’ axes of the helicoidal coordinates system around the z axis with respect to the Cartesian x and y axes by the angle −Az, where z = Λ corresponds to the full rotation angle. All lines parallel to the z axis in helical coordinates are helices in the Cartesian coordinate system with a pitch distance equal to Λ, which are left-handed for positive A. The inverse of the Jacobian matrix J − 1 used in this case is given by
J − 1 = [ cos ( A z ) − sin ( A z ) − A y ' sin ( A z ) cos ( A z ) A x ' 0 0 1 ] = [ 1 0 − A y ' 0 1 A x ' 0 0 1 ] [ cos ( A z ) − sin ( A z ) 0 sin ( A z ) cos ( A z ) 0 0 0 1 ] = [ 1 0 − A y ' 0 1 A x ' 0 0 1 ] R ( A z )
where R(Az) is the rotation matrix and det( J − 1 ) = 1. If the material properties of the twisted fiber are isotropic and therefore can be represented by scalars ε and µ, then according to Eqs. (1) and (4), the equivalent ε’ in helicoidal coordinates {x’, y’, z} can be expressed as [9].
ε ' ( x ' , y ' , z ) = ε ( x ' , y ' , z ) [ 1 + A 2 y ' 2 − A 2 x ' y ' − A y ' − A 2 x ' y ' 1 + A 2 x ' 2 A x ' − A y ' A x ' 1 ]
In this study, ε and ε (used for anisotropic materials) indicate values expressed in Cartesian coordinates, and ε’ is a corresponding value expressed in helical coordinates. In the following analysis, the same arguments (x’, y’, z) are used for ε, ε, and ε’ only to indicate the position in space. Equation (5) is z-independent if ε(x’, y’, z) can be expressed as ε(x’, y’), if its value in the Cartesian coordinate is a constant at a helix specified by a given x’ and y’. Such a condition is satisfied if the twist rate A, which defines the helicoidal coordinates in Eq. (3), is the same as that for the fiber twist. A similar relation holds for the scalar magnetic permeability µ. which turns the three-dimensional problem into a two-dimensional one and greatly simplifies the numerical calculations.

3. Applications of Chiral twisted fibers

Due to the above unique structure characteristics of chiral twisted fibers, it can be used to a variety of functional devices applications. In the following, the advantages of chiral twisted method combined with various functional fibers are discussed. Besides, the specific application and importance of functional chiral twisted fibers are further elaborated.

3.1. Fabracation of Chiral Twisted Fiber

To fabricate a twisted structure in fibers, there are some common methods to fabricate a twisted structure in fibers as shown in Figure 3. The first method involves using a high-temperature hydrogen-oxygen flame to heat and soften the fiber. By controlling the intensity of the flame and using motors at both ends, the fiber can be twisted and fabricated accordingly. Zhong et al. [4] proposed a method using a hydrogen-oxygen flame to etch twisted structure into fibers. The fabrication setup includes basic devices such as a high-precision rotator, two translational platforms, and a hydrogen-oxygen flame. These components are used to precisely control the twisting and etching process on the fiber surface. By utilizing this method, twisted fiber gratings can be fabricated in a stable manner, ensuring their long-term preservation. The controlled twisting and precise etching process enable the creation of durable and reliable twisted fiber gratings that can maintain their properties over an extended period of time. This stability and longevity make the fabricated gratings suitable for various applications in fiber optics and photonics. Another method for fabricating twisted fiber involves the use of a CO2 laser [10, 11, 12, 13]. The output power of the CO2 laser is computer-controlled, allowing for more precise and stable heating of the twisting region. Shin et al [14] fabricated a twisted single mode fiber with CO2 laser beam exposure and its characteristic was experimentally investigated. They achieved the formation of a periodic twisted structure by irradiating the fiber with a CO2 laser while uniformly rotating the motor along the fiber axis. This method enables precise control of the twisting period and allows for resonance to be generated within extremely short grating lengths. Automatic arc discharge technology is also utilized for the fabrication of twisted fiber. Sun et al first employed a commercial fusion splicer system to inscribe twisted structure in the conventional SMFs [15]. The system consists of two electrodes, a spiral motor, and a fixture for holding the fiber in place. By analyzing the influence of arc current on the growth of twisted fiber, they determined the appropriate current values to apply, resulting in clear resonance peaks and low insertion loss.

3.2. Traditional Single Core Chiral Twisted Fiber

Since the early stages of fiber optics, twisted-induced birefringence has been a prominent area of research. The concept of twisted fiber was proposed in 1979 by Ulrich et al [16]. They discussed the change in polarization along the twist direction. Using first principles, they employed perturbation methods to calculate the coupling between two degenerate modes. Furthermore, experimental results validated the correctness of this theory and provided an approximate calculation of the g-factor. Since then, research on twisted fiber has become increasingly rich and diverse.
Twisted SMFs undergo interesting changes in their polarization state due to the alteration of birefringence. After twisting, the single-mode fibers exhibit a significant degree of optical rotation, but they demonstrate almost no polarization anisotropy during the twisting process [17]. Therefore, twisted fiber can effectively eliminate polarization mode dispersion. Among them, the measurement of circular birefringence in twisted fiber is particularly important. Andrea [18] proposed a new method for circular birefringence measurement for long single-mode twisted fibers. The technique is based on polarization-sensitive optical time-domain reflectometry. The experimental results agree well with theoretical predictions. To further validate the fundamental effect of birefringence in twisted fiber, Diana [19] analyzed the developed birefringence matrix for the twisted fiber. They discovered that the Jones birefringence caused by twisting the birefringent optical fibers exceeds values of Jones birefringence caused by electric and/or magnetic fields in bulk birefringent material by several orders of magnitude. Furthermore, in Figure 4, they also found that the twisting of erbium-doped fibers has a greater impact on the fiber's polarization characteristics compared to non-doped fibers. This is attributed to the influence of the glass matrix composition and fiber structure.
The use of twisted optical fibers to construct HLPG structures has recently been proposed in multiple fields. Because of the grating's helical construction, clockwise or anticlockwise twisting can shorten or lengthen the grating's period, causing the resonance wavelength to shift in a different direction. Therefore, HLPG can be effectively applied in the fields of torsion, refractive index and temperature sensors [4,10,11,20,21,22,23,24,25]. Li [26] analyzed the effects of LPG and intermodal interference in chiral twisted single-mode fibers (CTSMF). In Figure 5, the LPG model established using mode resonance theory showed good agreement with experimental results. Furthermore, the response of CTSMF to external environmental factors was also analyzed. These outstanding results of CTSMF show that it is a strong contender in the sectors of sensing and communications. By controlling the length and direction of the twist pitch, effective applications of CTSMF in sensing can be achieved. An improved HLPG based was proposed by Zhao [21] to achieve real-time measurement of multiple parameters. To further enhance sensitivity, fiber taper was introduced in a twisted structure [20]. Experimental results indicate that when the fiber is twisted in different directions, the intensity of transmission peaks varies inversely. In 2020, to measure torsion and strain simultaneously, Xian [24] proposed a cascaded helical long-period grating (C-HLPG) with two distinct gratings that fabricate molten state duration durations (MSDTs) in Figure 6. It is proved that torsion and strain can be differentiated within the ranges of 0~1744µε and -240°~240° with accuracies of ~120µε and ~0.12 rad, respectively. The C-HLPG with various MSDTs provides exceptional opportunities as torsion and strain sensors as well as a future development for multiparameter fiber-optical sensors and new optical-fiber components.
In addition to sensing applications, CTSMF also plays a significant role in the generation and selection of modes [12,13,27]. A simple method for validating the mode-selection rules followed in a single-helix helical long-period fiber grating (SHLPG) has been demonstrated both theoretically and experimentally [28]. This is accomplished by investigating and analyzing the SHLPG's circular dichroism (CD) and polarization dependence loss (PDL) spectra. Moreover, CTSMF is considered a highly promising Orbital Angular Momentum (OAM) beam shaper and generator. A new approach for simultaneously generating first and second OAM modes has been developed and experimentally demonstrated utilizing two consecutively cascaded helical long-period fiber gratings (ccHLPGs) by Wang [29] in Figure 7. The first-order OAM mode with a conversion efficiency of 94% and the second-order (l = 2) OAM mode with an efficiency of 83% were effectively obtained. When the twisting angle changes, the excited OAM modes also vary accordingly. Based on oxyhydrogen-flame produced helical long-period fiber gratings (HLPFGs), Liu [30] present a class of all-fiber torsion-tunable orbital OAM mode generators. The single-mode fiber (SMF) and six-mode fiber (6MF) HLPFGs are used to excite the 1-order and 3-order OAM modes, respectively. The evolution of mode field distributions and its interference patterns with the Gaussian beams with varying torsion angles is shown in Figure 8.

3.3. Chiral Twisted Microstructured optical fibers

Compared to traditional SMFs, twisted structure in the form of MOFs offer more choices and greater possibilities in the field of twisted fiber applications due to their versatile and flexible structure. In addition to enhanced mode selection, mode field control, and OAM modes generation [31,32,33], Chiral twisted microstructured fiber (CTMOF) has also been found to have great potential in fields such as laser [34], sensing [35,36,37], and transmission [38,39,40]. Here, we have summarized some applications, including Chiral twisted photonics crystal fiber (CTPCF), Chiral twisted hollow core fiber (CTHCF), and Chiral twisted multicore fiber (CTMCF), and found that microstructured fibers play a crucial role in improving the the functionality of twisting.

3.1.1. Chiral Twisted Photonics Crystal Fiber

CTPCF exhibits peculiar optical phenomena due to its unique air channel [31,32,33,39,41]. Under the influence of the spiral lattice in the air-hole channel, the cladding light in the PCF is forced to follow a helical path. This results in a transfer of a portion of the axial momentum to the azimuthal direction, thereby creating discrete orbital angular momentum [42]. When the arrangement of air holes and the twisting angle changes, the topological phase of the core light and the degree of matching with the cladding leaky mode in terms of phase undergo changes, leading to the emergence of peculiar optical characteristics [40,43].
In 2012, Wong [44] proposed the excitation of OAM resonances in helically twisted PCF and the twisted structure is shown in Figure 9. They theoretically and experimentally analyzed the transmission spectra and mode-field states of CTPCF, laying the foundation for further research on CTPCF. Since then, further research has been conducted on generating and manipulating OAM using CTPCF. The effect of symmetry on coupling between core and cladding modes in twisted PCF was studied [45]. By conducting numerical simulations on CTPCF fibers, they analyzed the impact of cladding mode distribution on coupling. To further investigate the coupling between the core and cladding, Maciej [46,47] et al proposed an analytical model describing scaling properties of the CTMOFs. They related the conditions of this coupling model to the wavelength, the lattice pitch, the number of air hole rings, and the helix pitch. As a result, significant loss peaks can be observed over a wide range of wavelengths. Based on the above research, the generation of higher-order orbital OAM using CTMOF has sparked interest among researchers. Li [50] reported a high-order mode suppression effect that may cause dips in the transmission spectrum of a large-size six-hole helical microstructured fiber (HMSF). Cui [48] demonstrated a helically twisted pig-nose-shaped core PCF for high order OAM generation in Figure 10. Supermodes in the inner dual-core can be coupled to high-order modes in the outer ring-core in this fiber, generating OAM ring-shaped modes at different wavelengths, and several OAM modes at different twist rates.
Apart from the generation of OAM, the underlying mechanism behind this new effect warrants further investigation. In coreless PCF, a twisted periodic structure generates a helical channel, allowing the formation of guided modes despite the absence of any recognizable core structure [38]. As the twist rate increases, the mode field diameter decreases, and the refractive index increases. A twisted coreless PCF was reported which supported a family of guided helical Bloch modes (HBMs), each member of which had a unique transverse field distribution and harmonic spectrum [49]. By designing different stackings of air hole structures, it is possible to generate a variety of high-index HBMs. In 2023, Zeng et al [34] reported the stable oscillation of optical vortices and acoustic modes in a Brillouin laser based on chiral PCF, which robustly supports helical Bloch modes (HBMs) that convey circularly polarized optical vortices and exhibit circular birefringence as shown in Figure 11. It is implemented a narrow-linewidth Brillouin fiber laser that emits stable 1st- and 2nd-order vortex-carrying HBMs.
Due to its special circular birefringence effect, CTPCF becomes a good choice for fiber optic sensors. The feasibility of CTPCF as a current sensor was verified by determining the CTPCF structure with the maximum circular birefringence through numerical analysis [35], selecting appropriate shape and scale parameters. In order to develop high-sensitivity sensors, a fabrication method of a helical photonic crystal fiber (HPCF) and an inflated HPCF(IHPCF) by use of an inflation-assisted hydrogen-oxygen flame heating technique was proposed by Fu [36]. Modify the air holes before and after is shown in Figure 12. The experimental results indicate that increasing the size of the air holes can significantly enhance transverse-load sensitivity. Ramya [37] discovered that torsion can significantly enhance the sensitivity when the sensor is used for salinity testing.

3.1.2. Chiral Twisted Hollow Core Fiber

Hollow core fiber [51,52], as its transmission medium is air, utilizes the transmission mechanism of bandgap or anti-resonance, resulting in extremely low dispersion, loss, and other characteristics. At the same time, its distinctive cladding distribution structure enables it to play an important role in various fields such as transmission [53], amplification [54,55], lasers [56], and sensing [57]. When introducing twist into the Hollow Core Fiber (HCF) [58,59,60], it can maintain strong circular birefringence and stable circular polarization characteristics [61,62]. In addition, further exploration and research are warranted for its unique optical effects, such as the hybrid photonic bandgap effect [63] and the generation and preservation of OAM modes [64,65,66,67].
Strong circular dichroism is an important characteristic of CTHCF. Roth et al [68] demonstrating strong circular dichroism for the HE11-like core mode in helically twisted hollow-core single-ring photonic crystal fiber (SR-PCF), formed by spinning the preform during fiber drawing. The refractive index vs azimuthal mode order is shown in Figure 13. When twisted, the ring exhibits significant circular birefringence, allowing only one circular polarization state to couple to the core mode. The modulation and preservation of circular polarization states are equally important. Davtyan [65] presented a novel technique based on a helically twisted hollow-core photonic crystal fiber that exhibits circular birefringence and so stably maintains a circular polarization state in the face of external perturbations. The method based on CTHCF has the potential to be applied in the generation, modulation, and transmission of circularly polarized light from ultraviolet to mid-infrared wavelengths.
CTHCF can also induce mode conversion into OAM modes, allowing for a simple and tunable approach to generate OAM modes [66]. Tu [67] examined the orbital OAM mode generation process of a long-period onefold chiral fiber grating (L-1-CFG) based on a hollow-core anti-resonant fiber (HC-ARF). They theoretically and experimentally demonstrated that a first-order OAM mode can be generated simply by inputting a Gaussian beam. The process of mode evolution is illustrated in Figure 14. Additionally, an appropriate twisted pitch can suppress the fundamental mode and maintain the purity of higher-order modes [65]. This also provides a feasible solution for selecting specific modes.
The high robustness of HCF is also a major advantage in its applications. Compared to conventional HCF, CTHCF exhibits greater extinction ratio interference peaks, making it suitable for sensing applications. Zheng [69] proposed a helical HCF for bending sensing. In Figure 15, due to the isolation provided by the air gap, the bending sensitivity reaches -9.066nm/m-1, while being minimally affected by external temperatures. Davtyan et al [70] demonstrated a gas-filled twisted SR-PCF that offers a promising platform for precise excitation, robust polarization preservation, and effective Raman frequency conversion of optical vortices, as well as low-loss guidance.

3.1.3. Chiral Twisted Multicore Fiber

Due to their ability to support multiple guided channels, multicore fibers have attracted researchers' interest in the fields of transmission [71], amplification [72], and sensing [73,74]. CTMCF exhibits enhanced coupling between the fiber cores due to its helical structure [75], and its axial non-uniformity makes it outperform ordinary MCF in sensing [76,77,78], modulation of OAM modes [79], and other aspects.
Torsion sensor is an important application of CTHCF. Ordinary MCF can be used for torsion testing, but it cannot distinguish the direction of torsion. In torsion measurement, the pitch length of a pre-twisted MCF changes with different directions of torsion. Therefore, CTHCF [80,81,82,83,84,85] not only provides sensitivity in torsion testing but also allows for the determination of its direction. Zhang [78] proposed a directional torsion sensor based on a Mach-Zehnder interferometer generated in a helical structure (HS) multicore fiber (MCF). The cross-section parameters of the optical fiber and sensor structure are shown in Figure 16. In addition to achieving fiber circular asymmetry by using of this short helical structure, multiple interference was also significantly enhanced. Both simulation and experimental spectrum analysis revealed the different interferences caused by the interplay of the center core mode, outer core mode, and cladding mode. The suggested sensor's maximum torsion sensitivity is -0.118 nm/(rad/m) for twist rates between -17.094 rad/m and -15.669 rad/m. A highly sensitive strain sensor based on helical seven core fiber is proposed and experimentally demonstrated [86]. To create an in-line MZI, an all-solid heterogeneous seven core fiber was locally twisted into helical structures and then spliced between two short sections of multimode fibers (MMFs). Because of the helical structure, a maximum strain sensitivity of 61.8pm/με was reached. It is approximately 56 times greater than the equivalent MCF-based Mach-Zehnder interferometer.
To further enhance the sensing performance of CTMCF, researchers are attempting some mechanical treatments on the fiber. Tapered multicore fiber can further enhance the coupling between cores, making it considered as a promising method for enhancing sensitivity. In 2023, a highly sensitive torsion sensor based on MZI in helical seven-core fiber taper was proposed [77]. As shown in Figure 17, they created sensors with varying taper waists and helical pitches, and their transmission spectra were acquired and studied. With a helical structure, the sensitivity reaches 2.253 nm/(rad/m) and −1.123 nm/(rad/m). Furthermore, with a waist diameter of 48 m, the torsion sensitivity is raised to 5.391 nm/(rad/m) by reducing the taper waist and making the helix denser. They also calibrate the sensor's temperature properties, and the sensitivity is attained at 32 pm/℃, which means that tapered CTMCF can eliminate the cross-sensitivity to temperature. Song [87] also demonstrated this characteristic of CTMCF through experimental verification. Xiang [88] utilized the CO2 laser method to fabricate a helical LPG manufactured from MCF combined with twist, which also demonstrated low temperature cross-sensitivity.
Adding functional materials on the surface or inside of CTMCF can further explore its potential applications. Liu [89] attempted to coat gelatin on the surface of a four-core fiber (FCF) and deposited a gold film on its end face as a reflector. A helical structure was fabricated by twisting the FCF under continuous arc discharging. When the external environment's relative humidity (RH) varies, both the RI and the size of the gelatin film change, causing the effective RI of the FCF cladding and the strain of the sensor to change, resulting in the resonance dip wavelength change in the interference signal. In addition to coating materials on the surface, changing the core material of CTMCF can achieve other functionalities. CTMCF has been demonstrated to generate OAM modes [79]. Li [90] replaced the core of the twisted multicore PCF with Yb-doped material (YTMF) as shown in Figure 18 to achieve amplification of OAM light. The experimental results indicate that the fluorescence amplification properties of the doped material Yb3+ can be used to amplify the 1064nm laser. Furthermore, theoretical study shows that the modes in YTMF at 1064nm, which is in the amplified wavelength range, can accommodate nine OAM-carrying modes. The results indicate that combining doped materials with CTMCF enables the generation, amplification, and multiplexing of multiple beams of OAM light, providing new insights for the establishment of next-generation communication systems.

4. Summary and outlook of functional Chiral twisted fibers

Chiral Twisted Optical Fibers introduce unusual optical phenomena by incorporating a special twisted structure into the fiber. The twisted structure in SMF induces changes in birefringence, allowing the twisted fiber to exhibit similar behavior to fiber gratings. When combined with MOFs, they exhibit unexpectedly excellent results in the generation and selection of OAM beams due to their circular polarization properties. They also exhibit robust birefringence towards OAM beams, meaning that modes with different principal OAM orders have non-degenerate propagation constants. Particularly in hollow-core fibers, CTMOFs exhibit exceptional performance in mode filtering and selection, indicating their potential for stable OAM transmission. Furthermore, the transmission spectra of CTMOFs exhibit wavelength-dependent attenuation based on the twisting pitch, making them applicable in sensing applications. These changes not only enhance extinction ratio but also demonstrate significant advantages in directional discrimination. The combination of CTMOFs with functional materials expands their application scope, including external coating materials and internal core doping materials. Currently, the exploration of chiral twisted fibers is still in its early stages. In the near future, these applications may be realized and applied in real-life engineering. Due to their excellent performance in OAM birefringence and dispersion control, they hold tremendous potential for applications in nonlinear fiber optics, fiber lasers, amplifiers, and sensors.

Author Contributions

Conceptualization, Y.Z. and B.L.; investigation, T.H. and S.Z.; writing—original draft preparation, Y.Z.; writing—review and editing, B.L. and G.Z.; visualization, Y.Y.; funding acquisition, B.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Basic and Applied Basic Research Foundation of Guangdong Province, China, grant number 2022A1515110480, 2022A1515140054.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data available on request due to restrictions eg privacy or ethical.

Acknowledgments

We appreciate Yaoyao Liang's assistance with our English proofreading.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kopp, V.I.; Genack, A.Z. Chiral fibres: Adding twist. Nat. Photonics 2011, 5, 470–472. [Google Scholar] [CrossRef]
  2. Zhang, Y.; Zhang, W.; Wu, P.; Bie, L.; Kong, L.; Li, Z.; Zhang, Y.; Yan, T. Torsion bidirectional sensor based on tilted-arc long-period fiber grating. Opt. Express 2019, 27, 37695–37705. [Google Scholar] [CrossRef] [PubMed]
  3. Lu, C.; Jin, X.; Wang, S.; Xiang, Z.; Sun, C.; Chen, X.; Ma, Y.; Zhu, Q.; Tong, C.; Geng, T.; Sun, W.; Yuan, L. High Torsion Sensitivity Sensor Based on LPFG With Unique Geometric Structure. IEEE Sens. J. 2021, 21, 6217–6223. [Google Scholar] [CrossRef]
  4. Zhong, J.; Liu, S.; Zou, T.; Yan, W.; Chen, P.; Liu, B.; Sun, Z.; Wang, Y. High-Sensitivity Optical Fiber-Based Glucose Sensor Using Helical Intermediate-Period Fiber Grating. Sensors 2022, 22, 6824. [Google Scholar] [CrossRef] [PubMed]
  5. Wang, X.; Deng, H.; Yuan, L. Highly Sensitive Flexible Surface Plasmon Resonance Sensor Based on Side-Polishing Helical-Core Fiber: Theoretical Analysis and Experimental Demonstration. Adv. Photonics Res. 2021, 2(2), 2000054. [Google Scholar] [CrossRef]
  6. Li, B.; Zhang, Y.; Zhou, G.; Hou, Z.; Xia, C. The Surface Plasmon Resonance Polarizing Management in Helical Microstructure Fiber. Plasmonics 2020, 15, 995–1000. [Google Scholar] [CrossRef]
  7. Zhang, M.; Zhang, L.; Chen, Q.; Bai, G.; Li, S. A Designed Twist Sensor Based on the SPR Effect in the Thin-Gold-Film-Coated Helical Microstructured Optical Fibers. Sensors 2022, 22, 5668. [Google Scholar] [CrossRef]
  8. Li, C.; Xia, L.; Chen, X. Surface plasmon resonance effect in helical photonic crystal fiber using transformation optics formalism. 2017 25th Optical Fiber Sensors Conference (OFS), Jeju-Do, Korea, 24-28 April 2017. [Google Scholar]
  9. Napiorkowski, M.; Urbańczyk, W. Rigorous modeling of twisted anisotropic optical fibers with transformation optics formalism. Opt. Express 2021, 29, 15199–15216. [Google Scholar] [CrossRef]
  10. Zhu, T.; Chiang, K.S.; Rao, Y.; Shi, C.; Song, Y.; Liu, M. Characterization of Long-Period Fiber Gratings Written by CO2 Laser in Twisted Single-Mode Fibers. J. Lightwave Technol. 2009, 27, 4863–4869. [Google Scholar]
  11. Deng, M.; Xu, J.; Zhang, Z.; Bai, Z.; Liu, S.; Wang, Y.; Zhang, Y.; Liao, C.; Jin, W.; Peng, G.; Wang, Y. Long period fiber grating based on periodically screw-type distortions for torsion sensing. Opt. Express 2017, 25, 14308–14316. [Google Scholar] [CrossRef]
  12. Bai, Z.; Wang, Y.; Zhang, Y.; Fu, C.; Liu, S.; Li, M.; Liao, C.; Wang, Y.; He, J. Helical Long-Period Fiber Gratings as Wavelength-Tunable Orbital Angular Momentum Mode Generators. IEEE Photonic Technol. Lett. 2020, 32, 418–421. [Google Scholar] [CrossRef]
  13. Zhao, H.; Wang, P.; Yamakawa, T.; Li, H. All-fiber second-order orbital angular momentum generator based on a single-helix helical fiber grating. Opt. Lett. 2019, 44 21, 5370–5373. [Google Scholar] [CrossRef]
  14. Shin, W.; Yu, B.; Lee, Y.L.; Noh, Y.C.; Ko, D.; Lee, J. High strength coupling and low polarization-dependent long-period fiber gratings based on the helicoidal structure. Opt. Fiber Technol. 2008, 14, 323–327. [Google Scholar] [CrossRef]
  15. Sun, B.; Wei, W.; Liao, C.; Zhang, L.; Zhang, Z.; Chen, M.; Wang, Y. Automatic Arc Discharge-Induced Helical Long Period Fiber Gratings and Its Sensing Applications. IEEE Photonic Technol. Lett. 2017, 29, 873–876. [Google Scholar] [CrossRef]
  16. Ulrich, R.; Simon, A. Polarization optics of twisted single-mode fibers. Appl. Opt. 1979, 18, 2241–51. [Google Scholar] [CrossRef]
  17. Barlow, A.J.; Ramskov-Hansen, J.J.; Payne, D.N. Birefringence and polarization mode-dispersion in spun single-mode fibers. Appl. Opt. 1981, 20, 2962–8. [Google Scholar] [PubMed]
  18. Galtarossa, A.; Palmieri, L. Measure of twist-induced circular birefringence in long single-mode fibers: theory and experiments. J. Lightwave Technol. 2002, 20, 1149–1159. [Google Scholar] [CrossRef]
  19. Tentori, D.; García-Weidner, A. Jones birefringence in twisted single-mode optical fibers. Opt. Express 2013, 21, 31725–39. [Google Scholar] [CrossRef]
  20. Guo, Q.; Zhu, Y.; Shan, T.; Pan, X.; Liu, S.; Xue, Z.; Zheng, Z.; Chen, C.; Yu, Y. Intensity-modulated directional torsion sensor based on a helical fiber taper. Opt. Mater. Express 2020, 11, 80. [Google Scholar] [CrossRef]
  21. Zhao, Y.; Liu, S.; Luo, J.; Chen, Y.; Fu, C.; Xiong, C.; Wang, Y.; Jing, S.; Bai, Z.; Liao, C.; Wang, Y. Torsion, Refractive Index, and Temperature Sensors Based on An Improved Helical Long Period Fiber Grating. J. Lightwave Technol. 2020, 38, 2504–2510. [Google Scholar] [CrossRef]
  22. Cao, X.; Tian, D.; Liu, Y.; Zhang, L.; Wang, T. Sensing Characteristics of Helical Long-Period Gratings Written in the Double-Clad Fiber by CO2 Laser. IEEE Sens. J. 2018, 18, 7481–7485. [Google Scholar] [CrossRef]
  23. Zhang, H.; Zhang, W.; Chen, L.; Xie, Z.; Zhang, Z.; Yan, T.; Wang, B. Bidirectional Torsion Sensor Based on a Pair of Helical Long-Period Fiber Gratings. IEEE Photonic Technol. Lett. 2016, 28, 1700–1702. [Google Scholar] [CrossRef]
  24. Xian, L.; Wang, D.; Li, L. Torsion and strain simultaneous measurement using a cascaded helical long-period grating. J. Opt. Soc. Am. B. 2020, 37, 1307–1311. [Google Scholar] [CrossRef]
  25. Ivanov, O.V. Fabrication of long-period fiber gratings by twisting a standard single-mode fiber. Opt. Lett. 2005, 30, 3290–2. [Google Scholar] [CrossRef]
  26. Li, B.; Xia, R.; Shum, P.P.; Zhou, G. Long-Period Gratings and Multimode Interference in Helical Single-Mode Fiber. IEEE Photonic Technol. Lett. 2019, 31, 1956–1959. [Google Scholar] [CrossRef]
  27. Nakano, S.; Fujisawa, T.; Saitoh, K. The Effect of Core Offset on the Mode Converting Characteristics in Twisted Single Mode Fibers. J. Lightwave Technol. 2019, 37, 5479–5485. [Google Scholar] [CrossRef]
  28. Wang, P.; Zhao, H.; Detani, T.; Tsuyuki, Y.; Li, H. Demonstration of the mode-selection rules obeyed in a single-helix helical long-period fiber grating. Opt. Lett. 2020, 45, 1846–1849. [Google Scholar] [CrossRef]
  29. Wang, P.; Zhao, H.; Detani, T.; Li, H. Simultaneous Generation of the First- and Second- Order OAM Using the Cascaded HLPGs. IEEE Photonic Technol. Lett. 2020, 32, 685–688. [Google Scholar] [CrossRef]
  30. Liu, S.; Zhou, M.; Shao, L.; Zhang, Z.; Bai, Z.; Wang, Y. Torsion-tunable OAM mode generator based on oxyhydrogen-flame fabricated helical long-period fiber grating. Opt. Express 2022, 30, 21085–21093. [Google Scholar] [CrossRef]
  31. Fu, C.; Wang, Y.; Bai, Z.; Liu, S.; Zhang, Y.; Li, Z. Twist-direction-dependent orbital angular momentum generator based on inflation-assisted helical photonic crystal fiber. Opt. Lett. 2019, 44, 459–462. [Google Scholar] [CrossRef]
  32. Russell, P.S.; Chen, Y. Localization of Light in Multi-Helical Arrays of Discrete Coupled Waveguides. Laser Photonics Rev. 2022, 17, 2200570. [Google Scholar] [CrossRef]
  33. Zhang, S.; Liu, X.; Chen, L.; Zhang, C.; Bai, H.; Wu, J.; Shi, J.; Li, H.; Liu, Y. Wavelength Tunable Single-Circular-Polarization Twisted PCF. IEEE Photonic Technol. Lett. 2021, 33, 1355–1358. [Google Scholar] [CrossRef]
  34. Zeng, X.; Russell, P.S.; Chen, Y.; Wang, Z.; Wong, G.K.; Roth, P.; Frosz, M.H.; Stiller, B. Optical Vortex Brillouin Laser. Laser Photonics Rev. 2022, 17, 2200277. [Google Scholar] [CrossRef]
  35. Beravat, R.; Wong, G.K.; Xi, X.M.; Frosz, M.H.; St., J. Russell, P. Current sensing using circularly birefringent twisted solid-core photonic crystal fiber. Opt. Lett. 2016, 41, 1672–5. [Google Scholar] [CrossRef] [PubMed]
  36. Fu, C.; Wang, Y.; Liu, S.; Bai, Z.; Tang, J.; Shao, L.; Liu, X. Transverse-load, strain, temperature, and torsion sensors based on a helical photonic crystal fiber. Opt. Lett. 2019, 44, 1984–1987. [Google Scholar] [CrossRef]
  37. Ramya, K.C.; Monfared, Y.E.; Maheswar, R.; Dhasarathan, V. Dual-Core Twisted Photonic Crystal Fiber Salinity Sensor: A Numerical Investigation. IEEE Photonic Technol. Lett. 2020, 32, 616–619. [Google Scholar] [CrossRef]
  38. Beravat, R.; Wong, G.K.; Frosz, M.H.; Xi, X.M.; Russell, P.S. Twist-induced guidance in coreless photonic crystal fiber: A helical channel for light. Sci. Adv. 2016, 2, e1601421. [Google Scholar] [CrossRef]
  39. Fujisawa, T.; Saitoh, K. Off-axis core transmission characteristics of helically twisted photonic crystal fibers. Opt. Lett. 2018, 43, 4935–4938. [Google Scholar] [CrossRef]
  40. Nakano, S.; Fujisawa, T.; Sato, T.; Saitoh, K. Beam propagation analysis of optical activity and circular dichroism in helically twisted photonic crystal fiber. Jpn. J. Appl. Phys. 2017, 57, 08PF06. [Google Scholar] [CrossRef]
  41. Churikov, V.M.; Kopp, V.I.; Genack, A.Z. Chiral diffraction gratings in twisted microstructured fibers. Opt. Lett. 2010, 35, 342–4. [Google Scholar] [CrossRef]
  42. Russell, P.S.; Beravat, R.; Wong, G.K. Helically twisted photonic crystal fibres. Philosophical transactions. Philos. Trans. A Math. Phy.s Eng. Sci. 2017, 375, 20150440. [Google Scholar]
  43. Fujisawa, T.; Saitoh, K. Arbitrary polarization and orbital angular momentum generation based on spontaneously broken degeneracy in helically twisted ring-core photonic crystal fibers. Opt. Express 2021, 29, 31689–31705. [Google Scholar] [CrossRef]
  44. Wong, G.K.; Kang, M.S.; Lee, H.W.; Biancalana, F.; Conti, C.; Weiss, T.; Russell, P.S. Excitation of Orbital Angular Momentum Resonances in Helically Twisted Photonic Crystal Fiber. Science 2012, 337, 44–449. [Google Scholar] [CrossRef] [PubMed]
  45. Napiorkowski, M.; Urbańczyk, W. Role of symmetry in mode coupling in twisted microstructured optical fibers. Opt. Lett. 2018, 43, 395–398. [Google Scholar] [CrossRef] [PubMed]
  46. Napiorkowski, M.; Renversez, G.; Urbańczyk, W. Effect of cladding geometry on resonant coupling between fundamental and cladding modes in twisted microstructured fibers. Opt. Express 2019, 27, 5447–5460. [Google Scholar] [CrossRef] [PubMed]
  47. Napiorkowski, M.; Urbańczyk, W. Scaling effects in resonant coupling phenomena between fundamental and cladding modes in twisted microstructured optical fibers. Opt. Express 2018, 26, 12131–12143. [Google Scholar] [CrossRef]
  48. Cui, M.; Mo, Z.; Zhao, N.; Xia, C.; Hou, Z.; Zhou, G. High-order orbital angular momentum generation in a helically twisted pig-nose-shaped core microstructured optical fibers. Opt. Express 2021, 29, 6542–6552. [Google Scholar] [CrossRef]
  49. Roth, P.; Wong, G.K.; Frosz, M.H.; Ahmed, G.; Russell, P.S. Full-field characterization of helical Bloch modes guided in twisted coreless photonic crystal fiber. Opt. Lett. 2019, 44, 5049–5052. [Google Scholar] [CrossRef]
  50. Li, J.; Li, B.; Xia, C.; Hou, Z.; Zhou, G. High order modes suppression and manipulation in six-holes helical chiral microstructure fiber. Opt. Fiber Technol. 2021, 61, 102445. [Google Scholar] [CrossRef]
  51. Hong, Y.; Gao, S.; Ding, W.; Zhang, X.; Jia, A.; Sheng, Y.; Wang, P.; Wang, Y. Highly Birefringent Anti-Resonant Hollow-Core Fiber with a Bi-Thickness Fourfold Semi-Tube Structure. Laser Photonics Rev. 2022, 16, 2100365. [Google Scholar] [CrossRef]
  52. Gao, S.; Wang, Y.; Ding, W.; Hong, Y.; Wang, P. Conquering the Rayleigh Scattering Limit of Silica Glass Fiber at Visible Wavelengths with a Hollow-Core Fiber Approach. Laser Photonics Rev. 2019, 14, 1900241. [Google Scholar] [CrossRef]
  53. Michaud-Belleau, V.; Numkam Fokoua, E.R.; Bradley, T.D.; Hayes, J.R.; Chen, Y.; Poletti, F.; Richardson, D.J.; Genest, J.; Slavík, R. Backscattering in antiresonant hollow-core fibers: over 40 dB lower than in standard optical fibers. Optica 2021, 8, 216–219. [Google Scholar] [CrossRef]
  54. Belardi, W.; Sazio, P.J.; Bigot, L. Hollow core fibers for optical amplification. Opt. Lett. 2019, 44, 4127–4130. [Google Scholar] [CrossRef] [PubMed]
  55. Yang, F.; Gyger, F.; Thévenaz, L. Intense Brillouin amplification in gas using hollow-core waveguides. Nat. Photonics 2020, 14, 700–708. [Google Scholar] [CrossRef] [PubMed]
  56. Nampoothiri, A.V.; Jones, A.M.; Fourcade-Dutin, C.; Mao, C.; Dadashzadeh, N.; Baumgart, B.; Wang, Y.; Alharbi, M.; Bradley, T.D.; Campbell, N.S.; Benabid, F.; Washburn, B.R.; Corwin, K.L.; Rudolph, W. Hollow-core Optical Fiber Gas Lasers (HOFGLAS): a review [Invited]. Opt. Mater. Express 2012, 2, 948–961. [Google Scholar] [CrossRef]
  57. Förster, R.; Weidlich, S.; Nissen, M.; Wieduwilt, T.; Kobelke, J.; Goldfain, A.M.; Chiang, T.K.; Garmann, R.F.; Manoharan, V.N.; Lahini, Y.; Schmidt, M.A. Tracking and analysing the Brownian motion of nano-objects inside hollow core fibers. ACS Sens. 2020, 5, 879–886. [Google Scholar] [CrossRef]
  58. Stefani, A.; Fleming, S.C.; Kuhlmey, B.T. Terahertz orbital angular momentum modes with flexible twisted hollow core antiresonant fiber. APL Photonics 2017, 3, 051708. [Google Scholar] [CrossRef]
  59. Xie, S.; Sharma, A.; Romodina, M.N.; Joly, N.Y.; Russell, P.S. Tumbling and anomalous alignment of optically levitated anisotropic microparticles in chiral hollow-core photonic crystal fiber. Sci. Adv. 2021, 7, eabf6053. [Google Scholar] [CrossRef]
  60. Stefani, A.; Lwin, R.; Argyros, A.; Fleming, S. (2016, September). Hollow-Core Antiresonant Fibers with a Twist. Australian Conference on Optical Fibre Technology, Sydney, Australia, 5-8 September 2016. [Google Scholar]
  61. Davtyan, S.; Novoa, D.; Chen, Y.B.; Frosz, M.H.; Russell, P.S. Polarization-Tailored Raman Frequency Conversion in Chiral Gas-Filled Hollow-Core Photonic Crystal Fibers. Phys. Rev. Lett. 2019, 122, 143902. [Google Scholar] [CrossRef]
  62. Guerra, G.; Mousavi, S.M.; Taranta, A.; Fokoua, E.R.; Santagiustina, M.; Galtarossa, A.; Poletti, F.; Palmieri, L. A method to compute the local birefringence vector in twisted and bent antiresonant hollow-core fibers. 2023 Optical Fiber Communications Conference and Exhibition (OFC), San Diego California, United States, 5–9 March 2023; 2023. [Google Scholar]
  63. Zhu, Y.; Li, W.; Gao, F.; Xu, X.; Song, N. Hybrid photonic bandgap effect in twisted hollow-core photonic bandgap fibers. Opt. Lett. 2022, 47, 6161–6164. [Google Scholar] [CrossRef]
  64. Chattopadhyay, R.; Bhadra, S. K. Orbital Angular Momentum preserving guided mode in helically twisted hollow core photonic crystal fiber at Dirac point. arXiv preprint 2019, arXiv:1902.09117. [Google Scholar]
  65. Edavalath, N.N.; Günendi, M.C.; Beravat, R.; Wong, G.K.; Frosz, M.H.; Ménard, J.; St., J. Russell, P. Higher-order mode suppression in twisted single-ring hollow-core photonic crystal fibers. Opt. Lett. 2017, 42, 2074–2077. [Google Scholar] [CrossRef]
  66. Stefani, A.; Kuhlmey, B.T.; Fleming, S.C. Orbital angular momentum modes by twisting of a hollow core antiresonant fibe. 2017 Conference on Lasers and Electro-Optics Europe and European Quantum Electronics Conference (CLEO/Europe-EQEC, San Jose, United States, 14-19 May 2017. [Google Scholar]
  67. Tu, J.; Wu, J.; Huang, C.; Zhang, J.; Gao, S.; Liu, W.; Li, Z. OAM mode generation in helically twisted hollow-core antiresonant fiber. Opt. Lett. 2023, 48, 1634–1637. [Google Scholar] [CrossRef]
  68. Roth, P.; Chen, Y.; Günendi, M. C.; Beravat, R.; Edavalath, N. N.; Frosz, M. H.; Ahmed, G.; Wong, G.K. and Russell, P. S. J. Strong circular dichroism for the HE 11 mode in twisted single-ring hollow-core photonic crystal fiber. Optica 2018, 5, 1315–1321. [Google Scholar] [CrossRef]
  69. Zheng, Y.; Shum, P.P.; Li, B.; Zhang, H.; Auguste, J.; Humbert, G. Experimental Investigation of Bending Sensor Based on Helical Structure in Hollow Core Fiber. 2020 IEEE Photonics Conference (IPC), Vancouver, BC, Canada, 28 September-01 October 2020. [Google Scholar]
  70. Davtyan, S.; Chen, Y.B.; Frosz, M.H.; St.J. Russell, P.; Novoa, D. Robust excitation and Raman conversion of guided vortices in a chiral gas-filled photonic crystal fiber. Opt. Lett. 2020, 45, 1766–1769. [Google Scholar] [CrossRef] [PubMed]
  71. Puttnam, B. J.; Rademacher, G.; Luís, R. S. Space-division multiplexing for optical fiber communications. Optica 2021, 8, 1186–1203. [Google Scholar] [CrossRef]
  72. Jain, S.; Castro, C.; Jung, Y.; Hayes, J.R.; Sandoghchi, R.; Mizuno, T.; Sasaki, Y.; Amma, Y.; Miyamoto, Y.; Bohn, M.; Pulverer, K.; Nooruzzaman, Morioka T.; Alam, S.; Richardson, D.J. 32-core erbium/ytterbium-doped multicore fiber amplifier for next generation space-division multiplexed transmission system. Opt. Express 2017, 25, 32887–32896. [Google Scholar] [CrossRef]
  73. Meng, Y.; Fu, C.; Du, C.; Chen, L.; Zhong, H.; Li, P.; Xu, B.; Du, B.; He, J.; Wang, Y. Shape Sensing Using Two Outer Cores of Multicore Fiber and Optical Frequency Domain Reflectometer. J. Lightwave Technol. 2021, 39, 6624–6630. [Google Scholar] [CrossRef]
  74. Zhou, R.; Chen, F.; Li, S.; Wang, R.; Qiao, X. Three-Dimensional Vector Accelerometer Using a Multicore Fiber Inscribed With Three FBGs. J. Lightwave Technol. 2021, 39, 3244–3250. [Google Scholar] [CrossRef]
  75. Sakamoto, T.; Aozasa, S.; Mori, T.; Wada, M.; Yamamoto, T.; Nozoe, S.; Sagae, Y.; Tsujikawa, K.; Nakajima, K. Twisting-Rate-Controlled 125 μm Cladding Randomly Coupled Single-Mode 12-Core Fiber. J. Lightwave Technol. 2018, 36, 325–330. [Google Scholar] [CrossRef]
  76. Xu, Y.; Lin, H.; Zhou, A. A Pre-Twisted Taper in Dual-Side Hole Fiber for Torsion Measurement With High Sensitivity. IEEE Sens. J. 2020, 20, 7761–7765. [Google Scholar] [CrossRef]
  77. Wang, J.; Zeng, X.; Zhou, J.; Hao, J.; Yang, X.; Liu, Y.; Chen, W.; Li, S.; Yan, Y.; Geng, T.; Sun, W.; Yuan, L. Highly sensitive torsion sensor based on Mach–Zehnder interference in helical seven-core fiber taper. Chin. Opt. Lett. 2023, 21, 041205. [Google Scholar] [CrossRef]
  78. Zhang, H.; Wu, Z.; Shum, P.P.; Shao, X.; Wang, R.; Dinh, X.Q.; Fu, S.; Tong, W.; Tang, M. Directional torsion and temperature discrimination based on a multicore fiber with a helical structure. Opt. Express 2018, 26, 544–551. [Google Scholar] [CrossRef] [PubMed]
  79. Zhang, Y.; Li, B.; Xia, C.; Hou, Z.; Zhou, G. Orbit angular momentum supermode in chirality helical dual-core microstructure fiber. Opt. Commun. 2020, 475, 126245. [Google Scholar] [CrossRef]
  80. Parker, R.; Aceves, A. Standing-wave solutions in twisted multicore fibers. Phys. Rev. A 2021, 103, 053505. [Google Scholar] [CrossRef]
  81. Zhang, X. I. A. O.; Vysloukh, V. A.; Kartashov, Y. V.; Chen, X.; Ye, F. A. N. G. W. E. I.; Belić, M. R. PT symmetry in nonlinear twisted multicore fibers. Opt. Lett. 2017, 42, 2972–2975. [Google Scholar] [CrossRef]
  82. Zhang, H.; Wu, Z.; Ping Shum, P.; Wah Low, C.; Shao, X.; Wang, R.; Quyen Dinh, X.; Fu, S.; Tong, W.; Tang, M. Simultaneous Measurement of Torsion and Temperature Based on Helical Structure in Multicore Fiber. 2016 Asia Communications and Photonics Conference (ACP), Wuhan, China, 2–5 November 2016. [Google Scholar]
  83. Suchkov, S. V.; Chekhovskoy, I. S.; Shtyrina, O. V.; Wabnitz, S.; Fedoruk, M. P. Nonlinear twisted multicore fibers with PT-symmetry. Opt. Commun. 2023, 530, 129147. [Google Scholar] [CrossRef]
  84. Khan, F.; Barrera, D.; Sales, S.; Misra, S. Curvature, twist and pose measurements using fiber Bragg gratings in multi-core fiber: A comparative study between helical and straight core fibers. Sens. Actuators 2021, 317, 112442. [Google Scholar] [CrossRef]
  85. Yin, G.; Lu, L.; Zhou, L.; Shao, C.; Fu, Q.; Zhang, J.; Zhu, T. Distributed directional torsion sensing based on an optical frequency domain reflectometer and a helical multicore fiber. Opt. Express 2020, 28, 16140–16150. [Google Scholar] [CrossRef]
  86. Zhang, H.; Wu, Z.; Shum, P.P.; Dinh, X.Q.; Low, C.W.; Xu, Z.; Wang, R.; Shao, X.; Fu, S.; Tong, W.; Tang, M. Highly sensitive strain sensor based on helical structure combined with Mach-Zehnder interferometer in multicore fiber. Sci. Rep. 2017, 7, 46633. [Google Scholar] [CrossRef]
  87. Song, Z.; Li, Y.; Hu, J. Directional Torsion Sensor Based on a Two-Core Fiber with a Helical Structure. Sensors 2023, 23, 2874. [Google Scholar] [CrossRef] [PubMed]
  88. Xiang, S.; Xiongwei, H.; Luyun, Y.; Nengli, D.; Jianjun, W.; Fangfang, Z.; Jingang, P.; Haiqing, L.; Jinyan, L. Helical long-period grating manufactured with a CO2 laser on multicore fiber. Opt. Express 2017, 25, 10405–10412. [Google Scholar] [CrossRef] [PubMed]
  89. Liu, Y.; Zhou, A.; Yuan, L. Gelatin-Coated Michelson Interferometric Humidity Sensor Based on a Multicore Fiber With Helical Structure. J. Lightwave Technol. 2019, 37, 2452–2457. [Google Scholar] [CrossRef]
  90. Li, B.; Zhou, G.; Liu, J.; Xia, C.; Hou, Z. Orbital-angular-momentum-amplifying helical vector modes in Yb3+-doped three-core twisted microstructure fiber. Opt. Express 2020, 28, 21110–21120. [Google Scholar] [CrossRef] [PubMed]
Preprints 81017 g001
Figure 1. Illustration of twisted single core fiber.
Figure 1. Illustration of twisted single core fiber.
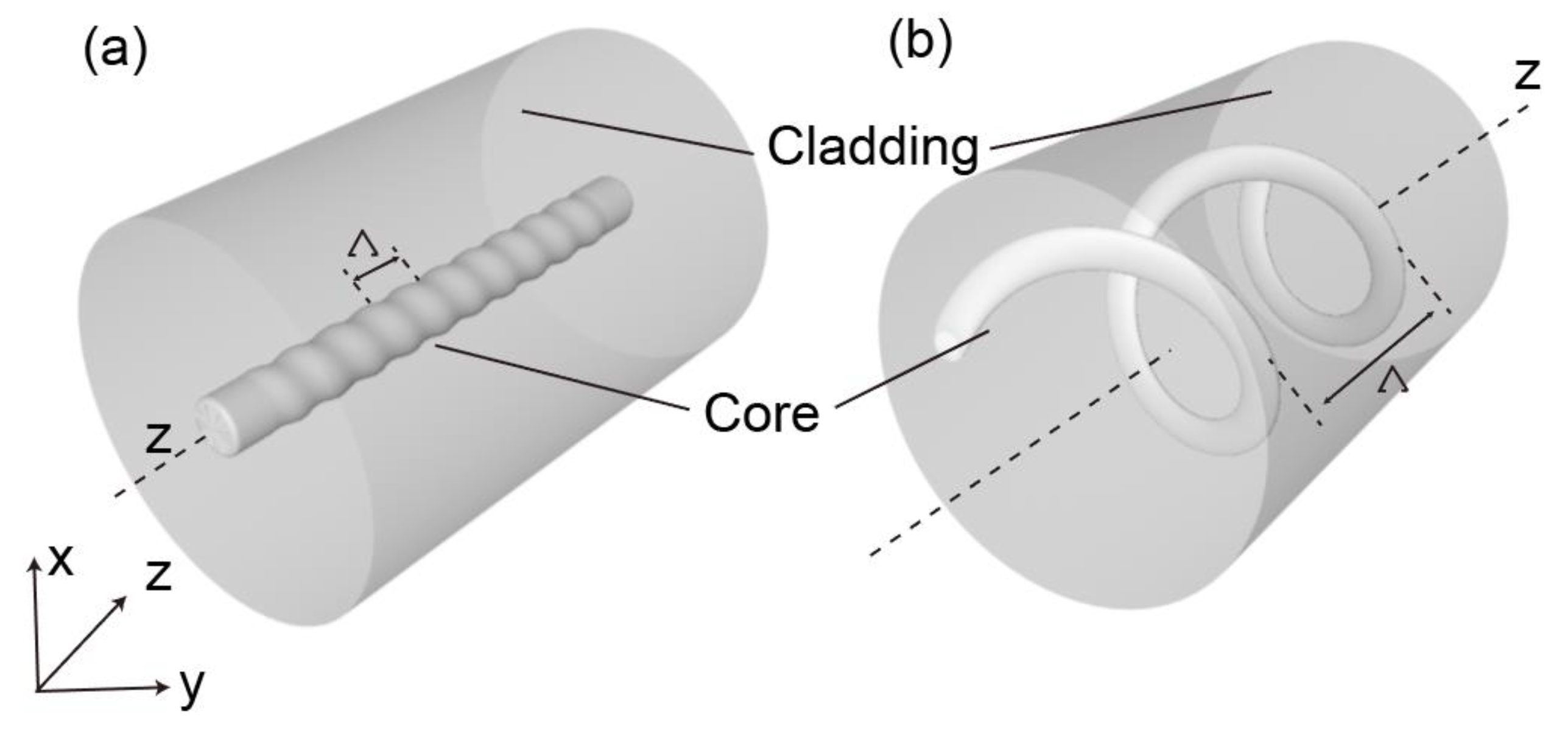
Preprints 81017 g001
Preprints 81017 g002
Figure 2. Schematic Diagram of Microstructured Optical Fiber Twist.
Figure 2. Schematic Diagram of Microstructured Optical Fiber Twist.
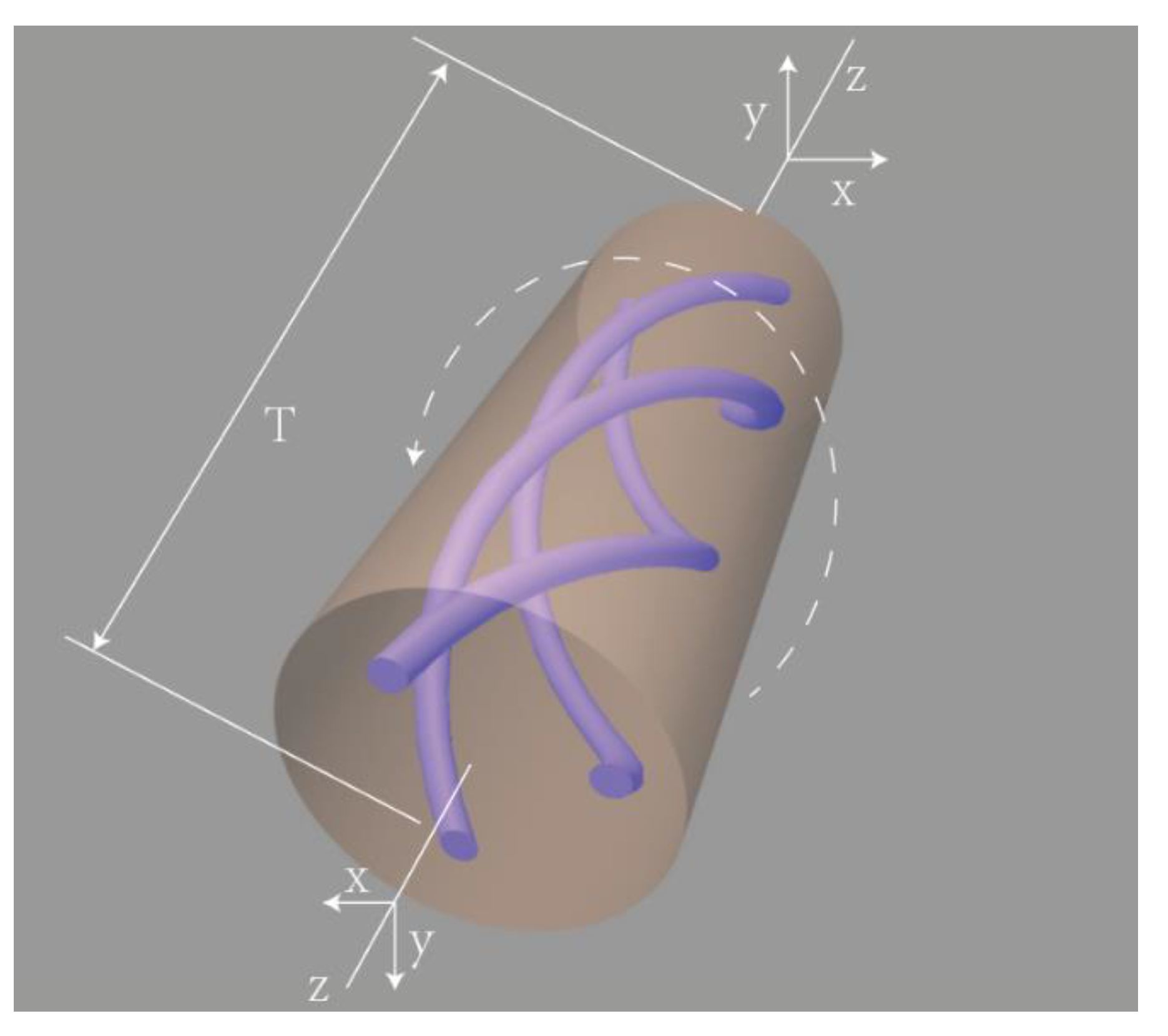
Preprints 81017 g002
Preprints 81017 g003
Figure 3. Methods for fabricating a helical optical fiber. (a) hydrogen-oxygen flame method. (b) CO2 laser beam method. (c) automatic arc discharge technology.
Figure 3. Methods for fabricating a helical optical fiber. (a) hydrogen-oxygen flame method. (b) CO2 laser beam method. (c) automatic arc discharge technology.
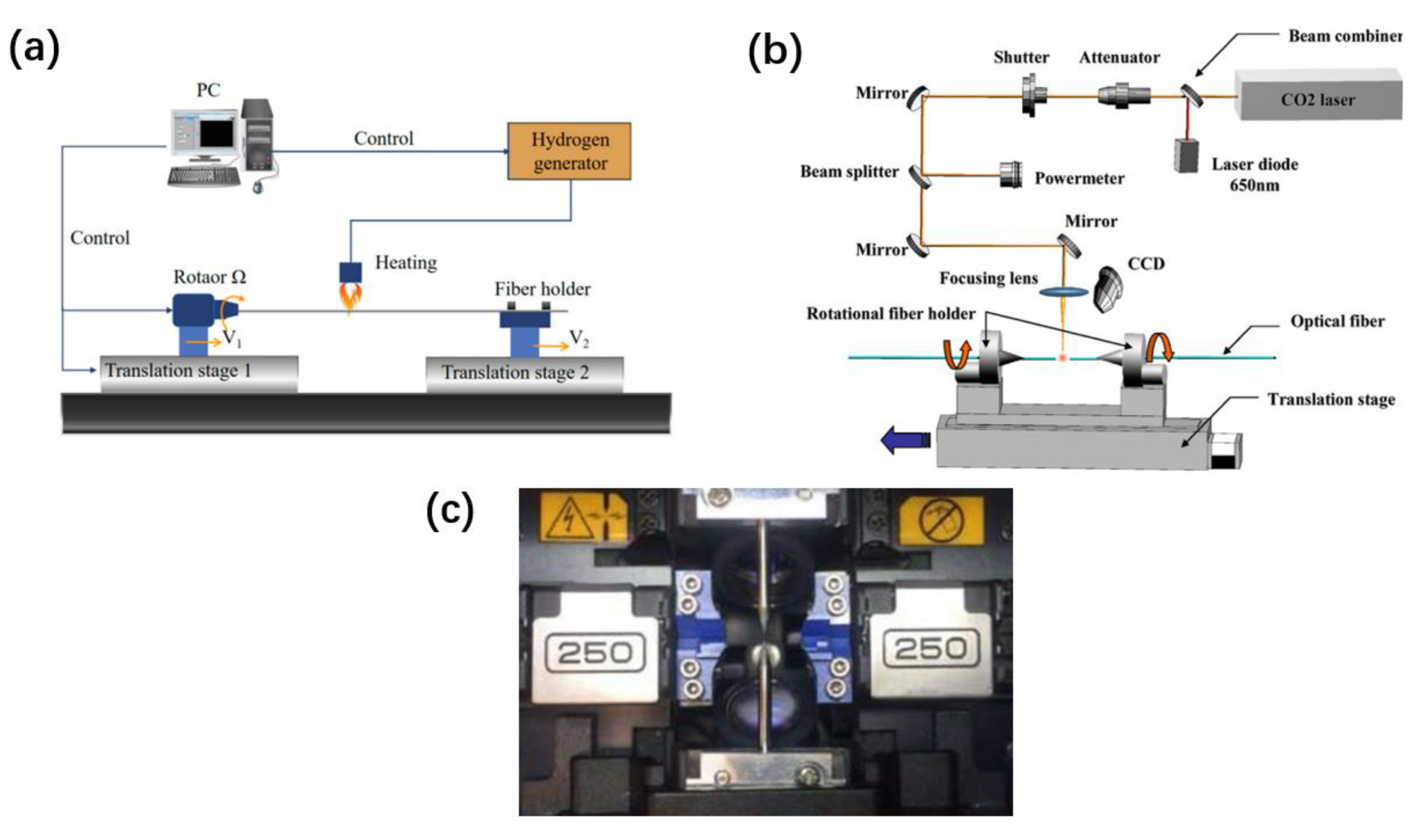
Preprints 81017 g003
Preprints 81017 g004
Figure 4. The change in output polarization state with varying twist angle was observed for both erbium-doped fiber (a) and standard single-mode fiber (b).
Figure 4. The change in output polarization state with varying twist angle was observed for both erbium-doped fiber (a) and standard single-mode fiber (b).
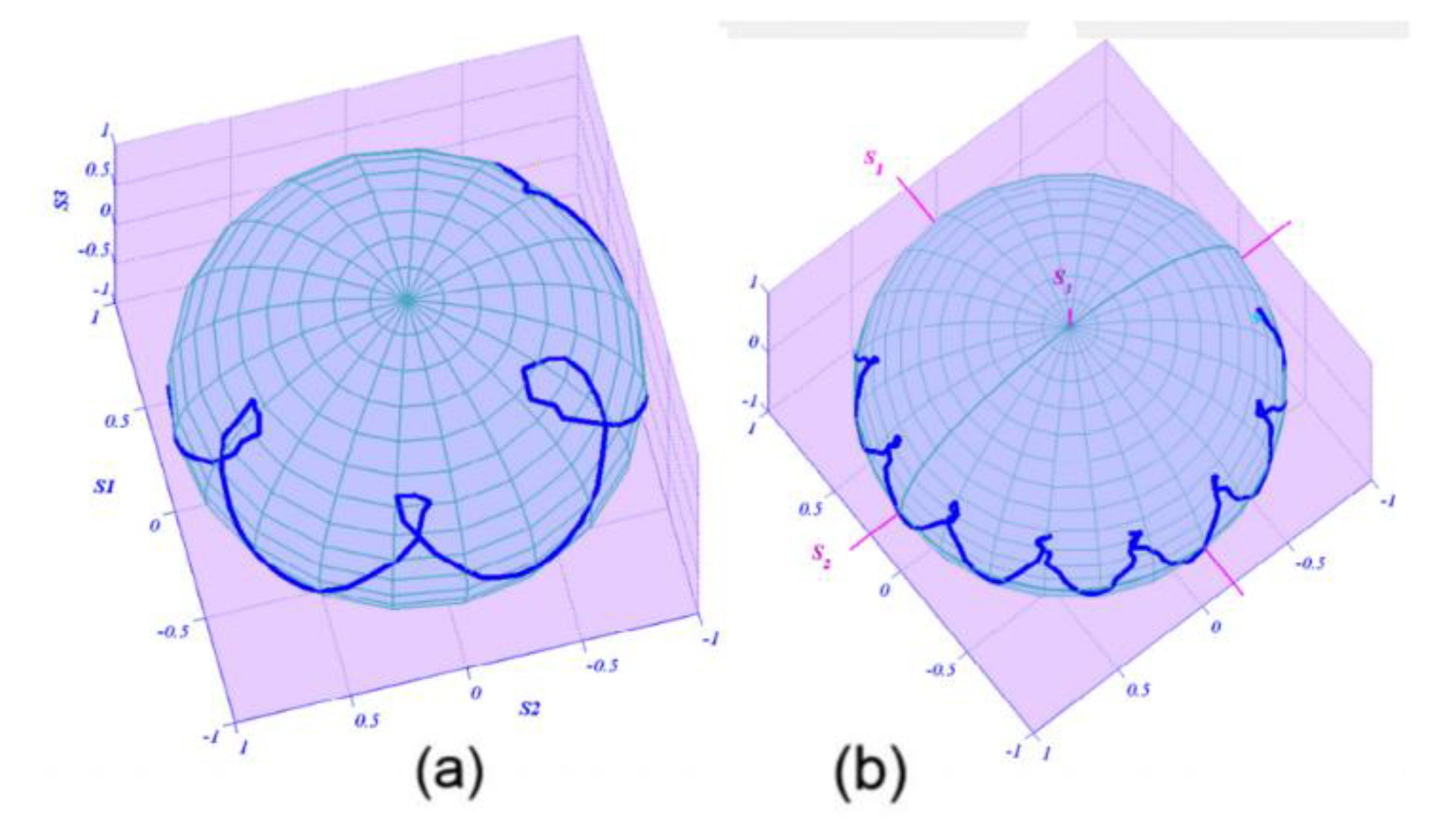
Preprints 81017 g004
Preprints 81017 g005
Figure 5. Results from experiments and theories are compared. The experimental result for LPG is at 1332 nm, whereas the theoretical dip is 1330 nm.
Figure 5. Results from experiments and theories are compared. The experimental result for LPG is at 1332 nm, whereas the theoretical dip is 1330 nm.
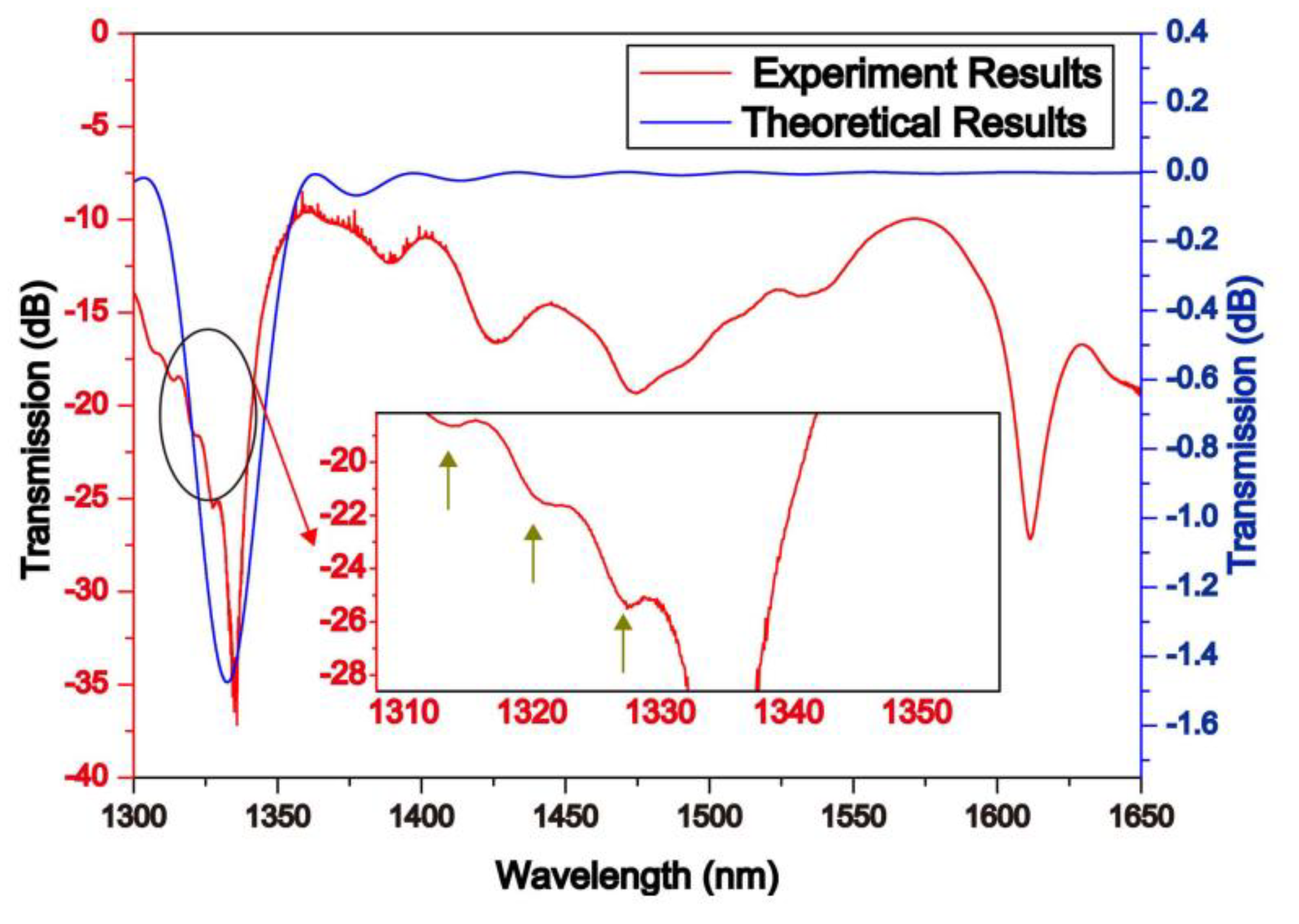
Preprints 81017 g005
Preprints 81017 g006
Figure 6. Torsion and strain measurement by using a cascaded HLPG.
Figure 6. Torsion and strain measurement by using a cascaded HLPG.
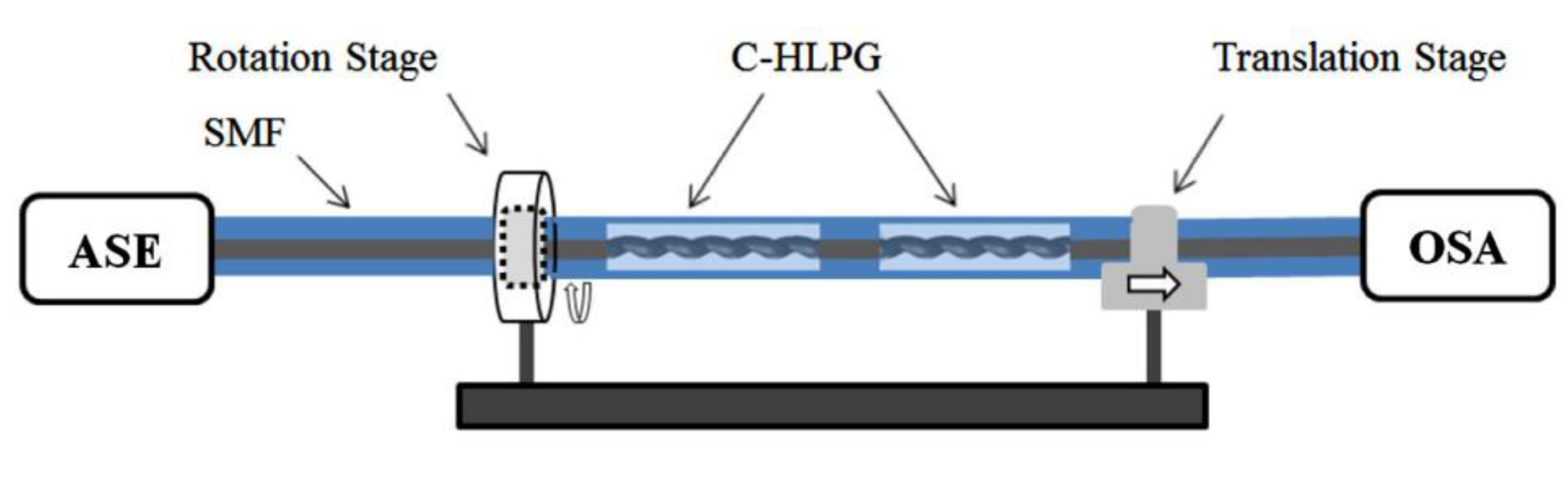
Preprints 81017 g006
Preprints 81017 g007
Figure 7. Schematic of the ccHLPGs-based OAM generator.
Figure 7. Schematic of the ccHLPGs-based OAM generator.
Preprints 81017 g007
Preprints 81017 g008
Figure 8. The evolution of mode field distributions and its interference patterns with the Gaussian beams with varying torsion angles.
Figure 8. The evolution of mode field distributions and its interference patterns with the Gaussian beams with varying torsion angles.
Preprints 81017 g008
Preprints 81017 g009
Figure 9. Helically twisted PCF and Local axial and azimuthal components of the refractive index of the fundamental space-filling Bloch mode in the twisted cladding.
Figure 9. Helically twisted PCF and Local axial and azimuthal components of the refractive index of the fundamental space-filling Bloch mode in the twisted cladding.
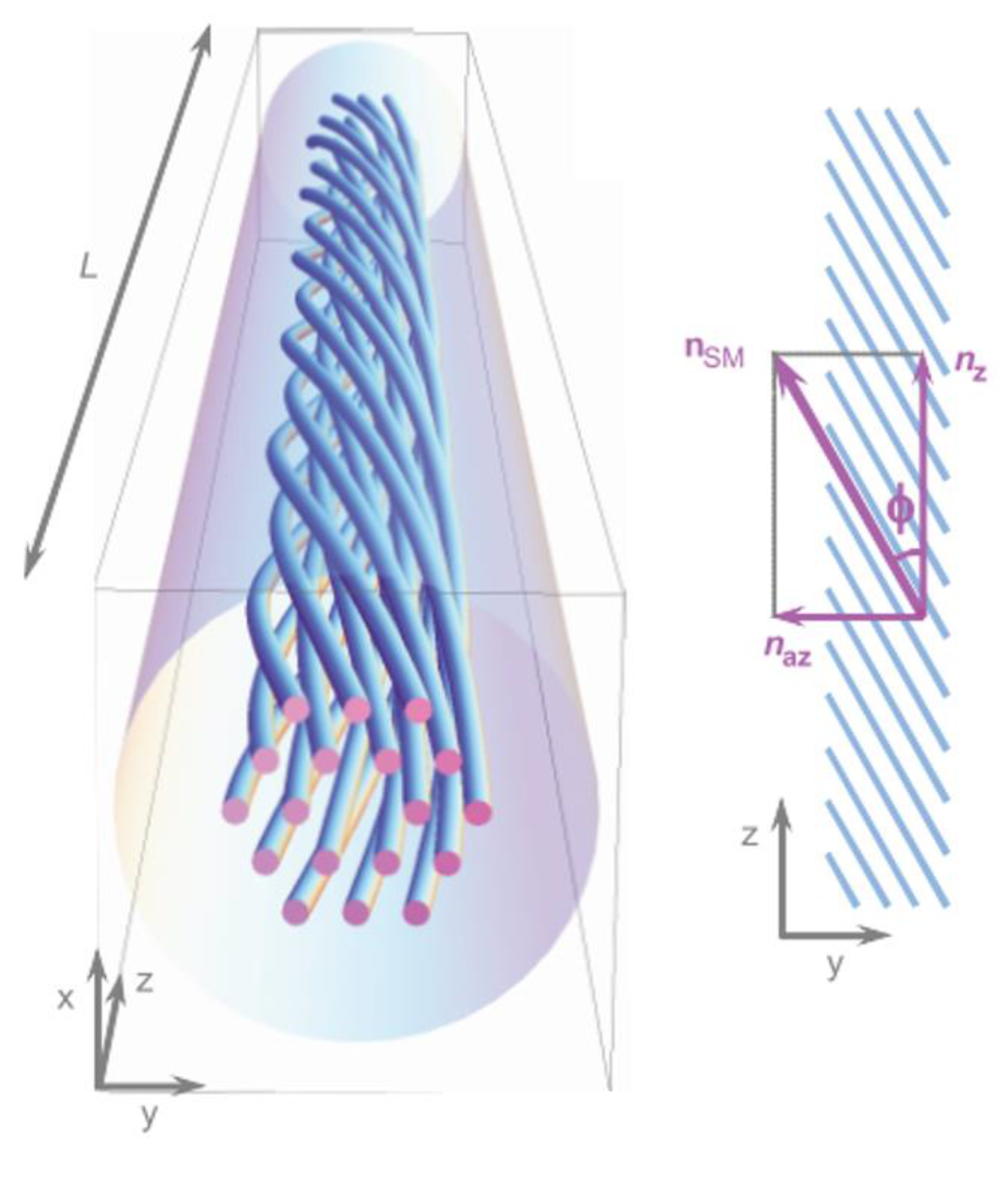
Preprints 81017 g009
Preprints 81017 g010
Figure 10. Cross-section and sketch of the HPC-MOF.
Figure 10. Cross-section and sketch of the HPC-MOF.
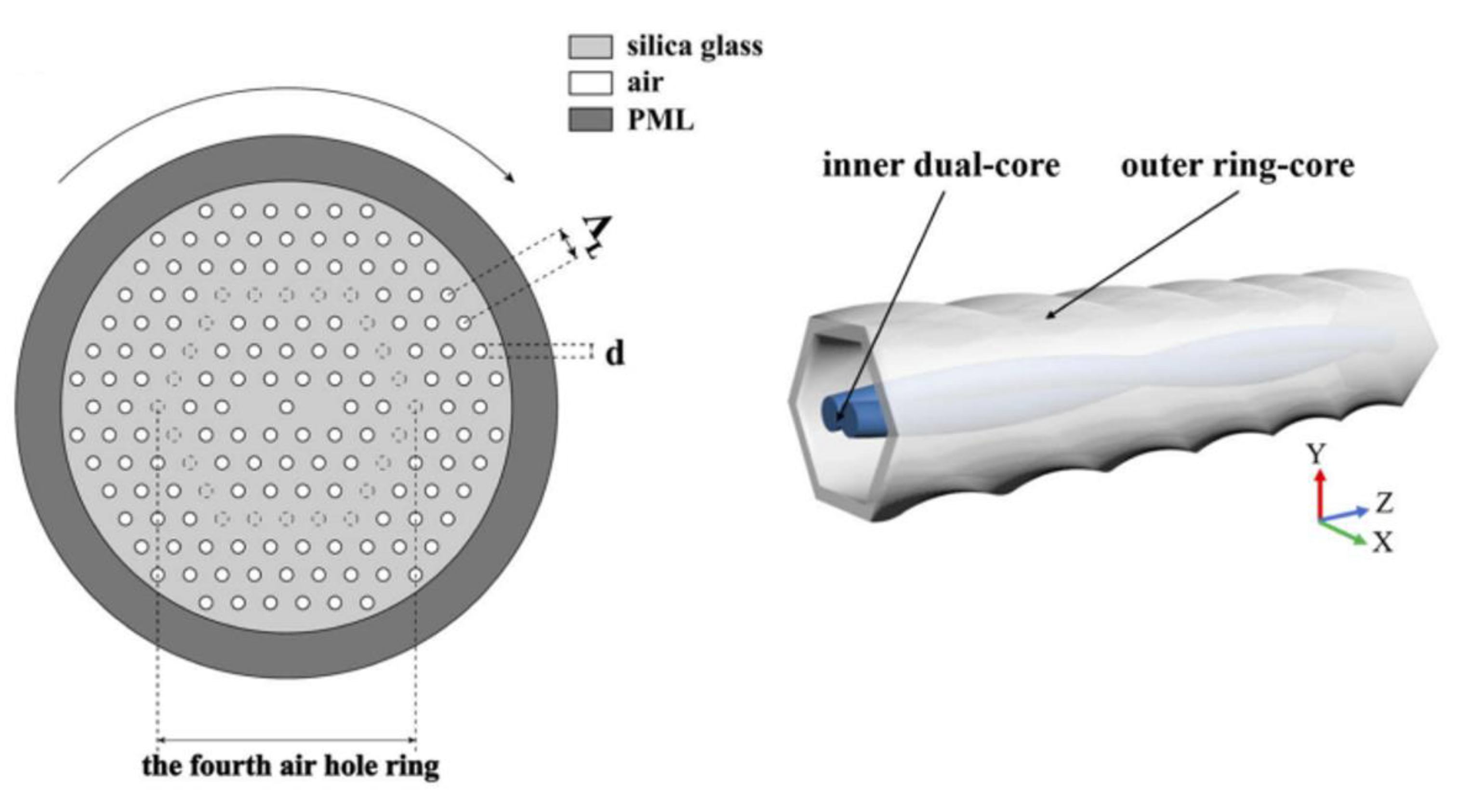
Preprints 81017 g010
Preprints 81017 g011
Figure 11. Experimental setup of vortex Brillouin laser.
Figure 11. Experimental setup of vortex Brillouin laser.
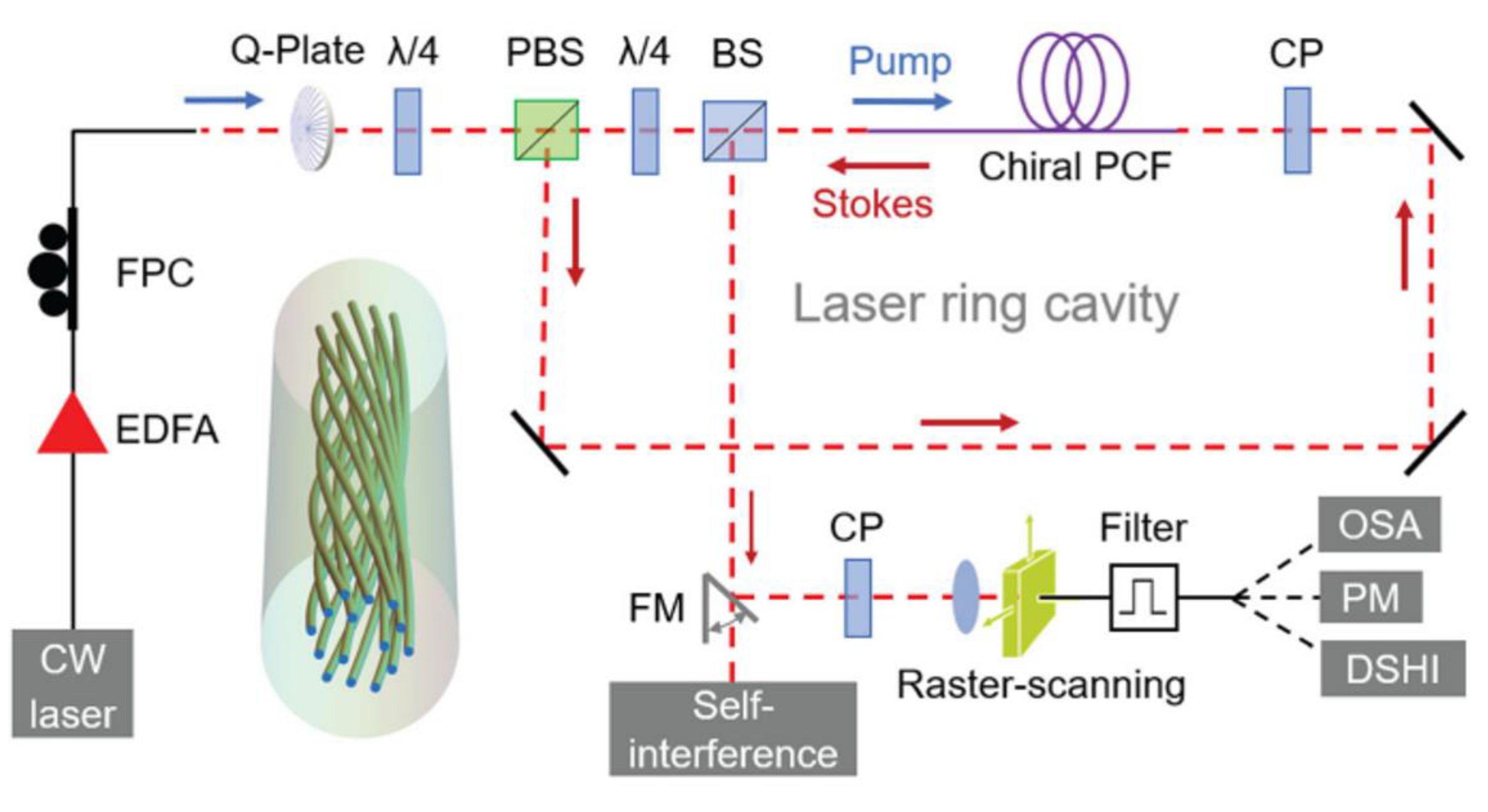
Preprints 81017 g011
Preprints 81017 g012
Figure 12. The scanning electron microscopy images on the cross sections of the achieved HPCF and IHPCF samples.
Figure 12. The scanning electron microscopy images on the cross sections of the achieved HPCF and IHPCF samples.
Preprints 81017 g012
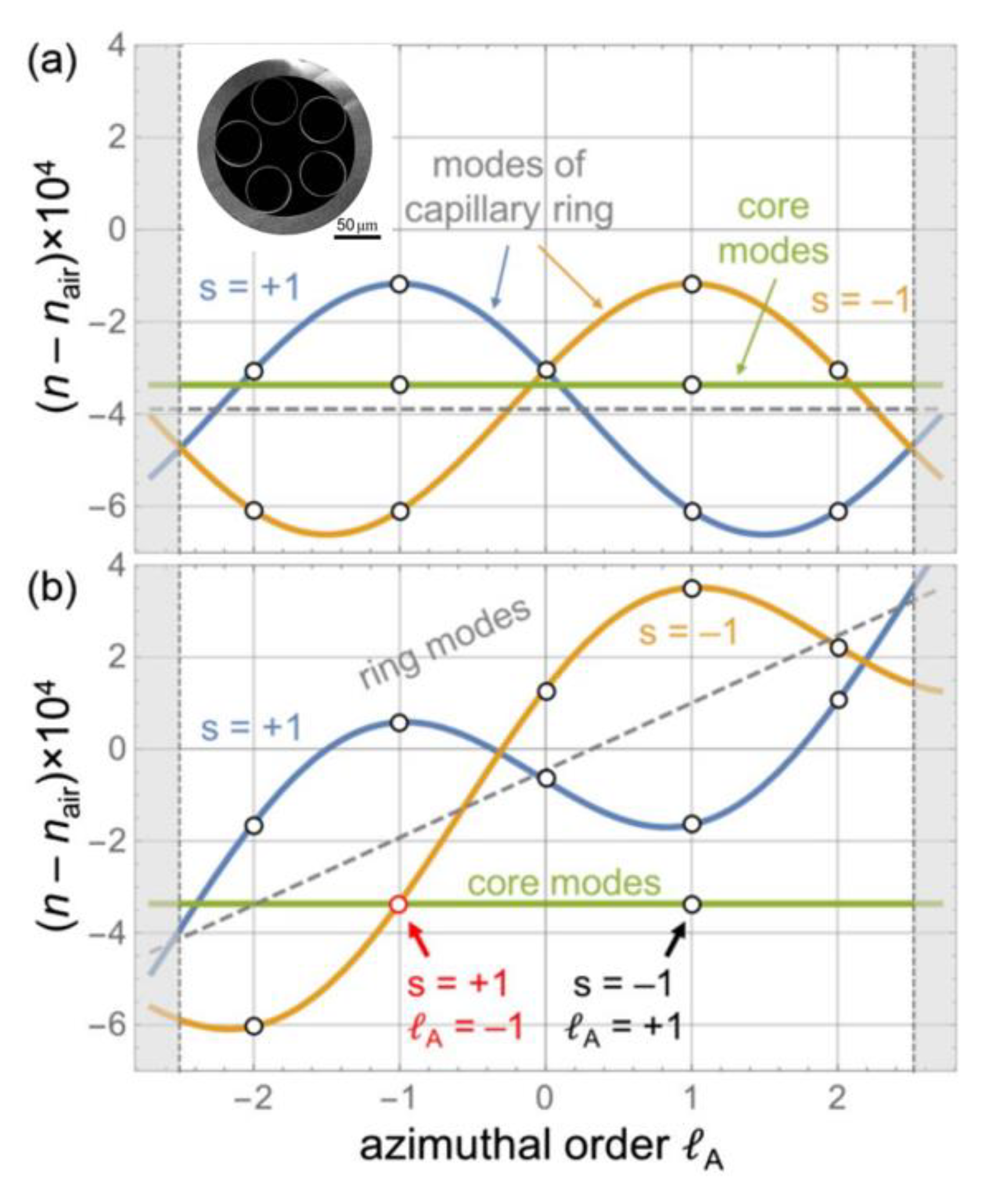
Preprints 81017 g013
Figure 13. Plots of modal refractive index vs azimuthal mode order in the first Brillouin zone for (a) untwisted and (b) twisted SR-PCFs.
Figure 13. Plots of modal refractive index vs azimuthal mode order in the first Brillouin zone for (a) untwisted and (b) twisted SR-PCFs.
Preprints 81017 g013
Preprints 81017 g014
Figure 14. (a), (d), (g) Input modes, (b), (e), (h) output modes, and (c), (f), (i) interference patterns of CTHCF.
Figure 14. (a), (d), (g) Input modes, (b), (e), (h) output modes, and (c), (f), (i) interference patterns of CTHCF.
Preprints 81017 g014
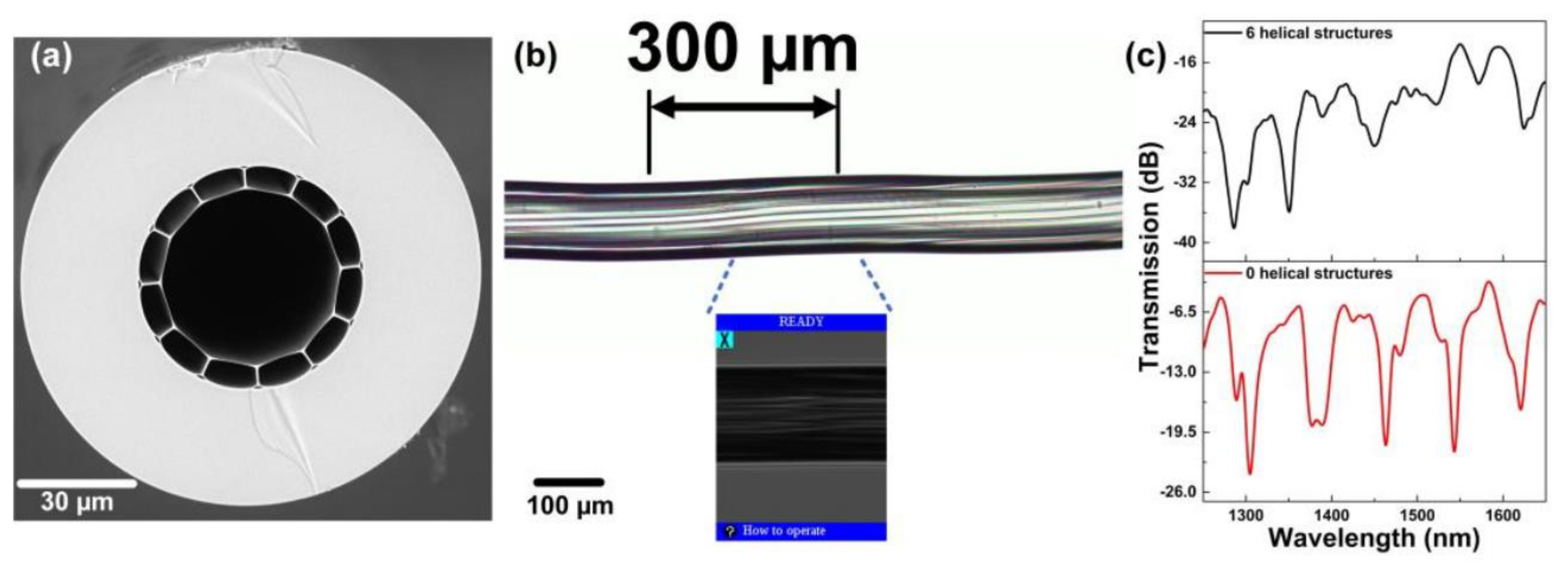
Preprints 81017 g015
Figure 15. (a) Cross-section of HCF. (b) Image of the HCF with HSs. (c) Transmission spectra of HCF with HSs and without HSs.
Figure 15. (a) Cross-section of HCF. (b) Image of the HCF with HSs. (c) Transmission spectra of HCF with HSs and without HSs.
Preprints 81017 g015
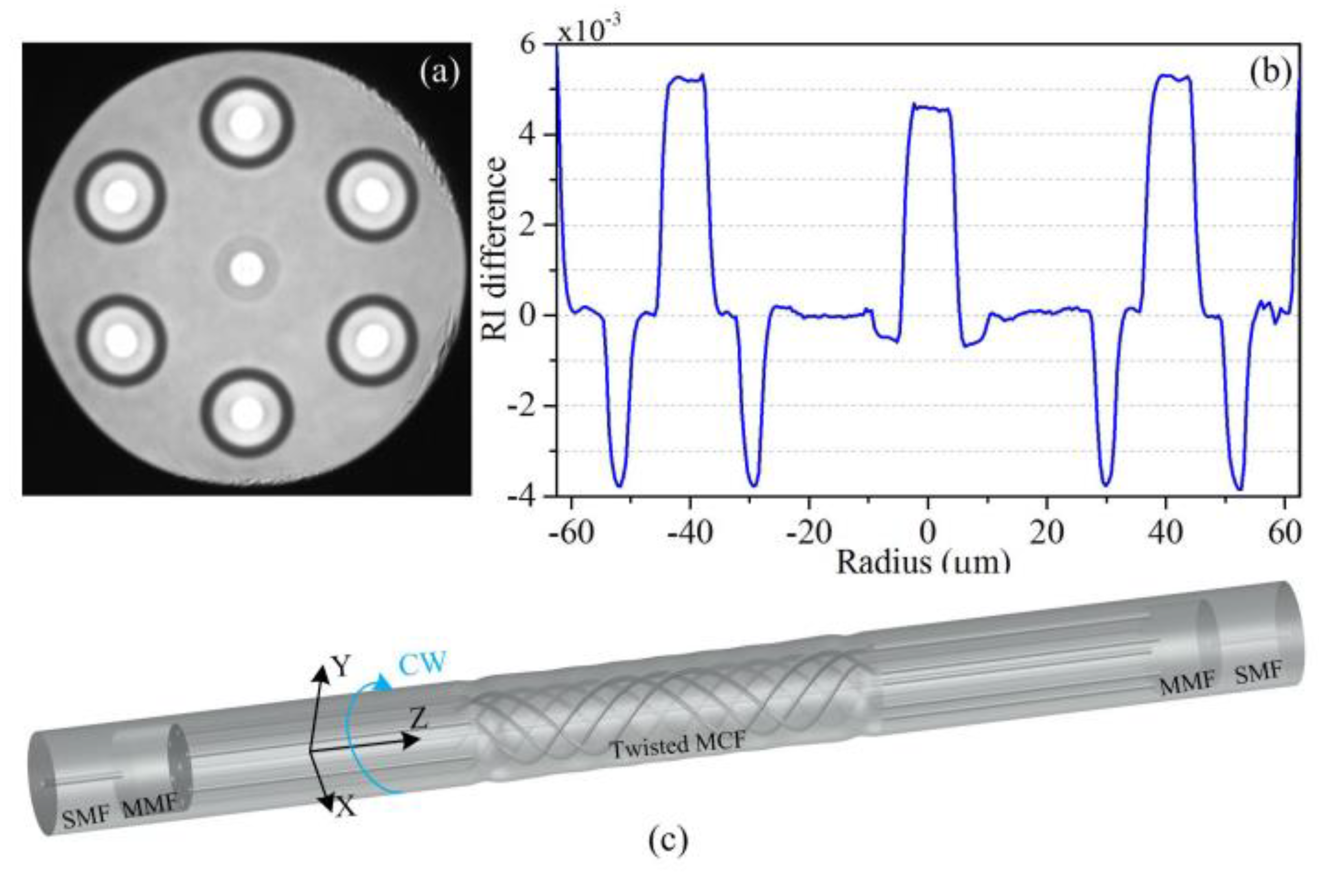
Preprints 81017 g016
Figure 16. (a) Cross-section of seven core fiber. (b) Refractive index of the proposed fiber. (c) The schematic diagram of the sensor structure.
Figure 16. (a) Cross-section of seven core fiber. (b) Refractive index of the proposed fiber. (c) The schematic diagram of the sensor structure.
Preprints 81017 g016
Preprints 81017 g017
Figure 17. (a) Schematic of the tapered twisted fiber; (b) micrograph of the sensor structure under phase contrast microscope; (c) Cross-section of the MCF.
Figure 17. (a) Schematic of the tapered twisted fiber; (b) micrograph of the sensor structure under phase contrast microscope; (c) Cross-section of the MCF.
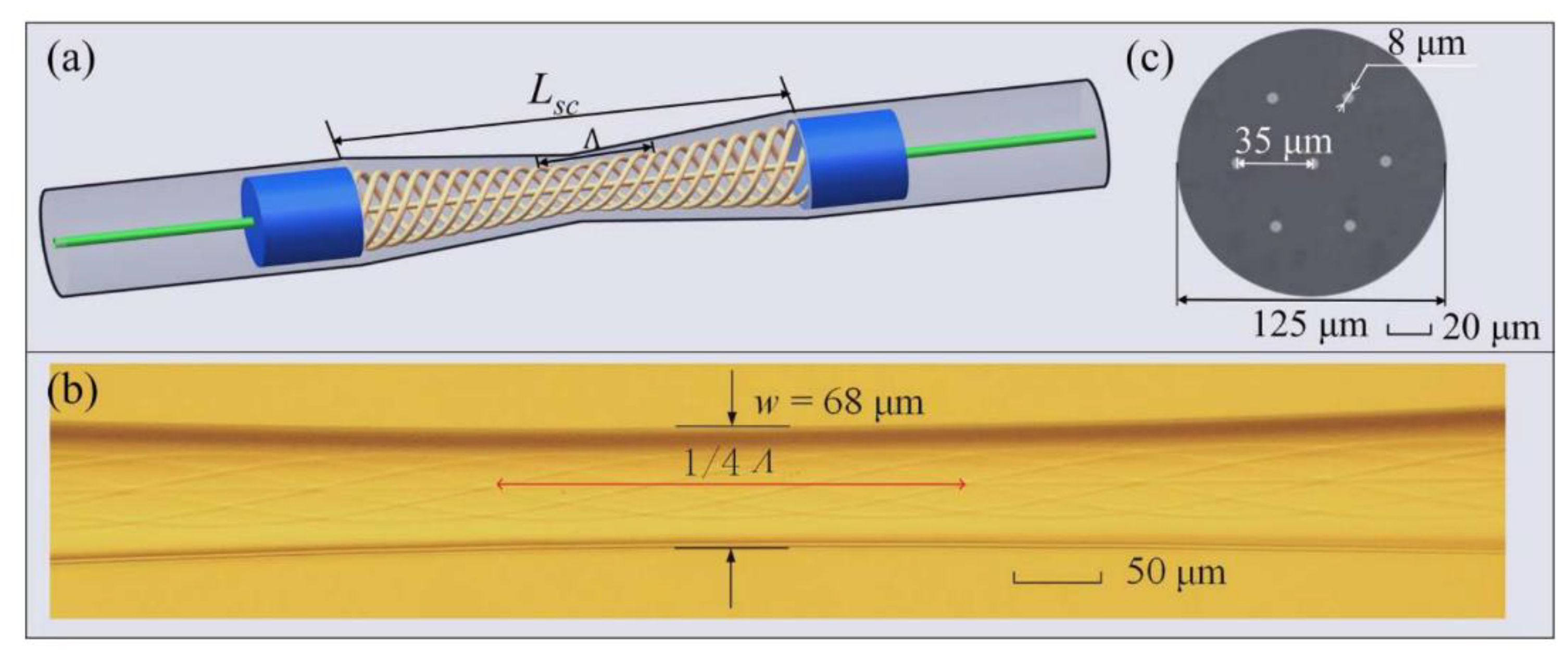
Preprints 81017 g017
Preprints 81017 g018
Figure 18. (a) Cross-section diagram of the YTMF; (b) Twisted machining diagram; (c) Lateral view of the twist sample.
Figure 18. (a) Cross-section diagram of the YTMF; (b) Twisted machining diagram; (c) Lateral view of the twist sample.
Preprints 81017 g018
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated