Prerpints.org logo
Preprint
Article

Dose-Dependent Shift in Relative Contribution of Homologous Recombination to DNA Repair after Low-LET Ionizing Radiation Exposure: Empirical Evidence and Numerical Simulation

Altmetrics

Downloads

117

Views

39

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

28 July 2023

Posted:

01 August 2023

You are already at the latest version

Alerts
Abstract
Relative contribution of different repair pathways to the radiation-induced DNA damage responses remains a challenging issue of studying the radiation injury endpoints. Comparative manifestation of homologous recombination (HR) after application of different radiation doses greatly determines an overall effectiveness of recovery in dividing cell after irradiation, since HR is an error-free mechanism intended for repair of DNA double strand breaks (DSB) during S/G2 phases of cell cycle. In this article, we present an experimentally observed evidence of dose-dependent shift in relative contribution of HR in human fibroblasts after X-ray exposure at doses 20-1000 mGy, which is also supported by quantitative modeling of DNA DSB repair. Our findings indicate that the radiation dose increase leads to dose-dependent decrease in relative contribution of HR into the entire repair process.
Keywords: 
Subject: Biology and Life Sciences  -   Biochemistry and Molecular Biology

1. Introduction

Ionizing radiation (IR) affects DNA structure by inducing various types of damage, of which DNA double-strand breaks (DSB) are considered to be the most deleterious ones [1,2]. DSBs are considered to be critical DNA lesions because their misrepair can lead to severe mutations, oncogenesis, cell death or senescence [3]. In this regards, selection of an optimal repair pathway is crucial for the cell in terms of a final outcome [4]. Non-homologous end joining (NHEJ) and homologous recombination (HR) are two major DSB repair pathways in mammalian and human cells. NHEJ fuses the two broken ends, with little regard for homology, leading to deletions and other rearrangements [5]. In contrast, HR typically copies the missing information from the sister chromatid into the break site, resulting in exact reconstitution of the original sequence [5]. In the last decades, at least three alternative pathways of DSB repair were suggested to be operational following the ionizing radiation exposure. These distinct pathways, the single-strand annealing (SSA), microhomology-mediated end-joining (MMEJ), and alternative end-joining (Alt-EJ), are distinguished based on the amount of DNA sequence complementarity used to align DNA ends [6].
Revealing the mechanistic nature of DSB repair pathways and evaluating their manifestation in response to different radiation doses aims to improve our understanding the deleterious effects of ionizing radiation and our ability to predict them [7,8]. Development of our predictive capabilities impacts the accuracy of radiotherapy, radiation-induced cancer risk estimations, as well as relevant for health issues of people living in areas with high background radiation and for future manned space exploration where astronauts can be exposed to complex radiation fields.
One of the initial events in the complex process of DNA repair from DSBs is the phosphorylation of the core histone H2AX by kinases of the PIKK family (phosphatidylinositol 3 kinase related kinases) ATM, ATR, DNA-PKcs in the flanking regions of DSBs of chromatin [9]. Dynamic microstructures containing thousands of copies of the phosphorylated histone H2AX (γ-H2AX) called “foci” in the literature are easily visualized using immunocytochemical staining [10-12]. Analysis of γH2AX foci provides information on the number of DNA repair sites from DSBs, their distribution over the nuclear volume, and on the kinetics of repair. However, it is equally important to evaluate not only changes in the total number of DSBs, but also the proportion of DSBs repaired by the HR correct pathway. For this purpose, the analysis of the key HR protein Rad51 foci is most often used [13].
Computational and mathematical modeling associated with cancer radiotherapy and radiation risk assessments has been undertaken for the decades and proceeds along with the new biophysics phenomena that have been identified [14-18]. Along with the modeling of radiation risk itself, there are a series of models designed to understand kinetics of radiation-induced DNA damage repair and associated secondary cancer risk. Combining the numerical simulation with experimental methods allows one to identify new mechanistic properties of the DNA repair process, which are hardly accessible to experimental studies but could be important for detailed understanding of the variety of outcomes induced by ionizing radiation.
One of the intriguing tasks being potentially solved via combining the experimental measurements with simulation techniques is the activation of specific DSB pathways following the low-dose radiation exposure. Currently, there are many works devoted to changes in the number of DNA damage foci in mammalian cells irradiated at low doses [19-21]. However, the question about DSB repair efficiency after low-dose radiation exposure is one of the most discussed and controversial topics in modern radiation biology.
The current study is aimed at the experimental probing of relative contribution of the HR pathway to DSB repair, induced by X-ray exposure in the dose range from 20 to 1000 mGy, with the subsequent numerical evaluation of γ-H2AX foci remaining considered as the main DSB repair marker.

2. Materials and Methods

2.1. Experimental study

2.1.1. Cell culture

The studies were performed with a human skin fibroblast culture (Cell Applications, United States, Cat.no. 106K-05a). Cells were cultured at 37°C and 5% CO2 in a standard DMEM culture medium with a high glucose content (4.5 g/L) (Thermo Fisher Scientific, United States) supplemented with 2 mmol/L L-glutamine (Thermo Fisher Scientific, United States), 100 U/mL penicillin, 100 μg/mL streptomycin (Thermo Fisher Scientific, United States) and 10% fetal bovine serum (Thermo Fisher Scientific, United States). Fibroblasts were then plated on 4 cm2 coverslips in 35 mm Petri dishes (SPL Lifesciences, South Korea) with a density of 104 cells/cm2. 3-5 passages of cells in the phase of exponential growth (cell population density ~ 60–70%) were used for the experiments.

2.1.2. Irradiation

The cells were irradiated using a RUB RUST-M1 X-irradiator (Russia), equipped with two X-ray emitters, at a dose rate of 40 mGy/min, voltage of 100 kV, current of 0.8 mA, 1.5 mm Al filter, and a temperature of 4°C (LAB ARMOR BEADS thermal granules were used for cooling). The error in the exposure dose was estimated to be within 15%. After irradiation, cells were incubated under the standard conditions of a CO2 incubator (37°C, 5% CO2) for 0.25–24 hours.

2.1.3. Immunocytochemistry

Cells were fixed on coverslips in 4% paraformaldehyde in PBS (pH 7.4) for 15 min at room temperature followed by two PBS rinses (pH 7.4) and permeabilization in 0.3% Triton-X100 (in PBS, pH 7.4) supplemented with 2% bovine serum albumin (BSA) to block non-specific antibody binding. For immunocytochemical staining, the slides were incubated for 1 hour at room temperature with a primary rabbit monoclonal antibody against γH2AX (dilution 1 : 200, clone EP854(2)Y, Merck-Millipore, United States), Rad51 (dilution 1 : 200, АВЕ257, Merck-Millipore, United States) or CENPF (dilution dilution 1:200, ab5, Abcam, USA) in PBS (рН 7.4), containing 1% BSA. After rinses with PBS, cells were incubated for 1 h at room temperature with the goat anti-mouse Alexa Fluor 488 conjugated secondary antibodies IgG (H + L) (Life Technologies, United States), dilution 1 : 600 and goat anti-rabbit rhodamine conjugated antibodies (Merck-Millipore, United States), dilution 1 : 400 in PBS (pH 7.4) with 1% BSA. ProLong Gold medium (Life Technologies, United States) was used with DAPI for DNA counter-staining and for the prevention of photo fading. Cells were viewed and imaged using a Nikon Eclipse Ni-U microscope (Nikon, Japan) equipped with a high definition ProgRes MFcool camera (Jenoptik AG, Germany). The filter sets UV-2E/C (340–380 nm excitation and 435–485 nm emission), B-2E/C (465–495 nm excitation and 515–555 nm emission) and Y-2E/C (540–580 nm excitation and 600–660 nm emission) were used. At least 200 cells were analyzed for each data point. γ-H2AX and Rad51 foci were counted by manual scoring and using DARFI (https://github.com/varnivey/darfi).

2.1.4. Statistical Analysis

Statistical and mathematical analyses of the data were conducted using the Statistica 8.0 software (StatSoft, Tulsa, OK, USA). The results are presented as means of three independent experiments ± standard error (SE).

2.2. Evaluating the percent contribution of HR to DSB repair

In order to evaluate the percent contribution of HR to the repair process, the quantitative model of radiation-induced DSB repair was used [22]. The model consists of five main parts. The first one evaluates the initial yield of radiation-induced DSBs. The other parts are the quantitative models of NHEJ, HR, SSA, and Alt-EJ repair systems. To simulate the processing of DNA lesions by repair enzymes the mass-action chemical kinetics approach is used.
The kinetics of DSB induction and repair is simulates as
d N 0 d t = α ( L ) d D d t N i r − V NHEJ − V HR − V SSA − V micro - SSA − V Alt - EJ
where N0 = NncDSB + NcDSB; VNHEJ, VHR, VSSA, Vmicro-SSA, and VAlt-EJ are the terms characterizing elimination of DSBs by the NHEJ, HR, SSA, micro-SSA, and Alt-EJ repair pathways respectively. Detalization of these terms is given in Eqs. A1 of Appendix A. In Eq. (1), Nir is the fraction of irreparable DSBs which corresponds to the level of γ-H2AX foci remained in the cell 24 h postirradiation. The rate of initial DSB induction is calculated as d N 0 / d t = α ( L ) d D / d t , similarly as it is done in [23-25]. Here, D is the dose of ionizing radiation (Gy) and α(L) is the slop coefficient of linear dose dependence which describes DSB induction per unit of dose (Gy–1 per cell).
Enzymatic interactions occurred in the course of repair are simulated as follows. Within the NHEJ pathway, the stage of Ku binding to a DSB is represented by the following kinetic equation
[ DSB ]   +   [ Ku ] ⇄ K − 1 K 1 [ DSB   ·   Ku ] ,
where quantities in brackets denote time-dependent intracellular concentrations of repair complexes; K values with an appropriate subscript used to represent the dimensional reaction rate-constants. Here [DSB] is the number of DSBs that undergo binding by Ku, [ DSB   ·   Ku ] is the level of resulting intermediate complex.
The stage of recruitment of the DNA-dependent protein kinase catalytic subunit (DNA-PKcs) and Artemis to a DSB site is described as
[ DSB   ·   Ku ]   +   [ DNA - PKcs ] ⇄ K − 2 K 2 [ DSB   ·   DNA - PK / Art ] ,
In this kinetic equation [DNA-PK] denotes a complex of Ku and DNA-PKcs. Art indicates that the mentioned intermediate complex is formed in the presence of Artemis.
The autophosphorylation of DNA-PKcs is represented by
[ DSB   ·   DNA - PK / Art ] → K 3 [ DSB   ·   DNA - PK / Art P ] ,
where the superscript P defines the phosphorylated DNA-PK product.
The subsequent end-bridging process is described as a junction of two [ DSB NHEJ   ·   DNA - PK / Art P ] constructs formed at the previous repair stage:
[ DSB   ·   DNA - PK / Art P ]   +   [ DSB   ·   DNA - PK / Art P ]   ⇄ K − 4 K 4   [ Bridge ] ,
Here the [Bridge] intermediate complex characterizes the final product of the reaction.
The further assembling of the NHEJ repair complex promotes the recruitment of LigIV with its associated factors XRCC4 and XLF, and subsequent involvement of the polynucleotide kinase phosphatase (PNKP) with a break site:
[ Bridge ]   +   [ LigIV / XRCC 4 / XLF ]   ⇄ K − 5 K 5   [ Bridge   ·   LigIV / XRCC 4 / XLF ] ,
[ Bridge   ·   LigIV / XRCC 4 / XLF ]   +   [ PNKP ]   ⇄ K − 6 K 6   [ Bridge   ·   LigIV / XRCC 4 / XLF   ·   PNKP ] .
The final step of the NHEJ pathway implying recruitment of a polymerase can be denoted as
[ Bridge · LigIV / XRCC 4 / XLF · PNKP ] + [ Pol ] ⇄ K − 7 K 7 [ Bridge · LigIV / XRCC 4 / XLF · PNKP · Pol ] → K 8                       → K 8 [ dsDNA ] + [ LigIV / XRCC 4 / XLF ] + [ Pol ] + [ PNKP ] +   [ DNA - PKcs ] + [ Ku ] .  
In this consideration, after gap filling and ligation are finalized, it is accepted that the repair complexes dissociate, leaving the recovered double-strand DNA (dsDNA).
The first stages of HR associated with action of MRN, its co-factors (CtlP, ExoI, Dna2) and ATM are described as follows in the model:
[ DSB ]   +   [ MRN / CtIP / ExoI / Dna 2 ] ⇄ P − 1 P 1 [ DSB · MRN / CtIP / ExoI / Dna 2 ] ,
[ ATM ] → P 2 [ ATM P ] ,
[ DSB · MRN / CtIP / ExoI / Dna 2 ] + [ ATM P ] ⇄ P − 3 P 3 [ DSB · MRN / CtIP / ExoI / Dna 2 · ATM P ] → P 4                                                                                               → P 4 [ ssDNA ] + [ MRN / CtIP / ExoI / Dna 2 ] + [ ATM P ]
where MRN (Mre11-Rad50-Nbs1) complex interacting with other repair factors is considered as a single complex and superscript P defines the phosphorylated species.
An involvement of the replication protein A (RPA) eliminating secondary structure of DNA and protecting single-stranded regions from other enzymatic activities is denoted by
[ ssDNA ]   +   [ RPA ] ⇄ P − 5 P 5 [ ssDNA   ·   RPA ] ,
The next HR step associated with formation of Rad51 filament is described with the following kinetic equation:
[ ssDNA   ·   RPA ]   + ​   [ Rad 51 / Rad 51 par / BRCA 2 ] ⇄ P − 6 P 6 [ ssDNA   ·   RPA   ·   Rad 51 / Rad 51 par / BRCA 2 ] → P 7                                                                                                 → P 7 [ Rad 51   filament ]   +   [ RPA ]    
where Rad51par abbreviation denotes five biologically important Rad51 paralogs (Rad51B, Rad51C, Rad51D, XRCC2, and XRCC3), and [Rad51 filament] defines the [ ssDNA   ·   Rad 51 / Rad 51 par / BRCA 2 ] complex.
Formation of a displacement loop (D-loop) and two ways of its subsequent resolution are represented as follows:
[ Rad 51   filament ]   + ​   [ DNA inc ] ⇄ P − 8 P 8 [ Rad 51   filament   ·   DNA inc ] → P 9                         → P 9 [ D - loop ]   +   [ Rad 51 / Rad 51 par / BRCA 2 ]
[ D - loop ]   → P 10 [ dHJ ] → P 11   [ dsDNA ]   +   [ DNA inc ] ,
[ D - loop ]   → P 12   [ dsDNA ]   +   [ DNA inc ] ,
where [DNAinc] defines the incoming DNA duplex, [ Rad 51   filament   ·   DNA inc ] complex is assumed to contain Rad54 protein, and dHJ denotes the double Holiday junction.
The SSA pathway is given as the following set of kinetics equations. The first step assuming interaction with Rad52 is denoted by
[ ssDNA   ·   RPA ]   +   [ Rad 52 ] ⇄ Q − 1 Q 1 [ ssDNA   ·   RPA   ·   Rad 52 ] ,
where the [ ssDNA   ·   RPA ]   complex is the same as in Eq. (12).
The junction between Rad52 heptamer rings and each ssDNA termini allowing formation of a flapped structure is represented as
[ ssDNA   ·   RPA   ·   Rad 52 ]   +   [ ssDNA   ·   RPA   ·   Rad 52 ]   → Q 2   [ Flap ]   +   [ RPA ] .
The cutting of the flapped ends by the ERCC1/XPF endonuclease and final ligation of a damaged site with LigIII complex are simulated by
  [ Flap ] + [ ERCC 1 / XPF ] ⇄ Q − 3 Q 3 [ Flap · ERCC 1 / XPF ] → Q 4 [ dsDNA nicks ] + [ Rad 52 ] + [ ERCC 1 / XPF ] ,   ( 19 )
[ dsDNA nicks ]   +   [ LigIII ]   ⇄ Q − 5 Q 5   [ dsDNA nicks ·   LigIII ]   → Q 6   [ dsDNA ]   +   [ LigIII ] .
Here, Rad52 and ERCC1/XPF assumed to dissociate from the processing site.
The simulation of the alternative end-joining pathways is based on the hypothesis suggesting two different Ku-independent repair mechanisms [26]. First of them is represented by MMEJ which is sometimes considered as an independent end-joining mechanism distinct from the other pathways. Meanwhile, experimental evidence suggests that this type of repair represents a specific subclass of the SSA pathway called as micro-SSA [27,28]. On the basis of these considerations, in our model, rejoining via MMEJ is simulated as the additional part of DSBs which follow the SSA pathway described above.
To simulate the Alt-EJ pathway, an additional mechanistic explanation is proposed. According to the recent hypothesis, Alt-EJ requires activity of MRX complex and possibly exhibits the same initiation steps as HR [26]. Therefore, the initial stages of Alt-EJ can be described by Eqs. (9)-(11). After the production of ssDNA, activity of PARP1 recruited to the DSB site is characterized by Eq. (21).
[ ssDNA ]   +   [ PARP 1 ]   ⇄ R − 1 R 1   [ ssDNA   ·   PARP 1 ]   .
The kinetics of microhomology production via a polymerase activity is simulated with
[ ssDNA   ·   PARP 1 ]   +   [ Pol ]   → R 2   [ ssDNA   ·   Pol ]   + [ PARP 1 ] ,
[ ssDNA   ·   Pol ] → R 3   [ MicroHomol ]   + [ Pol ] .
In Eq. (23), [MicroHomol] denotes the yield of microhomology produced.
The final step of Alt-EJ is believed to rely on LigI activity [26]. In the model, this stage is represented as follows
[ MicroHomol ] + [ LigI ] ⇄ R − 4 R 4 [ MicroHomol   ·   LigI ] → R 5 [ dsDNA ] + [ LigI ] .
Kinetics of induction of γ-H2AX foci is simulated by summing up all active forms of DNA-PKcs and ATM, which are considered in the model, similarly as it was done in [23]
V γ - H 2 AX + = K 9   [ Sum ]   [ H 2 AX ] K 10 + [ Sum ] ,
where [H2AX] is the level of histone variant H2AX and
            [ Sum ] = [ DSB   ·   DNA - PK / Art P ] + [ Bridge ] + [ Bridge   ·   LigIV / XRCC 4 / XLF ] + +   [ Bridge   ·   LigIV / XRCC 4 / XLF   ·   PNKP ] + [ Bridge · LigIV / XRCC 4 / XLF · PNKP · Pol ] +                                                       +   [ DSB · MRN / CtIP / ExoI / Dna 2 · ATM P ] .
The mechanism of γ-H2AX foci dephosphorylation is assumed to be proportional to the amount of repaired DNA and its spontaneous decay with the corresponding rate constants K11 and K12
V γ - H 2 AX − =   K 11 [ dsDNA ] + K 12 [ γ - H 2 AX ] .
To describe the interactions of repair enzymes with their substrates, the mass-action chemical kinetics approach was used. A dynamic change of intracellular concentrations of main repair complexes was expressed as the following differential equations
d X d t = V + ( X i , N 0 ) − V − ( X i , N 0 ) ,
where X i   ( i = 1 , ... , n ) is the intracellular level of the i-th repair complex, t is time, the functions V + and V − describe the complex accumulation and degradation, respectively. The dimensionless form of the system of ordinary differential equations (ODE) referred to simulation of NHEJ, HR, SSA and two alternative repair pathways as well as its parameters and initial conditions are presented in Appendix A. In the present study, the solution of the ODE system is performed using the fourth-order Runge–Kutta method. The integration time-step is chosen as 10–10 s in order to satisfy the fastest reactions being simulated in the model.
The initial yield (N0) of DSBs was calculated as
d N 0 d t = α ( L ) d D d t ,
where D is the radiation dose (Gy) and α ( L ) = a exp ( − b L ) is the slop coefficient of linear dose dependence which describes DSB induction per unit of dose (Gy–1 per cell). Parameters a and b used in this equation are also presented in Appendix A. The particular details of parameter evaluation as well as simulation of each repair pathway can be found in [22].
In order to simulate DSB rejoining in the asynchronous cell culture, we set a model cell cycle distribution similar to the distribution of HF19 cells observed in the work by [29] where 40% of cells were in G0/G1, <10% in S phase and 50% in G2/M. Assuming that S-phase cells include two equal sub-fractions of early-S and late-S cells, the final distribution was set as following: 45% of cells is in G0/G1 and early S phases, and 55% is in late S and G2/M. Based on the data discussed in [25,27,30,31], the model provides the following pathways for the repair of non-clustered and clustered DSBs. In G0/G1 and early S phases non-clustered DSBs are likely to follow rejoining via NHEJ, while the limited number of complex DSBs may undergo PARP1-dependent Alt-EJ. The other pathways are assumed to be unavailable or masked by NHEJ in these phases. In the late S and G2/M, non-clustered DSBs may follow NHEJ and may be a substrate for SSA and micro-SSA pathways. The clustered DSBs are suggested to proceed through HR, SSA, and Alt-EJ. Finally, in our calculations the models of corresponding repair mechanisms are processed according the following scheme
G 0 / G 1 ,   and   early   S     0.45   T N ncDSB →   NHEJ , 0.45   T N cDSB → Alt - EJ , late   S   and   G 2 / M   0.55   T N ncDSB →   NHEJ ,   SSA , 0.55   T N cDSB → HR ,   SSA ,   Alt - EJ ,
where numbers 0.45 and 0.55 represent the fractions of cells in G0/G1 and early S, and in late S and G2/M phases, respectively, NncDSB and NcDSB denote amounts of non-clustered and clustered DSBs, and T is the total size of the exponentially growing cell culture set to be 1×105 cells, as mentioned in [29]. The model accounts for the very cell cycle-dependence of the repair pathways through the initiating the computation procedure with the levels of NncDSB and NcDSB parameters according to the cell cycle distribution of the cell culture used in the experiment.
The evaluation of the percent contribution of HR to DSB repair was done through the obtaining the calculated time-courses of γ-H2AX and Rad51 foci for the particular dose of X-rays. The HR contribution to PHR was evaluated as the following ratio
P HR = 100 × y 9 ¯ /   x 14 ¯ ,
where y 9 ¯ and x 14 ¯ are the mean numbers of Rad51 and γ-H2AX foci respectively, counted per 24-hour simulation period.
To obtain a dependence of PHR on X-ray dose, the ODE system was run with a sufficiently small dose step equalling to 0.1 mGy within the range of 0–1000 mGy. This simulation procedure yielded a curve of PHR (D) dependence that is expressed by the formula
P HR ( D ) = 100 × y 9 ( D ) ¯ /   x 14 ( D ) ¯ .

3. Results

3.1. Experimental results

In Figure 1, γ-H2AX foci yields are shown, as scored at 0.25–24 h after exposure to different doses of X-rays ranged from 20 mGy to 1000 mGy. Foci yields scored in cells exposed to 500 mGy and 1000 mGy tend to peak values at 0.25–1.0 h, while exposure to doses of 20–250 mGy results in maximum levels of foci at 0.25–2.0 h. Closer to 4 h after exposure, the signal of γ-H2AX sharply decreases with time due to completion of the fast DSB repair being a feature of NHEJ. Then, up to 24 h after exposure, the slow DSB repair occurs, which is typically associated with complex DSBs being repaired via HR pathway.
It is noteworthy that 24 h after exposure to 40–80 mGy the level of γ-H2AX foci does not drop to control values, indicating a slowdown in the DSB repair kinetics following low doses of ionizing radiation. On the other hand, 24 h after exposure to 500 mGy and 1000 mGy the observed levels of γ-H2AX foci are slightly below the control values. A possible explanation is that the exposure to low and moderate doses of ionizing radiation affects cell proliferation in an oppositely directed manner. Low doses stimulate cell proliferation, while higher doses lead to its reduction.
One of the sources of DNA DSBs in proliferating cells is the collapse of replication forks in S phase of the cell cycle [32]. The repair of DSBs induced in this process follows through the HR pathway [32,33]. The histone H2AX in S phase is phosphorylated mainly by ATR kinase [34,35]. As a consequence, the percentage of cells in S phase contributes to the average amount of γ-H2AX foci in asynchronous cell populations. This leads to an overestimation of γ-H2AX foci level in cells exposed to low doses and to an underestimation of it in cells irradiated with moderate doses. The observed pattern generally meets our previous findings in human fibroblasts and mesenchymal stromal cells exposed to X-rays [36,37].
To estimate the contribution of HR to the entire process of DNA DSB repair, we analyzed changes in the level of radiation-induced Rad51 foci being the key marker of HR (Figure 2). A statistically significant increase in the number of Rad51 foci was observed 2 h after irradiation and reached its maximum values by 6 h. After 6 h, a decrease in the number of Rad51 foci was indicated, and by 24 h after irradiation, the level of foci dropped down to control values in cells exposed to 160–1000 mGy and remained higher than control in cells irradiated with doses of 40 mGy and 80 mGy.

3.2. Percent contribution of HR to DSB repair

To confirm the model validity for radiation doses in the range of 20–1000 mGy, the calculated time-courses of γ-H2AX and Rad51 foci were compared to the experimental data for normal human skin fibroblasts exposed to X-rays at the doses of 20, 40, 80, 160, 250, 500, and 1000 mGy. The results of comparison are shown in Figure 3 and Figure 4, which depict kinetics of these foci in the range of 0–24 h after irradiation.
Although the exposure to doses of 20–250 mGy results in relatively low absolute levels of γ-H2AX, the entire repair process does not seem to occur faster than in the case of higher considered doses. The proportion of γ-H2AX foci observed after exposure to 20–250 mGy remains elevated for a similarly long period as following the exposure to the doses of 500–1000 mGy. We hypothesize that the observed pattern of DSB repair occurs due to preferential activation of HR pathway, which takes longer to eliminate the damage.
Interestingly, that following the exposure to doses of 160 mGy and higher the levels of γ-H2AX foci remaining 24 h repair after irradiation were lower than the background value. This suggests that DSBs normally induced as a consequence of non-radiation factors can undergo a more effective elimination if cells enter into the process of radiation-induced DSB repair. In could be also expected that in cells that have successfully completed repair of a certain portion of radiation-induced DSBs the background levels of γ-H2AX foci can be suppressed as compared to non-irradiated cells at least for a residual period after exposure.
Overall juxtaposition of simulated and experimentally measured data suggests validity of the considered DSB repair model for relatively low radiation doses, enabling calculation of time-courses of γ-H2AX and Rad51 foci within the full dose range of interest (0–1000 mGy) to obtain a continuous dependence of PHR on D.
The results yielding the percent contribution of HR to DSB repair are shown in Figure 5. The general pattern of HR involvement in the DSB repair is characterized by near-exponentially decreasing function, which is supposed to depend on a cell line, type of ionizing radiation exposure and likely on other factors. The dependence of the HR on different factors requires more detailed examination.

3.3. Dose-dependent changes in the S/G2-phase сell fractions

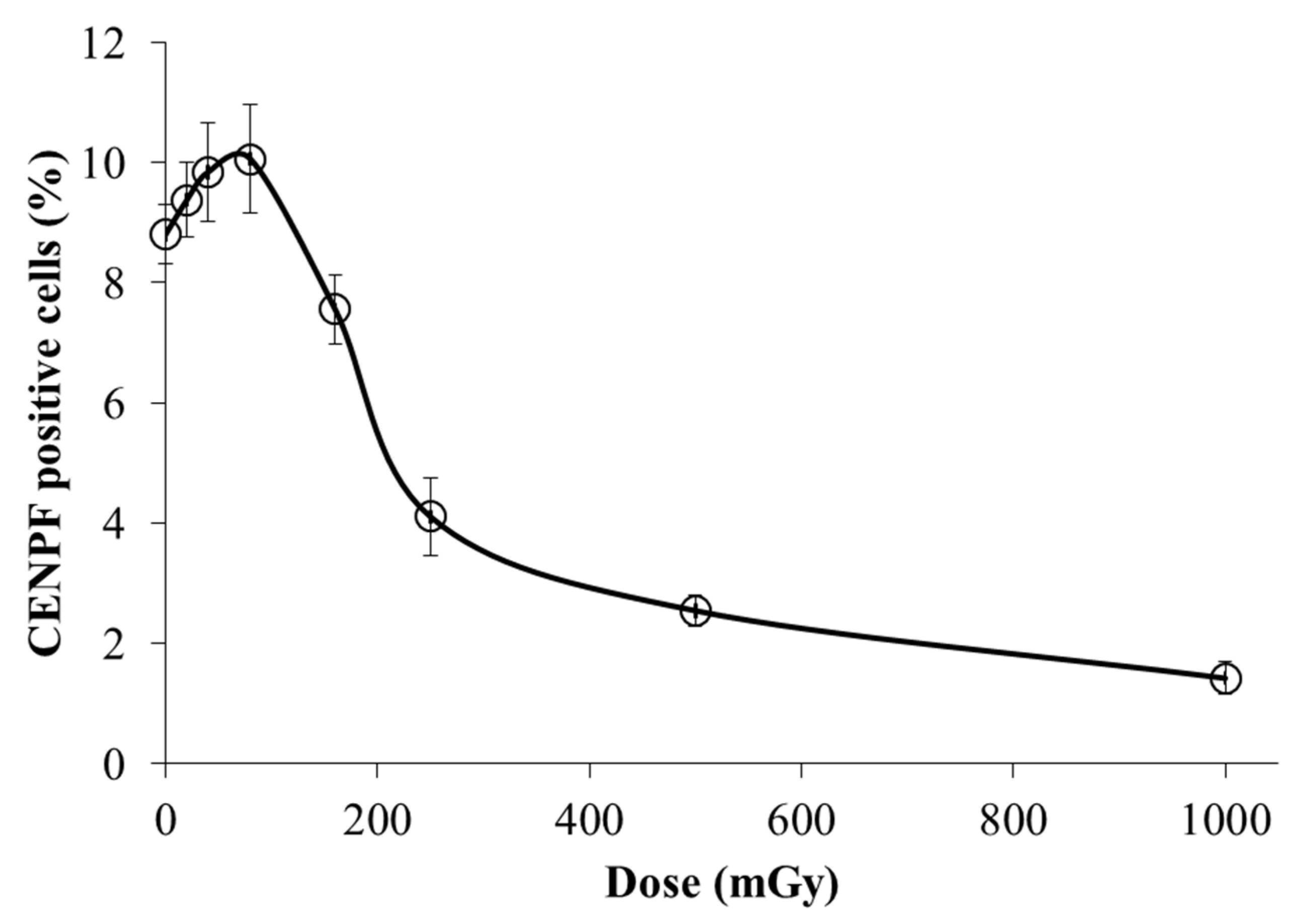
DNA repair by homologous recombination occurs predominantly in the S/G2 phases of the cell cycle. Therefore, for the correct interpretation of the obtained results, it was important to estimate the changes in the proportion of cells in the S/G2 phases in the irradiated cell populations. For this purpose, we used immunohistochemical analysis of a protein-marker of cells in S/G2 phases - Centromere protein F (CENPF). This protein, being a component of the nuclear matrix during G2 phase, has been used as a marker of S/G2 cells [38,39]. Its synthesis commences in early S phase and ceases in M phase, with a peak at G2 phase [39].
From the results presented in Figure 6, it can be seen that irradiation at low doses (20-80 mGy) leads to a slight increase in the proportion of CENPF positive cells. However, these changes are not statistically significant (p>0.05). Whereas irradiation at doses of 250, 500 and 1000 mGy leads to a significant decrease in the proportion of CENPF positive cells by 2.15 (p=0.004), 3.69 (p=0.0003) and 6.93 (p=0.0002) times, respectively (Figure 6). In general, after irradiation at doses of 160-1000 mGy, the pattern of change in the proportions of S/G2-phase fibroblasts is characterized by near-exponentially decreasing function. The obtained results are in good agreement with dose-dependent changes in the relative contribution of HR in irradiated cells.

4. Discussion

Our study reveals distinct patterns of γ-H2AX and Rad51 foci dynamics following the application of low and moderate doses of X-rays. We identified several parameters of foci dynamics, which demonstrate different regularities in response to low and moderate doses, including periods of reaching peak levels of γ-H2AX foci, numbers of γ-H2AX and Rad51 foci remaining 24 h post-irradiation as compared to control levels. All these characteristics of DNA DSB repair demonstrate a pronounced dose-dependent shift. Within the dose steps selected for the analysis, the dose-dependent shift associated with reaching peak levels of γ-H2AX foci is observed between 250 mGy and 500 mGy. The doses triggering the levels of remaining γ-H2AX and Rad51 foci appeared to be within the ranges of 80—500 mGy and of 80—160 mGy respectively.
Juxtaposition of our results with other findings [40] suggests another confirmation of a dose-dependent shift in the activity of DNA repair systems, at least with regards to the repair of radiation-induced DSBs. On the one hand, the number of DSBs increases linearly with radiation dose and the entire cell response depends on the correctness of DNA repair. Our results show that relatively low doses of low-LET ionizing radiation lead to a higher contribution of the error-free repair via HR pathway. Since HR takes longer than NHEJ, low-dose mediated activation of DNA repair mechanisms may not only protect DNA from the immediate damage, but also result in prolonged adaptive responses, protecting the cell from future oxidative insult (such as high-dose radiation), as is also confirmed in [40-46]. The observed shift to error-free HR allows restoration of the genome with maximum fidelity.
The mechanistic nature of the relative contribution of HR at low doses remains under debates. Nevertheless, our results support one of the possible models of DSB repair pathway engagement in responses to low doses of low-LET ionizing radiation [47]. According to these findings, error-prone pathways including NHEJ, Alt-EJ and SSA are partly or completely suppressed and likely only operate when HR fails to process the damage. Increase in the dose of low-LET ionizing radiation leads to the suppression of HR by mechanisms that remain to be identified, while the contribution of NHEJ increases and becomes the first choice. The decrease in the fraction of cells in the S/G2 phases of the cell cycle after irradiation at doses of 250–1000 mGy, shown in our work, suggests that the simplest mechanistic mechanism for reducing the contribution of HR with increasing radiation dose is G1/S arrest of the cell cycle. The dose-dependent G1/S cell cycle arrest leads to a decrease in the faction of cells in which HR repair is possible. Our study was limited to the radiation dose of 1 Gy, while the model in [47] postulates that DNA end resection remains active showing signs of suppression only above 20 Gy. Therefore, increased engagement of error-prone Alt-EJ and SSA under conditions of persisting resection and partially suppressed HR can be identified here only through the simulation approach.
Considering plenty of well-established facts on a strong compensatory power of the DBS repair in eukaryotes, it is unlikely to assume that the radiation effects related to DSB removal follow the linear dose dependence. Even the mechanistic nature of the assembly of DSB repair super-complexes in response to the appearance of radiation-induced lesions suggests a non-linear kinetics of this process, which may blur the resulting outcome within a certain dose range. It may suggest that genotoxicity and late risks associated with the quality of DSB repair after exposure to low-LET radiation can also undergo some radiation dose threshold.

Author Contributions

Conceptualization, A.N.O. and O.B.; methodology, A.C. and O.B.; software, A.C. and O.B.; validation, A.C. and O.B.; formal analysis, O.B., A.C., M.P. and A.O.; investigation, O.B., A.C., M.P., A.O., P.E., and N.V.; resources, A.N.O.; data curation, A.C. and O.B.; writing—original draft preparation, O.B.; writing—review and editing, A.N.O.; visualization, A.C., A.O. and O.B.; supervision, A.N.O.; project administration, A.N.O.; funding acquisition, A.N.O. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by RUSSIAN SCIENCE FOUNDATION, grant number 23-14-00078.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The authors would like to thank Dr. Daria Molodtsova for her help with preparing and editing the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A. Details the DSB repair model

Equations of the DSB model

The dynamical change in the levels of NHEJ repair complexes and γ-H2AX foci is described by the following system of ordinary differential equations:
d n 0 d τ = α ( L ) d D d t N i r − n 0 ( k 1 x 1 + p 1 y 1 ) + k − 1 x 2 + p − 1 y 2 , d x 2 d τ = k 1 N 0 x 1 − x 2 ( k − 1 + k 2 x 3 ) + k − 2 x 4 , d x 4 d τ = k 2 x 2 x 3 − x 4 ( k 3 + k − 2 ) , d x 5 d τ = k 3 x 4 − k 4 x 5 2 + k − 4 x 6 , d x 6 d τ = k 4 x 5 2 − x 6 ( k − 4 + k 5 x 7 ) + k − 5 x 8 , d x 8 d τ = k − 6 x 10 + k 5 x 6 x 7 − x 8 ( k − 5 + k 6 x 9 ) , d x 10 d τ = k − 7 x 12 + k 6 x 8 x 9 − x 10 ( k − 6 + k 7 x 11 ) , d x 12 d τ = k 7 x 10 x 11 − x 12 ( k 8 + k − 7 ) , d x 13 d τ = k 8 x 12 + p 12 y 14 + p 11 y 15 + q 6 z 8 + r 5 w 7 , d x 14 d τ = k 9 ( x 5 + x 6 + x 8 + x 10 + x 12 ) ⋅ x 15 k 10 + x 5 + x 6 + x 8 + x 10 + x 12 − k 11 x 13 − k 12 x 14 .
The initial conditions of this system for wild type cells are the following: n0(0) = α ( L ) D , x2(0) = x4(0) = x5(0) = x6(0) = x8(0) = x10(0) = x12(0) = x13(0) = x14(0) = 0. The values of variables x1, x3, x7, x9, x11, and x15 are set to be constant and equal to x1.
In Eqs. (A1) n0 is the scaled number of radiation-induced DBSs; Nir is the non-dimensional fraction of irreparable DSBs; x1, x3, x7, x9, and x11 are scaled intracellular concentrations of the Ku, DNA-PKcs, LigIV / XRCC 4 / XLF , PNK, and Pol enzymes respectively; x2, x4, x5, x6, x8, x10, x12, and x13, are normalized intracellular concentrations of intermediate complexes represented by [ DSB   ·   Ku ] , [ DSB   ·   DNA - PK / Art ] , [ DSB   ·   DNA - PK / Art P ] , [ Bridge ] , [ Bridge   ·   LigIV / XRCC 4 / XLF ] , [ Bridge   ·   LigIV / XRCC 4 / XLF   ·   PNKP ] , [ Bridge · LigIV / XRCC 4 / XLF · PNKP · Pol ] , and [ dsDNA ] ; x14 , x15, y5 , are the scaled levels of γ-H2AX foci, histone variant H2AX and [ DSB · MRN / CtIP / ExoI / Dna 2 · ATM P ] complex which contributes to the fluorescent signal upon the measurements of γ-H2AX foci induction; y15, z8, and w5 are the concentrations of the [dHJ], [ dsDNA nicks · LigIII ] , and [ MicroHomol · LigI ] ; and ki are scaled rate constants. The variables of the model are normalized per Ku total cellular level: n 0 = N 0 / X 1 , x i = X i / X 1 , y i = Y i / X 1 ,   z i = Z i / X 1 , and w i = W i / X 1 . In terms of molar concentration, this level was estimated as X 1 = N / ( N A V n u c l ) = 9.19 × 10 − 7 M , where N = 400 000 is the number of Ku molecules per cell [48], NA is the Avogadro constant, V n u c l = 7.23 × 10 − 13 L is an average volume of the cell nucleus in human fibroblasts [49]. In this consideration x1 = 1.
The kinetics of the HR repair complexes is described by the following system of ordinary differential equations:
d y 2 d τ = p 1 n 0 y 1 − y 2 ( p − 1 + p 3 y 4 ) + p − 3 y 5 , d y 4 d τ = p 2 y 3 − y 4 ( p − 2 + p 3 y 2 ) + y 5 ( p 4 + p − 3 ) , d y 5 d τ = p 3 y 2 y 4 − y 5 ( p 4 + p − 3 ) , d y 6 d τ = p 4 y 5 − y 6 ( p 5 y 7 + r 1 w 1 ) + p − 5 y 8 + r − 1 w 2 , d y 8 d τ = p − 6 y 10 + p 5 y 6 y 7 − y 8 ( p − 5 + p 6 y 9 + q 1 z 1 ) + q − 1 z 2 , d y 10 d τ = p 6 y 8 y 9 − y 10 ( p 7 + p − 6 ) , d y 11 d τ = p 7 y 10 − p 8 y 11 y 12 + p − 8 y 13 , d y 13 d τ = p 8 y 11 y 12 − y 13 ( p 9 + p − 8 ) , d y 14 d τ = p 9 y 13 − y 14 ( p 10 + p 12 ) , d y 15 d τ = p 10 y 14 − p 11 y 15 .
The initial conditions of this system for wild-type cells are the following: y2(0) = y4(0) = y5(0) = y6(0) = y8(0) = y10(0) = y11(0) = y13(0) = y14(0) = y15(0) = 0. The values of y1, y3, y7, y9, and y12 variables are set to be constant and equal to x1.
In Eqs. (A2), y1, y3, y4, y7, and y9 are scaled intracellular concentrations of the MRN, ATM, ATMP, RPA, and Rad 51 / Rad 51 par / BRCA 2 complexes respectively; y12 is the normalized level of incoming homologous sequence designated as [ DNA inc ] ; y2, y5, y6, y8, y10, y11, y13, y14 and y15 are normalized intracellular concentrations of the [ DSB · MRN / CtIP / ExoI / Dna 2 ] , [ DSB · MRN / CtIP / ExoI / Dna 2 · ATM P ] , [ ssDNA ] , [ ssDNA   ·   RPA ] , [ ssDNA   ·   RPA   ·   Rad 51 / Rad 51 par / BRCA 2 ] , [ Rad 51   filament ] , [ Rad 51   filament   ·   DNA inc ] , [ D - loop ] , and [ dHJ ] intermediate complexes respectively; and pi are scaled rate constants. The variables are also normalized per the Ku total cellular level as y i = Y i / X 1 .
The dimensionless form of the equations for SSA model is represented as
d z 2 d τ = q 1 y 8 z 1 − z 2 ( q − 1 + q 2 z 2 2 ) , d z 3 d τ = q 2 z 2 2 − q 3 z 3 z + 4 q − 3 z 5 , d z 5 d τ = q 3 z 3 z 4 − z 5 ( q 4 + q − 3 ) , d z 6 d τ = q 4 z 5 − q 5 z 6 z 7 + q − 5 z 8 , d z 8 d τ = q 5 z 6 z 7 − z 8 ( q 6 + q − 5 ) .
The initial conditions of this system for wild-type cells are the following: z2(0) = z3(0) = z5(0) = z6(0) = z8(0) = 0. The values of variables z1, z4, and z7 are set to be constant and equal to x1.
In Eqs. (A3), z1, z4, and z7 are scaled cellular levels of Rad52, ERCC 1 / XPF , and LigIII enzymes respectively; z2, z3, z5, z6, and z8 are scaled intracellular concentrations of the [ ssDNA   ·   RPA   ·   Rad 52 ] , [Flap], [ Flap   ·   ERCC 1 / XPF ] , [ dsDNA nicks ] , and [ dsDNA nicks ·   LigIII ]   intermediate complexes respectively; and qi are scaled rate constants. The variables are also normalized per Ku total cellular level as z i = Z i / X 1 .
The kinetics of the Alt-EJ intermediate complexes is described by the following system of ordinary differential equations:
d w 2 d τ = r 1 w 1 y 6 − w 2 ( r 2 + r − 1 ) , d w 4 d τ = r 2 w 2 w 3 − r 3 w 4 , d w 5 d τ = r 3 w 4 − r 4 w 5 w 6 + r − 4 w 7 , d w 7 d τ = r 4 w 5 w 6 − w 7 ( r 5 + r − 4 ) .
The initial conditions of this system for wild-type cells are the following: w2(0) = w4(0) = w5(0) = w7(0) = 0. The values of w1, w3, and w6 variables are set to be constant and equal to x1.
In Eqs. (A1), w1, w3, and w6 are scaled cellular levels of PARP1, Pol, and LigI respectively; w2, w4, w5 and w7 are scaled intracellular concentrations of the [ ssDNA   ·   PARP 1 ]   , [ ssDNA   ·   Pol ]   , [ MicroHomol ] , and [ MicroHomol   ·   LigI ] intermediate complexes respectively; and ri are scaled rate constants. The variables are also normalized per Ku total cellular level as w i = W i / X 1 .

Kinetic parameters of DSB repair model

The dimensionless parameters of Eqs. (A1) are k 1 = K 1 X 1 / K 8 , k − 1 = K − 1 / K 8 , k 2 = K 2 X 1 / K 8 , k − 2 = K − 2 / K 8 , k 3 = K 3 / K 8 , k 4 = K 4 X 1 / K 8 , k − 4 = K − 4 / K 8 , k 5 = K 5 X 1 / K 8 , k − 5 = K − 5 / K 8 , k 6 = K 6 X 1 / K 8 , k − 6 = K − 6 / K 8 , k 7 = K 7 X 1 / K 8 , k − 7 = K − 7 / K 8 , k 8 = K 8 / K 8 = 1 , k 9 = K 9 / K 8 , k 10 = K 10 / X 1 , k 11 = K 11 / K 8 , and k 12 = K 12 / K 8 . K8 here is the rate of final NHEJ process resulting in the production of the repaired dsDNA and unwinding of all repair factors. The reason for selection of this constant as a scaling factor is the assumed independence of this parameter on possible variations due to the competition of repair pathways at earlier stages. This assumption can be important mainly for future modifications of the model, when rate constants of early stages are planned to connect with the damage complexity.
The scaled reaction rates in Eqs. (A2) are p 1 = P 1 X 1 / K 8 , p − 1 = P − 1 / K 8 , p 2 = P 2 / K 8 , p 3 = P 3 X 1 / K 8 , p − 3 = P − 3 / K 8 , p 4 = P 4 / K 8 , p 5 = P 5 X 1 / K 8 , p − 5 = P − 5 / K 8 , p 6 = P 6 X 1 / K 8 , p − 6 = P − 6 / K 8 , p 7 = P 7 / K 8 , p 8 = P 8 X 1 / K 8 , p − 8 = P − 8 / K 8 , p 9 = X 1 / K 8 , p 10 = P 10 / K 8 , . p 11 = P 11 / K 8 ., and p 12 = P 12 / K 8 . The same scaling factors X1 and K8 are chosen for parameter normalization.
The scaled reaction rates in Eqs. (A3) are q 1 = Q 1 X 1 / K 8 , q − 1 = Q − 1 / K 8 , q 2 = Q 2 X 1 / K 8 , q 3 = Q 3 X 1 / K 8 , q − 3 = Q − 3 / K 8 , q 4 = Q 4 / K 8 , q 5 = Q 5 X 1 / K 8 , q − 5 = Q − 5 / K 8 , and q 6 = Q 6 / K 8 . In this case, the same factors X1 and K8 are used for scaling rate constants.
The scaled reaction rates in Eqs. (A4) are r 1 = R 1 X 1 / K 8 , r − 1 = R − 1 / K 8 , r 2 = R 2 X 1 / K 8 , r 3 = R 3 / K 8 , and r 4 = R 4 X 1 / K 8 , r − 4 = R − 4 / K 8 , and r 5 = R 5 / K 8 . As in the other models, the same scaling factors X1 and K8 are chosen for parameter normalization.
The majority of the rate constants of enzymatic reactions were determined by fitting the corresponding model curves produced using Eqs. (A1), (A2), (A3) and (A4) to the experimental data on kinetics of different stages of DSB repair. Other parameters characterizing the regularities of DSB induction were obtained directly from experimental measurements reviewed in the literature. For some of the parameters used, a dependence of their values on radiation dose is introduced. The functions representing these parameters are also shown in the Table A1.
In order to estimate α(L) we used three sets of experimental data on DSB induction in GM38 and GM57 lines of human skin fibroblasts within the LET values ranged from 0.2 to 440 keV/µm [50-52]. The total DSB yield measured in these studies as Gy–1 per 109 bp was recalculated to Gy–1 per cell taking into account that a diploid human cell in G1 phase contains about 5 × 109 bp of DNA [50]. The experimental data were approximated by the exponential function α ( L ) = a exp ( − b L ) to obtain a continuous function within the stated LET range. The parameters of the function given in Table A1 were evaluated by adjusting the curve for α(L) to the results of the above mentioned experimental measurements.
Table A1. Parameters of the model.
Table A1. Parameters of the model.
Parameter Value Parameter Value
a 27.5 P–5 8.82 × 10–5 h–1
b 2.43×10–3 P6 1.87×105 M–1 h–1
K1 11.05 M–1 h–1 P–6 1.55×10–3 h–1
K–1 6.6×10–4 h–1 P7 21.36 h–1
K2 18.83 × ( 1.09 − e − 21.42 / D 1.82 ) M–1 h–1 P8 1.20×104 M–1 h–1
K–2 5.26×10–1 h–1 P–8 2.49×10–4 h–1
K3 1.86 M–1 h–1 P9 1.11 × e 6.16 × 10 − 6 / D 2.68 − D 0.03 h–1
K4 1.20 + 4.48 × 10 5   e − 12.70   D 0.09 M–1 h–1 P10 7.20×10–3 h–1
K–4 3.86×10–4 h–1 P11 6.06×10–4 h–1
K5 15.24 M–1 h–1 P12 2.76×10–1 h–1
K–5 8.28 h–1 Q1 7.80×103 M–1 h–1
K6 18.06 M–1 h–1 Q–1 1.71×10–4 h–1
K–6 1.33 h–1 Q2 3.00×104 M–1 h–1
K7 2.73×105 M–1 h–1 Q3 6.00×103 M–1 h–1
K–7 3.20 h–1 Q–3 6.06×10–4 h–1
K8 5.52×10–1 h–1 Q4 1.66×10–6 h–1
K9 1.66×10–1 h–1 Q5 8.40×104 M–1 h–1
K10 1.93×10–7/Nir M Q–5 4.75×10–4 h–1
K11 7.50×10–2 h–1 Q6 11.58 h–1
K12 11.10 h–1 R1 2.39×103 M–1 h–1
P1 1.75×103 M–1 h–1 R–1 12.63 h–1
P–1 1.33×10–4 h–1 R2 4.07×104 M–1 h–1
P2 7.21 h–1 R3 9.82 h–1
P3 1.37×104 M–1 h–1 R4 1.47×105 M–1 h–1
P–3 2.34 h–1 R4 12.30 h–1
P4 5.52×10–2 h–1 R–4 2.72 h–1
P5 1.20×105 M–1 h–1 R5 1.65×10–1 h–1
Nirrep 0.12   e − 2.48   D 2.02 − 0.11   e − 5.43   D 0.76 ,   D < 1 0.01 ,   D ≥ 1

References

  1. Jeggo, P.A.; Löbrich, M. DNA double-strand breaks: their cellular and clinical impact? Oncogene 2007, 26, 7717–7719. [Google Scholar] [CrossRef] [PubMed]
  2. Bushmanov, A.; Vorobyeva, N.; Molodtsova, D.; Osipov, A.N. Utilization of DNA double-strand breaks for biodosimetry of ionizing radiation exposure. Environmental Advances 2022, 8. [Google Scholar] [CrossRef]
  3. Ackerson, S.M.; Romney, C.; Schuck, P.L.; Stewart, J.A. To Join or Not to Join: Decision Points Along the Pathway to Double-Strand Break Repair vs. Chromosome End Protection. Front Cell Dev Biol 2021, 9, 708763. [Google Scholar] [CrossRef] [PubMed]
  4. Her, J.; Bunting, S. How cells ensure correct repair of DNA double-strand breaks. Journal of Biological Chemistry 2018, 293, 10502–10511. [Google Scholar] [CrossRef] [PubMed]
  5. Li, Y.; Zhang, H.; Merkher, Y.; Chen, L.; Liu, N.; Leonov, S.; Chen, Y. Recent advances in therapeutic strategies for triple-negative breast cancer. Journal of Hematology & Oncology 2022, 15, 121. [Google Scholar] [CrossRef]
  6. Sallmyr, A.; Tomkinson, A. Repair of DNA double-strand breaks by mammalian alternative end-joining pathways. Journal of Biological Chemistry 2018, 293, 10536–10546. [Google Scholar] [CrossRef] [PubMed]
  7. Vitor, A.C.; Huertas, P.; Legube, G.; de Almeida, S.F. Studying DNA Double-Strand Break Repair: An Ever-Growing Toolbox. Front Mol Biosci 2020, 7. [Google Scholar] [CrossRef]
  8. Rich, T.; Allen, R.; Wyllie, A. Defying death after DNA damage. Nature 2000, 407, 777–783. [Google Scholar] [CrossRef]
  9. Kinner, A.; Wu, W.; Staudt, C.; Iliakis, G. -H2AX in recognition and signaling of DNA double-strand breaks in the context of chromatin. Nucleic Acids Research 2008, 36, 5678–5694. [Google Scholar] [CrossRef]
  10. Raavi, V.; Perumal, V.; F. D. Paul, S. Potential application of γ-H2AX as a biodosimetry tool for radiation triage. Mutation Research/Reviews in Mutation Research 2021, 787, 108350. [Google Scholar] [CrossRef] [PubMed]
  11. Rothkamm, K.; Barnard, S.; Moquet, J.; Ellender, M.; Rana, Z.; Burdak-Rothkamm, S. DNA damage foci: Meaning and significance. Environmental and Molecular Mutagenesis 2015, 56, 491–504. [Google Scholar] [CrossRef] [PubMed]
  12. Osipov, A.; Chigasova, A.; Yashkina, E.; Ignatov, M.; Fedotov, Y.; Molodtsova, D.; Vorobyeva, N.; Osipov, A.N. Residual Foci of DNA Damage Response Proteins in Relation to Cellular Senescence and Autophagy in X-Ray Irradiated Fibroblasts. Cells 2023, 12. [Google Scholar] [CrossRef]
  13. Tsvetkova, A.; Ozerov, I.V.; Pustovalova, M.; Grekhova, A.; Eremin, P.; Vorobyeva, N.; Eremin, I.; Pulin, A.; Zorin, V.; Kopnin, P.; et al. γH2AX, 53BP1 and Rad51 protein foci changes in mesenchymal stem cells during prolonged X-ray irradiation. Oncotarget 2017, 8, 64317–64329. [Google Scholar] [CrossRef] [PubMed]
  14. Smirnova, O.; Cucinotta, F. Dynamical modeling approach to risk assessment for radiogenic leukemia among astronauts engaged in interplanetary space missions. Life Sciences in Space Research 2018, 16, 76–83. [Google Scholar] [CrossRef] [PubMed]
  15. Talemi, S.; Kollarovic, G.; Lapytsko, A.; Schaber, J. Development of a robust DNA damage model including persistent telomere-associated damage with application to secondary cancer risk assessment. Scientific Reports 2015, 5. [Google Scholar] [CrossRef]
  16. Stewart, R. Two-lesion kinetic model of double-strand break rejoining and cell killing. Radiation Research 2001, 156, 365–378. [Google Scholar] [CrossRef] [PubMed]
  17. Sachs, R.; Hahnfeld, P.; Brenner, D. The link between low-LET dose-response relations and the underlying kinetics of damage production/repair/misrepair. International Journal of Radiation Biology 1997, 72, 351–374. [Google Scholar]
  18. Lea, D.E. Actions of Radiations on Living Cells; University Press: Cambridge, 1946. [Google Scholar]
  19. Osipov, A.N.; Pustovalova, M.; Grekhova, A.; Eremin, P.; Vorobyova, N.; Pulin, A.; Zhavoronkov, A.; Roumiantsev, S.; Klokov, D.Y.; Eremin, I. Low doses of X-rays induce prolonged and ATM-independent persistence of γH2AX foci in human gingival mesenchymal stem cells. Oncotarget 2015, 6, 27275–27287. [Google Scholar] [CrossRef]
  20. Pustovalova, M.; Astrelina, Т.A.; Grekhova, A.; Vorobyeva, N.; Tsvetkova, A.; Blokhina, T.; Nikitina, V.; Suchkova, Y.; Usupzhanova, D.; Brunchukov, V.; et al. Residual γH2AX foci induced by low dose x-ray radiation in bone marrow mesenchymal stem cells do not cause accelerated senescence in the progeny of irradiated cells. Aging 2017, 9, 2397–2410. [Google Scholar] [CrossRef]
  21. Jakl, L.; Marková, E.; Koláriková, L.; Belyaev, I. Biodosimetry of Low Dose Ionizing Radiation Using DNA Repair Foci in Human Lymphocytes. Genes 2020, 11, 58. [Google Scholar] [CrossRef]
  22. Belov, O.; Krasavin, E.; Lyashko, M.; Batmunkh, M.; Sweilam, N. A quantitative model of the major pathways for radiation-induced DNA double-strand break repair. Journal of Theoretical Biology 2015, 366, 115–130. [Google Scholar] [CrossRef] [PubMed]
  23. Cucinotta, F.A.; Pluth, J.M.; Anderson, J.A.; Harper, J.V.; O'Neill, P. Biochemical kinetics model of DSB repair and induction of gamma-H2AX foci by non-homologous end joining. Radiat Res 2008, 169, 214–222. [Google Scholar] [CrossRef] [PubMed]
  24. Taleei, R.; Weinfeld, M.; Nikjoo, H. Single strand annealing mathematical model for double strand break repair. journal of Molecular Engineering and Systems Biology 2012, 1. [Google Scholar] [CrossRef]
  25. Taleei, R.; Nikjoo, H. Biochemical DSB-repair model for mammalian cells in G1 and early S phases of the cell cycle. Mutation Research-Genetic Toxicology and Environmental Mutagenesis 2013, 756, 206–212. [Google Scholar] [CrossRef] [PubMed]
  26. Decottignies, A. Alternative end-joining mechanisms: a historical perspective. Front Genet 2013, 4, 48. [Google Scholar] [CrossRef]
  27. Decottignies, A. Microhomology-mediated end joining in fission yeast is repressed by Pku70 and relies on genes involved in homologous recombination. Genetics 2007, 176, 1403–1415. [Google Scholar] [CrossRef] [PubMed]
  28. Salles, D.; Mencalha, A.; Ireno, I.; Wiesmuller, L.; Abdelhay, E. BCR-ABL stimulates mutagenic homologous DNA double-strand break repair via the DNA-end-processing factor CtIP. Carcinogenesis 2011, 32, 27–34. [Google Scholar] [CrossRef] [PubMed]
  29. Anderson, J.; Harper, J.; Cucinotta, F.; O'Neill, P. Participation of DNA-PKcs in DSB Repair after Exposure to High- and Low-LET Radiation. Radiation Research 2010, 174, 195–205. [Google Scholar] [CrossRef]
  30. Moore, S.; Stanley, F.; Goodarzi, A. The repair of environmentally relevant DNA double strand breaks caused by high linear energy transfer irradiation - No simple task. DNA Repair 2014, 17, 64–73. [Google Scholar] [CrossRef] [PubMed]
  31. Bennardo, N.; Cheng, A.; Huang, N.; Stark, J. Alternative-NHEJ Is a Mechanistically Distinct Pathway of Mammalian Chromosome Break Repair. Plos Genetics 2008, 4. [Google Scholar] [CrossRef]
  32. Gelot, C.; Magdalou, I.; Lopez, B.S. Replication stress in Mammalian cells and its consequences for mitosis. Genes (Basel) 2015, 6, 267–298. [Google Scholar] [CrossRef] [PubMed]
  33. Kim, K.P.; Mirkin, E.V. So similar yet so different: The two ends of a double strand break. Mutation Research/Fundamental and Molecular Mechanisms of Mutagenesis 2018, 809, 70–80. [Google Scholar] [CrossRef] [PubMed]
  34. Ward, I.M.; Chen, J. Histone H2AX is phosphorylated in an ATR-dependent manner in response to replicational stress. J Biol Chem 2001, 276, 47759–47762. [Google Scholar] [CrossRef]
  35. Firsanov, D.V.; Solovjeva Lv Fau - Svetlova, M.P.; Svetlova, M.P. H2AX phosphorylation at the sites of DNA double-strand breaks in cultivated mammalian cells and tissues.
  36. Pustovalova, M.; Grekhova, A.; Astrelina, Т.; Nikitina, V.; Dobrovolskaya, E.; Suchkova, Y.; Kobzeva, I.; Usupzhanova, D.; Vorobyeva, N.; Samoylov, A.; et al. Accumulation of spontaneous γH2AX foci in long-term cultured mesenchymal stromal cells. Aging 2016, 8, 3498–3506. [Google Scholar] [CrossRef] [PubMed]
  37. Grekhova, A.K.; Pustovalova, M.V.; Eremin, P.S.; Ozerov, I.V.; Maksimova, O.A.; Gordeev, A.V.; Vorobyeva, N.Y.; Osipov, A.N. Evaluation of the Contribution of Homologous Recombination in DNA Double-Strand Break Repair in Human Fibroblasts after Exposure to Low and Intermediate Doses of X-ray Radiation. Biology Bulletin 2020, 46, 1496–1502. [Google Scholar] [CrossRef]
  38. Bee, L.; Fabris, S.; Cherubini, R.; Mognato, M.; Celotti, L. The efficiency of homologous recombination and non-homologous end joining systems in repairing double-strand breaks during cell cycle progression. PloS one 2013, 8, e69061. [Google Scholar] [CrossRef] [PubMed]
  39. Varis, A.; Salmela, A.L.; Kallio, M.J. Cenp-F (mitosin) is more than a mitotic marker. Chromosoma 2006, 115, 288–295. [Google Scholar] [CrossRef] [PubMed]
  40. Tharmalingam, S.; Sreetharan, S.; Brooks, A.L.; Boreham, D.R. Re-evaluation of the linear no-threshold (LNT) model using new paradigms and modern molecular studies. Chem Biol Interact 2019, 301, 54–67. [Google Scholar] [CrossRef] [PubMed]
  41. Boreham, D.R.; Dolling, J.A.; Somers, C.; Quinn, J.; Mitchel, R.E.J. The adaptive response and protection against heritable mutations and fetal malformation. Dose-Response 2006, 4, 317–326. [Google Scholar] [CrossRef]
  42. Murley, J.S.; Baker, K.L.; Miller, R.C.; Darga, T.E.; Weichselbaum, R.R.; Grdina, D.J. SOD2-mediated adaptive responses induced by low-dose ionizing radiation via TNF signaling and amifostine. Free Radical Biology and Medicine 2011, 51, 1918–1925. [Google Scholar] [CrossRef]
  43. Ojima, M.; Eto, H.; Ban, N.; Kai, M. Radiation-induced bystander effects induce radioadaptive response by low-dose radiation. Radiation Protection Dosimetry 2011, 146, 276–279. [Google Scholar] [CrossRef] [PubMed]
  44. Plews, M.; Simon, S.L.R.; Boreham, D.R.; Parchaliuk, D.; Wyatt, H.; Mantha, R.; Frost, K.; Lamoureux, L.; Stobart, M.; Czub, S.; et al. A radiation-induced adaptive response prolongs the survival of prion-infected mice. Free Radical Biology and Medicine 2010, 49, 1417–1421. [Google Scholar] [CrossRef] [PubMed]
  45. Taylor, K.; Lemon, J.A.; Boreham, D.R. Radiation-induced DNA damage and the relative biological effectiveness of 18F-FDG in wild-type mice. Mutagenesis 2014, 29, 279–287. [Google Scholar] [CrossRef] [PubMed]
  46. Veeraraghavan, J.; Natarajan, M.; Herman, T.S.; Aravindan, N. Low-dose γ-radiation-induced oxidative stress response in mouse brain and gut: Regulation by NFκB-MnSOD cross-signaling. Mutation Research - Genetic Toxicology and Environmental Mutagenesis 2011, 718, 44–55. [Google Scholar] [CrossRef] [PubMed]
  47. Mladenova, V.; Mladenov, E.; Stuschke, M.; Iliakis, G. DNA Damage Clustering after Ionizing Radiation and Consequences in the Processing of Chromatin Breaks. [CrossRef]
  48. Neal, J.A.; Meek, K. Choosing the right path: does DNA-PK help make the decision?
  49. Dos Santos, M.; Villagrasa, C.; Clairand, I.; Incerti, S. Influence of the DNA density on the number of clustered damages created by protons of different energies. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms 2013, 298, 47–54. [Google Scholar] [CrossRef]
  50. Rydberg, B. Clusters of DNA damage induced by ionizing radiation: Formation of short DNA fragments.2. Experimental detection. Radiation Research 1996, 145, 200–209. [Google Scholar] [CrossRef] [PubMed]
  51. Lobrich, M.; Cooper, P.; Rydberg, B. Non-random distribution of DNA double-strand breaks induced by particle irradiation. International Journal of Radiation Biology 1996, 70, 493–503. [Google Scholar] [CrossRef] [PubMed]
  52. Hoglund, E.; Blomquist, E.; Carlsson, J.; Stenerlow, B. DNA damage induced by radiation of different linear energy transfer: initial fragmentation. International Journal of Radiation Biology 2000, 76, 539–547. [Google Scholar] [CrossRef]
Preprints 80869 g001
Figure 1. Experimentally measured time-courses of γ-H2AX foci remaining in normal human skin fibroblasts after exposure to (a) 20 mGy, 40 mGy, 80 mGy, and (b) 160 mGy, 250 mGy, 500 mGy, 1000 mGy of X-rays in comparison with background level used as control (± SE).
Figure 1. Experimentally measured time-courses of γ-H2AX foci remaining in normal human skin fibroblasts after exposure to (a) 20 mGy, 40 mGy, 80 mGy, and (b) 160 mGy, 250 mGy, 500 mGy, 1000 mGy of X-rays in comparison with background level used as control (± SE).
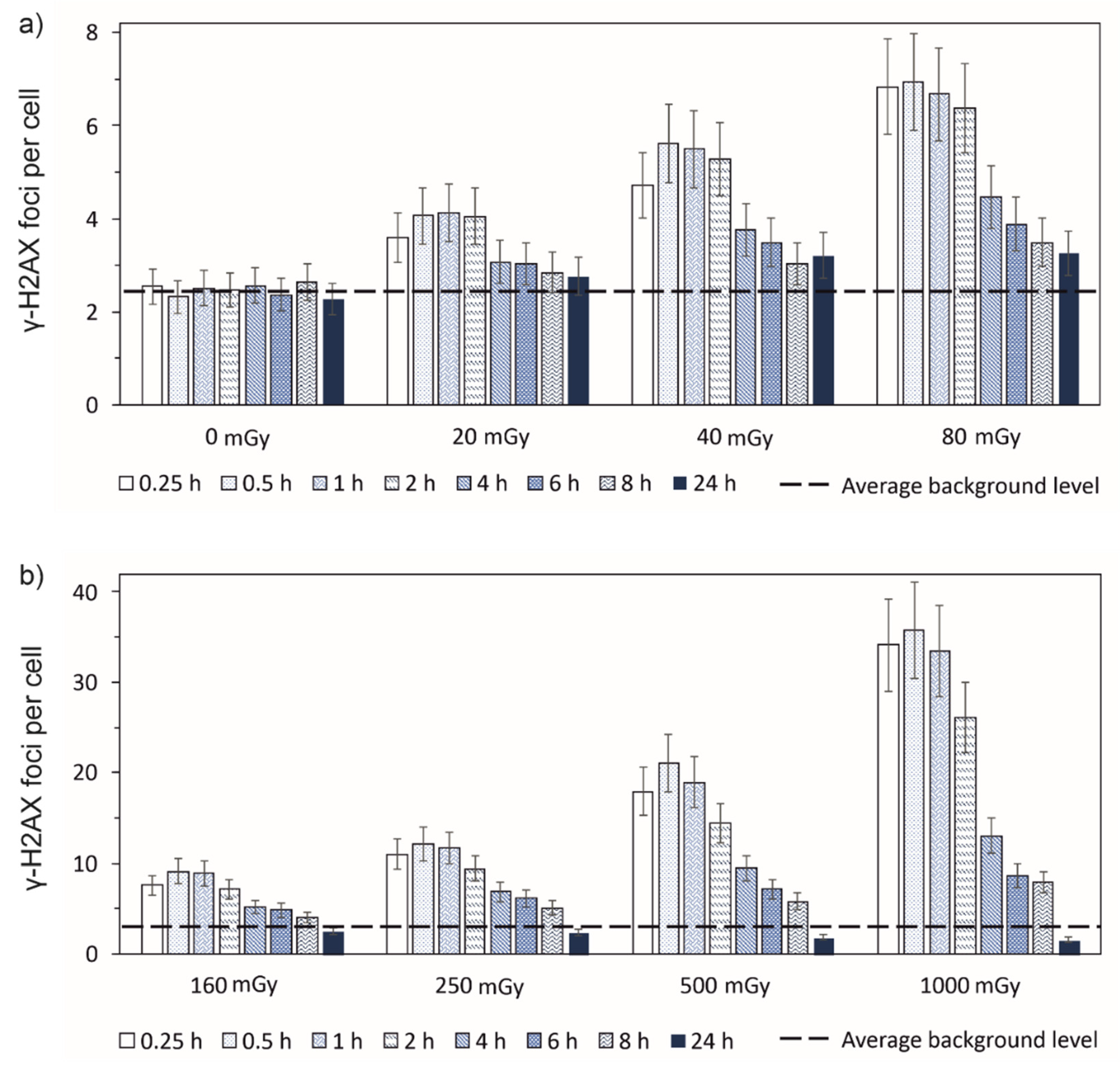
Preprints 80869 g001
Preprints 80869 g002
Figure 2. Experimentally measured time-courses of Rad51 foci remaining in normal human skin fibroblasts after exposure to (a) 20 mGy, 40 mGy, 80 mGy, and (b) 160 mGy, 250 mGy, 500 mGy, 1000 mGy of X-rays in comparison with background level used as control (± SE).
Figure 2. Experimentally measured time-courses of Rad51 foci remaining in normal human skin fibroblasts after exposure to (a) 20 mGy, 40 mGy, 80 mGy, and (b) 160 mGy, 250 mGy, 500 mGy, 1000 mGy of X-rays in comparison with background level used as control (± SE).
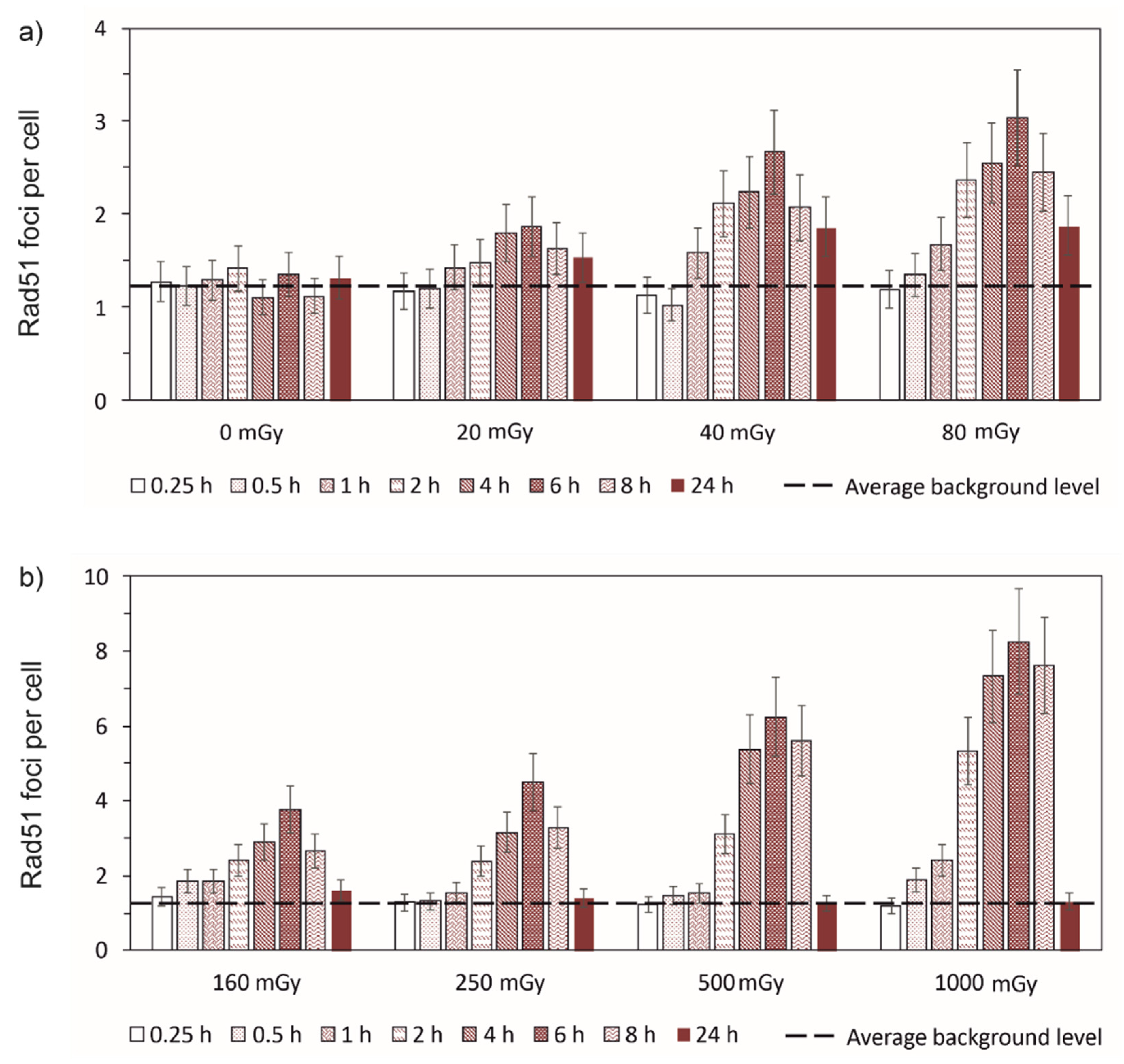
Preprints 80869 g002
Preprints 80869 g003
Figure 3. Time-courses of γ-H2AX foci remaining in normal human skin fibroblasts after exposure to different doses of X-rays. The curves are the calculated results; symbols are the experimental data (± SE). The data are normalized per maximum number of foci observed within the 24 h period.
Figure 3. Time-courses of γ-H2AX foci remaining in normal human skin fibroblasts after exposure to different doses of X-rays. The curves are the calculated results; symbols are the experimental data (± SE). The data are normalized per maximum number of foci observed within the 24 h period.
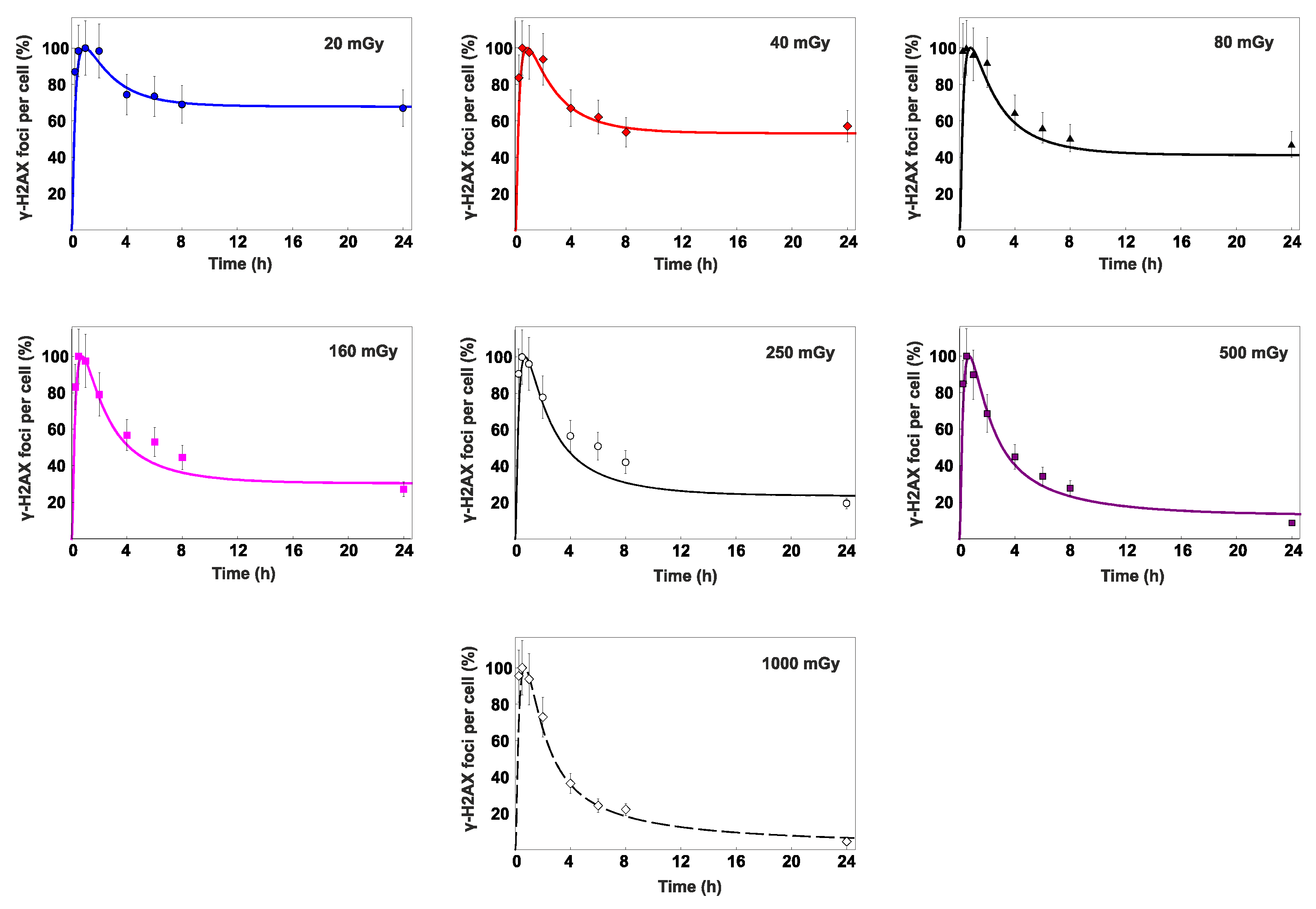
Preprints 80869 g003
Preprints 80869 g004
Figure 4. Time-courses of Rad-51 foci remaining in normal human skin fibroblasts after exposure to different doses of X-rays. The curves are the calculated results; symbols are the experimental data (± SE). The data are normalized per maximum number of foci observed within the 24 h period.
Figure 4. Time-courses of Rad-51 foci remaining in normal human skin fibroblasts after exposure to different doses of X-rays. The curves are the calculated results; symbols are the experimental data (± SE). The data are normalized per maximum number of foci observed within the 24 h period.
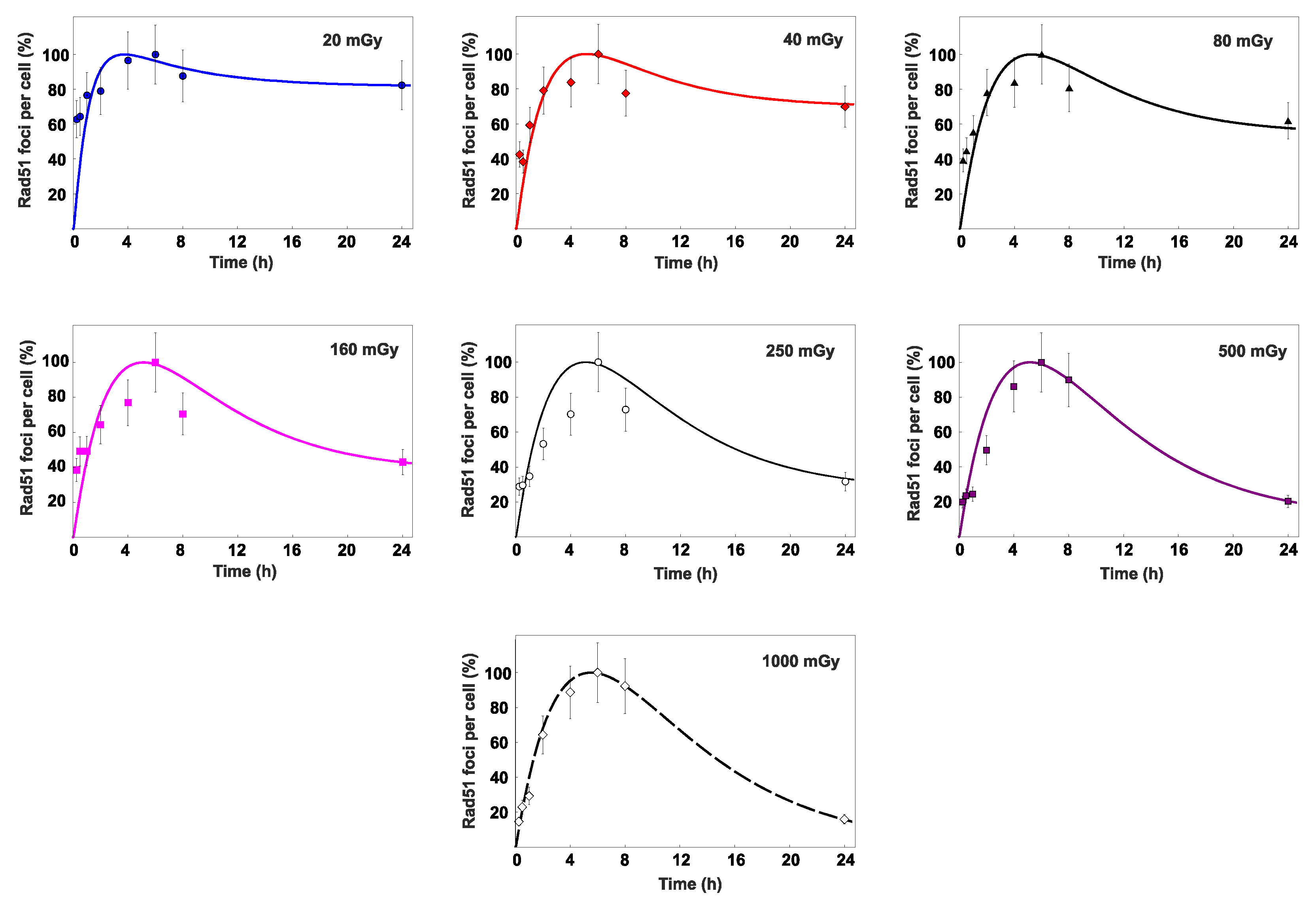
Preprints 80869 g004
Preprints 80869 g005
Figure 5. Dependence of the percent contribution of HR to DSB repair on radiation dose (PHR(D)). The curve is the calculated results; symbols are the experimental data.
Figure 5. Dependence of the percent contribution of HR to DSB repair on radiation dose (PHR(D)). The curve is the calculated results; symbols are the experimental data.
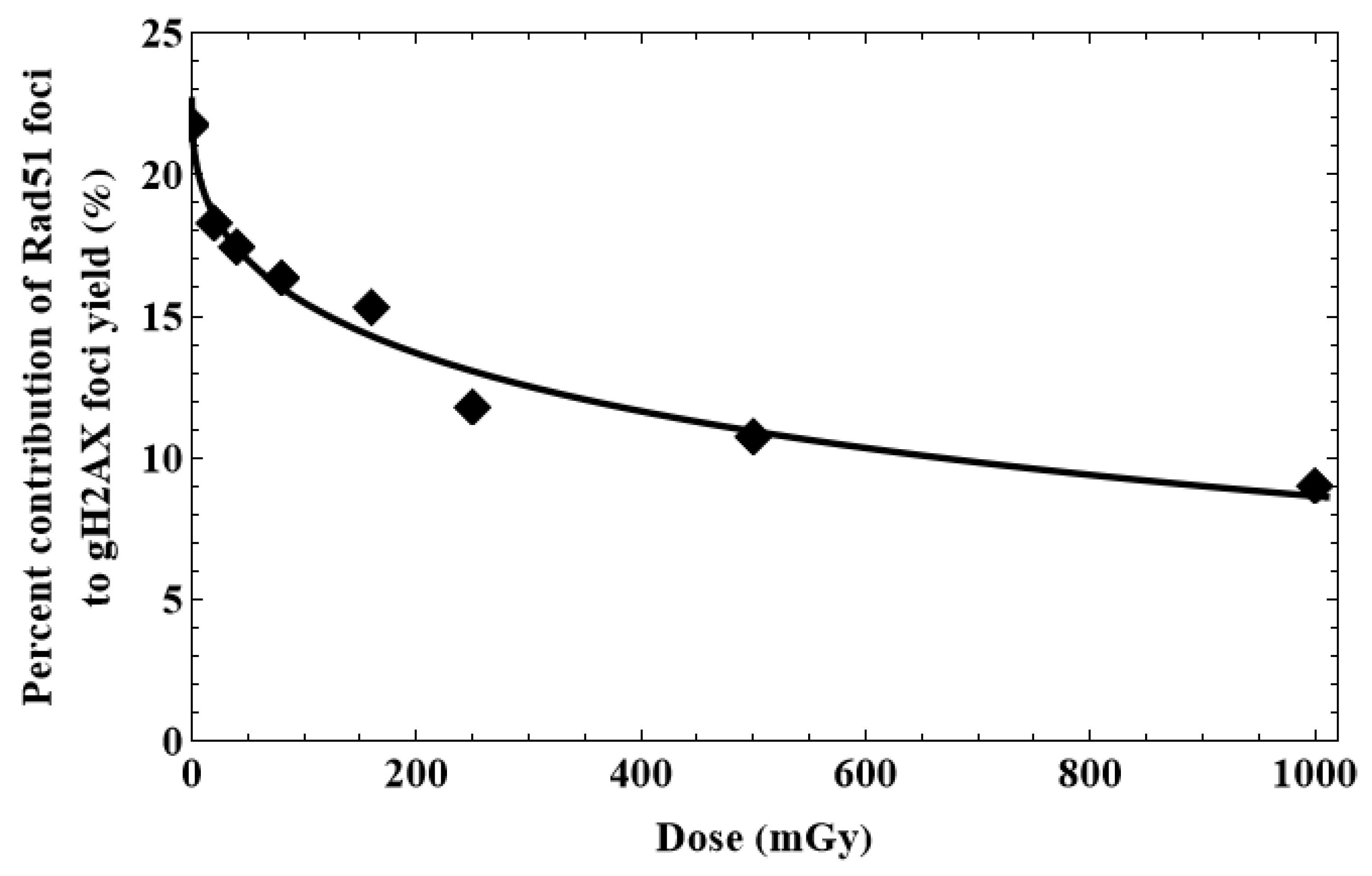
Preprints 80869 g005
Preprints 80869 g006
Figure 6. Dose-dependent changes in the S/G2-phase cell fractions (CENPF positive cells) 24 hours after irradiation of fibroblasts. Data are means ± SE of three independent experiments.
Figure 6. Dose-dependent changes in the S/G2-phase cell fractions (CENPF positive cells) 24 hours after irradiation of fibroblasts. Data are means ± SE of three independent experiments.
Preprints 80869 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated