Prerpints.org logo
Preprint
Article

Batch Simplification Algorithm for Trajectories over Road Networks

Altmetrics

Downloads

133

Views

19

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

31 July 2023

Posted:

01 August 2023

You are already at the latest version

Alerts
Abstract
The volume of vehicular traffic in large cities has increased in recent years, the devices that collect vehicular GPS data such as cameras, GPS receivers and others generate millions of records at every instant of time generating problems in processing and storage of these data which becomes important for researchers. Intelligent Transportation Systems perform vehicle monitoring and control by collecting GPS trajectories, this large volume of information is necessary to have an optimal storage process. Its processing by means of compression techniques and simplification algorithms allow to reduce the necessary storage space. This paper presents a GPS trajectory simplification algorithm that considers noise reduction, point simplification and analysis of road network information. The results obtained on two data sets from the cities of California and Beijing are satisfactory, achieving a higher compression ratio without affecting data quality
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Science

1. Introduction

The volume of generated data by global positioning systems (GPS) around the world is resulting in ever-increasing information storage requirements. Studies [1,2,3,4] have shown that, without compression and at 10-second collection intervals, 100 megabytes (MB) are stored for every 400 objects in a single day. Longer-term studies highlight that if you collect movement data from 10.000 users based on their geographic position every 15 seconds, you generate more than 50 million data per day and approximately 20 trillion data per year [5,6,7].
Data compression forms a crucial part of the data preparation and analysis phase [8]. Compression algorithms can be classified into two categories, lossless and lossy compression algorithms. Lossless compression algorithms perform a more accurate reconstruction of the original data without loss of information. In contrast, lossy compression algorithms exhibit inaccuracies compared to the original data [9].
The main advantage of lossy compression is that it can drastically reduce storage requirements while maintaining an acceptable degree of error [10,11]. If an acceptable error range can be maintained, lossy compression is effective when dealing with large volumes of data. This paper proposes a GPS vehicle trajectory simplification algorithm that considers noise reduction, point simplification and road network information analysis.
This article is organized as follows: Section 1 contains an introduction where the problem is identified, Section 2 contains related works that were identified in the literature and present different solutions to the problem are analyzed, Section 3 describes the proposed algorithm, Section 4 presents the obtained results, Section 5 discusses the results and finally Section 6 contains the conclusions and lines of future work.

2. Related work

A trajectory is represented as a discrete sequence of geographic coordinate points [2]. An example of trajectories are vehicular trajectories that are composed of thousands of points, since the stretches traveled in cities are usually long and with many stops, which implies a greater emission of coordinates generated from GPS devices.
There are currently active research related areas to GPS trajectories [12,13]. Among them is the area of trajectory pre-processing which studies trajectory simplification techniques and algorithms. The trajectory simplification algorithms eliminate some subtraces of the original trajectory [14]; which decreases the data storage space and the data transfer time[15,16,17]. A framework where these areas are observed is proposed in this paper [18].
Reducing the size of the data in a trajectory facilitates the acceleration of the information extraction process [10,19]. There are several path simplification methods and algorithms that are suitable for different types of data and yield different results [20]; but they all have the same principle in common: simplify the data by removing the redundancy of the data in the source file [21,22,23,24]. Meratnia et al. [25] define data compression as substantially reducing the amount of data without significant loss.
As can be seen, both terms have points of contact, so it is considered that in the consulted literature so far, the terms compression and simplification of GPS trajectories are used interchangeably to refer to the elimination of data redundancy. In the present work the term simplification is adopted when it refers to the elimination of redundancy of points of the original trajectory.
GPS trajectory simplification algorithms can be classified into: online algorithms and batch algorithms [26]. Online algorithms do not need to have the entire trajectory ready before starting the simplification, and are suitable for compressing trajectories in mobile device sensors [27,28,29,30]. Online algorithms not only have good compression ratios and deterministic error bounds, but are also easy to implement. They are widely used in practice, even for freely moving objects without the constraint of road networks [27,30,31,32].
Batch algorithms require all points in the trajectory before starting the simplification, which allows them to perform better processing and analysis of these [33]. The advantages of some of the analyzed algorithms [34] are:
  • Douglas-Peucker: Performs point simplification accurately in terms of the spatial error metric. By taking a parameter error threshold, it ensures that the error of the simplified trajectory is within the bounds of the target application [35];
  • TD-TR: By using the synchronous Euclidean distance for the calculations, this allows you to guarantee both a maximum spatial distance and a maximum temporal error distance;
  • Window opening algorithm: Processing time is very low;
  • ST-Trace: Uses the velocity and orientation of the trajectory points in the simplification step [36].
The noisy nature of GPS data is an important element to take into account, however, in the consulted literature there are few examples of GPS trajectory simplification algorithms that take this aspect into account. An example of this is proposed by Gomez et al. [37], where a Kalman filter is used to improve the accuracy of low-cost readers. That work shows that the use of a filtering technique, as a prior step, in the GPS trajectory simplification algorithm significantly improves the results of the simplification process. Data filtering is an important preliminary step to take into account and is one of the limitations of the currently proposed algorithms, which do not take into account the level of noise that a trajectory may have.
Two types of noises to which GPS trajectories are exposed and simplification algorithms do not take into account are exposed by Corcoran et al. [2]. The two types are:
  • Trajectories may contain outliers;
  • The points of a trajectory may have a localization error.
Ivanov [38] presented an online GPS trajectory simplification method, which explicitly states that it does not take into account the presented noise by the trajectory and therefore cannot be used for navigation.
The GPS trajectories obtained from the sensors on vehicles traveling on the road network contain information from this same network expressed in the form of geographic coordinates [39]. Several systems used to represent these trajectories (geographic information systems) contain among their layers the road network information layer. In this way it is possible to represent the trajectories on the map.
The GPS trajectory simplification algorithms proposed in the literature [40,41,42] only eliminate data that are considered redundant in the GPS trajectory in such a way that they do not affect its representation [43]. This process is performed without taking into account the information of the road network through which the traveled vehicle, however, the analysis of this information in the elimination of data resulting from the simplification process could be used to consider the relevance of keeping or eliminating a simplified data [44,45]. This analysis is not performed in the algorithms, described in the literature and there are works that use this information to improve the representation of simplified trajectories with the Douglas-Peucker algorithm [46].
Among the limitations of GPS trajectory simplification algorithms, described in the literature [34,40,47] are:
  • Douglas-Peucker: Only performs spatial analysis of the data;
  • Visvalingam: The compression ratio is reduced and only performs spatial analysis;
  • TD-TR: It presents a smaller margin of error in the trajectory simplification process and an acceptable compression ratio. A limitation is the processing time;
  • Lang: Its point elimination method is trivial, so it discards points considered significant, increasing its margin of error;
  • Window Aperture: Its main disadvantage is the frequent elimination or misrepresentation of important points such as acute angles. A secondary limitation is that straight lines are still over-represented. It requires high hardware performance for proper operation;
  • ST-Trace: Processing time is considerable and requires velocity information to characterize the trace.
From the documentary analysis performed, a set of common deficiencies in the aforementioned trajectory simplification algorithms were identified [48]. These deficiencies that undermine the effectiveness of the simplification algorithms are discussed below:
  • None of the analyzed algorithms consider the noise present in the trajectory data, which reduces the possibility of eliminating points that are not significant during the simplification process;
  • Only the Squish and Dots algorithms perform a rigorous analysis of the GPS trajectory decoding procedure, but do not consider the analysis of trajectory noise;
  • Douglas Peucker, Visvalingam and Window opening only perform spatial analysis of the data. This removes temporal information that provides data of importance to achieve a better compression ratio;
  • Visvalingam removes or misrepresents points, such as acute angles, so the resulting trajectory may lack important points for reconstructing a path;
  • None of the algorithms consider network information in trajectory simplification, missing the opportunity to perform an analysis that allows more points of little significance to be discarded from the original trajectory.
This paper proposes a GPS vehicle trajectory simplification algorithm that considers noise reduction, point simplification and road network information analysis. For this purpose, an area to be processed is selected according to the position of the GPS records within a road network. The area is delimited at the beginning of the process and its size depends on the number of identified outlier points and the zones to which they belong because they will be excluded from the area to be processed. Then, using a batch simplification technique that considers the temporal dimension, each GPS point of the trajectory is processed to reduce the noise present in the trajectory and an analysis is performed with the corresponding road network information to decide whether or not the GPS point is part of the final simplified trajectory. This algorithm can be used, along with other tools, for data compression methods that will allow intelligent transportation systems to improve the processing and storage of these large volumes of data. The proposed algorithm was used to process areas corresponding to GPS trajectories from two public datasets: Geolife and Mobile Century.

3. Materials and Methods

From the literature review, a set of common shortcomings in trajectory simplification algorithms have been identified. One of the main limitations is that these algorithms do not take into account the nature of the data and present compression ratio rates that can be improved. To improve the compression ratio rates, and based on a spatio-temporal batch simplification algorithm, the reduction of noise present in the trajectory and the simplification of points can be included with the analysis of road network information.
In this paper, a new GPS trajectory simplification algorithm called “GR Simplification” is proposed which considers noise reduction, point simplification and road network information analysis.

3.1. Noise reduction

The main objective of noise reduction is the elimination of outliers by correcting the points of the trajectory from an initial state, as the author of this work demonstrates by Reyes et al. [49]. For this purpose, the Kalman noise reduction logic is applied, which takes into account the characteristics of the problem to be treated. Initially, a model is constructed, closely related to the data of the trajectories to be analyzed in order to adjust the filter. The definition used in this article is supported by Lin et al. [50] because it makes use of the mathematical model for a 4-wheel vehicle.
The modeling of the motion problem for the Kalman filter logic is defined in this paper by the equations of motion (Equations (1) and (2)):
x k = x k − 1 + v k − 1 ∗ δ t
y k = y k − 1 + v k − 1 ∗ δ t
For the modeling of the problem to be solved, the type of data and the conditions of the problem must be taken into account. In the present work the a priori data are known and the GPS trajectories are composed basically of: velocity (which is calculated from the distance and time), time and position in the form of ( x , y ) coordinates. Once the initial time has been established, the problem has been properly modeled and the equations of motion have been established, the data is filtered using the Kalman filter, which consists of five main processes listed below:
  • Prediction of the next state of the system;
  • A priori covariance update;
  • Kalman gain calculation;
  • Estimation of the current state;
  • Update of the a posteriori covariance.
A flow chart for noise reduction is shown in Figure 1.

3.1.1. Brief description of kalman filter application for noise reduction

For the application of this filter, in the present work, the input data is defined as the initial state or state variables which contains the components of latitude, longitude and velocity present in the dynamics of the motion (Equation (3)).
X k = x x ˙ y y ˙
The covariance matrix is defined as the matrix C (Equation (4)):
C = 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1
The state matrix or transition matrix ME is defined in which the time variation between the previous state and the current state is represented together with the direction of the motion (Equation (5)):
M E = 1 δ t 0 0 0 1 0 δ t 0 0 1 0 0 0 0 1
The covariance matrix of the observed noise or observation matrix is obtained (Equation (6)).
R = C 0 0 0 0 0 C 0 0 0 0 0 C 0 0 0 0 0 C 0
Where C 0 represents the covariance of the observations. This covariance is calculated using the Equation (7):
C 0 = ∑ ( x i − x p r o m ) ( y i − y p r o m ) n − 1
So the prediction state is represented by the Equation (8):
X k + 1 = M E ∗ X k

3.2. Road network information

The road network information uses the topology of points and polygons connected by vectors for the spatial analysis of GPS points over vehicular road networks in the areas where the data are being analyzed [45], as evidenced by the author of the present research [51]. For the calculation of the distance between the GPS coordinates and the network information it is proposed to use the great circle distance. A flow chart for network analysis is shown in Figure 2.

3.3. Simplification of GPS points

The simplification is based on the simplification logic of the TD-TR algorithm, the Kalman noise reduction and the analysis of the road network information, in a hybrid way, to improve the presented results in the literature on the GPS trajectory simplification process. As a starting point, the simplification logic of Top Down Time Ratio is taken, a line is drawn between the first and last point of the trajectory and the Equations (9) and (10) are used to calculate the proposed intermediate points in the simplification logic.
x i ′ = x s + t i − t s t e − t s ( x e − x s )
y i ′ = y s + t i − t s t e − t s ( y e − y s )
For the calculation of the Synchronous Euclidean Distance (SED), the Equation (11).
S E D = ∑ i = 1 n ( x t i − x t i ′ ) 2 + ( y t i − y t i ′ ) 2
The maximum distance point is selected, marked to hold, and compared with a threshold value. If the point is greater than the threshold value it is evaluated considering the network information. For this purpose the author of this paper proposes the evaluation of this point with the network information. This evaluation consists of comparing the distance between this point with the neighboring points that are part of the road network information, selecting the point with the greatest distance. If the distance from this point to the line segment is greater than the defined tolerance, the point is accepted; otherwise, if it is less, all points that are not marked are discarded. The simplification is executed as long as there are unanalyzed GPS trajectory points and as a result the simplified GPS trajectory is obtained. Figure 3 shows the simplification flowchart.

3.3.1. Brief description of the application of point simplification with road network analysis

The simplification process of the proposed algorithm performs the application of the Kalman filter to the trajectory or segment being analyzed to then proceed to the simplification of the points. The points simplification process uses the logic of the TD-TR algorithm, which was selected as the basis for the proposal after performing an initial diagnosis in conjunction with other algorithms considered relevant by the author of this work; the logic of the TD-TR simplification process is taken as a basis in conjunction with the analysis of network information to reduce the number of points of the filtered trajectory and validate that these points are correct in the context of a vehicular road network. Simplification begins by plotting the segment, to which the Kalman filter will be applied to smooth the initial line segment between the first and last point. It then calculates by means of the synchronous Euclidean distance, the distances of all points to the line segment and identifies the point furthest from the line segment (or the maximum distance) and marks it to be kept. For this process, a obtained tolerance from the average of distances from one point to the next within the same trajectory has been selected. If the distance from the selected point to the line segment is less than the defined tolerance, all unmarked points are discarded, otherwise it selects the marked point to evaluate it with the network information and continues dividing the line segment with this point as shown in the Figure 4. This procedure is executed recursively until the value is less than the tolerance or the line segment can no longer be divided.
In case the point is marked, it is evaluated with the network information to decide whether or not it can be added to the final simplified trajectory. To evaluate a marked point, the distance from the great-circle of the point to all points in the network is calculated using the Equation (12):
cos ▵ σ = ( sin b 1 sin b 2 ) + ( cos b 1 cos b 2 cos | c | )
Two points P 1 ( a 1 , b 1 ) and P 2 ( a 2 , b 2 ) are used in the equation. Where a 1 , 2 and b 1 , 2 represent the longitudes and latitudes respectively in degrees and c represents the absolute value of the difference of the longitude axes ( a 1 − a 2 ) between the respective coordinates. The above formula expresses the result as a difference of angles, so to obtain the distance with respect to the circumference of the planet the Equation (13) is used:
d = r ▵ σ
A graphical representation of the simplification of the marked points and the evaluation with the points of the road networks is shown in Figure 5.
The road network information is used to discard points that are not within a lane on a road, a lane width of 4.5 meters has been considered for this work. As shown in Figure 6 the points of the trajectory P 2 and P 3 are eliminated keeping those that are in the lane width, thus keeping only the necessary points to trace the trajectory of a vehicle without affecting its correct representation.
The greater the width of the lane, the greater the possibility of accepting more points. The use of the great-circle distance in the analysis of network information allows more accurate calculations, since the distance between two points in Euclidean space is the length of a straight line between them, but on the sphere there are no straight lines. In spaces with curvature, straight lines are replaced by geodesics. Geodesics on the sphere are circles on the sphere whose centers coincide with the center of the sphere, and are called great circles [52].
The implementation of the proposed algorithm in a controlled environment is available from a public repository 1.

4. Results

4.1. Used data

4.1.1. Geolife

The “Geolife (Microsoft Research Asia)” dataset [53] consists of information from 182 users over a period of more than three years from April 2007 to August 2012. The GPS trajectories of this dataset contains the information of: “latitude”, “longitude”, “altitude”, “time” of each user record. The time is taken considering the GMT standard. This dataset contains 17.621 trajectories with a total distance of about 1,2 million kilometers and a total duration of more than 48.000 hours. These trajectories were recorded by different GPS loggers and GPS phones, and have a variety of sampling rates.

4.1.2. Mobile Century

The data set used “Mobile Century” data [54] collected on February 8, 2008 between 10 am and 6 pm on Interstate 880, CA as part of a joint UC Berkeley - Nokia project funded by the Department of Transportation to support exploration of the use of GPS-enabled sensor phones to monitor traffic. This data consists of individual “trips” in one direction on Interstate 880. Northbound trips are in the “NB_veh_files” folder and southbound trips are in the “SB_veh_files” folder. Each file contains the following five columns: “unixtime”, “latitude”, “longitude”, “postmile” and “speed”.

4.2. Initial diagnostics of batch GPS trajectory simplification algorithms

To evaluate the simplification algorithms in terms of processing time, compression ratio and margin of error, the author of this paper used two significant samples of GPS trajectory databases as follows:
From the “Mobile Century” dataset a sample of 100.169 spatial coordinates is used, which represent 10,95% of the original database data. A sample of 340 trajectories was used out of a total of 2.977 trajectories. For the selection of the sample, an area of approximately 24,51 x 24,45 km was delimited and the systematic sampling technique was used.
A sample of 417.056 spatial coordinates is used from the “Geolife Trajectories” dataset, which represents 1,68% of the original base size. A sample of 376 trajectories was used out of a total of 18.549 trajectories. For the selection of the sample, an area covering approximately 148,45 x 137,85 km was delimited, the same area where there is the highest concentration of trajectories, which would allow discarding many trajectories containing atypical points, and the systematic sampling technique was used.
For the initial diagnosis, the algorithms considered relevant by the author of this work were selected after the literature review; the algorithms were run on the samples obtained for the two data sets. A summary is shown in Table 1, showing the mean of the results obtained for each algorithm.
The obtained results in the initial diagnostic study led to the conclusion that:
  • The Visvalingam algorithm shows the worst compression ratio rates, being a very unstable algorithm in its behavior before different data sets;
  • The TD-TR algorithm is the second algorithm with the best compression ratio rate with an average of 86,01;
  • Douglas-Peucker obtains the best results in terms of compression ratio, however the processing time is longer than TD-TR and the margin of error is also higher, being 13,88 km while TD-TR presents 0,80 km;
  • The TD-TR algorithm is proposed in the literature as an improvement to the Douglas Peucker algorithm and presents better results in terms of margin of error and processing time.
As a result of the initial diagnosis in the present work, the TD-TR simplification logic is selected as the basis for the elaboration of the proposal. The author of the present work considers that it is the best option of the four algorithms analyzed, since it reported the second best compression ratio, the second best margin of error, considering that it is the only one that performs a spatio-temporal analysis and that the applicability of the present work is not based on the analysis of real-time trajectories, which are more focused on obtaining better times. The used metrics to perform the measurements to the “GR Simplification” algorithm, considering the application scenario in road networks and disconnected (batch) environments, are the compression ratio rate and the margin of error [26,55,56]. For the comparison of the “GR Simplification” algorithm and TDTR, the margin of error formula found in this paper [57] is used.

4.3. Obtained results from the GR Simplification algorithm for GPS trajectory simplification

To perform the measurements, the proposed algorithm “GR Simplification” was implemented in R language, which uses Kalman filtering logic, TD-TR simplification logic and road network information.
From the Datasets two samples are chosen whose trajectories are selected systematically, each sample uses the data corresponding to the GeoLife and Mobile Century datasets, with the following characteristics:
  • Sample 1 (Geolife): three hundred and seventy-six trajectories, each containing between 1 and 18.924 points;
  • Sample 2 (Mobile Century): three hundred and forty trajectories, each containing between 17 and 8.067 points.
In the two samples, the trajectories are selected systematically.
The calculations of the compression ratio and margin of error metrics were performed and a comparison is established with the obtained results by the TD-TR algorithm, as shown in Figure 7.
After performing the measurements in which the “GR Simplification” (denoted A1) and “TD-TR” (denoted A2) algorithms are executed, obtaining the values of compression ratio (metric 1) and margin of error (metric 2) for both algorithms, the average of the results, for the two samples, are shown in the Table 2. The obtained results are validated using the corresponding statistical tests.

5. Discussion

5.1. Assumption of normality

There are several methods for testing the fit to the normal distribution, among the best known are the Kolmogorov-Smirnov and Shapiro-Wilk’s test [58]. The latter, in the author’s opinion, is widely recommended and is used in the present work.
The null hypothesis (Ho) for validation is defined as “the groups of samples fit a normal distribution”, so that if the test yields a significant difference there is no fit to the normal distribution.
The Table 3 shows the obtained results after performing two tests to check the assumption of normality, both for the compression ratio metric and the margin of error metric.
When performing the Shapiro-Wilk’s test on the vectors, to check the assumption of normality of the obtained results in the compression ratio metric, it is evident that the values do not conform to a normal distribution; therefore, the null hypothesis (Ho) is rejected. In the same way it is observed that when performing the test to check the assumption of normality for the margin of error, it is evident that the values of the sample do not conform to a normal distribution, therefore the null hypothesis (Ho) is rejected. This can be seen visually by observing the p-value values and the density plots in Figure 8 and Figure 9.

5.2. Analysis of results for compression ratio metric

The Mann-Whitney test is a nonparametric test that allows comparison of two independent samples that do not conform to a normal distribution, as is the case for measurements made for the compression ratio in the two samples of the data sets. Three researchers, Mann, Whitney and Wilcoxon, separately refined a very similar nonparametric test that can determine whether samples can be considered identical or not on the basis of their ranges [59,60].
The result of applying this test to the two samples with respect to the compression ratio can be seen in Figure 10.
It is observed that all the values (p-values) are less than 0.05, which means that there are significant differences according to the test applied with a 95% confidence level, a obtained result for the two samples. Visual inspection shows that the median values are higher for the GR Simplification.

5.3. Analysis of results for the margin of error metric

To check whether the samples are identical, the nonparametric Mann-Whitney test (U-test) is applied. This test is applied in the present work to check that the samples are identical and thus verify the veracity of the results. The result of the application of this test for the two samples with respect to the margin of error can be seen in the Figure 11.
It is observed that all the values (p-values) are less than 0.05, which means that there are significant differences according to the applied test with a 95% confidence, obtained result for the two samples. Visual inspection shows that the median values are lower for the GR Simplification.
After performing the validation and hypothesis test on metric 1: compression ratio, it can be seen that there are significant differences between the “GR Simplification” and “TD-TR” algorithms. The box plots show that the median values are higher for “GR Simplification”. After performing the validation and hypothesis test on metric 2: margin of error, it is found that the means of the groups being compared have significant differences. The box plots show that the median values are lower for the “GR Simplification”. All tests are performed for 95% confidence.
It is evident that the compression ratio of the GR Simplification is better with respect to the TD-TR simplification. It is evident that the margin of error is lower, comparing the GR Simplification with respect to the TD-TR simplification.

6. Conclusions

The algorithm “GR Simplification” developed as a result of the present work, allows the simplification of GPS trajectory points, based on noise reduction, trajectory simplification and network information, increasing the data compression ratio compared to the TD-TR algorithm.
The measurements performed show that the GR trajectory simplification algorithm, based on noise reduction, trajectory simplification and network information proposed in this research, presents a higher compression ratio and even improves the margin of error with respect to its similar ones analyzed in the literature.
The validation of the obtained results through statistical tests allowed verifying that there is an increase in the compression ratio.
The results obtained from the “GR Simplification” algorithm show that it can be used in the processing of vehicle trajectories that have available information from the road network, allowing GPS trajectory analysis applications to optimally manage their storage space.
As lines of future work, it is proposed to improve the processing time of the GR Simplification algorithm, through a new implementation that considers a parallel processing approach of several trajectories. We also propose an implementation that includes the Kalman filter logic and the use of networks for online GPS trajectory simplification algorithms, considering the use of a temporary storage memory.

Author Contributions

The following statements should be used methodology, G.R. and V.E.; software, V.M.; validation, R.T.; formal analysis, R.T.; data curation, V.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Data Availability Statement

The Mobile Century Data presented in this study are openly available in Mobile Century Data at https://doi.org/10.1016/j.trc.2009.10.006. The Geolife GPS trajectory dataset analyzed in this study. This data can be found here: https://www.microsoft.com/en-us/research/publication/geolife-gps-trajectory-dataset-user-guide/

Acknowledgments

We would like to thank Dr. Antonio Cedeño Pozo and Dr. Ramón Santana Fernández for conceptual discussions on the programming part of the project. We would also like to thank the anonymous reviewers for their comments that helped to improve the work.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Muckell, J.; Patil, V.; Ping, F.; Hwang, J.H.; Lawson, C.T.; Ravi, S.S. SQUISH: An online approach for GPS trajectory compression. ACM, 2011, pp. 1–8. [CrossRef]
  2. Corcoran, P.; Mooney, P.; Huang, G. Unsupervised trajectory compression. 2016, pp. 3126–3132. [CrossRef]
  3. Rana, R.; Yang, M.; Wark, T.; Chou, C.T.; Hu, W. Simpletrack: Adaptive trajectory compression with deterministic projection matrix for mobile sensor networks. IEEE Sensors Journal 2015, 15, 365–373. [Google Scholar] [CrossRef]
  4. Trajcevski, G. Compression of Spatio-temporal Data. 2016, pp. 4–7. [CrossRef]
  5. Chen, Y.; Yu, P.; Chen, W.; Zheng, Z.; Guo, M. Embedding-Based Similarity Computation for Massive Vehicle Trajectory Data. IEEE Internet of Things Journal 2022, 9, 4650–4660. [Google Scholar] [CrossRef]
  6. Bashir, M.; Ashraf, J.; Habib, A.; Muzammil, M. An intelligent linear time trajectory data compression framework for smart planning of sustainable metropolitan cities. Transactions on Emerging Telecommunications Technologies 2022, 33, e3886. [Google Scholar] [CrossRef]
  7. Wang, Y.; Zhang, Z.; Liu, D. An optimization model for the transportation network with hierarchical structure: the case of China Post. Journal of Ambient Intelligence and Humanized Computing 2019 12:1 2019, 12, 167–182. [Google Scholar] [CrossRef]
  8. Richter, K.F.; Schmid, F.; Laube, P. Semantic trajectory compression: Representing urban movement in a nutshell. Journal of Spatial Information Science 2012, 3–10. [Google Scholar] [CrossRef]
  9. Souza, J.C.S.D.; Assis, T.M.L.; Pal, B.C. Data Compression in Smart Distribution Systems via Singular Value Decomposition. IEEE Transactions on Smart Grid 2017, 8, 275–284. [Google Scholar] [CrossRef]
  10. Muckell, J.; Olsen, P.W.; Hwang, J.H.; Lawson, C.T.; Ravi, S.S. Compression of trajectory data: A comprehensive evaluation and new approach. GeoInformatica 2014, 18, 435–460. [Google Scholar] [CrossRef]
  11. Nibali, A.; He, Z. Trajic: An Effective Compression System for Trajectory Data. IEEE Transactions on Knowledge and Data Engineering 2015, 27, 3138–3151. [Google Scholar] [CrossRef]
  12. Alowayr, A.D.; Alsalooli, L.A.; Alshahrani, A.M.; Akaichi, J. A review of trajectory data mining applications. 2021 International Conference of Women in Data Science at Taif University, WiDSTaif 2021, 2021. [Google Scholar] [CrossRef]
  13. Mazimpaka, J.D.; Timpf, S. Trajectory data mining: A review of methods and applications. Journal of Spatial Information Science 2016, 61–99. [Google Scholar] [CrossRef]
  14. Ji, Y.; Liu, H.; Liu, X.; Ding, Y.; Luo, W. A comparison of road-network-constrained trajectory compression methods. 2017, pp. 256–263. [CrossRef]
  15. Ouyang, Z.; Xue, L.; Ding, F.; Li, D. PSOTSC: A Global-Oriented Trajectory Segmentation and Compression Algorithm Based on Swarm Intelligence. ISPRS International Journal of Geo-Information 2021, 10. [Google Scholar] [CrossRef]
  16. Chen, H.; Chen, X. A Trajectory Ensemble-Compression Algorithm Based on Finite Element Method. ISPRS International Journal of Geo-Information 2021, 10. [Google Scholar] [CrossRef]
  17. Song, J.; Miao, R. A Novel Evaluation Approach for Line Simplification Algorithms towards Vector Map Visualization. ISPRS International Journal of Geo-Information 2016, 5. [Google Scholar] [CrossRef]
  18. Zheng, Y. Trajectory data mining: An overview. ACM Transactions on Intelligent Systems and Technology 2015, 6, 1–41. [Google Scholar] [CrossRef]
  19. Wang, S.; Zhong, E.; Li, K.; Song, G.; Cai, W. A Novel Dynamic Physical Storage Model for Vehicle Navigation Maps. ISPRS International Journal of Geo-Information 2016, 5. [Google Scholar] [CrossRef]
  20. Amigo, D.; Pedroche, D.S.; García, J.; Molina, J.M. Review and classification of trajectory summarisation algorithms: From compression to segmentation:. 2021; 17. [Google Scholar] [CrossRef]
  21. Salomon, D. Data compression: The complete reference, 4 ed.; Springer, 2014; pp. 1–1093. [CrossRef]
  22. Gudmundsson, J.; Katajainen, J.; Merrick, D.; Ong, C.; Wolle, T. Compressing spatio-temporal trajectories. Computational Geometry: Theory and Applications 2009, 42, 825–841. [Google Scholar] [CrossRef]
  23. Lv, C.; Chen, F.; Xu, Y.; Song, J.; Lv, P. A trajectory compression algorithm based on non-uniform quantization. IEEE, pp. 2469–2474. [CrossRef]
  24. Liu, D.; Wang, T.; Li, X.; Ni, Y.; Li, Y.; Jin, Z. A Multiresolution Vector Data Compression Algorithm Based on Space Division. ISPRS International Journal of Geo-Information 2020, 9. [Google Scholar] [CrossRef]
  25. Meratnia, N.; Rolf, A.; ITC, E. A new perspective on trajectory compression techniques. International Society for Photogrammetry and Remote Sensing, 2003, p. 2–3.
  26. Zheng, Y.; Zhou, X. Computing with Spatial Trajectories; Springer, 2011; pp. 1–306. [CrossRef]
  27. Lin, X.; Ma, S.; Zhang, H.; Wo, T.; Huai, J. One-pass error bounded trajectory simplification. ACM, 2017, Vol. 10, pp. 841–852. [CrossRef]
  28. Feldman, D.; Sugaya, A.; Rus, D. An effective coreset compression algorithm for large scale sensor networks. 2012, pp. 257–268. [CrossRef]
  29. Wang, Z.; Long, C.; Cong, G.; Zhang, Q. Error-Bounded Online Trajectory Simplification with Multi-Agent Reinforcement Learning. Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2021; 1758–1768. [Google Scholar] [CrossRef]
  30. Li, S.; Zhang, K.; Yin, H.; Yin, D.; Zu, H.; Gao, H. ROPW: An Online Trajectory Compression Algorithm. Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) 2021, 12680 LNCS, 16–28. [Google Scholar]
  31. Hendawi, A.M.; Khot, A.; Rustum, A.; Basalamah, A.; Teredesai, A.; Ali, M. A Map-Matching Aware Framework for Road Network Compression. 2015, Vol. 1, pp. 307–310. [CrossRef]
  32. Hussain, S.A.; Hassan, M.U.; Nasar, W.; Ghorashi, S.; Jamjoom, M.M.; Abdel-Aty, A.H.; Parveen, A.; Hameed, I.A. Efficient Trajectory Clustering with Road Network Constraints Based on Spatiotemporal Buffering. ISPRS International Journal of Geo-Information 2023, 12. [Google Scholar] [CrossRef]
  33. Song, R.; Sun, W.; Zheng, B.; Zheng, Y. A novel framework of trajectory compression in road networks. 2014, pp. 661–672. [CrossRef]
  34. Hunnik, R.V. Extensive Comparison of Trajectory Simplification Algorithms 2017. pp. 1–22.
  35. Lin, C.Y.; Hung, C.C.; Lei, P.R. A velocity-preserving trajectory simplification approach. IEEE Xplorer, 2016, pp. 58–65. [CrossRef]
  36. Kellaris, G.; Pelekis, N.; Theodoridis, Y. Trajectory compression under network constraints. Springer, 2009, pp. 392–398. [CrossRef]
  37. Gomez-Gil, J.; Ruiz-Gonzalez, R.; Alonso-Garcia, S.; Gomez-Gil, F.J. A Kalman filter implementation for precision improvement in Low-Cost GPS positioning of tractors. Sensors (Switzerland) 2013, 13, 15307–15323. [Google Scholar] [CrossRef]
  38. Ivanov, R. Real-time GPS track simplification algorithm for outdoor navigation of visually impaired. Journal of Network and Computer Applications 2012, 35, 1559–1567. [Google Scholar] [CrossRef]
  39. Chen, C.; Ding, Y.; Guo, S.; Wang, Y. DAVT: An Error-Bounded Vehicle Trajectory Data Representation and Compression Framework. IEEE Transactions on Vehicular Technology 2020, 69, 10606–10618. [Google Scholar] [CrossRef]
  40. Meratnia, N.; By, R.A.D. Spatiotemporal compression techniques for moving point objects. Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) 2004, 2992, 765–782. [Google Scholar] [CrossRef]
  41. Whyatt, J.D.; Wade, P.R. The Douglas-Peucker line simplification algorithm. Bulletin - Society of University Cartographers 1988, 22, 17–25. [Google Scholar]
  42. Visvalingam, M.; Whyatt, J.D. Line generalisation by repeated elimination of points. The Cartographic Journal 1993, 30, 46–51. [Google Scholar] [CrossRef]
  43. Buchin, M.; Driemel, A.; Van Kreveld, M.; Sacristan, V. Segmenting trajectories: A framework and algorithms using spatiotemporal criteria. Journal of Spatial Information Science, 2011; 33–63. [Google Scholar] [CrossRef]
  44. Bach, T.; Li, T.; Huang, R.; Chen, L.; Jensen, C.S.; Pedersen, T.B. Compression of Uncertain Trajectories in Road Networks. PVLDB 2020, 13, 1050–1063. [Google Scholar] [CrossRef]
  45. Weiss, R.; Weibel, R. Road network selection for small-scale maps using an improved centrality-based algorithm. Journal of Spatial Information Science 2014, 71–99. [Google Scholar] [CrossRef]
  46. Koegel, M.; Baselt, D.; Mauve, M.; Scheuermann, B. A comparison of vehicular trajectory encoding techniques. 2011, pp. 87–94. [CrossRef]
  47. Lawson, C.T. Compression and Mining of GPS Trace Data: New Techniques and Applications. Final Report: Region II University Transportation Research Center, 2011; 1–25. [Google Scholar]
  48. Reyes, G. Algoritmo de compresión de trayectorias GPS basado en el algoritmo Top Down Time Ratio (TD-TR). 2017, pp. 194–204.
  49. Reyes, G.; Estrada, V. Comparison Analysis On Noise Reduction In Gps Trajectories Simplification. Latin American and Caribbean Consortium of Engineering Institutions, 2021. [CrossRef]
  50. Lin, K.; Xu, Z.; Qiu, M.; Wang, X.; Han, T. Noise filtering, trajectory compression and trajectory segmentation on GPS data. 8 2016, pp. 490–495. [CrossRef]
  51. Reyes, G.; Crespo, C.; León-Granizo, O.; Bazán, W.; Horta, R. Propuesta de método de extracción de ubicaciones georreferenciales de una red de carreteras para el análisis de trayectorias GPS Proposal for a method to extract georeferenced locations from a road network for the analysis of GPS trajectories. Investigación, Tecnología E Innovación 2022, 14, 1–15. [Google Scholar]
  52. Fenn, R. , 2001; pp. 253–285. https://doi.org/10.1007/978-1-4471-0325-7_8.Geometry. In Geometry; Springer London: London, 2001; pp. 253–285. [Google Scholar] [CrossRef]
  53. Zheng, Y.; Fu, H.; Xie, X.; Ma, W.Y.; Li, Q. Geolife GPS trajectory dataset - User Guide, geolife gps trajectories 1.1 ed., 2011.
  54. Berkeley, U. Mobile Century data documentation 2009. pp. 1–6. [CrossRef]
  55. Reyes, G.; Maquilón, V.; Estrada, V. Relationships of Compression Ratio and Error in Trajectory Simplification Algorithms. Springer International Publishing, 2021, pp. 140–155.
  56. Muckell, J.; Olsen, P.W.; Hwang, J.H.; Ravi, S.S.; Lawson, C.T. A framework for efficient and convenient evaluation of trajectory compression algorithms. 2013, pp. 24–31. [CrossRef]
  57. Liu, M.; He, G.; Long, Y. A Semantics-Based Trajectory Segmentation Simplification Method. Journal of Geovisualization and Spatial Analysis 2021, 5. [Google Scholar] [CrossRef]
  58. Tapia, C.; Flores, K. Pruebas para comprobar la normalidad de datos en procesos productivos: Anderson-Darling, Ryan-Joiner, Shapiro-Wilk y Kologórov-Smirnov. Societas. Revista de Ciencias Sociales y Humanísticas 2021, 23, 83–97. [Google Scholar]
  59. Saldaña, M.R. Contraste de Hipótesis Comparación de dos medias independientes mediante pruebas no paramétricas: Prueba U de Mann-Whitney - Dialnet. Revista Enfermería del Trabajo 2013, 3, 77–84. [Google Scholar]
  60. Guillen, A.; a Araiza, L.; Cerna, E.; Valenzuela, J.; Uanl, J.L.; Nicolás, S.; Coah, S. Métodos No-Paramétricos de Uso Común ( Non Parametric Methods of Common Usage ). DAENA: International Journal of Good Conscience 2012, 7, 132–155. [Google Scholar]
1
Source code available at https://github.com/gary-reyes-zambrano/Algoritmo-de-simplificacion-GR
Preprints 81090 g001
Figure 1. Flowchart of the GR Simplification algorithm for noise reduction.
Figure 1. Flowchart of the GR Simplification algorithm for noise reduction.
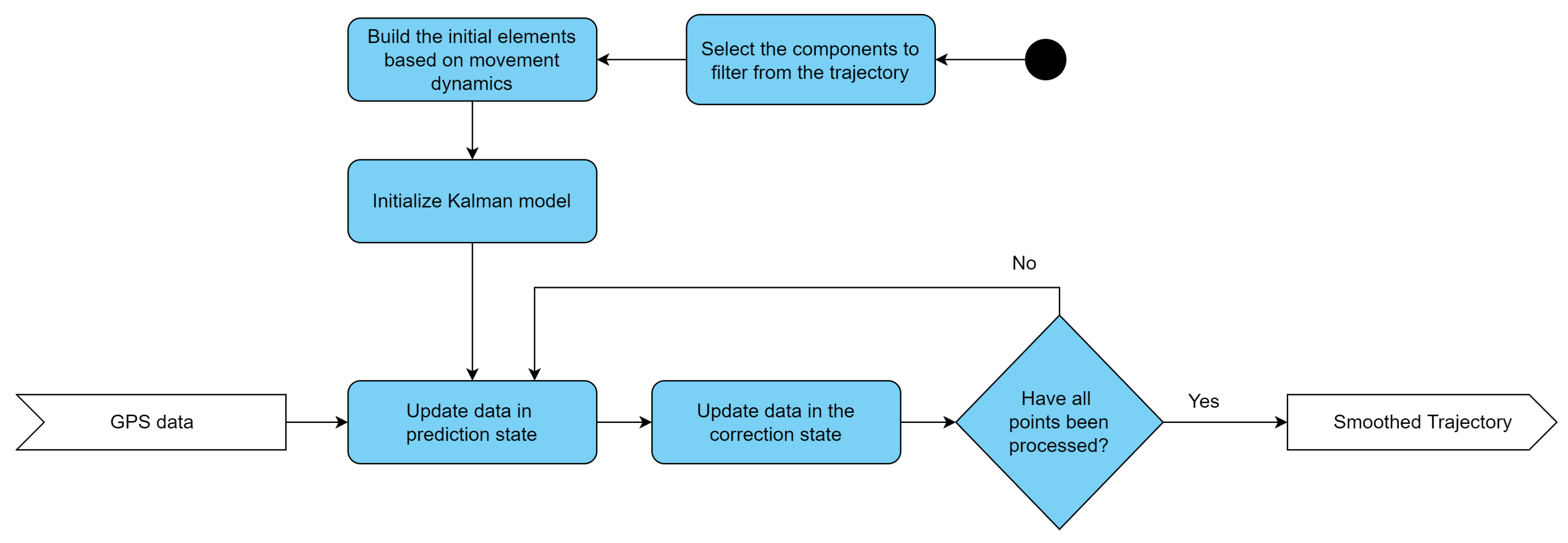
Preprints 81090 g001
Preprints 81090 g002
Figure 2. Flowchart of the GR Simplification algorithm for network analysis.
Figure 2. Flowchart of the GR Simplification algorithm for network analysis.
Preprints 81090 g002
Preprints 81090 g003
Figure 3. Flowchart of the GR Simplification algorithm for point simplification.
Figure 3. Flowchart of the GR Simplification algorithm for point simplification.
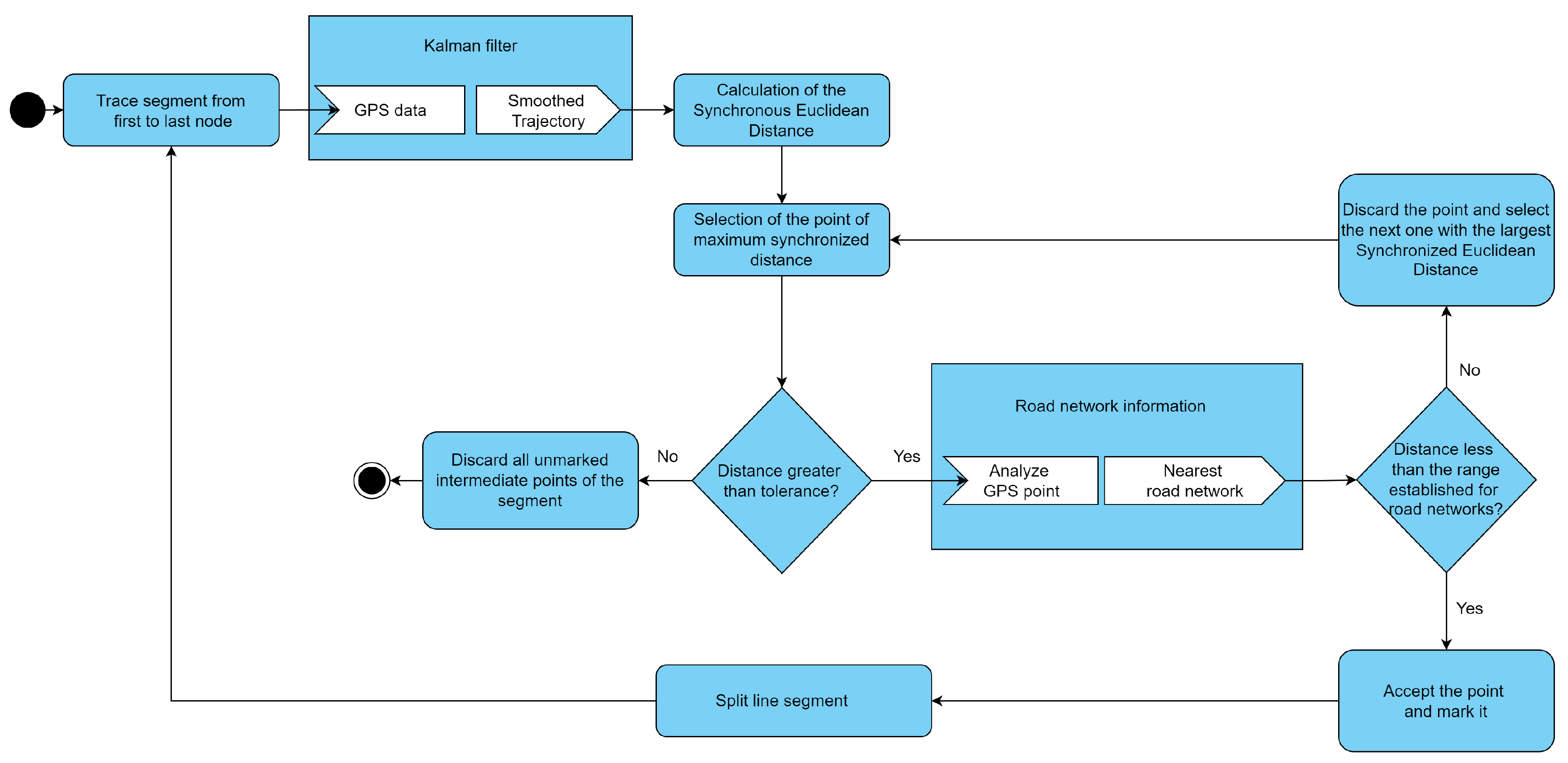
Preprints 81090 g003
Preprints 81090 g004
Figure 4. Simplification of points using synchronous Euclidean distance.
Figure 4. Simplification of points using synchronous Euclidean distance.
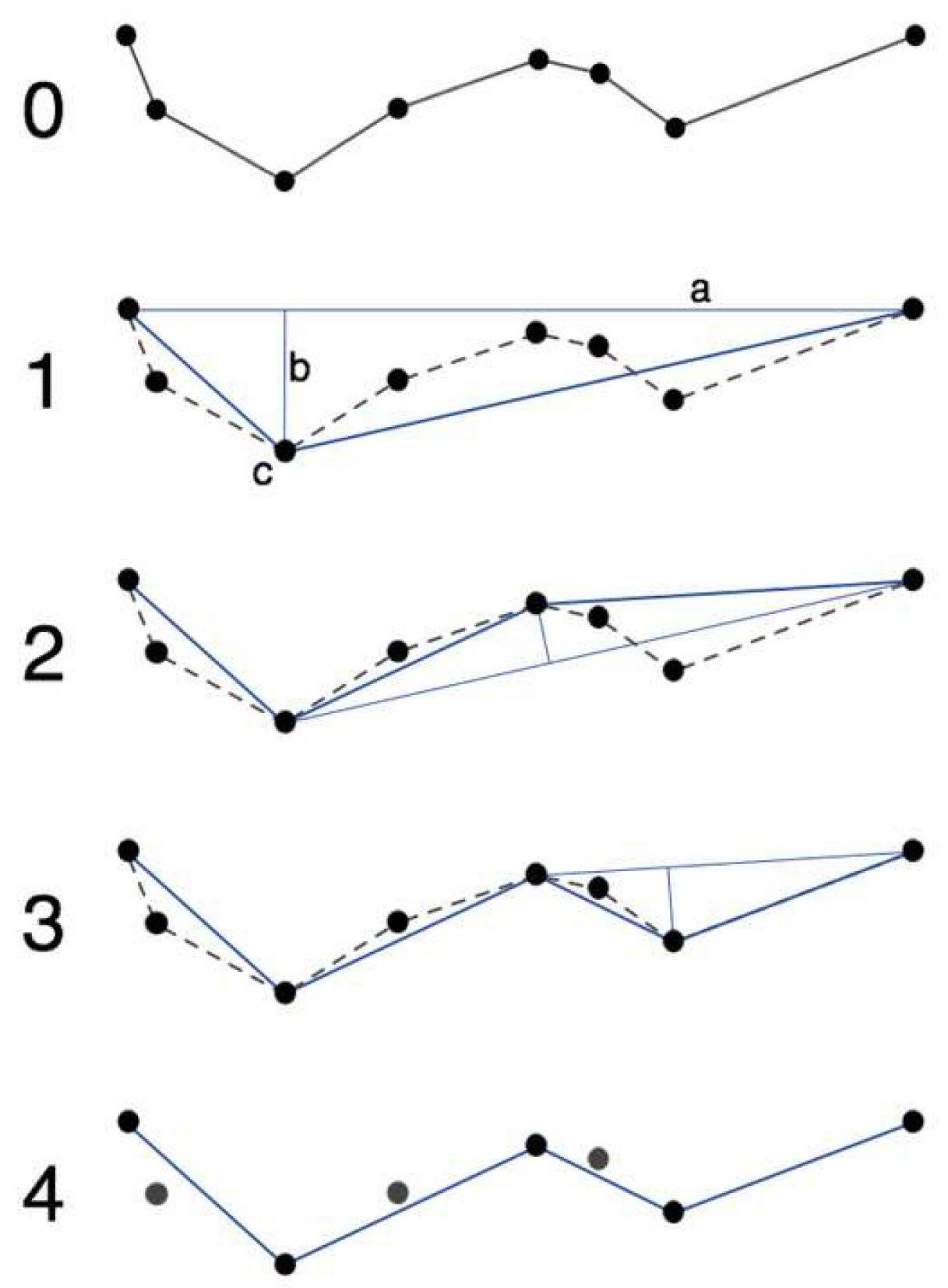
Preprints 81090 g004
Preprints 81090 g005
Figure 5. Evaluation of a point with network information.
Figure 5. Evaluation of a point with network information.
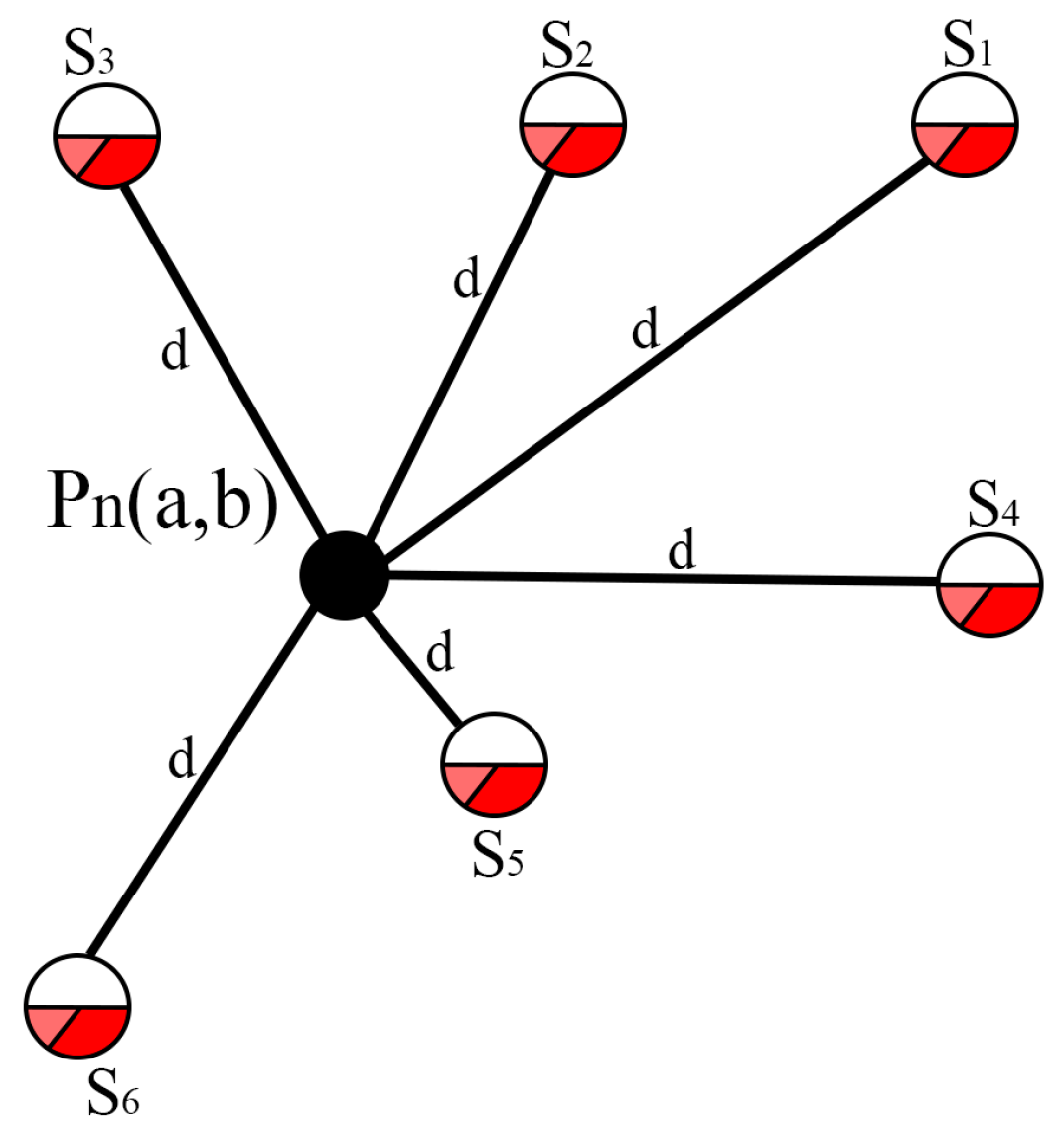
Preprints 81090 g005
Preprints 81090 g006
Figure 6. Network information associated with the street intersection.
Figure 6. Network information associated with the street intersection.
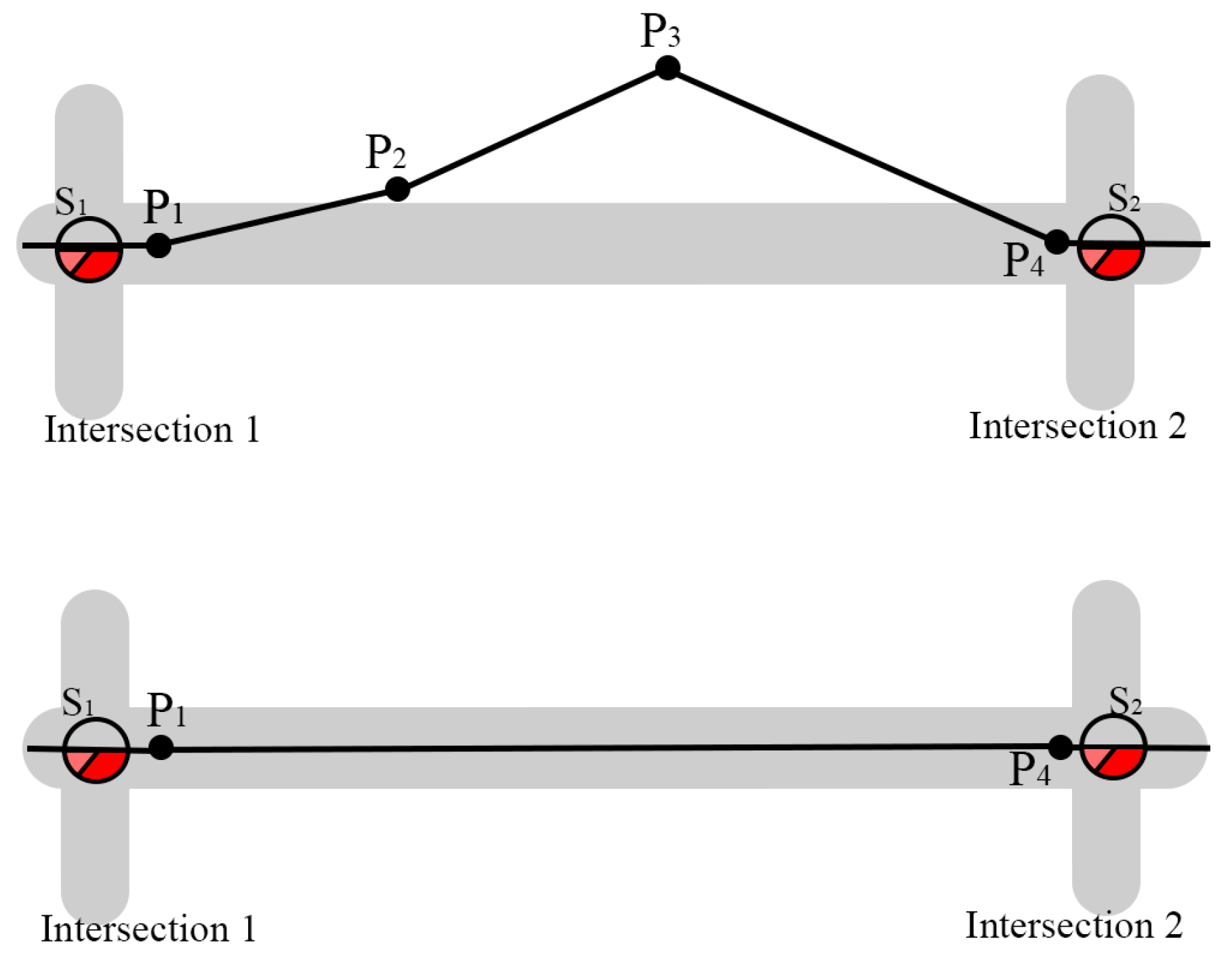
Preprints 81090 g006
Preprints 81090 g007
Figure 7. Comparison: GR Simplification vs TD-TR.
Figure 7. Comparison: GR Simplification vs TD-TR.
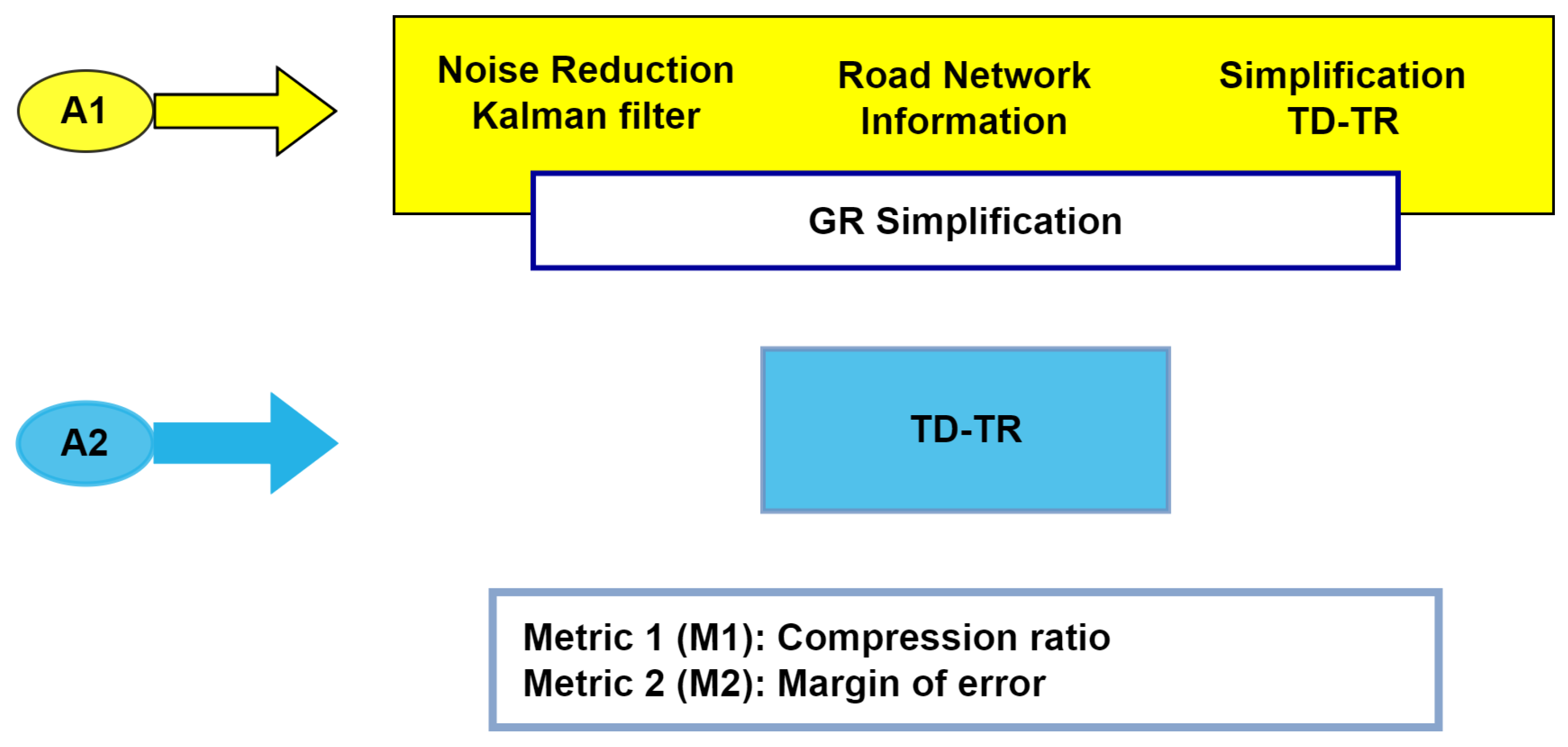
Preprints 81090 g007
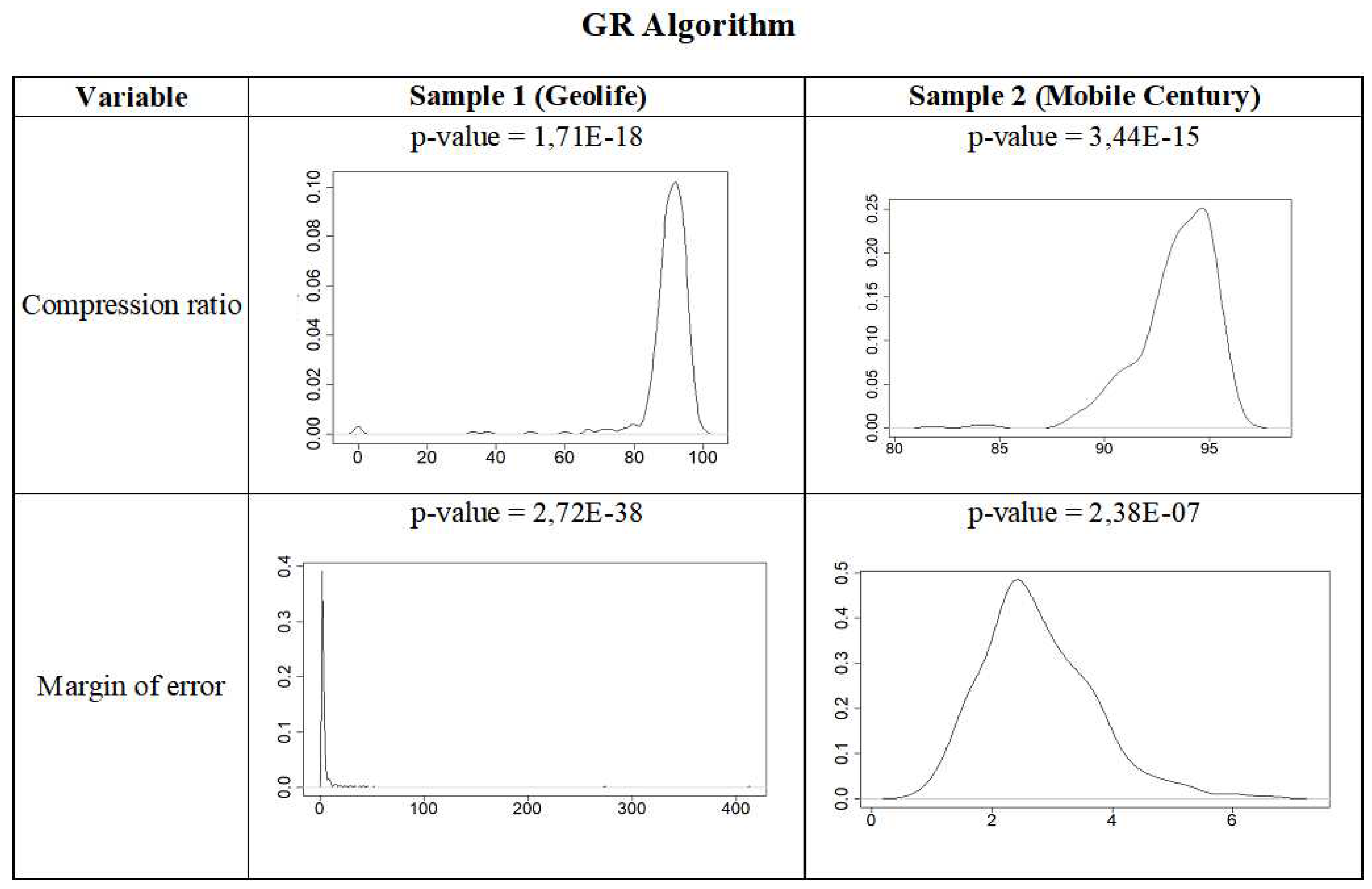
Preprints 81090 g008
Figure 8. Density plot of the obtained results with the GR algorithm.
Figure 8. Density plot of the obtained results with the GR algorithm.
Preprints 81090 g008
Preprints 81090 g009
Figure 9. Density plot of the obtained results with the TDTR algorithm.
Figure 9. Density plot of the obtained results with the TDTR algorithm.
Preprints 81090 g009
Preprints 81090 g010
Figure 10. Mann-Whitney test results for compression ratio.
Figure 10. Mann-Whitney test results for compression ratio.
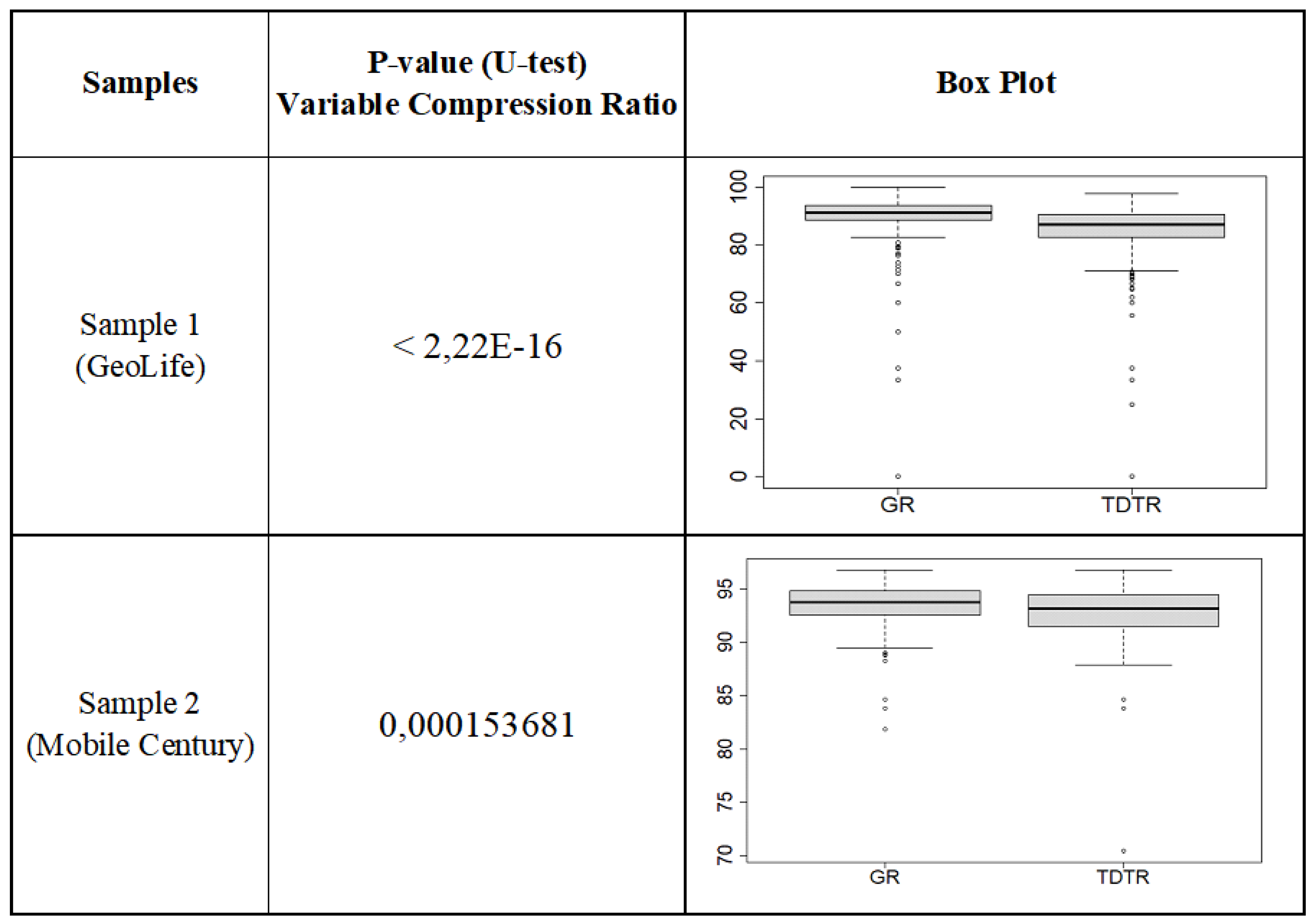
Preprints 81090 g010
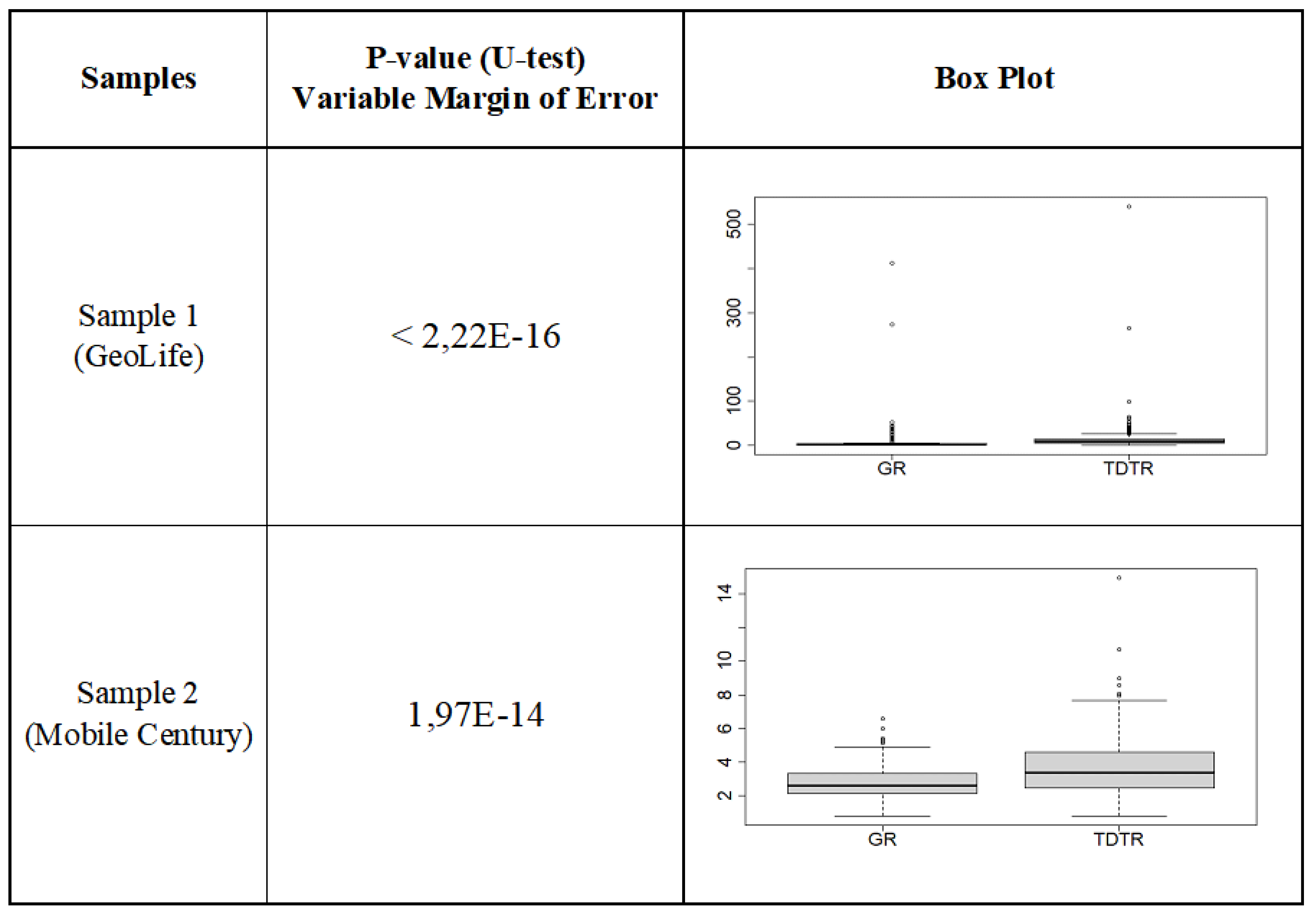
Preprints 81090 g011
Figure 11. Results of Mann-Whitney tests for margin of error.
Figure 11. Results of Mann-Whitney tests for margin of error.
Preprints 81090 g011
Table 1. Average of the results of the initial diagnosis of the simplification algorithms on the selected samples.
Table 1. Average of the results of the initial diagnosis of the simplification algorithms on the selected samples.
Algorithm Processing time (s) Compression ratio (percentage) Margin of error (km)
Douglas-Peucker 1.5011,75 91,60 13,88
Lang 3.159,65 76,19 4,75
Visvalingam 214,70 67,07 0,09
TD-TR 13.852,44 86,01 0,80
Table 2. Comparison of the average obtained results between the TD-TR and GR algorithms.
Table 2. Comparison of the average obtained results between the TD-TR and GR algorithms.
Compression ratio
(percentage)		 Margin of error
(meters)
TD-TR GR TD-TR GR
Sample 1 (Geolife) 85,485 90,214 14,22 6,47
Sample 2 (Mobile Century) 92,787 93,395 3,69 2,77
Average 89,136 91,804 8,955 4,62
Table 3. Shapiro-Wilk’s test results for the selected samples.
Table 3. Shapiro-Wilk’s test results for the selected samples.
Tests GR
(Ratio of
compression)		 GR
(Margin of error)		 TD-TR
(Ratio of
compression)		 TD-TR
(Margin of error)
Sample 1 (Geolife) Rejected Ho Rejected Ho Rejected Ho Rejected Ho
Sample 2 (Mobile Century) Rejected Ho Rejected Ho Rejected Ho Rejected Ho
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated