1. Introduction
In recent years, significant advancements have been made in the development of neural network architectures with reduced hard-coded priors or inductive biases. Traditional approaches, such as manually designing fixed features, e.g., SIFT, LBP [
1,
2,
3], have been replaced by automatic feature-learning strategies powered with more flexible architectures like Convolutional Neural Networks (CNNs) [
4]. Very recently, Vision transformers (ViTs) [
5] have further pushed the boundaries by eliminating hard-coded decisions like translation invariance and local connectivity commonly found in CNNs. However, such models always have huge computational complexity, are extremely data-hungry, and lack interpretability as the complex interactions and attention patterns within the self-attention mechanism. At the same time, such models require higher expert knowledge for adaptively designing neural architectures [
6,
7] for different applications. All of these, coupled with improved training schemes, have facilitated the reemergence of purely Multi-Layer Perceptron (MLP) architectures in computer vision tasks [
8,
9,
10,
11,
12]. Previously, MLPs were largely overlooked or disregarded in computer vision due to their computationally intensive nature. However, recent developments [
8,
9] have made it feasible to harness the potential of MLPs while achieving promising trade-offs between accuracy and design complexity in image classification tasks; for instance, MLPs [
8,
9] have got very promising results when trained and evaluated on large-scale dataset, ImageNet [
13].
However, it is worth noting that these neural network architectures, including MLPs, predominantly operate within the Euclidean space. Euclidean space represents the conventional generalization of our intuitive three-dimensional space but may not be the most suitable representation for all types of data [
14]. For instance, complex datasets such as social networks, human skeletons, sentences, and evolutionary relationships often exhibit hierarchical structures, leading to big distortion when embedding such data in the Euclidean space. Recognizing the limitations of Euclidean representation learning, researchers have explored alternative approaches that leverage hyperbolic spaces, which provide a natural fit for capturing the non-Euclidean nature of such data.
Hyperbolic deep learning [
14], based on the negative curvature of hyperbolic spaces [
15], has been successfully applied to various domains, including Natural Language Processing (NLP) and graph analysis [
16,
17]. Hyperbolic embeddings have been employed for tasks such as text classification [
18], entity typing [
19], word embeddings [
20,
21,
22] and some areas in graphs such as node classification [
17], graph classification [
16,
23], link prediction [
17], and graph embeddings [
24]. While it may not be immediately apparent that images possess a hierarchical data structure, several studies [
23,
25,
26,
27,
28] have demonstrated the effective utilization of hyperbolic spaces for learning image embeddings.
However, due to the challenges of extending hyperbolic neural networks to computer vision, most existing works [
23,
25] related to hyperbolic spaces in the context of computer vision rely on a hybrid framework, in which the Euclidean backbone is first applied to generate embeddings and then a hyperbolic layer is introduced to perform the final prediction. While this approach has shown promise, it still operates within an unable and hard-to-train hybrid setting. Therefore, fully hyperbolic networks that leverage hyperbolic operations and layers to learn feature embeddings need to be explored in the domain.
Therefore, this research is motivated to bridge the gap as we endeavor to address this deficiency by developing a fully hyperbolic neural network architecture without the usage of the tangent space, specifically tailored for computer vision tasks. By embracing the intrinsic hierarchical structures within images and harnessing the power of hyperbolic spaces, we expect that our proposed architecture will offer novel insights and potentially surpass traditional Euclidean-based models in certain scenarios. The contribution of this paper can be summarized as follows:
We present a brand new hyperbolic deep neural architecture, which is called hyperbolic ResMLP (HR-MLP), to explore the potential of the hyperbolic Perceptron to hierarchically model images for computer vision tasks.
The proposed HR-MLP is a fully hyperbolic neural network, which utilizes the Lorentz-based neural operation (Lorentz cross-patch and cross-channel layers), benefiting from its efficiency and manifold-preserving property.
We perform experiments on CIFAR10, CIFAR100, and MiniImageNet to demonstrate comparable and superior performance with their Euclidean counterpart while having much better interoperability.
2. Related Works
2.1. Image Classification in Euclidean space
Image classification is the process of categorizing and labeling images, which are commonly represented by groups of pixels or vectors. In terms of the availability of the class label during training, there are generally supervised and unsupervised Image classifications [
29]. Image classification models, which can be various machine learning methods/architectures, take an image as input and return a prediction about which class the image belongs to.
Before the advent of deep neural networks, especially Convolutional Neural Networks (CNNs), the traditional methods for image classification are heavily based on hand-crafted features, like Histogram of Oriented Gradients (HOG), Scale-Invariant Feature Transform (SIFT), and Local Binary Patterns (LBP) [
1,
2,
3,
30], or Bag-of-Visual-Words (BoVW) [
31], to represent the input images. After that, the feature will be further fed into a classifier, which can be Support Vector Machines (SVM) [
32] or Random Forests [
33], to predict the predefined labels. While traditional methods have been widely used for image classification tasks, they often face limitations in capturing the rich and hierarchical representations such that can not handle large-scale and complex datasets well. CNNs and other deep learning models have largely surpassed traditional methods in terms of accuracy and generalization, especially when applied to large-scale datasets like ImageNet [
13]. At the deep learning age, numerous neural architectures and techniques are proposed to automatically learn feature representations from a dataset, and in most cases feature learning and class prediction are combined in an end-to-end fashion. In terms of neural architectures, CNNs [
4] are now one of the most commonly used networks for images such as Residual Networks (ResNets) [
34], which introduces skip connections to alleviate the vanishing gradient problem, Inception Networks [
35], which utilize multiple parallel convolutional layers of different sizes to capture features at various scales, promoting the extraction of both fine-grained and high-level contextual information, DenseNet [
36], Squeeze-and-Excitation Networks (SENet) [
37] and EfficientNet [
38], which proposes a compound scaling method to achieve excellent trade-offs between model size and performance.
Recently, to further improve the representation ability of the neural network, self-attention mechanisms are introduced. Dosovitskiy et al. [
5] proposed an attention-based method, which is Vision Transformers (ViTs). The models process images in a patch-based manner (in which the image is treated as a sequence of tokens) and apply the self-attention mechanism to capture global correlations. This approach has achieved remarkable results in various image classification benchmarks. Unlike this, the Residual Multi-Layer Perceptrons (ResMLP) [
9] removed self-attention and expect to provide a much more efficient way to learn rich features. In particular, they combined the strengths of MLPs and residual connections and give more flexibility to the learning process. These models achieve competitive performance in image classification tasks while maintaining the simplicity and interpretability of MLPs.
Parallel to the design of the neural architectures, new techniques are also presented to improve the task. For instance, data augmentation techniques [
39], including different transformations, are commonly used to augment the training data and improve the generalization ability of image classifiers. Transfer learning techniques [
40], such as utilizing pre-trained models like VGG [
41], ResNet [
34], or InceptionNet [
35] trained on large-scale datasets like ImageNet [
13], have been widely adopted for image classification. By leveraging features learned from these models, transfer learning enables effective classification even with limited labeled data. Since designing neural architectures require high expert knowledge, both for deep neural networks with non-trivial optimizations and knowledge for a specific domain (e.g., segmentation, or different modalities), Neural Architecture Search (NAS) [
42] is introduced to automate the search for optimal network architectures for various datasets. NAS [
42] has been utilized to discover novel architectures that achieve state-of-the-art performance in image classification tasks.
It is worth that all of the methods here are in Euclidean space. These works highlight the extensive research efforts and advancements in image classification within the Euclidean space, leading to the development of highly effective and efficient neural network models for a wide range of applications. However, to give better interpretability, many attempts were made in constructing neural networks in the non-Euclidean space [
23,
25], while just turning to its tangent space, which has a huge space to improve.
2.2. Hyperbolic Deep Learning
Hyperbolic Deep Learning [
14] is a new research field of deep learning, which aims to learn compact and rich feature representation, utilizing hyperbolic spaces as the underlying mathematical structure for representing and processing data. Unlike traditional deep learning methods that primarily operate in Euclidean spaces, hyperbolic deep learning leverages the unique properties of hyperbolic geometries to handle data with hierarchical structures, non-Euclidean relationships [
16], and complex interconnectedness [
14,
17]. Hyperbolic deep learning has emerged as a promising paradigm in various domains, including graph analysis [
16,
17,
23,
43], Natural Language Processing (NLP)[
18,
19,
20,
21], and other complex data structures. Complex hierarchical relationships are prevalent in social networks, biological networks, and other graph data [
14]. By leveraging the negative curvature of hyperbolic spaces, in graph analysis, Hyperbolic deep learning has shown significant success in tasks such as node classification [
17], graph classification [
16,
23], and link prediction [
17], demonstrating significant potential to its Euclidean counterparts. For, instance, in the field of NLP, hyperbolic embeddings could provide extremely compact embedding (even 2 dimensions) [
22], which has demonstrated its efficacy in tasks like text classification, entity typing, word embeddings, and sentence representations.
In recent years, hyperbolic embeddings have gained attention in computer vision due to their ability to capture hierarchical relationships among data points. Several works have explored the application of hyperbolic learning in classical computer vision tasks.
One of the early attempts in utilizing hyperbolic embeddings for computer vision tasks comes from Khrulkov et al. [
25]. They argue that hierarchical relations between images are common in computer vision tasks, such as image retrieval and classification. In their work, they showed that feature embeddings of popular architectures, including ResNet [
34], VGG19 [
44], and InceptionV3 [
35], exhibit hyperbolicity on various datasets like CIFAR10, CIFAR100 [
45], CUB [
46], and MiniImageNet. However, their approach utilized hyperbolic layers along with Euclidean backbones, thus only partially leveraging the full potential of hyperbolic geometry.
Similarly, in [
23], a Poincaré ST-GCN was introduced for skeleton-based action recognition. They modeled the input sequence (skeletons) as a graph in the hyperbolic space, demonstrating the benefits of hyperbolic geometry for capturing spatial relationships. Nevertheless, their work mainly focused on applying hyperbolic transformations to specific components of the architecture without building a complete hyperbolic neural network.
Additionally, [
47] proposed hyperbolic manifolds as an alternative for image segmentation, enabling pixel-level classification with hierarchical formulation. Their work showed how hyperbolic spaces offer natural uncertainty estimation measures and improved zero-label generalization compared to Euclidean counterparts. However, similar to the previous works, they did not fully explore the potential of building a full hyperbolic neural network for computer vision tasks.
While the mentioned works have made significant strides in applying hyperbolic learning to computer vision, they have primarily used hyperbolic layers or transformations in conjunction with traditional Euclidean networks, limiting the realization of the full benefits of hyperbolic geometry. As a result, it is very valuable to develop a complete hyperbolic neural network for computer vision tasks. Building such a full hyperbolic neural network has the potential to enhance feature representations, improve generalization, and enable more efficient computations, opening new avenues for computer vision research.
3. Preliminary
Hyperbolic Geometry [
14], or the Lobachevsky-Bolyai-Gauss geometry, is a non-Euclidean geometry having a constant negative sectional curvature. This geometry satisfies all of Euclid’s five postulates except the last parallel postulate, as illustrated in
Figure 1.
Unlike Euclidean geometry, where the sum of the angles in a triangle is always 180 degrees, in hyperbolic geometry, the sum of the angles in a triangle is less than 180 degrees. This property is a consequence of the negative curvature of the hyperbolic plane. Distances in hyperbolic space grow exponentially as one moves away from a fixed point. As a result, objects in hyperbolic space appear to expand rapidly as they move away from an observer. The distance between two points in hyperbolic space is measured along the unique geodesic (the hyperbolic equivalent of a straight line) connecting them. Hyperbolic distance is often used to define similarity measures in hyperbolic embeddings. Hyperbolic geometry has found applications in various scientific fields, including physics, cosmology, computer graphics, and machine learning. In machine learning, hyperbolic geometry has been applied to design novel deep learning models, particularly in hyperbolic deep learning, to handle data with hierarchical or tree-like structures. By utilizing hyperbolic spaces, current studies aim to improve the representation and processing of complex data, such as graphs, hierarchical text data, and relational data, where traditional Euclidean spaces may not be the most suitable choice. Hyperbolic geometry provides a powerful and elegant mathematical framework to understand and analyze such intricate structures in a more efficient and expressive manner.
3.1. Topological Spaces and Manifold
A topological space [
14] is a set equipped with a collection of open sets that satisfy certain properties. Open sets are subsets of the space that are considered "open" in the sense that they contain a neighborhood around each of their points. These open sets must fulfill three conditions:
The entire space and the empty set are both open.
The intersection of any finite number of open sets is open.
The union of any number of open sets is open.
Based on this we provide the definition of a manifold. A d-dimensional manifold (which can be embedded in ) is a topological space that can be locally approximated by a d-dimensional Euclidean space . For any point , there is a homeomorphism between the neighborhood of x and the Euclidean space . Lines and circles are examples of one-dimensional manifolds. Planes and spheres are examples of two-dimensional manifolds which are called surfaces. The notion of the manifold is a generalization of surfaces in any dimension d. The tangent space at point is a d-dimensional hyperplane which is embedded in that locally approximates the manifold around the point x.
3.2. Isometric Models in the Hyperbolic Space
Hyperbolic space is a homogeneous space with constant negative curvature. It is a smooth Riemannian manifold and as such locally Euclidean space. The hyperbolic space can be modeled using the commonly used five isometric models [
48,
49], which are the Lorentz (hyperboloid) model, the Poincaré ball model, the Poincaré half-space model, the Klein model, and the hemishpere model. In the following parts, we will detail these models. Note that we describe the model by fixing the radius of the model to 1 for clarity, without loss of generality.
3.2.1. Lorentz Model
The Lorentz model
of an
n dimensional hyperbolic space is a manifold embedded in the
dimensional Minkowski space. The Lorentz model is defined as the upper sheet of a two-sheeted n-dimensional hyperbola with the metric
, which is
in which the
represents the Lorentzian inner product:
where
is a diagonal matrix with entries of 1s, except for the first element being -1. For any
, we can get that
. The distance in the Lorentz Model is defined as
The main advantage of this parameterization model is that it provides an efficient space for Riemannian optimization. An additional advantage is that its distance function avoids numerical instability, when compared to Poincaré model, in which the instability arises from the fraction.
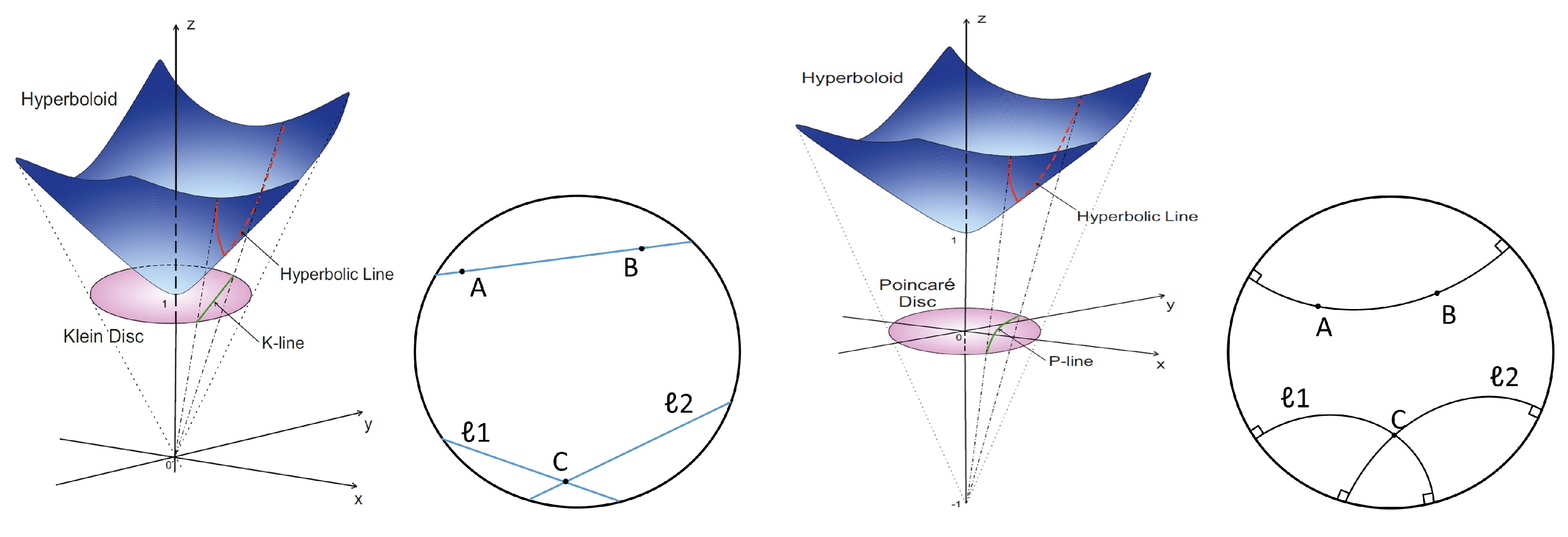
3.2.2. Klein Model
Klein model is also known as the Beltrami–Klein model, named after the Italian mathematician Eugenio Beltrami and German mathematician Felix Klein. The Klein model of hyperbolic space is a subset of
. As illustrated in
Figure 2. It is the isometric image of the Lorentz model under the stereographic projection [
49]. The Klein model is obtained by mapping
to the hyperplane
, using rays emanating from the origin. Formally, the Klein model is defined as
The distance is
A straight line,
e.g., line
in the second figure from the left of
Figure 2, in Klein model is an intersection of a plane with the disk, thus it is still straight like in Euclidean space. Therefore, the Klein model is commonly used to compute the middle point. This model is not conformal to the Euclidean model, which means that angles and circles are distorted,
3.2.3. Poincaré Model
The Poincaré model, as shown in
Figure 2, is given by projecting each point of
onto the hyperplane
, using the rays emanating from (-1, 0,..., 0). The Poincaré model
is a manifold equipped with a Riemannian metric
. This metric is conformal to the Euclidean metric
with the conformal factor
, and
. Formally, an
n dimensional Poincaré unit ball (manifold) is defined as
where
denotes the Euclidean norm. The distance between
is defined as:
3.2.4. Poincaré half plane Model
The closely related Poincaré half-plane model in hyperbolic space is a Riemannian manifold
, where
is the upper half space of an
n-dimensional Euclidean space. And the metric
is given by scaling the euclidean metric
. The model
can be obtained by taking the inverse of Poincaré model,
, with respect to a circle that has a radius twice that of
. The distance is
3.2.5. Hemisphere model
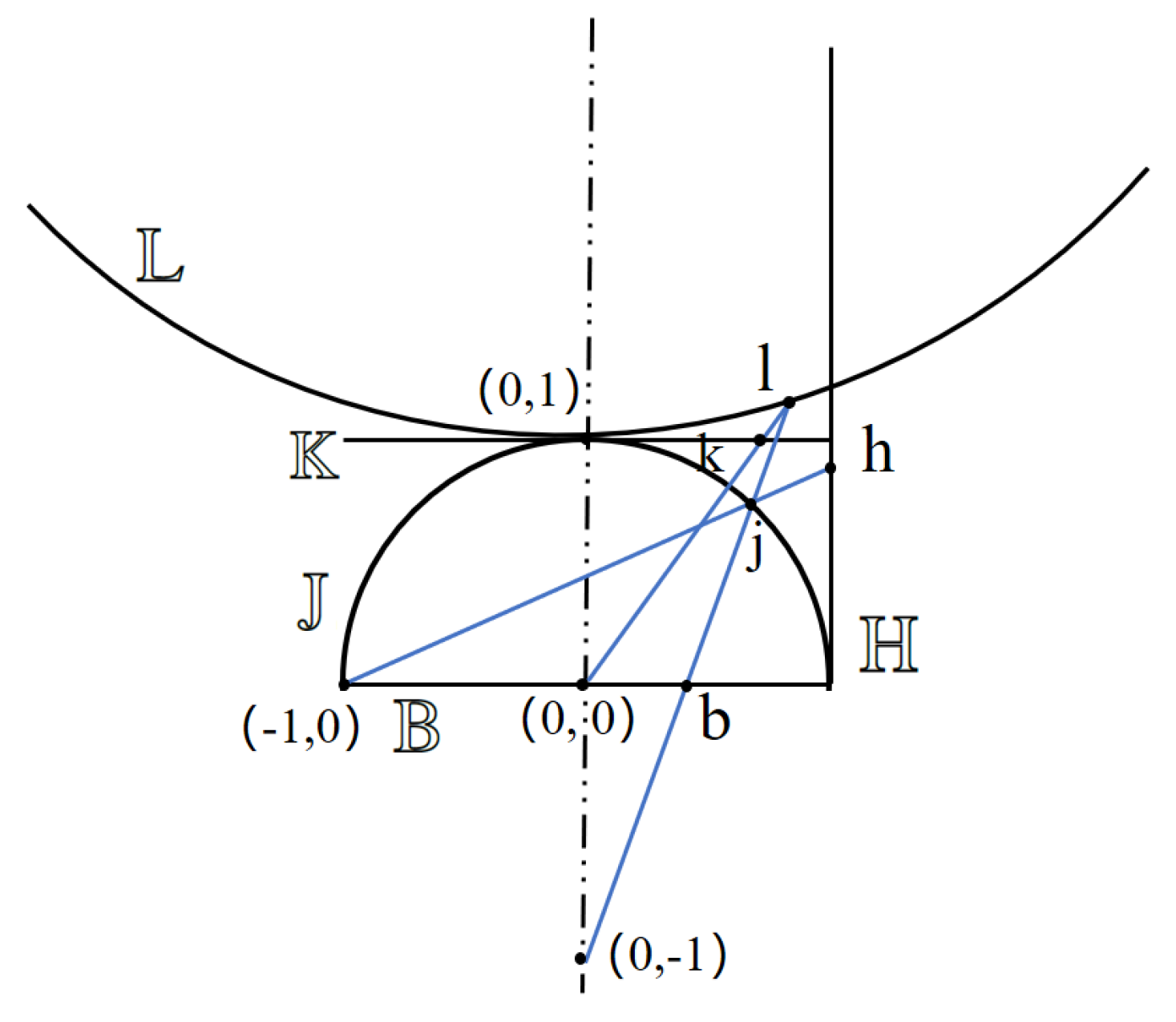
The hemisphere model is also called the Hemisphere model, which is not as common as the previous four models. Instead, this model is employed as a useful tool for visualizing transformations between other models. The hemisphere model is defined as
The five isometric models [
48,
49] are embedded sub-manifolds of ambient real vector spaces. In fact, these five models are equivalent models of the hyperbolic space. There are closed-form expressions for mapping between these hyperbolic models. As illustrated in
Figure 3, we display their model in a 2-dimensional space and demonstrate their relationship.
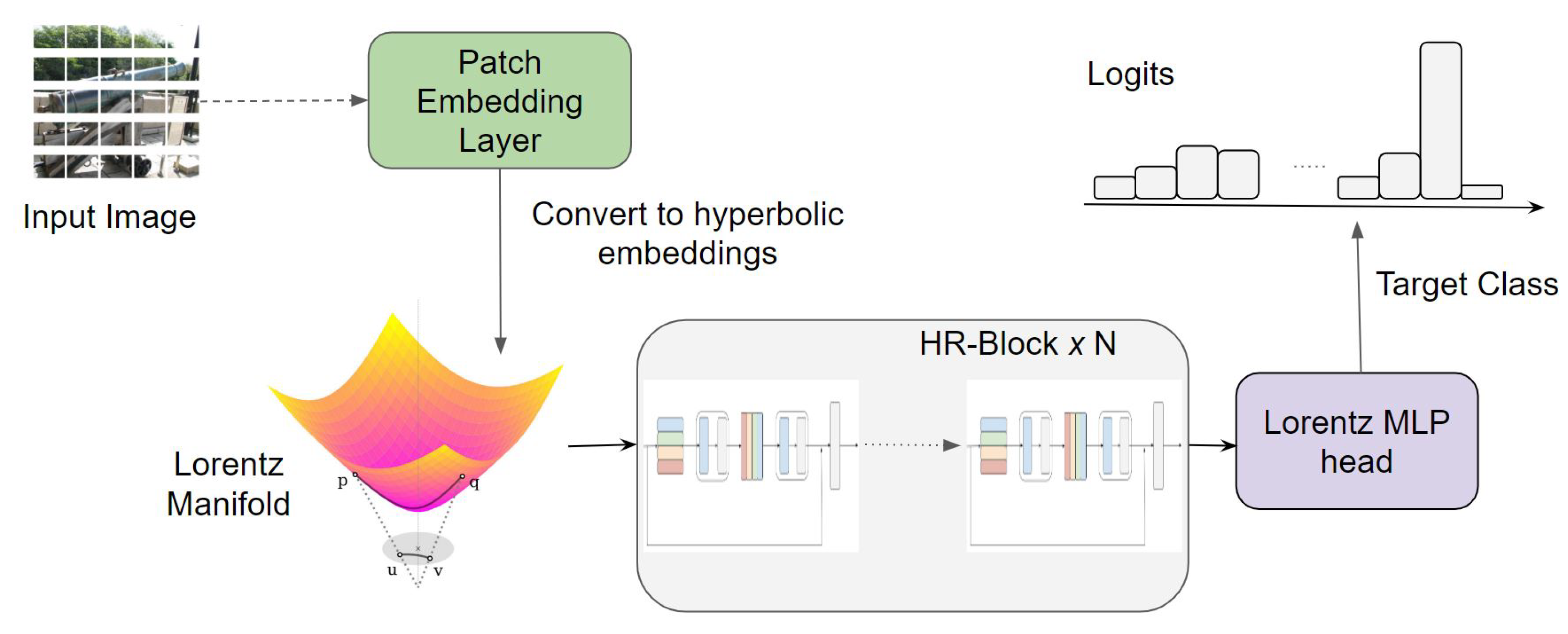
4. Methodology
In this section, we will describe our method, the efficient hyperbolic residual MLP, HR-MLP. The entire neural architecture is illustrated in
Figure 4. Initially, an image is taken as an input. It is divided into patches just like ViT, ResMLP, g-MLP, and MLP-mixer [
5,
8,
9,
10], then passed through a euclidean linear layer to create patch embeddings. Then the Euclidean embeddings are converted to the hyperbolic domain via exponential mapping, particularly using the Lorentz model, considering the representation ability and the optimization trade-off. The hyperbolic domains are passed to a block dubbed as HR-block that contains Lorentz linear layers for linear transformations in the hyperbolic domain. Finally, after passing through the block
the embeddings are then pooled using adaptive average pooling [
50]. Like HyboNet [
43], we use a hyperbolic MLP head to perform classification for the feature learned from the Lorentz model. In the following part, we will detail each neural component.
4.1. Lorentz Linear Embedding
Given an image
, we divide the image into overlapping patches [
51] by using convolution with zero padding which is our patch embedding layer. Specifically, an image
is fed to a convolution with stride
S, kernel size of
, padding size
, and the output channels
. The output size is
. We rearrange the output shape to
where P is the number of patches and it is calculated by
. Let
F be the feature learned from the patch embedding. As this feature
F is still in the Euclidean space, we need to lift the feature such that gets the corresponding feature in the Lorentz manifold. To this end, the exponential map function is applied, which is
in which we assume that the feature is at a tangent space of a feature point 0, which we choose the origin of the Lorentz model. The feature representation
F is then mapped to the Lorentz manifold. In this way, we get the feature representation that lies on the Lorentz manifold.
4.2. Lorentz Linear Layer
Basic operations, like addition, multiplication, and poolings, construct linear Layers. They are easy and efficient to be applied in the Euclidean space. The features F are now converted into the hyperbolic space where the Euclidean operations cannot be applied, as most are not manifold-preserving. So currently, we need to provide Lorentz operations that are able to keep the learned feature on the manifold after the transformation.
An alternative route is to transfer each point in the hyperbolic space to the tangent space, where the tangent space at that point is a Euclidean subspace. Therefore we can use Euclidean neural operations in this tangent subspace. Existing works [
52,
53], formalize most Euclidean operations for hyperbolic networks by transforming features between hyperbolic spaces and tangent spaces via logarithmic and exponential maps, such that neural network operations can directly be performed in the tangent spaces. However, tangent spaces are not the optimal choice for several reasons. First, the composition of these functions is complicated as features need continuously move back and forth between two spaces for each layer. Second, such transformation also leads to values ranging to infinity, which significantly reduces the stability of the model. Last but not least, tangent space is a linear approximation of hyperbolic space, which would not make full use of the advantages of non-Euclidean space.
To avoid such transformation between hyperbolic and tangent spaces, inspired by Chen et al. [
43], we proposed Lorentz (Hyperboloid) Linear Layer (
) fully in the hyperbolic space by formalizing Lorentz manifold-preserving operations for neural networks without using tangent spaces. Taking inspiration from the theory of special relativity which uses Minkowski space (Lorentz model), our framework selects the Lorentz model as the feature space. The operations are formalized via the relaxation of the Lorentz transformations to build hyperbolic neural networks including the linear layer, attention layer, etc. Additionally, from Chen et al. [
43] we know that performing linear transformation in the tangent space at the origin of hyperbolic spaces [
52,
53] is equivalent to performing a Lorentz rotation with relaxed restrictions. Therefore, by using this Lorentz rotation, we can build a Lorentz Linear Layer fully hyperbolic space, which is faster, more stable, and can achieve comparable or even better results than previous methods.
Here we introduce how to build the Lorentz Linear Layer. Simply, the linear layer can be a mapping matrix
, which can project the feature
from
dimension to
. As for the feature representation on the manifold, we can also decouple the linear operation into Lorentz boost and rotation parts, which are
. In this way, we can only let the operation perform on the rotation part while at the same time letting the extra boost part work as a regularizer, such that the entire features are always on the Lorentz manifold. The general formula is as follows
where
is the feature input from previous layer,
are linear operation mentioned above and
is the other operation functions, e.g., dropout, activation function, in the linear layer. This formula is derived from the Lorentz boost and Lorentz rotation which are polar decompositions of Lorentz transformation [
54]. One can easily verify that the norm of the feature is fixed and on the manifold. Compared to hyperbolic linear layers in Ganea et al. [
52] and Nickel and Kiela [
53], this linear layer is far more expressive, efficient, and stable as it does not use complicated logarithmic and exponential maps. They dub their transformation as pseudo-Lorentz rotation as it is a relaxation of the Lorentz transformations.
4.3. Lorentz cross-channel and cross-patch layers
Attention-based methods often involve cost computations to calculate the correlation across long-range positions. However, MLPs are trying to avoid such a burden while introducing a much more efficient way to perform information aggregation. Of which, the cross-channel and cross-patch layers are introduced as the fundamental components of MLP and its variants [
9].
The cross-channel and cross-patch layers are two function models, which are all-MLP architecture that uses linear layers to perform feature information updating. They consist of multiple layers of identical size (which means they will not change the feature resolutions). The first one is also called the channel-mixing MLP, which acts on rows (channels) of the feature and tries to exchange the feature information from different patches. This model is shared across all rows. As a comparison, the second MLP cross-patch layer, which also called token-mixing MLP. This acts on columns of each feature and performs the information across different channels. Combining this two, our method provides a much more efficient way to update the feature when compared with attention-based methods.
Our Lorentz cross-channel layer Uses Lorentz linear layer to perform transformations on all patches independently, to which the architecture is very similar. The only difference is the Lorentz Linear Layer () is followed to force the output features to be still on the manifold. Likewise, the Lorentz cross-patch layer is extended from its Euclidean counterpart, aiming to perform transformations on all channels independently. There is also a function to make sure the module is manifold-preserving.
Figure 5.
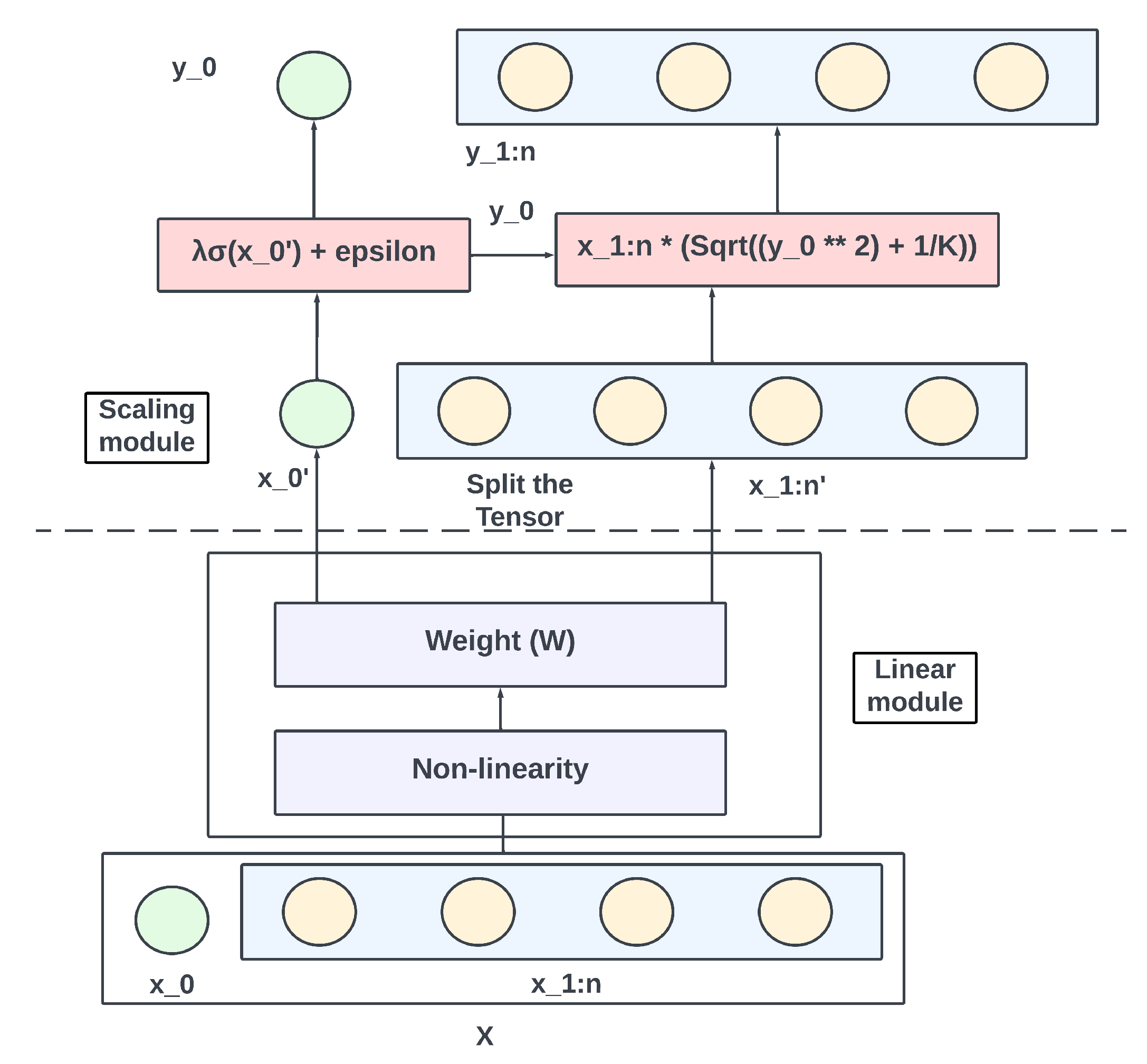
The Lorentz linear layer in the HR-block. There are two modules in this layer, which are the linear module and the scaling module, respectively. The former module performs the linear transformation for the input (nonr-linearity can be also applied) and the then following scaling module ensures the feature lie on the manifold.
Figure 5.
The Lorentz linear layer in the HR-block. There are two modules in this layer, which are the linear module and the scaling module, respectively. The former module performs the linear transformation for the input (nonr-linearity can be also applied) and the then following scaling module ensures the feature lie on the manifold.
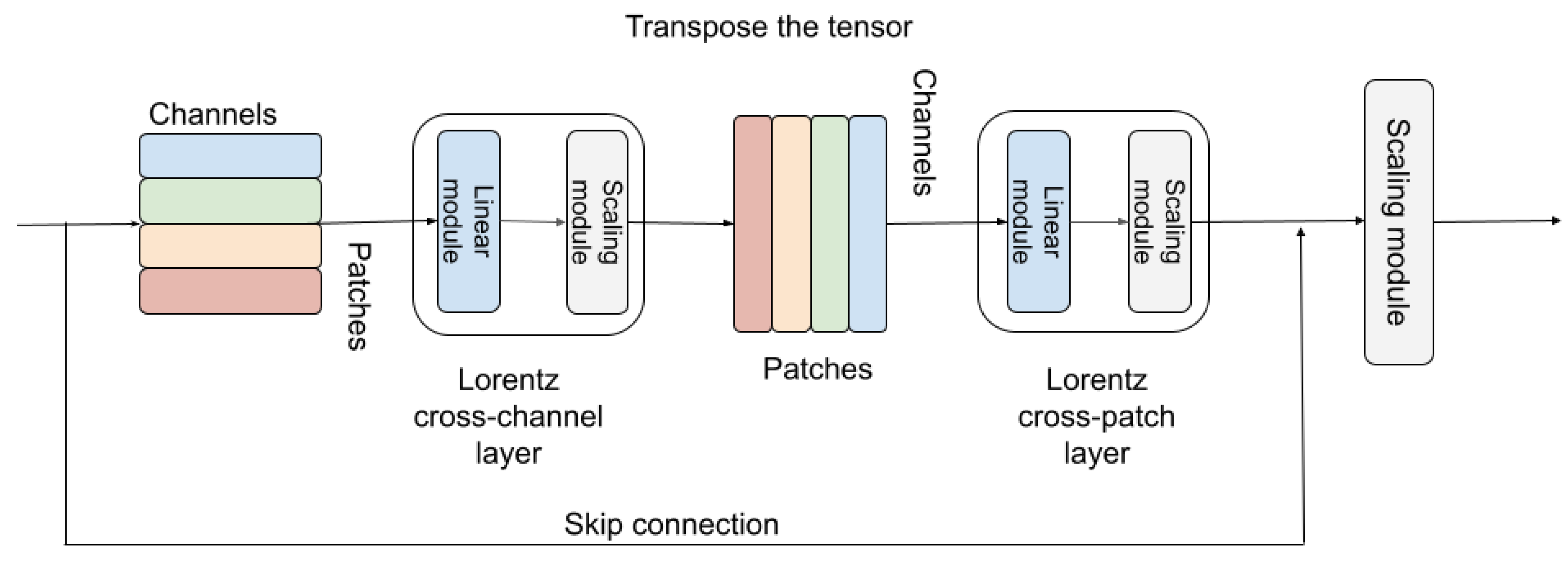
Figure 6.
The HR-Block in HR-MLP. The HR-block consists of the hyperbolic operations that transform the input features and ensure that features lie in the manifold. The features are first transformed via Lorentz cross-channel layer applied to patches. After transposing the tensor, it is passed through the Lorentz cross-patch layer applied to channels. Finally, after adding the transformed tensor with the input via skip connection, the result is passed through a scaling module which ensures that the features lie back in the Lorentz manifold.
Figure 6.
The HR-Block in HR-MLP. The HR-block consists of the hyperbolic operations that transform the input features and ensure that features lie in the manifold. The features are first transformed via Lorentz cross-channel layer applied to patches. After transposing the tensor, it is passed through the Lorentz cross-patch layer applied to channels. Finally, after adding the transformed tensor with the input via skip connection, the result is passed through a scaling module which ensures that the features lie back in the Lorentz manifold.
4.4. Hyperbolic MLP head
Once the feature is learned on the manifold, we will need to make the class prediction based on the feature representation of each sample, from the logits. However, as such features are lies in the non-Euclidean space, we cannot apply the Euclidean MLR to compute the logits of each category. Therefore, we build a Hyperbolic MLP head to make the class predictions based on the Lorentz feature. In particular, we build a learnable classification hyper-plane for each class. Then the Lorentz distances to each hyper-plane are computed based on Equation
3. Once we have the distances, we can make the prediction based on the shortest distance.
Compared with Vision transformer and its variants, our method is much more efficent as the replacement of self-attention sublayer by a linear layer with GELU non-linearity. This also makes the training more stable as the removal of batch-specific or cross-channel normalization, e.g., the BatchNorm, GroupNorm or LayerNorm, following the same training scheme as DeiT [
55].
5. Experiment
We train our HR-MLP model on CIFAR10, CIFAR100, and MiniImageNet for comparison. All the models have been trained from scratch and in the following subsection, we describe the hyperparameters we used to train on the dataset.
5.1. Datasets and metrics
The proposed method is evaluated on three publicly available datasets, i.e., CIFAR10 [
45], CIFAR100 [
45], and MiniImageNet [
56]. CIFAR10 and CIFAR100 are commonly used in image classification tasks. As indicated by the names, there are 10 classes and 100 classes for them. For MiniImageNet, the dataset is consisting of 60, 000 color images (RGB) of size
with 100 classes, of which each class has 600 examples. This dataset is more complex than CIFAR10 and CIFAR100, but fits in memory on modern machines, making it very convenient for rapid prototyping and experimentation.
We report the accuracy of the testing part of each dataset. We compared with state-of-the-art methods, including, CNN, MLP-Mixer [
8], and ResMLP [
9], in a compact setting (number of parameters is less than one million). Even though the neural architectures and embedding spaces are different, we make a fair comparison by constructing neural architectures with similar parameters.
5.2. Implementation
We used a batch size of 32 in all of our experiments. We used the cross entropy loss function with a label smoothing value of 0.1. All the models were trained on Tesla P100 16 GB GPU available on Kaggle. All the models used the GELU activation function [
57] for non-linearity. The HR-MLP model used Riemannian SGD [
58] with a learning rate value of 0.005 and weight decay of 0.05. While the ResMLP model used the Adamw [
59] optimizer with a learning rate value of 0.005 and weight decay value of 0.05. All the models were trained for a total of 150 epochs with a warmup for 20 epochs and a cosine annealing scheduler starting from epoch 40. The models were trained without any augmentation except for converting the images to tensors and normalizing the tensors. The model was evaluated based on the accuracy of the dataset’s test set.
6. Results
We compared different methods, including traditional CNN neural architecture and current advanced MLP neural architectures. As listed in
Table 1, we can see a clear advantage of the proposed method when compared with the other methods. The accuracy of our method is significantly higher than any other given method. For instance, when evaluating the CIFAR10 dataset, our method can be at least
higher than previous state-of-the-art methods, in the compact setting with similar parameters. This superiority could be even higher when compared with traditional architectures, like CNN. Moreover, with around 1M parameters, our method achieves
48.55% on the CIFAR100 dataset while CNN only gets 29.59%. On the more challenging dataset, MiniImageNet, our method achieves
37.47%, which is even 17.3% higher than CNN mehod and also better the previous state-of-the-art method, ResMLP, which clearly demonstrates the effectiveness of the proposed method using hyperbolic space.
To summarize, in this compact setting (which is valuable for local applications with limited resources), our method shows a clear superiority on different public datasets when compared with the baseline methods in the Euclidean space. This provides evidence for the potential of learning image embedding in the hyperbolic space for downstream tasks.
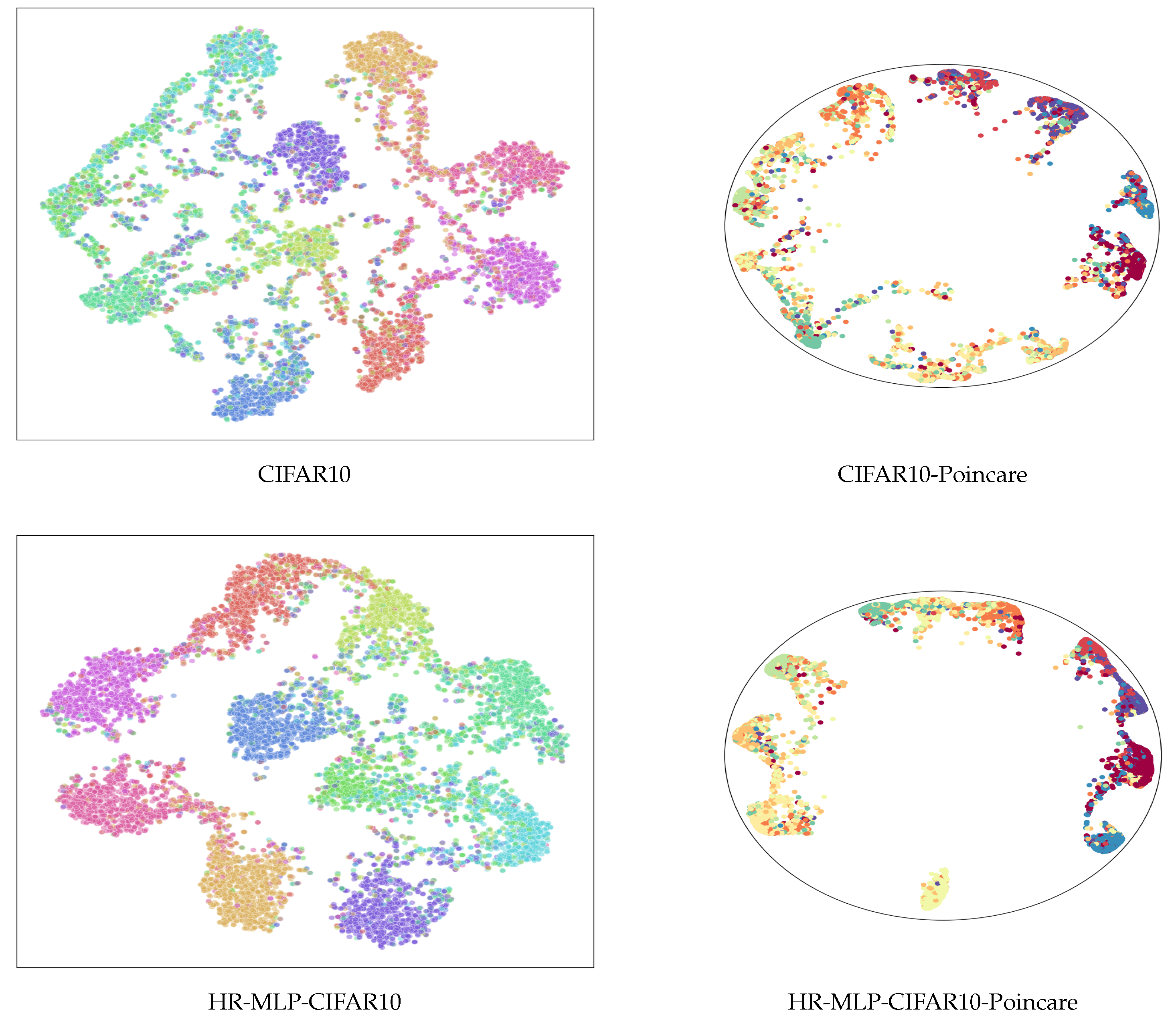
Here we also show the feature distribution using t-SNE [
60] to further demonstrate the advantage of the proposed hyperbolic neural network. As illustrated in
Figure 7, even though the models are very small, we can still observe clear clusters for different categories. However, for its Euclidean counterpart, it seems very struggling to computer distinguish patterns with such limited computational resources. This further proves the effectiveness of the proposed method.
7. Conclusions
This paper proposes a new totally new framework for image classification in the hyperbolic space. Inspired by success in graph learning using hyperbolic graph neural networks, we model the underlying hierarchical relationships using hyperbolic geometry. Our approach combines the success of the current recovery of MLP and the exponential growth of hyperbolic space, expecting to address the research gap surrounding the utilization of hyperbolic neural networks for computer vision tasks. The proposed method constructs ResMLP, including the cross-channel and cross-patch layers, in the hyperbolic space with neural operations fully performed in hyperbolic space, without the need for Euclidean/non-Euclidean space transformations back and forth. Our proposed methods offer several advantages for real-world image classification with hierarchies. They provide feature embedding with less distortion. Additionally, the models are generally much more compact than their Euclidean counterparts. Besides, such hyperbolic neural architectures also provide much better interpretability. The experimental results show that our methods achieve better performance on different datasets than previous methods in this compact setting. By embracing the hierarchical structures within images and leveraging the power of hyperbolic spaces, our work offers novel insights and presents a promising direction for advancing computer vision techniques.
However, a limitation of our hyperbolic methods is that they focus on compact models that provide better interpretability, neglecting the case that there are unlimited computational resources. It would be better if explore bigger hyperbolic neural models and compare their Euclidean counterparts. Despite this limitation, our approach proves effective in practice, as resources are limited in many. In the future, we plan to explore bigger neural network architectures as deep/big as neural architectures like ViT. Additionally, we aim to apply our method to various datasets and investigate strategies to improve the classification model as the diversity of training datasets increases.
Author Contributions
Methodology and Discussion, A.O.A. S.T. and W.P.; software, A.O.A.; writing—original draft, A.O.A.; writing—review and editing,A.O.A. S.T. and W.P.; supervision, W.P.; formal analysis, A.O.A. and W.P.: All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the 2005 IEEE computer society conference on computer vision and pattern recognition (CVPR’05); 2005; Volume 1, pp. 886–893. [Google Scholar]
- Ahonen, T.; Hadid, A.; Pietikäinen, M. Face recognition with local binary patterns. In Proceedings of the Computer Vision-ECCV 2004: 8th European Conference on Computer Vision, Prague, Czech Republic, 11–14 May 2004; pp. 469–481. [Google Scholar]
- Lindeberg, T. Scale invariant feature transform. 2012.
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Advances in neural information processing systems 2012, 25. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; Uszkoreit, J.; Houlsby, N. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. In Proceedings of the International Conference on Learning Representations; 2021. [Google Scholar]
- Peng, W.; Hong, X.; Chen, H.; Zhao, G. Learning graph convolutional network for skeleton-based human action recognition by neural searching. In Proceedings of the AAAI conference on artificial intelligence; 2020; Volume 34, pp. 2669–2676. [Google Scholar] [CrossRef]
- Peng, W.; Hong, X.; Zhao, G. Video action recognition via neural architecture searching. In Proceedings of the 2019 IEEE international conference on image processing (ICIP); 2019; pp. 11–15. [Google Scholar]
- Tolstikhin, I.O.; Houlsby, N.; Kolesnikov, A.; Beyer, L.; Zhai, X.; Unterthiner, T.; Yung, J.; Steiner, A.; Keysers, D.; Uszkoreit, J.; others. Mlp-mixer: An all-mlp architecture for vision. Advances in neural information processing systems 2021, 34, 24261–24272.
- Touvron, H.; Bojanowski, P.; Caron, M.; Cord, M.; El-Nouby, A.; Grave, E.; Izacard, G.; Joulin, A.; Synnaeve, G.; Verbeek, J.; others. Resmlp: Feedforward networks for image classification with data-efficient training. IEEE Transactions on Pattern Analysis and Machine Intelligence 2022. [CrossRef]
- Liu, H.; Dai, Z.; So, D.; Le, Q.V. Pay attention to mlps. Advances in Neural Information Processing Systems 2021, 34, 9204–9215. [Google Scholar]
- Melas-Kyriazi, L. Do you even need attention? a stack of feed-forward layers does surprisingly well on imagenet. arXiv 2021, arXiv:2105.02723. [Google Scholar]
- Peng, W.; Shi, J.; Varanka, T.; Zhao, G. Rethinking the ST-GCNs for 3D skeleton-based human action recognition. Neurocomputing 2021, 454, 45–53. [Google Scholar] [CrossRef]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; others. Imagenet large scale visual recognition challenge. International journal of computer vision 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Peng, W.; Varanka, T.; Mostafa, A.; Shi, H.; Zhao, G. Hyperbolic deep neural networks: A survey. IEEE Transactions on Pattern Analysis and Machine Intelligence 2021, 44, 10023–10044. [Google Scholar] [CrossRef]
- Bronstein, M.M.; Bruna, J.; LeCun, Y.; Szlam, A.; Vandergheynst, P. Geometric deep learning: going beyond euclidean data. IEEE Signal Processing Magazine 2017, 34, 18–42. [Google Scholar] [CrossRef]
- Liu, Q.; Nickel, M.; Kiela, D. Hyperbolic graph neural networks. Advances in neural information processing systems 2019, 32. [Google Scholar]
- Chami, I.; Ying, Z.; Ré, C.; Leskovec, J. Hyperbolic graph convolutional neural networks. Advances in neural information processing systems 2019, 32. [Google Scholar]
- Zhu, Y.; Zhou, D.; Xiao, J.; Jiang, X.; Chen, X.; Liu, Q. HyperText: Endowing FastText with Hyperbolic Geometry. In Proceedings of the Findings of the Association for Computational Linguistics: EMNLP 2020; Association for Computational Linguistics: Online, 2020; pp. 1166–1171. [Google Scholar] [CrossRef]
- López, F.; Heinzerling, B.; Strube, M. Fine-Grained Entity Typing in Hyperbolic Space. In Proceedings of the 4th Workshop on Representation Learning for NLP (RepL4NLP-2019); Association for Computational Linguistics: Florence, Italy, 2019; pp. 169–180. [Google Scholar] [CrossRef]
- Dhingra, B.; Shallue, C.; Norouzi, M.; Dai, A.; Dahl, G. Embedding Text in Hyperbolic Spaces. In Proceedings of the Twelfth Workshop on Graph-Based Methods for Natural Language Processing (TextGraphs-12); Association for Computational Linguistics: New Orleans, Louisiana, USA, 2018; pp. 59–69. [Google Scholar] [CrossRef]
- Tifrea, A.; Becigneul, G.; Ganea, O.E. Poincaré GloVe: Hyperbolic Word Embeddings. In Proceedings of the 7th International Conference on Learning Representations (ICLR); 2019. [Google Scholar]
- Nickel, M.; Kiela, D. Poincaré embeddings for learning hierarchical representations. Advances in neural information processing systems 2017, 30. [Google Scholar]
- Peng, W.; Shi, J.; Xia, Z.; Zhao, G. Mix dimension in poincaré geometry for 3d skeleton-based action recognition. In Proceedings of the 28th ACM International Conference on Multimedia; 2020; pp. 1432–1440. [Google Scholar]
- Bachmann, G.; Bécigneul, G.; Ganea, O. Constant curvature graph convolutional networks. In Proceedings of the International Conference on Machine Learning; 2020; pp. 486–496. [Google Scholar]
- Khrulkov, V.; Mirvakhabova, L.; Ustinova, E.; Oseledets, I.; Lempitsky, V. Hyperbolic image embeddings. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2020; pp. 6418–6428. [Google Scholar]
- Weber, M.; Zaheer, M.; Rawat, A.S.; Menon, A.K.; Kumar, S. Robust large-margin learning in hyperbolic space. Advances in Neural Information Processing Systems 2020, 33, 17863–17873. [Google Scholar]
- Mathieu, E.; Le Lan, C.; Maddison, C.J.; Tomioka, R.; Teh, Y.W. Continuous hierarchical representations with poincaré variational auto-encoders. Advances in neural information processing systems 2019, 32. [Google Scholar]
- Skopek, O.; Ganea, O.E.; Becigneul, G. Mixed-curvature Variational Autoencoders. In Proceedings of the 8th International Conference on Learning Representations (ICLR); 2020. [Google Scholar]
- Chen, X.; Duan, Y.; Houthooft, R.; Schulman, J.; Sutskever, I.; Abbeel, P. Infogan: Interpretable representation learning by information maximizing generative adversarial nets. Advances in neural information processing systems 2016, 29. [Google Scholar]
- Peng, W.; Hong, X.; Xu, Y.; Zhao, G. A boost in revealing subtle facial expressions: A consolidated eulerian framework. In Proceedings of the 2019 14th IEEE International Conference on Automatic Face & Gesture Recognition (FG 2019); 2019; pp. 1–5. [Google Scholar]
- Yang, J.; Jiang, Y.G.; Hauptmann, A.G.; Ngo, C.W. Evaluating bag-of-visual-words representations in scene classification. In Proceedings of the international workshop on Workshop on multimedia information retrieval; 2007; pp. 197–206. [Google Scholar]
- Hearst, M.A.; Dumais, S.T.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intelligent Systems and their applications 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Machine learning 2001, 45, 5–32. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition; 2016; pp. 770–778. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE conference on computer vision and pattern recognition; 2015; pp. 1–9. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE conference on computer vision and pattern recognition; 2017; pp. 4700–4708. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE conference on computer vision and pattern recognition; 2018; pp. 7132–7141. [Google Scholar]
- Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. In Proceedings of the International conference on machine learning; 2019; pp. 6105–6114. [Google Scholar]
- Mikołajczyk, A.; Grochowski, M. Data augmentation for improving deep learning in image classification problem. In Proceedings of the 2018 international interdisciplinary PhD workshop (IIPhDW); 2018; pp. 117–122. [Google Scholar]
- Shaha, M.; Pawar, M. Transfer learning for image classification. In Proceedings of the 2018 second international conference on electronics, communication and aerospace technology (ICECA); 2018; pp. 656–660. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015; Conference Track Proceedings. Bengio, Y., LeCun, Y., Eds.; 2015. [Google Scholar]
- Zoph, B.; Le, Q. Neural Architecture Search with Reinforcement Learning. In Proceedings of the International Conference on Learning Representations; 2017. [Google Scholar]
- Chen, W.; Han, X.; Lin, Y.; Zhao, H.; Liu, Z.; Li, P.; Sun, M.; Zhou, J. Fully Hyperbolic Neural Networks. In Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers); Association for Computational Linguistics: Dublin, Ireland, 2022; pp. 5672–5686. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Krizhevsky, A.; Hinton, G.; others. Learning multiple layers of features from tiny images. 2009.
- Wah, C.; Branson, S.; Welinder, P.; Perona, P.; Belongie, S. The caltech-ucsd birds-200-2011 dataset. 2011.
- Atigh, M.G.; Schoep, J.; Acar, E.; Van Noord, N.; Mettes, P. Hyperbolic image segmentation. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition; 2022; pp. 4453–4462. [Google Scholar]
- Beltrami, E. Teoria fondamentale degli spazii di curvatura costante memoria; Zanetti, F., Ed.; 1868. [Google Scholar]
- Cannon, J.W.; Floyd, W.J.; Kenyon, R.; Parry, W.R.; others. Hyperbolic geometry. Flavors of geometry 1997, 31, 2.
- van Wyk, G.J.; Bosman, A.S. Evolutionary neural architecture search for image restoration. In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN); 2019; pp. 1–8. [Google Scholar]
- Wang, W.; Xie, E.; Li, X.; Fan, D.P.; Song, K.; Liang, D.; Lu, T.; Luo, P.; Shao, L. Pvt v2: Improved baselines with pyramid vision transformer. Computational Visual Media 2022, 8, 415–424. [Google Scholar] [CrossRef]
- Ganea, O.; Bécigneul, G.; Hofmann, T. Hyperbolic neural networks. Advances in neural information processing systems 2018, 31. [Google Scholar]
- Nickel, M.; Kiela, D. Learning continuous hierarchies in the lorentz model of hyperbolic geometry. In Proceedings of the International Conference on Machine Learning; 2018; pp. 3779–3788. [Google Scholar]
- Moretti, V. The interplay of the polar decomposition theorem and the Lorentz group. arXiv 2002, arXiv:math-ph/0211047. [Google Scholar]
- Touvron, H.; Cord, M.; Douze, M.; Massa, F.; Sablayrolles, A.; Jégou, H. Training data-efficient image transformers & distillation through attention. In Proceedings of the International Conference on Machine Learning; 2021; pp. 10347–10357. [Google Scholar]
- Vinyals, O.; Blundell, C.; Lillicrap, T.; Wierstra, D.; others. Matching networks for one shot learning. Advances in neural information processing systems 2016, 29.
- Hendrycks, D.; Gimpel, K. Gaussian error linear units (gelus). arXiv 2016, arXiv:1606.08415. [Google Scholar]
- Becigneul, G.; Ganea, O.E. Riemannian Adaptive Optimization Methods. In Proceedings of the International Conference on Learning Representations; 2019. [Google Scholar]
- Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization. In Proceedings of the International Conference on Learning Representations; 2019. [Google Scholar]
- van der Maaten, L.; Hinton, G. Visualizing Data using t-SNE. Journal of Machine Learning Research 2008, 9, 2579–2605. [Google Scholar]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).