Prerpints.org logo
Preprint
Article

Comparative Analysis of Machine Learning Classification Algorithms for predicting Olive Anthracnose Disease

Altmetrics

Downloads

206

Views

142

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

31 July 2023

Posted:

02 August 2023

You are already at the latest version

Alerts
Abstract
Olive Anthracnose (OA) is the most important fungal disease of olive fruits worldwide. In the context of integrated pest management, the development of predictive models could be used for early diagnosis and control. In the current study, a dataset representing 58 cases (6 locations with 12 olive cultivars) was used to study the relationship between ΟΑ incidence (OAI) and 35 heterogeneous variables, including orchard characteristics, olive fruit parameters, foliar and soil nutrients, soil parameters and soil texture classes. The Random Forest-Recursive Feature Elimination with Cross Validation (RF-RFECV) feature selection method identified Location, Water Content, P, Ca, Mg, Exchangeable Mg, Trace Zn, Trace Cu as possible new indicators associated with OAI. Six different classification algorithms, namely Decision Tree (DT), Gradient Boosting (GB), Logistic Regression (LR), Random Forest (RF), K-Nearest Neighbors (KNN) and Support Vector Machine (SVM), were developed for predicting conditions leading to OAI >0% and 10%. Hyperparameter optimization using grid search was used to optimize the parameters of the models and finally the best parameters were applied to predict the OAI. The final models were evaluated in terms of several standard metrics, such as accuracy, sensitivity, specificity and ROC AUC score. Findings suggested that GB performance was superior compared to the other models for the prediction of the occurrence of OA disease (OAI>0%) with an accuracy of 86.7%, a sensitivity of 100%, a specificity of 75% and a ROC-AUC score of 93%, while for the prediction of the spread of the disease (OAI>10%), DT stood out with an accuracy of 86.7%, a sensitivity of 81.8%, a specificity of 100% and a ROC-AUC score of 91%. RF classifier performed very well in both cases, with an accuracy of 80%, a sensitivity of 85.7%, a specificity of 75% and a ROC-AUC score of 93% for the prediction of the occurrence of the disease (OAI>0%), and an accuracy of 86.7%, a sensitivity of 90.9%, a specificity of 75% and a ROC-AUC score of 84% for the prediction of the spread of the disease (OAI>10%).
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Olive Anthracnose (OA) caused by Colletotrichum species is a major fungal disease in olive oil producing countries, including Greece [1]. While the first OA incidence in Greece was reported in 1920 in Corfu, in recent years and similar to other countries, OA has become a grave concern for olive oil production in Greece [2]. The most affected regions are the Peloponnese and Crete. In fact, in the harvest year 2022 – 2023 the incidence was so high in areas of the Messinia region of the Peloponnese that olive mills often refused to process the damaged olive fruit, many shutting down their operations a month earlier than usual [3]. In Greece it is estimated that OA inflicts an annual loss of 300 million euros upon the olive oil sector [2].
The disease has a detrimental effect on the quality of olive oil as it affects its physicochemical and sensory properties [4,5,6,7]. A strong positive linear relationship has been found between OAI and acidity [7]. Furthermore, sensory defects are present even at a low disease incidence level [4]. Generally, the severity of quality degradation depends on the proportion of infected fruit, the specific Colletotrichum species causing the disease, and the olive cultivar [8].
OA incidence depends on factors including cultivar susceptibility [9], environmental conditions and the virulence of the pathogen [10]. The disease cycle begins with the infection of inflorescences and developing fruit through water-splashed conidia during the spring and summer seasons [11]. The infections in the developing fruit remain dormant until the fruit reaches the maturity stage in autumn and winter. The progression of the disease is heavily influenced by weather conditions [12], cultivar susceptibility [9,11], and the degree of fruit maturity [13,14]. A significant increase in anthracnose is anticipated when warm and moist conditions coincide with ripened fruit of susceptible olive cultivars [15]. Multiple Colletotrichum species also make disease control more challenging, as one or more species may be present in infected orchards [16]. Finally, the ability to persist and multiply without exhibiting noticeable symptoms may explain why anthracnose fungi often result in unforeseen losses in olive crops [14]. The complexity of anthracnose epidemiology highlights the necessity of ongoing research into disease management.
While the manual detection of a plant disease is time-consuming and may not always produce reliable results, the adoption of advanced technologies like Machine Learning (ML) and Deep Learning (DL) can address these challenges and facilitate early detection [17]. Over the last decade, there has been an increase in the number of publications relevant to this field. These can be divided into three categories of forecast models [18]: 1) based on image processing [19,20,21], 2) based on weather data [22,23,24] and, 3) based on distinct types of data coming from heterogeneous sources [25,26,27].
For the prediction of OA incidence, DL forecast models based on image analysis of symptomatic fruit have been developed [28,29]. In other studies, weather data combined with other parameters have been used for the prediction of the disease. For instance, [30] employed machine learning classification algorithms to predict OA disease combining weather data and symptoms. In another study [31], weather data was incorporated with cultivar susceptibility to develop three binary logistic models for predicting conditions leading to OAI>0, 1 and 5%, with overall accuracy of 81, 86, and 85% respectively.
Many researchers [7,31,32,33,34] have emphasized the importance of cultural management practices for the control of OA. These practices include irrigation, sanitation, pruning and balanced nutrition. It is well known that plants suffering nutrient stress are more susceptible to pests and diseases [34,35,36]. However, while balanced nutrition is recommended as a cultural practice, there is limited research on the role of soil amendments as well as the foliar application of nutrients between fruit set and harvest as a control strategy for OA [33]. [37] applied supervised machine learning methods, namely Orthogonal Least Squares Discriminant Analysis and the Random Forest (RF) algorithm, to identify the soil properties potentially associated with Banana Wilt disease incidence in banana plot lots in Venezuela, using a dataset of 78 soil samples and 16 soil variables. To our knowledge, no research has investigated whether soil nutrients are potentially associated and can be included in a predictive model for OA incidence.
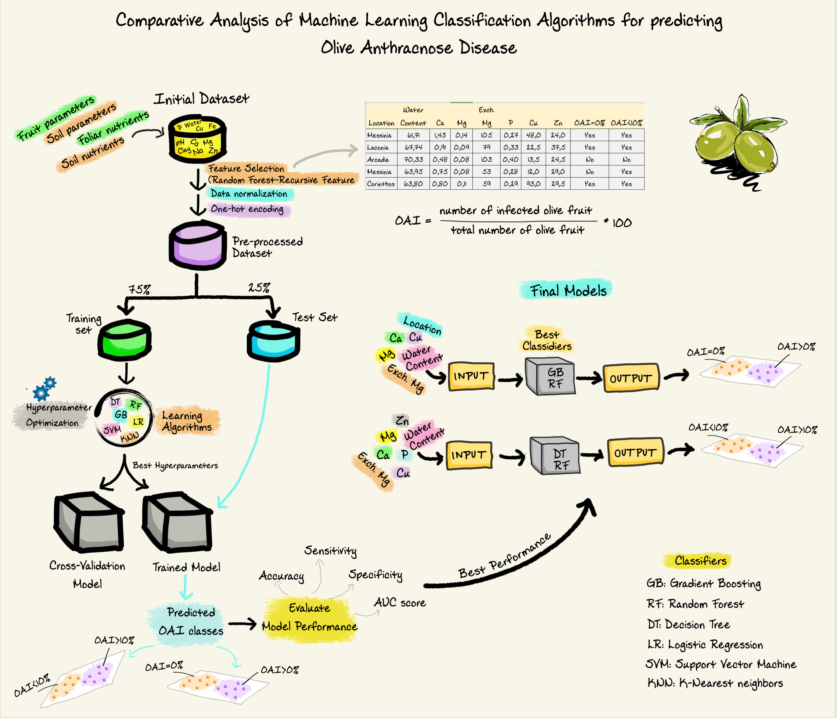
This research proposes forecast models based on high-dimensional and heterogeneous data for the prediction of OA incidence. This is so, because using such data can enhance the robustness and generalization capacity of the algorithms [18]. The dataset includes soil and foliar nutrients in combination with soil characteristics, the location of the orchard, olive cultivar, fruit maturity index and water content of fruit. As early detection of the disease is paramount for its control as well as for the yield and the quality of the harvest, the models aimed to predict OAI above 0% and 10%.
The Random Forest-Recursive Feature Elimination with Cross Validation (RF-RFECV) method was used to select the important features from the original dataset. Six different classification algorithms, that is Decision Tree (DT), Gradient Boosting (GB), Logistic Regression (LR), Random Forest (RF), K-Nearest Neighbors (KNN) and Support Vector Machine (SVM), were developed for predicting conditions leading to OAI >0% and 10%. Hyperparameter optimization using grid search was used to optimize the parameters of the models and finally the best parameters were applied to predict OAI. The final models were evaluated in terms of several standard metrics, such as accuracy, sensitivity, specificity and ROC AUC score.

2. Materials and Methods

2.1. Field Design

Olive fruit of ten Greek varieties (Koroneiki, Megaritiki, Kalamon, Manaki, Mavrolia, Asprolia, Myrtolia, Koytsourelia, Athinolia and Nemoutiana) and two Spanish varieties (Arbequina and Picual) were collected from 58 olive orchards from 5 different locations (Messinia, Corinthos, Laconia, Arcadia, Argolida) of the Peloponnese Region. Collection of olive fruits was carried out during the fruit harvest period of October 2021 until January 2022 and the maturity index of each sample was calculated immediately at the time of receipt [38].

2.2. Disease Assessment

Detection of latent anthracnose disease infection was conducted on asymptomatic and externally healthy detached olive drupes. Olive fruits were washed under running tap water, surface sterilized by immersion in a 5% solution of sodium hypochlorite (bleach) for 20 min, rinsed five times with sterile water and air-dried for 1 hour in a laminar cabinet before wounded with a sterile needle. An aliquot of 10 μl of sterilized distilled water was inoculated on the surface of each artificial wound. Olives from each sample were then transferred into plastic containers to maintain high relative humidity and stored in a well-ventilated cabinet at 25 ◦C for 6 days. A completely randomized design with three replicates per treatment and 20 fruit per replicate was used.
After six days of incubation the number of infected olive fruit was recorded, and disease incidence (OAI) was calculated according to the following formula [39]:
O A I % =   n u m b e r   o f   i n f e c t e d   o l i v e   f r u i t s t o t a l   n u m b e r   o f   o l i v e   f r u i t s ∗ 100
Fruits were considered affected by Colletotrichum spp. when typical symptoms of anthracnose disease appeared like round and ocher or brown lesion, with profuse production of orange masses of conidia or fruit rot. The average of the three replicates was used to calculate the OAI (%) per orchard.

2.3. Soil sampling and analysis

Soil samples were collected from fifty eight olive orchards from areas of Messinia, Laconia, Arcadia, Argolida and Corinthia of the Peloponnese Region. Each soil sample was taken in the zone of maximum root activity, from about 25 to 40 cm deep. The density of subsampling was 1-2 points per approximately 1,000 m2. The sampling points were random, and samples were taken by pressing into the soil a hand auger, combination type (Eijkelkamp, the Netherlands). Dry leaves, stems and other vegetal residuals on the soil surface were removed prior to sampling. Every sampling area contained similar soil types with trees of roughly uniform size and vigor. Subsamples of each orchard were thoroughly mixed in a plastic bucket in order to form a composite sample, which was then placed into a labeled bag until determination in the laboratory.
Soil samples were dried using forced air at ambient temperatures <36°C to constant weight and then passed through a 2 mm sieve (fine earth). Samples were saturated with deionized water and saturation percentage was determined [40,41]. Values of pH were measured in the soil/water slurry [42] using a Consort C835 multichannel analyzer. The exchangeable cations (Ca, Mg, K) were extracted with a 1 M NH4OAc solution at pH 7.00 [43,44,45] and their concentration was determined by a Shimadzu AA6200 atomic absorption spectrophotometer in an air-acetylene flame. Calcium and Magnesium were measured by adding La2O3 to both the standards and sample extraction to reach a concentration of 4,500 mg L-1 La [46]. Phosphorus was determined colorimetrically using a Shimadzu UV-1700 UV-visible spectrophotometer according to the Olsen method [47]. Organic matter concentration was measured according to the Walkley-Black method [48]. The particle size analysis (sand, silt and clay) was performed by the hydrometer method [49].

2.4. Leaf sampling and analysis

A sample of approximately 300 leaves per orchard were collected in July 2022. Each sample was comprised of randomly selected and peripherally collected mature healthy leaves from the middle portion of nonbearing current season shoots. The leaves were placed in paper bags, stored in a portable ice cooler, and transported to the laboratory.
Once in the laboratory, the leaves were pulverized in a grinder and 1 g of each sample was heated in a dry oven at 550°C for 4 hours in porcelain stoneware. The inorganic elements were extracted using 15 ml of 10% HCl solution and distilled water was added to up to 100 ml. The foliar nutrients Ca, Mg, K, Fe, Mn, Zn and Cu were determined using an atomic absorbance spectrophotometer Shimadzu AA6200. Total P and B were determined colorimetrically according to [50,51], respectively.

2.5. Dataset

The dataset had a total of 58 cases and 35 features, including numeric and categorical. The predictive targets were a) the occurrence of OA disease (OAI=0%, OAI>0%), where 0 indicated no occurrence (OAI=0%) and 1 indicated occurrence (OAI>0%) and b) the incidence of OA (OAI<10%, OAI>10%), where 0 indicated disease incidence lower than 10% and 1 greater than 10%.
The predictor variables (Table 1) included olive orchard characteristics (olive cultivar, location of the orchard), olive fruit parameters (olive fruit maturity index, water content of olive fruit), foliar nutrients (Total N, P, Ca, Mg, K, Fe, Mn, Zn, Cu and B), soil parameters (saturation percentage, pH, electrical conductivity, organic matter, Olsen P), soil macronutrients such as exchangeable cations (Ca, Mg, K, Na) and water-soluble cations (Water Soluble Mg, Water Soluble K), soil micronutrients or trace elements (B, Fe, Mn, Zn, Cu) and soil texture indicators (sand, silt, slay and soil textural class).

2.6. Data Preprocessing and Feature Selection

The dataset did not contain any missing values or user entry errors, so no imputation or data cleaning techniques were needed. Data scaling was applied on the numerical input features by rescaling the distribution of the values so that the mean of observed values was 0 and the standard deviation was 1. One-hot encoding was used to convert categorical variables into a format that could be readily used by the machine learning algorithms, that is creating a separate column for each type of category, with a value of 1 indicating that the row contains data about that category and a value of 0 indicating that it does not [52].
To overcome the problems associated with the high dimensionality and the multicollinearity between variables [53], we reduced the number of features of the original dataset by employing the Random Forest-Recursive Feature Elimination with Cross Validation (RF-RFECV) method [54]. To avoid overfitting and biased performance estimations due to data leakage, feature selection was only performed on the training data and not the complete dataset [55,56,57].
Random forest (RF) is a machine-learning technique that typically performs well with high dimensional data and can identify significant predictors without making assumptions about an underlying model [54,58]. However, the presence of correlated predictors, which is a common problem of high-dimensional data sets, impacts RF’s ability to identify the strongest predictors by decreasing the estimated importance scores of correlated variables. A suggested solution is the RF-RFECV algorithm [59] which was first developed for the gene selection process using the SVM classifier [60,61].
RFE is a wrapper-type feature selection method [62,63] which follows a greedy optimization approach to find a subset of features by first looking through every feature in the training dataset and then successfully removing features one at a time until the appropriate number of features is left. This is accomplished by first fitting the core model's machine learning algorithm, ranking the features according to relevance, eliminating the least important features [64], and then re-fitting the model. This process is repeated until a specified number of features remains. The number of features selected by RFE was chosen automatically by performing 5-fold cross-validation evaluation of several number of features and selecting the number of features that produced the best mean accuracy score.

2.7. Proposed Methodology

The aim of the current study was to optimize six classification machine learning algorithms, namely Decision Tree (DT), Gradient Boosting (GB), Logistic Regression (LR), Random Forest (RF), K-Nearest Neighbors (KNN) and Support Vector Machine (SVM), to develop prediction models for the occurrence of OA disease (OAI>0%) and its incidence level (OAI>10%).
To evaluate a model’s performance, some data (input) with known ground truth (labels) are required. In our case these labels were the values of the two binary target variables, (a) OA occurrence (0: OAI=0%, 1: OAI>0%) and (b) OA incidence (0: OAI<10%, 1: OAI>10%). The idea was to train the models on the data, for which the labels were known, and evaluate their performance on data, for which labels were unknown (unseen data to the model) [65]. To do so, the new dataset, as configured after data preprocessing and feature selection, was split into 75% training data (known labels) to train the models and 25% testing data (unknown labels) to evaluate the models, by comparing the predicted labels for this 25% data with the actual labels.
Grid search with 5-fold cross validation was applied on the 75% training data for hyperparameter tuning and model selection among the six candidate models. The values of the hyperparameters, which are the parameters that control the model's learning process, have a significant impact on the predictive performance of the machine learning model [66]. Therefore, it is essential to investigate the hyperparameter combinations that result in the best model. The hyperparameters were optimized using a tuning method called grid search. Grid search exhaustively explores the optimum values of hyperparameters while considering all possible combinations of user-specified hyperparameters [67]. The hyperparameters of the models (e.g., number of features to consider when looking for the best split for Gradient Boosting, number of trees in the forest for Random Forest etc.) were optimized through an internal 5-fold cross-validation on the training data by grid search over a range of values and the parameters that generated the best accuracy score were selected. GridSearchCV function that comes in Scikit-learn's model_selection package was used to find the best values for hyperparameters.
Standard 5-fold cross-validation was employed to address the overfitting issue, deal with the small sample size and increase the precision of the estimates, while still maintaining a small bias [68,69]. The 5-fold cross-validation was performed in the following steps: (a) the training dataset was split into 5 equal parts (folds). (b) 4 parts were used to train the model and the remaining one part to validate the model, (c) step (b) was repeated until each part was used for both the training and validation set, and (d) the performance of the model was finally computed as the average performance of the 5 estimations [68].
For each of the six learning algorithms (DT, GB, LR, RF, KNN, SVM), the hyperparameter setting which resulted in the highest 5-fold cross-validation score, was used to determine the best parameters for each algorithm and develop the final prediction model. The final models were then fitted on the entire training dataset (75% of the original data) and then tested on the 25% of the data, which were initially held-out from the original dataset to evaluate the final best models on data unseen to them during their learning phase.
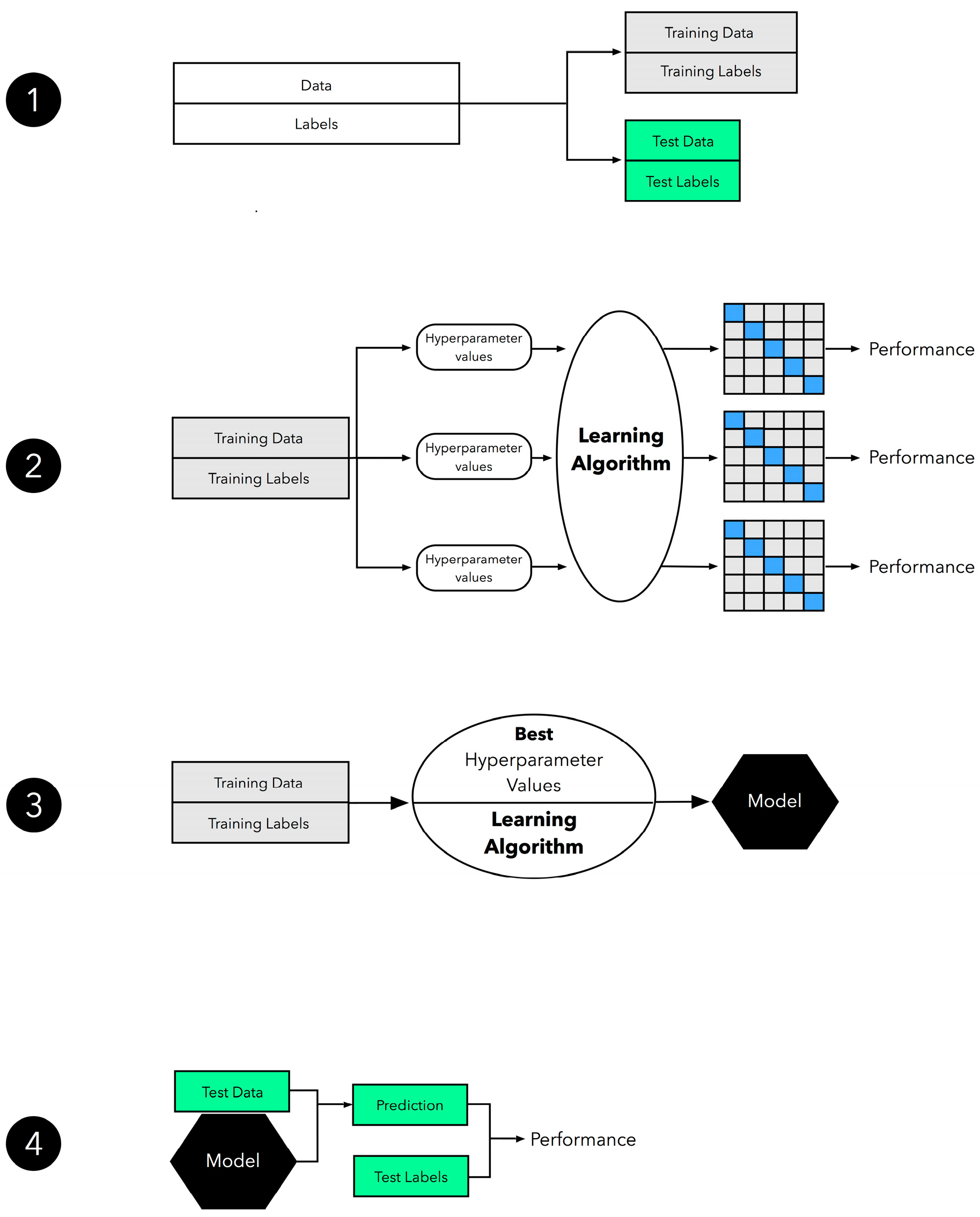
The methodology we applied to each of the six learning algorithms for model selection is summarized in 4 steps (Figure 1) [70]: (Step1): the original dataset was divided into a training set and an independent test set, with the test set being saved for the final model evaluation step. (Step 2): Grid Search was used in the second step to experiment with different hyperparameter settings. 5-fold cross-validation was employed on the training set to generate several models and performance estimates for each hyperparameter configuration. (Step 3): the entire training set was used for model fitting by selecting the hyperparameter values that corresponded to the best-performing model. (Step 4): the independent test set that was withheld in Step 1 was used to evaluate the model that was obtained from Step 3.

2.8. Machine Learning Models

Following the data collection and preprocessing steps, six machine learning algorithms (DT, GB, LR, RF, KNN, SVM) were developed and applied to the training set. All machine learning algorithms were run by the open-source Jupyter Notebook App in python 3.9.12.
Decision Tree (DT) is a non-parametric supervised learning method used both for classification and regression. Classification trees are generally applied to output variables which are categorical and mostly binary in nature. The objective is to learn straightforward decision rules derived from the data features in order to build a model that predicts the value of the target variable. Three different node types—a root node, a child node, and a leaf node—make up the tree. The procedure begins by selecting a root node from the relationships between each input and output variable that are the strongest. The selection of a child node is then made by computing Information Gain (IG), which is given by:
I G p a r e n t ,   c h i l d = E n t r o p y p a r e n t − p c 1 ∗ E n t r o p y c 1 + p c 2 ∗ E n t r o p y c 2 …
where E n t r o p y c i = − p c i ∗ l o g p c i and p c i is a probability of child node i. The parent for the following generation will then be the node with the highest IG. The process will continue until all children nodes are pure, or until the IG is 0 [71].
Gradient Boosting (GB) is an ensemble algorithm - a combination of weak individual models that together create a more powerful new model - based on decision trees, that is used in both regression and classification tasks. It is one of the most powerful algorithms in the field of machine learning because of its high prediction speed and accuracy. The weak learners are the individual decision trees which are connected in series and each tree tries to minimize the error of the previous tree. Boosting focuses on building up these weak learners successively and removing the observations that a learner correctly understands at each level [72]. In essence, the emphasis is on creating new, weak learners to manage the final, difficult observations at each step. The objective of the GB algorithm is to minimize the loss function i.e., the difference between the actual class and the predicted class, by using a gradient descent procedure. Classification algorithms frequently use logarithmic loss function whereas regression algorithms use squared errors [73].
Random Forest (RF) is an ensemble supervised machine learning algorithm that is used widely in both classification and regression problems. The Random Forest Classifier creates a set of decision trees from a randomly selected subset of the training set and then it collects the votes from different decision trees to decide the final prediction. Basically, each model is trained independently, and the final output is based on majority voting after combining the results of all models. By developing several decision-tree models, RF takes use of the decision tree algorithm's great speed and accuracy while dealing with classification problems. There is no link between the multiple decision trees, and errors are mutually reduced, leading to more precise and reliable classification findings [74].
K-Nearest Neighbors (KNN) is a non-parametric, lazy learning algorithm that works well with nonlinear data since it makes no assumptions about the input. It is a simple, easy to implement supervised machine learning algorithm that can be used to address both classification and regression tasks. KNN Classifier tries to predict the correct class for the test data by calculating the distance between the test data and all the training points. It finds the nearest neighbors by ranking points by increasing distance and finally votes on the predicted class labels based on the classes of the k nearest neighbors. The distance function and the value of k are the only two parameters necessary to implement KNN [75]. The most common distance function that is used to measure similarity is the Euclidian distance and it is defined by:
  d E u c l i d e a n x , y = ∑ i ( x i − y i ) 2
Logistic Regression (LR) is a supervised learning classification algorithm used to predict the probability of a target variable. The nature of the target variable is dichotomous, which means there would be only two possible classes (i.e., 0: uninfected, 1: infected). The function used by logistic regression to map predictions to probabilities is the sigmoid function:
σ ( y ) = 1 ( 1 + e − y )
y = b 0 x 0 + b 1 x 1 … … + b n x n
where ( x 0 ,   x 1 , … …   , x n )   is an instance of the dataset and bi are the coefficients values, which are estimated and updated by stochastic gradient descent. The sigmoid function returns a probability value between 0 and 1. In order to map this probability value to a discrete class (0/1, true/false), a threshold value, called ‘decision boundary’ is selected. The probability values above this threshold level are mapped into class 1 and below are mapped into class 0. Generally, the decision boundary is set to 0.5 [76].
Support Vector Machine (SVM) is a supervised machine learning algorithm which is used in both regression and classification tasks. However, it is mostly employed to solve classification problems. The SVM algorithm's objective is to establish the decision boundary (hyperplane) that can divide a n-dimensional space into classes, allowing new data points to be easily and correctly classified. SVMs are effective in high dimensional spaces as well as in cases where number of dimensions is greater than the number of samples. SVM algorithms use a set of mathematical functions (kernels) to transform data input into the required form. Gaussian radial basis function, linear, sigmoid and polynomial are several common kernel functions. Besides the kernel function, another important hyperparameter of SVM is the penalty parameter C which adds a penalty for each misclassified data and trades off correct classification of training examples against maximization of the decision function's margin [77].

2.9. Performance Evaluation

The considered classification models were evaluated by calculating several evaluation parameters - the number of correctly recognized class examples (true positives), the number of correctly recognized examples that do not belong to the class (true negatives), and examples that either were incorrectly assigned to the class (false positives) or that were not recognized as class examples (false negatives). For the case of the binary classification, these four counts constitute the confusion matrix displayed in Table 2. Based on the counts in the confusion matrix, the following performance measures were used to evaluate the classification models [78]:
Accuracy is the ratio of the number of correct predictions to the total number of input samples and reflects the overall effectiveness of a classifier.
A c c u r a c y = T P + T N T P + F P + T N + F N
Specificity is the ratio of the correctly classified negative samples to the total number of negative samples and describes the effectiveness of a classifier to identify negative labels. This proportion could also be called a True Negative Rate (TNR).
S p e c i f i c i t y = T N T N + F P
Sensitivity is the ratio of the correctly classified positive samples to the total number of positive samples and indicates the effectiveness of a classifier to identify positive labels. It is also known as the true positive rate (TPR) or recall.
S e n s i t i v i t y = T P T P + F N
While sensitivity and specificity are both important metrics in evaluating the performance of machine learning models, they represent different aspects of the model’s accuracy. As sensitivity increases, specificity decreases, and vice versa. This implies that both measurements cannot be optimized at the same time. To choose the optimum machine learning model for the task at hand, it is critical to consider both sensitivity and specificity. One measure could be more crucial than another in certain situations. For example, in disease diagnosis, it may be more important to have high sensitivity to avoid missing any true positive cases, even if it means a higher rate of false positives [79].
The Receiver Operating Characteristic (ROC) curve [80], a plot of sensitivity against 1-Specificity, was another useful metric used to assess the performance of the classifiers under consideration. ROC has been employed in recent years within the ML community to depict and assess the trade-off between the true positive rates and the false positive rates. This trade-off corresponds to all possible binary classifications that any dichotomization of the continuous outputs would allow. Consequently, ROC curves show a classifier's performance over a range of sensitivity and specificity thresholds. ROC curves are frequently summarized in a single value, the Area under the ROC Curve (AUC), which measures the entire two-dimensional area underneath the ROC curve and demonstrates the classifier’s ability to avoid false classification [81]. AUC values range from 0 to 1.0, where 1 is a perfect score and 0.5 means the model is as good as random. AUC provides an aggregate measure of performance across all possible classification thresholds and represents the degree of separability between classes [82].
To deal with the small amount of data available in the current study and its negative effect on the evaluation of the classifiers based solely on accuracy measurements [83], we used Permutations Tests to further assess the competence of the classifiers. The permutation test procedure measures how likely the observed statistic of interest (e.g., accuracy) would be obtained by chance. Traditional permutation tests propose the null hypothesis that the features and labels are independent, i.e., that there is no distinction between the classes. The null distribution under this null hypothesis is computed by randomly rearranging the labels in the data set. A p-value represents the fraction of random data sets under the null hypothesis where the classifier behaved as well as or better than in the original data [84]. Permutation tests are a non-parametric approach and do not use the chi-squared approximation, thereby avoiding the small expected frequency problem [85]. By directly calculating the distribution of the statistic of interest, permutation tests are ideal for small datasets as they do not require any assumptions about the distribution of the data, making them more flexible and robust to violations of assumptions. In the current study, we performed permutation tests on the training data for testing whether the models with the best hyperparameters, as derived from the optimization of the accuracy score through the hyperparameters Grid Search, had found a real class structure, that is, a real connection between the data and the class labels.
Following hyperparameter optimization, the final models with the best hyperparameters were fitted to the entire training dataset and evaluated on the hold-out set by measuring accuracy, specificity, sensitivity and AUC scores.

3. Results

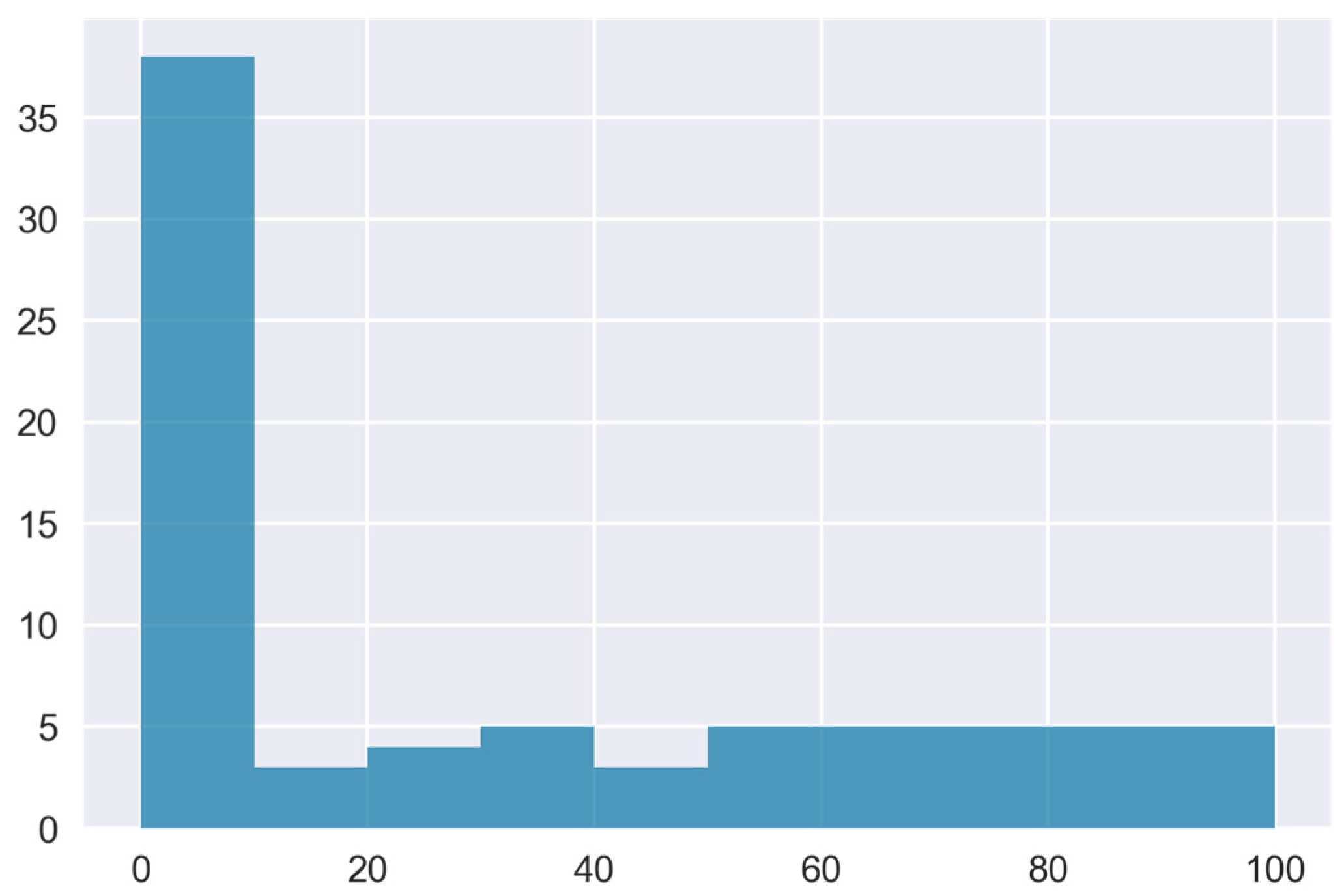
3.1. Statistical Analysis on the Initial Dataset

A quick overview of the dispersion and central tendency of the OA incidence (OAI) raw data is provided by the frequency distribution histogram in Figure 2.
A relatively balanced class distribution was observed in the data, with around 47% of the total cases having OA disease (OAI>0%) and roughly 34% having an OAI of more than 10%.
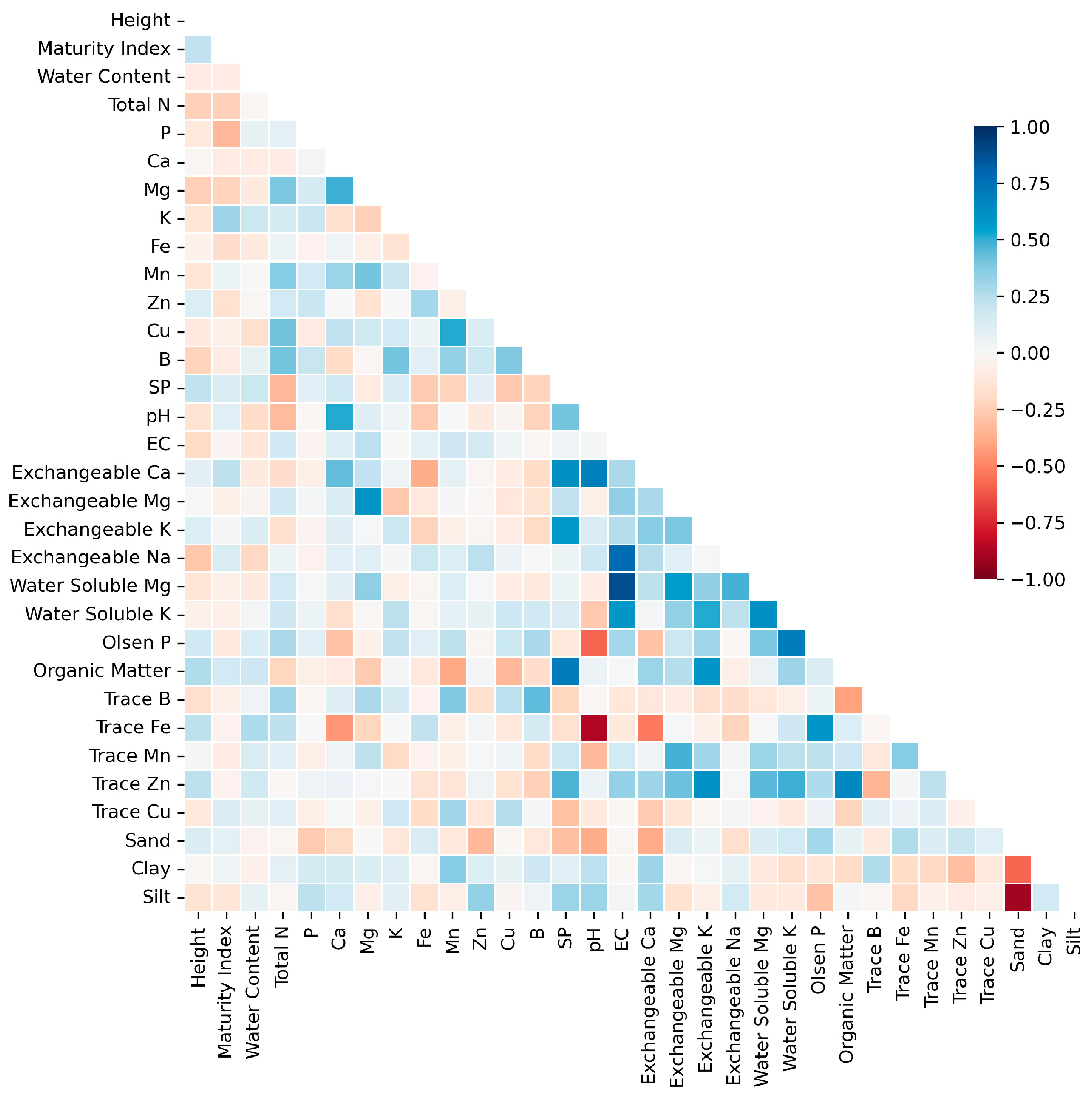
A correlation heatmap (Figure 3) was plotted to visualize the strength of the relationships between numerical variables. From the color-coding of the cells, it is obvious that variables such as Exchangeable Ca & pH, Organic Matter & SP, Exchangeable Na & EC, Water Soluble Mg & EC had strong positive correlation while variables such as Trace Fe & pH and Silt & Sand had strong negative correlations. Relative strong or medium correlations also existed between other variables in the dataset.
The univariate non-parametric Mann–Whitney U test was used to explore if there are statistically significant differences in the numerical predictor variables between infected (OAI>0%) and not infected (OAI=0%) cases, as well as between cases with OAI lower than 10% and those with OAI greater than 10%.
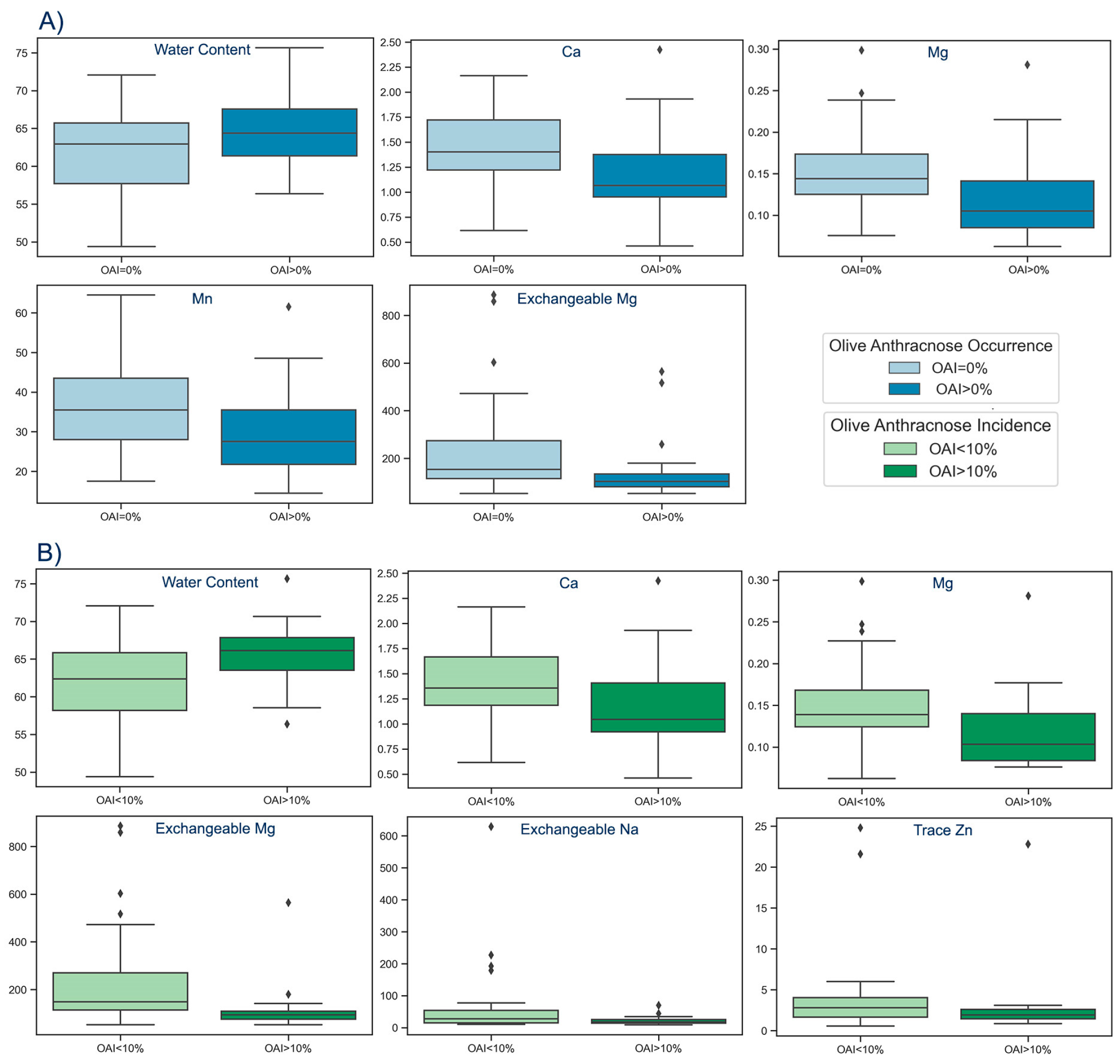
According to our findings, Water Content was statistically considerably higher in infected orchards (OAI>0%) compared to non-infected (OAI=0%), whereas Ca, Mg, Mn, and Exchangeable Mg were statistically significantly lower in infected orchards compared to not infected (Figure 4A, Table 3). Additionally, Mann-Whitney results indicated statistically significantly higher values of Water Content in orchards with OAI>10% compared to those with OAI<10%, as well as significantly lower values of Ca, Mg, Mn and Exchangeable Mg in orchards with OAI>10% compared to those with OAI<10% (Figure 4B, Table 3).
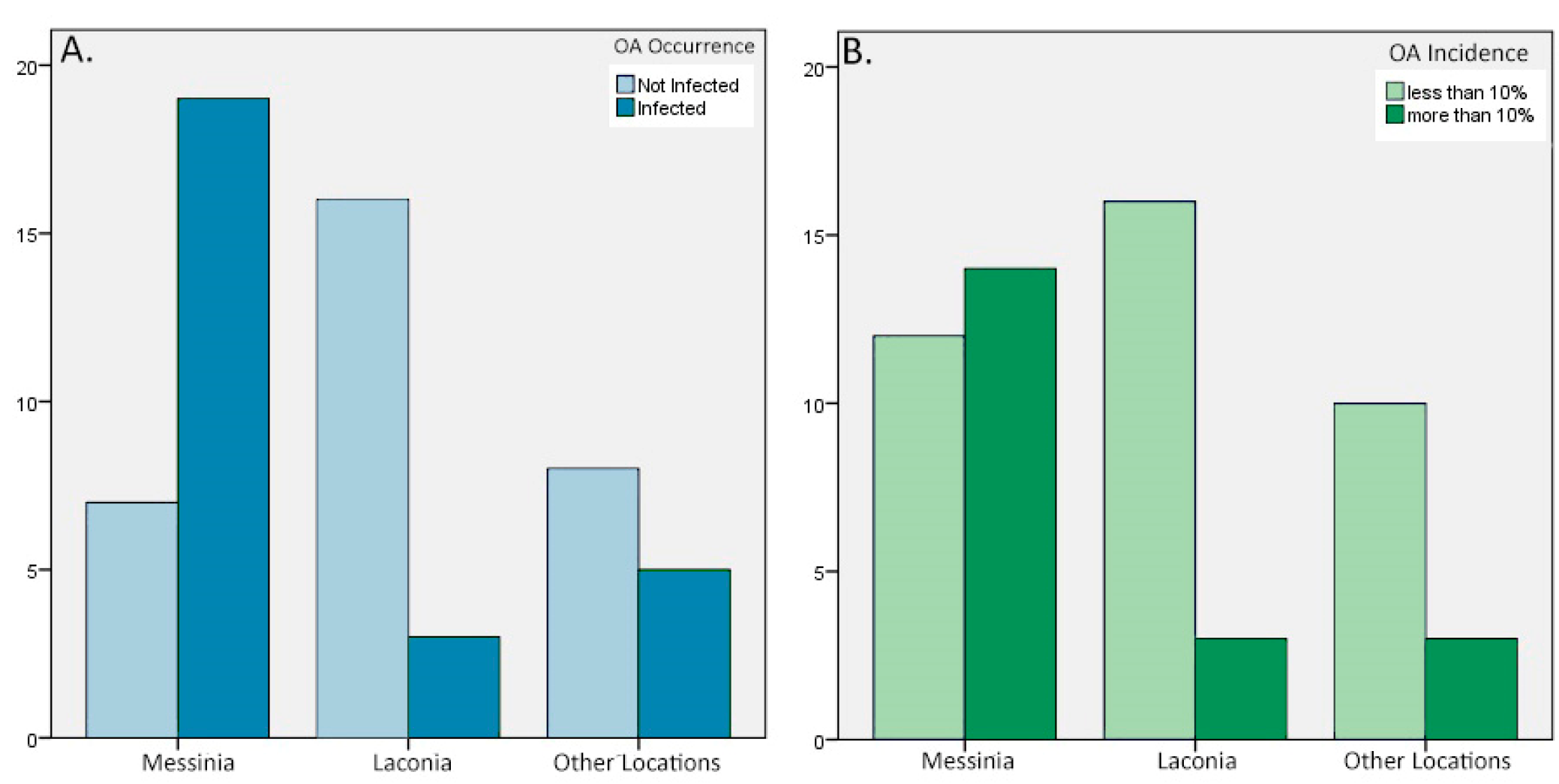
Furthermore, we conducted a Chi-square test to investigate the association between the location of olive orchards and the occurrence of OA disease (OAI=0%, OAI>0%). To meet the assumptions of the Chi-square test and address small sample size concerns, the categories Argolida, Corinthos, and Arcadia were merged into a single category named “Other Locations”. The Chi-square test revealed a significant association between the location of olive orchards and the occurrence of olive anthracnose disease (χ² = 14.921, df = 2, p = 0.001) (Table 4). Examining the adjusted residuals provided additional insights into the individual cells within the contingency table (Table 5) that played a significant role in the observed associations. Adjusted residuals highlighted that the categories “Messinia” and “Other Locations” showed higher prevalence of infected orchards, with adjusted residuals of 3.7 and 0.7, respectively. Conversely, “Laconia” had less infected orchards than expected, with an adjusted residual of -3.3. The Chi-square test results, and the adjusted residuals support the conclusion that the distribution of olive anthracnose disease significantly varies across different locations, with Messinia showing a notably higher prevalence of the disease (Figure 5A).
Similarly, we explored the association between the location of olive orchards and the incidence of olive anthracnose disease (OAI<10%, OAI>10%). The Chi-square test was conducted to examine the relationship between the variables, revealing a statistically significant association (χ² = 8.002, df = 2, p = 0.018) (Table 4). “Messinia” exhibited a negative adjusted residual of -2.8 for "OAI<10%" indicating fewer orchards than expected in this category. Conversely, “Laconia” showed a positive adjusted residual of 2.1 for “OAI<10%”, suggesting a higher prevalence. The "Other Locations" category displayed a positive adjusted residual of 1.0 for "OAI<10%", indicating that the number of orchards in this category was slightly higher than the expected (Table 5). The observed deviations, along with the statistical significance of the Chi-square test, emphasize that the incidence of olive anthracnose disease varies significantly across different locations. Specifically, “Messinia” demonstrated a relatively higher prevalence of orchards with disease incidence greater than 10%, while “Laconia” showed fewer orchards in the same category (Figure 5B).
Finally, Chi-square tests were employed to explore the potential associations between olive cultivar and OA occurrence and incidence, as well as between soil textural class and OA occurrence and incidence. The results were found to be not statistically significant, suggesting that there is no strong evidence of a direct relationship between the examined categorical variables and the presence or incidence of OA in the olive orchards.

3.2. Identification of Important Features

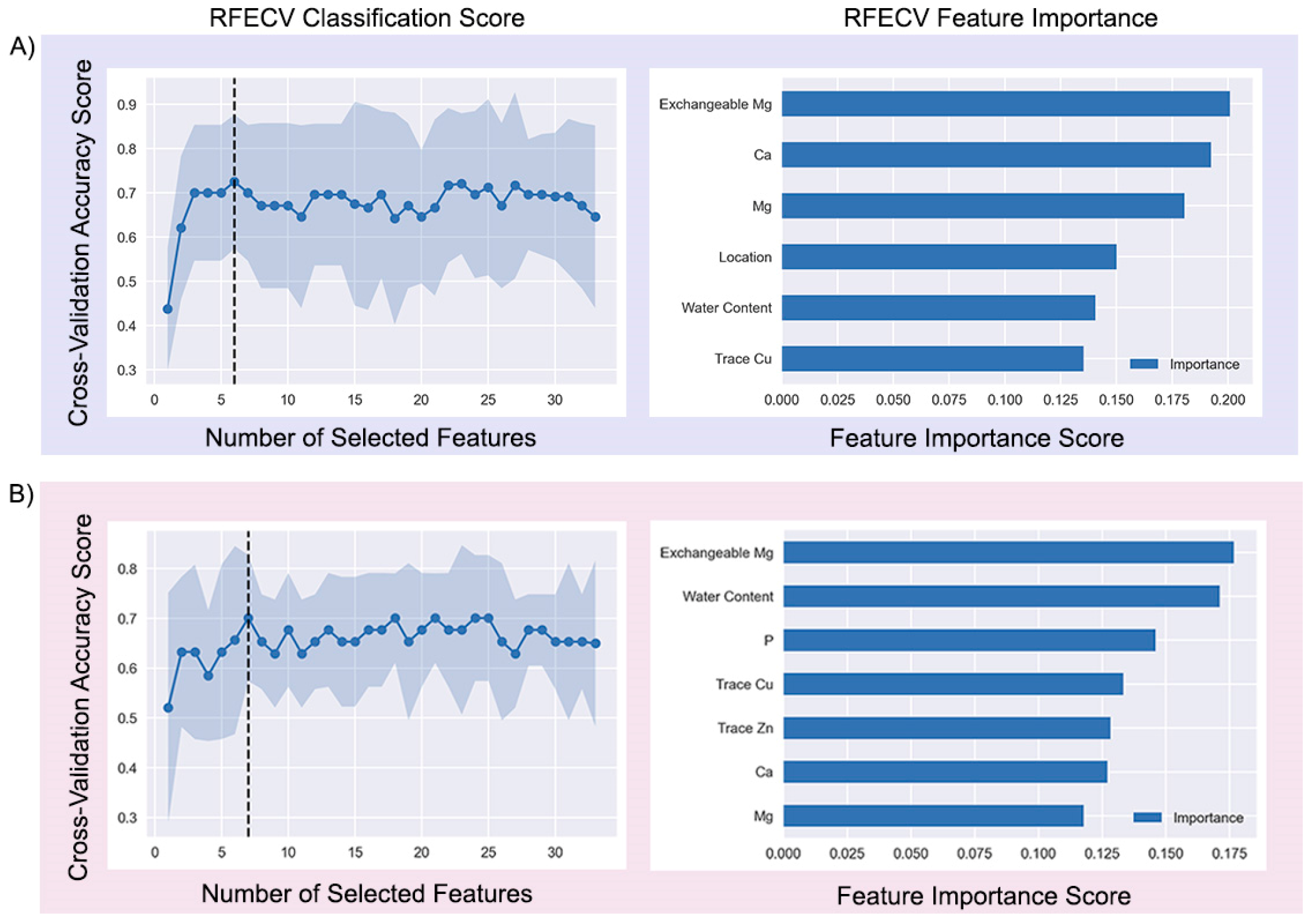
Six of the original thirty-three features—Exchangeable Mg, Ca, Mg, Location, Water Content, Trace Cu—were selected as the final predictor variables to accurately differentiate between infected (OAI>0%) and non-infected (OAI=0%) orchards, based on the results of the RF-RFECV approach (Figure 6A). Similarly, seven features, including Exchangeable Mg, Water Content, P, Trace Cu, Trace Zn, Ca and Mg were chosen as potential predictors for the distinction between the orchards with OAI<10% and OAI>10% (Figure 6B).
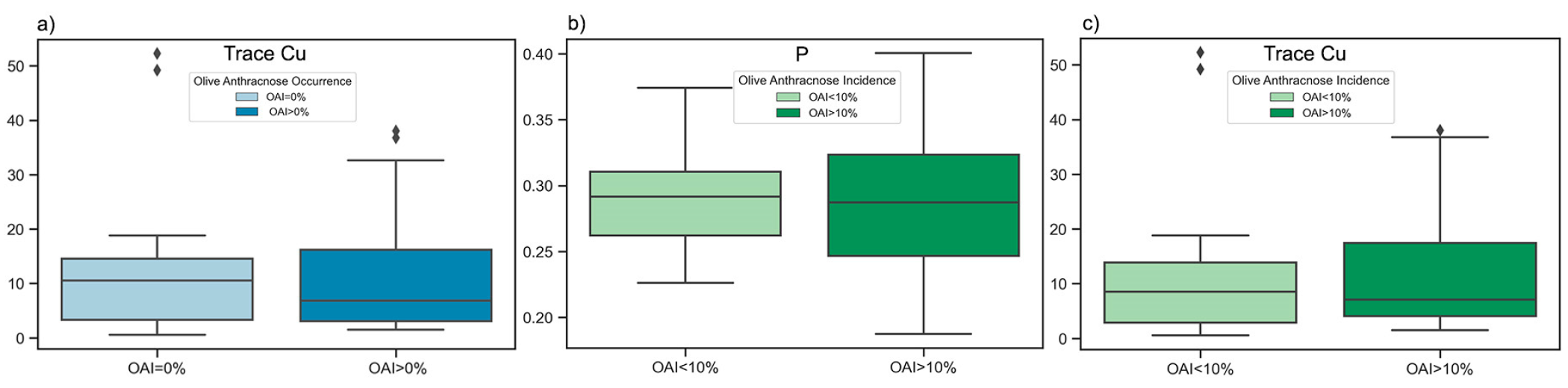
Despite P and Trace Cu being recognized as critical factors for the prediction of OAI, they were not found to be statistically significant, and hence not incorporated in the boxplots depicted in Figure 4. Supplementary boxplots (Figure 7) and five number summary statistics (Table 6) were generated to illustrate the intraclass dispersion of Trace Cu among infected and non-infected samples and that of P and Trace Cu among samples with OAI greater and less than 10%.

3.3. Performance of Classifiers

The grid search optimization method was used to fine-tune the parameters for each model in order to optimize the accuracy score. Table 7 shows the basics of the configuration space for the machine learning models developed for the prediction of OA occurrence (OAI>0%) and OA incidence (OAI>10%).
Table 8 presents the 5-fold cross-validation accuracy scores of the optimized machine learning models, used for predicting the occurrence (OAI>0%) and incidence of OA (OAI>10%). The results show that SVM (0.76) and GB (0.74) had the highest accuracy scores for predicting the occurrence of OA, followed by RF (0.73), DT (0.73), KNN (0.72), and LR (0.72). For predicting the incidence of OA, RF (0.81) and GB (0.77) were the models with the highest cross-validated scores, followed by KNN (0.74), DT (0.72), SVM (0.72), and LR (0.72).
After the grid search hyperparameter optimization, the models with the best hyperparameters were retrained on the complete training set (75% of the original data) and evaluated on the hold-out set (25% of the original data), using standard performance metrics (accuracy, specificity, sensitivity, AUC).
As shown in Table 9, GB classifier performed the best among all the models examined for the occurrence of OA (OAI>0%), with an accuracy of 87%, specificity of 100%, sensitivity of 75% and AUC score of 93%. RF also had an AUC score of 93%, indicating the classifier’s excellent ability to distinguish between infected and non-infected orchards, with an accuracy of 90%, a specificity of 86% and a sensitivity of 75%. Following GB and RF, SVM displayed an overall good performance, with an accuracy of 80%, a specificity of 86%, a sensitivity of 75% and an AUC score of 86%. KNN showed a remarkable specificity of 100%, indicating the classifier’s excellent ability to correctly classify non-infected samples, however due to its poor sensitivity of 50%, it was not considered effective for the identification of the disease. The low sensitivity of LR (62%) also indicated that the classifier was not useful in picking up the disease. DT classifier’s AUC score (0.65) indicated a poor discrimination capacity to distinguish between infected and non-infected samples.
Among the classifiers examined for the prediction of the OA incidence (OAI>10%), DT had the highest specificity (100%) and AUC score (91%), the highest accuracy (87%) together with RF and KNN and a sensitivity of 81%. Both RF and KNN demonstrated the highest sensitivity (91%) and the same accuracy (87%) and specificity (75%), although RF had a higher AUC score (84%) than KNN (77%). These classifiers stood out for their ability to identify 91% of the orchards with OA larger than 10%. GB had a fairly good performance with an accuracy of 80%, a specificity of 75%, a sensitivity of 81% and an AUC score of 77%. LR and SVM were the least effective classifiers with poor discrimination ability indicated by their low AUC scores (66% and 68% respectively) and a low specificity (50%) of LR, which made it inappropriate for the classification of the non-infected samples.
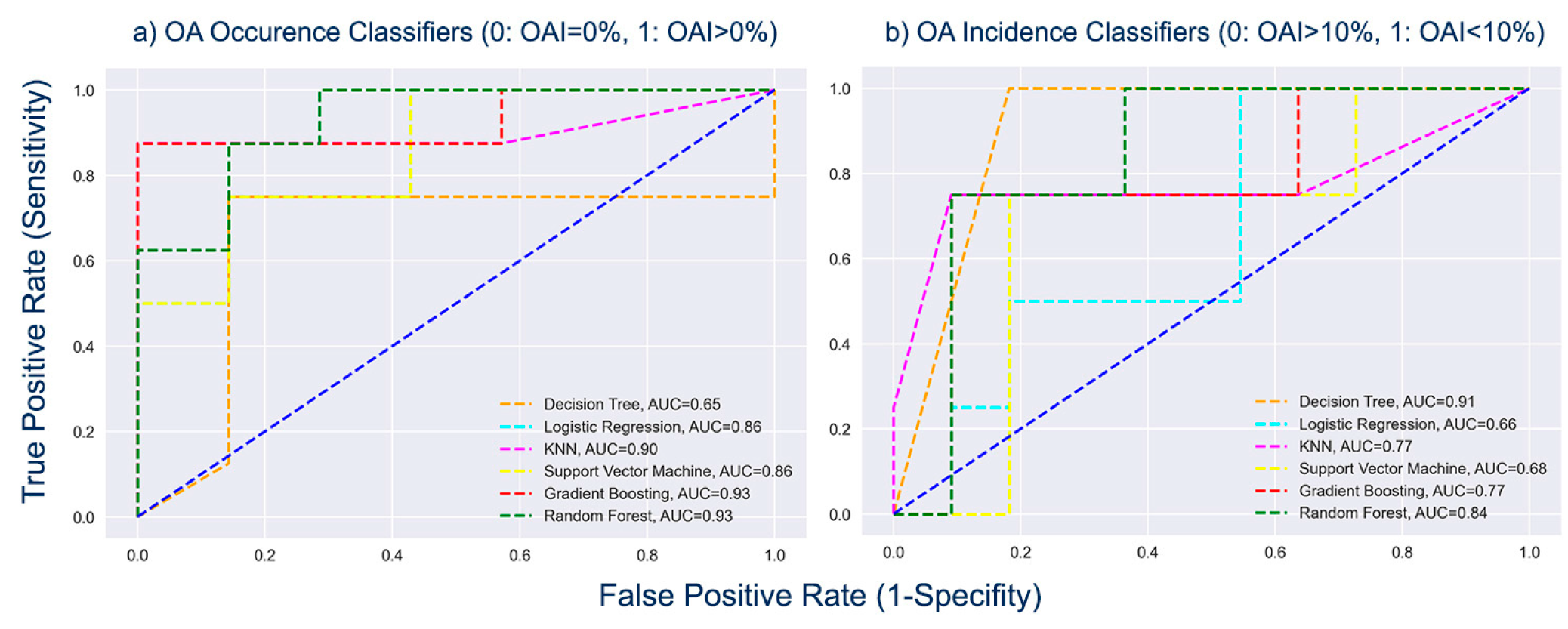
Figure 8 shows the Receiver Operating Characteristic (ROC) curves for the outputs of the classification models about OA occurrence (OAI>0%) and prediction of OA incidence (OAI>10%).
As shown in Figure 8a, among the classifiers for the occurrence of OA (OAI>0%), GB and RF achieved the highest AUC scores, equal to 0.93, demonstrating the models’ excellent ability to discriminate between the infected and non-infected samples. The classifiers DT and RF achieved the greatest AUC scores, equivalent to 0.91 and 0.84 respectively, when comparing the AUC scores of the classifiers developed for the prediction of OA incidence (OAI>10%) (Figure 8b), demonstrating their superior capacity to distinguish between olive orchards with OAI10% and those with OAI>10%.
Summarizing, GB performance was superior compared to the other models for the prediction of the occurrence of OA disease (OAI>0%) with an accuracy of 86.7%, a sensitivity of 100%, a specificity of 75% and a ROC-AUC score of 93%, while for the prediction of the spread of the disease (OAI>10%), DT stood out with an accuracy of 86.7%, a sensitivity of 81.8%, a specificity of 100% and a ROC-AUC score of 91%. The RF classifier performed very well in both cases, with an accuracy of 80%, a sensitivity of 85.7%, a specificity of 75% and a ROC-AUC score of 93% for the prediction of the occurrence of the disease (OAI>0%), and an accuracy of 86.7%, a sensitivity of 90.9%, a specificity of 75% and a ROC-AUC score of 84% for the prediction of the spread of the disease (OAI>10%).
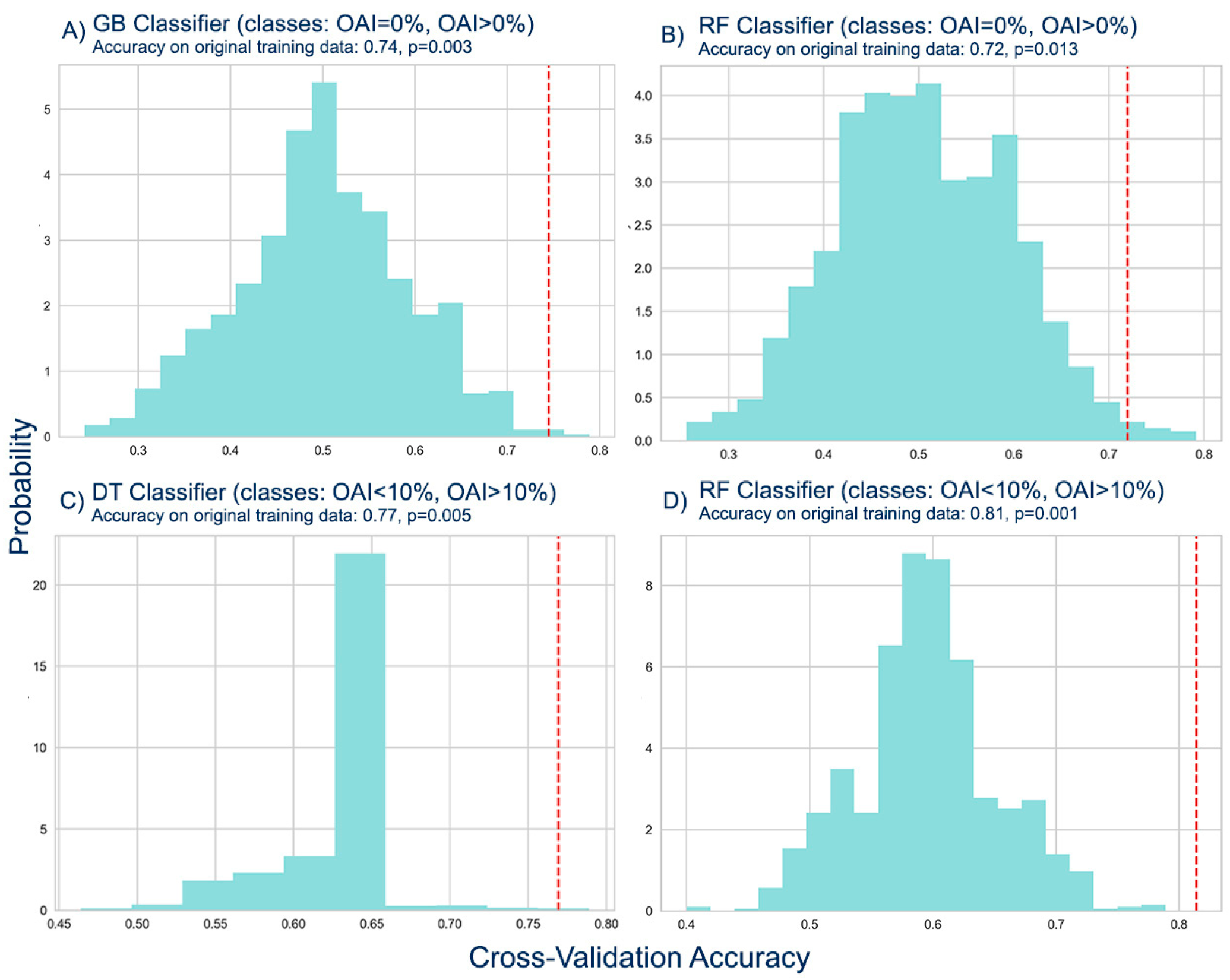
In order to verify that the best classifiers had in fact learned a significant predictive pattern in the data and that they were appropriate for the particular classification tasks, we conducted permutation tests. Specifically, we produced 1000 random permutations of the class labels for the training data sets used in the models' training. We then carried out the same 5-fold cross-validation procedure to obtain a classification accuracy score for each randomized dataset and generated a non-parametric null-distribution of accuracy values (Figure 9).
Based on the results of the permutation tests for the classification of the infected against non-infected orchards, we concluded that the accuracy scores of the GB (0.74) and RF (0.72) classifiers were statistically significant. With p-values of 0.003 and 0.013 respectively, we rejected the null hypothesis that the accuracy scores were due to chance. This means that the models’ accuracy scores on the original data are likely to generalize to new, unseen data. The permutation tests also provided evidence that the models were not overfitting to the training data.
The results of the permutation tests for the classification of the olive orchards with OAI<10% against those with OAI>10% demonstrated that the accuracy scores of the DT and RF classifiers were statistically significant with scores of 0.77 and 0.81, respectively. The null hypothesis was rejected with p-values of 0.005 and 0.001, suggesting that the accuracy scores were not due to chance. Thus, the accuracy scores for the original data are likely to be applicable to new, unseen data. The results of the permutation tests indicated that the models were not overfitting to the training data.

4. Discussion

Overall, the results suggested that the GB and RF Classifiers performed the best for the classification of OA infected and non-infected olive orchards. For the classification of the olive orchards with OAI<10% in relation to those with OAI>10%, the DT and RF classifiers had the highest performance.
The effectiveness of using the random forest classifier, combined with the recursive feature elimination technique, for feature selection derives from the high performance of the final models and the results obtained by the permutation tests. In summary, the permutation tests revealed that the selected features (Location, Water Content, Ca, Mg, Exchangeable Mg, Trace Cu) were effective at predicting the target class (OAI=0%, OAI>0%) for OA occurrence, while the chosen features (Water Content, P, Ca, Mg, Exchangeable Mg, Trace Zn, Trace Cu) were able to accurately predict the target class for OA incidence (OAI<10%, OAI>10%). This is in accordance with previous studies which claim that the random forest method provides a reliable and effective approach to feature selection from high-dimensional and heterogeneous data [86,87,88].
According to [88], the recursive partitioning process of random forests allows them to capture complex interactions between features. The trees in the ensemble consider multiple attributes simultaneously and identify interactions that may not be apparent in isolated feature evaluations. By exploiting the capabilities of random forests, we can gain insights into the importance of soil and foliar nutrient variables, considering their interactions and interdependencies. Many of the selected features in this study have been already linked to OAI incidence.
Our findings align with previous research [33,89] which has associated severe epidemic outbreaks of OA disease with high relative humidity and frequent rainfall during the flowering and fruit development stages. Specifically, we discovered that olive fruit from infected olive orchards had significantly higher water content (Median(IQR)=64.36(61.38-67.56%)) compared to non-infected (Median(IQR)=62.93(57.71-65.70%)). Similarly, olive fruit from orchards with OAI greater than 10% had significantly higher water content (Median(IQR)=66.13(63.50-67.84%)) compared to those with OAI<10% (Median(IQR)=62.38(58.17-65.84%)) (Table 3, Figure 4).
The location of the orchard emerged as another crucial factor for predicting OA disease, which is reasonable considering that different locations are associated with diverse microclimates and agronomical practices [10,11,15].
Furthermore, the results of this study agree with previous research, which suggests that resistance to OA is closely related to the health of plants and soil [16]. In certain regions of Portugal and southwest Spain, [10] found a potential connection between increased OA occurrence and low soil pH, which correlates with insufficient Ca levels. The statistical analysis of the data in this paper also revealed that Ca values were significantly lower in infected samples (Median(IQR)=1.06(0.95-1.37%)) and samples with OAI>10% (Median(IQR)=1.04(0.92-1.41%)), compared to non-infected (Median(IQR)=1.40(1.22-1.72%)) and those with OAI<10% (Median(IQR)=1.36(1.19-1.67%)), respectively (Table 3, Figure 4).
In regard to the micronutrient Cu, our findings showed that samples from olive orchards with copper levels above a certain limit (≈19 ppm) were almost all infected with OAI greater than 10% (Table 6, Figure 7). Previous research has shown that while the application of copper-based fungicides is the recommended measure for controlling anthracnose in olive groves, overuse can cause a build-up of copper in the soil and obstruct the uptake of other nutrients [90,91].
Our results showed that P levels between 0.23 to 0.37% were present in samples with OAI values both below and above 10%. Nevertheless, only samples with OAI values greater than 10% exhibited P levels that fell below 0.23 or exceeded 0.37% (Table 6, Figure 7). Furthermore, our research findings indicated that samples collected from orchards with OAI greater than 10% displayed significantly lower trace Zn values (Median(IQR)=1.92(1.43-2.60 mg kg-1)) compared to those collected from orchards with OAI<10% (Median(IQR)=2.80(1.65-4.05 mg kg-1)) (Table 3, Figure 4B).
Finally, Mg and Exchangeable Mg were also identified as two critical factors that could be used to predict the onset of OA disease. The Mg contents exhibited significant decreases in samples obtained from infected orchards (Median(IQR)=0.12(0.08-0.14%)), as opposed to non-infected ones (Median(IQR)=0.15(0.12-0.17%)). Similarly, samples from orchards with OAI>10% displayed lower Mg contents (Median(IQR)=0.10(0.08-0.14 %)) compared to orchards with OAI<10% (Median(IQR)=0.14(0.12-0.17%)) (Table 3, Figure 4). With regard to Exchangeable Mg, its concentrations demonstrated significant decreases in samples obtained from infected orchards (Median(IQR) = 103 (81-134 mg kg-1)), as opposed to non-infected (Median(IQR) = 154 (115.5-274 mg kg-1)). Likewise, samples from orchards with OAI>10% (Median(IQR) = 94 (75.75-108.75 mg kg-1)) displayed lower Exchangeable Mg contents relative to orchards with OAI<10% (Median(IQR) = 148.5 (114.75-270.5 mg kg-1)) (Table 3, Figure 4)
To our knowledge, there is no previous research exploring the relationship between P, Zn, Mg and OA disease. However, interactions among mineral nutrients occur frequently in the soil and at the plant level, leading to interdependencies. Consequently, a deficiency or excess of one nutrient can impact the absorption or utilization of another. Besides the functions of nutrients in plant metabolism, the plant tolerance or resistance to biotic or abiotic stresses can be affected by their status [92]. In all cases, our study demonstrated the importance of balanced nutrition for the control and management of OA disease [16,93].
Machine learning and deep learning models could play a significant role in creating and supporting targeted management plans for timely disease control. Our forecast models were based on distinct types of data coming from high-dimensional and heterogeneous data. However, the inclusion of weather variables and cultivar susceptibility level in the set of the predictive features of the proposed models could further enhance their performance. Finally, more data would improve the generalization of the proposed models.

Author Contributions

Conceptualization, Klimentia Kottaridi and Anna Milionis; Methodology, Klimentia Kottaridi; Software, Klimentia Kottaridi and Vasileios Nikolaidis; Validation, Klimentia Kottaridi; Formal Analysis, Klimentia Kottaridi and Vasileios Nikolaidis; Investigation, Klimentia Kottaridi, Anna Milionis, Polina C. Tsalgatidou, Athanasios Tsafouros, Anastasios Kotsiras, Alexandros Vithoulkas; Resources, Klimentia Kottaridi, Polina C. Tsalgatidou, Athanasios Tsafouros, Anastasios Kotsiras, Alexandros Vithoulkas; Data Curation, Klimentia Kottaridi; Writing – Original Draft Preparation, Klimentia Kottaridi and Anna Milionis; Writing – Review & Editing, Klimentia Kottaridi, Anna Milionis, Vasileios Nikolaidis, Polina C. Tsalgatidou, Athanasios Tsafouros, Alexandros Vithoulkas; Visualization, Klimentia Kottaridi; Supervision, Vasilis Demopoulos and Vasileios Nikolaidis; Project Administration, Klimentia Kottaridi and Anna Milionis; Funding Acquisition, Vasilis Demopoulos and Anna Milionis.

Funding

This work was funded by the Operational Program EPAnEK 2014 – 2020 Competitiveness – Entrepreneurship – Innovation, co-financed by Greece and the European Union in the context of the research program ‘Strategic Management of the Anthracnose Disease of Olive Cultivation in the Region of the Peloponnese’ (MIS 5046086).

Data Availability Statement

We encourage all authors of articles published in MDPI journals to share their research data. In this section, please provide details regarding where data supporting reported results can be found, including links to publicly archived datasets analyzed or generated during the study. Where no new data were created, or where data is unavailable due to privacy or ethical restrictions, a statement is still required. Suggested Data Availability Statements are available in section “MDPI Research Data Policies” at https://www.mdpi.com/ethics.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Romero, J., Santa-Bárbara, A. E., Moral, J., et al. (2022). Effect of latent and symptomatic infections by Colletotrichum godetiae on oil quality. Eur. J. Plant Pathol., 163(2), 545-556. [CrossRef]
  2. Kolainis, S., Koletti, A., Lykogianni, M., Karamanou, D., Gkizi, D., Tjamos, S. E., Paraskeuopoulos, A., & Aliferis, K. A. (2020). An integrated approach to improve plant protection against olive anthracnose caused by the Colletotrichum acutatum species complex. PLoS One, 15(5), e0233916. [CrossRef]
  3. https://www.tharrosnews.gr/2023/02/to-gloiosporio-efage-fetos-to-30-paragogis-sti-messinia/.
  4. Peres, F., Talhinhas, P., Afonso, H., Alegre, H., Oliveira, H., Ferreira-Dias, S. (2021). Olive Oils from Fruits Infected with Different Anthracnose Pathogens Show Sensory Defects Earlier Than Chemical Degradation. Agronomy, 11(6), 1041. [CrossRef]
  5. Carvalho, M. T., Simoes-Lopes, P., Silva, M. J. M. (2008). Influence of different olive infection rates of Colletotrichum acutatum on some important olive oil chemical parameters. Acta Hortic., 791, 555-559. [CrossRef]
  6. Moral, J., Xaviér, C., Roca, L. F., Romero, J., Moreda, W., Trapero, A. (2014). Olive Anthracnose and its effect on oil quality. Grasas Aceites, 65, e028. [CrossRef]
  7. Leoni, C., Bruzzone, J., Villamil, J. J., Martínez, C., Montelongo, M. J., Bentancur, O., Conde-Innamorato, P. (2018). Percentage of anthracnose (Colletotrichum acutatum s.s.) acceptable in olives for the production of extra virgin olive oil. Crop Prot., 108, 47-53. [CrossRef]
  8. Riolo, M., Pane, A., Santilli, E., Moricca, S., & Cacciola, S. O. (2023). Susceptibility of Italian olive cultivars to various Colletotrichum species associated with fruit anthracnose. Plant Pathol., 72, 255-267. [CrossRef]
  9. Moral, J., Xaviér, C. J., Viruega, J. R., Roca, L. F., Caballero, J., Trapero, A. (2017). Variability in susceptibility to anthracnose in the World Collection of Olive Cultivars of Cordoba (Spain). Front. Plant Sci., 8, 1892. [CrossRef]
  10. Talhinhas, P., Loureiro, A., & Oliveira, H. (2018). Olive anthracnose: a yield- and oil quality-degrading disease caused by several species of Colletotrichum that differ in virulence, host preference and geographical distribution. Mol. Plant Pathol., 19, 1797-1807. [CrossRef]
  11. Moral, J., Oliveira, R., Trapero-Casas, A. (2009). Elucidation of the Disease Cycle of Olive Anthracnose Caused by Colletotrichum acutatum. Phytopathology, 99, 548-556. [CrossRef]
  12. Moral, J., Trapero, A. (2012). Mummified fruit as a source of inoculum and disease dynamics of olive anthracnose caused by Colletotrichum spp. Phytopathology, 102(10), 982-989. [CrossRef]
  13. Moral, J., Bouhmidi, K., Trapero, A. (2008). Influence of fruit maturity, cultivar susceptibility, and inoculation method on infection of olive fruit by Colletotrichum acutatum. Plant Disease, 92, 1421-1426. [CrossRef]
  14. Moral, J., Agustí-Brisach, C., Raya, M.C., Jurado-Bello, J., López-Moral, A., Roca, L.F., Chattaoui, M., Rhouma, A., Nigro, F., Sergeeva, V., et al. (2021). Diversity of Colletotrichum Species Associated with Olive Anthracnose Worldwide. J. Fungi, 7, 741. [CrossRef]
  15. Cacciola, S.O., Faedda, R., Sinatra, F., Agosteo, G., Schena, L., Frisullo, S., Magnano di San Lio, G. (2012). Olive anthracnose. J. Plant Pathol., 94, 29-44.
  16. Sergeeva, V. (2014). The role of epidemiology data in developing integrated management of anthracnose in olives - A review. Acta Hortic., 1057, 163-168. [CrossRef]
  17. Shoaib, M., Shah, B., El-Sappagh, S., Ali, A., Ullah, A., Alenezi, F., Gechev, T., Hussain, T., & Ali, F. (2023). An advanced deep learning models-based plant disease detection: A review of recent research. Front. Plant Sci., 14, 1158933. [CrossRef]
  18. Fenu, G., & Malloci, F. (2021). Forecasting Plant and Crop Disease: An Explorative Study on Current Algorithms. Big Data Cogn. Comput., 5(2). [CrossRef]
  19. Hasan, N., Mustavi, M., Jubaer, A., Shahriar, M., & Ahmed, T. (2022). Plant Leaf Disease Detection Using Image Processing: A Comprehensive Review. Malays. J. Sci. Adv. Technol., 2(4), 174-182. [CrossRef]
  20. Guerrero-Ibañez, A., & Reyes-Muñoz, A. (2023). Monitoring Tomato Leaf Disease through Convolutional Neural Networks. Electronics, 12(1), 229. [CrossRef]
  21. Shoaib, M., Shah, B., El-Sappagh, S., Ali, A., Ullah, A., Alenezi, F., Gechev, T., Hussain, T., & Ali, F. (2023). An advanced deep learning models-based plant disease detection: A review of recent research. Front. Plant Sci., 14, 1158933. [CrossRef]
  22. Fenu, G., & Malloci, F. M. (2019). An Application of Machine Learning Technique in Forecasting Crop Disease. In Proceedings of the 2019 3rd International Conference on Big Data Research (pp. 76–82). Paris, France.
  23. Malicdem, A. R., & Fernandez, P. L. (2015). Rice blast disease forecasting for northern Philippines. WSEAS Trans. Inf. Sci. Appl., 12, 120–129.
  24. Bhatia, A., Chug, A., & Singh, A. P. (2020). Hybrid SVM-LR Classifier for Powdery Mildew Disease Prediction in Tomato Plant. In Proceedings of the 2020 7th International Conference on Signal Processing and Integrated Networks (SPIN). Noida, India. [CrossRef]
  25. Zhang, J., Pu, R., Yuan, L., Huang, W., Nie, C., Yang, G. (2014). Integrating Remotely Sensed and Meteorological Observations to Forecast Wheat Powdery Mildew at a Regional Scale. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens., 7(11), 4328-4339. [CrossRef]
  26. Rowlandson, T., Gleason, M., Sentelhas, P., Gillespie, T., Thomas, C., Hornbuckle, B. (2015). Reconsidering leaf wetness duration determination for plant disease management. Plant Dis., 99, 310–319. [CrossRef]
  27. Badnakhe, M.R., Durbha, S.S., Jagarlapudi, A., Gade, R.M. (2018). Evaluation of Citrus Gummosis disease dynamics and predictions with weather and inversion based leaf optical model. Comput. Electron. Agric., 155, 130–141. [CrossRef]
  28. Alruwaili, M., Alanazi, S., Abd ElGhany, S., Shehab, A. (2019). An Efficient Deep Learning Model for Olive Diseases Detection. Int. J. Adv. Comput. Sci. Appl., 10. [CrossRef]
  29. Fazari, A., Pellicer-Valero, O., Gómez-Sanchís, J., Bernardi, B., Cubero, S., Benalia, S., Zimbalatti, G., Blasco, J. (2021). Application of deep convolutional neural networks for the detection of anthracnose in olives using VIS/NIR hyperspectral images. Comput. Electron. Agric., 187, 106252. [CrossRef]
  30. Silva, R., Alves, L., & Bernardino, J. (2017). Using Data Mining to Predict Diseases in Vineyards and Olive Groves. [CrossRef]
  31. Romero, J., Moral, J., González-Domínguez, E., Agustí-Brisach, C., Roca, L., Rossi, V., Trapero-Casas, A. (2021). Logistic models to predict olive anthracnose under field conditions. Crop Protection, 148, 105714. [CrossRef]
  32. Sergeeva, V. (2011). Anthracnose in olives: symptoms, disease cycle, and management. In K.S. Chartzoulakis (Ed.), Proceedings of the 4th International Conference Olivebioteq 2011, Volume I.
  33. Sergeeva, V. (2011a). Integrated pest management of diseases in olives. Australian and New Zealand Olive Grower and Processor, 80, 16-21.
  34. Sergeeva, V. (2014). Anthracnose management factors influencing yield and quality of olives. Proceedings of the Australian National Conference, 17th-19th September 2014.
  35. Tripathi, R., Tewari, R., Singh, K., Keswani, C., Minkina, T., Singh, A., De Corato, U., Sansinenea, E. (2022). Plant mineral nutrition and disease resistance: A significant linkage for sustainable crop protection. Front. Plant Sci., 13, 883970. [CrossRef]
  36. Huber, D., Römheld, V., Weinmann, M. (2012). Relationship between Nutrition, Plant Diseases and Pests. Adv. Bot. Res., 62, 235-261. [CrossRef]
  37. Olivares, B., Lobo Luján, D., Rey, J.C., Landa, B., Gómez, J., Vega, A., Rueda Calderón, M. (2022). Identification of Soil Properties Associated with the Incidence of Banana Wilt Using Supervised Methods. Plants, 11(15), 2070. [CrossRef]
  38. Uceda, M., & Frias, L. (1975). Harvest dates: Evolution of the fruit oil content, oil composition and oil quality. In Proceedings of the II Seminario Oleicola Internacional (pp. 125-130). Cordoba, Spain: International Olive Oil Council.
  39. Tsalgatidou, P.C., Thomloudi, E.E., Baira, E., Papadimitriou, K., Skagia, A., Venieraki, A., Katinakis, P. (2022). Integrated Genomic and Metabolomic Analysis Illuminates Key Secreted Metabolites Produced by the Novel Endophyte Bacillus halotolerans Cal.l.30 Involved in Diverse Biological Control Activities. Microorganisms, 10(2), 399. [CrossRef]
  40. Klages, M.G. (1984). Reproducibility of saturation percentage of soils. Proc. Mont. Acad. Sci. 44, 6769.
  41. Rhoades, J.D. (1996). Salinity, electrical conductivity and total dissolved solids. In Methods of Soil Analysis. Part 3. Chemical Methods. SSSA Book Series No. 5. (WI, USA: ASA Madison), p.417–436.
  42. Kalra, Y.P. (1995). Determination of pH of soils by different methods: collaborative study. J. AOAC Int. 78, 310–321 10.1007/BF02348343.
  43. Van Reeuwijk, L.P. (2002). Procedures for Soil Analysis, 6th edn (Wageningen, The Netherlands: Technical Paper International Soil Reference and Information Centre), pp.120.
  44. Burt, R. (2004). Soil survey laboratory methods manual. Soil survey investigations report no. 42, version 4.0. (USDA-NRCS).
  45. Sumner, M.E., and Miller, W.P. (1996). Cation exchange capacity and exchange coefficients. In Methods of Soil Analysis, Part 3. Chemical Methods, Book Series no. 5 (Soil Science Society of America).
  46. Warncke, D., and Brown, J.R. (1982). Potassium and other basic cations. In Recommended Chemical Soil Test Procedures for the North Central Region (Columbia, MO: Missouri Agr. Exp. Sta. SB1001), p.31–33.
  47. Olsen, S.R., Cole, C.V., Watanabe, F.S., and Dean, L.A. (1954). Estimation of Available Phosphorus in Soils by Extraction with Sodium Bicarbonate. USDA Circular 939 (Washington, D.C.: U.S. Dept. of Agriculture), pp.18.
  48. Walkley, A., and Black, I.A. (1934). An examination of the Degtjareff method for determining soil organic matter and a proposed modification of the chromic acid titration method. Soil Sci. 37 (1), 29–38. [CrossRef]
  49. Miller, R.O., Kotuby-Amacher, J., and Rodriguez, J.B. (1998). Western States Laboratory Proficiency Testing Program Soil and Plant Analytical Methods. Ver 4.10.
  50. Murphy, J. and Riley, J.P. (1962) A Modified Single Solution Method for the Determination of Phosphate in Natural Waters. Anal. Chim. Acta, 27, 31-36. [CrossRef]
  51. Greweling, T. 1976. Chemical analysis of plant tissue. Search Vol. 6(8). 35 p. Cornell Univ. Agric. Exp. Station N.Y.S. Coll. of Agric. and Life Sciences.
  52. Fan, C., Chen, M., Wang, X., Wang, J., Huang, B. (2021). A Review on Data Preprocessing Techniques Toward Efficient and Reliable Knowledge Discovery From Building Operational Data. Front. Energy Res., 9, 652801. [CrossRef]
  53. Chan, J., Leow, S., Bea, K., Cheng, W. K., Phoong, S. W., Hong, Z. W., & Chen, Y. L. (2022). Mitigating the Multicollinearity Problem and Its Machine Learning Approach: A Review. Mathematics, 10(8), 1283. [CrossRef]
  54. Darst, B. F., Malecki, K. C., Engelman, C. D. (2018). Using recursive feature elimination in random forest to account for correlated variables in high dimensional data. BMC Genet., 19 (Suppl 1), 65. [CrossRef]
  55. Singhi, S., Liu, H. (2006). Feature subset selection bias for classification learning. In Proceedings of the 23rd International Conference on Machine Learning - ICML '06 (pp. 849-856).
  56. Ambroise, C., Mclachlan, G. (2002). Selection bias in gene extraction on the basis of microarray gene-expression data. Proceedings of the National Academy of Sciences of the United States of America, 99(10), 6562-6566. [CrossRef]
  57. Demircioğlu, A. (2021). Measuring the bias of incorrect application of feature selection when using cross-validation in radiomics. Insights Imaging, 12(1), 172. [CrossRef]
  58. Breiman, L. (2001). Random Forests. Mach. Learn., 45, 5-32. [CrossRef]
  59. Gregorutti, B., Michel, B., Saint-Pierre, P. (2017). Correlation and variable importance in random forests. Stat. Comput., 27, 659-678. [CrossRef]
  60. Pal, M., Foody, G. (2010). Feature Selection for Classification of Hyperspectral Data by SVM. IEEE Trans. Geosci. Remote Sens., 48: 2297-2307. [CrossRef]
  61. Bouchlaghem, Y., Akhiat, Y., Amjad, S. (2022). Feature Selection: A Review and Comparative Study. E3S Web of Conferences 351: 01046. [CrossRef]
  62. Akkaya, B. (2021). The Effect of Recursive Feature Elimination with Cross-Validation Method on Classification Performance with Different Sizes of Datasets.
  63. Kohavi, R., John, G. H. (1997). Wrappers for feature subset selection. Artif. Intell., 97(1-2), 273-324. [CrossRef]
  64. de Roda Husman, S., Sanden, J.J., Lhermitte, S., Eleveld, M. (2021). Integrating intensity and context for improved supervised river ice classification from dual-pol Sentinel-1 SAR data. Int. J. Appl. Earth Obs. Geoinf., 101, 102359. [CrossRef]
  65. Sarker, I.H. (2021). Machine Learning: Algorithms, Real-World Applications and Research Directions. SN Comput. Sci., 2, 160. [CrossRef]
  66. Li, Y., Shami, A. (2020). On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing, 415, 295-316. [CrossRef]
  67. Ali, Y. A., Awwad, E. M., Al-Razgan, M., Maarouf, A. (2023). Hyperparameter Search for Machine Learning Algorithms for Optimizing the Computational Complexity. Processes, 11(2), 349. [CrossRef]
  68. Montesinos López, O. A., Montesinos López, A., Crossa, J. (2022). Multivariate Statistical Machine Learning Methods for Genomic Prediction. In Overfitting, Model Tuning, and Evaluation of Prediction Performance. Cham (CH): Springer. Retrieved from https://www.ncbi.nlm.nih.gov/books/NBK583970/. [CrossRef]
  69. Vabalas, A., Gowen, E., Poliakoff, E., Casson, A. J. (2019). Machine learning algorithm validation with a limited sample size. PLOS ONE, 14(11), e0224365. [CrossRef]
  70. Raschka, S. (2018). Model Evaluation, Model Selection, and Algorithm Selection in Machine Learning. arXiv preprint arXiv:1811.12808.
  71. Charbuty, B., Abdulazeez, A. (2021). Classification Based on Decision Tree Algorithm for Machine Learning. J. Appl. Sci. Technol. Trends, 2(01), 20-28. [CrossRef]
  72. Schapire, R.E. (2003). The Boosting Approach to Machine Learning: An Overview. In D.D. Denison, M.H. Hansen, C.C. Holmes, B. Mallick, & B. Yu (Eds.), Nonlinear Estimation and Classification (pp. 37-64). Lecture Notes in Statistics, 171. Springer. [CrossRef]
  73. Hosen, M.S., Amin, R. (2021). Significance of Gradient Boosting Algorithm in Data Management System. Int. J. Eng., 9(2), 85-100. [CrossRef]
  74. Zhu, N., Zhu, C., Zhou, L., Zhu, Y., Zhang, X. (2022). Optimization of the Random Forest Hyperparameters for Power Industrial Control Systems Intrusion Occurrence Using an Improved Grid Search Algorithm. Appl. Sci., 12, 10456. [CrossRef]
  75. Kottaridi, K., Demopoulos, V., Sidiropoulos, A., Ihara, D., Nikolaidis, V., Antonopoulos, D. (2021). A Risk Assessment Tool for the Contamination of Aflatoxins on Dried Figs based on Machine Learning Algorithms. World Academy of Science, Engineering and Technology, Open Science Index 180, Int. j. food sci. nutr. eng., 15(12), 159 - 168.
  76. Peng, J., Lee, K., & Ingersoll, G. (2002). An Introduction to Logistic Regression Analysis and Reporting. J. Educ. Res., 96(1), 3-14. [CrossRef]
  77. Nayak, J., Naik, B., Behera, H. (2015). A Comprehensive Survey on Support Vector Machine in Data Mining Tasks: Applications & Challenges. Int. J. Database Theory Appl., 8, 169-186. [CrossRef]
  78. Cichosz, P. (2011). Assessing the quality of classification models: Performance measures and evaluation procedures. Open Eng., 1, 132-158. [CrossRef]
  79. Gogtay, N. J., Thatte, U. M. (2017). Statistical Evaluation of Diagnostic Tests (Part 1): Sensitivity, Specificity, Positive and Negative Predictive Values. J. Assoc. Physicians India, 65(6), 80-84.
  80. Fawcett, T. (2006). An Introduction to ROC Analysis. Pattern Recognit. Lett., 27, 861-874. [CrossRef]
  81. Nahm, F. S. (2022). Receiver operating characteristic curve: overview and practical use for clinicians. Korean Journal of Anesthesiology, 75(1), 25–36. [CrossRef]
  82. Hajian-Tilaki, K. (2013). Receiver Operating Characteristic (ROC) Curve Analysis for Medical Diagnostic Test Evaluation. Caspian Journal of Internal Medicine, 4(2), 627-635.
  83. Braga-Neto, U. M., & Dougherty, E. R. (2004). Is cross-validation valid for small-sample microarray classification? Bioinformatics, 20(3), 374-380. [CrossRef]
  84. Markus Ojala and Gemma C. Garriga. 2010. Permutation Tests for Studying Classifier Performance. J. Mach. Learn. Res. 11 (3/1/2010), 1833–1863. [CrossRef]
  85. Frank, E., Witten, I. (1998). Using a Permutation Test for Attribute Selection in Decision Trees. In Machine Learning: Proceedings of the Fifteenth International Conference (ICML 1998) (pp. 143-151).
  86. Speiser, J. L., Miller, M. E., Tooze, J., & Ip, E. (2019). A Comparison of Random Forest Variable Selection Methods for Classification Prediction Modeling. Expert Syst. Appl., 134, 93–101. [CrossRef]
  87. Chen, R. C., Dewi, C., Huang, S. W., et al. (2020). Selecting critical features for data classification based on machine learning methods. J. Big Data, 7, 52. [CrossRef]
  88. Reif, D. M., Motsinger, A. A., McKinney, B. A., Crowe, J. E., & Moore, J. H. (2006). Feature Selection using a Random Forests Classifier for the Integrated Analysis of Multiple Data Types. In 2006 IEEE Symposium on Computational Intelligence and Bioinformatics and Computational Biology (pp. 1-8). [CrossRef]
  89. Moral, J., Trapero, A. (2009). Assessing the Susceptibility of Olive Cultivars to Anthracnose Caused by Colletotrichum acutatum. Plant Dis., 93(10), 1028-1036. [CrossRef]
  90. Sergeeva, V. (2010). Using copper sprays to control olive diseases. Australian & New Zealand Olivegrower & Processor, 72 , 41-42.
  91. Roca, L., Moral, J., R., Viruega, A., Ávila, A., Oliveira, R., & Trapero-Casas, A. (2007). Copper fungicides in the control of olive diseases. Olea, 26, 48-50.
  92. Fernández-Escobar, R. (2019). Olive Nutritional Status and Tolerance to Biotic and Abiotic Stresses. Front, Plant Sci., 10, 1151. [CrossRef]
  93. Sergeeva V. (2011). Balanced plant nutrition may help reduce anthracnose. The Olive Press: Pests and Diseases, 23-24. https://olivediseases.com/balanced-plant-nutrition-may-help-reduce-anthracnose/.
Preprints 81062 g001
Figure 1. This image depicts model selection using Grid Search hyperparameter optimization with 5-fold cross-validation. Image downloaded from https://sebastianraschka.com/blog/2016/model-evaluation-selection-part1.html.
Figure 1. This image depicts model selection using Grid Search hyperparameter optimization with 5-fold cross-validation. Image downloaded from https://sebastianraschka.com/blog/2016/model-evaluation-selection-part1.html.
Preprints 81062 g001
Preprints 81062 g002
Figure 2. The frequency distribution histogram of OAI.
Figure 2. The frequency distribution histogram of OAI.
Preprints 81062 g002
Preprints 81062 g003
Figure 3. Heatmap Correlation Matrix of numeric features.
Figure 3. Heatmap Correlation Matrix of numeric features.
Preprints 81062 g003
Preprints 81062 g004
Figure 4. Boxplots visualizing statistically significant differences in A) Water Content, Ca, Mg, Mn and Exchangeable Mg between infected (OAI>0%) and non-infected (OAI=0%) orchards and B) Water Content, Ca, Mg, Exchangeable Mg, Exchangeable Na and Trace Zn between orchards with OAI<10% and orchards with OAI>10%.
Figure 4. Boxplots visualizing statistically significant differences in A) Water Content, Ca, Mg, Mn and Exchangeable Mg between infected (OAI>0%) and non-infected (OAI=0%) orchards and B) Water Content, Ca, Mg, Exchangeable Mg, Exchangeable Na and Trace Zn between orchards with OAI<10% and orchards with OAI>10%.
Preprints 81062 g004
Preprints 81062 g005
Figure 5. Distribution of A) Olive Anthracnose Occurrence across Different Locations and B) Olive Anthracnose Incidence across Different Locations.
Figure 5. Distribution of A) Olive Anthracnose Occurrence across Different Locations and B) Olive Anthracnose Incidence across Different Locations.
Preprints 81062 g005
Preprints 81062 g006
Figure 6. Recursive Feature Elimination with Cross-Validation (RFECV) to find optimal features for Random Forest classification of A) OA occurrence (0: OAI=0%, 1: OAI>0%) and B) OA incidence (0: OAI<10%, 1: OAI>10%).
Figure 6. Recursive Feature Elimination with Cross-Validation (RFECV) to find optimal features for Random Forest classification of A) OA occurrence (0: OAI=0%, 1: OAI>0%) and B) OA incidence (0: OAI<10%, 1: OAI>10%).
Preprints 81062 g006
Preprints 81062 g007
Figure 7. Boxplots visualizing differences in dispersion of a) Trace Cu data between infected (OAI>0%) and non-infected (OAI=0%) orchards and b) P data between orchards with OAI<10% and orchards with OAI>10% and c) Trace Cu data between orchards with OAI<10% and orchards with OAI>10%.
Figure 7. Boxplots visualizing differences in dispersion of a) Trace Cu data between infected (OAI>0%) and non-infected (OAI=0%) orchards and b) P data between orchards with OAI<10% and orchards with OAI>10% and c) Trace Cu data between orchards with OAI<10% and orchards with OAI>10%.
Preprints 81062 g007
Preprints 81062 g008
Figure 8. The comparison of the considered (a) OA occurrence (b) OA incidence models using AUC-ROC Curves. .
Figure 8. The comparison of the considered (a) OA occurrence (b) OA incidence models using AUC-ROC Curves. .
Preprints 81062 g008
Preprints 81062 g009
Figure 9. Generated null distributions of accuracy values from permutation tests where the class labels are randomly shuffled 1000 times and an accuracy value for each permutation is plotted. The vertical lines represent the observed accuracy values from the true class labels. (A, B) Generated null-distributions for the GB and RF classifications of infected (OAI>0%) against non-infected (OAI=0%) olive orchards. (C, D) Generated null-distributions for the DT and RF classification of olive orchards with OAI<10% against orchards with OAI>10%.
Figure 9. Generated null distributions of accuracy values from permutation tests where the class labels are randomly shuffled 1000 times and an accuracy value for each permutation is plotted. The vertical lines represent the observed accuracy values from the true class labels. (A, B) Generated null-distributions for the GB and RF classifications of infected (OAI>0%) against non-infected (OAI=0%) olive orchards. (C, D) Generated null-distributions for the DT and RF classification of olive orchards with OAI<10% against orchards with OAI>10%.
Preprints 81062 g009
Table 1. predictor variables used in this study.
Table 1. predictor variables used in this study.
Variable Type
Olive Orchard Characteristics
Olive Cultivar Categorical
Location Categorical
Olive Fruit Parameters
Maturity Index (%) Numerical
Water Content (%) Numerical
Foliar Nutrients
Total N (%) Numerical
P (%) Numerical
Ca (%) Numerical
Mg (%) Numerical
K (%) Numerical
Fe (ppm) Numerical
Mn (ppm) Numerical
Zn (ppm) Numerical
Cu (ppm) Numerical
B (ppm) Numerical
Soil Parameters
SP (%) Numerical
pH (0-14) Numerical
EC (mS/cm) Numerical
OM (%) Numerical
P Numerical
Soil Macronutrients
Exchangeable Cations (ppm) mg/kg
Ca Numerical
Mg Numerical
K Numerical
Na Numerical
Water Soluble Elements (ppm) mg/L
Mg Numerical
K Numerical
Soil Micronutrients (Trace elements) (ppm) mg/kg
B Numerical
Fe Numerical
Mn Numerical
Zn Numerical
Cu Numerical
Soil Texture Indicators (%)
Sand Numerical
Clay Numerical
Silt Numerical
Soil Textural Class Categorical
Table 2. Confusion matrix for binary classification.
Table 2. Confusion matrix for binary classification.
Actual
Positive Negative
Predicted Positive True Positives (TP) False Positives (FP)
Negative False Negatives (FN) True Negatives (TN)
Table 3. Five Number Summary Statistics and Mann-Whitney U tests results of statistically significant features for a) infected (oai>0%) and non-infected (oai=0%) orchards and b) orchards with oai<10% and oai>10%.
Table 3. Five Number Summary Statistics and Mann-Whitney U tests results of statistically significant features for a) infected (oai>0%) and non-infected (oai=0%) orchards and b) orchards with oai<10% and oai>10%.
Features Classes Min* Lower Quartile
(Q1)		 Median
(Q2)		 Upper Quartile
(Q3)		 Max* p**
A.
Water Content OAI=0% 49.39 57.71 62.93 65.70 72.07 .045
OAI>0% 56.38 61.38 64.36 67.56 75.67
Ca OAI=0% 0.62 1.22 1.40 1.72 2.16 .005
OAI>0% 0.46 0.95 1.06 1.37 1.93
Mg OAI=0% 0.08 0.12 0.15 0.17 0.24 .007
OAI>0% 0.06 0.08 0.12 0.14 0.22
Mn OAI=0% 17.5 28 35.5 43.5 64.5 .043
OAI>0% 14.5 21.75 27.5 35.5 48.5
Exch. Mg OAI=0% 53 115.5 154 274 472 .001
OAI>0% 53 81 103 134 180
B.
Water Content OAI<10% 49.39 58.17 62.38 65.84 72.07 .012
OAI>10% 58.53 63.50 66.13 67.84 70.66
Ca OAI<10% 0.62 1.19 1.36 1.67 2.16 .019
OAI>10% 0.46 0.92 1.04 1.41 1.93
Mg OAI<10% 0.06 0.12 0.14 0.17 0.23 .007
OAI>10% 0.08 0.08 0.10 0.14 0.18
Exch. Mg OAI<10% 53 114.75 148.5 270.5 472 .8 × 10-4
OAI>10% 53 75.75 94 108.75 142
Exch. Na OAI<10% 10 15 27.5 53.75 77 .037
OAI>10% 9 13.75 17.5 25.5 34
Trace Zn OAI<10% 0.58 1.65 2.80 4.05 6.02 .048
OAI>10% 0.86 1.43 1.92 2.6 3.10
*Outliers were excluded , **Statistically significant at the .05 level.
Table 4. Chi-square test results for the association between a) the location and oa occurrence and b) the location and oa incidence.
Table 4. Chi-square test results for the association between a) the location and oa occurrence and b) the location and oa incidence.
Categorical Variables Association Test Statistic Degrees of Freedom (df) p-value
A) Location & OA Occurrence Significant 14.921 2 .001
B) Location & OA Incidence Significant 8.216 2 .016
Table 5. contingency tables of a) location * oa occurrence and b) location * oa incidence.
Table 5. contingency tables of a) location * oa occurrence and b) location * oa incidence.
A. OA Occurrence OAI=0% OAI>0%
Location Messinia Count 7 19
Expected Count 13.9 12.1
Adjusted Residual -3.7 3.7
Laconia Count 16 3
Expected Count 10.2 8.8
Adjusted Residual 3.3 -3.3
Other Locations Count 8 5
Expected Count 6.9 6.1
Adjusted Residual .7 -.7
B. OA Incidence OAI<10% OAI>10%
Location Messinia Count 12 14
Expected Count 17 9
Adjusted Residual -2.8 2.8
Laconia Count 16 3
Expected Count 12.4 6.6
Adjusted Residual 2.1 -2.1
Other Locations Count 10 3
Expected Count 8.5 4.5
Adjusted Residual 1.0 -1.0
Table 6. Five Number Summary Statistics for p and trace cu by oai classes.
Table 6. Five Number Summary Statistics for p and trace cu by oai classes.
Features Min Lower Quartile
(Q1)		 Median
(Q2)		 Upper Quartile
(Q3)		 Max
Trace Cu OAI=0% 0.58 3.33 10.56 14.54 18.80
OAI>0% 1.48 3.09 6.80 16.17 32.60
P OAI<10% 0.23 0.26 0.29 0.31 0.37
OAI>10% 0.19 0.25 0.29 0.32 0.40
Trace Cu OAI<10% 0.58 2.86 8.55 13.86 18.80
OAI>10% 1.48 4.06 7.07 17.47 36.80
Table 7. the machine learning models hyperparameter configuration space.
Table 7. the machine learning models hyperparameter configuration space.
Model Hyperparameter Search Space Best parameters
OAI>0% OAI>10%
DT criterion
max_depth
ccp_alpha
max_features
min_samples_leaf
min_samples_split		 ['gini', 'entropy']
[None, 1,2,3,4,5]
[0, .01, .1, .3, 1, 2]
['auto', 'sqrt', 'log2', None]
[1,2,3,4]
[2,3,4]		 ‘entropy’
None
.01
‘sqrt’
3
2		 ‘gini’
None
.1
‘auto’
1
2
GB n_estimators
learning_rate
max_features
max_depth
min_samples_leaf
min_samples_split
subsample		 [15, 20, 22, 25]
[.1, .5, .8, 1]
['auto', 'sqrt', ‘log2’, None]
[None, 4, 5]
[1,2,3,4]
[.5, 6, 7]
[.8, 1]		 25
.5
sqrt
None
2
6
.8		 20
.1
sqrt
None
2
.5
.8
LR penalty
C
solver
max_iter		 [‘l1’, ‘l2’]
[.01, .1, .5, 1, 2]
[‘lbfgs’, ‘liblinear’]
[25, 30, 50, 100]		 ‘l2’
.1
‘liblinear’
30		 ‘l1’
.5
‘liblinear’
25
RF n_estimators
criterion
max_depth
min_samples_split
min_samples_leaf
max_features		 [10, 30,100]
[‘gini’, ‘entropy’]
[None, 1, 2, 3]
[2, 3, 4, 5, 10]
[1, 2, 3, 4]
['auto', 'sqrt', 'log2', None]		 100
‘gini’
None
10
1
‘sqrt’		 100
‘gini’
2
2
2
‘auto’
KNN n_neighbors
weights
metric		 [3, 4, 5, 6, 7, 8, 9]
[‘uniform’, ‘distance’]
[‘euklidean’, ‘manhattan’]		 4
‘distance’
‘manhattan’		 7
‘uniform’
‘manhattan’
SVM C
gamma
kernel		 [.1, .5, 1, 2, 3]
[‘scale’, .1, 1, 10, 100]
['linear', 'rbf', 'poly', 'sigmoid']		 .1
1
‘linear’		 .1
10
‘poly’
Table 8. the 5-fold cross-validation accuracy of the optimized models for the prediction of oa occurrence (Class 0: oai=0%, Class 1: oai>0%) and incidence (class 0: oai<10%, class 1: oai>10%).
Table 8. the 5-fold cross-validation accuracy of the optimized models for the prediction of oa occurrence (Class 0: oai=0%, Class 1: oai>0%) and incidence (class 0: oai<10%, class 1: oai>10%).
Accuracy
DT GB LR RF KNN SVM
OAΙ>0% 0.73 0.74 0.72 0.73 0.72 0.76
OAΙ>10% 0.72 0.77 0.72 0.81 0.74 0.72
Table 9. classification report of predictive models for oa occurrence (Class 0: oai=0%, Class 1: oai>0%) and oa incidence. (class 0: oai<10%, class 1: oai>10%).
Table 9. classification report of predictive models for oa occurrence (Class 0: oai=0%, Class 1: oai>0%) and oa incidence. (class 0: oai<10%, class 1: oai>10%).
Model Accuracy Specificity Sensitivity AUC
OAI>0%
DT 0.80 0.86 0.75 0.65
GB 0.87 1.00 0.75 0.93
LR 0.73 0.86 0.62 0.86
RF 0.80 0.86 0.75 0.93
KNN 0.73 1.00 0.50 0.90
SVM 0.80 0.86 0.75 0.86
OAI>10%
DT 0.87 1.00 0.81 0.91
GB 0.80 0.75 0.81 0.77
LR 0.73 0.50 0.81 0.66
RF 0.87 0.75 0.91 0.84
KNN 0.87 0.75 0.91 0.77
SVM 0.73 0.75 0.73 0.68
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated