Preprint
Article
A Theoretical Analysis of the Differential Chemical Reaction Results Caused by Chirality Induction
Altmetrics
Downloads
140
Views
130
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
31 July 2023
Posted:
01 August 2023
You are already at the latest version
Alerts
Abstract
The theory of electron spin has been proposed for a century, but the study of quantum effects in biological molecules is still in its infancy. Chirality-induced spin selectivity (CISS) is a very modern theory that can explain many biochemical phenomena. In this paper, we propose a new theoretical model based on CISS theory and quantum chemistry theory, which can well explain the theoretical explanation of the chiral selectivity of chiral proteins. Moreover, this theory can predict the spin state of corresponding chiral molecules. Taking L-DOPA and AADC enzyme as examples, this theoretical model solves the theoretical explanation of AADC enzyme's chiral catalysis selectivity problem and successfully predicts the spin state of L-DOPA and D-DOPA's valence electrons.
Keywords:
Subject: Computer Science and Mathematics - Mathematical and Computational Biology
1. Introduction
Research on chiral molecules has forged ahead since their discovery. In 1848, the concept of chiral molecules was first proposed by Louis Pasteur, who made the initial observation of optical rotation in substances. In 1961, the FDA approved the first chiral drug, thalidomide. However, it was later discovered that the levorotatory enantiomer of thalidomide can cause severe teratogenic effects, leading to a catastrophic event known as the „thalidomide tragedy” which resulted in a large number of newborn deformities. During the 1980s, with the advancement of chiral separation and synthesis techniques, the research on chiral drugs saw rapid development, contributing to the emergence of numerous novel chiral drugs. In 1992, the FDA issued guidance principles concerning chiral drugs, explicitly highlighting the significance of enantiomers in pharmacology and toxicology. Pharmaceutical companies were mandated to conduct thorough research on the chirality of drugs before their development and market launch. In 2000, Japan approved the sale of the chiral drug, pravastatin, making it the world’s first chiral drug to gain market approval. In recent years, as research on chiral drugs has deepened, an increasing number of chiral drugs have entered clinical research and been brought to the market, including moxifloxacin and levofloxacin, among others. Meanwhile, there is a growing focus on issues such as formulation, safety evaluation, and pharmacological efficacy assessment of chiral drugs.
Due to the chirality of the majority of drug molecules, different enantiomers of drug molecules may have distinct effects on the human body. Therefore, the synthesis of single enantiomers in drug molecules is of paramount importance in pharmaceutical development. In 1990, Elias J. Corey was awarded the Nobel Prize in Chemistry for his contributions to asymmetric synthesis. He introduced a novel organic synthesis method that involves designing and combining simple molecular units to achieve the asymmetric synthesis of complex molecules. This research provided new insights and approaches for the study of chiral drugs [1]. In 2001, William S. Knowles, Ryoji Noyori, and K. Barry Sharpless were winners of the Nobel Prize in Chemistry for their development of chiral catalysts. Among them, Ryoji Noyori published a paper titled „The Asymmetric Hydrogenation of β-Keto Carboxylic Esters Catalyzed by Chiral Ruthenium Complexes.” This paper investigated the application of chiral catalysts in asymmetric hydrogenation reactions with the purpose of synthesizing chiral drugs. The author first discovered that chiral catalysts can efficiently catalyze asymmetric hydrogenation reactions, yielding products with high yields and high enantioselectivity. This research provided essential means and theoretical foundations for the synthesis of chiral drugs [2].
In living organisms, the majority of biomolecules exhibit chirality. For instance, most proteins in the human body are composed of levorotatory amino acids which form peptide chains that undergo intricate folding, resulting in proteins with macroscopic levorotatory structures. However, the underlying reason for nature’s persistent selection of such a chiral preference remains unclear, despite the energetic costs associated with maintaining chirality. The rapid development of quantum mechanics in the 1920s facilitated the emergence of numerous interdisciplinary fields. In 1999, the first report on the dependence of electron transfer through chiral molecules on the electron’s spin was documented, later known as Chiral-Induced Spin Selectivity (CISS) [3]. The discovery of the CISS effect prompted the development of organic devices based on the manipulation of electron spin. At the Weizmann Institute of Science in Israel, Ron Naaman explored the relationship between electron spin and molecular chirality as well as their impact on vital biological processes, utilizing the CISS effect as a foundation. Naaman pointed to the crucial role of chiral molecular rotation in various biological processes, including protein folding and enzymatic catalytic activity. Furthermore, he discussed the advancements in employing chiral molecular spin to control electron transport and delved into the potential applications of these findings in the fields of biology and medicine [4].
Building upon the CISS theory, this paper proposes a theoretical explanation for the differential effects produced by drug molecules of different enantiomers on the human body. Theoretical calculations and explanatory discussions are conducted using L-DOPA and D-DOPA as examples, targeting the AADC enzyme. Finally, the relationship between optical rotation and the electron spin of chiral substances was briefly discussed.
2. Electron Spin and Chemical Reactions
The concept of electron spin was first introduced by physicists Samuel Goudsmit and George Uhlenbeck in their paper published in 1925. The paper proposed that electrons possess not only charge and mass but also intrinsic angular momentum [5]. Similar to electron charge, electron spin is an inherent property of electrons, dictating the behavior of electrons in external magnetic fields and influencing the properties and reactions of matter.
2.1. A simplified quantum mechanical explanation of the formation of covalent bonds
The essence of a chemical reaction lies in the transfer of electrons, leading to the formation or breaking of atomic bonds. In classical chemical theory, the process of a chemical reaction is solely based on the consideration of electron charge. However, in modern quantum chemical theory, factors such as the wave-like nature of electrons and electron spin are also taken into account, providing a more accurate and comprehensive explanation of chemical reactions.
Now, let us briefly discuss the formation of chemical bonds in quantum mechanics. Consider two molecules, A and B, which undergo a chemical reaction, resulting in the formation of a covalent bond between them. In chemical theory, the formation of a covalent bond involves the sharing of electron pairs between two atoms. Therefore, during the reaction process, only the two electrons participating in the reaction need to be considered. The other electrons within the molecules can be treated as a collective entity (similar to a nucleus) associated with molecules A and B. In this case, the interaction between the electron pairs in molecules A and B is equivalent to the interaction between the two equivalent positive charges constituted by A, B, and other electrons. When the two molecules come close enough, the orbitals of the valence electrons will overlap. At this point, the Hamiltonian operator for these two valence electrons can be expressed as:
Suppose these two electrons satisfy the Schrödinger equation:
As the two electrons share the same Hamiltonian operator, their orbital wave functions are identical and denoted as . Consequently, we can construct the total orbital wave functions satisfied by the two electrons as follows:
Here, is symmetric under exchange while is antisymmetric under exchange. From the second equation, it is apparent that the total orbital wave function of the electrons involved in forming the covalent bond can only be symmetric under exchange. The spin wave functions for two electrons with spin coupling are constructed as follows:
Among them, is antisymmetric under exchange while the other three spin-coupled wave functions are symmetric under exchange. Since electrons are fermions and constitute real matter, their wave functions must be antisymmetric under exchange. On the other hand, the total orbital wave function formed by the coupling of two valence electrons must be symmetric under exchange, and thus, the total spin wave function formed by coupling must be antisymmetric. After the formation of a covalent bond, the total wave function of the two electrons can only be expressed as:
From the expression of the total wave function, it can be observed that the spins of the two valence electrons involved in forming the covalent bond must be antiparallel, which can be illustrated through a chemical reaction.
As shown in Figure 1, two OH radicals undergo a chemical reaction. When the spins of the valence electrons on the two OH radicals are antiparallel, these radicals tend to form hydrogen peroxide molecules, resulting in covalent bond formation. The reaction outcome is depicted in the left diagram. Conversely, when the spins of the valence electrons on the two OH radicals are parallel, the total orbital wave function must be antisymmetric under exchange, meaning that these two valence electrons must couple in different orbitals, due to the fact that only spin-coupled wave functions such as and , which are symmetric under exchange, can be formed by the coupling of these valence electrons. Consequently, the reaction occurs on the triplet state surface. The formed chemical bond would be highly unstable, rapidly leading to the formation of molecular oxygen. The reaction outcome is illustrated in the right diagram. This result has been previously confirmed by Mtangi et al. in experimental studies [6].
2.2. Chiral-Induced Spin Selectivity (CISS)
In 1990, German physicists conducted an experiment where they emitted electrons towards the volatile odor molecules (a type of protein) of a camphor tree. They observed a slight bias in the spin of electrons passing through the molecules: electrons with spin pointing upward seemed to preferentially pass through left-handed chiral molecules, while electrons with spin pointing downward showed a preference for right-handed ones. This phenomenon is now known as „Chiral-Induced Spin Selectivity (CISS).”
The CISS effect has since drawn continuous attention from the scientific community. Although this phenomenon was initially observed in 1990, it was not systematically studied until 2013 [7]. In 2014, researchers found that this effect is related to the relative orientation of the chiral molecules and only occurs in molecules with a certain degree of symmetry [8]. In recent years, other scholars have discovered that the CISS effect also exists in more complex molecules and that its intensity can be controlled by adjusting the molecular structure. This research holds significant importance for designing novel chiral molecular materials [9]. Some have also pointed out that the CISS phenomenon has multiple impacts on biological systems. It can promote long-distance electron transfer, enhance biological affinity and enantioselectivity, and allow multi-electron oxidation-reduction processes to proceed effectively and selectively [10].
Currently, some theoretical assumptions have been proposed to expound the rationale behind the CISS effect. One theory posits that chiral molecules act more like spin polarizers rather than spin filters, as they cause all scattered (transmitted and reflected) electrons to polarize in the same direction, dependent on the chirality of the molecule and the incidence direction of the electron [11]. Some have analyzed the relationship between chiral-dependent spin polarization and the imaginary part of the effective single-electron Hamiltonian matrix for heavy-atom molecules [12]. Others have noted that aside from using an external magnetic field, there are other means to achieve spin polarization, with helical structures playing a key role in filtering electron spin [13]. Some researchers have validated all predictions based on quantum transport calculations of density functional theory, providing further quantitative insight within a single-particle framework [14]. However, consensus has not yet been reached theoretically to date [15]. Regardless of which hypothesis holds true, this effect remains crucial for furthering the applications of chiral molecules in fields such as life sciences and nanoelectronics.
For an in-depth discussion in the following sections, a semi-classical theory is employed here to provide a brief derivation of the CISS effect:
As shown in Figure 2, an electron moves in a helical trajectory along the Z-axis with a velocity V under the potential field of chiral molecules. The helical motion has a radius of a and a pitch of p. The equation of motion for the electron in this coordinate system can be written as:
The second derivative is as follows:
Based on the above equation and the classical force and effective spatial potential formula:
We can introduce them into the Hamiltonian operator of linear momentum and spin coupling:
Thus, the expression for can be derived. By using the commutation relations
We can determine the changes in spin during the transport process under spin-orbit coupling, as given by the following equations:
Here, θ represents the angle with respect to the Z-axis. g and b are coefficients related to the pitch p, radius a, and electron velocity V:
It seems equations (1) and (2) are able to explain the CISS effect well enough despite being derived with a semi-classical model. Equation (1) shows that the electron’s spin changes with the variation of the θ angle, implying that the spin distribution along the helical path is not uniform. Equation (2) demonstrates that the sign of the pitch p changes upon molecular chirality inversion, indicating the correlation between the CISS effect and molecular chirality. Through these two equations, it can be observed that electrons with spin pointing upward appear to preferentially pass through left-handed chiral molecules while electrons with spin pointing downward tend to pass through right-handed chiral molecules. This observation is consistent with experimental results.
For a more rigorous derivation, spin scattering theory and Green’s function should be employed, which, unfortunately, are beyond the scope of discussion in this paper [16].
2.3. Interaction of Electrically Neutral Molecules
Based on the CISS effect and the conclusions in Section 2.1, it can be observed that chiral molecules can selectively control which molecules participate in certain reactions by manipulating the spin of the electrons involved. This could potentially explain the phenomenon of biological recognition reactions [17]. It is noteworthy that similar effects can also occur when different chiral molecules interact with biomacromolecules possessing chiral structures.
The majority of chiral substances are organic compounds, which implies that these molecules are generally electrically neutral, i.e., non-polar molecules. Therefore, when two molecules gradually approach and are about to undergo a chemical reaction, the predominant forces acting on them are van der Waals forces, specifically London dispersion forces.
As shown in Figure 3, when two organic molecules approach each other, an electric dipole moment is induced, causing the charge centers of the reacting molecules to separate. The total energy of this system comprises the kinetic energy of the two molecules and the Coulomb potential energy. Therefore, the zero-point vibrational energy of the system corresponds to the Coulomb potential energy of the two molecules. This zero-point vibrational energy can be approximated as:
where the molecular polarizability coefficient is defined as:
From the expression of , it can be observed that the Van der Waals-London forces are attractive in nature. Furthermore, this attractive force rapidly increases as the molecules approach each other and is generated by the movement of charges within the two molecules. As a result, as the molecules come closer, the charge centers within the molecules deviate further from their original positions. This indicates that for point-neutral molecules, the internal charge distribution undergoes reorganization before a chemical reaction occurs. It is only when bonding begins that the deviation of charge centers within the molecules reaches its maximum.
2.4. Influence of Chiral Molecules on Chemical Reactions
According to the CISS effect, chiral molecules selectively affect the electron spin, with spin-up electrons being more likely to pass through left-handed chiral molecules, while spin-down electrons are more likely to pass through right-handed ones. Based on the analysis in Section 2.3, non-polar molecules undergo internal polarization currents before a chemical reaction occurs. If one of the molecules involved in the reaction is a chiral molecule, the internal polarization current within the molecule will be influenced by the CISS effect which will spontaneously lead to chemical reactions exhibiting selectivity towards electron spin. Moreover, experiments have suggested that reduction primarily occurs with electrons whose spin is antiparallel to their velocity [18]. For instance, if the reacting molecules are left-handed biomacromolecules, as the two reactants approach each other, the CISS effect will cause spin-up valence electrons to be more concentrated near the negative charge center of the molecule while spin-down electrons will be distributed more around the positive charge center. Similarly, for right-handed molecules, prior to the reaction, spin-down electrons will be more distributed near the negative charge center and spin-up electrons will be more distributed near the positive charge center.
At this point, if the spin of the electrons participating in the reaction with the chiral molecule is parallel to the electron spin at the bonding site of the chiral molecule, according to the conclusion in Section 2.1, the reaction will either be difficult to proceed or the resulting products will be unstable and prone to decomposition. Conversely, if the spin of the electrons participating in the reaction with the chiral molecule is antiparallel to the electron spin at the bonding site of the chiral molecule, then the two can easily undergo the formation of a covalent bond, meaning the chemical reaction can easily occur.
3. Chiral Selectivity of AADC Enzyme
As is widely known, AADC enzyme plays a crucial role in neural regulation in the human body. AADC enzyme belongs to a class of enzymes known as chiral enzymes which exhibit high enantioselectivity towards chiral substrates (such as L-amino acids), meaning they catalyze reactions selectively with one enantiomer over the other. However, as of now, there is no comprehensive theory that fully explains the chiral selectivity exhibited by chiral enzymes. In the following section, this paper will employ the theoretical framework established in Section 2 to elucidate the workings of the chiral selectivity of AADC enzyme.
3.1. Parkinson’s Disease and L-DOPA
Among the elderly population, Parkinson’s disease has a significantly high incidence rate. Up to the present, no fully curative medication has been discovered for this disease, rendering it an incurable condition. The underlying cause of Parkinson’s disease is an imbalance between dopamine and acetylcholine, with an increase in the excitatory effects of acetylcholine. The primary pathological characteristic involves the degeneration and death of dopaminergic neurons in the substantia nigra and the aggregation of α-synuclein in the brainstem neurons, forming Lewy bodies. In simple terms, Parkinson’s disease is a neurodegenerative disorder characterized by a reduction in dopamine secretion. Patients with Parkinson’s disease exhibit symptoms such as resting tremors, muscular rigidity, facial stiffness, and abnormal posture and gait. Additionally, a portion of patients (20% to 40%) may experience cognitive impairment, neuropsychiatric symptoms, and dementia during the course of the disease. As a result, Parkinson’s disease is considered a neurological disorder.
However, Parkinson’s patients cannot directly take dopamine to alleviate their symptoms. This is because dopamine cannot penetrate the blood-brain barrier to reach the brain. The blood-brain barrier is a structure composed of vascular endothelial cells and neuroglial cells, which restricts certain substances from entering the brain from the bloodstream, thus protecting the brain from harmful substances. Due to its large molecular size and strong polarity, dopamine cannot pass through the blood-brain barrier and, therefore, cannot be administered orally. To treat Parkinson’s disease, precursor drugs that can pass through the blood-brain barrier, such as L-DOPA, are typically used. Once metabolized, L-DOPA is converted into dopamine within the brain.
DOPA can be considered one of the earliest discovered chiral drugs in human history. Its corresponding chiral isomer is D-DOPA. If no artificial intervention is made during the pharmaceutical manufacturing process, an equal number of L-DOPA and D-DOPA molecules are naturally produced. However, only L-DOPA can be catalyzed by AADC enzyme. If an excessive amount of D-DOPA is ingested, it cannot be metabolized by the human body, leading to vascular blockage. Therefore, in the pharmaceutical manufacturing process, L-DOPA is selectively chosen for production.
As shown in Figure 4, the specific process by which L-DOPA is converted into dopamine in the human body remains elusive. However, it is generally believed that biologically active form of vitamin B6 - pyridoxal phosphate (PLP) - participates in the catalytic reaction. PLP serves as a coenzyme and forms a covalent bond with amino acid residues in AADC enzyme, thereby forming a catalytic intermediate that facilitates the decarboxylation of L-DOPA. Specifically, PLP undergoes a keto-enol tautomerization with the carboxyl group of L-DOPA, generating a keto-enol intermediate, which then undergoes decarboxylation to produce dopamine and CO2. In this process, PLP continuously receives and releases carboxyl and amino groups, thus enabling the conversion of L-DOPA to dopamine.
3.2. Simulation Method
With the rapid advancement of computer technology and quantum computational theory, it is now possible to conduct simulation studies of real molecular motion using computer simulation techniques. Since the discovery of electron wave properties, the resolution of human microscopes has increased dramatically, allowing for accurate representation of the structures of many biological molecules on computers. The use of probing methods for modeling significantly reduces the cost of manual modeling. The large molecular model data involved in this paper is obtained from the National Center for Biotechnology Information (NCBI). Some organic small molecules are self-modeled according to chemical formulas. The following section provides a brief introduction to the chemical organic molecular models used in the simulation calculations.
3.2.1. AADC and PLP
Although Section 3.1 briefly introduced the roles of AADC enzyme and PLP in the reaction process, in reality, the structure of AADC enzyme is highly complex. As shown in Figure 5, the AADC enzyme consists of two peptide chains, A-chain and B-chain, arranged symmetrically in a chiral manner. However, all the helical structures forming these peptide chains are levorotatory, suggesting that the amino acid molecules constituting these peptide chains are also entirely levorotatory. Therefore, AADC enzyme is a type of levorotatory enzyme.
Figure 6 illustrates the structure of AADC enzyme after structural optimization using the Forcite algorithm. From the figure, it is evident that the structure of AADC enzyme in Material Studio is extremely intricate, making it difficult to visually observe the folding and bending processes of the protein. However, in an overall perspective, the shapes of Figure 5 and Figure 6 are consistent. At the edges of AADC enzyme, there are some long carbon chains present on its surface.
Figure 7 illustrates the structures of LLP and PLP ligands formed on the AADC enzyme. As evident from Figure 8, both LLP and PLP ligands possess a benzene ring structure. These ligands are situated on opposite sides of the central crevice of the AADC enzyme. Consequently, the catalytic site for the conversion of L-DOPA is located at the vicinity of these ligands. The region surrounding these ligands is encompassed by protein structures with levorotatory conformations, creating a relatively enclosed reaction environment that favors the preservation of proper product molecular structures.
3.2.2. L-DOPA and D-DOPA
Figure 9 represent the optimized structures of the two chiral forms of dopamine molecules using the DMol3 algorithm. The chirality of these molecules arises from the presence of three different substituents attached to the third carbon atom of the benzene ring, leading to the optical rotation and other factors that contribute to the chiral selectivity of AADC enzyme.
3.2.3. Molecular Dynamics Simulation of Dopamine Molecules with AADC Enzyme
In order to simulate the real interaction between AADC enzyme and dopamine molecules in the human body, we employed the Monte Carlo algorithm to randomly place dopamine molecules in the vicinity of the AADC enzyme and searched for the configurations that minimized the overall system energy. We also set up several control groups with different quantities of L-(or D-) dopamine molecules, including 32, 100, 200, and 300, interacting with one AADC enzyme. The system temperature during the calculations was set to 310 K (approximately the normal body temperature), and 30 frames were output at each calculation.
3.2.4. Dynamic Simulation Results and Analysis Figures
Figure 10, Figure 11, Figure 12 and Figure 13 represent the outcomes of the dynamic simulation. The left-hand images depict the interaction between L-DOPA and AADC enzyme, while the right-hand images illustrate the interaction between D-DOPA and AADC enzyme. The AADC enzyme molecules are marked in yellow. As analyzed in Section 3.2.1, the active site for the interaction between AADC enzyme and DOPA molecules is located at the central concave region of the enzyme. From these four sets of images, it can be observed that D-DOPA exhibits a repulsive behavior relative to L-DOPA when interacting with the AADC enzyme molecules. Most D-DOPA molecules tend to distribute themselves on the opposite side of the AADC enzyme, away from the active site, whereas L-DOPA molecules tend to cluster around the concave region of the AADC enzyme. This indicates that D-DOPA molecules seem to be less inclined to react with the AADC enzyme.
To gain deeper insights into the reasons behind this phenomenon, we have calculated the total energy for each system:
From Figure 14, it can be observed that the total energy of the system consisting of D-DOPA and AADC enzyme is consistently higher than that of the system comprising L-DOPA and AADC enzyme. This indicates that the interaction energy between L-DOPA and AADC enzyme is smaller compared to the interaction between D-DOPA and AADC enzyme. The underlying reasons for this outcome can be analyzed using the theoretical model proposed in Section 2.
3.3. Theoretical Analysis of Results
Section 3.2.3 demonstrated that the interaction energy between AADC enzyme and D-DOPA molecules is greater than that between AADC enzyme and L-DOPA molecules. This observation suggests that AADC enzyme may exhibit chiral selectivity. However, it is noteworthy that L-DOPA and D-DOPA share identical chemical structures, indicating that their valence electron arrangements and chemical properties are exactly the same. Consequently, the underlying reason for this disparity can only be attributed to the electron spin of L-DOPA and D-DOPA molecules.
According to the theoretical analysis presented in Section 2, non-polar molecules undergo polarization currents during chemical reactions, resulting in electron redistribution within the molecules, whereas AADC enzyme is a levorotatory protein molecule. Based on the CISS effect, valence electrons with spin-up are more likely to accumulate near the negative charge center of the molecule, while valence electrons with spin-down are more distributed around the positive charge center. For stable, low-energy chemical bonding with AADC enzyme, the spin direction of the reactant’s valence electrons must be antiparallel to that of AADC enzyme. Since covalent bond formation involves the sharing of electron pairs, molecules that can form stable structures with AADC enzyme must carry valence electrons with the opposite spin direction to the negative charge center of AADC, i.e., spin-down valence electrons. Conversely, substances that form unstable interactions with AADC enzyme are expected to carry a higher proportion of spin-up valence electrons.
Therefore, a natural conjecture is that L-DOPA molecules carry valence electrons with spin-down, while D-DOPA molecules carry valence electrons with spin-up. Due to this characteristic, L-DOPA molecules are more prone to forming covalent bonds with AADC enzyme, making them more easily anchored at the catalytic site of AADC. S. By the same token, D-DOPA molecules require a transition to the triplet state surface when reacting with AADC enzyme. This transition necessitates one of the valence electrons to undergo a transition and emit to an energy level orbital that intersects with the other electron, forming an exchange anti-symmetric coupling orbital wave function, thus enabling the formation of an unstable chemical bond. Consequently, the interaction potential energy between D-DOPA molecules and AADC enzyme increases, generating an energy barrier. The barrier represents the energy required for the valence electron to transition to the nearest neighboring orbital. As a result, the difference in spin orientations of the electrons carried by the two molecules leads to the macroscopic phenomenon of chiral selectivity of AADC enzyme. Furthermore, it has been found that when spin in enzyme molecules is preferentially guided in a particular direction, charge recombination is reduced, which in turn improves charge transfer, thus enhancing the reaction rate [19].
3.3.1. Calculation of Charge Transfer in the Interaction of L-DOPA and D-DOPA with Peptide Chains
To validate the hypothesis proposed in Section 3.3, it is necessary to calculate the charge transfer between the enzyme molecule and L-DOPA, as well as D-DOPA, during the occurrence of the reaction. However, directly calculating the charge transfer between the large AADC enzyme molecule and L-DOPA or D-DOPA is impractical due to the sheer size of the enzyme. As AADC enzyme is composed of levorotatory peptide chains, for the convenience of computation, we calculated the charge transfer between levorotatory peptide chain molecules consisting of different numbers of amino acid units and L-DOPA or D-DOPA molecules. Prior to that, we need to analyze the active sites of L-DOPA and D-DOPA when undergoing a chemical reaction.
To determine the active sites, we calculated the Fukui indices of L-DOPA and D-DOPA molecules using the DMol3 [20,21] module in MS. The Fukui index provides a qualitative judgment of which functional group in the molecule is most likely to be involved in a chemical reaction. The larger the Fukui index of an atom, the higher its chemical reactivity will be. The Fukui indices are categorized into nucleophilic attack index (f+), electrophilic attack index (f-), and radical attack index (f0). The calculated results of the electrophilic attack index for L-DOPA and D-DOPA molecules are shown in the following figure:
The higher the electrophilic attack index, the more susceptible the atom is to losing electrons to other molecules. From Figure 15 and Figure 16, it can be observed that both L-DOPA and D-DOPA have the same sites that are prone to electron loss during the chemical reaction, specifically located on the oxygen atom of the benzene ring in the lower-left region of the figures. The electrophilic attack index at this site is 0.134 for L-DOPA and 0.131 for D-DOPA.
Based on the results, in the subsequent calculations, we positioned the benzene ring of L-DOPA and D-DOPA away from the levorotatory peptide chain to ensure that it is close to the side of the peptide chain. For comprehensive analysis, we also configured levorotatory peptide chains composed of 10, 15, 20, and 25 amino acid units, ensuring that the pitch and radius of each peptide chain are consistent. Additionally, we set the distance between the centers of L-DOPA and D-DOPA molecules and the centers of the peptide chain molecules to simulate the molecular approach during the chemical reaction. Due to the different exposed functional groups at the ends of the peptide chains, separate considerations are needed. Thus, we need to separately calculate the scenarios in which the N-terminus or the C-terminus of the peptide chains approaches L-DOPA and D-DOPA molecules.
As shown in Figure 17, this is one of the computed charge transfer models described above. The figure depicts the situation where the benzene ring side of the D-DOPA molecule approaches the C-terminus of a levorotatory peptide chain composed of 10 amino acids. We set the distance between the centers of the two molecules to be 15 angstroms. However, this distance is not the final value as the model needs to undergo structural optimization before calculating the electron population of the molecules. After structural optimization, the two molecules will be in the lowest energy state, which represents the most probable real-world scenario. At this point, the distance between the centers of the two molecules will change.
Due to the plethora of atoms and their valence electrons, it is difficult to discern the trend of charge transfer by directly analyzing the charge transfer data of each atom. Therefore, a method akin to calculating the center of mass of an object can be used to compute the positions of the positive and negative charge centers of the molecules. The calculation formula is as follows:
After performing the above calculation for each molecule, the positions of the positive and negative charge centers of the molecules are obtained. Then, the difference between the two position vectors is calculated and the magnitude of the resulting vector represents the distance between the positive and negative centers of the molecule in that specific scenario, which indicates the polarization strength of the molecule.
As shown in Figure 18, Figure 19, Figure 20 and Figure 21, it can be observed that the distance between the positive and negative charge centers of the D-DOPA molecule is smaller compared to that of the peptide molecule. By contrast, the distance between the positive and negative charge centers of the L-DOPA molecule is larger compared to the peptide molecule. Furthermore, the displacement distance of the positive and negative charge centers of the L-DOPA molecule is greater than that of D-DOPA. These findings indicate that L-DOPA is more prone to polarization compared to D-DOPA, while the difference in the positive and negative charge centers of the peptide molecule between the L-DOPA and D-DOPA comparison groups is not significant. This is attributed to the significantly larger molecular weight of the peptide molecule compared to L-DOPA and D-DOPA, which results in the presence of a larger number of electrons. Consequently, the changes in distance between the two molecules have a much greater impact on the variation in the positive and negative charge centers of the peptide molecule compared to the effects introduced by the different DOPA molecules.
By calculating the charge distribution of the molecules in their individual states and when in proximity to each other, and subsequently taking the difference between the two results, we can obtain the absolute value of charge transfer during the approaching process of the molecules. The computational results are presented as follows:
As depicted in Figure 22, Figure 23, Figure 24 and Figure 25, the following conclusions can be drawn: Firstly, the charge transfer of D-DOPA molecules increases with the rise in the peptide chain’s molecular weight whereas the charge transfer of L-DOPA molecules decreases with the decline in the peptide chain’s molecular weight. Secondly, the charge transfer of the peptide chain with both L-DOPA and D-DOPA molecules increases as the distance between them decreases. Moreover, the charge transfer of the peptide chain is generally greater than that of L-DOPA or D-DOPA. Furthermore, D-DOPA molecules are more prone to charge transfer compared to L-DOPA molecules, consistent with the analysis of charge centers. As the distance between the two molecules decreases, the difference in charge transfer between the peptide chain and L-DOPA, D-DOPA molecules becomes more pronounced.
These findings indicate that molecules carrying more charges exhibit larger internal charge transfer during chemical reactions. In the process of chemical reactions, due to the substantial molecular weight of the enzyme molecule, the CISS effect is expected to be significantly marked within the enzyme molecule.
3.3.2. Reaction Trends and CISS Effect
In Section 3.3.1, we analyzed the general trends of charge transfer for L-DOPA and D-DOPA when they approach peptide chains of different lengths. To provide more specific insights, we conducted separate calculations using data from electronic charge distributions for interactions between a peptide composed of 10 amino acids and L-DOPA, as well as D-DOPA. The results were used to create spatial representations of the positions of positive and negative charge centers when the molecules approach each other:
As shown in Figure 26, Figure 27, Figure 28 and Figure 29, these four graphs represent the positions of charge centers when the distance between the two molecules is consistent. These graphs are projections on the X-Y plane in three-dimensional space. From Figure 26 and Figure 27, it can be observed that the angle between the lines connecting the charge centers of the interacting molecules is significant. Thus, we can infer that the C-terminus of the polypeptide chain has a repulsive effect on both L-DOPA and D-DOPA, meaning that L-DOPA and D-DOPA are more inclined to react with the N-terminus of the polypeptide. Through these four graphs, we also find that both L-DOPA and D-DOPA approach the polypeptide with negative charge centers, which is consistent with the predictions based on the Fukui indices in Section 3.3.1. Furthermore, it can be observed that D-DOPA approaches the positive charge center of the polypeptide, while L-DOPA approaches the negative charge center. This finding aligns with the analysis in Section 3.3, indicating that L-DOPA tends to form covalent bonds with the polypeptide by sharing electrons whereas D-DOPA, due to charge-spin repulsion, can only approach the positive charge center of the polypeptide. This is because when the polypeptide approaches D-DOPA, the electrons with parallel spins are transferred to the molecule’s negative charge center, leaving behind the electrons with compatible spins at the positive charge center.
Based on the electronic population calculation data when the C-terminus of a 10-amino acid polypeptide molecule approaches D-DOPA, we performed polynomial fitting using the least squares method to establish the relationship between the distance of the positive and negative charge centers of the two molecules and the distance between their centers. As shown in Figure 30, it can be observed that initially, when the two molecules are relatively far apart, the distance between the positive and negative charge centers is very close. However, as the distance between them approaches a certain value, the distance between the charge centers suddenly increases.
According to equations (3) and (4) in Section 2.3, the intermolecular forces between nonpolar molecules are attractive, and the strength of these attractive forces increases with the polarization intensity of the molecules. Therefore, the rate of approach between nonpolar molecules during the reaction becomes faster. From Figure 30, it can be deduced that when the two molecules approach each other rapidly, the distance between their charge centers increases rapidly. Since positively charged atoms in nonpolar molecules are nearly stationary, this implies that the speed of electron transfer between the molecules increases as they come closer.
If one of the interacting molecules possesses a chiral structure, according to equations (1) and (2) in Section 2.2, it can be observed that the increased speed of electron transfer leads to a significant CISS effect.
Based on the above analysis, it can be concluded that when chiral molecules are involved as reactants, the CISS effect becomes very prominent when the two molecules are in close proximity. However, when the two molecules are relatively far apart, the manifestation of the CISS effect will be less significant.
3.4. Spin Theoretical Analysis and Verification of L-DOPA and D-DOPA
Based on the theoretical analysis in Section 3.3, it can be inferred that L-DOPA carries more electrons with spin oriented downward, while D-DOPA carries more electrons with spin oriented upward. To validate this inference, we employed the CASTEP [22] computational package to calculate the electronic spin state distribution of these two molecules. In order to achieve higher accuracy in the calculations, we considered the spin-orbit interaction of electrons. However, it should be noted that CASTEP supports calculations only for crystal cell structures.
As illustrated in Figure 31, we placed L-DOPA and D-DOPA molecules in sufficiently large crystal cells, ensuring that the intermolecular interactions can be neglected during the computations.
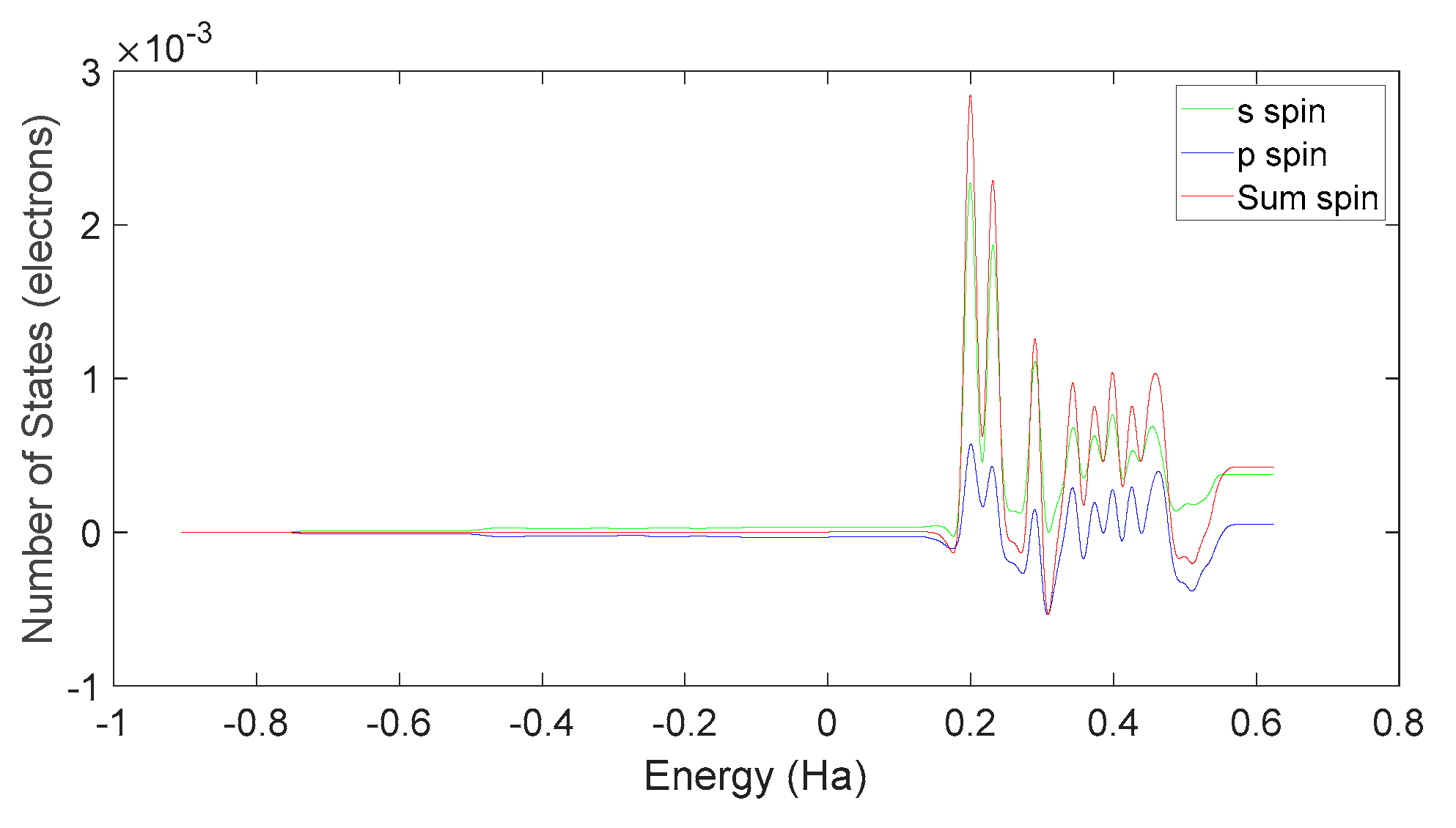
Based on Figure 34 and Figure 37, it can be observed that in L-DOPA molecules, the majority of higher-energy electrons have a spin orientation predominantly downward, while in D-DOPA molecules, the majority of higher-energy electrons have a spin orientation predominantly upward. This indicates that in L-DOPA molecules, the majority of valence electrons have a spin orientation downward, whereas in D-DOPA molecules, the majority of valence electrons have a spin orientation upward.
Further examination on Figure 35 and Figure 38 reveals that the downward spin orientation of valence electrons in L-DOPA molecules is mainly contributed by the P orbital, whereas the upward spin orientation of valence electrons in D-DOPA molecules is jointly provided by the S and P orbitals. As demonstrated in Figure 32 and Figure 33, the atoms primarily responsible for providing the spin-polarized electrons are oxygen and carbon atoms. Among these, the oxygen atom identified in Section 3.3.1 using Fukui indices analysis is included. The difference in electron spin orientations between L-DOPA and D-DOPA molecules is also consistent with the optical rotation of chiral substances.
Figure 32.
Spin electron distribution in L-DOPA molecule.
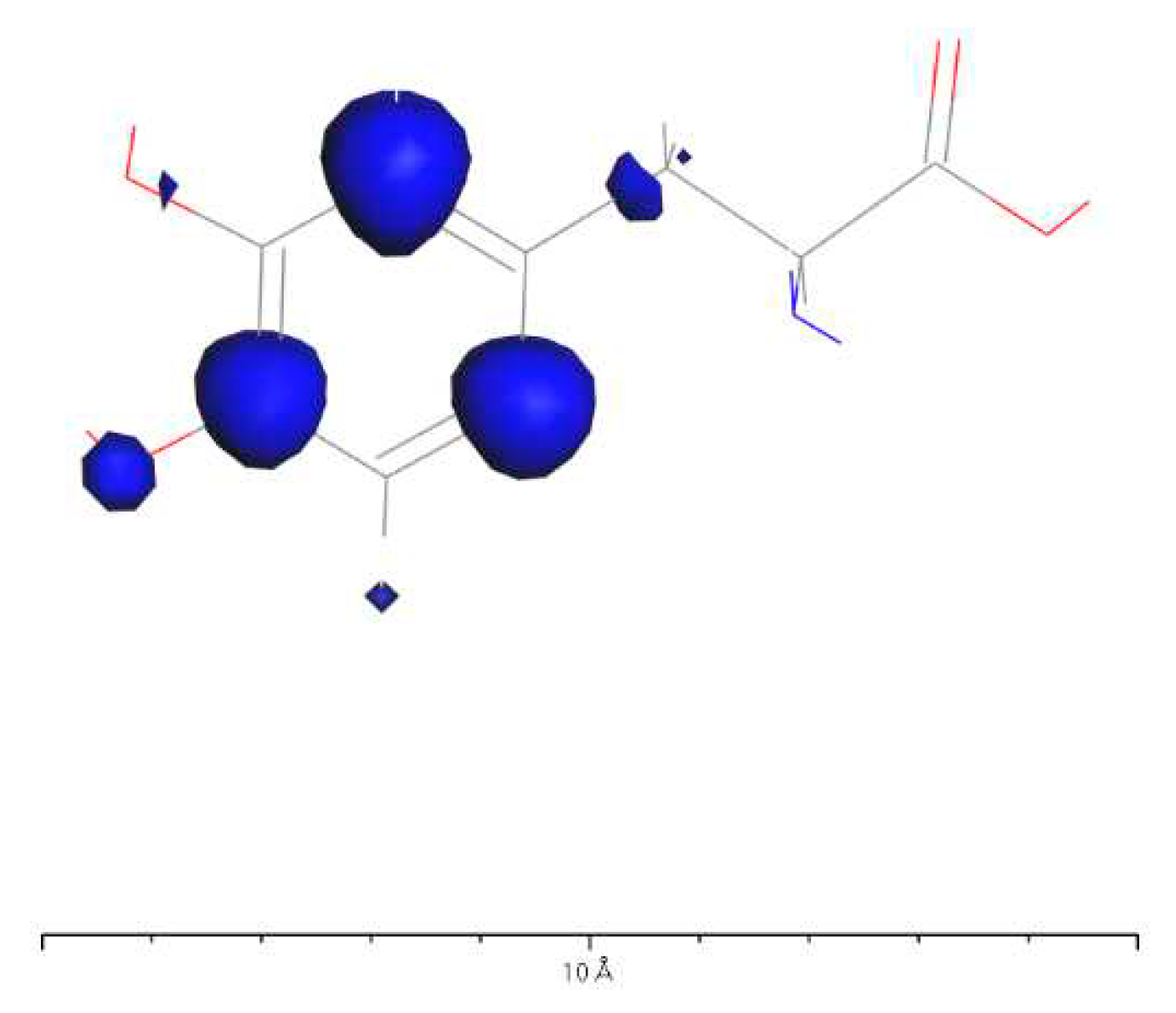
Figure 33.
Spin electron distribution in D-DOPA molecule.
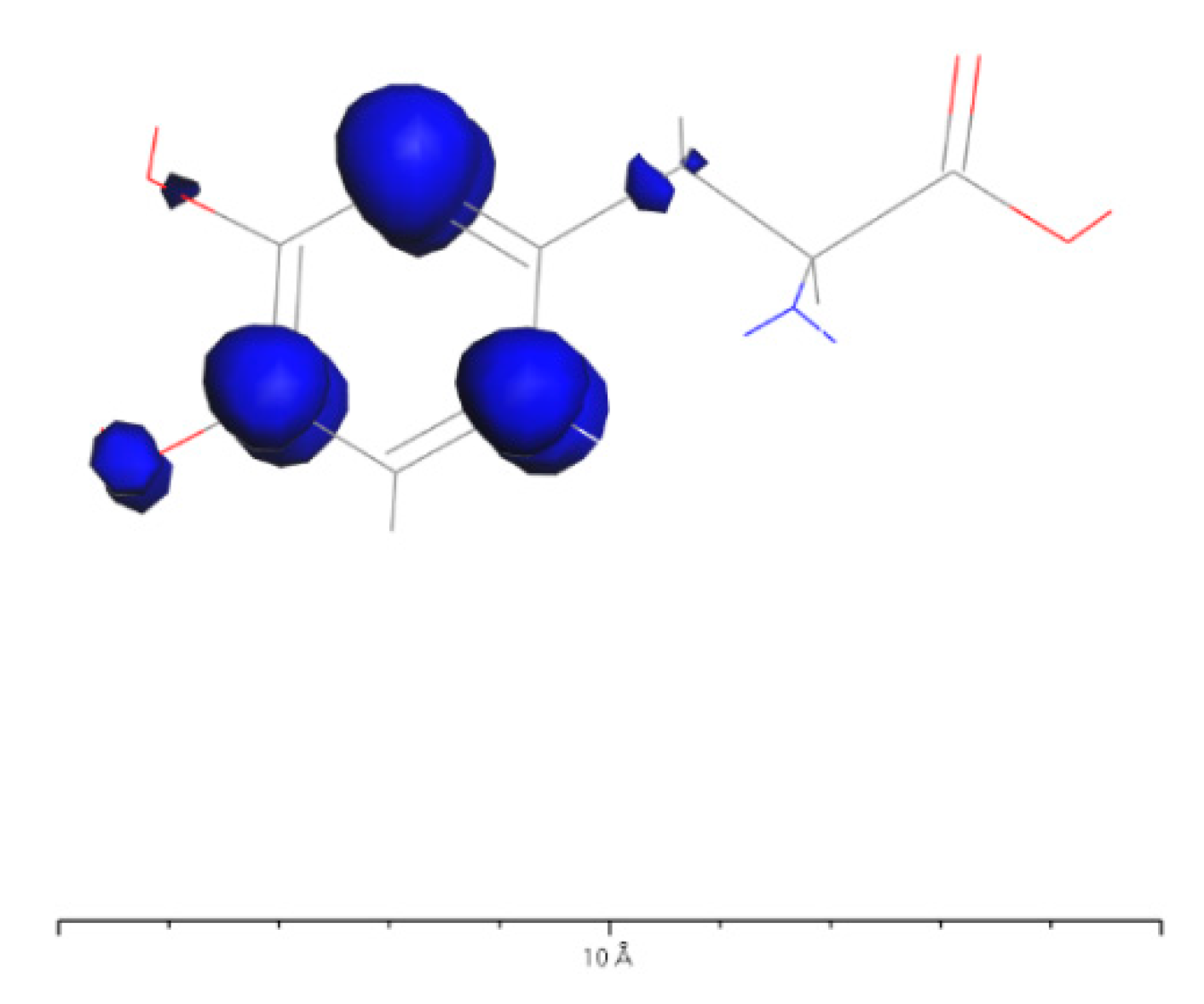
Figure 34.
Total spin state density in L-DOPA.
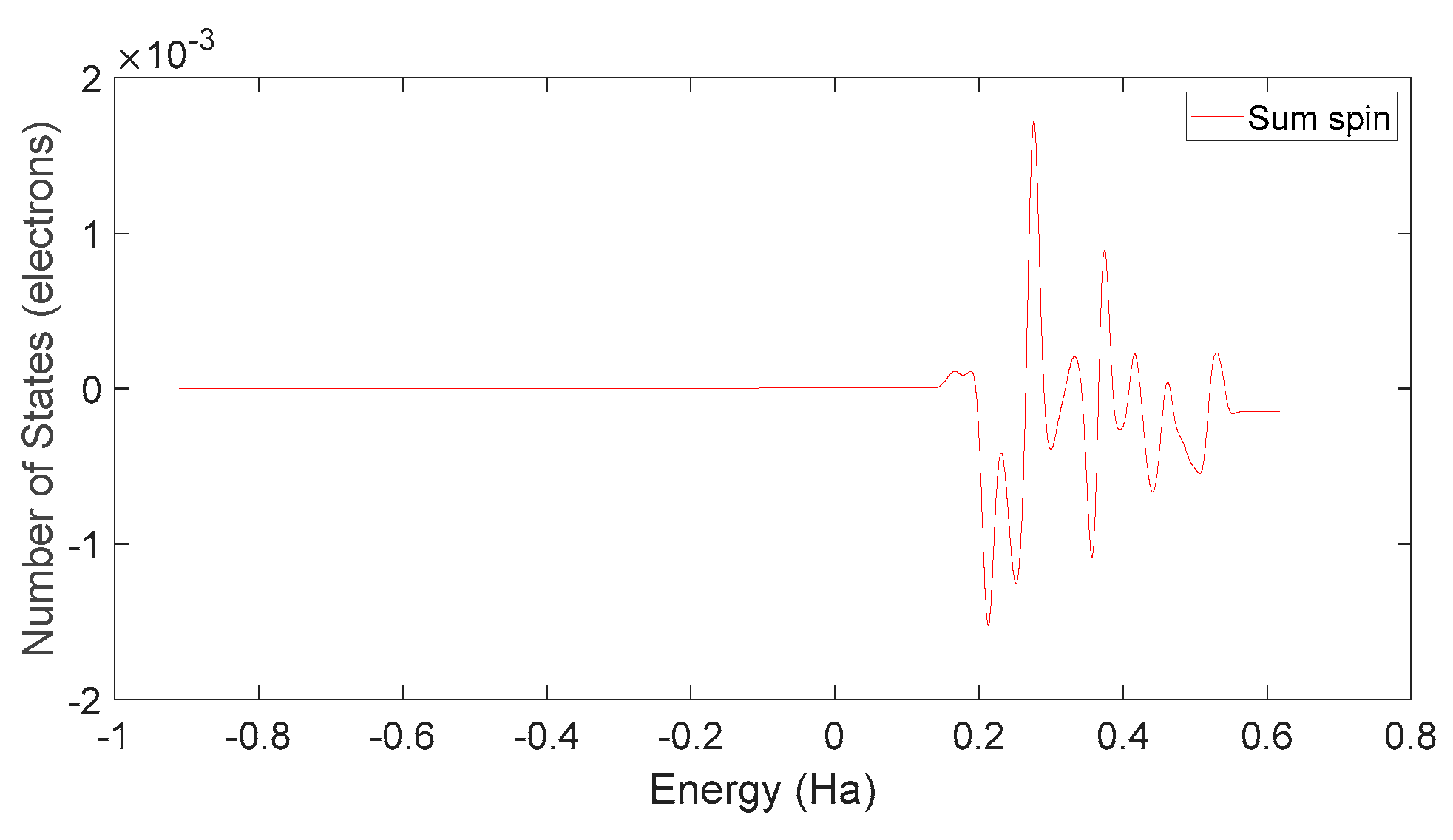
Figure 35.
Spin state density of S orbital and P orbital in L-DOPA.
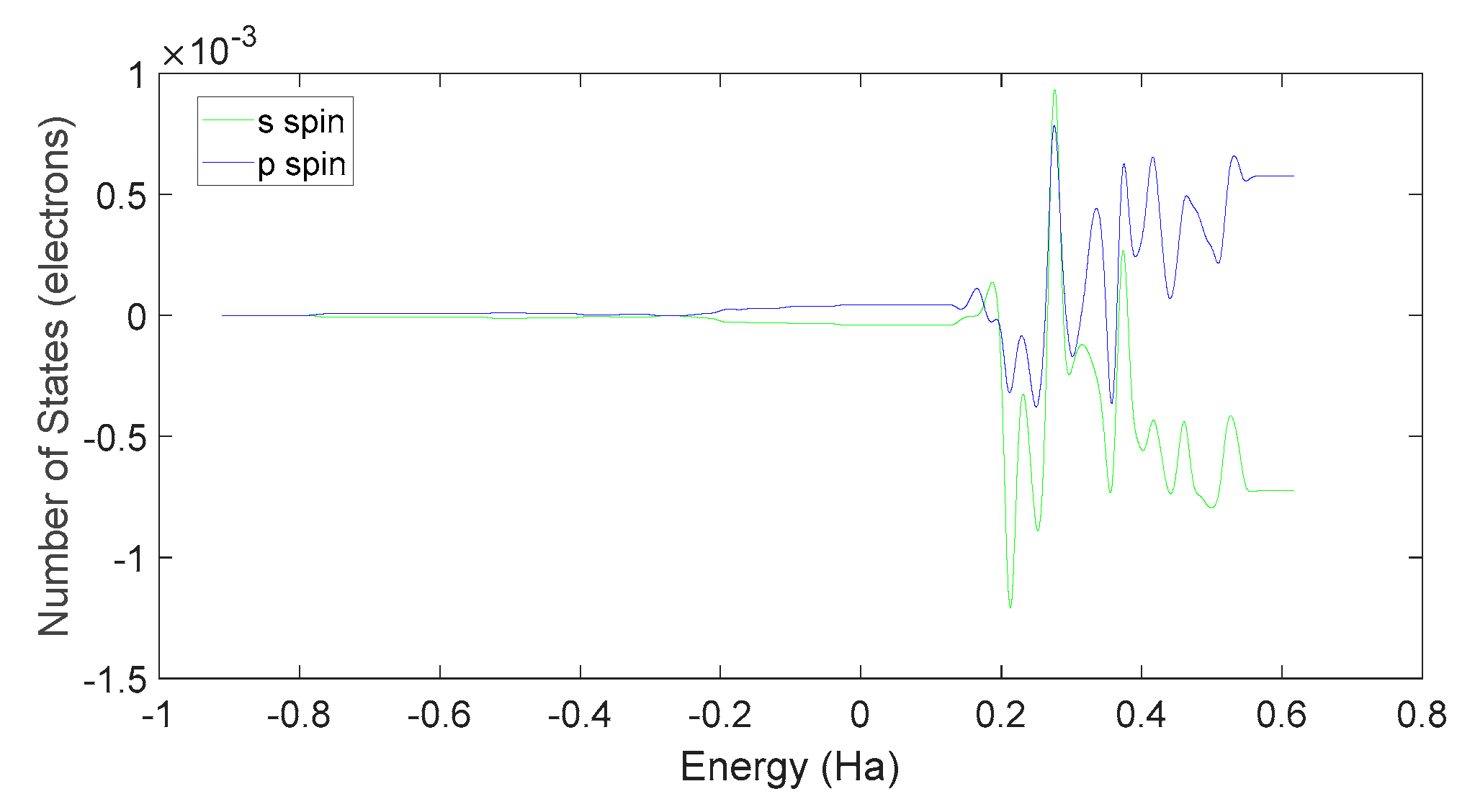
Figure 36.
Electron spin state density in L-DOPA.
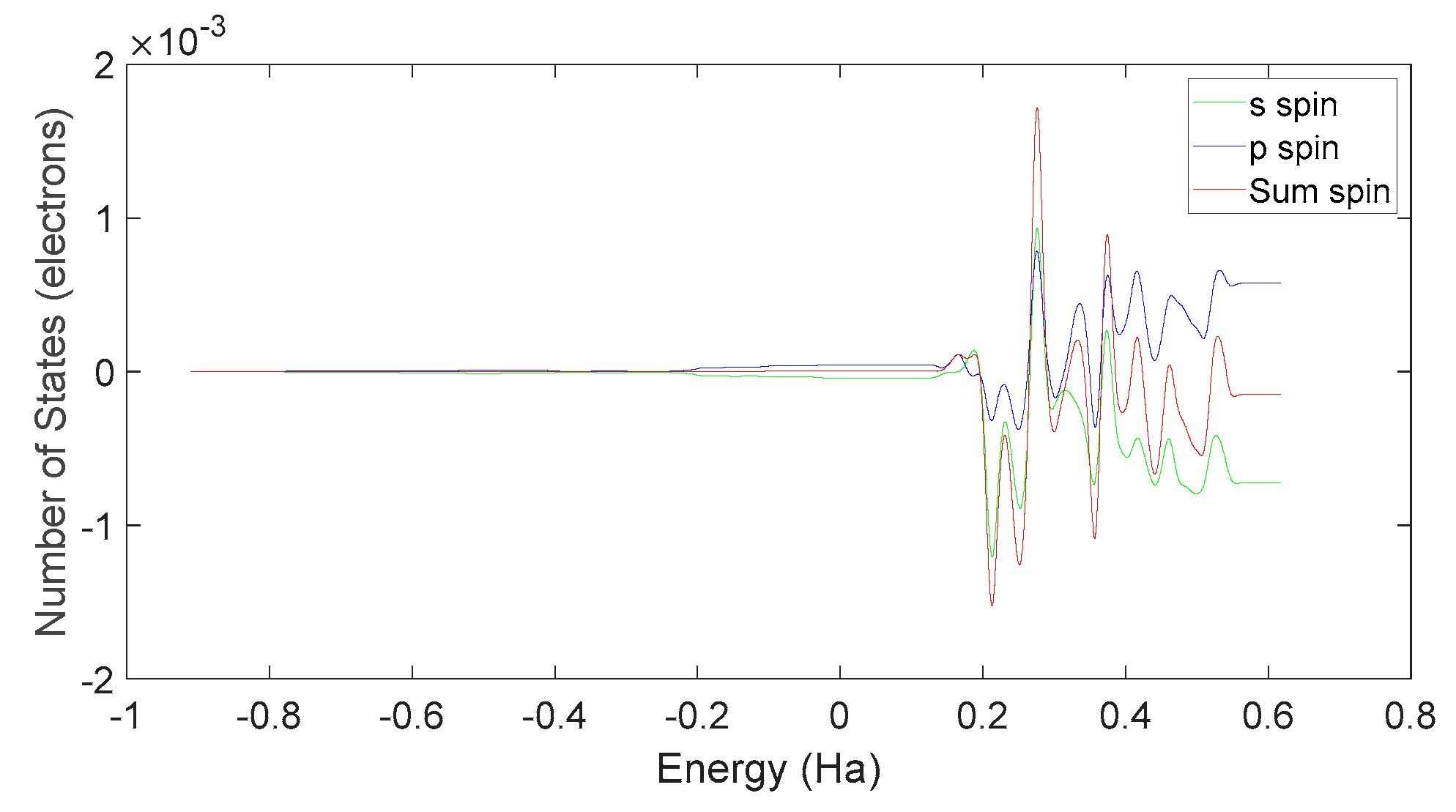
Figure 37.
Total spin state density in D-DOPA.
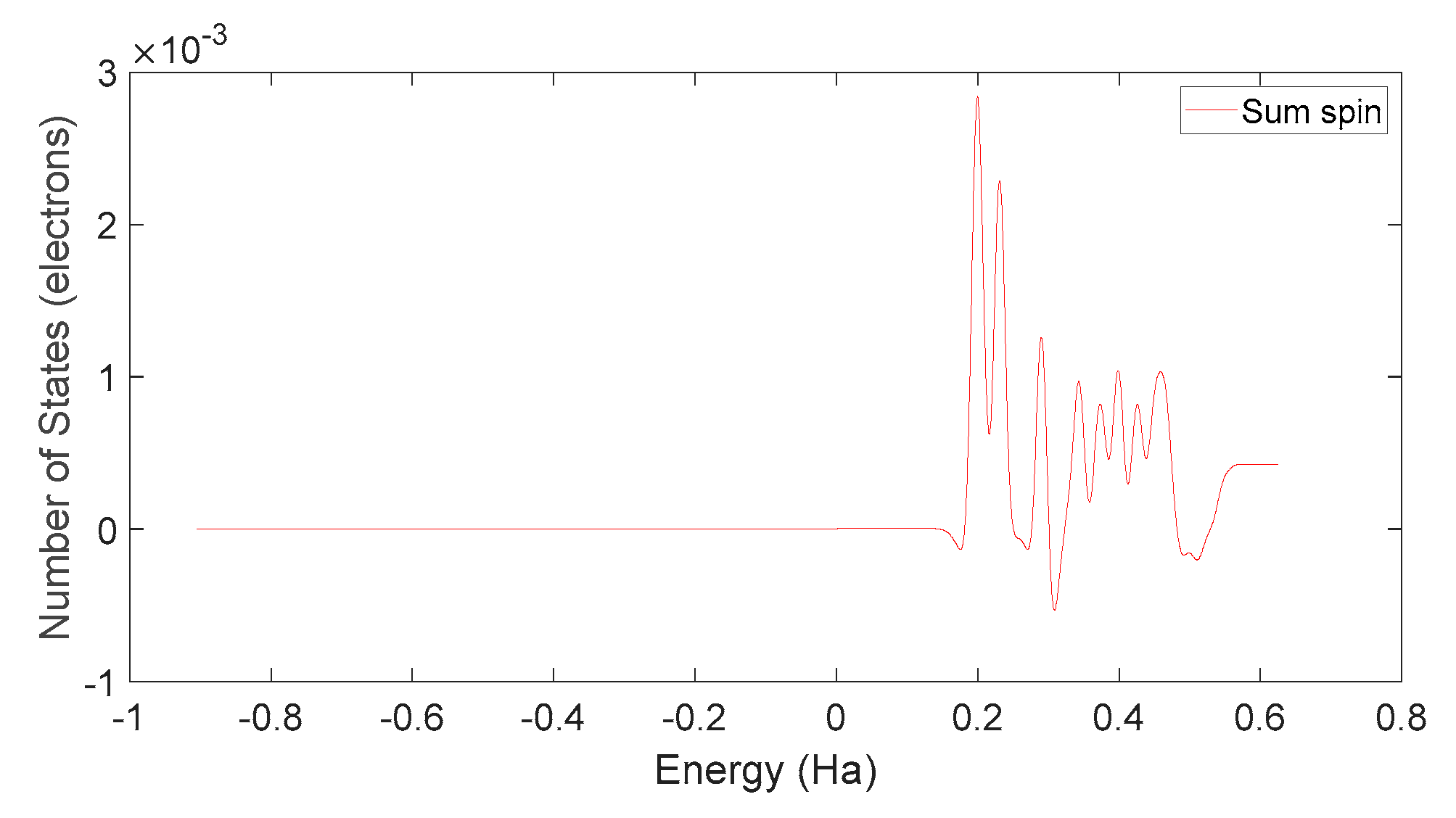
Figure 38.
Spin state density of S orbital and P orbital in D-DOPA.
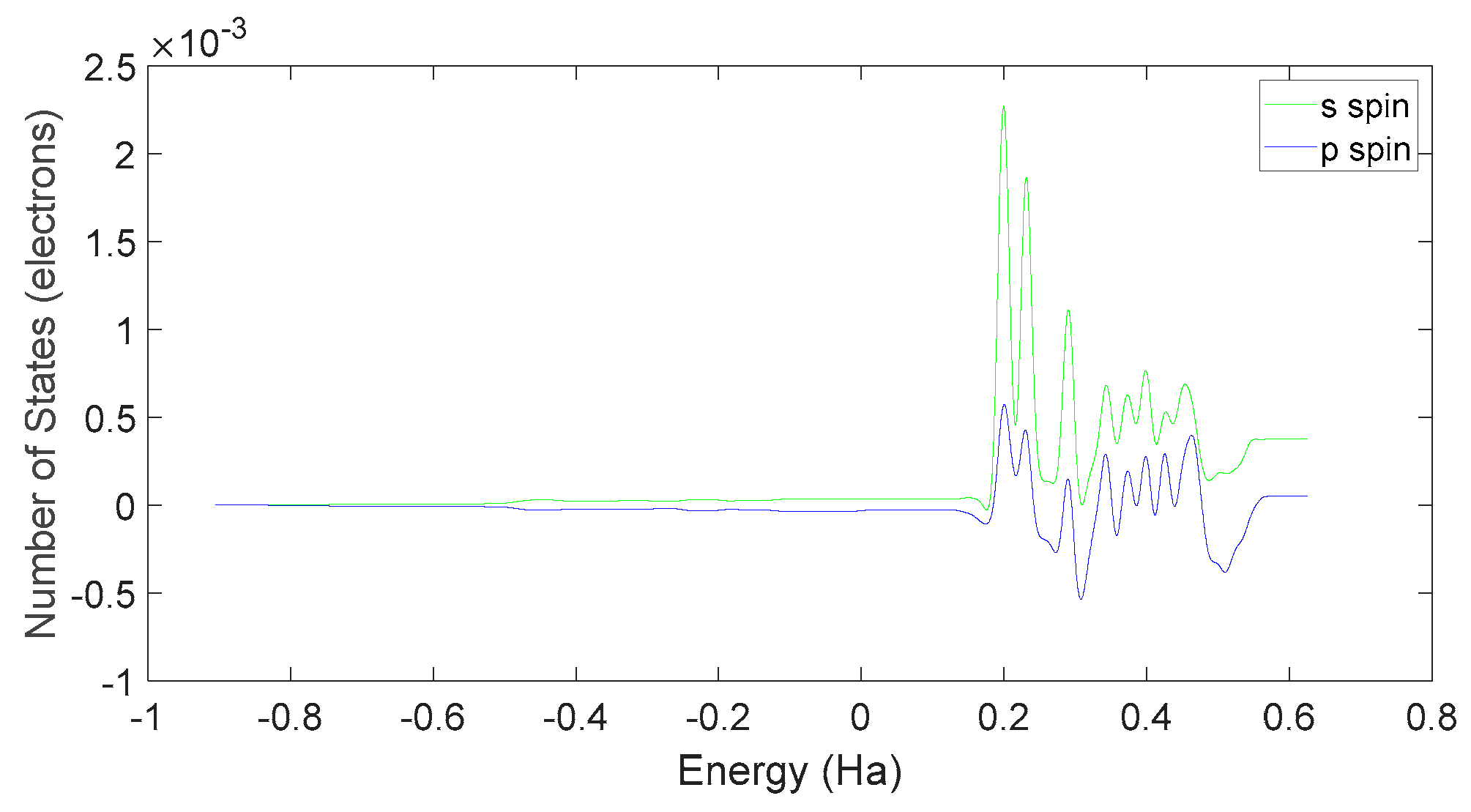
Figure 39.
Electron spin state density in D-DOPA.
As is well-known in the field of chemistry, chiral molecules often exhibit optical rotation. Currently, there are numerous theories explaining optical rotation [23]. When a solution of L-DOPA is irradiated with polarized light, the plane of polarization of light will rotate in the left-handed direction, whereas when a solution of D-DOPA is irradiated with polarized light, the plane of polarization will rotate in the right-handed direction.
This optical rotation does not require an external magnetic field, indicating that it is unrelated to the splitting of energy levels in a magnetic field. A beam of polarized light can be considered as a superposition of left-handed polarized light and right-handed polarized light. When the frequencies and intensities of the left-handed and right-handed polarized light are the same, the plane of polarization of the resulting beam of polarized light will remain unchanged. The optical rotation observed in L-DOPA and D-DOPA molecules are attributed to their different abilities to absorb left-handed and right-handed polarized light.
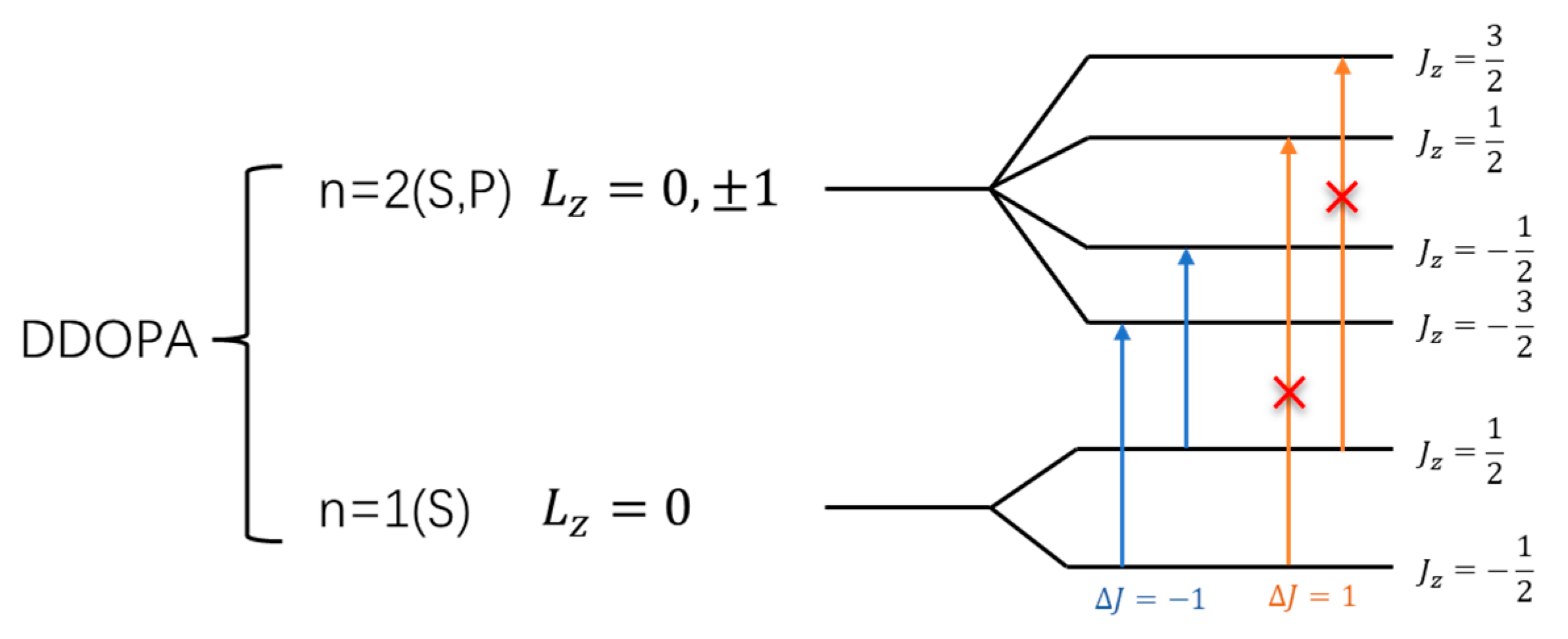
In both L-DOPA and D-DOPA molecules, the atoms with relatively high atomic numbers are oxygen and carbon. The electronic configurations of oxygen and carbon atoms are as follows: Oxygen - , Carbon - . As a result, their orbital energy levels can be depicted as shown in Figure 40 and 41. The electrons in atoms possess orbital angular momentum , which, when coupled with spin , gives rise to the total angular momentum . This results in the energy level diagram shown in the figure. It is worth noting that the coupled energy levels in the figure are shown together in the molecule since there is no external magnetic field to induce the Zeeman effect. Therefore, the energy levels depicted in Figure 40 and 41 are not separated by differences in energy levels.
When falling on the atoms, the light that satisfies the energy level difference will be absorbed. Although electronic transitions can occur between energy levels with the same principal quantum number, these transitions do not absorb light due to their small energy differences. Thus, light absorption transitions occur between energy levels with different principal quantum numbers, specifically when electrons transition from the n=1 level to the n=2 level, as depicted in the figure.
However, when electrons interact with photons, they must satisfy the conservation of angular momentum. Therefore, after absorbing right-circularly polarized light, electrons will undergo transitions with , as indicated by the orange arrows in Figure 40 and 41. Similarly, after absorbing left-circularly polarized light, electrons will undergo transitions with , as indicated by the blue arrows in Figure 40 and 41.
When the total electron spin on the atomic energy level is 0, the likelihood of absorbing left-circularly polarized light is the same as that of absorbing right-circularly polarized light. Based on the analysis in Figure 34, Figure 35, Figure 36, Figure 37, Figure 38 and Figure 39, as shown in Figure 40, most of the spin-down valence electrons in the L-DOPA molecule occupy states with and . Similarly, as shown in Figure 41, most of the spin-up valence electrons in the D-DOPA molecule occupy states with and . Given the Pauli exclusion principle, these already occupied states cannot accommodate more electrons, and thus, these transitions cannot occur. Consequently, the transitions with red crosses on the arrows in Figure 40 and 41 are less likely to occur for these molecules.
From the figures, it can be observed that L-DOPA molecules are more inclined to undergo transitions with , which means they are more likely to absorb right-circularly polarized light. On the other hand, D-DOPA molecules are more prone to undergo transitions with , making them more likely to absorb left-circularly polarized light.
By and large, the preferential absorption of right-circularly polarized light by L-DOPA molecules leads to a reduction in the intensity of right-circularly polarized light after transmission, causing the polarization plane of light to rotate to the left (left-handed rotation). Conversely, D-DOPA causes the polarization plane of light to rotate to the right (right-handed rotation). This phenomenon also explains the origins of their names.
Figure 32 reveals that most of the electrons with spin states in L-DOPA molecules are distributed on the benzene ring. This indicates that before the decarboxylation is completed to form a covalent bond, the benzene ring of L-DOPA molecules will be fixed on the AADC enzyme molecule. This can be likened to securing a patient to an operating table during surgery. Once the L-DOPA molecule is firmly fixed, PLP completes the decarboxylation with the exposed carboxyl group. After that, the L-DOPA molecule transforms into dopamine and the electron spin structure changes. Consequently, the dopamine molecule dissociates from AADC and goes on to exert its effects on other neurotransmitters. This is analogous to a patient recovering after surgery and leaving the hospital without turning back.
Based on the analysis above, it can be fully demonstrated that the chirality selectivity of enzyme molecules for the two chiral forms of dopamine is due to the different electron spin states they carry, which substantiates the theoretical analysis in Section 3.3.
4. Conclusion
This paper presents a creative approach that combines quantum mechanics with chemical reaction analysis and establishes a theoretical model based on CISS theory to explain the chiral selectivity of chiral molecules in chemical reactions. The model is able to effectively elucidate the chiral nature of the reaction between AADC enzyme and dopamine molecules, and successfully predicts the spin states of valence electrons in L-DOPA and D-DOPA molecules. Furthermore, the theory is verified through first-principles calculations and a theoretical explanation for the optical rotation of chiral substances is provided. These findings lay a theoretical foundation for the study of the pharmacological effects of chiral drugs.
Author Contributions
Feng-Yu Zhang is mainly responsible for model construction and article writing; Si-Cheng Liu helped to build the model and article writing; Anwei Huang helped to analyze the data and discuss the results; Yi-Ning Li and Xiao-Yan Liu participated in the discussion.
Funding
We are grateful to the project ZR2022MA017 supported by Shandong Provincial Natural Science for financial support.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The numerical calculations were performed on the supercomputing system at the Supercomputing Center, Shandong University, Weihai. Professional English-language editing support provided by AsiaEdit.
Conflicts of Interest
The Authors declare no Competing Financial or Non-Financial Interests.
Sample Availability
Samples of the compounds are available from the authors.
References
- Corey, E.J. The logic of chemical synthesis: Multistep synthesis of complex carbogenic molecules (Nobel lecture). Angewandte Chemie International Edition 1991, 30, 455–465. [Google Scholar]
- Noyori, R.; Kitamura, M. The asymmetric hydrogenation of β-keto carboxylic esters catalyzed by chiral ruthenium complexes. Journal of the American Chemical Society 1991, 113, 9885–9886. [Google Scholar]
- Naaman, R.; Waldeck, D.H. Title of the article. Annual Review of Physical Chemistry 2015, 66, 263–281. [Google Scholar] [PubMed]
- Michaeli, K.; Kantor-Uriel, N.; Naaman, R.; Waldeck, D.H. The electron’s spin and molecular chirality – how are they related and how do they affect life processes? . Chemical Society Reviews 2016, 45, 6478–6487. [Google Scholar] [PubMed]
- Goudsmit, S.; Uhlenbeck, G.E. The Quantum Theory of the Motion of Electrons. Physical Review 1925, 27, 359–364. [Google Scholar] [CrossRef]
- Mtangi, W.; Kiran, V.; Fontanesi, C.; Naaman, R. Title of the article. The Journal of Physical Chemistry Letters 2015, 6, 4916–4922. [Google Scholar] [PubMed]
- Simon, Y.C.; Srebro, M.; Jortner, J.; Naaman, R. Chiral-Induced Spin Selectivity: A Magnetic Property of Chiral Molecules. Nature 2013, 493, 216–220. [Google Scholar]
- Srebro, M.; Simon, Y.C.; Naaman, R. Chiral-Induced Spin Selectivity: On the Role of Symmetry. Journal of the American Chemical Society 2014, 136, 17682–17686. [Google Scholar]
- Capua, L.; Capua, M.; Naaman, R. Chiral-Induced Spin Selectivity in Electron Transport through Multilayered Chiral Structures. The Journal of Physical Chemistry Letters 2018, 9, 4344–4349. [Google Scholar]
- Naaman, R.; Paltiel, Y.; Waldeck, D.H. Chiral induced spin selectivity and its implications for biological functions. Annual Review of Biophysics 2022, 51, 99–114. [Google Scholar] [CrossRef] [PubMed]
- Wolf, Y.; Liu, Y.; Xiao, J.; Park, N.; Yan, B. Unusual Spin Polarization in the ChiralityInduced Spin Selectivity. ACS Nano 2022, 16, 18601–18607. [Google Scholar] [CrossRef] [PubMed]
- Zöllner, M.S.; Varela, S.; Medina, E.; Mujica, V.; Herrmann, C. Insight into the Origin of Chiral-Induced Spin Selectivity from a Symmetry Analysis of Electronic Transmission. Journal of Chemical Theory and Computation 2020, 16, 2914–2929. [Google Scholar] [CrossRef] [PubMed]
- Qi, D.; Kenaan, A.; Cui, D.; Song, J. Novel insights into the selection to electron’s spin of chiral structure. Nano Energy 2018, 52, 142–152. [Google Scholar] [CrossRef]
- Dednam, W.; García-Blázquez, M.A.; Zotti, L.A.; Lombardi, E.B.; Sabater, C.; Pakdel, S.; Palacios, J.J. A Group-Theoretic Approach to the Origin of Chirality-Induced Spin-Selectivity in Nonmagnetic Molecular Junctions. ACS Nano 2023, 17, 6452–6465. [Google Scholar] [CrossRef]
- Dalum, S.; Hedegård, P. Theory of Chiral Induced Spin Selectivity. Nano Letters 2019, 19, 5253–5259. [Google Scholar] [CrossRef] [PubMed]
- Sierra, M.A.; Sánchez, D.; Gutierrez, R.; Cuniberti, G.; Domínguez-Adame, F.; Díaz, E. Spin-Polarized Electron Transmission in DNA-Like Systems. Biomolecules 2019, 10, 49. [Google Scholar] [CrossRef]
- Kettner, M.; Artner, C.; Winkler, T.; Hohenester, U. Chiral Induced Spin Selectivity for the Identification and Classification of Biomolecules. The Journal of Physical Chemistry B 2019, 123, 4404–4411. [Google Scholar]
- Mondal, P.C.; Fontanesi, C.; Waldeck, D.H.; Naaman, R. Field and Chirality Effects on Electrochemical Charge Transfer Rates: Spin Dependent Electrochemistry. ACS Nano 2015, 9, 3377–3384. [Google Scholar] [CrossRef]
- Garcia, A.M.; Martínez, G.; Ruiz-Carretero, A. The Importance of Spin State in Chiral Supramolecular Electronics. Frontiers in Chemistry 2021, 9, Article 722727. [Google Scholar] [CrossRef]
- Delley, B. An all-electron numerical method for solving the local density functional for polyatomic molecules. The Journal of Chemical Physics 1990, 92, 508–517. [Google Scholar]
- Delley, B. From molecules to solids with the DMol3 approach. The Journal of Chemical Physics 2000, 113, 7756–7764. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Zeitschrift für Kristallographie - Crystalline Materials 2005, 220, 567–570. [Google Scholar]
- Pecul, M.; Ruud, K. The Ab Initio Calculation of Optical Rotation and Electronic Circular Dichroism. Advances in Quantum Chemistry 2005, 50, 186–210. [Google Scholar] [CrossRef]
Figure 1.
Reaction pathways of the OH radical in different spin states.
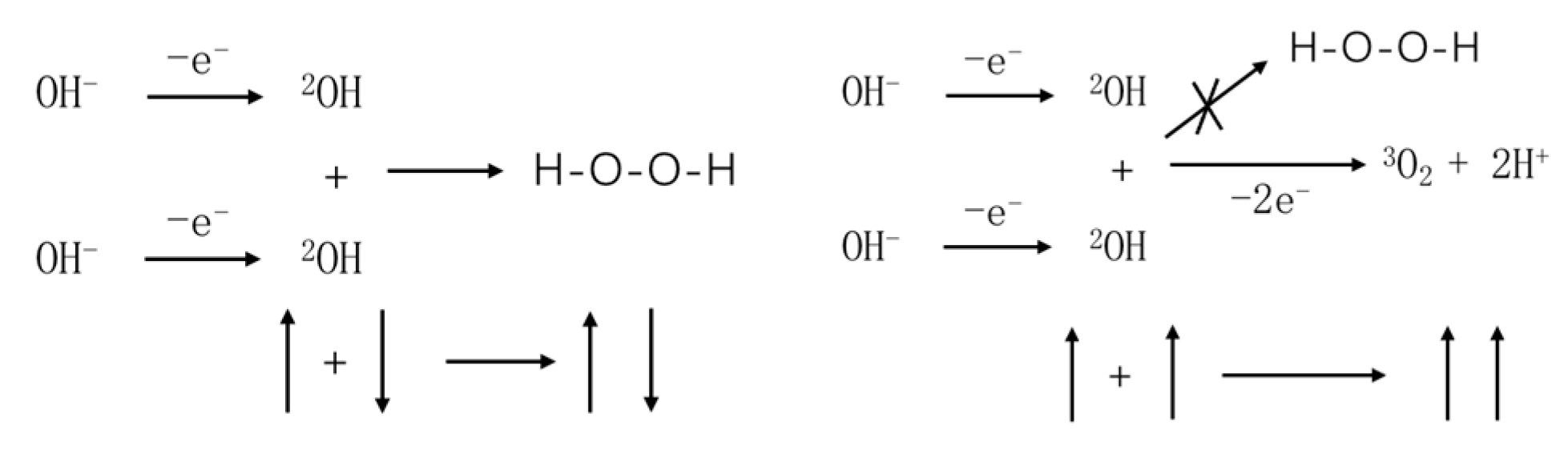
Figure 2.
The helical motion of electrons under the potential field of chiral molecules.
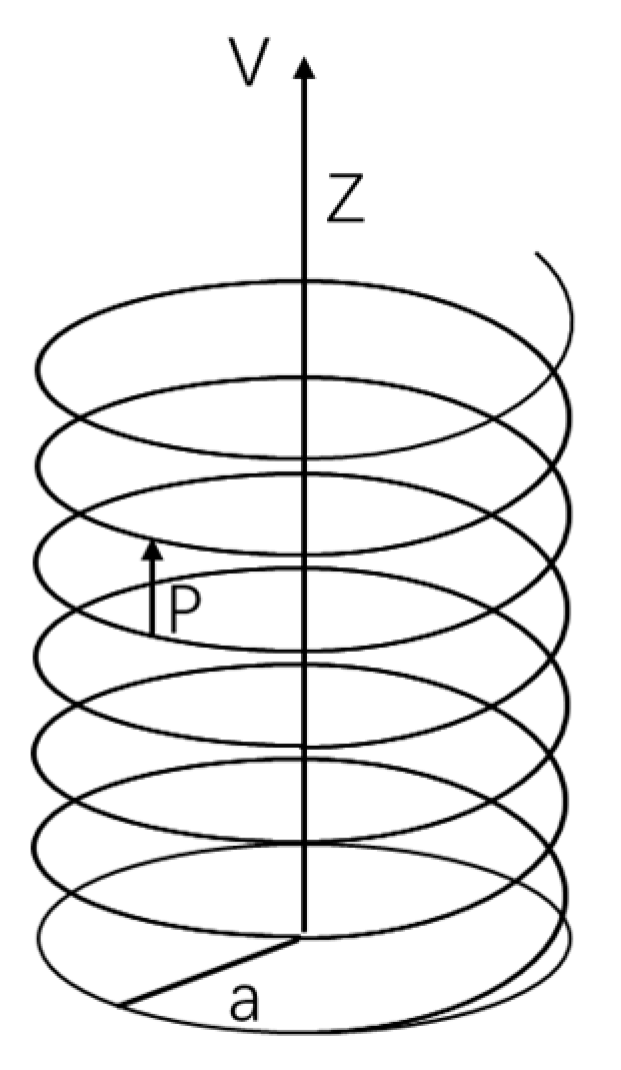
Figure 3.
Schematic of Van der Waals-London Forces.

Figure 4.
Schematic of AADC enzyme synthesizing DOPA molecules.
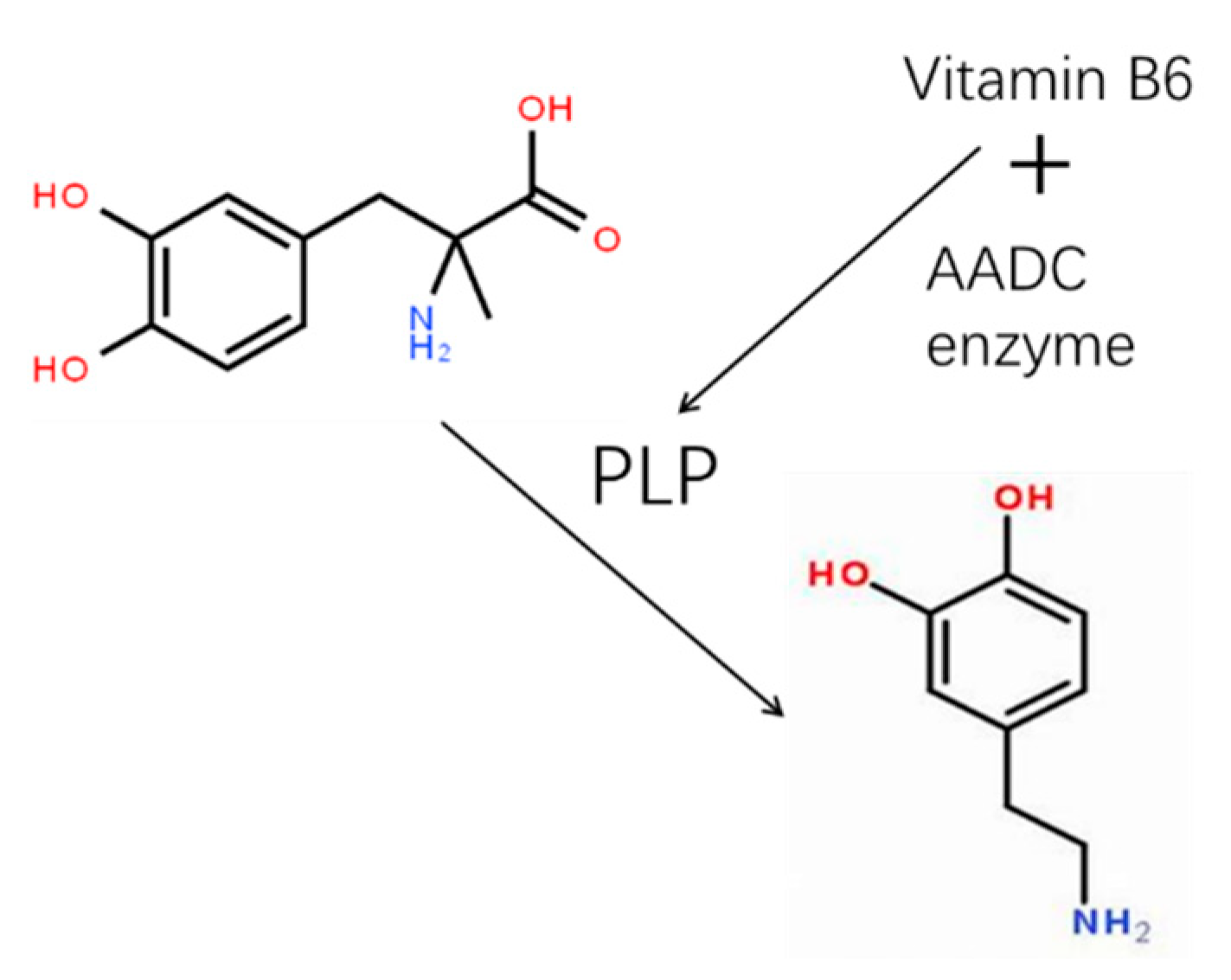
Figure 5.
Ribbon diagram of AADC enzyme.
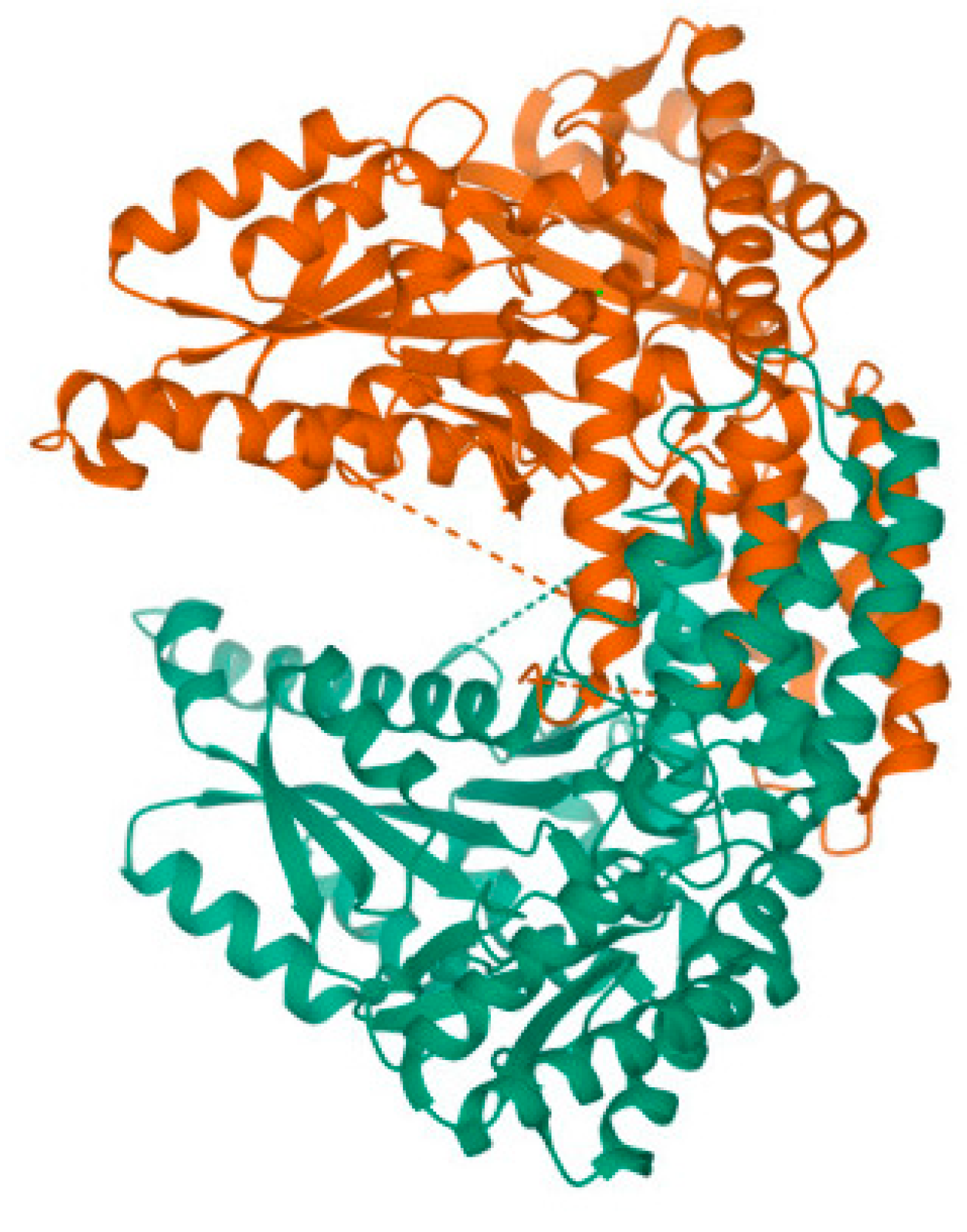
Figure 6.
Ball-and-stick model of AADC enzyme.
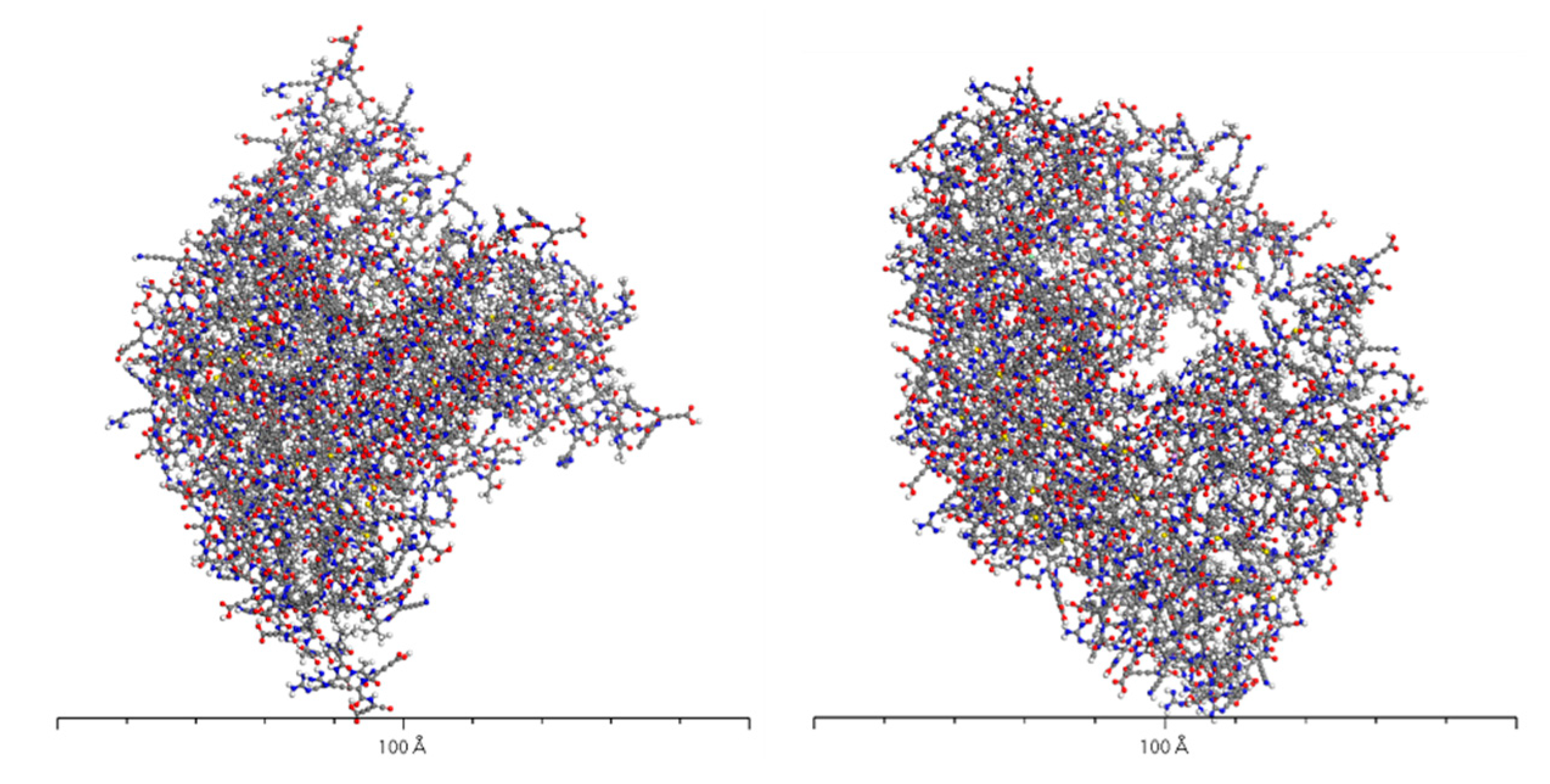
Figure 7.
Ribbon diagram of AADC enzyme complexed with PLP and LLP.
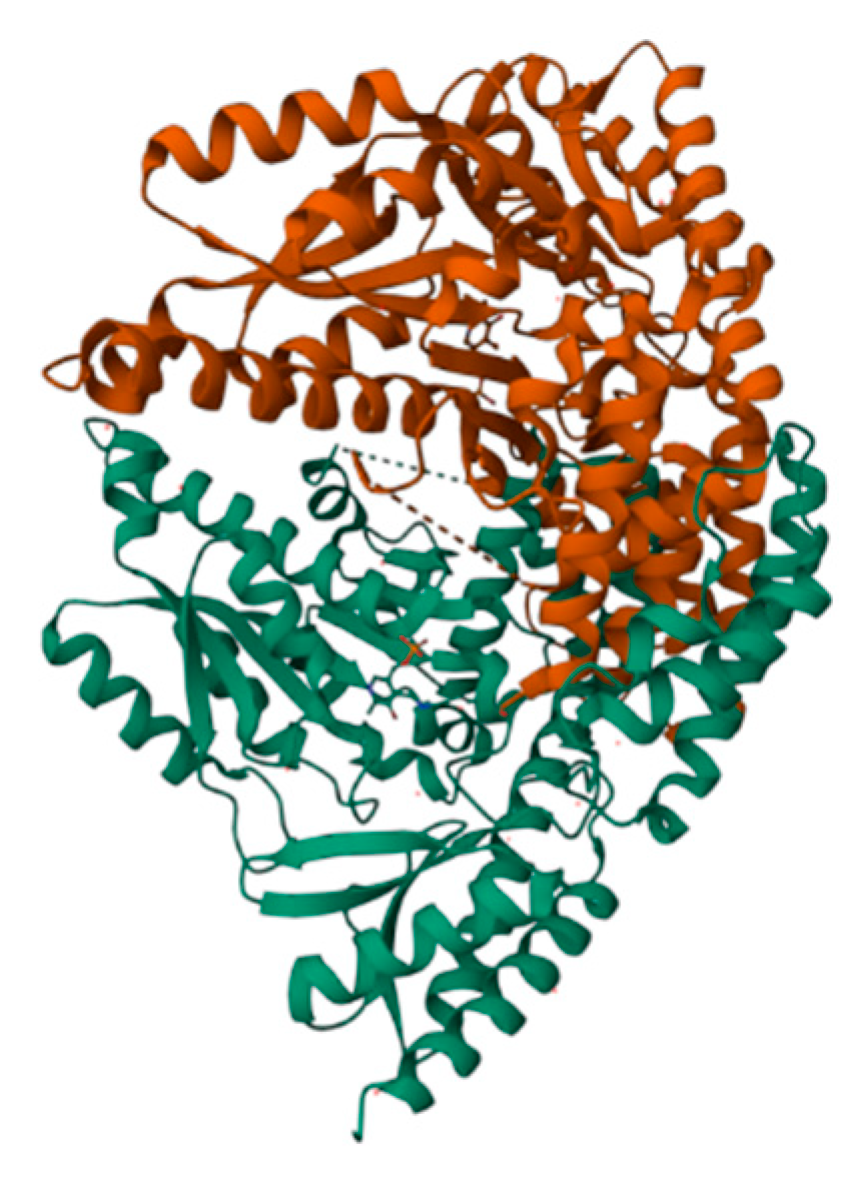
Figure 8.
PLP ligand (a) and LLP ligand (b).

Figure 9.
Molecular structure of DOPA. (a) L-DOPA. (b) D-DOPA.
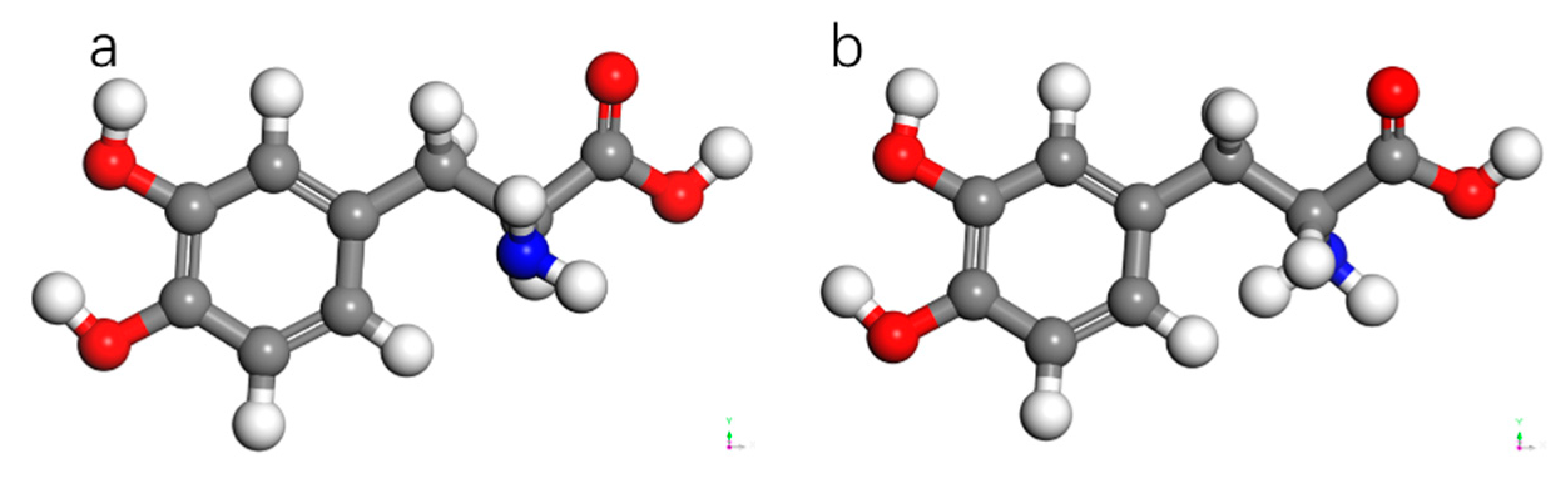
Figure 10.
AADC enzyme with 32 L-DOPA (a), and 32 D-DOPA (b).
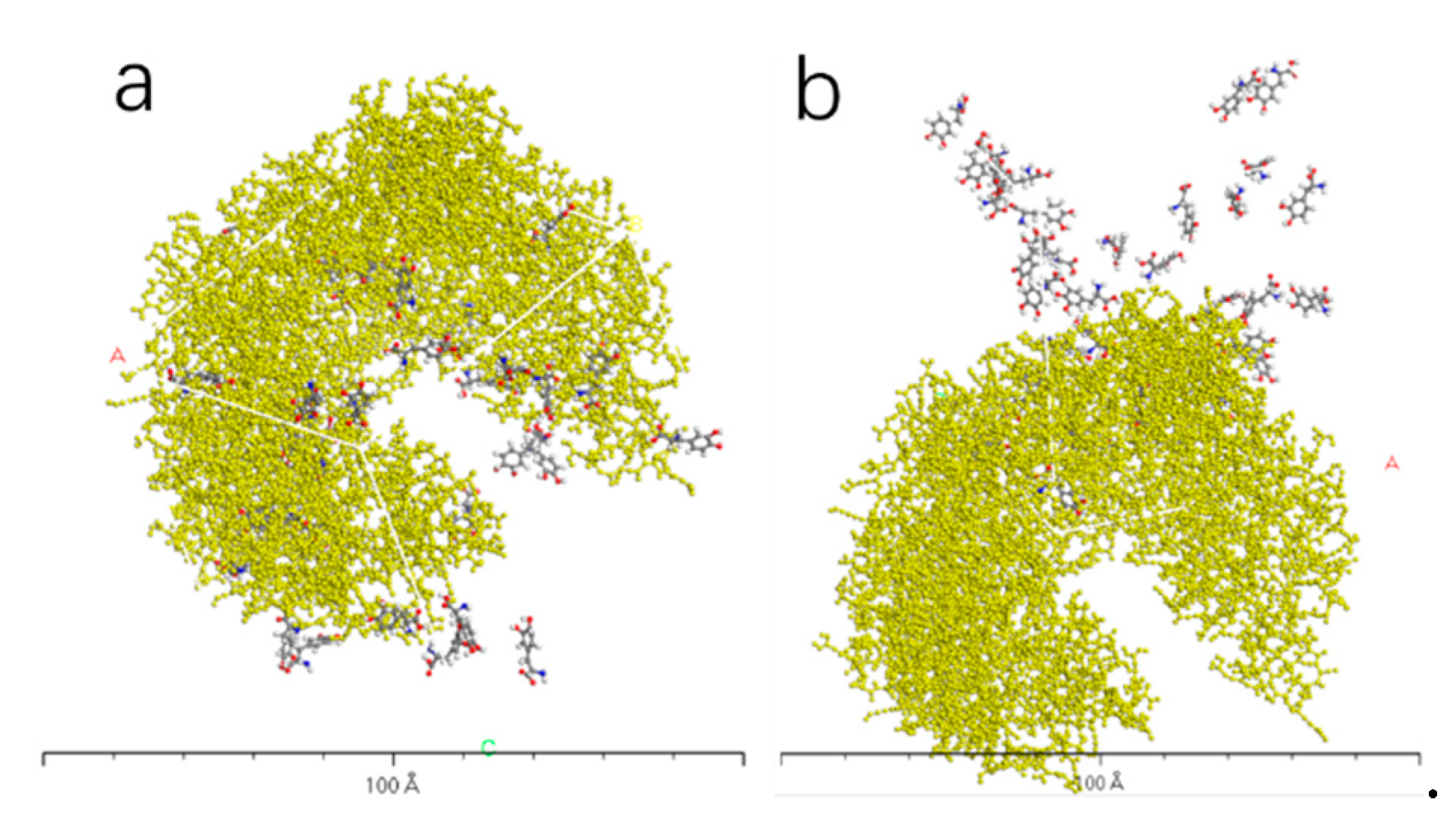
Figure 11.
AADC enzyme with 100 L-DOPA (a), and 100 D-DOPA (b).
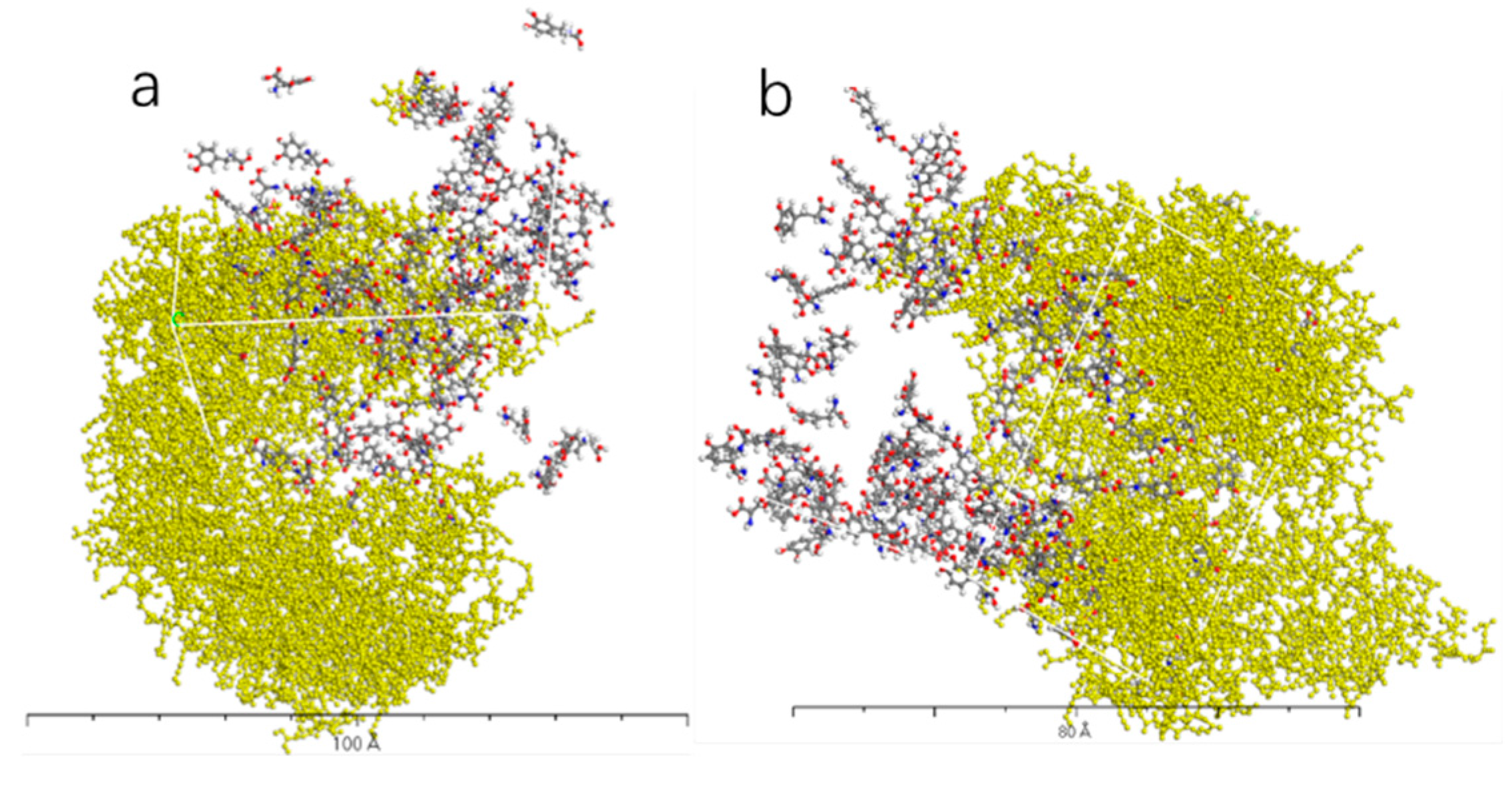
Figure 12.
AADC enzyme with 200 L-DOPA (a), and 200 D-DOPA (b).
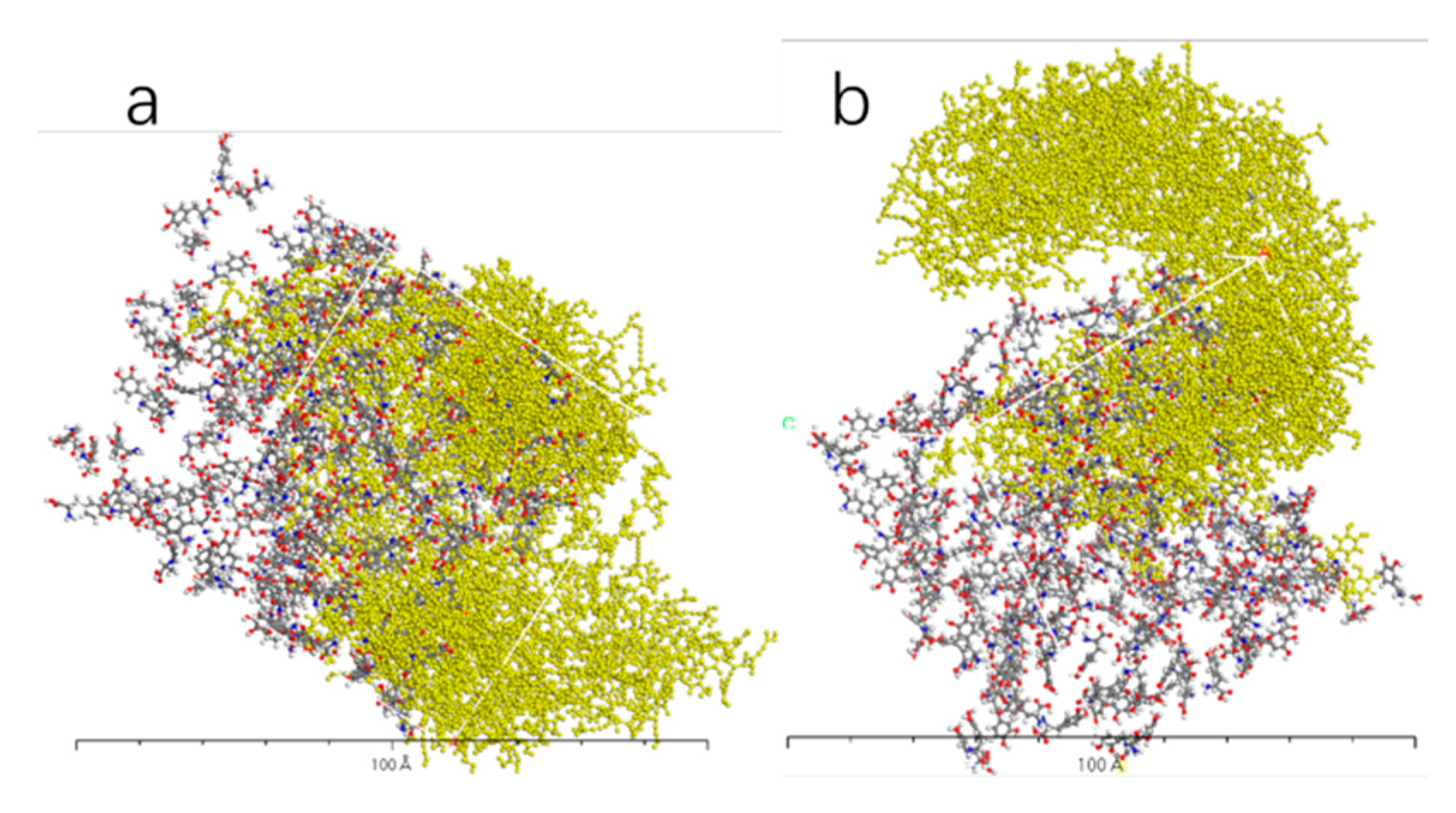
Figure 13.
AADC enzyme with 300 L-DOPA (a), and 300 D-DOPA (b).
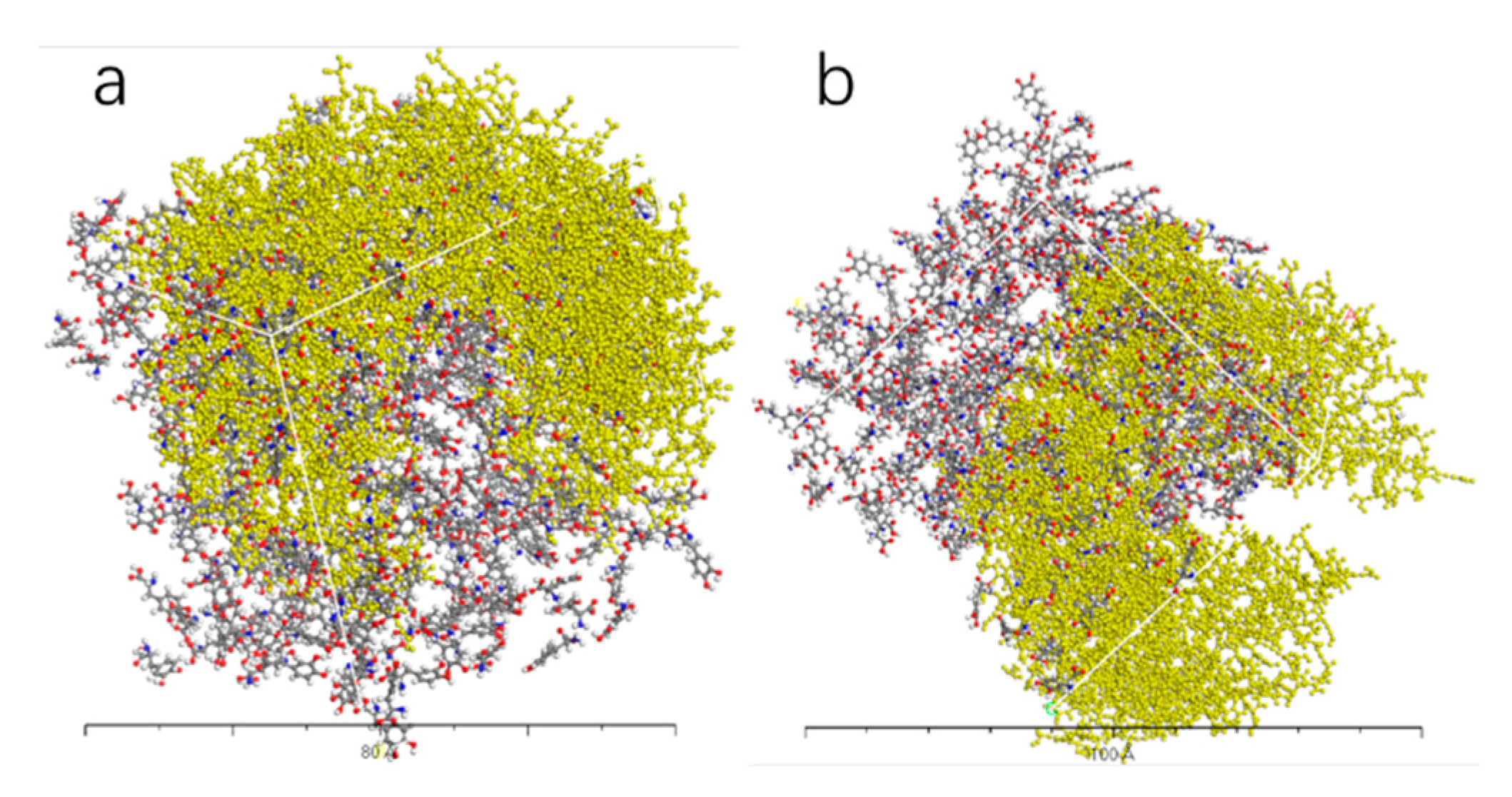
Figure 14.
The total energy of the system consisting of D-DOPA and AADC enzyme is consistently higher than that of the system comprising L-DOPA and AADC enzyme.
Figure 14.
The total energy of the system consisting of D-DOPA and AADC enzyme is consistently higher than that of the system comprising L-DOPA and AADC enzyme.
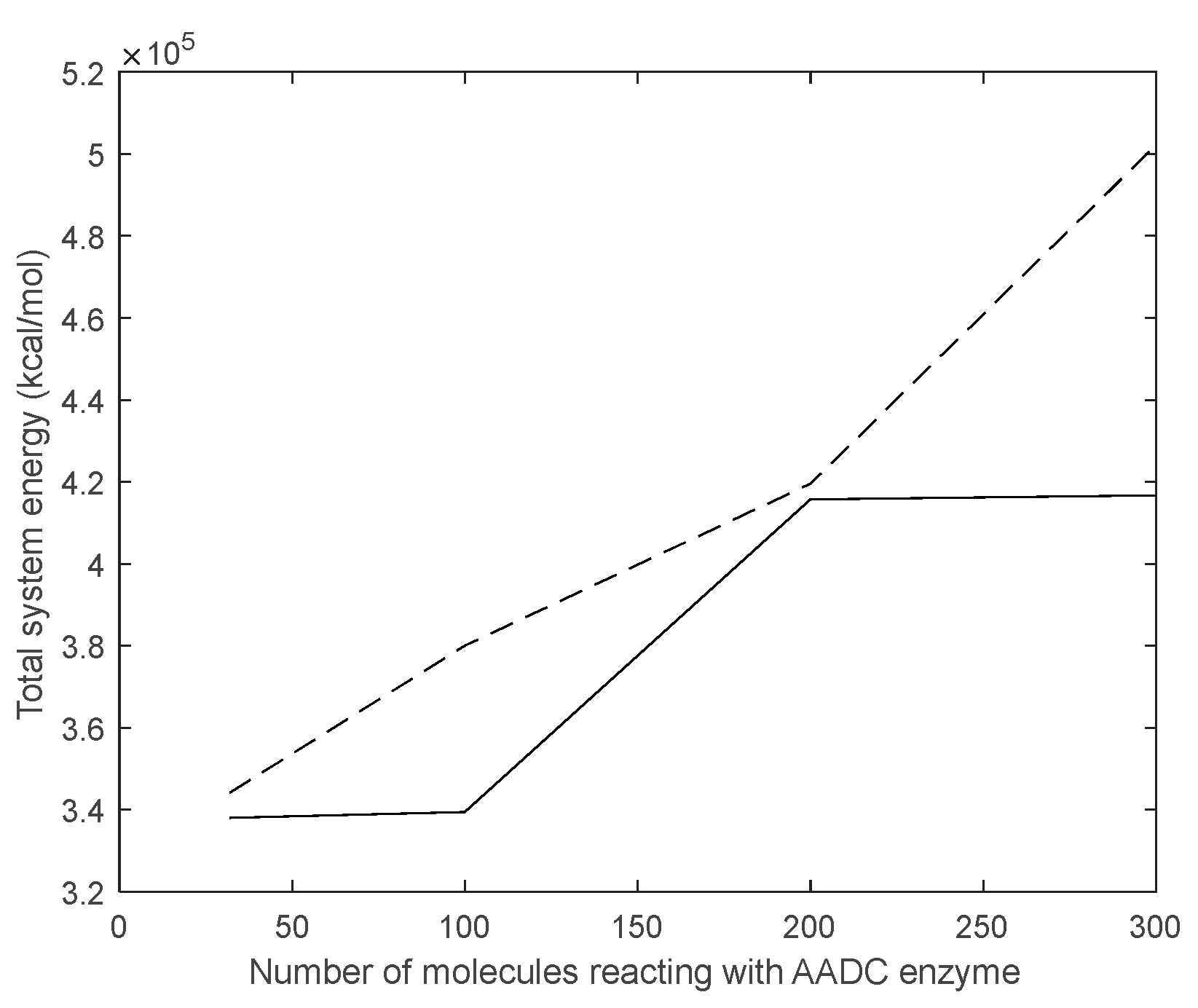
Figure 15.
Electrophilic attack index of L-DOPA.
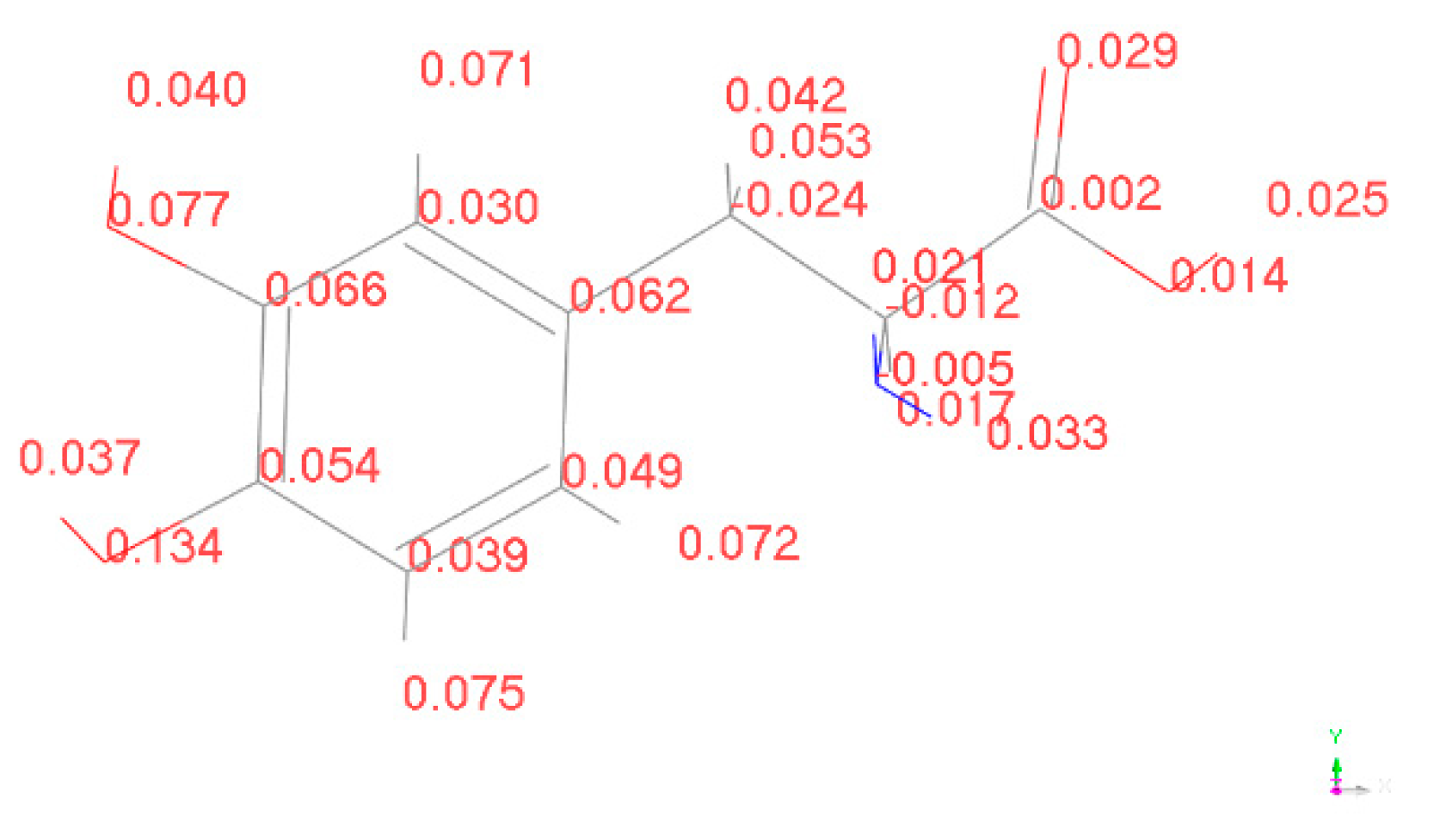
Figure 16.
Electrophilic attack index of D-DOPA.
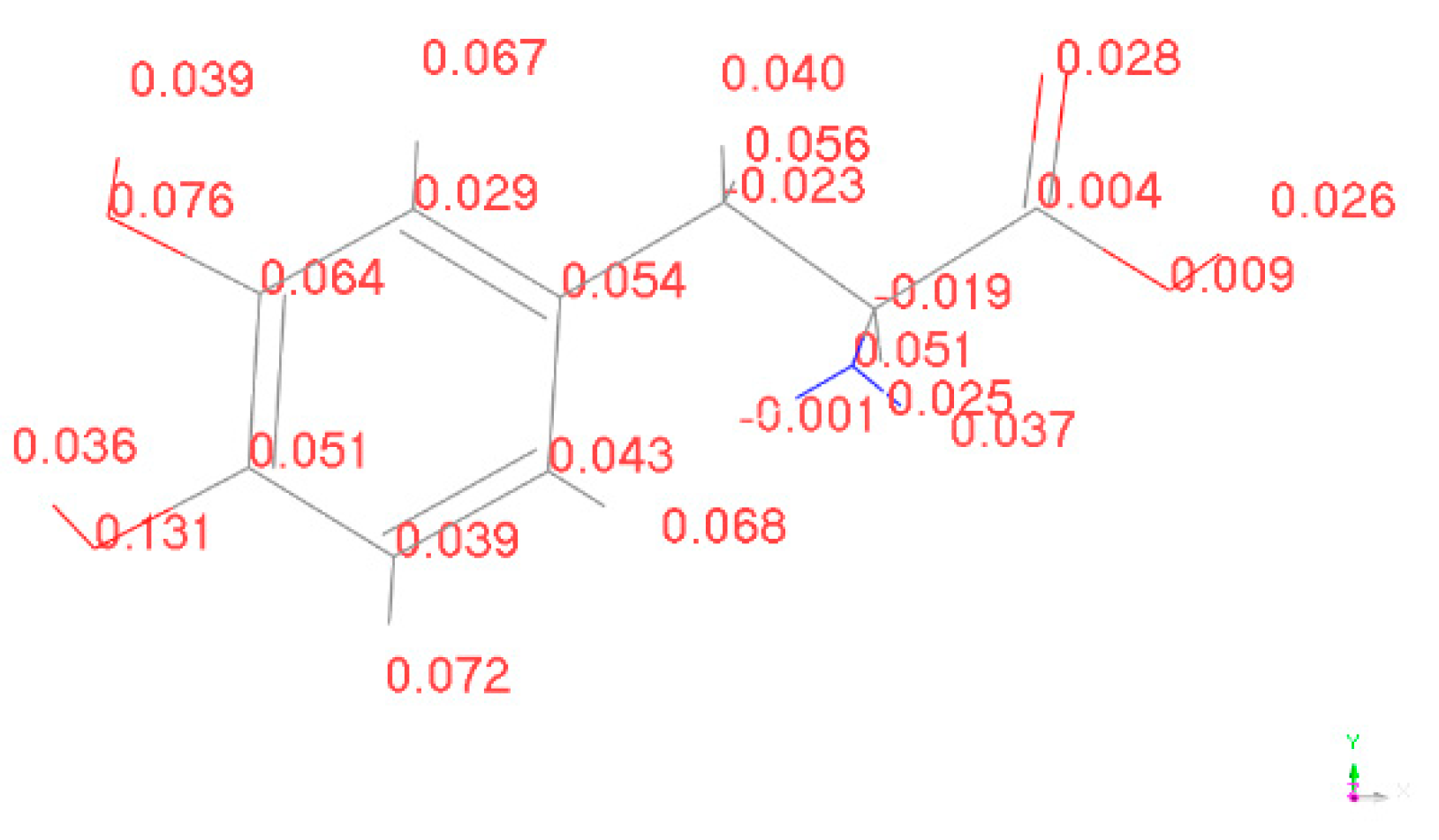
Figure 17.
D-DOPA approaching the C-terminus of a peptide chain composed of 10 amino acids.
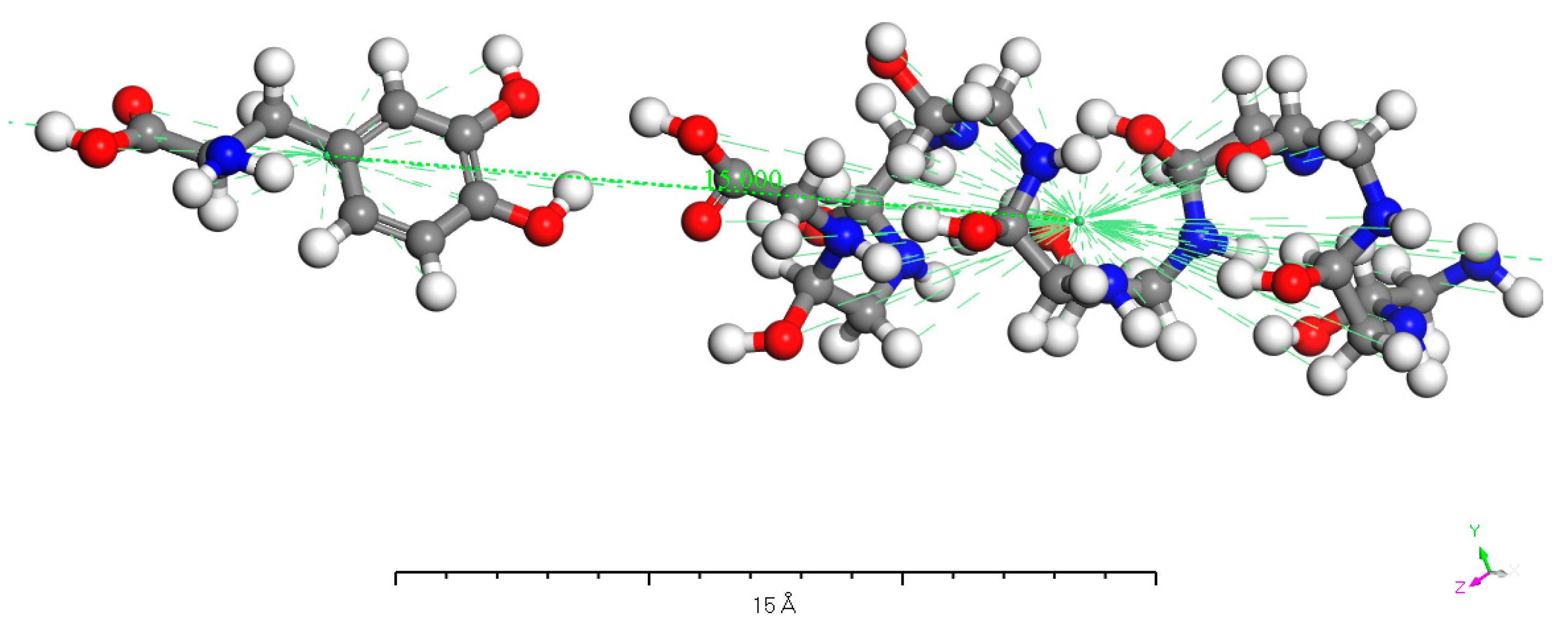
Figure 18.
Variation in distance as D-DOPA (—) approaches the C-terminus of the peptide chain (- -).
Figure 18.
Variation in distance as D-DOPA (—) approaches the C-terminus of the peptide chain (- -).
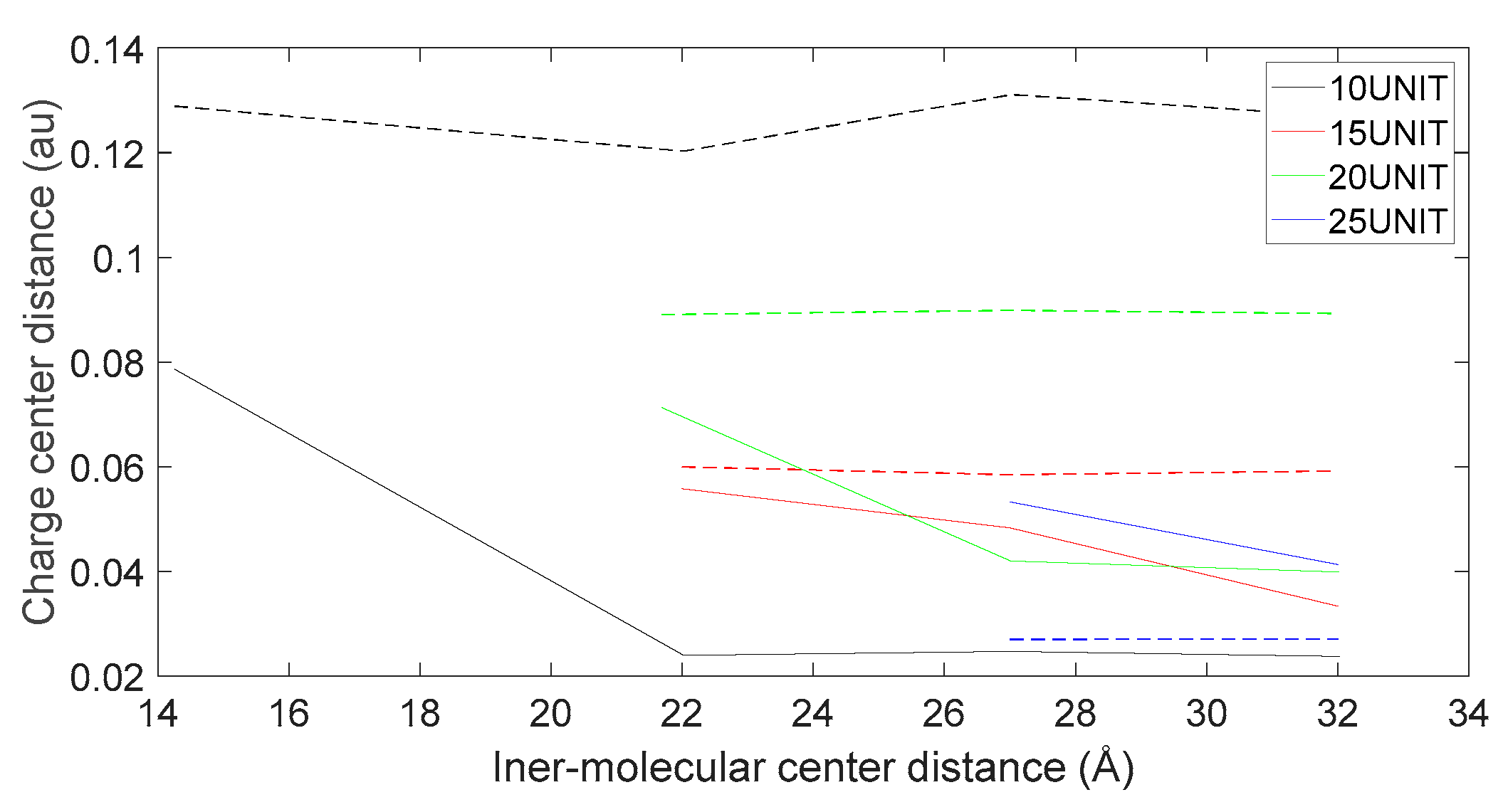
Figure 19.
Variation in distance as D-DOPA (—) approaches the N-terminus of the peptide chain (- -).
Figure 19.
Variation in distance as D-DOPA (—) approaches the N-terminus of the peptide chain (- -).
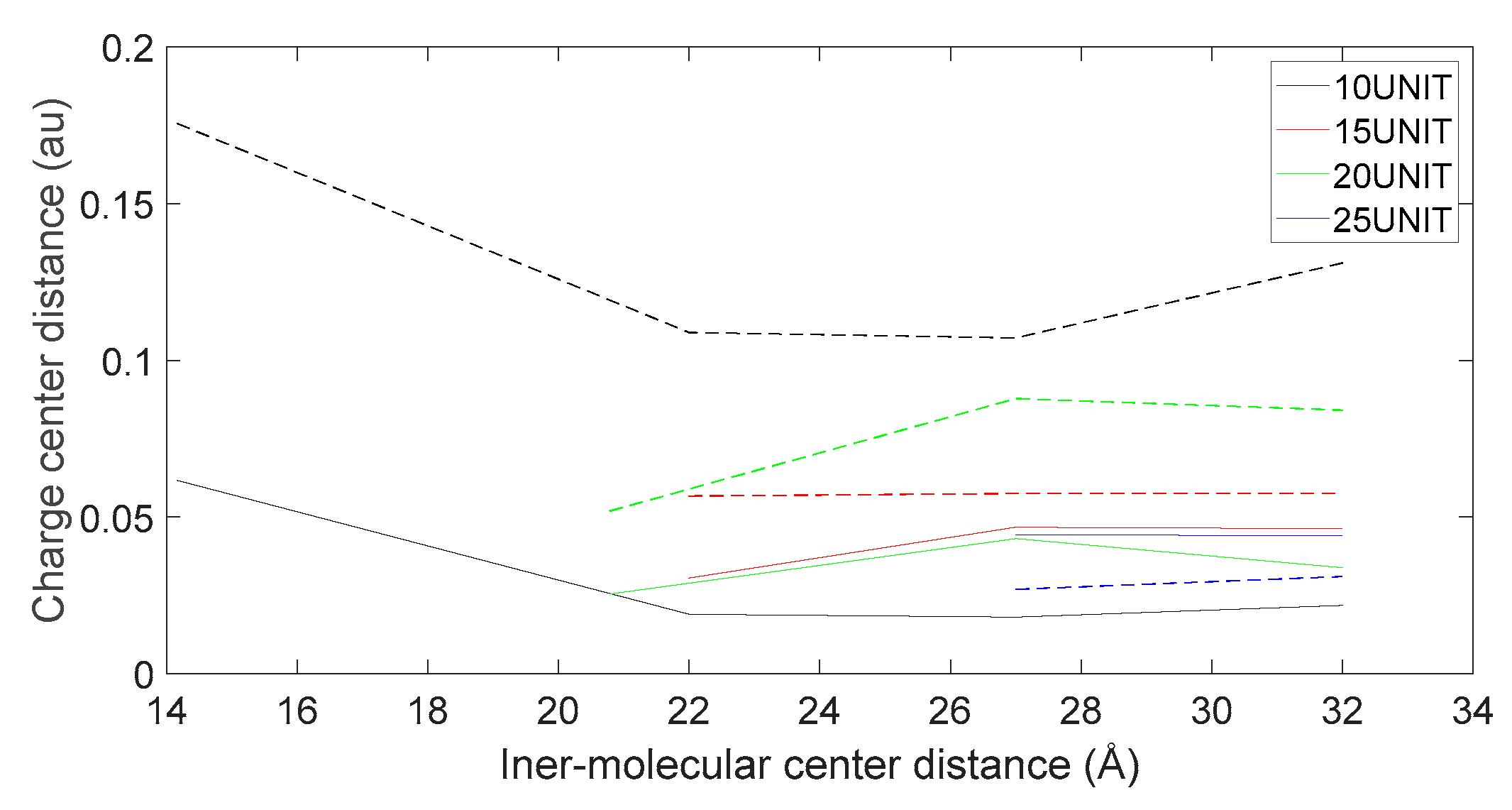
Figure 20.
Variation in distance as L-DOPA (—) approaches the C-terminus of the peptide chain (- -).
Figure 20.
Variation in distance as L-DOPA (—) approaches the C-terminus of the peptide chain (- -).
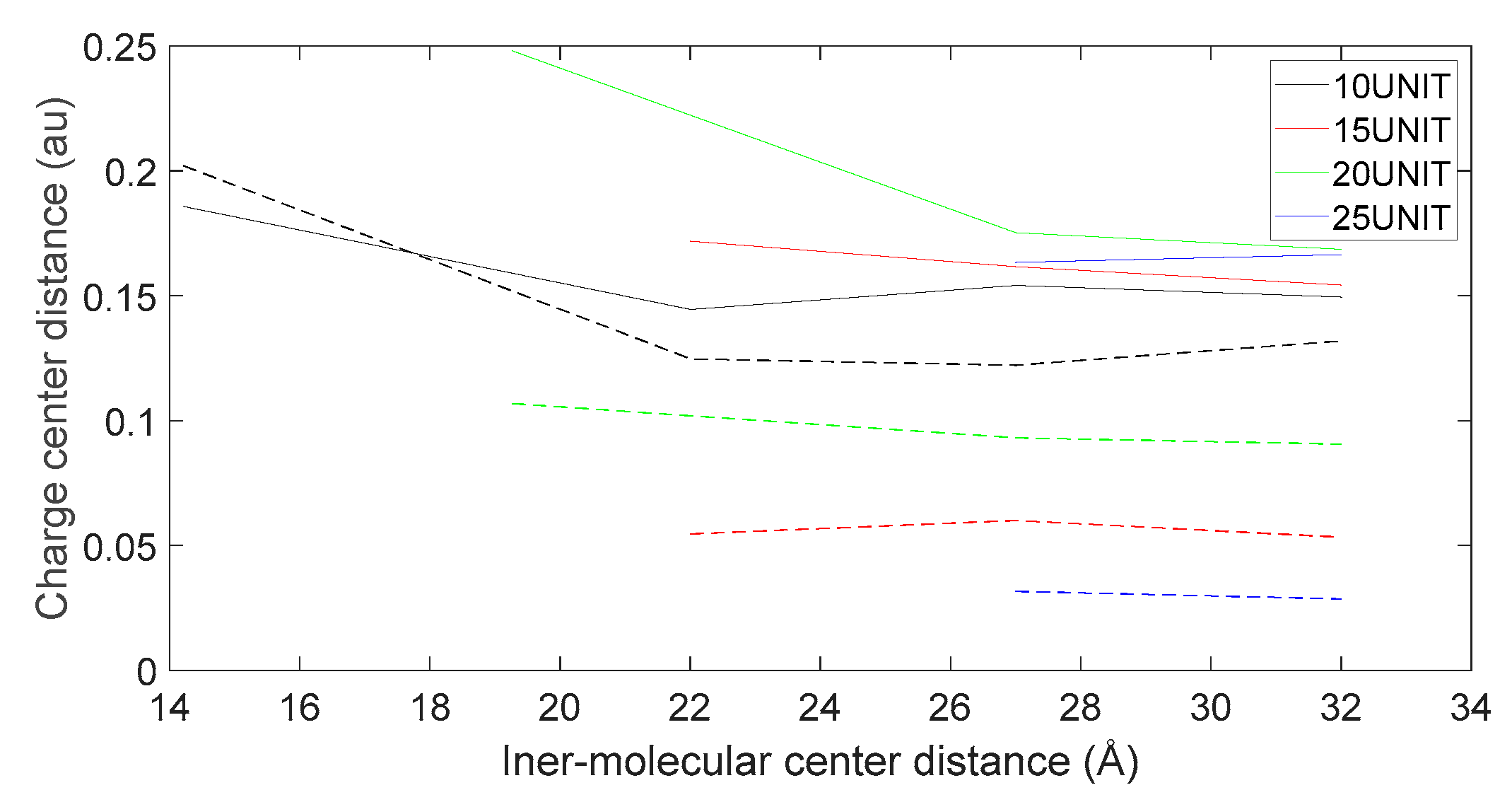
Figure 21.
Variation in distance as L-DOPA (—) approaches the N-terminus of the peptide chain (- -).
Figure 21.
Variation in distance as L-DOPA (—) approaches the N-terminus of the peptide chain (- -).
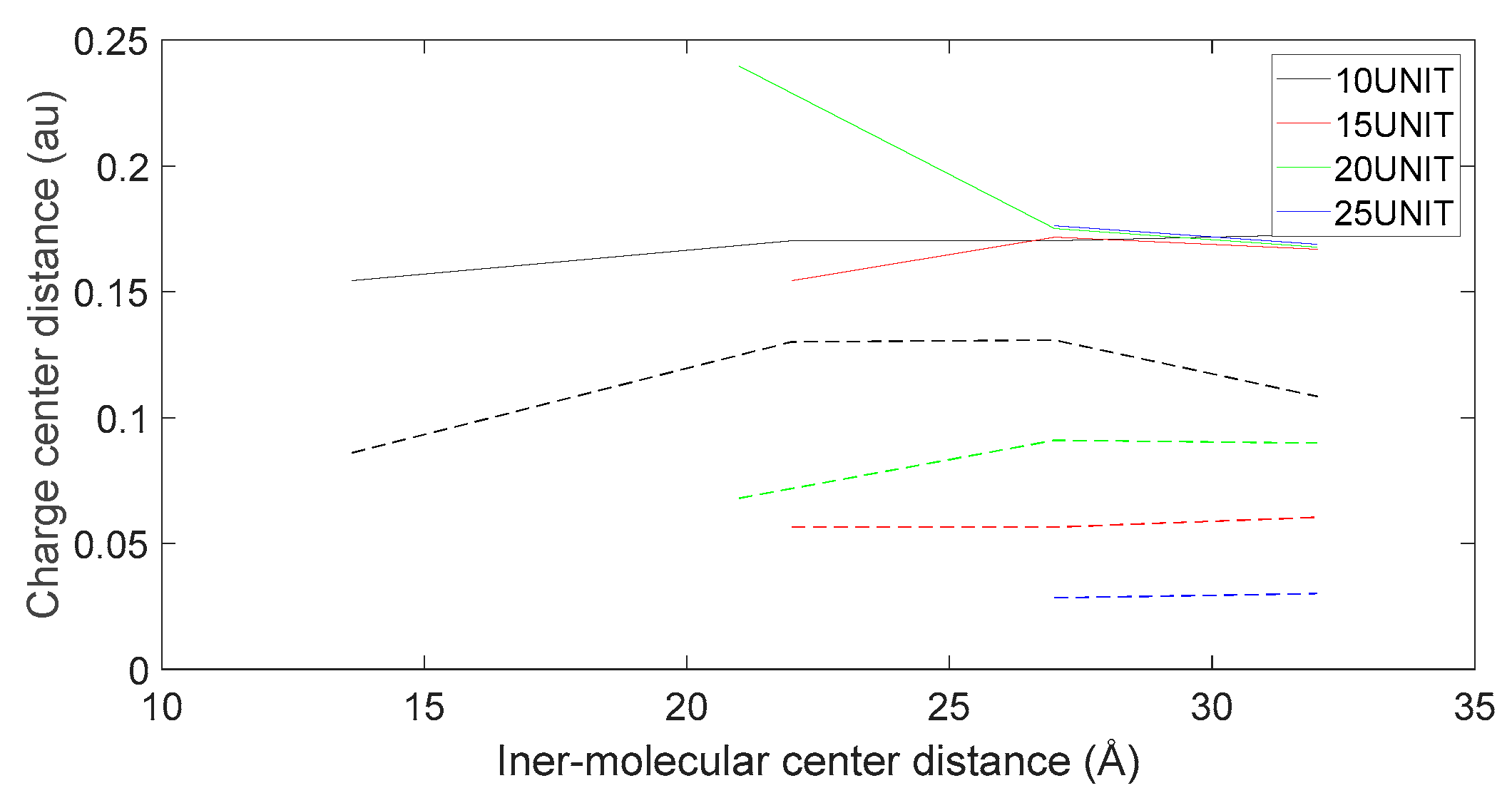
Figure 22.
The charge transfer as D-DOPA (—) approaches the C-terminus of the peptide chain (- -).
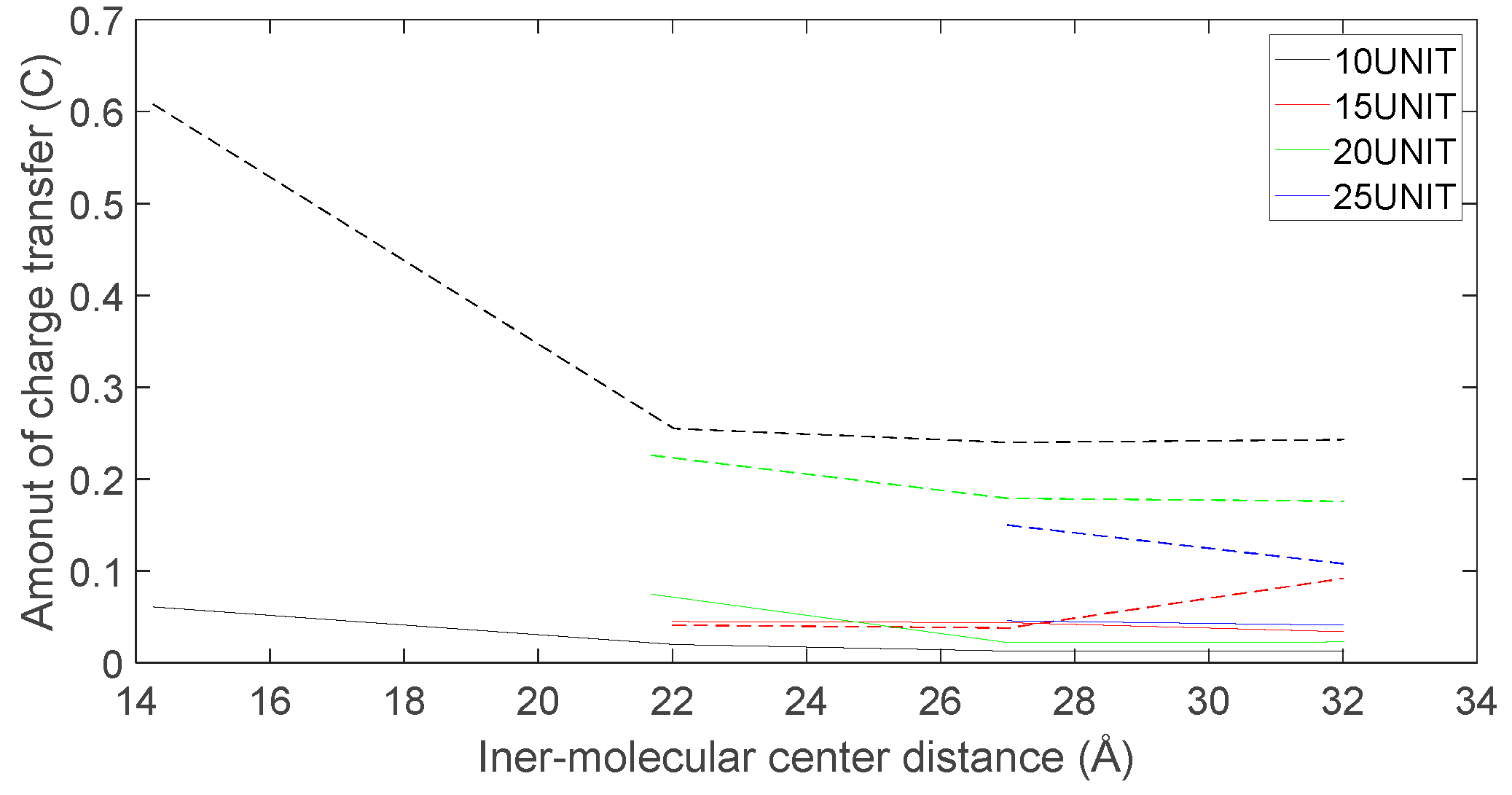
Figure 23.
The charge transfer as D-DOPA (—) approaches the N-terminus of the peptide chain (- -).
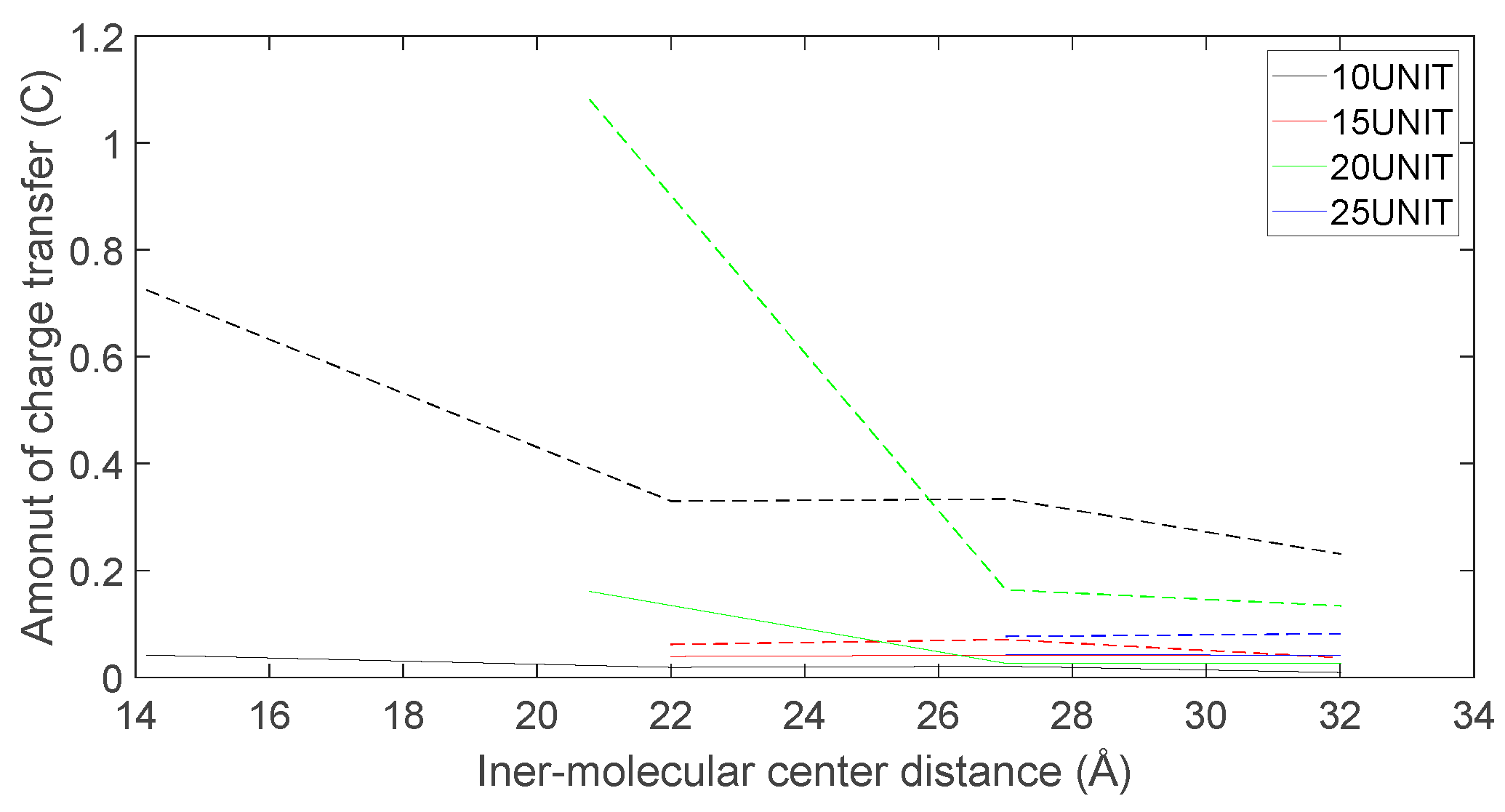
Figure 24.
The charge transfer as L-DOPA (—) approaches the C-terminus of the peptide chain (- -).
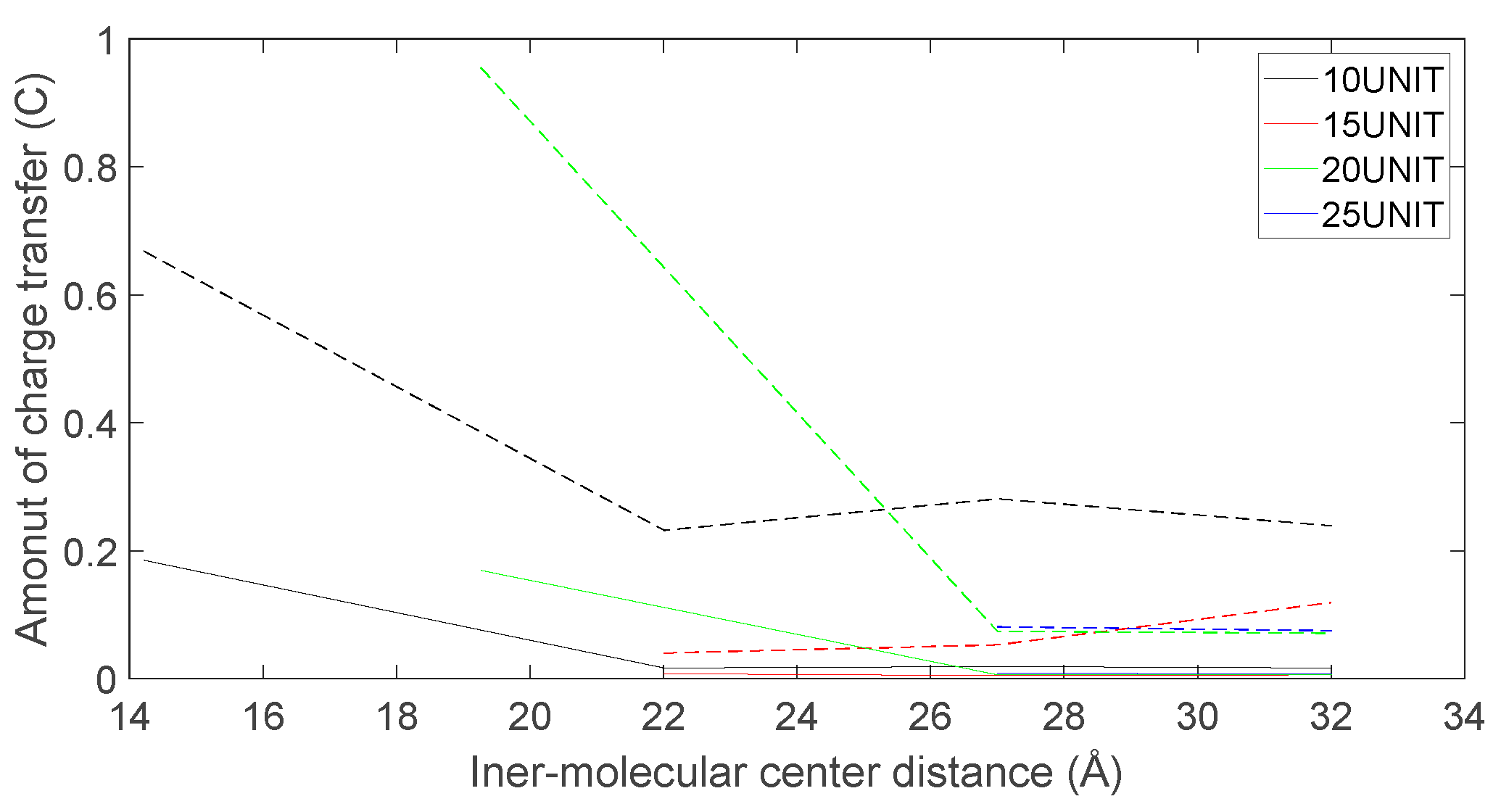
Figure 25.
The charge transfer as L-DOPA (—) approaches the N-terminus of the peptide chain (- -).
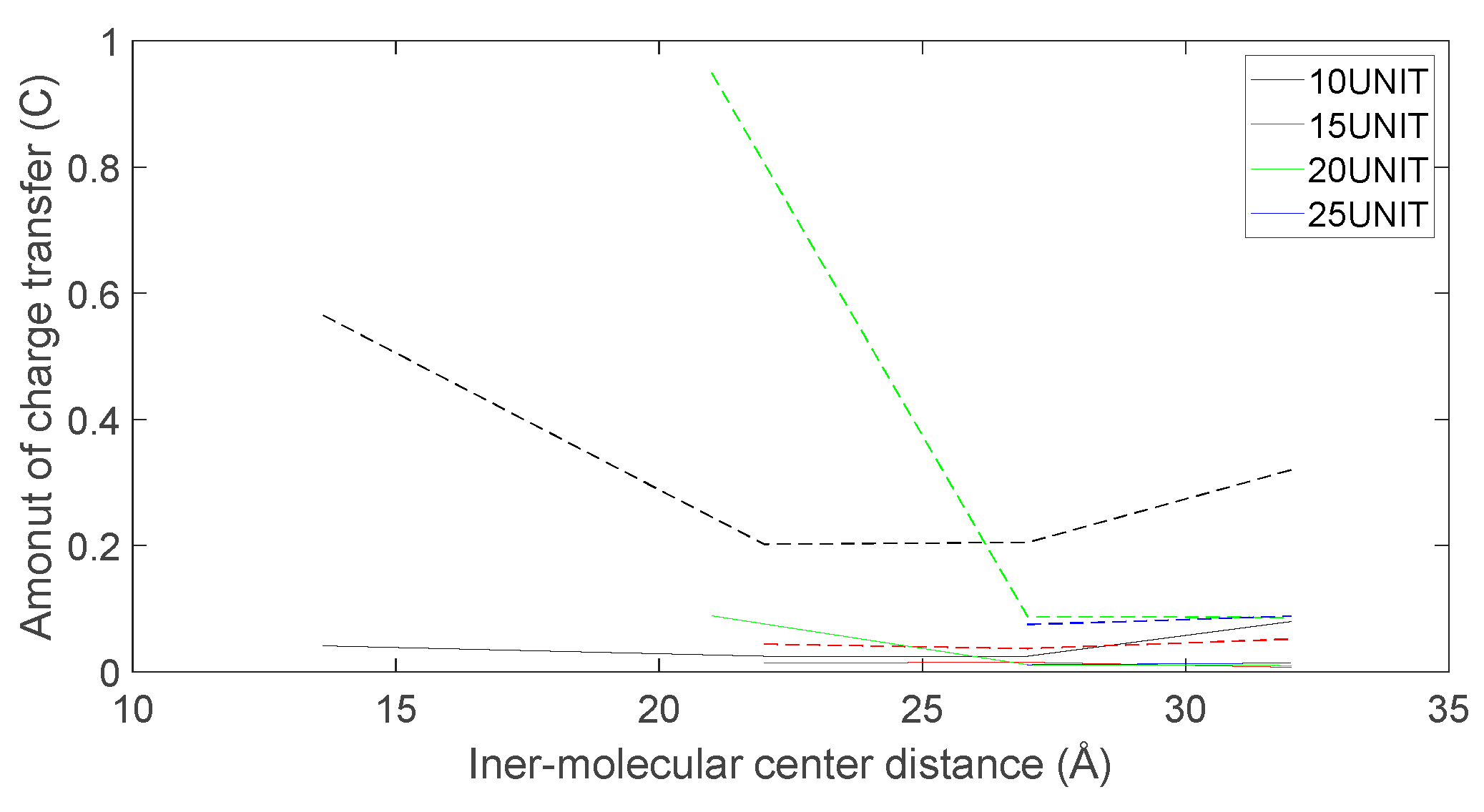
Figure 26.
The distribution of charge centers as D-DOPA approaches the C-terminus of the peptide chain.
Figure 26.
The distribution of charge centers as D-DOPA approaches the C-terminus of the peptide chain.
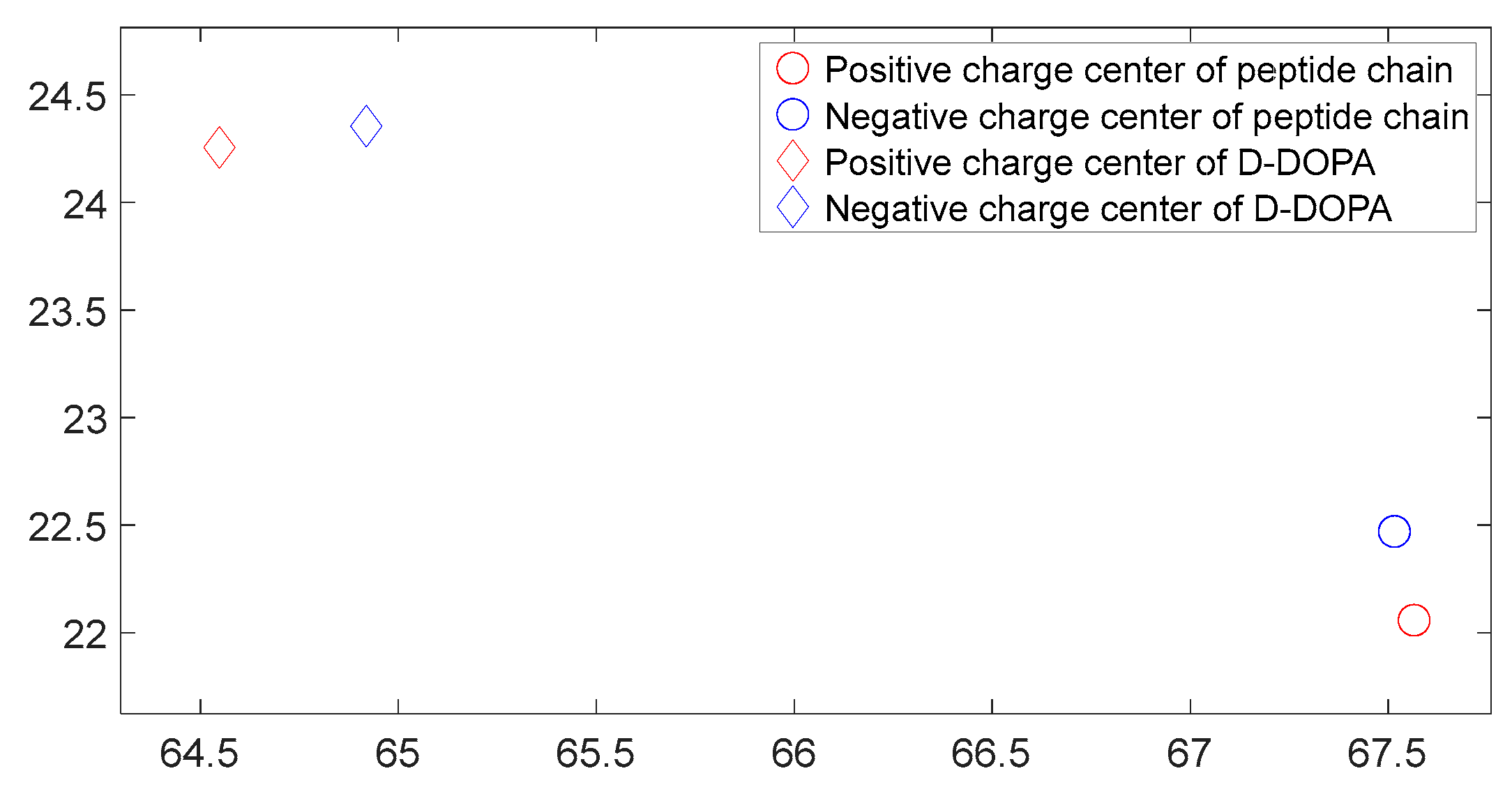
Figure 27.
The distribution of charge centers as L-DOPA approaches the C-terminus of the peptide chain.
Figure 27.
The distribution of charge centers as L-DOPA approaches the C-terminus of the peptide chain.
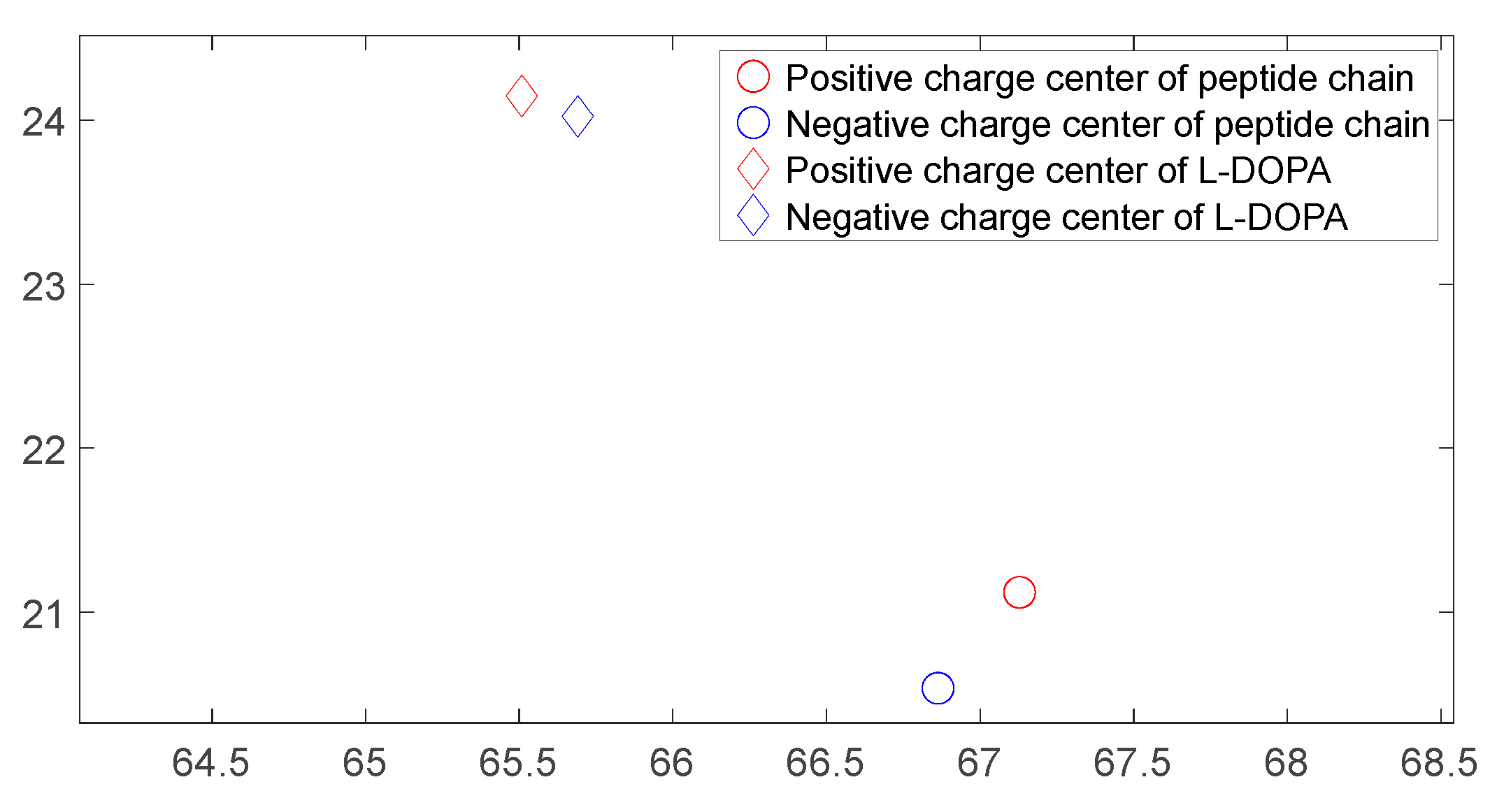
Figure 28.
The distribution of charge centers as D-DOPA approaches the N-terminus of the peptide chain.
Figure 28.
The distribution of charge centers as D-DOPA approaches the N-terminus of the peptide chain.
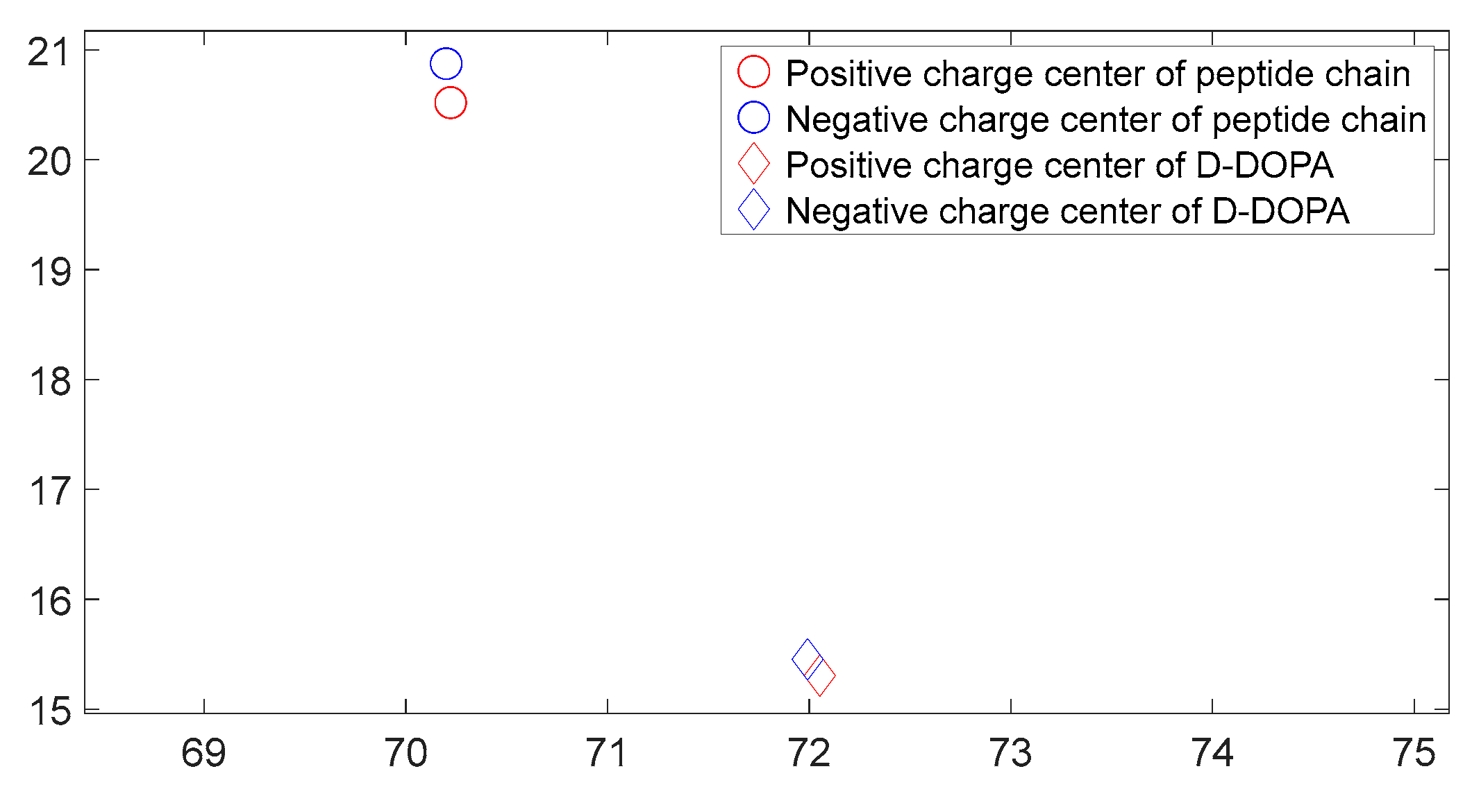
Figure 29.
The distribution of charge centers as L-DOPA approaches the N-terminus of the peptide chain.
Figure 29.
The distribution of charge centers as L-DOPA approaches the N-terminus of the peptide chain.
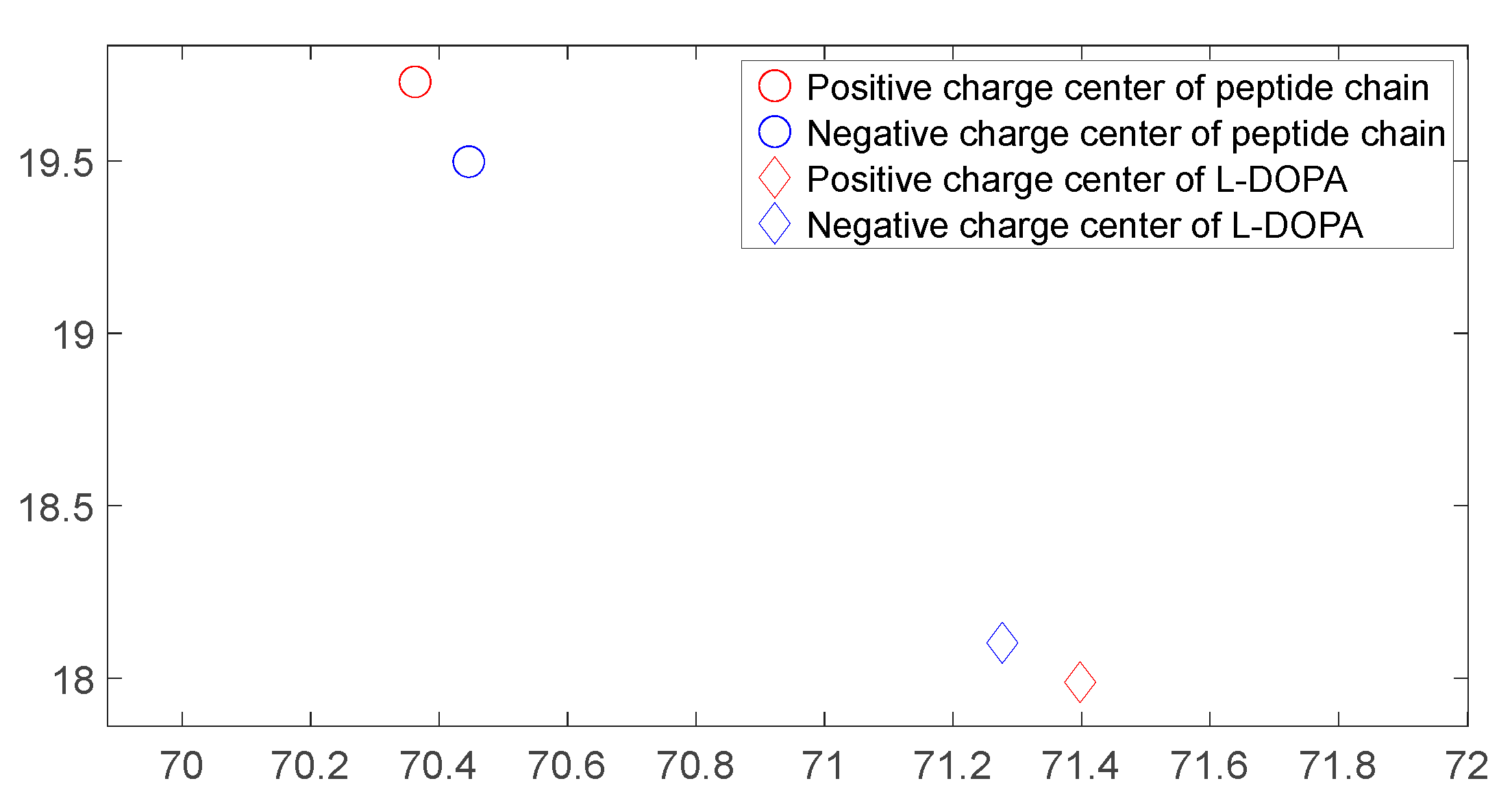
Figure 30.
Variation of charge center distance between D-DOPA molecule (—) and peptide chain (- -).
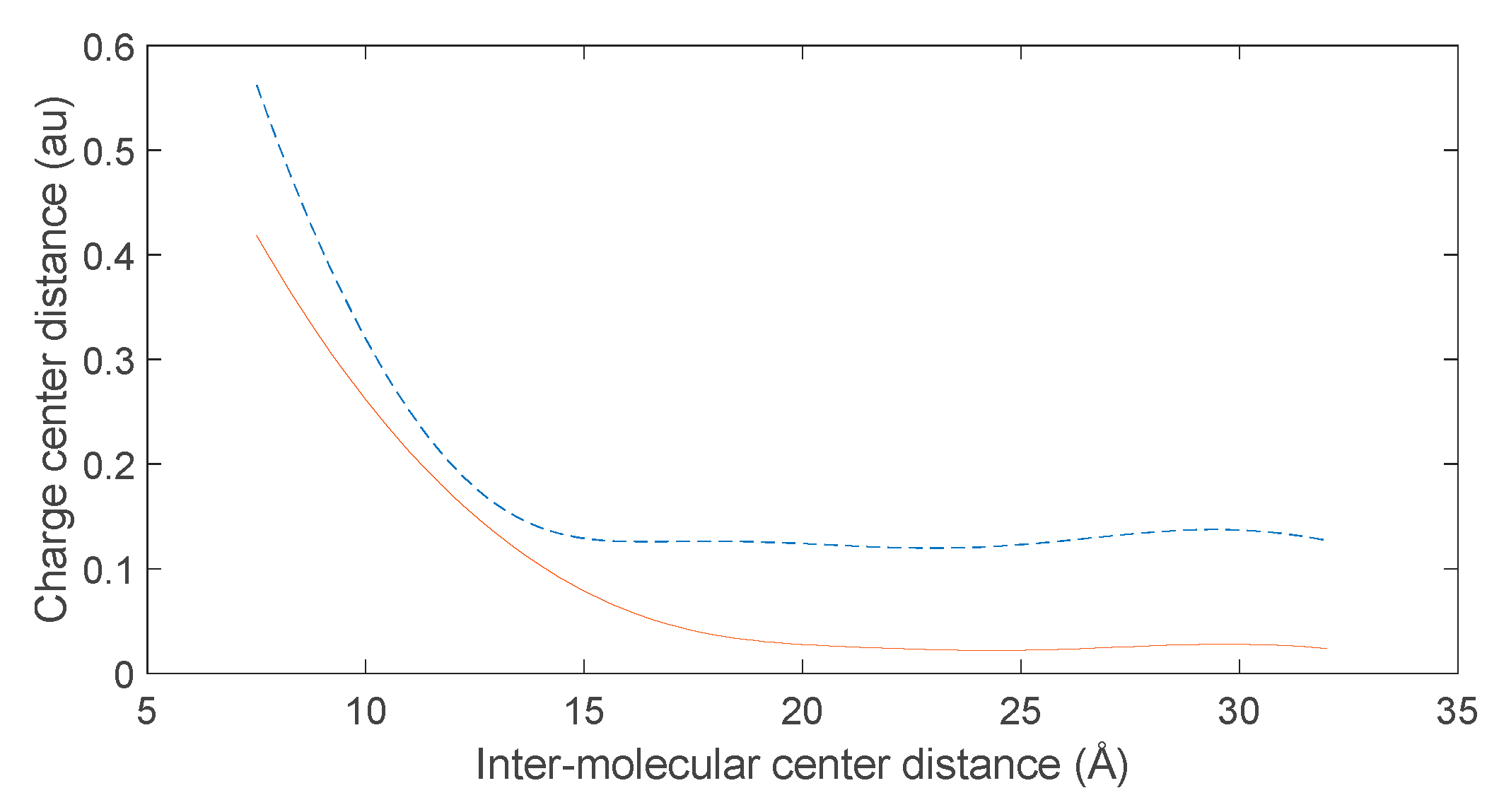
Figure 31.
A crystal cell containing one D-DOPA molecule.
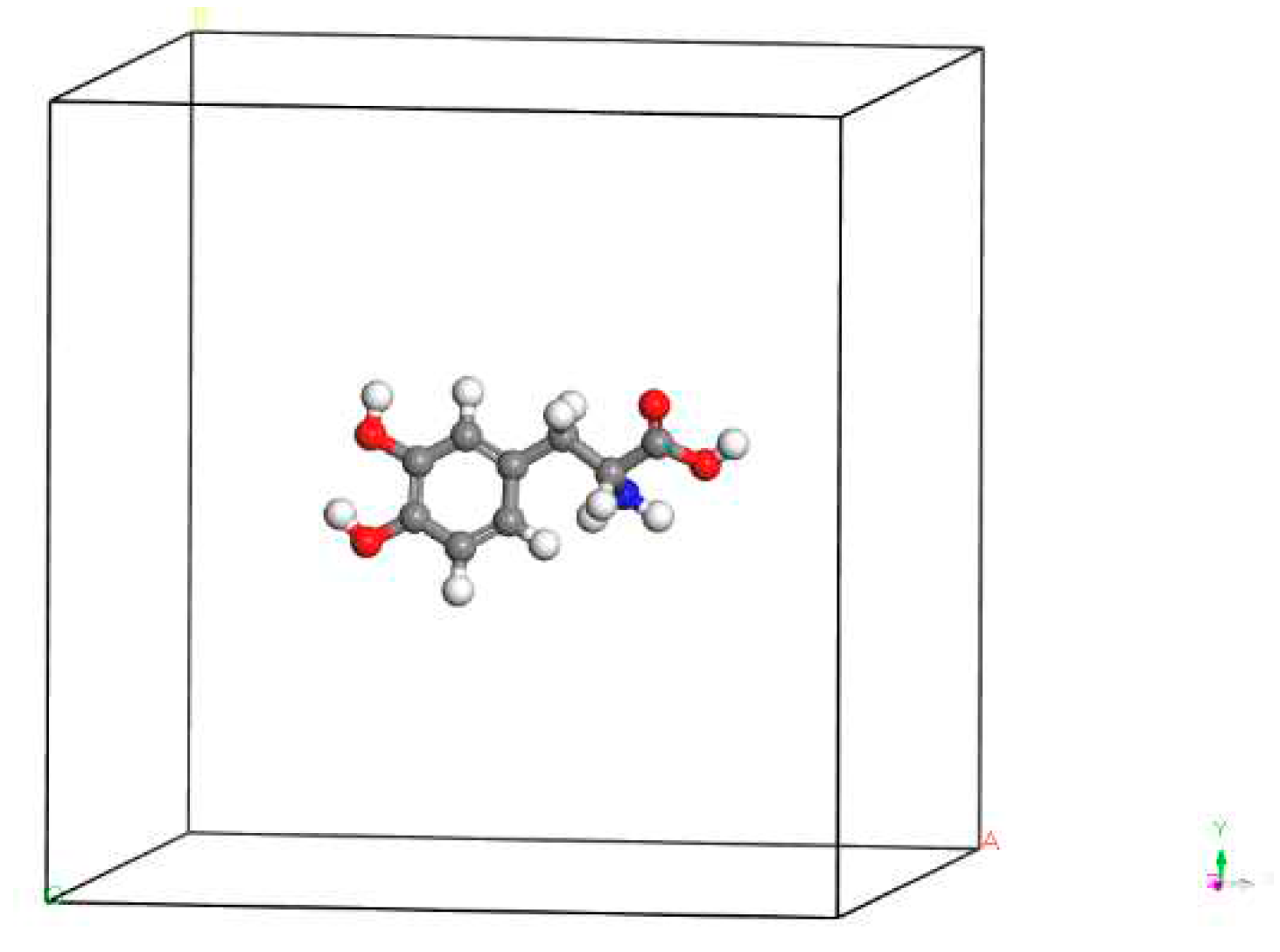
Figure 40.
Schematic of electron angular momentum in L-DOPA.
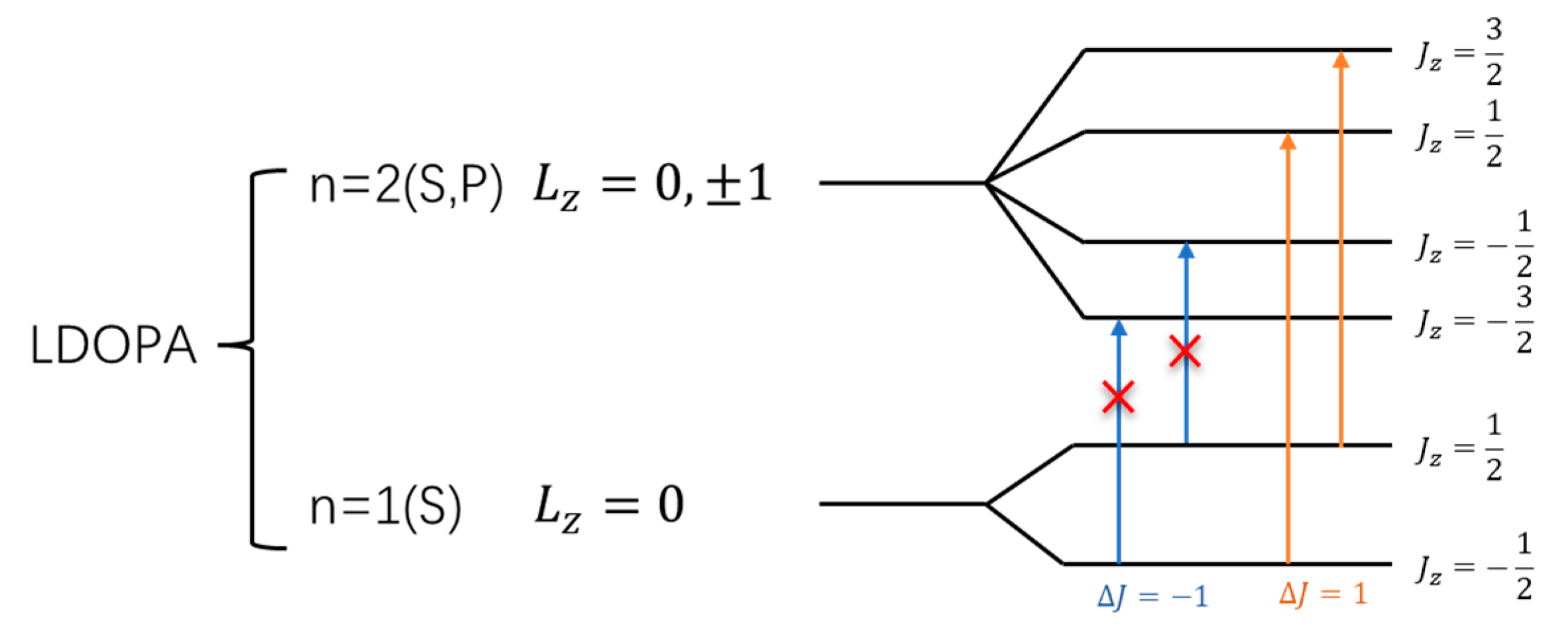
Figure 41.
Schematic of electron angular momentum in D-DOPA.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






