Prerpints.org logo
Preprint
Article

Position-dependent effective mass and asymmetry effects on the electronic and optical properties of quantum wells with improved Rosen-Morse potential

Altmetrics

Downloads

147

Views

46

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

31 July 2023

Posted:

02 August 2023

You are already at the latest version

Alerts
Abstract
In this study, we investigated, for the first time, the effects of the spatially varying effective mass, asymmetry parameter, and well width on the electronic and optical properties of the quantum well which has an improved Rosen-Morse potential. Calculations are made within the framework of the effective mass and parabolic band approximations. We have used the diagonalization method by choosing a wave function based on the trigonometric orthonormal functions to find eigenvalues and eigenfunctions of the electron confined within the improved Rosen-Morse potential. Our results show that the position-dependence mass, asymmetry, and confinement parameters cause significant changes in the electronic and optical properties of the structure we focus on since these effects create a significant increase in electron energies and a blue shift in the absorption spectrum. The increase in energy levels enables the development of optoelectronic devices that can operate at wider wavelengths and absorb higher energy photons. This offers potential advancements in fields such as optical communication, imaging technology, and solar cells.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

Constructing a universal empirical potential energy function for diatomic and/or polyatomic molecules holds significant importance. The fitting quality between the function and experimental data improves with an increased number of parameters in the analytical potential energy function. To illustrate, Morse proposed the first simple empirical analytical potential function in 1929 [1], which found utility in studying transition frequencies and intensities in diatomic and polyatomic molecules [2]. Several potential-energy functions, namely the Manning-Rosen, Schiöberg, Tietz, and Rosen-Morse potential functions, have been derived for diatomic molecules by explicitly incorporating the dissociation energy and equilibrium bond length as parameters [3,4,5].
The improved Rosen-Morse potential (IRMP) or exponential Rosen-Morse potential has independent fitting parameters for experimental data more than the trigonometric Rosen-Morse potential. Quantum well potentials are often used in combination with other materials to create heterostructures. By stacking different layers of materials with varying bandgaps and compositions, researchers can create quantum wells with different geometries. These heterostructures can provide additional degrees of freedom to control the electronic properties, enabling the design of advanced devices like high-electron-mobility transistors (HEMTs) and quantum cascade lasers. The significance of quantum well potentials with different geometries lies in their ability to manipulate electron energies, confinement effects, quantum tunneling, optical properties, and the creation of complex heterostructures.
By tailoring the geometry, researchers can engineer the desired electronic and optical characteristics for various applications in semiconductor devices and quantum technologies. Low-dimensional semiconductor heterostructures, in which position dependent mass (PDM) or spatially variable mass effects are taken into account, are of interest to researchers because of their importance in many branches of physics, especially in the study of electronic and optical properties of semiconductors [6,7,8,9,10,11,12,13]. The improved Rosen-Morse potential (IRMP) which can also call exponential RMP serves as a reliable model for describing the interaction between particles in various physical systems. By including more appropriate parameters, it provides a more flexible framework than trigonometric RM potential to accurately represent experimental data.
This study capitalizes on these advantages to explore the behavior of electrons in a quantum well, where the effective mass varies spatially. As known, understanding the electronic properties of confined electrons is crucial for developing advanced electronic devices and optoelectronic applications. Although there are a limited number of studies on the optical properties of quantum wells and quantum dots with trigonometric RM potential under external fields and without PDM [14,15,16], we have not found any studies on the optical properties of quantum well (QW) with IRM potential. Therefore, in this study, which we thought had never been studied except for the calculation of rotational-vibration energies of some diatomic molecules, we investigated, for the first time, the electronic and optical properties of an electron with a spatially varying effective mass, confined in a QW which has IRM (IRMQW) potential.
This work is arranged as follows: the theoretical framework is presented in Section 2, the results and discussion are outlined in Section 3, and the conclusions are given in Section 4.

2. Theoretical framework

In the effective mass approximation, Hamiltonian for the electron is given by
H = − ℏ 2 2 ∇ · 1 m ( z ) ∇ + V ( z ) ,
where m ( z ) is the position-dependent effective mass of the electron, and it is as defined below
m ( z ) = m * s e c h 2 π z d ,
where d-parameter describes the effective length of position dependence mass (PDM) distribution, and m * = 0 . 067 m 0 is the effective mass at z = 0 ( m 0 is the free electron mass). At sufficiently large d-values, the variable mass approaches the value of electron mass in the bulk material of interest, and the uniform behavior, stability, and spatial extension of the effective mass also increase. V ( z ) is the IRMQW potential, and its functional form is given as follows [17]
V ( z ) = V 0 1 − e z 0 / k + 1 e z / k + 1 2 ,
where V 0 is the depth of the quantum well, k-parameter is related to the well width. As z 0 increases, the minimum point of the potential shifts and barrier height on the right side slowly decreases, while the left side becomes sharper and rises to infinity. So, we defined the z 0 as an asymmetry parameter since it causes the IRMQW to turn into an asymmetrical structure. It should also be noted that using the IRMQW used in the literature to obtain the molecular energy spectrum of diatomic molecules, has been modified by us to investigate the electronic and optical properties of an electron confined within this potential.
Immediately after the energies and related wave functions are acquired, for transitions between any two electronic states, the linear and non-linear absorption coefficients are found by using the perturbation expansion and the density matrix methods. Using the relevant approaches mentioned before, expressions of the linear, third-order nonlinear, and total absorption coefficients (ACs) for the optical transitions are found, respectively, as follows [18,19,20,21].
β ( 1 ) ( ω ) = μ 0 ε r M i j 2 σ v η ω Γ i j ( E i j − η ω ) 2 + ( η Γ i j ) 2 ,
β ( 3 ) ( ω , I ) = − 2 μ 0 ε r I ε 0 n r c M i j 2 σ v η ω Γ i j ( E i j − η ω ) 2 + ( η Γ i j ) 2 1 − M j j − M i i 2 2 M i j 2 ( E i j − η ω ) 2 − ( η Γ i j ) 2 + E i j ( E i j − η ω ) E i j 2 + ( η Γ i j ) 2 ,
and
β ( ω ) = β ( 1 ) ( ω ) + β ( 3 ) ( ω ) ,
where ε r = n r 2 ε 0 is the real part of the permittivity, σ v is the carrier density in the system, μ 0 is the vacuum permeability, E i j = E j − E i is the energy difference between two impurity states, M i j = ψ i e z ψ j , ( i , j = 1 , 2 ) is the transition matrix element between the eigenstates ψ i and ψ j for incident radiation polarized in the z-direction, Γ i j ( = 1 / T i j ) is the relaxation rate, T i j is the inverse relaxation time, c is the speed of the light in free space, and I is the intensity of incident photon with the ω -angular frequency that leads to the intersubband optical transitions. It should be noted that diagonal (non-diagonal) matrix elements are zero (different zero) M i i = M j j = 0 , ( M i j ≠ 0 ) in the symmetric case for z 0 = 0 .

3. Results and Discussion

The parameter values in our numerical calculations are ε 0 = 12.58 μ 0 = 4 π × 10 − 7 H m − 1 , σ v = 3 . 0 × 10 22 m − 3 , and I = 5 . 0 × 10 8 W / m 2 . These parameters suit GaAs/GaAlAs heterostructures [6].
The changes in the shape of IRM type QW according to the z 0 -asymmetry parameter as a function of the z-coordinate are given in Figure 1. When the parameter- z 0 is zero, the structure has a symmetrical character; if z 0 is nonzero, it becomes an asymmetrical character; the parameter- z 0 also has a dominant effect on geometric confinement.
The variations of the energies corresponding to the first three levels of a confined electron within the IRMQW as a function of z 0 -parameter in the absence and presence of position dependence mass for k = 15 n m and k = 25 n m values are given in Figure 2a,b. In the absence and presence of PDM, energies are an increasing function of z 0 -parameter. As explained above, the energies also increase since the increase in the z 0 -parameter causes an increase in the geometric confinement. As seen in Equation (2), for small values of z 0 -parameter, the PDM of the electron is lower than that of the constant mass (CM), i.e., ( m ( z ) < m * ) , and so the energy values of the electron get larger the energy levels are always inversely proportional to the electron mass. However, for larger values of d-parameter, the energy values of the electron also approach to results of CM, since m ( z ) approaches m * -value. Furthermore, the electron with the E 3 -energy becomes unbound at z 0 ≥ 10 n m due to the increase in energies by the combined effects of the PDM and z 0 -parameter. The increase in the k-width parameter weakens the geometric confinement. Therefore, the energies decrease, and the electron with E 3 -energy becomes bound in the well at the same z 0 value for large d.
The variations of the energy differences between some energy levels of interest as a function of z 0 -parameter for the values of k = 15 n m and k = 25 n m are given in Figure 3a,b. As a natural consequence of the increase in energies as a function of z 0 , the energy differences between the two levels indicated at the inset of the figures also increase.
Figure 4a,b show the variation of total absorption coefficients for a transition that is called the (1-2) between the ground and first excited states of an electron confined within the quantum well with the improved Rosen-Morse confinement potential as a function of the incident photon energy for different z 0 -values for k = 15 n m and k = 25 n m respectively.
First of all, it should be noted that for z 0 = 0 , the IRMQW is symmetrical, and the (1-3) transition between the ground state and the second excited level is forbidden, other than that for all z 0 -values, all transitions are allowed since the structure is asymmetrical. Due to the delocalization of the electron that has E 3 -energy by the spatially varying mass and asymmetry effects, the (1-3) transition is not shown in the figures. The amplitude of the absorption peak corresponding to this transition is already very small due to the transition matrix element. For k = 15 n m , the total absorption peak positions corresponding to the (1-2) transition shift towards the blue with increasing z 0 -values. The peak positions shift first to blue with the effect of PDM, and for larger d-values, towards the peak positions corresponding to the results of the CM case, that is, to the red. For the CM case, the bleaching effect is observed in absorption peaks due to the increasing importance of the nonlinear contribution; the contribution of the nonlinear absorption coefficient decreases with increasing z 0 -value. In the case of PDM, the bleaching effect disappears, indicating that the nonlinear optical coefficient is negligible compared to the linear one. For k = 25 n m , all peaks shift to the red with decreasing magnitudes, and the contribution of the nonlinear term is bigger compared to the k = 15 n m .
Figure 5a,b have the same regulation as in Figure 4a,b, but the results given are for the (2-3) transition. It should be noted that the incident photon intensity for all the transitions in the Figure 4 and 5 is I = 5 . 0 × 10 8 W / m 2 . The bleaching effect is quite pronounced in the total absorption peaks corresponding to the (2-3) transition since the nonlinear term is greater than that of the linear term, and absorption peaks localize in lower photon energies than the (1-2) transition. Furthermore, the total absorption peaks for the (2-3) transition are not observed since the electron with the E 3 -energy unbound within the IRMQW for d = 30 n m .
As known, in linear absorption, the absorption properties of the material are independent of the light intensity. When the nonlinear absorption coefficient, which depends on the intensity of the incident light, is much larger than the linear absorption coefficient, the material exhibits a significantly stronger light absorption at high intensities compared to low intensities. This phenomenon is often observed in nonlinear optics. The material may exhibit strong absorption or even saturation effects at higher light intensities, leading to a higher light attenuation rate. This behavior can be exploited in applications such as optical limiting, optical switching, and nonlinear imaging, where controlling the intensity-dependent absorption is crucial. It’s worth noting that the specific mechanisms behind nonlinear absorption can vary depending on the material and the physical processes involved. Common examples include two-photon absorption, multiphoton absorption, and saturable absorption, each having different dependencies on the light intensity.
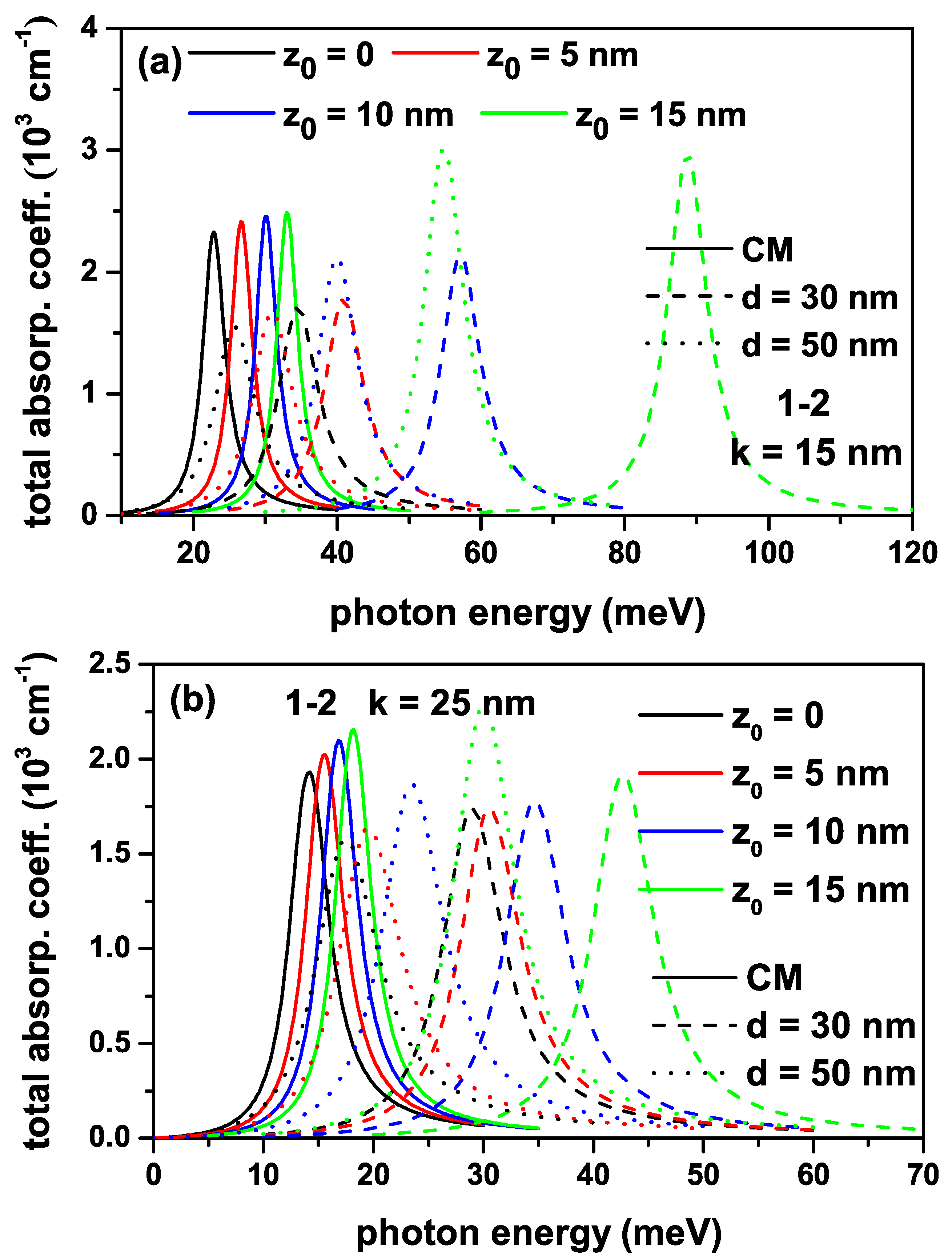
It is also well known that when the energy difference between any two states is sufficiently small, and the optical intensity which leads to the intersubband optical transitions is sufficiently high, the bleaching effect is observed. It is already known that the bleaching effect disappears using a smaller optic intensity than the one used here when the energy difference between the two energy levels is small. To see this, we added the new figures using a lower intensity for the photon, causing the intersubband transitions. Figure 6a,b have the same regulation as in Figure 4a,b, but the results are for the photon intensity I = 1 . 0 × 10 8 W / m 2 , and include only the (1-2) transition. There is already no bleaching effect in the presence of PDM. Still, as can be seen from the figures, when lower light intensity is used, the amplitude of all total ACs increases as the contribution of the third-order nonlinear term is reduced. Thus the bleaching effect observed in ACs without PDM is disappeared.

4. Conclusions

In this work, for the first time, the position-dependent effective mass, structure, and asymmetry parameter effects on the electronic and optical properties of an electron confined in both symmetric and asymmetric quantum wells that have improved an exponential Rosen-Morse potential are investigated. The position-dependent effective mass, asymmetry, and confinement parameters significantly increase electron energies, energy differences between the confined electron states, and a blue shift in the absorption spectrum. These results enable the development of optoelectronic devices that can operate at wider wavelengths and absorb higher energy photons. In the presence of the position-dependent mass, the bleaching effect disappears, which is observed in the case of constant mass. This behavior can be exploited in applications such as optical limiting, optical switching, and nonlinear imaging, where controlling the intensity-dependent absorption is crucial.

Author Contributions

E.K.: conceptualization, methodology, software, formal analysis, investigation, supervision, writing; M.B.Y.: conceptualization, methodology, software, formal analysis, writing; C.A.D.: formal analysis, writing. All authors have read and agreed to the published version of the manuscript.

Funding

CAD is grateful to Colombian agencies CODI-Universidad de Antioquia (Estrategia de Sostenibilidad de la Universidad de Antioquia and projects “Propiedades magneto-ópticas y óptica no lineal en superredes de Grafeno”, “Estudio de propiedades ópticas en sistemas semiconductores de dimensiones nanoscópicas”, “Propiedades de transporte, espintrónicas y térmicas en el sistema molecular ZincPorfirina”, and “Complejos excitónicos y propiedades de transporte en sistemas nanométricos de semiconductores con simetría axial”) and Facultad de Ciencias Exactas y Naturales-Universidad de Antioquia (CAD exclusive dedication project 2022-2023).

Institutional Review Board Statement

not applicable.

Informed Consent Statement

not applicable.

Data Availability Statement

No new data were created or analyzed in this study. Data sharing is not applicable to this article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. P. M. Morse, Diatomic Molecules According to the Wave Mechanics. II. Vibrational Levels, Phys. Rev. 34, 57 (1929). [CrossRef]
  2. Z. Rong, H. G. Kjaergaard, M. L. Sage, Comparison of the Morse and Deng-Fan potentials for X-H bonds in small molecules, Mol. Phys. 101, 2285 (2003). [CrossRef]
  3. C. S. Jia, Y. F. Diao, X. J. Liu, P. Q. Wang, J. Y. Liu, and G. D. Zhang, Equivalence of the Wei potential model and Tietz potential model for diatomic molecules, J. Chem. Phys. 137, 014101 (2012). [CrossRef]
  4. P. Q. Wang, L. H. Zhang, C. S. Jia, J. Y. Liu, Equivalence of the three empirical potential energy models for diatomic molecules. J. Mol. Spectrosc. 274, 5 (2012). [CrossRef]
  5. P. Q. Wang, J. Y. Liu, L. H. Zhang, S. Y. Cao, C. S. Jia, Improved expressions for the Schiöberg potential energy models for diatomic molecules, J. Mol. Spectroscopy. 278, 23 (2012). [CrossRef]
  6. H. Sari, E. Kasapoglu, S. Sakiroglu, I. Sökmen, Position-dependent mass effects on the optical responses of the quantum well with Tietz–Hua potential, Optik, 178 (2019)1280-1284. [CrossRef]
  7. H. Panahi, S. Golshani, M. Doostdar, Influence of position dependent effective mass on donor binding energy in square and V-shaped quantum wells in the presence of a magnetic field, Phys. B , 418 (2013) 47-51. [CrossRef]
  8. A. John Peter, K. Navaneethakrishnan, Effects of position-dependent effective mass and dielectric function of a hydrogenic donor in a quantum dot, Physica E , 40 (2008) 2747-2751. [CrossRef]
  9. H Dakhlaoui, W Belhadj, E Kasapoglu, F Ungan, Position-dependent-mass and laser field impact on the optical characteristics of Manning-like double quantum well, Physica E , 151 (2023) 115737. [CrossRef]
  10. E. Kasapoglu, C. A. Duque, Position dependent effective mass effect on the quantum wells with three-parameter modified Manning potential, Optik , 243 (2021) 166840. [CrossRef]
  11. K. Li, K. Guo, X. Jiang, M. Hu, Effect of position dependent effective mass on nonlinear optical properties in a quantum well, Optik, 132 (2017) 375-381. [CrossRef]
  12. A. Keshavarz, N. Zamani, Optical properties of spherical quantum dot with position-dependent effective mass, Superlattices Microst., 58 (2013) 191-197. [CrossRef]
  13. R. Khordad, Effect of position-dependent effective mass on linear and nonlinear optical properties of a cubic quantum dot, Physica B, 406 (2011) 3911-3916. [CrossRef]
  14. A Salman Durmuslar, A Turkoglu, M E Mora-Ramos, F Ungan, The non-resonant intense laser field effects on the binding energies and the nonlinear optical properties of a donor impurity in Rosen–Morse quantum well, Indian Journal of Physics 96 (2022) 3485–3492. [CrossRef]
  15. F. Ungan, M.K. Bahar, The laser field controlling on the nonlinear optical specifications of the electric field-triggered Rosen-Morse quantum well, Physics Letters A 384 (2020) 126400. [CrossRef]
  16. R. Khordad and B. Mirhosseini, Linear and nonlinear optical properties in spherical quantum dots: Rosen-Morse potential, Opt. Spectrosc. 117 (2014) 434-440. [CrossRef]
  17. Guang-Dong Zhang, Jian-Yi Liu, Lie-Hui Zhang, Wen Zhou, Chun-Sheng Jia, Modified Rosen-Morse potential-energy model for diatomic molecules, Physıcal Revıew A 86 (2012) 062510. [CrossRef]
  18. N. Zeiri, N. Sfina, S. Abdi-BenNasrallah, M. Said, Linear and non-linear optical properties in symmetric and asymmetric double quantum wells, Optik 124 (2013) 7044-7048. [CrossRef]
  19. N. Dinh Hien, Comparison of the nonlinear optical properties of asymmetrical and symmetrical quantum wells, The European Physical Journal B 95, 192 (2022). [CrossRef]
  20. A. AL-Naghmaish, H. Dakhlaoui, T. Ghrib, B. M.Wong, Effects of magnetic, electric, and intense laser fields on the optical properties of AlGaAs/GaAs quantum wells for terahertz photodetectors, Physica B 635 (2022) 413838. [CrossRef]
  21. H. Dakhlaoui, M. Nefzi, Tuning the linear and nonlinear optical properties in double and triple δ doped GaAs semiconductor: Impact of electric and magnetic field, Superlattice. Microst., 136 (2019) 106292. [CrossRef]
Preprints 81107 g001
Figure 1. For k = 0 . 15 and different z 0 -values, quantum well with the improved Rosen-Morse confinement potential, and squared wave function corresponding to the ground state of the electron localized in this well.
Figure 1. For k = 0 . 15 and different z 0 -values, quantum well with the improved Rosen-Morse confinement potential, and squared wave function corresponding to the ground state of the electron localized in this well.
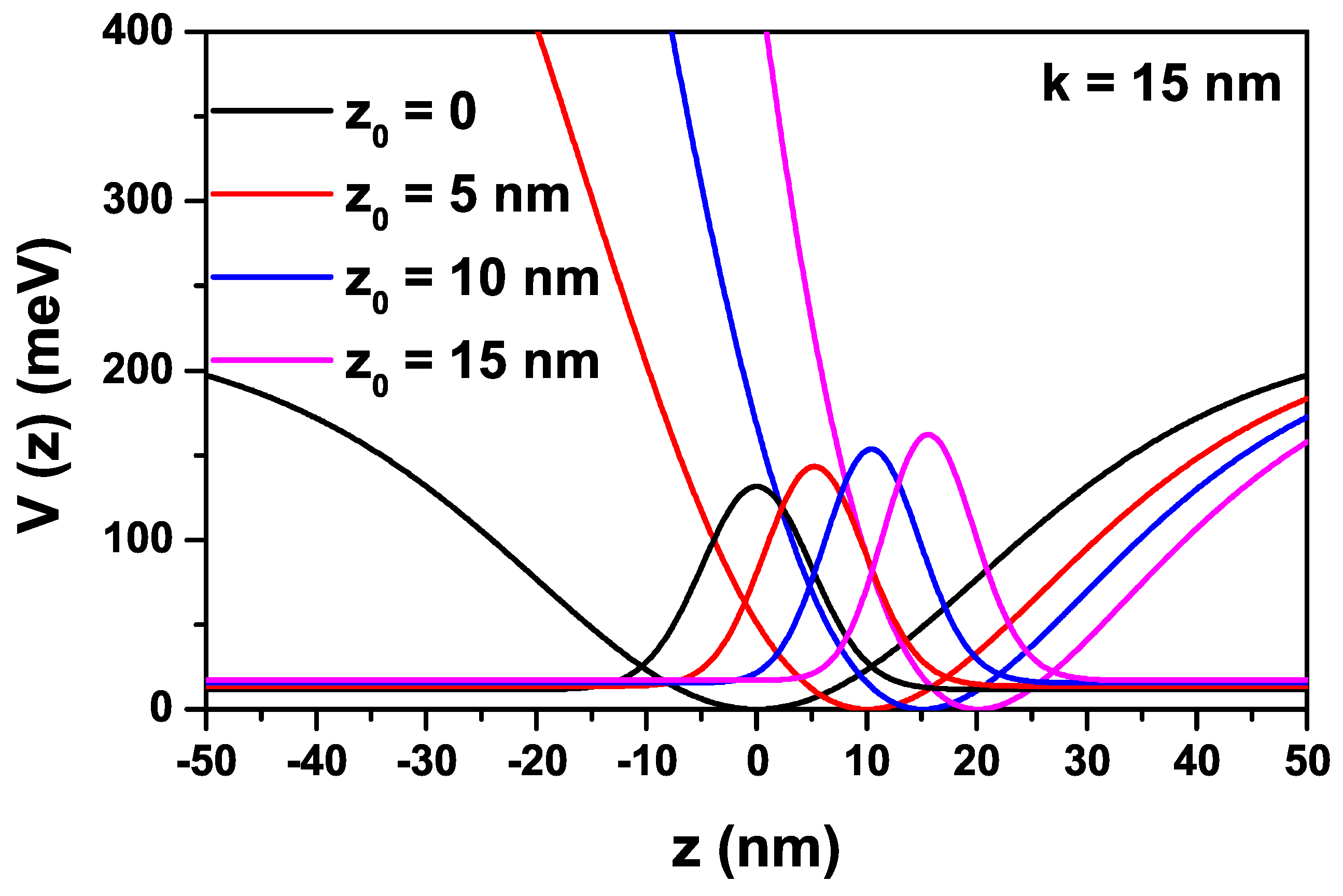
Preprints 81107 g001
Preprints 81107 g002
Figure 2. The variation of the energies corresponding to the first three energy levels of confined electron within the improved Rosen-Morse confinement potential as a function of z 0 -parameter in the absence and presence of position dependence mass: K = 15 n m (a), and K = 25 n m (b). Solid lines are for electron with constant mass (CM), dashed lines are for position dependence mass (PDM).
Figure 2. The variation of the energies corresponding to the first three energy levels of confined electron within the improved Rosen-Morse confinement potential as a function of z 0 -parameter in the absence and presence of position dependence mass: K = 15 n m (a), and K = 25 n m (b). Solid lines are for electron with constant mass (CM), dashed lines are for position dependence mass (PDM).
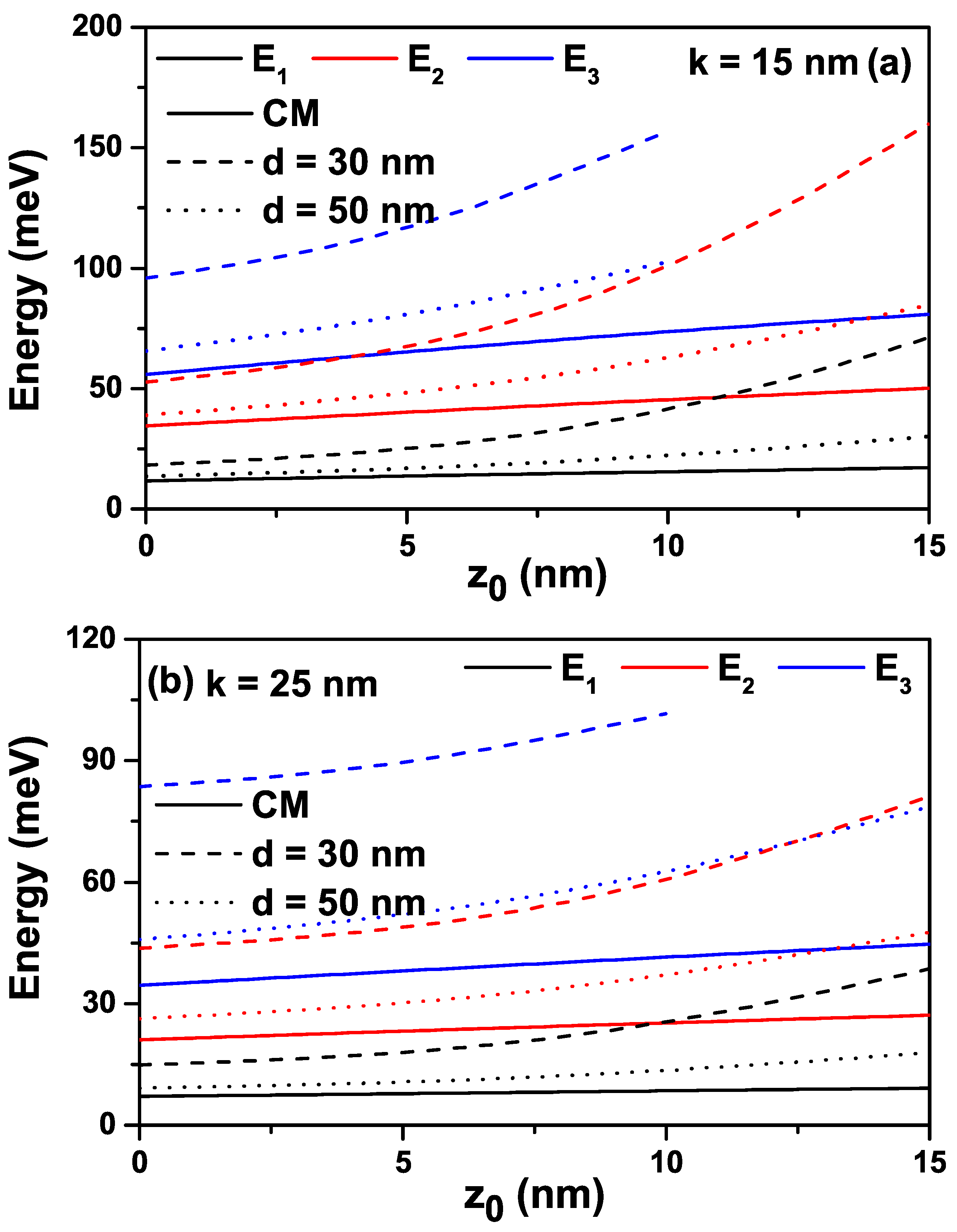
Preprints 81107 g002
Preprints 81107 g003
Figure 3. The variation of the energy differences between some energy levels of interest as a function of z 0 -parameter: K = 15 n m (a), and K = 25 n m (b).
Figure 3. The variation of the energy differences between some energy levels of interest as a function of z 0 -parameter: K = 15 n m (a), and K = 25 n m (b).
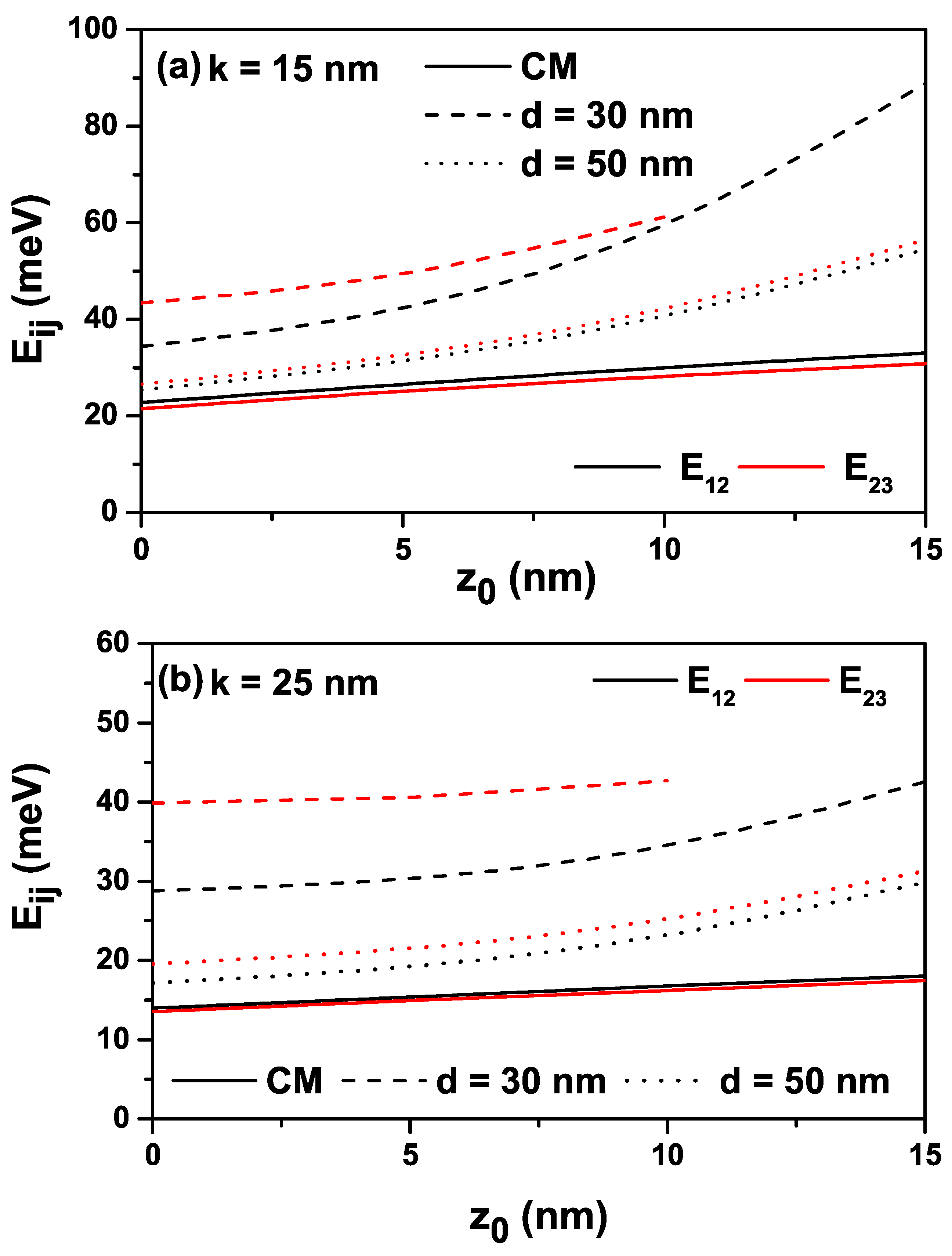
Preprints 81107 g003
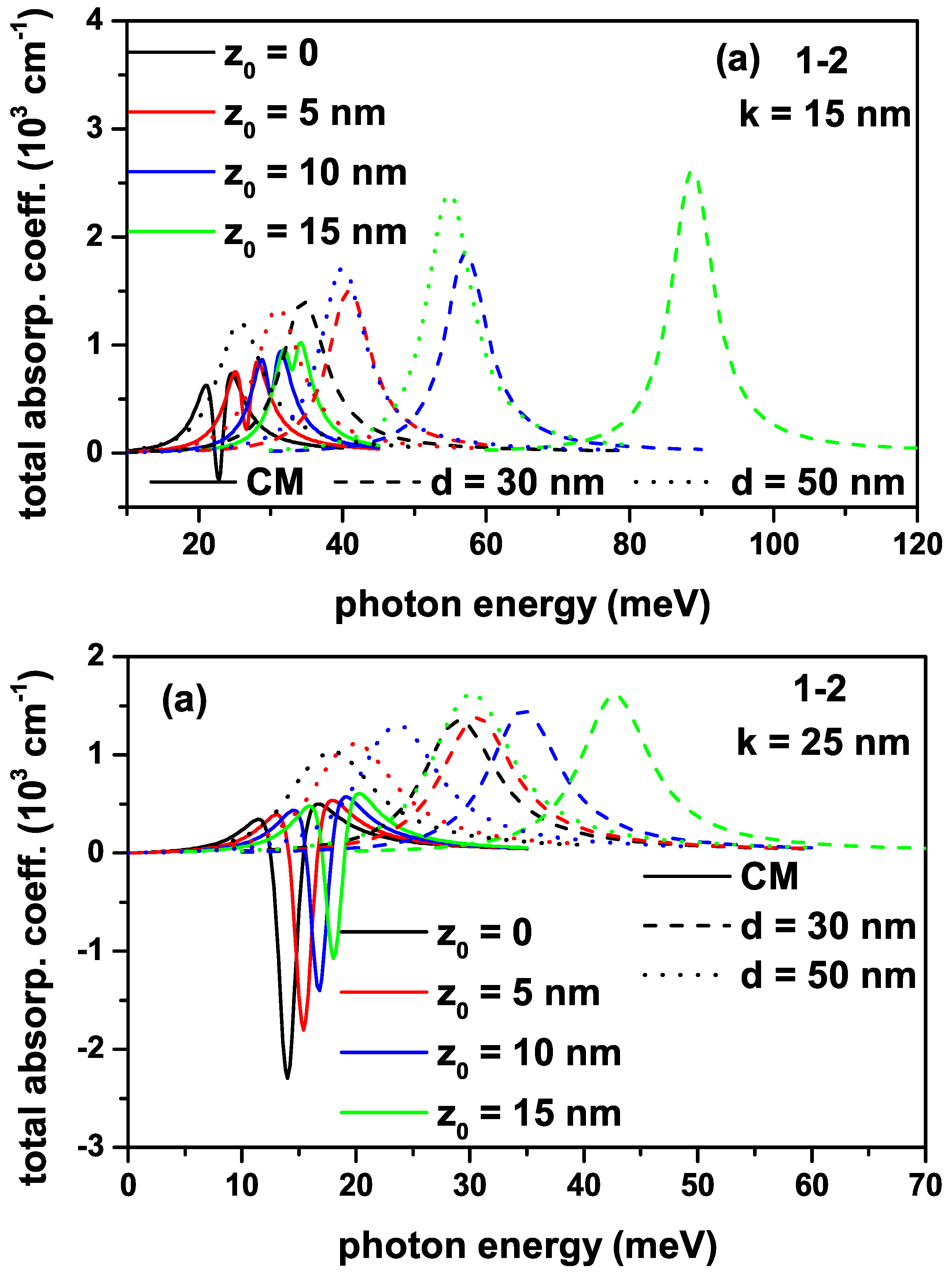
Preprints 81107 g004
Figure 4. The variation of total absorption coefficients for a transition that is called the (1-2) between the ground and first excited states of an electron confined within the quantum well with the improved Rosen-Morse confinement potential as a function of the incident photon energy with intensity I = 5 . 0 × 10 8 W / m 2 for different z 0 -values: k = 15 n m (a), and k = 25 n m (b).
Figure 4. The variation of total absorption coefficients for a transition that is called the (1-2) between the ground and first excited states of an electron confined within the quantum well with the improved Rosen-Morse confinement potential as a function of the incident photon energy with intensity I = 5 . 0 × 10 8 W / m 2 for different z 0 -values: k = 15 n m (a), and k = 25 n m (b).
Preprints 81107 g004
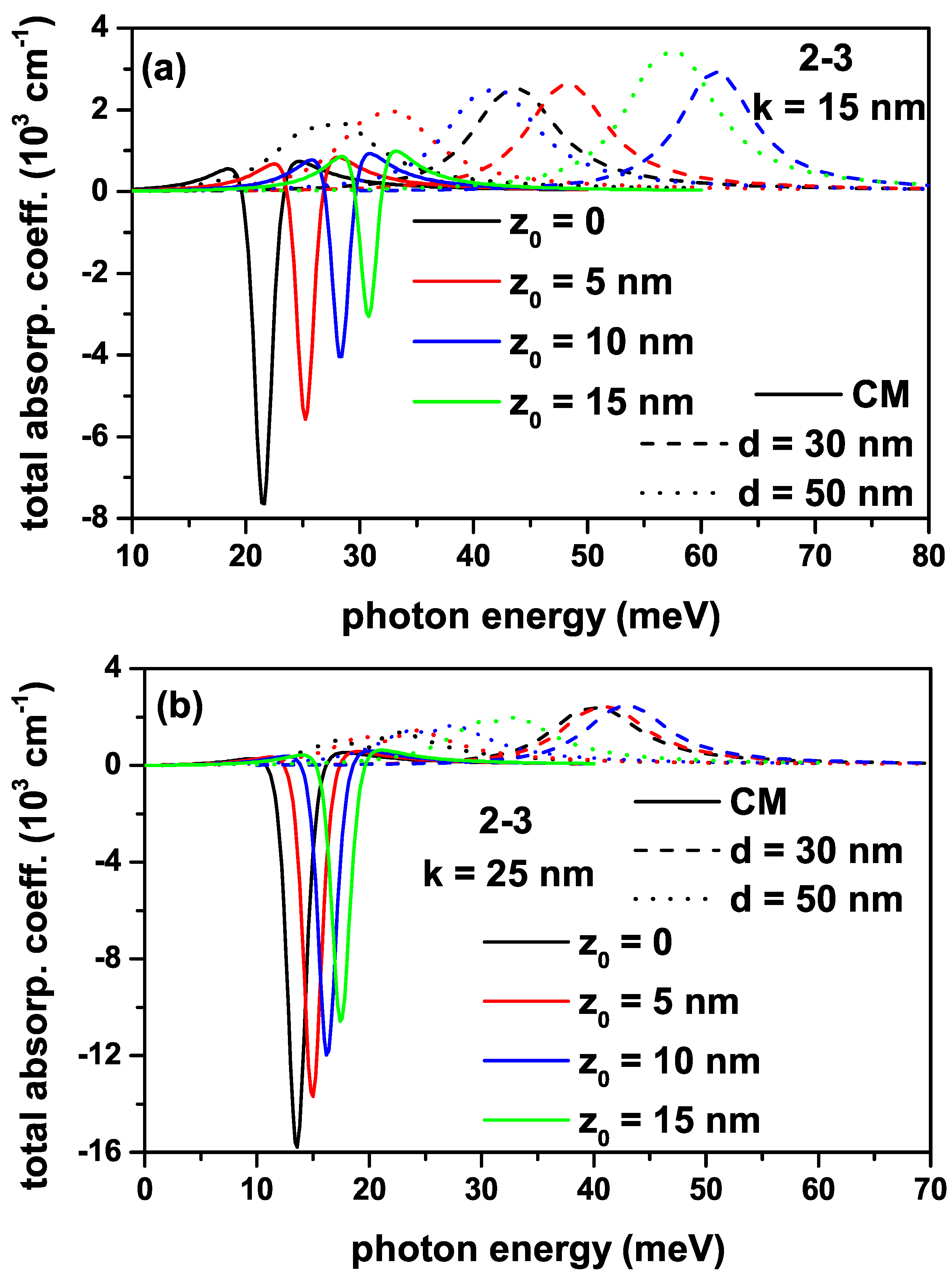
Preprints 81107 g005
Figure 5. The variation of total absorption coefficients for a transition that is called the (2-3) between the first and second excited states of an electron confined within the quantum well with the improved Rosen-Morse confinement potential as a function of the incident photon energy for different z 0 -values: k = 15 n m (a), and k = 25 n m (b).
Figure 5. The variation of total absorption coefficients for a transition that is called the (2-3) between the first and second excited states of an electron confined within the quantum well with the improved Rosen-Morse confinement potential as a function of the incident photon energy for different z 0 -values: k = 15 n m (a), and k = 25 n m (b).
Preprints 81107 g005
Preprints 81107 g006
Figure 6. The variation of total absorption coefficients for a transition that is called the (1-2) between the ground and first excited states of an electron confined within the quantum well with the improved Rosen-Morse confinement potential as a function of the incident photon energy with intensity I = 5 . 0 × 10 8 W / m 2 for different z 0 -values: k = 15 n m (a), and k = 25 n m (b).
Figure 6. The variation of total absorption coefficients for a transition that is called the (1-2) between the ground and first excited states of an electron confined within the quantum well with the improved Rosen-Morse confinement potential as a function of the incident photon energy with intensity I = 5 . 0 × 10 8 W / m 2 for different z 0 -values: k = 15 n m (a), and k = 25 n m (b).
Preprints 81107 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated