Preprint
Article
Questioning the mechanistic-universe paradigm using chaotic systems
Altmetrics
Downloads
299
Views
487
Comments
0
This version is not peer-reviewed
Submitted:
29 July 2023
Posted:
02 August 2023
Read the latest preprint version here
Alerts
Abstract
The following is undisputed:
1. The conceptual relation between QM, describing microscopic physics, and macroscopic irreversible physics, is as mysterious today as eighty years ago.
2. When propagating chaotic equations, arbitrarily small scales gradually become significant at arbitrarily large scales.
It follows that, the long-time behavior of chaotic systems is as mysterious today as eighty years ago. Previous work by the author sheds new light on the quantum-classical riddle, suggesting that quantum weirdness is a signature of a non mechanistic ontology, viz., one not describable by some generalized state-vector plus evolution rule thereof. It is argued that neither an empirical nor a theoretical case exists against such non mechanistic ontology manifesting in certain macroscopic chaotic systems. Bell's inequality violation by separated but previously coupled such systems is one example. More radically, it is hypothesized that certain systems could fuzzily `remember their future' in the sense that, a future perturbation applied to them could be inferred from their present behavior with probability>0.5. Experiments utilizing machine learning are proposed for testing such hypotheses.
Keywords:
Subject: Physical Sciences - Quantum Science and Technology
1. Introduction
Language shapes thought, and in no field is this more true than in physics. For over three centuries, the basic grammar of theoretical physics has remained that of Newton, consisting of two basic components: A ‘state vector’ representing the system at any given time, and an evolution equation for the state vector. Implicit in those two is also the way in which our actions in a ‘tabletop experiment’ are modeled: By choosing initial conditions for the state vector, and/or choosing parameters for the evolution equation, such as applying an external force or field.
Newtonian grammar1 (NG) even survived the 20th century turmoil. The quantum revolution only redefined the space of the state vector—n-dimensional configuration space ↦ infinite dimensional Hilbert space. More remarkably, even the relativistic revolution, which did away with the very notion of absolute time, did not seem to require a novel grammar.
Its robustness to paradigm shifts has erroneously promoted NG to an attribute of nature rather than that of our descriptive language, and physical models not expressible in NG are generally met with instinctive skepticism. However, the picture emerging from previous papers by the author suggests that, NG’s robustness to paradigm shifts might itself have been a product of wrongly shaped (Newtonian) thought. Maxwell-Lorentz Classical electrodynamics (CED) of point charges—an alleged success of NG—is ill-defined, and a century of attempts, expressed in NG, to cure its pathologies all failed. Currently, the only well-defined CED of interacting point-like charges (to the author’s best knowledge), dubbed ECD [1,2], is not expressible in NG. Precisely for this reason ECD can serve as a (classical) ontology underlying QM statistics without conflicting with various no-go theorems, all implicitly assuming an ontological description using NG [3]. There are also indications that advanced solutions of Maxwell’s equations, mandated by ECD, are at play not only in microscopic physics, where they create the illusion of ‘photons’ (among else) but also in astronomy’s missing mass problem [4]. And although advanced solutions per se are not in conflict with NG, their incorporation into a consitent mathematical formalism, involving both matter and radiation, certainly is—time-symmetric action-at-a-distance electrodynamics [5] being yet another, better known example.
The appearance of NG in macroscopic (classical) physics is explained by local constraints satisfied by the underlying (ECD) ontology—see, e.g., appendix D of [1] for how the Lorentz force equation is obtained as a local approximation for the center of an extended charge (The same is true for QM’s NG structure; see caption of Figure 1). The question of whether the underlying microscopic ontology is likewise described by NG, might therefore seem irrelevant to macroscopic physics. We argue to the contrary. Microscopic local constraints are just what they are: constraints; long-time integration of their manifestation in macroscopic, coarse grained quantities is not only unreliable due to the so-called butterfly effect, but moreover meaningless in a non NG universe, as is any statistics derived therefrom. This realization, in conjunction with the above indications of a non NG ontology, point to new experiments which might appear far-fetched, but only because of a NG bias. If the universe is indeed non mechanistic, the implications for physics and science in general would go far beyond quantum weirdness.
2. Non-machines and their statistics
The settings of what follows is the block-universe (BU): 4D spacetime hosting a locally conserved (symmetric) e-m tensor, constructed from the basic building blocks (fields in the case of ECD) of an ECD-like theory (Figure 1).
The BU is a highly redundant representation of a NG ontology as its content is fully encoded in any of its space-like slices. Philosophy aside, it is therefore an unnecessary complication even in relativistic theories. However, for a non-NG ontology, the BU is arguably the only faithful representation. Consider a non-machine—for lack of a better name: A system which, unlike a machine, does not admit an NG representation, viz., its contribution to the BU is not the result of propagating some initial conditions. To illustrate the basic idea while avoiding unnecessary complications specific to ECD (nor necessarily committing to ECD) consider the following (formal) toy non-machine action for
where K is any diagonal matrix of non compactly supported, once integrable symmetric functions, and denotes double differentiation. It is the non compactness of K which prevents translating the associated Euler-Lagrange equations,
into NG language2 . Nonetheless, twice integrating the first term in (2) by parts, we get the classical e.o.m.
with a residual term
vanishing in the ‘delta function limit’: , but simultaneously becoming infinitely non local. The same is true for the corresponding Noether currents which are exactly conserved even at finite hence better suited to be directly linked with observations. However, such exact local constraints don’t translate to an alternative mechanistic description of the system, which is the mistake alluded to in the introduction. For example,
appear in momentum conservation as ‘coarse grained positions’ and their ‘conjugate momenta’ resp., but only in the delta-function limit does there exists a Hamiltonian, for which .
For large enough , then, non-machines can be approximated arbitrarily well by machines. Without such quasi locality, the results of many experiments would not be reproducible, notwithstanding (spacetime-) translation covariance. However, in the case of chaotic potentials (more generally: chaotic systems) the time-scale, , over which a non-machine’s solution and that of its machine approximation remain close (t-wise less than some small constant) could grow very slowly with increasing especially if K has a long, i.e., algebraic tail (as is the case in ECD). The residue, R, plays the role of an external force in (3) which, when acting on q in unstable directions, leads to its subsequent exponential separation from the unperturbed path. The dimensionality, n, of the system plays a crucial role in tempering the growth of with increasing , as larger n implies (statistically) higher maximal Lyapunov exponent—and it only takes one such ultra unstable direction for even a meager R to rapidly drive an entire chaotic system ‘off course’. Now, practically speaking, there is no “unperturbed path”. And indeed, for sufficiently large most ‘coarse grained’ statistics associated with (2), e.g. attractor manifold and power spectrum, would most likely be experimentally indistinguishable from those of a noisy machine, viz. (3) with R a random noise. However, as R is far from being random, such noisy machine approximation becomes moot with regard to the global spacetime structure of (at least some) trajectories. In other words, a noise history reproducing a global path of (2) would need to be too ‘structured’, or non random, for any reasonable noise source (e.g. Gaussian White). Moreover, the solution set of a machine, such as (3) with , can be 1-to-1 mapped to a subset of , where the Liouville measure is a natural starting point for analyzing statistical aspects of ensembles, whereas that of (2) is some infinite dimensional function space having no obvious counterpart. The significance of this last point is illustrated clearly in a scattering experiment () of monoenergetic particles off a chaotic potential, e.g. a crystal lattice. In the non-machine case, uniformity over the impact parameter does not define an ensemble since two incoming particles can have identical (freely moving, asymptotic-) solutions yet different outgoing ones; As the two particles approach the target, their distinct future paths, gradually render their R’s non negligible and distinct. Such initial stage experimental ensembles, which are consistent with a local machine approximation yet not fully defined without global knowledge of V, including its value in the future relative to initiation, generalize to arbitrary n, motivating among else Bell’s inequality tests for previously interacting non-machines.
Single-system equations, such as (2), therefore cannot be a complete description of the experiment, necessitating a compatible statistical description of ensembles of solutions, not deriviable from the single-system theory alone, hence being equally fundamental. In [3] it is argued that QM is such a complementary theory.
Zooming out now from our toy model, insofar as a physicist obeys the physics of the systems he is studying—and there is no evidence to the contrary—he is represented by some (extended) world-line in the BU, and his free will is technically an illusion. This tension with one’s subjective feeling is present also in Newtonian-grammar physics, and this never disocuraged physicists from doing physics. But unlike its Newtonian counterpart, our physicist cannot meaningfully model this illusary free will by chosing the initial conditions of a system (or distribution thereof) from which the system (ensemble thereof resp.) then evolves. Instead, his ‘freely chosen’ actions constrain the global, spacetime structure of systems he is studying (in a way which depends on both the system and the actions) and in general, infinitely many such systems are compatible with a given constraint. His actions therefore only define an ensemble, with the relative frequency of each ensemble-member being a statistical property of the BU (revealed in a single lab only as a means of saving the hassle of sampling the whole BU for similarly constrained, spontaneously occurring systems [3]). Note that the Newtonian resolution can be viewed as a private case of ours.
In the case of closed systems, according to [3], QM provides a rich statistical description of the ensemble, encoded in the wave-function, which is therefore an attribute of the ensemble rather than of any single system (see caption of Figure 1). By “closed” it is meant that the system’s full energy-momentum balance is known and exactly incorporated into its Hamiltonian. In contrast, the statistical description of open systems [12] is currently not nearly as detailed and conceptually problematic. In one approach the openness of the system is modeled by treating it as a small subsystem of a large closed system, tracing out the extra degrees of freedom, not before making simplifying assumptions about their interaction with the subsystem and with one another. However, this attempt is no more reliable than similar attempts to model classical dissipation within the framework of Hamiltonian dynamics, if only because it ignores an essential source of dissipation and thermodynamic irreversibly: the radiation arrow-of-time (reflecting the system being out of equilibrium with the ECD zero-point-field [4]). Moreover, in the context of chaotic systems this approach (at best) leads back to the classical description [9] which, in turn, adds another layer of conceptual difficulties. Ergodic theory [11], for example, seeks a flow-invariant measure on phase/configuration space, and is indeed a valid starting point for predicting the steady-state distribution of certain chaotic systems. However, as it typically yields a fractal set which includes infinitely many (unstable) periodic orbits, neither ergodic theory nor its noisy versions, e.g. the associated Fokker-Planck equation, are sufficient for that. More relevant to out point, though (and as already pointed out) if this flow only locally approximates the 4D structure of chaotic systems, then ergodic theory is moot with regard to more complex statistics, e.g. the joint probability (density) of finding the system in state , and in state a fixed latter. A similar objection applies to ensemble propagation when used to predict the long-time behavior of chaotic systems, or to inter-system correlators of previously coupled chaotic systems (see Section 3.3).
Summarizing, when leaving the domain of closed quantum systems, QM becomes an unreliable tool. When then stepping into the realm of chaotic irreversible systems, one is already in largely uncharted territory. There, presumably, lies new physics.
3. Are there macroscopic non-machines?
To distinguish machines from non-machines, we first propose testing whether a system can ‘remember its future’. Machines can obviously remember their past, meaning that a perturbation, p, to a machine in its past can be inferred from its present state m (‘memory’). For simplicity, a binary type perturbations shall be used, labeled ‘L’(eft) and ‘R’(ight), and memory is exhibited by a machine if the m’s corresponding to the set are distinguishable from those of .
In contrast, machines cannot ‘remember’ their future. Inferring a future perturbation from a machine’s present state entails, among else, the following: The state, m, of a machine is measured, viz., projected onto the set at some initial time. The machine then propagates to a later time when its world-line intersects that of a random bit generator (RBG) applying a random to the machine, and miraculously . This must happen everywhere throughout the BU, to all copies of the machine, which is clearly not our BU.
This evident truth can be extended to non-deterministic machines in which the rest of the universe is (realistically) treated as the source of randomness and possibly dissipation. In this case, the machine’s stochastic evolution leads to a certain probability distribution over its future states, parametrically depending on the nature of the initial perturbation (L or R in our case, marginalized over possible additional ‘hidden variables’). If the two distributions are distinguishable, i.e., if a random perturbation, p, can be deduced from m with probability , then the machine is said to fuzzily remember a bit. As in the deterministic case, machines can fuzzily remember a past bit but not a future one.
Like machines, non-machines can remember their past. A sufficiently strong perturbation to a fully developed turbulence, for example, leaves an obvious signature on the streamlines for a short time thereafter. It is even conceivable that this ‘short term memory’ would extend much further into the past had only a different, more suitable signature been used—as in the case of seasonal weather forecasts which are based on large statistical tables rather than propagation of differential equations. But why should non-machines not remember their future, at least fuzzily?
3.1. Statistics in the BU
Our definition of fuzzy memory involves the repetition of an experiment. In the context of the BU this amounts to taking an ensemble of 4D structures, each corresponding to an instance of an experiment, and computing statistics thereof. A typical ensemble could consist of multiple ‘time slices’ from the (extended) world-line of a single non-machine, or single slices from multiple copies of a single type of non-machines (see Figure 1).
In the case of a binary type perturbation, there are four relevant sub ensembles of the full experiment ensemble, indexed by a pair with . The p(erturbation) index indicates which perturbation is finally applied to the non-machine, and the m(emory) is the result of some binary projection of an initial measurement, aimed at revealing the type of future perturbation. A fuzzy memory of a future random binary perturbation is demonstrated by a non-machine if
with being just the number of elements in the relevant sub-ensemble. Of course, the ensemble size should be large enough to exclude pure chance. Note that we now treat the perturbation as an attribute of the non-machine rather than the RBG, as in the machine case, for it constrains the global 4D structure of a non-machine. In contrast, a perturbation to a machine only constrains that irrelevant part of its world-line succeeding the perturbation. It follows that future memory of a non-machine, unlike that of a machine, does not involve its ‘conspiracy’ with RBG’s; It is just a statistical affinity, (4), between two segments of its (extended) world-line or, more accurately: A statistical property of spacetime structures, discriminating between the R and L ensembles of RBG’s in interaction with non-machines; Figure 2.
One instinctive (NG biased) push-back could be: Since the measurement, m, precedes the perturbation, p, the latter can be chosen non randomly so that . While this might be interpreted as an instance of ‘false memory’, it is not an argument against (fuzzy) future memory according to our definition (which machines are incapable of). So conditioning p on m corresponds to selectively choosing only the two sub-ensembles on the r.h.s. of (4) rather than all four. It might even render moot the original ensemble, consisting of spacetime structures of the type shown in Figure 2, as in this modified protocol a second e-m ‘bridge’ necessarily exists between non-machines and perturbers through which the latter is informed of m.
A different way of formulating the above objection involves so-called backwards-in-time signaling (BITS) [10], prima facie implied by future memory—p being the signal sent to the past, and m its (distorted) reception. BITS exclusion is normally taken as one of the tenets of any physical theory to exclude causal paradoxes, of the sort created by choosing when perfect future memory is possible. This reason clearly doesn’t apply to ‘fuzzy BIST’, facilitated by fuzzy future memory, but a weaker case can still be made against fuzzy BIST, on the premise that, whatever action m triggers, it must not affect the ‘fidelity of the communication channel’ (i.e. could completely ruin a near perfect channel). However, such action-independent channel fidelity proviso, borrowed from mundane communication, is inconsistent with the role of agency in a BU supporting non-machines (Section 2) hence BIST exclusion, as a tenet, is unjustified. In principle, then, future memory indeed facilitates BIST, provided the receiving side does not act to ruin the channel.
Yet another implausibility argument, involves the inevitable noise coming from the rest of the universe, and the variability in the act of measuring m. The long-time evolution of non-machines—a category allegedly including classically chaotic systems—are highly sensitive to both. As each member of an ensemble is affected by a distinct noise history and a member-specific measurement process, one may object to the very existence of a well-defined ensemble, comprising non-machines of a common type. However, the very formulation of this objection uses Newtonian grammar, which we have set out to refute. That each ensemble member corresponds to a distinct time-slice of the BU means that, should statistical regularities arise in the ensemble, environmental coupling would be incorporated into them (Kolmogorov scaling law and chaos universality are two such examples). This is precisely what allegedly happens in the case of systems faithfully described by QM according to [3].
One might also muster QM against future memory. By the standard collapse picture, the act of measuring m just updates the original wave-function in a way which is independent of any future interaction with the system. However, this argument (ideally) applies only to closed systems, (see caption of Figure 1). Moreover, the collapse picture is clearly a caricature of a much more complex, system dependent process, and it is conceivable, e.g., that a sufficiently massive, closed macroscopic chaotic system could be ‘looked at’ to obtain m—say, continuously and weakly coupled to some ‘recorder’ for a macroscopic time—in ways not captured by that simplified caricature.
With the above objections removed, the author can think of no reason why inequality (4) must not be satisfied by non-machines.
3.2. Schematic experiment for testing future memory
For the sake of concreteness, two types of analog, chaotic electric circuits shall serve as alleged non-machines (Figure 3) consisting of feedback topology and at least one nonlinear element which couples different scales—hence generically all scales (“scale" roughly refers to frequency components in the circuit’s currents/voltages). Such circuits should not be viewed as low-dimensional non-machines—small n in the language of Section 2—but rather as providing, though their voltages, a low dimensional projection of an effectively , dissipative non-machine; the dissipative counterpart of, say, the center-of-mass motion of a bound n-body system in an external chaotic potential.
The characteristics of the components together with Kirchhoff’s laws, jointly constrain the voltages, which can be seen as a point in configuration space, and in type-1 circuits these constraints locally (in time) translate to a chaotic flow on configuration space, i.e. take the form of coupled differential equations with a positive Lyapunov exponent (Note how the roles of system and its model are swapped when using analog computers to solve differential equation; analog circuits solving Hamilton’s equations should not be mistaken for closed systems). In type-2 circuits—so-called ‘noise sources’—no flow exists as components characteristics are too coarse of an abstraction, e.g., that of a Zener diode in reverse bias, just around its breakdown voltage (Nevertheless, the voltage of a type-2 circuit is also piece-wise mechanistic).
For lack of a better analytic option, we shall resort to machine learning (ML) in an attempt to prove future memory. The experiment consists of three stages: Data acquisition, followed by a training session (of, say, a deep neural network) on half of the data points and, finally, testing the trained ML against the remaining half of data points for future memory. The data acquisition stage begins with an initiation session, during which the circuit is brought to steady state. At the end of this prolonged stage (relative to all other time scales involved) a short voltages ‘clip’ of duration is recorded. It is important that the circuit be coupled to the ‘recorder’ (e.g. oscilloscope) throughout the entire experiment, so as to make it an integral part of the non-machine. The raw product of this stage is n measurements, which are predetermined projections of a clip. At a fixed later time, T, a perturbation is applied to the circuit in the form of some strong coupling to yet another (type L/R) circuit, manifestly affecting the circuit’s behavior. The perturbation type should be either randomly chosen or alternating , thereby reducing the effect of any systematic drift in experimental conditions. This cycle is repeated N times. Initiation and perturbation stages, jointly define our experiment ensemble.
Next, data points (cycles) are randomly chosen for the training session which seeks a function maximizing inequality (4). This optimal m is then tested for (4) violation on the remaining data points, and future memory is demonstrated if m passes the test with statistical significance.
For a sufficiently long initiation session the ‘local state’ of a circuit is assumed to converge to a fixed distribution irrespective of p. Defining as the time-scale over which the non-machine admits a reliable mechanistic approximation—in type-1 circuits the inverse Lyapunov exponent of the flow being a first guess—future memory detection therefore mandates or else the local state would uniquely determine the entire clip. Alternatively, and not mutually exclusive, a sufficiently large configuration space, guaranteeing an effectively infinite ‘ergodicity time’, might circumvent the condition.
Our assuption that the and subensebles of non-machine solutions are (statistically) distinuishable despite having identical configuarion-space distributions post initiation, parallels the QM case described in [3] section 4.2.2 (mind the arXiv erratum): Wave-function initiation leads to a charge/momentum steady-state distribution which is independent of any future interaction of the charge(s). However, for this assumption to be realistic, the measurement-to-perturbation time, T, must be much shorter than the duration of the initiation session (which must obviously be ) and as short as possible.
There are, of course, many possible variations on this protocol. For example. One can train an instead, where U stands for "Uncertain", in which case the data point is ignored in calculating the future memory ‘grade’ of m in both training and test sessions. More generally, a certainty mark which is valued in some continuous set can replace the discrete . Also worth noting is the possibility of testing past memory beyond the trivial ‘short-term’ mechanistic memory, using the proposed approach with p and m temporally interchanged.
3.3. Bell’s inequality test for entangled non-machines
The previous experimental approach can be used to test whether two such circuits, A and B, which are initially coupled, exhibit ‘spooky’ correlations after being decoupled. Decoupled machines would just propagate their states at decoupling, hence correlations post decoupling are bounded by those already existing in the joint distribution of these initial states, playing the role of the ‘hidden variable’ in Bell’s theorem. Bell quantified this mechanistic bound for a special case of post decoupling joint measurements, which aught to be respected by machines (“little robots" in his words3).
In contrast, the decoupling of non-machines is best understood as the branching of their joint, spacetime ‘tree’, and post decoupling correlations are just a statistical attribute of a ‘forest’ of such trees (Figure 4). More precisely: Four such forests are involved, corresponding to the four combinations of perturbations applied to a tree’s two ‘branches’, and , which in Bell’s case are the two possible polarizer’s orientations interacting with each particle. As each forest comes with its own set of trees, Bell’s theorem can’t be applied to the union of all four forests, treating a tree as a hidden variable to be sampled from a single distribution.
In the proposed counterpart to Bell’s test, the perturbation’s role is played by, say, coupling of circuit A to either circuit a or , and similarly for B. Howeever, unlike in the standard test (cf. [3] section 4.2.2) the ‘polarization measurements’ are virtual, as opposed to physical—a limitation of quantum systems only. Consequently, the data acquisition stage for each of the four forests— consisting of a long initiation session pre decoupling, followed by a shorter, though , post decoupling period and ending with two perturbations—does not yet involve polarization measurements. Only at the next stage, half the runs of each forest are randomly assigned for the training session where a virtual ‘polarization measurement’ of each circuit, in each run, is taken post decoupling, but either pre or post perturbation. To find the ‘best’ such choice of measurement, four neural networks,
are trained to maximize the l.h.s. of Bell-CHSH inequality
where the C’s are the relevant correlators, e.g.
with the sum running over all training trees in forest , and are the corresponding clip projections of post decoupling measurements. Then, violation of (6) is tested on the remaining half. Violation of the Tsirelson’s bound, i.e., (6) with a r.h.s. equal to , would prove—as with future memory—that macroscopic physics is even more non-local than permitted by QM.
Bell’s inequlity violation does not necessarily imply signaling across space-like separations which, at any any rate would not lead to causal paradoxes for exactly the same reason BIST doesn’t.4 Nor does non-violation imply no such signaling. Settling for the conditional probabilities needed to exclude/affirm such possibility, calculated from Bell’s test optimal m’s (5), is a mistake. One should instead optimize a single neural network to discriminate between and based on A’s data taken outside the future light-cone of the corresponding p.
Finally, it is possible to combine a Bell test with a future memory test, by training the neural network to predict whether two non-machines which are initially separated, are later brought into interaction. Note that future memory is, in fact, a private case of this last experiment; As (true) RNG’s are themselves (alleged) non-machines, the roles of perturbing and perturbed systems can be swapped in a future memory experiment.
3.4. Quantum computing
We conclude this section with insight into quantum computers (QC) which are, within the general framework of this paper, quintessentially non-machines, hence their superiority over digital classical computers (DCC) which are machines by design. Concretely, unlike a DCC, a QC doesn’t need to propagate the Schrödinger equation in order to compute at a final time from at some initial time—a task requiring computational resources, which increase exponentially with the ‘size’ of the system (e.g. number of qbits)5. Instead, QCs ‘sample’ ensembles of 4D structures, which indirectly leads to a sampling of at the final time.
Cleverly specified ensembles, defined by their initial wave-function and ‘Hamiltonian’, have been shown to result in great improvement over DCC algorithms in solving certain practical problems. In theory. In practice, decoherence (coupling to external, closed systems) and dissipation pose a formidable challenge to any substantial progress. Currently, to counter decoherence the plan is to use quantum error correcting codes (QECC) which, by definition, involve (multiple) measurements at intermediate times between the initial ‘wave function preparation’ and the final measurement. By our previous remarks, measuring a quantum system implies coupling a closed system to an open (macroscopic) one, i.e., leaving the arena of ensembles where QM (unitary) evolution alone determines . The extra component added to the description of involves the so-called collapse postulate of QM which, unlike the evolution operator, is only a caricature of an actual measurement (just recall how a Stern-Gerlach experiment ‘measures’ the spin of a particle to be ‘up’ or ‘down’).
Perhaps such machine-non-machine hybrid systems would eventually lead to practical quantum superiority. However, this is far from being experimentally settled, and ECD’s take on it isn’t optimistic: insofar as a qbit realization is well approximated by a closed system (hence its Hamiltonian), it is constantly radiating, with advanced and retarded radiation (statistically) canceling each other. A perfect qbit is therefore unavoidably coupled to its surroundings and, as a simple consequence of Maxwell’s equations, more so the nearer. Such essential ‘cross talking’, which is manifested in the (ECD) zero-point-field, can be prevented neither by a better qbit nor a shield thereof (whose constituent atoms likewise radiate). This renders unrealistic all QECC algorithms, which assume qbit wise noise-independence, in addition to the detrimental effect of uncontrolled qbits coupling.
Alternatively, if the previous experiments verify the existence of dissipative non-machines, a direct way of coping with environmental coupling in QC would be to search directly (theoretically and experimentally) for ‘XM’—that statistical description of irreversible systems—for various programmable (micro/meso-scopic) non-machines. Such XM’s already incorporate effects of decoherence and dissipation into their statistical description, doing so without sacrificing the one feature of QC responsible for its superiority over a DCC, viz., its ability to sample an ensemble of non-machines (And as with future memory, XM might even be more permissive than QM). Note that for an XM-based computer to be superior to any DCC, XM taking an analytic form must share QM’s exponential complexity growth with size (which is quite plausible). On the other hand, suppose the steady-state distribution of a simple chaotic system is known (e.g. via ergodic theory). Temporarily coupling n such systems, exponentially increases the ‘transient time’, T, before the combined system reaches steady-state and inter-system correlators become T-independent. This could pose a scalability barrier for XM computers and, according to our interpretation, should hold true also for reversible coupled systems, i.e., for (conventional) QCs.
Finally, should macroscopic non-machines prove to exist, the most profound implications would be for biology, viz., modeling of biological systems. To be sure, biological systems do have mechanistic components (or at the very least, components whose modeling by a machine is practically fruitful). However, biological systems are by far nature’s most complicated physical systems. The assumption that their current mind-boggling complexity has (mechanistically) evolved from some simple initial conditions in the early universe is quintessentially NG biased and highly speculative. Affirmation of non-machines’ existence might be a good opportunity to reconsider this mechanistic dogma. In particular, decades of research in brain science, done on the premise that brains are machines, have got us no closer to the answer for even the most basic questions. We still have no idea, e.g., how this alleged machine remembers, let alone creates original ideas.
4. Conclusion
In previous work by the author a detailed proposal was laid out for a classical ontology (ECD), of which QM is a very partial statistical description, applicable to ensembles of closed systems where the effects of the radiation arrow-of-time—an inescapable attribute of an ECD universe—are negligible. This view implies that current use of QM is grossly overreaching (and accordingly, with minimal empirical success to back it up). However, quantum weirdness allegedly lies in individual members of an ensemble, which are spacetime ‘structures’ associated with non-machines, whether closed or open. It is only QM’s statistics of ensembles of such structures which is applicable exclusively to simple closed systems. Quantum weirdness is therefore not expected to disappear altogether from macroscopic irreversible physics but, instead, take a new statistcal form, perhaps even weirder. The illusion of ‘dark matter’ is one example [4] with immediate, testable predictions. Non mechanistic correlations, proposed in the current paper, is another. The use of machine learning to this end is by no means essential, reflecting the author’s failure to hitherto come up with XM—that rich statistical description of irreversible systems. Nonetheless, it is certainly conceivable that none will be found and that, more generally, the days of new analytic laws of physics are numbered.
Data Availability Statement
No data to share.
Conflicts of Interest
YK declares no conflicts of interests.
References
- Knoll, Y. Quantum mechanics as a solution to the classical self-force problem. arXiv 2018, arXiv:0902.4606. [Google Scholar]
- Knoll, Y.; Yavneh, I. Scale covariant physics: a ‘quantum deformation’ of classical electrodynamics. J. Phys. A 2010, 43, 055401. [Google Scholar] [CrossRef]
- Knoll, Y. Quantum mechanics as a statistical description of classical electrodynamics. Found Phys 2017, arXiv:1804.0050947, 959. [Google Scholar] [CrossRef]
- Knoll, Y. Dark Matter as Variations in the Electromagnetic Zero-Point Field Induced by Baryonic Matter. Symmetry 2020, 12, 1534. [Google Scholar] [CrossRef]
- Wheeler, J.A.; Feynman, R.P. Classical Electrodynamics in Terms of Direct Interparticle Action.
- Price, H.; Wharton, K. A Live Alternative to Quantum Spooks. arXiv 2015, arXiv:1510.06712. [Google Scholar]
- Wharton, K.B.; Argaman, N. Colloquium: Bell’s theorem and locally mediated reformulations of quantum mechanics. Rev. Mod. Phys. 2020, 92. [Google Scholar] [CrossRef]
- Smolin, L. Physics World, June 2009; 21.
- Zurek, W.B. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 2003, 75, 715–775. [Google Scholar] [CrossRef]
- Guryanova, Y.; Silva, R.; Short, A.J.; Skrzypczyk, P.; Brunner, N.; Popescu, S. Exploring the limits of no backwards in time signalling. Quantum, 2019; 3, 211. [Google Scholar]
- Eckmann, J.-P.; Ruelle, D. Ergodic theory of chaos and strange attractors. Rev. Mod. Phys. 1985; 57, 617. [Google Scholar]
- Angel Rivas, Susana F. Huelga. Open Quantum Systems, 2011.
| 1 | "Newtonian Schema" is the term given to this structure of a physical theory by Lee Smolin [8]. We prefer "Grammar" as it highlights the thought shaping role of language. |
| 2 |
For a general system not derivable from a Lagrangian, (2) would be replaced by
for some vector F.
|
| 3 | Bell further assumes that the joint distribution of initial states of the ensemble of robot-couples, right after their decoupling, is independent of the orientation of the beam-splitters they later encounter. By relaxing this so-called independence/‘free will’ postulate, as certain ‘retro-causal’ models [6,7] do, any correlations can obviously be achieved by machines. In this case, however, initiation stage, too, must result in a joint distribution of states which depends on subsequent machines’ interaction (e.g. with beam-splitters) which most likely contradicts experiment. |
| 4 | Although not discussed in [3], the block-universal origin of QM (algebraic) no-signaling theorem implicitly appears in its section 4.2 . The c.o.m. associated with the marginal densities of any (spinning) particle, a, traces classical trajectories in a potential consisting of two parts: External, and some mean-field, inter-particle ensemble average, non vanishing inside the trap. Its motion can be first analyzed in region 1 of Figure 4 and then separately in regions , where the region-specific c.o.m encodes marginal ‘spin measurements’ in each arm of the experiment. No-signaling then follows under natural, i.e., non fine-tuned assumptions. This however has no bearing on signaling in our case, where measurements correspond to ‘clips’, and marginals of measurements are not encoded in the c.o.m. of fictitious particles. |
| 5 | Any analogue classical computer (ACC) which is patently a machine, by definition can be emulated by a DCC with resources that grow sub-exponentially with its size, hence is also inferior to QC. |
Figure 1.
BU time slices (left) allegedly involved in a single-particle—for simplisity—QM experiemnt. Thick vertical lines represent a crystal latice. Thin grey lines are initially left-to-right moving particles, some transmiting, others reflecting. By ‘superimposing’ all members of the ensemble (right), one gets various ensemble densities, e.g. charge density , from which the (statistical) results of any QM experiment can be deduced. From the constraints satisfied by individual members in the ensemble, equations for the ensemble densities can be derived [3], and, upon writing , QM wave equations for follow. Different ’s then describe different ensembles rather than any single system (hence Ehrenfest’s theorem, ‘scars’ and general amplitude amplification of wave-functions near classical periodic orbits, and the inevitale rapid wave-function delocalization of manifestly macroscopic but chaotic systems[9]). The NG nature of the Schrödinger evolution is a consequence of local e-m conservation, rather than being a property of individual systems. Note that different members are brought to a common time support so the Schrödinger evolution is fictitious—a mathematical tool for constructing ensemble densities; ensembles representing steady-state systems even correspond to multiple time slices of a single system. The construction in [3] only works for closed systems, hence the Hamiltonian. And indeed, when a closed system becomes coupled to the environment, as must be the case during its ‘measurement’, the initial wave-function and its evolution become nonsensical. Distinct ensembles, represented by distinct wave-functions, (left vs. right moving particles) must then be defined post measurement (insofar as QM is to be subsequently applied) and the collapse postulate is just that complementary statistical ingredient, bridging the pre-post measurement gap, giving weights to different ’s based on their corresponding macroscopic ‘pointer configuration’. Heisenberg’s uncertainty relations, reflecting certain properties of ensembles, are in line with the role of an agent in the BU, i.e., that its action—measurement in this case—defines an ensemble.
Figure 1.
BU time slices (left) allegedly involved in a single-particle—for simplisity—QM experiemnt. Thick vertical lines represent a crystal latice. Thin grey lines are initially left-to-right moving particles, some transmiting, others reflecting. By ‘superimposing’ all members of the ensemble (right), one gets various ensemble densities, e.g. charge density , from which the (statistical) results of any QM experiment can be deduced. From the constraints satisfied by individual members in the ensemble, equations for the ensemble densities can be derived [3], and, upon writing , QM wave equations for follow. Different ’s then describe different ensembles rather than any single system (hence Ehrenfest’s theorem, ‘scars’ and general amplitude amplification of wave-functions near classical periodic orbits, and the inevitale rapid wave-function delocalization of manifestly macroscopic but chaotic systems[9]). The NG nature of the Schrödinger evolution is a consequence of local e-m conservation, rather than being a property of individual systems. Note that different members are brought to a common time support so the Schrödinger evolution is fictitious—a mathematical tool for constructing ensemble densities; ensembles representing steady-state systems even correspond to multiple time slices of a single system. The construction in [3] only works for closed systems, hence the Hamiltonian. And indeed, when a closed system becomes coupled to the environment, as must be the case during its ‘measurement’, the initial wave-function and its evolution become nonsensical. Distinct ensembles, represented by distinct wave-functions, (left vs. right moving particles) must then be defined post measurement (insofar as QM is to be subsequently applied) and the collapse postulate is just that complementary statistical ingredient, bridging the pre-post measurement gap, giving weights to different ’s based on their corresponding macroscopic ‘pointer configuration’. Heisenberg’s uncertainty relations, reflecting certain properties of ensembles, are in line with the role of an agent in the BU, i.e., that its action—measurement in this case—defines an ensemble.

Figure 2.
Spacetime structures involving alleged non-machines (thin lines) interacting with a ‘perturber’ (thick lines), such as an RBG, in one of its two modes (R and L). Note the e-m bridge necessarily connecting the two. Seen form this perspective, future memory should not be attributed to any single non-machine type independently of an experimental context.
Figure 2.
Spacetime structures involving alleged non-machines (thin lines) interacting with a ‘perturber’ (thick lines), such as an RBG, in one of its two modes (R and L). Note the e-m bridge necessarily connecting the two. Seen form this perspective, future memory should not be attributed to any single non-machine type independently of an experimental context.
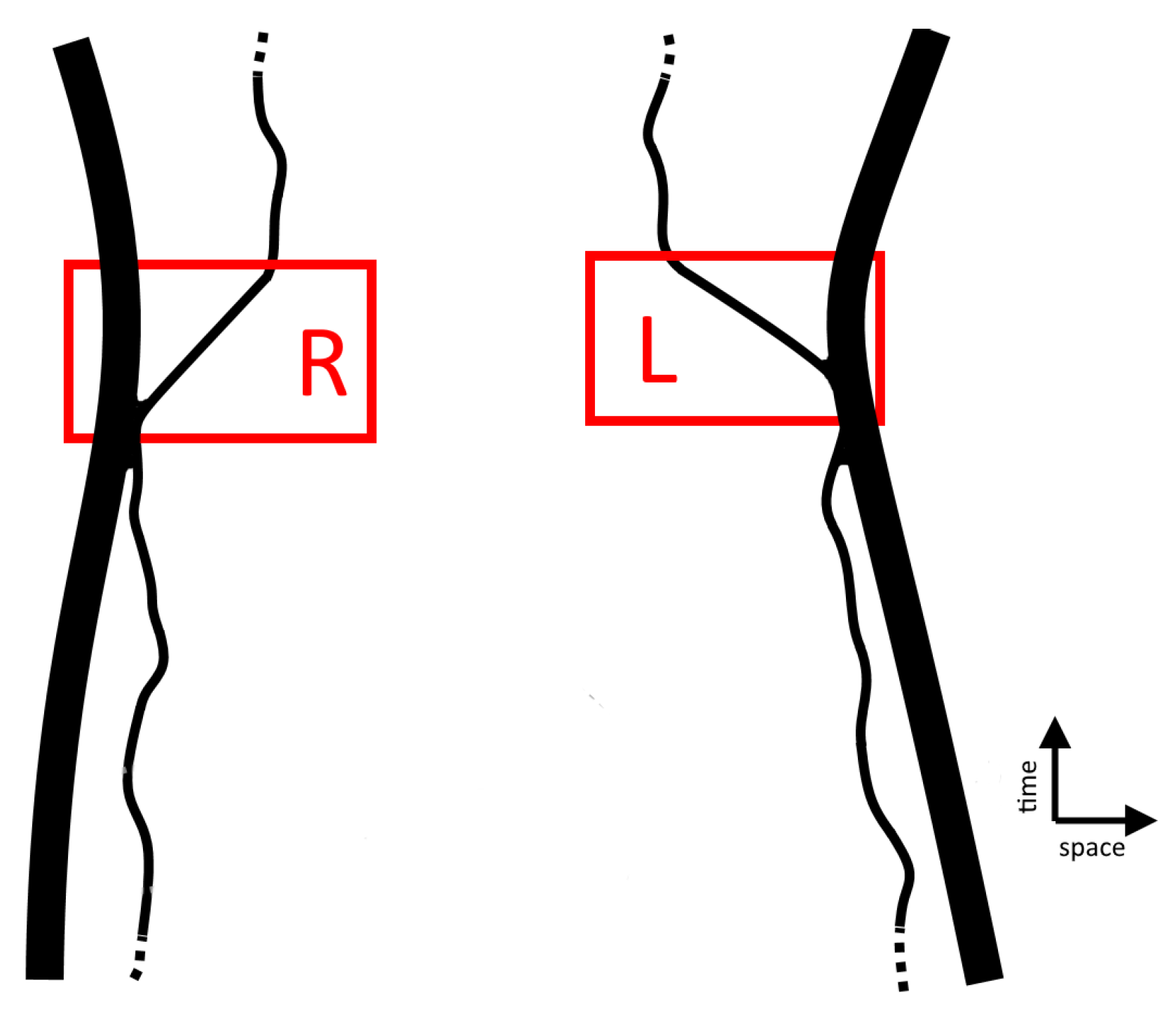
Figure 3.
Alleged non-machines. Type-1 circuits admit a local-in-time constraint in the form of a differential equation, Chau’s circuit being a simple example (the blue sub-circuit is one of several ‘non-linear resistor’ realizations). Type-2 circuits are so-called noise sources. A reversed biased Zener diode fluctuating around its breakdown voltage.
Figure 3.
Alleged non-machines. Type-1 circuits admit a local-in-time constraint in the form of a differential equation, Chau’s circuit being a simple example (the blue sub-circuit is one of several ‘non-linear resistor’ realizations). Type-2 circuits are so-called noise sources. A reversed biased Zener diode fluctuating around its breakdown voltage.
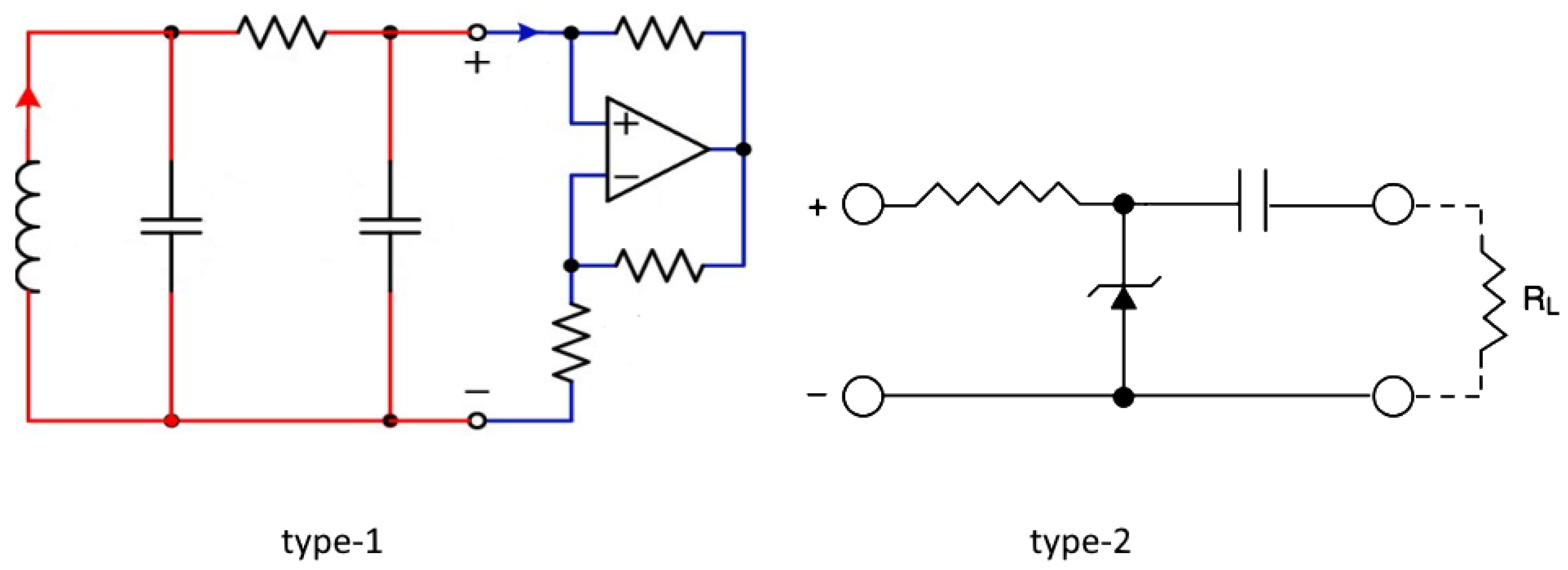
Figure 4.
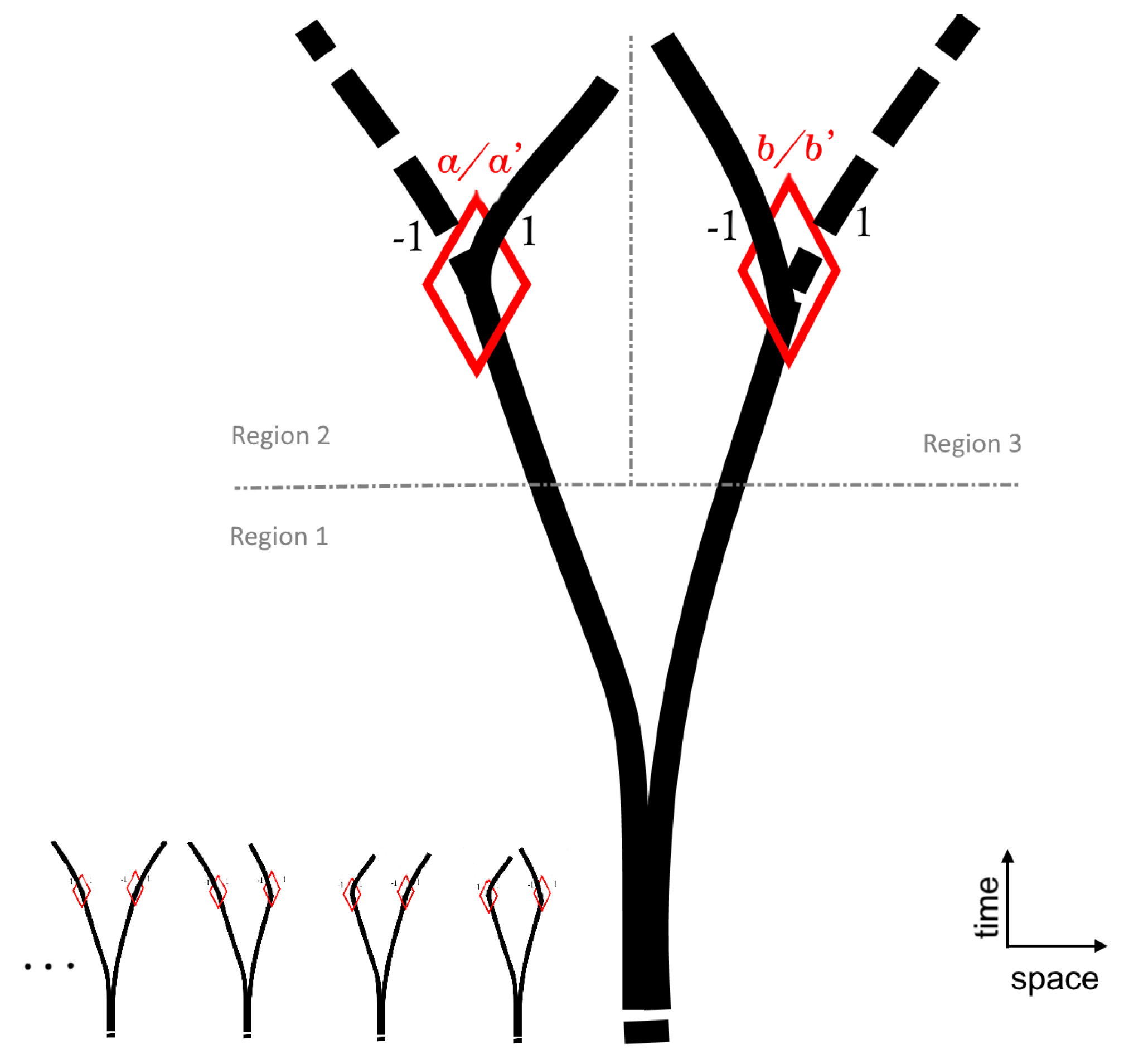
A typical Bell test consists of generating four ‘forests’ of ‘trees’ (samples shown bottom left) corresponding to the four combinations of perturbations applied to a tree’s two ‘branches’— and —which in Bell’s case correspond to two possible polarizer’s orientations interacting with a particle. A perturbation results in branch deformations of two types (). In the proposed Bell’s test, the classification scheme of each branch ( vs. 1 deformed) is not predetermined but instead optimized to violate the l.h.s. of Bell-CHSH inequality (7) on training data. The dashed grey line is only relevant to the discussion below of no-signaling.
Figure 4.
A typical Bell test consists of generating four ‘forests’ of ‘trees’ (samples shown bottom left) corresponding to the four combinations of perturbations applied to a tree’s two ‘branches’— and —which in Bell’s case correspond to two possible polarizer’s orientations interacting with a particle. A perturbation results in branch deformations of two types (). In the proposed Bell’s test, the classification scheme of each branch ( vs. 1 deformed) is not predetermined but instead optimized to violate the l.h.s. of Bell-CHSH inequality (7) on training data. The dashed grey line is only relevant to the discussion below of no-signaling.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated




