1. Introduction
Language shapes thought, and in no field is this more true than in physics. For over three centuries, the basic grammar of theoretical physics has remained that of Newton, consisting of two basic components: A `state vector’ representing the system at any given time, and an evolution equation for the state vector. Implicit in those two is also the way in which our actions in a `tabletop experiment’ are modeled: By choosing initial conditions for the state vector, and/or choosing parameters for the evolution equation, such as applying an external force or field.
Newtonian grammar
1 (NG) even survived the 20th century turmoil. The quantum revolution only redefined the space of the state vector—
n-dimensional configuration space ↦ infinite dimensional Hilbert space. More remarkably, even the relativistic revolution, which did away with the very notion of absolute time, did not seem to require a novel grammar.
Its robustness to paradigm shifts has erroneously promoted NG to an attribute of nature rather than that of our descriptive language, and physical models not expressible in NG are generally met with instinctive skepticism. However, the picture emerging from previous papers by the author suggests that, NG’s robustness to paradigm shifts might itself have been a product of wrongly shaped (Newtonian) thought. Maxwell-Lorentz Classical electrodynamics (CED) of point charges—an alleged success of NG—is ill-defined, and a century of attempts, expressed in NG, to cure its pathologies all failed. Currently, the only well-defined CED of interacting point-like charges (to the author’s best knowledge), dubbed ECD [
1,
2], is not expressible in NG. Precisely for this reason ECD can serve as a (classical) ontology underlying QM statistics without conflicting with various no-go theorems, all implicitly assuming an ontological description using NG [
3]. That QM
is an NG theory can be traced to local constraints, noatably energy-momentum conservation, satisfied by that ECD ontology; see caption of
Figure 1. Finally, there are indications that advanced solutions of Maxwell’s equations, mandated by ECD, are at play not only in microscopic physics, where they create the illusion of `photons’ (among else) but also in astronomy’s missing mass problem [
4]. And although advanced solutions per se are not in conflict with NG, their incorporation into a consitent mathematical formalism, involving both matter and radiation, certainly is—time-symmetric action-at-a-distance electrodynamics [
5] being yet another, better known example.
The appearance of NG in macroscopic (classical) physics is likewise explained by local constraints satisfied by the underlying (ECD) ontology—see, e.g., appendix D of [
1] for how the Lorentz force equation is obtained as a
local approximation for the center of an extended charge. The question of whether the underlying microscopic ontology is likewise described by NG, might therefore seem irrelevant to macroscopic physics. We argue to the contrary. Microscopic local constraints are just what they are: constraints; long-time integration of their manifestation in macroscopic, coarse grained quantities is not only often unreliable due to the so-called butterfly effect, but moreover
meaningless in a non NG universe, as are most statistics derived therefrom. This realization, in conjunction with the above indications of a non NG ontology, point to new experiments which might appear far-fetched, but only because of a NG bias. If the universe is indeed non mechanistic, the implications for physics and science in general would go far beyond quantum weirdness.
2. Non-Machines and Their Statistics
The settings of what follows is the block-universe (BU): 4D spacetime hosting a locally conserved (symmetric) energy-momentum tensor, constructed from the basic building blocks (fields in the case of ECD) of an ECD-like theory (
Figure 1).
The BU is an infinitely redundant representation of a NG ontology as its full content, statistical aspects included, can be faithfully reproduced from any of its space-like slices. Philosophy aside, it is therefore an unnecessary complication even in relativistic theories. However, for a non-NG ontology, the BU is arguably the only faithful representation. Consider a
non-machine—for lack of a better name: A system which, unlike a
machine, does not admit an NG representation, viz., its contribution to the BU is not the result of propagating some initial conditions. To illustrate the basic idea with as little technical complications as possible, consider the following (formal) non relativistic, toy non-machine action for
where
K is any diagonal matrix of non compactly supported, once integrable symmetric functions, and
denotes double differentiation. It is the non compactness of
K on
which prevents translating the associated Euler-Lagrange equations,
into NG language
2. Note that, in and of itself,
K’s non singular support does not necesserily lead to temporal paradoxes (although, importantly, unlike ECD, does violate scale covarince); More accurately: non tachyonic extrema of a relativistic version of (
1), e.g. the self-term in [
13], do not do so. It is violation of this no-tachyons condition which can create paradoxes
3 rather than a non-tachyonic
(
s a Lorentz scalar) functionally depending on
for
—hence also on
—which, at `worst’, can be labeled retro-causal, and does not entail a paradox, as explained below.
Nonetheless, twice integrating the first term in (
2) by parts, we get the classical e.o.m.
with a residual term
vanishing in the `delta function limit’:
(and is
for a finite
). A different way of seeing a machine in (
2) involves the Noether currents associated with the symmetries of action (
1), which are exactly conserved even at finite
. For sufficiently slowly varying
V on the scale set by
K’s extent, translation invariance, e.g., lends itself to a good mechanistic description of the coarse grained momenta and positions
viz.,
. Without such quasi locality it would be impossible to explain the reproducibility of many experiments notwithstanding (spacetime-) translation covariance. It would further allow to directly infer
with certainty future attributes of
V based on current behavior of
q, which would lead to a paradox whenever those attributes could still be altered.
Nonetheless, the local machine approximation, however good, is still only an approximation, whose validity strongly depends on the context in which it is used. For chaotic potentials (more generally: chaotic systems) the time-scale,
, over which a non-machine’s solution and that of its machine approximation remain close (
t-wise less than some small constant) could grow very slowly with increasing
especially if
K has a long, i.e., algebraic tail (as is the case in ECD). One way of seeing this lies in the residue,
R, playing the role of an external force in (
3) which, when acting on
q in unstable directions, leads to its subsequent exponential separation from the unperturbed path. The dimensionality,
n, of the system plays a crucial role in tempering the growth of
with increasing
, as larger
n implies (statistically) higher maximal Lyapunov exponent—and it only takes one such ultra unstable direction for even a meager
R to rapidly drive an entire chaotic system `off course’. Now, realistically speaking, there is no “unperturbed path”. And indeed, for a sufficiently large
most `coarse grained’ statistics associated with (
2), e.g. attractor manifold and power spectrum, would most likely be experimentally indistinguishable from those of a noisy machine, viz. (
3) with
R a random noise. However, as
R is far from being random, such noisy machine approximation becomes moot with regard to the
global spacetime structure of (at least some) trajectories. In other words, a noise history reproducing a global path of (
2) would need to be too `structured’, or non random, for any realistic noise source (e.g. Gaussian White).
Figure 1.
BU time slices (left) allegedly involved in a single-particle—for simplisity—QM experiemnt. Thick vertical lines represent a crystal latice. Thin grey lines are initially left-to-right moving particles, some transmiting, others reflecting. By `superimposing’ all members of the ensemble (right), one gets various ensemble densities, e.g. charge density
, from which the (statistical) results of any QM experiment can be deduced. From the constraints satisfied by individual members in the ensemble, equations for the ensemble densities can be derived [
3], and, upon writing
, QM wave equations for
follow. Different
’s then describe different ensembles rather than any single system (hence Ehrenfest’s theorem, `scars’ and general amplitude amplification of wave-functions near classical periodic orbits, and the inevitale rapid wave-function delocalization of manifestly macroscopic but chaotic systems[
9]). The NG nature of the Schrödinger evolution is a consequence of local energy-momentum conservation, rather than being a property of individual systems. Note that different members are brought to a common time support so the Schrödinger evolution is fictitious—a mathematical tool for constructing ensemble densities; ensembles representing steady-state systems even correspond to multiple time slices of a single system. The construction in [
3] only works for closed systems, hence the Hamiltonian. And indeed, when a closed system becomes coupled to the environment, as must be the case during its `measurement’, the initial wave-function and its evolution become nonsensical. Distinct ensembles, represented by distinct wave-functions,
must then be defined post measurement (insofar as QM is to be subsequently applied) and the collapse postulate is just that complementary statistical ingredient, bridging the pre-post measurement gap, giving weights to different
’s based on their corresponding macroscopic `pointer configuration’. Heisenberg’s uncertainty relations, reflecting certain properties of ensembles, are in line with the role of an agent in the BU, i.e., that its action—measurement in this case—defines an ensemble.
Figure 1.
BU time slices (left) allegedly involved in a single-particle—for simplisity—QM experiemnt. Thick vertical lines represent a crystal latice. Thin grey lines are initially left-to-right moving particles, some transmiting, others reflecting. By `superimposing’ all members of the ensemble (right), one gets various ensemble densities, e.g. charge density
, from which the (statistical) results of any QM experiment can be deduced. From the constraints satisfied by individual members in the ensemble, equations for the ensemble densities can be derived [
3], and, upon writing
, QM wave equations for
follow. Different
’s then describe different ensembles rather than any single system (hence Ehrenfest’s theorem, `scars’ and general amplitude amplification of wave-functions near classical periodic orbits, and the inevitale rapid wave-function delocalization of manifestly macroscopic but chaotic systems[
9]). The NG nature of the Schrödinger evolution is a consequence of local energy-momentum conservation, rather than being a property of individual systems. Note that different members are brought to a common time support so the Schrödinger evolution is fictitious—a mathematical tool for constructing ensemble densities; ensembles representing steady-state systems even correspond to multiple time slices of a single system. The construction in [
3] only works for closed systems, hence the Hamiltonian. And indeed, when a closed system becomes coupled to the environment, as must be the case during its `measurement’, the initial wave-function and its evolution become nonsensical. Distinct ensembles, represented by distinct wave-functions,
must then be defined post measurement (insofar as QM is to be subsequently applied) and the collapse postulate is just that complementary statistical ingredient, bridging the pre-post measurement gap, giving weights to different
’s based on their corresponding macroscopic `pointer configuration’. Heisenberg’s uncertainty relations, reflecting certain properties of ensembles, are in line with the role of an agent in the BU, i.e., that its action—measurement in this case—defines an ensemble.

However, the experiments proposed here do not attempt to `implicate’ individual spacetime structures as belonging to non-machines. Instead, a non mechanistic statistical signature is sought in ensembles of suspected structures, and there is a crucial difference in this regard between machines and non-machines. In the former, e.g. (
3) with
, its solution set can be 1-to-1 mapped to a subset of
equipped with a natural, i.e. Liouville measure. In contrast, the solution set of (
2) is some infinite dimensional function space having no obvious counterpart measure.
Single-system equations of non-machines, then, cannot be a complete description of the experiment, necessitating a compatible statistical description of ensembles of solutions, not deriviable from the single-system theory alone, hence being equally fundamental.
The significance of this last point is illustrated clearly in a scattering experiment (
) of monoenergetic particles off a chaotic potential, e.g. a crystal lattice. In the non-machine case, uniformity over the impact parameter does not define an ensemble since two incoming particles can have identical (freely moving, asymptotic-) solutions yet different outgoing ones; As the two particles approach the target, their distinct
future paths, gradually render their
R’s non negligible and distinct. Now, suppose that the past asymptotic motion takes place in some time-independent, chaotic potential
V. At some fixed plane orthogonal to the average propagation direction of the particles,
V transitions into either
or
. The BU statistical view of this scenario now involves
two ensembles of word-lines,
q, shifted in time such that
lies on the
interface plane. Define the
past ensemble as that collection of partial world-lines
for
. On time-scales shorter than
, any such partial world-line whose form is not excluded by (
3) with
could appear in either past ensemble. But does it? More accurately: Must its statistical weight (frequency of appearance) be the same in both? An NG physicist would answer in the affirmative, so long as the two ensembles originate from a common distribution of past initial conditions, but in a non mechanistic BU an ensemble can’t even be
mapped to such a distribution; past and future potentials seen by ensemble’s members are both relevant. A non mechanistic statistical signature should therefore be present in ensembles of non-machines even when individual members are examined on time-scales shorter than
. Obviously, one can do better by examining them on time-scales longer than
, hence the choice of a chaotic
V (almost any non chaotic
could do as well but the much longer
introduces much more noise which, in turn, requires greater statistical power to distinguish between the two ensembles).
Zooming out now from our toy model, insofar as a physicist obeys the physics of the systems he is studying—and there is no evidence to the contrary—he is represented by some (extended) world-line in the BU, and his free will is technically an illusion. This tension with one’s subjective feeling is present also in Newtonian-grammar physics, and this never disocuraged physicists from doing physics. But unlike its Newtonian counterpart, our physicist cannot meaningfully model this illusary free will by chosing the initial conditions of a system (or distribution thereof) from which the system (ensemble thereof resp.) then evolves. Instead, his `freely chosen’ actions constrain the
global, spacetime structure of systems he is studying (in a way which depends on both the system and the actions) and in general, infinitely many such systems are compatible with a given constraint. His actions therefore only define an
ensemble, with the relative frequency of each ensemble-member being a statistical property of the BU (revealed in a single lab only as a means of saving the hassle of sampling the whole BU for similarly constrained, spontaneously occurring systems [
3]). Note that the Newtonian resolution can be viewed as a private case of ours.
In the case of closed systems, according to [
3], QM provides a rich statistical description of the ensemble, encoded in the wave-function, which is therefore an attribute of the ensemble rather than of any single system (see caption of
Figure 1). By “closed” it is meant that the system’s full energy-momentum balance is known and exactly incorporated into its Hamiltonian. In contrast, the statistical description of open systems [
12] is currently not nearly as detailed and conceptually problematic. It boils down to treating an open system as a small subsystem of a large closed system, tracing out the extra degrees of freedom, not before making simplifying assumptions about their interaction with the subsystem and with one another. However, this attempt is no more reliable than similar attempts to model irreversibility within the framework of (classical) Hamiltonian dynamics, if only because it ignores an essential source of dissipation and thermodynamic irreversibly: the radiation arrow-of-time (manifested in ECD systems which are out of equilibrium with the zero-point-field [
4]). When used in the context of macroscopic irreversible systems it furthermore pushes the mysterious `collapse postulate’ of QM far beyond its empirically validated domain, making it even harder to defend: Is the `observer’—and what is meant by that—part of the environment? Moreover, when that irreversible system is chaotic, this approach, at best, would prove consistent with the classical description, which, in turn, comes with its own conceptual and practical difficulties. Ergodic theory [
11], for example, seeks a flow-invariant measure on phase/configuration space, and is indeed a valid starting point for predicting the steady-state distribution of those (exceptional) systems for which such flow exists (e.g. type-1 circuits in
Figure 3). However, as it typically yields a fractal set which includes infinitely many (unstable) periodic orbits, neither ergodic theory nor its noisy versions, e.g. the associated Fokker-Planck equation, are sufficient for that. More relevant to out point, though (and as already pointed out) if this flow only locally approximates the 4D structure of chaotic systems, then ergodic theory is mute with regard to more complex statistics, e.g., the measure on the past ensemble of chaotic solutions from the above example. A similar objection applies to ensemble propagation when used to predict the long-time behavior of chaotic systems, or to inter-system correlators of previously coupled chaotic systems (see sect.
3.3).
Summarizing, when leaving the domain of closed quantum systems, QM becomes an unreliable tool. When then stepping into the realm of chaotic irreversible systems, one is already in largely uncharted territory. There, presumably, lies new physics which is nevertheless consistent with well established theories.
3. Are There Macroscopic Non-Machines?
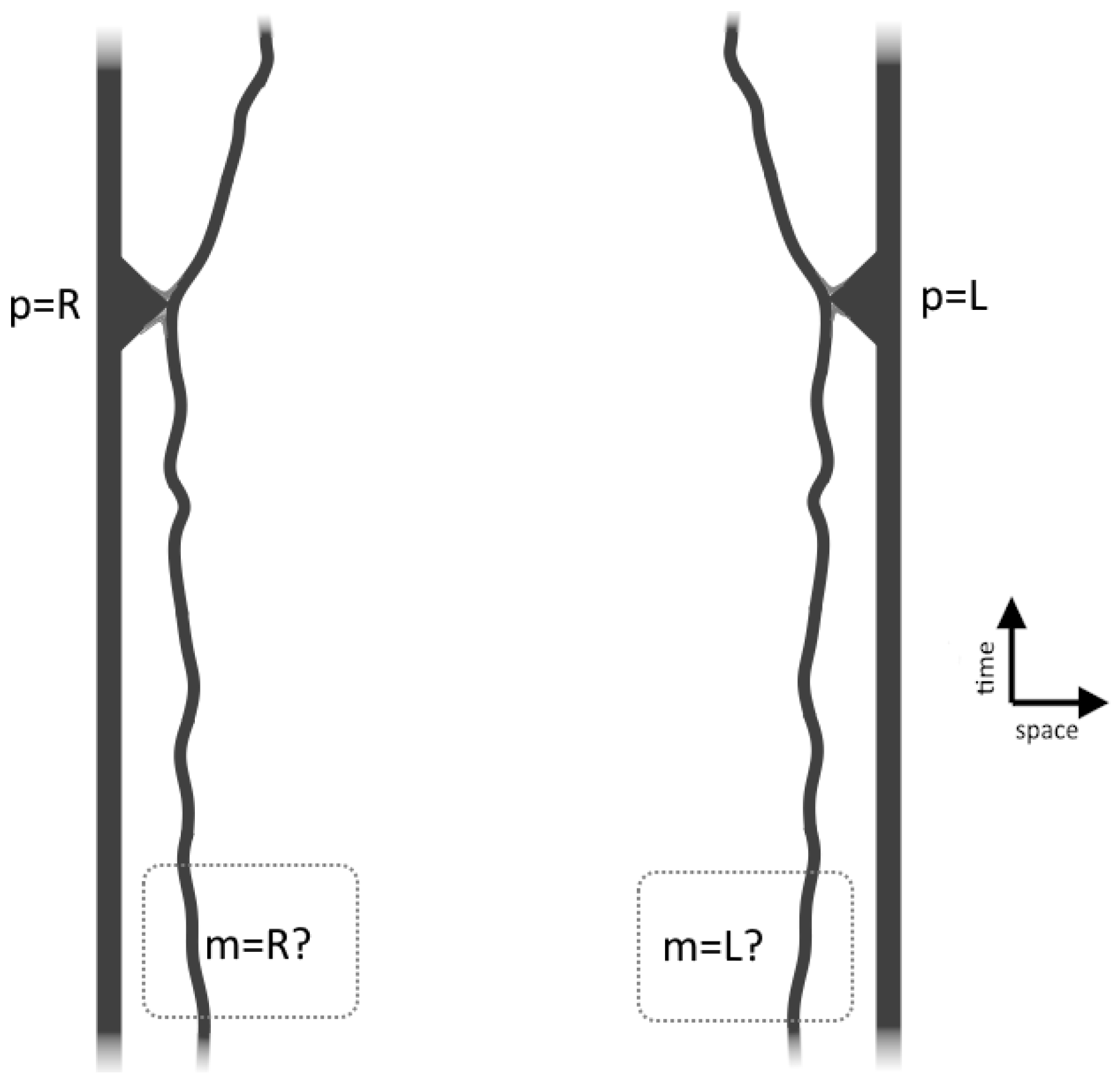
To distinguish machines from non-machines, we first propose testing whether a system can `remember its future’, diving deeper into the experiment described in sect.
2 and its consequences, but without committing to the toy model used there. Machines can obviously remember their past, meaning that a perturbation,
p, to a machine in its past can be inferred from its present state
m (`memory’). For simplicity, a binary type perturbations shall be used, labeled `
L’(eft) and `
R’(ight). In contrast, machines cannot `remember’ their future. Inferring a future perturbation from a machine’s present state entails, among else, the following: The state,
m, of a machine is measured and projected onto the set
at some initial time. The machine then propagates to a later time when its world-line intersects that of a random bit generator (RBG) applying a random
to it, and miraculously
. This must happen everywhere throughout the BU, to all copies of the machine, which is clearly not our BU.
This evident truth can be extended to non-deterministic machines in which the rest of the universe is (realistically) treated as the source of randomness and possibly dissipation. In this case, the machine’s stochastic evolution leads to a certain probability distribution over its future states, parametrically depending on the nature of the initial perturbation (L or R in our case, marginalized over possible additional `hidden variables’). If the two distributions are distinguishable, i.e., if a random perturbation, p, can be deduced from m with probability , then the machine is said to fuzzily remember a bit. As in the deterministic case, machines can fuzzily remember a past bit but not a future one.
Like machines, non-machines can remember their past. A sufficiently strong perturbation to a fully developed turbulence, for example, leaves an obvious signature on the streamlines for a short time thereafter. It is even conceivable that this `short term memory’ would extend much further into the past had only a different, more suitable signature been used—as in the case of seasonal weather forecasts which are based on large statistical tables rather than propagation of differential equations. But why should non-machines not remember their future, at least fuzzily?
3.1. Statistics in the BU
Our definition of fuzzy memory involves the repetition of an experiment. In the context of the BU this amounts to taking an ensemble of 4D structures, each corresponding to an instance of an experiment, and computing statistics thereof. A typical ensemble could consist of multiple `time slices’ from the (extended) world-line of a single non-machine, or single slices from multiple copies of a single type of non-machines (see
Figure 1).
In the case of a binary type perturbation, there are four relevant sub ensembles of the full experiment ensemble, indexed by a pair
with
. The p(erturbation) index indicates which perturbation is finally applied to the non-machine, and the m(emory) is the result of some binary projection of an initial measurement, aimed at revealing the type of future perturbation. A fuzzy memory of a future random binary perturbation is demonstrated by a non-machine if
with
being just the number of elements in the relevant sub-ensemble. Of course, the ensemble size should be large enough to exclude pure chance. Note that we now treat the perturbation as an attribute of the non-machine rather than the RBG, as in the machine case, for it constrains the
global 4D structure of a non-machine. In contrast, a perturbation to a machine only constrains that irrelevant part of its world-line succeeding the perturbation. It follows that future memory of a non-machine, unlike that of a machine, does not involve its `conspiracy’ with RBG’s; It is just a statistical affinity, (
4), between two segments of its (extended) world-line or, more accurately: A statistical property of spacetime structures, discriminating between the
R and
L ensembles of RBG’s in interaction with non-machines;
Figure 2.
One instinctive (NG biased) push-back could be: Since the measurement,
m, precedes the perturbation,
p, the latter can be chosen
non randomly so that
. While this might be interpreted as an instance of `false memory’, it is not an argument against (fuzzy) future memory according to our definition (which machines are incapable of). So conditioning
p on
m corresponds to selectively choosing only the two sub-ensembles on the r.h.s. of (
4) rather than all four. As a corollary we get the following consistency condition: For any
m and
p, and regardless of their mathematical representations within a physical theory, all four sets in (
4) must be non-empty—although an important caveat is that, conditioning
p on
m might render moot the original ensemble, consisting of spacetime structures of the type shown in
Figure 2, as in this modified protocol a second energy-momentum `bridge’ necessarily exists between non-machines and perturbers through which the latter is informed of
m.
A different way of formulating the above objection involves so-called backwards-in-time signaling (BITS) [
10], prima facie implied by future memory—
p being the signal sent to the past, and
m its (distorted) reception. BITS exclusion is normally taken as one of the tenets of any physical theory to exclude causal paradoxes, of the sort created by choosing
when perfect future memory is possible. This reason clearly doesn’t apply to `fuzzy BITS’, facilitated by fuzzy future memory, but a weaker case can still be made against fuzzy BITS, on the premise that, whatever action
m triggers, it must not affect the `fidelity of the communication channel’ (i.e.
could completely ruin a near perfect channel). However, such action-independent channel fidelity proviso, borrowed from mundane communication, is inconsistent with the role of agency in a BU supporting non-machines (sect.
2) hence BITS exclusion, as a tenet, is unjustified. In principle, then, future memory indeed facilitates BITS, provided the receiving side does not act to ruin the channel.
Yet another implausibility argument, involves the inevitable noise coming from the rest of the universe, and the variability in the act of measuring
m. The long-time evolution of non-machines—a category allegedly including classically chaotic systems—are highly sensitive to both. As each member of an ensemble is affected by a distinct noise history and a member-specific measurement process, one may object to the very existence of a well-defined ensemble, comprising non-machines of a common type. However, the very formulation of this objection uses Newtonian grammar, which we have set out to refute. That each ensemble member corresponds to a distinct time-slice of the BU means that, should statistical regularities arise in the ensemble, environmental coupling would be incorporated into them (Kolmogorov scaling law and chaos universality are two such examples). This is precisely what allegedly happens in the case of systems faithfully described by QM according to [
3].
One might also muster QM against future memory. By the standard collapse picture, the act of measuring
m just updates the original wave-function
in a way which is independent of any future interaction with the system. However, this argument (ideally) applies only to closed systems, (see caption of
Figure 1). Moreover, the collapse picture is clearly a caricature of a much more complex, system dependent process, and it is conceivable, e.g., that a sufficiently massive, closed macroscopic chaotic system could be `looked at’ to obtain
m—say, continuously and weakly coupled to some `recorder’ for a macroscopic time—in ways not captured by that simplified picture.
With the above objections removed, the author can think of no reason why inequality (
4) must not be satisfied by non-machines.
3.2. Schematic Proposal for Testing Future Memory
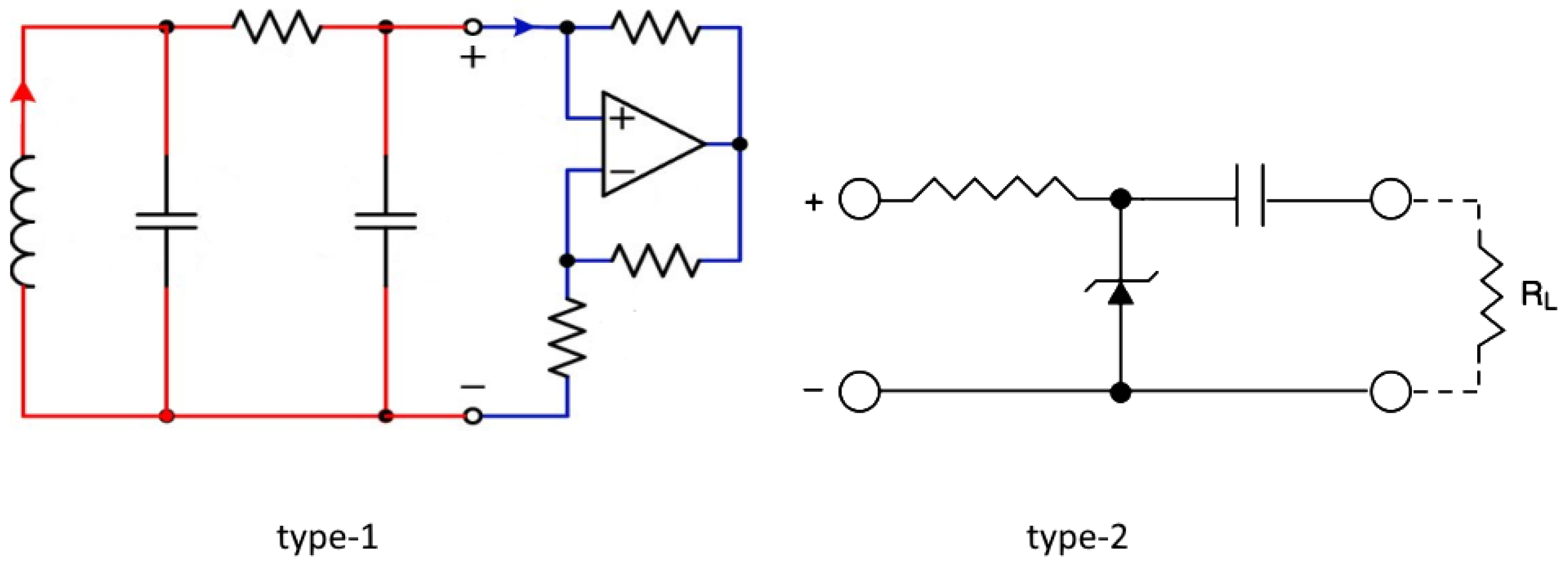
For the sake of concreteness, two types of analog, chaotic electric circuits shall serve as alleged non-machines (
Figure 3) consisting of some nonlinear `feedback principle’ coupling different scales—hence generically all scales (“scale" roughly refers to frequency components in the circuit’s currents/voltages). Such circuits should not be viewed as low-dimensional non-machines—small
n in the language of sect.
2—but rather as providing, though their voltages, a low dimensional projection of an effectively
, irreversible non-machine; the irreversible counterpart of, say, the center-of-mass motion of a bound
n-body system in an external chaotic potential.
The characteristics of the components together with Kirchhoff’s laws, jointly constrain the voltages, which can be seen as a point in configuration space, and in type-1 circuits these constraints locally (in time) translate to a chaotic flow on configuration space, i.e. take the form of coupled differential equations with a positive Lyapunov exponent (Note how the roles of system and its model are swapped when using analog computers to solve differential equation; analog circuits solving Hamilton’s equations should not be mistaken for closed systems). In type-2 circuits—so-called `noise sources’—no flow exists as components characteristics are too coarse of an abstraction, e.g., that of a Zener diode in reverse bias, just around its breakdown voltage. Nevertheless, the voltage of a type-2 circuit is also piece-wise mechanistic.
For lack of a better analytic option, we shall resort to machine learning (ML) in an attempt to prove future memory. The experiment consists of three stages: Data acquisition, followed by a training session of, say, a deep neural network on half of the data points and, finally, testing the trained network against the remaining half for future memory. The data acquisition stage begins with an
initiation session, during which the circuit is brought to steady state. At the end of this prolonged stage (relative to all other time scales involved) a short voltages `clip’ of duration
is recorded. It is important that the circuit be coupled to the `recorder’ (e.g. oscilloscope) throughout the entire experiment, so as to make it an integral part of the non-machine. The raw product of this stage is
n measurements,
which are predetermined projections of a clip. At a fixed later time,
T, a perturbation
is applied to the circuit in the form of some strong coupling to yet another (type
L/
R) circuit, manifestly affecting the circuit’s behavior. The perturbation type should be either randomly chosen or alternating
, thereby reducing the effect of any systematic drift in experimental conditions. This cycle is repeated
N times. Initiation session and the perturbation jointly define the experiment ensemble, hence there are two of them, presumably different.
Figure 3.
Alleged non-machines. Type-1 circuits admit a local-in-time constraint in the form of a differential equation, Chau’s circuit being a simple example (the blue sub-circuit is one of several `non-linear resistor’ realizations). Type-2 circuits are so-called noise sources. A reversed biased Zener diode fluctuating between insulator and conductor around its breakdown voltage.
Figure 3.
Alleged non-machines. Type-1 circuits admit a local-in-time constraint in the form of a differential equation, Chau’s circuit being a simple example (the blue sub-circuit is one of several `non-linear resistor’ realizations). Type-2 circuits are so-called noise sources. A reversed biased Zener diode fluctuating between insulator and conductor around its breakdown voltage.
Next,
data points (cycles) are randomly chosen for the training session which seeks a function
maximizing inequality (
4). This optimal
m is then tested for (
4) violation on the remaining
data points, and future memory is demonstrated if
m passes the test with statistical significance.
For a sufficiently long initiation session the `local state’ of a circuit is assumed to converge to a fixed distribution irrespective of p. Future memory detection therefore mandates or else the local state would uniquely determine the entire clip. Alternatively, and not mutually exclusive, a sufficiently large configuration space, guaranteeing an effectively infinite `ergodicity time’, might circumvent the condition. As for determining –in type-1 it is unknown a priori but is expected to be proportional to the inverse average Lyapunov exponent as components’ characteristics are varied; for type-2 it is the average duration of its piece-wise mechanistic behavior, which can be simply deduced and made very small. The tradeoff is that type-1 circuits are less sensitive to noise/environmental coupling than type-2.
Our assuption that the
and
experiemntal (sub-)ensebles of non-machine solutions are (statistically) distinct despite having identical configuarion-space distributions post initiation, parallels the QM case described in [
3] section 4.2.2 (mind the arXiv erratum): Wave-function initiation leads to a charge/momentum steady-state distribution which is independent of any future interaction of the charge(s). However, for this difference to be realistically detectable, the measurement-to-perturbation time,
T, must be much shorter than the duration of the initiation session (which must obviously be
) and as short as possible.
There are, of course, many possible variations on this protocol, e.g., m might take values in some continuous set instead of , reflecting a varying degree of certainty in p, etc. Also worth noting is the possibility of testing past memory beyond the trivial short-term mechanistic memory, using the proposed approach with p and m temporally interchanged.
3.3. Bell’s Inequality Test for Entangled Non-Machines
The previous experimental approach can be used to test whether two such circuits,
A and
B, which are initially coupled, exhibit `spooky’ correlations after being decoupled. Decoupled machines would just propagate their states at decoupling, hence correlations post decoupling are bounded by those already existing in the joint distribution of these initial states, playing the role of the `hidden variable’
in Bell’s theorem. Bell quantified this mechanistic bound for a special case of post decoupling joint measurements, which aught to be respected by machines (“little robots" in his words
4).
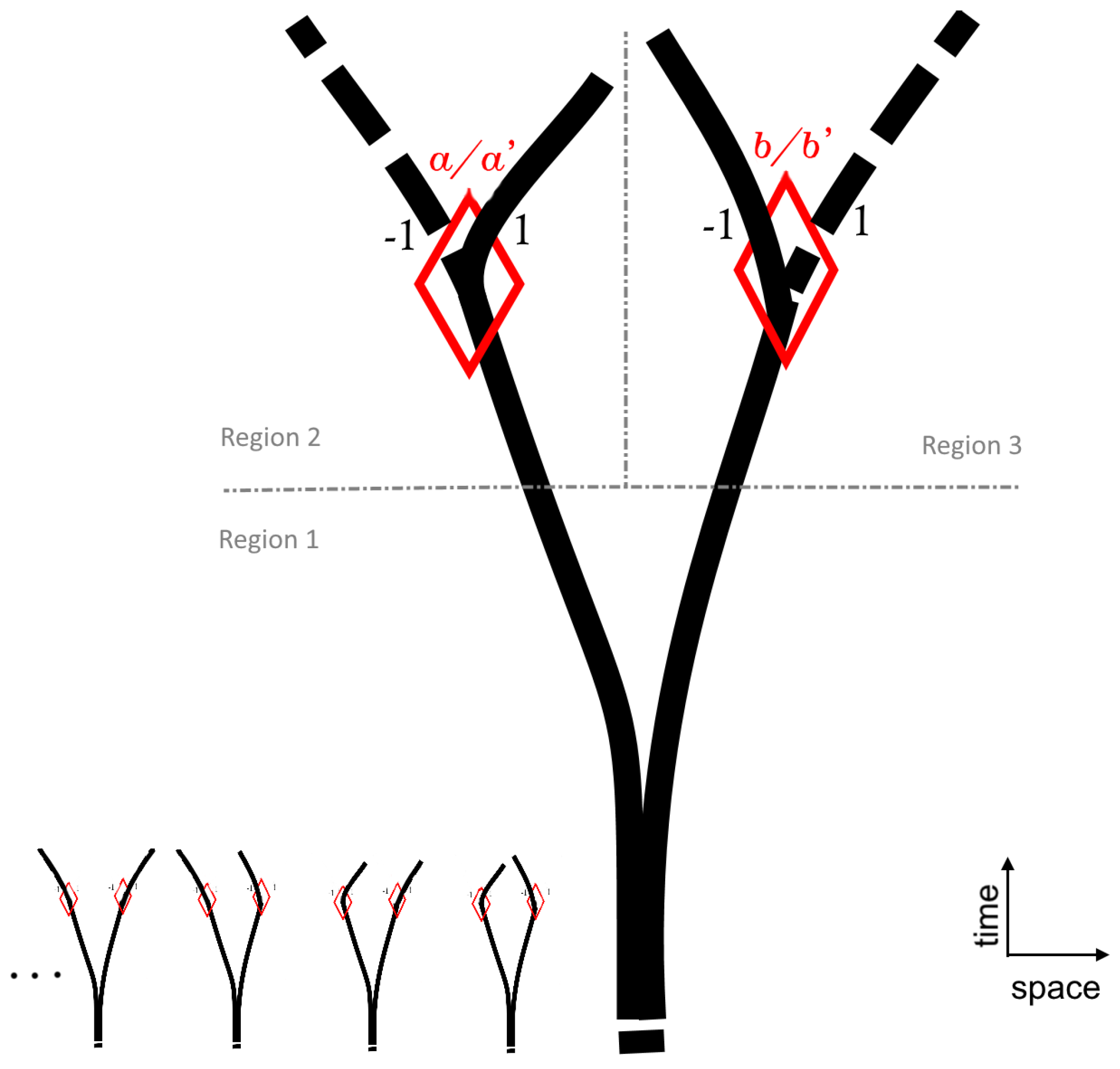
In contrast, the decoupling of non-machines is best understood as the branching of their joint, spacetime `tree’, and post decoupling correlations are just a statistical attribute of a `forest’ of such trees (
Figure 4). More precisely:
Four such forests are involved, corresponding to the four combinations of perturbations applied to a tree’s two `branches’,
and
, which in Bell’s case are the two possible polarizer’s orientations interacting with each particle. Note that, as each forest comes with its own set of trees, Bell’s theorem can neither be applied to the union of all four forests, treating this time a tree as a hidden variable to be sampled from a single distribution.
In the proposed counterpart to Bell’s test, the perturbation’s role is played by, say, coupling of circuit
A to either circuit
a or
, and similarly for
B. However, unlike in the standard test (cf.[
3] section 4.2.2) the `polarization measurements’ are virtual, as opposed to physical—a limitation of quantum systems only. Consequently, the data acquisition stage for each of the four forests— consisting of a long initiation session pre decoupling, followed by a shorter, though
, post decoupling period and ending with two perturbations—does not yet involve polarization measurements. Only at the next stage, half the runs of each forest are randomly assigned for the training session where a virtual `polarization measurement’
of each circuit, in each run, is taken post decoupling, but either pre or post perturbation. To find the `best’ such choice of measurement, four neural networks,
are trained to maximize the l.h.s. of Bell-CHSH inequality
where the
C’s are the relevant correlators, e.g.
with the sum running over all training trees in forest
, and
are the corresponding clip projections of post decoupling measurements. Then, violation of (
6) is tested on the remaining half. Violation of the Tsirelson’s bound, i.e., (
6) with a r.h.s. equal to
, would prove—as with future memory—that macroscopic physics is even more non-local than permitted by QM.
Bell’s inequlity violation does not necessarily imply signaling across space-like separations which, at any rate would not lead to causal paradoxes for exactly the same reason BITS doesn’t.
5 Nor does non-violation imply no such signaling. Settling for the conditional probabilities needed to exclude/affirm such possibility, calculated from Bell’s test optimal
m’s (
5), is a mistake. One should instead optimize a single neural network to discriminate between
and
based on
A’s data taken outside the future light-cone of the corresponding
p.
Finally, it is possible to combine a Bell test with a future memory test, by training the neural network to predict whether two non-machines which are initially separated, are later brought into interaction. Note that future memory is, in fact, a private case of this last experiment; As (true) RNG’s are themselves (alleged) non-machines, the roles of perturbing and perturbed systems can be swapped in a future memory experiment.
3.4. Quantum computing
We conclude this section with insight into quantum computers (QC) which are, within the general framework of this paper, quintessentially non-machines, hence their superiority over digital classical computers (DCC) which are machines by design. Concretely, unlike a DCC, a QC doesn’t need to propagate the Schrödinger equation in order to compute
at a final time from
at some initial time—a task requiring computational resources, which increase exponentially with the `size’ of the system (e.g. number of qbits)
6. Instead, QCs `sample’ ensembles of 4D structures, which indirectly leads to a sampling of
at the final time.
Cleverly specified ensembles, defined by their initial wave-function and `Hamiltonian’, have been shown to result in great improvement over DCC algorithms in solving certain practical problems. In theory. In practice, decoherence (coupling to external, closed systems) and dissipation pose a formidable challenge to any substantial progress. Currently, to counter decoherence the plan is to use quantum error correcting codes (QECC) which, by definition, involve (multiple) measurements at intermediate times between the initial `wave function preparation’ and the final measurement. By our previous remarks, measuring a quantum system implies coupling a closed system to an open (macroscopic) one, i.e., leaving the arena of ensembles where QM (unitary) evolution alone determines . The extra component added to the description of involves the so-called collapse postulate of QM which, unlike the evolution operator, is only a caricature of an actual measurement (just recall how a Stern-Gerlach experiment `measures’ the spin of a particle to be `up’ or `down’).
Perhaps such machine-non-machine hybrid systems would eventually lead to practical quantum superiority. However, this is far from being experimentally settled, and ECD’s take on it isn’t optimistic: insofar as a qbit realization is well approximated by a closed system (hence its Hamiltonian), it is constantly radiating, with advanced and retarded radiation (statistically) canceling each other. A perfect qbit is therefore unavoidably coupled to its surroundings and, as a simple consequence of Maxwell’s equations, more so the nearer. Such essential `cross talking’, which is manifested in the (ECD) zero-point-field, can be prevented neither by a better qbit nor a shield thereof (whose constituent atoms likewise radiate). This renders unrealistic all QECC algorithms, which assume qbit wise noise-independence, in addition to the detrimental effect of uncontrolled qbits coupling.
Alternatively, if the previous experiments verify the existence of irreversible non-machines, a direct way of coping with environmental coupling in QC would be to search directly (theoretically and experimentally) for `XM’—that statistical description of irreversible systems—for various programmable (micro/meso-scopic) non-machines. Such XM’s already incorporate effects of decoherence and dissipation into their statistical description, doing so without sacrificing the one feature of QC responsible for its superiority over a DCC, viz., its ability to sample an ensemble of non-machines (And as with future memory, XM might even be more permissive than QM). Note that for an XM-based computer to be superior to any DCC, XM taking an analytic form must share QM’s exponential complexity growth with size (which is quite plausible). On the other hand, suppose the steady-state distribution of a simple chaotic system is known (e.g. via ergodic theory). Temporarily coupling n such systems, exponentially increases the `transient time’, T, before the combined system reaches steady-state and inter-system correlators become T-independent. This could pose a scalability barrier for XM computers and, according to our interpretation, should hold true also for reversible coupled systems, i.e., for (conventional) QCs.
Yet another avenue possibly leading to an exponential advantage over DCCs might be to send, backwards in time, the result of a DCC heavy computation. However, in this case as well, the fuzziness of BITS is expected to increase with transmission-to-reception time hence might demand compensating resources, e.g. multiple BITS transmitters, which too grow exponentially with the size of the problem (notwithstanding error correcting codes). Similarly when trying to fight this rapid increase in fuzziness over time with multiple `relays’ at intermediate times between transmission and final reception.
Finally, should macroscopic non-machines prove to exist, the most profound implications would be for biology, viz., modeling of biological systems. To be sure, biological systems do have mechanistic components (or at the very least, components whose modeling by a machine is practically fruitful). However, biological systems are by far nature’s most complicated physical systems. The assumption that their current mind-boggling complexity has (mechanistically) evolved from some simple initial conditions in the early universe is quintessentially NG biased and highly speculative. Affirmation of non-machines’ existence might be a good opportunity to reconsider this mechanistic dogma. In particular, decades of research in brain science, done on the premise that brains are machines, have got us no closer to the answer for even the most basic questions. We still have no idea, e.g., how this alleged machine remembers, let alone creates original ideas.