A Method for Detecting Surface Damage of Large Reflector Antenna Wheel-Rail Based on Electromagnetic Ultrasonic Technology

Preprint

Article

A Method for Detecting Surface Damage of Large Reflector Antenna Wheel-Rail Based on Electromagnetic Ultrasonic Technology

Altmetrics

Downloads

125

Views

Comments

You Ban^*,

Cong Jin,Shufei Feng

You Ban^*,

Cong Jin,Shufei Feng

This version is not peer-reviewed

Submitted:

31 July 2023

Posted:

02 August 2023

You are already at the latest version

Alerts

Abstract

The azimuth wheel-rail of large aperture radio telescope is the key component, it not only sup-ports the whole weight of the antenna, but also directly affects the pointing performance of the antenna with its surface accuracy. The whole weight of the radio telescope is hundreds or even thousands of tons, its azimuth frame rollers have great contact stress with the wheel-rail surface, repeated rolling can cause rolling contact fatigue on the wheel-rail surface, resulting in wear, cracks and other damage to the wheel-rail, and even lead to failure or fracture of the wheel-rail in serious cases, so it is very important to monitor the damage of the antenna wheel-rail. In order to visually detect the use of antenna wheel-rail surface, this paper proposed the method using electromagnetic ultrasonic detection to detect the damage of antenna wheel-rail surface for the first time. Based on the electromagnetic ultrasonic nondestructive testing principle, the simplified wheel-rail model containing wear, corrosion and crack damage is simulated. The results show that this method can effectively detect the surface damage of the antenna wheel-rail surface, and it can provide an important reference for the research of wheel-rail damage detection of large radio telescope.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

With the rapid development of deep space exploration and radio astronomy, the radio telescope plays an increasingly prominent role and has become an indispensable and important equipment in related research directions [1]. At present, the world's famous radio telescopes are mainly constructed and used by big and powerful countries, China is also actively contributing to deep space exploration and radio astronomy research. For example, QTT (QiTai Radio Telescope), the world's largest fully movable high-performance radio telescope, is being built in Qitai, Xinjiang, China. With a diameter of 110 meters and a weight of about 6,000 tons, its operating frequency band is 150MHz-115GHz and it is expected to be completed in 2028 [2,3].

The radio telescope is heavy and usually uses a large wheel-rail to support its orientation operation, the Green Bank Telescope (GBT) of 110×100 meters in Figure 1a is a typical wheel-rail antenna, and its wheel-rail system is shown in Figure 1b. The azimuth operation of this kind of antenna has the characteristics of low speed and heavy load. After long-term operation, rolling contact fatigue occurs on the surface of the wheel-rail, and it suffers damages such as wear or cracks on its surface [4,5]. These damages will reduce its surface accuracy and reduce its service life [6,7]. For example, the American GBT antenna and the German Effelsberg 100m antenna have different degrees of wear on the track after several years of operation, which affects the performance and service life of the wheel-rail [8,9]; The 25m radio antenna in Sheshan, Shanghai, China, was found to have a large deformation of the track joints at the early stage of operation, which directly led to the reduction of the antenna's pointing accuracy [10].

The wheel-rail damage of radio telescope reduces its surface accuracy and directly affects the antenna pointing performance, so it is important to study the detection of damage to the wheel-rail surface. The GBT antenna in the U.S.A. was built and operated for a few years and had problems with wear on the surface of the substrate and wear plate, Anderson R et al. investigated this issue, designed and manufactured a new component system, and updated the antenna component in 2007, which greatly improved the performance and service life of the azimuth orbit of the GBT antenna [11,12]; Aiming at the mechanical behavior of the inclined joint track of GBT antenna and the fretting wear of the contact interface between wear-resistant plate and substrate, Juneja G et al. simulated the rolling situation of the roller by using the moving load method, and analyzed the force by using the finite element method, which provided a reference for the design and transformation of the antenna wheel-rail [13]; In order to make the antenna have good pointing performance, DR Smith et al. pointed out that attention must be paid to the wheel-rail design to make it have high hardness to withstand great contact pressure [14]; Antebi et al. used the finite element method to analyze and design the welding process of the Large Millimeter Telescope (LMT) antenna in Mexico, and through the testing of the mechanical properties, the impact of the welding process on the accuracy of the track was investigated [15]; Guo Hongwei et al. used Hertz contact theory and finite element method to analyze the stress of a radar wheel-rail type antenna mount, and did metallurgical analysis under the condition of satisfying the strength to determine the cause of cracks on the surface of the roller [16]; Kalker J. J defined the wheel-rail rolling contact area as an elliptic shape, studied the wheel-rail three-dimensional steady rolling contact problem by using the series method, and introduced the longitudinal and vertical creep rate and spin creep rate into the analysis of the influence of wheel-rail contact spots, thus developing the corresponding simplified theory [17,18].

The above researches of wheel-rail rolling contact applications and theories are based on the Hertz contact theory, it is difficult to visualize the damage of the antenna wheel-rail surface. To solve this problem, this paper proposed the method of electromagnetic ultrasonic non-destructive testing to detect the performance of antenna wheel-rail surface for the first time, combining the advantages of non-contact, non-coupling medium and high efficiency. The effectiveness of the proposed method is demonstrated by theoretical research and simulation analysis.

2. Principle and Method of Electromagnetic Ultrasonic Testing

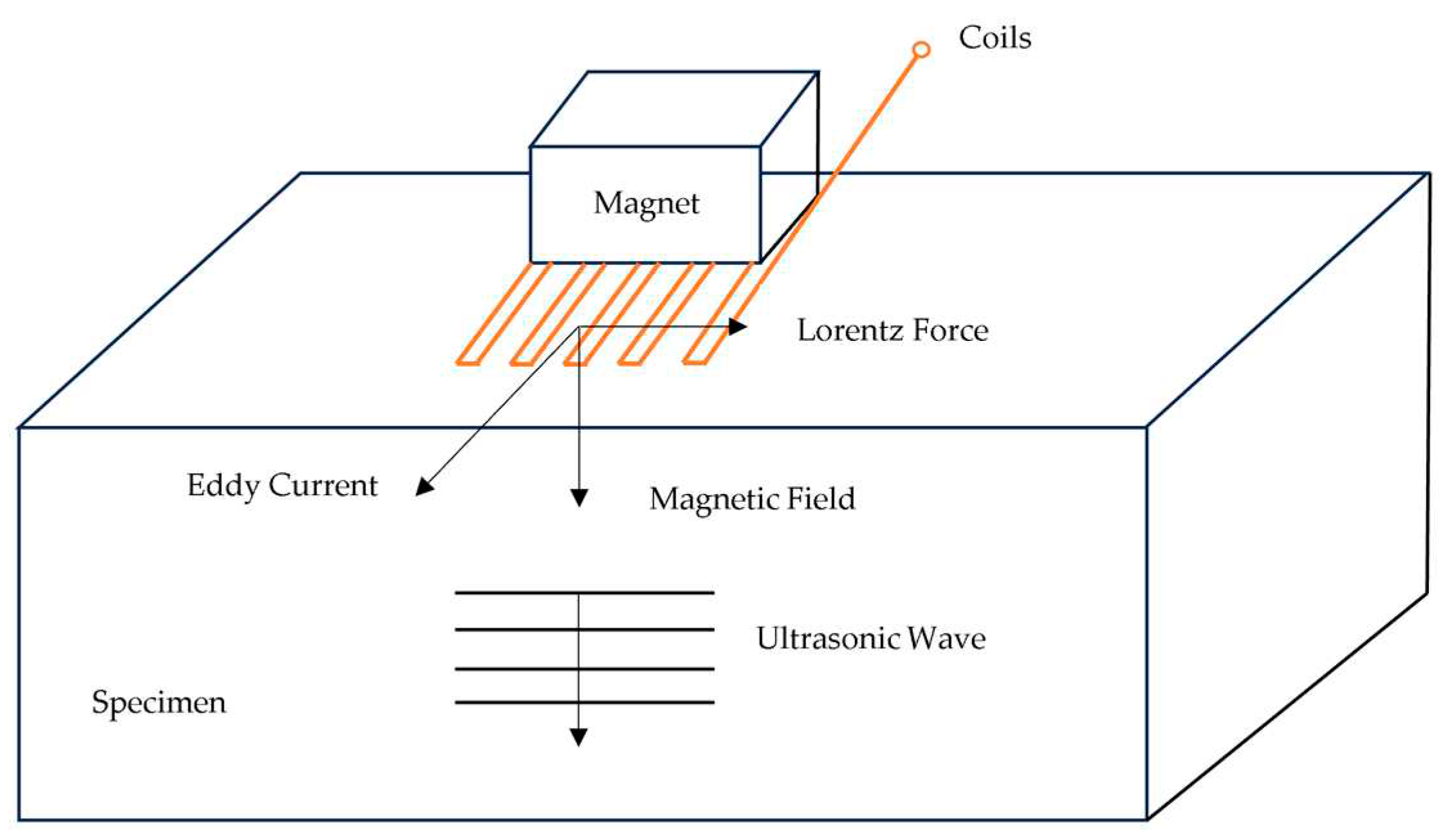
2.1. Basic Principles of Electromagnetic Ultrasonic Testing

The electromagnetic ultrasonic detection techniques dealt with in this paper all take electrical conductors as the measured objects, and their basic principles are based on electromagnetic induction phenomena, and the fundamental laws of macroscopic electromagnetic phenomena can be expressed very simply by Maxwell's equations [19], namely:

\nabla \times E = \frac{\partial B}{\partial t}

(1)

\nabla \times H = J + \frac{\partial D}{\partial t}

(2)

\nabla \times D = ρ

(3)

\nabla \times B = 0

(4)

where

E

is the electric field strength;

H

is the magnetic field strength;

D

is the electric flux density;

B

is the magnetic flux density;

J

is the current density;

ρ

is the charge density.

In general, the electromagnetic properties of a medium under the action of an electromagnetic field can also be expressed by the following relation:

B = μ H

(5)

J = σ E

(6)

D = ε E

(7)

where

σ

is the conductivity of the medium;

ε

is the dielectric constant of the medium;

μ

is the magnetic permeability of the medium.

Formulas (1) - (7) form the physical basis of the electromagnetic detection technique in this paper, and the solution of the electromagnetic detection problem can be found by combining the above formulas and by setting the boundary conditions of the specific model and applying the force.

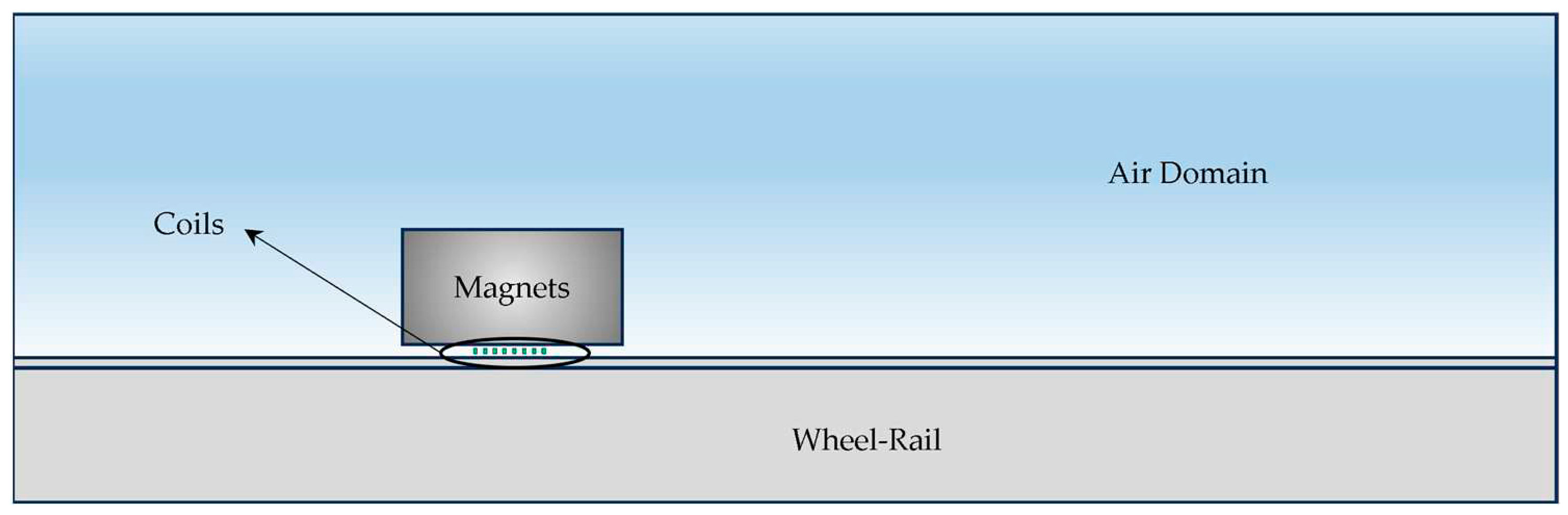
2.2. Antenna Wheel-Rail Electromagnetic Ultrasonic Inspection Mechanism

Electromagnetic ultrasonic detection mechanism is: in close proximity to the measured metal surface of the coil with high-frequency alternating current, the measured metal surface skin depth will produce a change in the electromagnetic field, and then in the surface will produce a same frequency of the induced eddy currents, the induced eddy currents in the applied bias magnetic field, resulting in the same frequency of the Lorentz force, which makes the specimen inside the point of the mass of the periodic vibration of the ultrasonic excitation, so as to detect the wheel-rail [20,21].

Electromagnetic Acoustic Transducer (EMAT) is a non-contact transducer that can be used to detect damage on the surface of an antenna wheel-rail by means of electromagnetic coupling. EMAT is a non-contact transducer, which excites and receives ultrasonic waves in a conductor by electromagnetic coupling, and can easily excite various types of ultrasonic waves. Among them, the body wave can well detect the internal defects of the specimen, but there is a blind spot for surface and near-surface defects [22]; while the energy of the surface wave is mainly concentrated in the skinning depth of the specimen surface when it is propagated, which is suitable for the detection of surface opening defects of thick plates [23,24]. The application in this paper is the detection of surface and near-surface defects by surface waves. EMAT is generally composed of a combination of a high-frequency coil, a biased magnetic field and a conductor under test. The principle is shown in Figure 2.

When the coil is passed through an alternating excitation current, a varying magnetic field is generated, and the alternating magnetic field induces eddy currents on the surface of the antenna wheel-rail, namely:

J_{W} = \nabla \times H

(8)

The Lorentz force is formed by the eddy currents in the wheel track under the action of the biased magnetic field

B

, namely:

F_{L} = J_{W} \times B_{P}

(9)

where

J_{W}

is the induced eddy current;

H

is the alternating magnetic field strength;

F_{L}

is the Lorentz force;

B_{P}

is the bias magnetic field strength.

The Lorentz force causes the mass inside the wheel-rail to vibrate, which generates ultrasonic waves. When there are no defects, the ultrasound waves propagate along the surface, and the energy attenuation on the propagation path is very small during acoustic wave detection, it allows the ultrasound guided waves to propagate over long distances on the surface of the antenna wheel-rail or inside the antenna wheel-rail. When there are defects on the surface or near surface of the wheel-rail, the ultrasonic waves encountering the defects will undergo reflection phenomena and transmission phenomena, which involves the fluctuation problem of elastic dynamics, the solution of it is based on the fundamental solution of elastic dynamics. The research models in this paper are all based on 2-D model of the antenna wheel-rail, and the assumption of 2-D plane strain problem is made here. It is assumed that the defects in the detected 2-D model are actually defective grooves in the direction of the perpendicular plate cross-section.

The following boundary integral equation for elastic dynamics can be introduced using the weighted residual method:

\frac{1}{2} [\begin{matrix} u \\ v \end{matrix}] + \int_{Γ} [\begin{matrix} T_{11} & T_{12} \\ T_{21} & T_{22} \end{matrix}] [\begin{matrix} u \\ v \end{matrix}] ds = \int [\begin{matrix} U_{11} & U_{12} \\ U_{21} & U_{21} \end{matrix}] [\begin{matrix} t_{x} \\ t_{y} \end{matrix}] ds

(10)

where

U_{jk}

and

T_{jk}

(j=1,2;k=1,2) are the elastic dynamics basis solutions, respectively represents the displacement and the surface force;

Γ

is the two-dimensional region boundary;

u

v

are the displacements in the

x

and

y

directions; and

t_{x}

t_{y}

are the surface forces of

F_{L}

in the

x

and

y

directions. According to the division of the boundary cells, the boundary equations with continuous integration over the whole boundary can be discretized into the following form:

\frac{1}{2} [\begin{matrix} u \\ v \end{matrix}] + \sum_{j = 1}^{N} \int_{Γ_{j}} [\begin{matrix} T_{11} & T_{12} \\ T_{21} & T_{22} \end{matrix}] [\begin{matrix} u \\ v \end{matrix}] d Γ_{j} = \sum_{j = 1}^{N} \int_{Γ_{j}} [\begin{matrix} U_{11} & U_{12} \\ U_{21} & U_{22} \end{matrix}] [\begin{matrix} t_{x} \\ t_{y} \end{matrix}] d Γ_{j}

(11)

where

N

is the total number of boundary cells.

Constant element is used in the boundary element program discussed in this paper. This element is geometrically represented as a straight line segment, and the physical quantity is constant on each element. Although the calculation accuracy of constant elements is not as high as that of more complex linear and higher-order elements, according to the research of Cho[25,26], the constant elements can also get better results in elastic wave problems.

If constant cells are used, the displacements and surface forces in the integral expressions contained in the boundary integral equations in discrete form can be referred to outside the integral sign, so that what needs to be solved is actually the integral of the underlying solution. The boundary integral in discrete form can be written as:

\frac{1}{2} u^{i} + \sum_{j = 1}^{N} {\hat{K}}_{ij} u^{j} = \sum_{j = 1}^{N} G_{ij} t^{j}

(12)

where:

u^{i} = {[\begin{matrix} u \\ v \end{matrix}]}^{i}

t^{j} = {[\begin{matrix} t_{x} \\ t_{y} \end{matrix}]}^{j}

{\hat{K}}_{ij} = [\begin{matrix} \int_{Γ_{j}} T_{11} d Γ_{j} & \int_{Γ_{j}} T_{12} d Γ_{j} \\ \int_{Γ_{j}} T_{21} d Γ_{j} & \int_{Γ_{j}} T_{22} d Γ_{j} \end{matrix}]

G_{ij} = [\begin{matrix} \int_{Γ_{j}} U_{11} d Γ_{j} & \int_{Γ_{j}} U_{12} d Γ_{j} \\ \int_{Γ_{j}} U_{21} d Γ_{j} & \int_{Γ_{j}} U_{22} d Γ_{j} \end{matrix}]

The unit number

i

is iterated within the unit number range

1 \leq i \leq N

(

i \in Z

), and finally

2 N

equations are obtained, which are sorted as follows:

K U = G T

(13)

where：

K = [\begin{matrix} {\hat{K}}_{11} & {\hat{K}}_{12} & \dots & {\hat{K}}_{1 N} \\ {\hat{K}}_{21} & {\hat{K}}_{22} & \dots & {\hat{K}}_{2 N} \\ ⋮ & ⋮ & ⋮ \\ {\hat{K}}_{N 1} & {\hat{K}}_{N 2} & \dots & {\hat{K}}_{N N} \end{matrix}] + \frac{1}{2} I

G = [\begin{matrix} G_{11} & G_{12} & \dots & G_{1 N} \\ G_{21} & G_{22} & \dots & G_{2 N} \\ ⋮ & ⋮ & ⋮ \\ G_{N 1} & G_{N 2} & \dots & G_{N N} \end{matrix}]

U = {[\begin{matrix} u^{1} & u^{2} & \dots & u^{N} \\ v^{1} & v^{2} & \dots & v^{N} \end{matrix}]}^{T}

T = {[\begin{matrix} t_{x}^{1} & t_{x}^{2} & \dots & t_{x}^{N} \\ t_{y}^{1} & t_{y}^{2} & \dots & t_{y}^{N} \end{matrix}]}^{T}

The solution of the elements of the coefficient matrices

K

and

G

needs to be discussed in two cases: 1) when

i \neq j

K

and

G

contain non-singular integrals, which can be solved directly by using the Gaussian product formula machine; 2) when

i = j

, the integrals in

K

and

G

have singularities at

r = 0

, which have to be dealt with in a special way.

After obtaining all the coefficients of the complex coefficient matrices

K

and

G

, it is necessary to introduce the boundary conditions to obtain the system of linear equations for the final required solution. The hybrid boundary element model of a rectangular defective slot is shown in Figure 3. Ultrasonic waves propagate within the elastic flat plate interface, the upper and lower surfaces of the plate and the defects are free boundaries with a surface force of 0; the so-called virtual boundary is established a certain distance away from the left and right sides of the defects, and the virtual boundary and the free surfaces together form a closed model area; the appropriate frequency thickness product is selected according to the design, so that a single-mode RAM wave is incident from the left virtual boundary into the model area and interacts with the defects, a part of the RAM wave reflects back to the left. The single mode Lamb wave is incident from the left virtual boundary and interacts with the defects, part of the Lamb wave is reflected back to the left virtual boundary, and the other part of the Lamb wave is transmitted to the right virtual boundary.

When a symmetric or antisymmetric mode Lamb wave of a certain frequency thickness and order is input to the left virtual boundary of the model as an incident mode, the reflection and transmission modes obtained after the interaction of the incident mode and the defect may contain any mode that can exist at that frequency thickness, as determined by the dispersion curve. For a linear material, the total displacement of the left boundary should be the sum of the incident mode displacements and the displacements of all possible reflection modes, expressed as follows:

u^{A} = u^{1} + u^{B S}

(14)

Similarly the right boundary displacement should be the sum of the displacements of all possible transmission modes with the following expression:

u^{A} = u^{F S}

(15)

where

u^{A}

is the total displacement;

u^{B S}

is the reflection mode displacement;

u^{F S}

is the transmission mode displacement.

3. Numerical Simulation and Result Analysis

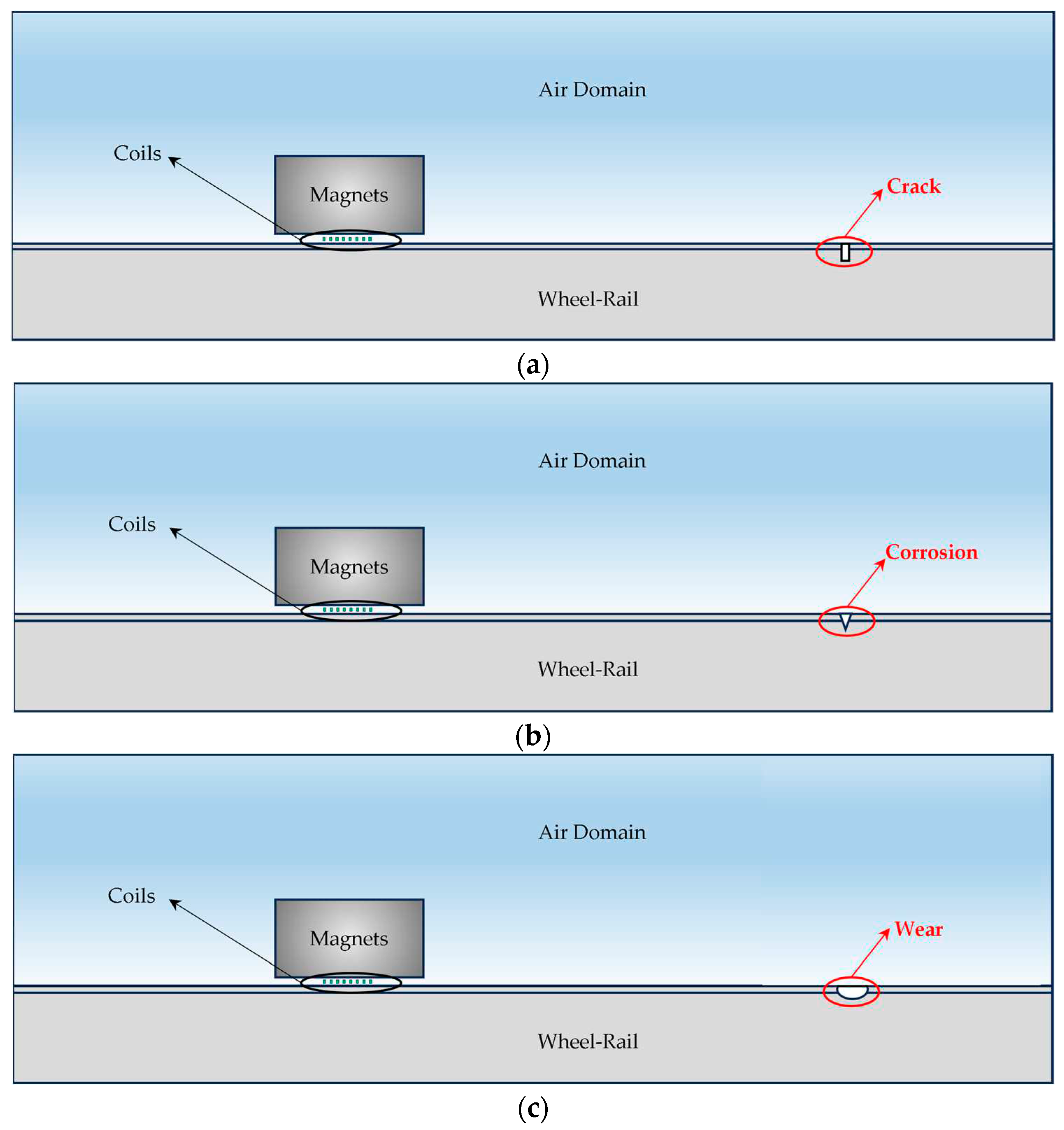
3.1. Antenna Wheel-Rail and Damage Forms

Large wheel-rail antenna azimuth track shown in Figure 4, its installation is generally divided into two kinds: splicing track technology and overall welding technology, different welding methods affect the service life of the track and pointing accuracy. Small aperture precision requirements are not high radio telescope usually use spliced track technology, segmented spliced track cost is low, but there are shortcomings such as stress concentration at the welded joints, and the overall rigidity of the track is poor, it is prone to serious deformation under the action of a large load, which results in a decline in precision [27]. The large-diameter, high-precision radio telescope track gradually adopts the overall welding technology, and the overall welding can reduce the welding deformation and shrink the weld, which in turn reduces the unevenness of the wheel-rail and improves the pointing accuracy of the wheel-rail. Most of the large antenna wheel-rail surface materials are made of forged 42CrMo and other structural steels, which are quenched and tempered by surface quenching and tempering, and have good contact strength and bending strength, but the carbon content and alloying elements in this type of material are high, which are prone to hot cracking, cold cracking, and delayed cracking.

Large wheel-rail type antenna seat frame is to use the friction between the roller and the track for transmission, so in the use of the antenna in the process of the roller and the track often have a great contact force between the wheel, will occur in the wheel-rail surfaces rolling contact fatigue, which is specifically manifested in the surface or sub-surface micro-cracks, and then continued to expand. In actual engineering, the material surface or internal defects will greatly reduce the load threshold of rolling contact fatigue, is the most common cause of failure. The final form of rolling contact fatigue of the wheel-rail is the fracture of the wheel-rail material, which can seriously affect the normal operation of the antenna. Through the research and analysis of the working damage situation of wheel-rails of radio telescopes in various countries, the wheel-rails of large aperture radio telescopes generally experience the following types of damage on the surface [4,5,6,7,8,9,10,11,12]:

Wheel-rail wear: wheel-rail surface contact force is too large, the roller in the track after a long period of operation will produce track surface wear, reduce the precision of the track;
fatigue cracks: roller and track long-term role, a point of stress concentration, gradually sprouting cracks;
wheel-rail corrosion: by the working environment as well as the influence of climate, the track surface is corroded, which seriously affects the precision of the wheel-rail, thus affecting the normal work of the antenna.

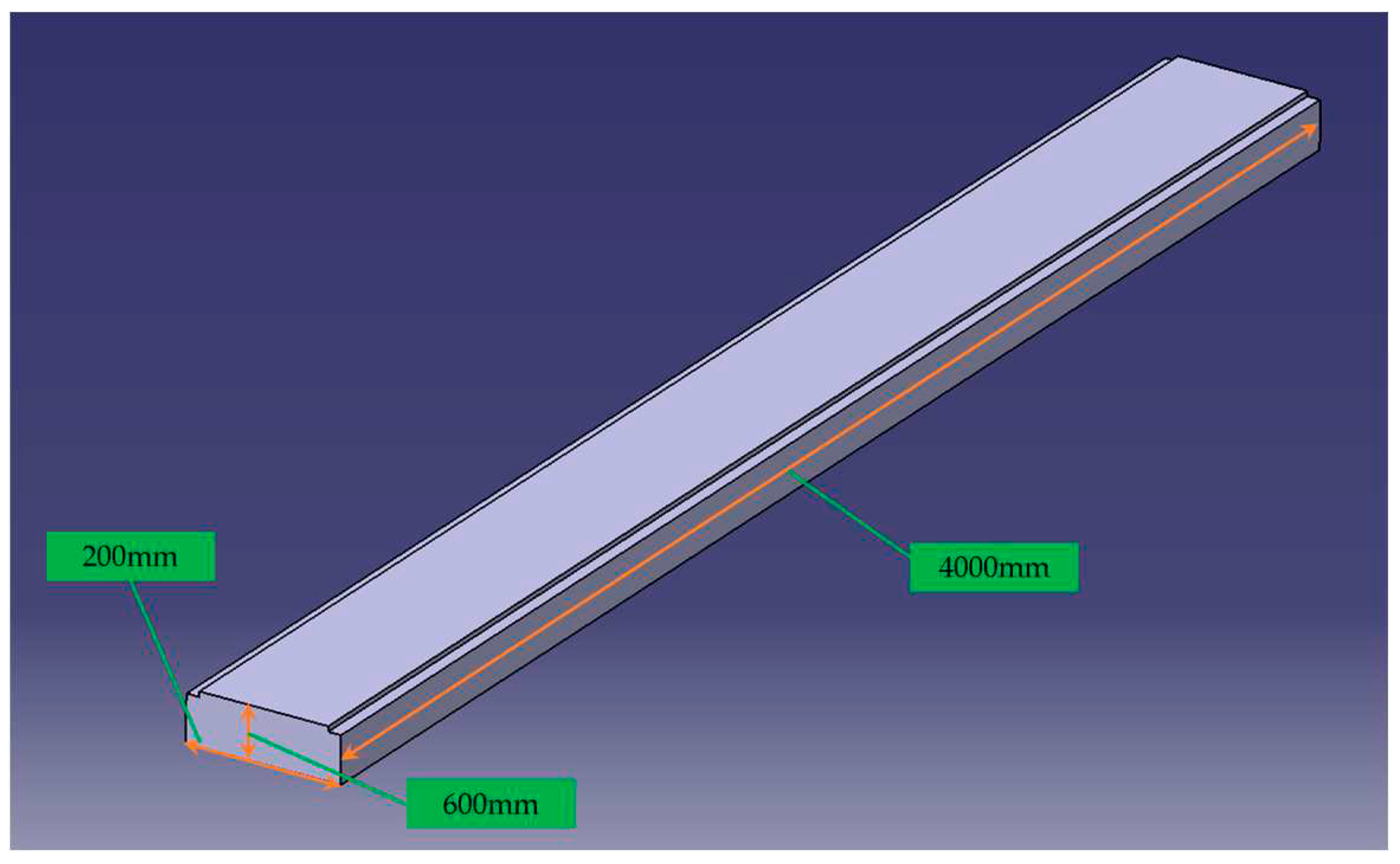
3.2 Construction of The Wheel-Rail Model

This paper focuses on the 110-meter aperture fully movable radio telescope QTT as the research object, and the simulation model is established based on the QTT. The QTT is a sharp tool for future astronomical research in radio astronomy in China, and it is also the basic support and necessary condition for the breakthrough of cutting-edge technology, and it has a significant role for China's modern astronomy to enter into the ranks of the world's advanced. The track of the QTT is made of a number of single-segment wheel rails spliced together, with each segment of the size of the wheel-rail is 4000mm*600mm*200mm (4m*0.6m*0.2m) [28]. According to the parameters of the antenna wheel-rail, the ideal 3-D wheel-rail model is established. Considering the overall structural layout of the track, the circular arc of the single section of the track is shorter, and in order to simplify the modeling process, the circular arc is ignored and only a part of the single section of the wheel-rail is selected for modeling, which effectively simplifies the model of the wheel-rail [5,29]. Figure 5 shows the schematic diagram of the wheel-rail model structure.

The purpose of this paper is to study the surface defects of the wheel-rail, so a simplified 2D wheel-rail model with a length of 200mm and a width of 10mm is established by intercepting 1/20 of the cross-section of a single section of QTT wheel-rail. Through the analysis of the basic theory of electromagnetic ultrasonic detection, the research in this paper is mainly based on the Lorentz force mechanism, the Lamb wave is excited on the surface of the wheel-rail, and the corresponding excitation frequency is selected according to the dispersion curve in order to avoid too much clutter affecting the results. In this paper, a single probe is used to realize the excitation and reception of ultrasonic waves, and the probe is placed at the left end of the specimen at a distance of 60mm.The two-dimensional simplified model of the QTT wheel-rail is shown in Figure 6.

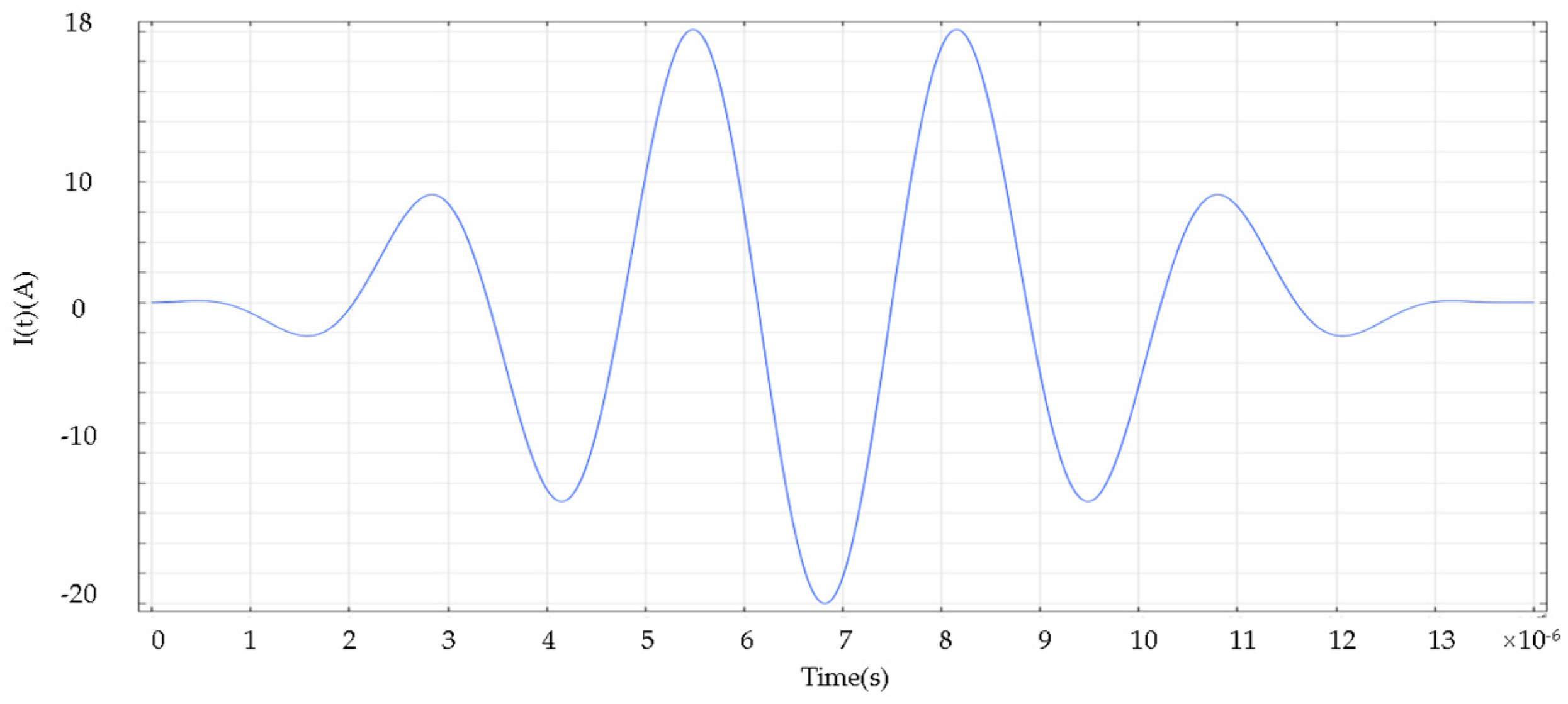
3.3 Electromagnetic Ultrasonic Excitation Process

In this paper, COMSOL Multiphysics finite element software is used as a carrier to study and analyze the established antenna wheel-rail model, which is divided into the following three phases:

Establish a simplified geometric model of the antenna wheel-rail. A low-reflection boundary is applied to the left and right boundaries of the model, and the reflections from the structural boundaries are neglected. The grid is divided into more than three layers in the skin depth, and other parts are appropriately coarsened;
Establish the electromagnetic field model. Set the appropriate step size and error in the transient solution to ensure the correctness and stability of the solution;
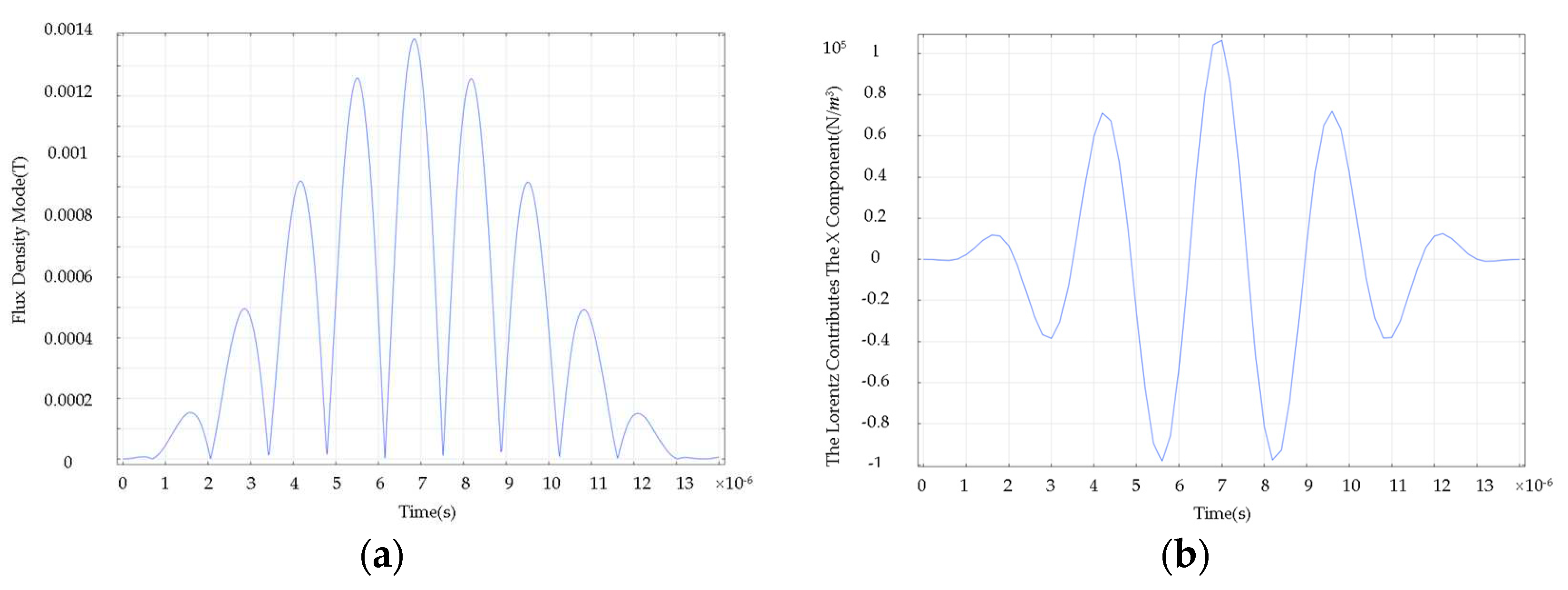
Establish the acoustic field model. This part uses the solid mechanics module to add the Lorentz force to realize the transformation of magnetic field to force field;
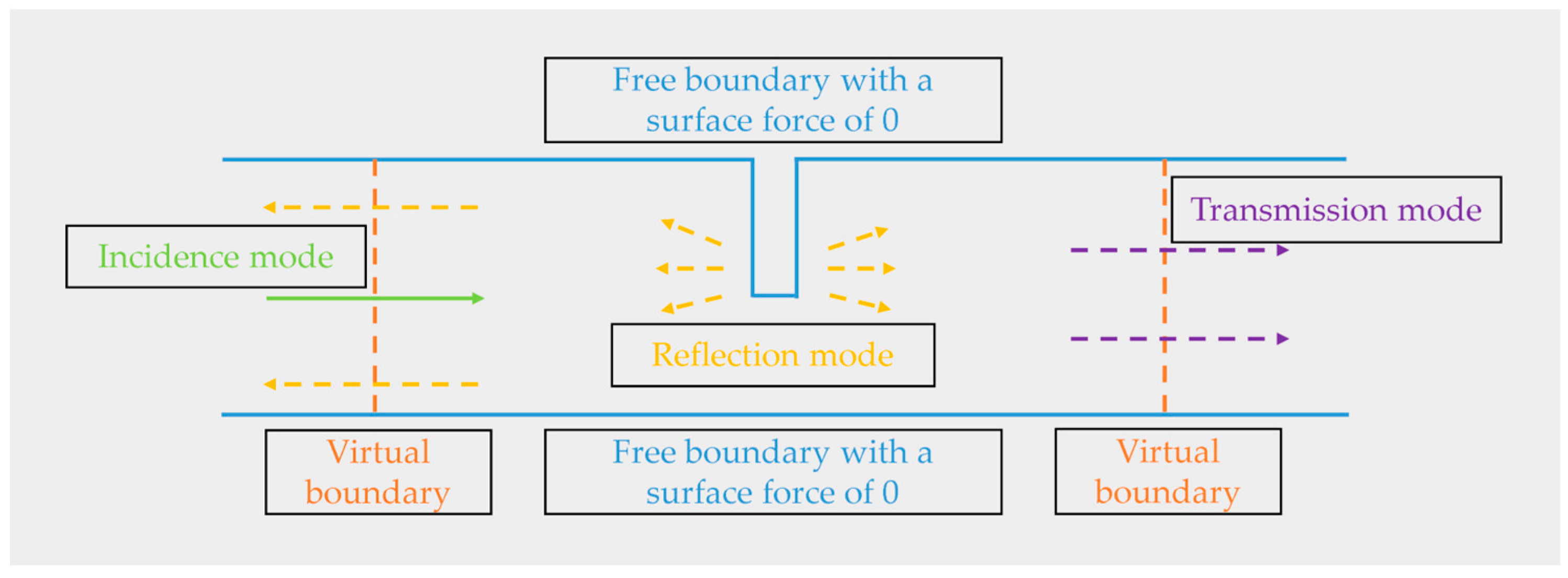
Multi-physics field coupling setup. The Lorentz force coupling setup is performed within the skin convergence depth of the specimen. The conversion of electric field-magnetic field-force field is realized by the above operations. The finite element simulation principle is shown in Figure 7.

In the process of solving the differential equations of the electromagnetic field, boundary conditions are set for the conductor under test. According to the excitation mechanism of electromagnetic ultrasound, an alternating current is used to apply excitation to the coil while neglecting the hysteresis effect and other secondary factors. The form of the excitation current is shown in Figure 8.

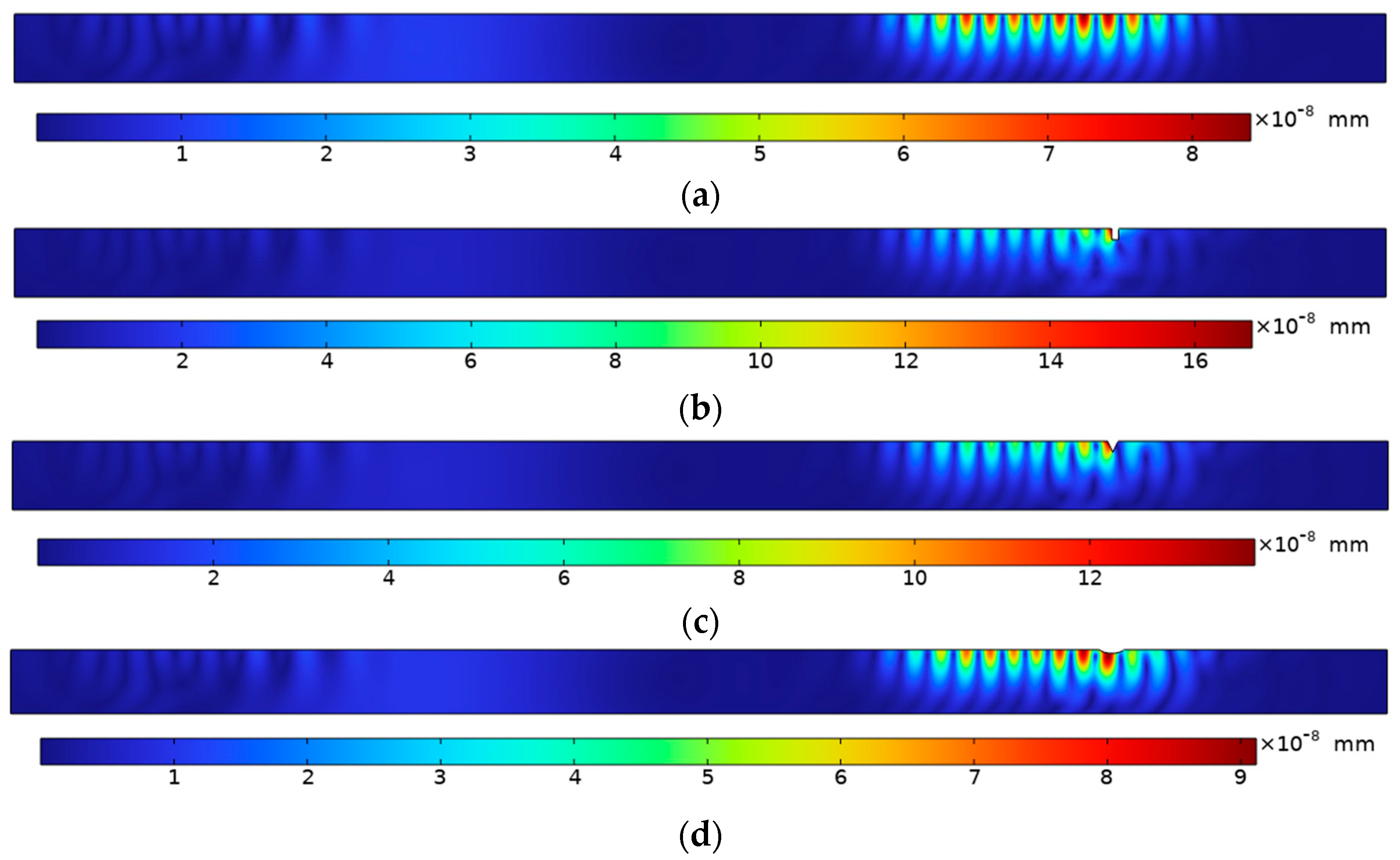
3.4 Setting of Wheel-Rail Surface Damage

For the possible defects on the surface of antenna wheel-rails, we constructed models of surface cracks, surface corrosion, surface wear, and intact wheel-rails. Liu Suzhen and HD Jeong et al. used rectangular slots instead of actual crack defects of aluminum plates in the detection of unidirectional surface waves on tiny defects of aluminum plates, with the width of the crack defects being 0.2 mm and the depth being 0.3 mm. The relationship between the defects and the reflection coefficient was analyzed by simulation, and the fitted curves were plotted, which well express the function relationship between the depth of the cracks and the reflection coefficient [30,31,32]; Ren XiaoKe also used rectangular slots instead of crack damages and triangular slots instead of corrosion damages in the simulation, simulation used rectangular slots instead of crack damage and triangular slots instead of corrosion damage, and through the detection of cracks, it was found that the detection rate of open defects was high [33]. Drawing on the previous research ideas, this paper adopts rectangular groove equivalent to the actual wheel-rail crack damage in the simulation analysis [30,31,32]; corrosion usually corrodes downward from the middle point and then expands to both sides, so the simulation adopts inverted triangular groove equivalent to the actual wheel-rail corrosion damage [33]; the wear is usually a concave arc, and elliptical groove equivalent to the actual wheel-rail wear damage is adopted in the simulation [34]. By analyzing and comparing the model results without defects and the simulation results of several defects, the existence of defects and the location of defects can be judged more clearly and intuitively.

The model with or without defects is based on selecting 1/20 of the QTT wheel-rail as the object of study, and setting a rectangular defect of 1mm*2mm at 140mm from the left end of the specimen to simulate defects such as weld seams or stress cracks with sharper shapes; when cracks and other sharp defects are taken into account, the antenna is affected by the climate and the working environment in practice, and a large number of defects are also formed due to construction defects or corrosion and other problems. And the formation of pit-type defects, so designed a width of 2mm, depth of 2mm triangular defects in the distance from the left end of the specimen 160mm; Finally, taking into account the surface of the wheel-rail surface force is large, often occurring a certain amount of abrasion and slippage, so a defect with 2mm long half-axis and 1mm short half-axis was set at 160mm from the left end of the specimen to represent damage such as wear and tear [35,36]. The three defects are shown in Figure 9a–c.

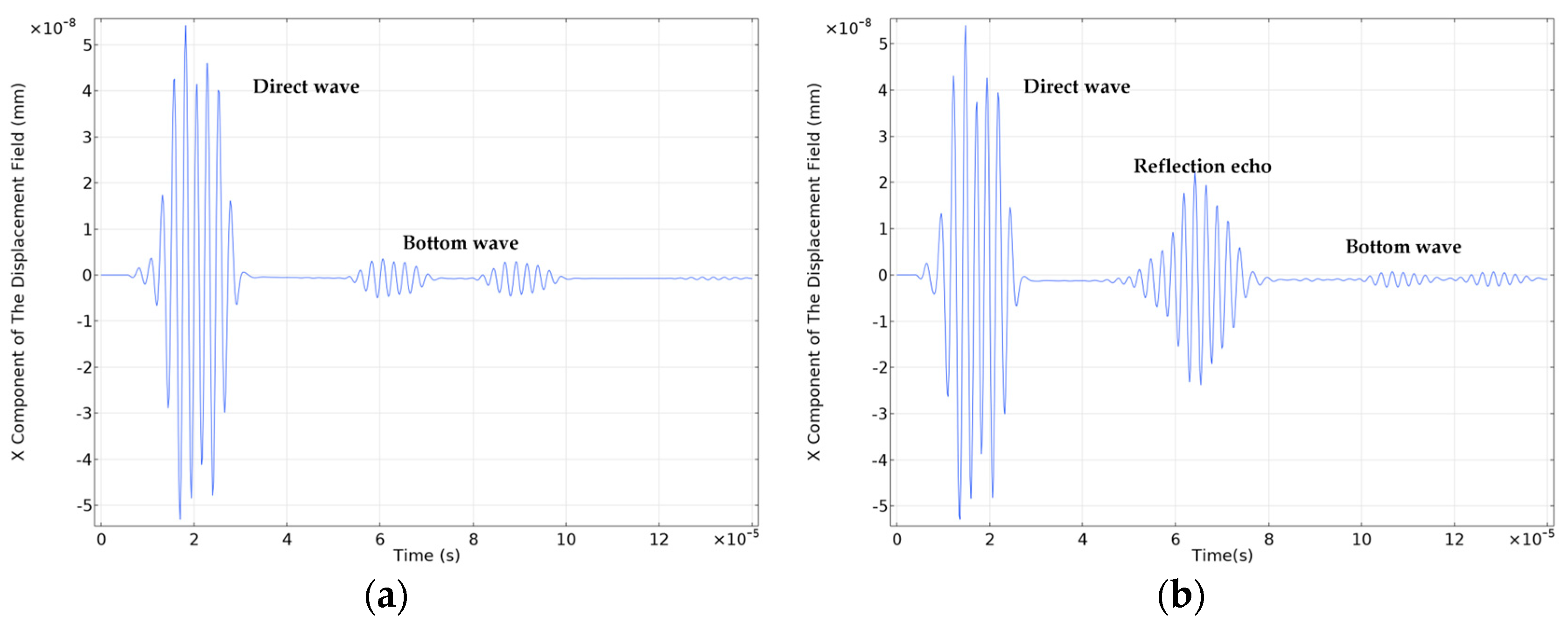
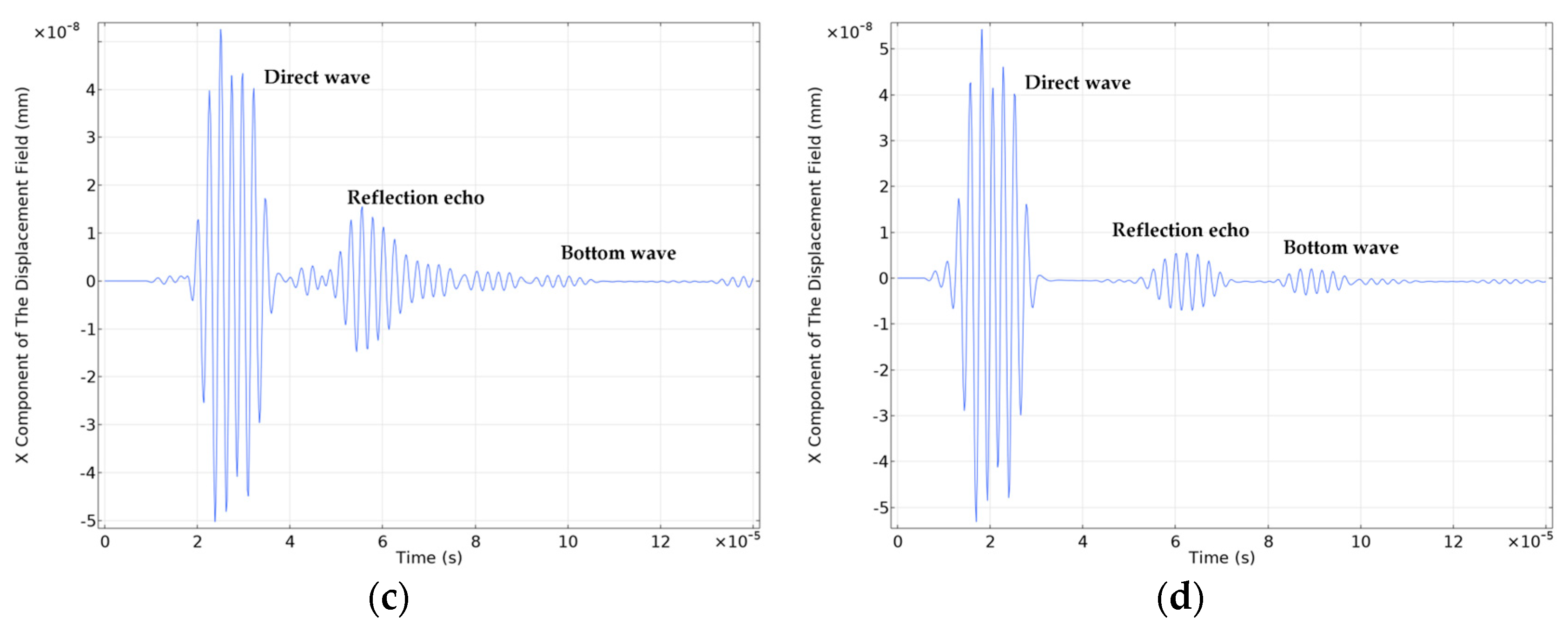
3.5 Wheel-Rail Damage Detection and Analysis

When the coil is excited by an alternating current source, an alternating electromagnetic field

H

is generated, and the magnetic induction of the alternating magnetic field is shown in Figure 10a. A biased magnetic field of

B_{0} = 1.0 T

is added to the air, and the induced eddy currents are subjected to a Lorentz force in the X-direction due to the biased static magnetic field, the amplitude of which varies with the strength of the eddy currents as shown in Figure 10b.

Figure 11a–d shows the 2-D cloud plots of the total displacement magnitude of the four simplified models of the wheel-rail at the moment of T=3.8E-5s. It is clear from the simulation results that the Lorentz force vibrates the internal plasmas of the wheel-rail, thus generating ultrasonic waves. Regardless of the presence of defects, the modes of the ultrasonic waves propagating to the left side are the same and are not affected by the defects. When there is no defect in the wheel-rail, the mass displacement continues uniformly in one direction, the ultrasonic waves propagate along the surface of the wheel-rail without reflection or transmission, and there is very little energy attenuation in the propagation path during acoustic wave detection, which allows the ultrasonic guided waves to propagate over long distances on the surface of the antenna wheel-rail or internally. When there are defects on the surface or near the surface of the wheel-rail, ultrasonic waves encountered by the defects will occur in the attenuation of energy, as well as the phenomenon of reflection and transmission phenomena. From the Formula (10)–(13), when there is a defect, the free boundary changes, the displacement

u

v

and surface force

t_{x}

t_{y}

size changes, the displacement size also changes; Figure 11b–d displacement amplitude relative to Figure 11a displacement amplitude increased a lot, this is because ultrasonic waves encountered defects after the reflection of the superposition of the result, and the deeper the depth of the defect the greater the amplitude of the displacement. Combined with Formulas (14) and (15), it can be seen that the total displacement of the left boundary of the defect is the sum of the displacements of the incident mode and all possible reflection modes, and the total displacement of the right boundary is the sum of the displacements of all possible transmission modes.

A point A (90, 10) is set on the surface of each model, and Figure 12a–d show the waveforms of the displacement X component at point A under the four models. It is generally recognized that the reflected wave between the start wave (direct wave) and the bottom wave is a defective wave. When there is no defect on the surface of the wheel-rail, there is only the beginning wave and the bottom wave; when there is a small defect on the surface of the wheel-rail, there is a defect in addition to the beginning wave and the bottom wave, and the defect wave and the bottom wave exist at the same time. Figure 12a shows the displacement waveform at point A when there is no defect, only the first wave packet can be observed as a direct wave, with an amplitude of 5.4×10-8mm, and the second and third wave packets are the primary bottom wave and the secondary bottom wave. Figure 12b shows the displacement waveform of point A under the crack defect, the first wave packet is a direct wave with an amplitude of 5.3×10-8mm, the second wave packet is a reflected wave reflected back after the defect with an amplitude of 1.3×10-8mm, and the wave packet after the defect wave is a bottom wave. Figure 12c shows the displacement waveform of point A under the corrosion defect, the first wave packet is the direct wave with the amplitude of 5.2×10-8mm, the second wave packet is the reflected wave reflected back through the defect with the amplitude of 1.8×10-8mm, and the wave packet after the defect wave is the bottom wave. Figure 12d shows the displacement waveform of point A under the wear defect, the first wave packet is the direct wave with the amplitude of 5.4×10-8mm, the second wave packet and the third wave packet are the reflected wave reflected back through the defect with the amplitude of 0.8×10-8mm, and the wave packet after the defect wave is the bottom wave. Through the Figure 12 b–d, it can be clearly seen that the direct wave is stronger than the reflected wave, and the bottom wave also changes with the defect, and the reflected wave can be analyzed to obtain the characteristics of the defect.

By comparing the three diagrams of Figure 12 b–d, it can be seen that Figure 12b is the waveform diagram of crack damage model on the surface of the wheel-rail, and its defective echo is higher, with more peaks, sharp and steep; Figure12c is the waveform diagram of corrosion damage model on the surface of the wheel-rail, and its defective echo is broader, steeper and straighter, and there is obvious dendritic shape; Figure 12d is the waveform diagram of abrasion damage model on the surface of the wheel-rail, and its defective echo is lower, with broader and sawtooth-shaped waveforms. Comparison of the three kinds of defective waves shows that with the increase of defect width, the reflected wave packet width also increases; with the increase of defect depth, the reflected wave packet amplitude also increases. Therefore, it can be concluded that when the width of the reflected wave packet is wider, it means that the defect width is longer, which affects the duration of the reflected wave; when the amplitude of the reflected wave is smaller, it means that the depth of the defect is shallower, and the surface wave can be easily transmitted from the shallower defect; when the depth of the defect is increased, the amplitude of the reflected wave is increased, which means that the deeper the defect is, the easier it is for the surface wave to be reflected back.

The waveform diagram can clearly determine the defects and the characteristics of the defects. The model and parameters need to be further optimized subsequently, so as to obtain more accurate defect information. In this paper, the first electromagnetic ultrasonic detection method for antenna wheel-rail surface defects is proposed. The current stage focuses on the simulation analysis of antenna wheel-rail surface defects and verifies the feasibility of the method. The theoretical phase of the study is started first, followed by further experimental research and analysis on the basis of the theoretical study.

4. Conclusions

This paper summarizes and analyzes the azimuthal track surface damage forms of large wheel-rail type antennas, and proposes for the first time to use electromagnetic ultrasonic nondestructive testing methods to detect antenna wheel-rail damage. The combination of theoretical analysis and numerical simulation is used to simulate and analyze different types of defects. By comparing the results of different models, the defects and the characteristics of the defects can be clearly determined, and the results show that the method can effectively detect the damage of the antenna wheel-rail surface, which can provide an important reference for the research of wheel-rail damage detection of large radio telescope.

Author Contributions

Conceptualization, Y.B. and C.J.; methodology, Y.B. and C.J.; software, C.J.; validation, Y.B., C.J. and S.F.; formal analysis, Y.B. and S.F.; data curation, Y.B. and C.J.; writing—original draft preparation, C.J.; writing—review and editing, Y.B., C.J. and S.F.; visualization, Y.B. and C.J.; supervision, Y.B. and S.F.; funding acquisition, Y.B. and S.F. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the National Natural Science Foundation of China (NSFC) (Grant no: 52165053); the China Postdoctoral Science Foundation (Grant no: 2021M702751); the Natural Science Foundation of Xinjiang Uygur Autonomous Region (Grant no: 2022D01C683); the Doctor Scientific Research Project of Xinjiang University(Grant no: 620320037); the Guangdong Basic and Applied Basic Research Foundation (2020A1515111043, 2023A1515010703).

Data Availability Statement

Not applicable.

Acknowledgments

We authors would like to express our gratitude to the Xinjiang Astronomical Observation, Chinese Academy of Sciences, Urumqi 830011, China. Additionally, we authors would like to express our appreciation to the anonymous reviewers for their insightful and constructive feedback, which greatly helped in improving the overall quality of this work.

Conflicts of Interest

The authors declare no conflict of interest.

References

de Pater, I.; Molter, E.M.; Moeckel, C.M. A Review of Radio Observations of the Giant Planets: Probing the Composition, Structure, and Dynamics of Their Deep Atmospheres. Remote Sens. 2023, 15, 1313. [CrossRef]
Wang, N. Xinjiang Qitai 110 m radio telescope. Scientia Sinica Physica, Mechanica & Astronomica. 2014, 44, 783-794. [CrossRef]
Xu, Q.; Wen, H.X.; Wang, N.; Li, L. Development challenges for the Xinjiang 110 m radio telescope (QTT) high accuracy panel structures. Scientia Sinica Physica, Mechanica & Astronomica. 2017, 47, 8-18. [CrossRef]
Gao, Y.L.; Wang, P.; Tian, G.Y.; Hao, S.S.; Xiong, L.H.; High-Speed Online Inspection Techniques of Rail Crack Defects Based on Electromagnetic Principle. NDT. 2012, 34, 1-11.
Wan, S.G.; Kon, D.Q.; Chen, Z.P. Contact in Wheel-Rail Systems for Large Radio Telescopes: A Review. Astronomical Research and Technology. 2014, 11, 27-33.
Liu, X.; AILI, Y.; Xiang, B.B.; Wang, C.S.; Xu, Q.; Wang, J. Analysis and Correction of the Influence of the Track Irregularity on Antenna Pointing. ACTA ASTRONOMICA SINICA. 2017, 58, 49-59.
Wu, J.; Wang, B. Influence of track irregularity on the pointing accuracy for large reflector antenna. Journal of Terahertz Science and Electronic Information Technology. 2017, 15, 634-639.
Kan, F.W.; Antebi, J. Slip and wear in multilayer azimuth track systems. Proceedings of SPIE. 2004, 549587. [CrossRef]
Prestage, R.M.; Maddalena, R.J. The Green Bank Telescope: current status and early results. Large Ground-Based Telescopes. SPIE. 2003, 4837, 944-953. [CrossRef]
Gu, J.X. Research on the antenna pointing error of 25m radio telescope. Annals of ShangHai Observatory Academia Sinica. 1994, 205-211.
Anderson, R.; Symmes, A.; Egan, D. Replacement of the Green Bank Telescope azimuth track. Proceedings of SPIE the International Society for Optical Engineering. 2008, 63, 3026-3030.
Symmes, A.; Anderson, R.; Egan, D. Improving the service life of the 100-meter green bank telescope azimuth track. In Ground-based and Airborne Telescopes. SPIE. 2008, 7012, 1225-1236. [CrossRef]
Juneja, G.; Kan, F.W.; Antebi, J. Update on slip and wear in multi-layer azimuth track systems. Proceedings of SPIE. 2006, 627318. [CrossRef]
Smith, D.R. Achievable alignment accuracy and surface hardness of a large welded azimuth track. Proceedings of SPIE. 2006, 627314. [CrossRef]
Antebi, J.; Kan, F.W. Precision continuous high-strength Azimuth track for large telescopes. San Jose: International Society for Optics and Photonics. 2003, 612-623. [CrossRef]
Guo, H.W. Analysis of Surface Crack on Wheel of a Rail Type Pedestal of Radar. Proceedings of the 2008 Electronic Machinery and Microwave Structure Technology Conference. 2008, 270-272.
Kalker, J.J. On the rolling contact of two elastic bodies in the presence of dry friction. 1967.
Kalker, J.J. Simplified theory of rolling contact. Delft Progress Rep. 1973, 1, 1-10. [CrossRef]
Huray, P.Y. Maxwell's equations. John Wiley & Sons. 2011.
Huang, S.L. Electromagnetic ultrasonic guided wave theory and application. Tsinghua University Press. 2013.
Ribaric.; Marijan. Conservation laws and open questions of classical electrodynamics. Singapore: World Scientific. 1990. [CrossRef]
Pei, C.; Fukuchi, T.; Zhu, H.; Koyama, K.; Demachi, K.; Uesaka, M. A study of internal defect testing with the laser-EMAT ultrasonic method. IEEE transactions on ultrasonics, ferroelectrics, and frequency control. 2012, 59, 2702-2708. [CrossRef]
Wang, S.J.; Kang, L.; Li, Z.C.; Zhai, G.; Zhang, L. 3-D modeling and analysis of meander-line-coil surface wave EMATs. Mechatronics. 2012, 22, 653-660. [CrossRef]
Zhang, Z.G.; Que, P.W.; Lei, H.M. Electromagnetic transducers for surface wave generation and their electroacoustic characteristics. Technical Acoustics. 2006, 25, 119-123.
Cho, Y.; Rose, J. A Boundary Element Solution for a Mode Conversion Study on the Edge Reflection of Lamb Waves. Journal of the Acoustical Society of America. 1996, 99, 2097-2109. [CrossRef]
Cho, Y.; Rose, J. An Elastodynamic Hybrid Boundary Element Study for Elastic Guided Wave Interactions with a Surface Breaking Defect. International Journal of Solids and Structures. 2000, 37, 4103—4124. [CrossRef]
Kong, D.Q. National Astronomical Observatories 50-meter radio antenna. National Astronomical Observatories data. 2008.
Xu, Q.; Hu, G.X.; Prediction of multi-layer and multi-pass welding Angle deformation under gravity bending moment of QTT antenna orbit. Transactions of The CHTNA Welding Institution. 2020, 41, 10-13+97-98.
Shi, H.Q.; Xu, Q.; Wang, N.; Wang, Z.J. Finite Element Analysis of Wheel-on-track Rolling Contact for Large Aperture Radio Telescope. Astronomical Research & Technology. 2022, 19, 95-102.
Liu, S.Z.; Dong, S.; Fang, Z.; Zhang, C. Tiny defect detection of aluminium plate by ultrasonic unidirectional surface electromagnetic wave. Technical Acoustics. 2019, 38(03).
Liu, S.Z.; Wang, S.J.; Zhang, C.; Jin, L.; Yang, Q.X. Simulation Analysis of Electromagnetic Acoustic Surface Wave of Steel Plate and Quantitative Defect Detection. Transactions of CHINA Electrotechnical Society. 2020, 35, 97-105.
Rose, J.; Shin, H.; Jeong, H. Detection of Defects in a Thin Steel Plate Using Ultrasonic Guided Wave. Proceedings of 15th World Conference on Non Destructive Testing, Rome. 2000.
Ren, X.K.; Li, J. Simulation research on electromagnetic acoustic NDT by ANSYS. Electronic Measurement Technology. 2008, 31, 26-28.
Bosso, N.; Magelli, M.; Zampieri, N. Simulation of wheel and rail profile wear: a review of numerical models. Railway Engineering Science. 2022, 30, 403-436. [CrossRef]
Zhang, Y.S.; Huang, S.L.; Zhao, W. Detection System About Steel Cracks Based on Electronic Ultrasonic. NDT. 2009, 31, 307-310.
Gharaibeh, Y.; Sanderson, R.; Mudge, P.; Ennaceur, C.; Balachandran, W. Investigation of the behaviour of selected ultrasonic guided wave modes to inspect rails for long-range testing and monitoring. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit. 2011, 225, 311-324. [CrossRef]

Figure 1. Typical wheel-rail radio telescope. (a) GBT wheel-rail antenna; (b) wheel-rail system for GBT antenna.

Figure 2. EMAT schematic.

Figure 3. Boundary element action mechanism diagram.

Figure 4. Azimuthal track for large wheel-rail antennas.

Figure 5. Simplified 3D model of the QTT wheel-rail.

Figure 6. QTT wheel-rail 2D simplified model.

Figure 7. Principle of finite element simulation.

Figure 8. Excitation current signal waveform.

Figure 9. Simplified model of wheel-rail for three defects. (a) Wheel- rail surface crack modeling; (b) Wheel-rail surface corrosion modeling; (c) Wheel-rail surface wear modeling.

Figure 10. (a) Magnetic induction of an alternating magnetic field; (b) Lorentz force.

Figure 11. 2-D cloud plot of total displacement of four simplified models of wheel-rail at T=3.8E-5s. (a) No-Defect wheel-rail model displacement; (b) Crack Defect wheel-rail model displacement; (c) Corrosion Defect wheel-rail model displacement; (d) Wear Defect wheel-rail model displacement.

Figure 12. 2-D cloud plot of total displacement of four simplified models of wheel-rail at T=3.8E-5s. (a) No-Defect wheel-rail model displacement; (b) Crack Defect wheel-rail model displacement; (c) Corrosion Defect wheel-rail model displacement; (d) Wear Defect wheel-rail model displacement.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Method for Detecting Surface Damage of Large Reflector Antenna Wheel-Rail Based on Electromagnetic Ultrasonic Technology

Abstract

1. Introduction

2. Principle and Method of Electromagnetic Ultrasonic Testing

2.1. Basic Principles of Electromagnetic Ultrasonic Testing

2.2. Antenna Wheel-Rail Electromagnetic Ultrasonic Inspection Mechanism

3. Numerical Simulation and Result Analysis

3.1. Antenna Wheel-Rail and Damage Forms

3.2 Construction of The Wheel-Rail Model

3.3 Electromagnetic Ultrasonic Excitation Process

3.4 Setting of Wheel-Rail Surface Damage

3.5 Wheel-Rail Damage Detection and Analysis

4. Conclusions

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe