Prerpints.org logo
Preprint
Article

Local Ratcheting at the Notch Region of Non-press-Fitted and Press-Fitted Al 7075-T6 Samples Undergoing Asymmetric Stress Cycles

Altmetrics

Downloads

73

Views

19

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

31 July 2023

Posted:

02 August 2023

You are already at the latest version

Alerts
Abstract
The present study evaluates ratcheting response of notched and press-fitted Al 7075-T6 specimens under stress-controlled asymmetric cycles. The degree of interference fit (DIF) directly influenced progressive plastic strain magnitude and rate at notch root region. Local ratcheting at the hole-pin interference region was analyzed by means of two kinematic hardening rules of Ahmadzadeh-Varvani (A-V) and Chaboche coupled with the Neuber rule. Ratcheting strains at notch root of aluminum samples with DIF=0 (non-press-fitting samples) were measured to be highest in magnitude. For the press-fitted samples, however ratcheting strains dropped noticeably as DIF increased from 1% to 2%. Press-fitted samples plastically deformed the perimeter edge of notches and improved materials locally at the notch edge, resulting in a better resistance against ratcheting progress. Local ratcheting at different distances of 0.5, 1.3 and 3.0 mm from the notch root were evaluated for both pinned and unpinned samples through the hardening rules and compared with those of measured values. The predicted ratcheting curves by means of the A-V and Chaboche hardening rules closely agreed with experimental data and respectively positioned above and below the measured data.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

The common approach for joining numerous important components in aerospace applications has been detachable mechanical joints of fastening and riveting. As a result of stress (and strain) concentration during service, fatigue cracks begin to form and spread from the fastener holes leading to failure of load-bearing components in-service. To alleviate the chance of premature failure, several techniques of clamping force application [1,2], cold expansion [3,4], interference fit [5,6], and combination of approaches [7,8] have been developed over last few decades. During part assembly, a larger fastener pin or bolt is put into the notch to create an interference fit (IF) around the notch. Interference fit is largely employed in automotive, aerospace, and manufacturing industries. The IF induces residual stresses on the hole-pin interface which can highly improve fatigue and ratcheting resistance of components undergoing stress cycles. The interaction of both notch and loading spectrum highly affects the plastic strain accumulation over the loading cycles in the interference and notch region. Ratcheting phenomenon refers to a progressive plastic strain under loading cycles with non-zero mean stress. Local ratcheting and stress relaxation at notch roots of metallic parts [9,10,11,12,13] have been studied lately. However, literature lacks a thorough ratcheting analysis at the hole-pin region. Varvani and coworkers [9,10] investigated local ratcheting at the notch root of 1045 steel plates with different-sized circular notches. They argued on how local ratcheting strain and its rate change as stress cycles proceeded. Local ratcheting and stress relaxation of notched samples were studied through use of a hardening framework controlling plastic strain progress over loading cycles [11]. Shekarian and Varvani [10,11,12,13] examined the ratcheting and stress relaxation at notch roots of steel plates through coupling the Chaboche [15] and A-V [16] kinematic hardening models and the Neuber rule [14]. They further employed these hardening frameworks along with Neuber rule to assess ratcheting at the roots of various elliptical and circular notches in 316 stainless steel specimens [13]. Steel specimens subjected to asymmetric loading cycles were studied by Wang and Rose [17]. To define the plastic shakedown rate while loading cycles continued, they proposed an integral approach. According to Hu et al. [18], local ratcheting and the rate of stress relaxation were intensified at the notch root as applied strain increased. They provided data on ratcheting and stress relaxation at notch roots that were consistent with predictions made using the Chaboche hardening rule. Ratcheting tests were carried out by Rahman and Hassan [19] on notched 304L steel plates with different notch geometries/ forms to assess the ratcheting response of notched specimens. They employed various hardening criteria developed by Chaboche [15], Ohno-Wang [20], and AbdelKarim-Ohno [21]. They reported that the simulated ratcheting values by Chaboche’s model closely agreed with experimental data at notch root. Firat [22] measured local strains at notched 1070 steel specimens through use of strain gauges mounted at the vicinity of notch roots. He used Neuber's rule and the Chaboche model to measure plastic strain values over asymmetric axial-torsional loading cycles. The local ratcheting strain prediction values at the notch root of 1070 steel specimens were found to be comparable to the observed values published in reference [23]. Liu et al [24] conducted cyclic tests on austenitic stainless steel elbow pipes. The local strains on the perimeter of pressurized elbows were measured using strain gauges installed around the diameter of elbow pipes closely agreed with those predicted through use of the Chen-Jiao-Kim (CJK) model [25]. In a recent study, Hatami and Varvani [26] assessed local ratcheting at notch root of 1045 steel samples subjected to uniaxial asymmetric loading cycles. They employed the A-V hardening framework coupled with the Neuber, Glinka, and Hoffman-Seeger (H-S) rules. They found that the use of Neuber’s rule along with the A-V model predicted local ratcheting more agreeable with those of experimental data as compared with the Glinka and H-S rules.
In this study, the local ratcheting response of Al 7075-T6 specimens at different distances from the notch root was predicted using the A-V and Chaboche hardening rules in conjunction with the Neuber rule. The ratcheting data for the interference fitted samples and at various distances from the notch roots were taken from an earlier work [27]. Pinned samples possessed DIF of 1% and 2%. The local ratcheting of press-fitted and non-press-fitted notched aluminum specimens was evaluated through use of the A-V and Chaboche kinematic hardening rules coupled with the Neuber rule. Local ratcheting results were analyzed at various DIFs, distances from the notch root, and applied stresses. As DIF increased from 0→ 1% →2%, local ratcheting strain dropped noticeably. An increase in the applied stress, promoted ratcheting at the hole-pine interference. The predicted ratcheting curves through the A-V model were placed above the measured values, while those predicted by the Chaboche hardening rule collapsed below experimental data. The lower ratcheting magnitude at press-fitted samples is attributed to the higher materials resistance against ratcheting developed at the hole-pin interference. The choice of press-fitted samples to control ratcheting at notch root of components are discussed.

2. Kinematic hardening rules and formulation

Strain Increments
The sum of the elastic and plastic strain increments yields:
d ε ̅ = d ε ¯ e + d ε ¯ p
Elastic strain increment is described through Hooke's law as:
d ε ¯ e = d σ ¯ 2 G − ϑ E ( d σ ¯ . I ¯ ) I ¯
Terms I and σ represent the unit and stress tensors, respectively, and E is the modulus of elasticity, G is the shear modulus, and ϑ is the Poisson's ratio.
The plastic strain increment and flow rule is described as:
d ε ¯ p = 1 H p ( d s ¯ .   n ¯ ) n ¯
where H p is the plastic modulus, d s ¯ is the deviatoric tensor increment, and n ¯ is the yield surface normal vector. The yield contour separates the elastic domain from the plastic region in the onset of yielding through:
f s ¯ , α , σ y = 3 2 s ¯ − α ¯ s ¯ − α ¯ − σ y 2
As the loading exceeds the elastic range, the yield surface is translated into deviatoric stress space via the backstress tensor α ¯ in equation (4).

2.1. The Ahmadzadeh-Varvani (A-V) kinematic hardening rule

The A-V nonlinear hardening model [16] was developed to control backstress increment evolution during loading paths. The yield surface is translated as loading exceeds elastic limit and backstress increment d α ¯ is controlled by contribution of an internal variable b ¯   in the dynamic recovery portion of model. Term ( α ¯ − δ b ¯ ) in the A-V rule controls magnitude and rate of yield surface translation in the deviatoric stress space and is expressed in a general form as:
d α ¯ = C d ε ¯ p − γ 1 ( α ¯ − δ b ¯ ) d p
d b ¯ = γ 2 ( α ¯ − b ¯ ) d p
In the dynamic recovery term, the internal variable, b ¯ , with an initial value of zero, is introduced to gradually control backstress α ¯ over loading cycles. A detailed explanation of how to calculate the variables in equations (5-a) and (5-b) is described in reference [16]. Term d p in equation (5) is expressed through a dot product of plastic strain increment d ε ¯ p through equation (6):
d p = d ε ¯ p . d ε ¯ p
The stress-controlled uniaxial stress-strain hysteresis loops are used to define coefficients C and γ 1 in equation (5). Material-dependent coefficient γ 2 is defined through use of experimental ratcheting data obtained over the proceeding stress cycles [28]. Under uniaxial loading cycles, coefficient δ is defined as ( α ¯ / k ) m . Equation (5a) is rewritten as:
d α ¯ = C d ε ¯ p − γ 1 ( α ¯ − ( α ¯ / k ) m b ¯ ) d p
where k is equal to k = C / γ 1 and exponent m falls between zero and unity 0 < m < 1.0 .

2.2. Neuber’s rule: Relating nominal stress/strain to Local components of stress and strain at notch root

Based on Neuber's rule, the theoretical stress concentration factor, K t , is related to the stress and strain concentration factors, K σ and K ε , as:
K σ K ε = K t 2
where
K σ = σ S
K ε = ε e
Equations (9) and (10) were substituted into equation (8) resulting in:
( K t S ) 2 = E σ ε
Equation (11) is rewritten as:
( K t ∆ S ) 2 E = ∆ σ ∆ ε
where ∆ S corresponds to the nominal stress range, and E is the modulus of elasticity. In the right-hand side of equation (12), ∆ ε and ∆ σ are respectively local stress and strain ranges.
Equation (12) was employed to relate nominal stress S and nominal strain e to local stress σ and strain ε at the notch root as notched samples are loaded, unloaded, and reloaded through paths O→A, A→B, and B→C:
( ε B L − ε A L ) ( σ B L − σ A L ) = K t 2 ( S B − S A ) ( e B − e A )      d ε ¯ p < 0
( ε C L − ε B L ) ( σ C L − σ B L ) = K t 2 ( S C − S B ) ( e C − e B )      d ε ¯ p ≥ 0
Term K t is the stress concentration factor, and the subscripts A, B, C correspond to the loads starting from zero to maximum load (point A), minimum load (point B), and maximum load (point C). Ramberg-Osgood [29] equation is employed to relate nominal strain and stress through:
∆ e = ∆ S E + 2 ( ∆ S 2 K ' ) 1 n '
where terms K ' and n ' correspond to cyclic hardening coefficient and cyclic hardening exponent, respectively.
A substitution of equation (15) into equations (13) and (14) yielded equations (16) and (17) relating local strains and stresses to equations [9,10,11,12]:
( ε B − ε A ) ( σ B − σ A ) = K t 2 ( S B − S A ) ( S B − S A E + 2 ( S B − S A 2 K ' ) 1 n ' ) ,      d ε ¯ p < 0
ε C − ε B σ C − σ B = K t 2 S C − S B ( S C − S B E + 2 ( S C − S B 2 K ' ) 1 n ' ) ,      d ε ¯ p ≥ 0
A local backstress component for half-cycle loads can be related to local stresses at turning points for components subject to uniaxial loads. Using equations (18-20), it can be used to determine the unloading (A→B) and reloading (B→C) conditions:
α A L = 2 3 ( σ A L − σ y )
α B L = 2 3 ( σ B L + σ y )
α C L = 2 3 ( σ C L − σ y )

2.3. The Chaboche kinematic hardening rule

Based on Chaboche's postulation [15], yield surface translation is defined by summation of backstress increments. This nonlinear kinematic hardening model translates the yield surface as backstress increments are integrated. As materials are deformed beyond their elastic limits, the yield surface is translated in the deviatoric stress space based on Chaboche's nonlinear model and expressed as:
d α ¯ = ∑ i = 1 3 d α ¯ i ,
d α ¯ i = 2 3 C i d ε ¯ p − γ i ' α ¯ i d p
Backstress components during unloading and reloading paths are defined as [15]:
α i = 2 C i 3 γ i ' + ( α i 0 − 2 C i 3 γ i ' ) e x p ⁡ [ − γ i ' ( ε p − ε p 0 ) ]      d ε p ≥ 0
α i = − 2 C i 3 γ i ' + ( α i 0 + 2 C i 3 γ i ' ) e x p ⁡ [ γ i ' ( ε p − ε p 0 ) ]      d ε p < 0
In this case, ε p 0 represents the initial plastic strain, while α i 0 represents the initial backstress. The Chaboche parameters are derived by simulating the lower half of the stabilized hysteresis curve from the strain-controlled cyclic test [15]. Using the slope of the initial part of the stabilized hysteresis curve with high plastic modulus at the yield point to determine parameter C 1 and the linear part of the same curve to determine parameter C 3 . Chaboche's rule requires a coefficient γ ' 1 that is large enough to stabilize the first hardening parameter.

3. Results and Discussion

3.1. Ratcheting Data

analytically evaluate ratcheting response of press-fitted and non-press fitted Al7075-T6 samples under asymmetric loading cycles, two sets of ratcheting data were employed (i) tests on notched aluminum sample with notch diameter d=5mm subjected to 155±155MPa with DIF=0 (non-press fitted), and (ii) tests conducted on notched aluminum samples (d=5mm) with different stress levels and DIF=1% and 2%. DIF was defined as the difference in diameters of notch on aluminum plate and the steel pin divided by the notch diameter. The former test set was conducted by the second author’s research group and the latter were reported by Chakherlou et al. [27]. In their cyclic tests, strain gauges were mounted at different distances from notch root to measure local strains. Press-fitted samples were tested at x=1.3, and 3mm distance from the notch roots. For the un-pinned sample, local strain was measured at a distance of x=0.5mm to technically represent local strain at notch root. Cyclic tests were carried out under stress control condition by a Roell fatigue testing machine at room temperature with a stress ratio of R=0. Tensile tests on Al7075-T6 resulted in yield stress of 503MPa and Modulus of elasticity of 71.5GPa.
Local ratcheting strains measured for un-pinned and pinned Al 7075-T6 samples at various stress levels presented in Figure 1.

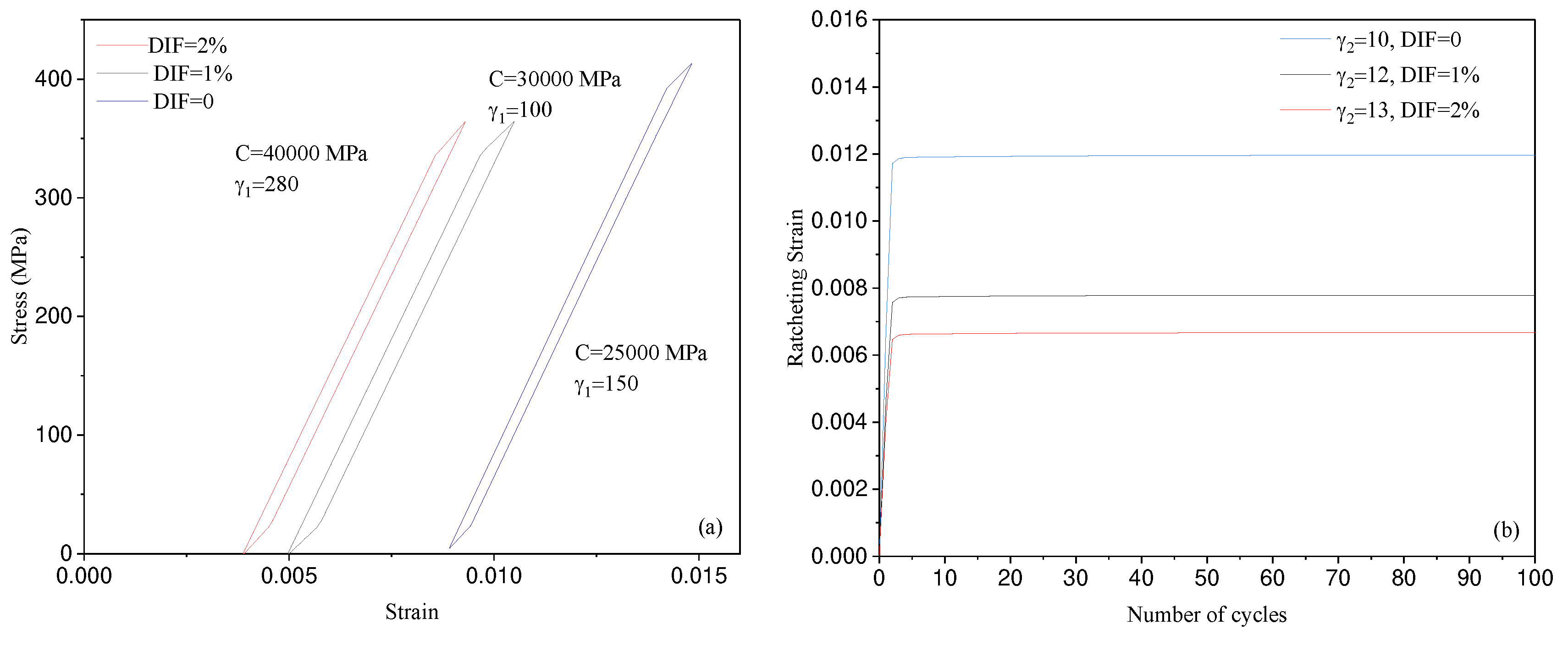
3.2. Kinematic Hardening Rule Coefficients:

Coefficients C, γ 1 , and γ 2 in the A-V kinematic hardening model were determined for Al7075-T6 at different DIFs of 0, 1% and 2%. Press-fitted samples less plastic deformation at the hole-pin interface. Figure 2 presents stress-controlled hysteresis loops generated for different DIF samples. Through the A-V model, the highest value of C=40000MPa was achieved for sample with DIF=2%, while this coefficient was found 30000 and 25000 MPa for DIF=1% and 0, respectively. This figure clearly depicts DIF=2% exhibiting the least amount of strain, whereas DIF=0 with the greatest amount of strain at the 2nd stress cycle. Coefficients C and γ 1 for different DIFs are presented in figure 2(a). Predicted ratcheting curves for DIF=0, 1%, and 2% are presented in figure 2(b), representing that the lower value of γ 2 in sample tested with DIF=0, resulted in a higher ratcheting magnitude. Coefficient γ 2 increased in magnitude as DIF increased representing greater resistance of notch-pin interface against ratcheting.
, and (b) coefficient γ 2 Coefficients of Chaboche's models ( C 1 , C 2 , C 3 and γ ' 1 , γ ' 2 , γ ' 3 ) were derived using the stress-strain hysteresis loop obtained from a strain-controlled test of ± 1.5 % . The lower half of the stabilised hysteresis curve from the strain-controlled test is used to determine Chaboche parameters. Different strain-controlled cyclic tests on Al7075-T6 samples with DIFs of 0, 1% and 2% resulted in three sets of C 1 − 3 and γ ' 1 − 3 coefficients as presented in figure 3.
and γ 1 − 3 * for un-pinned sample (DIF=0) and pinned samples (DIF=1% and 2%) of Al7075-T6 alloy [30]
3.3 Yield Surface Evolution
The onset of yield for Al 7075-T6 was defined by von-Mises criterion and isotropic hardening model expanded the surfaces with no changes in the position center of yield surfaces as stress magnitude exceeded materials yield point. Through kinematic hardening rule, yield surface was translated with increment of backstress term. Based on the A-V model, yield surface translation in the deviatoric stress space was further monitored by an internal variable b ¯ in term ( α ¯ − δ b ¯ ) , while backstress evolution is through integration of back stress components d α ¯ = ∑ i = 1 3 d α ¯ i . Both mechanisms act equivalently consistent in moving yield surfaces as loading over plastic domain increased. Figure 4 presents yield surface evolution based on the A-V hardening rule for different testing materials with DIFs of 0, 1% and 2%. This figure includes stress-strain curves developed by Ramberg-Osgood equation [29], at which materials constants for Al7075-T6 are taken from [31]. For different DIFs, the initial yield surfaces intercepted stress-strain curves at elastic limits representing the onset of yielding and were defined by the von-Mises criterion. The yield surfaces at hole-pin interface possessed different stress and strain values as materials at notch root of pinned and un-pinned samples show different resistance against deformation and materials yielding. Yield surface for DIF=0 initially owned lower onset of yielding where intercepted with the related stress-strain curve. Through the A-V hardening rule, the yield surface however was translated largely in the deviatoric stress space. For press-fitted specimens with initial larger yield stresses, this translation was found relatively lower in magnitude. This was consistent with the fact that the backstress increments dropped as degree of interference fit increased.

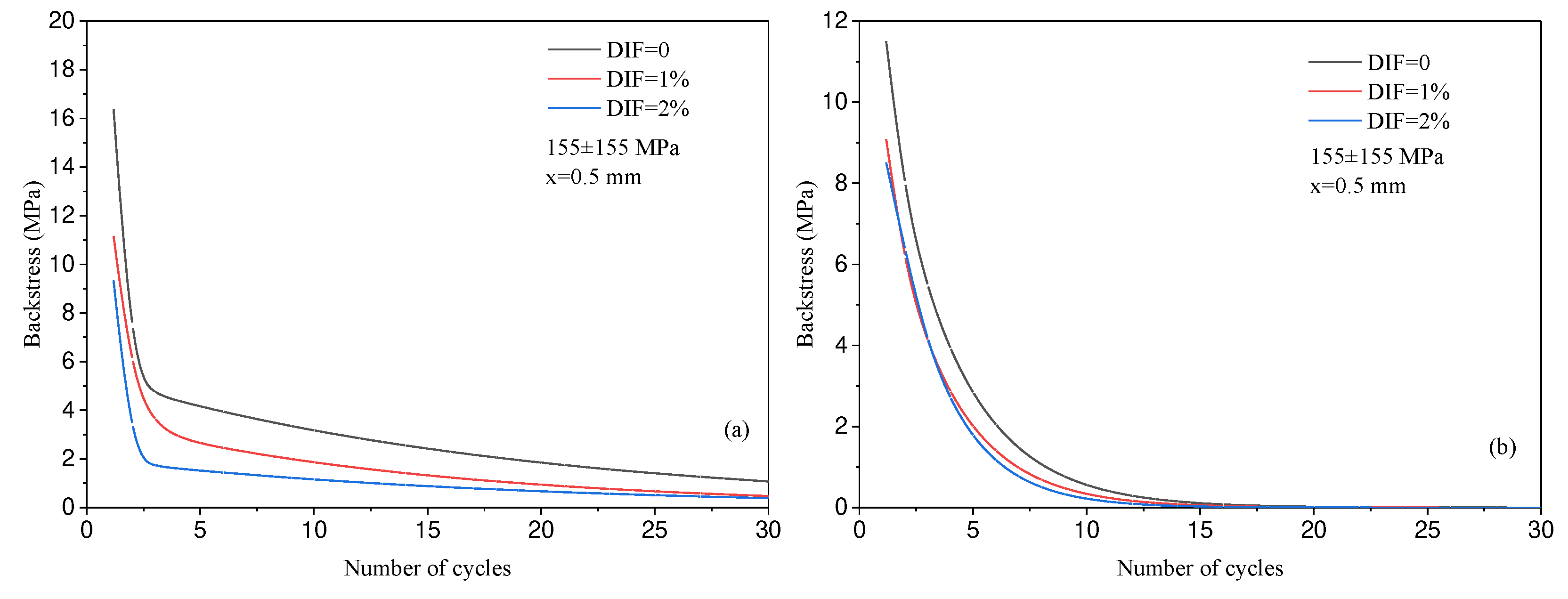
3.4. Backstress evolution with Loading

The A-V and Chaboche kinematic hardening rules were used to control the evolution of backstress during the loading cycles. The ratcheting and plastic strain increment d ε p , during asymmetric loading cycles, were controlled by backstress and internal variable b ¯ . In the dynamic recovery term of the A-V model, term ( α ¯ − 𝛿 b ¯ ) gradually got stabilized in magnitude as number of loading cycles was increased. Term ( α ¯ − 𝛿 b ¯ ) in the A-V model is comparable to Chaboche's integration of backstress increments d α ¯ = ∑ i = 1 3 d α ¯ i . Figure 5 illustrates the evolution of the backstress term ( α ¯ − 𝛿 b ¯ ) over the first 30 cycles of loading on Al7075-T6 samples with different DIFs. This graph demonstrates a sharp decline in term ( α ¯ − 𝛿 b ¯ ) over the first few cycles. After the initial cycles of loading, a steady-state was reached. The steady state in backstress evolution may be attributed to the interaction of dislocations beyond yielding point resulting in a reduction in the ratcheting strain rate. The graph clearly shows that backstress decreases with increasing DIF from 1% to 2%. The unpinned sample (DIF=0) possessed the highest backstress curve.

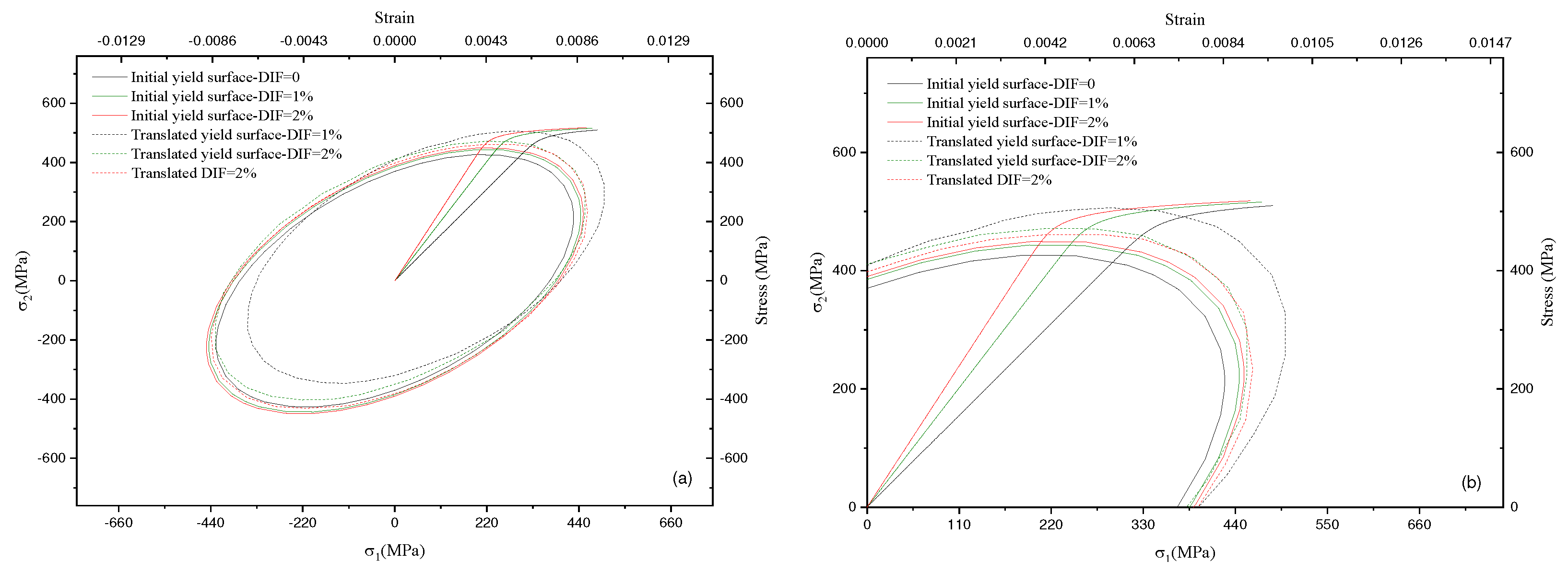
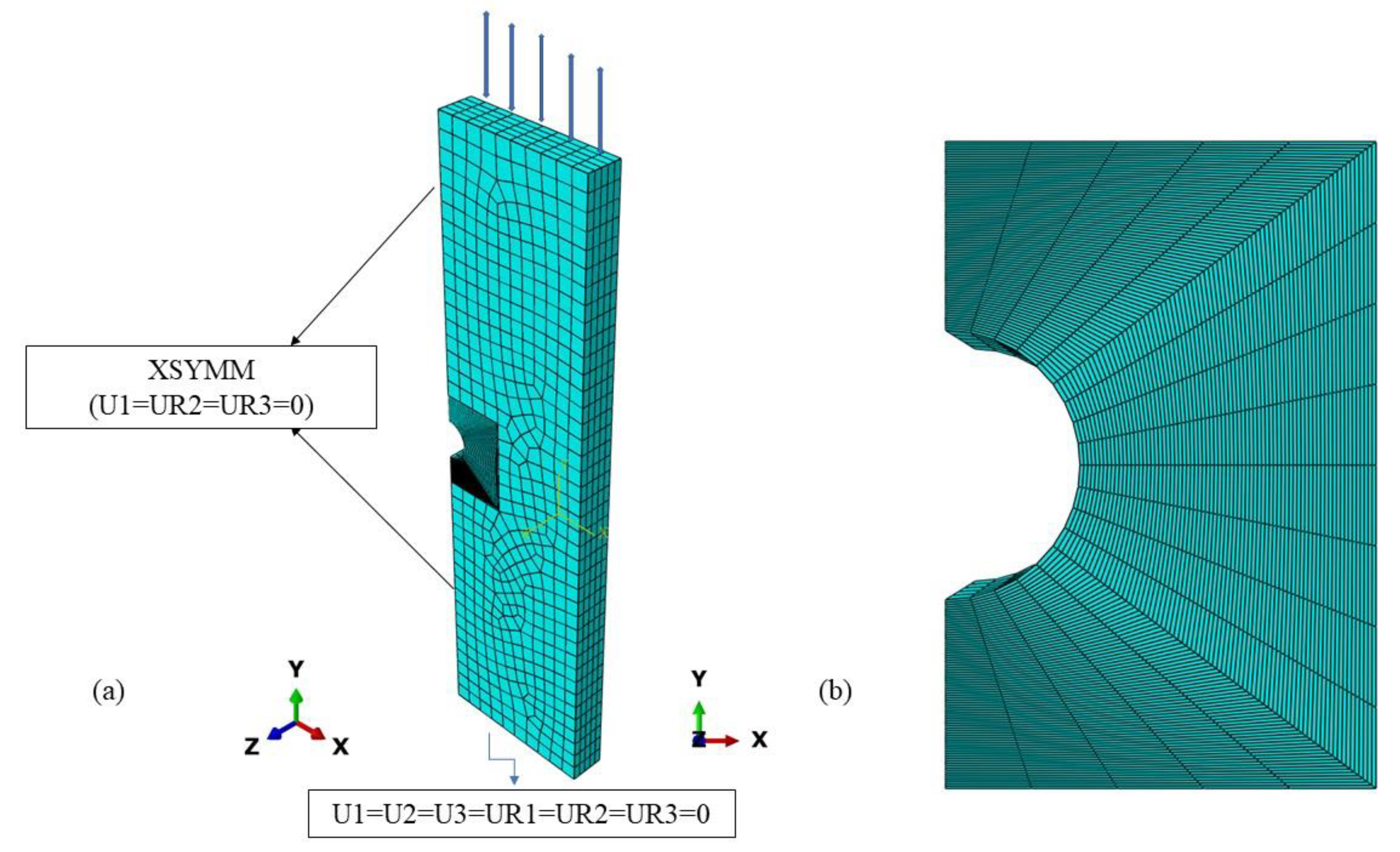
3.5. Finite Element Analysis and stress distribution

To contour the notch root region and to determine its stress distribution, finite element analysis was employed using ABAQUS software version 6.13 [32]. The notched specimen was meshed with quadratic elements, and the constraints were placed to block its motion at one end as shown in Figure 6. The upper end surface of the specimen had its translational and rotational axes restrained along the X- and Z-axes, while the specimen let to carry the load along the Y-axis. A uniaxial loading cycles were applied to the specimen upper end under stress-controlled condition with frequency of 10 Hz. Eight nodes per brick element were designed with quadratic elements of type C3D8R, and three degrees of freedom per node, resulted in 24 degrees of freedom. As the FE was run at various applied stress levels and notch sizes, taking a smallest size of 0.1 mm near the notch root led to a consistent convergence. The stress distribution curves over distance x from the notch root are presented in figure 7. This figure shows that as DIFs increase 0→1%→2% for various applied stress levels, curves fall to lower levels. The simulated stress values through FE analysis will be taken as input values of stress at given distance x to predict local ratcheting at notch-pin region of Al 7075-T6 samples.

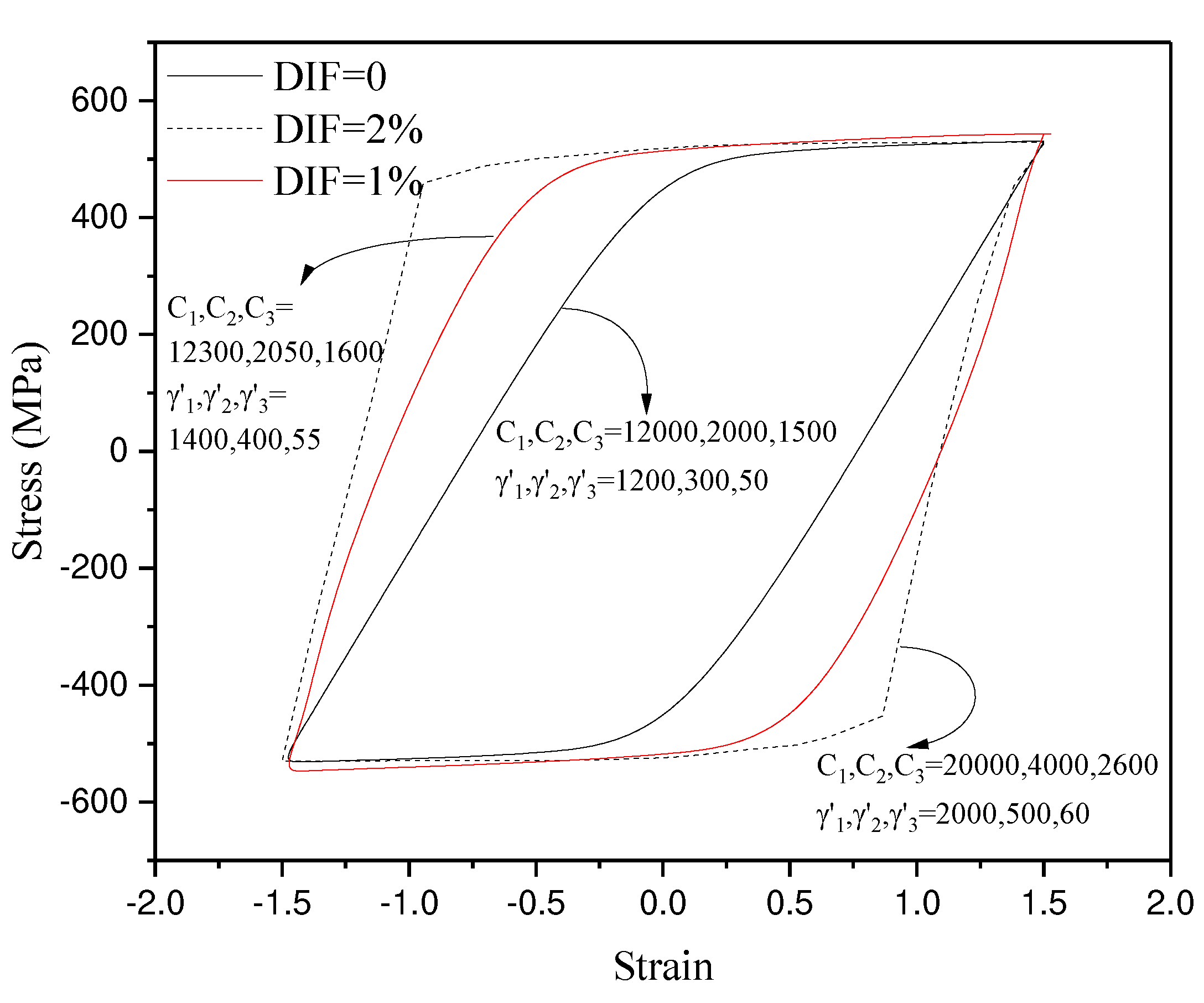
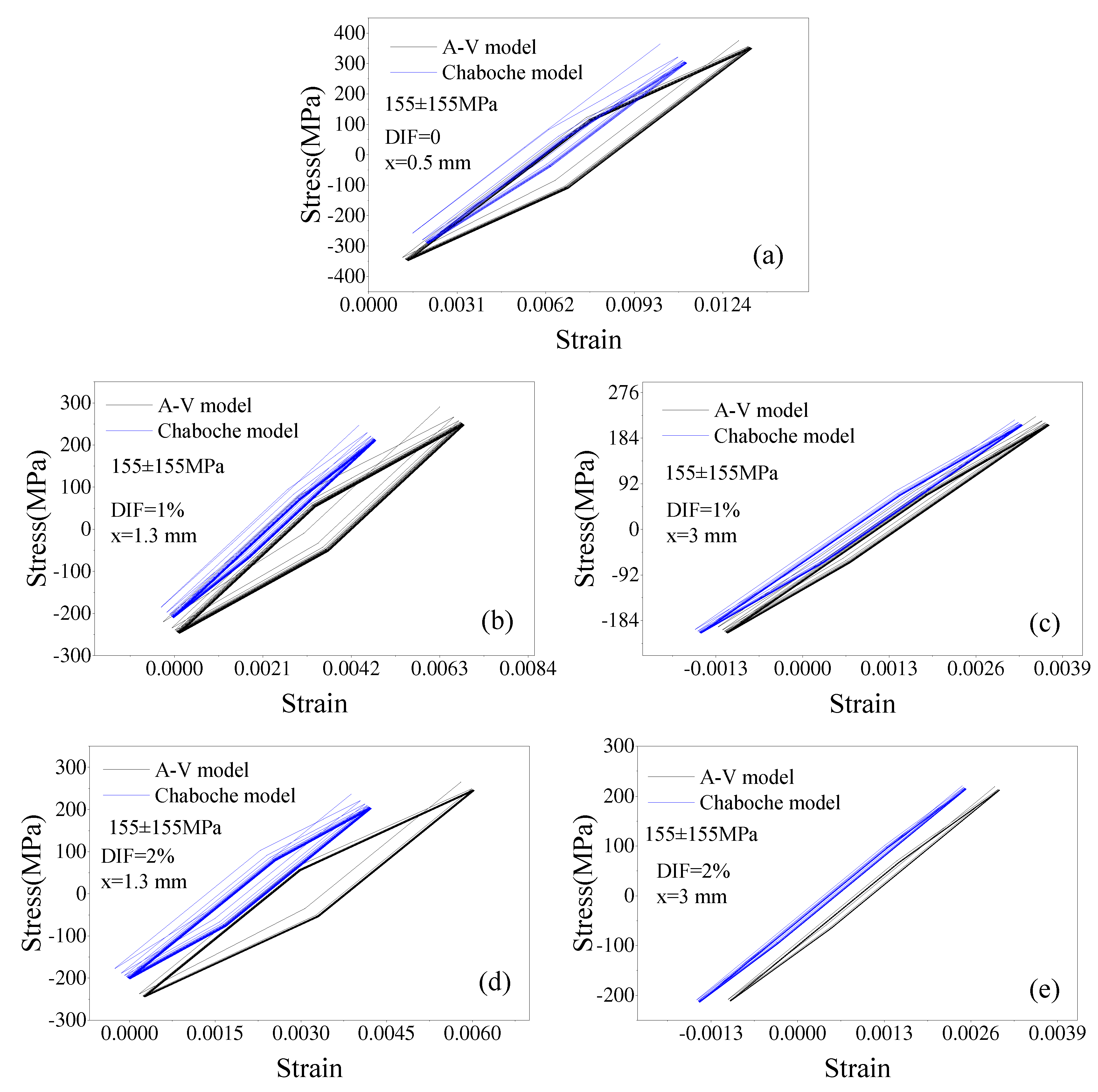
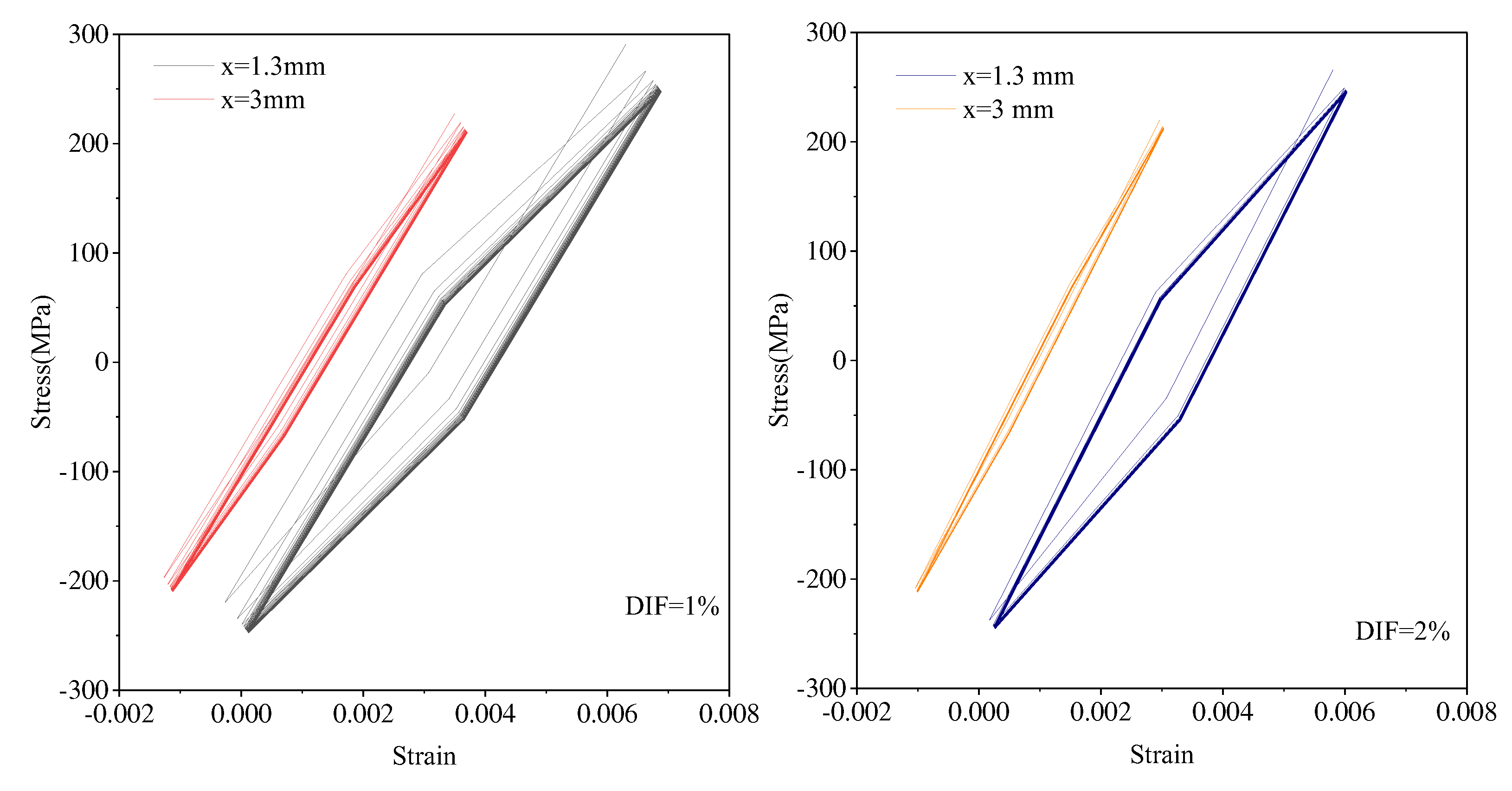
3.6. Predicted Hysteresis Loops

Stress-strain hysteresis loops of Al 7075-T6 samples tested at 155 ± 155 MPa with DIFs of 0, 1% and 2% are depicted in Figure 8. These loops are generated at distances of 0.5, 1.3, and 3 mm from the notch root and during 100 cycles. Vertical and horizontal axes in were scaled to be able to accurately compare/evaluate plastic strain range at the notch edge region. In this figure, DIF=2% test owned narrower hysteresis loops whereas the unpinned specimen (DIF=0) resulted in wider loops. At a given DIF, as distance x increases from 1.3mm to 3.0mm, both stress range and plastic strain range drop in magnitude. Figure 9 compares hysteresis loops generated at press-fitted samples at distances x=1.3 and 3mm for DIFs of 1% and 2%. The width of hysteresis loops generated for samples with DIF=1% through use of A-V model was found as large as four times for x=1.3mm than that of distance x=3.0mm. For DIF=2% this difference in plastic strain range at distances 1.3 and 3.0mm becomes as high as six times. In figures 8 and 9, as the number of cycles increased, the peaks of progressive loops joined, resulting in a stress relaxation for both unpinned and pinned samples.

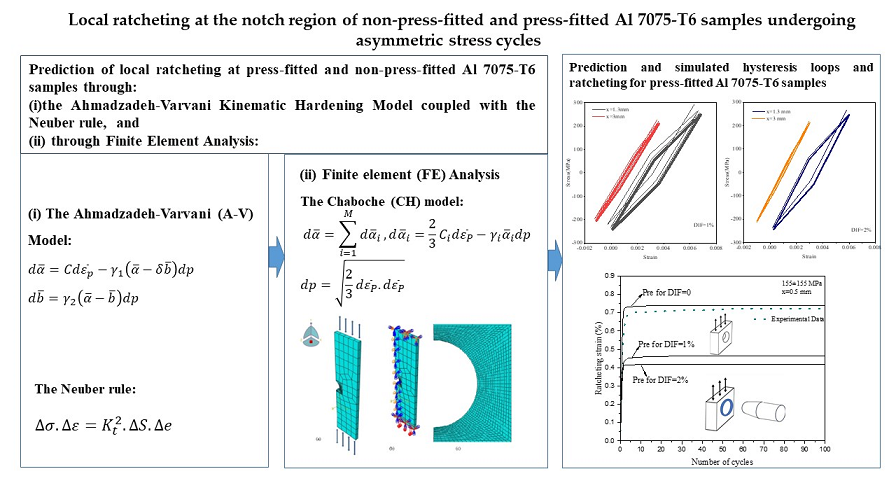
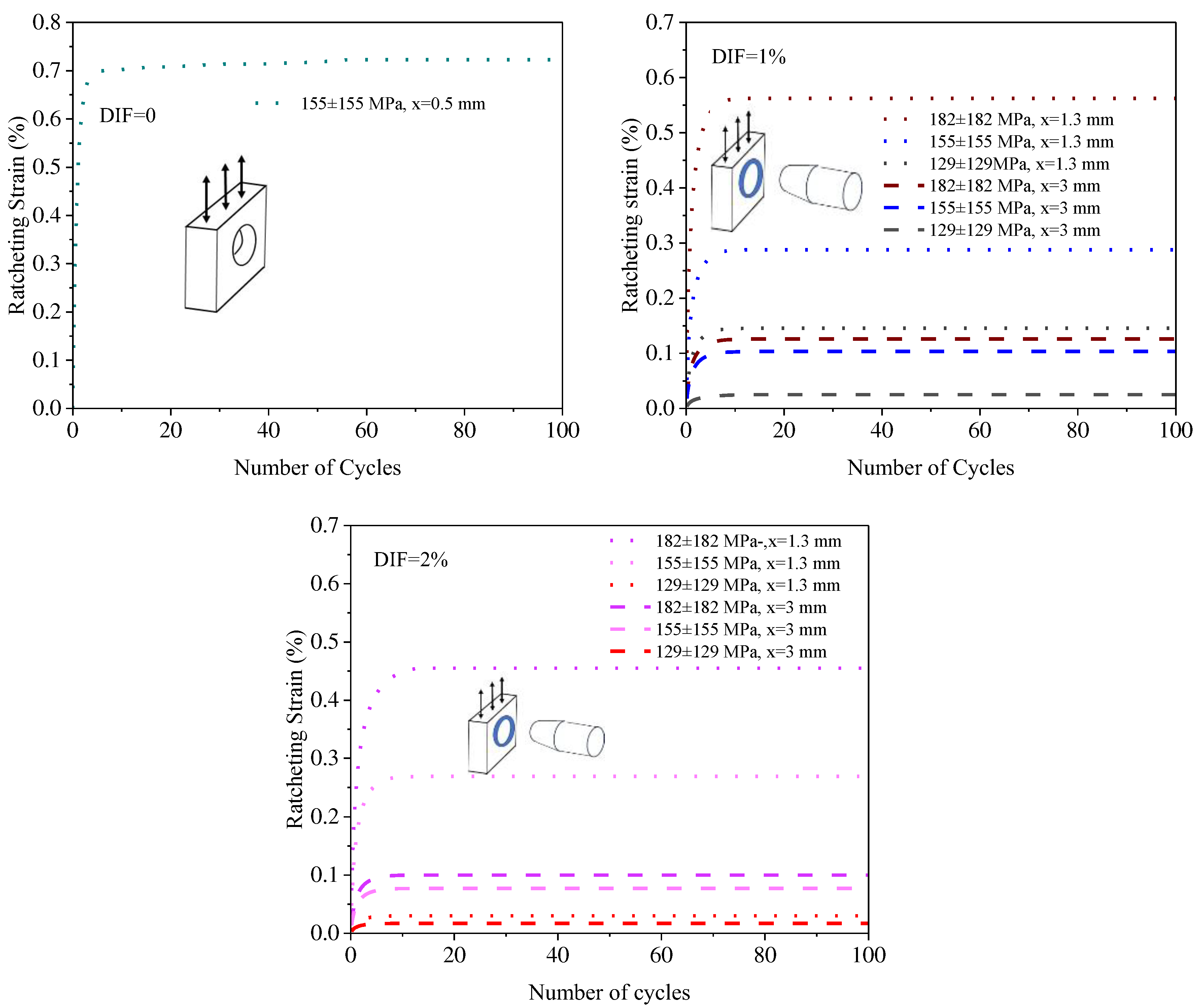
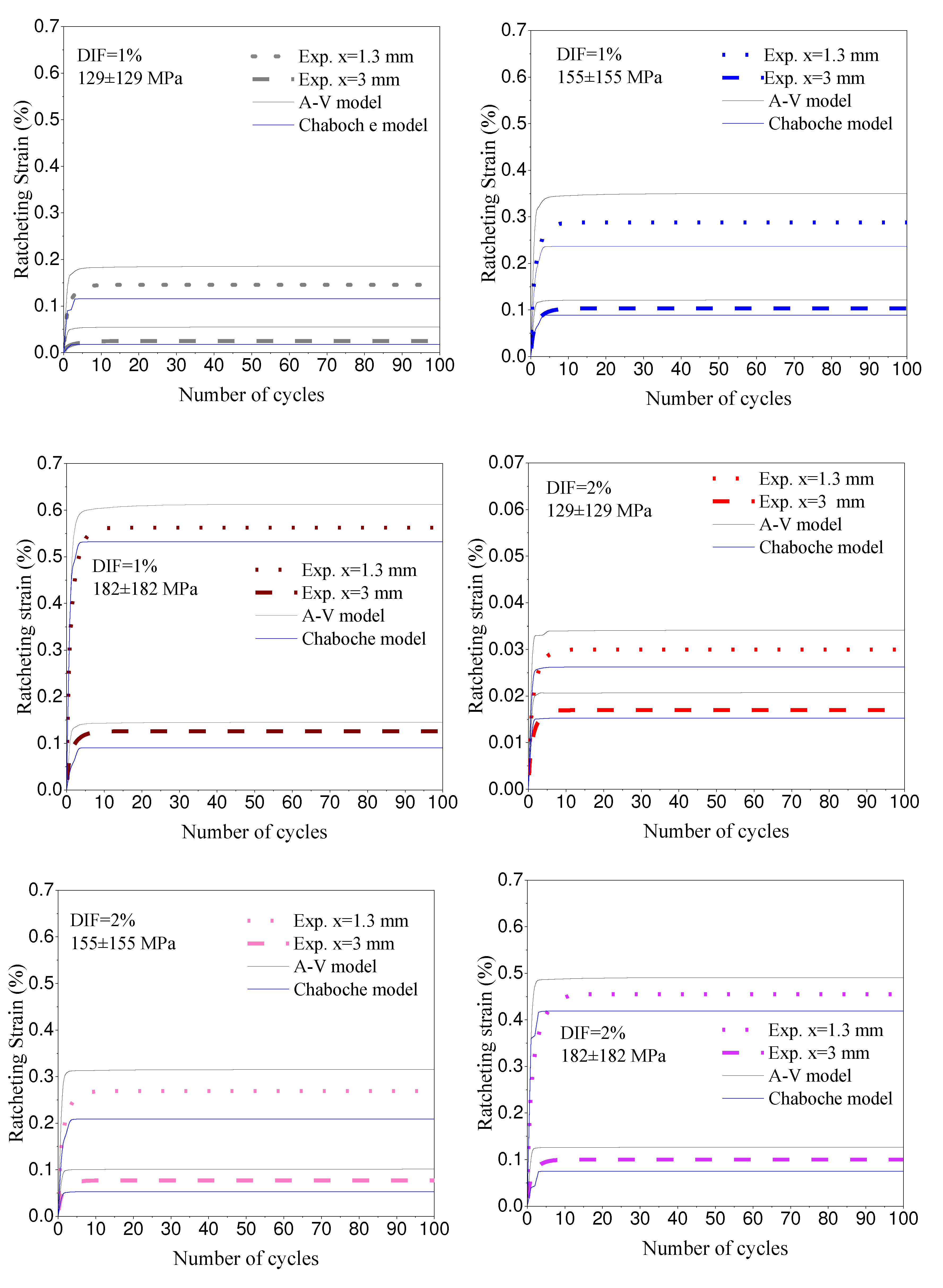
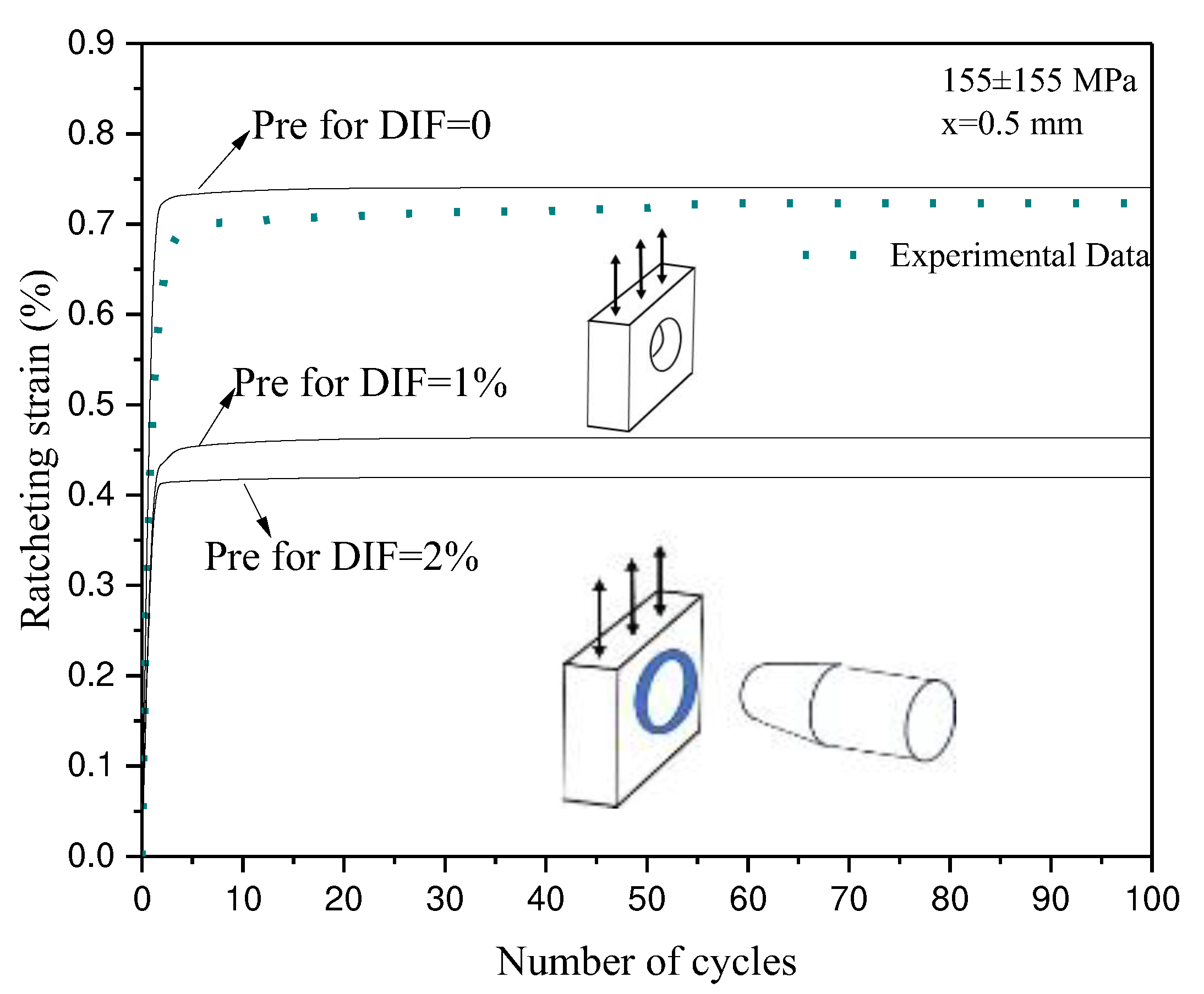
3.7. Local ratcheting strain prediction

To evaluate the ratcheting response of pinned and un-pinned Al 7075-T6 specimens subjected to asymmetric stress cycles, the A-V and Chaboche kinematic hardening rules coupled with Neuber’s rule were used. Figure 10 presents the predicted and experimental ratcheting results at various stress levels and DIFs. Over the first few cycles, predicted ratcheting strain showed a sudden increase; shortly after, the ratcheting rate dropped and the ratcheting progress rate remained almost constant as the number of cycles increased. The predicted ratcheting curves through the A-V kinematic hardening model shifted above the measured values while those predicted by Chaboche’s model fell below the experimental data consistently. Local ratcheting strain dropped in magnitude as distance x from the notch-pin interface increased. The applied cyclic stress level noticeably influenced ratcheting strain at notch region. For tests conducted with a DIF=1%, as stress level increased 129±129MPa→155±155MPa→182±182MPa, the A-V predicted ratcheting curve at x=1.3mm elevated respectively from 0.25%→0.35%→0.60%. The Predicted ratcheting through Chaboche’s model let to 0.12%→0.24%→0.53% at this distance. The predicted ratcheting curves at the notch edge x=0.5mm of unpinned (DIF=0) and pinned samples of Al 7075-T6 (DIF=1% and 2%) tested at 155±155MPa are presented in figure 11. This figure presents a set of measured data for DIF=0→1%→2%, the predicted local ratcheting magnitude at distance x=0.5mm decreases from 0.73%→0.46%→0.42%. These results show how press-fitting process as low as DIF=2% improve materials against ratcheting as high as 74%. The pinned samples hindered the progressive plastic strain over loading cycles and improves the life of notched samples.
The choice of interference fit noticeably improved materials against local ratcheting at the hole-pin interface. Implementing the press-fitting on notched perimeter increased onset of materials yielding at the notch region and shortened the yield surface motion as backstress increments dropped in magnitude. Stress-strain hysteresis loops generated on samples with DIF=2% possessed lower width as compared with loops of un-pinned samples (DIF=0). At farther distances the lower plastic strain range resulted in the formation of narrower loops. The higher DIFs led to lower backstress, and its evolution was stabilized at smaller number of cycles. At a given distance x from the notch root, an increase in DIF dropped the local stress level at notch region resulting in stress relaxation. This study intended to explore possibilities of minimizing materials damage and plastic deformation at notch root of samples undergoing asymmetric loading cycles through press-fitting holes with different degrees. Authors believe that investigation on the influence of press-fitting process on local ratcheting is promising and will promote a safe design of machinery components such as fastening and riveting against ratcheting phenomenon and failure. Nevertheless, there are several technical parameters and affecting variables in ratcheting of press-fitted samples to fully understand. Evaluation of local ratcheting of load-bearing notched components become crucial particularly in the presence of variables such as shape and size of stress raisers, elevated temperatures, multiaxial and load steps, and degree of press-fitting. As the next immediate research step, authors plan to conduct more experiments and promote research on ratcheting of press-fitted samples under various loading conditions.

4. Conclusions

Local ratcheting at hole-pin interface of Al 7075-T6 specimens subjected to various DIFs were studied. As DIF process on the test samples increased from 0→1%→2%, ratcheting at notch region dropped noticeably. Local ratcheting at non-press fitted and press-fitted samples were evaluated through use of the A-V and Chaboche hardening models coupled with the Neuber model. The highest magnitude of ratcheting was achieved for un-pinned samples (DIF=0). The press-fitted samples however resulted in lower ratcheting as DIF increased from 1% to 2%. Test samples with higher DIFs and farther distances from the notch edge possessed narrower stress-strain hysteresis loops and smaller ratcheting magnitudes. The predicted ratcheting curves by means of the A-V and Chaboche hardening rules respectively fall above and below the measured values. The lower ratcheting magnitude at press-fitted samples was attributed to the higher materials resistance against ratcheting developed at the hole-pin interference. The choice of press-fitted samples to control ratcheting at notch root of components were discussed.

Funding

This research was funded by Natural Sciences and Engineering Research Council of Canada (NSERC) through Prof. A. Varvani, grant number RGPIN-2021-03047”

Acknowledgments

Authors wish to acknowledge the financial support through Natural Sciences and Engineering Research Council of Canada (NSERC) through Dr. Varvani (RGPIN-2021-03047). A special thanks goes to Dr. A. Shekarian (the former PhD student, defended in 2021) for conducting ratcheting tests on notched Al7075-T6 samples.

Conflicts of Interest

Declare conflicts of interest or state “The authors declare no conflict of interest.” Authors must identify and declare any personal circumstances or interest that may be perceived as inappropriately influencing the representation or interpretation of reported research results. Any role of the funders in the design of the study; in the collection, analyses or interpretation of data; in the writing of the manuscript; or in the decision to publish the results must be declared in this section. If there is no role, please state “The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results”.

Nomenclature

d ε ̅ Total strain increment tensor
d ε ¯ e Elastic strain increment tensor
d ε ¯ p Plastic strain increment tensor
E Modulus of elasticity
H p Plastic modulus
α ¯ Backstress tensor
σ ¯ Stress tensor
𝐼̅ Unit tensor
ϑ Poisson’s ratio
G Shear modulus
s ¯ Deviatoric stress tensor
σ y Yield strength
D Circular notch diameter
γ 1 , γ 2 ,   C ,   δ Coefficients of the A-V model
C 1 − 3 , γ ' 1 − 3 Chaboche materials coefficients
K t Stress concentration factor
b ¯ Internal variable of the A-V model tensor
n ' , K '   Ramberg-Osgood coefficients
S,e Nominal stress and strain
R Stress ratio
K σ , K ε Stress and strain concentration factors
σ ,   ε Uniaxial local stress and strain at the notch root
W σ Strain energy per unit volume at the notch root
W S Elastic strain energy per unit volume due to the nominal remote stress

References

  1. Chakherlou, T. N.; Oskouei, R. H. and Vogwell, J. Experimental and numerical investigation of the effect of clamping force on the fatigue behaviour of bolted plates. Eng. Fail Anal. 2008, 15, 563–574. [Google Scholar] [CrossRef]
  2. Chakherlou, T. N.; Abazadeh, B. and Vogwell, J. The effect of bolt clamping force on the fracture strength and the stress intensity factor of a plate containing a fastener hole with edge cracks. Eng. Fail. Anal. 2009, 16, 242–253. [Google Scholar] [CrossRef]
  3. Chakherlou, T. N.; Vogwell, J. A novel method of cold expansion which creates near-uniform compressive tangential residual stress around a fastener hole. Fatigue Fract. Eng. Mater. Struct. 2004, 27, 343–351. [Google Scholar] [CrossRef]
  4. Chakherlou, T. N.; Aghdam, A. B. An experimental investigation on the effect of short time exposure to elevated temperature on fatigue life of cold expanded fastener holes. Mater. Design 2008, 29, 1504–1511. [Google Scholar] [CrossRef]
  5. Callinan, R. J.; Wang, C. H. On the fatigue enhancement of interference fitted stop drilled holes. Int. J. Fatigue 1999, 21, 865–72. [Google Scholar] [CrossRef]
  6. Chakherlou, T. N.; Mirzajanzadeh, M. and Saeedi, K. H. Fatigue crack growth and life prediction of a single interference fitted holed plate. Fatigue Fract. Eng. Mater. Struct. 2010, 33, 633–644. [Google Scholar]
  7. Iyer, K.; Rubin, C.A.; Hahn, G.T. Influence of interference and clamping on fretting fatigue in single rivet-row lap joints. J. Tribol ASME 2001, 123, 686–698. [Google Scholar] [CrossRef]
  8. Chakherlou, T. N.; Alvandi-Tabrizi, Y. and Kiani, A. On the fatigue behavior of cold expanded fastener holes subjected to bolt tightening. Int. J. Fatigue 2011, 33, 800–810. [Google Scholar]
  9. Kolasangiani, K.; Farhangdoost, K.; Shariati, M.; Varvani-Farahani, A. Ratcheting assessment of notched steel samples subjected to asymmetric loading cycles through coupled kinematic hardening-Neuber rules. Int. J. Mech. Sci. 2018, 144, 24–32. [Google Scholar] [CrossRef]
  10. Shekarian, A.; Varvani-Farahani, A. Ratcheting prediction at the notch root of steel samples over asymmetric loading cycles, J. Eng. Mater. Technol. Trans. 2020, 142(2), 1–23. [Google Scholar] [CrossRef]
  11. Shekarian, A.; Varvani-Farahani, A. Concurrent ratcheting and stress relaxation at the notch root of steel samples undergoing asymmetric tensile loading cycles, Fatigue Fract. Eng. Mater. Struct. 2019, 42, 1402–1413. [Google Scholar] [CrossRef]
  12. Shekarian, A.; Varvani-Farahani, A. Ratcheting behavior of notched stainless-steel samples subjected to asymmetric loading cycles. J. Iron Steel Res. Int. 2021, 28(1), 86–97. [Google Scholar] [CrossRef]
  13. Shekarian, A.; Varvani-Farahani, A. Ratcheting response of SS316 steel samples with different notch shapes under various loading spectra. J. Mater. Eng. Perform. 2021, 30(5), 3524–3535. [Google Scholar] [CrossRef]
  14. Neuber, H. Theory of stress concentration for shear-strained prismatical bodies with arbitrary nonlinear stress-strain law. J. Appl. Mech., 1961, 28, 544–550. [Google Scholar] [CrossRef]
  15. Chaboche, J. On some modifications of kinematic hardening to improve the description of ratcheting effects. Int. J. Plast. 1991, 7, 661–678. [Google Scholar] [CrossRef]
  16. Ahmadzadeh, G. R.; Varvani-Farahani, A. Ratcheting assessment of materials based on the modified Armstrong–Frederick hardening rule at various uniaxial stress levels, Fatigue Fract. Eng. Mater. Struct. 2013, 36(12), 1232–1245. [Google Scholar] [CrossRef]
  17. Wang, C.H.; Rose, L.R.F. Transient and steady-state deformation at notch root under cyclic loading, Mech. Mater. 1998, 30(3), 229–241. [Google Scholar]
  18. Hu, W.; Wang, C.H.; Barter, S. Analysis of cyclic mean stress relaxation and strain ratchetting behavior of aluminum 7050. Aeronautical and Maritime Research Lab Melbourne (Australia), 1999.
  19. Rahman, S.M.; Hassan, T. Advanced cyclic plasticity models in simulating ratcheting responses of straight and elbow piping components, and notched plates. ASME Pressure Vessels and Piping Conference 2005, 421–427. [Google Scholar]
  20. Ohno, N.; Wang, J.D. Kinematic hardening rules with critical state of dynamic recovery, part I: formulations and basic features for ratcheting behavior. Int. J. Plasticity 1993, 9, 375–390. [Google Scholar] [CrossRef]
  21. Ohno, N.; Abdel Karim, M. Uniaxial ratcheting of 316FR steel at room temperature – part II: Constitutive modeling and simulation. ASME J. Appl. Mech. 2000, 122, 35–41. [Google Scholar]
  22. Firat, M. A notch strain calculation of a notched specimen under axial-torsion loadings. Mater. Des. 2011, 32(7), 3876–3882. [Google Scholar] [CrossRef]
  23. Barkey, M.E. Calculation of notch strains under multiaxial nominal loading. PhD thesis, Department of Theoretical and Applied Mechanics, University of Illinois at Urbana-Champaign, Illinois, 1993.
  24. Liu, C.; Shi, S; Cai, Y. ; Chen, X. Ratcheting behavior of pressurized-bending elbow pipe after thermal aging. Int. J. Press. Vessel. Pip. 2019, 169, 160–169. [Google Scholar] [CrossRef]
  25. Chen, X.; Jiao, R.; Kim, K.S. ; On the Ohno-Wang kinematic hardening rules for multiaxial ratcheting modeling of medium carbon steel. Int. J. Plast. 2005, 21(1), 161–184. [Google Scholar] [CrossRef]
  26. Hatami, F; Varvani-Farahani, A; Accumulation of plastic strain at notch root of steel specimens undergoing asymmetric fatigue cycles: Analysis and simulation. Materials. 2023, 16(6), 2153. [CrossRef] [PubMed]
  27. Chakherlou, T. N.; AJRI, M. Strain ratcheting and stress relaxation around interference-fitted single-holed plates under cyclic loading: experimental and numerical investigations. Fatigue Fract Eng Mater Struct 2012, 327–339. [Google Scholar] [CrossRef]
  28. Varvani-Farahani, A. A comparative study in descriptions of coupled kinematic hardening rules and ratcheting assessment over asymmetric stress cycles. Fatigue Fract. Eng. Mater. Struct. 2017, 40(6), 882–893. [Google Scholar] [CrossRef]
  29. Ramberg, W.; Osgood, W.R. Description of stress-strain curves by three parameters. NACA Technical Note No. 902 ( 1943.
  30. Kolasangiani, K. Analysis of Local and Global Ratcheting Behavior of AISI 1045 Steel Specimens with Cutout. PhD thesis, department of Mechanical Engineering, Ferdowsi University of Mashhad, 2018.
  31. Benedetti, M.; Menapace, C.; Fontanari, V. and Santus, C. On the variability in static and cyclic mechanical properties of extruded 7075-T6 aluminum alloy. Fatigue Fract Eng Mater Struct 2021, 44, 2975–2989. [Google Scholar] [CrossRef]
  32. ABAQUS User’s manual, Version 6.13. Hibbitt, Karlsson and Sorensen (2016).
Preprints 81079 g001
Figure 1. Measured ratcheting data versus asymmetric loading cycles for Al 7075-T6 pinned and un-pinned samples tested at various stress levels and distances from notch roots. (a) un-pinned sample (DIF=0), x=0.5mm, (b) pinned samples (DIF=1%), x=1.3mm and x=3mm, and (c) pinned samples (DIF=2%), x=1.3mm and x=3mm [27].
Figure 1. Measured ratcheting data versus asymmetric loading cycles for Al 7075-T6 pinned and un-pinned samples tested at various stress levels and distances from notch roots. (a) un-pinned sample (DIF=0), x=0.5mm, (b) pinned samples (DIF=1%), x=1.3mm and x=3mm, and (c) pinned samples (DIF=2%), x=1.3mm and x=3mm [27].
Preprints 81079 g001
Preprints 81079 g002
Figure 2. Figure 2. The A-V hardening rule coefficients for un-pinned (DIF=0) and press-fitted/ pinned (DIF=1% and 2%) Al 7075-T6 samples: (a) coefficients C and γ 1
Figure 2. Figure 2. The A-V hardening rule coefficients for un-pinned (DIF=0) and press-fitted/ pinned (DIF=1% and 2%) Al 7075-T6 samples: (a) coefficients C and γ 1
Preprints 81079 g002
Preprints 81079 g003
Figure 3. Figure 3. strain-controlled test to determine Chaboche’s coefficients C 1 − 3  
Figure 3. Figure 3. strain-controlled test to determine Chaboche’s coefficients C 1 − 3  
Preprints 81079 g003
Preprints 81079 g004
Figure 4. Initial and translated yield surfaces based on the A-V hardening rule for different DIFs Al 7075-T6 samples (a) Yield surface evolution, and (b) intercepts of yield surfaces and stress-strain curves in the first quadrant.
Figure 4. Initial and translated yield surfaces based on the A-V hardening rule for different DIFs Al 7075-T6 samples (a) Yield surface evolution, and (b) intercepts of yield surfaces and stress-strain curves in the first quadrant.
Preprints 81079 g004
Preprints 81079 g005
Figure 5. The evolution of backstress over loading cycles on un-pinned sample (DIF=0) and Pinned samples (DIF=1% and 2%) of Al7075-T6 tested under 155±155 MPa based on (a) the A-V model and (b) the Chaboche model.
Figure 5. The evolution of backstress over loading cycles on un-pinned sample (DIF=0) and Pinned samples (DIF=1% and 2%) of Al7075-T6 tested under 155±155 MPa based on (a) the A-V model and (b) the Chaboche model.
Preprints 81079 g005
Preprints 81079 g006
Figure 6. (a) Meshed Notch sample, constraints and loading direction, and (b) quadratic elements at the notch edge and at various distances from the notch root.
Figure 6. (a) Meshed Notch sample, constraints and loading direction, and (b) quadratic elements at the notch edge and at various distances from the notch root.
Preprints 81079 g006
Preprints 81079 g007
Figure 7. Stress distribution for the first loading cycles as distance x from notch root increases for un-pinned sample (DIF=0) and pinned samples (DIF=1% and 2%) of Al7075-T6 tested under various applied stresses.
Figure 7. Stress distribution for the first loading cycles as distance x from notch root increases for un-pinned sample (DIF=0) and pinned samples (DIF=1% and 2%) of Al7075-T6 tested under various applied stresses.
Preprints 81079 g007
Preprints 81079 g008
Figure 8. Predicted hysteresis loops for pinned and un-pinned samples of Al7075-T6 tested at 155±155MPa by means of the A-V and Chaboche kinematic hardening rule: (a) DIF=0% and a distance of x=0.5mm from the notch root (b-c) DIF=1% and different distances of x=1.3mm and x=3mm, and (d-e) DIF=2% and different distances of x=1.3mm and x=3mm.
Figure 8. Predicted hysteresis loops for pinned and un-pinned samples of Al7075-T6 tested at 155±155MPa by means of the A-V and Chaboche kinematic hardening rule: (a) DIF=0% and a distance of x=0.5mm from the notch root (b-c) DIF=1% and different distances of x=1.3mm and x=3mm, and (d-e) DIF=2% and different distances of x=1.3mm and x=3mm.
Preprints 81079 g008
Preprints 81079 g009
Figure 9. Predicted stress-controlled hysteresis loops for pinned samples of Al7075-T6 tested at 155±155MPa by means of the A-V model: (a) comparison of the first 100 loops in DIF=1% samples at distances x=1.3 and 3mm, and (b) comparison of the first 100 loops in DIF=2% samples at distances x=1.3 and 3mm.
Figure 9. Predicted stress-controlled hysteresis loops for pinned samples of Al7075-T6 tested at 155±155MPa by means of the A-V model: (a) comparison of the first 100 loops in DIF=1% samples at distances x=1.3 and 3mm, and (b) comparison of the first 100 loops in DIF=2% samples at distances x=1.3 and 3mm.
Preprints 81079 g009
Preprints 81079 g010
Figure 10. Predicted ratcheting curves for pinned and un-peened samples of Al7075-T6 by means of the A-V and Chaboche kinematic hardening rules: (a-c) DIF=1% and different stress levels of 129±129MPa, 155±155MPa, and of 182±182MPa, (d-e) DIF=2% and different stress levels of 129±129MPa, 155±155MPa, and of 182±182MPa.
Figure 10. Predicted ratcheting curves for pinned and un-peened samples of Al7075-T6 by means of the A-V and Chaboche kinematic hardening rules: (a-c) DIF=1% and different stress levels of 129±129MPa, 155±155MPa, and of 182±182MPa, (d-e) DIF=2% and different stress levels of 129±129MPa, 155±155MPa, and of 182±182MPa.
Preprints 81079 g010
Preprints 81079 g011
Figure 11. Predicted ratcheting curves at the vicinity of notch root through the A-V model for un-pinned sample (DIF=0) and pinned samples (DIF=1% and 2%) of Al7075-T6 subjected to 155±155MPa.
Figure 11. Predicted ratcheting curves at the vicinity of notch root through the A-V model for un-pinned sample (DIF=0) and pinned samples (DIF=1% and 2%) of Al7075-T6 subjected to 155±155MPa.
Preprints 81079 g011
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated