Preprint
Article
An Improved Image Compression Algorithm Using 2D DWT and PCA with Canonical Huffman Encoding
Altmetrics
Downloads
163
Views
52
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
31 July 2023
Posted:
02 August 2023
You are already at the latest version
Alerts
Abstract
Image compression is a top priority today due to the need for faster encoding and decoding. To achieve this, the present study has proposed the use of Canonical Huffman Coding (CHC) as an entropy coder, which has a lower decoding time complexity than binary Huffman codes. For image compression, combining of the Discrete Wavelet Transform (DWT) and CHC with Principal Component Analysis (PCA) has been recommended. The lossy method has been introduced by using PCA, followed by DWT and CHC to enhance compression efficiency. By using DWT and CHC instead of PCA alone, the reconstructed image has been found to have a better peak signal-to-noise ratio (PSNR) value. This study has developed a hybrid compression model combining the advantages of DWT, CHC and PCA. With the increasing use of image data, better image compression techniques are necessary for efficient use of storage space. The proposed technique has achieved up to 60% compression while maintaining high visual quality. This method has also outperformed the currently available techniques in terms of both PSNR (in dB) and bit-per-pixel (bpp) scores. This approach has been tested on various color images, including Peppers 512×512 and Couple 256×256, showing improvement by 17 dB and 22 dB, respectively, while reducing bpp by 0.56 and 0.10, respectively. For grayscale images, i.e., Lena 512×512 and Boat 256×256, the proposed method has shown an improvement by 5 dB and 8 dB, respectively, with a decrease of 0.02 bpp in both cases.
Keywords:
Subject: Computer Science and Mathematics - Computer Science
1. Introduction
With phenomenal rise in the use of digital images in the Internet era, researchers are concentrating on image-processing applications [1,2]. The need for image compression has been growing, due to the pressing need to minimize data size for transmission as a result of the constrained capacity of the Internet. The primary objectives of image compression are to store large amounts of data in a small memory space and transfer data quickly [2].
There are primarily two types of image compression methods: lossless and lossy. Lossless compression guarantees that the original and reconstructed images are exactly the same. On the other hand, Lossy compression, although used in many domains, can result in data loss to a certain extent for greater redundancy reduction. Here, the original image is first transformed using the forward transform before quantizing the final image. The compressed image is then produced using entropy encoding. This process is shown in Figure 1.
Firstly, the direct image compression method, which works on sampling the image in a spatial domain. This method comprises techniques, such as, block truncation (Block Truncation Coding (BTC) [5], Absolute Moment Block Truncation (AMBTC) [6], Modified Block Truncation Coding (MBTC) [7], Improved Block Truncation Coding using K-means Quad Clustering (IBTC-KQ) [8], Adaptive Block Truncation Coding using edge-based quantization approach (ABTC-EQ) [9]) and vector quantization [10].
Secondly, the Image transformation method that comprises Singular Value Decomposition (SVD) [11], Principal Component Analysis (PCA) [12], Discrete Cosine Transform (DCT) [13] and Discrete Wavelet Transform (DWT) [14]. Through this method image samples are transformed from the spatial domain to the frequency domain to concentrate the energy of the image into a small number of coefficients.
Presently, researchers are emphasizing the DWT transformation tool due to its pyramidal or dyadic wavelet decomposition properties [15], facilitating high compression and superior-quality reconstructed images. The present study has also demonstrated the benefits of the DWT-based strategy using Canonical Huffman coding, which was explained as the entropy encoder in the preliminary work by the same authors [16]. A comparison of Canonical Huffman coding with the basic Huffman coding reveals that Canonical Huffman coding has a smaller code-book size and requires less processing time.
In the present study, the issue of enhancing the compression ratio has been resolved by improving quality of the reconstructed image and by thoroughly analyzing the necessary parameters, such as, PSNR, SSIM, CR and BPP, for standard test images. PCA, DWT, normalization, thresholding and Canonical Huffman coding methods have been employed to achieve high compression with excellent image quality. In course of the present study, Canonical Huffman coding has proved to be superior to both Huffman and arithmetic coding, as explained in Section III D.
The present authors have developed a lossy compression technique during the study using the PCA [12] which is marginally superior to the SVD method [23] and DWT [16] algorithms for both grayscale and color images. Canonical Huffman coding [16] has been used to compress the reconstructed image to a great extent. The authors have also compared the parameters, obtained in their proposed method with those provided in the block truncation [24] and the DCT-based approaches [25].
In the process of the study, the authors have also examined several frequently cited images in the available literature. Slice resolutions of 512x512 and 256x256 have been used, which are considered to be the minimum standards in the industry [26]. Also, the present authors have calculated the compression ratio and the PSNR values of their methods and have compared them to other research findings [5,6,7,8,9,16,19].
The present paper is based on the following structure. A Literature Review is presented in Section II. Section III discusses the approach adopted in the present study, which also covers the necessary concepts. Section IV details the proposed algorithm. The parameters for performance evaluation are discussed in Section V. Section VI presents the experiment findings while Section VII marks the conclusion.
2. Literature Review
An overview of several published works on this subject highlights various other methods, studied by many other researchers. One approach that has gained considerable attention among the research communities in recent years is a hybrid algorithm that combines DWT with other transformation tools [10]. S M Ahmed et al. [17] detailed their method of compressing ECG signals using a combination of SVD and DWT. Jayamol M. et al. [8] presented an improved method for block truncation coding of grayscale images, known as IBTC-KQ. This technique uses K-means quad clustering to achieve better results. Aldzjia et al. [18] presented a method for compressing color images using the DWT and Genetic Algorithm (GA). Messaoudi et al. [19] proposed a technique called DCT-DLUT, which involves using the discrete cosine transform and a lookup table, known as, DLUT to demarcate the difference between the indices. It is a quick and effective way to compress lossy color images.
Paul et al. [10] proposed a technique, called, DWT-VQ (Discrete Wavelet Transform-Vector Quantization) for generating an YCbCr image from an RGB image. This technique compresses images while maintaining their perceptual quality at levels that are acceptable in a clinical setting. A K Pandey et al. [20] presented a compression technique that uses the Haar wavelet transform to compress medical images. A method for compressing images using the Discrete Laguerre Wavelet Transform (DLWT) was introduced by J A Eleiwy [21]. However, this method concentrates only on approximate coefficients from four sub-bands of DLWT post-decomposition. As a result, this approach may affect the quality of the reconstructed images. In other words, maintaining a good image quality while achieving a high compression rate can prove to be a considerable challenge in image compression. Additionally, the author did not apply the Peak Signal-to-Noise Ratio (PSNR) or the Structural Similarity Index Measure (SSIM) index to evaluate the quality of the reconstructed image.
M. Alosta et al. [22] examined the arithmetic coding for data compression, where they measured the compression ratio and bit rate to determine the extent of the image compression. However, their study did not assess the quality of the compressed images, specifically the PSNR or SSIM values, which correspond to the compression rate (CR) or bits per pixel (BPP) values.
3. Fundamental Concepts
Various phases of the suggested strategy for the present study have been outlined in this section. These include Canonical Huffman coding, DWT and PCA. A transformation is a mathematical process through which a function, taken as an input, is mapped into itself. Transformation can extract hidden or valuable data from the original image. Moreover, in comparison with the original data, the transformed data may be more amenable to mathematical operations. Therefore, transformation tools are a significant means for image compression.
The most widely used transformation methods include the Karhunen-Loeve transform (KLT) [27], Walsh Hadamard transforms (WHT) [28], SVD [11], PCA [12], DCT [13], DWT [14] and Integer Wavelet Transform (IWT) [29].
The DCT method is commonly used for compressing images. However, it may result in image artifacts when compressed with JPEG. Moreover, DCT does not have the multi-resolution transform property. In all these respects, DWT is an improvement [30]. With DWT, one obtains the resulting filtered image after going through various levels of discrete wavelet decomposition. One can also collect statistics on the frequency domain for the following procedure via multi-level wavelet decomposition. By combining noise reduction and through information augmentation, better image reconstruction can be ensured following compression [2].
Accordingly, the preferred method of choice for image compression during the present study has been DWT [14]. Because of its high energy compaction property and lossy nature, the image compression technique can remove unnecessary data from an image to achieve the desired compression level. It produces wavelet coefficients iteratively by dividing an image into its low-pass and high-pass components. These wavelet coefficients de-correlate pixels and Canonical Huffman coding eliminates redundant data.
3.1. Principal Component
The principal components are a small number of uncorrelated variables, derived from many correlated variables by means of the PCA [12] transformation technique. The PCA technique explores the finer points in the data to highlight their similarities and differences. Once the patterns are found, datasets can be compressed by reducing their dimensions without losing the basic information. Therefore, the PCA technique is suitable for image compression with minimal data loss.
The idea of the PCA technique is to take only the values of the principal components and use them to generate other components.
In short:
- ❖
- PCA is a standard method for reducing the number of dimensions.
- ❖
- The variables are changed into a fresh set of data, known as primary components. These principal components are combinations of initial variables in linear form and they are orthogonal.
- ❖
- The first principal component accounts for the majority of the potential variation in the original data.
- ❖
- The second principal component addresses the data variance.
Mathematical Concepts of PCA
The PCA Algorithm: The following steps make the PCA Algorithm:
- Step-01
- : Obtaining data.
- Step-01
- Step-02: Determining the mean vector (µ).
- Step-01
- Step-03: Subtracting the mean value from the data.
- Step-01
- Step-04: Doing a covariance matrix calculation.
- Step-01
- Step-05: Determining the covariance matrix's Eigenvalues and Eigenvectors.
- Step-01
- Step-06: Assembling elements to create a feature vector.
- Step-01
- Step-07: Creating a novel data set.
Mathematical Example
Two-dimensional patterns have to be taken into account, i.e., (2, 1), (3, 5), (4, 3), (5, 6), (6, 7), and (7, 8). It has to be followed by the principal component calculation.
Step-01:
Data is obtained. x1 = (2, 1), x2 = (3, 5), x3 = (4, 3), x4 = (5, 6), x5 = (6, 7) & x6 = (7, 8).
The vectors provided are— .
Step-02:
The mean vector (µ) is identified.
Mean vector (µ) = ((2 + 3 + 4 + 5 + 6 + 7) / 6, (1 + 5 + 3 + 6 + 7 + 8) / 6) = (4.5, 5)
Step-03:
The mean vector (µ) is subtracted from the data.
x1 – µ = (2 – 4.5, 1 – 5) = (-2.5, -4)
Similarly other feature vectors are obtained.
After removing the mean vector (µ), the following feature vectors (xi) are obtained:
Step-04:
A covariance matrix calculation is done.
The covariance matrices are provided by—
Now,
Similarly the value of is calculated.
Covariance matrix is now equal to (m1 + m2 + m3 + m4 + m5 + m6) / 6.
The matrices above are added and divided by 6:
Step-05:
The Eigenvalues and Eigenvectors of covariance matrix are determined.
A value is considered to be an eigenvalue (λ) for a matrix M if it solves the defining equation |M- λ |=0.
Hence, one gets:,
By resolving this quadratic problem = 8.22, 0.38 is obtained.
Hence, eigenvalues λ1 and λ2 are 8.22 and 0.38, respectively.
It is obvious that the second eigenvalue is much smaller than the first eigenvalue.
Hence, it is possible to exclude the second eigenvector. The primary component is the eigenvector that corresponds to the highest eigenvalue in the given data set. As a result, the eigenvector is located matching eigenvalue λ1. To find the eigenvector, the equation is formulated.
X = Eigenvector, M = Covariance Matrix, and λ = Eigenvalue
By changing the values in the aforementioned equation, X2 =1 and X1=0.69 are obtained. Then these numbers are divided by the square root of the sum of their squares. The eigenvector V is .
Hence, the principal component of the presented data set is .
3.2. Discrete Wavelet Transform: The Operational Principle of DWT
The data matrix of the image is split into four sub-bands, which are LL (low pass vertical and horizontal filter), LH (low pass vertical and high pass horizontal filter), HL (high pass vertical and low pass horizontal filter) and HH (high pass vertical and horizontal filter). These sub-bands are used to apply wavelet transform in computing (DWT [14] and Wavelet [HAAR] [25]). The concept behind the decomposition of the image into the four sub-bands is explained in Figure 2.
The process involves dividing the image into rows and columns after convolution. The Wavelet decomposition and reconstruction phases make the DWT. The image input undergoes a process of convolution that includes both low and high pass reconstruction phases. Figure 3a describes a one-level DWT decomposition. In Figure 3b, the up arrow denotes the up-sampling procedure. The wavelet reconstruction is the opposite of the wavelet decomposition.
In the data processing, various wavelet families are commonly used such as Haar ('haar'), Daubechies ('db'), Coiflets ('coif'), Symlets ('sym'), Biorthogonal ('bior') and Meyer ('meyer') [20]. During the present study, the Haar wavelet transform was applied due to its comparatively modest computational needs [25].
3.3. Thresholding: Hard Thresholding
The hard-thresholding method is used frequently in image compression. The hard-threshold function works by keeping the input value if it is greater than the set threshold T. If the input value is less than or equal to the threshold, it is set at zero [31].
3.4. Entropy Encoder: Canonical Huffman coding
Canonical Huffman coding [16,32], is a significant subset of regular Huffman coding and has several advantages over other coding schemes (Huffman, Arithmetic). Advantages include faster computation times, superior compression and higher reconstruction quality. Many researchers are working with this coding because of these benefits. The information required for decoding is compactly stored since the codes are in lexicographic order.
For instance, if the Huffman code for 5 bits is "00010," only five will be used for canonical Huffman coding, equaling the entire number of bits available in the Huffman code [33].
4. Proposed Method
In course of the present study, various approaches for compressing images have been examined, including, transforming RGB color images into color images [34], PCA transformation, wavelet transformation and extra processing by using thresholding, normalization and Canonical Huffman coding.
4.1. Basic Procedure
To compress the image, the PCA approach has been applied first. Next the output of PCA has been decomposed using DWT. Finally, the image has been further decomposed using Canonical Huffman encoding. In order to breakdown 8-bit/24-bit key images with 256 x 256 and 512 x 512 pixel sizes, a 1-level Haar wavelet transform has been used.
4.2. PCA Based Compression
The PCA procedure involves mapping from an n-dimensional space to a k-dimensional space using orthogonal transformations (k<n). The principal components, which are unique orthogonal features in this case, are the k-dimensional features that include the majority of the characteristics of the original data set. Because of this, it is used in image compression.
PCA is a reliable image compression technique that ensures nominal information loss. Compared to the SVD approach, the PCA method produces better results.
PCA_Algorithm
Encoding
Input: The image ,
Here, the values x and y represent the coordinates of individual pixels in an image. Depending on the type, the value corresponds to the color or gray level.
Step 1: Image normalization has to be done.
The normalization is carried out on the image data set .
Here, is the column vector containing the mean value for to.
Step 2: Compute covariance matrix of
Here, m is the number of element y.
Step 3: Compute Eigenvectors and Eigenvalues of
Using SVD equation , eigenvectors and eigenvalues are calculated.
Here, "U" represents the eigenvectors of "", while the squared singular values in "D" are the eigenvalues of "". Eigenvector matrix denotes the principal feature of image data i.e. principal component.
Output: Image data with reduced dimension
Here, is the transpose of the eigenvectors matrix and is the adjusted original image datasets.
It can also be expressed as:
Here, 'm' and 'n' represent the matrix's rows and columns, while 'k' represents the number of principal components with.
Decoding
By reconstructing the image data, one gets
In PCA, the compression ratio (ρ) is calculated as:
4.3. DWT-CHC Based Compression
The DWT details show zero mean and a slight variation. The more significant DWT coefficients are used and the less significant ones are discarded by using a Canonical Huffman coding. The algorithm based on DWT is presented below.
Algorithm:
Input: An image in grayscale of size
Output: A reconstruction of a grayscale image of size
Encoding of Image
Step 1: The DWT is applied to separate the grayscale image into lower and higher sub bands.
Step 2: The equation=, is applied to normalize the lower and upper sub bands in the range of (0, 1), where is coefficient matrix of the image, is the data to be normalized, and nd are the maximum and minimum intensity values, respectively.
Step 3: Hard thresholding on the higher sub-band is used to save the important bits and throw away the unimportant ones.
Step 4: To acquire the lower and higher sub band coefficients, the lower sub band coefficient to the range of 0 to 127 and the higher sub band coefficient to the range of 0 to 63 are assigned.
Step 5: The canonical Huffman coding is applied to each band.
Step 6: Compressed bit streams are obtained.
Decoding of Image
- Step 1: Bit streams are compressed.
- Step 2: The reverse canonical Huffman coding process is applied to retrieve the reconstructed lower and higher sub band coefficient from the compressed bit streams of approximate and detail coefficients.
- Step 3: To get the normalized coefficients for the lower and higher sub bands, their respective coefficients are divided by 127 and 63.
- Step 4: The equation is applied to do inverse normalization on the normalized lower and higher sub band.
- Step 5: Inverse DWT is applied to obtain an image that has been rebuilt.
4.4. PCA-DWT-CHC Based Image Compression
The method involves first compressing the image through the PCA, followed by decomposing of the gray scale/color image by using a 1-level Haar wavelet transform. One gets approximate and detailed images by applying this method. To produce a digital data sequence, the approximation coefficients have to be normalized and encoded with Canonical Huffman coding. Moreover, while normalizing the detail coefficients, any insignificant coefficients are removed through hard thresholding. Finally, binary data is also obtained by using the Canonical Huffman coding.
The final compressed bit stream is created by combining all the binary data. This stream is then divided into approximate and detailed coefficient binary data to reconstruct the image. The qualitative loss is apparent only after a certain point by eliminating some principal components. This entire procedure is termed as the DWT-CHC method. During the present study, the proposed strategy has been found to work better when the PCA-based compression technique under the lossy method, was used with DWT-CHC. The DWT outperforms PCA in terms of compression ratios while the PCA outperforms the DWT in terms of the PSNR values. Evaluation of the necessary number of bits yields the CR value for the PCA algorithm.
During the present experimentation, initially, the image was compressed by using the PCA. The approximate image was then further compressed by using DWT-CHC. Accordingly, the image was initially decomposed using PCA, then a few principal components were removed. The reconstructed image was then computed. After that, the reconstructed image was used as the input image for the DWT-CHC segment of the proposed method.
When several primary components were dropped from the PCA segment of the proposed method, the compression ratio was found to be higher. The overall CR value was obtained by multiplying the CR values of the PCA and the DWT-CHC.
To analyze an image, it is first decomposed, applying a Haar wavelet to its approximation, horizontal, vertical and diagonal detail coefficients. Next, the approximation and the detail coefficients are coded with the DWT-CHC. Encoding is the compression process and decoding is the simple process of reversing the encoding stages from which the reconstructed image is derived. After quantization, the image is rebuilt using the inverse DWT-CHC of the quantized block.
This approach combines the PCA and the DWT-CHC to reach its full potential. It uses PCA, DWT and Canonical Huffman coding to achieve a high compression ratio while maintaining an excellent image quality. The structural layout of the proposed image compression approach is shown in Figure 4.
The steps in the suggested method are as follows:
Encoding:
Step 1:
- (i)
- For a C(x, y) grayscale image with an x×y pixel size, by using the PCA method, is decomposed first in order to obtain the Principal Component.
- (ii)
- If the image is in color, the color transform is used to change the RGB data into
using the formula.
To determine the Principal Component from the image, PCA decomposition is carried out.
Step 2: The image is reconstructed just by utilizing these principal components while taking into account only the principal component for compression.
Step 3: Compression ratio is obtained.
Step 4: The decomposition level is set at 1.
Step 5: By utilizing the HAAR wavelet, DWT generates four output matrices: LL (known as the approximate coefficients), LH, HL and HH (known as the detail coefficients). These matrices consist of three components: vertical, horizontal and diagonal details.
Step 6: To obtain bit streams, the DWT-CHC algorithm is applied to these coefficients (Compressed image).
Step 7: The compression ratio is calculated.
Step 8: To determine the final compression ratio of an image, the output from Steps 3 and 7 is multiplied.
Decoding:
Step 1: The DWT-CHC approach is applied in reverse to obtain the approximate and detailed coefficients.
Step 2: A reconstructed image is obtained.
Step 3: The PSNR value is determined.
The flowchart that follows further explains this idea:
5. Performance Assessment
A few of the parameters listed below can be used to gauge the efficacy of the lossy compression strategy.
Compression Ratio (CR): CR [35] is a parameter that measures compressibility.
Mathematically,
where = the dimension of the original image data, = A measure of the compressed image data's size (in bits).
Bitrate (BPP): BPP equals 24/CR for color images and 8/CR for grayscale images.
Peak Signal to Noise Ratio (PSNR): It is a common metric for calculating the compressed image's quality. Typically, the PSNR for 8-bit images is presented as [36]:
where 255 is the highest value that the image signal is capable of achieving. The term "MSE" in equation (1) refers to the image's mean squared error, written as
Here, the variable "m" represents the total number of pixels in the image. F (x, y) refers to the value of each pixel in the compressed image, while f (x, y) represents the value of each pixel in the original image.
Structural Similarity Index (SSIM): It is a process for determining how similar two images can be [37].
Luminance change,
Contrast change,
Structural change,
Here, SSIM can be evaluated as:
y displays the image that was recreated, and x displays the original image.
= average of x, = average of y
= Variance of x, = Variance of y
Two variables, and, are used to stabilise a division with a weak denominator.
, ,
, as a rule
In this case, the pixel values range from 0 to 255 and are represented by L. The SSIM index that is generated as a consequence ranges from -1 to 1.
6. Experiment Result
The outcomes of experiment for image compression, utilizing the PCA-DWT-CHC hybrid approach, are shown in this section. Additionally, a comparison between the suggested approach and other available methods (BTC [5], AMBTC [6], MBTC [7], IBTC-KQ [8], ABTC-EQ [9], DWT [16] and DCT-DLUT [19]) has been made in this part. All experiments were conducted using the 512 x 512 and 256 x 256 input images (8-bit grayscale images, which are Lena, Barbara, Baboon, Goldhill, Peppers, Cameraman, Boat and 24-bit color images, i.e., Aeroplane, Peppers, Lena, Couple, House, and Zelda), as presented in Figure 5 and Figure 6.
All experiments were run in the interim on the MATLAB software platform using the hardware configurations of an Intel Core i3-4005U processor running at 1.70 GHz, 4.00 GB of RAM and Windows 8.1 Pro 64-bit as the operating system.
The compression performance of images for various approaches is shown in the next part which is based on visual quality evaluation and objective image quality indexes, i.e., PSNR, SSIM, CR and BPP.
Two measurements, namely, CR and BPP, reflect common aspects of image compression. The PSNR and SSIM are used to assess the quality of the compressed image. Greater PSNR and SSIM values indicate better image reconstruction whereas higher compression ratios and lower bitrates indicate enhanced image compression.
The predictive approach was used to determine the threshold values, which were TH=0.10. For both color (256×256×3 & 512×512×3) and grayscale (256×256 & 512×512) images, the principal component values of 25, 25, 200 and 400 were taken, respectively, to reconstruct the image.
6.1. Visual Performance Evaluation of Proposed PCA-DWT-CHC Method
Based on the quality of the reconstructed images, the proposed hybrid PCA-DWT-CHC image compression method was compared to the existing approaches. The reconstructed images for visual quality comparison on the PSNR values, 34.78 dB, 33.31 dB, 33.43 dB and 37.99 dB with CR = 4.41, 4.04, 5.15 and 4.45 for the input grayscale images, i.e., ‘lena.bmp’ and ‘barbara.bmp’ of size 512×512 and ‘cameraman.bmp’ and ‘boat.bmp’ of size 256×256 are shown in Figures 7b,d and 8b,d. Figures 9a,b and 10a,b display the reconstructed image for visual quality comparison on the PSNR values 47.57 dB, 47.99 dB, 54.60 dB, and 53.47 dB with compression factors (in BPP) 0.27, 0.32, 0.69 and 0.70, respectively, for the input color images ‘airplane.bmp,’ and ‘peppers.bmp’ of size 512×512 and ‘couple.bmp’ and ‘house.bmp’ of size 256×256.
The results in Figure 7, Figure 8, Figure 9 and Figure 10 demonstrate that the proposed hybrid PCA-DWT-CHC method yielded superior quality image reconstruction as compared to other image compression methods for all input images. Based on the visual quality assessment of various standard test images, it has been demonstrated that the proposed hybrid PCA-DWT-CHC method is more efficient in reconstructing images as compared to the other available methods.
6.2. Objective Performance Evaluation of Proposed PCA-DWT-CHC Method
According to the experiment results, the suggested PCA, followed by the DWT-CHC approach, proved to be better in terms of PSNR, SSIM, BPP and CR values when compared to the other methods, as shown in Table 1 and Table 2.
In other words, from Table 1 and Table 2, one could conclude that the proposed method is superior to the BTC [5], AMBTC [6], MBTC [7], IBTC-KQ [8], ABTC-EQ [9] & DWT-CHC [16] and DCT-DLUT [19] for working on the grayscale and color images. This could be explained by the fact that among all the different compression methods, the PSNR and SSIM values in the proposed method are higher than the other available methods. Similarly, the CR value is higher than that of all other methods. Again, the bitrate values of the proposed method are noted to be less than all the other methods for color images.
The graphs in Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18 show the PSNR, SSIM, CR and the Compression factor (in bpp) results for eight grayscale images. Figure 19, Figure 20, Figure 21 and Figure 22, on the other hand, present graphs for the PSNR and Compression factor (in bpp) for six other color images. While comparing data from these graphs with the results of various other available techniques, the former demonstrated that the proposed method works better than the presently available ones.
Figure 11, Figure 14, Figure 19 and Figure 21 display the PSNR characteristics, while Figure 12 and Figure 16 show the SSIM index. The CR values are found in Figure 13 and Figure 17 and the compression factor (in bpp) can be seen in Figure 14, Figure 18, Figure 20 and Figure 22. It is evident from the four PSNR plots that the proposed hybrid PCA-DWT-CHC method performs better than the DWT and other existing approaches in terms of PSNR values. The hybrid PCA-DWT-CHC method displays significant improvements. When tested on the Lena image, it resulted in a gain of approximately 6 dB, -2 dB, -6 dB, -1 dB, -1 dB and 13 dB in PSNR. The CR values, on the other hand, showed a gain of 2, 1, 2.40, 0.4058, 0.4058 and 0.4058. The values for other standard test images can be obtained from Table 1 and Figure 11, Figure 14, Figure 19, Figure 21, Figure 13 and Figure 17.
The proposed method aims to enhance the image compression without compromising the image quality. In comparison to other methods, such as, DWT, ABTC-EQ, IBTC-KQ, MBTC, AMBTC and BTC, this process has proved to maintain or even improve the original image quality. The proposed hybrid PCA-DWT-CHC method for color images has revealed a significant increase in the PSNR values for Airplane, Peppers, Lena, Couple, House and Zelda images with gains of 16.41 dB, 16.80 dB, 16.30 dB, 21.98 dB, 30.20 dB and 21.73 dB. Additionally, this method has been found to reduce the compression factor (in bpp) by 0.21, 0.56, 0.37, 0.10, 0.09, 0.11 and 0.24. The parameters concerning the PSNR values are presented in Figure 19 and Figure 21 and concerning the compression factor (in bpp) are presented in Figure 20 and Figure 22.
The proposed method has also improved the SSIM index by 0.3734, 0.0161, 0.0058, 0.0146, 0.0450 and 0.0731 for the Goldhill grayscale image.
In other words, the suggested hybrid method has established with data that it could yield better-quality image reconstruction as compared to the other methods.
It has also shown improvement in image compression, as indicated by its higher CR values and lower compression factor (in bpp). Figure 12 and Figure 16 demonstrate that the SSIM characteristics, showing that the proposed hybrid PCA-DWT-CHC method ensure the highest SSIM values for all the test images. In other words, the proposed method is able to reconstruct all the images with greater similarity to the original ones as compared to the other available methods.
6.3. Time Complexity Analysis OF Proposed PCA-DWT-CHC Method
The speed of an entropy coder's encoding and decoding process is essential for real-time compression. In order to give a clear idea of whether entropy coders can be used in real-time applications, their time complexity needs to be explained. During the present study, the total time needed for an entropy coder to encode and decode data to ensure proper evaluation of its time complexity was assessed. The average time requirements were calculated and compared for analysis purposes. Table 3 presents the average time requirements of two entropy coders for encoding and decoding processes (ATTREDP). According to Table 3, the Canonical Huffman coding entropy coder is quicker than other entropy coders. Compared to the Huffman coding, the process of encoding and decoding of the four test images respectively takes 404.37, 388.05, 276.00 and 336.15 less time. The proposed hybrid PCA-DWT-CHC transform proves to be faster than other hybrid transform methods which use Huffman coding [16] as an entropy coder. Therefore, one could claim the proposed method to be effective for applications that require real-time image compression
7. Conclusion
The present study envisaged to develop a method that will improve the image quality and compression. By combining PCA, DWT and Canonical Huffman Coding, a new approach has been developed for compressing images. Accordingly, the proposed method has been able to outperform the existing methods, such as, BTC, AMBTC, MBTC, IBTC-KQ, ABTC-EQ, DWT and DCT-DLUT. Lower bit rates and better PSNR, CR and SSIM values indicate improved image quality. A comparison of the PSNR, SSIM, CR and BPP values, resulting from the proposed technique with that of the other available approaches confirms the superiority of the proposed method.
The findings from the objective and subjective tests indicate that the newly developed approach offers a more efficient image compression technique as compared to the existing techniques. For example, when working with grayscale images of 256×256 and 512×512 resolutions, improved results in metrics, such as, PSNR, SSIM, BPP and CR have been established. Again, in the case of color images of 256×256×3 and 512×512×3 resolutions, improved PSNR and lower BPP results have been noted. Hence, one could conclude that the proposed technique performs better than BTC, AMBTC, MBTC, IBTC-KQ, ABTC-EQ and DWT for grayscale images. Moreover, it is more useful with regard to the color images as compared to the ‘DCT-DLUT’. Therefore, this present research has the potential to greatly improve the storage and transmission of image data across the digital networks
References
- P. M. Latha and A. A. Fathima, “Collective Compression of Images using Averaging and Transform coding,” Measurement, vol. 135, pp. 795-805, Mar. 2019. [CrossRef]
- Sarah H. Farghaly, Samar M. Ismail, “Floating-point discrete wavelet transform-based image compression on FPGA,” AEU International Journal of Electronics and Communications, vol. 124, pp. 153363-73, Sep. 2020. [CrossRef]
- Messaoudi A, Srairi K, “Colour image compression algorithm based on the dct transform using difference lookup table.” Electron Lett. vol. 52, no. 20, pp. 1685–1686, Sep. 2016. [CrossRef]
- B. Ge, N. Bouguila, & W. Fan, “Single-target visual tracking using color compression and spatially weighted generalized Gaussian mixture models.” Pattern Anal Applic., vol. 25, pp. 285–304, Jan. 2022. [CrossRef]
- E. Delp and O. Mitchell, "Image Compression Using Block Truncation Coding," in IEEE Transactions on Communications, vol. 27, no. 9, pp. 1335-1342, Sep. 1979. [CrossRef]
- M. Lema and O. Mitchell, "Absolute Moment Block Truncation Coding and Its Application to Color Images," in IEEE Transactions on Communications, vol. 32, no. 10, pp. 1148-1157, Oct. 1984. [CrossRef]
- J. Mathews, M. S. Nair and L. Jo, "Modified BTC algorithm for gray scale images using max-min quantizer," 2013 International Mutli-Conference on Automation, Computing, Communication, Control and Compressed Sensing (iMac4s), Kottayam, India, 2013, pp. 377-382. [CrossRef]
- J. Mathews, M. S. Nair and L. Jo, “Improved BTC Algorithm for Gray Scale Images Using K-Means Quad Clustering,” In: proc. The 19th International Conference on Neural Information Processing, ICONIP 2012, Part IV, LNCS 7666, Doha, Qatar, 2012, pp. 9–17. [CrossRef]
- J. Mathews, M. S. Nair, “Adaptive block truncation coding technique using edge-based quantization approach,” Computers & Electrical Engineering, vol. 43, pp. 169-179, Apr. 2015. [CrossRef]
- P. N. T. Ammah, E. Owusu, “Robust medical image compression based on wavelet transform and vector quantization,” Informatics in Medicine Unlocked, vol. 15, pp. 100183 (1-11), Apr. 2019. [CrossRef]
- R. Kumar, U. Patbhaje, A. Kumar, “An efficient technique for image compression and quality retrieval using matrix completion,” Journal of King Saud University - Computer and Information Sciences, vol. 34, no. 4, pp. 1231-1239, Apr. 2022. [CrossRef]
- Zhou Wei, Sun Lijuan, Guo Jian, Liu Linfeng, “Image compression scheme based on PCA for wireless multimedia sensor networks,” The Journal of China Universities of Posts and Telecommunications, vol. 23, no. 1, pp. 22-30, Feb. 2016. [CrossRef]
- H. A. F. Almurib, T. N. Kumar and F. Lombardi, "Approximate DCT Image Compression Using Inexact Computing," IEEE Transactions on Computers, vol. 67, no. 2, pp. 149-159, Feb. 2018. [CrossRef]
- R. Ranjan, and P. Kumar, “An Efficient Compression of Gray Scale Images Using Wavelet Transform,” Wireless Pers. Commun., vol. 126, pp. 3195-3210, Jun. 2022. [CrossRef]
- P. A. Cheremkhin, E. A. Kurbatova, “Wavelet compression of off-axis digital holograms using real /imaginary and amplitude/phase parts.” Nature research, Scientific Reports, vol. 9, pp. 7561 (1-13), May 2019. [CrossRef]
- R. Ranjan, “Canonical Huffman Coding Based Image Compression using Wavelet,” Wireless Pers. Commun., vol. 117, no. 3, pp. 2193–2206, Apr. 2021. [CrossRef]
- S. M. Ahmed, Q. Al-Zoubi, M. Abo-Zahhad, “A hybrid ECG compression algorithm based on singular value decomposition and discrete wavelet transform,” J Med Eng Technol., vol. 31, no. 1, pp. 54– 61, Feb. 2007. [CrossRef]
- A. Boucetta, K. E. Melkemi, “DWT Based-Approach for Color Image Compression Using Genetic Algorithm,” In A. Elmoataz, D. Mammass, O. Lezoray, F. Nouboud & D. Aboutajdine (eds.), ICISP 2012, 2012, pp. 476-484.
- A. Messaoudi, K. Srairi, “Colour image compression algorithm based on the dct transform using difference lookup table,” Electron Lett., vol. 52, no. 20, pp. 1685-1686, Sep. 2016. [CrossRef]
- A. K. Pandey, J. Chaudhary, A. Sharma, H. C. Patel, P. D. Sharma, V. Baghel et al., “Optimum Value of Scale and threshold for Compression of 99m To-MDP bone scan image using Haar Wavelet Transform,” Indian J Nucl Med., vol. 37, no. 2, pp. 154-61, Apr. 2022. [CrossRef]
- Jabbar Abed Eleiwy, Characterizing wavelet coefficients with decomposition for medical images, Journal of Intelligent Systems and Internet of Things, Vol. 2, No. 1, (2021): 26-32. [CrossRef]
- Mahmud Alosta , Alireza Souri, Design of Effective Lossless Data Compression Technique for Multiple Genomic DNA Sequences, Fusion: Practice and Applications, Vol. 6 , No. 1 , (2021) : 17-25. [CrossRef]
- W. Renkjumnong, “SVD and PCA in Image Processing,” M. S. thesis, Dept. arts & sci., Georgia State Uni., Alanta, GA, USA, 2007.
- R. Ranjan and P. Kumar, “Absolute Moment Block Truncation Coding and Singular Value Decomposition-Based Image Compression Scheme Using Wavelet,” In: Sharma, H., Shrivastava, V., Kumari Bharti, K., Wang, L. (eds) Communication and Intelligent Systems. Lecture Notes in Networks and Systems, vol. 461, Springer, Singapore, Aug. 2022, PP. 919-931.
- R. Ranjan, P. Kumar, K. Naik and V. K. Singh, “ The HAAR-the JPEG based image compression technique using singular values decomposition,” 2022 2nd International Conference on Emerging Frontiers in Electrical and Electronic Technologies (ICEFEET), Patna, India, 2022, pp. 1-6.
- R. Boujelbene, L. Boubchir, Y. B. Jemaa, “Enhanced embedded zerotree wavelet algorithm for lossy image coding,” IET Image Process. vol. 13, no. 8, pp. 1364–1374, May 2019. [CrossRef]
- Y Nian, Ke Xu, J Wan, L Wang, Mi He, “Block-based KLT compression for multispectral Images,” International Journal of Wavelets, Multiresol Inf Process, vol. 14, no. 4, pp. 1650029, 2016. [CrossRef]
- A. D. Andrushia, R. Thangarjan, “Saliency-Based Image Compression Using Walsh–Hadamard Transform (WHT),” In: Hemanth, J., Balas , V. (eds) Biologically Rationalized Computing Techniques For Image Processing Applications. Lecture Notes in Computational Vision and Biomechanics, vol. 25, Springer, Cham, Aug. 2017, pp. 21-42.
- A. Shaik, V. Thanikaiselvan, “Comparative analysis of integer wavelet transforms in reversible data hiding using threshold based histogram modification,” Journal of King Saud University-Computer and Information Sciences, vol. 33, no. 7, pp. 878-889, Sep. 2021. [CrossRef]
- T. Liu and Y. Wu, "Multimedia Image Compression Method Based on Biorthogonal Wavelet and Edge Intelligent Analysis," in IEEE Access, vol. 8, pp. 67354-67365, 2020. [CrossRef]
- A. A. Nashat and N. M. Hussain Hassan, "Image compression based upon Wavelet Transform and a statistical threshold," 2016 International Conference on Optoelectronics and Image Processing (ICOIP), Warsaw, Poland, 2016, pp. 20-24.
- Szymon Grabowski, Dominik Köppl, Space-efficient Huffman codes revisited, Information Processing Letters, vol. 179, pp. 106274, 2023. [CrossRef]
- S. R. Khaitu and S. P. Panday, "Canonical Huffman Coding for Image Compression," 2018 IEEE 3rd International Conference on Computing, Communication and Security (ICCCS), Kathmandu, Nepal, 2018, pp. 184-190. [CrossRef]
- H. Tang, H. Zhu, H. Tao, C. Xie, “An Improved Algorithm for Low-Light Image Enhancement Based on RetinexNet.,” Appl. Sci. , vol. 12, pp. 7268, 2022. [CrossRef]
- A. Baviskar, S. Ashtekar, A. Chintawar, "Performance evaluation of high quality image compression techniques," 2014 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Delhi, India, 2014, pp. 1986-1990. [CrossRef]
- A. A. Jeny, M. B. Islam, M. S. Junayed and D. Das, "Improving Image Compression With Adjacent Attention and Refinement Block," in IEEE Access, vol. 11, pp. 17613-17625, 2023. [CrossRef]
- M. L. P. Rani, G. S. Rao and B. P. Rao, "Performance Analysis of Compression Techniques Using LM Algorithm and SVD for Medical Images," 2019 6th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 2019, pp. 654-659. [CrossRef]
Short Biography of Authors
 |
RAJIV RANJAN (Member, IEEE) holds a B. Tech in information technology, an M. Tech in computer science and engineering with a specialization in information security, and is currently pursuing a Ph. D. in computer science and engineering. He works as an Assistant Professor at BIT Sindri in Dhanbad, India. He has worked in numerous reputable technological institutions before that. He has 15 years of both teaching and research experience. He has published numerous articles in international journals and conferences as the author or coauthor. His areas of interest in study span cryptography, image compression, and data compression. |
 |
PRABHAT KUMAR (Senior Member, IEEE) is a Professor in Computer Science and Engineering Department at National Institute of Technology Patna, India. He is also the Professor-In-charge of the IT Services and Chairman of Computer and IT Purchase Committee, NIT Patna. He is the former Head of CSE Department, NIT Patna as well as former Bihar State Student Coordinator of Computer Society of India. He has over 100 publications in various reputed international journals and conferences. He is a member of NWG-13 (National Working Group 13) corresponding to ITU-T Study Group 13 “Future Networks, with focus on IMT-2020, cloud computing and trusted network infrastructures”. His research area includes Wireless Sensor Networks, Internet of Things, Social Networks, Operating Systems, Software Engineering, E-governance, Image Compression etc. He is a renowned scholar, reviewer, and teacher of excellence on a global scale. |
Figure 1.
Lossy Image Compression Block Diagram in General.

Figure 2.
Decomposition of discrete wavelets Transform: (a) Input Image, (b) Image Sub-bands, and (c) 1-Level DWT Decomposition.
Figure 2.
Decomposition of discrete wavelets Transform: (a) Input Image, (b) Image Sub-bands, and (c) 1-Level DWT Decomposition.
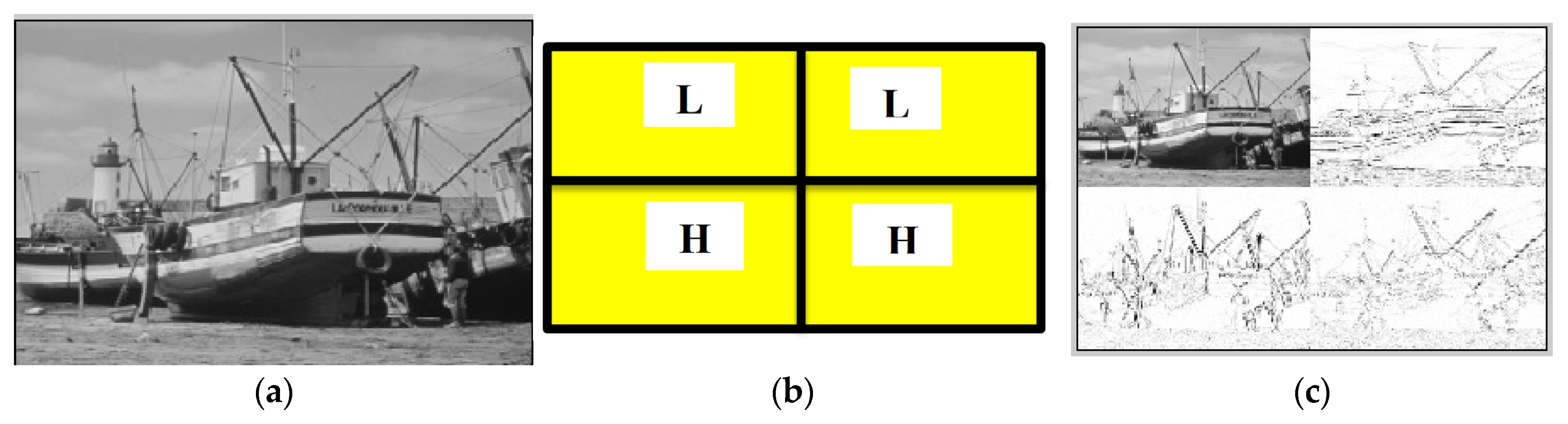
Figure 3.
(a) Decomposition and (b) Reconstruction of a One Level Discrete Wavelet Transform.

Figure 4.
The suggested method's encoder and decoder flowchart.
Figure 5.
Test images in grayscale for size 512×512 (a–d) & 256×256 (e–h).
Figure 6.
512x512 (a–c) and 256x256 (d–f) (color test images) in size.

Figure 7.
Results of compression for the 512×512 grayscale images of Lena and Barbara. (a) Lena image reconstruction using DWT with PSNR=29.90 dB and CR=2.43; (b) Lena image reconstruction using the proposed method with PSNR=34.78 dB and CR=4.41 (c) Barbara image reconstruction using DWT with PSNR=27.75 dB and CR=2.11 (d) Barbara image reconstruction using the proposed method with PSNR=33.31 dB and CR=4.04.
Figure 7.
Results of compression for the 512×512 grayscale images of Lena and Barbara. (a) Lena image reconstruction using DWT with PSNR=29.90 dB and CR=2.43; (b) Lena image reconstruction using the proposed method with PSNR=34.78 dB and CR=4.41 (c) Barbara image reconstruction using DWT with PSNR=27.75 dB and CR=2.11 (d) Barbara image reconstruction using the proposed method with PSNR=33.31 dB and CR=4.04.

Figure 8.
Compression outcomes for the grayscale images Cameraman & Boat of size 256×256 (a) Reconstructed Cameraman image by DWT with PSNR=26.43 dB, CR=2.86, (b) Reconstructed Cameraman image by Proposed Method with PSNR=33.43 dB, CR= 5.15 (c) Reconstructed Boat image by DWT with PSNR=29.65 dB, CR=2.35 (d) Reconstructed Boat image by Proposed Method with PSNR=37.99 dB, CR=4.45.
Figure 8.
Compression outcomes for the grayscale images Cameraman & Boat of size 256×256 (a) Reconstructed Cameraman image by DWT with PSNR=26.43 dB, CR=2.86, (b) Reconstructed Cameraman image by Proposed Method with PSNR=33.43 dB, CR= 5.15 (c) Reconstructed Boat image by DWT with PSNR=29.65 dB, CR=2.35 (d) Reconstructed Boat image by Proposed Method with PSNR=37.99 dB, CR=4.45.

Figure 9.
Results of compression for the 512×512 color images Airplane & Peppers. (a) Reconstructed image of an airplane using the proposed method, PSNR = 47.57 dB, and bpp = 0.27 (b) Peppers image reconstruction using the proposed method, PSNR = 47.99 dB, and bpp = 0.32.
Figure 9.
Results of compression for the 512×512 color images Airplane & Peppers. (a) Reconstructed image of an airplane using the proposed method, PSNR = 47.57 dB, and bpp = 0.27 (b) Peppers image reconstruction using the proposed method, PSNR = 47.99 dB, and bpp = 0.32.
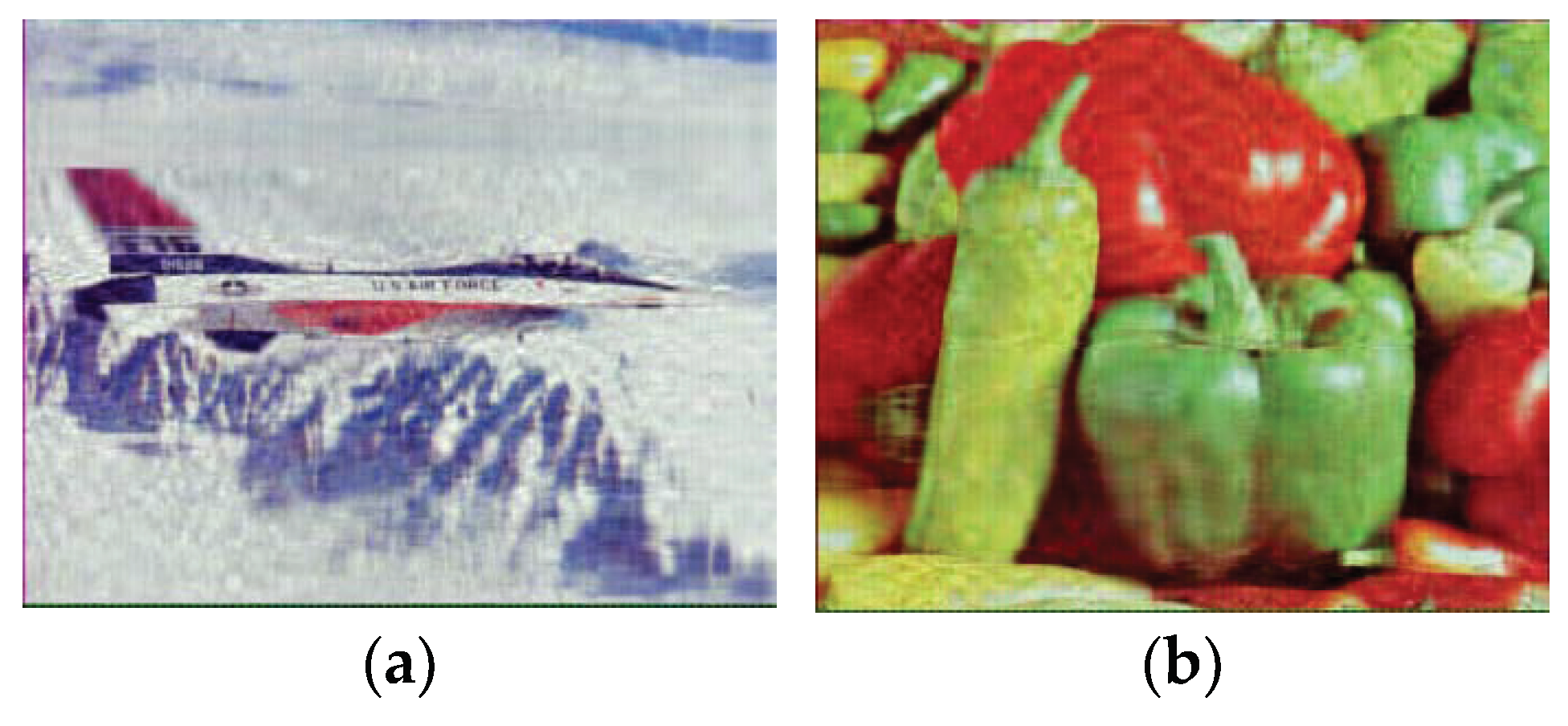
Figure 10.
Results of the color images' compression Couple & house with 256x256-sized (a) Reconstructed image of a couple with PSNR of 54.60 d Band bpp of 0.69; (b) Reconstructed image of a house with PSNR of 53.47 dB and bpp of 0.70.
Figure 10.
Results of the color images' compression Couple & house with 256x256-sized (a) Reconstructed image of a couple with PSNR of 54.60 d Band bpp of 0.69; (b) Reconstructed image of a house with PSNR of 53.47 dB and bpp of 0.70.

Figure 11.
Comparison of various compression techniques used on the different test grayscale images (Lena, Barbara, Baboon and Goldhill).
Figure 11.
Comparison of various compression techniques used on the different test grayscale images (Lena, Barbara, Baboon and Goldhill).
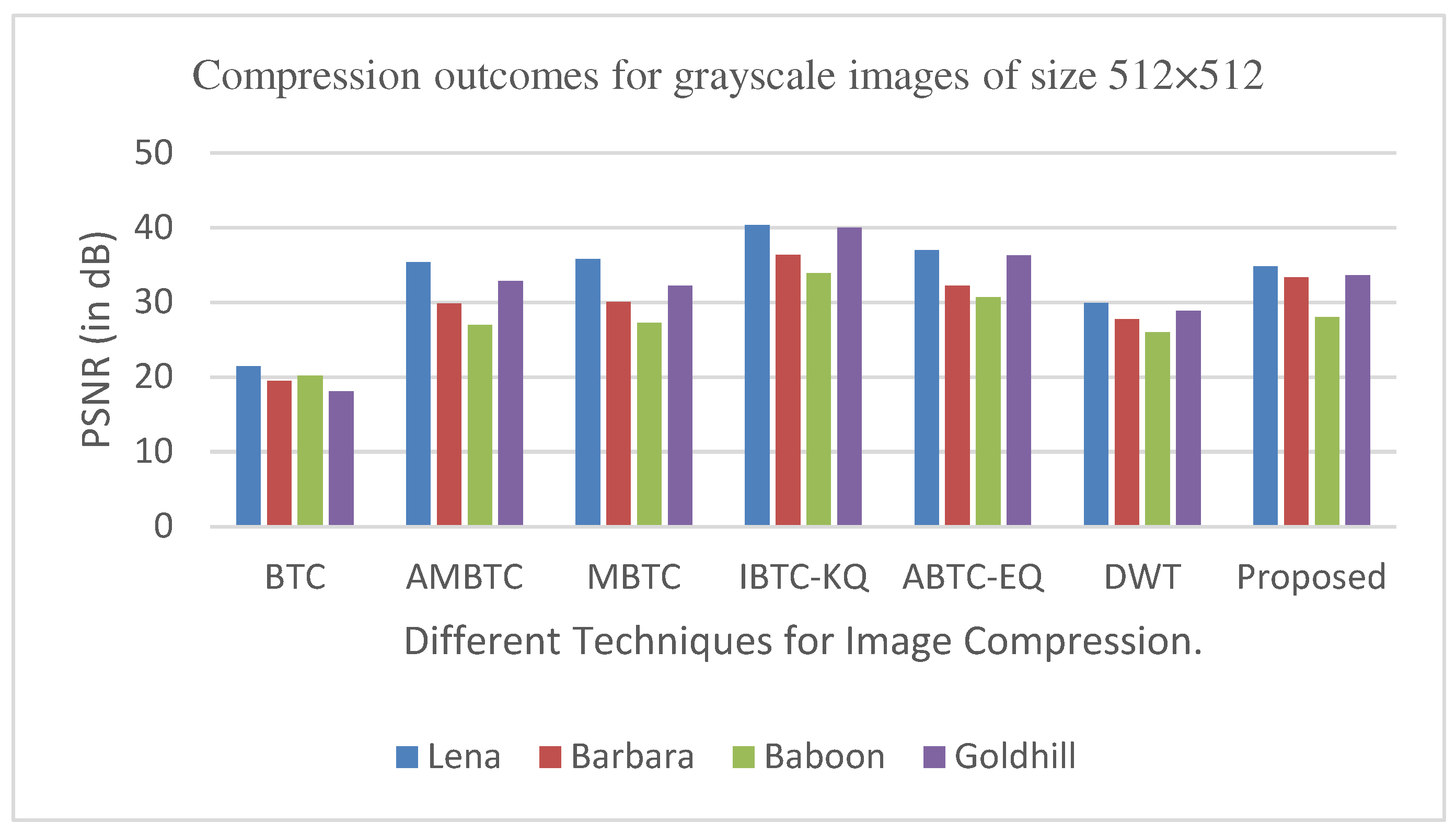
Figure 12.
Comparison of various compression techniques used on the different test grayscale images (Lena, Barbara, Baboon and Goldhill).
Figure 12.
Comparison of various compression techniques used on the different test grayscale images (Lena, Barbara, Baboon and Goldhill).
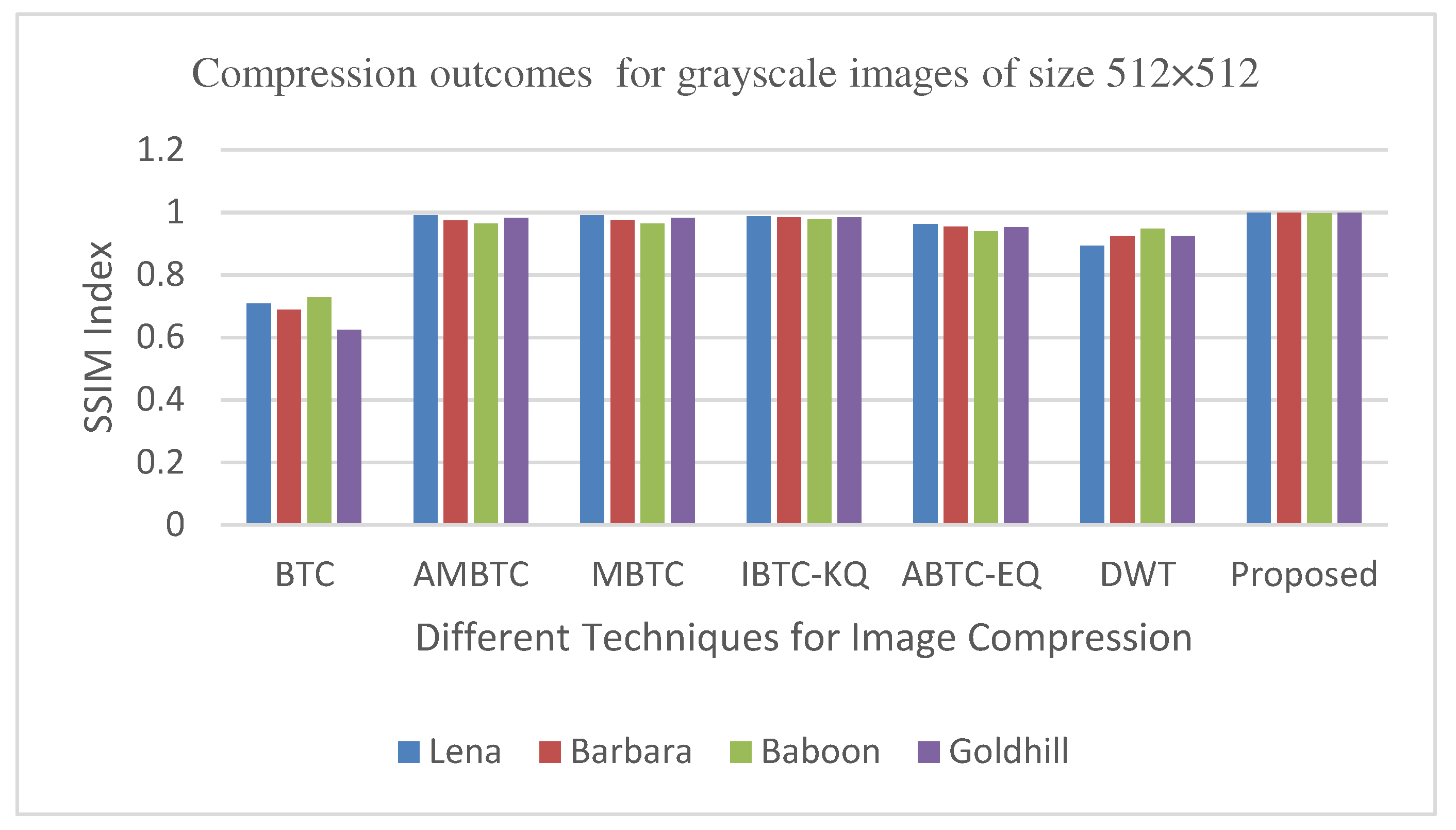
Figure 13.
Comparison of various compression techniques used on the different test grayscale images ( Lena, Barbara, Baboon and Goldhill).
Figure 13.
Comparison of various compression techniques used on the different test grayscale images ( Lena, Barbara, Baboon and Goldhill).
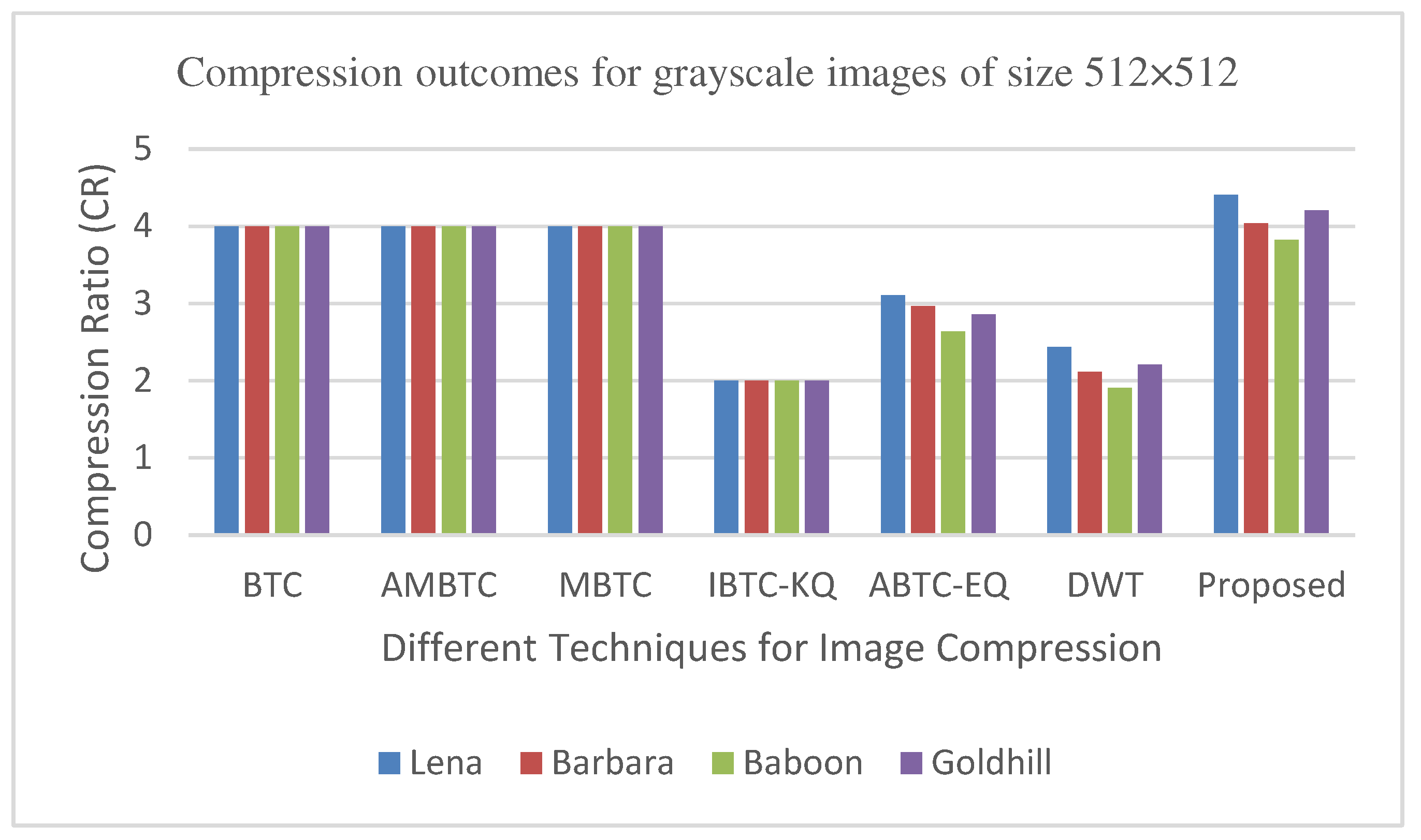
Figure 14.
Comparison of various compression techniques used on the different test grayscale images (Lena, Barbara, Baboon and Goldhill).
Figure 14.
Comparison of various compression techniques used on the different test grayscale images (Lena, Barbara, Baboon and Goldhill).
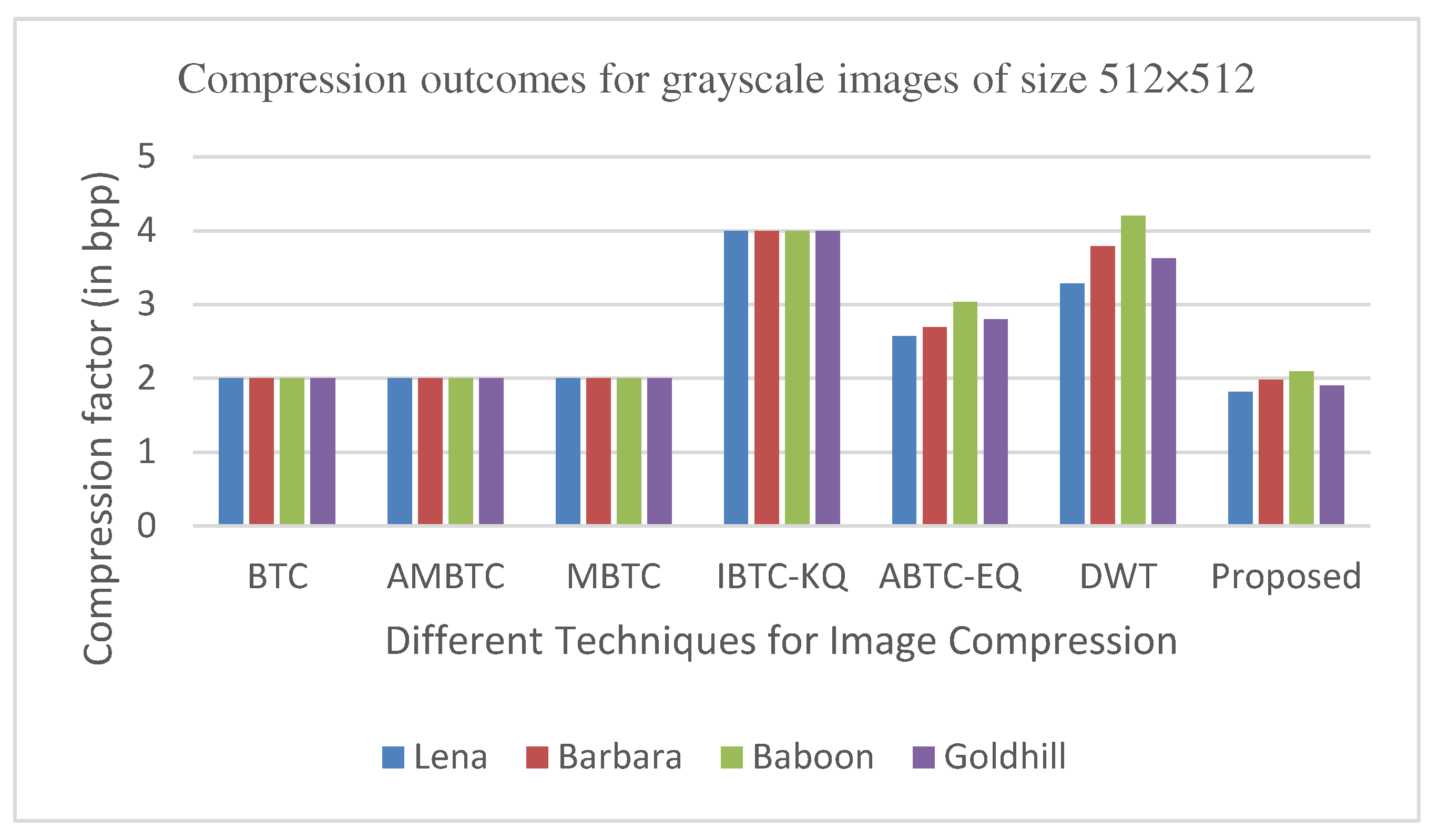
Figure 15.
Comparison of various compression techniques used on the different test grayscale images: 1- Lena, 2-Peppers, 3-Cameraman, and 4-Boat.
Figure 15.
Comparison of various compression techniques used on the different test grayscale images: 1- Lena, 2-Peppers, 3-Cameraman, and 4-Boat.

Figure 16.
Comparison of various compression techniques used on the different test grayscale images: 1- Lena, 2-Peppers, 3-Cameraman, and 4-Boat.
Figure 16.
Comparison of various compression techniques used on the different test grayscale images: 1- Lena, 2-Peppers, 3-Cameraman, and 4-Boat.
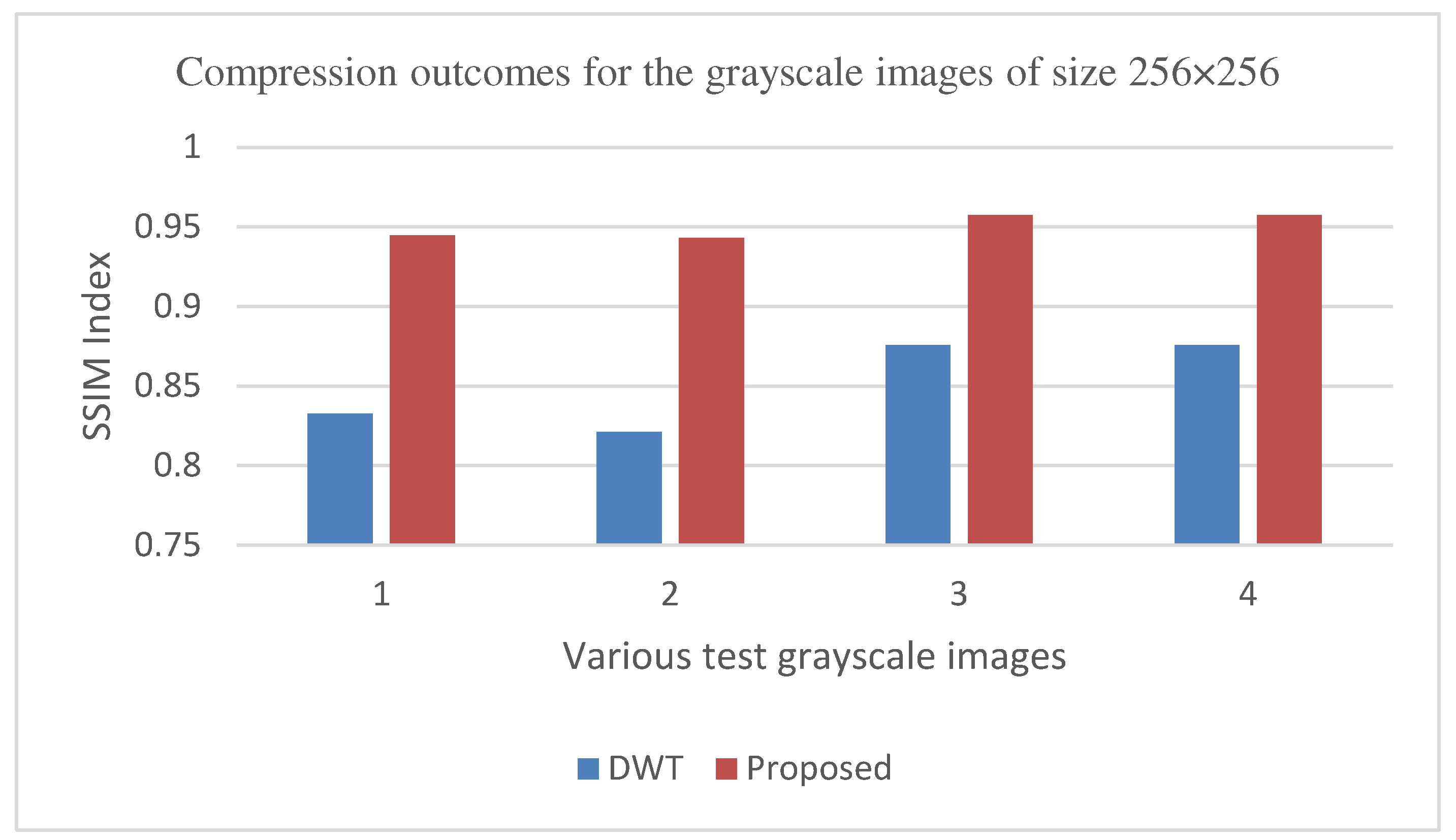
Figure 17.
Comparison of various compression techniques used on the different test grayscale images: 1- Lena, 2-Peppers, 3-Cameraman, and 4-Boat.
Figure 17.
Comparison of various compression techniques used on the different test grayscale images: 1- Lena, 2-Peppers, 3-Cameraman, and 4-Boat.
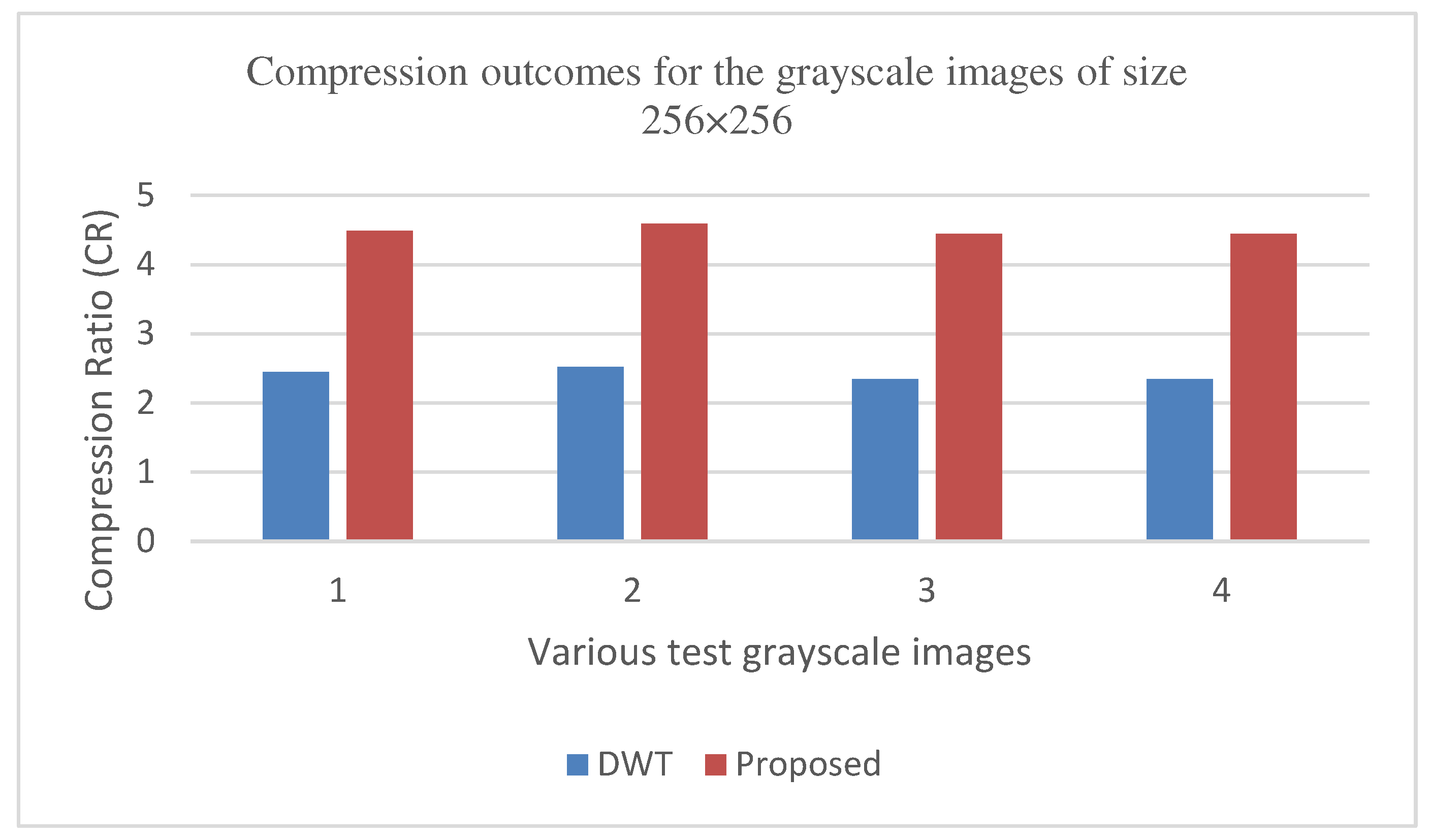
Figure 18.
Comparison of various compression techniques used on the different test grayscale images: 1- Lena, 2-Peppers, 3-Cameraman, and 4-Boat.
Figure 18.
Comparison of various compression techniques used on the different test grayscale images: 1- Lena, 2-Peppers, 3-Cameraman, and 4-Boat.
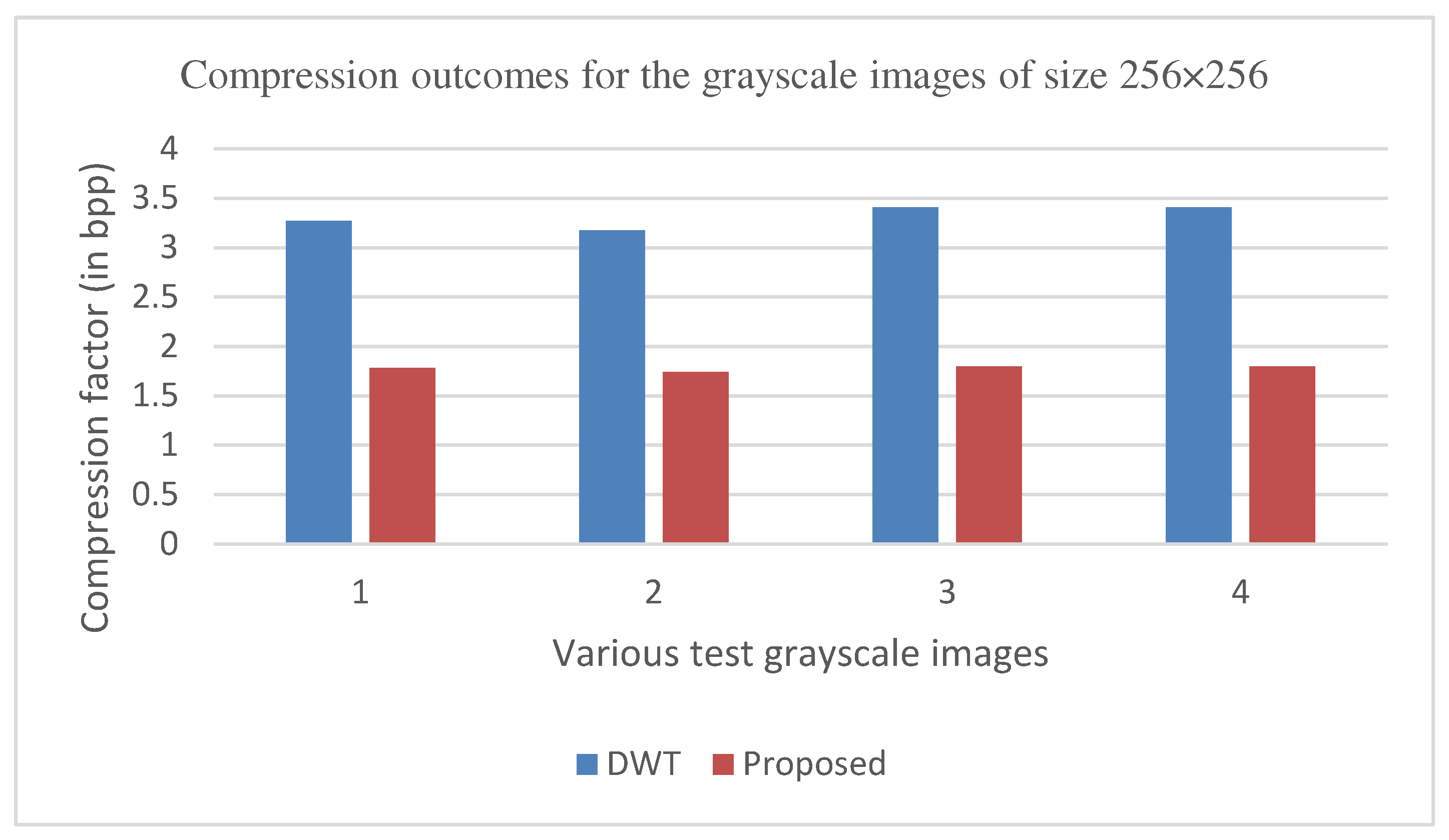
Figure 19.
Comparison of various compression techniques used on the different color test images: 1-airplane, 2-pepper, and 3-Lena.
Figure 19.
Comparison of various compression techniques used on the different color test images: 1-airplane, 2-pepper, and 3-Lena.
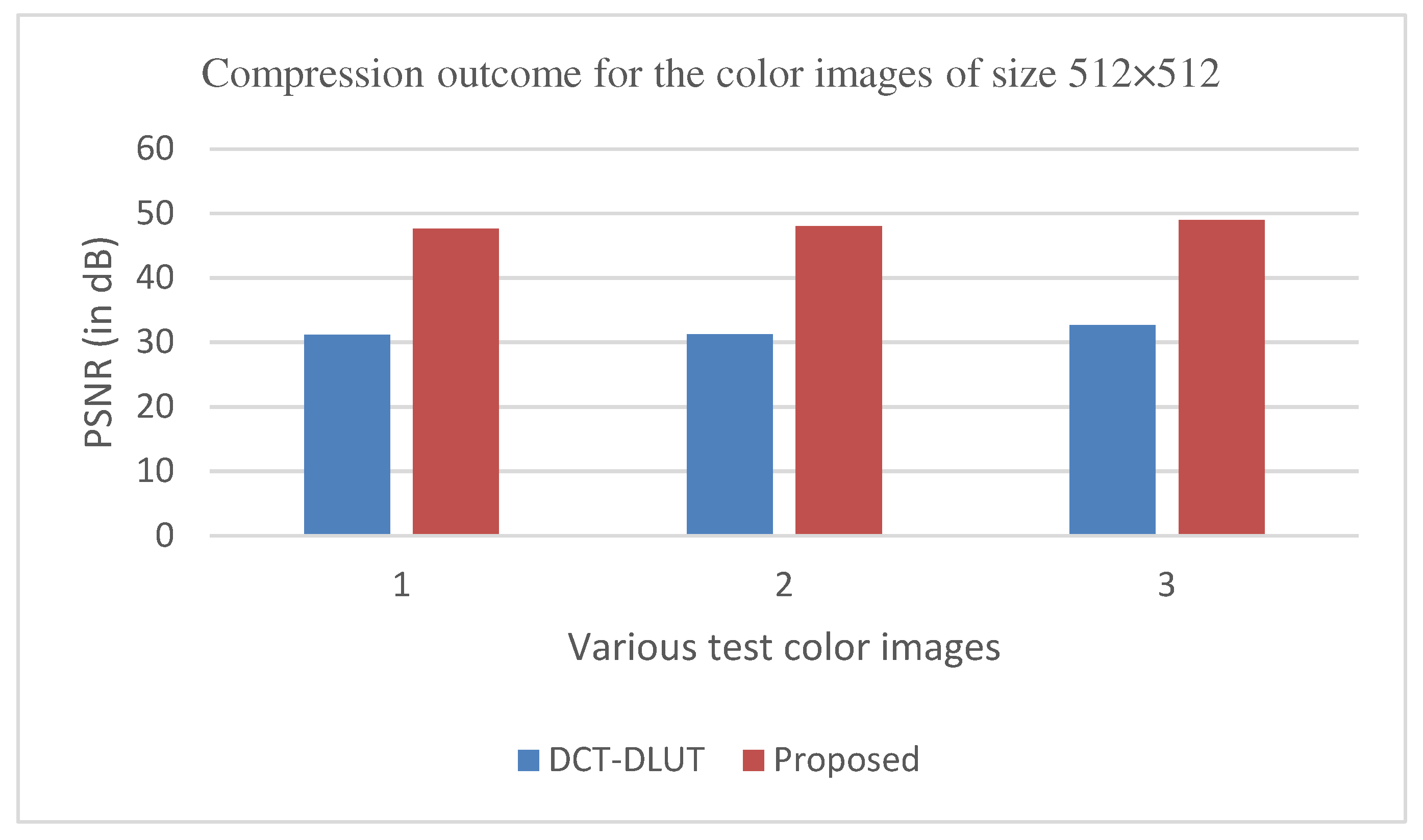
Figure 20.
Comparison of various compression techniques used on the different color test images: 1-airplane, 2-pepper, and 3-Lena.
Figure 20.
Comparison of various compression techniques used on the different color test images: 1-airplane, 2-pepper, and 3-Lena.
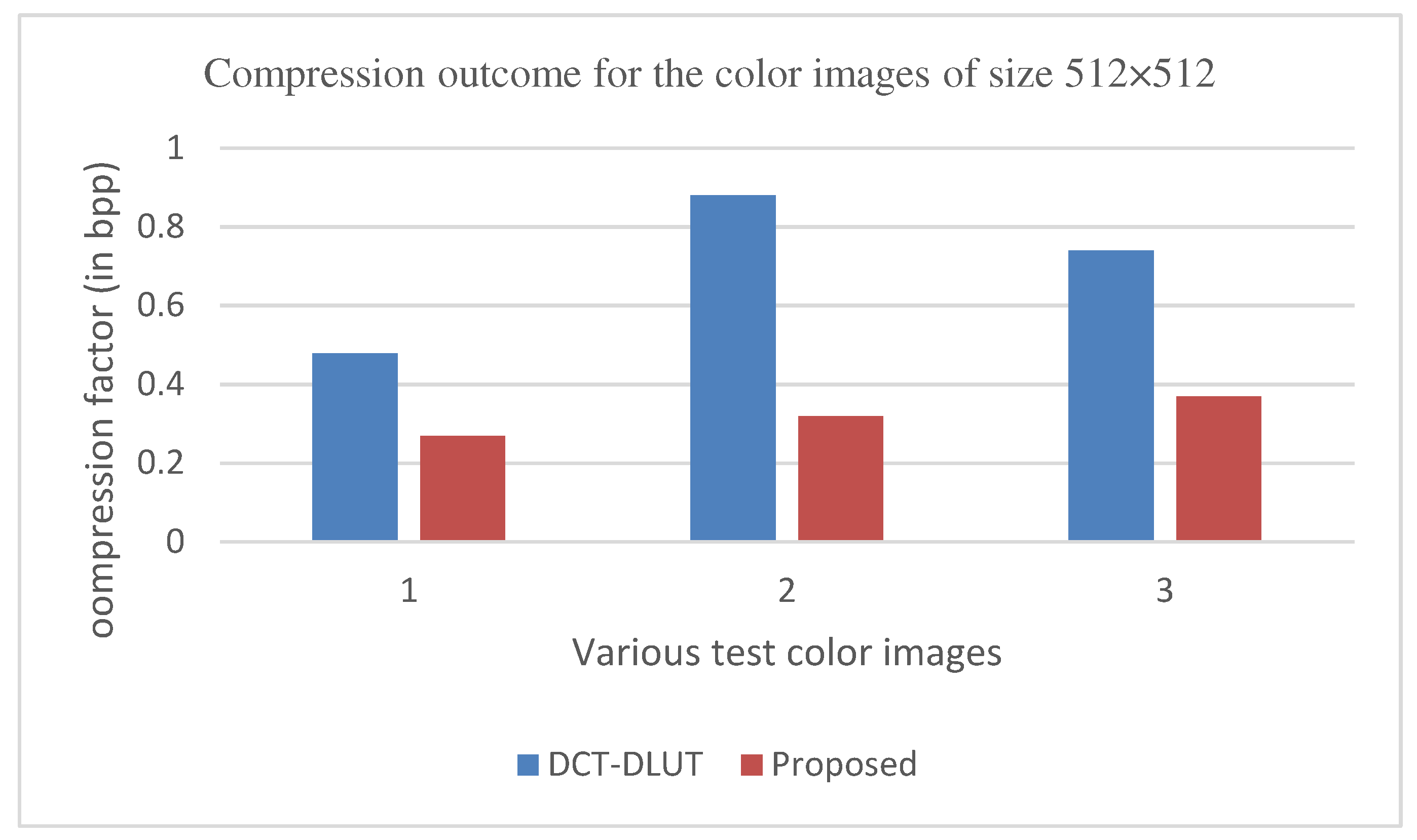
Figure 21.
Comparison of various compression techniques used on the different color test images: 1-Couple, 2-House, and 3-Zelda.
Figure 21.
Comparison of various compression techniques used on the different color test images: 1-Couple, 2-House, and 3-Zelda.
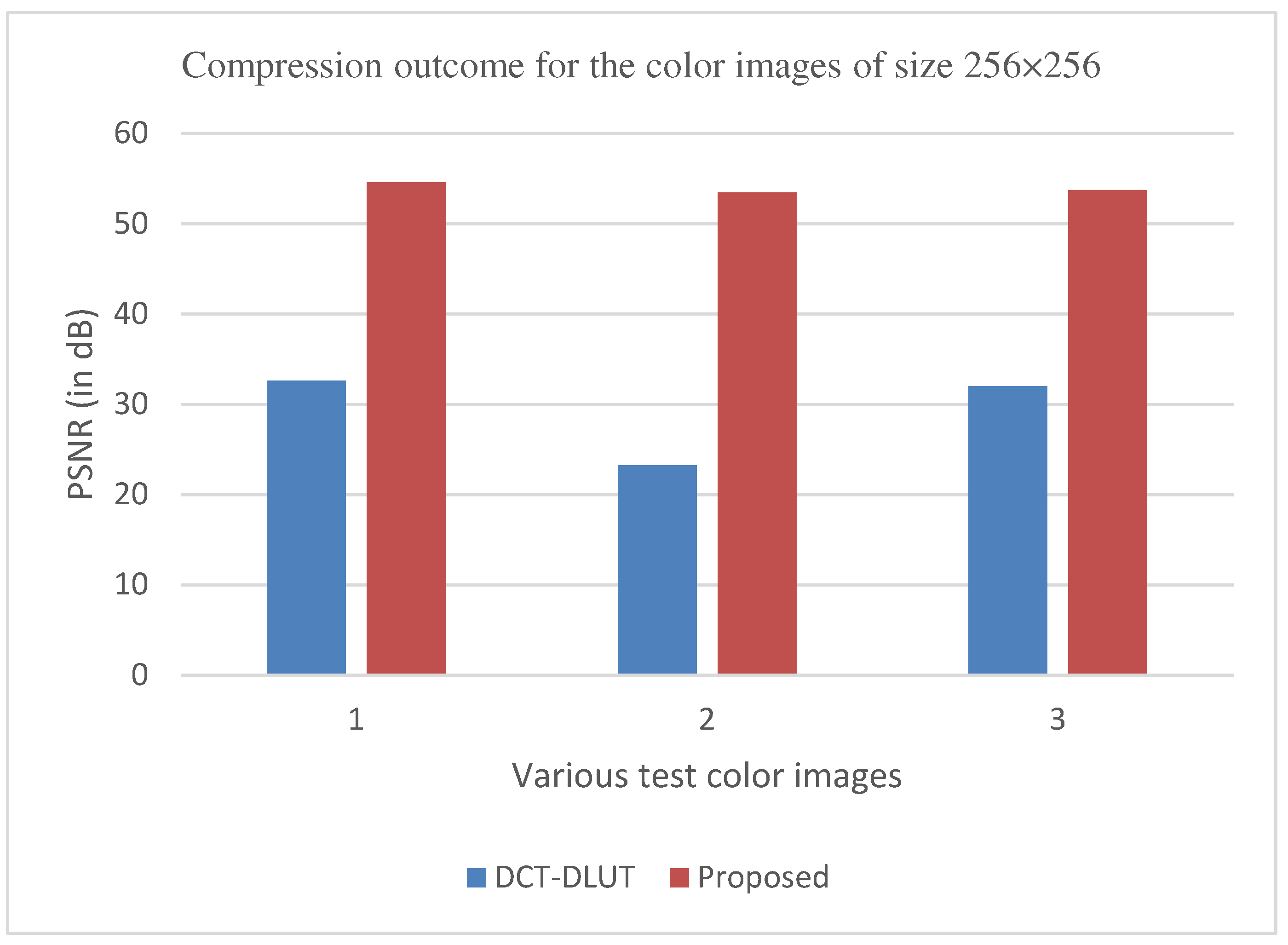
Figure 22.
Comparison of various compression techniques used on the different color test images: 1-Couple, 2-House, and 3-Zelda.
Figure 22.
Comparison of various compression techniques used on the different color test images: 1-Couple, 2-House, and 3-Zelda.
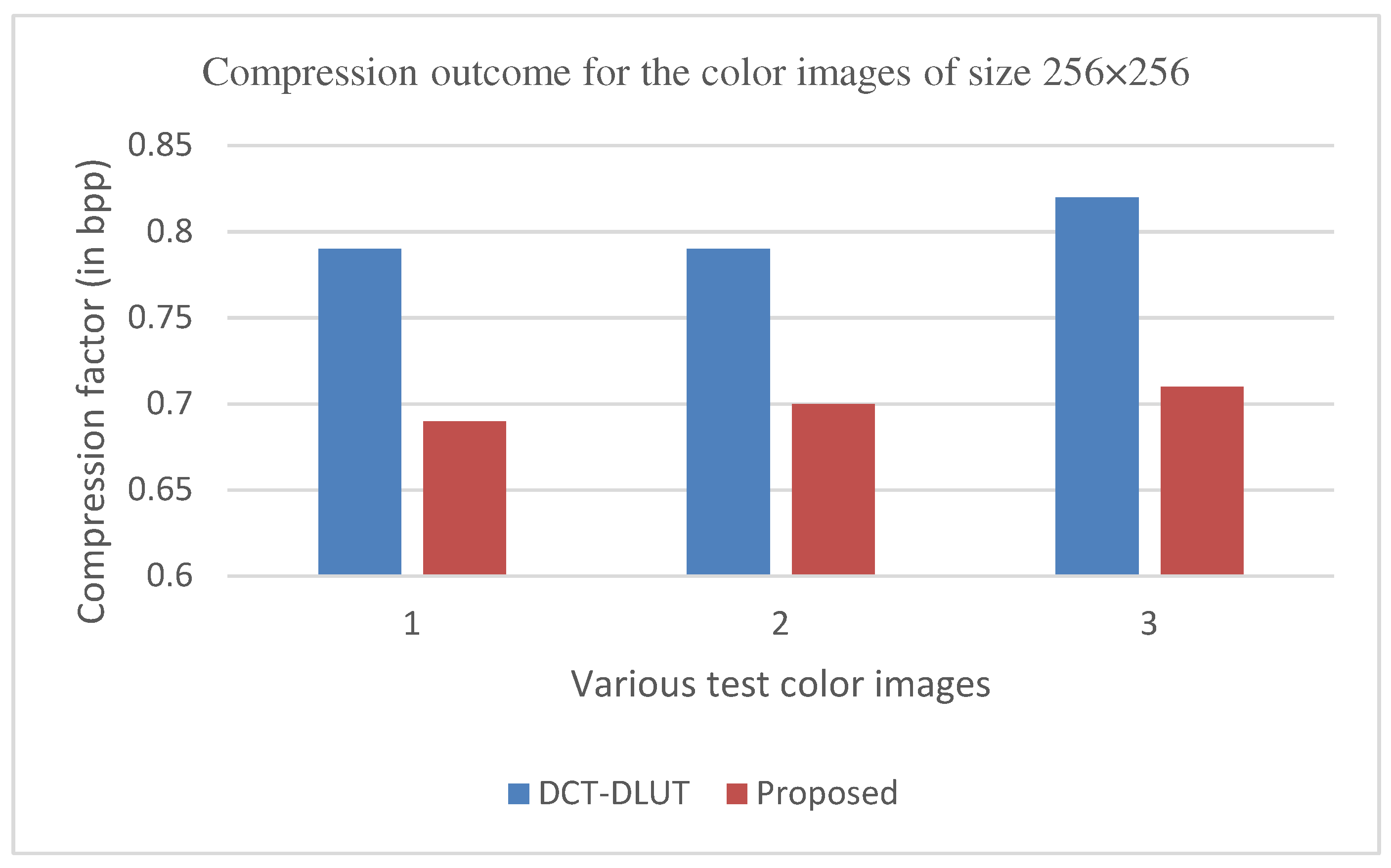
Table 1.
Comparative performance of BTC [5], AMBTC [6], MBTC [7], IBTC-KQ [8], ABTC-EQ [9], DWT [16] and proposed method for Gray Scale Images.
| Tested Image |
Method | Block Size (4×4) Pixels | Block Size (8×8) Pixels | ||||||
|---|---|---|---|---|---|---|---|---|---|
| PSNR | SSIM | BPP | CR | PSNR | SSIM | BPP | CR | ||
| Lena (512×512) |
BTC | 21.4520 | 0.7088 | 2 | 4 | 21.4520 | 0.7088 | 1.2500 | 6.4000 |
| AMBTC | 35.3706 | 0.9905 | 2 | 4 | 32.0885 | 0.9639 | 1.2500 | 6.4000 | |
| MBTC | 35.8137 | 0.9904 | 2 | 4 | 32.6268 | 0.9662 | 1.2500 | 6.4000 | |
| IBTC-KQ | 40.3478 | 0.9874 | 4 | 2 | 36.4511 | 0.9664 | 2.5000 | 3.2000 | |
| ABTC-EQ | 36.9919 | 0.9632 | 2.5734 | 3.1087 | 33.8401 | 0.9305 | 1.8267 | 4.3794 | |
| DWT | 29.9001 | 0.8943 | 3.2855 | 2.4349 | 29.9001 | 0.8943 | 3.2855 | 2.4349 | |
| Proposed | 34.7809 | 0.9985 | 1.8158 | 4.4058 | 34.7809 | 0.9985 | 1.8158 | 4.4058 | |
| Lena (256×256) |
DWT | 27.0772 | 0.8326 | 3.2713 | 2.4455 | 27.0772 | 0.8326 | 3.2713 | 2.4455 |
| Proposed | 36.9556 | 0.9447 | 1.7831 | 4.4865 | 36.9556 | 0.9447 | 1.7831 | 4.4865 | |
| Barbara (512×512) |
BTC | 19.4506 | 0.6894 | 2 | 4 | 19.4506 | 0.6894 | 1.2500 | 6.4000 |
| AMBTC | 29.8672 | 0.9747 | 2 | 4 | 27.8428 | 0.9429 | 1.2500 | 6.4000 | |
| MBTC | 30.0710 | 0.9757 | 2 | 4 | 28.1069 | 0.9451 | 1.2500 | 6.4000 | |
| IBTC-KQ | 36.3729 | 0.9847 | 4 | 2 | 33.5212 | 0.9632 | 2.5000 | 3.2000 | |
| ABTC-EQ | 32.1986 | 0.9551 | 2.6966 | 2.9667 | 30.5587 | 0.9244 | 1.9487 | 4.1053 | |
| DWT | 27.7496 | 0.9242 | 3.7896 | 2.1111 | 27.7496 | 0.9242 | 3.7896 | 2.1111 | |
| Proposed | 33.3092 | 0.9986 | 1.9806 | 4.0392 | 33.3092 | 0.9986 | 1.9806 | 4.0392 | |
| Baboon (512×512) |
BTC | 20.1671 | 0.7288 | 2 | 4 | 20.1671 | 0.7288 | 1.2500 | 6.4000 |
| AMBTC | 26.9827 | 0.9639 | 2 | 4 | 25.1842 | 0.9181 | 1.2500 | 6.4000 | |
| MBTC | 27.2264 | 0.9653 | 2 | 4 | 25.4677 | 0.9216 | 1.2500 | 6.4000 | |
| IBTC-KQ | 33.8605 | 0.9777 | 4 | 2 | 31.2925 | 0.9550 | 2.5000 | 3.2 | |
| ABTC-EQ | 30.6787 | 0.9400 | 3.0363 | 2.6348 | 28.7947 | 0.9089 | 2.1571 | 3.7086 | |
| DWT | 25.9806 | 0.9479 | 4.2012 | 1.9042 | 25.9806 | 0.9479 | 4.2012 | 1.9042 | |
| Proposed | 28.0266 | 0.9984 | 2.0917 | 3.8247 | 28.0266 | 0.9984 | 2.0917 | 3.8247 | |
| Goldhill (512×512) |
BTC | 18.0719 | 0.6252 | 2 | 4 | 18.0719 | 0.6252 | 1.2500 | 6.4000 |
| AMBTC | 32.8608 | 0.9825 | 2 | 4 | 29.9257 | 0.9438 | 1.2500 | 6.4000 | |
| MBTC | 32.2422 | 0.9828 | 2 | 4 | 30.3195 | 0.9472 | 1.2500 | 6.4000 | |
| IBTC-KQ | 39.9867 | 0.9840 | 4 | 2 | 36.1776 | 0.9599 | 2.5000 | 3.2000 | |
| ABTC-EQ | 36.3085 | 0.9536 | 2.7986 | 2.8586 | 33.6061 | 0.9210 | 2.0778 | 3.8502 | |
| DWT | 28.8597 | 0.9255 | 3.6259 | 2.2064 | 28.8597 | 0.9255 | 3.6259 | 2.2064 | |
| Proposed | 33.6289 | 0.9986 | 1.9020 | 4.2061 | 33.6289 | 0.9986 | 1.9020 | 4.2061 | |
| Peppers (256×256) |
BTC | 19.4540 | 0.6306 | 2 | 4 | 19.4540 | 0.6306 | 1.2500 | 6.4000 |
| AMBTC | 30.5655 | 0.9409 | 2 | 4 | 26.7127 | 0.8547 | 1.2500 | 6.4000 | |
| MBTC | 31.1372 | 0.9444 | 2 | 4 | 27.4445 | 0.8596 | 1.2500 | 6.4000 | |
| IBTC-KQ | ----------- | --------- | -------- | --------- | ----------- | --------- | -------- | --------- | |
| ABTC-EQ | 32.0306 | 0.9551 | 2.6966 | 2.9667 | 28.9805 | 0.8985 | 2.6966 | 4.0499 | |
| DWT | 27.3524 | 0.8212 | 3.1735 | 2.5209 | 27.3524 | 0.8212 | 3.1735 | 2.5209 | |
| Proposed | 37.1723 | 0.9431 | 1.7422 | 4.5918 | 37.1723 | 0.9431 | 1.7422 | 4.5918 | |
| Cameraman (256×256) |
BTC | 20.7083 | 0.7214 | 2 | 4 | 20.7083 | 0.7214 | 1.2500 | 6.4000 |
| AMBTC | 28.2699 | 0.9322 | 2 | 4 | 25.8654 | 0.8831 | 1.2500 | 6.4000 | |
| MBTC | 29.0746 | 0.9392 | 2 | 4 | 26.9365 | 0.8934 | 1.2500 | 6.4000 | |
| IBTC-KQ | 36.7714 | 0.9890 | 4 | 2 | 33.6339 | 0.9754 | 2.5000 | 3.2 | |
| ABTC-EQ | 33.9790 | 0.9725 | 2.6418 | 3.0282 | 31.2452 | 0.9531 | 1.8325 | 4.3656 | |
| DWT | 26.4333 | 0.7483 | 2.7925 | 2.8648 | 26.4333 | 0.7483 | 2.7925 | 2.8648 | |
| Proposed | 33.4238 | 0.8578 | 1.5536 | 5.1492 | 33.4238 | 0.8578 | 1.5536 | 5.1492 | |
| Boat (256×256) |
DWT | 29.6486 | 0.8758 | 3.4099 | 2.3461 | 29.6486 | 0.8758 | 3.4099 | 2.3461 |
| Proposed | 37.9922 | 0.9575 | 1.7985 | 4.4482 | 37.9922 | 0.9575 | 1.7985 | 4.4482 | |
Table 2.
Comparative Performance of Proposed Method and DCT-DLUT [19] for Color Images.
Table 2.
Comparative Performance of Proposed Method and DCT-DLUT [19] for Color Images.
| Image | Proposed method | DCT-DLUT | ||
|---|---|---|---|---|
| PSNR | Bpp | PSNR | Bpp | |
| Airplane (512×512) |
47.57 | 0.27 | 31.16 | 0.48 |
| Peppers (512×512) |
47.99 | 0.32 | 31.19 | 0.88 |
| Lena (512×512) |
48.95 | 0.37 | 32.65 | 0.74 |
| Couple (256×256) |
54.60 | 0.69 | 32.62 | 0.79 |
| House (256×256) |
53.47 | 0.70 | 23.27 | 0.79 |
| Zelda (256×256) |
53.74 | 0.71 | 32.01 | 0.82 |
| Average | 59.71 | 0.51 | 35.81 | 0.75 |
Table 3.
Time Complexity Comparison of Entropy Coders.
| Image (256×256) |
Canonical Huffman Coding Compression time (s) |
Huffman Coding Compression time (s) |
|---|---|---|
| Boat | 95.33 | 509.70 |
| Cameraman | 70.06 | 458.11 |
| Goldhill | 86.90 | 362.90 |
| Lena | 74.45 | 410.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







