Preprint
Article
First-Principles Investigation of Size Effects on Cohesive Energies of Transition-Metal Nanoparticles
Altmetrics
Downloads
98
Views
47
Comments
0
A peer-reviewed article of this preprint also exists.
supplementary.docx (945.45KB )
This version is not peer-reviewed
Submitted:
01 August 2023
Posted:
02 August 2023
You are already at the latest version
Alerts
Abstract
The cohesive energy of transition metal nanoparticles is crucial to understanding their stability and fundamental properties, which are essential for developing new technologies and applications in fields such as catalysis, electronics, energy storage, and biomedical engineering. In this study, we systematically investigate the size-dependent cohesive energies of all the 3d, 4d, and 5d transition-metal nanoparticles using first-principles density functional theory calculations. Our results show that the cohesive energies of nanoparticles decrease with decreasing size due to the increased surface-to-volume ratio and quantum confinement effects. We also find that the size-dependent cohesive energy trends are different for different transition metals, with some metals exhibiting stronger size effects than others. Our findings provide insights into the fundamental properties of transition-metal nanoparticles and have potential implications for their applications in various fields such as catalysis, electronics, and biomedical engineering.
Keywords:
Subject: Chemistry and Materials Science - Metals, Alloys and Metallurgy
1. Introduction
Nanoparticles have garnered considerable attention as promising tools for technological advancements across diverse disciplines [1,2,3,4,5,6,7,8,9]. Their distinct optical, electronic, magnetic, and reactive properties set them apart from bulk transition-metal structures [1,2]. This unique attribute has opened a wide range of potential applications, including drug delivery, therapeutics, environmental remediation, and energy storage, among others [2,3,4,5,6]. Of particular significance for our research focus, transition-metal nanoparticles have emerged as compelling candidates for catalytic applications in crucial industrial processes, such as methane reformation [10,11]. The catalytic potential of these nanoparticles holds great promise for enhancing efficiency and sustainability in various industries.
One of the most important physical properties of transition-metal nanoparticles is their cohesive energy, due to its interconnectedness with various other thermo-physical properties. These properties include but are not limited to melting temperature, melting enthalpy, creation and diffusion of vacancies of nanomaterials [12]. For instance, in the realm of catalysis, the cohesive energy plays a crucial role in determining the stability and robustness of transition-metal nanoparticles as catalysts [2,13]. Higher cohesive energy values signify greater stability, a crucial characteristic for successful catalysts that need to lower activation energy and accelerate reactions without self-destruction. Moreover, it is essential to acknowledge that the cohesive energy of transition-metal nanoparticles is influenced by their structural configuration and total number of atoms, making it vital to comprehend and predict cohesive energy trends across different nanoparticle sizes and configurations, especially for screening potential catalytic candidates.
Therefore, understanding and predicting the cohesive energy trends of transition-metal nanoparticles across different nanoparticle sizes and configurations is of vital importance in optimizing their performance and designing tailored materials for catalytic advancements. Prior studies have been carried out to understand the size and structural dependency of cohesive energy for a select group of transition-metal nanoparticles such as Ag, Al, W, Co, Mo, and Cu, Au [12,14]. These studies, however, mostly relied on empirical methods for calculating cohesive energy, such as the bond energy model (BEM) [12] and other simple models [14]. As a comparison, first-principles approach was employed to investigate various aspects of nanomaterials in previous studies. Specifically, it was used to study the geometries and stabilities of bimetallic nanoparticles, such as Fe-Ni nanoparticles [15] and doped Au clusters [16]. Additionally, this approach was utilized to explore the catalytic mechanism of specific nanoclusters, such as Ni4 [17] or three-atom metal clusters [9].
In our study, we conducted first-principles density functional theory (DFT) calculations to determine the size-dependent cohesive energies of all the 3d, 4d, and 5d transition-metal nanoparticles. This comprehensive investigation allowed us to unveil strong and applicable trends across diverse chemical species, nanoparticle sizes, and structures. By gaining these valuable insights, we can better evaluate and predict cohesive energy in transition-metal nanoparticles, especially those with potential significance in industrial catalysis. Our findings hold the potential to guide the selection of optimal transition-metal nanoparticle candidates for catalytic processes, ultimately contributing to advancements in various industrial applications.
2. Computational Details
The first-principles DFT electronic structure calculations were performed using the Vienna ab-initio simulation package [18,19]. The projector augmented wave potentials (PAW) were used for treating electron–ion interactions and the generalized gradient approximation parametrized by Perdew–Burke–Ernzerhof was used for exchange–correlation functional [20,21]. Structures were fully relaxed with a convergence tolerance of 0.01 meV per atom and a single k-point with the wavevector at the Γ point was used in our calculations. Other computational settings such as cut-off energy and appropriate entries for structural relaxations were generated and managed by the high-throughput computational software framework AFLOW code [22].
An illustration of geometrical structures of all the studied transition-metal nanoparticles (Xn, X = 3d, 4d, and 5d transition-metal elements) is shown in Figure 1. These structures were built based on a prior computational study of Pt nanoparticles conducted by Brunello et al. [23] These nanoparticle structures include 1-layer, 2-layer, and 3-layer cluster configurations, totaling 12 structures, each showcasing distinct arrangements of X atoms within the nanoparticles. This leads to a total number of 360 configurations for all the studied transition-metal nanoparticles. Through these configurations, insights into the nanoparticles' stability and properties at different sizes can be obtained. These nanoparticle models are placed in a cubic simulation box to mimic the bulk environment. To avoid interactions between periodic images, a vacuum region with a minimum distance of at least 10 Å is introduced between neighboring images of the nanoparticles. This ensures that the nanoparticles do not interact with their periodic replicas in the simulation, preventing artificial effects and providing an accurate representation of the isolated nanoparticles.
3. Results and Discussion
Cohesive energy refers to the energy needed to fully disassemble the constituent atoms of a substance, specifically in the case of a nanoparticle, and separate them from each other [24,25]. Consequently, the cohesive energy of transition-metal nanoparticle structures was determined through a two-step calculation process. First, the total energy of the entire nanoparticle system was obtained. This energy accounts for the interactions and bonding between atoms within the nanoparticle. Next, the energy of an individual metal atom (Eatom) was calculated separately. This energy represents the energy of an isolated metal atom. Finally, the cohesive energy per atom (Ecoh) was calculated by subtracting the energy of the individual atom from the total energy per atom of the nanoparticle system: Ecoh = Eatom – Etot/n, where Etot is the total energy of the nanoparticle structure and n is the number of atoms of the structure.
To succinctly depict the relationship between cohesive energy and nanoparticle size, we employed a natural logarithmic function for their approximation [12,14], as shown below:
In this logarithmic function, Y represents the cohesive energy per atom, n denotes the nanoparticle size, and a and b are parameters unique to each transition-metal element. A list of specific parameters a and b for all elements studied in this research is summarized in Table S1 of the Supplementary Information. In Figure 2, the plotted curve represents the fitted cohesive energy of transition-metal nanoparticles (Xn) as a function of nanoparticle size (n) for groups 3B to 8B. The curve is obtained through the natural logarithmic fitting, providing a concise representation of the cohesive energy trends within these groups. Here, the nanoparticle size (n) represents the number of atoms in the nanoparticle. Similarly, Figure 3 presents the fitted cohesive energy results for the groups 8B (X=Co, Rh, and Ir; X=Ni, Pd, and Pt), 1B (X=Cu, Ag, and Au), and 2B (X=Zn, Cd, and Hg). The calculated specific cohesive energy of each nanoparticle structure along with the fitted curve for all the studied transition-metal nanoparticles were shown in Figures S1–S6 of the Supplementary Information.
For all the groups, cohesive energy per atom increases with the size (n) of the nanoparticles, eventually approaching the values observed in the bulk material. This trend indicates a convergence towards the cohesive behavior characteristic of the corresponding bulk materials. This size-dependent increment in cohesive energy is attributed to the strengthening of interatomic interactions and enhanced bonding as the nanoparticle size expands. Specifically, as nanoparticles diminish in size, the decrease in cohesive energy can be attributed to the amplified surface-to-volume ratio and the effects of quantum confinement. A similar trend was also observed in a very recent study conducted by Sachin et al. [12], in which cohesive energy analysis was carried out for elements Ag, W, Co, and Mo via the bond energy model. In most of the studied groups, the cohesive energy displays a considerable range, spanning from 0.50 eV per atom to 6.00 eV per atom. This wide variability in cohesive energy values highlights the diverse nature of these transition-metal nanoparticles and their potential for applications in various fields. However, distinctive behaviors emerge in the last two groups, namely groups 1B and 2B, where the cohesive energy ranges are notably smaller. For group 1B, the cohesive energy values exhibit a more constrained range, varying from approximately 1.00 eV per atom to around 2.80 eV per atom. These values are also consistent with previously calculated average atomic binding energies of Pt-group-doped gold clusters in the range of 1.56 - 2.00 eV [16]. In the case of group 2B nanoparticles, the cohesive energy range is even narrower, spanning from about 0.05 eV per atom to approximately 0.58 eV per atom. This remarkable narrowing of cohesive energy values suggests unique characteristics within group 2B nanoparticles. Such nanoparticles may hold promise for specialized applications that require precise control over cohesive energy properties [26].
Analyzing the trends in cohesive energy per atom for individual groups yields the following observations:
i) In group 5B (X=V, Nb, and Ta), there is a consistent increase in cohesive energy per atom with the atomic number. Ta stands out with the highest cohesive energy per atom, while V exhibits the lowest, and Nb falls in between. This upward trend is also evident in other groups, including 6B (X=Cr, Mo, and W), 7B (X=Mn, Tc, and Re), 8B (X=Fe, Ru, Os), and 8B (X=Co, Rh, and Ir), reflecting a common pattern among these transition-metal nanoparticles.
ii) Group 4B (X=Ti, Zr, and Hf) presents a different trend. Surprisingly, the middle element, Zr, displays the lowest cohesive energy per atom, while the element with the highest atomic number, Hf, showcases the highest cohesive energy per atom. Ti, with the lowest atomic number, positions its cohesive energy per atom between that of Zr and Hf. Remarkably, this trend extends to Group 8B (X=Ni, Pd, and Pt) as well, further highlighting the unique behavior observed within this group.
iii) Another intriguing pattern emerges with group 3B (X=Sc, Y, and La). Here, the middle element, Y, exhibits the highest cohesive energy per atom, while the element with the lowest atomic number, Sc, demonstrates the lowest cohesive energy per atom. La, the element with the highest atomic number, displays cohesive energy per atom between that of Sc and Y. This behavior offers insights into the cohesive characteristics of these nanoparticles, reflecting a distinctive trend within this group.
iv) Group 1B (X=Cu, Ag, and Au) exhibits a highly distinctive trend compared to the other groups. The element with the lowest atomic number, Cu, surprisingly demonstrates the highest cohesive energy per atom. Conversely, the middle element, Ag, displays the lowest cohesive energy per atom among the three elements. Lastly, the element with the highest atomic number, Au, showcases cohesive energy per atom between that of Cu and Ag. This exceptional behavior adds to the complexity of cohesive energy trends within transition-metal nanoparticles.
v) The final group, 2B (X=Zn, Cd, and Hg), presents a trend opposite to that observed in point i). In this group, cohesive energy per atom decreases with the atomic number. Zn stands out with the highest cohesive energy per atom, while Hg exhibits the lowest cohesive energy, and Cd falls in between. This contrasting trend indicates the diverse cohesive energy behavior within these nanoparticles.
To present a clear and comprehensive comparison of cohesive energies among all the studied transition-metal elements, we plotted heat map illustrating the calculated cohesive energy values for transition-metal nanoparticles with structure X4, see Figure 4. It provides valuable insights into the cohesive energy trends across the various elements studied. For instance, one can observe that Hf has the highest cohesive energy, closely followed by Ta, while the nanoparticles of group 2B (X=Zn, Cd, and Hg) have low cohesive energy, with Hg exhibiting the lowest one among all the elements studied. The overall trend of the calculated cohesive energy of the X4 nanoparticles is generally consistent with the experimental values of the bulk transition metals in spite of some difference, as shown in the Figure S7 of the Supplementary Information. For instance, the bulk compound with the highest experimental cohesive energy values is W instead of Hf. Additionally, the cohesive energy values of Cr, Mo, Re, and Os are also higher than that of their nanoparticle counterparts. In short, our calculated results and the comparison with experimental bulk values provide a concise overview of the differences in cohesive energy values for both nanoparticles and bulk structures, shedding light on the unique properties exhibited by nanoparticles compared to their bulk counterparts.
4. Conclusion
In conclusion, we systematically explored the size-dependent cohesive energies of 3d, 4d, and 5d transition-metal nanoparticles using first-principles density functional theory calculations. Our investigation revealed a consistent trend of decreasing cohesive energies with decreasing nanoparticle size, which can be attributed to the increased surface-to-volume ratio and quantum confinement effects. Importantly, we observed variations in the size-dependent cohesive energy trends among different transition metals, with certain metals exhibiting more pronounced size effects than others. These findings offer valuable insights into the fundamental properties of transition-metal nanoparticles and have implications for their applications in fields such as catalysis, electronics, energy storage, and biomedical engineering.
Supplementary Materials
The following supporting information can be downloaded at the website of this paper posted on Preprints.org.
Acknowledgments
This work used the Expanse cluster at San Diego Supercomputer Center through allocation DMR160045 from the Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support (ACCESS) program, which is supported by National Science Foundation grants #2138259, #2138286, #2138307, #2137603, and #2138296. Acknowledgement is made to the donors of the American Chemical Society Petroleum Research Fund for support of this research. E.D acknowledges the Summer URS Ledell Family Research Scholarship for Science and Engineering at UC San Diego.
References
- Neugebauer, N.; Wang, Y.; Elm, M.T.; Hofmann, D.M.; Heiliger, C.; Ye, X.; Klar, P.J. Distance and size dependence of the interactions within highly ordered magnetic nanoparticle mesocrystals. Phys. Rev. B 2023, 107, 184410. [Google Scholar] [CrossRef]
- Tyo, E.C.; Vajda, S. Catalysis by clusters with precise numbers of atoms. Nat. Nanotechnol. 2015, 10, 577–588. [Google Scholar] [CrossRef] [PubMed]
- Oliver-Meseguer, J.; Cabrero-Antonino, J.R.; Domínguez, I.; Leyva-Pérez, A.; Corma, A. Small Gold Clusters Formed in Solution Give Reaction Turnover Numbers of 10 7 at Room Temperature. Science 2012, 338, 1452–1455. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Cheng, W.; Xin, H.; Liu, R.; Wang, Q.; Cai, W.; Peng, X.; Yang, F.; Xin, H. Nanoparticles advanced from preclinical studies to clinical trials for lung cancer therapy. Cancer Nanotechnol. 2023, 14, 1–25. [Google Scholar] [CrossRef]
- Ren, J.; Zhang, S.; Liu, S. Significance and implications of nanoparticle–biological corona fingerprints in diagnosis, prognosis, and therapeutics for diverse disorders. Nanoscale 2023, 15, 11422–11433. [Google Scholar] [CrossRef]
- Thomas, T.; Kuttoth, H.; Nair, R.V.; Sandhyarani, N. Electrochemical Approach for the Synthesis of Ultrasmall Cu13 Clusters and Their Application in the Detection of Endotoxin. Langmuir 2023, 39, 10011–10020. [Google Scholar] [CrossRef]
- Rice, P.S.; Hu, P. Understanding supported noble metal catalysts using first-principles calculations. J. Chem. Phys. 2019, 151, 180902. [Google Scholar] [CrossRef]
- Zhu, X.; Huang, H.; Zhang, H.; Zhang, Y.; Shi, P.; Qu, K.; Cheng, S.-B.; Wang, A.-L.; Lu, Q. Filling Mesopores of Conductive Metal–Organic Frameworks with Cu Clusters for Selective Nitrate Reduction to Ammonia. ACS Appl. Mater. Interfaces 2022, 14, 32176–32182. [Google Scholar] [CrossRef]
- Cui, C.; Zhang, H.; Cheng, R.; Huang, B.; Luo, Z. On the Nature of Three-Atom Metal Cluster Catalysis for N2 Reduction to Ammonia. ACS Catal. 2022, 12, 14964–14975. [Google Scholar] [CrossRef]
- Jones, G.; Jakobsen, J.G.; Shim, S.S.; Kleis, J.; Andersson, M.P.; Rossmeisl, J.; Abildpedersen, F.; Bligaard, T.; Helveg, S.; Hinnemann, B.; et al. First principles calculations and experimental insight into methane steam reforming over transition metal catalysts. J. Catal. 2008, 259, 147–160. [Google Scholar] [CrossRef]
- Wong, Y.; Halim, H.H.; Khairudin, N.F.; Pham, T.N.; Putra, S.E.M.; Hamamoto, Y.; Inagaki, K.; Hamada, I.; Mohamed, A.R.; Morikawa, Y. Dry Reforming of Methane on Cobalt Catalysts: DFT-Based Insights into Carbon Deposition Versus Removal. J. Phys. Chem. C 2021, 125, 21902–21913. [Google Scholar] [CrossRef]
- Sachin; Pandey, B. K.; Jaiswal, R.L. Dimensional effect on cohesive energy, melting temperature and Debye temperature of metallic nanoparticles. Phys. B: Condens. Matter 2023, 651. [Google Scholar] [CrossRef]
- Yang, X.-F.; Wang, A.; Qiao, B.; Li, J.; Liu, J.; Zhang, T. Single-Atom Catalysts: A New Frontier in Heterogeneous Catalysis. Accounts Chem. Res. 2013, 46, 1740–1748. [Google Scholar] [CrossRef] [PubMed]
- Qu, Y.D.; Liang, X.L.; Kong, X.Q.; Zhang, W.J. Size-dependent cohesive energy, melting temperature, and Debye temperature of spherical metallic nanoparticles. Phys. Met. Met. 2017, 118, 528–534. [Google Scholar] [CrossRef]
- Teeriniemi, J.; Melander, M.; Lipasti, S.; Hatz, R.; Laasonen, K. Fe–Ni Nanoparticles: A Multiscale First-Principles Study to Predict Geometry, Structure, and Catalytic Activity. J. Phys. Chem. C 2017, 121, 1667–1674. [Google Scholar] [CrossRef]
- Wang, S.J.; Kuang, X.Y.; Lu, C.; Li, Y.F.; Zhao, Y.R. Geometries, stabilities, and electronic properties of Pt-group-doped gold clusters, their relationship to cluster size, and comparison with pure gold clusters. Phys. Chem. Chem. Phys. 2011, 13, 10119–10130. [Google Scholar] [CrossRef]
- Roy, G.; Chattopadhyay, A.P. Dissociation of methane on Ni 4 cluster-A DFT study. Comput. Theor. Chem. 2017, 1106, 7–14. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes forab initiototal-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Curtarolo, S.; Setyawan, W.; Hart, G.L.; Jahnatek, M.; Chepulskii, R.V.; Taylor, R.H.; Wang, S.; Xue, J.; Yang, K.; Levy, O.; et al. AFLOW: An automatic framework for high-throughput materials discovery. Comput. Mater. Sci. 2012, 58, 218–226. [Google Scholar] [CrossRef]
- Brunello, G.F.; Lee, J.H.; Lee, S.G.; Choi, J.I.; Harvey, D.; Jang, S.S. Interactions of Pt nanoparticles with molecular components in polymer electrolyte membrane fuel cells: multi-scale modeling approach. RSC Adv. 2016, 6, 69670–69676. [Google Scholar] [CrossRef]
- Mizutani, U.; Inukai, M.; Sato, H.; Zijlstra, E. S. In Physical Metallurgy; Laughlin, D. E. , Hono, K., Eds.; Elsevier: Oxford, 2014. [Google Scholar]
- Glasser, L.; Sheppard, D.A. Cohesive Energies and Enthalpies: Complexities, Confusions, and Corrections. Inorg. Chem. 2016, 55, 7103–7110. [Google Scholar] [CrossRef]
- Lambie, S.; Steenbergen, K.G.; Gaston, N. Modulating the thermal and structural stability of galleneneviavariation of atomistic thickness. Nanoscale Adv. 2020, 3, 499–507. [Google Scholar] [CrossRef] [PubMed]
Figure 1.
Illustration of geometric structures of transition-metal (X) nanoparticles, with the first, second, and third rows corresponding to single-layer, two-layer, and three-layer nanoparticles, respectively.
Figure 1.
Illustration of geometric structures of transition-metal (X) nanoparticles, with the first, second, and third rows corresponding to single-layer, two-layer, and three-layer nanoparticles, respectively.
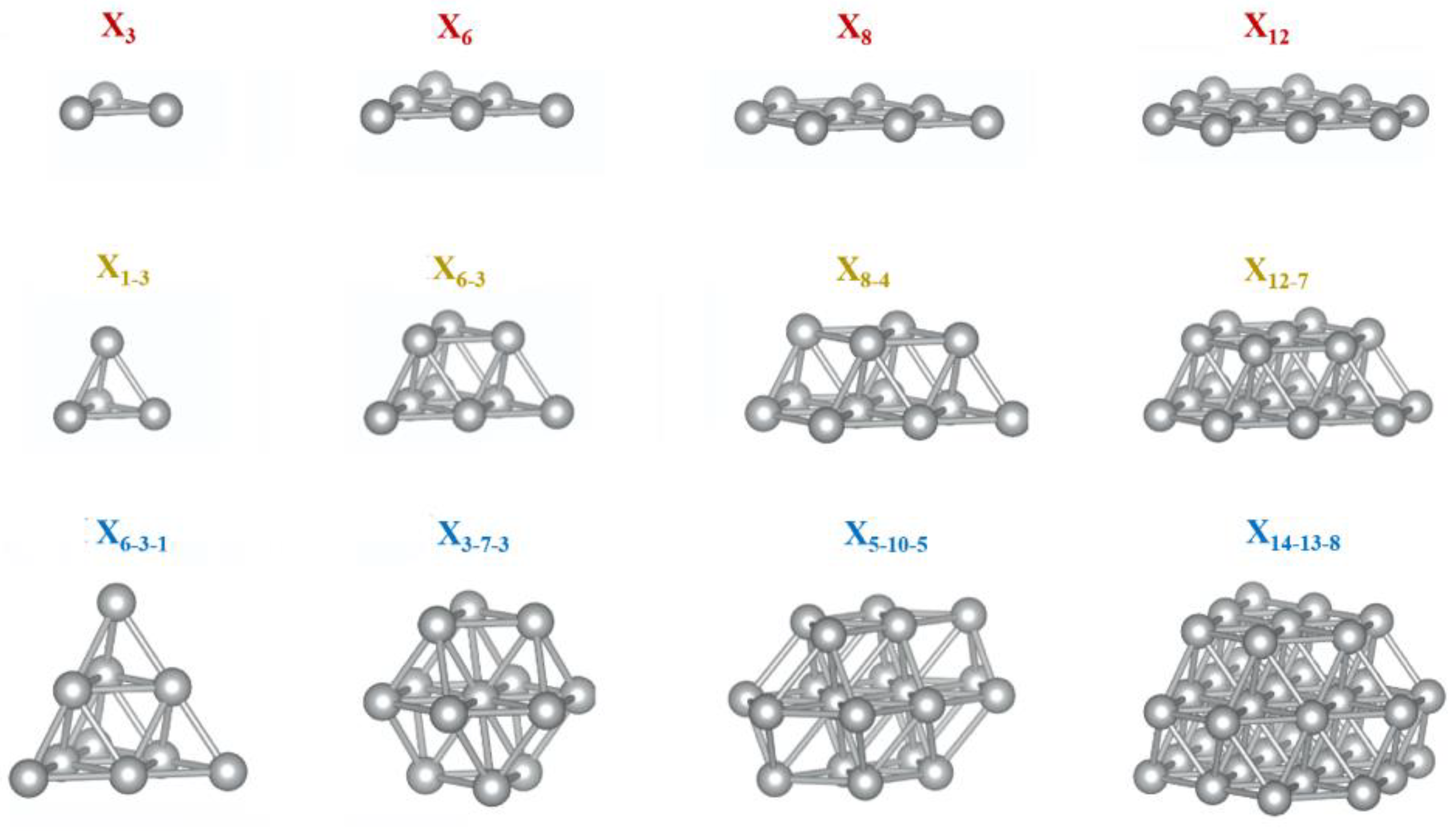
Figure 2.
Calculated cohesive energy per atom as a function of the nanoparticle size (n) for the transition-metal nanoparticles (Xn) in the group (a) 3B (X=Sc, Y, and La), (b) 4B (X=Ti, Zr, and Hf), (c) 5B (X=V, Nb, and Ta), (d) 6B (X=Cr, Mo, and W), (e) 7B (X=Mn, Tc, and Re), and (f) 8B (x=Fe, Ru, Os). The size n refers to the number of atoms of the nanoparticle.
Figure 2.
Calculated cohesive energy per atom as a function of the nanoparticle size (n) for the transition-metal nanoparticles (Xn) in the group (a) 3B (X=Sc, Y, and La), (b) 4B (X=Ti, Zr, and Hf), (c) 5B (X=V, Nb, and Ta), (d) 6B (X=Cr, Mo, and W), (e) 7B (X=Mn, Tc, and Re), and (f) 8B (x=Fe, Ru, Os). The size n refers to the number of atoms of the nanoparticle.
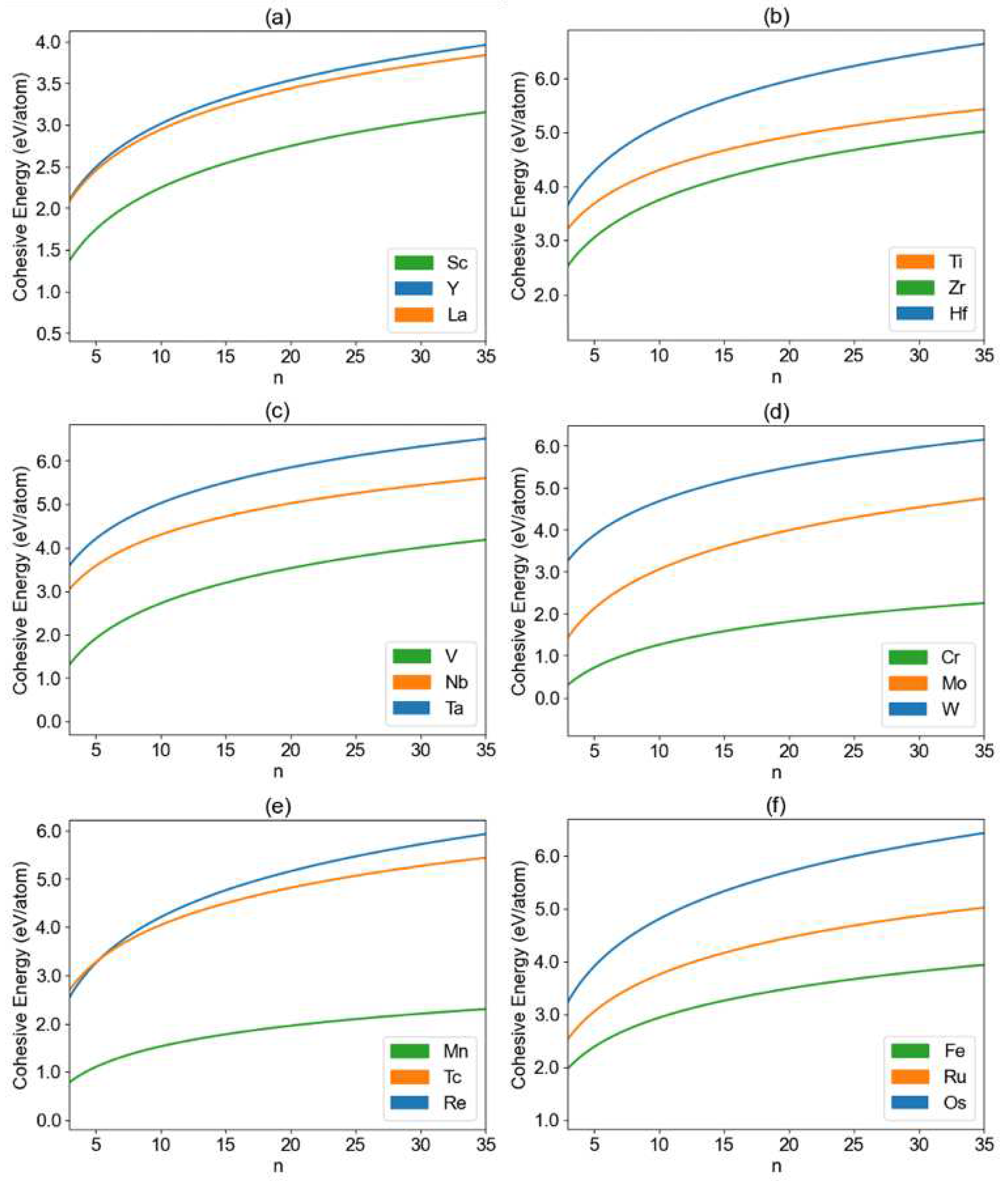
Figure 3.
Calculated cohesive energy per atom as a function of the nanoparticle size (n) for the transition-metal nanoparticles (Xn) in the group (a) 8B (X=Co, Rh, and Ir), (b) 8B (X=Ni, Pd, and Pt), (c) 1B (X=Cu, Ag, and Au), and (d) 2B (X=Zn, Cd, and Hg).
Figure 3.
Calculated cohesive energy per atom as a function of the nanoparticle size (n) for the transition-metal nanoparticles (Xn) in the group (a) 8B (X=Co, Rh, and Ir), (b) 8B (X=Ni, Pd, and Pt), (c) 1B (X=Cu, Ag, and Au), and (d) 2B (X=Zn, Cd, and Hg).
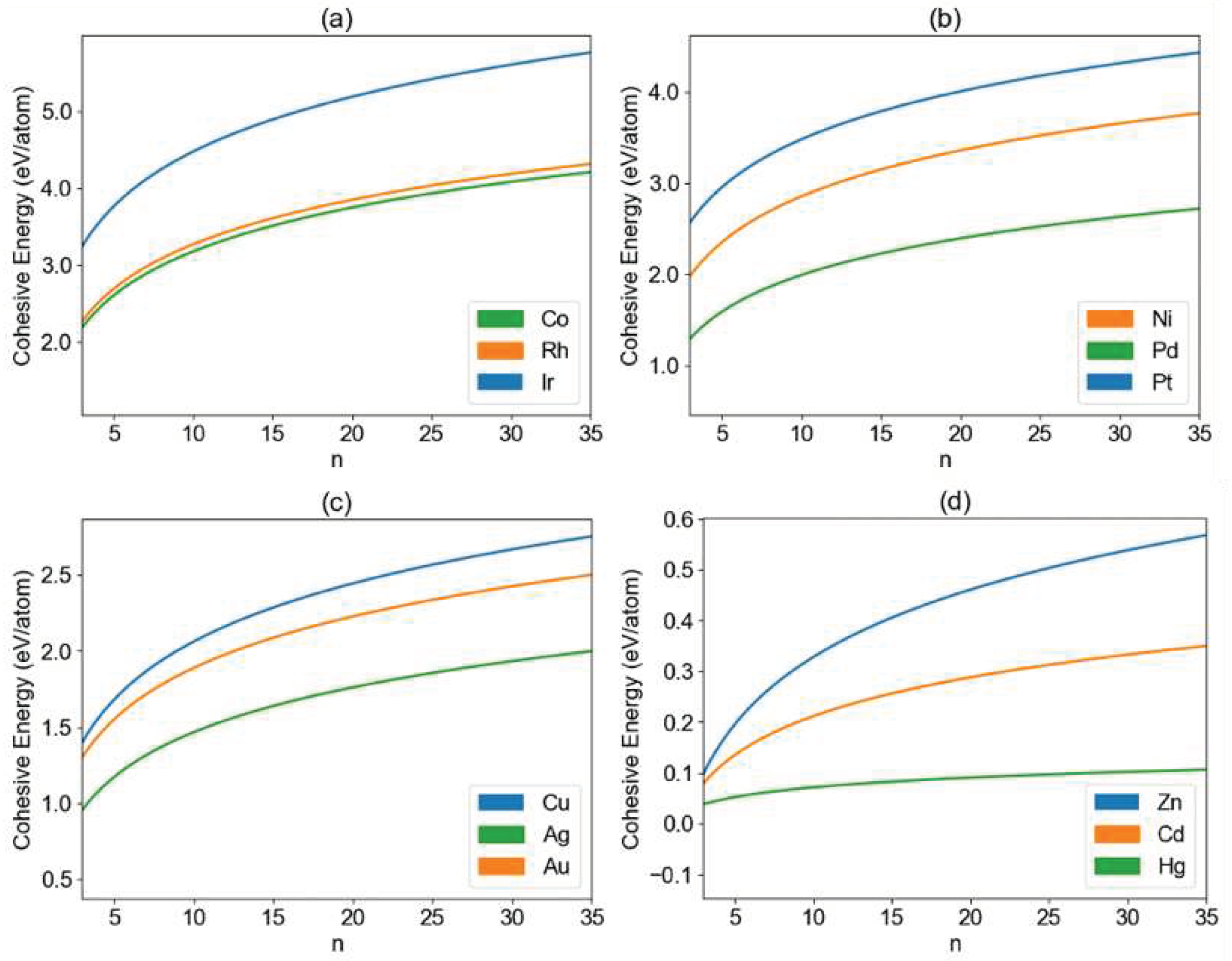
Figure 4.
Heat map illustrating the calculated cohesive energy per atom for transition-metal nanoparticles X4.
Figure 4.
Heat map illustrating the calculated cohesive energy per atom for transition-metal nanoparticles X4.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





