Course Prophet: A Machine Learning-Based System for Early Prediction of Student Failure in Numerical Methods Course in the Bachelor’s Degree in Engineering at the University of Córdoba, Colombia

Preprint

Article

Course Prophet: A Machine Learning-Based System for Early Prediction of Student Failure in Numerical Methods Course in the Bachelor’s Degree in Engineering at the University of Córdoba, Colombia

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Isaac Caicedo-Castro^*

This version is not peer-reviewed

Submitted:

30 July 2023

Posted:

03 August 2023

You are already at the latest version

Alerts

Abstract

In this paper, we address the following research question: Is feasibility to use an artificial intelligence system to predict the risk of student failure in a course based solely on their performance in prerequisite courses? Adopting a machine learning-based quantitative approach, we implement Course Prophet, the prototype of a predictive system that maps the input variables representing student performance to the target variable, i.e., the risk of course failure. We evaluate multiple machine learning methods and find that the Gaussian process with Matern kernel outperforms other methods, achieving the highest accuracy and a favorable trade-off between precision and recall. We conduct this research in the context of the students pursuing a Bachelor’s degree in Systems Engineering at the University of Córdoba, Colombia. In this context, we focus on predicting the risk of failing the Numerical Methods course. In conclusion, the main contribution of this research is the development of Course Prophet, providing an efficient and accurate tool for predicting student failure in the Numerical Methods course based on their academic history in prerequisite courses.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction and Background

In this study, our goal is designing an intelligence system that predicts if a given student is at-risk of failing the Numerical Methods course before the lectures start, based on the student’s performance in prerequisite courses.

Predicting whether a given student is at risk of failing a specific course in a Bachelor’s degree program enables all stakeholders, including the student, lecturers, academic policy makers, and others, to take precautions and prevent unsatisfactory performance or course dropouts. By implementing these precautions effectively, students can avoid psychological issues, frustration, and financial loss.

Motivated by the goal of preventing students from facing the unpleasant and undesirable consequences of failing a course, prior research has focused on identifying students at risk of course failure. Machine learning, particularly classification methods (i.e., a type supervised learning approaches), has been widely adopted in these studies. Various classifiers, including artificial neural networks or multilayer perceptron [1,2,3,4,5,6], support vector machines [1,2,6,7], logistic regression [2,6,7,8], decision trees [2,6,7,8], ensemble methods with different classification methods [1,4], random forest [2,3,4,6], gradient boosting [3], extreme gradient boosting (XGBoost) [3,4,6], variants of gradient boosting [3,7], namely CatBoost [9] and LightGBM [10], and Gaussian processes for classification [6].

Most of the previous research has been applied to online courses [1,2,4,5,8], namely Computer Networking and Web Design [1], Mathematics [8], and STEM (Science, Technology, Engineering, and Mathematics) in general [5]. In these research studies, failing is considered as dropping out such courses. The prediction is not carried out before the student starts the course; instead, failure forecasting is performed during the course development. This is based on student’s activities, such as, e.g., the number of course views, content downloads, and grades achieved in assignments, test, quizzes, projects, and so forth. However, the earlier the prediction is available, the better the stakeholders can plan and mitigate the risk of course failure. Therefore, the best scenario is identifying those students at risk of failing the course before it starts.

In another two studies, the prediction is performed before the course begins, using the grades achieved by the student in prerequisite courses [3,6]. One of these studies, grades are represented through ordinal data rather than quantitative data and the student’s age is used for predicting besides the grades [3]. In the other study, the input variables to predict the course failure are the student’s score in the admission test and the student’s grade in prerequisite courses [6]. This latter work specifically focused on the Numerical Methods course in the Bachelor’s degree program of Systems Engineering at the University of Córdoba in Colombia. In this paper, we have achieved improved results compared to the findings published in [6].

After evaluating several machine learning methods through 10-fold cross-validation (10FCV), in [6] the best mean values for accuracy, precision, recall, and harmonic mean (

F_{1}

) are 76.67%, 71.67%, 51.67%, and 57.67%, respectively. In this study, we collected more data, and conducted an evaluation based on 10FCV over various methods, which reveals that the best mean values for accuracy, precision, recall, and harmonic mean (

F_{1}

) are 80.45%, 83.33%, 66.5%, and 72.52%, respectively.

The contributions of our study are as follows:

(i): A larger dataset was used in the current study compared to the one collected in [6]. The dataset used in this study contains 103 instances, each with 39 variables. Out of these variables, 38 are independent variables, and one is the target variable. In contrast, the dataset used in [6] consists of 56 instances, which is a subset of the dataset used in the current study.
(ii): An intelligence system prototype, called Course Prophet, that utilizes Gaussian processes for classification to predict the probability of a student failing the Numerical Methods course. It achieves this by analyzing the student’s performance in prerequisite courses (e.g., Calculus, Physics, Computer Programming, etc).
(iii): The outcomes of an experimental evaluation that demonstrate that Gaussian processes outperform support vector machines, decision trees, and other machine learning methods in predicting the risk of course failure faced by individual students.

The remainder of this paper is outlined as follows: In Section 2, we present the methods adopted in this study, including the research context, formalization of the problem, assumptions, limitations, dataset collection, and the machine learning methods evaluated. Section 3 explains the experimental setting and provides a detailed analysis of the evaluation conducted on the machine learning methods. Finally, we conclude the paper in Section 4, summarizing the contributions and findings of this study, and outlining directions for future research.

2. Methods

In this study, our purpose is to predict the risk of course failure for students, and to achieve this, we adopt a quantitative approach using machine learning methods in lieu of solely relying on statistical approaches. To complement the dataset used in [6], we conducted a survey on students pursuing a bachelor’s degree in Systems Engineering at the University of Córdoba, Colombia. The data provided by the students were anonymized to protect their privacy, and we only consider their grades without including personal information such as, e.g., identification numbers, names, gender, and economic stratum.

Then, we evaluated several machine learning methods by adopting K-Fold Cross-Validation (KFCV). This afforded us the opportunity to evaluate each method K times using K different pairs of training and test datasets. Normally, K is equal to 10 or 30; we chose the former option to compare the results of the current study with those reported in [6], where the same choice was made. The purpose of this evaluation is to select the most effective machine learning method and identify the optimal hyper-parameter settings, including the regularization parameter for multilayer perceptrons and logistic regression.

2.1. Research Context and Problem Formalization

In many bachelor’s degree programs, courses are organized and grouped per semester, gradually increasing in complexity. Foundational subjects are typically taught in the first semester, followed by more advanced topics in the subsequent semesters. This organization of courses leads to the concept of prerequisite courses, where the successful completion of certain courses is assumed to be required for advancing to others.

Prerequisite courses play a crucial role in preparing students for more advanced subjects. They lay the groundwork and provide the necessary knowledge and skills for succeeding in later courses. For instance, a student who struggled to pass the Differential Calculus course might face challenges in the Differential Equations course, as the latter builds upon the concepts learned in the former.

The logical progression from prerequisite courses to advanced courses highlights the significance of a strong foundation in earlier subjects. Students who excel in prerequisite courses are more likely to perform well in subsequent, more complex courses, setting them on a path to academic success.

The relationship among courses and the results obtained in [6], where the prediction of course failure risk was based on students’ academic history and the outcomes obtained from the admission test, has motivated us to explore the following research question: Can an artificial intelligence system effectively learn patterns in students’ academic history to predict whether a given student is at risk of failing a course, based only on their performance in prerequisite courses?

To answer this question, we extended the research endeavor from [6], which focused on predicting course failure risk based on students’ academic history and admission test outcomes. Building upon the previous study, our goal in this study was to investigate whether an artificial intelligence system can effectively predict course failure risk solely based on students’ performance in prerequisite courses.

In the same context as [6], we collected additional data from students pursuing a Bachelor’s degree in Systems Engineering at the University of Córdoba in Colombia, a public university. The dataset now includes an expanded sample of students, to provide a more comprehensive representation of students’ academic performances.

We continued our examination of the numerical methods course, a critical subject in the curriculum, whose theoretical and practical topics depend on foundational courses such as calculus, physics, and computer programming. By focusing on this specific course, we aim to uncover the relationships between prerequisite courses and course failure risk, offering valuable insights to support academic interventions and enhance student success.

At Colombian universities, students pursuing any Bachelor’s degree are graded on a scale from 0 to 5. In our research context, the University of Córdoba requires students to maintain a global average grade of at least 3.3, as specified in Article 16 of the university’s student code [11]. However, the university’s code, particularly Article 28, outlines additional student retention policies for those whose global average grade falls below the above-mentioned thresholds (i.e., 3.3).

Therefore, students with a global average grade between 3 and 3.3 are placed on academic probation and must raise their grade to at least 3.3 in the next semester to maintain their student status. Failure to do so might result in dismissal from the university (cf., Article 16 in the student’s code [11]). Additionally, if a student’s grade falls below 3, they are automatically withdrawn from the university. The possibility of losing student status due to course failure is a significant concern and is commonly referred to as student dropout.

The performance of students in prerequisite courses is assessed based on their grades. For each prerequisite course, we consider three key input variables for the prediction, namely: (i) the number of semesters the student has attended the course until passing, (ii) the best grade achieved, and (iii) the worst grade received.

To represent the input variables corresponding to the ith student’s academic record, we use a real-valued D-dimensional vector

x_{i} \in X

, where

X = {x | x \in R^{D} \land 0 \leq x_{j} \leq 5,

\forall j = 1, \dots, D}

. Here,

D = 33

as we have ten prerequisite courses, and three variables are associated with each course. Each component of the vector

x_{i}

represents a specific input variable as follows:

$x_{i 1}$ is the best grade that a given student achieved in Calculus I course.
$x_{i 2}$ is the number of semester a given student has attended the Calculus I course.
$x_{i 3}$ is the worst that a given student achieved in Calculus I course.
$x_{i 4}$ is the best grade that a given student achieved in Calculus II course.
$x_{i 5}$ is the number of semester a given student has attended the Calculus II course.
$x_{i 6}$ is the worst that a given student achieved in Calculus II course.
$x_{i 7}$ is the best grade that a given student achieved in Calculus III course.
$x_{i 8}$ is the number of semester a given student has attended the calculus III course.
$x_{i 9}$ is the worst that a given student achieved in Calculus III course.
$x_{i, 10}$ is the best grade that a given student achieved in Linear Algebra course.
$x_{i, 11}$ is the number of semester a given student has attended the Linear Algebra course.
$x_{i, 12}$ is the worst that a given student achieved in Linear Algebra course.
$x_{i, 13}$ is the best grade that a given student achieved in Physics I course.
$x_{i, 14}$ is the number of semester a given student has attended the Physics I course.
$x_{i, 15}$ is the worst that a given student achieved in Physics I course.
$x_{i, 16}$ is the best grade that a given student achieved in Physics II course.
$x_{i, 17}$ is the number of semester a given student has attended the Physics II course.
$x_{i, 18}$ is the worst that a given student achieved in Physics II course.
$x_{i, 19}$ is the best grade that a given student achieved in Physics III course.
$x_{i, 20}$ is the number of semester a given student has attended the Physics III course.
$x_{i, 21}$ is the worst that a given student achieved in Physics III course.
$x_{i, 22}$ is the best grade that a given student achieved in Introduction to Computer Programming course.
$x_{i, 23}$ is the number of semester a given student has attended the Introduction to Computer Programming course.
$x_{i, 24}$ is the worst that a given student achieved in Introduction to Computer Programming course.
$x_{i, 25}$ is the best grade that a given student achieved in Computer Programming I course.
$x_{i, 26}$ is the number of semester a given student has attended the Computer Programming I course.
$x_{i, 27}$ is the worst that a given student achieved in Computer Programming I course.
$x_{i, 28}$ is the best grade that a given student achieved in Computer Programming II course.
$x_{i, 29}$ is the number of semester a given student has attended the Computer Programming II course.
$x_{i, 30}$ is the worst that a given student achieved in Computer Programming II course.
$x_{i, 31}$ is the best grade that a given student achieved in Computer Programming III course.
$x_{i, 32}$ is the number of semester a given student has attended the Computer Programming III course.
$x_{i, 33}$ is the worst that a given student achieved in Computer Programming III course.

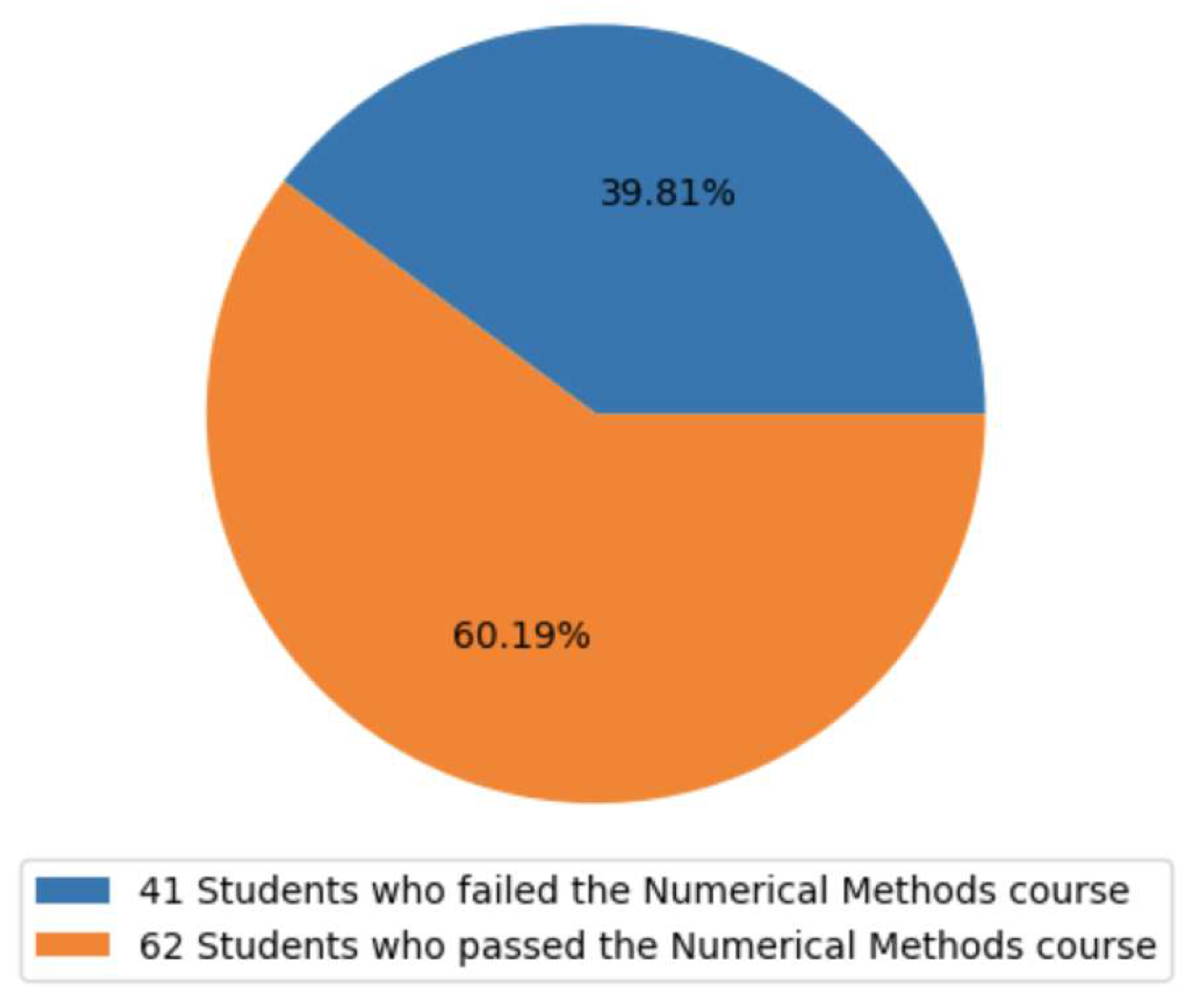
Moreover, it is essential to note that as part of the data collection process, we also obtained admission outcomes for each student. However, for the purpose of our current study, we decided not to incorporate these admission outcomes into our analysis as they fall outside the scope of our research question. Consequently, the dataset contains a total of 38 independent variables per student, of which we used 33 variables corresponding to the performance in prerequisite courses for our predictive models.

To formalize the problem, let

D = {(x_{i}, y_{i}) | x_{i} \in X \land y_{i} \in 0, 1 \forall i = 1, 2, \dots n}

be the training dataset, where n is the number of instances in the dataset (i.e., n is less than 103, or

n < 103

, due to a portion being set apart for evaluation). Each instance in

D

consists of a real-valued vector

x_{i}

representing the academic record of the ith student, along with the corresponding target variable

y_{i}

, which takes a value of one if the student either failed or dropped out of the numerical methods course (

y_{i} = 1

), and zero otherwise (

y_{i} = 0

The problem addressed in our study is to find the function f, such that

f : X \to 0, 1

, which maps the input variables in the academic record to the target variable, given the aforementioned training dataset. To tackle this problem, we have adopted a supervised learning approach, specifically employing classification methods.

2.2. Key Assumptions and Limitations

To conduct this research we have considered the following assumptions:

(i)

We assumed that a given students is at course failure risk as long as they might either fail or dropout the numerical methods course.

(ii)

We assumed that the student’s grades in prerequisite courses are sufficient input variables for forecasting the probability of course failure.

(iii)

We assumed that to succeed in Numerical Methods course, the prerequisites are Linear Algebra, Calculus I, II, III, Physics I, II, III, Introduction to Computer Programming, Computer Programming I, II, and III. The subjects included in the Numerical Methods course are as follows:

(a): Approximations and computer arithmetic: the concepts to understands these subjects are taught in Introduction to Computer Programming.
(b): Non-linear equations: students must have a working knowledge of integral calculus (taught in Calculus II), be able to program computers using iterative and selective control structures (skills taught in both Introduction to Computer Programming and Computer Programming I), and understand Taylor series, which is the foundation of the secant method, a numerical method used to solve non-linear equations.
(c): Systems of linear equations: the student must be familiar with matrix and vector operations taught in the Linear Algebra course in order to understand numerical methods such as, e.g., Gauss-Seidel or Jacobi. Besides, programming such methods are subjects dealt in Computer Programming II course.
(d): Interpolation: the student must know the topics taught in Calculus II to understand the background of the Taylor polynomial interpolation, and the subjects taught in courses such as Linear Algebra, Computer Programming I, and II to implement the other numerical methods for interpolation.
(e): Numerical integration: in this subject, algorithms are used for computing integrals which cannot be solved through analytic methods, hence, the student must know what integration is (taught in the Calculus II course), and how to calculate some integrals to understand this subject.
(f): Ordinary differential equations: In this subject, the student must know concepts from all prior mathematics courses. It would be appropriate if the student would have attended a differential equation course, however, in the context of this study, this course is simultaneously scheduled with numerical methods, so students attend both in the same semester.
(g): Numerical optimization: this subject is an introduction for more advanced courses such as, e.g., Statistics, Linear and Non-Linear Programming, Stochastic Methods courses, and Machine Learning. To understand this subject, the student must have mastered topics taught in courses, such as Computer Programming II and III, Linear Algebra, basic calculus, and vector calculus (which is taught in the Calculus III course).

The limitation of our research is two-fold:

(i): Studying the relevance of demographic and personal data to perform the prediction is out of the scope of this study.
(ii): Designing the action plans to prevent the student at-risk fails is beyond the scope of this research.

2.3. Machine Learning Methods

To solve the previously defined problem of predicting the risk of course failure, we have adopted classification methods, such as logistic regression, which is well-suited for binary outcome prediction tasks. Logistic regression utilizes the logistic function of the linear combination between input variables and weights, and the classifier is fitted by maximizing the objective function based on the log-likelihood of the training data given the binary outcome [12]. In our study, we employed the Limited-memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) algorithm [13,14] to efficiently fit the logistic regression classifier.

With the logistic regression method, it is assumed that a hyperplane exists to separate vectors into two classes within a multidimensional real-valued vector space. While this assumption might be reasonable taking into account the high dimensionality (i.e.,

D = 33

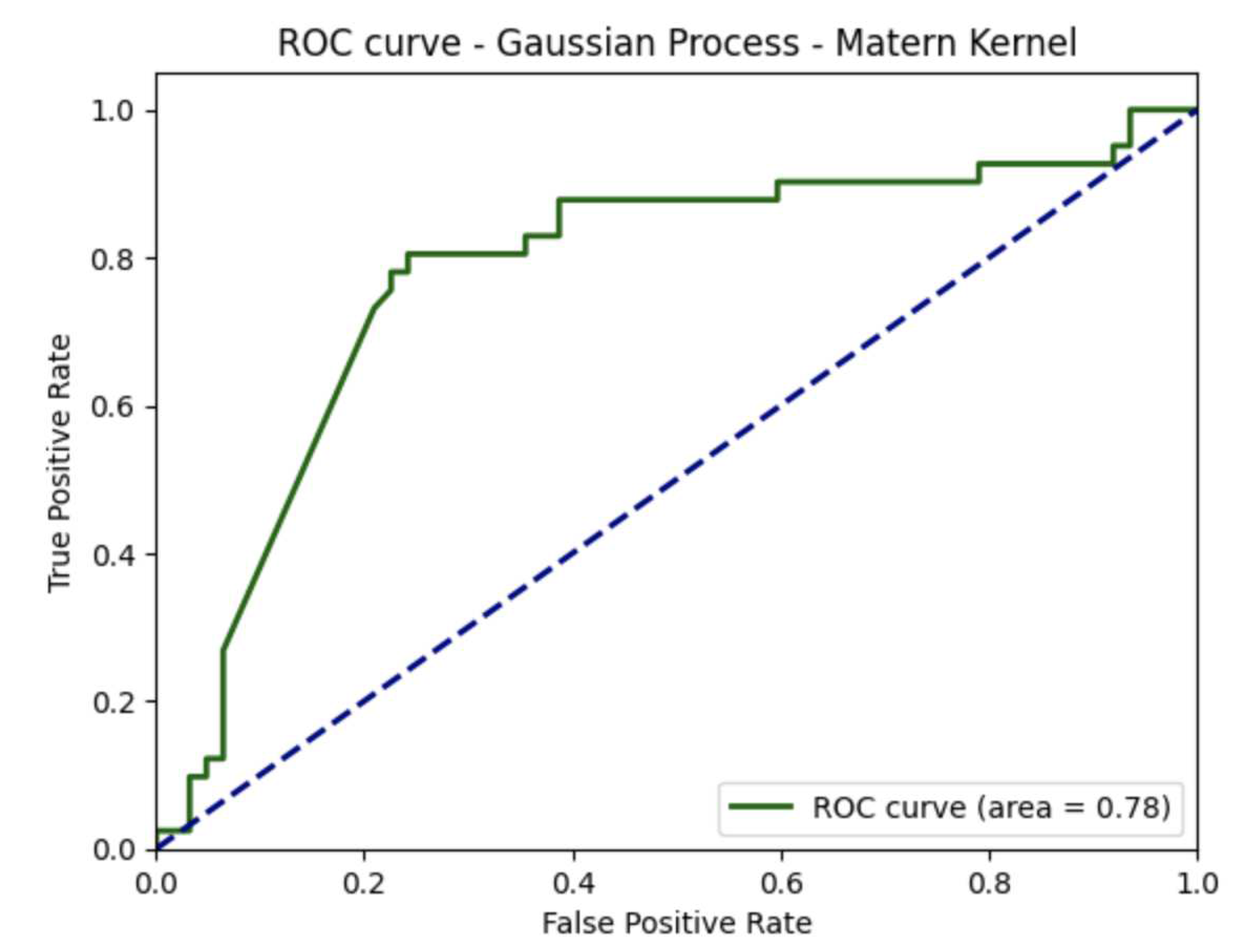
) of the dataset used in this study, we also adopted other classifiers more suited for non-linear classification problems, such as the Gaussian process classifier. The Gaussian process is a probabilistic method based on Bayesian inference, where the probability distribution of the target variable is Gaussian or normal, explaining the name of the method [15,16]. One of the main advantages of the Gaussian process classifier is its ability to incorporate prior knowledge about the problem, thereby improving its forecasting even with a small training dataset. Furthermore, in the context of this study, where the dataset is rather small, the Gaussian process classifier is a suitable choice.

In this study, we have used several kernels (a.k.a., covariant functions) with Gaussian processes. For instance, the radial basis function kernel, which is defined as follows:

k_{G} (x_{i}, x_{j}) = γ exp (- \frac{| | x_{j} - x_{i} {| |}^{2}}{2 σ^{2}}),

(1)

where

x_{i}, x_{j} \in R^{D}

are two D-dimensional vectors in real-valued space, and

γ, σ \in R

are scalars corresponding to the weight and length scale of the kernel, respectively.

Besides, we used the Matern kernel, which is defined as follows:

k_{M} (x_{i}, x_{j}) = γ \frac{1}{Γ (ν) 2^{ν - 1}} {(\frac{\sqrt{2 ν} | | x_{j} - x_{i} {| |}^{2}}{σ})}^{ν} K_{ν} (\frac{\sqrt{2 ν} | | x_{j} - x_{i} {| |}^{2}}{σ}),

(2)

where

K_{ν} (\cdot)

and

Γ (\cdot)

are the modified Bessel function and the gamma function, respectively. The hyperparameter

ν \in R

controls the smoothness of the kernel function.

Moreover, we employed rational quadratic kernel defined as follows:

k_{r} (x_{i}, x_{j}) = {(1 + \frac{| | x_{j} - x_{i} {| |}^{2}}{2 α σ^{2}})}^{- α},

(3)

where

σ

is used for the same purpose in Equation 1, while

α \in R

is the scale mixture parameter, such that

α > 0

Furthermore, we combined Matern and radial basis function kernels by summing both as follows:

k (x_{i}, x_{j}) = γ_{G} k_{G} (x_{i}, x_{j}) + γ_{M} k_{M} (x_{i}, x_{j}),

(4)

where

γ_{G}

and

γ_{M}

are the weights assigned to both kernels.

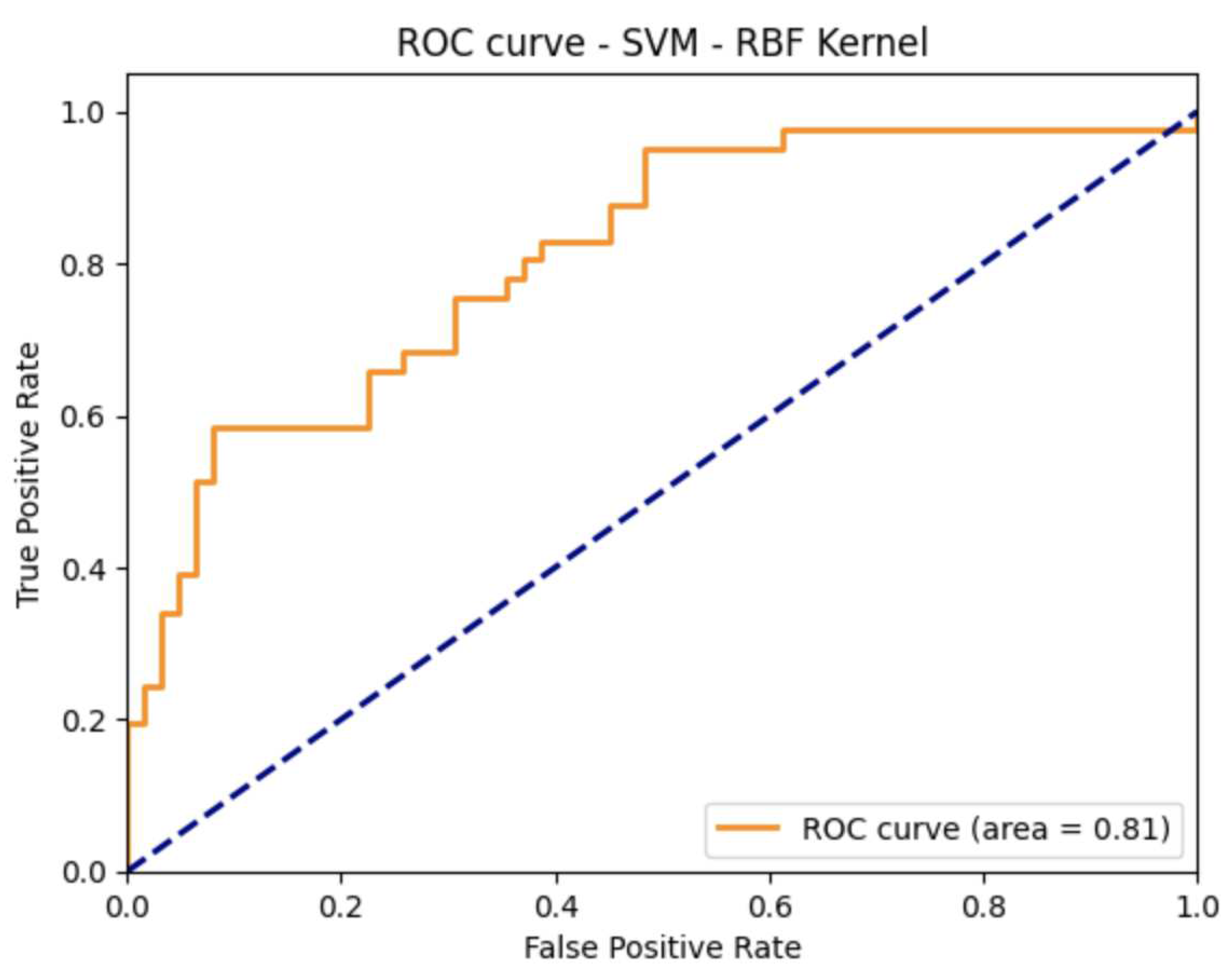
On the other hand, the support vector machines (SVM) method is so far the best theoretical motivated and one of the most successful methods in the practice of modern machine learning [17]. It is based on convex optimization, allowing for a global maximum solution to be found, which is its main advantage. However, SVM method is not well-suited for interpretation in data mining and is better suited for training accurate machine learning-based systems. A detailed description of this method is in [18].

Both SVM and logistic regression are linear classification methods that assume the input vector space can be separated by a linear decision boundary (or a hyperplane in the case of a multidimensional real-valued space). However, when this assumption is not satisfied, SVM can be used along with kernel methods to handle non-linear decision boundaries (see [18] for further details). In this study, we used the radial basis function kernel, which is similar to the one presented in Equation 1, and it is defined as follows:

k_{G} (x_{i}, x_{j}) = exp (- γ | | x_{j} - x_{i} {| |}^{2}),

(5)

where

γ

controls the radius of this spherical kernel, whose center is

x_{j}

. Additionally, we used polynomial and Sigmoid kernels defined in Equations , respectively. In Equation ,

d \in N

is the degree of the kernel, and

γ \in R

is the coefficient in Equation .

k_{p} (x_{i}, x_{j}) = {〈 x_{i}, x_{j} 〉}^{d}

(6)

k_{s} (x_{i}, x_{j}) = tanh (γ 〈 x_{i}, x_{j} 〉)

(7)

Although SVM method is considered one of the most successful methods in the practice of modern machine learning, multilayer perceptrons and their variants, which are artificial neural networks, are the most successful methods in the practice of deep learning and big data, particularly in tasks such as speech recognition, computer vision, natural language processing, and so forth. [19]. In this research, we have adopted the multilayer perceptrons fitted through back-propagated cross-entropy error [20], and the optimization algorithm known as Adam [21]. We used multilayer perceptrons with one and five hidden layers.

The multilayer perceptron method is a universal approximator (i.e., it is able to approximate any function for either classification or regression), which is its main advantage. However, its main disadvantage is that the objective function (a.k.a., loss function) based on the cross-entropy error is not convex. Therefore, the synaptic weights obtained through the fitting process might not converge to the most optimum solution because there are several local minima in the objective function. Thus, finding a solution depends on the random initialization of the synaptic weights. Furthermore, multilayer perceptrons have more hyperparameters to be tuned than other learning algorithms (e.g., support vector machines or naive Bayes), which is an additional shortcoming.

Except for the logistic regression method, all the above-mentioned methods are not easily interpretable. Therefore, we adopted decision trees, which are classification algorithms commonly used in data mining and knowledge discovery. In decision tree training, a tree is created using the dataset as input, where each internal node represents a test on an independent variable, each branch represents the result of the test, and leaves represent forecasted classes. The construction of the tree is carried out in a recursive way, beginning with the whole dataset as the root node, and at each iteration, the fitting algorithm selects the next attribute that best separates the data into different classes. The fitting algorithm can be stopped based on several criteria, such as when all the training data is classified or when the accuracy or performance of the classifier cannot be further improved.

Decision trees are fitted through heuristic algorithms, such as greedy algorithms, which may lead to several local optimal solutions at each node. This is one of the reasons why there is no guarantee that the learning algorithm will converge to the most optimal solution, as is also the case with the multilayer perceptrons algorithm. Therefore, this is the main drawback of decision trees, and it can cause completely different tree shapes due to small variations in the training dataset. The decision trees were proposed in 1984, in [22] Breiman et al. delve into the details of this method. We also adopted ensemble methods based on multiple decision trees such as, e.g., Adaboost (stands for adaptive boosting) [23], Random forest [24], and extreme gradient Boosting, a.k.a. XGBoost [25].

3. Evaluation

3.1. Experimental Setting

The test bed for the evaluation consists of a dataset with 103 instances, where each one contains 33 input variables and one target variable. Figure 1 shows the proportion of positive instances corresponding to students who failed the Numerical Methods course, and the negative examples that correspond to students who passed the course. This pie chart illustrates that the dataset is rather balanced; however, there are more negative examples, indicating a higher number of students who successfully passed the course compared to those who failed.

We centered each input variable by removing the mean and scaling to unit variance, using the training dataset during K-fold cross-validation (KFCV). Subsequently, we tuned the hyperparameter settings for each machine learning method through grid search within the KFCV process. We explored a set of possible values for each hyperparameter, and the best settings are presented as follows:

Gaussian process classifier with radial basis function kernel, the best values for $σ$ and $γ$ are 1 and $3.81 \times 10^{- 6}$ , respectively.
Gaussian process classifier with Matern kernel, the best values for $n u$ , $σ$ and $γ$ are 1.3, $2.5 \times 10^{- 1}$ and $3.81 \times 10^{- 6}$ , respectively.
Gaussian process classifier with the combination between radial basis function and Matern kernel as follows: $γ_{G}$ and $γ_{M}$ have the same value, i.e., $3.81 \times 10^{- 6}$ . The hyperparameter values used in the two previous kernels are also used in this combination.
Gaussian process classifier with rational quadratic kernel, where $σ$ and $α$ are $3.81 \times 10^{- 6}$ and 16, respectively.
SVM with radial basis function kernel, where $γ$ and C are $3.9 \times 10^{- 3}$ and 4, respectively.
SVM with polynomial kernel, where d (degree) and C are 1 and $7.59 \times 10^{- 1}$ , respectively.
Multilayer perceptron with a single hidden layer, with 600 neurons in the hidden layer. This was fitted with an initial learning rate and regularization parameter equal to $10^{- 4}$ and $10^{- 2}$ , respectively. The activation function used in the hidden layer is hyperbolic tangent function.
Multilayer perceptron with five hidden layers. The number of neurons in the first, second, third, fourth, and fifth layer are 600, 300, 100, 300, and 600, respectively. This was fitted with an initial learning rate and regularization parameter equal to $10^{- 4}$ and $10^{- 2}$ , respectively. The activation function used in the hidden layer is hyperbolic tangent function.
Logistic regression classifier was fitted with a regularization parameter of $10^{- 2}$ .
The decision trees were fitted using both the Gini and entropy indexes. The parameters used were the given by default in Scikit-Learn API.
XGBoost algorithm were fitted with a learning rate, maximum depth, and number of estimators equal to $1.13 \times 10^{- 1}$ , 3, and 50, respectively. Besides, we used the entropy index in the trees.
Adaboost algorithm were fitted with a learning rate and number of estimators equal to $3.13 \times 10^{- 2}$ and 110, respectively. Besides, we used the entropy index in the trees.
Random forest were fitted with 15 trees (with entropy index), at least one sample per leaf, minimum three samples per split, and a maximum depth of nine levels.

The above-mentioned hyperparameter settings were used to produce the results presented in Section 3.2. For prototyping, we utilized the Python programming language and the Scikit-Learn library [26] within Google Colaboratory [27].

3.2. Results

According to the results, Gaussian process (GP) with the Matern kernel outperformed the other machine learning methods in terms of accuracy and harmonic mean, as presented in Table 1 and Table 4. We chose decision trees (DT) as the baseline because it is a method that is typically less accurate but suitable for interpreting its output.

Table 2 shows that support vector machines (SVM) with the radial basis function kernel performs better than the other machine learning methods in terms of precision. However, it is outperformed by 8 out of 16 other methods in terms of recall, as revealed in Table 3. These results are consistent with the confusion matrices presented in Table 5 and Table 6, where SVM with the radial basis function fails to classify more students at risk than GP with the Matern kernel, leading to an increased number of false negatives and lower recall. Therefore, SVM with the radial basis function kernel does not have the highest harmonic mean (

F_{1}

) among the methods evaluated.

On the other hand, GP with the Matern kernel does not achieve the highest precision or recall individually. However, it stands out as one of the methods with high values in both metrics, resulting in a better trade-off between precision and recall, as evidenced by its harmonic mean (

F_{1}

), which is the highest one, as it is shown in Table 4.

Table 2. Mean Precision of the Machine Learning Methods Evaluated through Ten-Fold Cross-Validation.

Method	Mean Precision (%)	Variance (%)	Gain (%)
Decision Tree - Gini index
(baseline)	54.69	9.29	NA
Adaboost - Entropy index	57.33	3.87	4.60
Multilayer Perceptron
with a single hidden layer	60.45	1.09	10.53
Multilayer Perceptron
with five hidden layers	61.67	9.11	12.76
Gaussian Process
with Dot Product Kernel	64.83	2.68	18.54
Decision Tree - Entropy index	66.54	2.02	21.67
Random Forest - Entropy index	71.67	4.53	31.05
XGBoost	76.67	4.41	40.19
Gaussian Process with
the Radial Basis Function Kernel	81.33	2.47	48.71
Gaussian Process
with the Sum of Radial Basis
Function and Matern Kernels	81.33	2.47	48.71
Gaussian Process with
the Rational Quadratic Kernel	81.33	2.47	48.71
Gaussian Process
with the Matern Kernel	83.33	2.77	52.37
Logistic Regression	84.16	9.23	53.89
Support Vector Machines
with Sigmoid Kernel	85.00	10.25	55.42
Support Vector Machines
with Polynomial Kernel	85.00	10.25	55.42
Support Vector Machines
with Radial Basis Function Kernel	85.17	3.63	55.73

Table 3. Mean Recall of the Machine Learning Methods Evaluated through Ten-Fold Cross-Validation.

Method	Mean Recall (%)	Variance (%)	Gain (%)
Decision Tree - Gini index
(baseline)	41.50	6.25	NA
Logistic Regression	45.00	4.75	8.43
Support Vector Machines
with Sigmoid Kernel	45.00	4.75	8.43
Support Vector Machines
with Polynomial Kernel	45.00	4.75	8.43
Adaboost - Entropy index	49.00	2.59	18.07
Decision Tree - Entropy index	51.50	1.95	24.09
Multilayer Perceptron
with five hidden layers	54.50	7.57	31.33
Support Vector Machines
with Radial Basis Function Kernel	57.00	7.91	37.35
XGBoost	59.00	1.79	42.16
Multilayer Perceptron
with a single hidden layer	61.50	1.90	48.19
Gaussian Process with
the Radial Basis Function Kernel	64.00	4.39	54.22
Gaussian Process
with the Sum of Radial Basis
Function and Matern Kernels	64.00	4.39	54.22
Gaussian Process with
the Rational Quadratic Kernel	66.5	4.25	60.24
Gaussian Process
with the Matern Kernel	66.5	4.25	60.24
Random Forest - Entropy index	66.5	3.00	60.24
Gaussian Process
with Dot Product Kernel	67.00	5.51	61.44

Table 4. Mean Value of Harmonic Mean (

F_{1}

) of the Machine Learning Methods Evaluated through Ten-Fold Cross-Validation.

Table 4. Mean Value of Harmonic Mean (

F_{1}

) of the Machine Learning Methods Evaluated through Ten-Fold Cross-Validation.

Method	Mean $F_{1}$ (%)	Variance (%)	Gain (%)
Decision Tree - Gini index
(baseline)	44.42	5.85	NA
Adaboost - Entropy index	50.43	1.65	13.53
Multilayer Perceptron
with five hidden layers	53.97	5.04	21.49
Decision Tree - Entropy index	55.73	2.16	25.46
Logistic Regression	56.45	5.35	27.08
Support Vector Machines
with Sigmoid Kernel	56.81	5.89	27.89
Support Vector Machines
with Polynomial Kernel	56.81	5.89	27.89
Multilayer Perceptron
with a single hidden layer	59.81	0.82	34.65
Gaussian Process
with Dot Product Kernel	63.40	2.71	42.73
Support Vector Machines
with Radial Basis Function Kernel	63.88	5.24	43.81
XGBoost	64.33	1.23	44.82
Random Forest - Entropy index	67.47	2.30	51.89
Gaussian Process with
the Radial Basis Function Kernel	70.56	2.82	58.85
Gaussian Process
with the Sum of Radial Basis
Function and Matern Kernels	70.56	2.82	58.85
Gaussian Process with
the Rational Quadratic Kernel	71.41	2.08	60.76
Gaussian Process
with the Matern Kernel	72.52	2.58	63.26

Table 5. Confusion matrix for Gaussian process with the Matern kernel.

	Forecasted class
True class	Student without risk	Student at risk	Total
Student without risk	56	6	62
Student at risk	14	27	41
Total	70	33	103

Table 6. Confusion matrix for support vector machines with the radial basis function.

	Forecasted class
True class	Student without risk	Student at risk	Total
Student without risk	57	5	62
Student at risk	18	23	41
Total	75	28	103

In addition to the evaluation of accuracy, precision, recall, and harmonic mean (

F_{1}

) presented in Table 1, Table 2, Table 3, and Table 4, we further analyzed the receiver operating characteristics (ROC) curves for both GP with the Matern kernel and SVM with the radial basis function kernel, as depicted in Figure 2 and Figure 3, respectively. The area under the ROC curve (AUC) for GP with the Matern kernel was found to be 0.78, indicating that this classifier performs significantly better than random guessing and provides a good level of discrimination between positive and negative instances. Besides, Figure 3 shows that SVM with the radial basis function kernel has a greater AUC compared to GP with the Matern kernel.

These results suggest that the dataset size might be large enough to enable machine learning methods to learn the regular patterns between students’ course failure and their performance in prerequisite courses effectively. The combination of GP with the Matern kernel’s higher harmonic mean (

F_{1}

) and good discrimination ability, as shown in the ROC curve, supports its suitability as the best-performing classifier for predicting the risk of student failure in the Numerical Methods course based on their academic history in prerequisite courses.

3.3. Discussion

Based on the results obtained in this study, the optimal choice for implementing a system to forecast the risk of failing a course in our research context is Gaussian process (GP) with the Matern kernel. GP outperforms other machine learning methods in terms of accuracy, as well as achieving a favorable trade-off between precision and recall, as shown in Table 1, Table 2, and Table 3. One of the key advantages of GP is its probabilistic nature, which allows it to report the probability of a student failing the course. This predictive probability adds valuable insights, enabling better decision-making compared to methods like support vector machine (SVM), which lacks inherent probabilistic capabilities.

Therefore, GP ability to provide probabilistic risk estimates makes it the most suitable choice for building Course Prophet, the intelligence system for early prediction of student failure in the Numerical Methods course based on their academic history in prerequisite courses.

Reporting the probability of failure is valuable for determining the allocation of resources to support at-risk students. For instance, if a given student has a probability of failure around 54%, it might be unnecessary to recommend additional support or intervention measures to help improve their chances of success.

Finally, the paired t-test on the mean of each metric used to evaluate the machine learning methods reveals that there are no statistically significant differences between GP with the Matern kernel and SVM with the radial basis function kernel (i.e., p-value > 0.05), despite the former outperforming the latter in terms of accuracy and harmonic mean (

F_{1}

). Based on the paired t-test results, we draw the following conclusions:

There is solid statistical evidence that GP with the Matern kernel performs better than SVM with the polynomial and sigmoid kernel in terms of recall (i.e., p-value = 0.04 for both cases).
There is solid statistical evidence that GP with the Matern kernel performs better than GP with the dot product kernel in terms of precision (i.e., p-value = 0.02).
There is solid statistical evidence that GP with the Matern kernel is more accurate than multilayer perceptrons (MLP) with five hidden layers (i.e., p-value = 0.03).
There is solid statistical evidence that GP with the Matern kernel is more accurate than MLP with a single hidden layer (i.e., p-value = 0.01).
There is solid statistical evidence that GP with the Matern kernel outperforms MLP with a single hidden layer in terms of precision (i.e., p-value = 0.002).
There is solid statistical evidence that GP with the Matern kernel is more accurate than a decision tree (DT) with Gini index (i.e., p-value = 0.01), and outperforms it in terms of precision (i.e., p-value = 0.02), recall (i.e., p-value = 0.03), and harmonic mean (i.e., p-value = 0.009).
There is solid statistical evidence that GP with the Matern kernel is more accurate than DT with entropy index (i.e., p-value = 0.03), and outperforms it in terms of recall (i.e., p-value = 0.08) and harmonic mean (i.e., p-value = 0.03).
There is solid statistical evidence that GP with the Matern kernel is more accurate than AdaBoost with entropy index (i.e., p-value = 0.002), and outperforms it in terms of precision (i.e., p-value = 0.007) and harmonic mean (i.e., p-value = 0.004).
There is solid statistical evidence that GP with the Matern kernel performs better than logistic regression in terms of recall (i.e., p-value = 0.04).

4. Conclusions and Future Research

4.1. Contributions

In this research, our primary objective was to investigate the feasibility of accurately predicting whether a given student might fail a Bachelor’s degree course based on their performance in prerequisite courses. To achieve this goal, we adopted a quantitative research approach, focusing on machine learning methods. These methods allow us to map the input variables representing a student’s performance in prerequisite courses to the target variable, indicating whether the student is at-risk of failing the course or not. The study was conducted in the context of students pursuing the Bachelor’s degree in Systems Engineering at the University of Córdoba, Colombia. Specifically, we focused on the Numerical Methods course, which relies on several subjects taught in various prerequisite courses.

So the contributions of this research are as follows:

(i): A carefully curated dataset specifically designed to address the research problem, enabling the training and testing of the machine learning methods used in this study.
(ii): The development of Course Prophet, a machine learning-based system prototype, which offers early alerts to stakeholders at the University of Córdoba regarding students at risk of failing the Numerical Methods course. By providing timely warnings, stakeholders might implement appropriate measures to mitigate the risk of failure. Course Prophet uses the Gaussian process method and reports the probability of failure, providing additional valuable information for decision-making.
(iii): The findings of an extensive experimental evaluation, detailed in Section 4.2, providing valuable insights and results that contribute to a deeper understanding of the problem and the effectiveness of different machine learning methods in predicting course failure risk.

These contributions collectively advance the field of educational predictive analytics and offer practical solutions to enhance student success and educational outcomes.

4.2. Findings

In conclusion, in this study we found that:

Gaussian process with the Matern kernel demonstrates higher accuracy compared to the other machine learning methods. Although not all cases showed solid statistical evidence, the paired t-test results indicate that in our study’s context, Gaussian process with the Matern kernel outperforms multilayer perceptrons, decision trees, and AdaBoost in terms of accuracy, with p-values less than 0.05.
Gaussian process with the Matern kernel achieves the best trade-off between precision and recall, as evidenced by its highest harmonic mean ( $F_{1}$ ) value. This means it strikes a better balance between correctly identifying positive instances (precision) and capturing all relevant positive instances (recall).

These findings indicate that Gaussian process with the Matern kernel is a promising machine learning method for predicting course failure risk based on students’ performance in prerequisite courses. However, further research and validation with larger and diverse datasets could provide more robust and generalizable results. The proposed system, Course Prophet, offers valuable insights to stakeholders at the University of Córdoba in identifying students at risk and supporting their academic success.

4.3. Directions for Further Research

As a recommendation for future research, this study could be extended to encompass a broader range of courses and Bachelor’s degrees. Exploring the effectiveness of Course Prophet in predicting course failure risks across various disciplines would provide a more comprehensive understanding of its applicability and impact.

Moreover, conducting user assessments and gathering feedback from stakeholders, including educators, administrators, and students, would be crucial in evaluating Course Prophet’s practical usability and effectiveness. Understanding user satisfaction and identifying areas for improvement can lead to a more refined and user-friendly system.

Addressing the challenges associated with curriculum changes is essential to ensure the adaptability and relevance of Course Prophet in the long run. Developing strategies to seamlessly integrate curriculum updates into the system would enhance its sustainability and usefulness.

Furthermore, exploring the potential adaptation of Course Prophet into a recommender system for course selection based on individual student performance could greatly benefit students. Providing personalized course recommendations aligned with their academic strengths and needs would enhance their educational experience.

Lastly, investigating the impact of early identification of at-risk students raises important ethical considerations. Conducting in-depth research on the ethical and practical implications of using machine learning technology for educational decision-making is necessary to ensure responsible and informed adoption.

By addressing these points, future research can enrich the knowledge and applicability of Course Prophet, paving the way for more informed decision-making in educational institutions.

Funding

This research was funded by the University of Córdoba in Colombia grant number FI-01-22.

Institutional Review Board Statement

The study was approved by the Institutional Research Board of the University of Córdoba in Colombia (FI-01-22, January 22th of 2023).

Data Availability Statement

The dataset is available online to allow the reproduction of our study, and for further research [28].

Acknowledgments

Caicedo-Castro thanks the Lord Jesus Christ for blessing this project, and the Universidad de Córdoba in Colombia for supporting the Course Prophet Research Project (grant FI-01-22). In special, a deepest appreciation goes to Dr. Jairo Torres-Oviedo, rector of the University of Córdoba. Caicedo-Castro thanks all students who collaborated with us, answering the survey conducted for collecting the dataset, used to train the learning algorithms adopted in this research. Finally, Caicedo-Castro thanks the anonymous reviewers for their comments that contributed to improve the quality of this article.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:

Adaboost	Adaptive Boosting
AUC	Area Under the ROC Curve
DT	Decision Trees
GP	Gaussian Process
LR	Logistic Regression
KFCV	K-Fold Cross-Validation
RF	Random Forest
ROC	Receiver Operating Characteristics
SVM	Support Vector Machines
XGBoost	eXtreme Gradient Boosting

References

Lykourentzou, I.; Giannoukos, I.; Nikolopoulos, V.; Mpardis, G.; Loumos, V. Dropout prediction in e-learning courses through the combination of machine learning techniques. Computers and Education 2009, 53, 950–965. [Google Scholar] [CrossRef]
Kabathova, J.; Drlik, M. Towards Predicting Student’s Dropout in University Courses Using Different Machine Learning Techniques. Applied Sciences 2021, 11, 3130. [Google Scholar] [CrossRef]
da Silva, D.E.M.; Pires, E.J.S.; Reis, A.; de Moura Oliveira, P.B.; Barroso, J. Forecasting Students Dropout: A UTAD University Study. Future Internet 2022, 14, 1–14. [Google Scholar]
Niyogisubizo, J.; Liao, L.; Nziyumva, E.; Murwanashyaka, E.; Nshimyumukiza, P.C. Predicting student’s dropout in university classes using two-layer ensemble machine learning approach: A novel stacked generalization. Computers and Education: Artificial Intelligence 2022, 3, 100066. [Google Scholar] [CrossRef]
Čotić Poturić, V.; Bašić-Šiško, A.; Lulić, I. ARTIFICIAL NEURAL NETWORK MODEL FOR FORECASTING STUDENT FAILURE IN MATH COURSE. In Proceedings of the ICERI2022 Proceedings. IATED, 15th annual International Conference of Education, Research and Innovation; 2022; pp. 5872–5878. [Google Scholar] [CrossRef]
Caicedo-Castro, I.; Macea-Anaya, M.; Rivera-Castaño, S. Early Forecasting of At-Risk Students of Failing or Dropping Out of a Bachelor’s Course Given Their Academic History - The Case Study of Numerical Methods. In Proceedings of the PATTERNS 2023 : The Fifteenth International Conference on Pervasive Patterns and Applications. IARIA: International Academy, Research, and Industry Association, International Conferences on Pervasive Patterns and Applications; 2023; pp. 40–51. [Google Scholar]
Zihan, S.; Sung, S.H.; Park, D.M.; Park, B.K. All-Year Dropout Prediction Modeling and Analysis for University Students. Applied Sciences 2023, 13, 1143. [Google Scholar] [CrossRef]
Čotić Poturić, V.; Dražić, I.; Čandrlić, S. Identification of Predictive Factors for Student Failure in STEM Oriented Course. In Proceedings of the ICERI2022 Proceedings. IATED, 15th annual International Conference of Education, Research and Innovation; 2022; pp. 5831–5837. [Google Scholar] [CrossRef]
Dorogush, A.V.; Ershov, V.; Gulin, A. CatBoost: gradient boosting with categorical features support. arXiv 2018, arXiv:1810.11363. [Google Scholar]
Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the Advances in Neural Information Processing Systems; Guyon, I.; Luxburg, U.V.; Bengio, S.; Wallach, H.; Fergus, R.; Vishwanathan, S.; Garnett, R., Eds. Curran Associates, Inc., Vol. 30. 2017. [Google Scholar]
Pacheco-Arrieta, I.; et al. Agreement No. 004: Student’s code at the University of Córdoba in Colombia. 2004. Available online: http://www.unicordoba.edu.co/wp-content/uploads/2018/12/reglamento-academico.pdf (accessed on 24 July 2023).
Cox, D. The regression analysis of binary sequences. Journal of the Royal Statistical Society. Series B (Methodological) 1958, 20, 215–242. [Google Scholar] [CrossRef]
Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Mathematical Programming 1989, 45, 503–528. [Google Scholar] [CrossRef]
Byrd, R.; Lu, P.; Nocedal, J.; Zhu, C. A Limited Memory Algorithm for Bound Constrained Optimization. SIAM Journal on Scientific Computing 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
Williams, C.; Rasmussen, C. Gaussian Processes for Regression. In Proceedings of the Advances in Neural Information Processing Systems; Touretzky, D.; Mozer, M.; Hasselmo, M., Eds. MIT Press, Vol. 8; 1995; pp. 514–520. [Google Scholar]
Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press, 2006. [Google Scholar]
Mohri, M.; Rostamizadeh, A.; Talwalkar, A. Foundations of Machine Learning, 2nd ed.; The MIT Press, 2018. [Google Scholar]
Cortes, C.; Vapnik, V. Support Vector Networks. Machine Learning 1995, 20, 273–297. [Google Scholar] [CrossRef]
Aggarwal, C.C. Neural Networks and Deep Learning; Springer, 2018; p. 497. [Google Scholar]
Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back-propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. 2014. Available online: http://arxiv.org/abs/1412.6980 (accessed on 24 July 2023).
Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Wadsworth and Brooks: Monterey, CA, 1984. [Google Scholar]
Freund, Y.; Schapire, R.E. Experiments with a new boosting algorithm. In Proceedings of the ICML, Vol. 96; 1996; pp. 148–156. [Google Scholar]
Breiman, L. Random forests. In Proceedings of the Machine learning. Springer, Vol. 45; 2001; pp. 5–32. [Google Scholar]
Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining. ACM; 2016; pp. 785–794. [Google Scholar]
Pedregosa, F.; others. Scikit-learn: Machine Learning in Python. Journal of Machine Learning Research 2011, 12, 2825–2830. [Google Scholar]
Google Colaboratory. 2017. Available online: https://colab.research.google.com/ (accessed on 24 July 2023).
Caicedo-Castro, I. Dataset for Early Forecasting of At-Risk Students of Failing or Dropping Out of a Bachelor’s Course Given Their Academic History - The Case Study of Numerical Methods. 2023. Available online: https://www.example.com (accessed on 24 July 2023).

Figure 1. Proportion of students who failed or passed the Numerical Methods course in the dataset.

Figure 2. Receiver operating characteristics (ROC) curve for the Gaussian process with the Matern kernel.

Figure 3. Receiver operating characteristics (ROC) curve for the Support Vector Machines with the Radial Basis Function kernel.

Table 1. Mean Accuracy of the Machine Learning Methods Evaluated through Ten-Fold Cross-Validation.

Method	Mean Accuracy (%)	Variance (%)	Gain (%)
Decision Tree - Gini index
(baseline)	60.27	3.23	NA
Adaboost - Entropy index	62.45	1.07	3.62
Decision Tree - Entropy index	66.54	2.02	10.40
Multilayer Perceptron
with a single hidden layer	67.09	1.03	11.32
Multilayer Perceptron
with five hidden layers	68.18	1.18	13.12
Gaussian Process
with Dot Product Kernel	71.18	1.27	18.10
Random Forest - Entropy index	73.91	1.93	22.63
XGBoost	74.00	0.83	22.78
Logistic Regression	75.73	0.88	25.65
Support Vector Machines
with Sigmoid Kernel	75.91	1.18	25.95
Support Vector Machines
with Polynomial Kernel	75.91	1.17	25.95
Support Vector Machines
with Radial Basis Function Kernel	77.64	1.66	28.82
Gaussian Process with
the Radial Basis Function Kernel	79.45	1.38	31.82
Gaussian Process
with the Sum of Radial Basis
Function and Matern Kernels	79.45	1.38	31.82
Gaussian Process with
the Rational Quadratic Kernel	79.54	1.00	31.97
Gaussian Process
with the Matern Kernel	80.45	1.28	33.48

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Course Prophet: A Machine Learning-Based System for Early Prediction of Student Failure in Numerical Methods Course in the Bachelor’s Degree in Engineering at the University of Córdoba, Colombia

Abstract

1. Introduction and Background

2. Methods

2.1. Research Context and Problem Formalization

2.2. Key Assumptions and Limitations

2.3. Machine Learning Methods

3. Evaluation

3.1. Experimental Setting

3.2. Results

3.3. Discussion

4. Conclusions and Future Research

4.1. Contributions

4.2. Findings

4.3. Directions for Further Research

Funding

Institutional Review Board Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe