Prerpints.org logo
Preprint
Article

LightGBM and SVM algorithms for Predicting Synthetic Load Profiles Using a Non-Intrusive Approach

Altmetrics

Downloads

393

Views

98

Comments

0

Submitted:

01 August 2023

Posted:

03 August 2023

You are already at the latest version

Alerts
Abstract
Due to related uncertainties brought by changes in energy consumption and the integration of rooftop photovoltaic systems, the accuracy and availability of load profiling data are difficult to achieve. However, project managers and planners use a precise load profile as a crucial tool when determining whether the feeder must be updated or de-loaded. The paper aims to create a non-intrusive monitoring system that predicts the synthetic load profiles behavior of energy consumption using a Light Gradient Boosted and Support Vector Machine (SVM) machine learning technique. The most effective ML algorithm is chosen, and it has the potential to be assessed and verified using validation curves, residuals model generation, and prediction error metrics based on the following key statistical indicators: Mean Absolute Error, Mean Square Error, Root Mean Square Error, R-Square, Root Mean Squared Logarithmic Error, and Mean Absolute Percentage Error. The most effective ML has the potential to be assessed and verified using validation curves, residual model generation, and prediction error metrics based on the following key statistical indicators. The result shows that the estimation of the Irms avg -based on LightGBM is more accurate than the SVM because of its quick, economical, and difficult to overfit, particularly with high-dimensional data, speed, and efficiency of the MAE (3.0698), MSE (15.2757), RMSE (3.9020), RMSLE (0.1433), and MAPE (0.0049) respectively. Additionally, the machine learning model shows that, when compared to the SVM, the LightGBM model had the highest accurate prediction, with R-Square values of 89.8%, 90.3%, and 88.5% for Irms_A_avg, Irms_B_avg, and Irms_C_avg, respectively for Brakfontein Substation supply region, and best represents a diverse customer base.
Keywords: 
Subject: Engineering  -   Industrial and Manufacturing Engineering

1. Introduction

The complexity of power system construction, planning, and operation is increasing as the energy transition progresses. There are significant limitations with traditional manual analysis methods for quickly and accurately assessing the dynamic security region of power systems, such as rule roughness and low calculation efficiency, whereas data mining approaches could provide a novel way to overcome such issues [1]. The predictive ability accurately calculate load profiles is critical for building reliable and cost-effective power systems. It can cut operating expenses, optimize dispatching, and make unit maintenance and overhaul easier to schedule, achieving dispatching's economic logic [2]. It is challenging to predict daily load since it mostly depends on previous days' loads as well as other variables like temperature and calendar influence [3]. The industrial, commercial, and residential power consumption on the electrical grid demonstrates quick growth characteristics with a significant increase in economic and social levels. However, there are clear differences in the load characteristics of diverse consumers because production processes vary and because different industries use energy at different times of the day [4,5]. Specific loads experience significant swings in their peak and trough during brief periods [6]. Consequently, a crucial and difficult topic of research is how completely to evaluate the power load parameters for accurate load forecasting [7]. Demand predictions are the most important component of the demand-side idea of intelligent grids because they allow those in charge of the smart grid to make decisions.
Deep learning systems have recently shown promising results in predicting energy use. In terms of machine learning methods, some commonly used algorithms are artificial neural networks, support vector machines (SVM), and Gaussian processes (GP). The two most frequent methods are back propagation (BP) neural network and SVM [8]. Gradient boosting models are successful in estimating building energy usage in recent years. The authors of [9] integrated deep learning models like the temporal convolutional network (TCN) into the tree-based model LightGBM [10], which outperformed other artificial intelligence methods like the support vector regressor (SVR) and long short-term memory (LSTM). Aside from improved performance, the significance of features in tree-based ensemble models can be readily conveyed by a score representing the value of each feature as a splitting node in each tree. XGBoost [11] is another effective tree-based model for forecasting multi-step heat loads; it outperformed SVR and deep neural networks (DNNs) [12]. A similar day selection technique based on the XGBoost algorithm output feature importance score was proposed by [13]. The task of predicting load involves many different dimensions and aspects of ML algorithms are good at detecting patterns that appear to be random, numerical approaches like curve fitting are inaccurate. However, the preceding approaches do not consider time series correlation, therefore they cannot successfully converge when there are a large number of training samples.
A synthetic load that is generated from a profile can to some extent, resemble a real load. To synthesize load data, specific daily load profiles are created each year using hourly load data. By and analyzing the collected load data, it is feasible to determine the load profiles of the clients [14]. Metropolitan municipality’s primary goal is to improve its residents' quality of life by offering a range of services. The South African municipality can develop and carry out strategic initiatives to achieve its organizational goals, since it is one of the most important aspects of developing a reliable distribution network, an accurate load profile is essential. One way to provide services is to provide power to both formal and informal townships; this is accomplished through various programs and portfolios [15,16,17]. Ensure the dependability of the system, this entails keeping an eye on population expansion and enhancing the medium voltage (MV) distribution network. However, due to the surge in illegal electrical connections and people residing in their backyards, the City of Tshwane's Energy and Electrical Division (COT) is having difficulties in implementing these programs and portfolios. It is required to use a more thorough approach to computing and data analysis to ensure that the city's reliability management systems for the medium voltage (MV) distribution network are optimized to the maximum extent possible. The MV distribution network can generate synthetic load profiles using a computer application with the fewest possible human errors [18,19,20]. 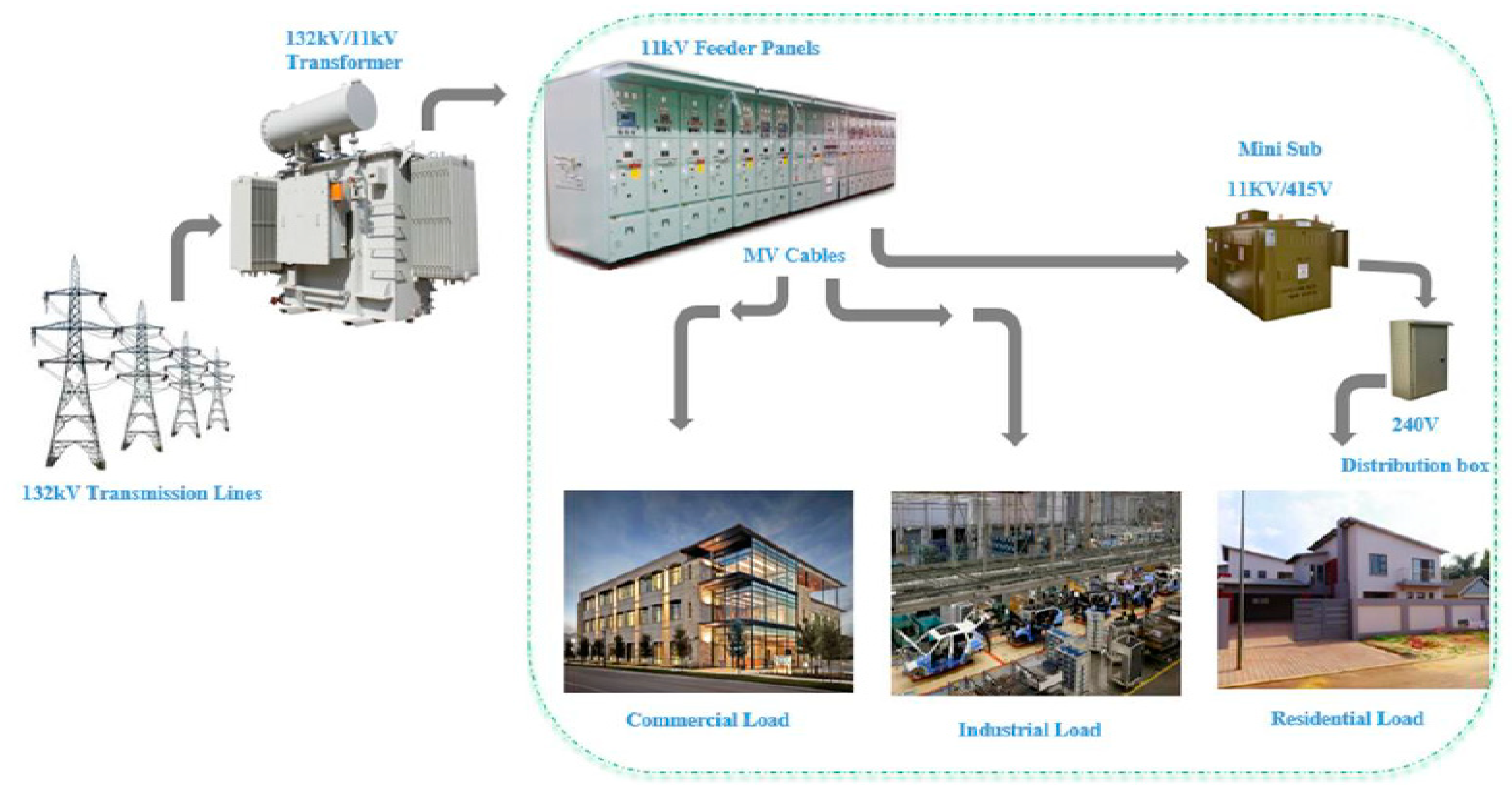Figure 1 shows the integration of the medium voltage network into the system using a typical distribution network configuration for COT.
Therefore, the paper proposes a non-intrusive monitoring system that analyzes the full house load demand curve using a Light Gradient Boosted and Support Vector Machine to evaluate the features of specific electric appliances. The main contributions of this paper are as follows.
1. We propose LightGBM and SVM algorithms and demonstrate that LightGBM is more accurate than the SVM because of its quick, economical, and difficult to overfit, particularly with high-dimensional data, speed, and efficiency.
2. We applied machine learning models to estimate the load profiles for the electric power distribution system using MLP, RBF, and linear SVM kernels to determine the load profiles for the electricity distribution network in Tshwane municipality.
3. We present a machine learning model that shows when compared to the SVM, the LightGBM model had the highest accurate prediction, with R-Square values of 89.8%, 90.3%, and 88.5% for Irms_A_avg, Irms_B_avg, and Irms_C_avg, respectively for Brakfontein Substation supply region, and best represents a diverse customer base.
The rest of this paper is structured as follows. Section 2 goes over studies on related works on current state of load profiling and power demand modeling techniques. Section 3 addresses the methods, while Section 4 discusses the results. Section 5 introduces the conclusion.

2. Related works on the Current State of Load Profiling and Power Demand Modeling Techniques

The electrical load patterns of users were previously grouped using models based on clustering methodologies to help with tariff design, short-term forecasting, and demand response programs to support management decisions. In developing countries, accurate electric load forecasting (ELF) is essential for carrying out energy policy effectively. Furthermore, accurate forecasts of the electric power load are essential for the management and planning of several organizations. For instance, it might have an impact on load shedding, contract evaluation, and infrastructure development. However, because the cost of an error is so high, it will be worthwhile to conduct research into forecasting strategies that could lower this by just a few percentage points [21]. Long-term load estimates often cover more than one year, while short-term load projections typically cover a period between one hour and one week. As a result, short-term forecasting is essential for keeping an eye on and managing electricity systems [22]. Projecting daily load, however, is challenging because it mostly depends on the load from the previous day, as well as other variables like temperature and the calendar [23]. The industrial, commercial, and residential power consumption on the electrical grid demonstrates quick growth characteristics with a significant increase in economic and social levels. However, there are noticeable differences in the load characteristics of diverse consumers due to the disparate manufacturing processes and peak and trough times of energy demand among industries [24,25].
The load characteristics of energy consumers also change depending on the time of year, the weather, average days, where power is consumed, and other factors. Because individual loads fluctuate greatly in a short amount of time, there is a big difference between peak and trough [26]. Consequently, a crucial and difficult topic of research is how to comprehensively evaluate the power load parameters for accurate load forecasting [27]. The general expansion of the energy infrastructure as well as population growth are responsible for the sharp increase in power demand. The use of "intelligent grids" is being made to successfully manage this increasing demand [28]. Demand predictions are the most important component of the demand-side idea of intelligent grids because they allow those in charge of the smart grid to make decisions. Short-term (from a few hours to a few days), medium-term, and long-term load forecasting are the three types available. The task of load forecasting involves many different dimensions and aspects. Because machine learning algorithms are so good at detecting patterns that appear to be random, numerical approaches like curve fitting are inaccurate. The paper aims to create a non-intrusive monitoring system that evaluates the behavior of each electric appliance based on a Light Gradient Boosted Machine (LightGBM) machine learning (ML) technique for producing synthetic load profiles.
Demand-side management and software control in the distribution network are empirical because every grid design may be simulated using different parameters. Electricity is produced and utilized on demand; it cannot be produced in large quantities and stored for use later. Several power demand modeling techniques that help with load prediction were explained in this section. The demand for residential, commercial, industrial, and other consumer characteristics may be predicted using a variety of machine learning and mathematical techniques for modeling electricity consumption [29,30,31,32,33]. Some of the methods utilized in earlier research include probability matrices and time series, linear auto-regression, Markov chains, Time-Use Survey data, autoregressive integrated moving average (ARIMA), artificial neural network (ANN), and multiple linear regression (MLR). These several techniques were used to cross-validate the results and were chosen depending on the type, quality, and quantity of available data. When a researcher has a lot of data gathered over a long enough period to cover the necessary population or sample size, for example, time series analysis is ideal since it accurately forecasts data [34]. The Holt-Winters (HWT) exponential smoothing model and Autoregressive Moving-Average (ARMA) approaches are the most used due to their ability to handle time-series data with patterns [35]. Fuzzy logic, on the other hand, is less ideal since expert systems rely on rules that are generated from the experiences of experts and operators. Another study focuses on modeling power demand regarding consumption patterns and cost and alternative energy sources. To explore the relationship between pricing and client consumption patterns, for instance, Author [36] built a multinomial logic model; the data were analyzed, and a response was produced. To regulate consumption patterns, a variety of pricing schemes (including fixed rate, variable rate, ladder pricing, single price, time-varying pricing, and others) have been studied. [37].
Adding useful features to energy consumption predictions can enhance accuracy. Because building energy consumption has multiple daily patterns, labeling various patterns can help increase forecasting accuracy. The most straightforward way is to identify the daily pattern of building energy usage with a time-series clustering algorithm such as k-shape [38], or k-means [39]. The historical energy data of a building can be separated into groups with various patterns using time-series clustering. The problem in applying a load pattern to STLF is that we cannot name the predicting day's pattern until we know the actual load numbers. As a result, previous studies solely used clustering techniques in the preprocessing step. Ref. [40] discovered that k-shape clustering can aid in appropriately labeling a building's principal space consumption to improve building performance benchmarking and analysis. The authors of [41] used cluster analysis to discover daily heating load trends for both the training and test sets. To circumvent the contradiction, academics have created other approaches for labeling forecasting day patterns.
Based on numerous findings from the literature, First, tree-based models such as SVM and LightGBM algorithms are promising; further research on feature engineering should be undertaken to increase their predicting performance. Second, most load pattern methods focus on day type and weather type, which are not equal to actual load patterns that are vital for building load forecasting. Because the forecasting day load is uncertain, a stochastic approach should be used to predefine the forecasting days' energy load pattern. Finally, a recursive multistep load forecasting algorithm produces better results, but at a higher calculation cost.

3. Methods

The two techniques of Gradient-Based Side Sampling and the EFB combine to provide the characteristics of the LightGBM Algorithm. The lightGBM was utilized in this study to predict the load profiles for the electricity distribution system. These algorithms include deep learning and shallow learning models, ensemble learning strategies, and traditional learning strategies like linear regression and support vector machines. They also include linear and nonlinear approaches. The Python program Pycaret is used to build the lightGBM model [42]. The construction of the Light Gradient Boosting Machine model for forecasting pillar stability, which was developed using Python 3.10 in Anaconda 3. It is easy to understand and use, resulting in skill estimations with less bias than previous methods. The training approach begins by reading three-phase power distribution systems' voltage and current datasets. The essential data used in this inquiry were load flow and voltage, current root-mean-square, and trend period information. The data for this research comes from the Brakfontein substation of the Tshwane electricity grid's supply region from August 29 2016 to September 19, 2017. The training dataset is then split into k subsets of 604 for cross-validation. This makes it feasible to produce identical k models without delay. Each model is then tested on the remaining partitions after being trained on k -10 partitions. The method parameter k denotes the number of groups that are created from a given data sample. The final evaluation performance is averaged k times to get the method's total performance. The results of this small dataset are then enhanced by cross-validation.

3.1. Light Gradient Boosted Machine Learning Algorithms

LightGBM, an upgraded form of Gradient Boosting Decision Tree (GBDT), was proposed in 2017 [9]. GBDT, an integrated algorithm, is made up of a succession of linear subset combinations. Based on the iteration concept, it takes the regression tree as the subset and adds the subsets one by one to reduce the learner's loss function. Equation (1) can be used to express GBDT.
F x x = ∑ i = 1 k f i ( x θ 1 ) ,
where f i ( x θ 1 ) is regression tress subsets in the i-th iteration; θ 1 = parameter of subsets; x is number of subsets; θ 1 is obtained by minimizing the loss functions by equation (2).
θ 1 = arg ⁡ min ⁡ L [ F i = 1 x + f i ( x θ 1 ) ] ,
where L is the loss function that the learner uses for prediction.
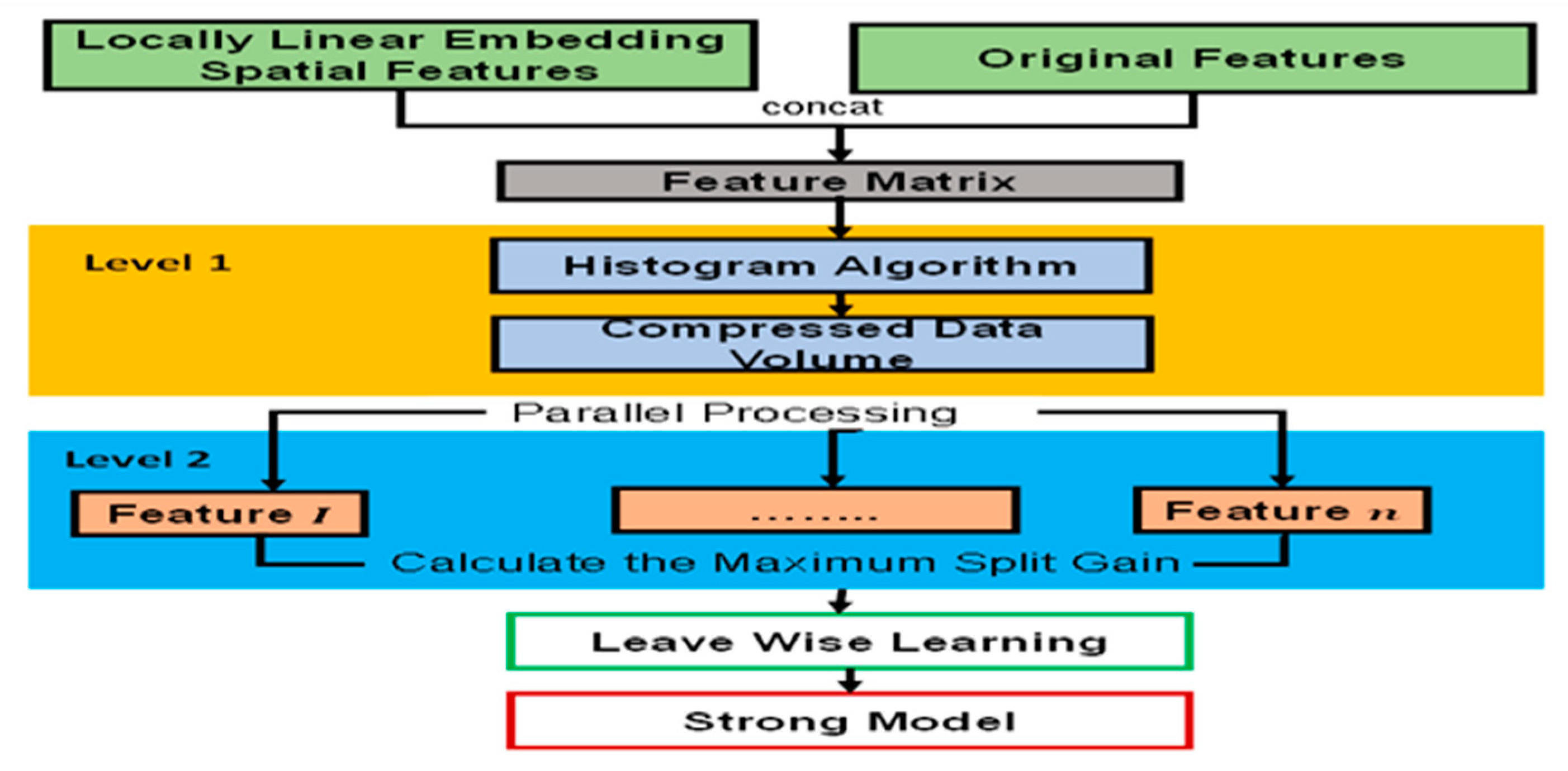
The algorithm enhances the gradient boosting technique employed by LightGBM by focusing on boosting situations with stronger gradients and using a type of autonomous feature selection. To get over the limitations of the histogram-based approach used GBDT frameworks, it also uses two cutting-edge techniques, Gradient-based One Side Sampling and Exclusive Feature Bundling (EFB). The histogram method and the leaf-wise strategy with depth limitation are the key advances of the LightGBM model. The histogram algorithm separates continuous data into K integers and creates a K-width histogram. The discretized value is accumulated in the histogram as an index during the traversal, and the best decision tree split point is then searched for. The Leaf-wise technique with depth limitation entails choosing the leaf with the highest gain to split and loop throughout each split. Simultaneously, by restricting the depth of the tree and the number of leaves, the model's complexity is minimized and overfitting is avoided. The LightGBM model is trained using the gradient boosting approach, and the grid search method is used to optimize the model's hyperparameters. The major hyperparameters of the LightGBM model optimized using the grid search approach are as follows: the number of weak regression trees is 200, the number of leaves is 50, the learning rate is 0.1, and the number of iterations is 2000. To better understand the flow diagram, Figure 2 describes how the flowchart shows the light gradient boosting machine learning establishment phases.

3.2. Support Vector Machine Algorithm

The support vector machines (SVM) method is excellent at resolving issues brought on by overfitting, a short sample size, nonlinear data, and extensive computing. For instance, in SVM, the most significant threshold in the feature set is used to first separate the good data grouping from the bad data. SVM is used in this dissertation with linear, RBF, and MLP kernels. By equation (3), the SVM algorithm, a classification algorithm based on linear discriminant function, was proposed in 1995 [7]. It uses convex optimization technologies to determine the best discriminant surface for sample categorization..
F x x = w T x + b ,
where w and b are the normal vector and displacement term of the hyperplane respectively; x is the sample data. Decision rule: if F x x > 0 , it is taken as a positive class, i.e., the black dots in Figure 3, namely the stable point; if F x x < 0 , as negative class.
Because most data are not linearly separable, SVM introduces a kernel function x, x to replace xx in equation (4) to translate the input space to a high-dimensional feature space, locate a hyperplane, and realize the classification function. SVM bypasses the high-dimensional transformation of data by calculating the inner product directly in the original input space, which circumvents the dimension explosion of high-dimensional space. SVM has an excellent classification impact, great interpretability, and generalization ability since it is based on the idea of structural risk reduction and the introduction of kernel function technology. When a linear kernel function is utilized, SVM can provide the expression of the classification hyperplane, i.e. the DSR border.
where is the relaxation variable, suggesting that the interval between the admissible samples and the hyperplane is less than the hard threshold 1, allowing for a given number of outliers; C, the penalty parameter indicating the significance of outliers; n, the number of training samples. When the number of features is enormous, however, the cost of SVM training is very high and overfitting is very likely. As a result, a feature selection process is required, and the quality of the outputs has a significant impact on SVM accuracy. Figure 3 depicts the fundamental principles of the SVM algorithm. The hyperparameter configurations of SVM are the kernel function, the penalty parameter C and the γ.
3.3 K-Folds Cross-Validation
Cross-validation is a model evaluation method that is superior to residual evaluations since it predicts how well the learner will perform when asked to make new predictions for data, which was handled by eliminating some of the data before training. After training, the data that was removed can be used to assess the learned model's performance on ''fresh'' data. The data set is divided into two parts: the training set and the testing set. The function approximator solely uses the training set to fit a function. The function approximator is then asked to forecast the output values for the data in the testing set (which it has never seen before).
The errors it makes are compounded in the same way as before to produce the mean absolute test set error, which is used to evaluate the model. The data set is partitioned into k subsets, and the holdout approach is applied to each one k times. Each time, one of the k subsets is utilized as the test set, while the remaining k − 1 subsets are combined to form the training set. The average error for all k trials is then computed. The advantage of this strategy is that it is less important how the data is separated. Every data point appears exactly once in a test set and k − 1 times in a training set. As k is increased, the variance of the resulting estimate decreases.
K-folds are frequently used in applied machine learning to compare and select a model for a predictive modeling issue. It produces skill estimates with less bias than other approaches since it is straightforward to understand and apply. Additionally, it is less biased than previous approaches because an average estimate of any characteristic is less biased than a single-shot estimate [43,44]. According to [43], the entire process of the K-Fold cross-validation technique employed in this area of the paper is broken down into four phases.
Step 1: If the total number of training instances in S sets is m , divide the entire training set S into K equal subgroups so that each subgroup contains m / k training examples.
Step 2: Select a model from the collection to serve as M i . Next, select k − 1 from the training subset S 1 , S 2 , S 3 , S j − 1 , S j + 1 , … , S k , . The last one left in the order is S j . For the hypothetical function h i j , practice with this k − 1 subset M i . Use the last S j as a test to see if you can encounter issues.
Step 3: Because we release S j (j from 1 to k) empirical errors one at a time. As a result, the mean of all k empirical errors are the empirical error for a M i ,. Consequently, the average produced is the K-Fold cross-validation performance metric in the loop.
Step 4: Pick the ones with the lowest average empirical error rate M i . Next, use all S to complete additional training for the final h i .

3.4. Sensitivity analysis

Performance is significantly impacted by how the learning algorithms' hyper-parameters are configured. The variety of hyper-parameter search and tuning techniques depends on the diversity of learning algorithms. The hyper-parameter values are adjusted for the validation set after training the machine learning models on the training set. The phrase "load model" refers to a mathematical relationship between the active or reactive power of a load bus and the same bus voltage. There are two methods for modeling loads: the first gauges the active and reactive powers' voltage and frequency sensitivity at the substation; the second builds a composite load model for a specific substation based on the mix of load classes at that substation. Static models and dynamic models are the two categories into which load models are separated.
The frequency-dependent model is derived by multiplying the exponential model by a factor that depends on the bus frequency [45]; the factor is responsible for the efficiency of the system data for the creation of the prediction model.
F a c t o r = [ 1 + a f ( f − f 0 ) ] ,
where f = The frequency of the bus voltage; f 0 =Nominal frequency; and a f =The frequency sensitivity parameter.
The active and reactive power responses to step disturbances of the bus voltage are represented in the ERL model; the load that recovers slowly over time is the right candidate for this model [46]. The ERL is modeled as a nonlinear first-order equation of the load response shown in the equation.
T p d x p d t = − x p + P 0 V V 0 N p s − P 0 V V 0 N p t ,
T p d x p d t = − x p + P 0 V V 0 N p s − P 0 V V 0 N p t ,
P d = x p + P 0 V V 0 N p t ,
T q d x q d t = − x q + Q 0 V V 0 N q s − Q 0 V V 0 N q t ,
Q d = x q + Q 0 V V 0 N q t ,
where x p and x q are state variables related to active and reactive power dynamics, T p and T q are time constants of the exponential recovery response, N p s and N q s are exponents related to the steady-state load response, N p t and N q t are exponents related to the transient load response. The equations above are responsible for computing the power load factor of the system data for the creation of the prediction model.
The measurement-based methodology adapted from [47] employs a step-by-step process. Getting measurement data is the first step, followed by choosing a load model structure, estimating parameters, and validating the load model. Under a specific set of circumstances and disturbances, the measurement is performed. By minimizing the discrepancy between the load model response and the field observations, the model parameters are finally computed.
Equation (10) explains how to express the measurement-based load model as a curve-fitting issue.
m i n 1 n ∑ i = 1 n P i m − P i e 2 + Q i m − Q i e 2 ,
P i e and Q i e are the modeled active and reactive power, P i m and Q i m are the measured active and reactive power, respectively. Least squares, Genetic techniques (GA), Support Vector Machines (SVM), Kalman Filter (KF), Levenberg-Marquardt method, and Simulated Annealing are some of the reliable techniques that can be used to determine the parameters.

3.5. Evaluation Criteria

The coefficient of determination ( R 2 ) is a standard metric in machine learning for evaluating the linear relationship between actual and predicted values. Furthermore, mean absolute error (MAE) and mean squared error (MSE) are popular model performance metrics. MAE and MSE calculated the mean of the absolute errors and the mean of the squared errors between the actual values and the model-predicted values on the data set. The Root Mean Squared Logarithmic Error (RMSLE) calculates the difference between predicted and actual results. These are their definitions:
M A E = ∑ i = 1 n y ^ i − y i n ,
M S E = ∑ i = 1 n y ^ i − y i 2 n ,
R 2 = 1 − ∑ i = 1 n y ^ i − y i 2 ∑ i = 1 n y i − y − 2 ,
R M S E = 1 n ∑ i − 1 n y i − y ^ 2 ,
R M S L E = 1 n ∑ i = 1 n log ⁡ y ^ i + 1 − log ⁡ y i + 1 2 ,
n is the total number of observations, y i represents the average value, y i the true value, and y ^ represents the predicted.

4. Results

The configurations of the hyper-parameters of the learning algorithms have a significant effect on the performance. The diversity of learning algorithms determines the variety of hyperparameter search and tuning methods. After training the machine learning models on the training set, the hyper-parameter settings are tweaked for the validation set. As used in power systems terminology, the load model describes a mathematical relationship between a load bus's active or reactive power and the same bus voltage. Two approaches exist for load modeling: the first measures the voltage and frequency sensitivity of the active and reactive powers at the substation; the second is to construct a composite load model for a given substation based on the mix of load classes substation. Load models are divided into two types: static models and dynamic models. Data pre-processing is a crucial first step in every machine-learning technique. In this paper, each regression model's leading training and prediction measure is distance. First, each data characteristic is normalized such that its contribution to the distance measure is proportional. Next, the calculation of a fresh weight is done to guarantee that the average difference between all locations remains consistent between weight sets. The data is then segregated into training, validation, and testing sets.
This section may be divided into subheadings. It should provide a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn.

4.1. Visualising Training Sets Results

The training and testing results for the residuals LGBM model show that both the train and test accuracy values are better than for the LGBM model, as shown in Table 1 is used to calculate the load profiles for Tshwane's energy grid's electric power distribution system. In applied machine learning, K-folds are often used to compare and choose a predictive modeling issue.

4.2. Evaluation cross-validation model Model Results

Table 2 and Table 3, respectively, illustrate the performance of the K-Fold cross-validation model for the SVM and Lightgbm models. The Mean Absolute Error (MAE), Mean Square Error (MSE), Root Mean Square Error (RMSE), R-Square (R2), Root Mean Squared Logarithmic Error (RMSLE), and Mean Absolute Percentage Error (MAPE) are all displayed in the tables. Due to its lower values of the MAE (3.0698), MSE (15.2757), RMSE (3.9020), RMSLE (0.1433), and MAPE (0.0049), respectively, the estimation-based lightGBM is shown to be more accurate than the SVM in this experiment.

4.3. Prediction Error Output and Residuals Model

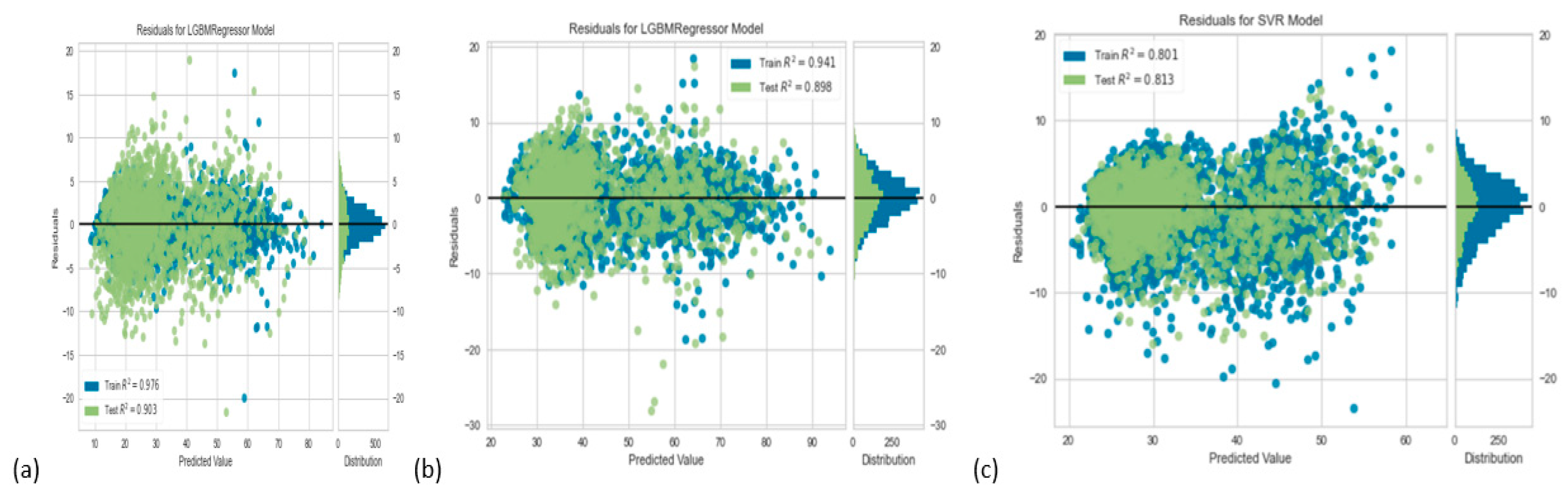
Figure 4 shows the estimated prediction error for the lightGBM model. Again, the Figures indicate that the lightGBM model had the most accurate prediction compared to their R-Square values of 89.8%, 90.3%, and 88.5%, respectively for Irms_A_avg, Irms_B_avg and Irms_C_avg.
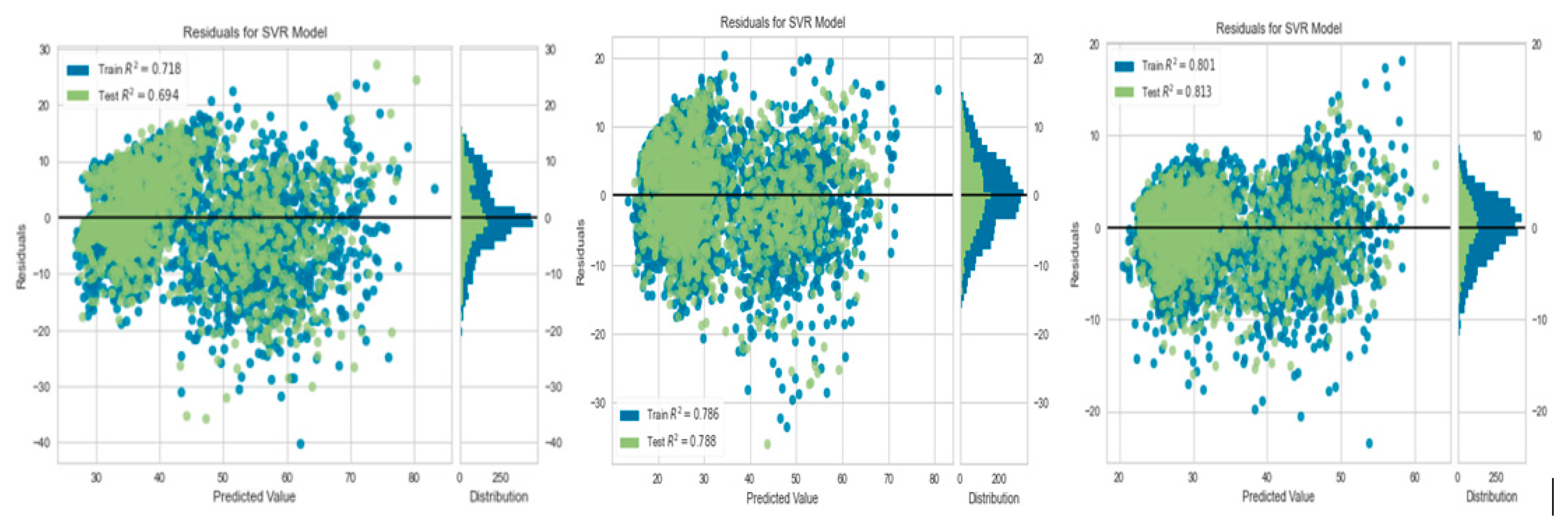
Figure 5 depicts the calculated residual model for the LGBM, according to the developed machine learning model, the training and testing residuals for LGBM models.
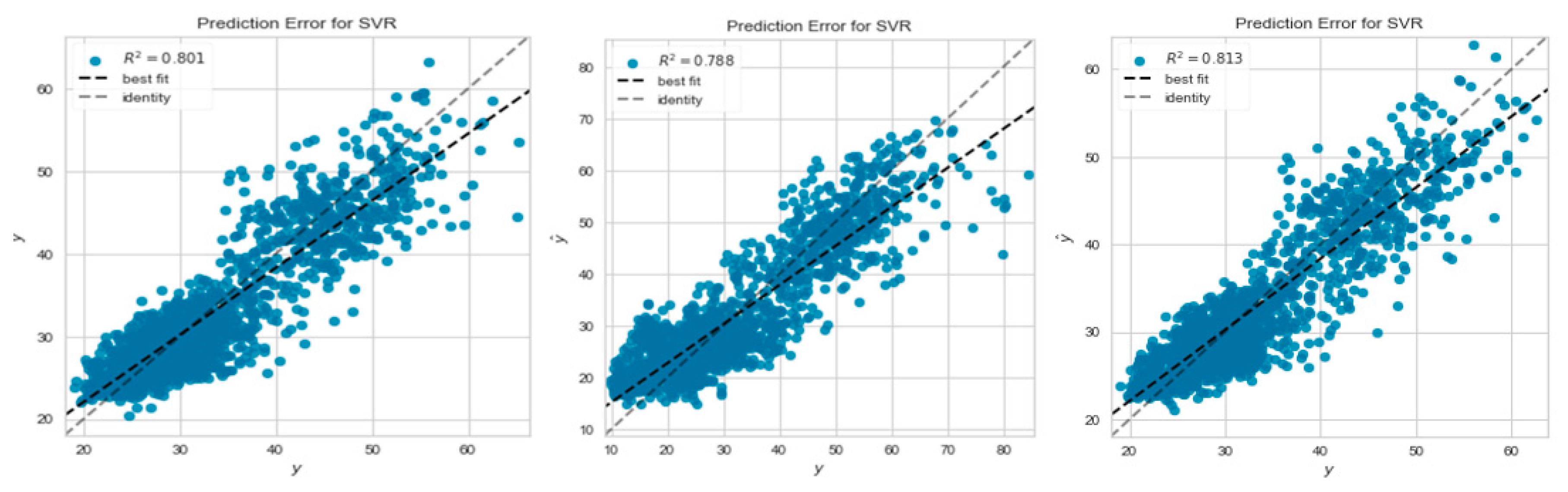
Figure 6 shows the estimated prediction error for the SVM models for the Irms_A_avg Output, Irms_B_avg Output, and Irms_C_avg Output. Figure 7 indicate that the SVM model predicted 80.1%, 78.8%, and 81.3%, respectively, owing to their R-Square values.

4.4. Prediction Error Output Validation

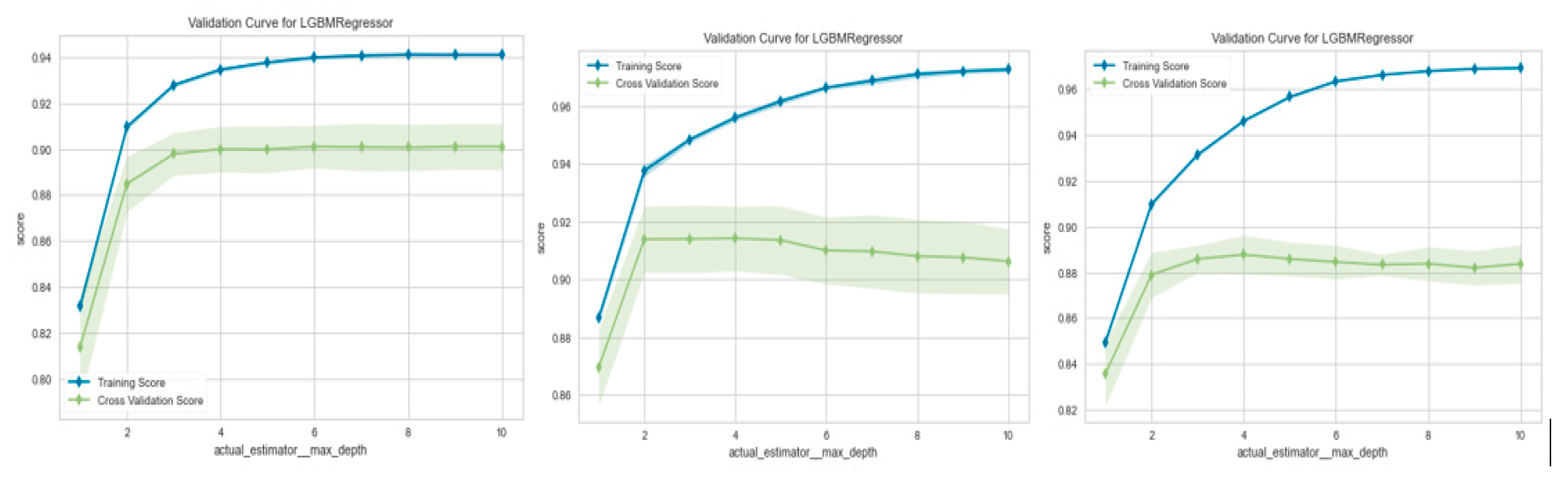
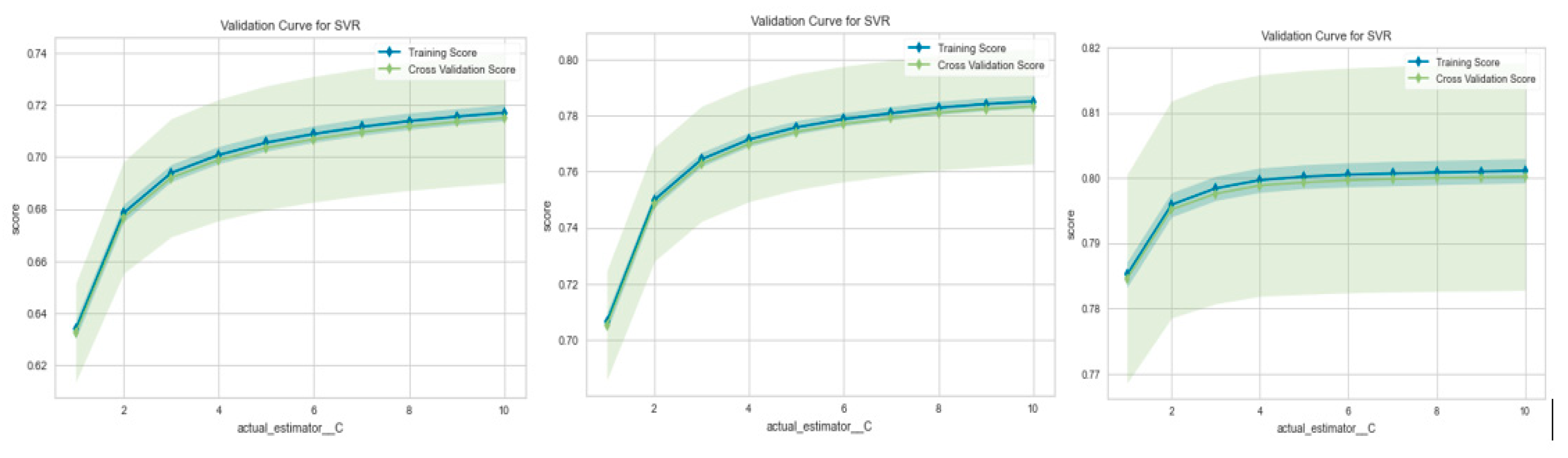
The relationship between a model parameter and the model score is often established using a validation curve. Two curves make up a validation curve: one for the cross-validation score and one for the training set score. This paper uses 10-fold cross-validation as its validation curve function. For Irms_A_avg Output, Irms_B_avg Output, and Irms_C_avg Output, respectively, Figure 8 displays the SVM validation curve. The curve in Figure 9 suggests that K = 10 would be the ideal value for K. The training and cross-validation results improve with increasing neighbors (K).
The training dataset is then split into K subsets of 604 for cross-validation. This makes it feasible to produce identical K models without delay. A validation test is presented to check the effectiveness of the proposed technique. The estimation-based lightGBM is more precise than the SVM since its MAE, MSE, RMSE, RMSLE, and MAPE values are more diminutive than SVM. However, as the number of neighbors (K) increases, the accuracy of the training and cross-validation scores decreases. In other words, the ideal value of K for the Irms A avg forecast would be 10.

5. Conclusions

In this paper, machine learning models are used to estimate the load profiles for the electric power distribution system in Tshwane municipality. The authors employ MLP, RBF, and linear SVM kernels. It determines the load profiles for the electricity distribution network in Tshwane. K-folds are frequently used in applied machine learning to compare and select a predictive modeling problem. Reading the root mean square voltage and current datasets for three-phase power distribution systems correspondingly is the first step in the training approach. For cross-validation, the training dataset is then split into K subsets of 604 each, yielding K identical models right away. Each model is then tested on the remaining partitions after being trained on K-1 partitions. The method parameter K denotes the number of groups that are created from a given data sample. The final evaluation performance is averaged K times to get the method's total performance. The results of this small dataset are then enhanced by cross-validation. It is mentioned how well the K-Fold cross-validation model performs for the SVM and LightGBM models. The relationship between a model parameter and the model score is often established using a validation curve. Two curves make up a validation curve: one for the cross-validation score and one for the training set score. Future work will look at recursive feature elimination with cross-validation (RFECV) to better understand what features will be included in the machine-learning model. Even though the data points used in this research are over 6040 by 20, more data is required to improve the accuracy of the prediction model.

Author Contributions

Conceptualization, A.M. and O.T.A.; methodology, A.M. and O.T.A.; software, A.M..; validation, A.M., O.T.A. O.M.P. and K.M.; formal analysis, A.M. and O.T.A.; investigation, O.T.A.; resources, A.M. and O.T.A.; data, A.M.; editing, K.M.; visualization, O.T.A.; supervision, O.T.A.O.M.P and K.M.; project administration, A.M.; funding acquisition, K.M. and O.M.P All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Research Foundation (NRF), grant number 123575, and the APC was funded by the Research Chair in Future Transport Manufacturing Technologies.

Acknowledgments

The researchers acknowledge the support and assistance of the Industrial Engineering Department of Tshwane University of Technology, Gibela Rail, and the National Research Foundation (123575) of South Africa for their financial and material assistance in executing this research project. The opinions that are presented in this paper are those of the authors and not the funders.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Ren, Z.; Hu, W.; Ma, K.; Zhang, Y.; Liu, W.; Xiong, J. Dynamic security region algorithm considering sample imbalance and misclassification cost. 2021. 1-6. [CrossRef]
  2. Juan, R.; Zhongping, Y.; Guiliang, G.; Guokang, Y.; Jin, Y. ; A CNN-LSTM-LightGBM based short-term wind power prediction method based on attention mechanism, Energy Reports, Volume 8, Supplement 5, 2022, Pages 437-443. [CrossRef]
  3. Lijing, W.; Cong, L. Short-term price forecasting based on PSO train BP neural network. Electric Power Science and Engineering, 2008. 24(10): p.21.
  4. Wang, Q.; Jiang, F. Integrating linear and nonlinear forecasting techniques based on grey theory and artificial intelligence to forecast shale gas monthly production in Pennsylvania and Texas of the United States. Energy, 2019.178: p.781-803. [CrossRef]
  5. Sengar, S.; Liu, X. An efficient load forecasting in predictive control strategy using hybrid neural network. Journal of Circuits, Systems and Computers, 2020. 29(01):2050010. [CrossRef]
  6. Bae, D.J; Kwon, B.S. .; Moon, C.H.; Woo, S.H.; Song, K.B. Short-term load forecasting algorithm on weekdays considering the amount of behind-the-meter generation. Journal of the Korean Institute of Illuminating and Electrical Installation Engineers, 2020.34(11): p.37-43. [CrossRef]
  7. Zhang, K.; Guo, W.; Feng, J.; Liu, M. Load Forecasting Method Based on Improved Deep Learning in Cloud Computing Environment. Scientific Programming, 2021. [CrossRef]
  8. Mbuli, N.; Mathonsi, M.; Seitshiro, M.; Pretorius, J.C. Decomposition forecasting methods: a review of applications in power systems, Energy Rep, 6 (9) (2020), pp. 298-306. [CrossRef]
  9. Wang, Y.; Chen, J.; Chen, X.; Zeng, X.; Kong, Y.; Sun, S. Short-Term Load Forecasting for Industrial Customers Based on TCN-LightGBM. IEEE Trans Power Syst 2020:1–1. [CrossRef]
  10. Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W. LightGBM: A Highly Efficient Gradient Boosting Decision Tree Adv. Neural. Inf. Process Syst., 30 (2017), pp. 3146-3154.
  11. Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System, 2016.
  12. Xue, P.; Jiang, Y.; Zhou, Z.; Chen, X.; Fang, X.; Liu, J. Multi-step ahead forecasting of heat load in district heating systems using machine learning algorithms Energy, 188 (2019), p. 11 6085. [CrossRef]
  13. Zheng, H.; Yuan, J.; Chen, L. Short-Term Load Forecasting Using EMD-LSTM Neural Networks with a Xgboost Algorithm for Feature Importance Evaluation Energies, 10 (2017), p. 1168. [Google Scholar] [CrossRef]
  14. Nousdilis, A.I.; Christoforidis, G.C.; Papagiannis, G.K. Active power management in low voltage networks with high photovoltaics penetration based on prosumers’ self-consumption. Applied energy, 2018. 229: p. 614-624. [CrossRef]
  15. Dent, I.; Craig, T.; Aickelin, U.; Rodden, T. Variability of Behaviour in Electricity Load Profile Clustering; Who Does Things at the Same Time Each Day?. In: Perner, P. (eds) Advances in Data Mining. Applications and Theoretical Aspects. ICDM 2014. Lecture Notes in Computer Science (), 2014. 8557. Springer, Cham. [CrossRef]
  16. Chicco, G.; Mazza, A. Load profiling revisited: prosumer profiling for local energy markets. In: Local Electricity Markets. Elsevier: 2021. p.215-242. [CrossRef]
  17. Mutanen, A.; Ruska, M.; Repo, S. Jarventausta, P. Customer classification and load profiling method for distribution systems. IEEE Transactions on Power Delivery, 2011. 26(3): p.1755-1763. [CrossRef]
  18. Bucher, C.; Andersson, G. Generation of domestic load profiles-an adaptive top-down approach. Proceedings of PMAPS. 2012. p.10-14.
  19. Pillai, G.G.; Putrus, G.A. Pearsall, N.M. Generation of synthetic benchmark electrical load profiles using publicly available load and weather data. International Journal of Electrical Power & Energy Systems, 2014. 61: p.1-10. [CrossRef]
  20. Toffanin, D. Generation of customer load profiles based on smart-metering time series, building-level data and aggregated measurements. 2016.
  21. Munshi, J. Illusory Statistical Power in Time Series Analysis. SSRN. 2016. [CrossRef]
  22. Sarhani, M.; El afia, A. Electric Load Forecasting Using Hybrid Machine Learning Approach Incorporating Feature Selection. BDCA. 2015.p.1-7.
  23. Taylor, J.W.; Mcsharry, P.E. Short-term load forecasting methods: An evaluation based on European data. IEEE Transactions on Power Systems, 2007. 22(4): p.2213-2219. [CrossRef]
  24. Lijing, W.; Cong, L. Short-term price forecasting based on PSO train BP neural network. Electric Power Science and Engineering, 2008. 24(10): p.21.
  25. Wang, Q.; Jiang, F. Integrating linear and nonlinear forecasting techniques based on grey theory and artificial intelligence to forecast shale gas monthly production in Pennsylvania and Texas of the United States. Energy, 2019.178: p.781-803. [CrossRef]
  26. Sengar, S.; Liu, X. An efficient load forecasting in predictive control strategy using hybrid neural network. Journal of Circuits, Systems and Computers, 2020. 29(01):2050010. [CrossRef]
  27. Evangelopoulos, V.A.; Georgilakis, P.S. Probabilistic Spatial Load Forecasting for Assessing the Impact of Electric Load Growth in Power Distribution Networks. Electric Power Systems Research 2022, 207, 107847. [Google Scholar] [CrossRef]
  28. Zhang, K.; Guo, W.; Feng, J.; Liu, M. Load Forecasting Method Based on Improved Deep Learning in Cloud Computing Environment. Scientific Programming, 2021. [CrossRef]
  29. Apostolos, G.N.; Skiadas, C.H. Forecasting the electricity consumption by applying stochastic modelling techniques: the case of Greece. In: Advances in Stochastic Modelling and Data Analysis. Springer: 1995. P.85-100.
  30. Ashyralyev, A,; Urun, M.; Parmaksizoglu, I. Mathematical modeling of the energy consumption problem. BULLETIN OF THE KARAGANDA UNIVERSITY-MATHEMATICS, 2022.105(1). [CrossRef]
  31. Bahn,.; Haurie, A.; Zachary, D. Mathematical modeling and simulation methods in energy systems. Les Cahiers du GERAD ISSN, 2004.711:2440.
  32. Pavlicko, M.; Vojteková, M.; Blažeková, O. Forecasting of Electrical Energy Consumption in Slovakia. Mathematics, 2022. 10(4):577. [CrossRef]
  33. Tilovska, S.; Tentov, A. Power consumption analyzes with mathematical models into the overall electrical network. International Journal of Electrical Power & Energy Systems, 2013.44(1): p.798-809. [CrossRef]
  34. Camurdan, Z. Ganiz, M.C. Machine learning based electricity demand forecasting. 2017 International Conference on Computer Science and Engineering (UBMK). IEEE: 2017. 412-417.
  35. Huang, J.; Srinivasan, D.; Zhang, D. Electricity Demand Forecasting Using HWT Model with Fourfold Seasonality. 2017 International Conference on Control, Artificial Intelligence, Robotics & Optimization (ICCAIRO). 2017. IEEE:254-258. [CrossRef]
  36. El-habil, A.M. An application on multinomial logistic regression model. Pakistan journal of statistics and operation research: 2012. p.271-291.
  37. Hou, J.; Liu, X.; Yu, J.; Lin, Z.; Yang, L.; Zhang, Z. Optimal Design of Electricity Plans for Active Demand Response of Power Demand Side. IEEE 3rd Conference on Energy Internet and Energy System Integration (EI2). IEEE: 2019. p. 2059-2064. [CrossRef]
  38. Paparrizos, J.; Gravano, L. k-Shape: efficient and accurate clustering of time series ACM SIGMOD Rec., 45 (1) (2016), pp. 69-76. [CrossRef]
  39. ajabi, A.; Eskandari, M.; Ghadi, M.J.; Li, L.; Zhang, J.; Siano P. A comparative study of clustering techniques for electrical load pattern segmentation Renew. Sustain. Energy Rev., 120 (2020), p. 109628. [CrossRef]
  40. Quintana, M.; Arjunan, P.; Miller, C. Islands of misfit buildings: Detecting uncharacteristic electricity use behavior using load shape clustering Build. Simul., 14 (1) (2021), pp. [CrossRef]
  41. Xue, P.; Jiang, Y.; Zhou, Z.; Chen, X.; Fang, X.; Liu, J. Multi-step ahead forecasting of heat load in district heating systems using machine learning algorithms Energy, 188 (2019), p. 116085,. [CrossRef]
  42. Ali, M. PyCaret: An open source, low-code machine learning library in Python, pyCaret version 1.0. 0. April 2020. PyCaret: An open source, low-code machine learning library in Python, pyCaret version 1.0. 0.
  43. Xiong, Z.; Cui, Y.; Liu, Z.; Zhao, Y.; Hu, M.; Hu, J. Evaluating explorative prediction power of machine learning algorithms for materials discovery using k-fold forward cross-validation. Computational Materials Science, 2020. 171:109203.
  44. Brownlee, J. A Gentle Introduction to k-fold Cross-Validation [available online: accessed August 3, 2020]. 2018, Available from: https://machinelearningmastery.com/k-fold-cross-validation/]. 3 August.
  45. Overbye, T. J. A power flow measure for unsolvable cases.” IEEE Transactions on Power Systems 1994.9: p.1359-1365. [CrossRef]
  46. Rouhani, A.; Abur, A. Real-time dynamic parameter estimation for an exponential dynamic load model. IEEE Transactions on Smart Grid, 2015.7(3): p.1530-1536. [CrossRef]
  47. Arif, A.; Wang, Z.; Wang, J.; Mather, B.; Bashualdo, H.; Zhao, D. Load modeling—A review. IEEE Transactions on Smart Grid, 2017. 9(6):5986-5999.
Preprints 81190 g001
Figure 1. Integration of the medium voltage network into the system using a typical distribution network configuration for COT.
Figure 1. Integration of the medium voltage network into the system using a typical distribution network configuration for COT.
Preprints 81190 g001
Preprints 81190 g002
Figure 2. Flowchart Showing the Light Gradient Boosting Machine Learning Establishment Phases.
Figure 2. Flowchart Showing the Light Gradient Boosting Machine Learning Establishment Phases.
Preprints 81190 g002
Preprints 81190 g003
Figure 3. Flowchart Illustrating Essential SVM Model Establishment Phases.
Figure 3. Flowchart Illustrating Essential SVM Model Establishment Phases.
Preprints 81190 g003
Preprints 81190 g004
Figure 4. Prediction Error for the Light Gradient Boosting Machine Model (a) Irms_A_avg Output Prediction Error; (b) Irms_B_avg Output Prediction Error; (c) Irms_C_avg Output Prediction Error.
Figure 4. Prediction Error for the Light Gradient Boosting Machine Model (a) Irms_A_avg Output Prediction Error; (b) Irms_B_avg Output Prediction Error; (c) Irms_C_avg Output Prediction Error.
Preprints 81190 g004
Preprints 81190 g005
Figure 5. Residuals for Light Gradient Boosting Machine Model (a) Irms_A_avg Output Prediction; (b) Irms_B_avg Output Prediction; (c) Irms_C_avg Output Prediction.
Figure 5. Residuals for Light Gradient Boosting Machine Model (a) Irms_A_avg Output Prediction; (b) Irms_B_avg Output Prediction; (c) Irms_C_avg Output Prediction.
Preprints 81190 g005
Preprints 81190 g006
Figure 6. Prediction Error for the SVM Model (a) Irms_A_avg Output Prediction Error; (b) Irms_B_avg Output Prediction Error; (c) Irms_C_avg Output Prediction Error.
Figure 6. Prediction Error for the SVM Model (a) Irms_A_avg Output Prediction Error; (b) Irms_B_avg Output Prediction Error; (c) Irms_C_avg Output Prediction Error.
Preprints 81190 g006
Preprints 81190 g007
Figure 7. Residuals for SVM Model (a) Irms_A_avg Output Prediction; (b) Irms_B_avg Output Prediction; (c) Irms_C_avg Output Prediction.
Figure 7. Residuals for SVM Model (a) Irms_A_avg Output Prediction; (b) Irms_B_avg Output Prediction; (c) Irms_C_avg Output Prediction.
Preprints 81190 g007
Preprints 81190 g008
Figure 8. Prediction Error for the Validation Curve for SVM Model (a) Irms_A_avg Output Prediction Validation; (b) Irms_B_avg Output Prediction Validation; (c) Irms_C_avg Output Prediction Validation.
Figure 8. Prediction Error for the Validation Curve for SVM Model (a) Irms_A_avg Output Prediction Validation; (b) Irms_B_avg Output Prediction Validation; (c) Irms_C_avg Output Prediction Validation.
Preprints 81190 g008
Preprints 81190 g009
Figure 9. Residuals for Validation Curve for SVM Model (a) Irms_A_avg Output Prediction Validation; (b) Irms_B_avg Output Prediction Validation; (c) Irms_C_avg Output Prediction Validation.
Figure 9. Residuals for Validation Curve for SVM Model (a) Irms_A_avg Output Prediction Validation; (b) Irms_B_avg Output Prediction Validation; (c) Irms_C_avg Output Prediction Validation.
Preprints 81190 g009
Table 1. Summary of Train and Test Results of the LGBM model.
Table 1. Summary of Train and Test Results of the LGBM model.
Irms_A_avg Residuals (R2) Irms_B_avg Residuals (R2) Irms_C_avg Residuals (R2)
Train 0.941 0.976 0.801
Test 0.898 0.903 0.813
Table 2. LightGBM Evaluation Model.
Table 2. LightGBM Evaluation Model.
Fold MAE MSE RMSE R2 RMLSE MAPE
0 3.1850 16.3168 4.0394 0.9212 0.1445 0.1175
1 3.1425 16.1701 4.0212 0.9159 0.1486 0.1195
2 2.8842 12.8020 3.5780 0.9258 0.1379 0.1141
3 2.8864 13.1910 3.6319 0.9180 0.1381 0.1122
4 3.1488 16.0548 4.0068 0.9143 0.1499 0.1207
5 3.2420 18.3126 4.2793 0.9150 0.1444 0.1144
6 3.1601 15.7749 3.9718 0.9183 0.1515 0.1246
7 3.1772 15.9247 3.9906 0.9096 0.1448 0.1199
8 3.0629 15.6130 3.9513 0.9203 0.1429 0.1145
9 2.8092 12.5966 3.5492 0.9320 0.1307 0.1063
Mean 3.0698 15.2757 3.9020 0.9190 0.1433 0.1164
Std 0.1450 1.7361 0.2245 0.0060 0.0060 0.0049
Table 3. SVM Evaluation Model.
Table 3. SVM Evaluation Model.
Fold MAE MSE RMSE R2 RMLSE MAPE
0 5.1526 45.2995 6.7305 0.7811 0.2217 0.1849
1 5.2075 44.9283 6.7029 0.7665 0.2373 0.2034
2 4.6869 36.2160 6.0180 0.7900 0.2155 0.1833
3 4.6784 34.8448 5.9029 0.7835 0.2136 0.1820
4 4.7701 37.9491 6.1603 0.7975 0.2225 0.1860
5 4.9934 42.8764 6.5480 0.8010 0.2125 0.1799
6 4.9565 40.8569 6.3919 0.7885 0.2295 0.1996
7 5.0272 41.4177 6.4357 0.7648 0.2248 0.1915
8 5.1403 46.0304 6.7846 0.7652 0.2253 0.1912
9 4.6993 36.8997 6.0745 0.8009 0.2080 0.1750
Mean 4.9312 40.7319 6.3749 0.7839 0.2211 0.1877
Std 0.1965 3.8615 0.3037 0.0136 0.0084 0.0084
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated