Preprint
Article
A Global Forecasting Approach to Large-Scale Crop Production Prediction with Time Series Transformers
Altmetrics
Downloads
313
Views
64
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
01 August 2023
Posted:
03 August 2023
You are already at the latest version
Alerts
Abstract
Accurate prediction of crop production is essential in effectively managing agricultural countries' food security and economic resilience. This study evaluates the performance of statistical and machine learning-based methods for large-scale crop production forecasting. We predict the quarterly production of 325 crops (including fruits, vegetables, cereals, non-food, and industrial crops) across 83 provinces in the Philippines. Using a comprehensive dataset of 10,949 time series over 13 years, we demonstrate that a global forecasting approach using a state-of-the-art deep learning architecture, the transformer, significantly outperforms traditional local forecasting approaches built on statistical and baseline methods. By leveraging cross-series information, our proposed way is scalable and works well even with time series that are short, sparse, intermittent, or exhibit structural breaks/regime shifts. The results of this study further advance the field of applied forecasting in agricultural production and provide a practical and effective decision-support tool for policymakers that oversee the farm sector on a national scale.
Keywords:
Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning
1. Introduction
Agriculture is a vital component of the Philippine economy, contributing about 9.1% of the gross domestic product (GDP) and employing about 24% of the labor force [1,2]. However, the sector, and in particular crop production, has been experiencing a decline in output due to the impacts of the COVID-19 pandemic and several typhoons that hit the country in 2020 and 2021 [3]. These challenges pose serious threats to the food security and economic resilience of the Philippine agriculture sector. To better optimize planning and improve decision making, more robust forecasting methodologies that leverage the latest developments in the field of artificial intelligence (AI) and machine learning (ML) should be adopted and integrated into the frameworks of policymakers and stakeholders in the sector.
A review of the literature reveals that much work has been done in applying traditional statistical and process-based models to the problem of forecasting crop production. Liu et al. examine the effects of climate change on crop failure, yield, and soil organic carbon on winter wheat and maize using the SPACSYS model in China [4]. Nazir et al. apply a phenology-based algorithm with linear regression in order to improve rice yield prediction using satellite data [5]. Florence et al. apply linear regression and gaussian process regression (GPR) to predict winter wheat yield using crop canopy properties (e.g. leaf area index or LAI, leaf chlorophyll content) [6]. These works demonstrate how careful analysis of exogenous variables and feature engineering can improve model performance in yield prediction problems and provide insight into their positive or negative impacts on crop yield.
With the emergence of larger datasets however, the use of machine learning has become the more prevalent approach to modeling prediction problems. Research on ML-based techniques has increased across a wide variety of critical economic fields such as energy demand prediction [7,8], water resource management [9,10,11], and multinational trade forecasting [12,13]. In the domain of agriculture, ML has also been explored in crop yield forecasting applications. Nosratabadi et al. compare the performance between an adaptive network-based fuzzy inference system (ANFIS) and multilayer perceptron (MLP) in predicting livestock and agricultural production in Iran [14]. Kamath et al. use a combination of data mining techniques and a random forest (RF) model to predict crop production in India [15]. Das et al. apply a hybrid ML method using multivariate adaptive regression spline (MARS) coupled with support vector regression (SVR) and artificial neural networks (ANN) to predict lentil grain yield in Kanpur, India [16].
Several works also specifically examine the use of ML models with vegetation and an assortment of meteorological data (e.g., temperature, rainfall). Sadenova et al. propose an ensemble ML algorithm combining traditional ML regressors (e.g., linear regression, SVR, RF) and a neural network (NN) to predict the yields of cereals, legumes, oilseeds, and forage crops in Kazakhstan using normalized difference vegetation index (NDVI) and meteorological data [17]. Sun et al. compare RF models and multiple linear regression (MLR) to estimate winter wheat yield in China using meteorological and geographic information [18]. Onwuchekwa-Henry et al. use a generalized additive model (GAM) to predict rice yield in Cambodia using NDVI and meteorological data [19]. Research in the field clearly points to the strengths of ML models in effectively incorporating exogenous variables from a wide variety of sources.
Deep learning specific approaches have also been explored in the literature. Tende et al. use a long short-term memory (LSTM) neural network to predict district-level end-of-season maize yields in Tanzania using NDVI and meteorological data [20]. Wang et al. apply LSTM neural networks using LAI as input data to improve winter wheat yield prediction in Henan, China [21]. Aside from recurrent neural networks (RNN), convolutional neural networks (CNN) have also been investigated. Wolanin et al. use explainable deep learning and convolutional neural networks (CNNs) to predict wheat yield in the Indian Wheat Belt using vegetation and meteorological data [22]. Bharadiya et al. compare a variety of deep learning architectures (e.g., CNN, LSTM, etc.) and traditional ML models (e.g., Gradient Boosted Trees, SVR, k-nearest neighbors, etc.) in forecasting crop yield via remote sensing [23]. Gavahi et al. propose DeepYield, a ConvLSTM-based deep learning architecture, to forecast the yield of soybean [24], the performance of which was compared against decision trees (DT), CNN + Gaussian process (GP), and a simpler CNN-LSTM. In general, neural networks have been identified as critical in building effective decision-making support tools in agriculture by helping stakeholders in forecasting production, classifying quality of harvested crops, and optimizing storage and transport processes [25].
Typically, studies in the literature (including the works mentioned above) focus on forecasting the production of one or even a few crops of interest. In practice, stakeholders in the agriculture sector may oversee monitoring the yields of many crops across several regions (e.g., national government agencies). Related to this, the work of Paudel et al. applies machine learning to predict the regional-level yield of 5 crops in 3 countries (the Netherlands, Germany, and France) [26]. This line of investigation was continued in [27], where the authors expand the analysis to 35 case studies, including 9 European countries that are major producers of 6 crops: soft wheat, spring barley, sunflower, grain maize, sugar beet, and potatoes. In both studies, they examine the performance of ridge regression, k-nearest neighbors (KNN) regression, SVR, and Gradient Boosted Trees (GBT).
In this work, we further push this line of research by substantially increasing the number of time series of interest. We propose a scalable method for predicting the quarterly production volume of 325 crops across 83 provinces in the Philippines. Using a total of 10,949-time series spanning 13 years, we show that a global forecasting approach using a state-of-the-art deep learning architecture, the transformer, significantly outperforms the traditional local forecasting approaches built on statistical and baseline techniques. We summarize the contributions of our work below:
- To the best of our knowledge, this is the first work that focuses on collectively forecasting large-scale disaggregated crop production comprising thousands of time series from diverse crops, including fruits, vegetables, cereals, root and tuber crops, non-food crops, and industrial crops.
- We demonstrate that a time series transformer trained via a global approach can achieve superior forecast accuracy compared to traditional local forecasting approaches. Empirical results show a significant 84.93%, 80.69%, and 79.54% improvement in normalized root mean squared error (NRMSE), normalized deviation (ND), and modified symmetric mean absolute percentage error (msMAPE), respectively, over the next best methods.
- Since only a single deep global model is optimized and trained, our proposed method scales more efficiently concerning the number of time series being predicted and the number of covariates and exogenous features being included.
- By leveraging cross-series information and learning patterns from a large pool of time series, our proposed method performs well even on time series that exhibit multiplicative seasonality, intermittent behavior, sparsity, or structural breaks/regime shifts.
2. Materials and Methods
2.1. Study Area
The Philippines is an archipelagic country in Southeast Asia, composed of more than 7,000 islands. It has a rich and diverse agricultural sector, producing a wide variety of crops for domestic consumption and export. The country has a total land area of about 300,000 square kilometers, of which about 42.5% is devoted to agriculture [28]. The country’s tropical and maritime climate is characterized by abundant rainfall, coupled with high temperatures and high humidity. The country has three major seasons: the wet season from June to November, the dry season from December to May, and the cool dry season from December to February [29]. The topography is also diverse, ranging from mountainous regions, plateaus, lowlands, coastal areas, and islands. These factors create a wide array of ecological zones that influence the types of crops that can be grown in each region.
2.2. Data Description
The data used in this study is taken from OpenSTAT and can be accessed through the following link: https://openstat.psa.gov.ph/. OpenSTAT is an open data platform under the Philippine Statistics Authority (PSA), the primary statistical arm of the Philippine government. We use a compilation of data from three surveys: the Palay Production Survey (PPS), Corn Production Survey (CPS), and Crops Production Survey (CrPS). These surveys report on quarterly production statistics for palay (the local term for rice prior to husking), corn, and other crops at the national and sub-national levels (i.e., regional, and provincial).
A total of 325 crops spread across 83 provinces are examined. The crops are broadly classified into four commodity groupings: Cereals, Fruit Crops, Vegetables and Root Crops, and Non-Food and Industrial Crops. Figure 1 illustrates the time series of some of the top produced crops in the Philippines. In this figure, palay and corn represent the top produced cereals in the country. Banana, pineapple, and mango represent some of the top produced fruit crops. Kamote (sweet potato) and eggplant represent some of the top produced vegetables and root crops. Sugarcane and coconut represent some of the top produced non-food and industrial crops. The full lists of crops, provinces, and regions are provided under Table A1 and Table A2 in Appendix A.
At the most disaggregated level (i.e., crops crossed with provinces), our dataset consists of 10,949 time series covering a 13-year period from 2010 to 2022. This is less than full 325 x 83 since each province only grows a certain subset of crops. Data on the volume of production (measured in metric tons) is collected quarterly, with each time series having 52 observations. For illustration, a sample of nine time series is shown in Figure 2. We note that the dataset consists of a large group of time series that capture a wide variety of dynamics and scales. While most time series show strong quarterly seasonality, some series also exhibit multiplicative seasonality, intermittent behavior, sparsity, or structural breaks/regime shifts. The combination of these dynamics makes using traditional approaches to time series modeling a challenging process, as each time series would have to be modeled individually or some level of aggregation would need to be performed, both of which are not ideal. In the former, it requires careful and meticulous feature engineering and model selection at a very large scale, while in the latter, information is sacrificed for feasibility. We discuss the main approach to solving this in Section 2.3.2.
Each time series is also accompanied by a set of covariates (summarized in Table 1) of which there are two types: static covariates and time features. Static covariates are integer-encoded categorical features consisting of identifiers for a time series’ crop type, province, and region. Time features are a type of dynamic covariate that explicitly captures temporal information (e.g., calendar information such as month of the year, day of the week, hour of the day). In this work, we include a Quarter variable to represent calendar seasonality and a monotonically increasing Age variable that measures the distance to the first observation in a time series.
2.3. Forecasting Methods
In this section we introduce the statistical and machine learning models used in this study and describe how their hyperparameters are tuned and selected. All methods described below are implemented in Python using the NumPy, Pandas, and Matplotlib libraries, as well as the PyTorch [30], Hugging Face Transformers [31], GluonTS [32], and StatsForecast [33] packages for the time series and deep learning methods. The code used in this study will be made publicly available upon publication.
2.3.1. Baseline and Statistical Methods
For our baseline and statistical techniques, we look at two approaches: a seasonal naïve forecast and ARIMA.
The seasonal naïve method constructs a forecast by repeating the observed values from the same “season” of the previous year [34],
where is the forecasted value -steps into the future, is the seasonal period, and is the integer part of . In this study, we set since the data consists of quarterly time series. Simply put, a seasonal naïve forecast for the test period is generated by repeating the observations in 2021 (i.e., we assume that next year is the same as the previous year). This type of naïve forecast is a common benchmark used in forecasting competitions [35,36], especially when time series exhibit strong seasonality.
For the statistical method, we use the autoregressive integrated moving average (ARIMA) model, a class of time series method used to model non-stationary stochastic processes. The AR term specifies that the current value of a time series is linearly dependent on its previous values, the I term defines the number of one-step differencing needed to eliminate the non-stationary behavior of the series, and the MA term specifies that the current value of the series is linearly dependent on previous values of the error term,
where is the I-differenced series, are the autoregressive parameters up to lag , are the moving average parameters up to lag , and is the error term assumed to be normally distributed. In this study, we use the AutoARIMA algorithm by Hyndman & Khandakar [37] which selects the best ARIMA model based on a series of statistical tests. ARIMA models are also similarly used as a benchmark for comparison against ML models, such as in [35,36,38].
2.3.2. Deep Learning and the Transformer
Deep learning (DL) is a sub-field of machine learning that combines the concepts of deep neural networks (DNNs) and representation learning. In this work, we focus on a seminal architecture, the transformer by Vaswani et al. [39]. Transformer models show state-of-the-art performance in several domains such as natural language processing [40,41,42], computer vision [43,44], audio signal processing [45,46], and recently, in time series forecasting [47,48,49,50].
The transformer (shown in Figure 3) is a neural network model that uses a self-attention mechanism to capture long-range dependencies and non-linear interactions in sequence data (e.g., text, time series). It consists of an encoder and a decoder network, each composed of stacked layers of multi-head attention blocks and feed-forward blocks with residual connections and layer normalization submodules.
In the context of time series modeling, the encoder takes the historical observations of the target time series as input and produces a learned embedding or latent representation. The decoder then generates a forecast of the target series by attending to the encoder’s output and its own previous outputs in an autoregressive fashion. The transformer also incorporates other contextual information, including static covariates (e.g., categorical identifiers) and dynamic covariates (e.g., related time series, calendar information). In the time series paradigm, the time features (e.g., month of the year, day of the week, hour of the day) are processed as positional encodings, which allows the transformer to explicitly capture information related to the sequence of the observations.
In this work, we use a time series transformer, a probabilistic neural network which closely follows the original transformer architecture that is adapted for time series data. Since the range of the time series values are continuous in nature, the time series transformer uses a swappable distribution head as its final layer (i.e., the model outputs the parameters of a continuous distribution) and is trained by minimizing its corresponding negative log-likelihood loss. At inference time, we can estimate the joint distribution of a multi-step forecast via ancestral sampling. That is, we generate multiple sample paths by autoregressively sampling from the decoder over the forecast horizon. From the collection of sample paths, we can then calculate the median at every time step along the forecast horizon to create a point forecast.
The hyperparameters of our time series transformer model were tuned manually and are summarized in Table 2. The forecast horizon describes the number of time steps to forecast. The lookback window indicates the conditioning length (i.e., how many lags are used as input to the encoder). The embedding dimension refers to the size of the learned embedding for each categorical feature. The transformer layer size describes the dimensionality of the learned embeddings inside each transformer layer. The number of transformer layers indicates how many transformer blocks are stacked in the encoder/decoder. The attention heads parameter refers to the number of heads inside each transformer layer. The transformer activation describes the activation function used inside each transformer layer. The dropout indicates the dropout probability used inside each transformer layer. For the output probability distribution, we use a Student's t distribution. For the optimizer, we use the AdamW optimizer [51] with a 1e-4 learning rate. Finally, we set the batch size to 256 and train the model for 500 epochs.
2.3.3. The Global Forecasting Approach
In the case of forecasting a group of time series, the traditional and parsimonious approach would be to assume that each time series comes from a different data generating process. In effect, the modeling task would be broken down into individual univariate forecasting problems (i.e., each time series would have its own model). This is called the local forecasting approach.
In contrast to this, recent research in the field of time series forecasting has shown that it is possible to fit a single model to a group of time series and achieve superior forecast accuracy. This is referred to as global forecasting [52] (also called the cross-learning approach [53]). Several important works in the forecasting literature have demonstrated the efficacy of such an approach. Notably, the top performers in the M4 forecasting competition [35], specifically the ES-RNN method of Smyl [53] and FFORMA method of Montero-Manso et al. [54], use a form of global forecasting via partial pooling with hybrid statistical-ML models. In this competition, contenders were tasked to forecast a group of 100,000 time series from various domains including business, finance, and economics. In response to this, the pure DL-based N-BEATS model of Oreshkin et al. [55], which uses a fully global approach, was shown to have improved accuracy compared with the top M4 winners. Following these results, many of the entrants in the M5 forecasting competition used both full and partial global approaches to modeling 42,840 time series of retail sales data [36]. Many of the winners utilized tree-based methods based on LightGBM [56] and recurrent neural network models [57]. In essence, empirical results show that globally trained ML and DL models have improved forecasting performance and better generalization.
We note that global forecasting in this context is still a univariate forecasting method (i.e., the model produces forecasts for each series one at a time) and is separate from multivariate forecasting, where we are interested in simultaneously predicting all time series of interest.
Global forecasting has become more relevant in the context of big data, where there are often thousands or millions of time series to forecast. It has several advantages over traditional local forecasting approaches which fit a separate model for each time series. First, global forecasting methods tend to be much more scalable, as it only requires training and maintaining one model instead of many. Second, global forecasting methods can leverage information across different time series, such as common trends, seasonality, or other patterns. Third, global forecasting methods can handle short and sparse time series better than local methods, as it can use information from other similar series that are longer or more complete. Lastly, global forecasting can even be used with heterogeneous time series which have different characteristics or data generating processes [58,59].
In this work, we train a time series transformer model using a global forecasting approach. That is, a single time series transformer is trained on all 10,949 time series and is used to produce forecasts for each series by conditioning on historically observed values, its related static identifiers, and the relevant time features.
2.4. Evaluating Model Performance
Since we are interested in forecasting a large group of time series with varying scales, we use three scale-independent error metrics to evaluate accuracy: modified symmetric mean absolute percentage error (msMAPE) [60], normalized root mean squared error (NRMSE) [61], and normalized deviation (ND) [61]. These are defined as,
where is the true value, is the forecasted value, is a smoothing parameter, and is the number of data points being forecasted.
We note that when evaluating forecasts of time series that may have intermittent characteristics, one needs to be careful about which metrics are used [60]. Metrics that optimize for the median (e.g., mean absolute error or MAE) are problematic since a naïve forecast of all zeros is often considered the “best”. Additionally, metrics with per-step scaling based on actual values (e.g., mean absolute percentage error or MAPE) or benchmark errors (e.g., mean absolute scaled error or MASE) can also be problematic because of potential divisions by zero.
3. Results and Discussion
In this work, we compare the performance of a time series transformer trained via a global forecasting approach against statistical and baseline techniques that use a traditional local forecasting approach. Observations from 2010 to 2021 are used as training data for all methods. Each method then generates a 4-step forecast for each time series, covering the hold-out testing period of 2022. Effectively, this amounts to 10,949 x 4 = 43,796-point forecasts per method. Error metrics are then calculated for each method using the equations defined in the previous section.
For the local ARIMA approach, the AutoARIMA algorithm is applied individually for every time series. That is, the optimal parameters for an ARIMA model are selected for each time series. For the seasonal naïve method, the observations for each time series in 2021 are repeated and used as a forecast of the testing period (i.e., the method assumes that 2022 is the same as 2021).
For the global forecasting approach with the time series transformer, all time series are pooled and used for fitting a single model (i.e., training of model parameters is done via batch gradient descent and backpropagation). Again, we note that the time series transformer is a probabilistic neural network model. That is, the model’s output corresponds to the parameters of a target distribution, in this case the Student’s t distribution. At inference time, the joint distribution of the 4-step forecast is estimated by autoregressively sampling paths (i.e., at each time step, a prediction is sampled from the output distribution of the model which is then fed back into the model to generate the conditional distribution of the next time step). For each time series, we sample 500 paths at test time and take the median to be the point forecast of the global model.
Analysis of Forecast Accuracy
We summarize the forecast accuracy of each method in Table 3. Overall, our results establish that the global time series transformer has significantly better forecast accuracy across all metrics compared with the local forecasting methods. In particular, the transformer model presents a substantial 84.93% and 80.69% improvement in NRMSE and ND respectively over the next best model, the locally trained and optimized ARIMA models. Similarly, the transformer shows a marked 79.54% improvement in msMAPE compared with the next best method, the seasonal naïve forecast. For illustration, Figure 4 depicts nine sample time series and each method’s corresponding one-year ahead forecasts (4-steps).
We see in the bottom three plots of Figure 4 that the transformer model does not always generate the best forecast. First, this suggests that hybrid or ensemble approaches can also potentially be explored to further improve forecast accuracy, which we leave for future work. We note however, that the bottom three plots in Figure 4 are of time series that exhibit extremely rigid intermittent patterns. In cases like this, simple naïve methods such as the seasonal naïve forecast can become very difficult to beat. Second, this also motivates us to dig further into model performance by also investigating the distribution of error measures. We focus specifically on the msMAPE metric and provide information about its distribution in Figure 5 and Table 4.
Figure 5 depicts a density plot that represents the distribution of msMAPE values for each forecasting method. A visual inspection reveals that the distribution of msMAPE values for the global time series transformer is significantly less skewed when compared with the local methods. This would indicate that the transformer model achieves better forecast accuracy across most of the dataset. A similar inference can be drawn from Table 4 which summarizes the summary statistics of the msMAPE distribution. We see that the transformer model exhibits substantially lower msMAPE values, with improvements of 57.48%, 68.67%, 74.81%, and 77.62% for each quartile and the maximum when compared with the next best method. Additionally, Table A3 in Appendix B summarizes the msMAPE metric stratified by region which also shows results consistent with our findings here and leads us to make comparable conclusions. These results further solidify our conclusion that a global time series transformer is the superior approach compared with traditional local forecasting approaches.
Interestingly, we observe in Table 3 that a seasonal naïve forecast achieves better average performance compared with locally optimized ARIMA models in terms of msMAPE. This can also be seen in Figure 5 and Table 4, where ARIMA shows worse performance across the quartiles of the msMAPE distribution. This seemingly benign result highlights the importance of including naïve and traditional statistical baselines when evaluating the model performance of ML and DL-based techniques. While our proposed global deep learning method exhibits great performance, many works in the crop yield forecasting literature neglect to include such baseline methods (including the studies mentioned in our review of the literature), and thus fail to properly contextualize the accuracy improvements (or even the validity) of a proposed method. This concern was also raised during an analysis of the results of the M5 forecasting competition, where a staggering 64.2% and 92.5% of the 2666 participating teams were unable to outperform a simple seasonal naïve forecast and the exponential smoothing benchmark (a classic statistical method), respectively [36]. We hope that our inclusion of naïve and statistical benchmarks will serve to encourage future works to incorporate them as well.
4. Conclusions
This study proposes using a global forecasting approach for large-scale prediction of crop production volume using time series transformers. We establish that our approach significantly improves forecast accuracy across a range of metrics compared with traditional local forecasting approaches based on statistical and baseline methods.
As larger datasets become more commonplace, we envision that methods such as ours will become even more vital in augmenting the decision-making process of policymakers and stakeholders in the agriculture sector. This is especially important for organizations that operate in and oversee large parts of the sector. National government agencies in charge of managing food security and the non-food industrial and commercial crop economy would greatly benefit from large-scale prediction models. Practically speaking, ML-based global forecasting methods can provide stakeholders with high-quality disaggregated predictions that allow for more granular planning in both long-term and short-term use cases. It also gives a better overall vision of the state of a country’s crop supply, which is crucial in effectively managing the health of the agricultural sector.
We suggest incorporating other exogenous variables such as meteorological and climate data (e.g., rainfall, El Niño, and La Niña climate indices) for future work. Adding such covariates is expected to improve forecast accuracy further and can even be used to perform more extensive counterfactual or what-if analyses. We also identify the potential for applying our proposed method to time series data of other countries. Lastly, while we expect global forecasting methods to perform better than local methods, there may be instances where specific datasets may benefit from hybrid or ensemble modeling approaches.
Author Contributions
Conceptualization, S.C.I. and C.P.M.; methodology, S.C.I.; software, S.C.I.; validation, S.C.I. and C.P.M.; formal analysis, S.C.I. and C.P.M.; investigation, S.C.I.; data curation, S.C.I.; writing—original draft preparation, S.C.I.; writing—review and editing, S.C.I. and C.P.M.; visualization, S.C.I.; supervision, C.P.M.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: https://openstat.psa.gov.ph/
Acknowledgments
The authors would like to acknowledge Daniel Stanley Tan and Gillian Uy for discussions and valuable insights.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Table A1.
List of crops used in this study.
| Crops | ||||
|---|---|---|---|---|
| Abaca | Carnation | Golden Melon | Marang | Samsamping |
| Abaca Leafsheath | Carrots | Gotocola | Mayana | San Francisco |
| Abiu | Cashew | Granada | Melon - Honey-dew | Basil - Sangig |
| African Palm Leaves | Cassava - Industrial Use | Grapes - Green | Melon - Muskmelon | Santan |
| Agitway | Cassava - Food | Grapes - Red | Mini Pineapple | Santol |
| Alugbati | Cassava Tops | Ubi | Mint | Sayung-sayong |
| Alubihod | Castor Beans | Green Corn Stalk | Mongo | Serial (Unclear) |
| Alucon | Cauliflower | Papaya, Green | Mushroom | Sesame |
| Ampalaya Fruit | Celery | Guava - Guaple | Mustard | Sineguelas |
| Ampalaya Leaves | Chayote Fruit | Guava - Native | Napier Grass | Sarali (Unclear) |
| Anonas | Chayote Tops | Guinea Grass | Ngalug | Snap Beans |
| Anthurium | Chai Sim | Guyabano | Nipa Leaves | Dracaena - Song of Korea |
| Apat-apat | Garbansos | Halib-on | Nipa Sap/Wine | Sorghum |
| Apatot | Chico | Hanlilika | Oil Palm - Fresh Fruit Bunch | Soybeans |
| Ariwat | Siling Labuyo | Heliconia | Onion Leeks | Spinach |
| Arrowroot | Chinese Malunggay | Hevi | Onion - Bermuda | Spraymum |
| Achuete | Chives | Ikmo | Onion - Native | Sibuyas |
| Asparagus | Chrysanthemum | Ilang-Ilang | Orange | Squash Fruit |
| Aster | Coconut Leaves | Ipil-Ipil Leaves | Oregano | Squash Tops |
| Atis | Coconut - Mature | Jackfruit - Young | Pahid | Starapple |
| Avocado | Coconut Sap | Jackfruit - Ripe | Palm Ornamentals | Statice |
| Azucena | Coconut - Young | Jatropha | Palong Manok | Strawberry |
| Baby's Breath | Coconut Pith | Jute Mallow | Pandan Fiber | Sitao |
| Bagbagkong Flower | Coffee - Dried Berries - Arabica | Kamias | Pandan-Mabango | Sugarcane - Basi/Vinegar |
| Bagbagkong Fruit | Coffee - Green Beans - Arabica | Kaong | Pangi | Sugarcane - Centrifugal Sugar |
| Bago Leaves | Coffee - Dried Berries - Excelsa | Kaong Sap | Pansit-Pansitan | Sugarcane - Chewing |
| Balimbing | Coffee - Green Beans - Excelsa | Kapok | Pao Galiang | Sugarcane - Ethanol |
| Ballaiba | Coffee - Dried Berries - Liberica | Karamay | Papait | Sugarcane - Panocha/Muscovado |
| Bamboo Shoots | Coffee - Green Beans - Liberica | Katuray | Papaya - Hawaiian | Sugod-sugod |
| Banaba | Coffee - Dried Berries - Robusta | Kentucky Beans | Papaya - Native | Kangkong |
| Banana Male Bud | Coffee - Green Beans - Robusta | Kidney Beans - Red | Papaya - Solo | Sweet Peas |
| Banana - Bungulan | Cogon | Kidney Beans - White | Parsley | Kamote |
| Banana - Cavendish | Coir | Kinchay | Passion Fruit | Tabon-tabon |
| Banana - Lakatan | Coriander | Kondol | Patola | Talinum |
| Banana - Latundan | Cotton | Kulibangbang | Peanut | Sampalok |
| Banana Leaves | Cowpea - Dry | Kulitis | Pears | Tamarind Flower |
| Banana - Others | Cowpea - Green | Labig Leaves | Pechay - Chinese | Tambis |
| Banana - Saba | Cowpea Tops | Okra | Pechay - Native | Gabi |
| Banana Pith | Cucumber | Lagundi | Pepper Chili Leaves | Tawri |
| Bariw Fiber | Dracaena - Marginata Color | Lanzones | Pepper - Bell | Tiger Grass |
| Basil | Dracaena - Sanderiana - White | Laurel | Pepper - Finger | Tikog |
| Batwan | Dracaena - Sanderiana - Yellow | Tambo/Laza | Persimmon | Tobacco - Native |
| Basil - Bawing Sulasi | Dahlia | Leatherleaf Fern | Pigeon Pea | Tobacco - Others |
| Beets | Daisy | Lemon | Pili Nut | Tobacco - Virginia |
| Betel Nut | Dawa | Lemon Grass | Pineapple | Tomato |
| Bignay | Orchids - Dendrobium | Lipote | Pineapple Fiber | Tugi |
| Black Beans | Dracaena | Lettuce | Suha | Turmeric |
| Black Pepper | Dragon Fruit | Likway | Potato | Singkamas |
| Blue Grass | Duhat | Patani | Puto-Puto | Orchids - Vanda |
| Upo | Durian | Lime | Labanos | Water Lily |
| Breadfruit | Pako | Longans | Radish Pods | Watercress |
| Broccoli | Eggplant | Sago Palm Pith | Rambutan | Watermelon |
| Bromeliad | Euphorbia | Lumbia Leaves | Rattan Fruits | Sigarilyas |
| Cabbage | Fishtail Palm | Lupo | Rattan Pith | Wonder Beans |
| Cacao | Flemingia | Mabolo | Red Beans | Yacon |
| Cactus | Dracaena - Florida Beauty | Maguey | Rensoni | Yam Beans |
| Calachuci | Taro Leaves with Stem | Makopa | Rice Hay | Yellow Bell |
| Calamansi | Gabi Runner | Malunggay Fruit | Romblon | Yerba Buena |
| Kalumpit | Garden Pea | Malunggay Leaves | Roses | Young Corn |
| Kamangeg | Garlic - Dried Bulb | Mandarin | Labog | Sapote |
| Kamansi | Garlic Leeks | Mango - Carabao | Rubber | Zucchini |
| Camachile | Gerbera | Mango - Others | Sabidokong | Irrigated Palay |
| Sweet Potato Tops | Ginger | Mango - Piko | Salago | Rainfed Palay |
| Canistel | Ginseng | Mangosteen | Saluyot | White Corn |
| Carabao Grass | Gladiola | Manzanita | Sampaguita | Yellow Corn |
Table A2.
List of regions and provinces.
| Region | Province |
|---|---|
| REGION I (ILOCOS REGION) | Ilocos Norte |
| Pangasinan | |
| Ilocos Sur | |
| La Union | |
| REGION II (CAGAYAN VALLEY) | Batanes |
| Cagayan | |
| Isabela | |
| Nueva Vizcaya | |
| Quirino | |
| REGION III (CENTRAL LUZON) | Aurora |
| Nueva Ecija | |
| Pampanga | |
| Zambales | |
| Bulacan | |
| Bataan | |
| Tarlac | |
| REGION IV-A (CALABARZON) | Rizal |
| Quezon | |
| Laguna | |
| Batangas | |
| Cavite | |
| REGION IX (ZAMBOANGA PENINSULA) | Zamboanga Sibugay |
| Zamboanga del Sur | |
| City of Zamboanga | |
| Zamboanga del Norte | |
| REGION V (BICOL REGION) | Masbate |
| Sorsogon | |
| Albay | |
| Catanduanes | |
| Camarines Sur | |
| Camarines Norte | |
| REGION VI (WESTERN VISAYAS) | Aklan |
| Antique | |
| Capiz | |
| Negros Occidental | |
| Iloilo | |
| Guimaras | |
| REGION VII (CENTRAL VISAYAS) | Cebu |
| Negros Oriental | |
| Bohol | |
| Siquijor | |
| REGION VIII (EASTERN VISAYAS) | Eastern Samar |
| Southern Leyte | |
| Northern Samar | |
| Samar | |
| Biliran | |
| Leyte | |
| REGION X (NORTHERN MINDANAO) | Lanao del Norte |
| Misamis Occidental | |
| Misamis Oriental | |
| Camiguin | |
| Bukidnon | |
| REGION XI (DAVAO REGION) | Davao del Norte |
| Davao Occidental | |
| Davao Oriental | |
| Davao de Oro | |
| Davao del Sur | |
| City of Davao | |
| REGION XII (SOCCSKSARGEN) | Cotabato |
| South Cotabato | |
| Sarangani | |
| Sultan Kudarat | |
| REGION XIII (CARAGA) | Dinagat Islands |
| Surigao del Sur | |
| Surigao del Norte | |
| Agusan del Sur | |
| Agusan del Norte | |
| BANGSAMORO AUTONOMOUS REGION IN MUSLIM MINDANAO (BARMM) | Tawi-tawi |
| Maguindanao | |
| Lanao del Sur | |
| Sulu | |
| Basilan | |
| CORDILLERA ADMINISTRATIVE REGION (CAR) | Benguet |
| Kalinga | |
| Abra | |
| Apayao | |
| Mountain Province | |
| Ifugao | |
| MIMAROPA REGION | Occidental Mindoro |
| Palawan | |
| Oriental Mindoro | |
| Romblon | |
| Marinduque |
Appendix B
Table A3 summarizes the recorded msMAPE values calculated on the test set, stratified by region. Notably, Region XIII (CARAGA) shows the worst performance across all three methods. Upon investigation, the agricultural sector of the region was found to exhibit a contraction in overall production in 2022. This is attributed to major weather disturbances causing prolonged impact to agricultural production in the region [62].
Table A3.
Recorded msMAPE metrics on the test set, stratified by region. The best metric is highlighted in boldface, while the next best metric is underlined. Lower is better.
Table A3.
Recorded msMAPE metrics on the test set, stratified by region. The best metric is highlighted in boldface, while the next best metric is underlined. Lower is better.
| Region | Seasonal Naïve |
ARIMA | Transformer | Number of Time Series |
|---|---|---|---|---|
| REGION I (ILOCOS REGION) | 6.0892 | 6.9896 | 2.7566 | 574 |
| REGION II (CAGAYAN VALLEY) | 9.1292 | 11.3719 | 2.8928 | 759 |
| REGION III (CENTRAL LUZON) | 10.8197 | 13.1275 | 2.9276 | 730 |
| REGION IV-A (CALABARZON) | 10.5602 | 12.5337 | 2.9033 | 596 |
| REGION V (BICOL REGION) | 15.6347 | 20.7075 | 2.9834 | 641 |
| REGION VI (WESTERN VISAYAS) | 9.8261 | 11.1632 | 2.4728 | 938 |
| REGION VII (CENTRAL VISAYAS) | 19.9428 | 21.9464 | 2.8230 | 582 |
| REGION VIII (EASTERN VISAYAS) | 14.1325 | 16.1343 | 2.5938 | 852 |
| REGION IX (ZAMBOANGA PENINSULA) | 9.2573 | 10.5922 | 2.3377 | 603 |
| REGION X (NORTHERN MINDANAO) | 10.3724 | 12.0962 | 2.6443 | 888 |
| REGION XI (DAVAO REGION) | 6.3099 | 8.4809 | 2.5301 | 909 |
| REGION XII (SOCCSKSARGEN) | 13.5562 | 15.0764 | 2.6834 | 763 |
| REGION XIII (CARAGA) | 20.1935 | 23.3830 | 3.4582 | 625 |
| BANGSAMORO AUTONOMOUS REGION IN MUSLIM MINDANAO (BARMM) | 6.3572 | 7.5493 | 2.4596 | 424 |
| CORDILLERA ADMINISTRATIVE REGION (CAR) | 9.5863 | 11.9596 | 2.8841 | 520 |
| MIMAROPA REGION | 16.4558 | 21.9118 | 3.1619 | 545 |
References
- Philippine Statistics Authority Gross National Income & Gross Domestic Product. Available online: https://psa.gov.ph/national-accounts/sector/Agriculture,%20Forestry%20and%20Fishing (accessed on 14 July 2023).
- Philippine Statistics Authority Unemployment Rate in December 2022 Is Estimated at 4.3 Percent. Available online: https://psa.gov.ph/content/unemployment-rate-december-2022-estimated-43-percent (accessed on 14 July 2023).
- 3. Alliance of Bioversity International and CIAT & World Food Programme. Philippine Climate Change and Food Security Analysis, 2021.
- Liu, C.; Yang, H.; Gongadze, K.; Harris, P.; Huang, M.; Wu, L. Climate Change Impacts on Crop Yield of Winter Wheat (Triticum Aestivum) and Maize (Zea Mays) and Soil Organic Carbon Stocks in Northern China. Agriculture 2022, 12, 614. [Google Scholar] [CrossRef]
- Nazir, A.; Ullah, S.; Saqib, Z.A.; Abbas, A.; Ali, A.; Iqbal, M.S.; Hussain, K.; Shakir, M.; Shah, M.; Butt, M.U. Estimation and Forecasting of Rice Yield Using Phenology-Based Algorithm and Linear Regression Model on Sentinel-II Satellite Data. Agriculture 2021, 11, 1026. [Google Scholar] [CrossRef]
- Florence, A.; Revill, A.; Hoad, S.; Rees, R.; Williams, M. The Effect of Antecedence on Empirical Model Forecasts of Crop Yield from Observations of Canopy Properties. Agriculture 2021, 11, 258. [Google Scholar] [CrossRef]
- Antonopoulos, I.; Robu, V.; Couraud, B.; Kirli, D.; Norbu, S.; Kiprakis, A.; Flynn, D.; Elizondo-Gonzalez, S.; Wattam, S. Artificial Intelligence and Machine Learning Approaches to Energy Demand-Side Response: A Systematic Review. Renew. Sustain. Energy Rev. 2020, 130, 109899. [Google Scholar] [CrossRef]
- Le, T.; Vo, M.T.; Vo, B.; Hwang, E.; Rho, S.; Baik, S.W. Improving Electric Energy Consumption Prediction Using CNN and Bi-LSTM. Appl. Sci. 2019, 9, 4237. [Google Scholar] [CrossRef]
- Ibañez, S.C.; Dajac, C.V.G.; Liponhay, M.P.; Legara, E.F.T.; Esteban, J.M.H.; Monterola, C.P. Forecasting Reservoir Water Levels Using Deep Neural Networks: A Case Study of Angat Dam in the Philippines. Water 2021, 14, 34. [Google Scholar] [CrossRef]
- Dailisan, D.; Liponhay, M.; Alis, C.; Monterola, C. Amenity Counts Significantly Improve Water Consumption Predictions. PLoS ONE 2022, 17, e0265771. [Google Scholar] [CrossRef]
- Javier, P.J.E.A.; Liponhay, M.P.; Dajac, C.V.G.; Monterola, C.P. Causal Network Inference in a Dam System and Its Implications on Feature Selection for Machine Learning Forecasting. Phys. A Stat. Mech. Appl. 2022, 604, 127893. [Google Scholar] [CrossRef]
- Shen, M.-L.; Lee, C.-F.; Liu, H.-H.; Chang, P.-Y.; Yang, C.-H. Effective Multinational Trade Forecasting Using LSTM Recurrent Neural Network. Expert Syst. Appl. 2021, 182, 115199. [Google Scholar] [CrossRef]
- Yang, C.-H.; Lee, C.-F.; Chang, P.-Y. Export- and Import-Based Economic Models for Predicting Global Trade Using Deep Learning. Expert Syst. Appl. 2023, 218, 119590. [Google Scholar] [CrossRef]
- Nosratabadi, S.; Ardabili, S.; Lakner, Z.; Mako, C.; Mosavi, A. Prediction of Food Production Using Machine Learning Algorithms of Multilayer Perceptron and ANFIS. Agriculture 2021, 11, 408. [Google Scholar] [CrossRef]
- Kamath, P.; Patil, P.; Sushma, S.S. Crop Yield Forecasting Using Data Mining. Glob. Transit. Proc. 2021, 2, 402–407. [Google Scholar] [CrossRef]
- Das, P.; Jha, G.K.; Lama, A.; Parsad, R. Crop Yield Prediction Using Hybrid Machine Learning Approach: A Case Study of Lentil (Lens Culinaris Medik). Agriculture 2023, 13, 596. [Google Scholar] [CrossRef]
- Sadenova, M.; Beisekenov, N.; Varbanov, P.S.; Pan, T. Application of Machine Learning and Neural Networks to Predict the Yield of Cereals, Legumes, Oilseeds and Forage Crops in Kazakhstan. Agriculture 2023, 13, 1195. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, S.; Tao, F.; Aboelenein, R.; Amer, A. Improving Winter Wheat Yield Forecasting Based on Multi-Source Data and Machine Learning. Agriculture 2022, 12, 571. [Google Scholar] [CrossRef]
- Onwuchekwa-Henry, C.B.; Ogtrop, F.V.; Roche, R.; Tan, D.K.Y. Model for Predicting Rice Yield from Reflectance Index and Weather Variables in Lowland Rice Fields. Agriculture 2022, 12, 130. [Google Scholar] [CrossRef]
- Tende, I.G.; Aburada, K.; Yamaba, H.; Katayama, T.; Okazaki, N. Development and Evaluation of a Deep Learning Based System to Predict District-Level Maize Yields in Tanzania. Agriculture 2023, 13, 627. [Google Scholar] [CrossRef]
- Wang, J.; Si, H.; Gao, Z.; Shi, L. Winter Wheat Yield Prediction Using an LSTM Model from MODIS LAI Products. Agriculture 2022, 12, 1707. [Google Scholar] [CrossRef]
- Wolanin, A.; Mateo-García, G.; Camps-Valls, G.; Gómez-Chova, L.; Meroni, M.; Duveiller, G.; Liangzhi, Y.; Guanter, L. Estimating and Understanding Crop Yields with Explainable Deep Learning in the Indian Wheat Belt. Environ. Res. Lett. 2020, 15, 024019. [Google Scholar] [CrossRef]
- Bharadiya, J.P.; Tzenios, N.T.; Reddy, M. Forecasting of Crop Yield Using Remote Sensing Data, Agrarian Factors and Machine Learning Approaches. JERR 2023, 24, 29–44. [Google Scholar] [CrossRef]
- Gavahi, K.; Abbaszadeh, P.; Moradkhani, H. DeepYield: A Combined Convolutional Neural Network with Long Short-Term Memory for Crop Yield Forecasting. Expert Syst. Appl. 2021, 184, 115511. [Google Scholar] [CrossRef]
- Kujawa, S.; Niedbała, G. Artificial Neural Networks in Agriculture. Agriculture 2021, 11, 497. [Google Scholar] [CrossRef]
- Paudel, D.; Boogaard, H.; De Wit, A.; Janssen, S.; Osinga, S.; Pylianidis, C.; Athanasiadis, I.N. Machine Learning for Large-Scale Crop Yield Forecasting. Agric. Syst. 2021, 187, 103016. [Google Scholar] [CrossRef]
- Paudel, D.; Boogaard, H.; De Wit, A.; Van Der Velde, M.; Claverie, M.; Nisini, L.; Janssen, S.; Osinga, S.; Athanasiadis, I.N. Machine Learning for Regional Crop Yield Forecasting in Europe. Field Crops Res. 2022, 276, 108377. [Google Scholar] [CrossRef]
- World Bank Agricultural Land (% of Land Area)—Philippines. Available online: https://data.worldbank.org/indicator/AG.LND.AGRI.ZS?locations=PH (accessed on 15 July 2023).
- Philippine Atmospheric, Geophysical and Astronomical Services Administration Climate of the Philippines. Available online: https://www.pagasa.dost.gov.ph/information/climate-philippines (accessed on 15 July 2023).
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. 2019.
- Wolf, T.; Debut, L.; Sanh, V.; Chaumond, J.; Delangue, C.; Moi, A.; Cistac, P.; Rault, T.; Louf, R.; Funtowicz, M.; et al. Transformers: State-of-the-Art Natural Language Processing. In Proceedings of the Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing: System Demonstrations; Association for Computational Linguistics: Online, 2020; pp. 38–45. [Google Scholar]
- Alexandrov, A.; Benidis, K.; Bohlke-Schneider, M.; Flunkert, V.; Gasthaus, J.; Januschowski, T.; Maddix, D.C.; Rangapuram, S.; Salinas, D.; Schulz, J.; et al. GluonTS: Probabilistic and Neural Time Series Modeling in Python.
- Garza, F.; Mergenthaler, M.; Challú, C.; Olivares, K.G. StatsForecast: Lightning Fast Forecasting with Statistical and Econometric Models 2022.
- Hyndman, R.; Athanasopoulos, G. Forecasting: Principles and Practice 2021.
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. The M4 Competition: 100,000 Time Series and 61 Forecasting Methods. Int. J. Forecast. 2020, 36, 54–74. [Google Scholar] [CrossRef]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. M5 Accuracy Competition: Results, Findings, and Conclusions. Int. J. Forecast. 2022, 38, 1346–1364. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Khandakar, Y. Automatic Time Series Forecasting: The Forecast Package for R. J. Stat. Soft. 2008, 27. [Google Scholar] [CrossRef]
- Godahewa, R.; Bergmeir, C.; Webb, G.I.; Hyndman, R.J.; Montero-Manso, P. Monash Time Series Forecasting Archive.
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need 2017.
- Devlin, J.; Chang, M.-W.; Lee, K.; Toutanova, K. BERT: Pre-Training of Deep Bidirectional Transformers for Language Understanding 2019.
- Lewis, M.; Liu, Y.; Goyal, N.; Ghazvininejad, M.; Mohamed, A.; Levy, O.; Stoyanov, V.; Zettlemoyer, L. BART: Denoising Sequence-to-Sequence Pre-Training for Natural Language Generation, Translation, and Comprehension 2019.
- Radford, A.; Narasimhan, K.; Salimans, T.; Sutskever, I. Improving Language Understanding by Generative Pre-Training.
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image Is Worth 16x16 Words: Transformers for Image Recognition at Scale 2021.
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-End Object Detection with Transformers 2020.
- Baevski, A.; Zhou, H.; Mohamed, A.; Auli, M. Wav2vec 2.0: A Framework for Self-Supervised Learning of Speech Representations 2020.
- Radford, A.; Kim, J.W.; Xu, T.; Brockman, G.; McLeavey, C.; Sutskever, I. Robust Speech Recognition via Large-Scale Weak Supervision.
- Li, S.; Jin, X.; Xuan, Y.; Zhou, X.; Chen, W.; Wang, Y.-X.; Yan, X. Enhancing the Locality and Breaking the Memory Bottleneck of Transformer on Time Series Forecasting.
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. AAAI 2021, 35, 11106–11115. [Google Scholar] [CrossRef]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting.
- Lim, B.; Arık, S.Ö.; Loeff, N.; Pfister, T. Temporal Fusion Transformers for Interpretable Multi-Horizon Time Series Forecasting. Int. J. Forecast. 2021, 37, 1748–1764. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization 2019.
- Salinas, D.; Flunkert, V.; Gasthaus, J.; Januschowski, T. DeepAR: Probabilistic Forecasting with Autoregressive Recurrent Networks. Int. J. Forecast. 2020, 36, 1181–1191. [Google Scholar] [CrossRef]
- Smyl, S. A Hybrid Method of Exponential Smoothing and Recurrent Neural Networks for Time Series Forecasting. Int. J. Forecast. 2020, 36, 75–85. [Google Scholar] [CrossRef]
- Montero-Manso, P.; Athanasopoulos, G.; Hyndman, R.J.; Talagala, T.S. FFORMA: Feature-Based Forecast Model Averaging. Int. J. Forecast. 2020, 36, 86–92. [Google Scholar] [CrossRef]
- Oreshkin, B.N.; Carpov, D.; Chapados, N.; Bengio, Y. N-BEATS: Neural Basis Expansion Analysis for Interpretable Time Series Forecasting 2020.
- In, Y.J.; Jung, J.Y. Simple Averaging of Direct and Recursive Forecasts via Partial Pooling Using Machine Learning. Int. J. Forecast. 2022, 38, 1386–1399. [Google Scholar] [CrossRef]
- Jeon, Y.; Seong, S. Robust Recurrent Network Model for Intermittent Time-Series Forecasting. Int. J. Forecast. 2022, 38, 1415–1425. [Google Scholar] [CrossRef]
- Montero-Manso, P.; Hyndman, R.J. Principles and Algorithms for Forecasting Groups of Time Series: Locality and Globality. Int. J. Forecast. 2021, 37, 1632–1653. [Google Scholar] [CrossRef]
- Hewamalage, H.; Bergmeir, C.; Bandara, K. Global Models for Time Series Forecasting: A Simulation Study 2021.
- Hewamalage, H.; Ackermann, K.; Bergmeir, C. Forecast Evaluation for Data Scientists: Common Pitfalls and Best Practices. Data Min Knowl Disc 2023, 37, 788–832. [Google Scholar] [CrossRef]
- Yu, H.-F.; Rao, N.; Dhillon, I.S. Temporal Regularized Matrix Factorization for High-Dimensional Time Series Prediction.
- National Economic and Development Authority Statement on the 2022 Economic Performance of the Caraga Region. Available online: https://nro13.neda.gov.ph/statement-on-the-2022-economic-performance-of-the-caraga-region/ (accessed on 28 July 2023).
Figure 1.
Nine time series representing some of the top produced crops in the Philippines covering the period from 2010 to 2022 with the crop name, province, and region listed, respectively. Observations are the quarterly production volume measured in metric tons. Palay and corn represent the top produced cereals. Banana, pineapple, and mango represent some of the top produced fruit crops. Kamote (sweet potato) and eggplant represent some of the top produced vegetables and root crops. Sugarcane and coconut represent some of the top produced non-food and industrial crops.
Figure 1.
Nine time series representing some of the top produced crops in the Philippines covering the period from 2010 to 2022 with the crop name, province, and region listed, respectively. Observations are the quarterly production volume measured in metric tons. Palay and corn represent the top produced cereals. Banana, pineapple, and mango represent some of the top produced fruit crops. Kamote (sweet potato) and eggplant represent some of the top produced vegetables and root crops. Sugarcane and coconut represent some of the top produced non-food and industrial crops.
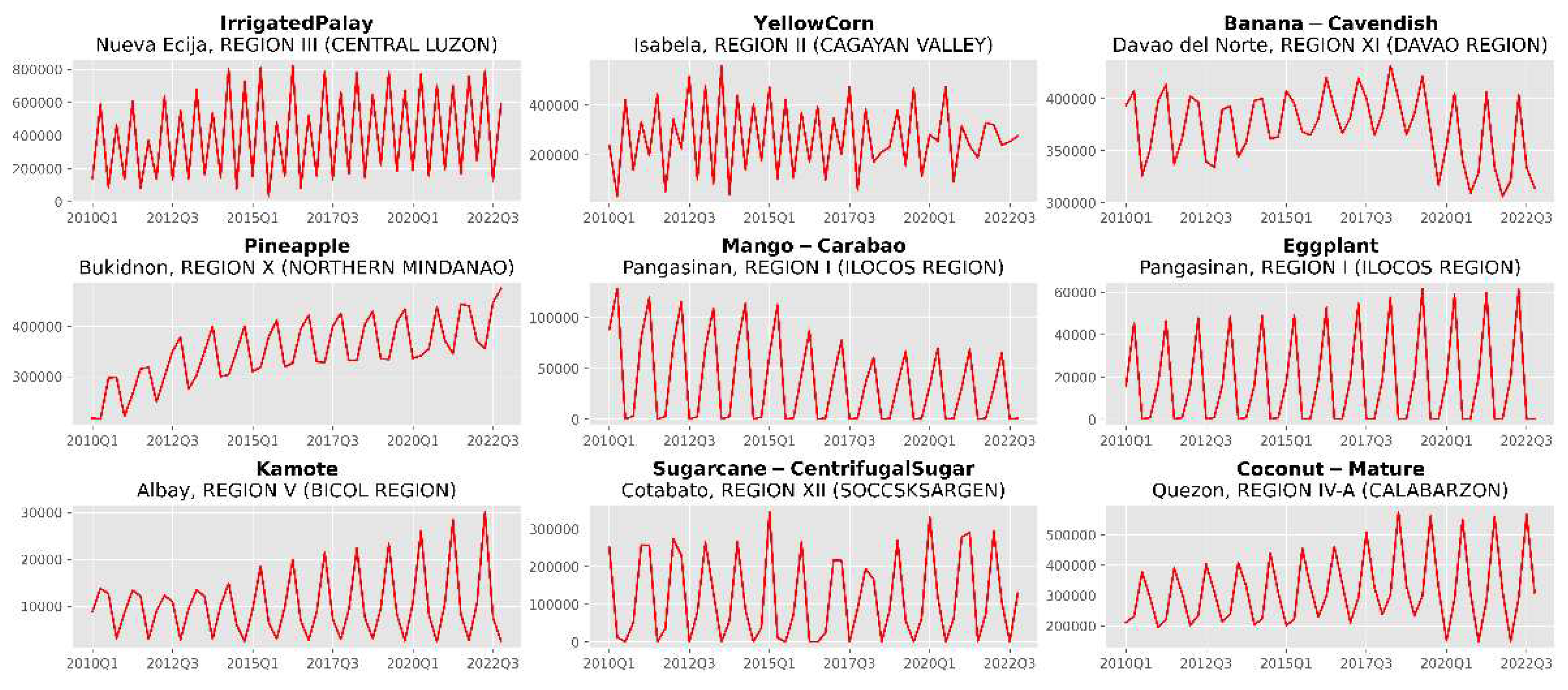
Figure 2.
Nine sample time series covering the period from 2010 to 2022 with the crop name, province, and region listed, respectively. Observations are the quarterly production volume measured in metric tons. The dataset consists of a large group of time series that capture a wide variety of dynamics and scales. While most time series show strong quarterly seasonality, some series also exhibit multiplicative seasonality, intermittent behavior, sparsity, or structural breaks/regime shifts.
Figure 2.
Nine sample time series covering the period from 2010 to 2022 with the crop name, province, and region listed, respectively. Observations are the quarterly production volume measured in metric tons. The dataset consists of a large group of time series that capture a wide variety of dynamics and scales. While most time series show strong quarterly seasonality, some series also exhibit multiplicative seasonality, intermittent behavior, sparsity, or structural breaks/regime shifts.
Figure 3.
The transformer architecture by Vaswani et al [39].
Figure 3.
The transformer architecture by Vaswani et al [39].
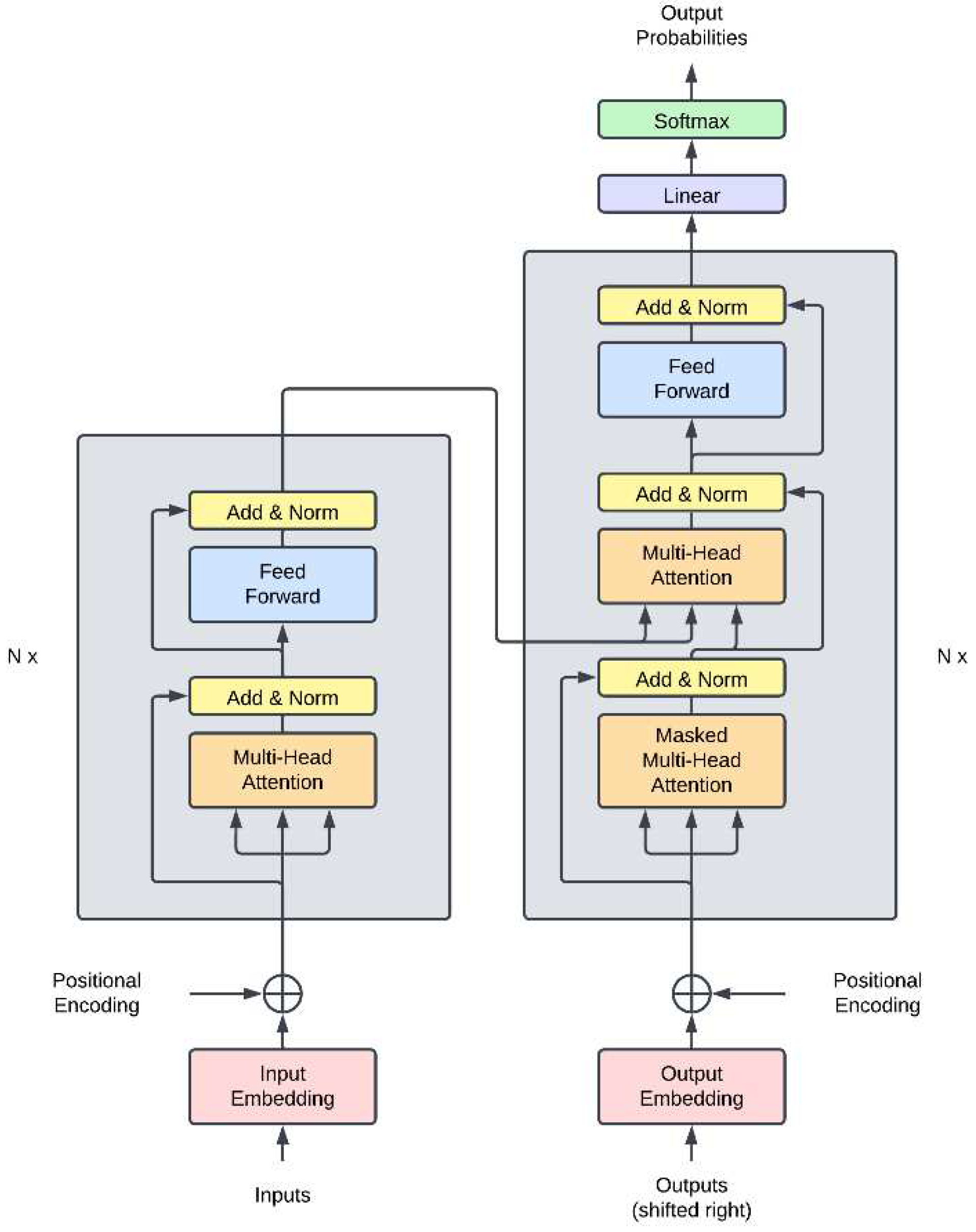
Figure 4.
Nine sample time series covering the period from 2019 to 2022 with the crop name, province, and region listed respectively. Observations are the quarterly production volume measured in metric tons. A one-year forecast (4-steps) was generated for each series, with the Seasonal Naïve in green, ARIMA in purple, and Transformer in blue. While the global time series transformer showed the highest accuracy across all metrics, it does not necessarily exhibit the best performance for all series, as shown in the bottom three plots.
Figure 4.
Nine sample time series covering the period from 2019 to 2022 with the crop name, province, and region listed respectively. Observations are the quarterly production volume measured in metric tons. A one-year forecast (4-steps) was generated for each series, with the Seasonal Naïve in green, ARIMA in purple, and Transformer in blue. While the global time series transformer showed the highest accuracy across all metrics, it does not necessarily exhibit the best performance for all series, as shown in the bottom three plots.

Figure 5.
A density plot representing the distribution of msMAPE values for each forecasting method. Visually, we see that the distribution of msMAPE values for the global time series transformer is significantly less skewed compared with the local methods, indicating that superior forecast accuracy is achieved across most of the dataset.
Figure 5.
A density plot representing the distribution of msMAPE values for each forecasting method. Visually, we see that the distribution of msMAPE values for the global time series transformer is significantly less skewed compared with the local methods, indicating that superior forecast accuracy is achieved across most of the dataset.
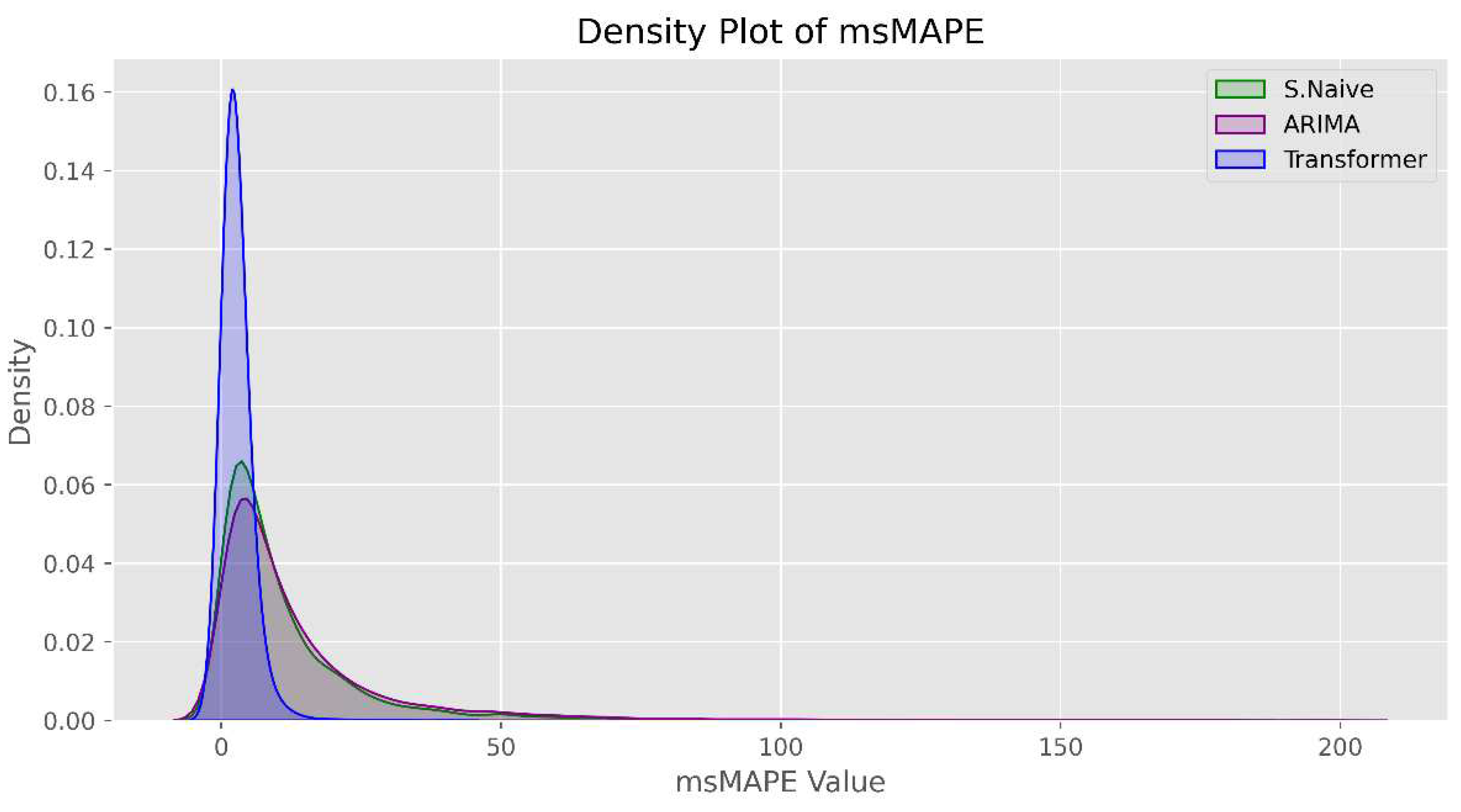
Table 1.
List of input features used in this study.
| Feature | Type | Training Period | Test Period |
|---|---|---|---|
| Volume | target | Q1 2010 to Q4 2021 |
Q1 2022 to Q4 2022 |
| Crop ID | static covariate | ||
| Province ID | static covariate | ||
| Region ID | static covariate | ||
| Quarter | time feature | ||
| Age | time feature |
Table 2.
Summary of model hyperparameters and training settings.
| Hyperparameter | Value |
|---|---|
| Forecast Horizon | 4 |
| Lookback Window | 12 |
| Embedding Dimension | [4, 4, 4] |
| Transformer Layer Size | 32 |
| No. Transformer Layers | 4 |
| Attention Heads | 2 |
| Transformer Activation | GELU |
| Dropout | 0.1 |
| Distribution Output | Student’s t |
| Loss | Negative log-likelihood |
| Optimizer | AdamW |
| Learning Rate | 1e-4 |
| Batch Size | 256 |
| Epochs | 500 |
Table 3.
Recorded msMAPE, NRMSE, and ND metrics on the test set. The best metric is highlighted in boldface, while the next best metric is underlined. Lower is better.
Table 3.
Recorded msMAPE, NRMSE, and ND metrics on the test set. The best metric is highlighted in boldface, while the next best metric is underlined. Lower is better.
| Model | msMAPE | NRMSE | ND |
|---|---|---|---|
| Seasonal Naïve | 13.5092 | 5.7848 | 0.1480 |
| ARIMA | 17.5130 | 4.8592 | 0.1450 |
| Transformer | 2.7639 | 0.7325 | 0.0280 |
Table 4.
Summary statistics of the distribution of msMAPE values for each forecasting method. We see that across all quartiles and the maximum, the global time series transformer shows a substantial improvement in forecast accuracy compared with the local methods. The best metric is highlighted in boldface, while the next best metric is underlined. Lower is better.
Table 4.
Summary statistics of the distribution of msMAPE values for each forecasting method. We see that across all quartiles and the maximum, the global time series transformer shows a substantial improvement in forecast accuracy compared with the local methods. The best metric is highlighted in boldface, while the next best metric is underlined. Lower is better.
| Model | Mean | Stdev | Min | 25% | 50% | 75% | Max |
|---|---|---|---|---|---|---|---|
| Seasonal Naïve | 11.66 | 15.35 | 0.00 | 2.94 | 6.83 | 14.13 | 181.07 |
| ARIMA | 13.91 | 18.25 | 0.00 | 3.51 | 7.88 | 16.55 | 199.95 |
| Transformer | 2.76 | 2.38 | 0.05 | 1.25 | 2.14 | 3.56 | 40.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






