Preprint
Article
Adaptive Control of M3C-Based Variable Speed Drive for Multiple PMSM-Driven Centrifugal Pumps
Altmetrics
Downloads
100
Views
49
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
02 August 2023
Posted:
03 August 2023
You are already at the latest version
Alerts
Abstract
There has been growing interest in using permanent magnet synchronous motors (PMSMs) for pumping applications to improve energy efficiency. One promising approach for powering these motors in variable speed applications is using modular multilevel cascaded converters based on a Triple-Star Bridge Cell (M3C) due to their inherent fault tolerance capability. However, M3C converters require a more complex control system than simpler converters. For instance, A basic M3C control system for power transmission requires seventeen (17) PI controllers, whose adjustment depends on the M3C’s dynamical model parameters’ value knowledge needing extensive and time-consuming testing to obtain them. To solve this control system issue, we propose an adaptive M3C control system for variable speed drives powering multiple PMSM-driven centrifugal pumps that reduces the number of controllers to six (6). Furthermore, the proposal does not require knowledge of the converter, motor, or load parameters, making it more practical and versatile. The proposal introduces an ad-hoc hybrid passivity-based model reference adaptive controller in cascade with a passivity-based control. It has been validated through theoretical stability proof and comparative simulation results with a basic control system under normal and fault operations. As a result, the proposal effectively follows the required rotor speed while enhancing performance by decreasing the current consumption and recovering from a 10% input phase imbalance, a cell short circuit, and an open cell.
Keywords:
Subject: Engineering - Electrical and Electronic Engineering
1. Introduction
In recent years, a growing emphasis has been on utilizing permanent magnet synchronous motors (PMSM) to enhance energy efficiency in pumping applications [1]. Compared to traditional induction motors (IM), PMSM motors have demonstrated superior efficiency, as evidenced by [1, Figure 3]. The work [2] proposes customizing PMSM design for this application, while [3,4] study a variable speed PMSM for water pumps powered by AC-AC converter fed by photovoltaic panels. The works [3,4] use a two-level voltage source inverter controlled by model reference adaptive control (MRAC).
However, the work [5] proposes several fault-tolerant multilevel converters. In this sense, the use of modular multilevel cascaded converter (MMCC) obtained popularity due to its many benefits, such as redundancy, high efficiency, robustness, lower output voltage TDH, and low maintenance [6,7,8]. Among these converters, the triple-star bridge cells (M3C) topology is particularly noteworthy. M3C employs smaller floating capacitors [6,9].
What sets M3C apart is its inherent fault tolerance characteristics, allowing it to continue proper operations even after having a power supply phase imbalance or a power cell failure [6,9]. It ensures energy balancing with low impact on the output currents [9]. Furthermore, it reduces current harmonics, enhances power factor and efficiency, [6,8,10], eliminates voltage fluctuations and ensures optimal operation at low output frequencies [11,12]. There are even several studies that propose fault detection and control under fault of M3C [13,14,15]. This manuscript focuses on controlling fault-tolerant M3C-based variable speed drive for PMSM-driven centrifugal pumps.
Figure 1 shows a commonly used M3C. It has modularity, the ability to reach high-voltage levels, power quality, bidirectional power conversion, and redundancy [16,17]. It has nine clusters (three per phase) that link the input phases (a, b, c) with the output phases (r, s, t), each consisting of three cells. Additionally, each cell has a full-bridge monophasic inverter. It has been widely utilized [18]; examples are to inject wind energy into an electrical network [17,19], and feed general loads [20].
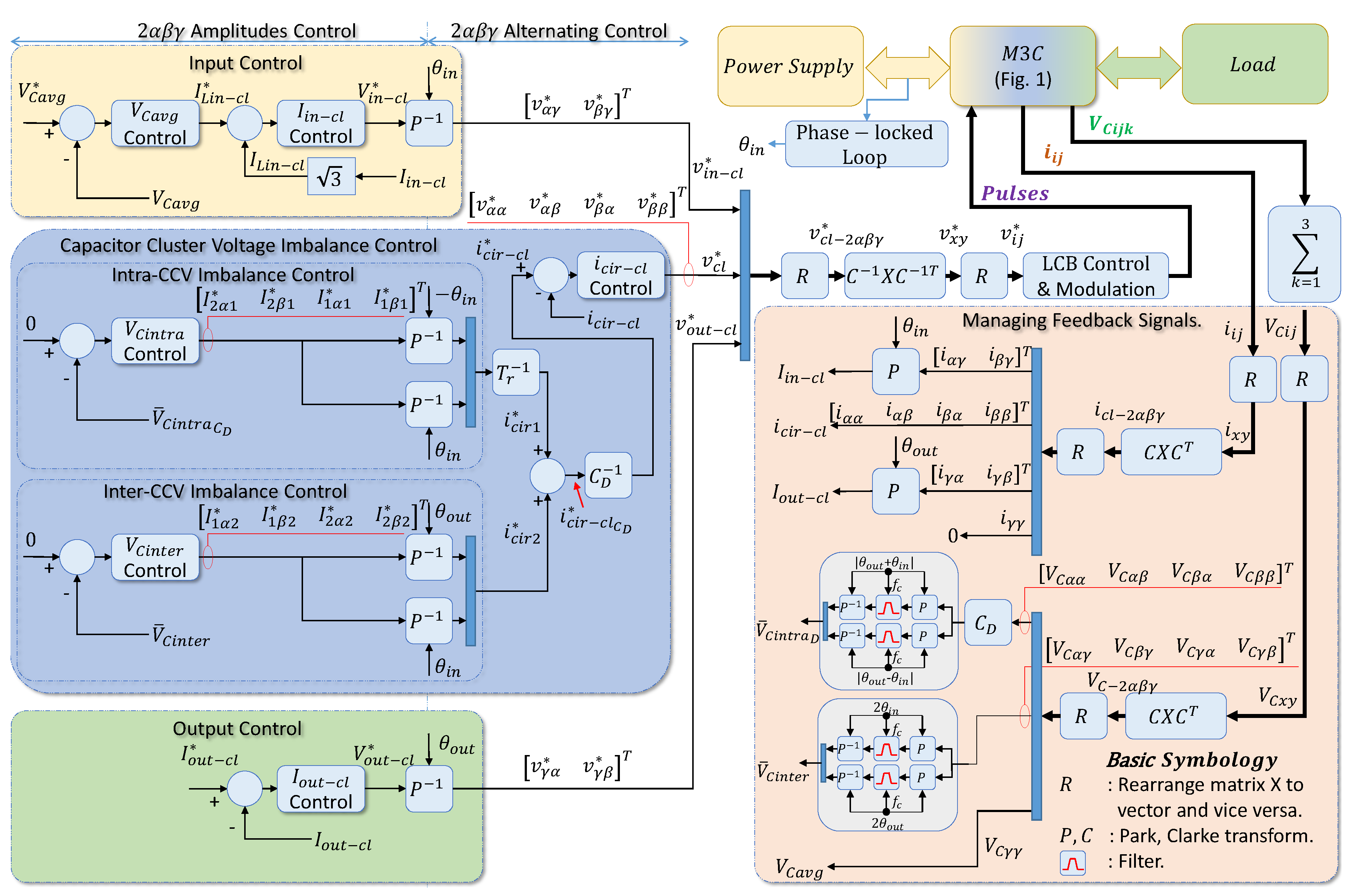
However, while having these fault-tolerant capabilities, controlling M3C is complex compared to simpler converters. Figure 2 describes how the control system of an M3C involves:
- Controlling the average capacitor voltage (ACV) in cascade with the input currents amplitude control, through the required input voltage .
- Keeping zero imbalance of the cluster capacitor voltage (CCV) in cascade with the circulating current control via the needed cluster voltage . It considers reducing to zero the Inter-CCV imbalances (CCV imbalance among clusters of different Sub-Converters) and the Intra-CCV imbalances (CCV imbalance among clusters inside the same Sub-Converters).
- Controlling a required output variable by adjusting the output voltage amplitude and frequency.
The control diagram of Figure 2 uses Park transform P[24], transform [22], doble transform of different matrix variables X[22], and the combined components transformation matrix [25]. Furthermore, the local cell balancing (LCB) and modulation block may use a phase-shifted (PS) pulse-wide modulation (PWM) technique [12,26], a space vector modulation (SVM) [27] or Predictive Control [11,21]. This manuscript controls an M3C with the most extensively used PS-PWM [6].
Regarding the controllers, the works [17,21,25,28,29] consider M3C has several single-input and single-output (SISO) subsystems and use Proportional Integer (PI) controllers for all variables except for the circulating current. Most reported control strategies for the circulating current regulation are based on a simple P controller [17,25,28]. However, some authors use a P-resonant (PR) controller [21,29] as described in [6]. As a result, there are thirteen (13) PI controllers and four (4) PR or P controllers. One (1) PI regulates the ACV direct component in cascade with two (2) PIs for the input current amplitude direct and quadrature components. Eight (8) PIs aim to reduce the CCV imbalance in cascade with four (4) PR or P circulating current controllers. Finally, two (2) PIs regulate the load output current amplitude direct and quadrature components for energy transfer applications between the power supply and the load [6].
Figure 2.
Basic control system of an M3C for transferring energy between the power supply and the load, which is based on [6,17,22,29].
The M3C has also been powering electrical motors with an output control strategy that differs from the one shown in Figure 2 and uses a speed control loop. The works [12,22,30] power IMs with an M3C, while [26] drives PMSMs. However, [12,22,26,30] do not describe the used output control strategy. In contrast, [31] clearly identifies a field-oriented control (FOC) strategy for an MMCC converter feeding IMs. Moreover, it presents multiple-input and multiple-output (MIMO) controllers, significantly reducing the number of controllers. All control systems proposed in [12,22,26,30,31] require knowledge of the plant parameters for their adjustment, which is typically obtained through extensive and time-consuming testing.
To overcome this issue and as the main contribution, this manuscript proposes a MIMO adaptive control of an M3C-based variable speed drive. It operates multiple PMSM-driven centrifugal pumps using a scalar control scheme () [32] for the output control, as FOC is unnecessary in pumping applications. Our proposal involves the following novelties:
- Obtaining the multivariable M3C state-space model for control. It is a MIMO dynamical system with a currents inner loop, a voltages outer loop, and an inner-outer interface. Appendix A of this manuscript details the model obtaining, which complements, describes, rearranges, and summarizes elements taken from [6,22,23,33]. In contrast to [6,22,23,33], herein we give details for control implementation, such as the matrix and vector operations (please see, for instance, the Managing feedback signals details given in Figure 2), and identify the state-space model form with inner and outer loops.
- Using MIMO adaptive controllers instead of non-adaptive SISO controllers [17,21,25,28,29,31]. We show it is a viable and more straightforward solution. The proposal gains the benefits discussed in [31] of reducing the number of controllers by using a MIMO approach for an MMCC but herein for the M3C. In contrast to the works [17,21,25,28,29,31], tuning adaptive controllers does not require plant parameters knowledge, decreasing the commissioning time. Moreover, they adapt to plant changes without compromising their effectiveness.
- Proposing a passivity-based hybrid MRAC called PBMRAC. In contrast to [3,4,34], it uses the MRAC as a low-pass filter for the noisy reference input signals. Moreover, PBMRAC introduces to MRAC a term of an adaptive passivity-based controller (APBC) [35] to attend to the closed-loop system response time. M3C control particularly needs it after having inner reference input noise periods more than sixty times distant from the M3C inner time constant.
- Presenting APBC in cascade with PBMRAC. It expands the Cascade MRAC [36] and the cascade APBC [37]. The first uses an outer SISO controller, whereas the M3C outer loop requires a MIMO controller. Moreover, as Figure 2 shows, the M3C has zero or constant outer references eliminating the need for the outer reference model; therefore, an outer APBC [37] ensures a faster outer loop’s time response.
The following manuscript sections describe the control preliminaries in Section 2. Section 3 details the proposed adaptive control algorithm. Section 4 exhibits the experimental setup and obtained results illustrating the proposal’s effectiveness. Finally, the Authors present concluding remarks in Section 5.
2. Preliminaries
This section commences by introducing the M3C state-space dynamical model. Subsequently, it presents the conventional PI tuning methods. Finally, it gives the requisite background information of the cascade MRAC to be extended with the proposal.
2.1. M3C State-Space Model
The M3C state-space model obtaining is detailed in Appendix A, resulting in the equations (A7) and (A13). The following dynamical equations describe it:
where in the inner loop, the output variables to control are the amplitudes of the input and output cluster currents and , and the instantaneous circulating current . Here, the input variables are the amplitudes of the input and output voltages and , and the instantaneous cluster voltage . The parameter is the coupling inductors inductance L. Finally, the time-varying and bounded disturbance terms for the input are and for the output currents, where and are rated voltages fluctuations.
For the outer loop, the output variables are the ACV , the intra-CCV imbalance , and the inter-CCV imbalance . The input variables are the amplitudes of the cluster input direct component , and the circulating currents and . There are also time-varying bounded disturbance terms , , and . Finally, the fixed parameters are the cells capacitor capacitance C and required capacitor voltage ; while the time-varying parameters are the cluster voltages amplitudes , , , and the capacitor voltage fluctuations .
The inner-outer interface links the direct component of the line input cluster current with the input cluster current . Moreover, it relates the circulating current amplitudes and with the instantaneous circulating current , after using the auxiliary transformation matrix [25] and the Park transformation matrix P[24] with the corresponding input and output angles dependence. Please see Appendix A and Figure 2 for details.
Regarding the operating points in this coordinate, the outer loops consider an ACV setpoint of [22, Definition given bellow Equation (26)], working at zero intra-CCV Imbalance and zero inter-CCV Imbalance [18]. Moreover, the output current reference would be for applications of energy transference between the power supply and the load [6].
The following section describes the PI controllers design for the M3C converter.
2.2. Basic Control Based PI Controllers
PI controllers design starts by assuming that plant parameters are constant, thus . Later, the method splits every equation (1) to (3) in scalar subsystems having each one the general form . Here, is the output variable, is the input, b represents the fixed subsystems parameter, and is the disturbance.
Then, Laplace transform is applied obtaining , not including the circulating current working in alternating current. Here, the corresponding open-loop transfer function is , after neglecting the disturbance term, i.e., .
After considering the PI transfer function acting in series with the , the feed forward transfer function is . Later, considering the feedback transfer function , you may obtain the following closed-loop transfer function as [38]:
where is the damping coefficient, and is the natural frequencies in .
The feedback sensor transfer function is often considered a unitary gain. Moreover, we can identify in (4) the equivalence terms and , between the general second-order equation of the right side and the obtained result of the center side. It allows adjusting the PI controllers as follows:
To tune all PI controllers based on (5), is usually considered [38, Section (5-3)]. However, there are different values of b, , and PI quantities for the distinct controlled variables, as Table 1 shows. Two (2) identical PI regulates the input and output current amplitude components d and q with , as described in (1) and (A7). One (1) PI controls the ACV with as can be seen in (3) and (A14). Four (4) PIs control the intra-CCV imbalance, where from (A14); thus, all components of the vector of are equal , having the same . Finally, also four (4) PI controls the inter-CCV imbalance. However, these have different values of b as described in Table 1, due to from (A14).
The alternating circulating current controller often considers four (4) P controllers adjusted as in (5) but a [23], and our case and .
Finally, for applications of energy transference between the power supply and the load [6,17,22,29], the output current amplitude control would have two PI controllers adjusted as in (5) and considering and .
Remark 1.
It is imperative to know the plant parameters value to adjust the PI controllers, as can be seen in equation (5) and Table 1. This knowledge is usually obtained through extensive testing, which can be time-consuming. It’s also crucial for the controllers to handle plant changes without compromising their effectiveness.
Finally, the output controller must be adjusted as we study pumping applications. Thus, the following P controller called scalar control scheme () is commonly used for a two-level voltage source inverter feeding PMSD-driven centrifugal pumps [32]:
Here, is the rated phase voltage from the motor data plate. is the motor-rated rotor speed in . The is a controller bias or offset (with a value up to of allowing the PMSM to deliver a certain amount of starting torque. The operates from minimum frequency (with a value up to of to the cut-frequency (with a value up to of ) [32].
Remark 2.
In order to attain the desired rotor angular frequency with a ramp-up, a two-level voltage source inverter necessitates a phase stator voltage amplitude of . However, the output voltage required for the M3C is in coordinates, utilizing a Power invariant transformation in lieu of Clarke’s transformation that preserves the amplitude [39]. This paper proposes utilizing equation (6) [32, Equation (1)] in conjunction with the subsequent equation:
The following section will give an overview of an adaptive controller that can maintain optimal performance while adapting to plant changes without requiring knowledge of plant parameters.
2.3. Cascade Adaptive Control Background
M3C modeled as (1) to (3) needs a cascade control system and the following cascade MRAC [36, Equations (14) - (22)] ensures the outputs and tracks the references and :
Here, the outer tracking error is and the inner tracking error is . The variables , are the outer and inner reference model outputs. The set point are and . The reference model parameters are and made equal ( and ) for an exact set point tracking without scaling. The adaptive external and internal controllers and depends on their adaptive parameters and and their corresponding information vectors and . The ideal adaptive parameters are and . The term refers to a vector with all its components equal to one. Besides the model reference parameters, the cascade MRAC has the following tuning parameters: adaptive law fixed-gains and , and adaptive law modification factors and .
Cascade MRAC (8)-(10) applies to time-varying cascade systems of the following form [36]:
where and are the outer and inner output variables, respectively. The inputs are for the outer loop and for the inner loop. Moreover, and are time-varying plant parameters, where and with and the modulus of each element of and .
Remark 3.
It is important to note that the cascade MRAC (8)-(10) uses an outer SISO controller, whereas the M3C outer loop (3) requires a MIMO controller. Additionally, Figure 2 shows that M3C has zero or constant outer references, eliminating the need for the outer reference model of (8), which would slow down the outer loop’s time response. Finally, the inner control loop receives noisy reference input signals with certain switching noise periods. Although the inner reference model of (10) could filter these signals, it would disregard the required inner loop response time, failing to ensure both needs.
These issues are solved by the controller proposed in the following section.
3. Proposal
This section proposes an adaptive controller for the following system that encompasses the M3C state-space model (1)-(3):
where and are the outer and inner output variables, respectively. The outer control input is and the inner is . Moreover, and are time-varying and unknown plant parameters, where and . Here, the matrix and are compose by the modulus of each element of and and are unknown. Furthermore, the matrix and are compose by the sign of each element of and and are known. The known interface nonlinear function is . Finally, and are the inner and outer bounded and unknown disturbances, respectively.
The following Theorem describes the proposal:
Theorem 1.
For systems of the form (12), the following adaptive controller ensures the outputs and tends to the constant references and , respectively:
Here, the outer tracking error is and the inner tracking error is . The variables and are the outer and inner reference model outputs, respectively. The set points are and . The inner and outer controllers and depends on their adaptive parameters and and their corresponding information vectors and . The unknown ideal adaptive parameters are defined as and . Moreover, and are Lyapunov-type energy terms.
Following, the adaptive controller tuning parameters settings are described. The outer APBC loop tunes the outer PB gain as , where is the process required stabilization time [32]. The adaptive law modification term is , depending on the identity matrix of order n. The adaptive law fixed-gain is . Moreover, the fine-tuning scalar factors are , and , with [36, Theorem 1]. Finally, APBC adjusts the adaptive law fixed-gain [32, Equation (11)] as follows:
The inner PBMRAC loop adjusts the model reference parameter as . The PB gain is computed as (over fifteen times faster than the outer loop), and the adaptive law modification terms . Here, are fine-tuning scalar adjusting factors, toguether with , , , where . Finally, the adaptive law fixed-gain is adjusted via the following equation [36]:
Following is the Theorem Proof.
Proof of Theorem 1.
As a result of applying the adaptive controllers (13) and (15) to the corresponding dynamical equation of (11), we obtain the closed-loop dynamical error equations whose require verification of their stability.
In detail, the term is added and subtracted to the right side of the outer loop equation of (11). The outer control law of (13) is then applied, the outer tracking error definition considered, and the terms regrouped conveniently. In regards to the inner loop, we subtract the inner reference model of (15) from the inner loop equation of (11). Later, we add and subtract the term to the right side and consider the inner tracking error definition . Moreover, we apply the inner control law of (15) and regroup terms. As a result, the following control error dynamical equations is obtained:
where and are the adaptive parameters errors. Obtaining now the first-time derivative of and , considering the definitions given in Theorem 1 for , , , and , these errors dynamical equations give:
These closed-loop dynamical error equations (18) and (19) have the following associated Lyapunov function:
Taking the first-time derivative of (20), considering the derivative property of the product in the trace, and replacing the control errors dynamical equations (18), we obtain:
Moreover, using the vector property , we can rewrite the following term . Moreover, we can also re express the term . Finally, considering that and (due to is diagonal), it gives the following expression:
Here, replacing the control parameters errors dynamical equation (19), canceling terms, and taking into account the expressions and , the Lyapunov function first-time derivative becomes:
Here, we have that , , , , and are positives; therefore the first five terms of (23) are negatives. However, although the terms and are also positives, there is nothing we can say about the sign of the last fourth terms of (23) at first sight. Therefore, we re-express equation (23) using some modulus and norm properties.
Using the Frobenius norm definition and the Cauchy–Schwarz inequality, we have that [40, Section 11.2.2]. Moreover, considering a positive A, . Therefore, the following terms become and
. Also, the last fourth terms fulfill ,
,
, and . Finally, using the property [40, Section 11.2.2], and conveniently adding the term to the right side of equation (23), the Lyapunov function first-time derivative (23) becomes:
where the plant parameters and their first-time derivatives are bounded. Therefore, and closed-loop dynamical error equations (18) and (19) are passive outside the region . This last, is the following instability hyper elliptical paraboloid that is compact, closed, and includes the origin:
Furthermore, substituting into (25), the terms and defined in (13) and (15), and using Lyapunov’s second method, we can conclude that the closed-loop dynamical error equations (18) and (19) are bounded outside . Suppose the errors are as minor as possible, resulting in within the instability compact and closed region , including the origin. In that case, they will be pushed back to a stable boundary. In practice, the values of and are chosen so the permanent errors are the possible lowest.
Thus, , and are bounded outside , i.e., outside . Since and are bounded, it implies that and are bounded, as and are bounded references. Moreover, and are bounded, and we have bounded plant parameters, then the adaptive parameters and are bounded, since and . Having all these bounded signals outside , and that , from (18) and (19), we have that Integrating both sides of in the interval , it gives
As V is bounded outside from the right-hand side of this last equation; we have that outside . Furthermore, as and and and , all outside , using Barbalat’s Lemma [34, Section 4.5.2] we have that and , both tend asymptotically to zero outside . Hence, and outside . We do not ensure parameter convergence. This concludes the proof. □
The following section applies the proposed controller to the M3C converter and describes the obtained results.
4. Simulation Results
This section applies the proposed control system shown in Figure 2 to the power topology of Figure 1 with three cells per cluster. It runs on a personal computer, in PLECS 4.7.2. The modeling settings are solver RADAU with variable-step, using a relative tolerance of .
The M3C load corresponds to four equal PMSMs electrically connected in parallel and moving a centrifugal pump each. Table 2 shows the motor-pump parameters.
Here, and are the rated stator voltage and current of the PMSM, respectively. The power factor is and is the electric required frequency of the PMSM for it to run at rated speed. P is the number of pole pairs and is the PMSM rated speed. The PMSM-rated torque and power are and , respectively. Moreover, , and are the resistance and inductance of the motor, is the magnetic flux induced by the motor magnets, is the motor inertia, is the inertia of the load. On the other hand, the load parameters are the initial load torque are zero speed and the constant , characterizing the pump model equation .
The M3C is designed to power these PMSMs-driven centrifugal pumps, having the same . Table 3 presents the plate data and parameters value of the M3C.
The reference capacitor voltage mean value is defined based on the M3C input and output rated voltages and and the number of cells. Here, , been divisible by 3 (number of cells per cluster). Therefore, .
Moreover, the Power supply has the rated voltage , the input frequency , and an input inductance . The load has the rated voltage equals the rated motor voltage , and an output frequency equals rated motor frequency . Finally, we have the cells with switching frequency and a capacitance capacitor C. The cluster coupling inductance is L.
The following two control systems are applied to the M3C-based variable speed drive for multiple PMSM-driven centrifugal pumps for comparison purposes:
The basic control includes sixteen (16) PI controllers, whose settings are calculated based on the definitions provided in equation (5) and Table 1:
-
Input Control:
- -
- One (1) PIs for the ACV Control:
-
- -
- Two (2) PIs for the input cluster line current amplitude direct and quadrature components:
-
CCV Imbalance Control.
- -
- Four (4) PIs for the Intra-CCV Imbalance Control [23, Outer controller of Figure 3]:
-
- -
- Four (4) PIs for the Inter-CCV Imbalance Control [23, Figure 4]:
-
- -
- Four (4) PIs controllers for the circulating current, considering only a P action [23, Inner controller of Figure 3]:
The adaptive control system consists of the following six (6) controllers, which are configured according to the definitions given in equations (13)-(15). These controllers utilize the Lyapunov-type energy terms and . Moreover, all base disturbances and are computed based on the equations (1) and (3) in a stable state (zero first-time-derivatives), considering rated values from Table 3 and unitary parameter values (taking the known disturbance portion).
-
Input Control.
- -
- One (1) APBC (13) for the ACV Control, with:
- -
- One (1) PBMRAC (15) for the input cluster line current, and filtering a 2 KHz reference input noise:
-
CCV Imbalance Control.
-
Output control.
The following sections present the comparative results of the M3C feeding the four PMSMs, each moving a centrifugal pump. The results were obtained with a simulation time of , under the following situations are described: normal operation, input phase imbalance, a cluster cell short-circuit, and an opened cluster cell.
For all cases, the set points in this coordinate are: , , and . Moreover, the reference rotor angular speed is between and , having a ramp up reaching at and kept constant the remaining time.
4.1. Results Under a Normal Operation
Figure 3 shows the comparative results under a normal operation. Here, we operate with the rated input and output voltages.
Figure 3 (a) and (g) demonstrate that the M3C adaptive proposal results in lower input and output current consumption (with a reduction of ) compared to the basis control that utilizes PI controllers. Moreover, the adaptive controllers also exhibit less input current overshoot than the PI controllers.
Figure 3 (b) shows that the proposed M3C adaptive control has a less CCV overshoot (with a reduction) than the basic solution. Both adaptive and basic solutions ensure that the rotor speed follows the reference, as shown in Figure 3 (h).
Regarding the directly controlled variables in double- coordinates, both adaptive and basic solution also follow the reference. However, the adaptive solution has lower overshoots of ACV in Figure 3 (c), input current amplitude in Figure 3 (d), intra and inter CCV Imbalance in Figure 3 (e), circulating current in Figure 3 (f). Moreover the adaptive proposal consumes less input and circulation currents. As for the basic solution, the adaptive one has a noisy input amplitude in double-.
4.2. Results Under an Input Phase Imbalance
Figure 4 displays the comparative results under an input phase imbalance. This first fault considers a drop of of the phase voltage, starting at 3 seconds.
Figure 4 (a) and (g) illustrates that prior to the fault, the M3C adaptive proposal results in lower input and output current consumption, with a reduction of compared to the basis control. The adaptive controllers also show less input current overshoot than the PI controllers. However, during the first second after the fault, the basic solution deteriorated while the adaptive approach recover its better performance faster.
Figure 4 (b) shows that the proposed M3C adaptive control has a less CCV overshoot (with a reduction) than the basic solution, similar to Figure 3 (b). However, the basic solution deteriorated after the fault while the adaptive approach tend to recover its performance.
Figure 4 (h) demonstrates that both the proposal and basic M3C controllers maintain the rotor speed in line with the reference, similar to Figure 3 (d). This is evident even when a fault occurs at the second 3, as it does not affect the pumping speed response.
Regarding the variables in double- coordinates; again, the adaptive solution has lower overshoots of ACV in Figure 3 (c), input current amplitude in Figure 3 (d), intra and inter CCV Imbalance in Figure 3 (e), circulating current in Figure 3 (f). Moreover, the adaptive proposal consumes less input and circulation currents before the fault. After the fault, the adaptive proposal completely recover its performance within in contrast to the basic solution.
4.3. Results Under a Cluster Cell Short Circuit
Figure 5 exhibits the comparative results under a cluster cell short circuit. This fault happens in cell one of the cluster at 3 seconds.
Figure 5 (a) and (g) show that prior to the fault, the M3C adaptive proposal results in lower input and output current consumption, with a reduction of compared to the basis control. However, during the first two seconds after the fault, the basic solution deteriorated and had a increase in input current consumption, increasing by compared to the adaptive approach.
Figure 5 (b) shows that the M3C adaptive control method has a reduction in CCV overshoot compared to the basic solution, reducing . This reduction is similar to the one shown in Figure 3 (b). However, the basic solution demonstrates a quicker CCV to recovery after the fault tending towards the CCV reference of .
Figure 5 (h) demonstrates that both the proposal and basic M3C controllers maintain the rotor speed in line with the reference, similar to Figure 3 (d) and Figure 4 (d). Again. this is observed even after the fault happens at the second 3, which does not have an impact on the pumping speed’s response.
Regarding the variables in double- coordinates; a similar behaviour than shown in Figure 3 is obtained. The adaptive solution has lower overshoots of ACV in Figure 5 (c), input current amplitude in Figure 5 (d), intra and inter CCV Imbalance in Figure 5 (e), and circulating current in Figure 5 (f). After the fault, the adaptive solution completely recover its performance within ; while the basic solution does not.
4.4. Results Under an Opened Cluster Cell
Figure 6 exhibits the comparative results under an opened cluster cell. This fault occurs in cell one of the cluster at 3 seconds.
Figure 6 describes a similar behaviour than in previously described faulty situations. However, both solutions have a lower degradation under this fault.
5. Conclusions
In this study, an adaptive control for an M3C-based variable speed drive powering multiple PMSM-driven centrifugal pumps was proposed. he study found that the adaptive proposal offers better performance and fault tolerance compared to the non-adaptive solution. The first step was to obtain the multivariable M3C state-space model for control, which allowed for the design and implementation of novel MIMO adaptive controllers.
Notably, the paper proposed and applied a novel cascade APBC-PBMRAC to the M3C. Simulation results demonstrate that the proposal and basic M3C controllers ensure the rotor speed follows the reference, even when a fault occurs. However, the proposal has several advantages over the basic solution:
- It reduces the number of non-adaptive PI controllers from thirteen (16) to five (5) MIMO adaptive controllers.
- It is a more straightforward solution that does not require plant parameters knowledge, reducing commissioning time.
- The proposed adaptive control has less overshoots than the basic solution.
- Additionally, it shows a more stable CCV response (less noisy), as expected due to the APBC-PBMRAC design.
- Finally, the basic solution tends to remain degraded after a fault, while the adaptive approach tends to recover quickly from any studied fault.
Author Contributions
Conceptualization, methodology, writing—original draft preparation, and visualization, R.M.-B. and J.C.T.-T.; investigation, formal analysis, supervision, project administration, data curation, and resources and funding acquisition, J.C.T.-T. and M.D.; validation, software, and writing—review and editing; R.M.-B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by FONDECYT Chile, grant 1220168; and FONDEQUIP Chile, grant EQM200234.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The Authors thank Abdiel Ricaldi-Morales for its technical support in the adaptive control implementation
Conflicts of Interest
The authors declare no conflict of interest.
Sample Availability
Not applicable.
Appendix A
This section starts by describing the M3C state-space dynamical model obtaining.
Appendix A.1. Inner control Loop M3C Dynamical model
The M3C inner loop dynamical model involves the following equation, obtained after applying Kirchhoff’s voltage law to the power system of Figure 1 [22, Figure 2], [25] and rearranging terms in a matrix form (for details, please see Appendix A.3):
where L is the coupling inductor inductance shown in Figure 1. Moreover, the instantaneous input phase voltage , cluster phase current , cluster phase voltage , output phase voltage , and neutral voltage are defined as follows:
where , , are the instantaneous phase voltages of the power supply. The instantaneous phase cluster currents and voltages are , , , , , , , , and , , , , , , , , respectively. Finally, , , are the instantaneous load phase voltages.
For independent control, a double- transformation [22] is applied to (A1). It consists in multiplying (A1) by the transform [22] from the left and the right side, with matrix X representing each phase variable , , , , and . As a result, we have:
where the transform [22], the input phase voltage , the cluster phase current , the cluster phase voltage , the output phase voltage , and the neutral voltage are following defined:
Here, , , are the phase voltages of the power supply in double- coordinates. The cluster phase currents and phase voltages in double- coordinates are , , , , , , , , and , , , , , , , , , respectively. Moreover, are the load phase voltages in double- coordinates.
Based on previous equations (A3) and (A4), the obtained decoupled state-space model for the input port, circulating currents, and output port is [6,25]:
with the instantaneous input phase voltage having an input frequency , and the instantaneous output phase voltage having an output frequency . These variables, joined the instantaneous cluster phase currents , , , and the instantaneous cluster voltages , , , are defined as:
Finally, multiplying the Park Transformation P[24] from the left by the input and output phase current equations of (A5), these are converted to their dq coordinates to allow their amplitudes control. The circulating phase current equation of (A5) remains the same for the control of this instantaneous variable. Moreover, we consider the input cluster line current control, related to the phase current as . As a result, the previous model (A5) takes the form:
where the Park Transformation P, the amplitudes of the input phase voltage , output phase voltage , cluster input line current , cluster output phase current , and cluster phase voltages , , all in d-q coordinates, are defined as:
where and are the amplitude components of the input coordinates of the cluster line currents. and are the amplitude components of the power supply phase voltage. and are the amplitude components of the input coordinates of the cluster phase voltages. and are the amplitude components of the output cluster phase currents. and are the amplitude components of the power supply phase voltage. Finally, and are the amplitude components of the output cluster phase voltages. The Park transformation uses for the input signals and for the output signals.
The following section describes the outer-loop M3C dynamical model obtaining.
Appendix A.2. Outer control Loop M3C Dynamical model
The outer loop M3C dynamical model considers the formula of an ideal capacitor instantaneous current , depending on the capacitance C and the capacitor voltage variation of a cell shown in Figure 1. Then, this last expression is re-expressed to obtain the variation rate of the cluster capacitor voltage in terms of the power through a cluster as [22, Equation (8)]. Finally, applying this concept to the M3C, assuming the clusters have three cells (summing their voltage variation expressions), are balanced, and all capacitors are the same, and that the average cluster capacitor voltage fluctuates times around its required value , the following matrix expression is obtained:
The reference cluster capacitor voltage mean value is , where is a multiple of 3 (number of cells per cluster). Moreover, the instantaneous cluster capacitor voltage and cluster power are defined as follows:
where the cluster capacitor instantaneous voltages are , , , , , , , , .
Again, for independent control, a double- transformation [22] is applied to (A9). Thus, (A9) is multiplied by the transform [22] from the left and the right side, with matrix X representing the instantaneous cluster capacitor voltage and the cluster instantaneous power (A10). Then, re-expressing the obtained result in a state space form, we have:
having the following variables definitions:
Here, in double- coordinates are , the cluster capacitor instantaneous voltages components, , , , , , , , and the instantaneous cluster power components are , , , , , , , , , which are clearly defined in [6]. However, there is an issue with the intra-CCV and inter-CCV imbalance control. Every power component could be controlled by controlling certain component of the circulating current (A6) but [6] that would be controlled by as [6]. Therefore, an extra auxiliary transformation is made after multiplying from the left the intra-CCV imbalance equation of (A11) by the matrix [25] as a solution to allow control. Moreover, the power formulas are re-expressed as a function of the phase voltages and phase currents as detailed in [6] separating the control terms from the rest, which are considered as a disturbance. Finally, the state-space form for control takes the following form:
where the auxiliary transformation matrix [25], capacitor voltage , , , the cluster voltage , , , the cluster current , , , and the disturbances , , , are following defined:
where the disturbance terms are obtained from the power expressions [6, Equations (38)-(45)], [22, Equations (17)-(25)], after separating the control terms components. The result gives:
The following section details the different vector and matrix transformations made in the previous state-space model obtaining.
Appendix A.3. Vector and Matrix Transformation Details
This section details the vector and matrix used transformations, starting from the managing feedback signals block located at the right lower side of Figure 2. First, the vector of the cluster capacitor voltages is obtained after summing the capacitor voltages per cell k inside each cluster as follows:
Then, the following rearrangements R are made to convert vectors to the matrix form to allow implementation. It applies to the measurement vectors of the cluster currents and the cluster capacitor voltage :
The matrix X previously obtained results are double- transformed [22]. The right lower side of Figure 2 shows these operations, multiplying X by the transform [22] from the left and right sides. Following, for and , it gives:
Moreover, there are other rearrangements R made to convert the matrix obtained in (A20) and (A21) to their vector form to allow implementation. The resulting vectors are demultiplexed in managing feedback signals block of Figure 2. It delivers the cluster instantaneous phase currents and capacitor voltages defined in (A6) and (A14) (, , , and , , ) as follows:
Additionally, the cluster instantaneous capacitor voltage intra-components are multiplied by the matrix [25]:
The outer signals of the Intra-CCV imbalance control are located at the left-center side of Figure 2. These are multiplied by the matrix to obtain to be sumed with . The result is multiplied by the inverse matrix to obtain the circulating current as follows:
Later, the output signal of the controllers (, , ) are multiplexed, considering , and the obtained vector is rearrangement R in the following matrix form:
The obtained matrix is then multiplied by the inverse transformation matrix [22] from the left and right sides, obtaining the required cluster voltage as follows:
A final rearrangement R is made to convert the obtained matrix to the required voltage vector form as follows:
References
- Beck, M.; Sperlich, A.; Blank, R.; Meyer, E.; Binz, R.; Ernst, M. Increasing energy efficiency in water collection systems by submersible PMSM well pumps. Water 2018, 10, 1310. [Google Scholar] [CrossRef]
- Candelo-Zuluaga, C.; Riba, J.R.; Espinosa, A.G.; Blanch, P.T. Customized PMSM design and optimization methodology for water pumping applications. IEEE Transactions on Energy Conversion 2021, 37, 454–465. [Google Scholar] [CrossRef]
- Kashif, M.; Singh, B. Reduced-Sensor-Based Multistage Model Reference Adaptive Control of PV-Fed PMSM Drive for Water Pump. IEEE Transactions on Industrial Electronics 2022, 70, 3782–3792. [Google Scholar] [CrossRef]
- Kashif, M.; Singh, B. Modified Active-Power MRAS Based Adaptive Control with Reduced Sensors for PMSM Operated Solar Water Pump. IEEE Transactions on Energy Conversion 2022. [Google Scholar] [CrossRef]
- Pires, V.F.; Cordeiro, A.; Foito, D.; Pires, A.J. Fault-tolerant multilevel converter to feed a switched reluctance machine. Machines 2022, 10, 35. [Google Scholar] [CrossRef]
- Diaz, M.; Cardenas, R.; Ibaceta, E.; Mora, A.; Urrutia, M.; Espinoza, M.; Rojas, F.; Wheeler, P. An Overview of Modelling Techniques and Control Strategies for Modular Multilevel Matrix Converters. Energies 2020, 13. [Google Scholar] [CrossRef]
- Kucka, J.; Karwatzki, D.; Mertens, A. AC/AC modular multilevel converters in wind energy applications: Design considerations 2016. pp. 1–10.
- Miura, Y.; Mizutani, T.; Ito, M.; Ise, T. Modular multilevel matrix converter for low frequency AC transmission 2013. pp. 2013, 1079–1084. [Google Scholar]
- Bontemps, P.; Milovanovic, S.; Dujic, D. Performance analysis of energy balancing methods for matrix modular multilevel converters. IEEE Transactions on Power Electronics 2022, 38, 2910–2924. [Google Scholar] [CrossRef]
- Fan, B.; Wang, K.; Wheeler, P.; Gu, C.; Li, Y. An optimal full frequency control strategy for the modular multilevel matrix converter based on predictive control. IEEE Transactions on Power Electronics 2017, 33, 6608–6621. [Google Scholar] [CrossRef]
- Fan, B.; Wang, K.; Wheeler, P.; Gu, C.; Li, Y. A branch current reallocation based energy balancing strategy for the modular multilevel matrix converter operating around equal frequency. IEEE Transactions on Power Electronics 2017, 33, 1105–1117. [Google Scholar] [CrossRef]
- Kawamura, W.; Chen, K.L.; Hagiwara, M.; Akagi, H. A low-speed, high-torque motor drive using a modular multilevel cascade converter based on triple-star bridge cells (MMCC-TSBC). IEEE Transactions on Industry Applications 2015, 51, 3965–3974. [Google Scholar] [CrossRef]
- Wang, C.; Zheng, Z.; Wang, K.; Li, Y. Fault detection and tolerant control of IGBT open-circuit failures in modular multilevel matrix converters. IEEE Journal of Emerging and Selected Topics in Power Electronics 2022, 10, 6714–6727. [Google Scholar] [CrossRef]
- Wang, C.; Zheng, Z.; Wang, K.; Yang, B.; Zhou, P.; Li, Y. Analysis and control of modular multilevel matrix converters under branch fault conditions. IEEE Transactions on Power Electronics 2021, 37, 1682–1699. [Google Scholar] [CrossRef]
- Wang, C.; Zheng, Z.; Wang, K.; Li, Y. Submodule Fault-Tolerant Control of Modular Multilevel Matrix Converters With Adaptive Optimum Common-Mode Voltage Injection. IEEE Transactions on Power Electronics 2022, 37, 7548–7554. [Google Scholar] [CrossRef]
- Erickson, R.W.; Al-Naseem, O.A. A new family of matrix converters 2001. 2, 1515–1520.
- Diaz, M.; Cardenas, R.; Espinoza, M.; Rojas, F.; Mora, A.; Clare, J.C.; Wheeler, P. Control of wind energy conversion systems based on the modular multilevel matrix converter. IEEE Transactions on Industrial Electronics 2017, 64, 8799–8810. [Google Scholar] [CrossRef]
- Diaz, M.; Cárdenas Dobson, R.; Ibaceta, E.; Mora, A.; Urrutia, M.; Espinoza, M.; Rojas, F.; Wheeler, P. An overview of applications of the modular multilevel matrix converter. Energies 2020, 13, 5546. [Google Scholar] [CrossRef]
- Guo, F.; Yu, J.; Ni, Q.; Zhang, Z.; Meng, J.; Wang, Y. Grid-forming control strategy for PMSG wind turbines connected to the low-frequency AC transmission system. Energy Reports 2023, 9, 1464–1472. [Google Scholar] [CrossRef]
- Bravo, P.; Pereda, J.; Merlin, M.M.; Neira, S.; Green, T.C.; Rojas, F. Modular Multilevel Matrix Converter as Solid State Transformer for Medium and High Voltage AC Substations. IEEE Transactions on Power Delivery 2022, 37, 5033–5043. [Google Scholar] [CrossRef]
- Mora, A.; Urrutia, M.; Cárdenas, R.; Angulo, A.; Espinoza, M.; Díaz, M.; Lezana, P. Model-predictive-control-based capacitor voltage balancing strategies for modular multilevel converters. IEEE Transactions on Industrial Electronics 2018, 66, 2432–2443. [Google Scholar] [CrossRef]
- Kawamura, W.; Hagiwara, M.; Akagi, H. Control and experiment of a modular multilevel cascade converter based on triple-star bridge cells. IEEE Transactions on Industry Applications 2014, 50, 3536–3548. [Google Scholar] [CrossRef]
- Diaz, M.; Cardenas, R.; Espinoza, M.; Hackl, C.M.; Rojas, F.; Clare, J.C.; Wheeler, P. Vector control of a modular multilevel matrix converter operating over the full output-frequency range. IEEE Transactions on Industrial Electronics 2018, 66, 5102–5114. [Google Scholar] [CrossRef]
- Park, R.H. Two-reaction theory of synchronous machines generalized method of analysis-part I. Transactions of the American Institute of Electrical Engineers 1929, 48, 716–727. [Google Scholar] [CrossRef]
- Kammerer, F.; Gommeringer, M.; Kolb, J.; Braun, M. Energy balancing of the modular multilevel matrix converter based on a new transformed arm power analysis. 2014 16th European Conference on Power Electronics and Applications; IEEE, 2014; pp. 1–10. [Google Scholar]
- Kawamura, W.; Chiba, Y.; Akagi, H. A broad range of speed control of a permanent magnet synchronous motor driven by a modular multilevel TSBC converter. IEEE Transactions on Industry Applications 2017, 53, 3821–3830. [Google Scholar] [CrossRef]
- Gili, L.C.; Dias, J.C.; Lazzarin, T.B. Review, Challenges and Potential of AC/AC Matrix Converters CMC, MMMC, and M3C. Energies 2022, 15, 9421. [Google Scholar] [CrossRef]
- Fan, B.; Wang, K.; Wheeler, P.; Gu, C.; Li, Y. An optimal full frequency control strategy for the modular multilevel matrix converter based on predictive control. IEEE Transactions on Power Electronics 2017, 33, 6608–6621. [Google Scholar] [CrossRef]
- Duran, A.; Ibaceta, E.; Diaz, M.; Rojas, F.; Cardenas, R.; Chavez, H. Control of a modular multilevel matrix converter for unified power flow controller applications. Energies 2020, 13, 953. [Google Scholar] [CrossRef]
- Kawamura, W.; Hagiwara, M.; Akagi, H.; Tsukakoshi, M.; Nakamura, R.; Kodama, S. AC-Inductors design for a modular multilevel TSBC converter, and performance of a low-speed high-torque motor drive using the converter. IEEE Transactions on Industry Applications 2017, 53, 4718–4729. [Google Scholar] [CrossRef]
- Arias-Esquivel, Y.; Cardenas, R.; Urrutia, M.; Diaz, M.; Tarisciotti, L.; Clare, J.C. Continuous control set model predictive control of a modular multilevel converter for drive applications. IEEE Transactions on Industrial Electronics 2022, 70, 8723–8733. [Google Scholar] [CrossRef]
- Travieso-Torres, J.C.; Vilaragut-Llanes, M.; Costa-Montiel, Á.; Duarte-Mermoud, M.A.; Aguila-Camacho, N.; Contreras-Jara, C.; Álvarez-Gracia, A. New adaptive high starting torque scalar control scheme for induction motors based on passivity. Energies 2020, 13, 1276. [Google Scholar] [CrossRef]
- Zhang, Z.; Jin, Y.; Xu, Z. Modeling and Control of Modular Multilevel Matrix Converter for Low-Frequency AC Transmission. Energies 2023, 16, 3474. [Google Scholar] [CrossRef]
- Narendra, K.S.; Annaswamy, A.M. Stable adaptive systems; Courier Corporation, 2012.
- Travieso-Torres, J.C.; Duarte-Mermoud, M.A.; Sepuleveda, D.I. Passivity-based control for stabilization, regulation and tracking purposes of a class of nonlinear systems. International Journal of adaptive control and signal processing 2007, 21, 582–602. [Google Scholar] [CrossRef]
- Travieso-Torres, J.C.; Ricaldi-Morales, A.; Véliz-Tejo, A.; Leiva-Silva, F. Robust Cascade MRAC for a Hybrid Grid-Connected Renewable Energy System. Processes 2023, 11, 1774. [Google Scholar] [CrossRef]
- Travieso-Torres, J.C.; Duarte-Mermoud, M.A.; Estrada, J.L. Tracking control of cascade systems based on passivity: the non-adaptive and adaptive cases. ISA transactions 2006, 45, 435–445. [Google Scholar] [CrossRef] [PubMed]
- Ogata, K.; et al. Modern control engineering; Prentice hall Upper Saddle River: NJ, 2010; Volume 5. [Google Scholar]
- Clarke, E. Circuit analysis of AC power systems: symmetrical and related components; Wiley, 1943; Volume 1. [Google Scholar]
- Eugene, L.; Kevin, W.; Howe, D. Robust and adaptive control with aerospace applications; Springer: London, England, 2013. [Google Scholar]
Figure 1.
Basic power topology of an M3C for transferring energy between the power supply and the load, which is based on [6,9,19,21,22].
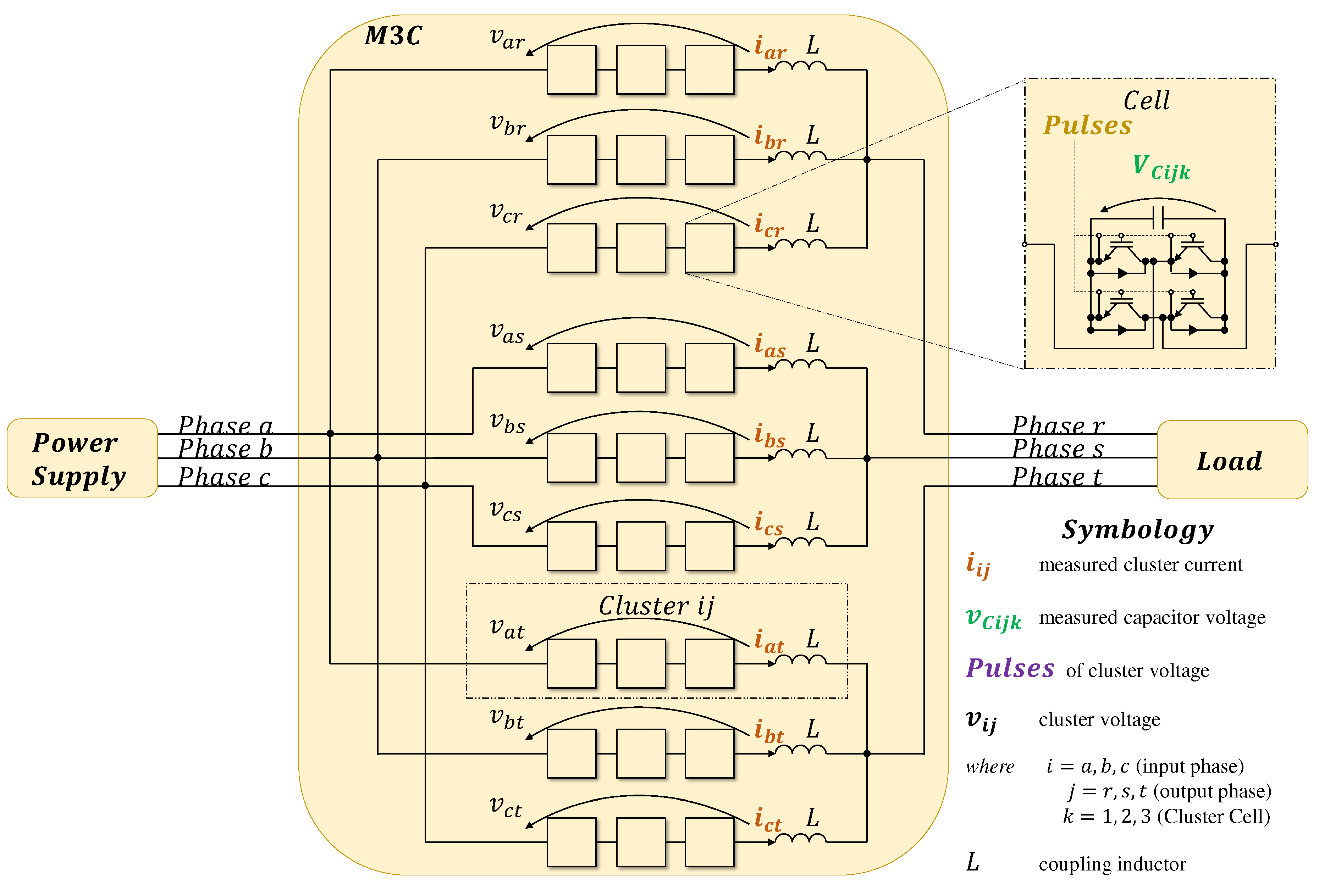
Figure 3.
Comparative results under normal operation, (a) Phase a input current, (b) Branch CCV, (c) Controlled ACV, (d) Controlled d component of the input current amplitude in , (e) Controlled intra and inter CCV imbalance in , (f) Controlled component of the circulating current in , (g) Phase r output current, (h) PMSM angular rotor speed.
Figure 3.
Comparative results under normal operation, (a) Phase a input current, (b) Branch CCV, (c) Controlled ACV, (d) Controlled d component of the input current amplitude in , (e) Controlled intra and inter CCV imbalance in , (f) Controlled component of the circulating current in , (g) Phase r output current, (h) PMSM angular rotor speed.
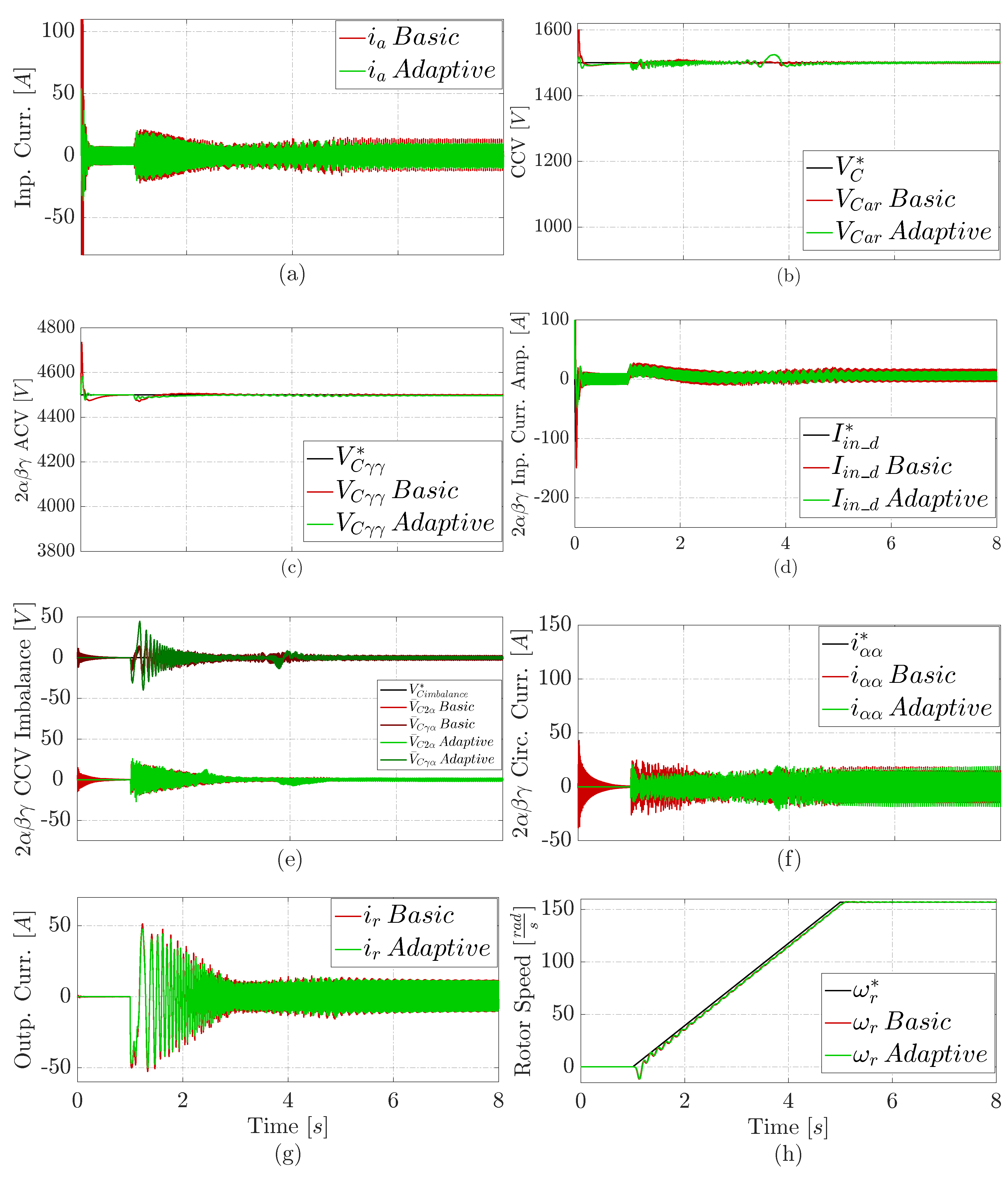
Figure 4.
Comparative results under an input voltage imbalance, with a voltage drop in phase a at 3 seconds, (a) Phase a input current, (b) Branch CCV, (c) Controlled ACV, (d) Controlled d component of the input current amplitude in , (e) Controlled intra and inter CCV imbalance in , (f) Controlled component of the circulating current in , (g) Phase r output current, (h) PMSM angular rotor speed.
Figure 4.
Comparative results under an input voltage imbalance, with a voltage drop in phase a at 3 seconds, (a) Phase a input current, (b) Branch CCV, (c) Controlled ACV, (d) Controlled d component of the input current amplitude in , (e) Controlled intra and inter CCV imbalance in , (f) Controlled component of the circulating current in , (g) Phase r output current, (h) PMSM angular rotor speed.
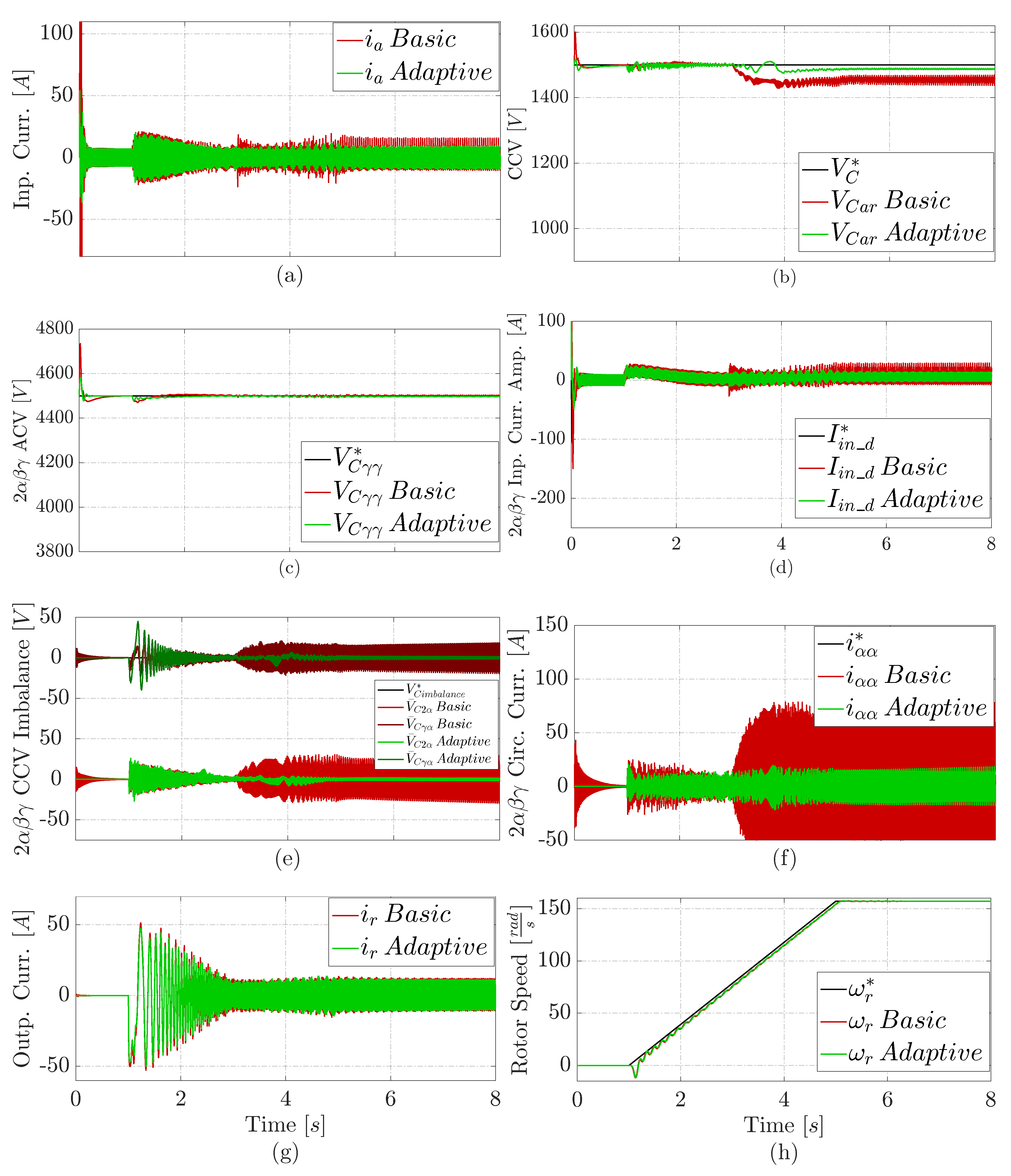
Figure 5.
Comparative results under a cluster short circuit at 3 seconds, (a) Phase a input current, (b) Branch CCV, (c) Controlled ACV, (d) Controlled d component of the input current amplitude in , (e) Controlled intra and inter CCV imbalance in , (f) Controlled component of the circulating current in , (g) Phase r output current, (h) PMSM angular rotor speed.
Figure 5.
Comparative results under a cluster short circuit at 3 seconds, (a) Phase a input current, (b) Branch CCV, (c) Controlled ACV, (d) Controlled d component of the input current amplitude in , (e) Controlled intra and inter CCV imbalance in , (f) Controlled component of the circulating current in , (g) Phase r output current, (h) PMSM angular rotor speed.
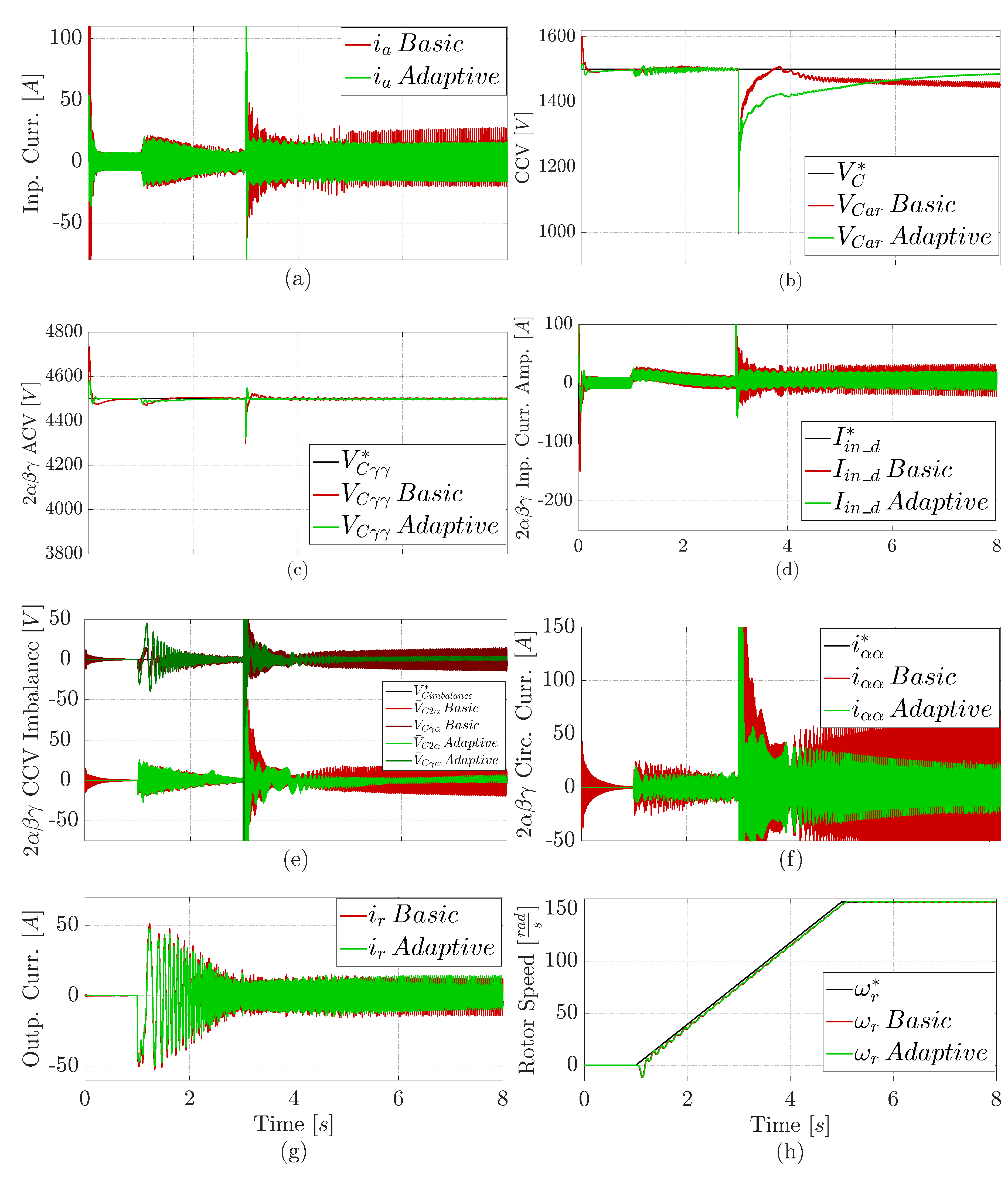
Figure 6.
Comparative results under a cluster open circuit at 3 seconds, (a) Phase a input current, (b) Branch CCV, (c) Controlled ACV, (d) Controlled d component of the input current amplitude in , (e) Controlled intra and inter CCV imbalance in , (f) Controlled component of the circulating current in , (g) Phase r output current, (h) PMSM angular rotor speed.
Figure 6.
Comparative results under a cluster open circuit at 3 seconds, (a) Phase a input current, (b) Branch CCV, (c) Controlled ACV, (d) Controlled d component of the input current amplitude in , (e) Controlled intra and inter CCV imbalance in , (f) Controlled component of the circulating current in , (g) Phase r output current, (h) PMSM angular rotor speed.
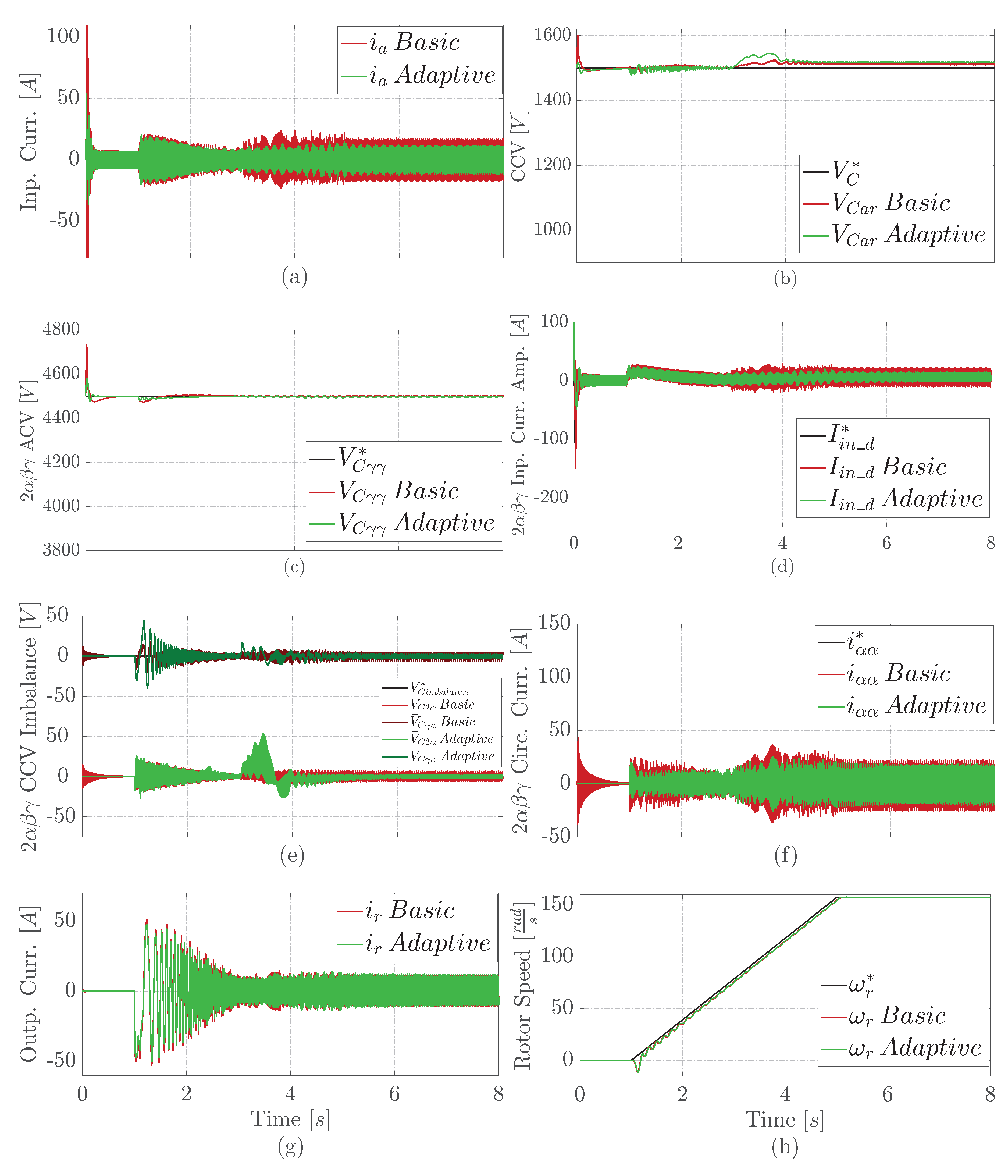
Table 1.
Values of b and for each controller.
| Controller | b | PI Quantity | |
|---|---|---|---|
| Input Current Amplitude Control | 2 | ||
| ACV Control d | (1 Hz) | 1 | |
| Intra-CCV Imbalance Control | (5 Hz) | 4 | |
| Inter-CCV Imbalance Control | (5 Hz) | 1 | |
| Inter-CCV Imbalance Control | (5 Hz) | 1 | |
| Inter-CCV Imbalance Control | (5 Hz) | 2 |
Table 2.
Motor-pump parameters.
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 644 [W] | 4.1 [N-m] | ||
| 165 [V] | 2.65 [A] | ||
| 75 [Hz] | 0.95 | ||
| P | 3 | 0.305 [Wb] | |
| 157.08[rad/s] | 0.0036 [Nms] | ||
| 6.2 [] | 0.0108 [Nms] | ||
| 25.025 [mH] | 93.053 [Kg m] | ||
| 40.17 [mH] | 0.41 [N-m] |
Table 3.
Plate data and parameters value of the M3C.
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 644 [W] | 1500 [V] | ||
| 220 [V] | 165 [V] | ||
| 50 [Hz] | 75 [Hz] | ||
| 1.5 [mH] | L | 1.0 [mH] | |
| 10 [KHz] | C | 3.3 [mF] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated








