Preprint
Article
Short-term Prediction of Multi-energy Loads Based on Copula Correlation Analysis and Model Fusions
Altmetrics
Downloads
68
Views
8
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
02 August 2023
Posted:
03 August 2023
You are already at the latest version
Alerts
Abstract
To improve the accuracy of short-term multi-energy load prediction models for integrated energy systems, the historical development law of the multi-energy loads must be considered. Moreover, understanding the complex coupling correlation of the different loads in the multi-energy systems and accounting for other load-influencing factors, such as weather, may further improve the forecasting performance of such models. In this study, a two-stage fuzzy optimization method is proposed for the feature selection and identification of the multi-energy loads. To enrich the information content of the prediction input feature, we introduced a copula correlation feature analysis in the proposed framework, which extracts the complex dynamic coupling correlation of multi-energy loads and applies Akaike information criterion (AIC) to evaluate the adaptability of the different copula models presented. Furthermore, we combined a NARX neural network with Bayesian optimization and an extreme learning machine model optimized using a genetic algorithm to effectively improve the feature fusion performances of the proposed multi-energy load prediction model. The effectiveness of the proposed short-term prediction model was confirmed by the experimental results obtained using the multi-energy load time-series data of an actual integrated energy system.
Keywords:
Subject: Engineering - Electrical and Electronic Engineering
1. Introduction
The safety, stability, and economic operations of traditional power systems depend on the short-term forecasting of power load, which has been extensively studied [1,2]. Further, other forms of load (cooling, heat, and gas energy) have some established foundations for research, mostly based on the pertinent aspects of this type of loads to conduct a single load prediction work [3,4,5,6,7,8]. The development of short-term load forecasting for integrated energy systems with different energy coupling characteristics is still in its infancy. On the one hand, the nature of the mandates as regards examining the complicated non-linear laws of cross-correlation between the historical development of the load and its influencing elements has not changed. Thus, the short-term prediction of multi-energy loads is implemented as an extension of short-term prediction of loads. On the other hand, the characteristics of energy coupling conversion, distributed energy access, users' flexible demand response, and other random influencing factors must be considered when making short-term predictions of the multi-energy loads. Consequently, further research is needed to improve the short-term multi-energy load prediction for the integrated energy systems [9].
Although traditional feature engineering methods in machine learning have certain advantages, the final interpretability of the obtained load features is not sufficiently straightforward [10,11,12,13]. The Douglas-Peucker (DP) algorithm, which is a classical method for curve feature extraction and compression, has advantages such as high computational efficiency and strong visibility. Thus, it is appropriate for the curve feature extraction and dimensionality reduction of the multi-energy loads. However, setting the threshold of this algorithm imposes certain limitations on the rationality of the feature extraction. This aspect must be sufficiently strengthened to satisfy the actual demand for accurate multi-energy load prediction models. Further, the existing multi-energy load correlation analysis methods mainly deal with the complex and dynamic coupling relationship between the linear and static multi-energy loads, wherein it is sometimes difficult to reflect their close relationship fully. Additionally, compared to the short-term prediction of a single energy load, the computational complexity of the short-term multi-energy load prediction is considerably higher. Hence, simple machine learning models are not suitable for effectively performing short-term multi-energy load prediction tasks. The concept of classical fusion in deep learning can further improve the performance of the multi-energy load prediction systems.
In this study, we developed a short-term prediction method for multi-energy loads based on the copula correlation feature analysis and model fusion. Fuzzy cluster analysis and two-stage fuzzy optimization load feature recognition algorithm were used to extract the features of the electrical, heating, and cooling load sequence data. Further, the principal component analysis (PCA) was used to extract the features from the data, including information on the multi-energy load influencing factors. The optimal dynamic copula correlation between the multi-energy loads was considered an extension feature. Additionally, a non-linear autoregressive exogenous (NARX) model, improved by Bayesian regularization (BR), and an extreme learning machine (ELM) model, improved using a genetic algorithm (GA), were used to improve the performance of the proposed prediction model by model fusion. Lastly, the generalization performance of the proposed model was verified in a short-term multi-energy load prediction task using experimental data.
2. Materials and Methods
2.1. Two-Stage Optimization Method for Features and Extraction for Multi-Energy Loads
In this study, to select the key features of the multi-energy loads, we combined a fuzzy c-means (FCM) [14] with a two-stage fuzzy-improved Douglas-Peucker (TFIDP) algorithm. This method includes a three-step process that can be applied to the feature recognition and extraction of a load. The first step comprises performing FCM clustering on the multi-energy loads. In the second step, based on similar load curves, the DP algorithm improved by a fuzzy optimization threshold performs the initial feature extraction of the load. Finally, by exploiting the concept of the statistical frequency distribution, a second feature extraction process is implemented based on the primary feature extraction.
2.1.1. Initial Feature Extraction Based on a Fuzzy Optimization- enhanced DP Algorithm
The classic DP algorithm extracts the feature points of a curve by setting the threshold value in advance. Further, the algorithm iteratively compares the vertical distance between the points of the updated target curve, first and last points, and set threshold size [15,16,17,18,19]. However, in practical applications, the threshold value needs to be specified using complicated factors that are difficult to quantify. Alternatively, the threshold value should be adjusted adaptively for different original datasets. Hence, it was essential to include an adaptive threshold to improve the TFIDP model.
The threshold value in the classical DP algorithm is usually set in the interval [0,1] based on the experience. For a series of curves with similar shape features, a reasonable threshold value must be set based on practical requirements. Hence, the DP algorithm threshold value can be set using fuzzy mathematics, which describes and models fuzzy concepts accurately to properly solve realistic problems. To improve the classical DP algorithm using the concept of fuzzy mathematics, we introduced a fuzzy optimized threshold value in the DP algorithm, which is the fundamental control standard for the final feature set extraction of curves. Further, by using the fuzzy mathematical concepts to optimize , the curve feature recognition and extraction process performed by the DP algorithm may improve in terms of generalizability.
The threshold value domain is defined as for the DP feature extraction algorithm. To simplify the operation, the threshold can assume a value in the range [0,1] at discrete intervals of 0.1. represents the membership degree of the threshold value of the DP algorithm for a cluster of similar curves and is expressed as follows:
where is the average matching degree between the curve features identified and extracted from the specified similar curve cluster and original curve, thereby reflecting the similarity between them. is the percentage value of the number of curve feature points divided by the number of original curve points, which is the average percentage ratio of the original curve extracted and compressed using curve features. a and b are the corresponding proportion coefficients. The threshold value membership degree in equation (1) comprises the sum of two parts and can be regarded as the overall curve feature extraction satisfaction for the specified similar curve cluster for a certain threshold value.
2.1.1.1. Average matching degree
Because the time dimension of the curve features is reduced compared to that of the original curve, it is no longer a one-to-one mapping relationship. Thus, we introduced the dynamic time warping (DTW) algorithm to calculate the matching degree between the curve features and original curve [20]. DTW is often used in speech recognition tasks to measure the similarity between two-time series with different lengths by calculating the DTW distance.
We define the original and characteristic sequences of the curve as and , respectively, with corresponding sequence lengths and , and the warped length , where ,. To satisfy the continuity and monotonicity at the boundary of the structured path, the main constraints are expressed as follows:
The cumulative distance of the warped length between the original sequence X and feature sequence Y can be calculated using equation (3).
The minimum value of the cumulative distance is reached for the optimal warped length and corresponds, in this case, to the DTW distance , which can be expressed as follows:
Based on the concept of dynamic programming, the cumulative distance of the optimal warped length can be calculated recursively using equation (5). Here, the value of calculated iteratively is equal to the DTW distance between X and Y.
In the limit case, the curve features only include the first and last points of the original curve. Here, we denote the line connecting the first and last points of the original curve as . Further, the between the curve features identified and extracted from the similar curve cluster and original curve is calculated as follows:
where n is the number of curves contained in the current similar curve cluster.
2.1.1.2. Average compression ratio
The average compression ratio between the curve features identified and extracted from the similar curve cluster and original curve is calculated as follows:
where the function represents the amount of data in the obtained sequence.
2.1.1.3. Proportion coefficients a and b
The selection of the proportion coefficients a and b is related to the importance of the terms and in equation (1). In this study, we set a = 0.7 and b = 0.3.
2.1.2. Secondary Feature Extraction Based on Statistical Frequency Distribution
After the DP algorithm based on the fuzzy-optimized threshold completes the initial extraction of the characteristics of all the load curves in a certain load curve cluster, it applies the concept of statistical frequency distribution to extract the overall characteristics of this type of load curve cluster twice. All the non-repeated load characteristics, which are generated in the process of the load feature identification and extraction from a load curve cluster, are denoted as with corresponding frequencies . The statistical frequency of each load characteristic for each load curve cluster can be calculated using equation (8). Equation (9) is used to assess whether this load feature is suitable as one of the overall characteristics for the selected type of load curve cluster. If equation (9) is satisfied, the corresponding is added to the feature number set of the updated load curve cluster, that is, .
Finally, the set obtained using the TFIDP exploiting the properties of the statistical frequency distribution is used as the representative feature of the selected load curve cluster.
2.2. Analysis of Multi-Energy Load Correlation Characteristics Based on the Copula Method
To improve the final prediction accuracy of the short-term multi-energy load forecasting, several aspects must be considered, including the characteristics of the internal load represented by the historical development laws of the multi-energy loads, coupling conversion relationship of the load, characteristics of the external load, and meteorological aspects. Compared to the number of studies on the historical development law of the multi-energy loads and correlation between the multi-energy loads and meteorological factors, only few studies address the characteristics of the complex and flexible coupling conversion of the multi-energy loads. Hence, more accurate characterization methods are needed to effectively optimize the overall performance of the proposed short-term multi-energy load forecasting model. In this study, copula theory is used to model and analyze the correlation characteristics of the non-linear coupling conversion of the time series of the multi-energy loads.
2.2.1. Definition of the Copula Function
The copula theory was developed to solve a joint distribution problem of random variables when their marginal distributions are known. The formulation of Sklar’s theorem introduced the concept of the copula function. Further, models based on the copula function have been widely used in finance and economics, new energy output characteristic analysis, and other fields owing to their ability to explain complex nonlinearities among variables [21,22].
Sklar’s theorem proves that the joint distribution function of multiple n-dimensional variables can be constructed by combining the marginal distribution function of these variables and associated copula function, which represents the complex correlation among variables. Considering an n-dimensional variable with a marginal distribution function in each dimension , the joint distribution and density functions of the n-dimensional variable can be expressed as follows:
where is the joint distribution function of the n-dimensional variable, the copula distribution function representing the complex correlation between n-dimensional variables, the density function of the variable in the dimension, the joint density function of the n-dimensional variable, and the copula density function.
Based on equations (10) and (11), the copula density function can be obtained by taking the derivative of the copula distribution function, as expressed in equation (12).
By calculating the copula distribution and density functions, the complex correlation between the multivariate random variables can be accurately described. Typical static copula distribution functions include N-, T-, Gumbel, Clayton, and Frank copula functions. Additionally, the dynamic N-, T-, Clayton, and SJC copula functions can be used to model dynamic copula distribution functions. Hence, the correlation characteristics of the random variables can be analyzed using different copula distribution functions, which can reflect different perspectives.
2.2.2. Correlation Analysis Based on Copula Functions
Generally, it is difficult to obtain a clear marginal distribution function because of the complexity of the multi-energy load time-series data. Hence, we applied the maximum likelihood estimation based on nonparametric kernel density (MLK) to estimate the correlation coefficient of the copula function [23,24]. The MLK method is not limited by the exact expression of the marginal distribution function. Instead, it uses the nonparametric kernel density estimation function of the analyzed variables.
For the normalized variable sequences Lp and Lc, the corresponding nonparametric kernel density estimation is conducted using the following equations:
where and represent the probability density functions of and , respectively. is the kernel function and T the size of the sequence of variables.
Using the MLK method, the static correlation coefficients can be obtained by substituting the marginal distributions with the probability density functions and in the likelihood function expressed in equation (15). Further, its extreme points can be calculated using equation (16).
However, to calculate the dynamic time-varying correlation coefficient series, a dynamic copula function must be considered. Further, the likelihood function must be obtained using the parameters of the dynamic distributions associated to the variables and corresponding evolution equations. Hence, we define the dynamic N-copula function using the dynamic distribution parameter and dynamic T-copula function with parameters and degrees of freedom. The correlation coefficient matrices of the dynamic N- and T-copula functions based on the DCC(1,1) decomposition can be expressed as follows:
where and its evolution equation is expressed as follows
where and represent the estimated evolution parameters, which satisfy the constraints , and , respectively. is the pseudo-inverse of the threshold distribution function.
The evolution equation of the dynamic Clayton copula function is defined as follows:
where , , and represent the estimated evolution parameters. is the restriction function.
The evolution equation of the dynamic SJC copula function is expressed as follows:
where is the upper-tail dependence coefficient, , , and the estimated parameters of the upper-tail evolution, the lower-tail dependence coefficient, and , , and the estimated parameters of the lower-tail evolution. The restriction function satisfies .
In this study, the Akaike information criterion (AIC) was used to evaluate the adaptability of the different copula models presented above. The AIC index is calculated as follows
where k represents the number of parameters of the copula function and S the associated maximum likelihood estimation.
2.2.3. Analysis of Multi-energy Load Characteristics Based on Copula Methods
The steps of the analysis of the multi-energy loads using the copula method are summarized in Table 1.
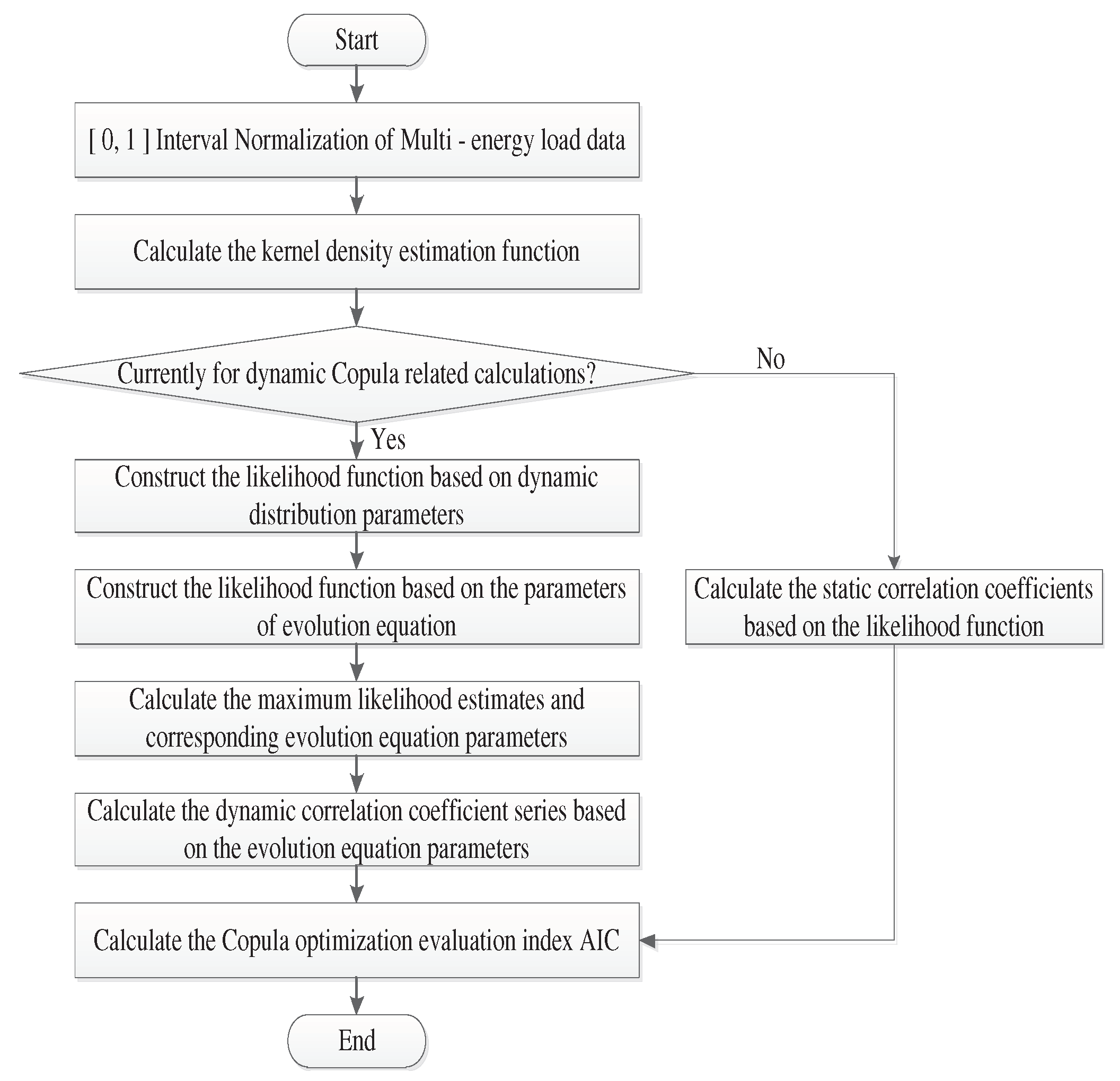
Copula functions can accurately describe the complex non-linear coupling relationship characterizing the multi-energy loads, which can considerably contribute to the improvement of the overall performance of the proposed short-term multi-energy load prediction model. As shown in Figure 1, the copula function-based feature analysis process proposed in this study includes the following steps:
- Multi-energy load data are normalized in the [0,1] interval to ensure data uniformity.
- The kernel density estimation function is calculated using the MLK method, which determines the marginal density function of the variable sequence.
To obtain static correlation coefficients, the marginal density copula functions are used to calculate the extreme points of the likelihood function.
- To obtain dynamic correlation coefficients, the dynamic copula distributions are used to construct the likelihood function considering the corresponding evolution equation parameters (, , and ).
- Once the maximum likelihood estimates and the corresponding evolution equation parameters are obtained, they are substituted into the evolution equation parameters to calculate the required time-varying cross-correlation coefficients.
- Simultaneously, the selected copula functions are optimized based on the maximum likelihood estimate, and later the optimal copula model is obtained by comparing the corresponding AIC indexes.
Figure 1.
Schematic of the copula feature analysis process.
2.3. Short-Term Forecasting Framework for Multi-Energy Loads Based on Model Fusion
The copula function-based analysis can capture effectively the intricate non-linear coupling between multi-energy loads. Using the optimal copula correlation measure, the input feature set of the proposed short-term prediction model for multi-energy loads can be enhanced with the interrelated characteristics of the multi-energy loads.
To further improve the performance of the multi-energy loads forecasting, we developed an approach that exploits model fusion in this study. For the first prediction step, we introduced a Bayesian regularization NARX (BR-NARX) neural network to predict the characteristics of the electrical, heating, and cooling loads. Based on the output of this primary prediction model, the secondary prediction is obtained using a GA-optimized ELM model that returns the final short-term prediction of electricity, heat, and cooling loads. Owing to this two-step process, the characteristics of the multi-energy loads are fully explored, thereby enhancing the accuracy level of the proposed short-term prediction model.
2.3.1. BR-NARX Model
Owing to its reasonable structural performance, the NARX neural network model effectively captures the nonlinearity of the time series. Further, its parallel distribution training mode improves fault tolerance and stability, thereby making this model more competitive than other typical machine learning approaches [25,26]. In this study, we introduced BR to further optimize the performance of the traditional NARX model.
Traditional neural network models often adopt the backpropagation algorithm to adjust network parameters during the training process. Here, the error performance function is usually defined as the sum of the mean squared errors as expressed below:
where is the expected value of the ith actual target, the ith output value predicted by the neural network, the ith absolute error of prediction, and n the total number of input samples trained by the neural network. By introducing the regularization optimization method for weight coefficients and threshold parameters, the performance of the neural network models can be enhanced in terms of limited overall parameter scale and improved generalization ability.
Based on the regularization optimization concept [27], the regularization optimization error performance function of the neural network is modified as follows:
where is the weight coefficient of the neural network, the sum of the squares of weight coefficients, and and the regularization optimization parameters weighting the contribution of and , respectively. The more is restricted, the stronger the generalization performance of the neural network will be. If the purpose of neural network training is to limit the size of network parameters, which may result in large training errors. On the contrary, if , equation (24) describes the typical mean squared error performance function, which may lead to overfitting. However, it is often difficult to practically determine the optimal size of the network parameters ω.
The Bayesian optimization theory, which is based on the Bayesian probability equation, can be used to infer and analyze the unknown regular optimization parameters and based on the expectation value and Bayesian probability estimation of the actual target [28] as expressed below:
where and represent the optimal regular optimization parameters, the minimum point of the network weight coefficient, the Hessian matrix of the BR objective function when the value of is minimal, γ the number of effective parameters of the neural network, and the trace of the matrix. During the neural network training, the regularized optimization parameters and are dynamically adjusted based on the above BR approach, thereby implementing an adaptive learning method that improves the overall generalization ability of the neural network using a limited training dataset. After the objective function is defined, the Levenberg–Marquardt algorithm is used to minimize it.
2.3.2. Combined Genetic Algorithm and Extreme Learning Machine Model
The ELM model introduces the concept of stochastic optimization in neural network applications. In this framework, the connection weights between the input and hidden layers and the bias values of the neurons in the hidden layers can be randomly generated. As opposed to the repeated training and adjustment that is typical of the gradient descent methods, the only parameter that needs to be set in the training of the ELM algorithm is the number of neurons of the hidden layer. The optimal solution under the corresponding conditions can be simply obtained by calculating the generalized inverse matrix, thereby resulting in several application advantages. Hence, the introduction of ELM has considerable advantages in terms of the training performance. However, it is difficult to ensure that the optimal parameters are selected for the actual prediction under the influence of unknown features. Moreover, the generalization ability of the model needs to be further improved.
Figure 2 summarizes the above optimization process of the ELM model using GA. The obtained GA-ELM optimization model represents the output layer of the proposed short-term multi-energy load prediction model.
2.3.3. Overall Modeling Framework
The complete framework of the proposed multi-energy load forecasting model, which was developed using copula function-based feature analysis and model fusion, is shown in Figure 3.
First, the feature extraction of the electrical, heating, and cooling loads series data is performed using the FCM-TFIDP method. Simultaneously, the meteorological and other daily varying relevant factors are extracted using PCA. The joint features obtained using the FCM-TFIDP method are used as the input vector of the BR-NARX layer, which is the first layer of the prediction model, to obtain the first prediction of the electrical, heating, and cooling load features. The output of this layer is then enhanced with the characteristics of the load-influencing factors extracted using PCA and the dynamic correlation characteristics of the optimal copula function. Further, the features are fused and used as the input vector of the GA-ELM prediction model in the second layer. Finally, optimizing the parameters of the entire prediction model gives the optimal prediction model, which is then used to predict the final features of the electrical, heating, and cooling multi-energy loads.
3. Results and Discussion
The original data used for the experiment performed in this study were obtained from the operating load data of the integrated energy system in a similar actual park from August 2019 to October 2020. Particularly, we used the total daily curve data of the electrical, heating, and cooling loads in the energy supply area of the system. The sampling interval of the multi-energy load data was set to 15 min (the daily load curve comprised 96 load points acquired from 00:00 to 23:45). To simplify the analysis, the measurement units of the cooling and heating loads were converted into MW (the unit of the electrical load). The load-influencing factors mainly included the meteorological information and other daily varying information. The meteorological data generally include daily temperature, humidity, air pressure, wind direction and speed. The daily varying data include information on working and rest days, and holidays.
In the proposed framework, data preprocessing is performed to convert the units of the other loads to that of the electrical load. Here, data cleaning is performed on the original data. The data is then normalized to obtain values in the interval [0,1]. Here, we used 80% of the data as the training set and the remaining 20% as the test set to evaluate the prediction performance of the proposed model. The reference input to predict the load at the time t of the day is obtained using the load at moment t that is forward to the adjacent 3 days (considering similar days) and at the times from t – 7 to t – 1 (considering relevant moments) in combination with the other energy load characteristic information of similar days (meteorological information and other daily varying information of similar and forecast days). For our experiment, we used a 3.00 GHz Intel Core I7 with 16 GB memory. The proposed model was implemented using MATLAB R2018b.
3.1. Copula-related Characteristic Analysis Based on Multi-energy Loads
Copula function-based characteristic analysis is considered from the perspective of multi-energy loads. Particularly, it is expected that the correlation between the multi-energy loads and external factors can be reasonably quantified through the optimal copula correlation coefficient under a certain measurement index. Consequently, the new characteristic connotation information can be introduced to provide a better reference, thus improving the accuracy of the proposed multi-energy load prediction model. To exploit the copula function correlation analysis, the optimal copula function between the electrical and cooling load series was selected among eight alternative copula functions based on the AIC criterion and maximum likelihood estimate values reported in Table 1.
The optimal copula function of the multi-energy loads is selected based on the AIC criterion and maximum likelihood estimate. In the optimal condition, the AIC value of the optimal copula function must be as small as possible, whereas the maximum likelihood estimate value must be as large as possible. From Table 1, the optimal copula function of the electrical and cooling loads series based on the selected criteria is the SJC copula function. In fact, its AIC value of –3284.187 is the smallest, and its maximum likelihood estimate value of 1648.263 is the largest among the values of all the other copula functions. Hence, it is reasonable and efficient to choose the SJC copula function to analyze the correlation characteristics of the electrical and cooling loads series.
The above optimization analysis of the copula functions for the electrical–heating and heating–cooling load series shows that the optimal copula functions for the multi-energy load series based on the selected criteria are the SJC copula functions. The SJC copula function reflects the static correlation characteristics of the multi-energy loads and provides an improved representation of their dynamic correlation characteristics. By analyzing the main dynamic distribution parameters and evolution equations of the SJC copula function, it can be observed that the dynamic coefficient of the tail dependence reflects the dynamic relationship of the time series, which is suitable for the extended input of multi-energy load forecasting. Hence, it provides a reference for the prediction model that considers the coupling characteristics of the multi-energy loads.
3.2. Model Parameter
To improve the prediction accuracy of the final prediction model, the parameters of each sub-model were optimized. The key parameters of the proposed model are summarized in Table 2.
For the BR-BARX neural network model in the first layer, a trial optimization method was adopted to determine the number of neurons in the key hidden layer and delay order. For the GA-ELM model in the second layer, the number of neurons in the hidden layer was determined using a method that combines trial optimization and GA algorithms.
3.3. Evaluation of the Model Performance
The performance evaluation metrics of the proposed prediction model adopted in this study include the relative error rate at the ith point of the load prediction, root-mean-squared error of total load prediction, and rate of the mean absolute error , accuracy of prediction , overall mean absolute error of multi-energy loads , and overall prediction accuracy of the multi-energy loads . These metrics are defined in equations (27)–(32), where represents the predicted value of the electrical load at the ith point and the actual value of the electrical load at a similar point. , and represent the rate of the overall mean absolute error of the electrical, heating, and cooling loads, respectively. , , and represent the rate of the overall prediction accuracy of the electrical, heating, and cooling loads, respectively. , , and are the energy allocation proportion coefficients of the electrical, heating, and cooling loads, respectively, which satisfy the relationship . In this study, the ratio coefficient of the electrical, heating, and cooling loads was set to 0.4:0.4:0.2 based on the actual energy configuration of the examined system.
3.4. Results
The daily electrical, heating, and cooling loads in a typical week of September 2020 (Jul. 2020.09.13) are selected as the prediction objects. Using the copula function feature analysis and model fusion layer of the proposed short-term multi-energy load prediction model, the multi-energy load prediction is performed. To analyze the prediction performance of the proposed model, we applied three other models to the collected dataset to compare the multi-energy load predictions in the selected period. The first model (group 1) was obtained considering the modules TFIDP, PCA, and BR-NARX only. The second model (group 2) included a similar module as the first one with the addition of the copula function-based characteristic analysis of the multi-energy loads. The third model (group 3) was obtained by adding to the second one the model fusion method with GA-ELM as the second layer of the prediction model. The fourth comparing model (group 4) was the complete short-term multi-energy load prediction model proposed in this study.
For the quantitative analysis, the metrics presented in Section 3 were used to evaluate the multi-energy load prediction performance of the comparison models. Further, to evaluate the differences in the prediction performance on weekdays and rest days, we performed a separate experiment using the four comparison models to evaluate the utility of the model components objectively and comprehensively.
From the evaluation of the multi-energy load prediction results of weekdays reported in Table 3, the overall effect on the predictions of the electrical and cooling loads is better than that of heating. In fact, the electrical and cooling loads often show a relatively stable evolution trend, while the heating load is driven by random energy demand and has the characteristics of time lag, thereby making the rule of change difficult to control.
Comparing the prediction results of groups 1–3 to those of the complete proposed model (group 4) confirmed that the copula function-based, BR-NARX, and GA-ELM modules fully benefitted from the feature extraction ability of the TFIDP–PCA method. Additionally, the copula correlation coefficient feature is introduced to expand the fusion feature, while the model fusion design is added simultaneously. The GA-ELM strong generalization ability is used for the analytic learning of fusion features. Thus, the prediction accuracy of the multi-energy load forecasting on weekdays is effectively improved.
The results reported in Table 4 show that, on rest days, the variation trend of the multi-energy loads is more random.
Hence, the accuracy of the multi-energy load prediction results on rest days is worse than that on weekdays. However, for the group 4 model, the values of the ERMSE and EMAPE of the cooling load prediction results were lower on rest days than on weekdays. To a certain extent, these results confirm that the proposed model has good generalization and strong anti-fluctuation abilities regardless of the type of day, which proves its practical effectiveness. Figure 4, Figure 5 and Figure 6 show the prediction results of the electrical, heating, and cooling loads of the integrated energy system considered in this study over one week for the four groups, further confirming that the complete prediction model of the multi-energy loads proposed in this study has the best performance. High prediction accuracy was achieved for the electrical and cooling loads by all the groups owing to their relatively stable variation trend. The heating load, which is characterized by a more random variation trend compared to that of the other loads was tracked more effectively by the full model, which provided improved prediction results compared to those obtained by groups 1–3.
By taking full advantage of the feature extraction ability of the TFIDP–PCA method, the improved feature fusion based on the copula correlation coefficient, and characterization of the multi-energy load coupling conversion relationship, the proposed model ensures high-accuracy prediction on both working and rest days, as confirmed by our experimental results.
From the analysis of the experimental results, we can conclude that the introduction of previous knowledge represents a key aspect for the improvement of the prediction accuracy of the multi-energy load forecasting. In fact, the multi-energy load characteristic correlation analysis considerably enhanced the multi-energy load prediction accuracy for the integrated energy system. Additionally, owing to the combined effect of the TFIDP–PCA method and BRNARX model, the proposed short-term prediction model effectively predicts the features of each load of the multi-energy integrated system independently.
4. Conclusions
In this study, the key features of the multi-energy load curves were selected by two-stage load feature identification and extraction. The non-linear coupling relationship of the multi-energy load features obtained using the copula correlation analysis was used to introduce the feature results and enhance the feature input. Further, using the model fusion, the prediction accuracy and performance of the proposed short-term multi-energy load prediction model were enhanced. Our experimental results confirmed that the copula correlation analysis could effectively quantify the coupling relationship of the multi-energy loads. Additionally, the time-varying copula correlation coefficient effectively enhanced the feature input of the multi-energy load prediction model by enriching the associated information content, thereby improving the prediction accuracy of the model. Lastly, by exploiting the model fusion, the advantages of the predictive models with different structures were effectively combined to improve the learning and processing ability for the multi-energy load feature fusion and generalization performance in practical applications of the proposed multi-energy load prediction model.
Funding
This work was supported in part by Guangdong Basic and Applied Basic Research Foundation(2022A1515240074 & 2021A1515012245) and Guangdong Provincial Basic and Applied Basic Research Fund (2022A1515240074).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nti, I.K.; Teimeh, M.; Nyarko-Boateng, O.; Adekoya, A.F. Electricity load forecasting: A systematic review. J Electr Syst Inf Technol. 2020, 7, 1–19. [CrossRef]
- Hammad, M.A.; Jereb, B.; Rosi, B.; Dragan, D. Methods and models for electric load forecasting: A comprehensive review. Logist Supply Chain Sustain Glob Chall. 2020, 11, 51–76. [CrossRef]
- Kim, J.H.; Seong, N.C.; Choi, W. Cooling load forecasting via predictive optimization of a non-linear autoregressive exogenous (NARX) neural network model. Sustainability. 2019, 11, 6535. [CrossRef]
- Fu, G. Deep belief network based ensemble approach for cooling load forecasting of air-conditioning system. Energy. 2018, 148, 269–282. [CrossRef]
- Li, F.; Zheng, H.; Li, X.; Yang, F. Day-ahead city natural gas load forecasting based on decomposition-fusion technique and diversified ensemble learning model. Appl Energy. 2021, 303, 117623. [CrossRef]
- Lu, H.; Azimi, M.; Iseley, T. Short-term load forecasting of urban gas using a hybrid model based on improved fruit fly optimization algorithm and support vector machine. Energy Rep. 2019, 5, 666–677. [CrossRef]
- Zhang, Z.; Liu, Y.; Cao, L.; Si, H. A forecasting method of district heat load based on improved wavelet neural network. J Energy Resour Technol. 2020, 142, 1–29. [CrossRef]
- Kannari, L.; Kiljander, J.; Piira, K.; Piippo, J.; Koponen, P. Building heat demand forecasting by training a common machine learning model with physics-based simulator. Forecasting. 2021, 3, 290–302. [CrossRef]
- Zhu, J.; Dong, H.; Zheng, W.; Li, S.; Huang, Y.; Xi, L. Review and prospect of data-driven techniques for load forecasting in integrated energy systems. Appl Energy. 2022, 321, 119269. [CrossRef]
- Liu, X.; Zhang, Z.; Song, Z. A comparative study of the data-driven day-ahead hourly provincial load forecasting methods: From classical data mining to deep learning. Renew Sustain Energy Rev. 2020, 119, 109632. [CrossRef]
- Chen, J.; Li, T.; Zou, Y.; Wang, G.; Ye, H.; Lv, F. An ensemble feature selection method for short-term electrical load forecasting. In Proceedings of the 2019 IEEE 3rd Conference on Energy Internet and Energy System Integration, 2019; Vol. EI2; pp. 1429–1432. [CrossRef]
- Salami, M.; Sobhani, F.M.; Ghazizadeh, M.S. A hybrid short-term load forecasting model developed by factor and feature selection algorithms using improved grasshopper optimization algorithm and principal component analysis. Electr Eng. 2020, 102, 437–460. [CrossRef]
- Yahaya, A.S.; Javaid, N.; Latif, K.; Rehman, A. An enhanced very short-term load forecasting scheme based on activation function. In International Conference on Computer and Information Sciences (ICCIS); IEEE Publications, 2019; pp. 1–6. [CrossRef]
- Kalkstein, L.S.; Tan, G.; Skindlov, J.A. An evaluation of three clustering procedures for use in synoptic climatological classification. J Climate Appl Meteor. 1987, 26, 717–730. [CrossRef]
- Douglas, D.H.; Peucker, T.K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature. Cartographica. 1973, 10, 112–122. [CrossRef]
- Visvalingam, M.; Whyatt, J.D. The Douglas-Peucker algorithm for line simplification: Re-evaluation through visualization. In Comput Graph Forum. 1990, 9, 213–225. [CrossRef]
- Hershberger, J.; Snoeyink, J. Speeding up the Douglas-Peucker line simplification algorithm. In Proceedings of the 5th International Syrnposium on Spatial Data Handling, 1992; pp. 134–143.
- Hershberger, J.; Snoeyink, J. An O(n log n) implementation of the Douglas-Peucker algorithm for line simplification. In Proceeding of the 10th Annual Symposium on Computational Geometry, 1994; pp. 383–384.
- Wang, J.; Liu, Z. Implementation and analysis of curve vector data compression algorithm. Geom Spat Inf Technol. 2006, 122–124.
- van der Vlist, R.; Taal, C.; Heusdens, R. Tracking recurring patterns in time series using dynamic time warping. In 27th European Signal Processing Conference (EUSIPCO), 2019; pp. 1–5. [CrossRef]
- Luo, M.; Tian, Y.; Li, C.; Chen, Y. The non-linear test and empirically study on the financial crisis contagion based on copula method. In 2nd International Conference on Artificial Intelligence, Management Science and Electronic Commerce (AIMSEC), 2011; pp. 2587–2591.
- Yundai, X.; Yue, Y. Analysis of aggregated wind power dependence based on optimal vine copula. In IEEE Innovative Smart Grid Technologies, Asia, I., Ed.; Asia Publishing, 2019; pp. 1788–1792. [CrossRef]
- Patton, A.J. Modelling asymmetric exchange rate dependence. Int Economic Rev. 2006, 47, 527–556. [CrossRef]
- Patton, A.J. Estimation of multivariate models for time series of possibly different lengths. J Appl Econ. 2006, 21, 147–173. [CrossRef]
- Leontaritis, I.J.; Billings, S.A. Input-output parametric models for non-linear systems part I: Deterministic non-linear systems. Int J Control. 1985, 41, 303–328. [CrossRef]
- Leontaritis, I.J.; Billings, S.A. Input-output parametric models for non-linear systems part II: Stochastic non-linear systems. Int J Control. 1985, 41, 329–344. [CrossRef]
- Wang, H.; Yeung, D.Y. Towards Bayesian deep learning: A framework and some existing methods. IEEE Trans Knowl Data Eng. 2016, 28, 3395–3408. [CrossRef]
- Mackay, D.J.C. Bayesian interpolation. Neural Comput. 1992, 4, 415–447. [CrossRef]
Figure 2.
Schematic of the GA-ELM prediction model execution process.
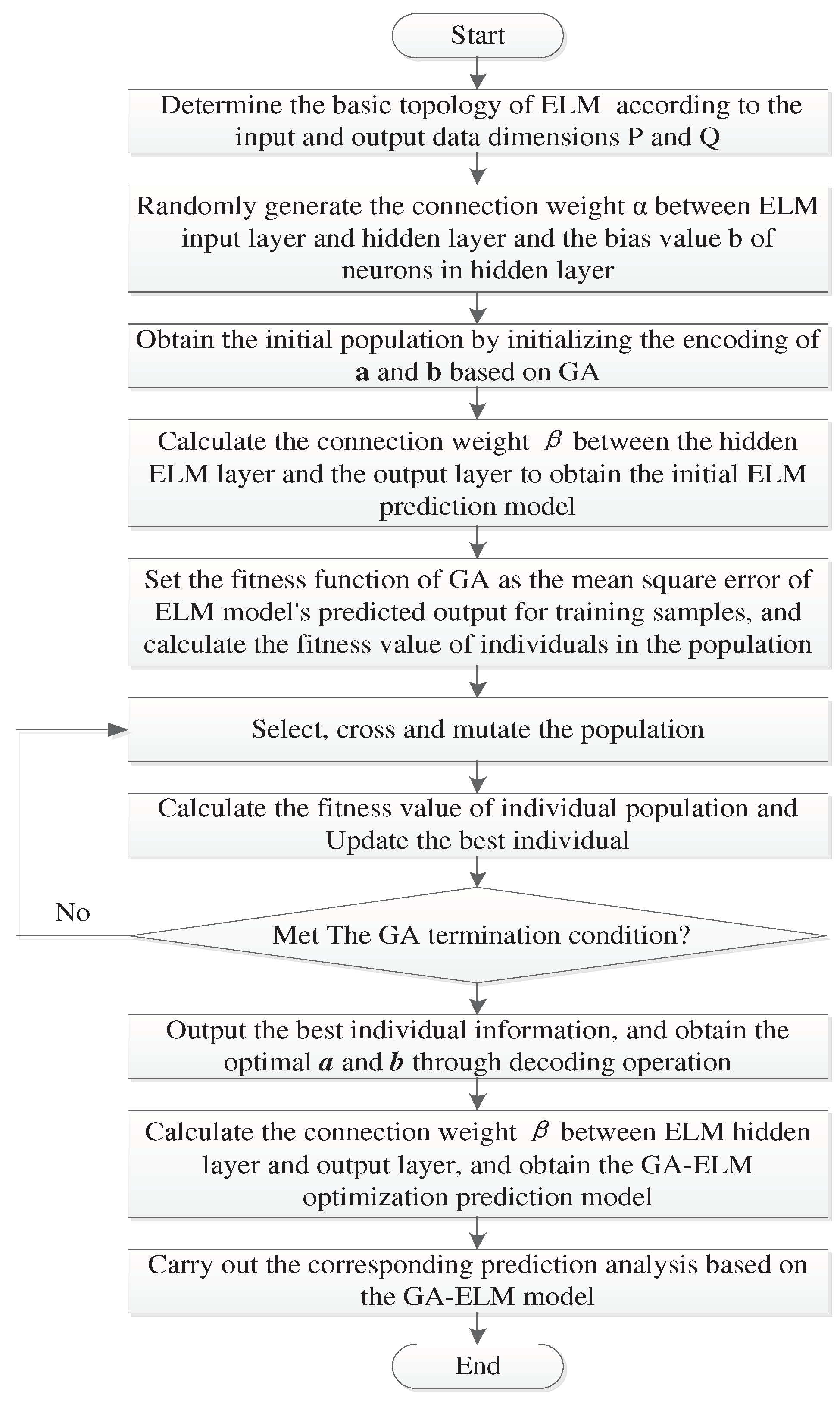
Figure 3.
Flow-chart of the proposed multi-energy load forecasting model.
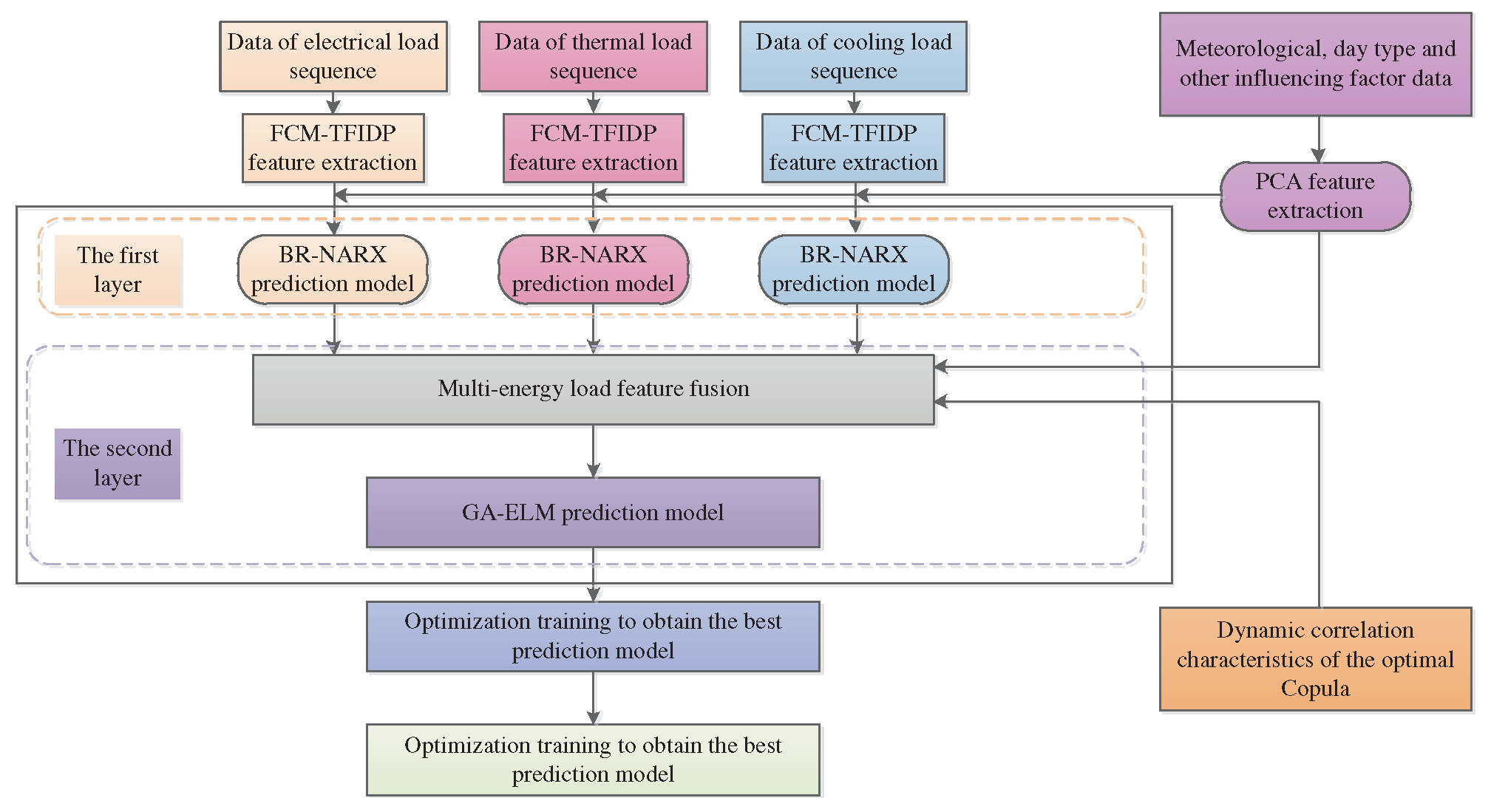
Figure 4.
Weekly electrical load forecast results.
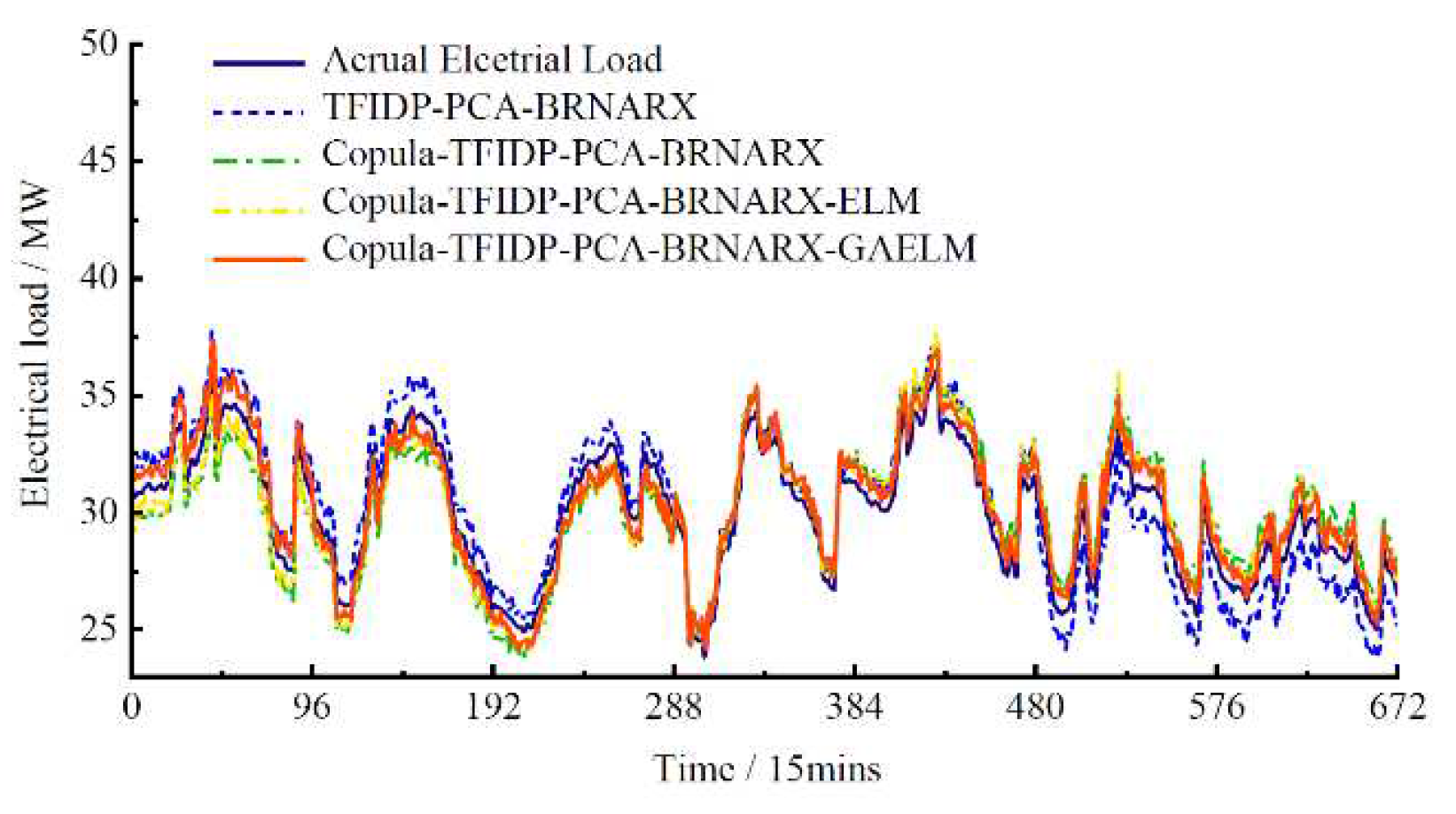
Figure 5.
Weekly heating load forecast results.
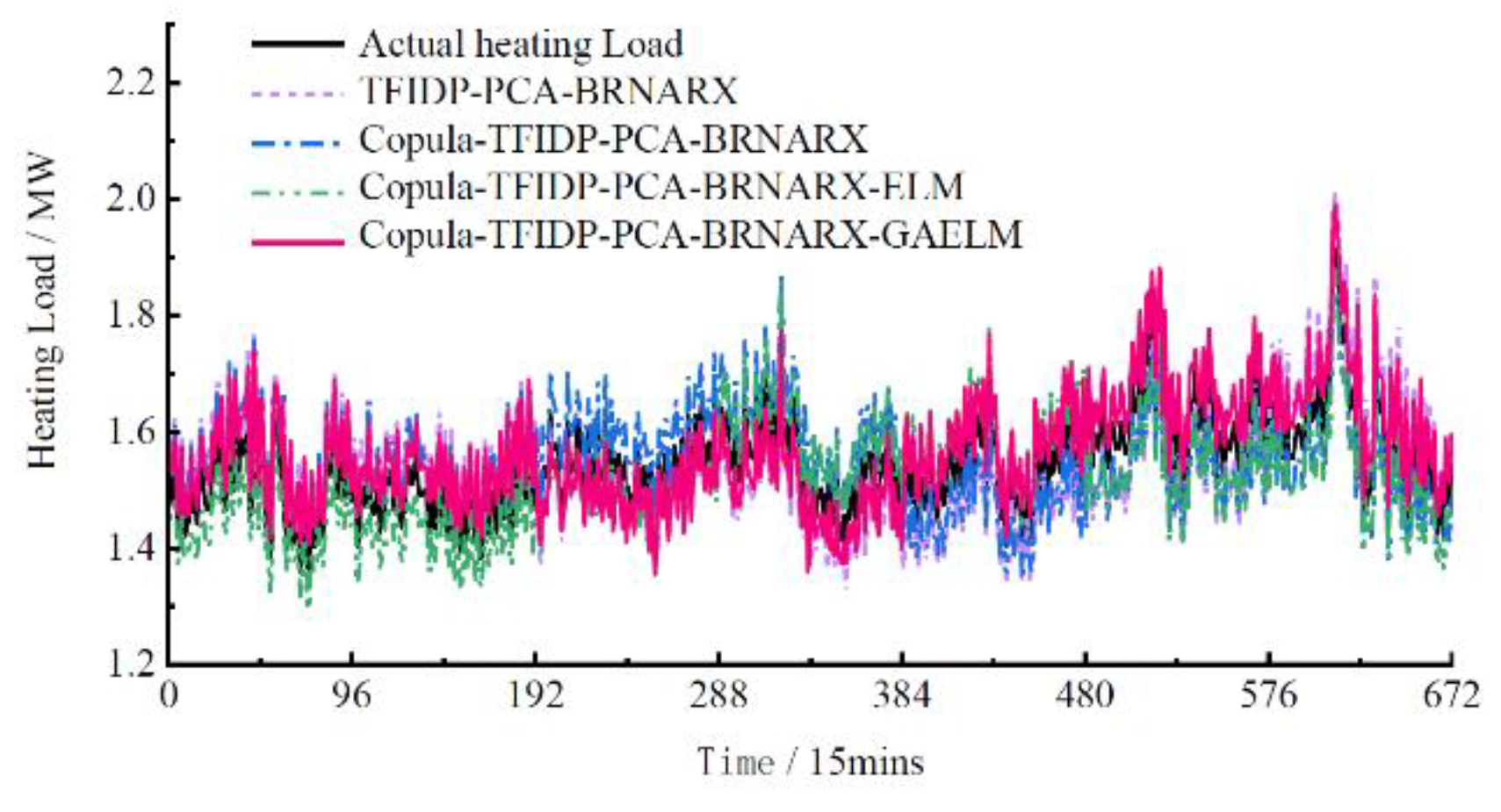
Figure 6.
Weekly cooling load forecast results.
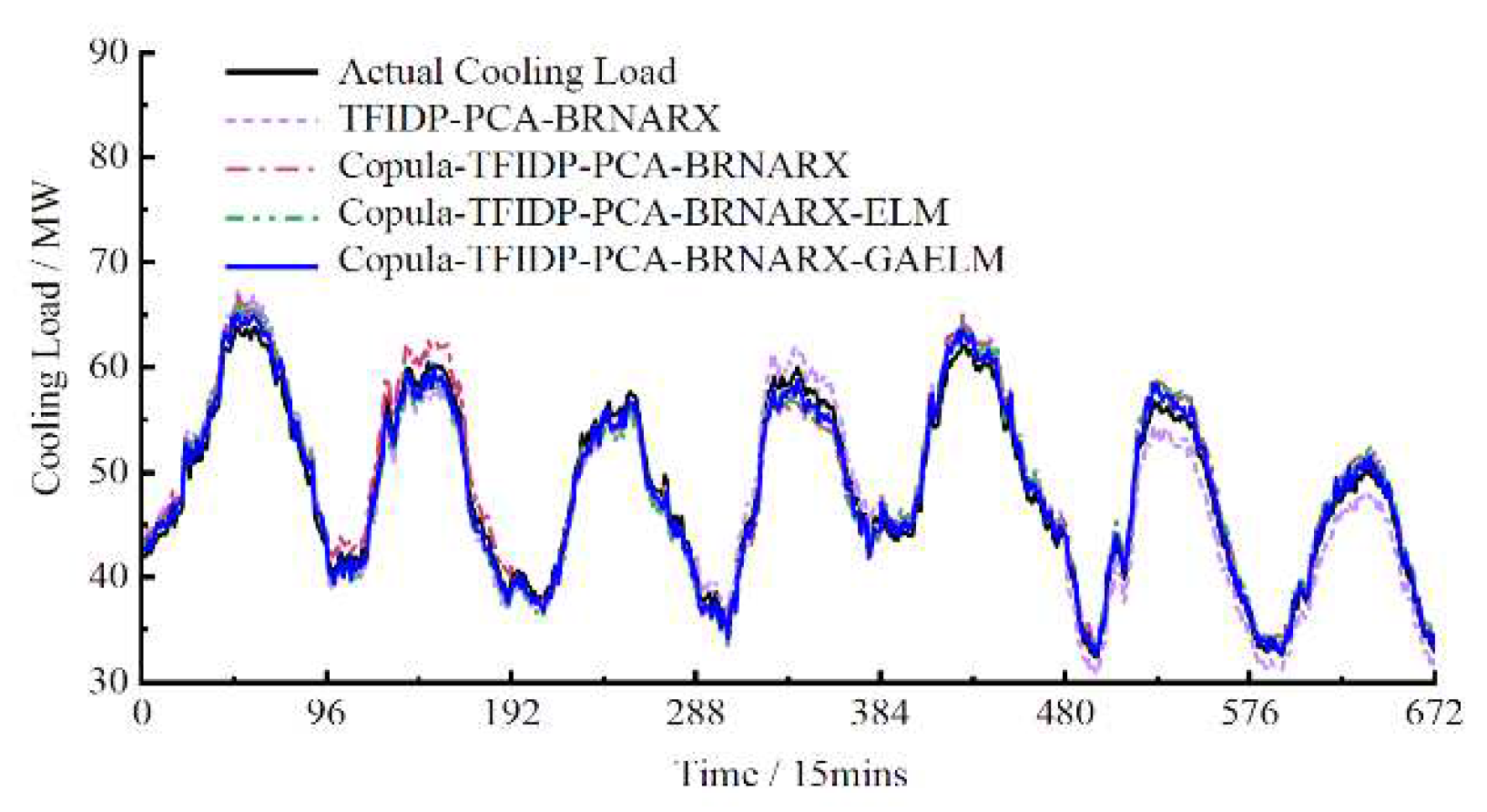
Table 1.
Performance comparison of copula functions (obtained for electrical and cooling loads data) based on the AIC and maximum likelihood estimate values.
Table 1.
Performance comparison of copula functions (obtained for electrical and cooling loads data) based on the AIC and maximum likelihood estimate values.
| Types of copula function | AIC | Maximum likelihood estimate |
| Static N-copula | 553.458 | -311.165 |
| Dynamic N-copula | -1725.336 | 851.325 |
| Static T-copula | 366.878 | -197.563 |
| Dynamic T-copula | -1935.928 | 937.112 |
| Static Clayton copula | 627.436 | -407.601 |
| Dynamic Clayton copula | -2817.727 | 1329.752 |
| Static SJC copula | -1622.901 | 677.244 |
| Dynamic SJC copula | -3284.187 | 1648.263 |
Table 2.
Key parameters of the model components.
| Model | Parameter | Parameter settings |
| BR-NARX | Total number of layers | 3 |
| Number of neurons in hidden layer | 18 | |
| Order of time delay | 7 | |
| GA | Population size | 40 |
| Number of iterations | 200 | |
| Crossover probability | 0.85 | |
| Mutation probability | 0.1 | |
| ELM | Number of neurons in input layer | 190 |
| Number of neurons in hidden layer | 25 | |
| Number of neurons in output layer | 96 |
Table 3.
Performance metric evaluation of the multi-energy load prediction results on weekdays.
| Evaluation index |
ERMSE (electrical/ heating/cooling) (MW) |
EMAPE (electrical/ heating/cooling) (%) |
ESUMMAPE (%) |
AccSUM (%) |
|
| Prediction model | |||||
| Group 1 | 1.077/0.066/1.816 | 3.280/4.212/3.411 | 3.519 | 96.329 | |
| Group 2 | 1.078/0.065/1.761 | 3.340/4.137/3.301 | 3.484 | 96.381 | |
| Group 3 | 0.928/0.053/1.533 | 2.831/3.411/2.905 | 2.977 | 96.892 | |
| Group 4 | 0.747/0.047/1.101 | 2.268/2.962/1.998 | 2.299 | 97.544 | |
Table 4.
Performance metric evaluation of multi-energy load prediction results on rest days.
| Evaluation index | ERMSE (electrical/ heating/cooling) (MW) |
EMAPE (electrical/ heating/cooling)(%) |
ESUMMAPE (%) |
AccSUM (%) |
|
| Prediction model |
|||||
| Group 1 | 1.390/0.078/2.044 | 4.811/4.751/4.596 | 4.713 | 95.199 | |
| Group 2 | 1.320/0.070/1.669 | 4.590/4.267/3.667 | 4.156 | 95.760 | |
| Group 3 | 0.975/0.074/1.488 | 3.308/4.483/3.276 | 3.530 | 96.371 | |
| Group 4 | 0.816/0.053/0.870 | 2.725/3.189/1.705 | 2.410 | 97.431 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





