Prerpints.org logo
Preprint
Article

Shaped-based Tightly Coupled IMU/Camera Object-level SLAM

Altmetrics

Downloads

151

Views

90

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

02 August 2023

Posted:

03 August 2023

You are already at the latest version

Alerts
Abstract
Object-level Simultaneous Localization and Mapping (SLAM) has gained popularity in recent years since it can provide a means for intelligent robot-to-environment interactions. However, most of these methods assume that the distribution of the errors is gaussian. This assumption is not valid under many circumstances. Further, these methods use a delayed initialization of the objects in the map. During this delayed period, the solution relies on the motion model provided by an Inertial Measurement Unit (IMU). Unfortunately, the errors tend to accumulate quickly due to the dead-reckoning nature of these motion models. Finally, the current solutions depend on a set of salient features on the object’s surface and not the object’s shape. This research proposes an accurate object-level solution to the SLAM problem with a 4.1 to 13.1 cm error in the position (0.005 to 0.021 of the total path). The developed solution is based on Rao-blackwellized Particle Filtering (RBPF) that does not assume any predefined error distribution for the parameters. Further, the solution relies on the shape and thus can be used for objects that lack texture on their surface. Finally, the developed tightly coupled IMU/camera solution is based on an undelayed initialization of the objects in the map.
Keywords: 
Subject: Engineering  -   Other

1. Introduction

The classical solutions to the SLAM problem rely on geometrical primitives (such as points, lines and planes) [1,2,3]. However, one of the challenges with these approaches is that such simple forms cannot be used for intelligent interactions of the robot with the environment. More recently, object-level methods are emerging as an alternative solution to the SLAM problem. In contrast to the classical methods, object-level solutions seek to represent the map of the environment using semantic objects. However, objects, unlike simpler geometrical forms, often are more difficult to represent, detect and track. Therefore, novel techniques and solutions are required to incorporate objects into the solution for the SLAM problem.
The state-of-the-art object-level solutions can be categorized based on different criteria. One possible categorization is based on the individual components. Such components include object detection/segmentation, object representation, and object-based pose estimation. Further, the solutions can be categorized based on the localization and mapping frameworks. In the following, the current research gaps and an overview of the developed object-level solution are provided.

1.1. Object-Level Mapping and Localization Framework

The earliest solutions to the object-level SLAM were based on Extended Kalman Filtering (EKF) [4,5,6]. One challenge with the EKF is that as a Dynamic Bayesian Filtering (DBF) method, this method processes the observations one at a time. Therefore, the propagation of error can lead to a reduction in the accuracy of the estimation. In order to address this challenge, more recent object-level solutions relied on the frontend/backend paradigm. In the frontend, an initial estimate of the solution is obtained using DBN or other techniques (one possible alternative to the DBN is to use keyframe-based Local Bundle Adjustment (LBA) [7]). The initial solution is further optimized in the backend using Global Bundle Adjustment (GBA), Factor Graphs (FG) [8], and others.
Current frameworks for object-level solutions can be categorized into two groups. The first group uses the obtained semantic information of the objects of interest to increase the accuracy of the classical solutions. A possible improvement can be achieved by using semantic information to improve the data correspondence. For example, in classical solutions to the SLAM problem, features such as FAST and Rotated BRIEF (ORB)[9] and Scale Invariant Feature Transformation (SIFT) [10] are often used for data correspondence. In some scenarios, false correspondence can occur if the two features have an identical visual signature but do not correspond to the same landmark on the map. However, in most cases, these features are detected on different objects. Therefore, adding a processing step of object class detection can result in avoiding false correspondences. Methods in this first group object-level solutions often use LBA in the frontend and FG [11,12,13] in the backend. These approaches only use semantic information to improve the classical approaches and, therefore, can be considered an extension of the classical solutions to the SLAM problem.
In the second group of solutions, the mapping and localization are performed by relying on the objects only. In these methods, the objects are inserted into the map with Six Degrees of Freedom (6DoF). In this category, methods have represented the objects in the map using ellipsoids [14,15], cuboids [18], and other forms. The geometrical forms of representation, such as ellipsoids, have the advantages that they can provide a simple observation model (defined as the mathematical model of the observations and the parameters to be estimated). Such models can be easily integrated into the process of FG [16] and GBA [17,18]. However, most of the current methods in the second group rely on an initially estimated position using classical solutions such as ORB SLAM [19].
Both groups of solutions assume that often the errors are gaussian or can be approximated as a gaussian distribution. However, the gaussian error assumption is not suitable in many circumstances. Due to this issue, the classical solutions to the SLAM problem, such as EKF-SLAM [20] and EIF-SLAM [21], were replaced with PF-SLAM [22], which does not depend on any assumptions about the distribution of the errors. Further, the efficiency of the PF-SLAM was later improved by the introduction of RBPF-SLAM [23,24]. In RBPF-SLAM for a given particle, the errors in the pose of the landmark (here object) are not correlated, thus reducing the computational cost of the algorithm greatly. RBPF-SLAM was originally implemented using rangefinders [23,24]. However, later its usage is extended to monocular cameras as well. These implementations use points [25], lines [26], and more recently, objects [27]. The developed RBPF-SLAM solution in this paper is closest to the method in [27]. Later in this section, the main differences between our method and the method in [27] are going to be highlighted.
One of the most important sensors nowadays is the monocular camera. This sensor provides abundant radiometric information (e.g., colour) and is often included in many platforms, such as mobile wheeled robots and handheld devices. The monocular camera suffers from scale ambiguity. Due to this ambiguity, this type of camera cannot observe the distance from the object of interest and, more importantly, cannot estimate the trajectory with a real scale. In order to resolve this ambiguity, the monocular camera should be fused with other sensors. One possible solution is to fuse this sensor with an IMU [28]. The developed object-level RBPF solution in this paper utilizes an IMU to predict the position of the particles in the next frame, while the images obtained using a monocular camera are used to update the weight of the particles. The sensor fusion is achieved in a tightly coupled fashion where the particle weighing is directly performed using the observation likelihood.
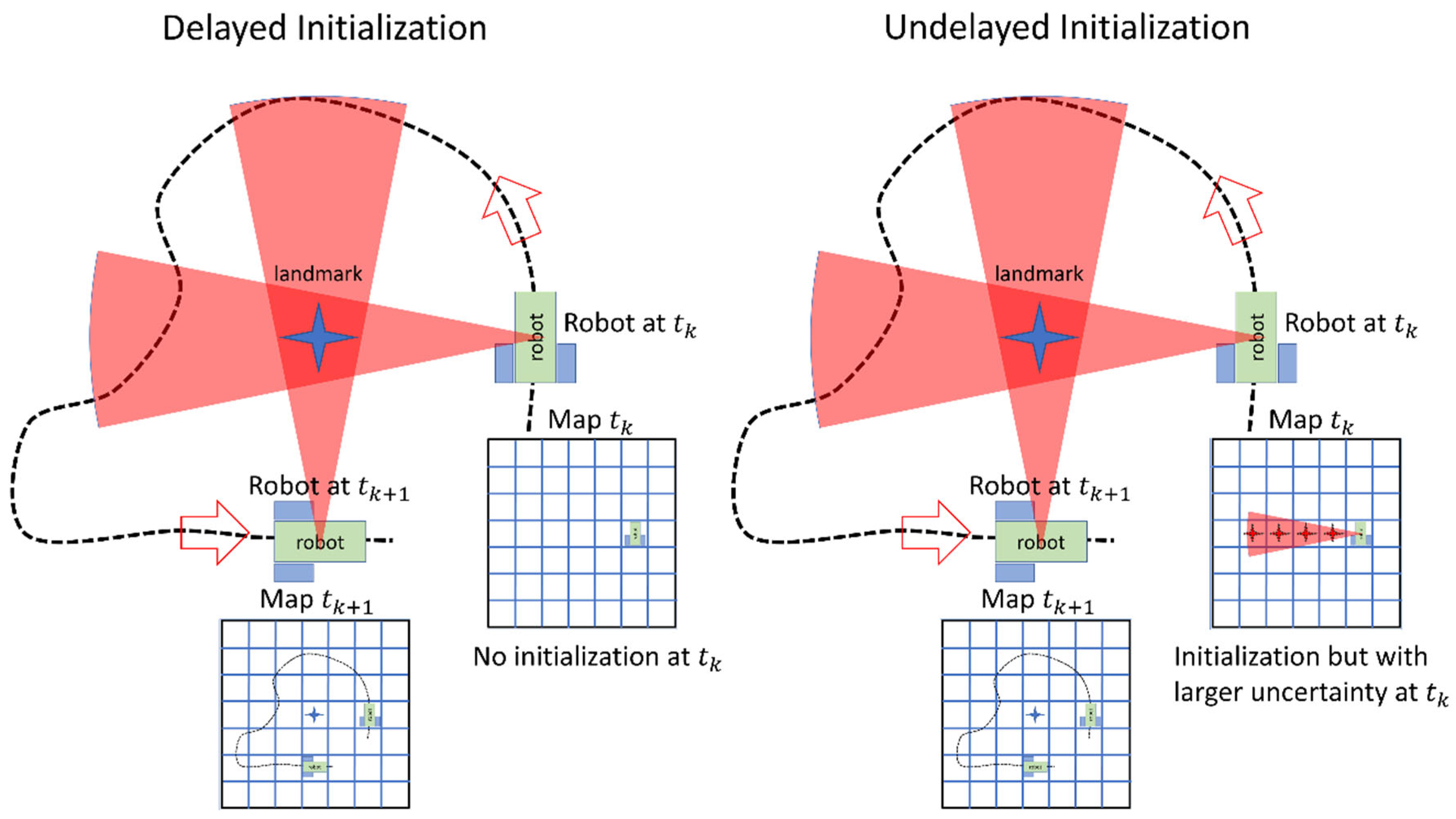
Unfortunately, the fusion of the IMU and the monocular cannot resolve the scale ambiguity using only a single observation. Thus, the observed landmarks (e.g., points, lines, objects) for the first time in the images cannot be inserted into the map with low uncertainty. In order to address this issue, delayed initialization has developed in the past [29,30,31]. In the delay initialization, the landmarks should be observed from different viewpoints. During the delayed period, the solution should remain dependent on the other sensors (e.g., IMU) if such sensors are available. If no other sensor is available, the solution should rely on a motion model heuristic (e.g., constant velocity [30]). Both types of solutions will result in the accumulation of errors typical of dead reckoning systems.
In order to address this issue, undelayed initialization methods have also been proposed in the past [32,33,34,35]. In the undelayed initialization, the landmark is inserted into the map with large uncertainty using the first image that is observed. It is reported that undelayed initialization can be used to provide a partial update to the estimated position and thus improve the accuracy of the trajectory estimation [25]. The two approaches are compared in Figure 1. In this figure, for the delayed initialization, the landmark cannot be inserted into robot’s map using one observation at a single epoch ( t k ). Thus, the initialization should be delayed until the object is also observed from a different viewpoint (such as t k + 1 ). During this period, no updates are available to the robot’s trajectory using the observations. In contrast, in the undelayed initialization, the landmark is inserted into the map in the first frame that they are observed ( t k ). As the robot moves and observes the object of interest, the uncertainty in the location of the landmark can decrease. The challenge with undelayed initialization is that uncertainty of the pose of the landmark is very large initially, and thus, a large number of particles are required to be sampled to ensure high accuracy of the estimation. In this research, a novel undelayed initialization is developed. The initialization of the object uses deep learning-based pose estimation to reduce the uncertainty in the device’s pose to an unknown distance of the camera from the objects. Further objects, unlike geometrical primitives (such as points, lines, and planes), can be assumed to have approximately known dimensions. Such an assumption helps reduce the scale ambiguity. This is explained more in Section 2.4.
The abovementioned methods rely on other important components in the object-level SLAM. One of these components is object representation. In this research work, the objects are represented using their shapes. The advantage of this approach over the state-of-the-art is explained in the following.

1.2. Object Representation

Object representation refers to prior information about the appearance and/or the shape of an object. The representation is required in many other components of an object-level SLAM. For example, object pose estimation is often performed by matching the detected/segmented object to this representation. One of the more ubiquitous solutions in object-level solutions is a representation using simpler geometrical shapes such as ellipsoids [15], cuboids [18], and others. These geometrical shapes provide the advantage of a simple observation model. However, these simpler shapes cannot represent most objects accurately. In contrast to the beforementioned methods, the objects can also be represented using detailed modelling. The solutions that have utilized these models can be categorized into two groups: online modelling and offline modelling. In the online methods, the model of the object is jointing estimated with the solution to the SLAM [36]. These approaches are computationally very costly.
In contrast, in offline methods, a representation of the object is built prior to the experiments. The offline methods can be divided into two subgroups: instance-based and category-based. The instance-based method model a specific instance of an object (such as an instance of a chair) [37,38,39], while the class-based method represents many objects belonging to the same class (such as the class of all chairs) [40,41].
The abovementioned method depends on a very simplistic representation of the object, or they rely on the object’s surface texture (the texture is the changes in the hue and intensity of the colour on the object’s surface, which can help identify salient features on the object’s surface). Unfortunately, in real-life scenarios, most objects do not have texture on their surface. Further, the object’s texture appearance can vary significantly due to the illumination conditions of the room. Finally, only a Computer-Aided Design (CAD) model of the objects is often available during the offline phase (when the representations are built), and such models often do not have an associated texture.
In contrast to the abovementioned method, alternative object representation techniques have been proposed in the past that depend on the detailed shape of the objects. The objects’ shapes, in these approaches, are represented using volumetric voxel girds [42,43] and implicit/ explicit parameterization [44,45]. However, such representation is not useful for monocular SLAM, as it is challenging to match the 3D shapes to the 2D contour segmented in the image. Thus, methods that represent the object as a set of 2D contours are preferred for monocular-camera-based solutions to the SLAM [46]. Such sets are built by capturing objects from different viewpoints. Unfortunately, object representation using images lacks robustness to the in-plane translation, rotation, and scale. Such geometrical variations are anticipated to be encountered when matching the segmented object in the image to the object representation. In order to address this issue, the 2D images of the objects are transformed into parameterized 2D contours known as shape-prior sets [47]. It is shown that these shape sets are capable of providing coarse pose estimation for objects in the camera frame. In this research, the method in [47] is used for object representation. Representing the object using the shape requires a novel approach to particle weighting and landmark initialization. This will be explained in detail in Section 2.2 and 2.3.
In summary, the developed solution in this research work is an object-level solution to the SLAM. This solution relies on RBPF and thus does not assume any errors in the distribution of the parameters (i.e., the poses of the device and objects). Further, the developed solution is based on the shape of the object. Finally, the objects are inserted into the map using undelayed initialization. The implementation of the RBPF-SLAM is proposed based on tightly coupled integration using a monocular camera and IMU for the first time. In this integration, particle weighting is performed directly using the observations. In Section 2, the methodology of the developed solution is provided in detail. In Section 3, the results are provided. In Section 4, the conclusions and pointers for further developments in the future are given.

2. Methodology

2.1. Overview

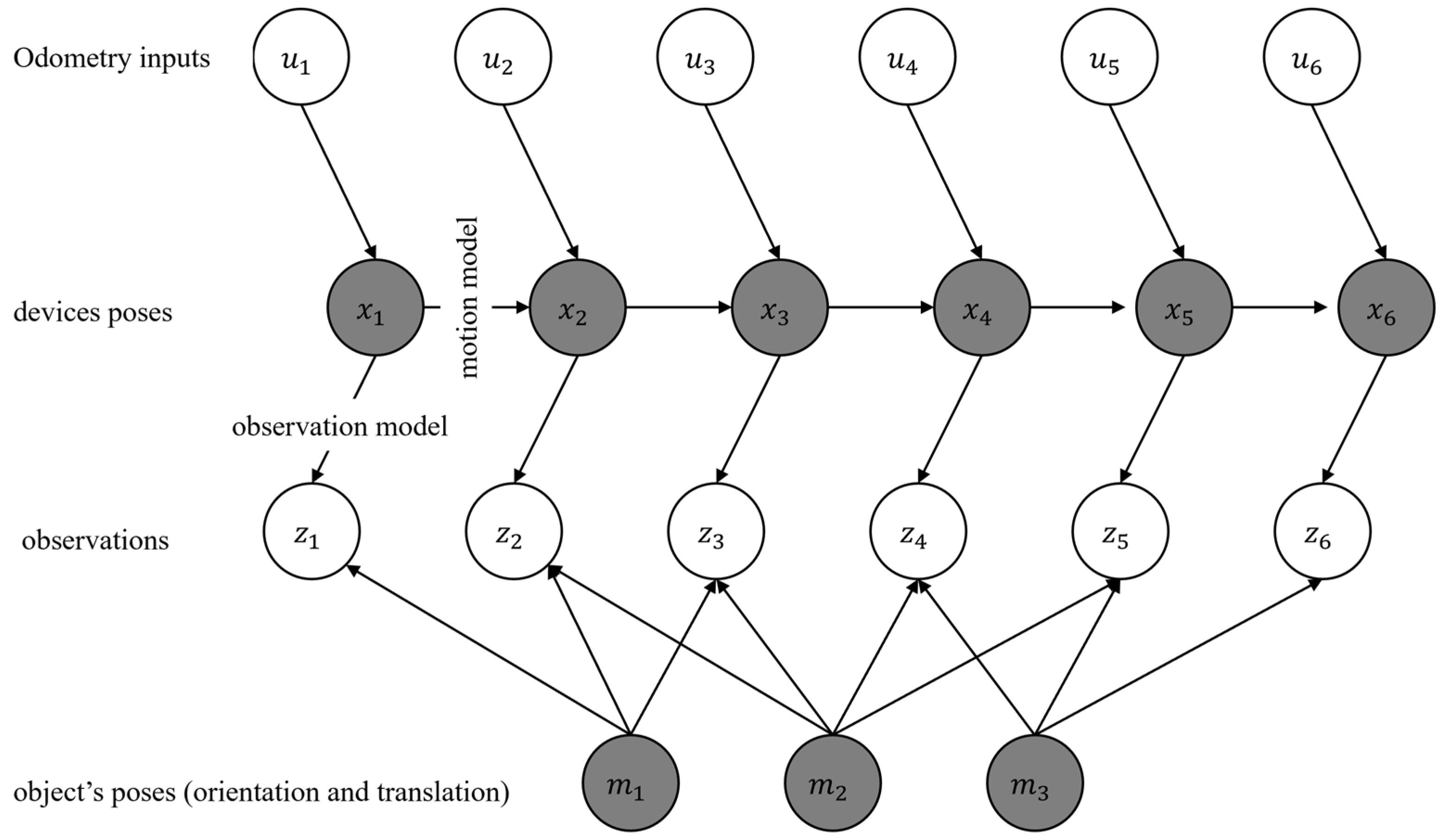
DBN in the past has been suggested as a possible solution to the SLAM problem. An overview of DBN is shown in Figure 2. In this figure, the landmarks, the robot’s states, the inputs to the robot, and the observations are denoted as m , x , u , and z . In Figure 2, the known variables are shown in white circles. These include the observations (such as images) or the input (such as the motion commands sent to a robot). Further, in Figure 2, the hidden variables are shown in gray circles. The hidden variables include the robot’s trajectory and the landmarks’ positions. These variables are not directly observed but can be inferred using the known variable. The goal in formalizing a solution to the SLAM problem using DBN is to estimate these hidden variables. In this research, each landmark is represented by six parameters. Three parameters are used to represent the position of a landmark, and three parameters are used to represent the orientation of the landmark. In contrast, in the classical point-based solutions to the SLAM, the landmarks are represented only using three parameters for the position.
Every DBN has two steps: prediction and update. In the prediction, a motion model is used to estimate the pose of a robot or a device. This motion model can be obtained using IMU mechanization [48], kinematic modelling of a robot, or motion heuristics (such as constant velocity or constant acceleration models). In the update step, the estimated pose of the robot is corrected with the help of an observation model. The observations can be images obtained from sensors such as monocular cameras, point clouds obtained using Light Detection and Ranging (LiDAR), and others. The two steps of prediction and update are repeated as more observations become available to the robot. DBN can be solved using many approaches. These include solutions based on EKF and PF. PF-based solutions can be applied in a wide variety of circumstances where the overall distribution of the errors is not known beforehand. In contrast, methods such as EKF assume that the errors have a gaussian distribution. However, the computational cost of implementing EKF is lower than PF.
PF-based solutions suffer from the Curse of Dimensionality (COD) [49]. The exact definition of COD is not within the scope of this research, and relevant research [50] can be investigated for more information. Due to the COD, increasing the number of dimensions results in an increase in the number of particles required to sample the solution space. Since in the SLAM problem, the unknowns (the robot’s trajectory and the landmarks’ poses) are often large, the number of particles should be increased substantially, and in order to implement PF, it is important to address the COD problem. One possible solution is to use RBPF, which is a computationally more efficient implementation of PF. RBPF has been used in the past as a solution to the SLAM problem. In RBPF-SLAM, similar to PF-SLAM, the state of the robot and the state of the landmarks are represented using particles. However, there are key differences between the two approaches. The RBPF-SLAM takes advantage of the structure of the SLAM. Due to this structure, for a given particle, the errors in the pose of the landmarks can be considered conditionally independent [24]. Therefore, the uncertainties in one landmark can be processed and stored independently of the other landmarks for a given particle. Such an approach can lead to a reduction in the required amount of computations.
In order to explain RBPF-SLAM mathematically, the notation in [51] is followed. Equation 1 shows the DBN for the SLAM problem formalized using RBPF-SLAM [51]. In this equation, the symbol x 1 : t corresponds to the estimated trajectory of the robot up to time step t . The a corresponds to the data association, and other symbols are consistent with their definitions provided earlier in this section. The data association is an important problem in the solutions to SLAM. The data association refers to the task of assigning observations to landmarks. An incorrect assignment will result in large errors and a possibility of the failure of the solution. In order to understand Equation 1, the right-hand side can be considered as two terms. The first term represents the posterior of the robot poses, and the second term represents the posterior of the map. It can be seen that for a given trajectory ( x 1 : t ), the posterior of each landmark is considered to be independent in RBPF-SLAM.
p x 1 : t , m a 1 : t , z 1 : t , u 1 : t =   p x 1 : t   a 1 : t , z 1 : t , u 1 : t ∏ j p ( m j | x 1 : t , a 1 : t , z 1 : t , u 1 : t )
In RBPF-SLAM, as implemented in [51], the data association is determined using a Maximum Likelihood Estimation (MLE) shown in Equation 2 (the superscript [ n ] corresponds to the weight of the n t h particle). The a ^ t [ n ] can be inserted in Equation 1, once it is known. In this research, the possibility of false data association is reduced by avoiding one-to-one point feature matching. This is explained in detail in Section 2.2.
a ^ t [ n ] =   a r g m a x a t p ( z t | a t , a ^ 1 : t − 1 [ n ] , x 1 : t [ n ] , z 1 : t − 1 , u 1 : t )
In order to update the estimated trajectory and the map, the particles are weighted (and resampled) in an RBPF-based solution. The particle weighting can be achieved using observation likelihood. This can be seen in Equation 3.
w t n ∝ p z t a ^ t [ n ] , x 1 : t n , z 1 : t − 1 , u 1 : t
If the weight update (and, in general, the update step in any DBN) is achieved directly using the observation likelihood (Equation 3), then the developed approach can be considered a tightly-coupled fusion of IMU and monocular camera [52]. If the weight update is obtained after an independent estimation of the robot’s pose using the camera and the IMU, then the method is deemed a loosely-coupled approach [52]. Since Equation 3 is directly evaluated in this research, the developed method can be considered a tightly-coupled solution. In order to summarize, the following four modules should be implemented:
  • Proposal distribution corresponds to the predicted state of the robot in a SLAM problem. The proposal distribution can be obtained using the motion model of a robot or a device. In this research, such a motion model is provided using IMU mechanization.
  • Particle weighting corresponds to the update step in DBN. The particles are weighted using observation likelihood. In this research, the actual and the predicted observations are obtained using semantic segmentation of the object and the predicted projection (onto the camera) of the object, respectively. This is explained in more detail in Section 2.2 and 2.3
  • Particle resampling is an important step in any PF-based solution. In the resampling, the particle with higher weights is duplicated, while particles with lower weights are discarded. In this research, classical Sequential Importance Resampling (SIR) [53] is used.
  • Based on the abovementioned processes, landmark initialization is another important topic that should be addressed in every solution to the SLAM problem, which is explained in Section 2.4.

2.2. Tightly-Coupled IMU/Camera Fusion

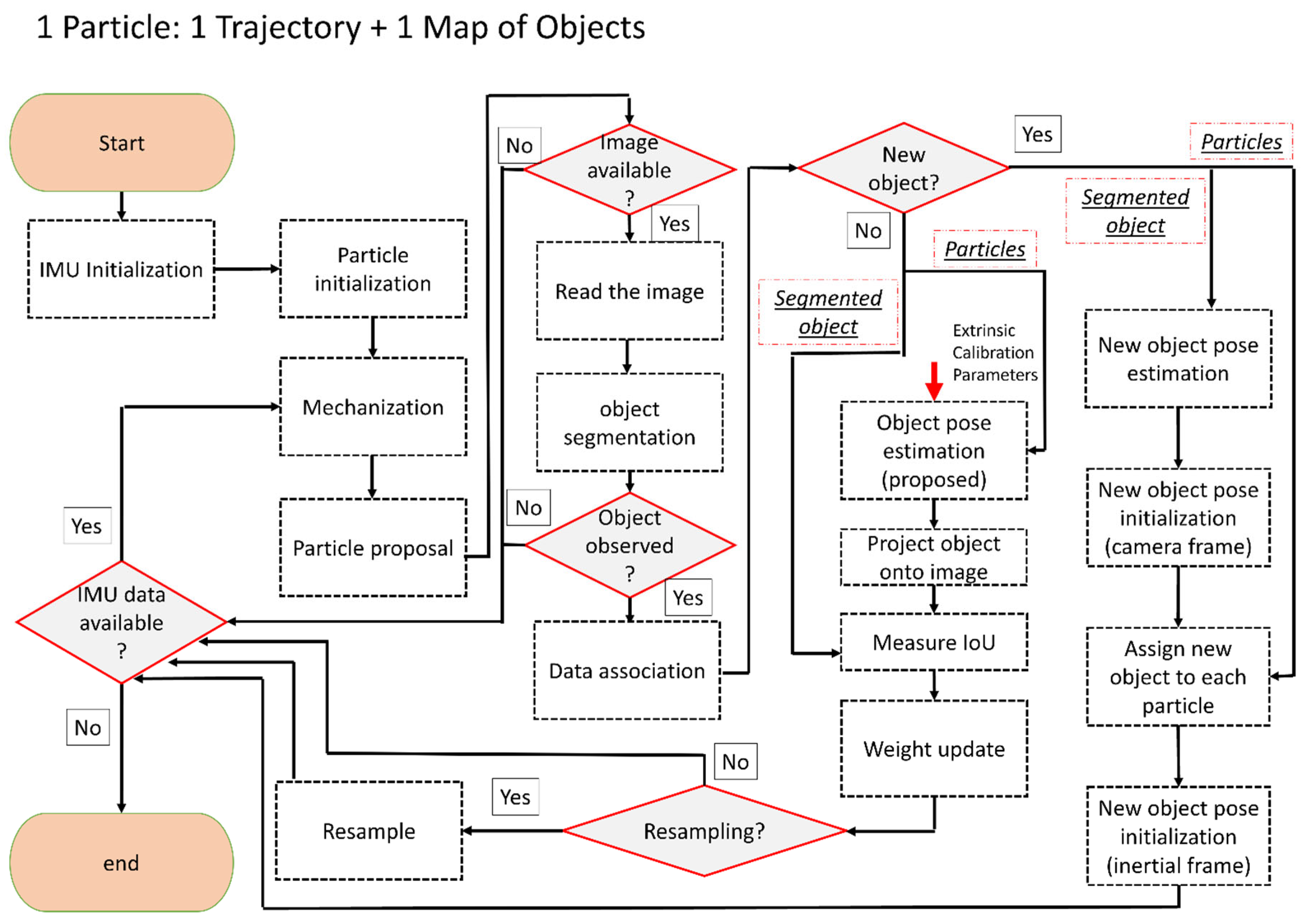
In the following, an overview of the tightly coupled fusion of IMU and a monocular camera is provided. The details about the mathematical derivation are also presented later in this section. The flowchart of the developed solution can be seen in Figure 3. The algorithm starts by initializing the particles in the map. Each particle includes an estimated pose of the device and poses of the objects (the particle initialization process is very similar to the landmark initialization, and it will be explained more in Section 2.4). It is assumed that at least one object is visible in the first image in order to achieve particle initialization. The segmented object in this image is used to estimate the pose of the camera. Once the pose of the camera is estimated up to an unknown scale, the particles are sampled around this pose with predetermined uncertainties in each direction. The uncertainties in this step should be provided by the user. It is important to note that the predetermined uncertainty should be larger in the direction from the camera’s center to the object(due to the explained scale ambiguity of the monocular camera). The other directions can be assigned with lower uncertainty. In the experiments, we have assigned 20 cm (standard deviation) in the direction from the camera center to the object and 5 cm (standard deviation) in other directions. However, uncertainties depend on the overall sizes of the objects used in the process of SLAM.
Once the particles are initialized in the map, their predicted positions are estimated using the IMU mechanization, as shown in Figure 3. This research follows the steps in [48] for mechanization, and it is assumed that the coordinate frame of the device (body frame) coincides with the IMU’s frame. The initial position of IMU is denoted as the inertial frame, and the robot’s trajectory is estimated in this frame. The mechanization will provide a predicted pose of the device in the inertial frame. Since mechanization is deterministic, a process noise term should be added to the predicted pose of the particles. Process noise is a very important consideration in incorporating uncertainties in the motion model. Such uncertainties can be due to errors in the readings of the IMU (both accelerometers and the gyroscopes). In order to include the process noise, the estimated noise variance for each of the sensors can be utilized. In this research, the noise term is sampled from a distribution with a variance corresponding to the provided information by the manufacturer of the IMU. This sampled value is added as noise to the raw measurement. The output of this step is the proposal distribution (see Figure 3).
The estimated poses of the particles obtained in the proposal distribution can be updated if an image with an initialized object is available. If this is the case, the observation likelihood shown in Equation 3 should be evaluated by comparing actual and predicted observations. The actual observation in this research is provided by object segmentation using deep learning-based [47]. Estimating the predicted contour is explained in Section 2.3. This contour is built by finding the boundary around the projected object (onto the image). This projection is achieved using the predicted pose of the particle (obtained from the particle proposal) and the camera calibration matrix of the camera. It is important to note this process assumes that the object of interest is already initialized in the map.
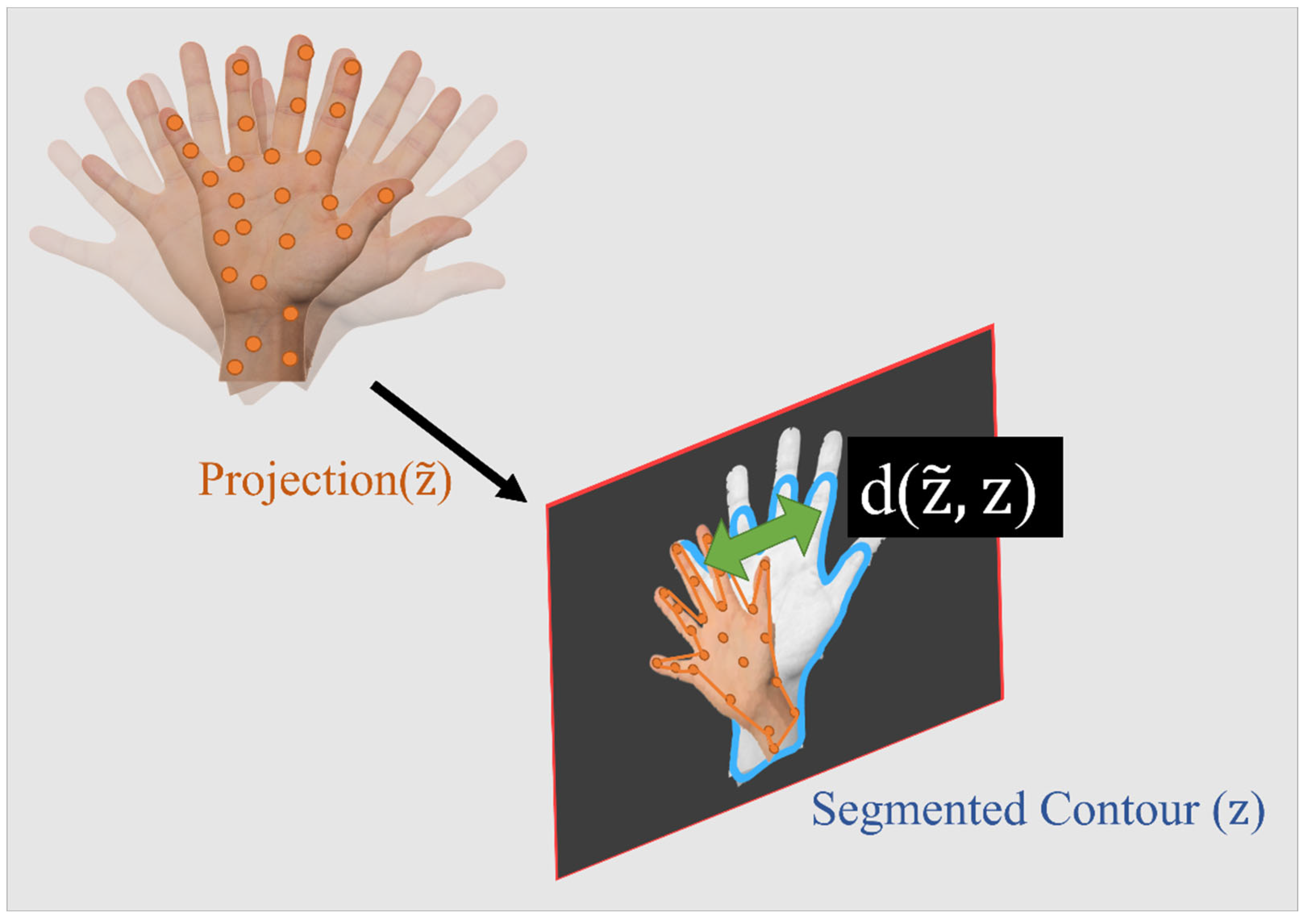
In order to assess the observation likelihood, the distance between the actual and the predicted observations (often known as the residuals) should be measured. Defining this distance depends on the type of observations. For most classical solutions (such as ORB-SLAM), where the landmarks are points, this is simply measured as the Euclidean distance between the points. However, the contour-based method used in this research does not provide such a point-to-point correspondence. Thus, a novel method of measuring the distance using Intersection over Union (IoU) is developed. The IoU is measured between the observed contour ( z k ) and the predicted contour ( z ~ k + 1 ) . The distance is inversely proportional to IoU, as shown in Equation 4. Finally, Equation 5 can be used, where the previous and current weights of the particles are denoted as w k [ n ] and w k + 1 [ n ] . The exponent term on the right hand is maximum when the two contours exactly coincide, and it becomes smallest when one contour completely residues outside of the other contour. The symbol η denotes the normalizing term, and it ensures that the weight of the particles sums to one. More information about a fast-weighting process and estimating IoU is provided in Section 2.3. Figure 4 shows a schematic of the object and its segmented and predicted contours. The weight update is only possible if the object is already initialized in the map. For the object that is not initialized, a different process should be followed (this is explained in Section 2.4). It is important to note that in the case that no objects are detected in the image, no updates are available. Under these circumstances, the solution should rely on IMU mechanization, which can lead to the accumulation of errors in a very short time.
d z ~ k + 1 n , z k + 1 = ( I o U ( z ~ k + 1 n , z k + 1 ) ) − 1
w k + 1 [ n ] = η   w k [ n ] e x p − 1 2 σ d d z ~ k + 1 n , z k + 1 − 1 2

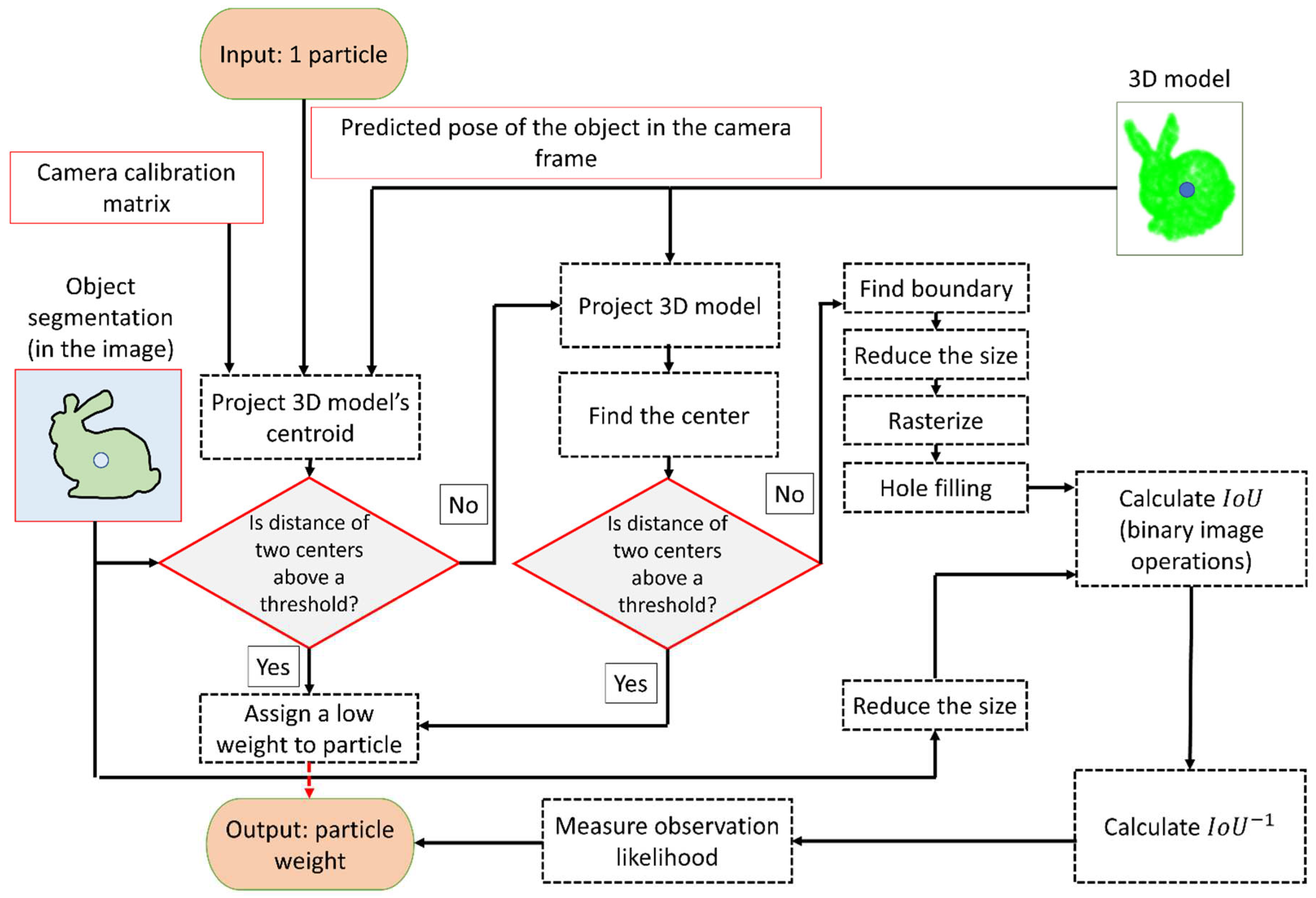
2.3. Measuring IoU

As mentioned, the predicted projection of an object’s boundary should be estimated to weigh the particles. Unfortunately, projecting the 3D model of the object onto the image and then finding the boundary of the object is computationally costly since this process should be repeated for each particle. In the following, a method is introduced that will greatly decrease the runtime of the algorithm. As a test step, the algorithm projects the centroid of the 3D object onto the camera. As mentioned, this projection is achieved by using the associated predicted pose of the particle and camera calibration matrix. If the distance between this centroid and the centroid of the segmented object (observed contour) is larger, it is more likely that the particle has a larger error in the pose. Thus, such a particle can be assigned to low weight without performing any additional step. In the second step, a downsampled 3D model of the object is projected onto the image. Similar to the previous step, the centroid of these projected points is compared to the centroid of the segmented object.If the distance is larger than a threshold, a low weight to the corresponding particle is assigned.
The boundary around the projected points should be estimated for all the remaining particles. A possible approach is to use the alpha-shape [54] based 2D boundary detection(e.g. as provided in MATLAB). This boundary can be rasterized (the boundary points can be inserted into an image, where the pixels belonging to the boundary are labelled as one and the pixels belonging to the background are labelled as zero). It is possible that the rasterized boundary will be disconnected. In order to address this issue, efficient morphological operations such as dilation can be used to create a connected boundary. Further, the hole-fill operation [55] can be used to assign ones to the points inside the boundary. As the segmented object in the image is already in the binary format, the abovementioned steps can be skipped for this image. Finally, once the two masks are available (the observed and the predicted), the IoU can be calculated using efficient logical operations for binary images. The process explained above is provided in Figure 5.

2.4. Landmark Initialization

In this section, the landmark initialization is explained. The landmark initialization is required if the object of interest is observed for the first time in the image. The initialization in the object-level SLAM should estimate the object’s position and orientation in the map. In this research, the undelayed initialization technique is utilized, which can improve the accuracy of the solution by providing partial updates immediately after the object is observed for the first time. As the monocular camera cannot observe the distance to the object, the object initialization can only be achieved up to an unknown scale. In order to estimate the pose of the object using one image, only the contours of the objects are used. Therefore, this approach is shape-based.
The developed initialization method depends on object segmentation. Object segmentation can be obtained with the help of deep learning methods. In this research work, the Fully Convolutional Network (FCN) U-Net [56] is utilized for the segmentation. The data is synthesized for this network using the method developed in [47]. The precision of this approach is reported to be over 0.94 (and a recall of over 0.85 )in many experiments.
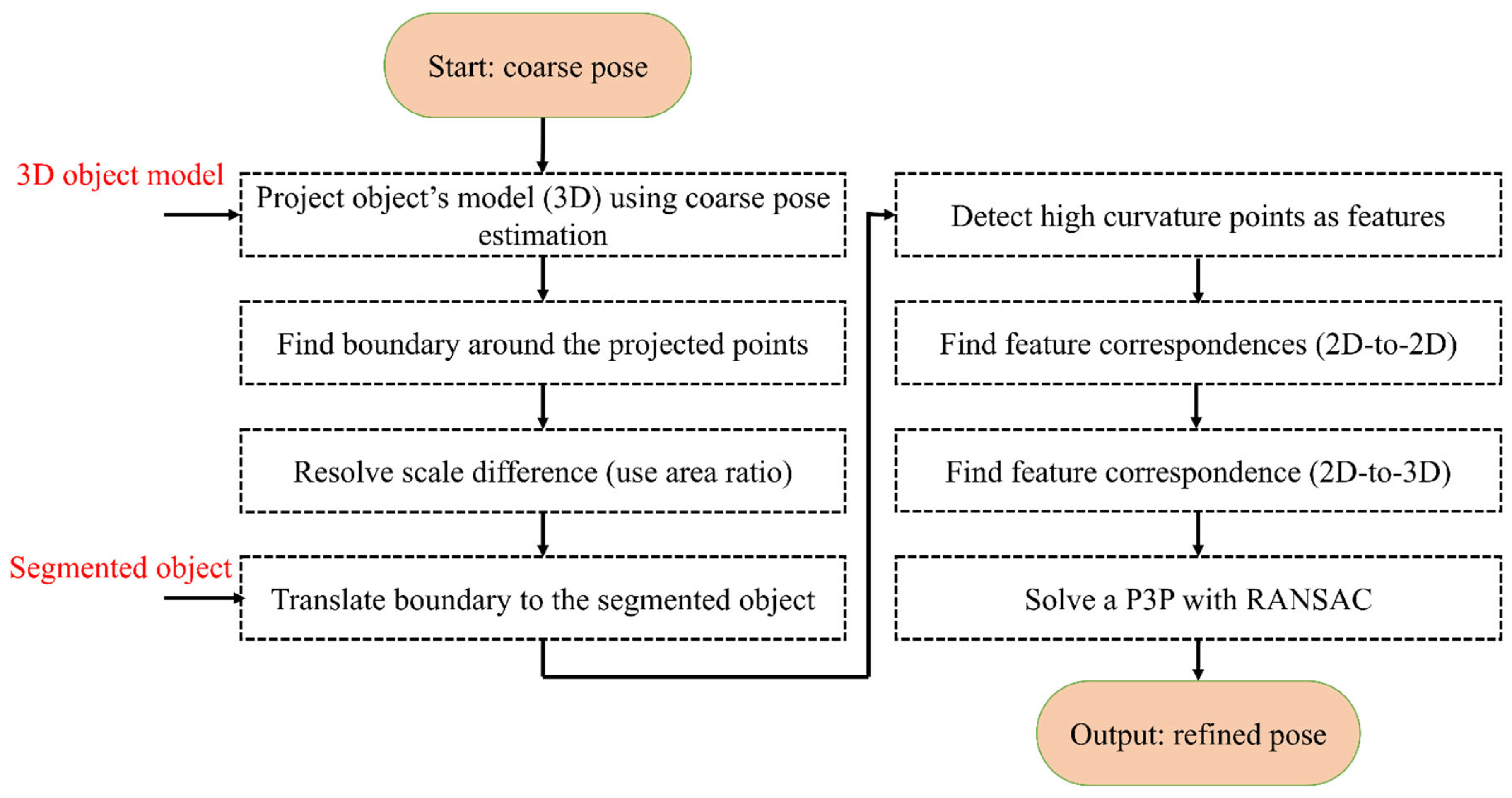
The pose estimation is obtained in a coarse-to-fine process. The coarse pose estimation follows the approach in [47] and, for brevity, is not explained here. The output of the coarse process is a rough estimate of the pose of the object in the camera frame. This estimation is only accurate if the camera center, the object of the center, and the projected center of the object in the image are aligned.
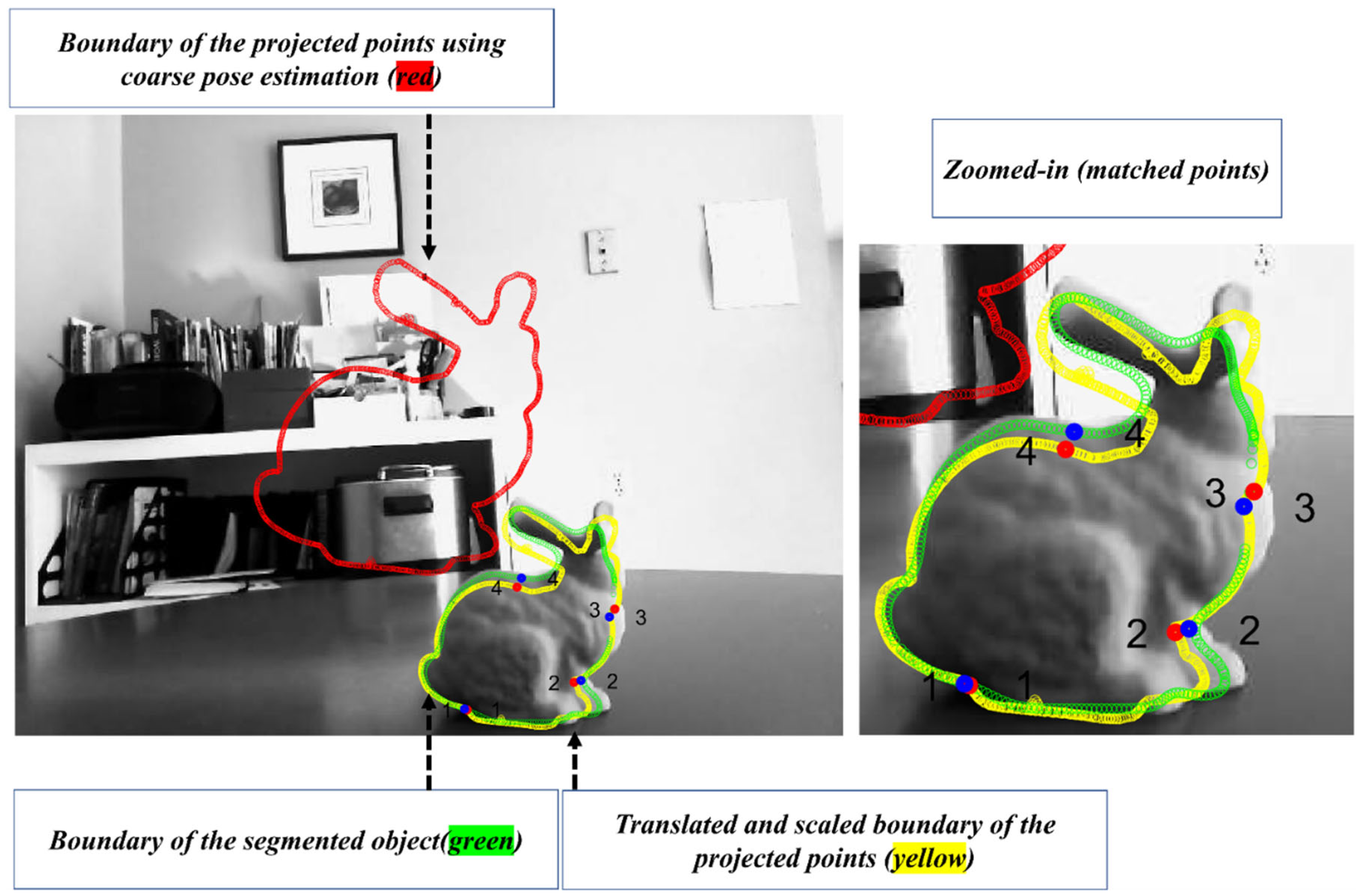
In order to improve the pose estimated in [47], a refinement step is developed in this section. In the classical pose refinement, the features detected on the object are matched to the 3D model of the object, and these matched features are used to solve a Perspective-n-Point (PnP). Unfortunately, since the developed method only assumes that the object’s contour is available, no features are detected on the object’s surface. In order to address this issue, the coarse pose estimation is used to project the object’s model (available in the CAD format) onto the image (see red points in Figure 6). In the image, a feature correspondence is established between the two contours (the segmented and the projected). This correspondence is established by identifying points with the highest curvature. Equation 6 is used to estimate the curvature of the points on the contour. In this equation, c ( x ) and c ( y ) are the estimated boundary of the object. The symbols x ′ , x ″ , y ′ , and y ″ correspond to the first and the second derivative with respect to the parameter of the curve ( s ) in the x and y directions.
κ = | x ′ ( s ) y ″ ( s ) − x ″ ( s ) y ′ ( s ) | x ′ s 2 + y ′ s 2 3 / 2
The identified high-curvature points on the boundary of the segmented object and the boundary of the projected object are utilized to establish a correspondence by first scaling and translating the projected boundary to the segmented object (see Figure 6, where the transformed and observed contours are shown in yellow and green). Once this transformation is achieved, the closest high-curvature points are declared as the corresponding features (the matched points are shown with numbers in Figure 6). The closest points can be found using nearest-neighbour methods such as kd-tree [57]. The established 2D-to-2D correspondence paves the path to establishing 2D-to-3D correspondence as well. This is possible as the correspondence between the project points and the 3D model is known. Finally, with the help of established 2D-to-3D correspondences, the pose of the object is refined using the P3P [58] and RANSAC [59]. The flowchart of the algorithm is provided in Figure 7.

2.5. Challenges Associated with Evaluation of Observation Likelihood

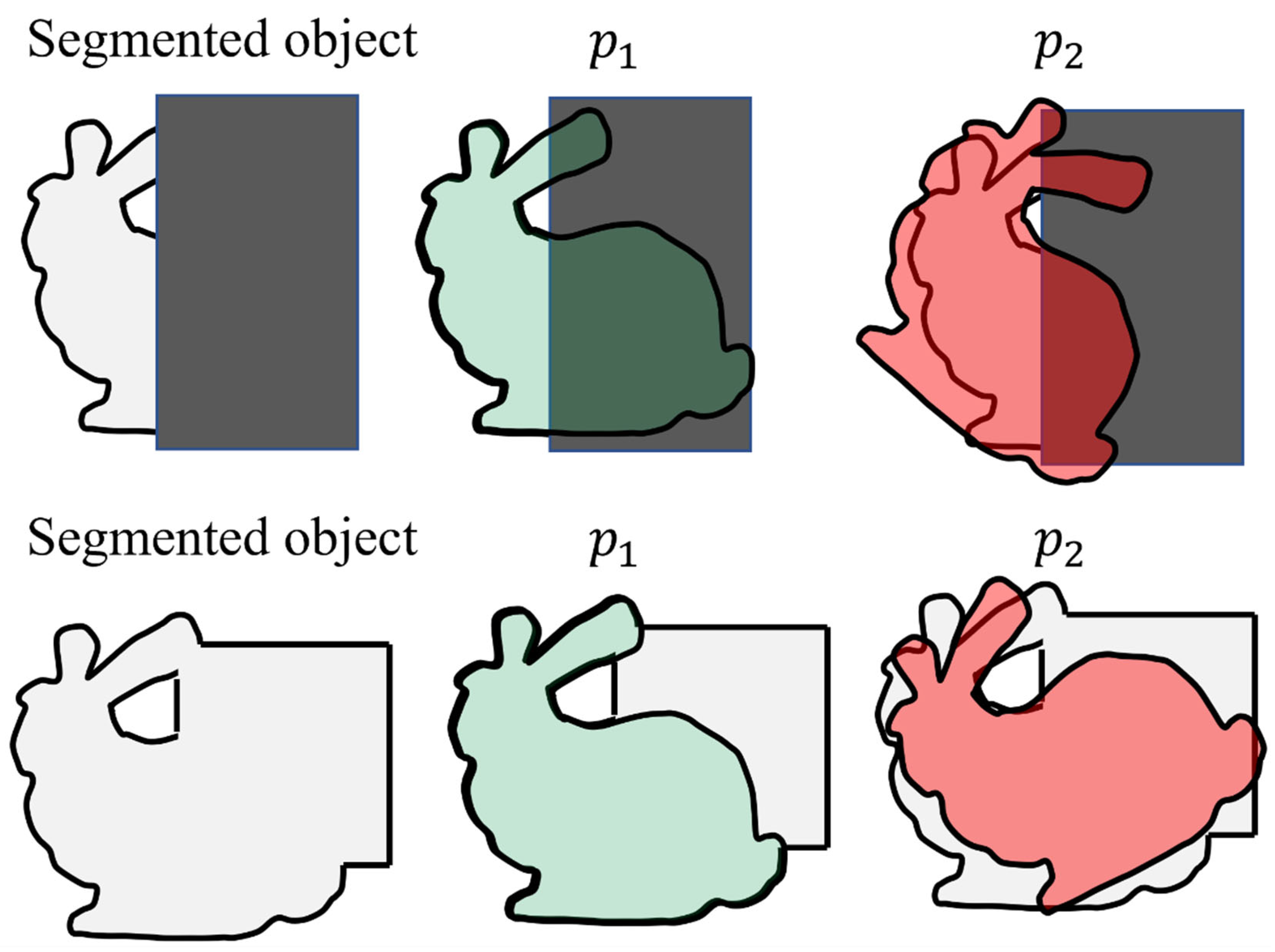
There are numerous challenges associated with the developed weighting process. These challenges are due to the utilization of the IoU for measuring the observation likelihood. The two most important challenges (Challenge I and Challenge II) are explained in detail in this section. Challenge I can occur when some of the pixels of the object are not identified during the object segmentation process. Possible reasons for this can be due to the occlusion of the object of interest, low-resolution images, or the long distance of the camera from the object of interest. Challenge I can frequently occur during the navigation. Figure 8 (first row) explains this problem schematically. In this figure, a schematic of the segmented and the predicted object in the image is shown. The occluded area is shown with a rectangular grey box. It can be seen that once the object of interest is occluded, particles p 1 and p 2 will result in a similar IoU (and lower than 1). However, particle p 1 is much closer to the actual observation. Problems such as these will lead to assigning similar weights to better and worst particles and thus challenge the developed algorithm.
Challenge II can occur when pixels belonging to the background clutter or another object is detected as part of the foreground. This challenge can occur if similar-looking objects are close-by to the object of interest. However, in our experiments, Challenge II is much less likely to be encountered than Challenge I. In order to illustrate Challenge II schematically, Figure 8 (bottom row) can be inspected. In this figure, the close-by rectangular object is segmented mistakenly as a part of the object. Both particles p 1 and p 2 are assigned a large weight. However, particle p 1 is closer to the correct observation. Challenge II can lead to larger weights in comparison to Challenge I.
In order to identify if Challenge I or Challenge II have occurred, a fault detection algorithm can be used. As mentioned, most particles will be assigned to lower IoU values if Challenge I occurs. Simply by testing the particle with the maximum weight, it is possible to detect the occurrence of Challenge I. In such circumstances, the observation can be discarded in order to avoid introducing erroneous updates to the process of particle filtering.
The detected false positive pixels in the background due to Challenge II are often not close to the foreground (object). Assuming that this is the case, a simple binary pixel grouping method can be used. Further, as the largest group is most likely to correspond to the segmented object, the smaller groups can be removed. Thus, they cannot contribute to measuring the particles’ weight.

3. Results and Discussion

The experiments are performed using a designed handheld device. This device includes Xsens mti-g-710 as the IMU sensor, which is a Micro-Electrical-Mechanical System (MEMS) device. The noise specification of this sensor is reported 60 μ g / √ H Z for the accelerometer and 0.01 degrees/s/ √ H Z for the gyroscope. The known 6-position calibration method [48] can be used to estimate deterministic errors such as bias, scale and non-orthogonality. However, since the developed system is robust, non-gaussian errors can also be handheld in the process of filtering. Thus, for the purpose of the algorithm identifying the bias of the accelerometer and gyroscope (which has the most significant error) is sufficient. The defined handheld device also includes a monocular camera. The electrical board for this sensor is developed by Arducam, and the sensor itself is an 8 Mega Pixel IMX219, which produces lower-quality images than most smartphones nowadays. The intrinsic parameters of the camera are obtained using MATLAB’s Camera Calibration toolbox.
The extrinsic calibration parameters between the IMU and the monocular camera are derived from the CAD model of the system, and it is also tested using Kalibr [60]. Kalibr is a known algorithm to estimate the extrinsic calibration of IMU and monocular cameras using special target boards. The data is collected on a Mini Desktop PC (BeeLink Mini S). Such Mini Desktop PCs are low-cost devices in comparison to smartphones. The specifications of the sensors and the calibration process are provided in Table 1. The image of the device is provided in Figure 9.
In the following, four sets of experiments are provided. In the first experiment, the coarse-to-fine pose estimation is assessed qualitatively. This process is independent of the RBPF-SLAM. In the second set of experiments, the performance of the RBPF-SLAM is evaluated. In the third experiment, the effect of increasing the number of particles on the accuracy of the solution is assessed. While all previous experiments were conducted using one object, the last experiment was conducted using two objects.
As mentioned, pose estimation is very important in the initialization of the object. In the first experiment, pose estimation is studied qualitatively. The camera is moved around the object of interest, and the pose is estimated in each image. The estimated coarse pose and the refined pose are used to project the 3D model of the object onto the image. The projected models are compared to the segmented object in the image. Results are provided in Figure 10. In this figure, the projected model using coarse estimation is shown in red. As discussed in Section 2.4, the coarse pose estimation always assumes that the camera center, the centroid of the 3D model of the object in the map, and the projected center of the object in the image are all lying on a line. The refined pose is shown in purple in Figure 10 (the segmented object using deep learning is shown in yellow). This figure demonstrates that the coarse pose estimation is very erroneous, while the final estimated pose is very close to the segmented object in the image. It is important to note that the refined pose is not a simple in-plane translation of the object in the image. This can be seen best in Figure 10 (third row/second column), where the object’s pose is refined substantially. Further, this initial estimation of the pose will be refined in the process of the tightly coupled solution.
The performance of tightly coupled solutions is evaluated using different metrics. The accuracy of the method is estimated by measuring the distance between the initial pose and the final pose and compared to the ground truth value. Since the developed method outputs particles, a method should be used to estimate a single pose using all the particles. One possible approach is using the weighted pose of the particles. This is denoted as the Expected Value (EV) in this section and estimated using Equation (7). The second method of estimating the pose is selecting the particle with the largest weight. This is denoted as Maximum A Posterior (MAP) estimation. Further, the accuracy of pose estimation is reported in terms of absolute error (reported in cm) and relative error (reported as the ratio of the error to the Total Travelled Path (TTP)).
E V = ∑ n ∈ { 1 : N } w t n x t [ n ]
Additional to errors in the position, other parameters are also utilized to assess the performance of the developed method. These assessment metrics are the average IoU of the particles throughout the motion of the device. This value can be one at maximum and can assume a minimum of zero. The second assessment criterion is the failure rate. As mentioned in Section 2.5, the developed method can fail due to many challenges. In order to avoid these failures, a fault detection algorithm is used. The failure rate is defined as the number of epochs where the particle update failed (due to either Challenge I or Challenge II) to the total number of epochs. The last metric of assessment is the runtime of the developed method. The dataset is captured in two indoor environments with varied levels of background clutter. Sample images are provided in Figure 11. Further, the camera’s distance to the object is also varied in these experiments. Both the distance of the object and the background clutter can affect the accuracy of the object segmentation and thus affect the performance of the developed method.
The results are summarized in Table 2, Table 3 and Table 4 for five experiments. Based on these results, the accuracy of the developed method is in the range from 4.1 to 13.1 cm (0.005 to 0.021 of TTP) using EV. The error varies in the range of 18.9 to 35.7 cm (0.023 to 0.052 of TTP) using MAP. The accuracy of the solution is not affected by the background clutter, the distance of the object from the camera, and the length of the trajectory. Thus, the developed solution is not diverging with longer trajectories. Similar accuracy is expected to be achievable for even longer trajectories if frequent updates are available using the monocular camera. The IoU is in the range of 0.747 to 0.821 (this value can be considered high). During the navigation, a few failure rates are detected (0.00 to 0.01). It is important to note that even in failed cases, the solution did not diverge (see Test 5).
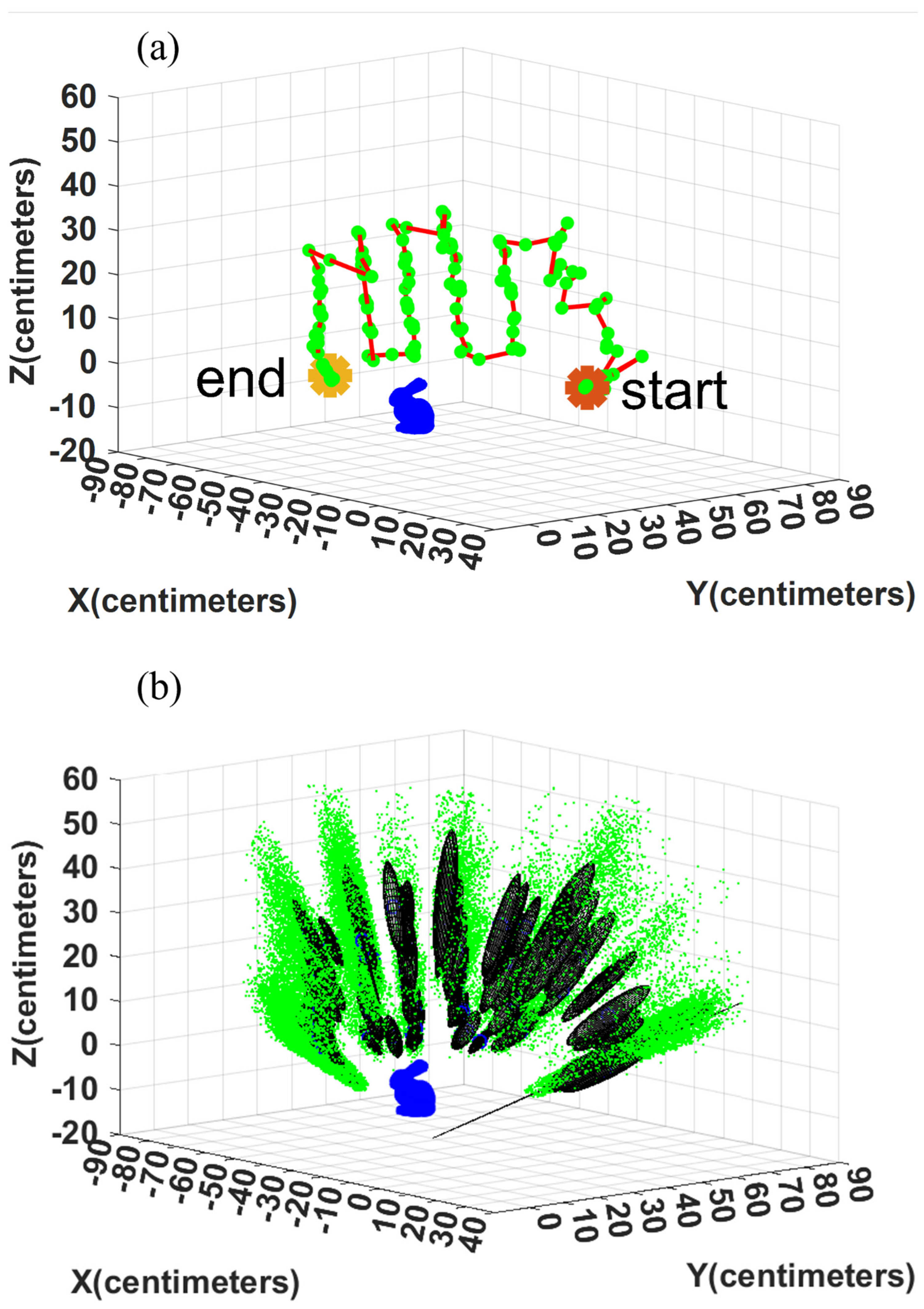
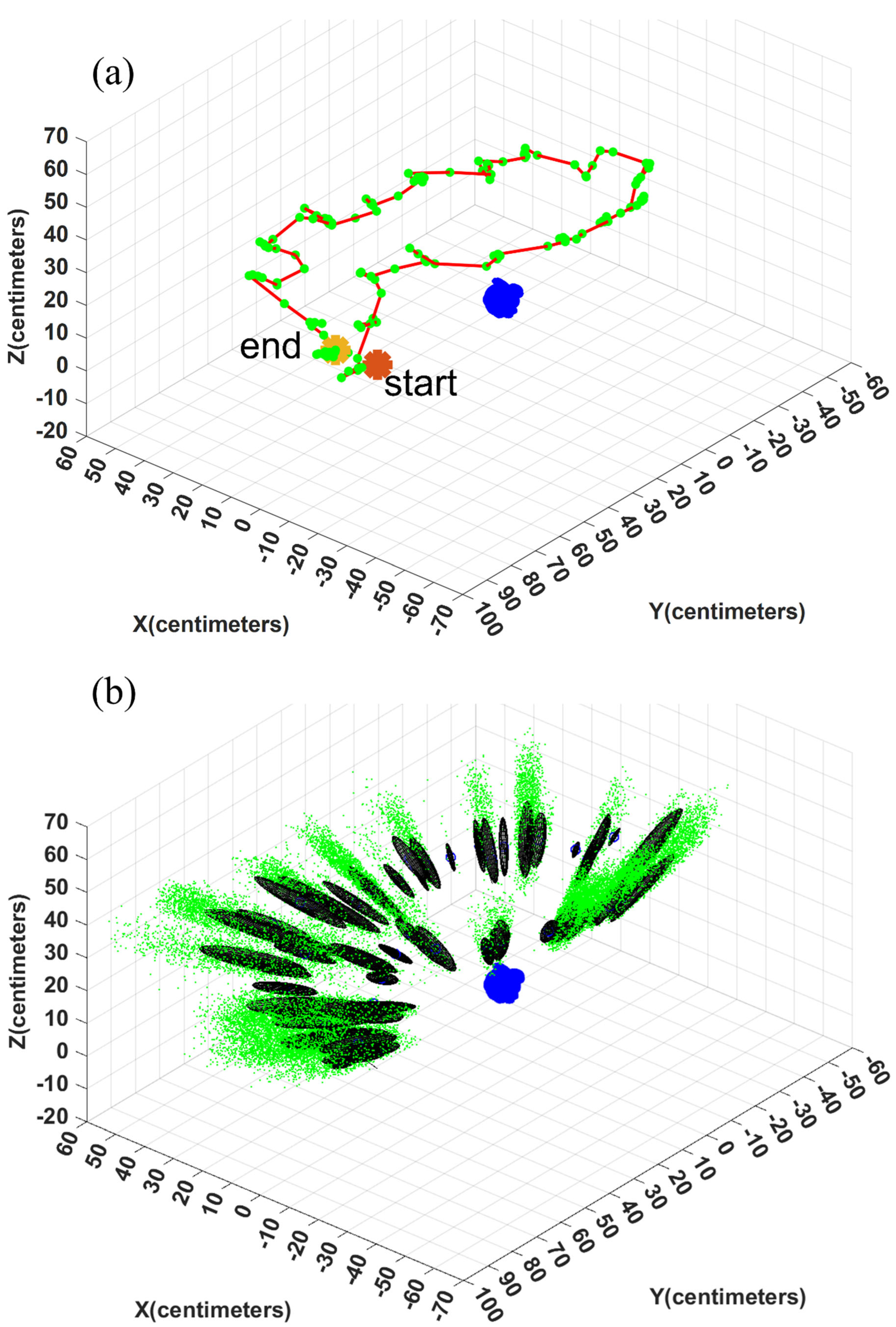
The estimated error ellipses and the robot’s trajectory are shown in Figure 12 and Figure 13 for Test 1 and 4, respectively. Figure 12(a) and Figure 13(a) show the trajectory and the camera’s positions in red and green, respectively. The initial and the final positions of the device are denoted as Start and End in this figure. In Figure 12(b) and Figure 13(b), the particles are shown in green. Further, the error ellipsoids, including 50% of the total weight, are shown as well. The figures show the uncertainty in the direction from the camera center toward the object is the highest.
The developed method can be compared to a similar IMU/camera fusion method in [61], where the reported error ranges from 0.01 to 0.037 (error ratio to TTP). This indicates a similar performance to the developed solution in this research. It is important to note that the method in [61] utilizes a stereo camera rig, while our solution utilizes a monocular camera.
In order to study the effect of the number of particles, experiments are performed by modifying the number of particles. The experiment’s results are summarized in Table 5. Based on these experiments changing the number of the particles from 5000 to 19000 did not seem to change the accuracy significantly. However, the runtime of the algorithm has increased substantially (from 6149.2 s to 13390.3 s).
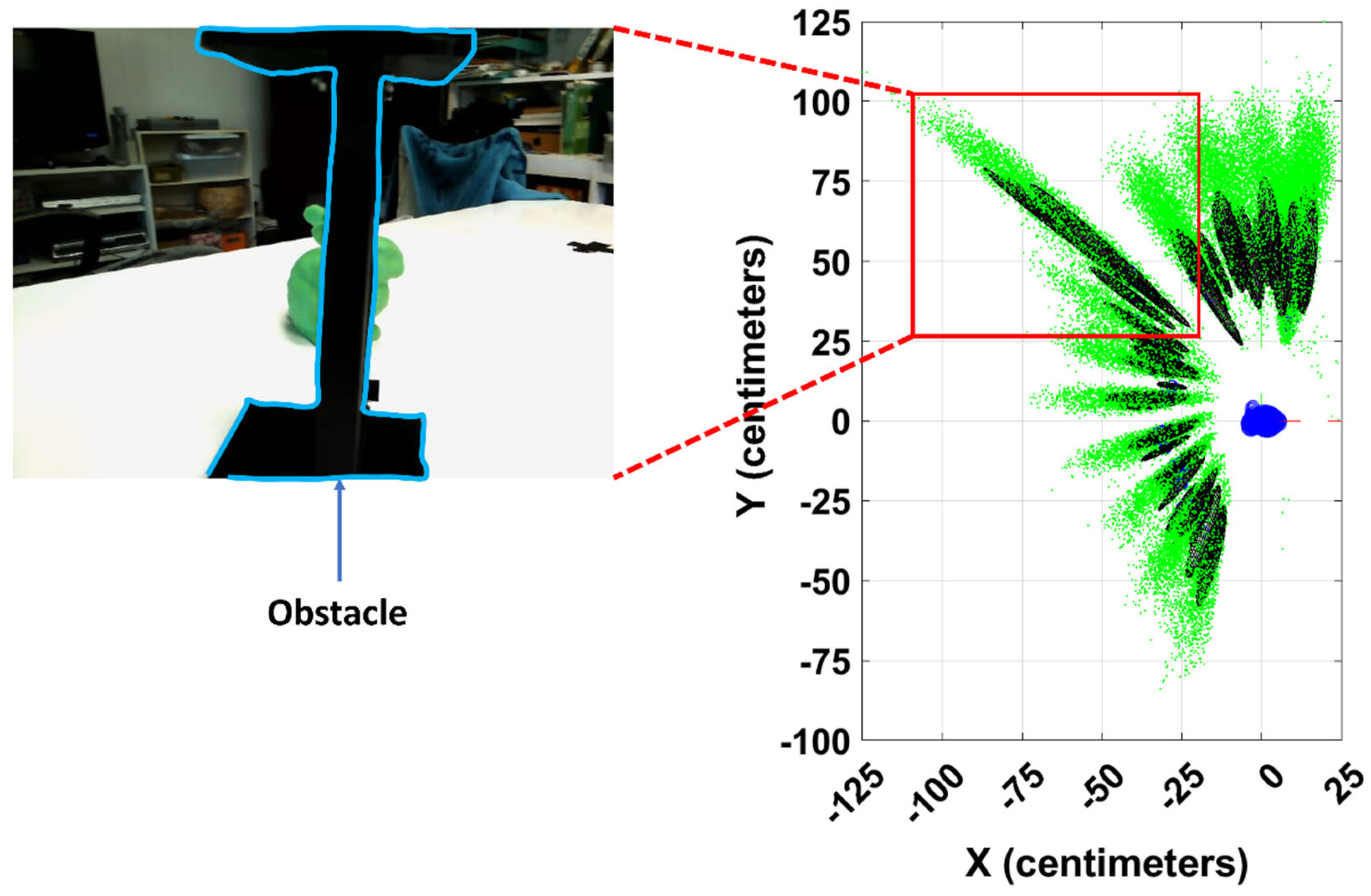
The objects can be severely occluded during the motion of the device. This will affect the performance of the solution. In the example shown in Figure 14, the object of interest (the green model of Stanford’s Bunny) is occluded by another object in some viewpoints. The estimated particles are shown in the plot on the right-hand side during the corresponding epochs inside a red box. It can be seen that based on this plot when the objects are occluded, the uncertainty in the solution has increased (as the error ellipses become more elongated). However, the algorithm does not diverge, and the uncertainty decreases as the object is not occluded in the later epochs.
The abovementioned tests have only utilized a single object to provide an object-level solution to the SLAM problem. While these results can provide evidence that the developed algorithm can produce relatively high accuracy in many circumstances, relying on a single object might lead to errors in real-life scenarios. For example, the object of interest may become occluded longer during the navigation. Therefore, relying on more than a single object can help improve the robustness of the algorithm to the errors caused by Challenge I and Challenge II. In the following, the results for using two objects are provided. The main difference between this experiment and the previous experiment is that more than single landmark initialization should be performed (one for each new object)
Throughout the navigation, there are two different cases that can occur when multiple objects are used. The first case occurs if only a single object is observed in the image. In this case, a data association procedure should be used to determine which landmark in the map the observation is associated with. Once such data association is performed, the following steps (particle proposal and the weight updates) are the same as using only a single object. In the second case, more than one object is observed in the images. In such circumstances, the IoU for the individual object should be estimated, and the object with the highest IoU should be used for updating the weight of the particles. This approach is not the only possible weight update strategy. However, since the developed solution can frequently encounter Challenge I (e.g., when one or more objects are occluded), using a single object with the highest IoU can improve the robustness of the developed solution. The results for the two objects are provided in Table 6. Based on these results, it can be seen that the error and IoU did not change using multiple objects in comparison to using only a single object.

4. Conclusions and Future Work

In this research, a novel tightly coupled IMU/camera object-level solution to the SLAM problem is developed. In the past, many of the object-level solutions relied on assumptions about the distribution of the errors (such as gaussian error assumption). Furthermore, these solutions are often an extension of the classical methods to the SLAM problem or do not offer a standalone object-level solution. The developed approach in this research shows that a standalone solution to the SLAM solution can be provided using RBPF. This DBN has been implemented in the past extensively using a laser rangefinder, but in the context of a monocular camera, it is only recently applied to objects. The biggest advantage of this approach is that no assumption about the distribution of the errors is made. Further, it is exhibited that the developed method can provide an accurate solution using a single object.
Object representation is an important component of an object-level SLAM. The state-of-the-art methods rely on simple geometrical shapes such as ellipsoids and cuboids to represent the object. However, these simpler forms are not suitable for many objects. Another commonly used approach is to detect feature points which require salient textures on the objects. In this research, instead of relying on simpler shapes or relying on salient features on the object’s surface, the objects are represented using their shape. The reliance on the shape is very useful when object segmentation is used. This is due to the fact that segmentation methods can only provide a contour around the object. With a shape-based object representation, we have developed a novel particle weighting method using IoU. The advantages and shortcomings of this particle weighting process are discussed as well. A key advantage of developed contour-based weighting is that one-to-one correspondence between the features is not required. Further, we have developed a coarse-to-fine pose estimation relying on the contour of the object. The pose estimation is a crucial element in the initialization phase.
The developed method provides a novel approach for the fusion of an IMU and a monocular camera for object-level solutions. In the past, the fusion of these sensors has been achieved using many methods. In these solutions, the IMU is used to predict the trajectory of the device, while the camera is used to correct the prediction and build a map of the environment. However, most of the state-of-the-art approaches rely on delayed landmark initialization. This technique can suffer from the accumulation of errors in the initialization phase. In contrast to these methods, the solution offered in this research is based on undelayed initialization. This approach can immediately provide updates to the position of the device once the objects are observed for the first time. Thus, it avoids relying only on the IMU mechanization for a longer period.
Based on the results shown, an error of 4.1 to 13.1 cm (0.005 to 0.021 of the TTP) can be achieved with the designed handheld device. It is also demonstrated that the IoU of the developed method is about 0.8. The failure rate of the algorithm is very low (within 0.00 to 0.01). The solution seems reliable under many different circumstances (such as different levels of background clutter and the camera’s distance from the object of interest). Finally, the solution is not degraded as the trajectory is longer. Similar results are expected to be obtained regardless of the trajectory if updates to the solution are available using images.
The effect of changing the number of particles is also investigated in this paper. It is shown that increasing the number of particles to more than 5000 does not decrease the error. These errors might be systematic errors (such as the ones caused by Challenge I and Challenge II) and cannot be addressed by increasing the number of particles. Finally, utilizing more than a single object does not improve position accuracy and the IoU.
One shortcoming of the developed method is the high computational cost. The computational cost has been reduced by using fast multi-step measurements of IoU. These steps can help assign low weights to particles with inaccurate poses without a requirement to measure the observation likelihood (measuring the observation likelihood is the major computational bottleneck of the developed method). In future research, it is important to reduce the computation cost further. One possible solution is a fusion with a rangefinder, such as an ultrasonic sensor. This fusion can help discard the particles that do not fall within a threshold of the observed distance from the object of interest. This elimination will help avoid calculating observation likelihood for many particles with inaccurate poses and thus substantially contributes to the computational cost reduction.

Funding

This research has been supported by the funding of Prof. Naser El-Sheimy from NSERC CREATE and Canada Research Chairs programs.

Acknowledgments

I will like to thank Dulcie Foofat for providing the opportunity to collect data for all the experiments in this research.

References

  1. Davison, Andrew J., Ian D. Reid, Nicholas D. Molton, and Olivier Stasse. “MonoSLAM: Real-time single camera SLAM.” IEEE transactions on pattern analysis and machine intelligence 29, no. 6 (2007): 1052-1067.
  2. Smith, Paul, Ian D. Reid, and Andrew J. Davison. “Real-time monocular SLAM with straight lines.” (2006). [CrossRef]
  3. Kaess, Michael. “Simultaneous localization and mapping with infinite planes.” In 2015 IEEE International Conference on Robotics and Automation (ICRA), pp. 4605-4611. IEEE, 2015.
  4. Ahn, Sunghwan, Minyong Choi, Jinwoo Choi, and Wan Kyun Chung. “Data association using visual object recognition for EKF-SLAM in home environment.” In 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 2588-2594. IEEE, 2006. [CrossRef]
  5. Castle, Robert Oliver, Georg Klein, and David William Murray. “Combining monoSLAM with object recognition for scene augmentation using a wearable camera.” Image and Vision Computing 28, no. 11 (2010): 1548-1556. [CrossRef]
  6. Civera, Javier, Dorian Gálvez-López, Luis Riazuelo, Juan D. Tardós, and Jose Maria Martinez Montiel. “Towards semantic SLAM using a monocular camera.” In 2011 IEEE/RSJ international conference on intelligent robots and systems, pp. 1277-1284. IEEE, 2011.
  7. Klein, G., & Murray, D. (2007). Parallel tracking and mapping for small AR workspaces. 2007 6th IEEE and ACM International Symposium on Mixed and Augmented Reality, ISMAR, 225–234. [CrossRef]
  8. Dellaert, Frank, and Michael Kaess. “Square Root SAM: Simultaneous localization and mapping via square root information smoothing.” The International Journal of Robotics Research 25, no. 12 (2006): 1181-1203. [CrossRef]
  9. Rublee, Ethan, Vincent Rabaud, Kurt Konolige, and Gary Bradski. “ORB: An efficient alternative to SIFT or SURF.” In 2011 International conference on computer vision, pp. 2564-2571. Ieee, 2011.
  10. Lowe, David G. “Object recognition from local scale-invariant features.” In Proceedings of the seventh IEEE international conference on computer vision, vol. 2, pp. 1150-1157. Ieee, 1999.
  11. Pillai, Sudeep, and John Leonard. “Monocular slam supported object recognition.” arXiv preprint arXiv:1506.01732 (2015). [CrossRef]
  12. Dharmasiri, Thanuja, Vincent Lui, and Tom Drummond. “MO-SLAM: Multi object slam with runtime object discovery through duplicates.” In 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp. 1214-1221. IEEE, 2016.
  13. Bowman, Sean L., Nikolay Atanasov, Kostas Daniilidis, and George J. Pappas. “Probabilistic data association for semantic slam.” In 2017 IEEE international conference on robotics and automation (ICRA), pp. 1722-1729. IEEE, 2017.
  14. Hosseinzadeh, Mehdi, Yasir Latif, Trung Pham, Niko Suenderhauf, and Ian Reid. “Structure aware slam using quadrics and planes.” In Computer Vision–ACCV 2018: 14th Asian Conference on Computer Vision, Perth, Australia, December 2–6, 2018, Revised Selected Papers, Part III 14, pp. 410-426. Springer International Publishing, 2019.
  15. Nicholson, Lachlan, Michael Milford, and Niko Sünderhauf. “Quadricslam: Dual quadrics from object detections as landmarks in object-oriented slam.” IEEE Robotics and Automation Letters 4, no. 1 (2018): 1-8. [CrossRef]
  16. Qian, Z., Patath, K., Fu, J., & Xiao, J. (2020). Semantic SLAM with autonomous object-level data association. ArXiv. [CrossRef]
  17. Ok, Kyel, Katherine Liu, Kris Frey, Jonathan P. How, and Nicholas Roy. “Robust object-based slam for high-speed autonomous navigation.” In 2019 International Conference on Robotics and Automation (ICRA), pp. 669-675. IEEE, 2019.
  18. Yang, Shichao, and Sebastian Scherer. “Cubeslam: Monocular 3-d object slam.” IEEE Transactions on Robotics 35, no. 4 (2019): 925-938. [CrossRef]
  19. Mur-Artal, Raul, and Juan D. Tardós. “Orb-slam2: An open-source slam system for monocular, stereo, and rgb-d cameras.” IEEE transactions on robotics 33, no. 5 (2017): 1255-1262.
  20. Smith, Randall C., and Peter Cheeseman. “On the representation and estimation of spatial uncertainty.” The international journal of Robotics Research 5, no. 4 (1986): 56-68. [CrossRef]
  21. Nettleton, Eric W., Hugh F. Durrant-Whyte, Peter W. Gibbens, and Ali H. Göktogan. “Multiple-platform localization and map building.” In Sensor Fusion and Decentralized Control in Robotic Systems III, vol. 4196, pp. 337-347. SPIE, 2000.
  22. Thrun, Sebastian, Dieter Fox, Wolfram Burgard, and Frank Dellaert. “Robust Monte Carlo localization for mobile robots.” Artificial intelligence 128, no. 1-2 (2001): 99-141. [CrossRef]
  23. Montemerlo, Michael, and Sebastian Thrun. “Simultaneous localization and mapping with unknown data association using FastSLAM.” In 2003 IEEE International Conference on Robotics and Automation (Cat. No. 03CH37422), vol. 2, pp. 1985-1991. IEEE, 2003. [CrossRef]
  24. Montemerlo, Michael, Sebastian Thrun, Daphne Koller, and Ben Wegbreit. “FastSLAM 2.0: An improved particle filtering algorithm for simultaneous localization and mapping that provably converges.” In IJCAI, vol. 3, no. 2003, pp. 1151-1156. 2003.
  25. Eade, Ethan, and Tom Drummond. "Scalable monocular SLAM." In 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), vol. 1, pp. 469-476. IEEE, 2006.
  26. Eade, Ethan, and Tom Drummond. “Edge landmarks in monocular SLAM.” Image and Vision Computing 27, no. 5 (2009): 588-596. [CrossRef]
  27. Deng, Xinke, Arsalan Mousavian, Yu Xiang, Fei Xia, Timothy Bretl, and Dieter Fox. “PoseRBPF: A Rao–Blackwellized particle filter for 6-D object pose tracking.” IEEE Transactions on Robotics 37, no. 5 (2021): 1328-1342. [CrossRef]
  28. Mourikis, Anastasios I., and Stergios I. Roumeliotis. “A multi-state constraint Kalman filter for vision-aided inertial navigation.” In Proceedings 2007 IEEE international conference on robotics and automation, pp. 3565-3572. IEEE, 2007.
  29. Bailey, Tim. “Constrained initialisation for bearing-only SLAM.” In 2003 IEEE International Conference on Robotics and Automation (Cat. No. 03CH37422), vol. 2, pp. 1966-1971. IEEE, 2003.
  30. Davison, Andrew J., Ian D. Reid, Nicholas D. Molton, and Olivier Stasse. “MonoSLAM: Real-time single camera SLAM.” IEEE transactions on pattern analysis and machine intelligence 29, no. 6 (2007): 1052-1067.
  31. Mungúia, R., & Grau, A. (2012). Monocular SLAM for visual odometry: A full approach to the delayed inverse-depth feature initialization method. Mathematical Problems in Engineering, 2012. [CrossRef]
  32. Gordon, Neil J., David J. Salmond, and Adrian FM Smith. “Novel approach to nonlinear/non-Gaussian Bayesian state estimation.” In IEE proceedings F (radar and signal processing), vol. 140, no. 2, pp. 107-113. IET Digital Library, 1993. [CrossRef]
  33. Kwok, Ngai Ming, and Gamini Dissanayake. “An efficient multiple hypothesis filter for bearing-only SLAM.” In 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS)(IEEE Cat. No. 04CH37566), vol. 1, pp. 736-741. IEEE, 2004.
  34. Sola, Joan, André Monin, Michel Devy, and Thomas Lemaire. “Undelayed initialization in bearing only SLAM.” In 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 2499-2504. IEEE, 2005.
  35. Munguia, Rodrigo, Bernardino Castillo-Toledo, and Antoni Grau. “A robust approach for a filter-based monocular simultaneous localization and mapping (SLAM) system.” Sensors 13, no. 7 (2013): 8501-8522. [CrossRef]
  36. Prisacariu, Victor Adrian, Olaf Kähler, David W. Murray, and Ian D. Reid. “Simultaneous 3D tracking and reconstruction on a mobile phone.” In 2013 IEEE International Symposium on Mixed and Augmented Reality (ISMAR), pp. 89-98. IEEE, 2013.
  37. Salas-Moreno, Renato F., Richard A. Newcombe, Hauke Strasdat, Paul HJ Kelly, and Andrew J. Davison. “Slam++: Simultaneous localisation and mapping at the level of objects.” In Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 1352-1359. 2013.
  38. Choudhary, Siddharth, Alexander JB Trevor, Henrik I. Christensen, and Frank Dellaert. “SLAM with object discovery, modeling and mapping.” In 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 1018-1025. IEEE, 2014.
  39. Caccamo, S., Ataer-Cansizoglu, E., & Taguchi, Y. (2017). Joint 3D reconstruction of a static scene and moving objects. 2017 International Conference on 3D Vision (3DV), 677–685. [CrossRef]
  40. Joshi, N., Sharma, Y., Parkhiya, P., Khawad, R., Krishna, K. M., & Bhowmick, B. (2018). Integrating objects into monocular slam: Line based category specific models. Proceedings of the 11th Indian Conference on Computer Vision, Graphics and Image Processing, 1–9.
  41. Parkhiya, P., Khawad, R., Murthy, J.K., Bhowmick, B. and Krishna, K.M., 2018, May. Constructing category-specific models for monocular object-slam. In 2018 IEEE International Conference on Robotics and Automation (ICRA) (pp. 4517-4524). IEEE.
  42. Gouiaa, R., & Meunier, J. (2014, May). 3D Reconstruction by Fusioning Shadow and Silhouette Information. Proceedings - Conference on Computer and Robot Vision, CRV 2014. [CrossRef]
  43. Asl Sabbaghian Hokmabadi, I., and N. El-Sheimy. “Probabilistic Silhouette-Based Close-Range Photogrammetry Using a Novel 3d Occupancy-Based Reconstruction.” The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences 43 (2022): 343-350. [CrossRef]
  44. Whitaker, Ross T. “A level-set approach to 3D reconstruction from range data.” International journal of computer vision 29 (1998): 203-231.
  45. Esteban, Carlos Hernández, and Francis Schmitt. “Silhouette and stereo fusion for 3D object modeling.” Computer Vision and Image Understanding 96, no. 3 (2004): 367-392. [CrossRef]
  46. Hinterstoisser, S., Lepetit, V., Ilic, S., Holzer, S., Bradski, G., Konolige, K., & Navab, N. (2013). Model based training, detection and pose estimation of texture-less 3d objects in heavily cluttered scenes. Computer Vision–ACCV 2012: 11th Asian Conference on Computer Vision, Daejeon, Korea, November 5-9, 2012, Revised Selected Papers, Part I 11, 548–562. [CrossRef]
  47. Hokmabadi, Ilyar Asl Sabbaghian, Mengchi Ai, Chrysostomos Minaretzis, Michael Sideris, and Naser El-Sheimy. “Accurate and Scalable Contour-based Camera Pose Estimation Using Deep Learning with Synthetic Data.” In 2023 IEEE/ION Position, Location and Navigation Symposium (PLANS), pp. 1385-1393. IEEE, 2023. [CrossRef]
  48. Noureldin, A., Karamat, T. B., & Georgy, J. (2012). Fundamentals of inertial navigation, satellite-based positioning and their integration. Springer Science & Business Media.
  49. Daum, F., & Huang, J. (2003). Curse of dimensionality and particle filters. 2003 IEEE Aerospace Conference Proceedings (Cat. No. 03TH8652), 4, 4_1979–4_1993.
  50. Asl Sabbaghian Hokmabadi, I. (2018). Localization on Smartphones Using Visual Fingerprinting. Master’s Dissertation, University of Calgary, 2018.
  51. Michael Montemerlo. "FastSLAM: A Factored Solution to the Simultaneous Localization and Mapping Problem with Unknown Data Association." PhD Thesis, CMU-RI-TR-03-28, Robotics Institute, Carnegie Mellon University, 2003.
  52. Henrik, Fåhraeus. “Fusion of IMU and Monocular-SLAM in a Loosely Coupled EKF.” (2017).
  53. Haug, Anton J. Bayesian estimation and tracking: a practical guide. John Wiley & Sons, 2012.
  54. Edelsbrunner, Herbert, and Ernst P. Mücke. “Three-dimensional alpha shapes.” ACM Transactions On Graphics (TOG) 13, no. 1 (1994): 43-72.
  55. E Woods, R., & C Gonzalez, R. (2008). Digital image processing. Pearson Education Ltd.
  56. Ronneberger, O., Fischer, P., & Brox, T. (2015). U-net: Convolutional networks for biomedical image segmentation. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, October 5-9, 2015, Proceedings, Part III 18, 234–241.
  57. Bentley, Jon Louis. “Multidimensional binary search trees used for associative searching.” Communications of the ACM 18, no. 9 (1975): 509-517. [CrossRef]
  58. Gao, X.-S., Hou, X.-R., Tang, J., & Cheng, H.-F. (2003). Complete solution classification for the perspective-three-point problem. IEEE Transactions on Pattern Analysis and Machine Intelligence, 25(8), 930–943. [CrossRef]
  59. Torr, P. H. S., & Zisserman, A. (2000). MLESAC: A new robust estimator with application to estimating image geometry. Computer Vision and Image Understanding, 78(1), 138–156. [CrossRef]
  60. Furgale, P., Rehder, J., & Siegwart, R. (2013). Unified temporal and spatial calibration for multi-sensor systems. 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, 1280–1286.
  61. Chermak, L., Aouf, N., Richardson, M., & Visentin, G. (2019). Real-time smart and standalone vision/IMU navigation sensor. Journal of Real-Time Image Processing, 16(4), 1189–1205. [CrossRef]
Preprints 81333 g001
Figure 1. A comparison of delayed and undelayed initialization.
Figure 1. A comparison of delayed and undelayed initialization.
Preprints 81333 g001
Preprints 81333 g002
Figure 2. The formalization of the SLAM problem as DBN.
Figure 2. The formalization of the SLAM problem as DBN.
Preprints 81333 g002
Preprints 81333 g003
Figure 3. The proposed IMU/monocular tightly coupled solution with initialization to SLAM.
Figure 3. The proposed IMU/monocular tightly coupled solution with initialization to SLAM.
Preprints 81333 g003
Preprints 81333 g004
Figure 4. An illustration of the defined distance between predicted and projected contours.
Figure 4. An illustration of the defined distance between predicted and projected contours.
Preprints 81333 g004
Preprints 81333 g005
Figure 5. The flowchart of the fast particle weighting process.
Figure 5. The flowchart of the fast particle weighting process.
Preprints 81333 g005
Preprints 81333 g006
Figure 6. Illustration of the procedure to establish point correspondences for pose refinement.
Figure 6. Illustration of the procedure to establish point correspondences for pose refinement.
Preprints 81333 g006
Preprints 81333 g007
Figure 7. The flowchart of coarse-to-fine pose estimation.
Figure 7. The flowchart of coarse-to-fine pose estimation.
Preprints 81333 g007
Preprints 81333 g008
Figure 8. Schematics of the challenges with the observation likelihood. The top row shows Challenge I, and the bottom: row shows Challenge II.
Figure 8. Schematics of the challenges with the observation likelihood. The top row shows Challenge I, and the bottom: row shows Challenge II.
Preprints 81333 g008
Preprints 81333 g009
Figure 9. Illustration of the handheld device used for the experiment.
Figure 9. Illustration of the handheld device used for the experiment.
Preprints 81333 g009
Preprints 81333 g010
Figure 10. Qualitative comparison of the projected object before and after pose refinement.
Figure 10. Qualitative comparison of the projected object before and after pose refinement.
Preprints 81333 g010
Preprints 81333 g011
Figure 11. This figure illustrates sample images of the environments of the experiments. The marked points indicate the initial and final positions of the device.
Figure 11. This figure illustrates sample images of the environments of the experiments. The marked points indicate the initial and final positions of the device.
Preprints 81333 g011
Preprints 81333 g012
Figure 12. The path (a) and the corresponding particles and ellipsoids (b).
Figure 12. The path (a) and the corresponding particles and ellipsoids (b).
Preprints 81333 g012
Preprints 81333 g013
Figure 13. The path (a) and the particles and the ellipsoids (b).
Figure 13. The path (a) and the particles and the ellipsoids (b).
Preprints 81333 g013
Preprints 81333 g014
Figure 14. The figure illustrates an increase in uncertainty when the object is severely occluded.
Figure 14. The figure illustrates an increase in uncertainty when the object is severely occluded.
Preprints 81333 g014
Table 1. A summary of the sensors, processor, and the power supply used for the experiments.
Table 1. A summary of the sensors, processor, and the power supply used for the experiments.
Sensor Intrinsic calibration Extrinsic calibration Additional information
Monocular camera MATLAB’s calibration toolbox Provided by 3D CAD model Arducam with 8MP IMX219
IMU 6-position static calibration Provided by 3D CAD model Xsens mti-g-710
Power supply N/A N/A Krisdonia Laptop Power Bank
Mini Desktop PC N/A N/A Beelink Mini S
Table 2. The errors in the position (cm) for five tests.
Table 2. The errors in the position (cm) for five tests.
Test Error in Position Distance
(camera to object)		 Experiments details
EV(cm) MAP(cm)
Test 1 7.8 22.4 short lower clutter, shorter trajectory
Test 2 4.1 18.9 long lower clutter, shorter trajectory
Test 3 12.3 35.7 medium higher clutter, longer trajectory
Test 4 13.1 32.7 medium higher clutter, longer trajectory
Test 5 12.3 25.5 medium higher clutter, average trajectory
Table 3. The ratio of the error in the position to the TTP.
Table 3. The ratio of the error in the position to the TTP.
Test Error in Position Distance
(camera to object)		 Experiments details
EV/ TTP MAP/ TTP
Test 1 0.015 0.043 short lower clutter, shorter trajectory
Test 2 0.005 0.023 long lower clutter, shorter trajectory
Test 3 0.018 0.052 medium higher clutter, longer trajectory
Test 4 0.021 0.052 medium higher clutter, longer trajectory
Test 5 0.014 0.029 medium higher clutter, average trajectory
Table 4. The IoU of the particles along the trajectory.
Table 4. The IoU of the particles along the trajectory.
Test Other Assessment Metrics Distance
(camera to object)		 Experiments details
IoU Fail rate
Test 1 0.805 0.00 short lower clutter, shorter trajectory
Test 2 0.805 0.00 long lower clutter, shorter trajectory
Test 3 0.819 0.00 medium higher clutter, longer trajectory
Test 4 0.821 0.00 medium higher clutter, longer trajectory
Test 5 0.747 0.01 medium higher clutter, average trajectory
Table 5. The performance of the developed tightly coupled solution for different particle numbers.
Table 5. The performance of the developed tightly coupled solution for different particle numbers.
Number of Particles Error in position Other Assessment Metrics
EV(cm) EV/ TTP IoU Time(s) Fail rate.
5000 12.4 0.018 0.813 6149.2 0.00
7000 11.4 0.020 0.821 8577.4 0.00
9000 10.9 0.019 0.824 9291.8 0.00
13000 10.8 0.018 0.830 11015.2 0.00
17000 13.4 0.022 0.835 12488.7 0.00
19000 11.0 0.018 0.837 13390.3 0.00
Table 6. The performance of the developed tightly coupled solution using two objects.
Table 6. The performance of the developed tightly coupled solution using two objects.
Test Error in position Other details
EV(cm) MAP(cm) EV/TTP MAP/TTP IoU Fail rate
Test 6 9.1 17.3 0.012 0.023 0.815 0.03
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated