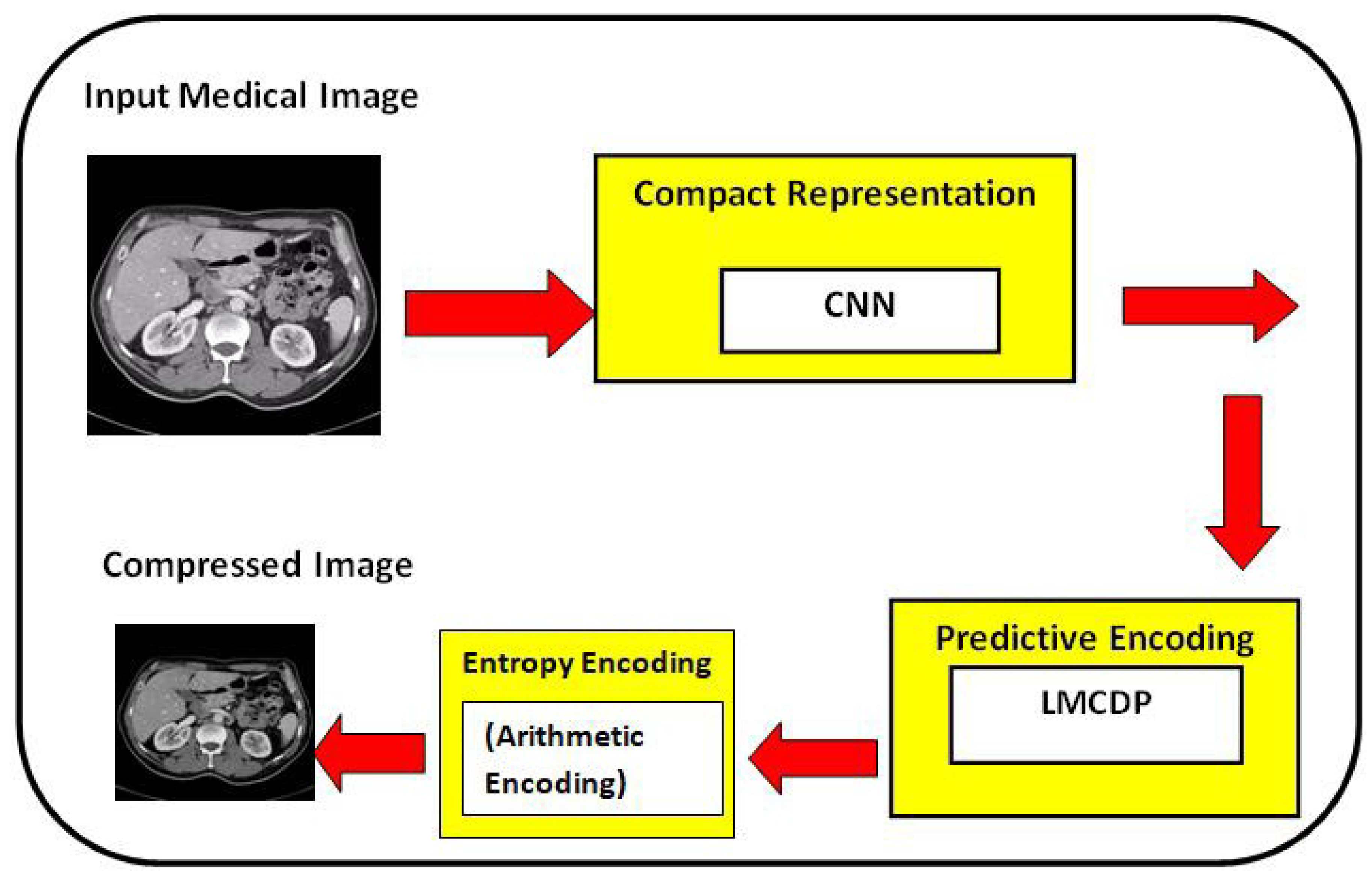
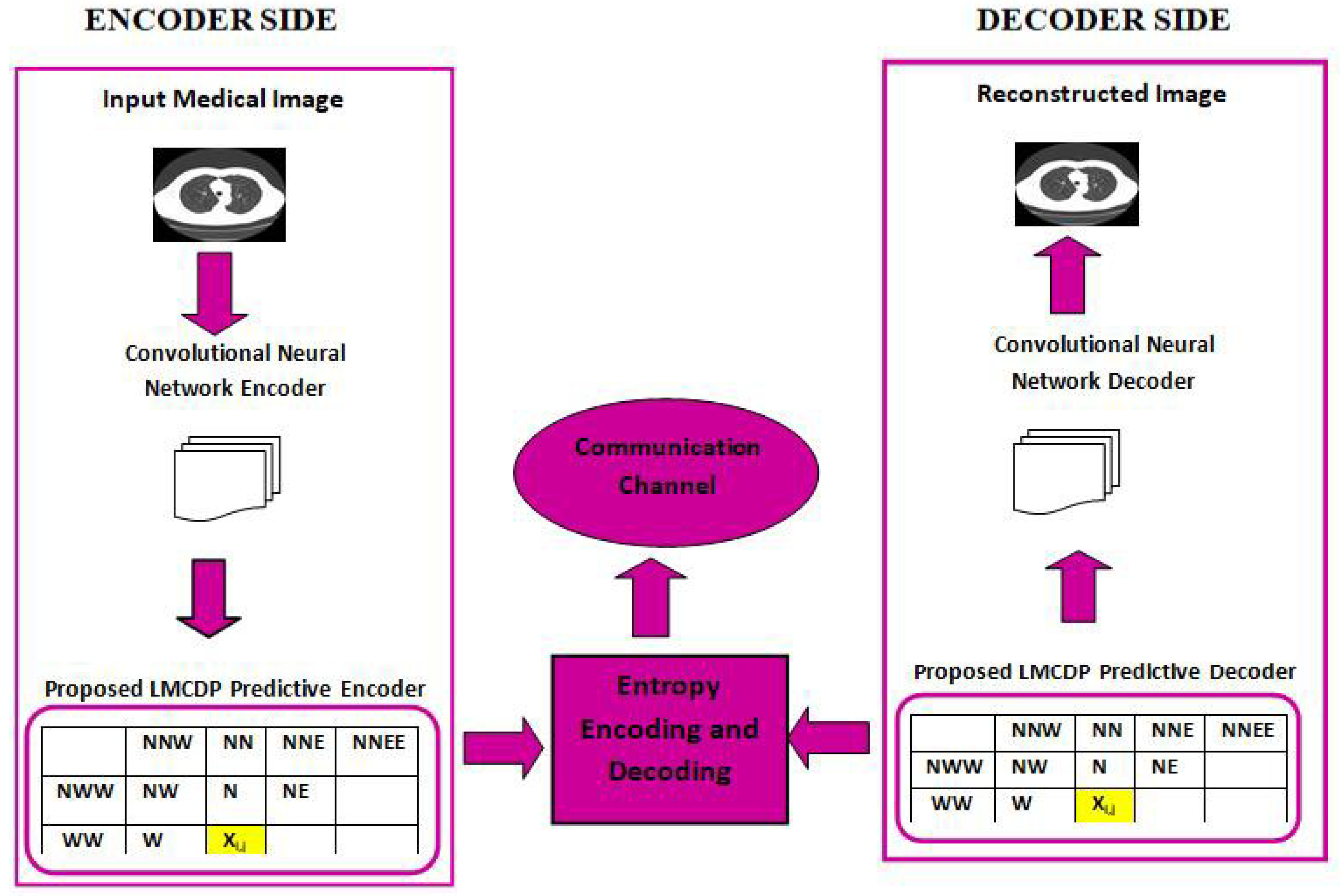
The proposed experimental works are conducted for 8 bit and 16 bit MRI and CT medical image samples. Various compression performance metrics such as CR, PSNR, MSE, BPP, SSIM, SC, NAE, NK and LMSE are used to validate the compression performance.
4.2. EXPERIMENTAL RESULTS
In this section, the experimental analysis is carried out for medical image datasets namely, CT-skull, MRI_ head, CT-Lung R13 (Grove, 2015), CT-Lung-R4 (Grove, 2015), MR-Neuro (Barboriak, 2015) and MR-Breast (Meyer, 2015) which are publicly available.
The CT-skull images used for testing are collected from CIPR dataset and MRI_ head samples from Computer Vision Group . CT-Lung R13, CT-Lung-R4, MR-Neuro and MR-Breast test samples of 16-bit depth are collected from Cancer Imaging Archive (Clark, 2013) dataset.
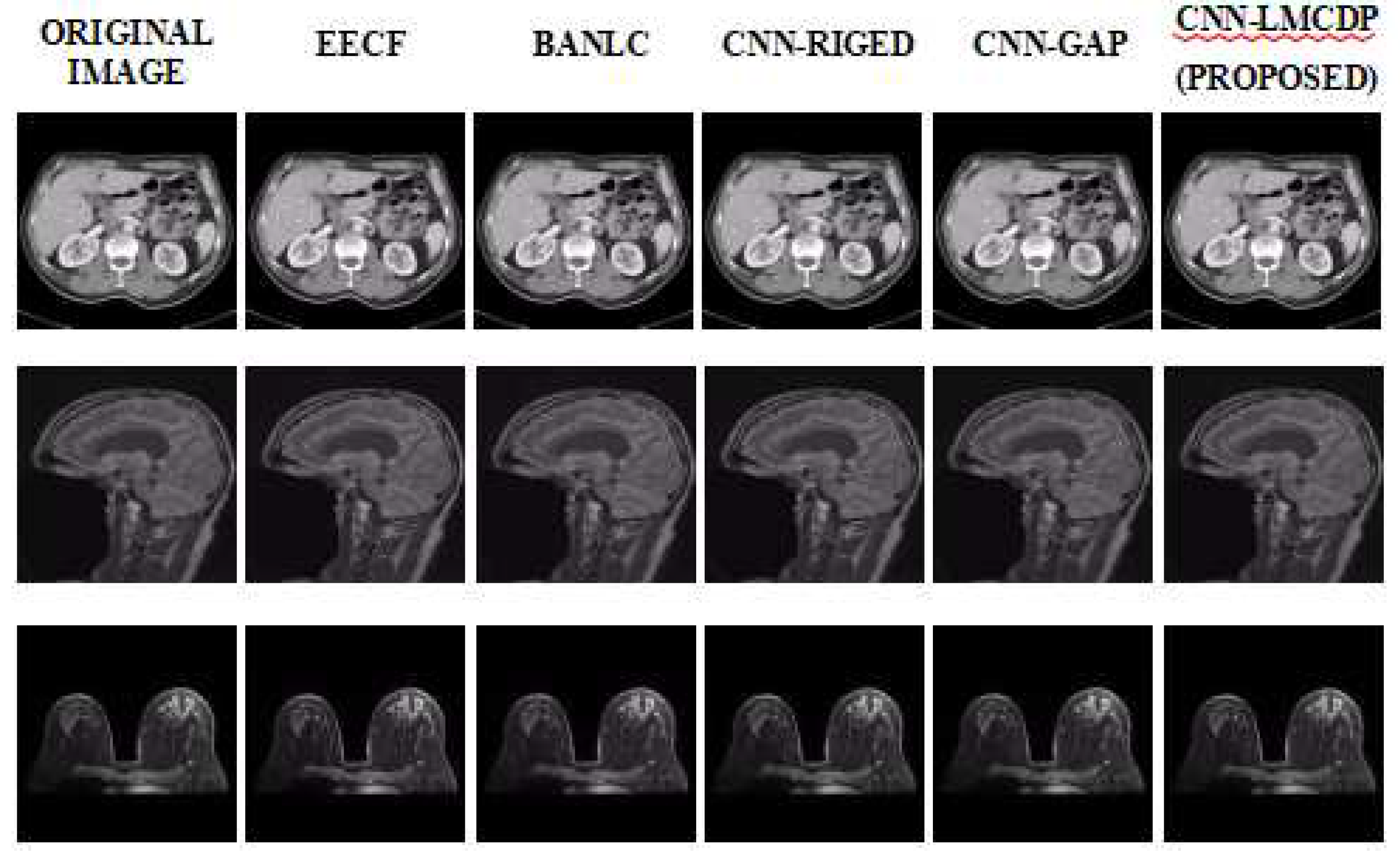
Figure 7 represents compression performance of various medical image samples. The proposed CNN-LMCDP method is compared with the existing techniques such as End to End Compression Framework (EECF) (Jiang, 2017), Block Adaptive Near Lossless Compression (BANLC) (Sharma,2020), CNN-RIGED and CNN-GAP respectively. From the figure, it is observed that the proposed work is better compared to the existing techniques.
Figure 7.
Comparison of CR (8 bit images) obtained by the proposed method with existing compression methods
Figure 7.
Comparison of CR (8 bit images) obtained by the proposed method with existing compression methods
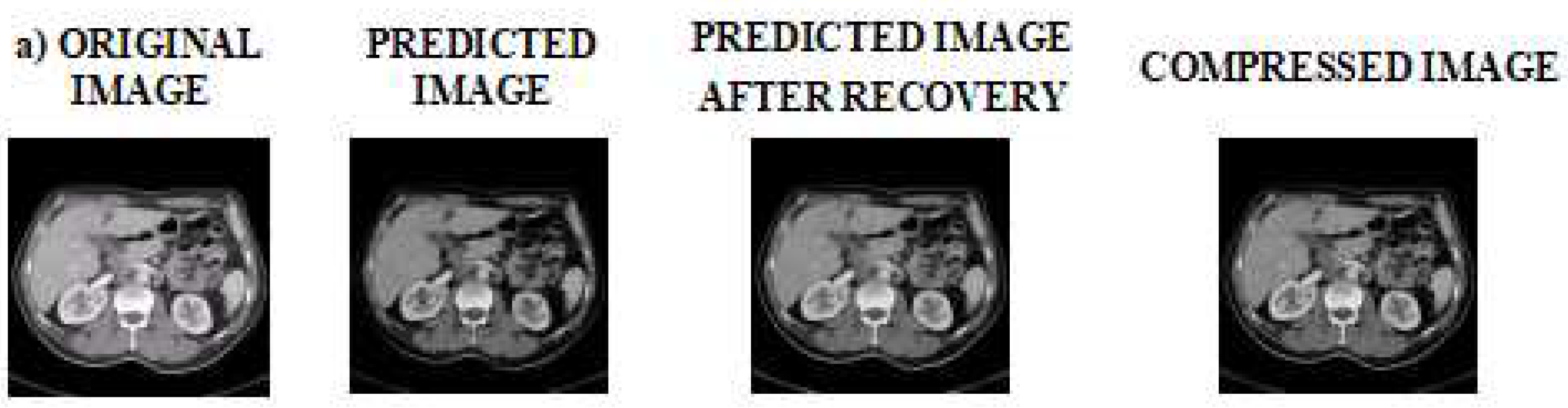
Figure 7 represents the sample outputs obtained while compressing various medical image samples. Firstly, the original image is fed into the encoder. Secondly, the predicted image is obtained after prediction. Thirdly, the predicted image is recovered and as a final step, the compressed image is obtained.
From the results obtained from Table 9, it is reported that the PSNR of the proposed CNN-LMCDP method for 16 bit depth images is compared with other existing approaches such as BANLC, EECF, CNN- RIGED and CNN-GAP. The proposed CNN-LMCDP method has achieved 1% improvement in the average PSNR results. Cancer Imaging Archive, a publicly available dataset reported in Table 9 have achieved 1% improvement in PSNR for the proposed work, when compared to BANLC method, 1% improvement in PSNR for EECF method, 1% improvement in PSNR for CNN-RIGED and 1% improvement in PSNR for CNN-GAP.
Table 9.
Comparison of PSNR values (16 bit images) for the proposed method with the existing compression methods
Table 9.
Comparison of PSNR values (16 bit images) for the proposed method with the existing compression methods
| DATASETS |
BANLC |
EECF |
CNN- RIGED |
CNN- GAP |
CNN-LMCDP (Proposed) |
| CT-Lung-R13 |
66.35 |
65.42 |
66.64 |
65.87 |
67.35 |
| CT-Lung-R4 |
67.30 |
67.02 |
67.60 |
66.81 |
68.32 |
| MR-Neuro |
64.46 |
65.16 |
63.74 |
63.99 |
65.43 |
| MR-Breast |
63.94 |
63.05 |
64.22 |
63.98 |
64.91 |
| Average |
65.51 |
65.16 |
65.55 |
65.16 |
66.50 |
CIPR, a publicly available dataset reported in Table 10 for MRI_head image sequences have achieved approximately 5% improvement in PSNR for the proposed work when compared to BANLC method, 1% improvement in PSNR for EECF, 1% improvement in PSNR for CNN- RIGED and 2% improvement in PSNR for CNN-GAP CIPR dataset of BANLC, EECF, CNN-RIGED and CNN-GAPreported in Table 10 for CT skull image sequences have achieved 5% improvement in PSNR when compared to BANLC method, 2% improvement in PSNR for EECF method, 1% improvement in PSNR for CNN-RIGED and 2% improvement in PSNR for CNN-GAP. From
Figure 8, it is observed that the PSNR values of the proposed work for 16 bit depth images has achieved better results when compared to the existing techniques. It is 4%, 2%, 1%, 1%, 1% and 1% better than Set Partitioning in Hierarchical Trees (SPIHT) (Said, 1996), JPEG 2000[65], BANLC, EECF, CNN-RIGED and CNN-GAP respectively.
Table 10.
Comparison of PSNR values (8 bit images) for the proposed method with the existing methods
Table 10.
Comparison of PSNR values (8 bit images) for the proposed method with the existing methods
| DATASETS |
BANLC |
EECF |
CNN- RIGED |
CNN- GAP |
CNN-LMCDP (Proposed) |
| MRI_head |
43.617 |
46.88 |
44.86 |
45.32 |
46.09 |
| CT-skull |
46.018 |
50.44 |
52.00 |
50.56 |
52.06 |
| Average |
44.8175 |
48.66 |
48.43 |
47.94 |
49.075 |
From Figure 9, it is observed that the PSNR value of the proposed work for 8 bit depth images is better when compared to the existing techniques. It is 5%, 5%, 5%, 1%, 1% and 2% better than SPIHT, JPEG 2000, BANLC, EECF, CNN-RIGED and CNN-GAP respectively.
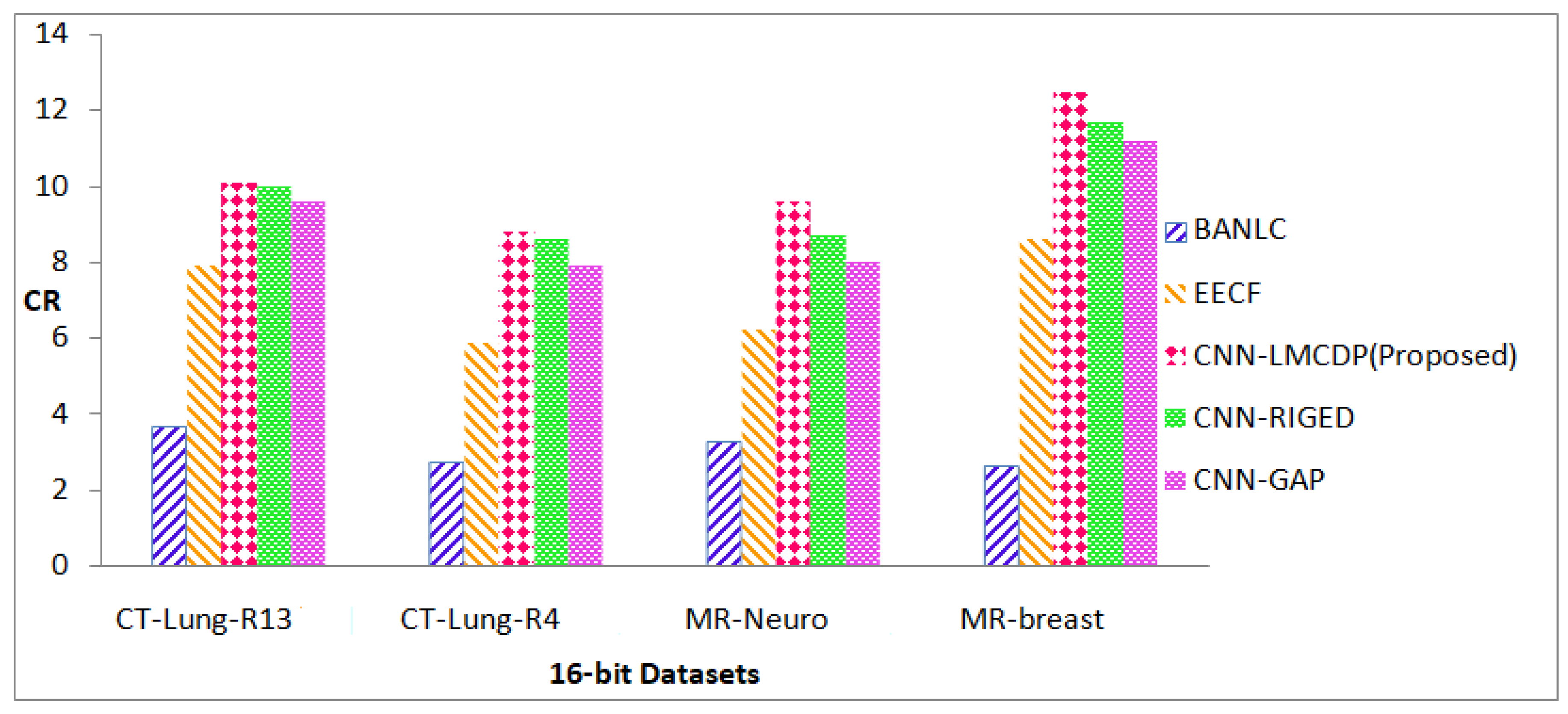
Various measures are taken into consideration to validate the proposed method results.CR is an effective measure which is used for assessing compression efficiency. Figure 4.17 and 4.18 represent the results obtained from various datasets for 16 bit and 8 bit images in terms of CR. Higher value of CR represents better compression and that is attained in the proposed work.From Figure 8, it is revealed that the proposed CNN-LMCDP method has achieved a maximum CR compared with other existing works. For the 16 bit test samples such as CT-Lung R13, CT-Lung-R4, MR-Neuro and MR-Breast images, the proposed CNN-LMCDP method has exhibited superior results with a higher average CR of 10.22.
CT-Lung R13 image sequences have achieved 7% improvement in CR for the proposed work, when compared to BANLC method, 2% improvement in CR for EECF method, 1% improvement in CR for CNN- RIGED and 2% improvement in CR for CNN-GAP. CT-Lung R4 image sequences have achieved 6% improvement in CR when compared to BANLC method, 3% improvement in CR for EECF method, 1% improvement in CR for CNN-RIGED and 1% improvement in CR for CNN-GAP.
Cancer Imaging Archive [27] dataset for MR-Neuro image sequences have achieved 6% improvement in CR when compared to BANLC method, 3% improvement in CR for EECF, 1% improvement in CR for CNN- RIGED and 2% improvement in CR for CNN-GAP. For MR-Breast image sequences, the dataset has achieved 9% improvement in CR when compared to BANLC method, 3% improvement in CR for EECF method, 1% improvement in CR for CNN-RIGED and 1% improvement in CR for CNN- GAP.
For all the other methods, the test images have achieved an average CR of 3.05,7.14,9.74 and 9.17 for BANLC, EECF, CNN-RIGED and CNN-GAP respectively, which is very less when compared to the proposed method.
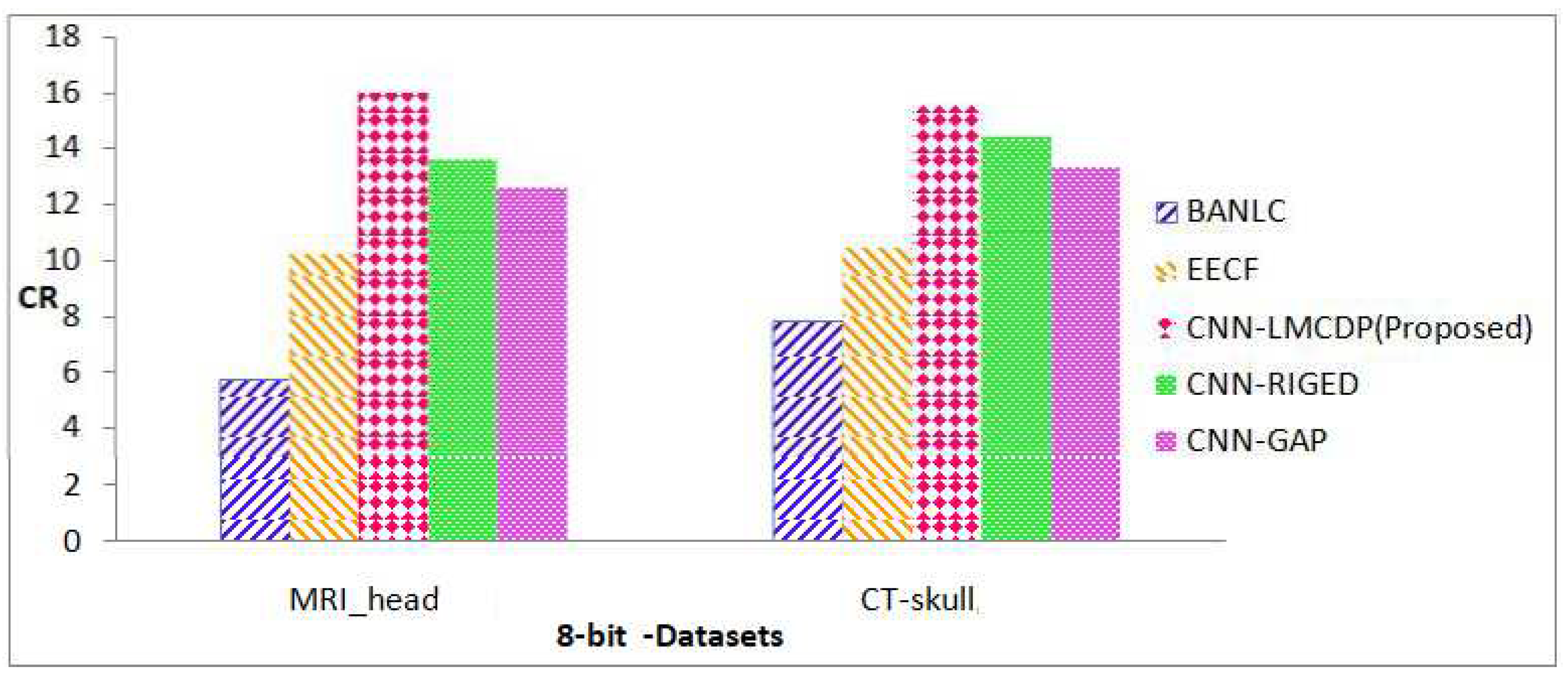
Figure 9 for MRI_head and CT-skull image sequences have achieved a maximum average CR of 15.75 bits which is an improvement of 9%, 5%, 1% and 3% for BANLC, EECF, CNN-RIGED and CNN-GAP respectively.
In the same manner, Figure 9 for 16 bit dataset images such as MRI_head and CT-skull, the proposed method excels with superior performance with an average CR of 10.22. There is an improvement by 8%, 8%, 7%, 3%, 1% and 1% for SPIHT, JPEG 2000, BANLC, EECF, CNN-RIGED and CNN-GAP respectively for the proposed method.
From Figure 10, it is observed that the proposed work for 8 bit depth images has achieved better CR results when compared to the existing techniques. It is 10%, 11%, 9%, 5%, 2% and 3% better than SPIHT, JPEG- 2000, BANLC, EECF, CNN-RIGED and CNN-GAP respectively.the proposed method is compared with state of art compression techniques
Figure 8.
1 BPP results (8 bit images) obtained by
the proposed method is compared with existing compression techniques for MRI_head and CT-skull datasets
Figure 8.
1 BPP results (8 bit images) obtained by
the proposed method is compared with existing compression techniques for MRI_head and CT-skull datasets
From Figure 11, it is observed that the proposed work for 8 bit depth images has achieved better CR results when compared to the existing techniques. It is 10%, 11%, 9%, 5%, 1% and 3% better than SPIHT, JPEG 2000, BANLC, EECF, CNN-RIGED and CNN-GAP respectively.
Figure 9.
2 BPP results (16 bit images) obtained by the proposed method is compared with existing compression techniques for MRI and CT Datasets
Figure 9.
2 BPP results (16 bit images) obtained by the proposed method is compared with existing compression techniques for MRI and CT Datasets
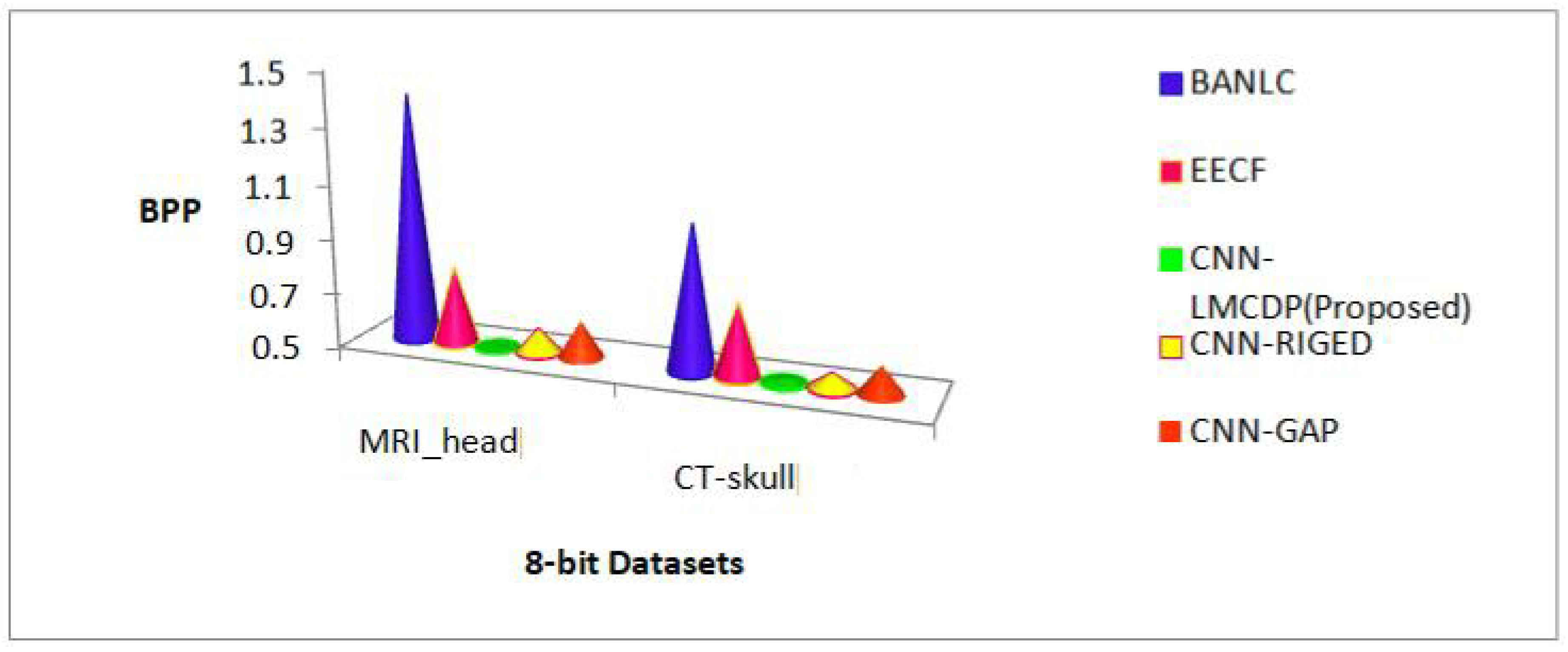
From Figure 12, it is observed that the proposed work for 16 bit depth images has achieved better BPP results of 0.79 bits when compared to the existing techniques. BPP results achieved by existing methods such as BANLC, EECF, CNN-RIGED and CNN-GAP are 2.67, 1.15, 0.83 and 0.89respectively.
In the same manner, Figure 13 for 16 bit test samples such as CT- Lung R13, CT-Lung-R4, MR-Neuro and MR-Breast images, the proposed CNN-LMCDP method has exhibited BPP results with a minimum average BPP of 0.7.
Figure 14 explains the result of the proposed method compared to the standard methods such as SPIHT and JPEG 2000 and with the existing methods like BANLC, EECF, CNN-RIGED and CNN-GAP. From the results, it is revealed that the BPP result for the proposed CNN-LMCDP method of 8- bit image samples outperform other methods. The BPP result achieved by the proposed LMCDP technique is 0.50 whereas the BPP results excels by the other methods such as SPIHT, JPEG 2000, BANLC, EECF, CNN-RIGED and CNN-GAP with 1.43, 1.81, 1.21, 0.77, 0.57 and 0.61 respectively.
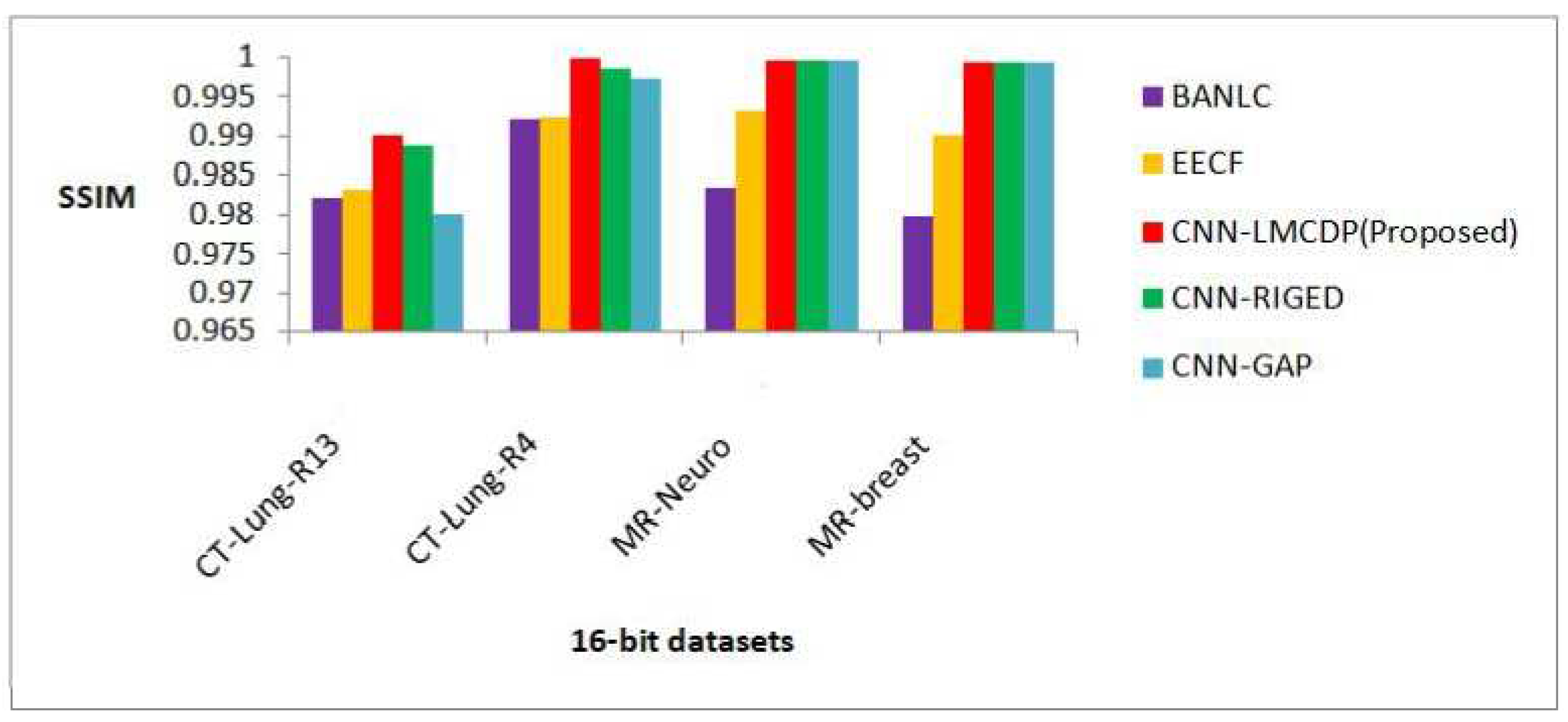
From Figure 15, it is revealed that the proposed CNN-LMCDP method has achieved the maximum average SSIM of 0.997 compared with other existing works for 16 bit test samples for different datasets such as CT- Lung R13, CT-Lung-R4, MR-Neuro and MR-breast images. For all the other methods, the test images have achieved an average SSIM of 0.984, 0.990, 0.996 and 0.990 for BANLC, EECF, CNN-RIGED and CNN-GAP respectively.
Figure 10.
5 Comparison of proposed method in terms of SSIM for 16 bit images over other compression techniques
Figure 10.
5 Comparison of proposed method in terms of SSIM for 16 bit images over other compression techniques
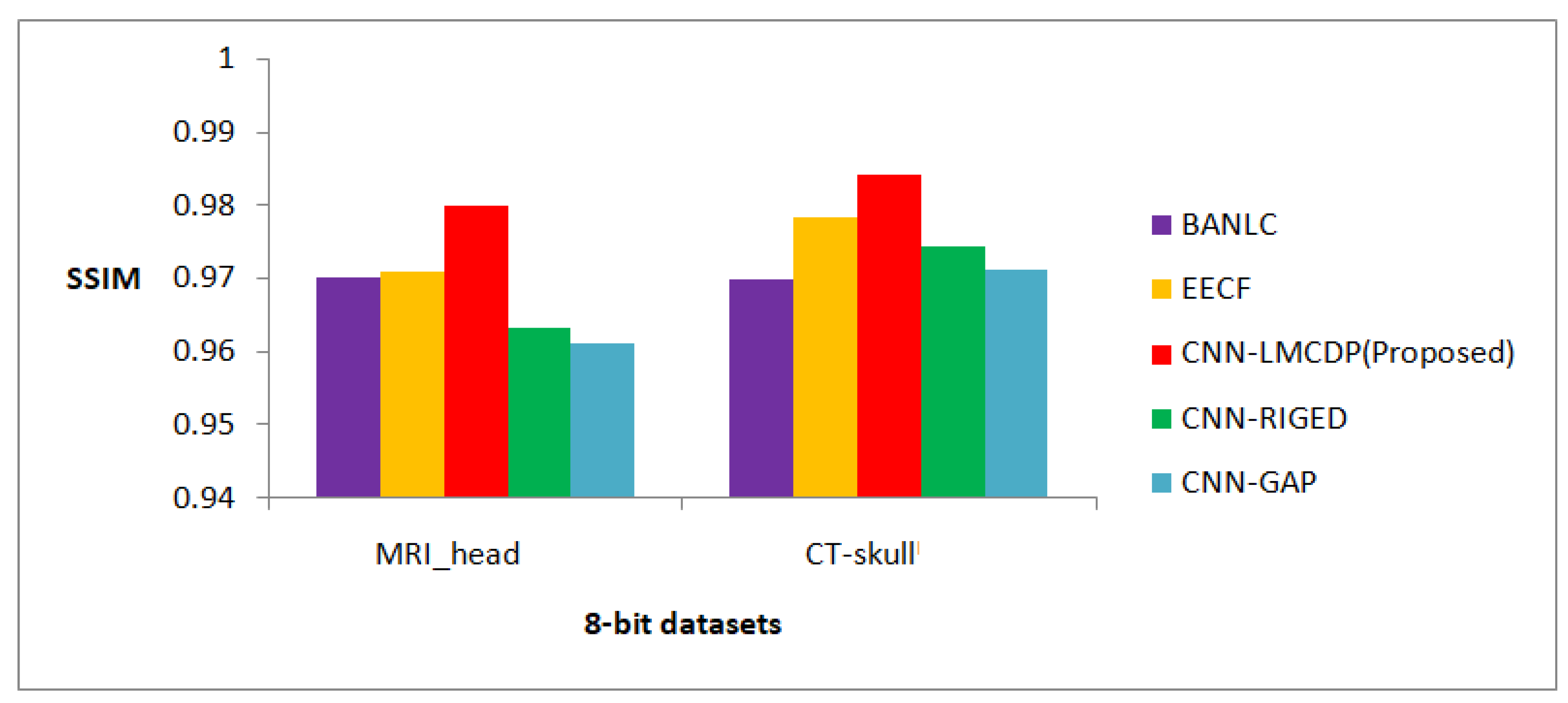
Figure 11.
Comparison of proposed method in terms of SSIM for 8 bit images over other compression techniques
Figure 11.
Comparison of proposed method in terms of SSIM for 8 bit images over other compression techniques
From Figure 13, it is obvious that for 8 bit dataset images such as MRI-head and CT-skull, the proposed CNN-LMCDP method has exhibited best result with an average SSIM of 0.982. For all the other methods, the test images have achieved an average SSIM of 0.970, 0.974, 0.968 and 0.966 for BANLC, EECF, CNN-RIGED and CNN-GAP respectively
Table 11.
Comparison of SC values for the proposed method over other existing compression techniques for various datasets
Table 11.
Comparison of SC values for the proposed method over other existing compression techniques for various datasets
| DATASETS |
BANLC |
EECF |
CNN- RIGED |
CNN- GAP |
CNN-LMCDP (Proposed) |
| CT-Lung-R13 |
0.9935 |
1.0067 |
0.98793 |
0.9744 |
1.0023 |
| CT-Lung-R4 |
0.9895 |
0.9895 |
1.0043 |
0.98054 |
0.9998 |
| MR-Neuro |
0.9997 |
0.9977 |
0.9922 |
0.9893 |
1.0045 |
| MR-breast |
0.9933 |
0.9905 |
0.9605 |
0.9751 |
0.9832 |
| MRI_head |
0.9531 |
0.9653 |
0.9622 |
0.9608 |
0.9727 |
| CT-skull |
0.9503 |
0.961 |
0.9711 |
0.963 |
0.9766 |
explains the SC value for the proposed work which is compared with the existing approaches such as BANLC, EECF, CNN-RIGED and CNN-GAP for different datasets such as CT-Lung R13, CT-Lung-R4, MR-Neuro, MR-Breast, MRI_ head and CT-skull images.
Table 12.
Comparison of NAE values for the proposed method over other existing compression techniques for various datasets
Table 12.
Comparison of NAE values for the proposed method over other existing compression techniques for various datasets
| DATASETS |
BANLC |
EECF |
CNN- RIGED |
CNN- GAP |
CNN- LMCDP (Proposed) |
| CT-Lung-R13 |
0.000617 |
0.000617 |
0.000617 |
0.000617 |
0.000617 |
| CT-Lung-R4 |
0.000619 |
0.000619 |
0.000619 |
0.000619 |
0.000619 |
| MR-Neuro |
0.000941 |
0.000941 |
0.000937 |
0.000937 |
0.000937 |
| MR-breast |
0.000628 |
0.000627 |
0.000627 |
0.000627 |
0.000626 |
| MRI_head |
0.001050 |
0.001050 |
0.001042 |
0.001042 |
0.001049 |
| CT-skull |
0.001044 |
0.001040 |
0.001040 |
0.001040 |
0.001038 |
The SC value for the proposed scheme for different datasets such as CT-Lung R13, CT-Lung-R4, MR-Neuro, MR-Breast and MRI_ head and CT- skull reported are 1.0023, 0.9998, 1.0045, 0.9832, 0.9727 and 0.97666 respectively. The SC value nearer to 1 indicates that the reconstructed image is of high quality and it is achieved by all the datasets and it is also superior compared to other methods.explains the NAE value for the proposed work and is compared with the existing approaches such as BANLC, EECF, CNN-RIGED and CNN-GAP. The NAE value for the proposed scheme for different datasets such as CT-Lung-R13, CT-Lung-R4, MR-Neuro, MR-Breast, MRI_head and CT-skull reported are 1.0023, 0.9998, 1.0045, 0.9832, 0.9727 and 0.97666 respectively.
Table 13.
Comparison of NCC values for the proposed method over other existing compression techniques for various datasets
Table 13.
Comparison of NCC values for the proposed method over other existing compression techniques for various datasets
| DATASETS |
BANLC |
EECF |
CNN- RIGED |
CNN-GAP |
CNN- LMCDP (Proposed) |
| CT-Lung-R13 |
0.98001 |
0.9889 |
0.9812 |
0.9799 |
0.9901 |
| CT-Lung-R4 |
0.9722 |
0.9844 |
0.98762 |
0.9712 |
0.9922 |
| MR-Neuro |
0.9844 |
0.9965 |
0.9901 |
0.9799 |
0.9955 |
| MR-breast |
0.9744 |
0.9803 |
0.9688 |
0.9611 |
0.9813 |
| MRI_head |
0.9512 |
0.9533 |
0.9677 |
0.9711 |
0.9733 |
| CT-skull |
0.9512 |
0.9599 |
0.9612 |
0.9599 |
0.9798 |
illustrates the NCC value for the proposed work and is compared with the existing approaches such as BANLC, EECF, CNN-RIGED and CNN-GAP for different datasets such as CT-Lung R13, CT-Lung-R4,
MR-Neuro, MR-Breast, MRI_ head and CT-skull images. The NK value for the proposed scheme for different datasets such as CT-Lung R13, CT-Lung- R4, MR-Neuro and MR-Breast reported are 1.0023, 0.9998, 1.0045, 0.9832,
Table 14.
Comparison of LMSE values for the proposed method over other existing compression techniques for various datasets
Table 14.
Comparison of LMSE values for the proposed method over other existing compression techniques for various datasets
| DATASETS |
BANLC |
EECF |
CNN- RIGED |
CNN- GAP |
CNN- LMCDP (Proposed) |
| CT-Lung-R13 |
0.001235 |
0.00124 |
0.00122 |
0.00121 |
0.00121 |
| CT-Lung-R4 |
0.001216 |
0.00122 |
0.0012 |
0.0012 |
0.00121 |
| MR-Neuro |
0.001321 |
0.00132 |
0.00131 |
0.00131 |
0.00131 |
| MR-breast |
0.001224 |
0.00119 |
0.00118 |
0.00118 |
0.00115 |
| MRI_head |
0.001578 |
0.00152 |
0.00152 |
0.00153 |
0.00150 |
| CT-skull |
0.001512 |
0.001498 |
0.001465 |
0.001467 |
0.001436 |
The LMSE value for the proposed work is compared with the existing approaches such as BANLC, EECF, CNN-RIGED and CNN-GAP with different datasets such as CT-Lung R13, CT-Lung-R4, MR-Neuro, MR- Breast, MRI_ head and CT-skull images which are shown in Table 4.6. The LMSE value for the proposed scheme for different datasets such as CT-Lung R13, CT-Lung-R4, MR-Neuro and MR-Breast reported are 1.0023, 0.9998, 1.0045, 0.9832, 0.9727 and 0.97666, respectively. For most of the data sets, the encoding time for RLE and AE is less when compared to the proposed work.
Table 15.
Comparison of MSE values for the proposed method over other existing compression techniques for various datasets
Table 15.
Comparison of MSE values for the proposed method over other existing compression techniques for various datasets
| DATASETS |
BANLC |
EECF |
CNN- RIGED |
CNN- GAP |
CNN- LMCDP (Proposed) |
| CT-Lung-R13 |
0.04605 |
0.04613 |
0.04601 |
0.04602 |
0.04501 |
| CT-Lung-R4 |
0.04512 |
0.04527 |
0.0453 |
0.0453 |
0.04513 |
| MR-Neuro |
0.04645 |
0.04622 |
0.04548 |
0.04548 |
0.04548 |
| MR-breast |
0.04683 |
0.04624 |
0.04378 |
0.04376 |
0.04591 |
| MRI_head |
0.05619 |
0.05366 |
0.0552 |
0.05592 |
0.05356 |
| CT-skull |
0.05326 |
0.05144 |
0.50394 |
0.05322 |
0.5034 |
The MSE value for the proposed work is compared with the existing approaches such as BANLC, EECF, CNN-RIGED and CNN-GAP with different datasets such as CT-Lung R13, CT-Lung-R4, MR-Neuro, MR- Breast, MRI_ head and CT-skull images which are shown in Table 4.7.
Table 16.
Comparison of PSNR values for the proposed method over other existing compression techniques for various datasets
Table 16.
Comparison of PSNR values for the proposed method over other existing compression techniques for various datasets
| DATASETS |
BANLC |
EECF |
CNN- RIGED |
CNN- GAP |
CNN-LMCDP (Proposed) |
| CT-Lung-R13 |
66.35 |
65.42 |
66.64 |
65.87 |
67.35 |
| CT-Lung-R4 |
67.30 |
67.02 |
67.60 |
66.81 |
68.32 |
| MR-Neuro |
64.46 |
65.16 |
63.74 |
63.99 |
65.43 |
| MR-Breast |
63.94 |
63.05 |
64.22 |
63.98 |
64.91 |
| MRI_head |
43.61 |
46.88 |
44.86 |
45.32 |
46.09 |
| CT-skull |
46.01 |
50.44 |
52.00 |
50.56 |
52.06 |
The MSE value for the proposed scheme for different datasets such as CT-Lung R13, CT-Lung-R4, MR-Neuro and MR-Breast reported are 1.0023, 0.9998, 1.0045, 0.9832, 0.9727 and 0.97666, respectively. The MSEvalue nearer to 1 indicates that the reconstructed image is of high quality and it is achieved by all the datasets for the proposed work. reports the PSNR value for the proposed work in comparison with the existing approaches such as BANLC, EECF, CNN- RIGED and CNN-GAP. The PSNR values of the proposed scheme for different datasets such as CT-Lung R13, CT-Lung-R4, MR-Neuro, MR- Breast, MRI_ head and CT-skull images reported are 67.35, 68.32, 65.43, 64.91, 46.09 and 52.06 respectively. The PSNR value is improved by 1%,2%,1%, and 2% for CT-Lung R13 and improved by 1%, 1%,1%, and 2% for CT-Lung R4 dataset.
Table 17.
Comparison of CR values for the proposed method over other existing encoding techniques of various datasets
Table 17.
Comparison of CR values for the proposed method over other existing encoding techniques of various datasets
| DATASETS |
BANLC |
EECF |
CNN- RIGED |
CNN- GAP |
CNN- LMCDP (Proposed) |
| CT-Lung-R13 |
3.64 |
7.89 |
10.00 |
9.59 |
10.06 |
| CT-Lung-R4 |
2.69 |
5.88 |
8.61 |
7.92 |
8.79 |
| MR-Neuro |
3.27 |
6.20 |
8.67 |
7.98 |
9.58 |
| MR-breast |
2.59 |
8.60 |
11.68 |
11.19 |
12.46 |
| MRI_head |
5.71 |
10.25 |
13.61 |
12.58 |
15.97 |
| CT-skull |
7.79 |
10.49 |
14.39 |
13.27 |
15.53 |
Similarly, the PSNR value is improved by 1%, 0.27%, 2% and 2% for MR-Neuro and is improved by 1%, 1%, 0.69% and 2% for MR-Breas dataset. And also, the PSNR value is improved by 3%, 0.79%, 2% and 1% for MR-head and improved by 6%, 2%, 0.06% and 2% for CT-skull dataset. The high PSNR value indicates that the reconstructed image is of high quality and it is achieved for all the datasets.discusses the CR value for the proposed work and is compared with the existing approaches suchas BANLC, EECF, CNN-RIGED and CNN-GAP. The CR value of the proposed scheme is superior for different datasets such as CT-Lung R13, CT-Lung-R4, MR-Neuro, MR- Breast, MRI_ head and CT-skull and the results reported are 10.06, 8.79, 9.58, 12.46, 15.97 and 15.53 respectively.
Table 18.
Comparison of BPP values for the proposed method over other existing compression techniques for various datasets
Table 18.
Comparison of BPP values for the proposed method over other existing compression techniques for various datasets
| DATASETS |
BANLC |
EECF |
CNN-RIGED |
CNN-GAP |
CNN-LMCDP (Proposed) |
| CT-Lung-R13 |
2.193 |
1.01 |
0.7999 |
0.83 |
0.795 |
| CT-Lung-R4 |
2.967 |
1.36 |
0.929 |
1.01 |
0.91 |
| MR-Neuro |
2.445 |
1.29 |
0.923 |
1.0031 |
0.835 |
| MR-breast |
3.082 |
0.93 |
0.685 |
0.715 |
0.642 |
| MRI_head |
1.4 |
0.78 |
0.588 |
0.636 |
0.501 |
| CT-skull |
1.026 |
0.762 |
0.556 |
0.603 |
0.515 |
0 explains the BPP value for the proposed work in comparison with the existing approaches such as BANLC, EECF, CNN- RIGED and CNN-GAP. The BPP value reported for the proposed scheme for different datasets such as CT-Lung R13, CT-Lung-R4, MR-Neuro, MR- Breast, MRI_ head and CT-skull are 0.795, 0.91, 0.835, 0.642, 0.501 and