Prerpints.org logo
Preprint
Article

A New Approach to Estimating the Parameters of Structural Formations in Polyethylene Reactor Powder

Altmetrics

Downloads

133

Views

41

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

02 August 2023

Posted:

04 August 2023

You are already at the latest version

Alerts
Abstract
The morphology of virgin reactor powder (RP) of high-density polyethylene HDPE with MW = 160,000 g/mol was investigated with the help of DSC, SEM, SAXS and WAXS methods. The morphological SEM analysis showed, that the main morphological units of RP are macro- and micro-shish kebab structures with significantly different geometric dimensions, as well as individual lamellae of folded chain crystals. Quantitative analysis of an asymmetric SAXS reflection made it possible to reveal the presence of several periodic morphoses in the RP with long periods from 20 nm to 60 nm and to correlate them with the observed powder morphology. According to the DSC crystallinity data, the thickness of the lamellae in each long period was estimated. Their surface energy was calculated in the framework of the Gibbs-Thompson theory. The presence of regular and irregular folds on the surface of the different shish-kebab lamellae is discussed. The percentage of identified morphoses in the RP was calculated. It has been suggested that the specific structure of HDPE RP is due to the peculiarity of polymer crystallization during suspension synthesis in a quasi-stationary regime, in which local overheating and inhomogeneous distribution of shear stresses in a chemical reactor are possible.
Keywords: 
Subject: Chemistry and Materials Science  -   Materials Science and Technology

1. Introduction

Ultra-high molecular weight polyethylene (UHMWPE) continues to be one of the most popular and widely used polymer materials due to its high chemical resistance to aggressive media, high wear resistance, low friction coefficient, high impact strength, ability to fiber formation and the possibility of obtaining high performance fibers, on the basis of which products for various purposes are created: from bulletproof vests and armor to boat hulls, towing ropes, medical implants, suture material, etc. As known, UHMWPE has a very high melt viscosity, which makes it impossible to process it by traditional methods such as ram extrusion and injection molding. Recently, it has become possible to process UHMWPE in the molten state by modified methods of ram extrusion and compression molding due to a significant increase in temperature (up to 200°C) and an increase in the residence time of the polymer at elevated temperature (up to 2 hours) [1]. However, the presence of the polymer for a long time at a high temperature inevitably leads to its destruction and deterioration of properties. To facilitate the processability of UHMWPE and modify its behavior one can mix it with polyethylene (PE) of lower MW.
For instance, a synthesized UHMWPE with a less entangled state and a commercial UHMWPE with a highly entangled state were blended with high-density polyethylene (HDPE) by melt blending, respectively [2]. It was demonstrated that the UHMWPE with the less entangled state was easy to be oriented at a given flow. More mechanical networks were achieved among the HDPE matrix and the UHMWPE chains due to the fewer entanglements of synthesized UHMWPE, improving the melting recovery of blends. However, the phase separation of blends was characterized when more weakly entangled UHMWPE was incorporated. In [3] the blends of high-density polyethylene (HDPE) with ultra-high molecular weight polyethylene (UHMWPE) were obtained by mixing in a melted state at concentrations ranging from 10 to 30% by weight in an intermeshing co-rotating twin screw extruder (ICTSE). The morphological analysis conducted by scanning electron microscopy showed that the UHMWPE is present in the HDPE matrix as a second phase, but there is a good interface between the two. In [4] blends of HDPE and UHMWPE, with a content of UHMWPE up to 20% wt, were prepared using two different types of processing apparatus, a single screw extruder and an internal mixer, as a function of mixing time. Evaluation of melt viscosity of the blends showed a double effect of UHMWPE due to its slight dissolution and to its presence as filler. Most methods of mixing polymers have their limitations and require special conditions.
Recently, interest has increased in the structure and properties of the nascent polymers, so-called reactor powders (synthesis products that have not been subjected to any impact influence) since a solution-free method of processing polymers and their mixtures into products from reactor powders directly is being actively developed. The possibility of manufacturing products from UHMWPE in particular, high-performance fibers, directly from the nascent reactor powder was discovered at the end of the 80s by P. Smith et al. [5,6] and is being successfully exploited at present [7,8,9,10,11]. The ability of reactor powders to monolithization and orientation drawing depends on their molecular and supermolecular structure. The sintering of reactor powders with subsequent high-temperature orientation drawing remains a much more acceptable method for processing UHMWPE high performance fibers.
At the same time there is different industrial demanding to the mechanical properties of UHMWPE products. These properties can be changed by adding the reactor powder with a lower molecular weight PE to the UHMWPE reactor powder (RP). Earlier, one of the co-authors of this article [12] attempted to obtain polymer-polymer mixtures by the method of two-stage PE synthesis in order to more homogeneously mix the components. The reactor powders of molecular composites consisting of UHMWPE (MW = 1 × 106 g/mol) and linear HDPE (1.6 × 105 g/mol) can be obtained by changing the synthesis conditions in the same reactor. It has been shown that the mechanical behavior of the molecular composited strongly depends on the content of the components and the sequence of synthesis. The best properties were demonstrated by the composites into which HDPE was synthesized at the first stage. While the structure of UHMWPE reactor powders is fairly well understood, the structure of HDPE reactor powders has not been sufficiently studied.
So, the aim of this work is to study the complicate hierarchical structure of the nascent HDPE at all levels of the molecular organization.

2. Materials and Methods

2.1. Objects of Study

For the study, reactor powder of a linear HDPE with a molecular weight 160,000 g/mol, synthesized on a metallocene catalyst (rac-(Me)2Si(Ind)2ZrCl2/methylalumoxane) at a temperature of 70°C at the Federal Research Center for Chemical Physics named after N.N. Semenov RAS was chosen.

2.2. Methods

2.2.1. Scanning Electron Microscopy

The morphology of the powder particles was studied using a Zeiss Supra 55VP scanning electron microscope. To avoid charge accumulation when scanning samples with an electron probe, the particles were placed on a conductive substrate and a thin layer of platinum was deposited onto them in an Q150T ES (Quorum Instruments, UK).

2.2.2. Thermal Analysis

Thermograms were recorded on a DSC-500 differential scanning calorimeter (Spetspribor, Samara). The temperature scale was calibrated by the melting points of ice (273.1 K) and indium (429.7 K), and the heat flux was calibrated by the heat capacity of sapphire. The scanning speed (V) varied from 1.0 to 10 K/min. The true melting temperature (Ttm), the true temperatures of the beginning (Tt1) and end (Tt2) of melting were obtained by extrapolating the dependences Tm(V1/2), T1(V1/2) and T2(V1/2) to zero heating rate (V=0), respectively [13]. According to this extrapolation, the methodological error ΔТ was estimated, which in this case was ΔТ = 1.6 K and which was taken into account in the calculations. The melting enthalpy (ΔHm) was calculated from the area of ​​the melting peak, and the degree of crystallinity χ was calculated from the relation χ = ΔHm/ΔH0m, where ΔH0m is the melting enthalpy of an ideal PE crystal (4.1 kJ/mol = 294 J/g) [14].

2.2.3. X-ray Diffraction Analysis at Small Angles (SAXS)

Small-angle X-ray scattering (SAXS) curves from the powder were recorded for reflection in the θ-2θ scanning mode (angle range 0 ≤ 2θ ≤ 2) on a Bruker D8 Discover diffractometer equipped with a rotating anode as an X-ray source. We used monochromatized CuKα1 radiation with a wavelength λ = 1.5406 Å. The reactor powder was placed in a standard cuvette and a drop of vaseline oil, having an electron density close to the electron density of polyethylene, was added there in order to create a flat surface of the sample to reduce diffuse X-ray scattering on a rough surface and suppress scattering on the pores. The resulting small-angle scattering curve was decomposed into elementary peaks using the Fityk 1.3.1 program, and for each peak, the value of the long period LSAXS was calculated. In scientific articles concerned with the study of the supermolecular structure of reactor PE powders, they usually write about the absence of a regular long-period structure in them. In fact, this is due to the masking effect of X-ray scattering in air in the pores of reactor particles with a loose packing of various morphological units.

2.2.4. X-ray Diffraction Analysis at Large Angles (WAXS)

X-ray diffractometry in the region of large angles from the studied HDPE reactor powder was carried out on a Bruker 2DPhaser powder diffractometer using a PSD detector and a nickel ß-filter (CuKa1 radiation, λ = 1.54 Å), voltage 30 kV and current 10 mA. Registration was carried out with a step of 0.036 degrees in the angular range of 60-84 degrees on the 2θ scale. The curve was recorded in the accumulation mode for 24 hours. The average sizes of crystallites in the direction perpendicular to the plane (D002) were calculated from the linear half-widths of the 002 reflection (Scherrer method).

3. Results and Dicussion

3.1. Scanning Electron Microscopy

Figure 1 and Figure 2 shows electron micrographs of the investigated reactor HDPE powder, taken at different magnifications.
It is quite clear from the given micrographs that in the particles of reactor powder various morphological structural units coexist, that is clearly visible at high magnifications. It is possible to distinguish a number of morphoses that are frequently encountered:
  • extended lamellar plates (Figure 1C is the enlarged area marked with a circle in Figure 1B). Since it can be seen in the selected area that the lamellae are deformed with the formation of fibrils, like classical single-crystal mats with simultaneous unfolding molecular folds at the transition boundary from lamella to fibrils, it can be assumed that they are formed by folded crystallites with regular folds;
  • the fibrils themselves, which are formed during the deformation of the lamellae under the action of tensile forces arising from the pressure of the polymer mass growing during the synthesis. The forces leading to the deformation of the lamellae do not arise from the very beginning of synthesis, but upon the accumulation of a certain mass of polymer at a certain stage of synthesis;
  • classic shish-kebab formations (Figure 1D), which, as is known, consist of a central shish and lamellar kebabs of folded crystals crystallizing on it [15];
  • it is important to note that the sizes of kebabs and the distance between them vary markedly. It is possible to distinguish at least three types of structures with transverse dimensions of about 200 nm, 100 nm and 50 nm (Figure 2);
  • central shishas, clearly visible in Figure 2A in yellow circles.
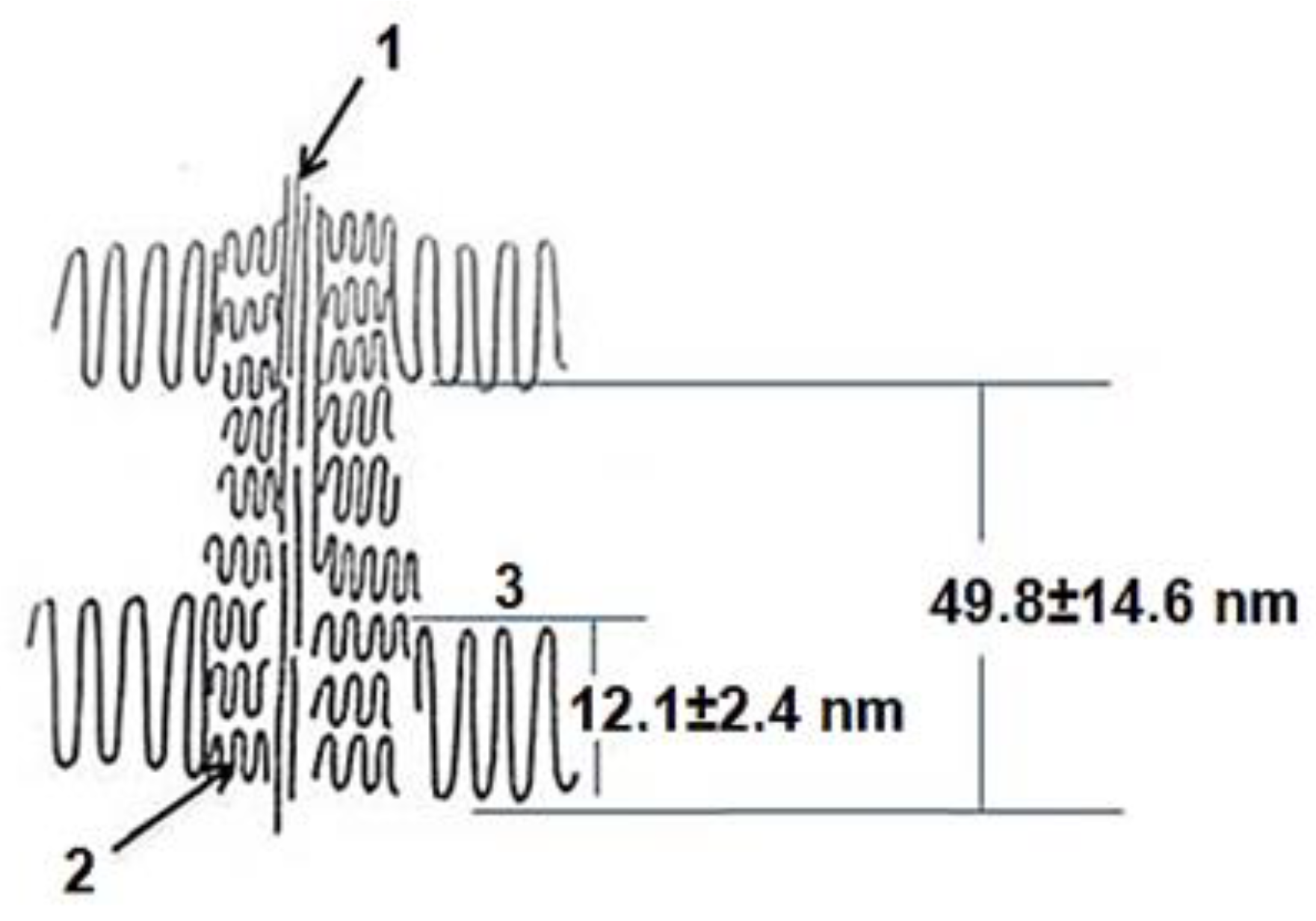
In addition, the central shish can have a complex structure and themself consists of a central thread formed by partially extended molecules (1), and micro-kebabs (2) growing on them (Figure 3).
Preprints 81394 g002
Figure 2. Enlarged area where shish-kebab morphological units are observed. The results of measurements of the thickness of individual kebabs (A) and measurements of the periodicity in kebabs location on the central shishas (B) are shown.
Figure 2. Enlarged area where shish-kebab morphological units are observed. The results of measurements of the thickness of individual kebabs (A) and measurements of the periodicity in kebabs location on the central shishas (B) are shown.
Preprints 81394 g002
The latter are not visualized on scanning micrographs, but one can presumably speak of the possibility of their existence, since the micro-shish-kebab structure was previously observed when studying polyethylene crystallized from a stirred solution using high-resolution transmission electron microscopy [15]. Note that the HDPE reactor powder we studied also crystallizes during suspension synthesis in a stirred solvent.
It is rather difficult to estimate the true percentage of the morphological units in the reactor powder using electron micrograph images. First, more statistics is needed. Second, the operators often pay more attention to the most expressive structural areas and can skip areas with less pronounced structure. Even if the operator is attentive to all possible structures, it is impossible to obtain reliable statistical results from SEM images, not to mention the fact that the ratio of different structures in the volume and on the surface of the polymer may differ. In addition, in determining the thickness of the lamellae, even in the images where the lamellae are oriented by sideways to the observer, there is a large uncertainty in the thickness of the platinum layer spattered to avoid charging of the sample.
We nevertheless took such measurements in order to compare them with small-angle X-ray data. The average thickness of lamellar macro-kebabs was 12.1 ± 2.4 nm, with their periodic arrangement along the central shish equal to 49.8 ± 14.6 nm. There is no polymer material between the macro-kebabs.
Preprints 81394 g003
Figure 3. Schematic representation of the central thread (1) with micro (2) and macro (3) shish-kebab structure.
Figure 3. Schematic representation of the central thread (1) with micro (2) and macro (3) shish-kebab structure.
Preprints 81394 g003
At the same time, scanning electron microscopy does not provide information on the distribution of crystalline and amorphous regions in morphological units. To quantify crystalline regions, disordered regions, and their location, it is necessary to involve such research methods as WAXS, SAXS and differential scanning calorimetry (DSC).
Often in the literature, a large period, determined from SAXS, is denoted by the letters L, the same as the thickness of the lamella (L), which sometimes leads to some confusion in understanding the data published. To clarify the experimental data obtained, we present below our model proposed earlier for lamellar structure [16] consisting of the lamellae themselves and the disordered regions separating them, formed by the ends of the molecules, regular and irregular folds, as well as tie molecules of different degrees of conformation (Figure 4).
LSAXS is the so-called long period (lcr+la+ 2linterphase), determined by SAXS; lcr (1) is the crystalline core size of the three-dimensional coherent scattering region in the direction of the chain (D002) determined by WAXS; linterphase (2) is the transition region between crystalline core and true amorphous region (la) consisting of a set of different conformers (irregular folds (3), strongly curved molecular molecules (4), ends of molecules (5), weakly curved molecular molecules (6), molecular folds connecting 2-3 molecules at the exit of the crystallite (7) and taut tie molecules (8); Llam is the thickness of the lamella (crystal core + two thicknesses of the more or less regular folded surface that melt simultaneously with the crystalline core). Obviously, LSAXS > Llam > lcr.
To estimate the parameters of the lamellar structure of the investigated HDPE reactor powder, the above listed experimental methods were used.

3.2. Small Angle X-ray Scattering (SAXS)

SAXS picture from the powder is presented in Figure 5.
Despite the fact that many authors, as a rule, do not detect a diffraction peak on SAXS of RP, it still exists. It is merely masked by air scattering on porous powders. We succeeded in its detection adding a drop of mineral oil to a powder sample which has an electron density close to that of PE. The peak is well seen in the inset in a right upper corner of Figure 5. The asymmetric profile of the observed peak implies the overlapping of lamellar stacks with different periodicity. It is possible to decompose the observed diffraction peak into elementary peaks with a known degree of reliability only in the range of angles 0.1 ≤ 2θ ≤ 1.0. The intensity in the range of angles 1 ≤ 2θ ≤ 2 is small and almost does not change. When taking the logarithm of the initial curve (lg I(2θ)), a rather high intensity is observed in this region, allowing to assume the presence of periodic structures with other (smaller) values ​​of long periods (Figure 6).
The periodic structures can be identified by decomposing the resulting curve (Figure 6) using Fityk 1.3.1 software (Figure 7).
The number of substantiated peaks in the decomposition was chosen in accordance with the number of different morphoses in the powder under study. It should be emphasized that the logarithmic scale makes it possible to obtain the elementary peaks without taking into account their real weight contribution. To estimate the real weight contribution, the decomposition of the original curve (Figure 8) was carried out with fixed angular positions of the peaks obtained by decomposing lg I(2θ) (Figure 7). As a profile function, the Pearson function was used.
As is known, a small-angle diffraction peak occurs when a stack of alternating regions with different electron densities (regions of order and disorder) is present in the object under study, the so-called long period (LSAXS), as it was mentioned above. In our case, the regions of order are lamellae (Llam) and disordered areas between them (la). Moreover, the intensity of low-angle peaks depends on the squared difference in the densities (ρ) of these areas (Δρ2) and the degree of stack regularity (ΔLSAXS/LSAXS). The diffraction peak distribution obtained (Figure 8) was recalculated to the long period size distribution using the Bragg equation 2Lsinθ = nλ (Figure 9).
The values of long periods LSAXS, calculated using the Bragg equation, and their weight contribution to the overall small-angle scattering curve in % are given in Table 1.
Comparison of the contributions of different long periods LSAXS calculated from the dependence I(LSAXS) with SEM data allows us to presumably attribute them to certain morphoses. So that, for example, large long LSAXS periods (peaks 1 and 2) are closest in size to macro-shish-kebabs, clearly visible on SEM of HDPE microphotographs in Figure 2B (49.8 ± 14.6 nm). However, there are not so many of them (7.2 and 11.0%), although the SEM images give the impression that macro-shish kebabs are the main structural elements in reactor powders. In addition, the intensity of these peaks is low compared to the intensity of the peaks related to LSAXS with a value of 21.0 – 27.0 nm (Figure 9), while from such structures with a huge difference in the density of the kebab and interkebab space (“voids” in SEM images), one could, on the contrary, expect the maximum scattering intensity.
Apparently, there are two reasons for the moderate contribution of these large LSAXS to the total scattering curve. Firstly, the preferred choice by the operator of the shooting area with the predominant localization of macro-shish-kebabs, while in another place on the surface there may be much less of them. Secondly, a large scatter in the thickness of kebabs and a scatter in the periodicity of their location along the central shish (which is clearly seen in SEM images) can significantly reduce the X-ray scattering intensity which will lead to a decrease in the peak area and, accordingly, a decrease in the estimate of the contribution of these peaks to the overall scattering curve.
Comparing the sizes and percentages of other elementary peaks given in the Table 1 with electron microscope images, we can assume that the structures with a frequency of 21.0 – 27.0 nm and the highest percentage (32.9 and 44.7%) are localized not along the central shish, but inside it and represent micro-kebabs (Figure 3), which were mentioned above. On SEM images of the RP (Figure 2A), micro-kebabs are not visualized due to the deposited metal layer, but they, apparently, still exist.
It is rather difficult to speak about the localization of structures with a periodicity of 10.7 – 16.3 nm, the contribution of which is very small (0.6% and 2.9%). These can be micro-kebabs with a large scatter of periodicity, and/or extended lamellae, occasionally found on SEM images of the RP (Figure 1C).
Knowing the degree of crystallinity (χ) calculated from the area of ​​the melting peak on the temperature dependence of the heat capacity obtained by DSC, it is possible to calculate the sizes of ordered regions (but not the regions of three-dimensional coherent scattering, the magnitude of which is determined from high-angle X-ray patterns (lcr), but regions that contribute to the enthalpy of melting (in our case, lamellae Llam; Llam = LSAXS × χ) and proper disordered regions (la = LSAXS - Llam).
The true dimensions of the crystalline core of the lamellae lcr in the direction of the chain were calculated from WAXS data for linear halfwidth of D002 reflex and were 6.2 nm. Half the difference between the lamella thickness and the size of the crystalline core ((Llam - lcr)/2) gives the value of the transition zones on both sides of the lamella, the thickness of the surface layer of the lamellae (linterphase).
The average degree of crystallinity χ of the studied HDPE, calculated from the dependence of heat capacity on temperature for a RP sample (m = 2.0 ± 0.1 mg) at a scanning rate of 2 K/min, was χ = 54%. However, taking into account the heterogeneity of the supermolecular structure of the studied RP, it can be assumed that the degree of crystallinity is unequal, especially for areas with a pronounced macro-shish-kebab structure. The schema on Figure 3 shows areas that are visible and invisible on microscopic images. We only see macro-kebabs alternating along the thick shish. There is no polymer material between them. Obviously, the crystalline part here is much less than 54%. You can estimate the "degree of crystallinity" of macro-kebabs: χ(1) = 12.1/49.8 = 24.3% (see Figure 3). At the same time, macro-kebabs account for 18.2% in the total set of various structures and, accordingly, somewhat underestimate the total crystallinity of the remaining structures. Then it is possible to estimate the crystallinity of macro-shish-kebab structures and the degree of crystallinity of all other periodic structures according to the relation below:
0.818 × χ(2) + 0.182 × 24.3 (%) = 54.0 (%),
χ(2) is the crystallinity of other structures. It is appeared to be to 60.6%.
Then for macro-shish-kebab structure Llam = 0.243 × LSAXS, and for other periodic structures Llam = 0.606 × LSAXS.
Knowing the values of the degree of crystallinity and the melting temperature, it is possible to calculate the values of the surface energy for each lamella found from the analysis SAXS data. The true melting temperature of the investigated HDPE was determined from the heat capacity peak taking into account the above-mentioned methodological error ΔТ = 1.2 K, and amounted to: Tm = 400.1 K. The surface energy σe can be calculated from the generalized Gibbs-Thomson equation [17], based on the balance of surface and volume energies
Tm(L) = T0 [1 – 2(σ/a + σ/b + σe/L)/ΔH0],
where a and b are the dimensions of the crystallite (the region of coherent scattering) in the plane of the section perpendicular to the longitudinal axis coinciding with the direction of the macromolecule; L is the longitudinal size of the crystallite; σ is the surface energy of the side surfaces of the crystallite; σe is the surface energy of the fold surface; ΔH0 is the heat of fusion.
In the supermolecular lamellar structure of the polymer, the parameters a and b >> L, therefore, in expression (1), the terms σ/a and σ/b can be neglected and it can be re-written in a simpler form:
Tm(L) = T0 [1 ̶ 2 σe /(ΔH0 L)]
or   σ e = ∆ H 0 L l a m 2 × 1 − T m T 0
The following data were used in further calculations: T0 = 415.5 K; ΔH0 = 279 J/g [14]. Since the long period LSAXS is determined by the SAXS, the longitudinal size of the crystalline part, more precisely the thickness of the lamella Llam in expression (2) is Llam = χ × LSAXS. Table 2 shows the parameters of the structures identified in the analysis of SAXS data and the surface energies calculated for them using equation (2).
As follows from the data given in the Table 2, the surface energy value (85.3 × 10-3 J/m2), which is closest to the energy of a regular fold (90 × 10-3 J/m2) [14], is observed in the thickest lamellae with a thickness of 16.5 nm, which, as we assume, are localized in micro-kebabs and make the largest contribution to the small-angle scattering curve (44.7 %). At the same time, the surface energy of lamellae of almost the same thickness (Llam = 15.2 nm), which form kebabs in macro-shish-kebab structures, also has a fairly high surface energy (78.6 × 10-3 J/m2), which allows us to assume a similar structure of the surface of the morphoses under consideration.
However, it is surprising that in these most perfect micro- and macro-bump formations with predominantly regular folds, according to the calculation within the Thompson Gibbs theory, the largest transition phase is observed (4.50 nm and 5.15 nm). The only explanation for this phenomenon can be the occurrence of strong distortions in the crystalline cores of the lamellae in the region of regular folds, which distort the crystallographic lattice in the near-surface layers of the lamellae.
In crystalline cores of lamellae with lower values ​​of surface energy (30–60 × 10-3 J/m2) and, accordingly, with a large number of irregular folds, such distortions are practically absent and the size of the transition zone near the lamella surface is smaller (1.85–3.35 nm).
Note that the investigated HDPE reactor powder was obtained by suspension synthesis in toluene at 70°C with stirring of the reaction liquid during synthesis. Polymerization and crystallization are exothermic processes. Therefore, in local regions of the reactor, even with intensive stirring, there may be temperature regions that differ from the average temperature. In addition, the emergence of a crystallization nucleus from segments of extended molecules (in shishas) leads to an instantaneous stress drop in the nearest environment [18,19], which allows folded crystals (kebabs) to crystallize in a quasi-stationary field. Thus, the crystallization of the resulting polymer occurs in shear fields with an inhomogeneous distribution of both shear stresses and temperature over the reactor volume. This, apparently, is the reason for such heterogeneity in the size of the lamellae and the difference in the structure of their surfaces.

4. Conclusions

Using a complex of SEM, SAXS, WAXS and DSC methods, a detailed study of the complex hierarchical structure of the reactor HDPE powder with MW = 160,000 g/mol, which is often used in a mixture with UHMWPE to modify its properties, was carried out. Based on the analysis of the all the data obtained, it was concluded that the main morphological units in the powder are macro- and micro-shish-kebab formations. Although micro-shish-kebabs are not visualized under a scanning electron microscope, their existence is indicated by small-angle X-ray scattering data. Micro-shish-kebab formations are part of the central shish, and macro-kebabs are really, like a culinary shish-kebab, strung on this complex central shish and separated by an empty space. Kebabs (lamellae) have different thicknesses and different energy characteristics of the surface, calculated in the framework of the Gibbs-Thompson theory. Based on the analysis of the surface energy values, it can be assumed that in the micro-shish-kebab structure, which makes up about 45% of the total reactor powder, the surface of the lamellae is formed by regular folds, which introduce significant distortions into the structure of the crystalline core of the lamellae. About 7% of macro-shish-kebabs have the same structure. The surface of the remaining lamellae in different morphoses is less ordered and is mostly formed by irregular folds and segments of molecular chains in various conformations. The formations of morphoses so different in their structural and energy characteristics during synthesis is apparently due to the heterogeneity of thermal and shear fields in the reactor in which the polymer is synthesized. The polymer factually undergoes a flow-induced non-isothermal crystallization process.

Author Contributions

“Conceptualization, L.M. and V.E.; methodology, Y.B.; software, S.G and K.D..; validation, T.U., K.D. and E.R.; formal analysis, L.N..; investigation, M.Y., E.I. and A.B..; re-sources, E.S. and T.U.; data curation, E.S.; writing—original draft preparation, L.M. and A.B.; writing—review and editing, L.M., V.M. and Y.B.; visualization, E.I. and S.G.; supervision, M.Y., E.R. and L.N.; project administration, V.M. and V.E.;. All authors have read and agreed to the published version of the manuscript.”.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

There are no financial and any other supports.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kurtz, S. M. The UHMWPE Handbook: Ultra-High Molecular Weight Polyethylene in Total Joint Replacement; Elsevier Academic Press: San Diego, CA, 2004.
  2. Yang, H.; Hui, L.; Zhang, J.; Chen, P.; Li, W. Effect of entangled state of nascent UHMWPE on structural and mechanical properties of HDPE/UHMWPE blends. Appl. Polym. Sci. 2017, 134, 44728. [CrossRef]
  3. Lucas, A.d.A.; Ambrósio, J.D.; Otaguro, H.; Costa, L.C.; Agnelli, J.A.M. Abrasive wear of HDPE/UHMWPE blends. Wear 2011, 270, 576-583. [CrossRef]
  4. Boscoletto, A.B.; Franco, R.; Scapin, M.; Tavan, M. An investigation on rheological and impact behavior of high density and ultra-high-molecular weight polyethylene mixtures Eur. Polym. J. 1997, 33, 97-105. [CrossRef]
  5. Smith, P.; Chanzy, H.D.; Rotzinger, B.P. Drawing of virgin ultrahigh molecular weight polyethylene: An alternative route to high strength/high modulus materials. J. Mater. Sci. 1987, 22, 523–531. [CrossRef]
  6. Rotzinger, B.P.; Chanzy, H.D.; Smith, P. High strength/high modulus polyethylene: synthesis and processing of ultra-high molecular weight virgin powders. Polymer 1989, 30, 1814-1819. [CrossRef]
  7. Selikhova, V.I; Zubov, Yu.-A.; Sinevich, E.A.; Chvalun. S.N.; Ivancheva, N.I.; Smol’yanova, O.V.; Ivanchev, S.S.; Bakeev, N.-F. Structure and thermodynamic characteristics of high modulus polyethylene produced by drawing of compacted reactor powders. Polym. Sci. Ser. A 1992, 34,151-159.
  8. Egorov, V.M.; Ivan’kova, E.M.; Marikhin, V.A.; Myasnikova, L.P.; Drews, A. Morphology and thermal properties of polyethylenes made by metallocene and Ziegler-Natta catalysts. J Macromol Sci., Part B, Phys. 2002, 41, 939-956. [CrossRef]
  9. Ronca, S,; Forte,G.; Tjaden, H.; Rastogi, S. Solvent-free solid-state-processed tapes of ultrahigh-molecular-weight polyethylene: influence of molar mass and molar mass distribution on the tensile properties. Ind. Eng. Chem. Res. 2015, 54, 7373-7381. [CrossRef]
  10. Myasnikova, L.P.; Boiko, Yu.M.; Ivan’kova, E.M., Lebedev, D.V.; Marikhin, V.A.; Radovanova, E.I.; Michler, G.H.; Seidewitz, V.; Goerlitz, S. Fine structure of UHMWPE reactor powder and its change in mechanical and thermal fields. In: Reactor Powder Morphology; Lemstra, P.-J.; Myasnikova, L.-P. (eds). Nova Science Publishers: New York, USA, 2011; pp 93-151. (open access).
  11. Ozerin, A.N.; Ivanchev, S.S.; Chvalun, S.N.; Aulov,V.A.; Ivancheva,N.I.; Bakeev,N.F. Properties of Oriented Film Tapes Prepared via Solid-State Processing of a Nascent Ultrahigh-Molecular-Weight Polyethylene Reactor Powder Synthesized with a Postmetallocene Catalyst Polym. Sci. Ser. A 2012, 54, 950-955. [CrossRef]
  12. Ushakova, T.M.; Starchak, E.E.; Gostev, S.S.; Grinev, V.G.; Krasheninnikov, V.G.; Gorenberg, A.Ya.; Novokshonova, L.A. All-polyethylene compositions based on ultrahigh molecular weight polyethylene: Synthesis and properties. J. Appl. Polym. Sci. 2020, 137, 49121-49130. [CrossRef]
  13. Bershtein, V.A.; Egorov, V.M. Differential Scanning Calorimetry of Polymers: Physics, Chemistry, Analysis, Technology. Ellis Horwood, N.Y. 1994; 253p.
  14. Wunderlich, B. Crystal Melting. Macromolecular Physics; Academic Press: New York, NY, 1980; Volume 3, pp 460.
  15. Keller, A.; Machin, M.J. Oriented Crystallization in Polymers. J. Macromol. Sci. B1 1967, 1, 41-91. [CrossRef]
  16. Yegorov, Ye. A.; Zhizhenkov, V. V.; Marikhin, V. A.; Myasnikova, L. P.; Popov, A. Structure of non-ordered regions in lamellae of linear polyethylene. VMS Ser. A. 1986, 25, 693-701.
  17. Hoffman, J. D. Treatise on Solid State Chemistry, Vol. 3; Plenum Press: New York, USA, 1976.
  18. Elyashevich, G.K. Thermodynamics and kinetics of orientational crystallization of flexible-chain polymers. Adv. Polym. Sci. 1982, 43, 205-245. [CrossRef]
  19. Frenkel, S.Ya.; Baranov, V.G.; Elyashevich, G.K. Probleme der Festigkeit von Polymeren: Paradoxen, Perspektiven, Prognosen. Acta Polymerica 1984, 35, ss.393-400. [CrossRef]
Preprints 81394 g001
Figure 1. Scanning electron micrographs of HDPE (A), (B), (C) and (D) at various magnifications, shown in the images with scale bars. 1C is the area circled in the image 1B.
Figure 1. Scanning electron micrographs of HDPE (A), (B), (C) and (D) at various magnifications, shown in the images with scale bars. 1C is the area circled in the image 1B.
Preprints 81394 g001
Preprints 81394 g004
Figure 4. Model of long period structure.
Figure 4. Model of long period structure.
Preprints 81394 g004
Preprints 81394 g005
Figure 5. Small angle scattering from HDPE reactor powder. The inset shows a part of the curve with a modified intensity scale (primary beam cut in height), which makes it possible to clearly observe the asymmetric diffraction maximum.
Figure 5. Small angle scattering from HDPE reactor powder. The inset shows a part of the curve with a modified intensity scale (primary beam cut in height), which makes it possible to clearly observe the asymmetric diffraction maximum.
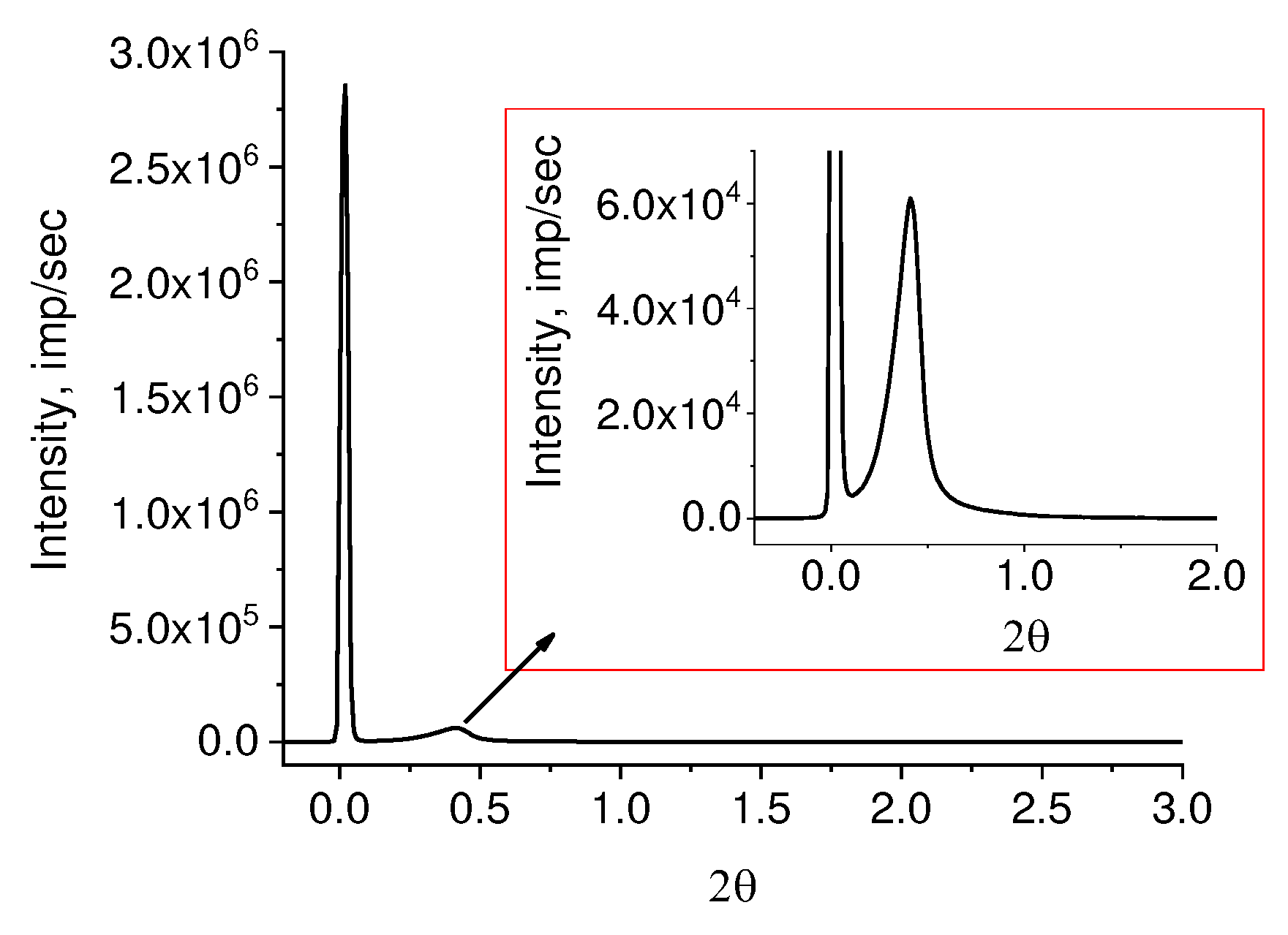
Preprints 81394 g005
Preprints 81394 g006
Figure 6. lg I(2θ) for HDPE reactor powder.
Figure 6. lg I(2θ) for HDPE reactor powder.
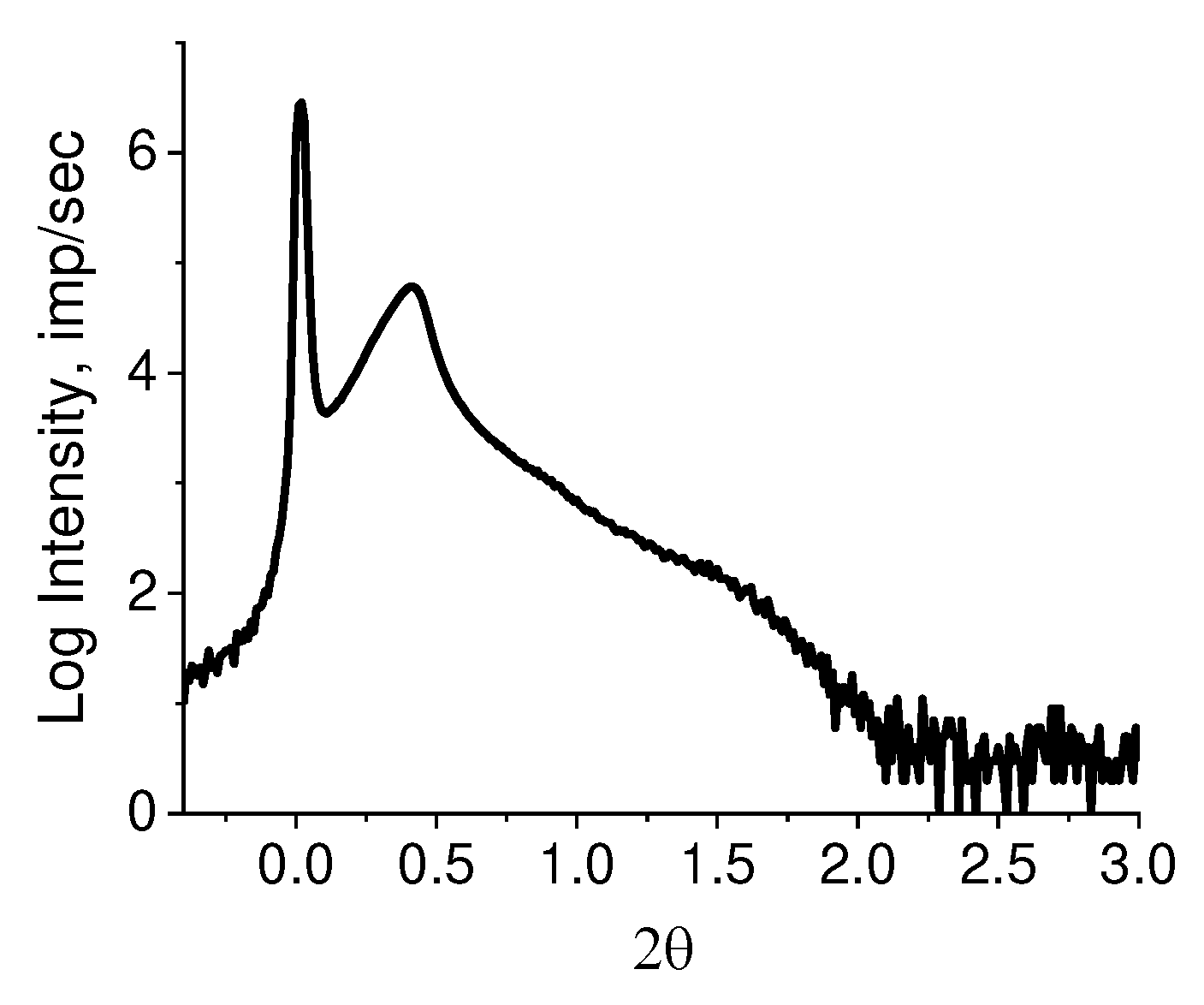
Preprints 81394 g006
Preprints 81394 g007
Figure 7. Decomposition of the dependency lg I(2θ) for HDPE reactor powder into elementary peaks using the Fityk 1.3.1 software.
Figure 7. Decomposition of the dependency lg I(2θ) for HDPE reactor powder into elementary peaks using the Fityk 1.3.1 software.
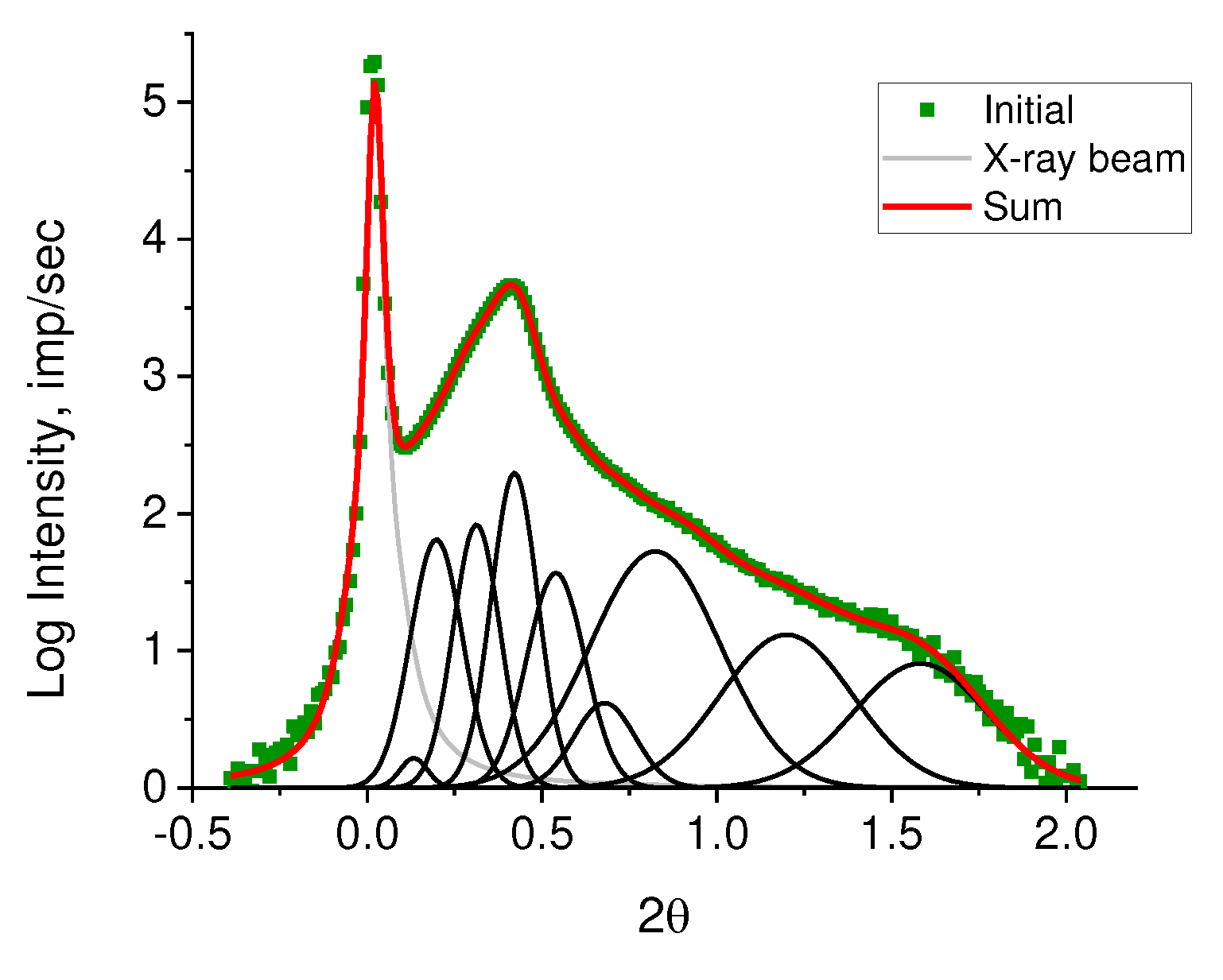
Preprints 81394 g007
Preprints 81394 g008
Figure 8. Decomposition of SAXS intensity I(2θ) of investigated RP into separate diffraction peaks, the angular position of which corresponds to the angular positions of the peaks in the lg I(2θ) decomposition.
Figure 8. Decomposition of SAXS intensity I(2θ) of investigated RP into separate diffraction peaks, the angular position of which corresponds to the angular positions of the peaks in the lg I(2θ) decomposition.
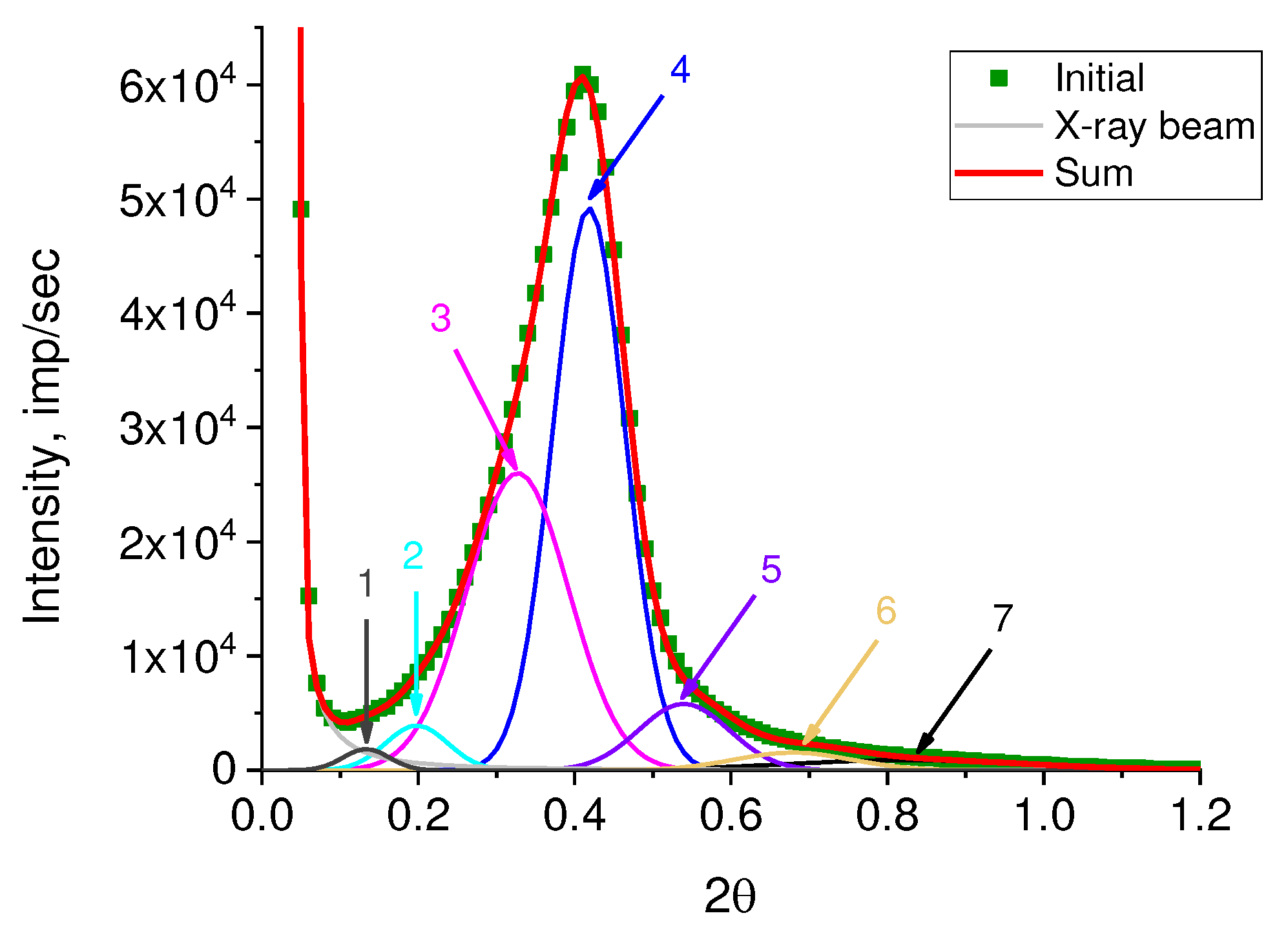
Preprints 81394 g008
Preprints 81394 g009
Figure 9. The long period (LSAXS) size distribution calculated from the data in Figure 8.
Figure 9. The long period (LSAXS) size distribution calculated from the data in Figure 8.
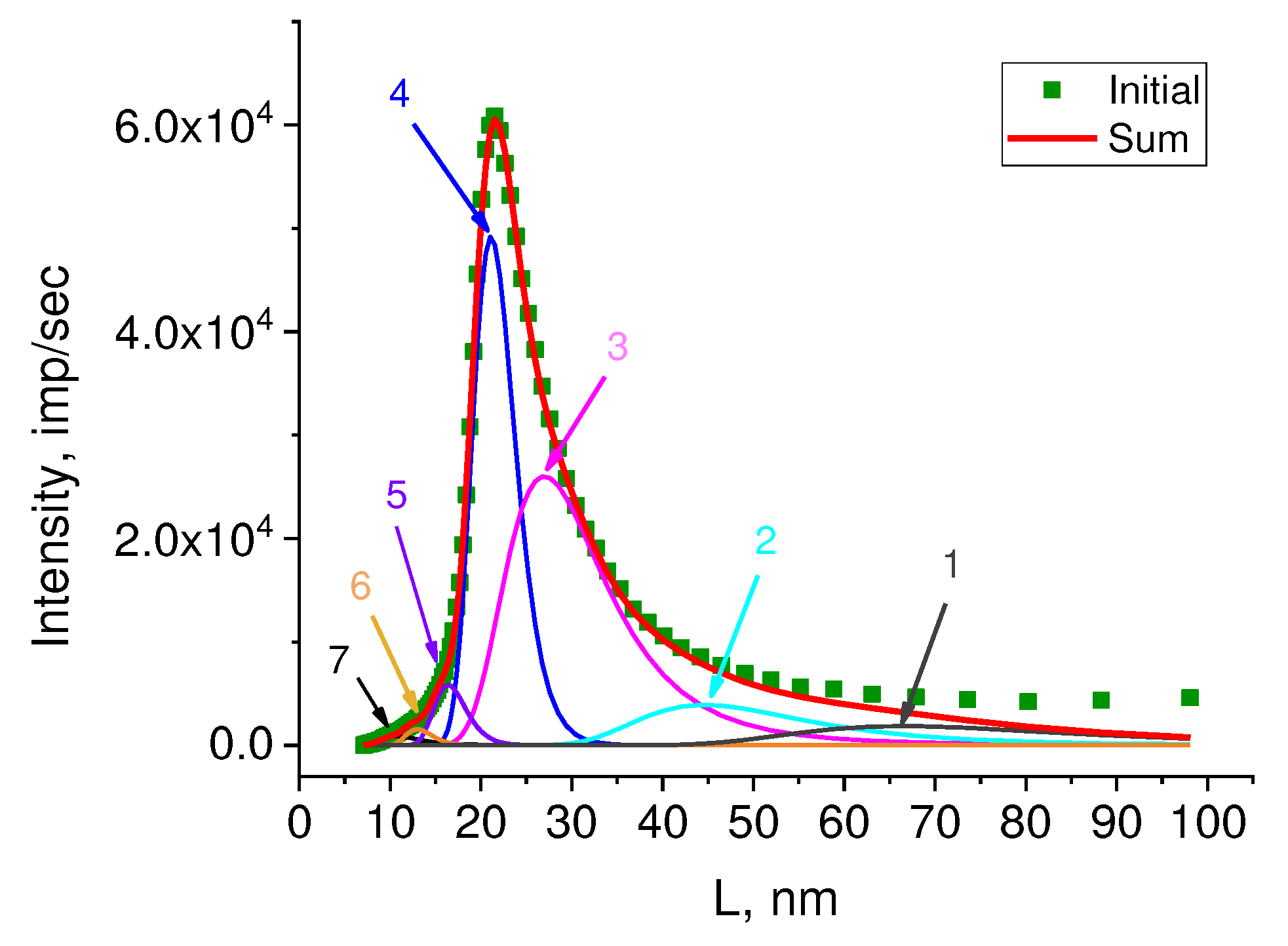
Preprints 81394 g009
Table 1. Parameters of the separated diffraction peaks.
Table 1. Parameters of the separated diffraction peaks.
Peak numbers 1 2 3 4 5 6 7
2θ, degrees 0.133 0.198 0.327 0.418 0.540 0.679 0.824
LSAXS, nm 66.3 44.6 27.0 21.0 16.3 13.0 10.7
Contribution to SAXS, % 7.2 11.0 44.7 32.9 2.9 0.6 0.6
Table 2. Values of the identified long periods, lamella thicknesses, and values of the surface energy for each component of the expansion of the SAXS curve.
Table 2. Values of the identified long periods, lamella thicknesses, and values of the surface energy for each component of the expansion of the SAXS curve.
LSAXS, nm Llam, nm linterphase*, nm Contribution to the total SAXS curve, % σe, 10-3 J/m2
10.7 6.5 0.15 0.6 33.6
13.0 7.9 0.85 0.6 40.8
16.3 9.9 1.85 2.9 51.2
21.1 12.9 3.35 32.9 66.7
27.0 16.5 5.15 44.7 85.3
44.6 10.3 2.05 11.0 53.3
66.3 15.2 4.50 7.2 78.6
*linterphase = (Llam - lcr)/2; lcr = 6.2 nm.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated