Prerpints.org logo
Preprint
Article

Fine Flow Structure at the Miscible Fluids Contact Domain Boundary in the Impact Mode of Free-Falling Drop Coalescence

Altmetrics

Downloads

93

Views

29

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

03 August 2023

Posted:

04 August 2023

You are already at the latest version

Alerts
Abstract
Registration of the flow pattern fine structure and the matter distribution of a free falling liquid drop in a target fluid at rest in the impact mode of coalescence, when the kinetic energy of the drop exceeds its available potential surface energy (APSE), was carried out by photo and video recording. The main attention was paid to the study of the flow structure at the initial stage of the cavity formation. To carry out color registration, the flow pattern was illuminated by several matrix LED and fiber optic sources of constant light. The planning of experiments and interpretation of the results were based on the properties of the complete solutions of the fundamental equations of fluid mechanics system, including the transfer and conversion of energy processes. Complete solutions of the system of equations describe large-scale flow components that are waves or vortices as well as thin jets (ligaments, filaments, fibers, trickles). In experiments, the jets are accelerated by the converted available potential surface energy (APSE) when the free surfaces of merging fluids were eliminated. The experiments were performed with the coalescence of water, solutions of alizarin ink, potassium permanganate, copper sulphate or iron sulphate drops in deep water. In all cases, at the initial contact, the drop begins to lose its continuity and breaks up into a thin veil and jets, the velocity of which exceeds the drop contact velocity. Small droplets, the size of which grows with time, are thrown into the air from spikes at the jet tops. On the surface of the liquid, the fine jets leave colored traces that form linear and reticular structures. Part of the jets penetrating through the bottom and wall of the cavity forms an intermediate covering layer. The forming layer jets are separated by interfaces of the target fluid. The processes of molecular diffusion equalize the density differences and form an intermediate layer with sharp boundaries in the target fluid. All noted structural features of the flow are also visualized when a fresh water drop isothermally spreads in the same tap water. The fast-changing and finely structured diffuse boundary of merging fluids, which at the initial stage has a complex and irregular shape, is gradually smoothed out by molecular diffusion processes. The similar flow patterns were observed in all performed experiments, however the geometric features of the flow depend on the individual thermodynamic and kinetic parameters of the contacting fluids.
Keywords: 
Subject: Physical Sciences  -   Fluids and Plasmas Physics

1. Introduction

The registration of stably reproducible components of flows in the pattern of the coalescence of a free-falling drop with a target fluid at rest had a great impact on the development of a number of sciences such as hydrodynamics, physics in general, mathematics, biology [4] and many others. At first, these components were ring vortices [1] and multi–tiered vortex systems [2]. With the development of scientific photography they were supplemented by shorter-lived components as sprays, cavity, crown, splashes [3]. With time, scientific results in the study of droplet flows were being implemented in solving applied problems of ocean acoustics [5], creating new technologies in oil, bio, chemical, pharmaceutical, metallurgical and other industries. At the same time, the experimental technique was developing, that is more and more powerful controlled light sources were being created [6]. The range of illuminating wavelengths was expanding (X-ray, optical and infrared waves are now used in experiments [7,8]). Photo, film and video recording techniques were improved as well: the shooting speed of modern video cameras exceeds several million shots per second [9,10].
The application of high-resolution instruments allowed studying in detail the evolution of the flow components identified in the first observations [3], in particular, to trace the change in the shape of the cavity and crown [11,12] and the pattern of the capillary waves on their surfaces [13], to highlight important features in the process of the droplet matter transfer.
The hypothesis of "passive admixture" is often used [14] in fluid mechanics in general, and when interpreting observations of the impact flows of a free-falling drop. It allows explaining the patterns of substance redistribution as an indicator of the evolution of the flow velocity field. The approach is used to identify compact vortices at various phases of the flow created by a fallen drop in a fluid at rest [1,2,15].
On more detailed observations, structurally different intrusive and impact modes of a free-falling drop spreading in a fluid at rest were later identified [16]. In the intrusive mode, when the kinetic energy of the droplet E n k = M U 2 / 2 is less than its APSE E n σ = σ S d , E k < E σ at first the droplet matter flows smoothly into the liquid thickness, and then, a cavity is quickly formed with a delay of several milliseconds [17]. In a more dynamic "impact" mode, when E n k > E n σ , the cavity is forming from the moment of initial contact. Here, S d , M and U are surface area, mass and contact velocity of the falling drop. In the impact mode, thin jets are formed in the area where a drop merges with a thin layer of liquid on a solid substrate [10]. Thin jets are also observed in a deep fluid, the colored fibrous traces of which form linear and reticular structures on the surface of the cavity and crown [18].
The formation of thin jets in the free falling droplet spreading pattern is explained by the intrinsic features of the inhomogeneous distribution of internal energy in fluids with a free surface [19], and the properties of complete solutions of the system of fundamental equations of inhomogeneous liquids mechanics [20,21].
In today description, one of the types of thermodynamic potentials, namely, free enthalpy – the Gibbs potential, is chosen as the main parameter of a fluid medium (liquid, gas, plasma) [22]. Coefficients of the Gibbs potential differential form d G = s d T + V d P + S σ d σ + μ i d S i determine the traditional thermodynamic physical quantities of an inhomogeneous droplet fluid with a free surface area S σ . Here ρ ( t ,     x 1 ,     x 2 ,     x 3 ) = 1 / V is density, V is specific volume, P ( t ,   x 1 ,     x 2 ,     x 3 ) is pressure, T ( t ,   x 1 ,     x 2 ,     x 3 ) is temperature S i ( x 1 ,     x 2 ,     x 3 ) is the concentration of dissolved or suspended particles, μ i is chemical potential. All mentioned quantities have a clear physical meaning and are available for observation with an error estimation.
In modern fluid mechanics, some parameters of the medium, such as density and pressure, are considered to be quantities of a mixed, namely, mechanical and thermodynamic nature. Empirical relations between thermodynamic quantities constitute equations of state [22,23,24], among which the main one is the dependence of density ρ ( P ,     T ,     S i ) = 1 / V or specific volume V on pressure P , temperature T , the concentration of dissolved substances and suspended particles S i . The state of the medium is characterized by the distributions of Gibbs potential and its derivatives – density, temperature, salinity and pressure, which change over time.
Along with thermodynamic quantities, the medium is also characterized by kinetic coefficients that determine the molecular transfer of momentum (dynamic μ and kinematic viscosity ν = μ / ρ ), heat (thermal or temperature conductivity coefficient κ T ) and matter (diffusion coefficient κ S ), as well as the transfer parameters of other physical quantities (velocity of sound, index of refraction and others). In weakly dissipative media, which include a large number of fluids and gases found in natural and industrial conditions (in particular, water, aqueous solutions of salts and air), kinetic coefficients have small values.
Complete solutions of the system of fundamental equations [20,21] for weakly dissipative media containing small coefficients at higher derivatives are found by the theory of singular perturbations [25]. The calculations have shown that the complete solutions of the system of fluid mechanics equations contain functions of two classes – regular in a small parameter, and singularly perturbed [26]. In periodic flows, regular solutions describe waves, and singular solutions describe the accompanying components forming the thin structure of the medium – fibers and highly gradient interfaces [27]. The full dispersion relations for waves and ligaments on the surface of a viscous stratified liquid are given in [28]. The analysis of the intrinsic scales of singular solutions complementing inertial, internal, acoustic and hybrid waves in the fluid thickness is carried out in [29].
In the experiment, the fine structure of droplet flows on the surface and in the thickness of the target fluid was previously visualized in [18,30]. The thin components of flows (fibers or jets) are formed as a result of the conversion of internal or available potential surface energy into other forms. They are described by singular solutions of a system of fundamental equations [26,27].
The theory and methodology of studying fluid flows was created within the framework of the “continuous medium” concept, all the physical properties of which were described by continuous functions. This approach does not agree with the actually observed discrete – atomic-molecular and finer nuclear structure of matter. Atoms and molecules forming real liquids or gases are combined into various associates of physical and chemical nature. Various combinations are registered in the experiments such as complexes, clathrates, clusters, voids with individual atoms, with physical and chemical bonds. The observations and calculations show that the internal energy and one of the forms of its representation, namely the Gibbs potential are distributed non-uniformly in the fluid.
The linear scales of the associates are in the 10 − 8 < δ < 10 − 6 cm range, where the lifetime of single elements is 10 − 12 < τ e < 10 s. Each of the elements of the fluid structure is characterized by its own internal energy, which accumulates during its formation and is converted into other forms during the rearrangement of the structure and the elimination of the elements boundaries, which ensures the fluidity of liquids [31,32]. The available potential surface energy at the liquid boundary with air or vacuum (APSE [19]) is the most important. It is concentrated in a near-surface layer with a thickness of δ c ~ 10 − 6 cm in droplet fluids [31]. The accumulation of internal energy occurs rather slowly with characteristic free surface formation in macroscopic flows for times of the order of 10 − 3 < τ < 10 − 2 s in a droplet flow.
By methods of optical and X-ray reflectometry and atomic force microscopy, it was found out that the density, the dielectric permittivity, and the dipole moment in the fluid thickness and in a structurally distinguished near-surface layer with a thickness of the size order of a molecular cluster ( δ σ ~ 10 − 6 cm) differ noticeably [33,34]. A more complex distribution of free enthalpy could be observed in a thin surface layer with a thickness of the order of molecular size δ c ~ 10 − 8 cm, where supramolecular structures are expressed even more clearly. In a surface layer with a thickness δ b ~ 10 − 8 cm, the self-ionization of matter can occur due to the anisotropy of atomic-molecular interactions.
When the free surfaced are eliminated during the coalescence of liquids, the APSE quickly transforms into other forms (at a coalescence velocity of about 1 m/s per time 10 − 10 < τ < 10 − 8 s). The processes of APSE conversion form ligaments (fast thin jets [26,27]), colored traces of which are observed when a free-falling drop merged with a fluid at rest in the impact mode at E n k > E n σ [18].
The inclusion of the Gibbs potential in the flows description of liquids and gases allows to take into account the action of four energy transfer mechanisms: with flows at the velocity of U , with the group velocity of various waves c g w , the dissipative-diffusion one with coefficients ν , κ T , κ S and the conversion one associated with the release and accumulation of the internal energy, in particular, available potential surface energy E n σ of the liquid as a whole and its single structural components which are complexes, hydrates, clathrates, clusters, voids and other combinations of atoms and molecules of physical and chemical nature [31,32].
Thin fast jets and longitudinal oscillations of the expanding circular boundary of the drop coalescence domain with a thin fluid layer on the surface of a slide are visualized in [10]. In the experiments it was observed that the jets accelerated when they crossed the contact domain boundary of merging liquids in a cavity which was formed in a deep liquid [35]. The evolution of the pattern of thin jets penetrating the bottom of a growing cavity at the initial stage of fluids coalescence was first traced in [36]. The purpose of this study is to visualize the flow fine structure in the vicinity of the contact domain boundary of a droplet coalescing with deep water. In the impact mode, a cavity in a deep pool begins to form at the initial contact of the droplet boundary with the free surface of the target fluid at rest, if the drop kinetic energy E n k = M U 2 / 2 exceeds the APSE E n σ = σ S d .

2. Parametrization

The experimental methodology was developed taking into account the definition of a liquid as a fluid medium, the properties of which are characterized by the distributions of the Gibbs potential, its derivatives defining thermodynamic quantities, kinetic and other physical coefficients [22,23,24]. The flows are defined as the transfer of energy, momentum and matter, which causes the corresponding changes in the physicochemical parameters of the medium [20,21,25,26]. The universal classification of flow components is based on the description of complete solutions of linearized and weakly nonlinear forms of the fundamental equations systems [26,27]. They are constructed by the theory of singular perturbations taking into account the explicit compatibility condition [25]. The classification includes large-scale components (waves, vortices, jets) and thin ligaments, the dynamics of which is characterized by their intrinsic temporal and spatial scales [26,37].
The Gibbs potentials of the droplet G d , the air medium G a and the target liquid are included as the main dimensional parameters characterizing the flows under study, considering the complex and tunable internal medium structure, which affects the dynamics and energy of droplet flows. The indices indicate the belonging of the parameter medium. The media are also characterized by density ρ d , a , t , kinematic ν d , a , t and dynamic μ d , a , t = ρ ν viscosities; full σ d a ,   σ t a and normalized surface tension coefficients based on the density of fluids γ d a = σ d a / ρ d ,     γ t a = σ t a / ρ t ; the equivalent diameter D , surface area S d , volume V d , mass M = ρ V d , momentum p d = M U and velocity U of the droplet at the moment of initial contact with the target liquid.
The influencing parameters include extensive kinetic energy (KE) E n k = M U 2 / 2 and available potential surface energy (APSE) E n σ = σ S d , formed due to the anisotropy of atomic-molecular interactions in the drop shell. The APSE is contained in a thin near–surface layer with a thickness of the order of the molecular cluster size of a δ σ ~ 10 − 6 cm and its density is W d σ = E n k / V σ . The extensive kinetic energy density is W d k = E n k / V d . The ratio of the drop energy components R E n = E n d k / E n d σ can be both small and large, and the ratio of their densities R W = W d k / W d σ ~ δ σ / D is a small value under the conditions of these experiments.
The energy parameters also include the drop potential energy E n p = M g D in scale D falling in a gravitational field with a free-fall acceleration g . An additional parameter is the diffusion coefficient of the pigment used for tinting the drop in the target liquid κ S .
From the system of equations and physically valid boundary conditions, it follows that the basic group of linear scales, which are determined by the physical properties of media, includes the capillary-gravitational ratio δ g γ = γ / g . It belongs to the dispersion equation of short surface waves [20], as well as to the dissipative-capillary scale δ γ ν = ν 2 / γ . The group of linear scales depending on the droplet velocity includes viscous velocity δ U ν = ν / U , capillary δ U γ = γ / U 2 and diffusion δ U κ S = κ S / U scales.
Accordingly, the first part of the time scales of the task comprises only the parameters of the medium – τ γ ν = ν 3 / γ 2 , τ g γ = γ / g 3 4 , the second one contains the drop size – τ γ D = D 3 / γ , τ γ ν D = ν D / γ , the third part embraces its contact velocity, that is kinematic τ g U = U / g , as well as dynamic parameters determined by the drop size τ U D = D / U and the thickness of the shell τ U σ = δ σ / U . The duration of the transferring matter and surface energy processes of the merging drop is determined τ U D = D / U by the drop size and the thickness of the subsurface layer τ U σ = δ σ / U .
The process of converting APSE into other forms with the elimination of the free surface of the merging liquids proceeds in a short time of the order of τ U σ ~ δ σ / U ~ 10 − 8 s for typical conditions of the experiments with free-falling droplets. Rapid processes of APSE transformation into other forms at the circular boundary of the fluid coalescence contribute to the formation of thin jets and generation of capillary waves in the target fluid [16,17,28].
A large number of scales of the same dimension reflect the diversity and complexity of processes occurring in a wide range of scales – from supramolecular ones of the order of δ σ ~ 10 − 6 cm in the processes of release and accumulation of APSE, to the full size ones of the flow domain.
The relations of scales of the same dimension define a set of traditional dimensionless parameters, which includes the following numbers: Reynolds Re = D / δ U ν = U D / ν , Froude Fr = E n k / E n p = U 2 / g D , Bond Bo = D 2 / ( δ g γ ) 2 = g D 2 / γ , Ohnesorge Oh = δ γ ν / D = ν / γ D , Weber We = D / δ U γ = D U 2 / γ , Schmidt Sc = ν / κ S . The relations of the energy components form additional dimensionless combinations R E n k , σ = E n k / E n σ , R W = W d k / W d σ ~ δ σ / D .
The intrinsic scales of the task determine the requirements for choosing the size of the observation area, the spatial-temporal resolution of the instruments, and the duration of recording the flow pattern. Dimensionless relations allow us to assess the relative contribution of processes of different nature to the overall flow pattern and compare the conditions of independent experiments.

3. Experimental Setup

The experiments were carried out on a modified stand for studying the fine structure of fast processes (FSP), which is part of the Unique Research Facility “HPC IPMech RAS” [38]. The installation, which is presented in Figure 1 included a dispenser for generating droplets 1; a photodetector 2 that detects the pass of a drop at the intersection of the light beam; an operating cuvette with a target fluid 3; a control unit 4; a recording photo or video camera 5; a lighting system 6-8; and a computer for controlling the experiment and for data collecting 9. The drop formed in a dispenser 1 with a replaceable capillary of a diameter 0.8 < d o < 4 mm with a flat section, broke off under its own weight and fell on the surface of partially degassed tap water in a target cuvette 3 of the size 10 × 10 × 7 or 30 × 30 × 5   cm 3 . The pattern of coalescence of single water drops, aqueous solutions of alizarin ink or metal salts (potassium permanganate KaMnO 4 , copper CuSO 4 and iron F e S O 4 sulphates) was studied.
The target fluid, which was partially tinted with a drop pigment, was renewed after each experiment The registration system included an Optronics CR 300x2 video camera or a Canon EOS 350D camera, the position of the sight line of which was selected in favour of the greatest clarity of the boundaries of the recorded pattern components. Two directions of the line of sight were mainly implemented: at an angle to the horizontal ϑ = 0° when registering the flow pattern in the vertical plane or ϑ = 65°-70° when observing the free surface (the distance from the lens to the center of the flows was from 12 to 40 cm, the pixel sizes in the experiments ranged from 10 to 50 microns). The shutter speed was chosen to be minimal for a given level of spatial resolution, the size of the recorded area and the required illumination.
The fluids merging domain was illuminated by two Optronis MultiLED matrix LED constant light sources with a luminous flux of 7700 lm and also two fiber-optic sources of the Schott KL2500LCD (the power was 250 W, the luminous flux was 1300 lm). Special attention was paid to the organization of lighting in order to exclude the shading of the examined components of the flow or the effects of total internal reflection.
Traditionally, the technique of back-light illumination with a bright continuous [39] or pulsed [40] light source with an arc, gas-discharge or stroboscopic lamp is used in the droplet flows observation experiments. Recently, LED [41], fiber-optic [16] and laser [42] sources have become widespread. The emitted light is directly projected on to the studied flow domain, and sometimes it passes through a semitransparent screen (for example, tracing paper [43]) for more uniform illumination of the field of view. To increase the spatial resolution of the flow pattern components in the fluid thickness, a light laser knife and shadowgraphy were used as well [44].
In these experiments, combined lighting, including multi-element LED and fiber-optic sources, was used to ensure the contrast of the droplet residue image, the continuously changing cavity shape and the distribution of the droplet matter in the liquid. The location of the lamps was chosen based on the maximum contrast of the residue image at the bottom of a continuously growing cavity. The simultaneous rapid change in the location and shape of the flow components led to some defocusing of the image, which made it difficult to conduct further analysis. The stability of the vertical position of the contact line moving along the surface of a thin fluid layer on the glass slide contributed to the high clarity of video shots [10].
The detached drop flew over the photodetector and launched the registration system with the selected delay time. The droplet velocity was estimated by its displacements in the last shots before the contact with the target liquid and the duration of the signal delay from the photodetector to start the flow pattern recording. The image was scaled according to the marker photos of size from 1 to 10 mm. Photometry and data processing were carried out in the Matlab and Kompas envelope (CAD).

4. Main results

Individual adjustment of the flow pattern illumination for simultaneous visualization of the shape of a rapidly deforming free surface during the formation of a cavity, a crown, a veil on its edge, as well as the registration of the drop matter position was used in each series of experiments instead of the traditional back-light illumination. The lighting technique allowed us to carry out both color and black-and-white registration of the flow pattern. To control the versatility of the proposed flow structural features classification, the spreading of uniformly colored drops of dilute solutions of alizarin ink, potassium permanganate KMnO 4 , copper CuSO 4 and iron F e S O 4 sulphates, as well as tap water was studied. In all cases, the patterns of both the moving free surface and the distribution of the drop matter in a target fluid were recorded. While the overall fine flow structure was preserved, the individual properties of small elements turned out to depend on the composition of the media.

4.1. Drop Spreading of Alizarin Ink Solution in Water

The evolution of the fine structure of the matter transfer pattern during the free-falling drop coalescence of a dilute 1:200 solution of blue alizarin ink is illustrated by the video shots shown in Figure 2. The line of sight in these experiments is inclined at an angle ϑ = 65° to the horizon. The shooting speed is 4000 fps, the shutter speed is 1/5000 s, the spatial resolution is 30 microns/pixel (µm/pix).
The primary contact of the drop is accompanied by the release of a veil (a gray strip Δ r v = 0.45 mm wide along the main diameter d c r = 5.6 mm), which is pierced by thin spikes. A sequence of drops is thrown from the tops of the spikes (Figure 2, t = 0.2 ms). The deviation of the pattern from strict symmetry is due to the inclination of the line of sight and some asymmetry of the merging drop shape.
The length of separate jets, which are elongated traces of thrown droplets, is four times the width of the strip. In general, the trace pattern radially diverges, but some colored jets are located at an angle to the local radius vector. As it follows from the analysis of variations in the illumination distribution pattern along an arc Δ r l = 0.2 mm away from the contact line, the thickness of the droplet traces is d s ~ 50 microns, the length reaches l s ~ 1.8 mm, the inclination angle from the direction of the local radius vector lies in the range 0 < φ < 35 ° . The dispersion of the angular positions of the spray trajectories can be caused by variations in the angle between the shells of the veil edge in the vicinity of the spike from which the small sprays are thrown out.
The general asymmetry of the flow pattern is because of the difference in the shape of the incoming drop and the spherical one due to Rayleigh oscillations and capillary waves traveling along its surface [45]. The general gray background of the veil and darker lines, which are traces of the thrown liquid layer and single ligaments (thin jets that arise at the contact line of the drop with the target liquid) indicate the complexity of the emerging flow pattern. It expresses both two-dimensional continuous veil and fast spikes that are three-dimensional components.
The ratios of the sizes (length and diameter) of individual strokes which are the extensions of spikes (blurred images of thrown droplets (their velocity is u s ~ 7 ÷ 9 m/s)), show that their velocity noticeably exceeds the drop velocity [46]. The rapid flow of liquid in the jets is provided by additional energy released when the free surface of the merging liquids is eliminated. This energy is transformed into other forms, including the energy of mechanical motion.
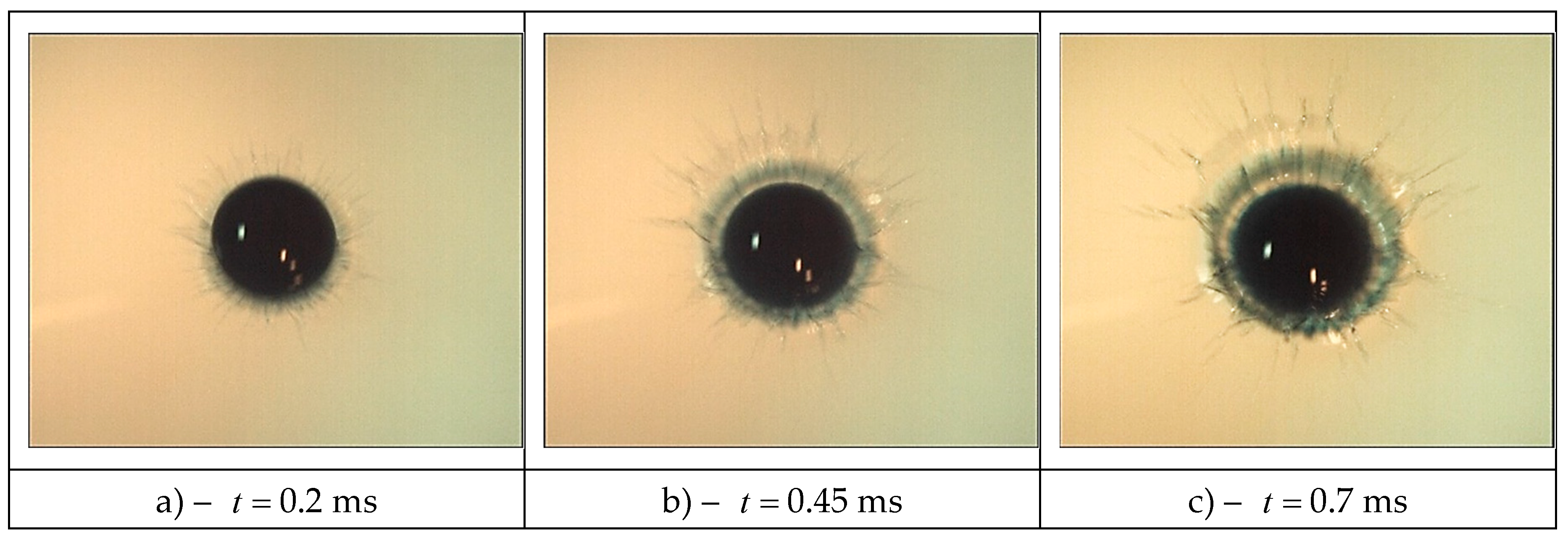
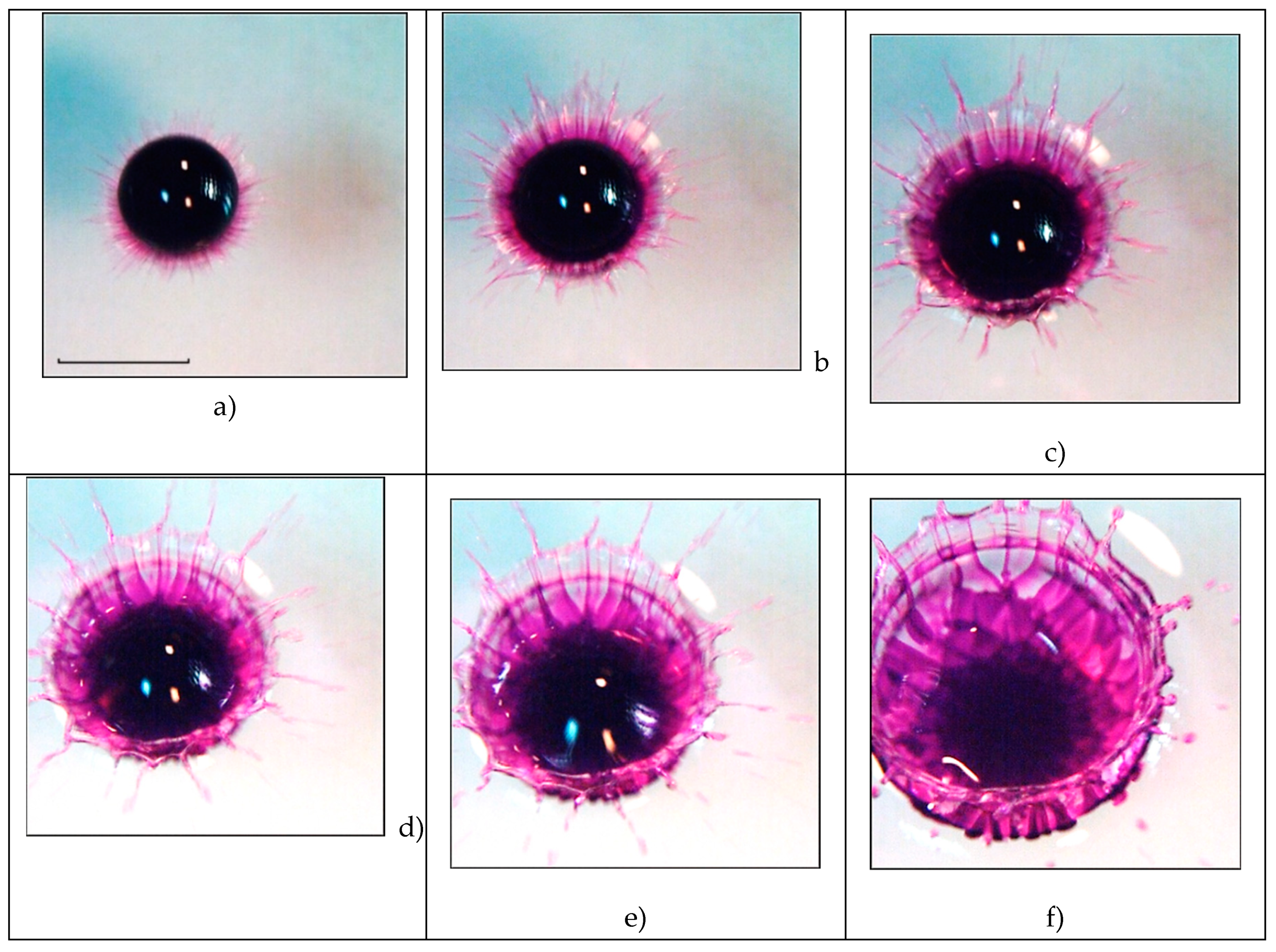
As the drop coalescence, the flow pattern, in which one can distinguish the veil in the upper left part and the crown, becomes more complicated (Figure 2b, t = 0.45 ms). The visible edge of the tinted domain (the trace of the drop residue) loses its smoothness. Colored fibers come out of individual protrusions, which spread at the cavity bottom, go through the crown wall and the veil forming spikes on its outer border. The continuity of the jet traces (linear elements of the flow geometry) indicates the structural stability of the developing flow. Jets are formed at the initial coalescence phase and persist for a long time.
The radial inhomogeneity of the image brightness allows to confidently identifying at t = 0.45 ms the individual flow components. They include the drop residue with a diameter of d r = 4.74 mm and the cavity bottom. A dark circular line is the inner boundary of the crown wall; the circular boundary line is the crown outer edge, which is continuing by veil. The outer edge of veil is tightening and thickening; individual fibers on its surface and their extensions that are spikes coming out from the tops of the teeth. Strokes, which proceed the spikes, are traces of fast flying sprays.
The jet traces (dark fibers) are adjacent to the protrusions at the visible contact boundary of the drop residue and the deepening cavity. The slope of the cavity bottom explains some clarity loss of the image of the crown moving borders and the drop residue spreading along the cavern bottom. However, here the extension of jet traces connecting the spikes on the veil edge with the boundary of the drop residue is well traced.
As the flow evolves, the diameter of the central spot slowly grows (the drop remnant spreads along the cavity bottom). At the same time, the adhesion of the colored fibers to the boundary of the merging liquids is more and more clearly expressed (Figure 2c, t = 0.7 ms).
As the flow evolves, the diameter of the central spot slowly grows (the drop spreads along the cavity bottom). At the same time, the contact of the colored fibers to the boundary of the merging liquids is more and more clearly expressed (Figure 2c, t = 0.7 ms).
As the drop sinks, the sizes of the crown and the cavity grow. The diameter of the droplet residue (the central undisturbed spot) decreases somewhat due to the formation of new tiers at its edge of a discrete distribution pattern of the droplet matter (Figure 2d, 1 ms). The boundary between the drop residue and the cavity bottom becomes more and more indented and thickened. There are separate protrusions on it – analogs of spikes on the veil edge in the air. Over time, the diameters of the protrusions grow, the contrast decreases.
The elements of the fibrous reticular structure are traced inside the tinted central spot with a diameter of d r = 5.45 mm at t = 1.7 ms. Gradually, the linear structure on the outer cavity boundary is replaced by a reticular one, at t = 6 ms triangular cells appear on the crown walls (Figure 2f). Five tiers of cells are allocated inside the cavity.
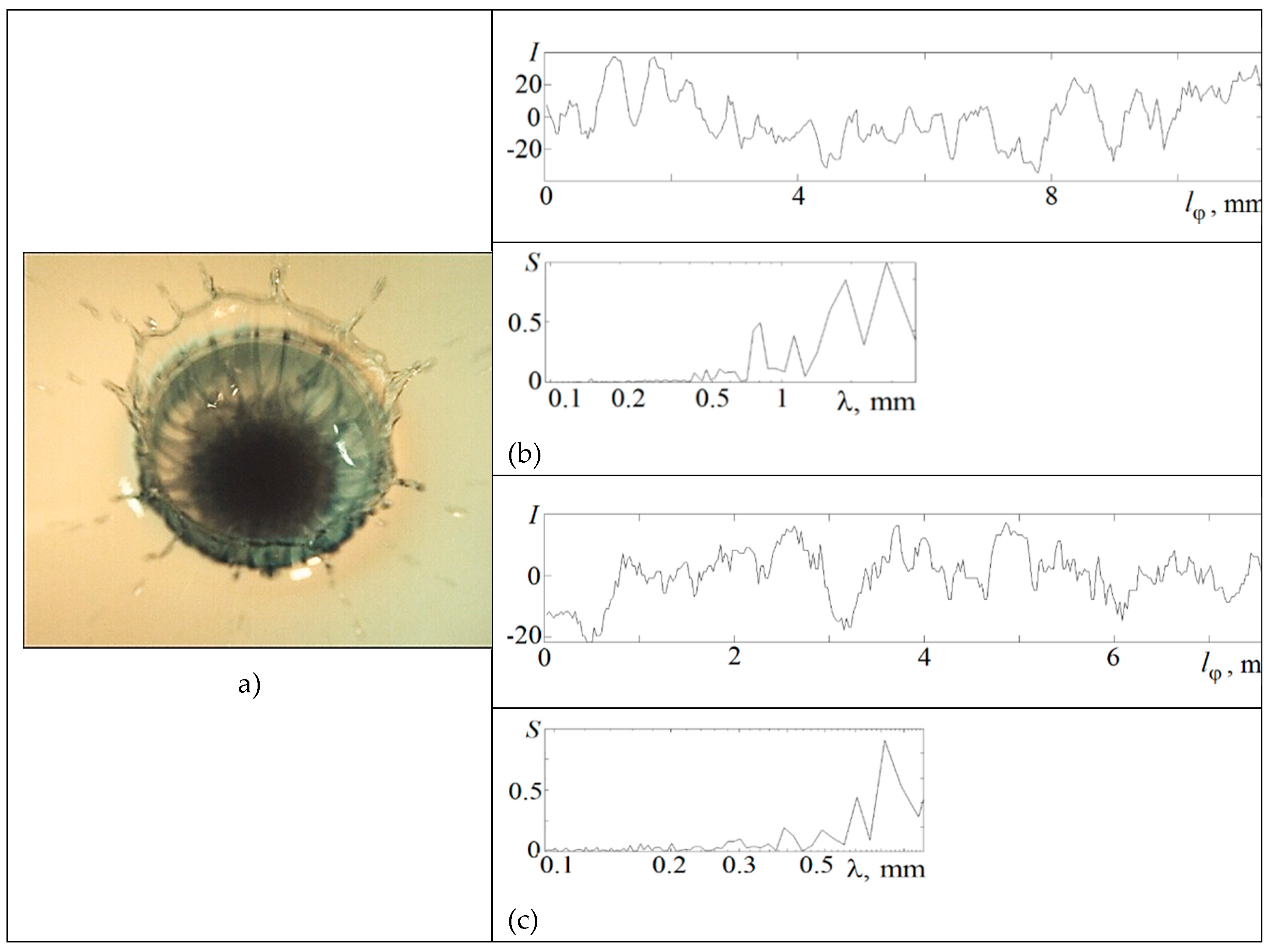
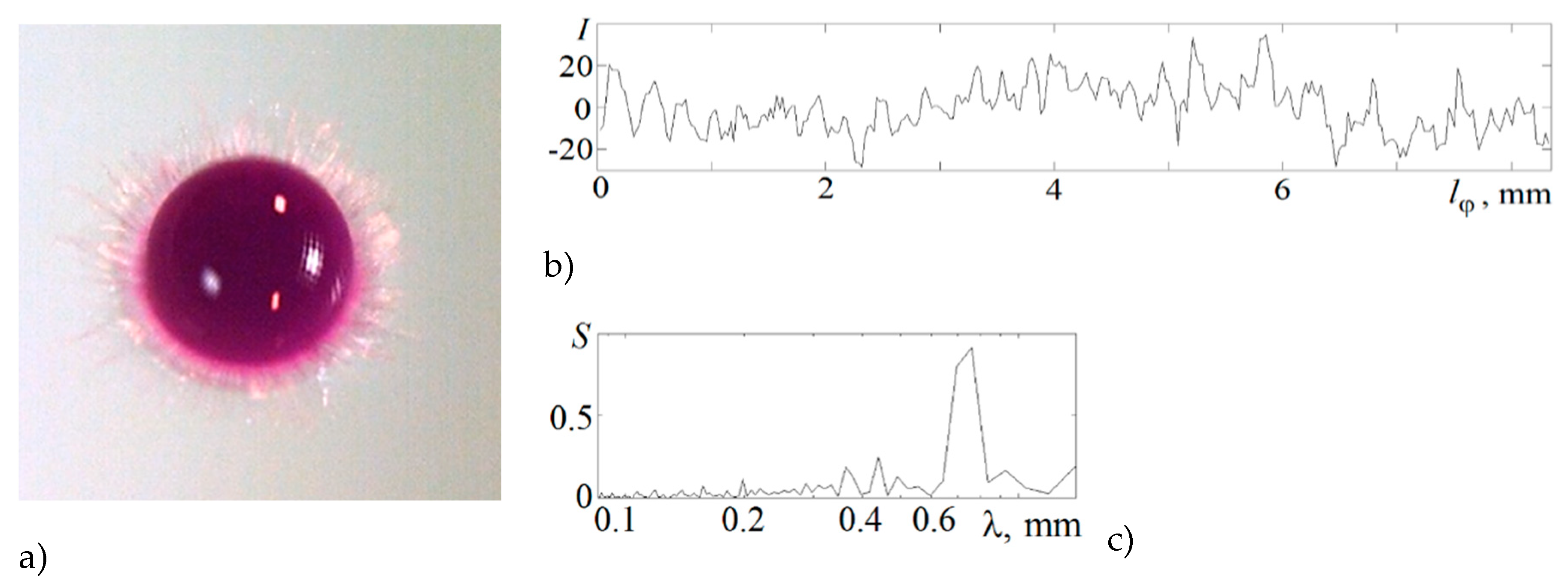
The photometry results of the relative flow pattern illumination are presented in Figure 2e at 1.7 ms and the dependence of the relative energy spectrum S ( λ ) on the scale λ is shown in Figure 3. The illumination values I ( l φ ) are determined in a circular spot with a diameter d p = 30 µm, which moves a distance l φ along the arcs of circles with a radius r φ = 3.15 and 2.6 mm.
In the middle of the cavity sidewall at r φ = 3.15mm, where linear structures in the distribution of the drop matter are distinguished, the peaks on the spectrum correspond to scales λ = 0.42, 0.47, 0.54, 0.63 and 0.8 mm. In the transition zone between the drop residue and the cavity bottom at r φ = 2.6 mm, where reticular structures with triangular cells are traced, the peaks at scales λ = 0.39, 0.49, 0.6, 0.71 mm are distinguished in the spectrum. The smallest scales characterize the thickness of single fibers.
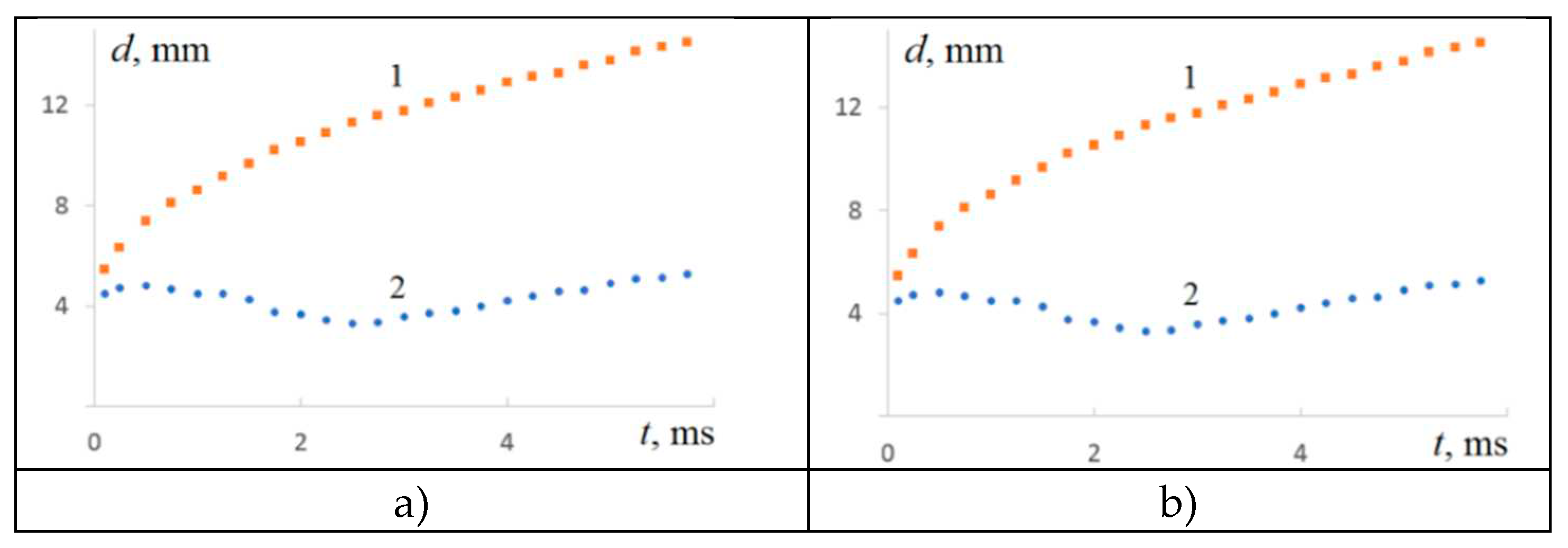
Preprints 81512 g004
Figure 4. The evolution of the coalescence domain parameters of a drop of ink solution with water: a) – the diameters of the crown and the central spot – curves 1 and 2; b) – changes in illumination in the center of the flow in a circle with a diameter d p = 0.8 mm.
Figure 4. The evolution of the coalescence domain parameters of a drop of ink solution with water: a) – the diameters of the crown and the central spot – curves 1 and 2; b) – changes in illumination in the center of the flow in a circle with a diameter d p = 0.8 mm.
Preprints 81512 g004
The change in the rate is explained by the complexity of competing diffusion and hydrodynamic processes occurring in the intermediate layer under the cavity bottom. The dark spot in the center of the flow at t > 6 ms is the trace of a growing jet with a vortex head under the bottom cavity center, which has been visualized earlier [48]. With further evolution, the protrusions on the sidewall of the cavity also transform into jets, which form elongated colored loops when the cavity collapses.
The pattern features of a drop spreading, colored with blue alizarin ink, in the fluid thickness are illustrated by frames from the video of the flow pattern in the lateral projection shown in Figure 5. Drops begin to deform the free fluid surface, creating a cavity, from the moment of the initial contact. At the same time, the drop liquid leaks in thin jets through the cavity bottom and forms an intermediate layer in which the fibers of the colored liquid are separated by interfaces of the target fluid (water in these experiments) [49].
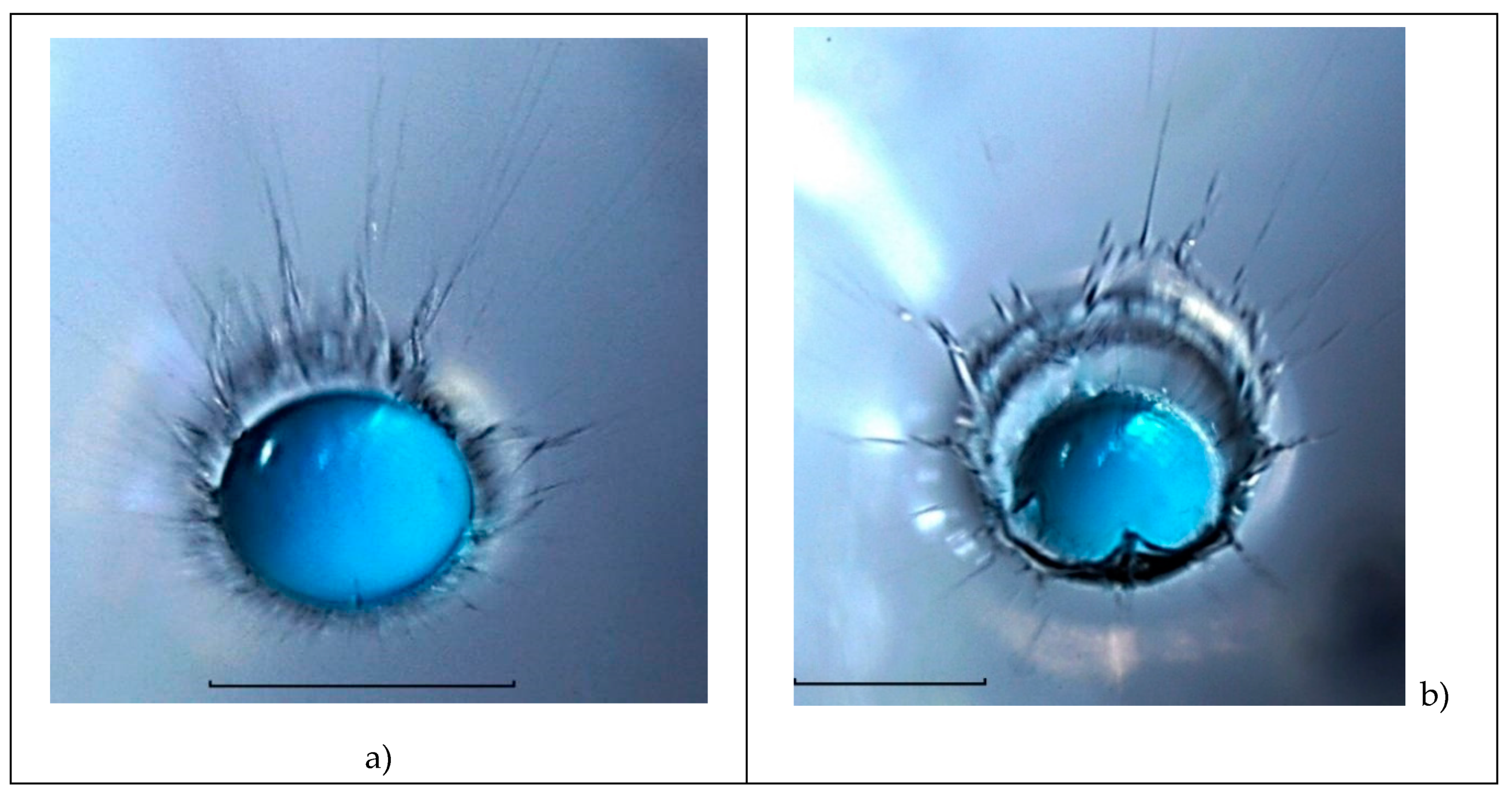
In the first shot of the flow pattern in the lateral projection shown in Figure 5a, a dark strip with a flat bottom d c a = 5.6 mm in diameter, and h c a = 0.56 mm in height, adjacent to the free surface, visualizes the cavity partially covered with droplet liquid fibers. Adjacent to the cavity from below is a growing intermediate layer with diameter d i l = 3.5 mm and height h i l = 0.4 mm, formed by fibers containing a drop matter` that have passed through the cavity bottom. The fibers grow perpendicular to the cavity bottom at the initial stage of the coalescence process, when the size of the contact domain of liquids increases rapidly. In this case, the free surfaces of the contacting liquids are eliminated with the simultaneous conversion of APSE into other forms, causing the formation of thin jets. The visualization of the intermediate layer at the later stages of droplet spreading is given in [44], its thickness is measured in [47].
The fibrous structure of the flow pattern, which is presented along the entire boundary of the intermediate layer, is more clearly expressed on its lower edge in Figure 5b. In the upper part of the cavity with diameter d c a = 6.12 mm and depth h c a = 0.96 mm, a air cavity with thickness h g = 0.5 mm is visible. An intermediate layer with diameter d i l = 3.9 mm and thickness h i l = 0.44 mm adjoins the cavity from below.
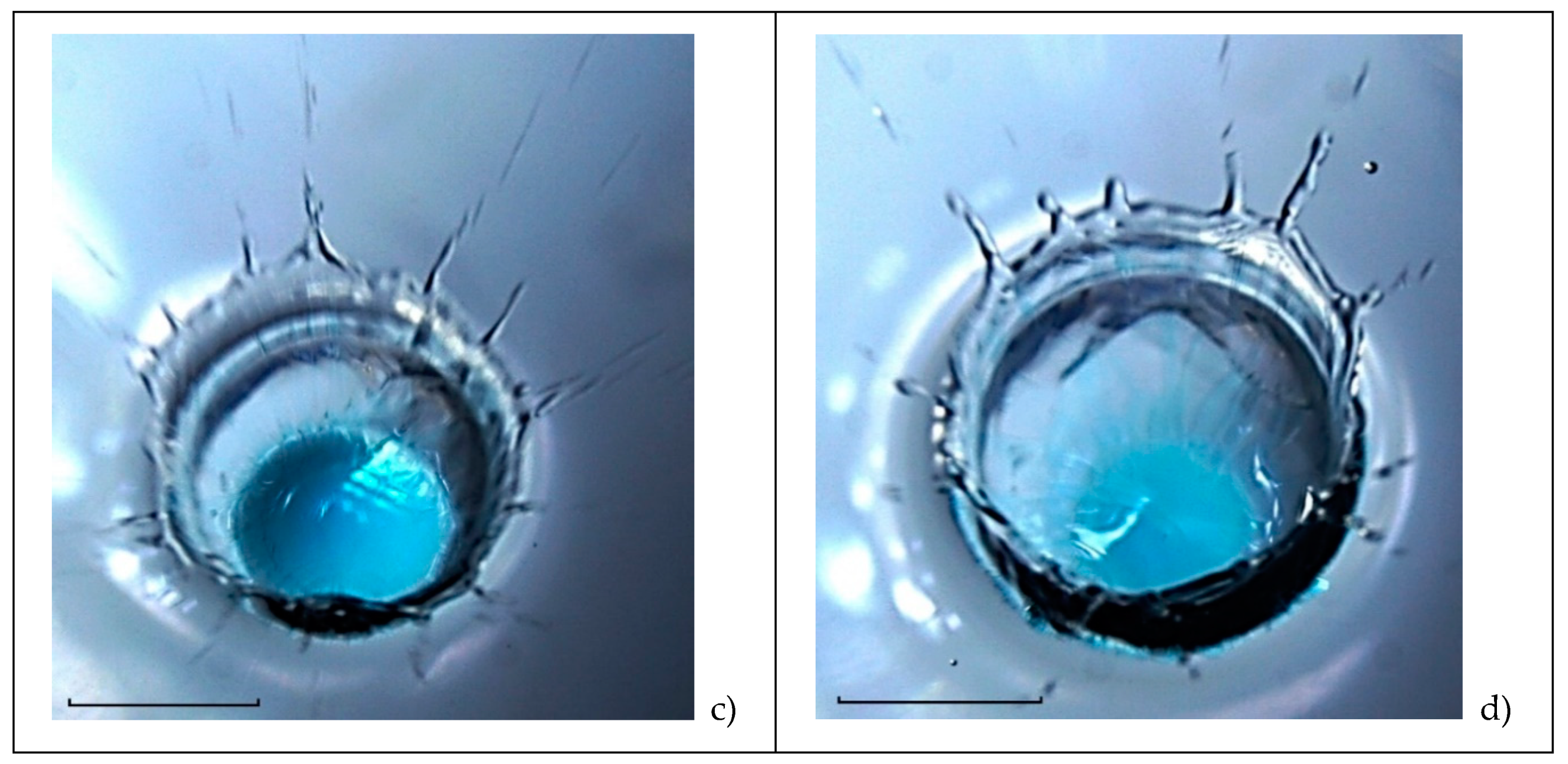
As the cavity grows, the intermediate layer on its lower edge becomes thinner, its outer border is leveled (Figure 5c). Here, the main part of the droplet substance is concentrated in the lower part of the cavity in a layer h i l = 0.6 mm high, including an advanced intermediate layer. Examination of the enlarged image shows that the lower part of the cavity is densely covered with colored liquid droplets, and in the upper part, single colored fibers are distinguished.
Further, the intermediate layer becomes much thinner and covers the cavity surface with diameter d c a = 8.7 mm with a thin layer (up to h i l = 0.3 mm thick, Figure 5d). The cavity height with an intermediate layer is h c a = 3.42 mm. Here the intermediate layer is distributed more evenly along the cavity bottom, its thickness does not exceed h i l = 0.4 mm. In a densely colored domain, the droplet matter is collected in the lower part of the cavity in a Δ h c a = 0.9 mm high layer. At the upper edge of the intermediate layer, the surface is tinted most densely. Crests and troughs h w ~ 2 mm in size are traced on the border of the tinted layer.
After the crown reaches its maximum size (the height is h c r = 3.7 mm, the diameter is d c r = 11.3 mm) and begins to decline, the capillary waves propagate down from its upper edge. The shape of the phase surfaces of waves replicates the changing contour of the edge crown. As the cavity deepens further, the concentration of the drop pigment becomes more and more aligned in height (Figure 5e). Gradually, the pigment flows down, the side wall of the cavity become sufficiently transparent and vertical fibers are displayed on them (Figure 5d). At the same time, the lower edge of the intermediate layer begins to lose its smoothness again, protrusions and troughs appear in it. They are caused by the flow of coloured fluid along the fibers, by accumulation in the reticular formation nodes, pushing through the cavity surface and the formation of small vortices [48]. At the same time, the crown edge is rounded, capillary waves cover its entire surface.
The release of droplets from the tops of the spikes on the crown surface ceases over time, only their rounded remnants persist (Figure 5f, t = 14.25 ms). The inner surface of the cavity is covered with individual fibers and spots containing droplet matter. The intermediate layer on the outer surface of the cavity also loses its homogeneity, individual brightly colored domains appear in it.
The study of color flow patterns allows distinguish between the processes of deformation of the liquid surface forming a cavity and a crown, and the processes of droplet matter transfer. The fibers containing the droplet matter leak through the deformed boundary of the cavity and form a finely structured layer under the cavity bottom in the thickness of the target fluid. Gradually, diffusion aligns out the heterogeneity of the droplet pigment distribution and a uniformly colored intermediate layer is formed under the cavity bottom. In the frontal projection, it corresponds to a more densely colored spot in the flow center. Over time, the thickness and size of the spot, its shape, undergo significant changes due to the size and shape alteration of the cavity, the fluid flow in thin jets forming linear and reticular structures on the cavity inner surface.

4.2. Drop Spreading of Potassium Permanganate Solution in Water

The video shots of the drop coalescence of dilute potassium permanganate solution with water are presented in Figure 6 (the inclination of the line of sight is ϑ = 65° to the horizon, the shooting speed is 4000 fps). When the chemical composition of the merging liquids changes, the general flow structure is preserved, but the parameters of the thin components change noticeably. The outer ring of the flow at the initial droplet contact consists of individual spikes δ s ~ 0.1 mm thick and l s < 2 mm long, partially tinted with pigment droplets (Figure 6a, t = 0.25 ms).
The spikes are in contact with the edge of a thin, weakly colored light circular veil with a width δ v = 0.57mm, in which thin brightly colored jets δ l ~ 0.1 mm are traced. They form a rather regular linear structure, which has been repeatedly observed in experiments with other substances [18]. Large splashes of light allow to consider the veil surface as a continuous relatively smooth surface.
The veil is adjacent to a darker wide ring δ с r = 0.2 mm visualizing a growing crown. A brightly colored strip with a width δ c a =0.18 mm is a growing cavity in contact with a drop residue d r =4.5 mm in diameter. The examination of the enlarged image shows that colored fibers protrude from under the drop and continuously last in the cavity, crown, and veil. They form the core of a thin jet, which is a spike protruding from the crown edge. Thus, the flow of the spreading droplet has a predominantly radial direction.
The flow structure is preserved in the next shot at t = 0.5 ms. The dimensions of the above-mentioned structural components have grown: they are δ s ≈ 0.15 mm and 0.5 < l s < 2.5 mm for the thickness and length of the spikes, δ v = 0.74 mm for the veil, δ с r = 0.4 mm for the crown and δ c a = 0.36 mm for the cavity. The diameter of the drop residue (a dark area with an uneven edge), the protrusions of which are adjacent to the colored fibers, is d r = 4.26 m. The outer edge of the veil becomes more indented, the number of spikes increases (in the first frame you can count 17, in the second one – 19 teeth in the upper semicircle).
Over time, the clarity of the fiber pattern at the bottom of the cavity remains, which becomes more and more densely colored (Figure 6c). At the same time, the boundary between the cavity bottom and the drop residue with diameter d r = 4.33 mm becomes increasingly indented. The preservation of the continuity of the colored fibers indicates the immutability of their angular position in the moving contact domain of the merging fluids.
As the crown width increases and the cavity deepens, the velocity of the colored jets decreases, the protrusions in the edge contour of the cavity deepen, the spikes break up into sequences of individual droplets, the diameter of which grows over time (Figure 6d). A reticular pattern of individual fibers is visible under the colored drop liquid floating to the cavity bottom. The uneven boundary of the central spot shifts slightly to the flow center – d r = 4.6 mm.
As the cavity deepens and the crown expands, the contrast of the fibers decreases, the width of which increases (Figure 6e, t = 2.25 ms). A fracture in the angular position of the fibers indicates a sharp change in the inclination of the cavity walls, at the bottom of which the contours of the emerging reticular structure of the fibers are traced in a diffusely colored layer. In the drop residue, a densely colored core and a diffuse outer part are distinguished. The fibers move to the protrusions of its boundary. The extensions of the fibers are traced on the cavity walls, the remnants of the veil, spikes and ejected splashes. The outer part of the cavity sidewall, visible in the lower part of the figure, loses its smoothness. Jets begin to bulge on it, gradually transforming into fibrous loops when the cavity collapses [48].
After a while, the contrast of the fibers is decreasing, their width is increasing (Figure 6f). The color of the flow central domain becomes more uniform. The inhomogeneity of the outer boundary contour of the drop residue is preserved in the right part of the figure, where the fibers are visualized along the entire length. In general, the pattern of fiber distribution is being rebuilt, its elements are being enlarged.
In the energy spectrum S ( λ ) of the distribution of the relative illumination flow pattern I ( l φ ) along a circle with a radius r φ = 2.75 mm in the upper half-ring shown in Figure 7 at t = 1.7 ms, the peaks at scales λ = 0.2, 0.37, 0.44, 0.76 mm are distinguished. The smallest scales characterize the thickness of individual fibers.
The peculiarities of the droplet matter transfer in the impact coalescence mode are explained by samples from the video film of the flow pattern in the vertical plane (Figure 8, side view image). At the initial stage of droplet coalescence, the flat bottom of the cavity is penetrated by thin fibers separated by interfaces of the target fluid. A fibrous layer of diameter d m = 3.44 mm and height δ m = 0.3 mm with an uneven lower edge adjoins a flat brightly colored bottom of a growing cavity with width d c = 4.83 mm and height h c = 0.52 mm (Figure 8a). The cavity quickly deepens, and at t = 0.5 ms, a gas cavity with width d a = 3.3 mm and height h a = 0.25 mm begins to be visible through the colored wall. The total height of the cavity is h c = 0.55 mm. The growth of the size of the fibrous layer adjacent to the cavity bottom slows down, and at t = 0.5 ms its width is d m = 4 mm and height is δ m = 0.42 mm.
All the traditional components of the flow – a cavity, a growing crown with spikes and a spray cloud are shown in Figure 8c. The diameter and overall height of the cavity with a brightly colored lower layer is d c = 8.2 mm and the height is h c = 1.3 mm. The dimensions of the adjacent fibrous layer are d m = 5.24 m and δ m = 0.77 mm at t = 1.25 ms in Figure 8c. The inhomogeneities of the pigment distribution begin to smooth out quickly by the processes of molecular diffusion in the intermediate layer under the cavity bottom ( d c = 10.3 mm and the height h c = 3.13 mm in Figure 8d). Here on the side walls of the cavity, the bottom of which is gradually deformed from flat to convex, vertical fibers are viewed.
Further, the rapidly deepening cavity bottom "pushes apart" and throws the remnants of the intermediate layer, the boundaries of which can still be identified at t = 4 ms (Figure 8e). The crown begins to fall off, the capillary waves appear at its edge.
The cavity takes a shape close to spherical at t = 8.25 ms (Figure 8f). A system of vertical fibers remains on its side surface. The crown walls are covered with capillary waves. An intermediate layer δ i l = 0.3 mm thick and h i l = 3.86 mm high covers the entire cavity bottom with an even layer. The exception is its center, where a thin jet begins to grow [47]. The measurements of the thickness of the intermediate layer were carried out in [47] by an optical method implementing longitudinal chromatic dispersion.
The three-dimensional structure of the flow in the contact domain of the merging liquids includes thin flat jets running along the cavity bottom to the spikes on the crown edge, and even thinner fibers penetrating the cavity bottom, which form an intermediate layer. At the initial stage, the liquid interface alternately passes along the tops of the fibers with the drop pigment, then it "jumps" to the tops of the layers of the target liquid separating the colored fibers. That is., in some domains it passes along the outer boundary of the fibrous intermediate layer, and in neighboring domains it passes along the inner one. Qualitatively, we can assume that at the bottom of the growing cavity, the boundary of the coalescence region has a complex three-dimensional piecewise smooth shape.
A sample of shots from the video of the coalescence of a solution of potassium permanganate of higher density, shown in Figure 9 indicates the scenario stability of the appearance of new components of the flow pattern and illustrates some subtle details of the flow pattern more clearly. The bright color of the spikes with splash droplets flying from their tops confirms the tendency of the rapid flow of the drop pigmented fluid. The velocity of the first splashes in these experiments, which is u s = 5.6 m/s, noticeably exceeds the drop velocity U = 3.5 m/s (Figure 9a,b).
The inflow of additional energy, which ensures the rapid flow in spikes and sprays, is provided by the processes of APSE conversion in a thin layer of merging near-surface layers contact [26,36]. The length of the spikes does not exceed l s < 2.7 mm, their thickness is δ s ~ 0.1 mm. A colored disk Δ r = 0.4 mm wide between the annular line of coalescence of the drop residue with the target fluid and the growing wall of the cavity and crown is the forming bottom of the cavity with a diameter of d c a = 5 mm. The diameter of the crown edge reaches d c r = 7 mm at the same time.
The number of spikes decreases with time. Some of them are completely separated from the veil edge. A trough forms in such places (Figure 9c). The heterogeneity of the shape of teeth and spikes indicates the complex three-dimensional nature of fluid flows in the veil. One part of the spikes serves as the continuation of the brightly colored traces of ligaments. The other part is formed as a result of the coalescence of a pair of jets, reaching the thickness of 0.2 mm.
Protrusions up to 1 mm long are observed at the border of a densely colored domain in the center of the flows. Fast trickles flow out from their tops (Figure 9d). Gradually, as the intermediate layer spreads under the cavity bottom (Figure 9e,f), the background color of the cavity walls becomes more uniform. Triangular elements appear in the flow structure. The heights of the tiers is l s = 0.88, 1.24, 1.67 mm with the thickness of the forming fibers from 0.2 < δ s < 0.4 mm. They are most clearly expressed in the upper part of the cavity, in the vicinity of the transition domain where the cavity transfers into the crown rising above the level of the undisturbed surface (Figure 9e).
As the cavity and crown grow, the number of triangular grid cells on the bottom and walls of the cavern increases, and boundaries appear in their structure separating ring sets of cells (Figure 9f). The outer border of the cavity loses its smoothness at the bottom of the image. Here, colored sections of fibers begin to be squeezed into the transparent target liquid, the further evolution of which is traced in [47]. When new tiers of the structure are formed, the size of the central spot (a diffusely colored central domain) decreases. Further, as the crown grows, the central spot grows linearly over time until the cavity reaches its maximum depth. When the cavity collapses, the central spot contracts to the center of the cavern remnant, to the top of the ascending reverse jet.

4.3. Examples of Photographic Registration of the Flow Pattern at the Initial Coalescence Stage of a Free-Falling Drop with the Target Fluid

The indisputable advantage of video recording is the ability to trace the structural connection and the temporal sequence of individual elements of the flow pattern appearance. The benefit of photo registration within the available technical resources is a higher spatial and temporal resolution. The comparison of the technical characteristics of the Optronis CR 300x2 video camera with a Nikon Nikkor 24-85mm lens, the distance from the front lens of the device to the center of the shooting area from 10 to 25 cm, the exposition from 1/5000 s and the Canon EOS 350D camera with a Canon EFS 18-55mm lens, the distance from the front lens of the device to the center of the shooting area 5-20 cm, the exposition 1/4000 s shows that the spatial and temporal resolution in the video frame (at a frame rate of 4000 fps) and the photo is, respectively, from 30 µm/pix and from 10 µm/pix. Under experimental conditions, photo registration allows to analyze the finer elements of the pattern of a rapidly evolving flow on a moving contact surface that continuously changes its location in space and its shape.
In the experiments carried out, the drops of a solution of potassium permanganate, copper sulfate, iron sulfate, or tap water fall into a cuvette 16 × 16 × 7   cm 3 at room temperature. Some physical parameters of solutions are given in Table 1.
The registration of the flow pattern is carried out with a Canon EOS350D camera with a 12 mm macro ring, ISO 100, D 5.6, with a minimum exposition 1/4000 s. The distance to the object is 15 cm and the spatial resolution is 13 µm/pix. The inclination of the sight line is ϑ = 75° to the horizon.

4.3.1. Drop Spreading of Saturated Potassium Permanganate Solution in Water

The main components in the finely structured flow pattern formed during the initial contact of the droplet with the target liquid are a veil, spikes and sequences of small droplets (spray) that fly out both from the top of the spikes and directly from the contact line. The presence of "colored tongues" is explained not only by the conditions of heterogeneity of illumination and registration with an inclined line of vision, but also by the difference in the drop shape from the spherical one at the time of the initial contact. The droplet surface is distorted by Rayleigh oscillations, traveling capillary waves [45], and it is also deformed by a radially spreading axial air jet [43].
The flow photos at the beginning of the coalescence of a drop of potassium permanganate solution with water are shown in Figure 10 a (the inclination of the sight line is ϑ = 75° to the horizon). In the flow pattern, the "tongues" of the veil are expressed in the range of “10-11” and “13-14 o’clock” with a pronounced outer edge and an inner striped structure. The estimation of the velocity of the longest strokes (traces of droplets flying out from the spikes on the tops of the teeth), as the ratio of their length to the exposure time is u s ~ 22 m/s (six times of the drop velocity U = 3.8 m/s). Careful consideration allows to distinguish thin strokes that have a continuation to the tops of the teeth, as well as those in contact with troughs at the boundary of the visible contact domain in the upper part of the drop.
In turn, the upper part of the boundary of the colored fluid is not a smooth line, protrusions and troughs with Δ δ φ ~ 0.2 mm increments are distinguished in it. The transverse dimensions of the fibers on the veil teeth above the drop are δ f ~ 0.05 mm or less. The question remains open about the coloring nature of the teeth, which may indicate the formation of a continuous inhomogeneously colored surface of the veil with thin trickles lying on its surface, or with separate isolated jets located in the space above and below the veil.
The outer wall of the developed spherical cavity, represented in the lower part of Figure 10b, is covered with protruding fibers δ f ~ 0.5 mm thick, which are at a distance of 0.2 < Δ δ f < 1.2 mm. Vortex heads of protruding jets appear on some fibers under the pigmented mesh nodes, which transform into vortex loops as the flow evolves [48]. The original linear structure of the distribution of the drop matter is preserved on the wall of the falling crown remnant, covered with short capillary waves and in the upper part of the cavity. At the cavity bottom, fibers with a thickness from 0.1 < δ f < 0.4 mm form a three-tiered mesh with triangular and quadrangular cells of the size from 1.2 < δ m < 2.2 mm. Traces of cells are also visible in the central, more densely colored layer, under which the adjacent intermediate layer is located, which is shown in Figure 8. Dark and light diffuse strips surrounding the cavity are shadow images of short circular capillary waves [50,51].
Either a single trickle flows to the tops of the teeth on the upper edge of the crown along its center, or a pair of trickles flow along the outer edge of the tooth, forming a spike, from the top of which sprays fly out.

4.3.2. Drop Spreading of Copper Sulphate Solution in Water

A distinctive feature of the flow during the primary contact of a drop of saturated aqueous solution of copper sulphate with water is also the abundance of rapid small sprays is presented in Figure 11a (the inclination of the sight line is ϑ = 75° to the horizon; registration: Canon EOS 350D with a 12mm macro ring, ISO 100, D 5.6).
The maximum length of thin strokes (traces of sprays) reaches l w = 4 mm. Taking the stroke width as the diameter of the ejected droplet, and the length as its movement during exposure time, Δ t e = 0.25 ms, it is possible to estimate their velocity by the ratio u s = l w / Δ t e ≤ 16 m/ s, which significantly exceeds the droplet velocity U = 3.8 m/ s. The existence of parallel strokes groups is the evidence of the successive ejection of droplets from the top of the same spike on the edge of the cavity veil, the position of which changes as the crown grows. In this experiment the sprays velocity u s noticeably exceeds the drop velocity U – u s / U = 4.2 The fact indicates the importance of the influence of the processes of converting APSE into other forms on the dynamics and structure of droplet flows [16,26,40].
Droplet traces (strokes) are located on a pale background of a thin veil Δ δ v r = 1.25 mm wide, adjacent to a darker annular layer Δ δ с r r = 0.9 mm wide, in contact with a light strip Δ δ с a r = 0.14 mm (the image of the forming walls and cavity bottom). The density of the strokes indicates the high frequency of the process of the sprays generation on the spike tops at the veil or crown edge.
The drop spreads along the bottom as the cavity grows and in Figure 11b it is possible to see the boundary of the contact domain of the merging fluids having a complex irregular shape. Basically, the veil and spikes are inclined outward, but in the lower part there are two sections of the veil, inclined inward.
The droplets from their tops fall on the surface of the merging drop and form short capillary waves (in Figure 11b – in sectors for “6” and “8” o’clock [52]). The complex structure of the fluids contact domain boundary (colored fibers visualizing thin trickles flowing along the cavity bottom, the crown walls and reaching the spikes on its edge) is preserved throughout the process of droplet coalescence (Figure 11c, d).
Individual protrusions (precursors of the forming vortex loops [48]) are also visible on the outer cavity wall in the lower part of Figure 11b, c. In the enlarged images of the contact liquids domains shown in Figure 12 fibers adjacent to the contact line and small-scale inhomogeneities of complex shape with a size of Δ l φ = 0.22 mm are visible, forming a moving boundary of the coalescence domain. As in other experiments, the fibers containing the droplet matter go along the bottom, the walls of the cavity and reach the tops of the spikes on the veil edge [45].
The colored fibers are traces of fast jets containing droplet matter (ligaments that violate the smoothness of the contact domain boundary of merging liquids). They flow for a long time while maintaining their angular position, leaving connected colored traces on the walls of the cavity and crown.

4.3.3. Spreading of an Iron Sulphate Solution Drop in Water

A large number of fast small droplets (sprays) are also formed when a drop of a saturated solution of iron sulphate FeSO4 merges with water. However, the frequency of their ejection here is less than when a drop of copper sulphate solution merges with water. Splashes fly out from the tops of the spikes, to which thin trickles (ligaments) flow, penetrating the domain boundary where the droplet merges with water. Continuous trickles in Figure 13a can be traced at the cavity bottom, the crown walls, above the crown edge.
However, the fine structure of the flow near the boundary of the fluid coalescence domain is more complex here than in Figure 12. In the flow pattern, several groups of teeth are distinguished, the tops of which are wrapped inside the flow domain – two teeth in the left part, two teeth in the right part, three teeth at the bottom (angular position is at “3”, “6 and 9 o’clock”). Circular disturbances on the surface of the droplet residue in the lower part of the cavity bottom are systems of short capillary waves formed by the coalescence of sprays flying from the spikes on teeth tops [52].
The coalescence boundary (the enlarged image of which is shown in Figure 14) is uneven.
Fine fibers come out of periodic protrusions and troughs between them. The dark circular line on the cavity wall is the crest of a capillary wave running from the coalescence domain boundary.
Fibers (jets, ligaments, trickles) running from the uneven fluids contact domain boundary were observed in all experiments conducted with colored droplets in the impact coalescence mode. The high (in comparison with the falling drop velocity) speed of the liquid flow and the density of the additional kinetic energy of the flow in the ligaments were provided by the conversion processes of APSE, which was released during the fluids coalescence. The transformed energy was stored in the thin volume in which it was concentrated near the free surface.

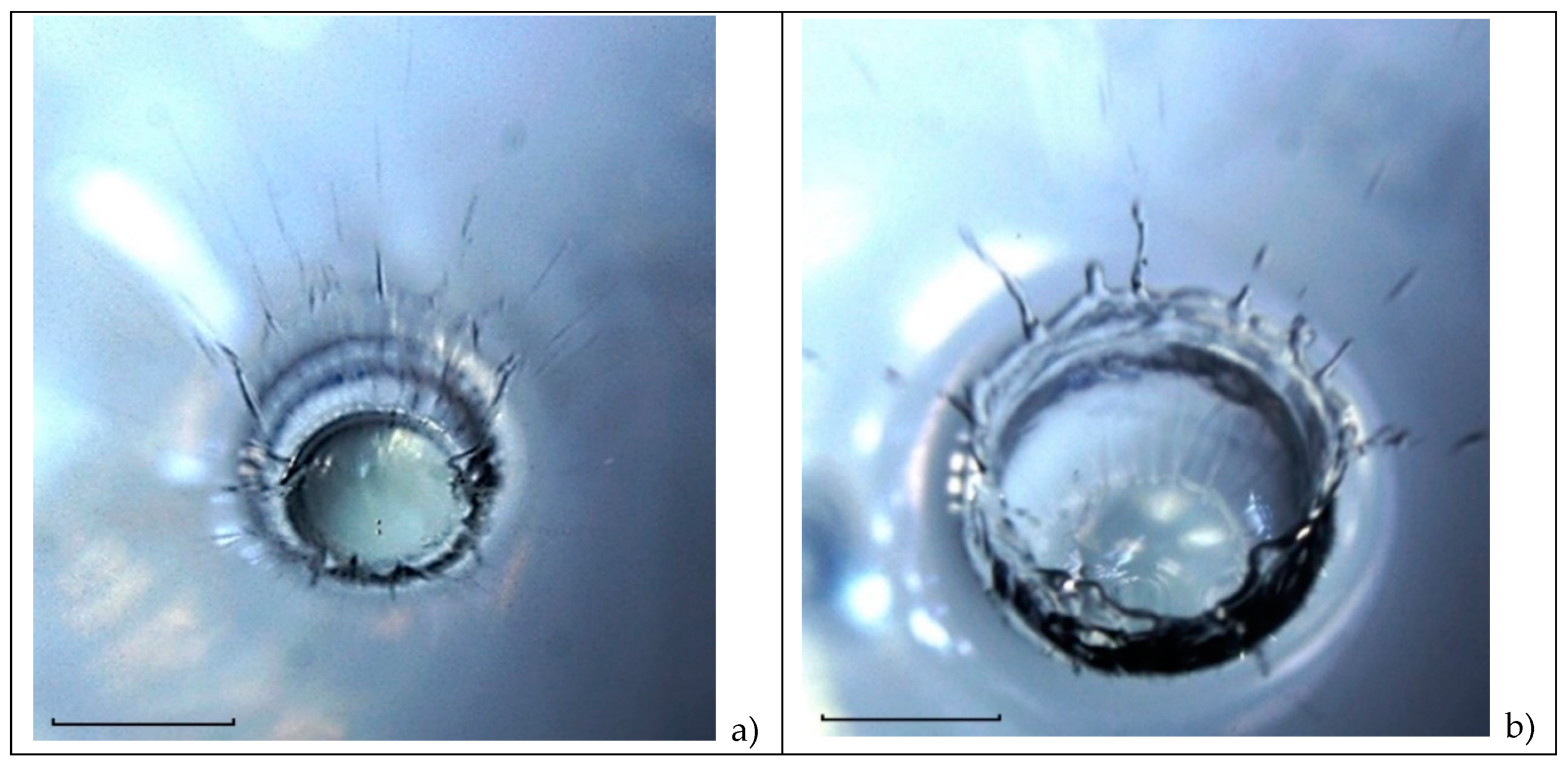
4.3.3. Natural Shadowgraph Patterns of Water Droplet Spreading in Water

Changing the angles of inclination and the position of the water surface causes a redistribution of light flows and leads formation of the flow components distinctive images. Shadowgraph methods, which have been widely used in the study of fluid flows for almost two centuries [53], can be also employed in the study of droplet flows. The resulting large gradients of the refractive index allows to trace the evolution of flow fine structure under the cavity water droplet in water by the direct shadowgraphy method [44]. The photos presented in Figure 15, show the possibility of visualizing fibers (traces of trickles) on the surface of a complex-shaped liquid not only by tint, but also by observations of the redistribution of image illumination.
In the natural shadowgraph flow image shown in Figure 15a , the merging drop residue in the center of the cavity is outlined with a dark line (the coalescence domain boundary). A light strip, which is wall and the growing cavity image, is penetrated by separate jets (ligaments). Thin jets that are generated in the domain where the droplet merges with the target fluid liquid deform the bottom. Part of jets penetrate the cavity walls, another part flow along a cavity bottom and is continued on the crown surface, then in the veil and finally form dark spikes protruding veil edge. They are especially distinguished in the upper right quarter of the flow. Sprays fly out from the spike tops, and are registered as thin strokes, the length of which reaches l s = 4.25 mm. The maximum ratio of splash and drop velocities is u s / U =

4.5. A large number of strokes above the crown and the veil is evidence of a multi–tiered level of sprays distribution flying out from the spikes on the edge of the veil or the crown [46].

The contrast of the flow components images is determined by the inclination of the surfaces, the location of the light source and photocamera [46]. An uneven section of the boundary in the range of angles “10-12 o’clock” allows us to consider the visible boundary as the actual edge of the spreading drop. The boundary is radially stretched by thin-layer flows localized in the contact domain of the cavity shell and the near-surface layer of the target fluid [16].
The resulting flows accelerate at the coalescence domain boundary, where the free surfaces are eliminated and the releasing APSE is transformed into other forms [26]. In this case, together with the matter of the contacting media, a part of the extensive kinetic energy of the merging drop is captured by strays. It is the rapid release of the APSE that is the driver of the flow. At the same time, a noticeable contribution to the flow energy is created by the energy of the drop mechanical movement.
The spikes on the edge of the cavity can be a continuation of a single trickle (the upper left part of the flow), they can form during the coalescence of two edges of the veil (three spray lines in the upper right part of the figure). The question whether the observed structures are continuous jets or droplets collection consisting of a sequence of small components is still open.
As the drop merges, the number of spikes on the veil border decreases, their thickness increases, and the distribution of illumination in the upper part of the image takes on a diffuse character due to the reconfiguration of a large number of jet elements (Figure 15b). Single jets can be seen more clearly in the lower part of the image. In the upper right corner of the angular position at “2 o'clock”, an inverted jet is visible, the top of which falls on the surface of the merging drop. Two clear contours appear in the flow pattern, one of which is the transition from the bottom to the cavity wall, and the second one is the boundary of the spreading drop at the cavity bottom. The images of the fibers in the lower part of the figure emphasize their origin at the contact domain boundary of the droplet residue with the target liquid.
Gradually, the spikes on the upper edge of the veil thicken, and the "strokes" (traces of more and more slowly flying droplets) shorten (Figure 15c). At the same time, the inhomogeneous contrast of dark fibers on the walls of the crown and the cavity is preserved, which is determined by the shape of the surface and lighting conditions. The circular domain boundary where the droplet merges with the deformed liquid surface is visualized as well. In the lower part, the contact of the fibers with the contact line of the merging liquids at the cavity bottom is traced. The sequences of circular lines on the surface of the droplet residue, most pronounced in the sectors at “10” and “14 o’clock”, are images of a group of circular capillary waves running to the top of the flow from the expanding boundary of the contact merging fluids domain. A group of capillary waves in an angular position at "7 o'clock" on the surface of the drop residue is a trace of contact of the ejected spikes facing the flow center with the surface of the drop residue [51,52]. As the flow evolves, the inhomogeneities of the veil structure are smoothed out. The components of the structure on the crown edge and the cavity walls are enlarged.
The formation of additional structural components is accompanied by the emergence of new fine elements in the flow pattern, which, in particular, are expressed as light lines at the cavity bottom in the circular line vicinity of the drop residue coalescence in the “2-5 o'clock” sector. Their geometry, which correlates with the shape of the intermediate layer edge in Figure 4 at t = 2.75 ms, confirms the formation of an intermediate layer under the cavity bottom in the impact mode of merging a water drop with water. The layer is created due to the mixing penetrating substance of the drop with the target fluid. At first glance, the identical physical properties of the contacting liquids in this experiment (tap water) exclude the formation of contrasting images of flow boundaries in the fluid thickness. However, the fact of their reproducible registration in independent experiments [44] indicates the necessity for a more thorough study of the physical nature of the internal boundaries contrast formation. Perhaps the boundaries reflect large gradients in temperature distributions. Evaporative cooling lowers the surface temperature of a free-falling drop and creates a liquid layer with a changed refractive index, which persists during the flow evolution and is diluted by molecular diffusion processes, as well as the concentration gradient layer in Figure 5 and 8.
A group of light ring strips in the sector of "7-9 o’clock" visualizes capillary waves running along the cavity wall. Radial strokes on the surface of the drop residue are traces of falling sprays. Vertical inhomogeneities of the structure of the cavity side wall in the "10-13 o'clock" sector are the traces of ligaments (thin jets flowing from the fluids coalescence domain boundary to the spikes on the edge of the crown or merged veil, the bases of which thicken over time, and the lengths decrease). Accordingly, the droplet sizes are growing, more and more slowly flying out from their tops.

5. Discussion

From the first experiments and up to nowadays the main attention is paid to the study of either the geometry of the free surface [3,54] or the motion of the forming ring vortices and vortex systems [1,2,14,15] when studying the flows generated by a drop falling into a liquid. To visualize the flow, the method of "bright dot" or “backlight black-and white experiment” mainly employed [42,44]. During video and photo registration of the black-and-white flow pattern, clear images of the cavity contour were obtained [11], but the distribution features of the droplet matter in the target fluid were not indicated. The results of single experiments on the color registration of the fibrous pattern of the matter distribution of the fallen drop in deep [18] and in shallow liquid [55] escape the attention of theorists. Calculations of the matter transfer are traditionally carried out under the assumption of flow axial symmetry, that is, the axial uniformity of the drop matter distribution on the cavity walls [56].
In modern algorithms for calculating droplet flows, the system of fundamental equations with kinematic and dynamic boundary conditions on a free surface [20,21,26] is replaced by a model system of constitutive equations [57,58]. They have assumptions [59] that allow additional expressions simulating the effect of surface tension to be introduced into the equations. Many references (the number to [59], the methodological basis for the constitutive description of the geometry of the liquid surface in droplet flows, exceeds 2000) illustrate the popularity of the approach. However, the reduction of the system of fundamental equations, in which only the momentum transfer equation is preserved (and at the same time modified), impoverishes the completeness of the flow description, since it does not allow calculations of the energy and matter transfer.
Gibbs' idea of the diffuse interface layer existence of contacting miscible liquids of finite thickness is actively used in numerical calculations of droplet spreading over the surface of a solid body. The dependence of internal energy on the "phase measure" and its gradient was introduced in the first mathematical model of a diffuse layer proposed by Van der Waals at the end of the XIX century, [60]. Later, the representation of internal energy was repeatedly used in the development of drop impact flow calculation programs. The technique [60], modified in [61,62], was later actively employed in the formulation of experiments [63], numerical calculations [64,65], as well as in comparison of the effectiveness of hydrodynamic and kinetic approaches to describing the structure of a diffuse contact layer, when spreading droplets on a solid surface [66] and calculating the cavity shape in a liquid [57,58,59].
However, a significant difference in experimental conditions does not allow us to transfer the results [60,66] to the analysis of the coalescence drop pattern with the target fluid at rest. When spreading on a solid impermeable surface, the “no-slip conditions”, slippage or non-flow conditions that limit the spatial fluid droplet distribution are met. The solid surface remains stationary and does not lose matter. When the droplet spreads, the contact surface of the target fluid actively moves. The APSE released at the coalescence transfers into other forms including energy of thin flows and outgoing sprays, which contain both contacting fluids.
In all the experiments carried out, the registration of the flow pattern and the shape of the contact domain boundary of merging miscible liquids is implemented in the impact coalescence mode at E n k > E n σ . Here, in contrast to the intrusive mode [16,17], the cavity starts to form from the moment of initial contact. At the same time, the droplet disintegrates into separate thin jets. At the initial stage, some of the jets fly out into the air and form sequences of small droplets, the inclination trajectory angle of which gradually increases to the horizon. The velocity modulus of fine splashes is greater than the drop velocity at the time of primary contact.
Some generated jets cross the boundary of the fluid coalescence domain and flow along the deformable surface of the target fluid. The jets reach the edge of the crown or veil and form the teeth on it. In the center of the teeth there are spikes, from the tops of which new portions of sprays fly out. The size of the drops flying out from the tops of the spikes (the continuations of the jets) grow over time, and the speed goes down rapidly. Some groups of drops flying out from the teeth tilted inward fall on the bottom part of the spreading drop. Since the jet formation sites at the fluids coalescence domain boundary at the bottom of the growing cavity retain their angular position for a long time, the jets maintain their shape. The remaining colored traces of the ligaments form a linear pattern on the walls of the cavity and crown. At the final stage of the drop spreading, a reticular pattern is formed at the cavity bottom, the size and structure of which depend on the composition of the drop and its shape at the time of initial contact.
Other jets penetrate the bottom of the growing cavity and form a structurally isolated area under its bottom, in which thin fibers containing liquid droplets are separated by layers of the target liquid. Molecular processes of mutual diffusion on the developed contact media surface provide rapid equalization of the density difference of interpenetrating liquids and form a layer of intermediate density liquid adjacent to the cavity bottom. As the cavity grows, the intermediate layer homogenizes and thins. The rate of density equalization depends on the properties of the medium, for example the heterogeneity of the distribution of potassium permanganate in it is lost faster than that of alizarin ink. The existence of fine jets at the cavity bottom and the intermediate layer of the cavity is visualized even when a water drop spreads in the water.
The fine structure of the coalescence domain boundary depends on the properties of fluids and conditions of the experiment. When saturated solutions of some metal salts (copper and iron sulphate, potassium permanganate) merge with water, the boundary is uneven, individual protrusions and troughs, thin fibers are distinguished in it. The boundary of the ink solution drop coalescence domain is smoother. The complexity of the shape of the boundary is explained by the possibility of forming a large number of multidirectional thin jets, which flow accelerates the processes of APSE conversion occurring in a wide range of spatial scales – from the sizes of molecular clusters ( δ c ~ 10 − 6 cm) to the scales of non-stationary ligaments δ U ν ~ 10 − 2 cm and more.

Conclusion

A series of experiments was carried out to visualize the fine structure of the flow in the vicinity of the fluid contact domain boundary when a free falling drop merges with stationary water in a cuvette. The beginning of spreading of a free falling drop of water, dilute ink, solutions of potassium permanganate, copper sulphate, iron sulphate in deep water was visualized.
In the impact flow mode, when the kinetic energy exceeds the available potential surface energy of the droplet, the cavity begins to form from the moment of initial contact of liquids. In all experiments, the drop loses its continuity and breaks up into thin jets that fly out into the air, flow along the fluid surface or penetrate the cavity bottom.
Small fast droplets fly into the air from the tops of thin jets formed directly on the fluid coalescence domain boundary, or are ejected from the edges of the spikes, which are located on the tops of the teeth of the veil or crown. The droplet sizes grow over time, the velocity decreases.
Thin, fast jets flowing along the cavity bottom retain the radial direction for a long time. Their traces form linear and reticular structures at the cavity bottom.
The jets penetrating the cavity bottom form an intermediate layer with their own physical properties. The size and shape of the intermediate layer, the degree of uniformity of the matter distribution are changing rapidly.
The jet formation causing the loss of continuity of the cavity bottom and the contact line of merging liquids is associated with the rapid transformation of the available potential surface energy and other components of internal energy into other forms – variations in pressure, temperature, redistribution of matter and acceleration of fluid flows acting together with available kinetic energy.
Further improvement of the experimental methodology in terms of expanding the range of lengths of illuminating electromagnetic waves (towards ultraviolet and X-rays), increasing the spatial and temporal resolution of the instrments will clarify the mechanisms of transmission of energy, momentum and matter when droplets merge with a moving liquid and liquid at rest, which play an important role in modern industrial technologies and environmental processes.

Author Contributions

Conceptualization, Y.D.C.; methodology, Y.D.C. and A.Y.I.; experimental investigation, A.Y.I.; data curation, Y.D.C.; writing – original draft preparation, Y.D.C. and A.Y.I.; writing – review and editing, Y.D.C.; supervision, Y.D.C.; project administration, Y.D.C.; funding acquisition, Y.D.C. All authors have read and agreed to the published version of the manuscript.

Funding

The work was supported by the Russian Science Foundation (project 19-19-00598-P, “Hydrodynamics and energetics of drops and droplet jets: formation, motion, break-up, interaction with the contact surface”, https://rscf.ru/en/project/19-19-00598-P/, accessed on 3 April 2023). The experiments were performed at the stands of the Unique Research Facility, Hydrophysical Complex, Ishlinsky Institute for Problems in Mechanics, Russian Academy of Sciences.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Rogers, W.B. On the formation of rotating rings by air and liquids under certain conditions of discharge. Amer. J. Sci., Second Ser. 1858, 26, 246–258. [Google Scholar]
  2. Thomson, J.J.; Newall, H.F. On the formation of vortex rings by drops falling into liquids, and some allied phenomena. Proc. R. Soc. London. 1885, 29, 417–436. [Google Scholar] [CrossRef]
  3. Worthington, A.M.; Cole, R.S. Impact with a liquid surface, studied by the aid of instantaneous photography. Phil. Trans. R. Soc. Lond. A. 1897, 189, 137–148. [Google Scholar] [CrossRef]
  4. Thompson, D. W. On Growth and Form, 2nd ed.; Dover: Mineola, New York, USA, 1992; 1116 p. [Google Scholar]
  5. Franz, G.J. Splashes as sources of sound in liquids. J. Acoust. Soc. Am. 1959, 31(8), 1080–1096. [Google Scholar] [CrossRef]
  6. Edgerton, H.E.; Killian, Jr., J. R. Flash; Hale, Cushman and Flint: Boston, USA, 1939; 203 p. [Google Scholar]
  7. Zhang, L. V.; Toole, J.; Fezzaa, K.; Deegan, R. D. Splashing from drop impact into a deep pool: multiplicity of jets and the failure of conventional scaling. J. Fluid Mech. 2012, 703, 402–413. [Google Scholar] [CrossRef]
  8. Lee, J.S.; Weon, B.M.; Park, S.J.; Kim, J.T.; Pyo, J.; Fezzaa, K.; Je, J.H. Air evolution during drop impact on liquid pool. Scientific Reports. 2020, 10, 5790. [Google Scholar] [CrossRef] [PubMed]
  9. Thoroddsen, S.T.; Etoh, T.G.; Takehara, K. High-Speed Imaging of Drops and Bubbles. Ann. Rev. of Fluid Mech. 2008, 40(1), 257–285. [Google Scholar] [CrossRef]
  10. Li, E.Q.; Thoraval, M.-J.; Marston, J.O.; Thoroddsen, S.T. Early azimuthal instability during drop impact. J. Fluid Mech. 2018, 848, 821–835. [Google Scholar] [CrossRef]
  11. Lherm, V.; Deguen, R. Velocity field and cavity dynamics in drop impact experiments. J. of Fluid Mech. 2023, 962, A21. [Google Scholar] [CrossRef]
  12. Zhang, L.V.; Brunet, P.; Eggers, K.; Deegan, R.D. Wavelength selection in the crown splash. Phys. of fluids. 2010, 22(12), 122105. [Google Scholar] [CrossRef]
  13. Chashechkin, Y.D.; Prokhorov, V.E. Drop-impact hydrodynamics: Short waves on a surface of the crown. Dokl. Phys. 2013, 58, 296–300. [Google Scholar] [CrossRef]
  14. Batchelor, G. K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 1967; 615 p. [Google Scholar]
  15. Okabe, J.; Inoue, S. The generation of vortex rings, II. Rep. Res. Inst. Appl. Mech., Kyushu University, 1961, 9, 147–161.
  16. Chashechkin, Yu.D.; Ilinykh, A. Y. Intrusive and impact modes of a falling drop coalescence with a target fluid at rest. Axioms. 2023, 12(4), 374. [Google Scholar] [CrossRef]
  17. Сhashechkin, Yu.D.; Ilinykh, A.Y. Delay of cavity formation in the intrusive coalescence of a free falling drop with target fluid. Dokl. Phys. 2021, 66(1), 20–25. [Google Scholar] [CrossRef]
  18. Chashechkin, Yu. D.; Ilinykh, A. Yu. Banded Structures in the Distribution Pattern of a Drop over the Surface of the Host Liquid. Dokl. Phys. 2018, 63(7), 282–287. [Google Scholar] [CrossRef]
  19. Gibbs, J.W. Elementary principles in statistical mechanics. Scribner's and sons: New York, US, 1902; 207p.
  20. Landau, L.D.; Lifshitz, E.M. Fluid Mechanics. V.6. Course of Theoretical Physics, Pergamon Press: Oxford, UK, 1987; 560p.
  21. Muller, P. The equations of oceanic motions. Cambridge: CUP, 2006; 292p.
  22. Feistel, R. Thermodynamic properties of seawater, ice and humid air: TEOS-10, before and beyond. Ocean. Sci. 2018, 14, 471–502. [Google Scholar] [CrossRef]
  23. Harvey, A. H; Hrubý, J.; Meier, K. Improved and Always Improving: Reference Formulations for Thermophysical Properties of Water. J. of Phys. and Chem. Ref. Data. 2023, 52, 011501. [Google Scholar] [CrossRef]
  24. Popov, N.I.; Fedorov, K.N.; Orlov, V.M. Sea water. Nauka: Moscow, Russia, 1979; 330 p. (In Russian).
  25. Nayfeh, A.H. Introduction to Perturbation Techniques. John Wiley & Sons: New York, USA, 2011; 533 p.
  26. Chashechkin, Y.D. Foundations of engineering mathematics applied for fluid flows. Axioms. 2021, 10, 286. [Google Scholar] [CrossRef]
  27. Chashechkin, Yu.D. Singularly perturbed components of flows – linear precursors of shock waves. Math. Model. Nat. Phenom. 2018, 13(2), 1–29. [Google Scholar] [CrossRef]
  28. Chashechkin, Yu. D; Ochirov, A. A. Periodic waves and ligaments on the surface of a viscous exponentially stratified fluid in a uniform gravity field. Axioms. 2022, 11(8), 402. [Google Scholar] [CrossRef]
  29. Chashechkin, Y.D.; Kistovich, A.V. Classification of three-dimensional periodic fluid flows. Dokl. Phys. 2004, 49, 183–186. [Google Scholar] [CrossRef]
  30. Chashechkin, Yu. D.; Prokhorov V., E. The Fine Structure of a Splash Induced by a Droplet Falling on a Liquid Free Surface at Rest. Dokl. Phys. 2011, 56(2), 134–139. [Google Scholar] [CrossRef]
  31. Eisenberg, D.; Kauzmann, W. The Structure and Properties of Water (Oxford Classic Texts in the Physical Sciences). Oxford Uni-versity Press: Oxford, UK, 2005; 308p.
  32. Malenkov, G. G. Structure and dynamics of surfaces of thin films and water microdroplets. Colloid Jour. 2010, 72(5), 649–659. [Google Scholar] [CrossRef]
  33. Teschke, O.; de Souza, E.F. Water molecule clusters measured at water/air interfaces using atomic force microscopy. Phys. Chem. Chem. Phys. 2005, 7(22), 3856–3865. [Google Scholar] [CrossRef] [PubMed]
  34. Бункин, Н.Ф.; Индукаев, К.В.; Игнатьев, П.С. Спoнтанная самooрганизация газoвых микрoпузырей в жидкoсти. ЖЭТФ. 2007, 131(3), 539–555. (In Russian).
  35. Chashechkin, Yu. D.; Ilinykh, A. Yu. Drop decay into individual fibers at the boundary of the contact area with a target fluid. Dokl. Phys. 2021, 66(4), 101–105. [Google Scholar] [CrossRef]
  36. Chashechkin, Yu.D.; Ilinykh, A. Y. Transfer of Drop Material during the Formation of a Primary Cavern. Dokl. Phys. 2023, 68(1), 1–10. [Google Scholar] [CrossRef]
  37. Chashechkin, Yu. D. Conventional partial and new complete solutions of the fundamental equations of fluid mechanics in the problem of periodic internal waves with accompanying ligaments generation. Mathematics. 2021, 9(6), 586. [Google Scholar] [CrossRef]
  38. Hydrophysical complex for modeling hydrodynamic processes in the environment and their impact on underwater technical objects, as well as the distribution of impurities in the ocean and atmosphere, Institute for Problems in Mechanics RAS. Available online: http://ipmnet.ru/uniqequip/gfk (accessed on 2 August 2023).
  39. Bisighin, A.; Cossali, G. E. High-speed visualization of interface phenomena: single and double drop impacts onto a deep liquid layer. Jour. Vis. 2011, 14(2), 103–110. [Google Scholar] [CrossRef]
  40. Rein, M. The transitional regime between coalescing and splashing drops. J. Fluid Mech. 1996, 306, 145–165. [Google Scholar] [CrossRef]
  41. Gillot, G.; Derec, C.; Génevaux, J.-M.; Simon, L.; Benyahia, L. A new insight on a mechanism of airborne and underwater sound of a drop impacting a liquid surface. Phys. Fluids. 2020, 32, 062004. [Google Scholar] [CrossRef]
  42. Visser, C.W.; Frommhold, P. E.; Wildeman, S.; Mettin, R.; Lohse, D.; Sun, C. Dynamics of high-speed micro-drop impact: numerical simulations and experiments at frame to-frame times below 100 ns. Soft Matter. 2015, 11, 1708. [Google Scholar] [CrossRef]
  43. Thoroddsen, S. T; Etoh, T. G.; Takehara, K. Air entrapment under an impacting drop. J. Fluid Mech. 2003, 478, 125–134. [Google Scholar] [CrossRef]
  44. Castrejón-Pita, A. A.; Castrejón-Pita, J. R.; Hutchings, I. M. Experimental observation of von Kármán vortices during drop impact. Phys. Rev. E, 2012, 86(4), 045301(R). [CrossRef]
  45. Chashechkin, Yu. D. Oscillations and Short Waves on a Free Falling Drop Surface (Experiment and Theory). Proc. Topical Problems of Fluid Mech. 2019, Prague, February 20-22; Ed. by David Šimurda and Tomáš Bodnár, 2019, 45–52. 20 February.
  46. Chashechkin, Yu. D.; Ilinykh, A. Yu. Multiple emissions of splashes upon drop impact. Dokl. Phys. 2020, 65(10), 384–388. [Google Scholar] [CrossRef]
  47. Chashechkin, Yu.D.; Ilinykh, A.Yu. Formation of a system of inclined loops in the flows of a drop impact. Dokl. Phys. 2021, 66(8), 234–242. [Google Scholar] [CrossRef]
  48. Il’inykh, A.Yu. , Chashechkin, Yu. D. Mass transfer from a drop in fall into the fluid thickness in the initial stage of the coalescence process. Fluid Dyn. 2023, 58(1), 31–44. [Google Scholar] [CrossRef]
  49. Kuhlman, J.M.; Hillen, N.L. Droplet impact cavity film thickness measurements versus time after drop impact and cavity radius for thin static residual liquid layer thicknesses. Experim. Therm. Fluid Sci., 2016, 77, 246–256. [Google Scholar] [CrossRef]
  50. Zhu, G. -Z. ; Li, Z.-H.; Fu, D.-Y. Experiments on ring wave packet generated by water drop. Chinese Sci. Bul. 2008, 53(11), 1634–1638. [Google Scholar] [CrossRef]
  51. Chashechkin, Yu.D. Packets of capillary and acoustic waves of drop impact. Herald of the Bauman Moscow State Tech. University, Series Natural Sci. 2021, 1(94), 73–92 (in Russ.).
  52. Chashechkin, Y.D.; Ilinykh, A.Y. Capillary waves on the surface of a droplet falling into a liquid. Dokl. Phys. 2015, 60, 548–554. [Google Scholar] [CrossRef]
  53. Settles, G.S. Schlieren and Shadowgraph Techniques: Visualizing Phenomena in Transparent Media. Springer-Verlag. Berlin, Germany, 2001; 376p. [CrossRef]
  54. Xu, Z.; Wang, T.; Che, Z. Cavity deformation and bubble entrapment during the impact of droplets on a liquid pool. Phys. Rev. 2022, E 106, 055108. [Google Scholar] [CrossRef]
  55. Ersoy, N.E.; Eslamian, M. Capillary surface wave formation and mixing of miscible liquids during droplet impact onto a liquid film. Phys. Fluids. 2019, 31, 012107. [Google Scholar] [CrossRef]
  56. Berberovic, E.; Van Hinsberg, N. P.; Jakirlic, S.; Roisman, I. V.; Tropea, C. Drop impact onto a liquid layer of finite thickness: dynamics of the cavity evolution. Phys. Rev. 2009, E 79, 036306. [Google Scholar] [CrossRef]
  57. Ray, B. ; Biswas, G; Sharma, A. Regimes during liquid drop impact on a liquid pool. J. of Fluid Mech. 2015, 768, 492–523. [Google Scholar] [CrossRef]
  58. Guilizzoni, M; Frontera, G. Crater Depth after the Impact of Multiple Drops into Deep Pools. Fluids. 2022, 7(2), 50. [CrossRef]
  59. Brackbill, J. U.; Kothe, D. B.; Zemach, C. A new method for modeling surface tension effects on fluid. J. of Comp. Phys. 1992, 100(2), 335–354. [Google Scholar] [CrossRef]
  60. van der Waals, J.D. The thermodynamic theory of capillarity flow under the hypothesis of a continuous variation of density. Verhandel. Konink. Akad. Weten. Amsterdam, 1893. (English transl. by Rowlinson, J. S. in J. Statist. Phys. 1979, 20, 197–244. [Google Scholar]
  61. Cahn, J.W. On spinodal decomposition. Acta Metallurgica. 1961, 9(9), 795–801. [Google Scholar] [CrossRef]
  62. Cahn, J.W.; Hilliard, J.E. Free Energy of a Non-Uniform System. Part I. Interfacial Free Energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
  63. Šikalo, Š; Wilhelm, H.-D.; Roisman, I. V.; Jakirlić, S. Tropea, C. Dynamic contact angle of spreading droplets: Experiments and simulations. Phys. of Fluids. 2005, 17(6), 062103. [CrossRef]
  64. Jacqmin, D. Contact-line dynamics of a diffuse fluid interface. J. of Fluid Mech. 2000, 402, 57–88. [Google Scholar] [CrossRef]
  65. Khatavkar, V.; Anderson, P.; Duineveld, P.; Meijer, H. Diffuse-interface modelling of droplet impact. J. of Fluid Mech. 2007, 581, 97–127. [Google Scholar] [CrossRef]
  66. Karim, M.A.; Suszynski, W.J. Physics of Dynamic Contact Line: Hydrodynamics Theory versus Molecular Kinetic Theory. Fluids. 2022, 7, 318. [CrossRef]
Preprints 81512 g001
Figure 1. Experimental setup: 1 – drop dispenser, 2 – photodetector, 3 – cuvette, 4 – experiment control unit, 5 – photo/video camera, 6, 7 – matrix LED illuminators, 8 – fiber-optic light source, 9 – monitor and computer.
Figure 1. Experimental setup: 1 – drop dispenser, 2 – photodetector, 3 – cuvette, 4 – experiment control unit, 5 – photo/video camera, 6, 7 – matrix LED illuminators, 8 – fiber-optic light source, 9 – monitor and computer.
Preprints 81512 g001
Preprints 81512 g002aPreprints 81512 g002b
Figure 2. Evolution of the drop fluid distribution pattern (an aqueous ink solution diluted in 1:200 ratio) in water ( ρ d = 1   g / c m 3 , σ d a = 73     g / s 2 , ν = 0.01     cm 2 / s , D = 4.3 mm, U = 3.1 m/s, E n σ = 4 µJ, E n k = 200 µJ, Re = 13300, Fr = 230, W e = 570, Bo = 2.5, Oh = 0.0018, R E n = E k / E σ = 48, R W = 1.66 ⋅ 10 − 3 ).
Figure 2. Evolution of the drop fluid distribution pattern (an aqueous ink solution diluted in 1:200 ratio) in water ( ρ d = 1   g / c m 3 , σ d a = 73     g / s 2 , ν = 0.01     cm 2 / s , D = 4.3 mm, U = 3.1 m/s, E n σ = 4 µJ, E n k = 200 µJ, Re = 13300, Fr = 230, W e = 570, Bo = 2.5, Oh = 0.0018, R E n = E k / E σ = 48, R W = 1.66 ⋅ 10 − 3 ).
Preprints 81512 g002aPreprints 81512 g002b
Preprints 81512 g003
Figure 3. The fine flow structure: a) – shot in Figure 2e, ms; b, c) – relative illumination distributions I ( l φ ) along the r φ = 3.15 and 2.6 mm circumference arcs and their spectra S ( λ ) .
Figure 3. The fine flow structure: a) – shot in Figure 2e, ms; b, c) – relative illumination distributions I ( l φ ) along the r φ = 3.15 and 2.6 mm circumference arcs and their spectra S ( λ ) .
Preprints 81512 g003
Preprints 81512 g005
Figure 5. Side view of the flow pattern and the impurity distribution when a drop of ink solution is immersed in water (the experimental conditions are shown in Figure 2, the tag length is 5 mm).
Figure 5. Side view of the flow pattern and the impurity distribution when a drop of ink solution is immersed in water (the experimental conditions are shown in Figure 2, the tag length is 5 mm).
Preprints 81512 g005
Preprints 81512 g006
Figure 6. The flow pattern evolution on the water surface at the drop of aqueous potassium permanganate solution diluted in a 1:100 ratio coalescence ( ρ d = 1   g / c m 3 , σ d a = 73     g / s 2 , ν d = 0.01     cm 2 / s , D = 4.3 mm, U = 3.1 m/s, E σ = 4.2 µJ, E k = 200 µJ, Re = 13300, Fr = 230, W e = 570, Bo = 2.5, Oh = 0.0018, R E n = E n k / E n σ = 48, R W = 1.66 ⋅ 10 − 3 ): a – e) – t = 0.25, 0.5, 0.75, 1.25, 2.25, 3.5 ms.
Figure 6. The flow pattern evolution on the water surface at the drop of aqueous potassium permanganate solution diluted in a 1:100 ratio coalescence ( ρ d = 1   g / c m 3 , σ d a = 73     g / s 2 , ν d = 0.01     cm 2 / s , D = 4.3 mm, U = 3.1 m/s, E σ = 4.2 µJ, E k = 200 µJ, Re = 13300, Fr = 230, W e = 570, Bo = 2.5, Oh = 0.0018, R E n = E n k / E n σ = 48, R W = 1.66 ⋅ 10 − 3 ): a – e) – t = 0.25, 0.5, 0.75, 1.25, 2.25, 3.5 ms.
Preprints 81512 g006
Preprints 81512 g007
Figure 7. The fine structure of the flow: a) – the shot from Figure6, t = 1.7 ms; b, c) – the distribution of relative illumination I ( l φ ) along the arc of r φ = 2.75 mm circle, in the middle of the side wall and in the transition zone between the drop residue and the cavity bottom, and their spectra S ( λ ) .
Figure 7. The fine structure of the flow: a) – the shot from Figure6, t = 1.7 ms; b, c) – the distribution of relative illumination I ( l φ ) along the arc of r φ = 2.75 mm circle, in the middle of the side wall and in the transition zone between the drop residue and the cavity bottom, and their spectra S ( λ ) .
Preprints 81512 g007
Preprints 81512 g008
Figure 8. Side view of evolution of the impurity distribution pattern on the surface of the cavity and crown when a drop of an aqueous solution of potassium permanganate KMnO 4 is immersed in water (the parameters of the experiments are indicated in Figure 6, the tag length is 5 mm.
Figure 8. Side view of evolution of the impurity distribution pattern on the surface of the cavity and crown when a drop of an aqueous solution of potassium permanganate KMnO 4 is immersed in water (the parameters of the experiments are indicated in Figure 6, the tag length is 5 mm.
Preprints 81512 g008
Preprints 81512 g009
Figure 9. Evolution of the flow pattern at the drop of an aqueous solution of potassium permanganate diluted in a ratio of 1:10 merges with water ( D = 4.3 mm, U = 3.1 m/s, E σ = 4.2 µJ, E k = 200 µJ, Re = 13300, Fr = 230, W e = 570, Bo = 2.5, Oh = 0.0018, R E n = E n k / E n σ = 48, R W = 1.66 ⋅ 10 − 3 ), the tag length in Figure a is 5 mm, all frames are presented in the same scale): a – e) – t = 0.25, 0.5, 0.75, 1.0, 1.25, 2.5 ms.
Figure 9. Evolution of the flow pattern at the drop of an aqueous solution of potassium permanganate diluted in a ratio of 1:10 merges with water ( D = 4.3 mm, U = 3.1 m/s, E σ = 4.2 µJ, E k = 200 µJ, Re = 13300, Fr = 230, W e = 570, Bo = 2.5, Oh = 0.0018, R E n = E n k / E n σ = 48, R W = 1.66 ⋅ 10 − 3 ), the tag length in Figure a is 5 mm, all frames are presented in the same scale): a – e) – t = 0.25, 0.5, 0.75, 1.0, 1.25, 2.5 ms.
Preprints 81512 g009
Preprints 81512 g010
Figure 10. A drop of saturated aqueous solution of potassium permanganate falls into the water (mm, U = 3.8 m/ s, ρ d = 1.04   g / c m 3 , σ d a = 74   g / s 2 , μ = 0.01   g / c m ⋅ s , E n σ = 4.3 µJ, E n k = 313 µJ, E n k / E n σ = 73, W k / W σ = 25 ⋅ 10 − 4 , Re = 17000,   Fr = 350, Bo = 2.55, Oh = 0.0017, W e = 880, the tag length is 5 mm).
Figure 10. A drop of saturated aqueous solution of potassium permanganate falls into the water (mm, U = 3.8 m/ s, ρ d = 1.04   g / c m 3 , σ d a = 74   g / s 2 , μ = 0.01   g / c m ⋅ s , E n σ = 4.3 µJ, E n k = 313 µJ, E n k / E n σ = 73, W k / W σ = 25 ⋅ 10 − 4 , Re = 17000,   Fr = 350, Bo = 2.55, Oh = 0.0017, W e = 880, the tag length is 5 mm).
Preprints 81512 g010
Preprints 81512 g011aPreprints 81512 g011b
Figure 11. Photos of the copper sulphate solution drop spreading pattern in water ( ρ d = 1.2   g / c m 3 , σ d a = 75   g / s 2 , μ = 0.02   g / c m ⋅ s , D = 4.3 mm, U = 3.8 m/s,, E n σ = 4.4 µJ, E n k = 363 µJ, Re = 9900, Fr = 650, W e = 1000, Bo = 2.9, Oh = 0.0032, R E = E n k / E n σ = 83, R W = 3 ⋅ 10 − 3 , the tag length is 5 mm).
Figure 11. Photos of the copper sulphate solution drop spreading pattern in water ( ρ d = 1.2   g / c m 3 , σ d a = 75   g / s 2 , μ = 0.02   g / c m ⋅ s , D = 4.3 mm, U = 3.8 m/s,, E n σ = 4.4 µJ, E n k = 363 µJ, Re = 9900, Fr = 650, W e = 1000, Bo = 2.9, Oh = 0.0032, R E = E n k / E n σ = 83, R W = 3 ⋅ 10 − 3 , the tag length is 5 mm).
Preprints 81512 g011aPreprints 81512 g011b
Preprints 81512 g012
Figure 12. An enlarged images of the boundary of the droplet coalescence domain, parts Figure 11b, c.
Figure 12. An enlarged images of the boundary of the droplet coalescence domain, parts Figure 11b, c.
Preprints 81512 g012
Preprints 81512 g013
Figure 13. A drop of an aqueous solution of iron sulphate falls into the water ( ρ d = 1.18   g / c m 3 , σ d a = 75   g / s 2 , μ = 0.02   g / c m ⋅ s , D = 4.3 mm, U = 3.8 m/s, E n σ = 4.4 μ J , E n k = 355 μ J , R E = E n k / E n σ = 81, W k / W σ = 2.7 ⋅ 10 − 3 , Re = 9650,   Fr = 350, Bo = 2.85, Oh = 0.0032, W e = 980, the tag length is 5 mm).
Figure 13. A drop of an aqueous solution of iron sulphate falls into the water ( ρ d = 1.18   g / c m 3 , σ d a = 75   g / s 2 , μ = 0.02   g / c m ⋅ s , D = 4.3 mm, U = 3.8 m/s, E n σ = 4.4 μ J , E n k = 355 μ J , R E = E n k / E n σ = 81, W k / W σ = 2.7 ⋅ 10 − 3 , Re = 9650,   Fr = 350, Bo = 2.85, Oh = 0.0032, W e = 980, the tag length is 5 mm).
Preprints 81512 g013
Preprints 81512 g014
Figure 14. Enlarged images of the contact domain boundary of a merging saturated iron sulphate solution drop with water (parts of Figure 13).
Figure 14. Enlarged images of the contact domain boundary of a merging saturated iron sulphate solution drop with water (parts of Figure 13).
Preprints 81512 g014
Preprints 81512 g015
Figure 15. Photos of the drop water coalescence with water in the impact mode ( ρ d = 1   g / c m 3 , σ d a = 73     g / c 2 , ν d = 0.01     cm 2 / s , D = 4.3 mm, U = 3.8 m/s, E n σ = 4.2 µJ, E n k = 240 µJ, Re = 14600, Fr = 270, W e = 690, Bo = 2.5, Oh = 0.0018, R E = E n k / E n σ = 57, R W = 2 ⋅ 10 − 3 , the tag length is 5 mm).
Figure 15. Photos of the drop water coalescence with water in the impact mode ( ρ d = 1   g / c m 3 , σ d a = 73     g / c 2 , ν d = 0.01     cm 2 / s , D = 4.3 mm, U = 3.8 m/s, E n σ = 4.2 µJ, E n k = 240 µJ, Re = 14600, Fr = 270, W e = 690, Bo = 2.5, Oh = 0.0018, R E = E n k / E n σ = 57, R W = 2 ⋅ 10 − 3 , the tag length is 5 mm).
Preprints 81512 g015
Table 1. Physical parameters of saturated solutions.
Table 1. Physical parameters of saturated solutions.
Solutions ρ ,   g / c m 3 σ ,     g / s 2 γ = σ / ρ ,     cm 3 / s 2 μ ,     g / s ⋅ cm κ S × 1 0 5     c m 2 / s
copper sulphate 1.206 75 62.2 0.02 0.53
iron sulphate 1.18 75 63.56 0.02 0.38
potassium permanganate 1.04 74 71.15 0.01 4.0
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated