1. Introduction
In today’s technological landscape, inter-vehicular communications play a pivotal role in various domains, including road safety, traffic management, and passenger comfort. These communications are enabled through Vehicular Ad-Hoc Networks (VANETs) [
1], where vehicles are equipped with on-board unit devices (OBUs) and employ two primary communication paradigms: Vehicle-to-Vehicle (V2V) and Vehicle-to-Infrastructure (V2I) communication. The V2I paradigm relies on roadside units (RSUs) positioned along roadsides to facilitate the transmission of data packets. However, the dynamic nature of VANETs, characterized by frequent changes in network topology due to high speeds and vehicle mobility, presents significant challenges for data transmission. These challenges stem from intermittent connection disruptions, interference from nearby vehicles in congested areas, signal attenuation caused by obstacles, and other factors. For instance, intermittent communication during the transmission of data packets from an emergency vehicle can result in delays, potentially compromising the patient’s timely arrival at the hospital and endangering their life.
This scientific paper addresses the challenge of determining the most reliable path for data packet transmission from emergency vehicles by utilizing artificial neural networks. Specifically, we propose a model that leverages these networks to estimate the Bit Error Rate (BER) based on the characteristics of the surrounding buildings. By considering the perceived building information (, , , ) as input, our model provides an output that represents the estimated BER.
The structure of this paper is organized as follows:
Section 2 provides a comprehensive literature review, focusing on relevant research in the field.
Section 3 introduces artificial neural networks, highlighting their significance and application in our study. In
Section 4, we detail the step-by-step process employed to develop the BER estimation model. Subsequently,
Section 5 presents the obtained results, accompanied by a meticulous analysis. Finally,
Section 6 concludes the paper, summarizing the key findings and discussing potential avenues for future research.
2. Related Work
Vehicular Ad Hoc Networks (VANETs) are specifically designed to ensure reliable data transmission for both safety and non-safety applications. The performance of VANETs during simulation is influenced by various factors, including the chosen simulation parameters and the accuracy of environmental conditions modeling. Several research studies in the literature have investigated the impact of simulation parameters on VANET scenarios. However, this paper focuses on exploring the effects of obstacles, particularly buildings, on the quality of data transmission in VANETs.
In the following sections, we present a comprehensive overview of relevant studies that contribute to our understanding of this particular aspect. These studies shed light on the challenges and potential solutions related to obstacles in VANETs, which can significantly affect the performance and reliability of data transmission. By reviewing these contributions, we aim to provide valuable insights and identify research gaps that need to be addressed in our study.
It is important to note that our investigation primarily focuses on the impact of buildings as obstacles, given their prevalence and potential interference in urban VANET scenarios. Nevertheless, we acknowledge that other types of obstacles, such as trees or geographical features, may also affect data transmission quality. However, due to the scope of this paper, we specifically concentrate on buildings as they are a prominent obstacle category.
By analyzing and synthesizing the existing body of work, we aim to contribute to the current knowledge by presenting novel approaches and techniques to mitigate the adverse effects of obstacles in VANETs. We believe that our study will not only enhance the understanding of VANET performance in the presence of obstacles but also pave the way for more efficient and reliable data transmission in future vehicular communication systems.
In their study, [
1] focuses on evaluating reception power in different scenarios by considering buildings as a significant parameter. Their approach involves utilizing the geometry of the environment as an input for the communication channel model. To account for the impact of buildings, they employ a 2D polygonal baseline that describes the boundaries of these structures. The baseline boundaries are stored in a recursive Binary Space Tree (BSP) to facilitate efficient data retrieval. This storage mechanism enables access to information about all buildings in the environment. Subsequently, the BSP algorithm utilizes the line of sight rectangle between the transmitter and receiver to identify buildings that have the potential to obstruct the signal propagation. By employing this method, they effectively analyze the influence of buildings on the reception of signals.
In [
2], the authors proposed a novel approach to model 3D vehicles as obstacles in the context of Line of Sight (LOS) analysis. They specifically investigated the impact of these obstacles on LOS by employing the knife-edge diffraction pattern. This work shed light on the influence of vehicles on wireless communication systems.
Building upon the research on obstacles in wireless communication, [
3] delved into studying the effects of additional attenuation caused by large trucks obstructing the LOS between the transmitter and the receiver. The authors analyzed the specific challenges posed by these obstructing vehicles, providing valuable insights into the impact of such obstacles on wireless signal propagation.
Furthermore, works presented in [
4] focused on modeling the influence of buildings on the communication channel in Vehicular Ad hoc Networks (VANETs). The authors conducted a comparative analysis of three different approaches to accurately represent the impact of buildings on the VANET communication channel model.
Several studies have focused on addressing the computational cost associated with the IEEE 802.11p [
5] shadowing radio model in urban areas. For instance, [
6] proposed an empirical simulation model that effectively minimizes computational overhead. The authors validated their model using real-world measurements obtained from IEEE 802.11p/DSRC devices, which enabled them to evaluate the impact of buildings and other obstacles on radio communications between vehicles. Their approach considers the geometric properties of the buildings and the positions of the transmitter and receiver. To define the boundaries of the buildings, the authors relied on widely available geographic databases, such as OpenStreetMap [
7].
While existing research has made notable contributions to analyzing the impact of obstacles on radio communications, to the best of our knowledge, no study has yet explored the use of artificial neural networks for this purpose. In contrast, our proposed model utilizes artificial neural networks to evaluate the impact of buildings on communication by estimating the bit error rate (BER) based on the building’s geometric characteristics. By employing neural networks, we aim to provide a more accurate and efficient approach to assess the influence of obstacles on wireless communication systems.
3. Artificial Neural Networks
Artificial Neural Networks (ANNs) are powerful models for statistical learning, drawing inspiration from the intricate workings of biological neural networks. ANNs have gained significant popularity in the field of machine learning [
8]. These networks are composed of interconnected "neurons" that communicate with each other via synapses, mimicking the neural connections found in living organisms. The strength of these connections can be adaptively modified based on input and output signals, rendering ANNs highly suitable for supervised learning tasks.
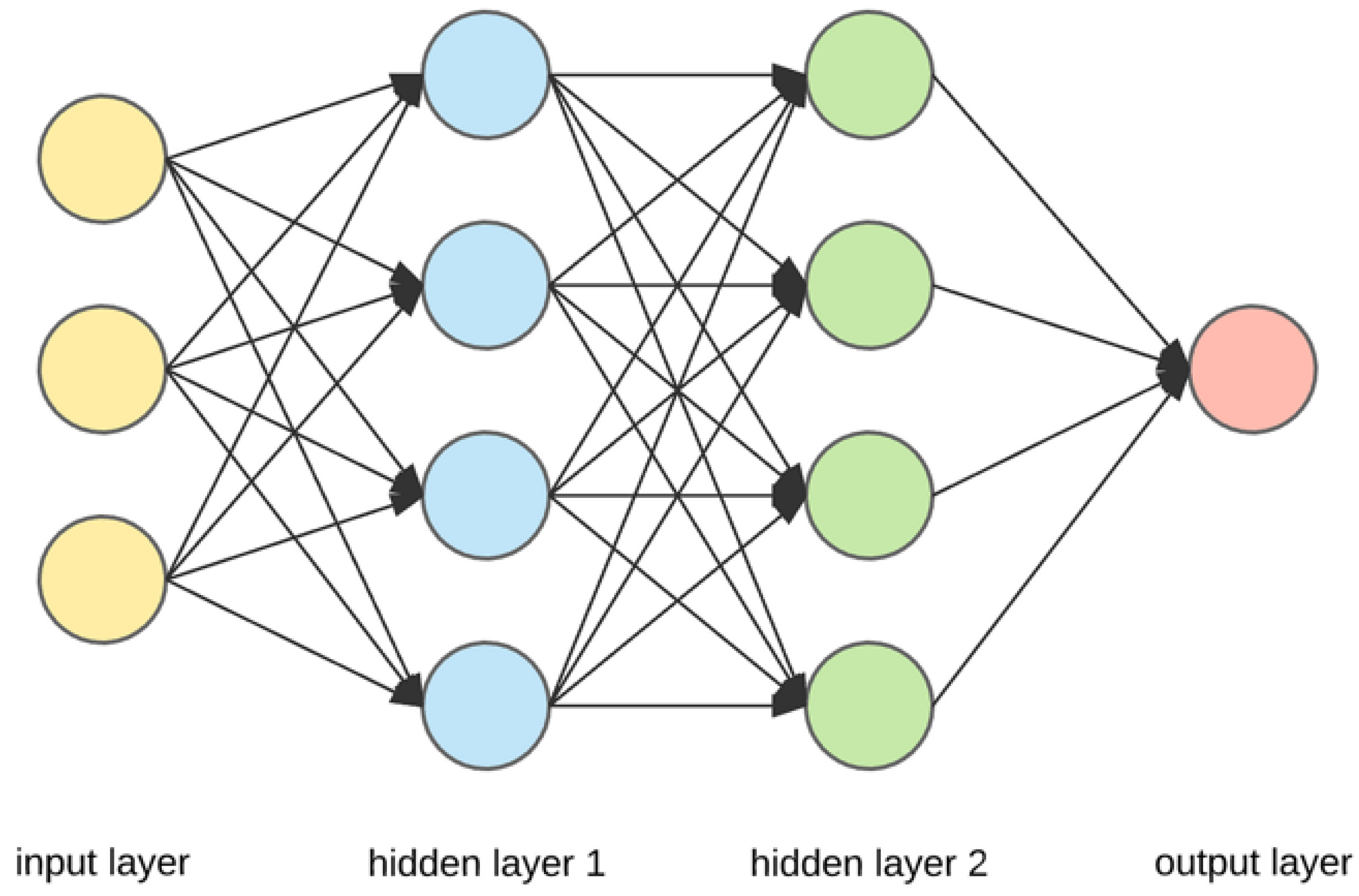
A typical neural network comprises three essential components: the input layer, the hidden layer(s), and the output layer. This structure can be envisioned as a black box, as illustrated in
Figure 1 below, encapsulating the intricate computations performed by the network. The input layer receives the initial data, which is then processed through the interconnected hidden layer(s), ultimately producing an output through the output layer.
4. Supervised Learning for Estimating the Bit Error Rate (BER)
In this subsection, we present our approach for applying supervised learning to address our research problem. Our approach encompasses seven key steps, outlined as follows:
4.1. Data Collection
The data collection phase serves the purpose of establishing a comprehensive knowledge base for machine learning. In our study, data is collected through simulations, enabling us to obtain essential information. This includes the geometric structure of the building (, , , ), the signal-to-noise ratio, the number of transmitted and received bits, the percentage of received bits, and the bit error rate (BER). These collected data points serve as the foundation for our subsequent machine learning analyses.
4.1.1. Experimental Environment for Data Collection
The experimental environment used for data collection consists of two simulators: a network simulator and a traffic simulator. To enable comprehensive studies based on the protocols under analysis, we have chosen NS-3 (Network Simulator 3) [
9] as our network simulator. NS-3 offers a wide range of network components that facilitate diverse investigations in the field of wireless network technologies [
10]. Moreover, NS-3 supports essential standards such as IEEE 802.11 PHY/MAC, 1609/WAVE, and 802.11p [
11], allowing for realistic studies on Vehicular Ad Hoc Networks (VANETs). Furthermore, NS-3 provides support for Dedicated Short Range Communication (DSRC) [
12], a technology widely employed in North America for real-world vehicle communications testing.
To incorporate a mobility model specific to vehicles, we have opted to utilize SUMO (Simulation of Urban MObility) [
13] as our traffic simulator. SUMO is a frequently employed tool in studies related to traffic analysis in road networks. Additionally, SUMO offers the capability to interact with external applications through a socket connection. This interaction is facilitated by TraCi (Traffic Control Interface), enabling simulations in a client/server mode.
Figure 2 provides a visual representation of our experimental environment.
4.1.2. Experiment Scenarios for Data Gathering
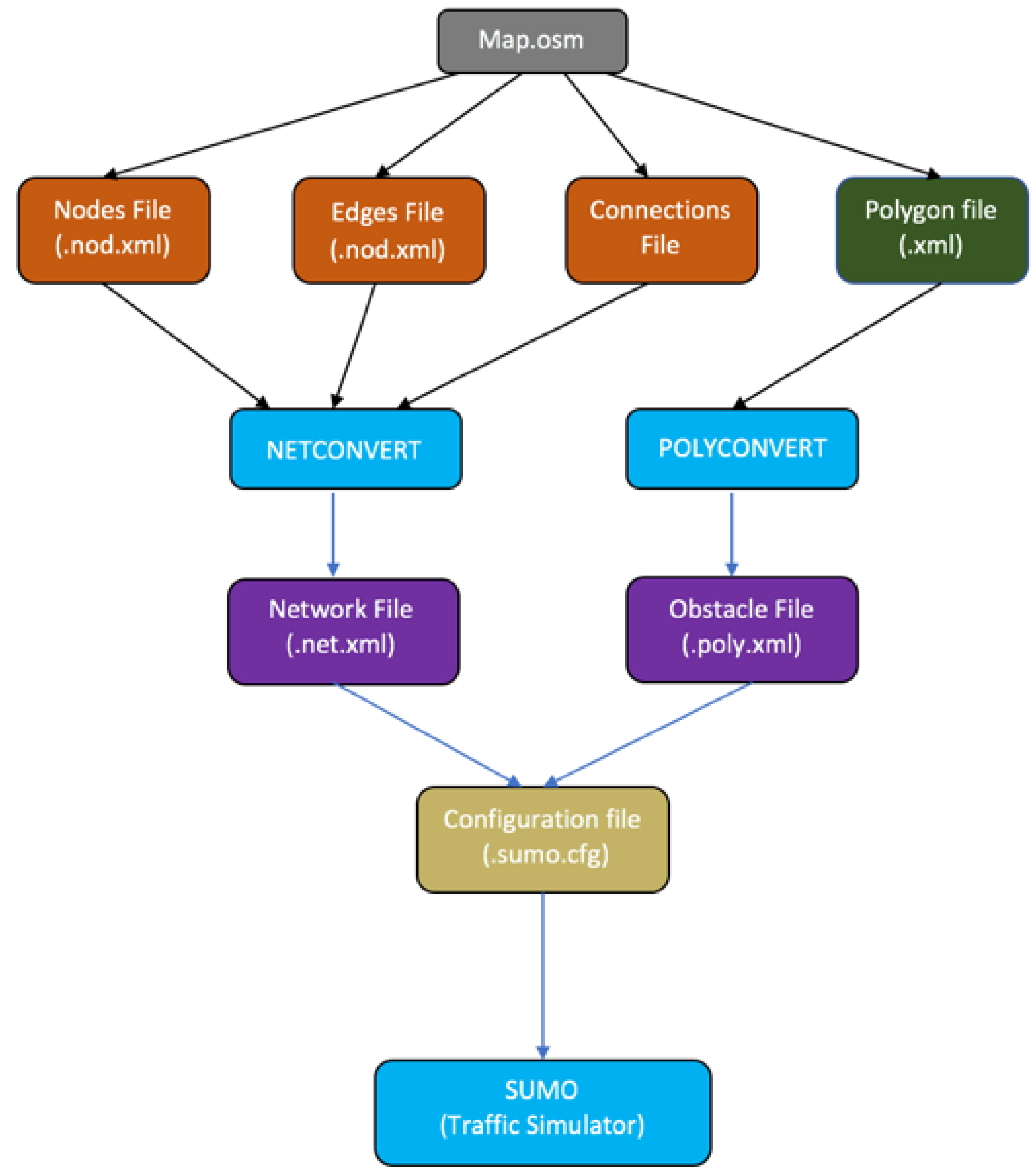
This subsection provides a concise overview of the approach employed to specify urban scenarios using the SUMO simulation framework. Within SUMO, a range of tools were utilized to define the urban components, including obstacles like buildings.
Figure 3 illustrates the process of generating urban scenarios in SUMO.
In our study, it is crucial to accurately represent the geometric structure of the network, considering urban elements such as buildings. To accomplish this, we leveraged the capabilities of the NETCONVERT and POLYCONVERT tools provided by the SUMO Traffic Simulator.
The NETCONVERT tool facilitated the conversion of files (e.g., OSM) containing information about the geometric structure of road networks from diverse sources into a format compatible with SUMO. Specifically, for our research, we imported the specifications of the geometric structure of the road network from the OpenStreetMap platform [
7].
The POLYCONVERT tool was employed to transform the geometric forms (i.e., buildings) obtained from various sources into a visualizable representation within the graphical interface of SUMO.
After defining the urban model, the subsequent task involves the development of a script in NS-3 that builds upon the aforementioned model.
4.1.3. Examples of Urban Model Specification using SUMO
In this subsection, we present two illustrative examples of urban model specification using SUMO.
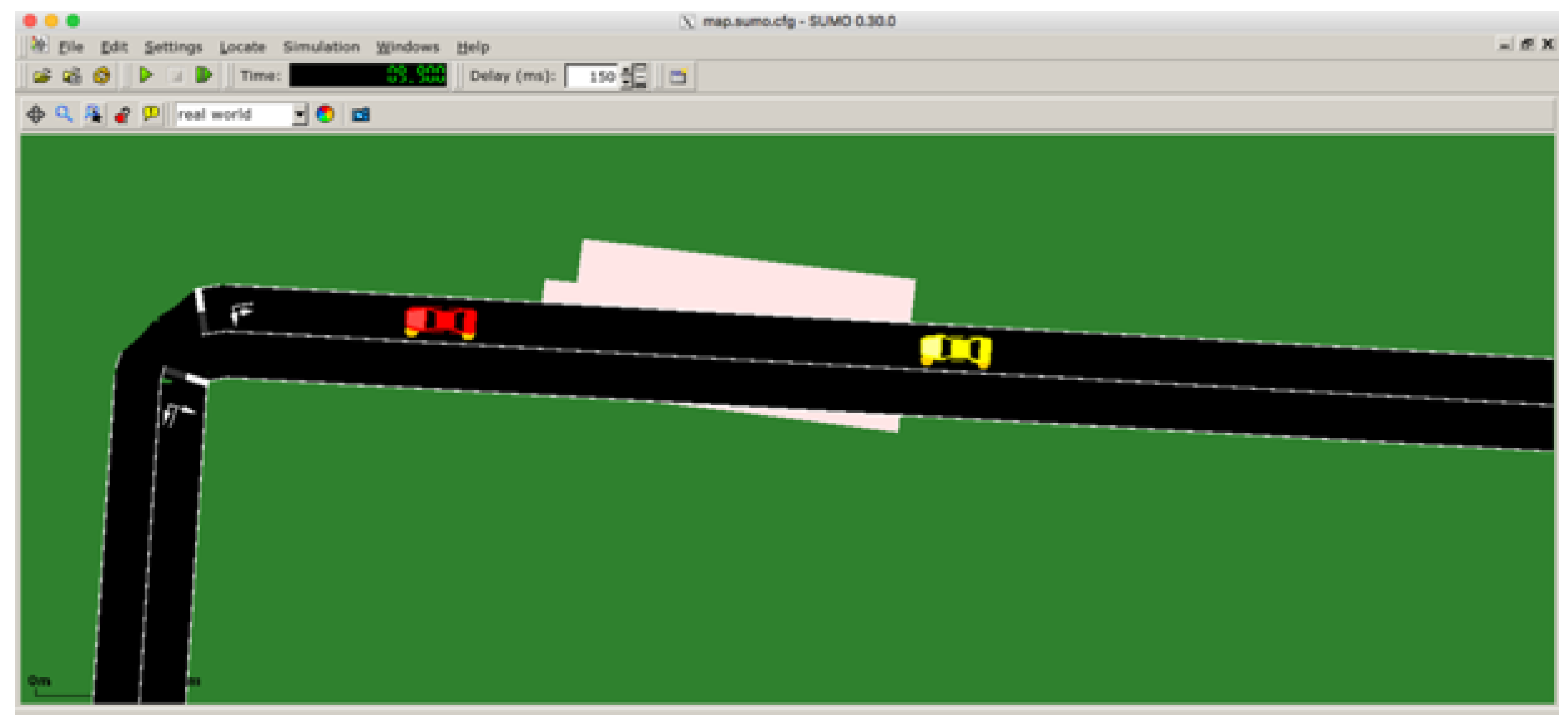
Signal Degradation between Two Vehicles due to Obstacle Presence
This specific scenario is described as follows: At time instant
, two vehicles,
and
, which act as the transmitter and receiver respectively, are located on a road segment. At
+
t, the transmission between
and
becomes disrupted due to the presence of an obstacle. This scenario effectively demonstrates the impact of obstacles such as walls or buildings on signal degradation. To effectively quantify the extent of signal degradation caused by an obstacle, our study focuses on the transmission between these two vehicles. By limiting the transmission to only two vehicles, we aim to gain a deeper understanding of the obstacle’s impact on the signal degradation phenomenon.
Figure 4 below visually depicts the aforementioned scenario using SUMO.
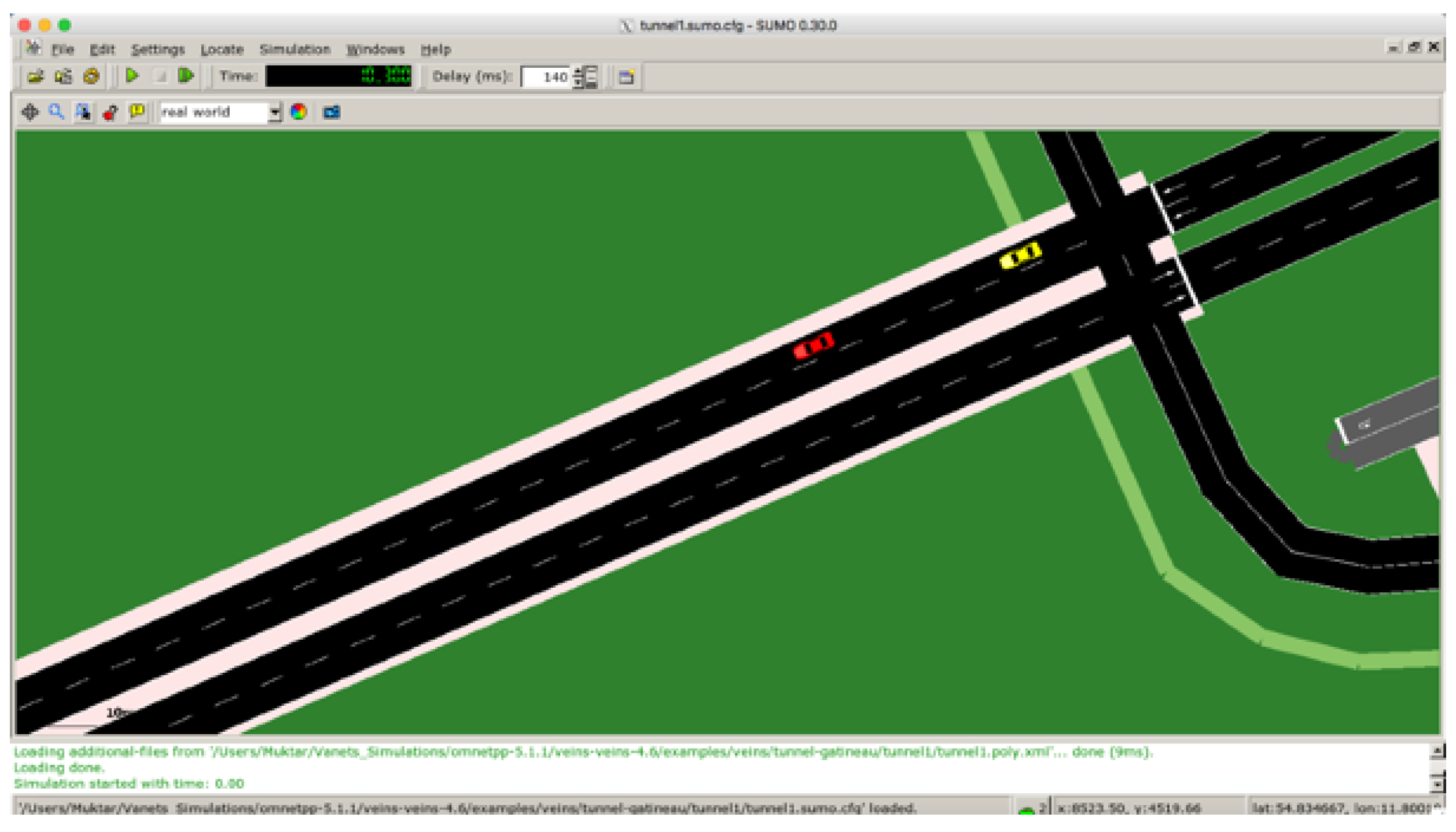
Signal Degradation Between Two Vehicles Caused by Bridge Presence
In this scenario, we consider two vehicles located within transmission range, traversing a two-lane bridge. The communication signal between these vehicles experiences attenuation due to the presence of the bridge. This scenario emphasizes the phenomenon of signal attenuation in an enclosed space, such as a bridge.
Figure 5 below depicts the described scenario, illustrating the signal attenuation caused by the presence of the bridge.
In
Figure 4 and
Figure 5, the vehicles
and
are depicted in red and yellow, respectively. The pink illustrations represent the obstacles that obstruct the transmission signal between
and
.
4.1.4. NS-3 Simulation Parameters for Data Collection
In this section, we provide a summary of the simulation parameters used in NS-3 to establish the foundational knowledge for our learning system.
Table 1 presents the experiment parameters utilized in the NS-3 simulations.
Furthermore,
Table 2 demonstrates a sample of the simulation results, highlighting the obtained data.
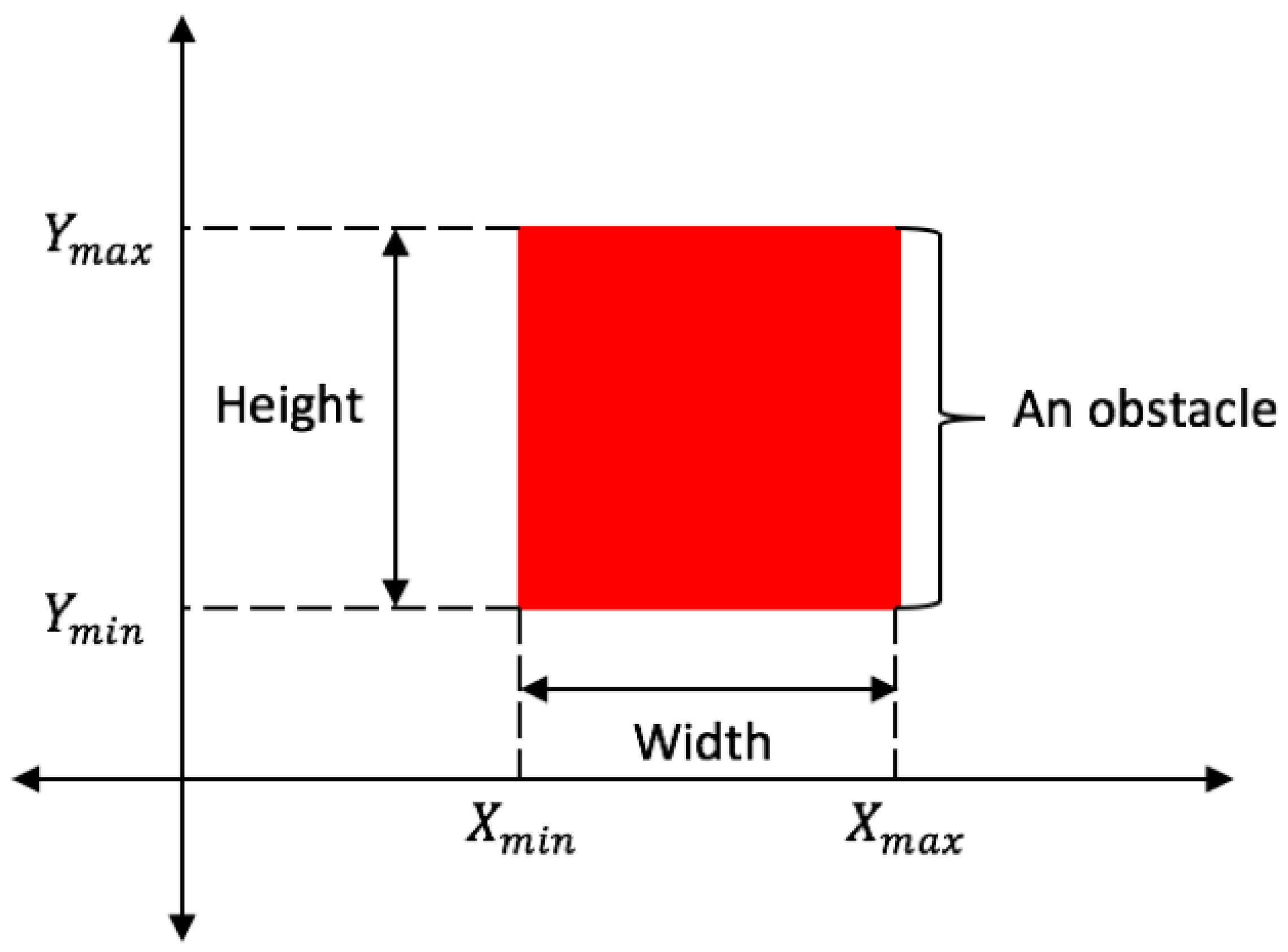
Figure 6 below illustrates the representation of an obstacle in our urban scenarios.
Where: = , = , = and =
Table 2 above demonstrates how each geometric structure of a building impacts the transmission quality. This information can be interpreted through qualitative variables such as SNR and BER.
4.2. Data Preprocessing
In this phase, we undertake data preprocessing to enhance the usability of the input and output parameters for the learning algorithm. Our preprocessing approach involves a transformation aimed at eliminating redundant information, specifically the inclusion of the number of received bits and the corresponding percentage of bits received. These details, being dependent on the estimated variable (Bit Error Rate or BER), are deemed non-essential for the learning system. By eliminating this extraneous information, we streamline the dataset for more effective analysis and model training.
4.3. Choice of Learning Function
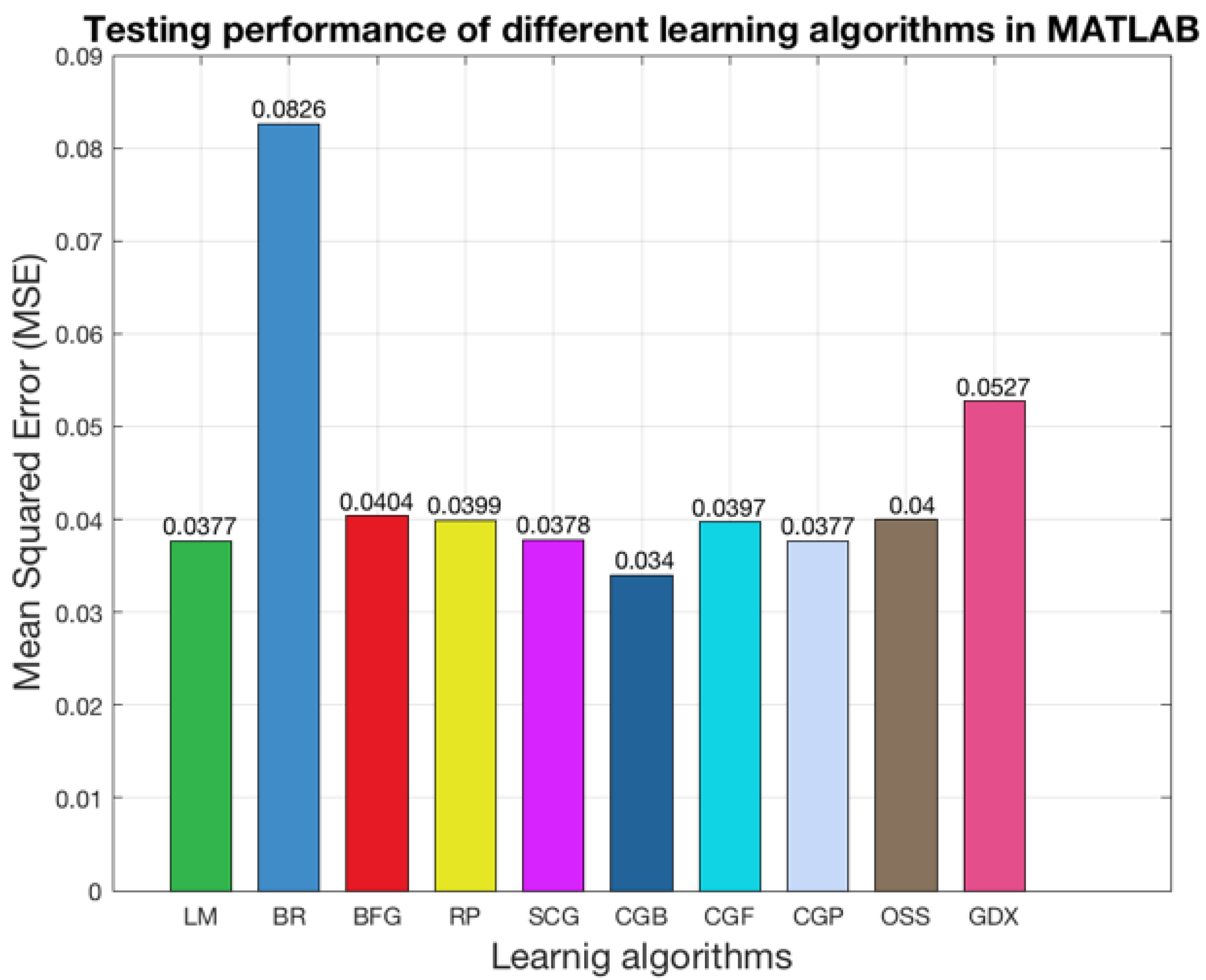
In this section, we discuss the selection of an appropriate learning function for our model. To determine the optimal choice, we employ the mean squared error (MSE) as our primary criterion.
Table 3 presents a comprehensive evaluation of various learning functions tested using MATLAB.
Based on our evaluation, we have selected the Conjugate Gradient with Powell/Beale Restarts learning function for our model due to its superior performance, indicated by the lowest MSE value. To visualize the performance of the different learning functions based on the MSE metric, refer to
Figure 7 below.
4.4. Data Splitting for Training, Testing, and Validation
To ensure proper evaluation and validation of our model, the gathered data is split into distinct subsets. This step allows us to allocate data for learning, testing, and validation purposes, ensuring robust performance assessment. The following example illustrates the distribution of the data:
70% of the data is allocated for the learning phase.
15% of the data is reserved for validation purposes.
Another 15% is dedicated to testing the model’s performance.
4.5. Model Evaluation
The evaluation step plays a crucial role in assessing the model’s capabilities using data that has not been previously utilized for learning. By subjecting the model to this independent dataset, we gain valuable insights into its real-world potential and how it would perform in practical scenarios.
4.6. Tuning Model Parameters
After the model evaluation, we engage in fine-tuning the learning process to enhance its performance. This step involves adjusting specific parameters within the model, such as the number of neurons, learning functions, synaptic weights, among others. By iteratively refining these parameters, we can optimize the model’s learning process and achieve improved overall performance.
4.7. Estimation of Bit Error Rate (BER)
In this step, we leverage the trained model to estimate the Bit Error Rate (BER) based on new data. Specifically, we feed 300 new samples into the model, and it generates an output corresponding to the estimated BER value.
5. Results and Analysis
In this subsection, we present the outcomes and provide an in-depth analysis resulting from the evaluation of our developed model.
5.1. Results
The results are presented in tabular form, showcasing the maximum, minimum, and average accuracy of the estimated BER values obtained from our model. These tables serve as a quantitative representation of the model’s performance in predicting the BER.
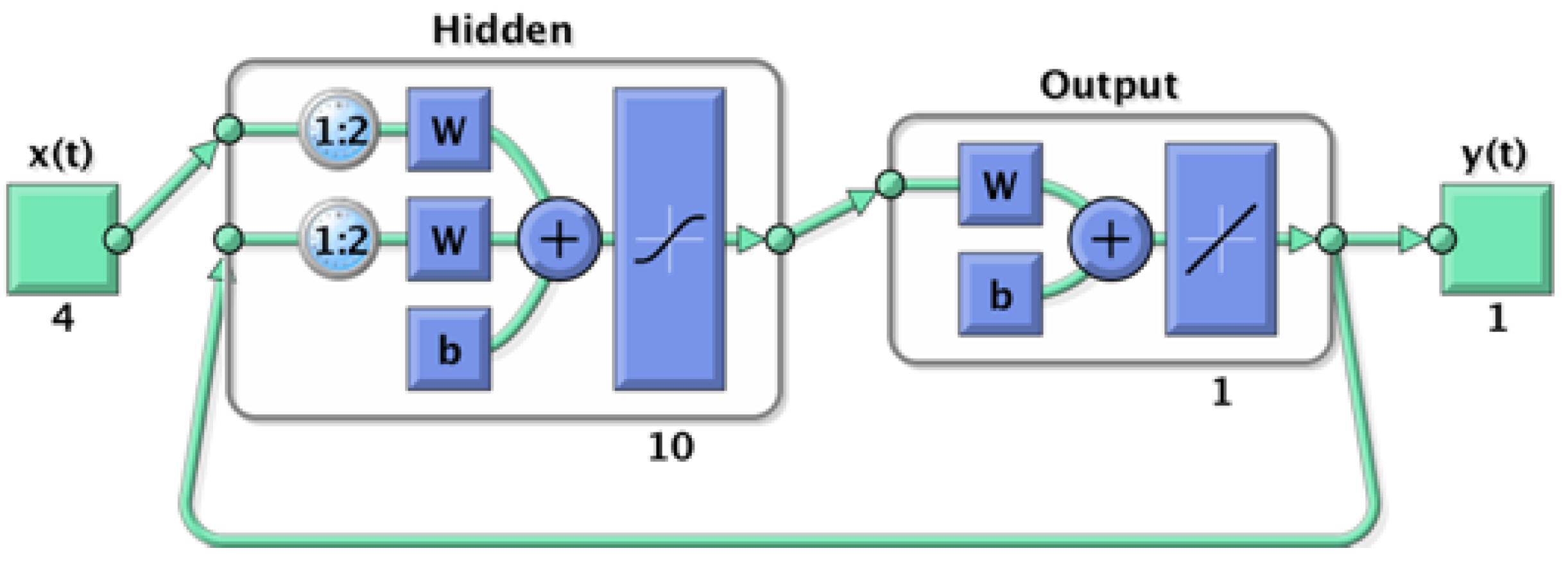
5.1.1. Parameter Selection for the Developed Neural Network Model
To configure the developed neural network, we carefully determined the parameters for optimal performance. The architecture of the model consists of ten hidden layers, as depicted in
Figure 8 (see below). We divided the dataset into three subsets, allocating 70% for the learning phase, 15% for validation, and the remaining 15% for testing purposes. The following results are obtained using this specific configuration.
5.1.2. Adjusting the Number of Hidden Neurons
In order to investigate the impact of the number of hidden neurons on the performance of the network, we conducted experiments using different configurations. For consistency, the distribution of the entire learning dataset in the following results was maintained according to the default values (70% for learning, 15% for validation, and 15% for testing), while the number of hidden neurons was varied.
5.2. Analysis
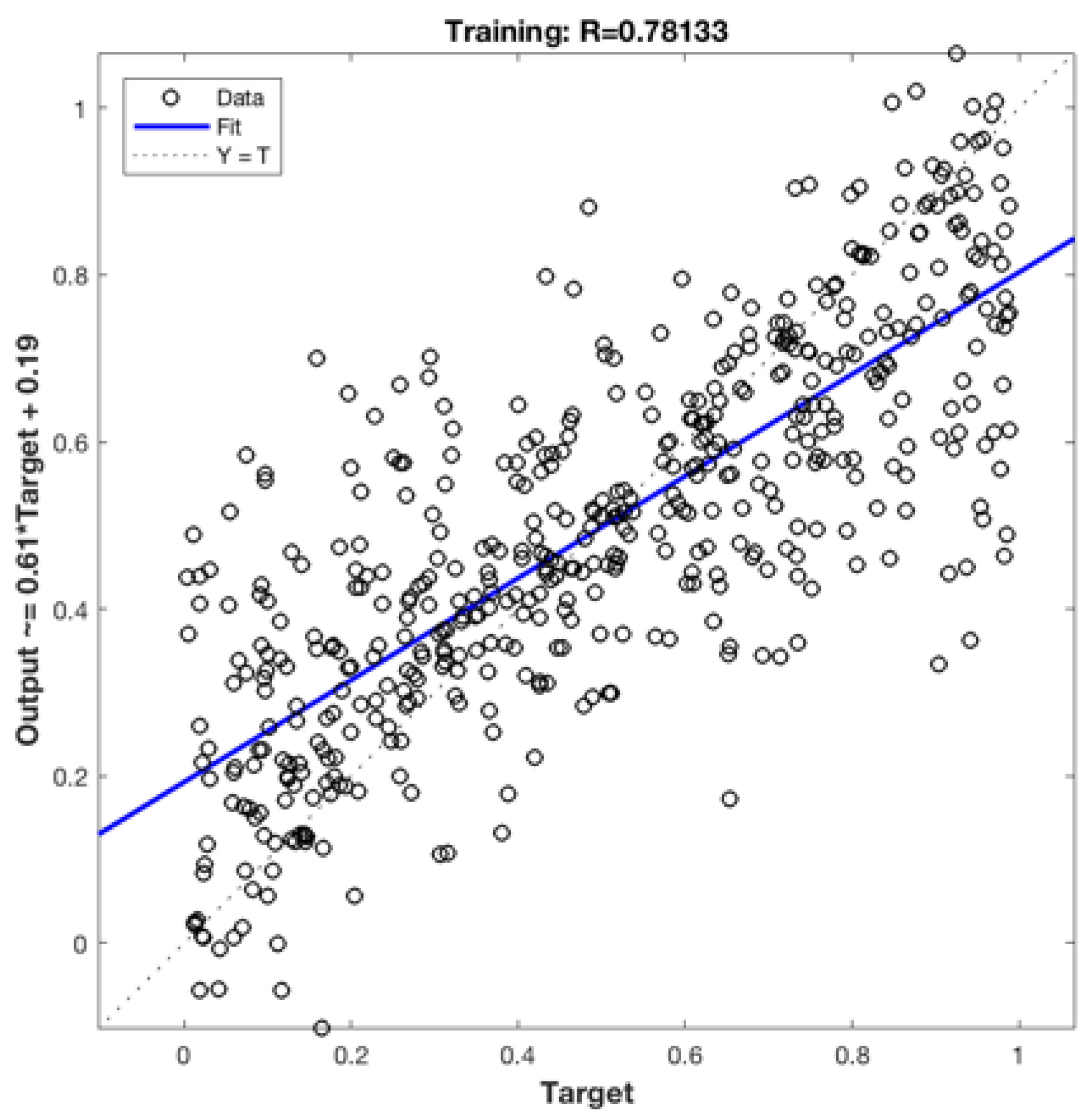
The results presented in
Figure 9 and
Figure 11 illustrate the regression plots for learning with 10 and 15 neurons, respectively. The correlation coefficient (R) is a measure of the relationship between the network outputs and the targets. A correlation coefficient close to 1 indicates good learning, while a value close to 0 suggests weak learning.
Figure 9.
Network Regression Plot Illustrating Learning Performance with 10 Neurons.
Figure 9.
Network Regression Plot Illustrating Learning Performance with 10 Neurons.
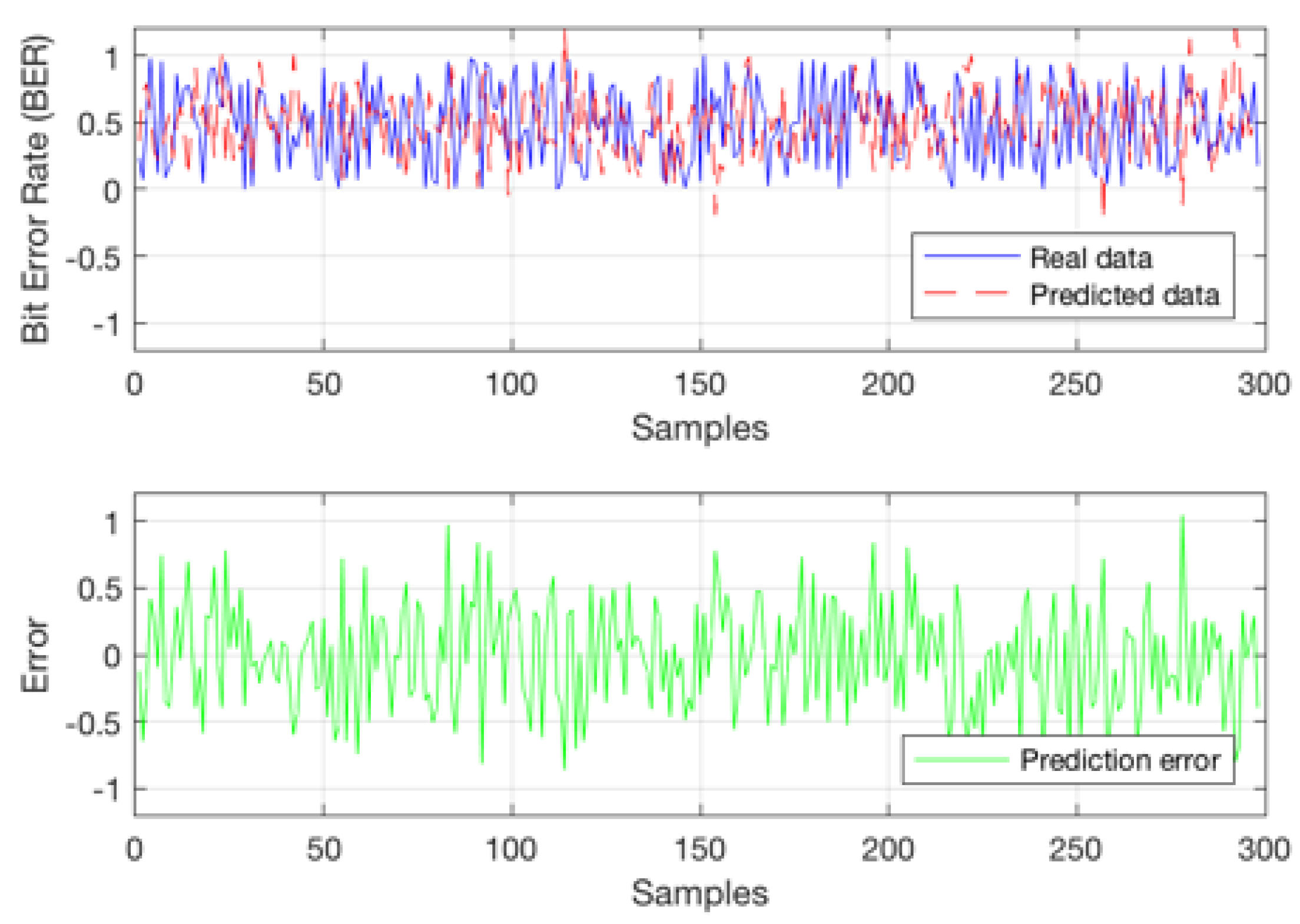
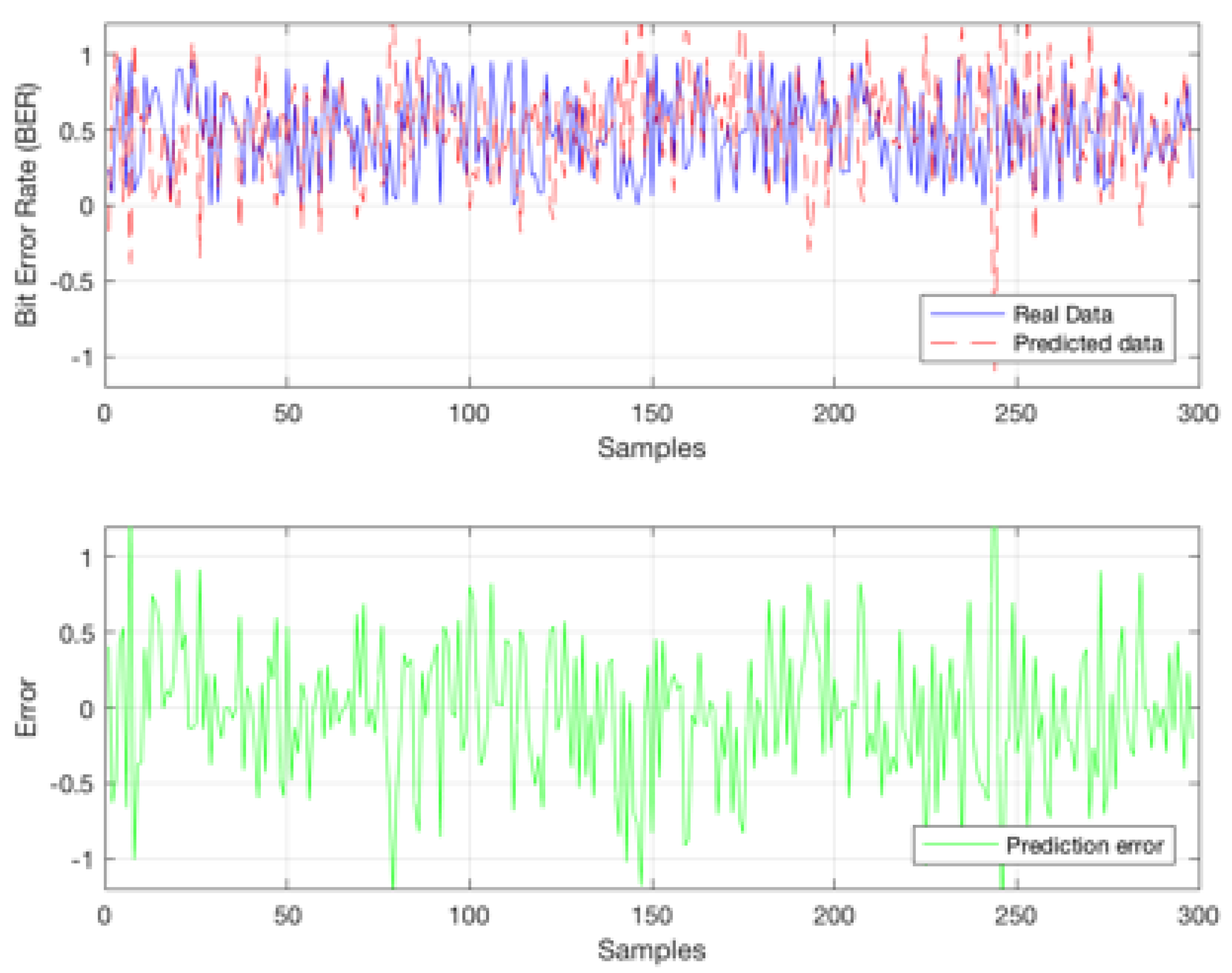
Figure 10.
Bit Error Rate (BER) Estimation Based on 300 Samples Utilizing a Network Architecture with 10 Neurons.
Figure 10.
Bit Error Rate (BER) Estimation Based on 300 Samples Utilizing a Network Architecture with 10 Neurons.
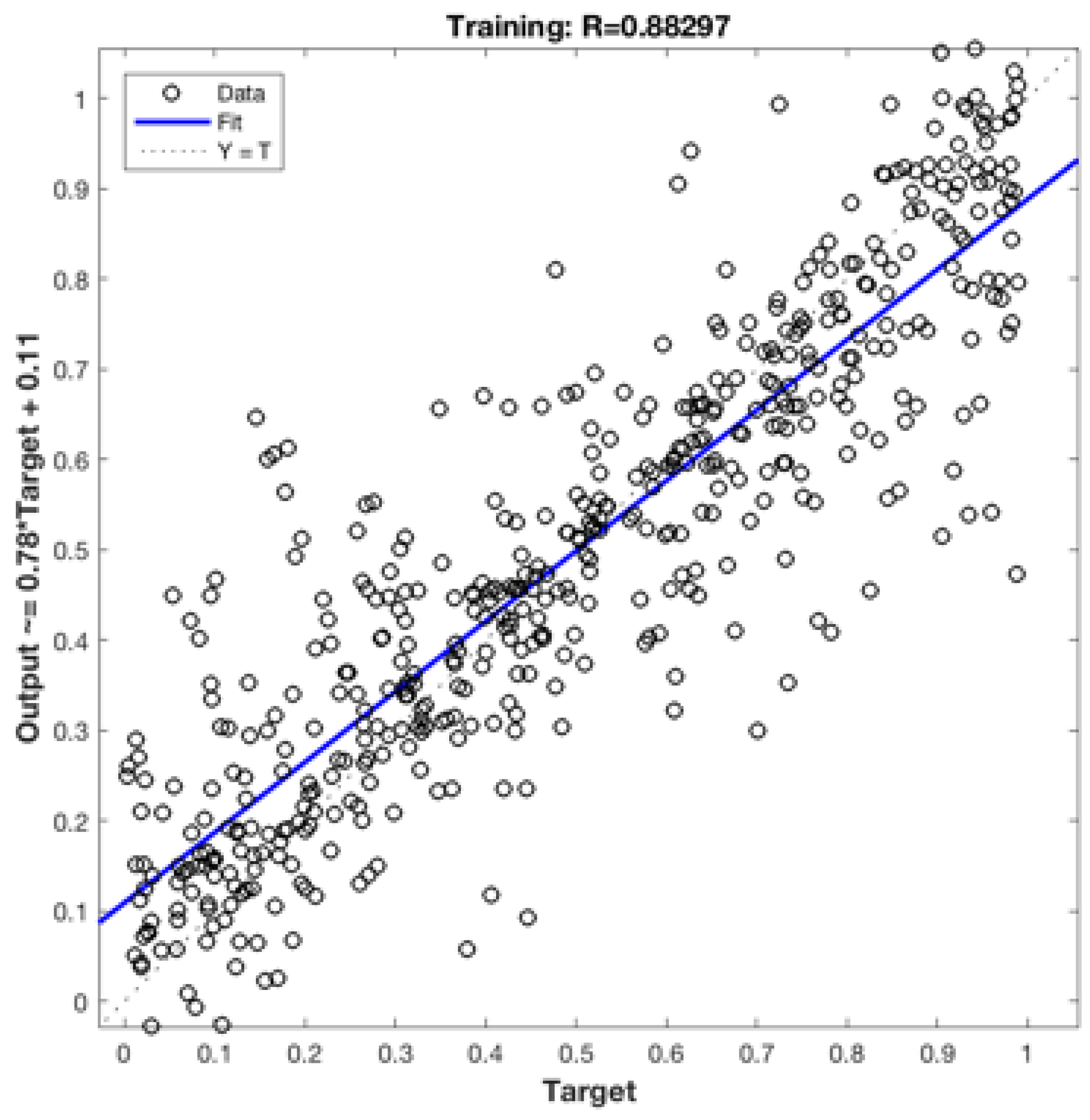
Figure 11.
Network Regression Plot Illustrating Learning Performance with 15 Neurons.
Figure 11.
Network Regression Plot Illustrating Learning Performance with 15 Neurons.
Regression plots provide a visual representation of the network outputs compared to the targets in a set of learning, validation, or test data. A perfect fit occurs when the data points align along the 45-degree line, indicating that the network outputs perfectly match the targets. In our study, the learning process achieved a correlation coefficient of R = 0.78 when utilizing 10 neurons and R = 0.88 when employing 15 neurons. These values indicate a strong performance in terms of learning.
Figure 10 and
Figure 12 demonstrate the impact of varying the number of hidden neurons on the estimated Bit Error Rate (BER) value. When employing 15 neurons, the correlation coefficient indicates a good learning performance (R = 0.88) compared to the network trained with 10 neurons (R = 0.78). However, the model’s generalization capacity, which refers to its ability to perform well on unseen data, diminishes when using 15 neurons as depicted in
Figure 12. In contrast, the model trained with 10 neurons (
Figure 10) exhibits greater precision, with errors ranging between -1 and 1. Conversely, the model trained with 15 neurons loses precision, leading to higher error values. This phenomenon is attributed to overfitting, wherein an increase in hidden neurons improves the learning process but compromises the accuracy of the model.
Thus, depending on the specific problem being studied, it is crucial to strike a balance between learning performance and model accuracy. In our case, the results indicate that the model based on 10 hidden neurons achieves a better compromise between the two. Consequently, for optimal prediction performance, it is recommended to calibrate the network with 10 hidden neurons.
In conclusion, based on our analysis, using 10 hidden neurons yields superior prediction performance in our case.
Table 5.
Network Accuracy for 15 Learning Sessions with Varying Numbers of Hidden Neurons.
Table 5.
Network Accuracy for 15 Learning Sessions with Varying Numbers of Hidden Neurons.
| Session |
Mean Squared Error (MSE) |
| |
Minimum |
Maximum |
Mean |
| 1 |
|
|
|
| 2 |
|
|
|
| 3 |
|
|
|
| 4 |
|
|
|
| 5 |
|
|
|
| 6 |
|
|
|
| 7 |
|
|
|
| 8 |
|
|
|
| 9 |
|
|
|
| 10 |
|
|
|
| 11 |
|
|
|
| 12 |
|
|
|
| 13 |
|
|
|
| 14 |
|
|
|
| 15 |
|
|
|
| Mean |
|
|
|
6. Conclusion
In this paper, we presented an empirical study based on neural networks, which allows to estimate BER according to the obstacles (buildings) perceived by a mobile vehicle in a VANET network. This study is motivated by QoS need for emergency communications in VANETs. By estimating BER based on information related the geometric structure of obstacles, vehicles will be able to optimize their data routing decisions.
For our future work, we plan to integrate the mechanism which allows to estimate BER with the CL-ANTHOCNET routing protocol that we have developed [
14], then we will evaluate its performance in a context of the critical situation involving the transmission of emergency vehicles.
Author Contributions
The structuring, methodology, writing, and implementation of the simulation using tools such as SUMO, NS-3, and Matlab were carried out by B.M. and V.F. The improvement of the writing and the analysis of the results were performed by M.Z. The published version of the manuscript was read and revised by all authors.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ANN |
Artificial Neural Network |
| BER |
Bit Error Rate |
| BSP |
Binary Space Tree |
| CBR |
Constant Bit Rate |
| CL-AntHocNet |
Cross-Layer AntHocNet |
| DSRC |
Dedicated Short Range Communications |
| LOS |
Line of Sight |
| MAC |
Media Access Control |
| MSE |
Mean Squared Error |
| NS-3 |
Network Simulator 3 |
| OBU |
On-Board Unit |
| OSM |
OpenStreetMap |
| PHY |
Physical Layer |
| QoS |
Quality of Service |
| SNR |
Signal-to-Noise Ratio |
| SUMO |
Simulation of Urban Mobility |
| TraCI |
Traffic Control Interface |
| UDP |
User Datagram Protocol |
| V2I |
Vehicle-to-Infrastructure |
| V2V |
Vehicle-to-Vehicle |
| VANET |
Vehicular Ad-Hoc Network |
| WAVE |
Wireless Access In Vehicular Environment |
References
- Nagel, R.; Eichler, S. Efficient and realistic mobility and channel modeling for VANET scenarios using OMNeT++ and INET-framework. In Proceedings of the Proceedings of the 1st international conference on Simulation tools and techniques for communications, networks and systems & workshops, 2008, pp. 1–8.
- Boban, M.; Vinhoza, T.T.; Ferreira, M.; Barros, J.; Tonguz, O.K. Impact of vehicles as obstacles in vehicular ad hoc networks. IEEE journal on selected areas in communications 2010, 29, 15–28. [CrossRef]
- Vlastaras, D.; Abbas, T.; Nilsson, M.; Whiton, R.; Olbäck, M.; Tufvesson, F. Impact of a truck as an obstacle on vehicle-to-vehicle communications in rural and highway scenarios. In Proceedings of the 2014 IEEE 6th International Symposium on Wireless Vehicular Communications (WiVeC 2014). IEEE, 2014, pp. 1–6.
- Urquiza-Aguiar, L.; Tripp-Barba, C.; Estrada-Jiménez, J.; Igartua, M.A. On the impact of building attenuation models in vanet simulations of urban scenarios. Electronics 2015, 4, 37–58. [CrossRef]
- Jiang, D.; Delgrossi, L. IEEE 802.11 p: Towards an international standard for wireless access in vehicular environments. In Proceedings of the VTC Spring 2008-IEEE vehicular technology conference. IEEE, 2008, pp. 2036–2040.
- Sommer, C.; Eckhoff, D.; German, R.; Dressler, F. A computationally inexpensive empirical model of IEEE 802.11 p radio shadowing in urban environments. In Proceedings of the 2011 Eighth international conference on wireless on-demand network systems and services. IEEE, 2011, pp. 84–90.
- Haklay, M.; Weber, P. Openstreetmap: User-generated street maps. IEEE Pervasive computing 2008, 7, 12–18. [CrossRef]
- Yegnanarayana, B. Artificial neural networks; PHI Learning Pvt. Ltd., 2009.
- Henderson, T.R.; Lacage, M.; Riley, G.F.; Dowell, C.; Kopena, J. Network simulations with the ns-3 simulator. SIGCOMM demonstration 2008, 14, 527.
- Arbabi, H.; Weigle, M.C. Highway mobility and vehicular ad-hoc networks in ns-3. In Proceedings of the Proceedings of the 2010 Winter Simulation Conference. IEEE, 2010, pp. 2991–3003.
- Bu, J.; Tan, G.; Ding, N.; Liu, M.; Son, C. Implementation and evaluation of wave 1609.4/802.11 p in ns-3. In Proceedings of the Proceedings of the 2014 Workshop on ns-3, 2014, pp. 1–8.
- Kenney, J.B. Dedicated short-range communications (DSRC) standards in the United States. Proceedings of the IEEE 2011, 99, 1162–1182. [CrossRef]
- Behrisch, M.; Bieker, L.; Erdmann, J.; Krajzewicz, D. SUMO–simulation of urban mobility: an overview. In Proceedings of the Proceedings of SIMUL 2011, The Third International Conference on Advances in System Simulation. ThinkMind, 2011.
- Benyahia, I.; Bappa, M.; Perrot, J. A Variant of the AnthocNet Routing Protocol: Empirical Study with Application to Communications between Emergency Vehicles. In Proceedings of the ITS World congress, 2017.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).