Prerpints.org logo
Preprint
Article

Perturbation-Based Non-Perturbative Method

Altmetrics

Downloads

167

Views

46

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

04 August 2023

Posted:

07 August 2023

You are already at the latest version

Alerts
Abstract
This paper presents a non-perturbative method for solving eigenproblems. This method applies to almost all potentials and provides non-perturbative approximations for any energy level. The method converts an eigenproblem into a perturbation problem, obtains perturbation solutions through standard perturbation theory, and then analytically continues the perturbative solution into a non-perturbative solution.
Keywords: 
Subject: Physical Sciences  -   Mathematical Physics

1. Introduction

Exact solutions are rare and require approximation methods. In quantum mechanics, approximation methods can be roughly divided into perturbation methods, such as the stationary perturbation theory, and non-perturbation methods, such as the variational method. The advantage of the perturbation method lies in its standardized procedures, but its limitation is that it is only effective for perturbation problems. Non-perturbation methods lack the universally standardized procedures like that in perturbation theory; for instance, in variational methods, the choice of trial wave functions relies entirely on guesswork without a systematic construction approach. In this paper, we establish a non-perturbation approximation method to solve the eigenvalue of the Hamiltonian
H = − ℏ 2 2 μ ∇ 2 + V .
This non-perturbation method has a standardized procedure like that in the perturbation theory, which can give an explicit non-perturbation approximate expression of the eigenvalues of the Hamiltonian.
The basic idea of the non-perturbation method proposed in this paper can be briefly divided into two steps:
(1) Converting an eigenproblem, a non-perturbation problem, into a perturbation problem and then using the standard perturbation method to calculate the eigenvalue.
(2) Analytically continuing the obtained perturbation results into a non-perturbation result.
The technical key of this method lies in step 2. In step 2, the perturbation result obtained in step 1 is analytically continued into a non-perturbation result.
Analytic continuation, theoretically, can be achieved as follows: first, calculate all orders of perturbation to obtain a perturbation series (which is always practically impossible); then, sum up the perturbation series to obtain a summation function (which is also highly impractical). This summation function is just the analytic continuation of the perturbative series solution. For instance, if the perturbation series is a power series, then the effective region of this power series is a disk with a radius equal to the convergence radius. The analytic region of the summation function obtained by summing up this power series will have an analytic region encompassing a larger area, including that disk. The region of convergence of a perturbative power series, such as the convergence disk of a power series, is the region where perturbation theory holds. The larger analytic region of the summation function obtained by analytic continuation is the non-perturbative region. Using this method, we start with a perturbative result and obtain a non-perturbative result through analytic continuation. However, generally speaking, we can neither obtain every term of an infinite perturbation series nor are we likely to be able to sum the series.
Perturbation theory usually only provides the first few terms of the perturbation series rather than the entire series. In other words, perturbation theory can only give a polynomial approximation. Therefore, what we need to do is to analytically continue an approximate polynomial, rather than a perturbation series, into a non-perturbative result, which requires an approximate analytic continuation. In this paper, we will use rational approximation to perform this approximate analytic continuation, analytically continuing the approximate polynomial obtained by perturbation theory to the non-perturbative region.
The idea of rational approximation was already present in Euler’s "Introduction to analysis of the infinite" [1]. Rational approximation is the use of rational expressions to approximate a function. In contrast, power series approximation uses a truncated power series, or a polynomial, to approximate a function.
The advantage of power series approximation lies in its operational convenience, as it has a standardized procedural procedure for calculating the coefficients of terms in a power series, such as Taylor expansions in mathematics and Feynman diagrammatic expansions and virial expansions in physics. Additionally, since the polynomial obtained by truncating the power series has no singularities, the information about singularities in the original function is lost after approximation.
The disadvantage of rational approximation is the lack of a procedural procedure for obtaining the coefficients of the approximating rational function. The advantage of rational approximation is that it is not limited to the perturbation region but applies to the non-perturbation region. Furthermore, the rational approximation can partially preserve information about singularities: the poles of the rational function are approximations of singularities in the original function [2].
The rational approximation adopted in this paper employs Padé approximation [3,4,5], where the coefficients of the rational function approximation are determined by the polynomial approximation given by perturbation theory. Of course, there are other methods for rational approximation besides the Padé approximation, such as determining the coefficients of the rational function through numerical fitting.
For the Schrödinger equation, some authors seek exact solutions. The exact solutions of 1 / r -, r 2 / 3 -, r 6 -, 1 / r 2 / 3 -, and r 6 -potential are obtained [6,7,8]. Methods for constructing exact solutions have been proposed, such as the dual transformation method [8,9]. In Ref. [10], the authors utilized the Nikiforov-Uvarov method and supersymmetric quantum mechanics to obtain analytical bound-state solutions of the radial Schrödinger equation for the combined potential obtained by adding a Hulthén potential term to the Manning-Rosen potential. Ref. [11] describes how nonlinear supersymmetric quantum mechanics provides two novel SUSY variable separation methods for various two-dimensional models; this approach can obtain partial or complete solutions for some two-dimensional models. Ref. [12] combines supersymmetric quantum mechanics with symplectic quantum mechanics to develop a new tool for solving quantum mechanical eigenproblems. Ref. [13] proposes a new quantization rule for solving bound state problems in quantum mechanics based on the parameterized Nikiforov-Uvarov method. Ref. [14] uses the factorization method to solve the 1 + 1 and 2 + 1 dimensional Dirac equation with a static external potential. The Painlevé V equation was solved using supersymmetric quantum mechanics in Ref. [15]. In Ref. [10], the authors apply the supersymmetric quantum mechanics method to the inverted oscillator potential. Inverted oscillator potential is commonly used as an unstable model in physics and can be seen as a mapping of the 2D string theory or a toy model to study early time evolution in inflationary models. Some authors seek quasi-exact solutions. In [16], the authors transform four different models, namely, the anharmonic singular potential, the generalized quantum isotonic oscillator, the soft-core Coulomb potential, and the non-polynomially modified oscillator, into the same basic ordinary differential equation. All these models are quasi-exactly solvable, and their solutions were given using the Bethe Ansatz method. In [17], the functional Bethe Ansatz method provides quasi-exact solutions for the inverse quartic, sextic, octic, and decatic power potentials. Ref. [18] reviews a series of one-dimensional quasi-exactly solvable Schrödinger equations. In Ref. [19], the author unifies modified Manning potentials with three parameters, Hyperbolic Razavy potential, and Double sinh-Gordon equation with two perturbation terms into a class of quasi-exactly solvable models. Ref. [20] presents a series of generalized isotonic oscillators based on quasi-exactly solvable methods. Ref. [21] provides a class of exactly solvable periodic potentials. Some authors seek approximate methods. In Ref. [22], a method for solving time-dependent Schrödinger equations is presented using the method of stationary states combined with a variational matrix method. Ref. [23] proposes a method for going beyond the WKB approximation in PT-symmetric quantum mechanics based on the ordinary differential equation/integrable model correspondence. Ref. [23] proposes a method beyond the WKB approximation in PT-symmetric quantum mechanics based on ordinary differential equation/integrable model correspondence.
In Section 2, we introduce the non-perturbative method. In Section 3, we calculate the non-perturbative eigenvalues. In Section 4, We consider the construction of auxiliary potentials. The summary is given in Section 5.

2. Non-Perturbative Method

The non-perturbative method proposed in this paper consists of two steps: (1) first converting a non-perturbative problem into a perturbative problem, and (2) then analytically continuing the obtained perturbative result to a non-perturbative one.

2.1. Step 1: Converting Non-Perturbation to Perturbation

The first step is to convert the eigenproblem of the Hamiltonian (1), a non-perturbation problem, to a perturbation problem.
By introducing an exactly solvable auxiliary potential U, we rewrite the Hamiltonian (1) into a perturbative form:
H λ = − ℏ 2 2 μ ∇ 2 + U + λ V − U = H 0 + λ Δ ,
where H 0 = − ℏ 2 2 μ ∇ 2 + U is exactly solvable. The eigenproblem of the auxiliary Hamiltonian H λ ,
H λ ψ n λ = E n λ ψ n λ ,
can be calculated by perturbation theory when the parameter λ is small. Note that what we are concerned about is the case of λ = 1 , i.e.,
H ( 1 ) = H ,
which is not a perturbation problem.
In the method presented in this paper, we first treat the parameter λ as a small parameter, allowing us to use the standard perturbation theory to solve the eigenequation (3). The eigenvalue given by perturbation theory is a truncated power series, i.e., a polynomial in λ ,
E n λ ≃ E n 0 + E n 1 λ + E n 2 λ 2 + ⋯ + E n N λ N ,
This result is only valid for λ ≪ 1 . When λ = 1 , the corresponding series does not converge.
In a word, in step 1, we use standard stationary perturbation theory to calculate a polynomial approximation of the eigenvalues of the auxiliary Hamiltonian H λ given by equation (6) under the assumption that λ < 1 . This polynomial approximation of the eigenvalue, similar to Equation (6), fails at λ = 1 . The next step is to use analytic continuation to obtain the result for λ = 1 from the perturbation result (5).

2.2. Step 2: Analytically Continuating Perturbation to Non-Perturbation

Perturbation theory does not yield a complete power series but rather a polynomial approximation obtained by truncating the power series. In this paper, we use a rational approximation to perform an approximative analytic continuation. The exact analytic continuation is unique, but the approximate analytic continuation is not. However, the difference between the analytic continuation results obtained from different rational approximations is often insignificant.
In our problem, rational approximation means using rational functions to approximate polynomials obtained from perturbation theory. In this paper, we use the Padé approximation to perform rational approximation. However, other methods can also be used to perform the rational approximation, such as determining the coefficients of the rational function through numerical fitting.
The Padé approximation is a rational approximation obtained through polynomial approximation. Perturbation theory approximates the exact solution using polynomials, while rational approximation approximates the exact solution using rational functions. The method of making an approximate analytic continuation using rational approximation is to use a rational function to approximate the approximate polynomial given by perturbation theory; that is, the rational approximation obtained this way is essentially an approximate analytic continuation of perturbation theory.
In a word, in step 2, we use the Padé approximation to analytically continue the perturbative result to a non-perturbative one valid at λ = 1 . When λ = 1 , H 1 = H , and E n 1 is a non-perturbative approximation of the eigenvalue of H.
The advantage of this method is that both the perturbation theory in step 1, such as the stationary perturbation theory, and the analytic continuation in step 2, such as the Padé approximation, have standard procedures.
Mathematical example. The convergence radius of the power series f x = 1 + x = ∑ n = 0 ∞ − 1 n + 1 2 n − 3 ! ! 2 n n ! x n is 1. Assuming that, as in perturbation theory, we only obtain the first four orders of this series, i.e., the polynomial approximation of f x is
f P x ≃ 1 + x 2 − x 2 8 + x 3 16 − 5 x 4 128 .
This approximation is only valid for x < 1 , and it fails outside the convergence radius of the series, i.e., in the region x > 1 , as shown in Figure 1.
If we approximate the polynomial f P x with a rational function f R x whose numerator and denominator are both second-order polynomials,
f R x ≃ 1 + 5 4 x + 5 16 x 2 1 + 3 4 x + x 2 16 ,
then for x < 1 , we have f R x ≃ f P x , that is, f R x is an approximate analytic continuation of f P x . f R x provides a good approximation of f x even when x > 1 , as shown in Figure 1.
This example demonstrates how to use a rational approximation based on Padé approximation to perform an approximate analytical continuation of a polynomial approximation.

3. Eigenvalue

3.1. Perturbative Approximation of Eigenvalue

Using the standard stationary perturbation theory to solve the eigenequation (3), we can obtain a polynomial approximation of the eigenvalues of the auxiliary Hamiltonian, H λ , of the form (5).
The Nth-order approximate eigenvalue, by the stationary perturbation theory, can be calculated directly:
E n N = ∑ m ≠ n = 1 Δ m n E n 0 − E m 0 K N − 1 , m , n , N ≥ 2 ,
where the zero-order approximation of the eigenvalue E n 0 is given by the exact solution of H 0 ψ n 0 = E n 0 ψ n 0 and
K N , m , n = E n N − ∑ j = 1 N − 1 E n j K N − j , m , n E n 0 − E m 0
with Δ m n = ψ m 0 Δ ψ n 0 and E n ( 1 ) = Δ n n .

3.2. Non-Perturbative Approximation of Eigenvalue

To perform an analytic continuation of the polynomial approximation of the eigenvalues obtained by perturbation theory, we approximate the polynomial (5) by a rational function:
E n L / M λ = P [ L / M ] ( λ ) Q [ L / M ] ( λ ) ≃ ∑ i = 0 N E n i λ i ,
where the numerator P [ L / M ] ( z ) = ∑ n = 0 L a l λ l is an Lth-order polynomial, the denominator Q [ L / M ] ( z ) = ∑ n = 0 M b m λ m is an Mth-order polynomial, and N = L + M . In the Padé approximation, the coefficient of the rational approximant is determined by the polynomial approximation:
P [ L / M ] ( λ ) = E n L − M + 1 E n L − M + 2 ⋯ E n L + 1 E n L − M + 2 E n L − M + 3 ⋯ E n L + 2 ⋮ ⋮ ⋱ ⋮ E n L − 1 E n L ⋯ E n L + M − 1 E n L E n L + 1 ⋯ E n L + M ∑ i = 0 L − M E n i λ M + i ∑ i = 0 L − M + 1 E n i λ M + i − 1 ⋯ ∑ i = 0 L E n i λ i ,
and
Q [ L / M ] ( λ ) = E n L − M + 1 E n L − M + 2 ⋯ E n L E n L + 1 E n L − M + 2 E n L − M + 3 ⋯ E n L + 1 E n L + 2 ⋮ ⋮ ⋱ ⋮ ⋮ E n L − 1 E n L ⋯ E n L + M − 2 E n L + M − 1 E n L E n L + 1 ⋯ E n L + M − 1 E n L + M λ M λ M − 1 ⋯ λ 1 .
E n L / M λ obtained in this way is an analytically continued result and remains valid at λ = 1 in the non-perturbative region. E n L / M λ with λ = 1 provides a non-perturbative approximative eigenvalues of the Hamiltonian (1):
E n = E n L / M 1 = P [ L / M ] ( 1 ) Q [ L / M ] ( 1 ) .

4. Construction of Auxiliary Hamiltonian

In order to convert a non-perturbative problem described by the Hamiltonian (1) into a perturbative problem, we need to rewrite the Hamiltonian (1) into a perturbative form like Equation (2). This requires introducing an auxiliary potential U as in Equation (2). In principle, the auxiliary potential U can be chosen arbitrarily, because in Eq. (2) we always have H ( 1 ) = H when λ = 1 , regardless of how U is chosen. However, a good choice of the auxiliary potential should (1) improve computational efficiency, i.e., achieving the same accuracy with fewer orders of perturbation, and (2) follow a standardized systematic procedure rather than relying solely on guesswork as in variational methods for choosing trial wavefunctions. This section will provide a systematic procedure for choosing the auxiliary potential.

4.1. Auxiliary Potential: Taylor Expansion

The method for constructing the auxiliary potential presented in this section applies to potentials with good analytical properties that can be expanded as power series. Here, we only consider potentials that can be Taylor expanded, but this method is not limited to this type of potential.
1) First, select an energy E within the range of interest. The choice of E determines which energy levels will have higher precision in the results. For example, for a potential with a minimum value of zero, roughly speaking, if choosing E = 0 , the calculated energy levels with high precision will be near the ground state. The higher the energy E, the higher the energy levels with high precision will be.
2) Expanding the potential V x around the energy E, up to 2th-order terms:
V x ≃ V x E + V ′ x E x + 1 2 V ′ ′ x E x 2 = 1 2 V ′ ′ x E x + V ′ x E V ′ ′ x E 2 + V x E − V ′ x E 2 2 V ′ ′ x E ,
where x E is given by V x E = E , as shown in Figure 2a, gives a harmonic oscillator potential with a vertex at − V ′ x E V ′ ′ x E , V x E − V ′ x E 2 2 V ′ ′ x E .
3) Shifting the vertex of the harmonic oscillator potential (14) along the x-axis to x = 0 results in a harmonic oscillator potential with vertex at 0 , V x E − V ′ x E 2 2 V ′ ′ x E : 1 2 V ′ ′ x E x 2 + V x E − V ′ x E 2 2 V ′ ′ x E . (Note that shifting the harmonic oscillator potential (14) does not affect the energy level, so it can be performed or omitted at discretion.) The constant V x E − V ′ x E 2 2 V ′ ′ x E in the potential only shifts energy levels and can be arbitrarily chosen. Taking the zero point of the potential to be V x E gives the auxiliary potential:
U x = 1 2 V ′ ′ x E x 2 + V x E ,
shown in Figure 2b. The auxiliary potential constructed in this way is a harmonic oscillator potential, which has exact solutions and facilitates perturbation theory.
According to Equation (2), we rewrite the Hamiltonian (1) into a perturbative form:
H λ = − ℏ 2 2 μ ∇ 2 + 1 2 V ′ ′ x E x 2 + V x E + λ V − 1 2 V ′ ′ x E x 2 − V x E .
Pöschl-Teller potential. We illustrate our method using the exactly solvable Pöschl-Teller potential as an example. The Pöschl-Teller potential is [24]
V ( x ) = − ℏ 2 2 μ β β + 1 sech 2 x ,
whose eigenvalue is E n = − ℏ 2 2 μ β − n 2 with n = 0 , 1 , … , β . In the following, we take ℏ 2 2 μ = 1 .
First, choose an energy value E. If interested in a higher excited state, select a larger value of E; otherwise, select a smaller one. Then, construct the auxiliary Hamiltonian according to Equation (16):
H PT λ = H 0 + λ Δ .
Here H 0 = − ℏ 2 2 μ ∇ 2 + ℏ 2 2 μ β ( β + 1 ) 2 sech 2 x E tanh 2 x E − sech 2 x E x 2 − sech 2 x E is an exactly solvable harmonic oscillator potential with the eigenvalue E n = ε 2 2 n + 1 , ε = 1 2 V ′ ′ x E 1 / 4 , and the eigenfunction ψ n x = ε 2 n n ! π 1 / 2 H n ( ε x ) exp − 1 2 ε 2 x 2 , where H n ( x ) is the Hermitian polynomial. The perturbative part Δ = − ℏ 2 2 μ β β + 1 [ sech 2 x + ( 2 sech 2 x E tanh 2 x E − sech 2 x E ) x 2 + sech 2 x E ] .
For the potential (17), we choose three values of energy and obtain the positions of the three expansion points, x E a = 0 , x E b = 0.3 , x E c = 0.55 , according to V x E i = E i . The auxiliary potentials are obtained by expanding and shifting at the three points x E a , x E b , and x E c , as shown in Figure 3.
The analytical continuation provides an explicit expression for the eigenvalue, Equation (13). In Figure 4, we plot the result for E n ≃ E n 8 / 8 1 = P [ 8 / 8 ] ( 1 ) Q [ 8 / 8 ] ( 1 ) with the parameter ℏ = 1 , μ = 1 2 , and β = 20 .
By comparing the three auxiliary potentials constructed at three different points, x E a , x E b , and x E c , we can see that the eigenvalues obtained from the auxiliary potential corresponding to E = 0 are highly accurate near the ground state, while those obtained from the auxiliary potential corresponding to larger E are highly accurate in higher excited states. To obtain more energy levels, we can construct more auxiliary potentials at more positions x E corresponding to different energies E, which can provide approximate solutions in different energy level intervals. In other words, by constructing auxiliary potentials corresponding to various E, we can calculate all eigenvalues with high precision.
In Figure 5, we compare the non-perturbative eigenvalues of the Pöschl-Teller potential given by different auxiliary potentials ( E a > E b > E c ).

4.2. Auxiliary potential: Laurent expansion

The potentials considered previously are those that can be Taylor expanded. Similar treatment also applies to potentials that can be Laurent expanded. In this section, we take the central potential as an example to illustrate.
Considering that the negative power law potentials α r n have bound states only when n < 2 , here we consider the case where the leading order of the Laurent expansion is the negative first power, i.e., the Coulomb potential. For the central potential, we perform a Laurent expansion around r = 0 :
V r = − α r + ⋯ .
In this case, the Coulomb potential is taken as the auxiliary potential,
U r = − α r .
According to Equation (2), we write the Hamiltonian for central potentials in the following perturbative form:
H λ = − ℏ 2 2 μ ∇ 2 − α r + λ V r + α r .
Here the Coulomb potential H 0 = − ℏ 2 2 μ ∇ 2 − α r is exactly solvable. Note that the discussion here is not limited to the three-dimensional case, but also applies to the one-dimensional Coulomb potential.
Hulthen potential. As an example, we consider the exactly solvable spherically symmetric Hulthen potential [24]
V r = − V 0 e − r / r 0 1 − e − r / r 0 ,
whose eigenvalue for l = 0 is E n = − V 0 β 2 − n 2 2 β n 2 with β 2 = 2 μ V 0 ℏ 2 r 0 2 and β 2 − n 2 > 0 .
The leading term of the Laurent expansion of the Hulthen potential (22) is − V 0 r 0 r . According to Section 4.2, we choose the Coulomb potential as the auxiliary potential,
U r = − V 0 r 0 r .
The auxiliary Hamiltonian for l = 0 , according to Equation (21), is chosen as
H λ = − ℏ 2 2 μ 1 r d 2 d r 2 r − V 0 r 0 r + λ − V 0 e − r / r 0 1 − e − r / r 0 + V 0 r 0 r .
Here H 0 = − ℏ 2 2 μ 1 r d 2 d r 2 r − V 0 r 0 r , whose eigenvalue E n = − r 0 V 0 2 a n 2 with a = ℏ 2 μ r 0 V 0 and eigenfunction ψ n r = 2 4 π a 3 / 2 n 2 n ! n − 1 ! e − r n a 1 F 1 − n + 1 , 2 , 2 r n a with 1 F 1 a , b , z the confluent hypergeometric function.
By Equation (13) we obtain the eigenvalue E n ≃ E n 8 / 8 1 = P [ 8 / 8 ] ( 1 ) Q [ 8 / 8 ] ( 1 ) , where we take ℏ = 1 , μ = 1 2 , V 0 = 2 , and r 0 = 3 . The comparison between the non-perturbative result and the exact solution is illustrated in Figure 6.

4.3. Auxiliary Potential: Numerical Fitting

For the potentials that cannot be Taylor or Laurent expanded, we suggest a fitting-based scheme for constructing auxiliary potentials.
Based on the form of the potential V, we first choose an exactly solvable auxiliary potential U which should contain some undetermined parameters k 1 , k 2 , ⋯ . Then we fit the auxiliary potential U to V to determine these parameters. After determining the parameters in the auxiliary potential U through fitting, we can calculate the energy levels using the method described. In the example in this section, we take the exactly solvable linear potential as the auxiliary potential.
2 3 -potential.Consider the exactly solvable 2 3 -potential
V r = r 2 / 3
as an example. For convenience, we only consider the asymptotic solutions of its eigenvalues: E n ≃ 4 6 3 n − 1 8 1 / 2 [7].
Take an exactly solvable linear potential as an auxiliary potential,
U r = k r + r 0 ,
where k and r 0 are fitting parameters to be determined. The auxiliary Hamiltonian reads ( ℏ 2 2 μ = 1 and l = 0 ):
H λ = − 1 r d 2 d r 2 r + k r + r 0 + λ r 2 / 3 − k r − r 0 .
The asymptotic solution of eigenvalue of H 0 = − 1 r d 2 d r 2 r + k r + r 0 is E n = 3 π k / 2 2 / 3 2 n − 1 / 2 2 / 3 + r 0 , the eigenfunction is ψ n r = C n Ai ξ with Ai ξ the Airy function, ξ = 2 1 / 3 k − 2 / 3 k r − E n t , C n = 2 k 1 / 6 / α n Ai − α n 2 + Ai ′ − α n 2 , and α n = 2 1 / 3 r 0 k − 2 / 3 + 1 2 3 π 4 n − 1 2 / 3 [24].
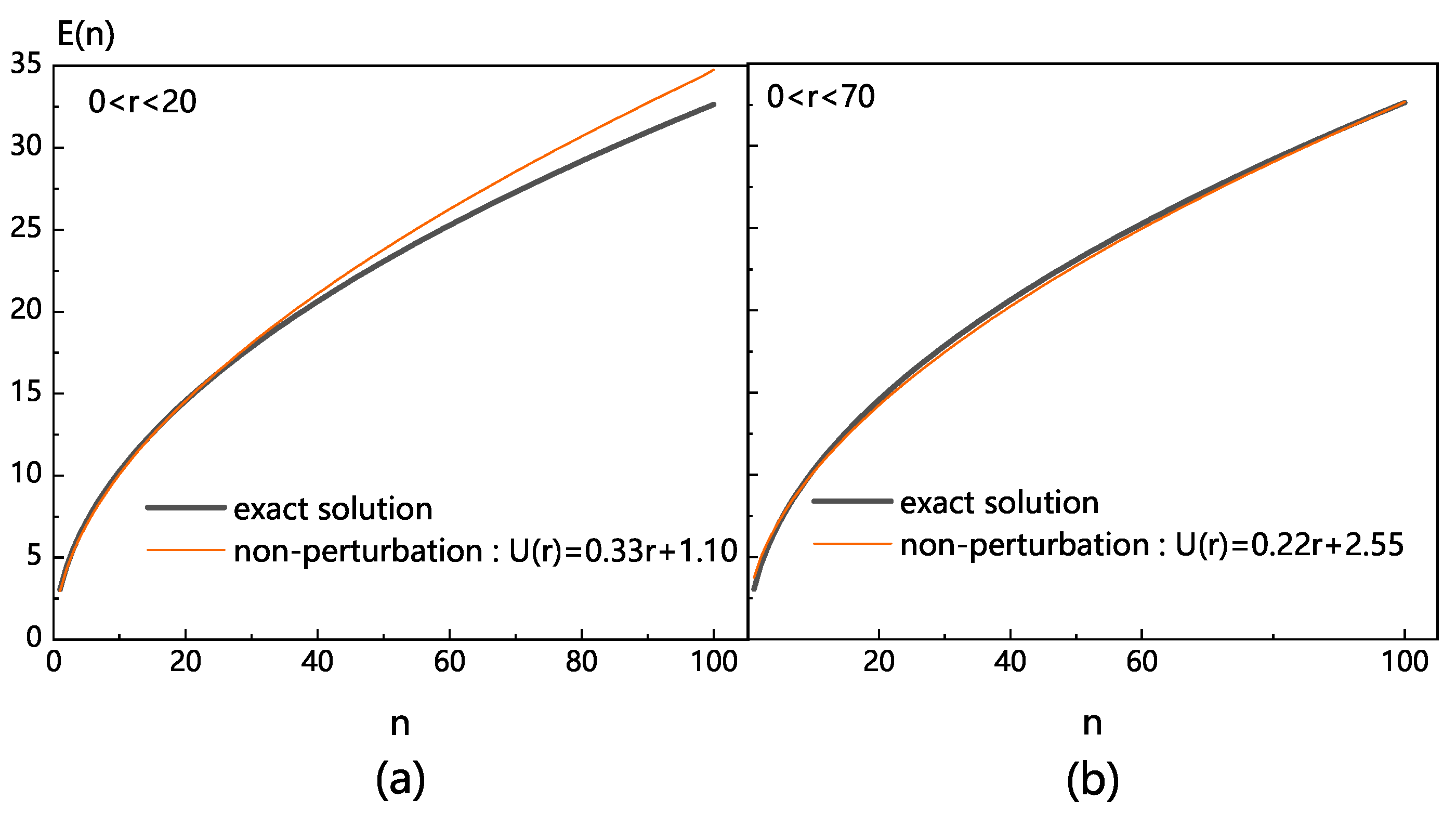
Different fitting ranges give different auxiliary potentials with different values of k and r 0 . In Figure 7, we plot two non-perturbative results, E n ≃ E n 8 / 8 1 = P [ 8 / 8 ] ( 1 ) Q [ 8 / 8 ] ( 1 ) , corresponding to two auxiliary potentials: (a) fitting range 0 < r < 20 gives the auxiliary potential U r = 0.331619 r + 1.10428 ; (b) fitting range 0 < r < 70 gives the auxiliary potential U r = U r = 0.2184 r + 2.54714 .
It can be seen that as the fitting range expands, the region of high precision shifts from low to high excited states.

5. Conclusion

In this paper, we propose a non-perturbative method for solving the eigenvalues of the Hamiltonian H = T + V for an arbitrary potential V. This method, like perturbation theory, has standardized procedures.
The basic idea of the method is to first (1) convert a non-perturbative problem into a perturbative one and (2) then analytically continue the perturbative results to the non-perturbative region. We utilize, but in principle not limited to, the rational approximation to perform approximative analytic continuations. As shown in the examples, this method yields very good results for a general class of potentials.
As a non-perturbative method, we can compare our approach with another non-perturbative method, the variational method. (1) The variational method is based on guessing trial wave functions, for which there is no standard procedure, and relies on isolated techniques. The variational method cannot be automatically carried out according to a standardized procedure like perturbation theory. In contrast, our method has a standardized procedure where the calculations proceed automatically, like in perturbation theory. (2) The variational method is only effective for the ground and low-excited states, while our method can calculate non-perturbative approximations for arbitrary energy levels.
In a previous work, we applied a similar approach to deal with phase transition problems. In that work, we used rational approximation to approximatively analytically continue the high-temperature results of quantum gases to the low-temperature region, providing information on the phase transition [2].
In this paper, we demonstrate this non-perturbative method using quantum mechanical eigenproblems as examples. The idea of this method can be applied to any field where perturbative treatments are well-established, such as quantum field theory and quantum statistical mechanics. In our future work, we will apply this approach to non-perturbative treatments in quantum field theory. Utilizing this method, we can convert perturbative techniques in quantum field theory, such as thermal field theory and Feynman diagrammatic expansions, into non-perturbative methods.
Perturbation theory is ineffective for strong coupling problems (coupling constants greater than 1). Perturbation theory results in a perturbation series, or more strictly speaking, a truncated series with a finite number of terms. Using perturbation theory based on a power series of the coupling constant, the effective range of the perturbation series is within the convergence circle of the power series. The necessary condition for convergence of the power series is that the coupling constant must be smaller than 1. Thus, (1) perturbation theory is not applicable for coupling constants greater than 1; (2) even if the coupling constant is smaller than 1, the perturbation series may not converge (because the condition that the coupling constant must be smaller than 1 is necessary but not sufficient). While, the rational function approximation obtained by analytic continuing perturbation theory not only applies at λ = 1 but is also valid when λ > 1 . We only use λ = 1 in the problem under consideration. This method can also be used to deal with non-perturbative strong coupling problems: first treating a strong coupling problem as a weak coupling problem which can be solved by perturbation theory, and then obtaining the strong coupling result through analytic continuation.

Acknowledgments

We are very indebted to Dr G. Zeitrauman for his encouragement. This work is supported in part by Special Funds for theoretical physics Research Program of the NSFC under Grant No. 11947124, and NSFC under Grant Nos. 11575125 and 11675119.

References

  1. Euler, L. Introduction to analysis of the infinite: Book I; Springer Science & Business Media, 2012. [Google Scholar]
  2. Tian, Y.-H.; Li, W.-D.; Shen, Y.; Dai, W.-S. Padé approximant approach to singular properties of quantum gases: the ideal cases. Communications in Theoretical Physics 2021, 73, 065602. [Google Scholar] [CrossRef]
  3. Baker, G.A.; Graves-Morris, P. Padé approximants; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
  4. Baker, G.A.; Gammel, J.L. The padé approximant. Journal of Mathematical Analysis and Applications 1961, 2, 21–30. [Google Scholar] [CrossRef]
  5. Baker, G.A.; Baker, G.A. Essentials of Padé approximants; Academic press New York: New York, NY, USA, 1975. [Google Scholar]
  6. Li, W.-D.; Dai, W.-S. Exact solution of inverse-square-root potential V (r)=- αr. Annals of Physics 2016, 373, 207–215. [Google Scholar] [CrossRef]
  7. Chen, Y.-J.; Li, S.-L.; Li, W.-D.; Dai, W.-S. Exact solution of two-thirds power potential. Europhysics Letters 2022, 138, 38002. [Google Scholar] [CrossRef]
  8. Chen, Y.-J.; Li, S.-L.; Li, W.-D.; Dai, W.-S. Solving eigenproblem by duality transform. Annals of Physics 2022, 443, 168962. [Google Scholar] [CrossRef]
  9. Li, W.-D.; Dai, W.-S. Duality family of scalar field. Nuclear Physics B 2021, 972. [Google Scholar] [CrossRef]
  10. A. Ahmadov, M. A. Ahmadov, M. Naeem, M. Qocayeva, and V. Tarverdiyeva, Analytical solutions of the Schrödinger equation for the Manning-Rosen plus Hulthén potential within SUSY quantum mechanics.
  11. Andrianov, A.; Ioffe, M. Nonlinear supersymmetric quantum mechanics: concepts and realizations. Journal of Physics A: Mathematical and Theoretical 2012, 45, 503001. [Google Scholar] [CrossRef]
  12. de Menezes, M.B.; Fernandes, M.; Graças, R.M.M.D.; Santana, A.; Vianna, J. Supersymmetric symplectic quantum mechanics. Annals of Physics 2018, 389, 111–135. [Google Scholar] [CrossRef]
  13. Kumar, P.R.; Dong, S.-H. A new quantization rule to the bound state problem in non-relativistic quantum mechanics. Physics Letters A 2021, 417, 127700. [Google Scholar] [CrossRef]
  14. Sanchez-Monroy, J.; Quimbay, C. Dirac equation in low dimensions: The factorization method. Annals of Physics 2014, 350, 69–83. [Google Scholar] [CrossRef]
  15. Bermudez, D.; Negro, J.; et al. Solutions to the Painlevé V equation through supersymmetric quantum mechanics. Journal of Physics A: Mathematical and Theoretical 2016, 49, 335203. [Google Scholar] [CrossRef]
  16. Agboola, D.; Zhang, Y.-Z. Unified derivation of exact solutions for a class of quasi-exactly solvable models. Journal of Mathematical Physics 2012, 53, 4. [Google Scholar] [CrossRef]
  17. Agboola, D.; Zhang, Y.-Z. Novel quasi-exactly solvable models with anharmonic singular potentials. Annals of Physics 2013, 330, 246–262. [Google Scholar] [CrossRef]
  18. Turbiner, A.V. One-dimensional quasi-exactly solvable Schrödinger equations. Physics Reports 2016, 642, 1–71. [Google Scholar] [CrossRef]
  19. N. Hatami and M. Setare, Exact solutions for a class of quasi-exactly solvable models: A unified treatment, The European Physical Journal Plus 132 (2017) 1–11.
  20. D. Agboola, J. D. Agboola, J. Links, I. Marquette, and Y.-Z. Zhang, New quasi-exactly solvable class of generalized isotonic oscillators, Journal of Physics A: Mathematical and Theoretical 47 (2014), no. 39 395305.
  21. Xie, Q.-T. New quasi-exactly solvable periodic potentials. Journal of Physics A: Mathematical and Theoretical 2011, 44, 285302. [Google Scholar] [CrossRef]
  22. Amore, P.; Aranda, A.; Fernández, F.M.; Jones, H. A new approximation method for time-dependent problems in quantum mechanics. Physics Letters A 2005, 340, 87–93. [Google Scholar] [CrossRef]
  23. Dorey, P.; Millican-Slater, A.; Tateo, R. Beyond the WKB approximation in-symmetric quantum mechanics. Journal of Physics A: Mathematical and General 2005, 38, 1305. [Google Scholar] [CrossRef]
  24. Fl, S.; et al. Practical quantum mechanics. Springer Science & Business Media, 1999; vol. 177. [Google Scholar]
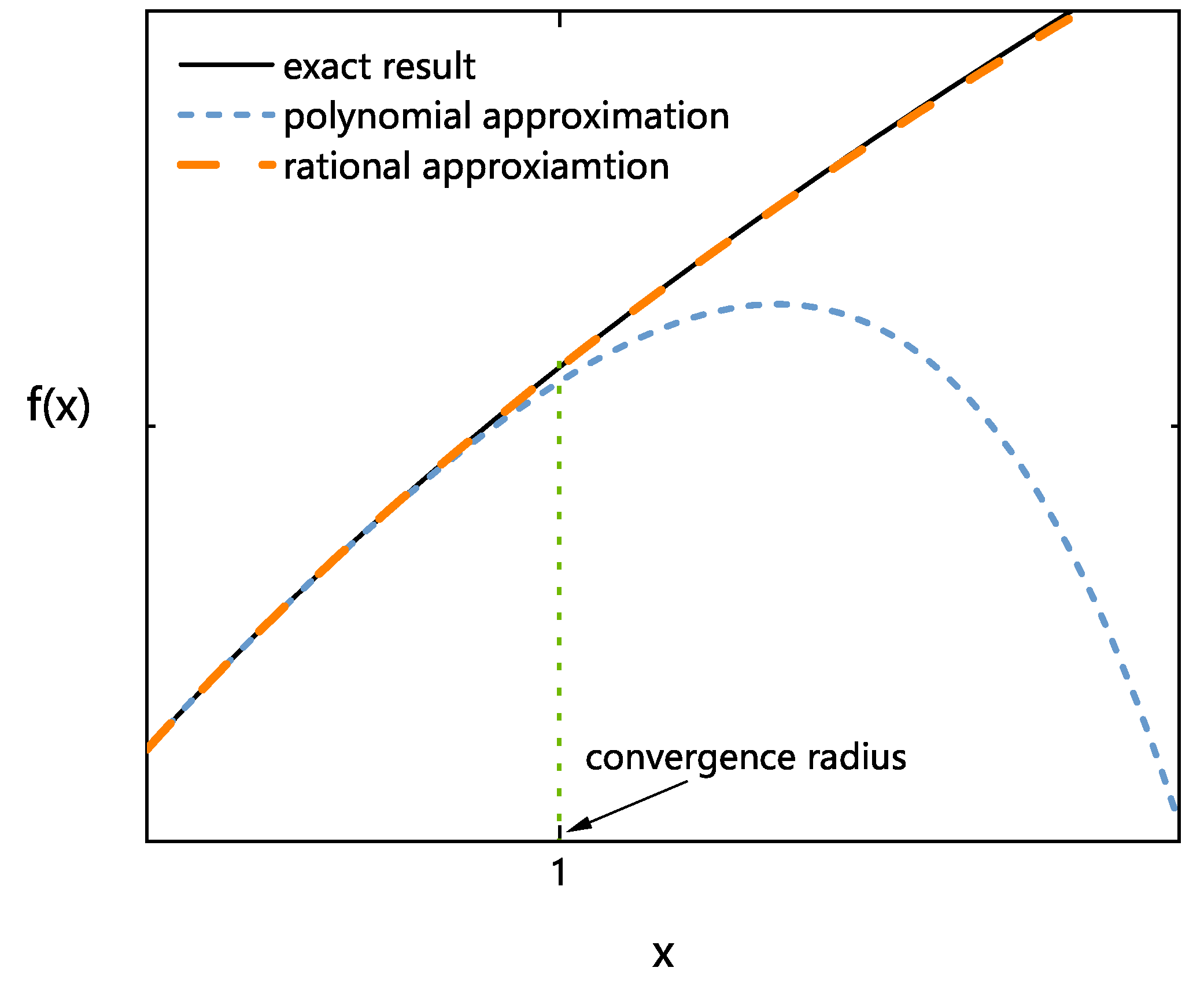
Preprints 81555 g001
Figure 1. Comparison of polynomial approximation, rational approximation, and exact value of f x = 1 + x .
Figure 1. Comparison of polynomial approximation, rational approximation, and exact value of f x = 1 + x .
Preprints 81555 g001
Preprints 81555 g002
Figure 2. Construction of the auxiliary potential. (a) Expanding the potential V x around x = x E ; (b) Obtaining the auxiliary potential, U x = 1 2 V ′ ′ x E x 2 + V x E , by a shifting.
Figure 2. Construction of the auxiliary potential. (a) Expanding the potential V x around x = x E ; (b) Obtaining the auxiliary potential, U x = 1 2 V ′ ′ x E x 2 + V x E , by a shifting.
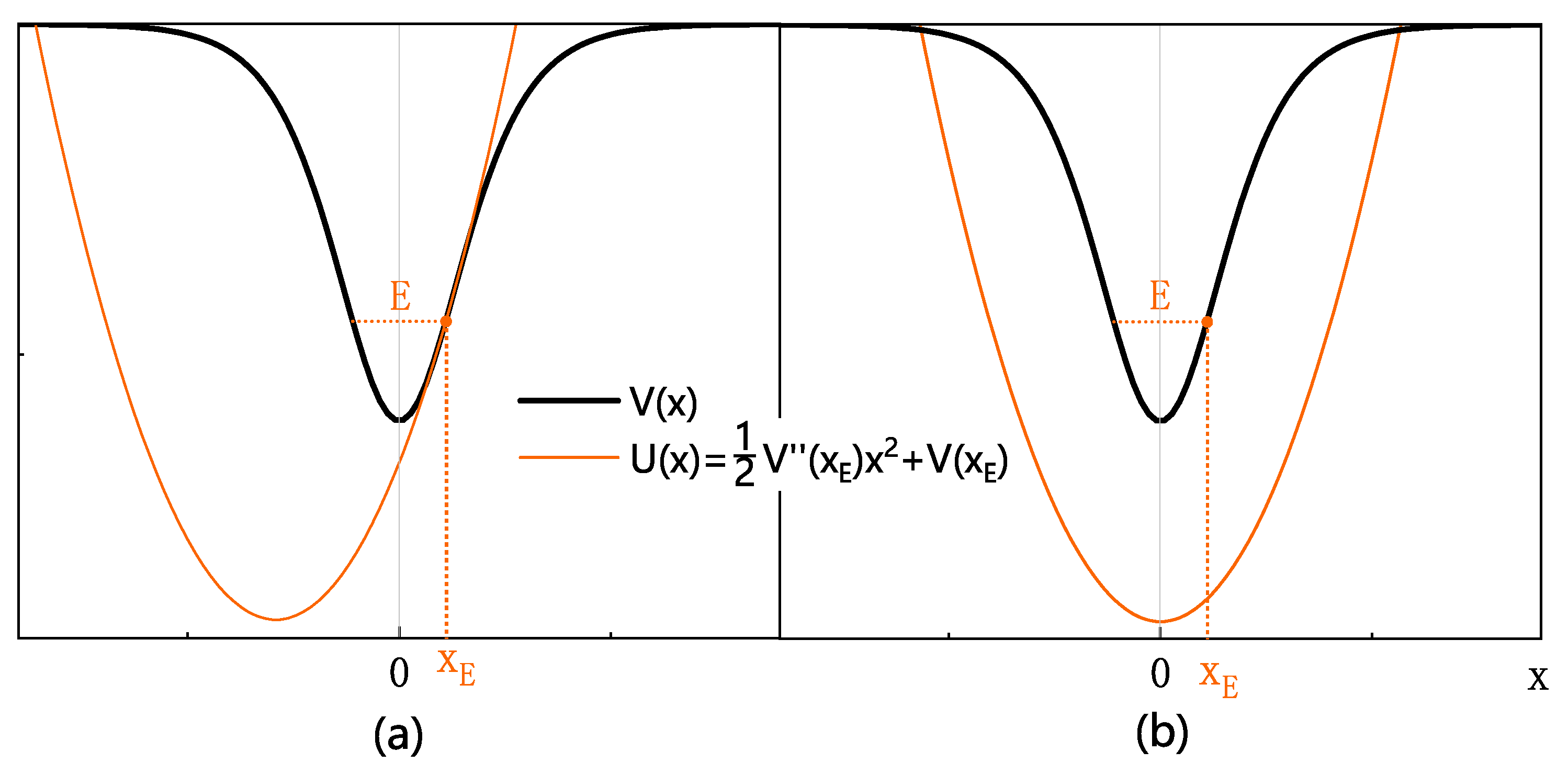
Preprints 81555 g002
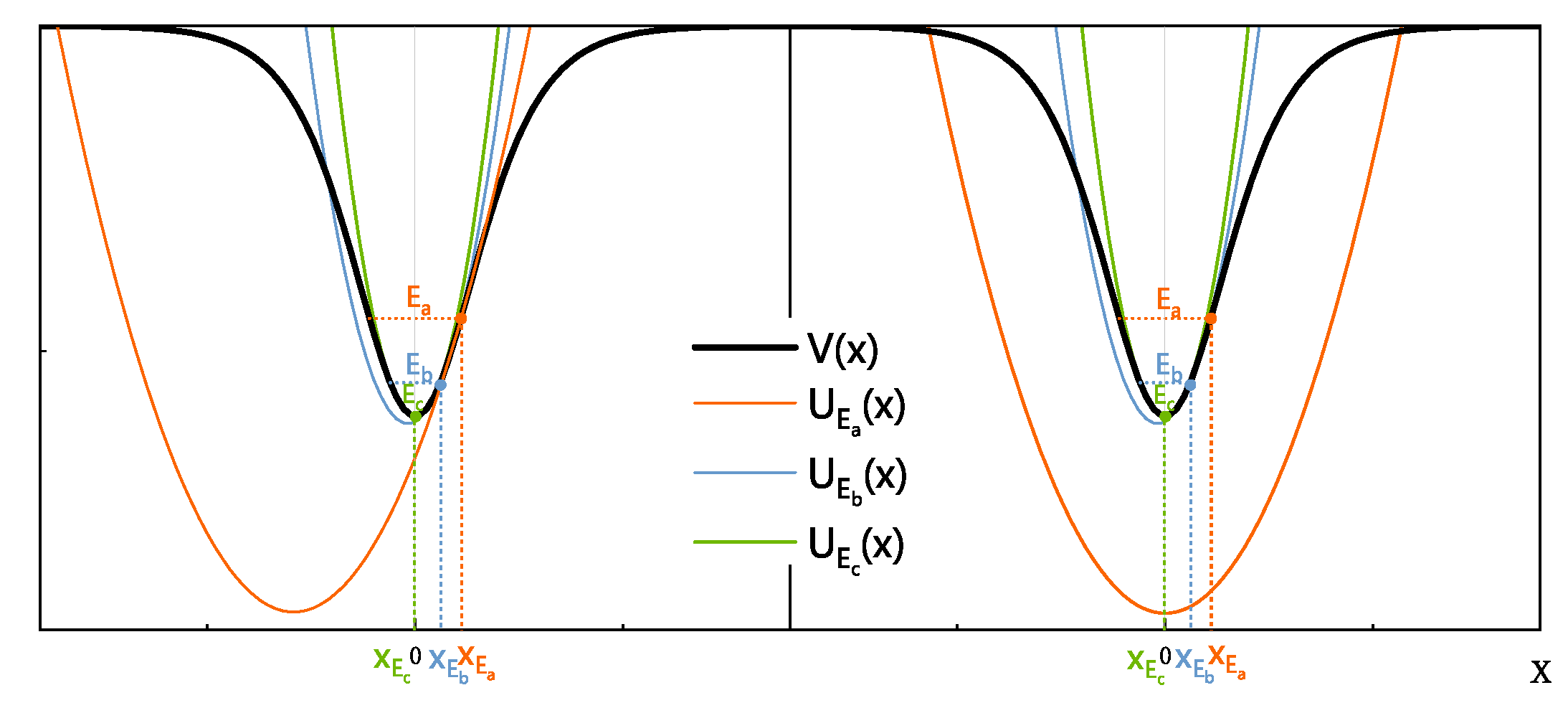
Preprints 81555 g003
Figure 3. Construction of auxiliary potentials for the Pöschl-Teller potential ( E a > E b > E c ).
Figure 3. Construction of auxiliary potentials for the Pöschl-Teller potential ( E a > E b > E c ).
Preprints 81555 g003
Preprints 81555 g004
Figure 4. Comparison of the non-perturbative eigenvalues of the Pöschl-Teller potential with the exact solution.
Figure 4. Comparison of the non-perturbative eigenvalues of the Pöschl-Teller potential with the exact solution.
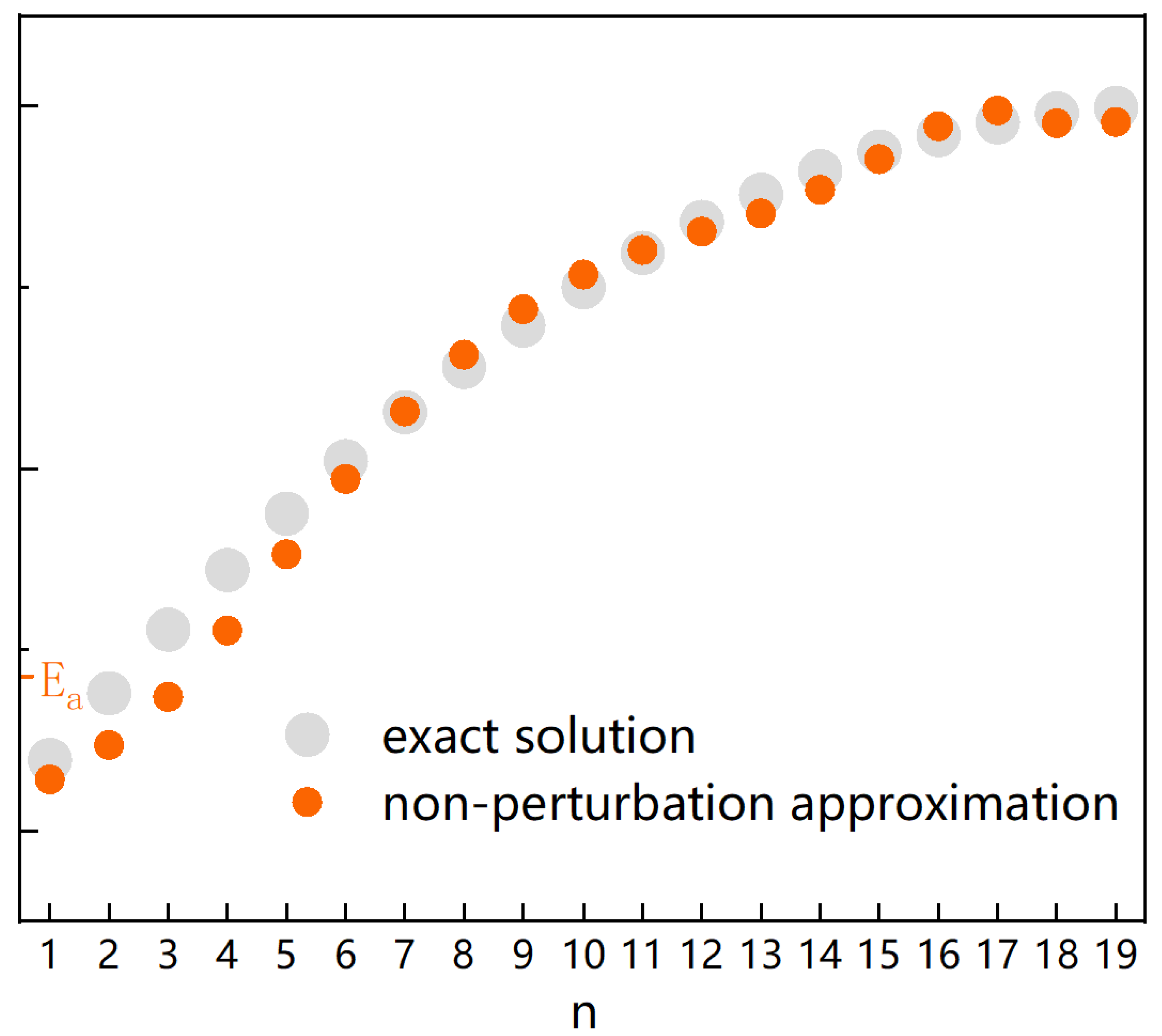
Preprints 81555 g004
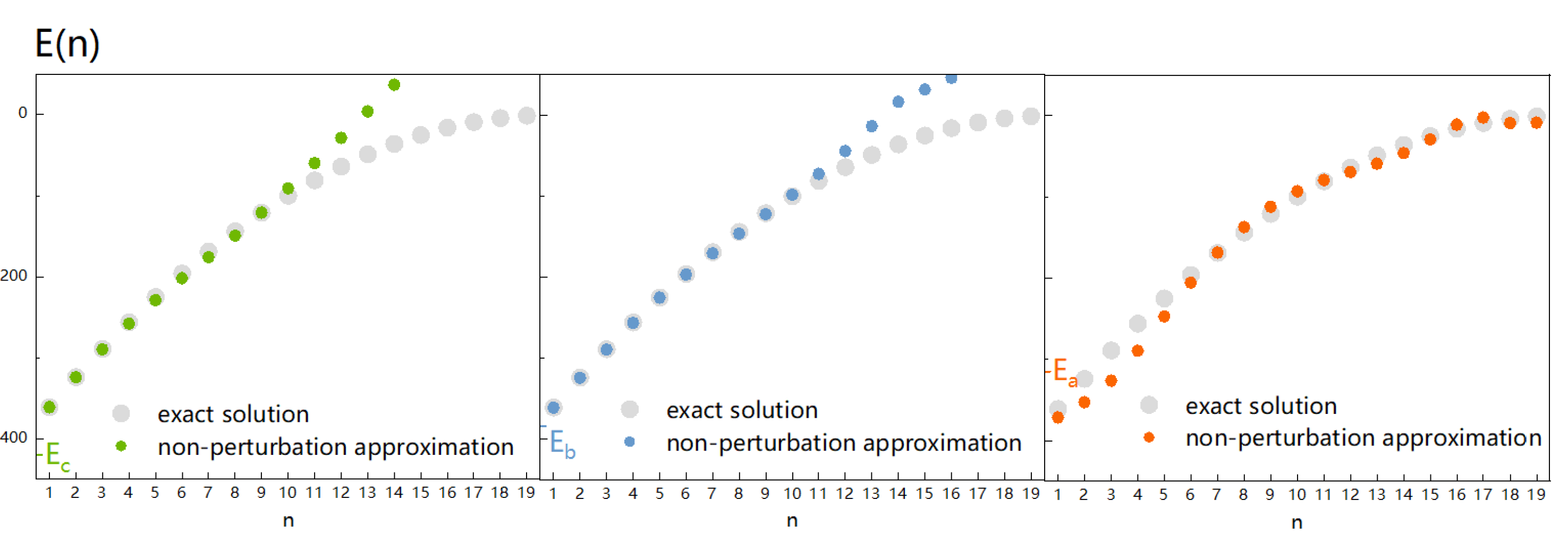
Preprints 81555 g005
Figure 5. Comparison of the non-perturbative eigenvalues of the Pöschl-Teller potential given by different auxiliary potentials ( E a > E b > E c ).
Figure 5. Comparison of the non-perturbative eigenvalues of the Pöschl-Teller potential given by different auxiliary potentials ( E a > E b > E c ).
Preprints 81555 g005
Preprints 81555 g006
Figure 6. Comparison of the non-perturbative result of eigenvalues of the Hulthen potential with the exact solution.
Figure 6. Comparison of the non-perturbative result of eigenvalues of the Hulthen potential with the exact solution.
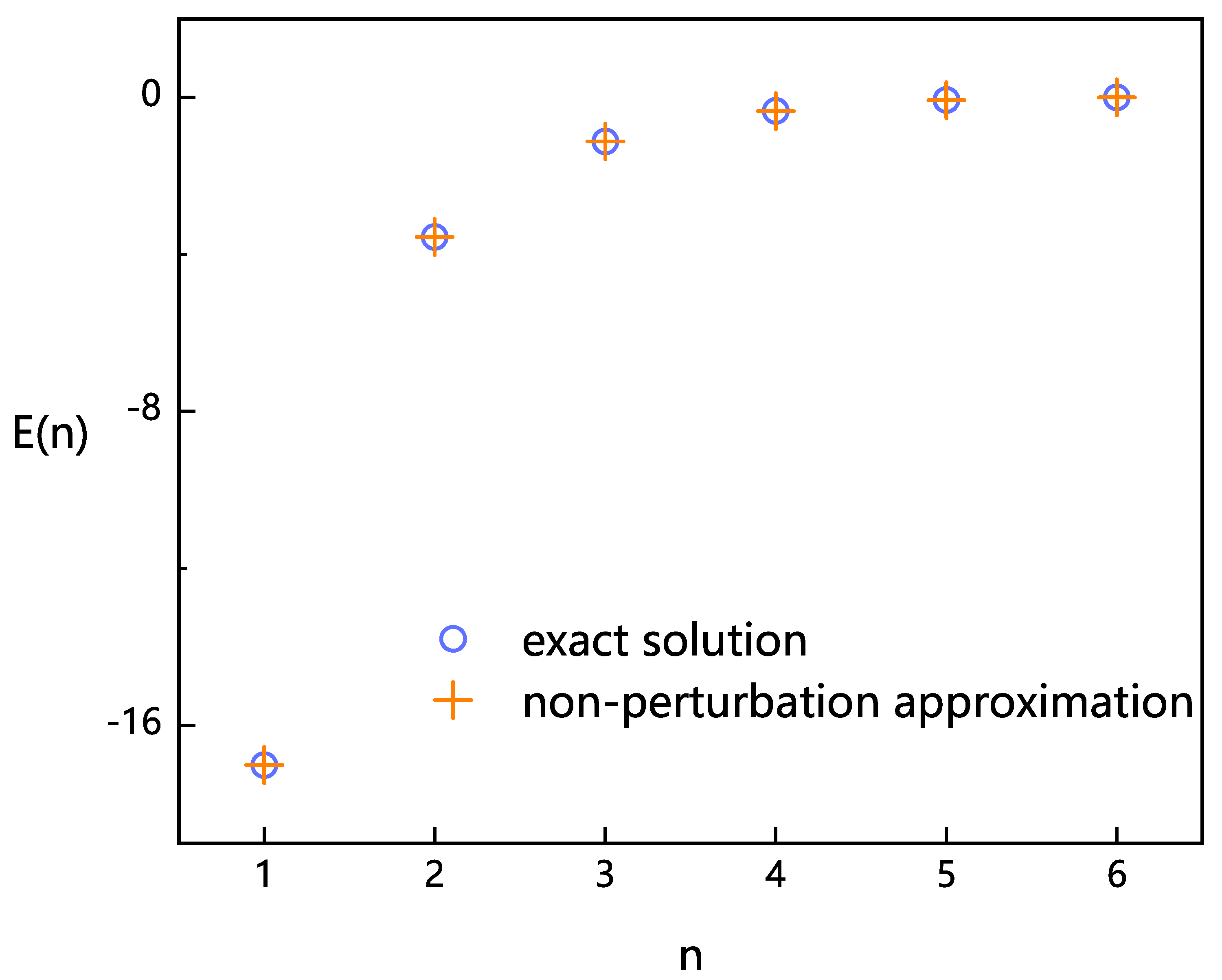
Preprints 81555 g006
Preprints 81555 g007
Figure 7. Comparison of the non-perturbative result of eigenvalues of the 2 3 -potential with the asymptotic solution.).
Figure 7. Comparison of the non-perturbative result of eigenvalues of the 2 3 -potential with the asymptotic solution.).
Preprints 81555 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated