Prerpints.org logo
Preprint
Article

Pipe Cavitation Parameters Reveal Bubble Embolism Dynamics in Maize Xylem Ducts Across Water Potential Gradients

Altmetrics

Downloads

104

Views

38

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

05 August 2023

Posted:

07 August 2023

You are already at the latest version

Alerts
Abstract
Maize, a crop of international relevance, frequently undergoes xylem embolism due to water shortage, negatively impacting growth, yield, and quality. Consequently, a refined comprehension of xylem embolism is vital for enhancing maize cultivation. Notwithstanding extensive research and the generation of analytical models for embolism mechanisms, prevalent models often disregard crop-specific hydraulic processes and the formation of embolisms via air bubbles in the xylem conduit. In this research, we present an inventive model applying pipe cavitation parameters to discern water potential and bubble formation in maize leaf xylem. The model integrates pivotal physiological traits of maize—leaf count, leaf vein count, and average leaf radius—demonstrating robust correlations. Furthermore, we constructed a percentage conductivity loss (PLC) curve based on pre-dawn leaf water potential and compared it with our model, offering interval data to observe embolisation events triggered by air bubbles. Utilizing experimental data, our novel cavitation-parameters based model effectively corresponds with observed bubble phenomena and appropriately characterizes water transport in plant xylem conduits. This method enabled us to observe the transition from bubble occurrence to cavitation embolism microscopically, which aligned with the embolism intervals provided by the model. This procedure reveals potential trends in bubble-induced embolism and deepens our knowledge of microscopic plant hydraulics and crop embolism. This work establishes a basis for understanding the generation of bubble embolisms in maize, assists in evaluating maize plant water status for efficient water supply management throughout the growth cycle, and contributes towards potential water management strategies for maize.
Keywords: 
Subject: Biology and Life Sciences  -   Agricultural Science and Agronomy

1. Introduction

Maize, also referred to as corn (Zea mays), is a versatile and extensively cultivated crop that has served as a vital food source for several millennia [1]. Due to its high nutritional content and ability to be processed into various products, corn has become a staple crop that holds a significant role in global agri-food systems [2,3,4]. However, maize production necessitates substantial amounts of water, and water scarcity may negatively impact plant growth and development, leading to smaller organs, inhibited flower production, and reduced seed filling [5]. The maintenance of optimal yield and quality of corn relies heavily on effective water management practices [6]. In this regard, assessing the water status of maize proves to be a valuable tool for managing water supply during crop growth. Among the various methods available, measuring pre-dawn leaf water potential to construct percentage loss of conductivities (PLC) as a superior technique, both in terms of simplicity and accuracy, when compared to relative evapotranspiration or soil water potential [7]. This underscores the criticality of leaf water in the growth of maize [8,9].
Plants rely on a complex network of xylem cells to transport water under negative pressure [10]. This negative pressure, however, makes the water column susceptible to interruption by large bubbles, leading to embolism formation and blockage of water flow within the plant [11]. Factors such as limited soil water or high evaporative demand can increase tension in the water column, making embolism formation more likely [12]. If water stress persists, the hydraulic conductivity of the xylem system progressively declines, eventually resulting in its failure, which can have serious consequences for the plant's photosynthetic performance and even lead to organ dieback [13].
Embolisms can form due to drought-induced tension reaching a critical threshold, where air is aspirated through pit membranes separating adjacent conduits or gas bubbles spontaneously nucleate from dissolved gas in the xylem sap [14]. The negative pressure inside the xylem conduits causes the gas to expand rapidly and forces water into connected neighboring conduits. Embolisms can also form following freeze-thaw events, where crystallization of liquid water forces dissolved gas out of solution, leaving gas bubbles that expand to fill the conduit when tension is subsequently applied to the xylem sap [15,16,17]. Wounding and pathogen infections can also result in air entry into the xylem network, leading to non-functional xylem conduits that disrupt the transport and distribution of water and nutrients throughout the plant [18]. Despite the negative physiological impacts, most plant species live with some proportion of their xylem rendered non-functional due to embolism [19].
Extensive research into plant xylem embolism has led to the development of models to analyse the state of bubbles at the time of embolism [20]. Cavitation is a process involving the formation, growth and collapse of gas and vapour filled bubbles in low pressure fluids and has been shown to be formed by the expansion of bubbles through pre-existing cracks or by the seeding of air in the pores of pit membranes [21]. The cavitation number serves as a predictive index of cavitation phenomena and potential impacts, illustrating the propensity for cavitation and enabling prediction of bubble states during cavitation [22]. In scenarios of unhindered soil moisture supply, sap flow rate correlates with solar radiation and vapor pressure disparity, culminating in peak transpiration rate and total daily transpiration. Conversely, under drought conditions, both stem water potential and sap flow rate experience significant reductions. Models grounded in field measurements have demonstrated a robust correlation between sap flow rate and water potential [23].
Rising global crop mortality rates, tied to climate change and weather events, underscore the need for a better understanding of crop mortality during water stress [24]. A recent breakthrough has identified xylem cavitation as a primary cause of plant mortality during drought [25]. Visualization of cavitation (xylem bubbles diffusion and formation within the xylem water column) showed varying susceptibility to cavitation between individuals, within individuals, and within tissues [26]. Xylem cavitation not only results in plant death but also slows recovery from drought, underlining its significance. Current hydraulic models offer valuable insights into complex plant water dynamics, such as leaf and soil water potentials, stomatal conductance, and transpiration, under various conditions [27,28,29]. these models leverage optimization principles and incorporate plant hydraulic properties to generate predictions of stomatal conductance, culminating in the construction of a Plant Hydraulic Conductance Curve (PLC) [30,31]. Persisting challenges lie predominantly in the detailed portrayal of microscopic bubble conduction within leaf xylem conduits, a process that triggers changes in water potential and incites embolism. Current modelling paradigms tend to concentrate on tree-specific hydraulic mechanisms [32,33,34], while often neglecting those pertinent to crops and falling short in accommodating embolism within the micro xylem canals. However, in this study, we advance our understanding by modelling bubble water potential and recording the preliminary observations of bubble emergence in alignment with the Percentage Loss of Conductivity (PLC) curves. The insights gleaned from this research undeniably fortify our knowledge of microscopic plant hydraulics. Furthermore, our findings offer essential implications for enhancing our grasp of crop embolism and provide a new assessment method for combating drought-induced embolism.

2. Materials and Methods

2.1. Materials

This experiment was conducted in a maize seed plantation in Mengrun Township, Mengla County, Xishuangbanna Dai Autonomous Prefecture, at latitude and longitude 21°56'N and 101°13'E, respectively, with maize selected for experimentation in March of each year from 2021-2023 (Table 1).the maize growth cycle was divided into seven growth stages, namely the germination and seedling stage, early ear expansion stage, late vegetative growth stage before flowering, flowering stage, lag phase, effective grain-filling stage, and late grain-filling stage. The maize specimens investigated in this study demonstrated swift growth during the initial five stages, leading to an increased susceptibility to damage due to their frail state. However, the final two stages were marked by a deceleration in growth, resulting in the plants and their foliage reaching a more durable and stable phase, optimal for experimental purposes. Consequently, our experiments focused on maize plants at the terminal grain-filling stage, including the late grain-filling stage.
Cultivation of the seedlings spanned a period of 15 days, followed by the random collection of mature leaves approximately 55 days post-transplantation, in line with the optimal growth parameters of this specific maize variety. In an attempt to simulate the plant's natural environment, the harvested leaves were submerged in water and propagated in plastic receptacles. The leaves were uniformly distributed in a well-ventilated room under visible light conditions, with a regulated temperature of 20±3°C. To maintain their inherent physiological conditions, all experimental procedures were executed within a 48-hour period following the leaf harvest. This rigorous approach facilitates a meticulous exploration of the maize growth cycle, ensuring accuracy and replicability.

2.2. Theory

Plant cavitation has been extensively investigated, although our understanding of the precise mechanisms underpinning bubble rupture in xylem conduits remains incomplete. Phenomena like embolism propagation via pits and similar duct structures have been noted in earlier work [35]. Moreover, previous research has dissected cavitation into two broad categories, encompassing three distinct mechanisms [36]. Essentially, cavitation within a conduit entails two primary stages: bubble expansion and subsequent explosion, the latter being a process exclusively confined to an intact, water-tense conduit [37]. This explosion stage necessitates comprehensive understanding due to its role in emboli spread.
For instance, in Oriental Red, experimental findings have demonstrated that bubble burst within intact xylem conduits results in the generation of acoustic or ultrasonic waves. Concurrently, conduit-contained water recedes under tension through guide walls, leading to rapid bubble dispersal and the formation of a turbid water-gas interface [38].
Cavitation, based on the structural and hydrodynamic attributes of the cavitation zone, can be subcategorized into four types: wandering, stationary, vortex, and oscillatory [39]. Stationary cavitation manifests post the incipient cavitation's critical state. When water is displaced from the sidewalls of a tortuous object or passage, unstable cavities form on the wall surface. These appear static to the unaided eye but are in reality continuously fluctuating. Stationary cavities may occasionally grow and refill from the rear, triggering a cyclic process of cavity collapse. Stationary cavitation is observed where the solid wall's pressure approximates the vapour pressure (or critical tensile strength), and local cavitation at this point facilitates fluid deviation and the formation of a stationary cavitation cavity.
The focus of this study is cavitation, a process that entails vapour bubble formation in a fluid's low-pressure region. Specifically, hydraulic cavitation involves the formation, enlargement, and eventual collapse of cavities or bubbles filled with a gas-vapour mix in a flowing fluid. This process is triggered as the system's flow rate accelerates and its pressure approximates the fluid's saturation vapour pressure at a given temperature [40]. To predict cavitation phenomena and assess its potential impacts, researchers utilize the Cavitation Number as a key parameter：
σ = P a − P v 1 2 ρ v e 2
where Pa is an ambient pressure; Pv is a vapor pressure of the liquid; Ve is the mean jet exit velocity; ρ is a liquid density .
The cavitation number can be calculated for any flow, and when cavitation begins within the flow, this number is known as the critical cavitation number or incipient cavitation number. As illustrated in Equation (1), cavitation will not occur when σ is large, which can be due to high rupture pressure or low flow velocity. By increasing flow velocity and reducing ambient pressure, the cavitation number can be decreased, and when it reaches a critical (incipient) level, cavitation bubbles start forming within the flow. The intensity of cavitation and the subsequent cavitation erosion are influenced as the cavitation number further decreases. To demonstrate the behavior at different rupture pressures and xylem flow rates, the values 1, 0.5, 0.1, and 0.05 are considered, representing incidental cavitation bubbles, the generation of cavitation bubbles, stable cavitation bubbles, and a large number of cavitation bubbles, respectively.
Following the reperfusion of embolized vessels, research shows that small air bubbles may reappear and adhere to hydrophobic cracks in the catheter wall [41]. Xylem pressure increases, extracting air from the fissures and resulting in the regeneration of bubbles. According to Henry's Law and Fick's Law, if the gas pressure within a bubble exceeds atmospheric pressure, the air must dissolve in the neighboring water and disperse. Based on the empirical formula by Yang and Tyree [42,43], it takes over 10 hours to fully recover conductivity when xylem pressure is at 0 kPa. In our experiments, injecting water into glass capillaries led to the observation that some bubbles persisted on the capillary walls for at least three days. As a result, we propose that air dissolution has a limited impact on the daily cavitation repair cycle compared to bubble expansion. We also infer that air dissolution in water is not an essential mechanism in cavitation, meaning that n remains constant during bubble expansion. In an effort to simplify our analysis [41], we assume that bubble expansion transpires isothermally. Therefore, in our examination, P relies exclusively on the bubble radius r.
P g = P 1 + 2 k / r
When a bubble reaches equilibrium, its rupture pressure (2k/r) is offset by the pressure differential between the gas pressure (Pg) and the absolute pressure of the xylem liquid at its surface (Pl).
A study discusses the observation of saplings growing on the edge of the Fraxino-Aceretum forest in western Germany, where a model was designed to directly link sap flow rates to water potential [44]. A strong correlation between measured sap flow rates and simulated sap flow rates was also confirmed, enabling the model to be employed for data interpretation between sap flow rates and water potential in xylem conduits (1).
W a t e r p o t e n t i a l M P a v % = 97 e − 1.33 Ψ w 2 − 1.649 Ψ w − o . 511 + 7
where v % is the percentage of maize sap flow; Ψ w is the maize water potential.
In contrast, maize is an herbaceous plant. The epidermis does not form a layer beneath the surface, and its thickness is negligible compared to the thickness of the xylem. The mean maximum flow rate, Vmax = 90.3 g h-1, was obtained from liquid flow monitoring tests conducted from the tassel stage to maturity. The liquid flow rate-water potential model was utilized to relate the water potential within the maize leaf to the xylem duct liquid flow rate, using the actual observed liquid flow rate to connect equation (1), resulting in:
σ = 4 k ρ r V m a x 97 e − 1.33 Ψ w   2 − 1.649 Ψ w − o . 511 + 7 / 100 2
where σ is the cavitation number；k=0.073 Nm-1 is the bubble pressure coefficient; r is the bubble radius; Vmax=90.3 g h-1 is the maximum daily stem flow rate; ρ is the sap flow density; and Ψ w is the maize water potential. The equation accurately demonstrates the bubble formation phenomenon within the primary xylem tube of maize, as influenced by sap flow rate and pressure (Figure 1).

2.3. Sample Processing

2.3.1. Physiological indicators

Maize, an angiosperm with slender leaves and well-structured transport tissues, exhibits an orderly arrangement of vascular bundles. Its main xylem is comprised of uniform vessels. Given its propensity to undergo cavitation under moderate water stress [45,46], maize serves as an exemplary subject for observing the bubble-producing cavitation process.
The daily average maximum sap flow rate in maize, as identified by the measurements Vmax = 90.3 g h-1, represents the average sap flow rate in the stem's xylem. To correlate this value with the flow rate in the xylem of maize leaves according to Equation (4), it is necessary to normalize it.
As depicted in Figure 1, the leaf's xylem is akin to a long cylindrical conduit. This necessitates the determination of several parameters, including the number of leaves (n1), the number of leaf veins (n2), and the radius of the xylem cross-sectional area within these veins (R). These parameters will enable calibration of the required sap flow rate in each xylem conduit of the maize leaf.
V m a x = ∫ 0 t q m d t n 1 n 2 ρ 4 π R 2
Sampling was conducted over three consecutive years: 2021, 2022, and 2023. Each year, seven maize plants were randomly chosen for sampling from the experimental field as illustrated in Figure 2 a, and the quantity of leaves on each maize plant was recorded. In the manner shown in Figure 2 b, a total of 21 maize plants were randomly selected across the three years. From each plant, five leaves were randomly picked. Post-sampling, leaves were immediately immersed in water. Images of the leaf veins were then captured using a Canon D550 camera, and the number of prominent leaf veins per leaf was manually tallied.
We show manual cross-sections of the lateral veins of maize leaves (Figure 2c). As in Figure c, the xylem cross-sectional area radius of the leaf veins was counted in the unstained state within 48 h, at 20°, maintaining the physiological activity of the maize leaves, and the sections were observed. We observed two large xylem vessels (V) in the lateral veins, each with a diameter close to 40 µm. Above the two large xylem vessels are protoxylem (arrows), which are approximately 20 µm in diameter (Figure 2c Unstained cross-section of lateral veins of maize leaves. Scale bar = μm50 ).
we present hand cross sections of a lateral vein of a maize leaf (Figure 2c). We observe two large metaxylem vessels (V) in the lateral vein, each with a diameter near 40 μm, and one protoxylem lacuna (arrow), with a diameter of approximately 20 μm. (Figure 2c Lateral veins of maize leaves without staining in cross-section .Scale = 50 μm )

2.3.2. Quantifying Hydraulic Conductivity Loss for Xylem Vulnerability Curve Generation

Leaf Vulnerability Curves and Xylem Anatomy: Utilizing the natural air-drying technique [47], we collected the lower leaves of maize cobs in the early morning. These leaves were isolated and placed in a chamber to undergo dehydration for varying durations to establish different water potential gradients. Leaf vulnerability curves were then derived by measuring the hydraulic conductivity corresponding to each water potential. The functional leaf intended for measurement was enveloped in tin foil to maintain equilibrium in the whole leaf's water potential. The xylem water potential was estimated by examining the leaf's end part, with water conductivity measured post a 15-minute equilibration period. We then cut the leaf end under water for a length of 15 cm and measured the water potential. Following this, we cut the leaf's middle underwater, ensuring it was 7 cm long, trimmed the vein segment to a width of 0.7 cm, and maintained a water head height between 40-50 cm. We defined the specific leaf hydraulic conductivity (Kl) as the ratio of initial hydraulic conductivity to the leaf area, and calculated the hydraulic conductivity per unit pressure gradient (Kh, MPa m-1) using the formula: Kh = F/(d P/dx), where F represents the water flow (kg s-1) and d P/dx is the hydraulic conductivity per unit stem length (MPa m-1).
We determined the percentage loss of hydraulic conductivity (PLC) as (1 - Kh/Kmax) × 100%, with the relationship between PLC and negative xylem pressure forming the leaf xylem vulnerability curve. We fitted the correlation between PLC and negative xylem pressure in stems using the Weibull distribution function:
P L C 100 = A * ( 1 − e x p ⁡ ( − ( k * x − x c ) ) ^ d )
In this function, the parameter xc is the absolute value of the negative xylem pressure correlating to a 64.2% loss of hydraulic conductivity, while the parameter d represents the curve's slope at a negative xylem pressure equivalent to -xc. A larger d value indicates a steeper curve.

2.3.3. Small Flow Method

We scrutinized the diameters of vascular conduits within the veins of maize leaves from the spring season of 2023. We formed three distinct experimental groups, each composed of nine leaves selectively chosen due to their vascular conduit diameters spanning between 60 to 65 µm. These leaves were subjected to a succession of experimental treatments to emulate the varying stages of primary leaf cavitation during their growth.
The Control Group (CG) maintained the lower half of the corn leaves submerged in water, simulating a water potential that precludes air bubble generation under standard physiological parameters. The Before Embolization Group (BE) involved a brief air exposure of the leaves for a minute post-immersion, imitating the onset of embolization within leaf vein conduits when minuscule air bubbles are created by air pressure. Lastly, the After Embolization Group (AE) allowed the leaves to remain exposed to air for an extended duration to enable close monitoring of the progression of embolization in these conduits. These distinct treatments were assigned randomly, and water potential measurements of individual leaves in each group were conducted three times to ensure reproducibility.
To quantify the water potential within leaf vein conduits at differing bubble formation stages, ten perforations in the upper third of each leaf were created using a 1 cm hole puncher. The perforated leaf discs were then soaked in a sucrose solution and placed in a 2 ml test tube containing a sucrose solution gradient. This mixture was thoroughly stirred and methyl blue was added. After aspirating 0.1 ml of this blend, it was reintroduced into the original sucrose solution tube. The final resting position of the leaf disc within the sucrose solution provided an approximation of the osmotic potential equivalence between the leaf and the solution at this stage.
ψw = ψπ = -CiRT
where, ψw refers to the osmotic potential, ψπ represents the leaf water potential, C denotes the small-scale current-stopped sucrose concentration in mol/L, R is the gas constant (0.008314 L-Pa/mol-K), T is the absolute temperature (293 K), and i is the dissociation coefficient, with the sucrose solution taking a value of 1.

3. Results

3.1. Physiological Parameters of Maize

Conducted between 2021 and 2023, our research involved the annual sampling of seven randomly selected maize plants from our experimental field (Figure 2 a). The leaf count of these specimens was duly noted.
During this triennial span, the leaf count for mature maize plants fluctuated mildly between 9.29 and 10.57, with the highest average appearing in 2021 (Table 1). The consistency of the data is striking; throughout the years, the leaf count for each mature maize plant remained steady, typically close to ten, with no significant yearly deviations. A robust positive correlation emerged between maize leaves and leaf vein counts across all categories (r = 0.82, p < 0.05), pointing towards effective photosynthesis, regular intra-plant transport exchange, and beneficial growth conditions for maize [48]. Physiological indicators, encompassing leaf and vein counts, and the diameters of leaf vein conduits, demonstrated varying trends across the years under differing environmental conditions. The peak values for these parameters were recorded in 2021, with an average leaf count of 10.5, a vein count of 43, and a mean leaf vein conduit diameter of 58 µm.
The average leaf diameter remained somewhat uniform, falling within 44.84 and 58 µm from 2021 to 2023. However, within the 2021 samples, leaf diameters presented a wide range from 32.79 to 97.20 µm. This variability likely arises from differing growth conditions within the maize sections from where the samples were randomly selected. Leaf length, a critical factor for estimating leaf area, maintained general stability over the three years, with lengths between 57.80 and 67.20 cm. On average, the diameters of mature maize leaves exhibited substantial overlap throughout the three years. A comprehensive analysis of maize samples from 2021, 2022, and 2023 revealed relative uniformity in the physiological indicators — leaf count, vein count, average leaf diameter, and leaf length — across the three years, affirming their appropriateness as parameters (Table 2).

3.2. Establishing the Bubble Radius-Sap Flow Rate-Water Potential Model

The formation of cavitation, or the explosive creation of air bubbles leading to embolism, is significantly influenced by the interplay of sap flow and water potential in maize leaf xylem [49]. Employing physiological indicators, the sap flow in maize xylem was converted, with the leaf count set to 10, the vein count to 40, and the average leaf diameter to 62.43 µm, to yield optimal preliminary xylem sap flow parameters, according to equation (5), which was then incorporated into equation 4.
During cavitation, a smaller initial cavitation number implies a lower likelihood of occurrence, while a larger initial number suggests a higher probability of cavitation due to bubble formation. At the moment of bubble inception, a smaller cavitation number is associated with increased bubble production and more pronounced cavitation, while a larger number signifies lesser bubble generation and a less intense cavitation. Theoretically, bubble generation should occur when σ ≤ 1, with stable bubbles forming when σ ≤ 0.5. We incorporated smaller cavitation numbers (0.1 and 0.05) to examine the initial stage of bubble generation preceding embolism, according to the model. This stage corresponds to the generation of numerous small bubbles and intense cavitation. The cavitation process occurs in tandem with variations in the bubble radius, leading to alterations in the sap flow rate and water potential within the xylem. This phenomenon occurs intensely at a cavitation number of 0.05, leading to bubble accumulation within maize leaf vascular conduits, subsequently transitioning to stable embolism as the bubbles enlarge and the cavitation coefficient increases beyond 1. It should also be noted that bubble formation is more likely under conditions of high sap flow and low water potential (Figure 3a).
The analysis, based on cavitation numbers, reveals that there are three bubble states preceding embolism during cavitation, namely, Incidental cavitation bubbles (Ib), Generation of cavitation bubbles (Gb), Stable cavitation bubbles (Sb), and a Large number of cavitation bubbles (Lb). These states correspond to cavitation parameters within the ranges of σ ≥ 1, 1 ≥ σ ≥ 0.5, 0.5 ≥ σ ≥ 0.1, and 0.1 ≥ σ ≥ 0.05, respectively. The moment bubble accumulation triggers cavitation, few bubbles are produced in the Ib state, making it difficult for embolism to form within the vascular conduits. The Gb state, however, begins to produce active bubbles, enabling bubble accumulation within this range. The Sb state is characterized by bubble stabilization, where an increased number of bubbles begin to connect via the phase boundary layer, naturally occurring in the Lb state. Here, large-radius bubbles accumulate, and cavitation generally occurs within the xylem, leading to the formation of one cavity after another, eventually expanding and merging to form larger cavities. This process results in the embolization of water channels and the loss of water transport function.
The model suggests that the conditions for cavitation are present at sap flow rates between 8-140 g h-1. Cavitation exists at varying water potentials and sap flow rates, with the Ib, Gb, Sb, and Lb sections defined by the cavitation number overlap, indicating that cavitation occurs at each sap flow rate and water potential. The bubbles produced are in various states and have different radii, suggesting that cavitation is a multi-core gas nucleus, with bubbles expanding at varying rates depending on their radii and the speed of their formation (Figure 3c). As more bubbles are produced, the sap flow rate decreases to the point immediately after bubble generation and then further drops until it reaches the region below the Gb level. At this point, cavitation reaches its endpoint, with the gas nucleus expanding to form a cavity, and the sap flow rate and water potential within the maize leaf xylem gradually stabilize, signifying the occurrence of a stable embolism (Figure 3b). During cavitation, in xylem sap flow of different leaf veins with identical water potential, larger air bubbles require a higher water potential when cavitation occurs in xylem with larger radii, implying that larger conduits are less susceptible to blockage (Figure 3d). Depending on the cavitation number, the region most likely to produce bubbles ranges from L to S to G to I, suggesting that smaller bubble radii are closer to the L region when cavitation occurs (Figure 3d).

3.3. Comparison of Cavitation Emergence in Leaf PLC and Model Predictions

Figure 4(a)presents the correlation between the percentage loss of conductivity (PLC) and negative xylem pressure (Ψs) in XueTian7401 leaf samples, utilizing the Weibull function. The analysis quantifies plant cavitation resistance by assessing the relationship between water potential and the corresponding degree of xylem conduit embolism. PLC was employed to explore the circumstances within the xylem conduits at each phase, compared to the previously constructed model view (Figure 4b). During the initial bubble generation stage (Lb), as PLC begins to rise to 27%, a marked decrease in hydraulic conductivity within the maize leaf vascular ducts is observed, with the concurrent formation of numerous small bubbles. This stage aligns with the Lb range of water potential, spanning from Ψs1 to Ψs2. As PLC further increases to 34%, a deceleration in the bubble growth rate is observed, with the phase boundary layer stabilizing. Upon further PLC increase to 50%, reaching the Gb range, corresponding to the water potential between Ψs3~Ψs4, an accumulation of bubbles within the conduit is noted. This occurrence leads to a significant increase in conduit PLC, a substantial decrease in hydraulic conductivity, the cessation of sap flow due to water scarcity, and air bubbles occupying substantial conduit space, disrupting plant homeostasis. At this stage, the accumulation of bubbles begins to disrupt the phase boundary layer with each newly formed air nucleus. As PLC continues to rise beyond 58%, when the water potential drops below Ψs4, air pockets within the maize leaf xylem start to interconnect, expanding into large sections of the duct cavity. Consequently, water transport ceases entirely, with air dominating the conduit space.

3.4. Observations of Leaf Conditions at Different Water Potentials during Cavitation

Given the invariability in the diameters of vascular bundle conduits in maize leaves from 2021 to 2023, the 2023 cohort was selected for analysis to guarantee leaf freshness during cavitation occurrence. Examination of the vascular bundle conduit diameters, using the OLYMPUS BX51 microscope, yielded an average diameter parameter of 62.43 µm for the simulation model. Consequently, conduits ranging from 60 to 65 µm in diameter were selected for the study.
Three conditions were simulated regarding the water potential (Ψs) in maize leaves during cavitation: Control Group (CG), Before Embolism Group (BE), and After Embolism Group (AE). Random images from each of these conditions were selected for presentation. The water potential values for these categories were aligned with the modeled values corresponding to XueTian7401 leaf Percentage Loss of Conductivity (PLC) within an acceptable margin of error. Preserve leaf activity, all measurements were performed within 24 h of leaf collection. Leaves in the CG were maintained through water immersion. The BE consisted of leaves observed within 1 min of air exposure, with water potential Ψ ranging from -0.72 MPa to -0.87 MPa, corresponding to the Lb region in the model. In the BE, small bubbles began to form in the conduit and the sap flow started to be influenced by the gas presence, corresponding to the Sb region in the model. Notably, large bubble sections were also observed, corroborating the model's prediction of multiple bubble states coexisting at the same water potential. AE group comprised leaves exposed to air for more than 3 min, at which point the extended air bubbles in the xylem conduit blocked sap flow, with water potential ranging from -1.16 MPa to -1.29 MPa. This stage corresponds to the Gb region in the model.
Comparing the CG, BE, and AE groups, a rapid decrease in leaf water potential was observed upon air exposure, with xylem cavitation ensuing. According to the experimental results, the water potential change caused by cavitation in maize leaves (AE) did not significantly differ from the trend in CG and BE. This discrepancy may be attributed to the atmospheric pressure in the in vitro environment being less than when cavitation occurs within the xylem ducts of maize leaves under natural conditions.
These changes in water potential due to leaf cavitation significantly impact the entire water transport network in maize plants, particularly under extreme water potential stress (Figure 5). We found a mean decrease of 0.24 MPa in water potential when small bubbles started to form within the ducts of the maize leaf xylem. The water potential dropped a further 0.18 MPa when bubble accumulation led to cavitation within the ducts, falling from -0.80 MPa before cavitation to -1.22 MPa after cavitation under normal physiological conditions (Figure 5). This transition marked a shift from the Lb to Gb interval within the maize leaf xylem ducts, denoting the establishment of a stable cavitation state within the ducts.

4. Discussion

Plant embolism has intrigued researchers for over a century, with microstructural analyses in recent years unveiling the crucial relationship between air bubbles and embolism formation [50,51]. Nevertheless, harmonizing macroscopic observations with microstructural findings using formulas has posed a considerable challenge. In response, we devised a novel formulation of the Bubble Radius-Sap Flow Rate-Water Potential Model for maize, offering insight into flow rate, water pressure, and bubble dynamics. Initial experimental measures substantiated various bubble alterations within the model's range, emphasizing the utility of the Bubble Radius-Sap Flow Rate-Water Potential Model in detecting xylem cavitation in maize leaves. Moreover, the model offers a platform for tracing potential bubble trends through water potential and sap flow rate investigations, thereby shedding light on the cavitation phenomenon;
Our model incorporates cavitation parameters to encapsulate the relationship with the liquid flow rate and uses the PLC as a comparative water indicator. This approach harmonizes the equation with experimental data. Built on maize plants, our study holds significant implications for understanding the relationships between water uptake and transport and photosynthesis. As such, our findings will play a crucial role in shaping models of maize growth, yield, and crop production mechanisms. They will also help anticipate future species distributions and plant responses to climate change. By aligning the flow rate of maize with the bubble radius-sap flow rate-water potential model, supported by available experimental data, we can better synchronize to reveal correlations between the maize's physiological state and subsequent yield;
The symbiotic relationship between plant water uptake and transport and photosynthesis has immense implications for maize growth, yield, crop production modeling, and climate change predictions[23,52,53]. Our experimental studies, based on environmental conditions, demonstrated the efficacy of the bubble radius-sap flow rate-water potential model in explaining the generation and expansion of air nuclei, sap flow rate, and leaf water potential within corn leaves under various treatments. This model aids in comprehending the conditions necessary for cavitation occurrence in maize leaves, laying the groundwork for understanding the formation process of cavitation at the onset of drought-induced embolism. This understanding could pave the way for stabilizing corn yield under such conditions.

Author Contributions

Conceptualization Y.R.; data curation Y.R. and S.G.; formal analysis Y.R., B.W., S.W. and Y.Z.; investigation Y.R. and Y.Z.; methodology Y.R.; software Y.R., B.W. and S.W.; writing—original draft Y.Z., Y.R., B.W., S.W., S.G. and W.G.; writing—review and editing Y.R., Y.Z., S.G, B.W., S.W. and W.G. All authors have read and agreed to the published version of the manuscript.

Funding

National Natural Science Foundation of China (NSFC) 31070651

Institutional Review Board Statement

Not applicable.

Data Availability Statement

The data used in the article are available from corresponding authors at request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Erenstein, O.; Jaleta, M.; Sonder, K.; Mottaleb, K.; Prasanna, B.M. Global Maize Production, Consumption and Trade: Trends and R&D Implications. Food Sec. 2022, 14, 1295–1319. [Google Scholar] [CrossRef]
  2. Shiferaw, B.; Prasanna, B.M.; Hellin, J.; Bänziger, M. Crops That Feed the World 6. Past Successes and Future Challenges to the Role Played by Maize in Global Food Security. Food Sec. 2011, 3, 307–327. [Google Scholar] [CrossRef]
  3. Jones-Garcia, E.; Krishna, V.V. Farmer Adoption of Sustainable Intensification Technologies in the Maize Systems of the Global South. A Review. Agron. Sustain. Dev. 2021, 41, 8. [Google Scholar] [CrossRef]
  4. Ranum, P.; Peña-Rosas, J.P.; Garcia-Casal, M.N. Global Maize Production, Utilization, and Consumption. Ann. N.Y. Acad. Sci. 2014, 1312, 105–112. [Google Scholar] [CrossRef] [PubMed]
  5. Farooq, M.; Wahid, A.; Kobayashi, N.; Fujita, D.; Basra, S.M.A. Plant Drought Stress: Effects, Mechanisms and Management. Agron. Sustain. Dev. 2009, 29, 185–212. [Google Scholar] [CrossRef]
  6. Prediction of Moisture Content in Corn Leaves Based on Hyperspectral Imaging and Chemometric Analysis. Trans. ASABE 2015, 531–537. [CrossRef]
  7. Katerji, N. Comparison of Corn Yield Response to Plant Water Stress Caused by Salinity and by Drought. Agricultural Water Management 2003. [Google Scholar] [CrossRef]
  8. Nilahyane, A.; Islam, M.A.; Mesbah, A.O.; Herbert, S.K.; Garcia y Garcia, A. Growth, Water Productivity, Nutritive Value, and Physiology Responses of Silage Corn to Water Stress. Agron. J. 2020, 112, 1625–1635. [Google Scholar] [CrossRef]
  9. Mahmoud, M.A.B.; Sharp, R.E.; Oliver, M.J.; Finke, D.L.; Ellersieck, M.R.; Hibbard, B.E. The Effect of Western Corn Rootworm (Coleoptera: Chrysomelidae) and Water Deficit on Maize Performance under Controlled Conditions. Journal of Economic Entomology 2016, 109, 684–698. [Google Scholar]
  10. Jansen, S.; Schenk, H.J. On the Ascent of Sap in the Presence of Bubbles. American Journal of Botany 2015, 102, 1561–1563. [Google Scholar] [CrossRef]
  11. Ponomarenko, A.; Vincent, O.; Pietriga, A.; Cochard, H.; Badel, E.; Marmottant, P. Ultrasonic Emissions Reveal Individual Cavitation Bubbles in Water-Stressed Wood. J. R. Soc. Interface 2014, 11, 20140480. [Google Scholar] [CrossRef]
  12. Torres-Ruiz, J.M.; Diaz-Espejo, A.; Morales-Sillero, A.; Martin-Palomo, M.J.; Mayr, S.; Beikircher, B.; Fernandez, J.E. Shoot Hydraulic Characteristics, Plant Water Status and Stomatal Response in Olive Trees under Different Soil Water Conditions. Plant Soil 2013, 373, 77–87. [Google Scholar] [CrossRef]
  13. Miyashita, K.; Tanakamaru, S.; Maitani, T.; Kimura, K. Recovery Responses of Photosynthesis, Transpiration, and Stomatal Conductance in Kidney Bean Following Drought Stress. Environ. Exp. Bot. 2005, 53, 205–214. [Google Scholar] [CrossRef]
  14. Schenk, H.J.; Steppe, K.; Jansen, S. Nanobubbles: A New Paradigm for Air-Seeding in Xylem. Trends Plant Sci. 2015, 20, 199–205. [Google Scholar] [CrossRef] [PubMed]
  15. TOGNETTIt, R.; Borghett, M. Formation and Seasonaloccurrence of Xylem Embolism in Alms Cordata. [CrossRef]
  16. Pratt, R.B.; Ewers, F.W.; Lawson, M.C.; Jacobsen, A.L.; Brediger, M.M.; Davis, S.D. Mechanisms for Tolerating Freeze–Thaw Stress of Two Evergreen Chaparral Species: Rhus Ovata and Malosma Laurina (Anacardiaceae). Am. J. Bot. 2005, 92, 1102–1113. [Google Scholar] [CrossRef] [PubMed]
  17. Umebayashi, T.; Fukuda, K. Seasonal Changes in the Occurrence of Embolisms among Broad-Leaved Trees in a Temperate Region. Botany 2018, 96, 873–881. [Google Scholar] [CrossRef]
  18. Ghosh, S.K.; Slot, J.C.; Visser, E.; Naidoo, S.; Sovic, M.; Conrad, A.O.; Bonello, P. How Abiotic Stress Plays Ally to Pathogenic Attack in Trees. In Proceedings of the PHYTOPATHOLOGY; AMER PHYTOPATHOLOGICAL SOC 3340 PILOT KNOB ROAD, ST PAUL, MN 55121 USA, 2021; Vol. 111, pp. 63–63. [Google Scholar]
  19. Simova-Stoilova, L.; Vassileva, V.; Feller, U. Selection and Breeding of Suitable Crop Genotypes for Drought and Heat Periods in a Changing Climate: Which Morphological and Physiological Properties Should Be Considered? Agriculture 2016, 6, 26. [Google Scholar] [CrossRef]
  20. Torres-Ruiz, J.M.; Cochard, H.; Mencuccini, M.; Delzon, S.; Badel, E. Direct Observation and Modelling of Embolism Spread between Xylem Conduits: A Case Study in Scots Pine. Plant Cell Environ. 2016, 39, 2774–2785. [Google Scholar] [CrossRef]
  21. Holtta, T.; Juurola, E.; Lindfors, L.; Porcar-Castell, A. Cavitation Induced by a Surfactant Leads to a Transient Release of Water Stress and Subsequent “run Away” Embolism in Scots Pine (Pinus Sylvestris) Seedlings. J. Exp. Bot. 2012, 63, 1057–1067. [Google Scholar] [CrossRef]
  22. Omelyanyuk, M.; Ukolov, A.; Pakhlyan, I.; Bukharin, N.; El Hassan, M. Experimental and Numerical Study of Cavitation Number Limitations for Hydrodynamic Cavitation Inception Prediction. Fluids 2022, 7, 198. [Google Scholar] [CrossRef]
  23. Zhao, L.; He, Z.; Zhao, W.; Yang, Q. Extensive Investigation of the Sap Flow of Maize Plants in an Oasis Farmland in the Middle Reach of the Heihe River, Northwest China. J Plant Res 2016, 129, 841–851. [Google Scholar] [CrossRef] [PubMed]
  24. Bibi, F.; Rahman, A. An Overview of Climate Change Impacts on Agriculture and Their Mitigation Strategies. Agriculture 2023, 13, 1508. [Google Scholar] [CrossRef]
  25. Lens, F.; Gleason, S.M.; Bortolami, G.; Brodersen, C.; Delzon, S.; Jansen, S. Functional Xylem Characteristics Associated with Drought-Induced Embolism in Angiosperms. New Phytol. 2022, 236, 2019–2036. [Google Scholar] [CrossRef] [PubMed]
  26. Rodriguez-Dominguez, C.M.; Carins Murphy, M.R.; Lucani, C.; Brodribb, T.J. Mapping Xylem Failure in Disparate Organs of Whole Plants Reveals Extreme Resistance in Olive Roots. New Phytol 2018, 218, 1025–1035. [Google Scholar] [CrossRef]
  27. Tardieu, F.; Simonneau, T.; Parent, B. Modelling the Coordination of the Controls of Stomatal Aperture, Transpiration, Leaf Growth, and Abscisic Acid: Update and Extension of the Tardieu–Davies Model. Journal of Experimental Botany 2015, 66, 2227–2237. [Google Scholar] [CrossRef]
  28. Venturas, M.D.; Sperry, J.S.; Love, D.M.; Frehner, E.H.; Allred, M.G.; Wang, Y.; Anderegg, W.R.L. A Stomatal Control Model Based on Optimization of Carbon Gain versus Hydraulic Risk Predicts Aspen Sapling Responses to Drought. New Phytol 2018, 220, 836–850. [Google Scholar] [CrossRef]
  29. Sperry, J.S.; Venturas, M.D.; Anderegg, W.R.L.; Mencuccini, M.; Mackay, D.S.; Wang, Y.; Love, D.M. Predicting Stomatal Responses to the Environment from the Optimization of Photosynthetic Gain and Hydraulic Cost: A Stomatal Optimization Model. Plant, Cell & Environment 2017, 40, 816–830. [Google Scholar] [CrossRef]
  30. Mencuccini, M. Modelling Water Fluxes in Plants: From Tissues to Biosphere. New Phytologist 2019. [Google Scholar] [CrossRef]
  31. Fan, D.-Y.; Dang, Q.-L.; Xu, C.-Y.; Jiang, C.-D.; Zhang, W.-F.; Xu, X.-W.; Yang, X.-F.; Zhang, S.-R. Stomatal Sensitivity to Vapor Pressure Deficit and the Loss of Hydraulic Conductivity Are Coordinated in Populus Euphratica, a Desert Phreatophyte Species. Front. Plant Sci. 2020, 11, 1248. [Google Scholar] [CrossRef]
  32. Phillips, N.G.; Oren, R.; Licata, J.; Linder, S. Time Series Diagnosis of Tree Hydraulic Characteristics. Tree Physiology 2004, 24, 879–890. [Google Scholar] [CrossRef]
  33. 36 10.1093@treephys@tpz070.Pdf.
  34. Giles, A.L.; Rowland, L.; Bittencourt, P.R.L.; Bartholomew, D.C.; Coughlin, I.; Costa, P.B.; Domingues, T.; Miatto, R.C.; Barros, F.V.; Ferreira, L.V.; et al. Small Understorey Trees Have Greater Capacity than Canopy Trees to Adjust Hydraulic Traits Following Prolonged Experimental Drought in a Tropical Forest. Tree Physiology 2022, 42, 537–556. [Google Scholar] [CrossRef]
  35. Wason, J.; Bouda, M.; Lee, E.F.; McElrone, A.J.; Phillips, R.J.; Shackel, K.A.; Matthews, M.A.; Brodersen, C. Xylem Network Connectivity and Embolism Spread in Grapevine( Vitis Vinifera L.). Plant Physiology 2021, 186, 373–387. [Google Scholar] [CrossRef]
  36. Shen, F. Analysis of Cavitation Processes in Xylem. JAMP 2020, 08, 1767–1778. [Google Scholar] [CrossRef]
  37. Shen, F.; Gao, R.; Liu, W.; Zhang, W. Physical Analysis of the Process of Cavitation in Xylem Sap. Tree Physiology 2002, 22, 655–659. [Google Scholar] [CrossRef]
  38. Shen, F.; Cheng, Y.; Zhang, L.; Gao, R.; Shao, X. Experimental Study of the Types of Cavitation by Air Seeding Using Light Microscopy. Tree Physiol 2015, 35, 1325–1332. [Google Scholar] [CrossRef] [PubMed]
  39. Huang, Jitang. Principles and Applications of Cavitation and Cavitation; Tsinghua University Press, 1991; ISBN 7-302-00670-9. [Google Scholar]
  40. Sperry, J.S.; Wang, Y.; Wolfe, B.T.; Mackay, D.S.; Anderegg, W.R.L.; McDowell, N.G.; Pockman, W.T. Pragmatic Hydraulic Theory Predicts Stomatal Responses to Climatic Water Deficits. New Phytol 2016, 212, 577–589. [Google Scholar] [CrossRef]
  41. Borghetti, M.; Grace, J.; Raschi, A. Water Transport in Plants under Climatic Stress; Cambridge University Press, 1993; ISBN 0-521-44219-2. [Google Scholar]
  42. Tyree, M.T.; Salleo, S.; Nardini, A.; Assunta Lo Gullo, M.; Mosca, R. Refilling of Embolized Vessels in Young Stems of Laurel. Do We Need a New Paradigm? Plant physiology 1999, 120, 11–22. [Google Scholar] [CrossRef]
  43. Yang, S.; Tyree, M.T. A Theoretical Model of Hydraulic Conductivity Recovery from Embolism with Comparison to Experimental Data on Acer Saccharum. Plant, Cell & Environment 1992, 15, 633–643. [Google Scholar] [CrossRef]
  44. Stohr, A.; Losch, R. Xylem Sap Flow and Drought Stress of Fraxinus Excelsior Saplings. Tree Physiology 2004, 24, 169–180. [Google Scholar] [CrossRef] [PubMed]
  45. Tyree, M.T.; Fiscus, E.L.; Wullschleger, S.; Dixon, M. Detection of Xylem Cavitation in Corn under Field Conditions. Plant Physiology 1986, 82, 597–599. [Google Scholar] [CrossRef] [PubMed]
  46. McCully, M.; Huang, C.; Ling, L. Daily Embolism and Refilling of Xylem Vessels in the Roots of Field-Grown Maize. The New Phytologist 1998, 138, 327–342. [Google Scholar] [CrossRef] [PubMed]
  47. Tyree, M.T.; Sperry, J.S. Vulnerability of Xylem to Cavitation and Embolism. Annual review of plant biology 1989, 40, 19–36. [Google Scholar] [CrossRef]
  48. Xiong, D.; Nadal, M. Linking Water Relations and Hydraulics with Photosynthesis. Plant J 2020, 101, 800–815. [Google Scholar] [CrossRef]
  49. McCully, M.E. Root Xylem Embolisms and Refilling. Relation to Water Potentials of Soil, Roots, and Leaves, and Osmotic Potentials of Root Xylem Sap. Plant physiology 1999, 119, 1001–1008. [Google Scholar] [CrossRef] [PubMed]
  50. Jones, H.G.; Sutherland, R.A. Stomatal Control of Xylem Embolism. Plant Cell Environ 1991, 14, 607–612. [Google Scholar] [CrossRef]
  51. Cochard, H.; Delzon, S.; Badel, E. X-Ray Microtomography (Micro-CT): A Reference Technology for High-Resolution Quantification of Xylem Embolism in Trees: A Reference Method for Xylem Embolism. Plant Cell Environ 2015, 38, 201–206. [Google Scholar] [CrossRef]
  52. Jia, Y.; Xiao, W.; Ye, Y.; Wang, X.; Liu, X.; Wang, G.; Li, G.; Wang, Y. Response of Photosynthetic Performance to Drought Duration and Re-Watering in Maize. Agronomy-Basel 2020, 10, 533. [Google Scholar] [CrossRef]
  53. Jiang, J.; Feng, S.; Ma, J.; Huo, Z.; Zhang, C. Irrigation Management for Spring Maize Grown on Saline Soil Based on SWAP Model. Field Crop. Res. 2016, 196, 85–97. [Google Scholar] [CrossRef]
Preprints 81676 g001
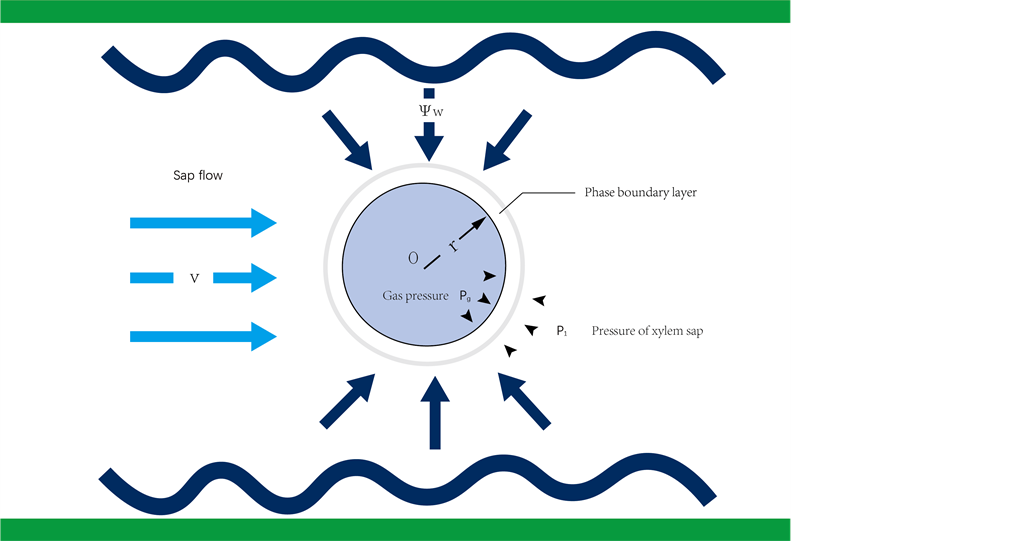
Figure 1. Illustrates the conditions for bubble generation within maize leaf xylem. V denotes the flow rate of sap within the xylem, Ψw signifies the pressure of the surrounding water potential, and r is the radius of the resulting bubble. Pg represents the gas pressure inside the air pie, and P1 is the pressure of the xylem sap, separated by the phase boundary layer.
Figure 1. Illustrates the conditions for bubble generation within maize leaf xylem. V denotes the flow rate of sap within the xylem, Ψw signifies the pressure of the surrounding water potential, and r is the radius of the resulting bubble. Pg represents the gas pressure inside the air pie, and P1 is the pressure of the xylem sap, separated by the phase boundary layer.
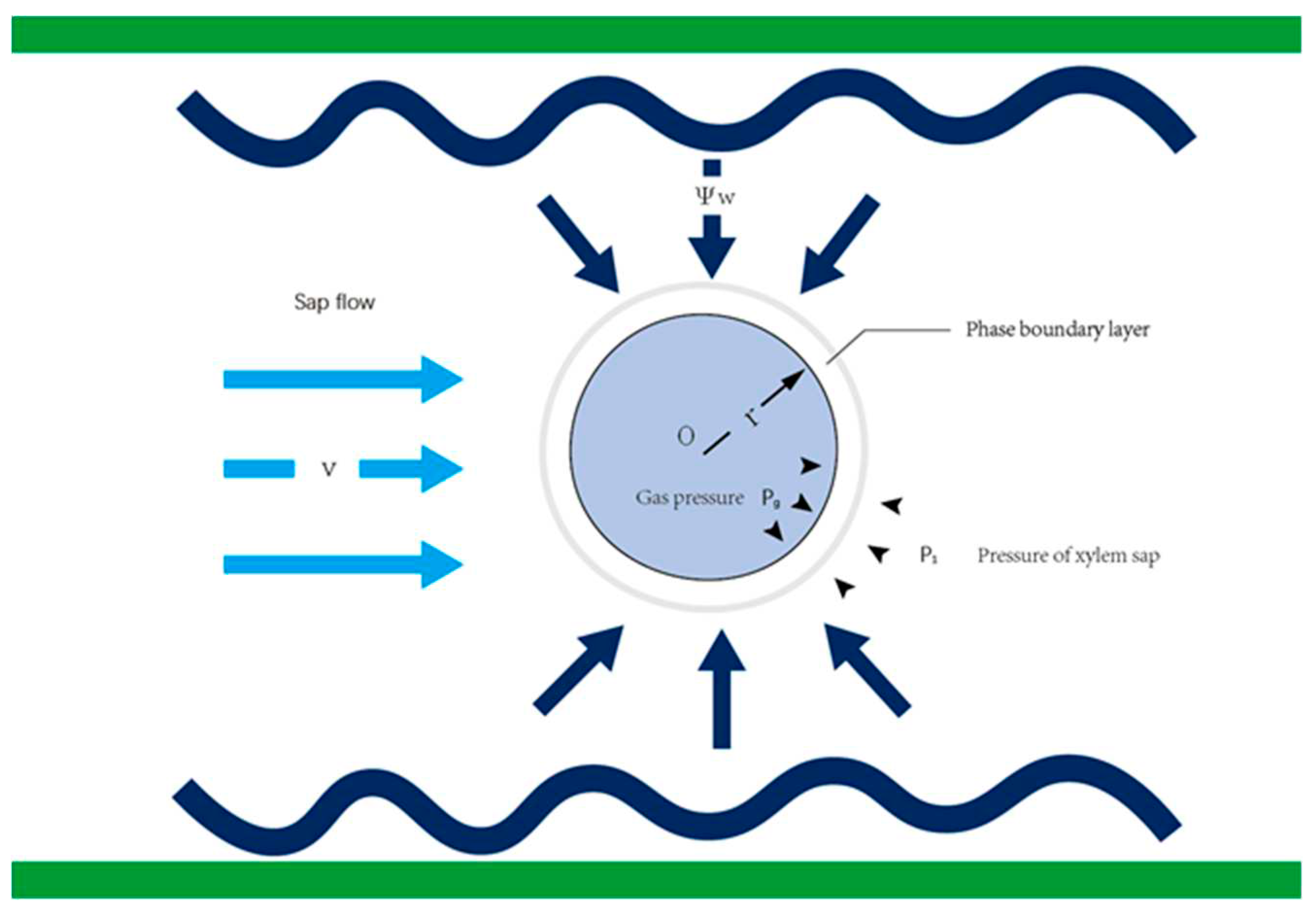
Preprints 81676 g001
Preprints 81676 g002
Figure 2. Investigative findings from trial maize plots in Mengrun Township. (a) Tally of leaf quantities in exemplar maize plots; (b) Examination of the principal lateral venation in maize foliage; (c) Cross-section study of the vascular bundles within maize leaf veins.
Figure 2. Investigative findings from trial maize plots in Mengrun Township. (a) Tally of leaf quantities in exemplar maize plots; (b) Examination of the principal lateral venation in maize foliage; (c) Cross-section study of the vascular bundles within maize leaf veins.
Preprints 81676 g002
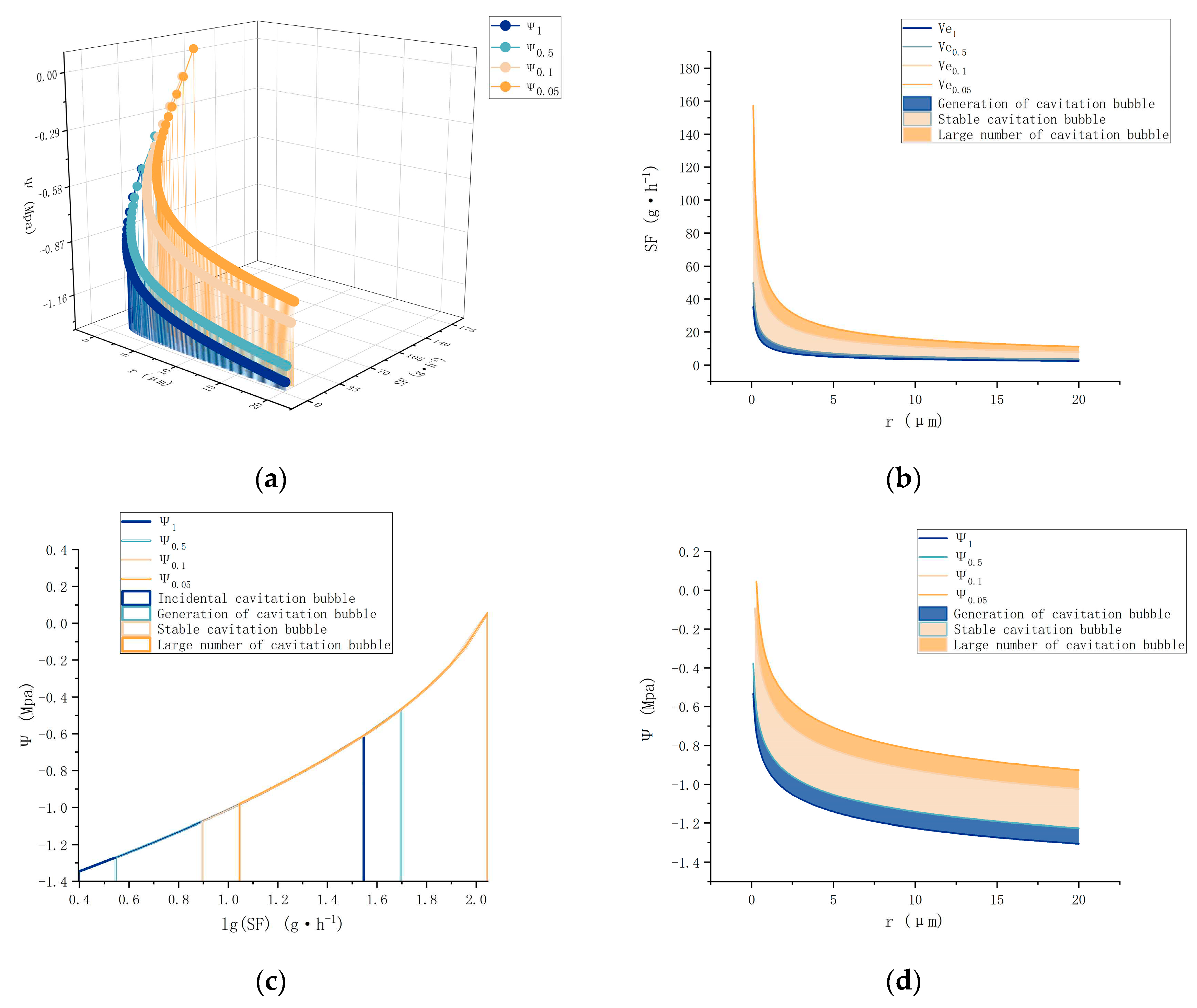
Preprints 81676 g003
Figure 3. Model demonstrating the interrelations between bubble radius, sap flow rate, and water potential in vascular xylem conduits within maize leaves. (a) A three-dimensional depiction of bubble radius, sap flow rate, and water potential under various simulated cavitation conditions. (b) The correlation between sap flow rate within the conduit and bubble radius under diverse cavitation parameters. (c)Depiction of varying sap flow rate intervals in relation to water potential under assorted cavitation states. (d) Demarcation of regions representing different cavitation states, based on bubble radius and water potential under distinct cavitation parameters.
Figure 3. Model demonstrating the interrelations between bubble radius, sap flow rate, and water potential in vascular xylem conduits within maize leaves. (a) A three-dimensional depiction of bubble radius, sap flow rate, and water potential under various simulated cavitation conditions. (b) The correlation between sap flow rate within the conduit and bubble radius under diverse cavitation parameters. (c)Depiction of varying sap flow rate intervals in relation to water potential under assorted cavitation states. (d) Demarcation of regions representing different cavitation states, based on bubble radius and water potential under distinct cavitation parameters.
Preprints 81676 g003
Preprints 81676 g004
Figure 4. (a) Correlation between Percentage Loss of Conductivity (PLC) and the water potential within maize leaves. (b) Mapping of the relationship between the derived model for maize leaves and the corresponding PLC, utilizing specific parameters.
Figure 4. (a) Correlation between Percentage Loss of Conductivity (PLC) and the water potential within maize leaves. (b) Mapping of the relationship between the derived model for maize leaves and the corresponding PLC, utilizing specific parameters.
Preprints 81676 g004
Preprints 81676 g005
Figure 5. Comparison of Water Potential in Maize Leaves under Physiological Conditions (CG), before Embolism (BE), and after Embolism (AE).
Figure 5. Comparison of Water Potential in Maize Leaves under Physiological Conditions (CG), before Embolism (BE), and after Embolism (AE).
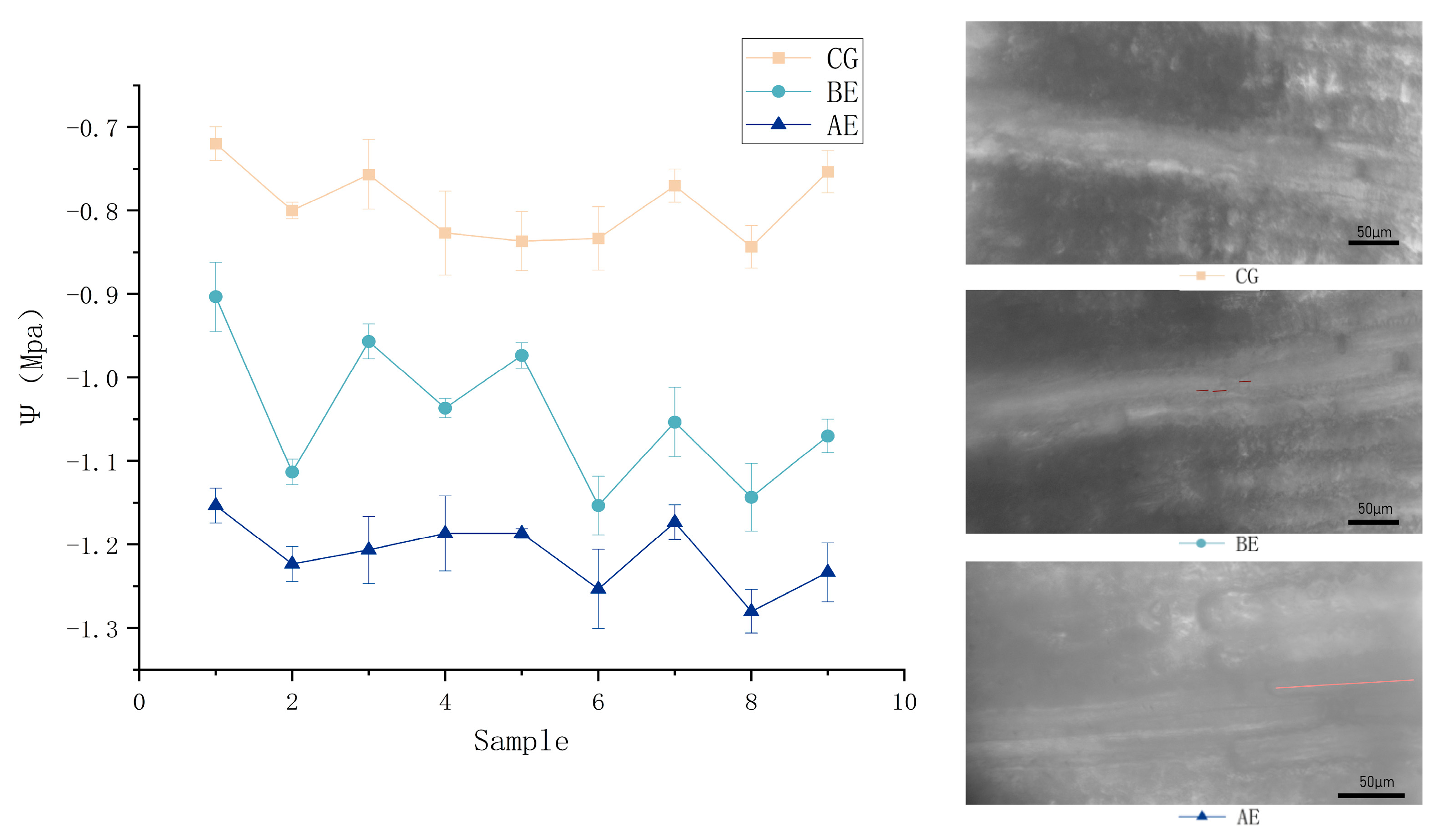
Preprints 81676 g005
Table 1. Climate conditions in the study area.
Table 1. Climate conditions in the study area.
Year Month Mean month air temperature (°C) Humidity range (%) Precipitation (mm) Mean wind speed (m s−1) Mean daily net radiation (W m−2)
2021 March 21.91 18.1-99.9 1.39 1.6 259.3
2022 March 23.12 25.4-99.9 79.33 1.6 206.1
2023 March 20.69 23.1-99.9 0.13 1.5 197.4
Table 2. An overview of growth characteristics, specifically leaf length, of a randomly selected sample of 21 maize plants observed from 2021 to 2023.
Table 2. An overview of growth characteristics, specifically leaf length, of a randomly selected sample of 21 maize plants observed from 2021 to 2023.
Year Number of leaves Number of veins Average leaf radius (μm) Maize leaf length(cm)
2021 12 45 66.02 ±2.10 74.95 ±1.21
9 38 42.01 ±3.33 56.50 ± 0.53
11 43 54.19 ±0.35 64.40 ±3.18
6 35 32.79 ±1.3 47.90 ±2.26
9 39 51.43 ±3.77 67.40 ±1.30
15 53 97.20 ±2.43 93.70 ± 2.11
12 48 62.36 ±1.27 66.40 ± 1.57
Average value 10.57 43 58.00 67.30
2022 11 45 69.03 ±0.98 78.40 ±0.43
7 34 27.64 ±1.85 41.55 ±3.53
8 35 33.98 ±1.24 49.60 ±1.73
10 38 41.72 ±3.79 56.10 ±3.12
12 47 69.29 ±1.43 75.35 ±1.83
7 29 23.12 ±1.26 40.75 ±0.86
10 40 49.11 ±2.36 62.75 ±1.48
Average value 9.29 38.29 44.84 57.80
2022 12 49 73.5 ±1.24 72.5 ±1.32
11 46 53.15 ±1.57 59.05 ±1.2
7 36 34.80 ±0.74 49.40 ±2.10
12 41 53.50 ±0.69 66.70 ±1.63
8 37 35.69 ±3.1 49.30 ±3.41
10 27 41.30 ±1.45 78.15 ±0.76
9 35 38.50 ±1.15 56.20 ±0.84
Average value 9.86 38.71 47.21 62.20
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated