Prerpints.org logo
Preprint
Article

Community-Based Matrix Factorization (CBMF) Approach for Enhancing Quality of Recommendations

Altmetrics

Downloads

98

Views

31

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

03 August 2023

Posted:

07 August 2023

You are already at the latest version

Alerts
Abstract
Matrix Factorization is a long established method employed for analyzing and extracting valuable insight recommendations from complex networks containing user ratings. The execution time and computational resources demanded by these algorithms pose limitations when confronted with large datasets. Community detection algorithms play a crucial role in identifying groups and communities within intricate networks. To overcome the challenge of extensive computing resources, we present a novel parallel computation framework utilizing community information available in the rating network. Our proposed approach named as Community-based Matrix Factorization(CBMF), parallelizes matrix factorization technique by dividing the network into communities using existing community detection algorithms. We prove that this parallel approach not only increases the quality of recommendations in connection with Root Mean Square Error (RMSE), but also yields substantial performance improvement. We empirically evaluate our idea on diverse datasets and present comprehensive experimental results. These results serve as empirical evidence of the effectiveness and performance gains offered by our parallel computation framework.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

To predict recommendations to the users based on past behavior and their preferences, a technique in recommender systems namely collaborative filtering is used [1]. The main objective is to suggest items or content to the users by considering their interactions or resemblances with other users. Due to the continuous growth in data availability and the interconnected nature of diverse systems, these techniques hold immense importance in revealing patterns, relationships, and significant insights [2].
Matrix Factorization (MF) is a technique utilized in collaborative filtering to break down a matrix of user-item ratings into lower-rank matrices capturing the latent factors, underlying the data [3,4]. The user-item rating matrix serves as a representation of user ratings assigned to different items [5]. The matrix is frequently sparse as users typically only rate a small subset of items. MF techniques strive to complete the missing entries in the matrix by decomposing it into lower-rank matrices, one capturing the user’s underlying preferences and the other reflecting the item’s latent characteristics [6]. The latent representations of users along with items can be used to estimate future ratings or calculate missing ratings once the matrix has been factorized.
In network analysis, community detection stands as a fundamental task, endeavoring to identify cohesive subsets of nodes, referred to as communities or modules within a network [7]. These communities in networks signify groups of nodes that display stronger interconnections amongst themselves compared to connections with nodes outside the community [8]. These communities provide insightful information on the structure, organization, and dynamics of complex systems [9,10]. The applications of community detection across various domains such as social network analysis, biological networks, online forums, and recommendation systems have garnered substantial attention [11]. Through the identification of communities, we gain insights into the underlying interaction patterns, discover influential groups, and develop a deeper comprehension of the network’s functionality [12].

1.1. Applications

Matrix Factorization techniques have been widely applied across diverse domains, demonstrating their versatility and effectiveness. Some of the notable applications of the matrix factorization techniques include
  • Natural Language Processing (NLP): Within the field of NLP, techniques for matrix factorization have been used in a variety of tasks in topic modeling, text classification, etc [13,14]. Through the decomposition of the document matrix, MF algorithms can reveal latent representations that effectively capture the underlying semantic structure of the textual data.
  • Social Network Analysis: MF techniques have been utilized in social network analysis to unveil communities of individuals sharing common interests or behaviors [15,16]. SVD++ facilitates the identification of friends, influencers, or interest-based communities by enhancing user experience and engagement on social media platforms. FANMF is used to uncover community structures and identify influential nodes within the network. FANMF can effectively detect the group of nodes by exposing hidden relationships and structures by factorizing them into non-negative adjacency matrices.
  • E-commerce: In the realm of e-commerce platforms, SVD++ is extensively utilized to deliver personalized product recommendations to users [17,18].By including implicit feedback, supplementary data, and user-item ratings, SVD++ can adeptly capture user preferences and item characteristics for accurate product recommendations [19].
  • Streaming Services: Streaming platforms including music or video services, SVD++ provide personalized content recommendations to the users. SVD++ significantly enhances the discovery and recommendation of relevant and captivating content. It ensures that the users are presented with content aligned with their individual tastes and preferences [20].
  • Image Processing: FANMF finds application in image processing tasks, where the image data is factored into non-negative matrices. By extraction, it improves image quality and facilitates the analysis of visual data. By decomposition, matrix factorization algorithms are capable of distinguishing noise from the underlying structure. It also completes missing parts, and extracts significant features for analysis and representation [21].
In essence, the applications of MF techniques have a broad scope of transforming the methods through which we analyze, comprehend, and leverage complex data [22]. The ongoing evolution of these techniques holds the potential to unlock fresh possibilities and propel advancements in numerous domains. It ultimately benefits individuals, organizations, and society at large.

2. Literature Review

In recent years, the MF method has garnered significant attention as a widely adopted and successful method for rating prediction in recommendation systems. The Netflix Prize competition, which was started in 2006, is one early piece of work noteworthy in relation to MF in recommender systems [23]. The fundamental matrix factorization model creates user and item latent feature matrices from the rating matrix, enhancing the accuracy of rating predictions through the understanding of possible connections between users and items.
As the information interconnection era has emerged, the basic MF model is no longer satisfied the demands of recommender systems. It thus leads to the emergence of numerous variants of this model. Excluding all the non-negative entries in latent features, a model Non-Negative Matrix Factorization (NMF) has been initiated by Paatero et al., and Tapper et al. in 1994 that improves the accuracy of the model [24]. R.Salakhuntidnov et al., and A.Mnih et al. in the year 2007 proposed Probabilistic Matrix Factorization (PMF) that utilizes probabilistic modeling to effectively capture uncertainties in user-item ratings, resulting in recommendations that are more reliable and precise [25]. The significance of the Singular Value Decomposition (SVD) technique is introduced by Eugenio Beltrami et al., and Camille Jordan et al. in 1857 and came into existence from 2006 [26]. The method has the ability to perform robust MF, enabling the identification of hidden features and effective dimensionality reduction in data analysis.
By integrating explicit and implicit feedback to enhance recommendation accuracy and personalization, Yehuda Koren et al. in the year 2008 introduced Advanced Singular Value Decomposition (SVD++) method [27]. Through the incorporation of user-item ratings and implicit feedback, SVD++ boosts the performance of the recommender systems, enabling better capture of user preferences and more effective recommendation generation. In 2015, Xiaohua Shi et al. introduced a method namely Pairwisely Constrained Nonnegative Symmetric Matrix Factorization (PCSNMF) that incorporates the symmetric community structures found in undirected networks but also leverages pairwise constraints derived from ground-truth group information [28]. By doing so, we enhance the accuracy of community detection. In 2017, Deep Matrix Factorization (DMF) is a significant technique introduced by Xiangnan He et al. that emerges the deep learning with MF [29]. This method enables the discovery of intricate patterns and the extraction of complex features from large-scale datasets. Kipf et al., and Welling et al. in the year 2018 combines the power of MF and graph convolutional neural network to capture both collaborative filtering patterns and graph structures in recommendation systems [30]. By incorporating the graph information, the recommendation accuracy is improved by leveraging the connectivity and relationships among users and items. In 2019, Factorized Asymmetric Non-Negative Matrix Factorization (FANMF) was introduced by Tosyali et al. by considering the asymmetric relationships between users and items [31]. It leads to enhanced recommendation quality, a deeper understanding of user preferences, and ultimately providing personalized user experiences in various data analysis tasks.
M. Girvan et al. and M. E. J. Newman et al. in 2002 proposed an algorithm namely Girvan-Neuman that is very significant because it uses edge betweenness centrality to iteratively remove edges and identify communities in a network [32]. In 2007 Raghavan et al., Albert et al., and Kumara et al. initiated a label propagation algorithm that is a straightforward and efficient approach, updating node labels iteratively based on the majority of their neighbors to effectively detect communities in a network [33]. Vincent D. Blondel et al., Jean-Loup Guillaume et al., Renaud Lambiotte et al., and Etienne Lefebvre et al. in 2008 proposed an algorithm Louvain that has the ability to efficiently optimize modularity, making it highly effective in detecting communities in large-scale networks while maintaining computational speed [34]. In 2011 by Pascal Pons et al.and Matthieu Latapy et al. introduced the Walktrap algorithm that is notable for its use of random walks to assess node similarities, providing an effective technique for locating communities in large networks [35]. The Leiden algorithm was bought up in 2019 by V.A.Traag et al., L.Waltman et al., and N. J. van Eck et al. to ensure there are connected communities, and iterative application results in a partition when local best assignments are made to all community subsets.

3. Methodology

In this work, we come up with a parallel framework for Matrix Factorization. This section first provides an elaborate exposition elucidating the various Matrix Factorization methods. Then discusses the community detection algorithms.

3.1. Matrix Factorization (MF)

In the early 2000 s , the concept of matrix factorization emerged from the field of linear algebra. It can be used in diverse domains like recommender systems and data analysis. Simon Funk’s work during the Netflix Prize competition in 2006 played a significant role in popularizing the use of matrix factorization algorithms for recommender systems [23].
In the MF method, we compute the latent features based on user-item interactions of which a matrix serves as a representation [36]. Ratings are used to describe the interactions between users and items in the matrix, which is created by placing people on one axis and items on the other [37]. The representation of the matrix is shown below.
r 11 . . r 1 b . . . . . . . . . . . . r m 1 . . r m n = m 11 . . m 1 k . . . . . . . . . . . . m a 1 . . m a k n 11 . . n 1 b . . . . . . . . . . . . n k 1 . . n k b
                             a × b                 a × k             k × b  a stands for users, b for items, and k for the number of features that were extracted. M is a matrix representing the latent features of the users, and N denotes the latent features of the items. The relation between R and R ˜ is shown in Equation 1.
R ≈ X Y T
R ˜ = X Y T
The user and item rating vectors are combined to create the original rating R as shown in Equation 2.
r a b ≈ m a n b T
The values of M and N are randomly distributed from 0 to 1. We compute the empty ratings in the matrix by minimization of the squared error as shown in Equation 3.
m i n ∑ a , b ( r a b − m a n b T ) 2
In order to avoid overfitting the squared error, the regularization term α is added as shown in Equation 4.
m i n ∑ a , b ( r a b − m a n b T ) 2 + α ( | | m a | | 2 + | | n b | | 2 )
where | | . | | is the frobenius norm. The approximation of this value is calculated using stochastic gradient descent or alternating least squares. For each rating in the training data, the prediction error is calculated using the stochastic gradient descent method as displayed in Equation 5.
e a b = r a b − m a n b T
Then update the values of n b and m a with β learning rate and α regularization constant is added as shown in Equation 6.
n b ⟵ n b + β ( e a b m a − α n b ) m a ⟵ m a + β ( e a b n b − α m a )
The dot product of the prediction matrix that is obtained and the latent feature matrices m a and n b as shown in Equation 7.
r ˜ = m a . n b
After computing the predicted rating matrix, the difference between the cells of R and R ˜ as shown in Equation 8 is computed as Root Mean Square (RMSE).
R M S E = 1 N ∑ r a b − r ˜ a b 2
where r a b is the original rating, r ˜ a b is the predicted rating, and N is the total number of predictions.

3.2. SVD++

It is an extension of the singular value decomposition method introduced by Yehuda Koren in 2008 [27]. He proposed this method as a part of his work improvement in the Netflix recommendation algorithm.
In the SVD++ method, implicit feedback is added to the user’s latent feature vector [38,39]. The implicit feedback P Q is added and is calculated as follows:
P Calculation:
In the P matrix, the values will be either 1 or 0. The value of P = [ p a b ] ∀ ( a , b ) is 1 if r a b is observed or else 0. Every non-zero entry in the P matrix is written as 1 | I i | which is a u × v matrix.
Q Calculation:
Q = [ q a b ] ∀ ( a , b ) which is similar to the item latent feature vector of order v × k .
Calculate the dot product of P and Q matrices and add it to the user latent feature matrix i.e., ( M + P Q ) . Then the deviation between the original rating R i.e., ( m a n b ) and the predicted rating matrix R ˜ i.e., ( ( m + p q ) a n b ) is computed as the RMSE value as shown in Eq. (8).

3.3. Factorized Asymmetric Non-Negative Matrix Factorization (FANMF)

In 2019, the FANMF method is introduced by Tosyali [31]. The main purpose of the FANMF method is to handle non-negative data that has an asymmetric nature. Data in the real world is often asymmetry, where the rows and columns are related in this way are not symmetrical [40]. In the FANMF method, a rating matrix is decomposed into two non-negative latent feature matrices. FANMF is different from the traditional methods, as it accommodates the feature matrices of different dimensions that enable to capture the of data that are asymmetric in nature. It also adds a sparsity constraint along with the non-negativity constraint, that contains only a limited number of non-zero elements.
FANMF extends NMF to asymmetric scenarios where the user and item bias are considered in addition to the user-item interactions to make the model more accurate and improve the recommendation quality. User item bias includes the inherent inclinations of users towards specific items or the inherent attractiveness of items to users, independent of their previous interactions or behaviors.
The original rating matrix is represented as the product of user and item rating vectors as shown in Equation 9.
r a b ≈ m a n b T
Update the values of M and N by using a multiplicative update algorithm that contains update values [41].
M = M · × ( ( R · / ( M × N + ( R = = 0 ) ) ) × N T ) N = N · × ( M T × ( R · / ( M × N + ( R = = 0 ) ) ) )
where M · × N is the dot product of M and N similarly M · /N is the dot division of M and N i.e., element wise division. M × N is the product of two matrices M and N. M T is the transpose of the matrix M. The term R = = 0 is included in the denominator to prevent division by zero.
Make the dot product of the updated latent feature matrices which is R ˜ . The deviation between the original and the predicted rating matrices is computed as RMSE value as shown in Equation 8.
In this work, we introduce parallelism in matrix factorization with the help of community information. Various community detection algorithms are available in the literature to divide a complex network into communities. The Girvan-Newman is one of the first popular algorithms that uses edge betweenness centrality to detect communities in networks, achieved through iterative removal of edges with high betweenness. The shortcoming of the above-mentioned algorithms is while it excels at identifying overlapping communities, it faces the drawback of being computationally expensive, particularly for large graphs, due to repeated edge removals and recalculations of betweenness. Louvain algorithm addresses these shortcomings by adopting an efficient approach centered around optimizing modularity. Through iterative modularity optimization with node movements, it achieves fast and scalable community detection, effectively capturing communities even in large-scale networks. Louvain’s superior optimization of modularity enables it to outperform Girvan-Newman in terms of speed and scalability, making it the preferred choice for real-world community detection tasks involving massive and complex networks. Therefore, we use the Louvain algorithm to divide the rating network into communities. Next section gives the details of Louvain.

3.4. Louvain Algorithm

The Louvain algorithm works effectively in covering large communities or groups that are densely interconnected in a network. It employs a modularity optimization process, iteratively refining the network’s community structure to maximize modularity.
Louvain algorithm has a 6 step procedure to find the appropriate communities. Each node in the initial step is attached to its own community. Next, rearrange the nodes between the communities that iteratively optimize the modularity score which elevates the standards of the community structure. By iteratively considering each node, evaluate the modularity score by relocating the nodes to nearby communities. It is followed until there is no change in the modularity score. A new graph is constructed by combining the nodes in each community by connecting the nodes and edges of different communities. All these steps are repeated until there is no change in the modularity score is observed.
The Louvain algorithm has become popular because of its efficiency in detecting communities in the network by achieving a high modularity score, all while maintaining computational efficiency [9]. A higher modularity score signifies a more robust community structure, characterized by tightly interconnected nodes within communities while having fewer connections between communities [42,43]. This indicates the algorithm’s successful identification of distinct and internally cohesive communities, demonstrating their meaningful organization within the network.

4. Proposed Method

In any type of MF method, the rating matrix is constructed by using users and items. The predicted rating matrix is obtained by using different update rules for the latent feature matrices in each kind of MF. The variation between the original and the predicted rating matrix is defined as the RMSE value. In order to run such huge rating matrices, the computational time and efficiency are very high. To reduce that, a combination of the MF method with the community detection algorithm "Louvain" is used.
The following procedure is carried out for using this approach as shown in Algorithm 1.
Algorithm 1: Community-based Matrix Factorization Algorithm (CBMF)
Preprints 81515 i001
A bipartite graph B G is constructed from users, and items in the dataset. The procedure followed for the construction of a bipartite graph is: Consider two sets of nodes, one for users and one for items. For each user node in one set, establish connections to every item node in the other set to represent the interactions or relationships between users and items in the dataset. If there exists a relation between the user and the item, there establishes an edge between the user and the item. For the bipartite graph that is constructed, the Louvain algorithm is applied and divided into communities. A rating matrix is formed by each community that is obtained from the graph. The size of the rating matrix is the same as the community size. For the rating matrices that are obtained, we apply MF (i.e., MF, SVD++, or FANMF) method, and by using the update rules we perform updation on the rating matrix, and the predicted rating matrices are formed. Combine all the predicted rating matrices into a single prediction rating matrix. RMSE value is calculated between the original rating matrix that is obtained before dividing into communities with the predicted rating matrix that is obtained. The flowchart of the overall approach is shown in Figure 1.
It is observed that we can get less RMSE value when dividing into communities by without division. At some times a constant RMSE value is maintained after a certain number of communities. The time taken for computing the RMSE value is also low due to parallel computation.
Hence, we can say that the computational time and efficiency are better as compared to only using the MF method. A combination of the MF method with community detection gives better results.

5. Time Complexity

In computer science and algorithm analysis, the definition of time complexity plays a vital role. By quantifying time complexity, we can compare various methods for problem-solving and assess their performance considering input sizes or limitations. This comparison facilitates algorithm selection and leads us to discover more efficient solutions. Let us consider the time complexities of our different matrix factorization methods (MF, SVD++, and FANMF) in this section.
For the Matrix Factorization method, let a × b be a rating matrix of a users, b items, and k latent features. The iterations are same for every method and are taken as constant. The time complexity required for calculating the MF method is typically considered to be O ( a b k ) [44]. The Louvain community detection method takes O ( a log a ) time complexity, where a is the graph’s number of nodes [45].
For a bipartite graph B G that contains users and items is taken as input for the louvain algorithm, the total of users and items will equal the number of nodes in the graph. Here, in this case, ( a + b ) will be the nodes in the graph. Therefore, the time complexity of the louvain algorithm will be O ( ( a + b ) log ( a + b ) ) . A flow graph G is constructed from the bipartite graph and is divided into appropriate community structures by using the louvain algorithm (say c 1 , c 2 , ⋯ , c c ). From each community, a small rating matrix will be obtained (say R 1 , R 2 , ⋯ , R c ). Apply MF time complexity for each rating matrix and we get a time complexity of O ( a 1 b 1 k 1 ) , O ( a 2 b 2 k 2 ) ,⋯, O ( a c b c k c ) , consider the maximum of all these time complexities. Suppose R p community rating matrix has the maximum value and the time complexity is O ( a p b p k p ) .
Hence, the overall time complexity for the MF method using the louvain community detection method is O ( ( a + b ) log ( a + b ) ) + O ( a p b p k p ) .
Similarly for SVD++ and FANMF methods, the time complexity is O ( a b k ) . Therefore the total time complexity that is required for the calculation of SVD++, and FANMF methods will be O ( ( a + b ) log ( a + b ) ) + O ( a p b p k p ) .

6. Dataset Statistics

To process our analysis, we have taken different datasets from different domains. Datasets namely Movie Lens-100K, Film Trust, Jester, Good Books, Wikilens, and Cell Phone Recommendation are taken. The dataset statistics of all these datasets are shown in Table 1.
All of these dataset’s distribution plots are displayed in Figure 2. The plots are drawn by taking the ratings, the X-axis represents users, while the Y-axis represents the count of each rating provided by those users. In the dataset movie lens-100K, the users are the people and the items are the movies in the dataset. The rating distribution is from 1 to 5 where the people have rated movies. It is observed in the plot that 34174 of the users had given a higher rating of four for the movies and a low rating of one is given by 6110 the users out of 100000 ratings. For the dataset film trust, the users are the people and the items are the films having a rating distribution from 0.5 to 4 where the people have rated films. It is observed in the plot that 9170 users had given a rating of five for films and a low rating of 0.5 is given by the users 1060 out of 35494 ratings. In the dataset jester, the users are the people and the items are jokes having a rating distribution from − 10 to + 10 where the people have rated the jokes. It is observed that there are above 4000 users who have rated + 10 in the dataset out of 1048575 ratings.
The wikilens dataset is shown in Figure 2 where the users are the people and the items are the wikipedia articles. The rating distribution is given from 0.5 to 5, where the users rated the items in wikipedia. From the plot, it is observed that a higher rating of four is given by 5721 users, and a low rating of 1.5 is given by 730 users out of 26936 ratings. In the dataset, good books people are the users, and the items are the books having a rating distribution from 1 to 5. The rating is given by the users on different books. From the plot, we can observe that 376467 of the users have given a higher rating of four for the books, and a low rating of one is given by 24676 users out of 1048575 ratings. For the cell phone recommendation dataset, the users are the people and the items are the cell phone id’s having a rating distribution from 1 to 10. The ratings are given by people on different cell phone id’s. From the plot, it is observed that a higher rating of eight is given by 196 users, and a low rating of three is given by 30 users out of 990 ratings.
In community detection algorithms, modularity plays a significant impact in determining the standard of the communities that are formed. Girvan and Neuman introduced the modularity measure to assess the standards of the communities that are formed and defined modularity as
G = 1 2 m ∑ ( i , j ) A i j − k i k j 2 m δ c i , c j
where m is the total number of edges in the graph, A i j is the edge weight between the nodes i and j, k i and k j are the degree of nodes i and j respectively, c i , c j are the communities to which nodes i and j belongs and, δ ( c i , c j ) is the Kronecker delta function which is equal to 1 if c i = c j and 0 otherwise. The term [ A i j − k i k j 2 m ] represents the difference between the observed number of edges between the nodes i and j and the expected number of edges under a null model where edges are placed at random. The values of modularity(G) varies between − 1 to + 1 .
Figure 3 shows the modularity score that is obtained from six different datasets namely Movie Lens-100K, Film Trust, Jester, Wikilens, Good Books, and Cell Phone Recommendation for Louvain algorithm. It is observed from all the datasets that, the modularity score is increasing as the communities are increased and maintained constant after a certain number of communities. The highest modularity score is maintained by the wikilens dataset, and the lowest modularity score is given by the movie lens-100K dataset. The time taken for calculating the modularity score is shown in Table 2.

7. Result Analysis

This section presents a series of experiments designed to demonstrate the validity of the hypothesis proposed in the paper. Using the Louvain community detection algorithm, three different matrix factorization methods (MF, SVD++, and FANMF) are employed to predict the missing entries in the rating matrix across six distinct datasets as shown in Table 1.
The computation of the root mean square error (RMSE) involves varying the number of latent features at values of k = 2 , 10 , 20 , 30 , 50 . Considering the random nature of the Louvain algorithm, each MF method is iterated for 25 communities and 25 iterations. The evaluation of different patterns in RMSE values, along with the total time taken to assess the MF method for six datasets is presented. The resulting graph depicts the relationship between the number of communities on the X-axis and the corresponding RMSE value on the Y-axis. Given that the cell phone recommendation dataset comprises only 99 users and 33 items, the value of k should be the minimum of number of users and items. Therefore, the iteration for k is limited to 30.
Figure 4 illustrates the variation in RMSE values across six distinct datasets when employing the MF method with different k values on a set of 25 communities. A notable observation from the graph is that, in all datasets, the absence of the Louvain algorithm results in the highest RMSE value when c = 1 . However, as the number of communities increases through the utilization of the Louvain algorithm i.e., c = 2 , 3 , ⋯ , 25 , a decline in the RMSE value is observed. Notably, the movie lens-100K, good books, and cell phone recommendation datasets exhibit an increase in the RMSE value with higher k values. Conversely, in the film trust and jester datasets, the RMSE value stabilizes after reaching a certain number of communities, regardless of the k value. Furthermore, in the wikilens dataset, there exhibit a constant relationship between the RMSE value for different communities as well as the k values. Overall, it is evident that the MF method consistently yields better RMSE values with lower k values across all datasets.
Figure 5 displays the computational time required to execute the MF method on six distinct datasets, employing different k values across a set of 25 communities. Across all datasets, a noticeable observation is that the computation time for the MF method, without the utilization of community division, exceeds that of the method with community division. As the number of communities increases, a reduction in computational time is observed. Interestingly, the evaluation time of the method remains constant as the number of communities expands, regardless of the specific k values employed.
Figure 6 presents the RMSE values across six distinct datasets when employing the SVD++ method with varying k values on a set of 25 communities. Notably, at c = 1 , a significantly high RMSE value is observed across all datasets. However, as the communities are divided, a decline in the RMSE value is observed, reaching a stable state after a certain number of communities. It is worth noting that in the SVD++ method, subtle variations in the RMSE value can be observed for different k values across all datasets.
Figure 7 displays the computational time required to execute the SVD++ method on six distinct datasets, employing different k values across a set of 25 communities. Noteworthy observations can be made across various datasets. In the movie lens-100K and good books datasets, an increase in the number of communities leads to a decrease in the evaluation time of the method. The maximum evaluation time is observed at c = 1 . Conversely, in the jester dataset, the maximum time is taken to evaluate the SVD++ method at c value 1, with slight fluctuations in time as the communities increase. Furthermore, for the film trust, wikilens, and cell phone recommendation datasets, it is observed that initially, evaluating the method without dividing into communities requires less time compared to the division into communities. However, after reaching a certain number of community divisions (i.e., k = 18 for film trust and wikilens datasets), the evaluation time becomes less than that at the time taken without community division and remains constant. Similarly, in the case of the cell phone recommendation dataset, the evaluation time becomes less than that at c value 1, and starting from c value 7 constant time is maintained for evaluation.
The obtained RMSE values from applying the FANMF method to six distinct datasets, using different values of k across a set of 25 communities are illustrated in Figure 8. In all datasets, it is evident that increasing the k value results in a decrease in the RMSE, regardless of the specific communities. Significantly, in the film trust, wikilens, and cell phone recommendation datasets, it is notable that the RMSE values stabilize after a certain number of communities. This stability is observed across all k values, indicating a consistent RMSE value. Moreover, across all datasets, it can be observed that a higher number of latent features leads to lower RMSE values when employing the FANMF method.
The computational time needed to run the FANMF method on six different datasets using various k values over a set of 25 communities is shown in Figure 9. A notable observation across all datasets is that the computation time for the community 2 exceeds that of the community 1. However, after reaching a certain number of communities, the computation time decreases compared to the c = 1 community for the film trust, wikilens, and good books datasets. Conversely, for the movie lens-100K and jester datasets, a constant computation time is maintained, which is higher than that of the c = 1 community.

8. Conclusions

In this study, we have delved into the realm of parallel computation. We proposed Community based Matrix Factorization(CBMF), which parallelizes matrix factorization utilizing community information. The experimental results obtained from our study provide compelling evidence of the scalability and speedup attained through CBMF, surpassing the performance of sequential implementations. These findings underscore the immense potential of parallel computation in effectively tackling the resources in the distributed environment. Looking ahead, the introduction of our parallel computation framework unlocks fresh opportunities for the efficient processing of large datasets. It empowers researchers and practitioners to extract valuable insights from intricate networks. This framework serves as a stepping stone for future advancements in providing accurate recommendations across diverse domains. It lays the foundation for future innovations and break-through in the realm of data-driven solutions.

Author Contributions

Concept and methodology by ST, MKE and TJL. ST compiled the primary data, implemented the model, and ran the simulations. Findings, Validation, and analysis by ST, MKE and TJL. ST and MKE wrote the manuscript. All authors have read and approved to the published version of the manuscript.

Funding

There is no external funding for this work.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

All the authors stated there is no conflict of interest.

Abbreviations

Abbreviations used in this paper are as follows:
BG Bipartite Graph
DMF Deep Matrix Factorization
FANMF Factorized Asymmetric Non-Negative Matrix Factorization
MF Matrix Factorization
NLP Natural Language Processing
NMF Non-Negative Matrix Factorization
PCSNMF Pairwisely Constrained Nonnegative Symmetric Matrix Factorization
RMSE Root Mean Square Error
SVD++ Advanced Singular Value Decomposition

References

  1. Adomavicius, G.; Tuzhilin, A. Toward the next generation of recommender systems: A survey of the state-of-the-art and possible extensions. IEEE transactions on knowledge and data engineering 2005, 17, 734–749. [Google Scholar] [CrossRef]
  2. Felfernig, A.; Jeran, M.; Ninaus, G.; Reinfrank, F.; Reiterer, S.; Stettinger, M. Basic approaches in recommendation systems. Recommendation Systems in Software Engineering 2014, 15–37. [Google Scholar] [CrossRef]
  3. Hintz, J. Matrix Factorization for Collaborative Filtering Recommender Systems. 2015. [Google Scholar]
  4. kumar Bokde, D.; Girase, S.; Mukhopadhyay, D. Role of matrix factorization model in collaborative filtering algorithm: A survey. CoRR, abs/1503.07475 2015. [Google Scholar]
  5. Koren, Y.; Bell, R.; Volinsky, C. Matrix factorization techniques for recommender systems. Computer 2009, 42, 30–37. [Google Scholar] [CrossRef]
  6. Mehta, R.; Rana, K. A review on matrix factorization techniques in recommender systems. In Proceedings of the 2017 2nd International Conference on Communication Systems, Computing and IT Applications (CSCITA), Mumbai, India, 7–8 April 2017; 274, pp. 269–274. [Google Scholar]
  7. Abdrabbah, S.B.; Ayachi, R.; Amor, N.B. Collaborative filtering based on dynamic community detection. Dynamic Networks and Knowledge Discovery 2014, 85. [Google Scholar]
  8. Kumar, P.; Chawla, P.; Rana, A. A review on community detection algorithms in social networks. In Proceedings of the 2018 4th International Conference on Applied and Theoretical Computing and Communication Technology (iCATccT), Mangalore, India, 6–8 September 2018; pp. 304–309. [Google Scholar]
  9. Bedi, P.; Sharma, C. Community detection in social networks. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery 2016, 6, 115–135. [Google Scholar] [CrossRef]
  10. Du, N.; Wu, B.; Pei, X.; Wang, B.; Xu, L. Community detection in large-scale social networks. In Proceedings of the 9th WebKDD and 1st SNA-KDD 2007 workshop on Web mining and social network analysis; 2007; pp. 16–25. [Google Scholar]
  11. Karataş, A.; Şahin, S. Application areas of community detection: A review. In Proceedings of the 2018 International congress on big data, deep learning and fighting cyber terrorism (IBIGDELFT); 2018; pp. 65–70. [Google Scholar]
  12. Lalwani, D.; Somayajulu, D.V.; Krishna, P.R. A community driven social recommendation system. In Proceedings of the 2015 IEEE International conference on big data (big data); 2015; pp. 821–826. [Google Scholar]
  13. Guo, W.; Gao, H.; Shi, J.; Long, B.; Zhang, L.; Chen, B.C.; Agarwal, D. Deep natural language processing for search and recommender systems. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining; 2019; pp. 3199–3200. [Google Scholar]
  14. Musto, C.; de Gemmis, M.; Lops, P.; Semeraro, G. Generating post hoc review-based natural language justifications for recommender systems. User Modeling and User-Adapted Interaction 2021, 31, 629–673. [Google Scholar] [CrossRef]
  15. Chen, S.; Owusu, S.; Zhou, L. Social network based recommendation systems: A short survey. In Proceedings of the 2013 international conference on social computing; 2013; pp. 882–885. [Google Scholar]
  16. Sun, Z.; Han, L.; Huang, W.; Wang, X.; Zeng, X.; Wang, M.; Yan, H. Recommender systems based on social networks. Journal of Systems and Software 2015, 99, 109–119. [Google Scholar] [CrossRef]
  17. Kim, J.K.; Cho, Y.H.; Kim, W.J.; Kim, J.R.; Suh, J.H. A personalized recommendation procedure for Internet shopping support. Electronic commerce research and applications 2002, 1, 301–313. [Google Scholar] [CrossRef]
  18. Wei, K.; Huang, J.; Fu, S. A survey of e-commerce recommender systems. In Proceedings of the 2007 international conference on service systems and service management; 2007; pp. 1–5. [Google Scholar]
  19. Kim, K.j.; Ahn, H. A recommender system using GA K-means clustering in an online shopping market. Expert systems with applications 2008, 34, 1200–1209. [Google Scholar] [CrossRef]
  20. Hasan, M.R.; Jha, A.K.; Liu, Y. Excessive use of online video streaming services: Impact of recommender system use, psychological factors, and motives. Computers in Human Behavior 2018, 80, 220–228. [Google Scholar] [CrossRef]
  21. Park, D.H.; Kim, H.K.; Choi, I.Y.; Kim, J.K. A literature review and classification of recommender systems research. Expert systems with applications 2012, 39, 10059–10072. [Google Scholar] [CrossRef]
  22. Isinkaye, F.O. Matrix factorization in recommender systems: algorithms, applications, and peculiar challenges. IETE Journal of Research 2021, 1–14. [Google Scholar] [CrossRef]
  23. Hallinan, B.; Striphas, T. Recommended for you: The Netflix Prize and the production of algorithmic culture. New media & society 2016, 18, 117–137. [Google Scholar]
  24. Paatero, P.; Tapper, U. Positive matrix factorization: A non-negative factor model with optimal utilization of error estimates of data values. Environmetrics 1994, 5, 111–126. [Google Scholar] [CrossRef]
  25. Mnih, A.; Salakhutdinov, R.R. Probabilistic matrix factorization. Advances in neural information processing systems 2007, 20. [Google Scholar]
  26. Mastorakis, N.E. The singular value decomposition (svd) in tensors (multidimensional arrays) as an optimization problem. solution via genetic algorithms and method of nelder-mead. WSEAS Transactions on Systems 2007, 6, 17–23. [Google Scholar]
  27. Hu, Y.; Koren, Y.; Volinsky, C. Collaborative filtering for implicit feedback datasets. In Proceedings of the 2008 Eighth IEEE international conference on data mining; 2008; pp. 263–272. [Google Scholar]
  28. Shi, X.; Lu, H.; He, Y.; He, S. Community detection in social network with pairwisely constrained symmetric non-negative matrix factorization. In Proceedings of the 2015 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining; 2015; pp. 541–546. [Google Scholar]
  29. Xue, H.J.; Dai, X.; Zhang, J.; Huang, S.; Chen, J. Deep matrix factorization models for recommender systems. IJCAI 2017, 17, 3203–3209. [Google Scholar]
  30. Schlichtkrull, M.; Kipf, T.N.; Bloem, P.; Van Den Berg, R.; Titov, I.; Welling, M. Modeling relational data with graph convolutional networks. In Proceedings of the Semantic Web: 15th International Conference, ESWC 2018, Heraklion, Crete, Greece, 3–7 June 2018; pp. 593–607. [Google Scholar]
  31. Tosyali, A.; Kim, J.; Choi, J.; Jeong, M.K. Regularized asymmetric nonnegative matrix factorization for clustering in directed networks. Pattern Recognition Letters 2019, 125, 750–757. [Google Scholar] [CrossRef]
  32. Girvan, M.; Newman, M.E. Community structure in social and biological networks. Proceedings of the national academy of sciences 2002, 99, 7821–7826. [Google Scholar] [CrossRef]
  33. Raghavan, U.N.; Albert, R.; Kumara, S. Near linear time algorithm to detect community structures in large-scale networks. Physical review E 2007, 76, 036106. [Google Scholar] [CrossRef] [PubMed]
  34. Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. Journal of statistical mechanics: theory and experiment 2008, 2008, P10008. [Google Scholar] [CrossRef]
  35. Pons, P.; Latapy, M. Post-processing hierarchical community structures: Quality improvements and multi-scale view. Theoretical Computer Science 2011, 412, 892–900. [Google Scholar] [CrossRef]
  36. Singh, A.P.; Gordon, G.J. A unified view of matrix factorization models. In Proceedings of the Machine Learning and Knowledge Discovery in Databases: European Conference, ECML PKDD 2008, Antwerp, Belgium, 15–19 September 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 358–373. [Google Scholar]
  37. Ivarsson, J.; Lindgren, M. Movie recommendations using matrix factorization. 2016. [Google Scholar]
  38. Kumar, R.; Verma, B.; Rastogi, S.S. Social popularity based SVD++ recommender system. International Journal of Computer Applications 2014, 87. [Google Scholar] [CrossRef]
  39. Rendle, S. Factorization machines. In Proceedings of the 2010 IEEE International conference on data mining; 2010; pp. 995–1000. [Google Scholar]
  40. Hosseinzadeh Aghdam, M.; Daryaie Zanjani, M. A novel regularized asymmetric non-negative matrix factorization for text clustering. 2021. [Google Scholar]
  41. Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef]
  42. Alzahrani, T.; Horadam, K.J. Community detection in bipartite networks: Algorithms and case studies. In Complex systems and networks: Dynamics, controls and applications; 2015; pp. 25–50. [Google Scholar]
  43. Gupta, S.; Singh, D.P. Recent trends on community detection algorithms: A survey. Modern Physics Letters B 2020, 34, 2050408. [Google Scholar] [CrossRef]
  44. He, X.; Zhang, H.; Kan, M.Y.; Chua, T.S. Fast matrix factorization for online recommendation with implicit feedback. In Proceedings of the 39th International ACM SIGIR conference on Research and Development in Information Retrieval; 2016; pp. 549–558. [Google Scholar]
  45. Seifikar, M.; Farzi, S.; Barati, M. C-blondel: an efficient louvain-based dynamic community detection algorithm. IEEE Transactions on Computational Social Systems 2020, 7, 308–318. [Google Scholar] [CrossRef]
Preprints 81515 g001
Figure 1. Community-based Matrix Factorization (CBMF) framework.
Figure 1. Community-based Matrix Factorization (CBMF) framework.
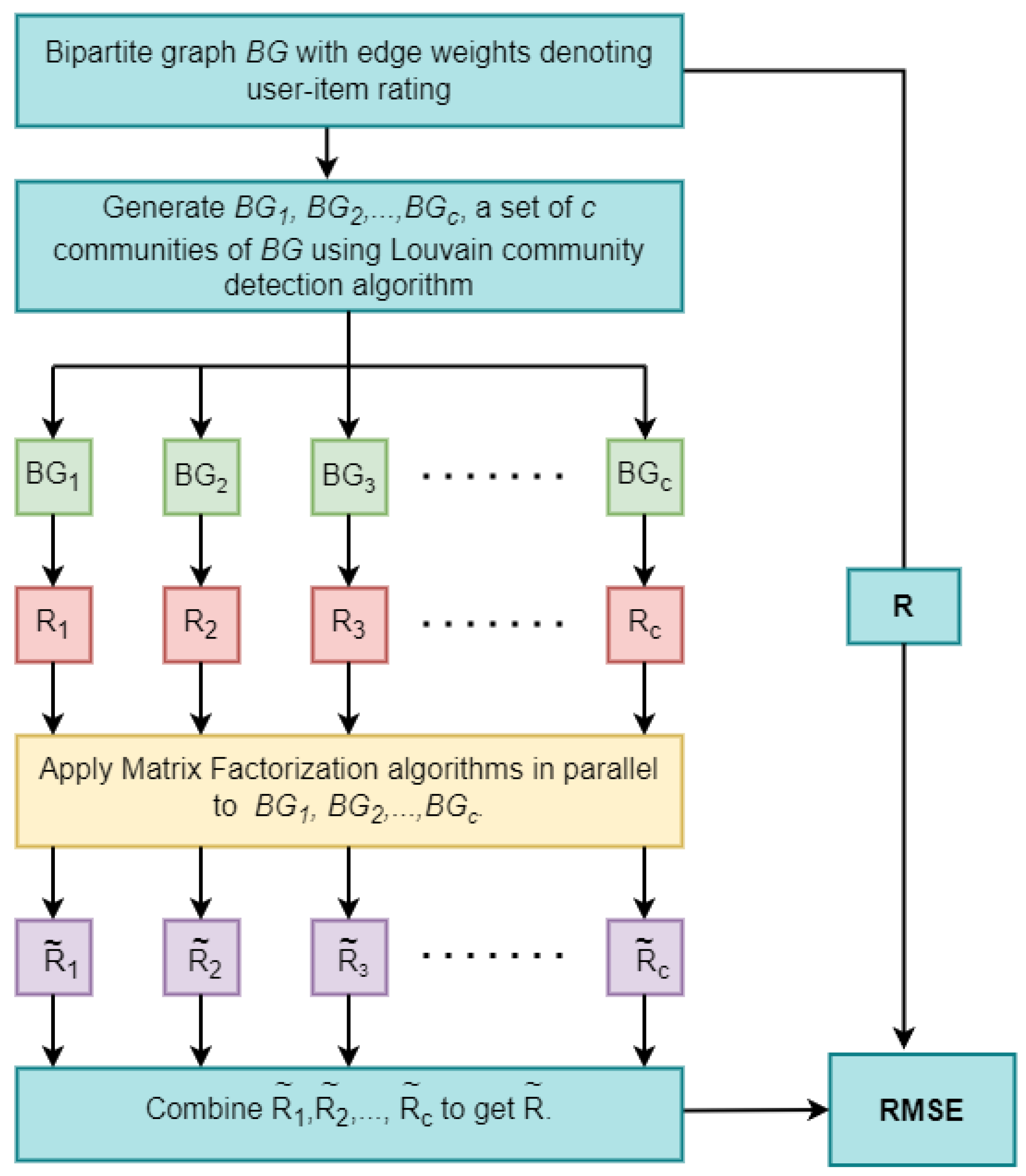
Preprints 81515 g001
Preprints 81515 g002
Figure 2. Rating plots distribution for six different datasets namely Movie Lens-100K, Film Trust, Jester, Wikilens, Good Books, and Cell Phone Recommendation
Figure 2. Rating plots distribution for six different datasets namely Movie Lens-100K, Film Trust, Jester, Wikilens, Good Books, and Cell Phone Recommendation
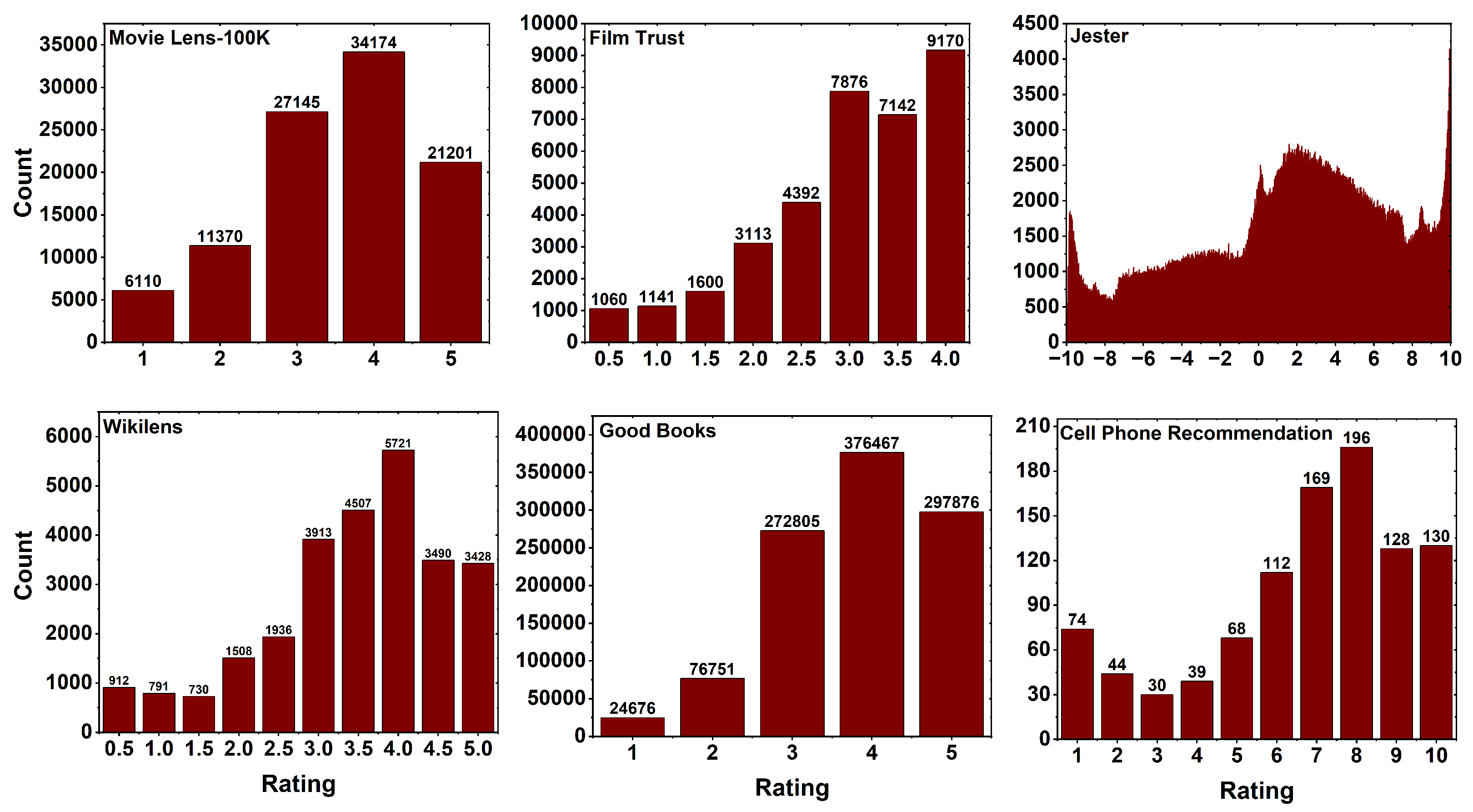
Preprints 81515 g002
Preprints 81515 g003
Figure 3. Modularity performance for six different datasets namely Movie Lens-100K, Film Trust, Jester, Wikilens, Good Books, and Cell Phone Recommendation for the Louvain algorithm.
Figure 3. Modularity performance for six different datasets namely Movie Lens-100K, Film Trust, Jester, Wikilens, Good Books, and Cell Phone Recommendation for the Louvain algorithm.
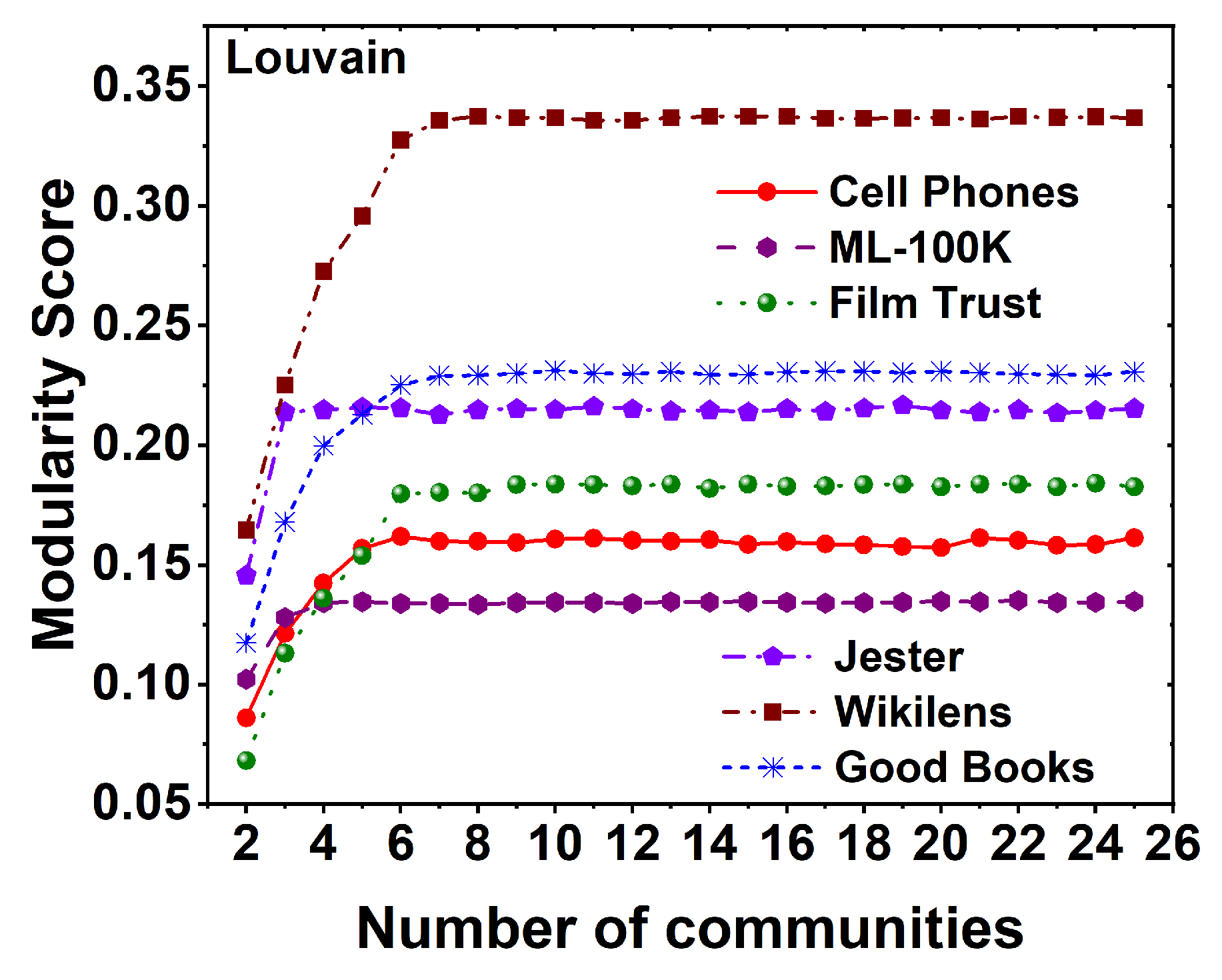
Preprints 81515 g003
Preprints 81515 g004
Figure 4. RMSE plots using MF method for six different datasets namely Movie Lens-100K, Film Trust, Jester, Wikilens, Good Books, and Cell Phone Recommendation with 25 communities and different k values.
Figure 4. RMSE plots using MF method for six different datasets namely Movie Lens-100K, Film Trust, Jester, Wikilens, Good Books, and Cell Phone Recommendation with 25 communities and different k values.
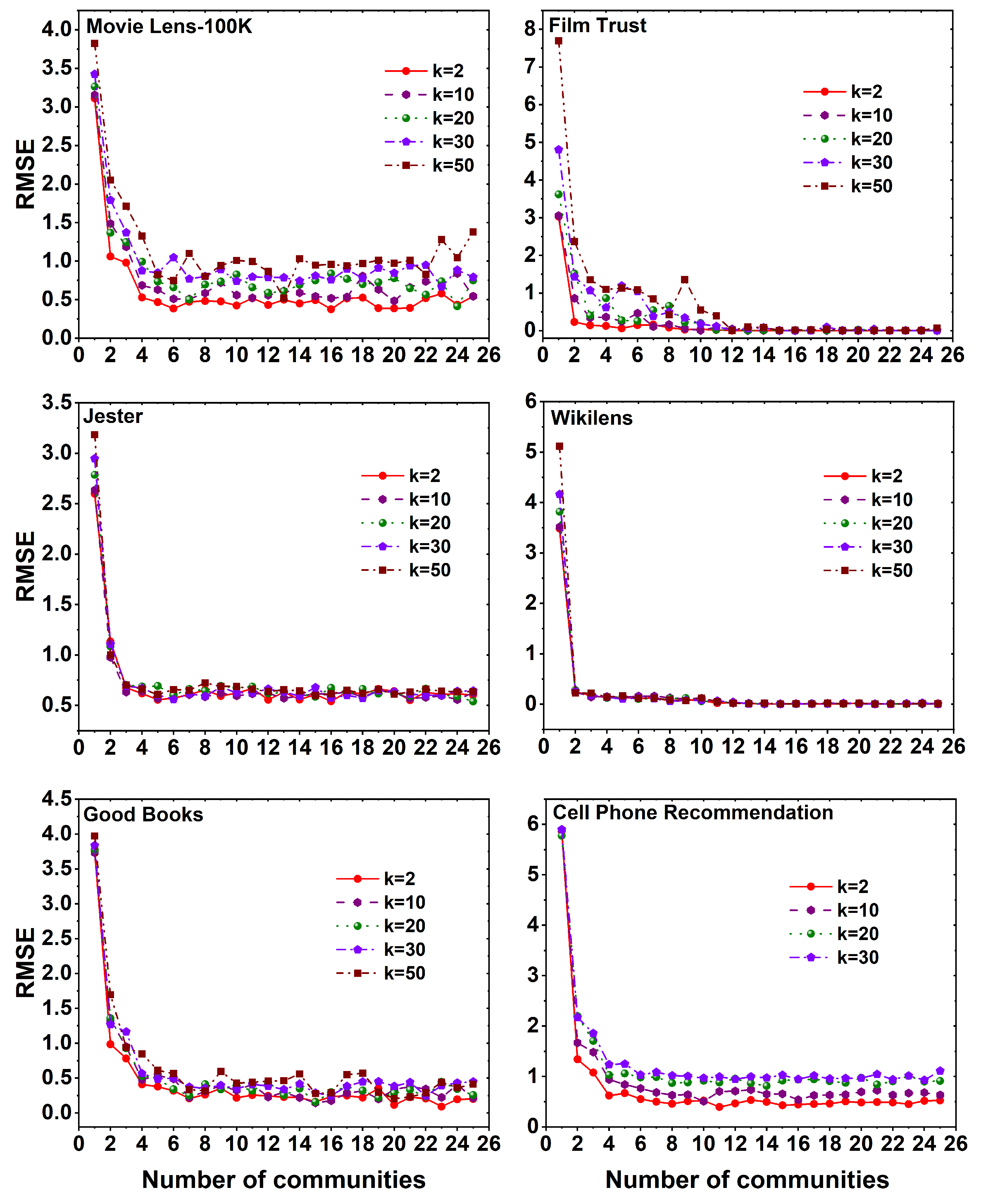
Preprints 81515 g004
Preprints 81515 g005
Figure 5. Time taken to calculate MF method for six different datasets namely Movie Lens-100K, Film Trust, Jester, Wikilens, Good Books, and Cell Phone Recommendation with 25 communities.
Figure 5. Time taken to calculate MF method for six different datasets namely Movie Lens-100K, Film Trust, Jester, Wikilens, Good Books, and Cell Phone Recommendation with 25 communities.
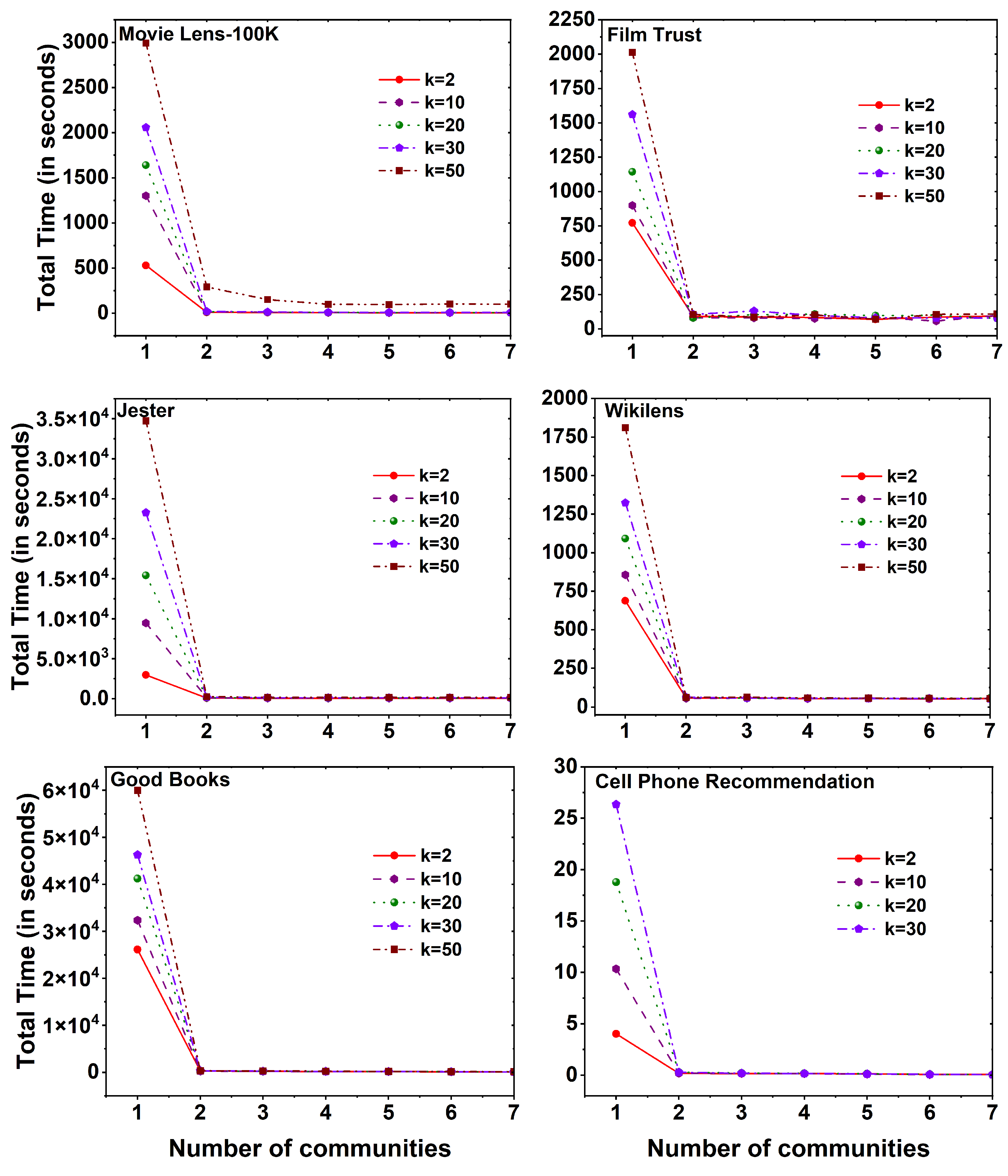
Preprints 81515 g005
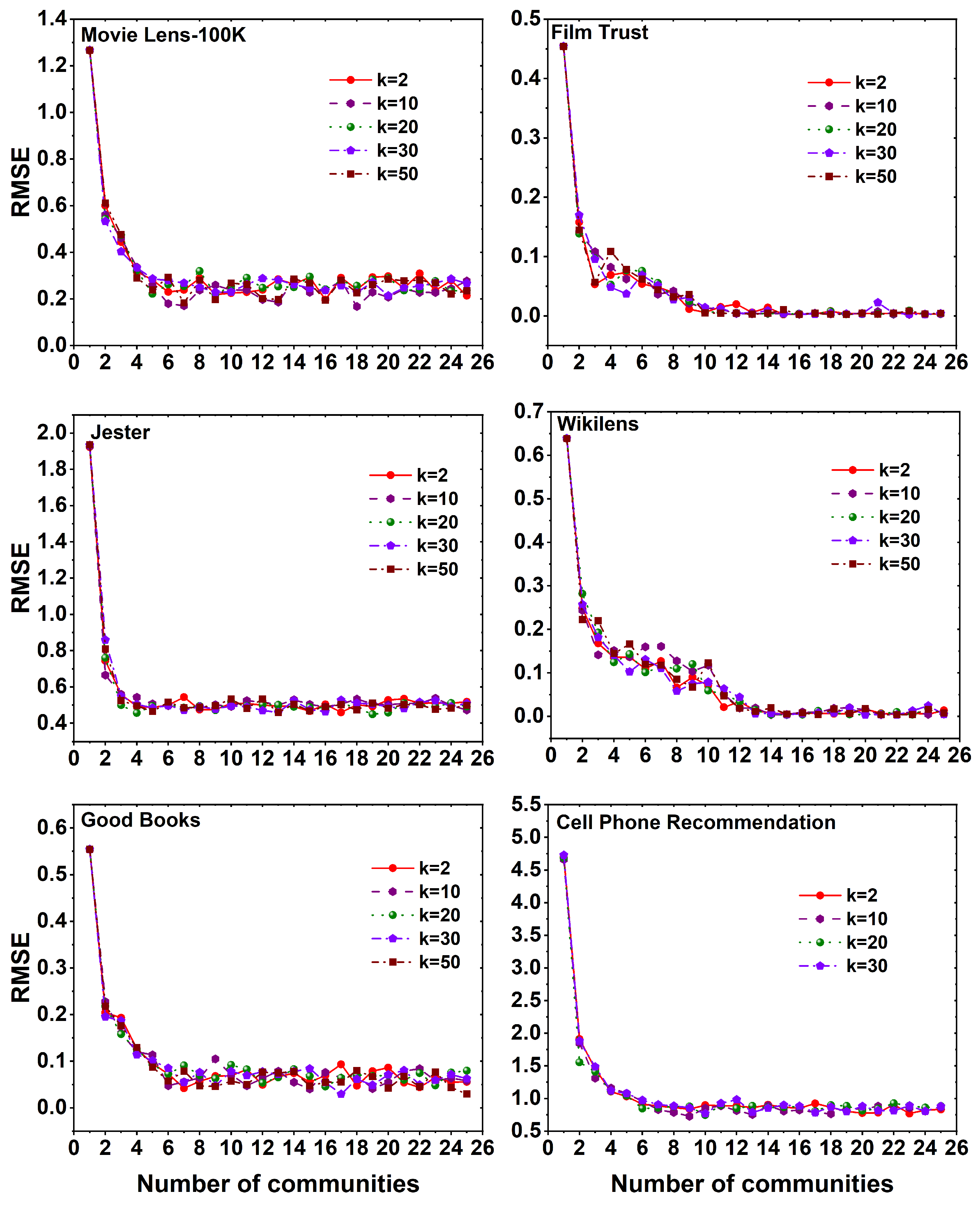
Preprints 81515 g006
Figure 6. RMSE plots using SVD++ method for six different datasets namely Movie Lens-100K, Film Trust, Jester, Wikilens, Good Books, and Cell Phone Recommendation with 25 communities.
Figure 6. RMSE plots using SVD++ method for six different datasets namely Movie Lens-100K, Film Trust, Jester, Wikilens, Good Books, and Cell Phone Recommendation with 25 communities.
Preprints 81515 g006
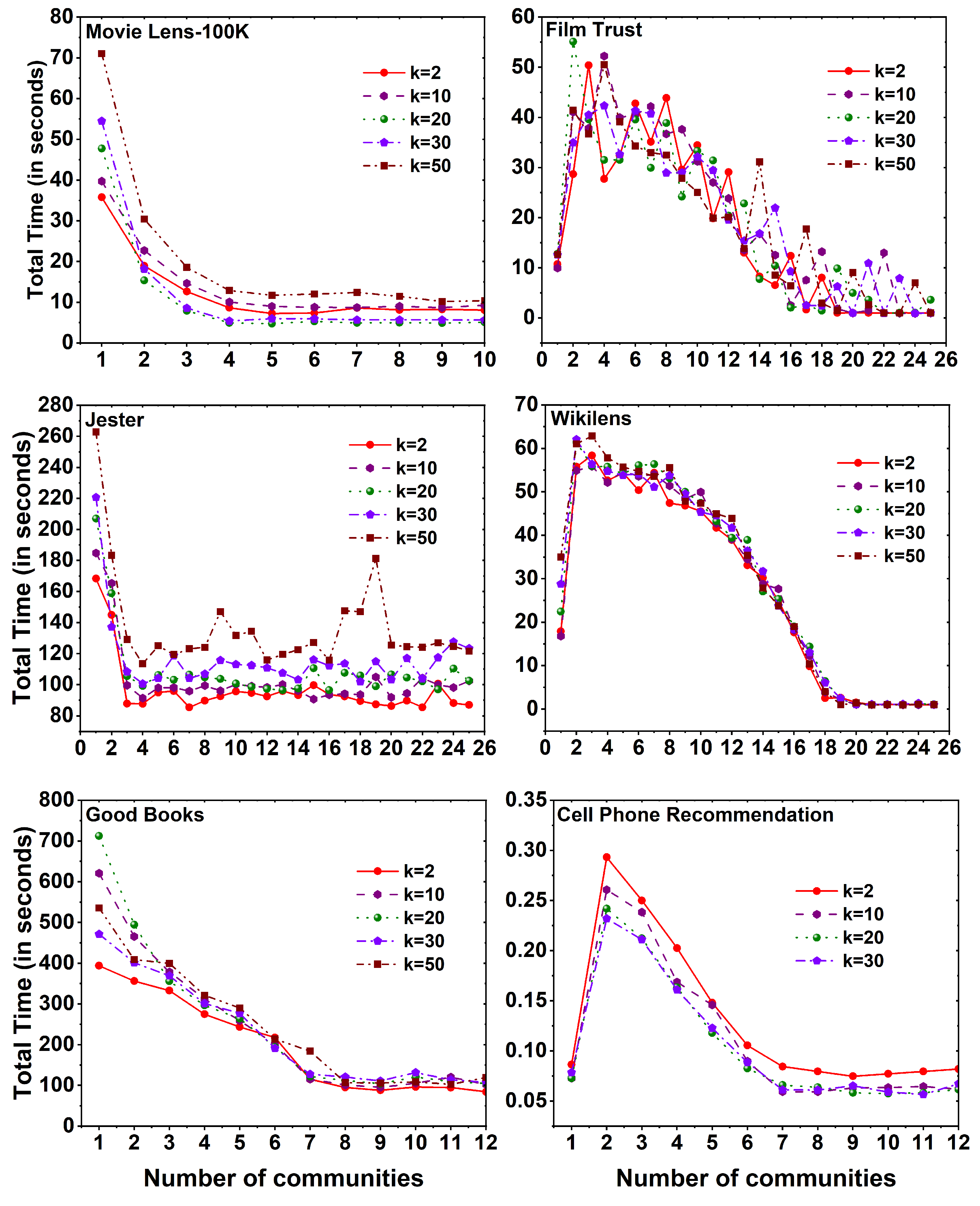
Preprints 81515 g007
Figure 7. Time taken to calculate SVD++ method for six different datasets namely Movie Lens-100K, Film Trust, Jester, Wikilens, Good Books, and Cell Phone Recommendation with 25 communities.
Figure 7. Time taken to calculate SVD++ method for six different datasets namely Movie Lens-100K, Film Trust, Jester, Wikilens, Good Books, and Cell Phone Recommendation with 25 communities.
Preprints 81515 g007
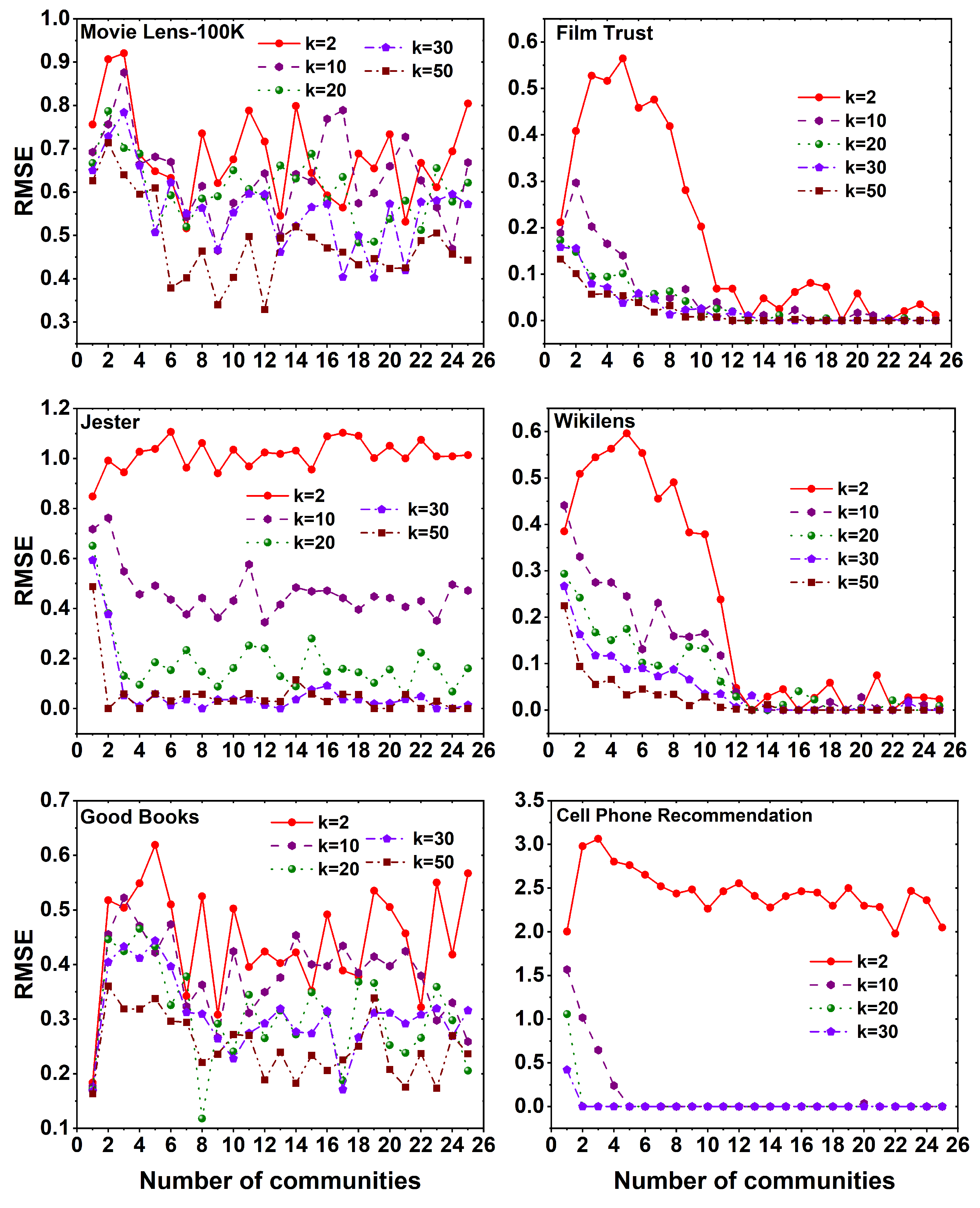
Preprints 81515 g008
Figure 8. RMSE plots using FANMF method for six different datasets namely Movie Lens-100K, Film Trust, Jester, Wikilens, Good Books, and Cell Phone Recommendation with 25 communities.
Figure 8. RMSE plots using FANMF method for six different datasets namely Movie Lens-100K, Film Trust, Jester, Wikilens, Good Books, and Cell Phone Recommendation with 25 communities.
Preprints 81515 g008
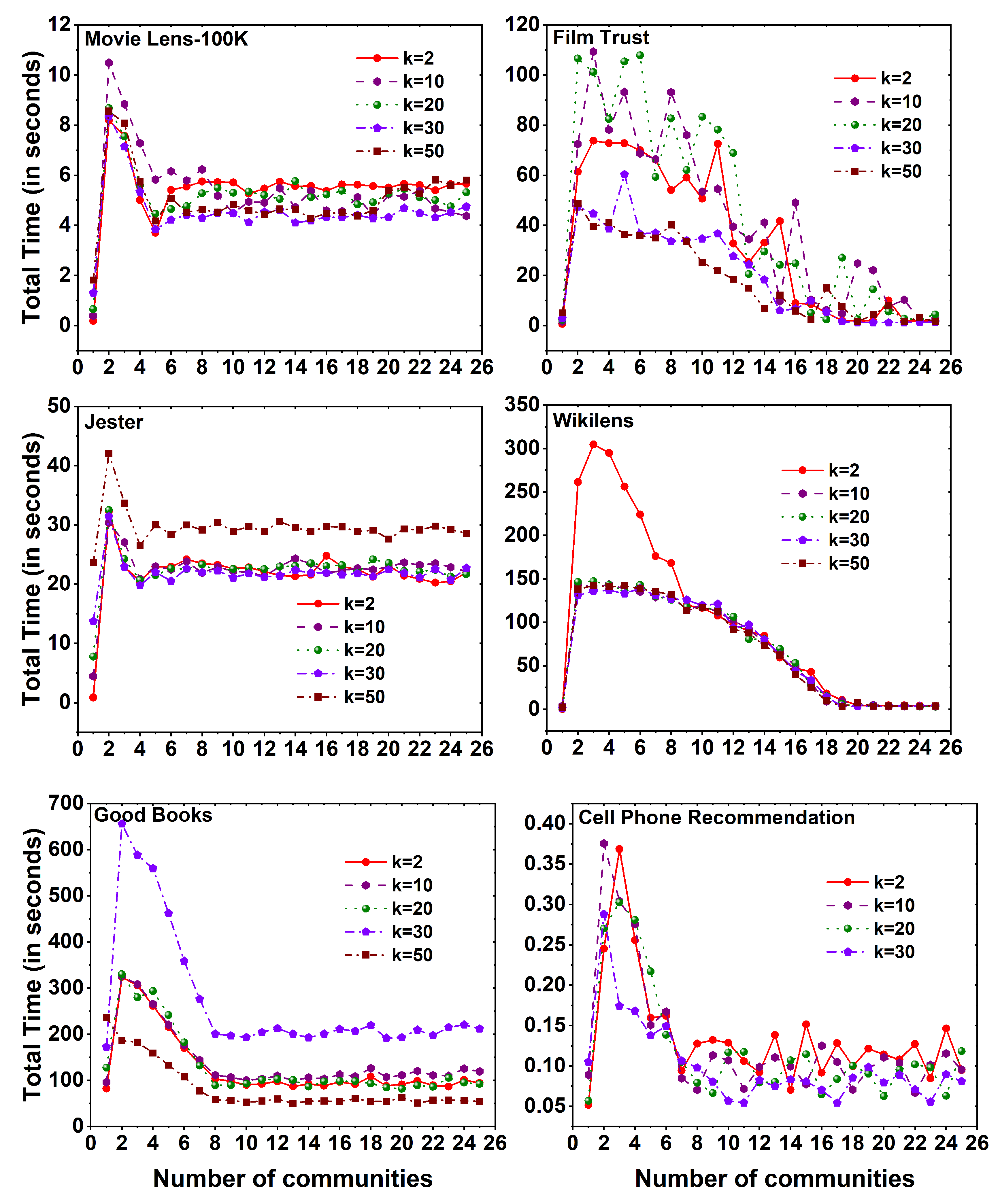
Preprints 81515 g009
Figure 9. Time taken to calculate FANMF method for six different datasets namely Movie Lens-100K, Film Trust, Jester, Wikilens, Good Books, and Cell Phone Recommendation with 25 communities.
Figure 9. Time taken to calculate FANMF method for six different datasets namely Movie Lens-100K, Film Trust, Jester, Wikilens, Good Books, and Cell Phone Recommendation with 25 communities.
Preprints 81515 g009
Table 1. Dataset statistics for six different datasets namely Movie Lens-100K, Film Trust, Jester, Wikilens, Good Books, and Cell Phone Recommendation datasets.
Table 1. Dataset statistics for six different datasets namely Movie Lens-100K, Film Trust, Jester, Wikilens, Good Books, and Cell Phone Recommendation datasets.
Dataset Number of Users Number of Items Number of Ratings Rating Range Average Rating Sparsity
Movie Lens-100K 943 1682 100000 1-5 3.529 0.937
Film Trust 1508 2071 35494 0.5-4 3.002 0.988
Jester 31958 140 1048575 -10 - +10 0.955 0.839
Wikilens 326 5111 26936 0.5-5 3.468 0.983
Good Books 13123 7774 1048575 1-5 3.806 0.989
Cell Phone Recommendation 99 33 990 1-10 6.689 0.708
Table 2. Time taken (in seconds) to calculate dividing community modularity score for six different datasets namely Movie Lens-100K, Film Trust, Jester, Wikilens, Good Books, and Cell Phone Recommendation datasets.
Table 2. Time taken (in seconds) to calculate dividing community modularity score for six different datasets namely Movie Lens-100K, Film Trust, Jester, Wikilens, Good Books, and Cell Phone Recommendation datasets.
Dataset Time (in sec)
Movie Lens-100K 1473.21
Film Trust 936.00
Jester 11714.99
Wikilens 1068.41
Good Books 43125.11
Cell Phone Recommendation 15.58
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated