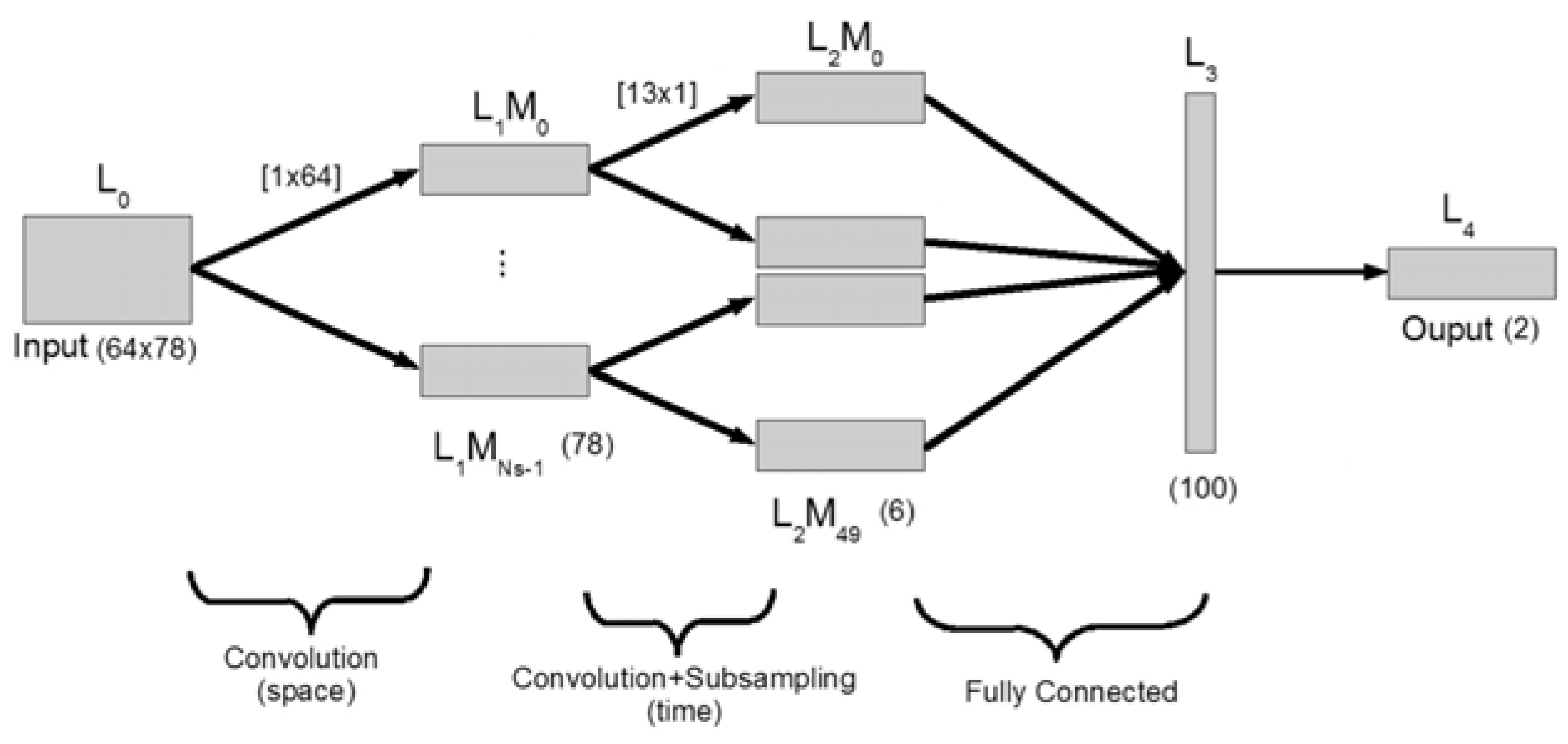
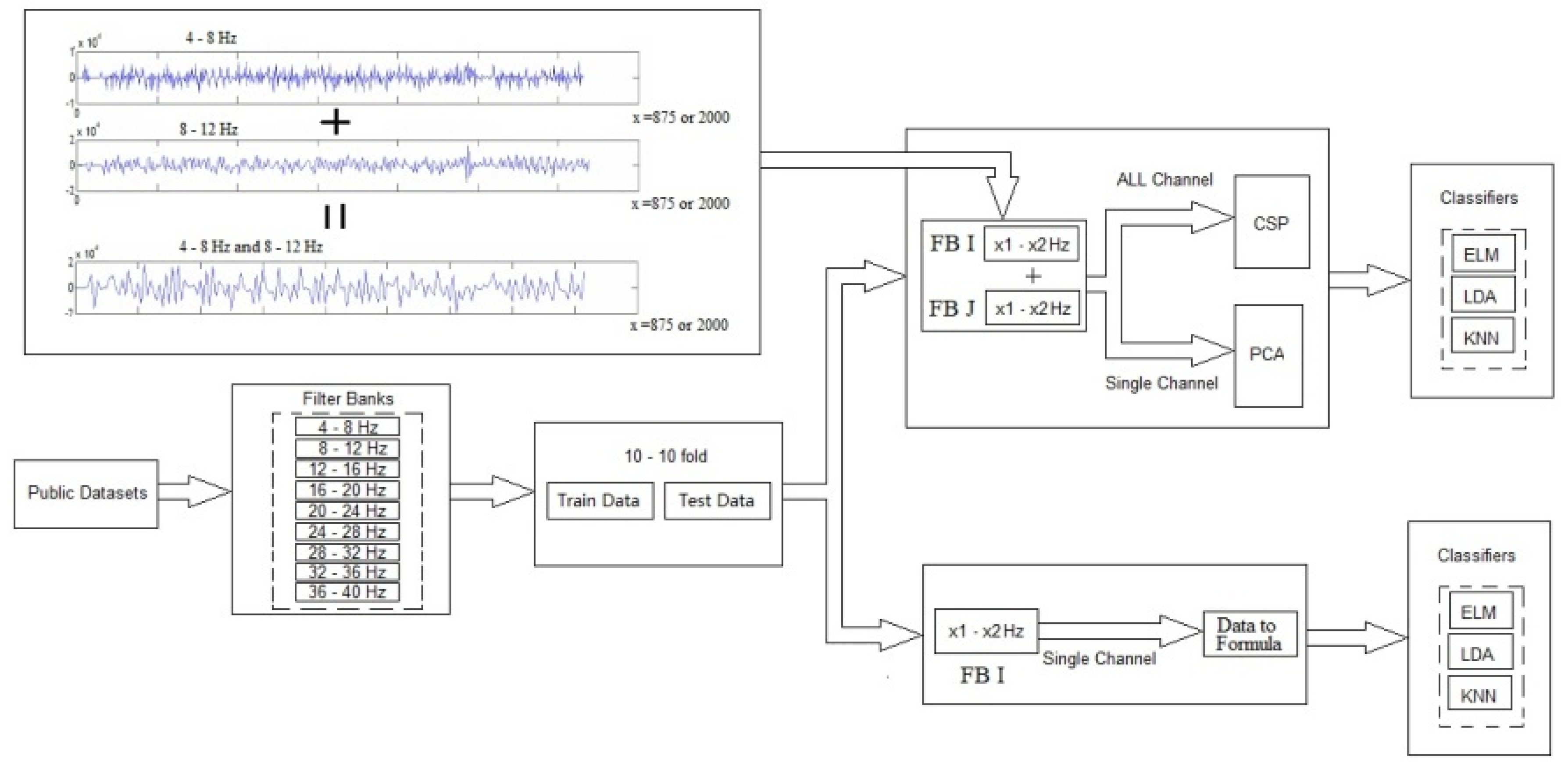
2.1. Speech Imagery Based on Mental Task
Before speech imagery research [
24], the essential part of the classification began in 2009. First, Charles S. Da Silva[
25] and all the video lectures of the two English characters researched with a practical mode for relaxation. In the second stage, Lee Wang and et. al [
26] formed their mental task with/without speech imagination. Some researchers implemented other ideas. But the main ones implemented. According to all research, five English characters (a, e, u, o, i) are possible for humans to create sounds in the brain. It is also difficult to imagine these vowels easily for more time. Each researcher considers only their language, such as English, Chinese, etc. It is impossible to imagine sound of other characters.
2.1.1. Speech Imagery Based on Lip-Sync
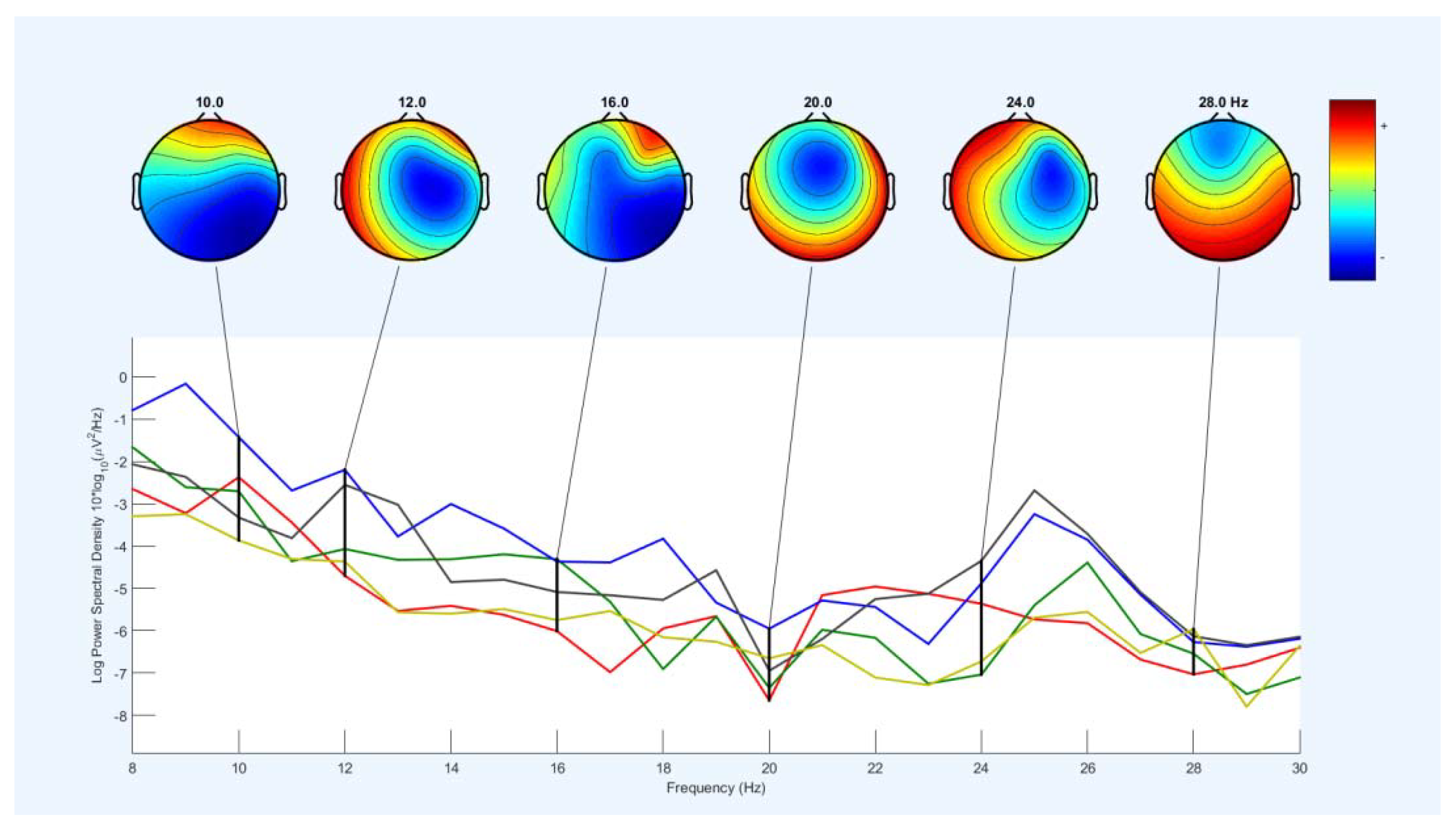
Our electrode cap has 32 channels related to the 10-20 international system. It is placed on the head to record EEG signals. The electrodes are distributed in different parts of the brain.
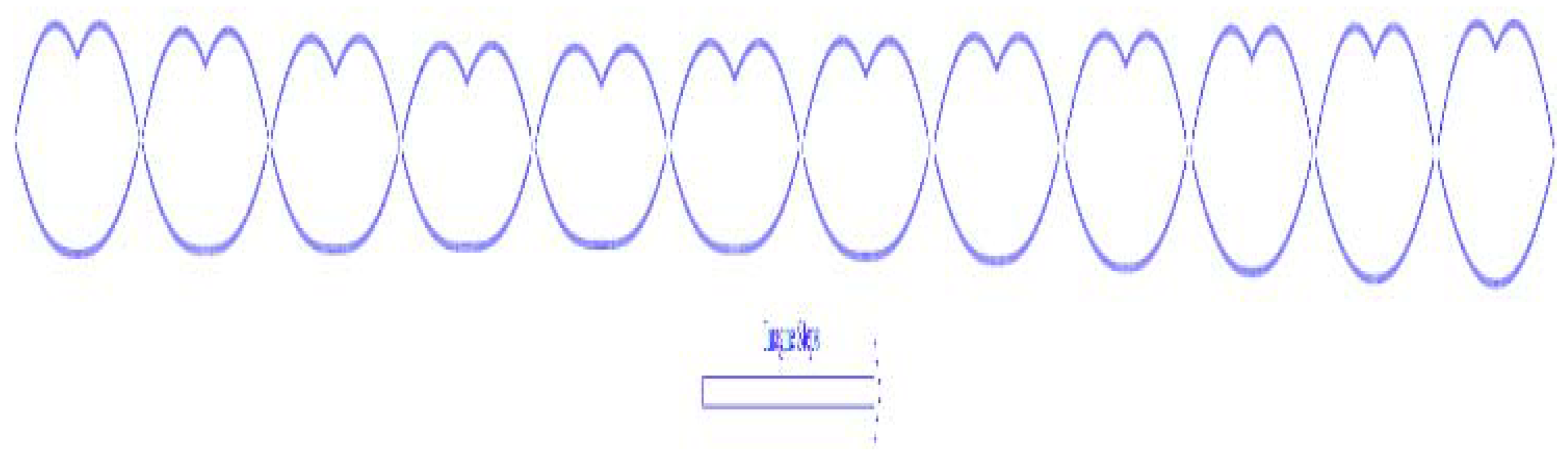
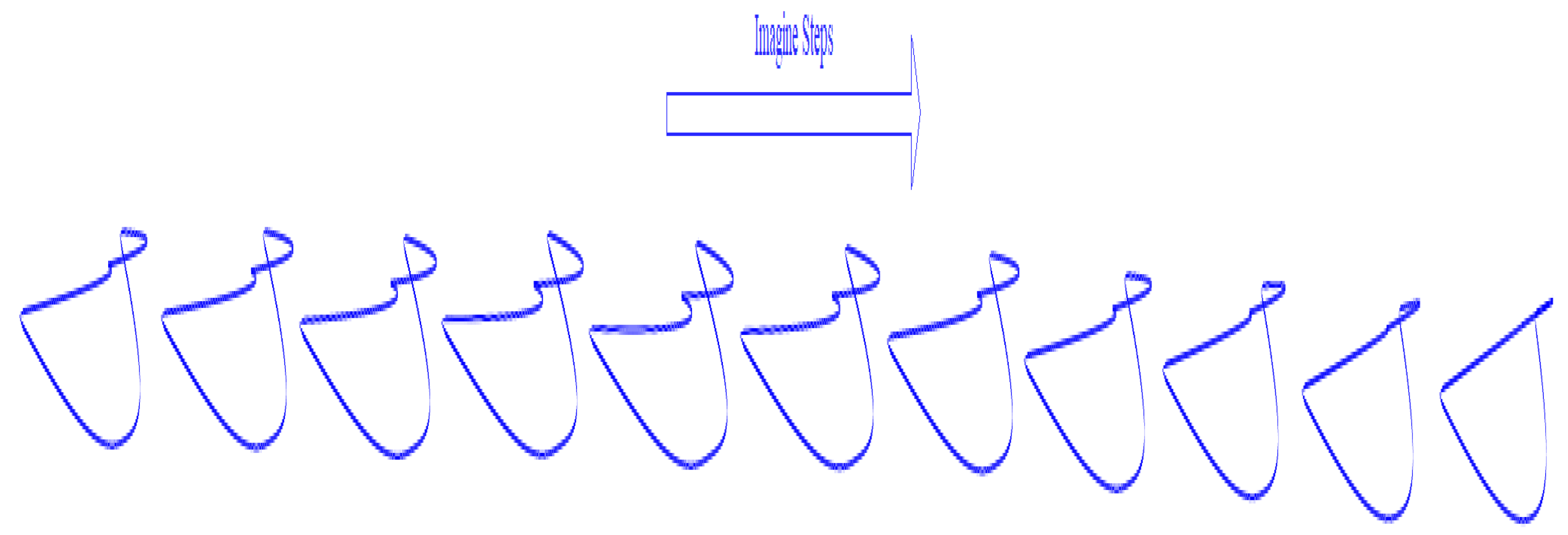
It is difficult for volunteers to imagine all the lips. Our research only considered the lip border as a line in 2D and a page in 3D to synchronize the language because it is easy to imagine and learn for all ages. The performance of these ideas depends on learning. This model is like the language of deaf people for all languages. Development this model for all sounds creates a new model for future communication. Our paper focuses on analyzing and classifying EEG signals from a mental task related to lip synchronization. The EEG signals collected the M and A sounds by lip synchronization with three Chinese volunteer students. Educated people are in good health.
Based on this idea, our model wants to create another idea for the communication person look like visual communication. This new idea uses lips and language synchronization. It can also be created based on one of them. But it is difficult for us to get a good result for it. Our model should make about 30 to 40 sounds for our area. First, it used a combination of them for this area with two basic sounds.
Lip synchronization is one way that some people can understand. Learning for any person is hard. Some articles have a formula for it.
The lip-sync [
71,
72,
73,
74,
75,
76,
77,
78,
79] contour formula is one of these formulas for detecting lip movement. Our model uses a lip liner for two created sounds.
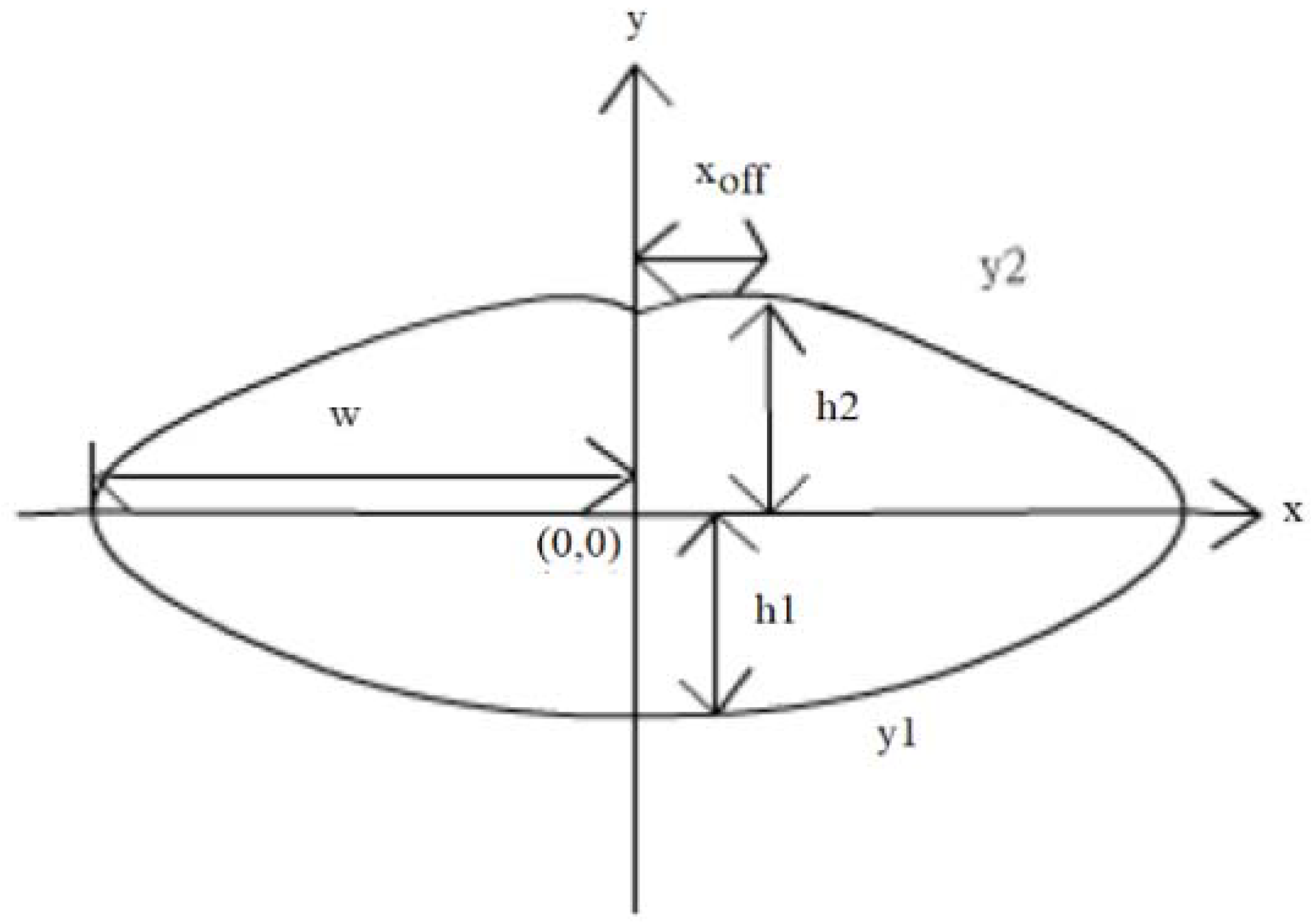
Figure 3,
Figure 4 and
Figure 5 show the steps of a sound based on lip and contour synchronization. Lip imagination is two-dimensional (2D) or three-dimensional (3D).
The formula of the contour of the lip is
H1 is the height of the lower lip, and H2 is the height of the upper lip. w is half of the mouth width. Xeff is the amount of curvature or the middle curve on the upper lip.
2.1.2. Signal Collection Datasets
Three Xian Jiaotong University volunteers collaborate with our experiment in a non-feedback the experiment. Their age is 30-40 years, the average age is about thirty five years old, and the standard deviation is three years. Our volunteer was in good health. They trained to work mentally with their lips and synchronize their language using video. The experiment is conducted under a test protocol under Xi’an Jiaotong University. All volunteers sign informed consent to the test. It explained for volunteers how to think and other details. People sit in a comfortable chair in a lab, about 1 meter in front of a 14-inch LCD monitor.
2.1.3. Filter in frequency Domain
Our electrode cap has 32 channels related to the 10-20 international system. It is placed on the head to record EEG signals. Based on some researches distributed electrodes in different brain parts such as the Broca and Wernicke area, the superior parietal lobe, and the primary motor area (M1). SynAmps system 2 EEG signals recorded. Vertical and horizontal electrooculogram (EOG) signals are recorded by two bipolar channels to control eye movements and blinking. EEG signals are recorded after passing through the 0.1 to 100 Hz bandwidth filter, and the sampling frequency set to 256 Hz. The skin impedance is also maintained below .
2.1.4. Independent component analysis (ICA)
Independent component analysis (ICA) is a very broad method for EEG signal preprocessing. This is a classic and efficient way to isolate the blind source, the first solution to the problem of cocktail parties. As researchers all know, similar to a cocktail party scene generally includes music, conversation, and unrelated types of noise. Although scene is very messy because the person himself can see someone with the content He speaks and hears, the man forces himself to identify himself and wants to instinct content of the signal source, but this scene is deadly of various kinds. Blind and sources signals mix to make target source signal cocktail effect. Independent component analysis algorithm proposed for that purpose and allows the computer to have the ability to complete the same ear of interest. Component-independent component analysis algorithms assume that each source component is statistically independent.
2.1.5. Common Spatial Pattern (CSP)
Koles and eta have introduced a Common Spatial Pattern (CSP) that can detect abnormal EEG activity. CSP tries to find the maximum discrimination between different classes by using signal conversion to variance matrix. EEG pattern detection performs using spatial information extracted with a space filter. CSP only requires more electrodes to operate and does not require specific frequency bands and knowledge of these bands. CSP is also very sensitive to the position of electrodes and artifacts. The same electrode positions in the training process are related to memorization to collect similar signals. It is effective for increasing accuracy as obsolete.
2.2. New Combination Signal Model with Four CommonMethods
Most researchers [
15,
16,
17,
18,
80] have used a large-scale frequency domain consisting of known brain activities and some noise representing unknown brain activities. A large-scale frequency filter could divide into overlapping narrow frequency filters to extract high discriminate features [
19,
20]. The disadvantage of decomposing the EEG signal into narrow-pass filters is the damage to the raw EEG signals. The essential information of each distribution event is in a large frequency band. The damage is related to removing more EEG frequency range for processing. The main EEG signals of the events are lost. The main goal of the model is to find the most important patterns of different events in small frequency bands and to find more frequency ranges of more similar patterns. Choosing an appropriate scale for frequency filters is essential to avoid damage to raw EEG signals and to reduce noise in EEG signals. Our model is reduced damage. For collecting important distinctive patterns of brain activities, it is necessary to combine several essential small-scale frequency bands for classification. The combination of two fixed filter banks introduces new combination signals. These models investigate three feature extraction methods and one feature selection method.
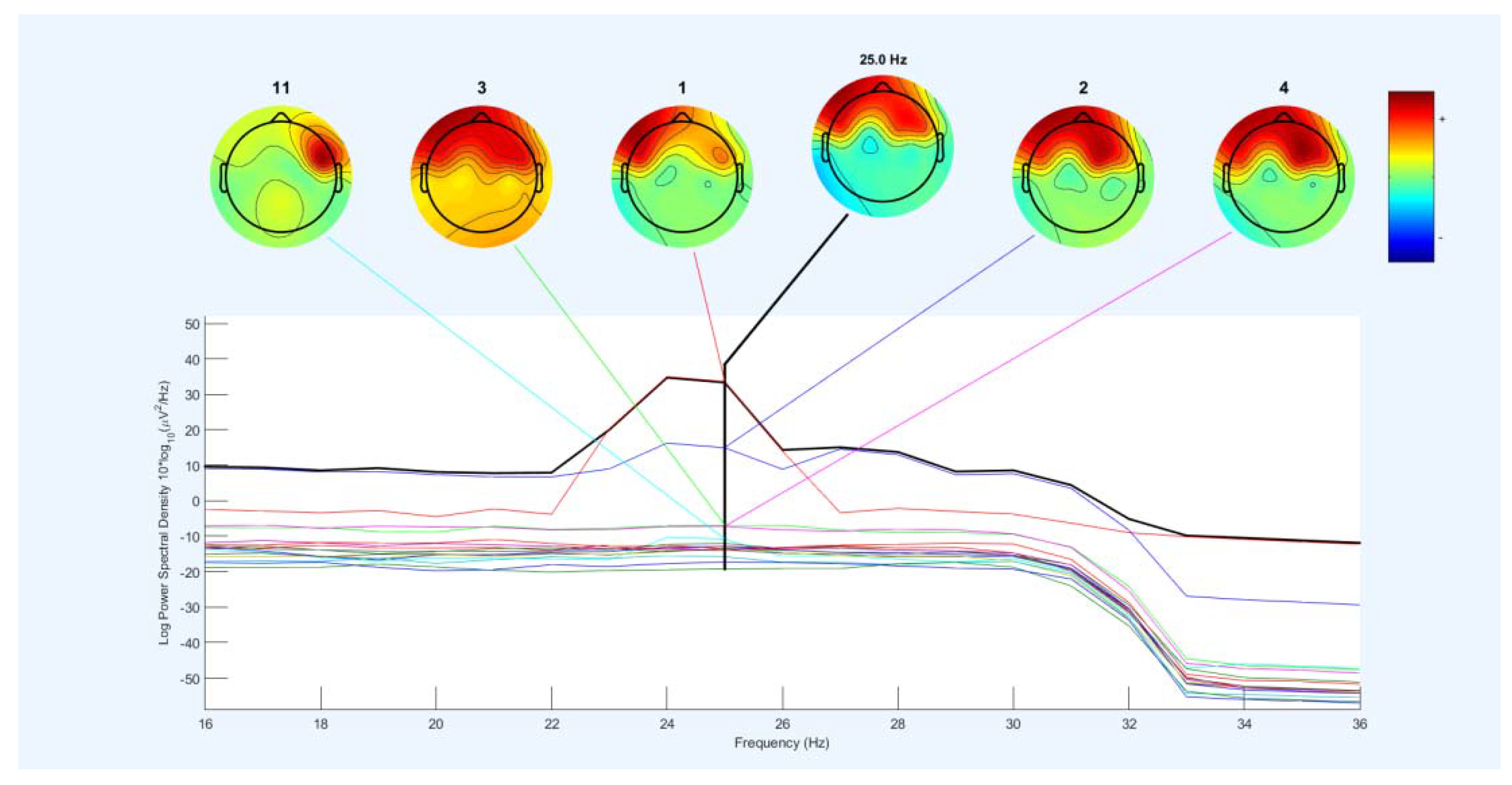
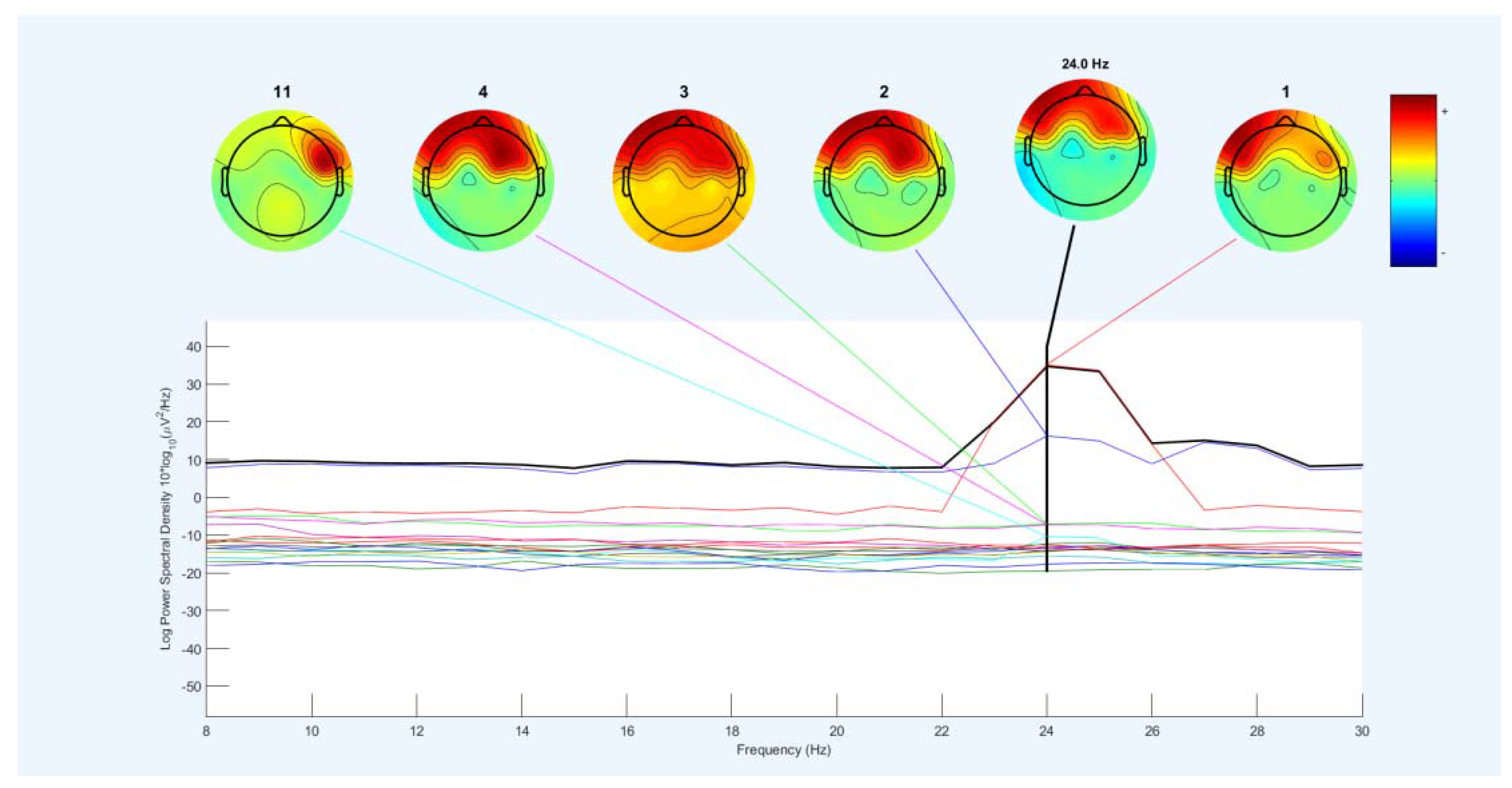
To the best of our knowledge, at the time of writing this paper, using the combination of two fixed filter banks with a 4Hz domain (limited frequency bands) is used for the first time with this scale in this paper. This leads to creating new combination signals with 8Hz domains in total. The accuracy performance of new signals has been studied by two feature extraction methods, i.e., CSP, FBCSP, and one feature selection, i.e., PCA. In addition to three common methods, a lagrangian polynomial equation is introduced to convert data structure to formula structure for classification. The purpose of the lagrangian polynomial is to detect important coefficients for increasing a distinction of brain activities. It may be noted that the concept of the lagrangian polynomial is different from Auto-regression (AR), in which features are coefficients for classification.
In the following subsections, we explain the details of the four main contributions of this paper by describing the models. We show an overview of four implemented models in
Figure 1,
Figure 2,
Figure 3 and
Figure 4.
Figure 5 provides an overview of the database, filter banks, and the model of the new combination signals with the classifiers.
2.2.1. CSP Using New Combination Signal
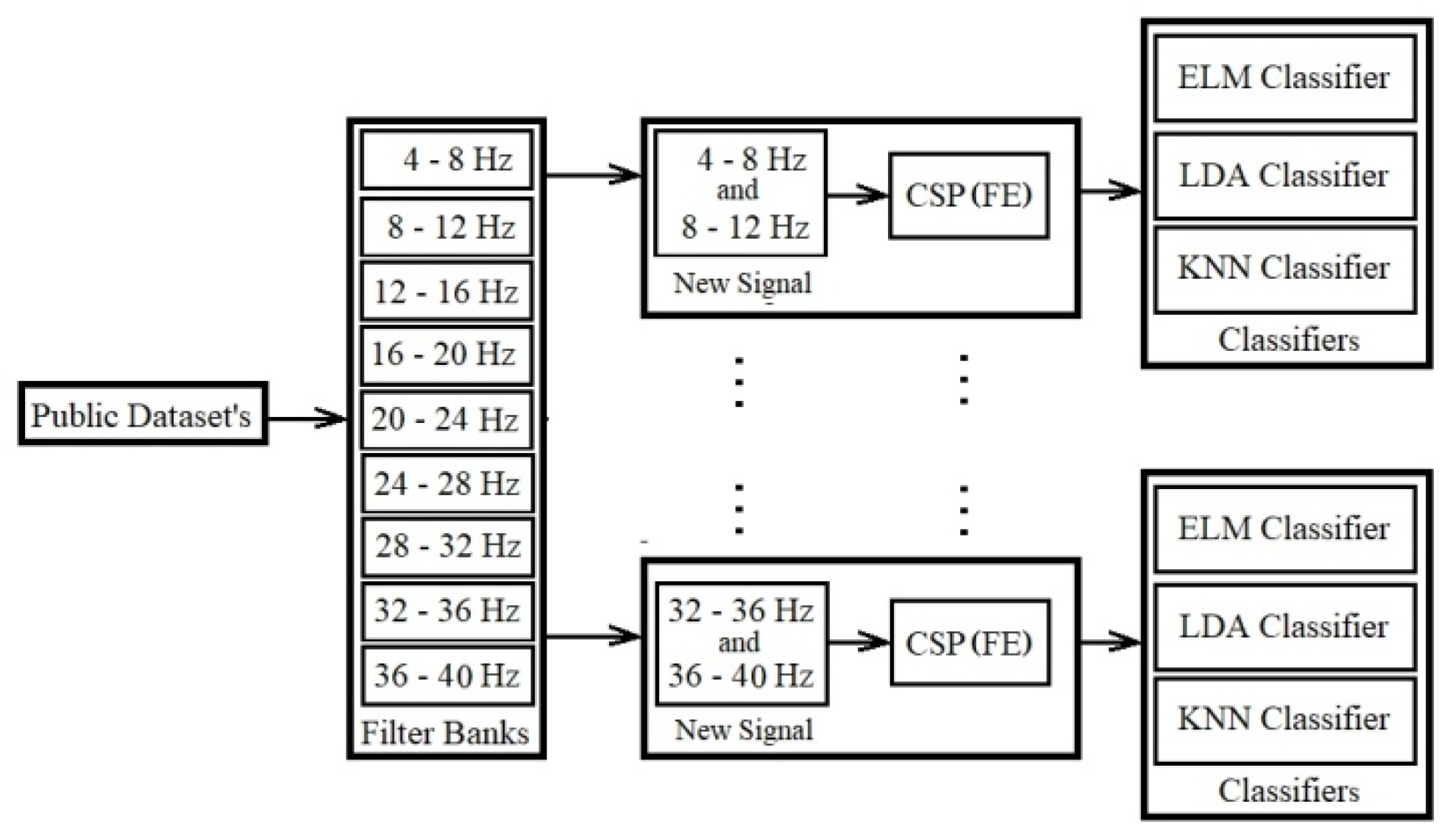
The first proposed model increases the extracted good distinctive features on the whole channel. In this model new combinational signals are created and applied individually in the classification. In this case, all of the electrodes are involved in extracting features. The model consists of four phases as presented in
Figure 6 and explained below:
1) Filtering data by Butterworth filter: In the first phase, using frequency filtering, noises and artifacts are removed with a filter bank. The domain of these filter banks is out of the noise and artifact domain. EEG measurements are decomposed into nine filter banks from 4-8Hz, 8-12Hz, …,36-40Hz. All of the data using the Butterworth filter is filtered by 100th order. Most of researcher use the Butterworth filter for filtering [
20,
21].
2) Creating new combination signals: The combination of the two fixed filter banks creates new combination signals. Each fixed filter bank has a 4-frequency range. For example, filter bank 5 starts with 20Hz (lower band) and ends with 24Hz (upper band). The new combination signal of filter banks 2 and 5 support the 8Hz to 12Hz and the 20Hz to 24Hz frequency ranges.
The formula of new signals for all of the electrodes is calculated as:
where FB(i,j,m) represents the ith and jth Filter bank of mth channel and n is the maximum electrodes of a dataset that data is recorded. Therefore, m and i variables indicate the selected channel and selected 4Hz-ranged domain frequency(for example, m=2 and i = 2, means channel 2 and 8Hz-12Hz frequency range).
3) Using CSP as the spatial filter and feature extraction: The common spatial pattern algorithm [
81,
82,
83,
84] is known as an efficient and effective EEG signal class analyzer. CSP is a feature extraction method that uses signals from several channels to maximizes the difference between classes and minimizes their similarities. This is accomplished by maximizing the variance of one class by minimizing the variance of another class.
The CSP calculation is done as follows
where C is the covariance of the normalized space of data input E, which provides raw data from a single imaging period. E is a N×T matrix where T is the number of electrodes or channels, and N is the number of samples in the channel. The apostrophe represents the transposition operator. Trace is also a set of diagonal elements of x.
The covariance matrix of both classes C1 and C2 is calculated by the average of several imaging periods of the EEG data, and the covariance of the combined space Cc is calculated as follows:
is real and symmetric and can be defined as follows:
where
is a matrix of eigenvectors and
is the diameter of the eigenvalues matrix.
The variances in space are equalized by
and all eigenvalues of
are set to 1.
and are common special sharers, provided that and and .
Eigenvalues are arranged in descending order. And the projection matrix
is defined as follows:
where and are transfer matrix and data.
The reflection matrix of each training is as follows
where rows are selected to represent each period of conception and the covariance of , components of the feature vectors are calculated for the nth instruction.
Normalized variance used in the algorithm is as follows:
4) Classification by Classifiers: Classification is done using three classifiers in our model, including LDA with a linear model, ELM with the sigmoid function using 20 nodes, and KNN with five neighborhoods (k=5).
Two public datasets are selected according to details described in next Section. After filtering data, the combinations of two filter banks based on formula (1) for all of the electrodes are created. Each combination of two filter banks is considered separately for the next steps. In the next step, CSP is applied for spatial filtering, removing artifacts, and extracting features on the new combination signal. The experimental model of train data and test data is presented in section 3.
2.2.2. FBCSP[85,86,87] Using New Combination Signal
The second proposed model increases the good extracted distinctive features on the whole channel, which have the additional step of feature selection to the first model. In this model new combination signals are created, and the best signals from both primary and new signals are selected using the feature selection and used the classification. All of the electrodes cooperate for noise and artifact filtering and extraction of features. This model consists of the following phases presented in
Figure 7 and explained below:
1) Filtering data by Butterworth filter: This step is the same as the first step in the previous section, i.e., 2.2.1.1.
2) Creating new combination signals: This step is the same as the second step in the previous section, i.e., 2.2.1.1.
3) CSP as the spatial filter and feature extraction: In this phase, the CSP algorithm extracts
pairs of CSP features from new combination signals. This is performed through spatial filtering by linearly transforming the EEG data. Then features of all new signals are collected in a feature vector for ith trial, i.e.:
where denotes the pairs of CSP features for the band-pass filtered EEG measurements, .
4) Features collection and selection: In this phase, an algorithm called Mutual Information Best Individual Features (MIBIF) is used as feature selection from the extracted features, and it selects the best features that are sorted (descending order) using class labels.
In general, the purpose of the mutual information index in MIBIF [
88,
89] is to obtain maximum accuracy k features are selected that from a subset of
which the primary set F includes d features. This approach maximizes the mutual information I(S; Ω). In the classification of features, input features, i.e., X, are usually continuous variables, and the Omega class (Ω) has discrete values. So the mutual information between the input features X and class Ω is calculated as:
Where
And the conditional entropy is calculated as:
Where the number of classes is Nω.
In general, there are two types of feature extraction approaches in mutual information technique, including wrapper and filter approach.
With a wrapper feature selection approach, conditional entropy simply is in the in (14):
P(ω|X) can be estimated easily from the data samples that are classified as class ω using the classifier over the total sample set.
Mutual information based on the filter approach is described briefly in three steps:
Step1: Initialization of set d feature and selected features set S=Null.
Step2: Compute MI features based on I(|Ω) for each i=1…d, and belong to F
Step3: Select k best features that maximize I(
|Ω) [
87,
88]
Step4: Repeat the previous steps until
5) Classification by Classifiers: This step is the same as the fourth step in the previous section, i.e., 2.2.1.1.
This model is applied to one public dataset (including left hand and right hand), which is described in next section. Most of the steps in the two models are the same. Except, one phase as feature selection is added between CSP and classifiers, which selects the best features by mutual information feature selection after collecting the extracting features of new combination signals. Selected features are about 10 to 100 features, which are sent to classifiers for classification.
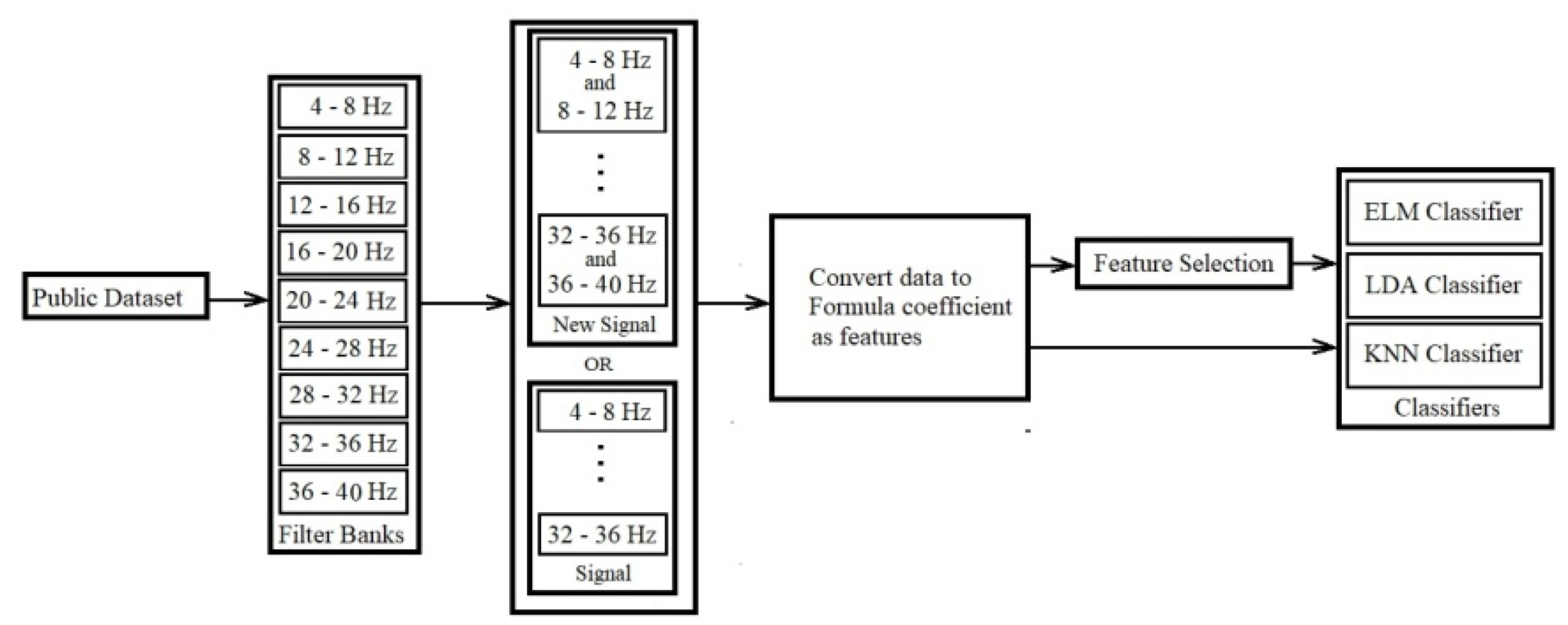
2.2.3. Lagrangian Polynomial Equation Using New Combination Signal
The third proposed model increases the good extracted distinctive features on every single channel separately. In this model, we a Lagrangian polynomial model for transforming the data into formulas that are then used as features in classifications. A single channel/electrode cooperates for extracting features and classification, as illustrated in
Figure 8 and explained in the following steps.
1) Filtering data by Butterworth filter: In the first phase using frequency filtering, the noises and artifacts are removed with a filter bank. This process is the same as the first step in section 2.2.1.1, with the difference that it involves single channels individually
2) Filter banks (sub-bands) signals or new combination signals: Two models are considered as input data, including sub-bands in the name of filter banks and new combination signals. New combination signals are created based on the following formula for a single electrode. This formula is used for the calculation of a single electrode or channel.
where represents the filter bank signal.
3) Convert data to the formula of coefficients with different order by the Lagrangian polynomial equation: The input data is about one second from 3.5 seconds imagination time. Lagrangian polynomial equation converts these input data of the two single channels to coefficients for classification.
Lagrangian polynomial is described as:
There is
data asset
, while each
is unique. The interpolation polynomial as a linear combination is in the Lagrange [
86,
87] form.
The structure of Lagrangian polynomial is described in the form of:
where
. In fact, in the initial assumption, two
aren’t the same, then (when
)
, therefore, this phrase is the appropriate definition. The reason pairs
with
are not allowed, so no interpolation function
such that
would exist, and the function gives unique value for each argument
. On the other hand, if also
, therefore
are the same value as one single point. For all
,
includes the term
in the numerator, so that with
the whole product will be zero,
is:
In other words, lagrangian polynomials are at Unlessit is as lack of the term. It follows that , so at each point , , shows that interpolates the function entirely.
The final formula is:
where
,
,…,
,
are coefficients of the Lagrangian polynomial, and n, n-1, n-2, …, 1 are the orders.
4) With/without feature selection methods: First, all features are used for the classification. Second, the best equation coefficients using the feature selection are selected for the classification.
5) Classification by Classifiers: In this phase, we perform classifications on features to determine accuracy using classifiers. This phase is similar to the last phase of the two above models.
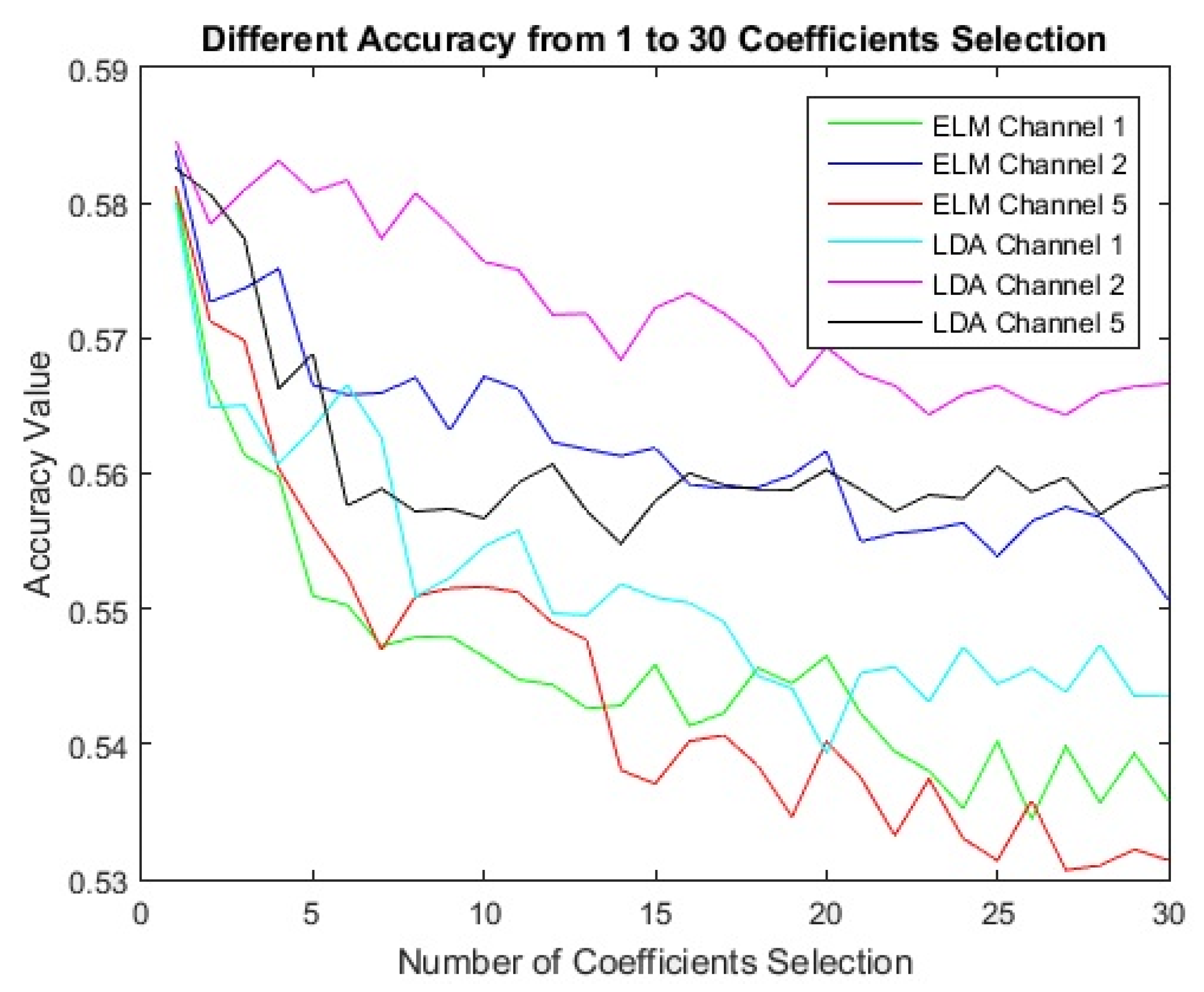
This model is examined on one public dataset (including left and right hand) for examination. We describe this public dataset in more detail in next section. Single channels are applied for processing. Then the combination of two filter banks based on formula (17) for single electrodes/channels is calculated. Each combination is considered separately for the next steps. In the next step, two procedures are considered for processing. The first procedure uses fixed filter banks of a single channel, and the second procedure uses the new combination signals of a single channel. Then each procedure uses the lagrangian polynomial equation for converting data to formula structures. The lagrangian coefficients are considered as features for the classification. The feature selection is not used in the first procedure, but it is used in the second procedure. Mutual information feature selection selects the best features from 1 to 30 features. And finally, the selected coefficients as most effective features are sent to LDA, KNN, and ELM classifiers for classification.
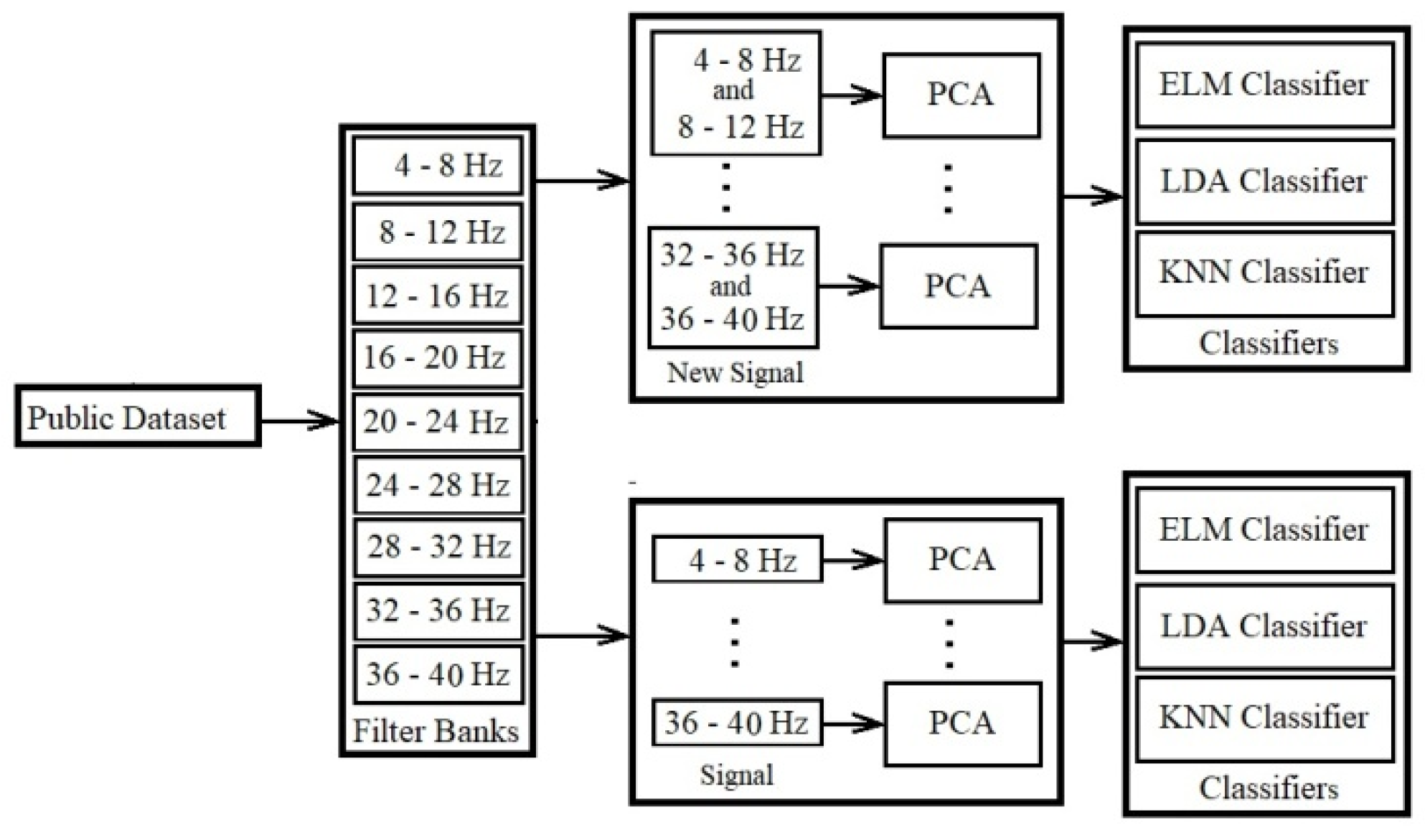
2.2.4. PCA Using New Combination Signal
The fourth proposed model increases the good extracted distinctive features separately single-channels. In this model using PCA, we sort the data without dimensional reduction based on the best features before the classification. A single electrode cooperates for sorting the features and transforming to a new space followed by the classification as illustrated in
Figure 9 and explained in the following steps:
Filtering data by Butterworth filter: The first phase is the same as the first phase of the previous model.
Filter banks (sub-bands) signals or new combination signals: The second phase is the same as the second phase of the previous model.
Sorting features by PCA: The purpose of PCA as an orthogonal linear transformation is to reduce the dimension by transferring data to a new space and sorting them. The greatest variance lies on the first coordinate as the first principal component and the second greatest variance as the second coordinate, and so on. PCA is introduced as one method for reducing primary features using the transformation of data to new space artificially [
88,
89,
90,
91].
The basic description of the PCA approach is as follows. Let’s define a data matrix
where
is the number of observations and
is the number of features. Then
is defined as the covariance matrix of matrix
:
Where: and .
Eigenvectors and eigenvalues matrix are produced by matrix
as:
Where
is a matrix of sorted eigenvalue
And
is a matrix of eigenvectors (each column corresponds to one eigenvalue from matrix
):
Finally, the matrix of principal components is defined as:
Each of features can be explained with parameters from matrix as a linear combination of first principal components:.
Classification by Classifiers: The fourth phase is the same as the fourth phase of the previous model, with differences in the scale of input data.
This model uses the entire 3.5 seconds as input with the PCA method. PCA is used for transferring data and sorting in our research.
Finally, we present the combination of filter banks in
Figure 10.
2.3. New Linear and Nonlinear Bond Graph Classifier
The bond graph classifier uses a distance calculation method for classification. This model is local and focuses on the structure. Boundary uses point data centrally. Our model has different steps: 1) Search for the minimum path of nodes (attributes). 2) Create the center of the arc with the node and the longest sub-nodes. 3) Calculate the boundary between the two centers. 5) Create the main structure to support all borders. In this section, this paper begins with a brief description of the new classifier model in the main structure. Our idea explains in the following.
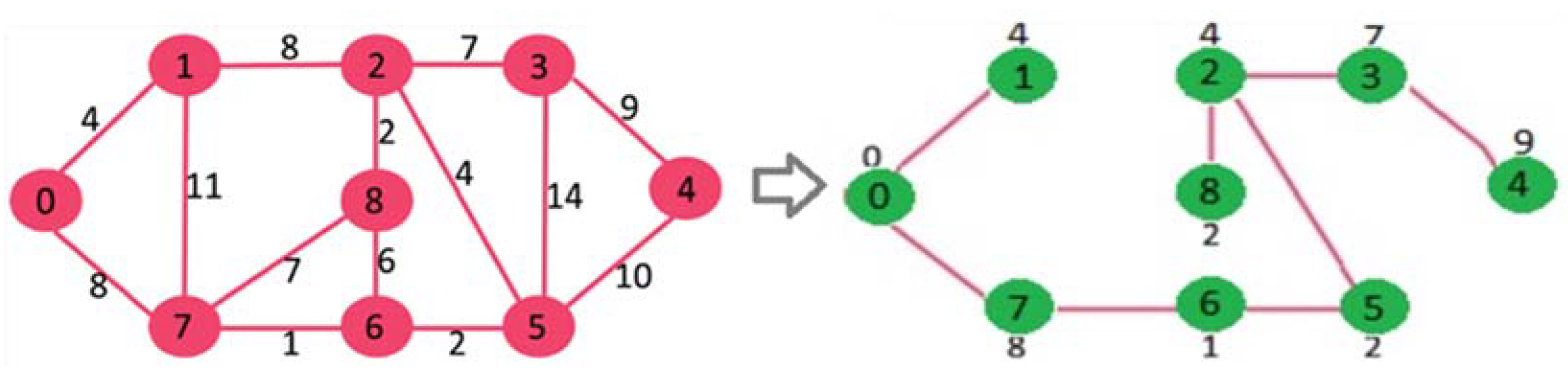
Our idea uses one of the greedy algorithms (Prim algorithm) to find the least spanning tree, which is weighted based on a directionless diagram. A subset of edges provides by the Prim algorithm to minimize the total weight of all tree edges. The algorithm arbitrarily starts the tree from one vertex to the vertex once. Then it adds the cheapest possible connection from the tree to the other vertex. Following the development of the algorithm in 1930 by the Czech mathematician Vojtěch Jarník, the algorithm was republished by computer scientists Robert C. Prim in 1957 and Edsger W. Dijkstra in 1959. These algorithms find at least a spanning diagram in a potentially truncated router. The most basic form of the Prim algorithm finds only minimal spanning trees in connected diagrams. In terms of asymptotic time complexity, these three algorithms are equally fast but slower than more complex algorithms. However, for graphs that are dense enough, the Prim algorithm can run in linear time, meeting or improving time limits for other algorithms. [
92,
93,
94,
95,
96] (
Figure 11).
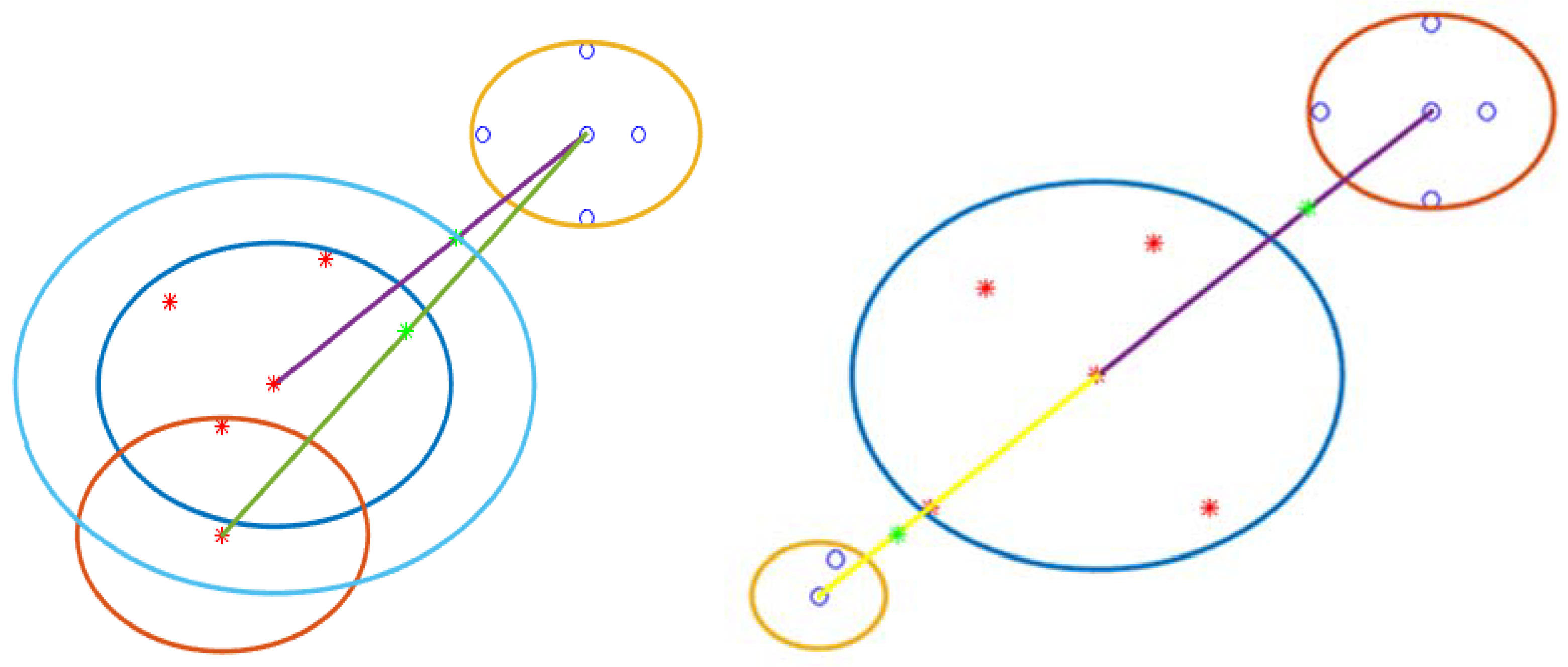
This tree matrix has some nodes above and below the nodes. Each head node finds the smallest distance from its sub-nodes. They then create a slightly larger arc than the longest (27).
All head nodes of different classes have arches to participate. The distribution of samples in the n-dimension creates the longest different arcs and various centers for arcs. Our model has three modes for detecting a boundary point. 1) Near the center can detect the border point. 2) The local center can detect the boundary point. 3) Near the node center, can recognizes the border point. In one case, it can find the boundary point for arches when the arc does not intersect. The distance between two different central classes calculates. It does not have an arc distance, in the middle of which the distance between nodes recognizes as a boundary point.
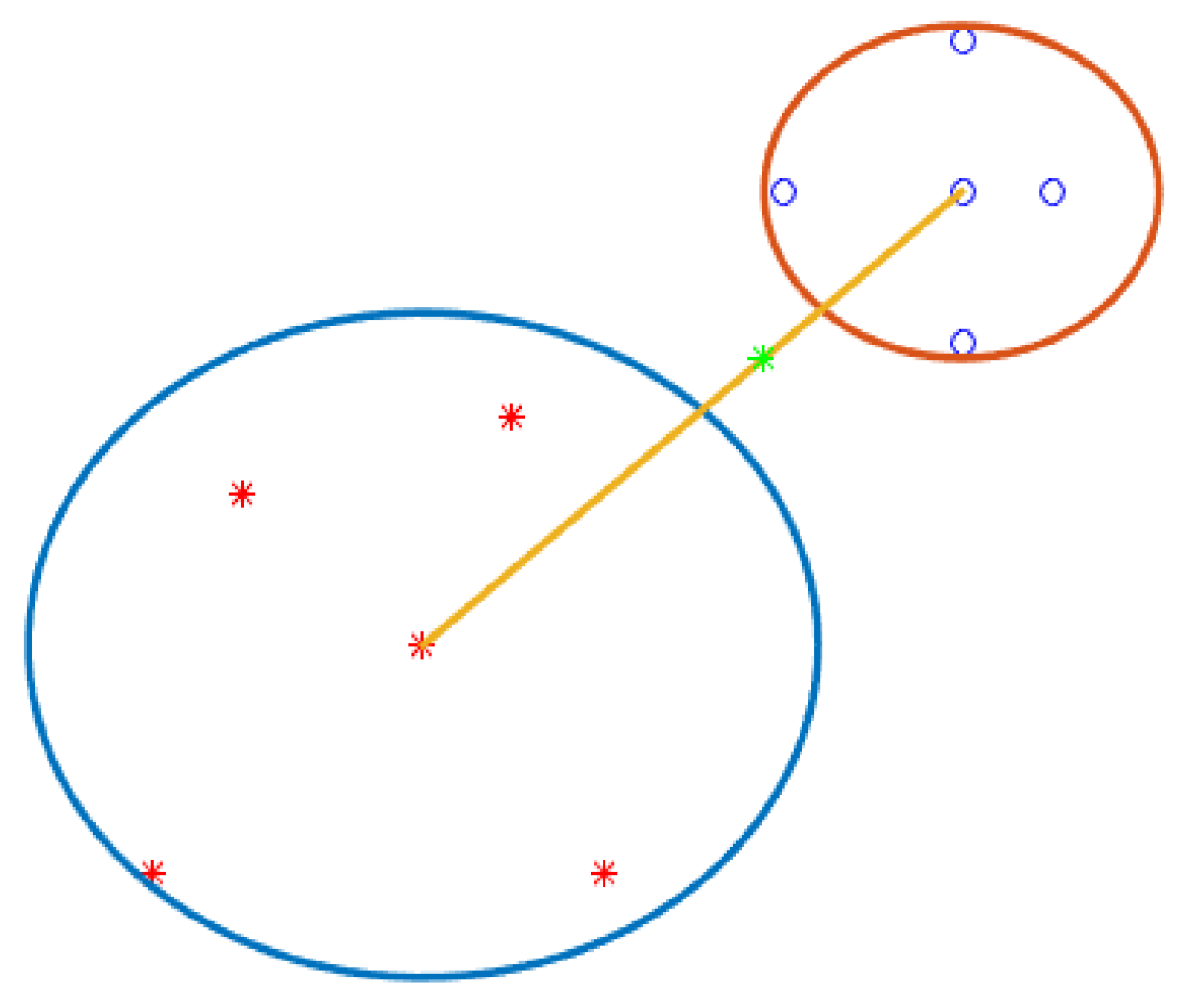
Figure 12 can show two different class centers. The blue and red dots respectfully belong to classes one and two. The two centers connect by a yellow line (the yellow line is the distance between the two centers). The red arc of class one and the blue arc of class two do not have a cross, and the border points with the green dot are in the middle of the two arches. Other states of the arc have intersections, in which case the arch must break and turn into small arches because only in the first case can this method detect the boundary point. This situation occurs when the distribution of samples is more at the border. The main question is, which arch needs to break? In
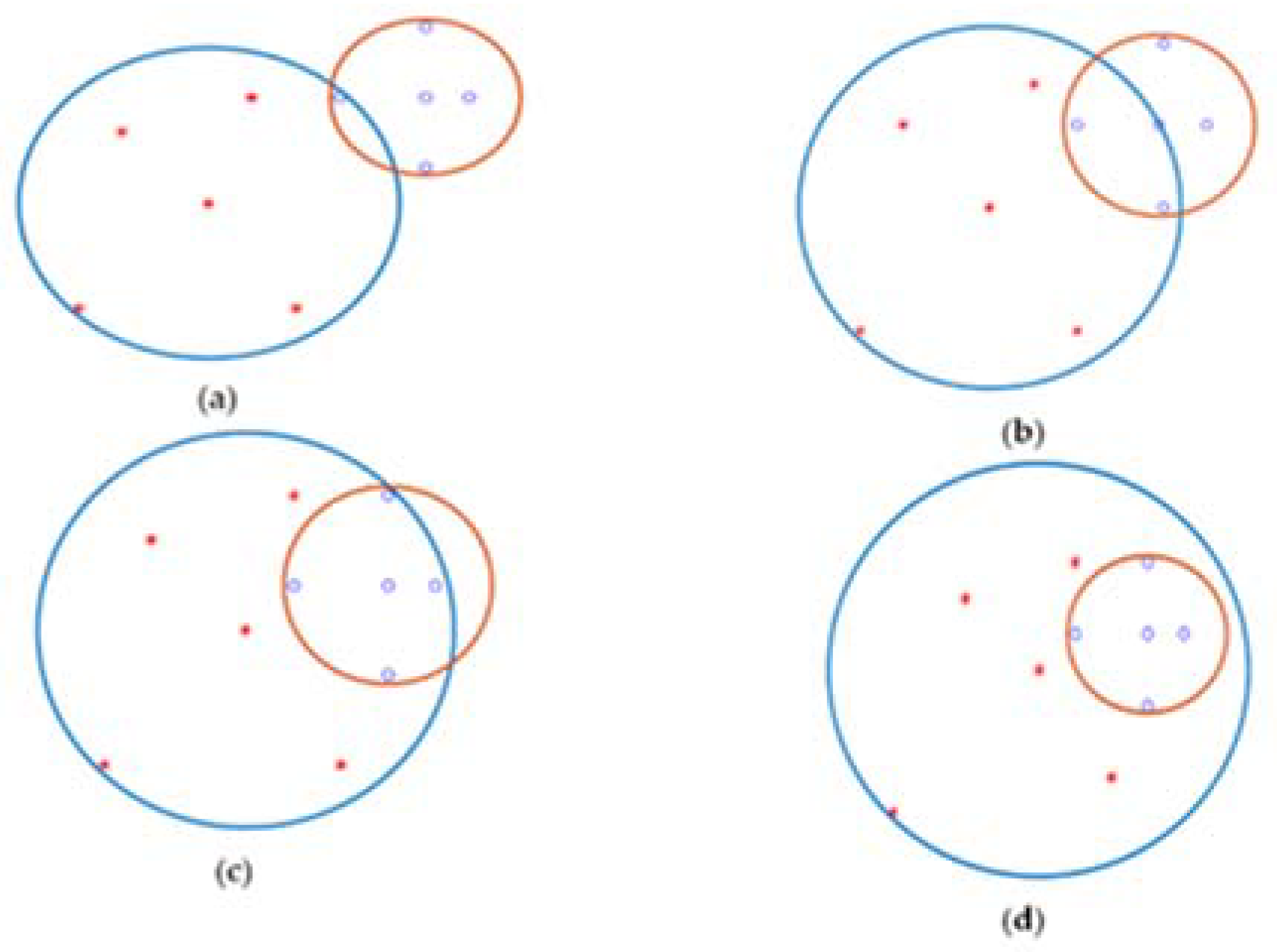
Figure 9, there are four modes for this situation. All of them are necessary to break the blue arc into two small arches. (
Figure 13).
After finding all the border points, some border points are not necessary. Therefore, they need to remove. In
Figure 14, two class two arcs and one class arc have two boundary points. One part of the program recognizes that some arches are necessary to stay, and another must delete because one boundary point also supports another boundary point. One green border point on the blue arc is light, and the other is the arc. It means that when two boundary points are in one direction, the other supports the other. In
Figure 8, two different directional boundaries and locations do not remove another boundary point. You might think that if another green dot in the blue-green dot arc was bright, another green dot should remove. It is essential for boundaries to remove some boundary points where only a Class I arc has some boundary points with some different Class II arcs. Class two is the same as class one. Our model stores tree data like a matrix to find the longest arc. Then create another table for it. Since arches and centers work together to find the boundary when it is about to break, You must return the first table to create two other (
Figure 15).
Then it finds the center of the hypothesis. First, the mean of two or more sample classes finds separately. Second, our model finds the distance between the central and the assumed points. It can see that 50 local concentrated locations are near the center of the hypothesis. Then it computes another hypothetical center based on these local focal points (the sample distribution is closer to the center. But it cannot find it exactly. Because it also has noisy samples. It is impossible not to have noisy features for EEG signals. Our model has a central assumption, then it adds the boundary points (around) of this center, and the other local center has noise, which means that the local and general nodes are noise because the node headbands support sub-nodes. Calculate the distance between the hypothetical axial and noisy axial points and calculate the existing noisy calculation.
In the following, our model has fully explained this classification.
Firstly, it explains the peso code of this model.
In the second step, the flow diagram clearly shows the details of this model.
1) Data collection: Collection of data from each field (collection of signal data from different areas and EEG signals (brain signals)).
2) Input data model (function): Two models intended for sending classification. 1) Raw data sends a classifier directly for classification (raw image data). 2) Processing data as filtering raw data sends the classifier for classification (filter signals). 2) Extract new features of raw data (raw image data and filter signals).
3) Select a data model for classification (function): This supports all models. In test marks, there are two models. 1) Data includes train and test data. 2) K-Fold model in which data divides into K parts. They consider one part of the test and the other part for training. All parts one time considered for testing. It executes K time.
4) Separate class data and random selection vectors (function): Two multi-class models can choose. 1) A class is first class, and other classes are a second class. It runs all these classes one by one. 2) A class is first class, and other classes are a second class. Once executed, that class deleted, and other classes used as public classes. Again, one class is considered a first-class general class and the other a second-class class. Our model runs until all classes are considered first class (First class). It executes these classes one by one.
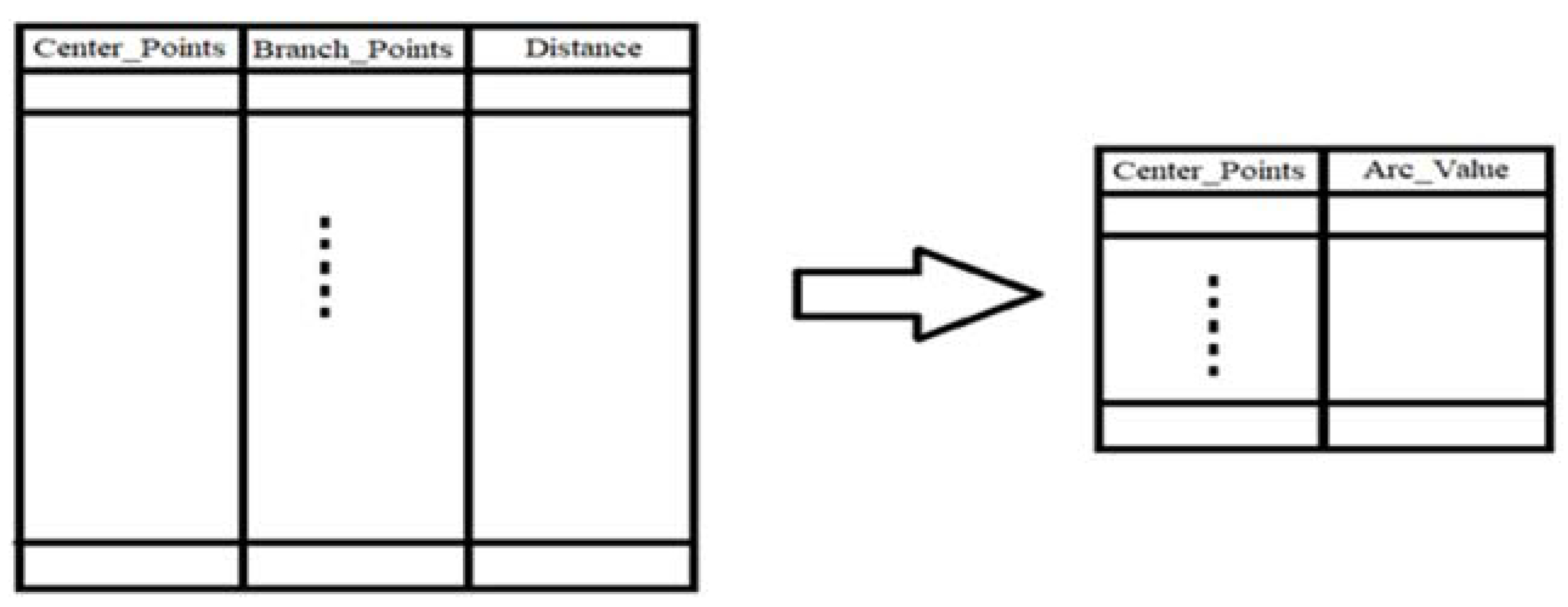
5) Find the minimum routing for each class (function) separately: All vectors of each class passes to function of the Prim algorithm (it is possible to implement a new algorithm for this idea. But in the first our model uses the Prim algorithm for our purpose.) Each vector is considered a node that has all information of the vectors. The output of a connection matrix is the nodes have the least routing, the first column is the number of nodes, and the second column is the number of neighbors, which includes the least routing. There is no number of leaves in the first column. They exist only in the second column. The original algorithm uses the Euclidean distance to calculate. This table arranged for further processing.
6) Create Arc (Function): Based on the last step matrix, this function creates an arc based on two models. 1) A arc of each node is created from the first column with the maximum distance of children. The high distance between children plus the amount of epsilon considered the size of the Arc to create in all dimensions. 2) A arc is created only in the first column with the maximum distance of children, and they only support leaf nodes. In this type, like the first model, the high distance of children plus the amount of epsilon is also considered the size of the arch to create in all dimensions.
7) Find centers and calculate boundary points (function): This function starts to find boundary points using centers and arcs of two classes. Finding boundary points involves three possible modes, which briefly describe in this section. These modes are in order:
7.1) this means that the boundary point is in the middle of the distance between the two arcs. The Euclidean distance between two equal:
These expression nodes in the two arches are completing noiseless.
7.2) If two arcs of two different classes are in contact and cover equal or less than a quarter of the other arc (area under the supporting arches) (this means that the Euclidean distance between the two centers is less than The first arc is plus, the center (the size of the second center arc). This mode is divided into two different models, respectively.
7.2.1) this model occurs when two centers do not locate in other arcs. In this case, the nodes belong to each center and its arches and do not place another. These nodes remove two. Other nodes consider finding boundary points. Ineffective nodes remove. They also do not have noisy knots. Noisy nodes are for border-to-border separation. Nodes and Central Nodes Special nodes with epsilon arcs of each class start finding boundary points (all nodes are central nodes with epsilon arcs).
This paragraph of our idea wants to prove the minimum and maximum nodes that can supports by the central nodes.
If the Euclidean distances a and b are equal to the Euclidean ab. Two modes occur. Mode 1: If node 3 is in zone 1, the central node cannot support node 3 (meaning that Node 3 does not have the minimum path to the central node). Mode 2: If Node 3 is in zone 2, Node 3 can support by the central node (this means that Node 3 has the least routing to the central node). But Node 2 can be supported by the central node. Node 2 connects node 3 (has minimal routing). If this path continues to all the space, the central node can support more nodes.
It does by examining the nodes with far and near distances. Each node can support angles between 60 and 120 degrees. If it considers the average of 90 degrees indicates that the number of nodes can be increased or decreased. But the number of nodes cannot increase the constant value, and if the minimum degree (60 degrees) or maximum degree considers for the nodes. The number of nodes is six nodes and three nodes, respectively.
7.2.2) When this model occurs, two arcs are touched. The big arc cannot fully support others (the small into the big). Under these conditions, all nodes are considered central. Then all the nodes go to the first mode and find the boundary points. These knots are a bit noisy. It exists right on the border. They may go to another class a little.
7.3) In this case, the center of the first class with its arc is placed in the center of another center class (meaning that the large fully supports the small. The Euclidean distance is also less than the arc scale. The Euclidean distance equals the absolute value of the size of one central arc (Class 1) minus the size of another center arc (Class 2). Use only the central node to find the boundary points. But another center breaks, and all nodes and centers become center nodes with epsilon values for their arcs. To the nodes, These nodes go to mode 1 to find the boundary points. Based on the Mathematica formula described above. The nodes locate away from the support of the other arc zone. These nodes remove before sending mode 1.
8) Effective and inefficient central boundary detection (function): This function supports two modes. 1) Boundary center detection for classification: All centers identify in the first case. But they are not exactly in the border area. They are not used to find border points. They removed. All centers in modes 2 and 3 are designed to find border points. 2) Identify the public center of each class: For all centers in the first case and all centers in the border support area to find the border, they are removed based on the deletion method. Based on the ranking of the total centers, the calculation leads to our center can find, which is close to the public center (it may have a central center. And then divide the sum of all ranking values). Find the general center assumption for calculating the noise intended for each node and will apply it to future work.
Figure 10 shows the flow diagram for the classification and noise detection of the two classes. This model becomes a multi-model by repeating this flow chart for more classes. For example, there are three classes. In Stage 1, the first class is Class 1, and the second and third classes are Class 2. In stage 2, the second class is class one, and the first and third classes call class two. In Stage 3, the third class is Class 1, and the first and second classes call Class 2. In this flowchart, our classifier uses the prim algorithm to find the least spanning tree. Anyone can use any algorithm that has a small chronological order. The best effect of this idea is that our model can use it as a steep descent to expand backward. For example, writing this idea and choosing a feature can be a great feature. And the sample noise is correct if more than 60 creatures do not have noise. The performance of this classification is more than 70% which is very well accuracy, and less than 50 is the worst. This classification is not very suitable for noise detection.
2.4. Deep Formula Detection With Extracting Formula Classifiers
2.4.1. Classification of deep formula coefficients by extracting formula coefficients in different layers along with prevalent classifiers
This section introduced a new model which converts the data into a formula in the first layer, and then the coefficients are extracted and selected in the other layers. After the last layer, the selected coefficients are sent as coefficients from the main formula to various classifiers. It is possible to apply classification to them. This model includes the following steps for definition, which are: (
Figure 6):
1) Data-to-formula conversion layer: The input layer is the input data-to-formula conversion layer. At first, windows with specific sizes define to convert data into formulas, and then the conversion is done. In other words, the data converts into a polynomial equation using Lagrange’s formula based on the defined window size (filter in deep learning). The jump also uses in such a way that they do not overlap. In this layer, the entire matrix or vectors convert into formulas.
2) Formula coefficients selection layers: These layers are defined similarly to convolution neural network layers to remove noise from coefficients. But in this implementation, only the sampling part is used for layers (sampling without noise removal using convolution neural networks). When the sampling function (without noise removal) uses in each layer. The only method of separating specific parts of polynomial formulas based on specific criteria is applied. In other words, the coefficients of formulas decreased. We have implemented this model as a prototype for our research.
3) Common and common classifiers for data: In this part, several common and common classifiers RF, KNN, SVM, and LDA used.
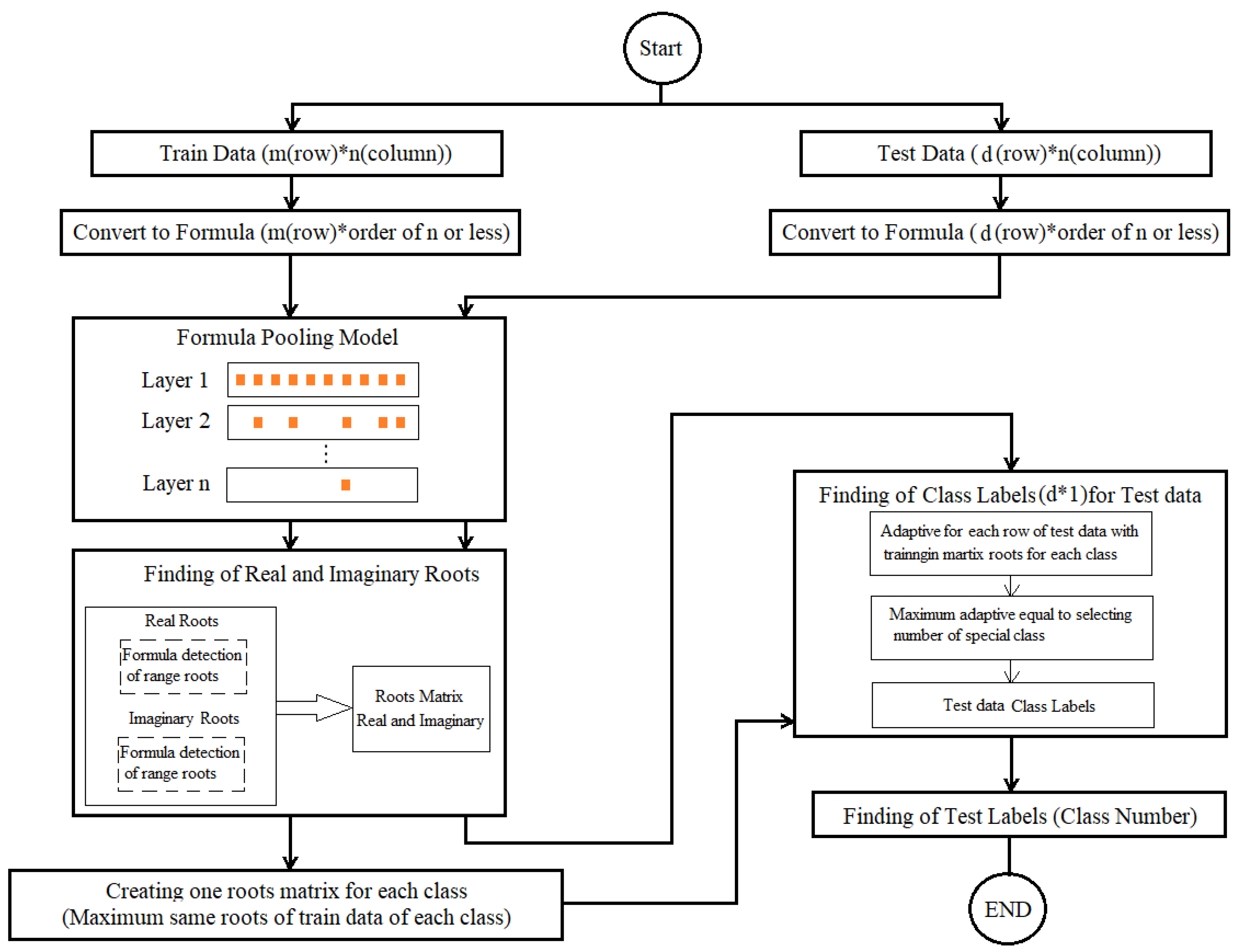
2.4.2. Detecting the range of deep formula roots by extracting coefficients of formulas in different layers along with the extraction of the roots ranges together with the classifiers of event formula roots
This section presents a new model which the data converts into a formula in the first layer, and then the coefficients are extracted and selected in the other layers. After the last layer, the coefficients are selected as coefficients from the original formula to the new interval extraction model. Test formulas sent to have classification applied to them for the same root interval basis. This model includes the following steps for definition, which are: (
Figure 16):
1) This layer is the same as the items defined in the first part of the section 2.2, which uses in the same way for the two specified items. The only difference can be the various selection of the coefficient selection function in different layers.
2) These layers are the same as those defined in the first part of the section 2.2, which uses in the same way for the two specified cases. The only difference can be the various selection of the coefficient selection function in different layers.
3) New classifier based on the rooting interval of formulas for classes: a new classifier introduced to extract and identify the roots of group members as a class based on the formula roots of the majority of members. In this way, the range of majority formula roots of members of each class is identified and recognized during learning. Based on the high similarity between the formula roots intervals of the experimental members using the root interval of the group members (classes), it is possible to identify and determine which belong to group members a class. Our experiment runs on the members of two classes.
Because it takes a lot of time to find the exact place of roots, for this reason, we have chosen the method of finding the roots of equations or polynomials at specific intervals, which requires less time. It does not need to find the exact positions. But we can discover roots at certain fixed and limited intervals where there is a root in this interval. Our classifier uses certain fixed bounded intervals of formula Roots instead of the exact place of formula roots for classification. Formula Roots are in certain fixed bounded intervals.
In the following, it is described new roots extraction and detection classifiers for more details.
Suppose the function
is given by the table in the figure below so that we have for
:
In this method, we assume that
each is a polynomial of degree n.
Where we have n for
That is, the polynomial (x) P defined by (1) holds in the condition .
The model for finding roots in a range is that the equation is divided into certain intervals. The range that has the condition of having a root is known as the root range, which must have the following conditions.
The following equation is used for real roots.
The following equation is used for imaginary roots.
We use the following method to establish the condition of the existence of the root in the specified interval.
If and , and ( is positive and is negative) or ( is negative and is positive), Lead to one root is value range.
2.4.3. Dataset and Experiments
Dataset IIa [
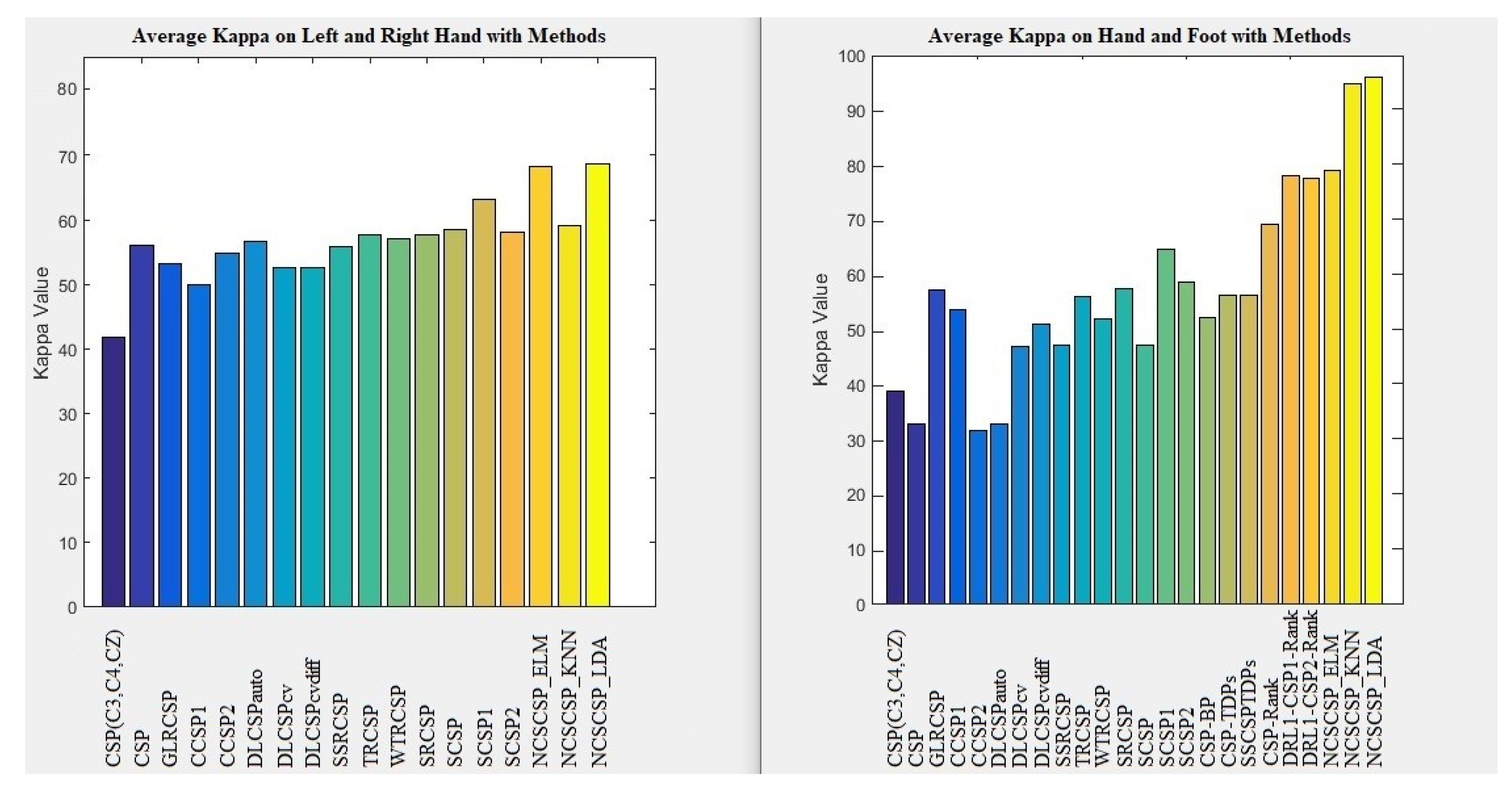
101], from BCI competition IV: It is included EEG signals from 9 subjects, and they performed four class imagery such as left hand, right hand, foot, and tongue motor imagery (MI). 22 electrodes for the recording of EEG signals on the scalp have been used. For our research, EEG signals of left and right-hands MI are considered. All training (72 trials) and testing (72 trials) sets are available for each subject. Our experiment used 280 trails. For our research, it is considered 10-10fold for experiments. This dataset is used for all four ideas.
The structure is easier to find the roots of the equation or polynomial in specific intervals. It means that it does not find the exact position of roots, it finds roots in fixed limited specific intervals and the current commonly used classifiers use different formulas to differentiate the extracted class property.
When entering the coefficients of the formulas into the classifier, the coefficients of the training and test formulas are separated with a specified function. This method is also executed with the Kfold10-10 method.
The root classifier detection section (test function) identifies the roots of the classes based on the most similar formula roots between the members of the same class, so the formula roots of each class are identified and recognized. Each test member belongs to a class that has a high similarity between the formula roots of that member and the roots of one of the classes.
This section describes the values assigned to variables and structures for practical implementation. This includes:
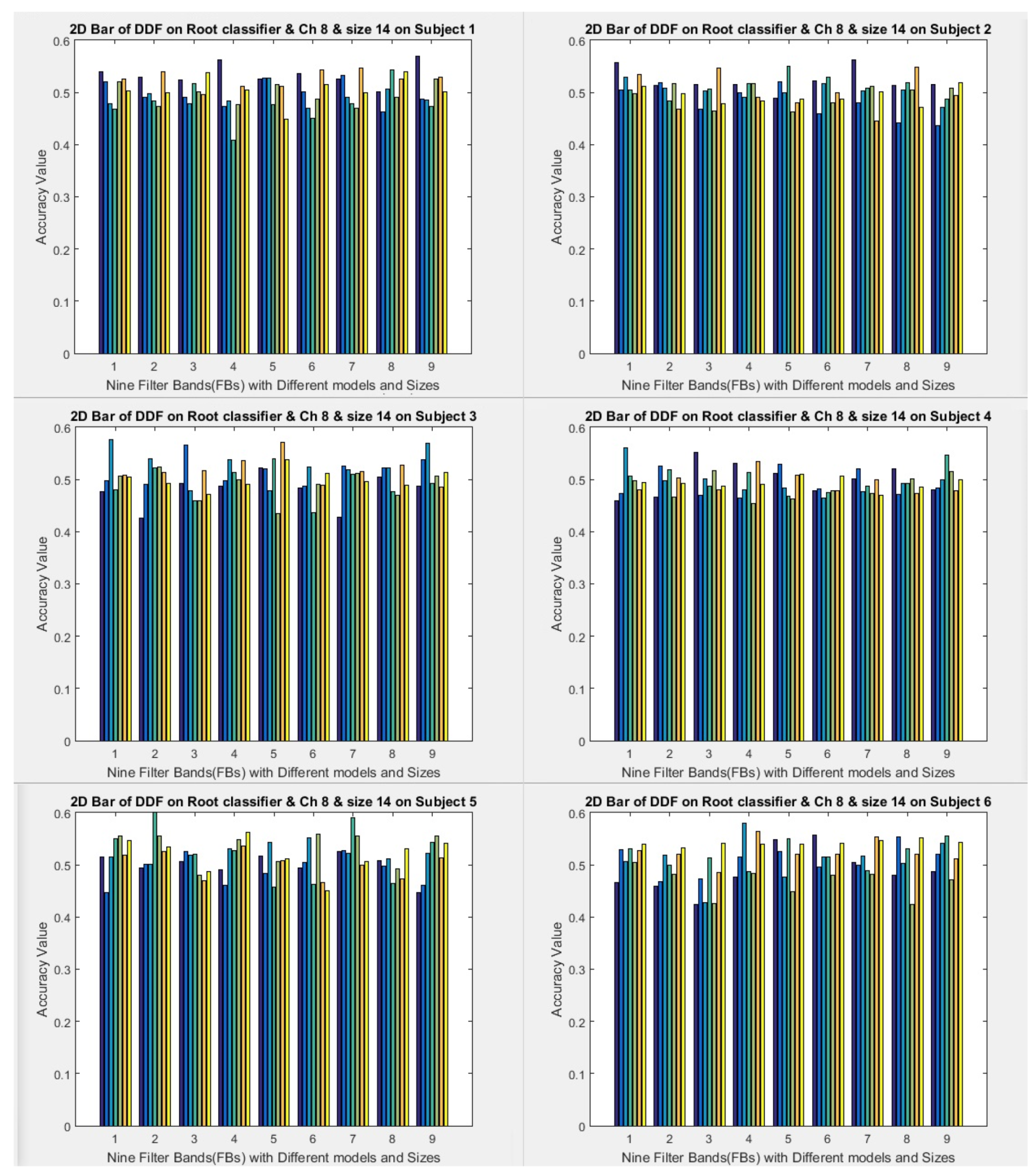
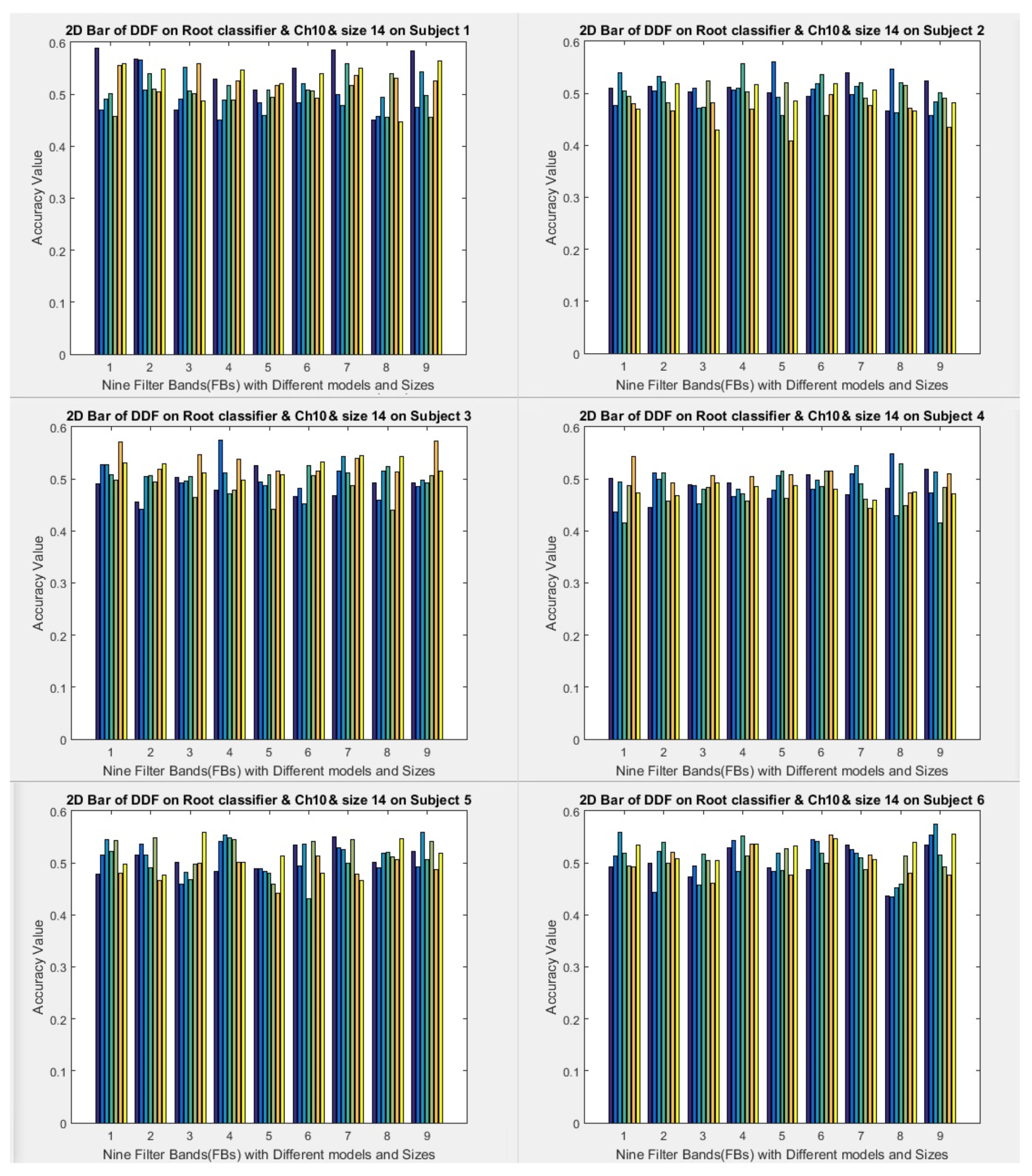
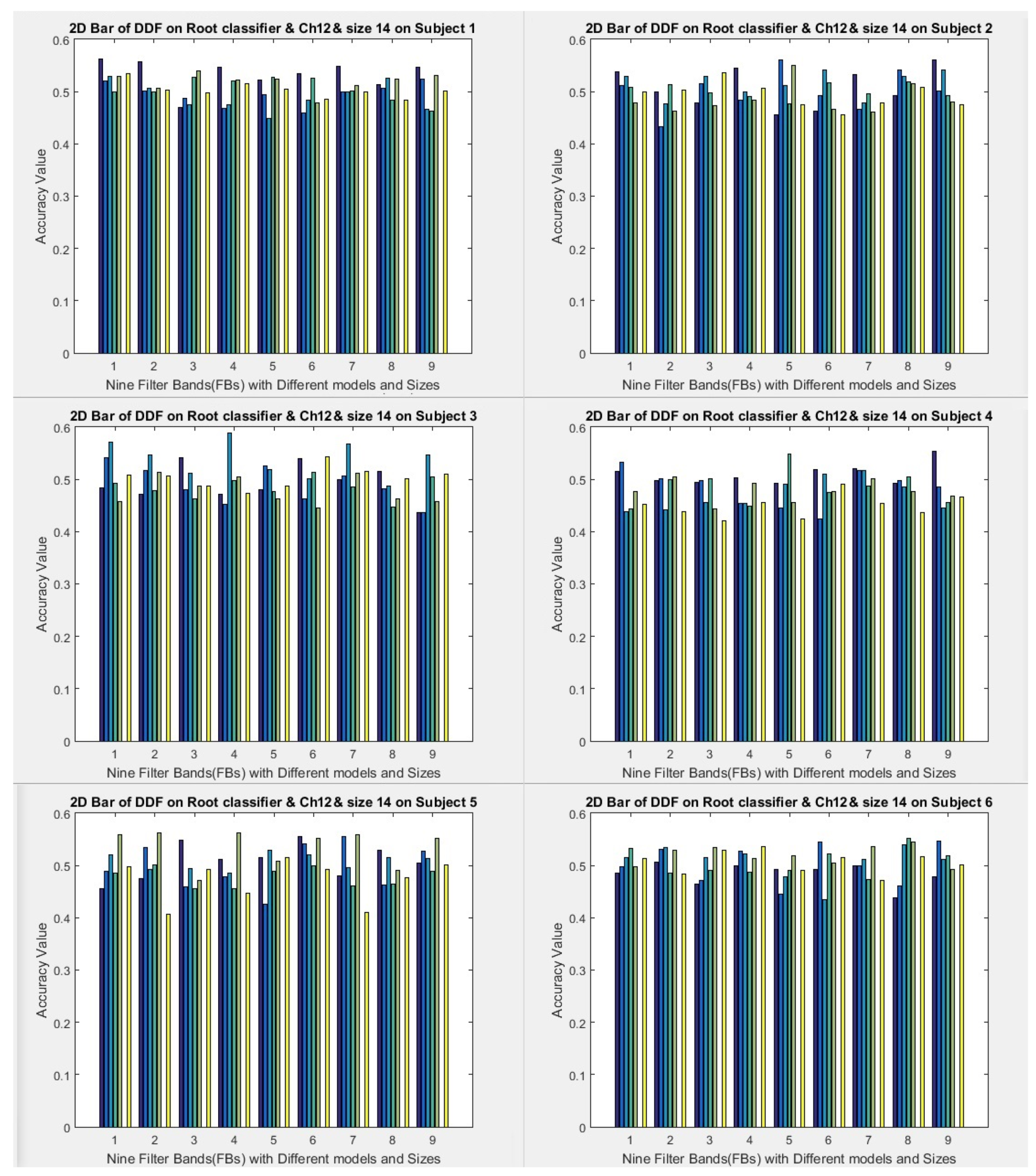
1) All filter banks (1 to 9) with three selected channels (8, 10, and 12) are used to run the models.
2) Two fixed window sizes (7 and 14) are used, which convert data into formulas in the first layer.
3) Window sampling size is used for the second and subsequent layers, respectively 3, 5, 7, 10, and 15 for size 7 (data to formula conversion). The window sampling size for the second layer and subsequent layers are 5, 10, and 14 the size of 14 (data to formula conversion), and various variables use for investigation. The results of the two cases mentioned above obtain. But this article shows the formula with a window size of 14.
4) The root folder has ten folders and ten executions. On average, all the results of 10 folders after execution are considered the final result. Therefore, it executes ten times, and the average of ten times is considered the final result. For the classifier, we set the root range (spin range) to 0.5 and can set it between 0.001 to 1. But the smaller the interval of these roots, the more time it will take to find the formula roots (our model considers only one mode).
Next, you can see an overview of the proposed new model with prevalent classifiers in
Figure 17.
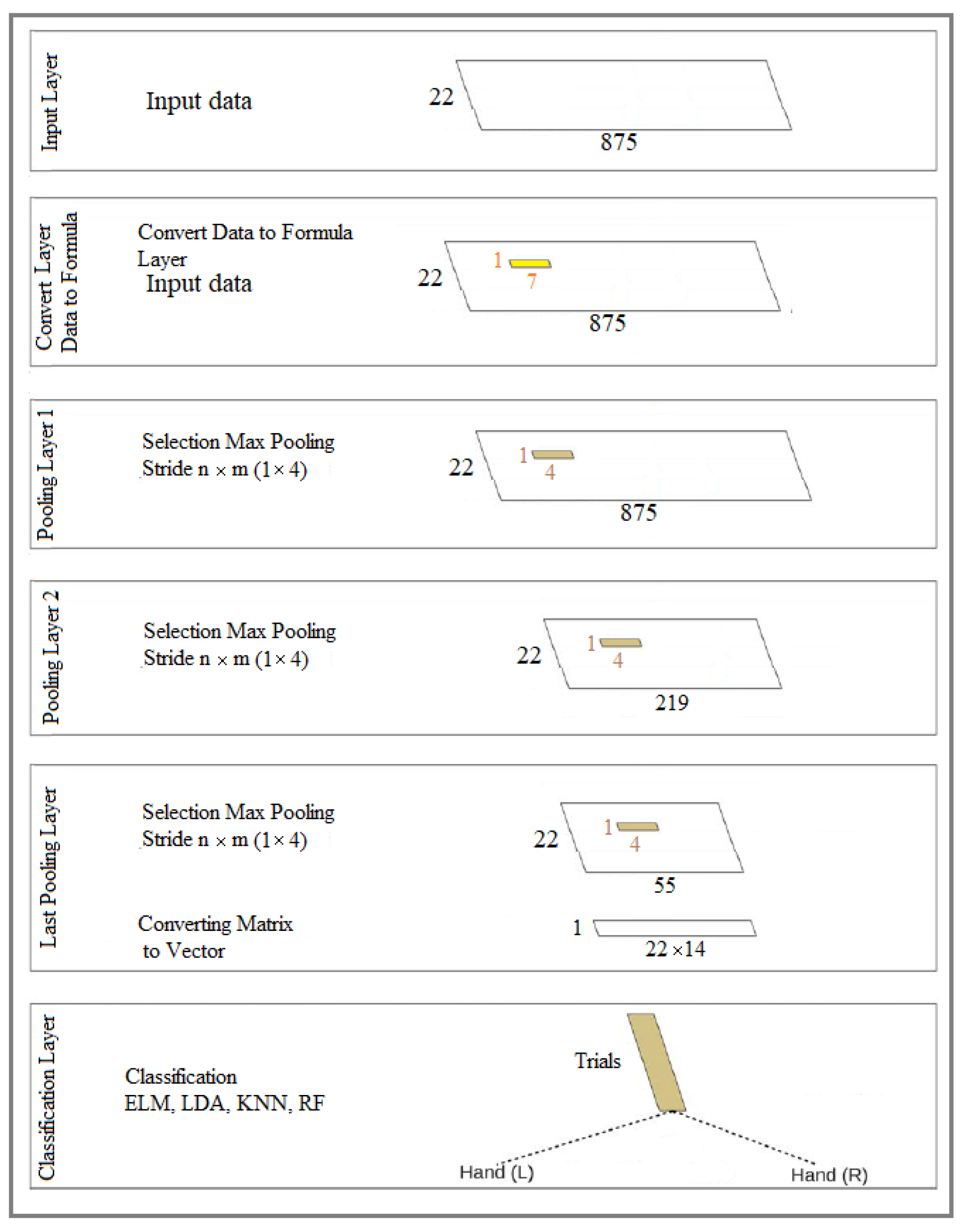
The size of the output layers and the filters used in four ways:
1) In all models, the input layer includes 288 mental images, nine filter banks, 22 channels, and 875 features for each channel during a mental imagination for each brain activity as left or right-hand. In other words, the total input data is 875x22x888x9x288 for a specific image such as the left or right hand. Therefore, the features are extracted from the original signal for each filter bank separately. In other words, the primary data stored by the electrodes for the EEG signal for each specific mental imagination (left or right hand) is equal to 875x22x288.
2) The second layer uses to extract spatial features. This way, a 22 x 1 filter applies to the channels, the output of which is 288 x 875. For all nine bank filters, feature extraction does separate. The second layer output for all models is 288x9x1x875.
3) The third layer removes in one of the models. So the third layer implements in two models. The third layer acts as an RNN layer. The jump operation is the same as the window size (filter size). The output of all models is 175x1, which includes two matrices in the form of a screen and nine bank filters, and the total network output results are 285x9x1x175.
4) The third layer uses only one model (the first model). The third layer input (the output of the second layer) directs to a fully connected neural network (MLP). The size for MLP is a 5x5 matrix. The last layer output is equal to the input to the neural network.
5) The data output of the last layer is collected for classification, and if it is in the form of a matrix, it converts into a one-dimensional vector. The number of features is equal to m, and the number of repetitions of brain activity is equal to 288. In other words, 288 × M, where m represents m = 175 × 2 × 9. Finally, a two-dimensional matrix sends to the classifier.
6) In the model where the third layer is disabled. The output of the second layer is sent directly to the ELM classifier for classification. The input data randomly divide into 50% and 50% training and testing parts. 20 neurons use for the ELM classifier.