Troubles With Gravitational Frequency Shift Derived From Energy Conservation

Preprint

Article

Troubles With Gravitational Frequency Shift Derived From Energy Conservation

Altmetrics

Downloads

172

Views

113

Comments

Germano D'Abramo^*

This version is not peer-reviewed

Submitted:

03 August 2023

Posted:

07 August 2023

Read the latest preprint version here

Alerts

Abstract

In physics, thought experiments are impressive heuristic tools. They are valuable instruments to help scientists find new results and to teach students the known ones. However, as we shall show, they should always be received with prudence, even when they are a shortcut to 'prove' well-established results. Here, we show that the most widely known thought experiments devised to derive the gravitational frequency shift from energy conservation are, in fact, problematic. Unfortunately, even some criticism of them found in the literature seems to share a similar fate. When properly set and correctly read, those thought experiments reveal that the existence of the gravitational frequency shift is, in fact, at odds with energy conservation. However, in light of the well-known experimental proofs of the gravitational redshift, our findings cannot be considered a confutation of the phenomenon. Nonetheless, our results may be of some epistemological interest and could serve as a warning sign on how thought experiments should be received and trusted.

Keywords:

Subject: Physical Sciences - Astronomy and Astrophysics

1. Introduction

In 1907, Einstein introduced the equivalence principle [1]. He used it to ‘extrapolate’ the effects of special relativity to systems at rest in a gravitational field via their alleged equivalence to uniformly accelerated systems. In that paper, Einstein first derived the gravitational redshift, the gravitational time dilation, and the influence of gravity on electromagnetic processes, like the variable velocity of light and the gravitational light deflection.

His first attempt to extend special relativity to gravitation was, according to Einstein himself, not particularly satisfying, and he returned to the topic in 1911, providing a much simpler derivation of the gravitational time dilation, redshift, and light deflection. Let us briefly review this second derivation of the gravitational redshift [2].

Consider two material systems,

S_{1}

and

S_{2}

, at rest in a local, uniform gravitational field

a

(Figure 1).

S_{1}

and

S_{2}

are separated by a distance d. Consider further a reference frame

K_{0}

. System

K_{0}

is a free-falling (gravitation-free) system located near

S_{2}

with an initial instantaneous velocity relative to

S_{2}

equal to zero.

Suppose further that a ray of light of frequency

ν_{2}

is emitted by

S_{2}

towards

S_{1}

when the relative velocity of the free-falling frame

K_{0}

with respect to

S_{2}

and

S_{1}

is still equal to zero. The ray of light reaches

S_{1}

after a time nearly equal to

d / c

. According to the principle of equivalence, this situation is physically equivalent to one in which

K_{0}

is at rest, and

S_{2}

and

S_{1}

accelerate with acceleration

- a

and initial velocity equal to zero. When the ray of light arrives at

S_{1}

, the velocity of

S_{1}

relative to the stationary frame

K_{0}

is equal to

v = a d / c

. Then, in the view of any observer in frame

K_{0}

, the ray of light received at

S_{1}

has a frequency

ν_{1}

as follows

ν_{1} = ν_{2} (1 + \frac{v}{c}) = ν_{2} (1 + \frac{a d}{c^{2}}),

(1)

where the second term is the Doppler formula for

v ≪ c

For

a d

, Einstein substituted the gravitational potential

Φ

S_{2}

, that of

S_{1}

is taken as zero, and assumed that the relation (1), deduced for a homogeneous gravitational field, would also hold for other forms of field. Then, Einstein arrived at the well-known (approximated) formula for the gravitational redshift (in this example, it is actually a blueshift)

ν_{1} = ν_{2} (1 + \frac{Φ}{c^{2}}) .

(2)

From this formula, Einstein also derived the gravitational time dilation formula. Suppose that, during the time interval

Δ t_{2}

(as measured by a clock at rest at

S_{2}

S_{2}

emits n waves. Then, from the definition of frequency, we have

n = ν_{2} Δ t_{2}

. Let

S_{1}

receive these same n waves during the time interval

Δ t_{1}

(as measured by a clock at rest at

S_{1}

). Then, again according to the definition of frequency, we have

n = ν_{1} Δ t_{1} = ν_{2} Δ t_{2}

. Hence, equation (2) leads to the gravitational time dilation formula

Δ t_{2} = Δ t_{1} (1 + \frac{Φ}{c^{2}}) .

(3)

In Section 2 of the 1911 paper, Einstein showed that, in general, energy is affected by a gravitational field and that, like the inertial mass, the gravitational mass of a body increases by

E / c^{2}

when the body absorbs an amount of energy equal to E. In that derivation, the setup is the same as in Figure 1. Einstein used the approximated relativistic energy transformation law [3]

E_{1} = E_{2} (1 + \frac{v}{c})

and, again, the equivalence principle. Moreover, by devising a clever thought experiment, he proved the following:

[...] hence, energy must possess a gravitational mass which is equal to its inertial mass. If a mass $M_{0}$ is suspended from a spring balance in the system $K^{'}$ [the system moving with acceleration $- a$ ], the balance will indicate the apparent weight $M_{0} a$ because of the inertia of $M_{0}$ . If the quantity of energy E is transferred to $M_{0}$ , the spring balance will indicate $(M_{0} + \frac{E}{c^{2}}) a$ , in accordance with the principle of the inertia of energy. According to our basic assumption [the principle of equivalence], exactly the same thing must happen if the experiment is repeated in the system K, i.e., in the gravitational field. [emphasis in the original]

It cannot escape us that this second derivation, together with the quantum formula for the energy of a photon of frequency

ν

E = h ν

, and some algebra, again gives the relation (2) for the gravitational frequency shift. However, although Einstein’s discovery of mass and energy dependence on gravitation is a crucial assumption, and his idealized experiment inspired the subsequent thought experiments analyzed in this paper, this last derivation does not strictly count as a derivation of the gravitational frequency shift from energy conservation. In fact, it is still a derivation from special relativity and the principle of equivalence. Instead, the typical (archetypal) derivations from energy conservation can be found, for instance, in the books by Born [4], Feynman, Leighton, and Sands [5], Weinberg [6], Misner, Thorne, and Wheeler [8], Rindler [9], and Schutz [10] (and many minor physics textbooks).

In the following section, we first explicitly list all the assumptions necessary for the derivation from energy conservation and outline the typical thought experiment widely used in literature, which extends those assumptions to the photon. We show why those types of derivation are problematic and are, in fact, the result of misconception and misinterpretation. Even if the previous assumptions were admissible for the photon, those derivations would be just as erroneous: when properly set and correctly read, the thought experiments lead to the non-existence of the gravitational frequency shift. We also discuss the criticism of the derivation from energy conservation advanced by Okun et al. [11] and show why we believe it is misdirected. We agree with Okun et al. reservations in applying the mentioned assumptions to the photon. However, we recall that a derivation from energy conservation that does not require these assumptions for the photon is possible. As representatives of such derivations, we analyze in more detail the thought experiments presented in Feynman, Leighton, and Sands [5], Weinberg [6], and Misner, Thorne, and Wheeler [8]. We show that, when revised and corrected, they, too, turn out to be troublesome for the very existence of the gravitational frequency shift.

In the last section, we discuss the significance of our results. Our findings may be instructive on how thought experiments should be received, most of all those which appear too good to be true: with initial skepticism and prudence. Sometimes, when we have other solid reasons to believe a physical phenomenon, thought experiments happen to be designed and interpreted in a biased way and are used as a heuristic and quick confirmation of a more complex (and not immediate) derivation. Therefore, although our results will hardly be received as a confutation of the physical existence of the gravitational frequency shift, we believe they should be taken anyway seriously from an epistemological point of view.

2. Gravitational frequency shift and the conservation of energy

The derivation of the gravitational frequency shift from energy conservation is generally seen as a confirmation of that phenomenon alternative to (and independent of) the classical one from special relativity and the principle of equivalence, and it can be found in many textbooks on general relativity.

Let us first list all the premises and commonly held beliefs explicitly or tacitly assumed in the derivation from energy conservation. They are crucial for the acceptance of its physical validity:

1): Not only can mass be converted into energy, but every kind of energy has mass as well (or can always be converted into mass) via the mass-energy equivalence formula $E = m_{0} c^{2}$ , where $m_{0}$ is the rest mass [1,2];
2): Inertial mass is equivalent to gravitational mass;
3): The energy of a light photon with frequency $ν$ is $E = h ν$ , where h is the Planck’s constant;
4): The principle of conservation of energy.

An example of derivation is the following. An `infinitesimal’ version of it can be found in the book by Rindler [9] and will be discussed later in the text. A receiver R is placed straight above an emitter of photons E at a distance d. Both are stationary in a uniform gravitational field g. The emitter E emits a photon of frequency

ν

, and energy

E = h ν

, towards R. Photons do not have rest mass, but for the sake of derivation, it is assumed that the emitted photon has an `effective’ gravitational mass m equal to its inertial mass obtained from the mass-energy equivalence,

m = \frac{E}{c^{2}} = \frac{h ν}{c^{2}}

(assumptions 1, 2, and 3). Since the emitted photon needs to climb a height d in the uniform gravitational field, its energy

E^{'}

at the receiver R is lower than E. Due to the conservation of energy (assumption 4), we necessarily have that

E^{'} = E - m g d,

(4)

where the potential energy

m g d

is the energy `spent’ by the photon climbing the distance d.

Equation (4) can be rewritten as follows,

ν^{'} = \frac{E^{'}}{h} = \frac{E - m g d}{h} = \frac{h ν - \frac{h ν}{c^{2}} g d}{h} = ν (1 - \frac{g d}{c^{2}}),

(5)

which is the sought-out gravitational frequency shift formula (1) (if the positions of E and R are reversed, the minus sign becomes a plus sign in the equation).

As far as this author knows, that type of derivation received few criticisms, with some notable exceptions like Weinberg [6], who affirms that the concept of gravitational potential energy for a photon is without foundation. Like Weinberg, Okun et al. [11] argue that any explanation of the gravitational frequency shift in terms of gravitational mass and gravitational potential energy of the photon is incorrect and misleading. Moreover, according to them, the only acceptable explanation is in the modification of the rate of a clock exposed to gravitational potential1. They further assert that the energy (and the frequency) of a photon is conserved as it propagates in a static gravitational field. Therefore, the light appears to be redshifted only relative to the frequency of the clock of the receiver. In fact, Okun et al. concentrate on past laboratory experiments for gravitational redshift detection [13,14] and ascribe the redshift to the increase in energy difference between two atomic levels of the receiver’s atoms with the distance from the center of gravity. They say verbatim that what is called the redshift of the photon is actually a blueshift of the atom, whatever it means.

However, Okun et al. do not provide any theoretical proof for their definitive rejection of the derivation from energy conservation. They only state that if the explanation in terms of gravitational attraction of the photon to the Earth were also correct, then one would be forced to expect a doubling of the redshift (the sum of the effects on the clock and the photon) in the Pound-type experiments.

We agree with some claims by Okun et al.. However, according to some basic physics principles, we believe that other claims are inconsistent and difficult to understand. Let us start with their objection that if the explanation in terms of gravitational attraction of the photon were correct, then one would be forced to expect a doubling of the redshift, the sum of the effects on the clock and the photon. In fact, it is a bit bizarre that Einstein himself derived the gravitational time dilation (clock rate dependence on gravitational potential) to explain how it was possible to have different radiation frequencies of the same radiation between two relatively stationary observers (the emitter and the receiver), see Section 1. Namely, he derived the effect of gravitation on clocks to explain the gravitational modification of the radiation frequency derived without appealing to energy conservation but only to special relativity and the equivalence principle. In Einstein’s 1911 derivation (Section 1), the stationary (or free-falling) observer

K_{0}

does not directly observe any frequency shift but infers that the accelerated (or stationary in a static gravitational field) observer

S_{1}

should see one due to the well-known Doppler effect (movement of

S_{1}

relative to the radiation instantaneously emitted by

S_{2}

). Now, in the equivalent case of

S_{2}

and

S_{1}

being stationary in a gravitational field, the free-falling observer

K_{0}

asks how a frequency shift in radiation exchanged between two relatively stationary observers is possible and comes up with the discovery of the gravitational time dilation (equation (3)). At this point, by following Okun et al., to avoid a doubling of the frequency shift, the observer

K_{0}

would be forced to negate any frequency shift of radiation he inferred at the beginning of the whole derivation (in the equivalent case in which

K_{0}

is at rest and

S_{2}

and

S_{1}

accelerating). But then, if that interpretation were correct, the very same necessity to introduce from the beginning a time dilation would disappear, leaving us with no gravitational time dilation and frequency shift. As a matter of fact, the only logical and meaningful conclusion of that reasoning would be that there is neither a gravitational frequency shift nor a gravitational time dilation from the outset. That is to say that we would have the `doubling issue’ even with Einstein’s original derivation.

Moreover, if Okun et al. were right when they say that the energy of the photon does not change as the photon propagates in a static gravitational field, that would make, by definition, the existence of gravitational redshift impossible. If the Planck-Einstein formula

E = h ν

and the value of Planck’s constant h must be the same everywhere, then we cannot understand how the receiver atoms cannot measure the same frequency of the photon as the emitter. If the photon energy E does not change between the emitter and the receiver, the receiver would necessarily measure the frequency

ν = \frac{E}{h}

, which is the same as that measured by the emitter, E and h being the same as those at the height of the emitter.

Incidentally, if correctly set and interpreted, even the widely used derivations that appeal to the criticized concepts of “photon mass” and “photon gravitational potential energy” do not imply any gravitational energy or frequency shift of the photon. For instance, Rindler [9] wrote:

[...] as light climbs up a gravitational gradient, its frequency decreases [...]. Of course, [this effect is] intuitive once we know that light consists of photons: We `only’ need to know the Planck-Einstein formula $E = h ν$ for the kinetic energy of a photon of frequency $ν$ , Einstein’s formula $E = m_{I} c^{2}$ relating energy to inertial mass, and the weak EP, $m_{I} = m_{G}$ . For the work done by a gravitational field with potential $Φ$ on a particle of gravitational mass $m_{G}$ as it traverses a potential difference $d Φ$ is $- m_{G} d Φ$ . This must equal $d E$ , the gain in the particle’s kinetic energy. For a photon, $d E = h d ν$ , and so

h d ν = - m_{G} d Φ = - m_{I} d Φ = - \frac{E}{c^{2}} d Φ = - \frac{h ν}{c^{2}} d Φ,

whence

\frac{d ν}{ν} = \frac{- d Φ}{c^{2}} .

In fact, the Planck-Einstein relation

E = h ν

gives the total energy or simply the energy of a photon of frequency

ν

, and the concept of the kinetic energy of a photon is misleading. As a matter of fact, if

E = h ν

were only the kinetic energy of the photon, the mass-energy equivalence would not provide us with the total effective inertial/gravitational mass of the photon since, in that case, any gravitational potential energy contribution (assumption 1) would not be included in the formula

E = h ν

, and the relation

m_{G} = m_{I} = \frac{h ν}{c^{2}}

would only give an indeterminate partial value of its effective mass.

Therefore, consider the following addition to Rindler’s derivation. By sticking to Rindler’s assumptions, we can equally reasonably apply his argument like this. When a photon of energy E, and effective inertial/gravitational mass

m_{G} = m_{I} = \frac{E}{c^{2}}

, climbs up a gravitational gradient

d Φ

, it also gains a gravitational potential energy equal to

+ m_{G} d Φ

. Therefore, the following term should be taken into account in the total variation of the photon energy,

d E = + m_{G} d Φ = + m_{I} d Φ = + \frac{E}{c^{2}} d Φ = + \frac{h ν}{c^{2}} d Φ .

The only possible way to count this energy in that of the photon is to count it in the energy

E = h ν

because it is the only energy a photon is identified by. In doing so, the total energy variation of the photon in traversing a gravitational gradient amounts to zero, and so does its frequency shift.

We agree with Okun et al. that since the photon has no rest mass, the appeal to its gravitational mass and potential energy may be a loose and not fully legitimate argument. However, it is possible to come up with a gravitational frequency shift derivation from energy conservation that does not appeal to those concepts like, for instance, the derivations in Feynman, Leighton, and Sands [5], Weinberg [6], Earman and Glymour [7], Misner, Thorne, and Wheeler [8], Schutz [10], and Koks [12].

As a representative of such derivations, consider first the thought experiment by Misner, Thorne, and Wheeler [8]. They recount Einstein’s 1911 realization of the interaction between light and gravity as follows (the speed of light is set as

c = 1

That a photon must be affected by a gravitational field Einstein (1911) showed from the law of conservation of energy, applied in the context of Newtonian gravitation theory. Let a particle of rest mass m start from rest in a gravitational field g at point $A$ and fall freely for a distance h to point $B$ . It gains kinetic energy $m g h$ . Its total energy, including rest mass, become

m + m g h .

Now, let the particle undergo an annihilation at $B$ , converting its total rest mass plus kinetic energy into a photon of the same energy. Let this photon travel upward in the gravitational field to $A$ . If it does not interact with gravity, it will have its original energy on arrival at $A$ . At this point it could be converted by a suitable apparatus into another particle of rest mass m (which could then repeat the whole process) plus an excess energy $m g h$ that costs nothing to produce. To avoid this contradiction of the principal [sic] of conservation of energy, which can also be stated in purely classical terms, Einstein saw that the photon must suffer a red shift.

In this derivation, nowhere reference is made to the gravitational mass or the gravitational potential energy of the photon. Energy has a mass only after absorption by a non-relativistic and macroscopic material body (the apparatus that converts it into a massive particle in the last part of the process). That is allowed by the widely-held interpretation of the mass-energy equivalence.

Unfortunately, even Misner, Thorne, and Wheeler’s argument is fallacious [15]. If a particle of rest mass m starts from rest in a gravitational field g at point

A

and falls freely for a distance h to point

B

, that particle posses also an energy equal to

m g h

already at point

A

. It is called gravitational potential energy. Therefore, owing to mass-energy equivalence, at point

A

, that particle already has a total mass/energy equal2 to

m + m g h

. Now, if the energy of the photon produced in the particle annihilation at point

B

and traveling upward does not have its original value on arrival at

A

(i.e.,

m + m g h

), the mass of the particle created by the suitable apparatus at the end of the process would not have the same mass as the original particle (again,

m + m g h

), and the total energy/mass would not be conserved. When Misner, Thorne, and Wheeler say that the particle “gains kinetic energy

m g h

” on arrival at point

B

, and “its total energy, including rest mass, becomes

m + m g h

”, they seem to forget that the particle already has gravitational potential energy

m g h

, and total energy

m + m g h

, just before starting to fall. That is demanded by the principle of conservation of energy. The same analysis with a few adjustments also applies to the derivations in Schutz [10] and Koks [12] with the same conclusion.

The intriguing part is that Misner, Thorne and Wheeler’s thought experiment and our correction to it are immune to the criticism of Okun et al. on the value and implications of the derivations from energy conservation. Misner, Thorne, and Wheeler do not make any reference to the gravitational mass, the gravitational potential energy, or the frequency of the photon. They refer only to the photon energy and the conversion of energy into mass and vice versa.

Even if Misner, Thorne, and Wheeler do not explicitly mention the Planck-Einstein formula

E = h ν

, the fact that the energy can be converted into a single photon or a finite (and definite) number of photons is a tacit but important further assumption. For if it were possible to convert energy into light in a `continuous’ way, the conservation of energy could still be re-established: in principle, if the emitter at point

B

continuously emitted a higher frequency radiation (higher intrinsic energy) for an interval

Δ t

and the receiver at point

A

continuously received a lower frequency radiation (lower intrinsic energy) for a suitably longer interval

Δ t^{'} > Δ t

, the total amount of energy could still be conserved (and the gravitational time dilation would necessarily get back into the game). However, the quantization of energy in light transmission has solid theoretical and experimental corroboration.

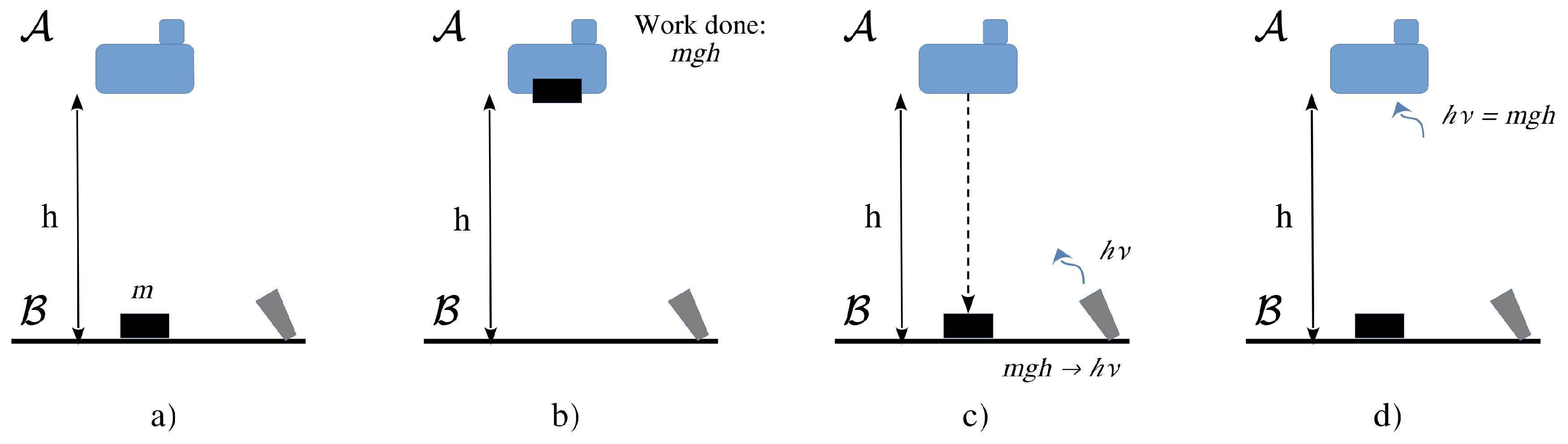
Incidentally, upon closer scrutiny, the mass-energy equivalence is not even necessary. Consider a body of mass m stationary at point

B

and a macroscopic apparatus stationary at point

A

at a height h above point

B

in a gravitational field g (Figure 2). Let the apparatus perform mechanical work on body m raising it to point

A

. The work done by the apparatus is equal to

m g h

, which is also equal to the gravitational potential energy of the body m relative to point

B

. Now, if the mass is lowered back to point

B

and its potential energy conventionally (and entirely) converted into electrical energy (and then into a single photon of energy

m g h

), the energy of the photon must always be the same while climbing up the gravitational field back to point

A

. The photon energy at point

A

must still be equal to

m g h

. That is demanded by the conservation of energy. Through photon absorption, the apparatus must regain the same energy expended at the beginning of the cycle on m. Therefore, owing to the Planck-Einstein formula, the photon frequency must be the same at points

A

and

B

Weinberg presented a derivation from energy conservation slightly different from that given by Misner, Thorne, and Wheeler but equally fallacious. It could be of some interest to go into detail. Weinberg writes (again, the speed of light is set as

c = 1

) [6]:

Incidentally, the gravitational red shift of light rising from a lower to a higher gravitational potential can to some extent be understood as a consequence of quantum theory, energy conservation, and the “weak” Principle of Equivalence. When a photon is produced at point 1 by some heavy nonrelativistic apparatus, an observer in a locally inertial coordinate system moving with the apparatus will see its internal energy and hence its inertial mass change by an amount related to the photon frequency $ν_{1}$ he observes, that is, by

Δ m_{1} = - h ν_{1}

where $h = 6.625 \times 10^{- 27}$ erg sec is Planck’s constant. Suppose that the photon is then absorbed at point 2 by a second heavy apparatus; an observer in a freely falling system will see the apparatus change in inertial mass by an amount related to the photon frequency $ν_{2}$ he observes, that is, by

Δ m_{2} = h ν_{2}

However, the total internal plus gravitational potential energy of the two pieces of apparatus must be the same before and after these events, so

0 = Δ m_{1} + ϕ_{1} Δ m_{1} + Δ m_{2} + ϕ_{2} Δ m_{2}

and therefore

\frac{ν_{2}}{ν_{1}} = \frac{1 + ϕ_{1}}{1 + ϕ_{2}} ≃ 1 + ϕ_{1} - ϕ_{2}

in agreement with our previous result. (Also, it makes no difference whether the photon frequencies are measured in locally inertial systems, because the gravitational field in any other frame will affect the rate of the observer’s standard clock in the same way as it affects the $ν$ ’s.)

Leaving aside the reference to the free-falling observer who will necessarily see a Doppler shift due to the motion relative to the stationary emitting apparatus, a thing that, in the humble opinion of this author, unnecessarily complicates the picture, Weinberg’s derivation seems to violate the conservation of energy just from the beginning. First, he states that, upon the photon emission, the apparatus will change its internal energy by an amount

h ν_{1} = | Δ m_{1} |

. But, then, he says that the variation of the total energy of the apparatus to consider upon emission is

| Δ m_{1} + ϕ_{1} Δ m_{1} |

. Namely, the apparatus emits energy equal to

| Δ m_{1} |

, but its total energy variation is

| Δ m_{1} + ϕ_{1} Δ m_{1} | \neq | Δ m_{1} |

. This already represents a violation of the energy conservation. If we reestablish the conservation of energy (

| Δ m_{1 / 2} + ϕ_{1 / 2} Δ m_{1 / 2} | = | h ν_{1 / 2} |

), no gravitational frequency shift is implied.

A similar oversight in the application of energy conservation also affects the derivation in Feynman, Leighton, and Sands [5]. They write:

We know that the gravitational force on an object is proportional to its mass M, which is related to its total internal energy E by $M = E / c^{2}$ . For instance, the masses of nuclei determined from the energies of nuclear reactions which transmute one nucleus into another agree with the masses obtained from atomic weights.

Now think of an atom which has a lowest energy state of total energy $E_{0}$ and a higher energy state $E_{1}$ , and which can go from the state $E_{1}$ to the state $E_{0}$ by emitting light. The frequency $ω$ of the light will be given by

ℏ ω = E_{1} - E_{0}

(42.7)

Now suppose we have such an atom in the state $E_{1}$ sitting on the floor, and we carry it from the floor to the height H. To do that we must do some work in carrying the mass $m_{1} = E_{1} / c^{2}$ up against the gravitational force. The amount of work done is

\frac{E_{1}}{c^{2}} g H

(42.8)

Then we let the atom emit a photon and go into the lower energy state $E_{0}$ . Afterward we carry the atom back to the floor. On the return trip the mass is $E_{0} / c^{2}$ ; we get back the energy

\frac{E_{0}}{c^{2}} g H,

(42.9)

so we have done a net amount of work equal to

Δ U = \frac{(E_{1} - E_{0})}{c^{2}} g H .

(42.10)

When the atom emitted the photon it gave up the energy $E_{1} - E_{0}$ . Now suppose that the photon happened to go down to the floor and be absorbed. How much energy would it deliver there? You might at first think that it would deliver just the energy $E_{1} - E_{0}$ . But that can’t be right if energy is conserved, as you can see from the following argument. We started with the energy $E_{1}$ at the floor. When we finish, the energy at the floor level is the energy $E_{0}$ of the atom in its lower state plus the energy $E_{p h}$ received from the photon. In the meantime we have had to supply the additional energy $Δ U$ of Eq. (42.10). If energy is conserved, the energy we end up with at the floor must be greater than we started with by just the work we have done. Namely, we must have that

E_{p h} + E_{0} = E_{1} + Δ U,

or

E_{p h} = (E_{1} - E_{0}) + Δ U .

(42.11)

It must be that the photon does not arrive at the floor with just the energy $E_{1} - E_{0}$ it started with, but with a little more energy. Otherwise some energy would have been lost. If we substitute in Eq. (42.11) the $Δ U$ we got in Eq. (42.10) we get that the photon arrives at the floor with the energy

E_{p h} = (E_{1} - E_{0}) (1 + \frac{g H}{c^{2}}) .

(42.12)

But a photon of energy $E_{p h}$ has the frequency $ω = E_{p h} / ℏ$ . Calling the frequency of the emitted photon $ω_{0}$ —which is by Eq. (42.7) equal to $(E_{1} - E_{0}) / ℏ$ —our result in Eq. (42.12) gives again the relation of (42.5) between the frequency of the photon when it is absorbed on the floor and the frequency with which it was emitted.

The weak link of the above inference chain is the assumption (42.9). The total energy of the atom sitting on the floor is

E_{1}

. After being carried to the height H, its total energy becomes

E_{1} + \frac{E_{1}}{c^{2}} g H

(its rest energy plus the work done on the atom). With the emission of a photon of energy

ℏ ω = E_{1} - E_{0}

, the total energy becomes

(E_{1} + \frac{E_{1}}{c^{2}} g H) - (E_{1} - E_{0}) = E_{0} + \frac{E_{1}}{c^{2}} g H

. According to the conservation of energy, that total energy must be conserved after the atom is carried back to the floor. Now, if we subtract the new rest energy

E_{0}

of the atom from this total energy, we get back the correct energy

\frac{E_{1}}{c^{2}} g H

, and the net amount of work we have done is

Δ U = 0

. Therefore, according to equation (42.11), the photon must arrive at the floor with just the energy

E_{1} - E_{0}

it started with at the height H.

In conclusion, our analysis and revision of, in particular, Misner, Thorne, and Wheeler’s, Weinberg’s, and Feynman, Leighton, and Sands’s thought experiments ultimately pit the existence of the gravitational frequency shift or, better, the dependence of the photon energy on gravitation against the conservation of energy. Moreover, the revised thought experiments can now be considered as the proof missing in the paper by Okun et al. of the fact that photon energy is unaffected by gravitation. However, contrary to Okun et al., we see all that as a problem for the very existence of the gravitational frequency shift. The reason has already been mentioned. The Planck-Einstein formula

E = h ν

must hold at every height in a gravitational field. Therefore, if

Δ E = 0

, the photon frequency

ν

must be the same at every height in a gravitational field, no matter what may happen to the observers (e.g., the atoms of the receiver) in that field.

3. Discussion and conclusions

In physics, thought experiments can be powerful heuristic tools. However, as we have shown in the present paper with the derivation of the gravitational frequency shift from energy conservation, they must be received with prudence. Sometimes, as they are conceived, they dangerously lend to being a rhetorical device to sustain what we already believe in or, at least, what seems reasonable to us from the beginning. Sometimes, even criticism of them may follow a similar fate, as we have shown with the paper by Okun et al.

By following a different approach, Florides [16,17] showed that even the standard argument introduced by Einstein in 1911 is fundamentally flawed. By deriving a more general formula for the Doppler shift, Florides showed that the frequency of the light received in

S_{1}

is equal to that emitted in

S_{2}

Before deriving his main result, Florides [17] stresses a premise: he reminds the reader that the gravitational redshift has been verified experimentally on the Earth’s surface (Pound and Rebka [13], and Pound and Snider [14]), and its existence is, therefore, beyond any doubt. He then concludes his paper with the following words:

[...] in view of the failure of the equivalence principle to predict the phenomenon of the gravitational red-shift, the question must be asked: Is the general theory of relativity wrong? The answer is, of course, an emphatic and resounding no. As is shown in every book on general relativity the full theory (including its field equations), irrespective of its origins, predicts simply and unambiguously the exact experimentally observed gravitational red-shift. Thus, by an ironic reversal of events, the non-validity of the equivalence principle, or at least its failure to predict the gravitational red-shift which gave the principle so much prominence in the first place, not only does it not invalidate the general theory of relativity but it strengthens it; for the full general theory of relativity alone predicts the observed gravitational red shift. [emphasis in the original]

Although it would be interesting, a treatment of the experimental confirmations of gravitational redshift, and a discussion on how Florides’s and our results confront them, is beyond the scope of the present paper. Given the complexity of each experiment, a thorough analysis would require an entire research project. However, we think the following comments on Florides’s stand can be useful, also because Florides’s view represents of a widespread way of thinking. From an epistemological point of view and first principles, we must confess our uneasiness with that position. How can we affirm with great complacency that the full-fledged theory of general relativity is correct beyond any reasonable doubt when the thought experiments that allowed us to discover the gravitational redshift and provided the only physical justification for its existence from the beginning have been misinterpreted and their conclusion turned out to be wrong? Those thought experiments convinced us that new phenomena must physically exist. Then, a lofty, apparently self-consistent mathematical theory was developed to include those phenomena. But, then, it turns out that the original thought experiments have been misconceived and no longer imply any gravitational redshift. Can all this be taken lightly?

We believe that the most intellectually honest reaction to all that should not be: “we now have a complete theory; therefore, we do not mind and sweep the wrong original derivations under the carpet”. And we should not have that reaction even if we now have allegedly solid experimental confirmations of the predicted phenomena. Like theoretical results, even experimental ones should be revised (and experiments re-done) whenever the theoretical premises that made us aware of the existence of the new phenomena under test turn out to be wrong. In general, when new elements emerge about a physical theory, we believe it would be wise to redo the experiments with that information because we all know that the experiments’ design, acquisition, and interpretation of (almost always indirect) data, and in the end, what they tell us, are not independent of the theoretical assumptions (e.g., the theory-ladenness of experiment sustained by Kuhn and Feyerabend [18]).

However, in light of the well-known and well-accepted experimental proofs of the gravitational redshift, it is hard to believe that what we have derived in the present paper will be felt as a confutation of the phenomenon. Nonetheless, we think it may be instructive as a warning sign on how thought experiments should be received and trusted, and therefore it could be of some epistemological interest and utility.

References

Einstein, A. On the relativity principle and the conclusions drawn from it. Jahrbuch der Radioaktivität 1907, 4, 411–462. English translation at https://einsteinpapers.press.princeton.edu/vol3-trans/266.
Einstein, A. On the influence of gravitation on the propagation of light. Ann. Phys. 1911, 35, 898–908. English translation at https://einsteinpapers.press.princeton.edu/vol3-trans/393.
Einstein, A. On the Electrodynamics of Moving Bodies. Ann. Phys. 1905, 18, 639–643. English translation at https://einsteinpapers.press.princeton.edu/vol2-trans/154.
Born, M. Die Relativitatstheorie Einstein; Springer-Verlag: Berlin, Heidelberg, Germany, 1964; p. 303.
R.P. Feynman, R.P.; Leighton, R.B.; Sands, M. The Feynman Lectures on Physics, Vol. II: The New Millennium Edition: Mainly Electromagnetism and Matter, First Trade Paper ed.; Basic Books: New York, USA, 2011; Sec. 42-6.
Weinberg, S. Gravitation and Cosmology; J.Wiley & Sons: New York, USA, 1972; Sec. 3.6, pp. 84–85.
Earman, J.; Glymour, C. The gravitational red shift as a test of general relativity: history and analysis. Stud. Hist. Phil. Sci. 1980, 2(3), pp. 175–214. [CrossRef]
Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W.H. Freeman: San Francisco, USA, 1973; Sec. 7.2, p. 187.
Rindler, W. Relativity: Special, General and Cosmological, 2nd Ed.; Oxford University Press: Oxford, UK, 2006; Sec. 1.16, p. 24.
Schutz, B. A first course in General Relativity; Cambridge University Press: Cambridge, UK, 2009; Section 5.1, p. 112.
Okun, L.B.; Selivanov. K.G.; Telegdi, V.L. On the interpretation of the redshift in a static gravitational field. Am. J. Phys. 2000, 68, pp. 115–119. [CrossRef]
Koks, D. The Uniformly Accelerated Frame as a Test Bed for Analysing the Gravitational Redshift. Universe 2021, 7(1), pp. 4–36. [CrossRef]
Pound, R.V.; Rebka, G.A. Apparent Weight of Photons. Phys. Rev. Lett. 1968, 4, pp. 337–341.
R.V. Pound, R.V.; Snider, J.L. Effect of Gravity on Nuclear Resonance. Phys. Rev. Lett. 1964, 13, pp. 539–540. [CrossRef]
D’Abramo, G. Einstein’s 1905 derivation of the mass-energy equivalence: is it valid? Is energy always equal to mass and vice versa? Physics of Particles and Nuclei 2023, 54, pp. 966–971.
Florides, P.A. Einstein’s Equivalence Principle and the Gravitational Red Shift. Int. J. Mod. Phys. A 2002, 17(20), p. 2759. [CrossRef]
Florides, P.A. Einstein’s Equivalence Principle and the Gravitational Red Shift II. arXiv 2013 (retrieved Dec., 2022).
Franklin, A. The Theory-Ladenness of Experiment. J. Gen. Philos. Sci. 2015, 49(1), pp. 155–166. [CrossRef]

That view is also shared by Koks [12], although he does not see anything wrong with functional concepts of gravitational mass and gravitational potential energy of a photon.

It can be shown that, in a uniform gravitational field g, the mass

m_{h}

of a particle at height h is

m_{h} = m e^{\frac{g h}{c^{2}}}

, where m is the proper mass at the height taken as zero. The total energy

E_{t o t}

, proper mass plus gravitational potential energy, at height h is given by

E_{t o t} = m c^{2} e^{\frac{g h}{c^{2}}}

. For small distances h, we have

m_{h} ≃ m + \frac{m g h}{c^{2}}

and

E_{t o t} ≃ m c^{2} + m g h

(a similar result is also present in [11]). By assuming

c = 1

, like in [8], we have that the mass and total energy of the particle at height h (point

A

) are

m + m g h

Figure 1. Material systems

S_{1}

and

S_{2}

are at rest in a local, uniform gravitational field

a

. The reference frame

K_{0}

is a free-falling (gravitation-free) system located near

S_{2}

with zero initial velocity relative to

S_{2}

. According to the equivalence principle, this is equivalent to systems

S_{1}

and

S_{2}

accelerating upward with acceleration

- a

and frame

K_{0}

being inertial and at rest.

Figure 1. Material systems

S_{1}

and

S_{2}

are at rest in a local, uniform gravitational field

a

. The reference frame

K_{0}

is a free-falling (gravitation-free) system located near

S_{2}

with zero initial velocity relative to

S_{2}

. According to the equivalence principle, this is equivalent to systems

S_{1}

and

S_{2}

accelerating upward with acceleration

- a

and frame

K_{0}

being inertial and at rest.

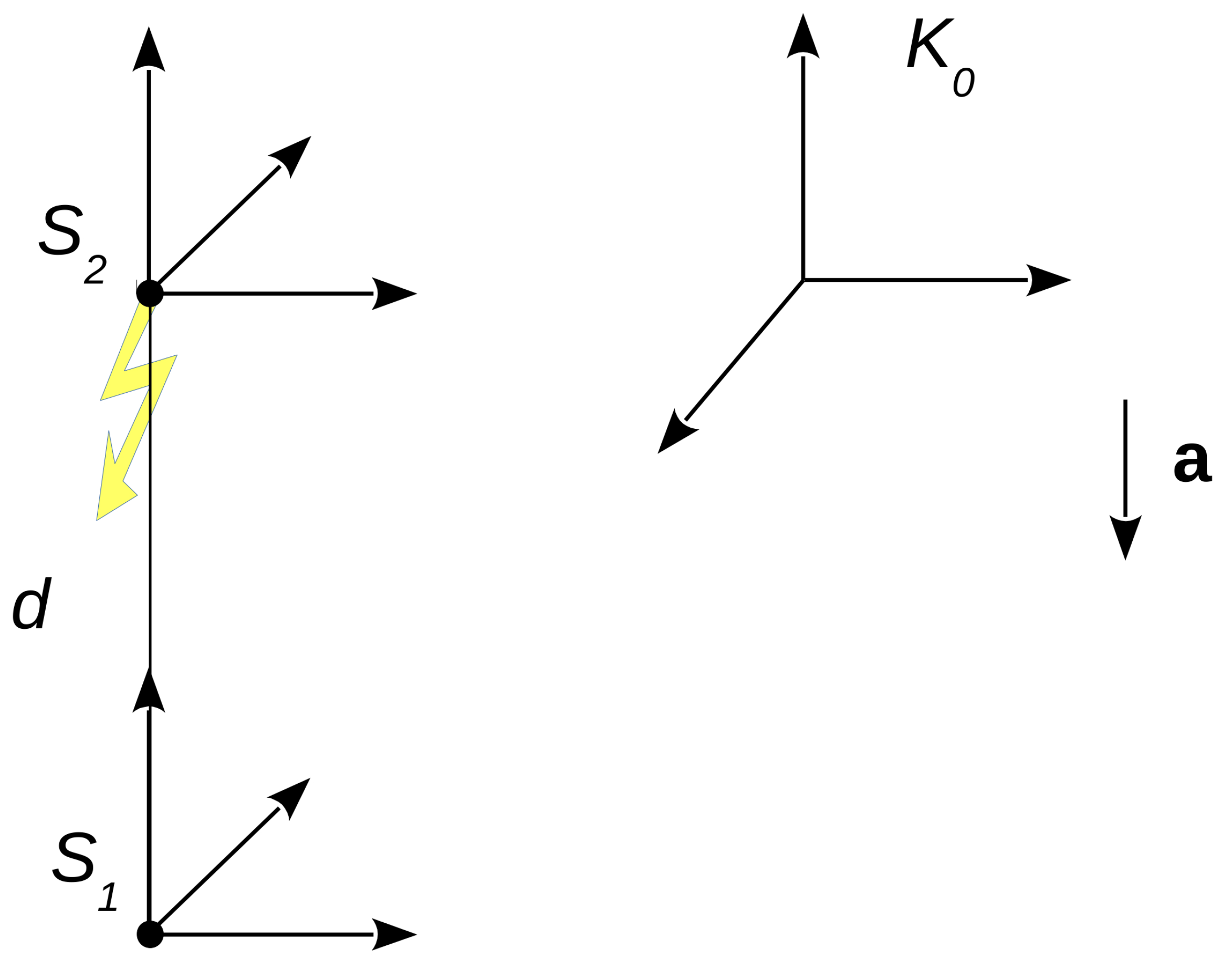
Figure 2. Pictorial representation of the thought experiment described in the text.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.