Road Descriptors for Fast Global localization on Rural Roads using OpenStreetMaps

Preprint

Article

Road Descriptors for Fast Global localization on Rural Roads using OpenStreetMaps

Altmetrics

Downloads

112

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

04 August 2023

Posted:

08 August 2023

You are already at the latest version

Alerts

Abstract

Accurate pose estimation is a fundamental ability that all mobile robots must posses in order to navigate a given environment. Much like a human, this ability is dependent on the robot's understanding of a given scene. For Autonomous Vehicles (AV's), detailed 3D maps created beforehand are widely used to augment the perceptive abilities and estimate pose based on current sensor measurements. This approach however is less suited for rural communities that are sparsely connected and cover large areas. Topological maps such as OpenStreetMaps have proven to be a useful alternative in these situations. However, vehicle localization using these maps is non-trivial, particularly for the global localization task, where the map spans large areas. To deal with this challenge, we propose road descriptors along with an initialization technique for localization that allows for fast global pose estimation. We test our algorithms on (real world) maps and benchmark them against other map based localization as well as SLAM algorithms. Our results show that the proposed method can narrow down the pose to within 50 centimeters of the ground truth significantly faster than the state of the art methods.

Keywords:

Subject: Engineering - Transportation Science and Technology

1. Introduction

Every Autonomous Vehicle needs to answer three fundamental questions - Where am I? Where am I going? and How do I get there? The process of answering the first question is what is commonly referred to as Localization. To solve the localization problem means to estimate a robot’s pose in a predefined map of the environment. In general, a vehicle’s ability to safely navigate a given environment is highly dependent on its understanding of the environment, and its pose within the environment. An accurate and reliable pose estimate is therefore critical for safe functioning of Autonomous Vehicles (AV’s).

A common approach [1] to solve the localization problem is through the use of pre-constructed environment maps, along with sensor and motion measurements. Depending on the sensors used by the vehicle, the map representation could be anything ranging from a simple position vector, containing positions of artifacts in the map frame, to more complex representation such as a dense 3D map containing point-wise annotations. As such, environment maps are useful not only for localization, but also for other functions such as motion and path planning, besides also improving robustness of the perception system.

In the context of Self Driving Vehicles, the map representation that is most often used is in the form of dense feature maps with detailed annotations for features such as lane markings and traffic signs. Although the use of such maps has been highly successful for structured environments such as urban roads, their advantage is less pronounced for rural driving scenarios because of three main reasons - structure, scale and sparsity of features, each of which is tied to the makeup of rural roads.

The first and most important distinction between urban and rural roads is their structure. While, urban roads usually have a well defined and consistent structure, rural roads can have large variations in structure such as - inconsistent road markings, varying road surfaces such as gravel or dirt roads apart from the usual asphalt or concrete found on urban Roads.

Another problem with using dense maps for rural roads is their scale and sparsity of features. Urban scenes generally contain a rich feature space composed of features such as traffic signs, buildings, curb and lane markings, to name a few. Compared to urban communities, rural communities span very large areas and have very low population densities. Because of this, rural roads are primarily surrounded by vegetation and any features useful for localization are few and far between. An example of this structural difference is shown in Figure 1. Notice that the urban scene has several useful landmarks such as buildings, sidewalks and lane markings.

Topological maps such as Open Street Maps have been shown to be useful for Autonomous Driving scenarios where the length of the trip is very large [2], or for locations where dense 3D maps are not available.

These maps however, do not contain low level features such as lane markings and traffic signs. Pose estimation using these maps alone is therefore a significant challenge.

Our focus in this paper is on developing localization algorithms for rural roads. Our approach is useful even when GPS signals are disrupted due to jamming (intentionally or unintentionally) [3,4], or while traveling through mountainous regions or in scenarios with challenging weather conditions [5,6]. Within this work, we propose a novel road descriptor as a concise feature representation for rural roads. We use these road descriptors to generate an initial pose belief which is then passed to a Particle filter for localization. The choice of initial belief significantly impacts the rate of convergence of Particle filter based localization algorithms, especially for global localization, where the search space is very large. The Road Descriptor Search (RDS) technique we introduce helps in the selection of this initial belief. We demonstrate this through simulations as well as real world tests by comparing the performance of the localization algorithm with and without the generation of an initial belief. Results show that our RDS initialization significantly reduces the time to convergence for global localization compared to the state of the art. The algorithm is also able to estimate the pose of an ego vehicle in a map spanning 36 sq. km with a mean error of 1.5 meters. Our software has been made open source and can be accessed here.

The rest of this paper is organized as follows: Section 2 contains a summary of the existing work on localization using topological maps. In Section 3, we introduce the road descriptor along with the Monte Carlo Localization Algorithm . Lastly, Section 4 contains results from both simulations and real-world tests to corroborate the effectiveness of our approach.

2. Related Work

The use of topological maps for localization has been widely researched as an alternative to traditional mapping. Hentschel et al. [7,8] used a Kalman filter for fusing noisy GPS observations with laser scans and a 2D line feature map, that enabled localization near buildings. In OpenStreetSLAM [9], the authors propose a chamfer matching algorithm to estimate a vehicles pose by matching the vehicle’s trajectory over a period of time to a sequence of edges on the map.

A common trend among recent works in this area is the use of a Particle Filter for localization, with different measurement models proposed to correlate visual information with the information available in OpenStreetMaps. Ruchti et al. [10] use road points from laser scans along with a zero mean gaussian for the observation model, similarly MapLite[11], proposes a signed distance function for the measurement model. Learning based methods have also been proposed to learn the measurement function. One such work is done by Chen et al. [12], in which the authors train a model to embed road images to their corresponding map tiles, which is then used as a measurement model.

More recently, the idea of descriptors has been proposed as an alternative to previously cited distance based measurement models. In [13], Image based Oriented and Rotated Brief (ORB) descriptors are used to generate a Bag of Words which is then queried for future measurements. A 4-bit descriptor encoding surrounding structural information such as intersections and buildings was introduced by Yan et al. [14]. This approach was further extended through the use of building descriptors as a unique feature vector for a pose on the map by Cho et al. [15]. This method measures the distance to surrounding building walls at a given pose to form a rotation invariant descriptor. Although, this method was successful for urban routes, it is less suitable for rural scenarios where building information is non-existent and most roads are open roads.

Since features such as buildings and landmarks are absent on rural roads, we propose a descriptor that utilizes a key feature that is consistent on all rural roads - road geometry. We do this by proposing road descriptors as a concise representation of road geometry for any given pose for rural roads. We then combine the advantages of descriptors as well as distance based measurement functions for fast and accurate global pose estimation on rural roads.

3. Methodology

Localization can be mathematically defined as the task of calculating the belief of a robot’s pose,

b e l (x_{t})

at time t, by combining information from previous sensor measurements

z_{1 : t}

, control inputs

u_{1 : t}

, and map information m. In other words,

b e l (x_{t}) = p (x_{t} | z_{1 : t}, u_{1 : t}, m) .

(1)

By applying Bayes rule, Equation (1) can be rewritten as,

p (x_{t} | z_{1 : t}, u_{1 : t}, m) = \frac{p (z_{t} | x_{t}, z_{1 : t - 1}, u_{1 : t}, m) p (x_{t} | z_{1 : t - 1}, u_{1 : t}, m)}{p (z_{t} | z_{1 : t - 1}, u_{1 : t}, m)} .

(2)

We can further simplify Equation (2) using a Markovian assumption and by applying the law of total probability to get a recursive function,

p (x_{t} | z_{1 : t}, u_{1 : t}, m) = \frac{p (z_{t} | x_{t}, m) \sum_{i} p (x_{t} | u_{t}, x_{t - 1}^{i}) b e l (x_{t - 1}^{i})}{p (z_{t} | m)} .

(3)

Equation (3) is commonly referred to as the Bayes filter equation, which can be divided into three components - the motion model which takes into account control input

u_{t}

represented by

\sum_{i} p (x_{t} | u_{t}, x_{t - 1}^{i}) b e l (x_{t - 1}^{i})

, the observation model, represented by

p (z_{t} | x_{t}, m)

, and the normalizing factor,

p (z_{t} | m)

which is to ensure that the total probability sums to one. Our implementation of the motion and observation models as well as the proposed Road Descriptors are discussed in the following subsections.

3.1. Road Descriptors and Motion Model

As seen in Equation (3), the motion model depends on the previous state

x_{t - 1}

and the input

u_{t}

. Since this is a recursive algorithm, the previous state will need to be initialized for the first iteration. The choice of initial belief significantly impacts the rate of convergence of these Monte Carlo style localization algorithms, especially for Global Localization tasks where the search space is very large (we demonstrate this later in the results section). To narrow down the search space and generate a better initial belief, we propose Road Descriptors which embed road geometry information at a given position on the map. For rural scenes, Roads are the visual features of choice because unlike urban scenes they most often do not contain other consistent features such as buildings.

The road descriptor for any point p on the map is a 2-dimensional binary array D with rows corresponding to the distances between p and the road features, and columns corresponding to the angle subtended by the position vectors of the road features with respect to p. The values in D are generated by a ray casting operation, as illustrated in Figure 2. To form one row of D, we project a ray of a length r, radially outwards, starting at p. This is done for all angles

θ

in intervals of size 1 degree. The value is then assigned depending on whether the ray terminates at a road point or not, based on the following rule:

D (r, θ) = \{\begin{matrix} 1, & if the ray lands on a road point \\ 0, & otherwise \end{matrix}

The result of this calculation for a given radius for two different positions on the road are shown in Figure 2. Repeating this operation for multiple radii, multiple rows can be generated and the Road Descriptor for the point p can be computed as shown in Figure 3. In our framework, such road descriptors are precomputed for each node on OpenStreetMap and stored in a lookup table for the initialization step.

Measurements

z_{t}

for the filter are Lidar Point Clouds with labels for road points. In order to correlate point cloud data with road descriptors, point clouds are transformed into lidar descriptors to enable a descriptor search during the initialization phase. For this, the point clouds are first projected to a Bird’s Eye View (BEV) image, as shown in Figure 4. The LiDAR descriptor L is then generated using the same ray casting process explained for Road Descriptors. The ray casting in this case is done starting from the center of the BEV image.

Now, to generate the initial belief

b e l (x_{t_{0}})

, a two step approach is used. The lidar point cloud is first converted into the descriptor form. This descriptor now acts as the query descriptor L, for the search steps. First, a search is done for the top 1500 positions on the map where the road descriptors are similar to the query descriptor.

Since descriptor values are dependent on orientation, they are flattened by computing the row sum for each row, and then converting them into a 1-dimensional vector, as shown in Figure 5.

This step makes them rotation invariant as explained in [15]. To find the top 1000 similar descriptors S and their corresponding positions, a similarity score for a query (L) and road descriptor (D) pair is defined, which is:

S i m i l a r i t y S c o r e = \frac{1}{| | L - {D | |}_{2}},

where

{| | x | |}_{2}

denotes the

L_{2}

-norm of x.

In the second step, to further reduce the number of matches for a given query descriptor, the orientation is also accounted for. The full 2 dimensional descriptors for L and R are used in this case. To do this, for each position in S, all orientations between 0 and

2 π

and their corresponding descriptors are considered. These are then sorted by their similarity score, and the top 1000 are selected as poses for initializing the particle filter.

For the motion model, we have the control input

u_{t} = {[d e, d n, d θ]}^{T}

which represents the estimated change in pose between time steps

t - 1

and t.

The control input

u_{t}

along with initial estimates,

x_{t - 1}

are used to generate a pose hypothesis,

{\bar{x}}_{t}

by sampling over the probability distribution as follows:

p (x_{t} | x_{t - 1}, u_{t}) = N (x_{t} + u_{t}, q)

(4)

where q represents the covariance of motion estimates.

3.2. Measurement Model

For the measurement model, a distance function is used to assign probability mass to each pose hypothesis

{\bar{x}}_{t} \in {\bar{X}}_{t}

. To calculate this distance function for a pose hypothesis

{\bar{x}}_{t}

, we transform the segmented point cloud to the map frame using the pose represented by

{\bar{x}}_{t}

, and based on the distance

d_{p_{r o a d, i}}

between the nearest road edge and a road point

p_{r o a d, i}

in the segmented cloud, we estimate

p (z_{t} | x_{t}, m)

as:

p (z_{t} | x_{t}, m) = \prod_{i = 1}^{1 = n} δ (d_{p_{r o a d, i}})

(5)

where n is the number of road points in the segmented point cloud and

δ

represents the distance function which is a Gaussian with zero mean and covariance r as proposed in [10].

δ (d_{p_{r o a d, i}}) = N (0, r) .

(6)

For non road points,

p_{n o n - r o a d, i}

, an inverse probabilistic rule is used such that,

δ (d_{p_{n o n - r o a d, i}}) = 1 - δ (d_{p_{r o a d, i}}) .

(7)

The distance function returns the maximum probability for projected points

p_{r o a d}

that are close to road edges on the map as illustrated in Figure 6. In effect, this means a greater probability mass will be assigned to poses where the road points

p_{r o a d}

are well aligned to the road geometry in the map. The probabilities of all pose hypotheses

{\bar{x}}_{t} \in {\bar{X}}_{t}

are updated in this way. The poses are then sampled based on the assigned probability mass. Finally, the pose estimate

x_{t}

is then estimated as the weighted average over all poses,

x_{t} = \frac{\sum_{i} p (x_{i}) x_{i}}{\sum_{i} p (x_{i})}

(8)

Figure 6. Returns from the distance function around a road edge on the map.

Figure 7. Example of data from the Texas A&M Autonomous Vehicle dataset.

4. Experimentation and Results

To demonstrate the advantage of using Road Descriptors for the initialization of prior belief, we perform two experiments. First, we simulate lidar road detection using Open Street Maps. This is done to evaluate the road descriptor method independent of the performance of the road segmentation algorithm. Second, we evaluate global localization performance of the Maplite algorithm [11] on real world data, with and without the Road Descriptors, to corroborate the performance of the proposed approach.

4.1. Simulation tests

For the simulation process, instead of using real world point clouds with road labels, as explained in Section 3, we generate a virtual BEV image from Open Street Maps. This image is simply a top down snapshot of the portion of the map around the true pose

x_{t}

. The virtual BEV image is used to generate the lidar descriptor L as explained in Section 3.1. The lidar descriptor is then used as the query descriptor for the road descriptor search process.

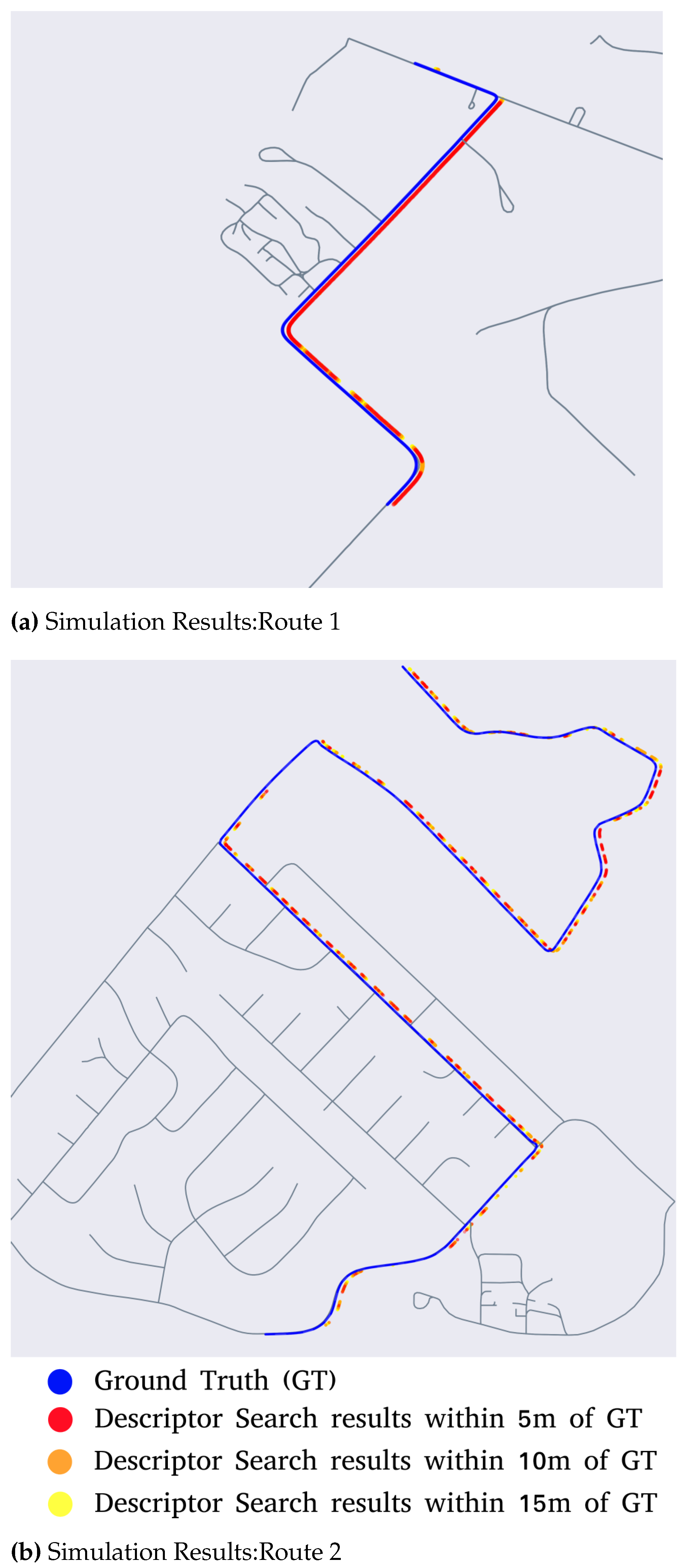
In order to simulate a route, position and orientation information from OpenSteetMap nodes is used to generate ground truth measurements. For each ground truth measurement, the road descriptor search is done over a segment of the map spanning 36 sq. km. The lidar descriptor generated from the virtual BEV image is used as the query descriptor. For each of the query descriptors, the top 1500 poses on the map that have similar descriptors are then found. If the true pose is within 5m of the top 1500 matches, the descriptor search is considered to have converged. The results from this simulation are depicted in Figure 9a. The segments of the route where RDS has converged are highlighted in red, orange or yellow - based on the distance to ground truth. If RDS does not converge to within 15 meters of the ground truth position, such nodes along the route are left uncolored.

From the simulation results, it can be seen that the descriptor search technique is most effective in segments of the route where there are road features such as turns and intersections; whereas it struggles in segments with only straight roads, this is prominent in the results from Route 2 (Figure 9b), where localization is lost in the straight portions of the route but subsequently regained at the portions with intersections and turns.

Figure 8. Vehicle platform used for realtime testing.

Figure 9. Results from LIDAR simulation tests.

4.2. Real world tests

The performance of the particle filter with and without the proposed initialization using Road Descriptor search is evaluated by testing it on real world data collected on two routes near Bryan, Texas. For data collection, a test vehicle (depicted in Figure 8) equipped with a 128 channel LIDAR sensor, a GNSS receiver with 2.0 meter horizontal sensing accuracy, wheel speed and steering angle sensor was used.

To detect the road surface, a Range Image based segmentation method based on RangeNet++ [16] was used. The model was trained on the Texas A&M Autonomous Vehicle rural road dataset [17]. The dataset contains 2800 Range Images (illustrated in Figure 7) labelled for detection of road points. It also includes vehicle bus data such as GPS, IMU, steering, brake, throttle inputs and wheel speed measurements. In all, the dataset contains around 15 minutes of driving data.

All the tests are run without using any of the GPS measurements. GPS logs are only used as ground truth for performance evaluation. The control input

u_{t}

in Equation 4, is generated using a bicycle model, based on wheel speed and steering angle measurements. To reduce runtimes, we down sample the point clouds using a voxel grid, with voxels of size

2 \times 2

meters, and pre-compute the distance to nearest edge for all points on the map. Similarly, road descriptors for all nodes on the map are pre-computed.

To demonstrate how the computational advantages of the proposed approach, the size of the search space on the map is varied. For each of the routes considered two tests are performed. For the first test, a search space of 9 sq. km is considered, followed by a 36 sq. km search space for the second test. For each of the tests, first the MapLite algorithm is initialized with 90,000 particles uniformly distributed over the entire search space. Next, MapLite is tested again, but this time with RDS initialization. In this case, particles are initialized around the top 1500 matches returned by the descriptor search algorithm. Further validation is done by comparing the localization results after convergence, with those obtained from SuMA SLAM [18].

The first route represents data that has been previously seen by the road segmentation model, as training data was collected on this route. The localization results from this route are shown in Figure 10. It can be seen that the time taken by the Maplite algorithm to converge to the true position is significantly longer than when RDS was used for particle initialization.

When RDS initialization is used, a distinct reduction in time to convergence is observed both for the 9 and 36 sq. km search spaces. Referring to Figure 10, for the 9 sq. km. search test, the MapLite algorithm converges only after it has seen road features upto turn B, which is indicated by the drop in error after around 400 time steps. In comparison, when RDS initialization is used, the algorithm quickly converges after around 100 time steps, when the vehicle reaches the turn ’A’ and is therefore much faster than the earlier case.

Owing to the larger search space, the algorithm takes longer time to converge for the 36 sq. km. search space. As seen in Figure 10c, when the algorithm is initialized without the descriptor search, it converges to an erroneous position on the map, which is indicated by the large position errors. This indicates that the number of particles used was inadequate with respect to the size of the search space. When road descriptors are used, the position estimate is close to the ground truth after the vehicle reaches turn A, however there is still a small amount of error. This is because there are a few clusters of particles concentrated elsewhere on the map. These are subsequently ruled out after the vehicle reaches turn B, causing the algorithm to converge to the ground truth. The Average Position Error (APE) after convergence for the proposed algorithm as well as popular SLAM algorithm SuMA-SLAM [18] is reported in Table 1. We observe that the pose tracking done by our algorithm is more accurate than the SLAM approach. This may be because of the lack of reliable feature points, given that the route is mostly surrounded by open fields.

Route 2 represents a more challenging test case because of the greater complexity and density of the road network in the region. This is also a previously unseen route for the road segmentation model. Similar to Route 1, we perform the two tests on MapLite and MapLite + RDS algorithms, the results of which are shown in Figure 11 and Figure 12. It can be seen that MapLite alone fails to converge for both the 9 sq. km. and 36 sq.km test cases, once again indicating that for the number of particles was too small in comparison to the size and complexity of the map in consideration. It can be seen that, when road descriptors are used for both these tests, the algorithm successfully converges to the true vehicle position. The large fluctuations in positional errors seen in Figure 11 in the initial phase is because of the presence of particles at other parts of the map that have a similar road geometry, such as turns C and E in Figure 11. However, when the vehicle reaches the intersection at D, those particle groups are eliminated and the pose estimate thus converges to the ground truth after approximately 500 time steps. From Table 2 we observe once again that after convergence, the proposed algorithm has a lower APE than pose estimates from SLAM on the same route.

5. Conclusion

In this paper, we present a localization algorithm to enable global localization on rural roads. The proposed algorithm enhances the state of the art by using road descriptors for generating an initial belief. The algorithm is used to implement a LIDAR based, GPS denied localization algorithm for global localization. Experimental results demonstrate that the algorithm can recover a vehicle’s pose, with a mean error as low as

0.5

meters in maps as large as 36 sq. km. The performance enhancement provided by the RDS initialization make this method suitable to deal with the kidnapping problem, especially for autonomous vehicles operating in regions with poor GPS reception.

Acknowledgments

Support for this research was provided in part by a grant from the U.S. Department of Transportation, University Transportation Centers Program to the Safety through Disruption University Transportation Center (451453-19C36).

Disclaimer

The contents of this paper reflect the views of the authors, who are responsible for the facts and the accuracy of the information presented herein. This document is disseminated in the interest of information exchange. The report is funded, partially or entirely, by a grant from the U.S. Department of Transportation’s University Transportation Centers Program. However, the U.S. Government assumes no liability for the contents or use thereof.

References

Levinson, J.; Thrun, S. Robust vehicle localization in urban environments using probabilistic maps. In Proceedings of the 2010 IEEE international conference on robotics and automation. IEEE; 2010; pp. 4372–4378. [Google Scholar]
Ziegler, J.; Bender, P.; Schreiber, M.; Lategahn, H.; Strauss, T.; Stiller, C.; Dang, T.; Franke, U.; Appenrodt, N.; Keller, C.G.; et al. Making Bertha Drive—An Autonomous Journey on a Historic Route. IEEE Intelligent Transportation Systems Magazine 2014, 6, 8–20. [Google Scholar] [CrossRef]
Kerns, A.J.; Shepard, D.P.; Bhatti, J.A.; Humphreys, T.E. Unmanned aircraft capture and control via GPS spoofing. Journal of Field Robotics 2014, 31, 617–636. [Google Scholar] [CrossRef]
Warwick, G. Lightsquared tests confirm GPS jamming. originally published online by Aviation Week on 09-Jun-2011, but only an archive still exists now at https://web.archive.org/web/20110812045607/http://www.aviationweek.com/aw/generic/story.jsp?id=news%2Fawx%2F2011%2F06%2F09%2Fawx_06_09_2011_p0-334122.xml&headline=LightSquared%20Tests%20Confirm%20GPS%20Jamming&channel=busav. [Online; accessed 30-Jul-2020].
Gregorius, T.L.H.; Blewitt, G. The Effect of Weather Fronts on GPS Measurements. In Proceedings of the Environmental Science; 1998. [Google Scholar]
Zhang, S.; He, L.; Wu, L. Statistical Study of Loss of GPS Signals Caused by Severe and Great Geomagnetic Storms. Journal of Geophysical Research: Space Physics 2020, 125, e2019JA027749. [Google Scholar] [CrossRef]
Hentschel, M.; Wulf, O.; Wagner, B. A GPS and laser-based localization for urban and non-urban outdoor environments. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems; 2008; pp. 149–154. [Google Scholar] [CrossRef]
Hentschel, M.; Wagner, B. Autonomous robot navigation based on openstreetmap geodata. In Proceedings of the 13th International IEEE Conference on Intelligent Transportation Systems. IEEE; 2010; pp. 1645–1650. [Google Scholar]
Floros, G.; Van Der Zander, B.; Leibe, B. Openstreetslam: Global vehicle localization using openstreetmaps. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation. IEEE; 2013; pp. 1054–1059. [Google Scholar]
Ruchti, P.; Steder, B.; Ruhnke, M.; Burgard, W. Localization on openstreetmap data using a 3d laser scanner. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA). IEEE; 2015; pp. 5260–5265. [Google Scholar]
Ort, T.; Murthy, K.; Banerjee, R.; Gottipati, S.K.; Bhatt, D.; Gilitschenski, I.; Paull, L.; Rus, D. Maplite: Autonomous intersection navigation without a detailed prior map. IEEE Robotics and Automation Letters 2019, 5, 556–563. [Google Scholar] [CrossRef]
Zhou, M.; Chen, X.; Samano, N.; Stachniss, C.; Calway, A. Efficient Localisation Using Images and OpenStreetMaps. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE; 2021; pp. 5507–5513. [Google Scholar]
Rangan, S.N.K.; Yalla, V.G.; Bacchet, D.; Domi, I. Improved localization using visual features and maps for Autonomous Cars. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV); 2018; pp. 623–629. [Google Scholar] [CrossRef]
Yan, F.; Vysotska, O.; Stachniss, C. Global Localization on OpenStreetMap Using 4-bit Semantic Descriptors. In Proceedings of the 2019 European Conference on Mobile Robots (ECMR); 2019; pp. 1–7. [Google Scholar] [CrossRef]
Cho, Y.; Kim, G.; Lee, S.; Ryu, J.H. OpenStreetMap-based LiDAR Global Localization in Urban Environment without a Prior LiDAR Map. IEEE Robotics and Automation Letters 2022, 7, 4999–5006. [Google Scholar] [CrossRef]
Milioto, A.; Vizzo, I.; Behley, J.; Stachniss, C. RangeNet ++: Fast and Accurate LiDAR Semantic Segmentation. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS); 2019; pp. 4213–4220. [Google Scholar] [CrossRef]
Ninan, S.; Rathinam, S. Autonomous Vehicle Rural Road Dataset (06-004) 2022. [CrossRef]
Chen, X.; Milioto, A.; Palazzolo, E.; Giguère, P.; Behley, J.; Stachniss, C. SuMa++: Efficient LiDAR-based Semantic SLAM. CoRR, 2021; abs/2105.11320, [2105.11320]. [Google Scholar]

Figure 1. Comparison between Urban and Rural Scenes.

Figure 2. Generating Road Descriptors from OpenStreet Maps.

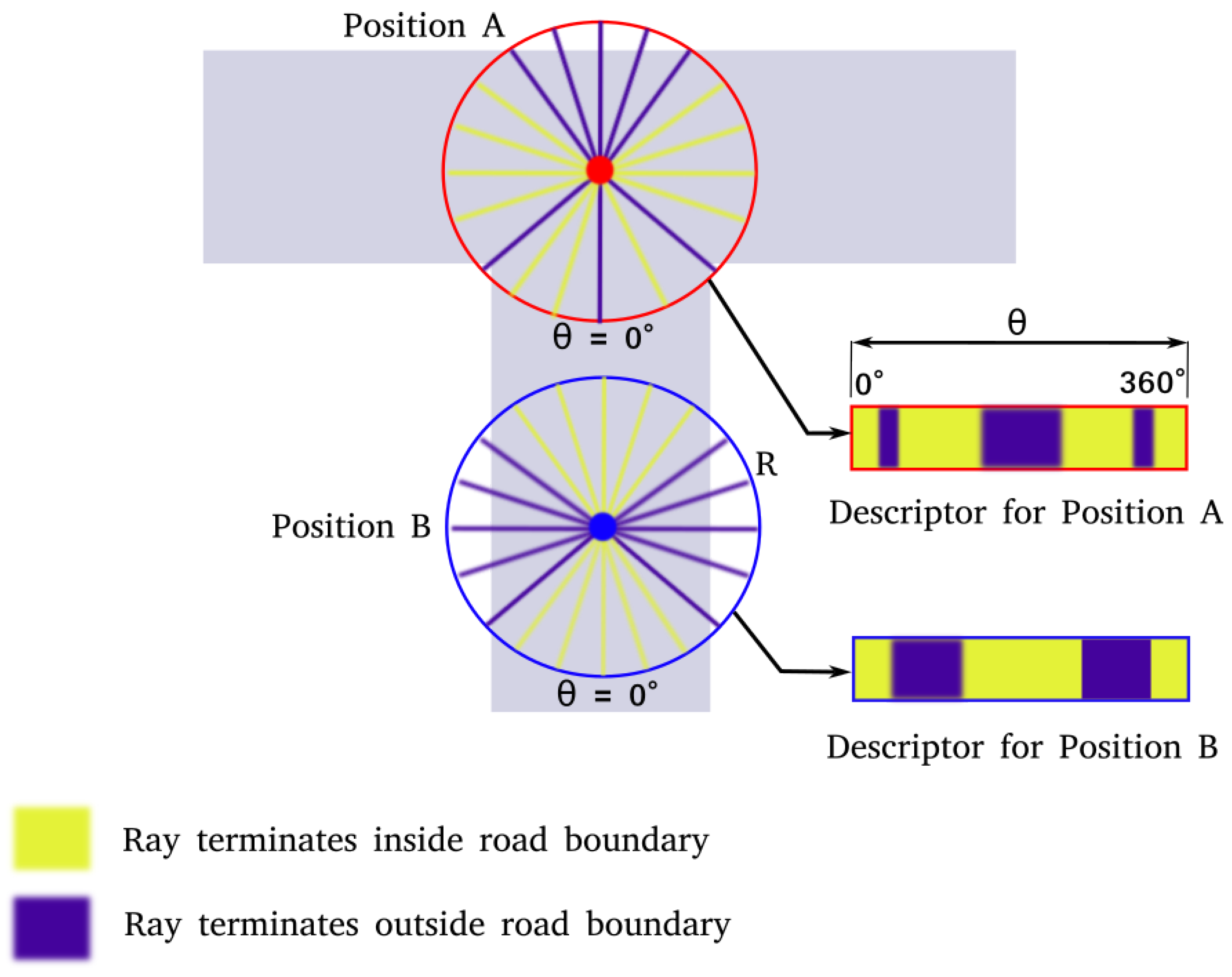
Figure 3. Concept of 2-Dimensional Road Descriptors.

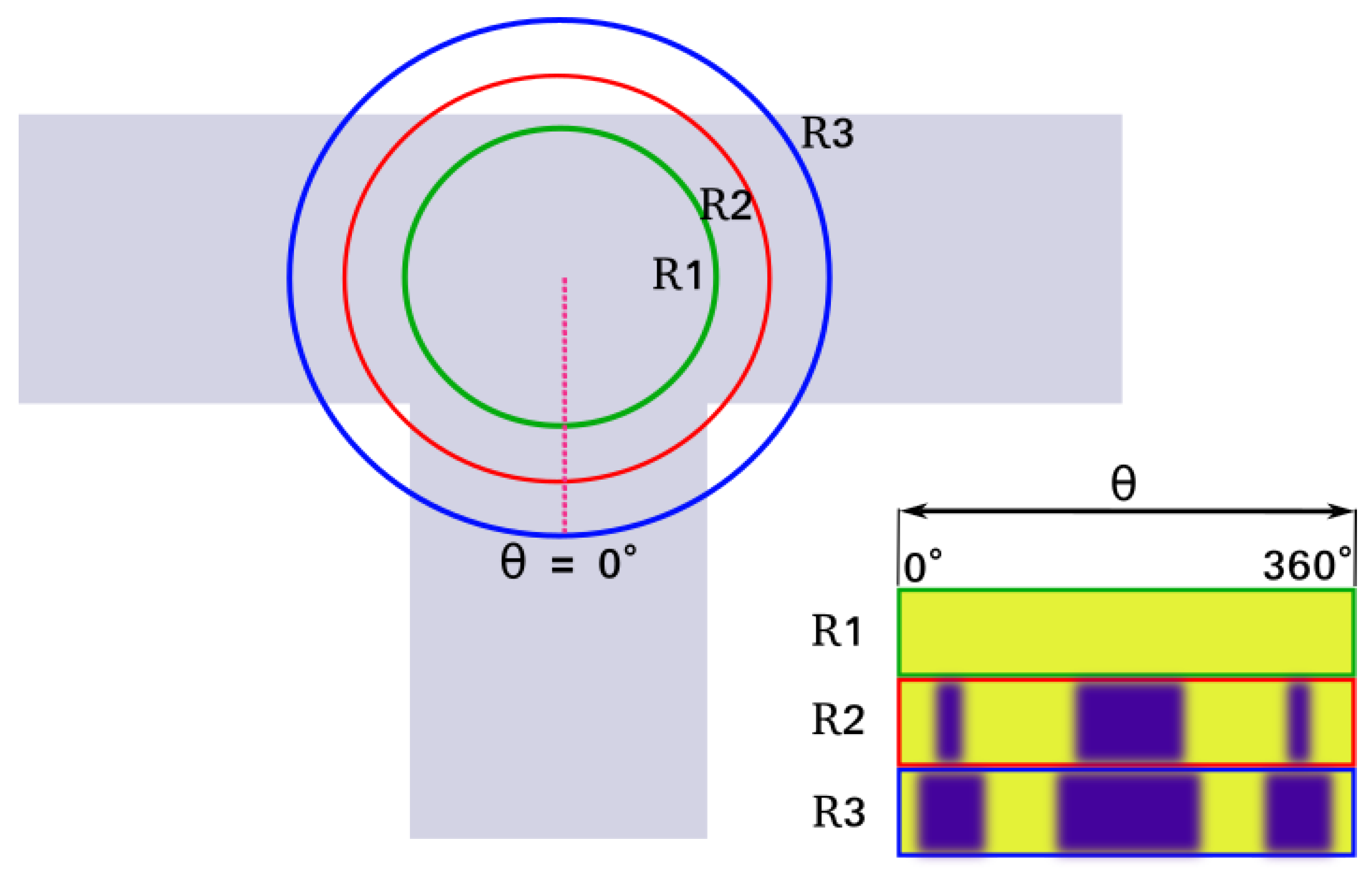
Figure 4. Generating Road Descriptors from Segmented Point Clouds.

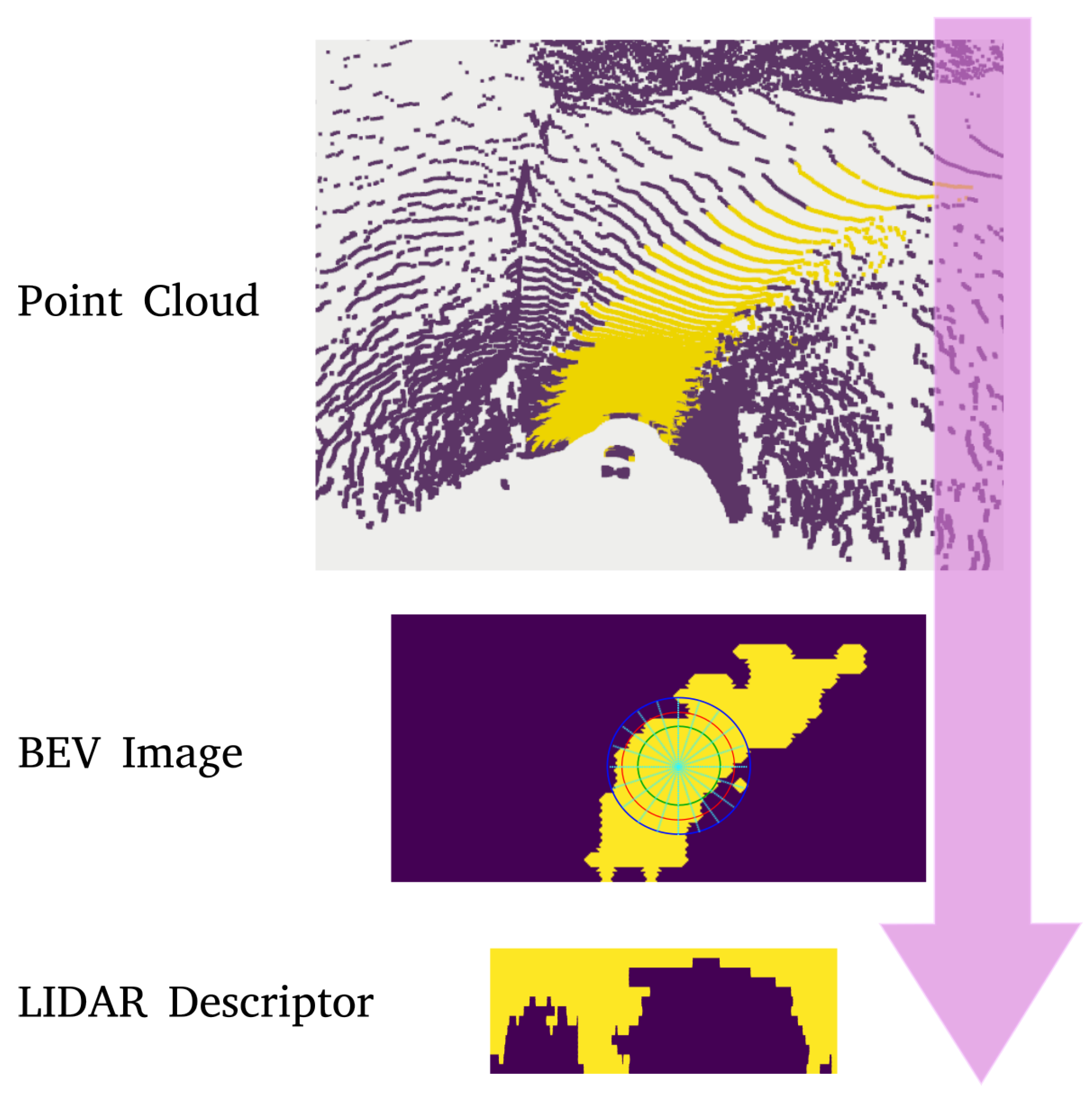
Figure 5. Descriptor Search process.

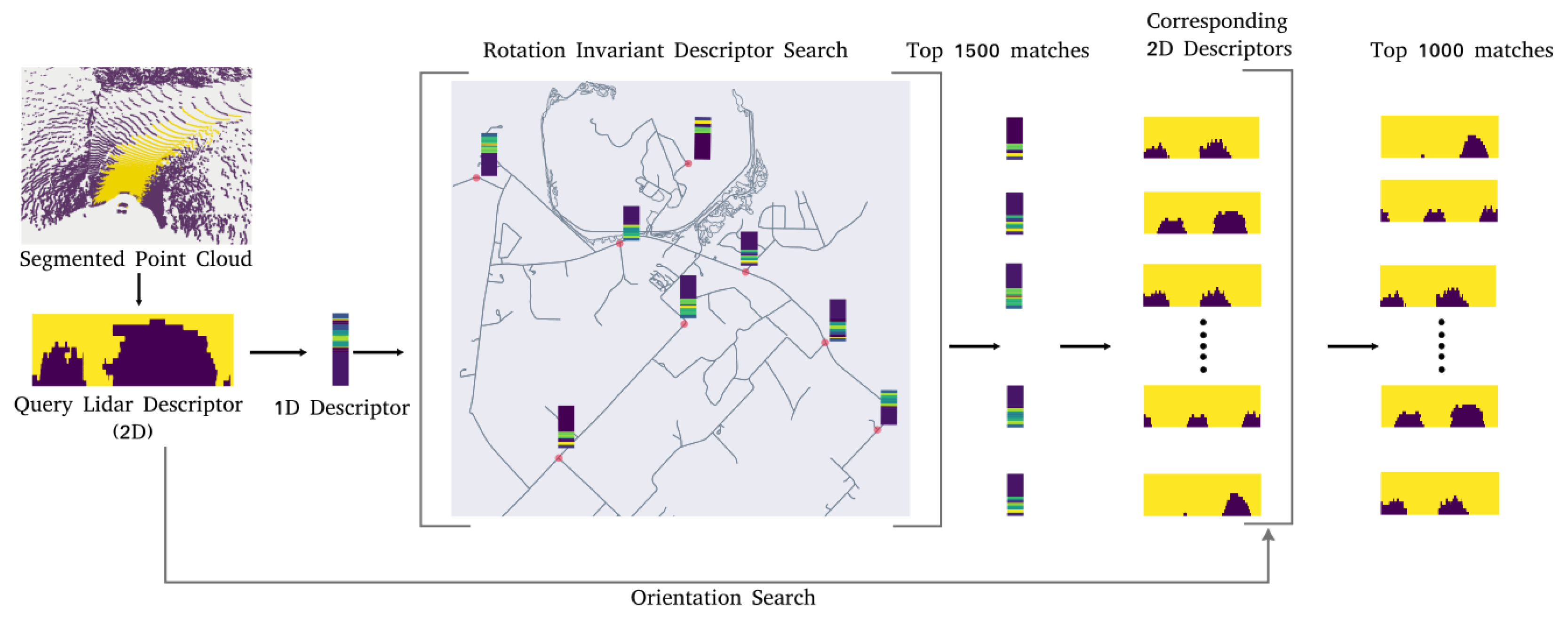
Figure 10. Localization Results for Route 1.

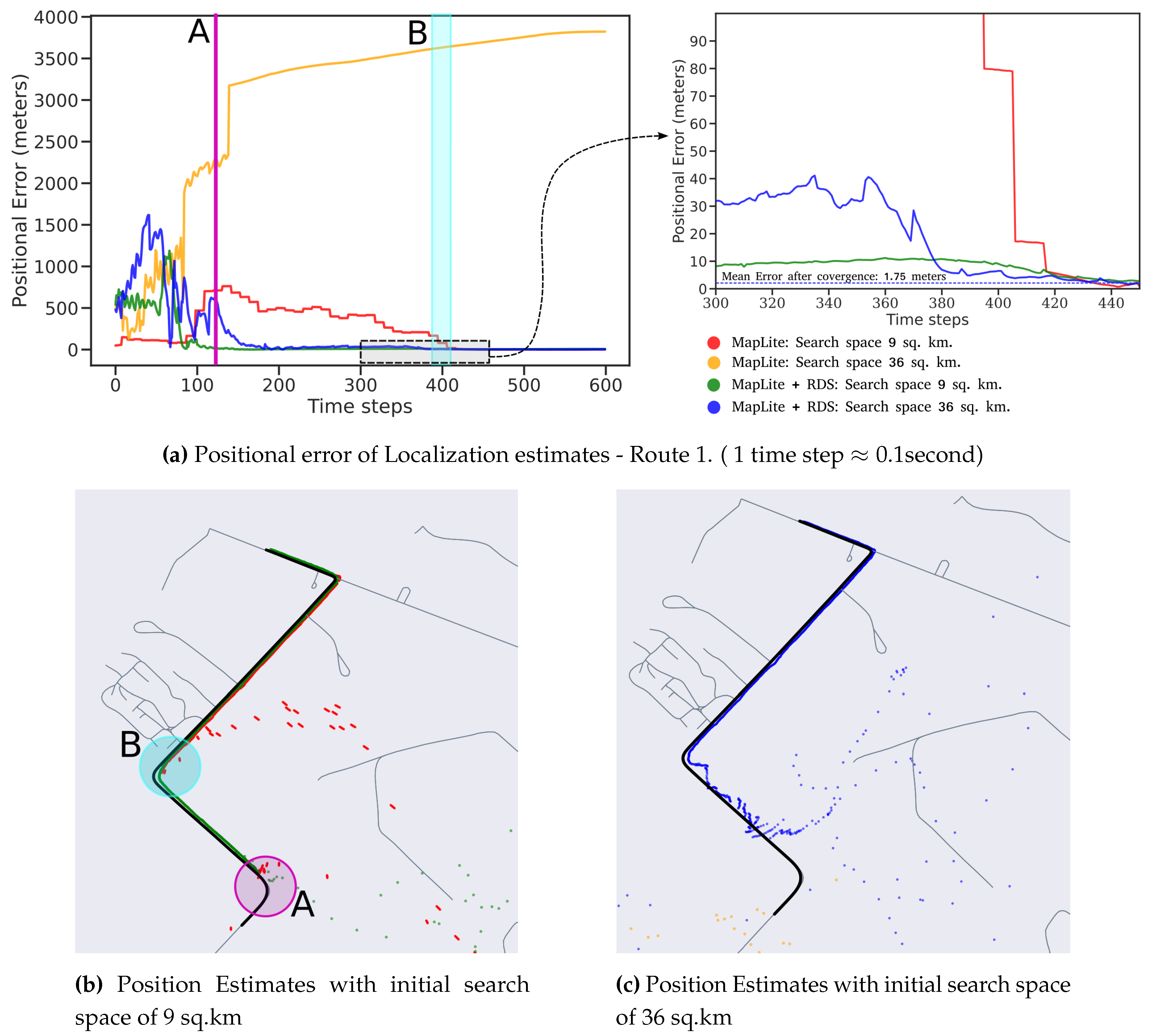
Figure 11. Positional Error of Localization estimates - Route 2. ( 1 time step

\approx 0.1 \sec ond

Figure 11. Positional Error of Localization estimates - Route 2. ( 1 time step

\approx 0.1 \sec ond

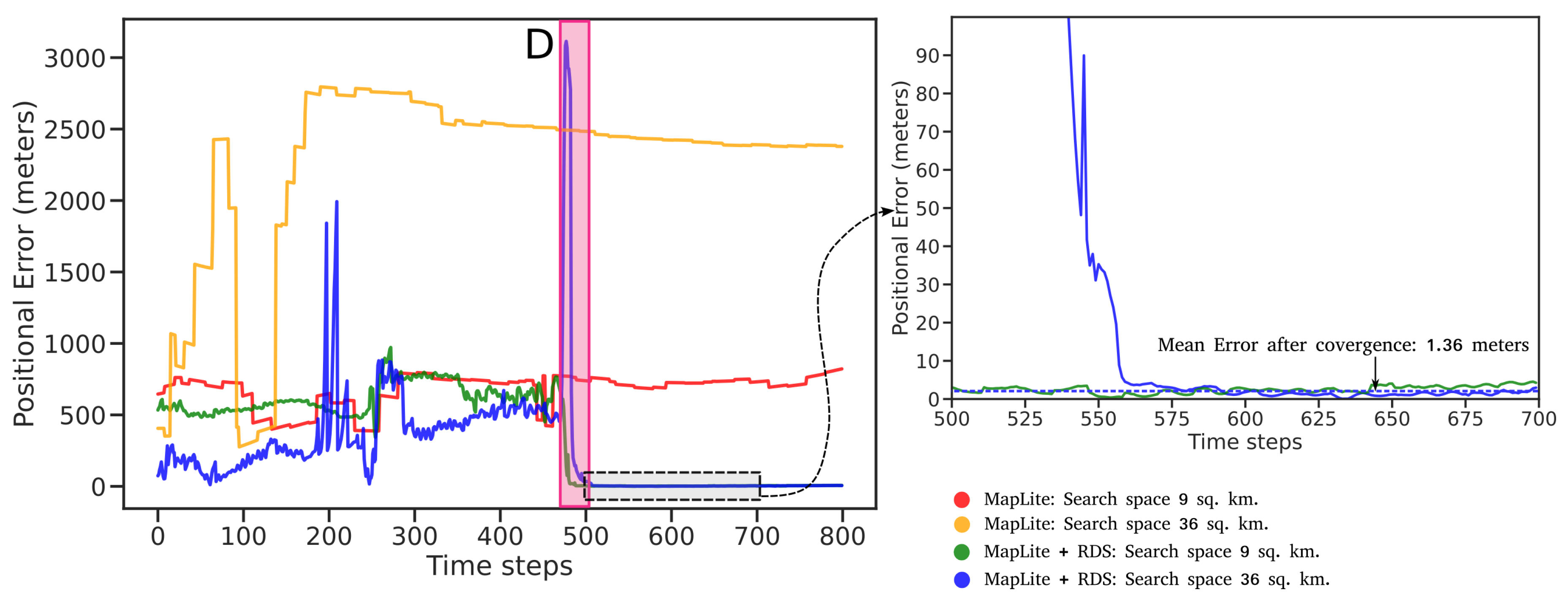
Figure 12. Left: Search space spanning 36 sq. km., Right: Position estimates after convergence for Route 2.

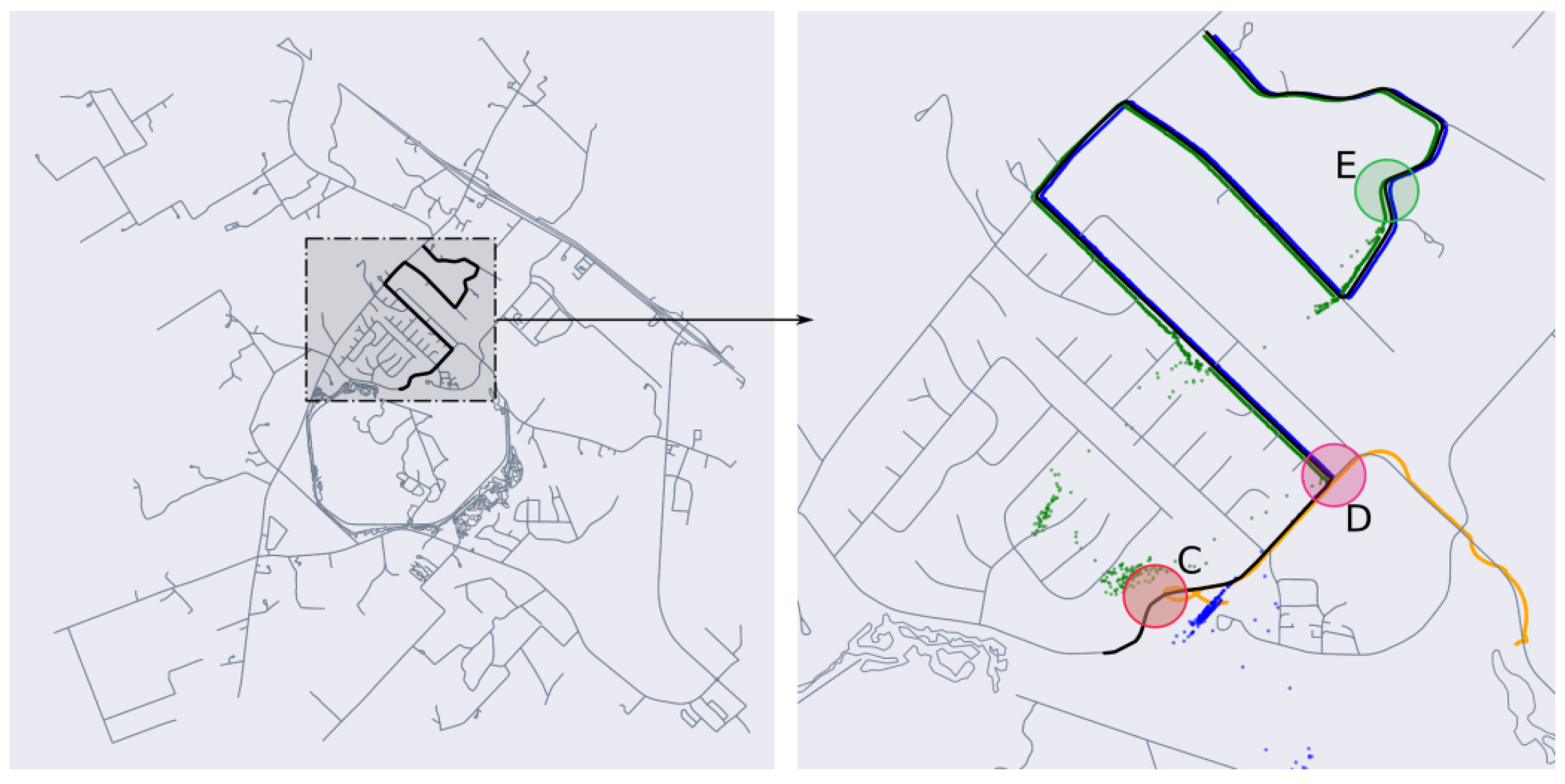
Table 1. Results after convergence:Route 1.

Method	Search space	APE (m)	RMSE	$σ$
Maplite	9 sq. km	1.0	1.2	0.63
Maplite+RDS	9 sq. km	0.7	0.85	0.46
Maplite	36 sq. km	0.61	0.76	0.45
Maplite+RDS	36 sq. km	0.5	0.54	0.21
$SuMA SLAM$	N/A	1.2	1.38	0.68

Table 2. Results after convergence:Route 2.

Method	Search space	APE(m)	RMSE	$σ$
Maplite	9 sq. km	-	-	-
Maplite+RDS	9 sq. km	0.81	0.7	0.45
Maplite	36 sq. km	-	-	-
Maplite+RDS	36 sq. km	0.81	1.08	0.7
$SuMA SLAM$	N/A	1.3	1.45	0.87

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Road Descriptors for Fast Global localization on Rural Roads using OpenStreetMaps

Abstract

1. Introduction

2. Related Work

3. Methodology

3.1. Road Descriptors and Motion Model

3.2. Measurement Model

4. Experimentation and Results

4.1. Simulation tests

4.2. Real world tests

5. Conclusion

Acknowledgments

Disclaimer

References

MDPI Initiatives

Important Links

Subscribe