Mutual Inductance and Load Identification of LCC-S IPT System Considering Equivalent Inductance of Rectifier Load

The variation of mutual inductance and load parameters will affect the transmission power and efficiency of the inductive power transfer (IPT) system. The identification of mutual inductance and load parameters is an essential part of establishing a stable and reliable IPT system. This paper presents a joint identification method of load and mutual inductance for LCC-S IPT system, which does not require the establishment of primary and secondary communication and related control. Firstly, the resistance-inductance characteristics of the equivalent load of the rectifier are analyzed by simulation, and then the rectifier and system load are equivalent to the circuit model of resistance and inductance in series. Secondly, the characteristics of the reflected impedance are analyzed, and the functional relationship between the transmitter impedance and the rectifier impedance is established by using the ratio of the real part to the imaginary part of the reflected impedance, which realizes the decoupling of the load and the mutual inductance. Thirdly, the functional relationship between the equivalent impedance of the rectifier and the load resistance of the system is obtained by data fitting. Then, the equations of the above two functional relationships are combined. By measuring the voltage of the parallel compensation capacitor at the transmitting side, the current of the transmitting coil and the phase difference between the two, the battery load can be solved first, and then the mutual inductance can be calculated, so that the high-precision identification of the load and mutual inductance can be realized. Finally, an experimental platform of LCC-S IPT system is built for experimental verification. The experimental results show that the maximum identification errors of mutual inductance and load are 5.20 % and 5.53 %, respectively, which proves that the proposed identification method can achieve high precision identification.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

With the development of science and technology, inductive power transfer (IPT) technology has attracted more and more attention. Compared with the traditional charging method, this technology is safe, reliable, flexible and convenient, and has strong adaptability [1,2,3,4]. As a new type of power supply, it is widely used in electric vehicle charging [5], electronic products charging [6], biomedical [7], underwater vehicle [8] and other fields. In addition, with the continuous development of IPT system, its application scenarios are also being further explored and expanded.

In the practical application of IPT system, the change of the relative position between the transmitter and the receiver will lead to the change of the mutual inductance of the coupler. And with the change of the charging state of the charging device itself or the switching of different devices, the load of the system is also in the process of dynamic change. The change of mutual inductance and load of the system will cause the change of the system reflection impedance, which will affect the transmission power and transmission efficiency of the system [9]. Therefore, in order to establish a more efficient and reliable IPT system, it is necessary to identify the parameter information of mutual inductance and load, and then guide the control of the system. The most critical problem is the identification of mutual inductance and load parameters [9,10].

At present, some scholars have carried out research on the identification of the load and mutual inductance parameters of the IPT system [11,12,13,14,15,16,17]. Ref. [11] establishes the steady-state circuit model of the SS type IPT system, uses the genetic algorithm to obtain the optimal solution of the load and then obtains the mutual inductance value. Ref. [12] makes the system work in two operating modes by switching capacitors, and then establishes a mathematical model based on these two modes to identify the load and mutual inductance parameters of the SS-type IPT system. Ref. [13,14,15] establish the energy supply, storage and dissipation functions and energy balance equation of the system based on the method of energy analysis. And then, propose a load parameter identification method for SS-type IPT system by analyzing the reflected impedance. In Ref. [16], a mutual inductance identification method based on LCC-S type IPT system is proposed by using the weighted particle swarm optimization algorithm. In Ref. [17], a mathematical model of LCC-S IPT system is established by combining phase shift control and AC impedance analysis. The parameter identification of mutual inductance and load is realized by combining classical genetic algorithm (GA) and particle swarm optimization (PSO).

The traditional parameter identification methods need to add additional communication equipment at the receiver, which will increase the complexity of the system [18]. Furthermore, in the existing research on mutual inductance and load parameter identification method of IPT system, there are mainly the following problems:

1 There are many researches on parameter identification of SS type IPT system, but few on LCC - S type IPT system.

2 Some parameter identification methods can only identify a single parameter.

3 The nonlinear characteristic of uncontrolled rectifier circuit is not considered in the traditional parameter identification research[19]. If the rectifier and its back-end are only regarded as pure resistors, the accuracy of the system model will be reduced, thus affecting the accuracy of parameter identification.

In order to achieve high-precision identification of mutual inductance and load parameters of IPT system, this paper proposes a joint identification method of mutual inductance and load parameters for LCC-S type IPT system. The rest of the article is arranged as follows: Section 2 analyzes the working principle of LCC-S IPT system. Section 3 analyzes the characteristics of the reflection impedance to realize the decoupling of mutual inductance and load. Then, a joint identification method of mutual inductance and load parameters is proposed, and the equivalent impedance of the rectifier is modeled by the method of data fitting. Section 4 gives the simulation and experimental verification analysis. And finally, the full article is summarized in Section 5.

2. Basic Analysis of LCC-S IPT System

Compared with the low-order compensation topology, the transmitter adopts the LCC topology, which can achieve constant voltage or constant current output by configuring the parameters of the compensation network and setting the operating frequency. This is in line with the practical application requirements of dynamic power supply, and it is easy to realize zero voltage switching (ZVS) [20] to reduce switching loss. The receiving side adopts an S-type topology, which is conducive to reducing the number of components and reducing the weight of the device. It has received extensive attention in the field of electric vehicle charging. Therefore, this paper takes the LCC-S IPT system as an example to study.

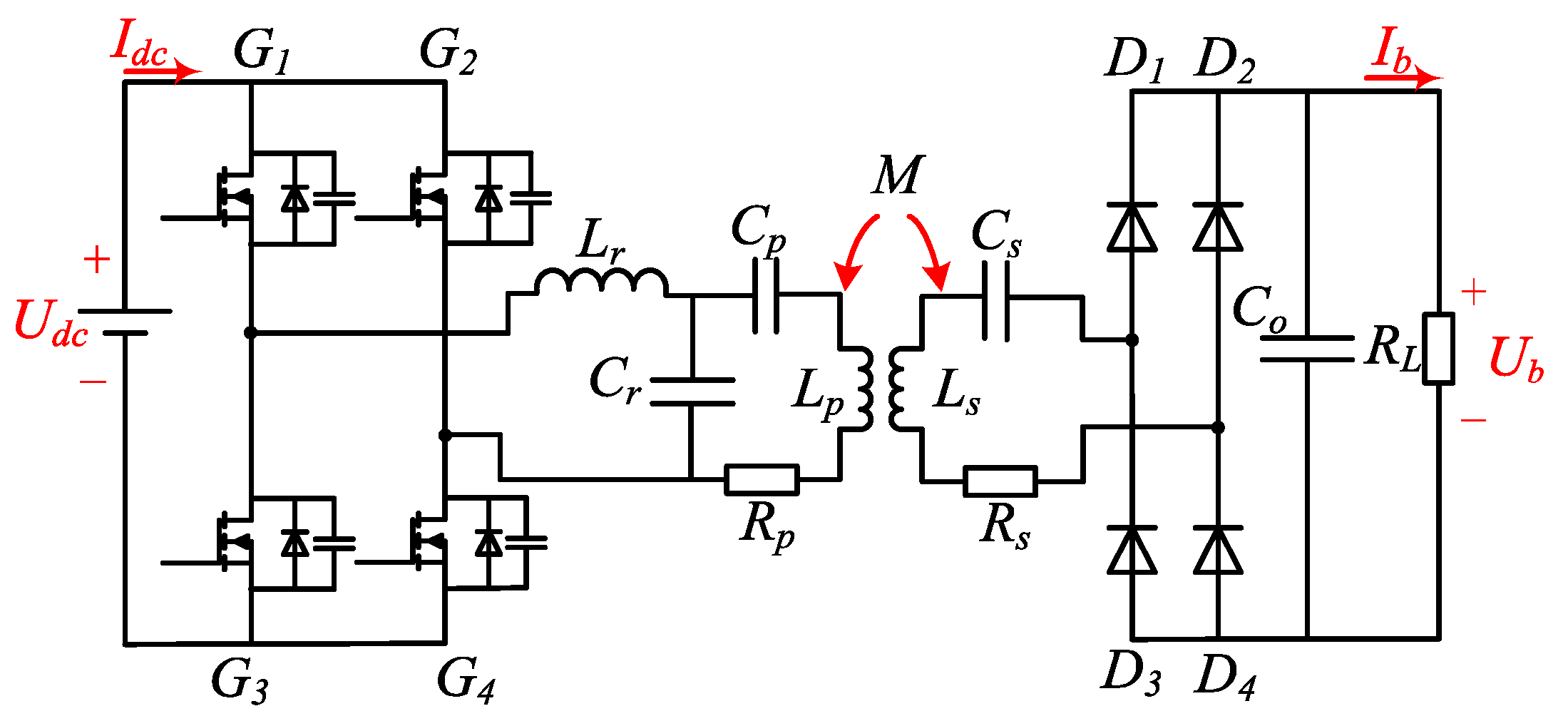
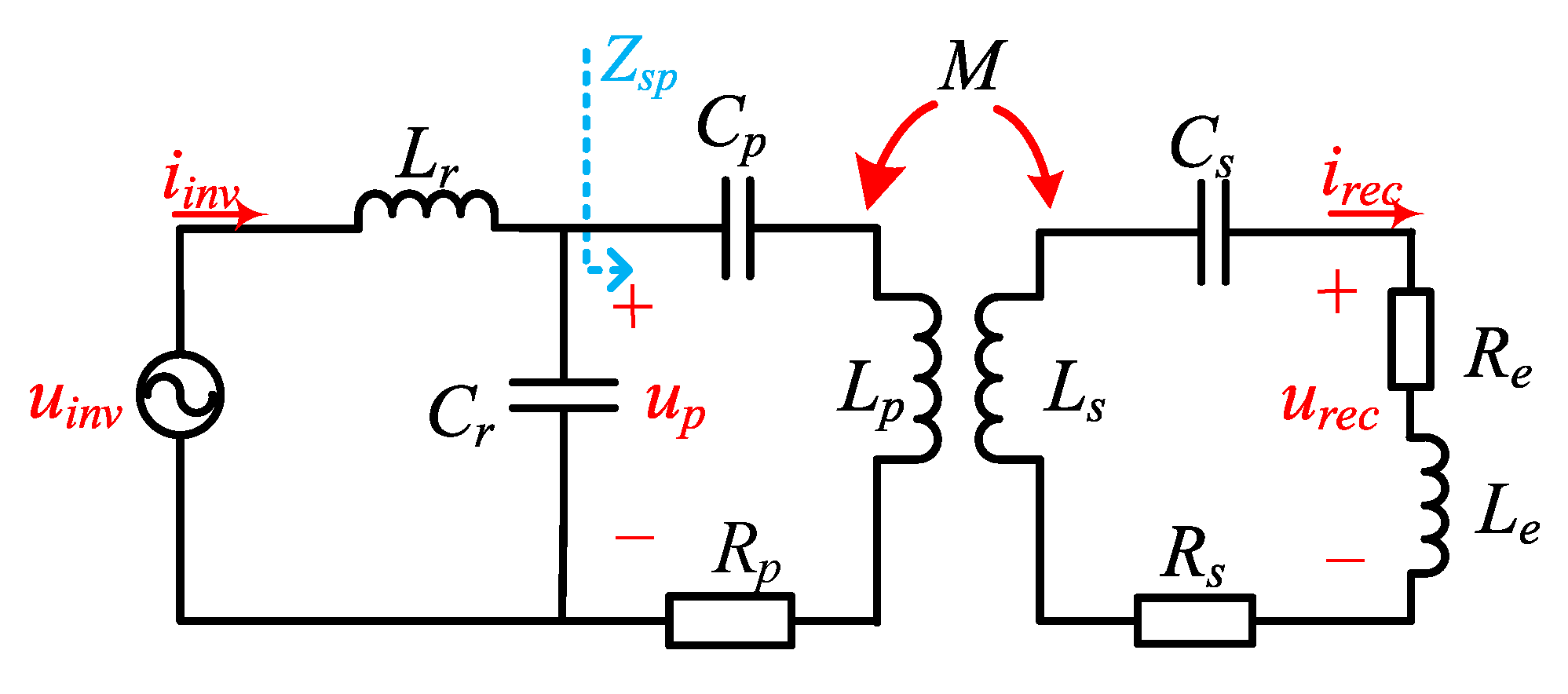
The circuit topology of LCC-S IPT system is shown in Figure 1. It is composed of DC power supply, full-bridge inverter circuit, coils, compensation network, uncontrolled rectifier circuit and load. L_p, L_s and M are the self-inductance of the transmitting coil, the self-inductance of the receiving coil and the mutual inductance between the two coils, respectively. L_r, C_r and C_p are the series compensation inductance, parallel compensation capacitance and series compensation capacitance of the primary side compensation network, respectively. C_s is the secondary side series compensation capacitor. R_p and R_s denote the equivalent internal resistance of the transmitting and receiving coils. U_b and I_b are the charging voltage and charging current of the load R_L. The working principle of the system is as follows : The DC voltage source U_dc provides the power input of the whole system. The the switches G₁～G₄ constitute a high-frequency inverter, which converts the DC voltage into a high-frequency square wave voltage and sends it to the original side compensation network. After filtering and reactive power compensation of the original side compensation network, the high-frequency alternating current is transmitted to the secondary side through the induction coil. Diodes D₁～D₄ and the filter capacitor C_o constitute the rectifier filter circuit. They rectify the high frequency alternating current on the secondary side to direct current, and then charge the system load.

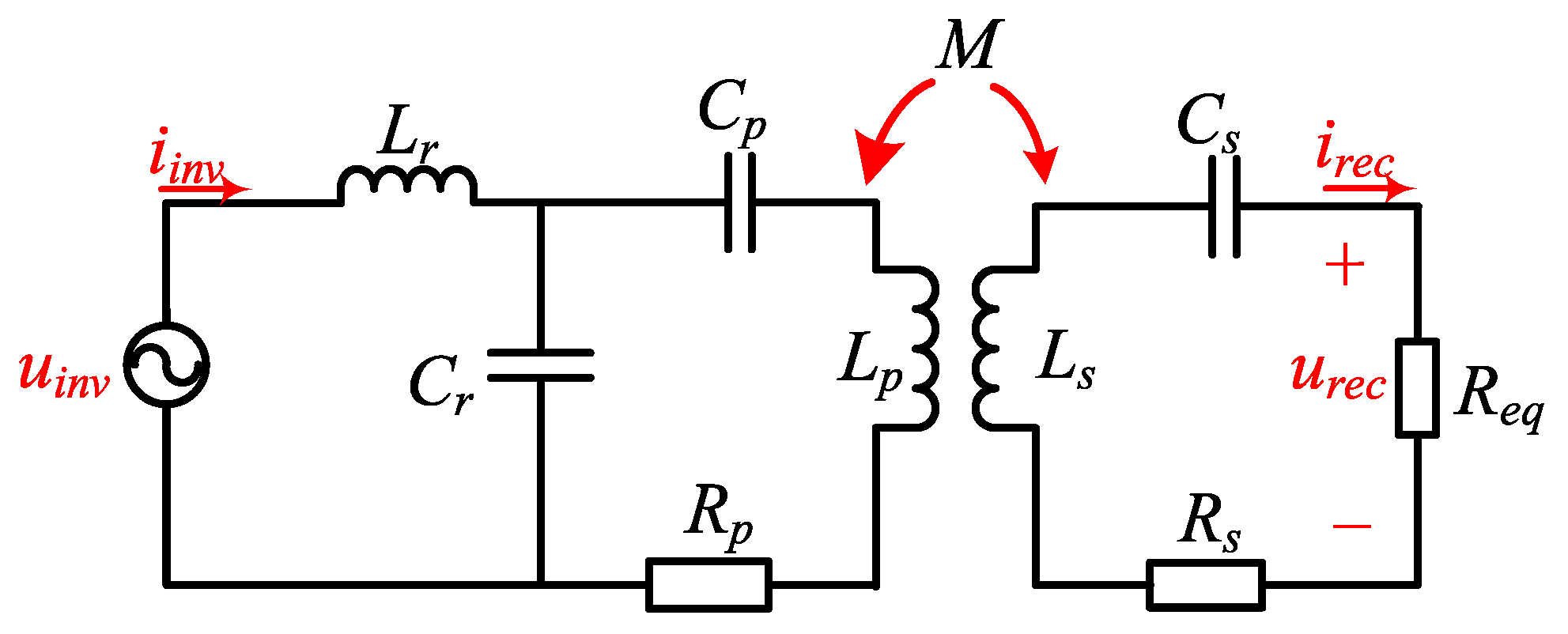
By simplifying the system of Figure 1, the equivalent circuit diagram of the system shown in Figure 2 can be obtained. u_inv and i_inv are inverter output voltage and current, respectively. u_rec and i_rec are the input voltage and current of equivalent load, respectively. u_p is the voltage on the parallel compensation capacitor C_r at the transmitter. i_p is the current of the transmitting coil. R_eq is the equivalent load resistance of the rectifier module and ω is the angular frequency of the system.

Based on Kirchhoff’s voltage law, the depiction of the LCC-S system can be obtained as follows:

\begin{matrix} \{\begin{matrix} j ω L_{r} {\dot{I}}_{i n v} + {\dot{I}}_{p} [j (ω L_{p} - \frac{1}{ω C_{p}}) + R_{p}] - j ω M {\dot{I}}_{r e c} = {\dot{U}}_{i n v} \\ j ω L_{r} {\dot{I}}_{i n v} + ({\dot{I}}_{i n v} - {\dot{I}}_{p}) \frac{1}{j ω C_{r}} = {\dot{U}}_{i n v} \\ {\dot{I}}_{r e c} [j (ω L_{s} - \frac{1}{ω C_{s}}) + R_{s} + R_{e q}] - j ω M {\dot{I}}_{p} = 0 \end{matrix} \end{matrix}

(1)

In order to improve the energy transmission efficiency of the system, the operating angular frequency ω of the system is generally made close to the natural resonant frequency of the circuit [21,22]. Therefore, the parameters of the coupler and compensation networks should satisfy the following relationship:

\{\begin{matrix} ω L_{r} = \frac{1}{ω C_{r}} \\ ω L_{s} = \frac{1}{ω C_{s}} \\ ω (L_{p} - L_{r}) = \frac{1}{ω C_{p}} \end{matrix}

(2)

Then, the current of each loop under the resonance condition can be determined in (3).

\{\begin{matrix} {\dot{I}}_{i n v} = \frac{C_{r} [(R_{s} + R_{e q}) R_{p} + ω^{2} M^{2}]}{L_{r} (R_{s} + R_{e q})} {\dot{U}}_{i n v} \\ {\dot{I}}_{p} = - j ω C_{r} {\dot{U}}_{i n v} \\ {\dot{I}}_{r e c} = \frac{M}{L_{r} (R_{s} + R_{e q})} {\dot{U}}_{i n v} \end{matrix}

(3)

Therefore, the voltage gain of the LCC-S system can be determined in (4), and the current gain of the LCC-S system can be determined in (5).

\begin{matrix} G_{v} = |\frac{{\dot{U}}_{r e c}}{{\dot{U}}_{i n v}}| = \frac{M R_{e q}}{L_{r} (R_{s} + R_{e q})} = \frac{M}{L_{r}} \end{matrix}

(4)

G_{i} = |\frac{{\dot{I}}_{r e c}}{{\dot{I}}_{i n v}}| = \frac{M}{C_{r} [(R_{s} + R_{e q}) R_{p} + ω^{2} M^{2}]}

(5)

From (4) and (5), it can be seen that the LCC-S type topology has the characteristics of constant current output at the primary side and constant voltage output at the secondary side under resonate conditions. Moreover, the voltage gain is only related to the topology network parameters and the mutual inductance of the coil, and is not affected by load changes. Therefore, it is suitable for dynamic charging and other application environments.

3. Joint Identification Method of Mutual Inductance and Load Parameters

This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn.

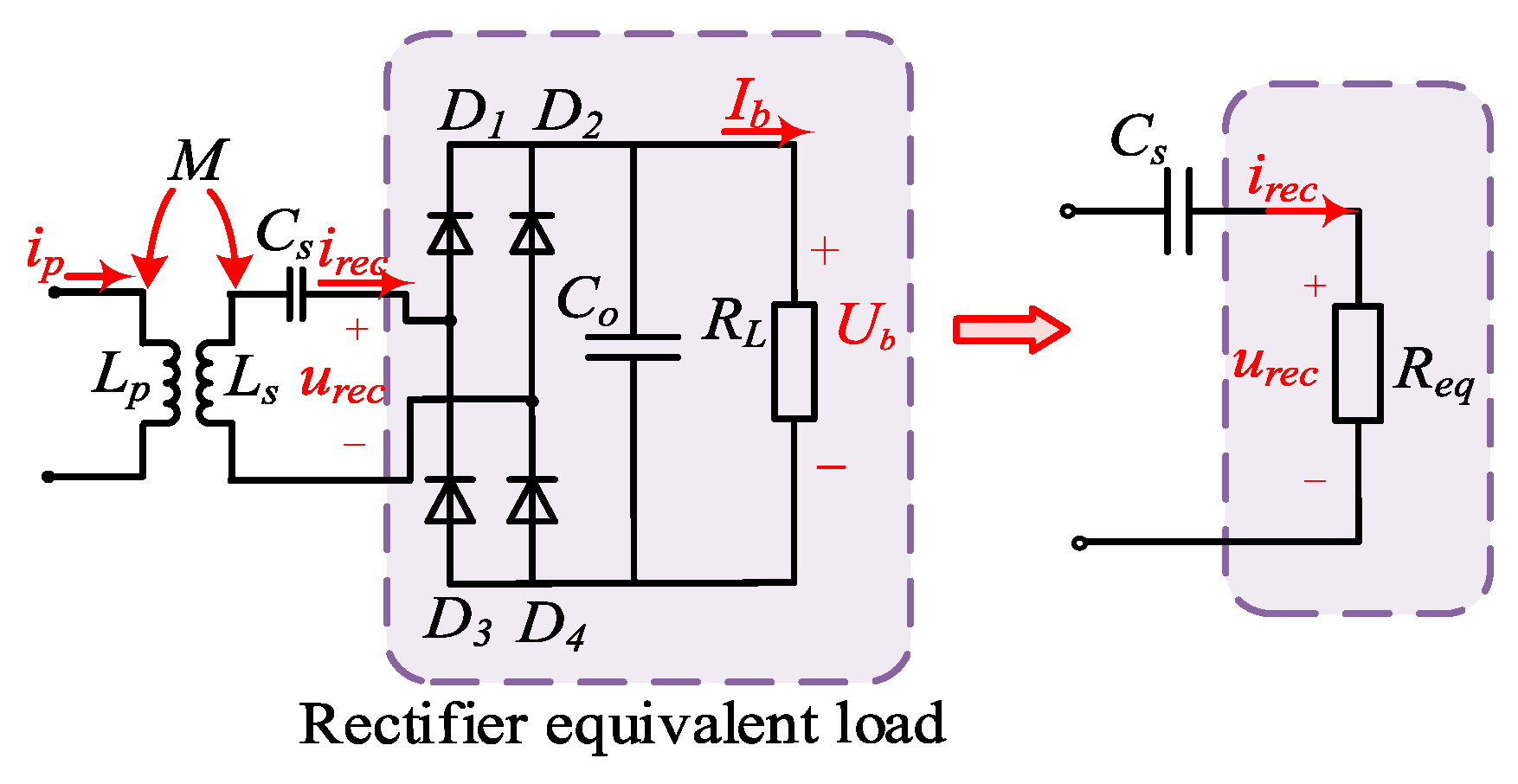
3.1. Rectifier Equivalent Load Analysis of LCC-S Type IPT System

In addition to system components, the performance of an IPT system is also affected by load characteristics. The diode has the advantages of simple structure, high stability, and no additional control, therefore, the receiver of the IPT system usually adopts a full-bridge uncontrolled rectifier circuit. The rectifier and the back-end circuit are usually equivalent to a resistor R_eq as shown in Figure 3 [13,14]. The relationship between the R_eq and R_L can be expressed by (6).

R_{e q} = \frac{8}{π^{2}} R_{L}

(6)

In fact, equivalent load model of rectifier also contains inductance components, so it is not accurate to equivalent it to a pure resistance. The rectifier and its back end should be represented as a series circuit consisting of an equivalent input resistance and an equivalent input inductance [15]. In addition, based on the double-sided LCC system, the quantitative relationship between the equivalent load resistance and the equivalent input impedance of rectifier is deduced by analyzing the relationship between the voltage on the parallel compensation capacitor at receiver, rectifier input voltage and rectifier input current. Therefore, the parameter identification with higher precision is realized for the double-sided LCC system.

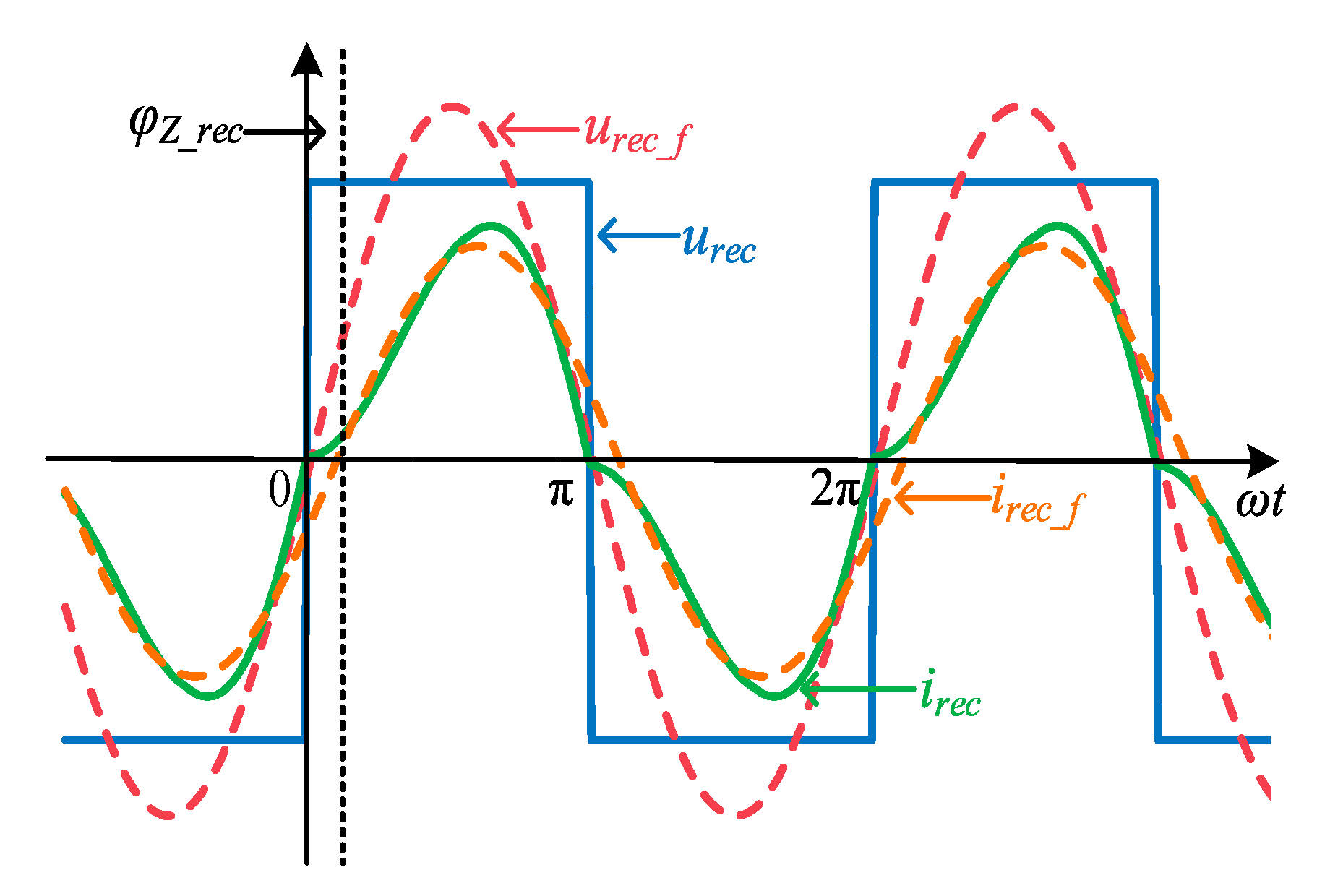
The input voltage and input current waveforms of the rectifier in the LCC-S type IPT system are shown in Figure 4. Here, u_rec and i_rec are the input voltage and current of the rectifier respectively; u_{rec_f} and i_{rec_f} are the fundamental components of the input voltage and current of the rectifier, respectively. It can be seen from Figure 4 that the input current waveform of the rectifier i_rec is not a standard sine wave, and there is a certain distortion. And compared with the fundamental component i_{rec_f}, its amplitude is to the right. This indicates that the equivalent load of the rectifier is not purely resistive. In addition, the phase of the fundamental wave of the input voltage of the rectifier is ahead of the phase of the fundamental wave of the input current of the rectifier, which can also indicate that the equivalent load of the rectifier is resistive. Therefore, it is not accurate that the rectifier and the back end are only equivalent to pure resistance in the process of parameter identification as shown in the Figure 3.

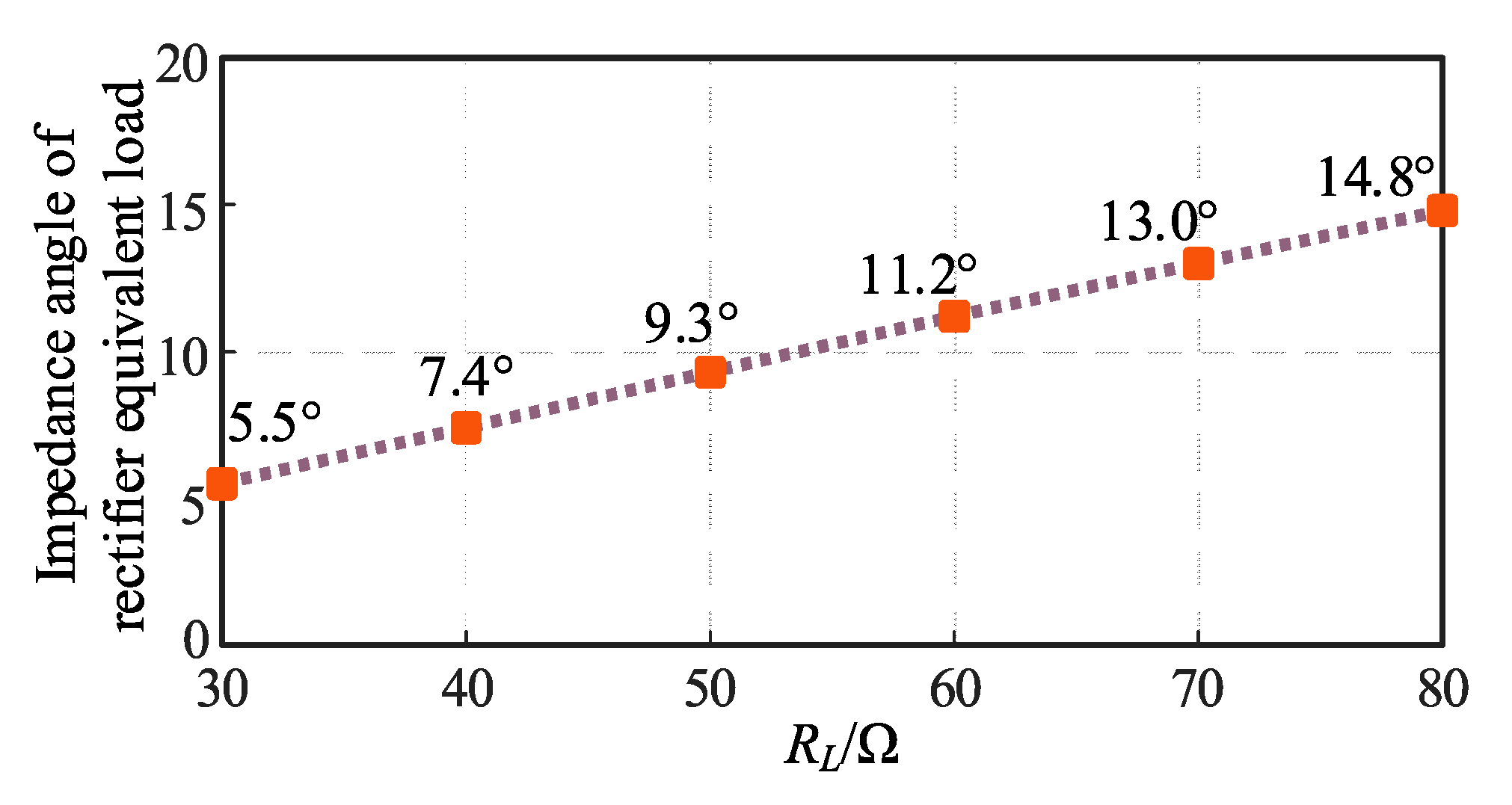
In order to verify the inductive component of the rectifier equivalent load module, a model of a IPT system as depicted in Figure 1 is built in the Matlab/Simulink environment and set the variation range of system load R_L to 30Ω～80Ω. The phase angle of the input voltage u_rec and the input current i_rec of the rectifier equivalent load module is obtained through Fast Fourier Transform (FFT), and then the impedance angle of the rectifier equivalent load φ_{Z_rec} under different load conditions is calculated. It can be seen from Figure 5 that in the range of load R_L, the impedance angle of the equivalent load of the rectifier is greater than zero, which further indicates that the equivalent load of the rectifier has resistance-inductance characteristics. And as the value of system load R_L increases, the impedance angle of the equivalent load of the rectifier φ_{Z_rec} also increases. It shows that the system load R_L will affect the inductance of the equivalent load of the rectifier.

The LCC-S type IPT system is different from the double-sided LCC system because there is no parallel compensation capacitor at the front end of the rectifier. The quantitative relationship between the system load resistance and the equivalent impedance of the rectifier derived in reference [15] cannot be used. Therefore, in the process of parameter identification of LCC-S type IPT system, in order to ensure the identification accuracy, the inductance component of the equivalent load module of the rectifier must be considered.

3.2. Joint identification of mutual inductance and load parameters

The equivalent load module of the rectifier is equivalent to a circuit model in which a resistor and an inductor are connected in series, as shown in Figure 6. R_e is the equivalent input resistance, and L_e is the equivalent input inductance. Define X_e as the equivalent reactance, where X_e=ωL_e.

Seen from Figure 5, as the load resistance increases, the impedance angle of the equivalent impedance of the rectifier φ_{Z_rec} increases monotonically. Although the variation law of the equivalent input impedance of the rectifier is uncertain, it can be reasonably inferred that there is a certain functional relationship between the equivalent input impedance of the rectifier and the system load. It means that R_e and X_e can be represented by R_L, as shown in (7).

\{\begin{matrix} R_{e} = f (R_{L}) \\ X_{e} = g (R_{L}) \end{matrix}

(7)

According to the circuit principle, the equivalent impedance of the receiver can be derived as:

Z_{s} = R_{s} + f (R_{L}) + j [ω L_{s} - \frac{1}{ω C_{s}} + g (R_{L})]

(8)

Then, the reflected impedance equivalent to the transmitter can be derived as:

Z_{r} = \frac{ω^{2} M^{2}}{Z_{s}}

(9)

Taking (8) into (9) and separating the real part and imaginary part of Z_r, (10) can be obtained.

Z_{r} = r e a l (Z_{r}) + i m a g (Z_{r}) j

(10)

Where

\{\begin{matrix} r e a l (Z_{r}) = \frac{ω^{2} M^{2}}{{[R_{s} + f (R_{L})]}^{2} + {[ω L_{s} - \frac{1}{ω C_{s}} + g (R_{L})]}^{2}} [R_{s} + f (R_{L})] \\ i m a g (Z_{r}) = \frac{- ω^{2} M^{2}}{{[R_{s} + f (R_{L})]}^{2} + {[ω L_{s} - \frac{1}{ω C_{s}} + g (R_{L})]}^{2}} [ω L_{s} - \frac{1}{ω C_{s}} + g (R_{L})] \end{matrix}

The coefficient α is defined as the ratio of the real part to the imaginary part of Z_r, as shown in (11). It can be seen that α is related to R_L and has nothing to do with the mutual inductance of the coil M, thus realizing the decoupling of R_L and M.

α = \frac{r e a l (Z_{r})}{i m a g (Z_{r})} = - \frac{R_{s} + f (R_{L})}{ω L_{s} - \frac{1}{ω C_{s}} + g (R_{L})}

(11)

Then according to the circuit principle, the transmitter impedance can be derived as:

Z_{s p} = R_{p} + j (ω L_{p} - \frac{1}{ω C_{p}}) + Z_{r}

(12)

Combining (10) and (12), the real part and imaginary part of Z_r can be expressed as:

\{\begin{matrix} r e a l (Z_{r}) = r e a l (Z_{s p}) - R_{p} \\ i m a g (Z_{r}) = i m a g (Z_{s p}) - ω L_{p} + \frac{1}{ω C_{p}} \end{matrix}

(13)

Taking (13) into (11), the relationship between the transmitter impedance Z_sp and the equivalent input impedances of the rectifier R_e and X_e can be established by the coefficient α, as shown in (14).

α = \frac{r e a l (Z_{s p}) - R_{p}}{i m a g (Z_{s p}) - ω L_{p} + \frac{1}{ω C_{p}}} = - \frac{R_{s} + f (R_{L})}{ω L_{s} - \frac{1}{ω C_{s}} + g (R_{L})}

(14)

Taking (7) into (14), the relationship between Z_sp and R_L is obtained, as shown in (15).

n f (R_{L}) + m g (R_{L}) = - n R_{s} - m (ω L_{s} - \frac{1}{ω C_{s}})

(15)

Where

\{\begin{matrix} m = r e a l (Z_{s p}) - R_{p} \\ n = i m a g (Z_{s p}) - ω L_{p} + \frac{1}{ω C_{p}} \end{matrix}

In (15), the circuit parameters such as self-inductance, internal resistance and compensation capacitance can be measured before identification, and there is no offset during the operation of the circuit basically. In addition, the real and imaginary parts of the transmitter impedance can be calculated by measuring the voltage on the parallel compensation capacitor at the transmitter u_p, the current of the transmitting coil i_p and the phase difference θ of the two, as shown in Equation (16). Videlicet, the value of R_L can be directly solved only by measuring the amplitude and phase of the voltage and current at the transmitter.

\{\begin{matrix} r e a l (Z_{s p}) = \frac{\dot{U_{p}}}{\dot{I_{p}}} c o s θ \\ i m a g (Z_{s p}) = \frac{\dot{U_{p}}}{\dot{I_{p}}} s i n θ \end{matrix}

(16)

After solving the R_L, then the equivalent input impedance of the rectifier R_e and X_e can be calculated according to (7). Next, the real part or imaginary part of the reflected impedance Z_r is calculated by (13), and then the mutual inductance M can be obtained, as shown in (17).

M = \sqrt{\frac{[r e a l (Z_{s p}) - R_{p}] {[R_{s} + f (R_{L})]}^{2} + {[ω L_{s} - \frac{1}{ω C_{s}} + g (R_{L})]}^{2}}{ω^{2} [R_{s} + f (R_{L})]}}

(17)

In conclusion, through the analysis of the real-imaginary ratio of the reflection impedance Z_r and the calculation of the transmitter impedance Z_sp, the decoupling of the load and the mutual inductance in the identification process is cleverly realized.So far, the specific steps of joint identification of mutual inductance and load parameters of LCC-S IPT system have been described. From (15) and (17), it can be seen that the joint identification of mutual inductance and load parameters can be realized only by measuring the amplitude and phase of the voltage and current at the transmitter. The focus of the next step is how to obtain the functional relationship between the equivalent input impedance of the rectifier and the system load, that is, the explicit expression of Equation (7).

3.3. Modeling of Rectifier Equivalent Load Based on Data Fitting Method

A model of a IPT system as depicted in Figure 1 is built in the Matlab/Simulink environment, and the parameters of the model are shown in Table 1.

The variation range of R_L is set to 20Ω～60Ω, then the amplitude A_u and phase φ_u of the rectifier input voltage u_rec and the amplitude A_i and phase φ_i of the rectifier input current i_rec can be measured by Fourier module, respectively. Thus, the equivalent input impedance of the rectifier can be calculated by (18)

\{\begin{matrix} R_{e} = |\frac{A_{u}}{A_{i}}| = \cos (φ_{u} - φ_{i}) \\ X_{e} = |\frac{A_{u}}{A_{i}}| = \sin (φ_{u} - φ_{i}) \end{matrix}

(18)

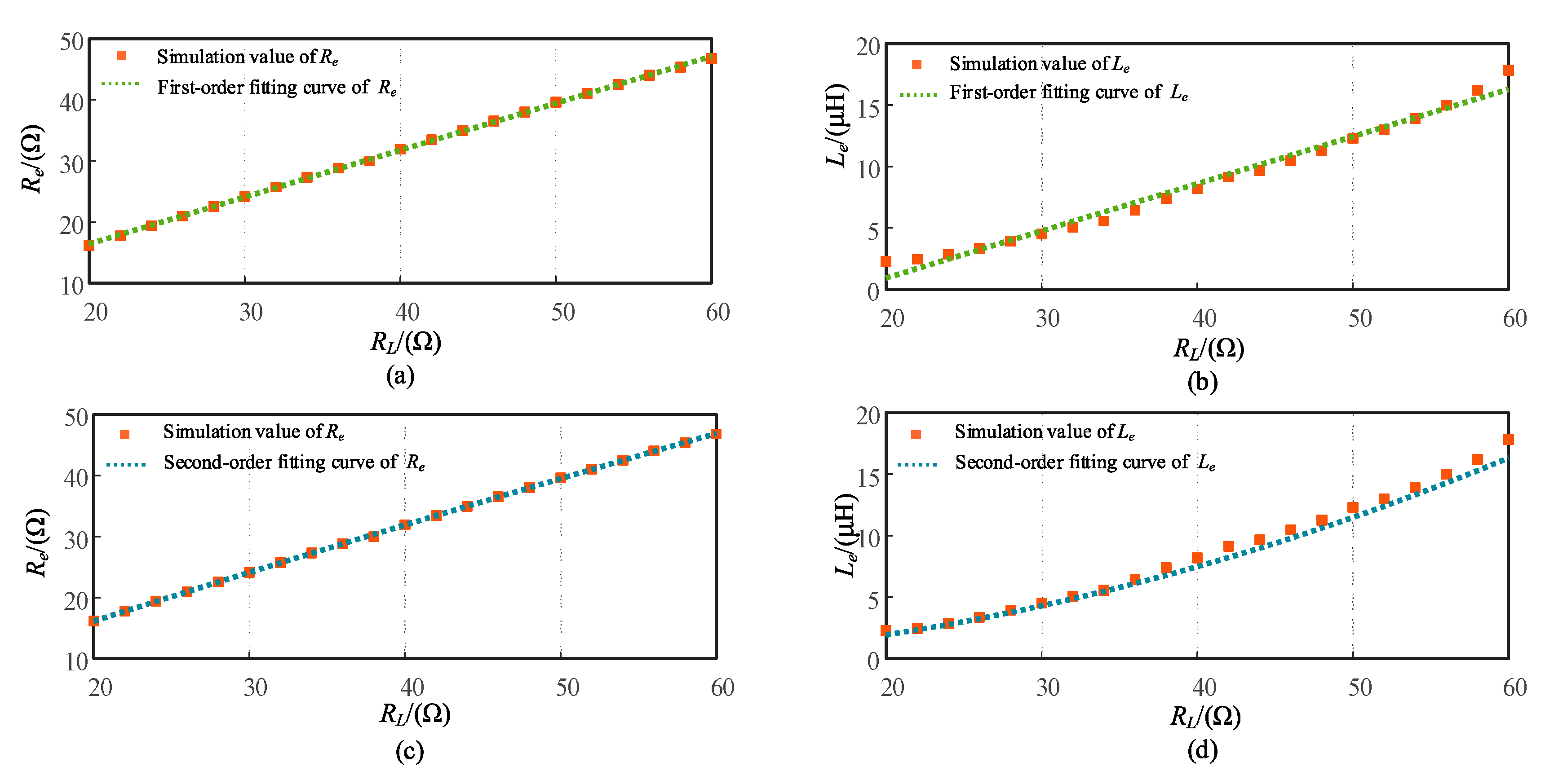
In order to describe the variation rule between the equivalent input impedance of the rectifier and the system load accurately, the polynomial data fitting method is proposed to fit the data in this paper. And the coefficients of the polynomial are determined by the least square method. The specific steps are as follows : Firstly, the equivalent resistance R_e and the equivalent inductance L_e calculated by formula ( 18 ) under different load conditions are drawn and plotted in the same coordinate diagram. Then, the calculated data R_e and L_e are fitted by first-order polynomial and second-order polynomial respectively. Finally, the data fitting diagram shown in Figure 7 can be obtained, and the fitting result is shown in Table 2.

As can be seen from Figure 7, the linearity between the rectifier equivalent input resistance R_e and the system load resistance R_L is high. Therefore, the fitting curves of first-order and second-order polynomials are basically consistent. As the system load resistance R_L increases, the linearity of the rectifier equivalent input reactance L_e gradually decreases. Therefore, the fitted curve is more consistent with the actual value when the order of the fitted curve is higher.

The data fitting results of the rectifier equivalent load are shown in Table 2. Usually, the goodness of fit is used to represent the fitting degree of the fitting curve to the actual value. In statistics, the statistic that measures the goodness of fit is the correlation coefficient R², which ranges from [0,100]. If the value of R² is closer to 100, it means that the fitting effect of the fitting curve to the actual value is better. It can be seen from Table 2 that the higher the order of the polynomial is, the closer the value of R² is to 1. That is, the higher the goodness of fit of the data, the better the fitting effect.

When the first-order polynomial fitting is adopted, the functional relationship between the equivalent input impedance of rectifier R_e and X_e and the system load R_L can be expressed as:

\{\begin{matrix} R_{e} = a_{1} R_{L} + b_{1} \\ X_{e} = ω L_{e} = a_{2} R_{L} + b_{2} \end{matrix}

(19)

Combining (15) and (19), the relationship between Z_sp and R_L can be derived as:

R_{L} = - \frac{b_{1} n + b_{2} m}{a_{1} n + a_{2} m}

(20)

According to (15) ~ (16), m and n in (20) can be obtained by measuring the voltage on the parallel compensation capacitor at the transmitter u_p, the current of the transmitting coil i_p and the phase difference θ between them, as shown in (21).

Where, U_p is the amplitude of u_p and I_p is the amplitude of i_p.

Therefore, after measuring the physical quantities above, the load R_L can be solved directly, and then the mutual inductance M of the system can be identified.

\{\begin{matrix} m = \frac{\dot{U_{p}}}{\dot{I_{p}}} c o s θ - R_{p} \\ n = \frac{\dot{U_{p}}}{\dot{I_{p}}} s i n θ - ω L_{p} + \frac{1}{ω C_{p}} \end{matrix}

(21)

Similarly, when the second-order polynomial fitting is adopted, the functional relationship between the equivalent input impedance of rectifier R_e and X_e and the system load R_L can be expressed as:

\{\begin{matrix} R_{e} = a_{1} {R_{L}}^{2} + b_{1} R_{L} + c_{1} \\ X_{e} = a_{2} {R_{L}}^{2} + b_{2} R_{L} + c_{2} \end{matrix}

(22)

Therefore, the relationship between Z_sp and R_L can be derived as:

(a_{2} m + a_{1} n) {R_{L}}^{2} + (b_{2} m + b_{1} n) R_{L} + c_{2} m + c_{1} n = 0

(23)

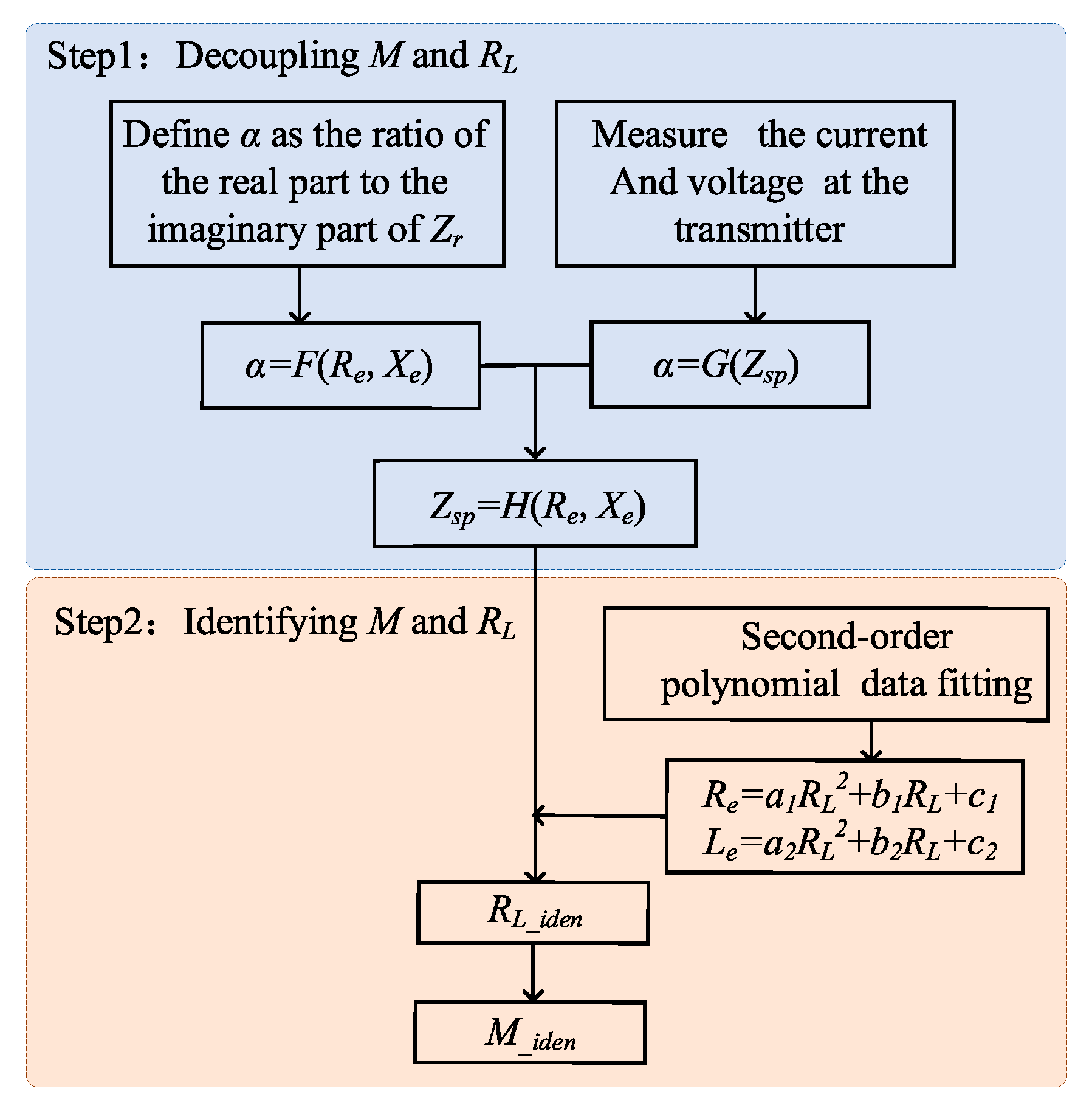
In summary, it can be seen from (20) and (23) that R_L can be solved by measuring the amplitude and phase of voltage on parallel compensating capacitor at transmitter and current of transmitting coil. Moreover, the higher the order of the polynomial used for fitting is, the more complex the fitting formula about. the equivalent input impedance of the rectifier module is. If used directly in the parameter identification process, it will increase the computational complexity greatly. Therefore, in order to facilitate the calculation and description, considering the goodness of data fitting and the simplicity of the parameter identification process comprehensively, this paper adopts the second-order polynomial fitting to analyze the equivalent load module of the rectifier. The identification process is shown in Figure 8.

Seen from Figure 8, firstly, the functional relationship between the impedance of the transmitter and the equivalent input impedance of the rectifier can be established by defining the ratio of the real part to the imaginary part of the reflected impedance. Secondly, the functional relationship between the equivalent input impedance of the rectifier and the system resistance can be obtained by fitting the data with a first-order polynomial. Then, M and R_L can be solved by combining the two functional relationships above into a equation group. That is to say, the joint identification of mutual inductance and load parameters is realized under the condition that only the voltage and current at the transmitter are measured.

4. Simulation Verification and Discussion

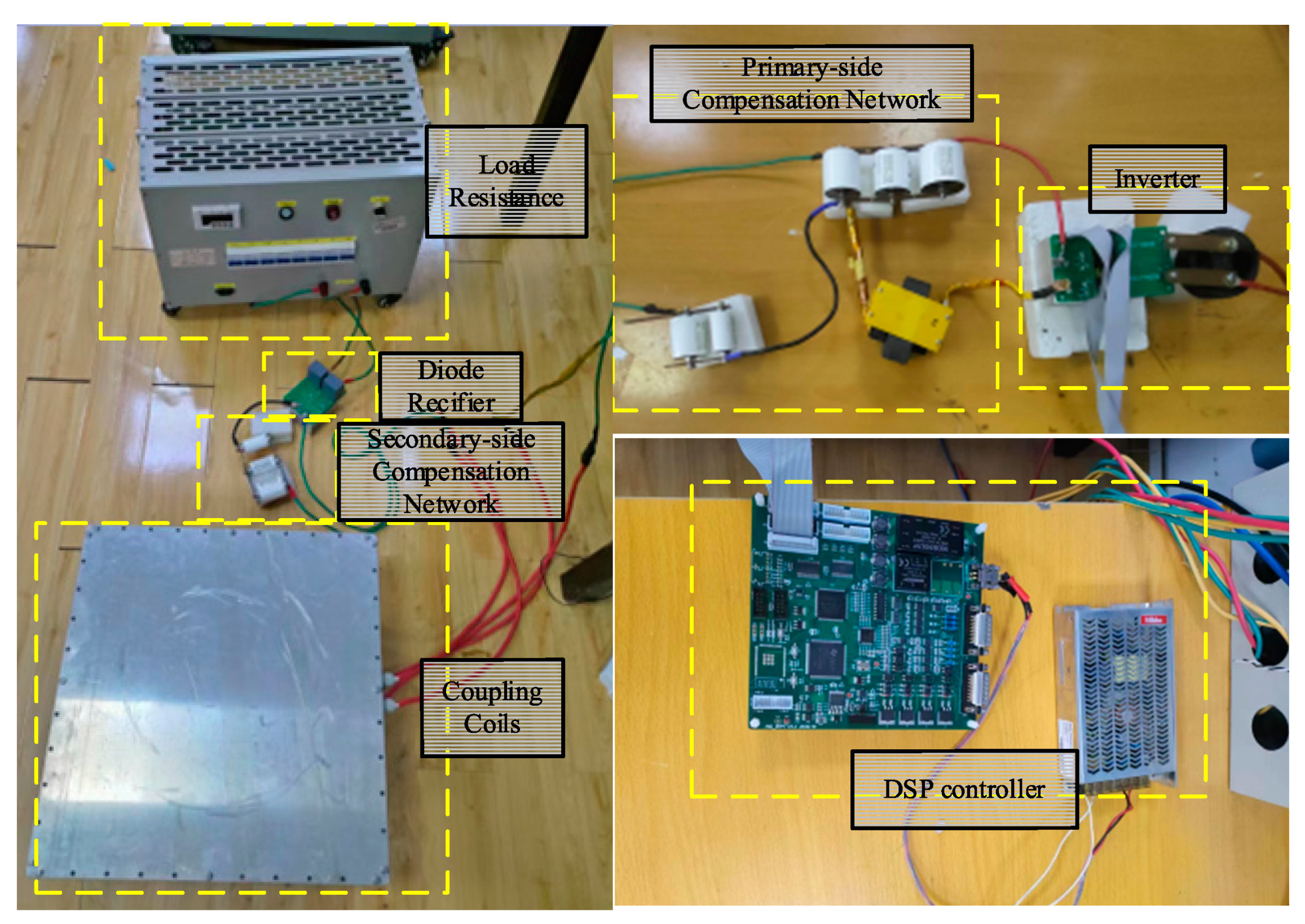
In order to verify the feasibility and identification effect of the proposed identification method, a LCC-S IPT experimental platform is built, as shown in Figure 9, and the system parameters are shown in Table 1.

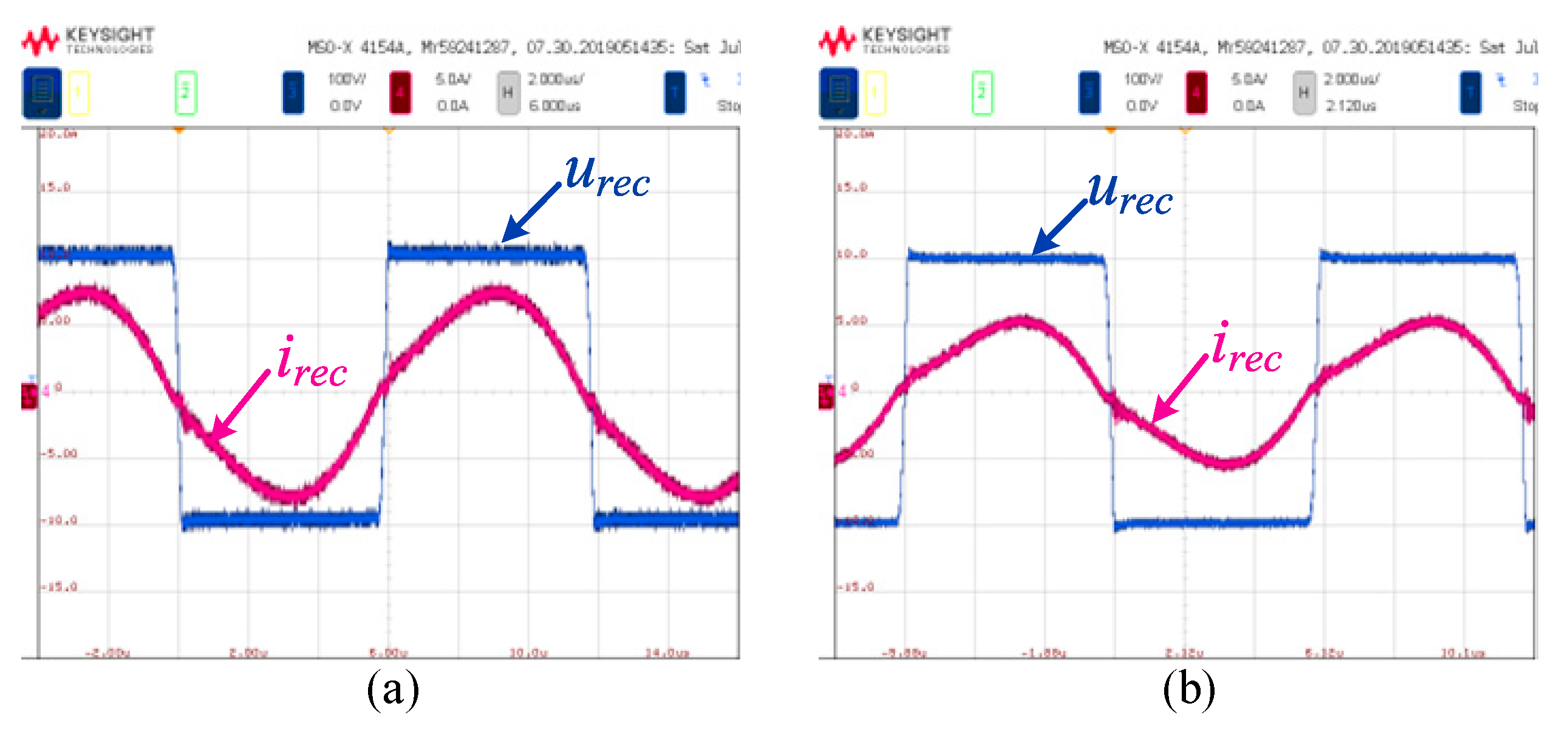
The voltage and current waveforms of the rectifier of the LCC-S type IPT system under different load conditions are shown in Figure 10, where u_rec is the rectifier input voltage and i_rec is the rectifier input current. It can be seen that the waveform of the input current of the rectifier i_rec has a certain distortion, which is not a standard sine wave, and its amplitude is to the right. This is consistent with the simulation analysis in section 2. This can indicate that there is an inductance component in the rectifier load.

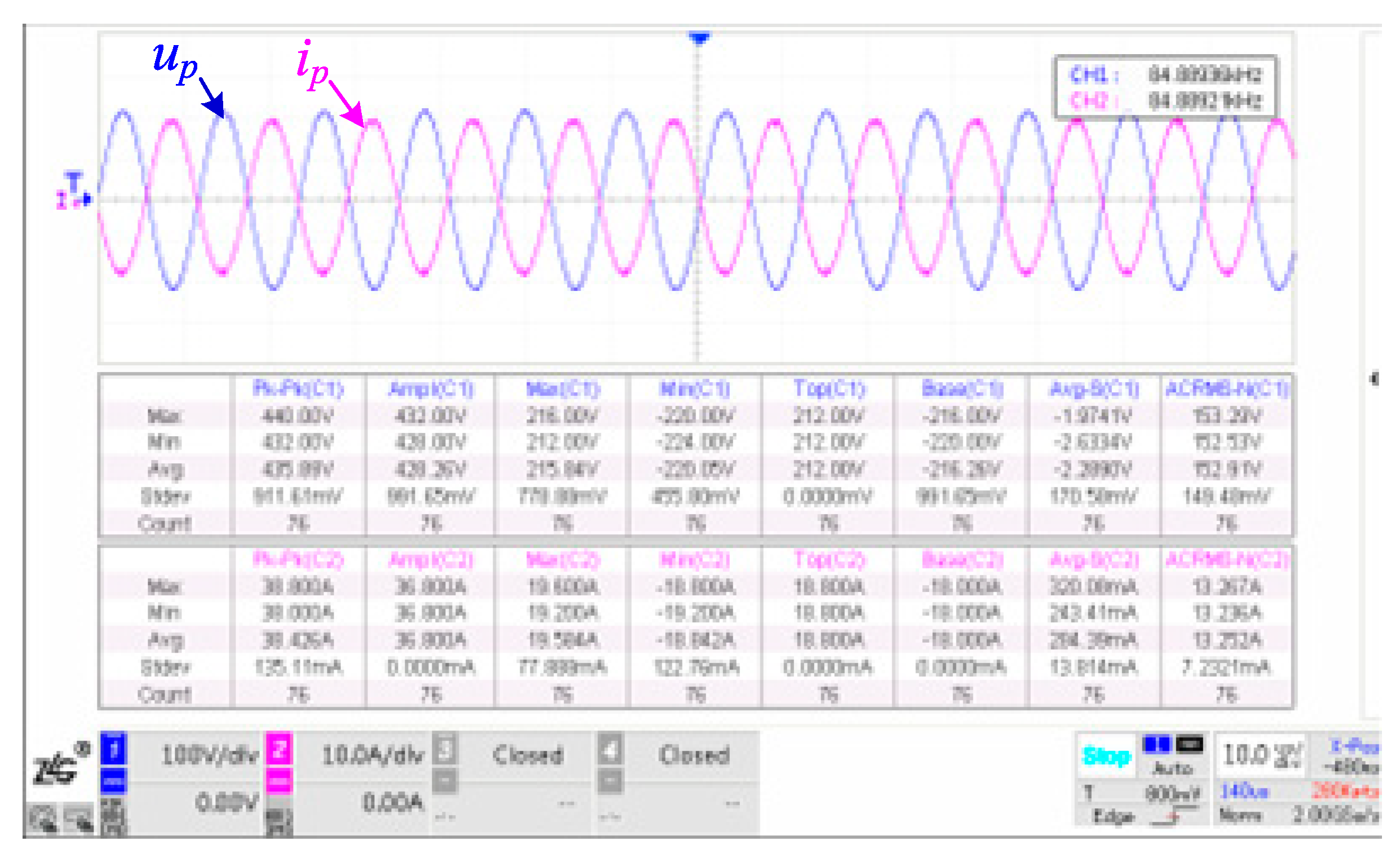
The waveforms of the voltage on the parallel compensation capacitor at the transmitter of the LCC topology u_p and the current of the transmitting coil i_p are shown in Figure 11. The experimental data of u_p and i_p are imported into Matlab for FFT (Fast Fourier transform) analysis, and then the amplitude and phase of the fundamental waves of u_p and i_p are extracted, and then the parameters are identified.

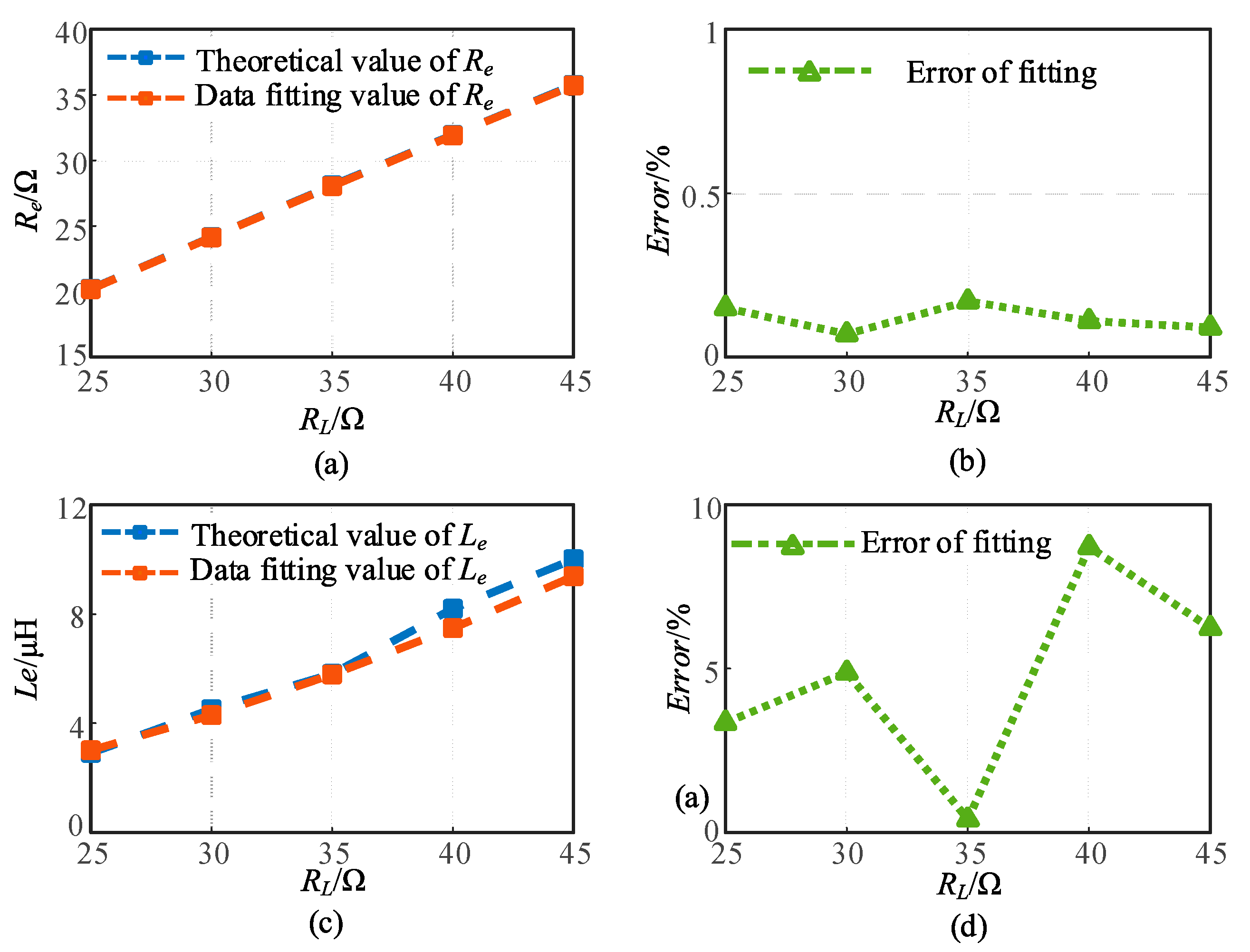
Compare the simulation value of R_e and L_e obtained in the Matlab/Simulink simulation with the data fitting value calculated by the second-order fitting formula (22). It can be seen that the maximum absolute error between the theoretical value and the fitted value of R_e is 0.048Ω and the maximum relative error of the two is 1.2%. Besides, the maximum absolute error between the theoretical value and the fitted value of L_e is 0.71μH and the maximum relative error of the two is 8.71%. When performing polynomial fitting on data, the higher the order of the polynomial used, the higher the fitting accuracy. Therefore, the errors above are mainly caused using second-order polynomial fitting in the data fitting process.

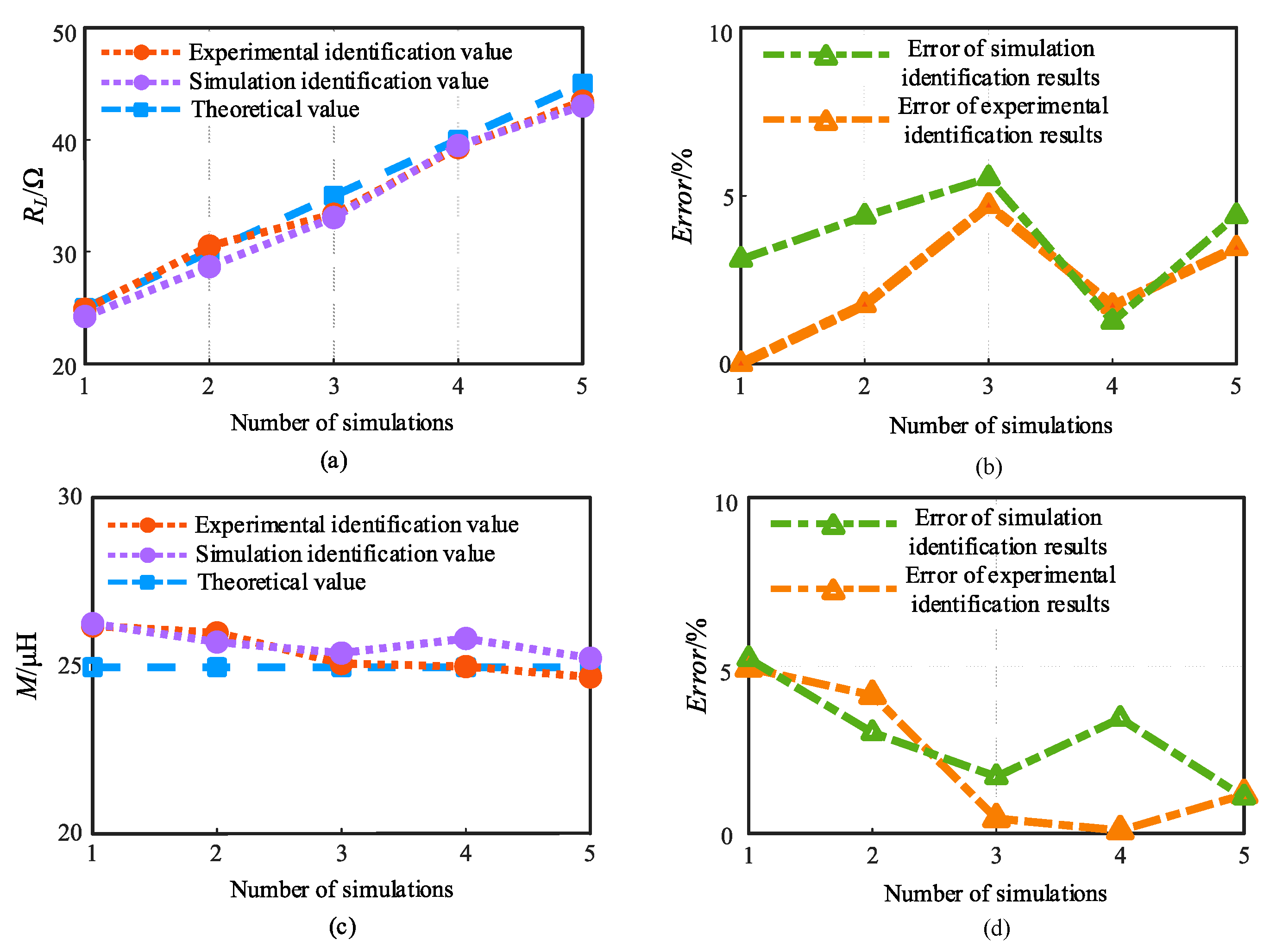
Figure 13 shows the identification results of M and R_L when the mutual inductance M is set to 24.95 μH and the variation range of load R_L is set to 25 Ω to 45 Ω with the size of 5 Ω per step. Compared with the theoretical value, the maximum relative error of the simulation identification result of the load R_L is 4.71 %, and the maximum relative error of the experimental identification result is 5.53 %. The maximum relative error of the simulation identification result of the mutual inductance M is 4.92 %, and the maximum relative error of the experimental identification result is 5.20 %.

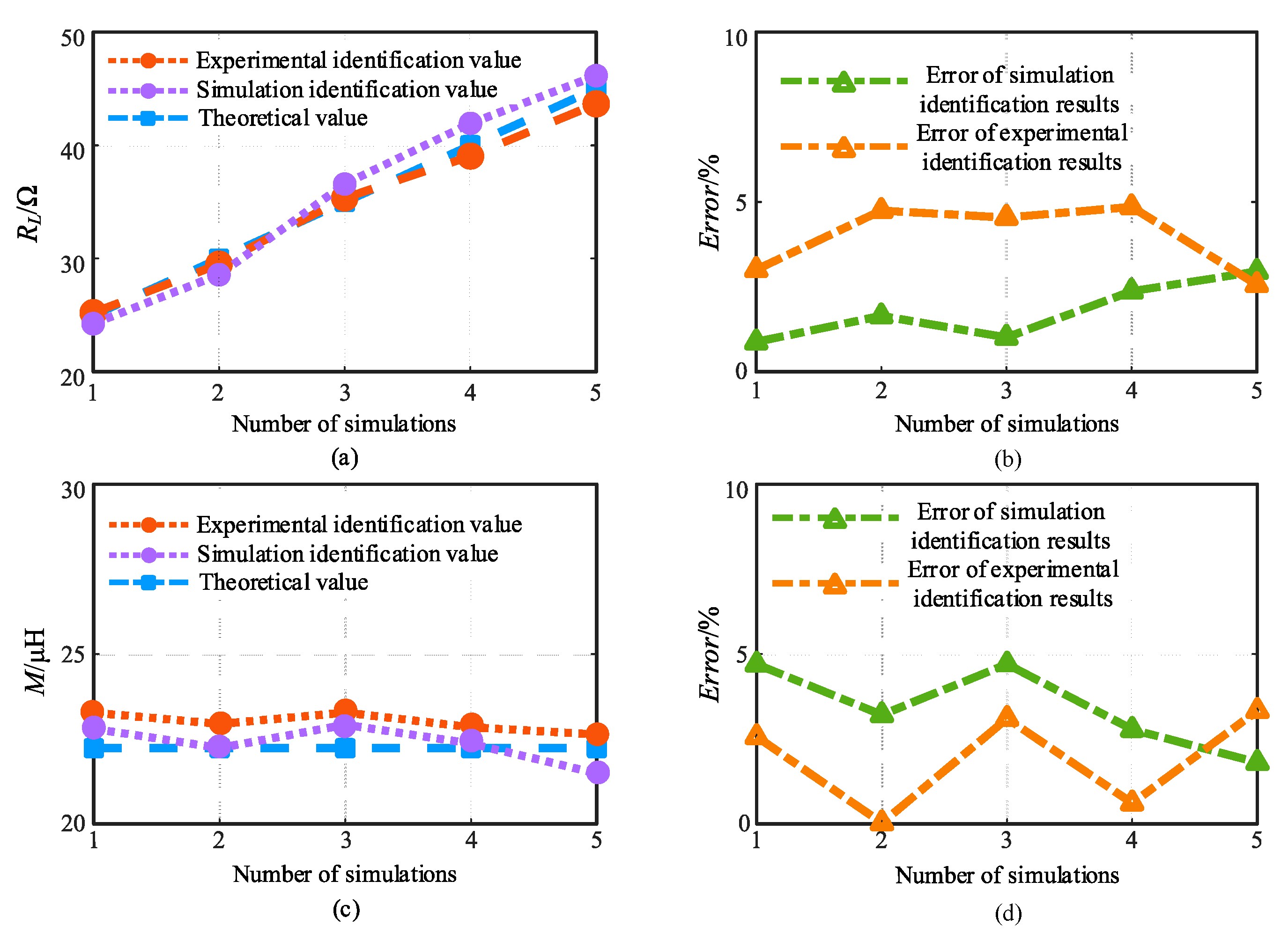
Figure 14 shows the identification results of M and R_L when the mutual inductance M is set to 22.23 μH and the variation range of load R_L is set to 25 Ω to 45 Ω with the size of 5 Ω per step. Compared with the theoretical value, the maximum relative error of the simulation identification result of the load R_L is 2.96 %, and the maximum relative error of the experimental identification result is 4.85 %. The maximum relative error of the simulation identification result of the mutual inductance M is 4.71 %, and the maximum relative error of the experimental identification result is 3.33%.

By analyzing the results of the mutual inductance and load identification above, it can be known that the maximum absolute error of the mutual inductance M identification is 1.22μH, and the maximum relative error is 5.2 %. The maximum absolute error of load RL identification is 1.94Ω, and the maximum relative error is 5.53 %. Since the second-order polynomial fitting is used for the input impedance of the rectifier during the identification process, and this will bring a certain identification error obviously. But these errors and differences are relatively small, so the universality and feasibility of the proposed identification method can be proved.

5. Conclusions

This paper presents a joint identification method of load and mutual inductance parameters for LCC-S type IPT system. Firstly, the rectifier and its back-end circuit are equivalent to a circuit model in which resistance and inductance are connected in series with a resistor and an inductor in series. Then, the mutual inductance and the load are decoupled by defining the ratio of the real part to the imaginary part of the system reflection impedance. Secondly, under the condition of knowing the quantitative relationship between the equivalent input impedance of the rectifier and the system load, the joint identification of the system load and mutual inductance parameters can be realized by measuring the voltage of the parallel compensation capacitor at the transmitting side, the current of the transmitting coil and the phase difference between the two. Meanwhile, the equivalent input impedance of rectifier is analyzed and modeled by data fitting method. The functional relationship between the equivalent input impedance of the rectifier and the system load is obtained by the second-order polynomial fitting method. Finally, the parameter identification of mutual inductance and load is realized. It not only ensures the accuracy of identification, but also simplifies the identification algorithm. A series of simulations and experiments are carried out to verify the proposed identification method. The load and mutual inductance identification results are in good agreement with the theoretical values, and the maximum errors are 5.53 % and 5.2 %, respectively, which proves the feasibility and accuracy of the identification method.

References

Solouma, N.H.; Kassahun, H.B.; Alsharafi, A.S.; et al. An Efficient Design of Inductive Transmitter and Receiver Coils for Wireless Power Transmission[J]. Electronics 2023, 12, 564. [Google Scholar] [CrossRef]
Zhang, B.; Shu, X.; Wu, L. Problems of wireless power transmission technology urgent to be solved and corresponding countermeasures[J]. Automation of Electric Power Systemd 2019, 43, 1–12. [Google Scholar]
Zhou, J.; Wang, J.; Yao, P.; et al. Design and Optimization of a Wireless Power Transfer System with a High Voltage Transfer Ratio[J]. Electronics 2022, 11, 2115. [Google Scholar] [CrossRef]
Zhang, Z.; Pang, H.; Georgiadis, A.; et al. Wireless Power Transfer—An Overview[J]. IEEE Transactions on Industrial Electronics 2019, 66, 1044–1058. [Google Scholar] [CrossRef]
Xian, Z.; Yuan, Z.; Yang, Q.; et al. Coil Design and Efficiency Analysis for Dynamic Wireless Charging System for Electric Vehicles[J]. IEEE Transactions on Magnetics 2016, 52, 1–4. [Google Scholar]
Arnitz, D.; Reynolds, M.S. MIMO Wireless Power Transfer for Mobile Devices[J]. IEEE Pervasive Computing 2016, 15, 36–44. [Google Scholar] [CrossRef]
Shaw, T.; Samanta, G.; Mitra, D. Efficient Wireless Power Transfer System for Implantable Medical Devices Using Circular Polarized Antennas[J]. IEEE Transactions on Antennas and Propagation 2020, 69, 4109–4122. [Google Scholar] [CrossRef]
Qiao, K.; Rong, E.; Sun, P.; Zhang, X.; Sun, J. Design of LCC-P Constant Current Topology Parameters for AUV Wireless Power Transfer. Energies 2022, 15, 5249. [Google Scholar] [CrossRef]
Liao, Z.; Sun, Y.; Ye, Z.; et al. Research on Resonance Mechanism and Resonant Point Distribution Characteristic of Magnetic Coupling Wireless Power Transfer Systems[J]. Transactions of China Electrotechnical Society 2020, 35, 215–224. [Google Scholar]
Basar, M.R.; Ahmad, M.Y.; Cho, J.; et al. Stable and High-Efficiency Wireless Power Transfer System for Robotic Capsule Using a Modified Helmholtz Coil[J]. IEEE Transactions on Industrial Electronics 2017, 64, 1113–1122. [Google Scholar] [CrossRef]
Su, Y.; Chen, L.; Wu, X.; et al. Load and Mutual Inductance Identification Method of SS-Type Magnetically-Coupled WPT System Based on Genetic Algorithm[J]. Transactions of China Electrotechnical Society 2018, 33, 4199–4206. [Google Scholar]
Su, Y.; Zhang, H.; Wang, Z.; et al. The Load Identification Method of Inductive Power Transfer System Based on Switching Capacitors[J]. IEEE Transactions on Power Electronics 2015, 30, 1–1. [Google Scholar] [CrossRef]
Dai, X.; Sun, Y.; Tang, C.; et al. Dynamic Parameters Identification Method for Inductively Coupled Power Transfer System[C]// IEEE International Conference on Sustainable Energy Technologies. IEEE, 2011.
Wang, Z.; Li, Y.; Sun, Y.; Tang, C.; Lv, X. Load Detection Model of Voltage-Fed Inductive Power Transfer System[J]. IEEE Transactions on Power Electronics 2013, 28. [Google Scholar] [CrossRef]
Lv, X.; Zhang, L.; Zou, D. An Approach for Detecting Illegal Load in Wireless Power Transfer System [C]//International Conference on Frontiers of Manufacturing Science and Measuring Technology. 2014.
Ma, S. Research on the Control Strategy of LCC-S Magnetic Coupled Resonant DWPT System[D]. Tiangong University, 2021.
Kuang, X. Research on Parameter Identification and Phase-shifted Output Voltage Control of MC-WPT System Based on LCC-S Topology[D]. Chongqing University, 2021.
Guo, Y.; Zhang, Y.; Li, S.; et al. Load Parameter Joint Identification of Wireless Power Transfer System Based on DC Input Current and Phase Shift Angle[J]. IEEE Transactions on Power Electronics 2020, 35, 10542–10553. [Google Scholar] [CrossRef]
Zhu, Y.; Zhang, H.; Wang, Z.; et al. Design of a High-Power High-Efficiency Multi-Receiver Wireless Power Transfer System [J]. Electronics 2021, 10, 1308. [Google Scholar] [CrossRef]
Liao, C.; Li, J.; Li, S. Design of LCC Impedance Matching Circuit for Wireless Power Transfer System Under Rectifier Load[J]. Cpss Transactions on Power Electronics & Applications 2017, 2, 237–245. [Google Scholar]
Su, Y.; Yang. J.; Dal, X.; et al. Load and mutual inductance identification method for MCR-WPT system based on TensorFlow neural network[J]. Automation of Electric Power Systems 2021, 45, 162–169. [Google Scholar]
Zhu, Y.; Wu, H.; Li, F.; et al. A Comparative Analysis of S-S and LCCL-S Compensation for Wireless Power Transfer with a Wide Range Load Variation[J]. Electronics 2022, 11, 420. [Google Scholar] [CrossRef]

Figure 1. Circuit structure of LCC-S IPT system.

Figure 2. Equivalent Circuit of LCC-S IPT System.

Figure 3. Traditional rectifier equivalent load circuit model.

Figure 4. Schematic of rectifier input voltage u_rec and current i_rec.

Figure 5. Impedance angle of rectifier load of LCC-S topology under different load conditions.

Figure 6. Equivalent circuit model of LCC-S type IPT system considering equivalent inductance of rectifier.

Figure 7. Fitting Curves of Equivalent Input Impedance of Rectifier：(a) First-order fitting curve of R_e; (b) First-order fitting curve of L_e; (c) Second-order fitting curve of R_e; (d) Second-order fitting curve of L_e.

Figure 8. Flow chart of parameter joint identification method.

Figure 9. The experimental platform diagram of LCC-S IPT system.

Figure 10. The voltage and current waveforms of the rectifier of the LCC-S IPT system: (a) R_L=40Ω;(b) R_L=60Ω.

Figure 11. Voltage and Current Waveform of LCC-S Type IPT System when M=22.23μH and R_L=40Ω.

Figure 12. Simulation results of rectifier equivalent input impedance when R_L changes (a) R_e data fitting results; (b) The error of data fitting of R_e; (c) L_e data fitting results; (d) The error of data fitting of L_e.

Figure 13. The identification results of mutual inductance and load when M=24.95μH (a) Identification results of R_L; (b) The error of R_L identification; (c) Identification results of M; (b) The error of M identification.

Figure 14. The identification results of mutual inductance and load when M=22.23μH (a) Identification results of R_L; (b) The error of R_L identification; (c) Identification results of M; (b) The error of M identification.

Table 1. Parametric Values of The IPT System.

Parameters	Values	Parameters	Values
U_dc (V)	200	f/kHz	85
L_p/μH	128.9	L_s/μH	117.61
R_p/Ω	0.376	R_s/Ω	0.350
C_p/nF	32.58	C_s/nF	29.64
L_r/μH	25.2	M/μH	24.95
C_r/nF	136.8

Table 2. Data Fitting Results of Equivalent Impedance of Rectifier.

Types of polynomials	Data fitting equations	$R^{2}$ /%
1st-order polynomial	$R_{e} = 0.7683 + 1.042$	99.97
1st-order polynomial	$L_{e} = 0.3838 R_{L} - 6.746$	98.31
2nd-order polynomial	$R_{e} = 0.0009394 {R_{L}}^{2} + 0.8343 R_{L} - 0.3231$ 6	99.99
2nd-order polynomial	$L_{e} = 0.004416 {R_{L}}^{2} + 0.03056 R_{L} - 0.3279$	99.83

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer