Prerpints.org logo
Preprint
Article

Rainfall Erosivity in Peru: A New Gridded Dataset Based on GPM-IMERG and Comprehensive Assessment (2000–2020)

Altmetrics

Downloads

145

Views

181

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

04 August 2023

Posted:

08 August 2023

You are already at the latest version

Alerts
Abstract
In soil erosion estimation models, the variable with the greatest impact is rainfall erosivity (RE), which is the measurement of precipitation energy and its potential capacity to cause erosion, and erosivity density (ED), which relates RE to precipitation. The RE requires high temporal resolution records for its estimation. However, due to the limited observed information and the increasing availability of rainfall estimates based on remote sensing, recent research has shown the usefulness of using observed-corrected satellite data for RE estimation. This study evaluates the performance of a new gridded dataset of RE and ED in Peru (PISCO_reed) by merging data from the IMERG v06 product, through a new calibration approach with hourly records of automatic weather stations, during the period of 2000-2020. By using this method, a correlation of 0.7 was found between the PISCO\_reed and RE obtained by the observed data. An average annual RE for Peru of 4831 MJ·mm·ha-1·h-1 was estimated with a general increase towards the lowland Amazon regions and high values are found on the north-coast Pacific area of Peru. The spatial identification of the most risk areas of erosion, was carried out through a relationship between the ED and rainfall. Both erosivity data sets will allow us to expand our fundamental understanding and quantify soil erosion with greater precision.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

Soil erosion is one of the greatest environmental threats worldwide Nearing et al. [1], Panagos et al. [2], Karlen et al. [3], Tripathi and Singh [4] presenting multiple issues such as reduced crop yields, deterioration of water quality due to transport of fertilizers and pesticides, the decreased storage capacity of reservoirs due to sediment production, as well as losses in soils for cultivation [5,6,7]. There are various categories of erosion such as water, wind, freezing, and mixed erosion, but the most frequent and highest proportion is water [8]. Water erosion of the soil damages the productive surface of the soil due to separation and transport processes, exposing the subsoil of the soil [9,10]. Therefore, the quality of the soil is affected by reducing its water retention capacity and amount of organic matter [11,12], endangering its various ecosystem services such as CO 2 fixation, agricultural productivity and flood risk reduction [13], which are expected to increase in demand due to urban expansion and changes in consumption patterns [14]. To prevent a worsening of soil erosion, the application of public soil conservation policies based on the monitoring of regions susceptible to RE is required to understand and mitigate its effects, such as the reduction of agricultural productivity, food, and water security, and the national economy [15,16,17,18].
The Intergovernmental Panel on Climate Change reports that a continuous increase in CO 2 emissions has occurred in recent decades [19]. On average, the global concentration of CO 2 in the atmosphere increased by 40% from a pre-industrial value in 2011. Evidence suggests that such an increase has resulted in an average increase in air temperature of 0.85 ∘ C (1880-2012), and according to the outputs of Global Climate Models, it is predicted that by the end of the 21st century the increase will reach 2 ∘ C with respect second half of the 19th century [19]. In this sense, it is expected that changes will occur in the hydrological cycle, and consequently, in the availability of water resources [19,20,21]. The change in the global water supply is expected to be ± 10% with more intense precipitation events, depending on the region of analysis [19,22,23]. In Peru, some investigations on the impact of climate change converged towards a scenario with increased rainfall rates in the summer months (December-March), which would increase the erosive potential of storms, favouring the loss of soil from the available agricultural area, during these months [24]. Another consequence is the increase in the occurrence of events associated with soil loss such as landslides [25,26]. For this reason, soil erosion in Peru should be part of Urgent National Policy, aiming at the identification and monitoring of areas more vulnerable to the loss of agricultural soils and promoting actions to prevent, mitigate or reverse its effects on desertification and soil degradation processes [27,28].
Soil erosion is caused by two physical processes: i) the separation of soil particles generated by the kinetic energy of the impact of raindrops and ii) the transport of sediments by surface flow [1]. The level of erosion depends on the regional physiographic, soil and precipitation characteristics [29], which is composed of two factors: the intensity of precipitation and its kinetic energy at the soil surface [18]. One of the widely used indicators to quantitatively represent and measure the level of soil erosion, sheet and rill, is the multi-annual index of RE [22,30,31,32] and the erosivity density (ED), computed as the ratio of RE and precipitation [33,34]. Generally, the RE is calculated in periods of less than 15 minutes, or adapted by means of statistical algorithms according to the available temporal resolution [35]. To predict soil erosion using RE, the empirical Revised Universal Soil Loss Equation (RUSLE) [34,36,37], which combines the influence of duration, magnitude, and intensity of storm events can be used. Although the RUSLE method is estimated at the annual average level, it can also be calculated on shorter time scales to assess its variability [38]. In its formulation, the most dynamic and reactive factor to changes in climatic conditions is RE, therefore identifying temporal variability provides a more realistic and accurate assessment of soil erosion, for example, the seasonal estimate of RE is used to assess erosion risk in various vulnerable regions [11,39,40].
The classic RE equation requires precipitation time series from 1 to 15 minutes, unfortunately, this information is scarce globally [41,42]. Nevertheless, through empirical equations, it is possible to use of hourly or 30-minute data. This convenient technique is commonly used in multiple regions [40,43]. More recently, a diversity of research has examined the use of observed data and Satellite Precipitation Product (SPP) for RE estimation, with their respective limitations due to the source, data derivation model and spatial scales [2,44,45]. Based on the above, the spatial estimation of RE can be grouped into three approaches: i) observed-based RE: local estimates of weather stations and subsequent geospatial interpolation [44,46,47]; ii) "satellite-based RE": the use of satellite-based precipitation products (SPPs) [48,49,50]; and, iii) "merged-based RE": a mix of both observed and simulated data sources, based on the correction of the RE obtained by the SPPs with respect to data from observed stations, at the national scale [8,18,51,52,53], regional [11,54] and global [40,52]. In this research, the "merged-based RE" method is used through seasonal satellite correction factors based on automatic weather stations (AWS) at a national scale. This procedure combines the advantages of AWS (accuracy at the hourly timescale) with that of the SPP (spatial variability), widely used as a complement in the analysis of various hydrological processes [55,56].
In South America, studies have been carried out with the observed-based RE methodology for the estimation of the RE. In Brazil, Sanchez-Moreno et al. [57] use that method because they have more availability of this information, obtaining a RE range from 1672 to 22,452 M J · m m · h a − 1 · h − 1 with an increase from east to west; likewise, Mello et al. [58] identify areas in the northwest with very high RE (>20,000 M J · m m · h a − 1 · h − 1 ) and in the northeast with medium RE rates (>2,000 M J · m m · h a − 1 · h − 1 ). Using "merged-based RE", in Ecuador Delgado et al. [59] estimated the RE based on observed stations and the Integrated Multi-satellitE Retrievals for GPM (IMERG) obtains a national average of 3,173 M J · m m · h a − 1 · h − 1 , in Chile central region Bonilla and Vidal [47] obtaining an RE range of 50 to 6,000 M J · m m · h a − 1 · h − 1 with an increase from north to south. Moreover, Lobo and Bonilla [60] based on the hourly precipitation from AWS estimates the RE at a point level with a range of 68 to 3,520 M J · m m · h a − 1 · h − 1 . In addition, he highlights that the use of rainfall at a higher temporal resolution results in a non-linear decrease in the RE.
In Peru, there are investigations that use the three methods. Based on the "observed-based RE", local studies such as that of Romero (2007) in the north of the Andean region, estimates an RE of 2950 M J · m m · h a − 1 · h − 1 at a point level, while Mejía-Marcacuzco et al. [61] on the south coast in Tacna estimates an RE of 1190 M J · m m · h a − 1 · h − 1 . Using the "satellite-based RE" method, some global studies determine an average RE in Peru of 2,246 M J · m m · h a − 1 · h − 1 [62]; on the other hand, through the Global Rainfall Erosivity Database (GloREDa) product developed by Panagos et al. [40] an RE range is estimated between 148 in the coastal region to 14226 M J · m m · h a − 1 · h − 1 in the lowland Amazon. Using the "merged-based RE" method, (Peru) [63], prepared a map of soil erosion intensity at a national scale, which was published by the National Institute of Natural Resources - INRENA, using cartographic information, represented by national charts, aerial photographs and images captured by radar and satellite. Also, Sabino Rojas et al. [64] developed a soil erosion atlas on an annual scale from 1981 to 2014, based on the information from PISCOp V1.0 product on a monthly scale Aybar et al. [65], finding an range from 0 to ±10000 M J · m m · h a − 1 · h − 1 .
In this study, PISCO_reed product was used through a seasonal calibration process based on AWS, in order to i) obtain a more accurate RE product on a national scale and ii) perform a regional assessment of erosivity, that allows us to identify the areas most at risk from the negative effects of soil loss. For this reason, the specific objectives of this research are: (a) To carry out a cross-validation of the RE database, and (b) to evaluate spatio-temporally erosivity by estimating trends and identifying danger zones. Finally, this study has the utility of demonstrating the application of precipitation data based on satellite products and observed stations to estimate the erosivity of precipitation at monthly, annual and multi-annual scales.

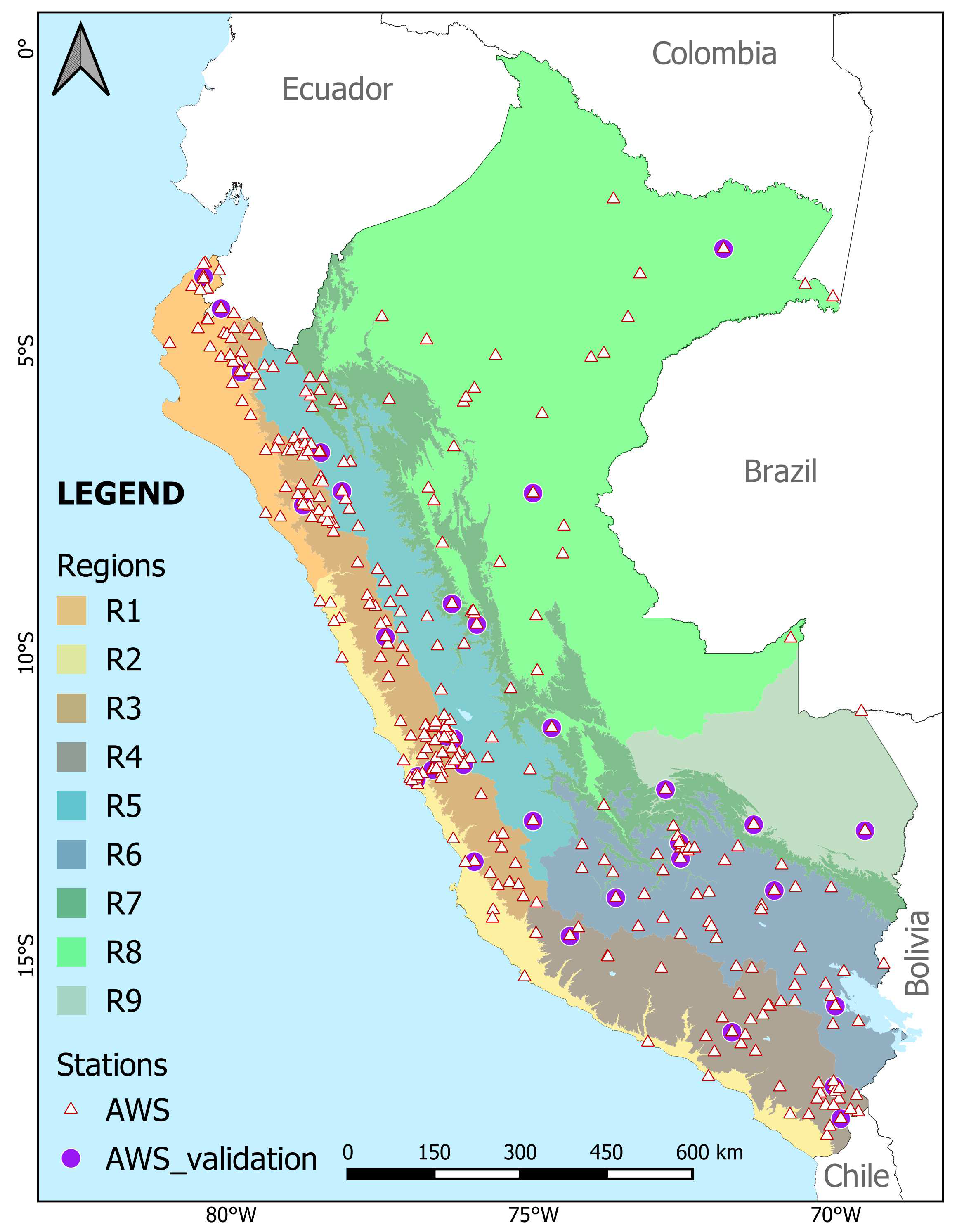
2. Study Area

The study was carried for the entire Peruvian territory, located on the west coast of South America and is between 0 ∘ 02N - 17 ∘ 50.2S and 68 ∘ 10.2W - 81 ∘ 90.2W, with an extension of 1,285 million km 2 . This territory is characterised by high topographic variability, with an elevation range from sea level to 6,685 meters above sea level (masl), with an average of 1,489 masl. Peru exhibits high variability of various climatic factors such as precipitation and temperature, as a result of the interaction of various influences and forcing factors such as synoptic-scale atmospheric currents, the complex orography of the Andes, the cold Humboldt Current System and El Niño Southern Oscillation [66,67,68,69].
In general, the average annual precipitation varies in the range of ± 1 mm on the southern coast, while in the lowland Amazon it reaches higher values of 4860 mm, the average is 1412 mm. Presenting the highest rainfall in the month of February and the minimum during the month of July. In addition, in the Peruvian Andes, the climate is complex and is mainly controlled by the orography that acts as a topographic barrier to the flow of moisture, causing the formation of strong precipitation gradients on the eastern flanks of the Andes [65]. The inter-Andean valleys (≳ 500 mm) are mainly dominated by convective processes that channel moisture intrusions from the Amazon. At the same time, the influence of the cold and dry air masses coming from the Humboldt Current System cause the driest conditions on the Pacific coast and on the western flanks of the Andes (≲ 500 mm). However, during the El Niño Southern Oscillation occurrence, the Humboldt Current System weakens and the formation of severe convective storms can occur, especially over the North Pacific Coast [65].
For the sake of clarity in the development and evaluation of PISCO_reed dataset, the study area was divided into different regions. This segmentation was based on: i) the classification of climatic sectors [70] and ii) on the availability of AWS (Figure 1), the regions were labeled as follows: North Pacific Coast (1), Central and South Pacific Coast (2), North Western Andes (3), Central and South Western Andes (4), North Eastern Andes (5), Central and South Eastern Andes (6), High Forest (7), Northern Low Forest (8) and Lowland Amazon center and south (9). These regions can be grouped into 3 zones: Region 1 and 2 (Pacific Coast), Region 3, 4, 5 and 6 (Andes) and Region 7, 8 and 9 (Amazon).

3. Materials and Methods

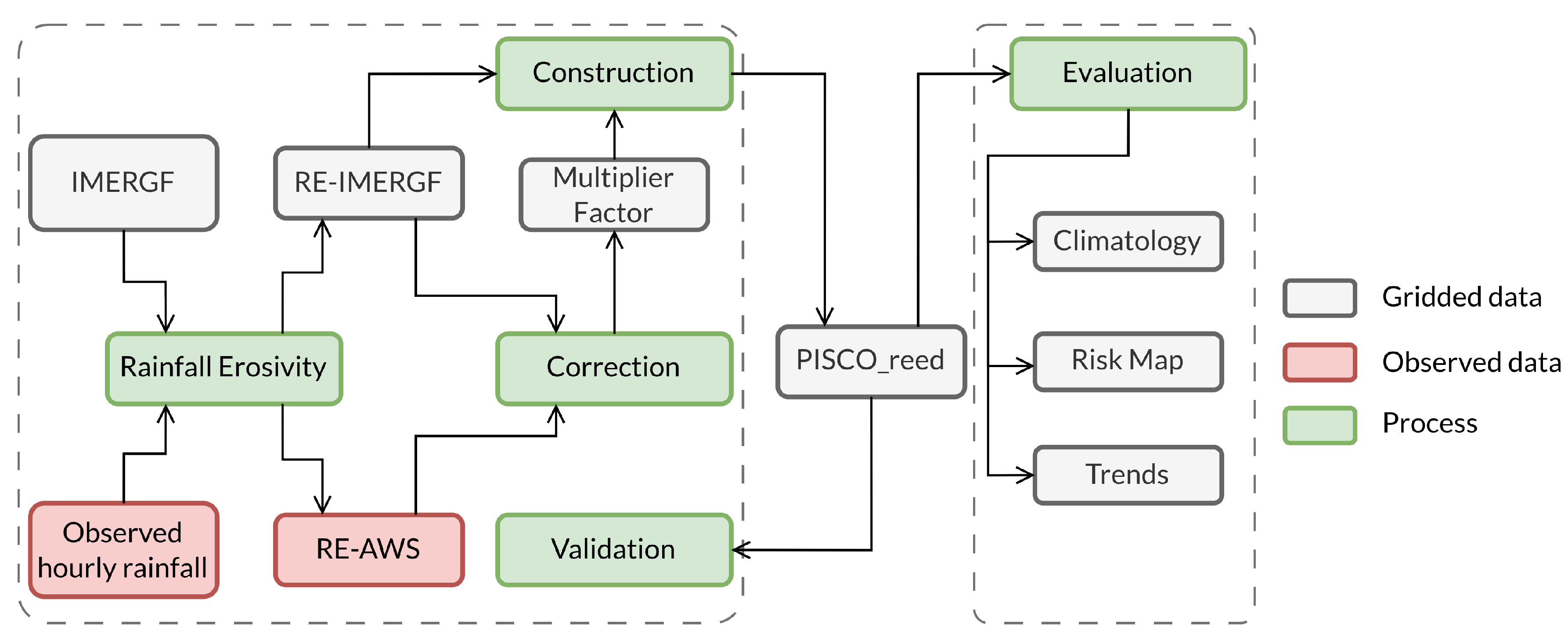
3.1. Overview

Stages, functions and gridded/observed data used in this research are shown in the flowchart (Figure 2), obtaining as results the PISCO_reed product and its evaluation. First, the RE of the AWS and the IMERGF product is estimated on an hourly scale using the conventional RUSLE method. Then, the IMERGF-RE series is reconstructed through a correction based on the observed-RE, with a validation of the interpolation of the multiplicative factor by seasonal periods. Next, the uncertainty of the erosivity products generated is evaluated taking the observed data as a reference. Secondly, the ED rates and the areas of greatest danger of erosivity are estimated. Moreover, trends of the annual RE series by region are estimated.

3.2. Data

The estimation and evaluation of the RE in Peru required gridded products and observed precipitation data: (i) SPP IMERG, (ii) AWS from SENAMHI, and iii) Global RE gridded products. These data sets were used in this study for the development of the methodology.

3.2.1. IMERG V06

The increased accessibility to high spatio-temporal resolution SPPs, such as the Global Precipitation Measurement (GPM) mission, has facilitated the development of hydrological research. GPM jointly developed by the National Aeronautics and Space Administration (NASA) and the Japan Aerospace Exploration Agency (JAXA) (Hoe, 2014), was put into orbit and has been in operation since 2014 as a successor to TRMM (deployed in 1997), to unite and increase precipitation estimates from a constellation of satellites [71]. NASA’s Goddard Earth Sciences Data and Information Services Center (GES DISC) provides access to GPM-derived products through multiple applications that contribute to knowledge about the water cycle and its impact from extreme natural events [45,72]. NASA’s Earth Observing System Data and Information System has defined three levels of products for the distribution and labeling of GPM products, level 3 is called IMERG. For precipitation estimation, IMERG is based on an algorithm that uses GPM microwave observations as a reference for combining, using a number of interpolation methods such as CMORPH-KF [73], with multiple satellite data such as passive microwave (PMW), geosynchronous infrared (IR), TRMM microwave imager estimates. (TMI), among others. Therefore, it presents advantages with respect to TRMM in terms of temporal resolution (3 to 0.5 hours), spatial resolution (0.25 ∘ to 0.1 ∘ ), and area covered (60 ∘ S–60 ∘ N). In addition, IMERG version 6 features two enhancements. The first is the length of the period covered by GPM, using TRMM estimates (2000-2014) to obtain hourly rainfall from June 2000 to the present [71]. The second is the distinction between liquid and non-liquid precipitation, to calculate the precipitation from this first ratio. IMERG classifies its products according to latency periods: Early, Late and Final with ±4 hours, ±14 hours and ±3.5 months, respectively [74]. The Early and Late versions only have a calibration for observed climatology, while the Final version uses the observed monthly rainfall from the Global Precipitation Climatology Center (GPCC) for bias correction. GPM-IMERG-V06-Final (IMERGF) contains the variable PrecipitationCal, calibrated precipitation with observed stations, expressed in mm/h. To estimate the RE, this research uses IMERGF data from September 2000 to August 2020. The product is available in NCDF4 format, freely downloadable from the portal https://disc.gsfc.nasagov/datasets (accessed on 1 April 2023).

3.2.2. Observed Rainfall

The observed hourly precipitation used in this study was obtained from the National Hydrology and Meteorology Service of Peru (SENAMHI). The data were extracted from 322 AWS, located at altitudes ranging from 100 to 5,000 masl, with an average of 2,000 masl (Figure 1). The amount of AWS has increased in recent years, from 120 in 2014 to 320 in 2021. In addition, the temporal period of the seasons is from 1.5 to 6 years, with an average of 3.5 (Figure A1), therefore, this is the most extensive hourly data set for the estimation of the RE in Peru. The analysis of the results derived from the AWS is classified in the nine climatic regions, obtaining a total of 180, 90 and 40 AWS in the Coast, Andes and Amazon zones, respectively. SENAMHI provides this information with a basic quality control (QC), with a procedure that can be divided into two stages: i) filtering by extreme physical, national limits (401 mm/h) and internal consistency control; ii) visual inspection of the hourly, daily, monthly and annual series, to validate internal consistency and homogeneity. The reliability of the AWS data has been successfully tested in various investigations that evaluate the performance and accuracy of the SPPs in Peru [56].

3.2.3. Global RE products

This study uses global RE products such as GloREDa and CMORPH for comparison purposes. GloREDa is based on observed data of high temporal resolution (1 to 60 min) that mainly cover the period from 2000 to 2010, collected from various countries of different regions and climates, however in South America the number of stations only represents 5% with an irregular geographic distribution [40]. The resulting global RE product has a spatial resolution of 0.1 ∘ and can be accessed through the European Soil Data Center website (https://esdac.jrc.ec.europa.eu/). On the other hand, CMORPH is a global precipitation reanalysis product, based on geostationary, low-orbit and PMW satellites [18], with temporal resolution (0.5 h), spatial resolution (0.8km × 0.8km), temporal period (1998 to present), and coverage area (60 ∘ S–60 ∘ N), developed by the National Oceanic and Atmospheric Administration. (NOAA) [75,76]. This product has been applied for the identification of extreme hydrological processes such as RE, Bezak et al. [52] obtained this variable by pixel level using the RUSLE method [77].

3.3. Methodology

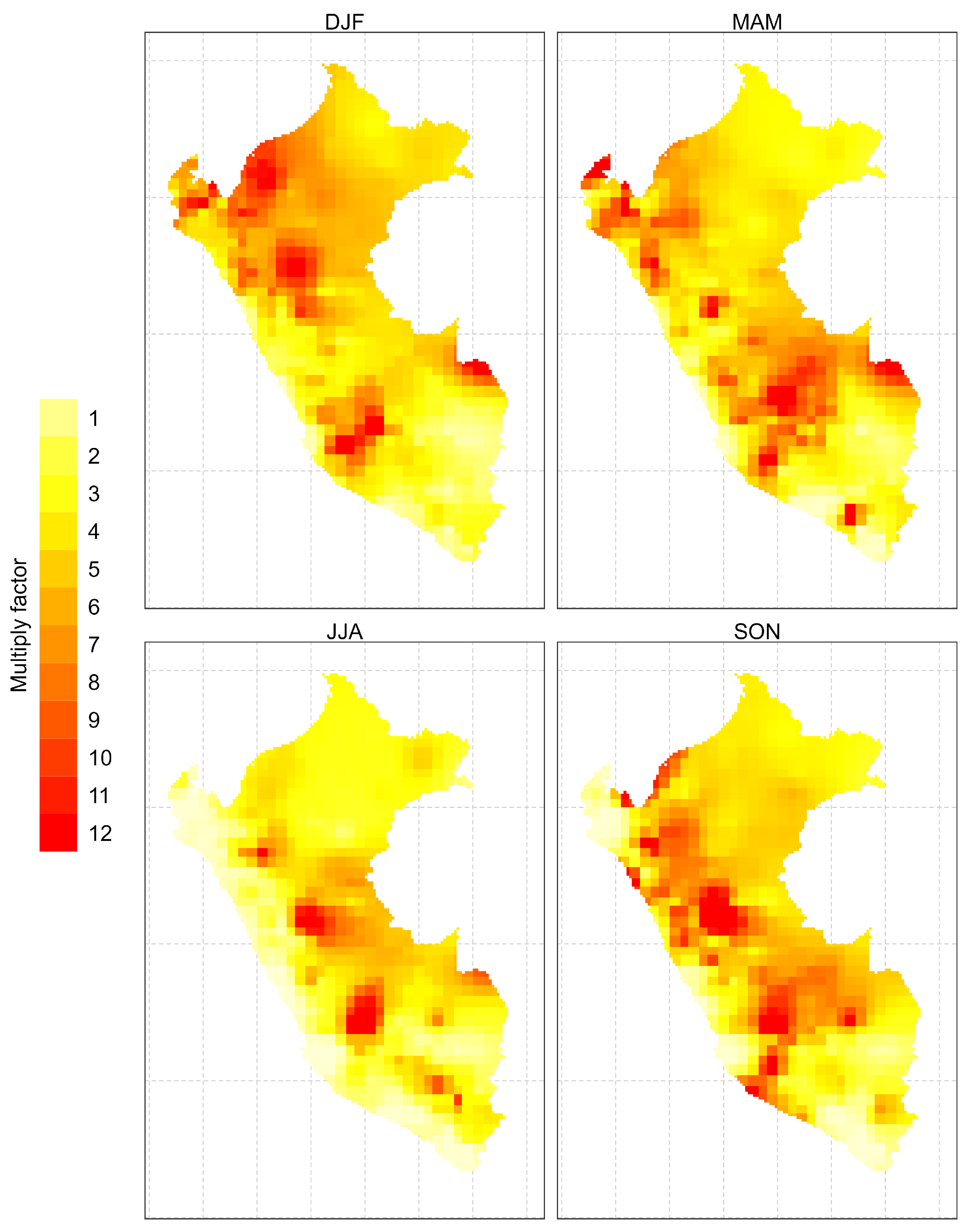
3.3.1. Gridded product construction

Estimation RE

The estimation of the RE requires a minimum period of 20 years of information in order to reduce the uncertainties and biases generated by dry and wet years Wischmeier and Smith [30]. In addition, this indicator carries out the analysis of each storm event separately, therefore, Wischmeier and Smith [30] recommends as storm identification requirements: i) use a minimum time interval (TMI) of 6 hours between each event, ii) hourly rainfall greater than 0.2 mm at the hourly level and 0.1 mm at the 30 minute level, iii) finally, the accumulated volume of each event must be greater than 0.2 mm (Figure A2).
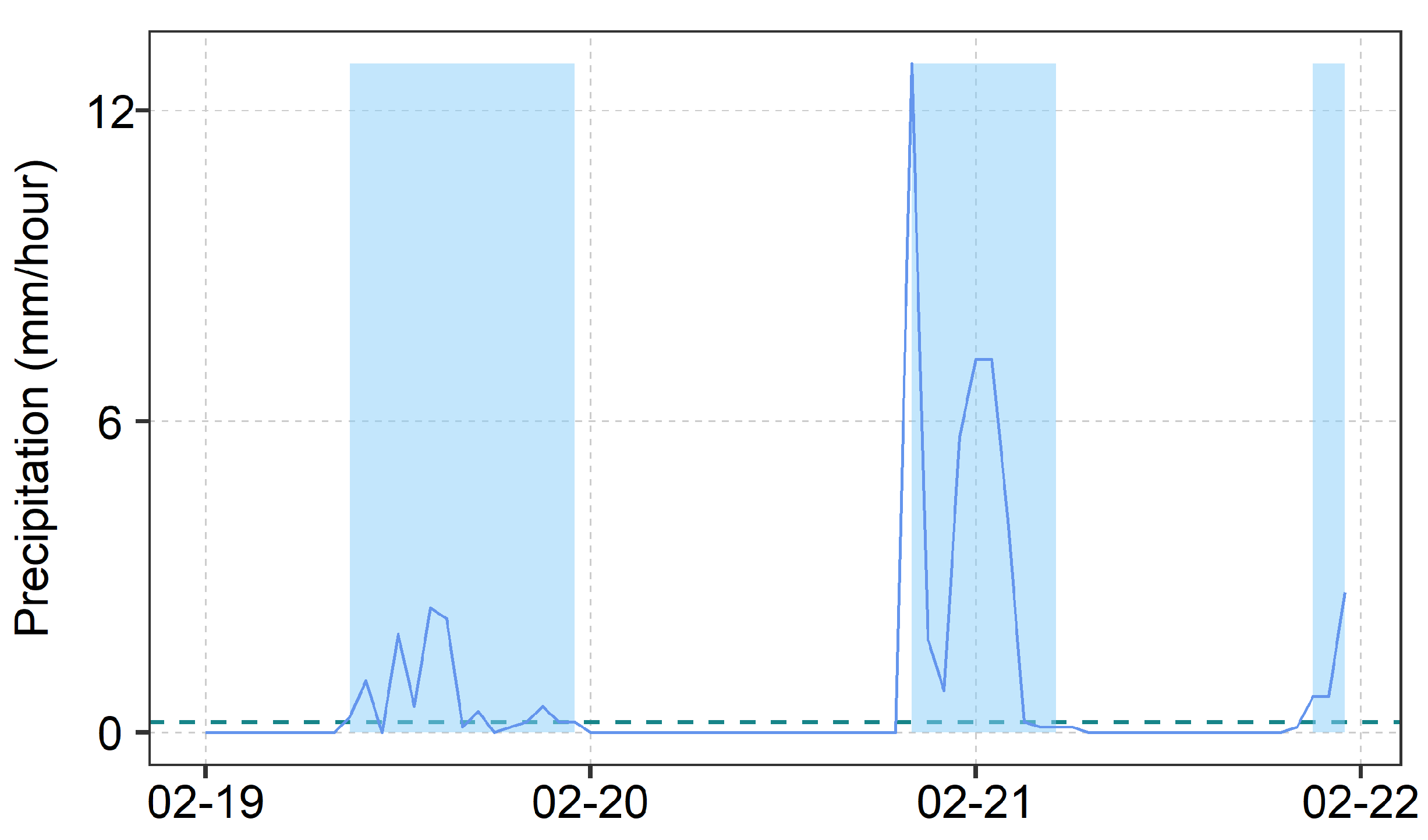
Preprints 81660 g003
Figure 3. An example of the identification of storm events, during February 2020 at the Alamor AWS. Blue spaces represent storm events.
Figure 3. An example of the identification of storm events, during February 2020 at the Alamor AWS. Blue spaces represent storm events.
Preprints 81660 g003
The precipitation intensity (I) for the hourly and sub-hourly scales was obtained through the relationship of the accumulated precipitation and its corresponding recording time (1).
I = P T
Where, I indicates the intensity of precipitation in mm/h, P the precipitation in mm and T as the recording time in hours. In each storm event, according to Wischmeier and Smith [30], the unit measure of kinetic energy ( e r ) is estimated at each chosen time resolution interval, Equation 2.
e r = 0.29 [ 1 − 0.72 × e x p ( − 0.05 i r ) ]
Where, i r is the precipitation intensity during the time interval in m m / h . The sum of the unit kinetic energy, multiplied by the rainfall volume for each time interval in a storm event, result to its total kinetic energy E, expressed in the next Equation 3.
E = ∑ r = 1 m e r Δ V r
Where, E is expressed in M J / h a and V r is the rainfall in mm, during an event. Subsequently, Brown and Foster [36] defines the RE ( E I 30 ), as the result of the multiplication of E with the maximum intensity in 30 minutes of each storm event, as indicated in Equation 4.
R E = E I 30 = E I 30 m a x
Where, R E is expressed in M J · m m · h a − 1 · h − 1 . y r − 1 and I 30 is the maximum rainfall intensity by storm event in m m / h . In the case of only having temporal resolutions of 60 minutes Panagos et al. [11], Yin et al. [53], suggest multiplying E × I60max with a correction coefficient ( C C 60 ), this value varies between 1.15 and 3.37 (Equation 5).
R E = E I 30 = E × I 60 m a x × C C 60
Where I 30 m a x corresponds to the maximum intensity of 30 minutes identified in each storm event. E I 30 is the equivalent to the RE of RUSLE and CC60 is the correction coefficient.
As part of the methodology, C C 60 was estimated by means of correlations between the RE obtained from the AWS of 10 minutes added to 30 minutes, with those obtained from the temporal resolution of 60 minutes. Fischer et al. [78] identified an underestimation of the RE of RUSLE, when using precipitation series with a temporal resolution greater than 30 minutes.

Estimation ED

The erosivity needs to be evaluated with long periods of hourly precipitation, to solve these deficiencies, Foster et al. [79] introduced the ED function. This erosivity index is more stable and independent of the length of precipitation information, it is also used to evaluate erosion patterns Panagos et al. [11], it is also more dependent on the number of erosive events and the intensity of precipitation [79]. Although, the RE provides information on the erosive potential of rainfall, it does not provide information on the concentration of extreme storms during the year, on the other hand, the ED better represents the RE patterns and the type of precipitation during erosive events (Zu et al., 2020). Very high ED values indicate high runoff, which implies an area more prone to the occurrence of floods and intense storms [37,45,80]. The ED is the ratio of RE to precipitation [79]. Expressed through Equation 6.
E D = R E P
Where the annual accumulated precipitation is measured in mm.yr-1 and the annual RE in M J · m m · h a − 1 · h − 1 . y r − 1 , the equation will be applied on a monthly and annual scale. The estimation of the RE from the IMERGF product (RE-IMERGF) was carried out pixel by pixel, while the one obtained by the AWS (RE-AWS) was calculated in a specific way, both results were classified by region.

Reconstruction and validation of rainfall erosivity

Various studies show a high correlation between the precipitation characteristics obtained from SPPs and observed stations, likewise, its spatial distribution shows a good correlation with the annual RE [51,65]. Therefore, there is evidence of using the IMERGF precipitation to estimate the temporal variability of the RE. However, it is necessary to perform a bias correction, with respect to the observed values [51]). Correction of simulated data based on observed stations is widely used to improve the accuracy in the generation of precipitation products [75,81,82].
Several studies identified a high correlation in the spatiotemporal variability between precipitation and RE [23,51,62], therefore, the correction of the RE from IMERGF was performed by reescaling precipitation with observed data, for each independent pixel, using an annual factor average by season. By extending the approach of Chen et al. [51], the correction process was as follows: i) obtention of the calibration factor by grouping the monthly series at the seasonal level DJF, MAM, JJA, SON in the same period 2015-2020. ii) building a linear model between the point-gridded values from RE-AWS and RE-IMERGF in the four seasonal periods to obtain the slope of each linear model defined as the seasonal multiplicative factor (FME). iii) spatial interpolation of the FME point values by using the inverse distance weighted interpolation (IDW) method, at the same native spatial resolution of IMERGF (0.1 ∘ C), iv) spatial aggregation was applied to reduce the spatial resolution from 0.1 ∘ to 0.25 ∘ , with the aim of avoiding spatial inconsistencies as a consequence of the high variability of the multiply factor. iii) Finally, RE-COR was obtained as a result of multiplying RE-IMERGF by the FDM maps. The validation was carried out at the pixel level with the observed data from RE-AWS during the common period 2015-2020.

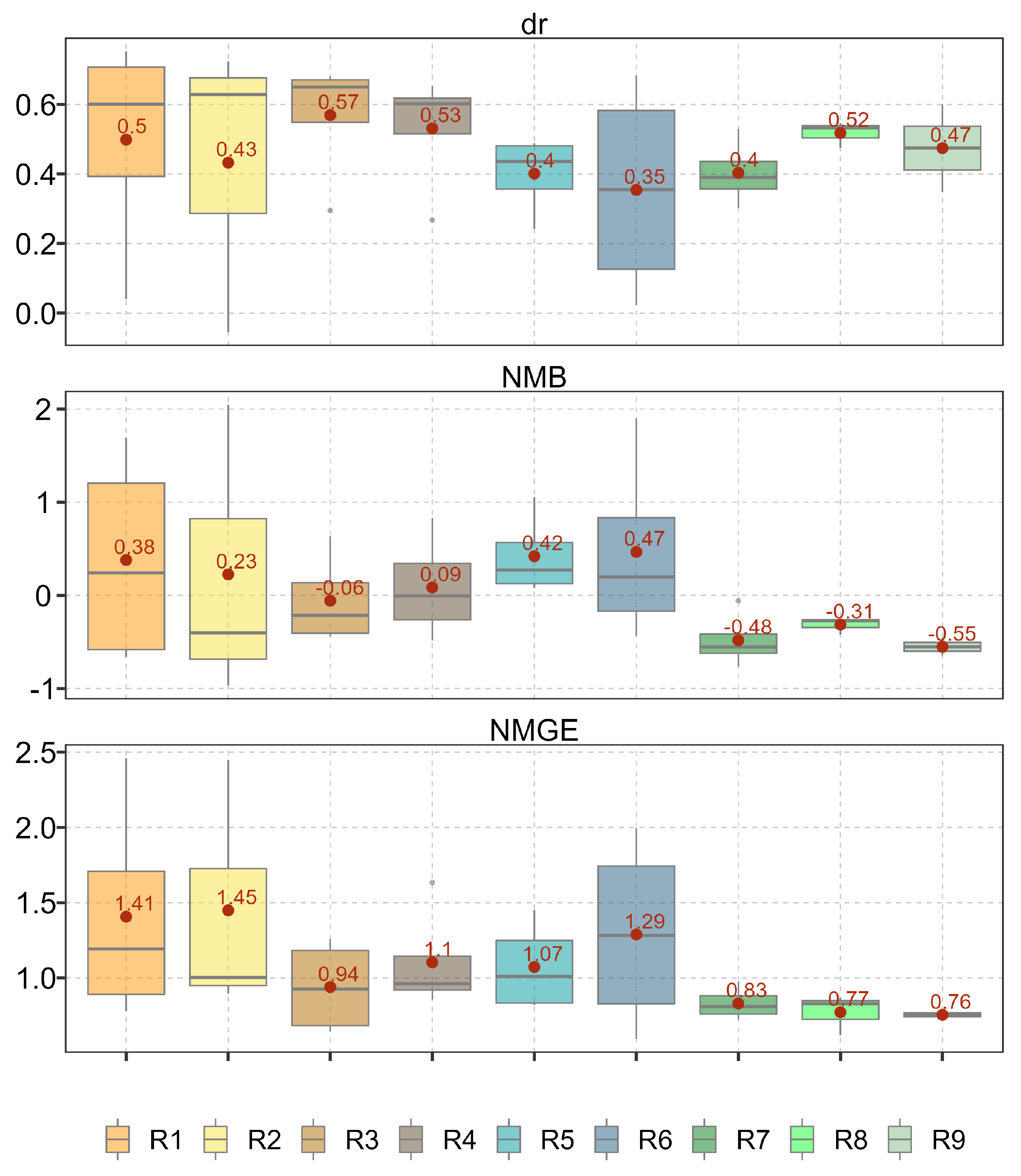
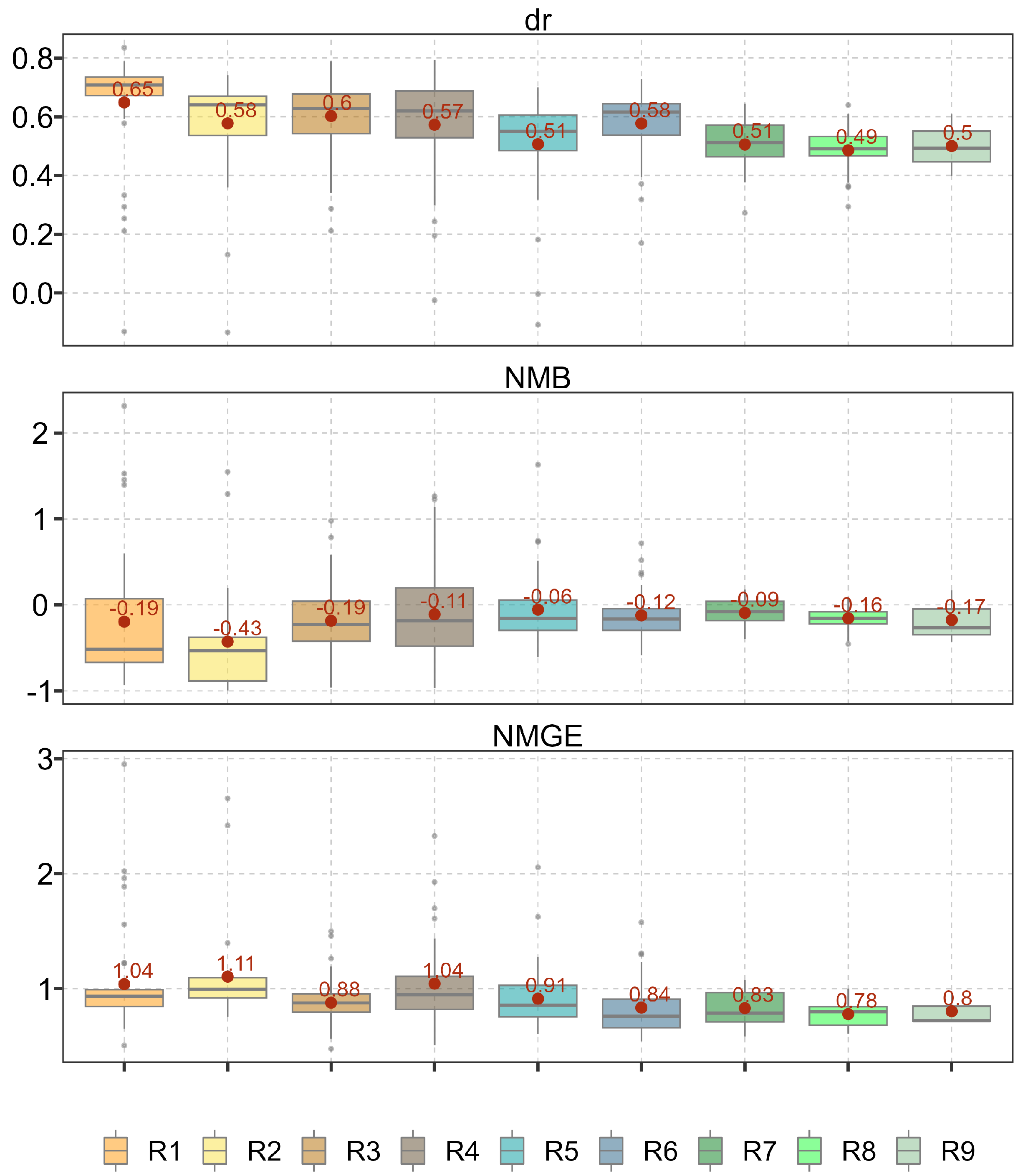
Metrics validation

The performance of PISCO was evaluated by regions with reference to RE-AWS, both database was comparing by statistical correlation and magnitude difference. The metrics statistics used are Pearson correlation coefficient (r) and the aggregation index (dr) [83]. The coefficient r is a measure of the relationship of strength between two variables where a result of 1 indicates a perfect relationship with a positive slope, while -1 indicates a relationship with a negative slope. The dr is similar to a correlation coefficient, except that it varies between -1 and 1, a high value (>0.5) indicating both high correlation and low absolute differences between the observed and simulated time series. On the other hand, due to the difference between the magnitudes of the hydrological variables in the study regions, it was necessary to have a statistic that indicates the relative difference between the observed and simulated data, through a normalization process. In the comparison of the samples the relative differences are normalized by the observed sample. The “Normalized mean gross error” (NMGE) and “Normalized Mean Bias” (NMB) statistics were selected. NMGE is a measure of the mean relative deviation from the observed values and is independent of the magnitude of the hydrological variable, suitable for comparison between arid and humid regions. While NMB is useful for evaluating the RE of different monthly rates, since the mean bias is normalized by dividing it by the observed RE.

3.3.2. Erosivity evaluation

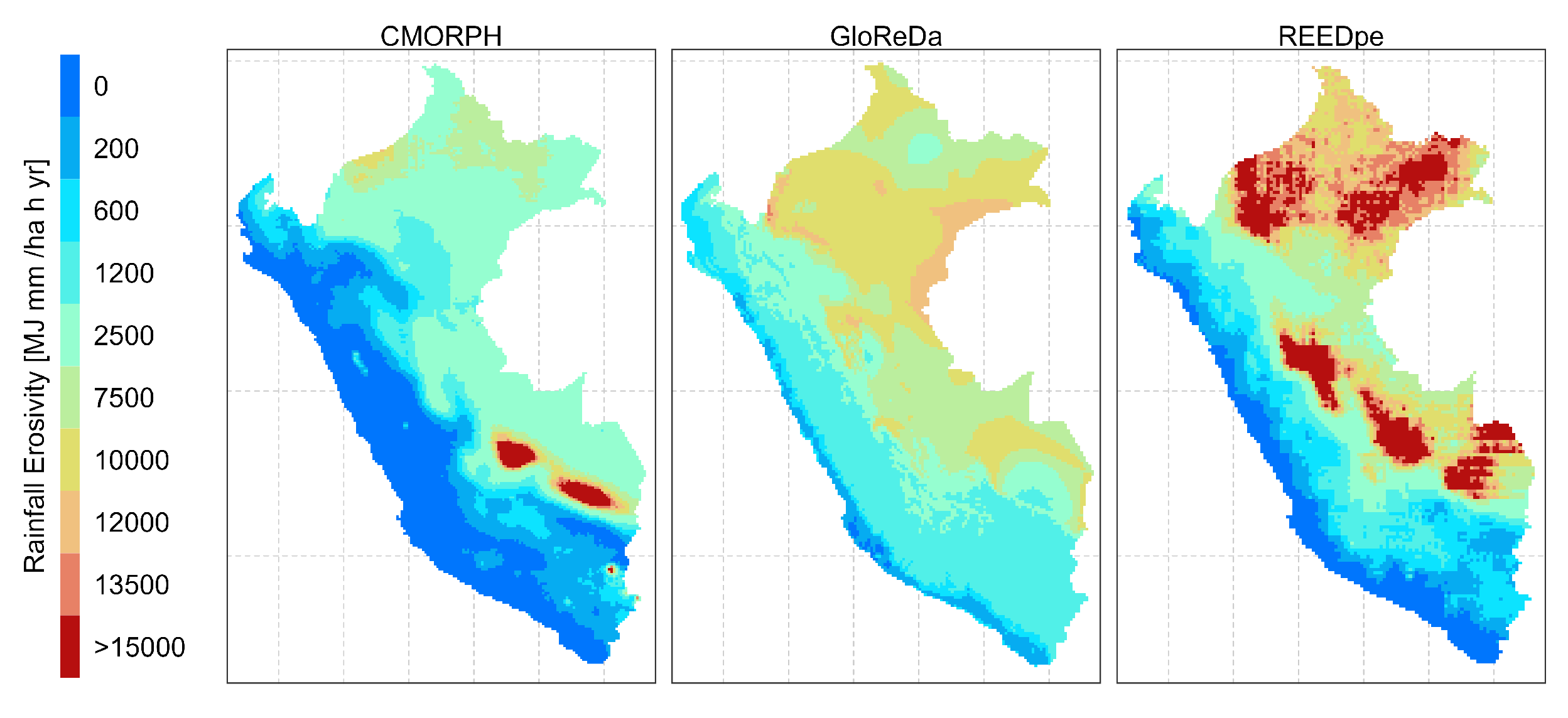
Global and national comparative analysis

The evaluation of the performance of the IMERGF in the estimation of the RE and its characteristics, such as the intensity of precipitation, duration, accumulated precipitation and number of events during 2015-2020, was carried out using a statistical approach based on the results obtained by the AWS. In addition, a comparison was made in statistical terms at the pixel scale between the observed data, the generated RE product, and other global products that use the same RE estimation method [30], such as the GloREDa product [2], derived from the observed ER-corrected ERA5 precipitation from globally distributed AWS for the period 1998–2019; and the global RE product obtained by Bezak et al. [52], based on the CMORPH precipitation product and observed stations for the period 1998-2019, both products with a spatial resolution of 0.1 ∘ . The temporary availability of global products is different, therefore, the RE was contrasted by means of the multi-year average; in the case of the correlation, a symmetric line with origin at 0 was used as reference.

Risk map

In this study we use ED to evaluate erosivity patterns and their effect under different ranges of precipitation, through a hazard map [2]. Based on the combination of quartiles of the variables at a multi-year scale of ED and P, we obtain 16 classes to characterise the susceptibility to soil erosivity Das et al. [45]. In this range, areas with very high ED and very high to very low mean precipitation are the most vulnerable, while areas with very low ED, regardless of the precipitation rate, can be considered as those with less prone to soil erosion Panagos et al. [2].

4. Results

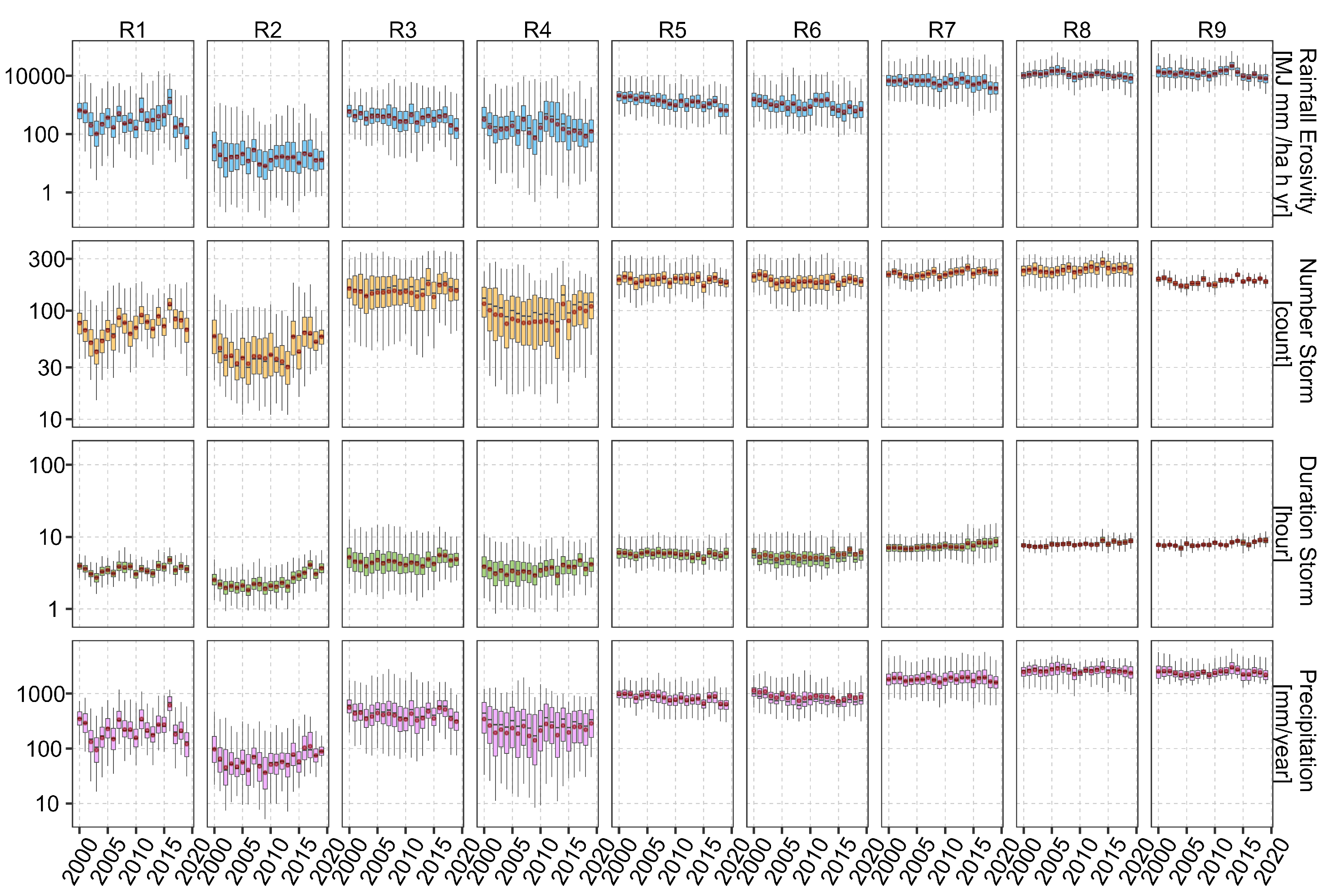
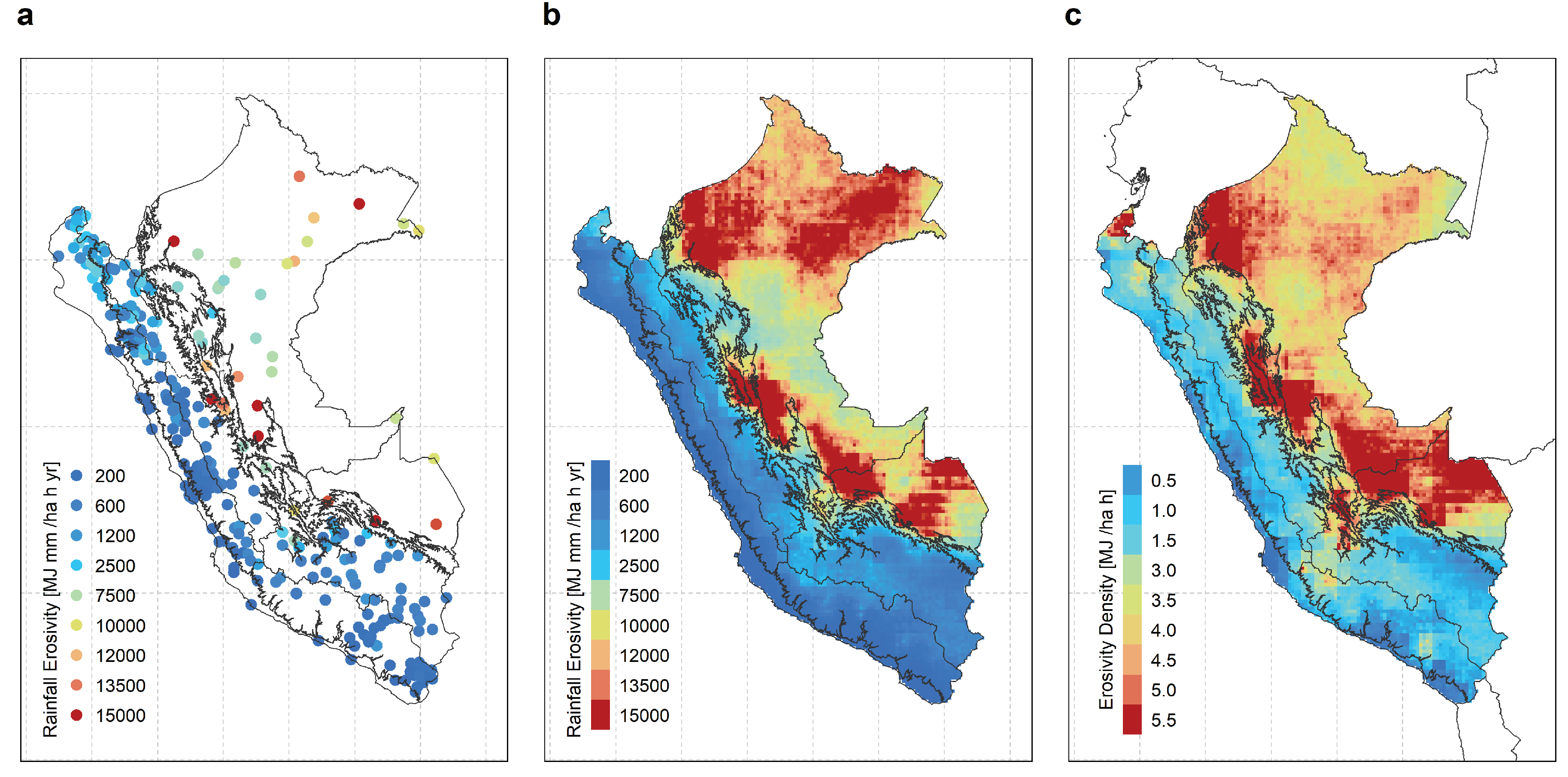
4.1. Spatiotemporal distribution of RE and ED

In Figure 4, the properties of the rain erosivity events are compared, such as the average accumulated precipitation, maximum intensity, total number, average duration, average annual precipitation, RE and ED obtained with the IMERG product, with respect to that obtained by the stations observed during the 2015-2020 period. The precipitation during the events and the accumulated annual precipitation is slightly underestimated in part of the Coast and Amazon, according to Derin et al. [92]. On the contrary, the duration of the events is overestimated at the national level by the IMERGF product, in a ratio of up to 3 to 1 in the Andean regions. However, the greatest disagreement of magnitudes is found in the identification of the maximum intensities, with a high correlation by underestimation up to 5 times in all the regions, which has a more relevant impact on the estimation of the RE and ED, the maximum underestimations are found in the lowland forest region reaching -80%, that is, in 12000 M J · m m · h a − 1 · h − 1 . In summary, this comparison shows a significant discrepancy in the identification of magnitudes of storm properties, since they require greater temporal resolution as Chen et al. [51] demonstrates, presenting correlations from 0.47 in the average duration of the events to 0.85 in the total annual number of storm events.
The precision of the annual RE estimates using the IMERGF precipitation-based data was also evaluated and compared with the observed stations. The correlation coefficient of the mean annual RE based on the observed precipitation data and IMERGF is 0.84. In general, taking the observed data as a reference, the values based on IMERG indicate an underestimation of the RE, present in all the analysis regions, with IMERGF values in region 1 and maximum values in 7 and 9.
Based on the comparison of the IMERGF RE and the AWS at a seasonal scale for the period 2015-2020, the multiplicative factors for each AWS were calculated (Figure 5). Values less than 1 indicate an underestimation of IMERGF, while values greater than 1 indicate an overestimation. Figure 5 shows a variability between 0 to 28 with a central value of 5.5. There is a smaller amount of multiplicative factors < 1 ( 4% on average) that indicate the overestimation of the RE, mainly in the coastal regions during the winter and spring seasons. Whereas, the regions with the greatest underestimation of the RE are 3, 4, 5, 6 and 9, precisely where the most intense storm events are recorded. The interpolation of the multiplicative factors was added to reduce the spatial resolution to 0.4º, in order to reduce the factors with the greatest difference and proximity (Figure 5). Subsequently, the IMERGF is corrected, through seasonal multiplication with the multiplicative factor map.
The corrected RE from 2015-2020 was compared with the AWS data in Figure 6. The results show an improvement in the dr, with means in the range of 0.5 in region 9, up to 0.65 in region 1. Also, the underestimation of the product is improved with means of NMB from -0.06 to -0.43. On the other hand, the NMGE medians range from 0.78 to 1.11, indicating an adequate performance of the final RE product, which will be analysed at a regional scale in the following sections. In addition, together with the ED product, both on a monthly scale, the PISCO_reed product was formed.

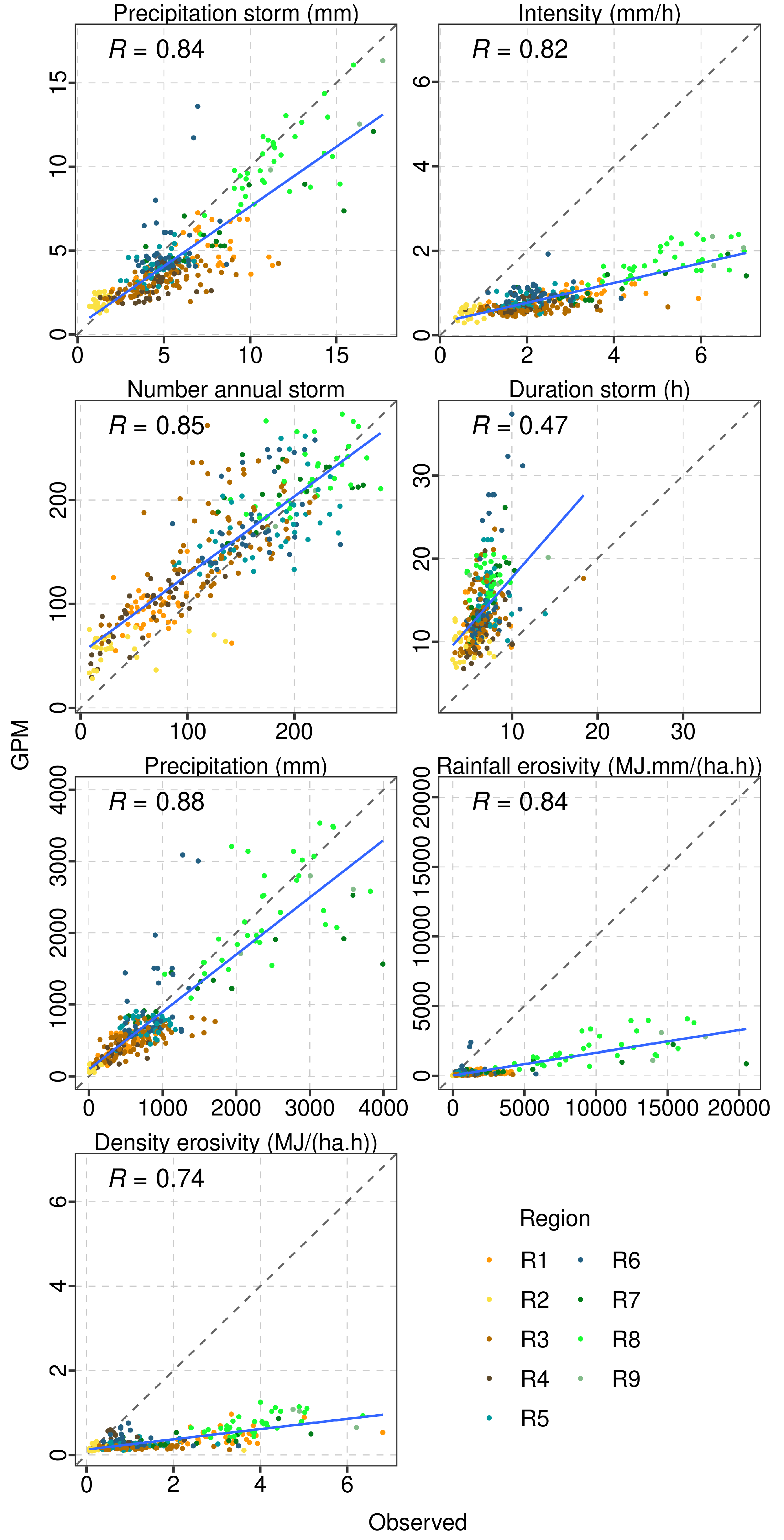
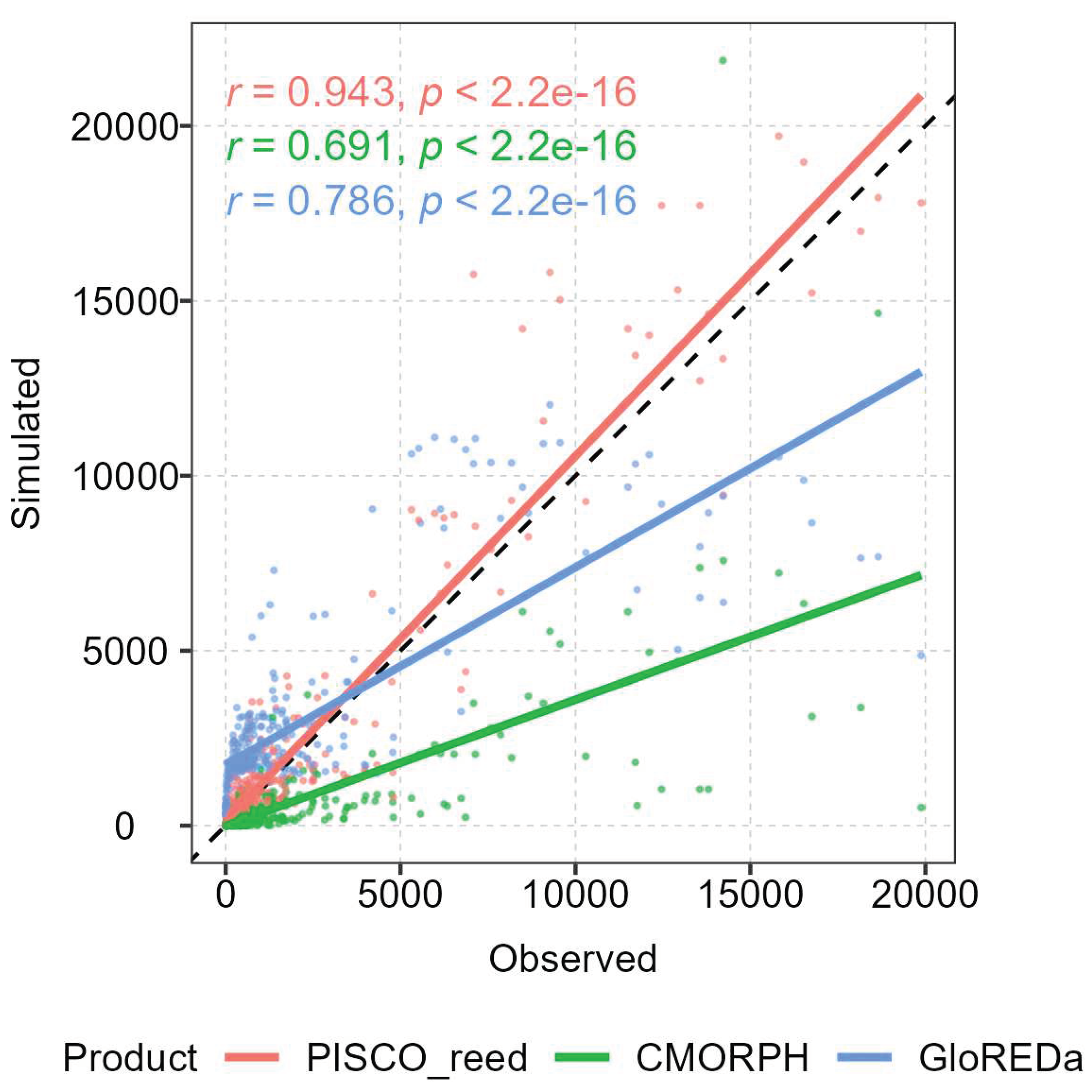
4.1.1. Comparison with global products

When comparing the PISCO_reed product with the global products GloREDa and CMORPH obtained from the multi-year average, taking as reference the observed data from the AWS (Figure 7 and Figure A3), a higher correlation is found in the PISCO_reed product (r = 0.94), finding slight overestimations in some regions. On the other hand, the CMORPH product has a greater underestimation in all regions, mainly in regions 3, 4, 5 and 6. This underestimation is also observed in GloREDa, with the particularity of a marked overestimation of the RE in regions 1 and 2, where the RE is less than 3,000 M J · m m · h a − 1 · h − 1 .

4.1.2. National analysis

Figure 8 shows the observed RE of the AWS, the map of RE and ED for Peru. The RE and ED map was presented with a spatial resolution of 0.1 ∘ or ∼ 10 km. The mean RE value is 7,118 M J · m m · h a − 1 · h − 1 with a high variability that can be expressed by the standard deviation of 6231 M J · m m · h a − 1 · h − 1 or a coefficient of variation of 0.88. The median RE is 7,161 MJ. The first quartile is 841 MJ, and the third is 12,377 M J · m m · h a − 1 · h − 1 . In the same way, the ED has an average value of 3.18 MJ.ha-1.h-1 with a coefficient of variation of 0.62, in addition, the 25th, 50th and 75th percentiles are 1.33, 3.48 and 4.49 MJ.ha-1.h-1, respectively.
The RE climatology map in Figure 9 shows that the month with the highest erosiveness is March (954 M J · m m · h a − 1 · h − 1 ), followed by December, January and February (793 to 846 M J · m m · h a − 1 · h − 1 ). The RE shows its lowest values in the period from June to September (224 to 397 M J · m m · h a − 1 · h − 1 ), coinciding with the variability of precipitation climatologies. Likewise, the spatial distribution of the RE shows a notable difference between the regions of the eastern Andes and the Amazon, with respect to the formerly western and coastal regions, with the high rates of erosivity in the first years.

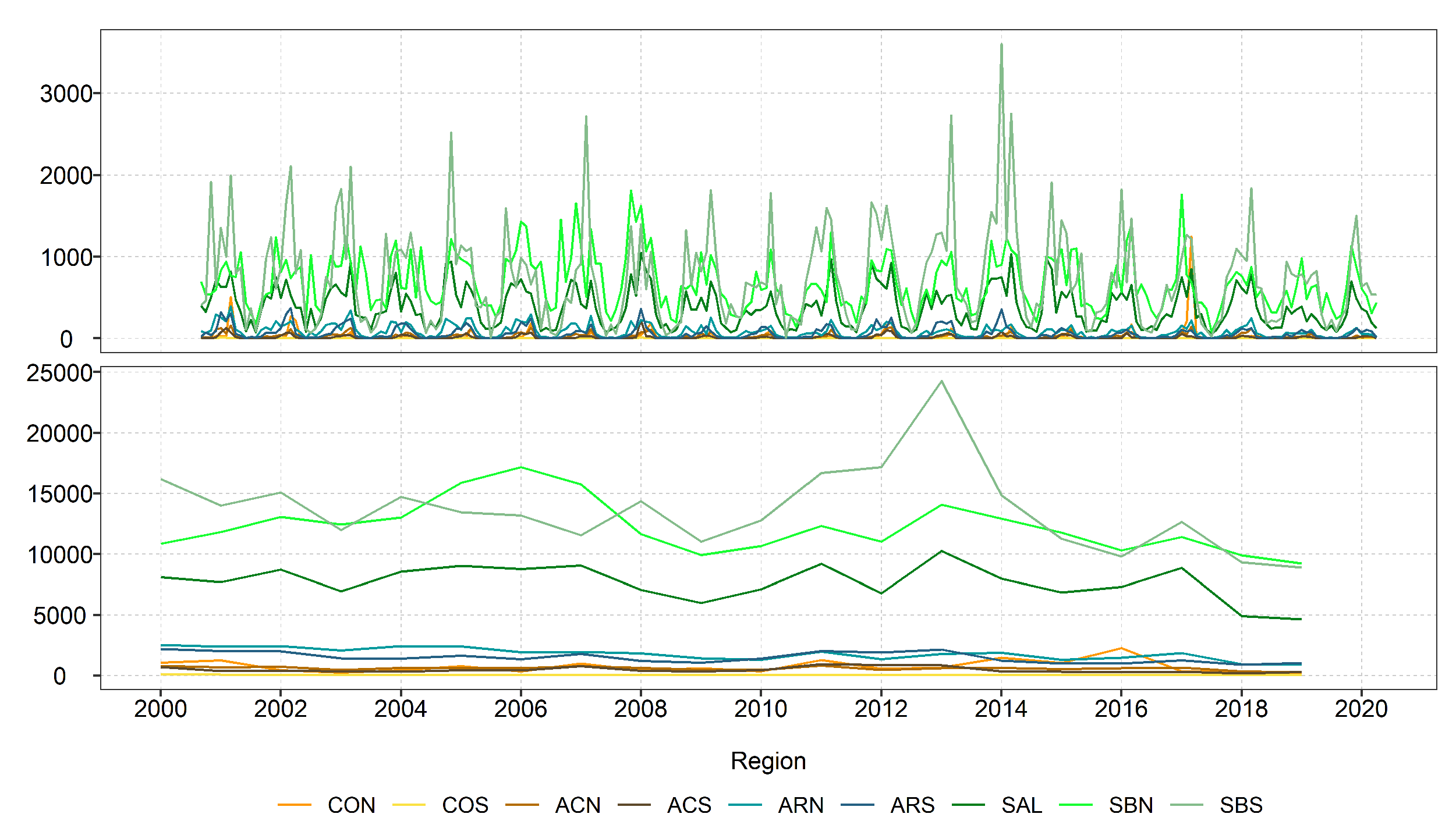
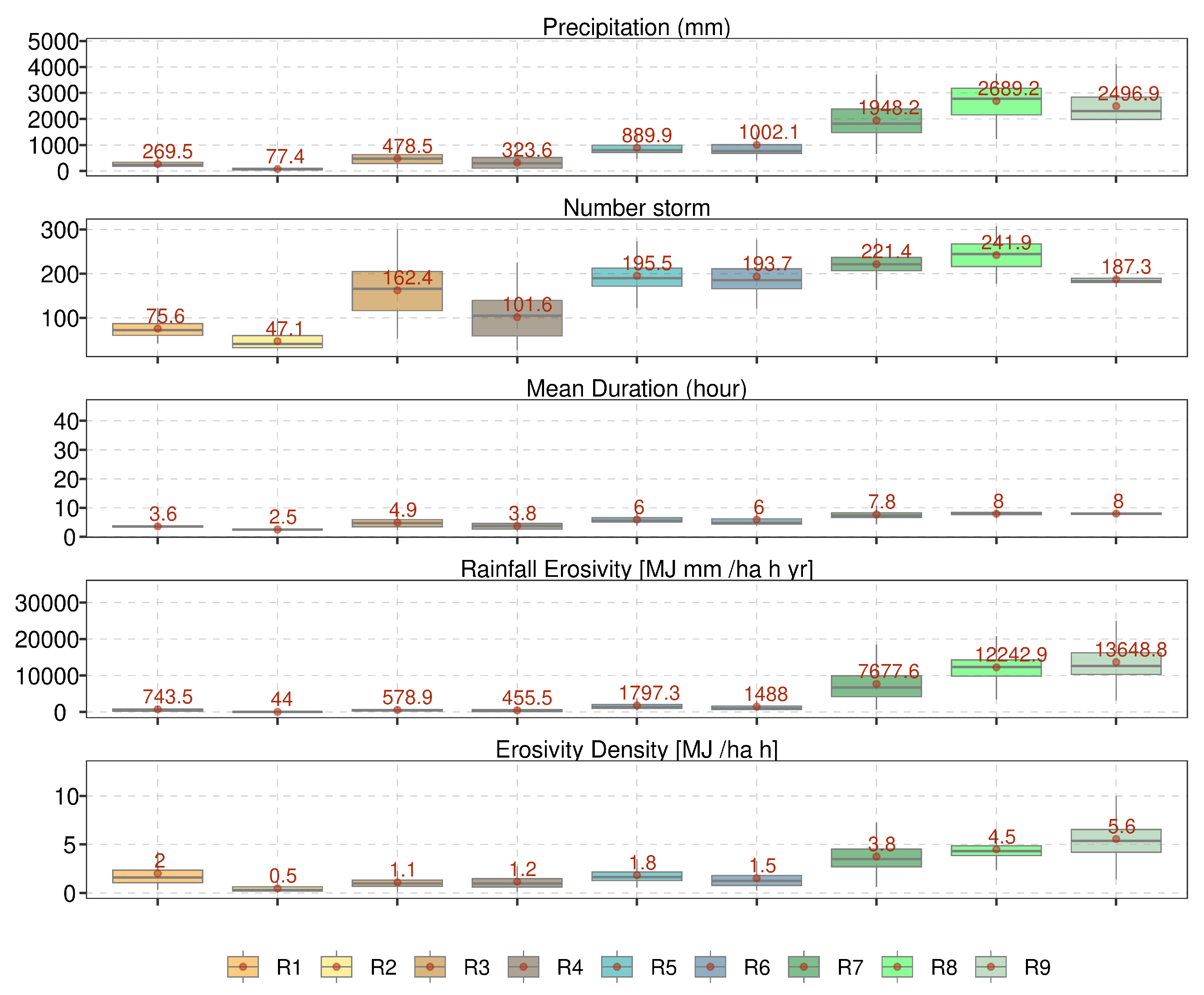
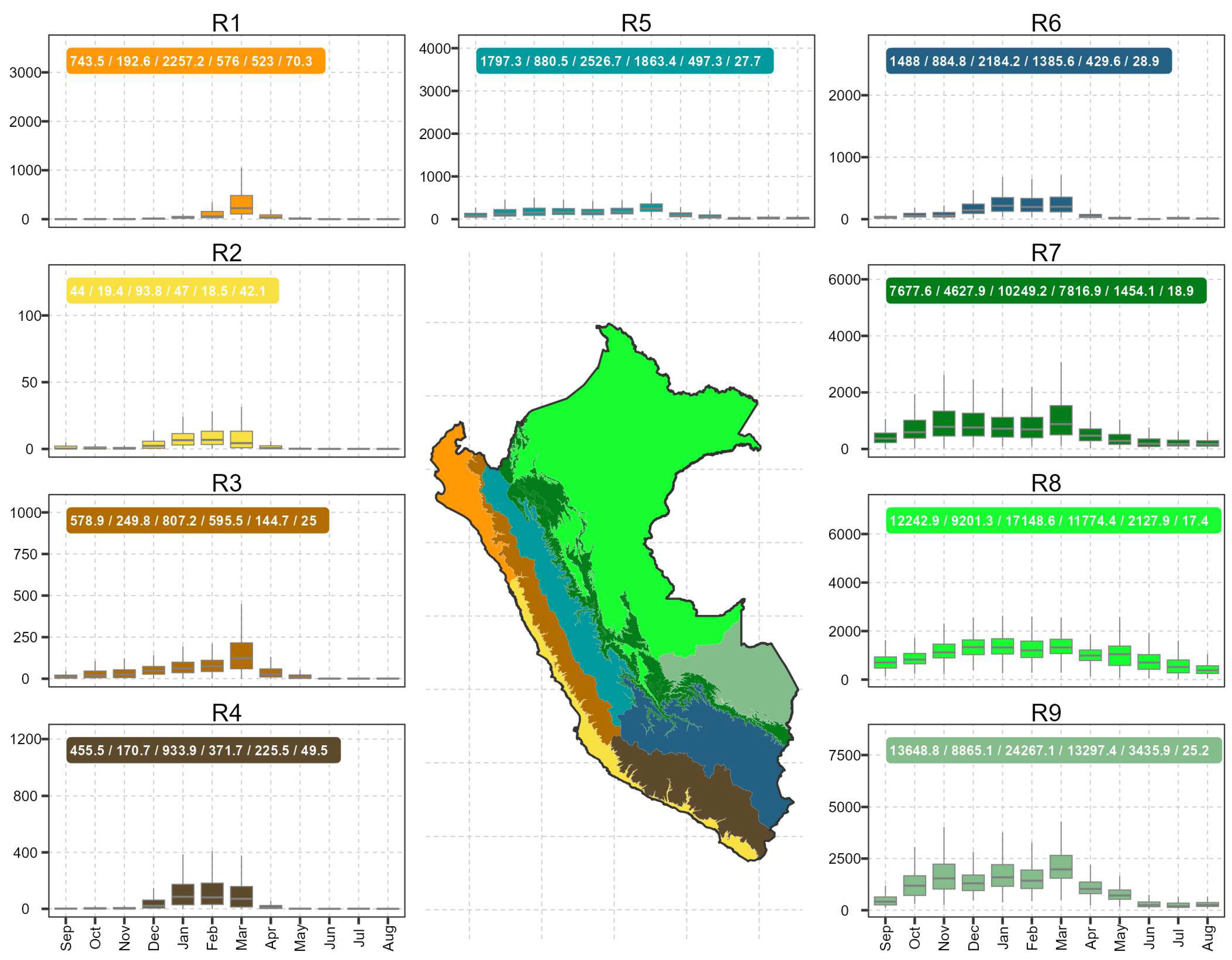
4.1.3. Regional analysis

Figure A4 shows, at the regional level, the 2000-2020 annual variability of storm properties such as total precipitation from erosive events, average storm duration, number of storm events, RE and ED. In 2001, 2012 and 2017 where the RE reached its highest annual values, the total precipitation, the number and duration of storm events were also higher than in the other years. The mean annual duration of storm events is in the range of 3 and 10 hours, the mean annual number of storms ranges from 40 to 280, the total precipitation ranges from 50 to 2,500 mm, and the mean annual RE ranges from 40 to 11,000 M J · m m · h a − 1 · h − 1 .
The properties of the average annual storm events are analyzed at the regional scale in Figure 10. The average number of storm events varies gradually from 47 in region 2 to 242 in 8, that gradual scale in the regions is also shown in the average duration of the storms with the range of 2.5 to 8 hours. The Amazon regions have a higher RE (7,677 to 13,648 M J · m m · h a − 1 · h − 1 ), compared to the coastal and Andean regions (44 to 1488 M J · m m · h a − 1 · h − 1 ). This contrast is mainly due to the total precipitation, which on average is up to 13 times higher between the regions of the respective groups. In the same way, the analysis of the DE shows average rates of 0.5 to 2 MJ.ha-1.h-1 in the coastal and Andean regions, while in the Amazon the average ED varies from 3.8 MJ.ha-1.h-1 in region 7 to 5.6 MJ.ha-1.h-1 en 9.
Figure 11 shows the monthly RE by region. The seasonality of the RE is visible in the regions, presenting the highest values of the RE during the wet season from December to April (average 510 M J · m m · h a − 1 · h − 1 ), with maximum values in the month of March. While the low RE values were found during the dry season from June to September (average 152 M J · m m · h a − 1 · h − 1 ), with minimums during the months of July or August. Finally, a descriptive statistical summary is shown in Figure 11 and Figure A5.

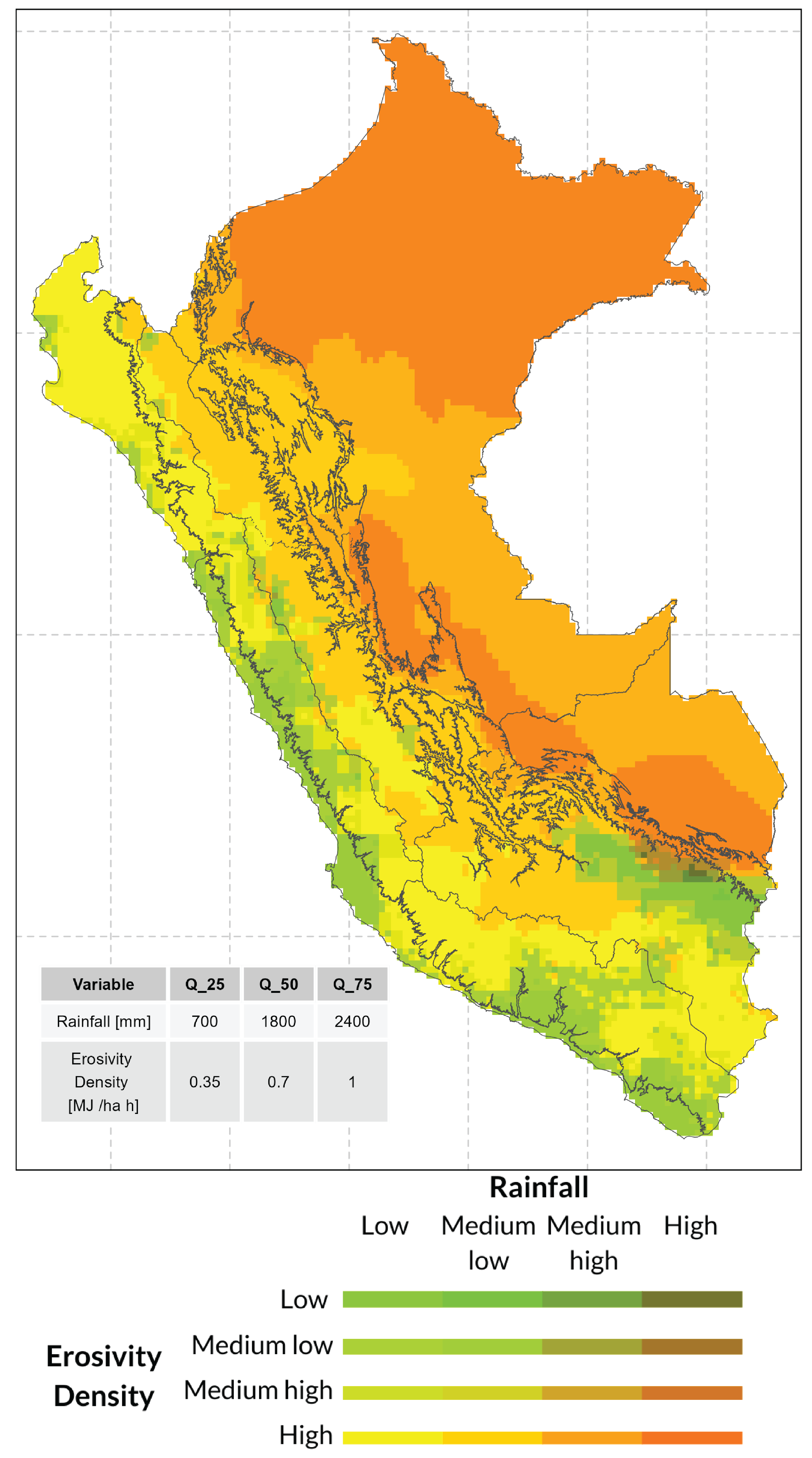
4.2. Spatial variation of risk areas

The spatial variation of the danger areas, classified into 16 classes in Peru is shown in Figure A1. The high-risk areas are found mainly in the region 8 and 9, only some areas were identified in region 7, due to their high rates of precipitation and ED. These transition areas to the Amazon plain are associated with areas of high soil erosion and landslides, depending on the physiography. The rest of the high Amazon, eastern and western Andes belong to the medium precipitation classification, but with high rates of ED associated with a medium danger of erosion. These regions are the ones that are frequently affected by soil erosion and mass movements, due to their physiography with steep slopes and intense rainfall. In the Andean regions, during the period 2004-2013, 38 land movements were registered with fatal consequences for the local population and high damage to the supply network at the national level [93]. In addition, the Andean regions have multiple geological faults, anthropogenic soil erosion activities, and are affected by extreme hydrological events such as ENSO, which due to climate change are accentuating their intensity and frequency.
Preprints 81660 g012
Figure 12. Risk map of erosivity in Peru as a function rainfall (mm) and Erosivity Density ( M J · m m · h a − 1 · h − 1 ). The quartile of these hydrological variables are presented in a table.
Figure 12. Risk map of erosivity in Peru as a function rainfall (mm) and Erosivity Density ( M J · m m · h a − 1 · h − 1 ). The quartile of these hydrological variables are presented in a table.
Preprints 81660 g012

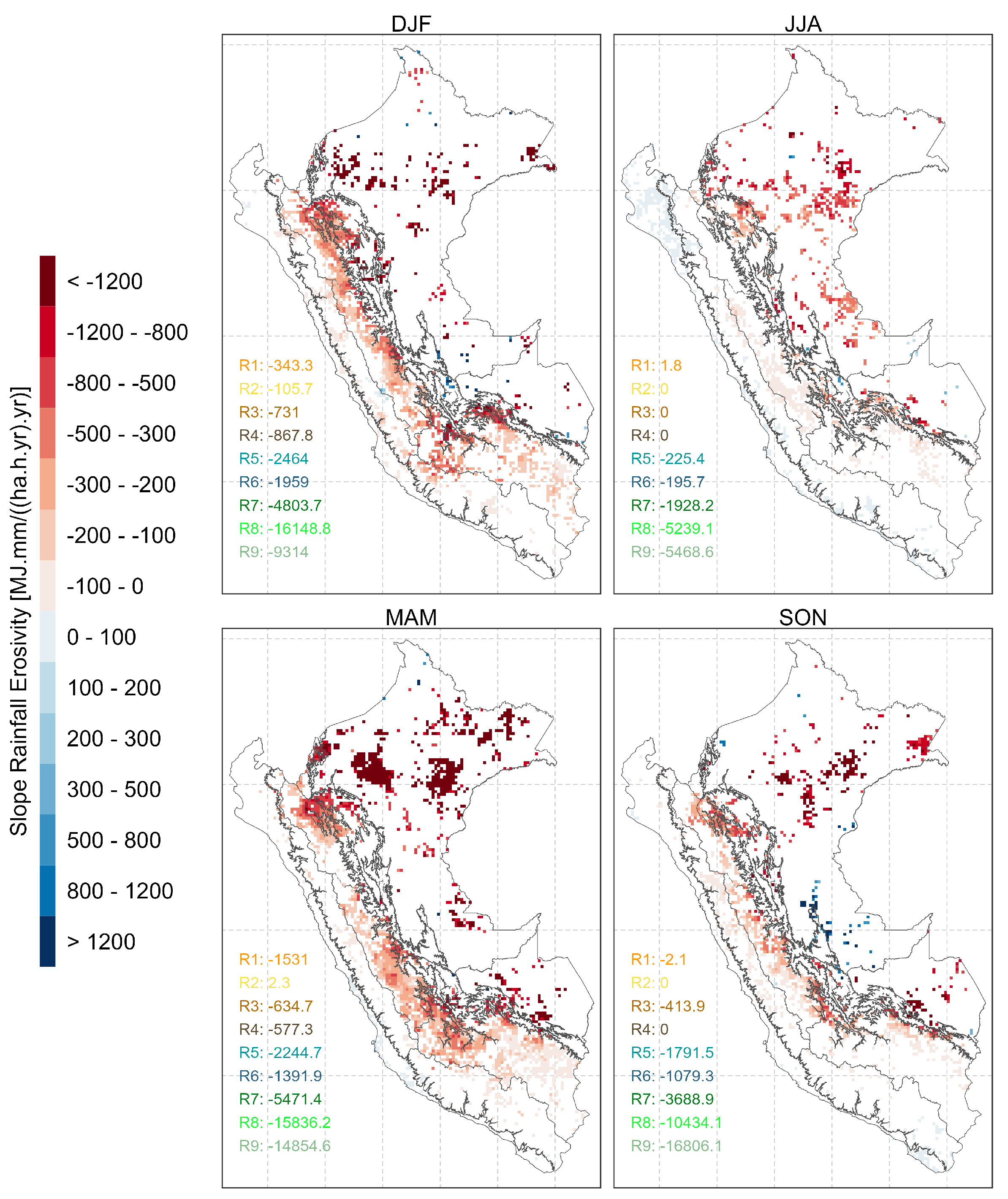
4.3. RE seasonal trend

The spatial variation of the seasonal trends of the RE evaluated at the pixel level with a significance level of 0.95% (p < 0.05) and the regional averages are shown in Figure A2. The seasonal periods of SON and DJF show an increase in the central low and high Amazon regions with positive annual changes greater than 50 M J · m m · h a − 1 · h − 1 , while in the southern and northern low Amazon regions the change is negative at rates of 80 M J · m m · h a − 1 · h − 1 . In the rest of the country, such as in the coastal and western Andean regions, no significant changes (+/- 10 M J · m m · h a − 1 · h − 1 ) are observed during all seasons. This same pattern is observed in the western Andes in the SON and JJA stations, however, during the MAM and DJF stations a slight increase in areas with trends of up to -20 M J · m m · h a − 1 · h − 1 is identified. Finally, it is highlighted that the lowland forest regions are the ones with the widest range of trends (<120 to >120 M J · m m · h a − 1 · h − 1 ), becoming more accentuated during the DJF and SON seasons, on the other hand, the range is reduced from -80 to 50 M J · m m · h a − 1 · h − 1 during the JJA or winter season.
Preprints 81660 g013
Figure 13. RE trends at 95% significance, p.value < 0.05 and meadian trend by region.
Figure 13. RE trends at 95% significance, p.value < 0.05 and meadian trend by region.
Preprints 81660 g013

5. Discussion

5.1. Comparison with other studies and analysis of causes

Observed sub-daily station data is a fundamental source of information on rainfall frequency and amount (Chen et al, 2021). However, the scarce availability, irregular distribution and spatial inconsistencies, in steep regions, limit the use of the observed rainfall [94]. Therefore, SPPs are an alternative solution to precipitation estimation, since they provide spatially continuous information over large geographic areas [95]. The complementary use of this information is already used in South America, for the estimation of the RE with the RUSLE method on a monthly and annual scale [47,59]. The evaluation of the product obtained from RE in this study is compared with the hourly rainfall data, suitable for evaluating hydrological products based on hourly information such as RE [45], which constitute the longest, most numerous hourly base and with quality control in Peru.
The main factors of uncertainty in the generation of the RE are the precision of precipitation data, the estimation model of the RE and the correction factor in the conversion of time scales [8]. Furthermore, Catari et al. [96], identifies the sources of the error in the estimation of the RE: erroneous measurements of precipitation, efficiency of the kinetic energy equation of storms as a function of intensity and the variation of spatial patterns.
This study is consistent with the RE obtained by Barurén [97], however, the maximum average RE are higher than our product (41106 M J · m m · h a − 1 · h − 1 ). This may be due to the fact that the analysis periods are different, altering the final result of the multi-year product. In addition, Rosas and Gutierrez [98] coincides with the quantification of erosion variability, finding an increase in erosion in the direction of region 4 to 3, the latter region being the region with the highest erosion in the western Andes of Peru. In region 2, the results are in the range obtained by Mejía-Marcacuzco et al. [61], with an analysis period within the years of analysis of this study 1997-2020. In the South American region, one of the global RE products is GloREDa, which estimates this variable using globally observed data and the ERA5 precipitation reanalysis product, however, the largest differences between RE and GloREDa estimates were observed in South America due to underestimation of precipitation in mountainous regions such as the Andes [52]. The observed stations used for the elaboration of this product are mainly from the Brazilian Amazon.

5.2. Limitations

In this research, the hourly precipitation data at hourly temporal resolution are based on the SPP IMERG, evaluations of the performance of this product in the analysis of storm events have been carried out in multiple regions of the world. According to Derin et al. [92], Manz et al. [99], IMERG is better than other products such as TMPA-V7 in terms of precision of the estimation of the frequency of occurrence and intensity of distribution of rainfall in the Andean regions. Regarding the detection of daily rainfall volumes, Das et al. [45] find that IMERG is sensitive in identifying light and null rainfall conditions. On the contrary, in the detection of extreme rainfall, the global average is satisfactory due to the correction of biases based on the observed stations [100], for the geographical conditions of the Andean zone of Peru, Derin et al. [92] identifies slight overestimations. These biases influence the underestimation of the RE in regions 1, 6 and 4, since IMERG has limitations to detect extreme storms.
The IMERG product, being a high spatial resolution dataset, reduces the uncertainties in the spatial patterns caused by the punctual interpolation of rainfall and its derivatives in geographical areas with low AWS density [45]. However, the scarcity of AWS in region 8 limits the bias correction of the ER, although these zones are more resilient to erosion due to their flat land cover and physiography. These zones have a lower level of danger in the generation of extreme events as identified in the domain area of the SILVIA product (Potential Mass Movement Monitoring System generated by Intense Rain) for the identification of earth movement events [26].
The RE estimate is sensitive to the temporal resolution of the rainfall [45], which originally required 30 minutes for its calculation. Therefore, if we use a different temporal resolution, it is necessary to apply an appropriate regression function to obtain a result equivalent to the estimate of the RE. Various studies develop a correlation function based on 30-minute resolutions, in areas where sub-hourly rainfall is not available. Panagos et al. [2] finds a high underestimation of the RE ( 56%) when using hourly rainfall without correction, but when using a correction factor a good correlation is obtained. The use of an erroneous function, or a low and irregular distribution of sub-hourly stations for its development, can increase the bias of your estimate [45]. In this investigation, information from stations with 10-minute temporal resolution of the rains was used for the first time, to find an adequate correction factor for the hourly RE, finding a factor greater than 1.5, which indicates an underestimation of the RE, compared to the original calculation with 30-minute rains.

5.3. Applications

RE is a key factor in estimating soil erosion [23]. Rain and its kinetic energy is the main driver of soil water erosion processes. These processes are associated with the detachment of soil particles, the generation of runoff and the triggering of mass movements [101,102]. On the other hand, agricultural practices without soil conservation measures together with the increase in the intensity of severe storms [23,103], would cause erosion and increase the amount of solids in suspension in rivers, which could clog reservoirs, raise riverbeds and affect water quality, due to high turbidity levels in the rainy season.
High erosion rates have effects on the ground as well as effects external to it [11]. As a consequence they are responsible for contamination and low productivity of farmland [104]. It is expected that the rain erosivity results developed in this research can be used to update the maps and identify regions vulnerable to this mode of erosion. We must understand the physical processes of soil erosion, for this reason it is important to implement a monitoring system for erosion and sediment production in experimental basins. The results of this study can be considered in the planning of public policies to reduce erosion aimed at conserving soil productivity [105] and maintaining soil ecosystem services at a tolerable level [106], especially in regions where a large increase was detected.
In Peru, data from AWS are spatially scarce. Therefore, SENAMHI projects the installation of rain radars, which will make it possible to have high-resolution spatiotemporal information. This could potentially improve [107] estimates of RE [108].

6. Conclusions

In this research, the RE was estimated in the 9 climatic regions of Peru, using the RUSLE methodology, based on a correction of the IMERG product based on the hourly and sub-hourly AWS in the period 2000 to 2020. The following is concluded: through the spatial calibration of the IMERGF-RE based on the observed RE, it was possible to reduce the biases, to analyze its spatial distribution at the national and regional level, on various time scales (climatology, monthly, and annual). At the national level, the RE mean was 7,840 M J · m m · h a − 1 · h − 1 , in the range of 0 in region 2 to 60,000 M J · m m · h a − 1 · h − 1 in region 9, with a spatial distribution similar to rainfall. The results of this study indicate that the previous analyzes underestimated the RE, due to the underestimation of the maximum intensities by the use of daily rainfall data, however, the RE obtained is in the range of regional studies in the Amazon and the South and North Pacific that use similar methodologies.
The PISCO_reed product has the advantage of quick and simple access to information for the characterization and identification of zones vulnerable to erosion and trends at a grid level (0.1 ∘ ) on a climatological, monthly, and annual scale. This information is necessary for the implementation of soil conservation and management policies, water administration, disaster prevention, agricultural or forestry planning and other applications for the management of hydrographic basins, especially in the regions and seasonal periods where a significant increase in the trend has been identified in regions 5 and 6.
In the coming years, through the use of radars for the identification of observed hourly precipitation, storm events will be able to be analysed with greater precision, improving the accuracy of the PISCO_reed product.

Author Contributions

Conceptualization, L.G. and W.L.-C.; methodology, L.G., W.L.-C., A.H. and E.S.; software, L.G.; validation, L.G., A.H. and W.L.-C.; formal analysis, L.G. and W.L.-C.; investigation, L.G., A.H., E.S. and W.L.-C.; resources, W.L.-C. and L.B.; data curation, L.G., A.H., and E.S.; writing—original draft preparation, L.G.; writing—review and editing, L.G., A.H., E.S., L.B., F.F., and W.L.-C.; visualization, L.G. and A.H.; supervision, W.L.-C. and A.H.; project administration, W.L.-C.; funding acquisition, L.B. and F.F. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funding by the National Hydrology and Meteorology Service (SENAMHI) of the Ministry of the Environment of Peru and the Research Institute for Development (IRD) of France.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

The PISCO_reed gridded product is available in the following repository https://github.com/lgutierrezl/PISCO_reed.

Acknowledgments

The authors extend their appreciation to the anonymous reviewers for their thoughtful comments and valuable advice.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Appendix A.1

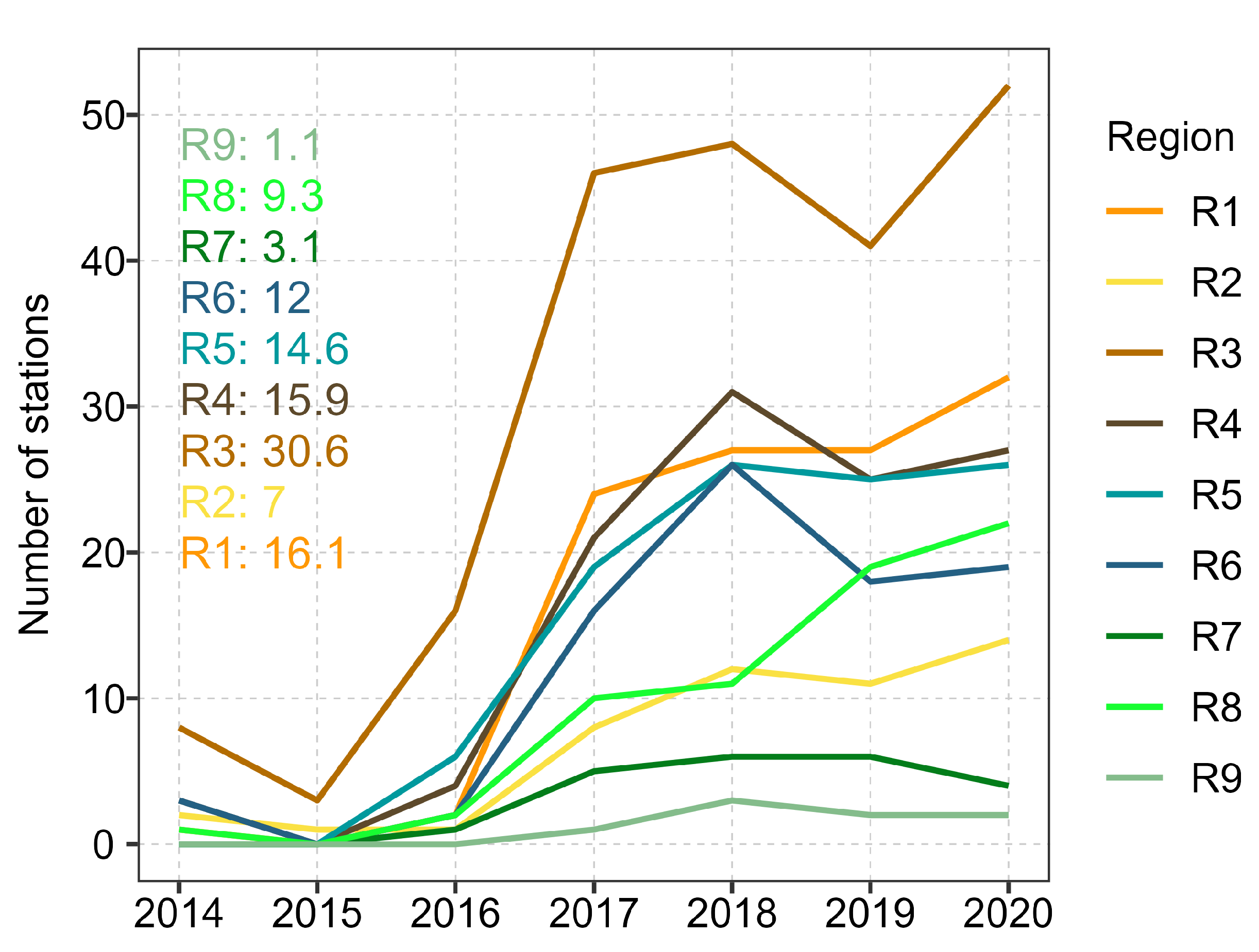
Preprints 81660 g0a1
Figure A1. Number of automatic weather stations with availability of information by year.
Figure A1. Number of automatic weather stations with availability of information by year.
Preprints 81660 g0a1
Preprints 81660 g0a2
Figure A2. Cross validation of the correction factor from corrected IMERG=RE and the RE from AWS by means of (a) Aggregation index, (b) Normalized Mean Bias and (c) Normalized mean gross error.
Figure A2. Cross validation of the correction factor from corrected IMERG=RE and the RE from AWS by means of (a) Aggregation index, (b) Normalized Mean Bias and (c) Normalized mean gross error.
Preprints 81660 g0a2
Preprints 81660 g0a3
Figure A3. Map plot of PISCO_reed, GloREDa, and CMORPH rainfall erosivity, based on observed data from weather automatic stations for 2015–2020.
Figure A3. Map plot of PISCO_reed, GloREDa, and CMORPH rainfall erosivity, based on observed data from weather automatic stations for 2015–2020.
Preprints 81660 g0a3
Preprints 81660 g0a4
Figure A4. Characterization storm events by year at regional scale.
Figure A4. Characterization storm events by year at regional scale.
Preprints 81660 g0a4
Preprints 81660 g0a5
Figure A5. Variation of regional RE at yearly and monthly scale.
Figure A5. Variation of regional RE at yearly and monthly scale.
Preprints 81660 g0a5

References

  1. Nearing, M.; Lane, L.; Lopes, V. Modelling Soil Erosion, Soil Erosion Research Methods, R. Lal, St, 1994.
  2. Panagos, P.; Borrelli, P.; Poesen, J.; Ballabio, C.; Lugato, E.; Meusburger, K.; Montanarella, L.; Alewell, C. The new assessment of soil loss by water erosion in Europe. Environ. Sci. Policy 2015, 54, 438–447. [Google Scholar] [CrossRef]
  3. Karlen, D.L.; Ditzler, C.A.; Andrews, S.S. Soil quality: why and how? Geoderma 2003, 114, 145–156. [Google Scholar] [CrossRef]
  4. Tripathi, R.; Singh, H. Soil Erosion and Conservation; Wiley Eastern Limited: Hoboken, NJ, USA, 1993. [Google Scholar]
  5. Sparovek, G.; Schnug, E. Temporal erosion-induced soil degradation and yield loss. Soil Sci. Soc. Am. J. 2001, 65, 1479–1486. [Google Scholar] [CrossRef]
  6. Pimentel, D. Soil erosion: A food and environmental threat. Environ. Dev. Sustain. 2006, 8, 119–137. [Google Scholar] [CrossRef]
  7. Lukić, T.; Lukić, A.; Basarin, B.; Ponjiger, T.M.; Blagojević, D.; Mesaroš, M.; Milanović, M.; Gavrilov, M.; Pavić, D.; Zorn, M.; et al. Rainfall erosivity and extreme precipitation in the Pannonian basin. Open Geosci. 2019, 11, 664–681. [Google Scholar] [CrossRef]
  8. Chen, Y.; Xu, M.; Wang, Z.; Gao, P.; Lai, C. Applicability of two satellite-based precipitation products for assessing rainfall erosivity in China. Sci. Total Environ. 2021, 757, 143975. [Google Scholar] [CrossRef]
  9. Jain, M.K.; Kothyari, U.C.; Raju, K.G. GIS based distributed model for soil erosion and rate of sediment outflow from catchments. J. Hydraul. Eng. 2005, 131, 755–769. [Google Scholar] [CrossRef]
  10. Lee, J.H.; Heo, J.H. Evaluation of estimation methods for rainfall erosivity based on annual precipitation in Korea. J. Hydrol. 2011, 409, 30–48. [Google Scholar] [CrossRef]
  11. Panagos, P.; Ballabio, C.; Borrelli, P.; Meusburger, K.; Klik, A.; Rousseva, S.; Tadić, M.P.; Michaelides, S.; Hrabalíková, M.; Olsen, P.; et al. Rainfall erosivity in Europe. Sci. Total Environ. 2015, 511, 801–814. [Google Scholar] [CrossRef]
  12. Pimentel, D.; Kounang, N. Ecology of soil erosion in ecosystems. Ecosystems 1998, 1, 416–426. [Google Scholar] [CrossRef]
  13. Diodato, N.; Bellocchi, G. Assessing and modelling changes in rainfall erosivity at different climate scales. Earth Surf. Process. Landforms 2009, 34, 969–980. [Google Scholar] [CrossRef]
  14. Tilman, D.; Fargione, J.; Wolff, B.; D’antonio, C.; Dobson, A.; Howarth, R.; Schindler, D.; Schlesinger, W.H.; Simberloff, D.; Swackhamer, D. Forecasting agriculturally driven global environmental change. science 2001, 292, 281–284. [Google Scholar] [CrossRef] [PubMed]
  15. Schulze, K.; Alder, J.; Cramer, W.; Masui, T.; van Vuuren, D.; Ringler, C.; Alcamo, J. Changes in Nature’s Balance Sheet: Model-based Estimates of Future Worldwide Ecosystem Services; 2005.
  16. Colombo, S.; Hanley, N.; Calatrava-Requena, J. Designing policy for reducing the off-farm effects of soil erosion using choice experiments. J. Agric. Econ. 2005, 56, 81–95. [Google Scholar] [CrossRef]
  17. Conner, W.H.; Day, J.W.; Baumann, R.H.; Randall, J.M. Influence of hurricanes on coastal ecosystems along the northern Gulf of Mexico. Wetl. Ecol. Manag. 1989, 1, 45–56. [Google Scholar] [CrossRef]
  18. Kim, J.; Han, H.; Kim, B.; Chen, H.; Lee, J.H. Use of a high-resolution-satellite-based precipitation product in mapping continental-scale rainfall erosivity: A case study of the United States. Catena 2020, 193, 104602. [Google Scholar] [CrossRef]
  19. Change, I.C. The physical science basis. 2013.
  20. Buytaert, W.; De Bièvre, B. Water for cities: The impact of climate change and demographic growth in the tropical Andes. Water Resources Research 2012, 48. [Google Scholar] [CrossRef]
  21. Vuille, M. Climate change and water resources in the tropical Andes. 2013.
  22. Field, C.B.; Barros, V.; Stocker, T.F.; Dahe, Q. Managing the risks of extreme events and disasters to advance climate change adaptation: special report of the intergovernmental panel on climate change; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
  23. Micić Ponjiger, T.; Lukić, T.; Basarin, B.; Jokić, M.; Wilby, R.L.; Pavić, D.; Mesaroš, M.; Valjarević, A.; Milanović, M.M.; Morar, C. Detailed Analysis of Spatial–Temporal Variability of Rainfall Erosivity and Erosivity Density in the Central and Southern Pannonian Basin. Sustainability 2021, 13, 13355. [Google Scholar] [CrossRef]
  24. Almazroui, M.; Ashfaq, M.; Islam, M.N.; Rashid, I.U.; Kamil, S.; Abid, M.A.; O’Brien, E.; Ismail, M.; Reboita, M.S.; Sörensson, A.A.; et al. Assessment of CMIP6 performance and projected temperature and precipitation changes over South America. Earth Syst. Environ. 2021, 5, 155–183. [Google Scholar] [CrossRef]
  25. de Defensa Civil (Peru), I.N. Compendio estadístico del INDECI 2019, en la preparación, respuesta y rehabilitación de la GRD; Instituto Nacional de Defensa Civil-INDECI. 2019.
  26. Millán-Arancibia, C.; Lavado-Casimiro, W. Rainfall thresholds estimation for shallow landslides in Peru from gridded daily data. Nat. Hazards Earth Syst. Sci. Discuss. 2022, 2022, 1–22. [Google Scholar] [CrossRef]
  27. Huerta, A.; Lavado, W. ATLAS Zonas Áridas del Perú. 2019.
  28. del Ambiente (Peru), M. Climático, Cambio. 2009.
  29. Jayawardena, A.; Rezaur, R. Drop size distribution and kinetic energy load of rainstorms in Hong Kong. Hydrol. Process. 2000, 14, 1069–1082. [Google Scholar] [CrossRef]
  30. Wischmeier, W.; Smith, D. Predicting rainfall erosion losses: a guide to conservation planning; Number 537, 1978.
  31. Panagos, P.; Ballabio, C.; Borrelli, P.; Meusburger, K. Spatio-temporal analysis of rainfall erosivity and erosivity density in Greece. Catena 2016, 137, 161–172. [Google Scholar] [CrossRef]
  32. Goovaerts, P. Using elevation to aid the geostatistical mapping of rainfall erosivity. Catena 1999, 34, 227–242. [Google Scholar] [CrossRef]
  33. Xu, Z.; Pan, B.; Han, M.; Zhu, J.; Tian, L. Spatial–temporal distribution of rainfall erosivity, erosivity density and correlation with El Niño–Southern Oscillation in the Huaihe River Basin, China. Ecol. Informatics 2019, 52, 14–25. [Google Scholar] [CrossRef]
  34. Renard, K.G.; Freimund, J.R. Using monthly precipitation data to estimate the R-factor in the revised USLE. J. Hydrol. 1994, 157, 287–306. [Google Scholar] [CrossRef]
  35. Zhang, W.B.; Xie, Y.; Liu, B.Y. Rainfall erosivity estimation using daily rainfall amounts. Sci. Geogr. Sinica/Dili Kexue 2002, 22, 711–716. [Google Scholar]
  36. Brown, L.; Foster, G. Storm erosivity using idealized intensity distributions. Trans. ASAE 1987, 30, 379–0386. [Google Scholar] [CrossRef]
  37. Kinnell, P. Event soil loss, runoff and the Universal Soil Loss Equation family of models: A review. J. Hydrol. 2010, 385, 384–397. [Google Scholar] [CrossRef]
  38. Vrieling, A.; Hoedjes, J.C.; van der Velde, M. Towards large-scale monitoring of soil erosion in Africa: Accounting for the dynamics of rainfall erosivity. Global Planet. Chang. 2014, 115, 33–43. [Google Scholar] [CrossRef]
  39. Meusburger, K.; Steel, A.; Panagos, P.; Montanarella, L.; Alewell, C. Spatial and temporal variability of rainfall erosivity factor for Switzerland. Hydrol. Earth Syst. Sci. 2012, 16, 167–177. [Google Scholar] [CrossRef]
  40. Panagos, P.; Borrelli, P.; Meusburger, K.; Yu, B.; Klik, A.; Jae Lim, K.; Yang, J.E.; Ni, J.; Miao, C.; Chattopadhyay, N.; et al. Global rainfall erosivity assessment based on high-temporal resolution rainfall records. Sci. Rep. 2017, 7, 1–12. [Google Scholar] [CrossRef]
  41. Williams, R.; Sheridan, J. Effect of rainfall measurement time and depth resolution on EI calculation. Trans. ASAE 1991, 34, 402–0406. [Google Scholar] [CrossRef]
  42. Angulo-Martínez, M.; Beguería, S. Estimating rainfall erosivity from daily precipitation records: A comparison among methods using data from the Ebro Basin (NE Spain). J. Hydrol. 2009, 379, 111–121. [Google Scholar] [CrossRef]
  43. Padulano, R.; Rianna, G.; Santini, M. Datasets and approaches for the estimation of rainfall erosivity over Italy: A comprehensive comparison study and a new method. J. Hydrol. Reg. Stud. 2021, 34, 100788. [Google Scholar] [CrossRef]
  44. Wang, Z.; Zhong, R.; Lai, C.; Chen, J. Evaluation of the GPM IMERG satellite-based precipitation products and the hydrological utility. Atmos. Res. 2017, 196, 151–163. [Google Scholar] [CrossRef]
  45. Das, S.; Jain, M.K.; Gupta, V. A step towards mapping rainfall erosivity for India using high-resolution GPM satellite rainfall products. CATENA 2022, 212, 106067. [Google Scholar] [CrossRef]
  46. Agnese, C.; Bagarello, V.; Corrao, C.; d’Agostino, L.; d’Asaro, F. Influence of the rainfall measurement interval on the erosivity determinations in the Mediterranean area. J. Hydrol. 2006, 329, 39–48. [Google Scholar] [CrossRef]
  47. Bonilla, C.A.; Vidal, K.L. Rainfall erosivity in central Chile. J. Hydrol. 2011, 410, 126–133. [Google Scholar] [CrossRef]
  48. Chen, M.; Shi, W.; Xie, P.; Silva, V.B.; Kousky, V.E.; Wayne Higgins, R.; Janowiak, J.E. Assessing objective techniques for gauge-based analyses of global daily precipitation. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
  49. Yan, S.; Mingnong, F.; Hongzheng, Z.; Feng, G. Interpolation methods of China daily precipitation data. 应用气象学报 2010, 21, 279–286. [Google Scholar]
  50. Tapiador, F.J.; Turk, F.J.; Petersen, W.; Hou, A.Y.; García-Ortega, E.; Machado, L.A.; Angelis, C.F.; Salio, P.; Kidd, C.; Huffman, G.J.; et al. Global precipitation measurement: Methods, datasets and applications. Atmos. Res. 2012, 104, 70–97. [Google Scholar] [CrossRef]
  51. Chen, Y.; Duan, X.; Ding, M.; Qi, W.; Wei, T.; Li, J.; Xie, Y. New gridded dataset of rainfall erosivity (1950–2020) on the Tibetan Plateau. Earth Syst. Sci. Data 2022, 14, 2681–2695. [Google Scholar]
  52. Bezak, N.; Borrelli, P.; Panagos, P. Exploring the possible role of satellite-based rainfall data in estimating inter-and intra-annual global rainfall erosivity. Hydrol. Earth Syst. Sci. 2022, 26, 1907–1924. [Google Scholar] [CrossRef]
  53. Yin, S.; Xie, Y.; Nearing, M.; Wang, C. Estimation of rainfall erosivity using 5-to 60-minute fixed-interval rainfall data from China. Catena 2007, 70, 306–312. [Google Scholar] [CrossRef]
  54. Vrieling, A.; Sterk, G.; de Jong, S.M. Satellite-based estimation of rainfall erosivity for Africa. J. Hydrol. 2010, 395, 235–241. [Google Scholar] [CrossRef]
  55. Herrera, S.; Kotlarski, S.; Soares, P.M.; Cardoso, R.M.; Jaczewski, A.; Gutiérrez, J.M.; Maraun, D. Uncertainty in gridded precipitation products: Influence of station density, interpolation method and grid resolution. Int. J. Climatol. 2019, 39, 3717–3729. [Google Scholar] [CrossRef]
  56. Huerta, A.; Lavado-Casimiro, W.; Felipe-Obando, O. High-resolution gridded hourly precipitation dataset for Peru (PISCOp_h). Data Brief 2022, 45, 108570. [Google Scholar] [CrossRef]
  57. Sanchez-Moreno, J.F.; Mannaerts, C.M.; Jetten, V. Rainfall erosivity mapping for Santiago island, Cape Verde. Geoderma 2014, 217, 74–82. [Google Scholar] [CrossRef]
  58. Mello, C.d.; Viola, M.; Beskow, S.; Norton, L. Multivariate models for annual rainfall erosivity in Brazil. Geoderma 2013, 202, 88–102. [Google Scholar] [CrossRef]
  59. Delgado, D.; Sadaoui, M.; Ludwig, W.; Méndez, W. Spatio-temporal assessment of rainfall erosivity in Ecuador based on RUSLE using satellite-based high frequency GPM-IMERG precipitation data. CATENA 2022, 219, 106597. [Google Scholar] [CrossRef]
  60. Lobo, G.P.; Bonilla, C.A. Effect of temporal resolution on rainfall erosivity estimates in zones of precipitation caused by frontal systems. Catena 2015, 135, 202–207. [Google Scholar] [CrossRef]
  61. Mejía-Marcacuzco, J.; Pino-Vargas, E.; Guevara-Pérez, E.; Olivos-Alvites, V.; Condori-Ventura, M. Predicción espacial de la erosión del suelo en zonas áridas mediante teledetección. Estudio de caso: Quebrada del Diablo, Tacna, Perú. Revista Ingeniería UC 2021, 28, 252–264. [Google Scholar] [CrossRef]
  62. Riquetti, N.B.; Mello, C.R.; Beskow, S.; Viola, M.R. Rainfall erosivity in South America: Current patterns and future perspectives. Sci. Total Environ. 2020, 724, 138315. [Google Scholar] [CrossRef] [PubMed]
  63. (Peru), I. Informe técnico del estudio de inventario y evaluación de andenes. 1996.
  64. Sabino Rojas, E.; Felipe-Obando, O.; Lavado-Casimiro, W. Atlas de erosión de suelos por regiones hidrológicas del Perú. Nota Técnica Nº 002 SENAMHI-DHI-2017. 2017.
  65. Aybar, C.; Fernández, C.; Huerta, A.; Lavado, W.; Vega, F.; Felipe-Obando, O. Construction of a high-resolution gridded rainfall dataset for Peru from 1981 to the present day. Hydrol. Sci. J. 2020, 65, 770–785. [Google Scholar] [CrossRef]
  66. Garreaud, R. The Andes climate and weather. Adv. Geosci. 2009, 22, 3–11. [Google Scholar] [CrossRef]
  67. Lavado-Casimiro, W.; Espinoza, J.C. Impactos de El Niño y La Niña en las lluvias del Perú (1965-2007). Rev. Bras. Meteorol. 2014, 29, 171–182. [Google Scholar] [CrossRef]
  68. Bourrel, L.; Rau, P.; Dewitte, B.; Labat, D.; Lavado, W.; Coutaud, A.; Vera, A.; Alvarado, A.; Ordoñez, J. Low-frequency modulation and trend of the relationship between ENSO and precipitation along the northern to centre Peruvian Pacific coast. Hydrol. Process. 2015, 29, 1252–1266. [Google Scholar] [CrossRef]
  69. Rau, P.; Bourrel, L.; Labat, D.; Melo, P.; Dewitte, B.; Frappart, F.; Lavado, W.; Felipe, O. Regionalization of rainfall over the Peruvian Pacific slope and coast. Int. J. Climatol. 2017, 37, 143–158. [Google Scholar] [CrossRef]
  70. Cubas Saucedo, F. Sectorización climática del territorio peruano. Nota Técnica N° 001-2020/SENAMHI/DMA/SPC (marzo 2020). 2021.
  71. Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.L.; Joyce, R.J.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Stocker, E.F.; Tan, J.; et al. Integrated multi-satellite retrievals for the global precipitation measurement (GPM) mission (IMERG). Satell. Precip. Meas. 2020, 1, 343–353. [Google Scholar]
  72. Tan, J.; Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J. IMERG V06: Changes to the morphing algorithm. J. Atmos. Ocean. Technol. 2019, 36, 2471–2482. [Google Scholar] [CrossRef]
  73. Huffman, G.; Bolvin, D.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Sorooshian, S.; Xie, P.; Yoo, S. The Day-1 GPM Combined Precipitation Algorithm: IMERG. Proc. AGU Fall Meet. Abstr. 2011, 2011, H41L–08. [Google Scholar]
  74. Huffman, G.J.; The transition in multi-satellite products from TRMM to GPM (TMPA to IMERG). Algorithm Information Document. 2019. Available online: https://docserver. gesdisc. eosdis. nasa.gov/public/project/GPM/TMPA-to-IMERG_transition. pdf (accessed on 2 November 2021).
  75. Xie, P.; Joyce, R.; Wu, S.; Yoo, S.H.; Yarosh, Y.; Sun, F.; Lin, R. Reprocessed, bias-corrected CMORPH global high-resolution precipitation estimates from 1998. J. Hydrometeorol. 2017, 18, 1617–1641. [Google Scholar] [CrossRef]
  76. Xie, P.; Joyce, R.; Wu, S.; Yoo, S.; Yarosh, Y.; Sun, F.; Lin, R.; et al. NOAA climate data record (CDR) of CPC morphing technique (CMORPH) high resolution global precipitation estimates. Version 2021, 1, w9va–q159. [Google Scholar]
  77. Renard, K.G. Predicting soil erosion by water: a guide to conservation planning with the Revised Universal Soil Loss Equation (RUSLE); US Department of Agriculture, Agricultural Research Service: 1997.
  78. Fischer, F.K.; Winterrath, T.; Auerswald, K. Temporal-and spatial-scale and positional effects on rain erosivity derived from point-scale and contiguous rain data. Hydrol. Earth Syst. Sci. 2018, 22, 6505–6518. [Google Scholar] [CrossRef]
  79. Foster, G.; Yoder, D.; Weesies, G.; McCool, D.; McGregor, K.; Bingner, R. User’s Guide—revised universal soil loss equation version 2 (RUSLE 2); USDA–Agricultural Research Service: Washington, DC, USA, 2002. [Google Scholar]
  80. Dabney, S.M.; Yoder, D.C.; Vieira, D.A.N.; Bingner, R.L. Enhancing RUSLE to include runoff-driven phenomena. Hydrol. Process. 2011, 25, 1373–1390. [Google Scholar] [CrossRef]
  81. Fick, S.E.; Hijmans, R.J. WorldClim 2: new 1-km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
  82. Cucchi, M.; Weedon, G.P.; Amici, A.; Bellouin, N.; Lange, S.; Müller Schmied, H.; Hersbach, H.; Buontempo, C. WFDE5: bias-adjusted ERA5 reanalysis data for impact studies. Earth Syst. Sci. Data 2020, 12, 2097–2120. [Google Scholar] [CrossRef]
  83. Willmott, C.J.; Robeson, S.M.; Matsuura, K. A refined index of model performance. Int. J. Climatol. 2012, 32, 2088–2094. [Google Scholar] [CrossRef]
  84. Mann, H.B. Nonparametric tests against trend. Econom. J. Econom. Soc. 1945, 13, 245–259. [Google Scholar] [CrossRef]
  85. Kendall, M.G. Rank correlation methods. 1948.
  86. Hirsch, R.; Scott, A.G.; Wyant, T. Investigation of trends in flooding in the Tug Fork basin of Kentucky, Virginia, and West Virginia; Technical Report; US Geological Survey: Reston, VA, USA, 1982. [Google Scholar]
  87. Ashraf, M.; Routray, J.L. Spatio-temporal characteristics of precipitation and drought in Balochistan Province, Pakistan. Nat. Hazards 2015, 77, 229–254. [Google Scholar] [CrossRef]
  88. Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
  89. Collaud Coen, M.; Andrews, E.; Bigi, A.; Martucci, G.; Romanens, G.; Vogt, F.; Vuilleumier, L. Effects of the prewhitening method, the time granularity, and the time segmentation on the Mann–Kendall trend detection and the associated Sen’s slope. Atmos. Meas. Tech. 2020, 13, 6945–6964. [Google Scholar] [CrossRef]
  90. Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
  91. Theil, H. A rank-invariant method of linear and polynomial regression analysis. In Henri Theil’s contributions to economics and econometrics: Econometric theory and methodology; Springer: Berlin/Heidelberg, Germany, 1992; pp. 345–381. [Google Scholar]
  92. Derin, Y.; Anagnostou, E.; Berne, A.; Borga, M.; Boudevillain, B.; Buytaert, W.; Chang, C.H.; Chen, H.; Delrieu, G.; Hsu, Y.C.; et al. Evaluation of GPM-era global satellite precipitation products over multiple complex terrain regions. Remote Sens. 2019, 11, 2936. [Google Scholar] [CrossRef]
  93. Sepúlveda, S.A.; Petley, D.N. Regional trends and controlling factors of fatal landslides in Latin America and the Caribbean. Nat. Hazards Earth Syst. Sci. 2015, 15, 1821–1833. [Google Scholar] [CrossRef]
  94. Kühnlein, M.; Appelhans, T.; Thies, B.; Nauss, T. Improving the accuracy of rainfall rates from optical satellite sensors with machine learning—A random forests-based approach applied to MSG SEVIRI. Remote Sens. Environ. 2014, 141, 129–143. [Google Scholar] [CrossRef]
  95. Zhu, Q.; Chen, X.; Fan, Q.; Jin, H.; Li, J. A new procedure to estimate the rainfall erosivity factor based on Tropical Rainfall Measuring Mission (TRMM) data. Sci. China Technol. Sci. 2011, 54, 2437–2445. [Google Scholar] [CrossRef]
  96. Catari, G.; Latron, J.; Gallart, F. Assessing the sources of uncertainty associated with the calculation of rainfall kinetic energy and erosivity–application to the Upper Llobregat Basin, NE Spain. Hydrol. Earth Syst. Sci. 2011, 15, 679–688. [Google Scholar] [CrossRef]
  97. Barurén, M.A.R. Cuantificación de la erosión hídrica en el Perú y los costos ambientales asociados; Pontificia Universidad Catolica del Peru (Peru): 2016.
  98. Rosas, M.A.; Gutierrez, R.R. Assessing soil erosion risk at national scale in developing countries: The technical challenges, a proposed methodology, and a case history. Sci. Total Environ. 2020, 703, 135474. [Google Scholar] [CrossRef]
  99. Manz, B.; Páez-Bimos, S.; Horna, N.; Buytaert, W.; Ochoa-Tocachi, B.; Lavado-Casimiro, W.; Willems, B. Comparative ground validation of IMERG and TMPA at variable spatiotemporal scales in the tropical Andes. J. Hydrometeorol. 2017, 18, 2469–2489. [Google Scholar] [CrossRef]
  100. Ning, S.; Wang, J.; Jin, J.; Ishidaira, H. Assessment of the latest GPM-Era high-resolution satellite precipitation products by comparison with observation gauge data over the Chinese mainland. Water 2016, 8, 481. [Google Scholar] [CrossRef]
  101. Klik, A.; Haas, K.; Dvorackova, A.; Fuller, I.C. Spatial and temporal distribution of rainfall erosivity in New Zealand. Soil Res. 2015, 53, 815. [Google Scholar] [CrossRef]
  102. Nyssen, J.; Vandenreyken, H.; Poesen, J.; Moeyersons, J.; Deckers, J.; Haile, M.; Salles, C.; Govers, G. Rainfall erosivity and variability in the Northern Ethiopian Highlands. J. Hydrol. 2005, 311, 172–187. [Google Scholar] [CrossRef]
  103. Lenzi, M.; Di Luzio, M. Surface runoff, soil erosion and water quality modelling in the Alpone watershed using AGNPS integrated with a Geographic Information System. Eur. J. Agron. 1997, 6, 1–14. [Google Scholar] [CrossRef]
  104. Issaka, S.; Ashraf, M.A. Impact of soil erosion and degradation on water quality: a review. Geol. Ecol. Landscapes 2017, 1, 1–11. [Google Scholar] [CrossRef]
  105. Blanco-Canqui, H. Energy crops and their implications on soil and environment. Agron. J. 2010, 102, 403–419. [Google Scholar] [CrossRef]
  106. Grillakis, M.G.; Polykretis, C.; Alexakis, D.D. Past and projected climate change impacts on rainfall erosivity: Advancing our knowledge for the eastern Mediterranean island of Crete. CATENA 2020, 193, 104625. [Google Scholar] [CrossRef]
  107. Auerswald, K.; Fischer, F.K.; Winterrath, T.; Brandhuber, R. Rain erosivity map for Germany derived from contiguous radar rain data. Hydrol. Earth Syst. Sci. 2019, 23, 1819–1832. [Google Scholar] [CrossRef]
  108. Kreklow, J.; Steinhoff-Knopp, B.; Friedrich, K.; Tetzlaff, B. Comparing Rainfall Erosivity Estimation Methods Using Weather Radar Data for the State of Hesse (Germany). Water 2020, 12, 1424. [Google Scholar] [CrossRef]
Preprints 81660 g001
Figure 1. Regions in the study area and location of automatic weather stations with hourly rainfall data. Triangles represent automatic weather stations (AWS) and circles the AWS for cross validation.
Figure 1. Regions in the study area and location of automatic weather stations with hourly rainfall data. Triangles represent automatic weather stations (AWS) and circles the AWS for cross validation.
Preprints 81660 g001
Preprints 81660 g002
Figure 2. Rainfall erosivity analysis methodology. RE-IMERGF and RE-AWS is the rainfall erosivity obtained from IMERGF and AWS source.
Figure 2. Rainfall erosivity analysis methodology. RE-IMERGF and RE-AWS is the rainfall erosivity obtained from IMERGF and AWS source.
Preprints 81660 g002
Preprints 81660 g004
Figure 4. Seasonally based annual average scatter plots of (a) total precipitation amount, (b) average number of storm events, (c) average duration of storm events, (d) maximum storm intensity, (e) precipitation erosivity, and (f) erosivity density relative to those derived from IMERGF data at the corresponding pixels in 2015-2020.
Figure 4. Seasonally based annual average scatter plots of (a) total precipitation amount, (b) average number of storm events, (c) average duration of storm events, (d) maximum storm intensity, (e) precipitation erosivity, and (f) erosivity density relative to those derived from IMERGF data at the corresponding pixels in 2015-2020.
Preprints 81660 g004
Preprints 81660 g005
Figure 5. (a) Map of the seasonal multiplicative factor and its respective, (b) histograms.
Figure 5. (a) Map of the seasonal multiplicative factor and its respective, (b) histograms.
Preprints 81660 g005
Preprints 81660 g006
Figure 6. Comparison of PISCO_reed and the observed rainfall erosivity. (a) Aggregation index, (b) Normalized Mean Bias y (c) Normalised mean gross error.
Figure 6. Comparison of PISCO_reed and the observed rainfall erosivity. (a) Aggregation index, (b) Normalized Mean Bias y (c) Normalised mean gross error.
Preprints 81660 g006
Preprints 81660 g007
Figure 7. Scatterplot of PISCO_reed, GloREDa, and CMORPH product precipitation erosivity, based on observed data from 321 stations for 2015–2020.
Figure 7. Scatterplot of PISCO_reed, GloREDa, and CMORPH product precipitation erosivity, based on observed data from 321 stations for 2015–2020.
Preprints 81660 g007
Preprints 81660 g008
Figure 8. (a) Precipitation erosivity of the observed stations and PISCO_reed product: (b) precipitation erosivity and (c) erosive density.
Figure 8. (a) Precipitation erosivity of the observed stations and PISCO_reed product: (b) precipitation erosivity and (c) erosive density.
Preprints 81660 g008
Preprints 81660 g009
Figure 9. Climatology of precipitation erosivity.
Figure 9. Climatology of precipitation erosivity.
Preprints 81660 g009
Preprints 81660 g010
Figure 10. Boxplots of PISCO_reed, GloREDa, and CMORPH product precipitation erosivity, based on automatic weather stations for 2015–2020.
Figure 10. Boxplots of PISCO_reed, GloREDa, and CMORPH product precipitation erosivity, based on automatic weather stations for 2015–2020.
Preprints 81660 g010
Preprints 81660 g011
Figure 11. Climatology of precipitation erosivity. Moreover, show following RE multiannual stats by region: mean, minimum, maximum, median, SD, CV.
Figure 11. Climatology of precipitation erosivity. Moreover, show following RE multiannual stats by region: mean, minimum, maximum, median, SD, CV.
Preprints 81660 g011
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated