Preprint
Article
Examining the Impact of Urban Morphology on Seasonal Land Surface Temperatures: Comparing Grid‐ and Block‐Based Approaches
Altmetrics
Downloads
223
Views
153
Comments
0
A peer-reviewed article of this preprint also exists.
supplementary.docx (96.83KB )
This version is not peer-reviewed
Submitted:
03 August 2023
Posted:
08 August 2023
You are already at the latest version
Alerts
Abstract
Climate change is expected to result in rising temperatures, leading to increased occurrences of extreme weather events like heat waves and cold spells. Urban planning responses are crucial for improving the adaptive capacity of cities and communities in dealing with significant temperature variations across seasons. This study aims to investigate the relationship between urban temperature fluctuations and urban morphology throughout the four seasons. Through quadrant and statistical analyses, the study identifies built-environment factors that contribute to moderate seasonal land surface temperatures (LST). The research focuses on Seoul, South Korea as a case study and calculates seasonal LST values at both the grid level (100m×100m) and street-block level, incorporating factors such as vegetation density, land use patterns, albedo, two- and three-dimensional building forms, and gravity indices for natural reserves. The quadrant analysis reveals spatial segregation between areas demonstrating high LST adaptability (cooler summers and warmer winters) and those displaying LST vulnerability (hotter summers and colder winters), with significant differences in vegetation and building forms. The spatial regression analysis demonstrates that higher vegetation density and proximity to water bodies play key roles in moderating LST, leading to cooler summers and warmer winters. Building characteristics have an invariant impact on LST across all seasons, where horizontal expansion contributes to higher LST, while vertical expansion reduces LST. These findings are consistent for both grid- and block-level analyses. The study emphasizes the flexible role of the natural environment in moderating temperatures.
Keywords:
Subject: Environmental and Earth Sciences - Remote Sensing
1. Introduction
Global warming and climate change are leading to an increase in extreme weather events worldwide. New climate norms caused by global warming can take various forms, including the largest number of meteorological droughts since 1974, an early summer heat wave occurring in spring, and a strong cold shock in fall (KMA, 2023; Park and Song, 2023). These severe weather events, both heatwaves and cold waves, are closely related to human health and well-being. According to the World Health Organization (WHO, 2014), climate change is expected to cause about 250,000 deaths per year from 2030 to 2050. With continued urbanization, the temperature rise in urban centers will likely accelerate, necessitating appropriate mitigation measures and environmental adaptation strategies.
In urban temperature research, atmospheric temperature (AT) and land surface temperature (LST) are often mixed, but the latter is directly affected by the spatial and temporal traits of microscale urban morphology and surface composition (Turner et al., 2022). Therefore, many studies have used LST as an indicator to understand thermal variability in response to urban changes. Artificial urban structures, such as buildings and roads, significantly contribute to urban warming (Liu et al., 2022; Moazzam et al., 2022). Identifying and analyzing the components of a city and their varying impacts on thermal conditions are fundamental steps in sustainable urban design (Boeing et al., 2018; Kang, 2022; Zhao et al., 2023b). Urban form analysis can also assess the adaptability of cities to extreme temperatures (Choi et al., 2018; Kim et al., 2022). Thus, understanding urban form factors closely related to LST variance over seasons is crucial for urban management.
Urban LST is influenced by multiple factors, ranging from land cover materials to planar and vertical urban geometry, and their effects may depend on the seasonal and spatial context (Guo et al., 2023; Liu et al., 2023). For example, urban forests and woods are beneficial for urban cooling due to active evapotranspiration and shading, but their impacts in cold months are less known. Similarly, urban water bodies, such as lakes and ponds, keep lower surface temperatures than their surroundings in summer, but the thermal impact of large stretching rivers is less understood (Firozjaei et al., 2023; Zhao et al., 2023a; Zhou et al., 2023). The influences of conserving and restoring urban blue spaces throughout the seasons need to be better understood. Additionally, the correlation between LST and its associated factors has only been examined on a grid system, and research on the suitability of using grid-based data aggregation to explain LST variability is lacking (Yao et al., 2020). This study aims to identify the impacts of multi-dimensional urban form and spatial indicators on seasonal LST using two data aggregation systems – grid and areal units – and to explore desirable urban forms that can be flexibly adapted to different seasons.
The research goals of this paper, focusing on the city of Seoul, South Korea as the study area, are as follows: First, explaining seasonal LST as a combination of multiple urban factors considering biophysical, manmade 2D/3D structures, and proximity to green-blue spaces. Second, intersecting summer and winter LSTs to obtain four thermal quadrants and identify areas exhibiting seasonally flexible versus seasonally vulnerable thermal patterns. Finally, applying spatial regression analysis to both grid-based and block-based datasets to explore the impact of spatial unit choice on understanding LST while controlling for spatial autocorrelation.
2. Literature Review
According to existing studies, urban land surface temperature (LST) results from various built environment dimensions, including surface biophysical composition, landscape characteristics, and building form (Li et al., 20221a; Shao et al., 2023). Surface biophysical composition refers to the land cover, such as vegetation, asphalt, concrete, bare soil, and water. Converting natural land cover into urbanized impervious areas significantly increases LST, closely linked to thermal mass and albedo (Dai et al., 2018; Li et al., 2021b). Surface albedo significantly influences LST by altering solar radiation absorption (Adilkhanova et al., 2023; HosseiniHaghighi et al., 2020). Urban features like buildings and roads with low albedo absorb heat and release longwave heat energy, exacerbating the urban heat island effect (Liu et al., 2023).
Land cover composition is quantified using remotely sensed spectral indices, including NDVI, NDBI, and MNDWI. These indices consistently and significantly influence LST in summer and seasonal variations (Fan et al., 2023; Ge et al., 2021; Kafy et al., 2021). NDVI helps regulate LST against seasonal temperature changes, reducing LST in summer while increasing it in winter (Chun and Guldmann, 2018). Built-up surfaces in cities can reduce the cooling effect of vegetation's evapotranspiration, intensifying urban warming (Fan et al., 2023). MNDWI (percent water content) is negatively correlated with LST (Dai et al., 2018; Ge et al., 2020; Wu et al., 2021). Another approach to quantifying land cover composition is calculating proportions and spatial arrangements of land use and land cover (LULC) types using landscape metrics (Peng et al., 2018). While metrics summarize distinct LULC patterns, results regarding individual metrics' effects lack coherent understanding due to differences in metric subsets and grid sizes (Han et al., 2023; Li et al., 2021b; Shao et al., 2023). The percentages and mix of distinct LULC types may provide a comparable control for LST effects and facilitate interpretation.
Building form significantly impacts spatial LST distribution through vertical form, planar spacing, and urban canyon characteristics, affecting thermal mass, shadow casting, wind swirling, and waste heat release (Alavipanah et al., 2018; Hu et al., 2020; Hwang et al., 2021; Park et al., 2021). Studies on building form's effects on seasonal LST find that building density increases LST, while building height (BH) decreases it, and these effects remain stable across seasons (Cai et al., 2018; Chen et al., 2023; Han et al., 2022; Li et al., 2021a). Taller buildings can reduce summertime LST by casting shadows on adjacent buildings and grounds (Park et al., 2021; Yang et al., 2021; Yu et al., 2019). The transition point for BH’s impact on LST occurs around 10m, above which BH reduces LST due to increased shade (Li et al., 2021a). However, there are mixed findings for other building indices, such as SVF, frontal area index, floor area ratio, and building coverage ratio, whose nonlinear effects may vary by season and location (Hu et al., 2020; Li et al., 2021a; Liu et al., 2022; Liu et al., 2023).
The local LST characteristics of an area are influenced by adjacent areas due to air convection and wind flow, resulting in spatial autocorrelation (Baek et al., 2022; Park et al., 2022). However, this spatial spillover has rarely been considered in modeling seasonal LST variations. Another source of LST autocorrelation is the propagation of heat and cooling loads, where large natural areas can influence neighboring areas by dissipating additional cooling or warming effects (Cureau et al., 2023; Firozjaei et al., 2023; Tang et al., 2023; Wang et al., 2019; Zhou et al., 2023). Investigating the cooling effect of river bodies, Cai et al. (2018) observe that the relationship between building form and seasonal LST becomes stronger with an increasing distance to the closest river corridors. Hu et al. (2020) utilize a gravity index based on the distance to and area of nearby parks in each LST grid cell, finding that larger park areas in closer proximity result in a stronger cooling effect on LST, albeit significant only in spring and summer. Few studies account for the area and proximity of large natural zones such as forests and rivers simultaneously in modeling seasonal LST, and whether thermal propagation from those natural reserves to urban settlements is positive or not remains underexplored.
The spatial unit of analysis used to quantify urban form vary among studies. Previous investigations of the relationship between seasonal LST and urban factors have primarily utilized data aggregated over uniform grid cells (Ge et al., 2020). Some studies have tested the effect of grid scale on LST estimation (Chen et al., 2023; Chun and Guldmann, 2018; Dai et al., 2018; Han et al., 2022; Li et al., 2021a) with varied conclusions on the optimal grid size. While this grid processing is natural due to the availability of satellite thermal infrared observations in grid format, it requires truncating the spatially continuous urban form into discrete pieces to align with the grid cells (Zhu et al., 2023). Urban planning and development occur at a site or block scale, typically encompassing street segments and natural corridors. A street block represents a homogeneous area in terms of buildings and land use/land cover (LULC) but varies in size (Zhang et al., 2023). Research exploring whether block-level data aggregation and modeling of LST produce results consistent with conventional grid-based analysis is scarce.
To address these gaps in prior studies, this study aims to explore the impacts of three groups of urban form factors on seasonal LST by comparing both grid- and street-block-based data aggregations. The urban form factors considered include NDVI, surface albedo, land-use proportions and diversity, 2D/3D building form, and proximity to natural zones. Their individual effects will be estimated using spatial models that control for spatial autocorrelation. Additionally, this study examines whether there are significant similarities and dissimilarities among areas with favorable thermal conditions, mitigating summer heat and winter cold, and those with the least favorable thermal conditions.
3. Methodology
3.1. Study Area
The study area is the City of Seoul, South Korea. As the capital of South Korea, Seoul serves as the epicenter of commercial and business activities, intertwined with densely developed and diverse residential districts. With an area of 605.2 km2, Seoul represents 0.6% of the national territory, yet it accommodates approximately 17% of the nation's total population. Geographically, the city is situated in the northwestern part of South Korea, along the Han River, which flows through the city from east to west (Figure 1). Surrounded by mountains, Seoul lies in a basin, with several smaller tributaries feeding into the Han River (Figure 3). The city features numerous bridges that facilitate transportation between different areas. Seoul experiences four distinct seasons, characterized by hot and humid summers, with temperatures occasionally surpassing 30°C, and cold winters, where average temperatures fall below freezing, accompanied by intermittent snowfall. Given these diverse seasonal conditions, Seoul presents an ideal case study to explore the influence of complex urban built-up form characteristics on seasonal thermal environments.
3.2. Data Sources and Processing
3.2.1. Grid cells versus street blocks
LST exhibit spatial variations influenced by local physical characteristics, and various spatial units are employed to delineate these locations and process local attributes. Geospatial data are commonly distributed in raster or lattice (areal vector) format. Raster-grid-based analysis has been extensively utilized for LST data analysis, owing to its efficiency in handling large-scale continuous geospatial information, particularly since LST images are initially generated as collections of image pixels.
Despite the advantages of grid-based data processing, it involves dividing physical elements into uniformly-sized grid cells, leading to artificial truncation that may introduce biases in LST estimation using physical variables. The grid size is determined by sensor capabilities rather than scientific rationale. Thus, this study explores whether lattice-based analysis yields different results compared to the grid-based approach (Figure 2). Urban landscapes are divided into homogenous blocks by streets and roads, creating coherent spatial units in terms of land use and buildings. These street-enclosed blocks likely represent homogeneous neighborhoods governed by similar land use regulations, including design codes and caps for building coverage ratio (BCR) and floor area ratio (FAR). Consequently, we also utilize street-enclosed neighborhood blocks as alternative spatial units for LST analysis and compare the results obtained from each approach. The Ministry of the Interior and Safety has recently developed a street block unit system known as the state basic district (SBD), where boundaries are delineated based primarily on transportation and river networks. In this study, we select and compare the grid and street blocks as spatial units of analysis.
3.2.2. Land surface temperatures
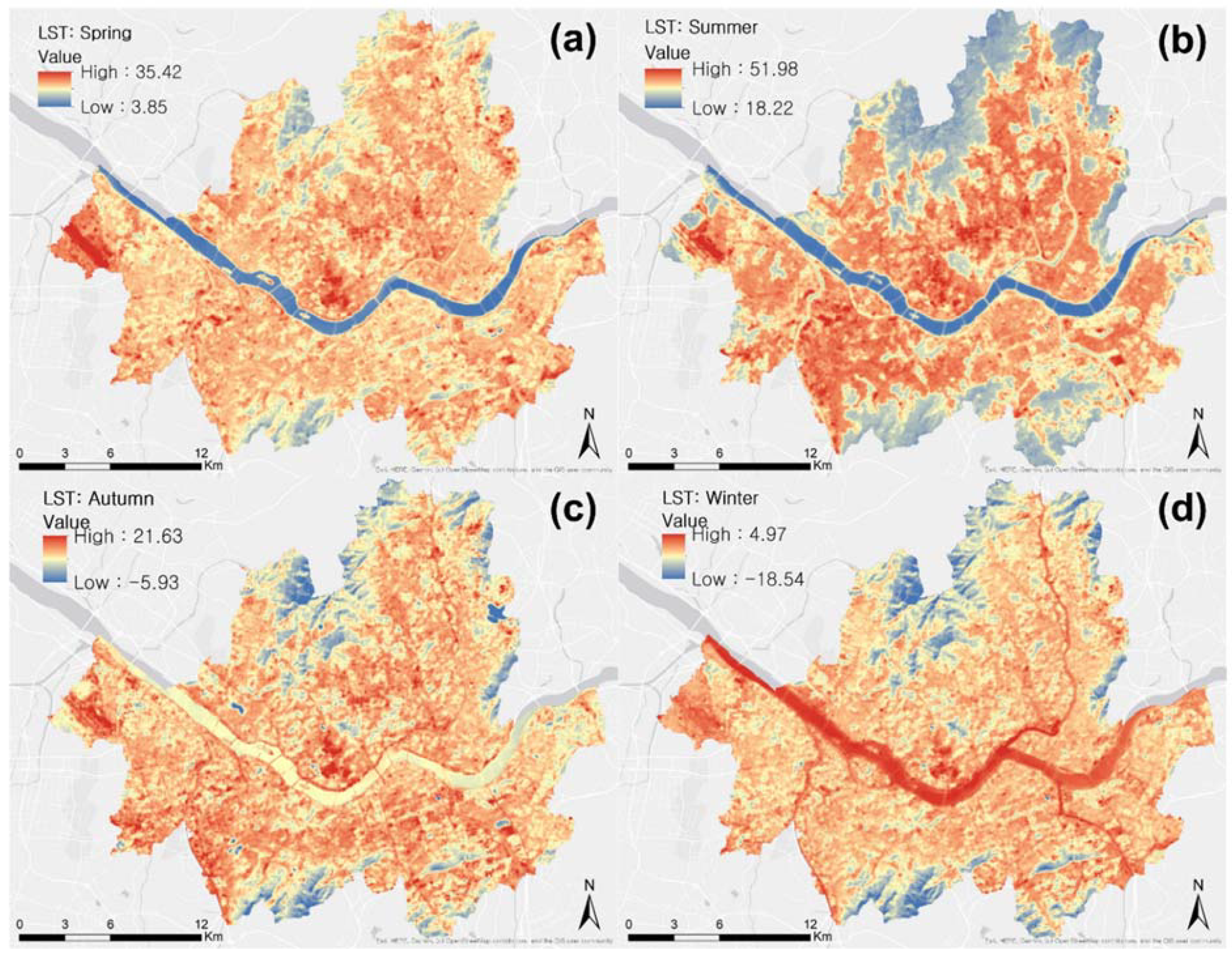
The seasonal LST values across Seoul were extracted from Landsat 8 Thermal Infrared Sensors (TIRS) Collection-2 Level-2 products, featuring a 30m spatial resolution, accessed through Earth Explorer, the data distribution platform operated by the United States Geological Survey (USGS). This dataset comprises atmospherically corrected surface reflectance and surface temperature values derived from Level-1 inputs meeting specific technical criteria to ensure scientific validity. Remotely sensed (RS) LST data allows for spatially continuous analysis and exhibits a strong correlation with AT measures, which are typically available from only a limited number of meteorological stations. To ensure image quality, it is crucial to select imagery with minimal cloud cover. For this study, clear atmospheric conditions representative of the four seasons in Seoul were available for the year 2017 (Figure 3). Table 1 presents the date and time of data collection.
Seoul boasts extensive nature preserves, with approximately 13% of the city's area covered by public waters, such as rivers and tributaries, and an additional 25.3% covered by forests and woods. In total, approximately 38% of the city comprises uninhabited natural preserves. As these areas lack urban built-up form variables, they were excluded from the subsequent analysis to avoid zero-inflation issues in the dataset. Moreover, the LST patterns of natural features differ significantly from those of urbanized areas. Hence, this study focuses exclusively on the built-up morphology of urban areas and its impact on LST. To address the spillover effects of nearby natural features on the LST of adjacent urban areas, the final dataset includes variables quantifying the proximity to forests, rivers, small green spaces, and water bodies as distinct land-use types.
For the grid-based analysis, the LST cells with a 30m resolution were resampled to 100m by 100m, using bilinear interpolation in ArcGIS to align with building geometry and density information, where the smallest unit of distribution is a 100m grid. On the other hand, for the block-level analysis, the mean LST values were calculated for each individual block. In Seoul, a total of 34,135 grid cells and 4,553 street-blocks were considered for this study.
Figure 3.
Seasonal distribution of urban land surface temperature in 2017, Seoul, South Korea: (a) spring, (b) summer, (c) autumn, (d) winter.
Figure 3.
Seasonal distribution of urban land surface temperature in 2017, Seoul, South Korea: (a) spring, (b) summer, (c) autumn, (d) winter.
3.2.3. NDVI and albedo
The Normalized Difference Vegetation Index (NDVI) is a widely used indicator of vegetation density or photosynthetic activity, and is calculated as follows:
where RED and NIR are the surface reflectance in
the red and near-infrared bands. These SR values are in eq. (2) obtained from
Landsat 8 data at a 30m resolution, and NDVI values are calculated for each of
the four seasons. NDVI values range from -1.0 to 1.0, with higher values
indicating higher vegetation density and health, whereas lower values
indicating impervious land with limited vegetation or water content.
Surface albedo quantifies the extent to which a surface reflects solar radiation and is expressed as a percentage ranging from 0 (indicating no reflection) to 100 (indicating complete reflection). Surfaces with high albedo values include white materials like snow and clouds, which remain cooler due to their ability to reflect a significant portion of incoming solar radiation. Conversely, darker surfaces, such as asphalt, dark trees, and soil, exhibit low albedo values and tend to absorb a larger portion of solar energy, leading to increased warmth. Given the influence of surface albedo on surface temperature, it becomes essential to account for this characteristic when modeling LST. The calculation of albedo is based on Landsat SR bands, utilizing the formula proposed by Liang (2001):
where NIR is near-infrared and SWIR 1 and 2 represent short-wave infrared in different bandwidths. Both of the seasonal NDVI and surface albedo values are aggregated at the grid level of 100m and the block level, respectively.
3.2.4. Land uses and buildings
Land use classification data available at the land parcel level in vector form is downloaded from the Korean Ministry of Environment’s website, Environmental Geographic Information Service (EGIS). The classification is conducted via manual digitization based on very-high-resolution orthorectified aerial images (0.25m/pixel). In this study, seven land-use categories are considered – residential, commercial, industrial, cultural & recreational, transport, public, and others (non-urban uses), and their proportions within each grid and block are correlated with seasonal LST changes. In addition, the entropy index is used as a metric to measure the level of land-use diversity, and is calculated as follows:
where is the percentage of land use type j in the grid cell (block) and k is the total number of land-use types considered. It ranges from 0 to 1, higher values indicating a balanced mix of different land uses.
This study gathered GIS data on various building characteristics in Seoul, including the number of buildings, the percentage of aged buildings, building coverage ratio, total floor area, floor area ratio, and building height. The data was obtained from the National Geographic Information Institute (NGII), which provides building information in two different data formats: grid cells of varying sizes and lattice formats encompassing State Basic Districts (SBDs), census tracts, ZIP code areas, villages, and municipalities. To ensure data consistency, the finest spatial unit from each format was selected for data acquisition, resulting in a grid size of 100m and the use of SBDs. While individual building information would have been valuable, it was unfortunately unavailable for the study area. Therefore, building form indicators, as processed by the NGII, were retained along with land-use proportions and land-use diversity variables for subsequent statistical analyses. The study employs six building indicators, three related to two-dimensional aspects, and the remaining three concerning three-dimensional volumes.
3.2.5. Gravity Index
Two gravity indices are calculated for the grid and block level analyses: gravity index for urban forests and for water bodies. The gravity index measures the distance-decay impacts of urban forests and water bodies on LST. First, a 1,000 m buffer is constructed around the centroid of grid cell or street-block i, and the areas of urban forests and water bodies are converted into points for every 30m in GIS. Let be the buffer of centroid i, j a point within this buffer, the distance between the centroid i and point j, the area, either forests or waters, represented by point j (900m2), and α a positive exponent. The gravity index is defined as follows:
This gravity index (GI) accounts for the fact that the influence of forests on LST may be reduced by the distances of these areas, and the effect of distance is discounted by exponent α. Higher α values decrease the importance of farther-away forests (waters) while increasing the influence of nearby ones. Several α values (1.0, 1.5, 2.0, 2.5, 3.0) were tried, with α = 1.5 providing the best statistical fit. The mapping of the gravity indices for urban forests (GIUF) and for water bodies (GIWB) is presented in Figure 4 and Figure 5. The final set of variables estimating LST, and their sources are presented in Table 2.
Table 2.
List of variables and descriptions.
| Category | Variables | Unit | Source | ||
| Dependent | Seasonal land surface temperature (LST) | ℃ | Landsat 8 TIR | ||
| Explanatory | Vegetation | Seasonal normalized difference in vegetation index (NDVI) | [0~1] | Landsat 8 OLI | |
| Land use | Land use type proportion | Residential | % | Korea Environmental Geographic Information Service (EGIS) 2017 |
|
| Commercial | % | ||||
| Industrial | % | ||||
| Cultural & Recreational | % | ||||
| Transport | % | ||||
| Public | % | ||||
| Other uses | % | ||||
| Land use diversity | Entropy index | [0~3] | |||
| Reflectance | Albedo | % | Landsat 8 OLI | ||
| Building | 2-D | Number of buildings | - | Korea National Geographic Information Institute (NGII) 2017 |
|
| Percent old buildings (+35 years) |
% | ||||
| Average building coverage ratio (BCR) | % | ||||
| 3-D | Average floor area ratio (FAR) | % | |||
| Average total floor area | m2 | ||||
| Average building height | m | ||||
| Natural Area |
Proximity to natural areas | Gravity index for urban forests | - | EGIS 2017 |
|
| Gravity index for rivers and streams | - | ||||
Table 2.
Descriptive statistics of LST and the explanatory variables aggregated at the grid level (100m×100m) (N=34,136).
Table 2.
Descriptive statistics of LST and the explanatory variables aggregated at the grid level (100m×100m) (N=34,136).
| Category | Variable | Mean | Std. Dev. | Min. | Max. | |
| LST | LST (℃) | Spring | 20.72 | 1.65 | 10.99 | 31.2 |
| Summer | 37.32 | 2.37 | 25.25 | 49.86 | ||
| Autumn | 13.35 | 1.09 | -2.68 | 20.22 | ||
| Winter | -2.27 | 1.11 | -11.77 | 3.90 | ||
| Vegetation | NDVI | Spring | 0.31 | 0.04 | 0.18 | 0.71 |
| Summer | 0.43 | 0.09 | 0.25 | 0.93 | ||
| Autumn | 0.28 | 0.04 | 0.18 | 0.52 | ||
| Winter | 0.17 | 0.02 | 0.11 | 0.43 | ||
| Land | Albedo | Spring | 10.39 | 1.59 | 0.00 | 32.59 |
| Summer | 12.48 | 2.08 | 0.00 | 45.44 | ||
| Autumn | 6.66 | 1.37 | 0.00 | 31.23 | ||
| Winter | 5.23 | 1.34 | 0.00 | 28.54 | ||
| Land use type proportion |
Residential | 19.73 | 21.6 | 0.00 | 97.27 | |
| Commercial | 12.45 | 15.52 | 0.00 | 100.0 | ||
| Industrial | 0.27 | 2.77 | 0.00 | 99.29 | ||
| Cultural & Recreational | 1.49 | 5.79 | 0.00 | 100.0 | ||
| Transport | 40.51 | 19.35 | 0.00 | 100.0 | ||
| Public | 3.35 | 7.52 | 0.00 | 100.0 | ||
| Other uses | 22.20 | 26.09 | 0.00 | 100.0 | ||
| Land use diversity | Entropy Index | 0.49 | 0.16 | 0.00 | 0.88 | |
| Building | 2-D form | Count of buildings | 15.43 | 17.38 | 0.00 | 180 |
| % of old buildings (+35 years) | 17.52 | 24.49 | 0.00 | 100 | ||
| Average building coverage ratio | 33.14 | 25.96 | 0.00 | 90.0 | ||
| 3-D form | Average floor area ratio | 121.17 | 124.07 | 0.00 | 1420.19 | |
| Average total floor area | 3071.25 | 10294.12 | 0.00 | 426719.2 | ||
| Average building height | 14.24 | 17.26 | 0.00 | 284.0 | ||
| Natural Area | Proximity to nature | Gravity index for urban forests | 18.53 | 26.73 | 0.00 | 196.51 |
| Gravity index for rivers and streams | 15.85 | 36.30 | 0.00 | 3290.23 | ||
Table 3.
Descriptive statistics of LST and the explanatory variables aggregated at the street-block level (N=4,098).
Table 3.
Descriptive statistics of LST and the explanatory variables aggregated at the street-block level (N=4,098).
| Category | Variable | Mean | Std. Dev. | Min. | Max. | |
| Block | Street-block area (m2) | 65,611.1 | 71,397.9 | 3,071.2 | 2,494,292.3 | |
| LST | LST (℃) | Spring | 20.44 | 1.17 | 15.32 | 25.93 |
| Summer | 37.62 | 1.81 | 28.95 | 45.21 | ||
| Autumn | 13.30 | 0.80 | 8.70 | 17.04 | ||
| Winter | -2.51 | 0.78 | -6.29 | 1.07 | ||
| Vegetation | NDVI | Spring | 0.30 | 0.03 | 0.21 | 0.47 |
| Summer | 0.41 | 0.06 | 0.31 | 0.74 | ||
| Autumn | 0.27 | 0.02 | 0.21 | 0.41 | ||
| Winter | 0.17 | 0.01 | 0.13 | 0.26 | ||
| Land | Albedo (%) |
Spring | 9.99 | 0.85 | 7.39 | 15.00 |
| Summer | 11.99 | 1.16 | 8.05 | 22.38 | ||
| Autumn | 6.33 | 0.71 | 3.53 | 11.49 | ||
| Winter | 4.90 | 0.70 | 2.83 | 12.53 | ||
| Land use type proportion (%) |
Residential | 24.87 | 18.64 | 0.00 | 83.98 | |
| Commercial | 15.71 | 13.35 | 0.00 | 74.37 | ||
| Industrial | 0.20 | 1.82 | 0.00 | 49.00 | ||
| Cultural & Recreational | 1.10 | 2.36 | 0.00 | 31.85 | ||
| Transport | 40.07 | 13.26 | 0.18 | 91.96 | ||
| Public | 3.08 | 4.08 | 0.00 | 48.96 | ||
| Other uses | 14.97 | 18.06 | 0.00 | 99.82 | ||
| Land use diversity | Entropy Index | 0.60 | 0.11 | 0.01 | 0.91 | |
| Building | 2-D form | Building density (km2) | 20.57 | 15.99 | 0.00 | 95.80 |
| % of old buildings (+35 years) | 21.43 | 19.30 | 0.00 | 100.00 | ||
| Average building coverage ratio | 49.13 | 14.68 | 0.00 | 80.23 | ||
| 3-D form | Average floor area ratio | 183.80 | 113.95 | 0.00 | 1409.8 | |
| Average total floor area | 3554.87 | 13344.02 | 0.00 | 426719.2 | ||
| Average building height | 18.26 | 15.32 | 0.00 | 250.73 | ||
| Natural Area | Proximity to nature | Gravity index for urban forests | 23.67 | 39.64 | 0.00 | 1057.1 |
| Gravity index for rivers and streams | 7.27 | 12.78 | 0.00 | 98.85 | ||
3.3. Statistical Analyses
The study investigates the relationships between LST and urban built-up morphological traits at both the grid-cell and street-block levels, employing two analytical methods: quadrant and spatial regression analyses.
3.3.1. Quadrant analysis
The quadrant analysis involves the division of grid cells and blocks into four groups based on the intersection of summer LST on the x-axis and winter LST on the y-axis (Figure 6). These quadrants are characterized as follows: the first quadrant exhibits hotter LST in summer and warmer LST in winter compared to the other areas; the second quadrant represents the most desirable condition, with cooler summer LST and warmer winter LST; the third quadrant contains cooler LST in both summer and winter; and the fourth quadrant indicates the worst case of LST variations, with areas experiencing higher temperatures in summer and colder temperatures in winter. The study explores the spatial distributions of these quadrants across Seoul and assesses whether there are significant statistical dissimilarities among them in terms of vegetation and built-up morphology. To achieve this, the one-way ANOVA test and post hoc tests are employed to determine specific pairs of quadrants with significant differences in mean values.
3.3.2. Regression analysis
The regression analysis is conducted to estimate the relationship between LST and each urban morphological attribute over the four seasons. Applying regression models to a large LST dataset allows for identifying the independent, disaggregated effect of each explanatory variable while controlling for the influence of the other variables and geographically neighboring areas.
Different forms of regression are considered: the ordinary least square model (OLS), the spatial lag model (SLM), the spatial error model (SEM), and the general spatial model (GSM), incorporating SLM and SEM. Each of these models is estimated in a sequence suggested by LeSage (1999) and Anselin (2005). The LST in each cell is likely to be closely related to LST values at nearby cells, because of thermal conduction and air circulation. This spatial autocorrelation (SA) can be accounted for in spatial regression models. The basic specification of the OLS model is:
where Y (i.e., LST) is the column vector of the dependent variable, X a matrix of the explanatory variables, a vector of coefficients, and a vector of normally and independently distributed random errors. The Moran’s I test is used to test whether SA exists among OLS residuals. If so, spatial regression models are needed. The SLM assumes that SA exists in the distribution of the dependent variable, with:
where is the spatial lag factor, a measure of the
spatial autocorrelation, W a spatial weight matrix defined by spatial
contiguity of the first order and in a row-stochastic form, and the vector of the spatially lagged dependent
variable. The SEM assumes that only the error terms are spatially
autocorrelated, with:
where is a measure of the SA. The GSM assumes that both
the dependent variable and the error terms are spatially autocorrelated, with:
where measures the magnitude of the influence of the
adjacent LST values on the central cell LST, and represents the effects of the unobserved variables nearby that are captured by the error term. The most appropriate model is determined based on three statistical criteria: R², Akaike Information Criterion (AIC), and Lagrange Multiplier (LM) test. To select and implement spatial regression models, two software packages are used: Matlab and GeoDa.
4. Results
This section first presents the LST quadrant analyses conducted at both the grid and block levels. The ANOVA tests applied to the variables across the quadrants reveal a noteworthy correlation between urban built-up form characteristics and seasonal LST variations. To model the relationships between seasonal LST and urban spatial form indicators, a dataset consisting of 34,135 grid cells and 4,553 street blocks is utilized for multivariate regression analysis. Given the identification of significant SA in OLS models, spatial regression models are employed for estimation.
4.1. Quadrant analysis
Based on the average summer LST (37.3℃) and the average winter LST (-2.2℃), grid cells and blocks are categorized into four quadrants. Quadrant 1 (Q1) represents higher LST in both summer and winter, while Quadrant 3 (Q3) exhibits lower LST in both seasons. Ideally, Quadrant 2 (Q2) is the most favored, displaying cooler summer LST and warmer winter LST, while Quadrant 4 (Q4) represents the least favored combination, with hotter summer and colder winter temperatures.
The results of the summer and winter LST quadrant analysis presented in Table 4 reveal that Quadrant 1 is the most prevalent type, encompassing the largest number of grid cells (31.5%) and blocks (37.9%), followed by Q3, which includes 27.7% of the grid cells and 29.3% of the street blocks. This indicates that approximately 60% to 66% of the entire city consistently experiences warmer or colder LST in both summer and winter compared to other areas. Areas with relatively cooler summer and warmer winter temperatures (Q2) account for approximately 17.3% at the grid level and 14.6% at the block level. Meanwhile, areas with the least favorable LST conditions, being warmer in summer and colder in winter (Q4), account for approximately 23.6% at the grid level and 18.3% at the block level.
The spatial distribution of these four quadrants across Seoul's 25 local districts shows significant clustering, with spatial disparities among the districts in terms of quadrant proportions (Figure 7). Some districts located northeast and southwest of Seoul exhibit disproportionately larger numbers of Q4, indicating a large contiguous cluster of grid cells and blocks with unfavorable LST conditions. On the other hand, some other districts located southeast of Seoul show very few traces of Q4. The three districts with the fewest number of Q4 consist of socioeconomically well-to-do communities and high-end commercial centers in Seoul, typically characterized by higher property values and well-maintained green infrastructure. These districts predominantly comprise Q2, Q3, and Q1.
Notably, Q2 (cooler summer and warmer winter LST) tends to be more located along the rivers and streams, particularly the Han River that cuts through Seoul. Q3 (cooler summer and colder winter LST) also exhibits a similar spatial pattern, being situated close to water bodies, but it is more densely clustered near urban forests and mountains north and northwest of Seoul. Additionally, some districts to the east and northwest of Seoul are predominantly composed of Q1 and Q4, indicating vulnerable thermal conditions in summer and winter. These areas coincide with large local clusters of affordable residential areas in Seoul, indicating an inequitable social distribution of summer heat and winter cold.
The comparison of mean values of urban form variables, including NDVI, building form indicators, and proximity to forests and water bodies, provides further insights into the characteristics of each quadrant (Table 4). Quadrant 2 (Q2) exhibits the highest vegetation density in both summer and winter. It also has greater access to large water bodies in its vicinity compared to the other quadrants, as well as moderate access to urban forests nearby. Quadrant 3 (Q3) ranks second to Q2 in terms of vegetation density in both seasons and access to water bodies, but it excels in its proximity to urban forests. It appears that urban nature elements such as greenery and waterfront areas are closely associated with pleasant changes in LST between summer and winter.
Table 4.
Comparison of means among LST quadrants: grid-level versus block-level.
| Variables | Summer-winter LST quadrants | |||
| Quadrant 1 (hot-warm) |
Quadrant 2( cool-warm) |
Quadrant 3 (cool-cold) |
Quadrant 4 (hot-cold) |
|
| Grid-level (N=34,135) | ||||
| Count | 10,747 (31.5%) | 5,891 (17.3%) | 9,457 (27.7%) | 8,040 (23.6%) |
| Summer LST * | 39.32** | 35.09** | 35.42** | 38.50** |
| Winter LST * | -1.45** | -1.36** | -3.31** | -2.82** |
| Summer NDVI * | 0.40** | 0.52** | 0.45** | 0.39** |
| Winter NDVI * | 0.17** | 0.19** | 0.17** | 0.16** |
| Count of buildings * | 21.05** | 3.14** | 7.41** | 26.38** |
| Percent old buildings * | 23.30** | 7.90** | 11.65** | 23.75** |
| Average BCR * | 40.10** | 12.73** | 23.71** | 49.89** |
| Average FAR * | 128.84** | 54.29** | 112.80** | 169.79** |
| Average TFA * | 1487.5** | 2495.1** | 6362.3** | 1739.3** |
| Average BH * | 11.04** | 8.62** | 21.23** | 14.40** |
| GIUF * | 14.77** | 17.82** | 24.59** | 16.94** |
| GIWB * | 12.48** | 35.60** | 13.94** | 8.12** |
| Block-level (N=4,553) | ||||
| Count | 1,727 (37.9%) | 663 (14.6%) | 1,332 (29.3%) | 831 (18.3%) |
| Summer LST * | 39.07** | 36.30** | 35.84** | 38.52** |
| Winter LST * | -1.94** | -1.98** | -3.29** | -2.89** |
| Summer NDVI * | 0.39** | 0.45** | 0.44** | 0.39** |
| Winter NDVI * | 0.17** | 0.18** | 0.17** | 0.16** |
| Building density * | 28.44** | 10.32** | 10.54** | 28.45** |
| Percent old buildings * | 27.27** | 16.35** | 14.08** | 25.12** |
| Average BCR * | 53.75** | 43.26** | 42.74** | 54.48** |
| Average FAR * | 172.46** | 178.84** | 199.84** | 185.62** |
| Average TFA * | 1250.9** | 4906.4** | 7260.7** | 1324.6** |
| Average BH * | 13.61** | 19.48** | 25.95** | 14.65** |
| GIUF * | 13.67** | 33.19** | 37.18** | 15.20** |
| GIWB * | 8.01** | 11.00** | 5.68** | 5.29** |
| * According to one-way ANOVA test, mean differences between quadrants are statistically significant (p<0.01). ** The mean differences against at least two other groups are statistically significant (p<0.05) | ||||
Furthermore, the quadrants significantly differ in terms of building form and geometry. Q2 and Q3 have lower building density, percent of aged buildings, and building coverage ratio (BCR) than Q1 and Q4, but they boast higher or comparable average building height and volumes. This indicates that Q1 and Q4 include areas with high population density, characterized by mid-to-low rise buildings situated close to one another and located farther away from rivers and forests within the city. On the other hand, Q2 and Q3 areas exhibit more spaced-out, taller buildings and have better access to urban green spaces and water features.
4.2. Regression analyses of LST
4.2.1. Model Selection
Multivariate regression models are employed to investigate the impact of individual urban built-up form variables on seasonal LST variations. Given the observed spatial correlation between LST and urban form indicators, spatial regression models are explored. The Queen contiguity criterion is adopted for the spatial weight matrix, defining adjacency between areas when they share a vertex or line segment. Moran's I statistics indicate significant SA in the error term of the OLS models for both grid- and block-level analyses across all four seasons. This points to the necessity of controlling for spatial autocorrelation (Table 5). The Lagrange multiplier (LM) test confirms that both lambda (λ) in the spatial error term (λWω) and rho (ρ) in the spatial lag term (ρWY) have statistically significant values (λ≠0 and ρ≠0), indicating the suitability of SEM and SLM over OLS at both grid and block scales for all seasons. To determine the relative fit of SEM and SLM, the Robust LM test is applied. Robust LM error assesses whether the spatial error term remains statistically significant (λ≠0) when the spatial lag term is included in the model (ρ≠0), while Robust LM lag assesses whether it is still appropriate to include the spatial lag term when the spatial error term is controlled for. The Robust LM test of the four-season LST models at the grid and block levels shows that both Robust LM error and lag statistics are significant, with the former higher than the latter in all cases. This suggests that the GSM that integrates both error and lag terms is preferred. Consequently, subsequent regression analysis of seasonal LST at grid and block scales is conducted using GSM.
Table 5.
Statistics for spatial regression model selection at grid and block levels.
| Unit | Statistics | Spring LST | Summer LST | Autumn LST | Winter LST |
| Grid | Moran’s I (error) | 231.6*** | 242.7*** | 252.9*** | 221.1** |
| Lagrange Multiplier (lag) | 23347.6*** | 17587.1*** | 28046.9*** | 43904.2** | |
| Robust LM (lag) | 1185.5*** | 867.7*** | 198.6*** | 2364.5** | |
| Lagrange Multiplier (error) | 53517.2*** | 58793.9*** | 63801.3*** | 48794.3** | |
| Robust LM (error) | 31355.2*** | 42074.5*** | 35953.0*** | 7254.6** | |
| Block | Moran’s I (error) | 47.8*** | 49.9*** | 53.5*** | 45.3*** |
| Lagrange Multiplier (lag) | 249.7*** | 198.4*** | 368.0*** | 1432.9*** | |
| Robust LM (lag) | 6.7*** | 16.3*** | 3.2* | 42.2*** | |
| Lagrange Multiplier (error) | 2263.0*** | 2466.2*** | 2827.1*** | 2027.0*** | |
| Robust LM (error) | 2020.0*** | 2284.2*** | 2462.3*** | 636.3*** | |
| ***: p-value <0.01, **: p-value<0.05, *: p-value<0.1 | |||||
4.2.2. Model Estimation: Grid Level
The GSM is employed to explain LST variations across all four seasons, utilizing both grid and block-level databases (Table 6 and Table 7). The spatial error and lag terms demonstrate statistical significance with substantial coefficients, affirming the suitability of spatial regression over OLS. The results indicate that the model for summer LST exhibits the highest goodness of fit statistics, including R2 and AIC, with all explanatory variables being statistically significant, followed by the spring LST model. In contrast, the winter LST model shows the lowest model fit compared to the other seasons, suggesting that winter temperatures are more challenging to explain based on urban built-up form indicators, such as vegetation, land use, building characteristics, and proximity to nature. The variance in LST is much smaller in winter than in other seasons, indicating a stronger association between urban form and heat rather than cold (Table 3 and Table 4). Summer experiences the most substantial impact from urban natural and artificial environments.
The results of the grid-based GSM estimation reveal that two urban built-up form factors play a crucial role in the city's adaptive capacity to temperature changes across the four seasons: vegetation density, represented by NDVI, and proximity to water bodies, represented by the gravity index for rivers and streams (GIWB) (Table 6). These two variables exhibit opposite coefficient directions between summer and other seasons. Higher vegetation density leads to cooler summer and warmer winter LSTs. However, a higher winter NDVI, suggesting a higher density of evergreen trees and lawns, increases LST significantly. Additionally, closer proximity to water bodies reduces LST in summer and spring but increases LST in winter and fall. This indicates that areas located near rivers, streams, and other water bodies are more likely to experience lower temperatures in summer and warmer temperatures in winter compared to areas without such proximity (within 1km). Careful management of vegetation health and water content in urban areas holds significant potential to mitigate temperature extremes and naturally regulate heat and cold. However, proximity to urban forests and mountains consistently decreases LST across all seasons. Unlike urban greenery, hilly mountains covered by forests block sunlight and trap cold air near the ground, leading to overall colder conditions. Moreover, forests contribute to increased humidity due to evaporation, intensifying the perception of cold temperatures. Seoul's urban forests, usually situated at higher altitudes, lead to temperature drops both within the forests and in adjacent areas.
Regarding other urban form variables, except for NDVI and GIWB, their effects on LST remain consistent across all seasons without flexible switching. Concerning land use types, all urban land uses increase LST in all seasons. Industrial and cultural/recreational uses tend to have a more significant impact on increasing LST, likely due to the expansive building interior spaces required for industrial production and recreational facilities. Residential and commercial uses, as well as roads and parking lots, also contribute to elevated LST in all seasons compared to non-urban land uses, such as agricultural open spaces. However, the level of land use mixture is associated with LST reductions. The entropy index, representing land use diversity, shows that LST is likely to decrease as the land use mix increases in all seasons. Increasing land use diversity at a compact scale (100m×100m) may help reduce LST in summer and spring but may not be as favorable in fall and winter.
Regarding building morphology, two- and three-dimensional factors exert opposing impacts on LST. Horizontal expansion of building space increases LST in all seasons. The count of buildings is positively associated with higher LST. A higher BCR, indicating less open space and limited spacing between buildings, also leads to increased LST in all seasons. Moreover, an increased number of buildings aged over 35 years results in a further increase in LST, possibly due to heat-prone materials and designs. Conversely, vertical expansion of buildings consistently reduces LST across seasons, with a more significant decrease observed in warmer seasons. A higher FAR and TFA, representing larger building floors and volumes, and greater building height, all contribute to a significant decrease in LST, possibly because taller buildings cast long shadows on streets and surrounding areas, blocking sunlight. The effects of building morphology on LST remain consistent throughout all seasons.
Table 6.
General spatial model (GSM) estimation results at the grid level (N=34,135).
| Variable | Spring LST |
Summer LST | Autumn LST | Winter LST |
|
| Constant | 2.0475*** | 11.759*** | 1.4901*** | -3.4028*** | |
| NDVI | 3.5077*** | -3.6698*** | 4.0788*** | 9.1573*** | |
| Albedo | 0.1341*** | 0.0573*** | 0.1316*** | 0.1714*** | |
| Land use type proportion |
Residential | 0.0005 | 0.0093*** | 0.0060*** | 0.0028*** |
| Commercial | 0.0065*** | 0.0153*** | 0.0071*** | 0.0036*** | |
| Industrial | 0.0186*** | 0.0340*** | 0.0159*** | 0.0067*** | |
| Cultural & Recreational | 0.0193*** | 0.0303*** | 0.0115*** | 0.0076*** | |
| Transport | 0.0031*** | 0.0101*** | 0.0073*** | 0.0062*** | |
| Public | 0.0071*** | 0.0184*** | 0.0064*** | 0.0020*** | |
| Land use mix | Entropy Index | -0.5538*** | -0.2345*** | -0.2339*** | -0.2575*** |
| Building 2-D form |
Count of buildings | 0.0072*** | 0.0100*** | 0.0050*** | 0.0035*** |
| % of old buildings (+35 years) | 0.0017*** | 0.0032*** | 0.0009*** | 0.0006*** | |
| Average building coverage ratio | 0.0034*** | 0.0051*** | 0.0013*** | 0.0008*** | |
| Building 3-D form |
Average floor area ratio | -0.0004*** | -0.0006*** | -0.0001*** | -0.0001 |
| Average total floor area | -1.0e-06** | -1.0e-06** | -2.0e-06*** | -2.0e-06*** | |
| Average building height | -0.0039*** | -0.0052*** | -0.0005** | -0.0003 | |
| Natural area |
Gravity index for urban forests | -0.0018*** | -0.0113*** | -0.0022*** | -0.0030*** |
| Gravity index for water bodies | -0.0002** | -0.0018*** | 0.0001* | 0.0009*** | |
| Rho (ρ) | 0.777*** | 0.685*** | 0.701*** | 0.702*** | |
| Lambda (λ) | 0.647*** | 0.769*** | 0.748*** | 0.662*** | |
| Adj. R2 | 0.892 | 0.923 | 0.857 | 0.841 | |
| Std. Err. | 0.54 | 0.66 | 0.41 | 0.44 | |
| AIC | 37,325 | 51,139 | 19,431 | 23,078 | |
| ***: p-value <0.01, **: p-value<0.05, *: p-value<0.1 | |||||
4.2.3. Model Estimation: Block Level
The R² values of the GSM models for the block-based approach indicate a lower explanatory power compared to the grid-based models. This difference is attributed to the smaller level of spatial autocorrelation observed in the block-based data. Street blocks, being larger in size and enclosed by roads, experience reduced interaction with neighboring blocks, leading to lower spatial autocorrelation. Despite this, the coefficient signs and relative magnitudes of the individual variables in both the block- and grid-based approaches produce similar results. This suggests that grid-based data processing does not lead to distorted results compared to zonal approaches like street blocks. Hence, the choice of spatial unit of analysis does not significantly bias the analysis of LST.
Table 7.
General spatial model (GSM) estimation results at the block level (N=4,553) .
| Variable | Spring LST |
Summer LST | Autumn LST | Winter LST |
|
| Constant | 6.6525*** | 21.347*** | 4.0591*** | -6.499*** | |
| NDVI | 2.9606*** | -5.3722*** | 6.8056*** | 9.1059*** | |
| Albedo | 0.4429*** | 0.1354*** | 0.3110*** | 0.4796*** | |
| Land use type proportion |
Residential | 0.0006*** | 0.0179*** | 0.0104*** | 0.0061*** |
| Commercial | 0.0123*** | 0.0291*** | 0.0160*** | 0.0095*** | |
| Industrial | 0.0420*** | 0.0972*** | 0.0394*** | 0.0160*** | |
| Cultural & Recreational | 0.0463*** | 0.0651*** | 0.0226*** | 0.0192*** | |
| Transport | 0.0029*** | 0.0212*** | 0.0114*** | 0.0097*** | |
| Public | 0.0052* | 0.0407*** | 0.0066*** | -0.0071*** | |
| Land use mix | Entropy Index | -0.4084*** | 0.1690 | -0.1940** | -0.1257 |
| Building 2-D form |
Building density (100m2) | 0.0169*** | 0.0268*** | 0.0094*** | 0.0060*** |
| % of old buildings (+35 years) | 0.0046*** | 0.0074*** | 0.0009** | 0.0003 | |
| Average building coverage ratio | 0.0044*** | 0.0044*** | 0.0019*** | 0.0010 | |
| Building 3-D form |
Average floor area ratio | -0.0007*** | -0.0010*** | -0.0002 | 1.0e-05 |
| Average total floor area | 4.0e-06*** | 4.0e-06*** | 0.000 | -1.0e-06 | |
| Average building height | -0.0083*** | -0.0108*** | -0.0023*** | -0.0029*** | |
| Natural area |
Gravity index for urban forests | -0.0005* | -0.0059*** | -0.0016*** | -0.0021*** |
| Gravity index for water bodies | 0.0013 | -0.0044*** | 0.0025*** | 0.0075*** | |
| Rho (ρ) | 0.388*** | 0.381*** | 0.323*** | 0.259*** | |
| Lambda (λ) | 0.407*** | 0.439*** | 0.539*** | 0.494*** | |
| Adj. R2 | 0.731 | 0.826 | 0.691 | 0.638 | |
| Std. Err. | 0.61 | 0.75 | 0.45 | 0.47 | |
| AIC | 5,655 | 7,664 | 2,962 | 3,312 | |
| ***: p-value <0.01, **: p-value<0.05, *: p-value<0.1 | |||||
In most cases, the grid- and block-based analyses yield similar findings, particularly for variables related to vegetation density and proximity to large water bodies, which help areas mitigate temperature extremes by reducing LST in warm seasons while increasing LST in cold months. However, there are differences in the results, particularly concerning variables related to building morphology. In the block-based results, the LST effects of several building-related variables become insignificant for fall and winter, with only building density and height remaining significant for LST. Higher building density leads to elevated LST, while increased average building height reduces LST consistently across all seasons.
Another disparity between the grid- and block-based results involves the sign of TFA, which switches to positive in summer, while it remains negative in the grid-based analysis. This discrepancy can be explained by the fact that block-level calculations of TFA capture the net effect of gross building floor area, incorporating shade casting, wind channeling, and thermal mass effects of the buildings within blocks. On the other hand, grid-level analysis involves the truncation of building mass into two or more grid cells, making it challenging for a single cell to capture all potential effects of those buildings. As a result, different cells may reflect different influences of building volume on LST. The block-level analysis, which conserves building shape without truncation, suggests that the net effect of building volume is likely to increase LST rather than decrease it, although this effect is only valid for spring and summer.
Overall, the block-based analysis reveals a smaller number of significant variables compared to the grid-based counterpart. This may be due to local variations in LST attributable to urban form geometry, which are likely averaged out with block-level calculations that are better suited to identify the net effect of urban form.
5. Discussion
The seasonal variations of temperature present a challenge for climate change adaptation, particularly in regions with four distinct seasons. This study investigates the relationship between the spatial variations of urban Land Surface Temperature (LST) during the four seasons and urban built-up form indicators in Seoul, South Korea. Urban greenery, land use types, 2D and 3D building geometry, and access to natural areas are quantified and analyzed to assess their influence on LST across the four seasons and to compare results between grid-based and street-block-based approaches.
The LST quadrant analysis identifies communities experiencing different heat and cold conditions between summer and winter. While some communities consistently remain warmer (Q1) or colder (Q3) than others, others enjoy favorable thermal conditions with cool summers and moderate winter temperatures (Q2). However, this favorable condition is spatially unevenly distributed, predominantly clustering within affluent residential districts. Conversely, areas characterized by hot summers and cold winters (Q4) tend to be spatially concentrated within lower-income residential districts, indicating that communities at thermal risk are exposed to both heat and cold. Policy interventions targeting extreme heat and cold can contribute to improving environmental justice, as strategies focusing solely on warming or cooling may not effectively address seasonal thermal vulnerability.
The quadrants exhibit different levels of vegetation and building density, indicating their significance in the seasonal adaptation of the thermal environment. Building upon these findings, spatial regression analyses are conducted to assess the individual effects of the urban built-up form variables. The estimated coefficients confirm the significance of all variables, most of which contribute to increasing LST, particularly in summer. LST reductions are only observed with increasing vegetation density and access to water bodies, land use mix, and building height. The first two variables are the only ones that adapt flexibly across the four seasons, helping to mitigate heat and cold shocks.
Building morphology has a significant impact on LST and these effects remain consistent across seasons. It is crucial to distinguish between 2D and 3D variables when analyzing building morphology. A larger ground coverage of buildings is associated with increased LST, while increasing building height has a counteractive effect, leading to LST reduction. This contrasting interaction of building geometry with LST can be attributed to the fact that the 2D volume of buildings is closely linked to thermal mass heat absorption and reduction of green space, whereas the 3D rise of buildings contributes to shade and wind funneling, often referred to as the 'urban canyon' effect. Taller buildings cast shadows and create wind channels that direct cold air through the streets, resulting in increased wind speeds and cooler temperatures compared to open areas with fewer obstructions to the wind flow.
Manipulating building form can influence LST, with its effects remaining consistent across seasons. Surface warming can be mitigated by increasing open and green spaces, while reducing vertical building growth and implementing vegetation can alleviate frigid surface climates. Nature-based solutions like blue-green infrastructure show great potential in mitigating temperature extremes and shocks, surpassing building modification and land use mix, which may only contribute to warming or cooling effects. Tree canopies and vegetation offer multiple ecosystem services, including shading and evapotranspiration during summer, and acting as wind shields while enabling relatively more sunlight during winter.
The findings from both grid- and block-based approaches yield consistent results, providing empirical evidence that the choice of spatial unit for LST analysis seldom introduces biases in a seasonal cycle. When selecting the analysis unit, one should carefully consider the strengths and limitations of each approach. Grid-based methods reduce data distortion and processing effort due to the widespread use of raster-format thermal infrared data. The uniform grid cell size helps avoid concerns related to averaging out local variations and other potential Modifiable Areal Unit Problems (MAUP). On the other hand, block-based approaches facilitate the integration of thermal data with socioeconomic databases, typically available in lattice format for administrative areas. In both methods, significant SA is detected. To assess the unbiased effects of the variables considered, spatial regression models or other analytical measures must be employed to control this SA.
The study offers valuable insights for policy interventions in urban planning and design aimed at enhancing adaptation to extreme temperatures. First, incorporating urban greenery, such as evergreen trees, gardens, and hedges, facilitates flexible adaptation to both hotter and colder climates. Second, urban design strategies that provide greater public access to blue elements, including rivers, canals, ponds, wetlands, and lakes, present rare opportunities for improving seasonal temperature adaptation. Last, while increasing compact mixed-use developments can help reduce LST, it is crucial to ensure adequate provision of green and blue spaces to protect against cold weather conditions.
This study has several limitations. First, the thermal data used in this study are LST readings observed at 11:30 am for all seasons. Further research is needed to investigate the applicability of the estimated variables to spatial LST variations at other times before and after 11:30 am. Additionally, considering the impacts of these variables in relation to air and mean radiant temperatures affecting human thermal comfort is essential. Second, due to the unavailability of building-related data for each individual building, finer spatial-scale building geometry calculations, such as SVF, orientation, and variance in building height, were not possible. These aspects could provide further insight into the local shift of LST in response to the built-up environment. Third, this study does not account for artificial heat emissions released by human activities, such as transport, heating, and production, which have been reported as significant factors affecting LST in prior research. Each aspect of building form can influence different sources of waste heat emissions, directly or indirectly. For example, building density predicts transportation activities, directly impacting vehicle heat emissions, while it also indirectly affects building heat release. This anthropogenic dimension requires further research.
6. Conclusions
Climate change will cause temperatures to rise, resulting in more extreme weather events like heat waves and cold spells. Urban planning is crucial for improving cities' and communities' ability to adapt to these temperature variations across seasons. This study investigates the relationship between urban temperature fluctuations and urban morphology throughout the four seasons in Seoul, South Korea. Using quadrant and statistical analyses, the research identifies built environmental factors that influence the moderation of LST in different seasons. Factors such as vegetation density, land use patterns, albedo, and building forms (both two- and three-dimensional) are considered, along with spatially discounted effects of urban forests and rivers. The study finds spatial segregation between areas with high LST adaptability (cooler summers and warmer winters) and those with LST vulnerability (hotter summers and colder winters), with significant differences in vegetation and building forms. The analysis shows that higher vegetation density and proximity to water bodies play a key role in moderating LST, leading to cooler summers and warmer winters. Building characteristics have a rigid impact on LST across all seasons, implying that buildings’ planar expansion contributes to higher LST, and their vertical expansion contributes to reducing it. These findings apply to both grid- and block-level analyses, highlighting the natural environment's flexible role in moderating urban temperatures.
| 1 | Korea Meteorological Administration (KMA) weather history: https://www.weather.go.kr/w/obs-climate/land/past-obs/obs-by-day.do
|
References
- Adilkhanova, I.; Santamouris, M.; Yun, G.Y. Coupling urban climate modeling and city-scale building energy simulations with the statistical analysis: Climate and energy implications of high albedo materials in Seoul. Energy Build. 2023, 290, 113092. [Google Scholar] [CrossRef]
- Alavipanah, S.; Schreyer, J.; Haase, D.; Lakes, T.; Qureshi, S. The effect of multi-dimensional indicators on urban thermal conditions. J. Clean. Prod. 2018, 177, 115–123. [Google Scholar] [CrossRef]
- Anselin, L. Exploring spatial data with GeoDaTM: A workbook. Center for spatially integrated social science 2005, 165–223. [Google Scholar]
- Baek, J.; Kim, S.; Kang, D.; Ko, A.; Aida, A.; Choi, J.; Park, C. Prediction of Micro-climate Impact by Floor Height Change Scenarios in Housing Renewal Site: Focusing on the Temperature, Particulate Matter (PM10), Fine Particulate Matter (PM2. 5). Journal of Korea Planning Association 2022, 57, 124–137. [Google Scholar] [CrossRef]
- Boeing, G. Measuring the complexity of urban form and design. Urban Des. Int. 2018, 23, 281–292. [Google Scholar] [CrossRef]
- Cai, Z.; Han, G.; Chen, M. Do water bodies play an important role in the relationship between urban form and land surface temperature? Sustainable Cities and Society 2018, 39, 487–498. [Google Scholar]
- Chen, Y.; Yang, J.; Yu, W.; Ren, J.; Xiao, X.; Xia, J.C. Relationship between urban spatial form and seasonal land surface temperature under different grid scales. Sustain. Cities Soc. 2023, 89, 104374. [Google Scholar] [CrossRef]
- Choi, Y.; Kim, J. & Lim, U. An analysis on the spatial patterns of heat wave vulnerable areas and adaptive capacity vulnerable areas in Seoul. J. Korea Plan. Assoc. 2018, 53, 87–107. [Google Scholar] [CrossRef]
- Chun, B.; Guldmann, J.M. Impact of greening on the urban heat island: Seasonal variations and mitigation strategies. Computers, Environment and Urban Systems 2018, 71, 165–176. [Google Scholar] [CrossRef]
- Cureau, R.J.; Pigliautile, I. and Pisello, A.L. Seasonal and diurnal variability of a water body's effects on the urban microclimate in a coastal city in Italy. Urban Clim. 2023, 49, 101437. [Google Scholar] [CrossRef]
- Dai, Z.; Guldmann, J.M.; Hu, Y. Spatial regression models of park and land-use impacts on the urban heat island in central Beijing. Sci. Total Environ. 2018, 626, 1136–1147. [Google Scholar] [CrossRef]
- Fan, C.; Que, X.; Wang, Z.; Ma, X. Land Cover Impacts on Surface Temperatures: Evaluation and Application of a Novel Spatiotemporal Weighted Regression Approach. ISPRS Int. J. Geo-Inf. 2023, 12, 151. [Google Scholar] [CrossRef]
- Firozjaei, M.K.; Sedighi, A.; Mijani, N.; Kazemi, Y.; Amiraslani, F. Seasonal and daily effects of the sea on the surface urban heat island intensity: A case study of cities in the Caspian Sea Plain. Urban Clim. 2023, 51, 101603. [Google Scholar] [CrossRef]
- Ge, X.; Mauree, D.; Castello, R.; Scartezzini, J.L. Spatio-temporal relationship between land cover and land surface temperature in urban areas: A case study in Geneva and Paris. ISPRS Int. J. Geo-Inf. 2020, 9, 593. [Google Scholar] [CrossRef]
- Guo, F.; Schlink, U.; Wu, W.; Hu, D.; Sun, J. (2023). Scale-dependent and season-dependent impacts of 2D/3D building morphology on land surface temperature. Sustainable Cities and Society, 104788.
- Han, D.; An, H.; Wang, F.; Xu, X.; Qiao, Z.; Wang, M. . & Liu, Y. Understanding seasonal contributions of urban morphology to thermal environment based on boosted regression tree approach. Build. Environ. 2022, 226, 109770. [Google Scholar]
- Han, S.; Hou, H.; Estoque, R.C.; Zheng, Y.; Shen, C.; Murayama, Y.; Pan, J.; Wang, B. and Hu, T. Seasonal effects of urban morphology on land surface temperature in a three-dimensional perspective: A case study in Hangzhou, China. Build. Environ. 2023, 228, 109913. [Google Scholar] [CrossRef]
- HosseiniHaghighi, S.; Izadi, F.; Padsala, R.; Eicker, U. Using climate-sensitive 3D city modeling to analyze outdoor thermal comfort in urban areas. ISPRS Int. J. Geo-Inf. 2020, 9, 688. [Google Scholar] [CrossRef]
- Hu, Y.; Dai, Z.; Guldmann, J.M. Modeling the impact of 2D/3D urban indicators on the urban heat island over different seasons: A boosted regression tree approach. J. Environ. Manag. 2020, 266, 110424. [Google Scholar] [CrossRef]
- Hwang, R.L.; Lin, T.P.; Matzarakis, A. Seasonal effects of urban street shading on long-term outdoor thermal comfort. Build. Environ. 2011, 46, 863–870. [Google Scholar] [CrossRef]
- Kafy, A.A.; Shuvo, R.M.; Naim, M.N.H.; Sikdar, M.S.; Chowdhury, R.R.; Islam, M.A.; Sarker, M.H.S.; Khan, M.H.H. and Kona, M.A. Remote sensing approach to simulate the land use/land cover and seasonal land surface temperature change using machine learning algorithms in a fastest-growing megacity of Bangladesh. Remote Sens. Appl. : Soc. Environ. 2021, 21, 100463. [Google Scholar]
- Kang. C-D. Effects of urban form indicators on land prices in Seoul, Republic of Korea: An urban morphometric approach. J. Real Estate Anal. 2022, 8, 73–101. [Google Scholar] [CrossRef]
- Kim, M.; Kwon, I.; Yoo, S. A Study on the Typological Characteristics of Deteriorated Low-rise Residential Areas in Seoul. J. Korea Plan. Assoc. 2022, 57, 5–25. [Google Scholar] [CrossRef]
- KMA 2022 Extreme climate report. Korea Meteorological Administration (KMA): Daejeon, Korea, 2020.
- Li, H.; Li, Y.; Wang, T.; Wang, Z.; Gao, M.; Shen, H. (2021a). Quantifying 3D building form effects on urban land surface temperature and modeling seasonal correlation patterns. Build. Environ. 2023, 204, 108132. [Google Scholar] [CrossRef]
- Li, T.; Xu, Y.; Yao, L. Detecting urban landscape factors controlling seasonal land surface temperature: From the perspective of urban function zones. Environ. Sci. Pollut. Res. 2021, 28, 41191–41206. [Google Scholar] [CrossRef] [PubMed]
- Liang, S. Narrowband to broadband conversions of land surface albedo I: Algorithms. Remote sensing of environment 2001, 76, 213–238. [Google Scholar] [CrossRef]
- Liu, X.; Ming, Y.; Liu, Y.; Yue, W.; Han, G. Influences of landform and urban form factors on urban heat island: Comparative case study between Chengdu and Chongqing. Sci. Total Environ. 2022, 820, 153395. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Guo, X.; Jiang, J. How Urban Morphology Relates to the Urban Heat Island Effect: A Multi-Indicator Study. Sustainability 2023, 15, 10787. [Google Scholar] [CrossRef]
- Moazzam, M.F. U.; Doh, Y.H.; Lee, B.G. Impact of urbanization on land surface temperature and surface urban heat Island using optical remote sensing data: A case study of Jeju Island, Republic of Korea. Build. Environ. 2022, 222, 109368. [Google Scholar] [CrossRef]
- Park, H.; Song, J. Relationship between Flood Damage and Flood Vulnerability Focusing on Property Damage and Human Casualties. J. Korea Plan. Assoc. 2023, 58, 149–166. [Google Scholar] [CrossRef]
- Park, Y.; Guldmann, J.M.; Liu, D. Impacts of tree and building shades on the urban heat island: Combining remote sensing, 3D digital city and spatial regression approaches. Computers, Environment and Urban Systems 2021, 88, 101655. [Google Scholar] [CrossRef]
- Park, Y.; Zhao, Q.; Guldmann, J.M.; Wentz, E. (2022). Quantifying the Cumulative Cooling Effects of 3D Building and Tree Shades with High Resolution Thermal Imagery in a Hot Arid Urban Climate. Preprint.
- Peng, J.; Jia, J.; Liu, Y.; Li, H.; Wu, J. Seasonal contrast of the dominant factors for spatial distribution of land surface temperature in urban areas. Remote Sens. Environ. 2018, 215, 255–267. [Google Scholar] [CrossRef]
- Qiao, Z.; Tian, G.; Xiao, L. Diurnal and seasonal impacts of urbanization on the urban thermal environment: A case study of Beijing using MODIS data. ISPRS J. Photogramm. Remote Sens. 2013, 85, 93–101. [Google Scholar] [CrossRef]
- Shao, L.; Liao, W.; Li, P.; Luo, M.; Xiong, X.; Liu, X. Drivers of global surface urban heat islands: Surface property, climate background, and 2D/3D urban morphologies. Building and Environment 2023, 110581. [Google Scholar] [CrossRef]
- Tang, L.; Zhan, Q.; Fan, Y.; Liu, H. and Fan, Z. Exploring the impacts of greenspace spatial patterns on land surface temperature across different urban functional zones: A case study in Wuhan metropolitan area, China. Ecol. Indic. 2023, 146, 109787. [Google Scholar] [CrossRef]
- Turner, K.V.; Rogers, M.L.; Zhang, Y.; Middel, A.; Schneider, F.A.; Ocón, J.P. . &Dialesandro, J. More than surface temperature: Mitigating thermal exposure in hyper-local land system. J. Land Use Sci. 2022, 17, 79–99. [Google Scholar]
- Wang, C.; Li, Y.; Myint, S.W.; Zhao, Q.; Wentz, E.A. Impacts of spatial clustering of urban land cover on land surface temperature across Köppen climate zones in the contiguous United States. Landsc. Urban Plan. 2019, 192, 103668. [Google Scholar] [CrossRef]
- World Health Organization. (2014). Quantitative risk assessment of the effects of climate change on selected causes of death, 2030s and 2050s. World Health Organization.
- Wu, W.; Li, L.; Li, C. Seasonal variation in the effects of urban environmental factors on land surface temperature in a winter city. J. Clean. Prod. 2021, 299, 126897. [Google Scholar] [CrossRef]
- Yang, J.; Shi, Q.; Menenti, M.; Wong, M.S.; Wu, Z.; Zhao, Q.; Abbas, S. and Xu, Y. Observing the impact of urban morphology and building geometry on thermal environment by high spatial resolution thermal images. Urban Clim. 2021, 39, 100937. [Google Scholar] [CrossRef]
- Yao, L.; Li, T.; Xu, M.; Xu, Y. How the landscape features of urban green space impact seasonal land surface temperatures at a city-block-scale: An urban heat island study in Beijing, China. Urban For. Urban Green. 2020, 52, 126704. [Google Scholar] [CrossRef]
- Yu, K.; Chen, Y.; Wang, D.; Chen, Z.; Gong, A.; Li, J. Study of the seasonal effect of building shadows on urban land surface temperatures based on remote sensing data. remote sensing 2019, 11, 497. [Google Scholar] [CrossRef]
- Zhang, Z.; Luan, W.; Yang, J.; Guo, A.; Su, M.; Tian, C. The influences of 2D/3D urban morphology on land surface temperature at the block scale in Chinese megacities. Urban Clim. 2023, 49, 101553. [Google Scholar] [CrossRef]
- Zhao, L.; Li, T.; Przybysz, A.; Liu, H.; Zhang, B.; An, W. and Zhu, C. Effects of urban lakes and neighbouring green spaces on air temperature and humidity and seasonal variabilities. Sustain. Cities Soc. 2023, 91, 104438. [Google Scholar] [CrossRef]
- Zhao, Y.; Sen, S.; Susca, T.; Iaria, J.; Kubilay, A.; Gunawarden, K.; Zhou, X.; Takane, Y.; Park, Y.; Wang, X. and Rubin, A. Beating the Heat: Solution Sets for Developed Cities. 2023, Preprint.
- Zhou, W.; Cao, W.; Wu, T.; Zhang, T. The win-win interaction between integrated blue and green space on urban cooling. Sci. Total Environ. 2023, 863, 160712. [Google Scholar] [CrossRef]
- Zhu, Z.; Shen, Y.; Fu, W.; Zheng, D.; Huang, P.; Li, J.; Lan, Y.; Chen, Z.; Liu, Q.; Xu, X. and Yao, X. How does 2D and 3D of urban morphology affect the seasonal land surface temperature in Island City? A block-scale perspective. Ecol. Indic. 2023, 150, 110221. [Google Scholar] [CrossRef] [PubMed]
Figure 1.
Geographic location of the study area.
Figure 2.
Comparison of grid-based versus street-block-based units: (a) grid unit, (b) block unit.
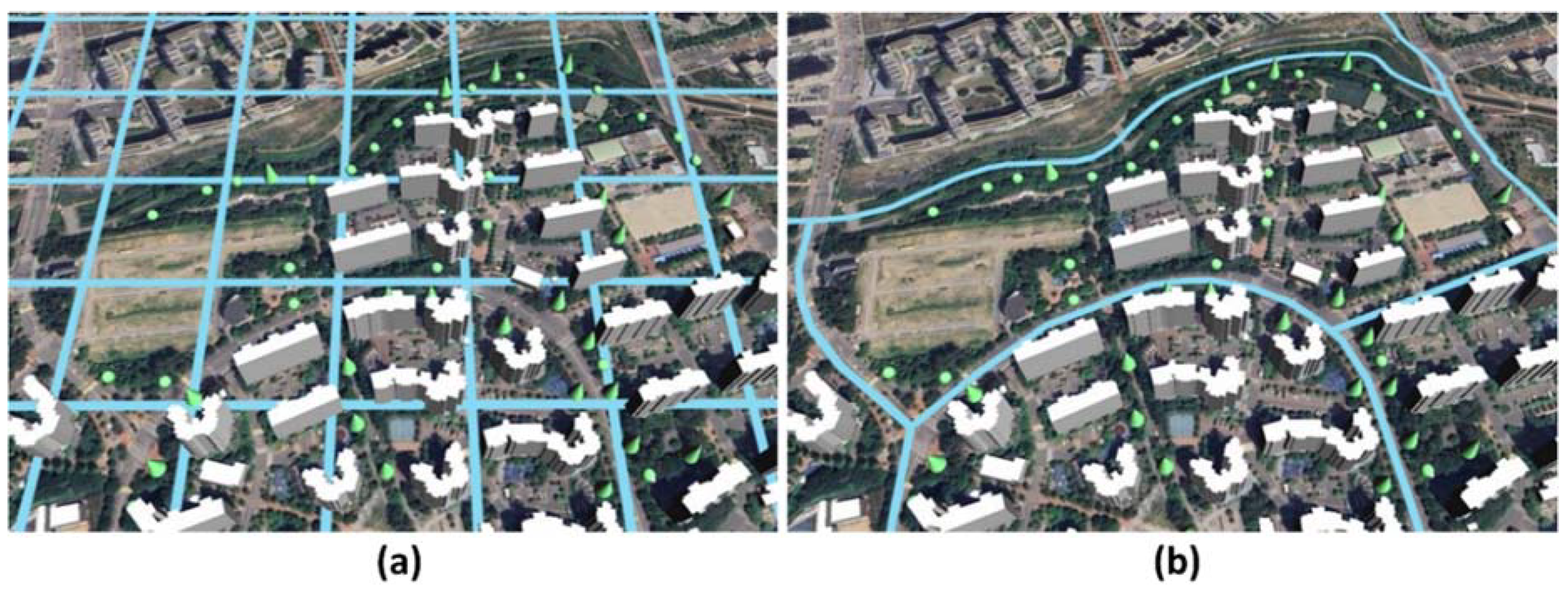
Figure 4.
Gravity index for urban forests (GIUF): (a) grid-level, (b) block-level.
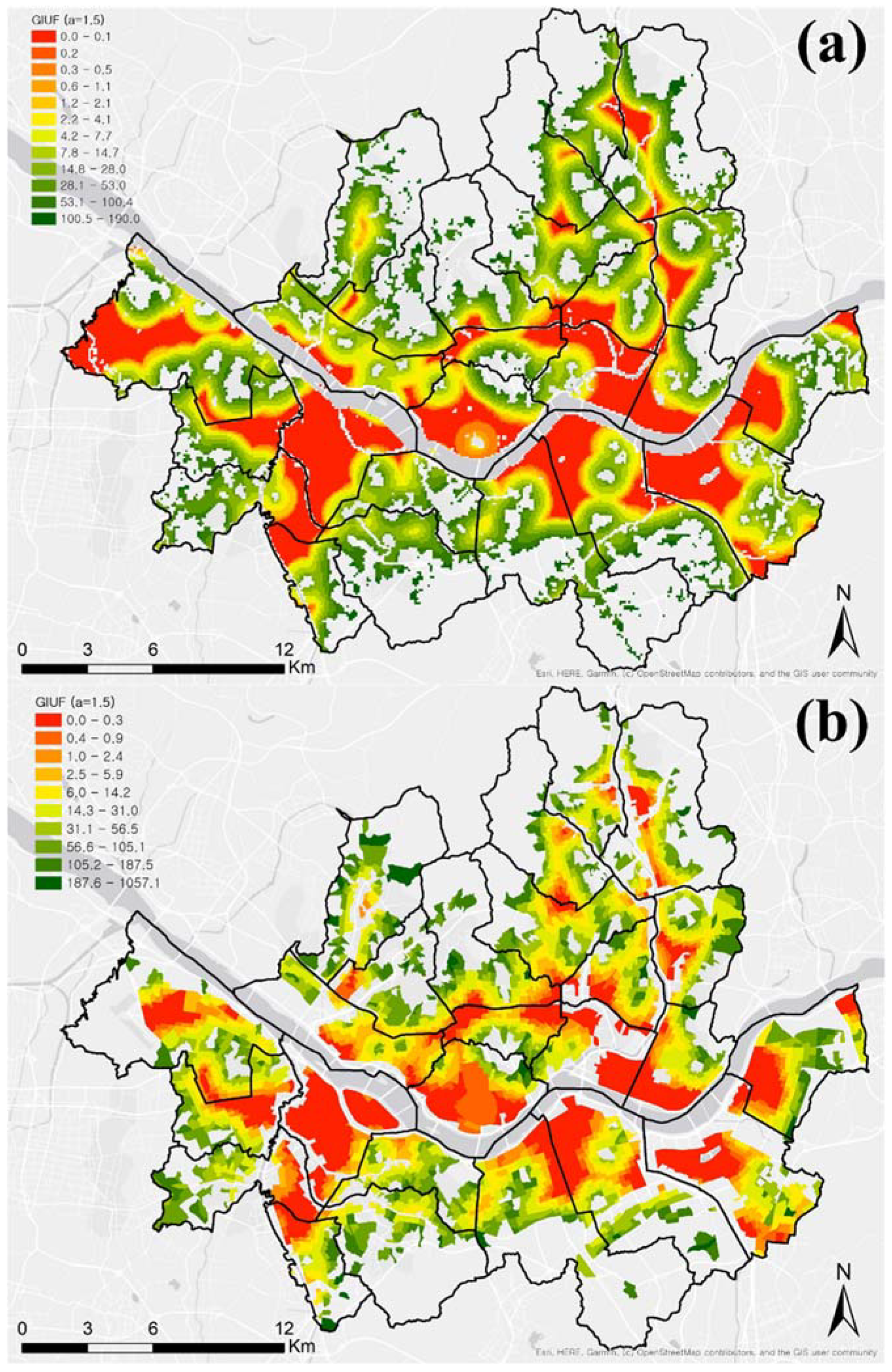
Figure 5.
Gravity index for water bodies (GIWB): (a) grid-level, (b) block-level.
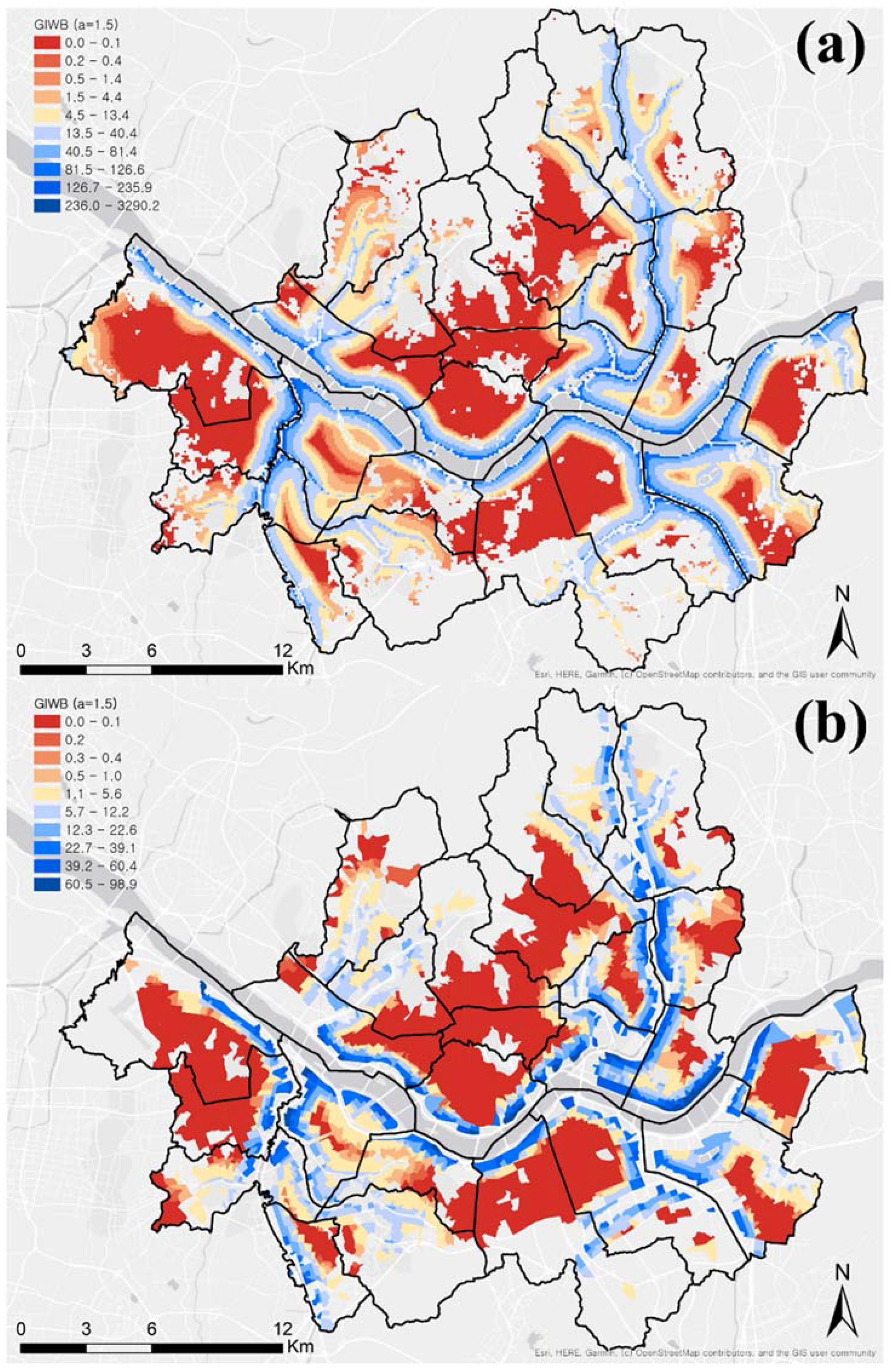
Figure 6.
Partition of four quadrants as the intersection of summer and winter LSTs.
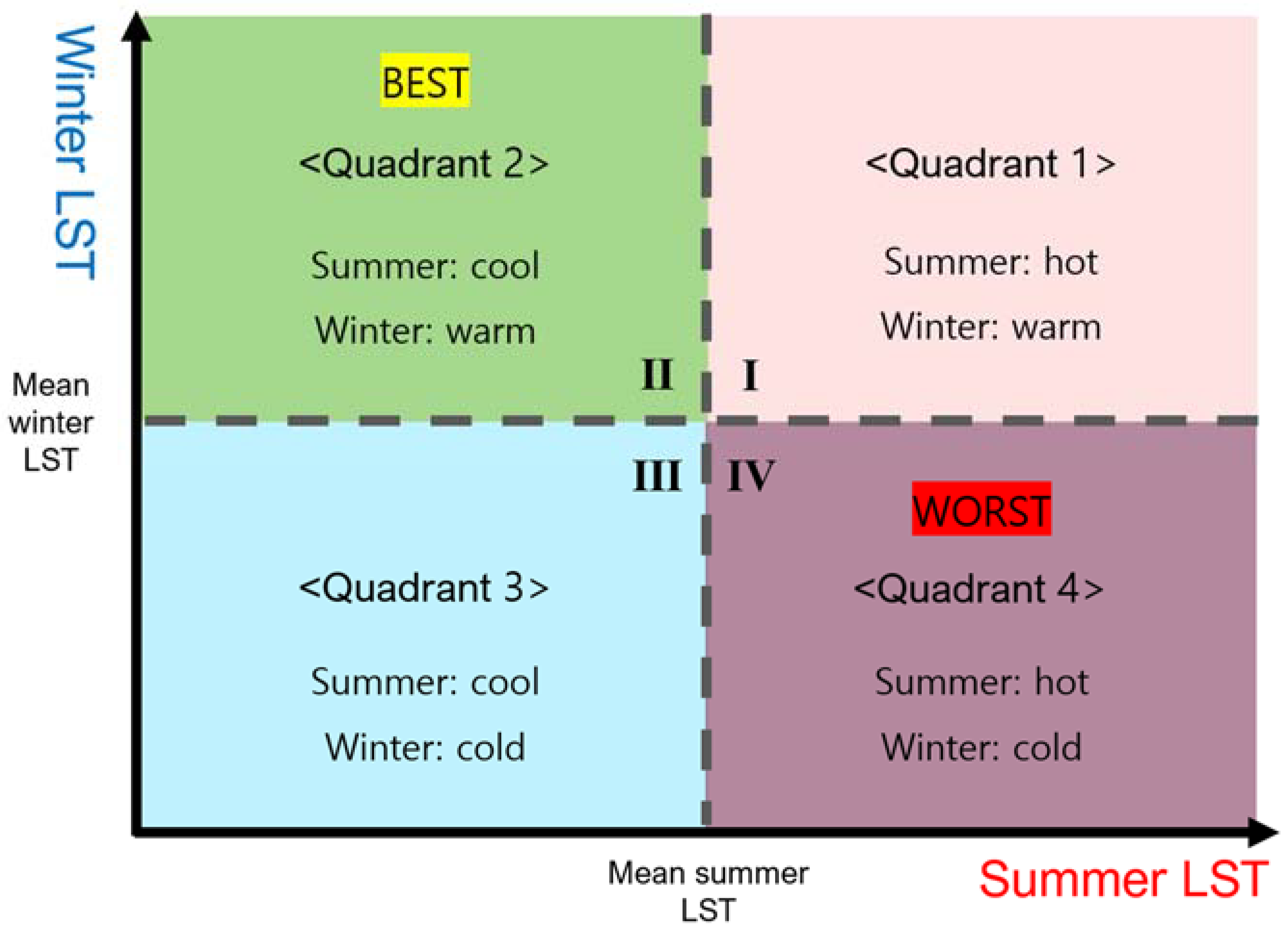
Figure 7.
Spatial distribution of the summer-winter LST quadrants in Seoul: (A) grid-cell level; (B) street-block level results.
Figure 7.
Spatial distribution of the summer-winter LST quadrants in Seoul: (A) grid-cell level; (B) street-block level results.
Table 1.
The date and time of Landsat 8 thermal infrared (TIR) image collection.
| Collection | Spring | Summer | Autumn | Winter | |
| Date | 2017.03.19 | 2017.08.26 | 2017.11.14 | 2017.01.14 | |
| Time | 11:10 AM | 11:10 AM | 11:10 AM | 11:11 AM | |
| LST (℃) |
Mean | 19.8 | 34.5 | 12.8 | -2.7 |
| Max | 35.4 | 52.0 | 21.6 | 5.0 | |
| Min | 3.9 | 18.2 | -5.9 | -18.5 | |
| AT1 (℃) |
Mean | 10.9 | 24.2 | 7.5 | -8.4 |
| Max | 18.9 | 29.2 | 11.4 | -5.4 | |
| Min | 3.2 | 19.0 | 2.9 | -10.4 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






