Prerpints.org logo
Preprint
Article

CFD Thermo-hydraulic Evaluation of Liquid Hydrogen Storage Tank with Different Insulation Thickness of Small-scale Hydrogen liquefier

This version is not peer-reviewed.

Submitted:

07 August 2023

Posted:

09 August 2023

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Accurate evaluation of thermo-fluid dynamic characteristics in tank are critically important for designing liquid hydrogen tank of small-scale hydrogen liquefier to minimize heat in-leak into the liquid and ullage. Due to the huge cost, most future liquid hydrogen storage tank designs will have to rely on predictive computational models for storage tank pressurization and heat-leak minimization. Thus, reliable on predictive numerical models to aid design process of tank design have been required. Therefore, in this study, in order to improve the storage efficiency of the small-scale hydrogen liquefier, a three-dimensional CFD model that can predict the boil-off rate and the thermo-fluid characteristics due to heat penetration has been developed. The prediction performance and accuracy of the CFD model is validated on the basis of the comparisons between its results and previous experimental data and a good agreement is obtained. To evaluate insulation performance of polyurethane foam according to thickness, the pressure change and thermo-fluid characteristics in a partially liquid hydrogen tank, subject to fixed ambient temperature and wind velocity, has been investigated numerically. Three different insulation thickness were considered to investigate not only interfacial characteristics between liquid and ullage but thermo-fluid dynamics in hydrogen storage tank for various heat-leak situation. The results indicate that as the insulation thickness becomes thinner and more heat penetration exists, natural convection by buoyancy develops stronger, so strong vortices are created near the interfacial zone by upward flow driven by buoyancy. In particular, as the amount of heat in-leak increased, wider and stronger heat accumulation was found in the top dished head area of the ullage area. In addition, it was confirmed that the CFD model developed in this study could well describe the phenomenon in which the temperature of the tank wall and the insulation mat increased at a faster rate due to faster heat transfer from the vapor and interface. In the future, the numerical model developed in this study will be used for optimizing insulation system of storage tank for small-scale hydrogen which is cost-effective and highly efficient.
Keywords: 
Subject: 
Engineering  -   Energy and Fuel Technology

1. Introduction

Liquid hydrogen has the best storage capacity per unit mass and is economical among methods for using hydrogen as fuel. [12,43]. Thus, in recent, great efforts have been made to apply liquified hydrogen tank as a fuel storage method for launch vehicle applications, subsonic transport aircraft [42], unmanned aerial vehicles [17,18] and liquid hydrogen-fueled automobile [12,16].
Although the small-scale hydrogen liquefier market is not yet active, the advent of the hydrogen economy is imminent and demand for it is rapidly increasing, so it is expected that a new market will be formed in the near future, and companies with existing hydrogen liquefaction technology can enter. However, when production of small-capacity liquid hydrogen is required, CAPEX & OPEX are too large to apply the cycle base technology for large-scale hydrogen liquefaction, and the business feasibility falls [40]. Therefore, it is necessary to preoccupy the market through the development of a direct cooling-based small-scale hydrogen liquefier. In the design of a small-scale hydrogen liquefier, securing the insulation performance of the liquid hydrogen storage tank is very important in terms of storage and production efficiency. However, since hydrogen has a very low boiling point, it is vulnerable to heat penetration from the environment.
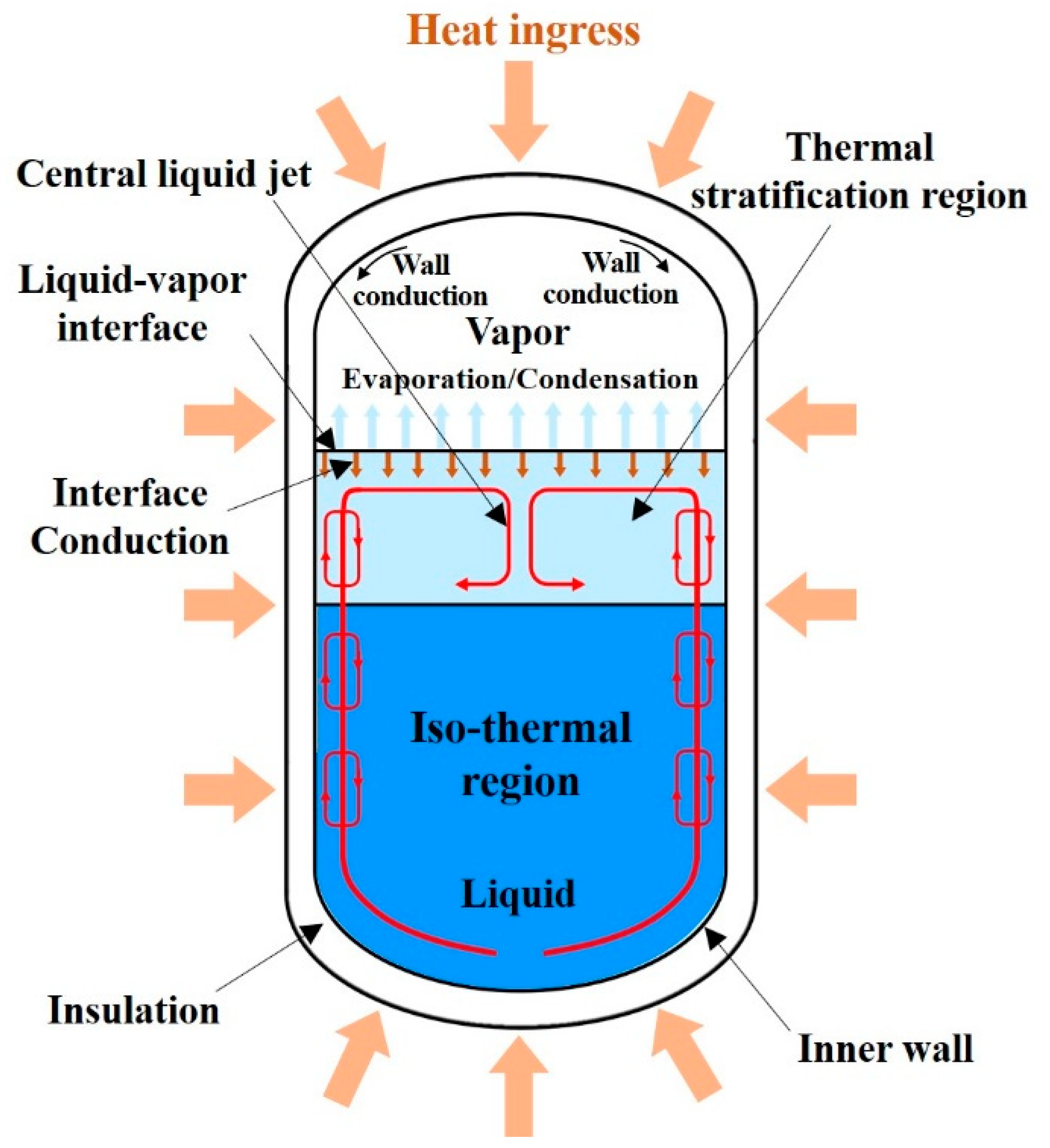
When these heat leaks penetrate the tank, the hydrogen evaporates intensively, increasing the tank pressure, causing not only serious security problems such as overpressure explosion but also serious deterioration of storage capacity of liquid hydrogen tank. It is well known that tank pressure increasing results in additional heat input to the tank because pressurization sub-cools the liquid and raises the temperature difference between liquid and vapor, increasing the axial temperature gradient near the interface which leads to high level of interfacial conduction heat flux.
This interfacial conduction heat flux also makes the liquid nearby interface warmer because of further increasing the liquid temperature. As time elapses, the axial temperature gradient in liquid called thermal stratification increases due to heat leaks-in from the environment. Fig.1 shows schematic the evolution of thermal stratification in a typical liquid hydrogen tank due to various external heat sources is shown in Fig. 1.
In the development of a high-efficiency direct-cooled small-scale hydrogen liquefier, evaporation of liquefied hydrogen by thermal stratification, which is called boil-off is a major cause of deterioration of storage efficiency as well as liquefaction efficiency. Therefore, boil-off losses control of liquid hydrogen is of significance for design of small-scale hydrogen liquefier. Thus, it is important to have prior knowledge about the pressurization and thermo-fluid characteristics inside the tank due to heat penetration through the development of a numerical model to predict the insulation efficiency and boil-off loss of the direct-cooled hydrogen liquefier [30].
In order to develop a liquefied hydrogen storage tank that is cost-effective and has high adiabatic performance, various numerical analysis models have been developed, and the reliance on computational models are ever-increasing.
Thus, reliable on predictive numerical models to aid design process of tank design have been required.
However, the physical mechanism that occurs in the liquefied hydrogen tank with heat penetration from the environment is controlled by the kinetics of the phase change and buoyancy-driven turbulent flows in the vapor and liquid phases.
Therefore, various numerical and experimental literatures have been reported so far to analyze the thermos-physical phenomena in the liquefied hydrogen tank according to heat penetration from the outside.
M. Kang [17,18] simulated thermal stratification by various heat ingresses in a conventional LNG tank using the finite element analysis(FEA) and verified the accuracy of the analysis by measuring the axial temperature distribution through experiments. The numerical results were in good agreement with the experimental values and showed that thermal stratification is strongly influenced by the thermal aspect ratio determined by the filling height of the storage tank.
On the other hand, calculating multi-dimensional N-S type governing equations using finite element method or finite difference method such as FEA is very time-consuming and expensive, so there are many limitations in terms of design time compared to experimental methods. Therefore, several thermodynamic equilibrium lumped (0-D) models [19,32,33] with varying levels of accuracy and complexity have been developed to predict the adiabatic performance and temperature distributions in partially filled liquid hydrogen tanks under various heat ingress conditions for long duration.
These 0-D models provided valuable design ideas and engineering insights for the adiabatic conditions to the designers of liquefied hydrogen storage under various conditions caused by long-term heat penetration. Panzarella [32,33] studied that the long-term pressurization of a large LH2 storage tank in microgravity by using coupling strategy in which combined lumped energy and lumped mass equations of the ullage to the Navier-stokes and energy equations in the liquid in their CFD model. Barsi and Kassemi [4] also used the coupling strategy of Panzarella and Kassemi [32] and coupled the incompressible N-S type equations based on Boussinesq approximation in the liquid to a 0-D lumped energy and mass model of the ullage. By using this lumped strategy, they describe the thermos-physical behavior of a partially filled LH2 tank in normal gravity. Liu and Li [29] developed a stratification model based on transient analytical thermodynamic lumped method to predict temporal growth of stratified layer and mass under constant wall temperature.
Recently, Joseph [15] developed a one-dimensional unsteady thermodynamic lumped model based on a software package named SINDA/FLUINT to study the thermal stratification inside a liquefied hydrogen storage tank for various insulation thickness. They calculated the ullage part by 1-D axial discretization , while the liquid part was discretized in the radial direction by dividing it into three parts. The accuracy of the 1-D model for simulating boil-off and thermo-fluid characteristics in the tank was validated by open literature and a good agreement was shown.
With the help of highly efficient numerical techniques and advanced computational resources, CFD approaches have been actively used since the early 2000s to study thermal stratification and boil-off losses in cryogenic storage tanks.
Adnani and Jennings [3] used a commercial CFD software FLUENT to simulate the temporal variation of pressure and pressurant gas requirement in liquid hydrogen tank. In this model, liquid phase inside the tank was not modeled, and treated as stationary liquid with constant temperature.
Meanwhile, multi-dimensional CFD analysis has been performed to study the effect of geometric variation of cryogenic tanks on the transient natural convection in cryogenic tank [34]. They pointed out that the interfacial heat and mass transfer strongly depend on the liquid-solid contact area in the tank. However, numerical modeling of interfacial heat and mass transfer at free surface due to thermal stratification, which is essential to reach this conclusion, was not considered in this study.
From the results of the previous literature mentioned above, the most important work in numerical analysis to achieve heat leak minimization due to heat penetration of the cryogenic storage tank is how to model the interfacial heat and mass transfer phenomenon at the free surface.
Recently, numerous previous studies [6,11,12,21,23] have actively investigated the relationship between buoyancy-driven turbulent flow and boil-off loss due to heat leaks using a CFD model that considers heat and mass transfer on the free surface of a liquefied hydrogen storage tank.
Numerical models that CFD technique have been widely adopted for describing the vapor-liquid interface phase change at free surface until recently are Volume of Fluid (VOF) [6,12,23,24,44] and a sharp interface model based on Schrage molecular mass transfer model [21,36].
In the meantime, the CFD model based on VOF has been used to investigate the effect of variations in geometric shapes such as the aspect ratio of a liquefied hydrogen storage tank [24] and changes in the position of baffles to suppress sloshing on boil-off rate and buoyancy-driven turbulent flow in the tank [11].
In very recent, the scope of application of the CFD model based on VOF has been extended to investigate the effect of the excitation of outside the cryogenic fuel tank on the sloshing pattern of liquid and pressurization of the ullage area [10,22].
he CFD model based on Schrage molecular mass transfer model was also actively used in the study of thermal stratification by heat leaks in liquefied hydrogen tanks. However, in order to use this model accurately, the model's coefficients must be calibrated by a trial-and-error method [21,48], and the difficulty of relieving the numerical stiffness must be overcome [52]. In addition, this model has a disadvantage that the sloshing effect cannot be considered.
Multi-layer insulation (MLI), which has excellent thermal insulation properties, is lightweight and environmentally friendly, has been extensively applied to LH2 tanks.
Hence, a large number of experimental and numerical studies under various ambient conditions have been performed and computational models for predicting the adiabatic and thermal performance of MLI have been reported in the literature [20,26,28,37]. In addition, since the insulation performance of MLI and the degree of vacuum are very closely related, Li [25] conducted numerical and experimental studies on thermal stratification inside the tank according to the degree of vacuum and reported that vacuum loss caused rapid thermal stratification. However, most of the aforementioned investigations used simple empirical models to evaluate only the insulating performance of MLI.
In the design of the insulation of the LH2 tank, the most recent focus has been on the thickness of the insulation.
Particularly, the one-dimensional thermodynamic lumped model was recently applied to investigate the effect of insulation thickness on thermal and adiabatic performance under fixed ambient temperature and wind velocity [15]. In their model, ullage space was considered temporally varying and axially one-dimensional. However, it was reported that the average temperature of each computational element overestimates the heat transfer from the ullage to the liquid at the interface due to one-dimensional limitations [44]. Additionally, prediction performance of this model was not validated in terms of self-pressurization in the tank, which was affected by the fluid dynamics of the buoyancy-driven turbulent flows in the liquid and vapor phases [43]. Therefore, the existing 0-D and 1-D models do not appear to be valid for predicting the effect of the cryogenic tank's thermal insulation performance on thermo-fluid characteristics in the liquid and vapor as well as self-pressurization. Furthermore, the above-mentioned thermo-fluid characteristics can only be displayed by the CFD model with interfacial treatments such as VOF and shape interface model with Schrage equation.
In this study, in order to develop a more compact and cost-effective small hydrogen liquefier (1.3liter/hr), a numerical analysis model was developed that can accurately evaluate the insulation performance of various insulation materials. It is well known that insulation performance is a very important design factor in terms of production efficiency and storage performance through boil-off prevention in the design of small hydrogen liquefiers.
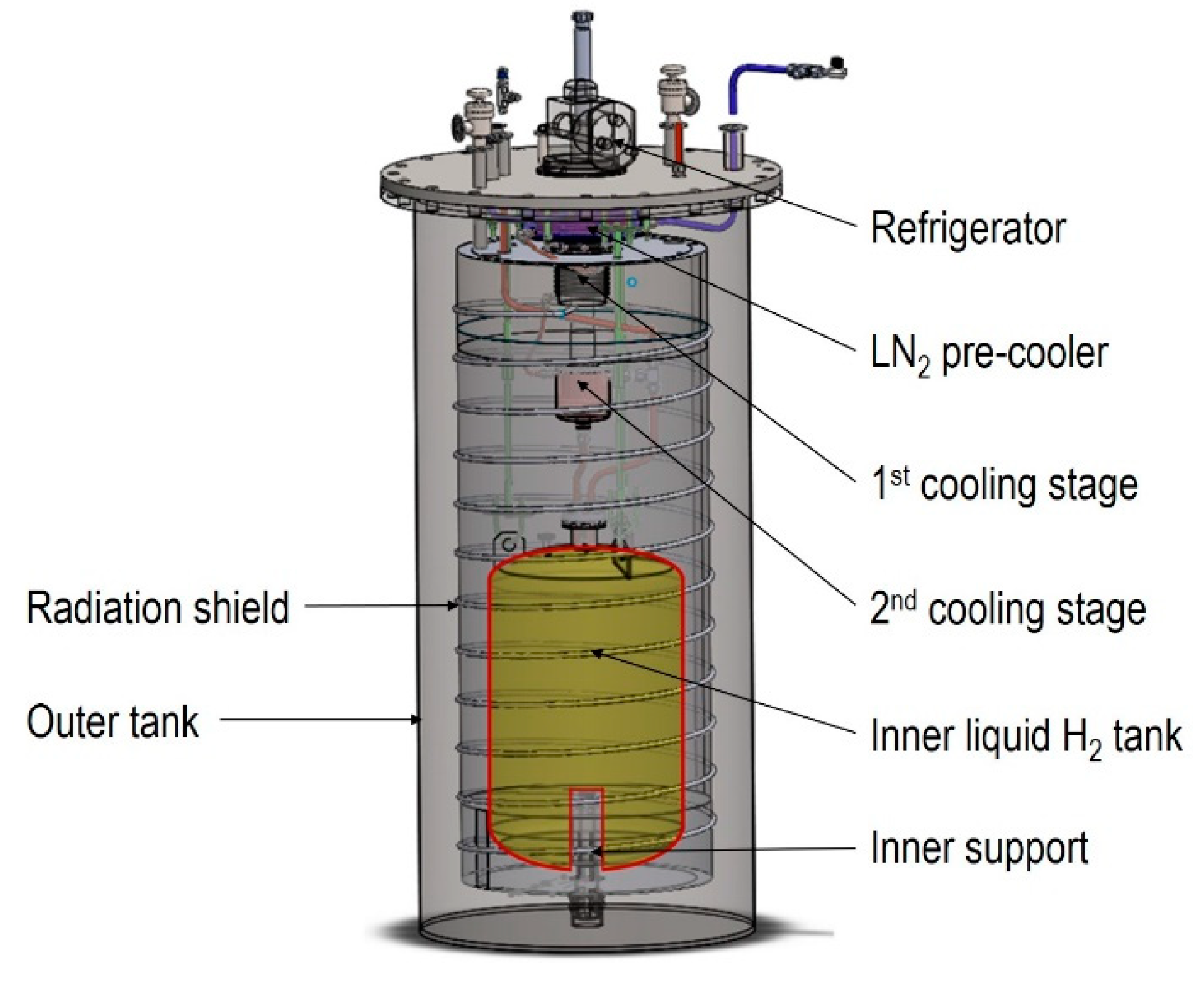
Figure 2 shows the small-scale hydrogen liquefier system considered in this study. As shown in the figure, this small-scale hydrogen liquefier is designed in such a way that the cryocooler with 1st and 2nd cooling stage, LN2 (Liquid Nitrogen) precooler, inner tank, and radiation shield are installed inside the outer tank. In this liquefier, gaseous hydrogen supplied to the liquefier is cooled to 77K by passing through the LN2 precooler and then liquefied at 20K, 1atm while passing through the 1st cooling stage and 2nd cooling stage directly in contact with the cold head of cryocooler and stored in the inner liquid hydrogen storage tank. In addition, the radiation shield prevents radiant heat emitted from the outside. The main parts described above (LN2 precooler, two stage cryocooler, inner tank) are covered with multi-layer thin film insulation (25 layers/inch) to prevent heat leakage.
Preprints 81739 g001
Figure 1. Self-pressurization subject to a liquid and vapor heat flu.
Figure 1. Self-pressurization subject to a liquid and vapor heat flu.
Preprints 81739 g001
In the case of liquefied hydrogen storage, MLI has been applied, which causes the price of small-scale liquefiers to rise. In the case of MLI, it has very good insulation performance, but as shown in Figure 2, since the surroundings must be kept in a vacuum, an outer tank must be installed, requiring high installation costs and a large space. Therefore, it is necessary to develop a cost-effective, high-efficiency insulation material comparable to MLI that does not require an outer tank and radiation shield, and to develop a three-dimensional CFD model that can evaluate the insulation and thermodynamic performance of various insulation materials.
Therefore, in this study, a three-dimensional CFD model with interfacial treatment based on the VOF was developed that can predict the thermo-fluid characteristics of liquid and ullage hydrogen stored inside the tank as well as the insulation performance of various materials applied to the liquefied hydrogen tank.
As mentioned above, the CFD approach has been heavily applied in the study of thermal stratification and self-pressurization of LH2 tanks, there is no previously published literature on a comprehensive investigation of the three-dimensional effect of insulation thickness on turbulence at not only interface but also liquid and ullage, thermal stratification and tank pressurization by a CFD approach.
Therefore, in this study, the effect of changes in the thickness of polyurethane insulation on interfacial thermo-fluid dynamics, mass transfer, and temporal variation of pressure in 50 liter liquid hydrogen storage tank has been focused in detail using the three-dimensional CFD model. The scenario used in this study is an extreme condition in the atmosphere with mild wind breezing.

2. Numerical Modeling

In this section, the main features of the three-dimensional CFD model with two-phase VOF models for LH2 tank are presented in this section. For more detailed description of the numerical model the reference can be made to the open literatures [16,21,23,52].

2.1. Modeling description

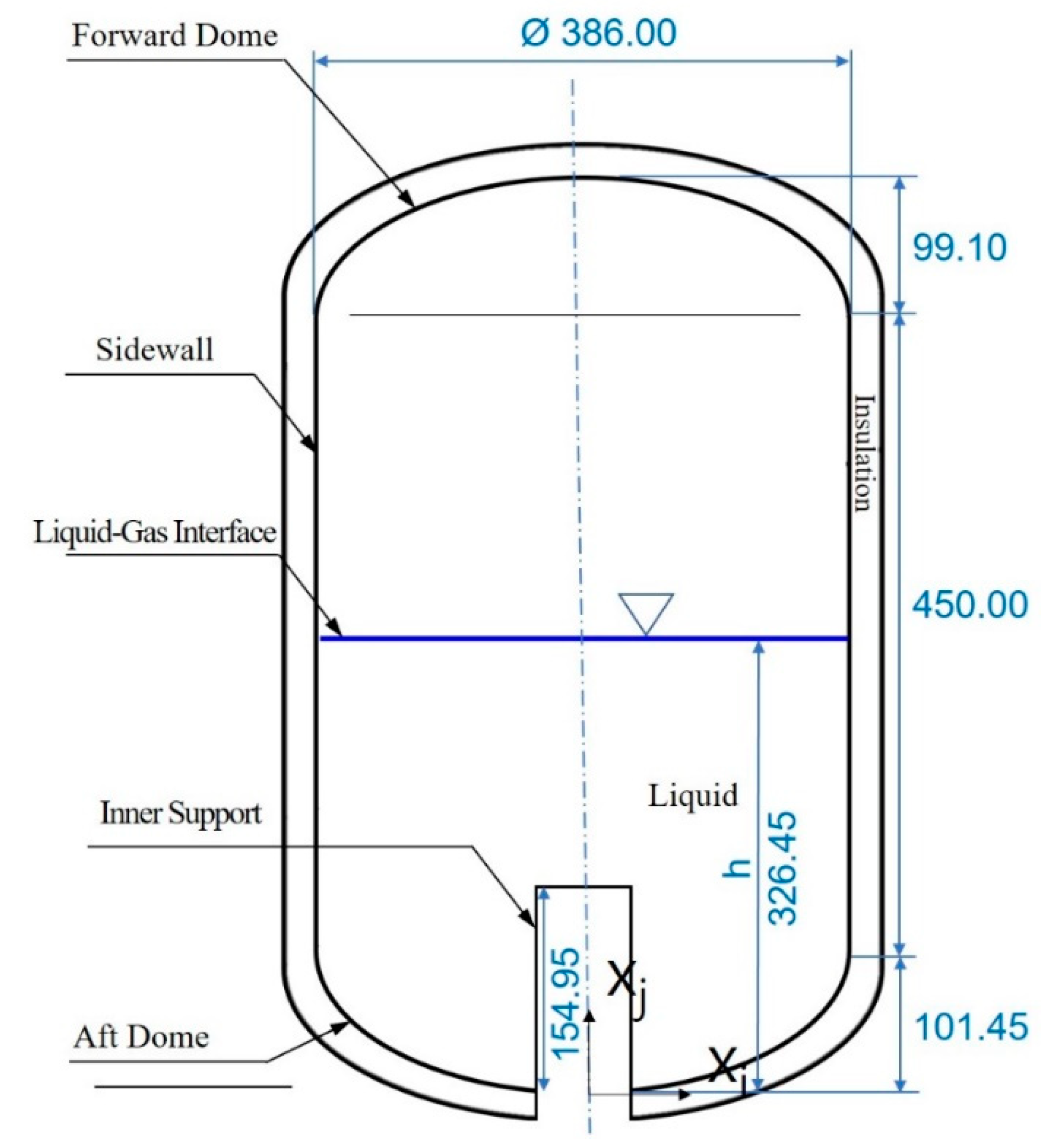
Figure 3 shows the schematic diagram of a LH2 tank(50liter) for the small-scale liquefier. The tank consists of a cylinder with a diameter of 386 mm and a height of 450 mm and two dome heads with a height of 99.1 mm and 101.45mm, respectively. A sheet of 2219 aluminum with a thickness of 3 mm is used to construct the tank walls.
Additionally, there is a cylindrical groove under the tank for inserting the support which can guarantee the stability of storage tank entirety and can be related to whole equipment safely and steadily run.
To reduce the heat ingress from the environment, various foam insulation thickness of 10mm, 20mm, and 30mm are applied to the surface of the tank. The reason for the parametric study using polyurethane foam as an insulation material in this study is that polyurethane foam provides a high strength-to-weight ratio and a stable insulation performance for a wide vacuum range and may be cheaper than other insulation materials and is feasible to store for a short period of time.
In the current simulation, the tank is filled to 50% of the liquid level by volume. Differing from the previous analysis [11,16,21,52], the wall heating is computed based on stable heat conduction to determine the tank wall temperature assuming external convective heat transfer with an increasingly adiabatic heat conduction tendency [24]. All of the fluid thermal properties in this study are defined as functions of temperature and corresponding ullage pressure taken from NIST [27], and updated with time. Since the foam material has low thermal conductivity, a large temperature gradient exists in the thermal insulation layer. Hence a fine mesh is required for the foam area. In order to reduce large computational burdens, the mesh gets progressively coarser as it moves away from the wall. The internal regions of the ellipsoidal top and bottom are meshed with hexahedron grids. After checking its grid dependency, the total number of grids used in this numerical model was 40,000. The physical and geometry parameters that compose the tank are presented in Table 1.

2.2. Governing Equation and Numerical Modeling

Thermo-fluid and mass transfer in the tank are described by the continuity, Navier-Stokes, energy equations and phase equations for two phases:
∂ ρ ∂ t + ▽ ㆍ ρ u = S ˙ m , c - S ˙ m , e                                                    
∂ ∂ t ρ u j + ∂ ∂ x j ρ u i u j = - ∂ P ∂ x j + μ eff ∂ u i ∂ x j + ∂ u j ∂ u i + ρ g i + f σ            
∂ ρ E ∂ t + ▽ ㆍ u ρ E + P = ▽ ㆍ k eff ∇ T + S ˙ q , c - S ˙ q , e            
∂ ∂ t ρ χ q + ∂ ∂ x i ρ u i χ q            
q = 1 : vapor, q = 2 : liquid
S ˙ m , e and S ˙ m , c represent the mass source terms resulting from liquid vaporization and vapor condensation, respectively. S ˙ q , e and S ˙ q , c represent the heat source terms from evaporation and condensation, respectively.
The liquid phase is assumed as incompressible with properties that vary with temperature except for density. The liquid density can vary linearly with temperature in the body term of the momentum equation based on the Boussinesq approximation. The vapor is modeled as a compressible ideal gas. The tracking of the liquid-vapor interface is carried out using the VOF method [13]. This model is a numerical technique for tracing the interface between the liquid phase and the gas phase of an immiscible fluid with large particles compared to the grid size. This numerical technique can use the same momentum and energy equations for both the liquid phase and gas phase domains. In other words, it is very economical because it can share the same pressure, temperature, and velocity field in each phase, and many researchers have used it, and its analysis accuracy has been proven. Therefore, in the present study, there are only the vapor and the liquid in the computational domain.
α l + α g = 1
The mixing density and dynamic viscositys of liquid phase and gas phase in each calculation cell can be expressed by the equation below.
ρ = α g ρ g + 1 - α g ρ l
μ = α g μ g + 1 - α g μ l
Energy term (E) in Eq. (2) is treated as mass-averaged variables:
E = α g ρ g E g + α l ρ l E l α g ρ g + α l ρ l
In the VOF model, the surface tension is calculated as a volume term( f σ ) acting on the calculation cell included in the interface. In this study, the CSF (Continuum Surface Force) model [33] is used to calculate the surface tension. A large pressure jump is formed at the interface between the liquid phase and the gas phase, and in an equilibrium state, the pressure gradient due to this pressure jump must have the same magnitude as the extra buoyancy term included in the momentum equation (2). Therefore, the force due to the pressure gradient that appears prominently at the phase interface is expressed by the equation below.
f σ = - σ ▽ ㆍ ▽ α α ▽ α
Therefore, it is necessary to know the vapor volume fraction in the entire computational domain. Tracking the interface between the liquid phase and the gas phase is achieved from the result of the continuity equation for the volume fraction as follows:
∂ α ∂ t + u i ∂ α ∂ x i = - S ˙ m , e + S ˙ m , c
When computational cell is completely occupied with vapor phase, α is equal one and vice versa. The range of volume fractions of cells in an interface fall 0 < α < 1 . S ˙ m , e and S ˙ m , c represent the liquid and vapor interface due to evaporation of liquid and condensation of vapor.
In present study, to express the mass interfacial exchange which controls how mass is exchanged between phases, Ranz-Marshall model [7,35] was selected. The governing equations are solved by using the commercial CFD code FIRE [2]. It is modified to include Ranz-Marshall model and all the thermo-physical and thermodynamic properties with respect to temperature and pressure which are taken from NIST [32]. The Nusselt number, Nu, is calculated as :
            Nu = 2.0 + 0.6   R e 1 2 Pr 1 3
            S ˙ m , e = C evap C A k l D d Nu A i ‴ h fg T l - T sat = S ˙ m , e ,   T l ≥ T sat
            S ˙ m , c = C cond C A k l D d Nu A i ‴ h fg T v - T sat = S ˙ m , c ,   T v ≥ T sat
where, h f g are respectively the latent heat; D d is the dispersed phase diameter. C e v a p and C c o n d are the closure coefficients for evaporation and condensation, respectively. A i ‴ is the interfacial area density described by the equation as :
A i ‴ = 6 α d D d
where α d is dispersed phase volume fraction. There is an additional closure variable, C A , which is used to correct for the effective mass change interfacial area density. It is defined as:
C A = 1 - α d + α min α pack + α min
where α p a c k is the packing limit, and α m i n is the minimum volume fraction. Therefore, the energy source terms included in Equation (3) are as follows:
  S ˙ q , e = S ˙ m , e h fg  
S ˙ q , c = S ˙ m , c h fg    

2.3. Initial & Boundary Conditions

It is assumed that stationary saturation conditions are dominant before the heat flux is applied at the surface of tank. The initial conditions at t=0 are:
  u i ,   j =   u i =   u j = 0  
The initial pressure is set to atmospheric pressure and the initial temperature is considered as the hydrogen saturation temperature at that pressure (20.268K). The initial temperature is assumed to be the same throughout the liquid and vapor.
In this study, there are three kinds of boundary conditions: symmetric conditions, adiabatic conditions and wall boundary conditions. The symmetry condition can be applied due to the cylindrical geometry, the applied boundary conditions, and the physics of the problem. Therefore, the flow and temperature fields are numerically considered as axisymmetric.
In this study, the harsh conditions in which there is no outer tank and radiation shield shown in Fig. 1 and the insulation foam at the outermost part of the tank is exposed to at normal temperature and pressure with light breeze were considered.
During the self-pressurization, LH2 tank is subjected to external forced convection with wind velocity of 2 m/s for the entire surface of the tank.
As mentioned earlier, since the outside of the liquid hydrogen storage tank of the small-scale liquefier, which is the subject of this study, uses MLI as an insulator, an outer tank exists to create a vacuum atmosphere. However, in this case, the amount of heat ingress is very small, so it takes a very long computational time to evaluate prediction performance of the numerical model and investigate the effect of insulation thickness. Therefore, in this study, this atmospheric temperature situation, which is a more severe situation, was used as a boundary condition to simulate the case where the heat penetration proceeds more rapidly.
Therefore, on the external insulation surfaces, the Robin boundary conditions is formulated as
- k ∂ T ∂ n = q w   ,   q w = h conv T ∞ - T w
where qw is the forced convection heat flux (=heat ingress). The characteristic temperature in this formula is the average temperature of the tank wall temperature, Tw and wind velocity temperature T∞ (283.15K). Tank inner diameter is used as characteristic length. In this study, the convective heat transfer coefficient of the tank cylinder surface, hconv is calculated by using the Churchill and Burnstein formula, which can take into account the ambient temperature and air flow [8].
However, it is known that this relation somewhat underestimates Nu in the middle Reynolds number region of 20,000 and 400,000. In the case of this study, the Re number of the flow passing through the tank cylinder surface is included in this range, so the following modified equation was used [5].
Nu = 0.3 + 0.62 Re 1 / 2 Pr 1 / 3 1 + ( 0.4 / Pr ) 2 / 3 1 / 4 1 + Re 282 , 000 5 / 8 4 / 5
Equilibrium heat conduction is assumed to calculate the tank wall temperature in equation (19) as follows:
q cond = k T w - T ∞ δ  
where k is the insulation thermal conductivity, and δ is the insulation thickness. It is assumed that external convection heat transfer tends to the insulation heat conduction gradually with long time soaking. Thus, q c o n v ≈ q c o n d .
The trial and error method is used to solve the insulation outer surface temperature [24]. The computation started in guessing appropriate initial Tw. Then qconv and qcond are computed with this guessed initial Tw. If both values, qconv and qcond are not equal with each other, the guessed initial Ts is corrected by increase or decrease of the guessed value. The iteration has been running until both qconv and qcond are almost equal, namely, convergence criterion ( q conv - q cond q conv + q conv / 2 < 0.5 % ) is meet. For more detail information can be found in the open literature [24].
Computed with the above numerical procedure, when the insulation thickness varies from 10mm to 30mm, the range of hconv is 9.4〜9.6 W/(m2‧K), and the external surface insulation temperature ranges from 220K to 268K. For the top and bottom dished heads, the heat transfer correlation [45] with flow over sphere is used. The rest of the computational procedure for obtaining the wall temperature is the same as for the cylinder tank wall.
The surfaces of inner support are assumed to be insulated and an adiabatic boundary condition is thus valid:
∂ T ∂ n = 0
The pressure in the liquid is taken as a function of the height and density. No slip boundary conditions are imposed on the sidewalls of the tank.

2.4. Turbulence Model

The previous literatures report that modeling heat exchange between ullage gas and tank wall plays a dominant role in the prediction of a thermo-fluid characteristics due to heat ingress [11,24,26,28], thus more attention should be paid to the fluid-wall heat transfer issue. Recently, many studies have reported that low-Re k-ε models have been successfully applied to the conjugate heat transfer region between liquid and wall. The nature of buoyancy-driven turbulent flow inside the tank by heat ingress is that the low Reynolds effect is prevalent and the basic assumption of the wall function for high Reynolds flow is no longer valid. [26,28,44,46,47]. However, low Re k-ε turbulence modeling tends to have a major drawback, requiring a dense grid such that the center of the wall-adjacent cell lies within the viscous sublayer region where the first wall-near cell is placed at y+≈1 [49]. Hence, it is very difficult to build near-wall grid system successfully for complex shapes.
In addition, a common drawback of low-Re turbulence models is the use of an ad-hoc viscous damping functions that represent wall proximity effects on turbulence and evading kinematic wall blocking effects.
The noteworthy features of the damping functions are that they use non-linear exponential relationships [22]. As a result, numerical stiffness can be introduced, and therefore, a strong under-relaxation factor is required and a lot of computation time is required to obtain a converged solution.
Therefore, in this study, the k-ζ-f model [14] was selected as a turbulence model, considering its high accuracy and convergence stability optimized in the near-wall turbulence closure model proposed by Durbin [9]. This is a model with the same characteristics as the low-Re turbulence model. The k-ζ-f model incorporates the near-wall turbulent anisotropy and non-local pressure-strain effects by introducing the wall-normal velocity fluctuation v2 and the source term f as variables in addition to the turbulent kinetic energy and dissipation rate of the standard k-ε turbulence model. Hence, careful introduction of this kind of relaxation avoids the need for a damping function [31]. This model improves the numerical stability of the original v2-f model by solving the transport equation for the velocity scale ratio ζ=v2/k opposite to the velocity scale v2. Numerical stability is a very important factor of low-Re version of turbulence model in predicting the buoyancy-driven turbulent flow by thermal penetration in a liquid hydrogen tank having a turbulent flow structure with strong anisotropy.
During the evaporative process at interface, the process of turbulent mixing between the evaporation gas and ambient gas in the LH2 tank is strongly influenced by the high gradient of thermophysical properties and the evaporation process on the interface. In particular, strong upward flow in both liquid and gas regimes based on natural convection by heat penetration thickens the boundary layer, potentially leading to a highly anisotropic turbulent structure. Therefore, to consider anisotropic turbulence, the k-ζ-f model is expected to have much better predictive ability than the k-ε model. It has also been reported that the k-ζ-f model has better prediction performance than the conventional k-ε turbulence model for many engineering problems [50].
In the meantime, several researchers have investigated the prediction performance of RANS type turbulence models along with VOF models for simulating the thermal and fluid characteristics in liquefied hydrogen storage containers with thermal penetration.
Kassemi [21] investigated the effect of turbulence on the pressure and temperature predictions of the liquid and gas phases in an aluminium LH2 tank subjected to a constant wall heat flux ranging from 2 to 3.5 W/m2. The CFD predictions using Menter's k-w SST turbulence model with wall functions were compared with temporal evolution of pressure results from the NASA GRC K-site facility. The results of this study report that the analysis results underestimate the pressure rise rate and thermal stratification at the ullage because the influence of turbulence at the interface and vapor misrepresents the degree of heat transfer to the ullage.
As shown in this result, the reason why VOF and k-e based turbulence models underestimate the evaporation rate, pressure rise rate and thermal stratification in the tank is that they overestimate the mixing in the ullage and underestimate the turbulent dissipation rate at the free surface.
Therefore, to overcome the above-mentioned errors of the two-equation RANS turbulence models, such as k-ε and SST k-ω in predicting thermo-physical phenomena in LH2 tank, the k-ζ-f model is adopted in this study.

2.5. Numerical Implementation

The mass and heat transfer equations at the interface used with VOF and the mass transfer and energy balances by evaporation and condensation are presented in the governing equations ((4)-(10)). In this study, an in-house modified version of the commercial CFD code, AVL FIRE™ was used as a solver and grid generator to numerically calculate the governing equations (11)-(14).
The liquid hydrogen storage tank geometry is modeled in 2-dimensional axial-symmetric, which could reflect the 3-dimensional results with saving much more computing resource and time. The all computational domain is divided into hexahedron structured grids with the near wall region refined into the boundary layer mesh. A second-order upwind TVD (Total Variation Diminishing) scheme with Roe's MINMOD limiter is used to discretize convective terms. The iterative SIMPLE-like (Semi-Implicit Method for Pressure-Linked Equations) pressure–velocity coupling scheme is used to compute the pressure field. Crank-Nicolson time integration is used for time discretization with the VOF model and the CFL (Courant Friedrichs Lewy) number for time step size is in ranging from 0.05 to 0.15.
The solution is iterated until the convergence criteria are met. When the residuals of the momentum equation, the turbulent kinetic energy and the turbulent energy dissipation rate fall below 10−6 and the energy equation residual below 10−8, it is considered to meet convergence criteria.

2.6. Model Validation

2.6.1. Numerical Validation

In order to verify the computational methodology and accuracy of the numerical model presented in this study, the predictions were compared with previous computational results by [11,38] for a liquid hydrogen tank. Here a cylindrical tank with a diameter of 0.5 m and a height of 1 m was studied. 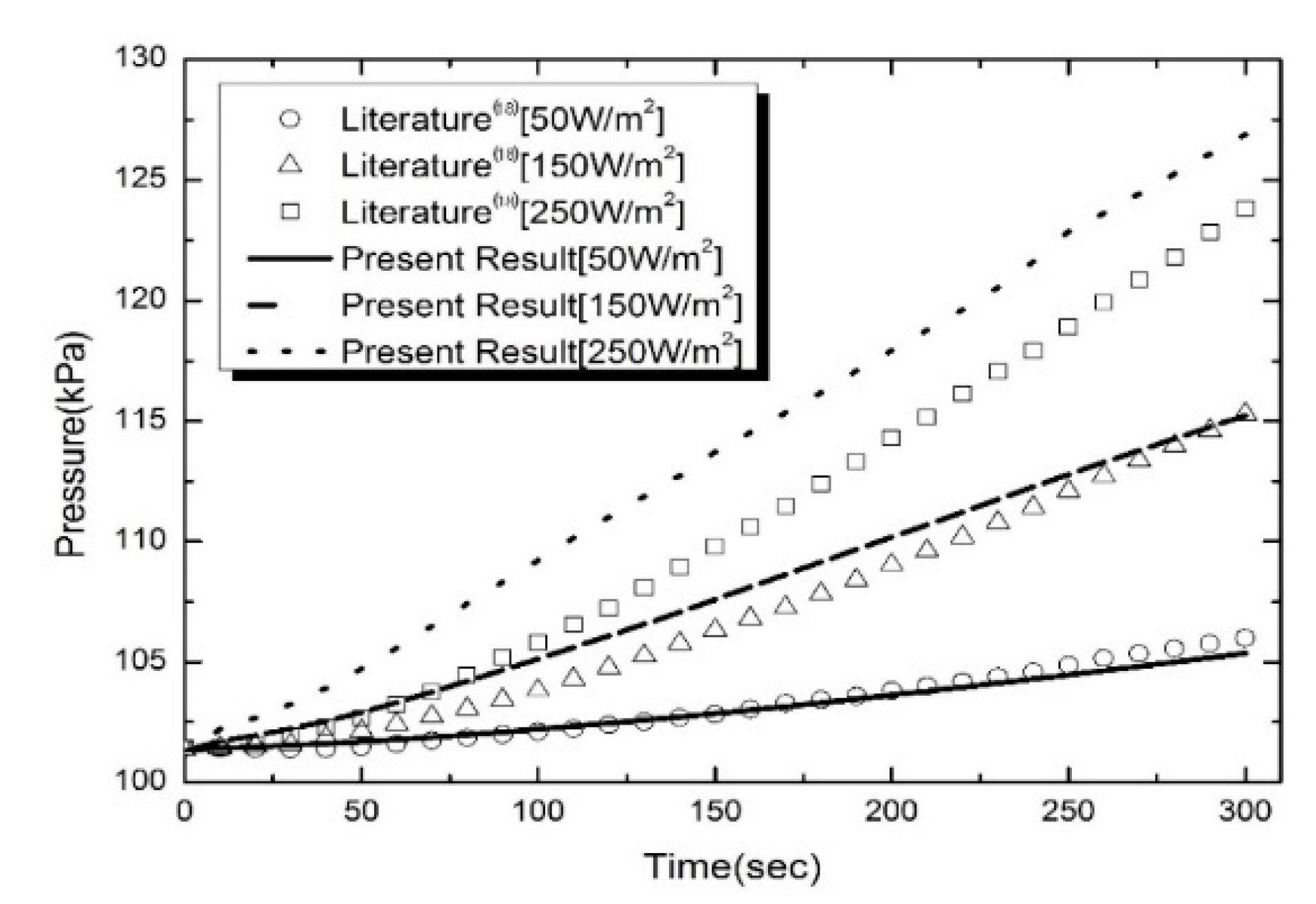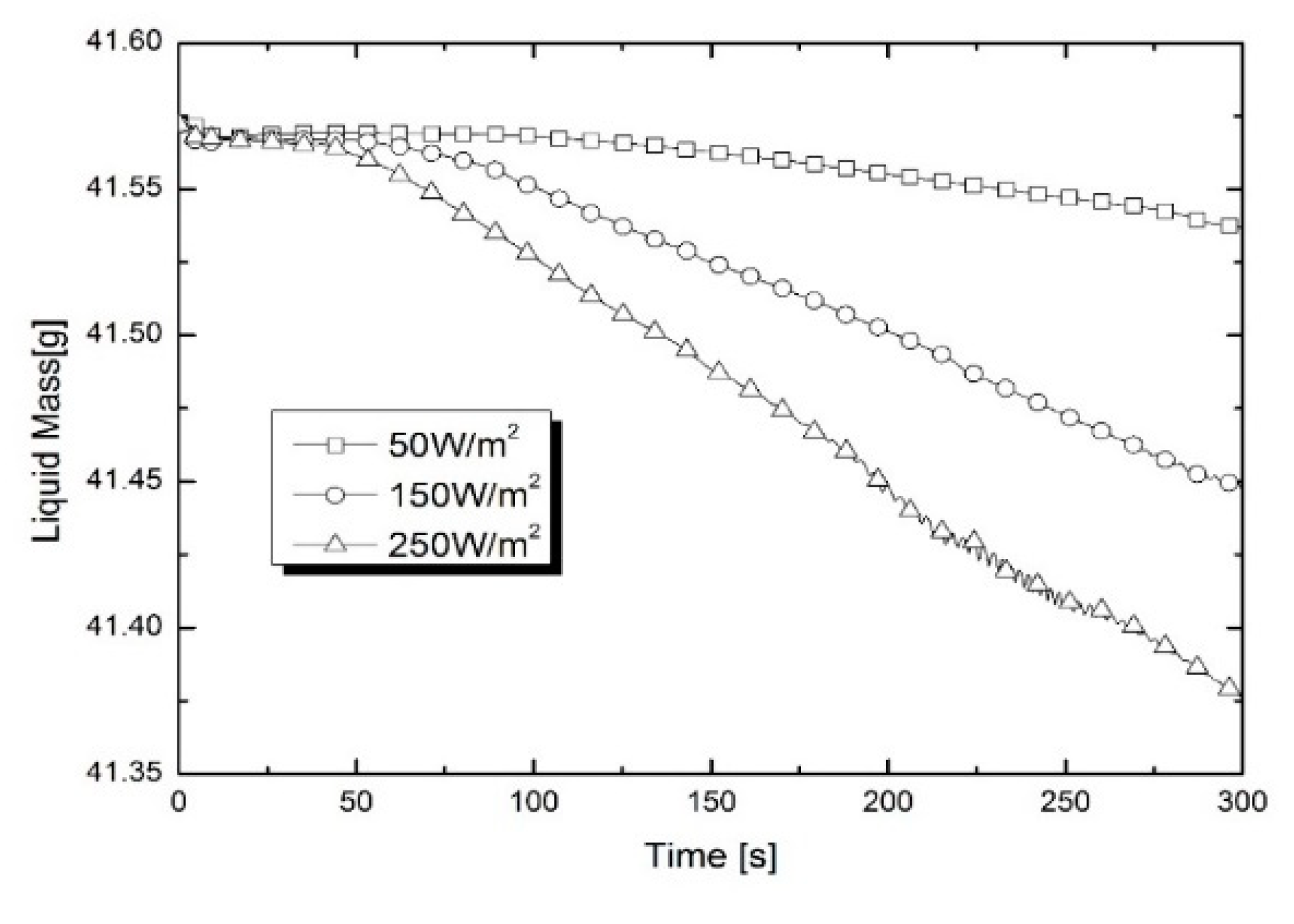It is filled with liquid hydrogen up to the level of 50%, with three constant heat flux boundary conditions of 50 W/m2, 150 W/m2 and 250 W/m2 which was imposed directly at the tank outer surface. For description of turbulent effect in the tank, this work adopted standard k-ε model. The initial pressure was 101.32 kPa and the temperature corresponded to the saturation value at this pressure. The comparison of the present computational results with the previous one for the temporal variations of pressure in the tank for various heat ingress is presented in Figure 4. It can be seen that the tendency of the tank to be pressurized is well expressed in the case of the two models. As the heat flux increases, the pressure rise rate and pressure increase. It should be noted that the present numerical pressure is larger than the previous one [11,38] particularly in case of the higher heat leakage (150, 250W/m2). As described above, this discrepancy is due to the fact that the turbulence models of the k-e model series underestimate the pressure rise rate and thermal stratification at the ullage in the tank. As mentioned above, the previous literature [21] reported that two equation RANS Turbulent models such as k–ε and SST k-ω under-predict the pressurization rate. Hence, we could reason from the previous results and this comparison to the fact that the k-ζ-f model adopted in this study has the much better prediction capability compared to the k-ε model for predicting impact of interfacial and vapor side turbulence on transport of heat into ullage and self-pressurization in the cryogenic tank. The details of the merits of the k-ζ-f model used in the present study have been mentioned before, so it will not be discussed further here.
The previous literature [1] reported that the analysis results using a standard k-ε turbulence model with a wall function showed that the Nu was underestimated when inputting the temperature difference into both sides in a closed square space similar to this study. Therefore, previous study results that used the standard k-ε turbulence model and wall function [11,38] underestimated the thermal stratification in the ullage due to heat flux from the wall, thereby predicting a low self-pressurization. On the contrary, in this study, calculating the eddy viscosity near the wall can effectively gauge the anisotropic effect of speed change near the wall by using v 2 ¯ , an equation without using a wall function. Therefore, accurate prediction performance is expected in the flow where strong buoyancy is dominant [39,51].
However, the prediction for low heat-leak case (50 W/m2) is observed to be in better agreement with the previous data [38] with an average error about 1% but locally somewhat higher. Figure 5 shows comparison of liquid mass amounts left in tank with time for various uniform wall heat fluxes. Comparing to Figure 5, it can be seen that marginal evaporation periods exists due to a coupling between the buoyancy force and convective cooling. After this period, vigorous evaporation occurs and the pressure start to rises gradually. As heat penetration increases, this delay before evaporation begins becomes shorter, and after evaporation begins, the rate of pressure and evaporation rise steepens. Since such a physical phenomenon was well-known from the previous study results [11,21,38], the analysis model developed in this study can physically validate the pressure behavior caused by evaporation in the tank according to the amount of heat ingress coming from outside.

2.6.2. Experimental Validation

In this study, AS-203 flight experiment [51] results were used for the second verification of the numerical model. The main purpose of AS-203 was to investigate how the fuel in the tank of the second stage rocket S-IVB reacts to low gravity conditions of this experiment. Based on the results of the existing Saturn AS-203 test flight, the phenomenon of pressurization of the inside of the tank due to propellant boil-off by an external heat penetration was simulated. Approximately 160g of LH2 remained in the tank at the beginning of this part of the experiment, and the tank pressure was 85.5 kPa. The analysis of this LH2 tank experiment using the CFD model included several simplifications. First of all, it was assumed that a constant gravity level of 1.0x10-4g was used during the entire simulation period, and that the incoming heat flux from each part of the tank was uniformly introduced over the entire tank surface with a uniform heat flux of 40 kW.
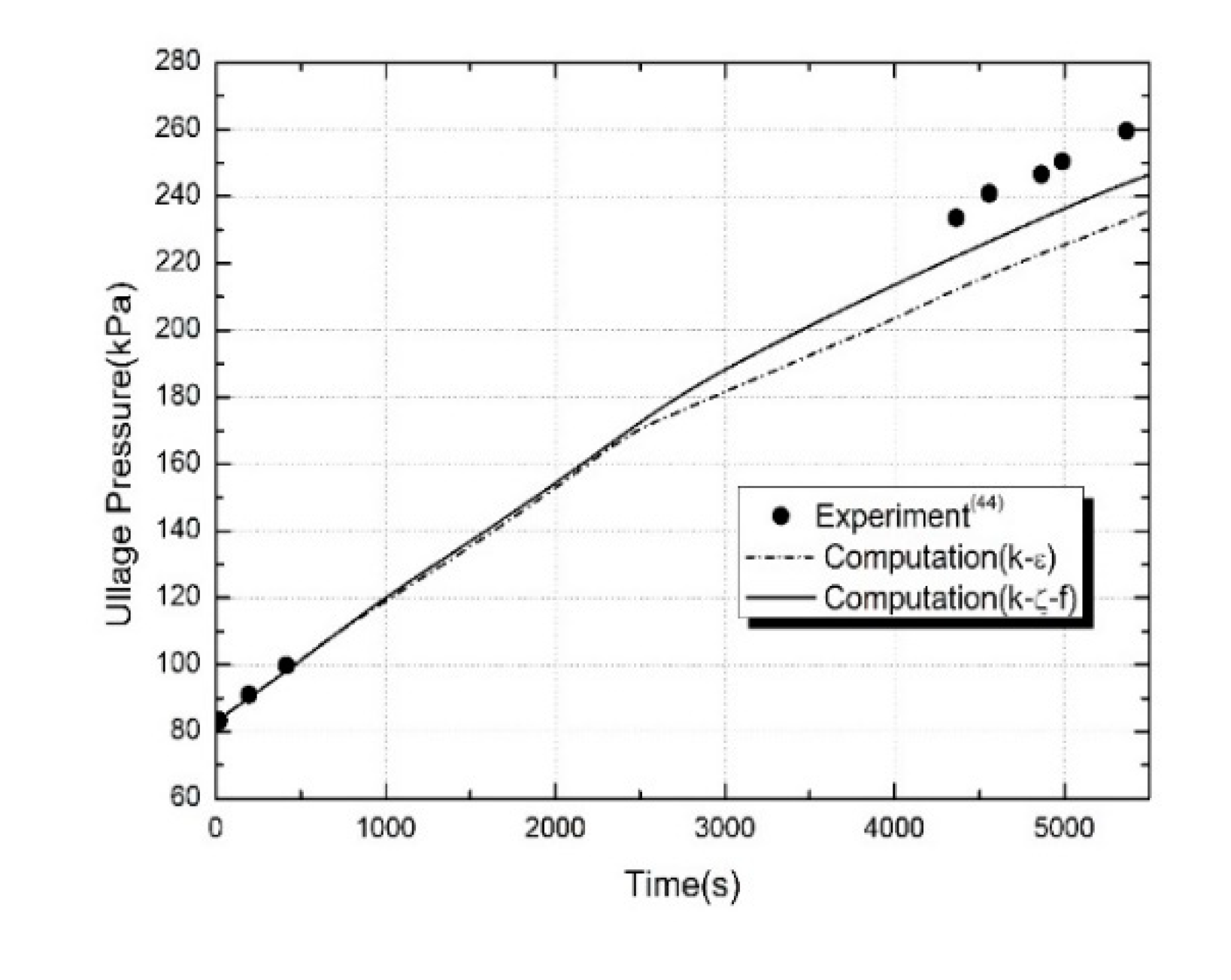
The experimental ullage pressure histories from Ref. [51] were given in Figure 6 (a) with the CFD model prediction overlaid for k-ε and k-ζ-f turbulent model. It can be clearly seen that two turbulent models have a tendency of under-predicts the experimental pressurization rate but the calculation results obtained by k-ζ-f turbulent model are in better agreement with the experimental data [51]. It is interesting to note that after t = 2500 s there is still a growing discrepancy between the slope of the measured and calculated pressure rises. This lack of agreement may be due to the imposition of a constant heat flux boundary condition, the assumption of continuity in the turbulence quantities across the interface by the VOF model, and inadequacies associated with turbulence models in the region of ullage. In addition, as explained by M. Kassemi and O. Kartuzova [21], this could be also due to the fact that the k-ε model series underestimate the pressure rise rate and thermal stratification at the ullage in the tank.
The pressure error at the end of the experiment compared with simulation with k-ζ-f turbulent model is approximately 6% which is considered as good with consideration of the simplified boundary conditions and assumptions. On the other hand, the prediction errors of k-ε turbulent model at the end of the experiment shows 10.34% for tank pressurization. This large discrepancies of two turbulence models are closely related to the fact that the two turbulence models do not adequately reflect the non-uniform wall shear stress caused by buoyancy, although it is closely related to the local flow structure and the turbulent quantities to express the actual heat transfer phenomenon. These limitations are due to the fact that many RANS turbulence models are built on the concept of isotropic eddy viscosity. However, it can be observed that the predictions by the k-ζ-f model adopted in this study show better accuracy because the introduction of the velocity scale v2 makes the V2F k-ε turbulence model reflect the effect of anisotropy of the velocity fluctuation near the wall.
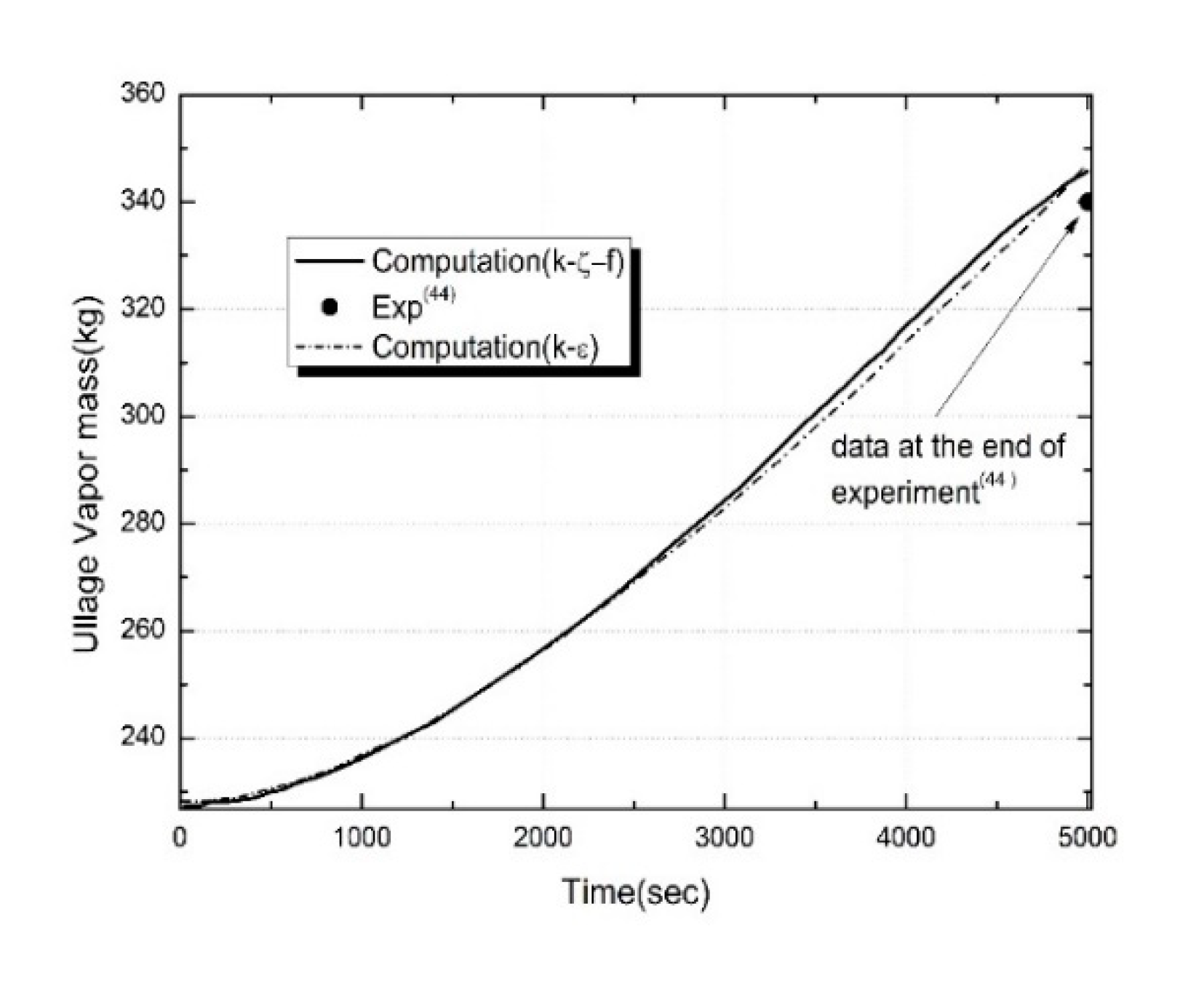
Figure 6 (b) shows comparison of evolution of ullage vapor mass between experimental data [44] and numerical predictions with two turbulent models. As shown in Figure, the temporal variations of evaporative vapor mass curves for ullage shows a rather short initial transient period resulting in an almost exponential rate of vapor mass increase as time elapsed. It could be found that the two turbulence models indicate that net interfacial mass transfer essentially evaporates throughout the test run. The increased rates of vapor mass to which two turbulence models were applied did not show a significant difference. The difference from experimental data with the k-ε turbulent model at the end of the experiment was on the higher side by 2.1%, while the result with the k-ζ-f turbulent model was predicted higher by 1.7%. By comparing the temporal variations of the mass transfer rate and pressure rise results by evaporation using two different turbulence models, it can be observed that the prediction of the k-e model underestimating the pressure rise is not due to misrepresentation in the evaporation rate at the interface. It can be clearly seen that the reason is more predominantly due to miscalculation of the influence of the turbulent effect at the interface and ullage on the heat transfer to the ullage [26,28]. It could be also noted that the prediction of pressurization rate is more sensitive to eddy viscosity formulation and near wall treatment of turbulent model than prediction of interfacial mass transfer.

3. Results and Discussion

A calibrated three-dimensional CFD model is built to investigate the influence of insulation thickness on the temporal evolution of the complex thermo-fluid characteristics of liquid and vapor in liquid hydrogen (LH2) tank. The pressure change and thermo-fluid characteristics in a partially liquid hydrogen storage tank, subject to ambient condition with wind blowing, has been investigated numerically. The results simulated from the analyses are discussed below.

3.1. Thermo-fluid Characteristics in a Tank

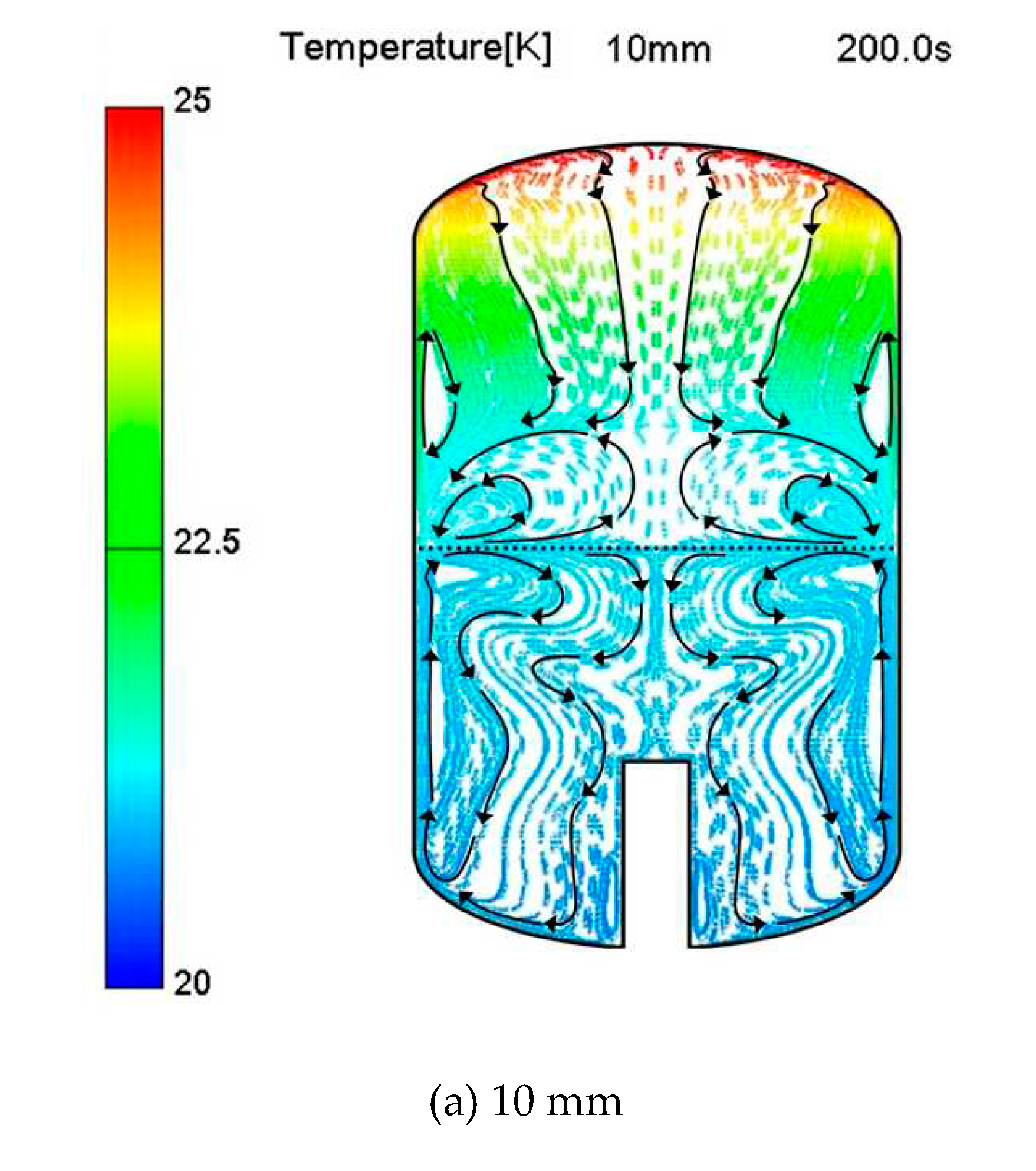
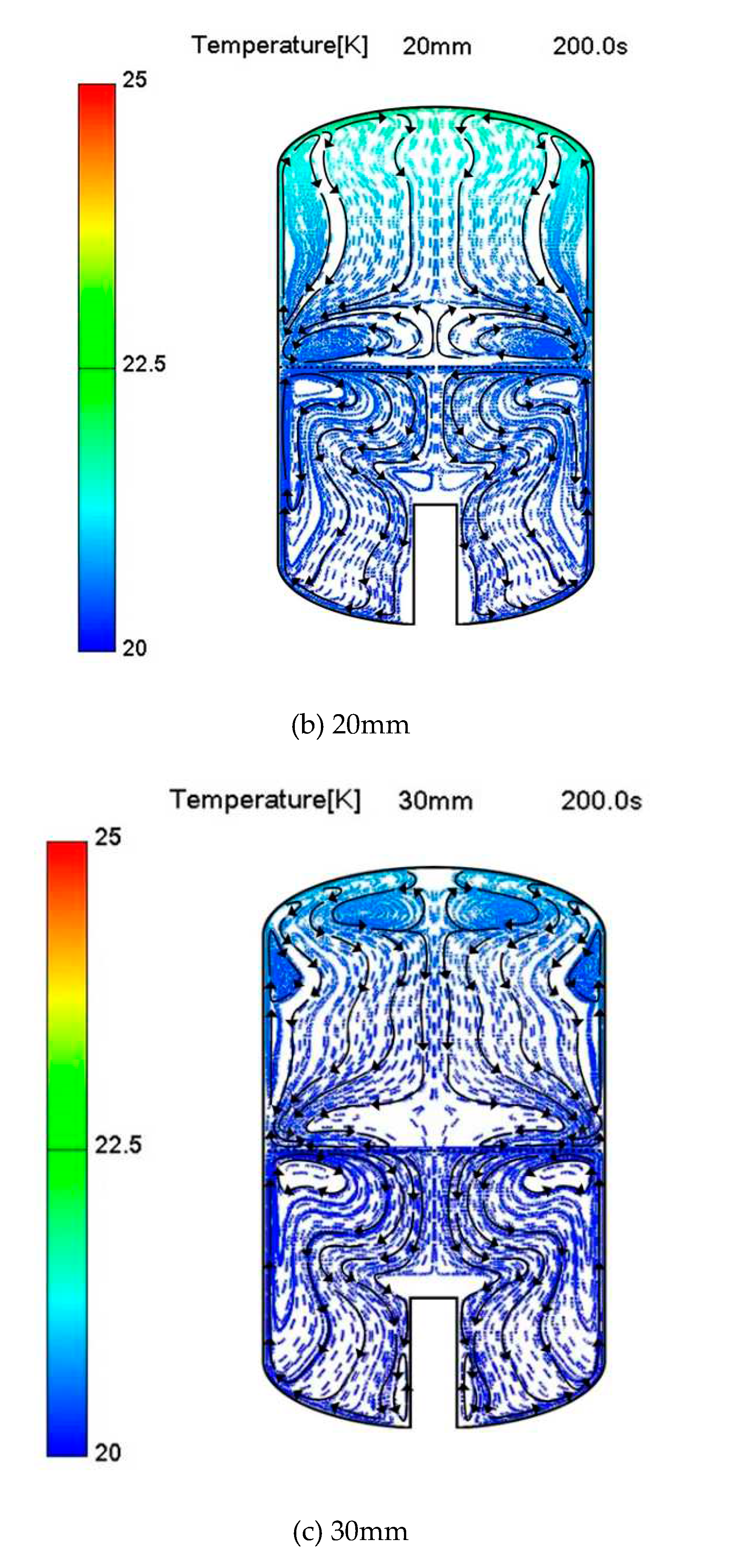
Figure 7 shows the streamlines and temperature distribution of liquid and vapor formed inside the tank according to insulation thickness for 200 seconds. The area of insulation material was omitted in the figure to detail the heat and flow characteristics caused by thermal penetration inside the tank.
From the results of the figures, it can be seen that the important physical phenomena that make up thermal stratification are well represented in succession. That is, when thermal leakage penetrates the tank, the heat load is mainly used to increase the tank pressure by gas expansion, increase the liquid temperature, and cause a phase change. Initially, the liquid close to the walls is heated by the heat input. Afterwards, the hot liquid near the heated wall moves upward under the influence of upward buoyancy-driven flow, mixes with the cold liquid near the interface, cools down, and eventually flows downward in the central area of the tank. As this process proceeds iteratively, it can be seen that increasingly warmer liquid accumulates at the liquid-vapor interface and provides a warmer liquid layer along the axial direction, illustrating the progress of thermal stratification. In the liquid region, the heat conducted through the insulation from the sidewall was transferred into the thermal boundary layer near the wall, and some of the heat inflated fluid to form an upward jet flow by buoyance and flew upward before being cooled near the free surface. It then moved to the central axis of the tank and became dense, ultimately descending to form a pair of recirculation zone nearby both sides of walls. Noteworthy feature of this study is that the descending flow at the central axis showed a radially distorted streamline and wake flow due to the existence of cylindrical support groove. At this time, in case the insulation thickness was thin (10 mm) where heat flux flowed excessively to the wall due to thin insulation, a weak and slow down flow which was not sufficiently cooled formed a highly curved streamline and large recirculation zone before the support groove. Meanwhile, in the case of (b) and (c), where the heat flux flowing into the liquid phase was relatively small due to the thick insulation, a stronger downward flow existed. In addition, a pair of vortices was formed before the support groove, which made the flow stagnant. The stagnant flow due to the support groove prevents the mixing of the cooled downflow with the hot fluid near the wall, which can cause non-uniform temperature distribution in the liquid phase, and especially increases the temperature near the wall, which can eventually increase the amount of boil-off. In particular, in the case of a 10 mm insulation thickness with a large heat ingress, a downward flow with low momentum is created due to insufficient cooling on the free surface, resulting in a wide stagnation region in front of the support groove. This can be considered as a dead zone because mixing with hot fluid is impossible in this region. Moreover, the rapidly rising flow near the wall caused fast flow at the liquid-vapor interface and accelerated vaporization.
Since the gaseous hydrogen evaporated from the interface moved to the central axis while heated on the liquid surface, the liquid hydrogen caused the highest temperature at the center of the free surface, so some of it moved to the vortex side and descended while some other portion vaporized and ascended along the central axis. Therefore, most of the external heat-ingress are accumulated under top dished head. Particularly, as shown in Figure7 (a), having very thin insulation thickness (10 mm) it can be observed that very strong thermal accumulation is formed obviously in the vapor region with the highest temperature in the top dished head because of natural convection. A large recirculation area existed near the free surface since the upward vapor flow generated by the strong heat energy supplied from the free surface of liquid side is hindered by heat accumulation in the top dished head.
In the case of Figure 7 (b) and (c), the penetrating heat leakage was small, so the vapor rising after evaporation became sufficiently cooled, forming a stable downward flow along both the walls and center, and descended toward the free surface. Therefore, the recirculation area above the free surface was reduced. In the case of Figure 7 (c), the amount of heat flowing into the tank was smaller, so it could not be evaporated upward from the center of the liquid-vapor interface, but it was evaporated around the wall where the thermal boundary layer existed.
As the gas rose upward and a weak thermal stratification region existed at the tank top, a pair of vortices were formed and stagnant in this region. A downward flow occurred at the wall because the area’s temperature where the vortex occurred was higher than the thermal boundary layer. Therefore, a pair of vortices was also formed on the gaseous wall surface. Since the amount of thermal accumulation at the tank top increased as the insulation became thinner, a strong temperature gradient was formed. The heated and up-rising vapor could not move to the tank top, leading to forming a pair of vortices on the liquid-vapor interface.
Additionally, as the thickness of the insulation decreases, more thermal energy is introduced into the tank, forming a strong buoyancy-driven force, allowing fully developed natural convection to occur in both the liquid and vapor domains. This improves the heat transfer rate by natural convection in each phase and the heat transfer from the free surface to the ullage by turbulence, resulting in faster heat transfer from the steam and interface.
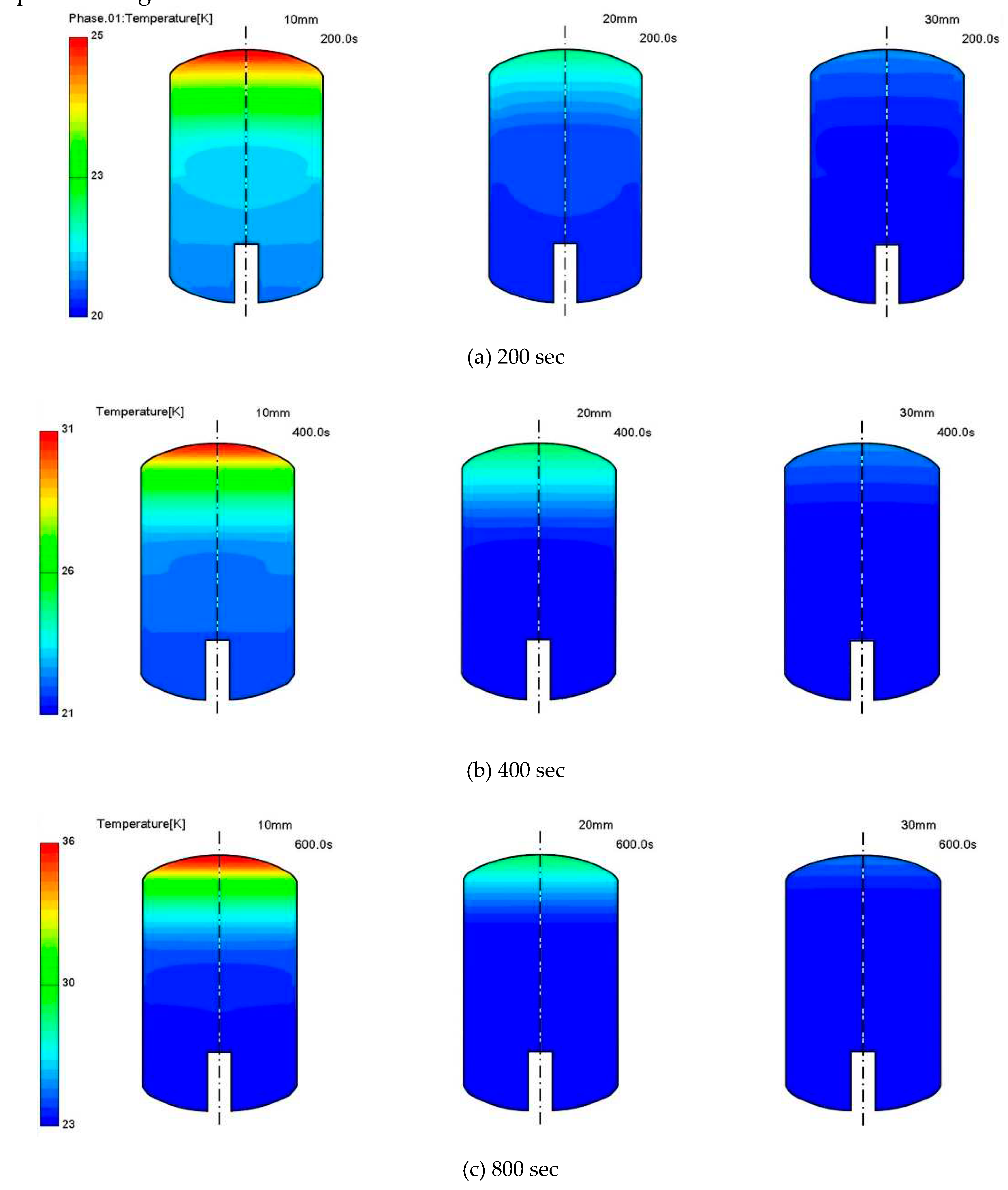
Figure 8 shows the thermal fields formed inside the tank when three different insulation thicknesses were applied at 200s, 400s, and 800s. As in the case of Figure 7, the figure shows the calculation results of the tank wall surface and inner area, excluding the insulating material area. A comprehensive analysis of the above results, in terms of temperature gradient in the liquid region inside the tank, showed that a radial temperature gradient gradually decreased with time starting from the heat leakage, but an axial temperature gradient was strongly formed. In particular, it can be observed that the existence of the mixing dead zone due to the support groove intensifies the radial temperature gradient. In the case of a 10mm insulation thickness with a large heat ingress into the tank, a large stagnant region exists in front of the support groove, so the radial temperature gradient in this region can be confirmed even at 600 s, which means that the temperature mixing proceeds very slowly. Therefore, in the future, a study on optimizing the shape of the support groove, which can minimize flow interference, will be conducted. In addition, the amount of heat accumulation in the vapor region increased with time at the tank top due to the rise of vapor evaporated at the liquid-vapor interface and expanded vapor near the wall surface, causing a sharp temperature gradient near the tank top. This phenomenon became more evident as the insulating thickness turned thinner where the heat leak was large. In the case of the insulating thickness of 1 0mm, a strong buoyancy-induced flow occurred at the liquid wall surface and transferred heat to the interfacial surface since it had the most significant heat leak. The radial temperature gradient by flow pattern, which was cooled at the central axis and flowed down, was large at 200s and 400s near the liquid-vapor interface. It could be confirmed from the above result that a thermal stratified layer was well-developed.
progressed further, the radial temperature gradient was considerably alleviated. On the contrary, with the thicker insulation of 20 mm and 30 mm, the thermal penetration was slight, and a weaker radial temperature gradient occurred compared to that of 10 mm. In the case of vapor, as explained before, a sharp and dense temperature gradient is created at the tank top dished head due to thermal accumulation as the insulating thickness decreases. In the case of the insulating thickness of 10mm at 400s and 800s, the thermal accumulation of the tank top was enormously expanded, which directly made liquid evaporate at the interface.
From the results of Figure 8, it can be also deduced that as most of the penetrated thermal energy is driven under the buoyancy force and accumulated on the top of the tank, the heat transfer capacity from the vapor to the interface that can be used for thermal stratification is reduced. Therefore, the thermal energy supplied for the thermal stratification of the liquid phase from the ullage is reduced. 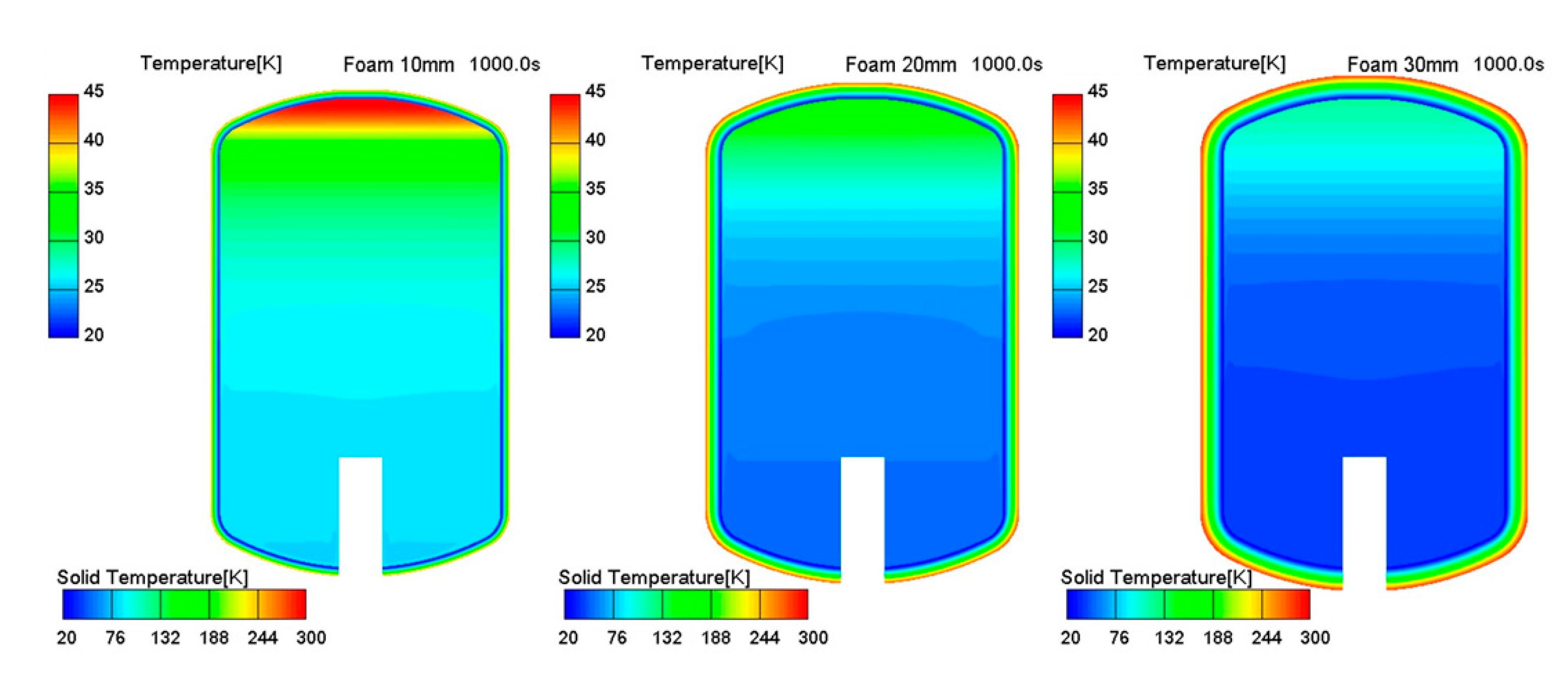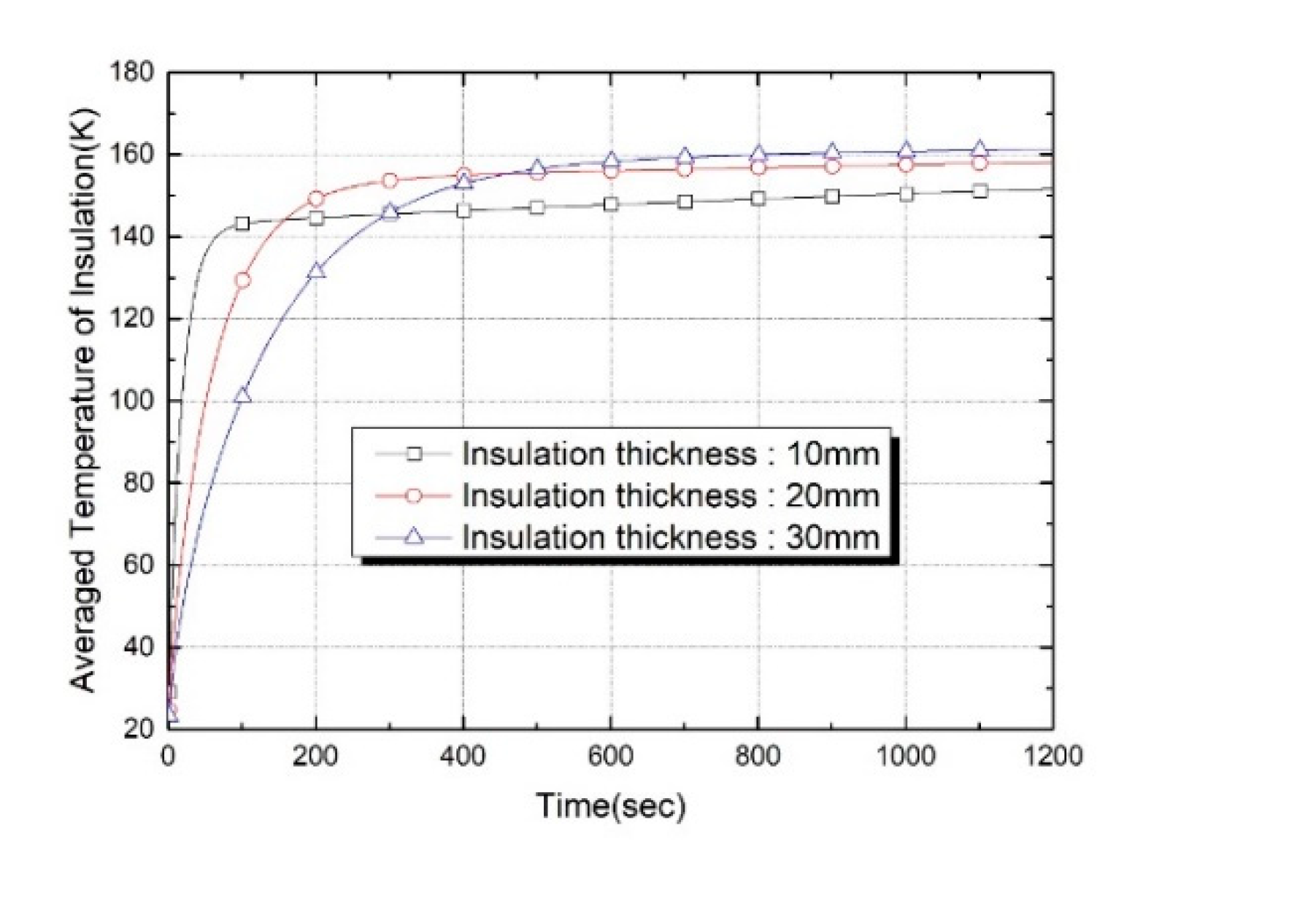Figure 9 shows the temperature distribution according to the three insulation thicknesses, including the insulation mat at t = 1000s. Since temperature scales distributed inside the tank and insulation materials were quite different, each scale was indicated differently. The results indicates that the insulation thickness has a dominant effect on the axial temperature gradient, which is due to the difference in the degree of energy mixing due to buoyancy force in the liquid phase and the gas phase. It is evident from Figure 9 that the presence of a constant heat flux on the surface of the insulation raises the temperature inside insulation, thereby increasing the conductive heat flux passing through the insulator, eventually increasing the heat ingress.
In further detail, it can be confirmed that there is a close relationship between heat leakage and the rise in surface temperature of the insulation. A substantial temperature gradient was formed in the insulation material due to the conductive heat flux passing through the insulation material. At a thickness of 10 mm with a significant thermal penetration due to a small thermal capacitance, a high thermal accumulation and a high-temperature gradient were observed near the tank top. On the contrary, in the case of thick insulation material of 30 mm having a high thermal capacitance, the radial temperature gradient at the tank top was greatly alleviated. Heat diffusion significantly progressed at 1000s, developing an axial temperature gradient more clearly than a radial temperature gradient.
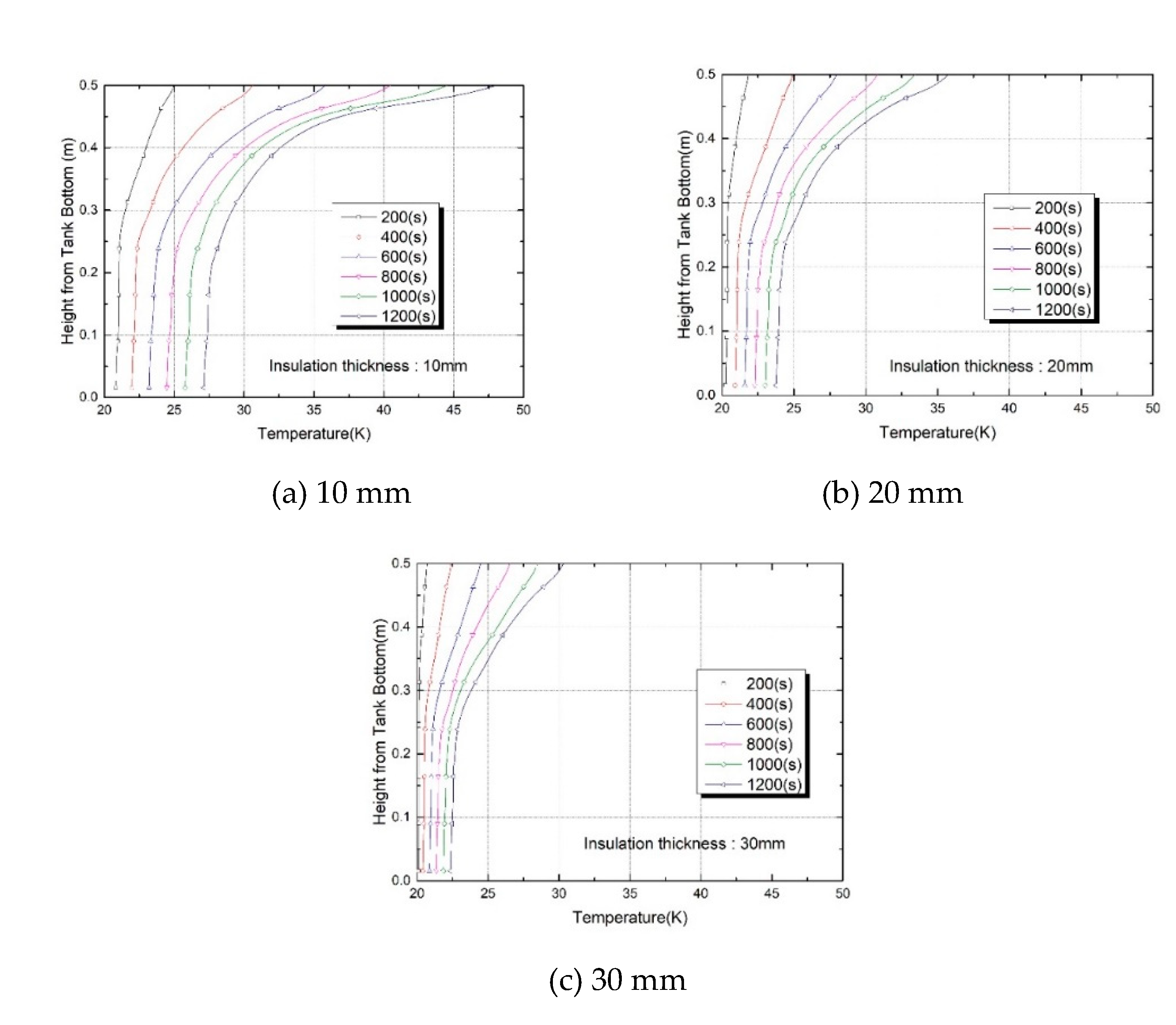
Central vertical temperature profiles at various times for three different insulation thicknesses are shown in Figure 10. It is clearly seen that the temperature of liquids and vapors increase at a faster rate as the thickness of the insulation becomes thinner. In addition, as the insulation thickness decreased and time lapsed, a large temperature gradient near the tank top was formed due to thermal accumulation. The results also show that the degree of thermal stratification in the vapor phase and the degree of thermal energy mixing between the liquid phase and the vapor phase through the interface according to the difference in the thermal energy transferred to the liquid phase vary greatly depending on the insulation thickness. The temperature was changed with time that when insulation thickness increased, so did the thermal capacitance. The heat leak penetration speed was delayed, causing a delay in temperature increase inside the tank. Significantly, as shown in Figure 10 (a), in the case of insulation thickness at 10 mm with a small thermal capacitance, a large heat penetrated the tank and conduction flux in-flowed to the liquid-vapor interface, causing the liquid temperature at the interface to exceed the saturation temperature. When the side wall heat ingress is large due to thin insulation thickness, not only increases the free surface temperature but also initiates evaporation before the thermal stratification build-ups. However, the temperature increase at the free surface was considerably delayed in the case of an insulation thickness of 30 mm. Volume averaged temperature-time histories for three different Figure 10. Temperature profiles at the central axis for three different times and insulation thickness insulation thickness are shown in Figure 11. 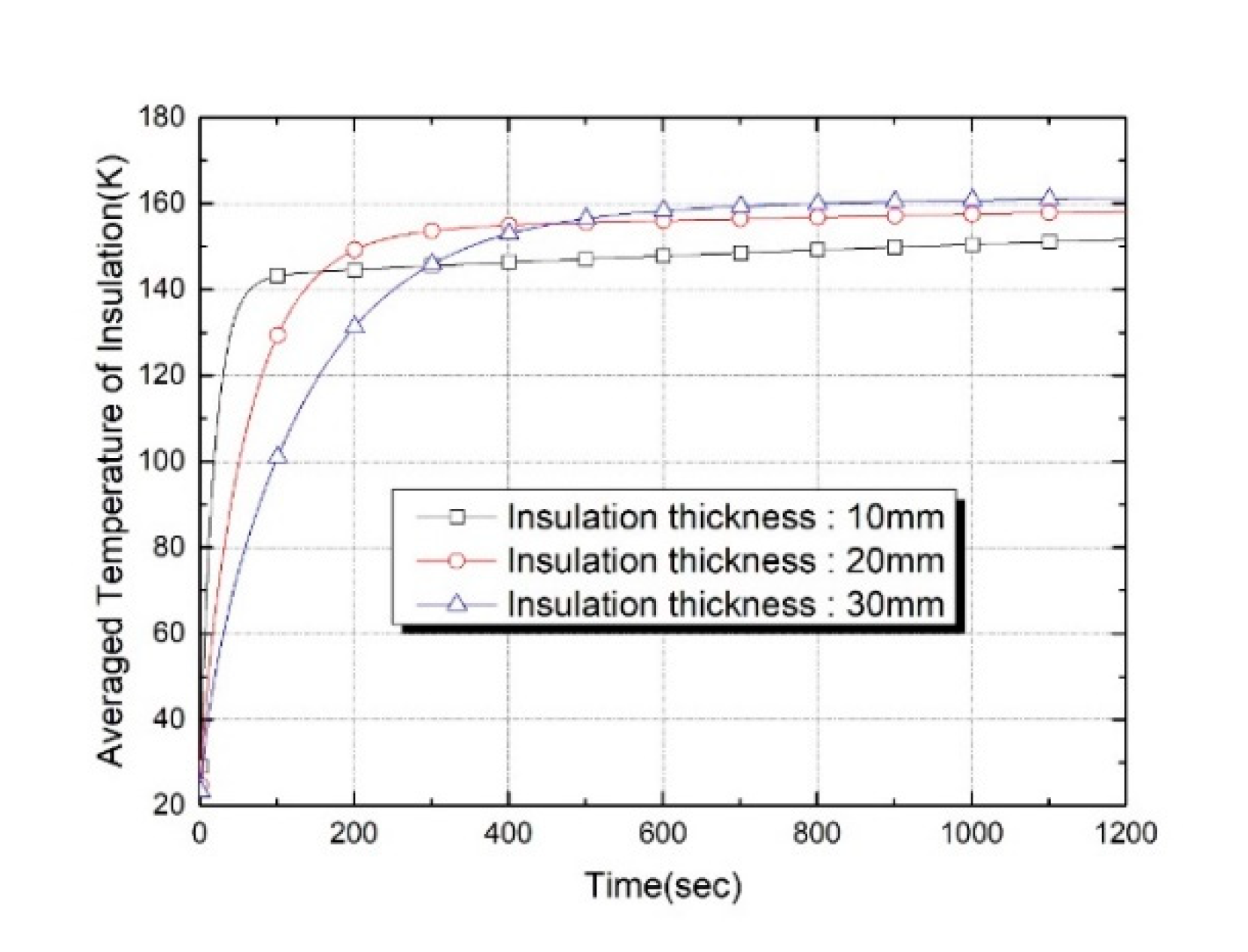Figure 11 shows that small thermal capacitance by reducing insulation thickness shortened the time to the near-steady-state condition of the inner temperature of insulation material. As the insulation thickness increased from 10 mm to 20 mm, the time to reach normal condition could be delayed by 215%. Again, when the insulation thickness increased to 30mm, the time to reach normal condition was delayed by 550%, delaying the entering speed of the heat penetration into the tank. Therefore, by increasing the insulation thickness, the elapsed time from the heat load input until the pressure increase was elevated, ultimately restricting the boil-off and self-pressurization.
From the above results, it can be seen that when the heat leakage penetrates the tank, the heat load is mainly used to increase the tank wall temperature and thermal insulation material, increase the liquid temperature and cause a phase change, resulting in self-pressurization.
Figure 12 displays the temporal evolution of volume averaged temperature profiles of tank wall for three different insulation thickness. From the figure, as the liquid surface is reduced by evaporation due to heat ingress, the area available for heat transfer between the warmer vapor with heat accumulation and the tank wall increases, improving heat transfer from the ullage to the tank wall. Therefore, a linear rise in the tank wall temperature can be due to the continuous rise of the heat exchange rate at both the fluid-wall interface and the wall-foam interface.
As predicted, as the insulation thickness became thinner, the amount of heat leakage became enormous, so the heat penetrated quickly into the tank wall. As time elapsed, the temperature rose almost linearly with a sharp temperature gradient. The temperature rose with an alleviated temperature gradient when the insulation grew thick. From Figure 11, it is clear that the temperature of the tank wall increases at a steeper rate with a thinner insulation thickness. As already mentioned, this is due to not only high levels of heat leakage into the bulk liquid and ullage but also low thermal capacitance of insulation material.
In the case of the thinnest tank wall at 10mm, the temperature rise gradient was about 0.0128 (K/sec), which was higher by 138% than that of the tank wall at 30mm, which was 3 times thicker. It was increased by 66.9% more than that of the double tank wall thickness.
According to three different insulation thicknesses, evaporation losses at 600s and 1200s are presented in Table 2. The thermal capacitance, which increased according to the insulation thickness and evaporation, changed as the insulation thickness increased from 10 mm to 20 mm in 600 seconds. The thermal capacitance doubled, and thus the evaporation decreased by about 1/2. If the insulation thickness at 30mm, the evaporation reduced to a quarter. Similarly, in the 1200s, evaporation was reduced according to the insulation thickness increases. With the insulation thicknesses of 20 mm and 30 mm, the evaporations decreased to 43% and 25% each compared to 10 mm.
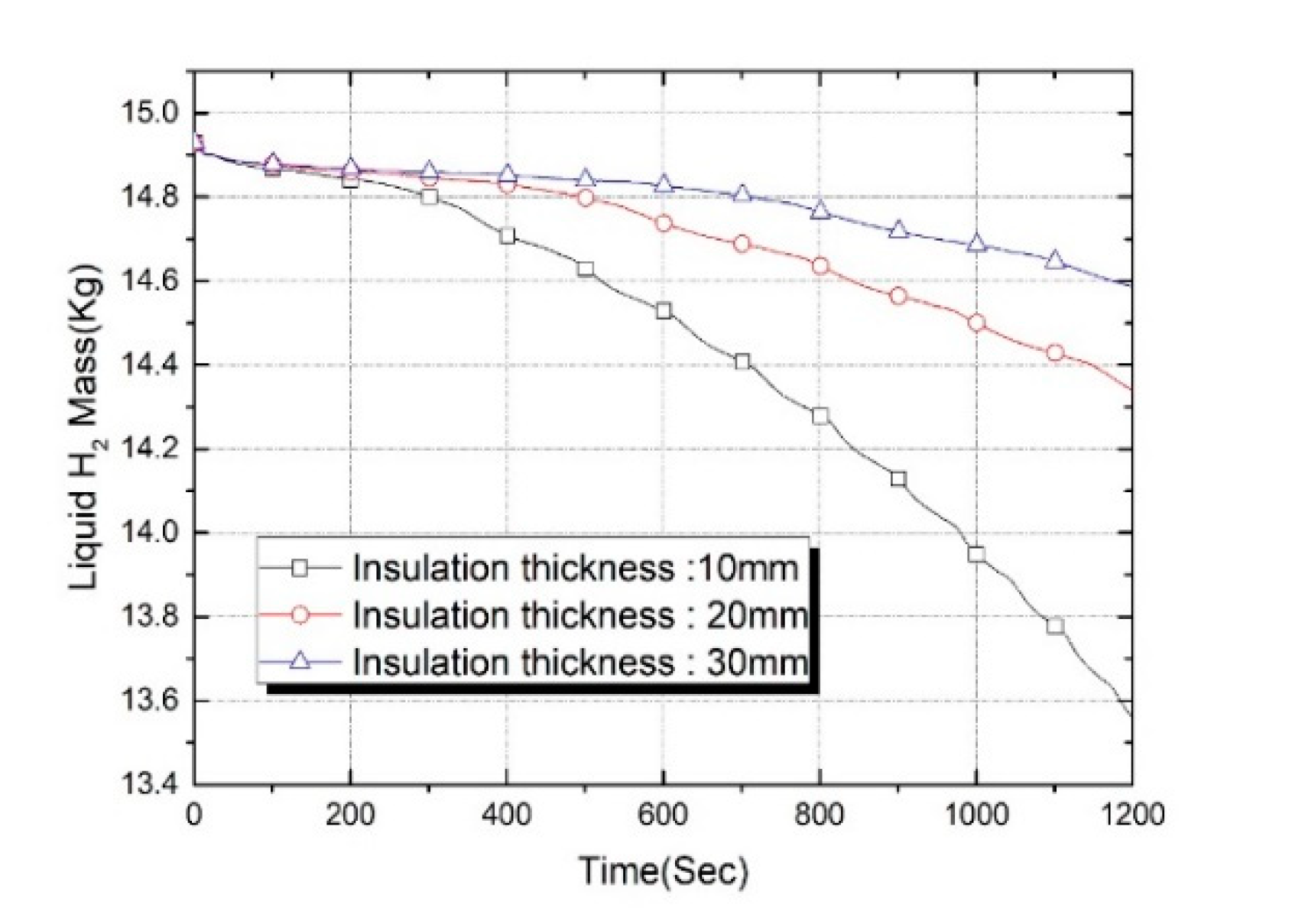
The changes in liquid mass according to three types of insulation thicknesses with time are presented in Figure 13. The liquid mass of the LH2 left in the tank decreased as the evaporation proceeds. As depicted in the figure, as the insulation thickness became thinner, the heat ingress penetrating the wall surface increased, which shortened the elapsed time, and evaporation took place quickly. Thermal leakage into the wall increases, and the buoyancy near the wall causes the warm liquid to rise and reach the interface in a shorter time. As a result, the rapid coupling of buoyancy and convection caused the enthalpy inside liquid hydrogen to increase rapidly, accelerating the onset of evaporation. After 600s, when the evaporation significantly progressed, the evaporation became relatively high with thinner insulation. Figure 14 shows the pressure rise versus time in the LH2 tank for three different insulation thickness. The results evidence that pressurization rates behave increasing with decreasing thickness. This is because as time elapses, for the lesser insulation thickness, the larger heat ingress into the tank leads to an increase in the internal energy of the two phases, resulting in a much more rapid rise in tank pressure. This behavior was also reported experimentally in previous literature [41], higher pressurization rates were measured for increased heat penetration into the tank. From the results of figure 14, it is observed that the pressure starts to rise after a certain time in all cases. This is because the warm liquid generated by the sidewall heat flux needs some time to flow upwards and reach the interface, and the enthalpy also increases [38]. It is also observed that as the thickness of the insulation decreases, the delay period before evaporation begins becomes shorter.

4. Conclusion

In this study, three-dimensional CFD model to accurately evaluate insulation performance and thermo-fluid characteristics in the partially filled liquid hydrogens tank of small-scale hydrogen liquefier has been developed and used to investigate the effect of insulation thickness ranging from 10 to 30mm on thermo-physical characteristics and evaporation loss. The proposed CFD model in this study describes not only thermo-fluid and mass transport phenomena in the ullage and liquid but also at the interface by solving N-S type governing equations with empirical correlation for mass interfacial exchange at free surface. The interfacial surface between liquid and vapor is represented and tracked using the VOF method. In addition, the proposed numerical model also includes a complex conjugated heat transfer problem coupled with a k-ξ-f turbulence model for simulating the near wall heat and fluid flow. To prove thermo-physical consistency and prediction accuracy, the propose model is validated with temporal history of pressure and evaporative mass data from experiments and computational results previously reported in literatures. It was confirmed that the numerical results in this study and the experimental results were in good agreement, and also noted that the prediction of pressurization rate is more sensitive to eddy viscosity formulation and near wall treatment of turbulent model than prediction of interfacial mass transfer.
From the results of this study, it is observed that with insulation thickness decreases, the enthalpy inside the liquid hydrogen quickly increased due to a fast coupling between the buoyance and convective, which made evaporation start faster. It can be also found that a radial temperature gradient rapidly decreased with time elapsed, but an axial temperature gradient was more strongly formed, causing a stronger temperature gradient and the thermal accumulation near the tank top in the vapor region.
It is also found that the stagnant flow due to the support groove prevents the mixing of the cooled downflow with the hot fluid near the wall, which can cause non-uniform temperature distribution in the liquid phase, and especially increases the temperature near the wall, which can eventually increase the amount of boil-off. As a result, pressurization rates due to evaporation behave increasing with decreasing thickness because of smaller thermal capacitance of insulation.
In the future, the numerical model developed in this study will be used to evaluates the insulation performance of the storage tank of the small-scale hydrogen liquefier to which the new insulation material is applied, and investigate the effect of inner structures such as support grooves on the temperature distribution and boil-off in the storage tank.

Author Contributions

Conceptualization, S-J. J. and S-J.L.; methodology, S-J.J.; software, S-J.J.; validation, S-J.J.; formal analysis, S-J.J. and S-J.L.; investigation, S-J.J. and S-J.L.; resources, S-J.J. and S-J. L.; writing—original draft preparation, S-J.J.; writing—review and editing, S-J.L.;S-J.L and S-J.M.; visualization, S-J.J and S-J.M.; supervision, S-J.J.; funding acquisition, S-J.J. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Material and parts technology development project of Korea Evaluation Institute of Industrial Technology, funded by the Korean government (Grant No. 20004900).

Acknowledgments

The authors also thank the AVL Korea, with whom they collaborated during 805 the initial stages of this work.

Conflicts of Interest

The authors declare no conflict of interest.

Nomenclature

The following nomenclatures are used in this manuscript:
g Gravitational acceleration [m2/s]
h Heat transfer coefficient [W/m2K]
k Conductivity [W/mK]
v 2 ¯ Wall normal fluctuations
D Diameter of tank or diffusivity [m, m2/s]
H Height of tank [m]
n Normal direction
α Volume fraction
ρ Density
μ Viscosity
δ Insulation thickness
ν Kinematic viscosity
χ Species mass fraction

Subscripts

The following subscripts are used in this manuscript:
air Air
Amb Ambient
c condensation
e f f Effective
e Evaporation
g Gas
i, j Coordinate
ℓ Liquid
m mass concentration
s Tank outer surface
sat Saturation
v Vapour
o Surface
s Surface
w Wall

References

  1. Altac, Z.; Ugurlubilek, N. Assessment of turbulence models in natural convection from two- and three-dimensional rectangular enclosures. Int. J. Therm. Sci. 2016, 107, 237–246. [Google Scholar] [CrossRef]
  2. FIRE ver. 2019 R2 main program user manual. AVL.com (accessed on December. 10. 2022).
  3. Adnani, P.; Jennings, R. W. Pressurization analysis of cryogenic propulsion systems. AIAA 2000, AIAA-2000-3788.
  4. Barsi, S.; Kassemi, M. Numerical and experimental comparison of the self-pressurization behavior of an LH2 tank in normal gravity. Cryogenics 2008, 48, 122–129. [Google Scholar] [CrossRef]
  5. Bergman, T. L.; Lavine, A. S.; Incropera, F. P.; Dewitt, D. P. Fundamentals of heat and mass transfer. 8th edn. John Wiley & Sons Inc., Massachusetts, USA, 2018, ISBN: 978-1-119-35388-1.
  6. Chen, L.; Liang, G. Z. Simulation research of vaporization and pressure variation in a cryogenic propellant tank at the launch site. Microgravity Sci. Technol. 2013, 25, 203–211. [Google Scholar]
  7. Chu, Xi.; Chen, W.; Shang, Y.; Hao, J.; Zhang, D. CFD investigation on reverse flow characteristics in U-tubes under two-phase natural circulation. Prog. Nucl. Energ. 2019, 114, 145–154. [Google Scholar] [CrossRef]
  8. Churchill, S. W.; Bernstein, M. A Correlating Equation for Forced Convection from Gases and Liquids to a Circular Cylinder in Crossflow. J. Heat Transfer 1977, 99, 300–306. [Google Scholar] [CrossRef]
  9. Durbin, P. A. Near-wall turbulence closure modeling without “damping functions”. Theor. Comput. Fluid Dyn. 1991, 3, 1–13. [Google Scholar]
  10. Duan, Z.; Zhu, Y.; Wang, C.; Yuan, Y.; Xue, H.; Tang, W. Numerical and Theoretical Prediction of the Thermodynamic Response in Marine LNG Fuel Tanks under Sloshing Conditions. Energy 2023, 270, 126935–126949. [Google Scholar] [CrossRef]
  11. Fu, J.; Sunden, B.; Chen, X. Influence of wall ribs on the thermal stratification and self-pressurization in a cryogenic liquid tank. Appl. Therm. Eng. 2014, 73, 1421–1431. [Google Scholar] [CrossRef]
  12. Gruz, M.; Baltacioglu, E.; Hames, Y.; Kaya, K. The meeting of hydrogen and automotive: a review. Int. J. Hydrogen Energy 2017, 42, 23334–23346. [Google Scholar] [CrossRef]
  13. Hardt, S.; Wondra, F. Evaporation model for interfacial flows based on a continuum-field representation of the source terms. J. Comput. Phys. 2008, 227, 5871–5895. [Google Scholar] [CrossRef]
  14. Hanjalić, K.; Popovac, M.; Hadžiabdić, M. A robust near-wall elliptic-relaxation eddy-viscosity turbulence model for CFD. Int. J. Heat Fluid Flow 2004, 25, 1047–1051. [Google Scholar] [CrossRef]
  15. Joseph, J.; Agrawal, G.; Agarwal, D. K.; Pisharady, J. C.; Kumar, S. S. Effect of insulation thickness on pressure evolution and thermal stratification in a cryogenic tank. Appl. Therm. Eng . 2017, 111, 1629–1639. [Google Scholar]
  16. 16. Jeong, S-J.; Moon S-J.; Park, K. W; Moon, S-J. Development of the three-dimensional numerical model for predicting thermal physical performance in liquified hydrogen tank for hydrogen fueled vehicle. Trans. Korean Society of Automotive Engineers, 2020; 28, 203–210.
  17. Kang, M.; Kim, J.; You, H.; Chang, D. Experimental investigation of thermal stratification in cryogenic tanks. Experimental Thermal and Fluid Science 2018, 96, 371–382. [Google Scholar] [CrossRef]
  18. Kang, H.; Kim, S. Y. Thermal design analysis of a 1 L cryogenic liquid hydrogen tank for an unmanned aerial vehicle. Int. J. Hydrogen Energy 2018, 39, 20009–20016. [Google Scholar] [CrossRef]
  19. Karimi, H.; Nassirharand, A.; Mohseni, M. Modeling and simulation of a class of liquid propellant engine pressurization systems. Acta Astrongautica 2010, 66, 539–549. [Google Scholar] [CrossRef]
  20. Krishnaprakas, C. K.; Badari Narayana, K.; Dutta, P. Heat transfer correlations for multilayer insulation systems. Cryogenics 2000, 40, 431. [Google Scholar] [CrossRef]
  21. Kassemi, M.; Kartuzova, O. Effect of interfacial turbulence and accommodation coefficient on CFD predictions of pressurization and pressure control in cryogenic storage tank. Cryogenics 2016, 74, 138–153. [Google Scholar] [CrossRef]
  22. Liu, Z.; and Li, Y. Thermal physical performance in liquid hydrogen tank under constant wall temperature. Renewable Energy 2019, 130, 601–612. [Google Scholar] [CrossRef]
  23. Liu, Z.; Li, C. Influence of slosh baffles on thermodynamic performance in liquid hydrogen tank. J. Hazard. Mater. 2018, 346, 253–262. [Google Scholar] [CrossRef]
  24. Liu, Z.; Li, Y.; Jin, Y.; Li, C. Thermodynamic performance of pre-pressurization in a cryogenic tank. Appl. Therm. Eng. 2017, 112, 801–810. [Google Scholar] [CrossRef]
  25. Li, X.; Xie, G.; Wang, R. Experimental and numerical investigations of fluid flow and heat transfer in a cryogenic tank at loss of vacuum. Heat Mass Transf. 2010, 46, 395–404. [Google Scholar] [CrossRef]
  26. Liu, Z.; Li, Y.; Xie, F.; Zhou, K. Thermal performance of foam/MLI for cryogenic liquid hydrogen tank during the ascent and on orbit period. Appl. Therm. Eng. 2016, 98, 430–439. [Google Scholar] [CrossRef]
  27. Lemmon, E. W.; McLinden, M. O.; Friend, D. G.; Linstrom, P.; Mallard, W. NIST chemistry WebBook, Nist standard reference database number 69. National Institute of Standards and Technology 2011.
  28. Liu, Z.; Li, Y.; Jin, Y. Pressurization performance and temperature stratification in cryogenic final stage propellant tank. Appl. Therm. Eng. 2016, 106, 211–220. [Google Scholar] [CrossRef]
  29. Liu, Z.; Feng, Y.; Lei, G.; Li, Y. Sloshing hydrodynamic performance in cryogenic liquid oxygen tanks under different amplitudes. Appl. Therm. Eng. 2019, 150, 359–371. [Google Scholar] [CrossRef]
  30. Masters, P. A. Computer programs for pressurization (RAMP) and pressurized expulsion from a cryogenic liquid propellant tank. 1974, NASA TN D-7504.
  31. Nzebuka, G. G.; Waheed, M. A. Thermal evolution in the direct chill casting of an Al-4 pct Cu alloy using the low-Reynolds number turbulence model. Int. J. Therm. Sci. 2020, 147, 106152. [Google Scholar] [CrossRef]
  32. Panzarella, C.; Kassemi, M. On the validity of purely thermodynamic descriptions of two-phase cryogenic fluid storage. J. Fluid Mech. 2003, 484, 41–68. [Google Scholar] [CrossRef]
  33. Panzarella, C.; Plachta, D.; Kassemi, M. Pressure control of large cryogenic tanks in microgravity. Cryogenics 2004, 44, 475–483. [Google Scholar] [CrossRef]
  34. Roh, S.; Son, G. Numerical study of natural convection in a liquefied natural gas tank. J. Mech. Sci. Technol. 2012, 26, 3133–3140. [Google Scholar] [CrossRef]
  35. Ranz, W.; Marshall, W. R. Modeling the interaction between a thermal flow and a liquid: review and future eulerian-lagrangian approaches. Chem. Eng. Prog. 1952, 48, 141–146. [Google Scholar]
  36. Schrage, RW. A theoretical study of interphase mass transfer, Columbia University Press, New York, 1953.
  37. Sun, P.; Wu, J. Y.; Zhang, P.; Xu, L.; Jiang, M. Experimental study of the influences of degraded vacuum on multilayer insulation blankets. Cryogenics 2009, 49, 719–726. [Google Scholar] [CrossRef]
  38. Sundén, B.; Fu, J. Heat transfer in aerospace applications, Academic Press, Massachusetts, USA, 2017.
  39. Spall, E.; Richards, A.; McEligot, D. M. An assessment of k-w and v2-f turbulence models for strongly heated internal gas flows. Numerical Heat Transfer 2004, 46, 831–849. [Google Scholar] [CrossRef]
  40. Saif, ZS.; Stephanie, M.; Umberto, C.; Eric, F.M. Hydrogen liquefaction: a review of the fundamental physics, engineering practice and future opportunities. Energy & Environmental Sci. 2022, 15, 2690–2731. [Google Scholar]
  41. Van Dresar, N.; Lin, C.; Hasan, M. Self-pressurization of a flight weight liquid hydrogen tank: effects of fill level at low wall heat flux. 1992, NASA TM-105411.
  42. Verstraete, D.; Hendrick, P.; Pilidis, P.; Ramsden, K. Hydrogen fuel for subsonic transport aircraft. Int. J. Hydrogen Energy 2010, 35, 11085–11098. [Google Scholar] [CrossRef]
  43. White, C.; Steeper, R.; Lutz, A. The hydrogen-fueled internal combustion engine: a technical review. Int. J. Hydrogen Energy 2006, 31, 1292–1305. [Google Scholar] [CrossRef]
  44. Wang, L.; Ye, S.; Ma, Y.; Wang, J.; Li, Y. CFD investigation on helium pressurization behaviors in liquid hydrogen tank. J. Hydrogen Energy 2017, 42, 30792–30803. [Google Scholar] [CrossRef]
  45. Whitaker, S. Forced convection heat transfer correlations for flow in pipes, past flat plates, single cylinders, single spheres, and for flow in packed beds and tube bundles. AIChE J. 1972, 18, 361–371. [Google Scholar] [CrossRef]
  46. Wang, L.; Li, Y.; Li, C.; Zhao, Z. CFD investigation of thermal and pressurization performance in LH2 tank during discharge. Cryogenics 2013, 57, 63–73. [Google Scholar] [CrossRef]
  47. Wang, Y.; Li, Y.; Zhu, K.; Jin, Y. Comparison of three computational models for predicting pressurization characteristics of cryogenic tank during discharge. Cryogenics 2015, 65, 16–25. [Google Scholar]
  48. Wang, H.; Wang, B.; Li, R.; Shen, X.; Wu, Y.; Pan, Q.; He, Y.; Zhou, W.; Gan, Z. Theoretical Investigation on Heat Leakage Distribution between Vapor and Liquid in Liquid Hydrogen Tanks. Int. J. Hydrogen Energy 2023, 48, 17187–17201. [Google Scholar]
  49. Wilcox, D. C. Turbulence modeling for CFD. 2nd. Ed. DCW Industries Inc., California.
  50. Wu, X.; Durbin, P. A. Numerical simulation of heat transfer in a transitional boundary layer with passing wakes. J. Heat Transfer . 1991, 122, 248–257. [Google Scholar]
  51. Ward, W. D. Evaluation of AS-203 low-gravity orbital experiment. NASA CR-94045 Chrysler Corp. Space Div. Technical Report, 1967.
  52. Zuo, Z.; Jiang, W.; Qin, X.; Huang, Y. A numerical model for liquid-vapor transition in self-pressurized cyogenic containers. Appl. Therm. Eng. 2021, 193, 117005–117015. [Google Scholar] [CrossRef]
Preprints 81739 g002
Figure 2. Schematic diagram of the small-scale (1.3 liter/hr) hydrogen liquefier.
Figure 2. Schematic diagram of the small-scale (1.3 liter/hr) hydrogen liquefier.
Preprints 81739 g002
Preprints 81739 g003
Figure 3. Schematic diagram of the inner liquid H2 tank.
Figure 3. Schematic diagram of the inner liquid H2 tank.
Preprints 81739 g003
Preprints 81739 g004
Figure 4. Prediction for temporal evolution of pressure for the pressurization of the 50% filling level of tank subjected to various sidewall heat ingress: comparison of predictions against previous computational results by [11].
Figure 4. Prediction for temporal evolution of pressure for the pressurization of the 50% filling level of tank subjected to various sidewall heat ingress: comparison of predictions against previous computational results by [11].
Preprints 81739 g004
Preprints 81739 g005
Figure 5. Comparison of liquid mass amounts with time for various uniform wall heat fluxes.
Figure 5. Comparison of liquid mass amounts with time for various uniform wall heat fluxes.
Preprints 81739 g005
Preprints 81739 g006aPreprints 81739 g006b
Figure 6. Comparison of k-ε and k-ζ-f turbulence model employed VOF model’s predictions against experimental results [51].
Figure 6. Comparison of k-ε and k-ζ-f turbulence model employed VOF model’s predictions against experimental results [51].
Preprints 81739 g006aPreprints 81739 g006b
Preprints 81739 g007aPreprints 81739 g007b
Figure 7. Comparison of streamlines in a tank for various insulation thickness.
Figure 7. Comparison of streamlines in a tank for various insulation thickness.
Preprints 81739 g007aPreprints 81739 g007b
Preprints 81739 g008
Figure 8. Temporal variations of temperature contours for the three different insulation thickness (insulation mat is not displayed). In 800s, when the thermal energy mix.
Figure 8. Temporal variations of temperature contours for the three different insulation thickness (insulation mat is not displayed). In 800s, when the thermal energy mix.
Preprints 81739 g008
Preprints 81739 g009
Figure 9. Temperature contours for three different insulation thickness at 1000s (including insulation mat).
Figure 9. Temperature contours for three different insulation thickness at 1000s (including insulation mat).
Preprints 81739 g009
Preprints 81739 g010
Figure 10. Temperature profiles at the central axis for three different times and insulation thickness.
Figure 10. Temperature profiles at the central axis for three different times and insulation thickness.
Preprints 81739 g010
Preprints 81739 g011
Figure 11. Temporal variations of averaged temperature of insulation for three different insulation thickness.
Figure 11. Temporal variations of averaged temperature of insulation for three different insulation thickness.
Preprints 81739 g011
Preprints 81739 g012
Figure 12. Temporal evolution of averaged temperature profiles of tank wall for three different insulation thickness.
Figure 12. Temporal evolution of averaged temperature profiles of tank wall for three different insulation thickness.
Preprints 81739 g012
Preprints 81739 g013
Figure 13. Comparison of liquid mass amounts with time for various insulation thickness.
Figure 13. Comparison of liquid mass amounts with time for various insulation thickness.
Preprints 81739 g013
Preprints 81739 g014
Figure 14. Prediction for evolution of pressure for the self-pressurization of the 50% filled tank subjected to various insulation thickness.
Figure 14. Prediction for evolution of pressure for the self-pressurization of the 50% filled tank subjected to various insulation thickness.
Preprints 81739 g014
Table 1. Geometrical dimensions and physical properties.
Table 1. Geometrical dimensions and physical properties.
Properties Tank wall (2219 Al alloy) Insulation foam
Thickness [mm]
Density [kg/m2]		 3
2,840		 10 ~ 30
35
Specific heat [J/(kgK)]
Thermal conductivity [W/(m·k)]		 864
143
 1,674
0.02
Table 2. Interface evaporation loss at t = 600s and t = 1,200s for three different insulation thicknesses.
Table 2. Interface evaporation loss at t = 600s and t = 1,200s for three different insulation thicknesses.
Insulation thickness [mm] Thermal capacitance [J/K] Evaporation loss (g) at t = 600s Evaporation loss (g) at t = 1,200s
10
20
30		 174.2
366.3
577.4		 0.398
0.190
0.101		 1.360
0.588
0.341
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated