Prerpints.org logo
Preprint
Article

Nonlinear Optical Absorption of Impurities in Hexagonal Quantum Wires: Electric and Magnetic Field Effects

Altmetrics

Downloads

172

Views

94

Comments

0

supplementary.bib (56.09KB )

Submitted:

31 July 2023

Posted:

08 August 2023

You are already at the latest version

Alerts
Abstract
Intraband energy transitions of an electron in GaAs/AlGaAs hexagonal quantum well wires in the presence of external electric and magnetic fields are presented. We consider the effects of the revolve of the quantum well wires via a geometric factor that converts the quantum wires straight and symmetric with respect to the z−axis, into a curved wires that no longer has this symmetry. In addition, the influence of having a shallow donor impurity on (off) is calculated. The shape of this quantum string corresponds to the core/shell structure. The energy levels and wave functions of the electron in the heterostructure with a finite potential between the shells are calculated using the effective mass approximation and the finite element method. The calculations of the optical properties are obtained from the compact density matrix and an iterative method. The direction of the applied external fields is parallel (anti-parallel) to the z−direction. The results reveal a significant dependence of the physical properties calculated with the deformation parameter, the dimensions of the quantum well wires and the presence or not of the impurity. The electronic transitions are in a range between 4.90 meV to 41.50 meV under the effect of the electric field, this corresponds to a range of frequencies of optical responses between 1.20 to 10 THz, that is, the mid-infrared. For the magnetic field the range is between 1.24 meV to 14 meV, that is, in frequencies from 0.36 to 3.38 THz, that is, in the far-infrared.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

Quantum wire structures have been an area of intensive research in the field of nanophysics due to their potential for revolutionizing a myriad of technological applications [1,2,3,4,5]. As the miniaturization trend in electronics continues, quantum wires and other low-dimensional structures exhibit unique properties that could substantially enhance device performance [6,7,8,9]. Among such structures, core/shell [10,11,12] semiconductor quantum wires, such as those based on Gallium Arsenide (GaAs) and Aluminum Gallium Arsenide (AlGaAs), have garnered particular interest. Their intriguing properties, such as high electron mobility and unique energy band structure, make them suitable for applications in quantum computing [13], optoelectronics [14], and other advanced electronic devices [15].
The properties of these quantum wires are not solely dependent on their material composition but also on their size, shape, and the external conditions they are subjected. For instance, when external electric and magnetic fields are applied, these can significantly modify the electronic and optical properties of the quantum wire [16,17,18,19,20,21,22]. Moreover, the presence of impurities, such as shallow donor atoms, can also have a considerable impact on the quantum wire’s behavior [23,24]. Understanding these effects is crucial for the design and optimization of quantum wire-based devices [25,26].
Such structures have been highlighted in several noteworthy and intriguing studies that have emerged in recent times. For example, Fonseka et al. [27], in one of their latest works, used nanowires as a basis for developing novel architectures. In figure 1 of their paper, they present a Scanning Electron Microscopy (SEM) [16] image of nanowires exhibiting a mild curvature. This particular feature spurred the motivation for the current study, given the prevalence and potential applications of these structures.
In this paper, we delve into the intricacies of GaAs/AlGaAs hexagonal quantum well wires under the influence of external magnetic and electric fields. More specifically, we study the intraband energy transitions of an electron in these wires and determine how these transitions are affected by the wire size and the presence of a shallow donor impurity. These analyses, carried out in the effective mass approximation, aim to provide a more nuanced understanding of the optical absorption coefficient.
To achieve this, we use the Finite Element Method (FEM) follow Vinasco et al. [28,29,30] via the licensed COMSOL-Multiphysics software [31,32] to calculate the electron energy levels and their corresponding wave functions. By leveraging the advanced computational capabilities of this software, we are able to accurately simulate the conditions within these quantum wires and obtain detailed insights into their behavior.
This paper presents the results of our investigations, revealing a significant dependence of the calculated physical properties on the presence of the impurity and the intensities of the applied electric and magnetic fields. Through this study, we hope to contribute to the body of knowledge on quantum wire structures, and provide valuable insights for future design and application of these advanced materials in various technological realms.

2. Materials and Methods

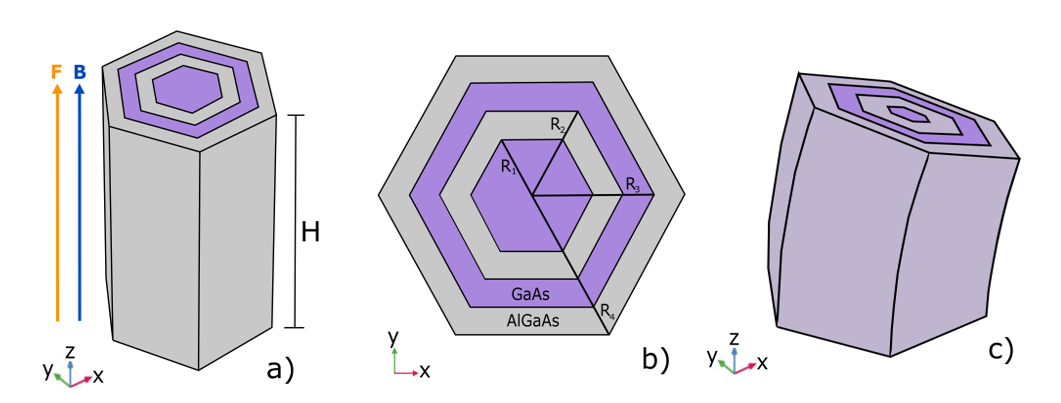
Figure 1(a) illustrates the structure of GaAs/AlGaAs hexagonal quantum wires without any revolution. The hexagonal arrangement consists of alternating GaAs semiconductor material (purple color in the first and third hexagon) and AlGaAs material (gray color in the second and fourth hexagon). The potential is set to zero within the GaAs material V w , while in the AlGaAs material, it is represented by V b . Additionally, a magnetic field B and an electric field F are applied in the z − direction. These external fields play a crucial role in the confinement and manipulation of charge carriers within the quantum wire system.
To further investigate the properties of the system, Figure 1(b) presents the hexagonal quantum wire at z = 0 , providing a clear visualization of the system’s geometry. The key parameters involved in the problem are indicated, including R 1 , R 2 , R 3 , and R 4 , which represent the radii of the four hexagons of the quantum wire. By specifying these parameters, we can precisely control the shape dimensions and geometry of the quantum wire structure, which in turn influences the electronic and optical properties under investigation.
To explore the effects of rotation on the quantum wire system, Figure 1(c) showcases the hexagonal quantum wire after rotation. A rotational transformation is applied with a radius of revolution, R * , and an angle of rotation, θ * . This rotational operation introduces a modified curvature to the wire while preserving the arc length. The introduction of an adimensional factor, k s the revolve parameter, allows us to adjust the curvature while maintaining the desired wire length along the z − direction. The relationships governing this modified curvature are expressed as R * = R k s , θ * = θ k s . It does not make sense to express the height of the quantum thread along z with H, but rather the product S = R θ . This rotational transformation enables the study of the influence of wire curvature on the electronic and optical properties of the system.
To numerically investigate the GaAs/AlGaAs hexagonal quantum wire system, we employ the powerful computational tool, Comsol Multiphysics. Specifically, we utilize the software’s Revolve functionality, which integrates the FEM to accurately solve the governing equations. The Revolve functionality is well-suited for modeling rotational symmetry in the system, allowing for a comprehensive analysis of the quantum wire’s properties.
In our simulation setup, Dirichlet boundary conditions are imposed on the sides of the last AlGaAs hexagon (with R 4 ), as well as on the front and rear covers of the system. These boundary conditions provide a physically realistic representation of the wire system and ensure accurate calculations of the electronic states and optical properties.
The electronic structure and optical properties of the system are elucidated by solving the Hamiltonian governing the quantum wire. The Hamiltonian is expressed as:
H = 1 2 m w , b * p → + e c A → ( r → ) 2 + V w , b ( x , y , z ) + e z F − κ e 2 4 π ϵ 0 ϵ r w , b r
where m w , b is the electron effective mass, ϵ r w , b is the static dielectric constant (the index w, b indicates the core or shell materials respectively). Within this Hamiltonian, the confinement potential is defined as V w ( x , y , z ) for GaAs quantum wire wells and V b ( x , y , z ) for AlGaAs quantum wires barriers. The first term in the Hamiltonian accounts for the kinetic energy of the charge carriers, including the momentum p → = − i ℏ ∇ → and the vector potential of the magnetic field A → . Besides, A → = B 2 ( y i ^ − x j ^ ) represents the potential vector associated to the applied magnetic field, where B → = ∇ → × A → comes from the gauge. The second term represents the confinement potential, which differs between GaAs and AlGaAs regions. The third term accounts for the interaction of the electric field with the charge carriers, where e represents the charge of the electron and F denotes the magnitude of the electric field in the z − direction. The final term in the Hamiltonian captures the Coulomb interaction between charges, with e representing the impurity charge and r denoting the distance between electron-impurity, with the impurity at a fixed point ( 0 , 0 , z i ) . Here, κ is a parameter that controls the presence or absence of the shallow donor impurity ( κ = 0 removes the impurity effects whereas κ = 1 turns them on).
To accurately describe the electronic and optical properties of the system, it is essential to consider the effective masses of the charge carriers. In our study, we utilize an effective mass of m w * for GaAs and m b * for AlGaAs. These effective masses account for the differences in carrier behavior between the two materials.
At the interface between GaAs and AlGaAs, the boundary conditions follow the approach established by Ben-Daniel and Duke [33,34]. These boundary conditions ensure a smooth transition of the electronic states across the material interface and provide a realistic representation of the heterostructure.
By solving the Hamiltonian using the FEM-based Comsol Multiphysics software, we obtain the electron states and corresponding wave functions for the system. These electron states are then utilized to evaluate the optical properties, particularly the transitions from the ground state to excited states.
Furthermore, we analyze the nonlinear optical absorption coefficients, following the framework proposed by Ahn and Chuang [35,36]. These coefficients, denoted as α i j ( ω ) , capture the intensity of the absorption process at different frequencies. They depend on various factors such as the incident photon frequency ω , the electron density ρ , and the matrix elements of the dipole moment M i j . The damping term, Γ i j , is inversely related to the relaxation time τ i j of the excited states.
α i j ( ω ) = ω e 2 μ 0 ε 0 ε r ρ ℏ Γ i j | M i j | 2 ( E i j − ℏ ω ) 2 + ( ℏ Γ i j ) 2 ,
In our calculations, we account for fundamental physical constants such as the permeability of free space ( μ 0 ), the vacuum permittivity ( ε 0 ), and the speed of light (c). The relative permittivity of the material, ε r , characterizes the dielectric properties of the quantum wire system. The elements of the dipole matrix moment for light polarized along the z − direction are calculated using the following:
M i j = 〈 ψ j | z | ψ i 〉
The calculated matrix elements provide insights into the strength and nature of the optical transitions occurring within the quantum wire system.
Finally, we emphasize that this study focuses on exploring the electron confinement effects related to the dimensions of quantum wires and the impact of externally applied electric and magnetic fields. Additionally, we investigate the influence of shallow donor impurity effects on the semiconductor nanostructure properties.

3. Results and Discussion

To further investigate the properties of the system, the key parameters involved in the problem are indicated, including R 1 = 4 nm for the GaAs core, R 2 = 10 nm (AlGaAs shell), R 3 = 15 nm (GaAs shell) and R 4 = 20 nm (AlGaAs shell), which represent the radii of the four hexagons in the quantum wire, see Figure 1 presents the hexagonal quantum wire base at z = 0 plane, providing a clear visualization of the semiconductor nanostructure geometry. R = 100 nm and revolve effect parameter k s = 0.9 fixed and θ = π 9 rad. The setup for the potential energy and effective mass are V w ( x , y , z ) = 0 and m w * = 0.067 m 0 for GaAs and V b ( x , y , z ) = 262 meV and m b * = 0.092 m 0 for AlGaAs, where m 0 corresponds to the mass of a free electron. In our calculations, we account for the relative permittivity value ε r = 12.53 , the nonlinear optical absorption coefficients for light polarized along the z − direction are calculated using the following: The damping term, Γ i j = 0.60 ps, is inversely related to the relaxation time τ i j = 1 / Γ i j of the excited states and density ρ = 3.5 × 10 23 m − 3 . The other variables are the fundamental physical constants such as the permeability of free space μ 0 , the vacuum permittivity ε 0 , e represents the charge of the electron and the speed of light c.
A pictorial view of the electron ground state wave function projections corresponds to the intersection of the hexagonal GaAs/AlGaAs quantum wire and a revolve effect, with the planes at z = 30 nm, the lower one at z = 10 nm, shown in Figure 2, without electric and magnetic fields effects.
In Figure 2(a) the wave function correspond to the case without donor impurity, it is observed that the wave function mostly spreads in the region of the GaAs shell with radius R 3 , this means that the electron is confined between the AlGaAs shells that forms a region of hexagonal barriers. It is observed that the highest probability of finding this with an intense red color in the plane z = 10 nm and in yellow color a lower probability is observed in the z = 30 nm plane, in these case the wave function only occupies a V-type region.
When we place a donor impurity at z i = 17.50 nm, the electron is most likely confined to the GaAs nucleus with radius R 1 , the intense red color region (a virtual quantum dot) to the bottom of the quantum wire (at z = 10 nm) appear, see Figure 2(b). Some probability minor is seen in the hexagonal region between R 2 and R 4 that cut z = 30 nm, these very low probability of the localize the electron are in the region in V-type form weakly painted in white color is observed, from here we can say that the presence of the impurity confines the electron in the lower region of the quantum wire close to the base in z = 0 .
In Figure 3 we present the wave function of the ground state and the first two excited states of an electron confined in a quantum wire without impurity. Figure 3 (a, b, c) show the effect of an electric field of F = 5 kV/cm, applied parallel to the positive z − axis and Figure 3 (d, e, f) F = − 5 kV/cm, that is, applied anti-parallel to the positive z − axis. Figure 3 (a, b, c) confirm the fact that a positive electric field repels the electron confining it towards the region of the base of the quantum wire, this is observed by the maximum probabilities (in red color) in the plane z = 10 nm and practically zero probability in the plane z = 30 nm (in blue color). In Figure 3(a) we have the fundamental state E 1 , in Figure 3(b) the first excited E 2 and in Figure 3(c) the second excited E 3 , regarding the excited states it can be see that its probability is "rotated by 90°", this is because all wave functions (and their projections) are orthogonal and normalized, this behavior explains why in Figure 4(a) the energy curves E 2 and E 3 are degenerate in the range from F = 0 kV/cm to F = 50 kV/cm, keeping the electron confined in this region.
Figure 3(d, e, f) illustrates the electron wave functions for an electric field of F = − 5 kV/cm, corresponds to first, second and third states, respectively. In Figure 3(d) the clear effect on the charge location probability within the system is evident. When the electric field is applied in the direction opposite to the z − axis, we can see the formation of a virtual V-groove quantum dot (intense red color) becomes apparent in plane z = 30 nm, while in z = 10 nm a slight probability appears, with a tendency to zero, in white color, these phenomenon influenced by the unique asymmetry that revolve parameter induces. On the other hand, in Figure 3(e, f) exhibits this same effect but with the activation the wave function in both cuts, distributing the probabilities of locating the electron in some regions in the hexagons, it is important to note that the differences with the wave functions shown in Figure 3(b, c), explain why in this case the states E 2 and E 3 are not degenerate in the entire range between -50 kv/cm and 0 in Figure 4(a).
In Figure 4 are shown (a) the electron energies, (b) dipole elements and (c) absorption coefficients as a function of the electric field strength F, without donor impurity ( κ = 0 ) in hexagonal GaAs/AlGaAs quantum wires. In this case we have fixed the geometrical dimensions of the quantum wire: R 1 = 4 nm, R 2 = 10 nm, R 3 = 15 nm, and R 4 = 20 nm which represent the radii of the four hexagons of the quantum wire and R = 100 nm, θ = π 9 rad and k s = 0.9 .
In the Figure 4(a) depicts the energies corresponding to the lowest energy states of the electron confined within a multi-layered quantum wire, as a function of an external electric field applied along the z − axis. The magnitude of this field varies from -50 kV/cm to zero, for anti-parallel to z − axis and from zero to F = 50 kV/cm in direction parallel to z − axis. Given the asymmetry introduced by the revolve factor k s , these electron energies curves are also asymmetric. This asymmetry can be observed, for instance, in the ground state, where the electron’s energy approximates E 1 = 44 meV at F = − 50 kV/cm and approximates E 1 = 56 meV at F = 50 kV/cm. The same asymmetric behavior applies to for all excited states. We observe the special effect of the geometrical asymmetric in combination whit the electric field over the first and second excited states, in the regimen of the anti-parallel direction these energies are separated for a 10 meV of difference, but in the parallel direction, after the electric field strength in zero values these energies are degenerates until F = 50 kV/cm. For fourth, fifth and sixth excited states, the energies curves present anti-crossing phenomena between their in several points correspond with the both parallel and anti-parallel regime, can see at round to 0, 10 kV/cm, 20 kV/cm and 40 kV/cm. The energies that correspond to seventh and eighth states only have tree point with anti-crossing and both curves are totally asymmetric. In a hypothetical scenario where the hexagonal quantum wire was upright, meaning that the axis of the quantum wire would align with the z − axis, the energy curves presented would be symmetric and degenerated in accordance with the symmetry delineated in Figure 1(a). When the electric field is applied in the same direction as the z − axis, i.e., in the range of 0 to F = 50 kV/cm, the electron, repelled by the electric field, demonstrates a probability to localize its wave function in the lower region of the quantum wire. This area represents the region of maximum geometric confinement, caused by the parameter k s .
For the third excited state ( E 4 ), in Figure 4(a), there is an inflection point at approximately F = 0 kV/cm, while in Figure 6(a), this same state presents a maximum, and the same behavior of changing critical points occurs in states E 6 and E 7 . At the same time, when the impurity is not present, E 4 is degenerate to E 5 , except between F = − 20 kV/cm and F = 10 kV/cm, where they are not. Conversely, when there is the presence of impurity, E 4 is always degenerate to E 5 , and even between F = 0 kV/cm and F = 15 kV/cm, E 3 and E 4 are degenerate. Another interesting detail is that, given the crossings between the first and second excited state at approximately F = − 13 kV/cm and F = 13 kV/cm, they favor the emergence of a transition probability between the ground state and the first excited state that previously did not exist in Figure 4(a).
The elements of the dipole matrix M 1 j , j = 3 , 4 , 5 , 6 , 7 , 8 depending on the magnitude of the electric field are presented in Figure 4(b), this allows to study the transitions allowed between the ground state and the corresponding excited states for which this occurs. Linear polarization along the z − axis has been considered to analyze the relationship with the electric field in both regimes.A non-uniform oscillatory behavior can be observed in the curves of the dipole elements, this behavior is associated with the crossings that have the states with energies E 3 to E 8 as can be seen in Figure 4(a). The dipole element M 13 has positive values from F = − 50 kV/cm and then drops to zero at F = 13 kV/cm. M 14 is different from zero in the range from -19 kV/cm to 16 kV/cm, and is also the largest magnitude, M 15 it only has a few points where it is different from zero, at: -40 kV/cm, -20 kV/cm and 13 kV/cm, which he understands by E 5 to be a state that is degenerate with E 6 for values greater than F > 13 kV/cm. The ranges where M 16 is different from zero are from -33 kV/cm to -20 kV/cm and then between 17 kV/cm to 19 kV/cm, M 17 between -50 kV/cm to -35 kV/cm and from 20 kV/cm to 37 kV/cm, finally M 18 is only different from zero between 40 kV/cm to 50 kV/cm. The crossings observed in the energy curves in Figure 4(a) cause, for example, that the positive values of the dipole elements from M 14 to M 18 to form a "curve" of positive values, making it possible to add the respective values of the absorption coefficients α 14 to α 18 .
In Figure 4(c), the transition energy effects ( E 1 f ) over the optical absorption coefficients, α a and α b , can be observed. The amplitude of these absorption coefficients is proportional to the product of the squared dipole moment and the transition energy, i.e. E 1 j × M 1 j 2 . For α a , represented by α 13 plus α 15 , a redshift is noticeable as the field becomes smaller for negative values of F, between 22.70 meV at -50 kV/cm and 5.70 meV at 12 kV/cm, respectively, after this electric field value the dipole M 13 becomes zero, therefore there are no absorption coefficient peaks. For α b , represented the sum of α 14 , α 16 , α 17 , and α 18 , the behavior demonstrates a redshift while under a negative electric field, from 40 meV at -50 kV/cm to 14 meV at 0 kV/cm, where is also the maximum amplitude of all the peaks of the optical absorption coefficients presented here and a blueshift when the electric field carries positive values, from the value corresponding to zero of the electric field to 41.50 meV at 50 kV/cm. The locations of the peaks of the optical absorption coefficients are in the range of allowed energy transitions, which correspond to the far infrared, between 1.38 THz and 10 THz, that is, to a semiconductor nanostructure such as this quantum wire with revolve effect, its optical response can be modulated with effects of electric fields, such as are presented in this work.
In Figure 5, they are presented in the same geometric conditions and applied electric field values as in Figure 3, the fundamental difference is that a donor impurity is placed at the point ( x = 0 , y = 0 , z i = 17.5 ) nm. As can be seen in the figures (a, b, c), the presence of the donor impurity repels the electron and the effect of the electric field of F = 5 kV/cm is reinforced, confining the electron near the cutting plane at z = 10 nm. In the ground state (a) and first excited (b) the combined effects of impurity and electric field locate the electronic probability in the central hexagon (or core), in a virtual quantum dot, the second is excited (c), it is located in the same plane, but rotated 90° with respect to the Figure 3(c), an effect that is essentially due to impurity. In this case it can be seen that the electron wave functions, although they are orthonormal, correspond to values where the associated energies are not degenerate, precisely because of the notorious differences between (b) and (c), (e) and (f). It is also important to clarify that at small values of the electric field (positive or negative) or in a weak regime, the presence of the impurity dominates the location of the electronic probability in the hexagonal core ( R 1 of GaAs, while for the strong regime of the electric field (for example | 50 | kV/cm), the effect of the field is dominant over that of the impurity.
In Figure 6, the same panels as in Figure 4 are presented, but in this case, within the hexagonal quantum wire system, there is a donor impurity at a height in the z i = 17.50 nm. Thus, for Figure 6(a), the first noticeable effect of the donor impurity is that the energies of both the ground state and the excited state decrease by approximately 9 meV (see the vertical axis in Figure 6 vs. Figure 4), due to the confinement the impurity grants to the electron. Another interesting effect that can be observed is that while in Figure 4(a), the first and second excited states ( E 2 and E 3 respectively) are degenerate for positive values of the electric field, in the case of Figure 6(a), these are barely degenerate for values greater than approximately 12 kV/cm.
Figure 6(b) shows the elements of the dipole matrix with the same configuration as Figure 4(b), considering the presence of impurity ( κ = 1 ), oscillations in the curves of these dipoles are also observed, the three main facts being: The values of all the dipoles drop by almost 1 nm on average, the second is that the M 12 dipole appears with a non-zero value between -15 kV/cm and 15 kV/cm and the third news is that a change occurs between the M 14 and M 15 dipole curves (compared to those of Figure 4(b)). This causes the appearance of a permitted transition formed by the dipoles M 12 , M 13 and M 14 . This behavior is responsible for the appearance of peaks in the optical absorption coefficients up to 40 kV/cm, a fact that does not occur when the impurity is off ( κ = 0 ), this due to the location of the electronic probability by the impurity along the z-axis.
In Figure 6(c), we can study the optical absorption coefficients α a = α 12 + α 13 + α 14 and α b = α 15 + α 16 + α 18 associated with the changes in transition energy for due to the presence of a donor impurity. If this graph is compared with Figure 4(c), though the amplitude of these in Figure 6(c) is less prominent than that shown in Figure 4(c). In α a , for positive electric field values, there exists a small peak not found in Figure 4(c). This is attributed to the probability of a transition between the ground state and the third excited state ( M 14 ), which did not exist previously in the absence of impurity, this is α a in figures presents a redshift for negative electric field values, from 23 meV at -50 kV/cm to 4.10 meV at zero and a blueshift for positive values, from 23 meV at -50 kV/cm to 13.10 meV at 40 kV/cm, from this value to 50 kV/cm the dipoles become zero, that is, energy transitions are not allowed in that range of electric field values between the first three excited states and the ground state, respectively. However, the path followed by the optical absorption coefficient α b in Figure 6(c) is 3 meV less compared to its counterpart in Figure 4(c), this can be attributed to the impurity which, as observed in Figure 6(a), causes lower energy values; also note that there is a redshift for negative values of the electric field and a blueshift for positive values.
Figure 7 show the wave function of the ground state of the electron. Upper panel (a, b, c, d) without donor impurity, lower panel (e, f, g, h) with donor impurity (at z i = 17.50 nm). The effects of the external magnetic field are shown in the following order: At (a, e) B = 1 T, at (b, f) B = 5 T, at (c, g) B = 10 T and in (d, h) B = 30 T, in GaAs/AlGaAs hexagonal quantum wires with revolution parameter k s = 0.9 and the fixed geometry related in this work. The magnetic field is applied in the positive direction of the z − axis.
In the Figure 7 of the upper panel without impurity ( κ = 0 ), three fundamental effects are noted, the first that the increase in the magnetic field B from 1 T, to 5T, 10 T and finally 30 T, leads to the location of the wave function of the electron to be confined in a virtual quantum ring for the weak regime of B in the region of the hexagon of radius R 3 (the third shell), until forming coupled points, this in the cut of the plane at z = 10 nm, with the quantum thread. The second is that when the value of B increases, the probability of locating the electron in the z = 30 nm plane becomes lower, the third effect is that this type of confinement evolution causes the energy of the ground state to increase and have smooth oscillations, see Figure 8(a), black curve ( E 1 ).
In the case of the lower panel, where there is the active donor impurity ( κ = 1 ), it is noted that by increasing the B value, the electron wave function is very well located in the cut of the hexagon of radius R 1 (core), of the quantum wire, with the plane at z = 10 nm, that is, the magnetic field confines the electron in a virtual quantum dot, combined with the presence of the donor impurity that rejects the electron towards that lower region of the nanostructure. It is clearly seen that the probability of locating the electron in the z = 30 nm plane becomes zero as B increases .Another quite noticeable effect of the combination of a magnetic field and the presence of the donor impurity is that the oscillations of the ground state, black curve E 1 , and the first excited state, red curve E 2 , tend to disappear,see Figure 9(a).
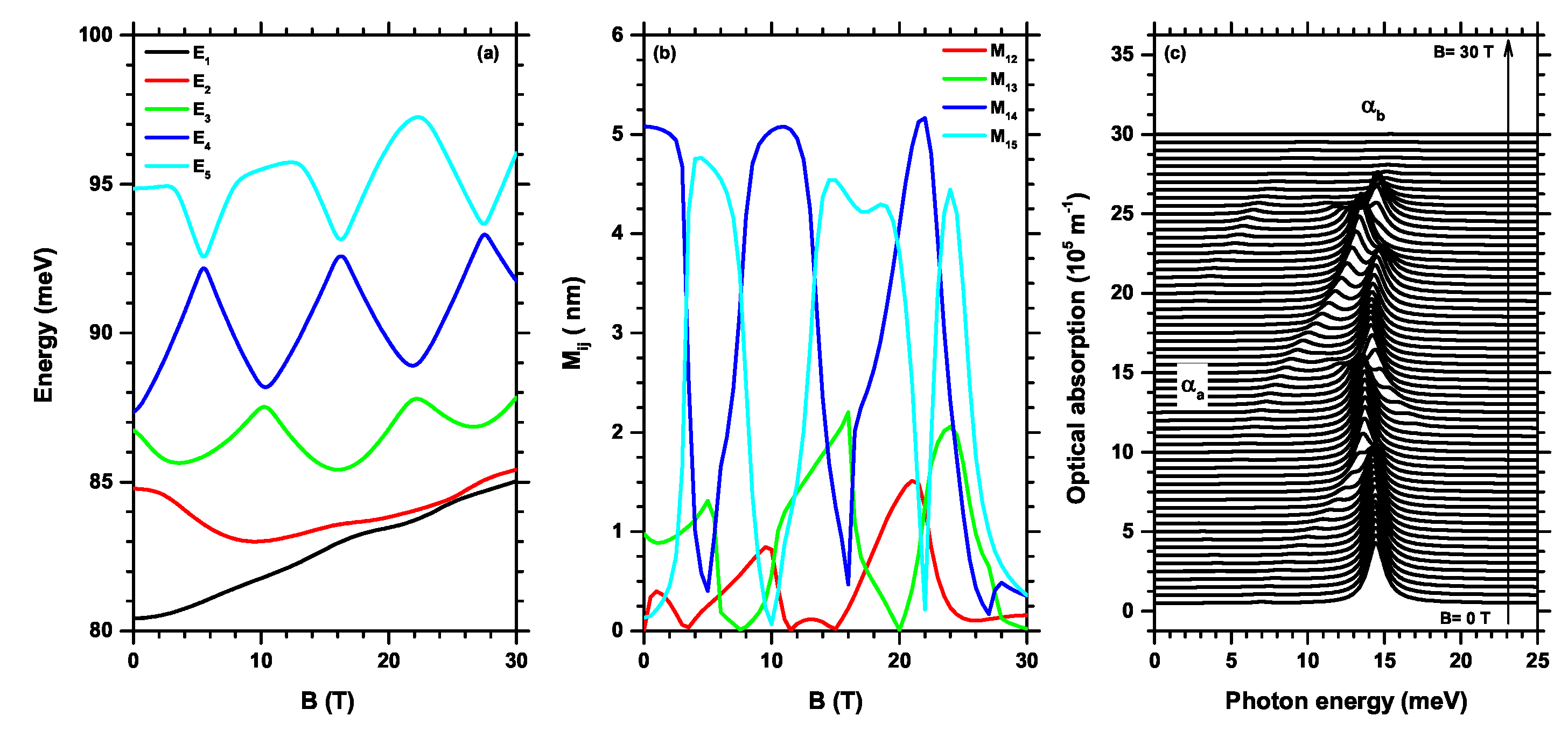
In Figure 8, the effect of the magnetic field is analyzed for (a) electron energies, (b) dipole elements and (c) optical absorption coefficients. Particularly in Figure 8(a), the energy levels of an electron confined within a hexagonal quantum wire, under the influence of a magnetic field applied in the z direction, are displayed. The magnitude of this field varies from 0 to B = 30 T. The energy range of the first five states is between 92 meV and 109 meV, much smaller than the range due to the electric field. The figure clearly depicts the oscillations induced by the magnetic field in the energies of the excited states, and to a lesser extent, in the ground state. Concurrently, it becomes apparent that as the field intensity increases, the energy levels increase. for B = 0 , it can be observed that the energies of the first two excited states are degenerate, the only time it occurs in the first five states shown here. However, this degeneracy was broken when a magnetic field was applied and multiple crossovers occurred between all energy levels for particular magnetic field values, causing accidental degeneracies. This resulted in an oscillating pattern of energies as a function of B, and at the crossing points, the wave functions are swapped at those points correspondingly.
Figure 8(b) shows the oscillating behavior of the elements of the dipole matrix as a function of the magnetic field, the ones with the greatest amplitude being those of the elements M 14 (blue color curve) and M 15 (cyan color curve), the maximum values of these dipoles alternate around 5 nm and 6 nm. Another group of dipoles is formed by M 12 (red color curve) and M 13 (green color curve), their maximum amplitude range is between 2 nm and 3 nm, respectively, throughout the B scan. These dipoles are associated with transitions with a non-zero probability of occurring when a magnetic field is applied.
Figure 8(c) shows two groups of nonlinear optical absorption coefficients ( α a = α 12 + α 13 and α b = α 14 + α 15 ) depending on the energy of the incident photons for different values of the magnetic field between 0 and 30 T, associated with the differences between the energies E 1 j = E j − E 1 shown in the curves of Figure 8(a) and the squares of the dipole elements M 1 j in Figure 8(b). For the coefficients grouped in α a it is observed that the optical absorption peaks oscillate as do the energies and the dipoles, these coefficients present a shift towards the blue in general, but their amplitudes are smaller because they come from the dipole elements M 12 and M 13 , the lowest value peak, which coincides with the energy of the photons at E 12 = ℏ ω = 4.1 meV which corresponds to 1 THz. The coefficients α b are mainly located at 12 meV for B = 0 and 14 meV at B = 30 T, with small oscillations that vary according to the transition energies E 14 and E 15 multiplied with the squares of the M 14 and and M 15 dipoles, correspondingly, these coefficients have their peaks almost centrally aligned. For these optical responses the frequencies are oscillating around 3.36 THz, in the far infrared.
Finally, Figure 9 shows the combined effects of a magnetic field with the presence of a donor impurity in the semiconductor nanostructure of a core/shell/shell type quantum wire, on the energies of the first five electronic states (a), the elements of the dipole matrix (b) and the optical absorption coefficients (c) associated with the allowed transitions. The configurations of the geometry and the values of the magnetic field are the same as those considered in Figure 8 and the active impurity in at z i = 17.50 nm. In Figure 9(a), the energy curves of the first five states generally lower their value, compared to those presented in Figure 8(a), this can be seen in all extreme values of the magnetic field, in general, the range of energies is between 80.50 meV at B = 0 for the ground state ( E 1 ) and 97.50 meV at B = 24 T for the fourth excited state ( E 5 ). In this energies range, the energy transitions occur if the corresponding dipole is different from zero. On the other hand, the effect of the magnetic field combined with the donor impurity, causes the electron to be confined in the R 1 region, which is the core of the structure, causing the curves of both the ground state and the first excited state to "smooth", losing the typical oscillations caused by the magnetic field only. The other three excited states keep this characteristic behavior, favoring the typical crossings for some specific values of the magnetic field.
The dipole elements are presented in Figure 9(b), it is observed that the group of elements M 14 and M 15 also present the oscillatory behavior and their maximums are between 4 and 5 nm, that is, they have dropped almost 1 nm, if compare with those of Figure 8(b). for the group M 12 and M 13 , which have their maximums between 1 nm and 2 nm, there is also an equal decrease, 1 nm, in their magnitude, an effect due to the presence of the donor impurity, it is also noteworthy that all the dipoles fall towards zero, after B = 24 T, a fact that converts the optical absorption coefficients to zero between 24 T and 30 T, as can be seen in Figure 9(c).
The optical absorption coefficients presented in Figure 9(c), are associated with the energy transitions and the corresponding dipole elements, thus in α a with the α 12 proportional to E 12 M 12 2 added with the α 13 which are proportional to E 13 M 13 2 , equal for α b = α 14 + α 15 . The optical absorption coefficients α b present their peaks oscillating around a central value of 14 meV, with small shifts towards the blue, which do not exceed 15 meV, very similar to the previous case with a magnetic field, but without impurity, however, in this case, with donor impurity present, the coefficients disappear after 24 T and the peaks appear more aligned, obviously of greater amplitude than those of the coefficients labeled α a . With a small amplitude and with a blue shift. the coefficients α a are observed, their peaks are located in corresponding regions of photon energy between 1.24 meV and 9.30 meV close to 28.50 T. These energy ranges correspond to photon frequencies between 0.36 and 3.38 THz.

4. Conclusions

By utilizing the aforementioned methodologies, including the Comsol Multiphysics software and the FEM approach, we are able to investigate and elucidate the intricate interplay between the structural, electronic, and optical properties of the GaAs/AlGaAs hexagonal quantum wire nanostructure.
We observe a very interesting effect related to the presence of the impurity in the structure, since without impurity we have the probability of the electron distributed in a ring, that is, a virtual quantum ring with geometric confinement. On the other hand, when the impurity is activated, the ground state is confined to the cylindrical hexagon in the core, which indicates that we have turned that ring into a virtual quantum dot, but we can also say that, being a 3D structure, we go to have a quantum wire.
The results reveal a significant dependence of the electronic transitions are in a range between 4.90 meV to 41.50 meV under the effect of the electric field, this corresponds to a range of frequencies of optical responses between 1.20 to 10 THz, that is, the mid-infrared. For the magnetic field the range from 0 to 30 T is between 1.24 meV to 14 meV, that is, in frequencies from 0.36 to 3.38 THz, that is, in the far-infrared.
This comprehensive analysis provides valuable insights into the behavior of charge carriers in confined geometries and under the influence of external electric and magnetic fields, paving the way for potential applications in nanoscale electronic and optoelectronic devices.

Author Contributions

C.A.D., A.S.G.N., T.S.G, J.A. V., R.L.R., A.L.M.: Conceptualization, methodology, software, formal analysis, research, writing; A.L.M., C.A.D.: Research, supervision, writing. All authors have read and agreed to the published version of the manuscript.

Funding

A.L.M., J.A.V. and C.A.D. are grateful to the Colombian Agencies: CODI-Universidad de Antioquia (Estrategia de Sostenibilidad de la Universidad de Antioquia and projects “Propiedades magneto-ópticas y óptica no lineal en superredes de Grafeno”, “Estudio de propiedades ópticas en sistemas semiconductores de dimensiones nanoscópicas”, “Propiedades de transporte, espintrónicas y térmicas en el sistema molecular ZincPorfirina”, and “Complejos excitónicos y propiedades de transporte en sistemas nanométricos de semiconductores con simetría axial”), and Facultad de Ciencias Exactas y Naturales-Universidad de Antioquia (A.L.M. and C.A.D. exclusive dedication projects 2022–2023). M.E.M.-R. acknowledges Mexican CONAHCYT for support through subsidy CB/2017-2018 and Grant A1-S-8218. R.L.R. is grateful to the permanent support of the Universida EIA.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

No new data were created or analyzed in this study. Data sharing is not applicable to this article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Jiang, Q.G.; Ao, Z.M. Density Functional Theory Study on the Ultrathin InAs/GaAs Core/Shell Nanowires for Solar Cell Applications. IOP Conference Series: Materials Science and Engineering 2018, 382. [Google Scholar] [CrossRef]
  2. Gu, Z.; Prete, P.; Lovergine, N.; Nabet, B. On optical properties of GaAs and GaAs/AlGaAs core-shell periodic nanowire arrays. Journal of Applied Physics 2011, 109. [Google Scholar] [CrossRef]
  3. Litvin, A.P.; Martynenko, I.V.; Purcell-Milton, F.; Baranov, A.V.; Fedorov, A.V.; Gun’Ko, Y.K. Colloidal quantum dots for optoelectronics. Journal of Materials Chemistry A 2017, 5, 13252–13275. [Google Scholar] [CrossRef]
  4. Lu, W.; Guo, X.; Luo, Y.; Li, Q.; Zhu, R.; Pang, H. Core-shell materials for advanced batteries. Chemical Engineering Journal 2019, 355, 208–237. [Google Scholar] [CrossRef]
  5. Vasudevan, D.; Gaddam, R.R.; Trinchi, A.; Cole, I. Core-shell quantum dots: Properties and applications. Journal of Alloys and Compounds 2015, 636, 395–404. [Google Scholar] [CrossRef]
  6. Li, J.J.; Wang, Y.A.; Guo, W.; Keay, J.C.; Mishima, T.D.; Johnson, M.B.; Peng, X. Large-scale synthesis of nearly monodisperse CdSe/CdS core/shell nanocrystals using air-stable reagents via successive ion layer adsorption and reaction. Journal of the American Chemical Society 2003, 125, 12567–12575. [Google Scholar] [CrossRef]
  7. Xie, R.; Kolb, U.; Li, J.; Basché, T.; Mews, A. Synthesis and characterization of highly luminescent CdSe-core CdS/Zn 0.5Cd0.5S/ZnS multishell nanocrystals. Journal of the American Chemical Society 2005, 127, 7480–7488. [Google Scholar] [CrossRef]
  8. Gadalla, A.; El-Sadek, M.S.; Hamood, R. Synthesis and optical properties of CdSe/CdS core/shell nanocrystals. Materials Science- Poland 2019, 37, 149–157. [Google Scholar] [CrossRef]
  9. Mandal, T.; Dasgupta, C.; Maiti, P.K. Tunable mechanical and thermal properties of ZnS/CdS core/shell nanowires. Physical Review B - Condensed Matter and Materials Physics 2015, 91. [Google Scholar] [CrossRef]
  10. Mayo, D.C.; Marvinney, C.E.; Bililign, E.S.; McBride, J.R.; Mu, R.R.; Haglund, R.F. Surface-plasmon mediated photoluminescence from Ag-coated ZnO/MgO core–shell nanowires. Thin Solid Films 2014, 553, 132–137. [Google Scholar] [CrossRef]
  11. Zheng, J.; Li, E.; Yan, J.; Cui, Z.; Ma, D. Electronic and optical properties of GaN/AlN core-shell nanowires. Modern Physics Letters B 2020, 34. [Google Scholar] [CrossRef]
  12. She, C.; Demortière, A.; Shevchenko, E.V.; Pelton, M. Using shape to control photoluminescence from CdSe/CdS core/shell nanorods. Journal of Physical Chemistry Letters 2011, 2, 1469–1475. [Google Scholar] [CrossRef]
  13. Yakimenko, I.I.; Yakimenko, I.P. Electronic properties of semiconductor quantum wires for shallow symmetric and asymmetric confinements. Journal of Physics Condensed Matter 2022, 34. [Google Scholar] [CrossRef] [PubMed]
  14. Zeiri, N.; Naifar, A.; Nasrallah, S.A.B.; Said, M. Third nonlinear optical susceptibility of CdS/ZnS core-shell spherical quantum dots for optoelectronic devices. Optik 2019, 176, 162–167. [Google Scholar] [CrossRef]
  15. Kagan, C.R.; Lifshitz, E.; Sargent, E.H.; Talapin, D.V. Building devices from colloidal quantum dots. Science 2016, 353. [Google Scholar] [CrossRef]
  16. Evangelou, S. Nonlinear optical absorption coefficient and refractive index change in symmetric semiconductor nanostructures: Comparison between different methods. Physica E: Low-dimensional Systems and Nanostructures 2020, 124, 114307. [Google Scholar] [CrossRef]
  17. Ungan, F. Effects of applied electric and magnetic fields on the nonlinear optical rectification and second-harmonic generation in a graded quantum well under intense laser field. Eur. Phys. J. B 2017, 90, 12. [Google Scholar] [CrossRef]
  18. Dakhlaoui, H.; Altuntas, I.; Mora-Ramos, M.E.; Ungan, F. Numerical simulation of linear and nonlinear optical properties in heterostructure based on triple Gaussian quantum wells: effects of applied external fields and structural parameters. Eur. Phys. J. Plus 2021, 136, 894. [Google Scholar] [CrossRef]
  19. Al, E.B.; Ungan, F.; Yesilgul, U.; Kasapoglu, E.; Sari, H.; Sökmen, I. Effects of applied electric and magnetic fields on the nonlinear optical properties of asymmetric GaAs/Ga1-xAlxAs double inverse parabolic quantum well. Optical Materials 2015, 47, 1–6. [Google Scholar] [CrossRef]
  20. Perez-Gonzalez, J.; Rojas-Brise˜no, J.G.; Nava-Maldonado, F.M.; Santiago, A.D.R.D.; Ungan, F.; Dakhlaoui, H.; Martınez-Orozco, J.C. In plane magnetic field and intense laser field effects on second harmonic generation of asymmetric AlGaAs/GaAs double quantum well. Revista Mexicana de Fisica 2022, 68. [Google Scholar] [CrossRef]
  21. Phuc, H.V.; Tung, L.V.; Vinh, P.T.; Dinh, L. Nonlinear optical absorption via two-photon process in asymmetrical Gaussian potential quantum wells. Superlattices and Microstructures 2015, 77, 267–275. [Google Scholar] [CrossRef]
  22. Phuc, H.V.; Khoa, D.Q.; Hieu, N.V.; Hieu, N.N. Linear and nonlinear magneto-optical absorption in parabolic quantum well. Optik 2016, 127, 10519–10526. [Google Scholar] [CrossRef]
  23. Loitsch, B.; Winnerl, J.; Grimaldi, G.; Wierzbowski, J.; Rudolph, D.; Morkötter, S.; Döblinger, M.; Abstreiter, G.; Koblmüller, G.; Finley, J.J. Crystal Phase Quantum Dots in the Ultrathin Core of GaAs-AlGaAs Core-Shell Nanowires. Nano Letters 2015, 15, 7544–7551. [Google Scholar] [CrossRef] [PubMed]
  24. Mantashian, G.A.; Zaqaryan, N.A.; Mantashyan, P.A.; Sarkisyan, H.A.; Baskoutas, S.; Hayrapetyan, D.B. Linear and nonlinear optical absorption of cdse/cds core/shell quantum dots in the presence of donor impurity. Atoms 2021, 9. [Google Scholar] [CrossRef]
  25. Hoang, T.; Titova, L.; Jackson, H.; Smith, L.; Yarrison-Rice, J.; Kim, Y.; Joyce, H.; Jagadish, C. Imaging and optical properties of single core-shell GaAs-AlGaAs nanowires. 2006 Sixth IEEE Conference on Nanotechnology 2006, 1, 116–118. [Google Scholar] [CrossRef]
  26. Kria, M.; Feddi, K.; Aghoutane, N.; El-Yadri, M.; Pérez, L.M.; Laroze, D.; Dujardin, F.; Feddi, E. Thermodynamic properties of SnO2/GaAs core/shell nanofiber. Physica A: Statistical Mechanics and its Applications 2020, 560. [Google Scholar] [CrossRef]
  27. Fonseka, H.A.; Velichko, A.V.; Zhang, Y.; Gott, J.A.; Davis, G.D.; Beanland, R.; Liu, H.; Mowbray, D.J.; Sanchez, A.M. Self-Formed Quantum Wires and Dots in GaAsP-GaAsP Core-Shell Nanowires. Nano Letters 2019, 19, 4158–4165. [Google Scholar] [CrossRef]
  28. Vinasco, J.A.; Londoño, M.A.; Restrepo, R.L.; Mora-Ramos, M.E.; Feddi, E.M.; Radu, A.; Kasapoglu, E.; Morales, A.L.; Duque, C.A. Optical Absorption and Electroabsorption Related to Electronic and Single Dopant Transitions in Holey Elliptical GaAs Quantum Dots. physica status solidi (b) 2018, 255, 1700470. [Google Scholar] [CrossRef]
  29. Vinasco, J.A.; Radu, A.; Niculescu, E.; Mora-Ramos, M.E.; Feddi, E.; Tulupenko, V.; Restrepo, R.L.; Kasapoglu, E.; Morales, A.L.; Duque, C.A. Electronic states in GaAs-(Al,Ga)As eccentric quantum rings under nonresonant intense laser and magnetic fields. Scientific Reports 2019, 9, 1427. [Google Scholar] [CrossRef]
  30. Altun, D.; Ozturk, O.; Alaydin, B.O.; Ozturk, E. Linear and nonlinear optical properties of a superlattice with periodically increased well width under electric and magnetic fields. Micro and Nanostructures 2022, 166. [Google Scholar] [CrossRef]
  31. Inc., C. COMSOL, 2020.
  32. Multiphysics, C. Introduction to COMSOL multiphysics®. COMSOL Multiphysics, Burlington, MA, accessed Feb 1998, 9, 2018. [Google Scholar]
  33. BenDaniel, D.J.; Duke, C.B. Space-Charge Effects on Electron Tunneling. Phys. Rev. 1966, 152, 683–692. [Google Scholar] [CrossRef]
  34. Li, T.L.; Kuhn, K.J. Band-offset ratio dependence on the effective-mass Hamiltonian based on a modified profile of the GaAs-AlxGa1-xAs quantum well. Phys. Rev. B 1993, 47, 12760–12770. [Google Scholar] [CrossRef] [PubMed]
  35. Ahn, D.; Chuang, S.L. Intersubband optical absorption in a quantum well with an applied electric field. Phys. Rev. B 1987, 35, 4149–4151. [Google Scholar] [CrossRef] [PubMed]
  36. Baskoutas, S.; Terzis, A.F. Size-dependent band gap of colloidal quantum dots. Journal of Applied Physics 2006, 99. [Google Scholar] [CrossRef]
Preprints 81104 g001
Figure 1. (a) GaAs/AlGaAs hexagonal (the shape) quantum wires and the direction of the electric and magnetic fields. In (b) the dimensions of the quantum wire are indicated together with the name of each hexagonal semiconductor material. In (c) is shown the revolve effect in the quantum wire as designed for this job.
Figure 1. (a) GaAs/AlGaAs hexagonal (the shape) quantum wires and the direction of the electric and magnetic fields. In (b) the dimensions of the quantum wire are indicated together with the name of each hexagonal semiconductor material. In (c) is shown the revolve effect in the quantum wire as designed for this job.
Preprints 81104 g001
Preprints 81104 g002
Figure 2. The electron ground state wave function in hexagonal a GaAs/AlGaAs quantum wires with revolve effect parameter k s = 0.9 fixed. In (a) without donor impurity (b) with impurity in z i = 17.50 nm. We have taken two cutting planes that intersect with the quantum wire to visualize the wave function, the upper one corresponds to the plane at z = 30 nm, the lower one at z = 10 nm. In the scale of colors, the blue indicates the zero value of the wave function whereas the red are associated to the maxima, respectively.
Figure 2. The electron ground state wave function in hexagonal a GaAs/AlGaAs quantum wires with revolve effect parameter k s = 0.9 fixed. In (a) without donor impurity (b) with impurity in z i = 17.50 nm. We have taken two cutting planes that intersect with the quantum wire to visualize the wave function, the upper one corresponds to the plane at z = 30 nm, the lower one at z = 10 nm. In the scale of colors, the blue indicates the zero value of the wave function whereas the red are associated to the maxima, respectively.
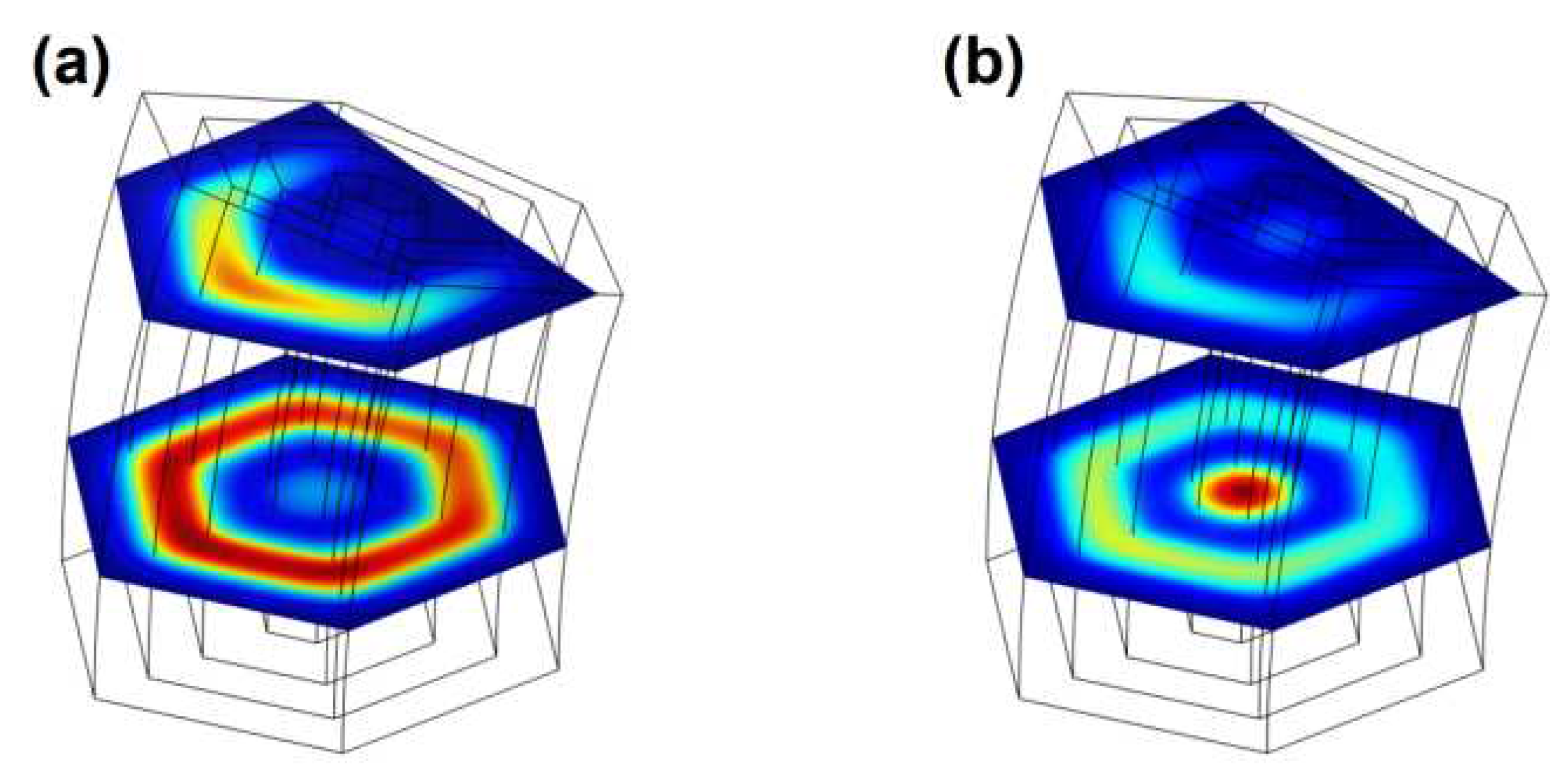
Preprints 81104 g002
Preprints 81104 g003
Figure 3. The electron ground and two first excited state wavefunctions in hexagonal a GaAs/AlGaAs quantum wires as a function of the electric field strength F with parameter k s = 0.9 fixed, without donor impurity. Panel (a, b, c) with F = 5 kV/cm and (d, e, f) with F = − 5 kV/cm.
Figure 3. The electron ground and two first excited state wavefunctions in hexagonal a GaAs/AlGaAs quantum wires as a function of the electric field strength F with parameter k s = 0.9 fixed, without donor impurity. Panel (a, b, c) with F = 5 kV/cm and (d, e, f) with F = − 5 kV/cm.
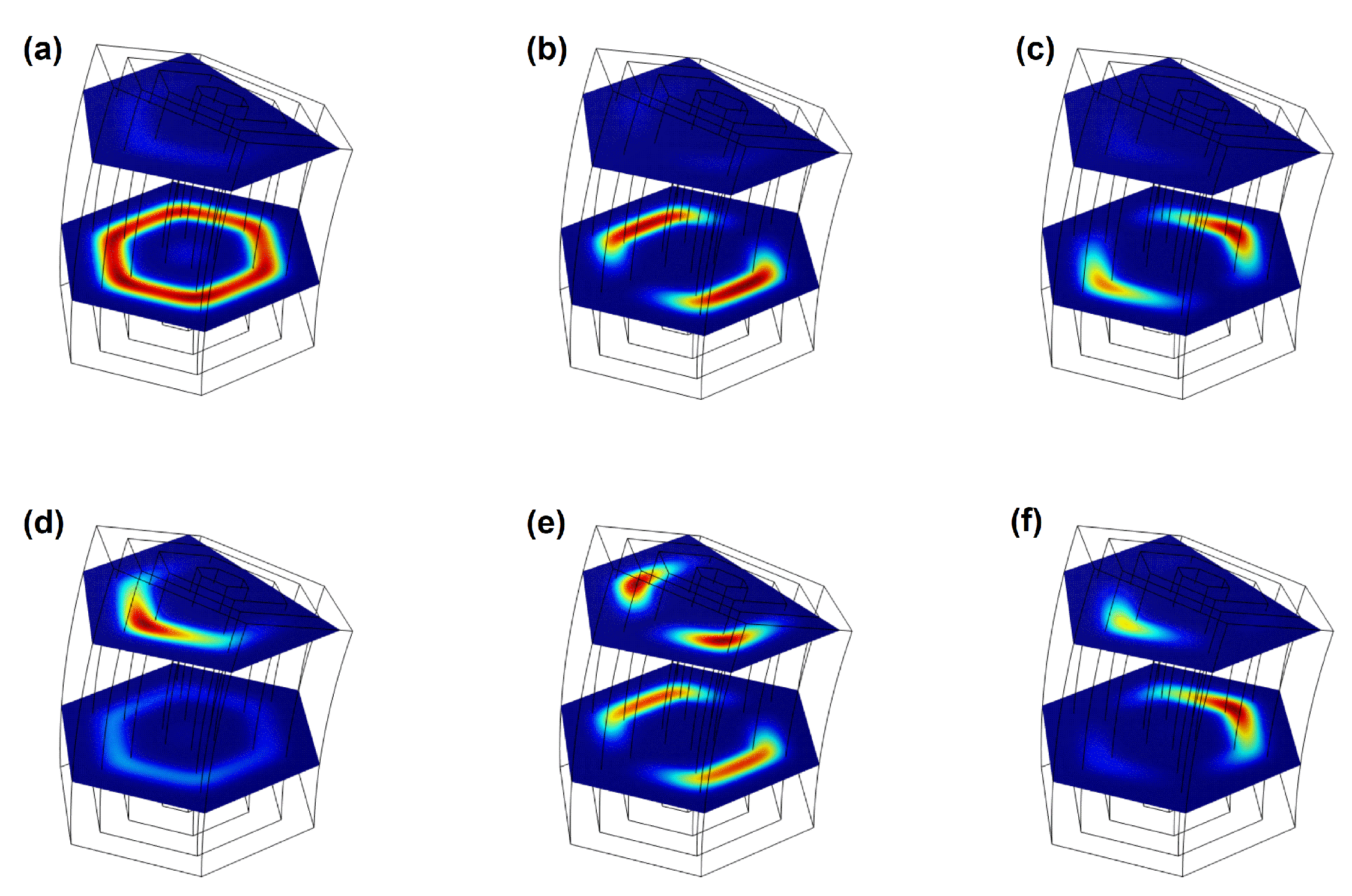
Preprints 81104 g003
Preprints 81104 g004
Figure 4. (a) The lowest energy states of the electron, (b) dipole elements and (c) absorption coefficients as a function of the electric field strength F with parameter k s = 0.9 fixed and without donor impurity in hexagonal GaAs/AlGaAs quantum wires.
Figure 4. (a) The lowest energy states of the electron, (b) dipole elements and (c) absorption coefficients as a function of the electric field strength F with parameter k s = 0.9 fixed and without donor impurity in hexagonal GaAs/AlGaAs quantum wires.
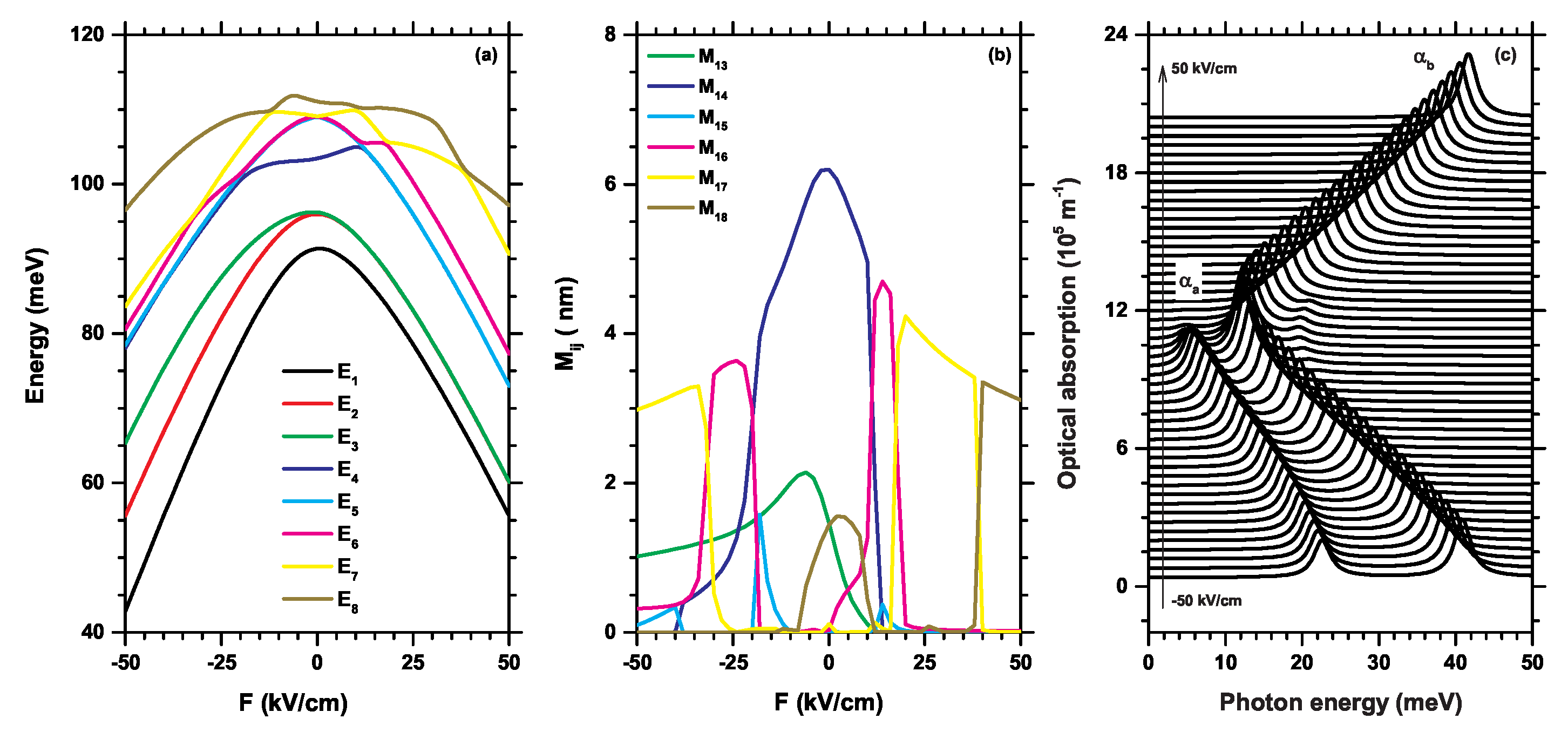
Preprints 81104 g004
Preprints 81104 g005
Figure 5. The electron ground and two first excited state wavefunctions in hexagonal a GaAs/AlGaAs quantum wires with parameter k s = 0.9 fixed as a function of the electric field strength F, with donor impurity ( z i = 17.50 nm). Panel (a, b, c) with F = 5 kV/cm and (d, e, f) with F = − 5 kV/cm.
Figure 5. The electron ground and two first excited state wavefunctions in hexagonal a GaAs/AlGaAs quantum wires with parameter k s = 0.9 fixed as a function of the electric field strength F, with donor impurity ( z i = 17.50 nm). Panel (a, b, c) with F = 5 kV/cm and (d, e, f) with F = − 5 kV/cm.
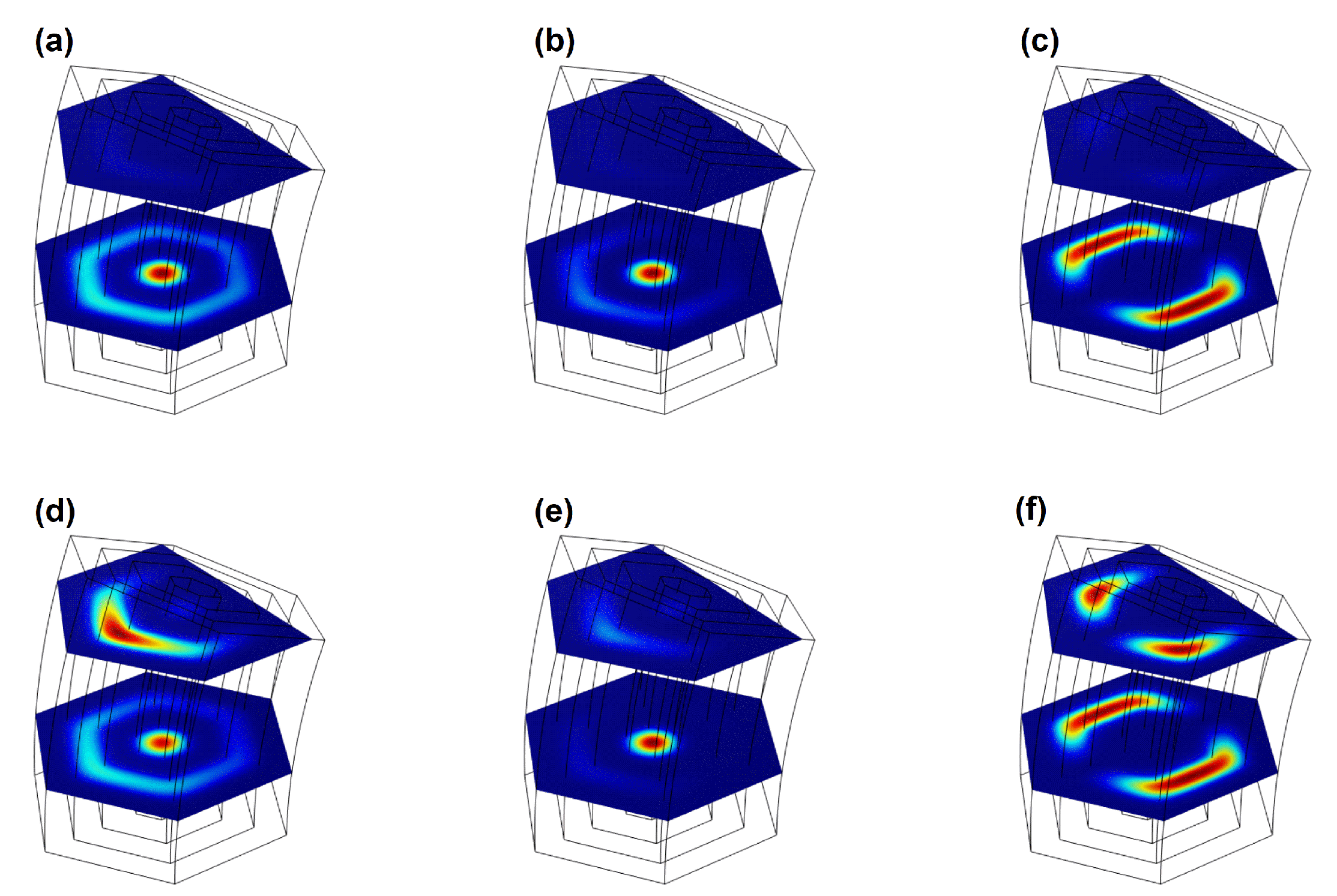
Preprints 81104 g005
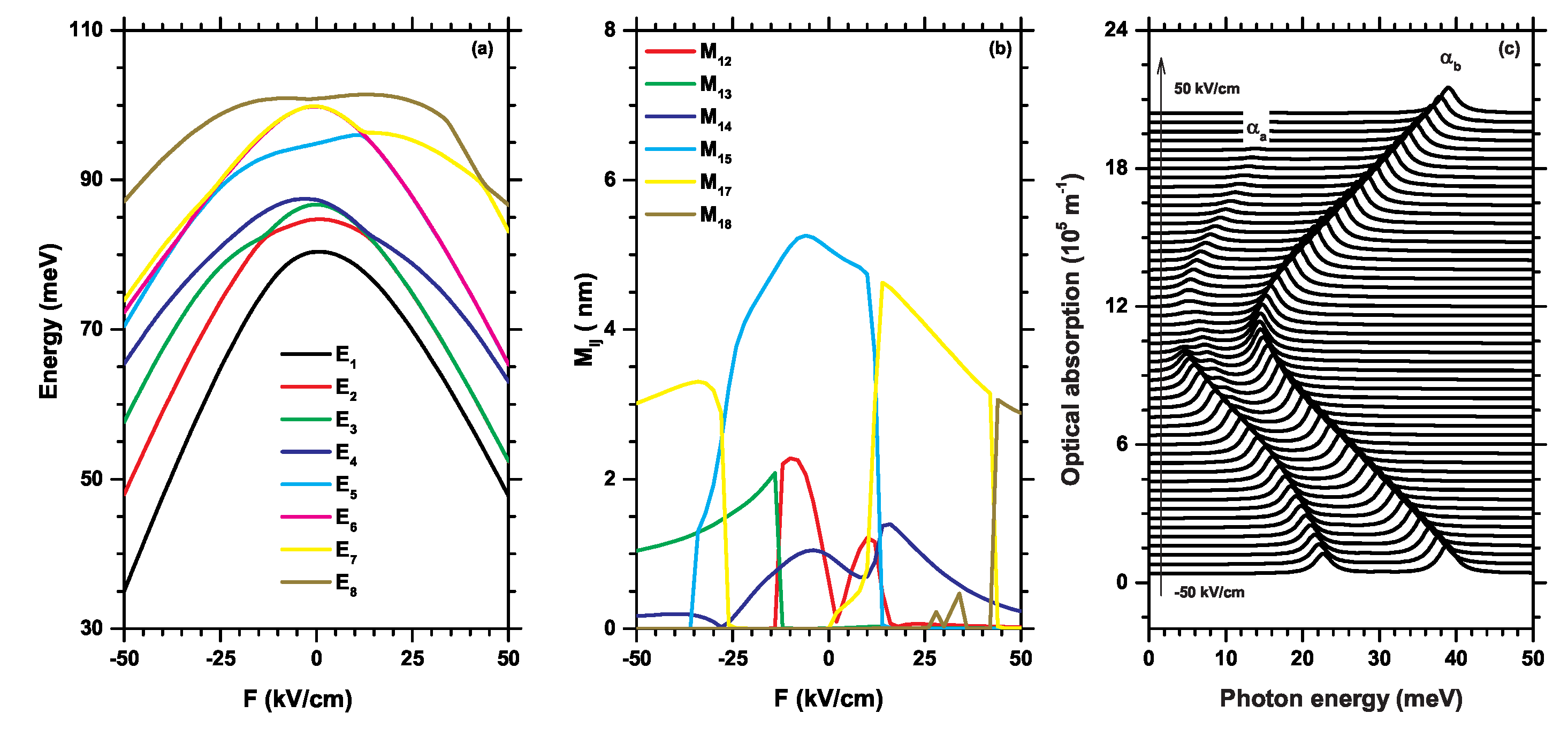
Preprints 81104 g006
Figure 6. (a) Energies, (b) dipole elements and (c) absorption coefficients as a function of the electric field strength F, with donor impurity (at z i = 17.50 nm) in hexagonal GaAs/AlGaAs quantum wires with revolve parameter k s = 0.9 .
Figure 6. (a) Energies, (b) dipole elements and (c) absorption coefficients as a function of the electric field strength F, with donor impurity (at z i = 17.50 nm) in hexagonal GaAs/AlGaAs quantum wires with revolve parameter k s = 0.9 .
Preprints 81104 g006
Preprints 81104 g007
Figure 7. The electron ground state wavefunction in hexagonal GaAs/AlGaAs quantum wires with revolve parameter k s = 0.9 . Upper Panel (a, b, c, d) without donor impurity, lower panel (e, f, g, h) with donor impurity (at z i = 17.50 nm). In (a, e) B = 1 T, in (b, f) B = 5 T, in (c, g) B = 10 T and in (d, h) B = 30 T.
Figure 7. The electron ground state wavefunction in hexagonal GaAs/AlGaAs quantum wires with revolve parameter k s = 0.9 . Upper Panel (a, b, c, d) without donor impurity, lower panel (e, f, g, h) with donor impurity (at z i = 17.50 nm). In (a, e) B = 1 T, in (b, f) B = 5 T, in (c, g) B = 10 T and in (d, h) B = 30 T.
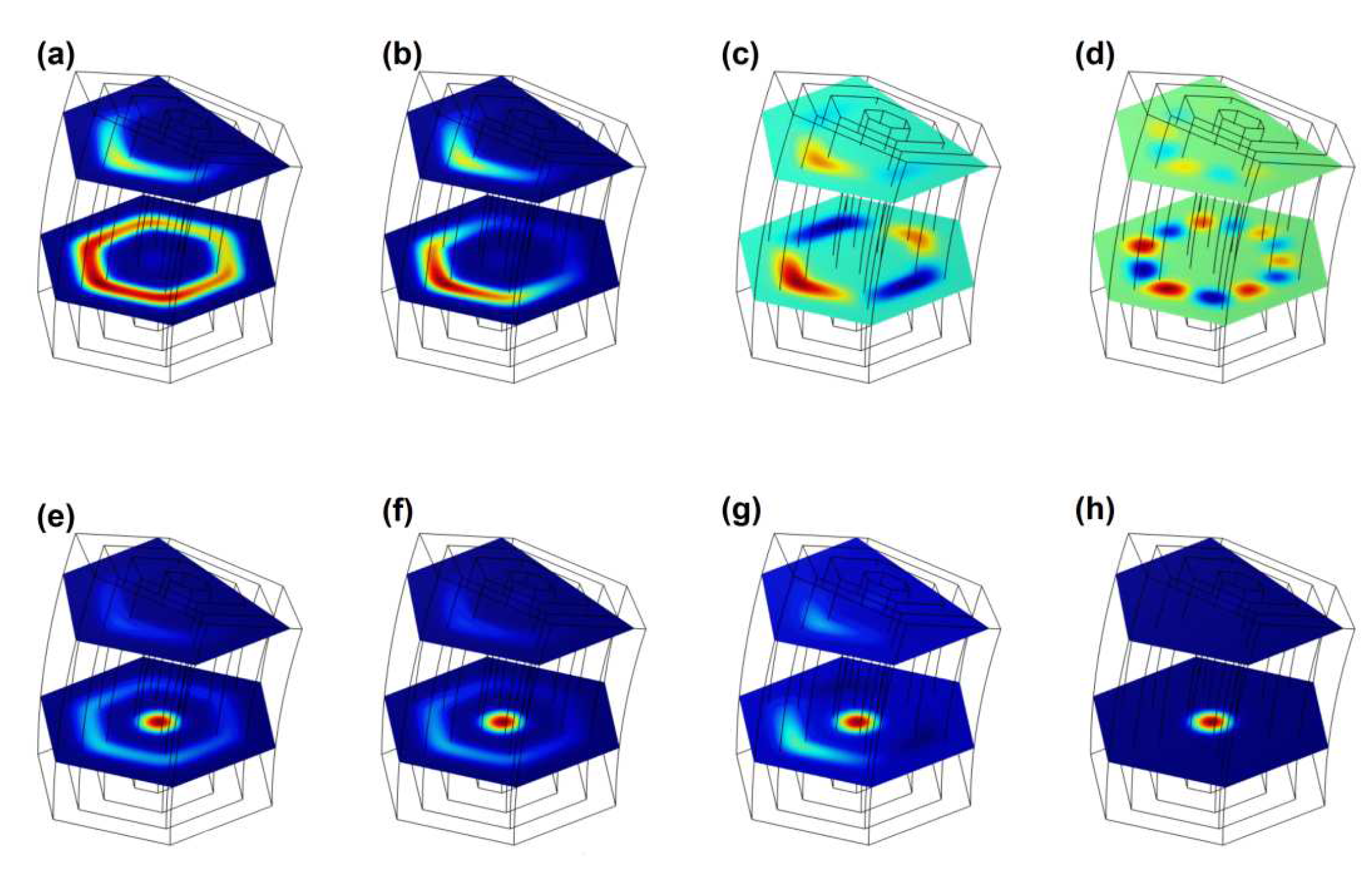
Preprints 81104 g007
Preprints 81104 g008
Figure 8. (a) Energies, (b) dipole elements and (c) absorption coefficients as a function of the magnetic field strength B with revolve parameter k s = 0.9 , without donor impurity in hexagonal GaAs/AlGaAs quantum wires.
Figure 8. (a) Energies, (b) dipole elements and (c) absorption coefficients as a function of the magnetic field strength B with revolve parameter k s = 0.9 , without donor impurity in hexagonal GaAs/AlGaAs quantum wires.
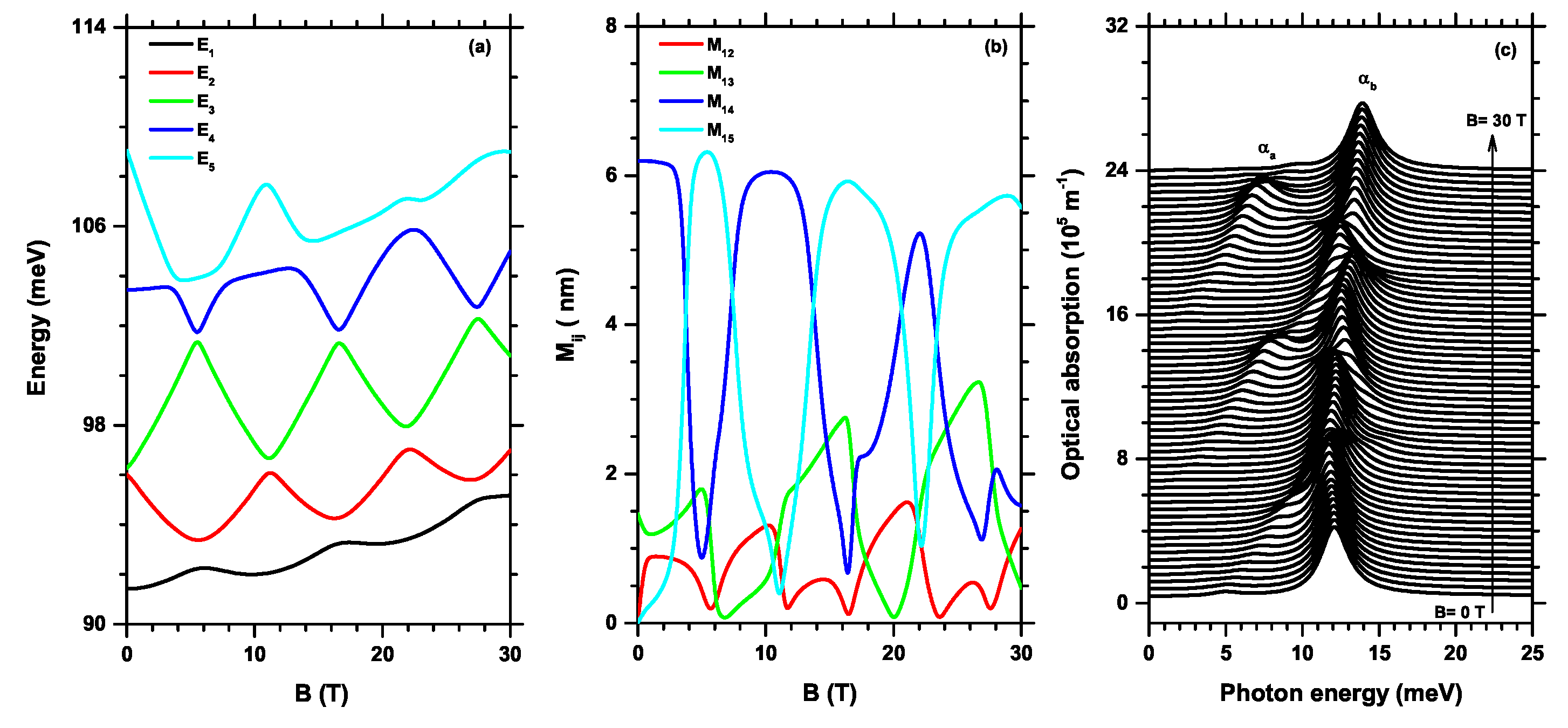
Preprints 81104 g008
Preprints 81104 g009
Figure 9. (a) Energies, (b) dipole elements and (c) absorption coefficients as a function of the magnetic field strength B with revolve parameter k s = 0.9 , with donor impurity (at z i = 17.5 nm) in hexagonal GaAs/AlGaAs quantum wires.
Figure 9. (a) Energies, (b) dipole elements and (c) absorption coefficients as a function of the magnetic field strength B with revolve parameter k s = 0.9 , with donor impurity (at z i = 17.5 nm) in hexagonal GaAs/AlGaAs quantum wires.
Preprints 81104 g009
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated