Prerpints.org logo
Preprint
Article

Comparative study of musical timbral variations: Crescendo and Vibrato using FFT-Acoustic Descriptor

Altmetrics

Downloads

77

Views

29

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

07 August 2023

Posted:

08 August 2023

You are already at the latest version

Alerts
Abstract
Quantitative evaluation of the musical timbre and its variations is important for the analysis of audio recordings and computer-aided music composition. Using the FFT acoustic descriptors and their representation in an abstract timbral space, variations of a sample of monophonic sounds of chordophones (violin, cello) and aerophones (trumpet, transverse flute, and clarinet) sounds are analyzed. It is concluded that the FFT acoustic descriptors allow us to distinguish the timbral variations of the musical dynamics, including crescendo and vibrato. Furthermore, using the Random Forest algorithm, it is shown that the FFT-Acoustic provides a statistically significant classification to distinguish musical instruments, family of instruments, and dynamics. We observed a better behavior for the FFT-Acoustic descriptors when classifying pitch compared to some timbral features of Librosa.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Science

1. Introduction

Various techniques are used in musical composition to add expressiveness to the performance; the most common being those generated by subtle variations in dynamics and pitch. In musical instruments, the intensity variations of the impulse (tension in the strings or air pressure) and/or variations in the frequency of the pulsation produce secondary waves of sounds that propagate through the musical instrument; in the boxes and resonance tubes of chordophones and aerophones, respectively. When sound propagates in the resonant cavities of musical instruments, reflection, diffraction, and interference phenomena take place, which generally produce secondary sound waves, which overlap the fundamental frequency of the natural vibration mode (characteristic of each musical sound). Therefore, the timbre of the instrument will present variations with respect to the sounds of a particular instrument. Such timbre variations are due to changes in the envelope of the wave that forms the musical sound.
The most common variation in dynamics in music is the crescendo or gradual increase in the intensity of the sound, that is, a transitional dynamic nuance [1-2]. From an acoustic point of view, a crescendo occurs in aerophones when the musician gradually increases the amount of air blown into the instrument, thereby increasing the amplitude of the sound waves produced. The intensity of the sound produced depends on the amount of air entering the instrument and the pressure exerted by the musician's lips and tongue. As the musician increases the intensity of the musical note, they can change the pressure exerted by the lips and tongue to maintain the desired tonal quality. Similarly, in chordophones, the crescendo is produced when the musician gradually increases the pressure exerted on the strings of the instrument, which increases the amplitude of the sound waves produced. The intensity of the sound produced will depend on the pressure exerted on the strings and the position and speed of the musician's hand on the fingerboard and frets. When a musician uses the crescendo technique on bowed string instruments, the musician gradually increases the pressure exerted by the bow on the strings, increasing the amplitude of the sound waves produced. The crescendo technique can also affect the tonal quality of the sound produced. As the player increases the intensity of the note, the musician can slightly change the position of the hand on the fingerboard to maintain the desired tonal quality.
In addition, in acoustic terms, vibrato [1,3] occurs when the player oscillates the frequency of the played note by a small amount around its fundamental frequency. The frequency of the musical note produced in aerophones depends on the length of the tube and the tension of the musician's lips. When the musician uses the vibrato technique, she or he modulates the tension of the lips and the speed of the blowing air, which alters the frequency of the note. Vibrato on aerophones produces a series of additional formants and harmonics that overlap the fundamental note. These secondary transverse waves can be stronger or weaker depending on the speed and amplitude of the vibrato, and can contribute to the tonal quality and harmonic richness of the sound. In chordophones, the sound frequency depends on the length, tension, and mass of the strings, as well as the way they are played. When the musician uses the vibrato technique, they slightly move their finger up and down the string in the fingerboards, which alters the effective length of the string and, therefore, the frequency of the note. Consequently, a series of additional formants and harmonics are produced that are superimposed on the fundamental note, as a result of the interaction of the string pulse with the resonant box. These harmonics can be stronger or weaker depending on the speed and amplitude of the vibrato and can contribute to the tonal quality and harmonic richness of the sound produced. In addition, vibrato can also affect the intensity and duration of the note, since the movement of the finger on the string can influence how much energy is transmitted to the string and how it is released.
On the other hand, the main timbral characteristics of the digital audio records must be somehow inscribed within the FFT through the succession of pairs of amplitude and frequencies of the sinusoidal components that compose it and that enables the recording and subsequent reproduction of musical sound. The collection of amplitude and frequency pairs in the FFT represents the intensities and tonal components of the audio recordings. Consequently, the timbre characteristics of digitized musical audio, which allow discrimination between musical sounds, octaves, instruments, and dynamics, must be contained in some way in the FFT [4-5]. Several representations of timbre descriptors can be computationally derived from statistical spectrum analysis (FFT). As many of them are derivatives or combinations of others and, in general, are correlated among themselves [6-7], we adopt the dimensionless acoustic descriptors proposed in [4,8], to describe the timbral variations of the playing techniques associated with the only existing magnitudes in the FFT: amplitudes (crescendo) and frequencies (vibrato).
The objective of this paper is to use acoustic descriptors to compare timbre variations in a sample of monophonic audio recordings, corresponding to the aerophones clarinet, transverse flute, and trumpet, as well as the chordophones violin and violoncello. For them, we will describe the methodology in the next section. Then the results and a brief discussion are shown in Section 3, covering the comparison by the family of instruments (Section 3.1) by musical dynamics (Section 3.2) by timbre variations in amplitude or crescendo (Section 3.3) and timbre variations in frequencies or vibrato (Section 3.4). The accuracy of the FFT acoustic descriptors is then compared with other timbral coefficients of statistical features, through the Random Forest machine learning algorithm (Section 4) and the conclusions in the last section.

2. Databases and general formalism

We used the Good-Sounds dataset [9], which contained monophonic recordings of single notes with different timbral characteristics (in mezzo-forte musical dynamics: mf, crescendo, and vibrato modes). Only the fourth-octave musical was used: C4, C#4, D4, D#4, E4, F4, F#4, G4, G#4, A4, A#4, and B4; in the musical scale of equal temperament, the most typical in western music. The selection of musical instruments corresponding to the aerophones clarinet, transverse flute, and trumpet, and the chordophones violin and violoncello. The Tynisol database [ 5,10 ] in dynamic pianissimo (pp) and fortissimo (ff) is also used as a comparison reference for these musical instruments. Also, the Tynisol database is used in Section 4 for the Random Forest algorithm of automatic classifications and is compared with other timbral features.
For each audio record, we obtain the FFT spectrum normalized by the ratio of the greatest amplitude of each spectrum. Noise in the spectrum is also reduced by considering only amplitudes greater than 10% of the maximum amplitude. Then each monophonic audio record is digitized by FFT as a discrete, finite, and countable collection of pairs of numbers that represent the relative amplitudes and frequencies, in Hertz, of the spectral components and the fundamental frequency (f0).
To describe the timbre in each FFT spectrum, we use the fundamental frequency (f0) and its amplitude (a0) plus a set of six dimensionless magnitudes denominated timbral coefficients [4,5,8]: "Affinity" A, "Sharpness" S, "Mean Affinity" MA, "Mean Contrast" MC, "Harmonicity" H, and "Monotony” M. The A and S timbral coefficients provide a measure of the frequency and relative amplitude of the fundamental signal with respect to the FFT spectrum. The coefficient H is a measure of the quantity and the quality of the harmonics present in a spectral distribution. The coefficient M describes the average increase-decrease of the spectrum envelope. The MA and MC coefficients provide a measure of the mean frequency and mean amplitude of the spectral distribution, respectively (see [5,8] for details). Figure 1 shows the timbral coefficients as a function of musical sounds and frequencies, for the instruments selected from the Goodsound database, fourth octave, mezzo-forte.
Then each FFT spectrum can be represented by a mean 7-tuple (f0, A, S, H, M, MA, MC) in an abstract configurational space. These 7-tuples that characterize the amplitude-frequency distribution present in each FFT spectrum provide a morphism between the frequency space and the seven-dimensional vector space. This 7-space, we can call it timbral space, since the musical timbre consists precisely of the set of spatial frequencies (formants and harmonics) that accompany each musical sound produced by a certain musical instrument, a certain dynamic, and the set of techniques of the performing musician. Note that the 7-tuples are real numbers and admit the definition of a module or Euclidean norm along with equivalence relations; therefore, they formally constitute a Moduli space, represented by a geometrical place that parametrizes the family of related algebraic objects [11].

3. Euclidean metric in Timbral Space.

Below are the timbral variations of the same musical sound due to the considered instrument (Section 3.1), to the musical dynamics (Section 3.2), and to the musical performance techniques used by the player: crescendo (Section 3.3) and vibrato (Section 3.4), they are shown below through the Euclidean distance between the characteristic vectors of each FFT of the audio record, classified by musical sound (among the 12 possible in the fourth octave of the tempered scale).

3.1. Instruments

Figure 2 shows the distances between monophonic audio recordings of instruments grouped by musical sounds. We observe that the registers are separated by notes, and the distance is a function of the tempered-scale sequence. The difference between the tables is due to the specific values of the timbral coefficients, as shown in Figure 1. Each musical sound corresponding to an instrument occupies a single point of timbre space.
The distances between different instruments, grouped by musical sounds, are illustrated with various examples in Figure 3. Note that for the same musical notes (diagonal), the distances are smaller between instruments of the same type: flute and clarinet, both wooden aerophones (panel a). It is greater between aerophones and chordophones (panel b), between the chordophone and the wooden aerophone (panel c) and between the metal aerophone and the wooden aerophone (panel d).
On the other hand, the results show that some sounds seem close to each other for different musical instruments and of different classifications, for example, the B4 sound. Figure 4 shows the FFTs for that sound. Notice the decrease in pulses, the number, and position of the partial frequencies. It cannot be affirmed that there is timbre similarity only because of the distance, since what defines the timbre is the vector and not only its module, and although the distance is equivalent, between violin-trumpet and Clarinet-Trumpet, the sounds of these three instruments are in different regions of the timbre space (different clusters). To have timbral similarity, the sounds must be in the same cluster or region of the timbral space and must also be close to each other [4]. This is equivalent to saying that they must be from audio recordings of the same instrument or type of instrument, and also with a distance less than the distance between adjacent musical sounds.

3.2. Musical Dynamics

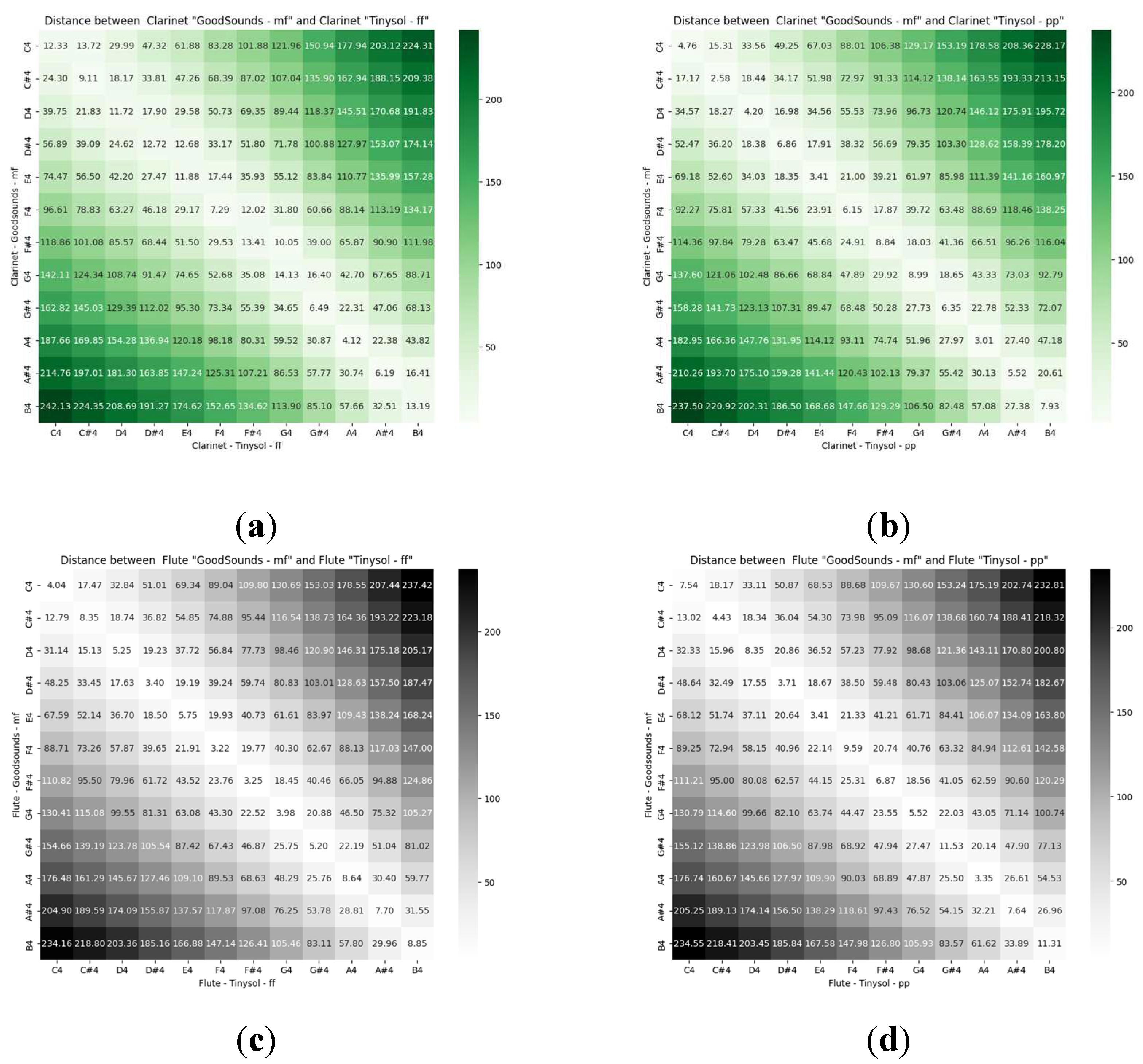
Given a musical sound and an instrument, the variations in the intensity of the performance (musical dynamics) should produce timbrally similar sounds, and consequently, their timbral representation should be close to the mezzo-forte sound. Indeed, that is what is observed in Figure 4 for the sounds of the Goodsound database, compared to the Tinysol database records for different dynamics. Note that the minimum distances are always on the diagonal and are less than 15.6, which is the minimum separation between two different musical notes of the tempered scale (between C4 and C#4), and therefore it is also less than any other pair of sounds (in the fourth octave).
Preprints 81858 g005
Figure 5. Matrix of Euclidean distances between musical sounds mezzo-forte Goodsounds and their dynamics of the clusters using the Tynisol dataset with the proper subspace of each musical instrument: (a) Clarinet fortissimo (b) Clarinet pianissimo (c) Flute and fortissimo (d) Flute pianissimo.
Figure 5. Matrix of Euclidean distances between musical sounds mezzo-forte Goodsounds and their dynamics of the clusters using the Tynisol dataset with the proper subspace of each musical instrument: (a) Clarinet fortissimo (b) Clarinet pianissimo (c) Flute and fortissimo (d) Flute pianissimo.
Preprints 81858 g005
Timbral variations due to musical dynamics are manifested in that more formants and harmonics appear in the FFT, as we increase the intensity. Thus, the envelope of the FFT spectrum must be more extended, and the average value of the amplitudes changes. Hence, the acoustic descriptor of Medium Contrast; Timbral coefficient MC, must vary in all musical sounds for the same instrument. As shown in Figure 6, for clarinet and flute.

3.3. Crescendo

The crescendo is an instrumental performance technique that consists of the gradual variation of the musical dynamics. Consequently, the timbre effect with respect to timbre in the mezzo forte audio recordings should be similar. For the flute and the clarinet, we can see in Figure 6 how a decrease in the Mean Contrast (MC) occurs when we compare the dynamics of pianissimo and mezzo-forte, also observing in the clarinet that the behavior of the crescendo effect decreases when we advance in frequencies. Figure 7 exhibits the same effect for the other instruments in the sample, so we can conjecture that, in general, the crescendo modifies the timbre coefficient of MC, by incorporating more secondary frequencies in all instruments.
The right panel of Figure 7 shows the values of the timbre coefficient M in the Crescendo technique with respect to mezzo-forte audio recordings for both aerophones and chordophones. We notice that the timbral variation of Crescendo reduces the Monotony value, which is a timbre coefficient that quantizes the envelope in the FFT. A decrease in the absolute value of Monotony implies that the envelope softens, that is , that the average value of the variations in amplitude with respect to the fundamental frequency decreases.
The audio recordings made with the crescendo technique must, similar to the dynamic musical variations, be close to the corresponding sounds in mezzo-forte. To illustrate this proximity, the matrix of Euclidean distances in the timbral space is shown in Figure 8. Note again that the minimum distances are on the diagonal and are less than 15.6 (separation between C4 and C#4 sounds).
The Crescendo technique increases the average intensity of the sounds, this implies that the formants and harmonics increase in intensity and, therefore, the value of the timbral coefficient of Affinity A, Mean Affinity MA, and Harmonicity H increases with respect to the values in mezzo-forte dynamics, as observed in the FFT of the audio recordings of Figure 9 for the aerophones.
In the upper panel of Figure 12, it is observed that H does not always increase in the chordophones. This may be due to the interaction with the resonance box of the instrument, since the vibrations of some harmonics can have destructive interference with the formants generated due to the geometry of the musical instrument considered. However, the change due to musical dynamics is evidenced by the increase in Mean Affinity even for chordophones. The variation in the Affinity is not conclusive, since in this technique as also in vibrato, the musical performer can, at his discretion and personal taste, modify the fundamental frequency during the performance of the crescendo, if he does that, the information is not recorded in the Goodsound datasets.

3.4. Vibrato

During the vibrato, there is a slight variation of the fundamental frequency of the corresponding musical sound. Consequently, secondary frequencies that accompany the fundamental must appear, then the Affinity A and Mean Affinity MA coefficients must change since they explicitly depend on the values of the frequencies of the audio record. Figure 9 compares the Mean Affinity values with the Goodsound mezzo-forte records. Although the change in the value of MA is uniform with respect to the musical sounds of the fourth octave, it is not the same for all instruments. Vibrato increases the MA value on the cello and decreases it on the clarinet and violin. Similarly, Figure 10 shows that vibrato also modifies Monotony, as expected because an increase in partial frequencies leads to a change in the envelope of the FFT spectrum.
The details of why some instruments increase the average of the partial frequencies (MA) and others decrease them are related to the geometry of the chordophone resonance box. The acoustics of chordophones is especially complicated because the wave generated by the vibration of the strings propagates in the air as a transversal wave, but in the sound-box, this pulsation originates transversal and longitudinal waves in the solid of the resonant cavity in addition to the transversal sound waves inside the air chamber. Therefore, it is beyond the objectives of this communication to elucidate this issue.
Also, since the variations in the frequency of the vibrato are less than the variation between adjacent musical notes in the tempered scale, it would be expected that the vibrato audio recordings would be at relatively close distances to the Goodsounds mezzo-forte recordings. We see that it is so in Figure 11 for the clarinet, but in the case of the violin, greater distances appear in some sounds (diagonal elements with distances greater than 15.6). This can be due to an incorrect musical performance of the vibrato or due to the effects of the violin sound box. Unlike the cello, the violin is more diverse in its musical performance of vibrato, due to the addition of the bow to the tension of the string by hand and due to the influence of the jaw resting on the body of the violin, which can modify the vibration modes of the formants.
It is understandable that the oscillation of the main frequency in the vibrato increases the coefficient H since the partial frequencies that are generated will not be harmonic (greater H, less harmonicity), as can be seen in the lower panel of Figure 9 and Figure 12. Figure 12 also shows that vibrato decreases the value of the Mean Affinity MA for chordophones.
Vibrato has not only caused a variation in frequency, but has also oscillated the timbre of the sound, that is, the greater or lesser prevalence of one component or another. This oscillation of the sound quality that the vibrato violin has is a characteristic feature of this instrument. The acoustic explanation of this feature of the violin lies in the properties of its sound box, which responds differently to very close frequency components. Finally, all instruments allow the performer to make his own vibrato, and this is a resource that is a very important part of characterizing the sound.
We have seen that the timbral coefficients allow characterizing the timbral variations; however, it is worth asking how these acoustically motivated descriptors compare with other descriptors of the FFT based on statistical distributions. This aspect is discussed in the next section.

4. Automatic classification of musical timbres

The problems of classification can be performed using supervised learning. These classification algorithms have been used in music style recognition problems through music feature extraction [12], musical instrument classification problems [13], and an intelligent system for piano timbre recognition [14], among others. Now, we are going to compare the classification capacities of the timbral coefficients proposed by González and Prati [8] with some timbral features extracted using Librosa: Chroma stft, spectral contrast, spectral flatness, poly features, spectral centroid, spectral rolloff, and spectral bandwidth [15].
For this, we use the TinySol database through the MIRDATA library [16], which offers a standardization to work with audio attributes more efficiently. After defining the meta-attributes, we explore timbral classification capabilities by considering some variations such as instruments (violin, cello, transverse flute, clarinet, and trumpet), dynamics (pianissimo, mezzo-forte, and fortissimo), musical notes (considering the entire range of each instrument) and instrument families (chordophones, wooden aerophones, and metal aerophones).
We have evaluated some classification algorithms such as Random Forest (RF), Support Vector Classifier (SVC), K-Nearest Neighbor (KNN), and logistic regression, and we observe better statistical behavior in terms of classification for our subject of study with the Random Forest algorithm, this behavior occurs in benchmark tests [17]. This is a conjoint learning method that combines multiple decision trees to create a more robust and accurate predictive model [18].
We use the data split provided in the MIRDATA library, which divides the data into 5 folds. We applied a 5-fold cross-validation, where in each iteration, one fold is used for testing and the remaining for training. The process is repeated five times, using a different test split each time. Using the Random Forest algorithm, we computed the mean accuracy using the timbral coefficients and the LibRosa features. Table 1 presents these results.
To compare the results statistically, we use a paired T-test for each possible class. The last row of Table 1 shows the p-value of the test., Statistically significant difference is observed for the timbral coefficients when compared with Librosa in the classification by musical notes (pitch); this may be because the musical timbre, as an acoustic characteristic, is a frequency-independent property of the musical timbre. On the other hand, if we consider a significance interval of 99%, we can see that the timbral coefficients behave well when classifying instruments and families of instruments, and are better in the classification by dynamics with respect to Timbral Features (Librosa).

5. Conclusions

Timbral variations in monophonic musical sounds can be characterized from FFT analysis of audio recordings. More particularly, due to the techniques of musical performance of variations in amplitude (crescendo) and frequency (vibrato), these timbre variations differ in each particular instrument according to its acoustic characteristics.
The acoustic FFT descriptors proposed by Gonzalez and Prati [4,8] provide a representation of the characteristic timbral space of each audio record. Its position in the timbral space [4] and the Euclidean distance between the registers allow us to distinguish the timbral variations, due to the family of instruments, the musical dynamics, and the variations in the execution technique. The latter modify the envelope of the FFT and consequently change the values of Monotonicity (M) and Harmonicity (H). The crescendo modifies the Mean Contrast (MC) coefficient and the vibrato modifies the Affinity (A).
The Random Forest technique applied to evaluate the accuracy of the proposed classification shows statistically significant results for FFT-Acoustic descriptors and timbral features of Librosa when classifying instruments, dynamics, and families of instruments, observing a better classification by pitch in the FFT-Acoustic descriptors when comparing them with Librosa features. It is important to perceive that the Librosa does not discriminate between the dynamic variations of crescendo and vibrato, while the FFT-Acoustic descriptors do allow them to be discriminated.

Author Contributions

Author Contributions: Conceptualization, Y.G. and R.C.P.; methodology, Y.G. and R.C.P.; software, Y.G. and R.C.P.; validation, Y.G. and R.C.P.; formal analysis, Y.G. and R.C.P.; investigation, Y.G. and R.C.P.; resources, Y.G. and R.C.P.; data curation, Y.G. and R.C.P.; writing—original draft preparation, Y.G.; writing—review and editing, Y.G. and R.C.P.; visualization, Y.G.; supervision, R.C.P.; project administration, Y.G. and R.C.P.; funding acquisition, Y.G. and R.C.P. All authors have read and agreed to the published version of the manuscript.

Funding

This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de nível Superior—Brasil (CAPES)—Finance Code 001.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The sounds used in this work are available at the following link: https://zenodo.org/record/3685367#.XnFp5i2h1IU%22, accessed on 15 May 2023.

References

  1. Randel, D.M. The Harvard Dictionary of Music; Harvard University Press: Cambridge, MA, USA, 2003; p. 224. [Google Scholar]
  2. Gough, C. Musical acoustics. In Springer Handbook of Acoustics; Springer: New York, NY, USA, 2014; pp. 567–701. [Google Scholar]
  3. Almeida, A.; Schubert, E.; Wolfe, J. Timbre Vibrato Perception and Description. Music Percept. 2021 38, 282–292. [CrossRef]
  4. Gonzalez, Y.; Prati, R.C. Similarity of musical timbres using FFT-acoustic descriptor analysis and machine learning. Eng 2023, 4, 555–568. [Google Scholar] [CrossRef]
  5. Gonzalez, Y.; Prati, R. Acoustic Analysis of Musical Timbre of Wooden Aerophones. Rom. J. Acoust. Vib. 2023, 19, 134–142. [Google Scholar]
  6. McAdams, S. The perceptual representation of timbre. In Timbre: Acoustics, Perception, and Cognition; Springer: Cham, Switzerland, 2019; pp. 23–57. [Google Scholar]
  7. Peeters, G.; Giordano, B.L.; Susini, P.; Misdariis, N.; McAdams, S. The timbre toolbox: Extracting audio descriptors from musical signals. JASA 2011, 130, 2902–2916. [Google Scholar] [CrossRef] [PubMed]
  8. Gonzalez, Y.; Prati, R.C. Acoustic descriptors for characterization of musical timbre using the Fast Fourier Transform. Electronics 2022, 11, 1405. [Google Scholar] [CrossRef]
  9. Romaní Picas, O.; Parra-Rodriguez, H.; Dabiri, D.; Tokuda, H.; Hariya, W.; Oishi, K.; Serra, X. A real-time system for measuring sound goodness in instrumental sounds. In Proceedings of the 138th Audio Engineering Society Convention, AES 2015, Warsaw, Poland; 2015; pp. 1106–1111. [Google Scholar]
  10. Carmine, E.; Ghisi, D.; Lostanlen, V.; Lévy, F.; Fineberg, J.; Maresz, Y. TinySOL: An Audio Dataset of Isolated Musical Notes.
  11. Zenodo 2020. Available online: https://zenodo.org/record/3632193#.Y-QrSnbMLIU (accessed on 15 May 2022).
  12. Kollár, J. Moduli of varieties of general type. In Handbook of moduli; Int. Press: Somerville, MA, USA, 2013; pp. 131–157. [Google Scholar]
  13. Zhang, K. Music style classification algorithm based on music feature extraction and deep neural network. In Wireless Communications and Mobile Computing; 2021.
  14. Chakraborty, S.S.; Parekh, R. Improved musical instrument classification using cepstral coefficients and neural networks. In Methodologies and Application Issues of Contemporary Computing Framework; Springer: Singapore, 2018; pp. 123–138. [Google Scholar]
  15. Lu, Y.; Chu, C. A Novel Piano Arrangement Timbre Intelligent Recognition System Using Multilabel Classification Technology and KNN Algorithm. Comput Intell Neurosci. 2022, 2205936. [Google Scholar] [CrossRef] [PubMed]
  16. McFee, B.; Raffel, C.; Liang, D.; Ellis, D.P.; McVicar, M.; Battenberg, E.; Nieto, O. librosa: Audio and music signal analysis in python. In Proceedings of the 14th python in science conference; 2015; pp. 18–25. [Google Scholar]
  17. Bittner, R.M.; Fuentes, M.; Rubinstein, D.; Jansson, A.; Choi, K.; Kell, T. Mirdata: Software for Reproducible Usage of Datasets. In Proceedings of the 20th International Society for Music Information Retrieval (ISMIR) Conference; 2019. [Google Scholar]
  18. Fernández-Delgado, M.; Cernadas, E.; Barro, S.; Amorim, D. Do we need hundreds of classifiers to solve real world classification problems? J. Mach. Learn. Res. 2014, 15, 3133–3181. [Google Scholar]
  19. Michalski, R.S.; Carbonell, J.G.; Mitchell, T.M. Machine learning: An artificial intelligence approach; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
Preprints 81858 g001
Figure 1. Representations in the frequency of the FFT-acoustic descriptors (Timbral Coefficients) for the Goodsound dataset.
Figure 1. Representations in the frequency of the FFT-acoustic descriptors (Timbral Coefficients) for the Goodsound dataset.
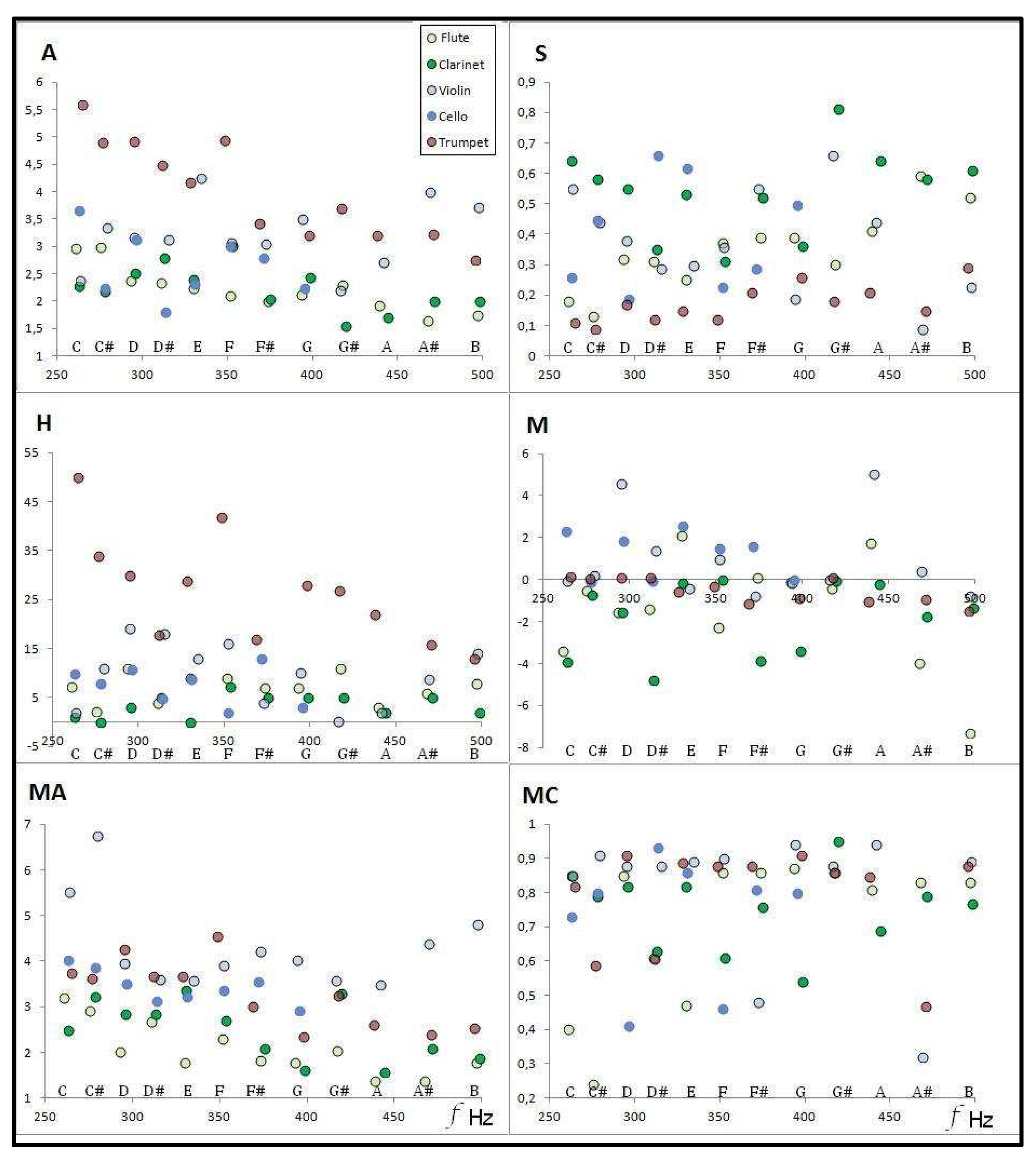
Preprints 81858 g001
Preprints 81858 g002
Figure 2. Matrix of Euclidean distances between musical sounds of the clusters that make up the proper subspace of each musical instrument: (a) Clarinet (b) Violin (c) Flute and (d) Trumpet.
Figure 2. Matrix of Euclidean distances between musical sounds of the clusters that make up the proper subspace of each musical instrument: (a) Clarinet (b) Violin (c) Flute and (d) Trumpet.
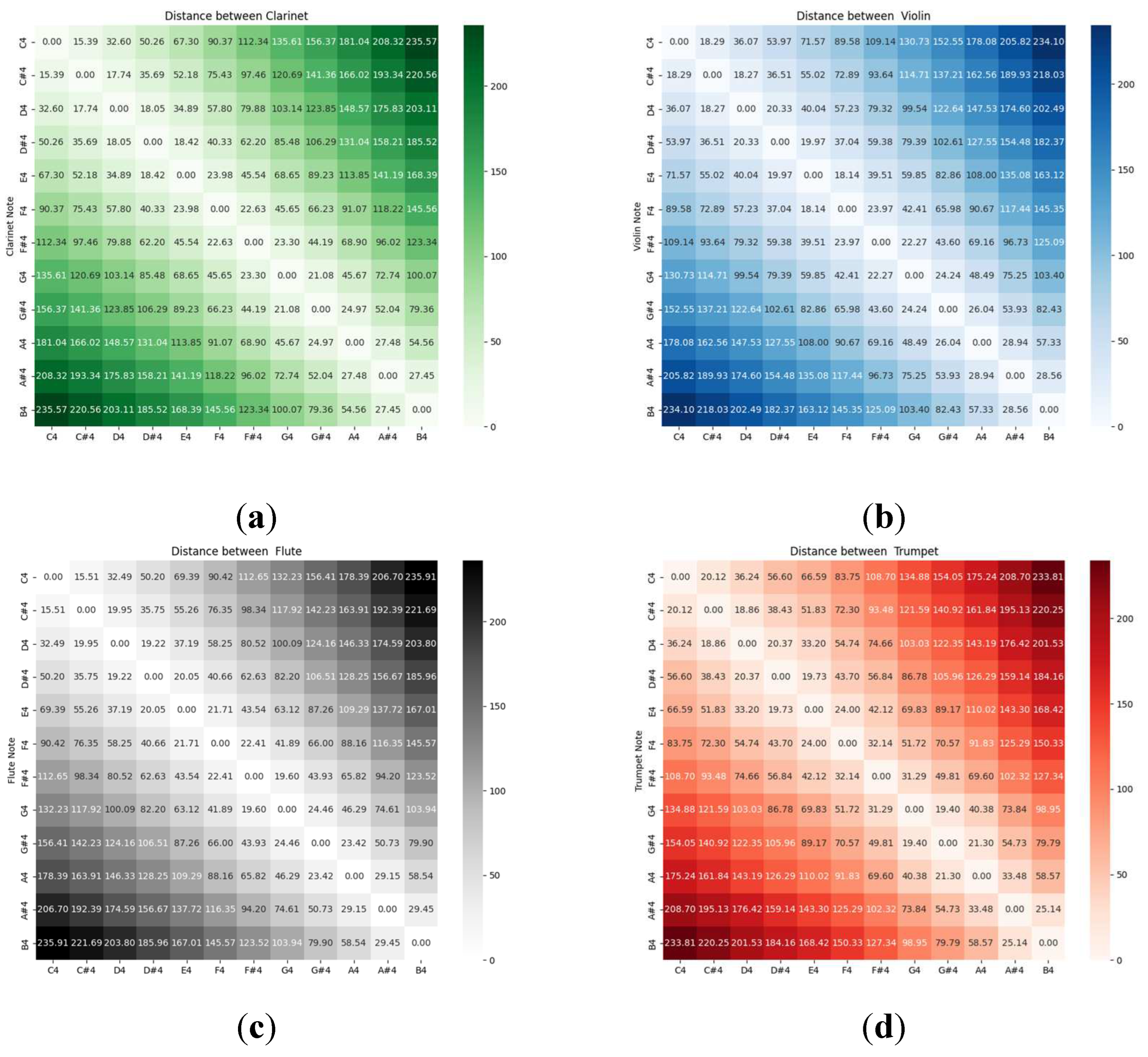
Preprints 81858 g002
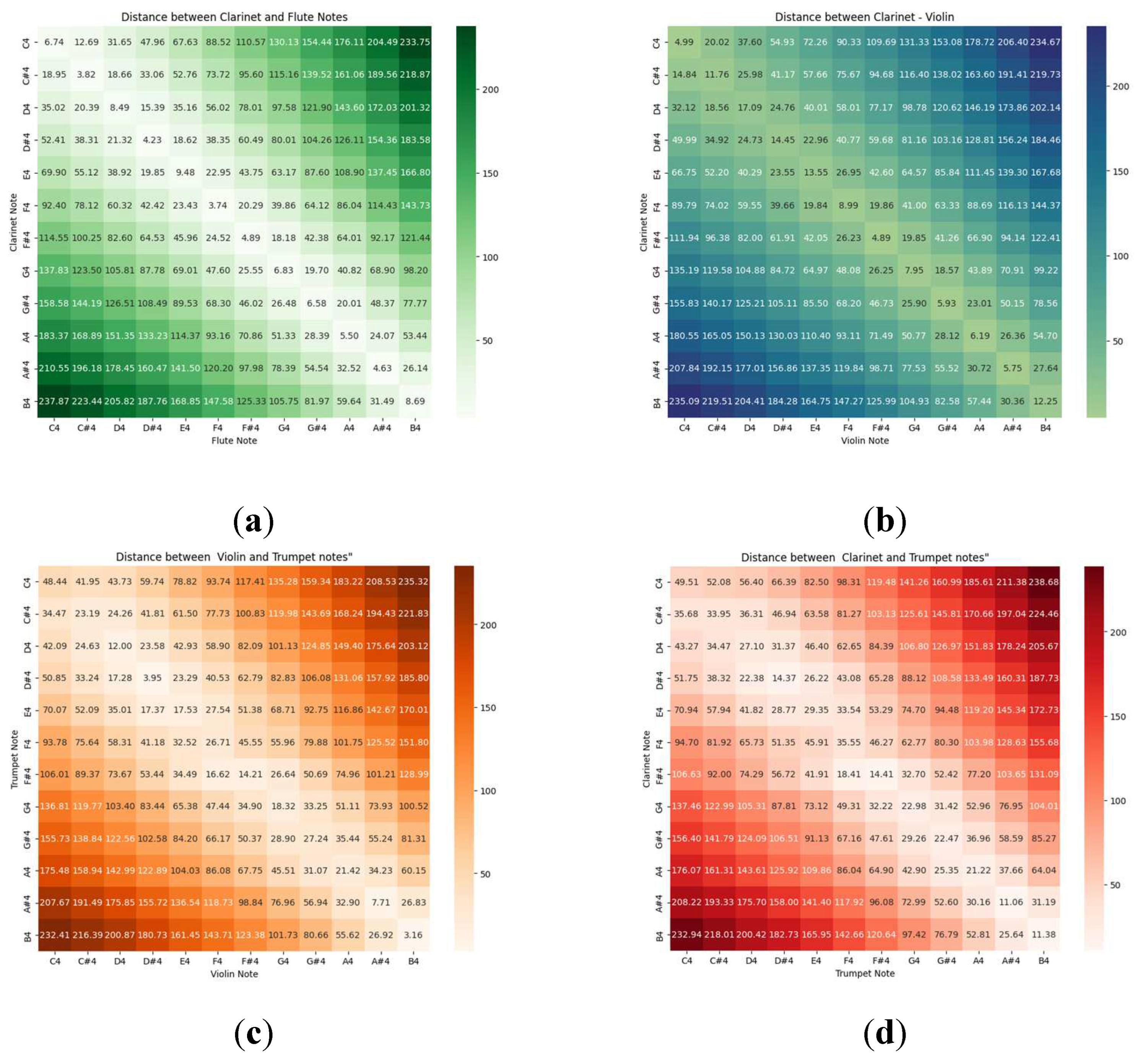
Preprints 81858 g003
Figure 3. Comparison of Euclidean distances between musical sounds of different instruments. (a) Clarinet-Flute (b) Clarinet-Violin (c) Violin-Trumpet and (d) Clarinet-Trumpet.
Figure 3. Comparison of Euclidean distances between musical sounds of different instruments. (a) Clarinet-Flute (b) Clarinet-Violin (c) Violin-Trumpet and (d) Clarinet-Trumpet.
Preprints 81858 g003
Preprints 81858 g004
Figure 4. Fourier Transforms of the B4 Goodsound for different instruments. See the text for details.
Figure 4. Fourier Transforms of the B4 Goodsound for different instruments. See the text for details.
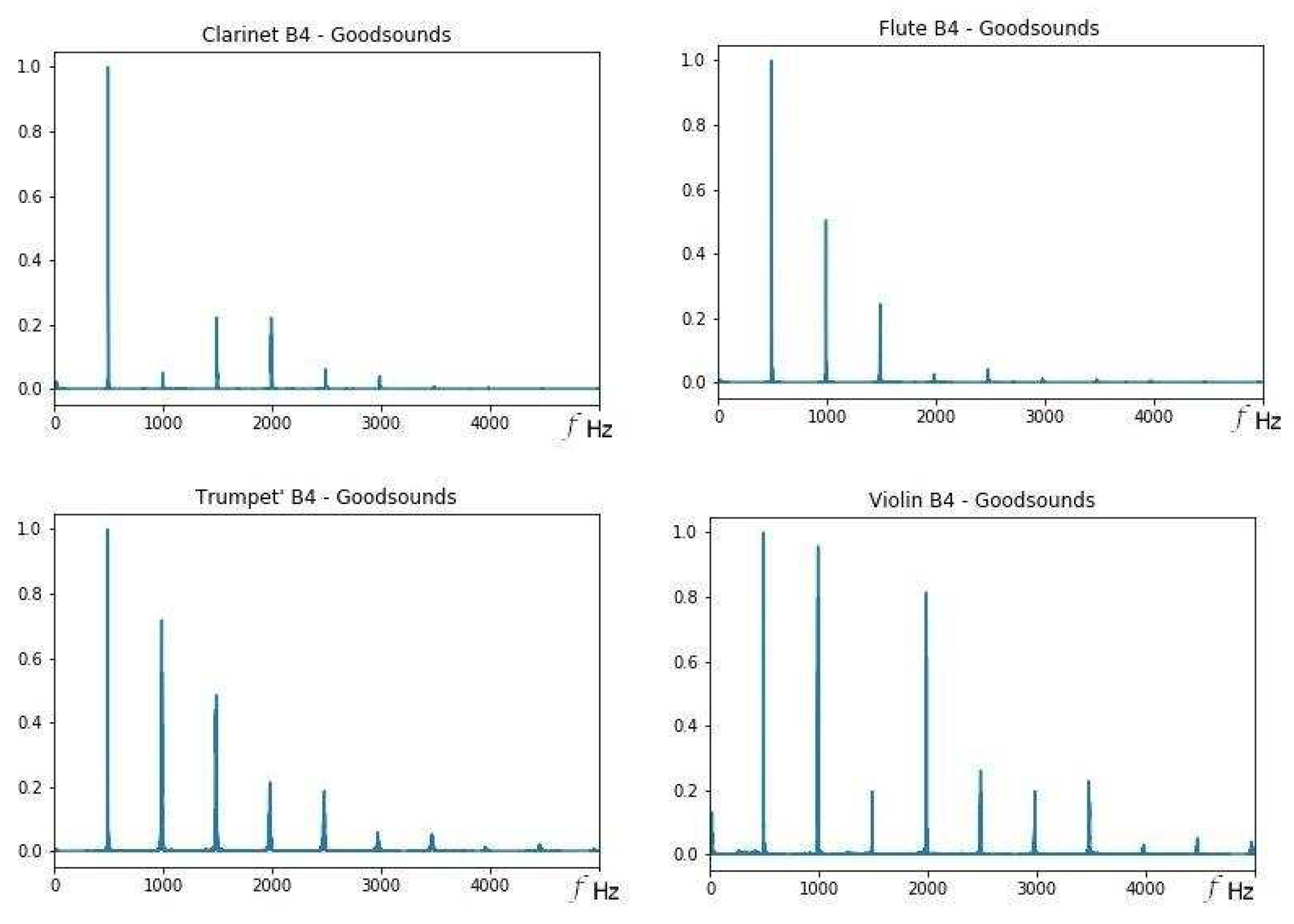
Preprints 81858 g004
Preprints 81858 g006
Figure 6. Variation of the MC timbre coefficient as a function of musical dynamics: clarinet, upper panel; and flute, lower panel. Also, note the variation of M when performing the Crescendo technique (Section 3.3)
Figure 6. Variation of the MC timbre coefficient as a function of musical dynamics: clarinet, upper panel; and flute, lower panel. Also, note the variation of M when performing the Crescendo technique (Section 3.3)
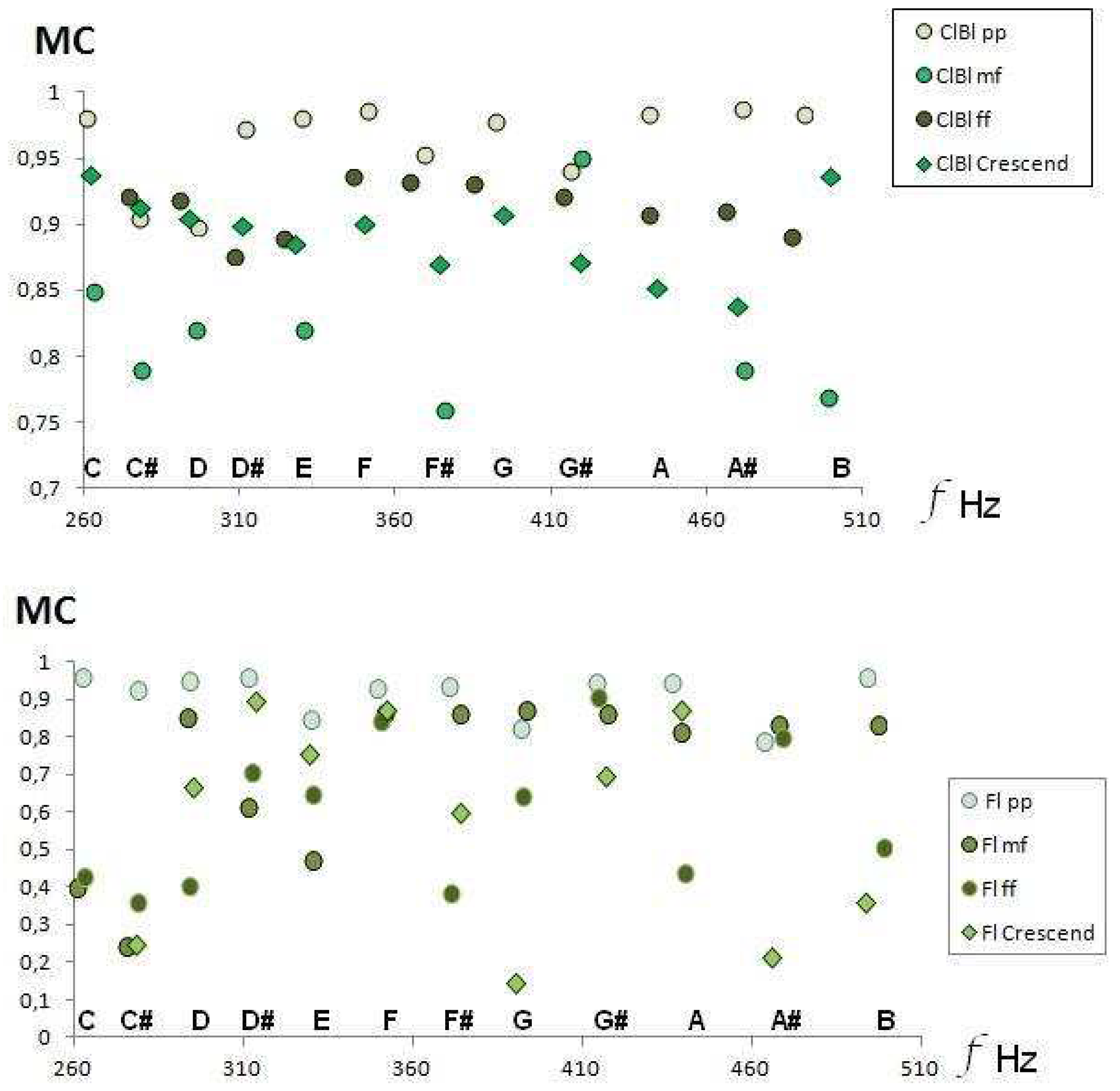
Preprints 81858 g006
Preprints 81858 g007
Figure 7. Medium Contrast (left panel) and Monotony (right panel) timbral coefficients, in the Goodsound database audios, of Violin (top) Cello (center) and Trumpet (bottom).
Figure 7. Medium Contrast (left panel) and Monotony (right panel) timbral coefficients, in the Goodsound database audios, of Violin (top) Cello (center) and Trumpet (bottom).
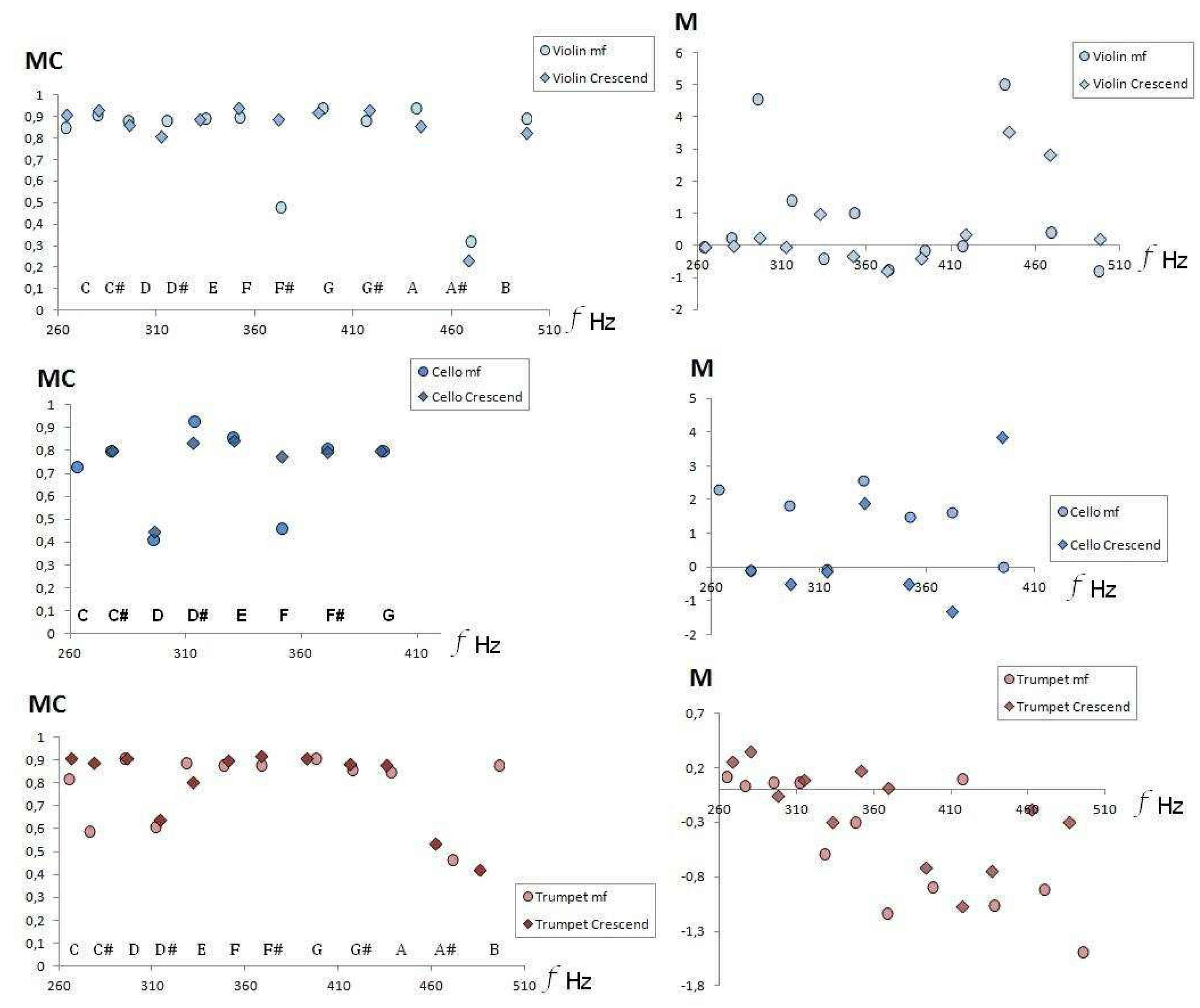
Preprints 81858 g007
Preprints 81858 g008
Figure 8. Matrix of Euclidean distances between the musical sounds of the Crescendo and Mezzoforte Goodsound audio records: (a) Clarinet (b) Violin.
Figure 8. Matrix of Euclidean distances between the musical sounds of the Crescendo and Mezzoforte Goodsound audio records: (a) Clarinet (b) Violin.
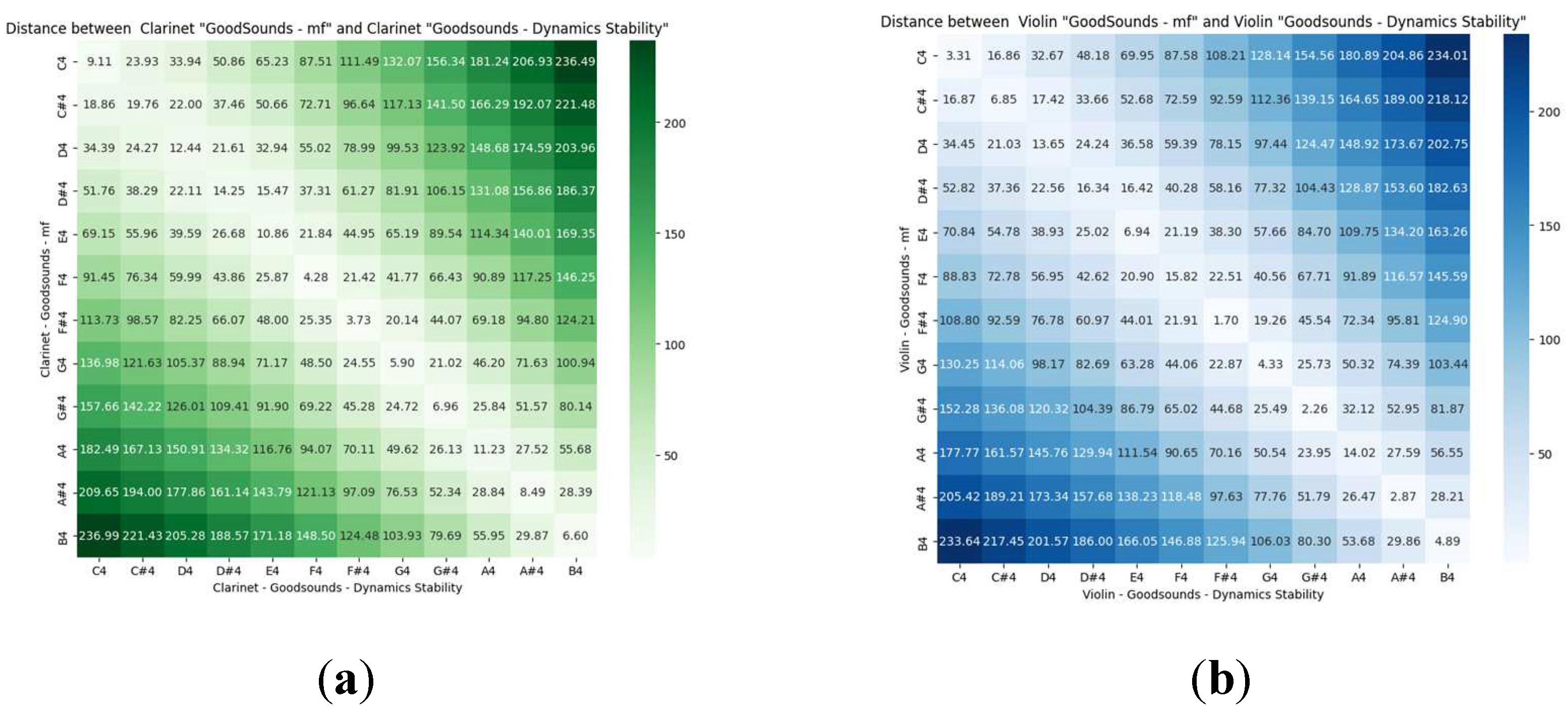
Preprints 81858 g008
Preprints 81858 g009
Figure 9. FFTs G4 Sound of Clarinet (Left Column) Flute (Central Column) and Trumpet (Right Column); normal register mezzo-forte (middle row), with crescendo technique (upper row) and vibrato (lower row). The values of the timbral coefficients of the Mean Affinity MA, Harmonicity H, and Affinity A are highlighted.
Figure 9. FFTs G4 Sound of Clarinet (Left Column) Flute (Central Column) and Trumpet (Right Column); normal register mezzo-forte (middle row), with crescendo technique (upper row) and vibrato (lower row). The values of the timbral coefficients of the Mean Affinity MA, Harmonicity H, and Affinity A are highlighted.
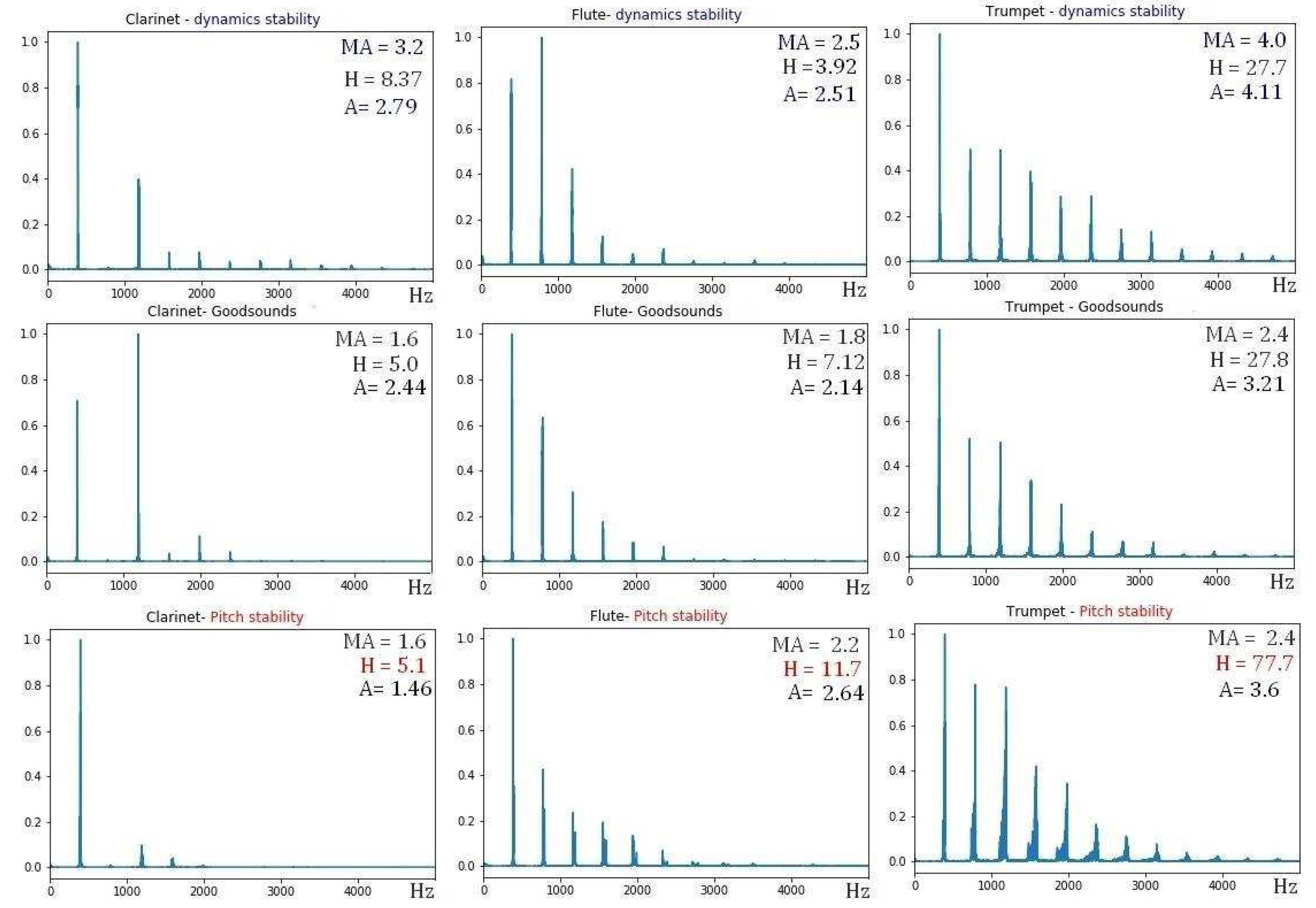
Preprints 81858 g009
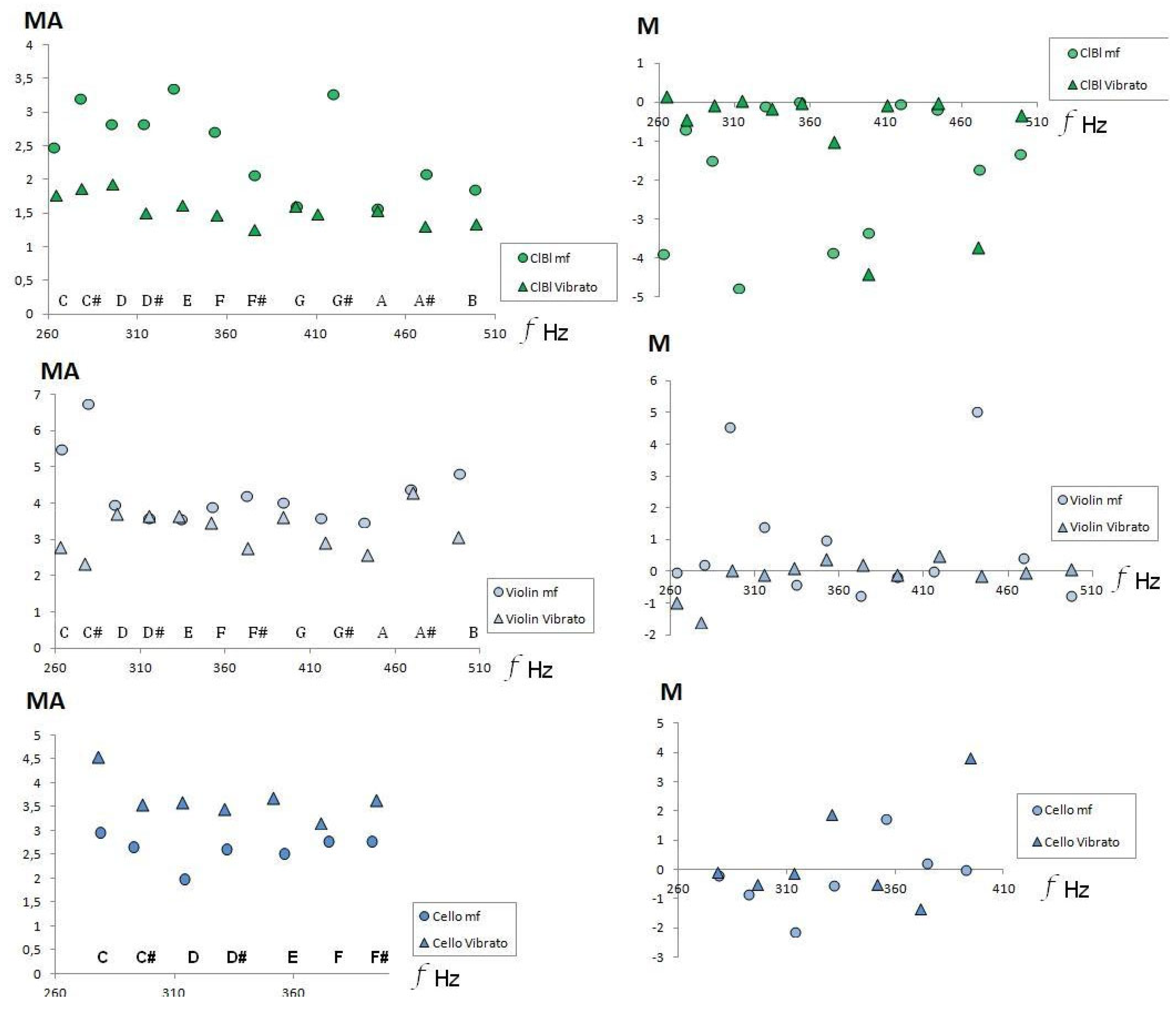
Preprints 81858 g010
Figure 10. Medium Affinity (left panel) and Monotony (right panel) timbral coefficients, in the Goodsound database audios, of Clarinet (top), Violin (center), and Cello (bottom).
Figure 10. Medium Affinity (left panel) and Monotony (right panel) timbral coefficients, in the Goodsound database audios, of Clarinet (top), Violin (center), and Cello (bottom).
Preprints 81858 g010
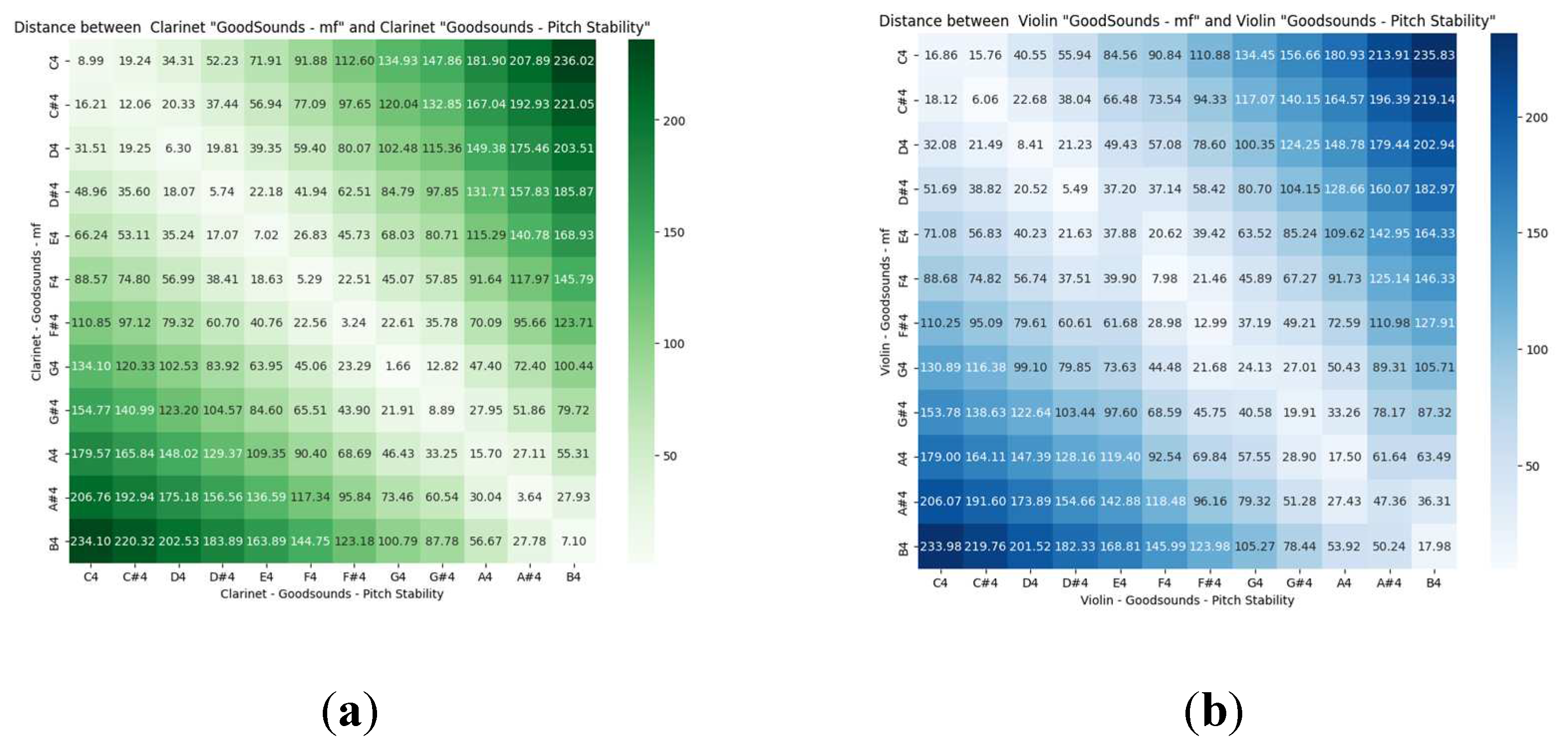
Preprints 81858 g011
Figure 11. Matrix of Euclidean distances between the musical sounds of the Vibrato and Mezzoforte Goodsound audio records: (a) Clarinet (b) Violin.
Figure 11. Matrix of Euclidean distances between the musical sounds of the Vibrato and Mezzoforte Goodsound audio records: (a) Clarinet (b) Violin.
Preprints 81858 g011
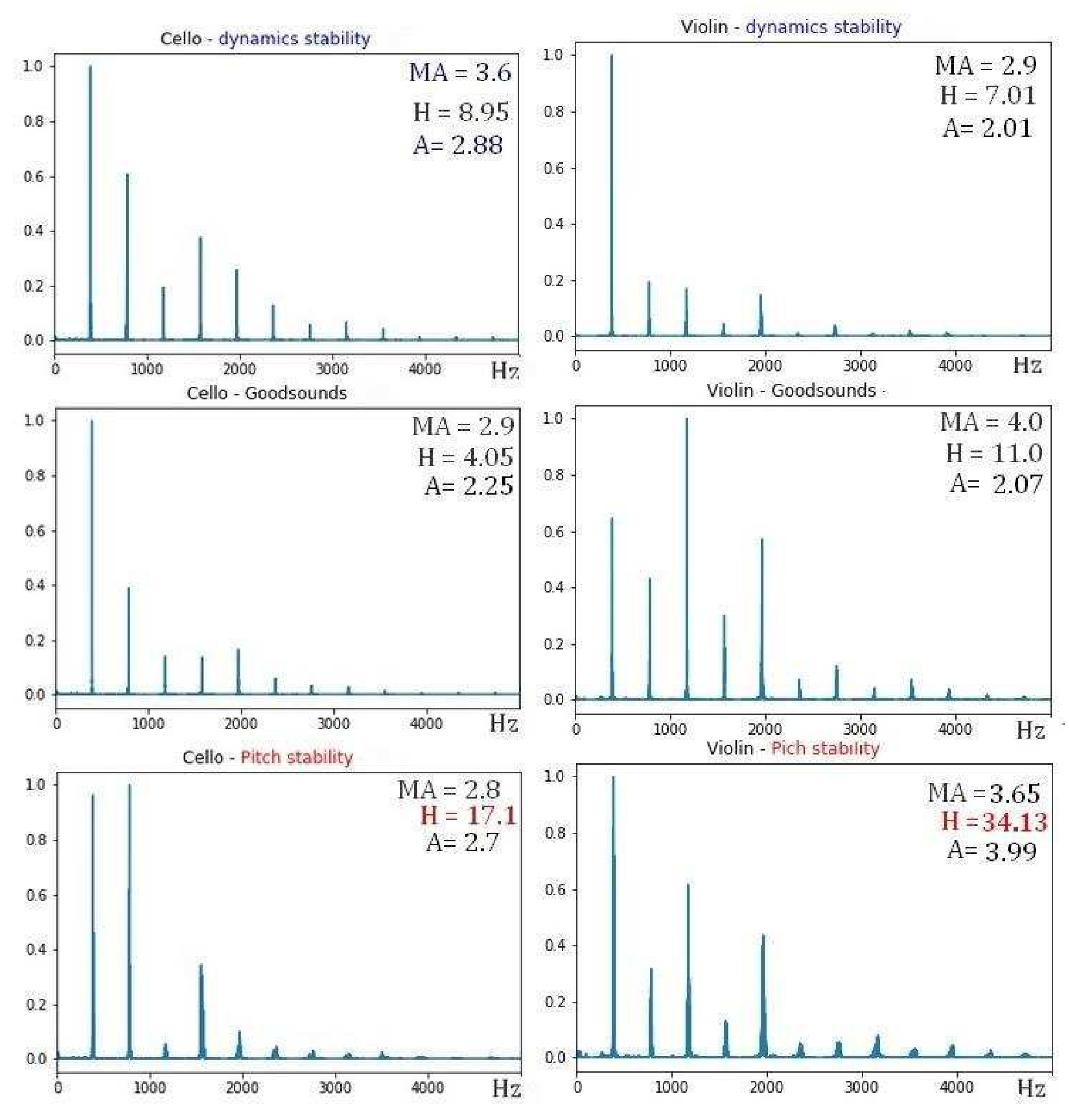
Preprints 81858 g012
Figure 12. FFTs of G4 sound: Cello (Left Column)) and Violin (Right Column); normal register mezzo-forte (middle row), with crescendo technique (upper row) and vibrato (lower row). The values of the timbral coefficients of Mean Affinity MA, Harmonicity H, and Affinity A are highlighted.
Figure 12. FFTs of G4 sound: Cello (Left Column)) and Violin (Right Column); normal register mezzo-forte (middle row), with crescendo technique (upper row) and vibrato (lower row). The values of the timbral coefficients of Mean Affinity MA, Harmonicity H, and Affinity A are highlighted.
Preprints 81858 g012
Table 1. Comparative results of the Random Forest classification algorithm (mean accuracy ± Standard Deviation) for categories recognition: musical instrument, musical dynamics, musical note, and musical instrument Families.
Table 1. Comparative results of the Random Forest classification algorithm (mean accuracy ± Standard Deviation) for categories recognition: musical instrument, musical dynamics, musical note, and musical instrument Families.
Instrument Dynamics Pitch Family
Timbral Coefficients [8] 0.78 ± 0.02 0.63 ± 0.038 0.65 ± 0.046 0.92 ± 0.017
Timbral features (Librosa) 0.89 ± 0.029 0.97 ± 0.011 0.22 ± 0.014 0.91 ± 0-018
Test T (p-value) 0.0000209 0.0000136 0.000115 0.0185
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated