Economic Model of Ancillary Services in Real Time for Frequency Control

Preprint

Article

Economic Model of Ancillary Services in Real Time for Frequency Control

Altmetrics

Downloads

125

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

07 August 2023

Posted:

08 August 2023

You are already at the latest version

Alerts

Abstract

Modern electrical power systems integrate ancillary services to provide security and quality of service in real-time operation because of the intense variations in frequency caused by the massive development and uncertainty of solar-wind generation. Therefore, this ancillary services market focuses on power reserves for secondary and tertiary frequency control. Adjusting reserves and dispatching plants is a manual instruction executed by the system operator to maintain the frequency in the normal operating state (49.80≤f≤50.20 Hz). However, in the absence of an economic model for real-time power reserve reallocation in the ancillary services market, the reserve adjustments made by the system operator are not always optimal since they generate a displacement between the scheduled and actual marginal costs. Then, this work proposes a methodology for operating the ancillary services market in real-time through a dynamic and hourly mathematical model that integrates the variability of solar-wind generation, the demand monitoring curve, and the trajectory of the marginal cost. This model minimizes power reserve costs, which are governed by hourly price auctions, for candidate plants classified as supra/infra-marginal and can optimally reallocate power reserves for secondary and tertiary frequency control.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

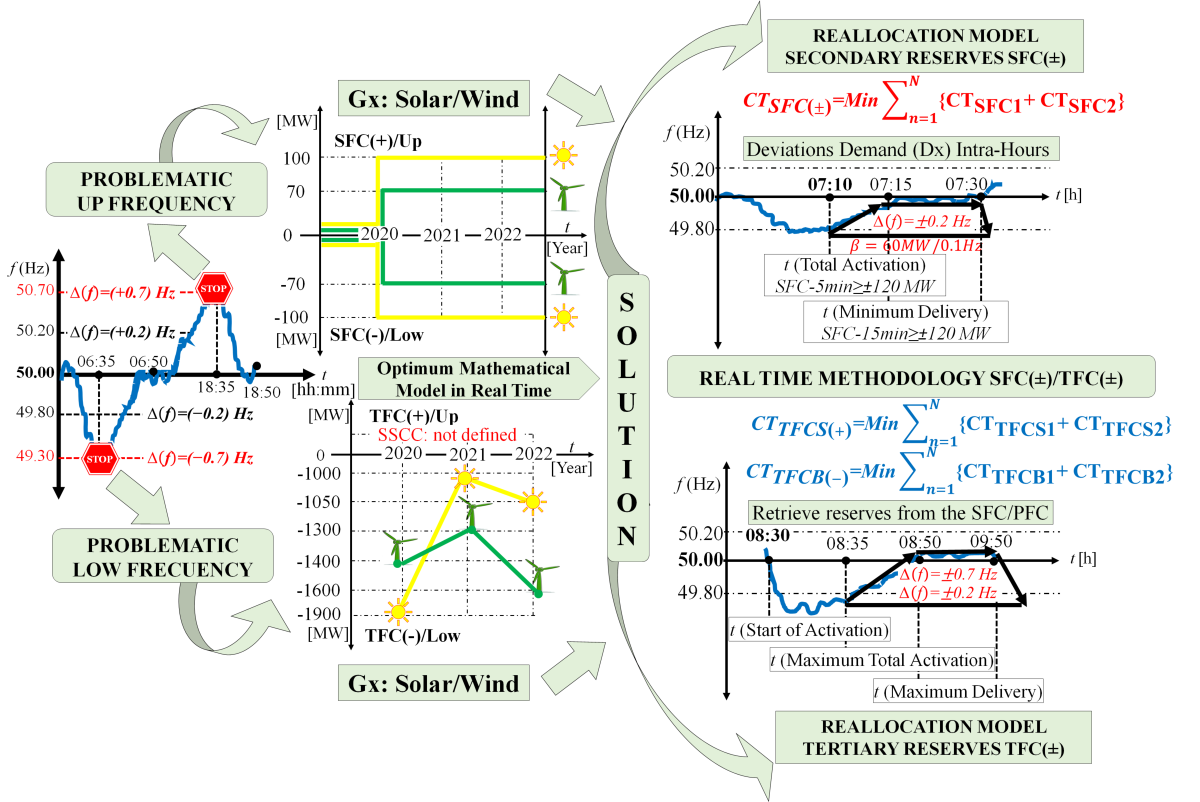
1. Introduction of real-time complementary services for frequency control

The energy transition and environmental policies due to climate change point towards carbon neutrality that proposes the definitive retirement of coal-fired thermal power plants, allowing the development of an emission-free energy matrix in the short and medium term [1]. The energy transition challenge focuses on developing modern technologies such as solar and wind power to displace fossil fuel thermal generation. Chile has been developing solar and wind generation for over a decade, registering a penetration of renewable energies of more than 40% of its total generation by 2022, becoming a world leader as the country with the most significant potential and development in solar generation [2].

However, the energy transition is in full implementation linked to the energy market, which aims to supply the demand with new economic and emission-free generation technologies. The problem lies in decoupling thermal generation and integrating renewable generation into this new ancillary services (AS) market. This market was designed to offer security and quality service to electric power systems. Currently, the operation of this market has a monopolistic structure exercised by the conventional generation.

While the ramification of renewable energies has opened an opportunity for complementary services, allowing to offer the same conditions of technical and economic competences that conventional generation delivers. The problem of renewable generation, demand and system failures, have a high level of uncertainty that cause severe frequency deviations that force the system operator to apply power reserves arbitrarily to mitigate frequency instability. Therefore, this inefficient mechanism of arbitrary power reserves with unjustified dispatches of power plants translates into an additional cost to the market that makes the overall operation of the system more expensive. Frequency control is the most critical variable in the ancillary services market. It is responsible for ensuring system stability through the action of three categories of operation in the following order: primary frequency control (PFC), secondary frequency control (SFC), and tertiary frequency control (TFC). Therefore, frequency control depends on those power plants that have the ability to deliver power reserves in the shortest response time to ramp up and down their generation [3]. However, the market for ancillary services must be able to incentivize and integrate conventional and renewable generation through an economic model that monetizes investment costs, implements control designs, and avoids arbitrary and unjustified dispatches of plants that control the frequency in real-time [4,5].

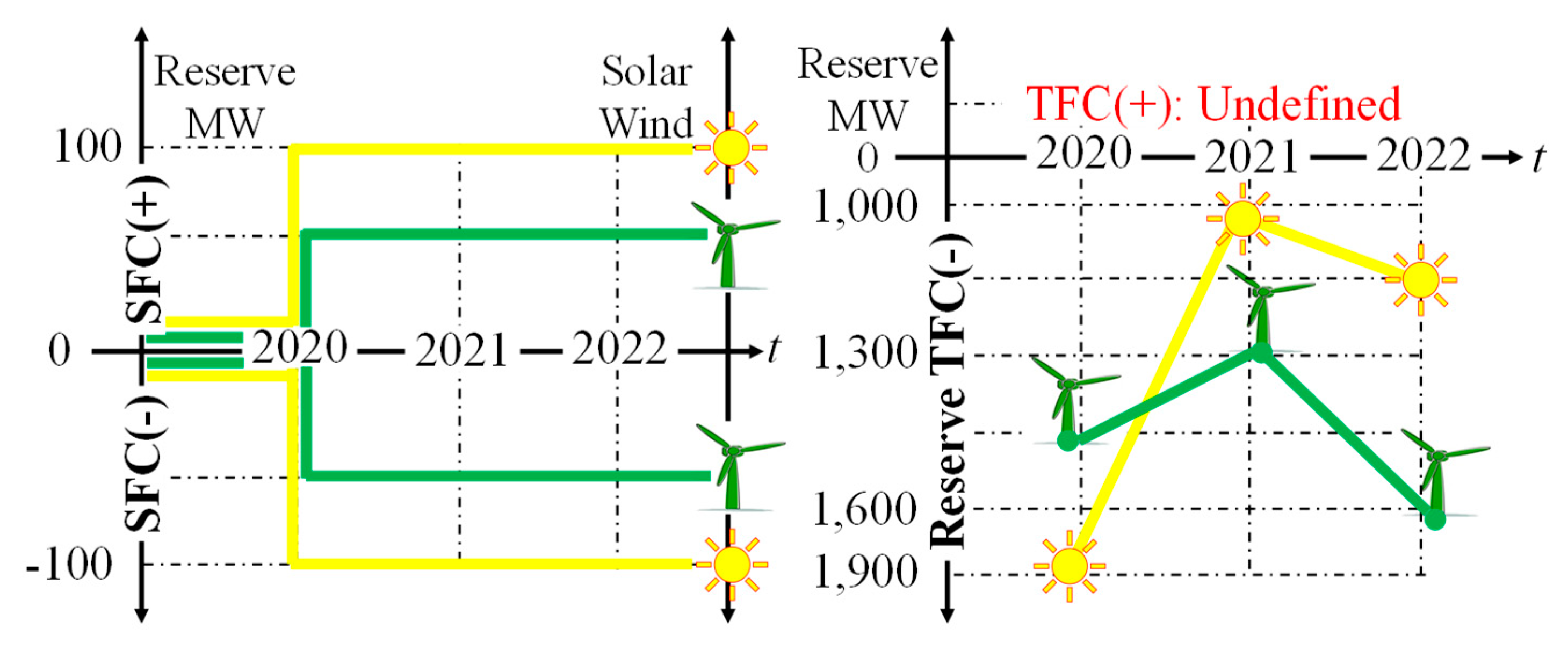
Both in Latin America and Chile, there is an unlimited resource for the development of solar and wind renewable energies that allow delivering large capacities of power reserves for secondary and tertiary frequency control, as shown in Figure 1, which shows an annual evolution of the entire capacity of power reserves of renewable resources in Chile that have not yet been fully allocated to frequency control.

The challenge of this market is focused on developing technical and economic mechanisms for the distribution of these power reserves for frequency control in real-time operation that allows balancing the energy market and the market for ancillary services. Therefore, the proposal of this work is novel because it proposes an hourly dynamic mathematical model that, through the demand curve tracking, minimizes the costs of reallocating power reserves for real-time frequency control in the market of ancillary services. This model considers the optimal dispatch of renewable and conventional power plants ordered in an economic merit list to adjust the minimum power reserves destined for SFC and TFC.

2. State of the art of ancillary services in the use of reserves for frequency control

The beginnings of the ancillary services markets were always linked to conventional hydrothermal generation and without market rules for its use. The massive entry of solar photovoltaic and wind generation requires participation in this market to displace thermal generation completely. Chile, for example, is one of the world leaders in the development of solar generation (Figure 2). However, the business model of renewable generation must integrate remuneration mechanisms, starting from investment, energy sales, and operating costs, to economic incentives dedicated to frequency control as an objective of the ancillary services market. In the ancillary services market in countries with higher energy development, renewable generation displaces the dispatches of conventional power plants by reducing the marginal cost, operation cost, and frequency regulation of the rotational axis; and guaranteeing the N-1 safety criteria in the transmission lines. Next, the most relevant bibliographic selection for this proposal is presented, showing the state of the art of works associated with the market of complementary services that use power reserves for real-time frequency control.

2.1. Bidding and auction market for frequency control power reserves

The availability of renewable generation implies modifications to the energy market rules to integrate its participation in ancillary services [6]. The ancillary services market should be designed with an economically attractive bidding and auction model to decouple renewable generation that can deliver power reserves for frequency control from the energy market [7].

In Europe, transmission system operators (TSO) reduce costs and optimize reserves for SFC in real-time operation, with bidding models and hourly auctions, as is the case of the Iberian Electricity System of Portugal [7]. Also, the TSO defines the market contracts in three operational aspects for power reserves (capacity, allocation, and activation) to avoid deserted auctions when no generation is available [8]. In Portugal, Spain, and France, bids and auctions of power reserves for frequency control are traded in €/MW involving three transmission system operators and the English TSO of the National Grid [9,10]. Although the bidding and auction model is efficient in a programmed systemic scenario, in real-time, it lacks flexibility because the bid values are static for each plant and do not change over time, causing an operating cost overrun, always leaving the option to those plants that monopolize the bids and auctions in the programmed operation.

These ancillary services market models’ characteristics are that they function prior to dispatch and aggregate renewable generation. The prices in the submitted bids are fixed, and participants can change the energy volumes in their bid between 1 to 5 minutes before the scheduled dispatch interval begins [11]. Like the pre-dispatch problem, the real-time ancillary services market is complex to implement due to its size, and human and technological effort [12] because variable bids are received every couple of minutes, and the market is settled accordingly to obtain the price and quantity values every 5 minutes before the dispatch and retirement of the plants [13]. This bidding and auction mechanism for real-time operation demonstrates that power reserve adjustments can be made because of system deviations that limit the resources to perform frequency control. The limitations of this methodology are associated with the fact that the system operator’s technological and human efforts are subjected to high-stress levels when testing real-time scenarios with reallocations of less than 5 minutes. This extreme methodology of the real-time availability of bids and auctions is practical if an oversizing of complementary services is applied to instantly adjust the frequency control reserves and avoid the stress of real-time operation. This would immediately cause an operation cost overrun and erroneous decisions by the system operators.

2.2. Mechanisms and economic models to reallocate power reserves in real time

The complex search for economic mechanisms to theoretically support power reserve reallocations for real-time frequency control, especially with specific cases in secondary and tertiary frequency control, allows relating the problem to other models with some similarities in their solution. For example, there are game theory algorithms based on the opportunity cost arising between energy payments and bid manipulation [14]. This game theory methodology applies to those plants dedicated to the sale of energy in a spot market when they are not governed by the marginalist theory, i.e., in a power market based on auctions or power exchanges. However, this method is slightly similar to the ancillary services market in definitions of opportunity cost based on the fixed offer of power reserves. Its primary deficit is the absence of an economic mechanism in real-time to encourage those plants that are generating close to the marginal cost and dedicate part of their power in reserves for frequency control.

There are other similar market techniques that perform an optimized allocation to distribute power reserves with a commercial categorization that are obtained through long-term contracts and regular reserves are purchased with daily or hourly auctions with frequency regulation market prices [15]. Also, ERCOT, California ISO, and Midcontinent ISO systems present an optimal model not in real-time but executing a co-optimization of reserves at different frequency controls with varied time scales (0.5 s, 10 s, 10 min, 15 min, and 30 min) [16]. The optimization of reserves in scheduled operations performed by system operators is efficient and optimizes the generation of resources dedicated to providing power reserves. However, adapting it to a real-time model is complex due to the size and operational effort involved. Even this mechanism challenges the flexibility of the generation, and the technical restrictions of switching on and off increase, causing an increase in the significant maintenance of the power plants and an extra cost for purchasing unscheduled energy in the spot market.

Other authors optimize generation resources by combining secondary and tertiary frequency control reserve reallocations for the same plant, using an economic dispatch solved by the lambda method that satisfies the supply-demand balance [17]. This method also solves the real-time power reserve reallocation by running a distributed economic dispatch by linear programming with Wasserstein’s metric-based robust distribution optimization technique [18]. This methodology is excellent for reallocating power reserves in real-time since it uses the theoretical foundations of economic dispatch to find the lowest cost of reserve reallocation. The problem with this model is its static structure that does not perceive in time the changes of new power plants that can acquire the reserve reallocations through an opportunity cost that can follow the marginal cost. This instantaneous method partially solves the reserve changes for frequency control in real-time. However, it still lacks improvements that guarantee its optimization in time.

2.3. Model of monopolistic structure of power reserves for frequency control

Several transmission system operators apply the use of reserves for frequency control, being influenced by generator eligibility rules. This causes energy prices to increase and each power plant’s revenues to be affected, even for units not actively providing reserves [19]. Currently, there are models for ancillary services markets that avoid generator eligibility rules, such as the agent-based modeling framework, which provides design parameters and strategies to the market operator in real-time, such as clearing algorithms for the day-ahead market, intraday dispatch and redispatch [20]. That is, when the conditions of competition in a market equilibrium are not met, generation companies tend to have a monopolistic structure in providing their services. The problem in this methodology is the reallocation of power reserves for frequency control in those plants of the same company that modify the scenarios in real-time in the energy market to be awarded the complementary services and receive the maximum profits to the detriment of other plants without the possibility of awarding. Thus, monitoring competition in real-time is essential to stop this type of action and has the mission to regulate the energy market and complementary services.

However, linear optimization can mitigate this problem to calculate the optimal daily and intraday market bids through a real-time predictive control model for uncertain reserve auctions due to the energy market’s priority [21]. In [22], a real-time integral post-operation method is proposed that minimizes the gap between the net payments of power plants and a penalty factor at different time scales (5 s, 15 s, up to 60 s) when they do not meet the market bids at the time of allocating frequency regulation. Both methods are effective when applied to supply the demand, and the minimum hourly reserves are not met in the scheduled dispatch. In the case of complementary services in real-time, their implementation becomes more complex because the specific calculation of costs or economic gaps between the reallocation of reserves in less than one minute becomes impracticable due to the system’s dynamics.

Classical pre-dispatch models with security constraints are also used with power reserve for frequency control and then co-optimization of energy with power reserve for ancillary services in the 24-hour day-ahead market schedule, and then migrate to a 15-minute or hourly real-time redispatch model using marginal busbar costs [23]. This real-time model applies a mechanism for reallocating reserves through direct instruction by the system operator based solely on availability, capacity, and the time to provide reserves with plants out of economic order.

The costs involved in this direct instruction mechanism are reflected in the global operation of the system, due to the incense burner dephasing of the marginal cost and the excess of plants operating at the technical minimum with ancillary services without justification, increasing the operating cost of supplying the demand.

2.4. Efficient real-time power reserve reallocation model

Implementing economic mechanisms dedicated to using power reserves in frequency control is complex. For generation plants, remuneration, and profitability are essential to enter this ancillary services market. Currently, there are models based on bids and auctions to establish the power reserves for frequency control. However, most reserve reallocation models have a static profile in the prices established by bids and auctions. This mechanism satisfactorily fulfills the reallocation of power reserves but does not follow a dynamic price metric that evidences a minimum total cost of reserves in the system.

Unlike Chile, Latin American power systems such as Peru, Argentina, Colombia, and others do not yet have a fully developed ancillary services market that can unify power reserves for frequency control and integrate renewable generation. Although a broad scientific field exists in ancillary services markets, the problem is not yet fully solved. Therefore, this work proposes a model adapted to the ancillary services market for frequency control that overcomes the traditional auction and hourly bidding methods with modeling in non-real scheduling scenarios. This is a dynamic method that allows minimizing the total hourly costs of power reserve reallocations of the candidate plants called Supramarginal (SMg) and Inframarginal (IMg) for secondary and tertiary frequency control, which depend exclusively on the marginal cost path (MgC), demand trend and the opportunity cost presented to the awarded plants guaranteeing the minimum cost of system operation.

3. Theoretical framework and methodology of a real-time reserve allocation model for frequency control

The theoretical framework defines the structure and technical conditions for applying the power reserves of power plants intended to raise or lower generation in the ancillary services market for secondary and tertiary frequency control. This theoretical scope governs the proposed economic methodology and the validation of the model using real case studies, intending to respect the margins of symmetrical, asymmetrical power reserves, activation times, delivery times, and power ramps.

3.1. Secondary frequency control symmetrical reserves

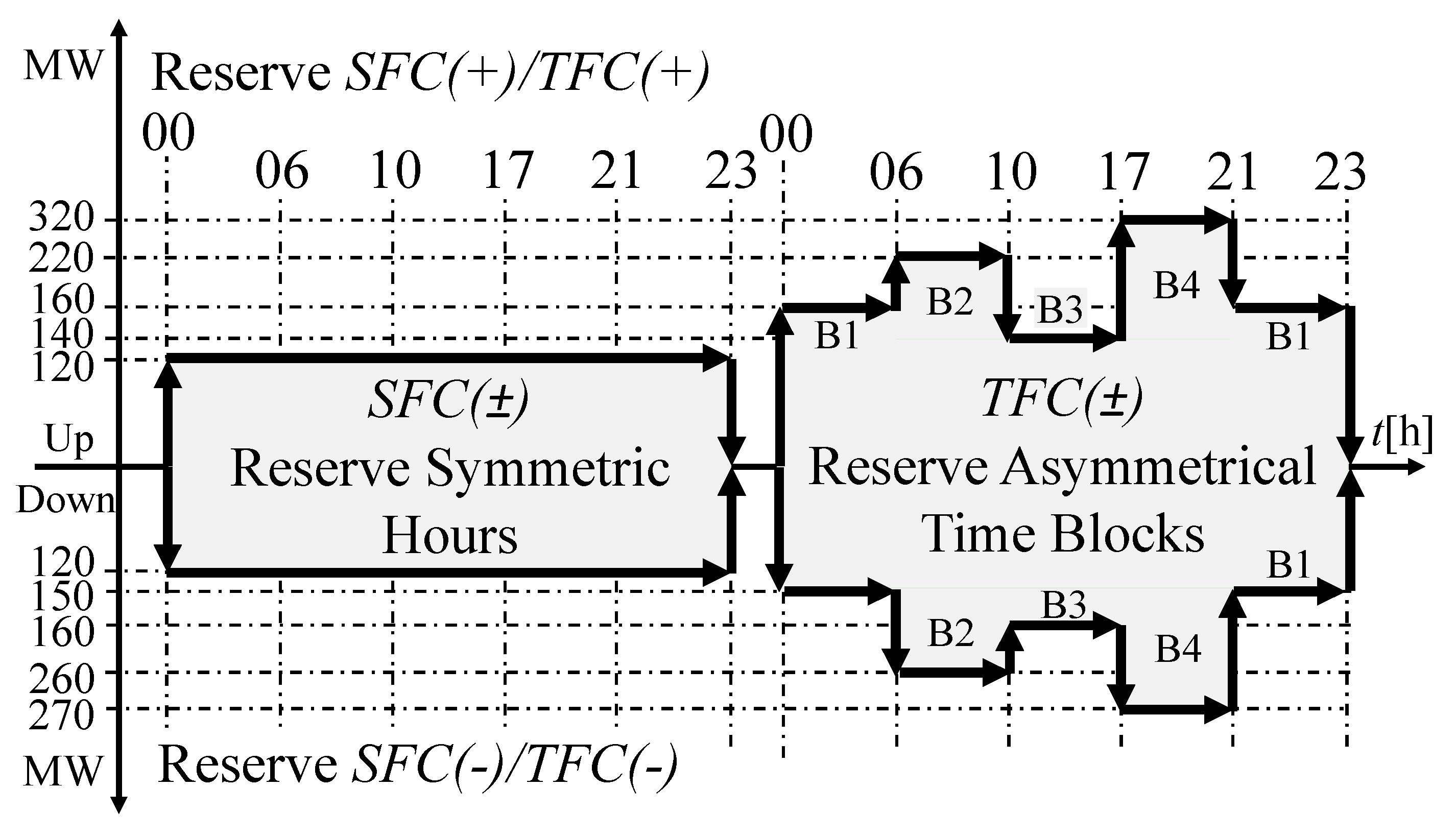
The complementary service for secondary frequency control, hereinafter SFC(±), corresponds to the capacity of power reserves to raise or lower generation to maintain the frequency in a normal operating state in a range of 49.80 to 50.20 Hz. This frequency control operates in manual mode or automatic generation control (AGC). These SFC(±) reserves are symmetrical with a value of ±120 MW during the entire period of its use and with a power ramp ranging between ±24 MW/min, as shown in Figure 3. In addition, this ancillary service is governed by a total activation time of 5 minutes and a minimum delivery time of 15 minutes, as shown in Figure 4.

The economic mechanism of this ancillary service is subdivided into two categories of operation, the first case being the secondary frequency control to increase generation, hereinafter SFC(+). According to Table 1, the increase in the generation of this ancillary service SFC(+) is in increasing order of the variable costs of the plants that were awarded from the economic merit list. While the second case is the secondary frequency control to lower generation, hereinafter SFC(-). The decrease of generation of this ancillary service SFC(-) is in increasing order of the values offered by the plants that were awarded from the priority list of activation of lowering of generation, as shown in Table 1.

3.2. Asymmetrical tertiary frequency control reserves

The ancillary service for tertiary frequency control, hereinafter referred to as TFC(±), corresponds to the spinning or cold power reserves for raising or lowering generation. This ancillary service acts in an emergency state when the system frequency oscillates between ± 0.7 Hz concerning its nominal value of 50.00 Hz. The purpose of the TFC(±) is to restore the frequency when the power reserves of the primary and secondary frequency control are depleted. The operation of the tertiary frequency control is manual. The TFC(±) reserves are asymmetrical with values from ±150 to ±320 MW in different operating time blocks, as shown in Figure 3. In addition, this ancillary service is governed by a maximum synchronization time between 5 and 15 minutes and a maximum delivery time of one hour, as shown in Figure 4.

The economic mechanism of this ancillary service is subdivided into two categories of operation, the first case being the tertiary frequency control to increase generation, hereinafter TFC(+). The increase of generation of this ancillary service TFC(+) is in increasing order of the variable costs of the plants that were awarded from the economic merit list, according to Table 1. While the second case is the tertiary frequency control to lower generation, hereinafter TFC(-). The decrease of generation of this ancillary service TFC(-) is in increasing order of the values offered by the plants that were awarded from the priority list of activation of lowering of generation, as shown in Table 1.

3.3. Methodology of a real-time reserve allocation model for frequency control

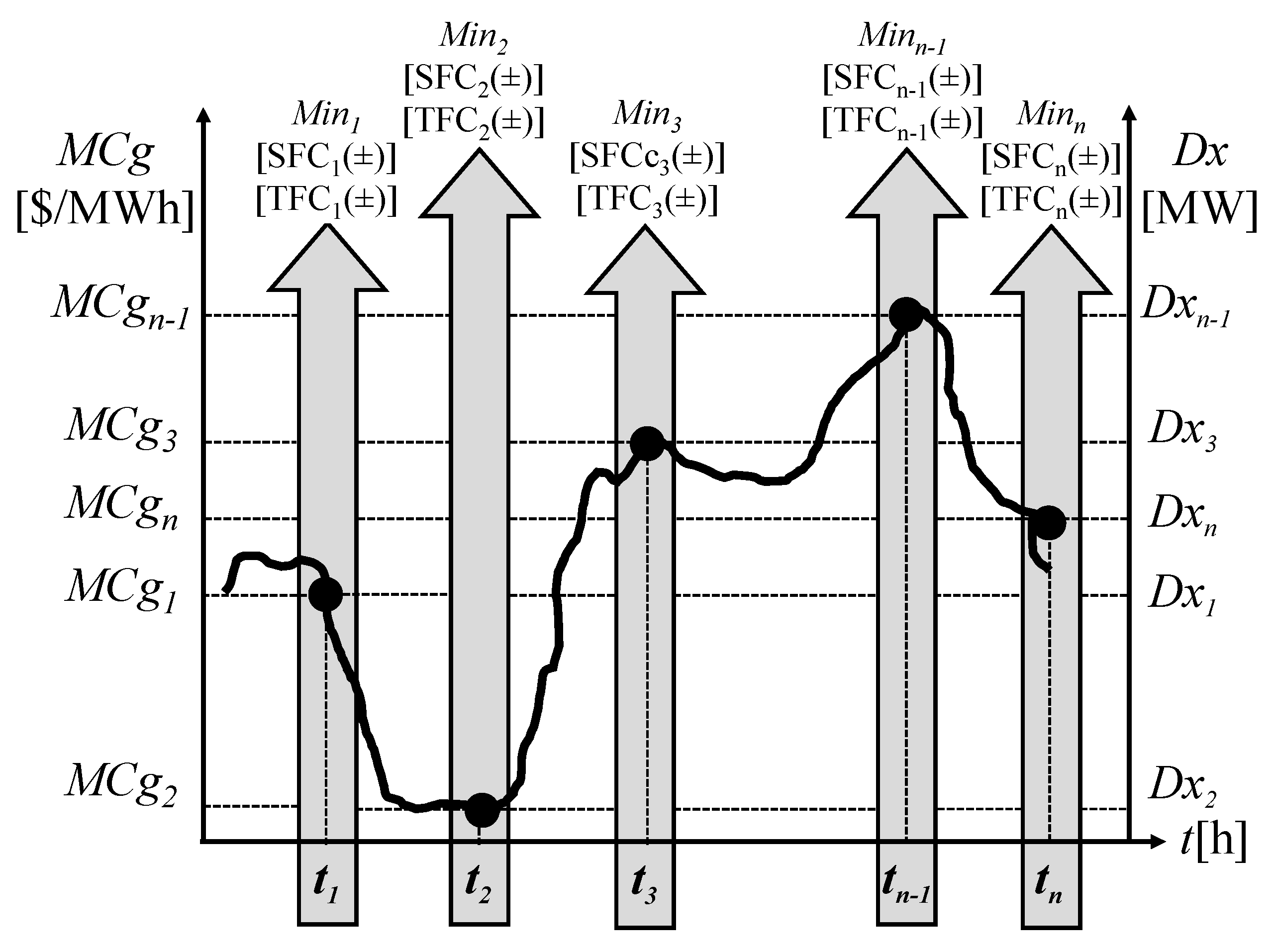
The methodology develops an hourly dynamic mathematical model that minimizes the total cost of power reserves for the ancillary services market, using reallocations of power reserves of those plants enabled for real-time secondary and tertiary frequency control. The model uses the available plants for real-time operation ordered from the lowest to the highest variable generation cost. The selection of these plants is categorized as Supramarginal (SMg) when the variable cost of generation of each plant is greater than the marginal cost (MgC) of the system, and Inframarginal (IMg) if the variable cost of generation is less than the marginal cost (MgC). Therefore, the marginal cost of the system is a consequence of the dispatch of plants due to the variation in demand.

This methodology allows minimizing hourly reserve costs in real-time as a function of the MgC and the demand curve (Dx), as opposed to a static and inefficient reallocation that does not perceive those changes in power reserves. However, the system MgC evolves over time. In other words, to cover the power reserve deficits for secondary and tertiary frequency control, the candidate plants SMg and IMg close to the MgC of the system are used. The reserve costs of each plant are calculated, and the reserve power value is reallocated hourly, considering the minimization of the cost function of one or more plants. As the demand curve and marginal costs shift over time, new cost minimization is performed to reallocate power reserves, as shown in Figure 5.

3.4. Mathematical method for reallocation secondary frequency control reserves

Mathematically, the methodology is a real-time economic model that minimizes hourly the total cost of power reserve reallocations for the new candidate plants selected as Supramarginal and Inframarginal for secondary frequency control to step-up and step-down generation as indicated in Eqs. (1)-(3).

{T C}_{t}^{S F C} = \min \sum_{n \in N} ({T C}_{n, t}^{S F C - S M g} + {T C}_{n, t}^{S F C - I M g}) \forall t \in T

(1)

{T C}_{n, t}^{S F C - S M g} = ({V C}_{n} - M {g C}_{t}) \cdot R e s^{(-)} \cdot H O p e

(2)

{T C}_{n, t}^{S F C - I M g} = (M {g C}_{t} - {V C}_{n}) \cdot R e s^{(+)} \cdot H O p e

(3)

Where the objective function (1) represents the minimization of the total cost

{T C}_{t}^{S F C}

of the power reserve for secondary frequency control for the N power plants named Supramarginal (SMg) and Inframarginal (IMg) in an hourly period t. Equation (2) corresponds to the costs of power reserves

{T C}_{n, t}^{S F C - S M g}

for secondary frequency control of Supramarginal power plants. While Equation (3) represents the cost of power reserves

{T C}_{n, t}^{C S F - I M g}

of secondary frequency control of Inframarginal power plants. Finally, Eqs. (2) and (3) depend on the hourly marginal cost

M {g C}_{t}

, variable cost

{V C}_{n}

, power reserve amount

R e s^{(-)}

R e s^{(+)}

, and operating hours

H O p e

3.5. Mathematical method for reallocation tertiary frequency control reserves

Mathematically, the power reserves for tertiary frequency control for up and down generation are calculated using a real-time economic model that minimizes hourly the total cost of power reserve reallocations to the new candidate plants selected as Supramarginal and Inframarginal, as shown in Eqs. (4)-(9).

{T C}_{t}^{T F C, u p} = \min \sum_{n \in N} ({T C}_{n, t}^{T F C, u p - S M g} + {T C}_{n, t}^{T F C, u p - I M g}) \forall t \in T

(4)

{T C}_{n, t}^{T F C, u p - S M g} = ({V C}_{n} - M {g C}_{t}) \cdot R e s \cdot H O p e + C P

(5)

{T C}_{n, t}^{T F C, u p - I M g} = (M {g C}_{t} - {V C}_{n}) \cdot R e s \cdot H O p e

(6)

{T C}_{t}^{T F C, d o w n} = \min \sum_{n \in N} ({T C}_{n, t}^{T F C, d o w n - S M g} + {T C}_{n, t}^{T F C - I M g}) \forall t \in T

(7)

{T C}_{n, t}^{T F C, d o w n - S M g} = ({V C}_{n} - M {g C}_{t}) \cdot R e s \cdot H O p e

(8)

{T C}_{n, t}^{T F C, d o w n - I M g} = (M {g C}_{t} - V_{n} C) \cdot R e s \cdot H O p e

(9)

Where Equation (4) and (7) represent the minimization of the total cost

{T C}_{t}^{C T F, u p}

and

{T C}_{t}^{C T F, d o w n}

of the power reserve reallocations for up/down generation of the tertiary frequency control of the

N

power plants named Supramarginal (SMg) and Inframarginal (IMg) for a period

t

. While (5) and (6) correspond to the costs

{T C}_{n, t}^{C T F, u p - S M g}

and

{T C}_{n, t}^{C T F, u p - I M g}

of the candidate plants SMg and IMg intended as power reserves for raising generation. Finally, (8) and (9) represent the costs

{T C}_{n, t}^{C T F, d o w n - S M g}

and

{T C}_{n, t}^{C T F, d o w n - I M g}

of the candidate SMg and IMg plants destined as power reserves to lower generation.

4. Simulation of real scenarios and discussion of the results

The methodology is validated using three scenarios of real-time operation to apply reallocation and activation of power reserves for frequency control with authentic data [24], as shown in Table 1. The methodology and validation of the model can be tested in any real system or experimental system using the initial conditions of variable generation costs (VC), marginal cost (MgC), auctions for ancillary services, and the power reserves of the secondary control SFC(±) and tertiary control TFC(±) of frequency of each system.

The first real scenario is a reallocation of power reserves for generation raising using the secondary frequency control for generation raising SFC(+). While the second real scenario is an activation of the power reserves for generation raising/lowering, known as the spinning reserves, and obeying the tertiary frequency control TFC(±). Finally, the third real scenario is a reallocation of power reserves for raising generation in the tertiary frequency control TFC (+).

4.1. Gas depletion in combined cycle plants implies reallocation reserves to increase generation in secondary frequency control

A reallocation for SFC(+) is performed with real-time operation data [24], using the actual hourly marginal cost (MgC) of 29.2 USD/MWh corresponding to the G-8 plant, according to Table 1. Therefore, in the event of a failure in the generation system, power reserve reallocations must be performed for frequency control. Thus, if the G-4 plant is without power reserve for the SFC(+) in 28 MW for one hour or several hours, then the 28 MW of SFC(+) of the G-4 plant must be replaced.

Currently, real-time power reserve resignations are solved with inefficient methods that increase the overall system operation cost. The most usual method is using the economic merit list (EML), which uses the most economical plants in the energy market, directly harming the plants in a deficit state to fulfill energy sale contracts with plants in the spot market. The second method corresponds to using plants at minimum technical cost (MT) or higher variable generation cost, causing an unnecessary displacement of the marginal cost and the exponential increase of the operating cost due to the excess of plants operating at minimum technical cost. However, this work proposes a novel and efficient solution using the Supramarginal (SMg) and Inframarginal (IMg) candidate plants that minimizes the total cost of reserves for reallocation. It is important to note that the plants selected as candidates for reserve reallocation acquire an opportunity cost as the variable cost of generation (VC) is close to the system’s actual marginal cost (MgC). The validation of the model with the inefficient reserve reallocation methods and the proposed methodology using Inframarginal and Supramarginal plants is presented below, as shown in Table 2.

4.1.1. Economic merit list method for calculating the cost of raising the generation in SFC

This technique involves using the most economical plants in the merit list to reallocate reserves according to the amount of reserves available for each plant in order of lowest to highest variable generation cost. The plants with the lowest marginal cost, i.e., G-1, G-2, G-3, and G-4, are used by calculating the reserve cost of Equation (3).

Plant G-1 (PV):

${TC}_{SFC - EML} = (29.2 - 0) \cdot 28 \cdot 1 = 818 U S D$ . It has a maximum margin of $S F C (+) = 100 M W$
Plant G-2 (PV):

${TC}_{SFC - EML} = (29.2 - 0) \cdot 28 \cdot 1 = 818 U S D$ . It has a maximum margin of $S F C (+) = 90 M W$
Plant G-3 (Wind):

${TC}_{SFC - EML} = (29.2 - 0) \cdot 28 \cdot 1 = 818 U S D$ . It has a maximum margin of $S F C (+) = 60 M W$
Plant G-4 (Gas):

${T C}_{SFC - EML} = (29.2 - 28.6) \cdot 28 \cdot 1 = 17 U S D$ . It has a maximum margin of $S F C (+) = 28 M W$ and runs out of SFC(+) reserve.

4.1.2. Technical minimum method to calculate the cost of raising generation in SFC

This technique involves using the plants operating at a technical minimum or out of service. It corresponds to the plants with the highest variable generation cost in the energy market since their provision is the ancillary services market. In order to reallocate the power reserves, plants G-16, G-17, G-18, and G-19 are used by calculating the reserve cost of Equation (2).

Plant G-16 (Hydro):

${TC}_{SFC - TM} = (40.9 - 29.2) \cdot 28 \cdot 1 = 328 U S D . It has a maximum margin of S F C (+) = 100 M W$
Plant G-17 (Coal):

${TC}_{SFC - TM} = (44.5 - 29.2) \cdot 28 \cdot 1 = 428 U S D$ . It has a maximum margin of $S F C (+) = 5 M W$
Plant G-18 (Hydro):

${TC}_{SFC - TM} = (47.2 - 29.2) \cdot 28 \cdot 1 = 504 U S D$ . It has a maximum margin of $S F C (+) = 100 M W$
Plant G-19 (Gas):

${TC}_{SFC - TM} = (77.0 - 29.2) \cdot 28 \cdot 1 = 1338 U S D$ . It has a maximum margin of $S F C (+) = 40 M W$ .

4.1.3. Methodology with inframarginal plants to calculate the cost of increasing generation in SFC

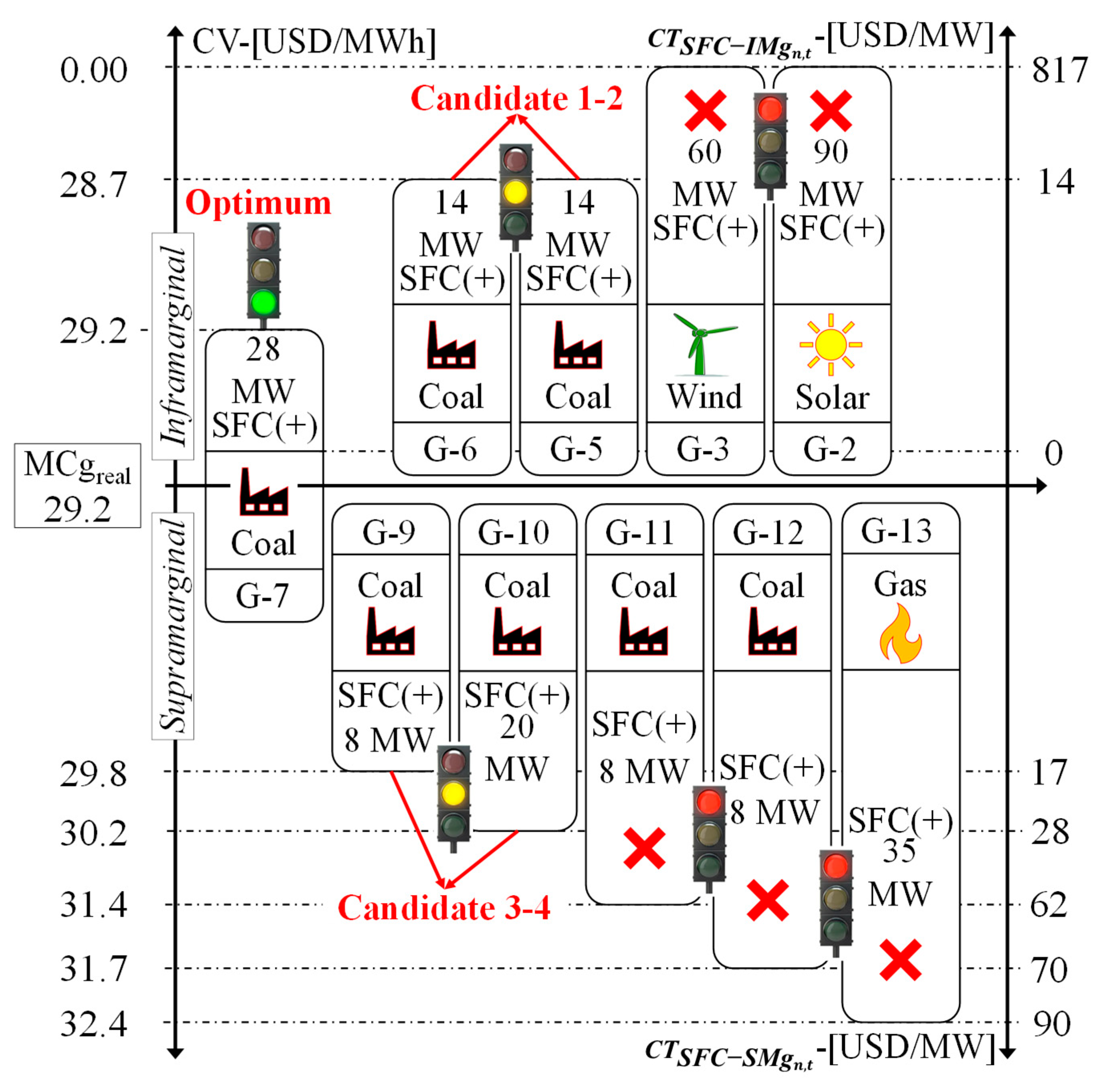
The IMg plants with

M g C > V C

that are close to the hourly

M {g C}_{t}

(G-8=29.2 USD/MWh) are used to award the SFC(+) reserve reallocation for one hour, according to Table 2. The selected plants are G-2, G-3, G-5. G-6 and G-7 by calculating the reserve cost of Equation (3).

Plant G-2 (PV):

${T C}_{2,1}^{S F C - I M g} = (29.2 - 0) \cdot 28 \cdot 1 = 818 U S D$ . It has a maximum margin of $S F C (+) = 90 M W$ .
Plant G-3 (Wind):

${T C}_{3,1}^{S F C - I M g} = (29.2 - 0) \cdot 28 \cdot 1 = 818 U S D$ . It has a maximum margin of $S F C (+) = 60 M W$ .
Plant G-5 (Coal):

${T C}_{5,1}^{S F C - I M g} = (29.2 - 28.7) \cdot 28 \cdot 1 = 14 U S D$ . It has a maximum margin of $S F C (+) = 14 M W$ .
Plant G-6 (Coal):

${T C}_{6,1}^{S F C - I M g} = (29.2 - 28.7) \cdot 28 \cdot 1 = 14 U S D$ . It has a maximum margin of $S F C (+) = 14 M W$ .
Plant G-7 (Coal):

${T C}_{7,1}^{S F C - I M g} = (29.2 - 29.2) \cdot 28 \cdot 1 = 0 U S D$ . It has a maximum margin of $S F C (+) = 35 M W$ .

The results indicate that the Inframarginal G-2 and G-3 solar/wind renewable power plants have sufficient capacity to replace the SFC(+) reserve reallocations. However, they are not selected as candidates as their reserve cost (818 USD) exceeds the G-5 and G-6 plants. Although the G-5 and G-6 plants are candidate plants for reserve reallocation, and together they can achieve the SFC(+) of 28 MW, contributing 14 MW each, they still do not satisfy the minimum value of the reserve power reallocation cost (28 USD in total for G-5 and G-6) compared to the G-7 plant. Finally, the optimum corresponds to the G-7 power plant that has a SFC(+) capacity of 35 MW in total to replace the 28 MW SFC(+) of the G-4 power plant with a cost

{T C}_{7,1}^{S F C - I M g}

of 0 USD due to the proximity (opportunity cost) it has with the real-time marginal cost MgC (29.2 USD/MWh). Then, the system operator considers the calculation obtained for the Inframarginal plants as a reallocation alternative before being executed in real-time. That is to say:

The G-7 power plant can perform SFC(+) of 28 MW in replacement of the G-4 power plant.
Total cost of the reserve to be replaced: ${T C}_{7,1}^{S F C - I M g} = 0$ USD.

4.1.4. Methodology with supramarginal plants to calculate the cost of increasing generation in SFC

The candidate SMg plants with

M g C < V C

, which are close to the hourly

M {g C}_{t}

(G-8=29.2 USD/MWh), as shown in Table 1, are used to reallocate 28 MW of SFC(+) reserve power from the G-4 plant. The selected plants are G-9, G-10, G-11, G-12, and G-13 by calculating the reserve cost of Equation (2).

Plant G-9 (Coal):

${T C}_{9,1}^{S F C - S M g} = (29.8 - 29.2) \cdot 28 \cdot 1 = 17$ USD. It has a maximum margin of $S F C (+) = 8 M W$
Plant G-10 (Coal):

${T C}_{10,1}^{S F C - S M g} = (30.2 - 29.2) \cdot 28 \cdot 1 = 28$ USD. It has a maximum margin of $S F C (+) = 30 M W$
Plant G-11 (Coal):

${T C}_{11,1}^{S F C - S M g} = (31.4 - 29.2) \cdot 28 \cdot 1 = 62$ USD. It has a maximum margin of $S F C (+) = 8 M W$
Plant G-12 (Coal):

${T C}_{12,1}^{S F C - S M g} = (31.7 - 29.2) \cdot 28 \cdot 1 = 70 U S D$ . It has a maximum margin of $S F C (+) = 8 M W$ .
Plant G-13 (Gas):

${T C}_{13,1}^{S F C - S M g} = (32.4 - 29.2) \cdot 28 \cdot 1 = 90 U S D$ . It has a maximum margin of $S F C (+) = 35 M W$ .

The results indicate that the Supramarginal G-11, G-12, and G-13 thermal plants have sufficient capacity to replace the 28 MW SFC(+) reserve reallocations of the G-4 plant. However, they are not selected as candidate plants as their standby cost ranges from USD 62 to 90, exceeding the reallocation costs offered by G-9 and G-10 plants. Finally, the optimum for power reserve reallocation corresponds to the G-9 and G-10 plants, which have a maximum SFC(+) capacity of 8 and 30 MW respectively with a reserve cost per plant of

{T C}_{9,1}^{C S F - S M g}

=17 USD and

{T C}_{10,1}^{C S F - S M g}

=28 USD. Then, the system operator considers the calculation obtained for the Supramarginal plants as a reallocation alternative before being executed in real-time. That is:

The G-9 plant can perform 8 MW SFC(+) in replacement of the G-4 plant.
The G-10 power plant can perform 20 MW SFC(+) in replacement of the G-4 power plant.
Total cost of reserve to be replaced: ${T C}_{9,1}^{C S F - S M g} + {T C}_{10,1}^{C S F - S M g} = 45$ USD.

4.1.5. Discussion and analysis of the calculation methods and the results of the reallocation of reserves for SFC

The Economic Merit List and Technical Minimum methods can satisfy the missing reserves for reallocating the 28 MW secondary frequency control of the G-4 plant. However, the selected plants of both methods fail to compete with the costs of the proposed methodology because the results of the reserve costs range from 17 to 818 USD/MW for the merit list method. The reserve cost ranges from 328 to 1,338 USD/MW for the technical minimum method.

The results proved more economical in the proposed model tested than the other inefficient methods. The proposed methodology results show that the total costs of power reserve reallocations for real-time secondary frequency control using candidate Inframarginal and Supramarginal plants range from 0 to 45 USD/MW. As the selection of candidate plants moves away from the marginal cost in the direction above or below the reference value, the opportunity cost increases, and therefore the total costs of reserves for real-time reallocation are not optimal because they range from 90 to 817 USD/MW, which corresponds to the high opportunity costs of renewable energies.

Mathematically, the results respond to the methodology of the real-time economic model that minimizes the total cost

{T C}_{t}^{C S F}

of power reserve reallocations of the set of selected candidate power plants of type SMg and IMg, as described in Equation (1). As the real-time marginal cost MgC changes, the cost minimization calculation of the power reserve reallocations cost should be modified with the selection of new candidate power plants SMg and IMg respectively. Finally, Figure 6 and Table 3 detail all the results of the reserve calculations for reallocating the 28 MW of the G-4 plant.

4.2. Severe frequency variations involve activating the power reserves of the TFC

For this type of factual scenario, an empirical methodology is used that is supported by the economic mechanisms of the merit list to increase generation and the TFC(-) auction list for plants that have to decrease generation, as shown in Table 1.

4.2.1. Method for activating power reserves to raise TFC generation

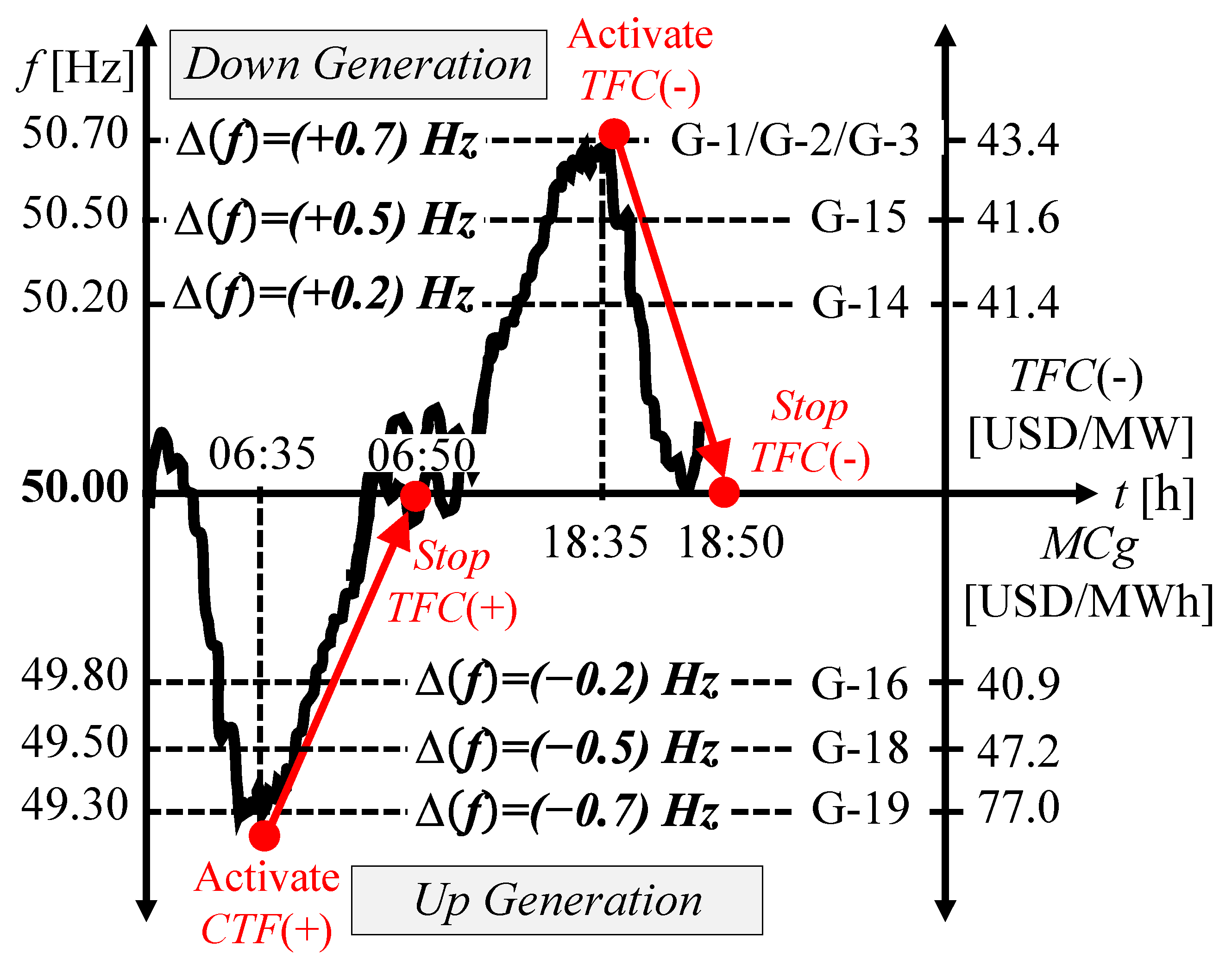
If the actual MgC of the system is 44.5 USD/MWh corresponding to the G-17 plant and the frequency variations are lower than 49.80 Hz with a duration time of more than 5 minutes, then the methodology of activating the TFC(+) reserves is applied using the ranking of the plants by the economic merit list, according to Table 1. Therefore, the candidate plant to increase generation is the G-16 plant (40.9 USD/MWh). If the reserves are insufficient, the next plant is ranked according to the same economic price criteria. That is, the G-18 plant (47.2 USD/MWh) and then the G19 plant (77.0 USD/MWh), as shown in Figure 7. If the real MgC of the system is 44.5 USD/MWh corresponding to the G-17 plant and the frequency variations are lower than 49.80 Hz with a duration time of more than 5 minutes. Then, according to Table 1, the methodology of activating the TFC(+) reserves is applied using the ranking of the plants through the economic merit list. Therefore, the candidate plant to increase generation is the G-16 plant (40.9 USD/MWh). If the reserves are not sufficient, the next plant in the ranking is followed by the next plant in the same economic price criterion. That is, the G-18 plant (47.2 USD/MWh) and then the G19 plant (77.0 USD/MWh), as shown in Figure 7.

4.2.2. Method to activate power reserves to decrease generation in TFC

If the actual MgC of the system is 77.0 USD/MWh corresponding to the G-19 plant and the frequency variations exceed 50.20 Hz for more than 5 minutes, then the methodology of activating the TFC(-) reserves is applied using the TFC(-) activation priority list, which goes from the lowest to the highest price offered to provide the TFC(-) service, according to Table 1. The candidate plant for reducing generation is the G-14 plant (41.4 USD/MWh). If the reserves are not restored, the next plant is followed by the next plant with the same economic criteria of auctioned prices. That is, G-15 (41.6 USD/MWh), G-1/G-2/G-3 (43.4 USD/MWh), and G-4 (49.0 USD/MWh), as shown in Figure 7.

4.2.3. Discussion and analysis of the results of the activation of reserves for TFC

The numerical results of this methodology of activating power reserves for tertiary frequency control for raising and reducing generation satisfy the equilibrium conditions between the energy market and ancillary services. For the case of activation of tertiary reserves to raise generation, the costs range from 40.9 to 77.0 USD/MWh in the vicinity of the marginal cost with the economic merit list mechanism, and for the activation of tertiary reserves to lower generation, the costs range from 41 to 43.4 USD/MWh depending on the bidding auction list, as shown in Figure 7.

4.3. Bidding and auction market for frequency control power reserves

A reallocation of reserves for TFC(+) is performed with real-time operation data [24], using a real hourly MgC of 29.2 USD/MWh corresponding to the G-8 plant, according to Table 1. Therefore, in the event of a failure in the generation system, power reserve reallocations must be performed for frequency control. If the G-18 plant lacks power reserve for the TFC(+) in 100 MW for one hour, then the 100 MW of TFC(+) of the G-18 plant must be replaced.

As in the problem of power reserve reallocation for secondary frequency control, this problem of power reserve reallocation for tertiary frequency control is solved using the economic merit list (EML) method and the technical minimum (TM) power plant method. The proposed methodology is also applied using the Supramarginal (SMg) and Inframarginal (IMg) candidate plants, which allows minimizing the total cost of reserves for tertiary reserve reallocation. It is essential to highlight that the plants selected as Supramarginal and Inframarginal candidates for reserve reallocation acquire an opportunity cost as the variable cost of generation (VC) is close to the actual marginal cost (MgC) of the system, as shown in Table 1. Next, the validation of the model with the inefficient methods of reserve reallocation and the proposed methodology using Inframarginal and Supramarginal plants is presented.

4.3.1. Economic merit list method for calculating the cost of raising generation in TFC

Plant G-1 (PV):

${TC}_{TFC, up - EML} = (29.2 - 0) \cdot 100 \cdot 1 = 2920 U S D$ . It has a maximum margin of $T F C (+) = 140 M W$ .
Plant G-2 (PV):

${TC}_{TFC, up - EML} = (29.2 - 0) \cdot 100 \cdot 1 = 2920 U S D$ . It has a maximum margin of $T F C (+) = 90 M W$ .
Plant G-3 (Wind):

${TC}_{TFC, up - EML} = (29.2 - 0) \cdot 100 \cdot 1 = 2920 U S D$ . It has a maximum margin of $T F C (+) = 80 M W$ .
Plant G-4 (Gas):

${TC}_{TFC, up - EML} = (29.2 - 28.6) \cdot 100 \cdot 1 = 60 U S D$ . It has a maximum margin of $T F C (+) = 45 M W$ .

4.3.2. Technical minimum method to calculate the cost of raising the generation in TFC

This technique involves using the plants operating at a technical minimum or out of service and corresponding to the plants with the highest variable generation cost in the energy market. To reallocate the power reserves, the G-16, G-17, G-18, and G-19 plants are used to calculate the reserve cost of Equation (5).

Plant G-16 (Hydro):

${TC}_{TFC, up - TM} = (40.9 - 29.2) \cdot 100 \cdot 1 = 1,170 U S D$ . It has a maximum margin of $C S F (+) = 100 M W$ .
Plant G-17 (Coal):

${TC}_{TFC, up - TM} = (44.5 - 29.2) \cdot 100 \cdot 1 = 1,530 U S D$ . It has a maximum margin of $C S F (+) = 20 M W$ .
Plant G-18 (Hydro):

${T C}_{TFC, up - TM} = (47.2 - 29.2) \cdot 100 \cdot 1 = 1,800 U S D$ . It has a maximum margin of $C S F (+) = 100 M W$ and runs out of TFC(+) reserve.
Plant G-19 (Gas):

${TC}_{TFC, up - TM} = (77.0 - 29.2) \cdot 100 \cdot 1 = 4,780 U S D$ . It has a maximum margin of $C S F (+) = 40 M W$ .

4.3.3. Methodology with inframarginal plants to calculate the cost of increasing generation in TFC

The IMg candidate plants to deliver the missing 100 MW reserve of the G-18 plant must lower their generation and evaluate the total cost of the reserve to reallocate the TFC(+) service. Then from Table 1, the candidate plants G-7, G-6, G-5, and G-4 are selected due to the closer proximity concerning the actual MgC of 29.2 USD/MWh that corresponds to the G-8 plant. Their calculation methodology is obtained according to Equation (6). The IMg candidate plants, to deliver the missing 100 MW reserve of the G-18 plant, must lower their generation and evaluate the total cost of the reserve to reallocate the TFC(+) service. Then, from Table 1, the candidate plants G-7, G-6, G-5, and G-4 are selected due to the closer proximity concerning the actual MgC of 29.2 USD/MWh that corresponds to the G-8 plant. Their calculation methodology is obtained according to Equation (6).

Plant G-7 (Coal):

${T C}_{7,1}^{T F C, u p - I M g} = (29.2 - 29.2) \cdot 100 \cdot 1 = 0 U S D$ . It has a maximum margin of $T F C (+) = 15 M W$ .
Plant G-6 (Coal):

${T C}_{6,1}^{T F C, u p - I M g} = (29.2 - 28.7) \cdot 100 \cdot 1 = 50 U S D$ . It has a maximum margin of $T F C (+) = 20 M W$ .
Plant G-5 (Coal):

${T C}_{5,1}^{T F C, u p - I M g} = (29.2 - 28.7) \cdot 100 \cdot 1 = 50 U S D$ . It has a maximum margin of $T F C (+) = 20 M W$ .
Plant G-4 (Gas):

${T C}_{4,1}^{T F C, u p - I M g} = (29.2 - 28.6) \cdot 100 \cdot 1 = 60 U S D$ . It has a maximum margin of $T F C (+) = 45 M W$ .
Plant G-3 (Wind), G-2 (Solar) and G-1 (Solar):

${T C}_{(3,2, 1), 1}^{T F C, u p - I M g} = (29.2 - 0) \cdot 100 \cdot 1 = 2920 U S D$ . Each renewable plant (G-3, G-2 and G-1) has a maximum margin of TFC(+) = 80, 90 and 100 MW, respectively. However, these plants are left out of the selection due to their high cost.

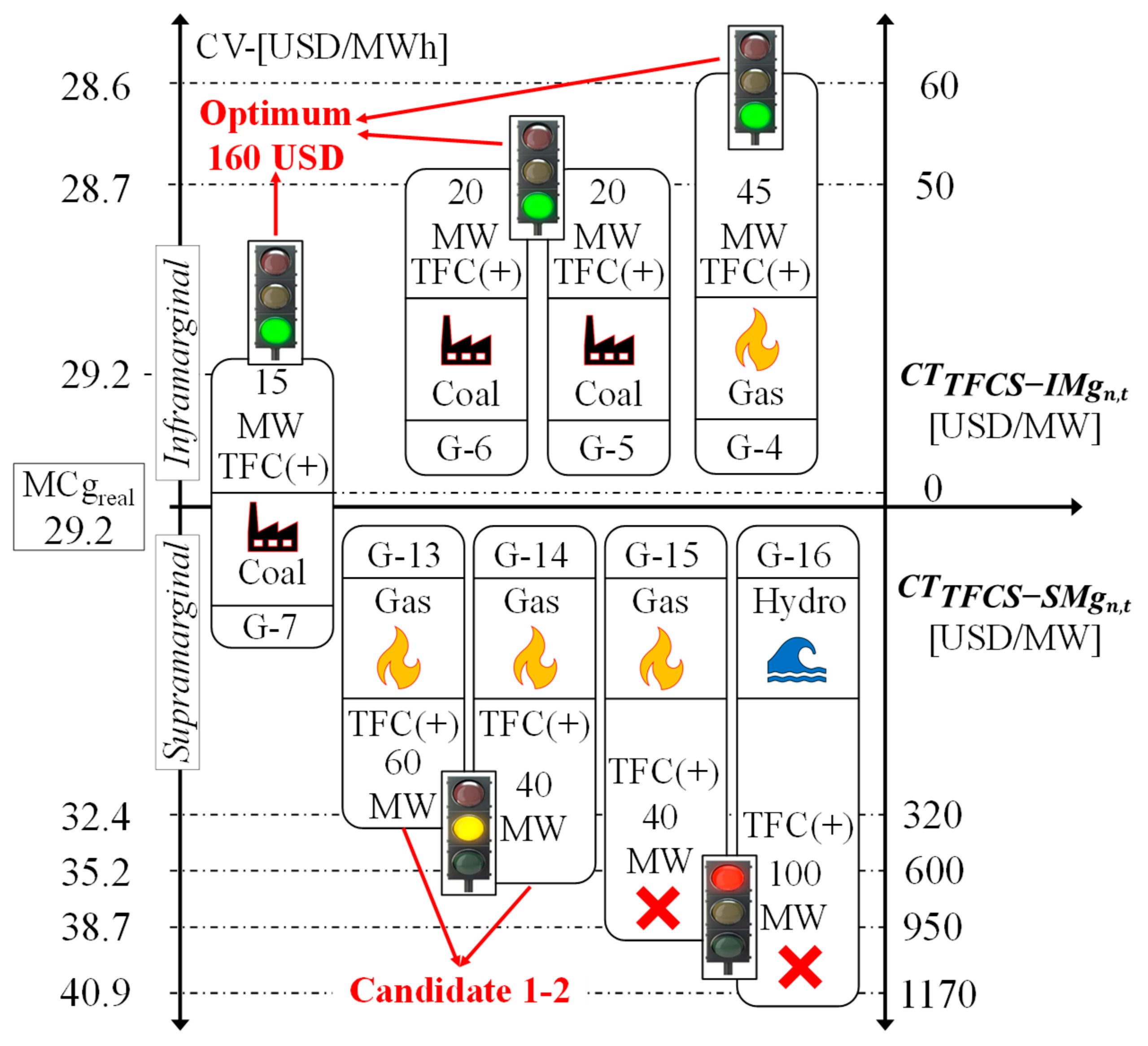
To supply the missing 100 MW reserve of the G-18 plant, the candidate IMg plants to replace the TFC(+) are the G-7, G-6, G-5 and G-4 plants with a total cost of

{T C}_{(7,6, 5,4), 1}^{C S F, u p - I M g}

= 160 USD. However, the renewable power plants G-3, G-2, and G-1 have variable costs of 0 USD/MWh and 100% TFC(+) reserve capacity. However, unfortunately, the cost of power reserve reallocations is higher than the rest of the conventional power plants, reaching a value of

{T C}_{(3,2, 1), 1}^{C S F, u p - I M g}

= 2920 USD for each renewable power plant. Then, the system operator considers the calculation obtained for the Inframarginal power plants as a reallocation alternative before being executed in real-time. Thus:

G-7, G-6, G-5 and G-4 power plants can perform TFC(+) of 100 MW to replace the G-18 power plant.
Total cost of the reserve to be replaced: ${T C}_{(7,6, 5,4), 1}^{C S F, u p - I M g}$ = 160 USD.

4.3.4. Methodology with supramarginal power plants to calculate the cost of increasing the generation in TFC

SMg candidate plants from Table 1 are used to deliver the missing 100 MW reserve of the G-18 plant. The selected plants must evaluate the total cost of raising generation to deliver the TFC(+) reserve capacity. Then the candidate plants, according to their available reserve capacity, are G-13, G-14, G-15, and G-16 because they have the closest proximity to the actual MgC of 29.2 USD/MWh corresponding to the G-8 plant. Therefore, their calculation methodology is obtained according to Equation (5).

Plant G-13 (Gas):

{T C}_{13,1}^{T F C, u p - S M g} = (32.4 - 29.2) \cdot 100 \cdot 1 = 320 U S D

It has a maximum margin of

C T F (+) = 60 M W

Plant G-14 (Gas):

{T C}_{14,1}^{T F C, u p - S M g} = (35.2 - 29.2) \cdot 100 \cdot 1 = 600 U S D

. It has a maximum margin of

C T F (+) = 40 M W

Plant G-15 (Gas):

{T C}_{15,1}^{T F C, u p - S M g} = (38.7 - 29.2) \cdot 100 \cdot 1 = 950 U S D

. It has a maximum margin of

C T F (+) = 40 M W

Plant G-16 (Hydro):

{T C}_{16,1}^{T F C, u p - S M g} = (40.9 - 29.2) \cdot 100 \cdot 1 = 1170 U S D

. It has a maximum margin of

C T F (+) = 100 M W

The results indicate that the optimum for power reserve reallocation corresponds to plants G-13 and G-14 which have a maximum TFC(+) capacity of 60 and 40 MW, respectively, with a reserve cost per plant of

C T_{13,1}^{C T F, u p - S M g}

=320 USD and

C T_{14,1}^{C T F, u p - S M g}

=600 USD. Then, the system operator considers the calculation obtained for the Supramarginal plants as a reallocation alternative before being executed in real-time. That is:

The G-13 plant can perform 60 MW TFC(+) in replacement of the G-18 plant.
The G-14 power plant can perform TFC(+) of 40 MW to replace the G-18 power plant.
Total cost of the reserve to be replaced ${T C}_{13,1}^{C T F, u p - S M g} + {T C}_{14,1}^{C T F, u p - S M g} = 920 U S D$ .

4.3.5. Discussion and analysis of the calculation methods and the result of the reallocation of reserve for TFC

The Economic Merit List and Technical Minimum methods can satisfy the missing reserves for reallocating the 100 MW tertiary frequency control of the G-18 plant. However, the selected plants from both inefficient methods fail to compete with the proposed methodology because the results of the reserve costs range from 60 to 2,920 USD/MW for the Merit List Method (LME) and the Technical Minimum Method (TM) the reserve cost ranges from 1,170 to 4,780 USD/MW.

Therefore, the proposed economic optimization model suits real-time power reserve reallocations for tertiary frequency control. From the results obtained, the candidate plants with spinning and cold reserves are identified. The main difference of this ancillary service is the duration time, which must sustain the required or reallocated power reserve of less than or equal to one hour. This implies that the reserve reallocation is with the minimum adjustment error by the system operator as it is a manual action mechanism. The execution of an undesired manual control action of tertiary reserves immediately causes an increase in the cost of operation in unnecessary time due to the inefficient dispatch of plants that operate at the technical minimum and out of price.

Mathematically, the results of the real-time economic model methodology allow minimizing the total cost

{T C}_{t}^{C T F, u p}

of power reserve reallocations of the set of candidate power plants of type SMg and IMg, as described in Equation (4). As the real-time marginal cost MgC shifts, the cost minimization calculation of power reserve reallocations cost should be modified with the selection of new candidate power plants SMg and IMg respectively. Table 4 and Figure 8 detail all the results of the reserve calculations for reallocating the 100 MW of the G-18 power plant.

5. Conclusion and future work on the real-time power reserve reallocation model

In this work, the main advances and contributions were discussed, identifying advantages, disadvantages, and what remains to be developed in this market in terms of bids and auctions of generation resources for frequency control, identifying the economic mechanisms for reallocations of power reserves in real-time and the structure of the allocation of power reserves in a conventional generation market of monopolistic character. The development of this real-time market model for ancillary services uses an economic mechanism that allows remunerating and making profitable the generation plants linked to the quality of service and the technical operation of an electric system in stability phenomena through the adequate use of frequency control with dispatches and retirements of plants capable of delivering the necessary power reserves to guarantee the security of the system.

5.1. Pioneering real-time economic model for reserve reallocation in the ancillary services market

The real-time reserve reallocation model is economically reliable and generates immediate flexibility to the system operator’s decisions, overlapping the traditional methods of the economic merit list, the technical minimum method, and the auctions and static bids methodologies, which allows to meet the reserve quantities, but with an overpricing of plants that divert the marginal costs and operating costs concerning the energy market. This real-time reallocation model is a novelty for the ancillary services market. It reduces the operating costs of reserves by more than 60% concerning non-candidate plants. It minimizes marginal cost shifts of 10 to 40% concerning the demand trend and randomly unjustified dispatches from the economic merit list. In addition, the real-time reserve reallocation model avoids the misuse of tertiary frequency control to forcibly stagnate the marginal cost of the system, covering the demand unnecessarily with dispatches from plants destined to deliver spinning reserve, non-spinning reserve, and replacement reserve that are exclusively for emergency purposes.

5.2. The validation of the model is consolidated with the analysis and discussion of the results obtained

Real-time power reserve reallocations depend on system marginal costs, and these cause the opportunity cost for renewable power plants not to be selected candidates in the short term to replace the ancillary services of the conventional generation that is monopolistically in the market due to system inertia constraints. Therefore, from the actual case studies, the model validation can optimally respond to power reserve reallocations for secondary frequency control with the use of inframarginal and supramarginal candidate plants with reserve costs ranging from 0 to 45 USD/MW as opposed to renewable plant reserve costs ranging from 90 to 817 USD/MW. In contrast, power reserve reallocations for tertiary frequency control avoid cost overruns ranging from 60 to 1,170 USD/MW. However, this work can identify the available solar and wind generation resources to actively participate in this market, with reserve capacities ranging from 70 to 100 MW for secondary frequency control and reserves from 1,000 to 1,900 MW for tertiary frequency control. As the ramp-up of renewable solar and wind generation becomes established in the market, its development will allow it to displace conventional generation in the power market, and there will be an absolute model of ancillary services for frequency control with 100% renewable generation.

5.3. Opportunities for improvement and future work on the real-time frequency control reserve reallocation model

The complex action to ensure system security is using power reserves for real-time frequency control. However, this security condition is directly related to the energy market that optimally utilizes power plant start-ups/shutdowns to reduce marginal and operating costs. This proposed model solves a large part of this problem of reallocating power reserves at minimum cost. However, the opportunity costs of the plants for the reallocation of reserves are subject to conventional generation through a monopolistic structure and the negligent use of the system’s inertia that conditions the plants out of economic order operating at the technical minimum. The model proposed in this situation does not allow the selection of these plants since they operate far from marginal cost and are not cataloged as Supramarginal and Inframarginal candidate plants. However, there is a forced reallocation of power reserves to justify the excess of plants in technical minimum that disagree with the proposed model. Therefore, it is important to define as future work a model that can monitor and avoid monopolistic actions with the use of unjustified plants in both markets and a real-time economic model for plants with reactive power reserve capacities to optimize the costs of modifying the P-Q curves in a dynamic state of the dispatches of plants that maintain voltage control in real-time.

Author Contributions

Conceptualization, K.B.; methodology, K.B.; validation, K.B.; formal analysis, K.B.; investigation, K.B.; writing—original draft preparation, K.B.; writing—review and editing, K.B., J.L., D.W.; visualization, K.B.; supervision, D.W. All authors have read and agreed to the published version of the manuscript.

Acknowledgments

The authors acknowledge the support and funding from Conicyt-Fondecyt 1221943 and Conicyt-FONDAP 1522A0006 (SERC Chile). Acknowledgments are extended to the Real-Time Dispatch and Control Center (CDC) of the National Electric Coordinator of Chile for the transparent information provided to develop this article.

Conflicts of Interest

The authors declare no conflict of interest.

References

Planificación y Desarrollo, “Estudio de Operación y Desarrollo del SEN sin centrales a carbón,” Coordinador Eléctrico Nacional, Santiago, 2019. Available online: https://www.coordinador.cl/.
Mapa del sector energético, “Mapa Normativo del Sector Energético Chileno,” Ministerio de Energía, Santiago, 2021. Available online: https://energia.gob.cl/.Available in: https://www.coordinador.cl/.
D. Fernández-Muñoz, J. Pérez-Díaz, I. Guisández, M. Chazarra and A. Fernández-Espina, “Fast frequency control ancillary services: An international review,” Renewable and Sustainable Energy Reviews, vol. 120, Mar. 2020.
Kumar, T.B.; Singh, A. Ancillary services in the Indian power sector – A look at recent developments and prospects. Energy Policy 2021, 149, 112020. [Google Scholar] [CrossRef]
Balzer, K.; Watts, D. Primary Frequency Control in an Ancillary Services Market in Real Time and its Relationship with Solar-Wind Generation. IEEE Lat. Am. Trans. 2021, 20, 553–561. [Google Scholar] [CrossRef]
Rancilio, G.; Rossi, A.; Falabretti, D.; Galliani, A.; Merlo, M. Ancillary services markets in europe: Evolution and regulatory trade-offs. Renew. Sustain. Energy Rev. 2022, 154, 111850. [Google Scholar] [CrossRef]
Frade, P.M.; Osório, G.J.; Santana, J.J.; Catalão, J.P. Regional coordination in ancillary services: An innovative study for secondary control in the Iberian electrical system. Int. J. Electr. Power Energy Syst. 2019, 109, 513–525. [Google Scholar] [CrossRef]
Hermans, M.; Bruninx, K.; Bergh, K.V.D.; Poncelet, K.; Delarue, E. On the temporal granularity of joint energy-reserve markets in a high-RES system. Appl. Energy 2021, 297, 117172. [Google Scholar] [CrossRef]
Frade, P.; Santana, J.; Shafie-Khah, M.; Catalão, J. Impact of tertiary reserve sharing in Portugal. Util. Policy 2018, 55, 167–177. [Google Scholar] [CrossRef]
Frade, P.; Shafie-Khah, M.; Santana, J.; Catalão, J. Cooperation in ancillary services: Portuguese strategic perspective on replacement reserves. Energy Strat. Rev. 2019, 23, 142–151. [Google Scholar] [CrossRef]
Prakash, A.; Bruce, A.; MacGill, I. Insights on designing effective and efficient frequency control arrangements from the Australian National Electricity Market. Renew. Sustain. Energy Rev. 2022, 161, 112303. [Google Scholar] [CrossRef]
De Zotti, G.; Pourmousavi, S.A.; Madsen, H.; Poulsen, N.K. Ancillary Services 4.0: A Top-to-Bottom Control-Based Approach for Solving Ancillary Services Problems in Smart Grids. IEEE Access 2018, 6, 11694–11706. [Google Scholar] [CrossRef]
De Zotti, G.; Pourmousavi, S.A.; Morales, J.M.; Madsen, H.; Poulsen, N.K. A Control-Based Method to Meet TSO and DSO Ancillary Services Needs by Flexible End-Users. IEEE Trans. Power Syst. 2020, 35, 1868–1880. [Google Scholar] [CrossRef]
Rayati, M.; Sheikhi, A.; Ranjbar, A.M. Optimal Contract Design for Purchasing From Frequency Regulation Service Providers With Private Information. IEEE Trans. Power Syst. 2019, 34, 2445–2448. [Google Scholar] [CrossRef]
Sun, K.; Xiao, H.; Liu, Y. Optimized allocation method of the VSC-MTDC system for frequency regulation reserves considering ancillary service cost. CSEE J. Power Energy Syst. 2022, 8, 53–63. [Google Scholar]
Du, P.; Mago, N.V.; Li, W.; Sharma, S.; Hu, Q.; Ding, T. New Ancillary Service Market for ERCOT. IEEE Access 2020, 8, 178391–178401. [Google Scholar] [CrossRef]
Jie, B.; Tsuji, T.; Uchida, K. Secondary Tertiary Balancing Power Generations Integration Feasibility Analysis Based on AGC30 Model with PV Penetration. European Energy Market (EEM) 2019. [Google Scholar] [CrossRef]
Liu, L.; Hu, Z.; Duan, X.; Pathak, N. Data-Driven Distributionally Robust Optimization for Real-Time Economic Dispatch Considering Secondary Frequency Regulation Cost. IEEE Trans. Power Syst. 2021, 36, 4172–4184. [Google Scholar] [CrossRef]
Frew, B.; Brinkman, G.; Denholm, P.; Narwade, V.; Stephen, G.; Bloom, A.; Lau, J. Impact of operating reserve rules on electricity prices with high penetrations of renewable energy. Energy Policy 2021, 156, 112443. [Google Scholar] [CrossRef]
G. Glismann, “Ancillary Services Acquisition Model: Considering market interactions in policy design,” Applied Energy, vol. 304, Dec. 2021.
Gonzalez-Garrido, A.; Saez-De-Ibarra, A.; Gaztanaga, H.; Milo, A.; Eguia, P. Annual Optimized Bidding and Operation Strategy in Energy and Secondary Reserve Markets for Solar Plants With Storage Systems. IEEE Trans. Power Syst. 2019, 34, 5115–5124. [Google Scholar] [CrossRef]
Attya, A.B.T.; Dominguez-Garcia, J.L. A Novel Method to Valorize Frequency Support Procurement by Wind Power Plants. IEEE Trans. Sustain. Energy 2020, 11, 239–249. [Google Scholar] [CrossRef]
Zhang, G.; Ela, E.; Wang, Q. Market Scheduling and Pricing for Primary and Secondary Frequency Reserve. IEEE Trans. Power Syst. 2019, 34, 2914–2924. [Google Scholar] [CrossRef]
Operación, “Programa Histórico de Operación,” Coordinador Eléctrico Nacional, Santiago, 2020. Available online: https://www.coordinador.cl/operacion/documentos/programas-de-operacion/.

Figure 1. Solar and wind reserve capacity for SFC and TFC.

Figure 2. Duck Curve projecting solar generation penetration per year in the National Electric System of Chile.

Figure 3. Symmetric and asymmetric power reserves of the SFC(±) and TFC(±).

Figure 4. SFC(+) and TFC(+) activation and delivery time at Δ(f) ±0.2-0.7 Hz.

Figure 5. Ancillary service model methodology for real-time SFC(±)/TFC(±).

Figure 6. Results of reserve reallocations for SFC(+)/Up.

Figure 7. Methodology for activating power reserves of the TFC(±) Up/Down.

Figure 8. Real-time power reserve reallocation for TFC(+) /Raise assigned to IMg G7, G6, G5 and G4 plants.

Table 1. List of economic merit and priority of TFC/down.

Gx-n	SFC(±) [MW]	TFC(±) [MW]	Type	CMg [USD/MWh]	TFC(+) Ranking	TFC(-) [USD/MW]
G-1	100	140	Solar	0	-	43.4
G-2	90	90	Solar	0	-	43.4
G-3	60	80	Wind	0	-	43.4
G-4	28	45	Gas	28.6	-	49.0
G-5	14	20	Coal	28.7	-	-
G-6	14	20	Coal	28.7	-	-
G-7	35	15	Coal	29.2	-	-
G-8	8	15	Coal	29.2	-	-
G-9	8	0	Coal	29.8	-	-
G-10	30	0	Coal	30.2	-	-
G-11	8	0	Coal	31.4	-	-
G-12	8	0	Coal	31.7	-	-
G-13	35	60	Gas	32.4	-	-
G-14	30	40	Gas	35.2	-	41.4
G-15	30	40	Gas	38.7	-	41.6
G-16	100	100	Hydro	40.9	1°	-
G-17	5	20	Coal	44.5	-	-
G-18	100	100	Hydro	47.2	2°	-
G-19	40	40	Gas	77.0	3°	-

Table 2. Methods for resolving power reserve reallocations.

Method	Symb.	State	Marginal Cost	Operation Cost
Economic merit list	EML	Inefficient	High	High
Technical minimum	TM	Inefficient	Down	High
Inframarginal Methodology	IMg	Proposal	Optimum	Optimum
Supramarginal Methodology	SMg	Proposal	Optimum	Optimum

Table 3. Results of the reallocation of reserves for SFC(+).

Plant	Type	Method	${T C}_{t}^{C S F}$ [USD]	SFC(+)[MW]	ReallocationSFC(+)
G-1	Solar	LME	817	28	Non-optimal
G-2	Solar	LME	817	28	Non-optimal
G-3	Wind	LME	817	28	Non-optimal
G-4	Gas	LME	817	28	No reserve
G-5	Coal	IMg	14	14	Candidate 1
G-6	Coal	IMg	14	14	Candidate 2
G-7	Coal	IMg	0	28	Optimal
G-9	Coal	SMg	17	8	Candidate 3
G-10	Coal	SMg	28	20	Candidate 4
G-11	Coal	SMg	62	8	Non-optimal
G-12	Coal	SMg	70	8	Non-optimal
G-13	Gas	SMg	90	35	Non-optimal
G-16	Hydro	MT	338	28	Non-optimal
G-17	Coal	MT	428	5	Non-optimal
G-18	Hydro	MT	504	28	Non-optimal
G-19	Gas	MT	1.338	28	Non-optimal

Table 4. Results of the reallocation of reserves for TFC(+).

Plant	Type	Method	TC_TFCS [USD]	TFC(+) [MW]	Reallocation TFC(+)
G-1	Solar	LME	2,920	14	Non-optimal
G-2	Solar	LME	2,920	14	Non-optimal
G-3	Wind	LME	2,920	14	Non-optimal
G-4	Gas	LME	60	45	Optimum
G-5	Coal	IMg	50	20	Optimum
G-6	Coal	IMg	50	20	Optimum
G-7	Coal	IMg	0	15	Optimum
G-13	Gas	SMg	320	60	Candidate 1
G-14	Gas	SMg	600	40	Candidate 2
G-15	Gas	SMg	950	40	Non-optimal
G-16	Hydro	MT	1,170	100	Non-optimal
G-17	Coal	MT	1,530	20	Non-optimal
G-18	Hydro	MT	1,800	100	No reserve
G-19	Gas	MT	4,780	40	Non-optimal

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Economic Model of Ancillary Services in Real Time for Frequency Control

Abstract

1. Introduction of real-time complementary services for frequency control

2. State of the art of ancillary services in the use of reserves for frequency control

2.1. Bidding and auction market for frequency control power reserves

2.2. Mechanisms and economic models to reallocate power reserves in real time

2.3. Model of monopolistic structure of power reserves for frequency control

2.4. Efficient real-time power reserve reallocation model

3. Theoretical framework and methodology of a real-time reserve allocation model for frequency control

3.1. Secondary frequency control symmetrical reserves

3.2. Asymmetrical tertiary frequency control reserves

3.3. Methodology of a real-time reserve allocation model for frequency control

3.4. Mathematical method for reallocation secondary frequency control reserves

3.5. Mathematical method for reallocation tertiary frequency control reserves

4. Simulation of real scenarios and discussion of the results

4.1. Gas depletion in combined cycle plants implies reallocation reserves to increase generation in secondary frequency control

4.1.1. Economic merit list method for calculating the cost of raising the generation in SFC

4.1.2. Technical minimum method to calculate the cost of raising generation in SFC

4.1.3. Methodology with inframarginal plants to calculate the cost of increasing generation in SFC

4.1.4. Methodology with supramarginal plants to calculate the cost of increasing generation in SFC

4.1.5. Discussion and analysis of the calculation methods and the results of the reallocation of reserves for SFC

4.2. Severe frequency variations involve activating the power reserves of the TFC

4.2.1. Method for activating power reserves to raise TFC generation

4.2.2. Method to activate power reserves to decrease generation in TFC

4.2.3. Discussion and analysis of the results of the activation of reserves for TFC

4.3. Bidding and auction market for frequency control power reserves

4.3.1. Economic merit list method for calculating the cost of raising generation in TFC

4.3.2. Technical minimum method to calculate the cost of raising the generation in TFC

4.3.3. Methodology with inframarginal plants to calculate the cost of increasing generation in TFC

4.3.4. Methodology with supramarginal power plants to calculate the cost of increasing the generation in TFC

4.3.5. Discussion and analysis of the calculation methods and the result of the reallocation of reserve for TFC

5. Conclusion and future work on the real-time power reserve reallocation model

5.1. Pioneering real-time economic model for reserve reallocation in the ancillary services market

5.2. The validation of the model is consolidated with the analysis and discussion of the results obtained

5.3. Opportunities for improvement and future work on the real-time frequency control reserve reallocation model

Author Contributions

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe