Prerpints.org logo
Preprint
Article

Machine Learning Dynamic Ensemble Methods for Solar Irradiance and Wind Speed Predictions

Altmetrics

Downloads

143

Views

79

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

07 August 2023

Posted:

09 August 2023

You are already at the latest version

Alerts
Abstract
In this paper, solar irradiance and wind speed forecasts were performed considering time horizons ranging from 10 min to 60 min, under a 10 min time-step. Global horizontal irradiance (GHI) and wind speed were computed using four forecasting models (Random Forest, k-Nearest Neighbours, Support Vector Regression, and Elastic Net) to compare their performance against two alternative dynamic ensemble methods (windowing and arbitrating). Forecasting models and dynamic forecasting ensembles were implemented in Python for performance evaluation. The performance comparison between the prediction models and the dynamic ensemble methods was carried out by evaluating the RMSE, MAE, R² and MAPE, to evaluate whether the dynamic ensemble forecasting method obtained greater. According to the results obtained windowing dynamic ensemble method was the most efficient among the tested. For the wind speed data, by varying its parameter λ (from 1 to 100), a variable performance profile was obtained, where from λ =1 to λ = 74, windowing proved to be the most efficient, reaching maximum efficiency for λ = 19. Windowing was the best method for the GHI analysis, reaching its best performance for λ = 1. The efficiency gain using windowing was 0.56% when using the wind speed model and 1.96% for GHI.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

The Electricity generated by fossil fuel sources has been the main driver of climate change, probably over 70% of greenhouse gas emissions and over 90% of all carbon gas emissions. The alternative of decarbonizing the world’s electricity generation system is a trend focused on alert sources of renewable energy, whose generation costs are increasingly accessible [1].
A very undesired effect when it comes to electrical generation from alternative resources is the impact of intermittency generation on the electrical grid, since this generation is dependent on weather conditions, and one of the means to eliminate or reduce its uncertainties is the availability prediction of these resources [2].
The influences of atmospheric factors on the generation of electrical energy from solarand wind sources are usually the main problem in the generation of smart grids, where large-scale generation plants need to be integrated into the electrical grid, which directly affects planning, investment, and decision-making purposes. Forecast models can minimize that problematic through machine learning models [3].
The benefits of optimizing the forecast of generation from wind and solar sources using models is also an economic factor, as it gives greater security to the electricity sector through the improvement of renewable energy purchase contracts [4].
A 14-year-long data set was explored in [5], containing daily values of meteorological variables. It was used to train three artificial neural networks (ANNs) in several time horizons to predict the global solar radiation for Fortaleza, in the Brazilian Northeastern region. The accuracy of the predictions was considered excellent according to its normalized root-mean-squared error (nRMSE) values and good relative to mean absolute percentage error (MAPE) values.
The variability of mathematical prediction models has individual importance inherent to each one of the methods employed and, in this scenario, dynamic ensemble models emerge, which present potential better performance when compared to individual models, since they seek maximum optimization by considering the best of the individual models. This approach is currently very successfully used in research and industrial areas. Several dynamic ensemble methods have been developed for forecasting energy generation from renewable sources in which they use the presence of well-known forecast models such as random forest regression (RF), support vector regression (SVR), and k-nearest neighbors (kNN), which are applied to integrate optimizations for use in dynamic ensemble methods [6].
The Support Vector Machine was first developed for classification models and is largely discussed [7,8], in recent approaches [9] to develop a novel method for the maximum power point tracking of a photovoltaic panel and in [10], where it is discussed the solar radiation estimation by five different machine learning approaches.
The KNN method predicts a new sample using the K-closest samples. Recently this approach has been used in [11], where Virtual Meteorological Masts use calibrated numerical data to provide precise wind estimates during all phases of a wind energy project to reproduce optimal site-specific environmental conditions.
Most studies have focused on accurate wind power forecasting, where random fluctuations and uncertainties involved are considered. The study in [12] proposes a novel ultra-short-term probabilistic wind power forecasting using an error correction modeling by the random forest approach.
The Elastic Net is a regularized regression method that linearly combines the penalties of the LASSO and Ridge methods. In [13] the study uses forecast combinations that are obtained by applying regional data from Germany for both solar photovoltaic and wind through the Elastic Net model, with cross-validation and rolling window estimation, in the context of renewable energy forecasts.
The state-of-the-art uses dynamic ensemble methods in a meta-learning approach such as arbitrating, which combines the output of experts according to predictions of the loss they will incur, and also windowing approaches, which have parameterizations for adjusting the degree of data to be considered [14].
In [15], the global climate model (GCM) is studied to improve a near-surface wind speed (WS) simulation through 28 coupled model intercomparison using dynamical components.
In [16], a hybrid transfer learning model based on a convolutional neural network and a gated recurrent neural network is proposed to predict short-term canyon wind speed with fewer observation data. The method uses a time sliding window to extract time series from historical wind speed data and temperature data of adjacent cities as the input of the neural network.
In [17] is explored the Multi-GRU-RCN, an ensemble model to get significant information such as precipitation and solar irradiation through short-time cloud motion predictions from a cloud image. The ensemble modeling used in [18] integrates wind and solar forecasting methodologies applied to two locations with different latitudes and climatic profiles. The obtained results reduce the forecast errors and can be useful in optimizing the planning for using intermittent solar and wind resources in the electrical matrices.
A proposed new ensemble model in [19] was based on Graph Attention Network (GAT) and GraphSAGE to predict wind speed in a bi-dimensional approach using a Dutch dataset considering several time horizons, timelags, and weather influences. The results showed that the ensemble model proposed was equivalent to or outperformed all benchmarking models and had smaller error values than those found in reference literature.
Under a 5 min time-step, in [20] it was applied time horizons ranging from 5 min to 30 min in evaluating the solar irradiance short-term forecasts to Global Horizontal Irradiance (GHI) and Direct Normal Irradiance (DNI) using deep neural networks with 1-dimensional convolutional neural network (CNN-1D), long short-term memory (LSTM), and CNN-LSTM. The metrics used were the mean absolute error (MAE), mean bias error (MBE), root-mean-squared error (RMSE), relative root mean squared error (rRMSE), and coefficient of determination (R²). The best accuracy was obtained for a horizon of 10 min, improving 11.15% on this error metric compared to the persistence model.
In front of this, the main contribution of this article is to demonstrate the influence of dynamic ensemble arbitrating and windowing methods on machine learning methods traditionally used for predicting electrical generation. We also present their greater efficiency, using data of interest for energy production with input variable of wind speed and solar irradiance, used, respectively, for both wind and solar farms. We have followed this approach because of its advantage in exploring dynamic ensemble methods, since these seek the best pre-existing efficiency for generating a unique and more effective predictability model.

2. Location and data

In this paper, two data types were used to carry out the analysis, which were acquired from solarimetric and anemometric station located in Petrolina – PE. The data were collected from the SONDA network (National Organization of Environmental Data System) [21], which was a joint collaboration of several institutions and was created for the implementation of physical infrastructure and human resources, aiming at raising and improving the database of solar and wind energy resources in Brazil.
In Table 1, information on the solarimetric and anemometric station can be found, and its location on the map is shown in Figure 1.

2.1. Wind speed data

The wind speed data was obtained in m/s from a meteorological station, which has anemometric sensors at altitudes of 25 m and 50 m from the ground. The highest altitude was chosen for this study, aiming to reduce the effects of the terrain and closer to the altitudes currently in practice for wind turbines [22].

2.2. Irradiance data

The Global Horizontal Irradiance (GHI) data acquired from the solarimetric station were used in this study, and the clear-sky coefficient was considered, in order to remove dependence on air mass in the irradiance values that reach the sensors [23], through the use of the clear-sky factor (Ics) [24], using the polinomial fit model [27]. The work [25] obtained promising results from the same database using two machine learning estimation models for (GHI).
In order to obtain irradiance data independent of air mass variations, we used kt, which is defined by the ratio between the Global Horizontal Irradiance value (GHI) (I) and clear sky factor (Ics), as shown in Equation 1.
k t = I I c s

3. Methodology

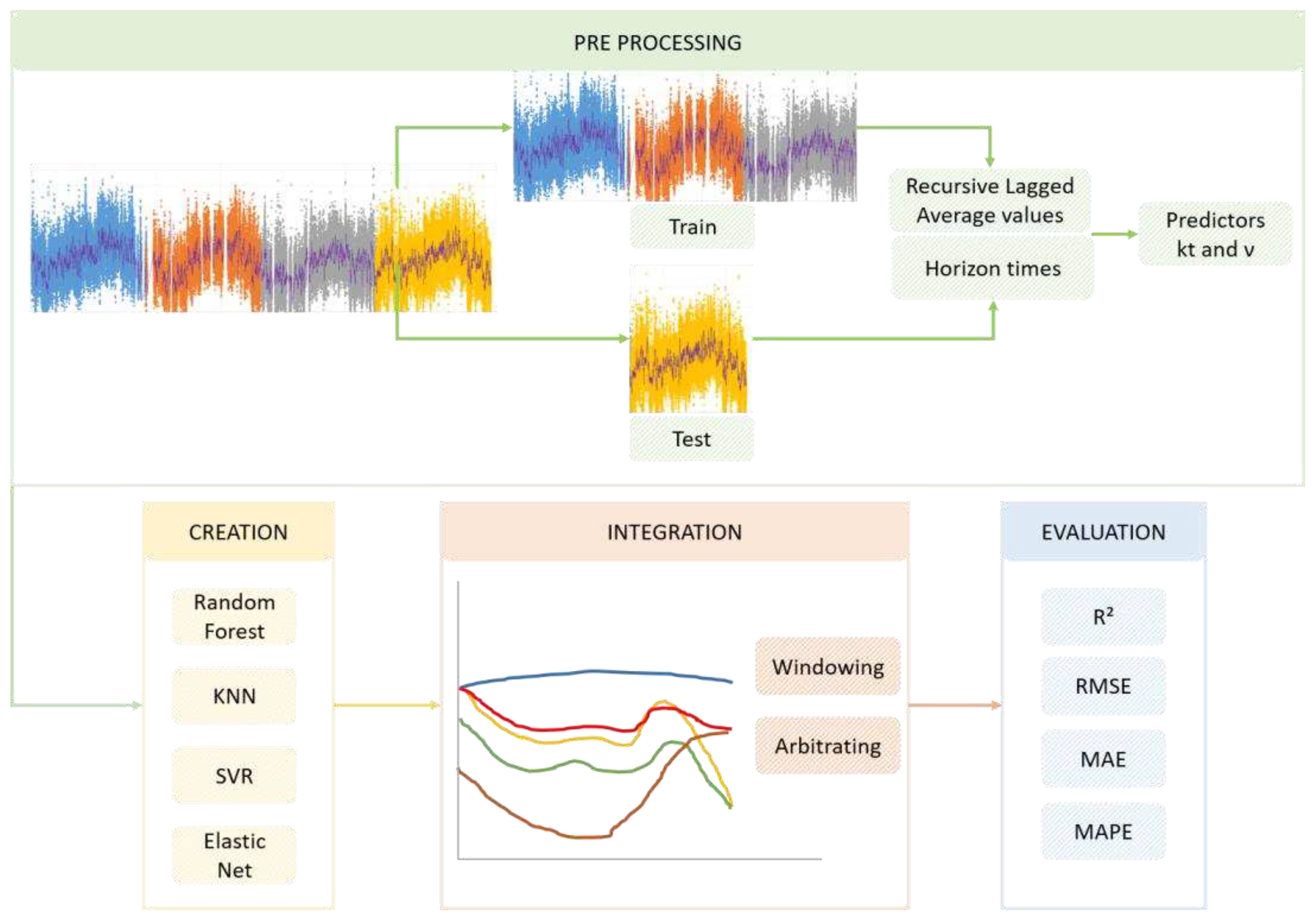
Initially, wind speed and irradiance data were acquired and the intervals for the test and training sets were determined. For wind speed data, in a measurement period from 2007 to 2010, the first three years were used as the training data set and the last year as the test set. In order to allow the evaluation of the performance of the tested forecasting models and also of dynamic ensemble methods, a computational code was developed in Python to evaluate the output values obtained by the well-known Machine Learning forecasting methods: Random Forest, k- Nearest Neighbors (kNN), Support vector Regression (SVR), and Elastic Net. For each of the methods, the best performance parameters (lower Root Mean Squared Error (RMSE)) were evaluated. Right after the stage of acquisition and determination of the optimal parameters for each of the models, the methods of dynamic ensemble windowing and arbitrating were executed, from which performance metrics values were also obtained: Coefficient of Determination (R²), Root Mean Squared Error (RMSE), Mean Absolute Error (MAE) and Mean Absolute Percentage Error (MAPE). These values were compared to evaluate the efficiency of the dynamic ensemble methods compared to other stand-alone models. It was also evaluated the variation of the lambda parameter for windowing, which is the length used for the extension of the values considered in the data forecast. The methodology used can be seen in Figure 2.
In the data pre-processing, a recursive approach of Lagged Average values for kt and ν time series was applied: this feature is given by the vector L(t) with components calculated using Equation (2).
L i ( t ) = 1 N   ∑ t ∈ ] t − i δ − T ,   t − ( i − 1 ) δ − T ] x ( t )  

3.1. Windowing method

The diversity of the models makes the forecast analysis rich and complex, since each model has strong points and other weaknesses, in the sense that from this combination, the best results can be treated and considered to obtain more accurate forecasts. To perform this combination, it is necessary to know how to estimate at which points certain specific models perform better.
Windowing [14] is a dynamic ensemble model, where weights are calculated based on the performance of each individual model, evaluated in a data window referring to immediately previous data. The size of this window is parameterized by the λ value. This means that the weights of each model are re-evaluated at each time step, and then they are classified to catalogue only the best performance results, generating a hybrid model.

3.2. Arbitrating method

Arbitrating [28] uses the metalearning method strategy to learn and predict the classifiers. In this study it regards the weights based on each model’s performance for a given time step. At each simulation instant, the most reliable model is selected and included in the prediction process.

3.3. Machine learning prediction models and dynamic ensemble method parameters

In the data training stage, GridSearch was used with 5-fold cross validation. The search parameters are shown in Table 2.

3.4. Performance Metrics Comparison Criteria

As the purpose of this work is to evaluate the performance of dynamic ensemble methods against other methods, performance metrics had to be determined to allow it. The metrics used were those of Equations 3, 4, 5 and 6.
  • Coefficient of Determination (R²)
R = 1 − ∑ i = 1 N ( y i − y i ^ ) ∑ i = 1 N ( y i − y i ¯ )
  • Root Mean Squared Error (RMSE)
R M S E = ∑ i = 1 N ( y i ^ − y i )
  • Mean Absolute Error (MAE)
R M S E = 1 N ∑ i = 1 N y i ^ − y i
  • Mean absolute percentage error (MAPE)
M A P E = 1 n ∑ i = 1 n y i − y i ^ y i

4. Results and Discussion

Discussions are carried out around the results generated regarding the analysis of efficiency metrics for the machine learning methods discussed here, in an attempt to determine which method/parameters obtains the best performance in the application for wind speed and solar irradiance data.

4.1. Wind Speed Predictions

During the search for best-performance methods, the optimized parameters for each of the tested methods needed to be known. This allows the elaboration of the dynamic ensemble, which is built upon the merging of the best-performance results at each time step and for all the methods in question. The optimal parameters found for each of the time horizons are shown in Table 3.
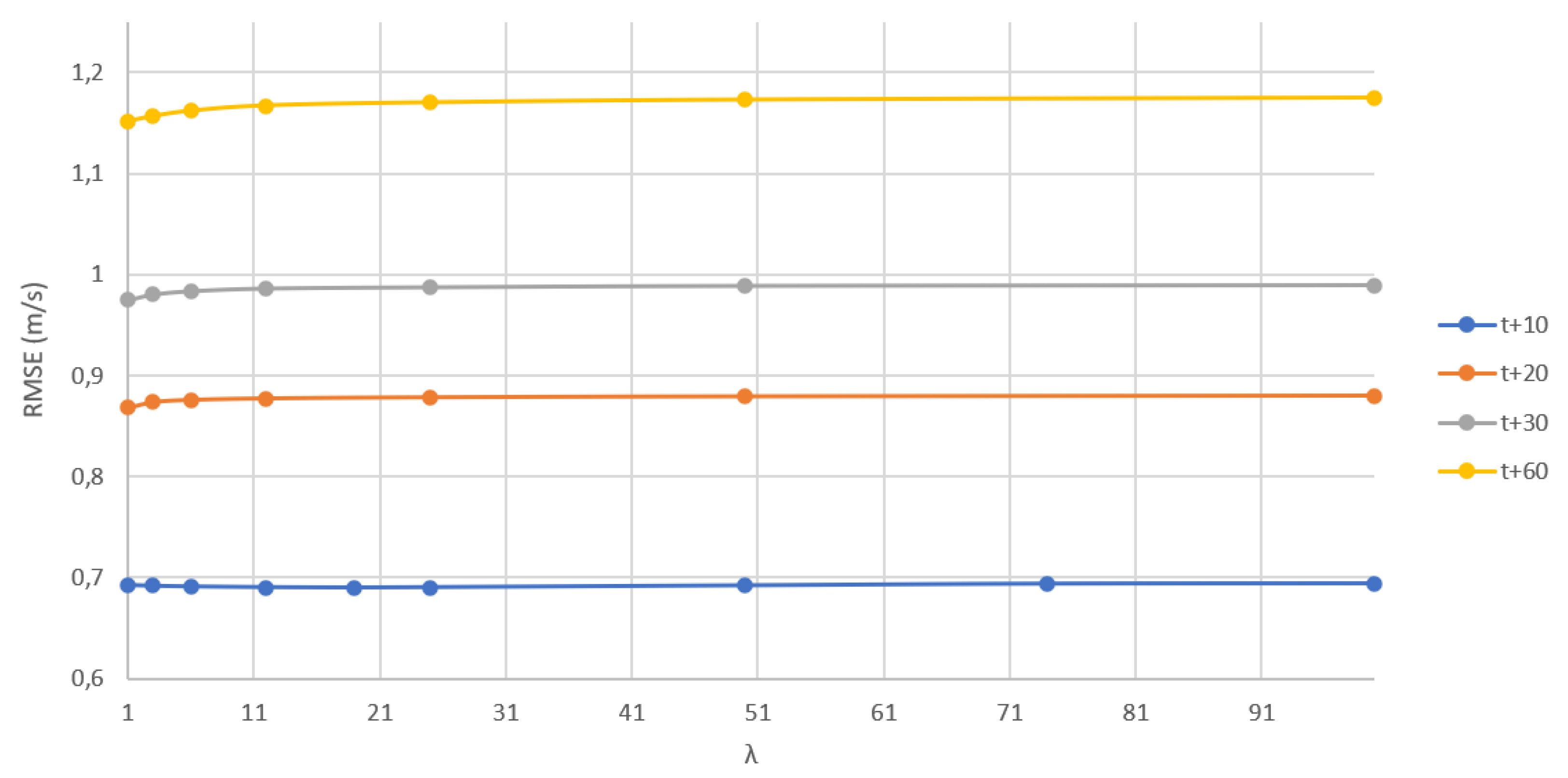
Efficiency evaluations for each of the forecasting methods were based on performance metrics evaluations for each time horizon under study (t+10, t+20, t+30 and t+60). Initially, for all time horizons, windowing proved to be the most efficient method. Then, a fine-tuning evaluation was performed based on the variation of the windowing parameter to assess its influence on performance. The predominance of better performance for windowing in all time horizons and its comparisons can be seen in Table 4 and Figure 3.
Elastic Net is a penalized linear regression model that is a combination of Ridge and Lasso regression into a single algorithm and uses best_l1_ratio as a penalty parameter during the training step, being 0 for Ridge and 1 value for Lasso regression. From Table 3, the parameter obtained the value of 1, which means that Lasso regression was used in its entirety.
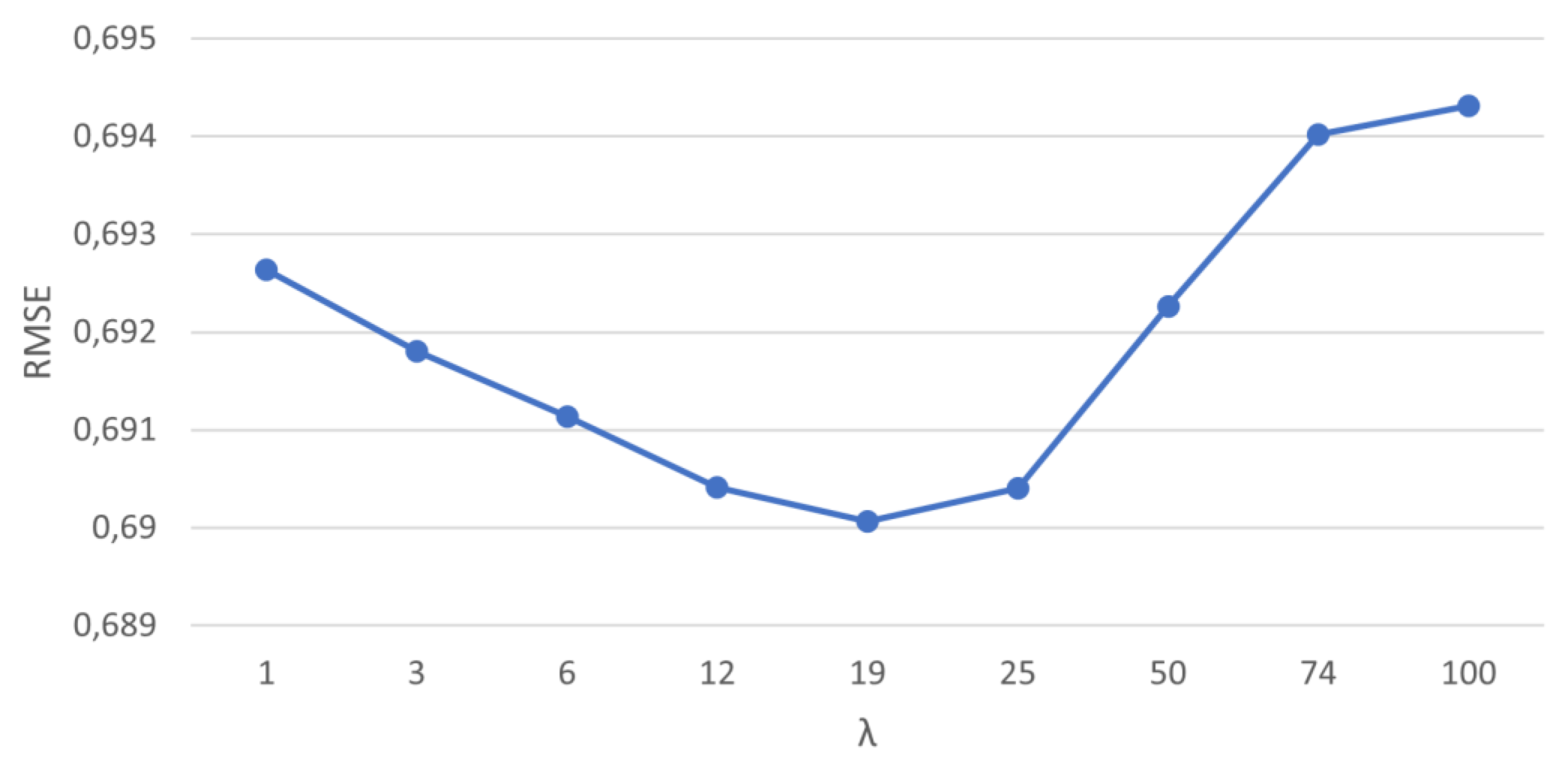
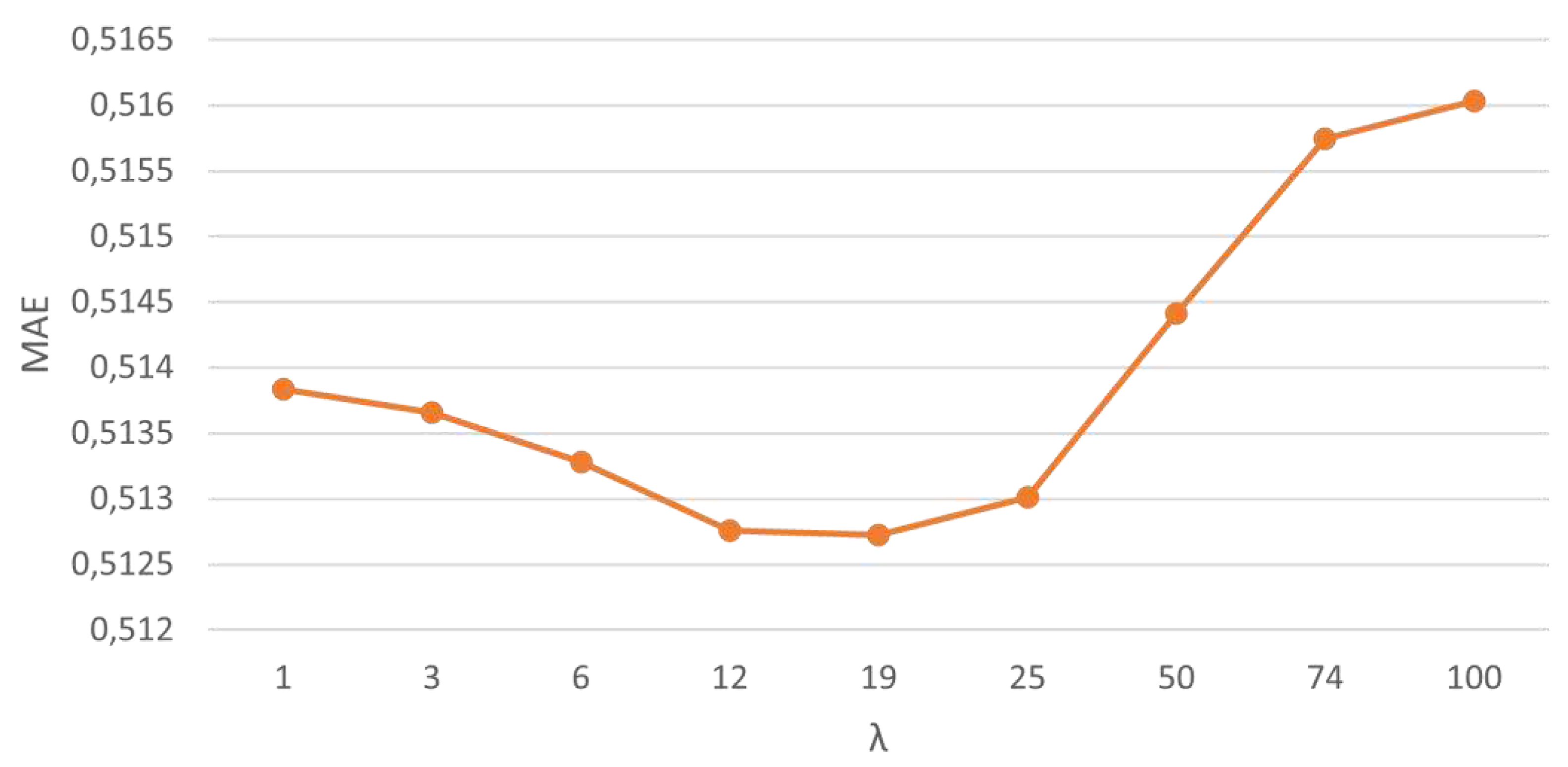
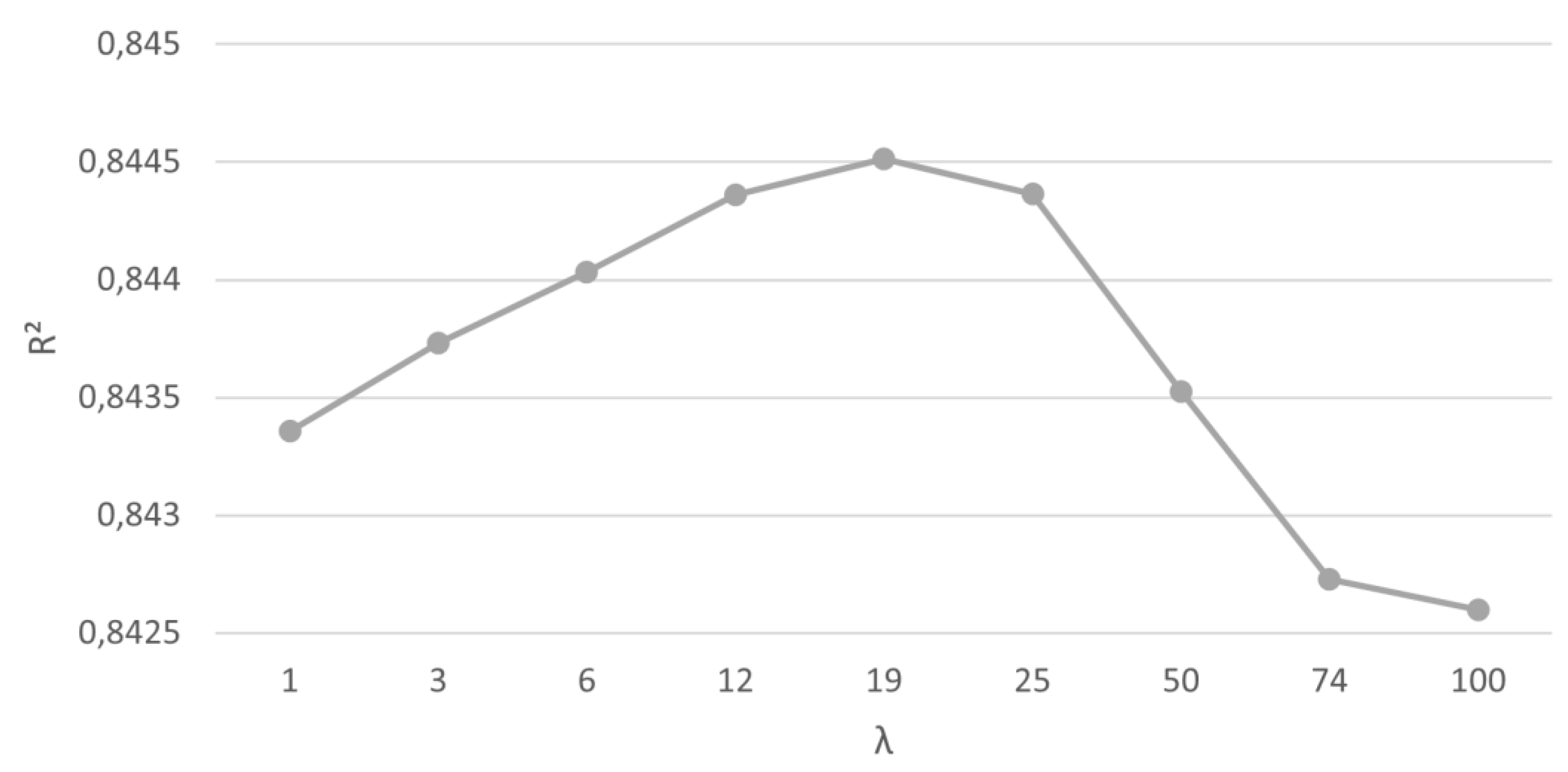
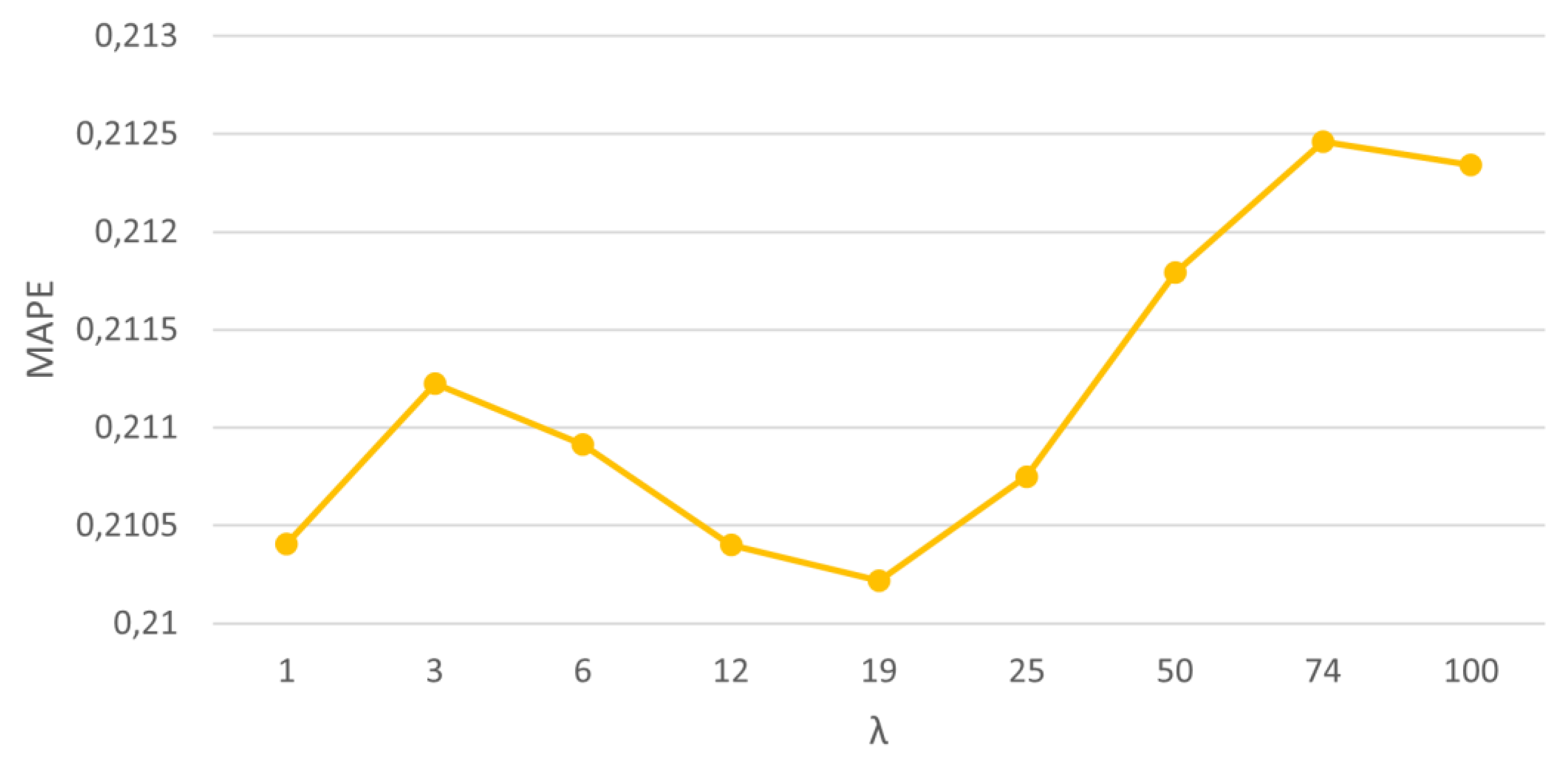
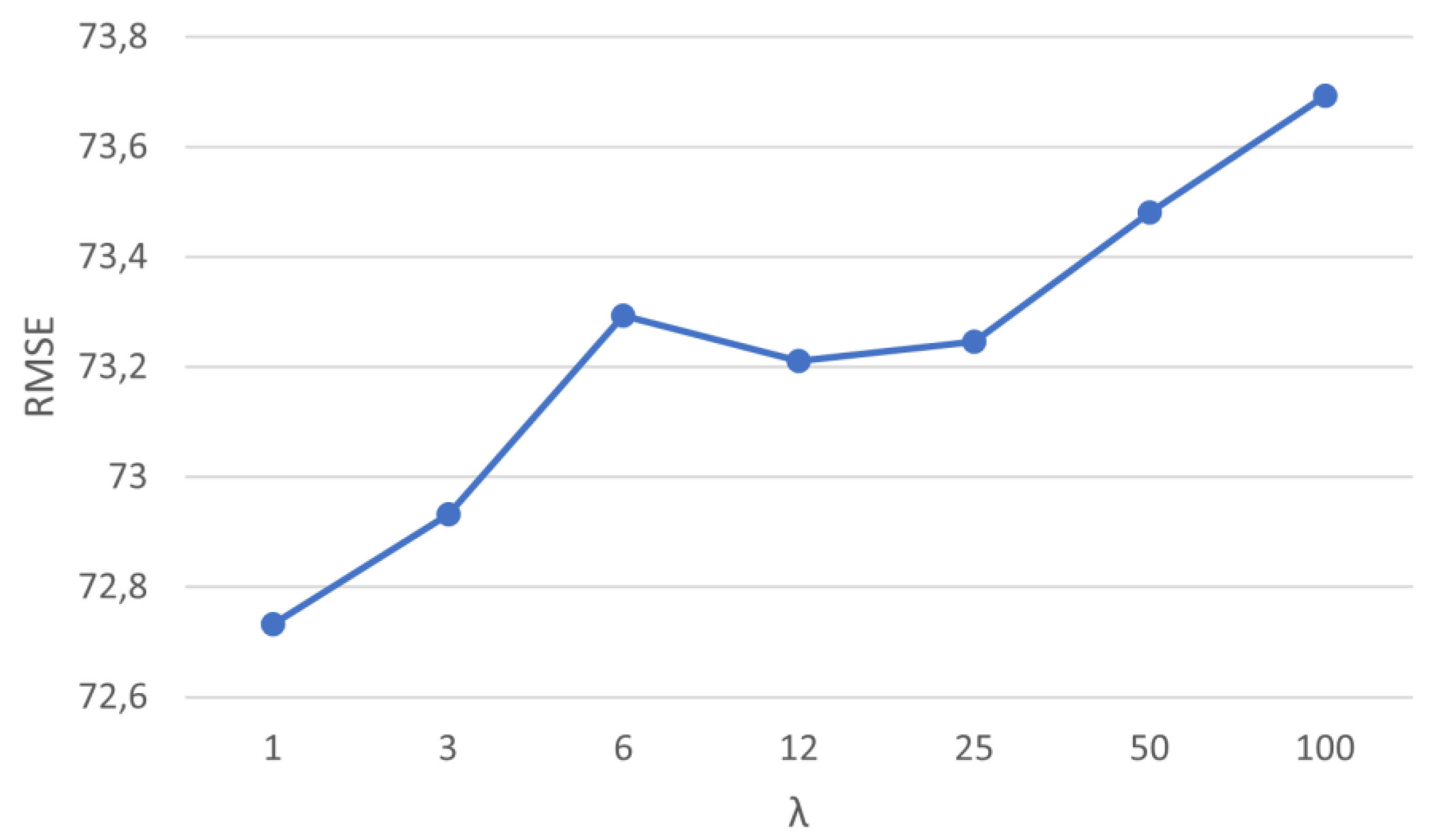
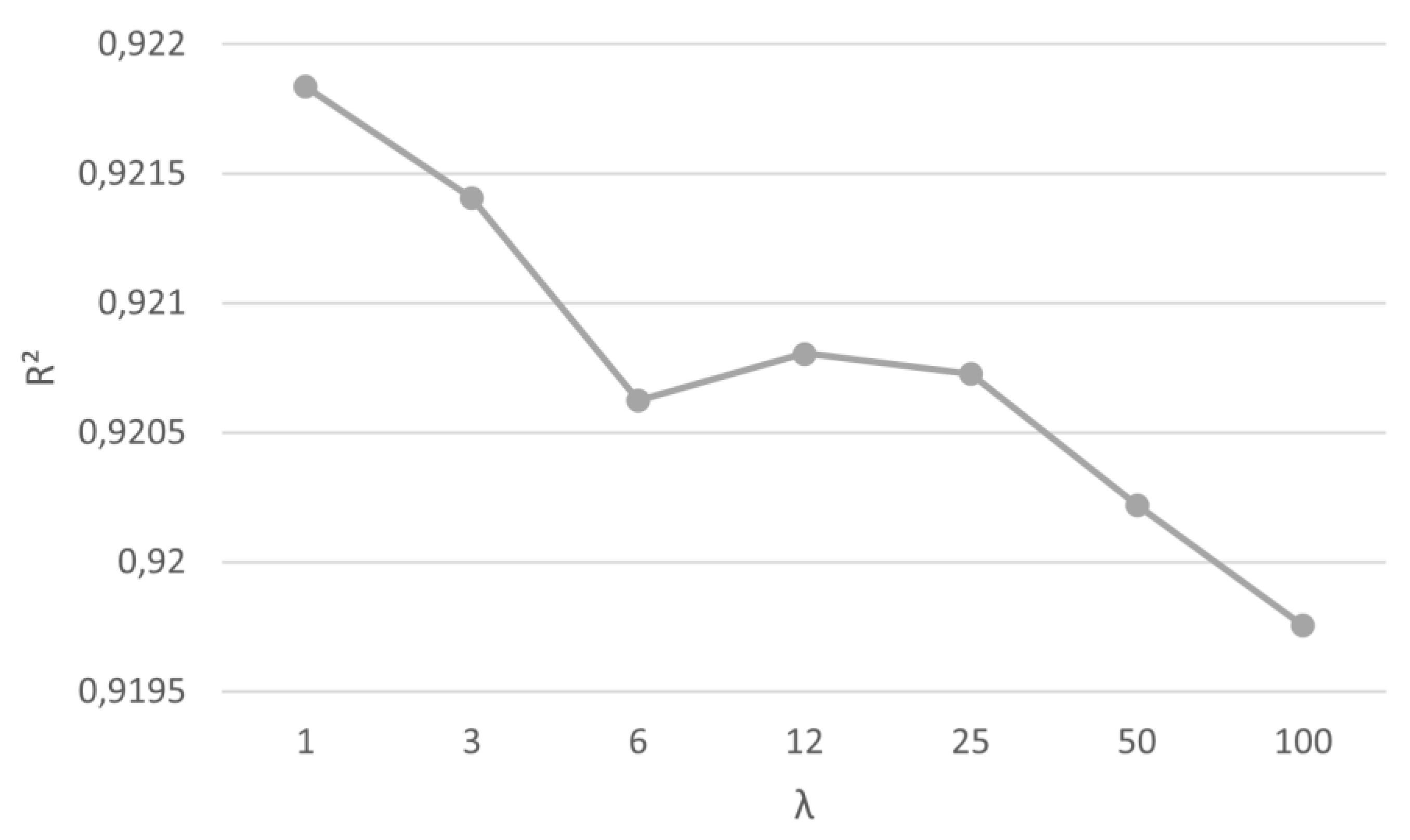
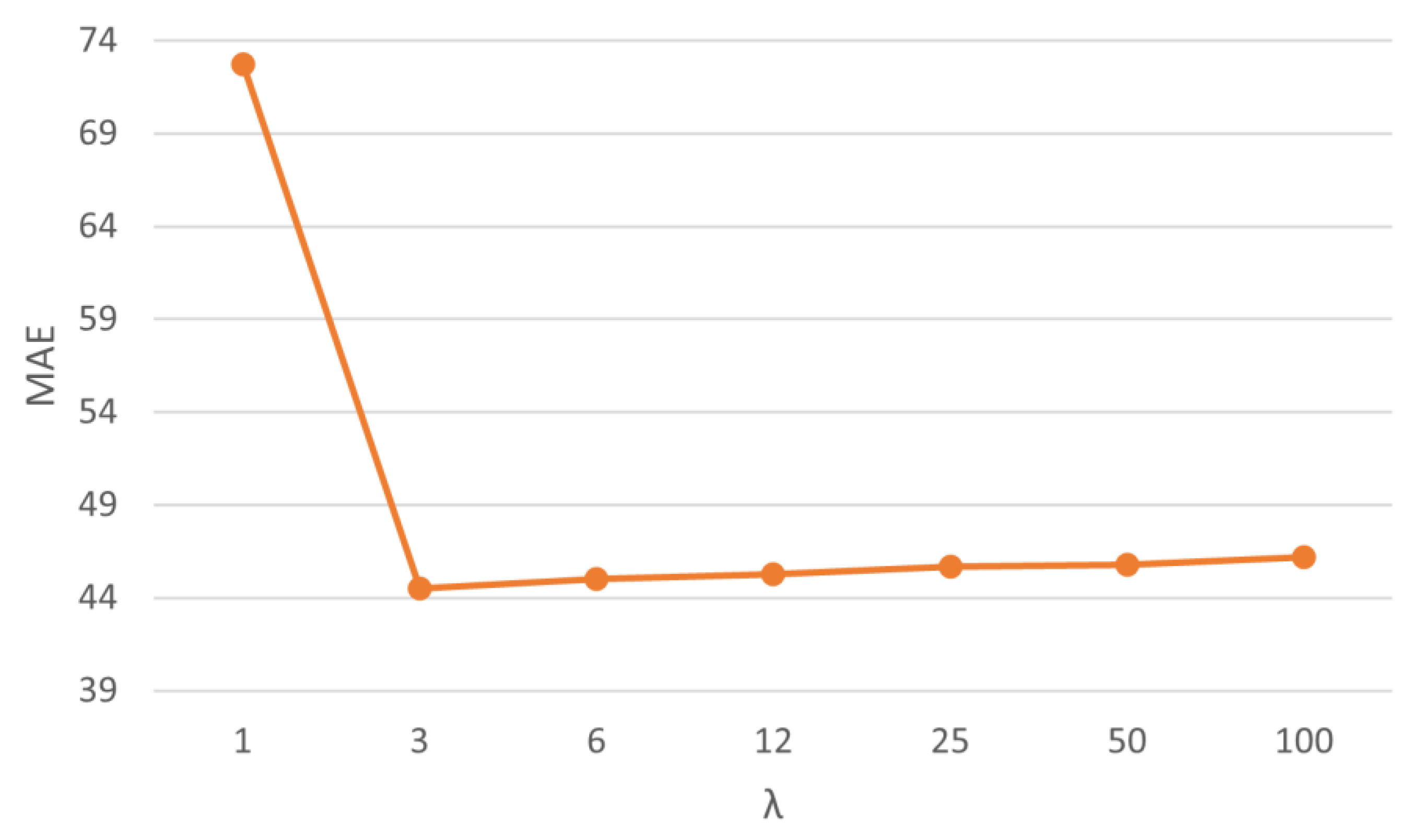
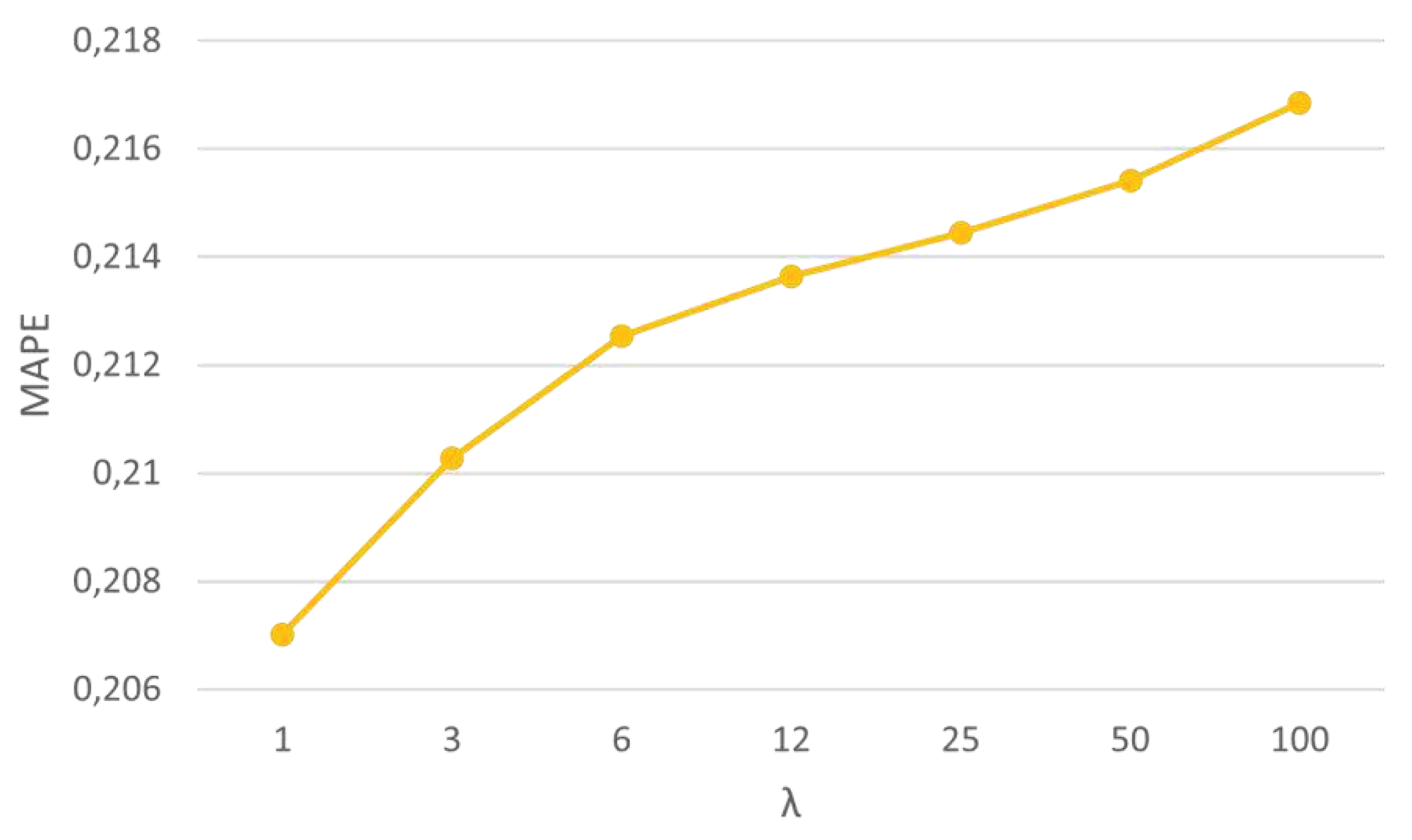
As with the evaluation carried out by the RMSE, the values of R², MAE and MAPE were also assessed. Once the best performance was found for the windowing ensemble method, an in-depth analysis was performed based on the variation of its parameter ʎ to assess the influence on its internal performance. Since the time horizon that presented the best performance was t+10, this was the focus of the analysis, as shown in Figure 4, Figure 5, Figure 6 and Figure 7. The detailed data for all the horizons is shown in Table 5, Table 6 and Table 7.
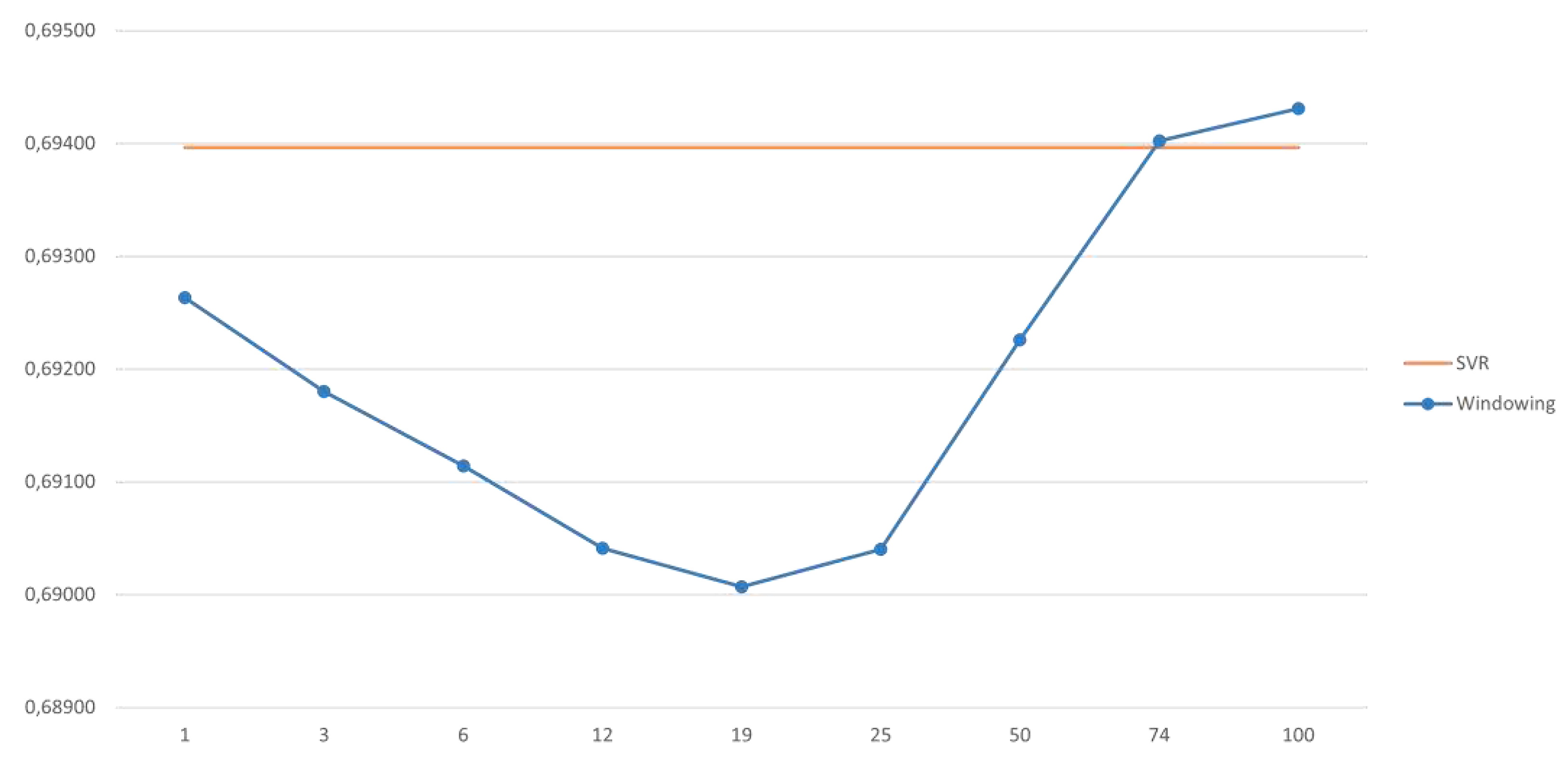
When we check the influence of the ʎ parameter on the windowing method performance, it was found that from ʎ = 74 it is no longer the most efficient method, where SVR becomes the best one, due to its lowest RMSE value. Anyway, it is important to highlight that the best performance value for the windowing method, which is the best performance overall, was found for ʎ = 19. The performance comparison between the two methods can be seen in Figure 8.

4.2. Irradiance Predictions

During the search for best-performance methods, the optimized parameters of each of these methods needed to be known to allow the elaboration of the dynamic ensemble, which is built from merging the best-performance results at each instant and for each of the methods in question. The optimal parameters for each time horizon are shown in Table 8.
Efficiency evaluation for each of the solar irradiance forecasting methods were based on performance metrics for each time horizon under study (t+10, t+20, t+30 and t+60). Again, windowing proved to be the most efficient method for all time horizons, with the best method being found for the t+10 time horizon, having the lowest RMSE value, using its parameterizations with ʎ = 50 initially. Then, fine-tuning was performed based on the variation of the windowing parameter to assess its influence on performance. The predominance of better performance for windowing in all time horizons and its comparisons can be seen in Table 9 and Figure 9.
Just like the evaluation carried out by the RMSE, the values of R², MAE, and MAPE were also analyzed. After the best performance was found for the windowing method, an in-depth analysis was performed based on the variation of its parameter ʎ to assess the influence on its internal performance. Since the time horizon that presented the best performance was t+10, this was the focus of the analysis, as shown in Figure 9, Figure 10, Figure 11 and Figure 12. The detailed data for all tested time horizons is shown in Table 10, Table 11 and Table 12.
Some authors applied Elastic Net in time-varying combinations [13], using RMSE as a performance metric. They found that, for PV forecasts, it has been reached 13.4% more precise forecasts than the simple average and for the wind forecast, it has been reached 6.1% better forecasts.
In [18] an ensemble method was studied, which used MAPE as the comparative efficiency metric for wind speed data, with a value of 9.345% and solar with 7.186%, which proved to be the most efficient.
In this study, performance improvements were obtained for the most efficient method (windowing) compared to the second most efficient for wind speed of 0,56% and, for solar irradiation, 1.86%.

4.3. Comparison with results from the literature

The performance of the windowing approach was compared with other wind forecasting models found in the literature. It is important to disclose that a direct comparison between different predictive models is not an easy task, once each applied approach has its own objectives, hyperparameters, and input data [19].
The results found in literature for wind speed forecasting are compiled and presented in Table 13, where RMSE and MAE are in m/s.
Analyzing the results for reference [19], in which wind speed was forecasted for the Netherlands using an ensemble approach merging graph theory and attention-based deep learning, we can observe that the proposed windowing ensemble model is not able to surpass the results for RMSE nor MAE for t+60 forecasting horizon. The accentuated difference between these two models can be explained because the GNN SAGE GAT model, being developed to handle graph-like data structure, excels in retrieving complex spatiotemporal relationships underlaying the dataset, drastically improving its forecasting capacity when compared with other ML and DL models alike.
In reference [29], the authors proposed a wind forecasting for a location in Sweden, with a model based on a bi-directional recurrent neural network, a hierarchical decomposition technique, and an optimisation algorithm. When compared with their results, the windowing model proposed in this paper offer improvement over the reference results for t+10 forecasting horizon by 1% and by 20% for t+60. Analysing MAE and MAPE, the windowing indicates improvement over these metrics for t+10 and t+60, increasing by 28% the MAE value for t+10, and 9% for t+60. Regarding MAPE, the improvement is 64% for t+10 and 95% for t+60.
In the work of Liu et al. [31], other deep learning-based predictive model was proposed. It used a hybrid approach composed of data area division to extract historical wind speed information, and an LSTM layer optimized by a genetic algorithm to process the temporal aspect of the dataset to forecast wind speed in Japan. Compared to this reference, the windowing model showed no improvement for wind speed forecasting. However, the windowing approach offers competitive forecasting for the assessed time windows, being in the same order of magnitude as the ones in the reference. In work [32], the authors proposed the employment of another hybrid forecasting architecture composed of CNN and LSTM deep learning models for wind speed estimation in the USA. Their results, when compared against the windowing methodology, are very similar for all forecasting horizons, showing that both windowing and CNN-LSTM offer good results for wind speed estimation for these time intervals.
In Dowell et al. [30], a statistical model for estimation of future wind speed values in the Netherlands was proposed. For the available t+60 time horizon we observe that, again, the forecasted wind speed for the reference and proposed windowing models are very similar, deeming both models as valuable tools for wind speed forecasting.
For GHI forecasting, the results found in the literature are presented in Table 14.
In work [20], the deep learning standalone model of CNN was applied to estimate future GHI values in the USA. Comparing the GHI forecasting results achieved by windowing with this reference, we observe that the proposed model was not able to provide superior forecasting performance. However, the windowing results are still competitive since both approaches were able to reach elevated coefficient of determination values for all the assessed forecasting horizons, with a slight advantage for the deep learning model.
In reference [35], the authors combined principal component analysis (PCA) with multivariate empirical model decomposition (MEMD) and gated recurrent unit (GRU) to predict GHI in India. In their methodology, the PCA extracted the most relevant features from the dataset after it was filtered by the MEMD algorithm. Lastly, the future irradiance was estimated by the deep learning model of GRU. Compared to their approach, the windowing model could not improve the GHI forecasting considering t+60 time window. Also, the reference model MEMD-PCA-GRU provided elevated R2 value of 99%, showing clearly superior performance over the proposed ensemble model.
Compared with the physical-based forecasting models proposed in [36] and [37], we can conclude that windowing can achieve similar results for time horizons of t+30 and t+60. In [36], authors used the FY-4A-Heliosat method for satellite imagery to estimate GHI in China. Although the windowing model could not improve the GHI forecasting for t+30 and t+60 time windows, the proposed model is able to return relevant results for irradiance estimation in both cases. The second physical-based model proposed in [37] was applied to estimate GHI in Finland. In their methodology, the Heliosat method is again employed, together with geostationary weather data from satellite images. Compared to their proposed approach, the windowing model can improve the GHI forecasting for t+60 in 8%, providing significant advance in the irradiance estimation.
In work [33], the authors used the state-of-the-art transformer deep learning architecture together with sky images [34] to GHI estimation in the USA. Analyzing their results and the ones provided by the windowing method, we observe that the transformer-based model reaches the best GHI forecasting values for RMSE in all the assessed time windows.
After the comparison of the ensemble windowing approach with reference models found in the literature, we see that wind speed prediction is often competitive and usually improves wind speed prediction for the assessed forecasting horizons. The results for wind speed prediction using the ensemble model corroborate the results found in the literature, where the ensemble approach often reaches state-of-the-art forecasting in time-series prediction applications [18,38,39,40]. Their improved performance comes from the combination of weaker predictive models to improve their overall forecasting capacity, also reducing the ensembled model’s variance [41,42].
However, the proposed dynamic ensembled approach faced increased difficulty when determining future GHI values. This may be an indication that the irradiance forecasting is a more complex non-linear natural phenomenon, requiring improved extraction of spatiotemporal information from the dataset. Since the proposed ensemble model does not have a deep learning model in its architecture it cannot properly identify and extract spatiotemporal information underlying the dataset, lacking in providing better irradiance estimation. Deep learning model can often excel in this type of task, as proved in the results from Table 14. Extensive literature can be found regarding improvements of time-series forecasting problems when complex and deep approaches are employed [19,20,43,44].

5. Conclusions

This work proposes to evaluate the performance of two ML methods of dynamic ensemble, using wind speed and solar irradiance data separately as inputs. Initially, wind speed and irradiance data from the same meteorological station were collected, the time horizons to be studied were determined (t+10 min, t+20 min, t+30 min and t+60 min), then a recursive approach of Lagged Average values was applied to evaluate the models’ predictors.
ML methods well known in other energy forecasting works and applied to wind and irradiance data were selected to compare efficiency with two other methods that use a dynamic ensemble approach (windowing and arbitrating). The programming code in Python was developed to catalog the optimal efficiency parameters of each previously known model, based on error metrics and coefficient of determination. The dynamic ensemble methods (windowing and arbitrating), based on the optimal parameters of each previously calibrated models (Random Forest, k-Nearest Neighbors, Support Vector Regression, and Elastic Net), generated a single model with greater efficiency for both wind and solar irradiance data.
For forecasting wind speed data, the most efficient method was found to be windowing for all time horizons, when evaluated by the criterion of the lowest RMSE value, and specifically for the time horizon t+10, as evidenced in Figure 3. The greater efficiency was found in an interval of 1 to 74 for the ʎ parameter, reaching maximum performance for the value ʎ = 19, as seen in Figure 8, which suggests that the windowing parameterization directly influences the method's performance.
For the solar irradiation forecasting, the most efficient method was also windowing and the t+10 min time horizon reached the lowest RMSE value. Differently from what was found for the wind speed data, a greater linearity in the trend was perceived from the ʎ windowing parameter variation graph when analyzing its RMSE values. Looking for the ʎ interval under study, the best performance value (using RMSE criteria) of ʎ = 1 was found, as can be seen in Figure 10.
Using wind speed data, the efficiency gain of the most efficient model (windowing for the time horizon t+10 min and ʎ = 19, see Table 4), when compared to the second highest efficiency (SVR) was 0.56%, when using the lowest value RMSE metric. A similar trend could be observed for the model using solar irradiance data. The efficiency increase, comparing the most efficient model (windowing for the time horizon t+10 min and ʎ = 1, see Table 9) to the second highest efficiency (Arbitrating) was about 1.72%, and when compared to the third most efficient method (SVR), it was about 1.96%.
Also, extensive comparisons with spatiotemporal models found in the literature show that the dynamic ensemble model for wind speed often provides superior forecasting performance for the assessed time horizons, deeming the proposed approach as a valuable tool for wind speed estimation. Regarding irradiance forecasting, the dynamic ensemble architecture proposed in this study could not surpass the deep learning-based models, which showed superior spatiotemporal identification, and consequently better estimated GHI values. However, the proposed windowing approach can provide competitive results and superior GHI forecasting when compared to physics-based predictive models.
For future works, the dynamic ensemble architecture can be improved with the addition of more complex machine learning models, such as deep learning and graph-based approaches. This may boost the windowing forecasting capacity for GHI and wind speed estimation once it will be able to benefit from spatiotemporal data information underlying the dataset. The development of an ensemble model able to provide accurate and precise estimations can then be employed in the development of real-time forecasting applications, helping the evaluation of wind and solar farm installation.

Author Contributions

Conceptualization, F.D.V.B., F.P.M. and P.A.C.R.; data curation, F.D.V.B. F.P.M.; formal analysis, P.A.C.R.; methodology, F.D.V.B., F.P.M. and P.A.C.R.; software, F.D.V.B. and F.P.M.; supervision, P.A.C.R.; validation, P.A.C.R., J.V.G.T. and B.G.; visualization, P.A.C.R., J.V.G.T. and B.G.; writing—original draft, F.D.V.B., F.P.M. and V.O.S.; writing—review and editing, F.D.V.B., F.P.M., P.A.C.R., V.O.S., J.V.G.T. and B.G.; project administration, P.A.C.R.; funding acquisition, P.A.C.R., B.G and J.V.G.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Natural Sciences and Engineering Research Council of Canada (NSERC) Alliance, grant No. 401643, in association with Lakes Environmental Software Inc., by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brasil (CAPES)—Finance Code (Grant No. 001), and by the Conselho Nacional de Desenvolvimento Científico e Tecnológico—Brasil (CNPq), grant no. 303585/2022-6.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data of wind speed and irradiation from Petrolina - PE - Brazil are downloaded from SONDA (National Organization of Environmental Data System) \\portal (http://sonda.ccst.inpe.br/, accessed on 12 July 2023).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Osman, A. I., Chen, L., Yang, M., Msigwa, G., Farghali, M., Fawzy, S., Rooney, D. W., 38; Yap, P. S. (2022). Cost, environmentalimpact, and resilience of renewable energy under a changing climate: a review. Environmental Chemistry Letters. [CrossRef]
  2. Carneiro, T. C., de Carvalho, P. C. M., dos Santos, H. A., Lima, M. A. F. B., 38; de Souza Braga, A. P. (2022). Review on Photovoltaic Power and Solar Resource Forecasting: Current Status and Trends. In Journal of Solar Energy Engineering, Transactions of the ASME (Vol. 144, Issue 1). [CrossRef]
  3. Meenal, R., Binu, D., Ramya, K. C., Michael, P. A., Vinoth Kumar, K., Rajasekaran, E., 38; Sangeetha, B. (2022). Weather Forecasting for Renewable Energy System: A Review. Archives of Computational Methods in Engineering, 29(5). [CrossRef]
  4. Mesa-Jiménez, J. J., Tzianoumis, A. L., Stokes, L., Yang, Q., 38; Livina, V. N. (2023). Long-term wind and solar energy generationforecasts, and optimisation of Power Purchase Agreements. Energy Reports, 9. [CrossRef]
  5. Rocha, P. A. C., Fernandes, J. L., Modolo, A. B., Lima, R. J. P., da Silva, M. E. V., 38; Bezerra, C. A. D. (2019). Estimation of daily,weekly and monthly global solar radiation using ANNs and a long data set: a case study of Fortaleza, in Brazilian Northeast region. International Journal of Energy and Environmental Engineering, 10(3). [CrossRef]
  6. Du, L., Gao, R., Suganthan, P. N., Wang, D. Z. W. (2022). Bayesian optimization based dynamic ensemble for time series forecasting. Information Sciences, 591. [CrossRef]
  7. Vapnik, V. N. (1995). The Nature of Statistical Learning Theory. Springer-Verlag. In Adaptive and learning Systems for SignalProcessing, Communications and Control.
  8. Smola, A. (1996). Regression estimation with support vector learning machines. Master’s Thesis, Technische Universit at Munchen.
  9. Mahesh, P. V., Meyyappan, S., 38; Alia, R. K. R. (2023). Support Vector Regression Machine Learning based Maximum PowerPoint Tracking for Solar Photovoltaic systems. International Journal of Electrical and Computer Engineering Systems, 14(1). [CrossRef]
  10. Demir, V., 38; Citakoglu, H. (2023). Forecasting of solar radiation using different machine learning approaches. Neural Computing and Applications, 35(1). [CrossRef]
  11. Schwegmann, S., Faulhaber, J., Pfaffel, S., Yu, Z., Dörenkämper, M., Kersting, K., 38; Gottschall, J. (2023). Enabling Virtual Met Masts for wind energy applications through machine learning-methods. Energy and AI, 11. [CrossRef]
  12. Che, J., Yuan, F., Deng, D., 38; Jiang, Z. (2023). Ultra-short-term probabilistic wind power forecasting with spatial-temporalmulti-scale features and K-FSDW based weight. Applied Energy, 331. [CrossRef]
  13. Nikodinoska, D., Käso, M., 38; Müsgens, F. (2022). Solar and wind power generation forecasts using elastic net in time-varyingforecast combinations. Applied Energy, 306. [CrossRef]
  14. Cerqueira, V., Torgo, L., Pinto, F., Soares, C. (2019). Arbitrage of forecasting experts. Machine Learning, 108(6). [CrossRef]
  15. Lakku, N. K. G., 38; Behera, M. R. (2022). Skill and Intercomparison of Global Climate Models in Simulating Wind Speed, andFuture Changes in Wind Speed over South Asian Domain. Atmosphere, 13(6). [CrossRef]
  16. Ji, L. , Fu, C., Ju, Z., Shi, Y., Wu, S., 38; Tao, L. (2022). Short-Term Canyon Wind Speed Prediction Based on CNN—GRU TransferLearning. Atmosphere, 13(5). [CrossRef]
  17. Su, X. , Li, T., An, C., 38; Wang, G. (2020). Prediction of short-time cloud motion using a deep-learning model. Atmosphere, 11(11). [CrossRef]
  18. Carneiro, T. C., Rocha, P. A. C., Carvalho, P. C. M., 38; Fernández-Ramírez, L. M. (2022). Ridge regression ensemble of machinelearning models applied to solar and wind forecasting in Brazil and Spain. Applied Energy, 314. [CrossRef]
  19. Santos, V. O. , Rocha, P. A. C., Scott, J., Thé, J. V. G., Gharabaghi, B. (2023). Spatiotemporal analysis of bidimensional wind speedforecasting: Development and thorough assessment of LSTM and ensemble graph neural networks on the Dutch database. Energy, 278, 127852. [CrossRef]
  20. Marinho, F. P. , Rocha, P. A. C., Neto, A. R., 38; Bezerra, F. D. V. (2023). Short-Term Solar Irradiance Forecasting Using CNN-1D, LSTM, and CNN-LSTM Deep Neural Networks: A Case Study with the Folsom (USA) Dataset. Journal of Solar Energy Engineering, Transactions of the ASME, 145(4). [CrossRef]
  21. INPE, S. (2012). Sistema De Organização Nacional de Dados Ambientais. Available online: http://sonda.ccst.inpe.br/.
  22. Landberg, L. , Myllerup, L., Rathmann, O., Petersen, E. L., Jørgensen, B. H., Badger, J., 38; Mortensen, N. G. (2003). Wind resourceestimation - An overview. In Wind Energy (Vol. 6, Issue 3). [CrossRef]
  23. Kasten, F., 38; Czeplak, G. (1980). Solar and terrestrial radiation dependent on the amount and type of cloud. Solar Energy, 24(2). [CrossRef]
  24. Ineichen, P. , Perez, R. (2002). A new airmass independent formulation for the linke turbidity coefficient. Solar Energy, 73(3). [CrossRef]
  25. Rocha, P. A. C., 38; Santos, V. O. (2022). Global horizontal and direct normal solar irradiance modeling by the machine learningmethods XGBoost and deep neural networks with CNN-LSTM layers: a case study using the GOES-16 satellite imagery. International Journal of Energy and Environmental Engineering, 13(4). [CrossRef]
  26. GOOGLE. Google Earth website. Available online: http://earth.google.com/ (accessed on 12 July 2023).
  27. Marquez, R. , Coimbra, C. F. M. (2013). Proposed metric for evaluation of solar forecasting models. Journal of Solar Energy Engineering, Transactions of the ASME. [CrossRef]
  28. Cerqueira, V. , Torgo, L., & Soares, C. (2017). Arbitrated ensemble for solar radiation forecasting. Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics). [CrossRef]
  29. Neshat, M. , Nezhad, M. M., Abbasnejad, E., Mirjalili, S., Tjernberg, L. B., Astiaso Garcia, D., Alexander, B., & Wagner, M. (2021). A deep learning-based evolutionary model for short-term wind speed forecasting: A case study of the Lillgrund offshore wind farm. Energy Conversion and Management. [CrossRef]
  30. Dowell, J. , Weiss, S., & Infield, D. (2014). Spatio-temporal prediction of wind speed and direction by continuous directional regime. 2014 International Conference on Probabilistic Methods Applied to Power Systems, PMAPS 2014 - Conference Proceedings. [CrossRef]
  31. Liu, Z. , Hara, R., & Kita, H. (2021). Hybrid forecasting system based on data area division and deep learning neural network for short-term wind speed forecasting. Energy Conversion and Management. [CrossRef]
  32. Zhu, Q. , Chen, J., Shi, D., Zhu, L., Bai, X., Duan, X., & Liu, Y. (2020). Learning Temporal and Spatial Correlations Jointly: A Unified Framework for Wind Speed Prediction. IEEE Transactions on Sustainable Energy. [CrossRef]
  33. J. Liu, H. J. Liu, H. Zang, L. Cheng, T. Ding, Z. Wei, and G. Sun, “A Transformer-based multimodal-learning framework using sky images for ultra-short-term solar irradiance forecasting,” Applied Energy, vol. 342, p. 121 160, 2023, issn: 0306-2619.
  34. Vaswani, A. , Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, Ł., & Polosukhin, I. (2017). Attention is all you need. Advances in Neural Information Processing Systems.
  35. Gupta, P. , & Singh, R. (2023). Combining a deep learning model with multivariate empirical mode decomposition for hourly global horizontal irradiance forecasting. Renewable Energy. [CrossRef]
  36. Yang, L. , Gao, X., Hua, J., & Wang, L. (2022). Intra-day global horizontal irradiance forecast using FY-4A clear sky index. Sustainable Energy Technologies and Assessments. [CrossRef]
  37. Kallio-Myers, V. , Riihelä, A., Lahtinen, P., & Lindfors, A. (2020). Global horizontal irradiance forecast for Finland based on geostationary weather satellite data. Solar Energy. [CrossRef]
  38. Peng, Z. , Peng, S., Fu, L., Lu, B., Tang, J., Wang, K., & Li, W. (2020). A novel deep learning ensemble model with data denoising for short-term wind speed forecasting. Energy Conversion and Management. [CrossRef]
  39. Abdellatif, A. , Mubarak, H., Ahmad, S., Ahmed, T., Shafiullah, G. M., Hammoudeh, A., Abdellatef, H., Rahman, M. M., & Gheni, H. M. (2022). Forecasting Photovoltaic Power Generation with a Stacking Ensemble Model. Sustainability (Switzerland). [CrossRef]
  40. Wu, H. , & Levinson, D. (2021). The ensemble approach to forecasting: A review and synthesis. Transportation Research Part C: Emerging Technologies. [CrossRef]
  41. Ghojogh B, Crowley M. The Theory BehindOverfitting, Cross Validation, Regularization,Bagging and Boosting: Tutorial. Available online: https://arxiv.org/abs/1905.12787:arXiv.
  42. Chen, T. , & Guestrin, C. (2016). XGBoost: A scalable tree boosting system. Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. [CrossRef]
  43. Oliveira Santos, V. , Costa Rocha, P. A., Scott, J., Van Griensven Thé, J., & Gharabaghi, B. (2023). Spatiotemporal Air Pollution Forecasting in Houston-TX: A Case Study for Ozone Using Deep Graph Neural Networks. Atmosphere. [CrossRef]
  44. Oliveira Santos, V.; Costa Rocha, P.A.; Scott, J.; Thé, J.V.G.; Gharabaghi, B. A New Graph-Based Deep Learning Model to Predict Flooding with Validation on a Case Study on the Humber River. Water 2023, 15, 1827. [Google Scholar] [CrossRef]
Preprints 81846 g001
Figure 1. Map of the Northeast of Brazil. The Petrolina measurement site is highlighted [26].
Figure 1. Map of the Northeast of Brazil. The Petrolina measurement site is highlighted [26].
Preprints 81846 g001
Preprints 81846 g002
Figure 2. Diagram of the data flow for the applied methodology.
Figure 2. Diagram of the data flow for the applied methodology.
Preprints 81846 g002
Preprints 81846 g003
Figure 3. Windowing λ parameter variation influence in RMSE for different time horizons in wind speed data analysis for all the studied time horizons.
Figure 3. Windowing λ parameter variation influence in RMSE for different time horizons in wind speed data analysis for all the studied time horizons.
Preprints 81846 g003
Preprints 81846 g004
Figure 4. Windowing λ parameter influence on RMSE value for the time horizon t+10.
Figure 4. Windowing λ parameter influence on RMSE value for the time horizon t+10.
Preprints 81846 g004
Preprints 81846 g005
Figure 5. Windowing λ parameter influence in MAE value for the time horizon t+10.
Figure 5. Windowing λ parameter influence in MAE value for the time horizon t+10.
Preprints 81846 g005
Preprints 81846 g006
Figure 6. Windowing λ parameter influence in R² value for the time horizon t+10.
Figure 6. Windowing λ parameter influence in R² value for the time horizon t+10.
Preprints 81846 g006
Preprints 81846 g007
Figure 7. Windowing λ parameter influence in MAPE value for the time horizon t+10.
Figure 7. Windowing λ parameter influence in MAPE value for the time horizon t+10.
Preprints 81846 g007
Preprints 81846 g008
Figure 8. Parameter λ variance effect in method performance. SVR result is shown for reference.
Figure 8. Parameter λ variance effect in method performance. SVR result is shown for reference.
Preprints 81846 g008
Preprints 81846 g009
Figure 9. Windowing λ parameter variation influence in RMSE for all the studied time horizons in solar irradiation data analysis.
Figure 9. Windowing λ parameter variation influence in RMSE for all the studied time horizons in solar irradiation data analysis.
Preprints 81846 g009
Figure 10. Windowing λ parameter influence in RMSE value in time horizon t+10.
Preprints 81846 g011
Figure 11. Windowing λ parameter influence in R² value in time horizon t+10.
Figure 11. Windowing λ parameter influence in R² value in time horizon t+10.
Preprints 81846 g011
Preprints 81846 g012
Figure 12. Windowing λ parameter influence in R² value in time horizon t+10.
Figure 12. Windowing λ parameter influence in R² value in time horizon t+10.
Preprints 81846 g012
Preprints 81846 g013
Figure 13. Windowing λ parameter influence in MAPE value in time horizon t+10.
Figure 13. Windowing λ parameter influence in MAPE value in time horizon t+10.
Preprints 81846 g013
Table 1. Geographic coordinates, altitude in relation to the sea level, measurement intervals, and measurement periods of the data collected from the Petrolina station. MI and MP stand for, respectively, “measurement interval” and “measurement period”.
Table 1. Geographic coordinates, altitude in relation to the sea level, measurement intervals, and measurement periods of the data collected from the Petrolina station. MI and MP stand for, respectively, “measurement interval” and “measurement period”.
Type Lat. (◦) Long. (◦) Alt. (m) MI (min) MP
Anemometric 09° 04’ 08" S 40° 19’ 11" O 387 10 01/Jan/2007 to 12/Dec/2010
Solarimetric 01/Jan/2010 to 12/Dec/2010
Table 2. Search parameters and grid values applied to the tested methods.
Table 2. Search parameters and grid values applied to the tested methods.
Method Search parameter Grid values
Random Forest maxdepth [2, 5, 7, 9, 11, 13, 15, 21, 35]
KNN nearest neighbours k 1 ≤ k ≤ 50, k integer
SVR penalty term C [0.1, 1, 10, 100, 1000]
coefficient λ [1, 0.1. 0.01, 0.001, 0.0001]
Elastic Net regularization term λ [1, 0.1. 0.01, 0.001, 0.0001]
Windowing Λ [1, 3, 6, 12, 25, 50, 100]
Arbitrating *
*: By using a meta-heuristic methodology, the initial parameter was not needed.
Table 3. Best parameters for each machine learning method.
Table 3. Best parameters for each machine learning method.
Method Parameter t+10 t+20 t+30 t+60
Random Forest best_max_depth 7
best_n_estimators 20
KNN best_n_neighbors 49
SVR best_ C 1
best_epsilon 0.1 1 0.1
Elastic Net best_l1_ratio 1
Table 4. Comparison of RMSE values, using different methods for different time horizons andwindowing ʎ parameter variation. The best results for each time horizon are in bold.
Table 4. Comparison of RMSE values, using different methods for different time horizons andwindowing ʎ parameter variation. The best results for each time horizon are in bold.
Time horizon ʎ RF KNN SVR Elastic Net Windowing Arbitrating
t+10 min 1 0.69458 0.71040 0.69396 0.69828 0.69263 0.69447
3 0.69180
6 0.69114
12 0.69041
19 0.69007
25 0.69040
50 0.69226
74 0.69402
100 0.69431
t+20 min 1 0.88310 0.89332 0.88372 0.88554 0.86817 0.88315
3 0.87353
6 0.87563
12 0.87699
25 0.87803
50 0.87889
100 0.87960
t+30 min 1 0.99469 0.99859 0.99130 0.99660 0.97497 0.99091
3 0.98017
6 0.98333
12 0.98583
25 0.98702
50 0.98832
100 0.98902
t+60 min 1 1.18092 1.19527 1.17764 1.18281 1.15150 1.18156
3 1.15647
6 1.16170
12 1.16685
25 1.16987
50 1.17254
100 1.17455
Table 5. Comparison of MAE values, using different methods in different time horizons and windowing λ parameter variation. The best results for each time horizon are in bold.
Table 5. Comparison of MAE values, using different methods in different time horizons and windowing λ parameter variation. The best results for each time horizon are in bold.
Time horizon ʎ RF KNN SVR Elastic Net Windowing Arbitrating
t+10 min 1 0.51592 0.53216 0.51438 0.51853 0.51384 0.51711
3 0.51366
6 0.51328
12 0.51276
19 0.51272
25 0.51301
50 0.51441
74 0.51574
100 0.51603
t+20 min 1 0.65845 0.66882 0.66040 0.65990 0.64663 0.65936
3 0.65140
6 0.65332
12 0.65435
25 0.65554
50 0.65637
100 0.65695
t+30 min 1 0.74250 0.74735 0.74125 0.74347 0.72594 0.74097
3 0.73105
6 0.73402
12 0.73625
25 0.73732
50 0.73846
100 0.73902
t+60 min 1 0.89496 0.90753 0.89179 0.89589 0.86784 0.89570
3 0.87277
6 0.87826
12 0.88307
25 0.88580
50 0.88813
100 0.88963
Table 6. Comparison of R² values, using different methods in different time horizons and windowing λ parameter variation. The best results for each time horizon are in bold.
Table 6. Comparison of R² values, using different methods in different time horizons and windowing λ parameter variation. The best results for each time horizon are in bold.
Time horizon ʎ RF KNN SVR Elastic Net Windowing Arbitrating
t+10 min 1 0.84248 0.83522 0.84275 0.84079 0.84336 0.84252
3 0.84373
6 0.84403
12 0.84436
19 0.84451
25 0.84436
50 0.84353
74 0.84273
100 0.84260
t+20 min 1 0.74534 0.73941 0.74498 0.74393 0.75388 0.74531
3 0.75083
6 0.74963
12 0.74885
25 0.74825
50 0.74776
100 0.74736
t+30 min 1 0.67690 0.67436 0.67909 0.67566 0.68958 0.67935
3 0.68626
6 0.68423
12 0.68262
25 0.68186
50 0.68102
100 0.68057
t+60 min 1 0.54443 0.53329 0.54695 0.54297 0.56685 0.54393
3 0.56310
6 0.55914
12 0.55522
25 0.55291
50 0.55087
100 0.54933
Table 7. Comparison of MAPE values, using different methods in different time horizons and windowing λ parameter variation. The best results for each time horizon are in bold.
Table 7. Comparison of MAPE values, using different methods in different time horizons and windowing λ parameter variation. The best results for each time horizon are in bold.
Time horizon ʎ RF KNN SVR Elastic Net Windowing Arbitrating
t+10 min 1 0.21277 0.25360 0.20257 0.21848 0.21040 0.21634
3 0.21122
6 0.21092
12 0.21040
19 0.21022
25 0.21075
50 0.21179
74 0.21246
100 0.21234
t+20 min 1 0.31534 0.33823 0.34178 0.31206 0.31280 0.32577
3 0.31558
6 0.31658
12 0.31745
25 0.31906
50 0.31990
100 0.32101
t+30 min 1 0.38089 0.39786 0.37520 0.37064 0.36711 0.38499
3 0.36968
6 0.37245
12 0.37227
25 0.37367
50 0.37352
100 0.37538
t+60 min 1 0.52320 0.53567 0.51731 0.51284 0.50552 0.52440
3 0.50730
6 0.51189
12 0.51289
25 0.51480
50 0.51571
100 0.51872
Table 8. Best parameters for each machine learning method.
Table 8. Best parameters for each machine learning method.
Method Parameter t+10 t+20 t+30 t+60
Random Forest best_max_depth 5
best_n_estimators 20
KNN best_n_neighbors 37 49 48
SVR best_ C 0.1
best_epsilon 0.1
Elastic Net best_l1_ratio 1
Table 9. Comparison of RMSE values, using different methods in different time horizons and windowing λ parameter variation. The best results for each time horizon are in bold.
Table 9. Comparison of RMSE values, using different methods in different time horizons and windowing λ parameter variation. The best results for each time horizon are in bold.
Time horizon ʎ RF KNN SVR Elastic Net Windowing Arbitrating
t+10 min 1 75.02000 75.26000 74.19000 74.98000 72.73186 74.01000
3 72.93221
6 73.29363
12 73.21035
25 73.24620
50 73.48055
100 73.69330
t+20 min 1 90.94000 83.50000 84.45000 84.53000 80.07000 83.19000
3 80.63000
6 81.19000
12 81.87000
25 82.56000
50 82.11000
100 82.57000
t+30 min 1 90.15000 90.50000 91.49000 93.49000 86.25000 89.70000
3 87.00000
6 87.75000
12 88.33000
25 88.95000
50 88.70000
100 89.01000
t+60 min 1 112.05000 112.13000 112.76000 118.08000 105.51000 111.13000
3 106.62000
6 107.76000
12 108.89000
25 109.32000
50 110.12000
100 110.30000
Table 10. Comparison of R² values, using different methods in different time horizons and windowing λ parameter variation. The best results for each time horizon are in bold.
Table 10. Comparison of R² values, using different methods in different time horizons and windowing λ parameter variation. The best results for each time horizon are in bold.
Time horizon λ RF KNN SVR Elastic Net Windowing Arbitrating
t+10 min 1 0.92000 0.92000 0.92000 0.92000 0.92184 0.92000
3 0.92141
6 0.92062
12 0.92080
25 0.92073
50 0.92022
100 0.91976
t+20 min 1 0.88000 0.90000 0.90000 0.90000 0.91000 0.90000
3 0.91000
6 0.90000
12 0.90000
25 0.90000
50 0.90000
100 0.90000
t+30 min 1 0.88000 0.88000 0.88000 0.87000 0.89000 0.88000
3 0.89000
6 0.89000
12 0.89000
25 0.89000
50 0.88000
100 0.89000
t+60 min 1 0.83000 0.83000 0.82000 0.51223 0.85000 0.83000
3 0.84000
6 0.84000
12 0.84000
25 0.83000
50 0.83000
100 0.83000
Table 11. Comparison of MAE values, using different methods in different time horizons and windowing λ parameter variation. The best results for each time horizon are in bold.
Table 11. Comparison of MAE values, using different methods in different time horizons and windowing λ parameter variation. The best results for each time horizon are in bold.
Time horizon λ RF KNN SVR Elastic Net Windowing Arbitrating
t+10 min 1 48.29000 48.47000 44.16000 49.31000 72.73186 46.24000
3 44.52301
6 45.00717
12 45.27759
25 45.67924
50 45.79140
10 46.16632
t+20 min 1 65.19000 55.63000 59.67000 58.86000 52.53000 56.20000
3 53.31000
6 54.12000
12 55.27000
25 56.88000
50 55.59000
10 56.79000
t+30 min 1 62.09000 61.58000 64.77000 67.13000 58.14000 60.91000
3 59.02000
6 59.91000
12 60.85000
25 61.34000
50 61.84000
10 61.51000
t+60 min 1 81.28000 79.84000 81.44000 89.07000 74.59000 79.80000
3 7592000
6 77.11000
12 78.47000
25 79.08000
50 79.48000
10 79.63000
Table 12. Comparison of MAPE values, using different methods in different time horizons and windowing λ parameter variation. The best results for each time horizon are in bold.
Table 12. Comparison of MAPE values, using different methods in different time horizons and windowing λ parameter variation. The best results for each time horizon are in bold.
Time horizon λ RF KNN SVR Elastic Net Windowing Arbitrating
t+10 min 1 0.22000 0.24000 0.21000 0.23000 0.20701 0.22000
3 0.21027
6 0.21254
12 0.21364
25 0.21444
50 0.21541
100 0.21684
t+20 min 1 0.32000 0.28000 0.28000 0.27000 0.25000 0.27000
3 0.25000
6 0.26000
12 0.26000
25 0.27000
50 0.26000
100 0.27000
t+30 min 1 0.29000 0.30000 0.29000 0.33000 0.27000 0.29000
3 0.28000
6 0.28000
12 0.28000
25 0.29000
50 0.29000
100 0.29000
t+60 min 1 0.34000 0.35000 0.34000 0.54747 0.32000 0.34000
3 0.32000
6 0.33000
12 0.33000
25 0.34000
50 0.34000
100 0.34000
Table 13. Compilation of results for wind speed forecasting.
Table 13. Compilation of results for wind speed forecasting.
Model Metric Value Author
GNN SAGE GAT RMSE
0.638 for t+60 forecasting horizon
MAE
0.458 for t+60 forecasting horizon		 Oliveira Santos et al. [19]
ED-HGNDO-BiLSTM RMSE
0.696 average for t+10 forecasting horizon
1.445 average for t+60 forecasting horizon
MAE
0.717 average for t+10 forecasting horizon
0.953 average for t+60 forecasting horizon
MAPE
0.590 average for t+10 forecasting horizon
9.769 average for t+60 forecasting horizon		 Neshat et al. [29]
Statistical model for wind speed forecasting RMSE
1.090 for t+60 forecasting horizon		 Dowell et al. [30]
Hybrid wind speed forecasting model using area division (DAD) method and a deep learning neural network RMSE
0.291 average for t+10 forecasting horizon
0.355 average for t+30 forecasting horizon
0.426 average for t+60 forecasting horizon
MAE
0.221 average for t+10 forecasting horizon
0.293 average for t+30 forecasting horizon
0.364 average for t+60 forecasting horizon		 Liu et al. [31]
Hybrid model CNN-LSTM RMSE
0.547 for t+10 forecasting horizon
0.802 for t+20 forecasting horizon
0.895 for t+30 forecasting horizon
1.114 for t+60 forecasting horizon
MAPE
4.385 for t+10 forecasting horizon
6.023 for t+20 forecasting horizon
7.510 for t+30 forecasting horizon
11.127 for t+60 forecasting horizon		 Zhu et al. [32]
Table 14. Compilation of results for GHI forecasting.
Table 14. Compilation of results for GHI forecasting.
Model Metric Value Author
CNN-1D RMSE (R2)
36.24 (0.98) for t+10 forecasting horizon
39.00 (0.98) for t+20 forecasting horizon
38.46 (0.98) for t+30 forecasting horizon		 Marinho et al. [20]
MEMD-PCA-GRU RMSE (R2)
31.92 (0.99) for t+60 forecasting horizon		 Gupta and Singh [35]
Physical-based forecasting model RMSE
75.91 for t+30 forecasting horizon
89.81 for t+60 forecasting horizon
MAE
48.85 for t+30 forecasting horizon
57.01 for t+60 forecasting horizon		 Yang et al. [36]
Physical-based forecasting model RMSE
114.06 for t+60 forecasting horizon		 Kallio-Meyers et al. [37]
Deep learning transformer-based forecasting model MAE
34.21 for t+10 forecasting horizon
43.64 for t+20 forecasting horizon
49.53 for t+30 forecasting horizon		 Liu et al. [33]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated