Preprint
Article
Unveiling Inertia Constants by Exploring Mass Distribution in Wind Turbine Blades and Review of the Drive Train Parameters
Altmetrics
Downloads
93
Views
19
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
07 August 2023
Posted:
09 August 2023
You are already at the latest version
Alerts
Abstract
In studies of dynamic stability and power quality, it is necessary to know the mechanical parameters that determine the transient response of a wind turbine. The exact value of these parameters is not as decisive as the power curve can be, but an estimate that is far from reality can distort or even invalidate the simulation results. Despite its importance, this information, especially the inertia, but also the stiffness and damping constant of the drive-train, is hardly available for the turbine model under investigation.
In this work, the different bibliographical sources that provide values of blade inertia in kg·m2 will be reviewed, and above all, those that provide a distribution of masses along the span of the blade.
With this, different reliable relations will be obtained that allow calculating the inertia of the turbine rotor, based on the mass and length of the blade. When the center of gravity is also available, a very correlated expression is provided to obtain the inertia.
The even rarer references to the stiffness and damping constant of the drive-train will also be reviewed.
Keywords:
Subject: Environmental and Earth Sciences - Sustainable Science and Technology
1. Introduction
In power system stability studies, it is important to have an appropriate model for the characterization of a physical phenomenon of interest. Depending on the analysis to be carried out, the corresponding models may be different. According to the time scale of interest for stability studies, the models can be classified as electromagnetic models (to scale short time frames) or electromechanical models to investigate slower events. The influence that modeling can have on the results of the study can be seen in [1].
With regard to the electromechanical models, the most important components to take into account are the turbine inertia, the generator inertia, and the coupling between both moving masses. In general, the inertia in AC electrical power system represents the kinetic energy stored in large rotating generators and synchronous motors, providing them with the tendency to maintain continuous rotation. In the case of additional rotating masses (steam turbine in the case of thermal units, Francis/Kaplan/Pelton turbine in the case of hydro units or blades in the case of wind turbines), the corresponding inertia must be added to the generator one.
A system that possesses a sufficient natural rotational inertia is able to maintain the grid frequency in its rated values, since this frequency is really an electromechanical variable that is linked to the mechanical speed of rotation of the generators. When a sudden power imbalance between generation and demand occurs in the grid, a frequency deviation typically appears, and if the contingency is not serious, this stored kinetic energy allows for a rapid response, permitting a transfer of energy to balance generation and load before the frequency deviation exceeds permitted values. On the other hand, in normal operation, small variations are permitted in the electrical frequency in real time to ensure an adequate balance of active generation and load. In both cases, abrupt or slow power imbalance, the inertia plays a determining role during the balancing transient.
This kinetic energy is
where is the rotational speed of the electrical generator. It allows us to define the inertia time constant H of a generator as the ratio between the stored kinetic energy and its rated power, and determines the time interval during which an electrical generator can supply its rated power only by using the kinetic energy stored in its rotating masses [2].
Additionally, the current paradigm shift, with the incorporation of wind power and photovoltaics into the power system is achieved using power-electronic converters that do not possess natural rotational inertia, unlike a synchronous generator (SG). Consequently, renewable generators displace synchronous generation and reduces the amount of rotating mass in the system. Consequently, system operators need to model these electrical systems with low rotational inertia, adding significant challenges to controlling the system stability [3,4].
The availability of precise inertia data permits the system operator to make appropriate decisions, and facilitates improved planning and operation of the system, ensuring the stability and resilience of the network and enabling the efficient integration of larger amounts of renewable generators without compromising system security or power quality.
The importance of inertia in stability studies is addressed by many authors. Ekanayake in [5] shows how, with proper control of the power electronics connected to the rotor of a doubly-fed induction generator (DFIG), inertia allows the recovery of a significant amount of kinetic energy that alleviates the effect of a frequency drop in the network system.
In the case of fixed speed induction generators (squirrel-cage type), the recovered kinetic energy is much lower since the range of operating rotation speeds is reduced to +1%-3% above the synchronous speed. At the other extreme, SGs allow a much wider speed range, and there is a decoupling between the mechanical part and the transient phenomena that occur on the network side [6], due to the IGBT-converters . Initially, this decoupling could lead to a reduction in inertia seen by the network, and therefore less damping against abrupt changes in generation and charging patterns [7,8]. This has given rise to a multitude of articles on frequency control strategies to effectively integrate wind energy systems into the grid. In any case, for the evaluation of the kinetic storage capacity, it is necessary to know, as precisely as possible, the inertia of the turbine and the generator, as well as the mechanism for the transmission of kinetic energy between both components through the coupling, for which it is necessary to know its characteristics of stiffness and damping.
Despite their importance in system stability and power quality studies, these parameters, especially the inertia, but also the stiffness and damping constant of the drive-train, are hardly available for the turbine model under investigation, for so often the researcher must carry out a study on which parameters to use in order to faithfully reproduce the actual situation or rely on the value used by other researchers, without being sure that they can adapt them to the characteristics of power, length or weight of their own system. Consequently, it is highly desirable that future studies on stability and in general on the dynamic behavior of wind turbines contain reliable data so that the modeling of the system is as realistic as possible. These parameters logically depend on the size of the turbine. Even using a dimensionless formulation, which converts the magnitudes into per unit (p.u.), these parameters have a certain dependence on power, and as power grows over the years, it is necessary to update the available databases with the values that can be extracted from modern machines. Guillamon in [9] performs a review of inertia data, although providing its dimensionless value, and in some references it is difficult to trace which ones have been reliably obtained. Other authors such as Morren in [6], in the absence of reliable data, assume that the geometry of the blade is very complicated, and approximates it to a bar of constant chord and constant, with which they obtain a simple expression to calculate the inertia as a function of power.
In this article, in addition to reviewing realistic data on inertia, mainly from multi-Megawatt turbines, it is intended to trace the references that provide data on the density distribution (DD) of real blades, or with designs based on realistic dynamic and structural analyses. From these, the calculation of the inertia of the blade will be made, and a relationship with some specific magnitude of the geometry will be deduced, such as the position of the center of gravity (CoG).
Although minor, other components have also influence on the dynamics of the mechanical system, whose precision will depend on the number of masses with which the mechanical part of the turbine is modeled [10,11], and their values are even more difficult to obtain: generator inertia, hub inertia, and stiffness/damping of the power transmission shafts between turbine and generator. The relationship between the different mechanical variables through these parameters will be reviewed, and the corresponding expressions converted into dimensionless. In [11] it is stated that it is possible to reduce the number of masses of the drive-train model, without large deviations.
The rest of the article is explained below. In Section 2, the mechanical equations that govern the rotation movement of each component are reviewed, the expressions that transform each variable and parameter into its value in p.u are shown, and certain distinguishing general characteristics of each parameter are described. In Section 3, all the data retrieved on the DD of twenty-one blade models are organized and a relation is provided that links the inertia with the position of the centre of gravity of the blade. The values obtained for the other parameters reviewed are also organized. Finally, in Section 4, the results obtained are evaluated, exposing the achievements obtained as well as their limitations.
2. Methods
This section formulates the expressions governing the dynamics of the interaction rotor–generator, how they can be converted in p.u., and anticipates some issues to take into account prior to listing the revised data.
Hereinafter, the set of blades plus hub will be named as the turbine rotor or simply turbine, and it will appear referenced in the expressions as T. A blade will be designated as , the generator as G, and the gearbox as . Magnitudes and parameters with dimension will appear in upper case, and their conversion to p.u. will be displayed in lower case.
2.1. Dynamics Rotor – Generator
Once the blades extract the aerodynamic energy from the wind, and transform it into a rotation torque exerted at the turbine speed , these magnitudes drive the dynamics of the system until producing a torque on generator which will rotate at speed . This speed will be given by the grid frequency f divided by the number of pole pairs , and will be exactly equal to this value in the case of SGs, or slightly higher (due to slip) in the case of IGs in normal operation.
With regard to IGs, a high number of poles would increase the magnetization losses, so this value is reduced to not more than or . Since the rotational speed in rpm is equal (or very close) to with f being the grid frequency, it yields an impermissible value for blade rotation. It is therefore necessary to include a gear box that accommodates both speeds. This new element introduces new equations in the dynamics of the system.
Permanent Magnet Synchronous Generators (PMSG), which are the most frequent type of SGs in wind turbines (WT), allow a high number of poles, thereby reducing the speed on their axis to the point that it can be the same value as the speed of rotation of the blades. In the latter case it would not be necessary to use a gear box. This setup is referred to as direct drive. In other cases, the number of pairs of poles is not high enough to obtain the adequate speed, although in any case the required transmission ratio decreases, and with it the dimensions and stages of the gear box.
Other elements that are part of this transmission are the brake and the couplings that account for the misalignment between rotation axes, although they are generally not included in the dynamic analysis of the system.
Figure 1 represents the interior of the nacelle with the transmission chain from the turbine rotor to the generator. The scheme corresponds to an IG, or a PMSG with a reduced number of poles. In this case, to accommodate the high speed in the generator shaft with the low speed of the blades, it is necessary to include a gearbox, with a ratio that increases with the turbine rotor diameter and decreases with the number of poles. The Figure 2.a corresponds to this dynamic scheme, called three masses, where:
- is the inertia of the turbine rotor due to the distribution of masses in the blades and, to a lesser extent, in the hub,
- is the coefficient of friction due to the aerodynamic resistance offered by the blades,
- is the stiffness constant in the slow axis that joins the hub and the gearbox,
- is the damping constant of the torsional movement of the slow axis,
- is the inertia of the gear box discs, measured from the slow shaft,
- is the coefficient of friction due to friction in the gear box, measured from the slow shaft,
- is the inertia of the rotor of the electric generator and the brake,
- is the coefficient of friction due to friction in the generator and ventilation losses,
- is the stiffness constant in the fast axis that joins the gearbox and the generator,
- is the damping constant of the torsion motion of the fast axis,
2.2. Mechanical equations
The equations that govern the dynamics in a system formed by the turbine rotor, the slow shaft, the gear box, the fast shaft and the generator are those that correspond to the left side of the following expressions:
where superscripts and stand respectively for low-speed shaft and high-speed shaft (as an example, is the torque available in the LSS), is the twist angle in the or , and is the gearbox ratio. The variables and magnitudes on the right hand are the same expressions, although referred to their base magnitudes; they are explained following.
2.3. Referring to base magnitudes
On many occasions, the value of a magnitude expressed in a measurement system (eg MKS) does not provide information on the operating range in which it is working, having to compare with its rated value. This is why it is customary to refer magnitudes, electrical or mechanical in our case, to their rated values, so that when working below rated conditions, it will be between 0 and 1. It usually entails adimensionalization also of the parameters that intervene in the relations between magnitudes. In most cases, the new magnitudes and parameters lose their dimensions and we then work in p.u. This facilitates computational manipulation, makes the variables independent, to a certain extent, of the capacity of the turbine, or offers a better view of how close is the operation to overload or idle. In the case of an ideal one, it disappears when operating in p.u. The expressions, once transformed into p.u, are those found on the right side of (2–10), where uppercase has been used for values with dimension and lowercase for values in p.u.
In the following subsections, a set of dimensionless values for the different parameters of these equations (inertia, damping coefficients and friction coefficients) will be listed, and it will be easy to identify outlier values and mark them as unreliable. If the adimensionalization is not carried out, the normality range for each parameter depends on other variables (power, speed, ), so its identification is more difficult.
The relationships between variables with dimensions and in p.u. are the following:
where P is the turbine rated capacity. This determines the transformation to p.u. of the different parameters (inertias, stiffness, friction or damping), different according to whether they are given in the or the .
It should be mentioned that there are cases such as that of the inertia constant J, in which a complete adimensionalization does not make practical sense, and although it is transformed to a value referred to rated conditions, it has a magnitude of s. In any case, and although it would be more accurate to speak of magnitudes referred to base values, the term p.u. will continue to be used, despite not being strictly correct for some parameters. Its reference to rated values (H) appears, also as an exception, in capital letters.
For the parameters in the , the transformations yield
For the parameters in the , the transformations yield
It is worth mentioning that some authors use the turbine rotation speed provided by the manufacturer as to transform the dimensioned parameters to p.u parameters. which is true for turbines driving PMSGs. However, for turbines with IGs, catalogues generally do not exactly show the speed value at rated conditions, but , so once again it is correct to use the value obtained from catalogues as . However, some other sources have also been identified in which these two values differ, although the deviation is small, less than 5%. This deviation is due to the slip s, of reduced value in high power generators since this slip determines the rotor losses due to the Joule effect. Consequently, there is a certain error in turbines with IGs when considering the rotational speed of the turbine as the base of the slow shaft speed. This error, although small, can be avoided by adopting as the base speed.
2.4. System of two masses
In the case of multipole PMSM generators with direct drive, there would be no gear box and all the measurements would refer to a single axis. In this case, it is usual to group the different constants in such a way that one works with a model of two masses as in the Figure 2.b). The error committed is not usually significant in stability studies [11].
Even when there is a gear ratio, all constants also tend to refer to a single axis, thus simplifying the analysis of the dynamics and making it possible to compare parameters between turbines with different gearbox ratios. In addition, the system is simplified if, as indicated in [11], the coupling on the fast axis is considered infinitely rigid, with which . As shown in Figure 2b, parameters measured in the HSS can be converted to the LSS (or vice versa), simply by multiplying (or dividing) by . This is,
where is a coefficient of inertia, stiffness, friction or damping. This is coherent with the expressions (22–29)
The different constants could be grouped into equivalent values according to [10], which in the case of using variables in p.u. is more simplified.
where refers to the equivalent value that includes all the components to the right of the rotor. It would constitute mass 2 against mass 1 which is that of the turbine.
From the grouped values of , and , the critical damping for the torsional dynamics can be obtained:
where for the study of damping in torsional dynamics [10,12], it must be used
From (22) and (23), can be obtained as a dimensionless value. Assuming, without loss of generality, that the values are referred to the LSS, it would be
From (24), it results:
where f is the network frequency. In the event that the values were referred to the fast axis, it would be necessary to multiply and by , but at the same time, the damping would also be divided by , so the expression would still be valid.
The resonant frequency is:
similar to that obtained in [13].
2.5. Evaluation of the blade inertia
Figure 3 represents the typical blade aspect composed of sections of different airfoils. Different regions can be established: root, a transition zone and the aerodynamic zone, from which the tip part can also be distinguished. The root region is the zone that is assembled to the hub through a bolted joint. It is cylindrical for structural reasons and to facilitate pitch control; hence has the lower aerodynamical efficiency. Consists of thick aerofoil profiles to provide greater structural integrity since this region is the one that supports the largest edgewise moments (due to the weight) and flapwise bending moments (due to aerodynamical forces). A transition region adapts the geometry from the cylindrical shape to the aerodynamical profile. This geometry is not as structurally efficient as the circular one, but it has to withstand practically the same moments, which is why it is the most structurally requested area and carries the highest loads, especially at high-pressure side [14,15]. Next is the aerodynamic zone, where the geometry is designed to be able to resist the design loads according to the IEC Class in which it is framed. Once this restriction is overcome, the design focus on maximizing the lift to drag ratio. In general a larger chord length close to the root would increase energy capture, but it results in higher moments when the turbine is parked in extreme wind conditions. The tip is a compromise between aerodynamics, aeroacoustics and deflection control. A less tapered tip can increase the lift, but also the noise and thrust forces, which will give larger tip deflections and bending moments.
In addition to these design requisites, manufacturers also introduce modification in the design and skin material to reduce the effect of the leading-edge soiling on airfoil performance.
In order to obtain reliable blade inertia data, and also to be able to deduce realistic expressions that allow their estimation, repositories and the literature have been reviewed in search of blade models that provide the distribution of mass along the blade span. It has been interpolated to produce uniform distributions over 101 positions of each blade and the result has been uploaded to [16] as a csv file. It is also accompanied by the Matlab/Octave code that allows them to be recovered. Section 3 shows the result of the analysis performed.
In the event that the moment of inertia is provided with respect to the root of the blade , instead of with respect to the axis of rotation (AoR) , this inertia would have to be transferred by the amount equivalent to the radius of the hub (see Figure 3). Applying Steiner’s theorem, and passing first through the centre of gravity (CoG), we have
where is the inertia about the CoG, is the blade mass, and is the distance from the CoG up to the blade root.
2.6. Modelling the drive train
A precise study of the behavior of the drive-train dynamics requires a model of 5 masses [10], referred to the turbine rotor Figure 2b, whose minimum requirements are outlined in IEC 61400-4. However, as mentioned in Section 2.4, a two-mass model is preferentially used in stability studies. Even for this simplified model, it is very difficult to find data ofr stiffness, and even worse, damping of the coupling between rotor and generator. In fact, the drivetrain torsional damping is often estimated, as in [17] for the NREL-5MW reference model, by assuming a relative damping . Hence,
with deduced from (38).
2.7. Generator inertia
The different types of generator used in megawatt WTs are listed in [18], along with their generic characteristics, and resumed in Table 1. Typical speeds, in concordance to [19] appear in the third column. Relationships between the mass and the power of the generator have also been extracted from this reference (fifth column). Data of the remaining columns have been extracted from [20], from [21] and other scattered catalogues .
The expressions in the last column of Table 1 can also be reached with a constructive and functional analysis of the generators, although what appears in this column is the mass of the entire machine and, in fact , only the mass and geometry of the rotor are required for the inertia. Therefore, the mass of the frame and that of the generator should have been subtracted. As a rule of thumb, many authors assume the same mass for the three components, although the ratio between the mass of the rotor with respect to the stator increases with the number of pairs of poles.
In general, for IGs, the torque and speed are determined respectively by the stator current, and the voltage. The first magnitude determines the section of Cu, and the second, the number of turns; hence, the power increases with the mass of Cu. On the other hand, to achieve a certain torque, Lorentz’s law indicates that the force is proportional to the length of the conductor (that is, the length of the machine and the number of windings that fit in the periphery), while the arm is related with the radius. Consequently, the power will be roughly proportional to the volume of the machine. Assuming that diameter and depth are scaled equally, we have
since the speed of the generator rotor depends on its number of pairs of poles which is independent of the power.
For slow synchronous generators, the speed is given by the inverse of the , and this number in turn determines the circumference length of the generator rotor.
On the other hand, an increase in the power of an electric machine implies a roughly proportional increase in weight. Consequently, as far as inertia is concerned, we have
3. Results
In this section, different expressions and relationships will be released that link different aspects related to blade design: power of the turbine that would mount that blade, rotor diameter, blade length, blade mass... Subsequently, the results found relative to the different elements of the turbine dynamics will be shown, especially the inertia of the blades.
3.1. Expressions relating weight and blade length
Each blade model is designed for certain wind conditions, which determine its geometry and mass, and therefore its inertia. The different conditions are included in the IEC 61400 standard, which distinguishes several classes depending on the average speed (IEC Class I, II and III) and turbulence (subclasses A and B), class IA being the most demanding in terms of design requirements. Table 2 shows a comparison of the average mass of a blade as a function of wind class and power. An additional class T is for areas with typhoons and sometimes class S is also indicated, alone or in combination with another class, for non-standard conditions specified by the manufacturer. Different versions are often made of a blade model, each one adapted to a certain class.
The left-hand plot of Figure 4 shows the dependence between the mass and the length of the blade for different classes of design. Some weight reduction is observed for class III turbines, but contrary to what is shown in Table 2, there is no significant difference between class I and class II turbines.
On the other hand, the experience and trajectory of each blade manufacturer usually leads to using a different material and method for its structure. At first it was mainly polyester resin reinforced with glass fibres, whose matrix has been displaced by epoxy resin whose composites exhibit better properties than polyester resin. Both of them are considered as glass fibre reinforced polymer (GFRP). Later, carbon fibres reinforced polymer (CFRP) have been introduced to substitute glass or have been combined to form hybrid glass-carbon blades (Gl-C/Ep) [22,23].
In the right-hand plot of Figure 4, the blades have been classified according to the essential material employed in their manufacture. In the set of study it was observed that composite materials based on fibres and polymers have displaced metals or wood, with a clear predominance of blades using GFRP, being difficult to determine whether the matrix is polyester or epoxy. Blades based on CFRP, are less frequent and usually appear as hybrid composites (CFRP/GFRP). For this material a certain decrease in the weight of the blade is observed. The opposite occurs for steel blades, significantly heavier, although it should be mentioned that these are two-blade turbines.
Table 3 list the relationship between M and L found for every case of study, with M expressed in kg and L in m.
The relative bad correlation (0.865) found in turbines larger than 3 MW indicates that there is great variability due to design conditions and material, so it is convenient to know the IEC class and the material to have a good estimate of the weight, if this is unknown.
3.2. Inertia obtained from density distribution
The most distinctive aspect of this work is to offer a set of inertia values obtained by DDs of different models of blade found in the literature. This distribution is not arbitrary, but a consequence of a detailed structural and aerodynamical analysis. These data are organized in the Mendeley [16] repository, along with a Matlab script to retrieve the data. From them, the inertia has been calculated for each of the blade models presented, as well as the position of the CoG with respect to the centre of rotation.
Figure 5 represents the mass distribution along the blade for twenty-one blade models. Data have been interpolated for each model in order to provide 101 values uniformly separated between 0 and 1, where 0 is the blade root and 1 is its tip.
The result of operating with these data is shown in Table 4. The meaning of each column is the following:
- Capacity of the turbine for which the blade is designed.
- Maximum rotational speed. It matches the rated rotor speed of the turbine.
- Blade Mass, as extracted from the reference (up) and calculated by integration (down).
- Inertia of the blade, as extracted from the reference (up)1 and calculated by integration (down).
- Inertia of the three blades, as extracted from the reference (up) and calculated by integration (down). Extracted data have been moved, when necessary, to the rotation axis.
- Position of the CoG with respect to the rotation axis, as extracted from the reference (up)1 and calculated by integration (down).
- Calculated position of the CoG, divided by the the rotor radius.
- Value for the coefficient .
- Time constant of Inertia H.
- Reference where data have been obtained.
1 A value of CoG or Inertia appears in cursive when it is referred to the blade root instead of to the rotation axis.
In many cases, the inertia value does not appear as such, but as "First Mass moment of inertia", as in [24]. In this case, it must be divided by . Also, attention must be paid to whether the CoG value refers to the axis of rotation or to the root of the blade. In the latter case, for purposes of inertia of the rotor as a whole, must be added. The latter also applies to inertia (also designated as "Second mass moment of inertia"), and (40) should be applied.
Other inertia values obtained from the literature, although without providing the mass distribution, are included in Table 5. Only data originally provided in , not in s, are included.
As discussed previously, there are different airfoils along the blade span, grouped in four regions. The first region, the root, is the one with the assembly structure with the hub, and the one that must withstand the greatest moments. It is this zone in which a higher density is observed in , and this difference is notable from one model to another. Anyway, since this region is close to the AoR, its influence on inertia is small.
If one tries to find some type of relationship between the inertia J of the blade as a function of the mass and the length of the blade, expressions are obtained with an apparently good correlation. Thus, looking for a relation of the type , it yields
A relationship of the type has also been tested, with the result
Figure 6 represents in blue the inertia values obtained from the mass distribution extracted from the references in Table 4, and which is taken as reference. In purple and green, the direct estimates of inertia from the expressions (45) and (46), respectively, are shown respectively. It is observed that for these estimates, obtained without taking geometry into account, there is a deviation of the estimated values (purple and green points) with respect to the value taken as reference (blue).
In the following, the blade geometry will be included in the inertia estimation through the CoG position. Accordingly, a more precise estimation of the blade inertia is obtained comparing columns 7 () and 8 () of Table 4. It is represented in Figure 7 with a good correlation between them (), in the form
and
The result of applying (50) is observed in Figure 6 as the items with red marker, and compared to the results of applying (45) and (46). As can be seen, the values obtained from the CoG (red marker) are very similar to the ones calculated from the DD (in blue). Consequently, expression (50) allows for a precise estimate of the inertia once the mass, length and CoG positions are known.
It should be mentioned that when the value of is used as abscissa instead of , a similar relationship is obtained, although with a somewhat lower correlation (). However, there is no observed dependence between the turbine capacity, identified through the marker colour in Figure 7, and .
3.3. Drive Train
Based on data obtained from [20], it can be seen that medium-speed wind turbines use planetary gears, with 1 or 2 stages. Clipper wind turbines, with 4 synchronous generators per turbine, and those that mount the WinDrive system are practically the only high-speed models with 2 stages. All others with speed above 1000 rpm have 3 stages, mainly combining spur and planetary, specifically 181 models of 241. There are some other models (37/241) with planetary gears along with helical, spur gears only (7/241) or just planetary (6/241). Each type has a transmission structure that gives different stiffness constants [43].
The values found are very scarce, and in many cases they do not really provide adequate reliability on the origin of their obtaining. They are represented in Table 6, where dimensional values are in uppercase and p.u. are lowercase. The parameters are those indicated in Figure 2.
Most of these values are in the range specified by Gonzalez-Longatt in [11]: LSS stiffness, (p.u./) 0.35-0.70; HSS stiffness, (p.u./) (p.u.) 2.00 - 4.00. In general, the coupling on the slow shaft is, less rigid than that of the fast shaft. Also, within their wide ranges, the turbines with active-stall control typically occupy the upper values, and those with pitch control occupy the lower ones.
3.4. Hub inertia
The hub is the weightier rotating component, and therefore its inertia must be taken into account or, at least, analyzed. Table 7 lists some values found in the literature.
Although the weight of the hub is on the order of twice that of a blade, its concentration around the axis of rotation means that the inertia, expressed in s, does not have a representative value with respect to the general dynamics.
3.5. Generator inertia
This component, although not as heavy as the hub, will add significant inertia to the system dynamics, since, except in the case of direct coupled turbines, there will be a gear box to accommodate the rotor and generator speeds. Thus, although the inertia of the generator in is not that high, when viewed from the slow axis of the gear box, its apparent inertia is multiplied by the gear ratio squared. In this case, the time constant is obtained from the expression (26). Table 8 lists some representative values.
Other values, supplied directly in s, are: for a 2 MW DFIG [53]; for a 0.6 MW DFIG [47]; for a 0.75 MW DGIG [10]; for a 1.5 MW PMSG [49]; for a 1.67 MW DFIG [13]; for a 2 MW PMSG [54]; for a 5 MW DFIG [50].
These values are more significant to those from the hub, and should be considered in dynamic studies. It is also observed that there is a great variability in the value of H, and it will be difficult to extract some generic law because the inertia will depend on the constructive characteristics of the rotor, mainly depending on whether the generator is an IG or a PMSG.
4. Discussion
The main focus of this article has been to provide reliable inertia data for the wind turbine. For this reason, values recovered from the bibliographic search have not been included.
An expression has been proposed that quite accurately links inertia to the mass of the blade, its length, and the position of the center of gravity, although the latter is only slightly easier to find than the inertia itself. Two expressions have also been proposed, very similar in their results, which do not require CoG data, although there is a deviation for some blade models with less conventional geometry.
In order to model the mechanical power transmission dynamics, the secondary purpose is to establish an end-to-end dimensionless framework of the mechanical magnitudes that come into play in the turbine dynamics, and collect existing data on the inertia of the rest of the components and other mechanical parameters such as stiffness, friction and damping. Since the data found are scarcer, values in p.u. found in the literature have been incorporated to the review, despite the fact that many are not entirely reliable, or have not been defined very well the base magnitudes of the adimensionalization.
Author Contributions
Conceptualization, Angel Gonzalez-Rodriguez and Juan Roldan-Fernandez; Data curation, Angel Gonzalez-Rodriguez and Luis Nieto-Nieto; Formal analysis, Angel Gonzalez-Rodriguez and Juan Roldan-Fernandez; Investigation, Angel Gonzalez-Rodriguez and Luis Nieto-Nieto; Methodology, Angel Gonzalez-Rodriguez and Luis Nieto-Nieto; Project administration, Angel Gonzalez-Rodriguez; Resources, Luis Nieto-Nieto; Software, Angel Gonzalez-Rodriguez and Luis Nieto-Nieto; Supervision, Juan Roldan-Fernandez; Validation, Angel Gonzalez-Rodriguez and Luis Nieto-Nieto; Visualization, Angel Gonzalez-Rodriguez and Juan Roldan-Fernandez; Writing – original draft, Angel Gonzalez-Rodriguez; Writing – review & editing, Juan Roldan-Fernandez. - All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Data with the DD and other data related to blade models can be found in [16].
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AoR | Axis of rotation |
| B | Blade |
| CoG | Center of gravity |
| DD | Density distribution |
| DFIG | Doubly-fed induction generator |
| G | Generator |
| GB | Gear Box |
| IG | Induction generator |
| number of pole pairs | |
| gearbox ratio | |
| HSS | High Speed Shaft |
| LSS | Low Speed Shaft |
| P | Turbine rated capacity |
| PMSG | Permanent magnet synchronous generator |
| T | Turbine or turbine rotor |
| W | Wind |
| WT | Wind Turbine |
The following variables are used in this manuscript:
| Magnitude | Symbol [units] | Referred to base [units] |
| Inertia | J | H |
| Torsion stiffness | K | k |
| Mutual damping | C | c |
| Shelf damping | D | d |
References
- Li, H.; Zhao, B.; Yang, C.; Chen, H.W.; Chen, Z. Analysis and estimation of transient stability for a grid-connected wind turbine with induction generator. Renew. Energy 2011, 36, 1469–1476. [Google Scholar] [CrossRef]
- Fernández-Guillamón, A.; Vigueras-Rodríguez, A.; Molina-García, Á. Analysis of power system inertia estimation in high wind power plant integration scenarios. IET Renew. Power Gener. 2019, 13, 2807–2816. [Google Scholar] [CrossRef]
- Miao, L.; Wen, J.; Xie, H.; Yue, C.; Lee, W.J. Coordinated Control Strategy of Wind Turbine Generator and Energy Storage Equipment for Frequency Support. IEEE Transactions on Industry Applications 2015, 51, 2732–2742. [Google Scholar] [CrossRef]
- He, X.; Geng, H.; Mu, G. Modeling of wind turbine generators for power system stability studies: A review. Renew. Sustain. Energy Rev. 2021, 143, 110865. [Google Scholar] [CrossRef]
- Ekanayake, J.; Jenkins, N. Comparison of the response of doubly fed and fixed-speed induction generator wind turbines to changes in network frequency. IEEE Trans. Energy Convers. 2004, 19, 800–802. [Google Scholar] [CrossRef]
- Morren, J.; Pierik, J.; de Haan, S.W. Inertial response of variable speed wind turbines. Electric Power Systems Research 2006, 76, 980–987. [Google Scholar] [CrossRef]
- Tielens, P.; Van Hertem, D. The relevance of inertia in power systems. Renew. Sustain. Energy Rev. 2016, 55, 999–1009. [Google Scholar] [CrossRef]
- Gonzalez-Longatt, F.M. Effects of the synthetic inertia from wind power on the total system inertia: Simulation study. 2nd Int. Symp. Environ. Friendly Energies Appl. EFEA 2012 2012, pp. 389–395. [CrossRef]
- Fernández-Guillamón, A.; Gómez-Lázaro, E.; Muljadi, E.; Molina-García, Á. Power systems with high renewable energy sources: A review of inertia and frequency control strategies over time. Renew. Sustain. Energy Rev. 2019, 115. [Google Scholar] [CrossRef]
- Girsang, I.P.; Dhupia, J.S.; Muljadi, E.; Singh, M.; Pao, L.Y. Gearbox and drivetrain models to study dynamic effects of modern wind turbines. IEEE Trans. Ind. Appl. 2014, 50, 3777–3786. [Google Scholar] [CrossRef]
- Gonzalez-Longatt, F.; Regulski, P.; Novanda, H.; Terzija, P. Effect of the shaft stiffness on the inertial response of the fixed speed wind turbines and its contribution to the system inertia. APAP 2011 - Proceedings: 2011 International Conference on Advanced Power System Automation and Protection, 2011, Vol. 2. [CrossRef]
- Akhmatov, V.; Knudsen, H. An aggregate model of a grid connected, large scale, offshore wind farm for power stability investigations - importance of windmill mechanical system. Electrical Power and Energy Systems 2002, 24, 709–717. [Google Scholar] [CrossRef]
- Rahimi, M. Drive train dynamics assessment and speed controller design in variable speed wind turbines. Renew. Energy 2016, 89, 716–729. [Google Scholar] [CrossRef]
- Frøyd, L.; Dahlhaug, O.G. Rotor design for a 10 MW offshore wind turbine. Proc. Int. Offshore Polar Eng. Conf. 2011, 8, 327–334. [Google Scholar]
- Schubel, P.; Crossley, R. Wind Turbine Blade Design Review. Wind Engineering 2012, 36, 365–388. [Google Scholar] [CrossRef]
- Gonzalez-Rodriguez, A.G. Review of mass distribution of wind turbine blades. Mendeley Data, V1, 2023. [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW reference wind turbine for offshore system development. Technical report, NREL, 2009. [CrossRef]
- Bywaters, G.; John, V.; Lynch, J.; Mattila, P.; Norton, G.; Stowell, J.; Salata, M.; Labath, O.; Chertok, A.; Hablanian, D. Northern Power Systems WindPACT Drive Train Alternative Design Study Report. Technical Report October 2004, NREL, 2004. [Google Scholar]
- Fingersh, L.; Hand, M.; Laxson, A. Wind Turbine Design Cost and Scaling Model. NREL 2006, 29, 1–43. [Google Scholar]
- Windturbines database. https://en.wind-turbine-models.com/turbines, accessed on June 2023.
- https://4coffshore.com, accessed on June 2023.
- Lekou, D.J.; Cres, D.C. Results of the benchmark for blade structural models. Technical Report November 2012, InnWind.EU, 2013. [Google Scholar]
- Jackson, K.J.; Zuteck, M.D.; Van Dam, C.P.; Standish, K.J.; Berry, D. Innovative design approaches for large wind turbine blades. Wind Energy 2005, 8, 141–171. [Google Scholar] [CrossRef]
- Rinker, J.; Dykes, K. WindPACT Reference Wind Turbines, 2018.
- Griffin, D.A. Evaluation of Design Concepts for Adaptive Wind Turbine Blades. Technical report, Sandia National Lab, 2002. [CrossRef]
- Bortolotti, P.; Tarres, H.C.; Dykes, K.; Merz, K.; Sethuraman, L.; Verelst, D.; Zahle, F. IEA Wind Task 37 on Systems Engineering in Wind Energy – WP2.1 Reference Wind Turbines. https://github.com/IEAWindTask37/IEA-3.4-130-RWT/tree/master/hawc2/data, accessed on June, 2023. https://www.nrel.gov/docs/fy19osti/73492.pdf.
- Resor, B.R. Definition of a 5MW/61.5 m wind turbine blade reference model. Albuquerque, New Mex. USA, Sandia Natl. Lab. SAND2013-2569 2013 2013, 2013, 50. [Google Scholar]
- Lindenburg, C. Aeroelastic Analysis of the LMH64-5 Blade Concept. Technical Report June, Energy research Centre of the Netherlands ECN, 2003.
- Bak, C.; Zahle, F.; Bitsche, R.; Kim, T.; Yde, A.; Henriksen, L.C.; Hansen, M.H.; Blasques, J.P.A.A.; Gaunaa, M.; Natarajan, A. The DTU 10-MW Reference Wind Turbine. https://github.com/Seager1989/DTU10MW_FAST_LIN/blob/main/Rotor/DTU_10MW_ElastoDyn_Blades.dat, accessed on July/2023.
- Bortolotti, P.; Tarres, H.C.; Dykes, K.; Merz, K.; Sethuraman, L.; Verelst, D.; Zahle, F. IEA Wind Task 37 on Systems Engineering in Wind Energy – WP2.1 Reference Wind Turbines. https://github.com/IEAWindTask37/IEA-10.0-198-RWT/tree/master/hawc2/data, accessed on June, 2023. https://www.nrel.gov/docs/fy19osti/73492.pdf.
- Griffith, D.T.; Ashwill, T.D. The Sandia 100-meter All-glass Baseline Wind Turbine Blade : SNL100-00, 2011.
- IEA Wind - Offshore Reference Wind - 15MW. https://github.com/IEAWindTask37/IEA-15-240-RWT/blob/master/HAWC2/IEA-15-240-RWT/IEA_15MW_RWT_Blade_st_FPM.st, accessed on June 2023.
- Gaertner, E.; Rinker, J.; Sethuraman, L.; Zahle, F.; Anderson, B.; Barter, G.; Abbas, N.; Meng, F.; Bortolotti, P.; Skrzypinski, W.; Scott, G.; Feil, R.; Bredmose, H.; Dykes, K.; Shields, M.; Allen, C.; Viselli, A. IEA Wind - Offshore Reference Wind - 15MW, 2020.
- Scott, S.; Greaves, P.; Macquart, T.; Pirrera, A. Comparison of blade optimisation strategies for the IEA 15MW reference turbine. J. Phys. Conf. Ser. 2022, 2265, https://github.com/IEAWindTask37/IEA-15-240-RWT/blob/master/HAWC2/IEA-15-240–RWT. [Google Scholar] [CrossRef]
- Sørensen, P.; Madsen, P.; Vikkelsø, A.; Jensen, K.; Fathima, K.; Unnikrishnan, A.; Lakaparampil, Z. Power quality and integration of wind farms in weak grids in India, 2000.
- Carrillo, C.; Feijoo, A.; Cidras, J.; Gonzalez, J. Power fluctuations in an isolated wind plant. IEEE Transactions on Energy Conversion 2004, 19, 217–221. [Google Scholar] [CrossRef]
- Chedid, R.; F. Mrad. Intelligent Control of a Class of Wind Energy Conversion Systems. IEEE Transactions on Energy Conversion 1999, Vol. 14, 1597–1604. [Google Scholar] [CrossRef]
- Garcia, H.; Segundo, J.; Rodríguez, O.; Campos-Amezcua, R.; Jaramillo, O. Harmonic Modelling of the Wind Turbine Induction Generator for Dynamic Analysis of Power Quality. Energies 2018, 11, 104. [Google Scholar] [CrossRef]
- Kayikçi, M.; Milanović, J.V. Dynamic contribution of DFIG-based wind plants to system frequency disturbances. IEEE Trans. Power Syst. 2009, 24, 859–867. [Google Scholar] [CrossRef]
- Licari, J.; Ekanayake, J.; Moore, I. Inertia response from full-power converter-based permanent magnet wind generators. Journal of Modern Power Systems and Clean Energy 2013, 1, 26–33. [Google Scholar] [CrossRef]
- Harrison, S.; Papadopoulos, P.N.; Silva, R.D.; Kinsella, A.; Gutierrez, I.; Egea-Alvarez, A. Impact of Wind Variation on the Measurement of Wind Turbine Inertia Provision. IEEE Access 2021, 9, 122166–122179. [Google Scholar] [CrossRef]
- Mercado-Vargas, M.; Gómez-Lorente, D.; Rabaza, O.; Alameda-Hernandez, E. Aggregated models of permanent magnet synchronous generators wind farms. Renewable Energy 2015, 83, 1287–1298. [Google Scholar] [CrossRef]
- Peeters, J.L.M.; Vandepitte, D.; Sas, P. Analysis of internal drive train dynamics in a wind turbine. Wind Energy 2006, 9, 141–161. [Google Scholar] [CrossRef]
- Petru, T.; Thiringer, T. Modeling of wind turbines for power system studies. IEEE Transactions on Power Systems 2002, 17, 1132–1139. [Google Scholar] [CrossRef]
- Papathanassiou, S.; Papadopoulos, M. Dynamic behavior of variable speed wind turbines under stochastic wind. IEEE Transactions on Energy Conversion 1999, 14, 1617–1623. [Google Scholar] [CrossRef]
- Vilar, C.; Usaola, J.; Amarís, H. A frequency domain approach to wind turbines for flicker analysis. IEEE Trans. Energy Convers. 2003, 18, 335–341. [Google Scholar] [CrossRef]
- Rodriguez, J.; Fernandez, J.; Beato, D.; Iturbe, R.; Usaola, J.; Ledesma, P.; Wilhelmi, J. Incidence on power system dynamics of high penetration of fixed speed and doubly fed wind energy systems: study of the Spanish case. IEEE Transactions on Power Systems 2002, 17, 1089–1095. [Google Scholar] [CrossRef]
- Rahim, Y.; Al-Sabbagh, A. Controlled power transfer from wind driven reluctance generator. IEEE Transactions on Energy Conversion 1997, 12, 275–281. [Google Scholar] [CrossRef]
- Xi, J.; Geng, H.; Yang, G.; Ma, S. Inertial response analysis of PMSG-based WECS with VSG control. The Journal of Engineering 2017, 2017, 897–901. [Google Scholar] [CrossRef]
- Mancilla-David, F.; Domínguez-García, J.L.; De Prada, M.; Gomis-Bellmunt, O.; Singh, M.; Muljadi, E. Modeling and control of Type-2 wind turbines for sub-synchronous resonance damping. Energy Conversion and Management 2015, 97, 315–322. [Google Scholar] [CrossRef]
- Kooijman, H.; Lindenburg, C.; Winkelaar, D.; Hooft. DOWEC 6 MW PRE-DESIGN Aero-elastic modelling of the DOWEC 6 MW pre-design in PHATAS Acknowledgement / Preface, 2003.
- Sethuraman, L.; Xing, Y.; Gao, Z.; Venugopal, V.; Mueller, M.; Moan, T. A 5MW direct-drive generator for floating spar-buoy wind turbine: Development and analysis of a fully coupled Mechanical model. Proc. Inst. Mech. Eng. Part A J. Power Energy 2014, 228, 718–741. [Google Scholar] [CrossRef]
- Zhao, M.; Yuan, X.; Hu, J. Modeling of DFIG Wind Turbine Based on Internal Voltage Motion Equation in Power Systems Phase-Amplitude Dynamics Analysis. IEEE Transactions on Power Systems 2018, 33, 1484–1495. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Z.; Wong, K.P. Advanced Control Strategies of PMSG-Based Wind Turbines for System Inertia Support. IEEE Trans. Power Syst. 2017, 32, 3027–3037. [Google Scholar] [CrossRef]
Figure 1.
Typical components in a wind turbine drive train.

Figure 2.
a) Schematic diagram of the traditional three-mass and b) two-mass equivalent model of a wind turbine. In the two-mass equivalent model, HSS-side values are translated to LSS-side.
Figure 2.
a) Schematic diagram of the traditional three-mass and b) two-mass equivalent model of a wind turbine. In the two-mass equivalent model, HSS-side values are translated to LSS-side.
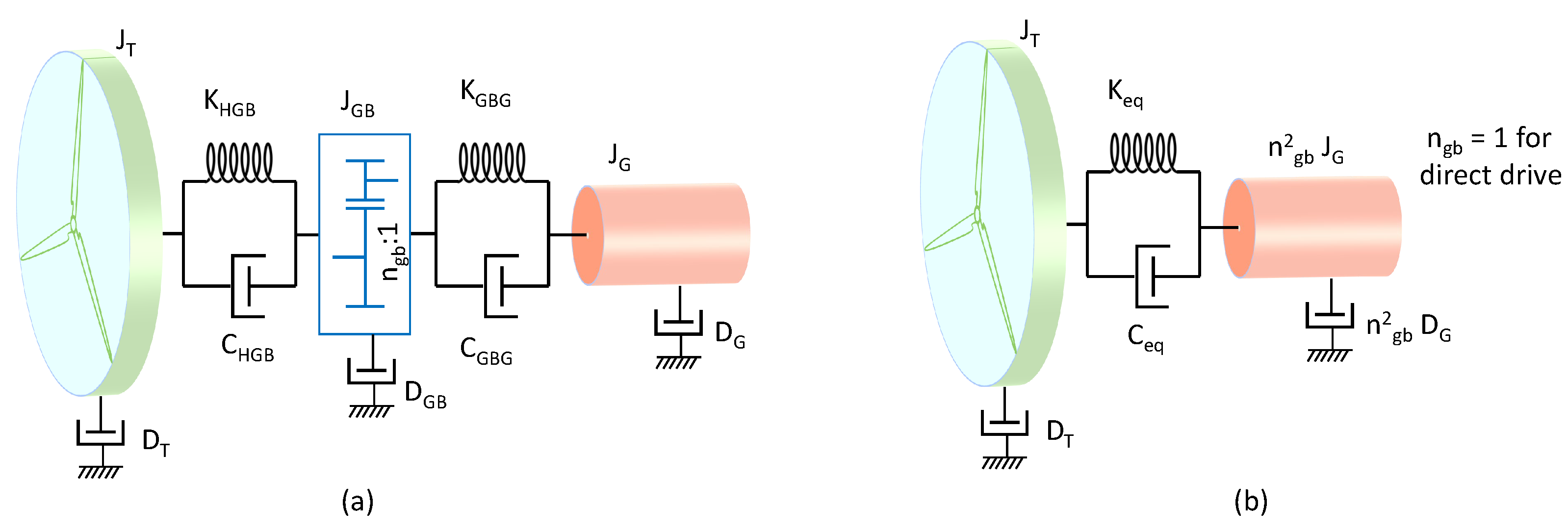
Figure 3.
Position of the CoG with respect to the blade root and the AoR.

Figure 4.
Blade mass as a function of the length: a) for different IEC Class; b) for different materials.
Figure 4.
Blade mass as a function of the length: a) for different IEC Class; b) for different materials.
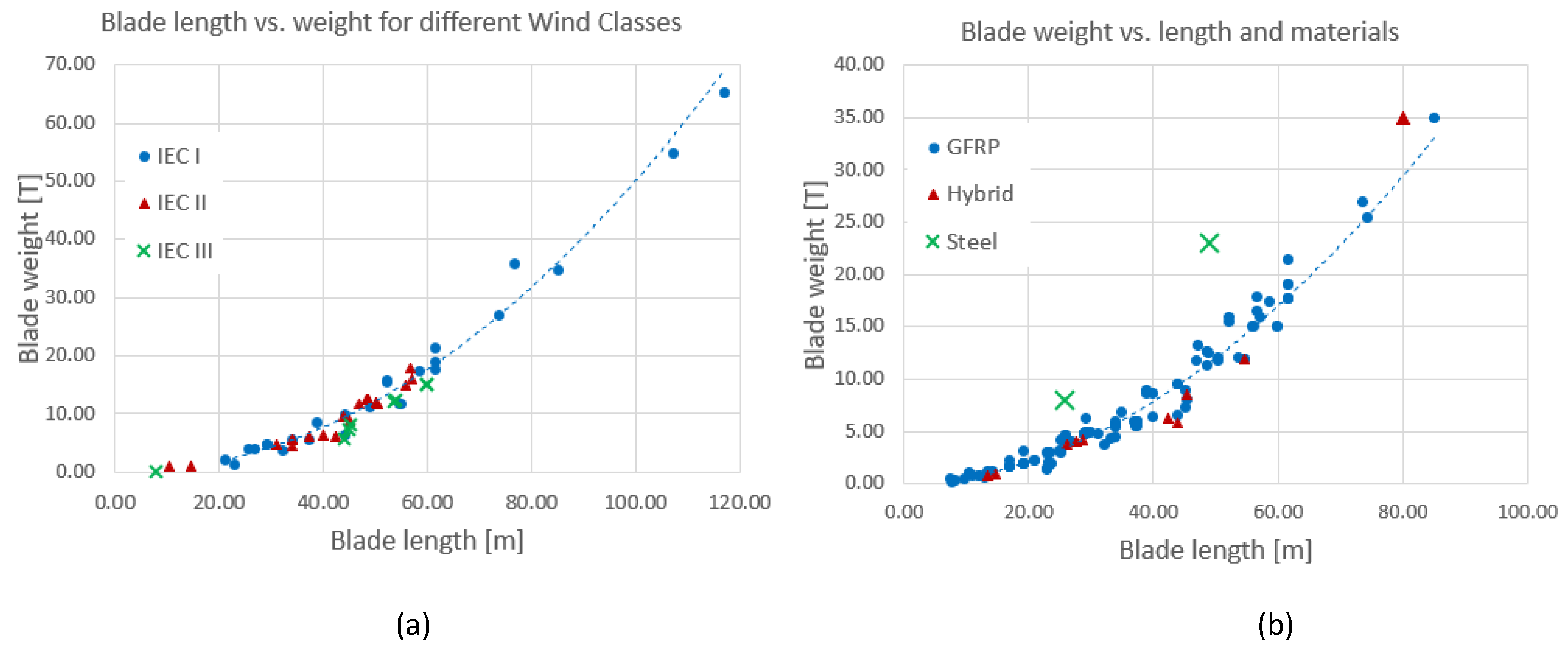
Figure 5.
Mass distribution along the blade for different models. The position along the blade is normalized by dividing into the blade length, starting from the root. The following references apply: Rinker 0.75/1.5/3/5MW [24]; Griffin 1.5MW [25]; Jackson 2.4 Carbon/E-glass [23], Bortolotti 3.4MW [26], Jonkman 5MW [17], Resor 5MW [27], Lindenburg 6MW [28], DTU 10 MW [29], Bortolotti 10MW [30], Lekou 10MW [22], Griffith 10/13.2/15 MW [31], Froyd 10MW [14], Scott 15MW [32], Gaertner 15 MW [33].
Figure 5.
Mass distribution along the blade for different models. The position along the blade is normalized by dividing into the blade length, starting from the root. The following references apply: Rinker 0.75/1.5/3/5MW [24]; Griffin 1.5MW [25]; Jackson 2.4 Carbon/E-glass [23], Bortolotti 3.4MW [26], Jonkman 5MW [17], Resor 5MW [27], Lindenburg 6MW [28], DTU 10 MW [29], Bortolotti 10MW [30], Lekou 10MW [22], Griffith 10/13.2/15 MW [31], Froyd 10MW [14], Scott 15MW [32], Gaertner 15 MW [33].
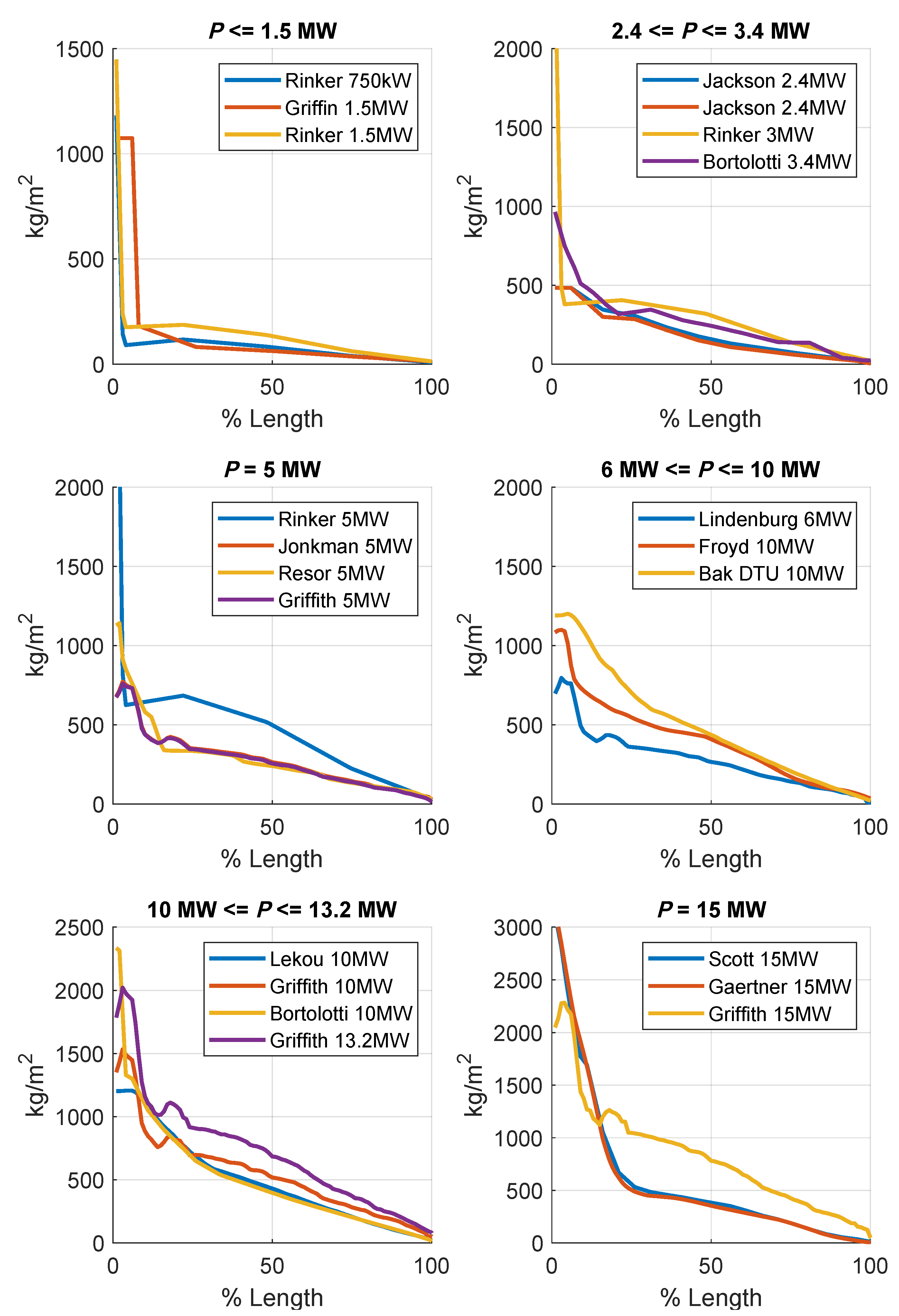
Figure 6.
Comparison of several estimates to obtain J with respect to the value calculated from the DD (blue). In purple, estimate from (45). In green, estimate from (46). In red, estimation from kJ obtained from CoG (50).

Figure 7.
Correlation between the position of the Center of Gravity and the Inertia, obtained from the mass distributions found in the literature. The value L is half the rotor diameter.
Figure 7.
Correlation between the position of the Center of Gravity and the Inertia, obtained from the mass distributions found in the literature. The value L is half the rotor diameter.

Table 1.
Types of generators and corresponding coupling to the turbine rotor.
| Type | Pole pairs | Speed | Drive-Train | Ratio P(kW) M(kg) |
|---|---|---|---|---|
| Squirrel cage induction | 2÷3 | 1000÷1800 rpm | Three stages, >50 | 2 |
| Wound rotor induction | 2÷3 | 1000÷1800 rpm | Three stages, >50 | |
| Synchronous | 5÷12 | 300÷600 rpm1 | Two stages = 12÷45 | |
| Synchronous | 10÷40 | 100÷160 rpm | One stage = 10 | |
| Synchronous | 200÷350 | 10 ÷20 | Direct-drive |
1 Manufacturers as Clipper, Eno Energy or Catum mount fast synchronous machines up to 1600 rpm. 2 The exponent 0.92 for induction generators is coherent with the statement that M ∝ P.
Table 2.
Comparison of blade mass per length depending on the IEC wind class.
| Class I (kg/m) | Class II (kg/m) | Class III (kg/m) | Class IV (kg/m) | Ref | |
|---|---|---|---|---|---|
| 1.5 MW | 163 | 159 | 143 | [22] | |
| 2 MW | 168 | 145 | 131 | [22] | |
| 3 MW | 201.7 | 164.8 | 144.1 | 119.0 | [23] |
Table 3.
Expressions linking M in kg and L in m.
| Designed for | Expression | Correlation |
|---|---|---|
| 0.936 | ||
| 0.865 | ||
| IEC Class I | 0.959 | |
| IEC Class II | 0.944 | |
| IEC Class III | 0.994 | |
| GFRP | 0.961 | |
| Hybrid | 0.909 |
Table 4.
Values relative to mass, length and inertia of several blade models extracted from literature, and compared with the values obtained from the DD appearing in the corresponding reference.
Table 4.
Values relative to mass, length and inertia of several blade models extracted from literature, and compared with the values obtained from the DD appearing in the corresponding reference.
| MW | (rpm) | M (kg) | Ref. | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.750 | 28.65 | 1941 1940 | 1.806E5 2.180E5 | 6.786E5 6.540E5 | 8.770 8.764 | 0.351 | 0.180 | 3.924 | [24] |
| 1.500 | 22.50 | 2530 4408 | - 6.360E5 | - 1.908E6 | - 8.607 | 0.234 | 0.107 | 3.531 | [25] |
| 1.500 | 20.46 | 4336 4332 | 7.985E5 9.653E5 | 3.003E6 2.896E6 | 12.47 12.46 | 0.356 | 0.182 | 4.432 | [24] |
| 2.400 | - | 8799 9560 | - 3.910E6 | - 1.173E7 | - 16.71 | 0.321 | 0.151 | - | [23] |
| 2.400 | - | 7920 8721 | - 3.388E6 | - 1.016E7 | - 16.16 | 0.311 | 0.144 | - | [23] |
| 3.000 | 14.47 | 13238 13230 | 5.012E6 6.070E6 | 1.884E7 1.821E7 | 18.12 18.11 | 0.366 | 0.187 | 6.968 | [24] |
| 3.400 | 8.679 | 16441 16466 | - 1.179E7 | - 3.537E7 | - 21.78 | 0.335 | 0.169 | 4.297 | [26] |
| 5.000 | 11.19 | 27854 27880 | 1.748E7 2.121E7 | 6.579E7 6.362E7 | 23.42 23.38 | 0.365 | 0.186 | 8.737 | [24] |
| 5.000 | 12.10 | 17740 16838 | 1.178E7 1.216E7 | 3.896E7 3.648E7 | 21.98 21.99 | 0.349 | 0.182 | 5.857 | [17] |
| 5.000 | 11.84 | 17700 17012 | 1.178E7 1.159E7 | 3.876E7 3.477E7 | 0.500 20.77 | 0.330 | 0.172 | 5.348 | [27] |
| 5.000 | 12.10 | 17740 16430 | - 1.158E7 | - 3.474E7 | 20.50 21.70 | 0.344 | 0.178 | 5.578 | [31] |
| 6.000 | 11.84 | 17334 17337 | 1.284E7 1.330E7 | 3.850E7 3.990E7 | - 22.97 | 0.353 | 0.181 | 5.115 | [28] |
| 10.000 | 12.95 | 27200 26773 | - 2.351E7 | - 7.053E7 | - 24.75 | 0.349 | 0.175 | 6.485 | [14] |
| 10.000 | 9.600 | - 41699 | - 5.163E7 | - 1.549E8 | - 28.89 | 0.324 | 0.156 | 7.827 | [29] |
| 10.000 | 9.600 | 42363 41620 | - 5.072E7 | - 1.522E8 | 31.60 28.61 | 0.322 | 0.155 | 7.690 | [22] |
| 10.000 | 8.560 | 50184 47104 | - 6.714E7 | - 2.014E8 | 29.00 30.91 | 0.347 | 0.180 | 8.092 | [31] |
| 10.000 | 8.680 | 47700 47943 | - 6.717E7 | - 2.015E8 | - 29.57 | 0.299 | 0.143 | 8.325 | [30] |
| 13.200 | 7.440 | 76402 71234 | - 1.340E8 | - 4.020E8 | 33.40 35.52 | 0.347 | 0.179 | 9.244 | [31] |
| 15.000 | 7.560 | 68415 67003 | - 1.126E8 | - 3.378E8 | - 31.34 | 0.259 | 0.115 | 7.058 | [34] |
| 15.000 | 7.560 | 65250 65417 | - 1.053E8 | - 3.160E8 | 2.970 30.40 | 0.251 | 0.110 | 6.603 | [33] |
| 15.000 | 6.990 | 92131 86626 | - 1.855E8 | - 5.565E8 | 35.60 37.87 | 0.347 | 0.180 | 9.939 | [31] |
Table 5.
Other values relative to mass, length and inertia of several blade models extracted from literature.
Table 5.
Other values relative to mass, length and inertia of several blade models extracted from literature.
| MW | (rpm) | J() | H(s) | Ref. | |
|---|---|---|---|---|---|
| 0.225 | 42.74 | 23.40:1 | 66000 | 2.937 | [35] |
| 0.225 | 41.00 | 23.40:1 | 66058 | 2.706 | [36] |
| 0.350 | 19.21 | 21.81:1 | 3.500E5 | 2.023 | [37] |
| 0.900 | 22.22 | 67.50:1 | 1.600E6 | 4.814 | [38] |
| 1.270 | 20.00 | 90.00:1 | 3.716E6 | 6.417 | [39] |
| 2.000 | 18.00 | 83.33:1 | 6.029E6 | 5.355 | [40] |
| 3.000 | 16.67 | 3.00:1 | 1.300E7 | 6.600 1 | [41] |
| 5.000 | 15.00 | 1.00:1 | 2.530E7 | 6.243 2 | [42] |
1 A direct drive is claimed in the article, but this would lead to a tip speed of 227 m/s. H has been obtained assuming a tip speed of 76 m/s. 2 The number of poles found in the reference is 200, but with this value, the tip speed is 196 m/s. It has been assumed that 200 is the number of pole pairs.
Table 6.
Values for the drive train components of Figure 2, obtained from the literature.
Table 6.
Values for the drive train components of Figure 2, obtained from the literature.
| MW | (rpm) | (Nm/rad) (pu/el.rad) | (Nm/rad) (pu/el.rad) | or (Nms/rad) or (pu) | (Nms/rad) (pu) | Ref. | |
|---|---|---|---|---|---|---|---|
| 0.180 | 42.00 | 24 | - | 2700.0 0.52 | - / - | - / - / - | [44] |
| 0.200 | 57.69 | 26 | - | - | 3.500/ 10.00 | 0.022/ 0.020/ 0.010 | [45] |
| 0.225 | 42.74 | 23 | 5.10E+06 1.4 | - | - / - | - / - / - | [35] |
| 0.225 | 41.00 | 23 | - | 2242.0 0.33 | - / - | 334/ - /0.61 0.027/ - / 0.027 | [36] |
| 0.330 | 34.00 | - | 3.181 | 2.301 | 32.19/ - | 0.004/ - / 0.004 | [46] |
| 0.500 | - | - | 54.8 | 1834.1 | 3.500/ 10.00 | 0.022/ 0.022/ 0.035 | [11] |
| 0.600 | - | - | 50.0 | 1834.1 | 1.000/ 10.00 | 0.005/ 0.022/ 0.005 | [47] |
| 0.750 | 28.65 | 63 | 1.30E+08 4.1 | - | 2.78E+05 3.3 | - / - / - | [24] |
| 0.900 | 22.22 | 68 | 6.00E+07 1.1 | - | 1.00E+06 6 | - / - / - | [38] |
| 1.000 | 41.78 | 22 | - | 1.00E+06 24 | - / - | - / - / - | [48] |
| 1.270 | 20.00 | 90 | 2.74E+08 2.5 | - | 5.02E+05 1.7 | - / - / - | [39] |
| 1.500 | 20.46 | 88 | 4.83E+08 3.9 | - | 1.36E+06 4.2 | - / - / - | [24] |
| 1.500 | 20.70 | 1.0 | 2.00 | - | - / - | - / - / - | [49] |
| 1.670 | 16.00 | 75 | 0.60 | - | 1.200 | - / - / - | [13] |
| 2.000 | 18.00 | 83 | 1.60E+08 0.9 | - | 2.50E+05 0.44 | - / - / - | [40] |
| 3.000 | 14.47 | 124.4 | 1.04E+09 2.1 | - | 4.99E+06 3.8 | - / - / - | [24] |
| 5.000 | 12.10 | 97 | 8.68E+08 0.74 | - | 6.22E+06 2/ - | - / - / - | [17] |
| 5.000 | 11.19 | 160.8 | 2.30E+09 1.7 | - | 1.49E+07 4.1 | - / - / - | [24] |
| 5.000 | 12.37 | 145.5 | 0.30 | - | 0.00372 | - / - / - | [50] |
| 6.000 | 11.84 | 93 | 3.29E+08 0.22 | 2.78E+06 16 | - / - | - / - / - | [51] |
Table 7.
Values for hub inertia obtained from the literature.
| MW | (rpm) | J() | H(s) | Ref. | |
|---|---|---|---|---|---|
| 0.750 | 28.65 | 62.832:1 | 5160 | 0.031 | [24] |
| 1.500 | 20.46 | 87.965:1 | 2.998E4 | 0.046 | [24] |
| 3.000 | 14.47 | 124.407:1 | 1.980E5 | 0.076 | [24] |
| 5.000 | 11.19 | 160.85:1 | 6.685E5 | 0.092 | [24] |
| 5.000 | 12.10 | 97.1:1 | 1.160E5 | 0.0191 | [31] |
| 5.000 | 12.10 | 97.1:1 | 1.159E5 | 0.0191 | [17] |
| 6.000 | 11.84 | 92.873:1 | 5.070E4 | 0.006 | [51] |
| 10.000 | 8.560 | 137.256:1 | 4.640E5 | 0.0191 | [31] |
| 13.200 | 7.440 | 157.918:1 | 8.120E5 | 0.0191 | [31] |
| 15.000 | 6.990 | 168.084:1 | 1.040E6 | 0.0191 | [31] |
1 The references of [31] are equal to each other, and equal to that of [17] since for this study the NREL 5MW model has been taken as a reference, and the mass moments of inertia were scaled with the fourth power of the diameter scale factor, which in turn inversely determines the speed of rotation.
Table 8.
Values for generator inertia obtained from the literature
| MW | (rpm) | J() | H(s) | f (Hz) | Ref. | ||
|---|---|---|---|---|---|---|---|
| 0.180 | 42.00 | 23.75:1 | 4.500 | 0.136 | 3 | - | [44] |
| 0.225 | 41.00 | 23.40:1 | 10.00 | 0.224 | 3 | 50 | [36] |
| 0.750 | 28.65 | 62.80:1 | 16.65 | 0.394 | 2 | 60 | [24] |
| 0.900 | 22.22 | 67.50:1 | 35184 1 | 0.106 | 2 | 50 | [38] |
| 1.270 | 20.00 | 90.00:1 | 84.08 | 1.176 | 2 | - | [39] |
| 1.500 | 20.46 | 88.00:1 | 56.44 | 0.669 | 2 | 60 | [24] |
| 2.000 | 18.00 | 83.33:1 | 416.6 | 2.570 | 2 | - | [40] |
| 3.000 | 14.47 | 124.40:1 | 177.9 | 1.053 | 2 | 60 | [24] |
| 3.000 | 16.67 | 3.00:1 2 | 1.400E6 | 6.397 | 60 | 50 | [41] |
| 5.000 | 12.10 | 97.10:1 | 534.1 | 0.809 | 3 | - | [17] |
| 5.000 | 11.19 | 160.80:1 | 438.9 | 1.558 | 2 | 60 | [24] |
| 5.000 | 12.10 | 97.10:1 | 534.1 | 0.809 | 3 | - | [31] |
| 5.000 | 12.10 | 1.00:1 | 3.790E5 | 0.061 | 248.0 | - | [52] |
| 10.000 | 8.560 | 137.26:1 | 2140 | 1.620 | 3 | - | [31] |
| 13.200 | 7.440 | 157.92:1 | 3740 | 2.145 | 3 | - | [31] |
| 15.000 | 6.990 | 168.08:1 | 4800 | 2.422 | 3 | - | [31] |
1 The value seems to be referred to the LSS, and consequently expression (22) has been used to obtain H. 2 Appears as direct drive, but with nGB = 1, the tip speed is 227 m/s. Assuming nGB = 3, the tip speed is 75, which is more feasible. The value for JG has been correspondingly divided by
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated








