Preprint
Article
A Comprehensive Design Analysis of MEMS Vibrating Ring Gyroscopes
This is a preprint, it has not been peer-reviewed.
Submitted:
09 August 2023
Posted:
09 August 2023
You are already at the latest version
A peer-reviewed article of this preprint also exists.
Abstract
Microelectromechanical System (MEMS) vibrating gyroscope design considerations are always intriguing due to their microscale mechanical, electrical, and material behavior. MEMS vibrating ring gyroscopes have become important inertial sensors in inertial measurement units (IMU) for navigation and sensing applications. The design of a MEMS vibrating ring gyroscope incorporates an oscillating ring structure as a proof mass, reflecting unique design challenges and possibilities. This paper presents a comprehensive design analysis of the MEMS vibrating ring gyroscope from the mechanical, electrical, and damping perspectives. The mechanical design of the MEMS vibrating ring gyroscope investigates the various frame designs of the vibrating ring structure, as well as the various beam structures, including curved, rectangular, and semicircular beam structures, which are analyzed using mathematical models and finite element analysis (FEA) simulations that provide an in-depth analysis of the stiffness and deflection of the vibrating structures. The electrical designs of the MEMS vibrating ring gyroscope were analyzed using various electrode configurations, electrostatic actuation, and capacitive detection mechanisms, respectively. The design analysis of various forms of damping, including viscous, structural, thermoelastic, and anchor damping, has been discussed. The variety of design structures investigated for MEMS vibrating ring gyroscopes' mechanical, electrical, and damping performance.
Keywords:
-
1. Introduction
The microelectromechanical systems (MEMS) vibrating ring gyroscope contributes significantly to inertial sensing and navigation in various household and space applications [1,2,3,4,5,6,7]. The MEMS vibrating ring gyroscope's symmetric design structure provides numerous advantages over other vibrating gyroscopes. The symmetric design offers greater precision, resolution, mode matching at resonance frequencies, thermal stability, and gyroscope sensitivity [8,9,10,11].
Continuous design innovation contributed to the evolution of MEMS vibrating gyroscopes from the first developed single-ring resonator gyroscope with eight springs and anchor support to the new complex design structures. Single-ring resonators [12,13,14], multi-ring resonators [15], disk resonators [16,17,18], star shaped resonators [19], cobweb shaped resonators [20,21], cylindrically shaped resonators [22,23,24], etc., are some of the possible geometrical classifications for ring resonators. These design variations have been investigated to achieve optimal gyroscope performance [25].
The design's mechanical, electrical, and damping properties are crucial to the operation of the MEMS vibrating gyroscope. The mechanical integrity ensures the design's reliability under inconsistent conditions without compromising the gyroscope's sensitivity [12,26,27]. The electrical design components translate and provide continuous actuation to the motion of vibrating mechanical systems, as well as detect the motion and convert it into electrical signals for the operation of the gyroscope [28]. The damping design analysis is crucial for controlling the vibrational energy, as it provides a system that can withstand severe environments and vibrate without causing damage. The mechanical, electrical, and damping design analyses for MEMS vibrating ring gyroscopes are described below.
2. Mechanical Design
There are numerous mechanical vibrating structures presented for MEMS vibrating gyroscopes [29]. Four common types of MEMS vibrating gyroscopes were discussed in detailed [25]. This paper aims to provide readers with a comprehension of the mechanical and electrical design fundamentals of the MEMS vibrating ring gyroscope. MEMS vibrating gyroscopes have a highly sensitive ring structure. The symmetric design of the vibratory ring gyroscope eliminates the cross-axis sensitivity, which is a major issue for other design structures. Additionally, the mechanical design provides temperature stability and enhanced shock resistance for harsh environments.
In Figure 1, the basic design structure of the MEMS vibrating ring gyroscope is depicted schematically. The ring structure acts as the system's proof mass; beam support structures typically support the ring mass structure, and a centrally placed anchor holds up the entire vibrating structure. Several electrodes are positioned around the ring structure for driving, sensing, and tuning purposes. Figure 1 depicts the rectangular beams attached to the outer ring function as the system's proof mass.
2.1. Dynamic Design System
The typical MEMS vibrating ring gyroscope design consists of the driving and sensing suspension systems. The driving suspension system has a set of driving electrodes, whereas the sensing suspension system has a set of sensing electrodes. The respective structure is positioned on top of the substrate. The driving and sensing electrodes are positioned at an angle of 45 degrees. Typically, the vibrating ring gyroscope has an elliptical mode shape. The driving oscillation elliptical shape appears on the 45-degree node of the ring when the device is subjected to Z-axis rotation. The sensing electrodes detect the change in displacement and transmit the signal to the system in order to realign its position to its initial state. Figure 2 depicts the vibrating ring design structure's schematic diagram.
2.2. Beam Structures
Microelectromechanical systems (MEMS) gyroscopes play a pivotal role as essential inertial sensors in a wide range of applications, encompassing navigation systems, mobile devices, digital cameras, gaming peripherals, and numerous other domains. The beam structures of these sensors consist of essential components. The design, selection of materials, and manufacturing processes employed in constructing these beam structures are crucial factors that significantly impact the reliability and operational effectiveness of the gyroscope. The beam structures facilitate the oscillation of the gyroscope mass in two opposing directions: the driving direction and the external rotation detecting direction. The driving and sensing systems utilize the same gyroscope mass for their operation. In order to ensure proper functioning, it is necessary for the gyroscope proof mass to possess the ability to oscillate freely along two axes.
The proof mass should also be constrained in one vibrational mode while oscillating in the other direction. The dynamic gyroscopic suspension system's design has significance in achieving these objectives, as it assumes the responsibility of suspending the proof mass above the substrate. Several elastic beam structures are frequently employed in MEMS vibrating gyroscopes, and a selection of these structures is provided below.
2.2.1. Rectangular Straight Beam
A rectangular straight beam refers to a beam with a rectangular cross-section that maintains a straight shape. The suspended gyroscope construction consists of a proof mass that is connected to micro elastic beams. These beams are microfabricated using the same structural layer as the suspension system used in MEMS vibrating gyroscopes. The compliance of these elastic beams occurs along the driving direction while they remain stiff in the other sensing direction in the absence of rotation. Rectangular-shaped beams are frequently used in the domain of MEMS vibrating gyroscopes for translational oscillation. The rectangular beam structures are integrated with other beam structures in order to provide structural support for intricate gyroscope designs. Figure 3 shows the typical rectangular straight beam.
The length of the rectangular beam is denoted as L when it is suspended along the X-axis. The width of the beam, suspended along the Y-axis, is represented as w. The height of the beam along the Z-axis is shown as h. The equation for the deflection of a rectangular beam can be stated as follows:
Where is the force applied towards the beam, is the stiffness constant, and is the deflection occurred when the beam is exposed to the applied force. The equation can be written as
Where is the young modulus is the moment of inertia, and L is the length of the rectangular beam. The moment of inertia is expressed in the axis differently. If the force is applied along the X-axis, the is mathematically expressed as
We can write stiffness constants for the rectangular beams along the three axes.
In the same way, the rectangular beam experiences a shear force, and therefore it is needed to find the stiffness constant because of the shear force exposed to the rectangular beam. The deflection occurs due to the applied force for the rectangular beam is given as
Where is the deflection due to the shear force, is the shear force, is the shear modulus , is the Poisson's ratio, is the length of the beam, and is the cross-sectional area of the rectangular beam. The stiffness constant due to the shear force can be written as
2.2.2. Curved Shaped Beam
There are many beam designs to consider for MEMS vibrating ring gyroscopes, with the curve-shaped beam being the most popular for vibrating ring gyroscopes. Figure 4 demonstrates the curved beam's schematic diagram.
The curved beams are subjected to experience applied force Fa and bending moments Mc. The stiffness constant kt for curved beams is the sum of the stiffness constant kt due to the applied force and stiffness constant due to bending moment kb. The schematic view of the curved beam under applied force and bending moment is shown in Figure 5.
When a curved beam is subjected to applied force or external rotation, it experiences bending moment and normal forces; the stiffness constant for the curved beam can be calculated using the strain energy equation [30].
Where is the stress, is the strain, and is the strain energy under applied force. The same equation can be written as
Where is the moment of inertia, is the distance from the neutral axis, is the width of the beam, is the height of the beam, is the bending moment, is the Young’s modulus of the material, and is the differential length of the beam.
The deflection of the curved beam can be described as
The length “L” of the curved beam can be described as
Where is the defined radius of the curved beam, and is the angle in the curved beam. Only half of the curved beam will be considered because of the symmetrical structure design of the curved beam. The schematic view is shown in Figure 6.
The deflection of the curved beam due to the applied force can be derived from the given equations shown below.
The curved shape beam is cut in half, and the bending moment with the angle is given [31].
The half section of the curved shape beam experienced an imaginary bending moment due to the strain energy. The strain energy for the half section of the curved beam is shown below.
Since the above equation is for the half section of the curved beam, and if we have to find the strain energy of the complete curved beam , the final equation becomes.
The structure is symmetric, so and
Equation (28) substitutes into Equation (22)
The partial derivative is taken with respect to the applied force .
Equations (29) and (30) substitute into Equation (21).
The stiffness constant due to the applied and reaction forces of the curved shape beam can be expressed as Equation (34).
The curved beam deflection due to the bending moments refers to Figure 5. (c) is investigated by the strain energy equation method, as shown below.
As we know that the energy is equal to the work done on the system; therefore, we can write as . Substituting the energy equation into the Equation (36).
Similarly, Figure 5. (c) the bending moment value of substituted into equation (37). The final deflection equation for the bending moment is given as equation (38).
The curved shape beam’s stiffness constant caused due to bending moments, and it can be determined by using Equation (39).
2.2.3. Semicircular Support Spring Structure
Semicircular support springs are commonly used in MEMS vibrating ring gyroscopes as support beams. This beam's design structure consists of a combination of a curved beam and two rectangular beams. In earlier sections, the deflection and stiffness constant equations were presented. Figure 7 demonstrates the semicircular beam's fundamental design. Typically, one end of the beam is connected to the anchor support as a fixed support, and the other is attached to the resonating structure.
Applying the previously presented equations can determine the semicircular beam's deflection. As the semicircular beam experiences applied forces, reaction forces, and bending moments, it undergoes deformation. To determine the deflections, we must use multiple equations presented in Table 1 for beam structures.
2.2.4. Beam Structural Analysis
The analysis of semicircular beam deflection is conducted using Ansys software. The study is being conducted using the static structural module. The semicircular beam is composed of two rectangular beams and a curved-shaped beam. The semicircular beam used in the comparison experiments has a radius of 75 µm and a length of 60 µm. The heights of the beam vary between 30 µm and 60 µm. The semicircular beam was subjected to an applied force ranging from 100 µN to 1500 µN. The deflections of the beams were simulated, and analytical results were achieved by using the derived equations. The comparative results obtained from varying beam heights are presented in Figure 8.
The frequency analysis of the semicircular beam is examined using both ANSYS software and analytical methods. The measured frequency observed in the simulation was 5.25 MHz, while the calculated natural frequency was determined to be 5.57 MHz. Table 2 displays the stiffness constant findings obtained from the modeled and analytical methods for the semicircular beam. The minimal percent errors for the frequency and the stiffness constant shows the reliability of the derived analytical equations for the semicircular beam and the comparison of the results with Ansys (FEA) software. Figure 9 illustrates the modal frequency of the semicircular beam.
2.3. Design Frames for MEMS Vibrating Ring Gyroscopes
The frame structures of MEMS vibrating ring gyroscopes are crucial parameters for improving performance, reliability, and decoupling vibrational modes. The frame structures are mainly divided into two broad categories: internal ring structure and outer ring structure. Both of the design frames are discussed below.
2.3.1. Internal Ring Frame Design
In internal ring designs, the anchor support is placed outside the vibrating structure, and the ring structure is connected to the fixed anchor support pillar via flexible elastic beams [32]. By isolating the vibrating structure from any undesirable external vibrations, this internal ring design configuration has the potential to enhance the gyroscope's performance. Internal ring structures are highly adaptable and durable, making them crucial inertial sensors for severe, harsh environments. They are well-suited for use in spacecraft and other related applications that may be exposed to harsh environments due to their resistance to unwanted vibrations. The schematic representation of the internal ring frame design is shown in Figure 10.
2.3.2. External Ring Frame Design
Incorporating an external ring frame is a common design technique utilized in designing and developing MEMS vibrating ring gyroscopes. The design of the external ring frame included the placement of the support anchor and the elastic beam structure inside the ring structure. Significantly enhancing the overall sensitivity of the gyroscope, this design approach's ability to accommodate a reasonably larger vibrating structure is a significant advantage. In contrast to the internal ring frame design, however, this particular design approach presents numerous challenges, particularly in its robustness in harsh environments. A schematic diagram of the external ring frame design is shown in Figure 11.
Numerous designs of vibrating ring gyroscopes can benefit from the use of internal and external ring frame designs. The structures include single-ring gyroscopes, multi-ring gyroscopes, disk resonator gyroscopes, cylindrical shapes, shell forms, and star-shaped structures. The design of the external ring frame can accommodate all of these gyroscope structures. In contrast, the internal ring design of single-ring gyroscopes is quite advantageous. The internal area could be used to install additional tuning electrodes or to deploy and design a small inertial sensor in that space, such as an accelerometer or magnetometer.
3. Electrical Design
MEMS vibrating ring gyroscopes are those MEMS devices that requires a constant force to operate. In general, MEMS gyroscopes require an actuation mechanism for continuous oscillation and a detecting system when the gyroscope is subjected to external rotation. The MEMS vibrating ring gyroscope is typically operated using a variety of actuation and detecting techniques. The actuation mechanisms include piezoelectric, magnetic, electrostatic, and thermo-actuation, whereas the detecting mechanisms include piezoelectric, capacitive, optical, and magnetic.
The electrode setup is also very significant when developing a gyroscope design, as the designed electrodes provide actuation and detecting mechanisms. The electrode setup design for the MEMS vibrating ring gyroscope is discussed in detail below.
3.1. Electrodes Setup
The vibrating ring structure is the most essential part of the MEMS vibrating ring gyroscope design. Multiple electrodes encompass the structure of the vibrating ring for driving and sensing purposes. The driving electrodes provide a continuous motion in two orthogonal axes. On the other hand, the sensing electrodes detect the change in displacement between the ring and the sensing electrode when the gyroscope is exposed to external rotation. There are many ways in which electrodes could be placed around the vibrating ring structure. Some of the common electrode placements in vibrating ring gyroscopes are discussed below.
3.1.1. Outside placement
In this configuration, the electrodes are positioned outside of the vibrating ring structure, while the inner portion of the ring is sustained by flexible beams with a central anchor. This configuration offers numerous advantages, including simple design, efficient connection, simple fabrication, and reduced electronic complexity. However, this design configuration tends to increase device size, which could restrict its use in many electronic applications due to space constraints.
3.1.2. Inside placement
In this design configuration, the electrodes are positioned within the vibrating ring structure, while the ring's exterior is covered and supported by flexible beams with an outer placed anchor. This design configuration accommodates a compact device area, making it suitable for miniaturized electronic devices. However, positioning electrodes within the ring structure complicates the design and requires intricate microfabrication processes.
3.1.3. Both Inside and Outside
In this design configuration, electrodes are positioned inside and outside the vibrating ring structure for optimal results. This type of design configuration effectively minimizes undesirable errors, such as geometrical imperfections caused by microfabrication tolerances, matches resonance frequencies, and eliminates other related errors. However, the complexity of the device's design, fabrication, and electronic circuitry is increased by this design configuration.
All three electrode setup designs are shown in Figure 12.
The design configuration of electrodes can be utilized for a variety of purposes. The advantage of the ring structure is the placement of numerous electrodes around the vibrating structure. Some of the primary functions of electrodes are listed below.
- Driving Electrode: The driving electrodes apply a continuous electrostatic actuation force to the ring's structure, causing it to oscillate in the driving direction.
- Sensing Electrode: These electrodes detect the change in displacement when the device is subjected to rotation via an electrostatic detection mechanism.
- Tuning Electrode: This type of electrode adjusts the resonance frequency to achieve optimal results, thereby enhancing the ring gyroscope's sensitivity.
- Quadrature Electrode: These electrodes mitigate the quadrature error that arises as a result of microfabrication or geometrical inaccuracies.
Considering the portion of the vibrating ring with the electrode as parallel plate capacitors driving and sensing mechanisms in the MEMS vibrating ring gyroscopes. The concept of moving parallel plate capacitors is most commonly employed for MEMS vibrating gyroscopes. The capacitors store charge when the voltage is applied to their terminals. The stored charge between the two parallel plates can be expressed as Equation (40).
𝑄=𝐶𝑉
The two parallel plate capacitors for a portion of the vibrating ring structure with the electrode are shown in Figure 13. The capacitance between the ring structure is given as Equation (41). Where represents the gap between the two electrodes, is the same width for both electrodes, is the same height for both electrodes, and is the free space permittivity constant.
The energy stored in the capacitor is usually found as a function of charge and by using Equation (42).
In the same way, the energy stored in terms of voltage can be determined by using the above equation as the function of voltage.
MEMS vibrating ring gyroscopes require actuation and detection mechanisms for their operations. The most popular and easy-to-implement method is electrostatic for actuation and capacitive for detection. Electrostatic actuation and capacitive detection offer many advantages over other methods as they provide good results and are easy to implement. This section will cover the electrostatic actuation and capacitive detection mechanisms for MEMS vibrating ring gyroscopes.
3.2. Basics of Electrostatic Actuation
Electrostatic actuation is a common mechanism to be utilized in the operation of MEMS vibrating gyroscopes. This mechanism generates electrostatic forces between the two closely placed electrodes. The generated electrostatic forces induce oscillations in the ring structure and maintain those oscillations for driving and sensing purposes. The parallel plate electrodes cause this electrostatic actuation. The electrostatic force field arises when the voltages are applied between the two parallel electrodes.
In the MEMS vibrating ring gyroscope, the electrostatic actuation force provides and regulates the ring structure's continuous oscillation. The parallel plate electrodes generate the electrostatic force via actuation, creating a conservative force between the parallel electrodes. The voltage around the parallel plate electrodes is precisely controlled. The generated electrostatic force is expressed below.
Where is the electrostatic force, is the permittivity of free space, is the height of the electrode, is the width of the electrode, is the gap between the parallel electrodes, and is the displacement of the ring that ultimately reduces the gap between the parallel plates. The schematic diagram of the two parallel plates is shown in Figure 14.
3.2.1. MEMS Vibrating Ring Gyroscope Actuation.
The ring structure in the MEMS vibrating ring gyroscope oscillates by an electrostatic actuation that is generated by applying a voltage across the parallel plate capacitors. The electrostatic actuation force generated by the set of electrodes is directly proportional to the square of the applied voltage difference. When a sinusoidal actuation force is needed, the actuation applied voltages must be selected appropriately to linearize the driving force. The total electrostatic force equation generated by the two opposite parallel plate capacitors and is given below.
The net balanced electrostatic actuation is a widely used strategy to compensate the force as linear with respect to the steady bias voltage VDC and an alternating voltage vAC. This technique involves applying a voltage to one set of driving electrodes and a voltage to the opposite set of driving electrodes, as presented schematically in Figure 15. In a symmetrical vibrating ring gyroscope, the overall electrostatic force simplifies to
The MEMS vibrating ring gyroscope's electrostatic actuator structure can be determined using Equation (48).
Where is the net electrostatic actuation force for the MEMS vibrating ring gyroscope, is the number of driving electrodes and ring portion, is the gap between the two electrodes, is the steady bias voltage, and is an alternating voltage.
3.3. Basics of Capacitive Detection
There are various methods to detect the deflection at sensing electrodes of the MEMS vibrating ring gyroscope. The capacitive detection method is quite popular and easy to design for gyroscopic operation. The capacitance of the parallel plate capacitors with a gap and overlap area is expressed as an equation (49).
Where is the dielectric value of the material between the parallel plate capacitors, the deflection of the ring structure changes the gap between the electrodes. The microfabrication requirements usually determine the ring to electrode gap, this gap usually ranges from a few micrometers to sub-micrometer value. Even a very small deflection provides a high capacitance value.
The capacitance is a nonlinear function of the deflection in capacitive detection for parallel plate capacitors. Although, the change in capacitance can be linearized because the deflections used to be very small as compared to the gap between the two electrodes. Let denote the deflection as , which is assumed to be very small compared to the gap. The change in capacitance can be determined by using Equation (50).
3.3.1. MEMS Vibrating Ring Gyroscope Differential Detection.
The ring structure oscillates as an elliptical shape, and when the gyroscope is exposed to the external rotation, the same elliptical shape of deflection starts to appear on the sensing electrodes. The sensing electrodes sense the deflection as capacitive detection between two parallel plate electrodes. The deflection appears orthogonally on the sensing electrodes in the MEMS vibrating ring gyroscope design. The change in capacitance detects on two orthogonally sets of electrodes. Differential capacitance detection is used to linearize the change in capacitance with deflections. The symmetrical sets of sensing electrodes are placed around the vibrating ring structure. The schematic diagram of the capacitive detection for MEMS vibrating ring gyroscope is shown in Figure 16.
When the vibrating ring gyroscope oscillates in the sensing direction, the opposite sets of symmetrical electrodes sense the positive deflection along the sensing electrodes and the higher capacitance at those respective electrodes. At the same time elliptical ring is away from the other set of sensing electrodes, then the lower capacitance value is detected on those electrodes. In this way, the differential detection method is expressed mathematically below.
In Equation (53), the change in capacitance is inversely proportional to the square of the gap between the two parallel plate electrodes. Therefore, it is believed to minimize the gap between the electrodes to enhance the sensitivity and performance of the vibrating ring gyroscopes.
4. Damping Design
Damping in the MEMS vibrating gyroscopes means a decrease in the amplitude of the oscillations in the gyroscope operation over time. It is the energy that is being lost to the surrounding. In any oscillatory system like a gyroscope, damping is one of the important parameters to control the vibrations and stabilize the system. The following types of damping are discussed below for the MEMS vibrating ring gyroscope.
4.1. Viscous Damping
Vibrating structures are subject to viscous damping phenomena due to the resistance offered by the surrounding gases. The vibrating ring, stationary electrodes, and anchor placements cause the viscous damping in the MEMS vibrating ring gyroscope. Due to the drag force in the gyroscope's stationary and oscillating systems, the motion of the ring structure through the atmosphere results in energy dissipation. Typically, viscous damping is linear and proportional to the vibrating ring structure's velocity.
Squeeze film damping is a type of viscous damping. It occurs when two parallel plate surfaces move toward one another and compress the gas-filled space between them. The concept of squeeze film damping for the MEMS vibrating ring gyroscope is quite complex due to the energy dissipation and system stiffness effects. The effective viscosity is crucial for describing the behavior of a gas or its rarefaction effects in squeeze film damping. The term effective viscosity in squeeze film damping is given by [33].
Where is the actual velocity of the gas, and is the Knudsen number which defines the rarefaction effect, and it is dimensionless. The solution of the linearized Reynolds equation attributes one of the forces inphase with the movement of the parallel plates, and the other force is outphase. Both inphase and outphase forces are spring and damping forces , respectively. The equations for the respective forces are given by [34], which are shown below.
Where is the deflection of the plate, is the spacing between the plates, m and n are odd integers, is the area of the parallel plate, and is the height, and is the length of the plate, and is the ambient pressure. The squeeze number is given by [35]. Where is the angular frequency.
4.2. Structural Damping
Structural damping for the MEMS vibrating gyroscope depends on the material's in-ternal structure. This kind of damping is quite a complex model. An easy method is to de-scribe first the material’s properties and then proceed to the damping properties. The model could be analyzed using finite element analysis (FEA) software.
𝐹𝑠𝑑= −𝜏 𝜔 𝑦
Where is the structural damping force, is the loss parameter related to the material's internal friction, is the frequency, is the deflection of the vibrating element.
4.3. Thermoelastic Damping
Thermoelastic damping is one of the main damping mechanisms under vacuum conditions. It is a phenomenon of the material's intrinsic behavior in which the system dissipates thermal energy because of the elastic deformation in the system. In the vibrating ring structure, the tensile and compressive forces generate heat dissipation in the vibrating system that finally affects the vibrational energy of the system. Thermoelastic damping significantly affects the gyroscope quality factor under vacuum conditions ranging from 100k to 200k values. The thermoelastic loss factor can be determined by the given equation (59).
Where is the coefficient of thermal expansion, is the shear modulus of the material, is the density of the material, is the specific heat at constant pressure, is the volume, is the stress, and is the operating temperature of the vibrating system.
4.4. Anchor Damping
Anchor damping could be determined by modeling with consideration of the energy losses at the anchor points through the anchor's design and material properties. This type of damping can be predicted through an accurate finite element analysis. The following simple equation could be used for evaluating anchor damping.
𝐹𝑎𝑑=−𝜏𝑎 𝑦
Where is the damping force, is the anchor loss factor, and is the deflection of the vibrating structure in the MEMS vibrating gyroscope.
5. Conclusion
This paper presents an exhaustive analysis of the MEMS vibrating ring gyroscopes, exploring the complexities of mechanical, electrical, and damping design considerations. A number of different setups of electrode designs, beam structures designs, and frame designs have been studied; each design finding presented its own set of difficulties and opportunities in the MEMS gyroscope field. The paper further investigated the effects of various types of damping, including viscous, structural, thermoelastic, and anchor damping, and their roles on the performance of the vibrating ring gyroscope. These findings contribute to a better understanding of the MEMS vibrating ring gyroscope technology and make avenues for further future investigations in the fields such as navigation systems and other related electronics applications. The research analysis between design complexity, performance, and size limitations was an important objective, highlighting the complexity of MEMS vibrating ring gyroscope design.
Supplementary Materials
The following supporting information can be downloaded at the website of this paper posted on Preprints.org.
Author Contributions
The conceptualization given by K. McKee and I. Howard. All the designing, findings, and preparation of the figures was done by W. A. Gill. Writing: Review and editing the final draft done by W. A. Gill. Supervision done by I. Howard, I. Mazhar and K. McKee.
Funding
The research support funded by research training program (RTP) by Australian government through Curtin University.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shaeffer, D.K. MEMS inertial sensors: A tutorial overview. IEEE Commun. Mag. 2013, 51, 100–109. [Google Scholar] [CrossRef]
- Piyabongkarn, D.; Rajamani, R.; Greminger, M. The development of a MEMS gyroscope for absolute angle measurement. IEEE Trans. Control. Syst. Technol. 2005, 13, 185–195. [Google Scholar] [CrossRef]
- Acar, C.; Schofield, A.R.; Trusov, A.A.; Costlow, L.E.; Shkel, A.M. Environmentally Robust MEMS Vibratory Gyroscopes for Automotive Applications. IEEE Sensors J. 2009, 9, 1895–1906. [Google Scholar] [CrossRef]
- Ren, X.; Zhou, X.; Yu, S.; Wu, X.; Xiao, D. Frequency-Modulated MEMS Gyroscopes: A Review. IEEE Sensors J. 2021, 21, 26426–26446. [Google Scholar] [CrossRef]
- Xia, D.; Yu, C.; Kong, L. The Development of Micromachined Gyroscope Structure and Circuitry Technology. Sensors 2014, 14, 1394–1473. [Google Scholar] [CrossRef]
- Liu K, Zhang W, Chen W, Li K, Dai F, Cui F, et al. The development of micro-gyroscope technology. Journal of Micromechanics and Microengineering 2009, 19, 113001.
- Hyun An B, Gill WA, Lee JS, Han S, Chang HK, Chatterjee AN, et al. Micro-electromechanical vibrating ring gyroscope with structural mode-matching in (100) silicon. sens lett. 2018, 16, 548–551. [CrossRef]
- Jia, J.; Ding, X.; Qin, Z.; Ruan, Z.; Li, W.; Liu, X.; Li, H. Overview and analysis of MEMS Coriolis vibratory ring gyroscope. Measurement 2021, 182, 109704. [Google Scholar] [CrossRef]
- Gill, W.A.; Ali, D.; An, B.H.; Syed, W.U.; Saeed, N.; Al-Shaibah, M.; Elfadel, I.M.; Al Dahmani, S.; Choi, D.S. MEMS multi-vibrating ring gyroscope for space applications. Microsyst. Technol. 2020, 26, 2527–2533. [Google Scholar] [CrossRef]
- Ayazi, F.; Najafi, K. A HARPSS polysilicon vibrating ring gyroscope. J. Microelectromechanical Syst. 2001, 10, 169–179. [Google Scholar] [CrossRef]
- Cao, H.; Liu, Y.; Kou, Z.; Zhang, Y.; Shao, X.; Gao, J.; Huang, K.; Shi, Y.; Tang, J.; Shen, C.; et al. Design, Fabrication and Experiment of Double U-Beam MEMS Vibration Ring Gyroscope. Micromachines 2019, 10, 186. [Google Scholar] [CrossRef]
- Ayazi F, Najafi K, editors. Design and fabrication of high-performance polysilicon vibrating ring gyroscope. Proceedings MEMS 98 IEEE Eleventh Annual International Workshop on Micro Electro Mechanical Systems An Investigation of Micro Structures, Sensors, Actuators, Machines and Systems (Cat No 98CH36176; 1998: IEEE.
- Kou, Z.; Liu, J.; Cao, H.; Shi, Y.; Ren, J.; Zhang, Y. A novel MEMS S-springs vibrating ring gyroscope with atmosphere package. AIP Adv. 2017, 7. [Google Scholar] [CrossRef]
- Syed, W.U.; An, B.H.; Gill, W.A.; Saeed, N.; Al-Shaibah, M.S.; Al Dahmani, S.; Choi, D.S.; Elfadel, I.A.M. Sensor Design Migration: The Case of a VRG. IEEE Sensors J. 2019, 19, 10336–10346. [Google Scholar] [CrossRef]
- Gill, W.A.; Howard, I.; Mazhar, I.; McKee, K. MEMS Vibrating Ring Gyroscope with Worm-Shaped Support Springs for Space Applications. 2022, 31, 2. [CrossRef]
- Challoner AD, Howard HG, Liu JY, editors. Boeing disc resonator gyroscope. 2014 IEEE/ION Position, Location and Navigation Symposium-PLANS 2014; 2014: IEEE.
- Su, T.-H.; Nitzan, S.H.; Taheri-Tehrani, P.; Kline, M.H.; Boser, B.E.; Horsley, D.A. Silicon MEMS Disk Resonator Gyroscope With an Integrated CMOS Analog Front-End. IEEE Sensors J. 2014, 14, 3426–3432. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Q.; Wang, P.; Zhang, Y.; Zhou, X.; Yu, L.; Wu, X.; Xiao, D. 0.015 Degree-Per-Hour Honeycomb Disk Resonator Gyroscope. IEEE Sensors J. 2020, 21, 7326–7338. [Google Scholar] [CrossRef]
- Zaman, M.F.; Sharma, A.; Ayazi, F. The Resonating Star Gyroscope: A Novel Multiple-Shell Silicon Gyroscope With Sub-5 deg/hr Allan Deviation Bias Instability. IEEE Sensors J. 2009, 9, 616–624. [Google Scholar] [CrossRef]
- Chen, F.; Wen, Z.; Xu, D.; Zhou, W.; Li, X. An Anti-Aliasing and Self-Clocking ΣΔM Cobweb-Like Disk Resonant MEMS Gyroscope with Extended Input Range. 2021, 334–337. [CrossRef]
- Fan, B.; Guo, S.; Cheng, M.; Yu, L.; Zhou, M.; Hu, W.; Zheng, F.; Bu, F.; Xu, D. Frequency Symmetry Comparison of Cobweb-Like Disk Resonator Gyroscope With Ring-Like Disk Resonator Gyroscope. IEEE Electron Device Lett. 2019, 40, 1515–1518. [Google Scholar] [CrossRef]
- Wu X, Xi X, Wu Y, Xiao D. Cylindrical Vibratory Gyroscope: Springer; 2021.
- Basarab, M.A.; Lunin, B.S.; Matveev, V.A.; Chumankin, E.A. Static balancing of metal resonators of cylindrical resonator gyroscopes. Gyroscopy Navig. 2014, 5, 213–218. [Google Scholar] [CrossRef]
- Lee, J.S.; An, B.H.; Mansouri, M.; Al Yassi, H.; Taha, I.; Gill, W.A.; Choi, D.S. MEMS vibrating wheel on gimbal gyroscope with high scale factor. Microsyst. Technol. 2019, 25, 4645–4650. [Google Scholar] [CrossRef]
- Gill, W.A.; Howard, I.; Mazhar, I.; McKee, K. A Review of MEMS Vibrating Gyroscopes and Their Reliability Issues in Harsh Environments. Sensors 2022, 22, 7405. [Google Scholar] [CrossRef] [PubMed]
- Khan, I.; Ting, D.S.K.; Ahamed, M.J. Design and development of a MEMS vibrating ring resonator with inner rose petal spring supports. Microsyst. Technol. 2020, 27, 985–995. [Google Scholar] [CrossRef]
- He G, Najafi K, editors. A single-crystal silicon vibrating ring gyroscope. Technical Digest MEMS 2002 IEEE International Conference Fifteenth IEEE International Conference on Micro Electro Mechanical Systems (Cat No 02CH37266); 2002: IEEE.
- Shkel AM, Horowitz R, Seshia AA, Park S, Howe RT, editors. Dynamics and control of micromachined gyroscopes. Proceedings of the 1999 American Control Conference (Cat No 99CH36251); 1999: IEEE.
- Acar C, Shkel A. Mechanical design of MEMS gyroscopes. MEMS Vibratory Gyroscopes: Structural Approaches to Improve Robustness. 2009:1-38.
- Hearn, EJ. Mechanics of Materials 2: The mechanics of elastic and plastic deformation of solids and structural materials: Elsevier; 1997.
- Hagedorn P, DasGupta A. Vibrations and waves in continuous mechanical systems: John Wiley & Sons; 2007.
- Gill, W.A.; Howard, I.; Mazhar, I.; McKee, K. Development of Starfish-Shaped Two-Ring Microelectromechanical Systems (MEMS) Vibratory Ring Gyroscope with C-Shaped Springs for Higher Sensitivity. 2022, 27, 36. [CrossRef]
- Veijola, T.; Kuisma, H.; Lahdenperä, J.; Ryhänen, T. Equivalent-circuit model of the squeezed gas film in a silicon accelerometer. Sensors Actuators A: Phys. 1995, 48, 239–248. [Google Scholar] [CrossRef]
- Blech, J.J. On Isothermal Squeeze Films. J. Lubr. Technol. 1983, 105, 615–620. [Google Scholar] [CrossRef]
- Griffin, W.S.; Richardson, H.H.; Yamanami, S. A Study of Fluid Squeeze-Film Damping. J. Basic Eng. 1966, 88, 451–456. [Google Scholar] [CrossRef]
Figure 1.
A schematic view of a simple vibrating ring gyroscope a) Gyroscope with electrodes b) Electrodes only c) Vibrating ring, beam support, and anchor support.
Figure 1.
A schematic view of a simple vibrating ring gyroscope a) Gyroscope with electrodes b) Electrodes only c) Vibrating ring, beam support, and anchor support.
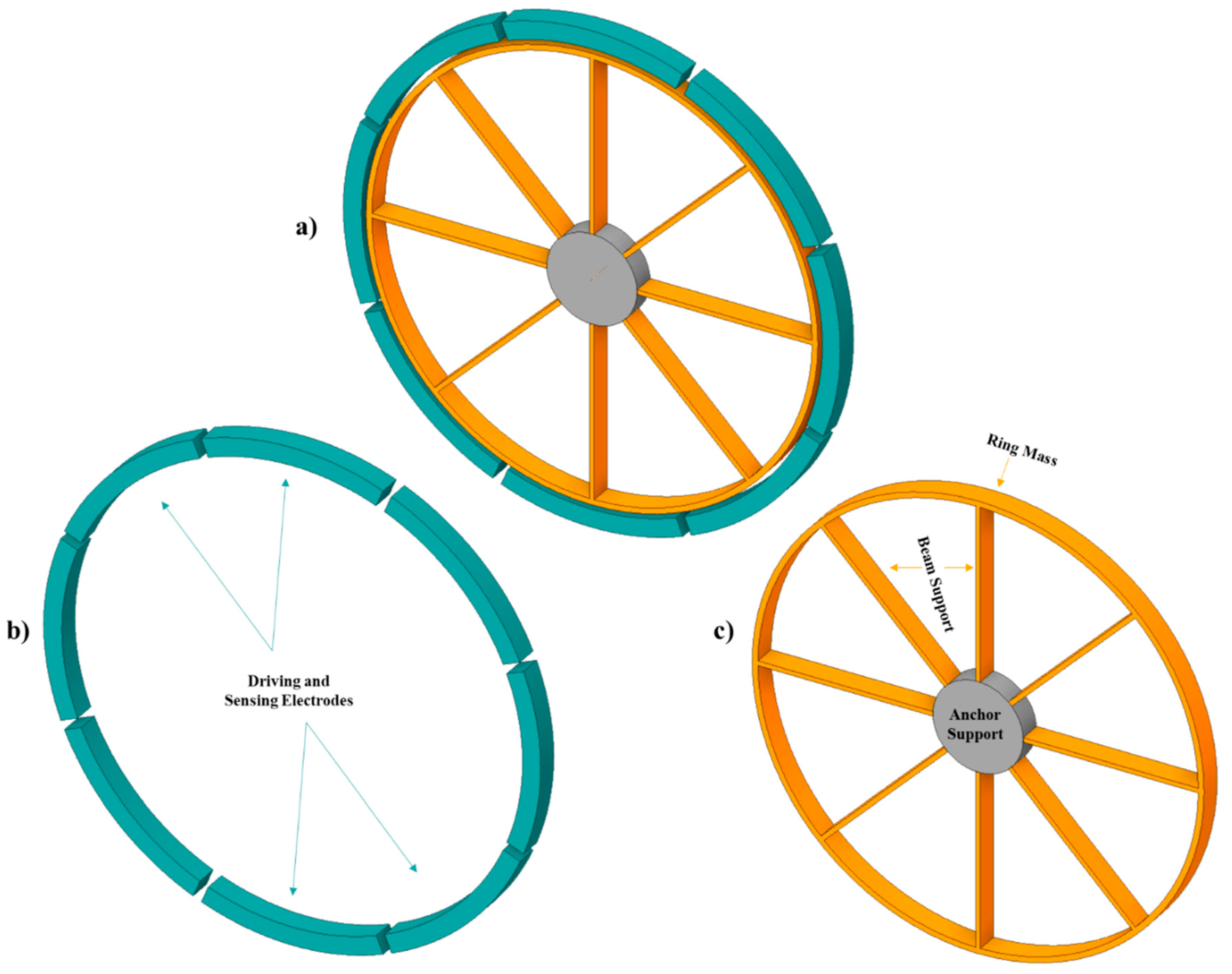
Figure 2.
A schematic view of a Simple Vibrating Ring Gyroscope patterned on the substrate.
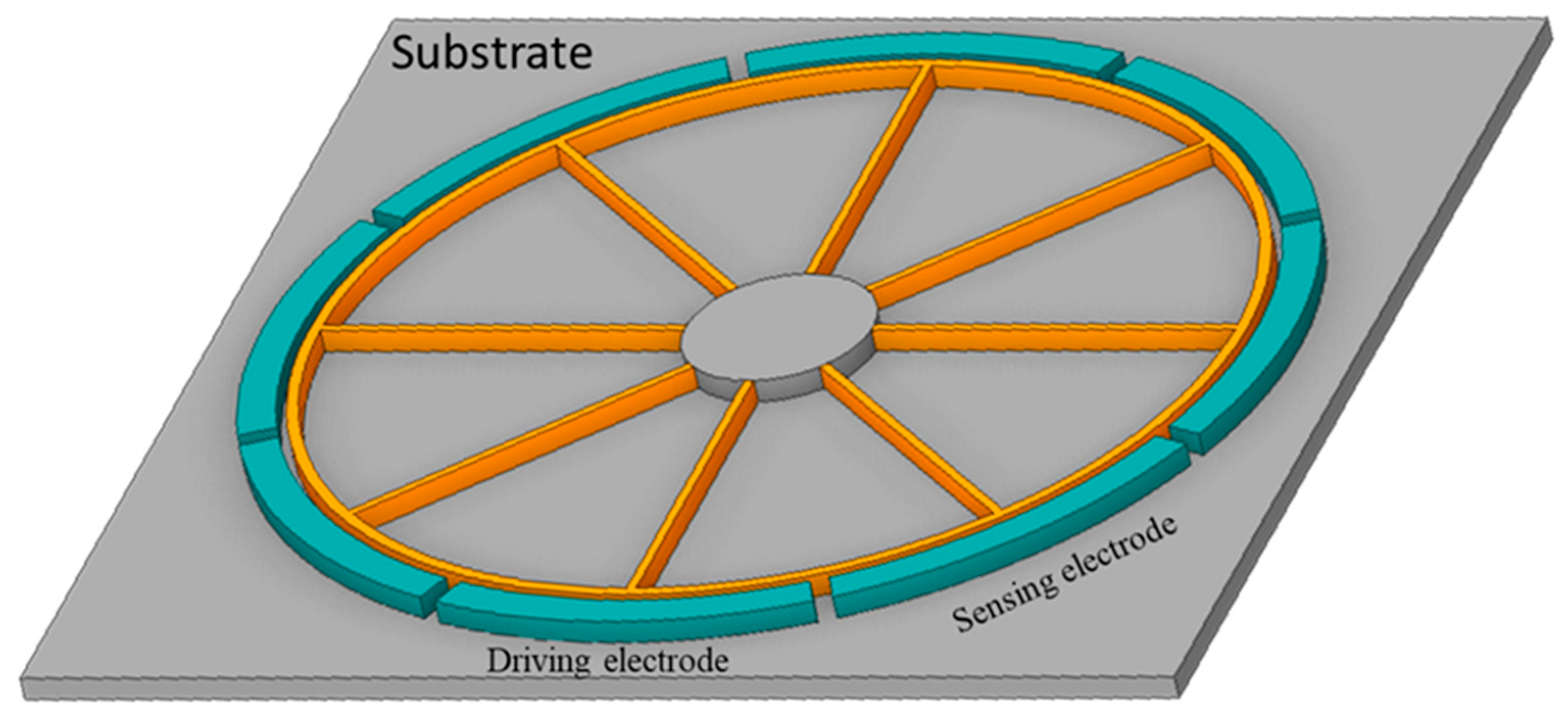
Figure 3.
A schematic diagram of a rectangular shaped beam.
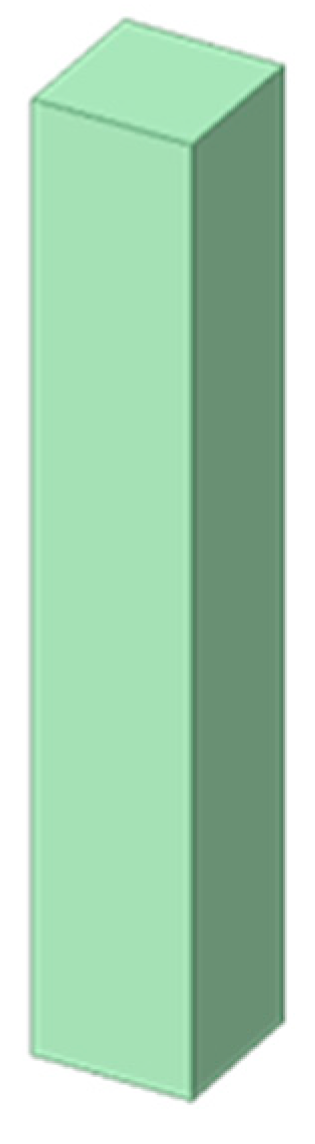
Figure 4.
A schematic diagram of a curved shaped beam structure.

Figure 5.
A schematic illustration of a curved beam subjected to (b) applied force and (c) bending moments.
Figure 5.
A schematic illustration of a curved beam subjected to (b) applied force and (c) bending moments.
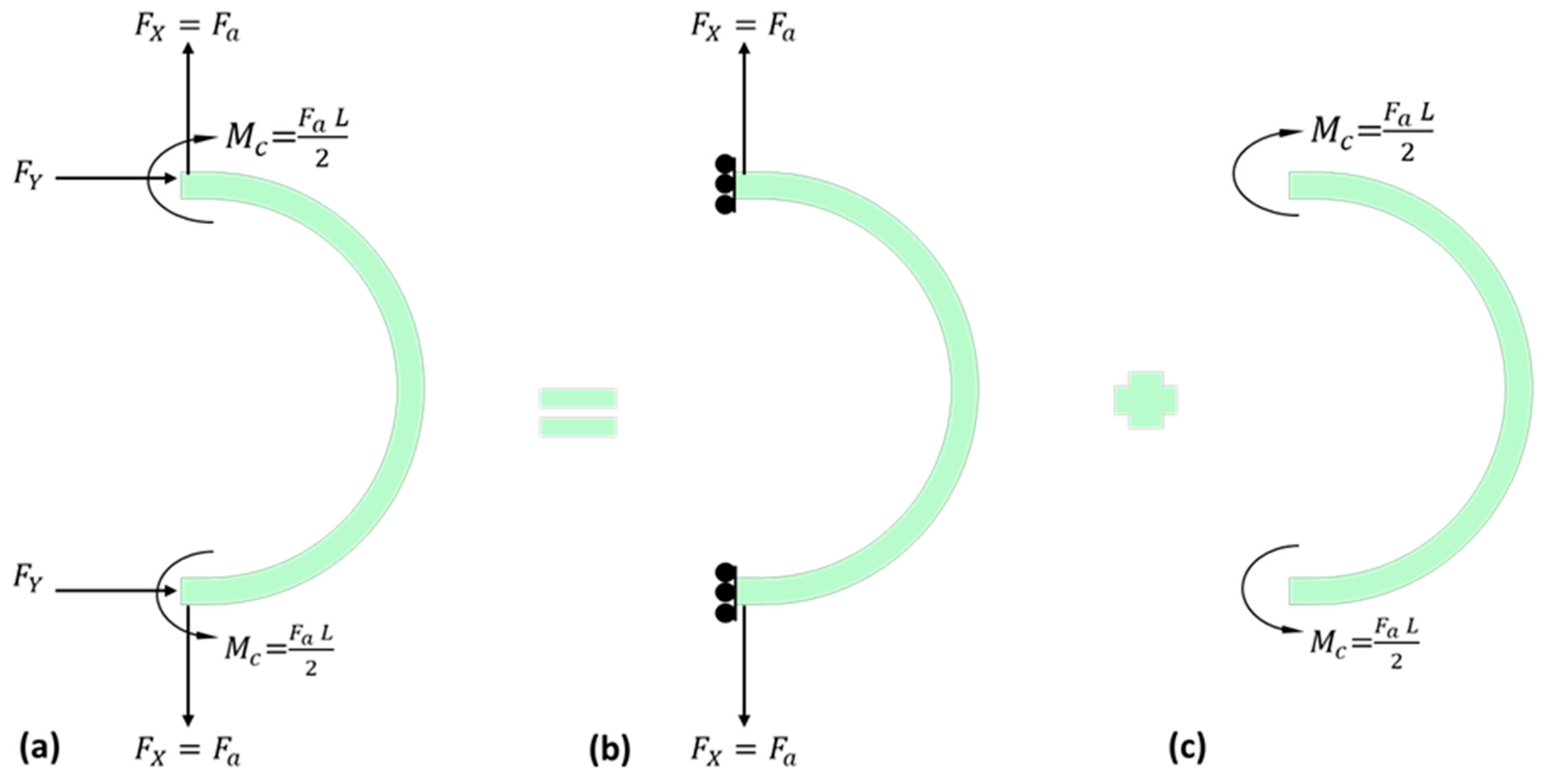
Figure 6.
A schematic representation of a curved shaped beam exposed to the applied force.
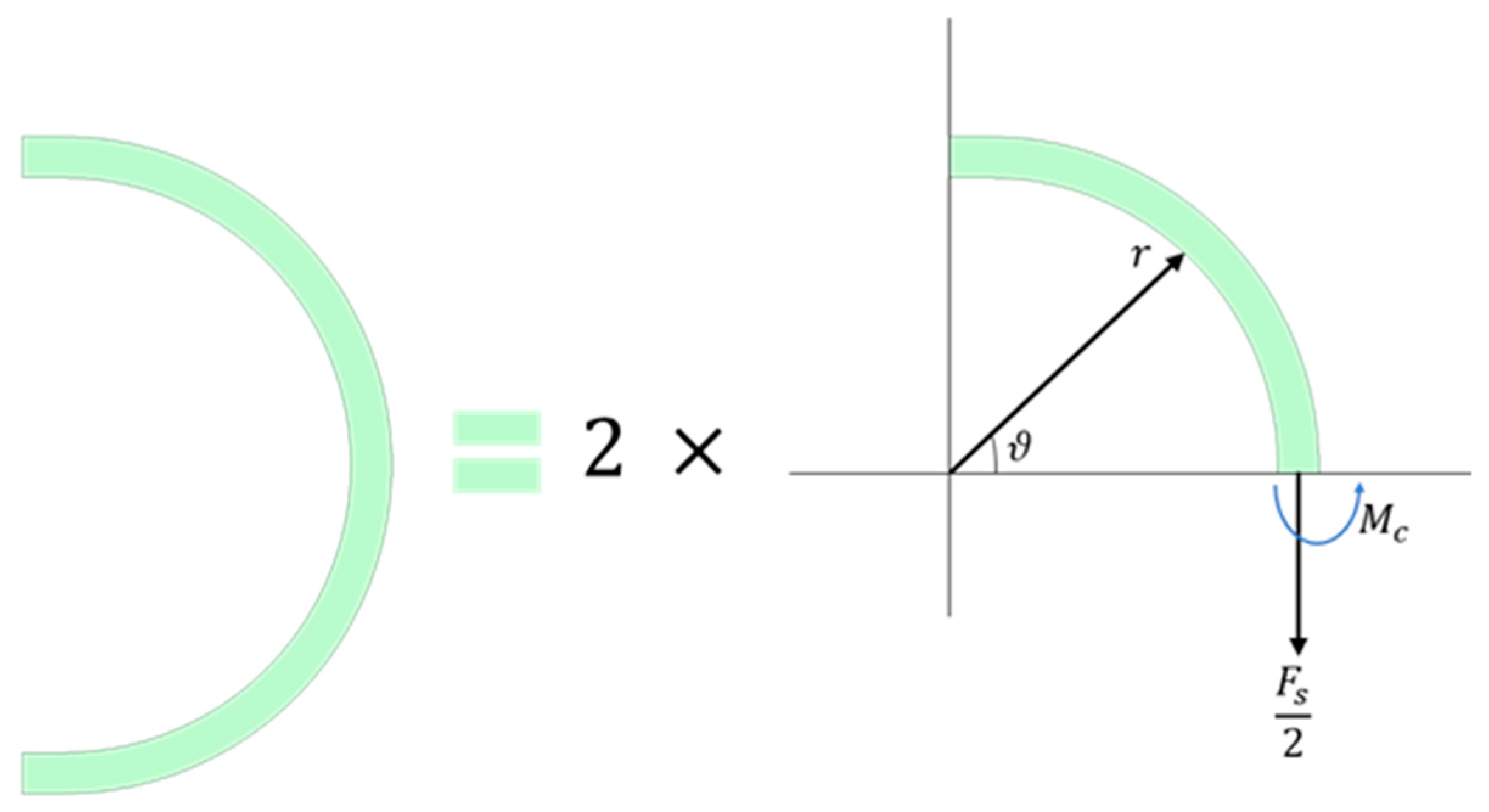
Figure 7.
A schematic view of semicircular support spring (a) 3D view (b) with its design description.
Figure 7.
A schematic view of semicircular support spring (a) 3D view (b) with its design description.
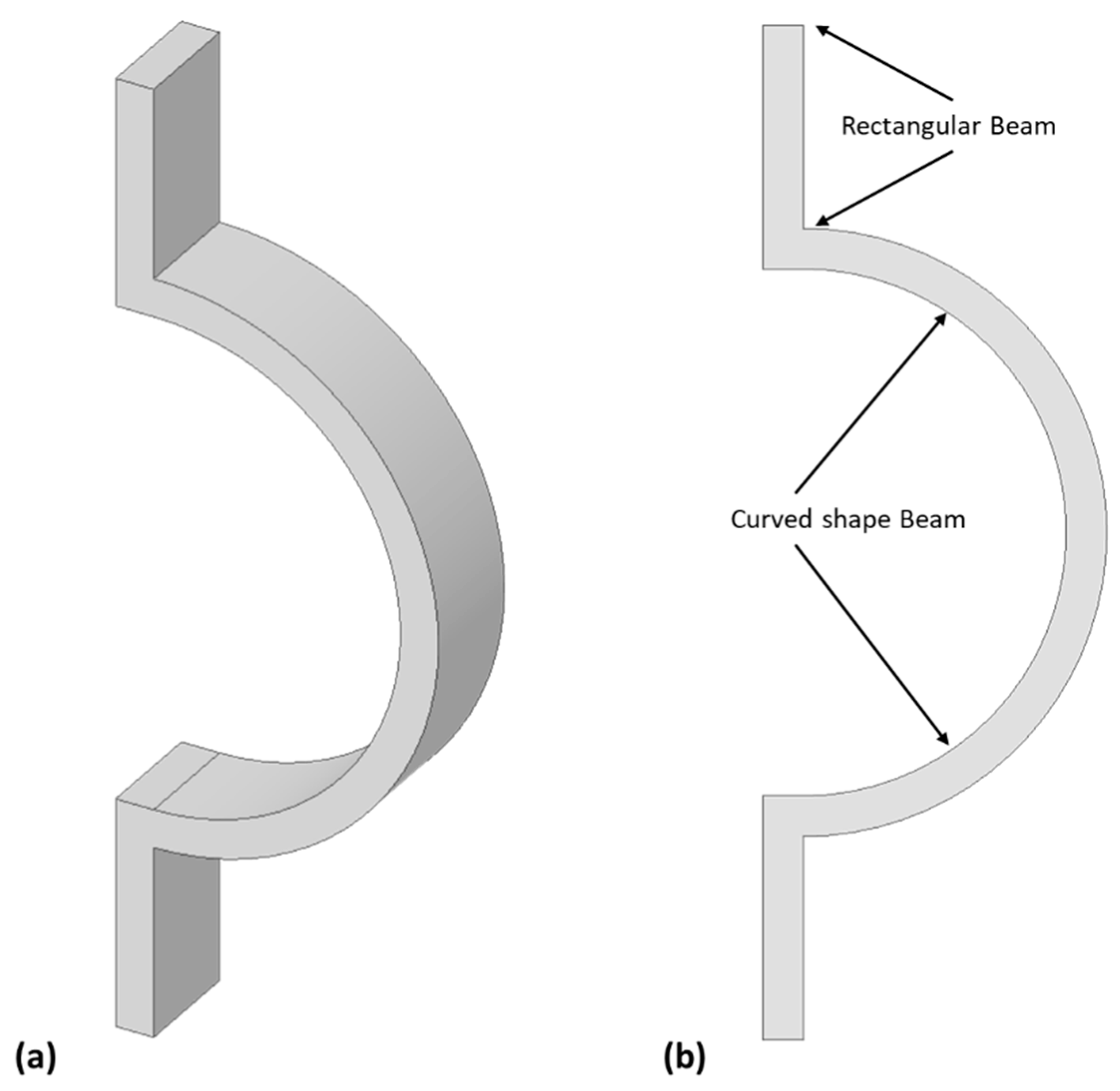
Figure 8.
The semicircular beam's deflection results in a comparison of Finite element analysis (FEA) and analytical results.
Figure 8.
The semicircular beam's deflection results in a comparison of Finite element analysis (FEA) and analytical results.
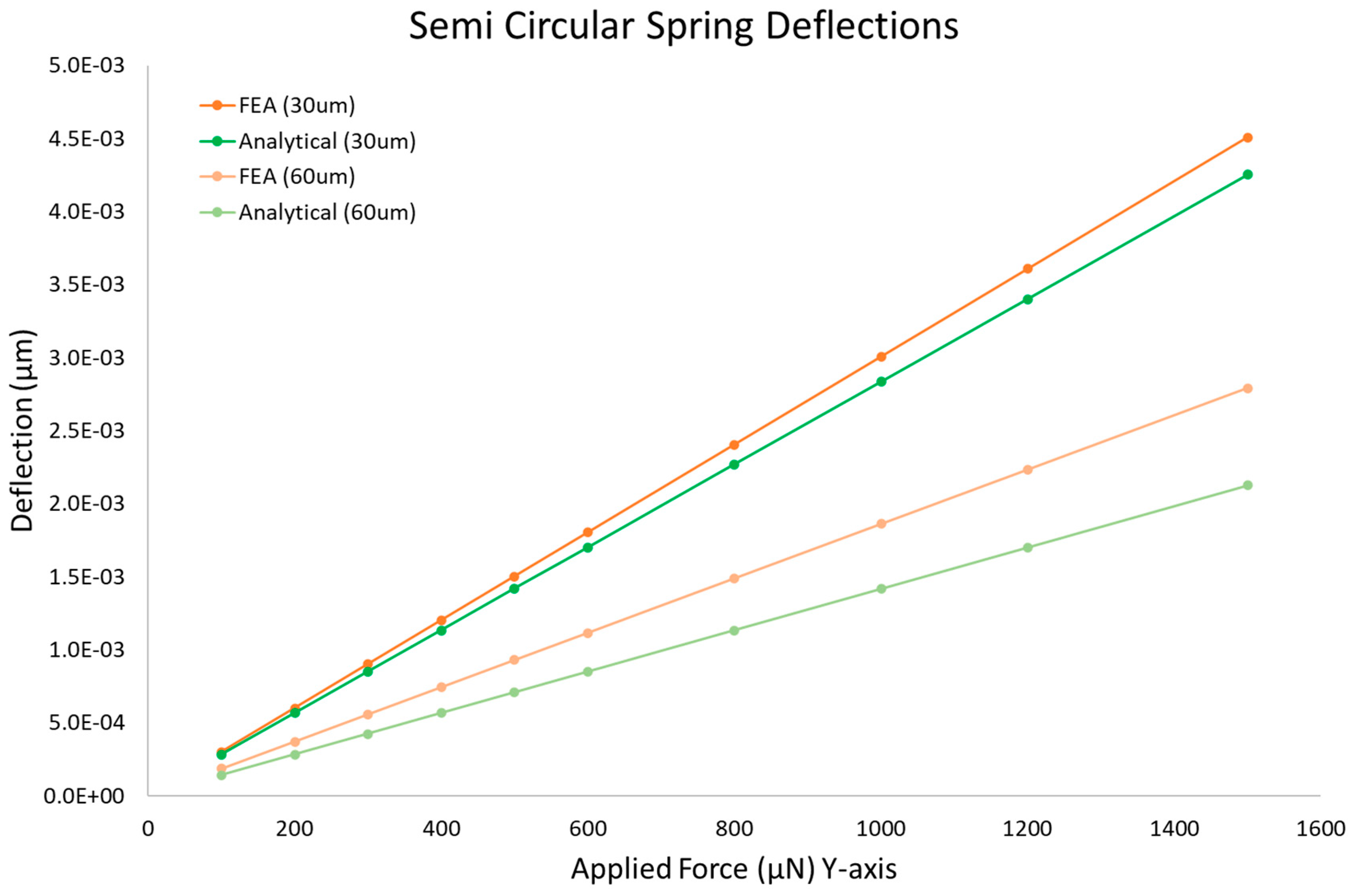
Figure 9.
Modal frequency of the semicircular beam.
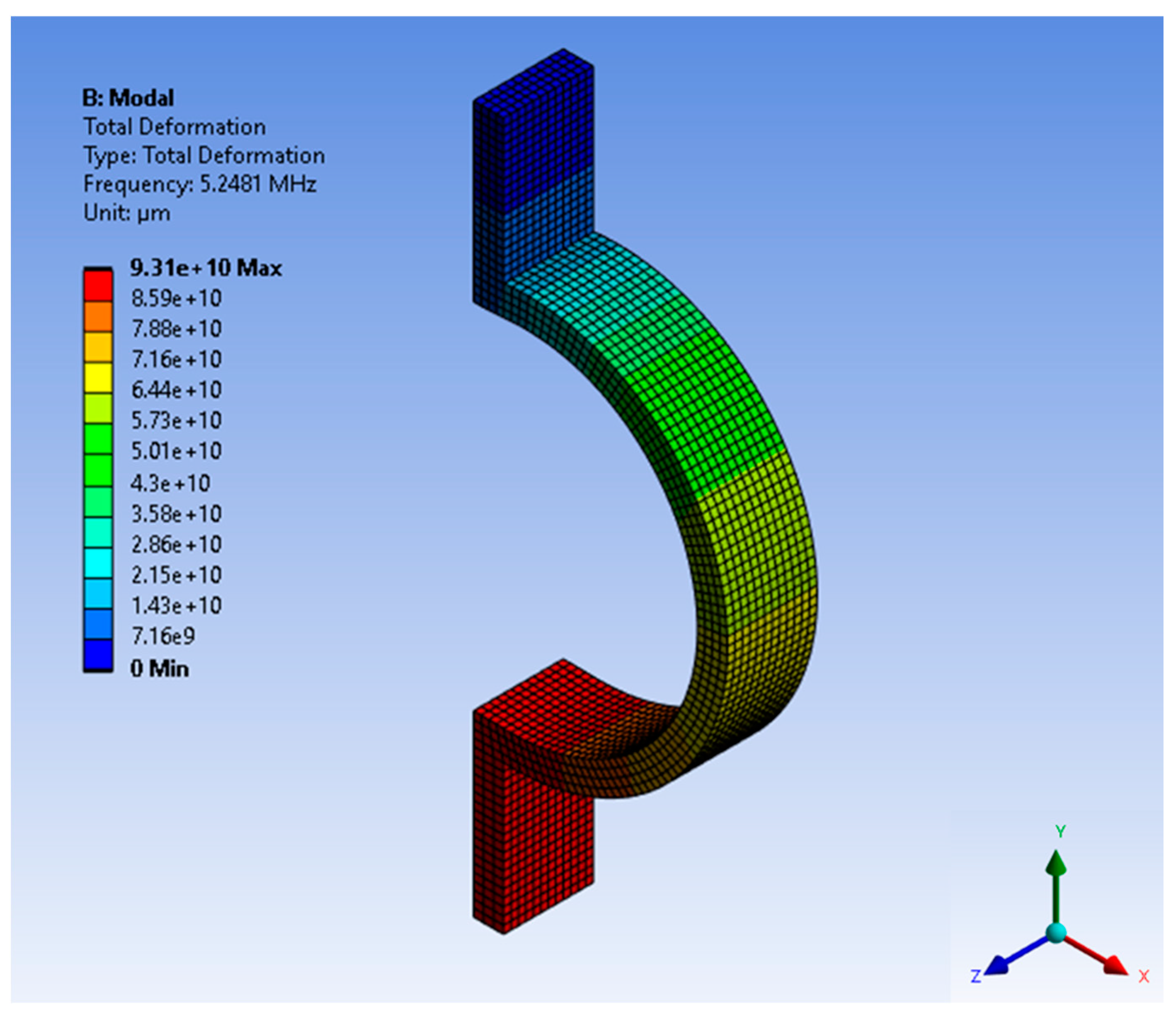
Figure 10.
A schematic diagram of the inner ring frame design (a) in 3D view (b) with design description.
Figure 10.
A schematic diagram of the inner ring frame design (a) in 3D view (b) with design description.
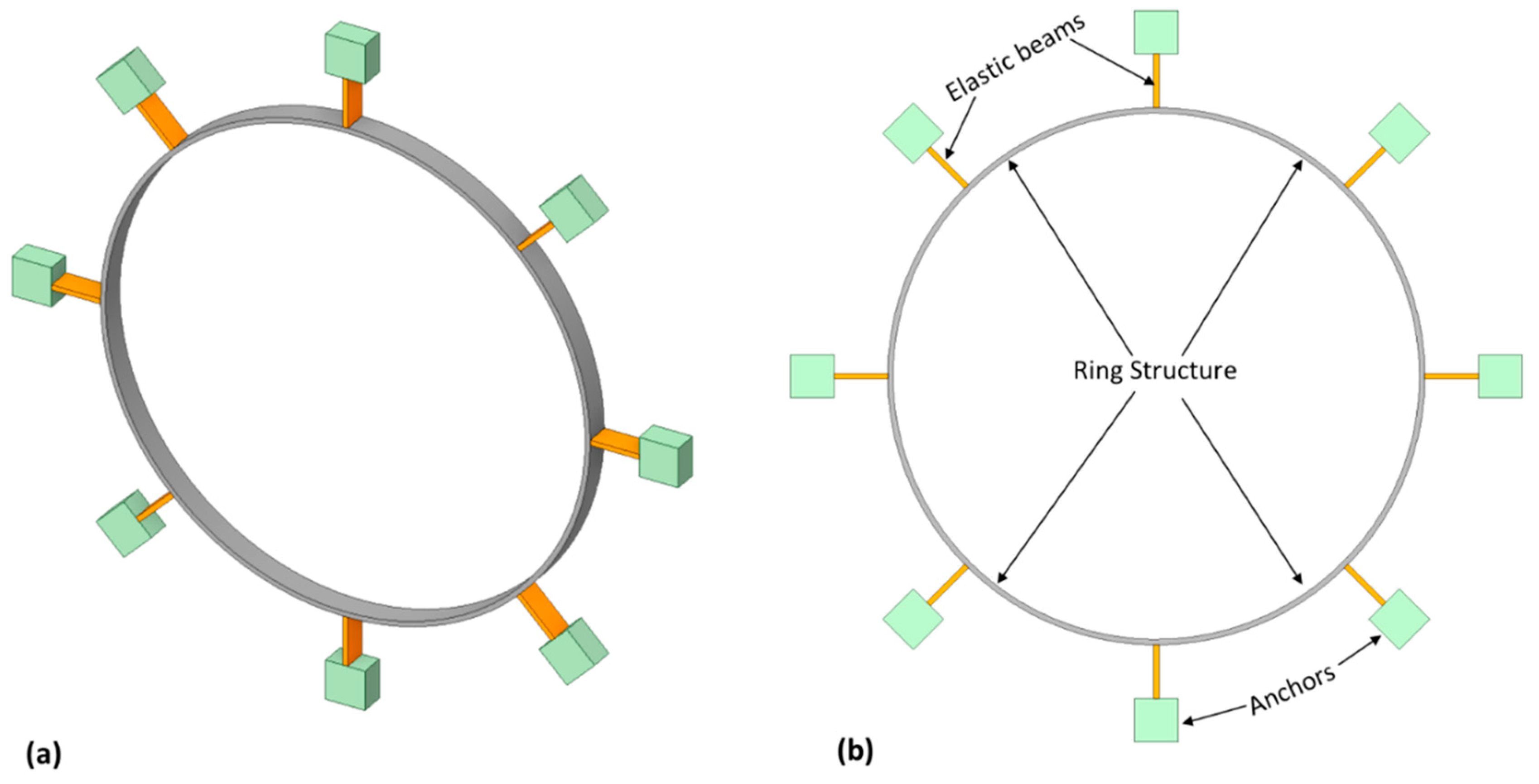
Figure 11.
A schematic diagram of the external ring frame design (a) in 3D view (b) with design description.
Figure 11.
A schematic diagram of the external ring frame design (a) in 3D view (b) with design description.
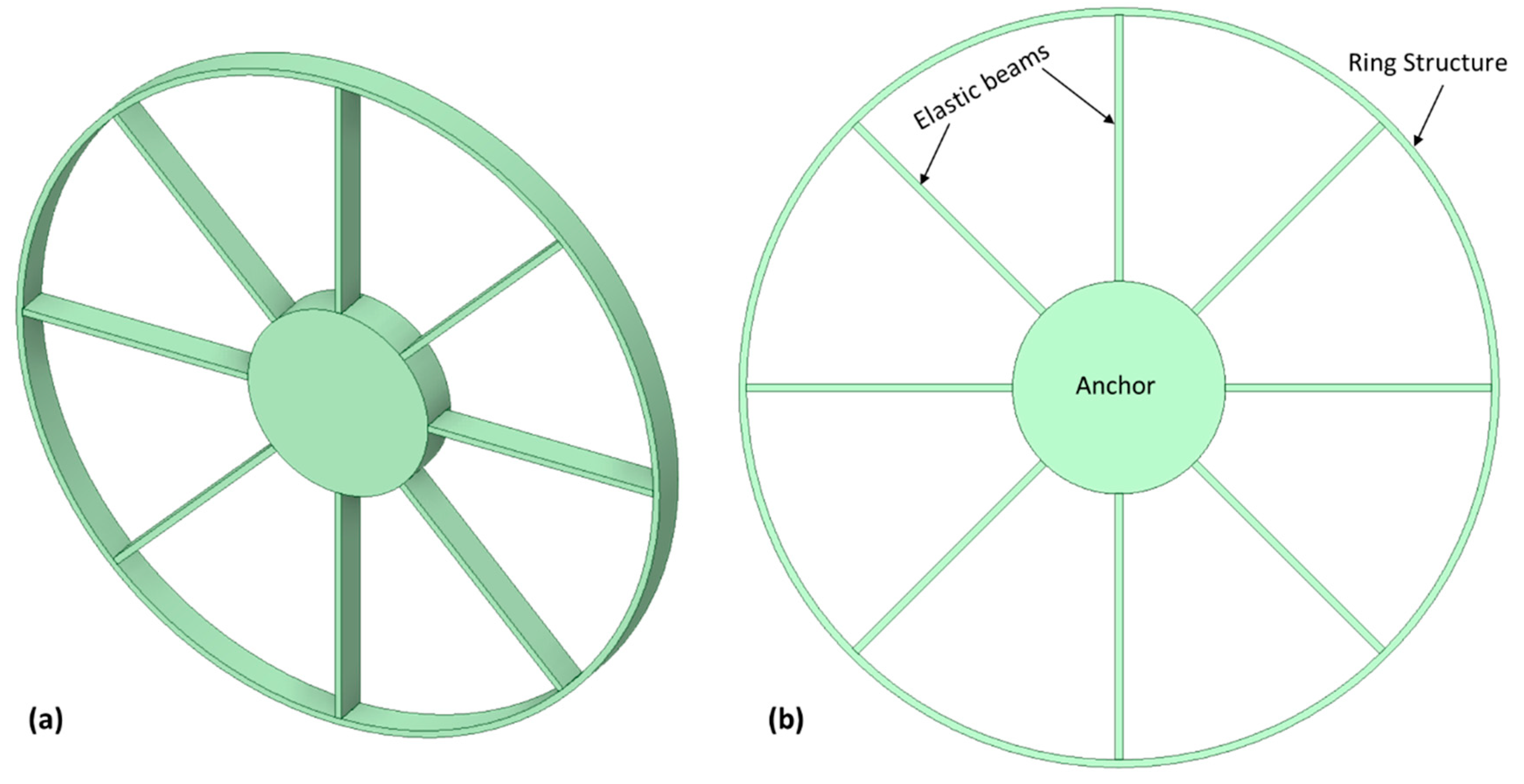
Figure 12.
Electrodes design configuration for MEMS vibrating ring gyroscope (a) Outside placement (b) Inside placement, and (c) Both inside and outside placement.
Figure 12.
Electrodes design configuration for MEMS vibrating ring gyroscope (a) Outside placement (b) Inside placement, and (c) Both inside and outside placement.
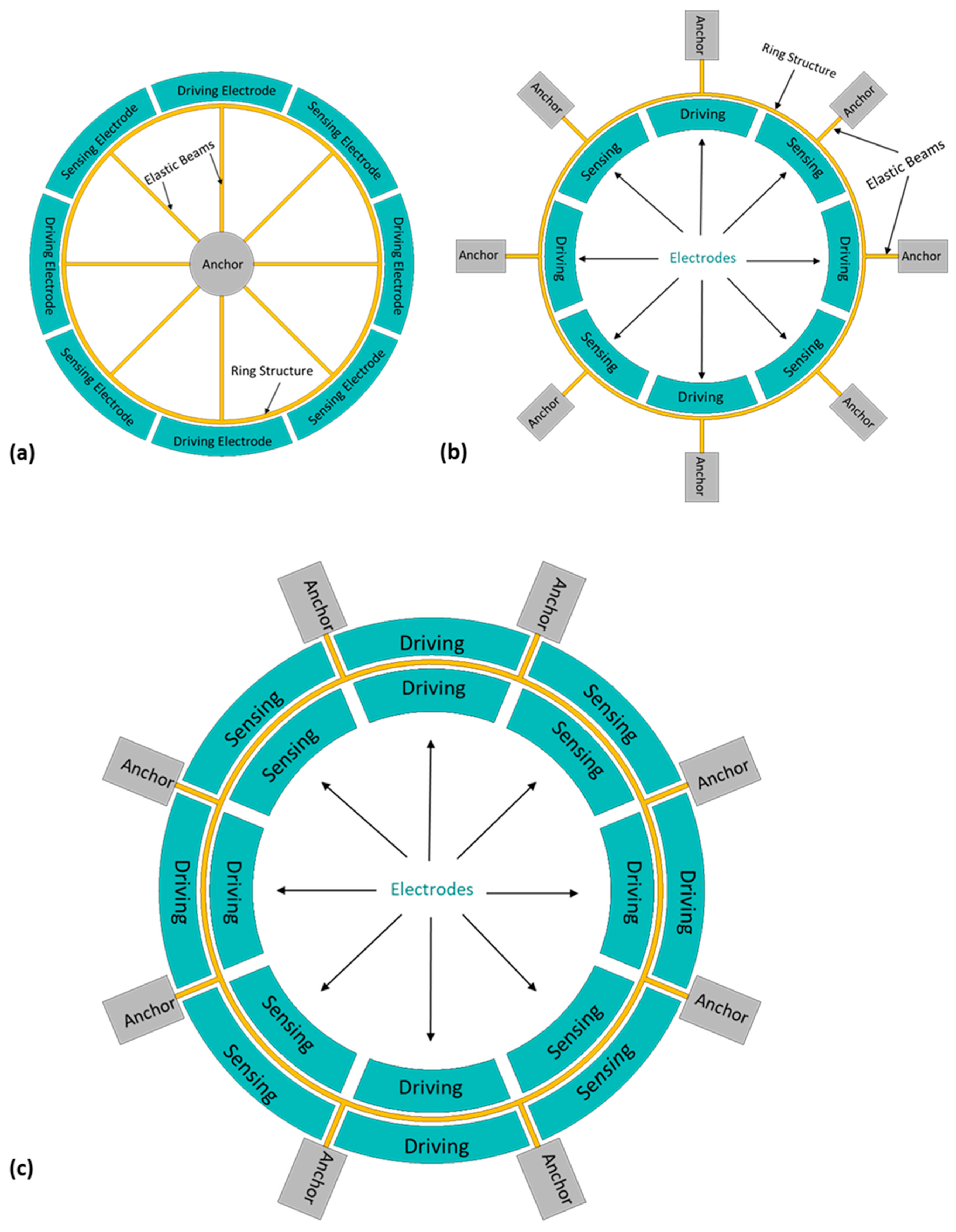
Figure 13.
A schematic view of parallel plate capacitor for MEMS vibrating ring gyroscope.

Figure 14.
A schematic electrostatic actuation model for MEMS vibrating ring gyroscope.
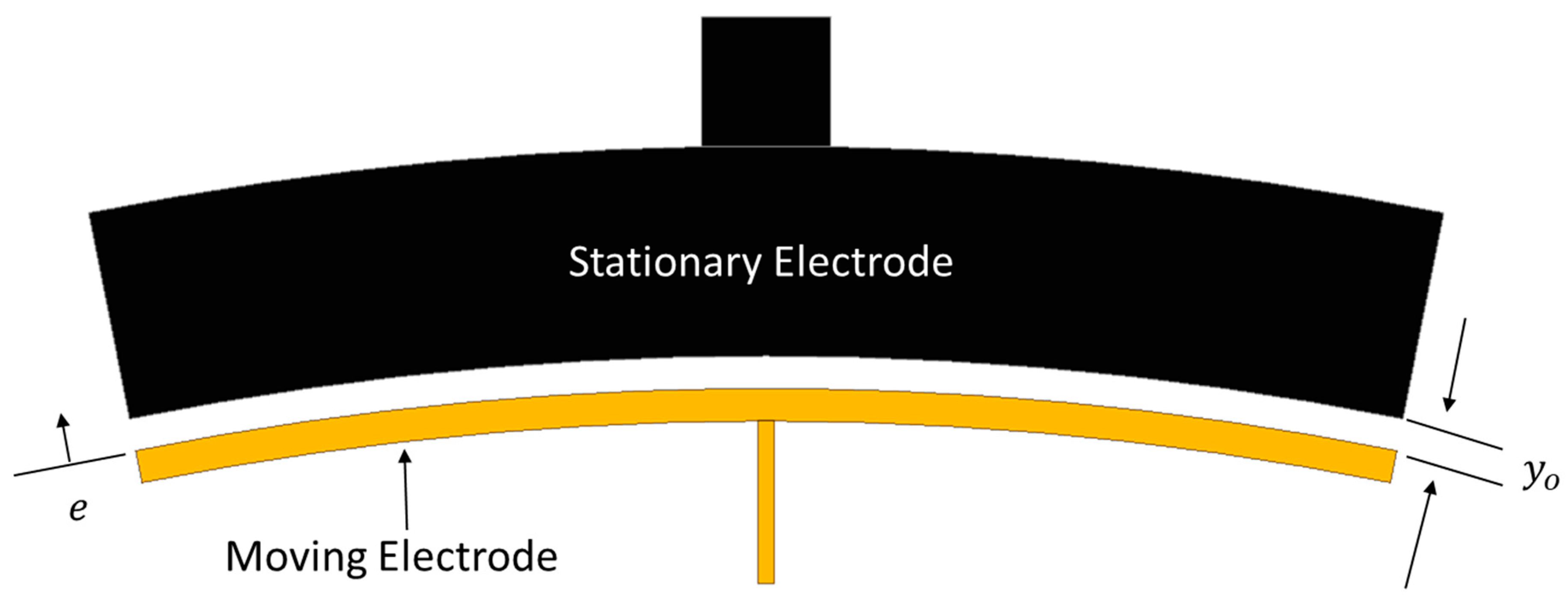
Figure 15.
A schematic representation of the balanced electrostatic actuation method for the vibrating ring gyroscope.
Figure 15.
A schematic representation of the balanced electrostatic actuation method for the vibrating ring gyroscope.
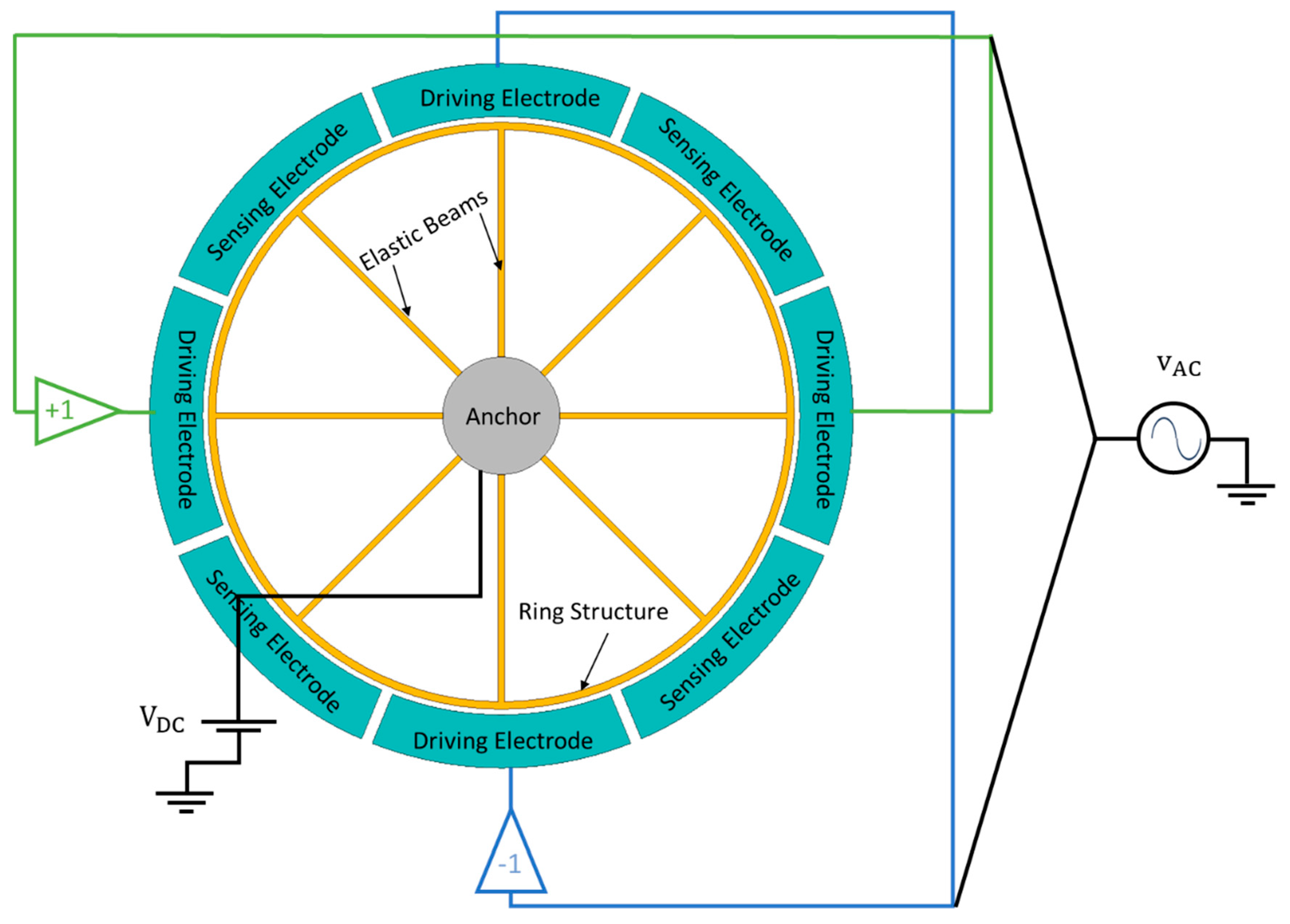
Figure 16.
A schematic representation of the differential detection method for the vibrating ring gyroscope.
Figure 16.
A schematic representation of the differential detection method for the vibrating ring gyroscope.
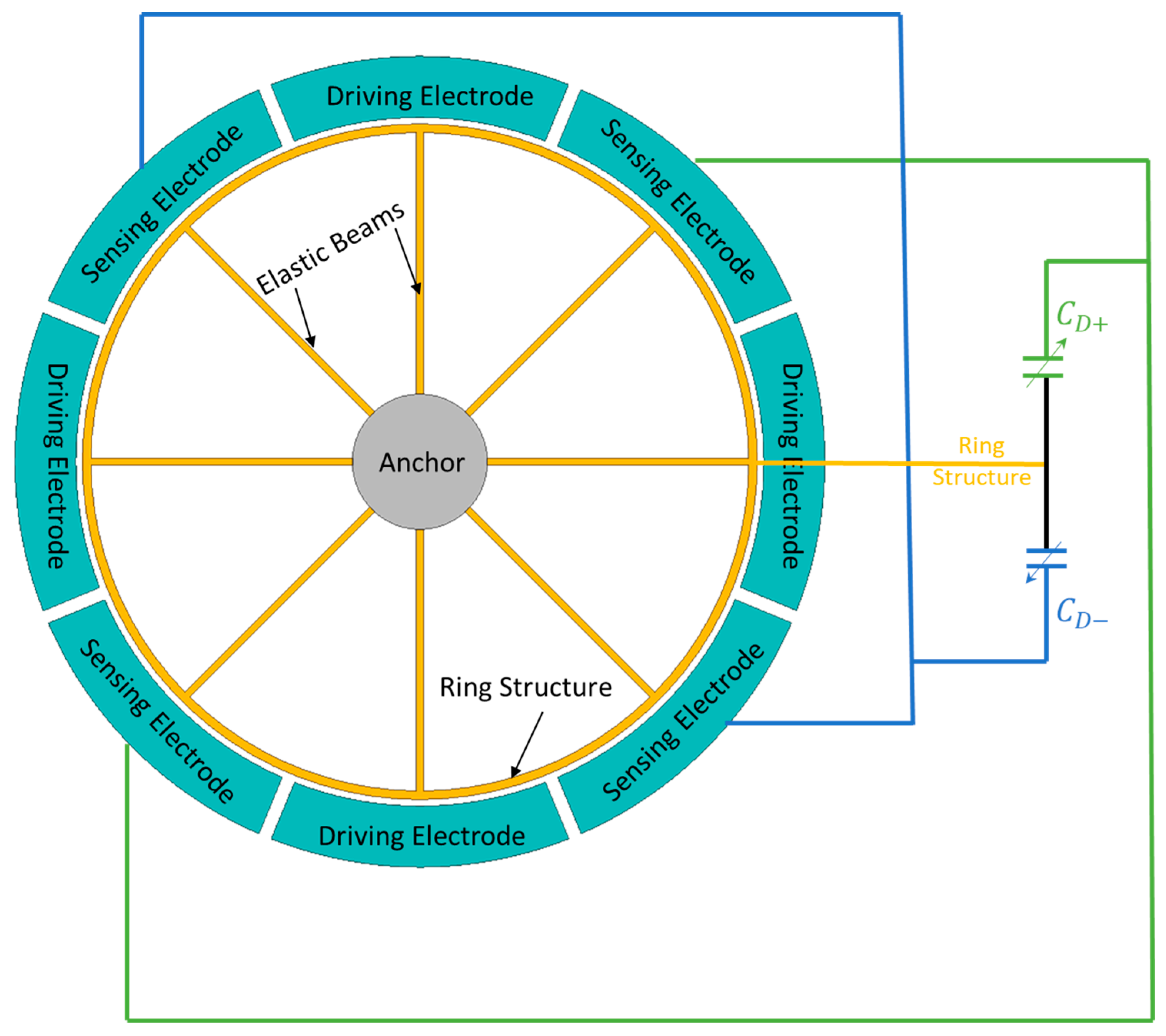
Table 1.
Various Beams design descriptions.
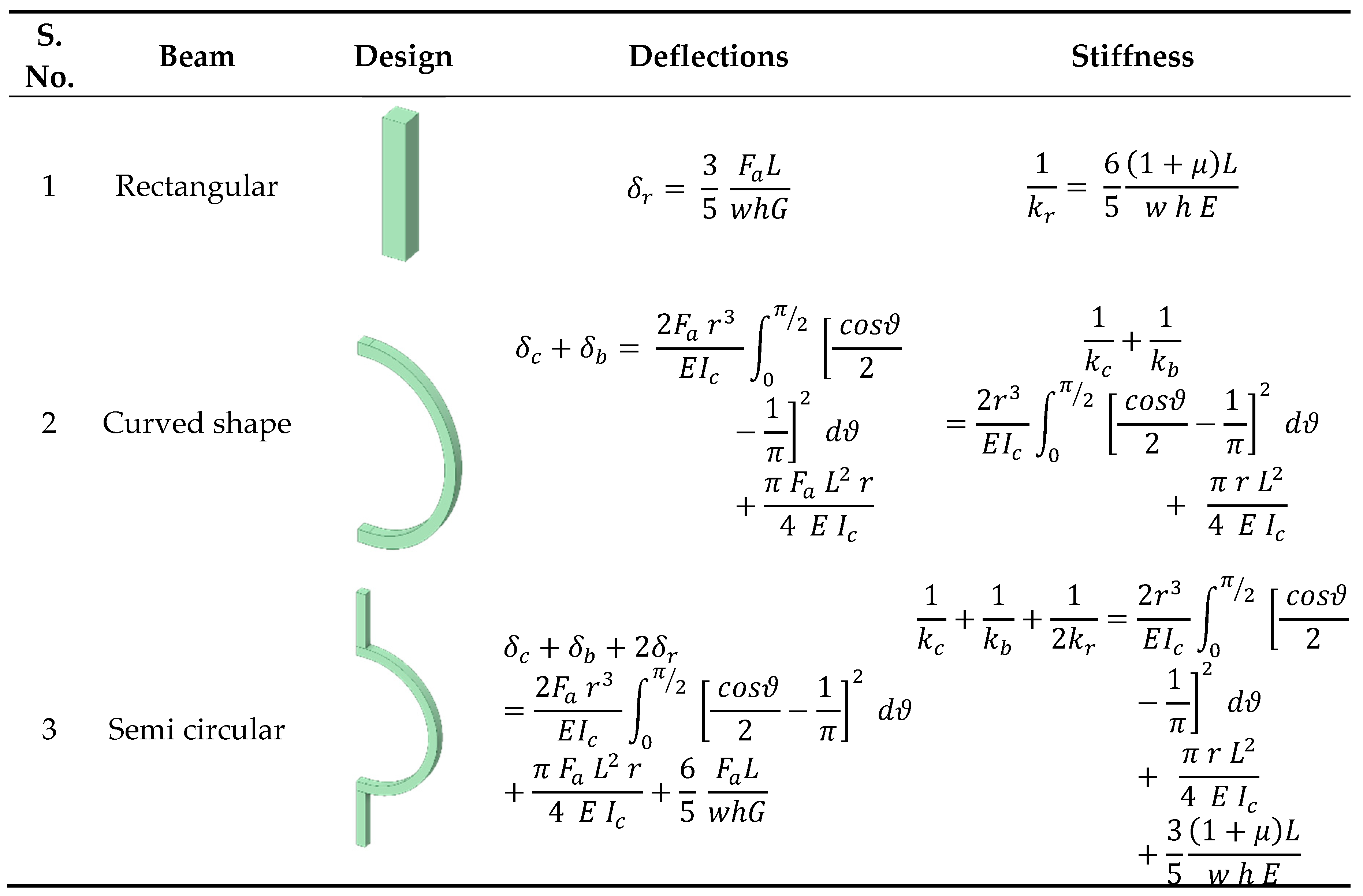
Table 2.
Comparative design results for semicircular beam.
| Frequency (MHz) | Error | Stiffness Constant (kN/m) | Error | |
|---|---|---|---|---|
| ANSYS | 5.25 | 5.74 % | 353.6 | 1.61% |
| Analytical | 5.57 | 347.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







