Prerpints.org logo
Preprint
Article

Ceramic Grinding Kinetics of Fine Magnetite Ores in the Batch Ball Mill

Altmetrics

Downloads

105

Views

46

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

07 August 2023

Posted:

10 August 2023

You are already at the latest version

Alerts
Abstract
Aiming to reveal the kinetic characteristics of ceramic ball grinding of fine magnetite comprehensively, two types of ceramic balls ground with the same filling rate and total weight as steel balls were researched. The results show that the breakage rate of ceramic ball grinding is only half of that of steel ball grinding with the same media filling rate. With the same total media weight and the feed size less than 0.212 mm, the breakage rate of the ceramic ball grinding approaches the steel ball grinding and is 21.43% higher than that of the steel ball grinding. The main crushing form of magnetite changed from impact to abrasion in ceramic ball grinding compared with steel ball grinding, which significantly affected the value of the zero-order output constant a. Consequently, there is a noticeable difference in the variation of the parameter β related to the fines generation rate of the ceramic ball grinding compared with the steel ball grinding.
Keywords: 
Subject: Engineering  -   Mining and Mineral Processing

1. Introduction

Iron ore is a vital resource for human survival and development, and magnetite as iron-bearing minerals are an important part of iron resources. The mining and processing of magnetite require a lot of energy, particularly given the decreasing proportion of high-grade magnetite available today[1]. Grinding represents the most energy-intensive operation in a mineral processing plant, accounting for 60% of the total energy consumption. In addition, the distribution of iron ore is more complex than in the past decade or so, placing higher demands on the grinding operation[2,3]. In order to reduce the energy consumption in magnetite processing, we propose to use ceramic grinding in the secondary ball mill. Ceramic grinding is a grinding process that uses ceramic balls instead of steel balls as the grinding medium of ball mills. The ceramic balls grinding process has been successfully applied in a well-known magnetite processing plant in China, resulting in over 30% energy savings and substantial cost reductions [4,5,6]. Given the recent emergence of ceramic grinding technology, the behavioral characteristics of its grinding kinetics remain have not yet been revealed.
As grinding powder technology advances, many grinding kinetic models have emerged, among which PBM (population balance model) is the most recognized and widely used model. The origin of PBM can be traced back to 1948 when Epstein [7] introduced two basic comminution functions, one of which is the breakage rate function (S) and the other is the cumulative breakage distribution function (Bij). In 1953 Sedlatschek and Bass [8] presented the first population balance model for time-continuous and size-discrete batch grinding on these two functions. Subsequently, Reid [9] found the analytical solution to the model in 1965.
The breakage rate function S was derived by linearly fitting the semi-logarithmic equation [10]. As for the calculation of the cumulative breakage distribution functions Bij, various methods have been proposed by experts in the field. The G-H algorithm [11,12,13] was proposed in a short communication by Kapur in 1970 and was guided by the idea of transforming the population balance model into two functions, G and H, performing iterative operations to solve the value of Bij by computers. the B-algorithm [14] was proposed by Austin in 1971 with three different forms: BⅠ, BⅡ, and BⅢ. BⅡ and BⅢ were modified for secondary breakage, with BⅡ having the widest range of applications. In 1999, the empirical formula algorithm [15] was proposed by Austin, which was a modification of Reid's analytical solution to enhance its suitability for computer simulations. This algorithm has become the most commonly used in current simulation studies [16,17,18,19,20].
PBM has been playing an important role in the study of grinding characteristics of single minerals with narrow size distributions. Herbst [21] studied the fragmentation characteristics of dolomite using a dry ball mill. The findings revealed that the breakage rate function was proportional to the power input of the ball mill while the breakage distribution function was constant. The study was subsequently extended to carbonate and silicate minerals, yielding consistent conclusions. Qian [22] studied the effects of grinding media shapes on the grinding kinetics of cement clinker in ball mills. The result showing that cement clinker followed first-order grinding kinetics and the primary breakage distribution parameters were dependent on the initial feed size. Li [23] made a comparison of the grinding effect of tungsten carbide balls (WC balls) and ordinary steel balls on narrow size quartz, the simulated results demonstrated that WC balls had higher throughput for coarse particles and lower energy efficiency for fine particles.
In this paper, the grinding kinetics of five narrow-size classes magnetite ores are investigated to compare the differences between ceramic ball grinding and steel ball grinding with the same media filling rate and the same total weight of loaded balls.

2. Theoretical Background

2.1. Population Balance Model

In batch milling, the population balance model was obtained on the basis of the principle that the mass of a given particle size of material after grinding is equal to the sum of its generated mass and the mass remaining after crushing [9]:
d m i ( t ) d t = − S i t × m i t + ∑ j = 1 i − 1 b i j S j ( t ) m j ( t )
Where mi(t) is the mass fraction of the size class i at time t in the discharge; Si(t) is the breakage rate function of the size class i at time t; bij is the breakage distribution function that describes the mass fraction after the size class j in the feed being crushed to the size class i in the discharge (j≧i).
For ease of calculation, breakage distribution function (bij) is often denoted by cumulative breakage distribution function (Bij):
B i j = ∑ k = n i b k j
S1(t) and Bij are required to solve Equation (1). The − S i t × m i t represents the amount of residual ore of this size class after t time of grinding. S i t is, the breakage rate function that can be obtained from the following equation:
d m 1 ( t ) d t = − S 1 ( t ) × m 1 t
The ∑ j = 1 i − 1 b i j S j ( t ) m j ( t ) represents the amount of new ore added to this size class after t time of grinding., Bi1 can be calculated in two ways:
G-H algorithm created by Kapur[11]:
l n M i ( t ) l n M 1 ( t ) = B i 1 − H i 2 S 1 t
Where Mi(t) is the cumulative mass fraction coarser than the size class i at time t. A linear regression analysis of Equation (4) leads to the value of Bi1, which is the intercept of the function with lnMi(t) as its vertical axis and t as its horizontal axis.
BⅡ algorithm created by Austin[14]:
B i 1 = l n ⁡ [ 1 − Y i t 1 − Y i 0 ] l n ⁡ [ 1 − Y 2 t 1 − Y 2 0 ]
Where Yi(t) is the cumulative mass fraction finer than the size class i at time t. BⅡ algorithm can be seen as a special form of G-H algorithm with a premise of no repeated fragmentation.
Since the Austin empirical formula is the most widely used, the results for Bi1 are exhibited with this formula[15]:
B i 1 = φ ( x i − 1 x 1 ) γ + ( 1 − φ ) ( x i − 1 x 1 ) β

2.2. Zero-Order Output Characteristics

In the characterization of mineral crushing behavior, apart from two crucial parameters, the breakage rate function (which describes the rate of mineral size reduction) and the cumulative distribution function (which represents the percentage distribution of minerals after mineral crushing), the production rate of fine minerals holds equal importance[24-26]. The zero-order output characteristic constants are obtained by establishing the relationship between the fines generation rate and particle size, and thus enables the understanding of the differences in the fines generation characteristics of different minerals after the grinding process [27-29]. The output of the fines in the discharge is consistent with zero-order output if the minerals are ground for a shorter duration (no more than 65% fragmentation of the single or coarsest size class):
d P ( x , t ) d t = F ( x )
where P(x,t) is the cumulative yield under the sieve for size x at t. F(x) denotes the zero-order cumulative yield rate constant for size x, which varies with size. Typically, there is a relationship between F(x) and size x as follows:
F x i = k x i a
Where k and a are constants, the value of a is related to the grinding characteristics of the material itself, and its correlation with the condition of ball mills is weak.

3. Methodology

3.1. Material

The magnetite ore used in this study were sourced from Guangdong, China. The bulk density of the magnetite was measured 2980 kg/m3 by helium replacement method. Table 1 shows the composition of the compounds of the magnetite ore used in the experiment. Notably, the magnetite (Fe3O4) content exceeds 90%, indicating the high purity of the ore in this experiment and its ability to represent the fracture characteristics of magnetite.
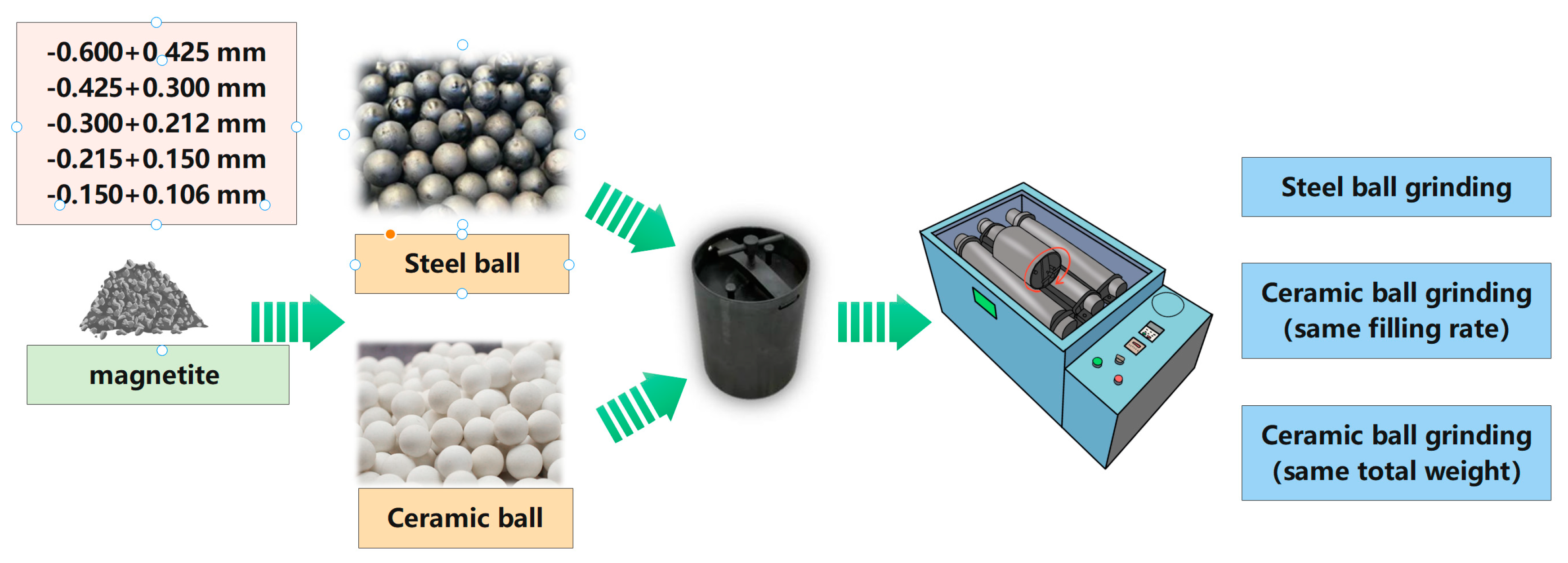
Large magnetite rocks were initially crushed by a laboratory jaw crusher. Then, as Gupta[30] warned against jaw crushing in preparation for batch testing, a laboratory grinding roller was subsequently employed in the second stage to ensure that particles did not have internal cracks that would weaken them and thus bias the results. Subsequently, the feed was classified with a sieve shaker and the size classes of feeds for the experiment were -0.600+0.425 mm, -0.425+0.300 mm, -0.300+0.212 mm, -0.212+0.150 mm and -0.150+0.106 mm.
The grinding media used in this experiment are conventional steel balls and ceramic balls whose diameter are both 18 mm, and the relevant physical parameters of the two grinding media are shown in Table 2. The bulk density and true density of the ceramic ball is only about half of those of the steel ball, but its surface Mohs hardness is about 1.5 times of the steel ball, which is a major characteristic of the ceramic ball.

3.2. Experimental Method

In this study, a batch wet ball mill was used. The tests were carried out in an XBM ball mill with a speed of 86 r/min and a cylinder volume of 2.5 L (D×L=140 mm×160 mm). The amount of ore fed into the mill for each experiment was 200 g and the mass concentration of the mill was 67%, both of which were constant parameters. Firstly, the steel ball milling experiment was carried out, and the steel ball filling rate for this experiment was 20% (2425 g) with the grinding time of 2 min, 4 min, 6 min, 8 min and 10 min respectively. Then the same filling rate of ceramic ball grinding were carried out in the experiment. Besides, the ceramic ball filling rate remained 20% and the grinding time was set for 2 min, 4 min, 6 min, 8 min and 10 min, respectively. Finally, in the ceramic ball grinding experiments with the same total weight of grinding media, only the total weight of ceramic ball loading ball was changed to 2425 g, while other conditions are remained the same. Each of the five particle sizes of magnetite requires these 15 sets of grinding experiments, resulting in a total of 75 sets of batch grinding experiments. The specific experimental method is shown in Figure 1.
The particle size distribution of grinding products was measured by standard sieves and the interval was 2-1/2 (0.425 mm, 0.300 mm, 0.212 mm, 0.150 mm, 0.106 mm, 0.075 mm, 0.053 mm, 0.045 mm and 0.038 mm), accounting for the most satisfactory for the first-order grinding kinetics[31]. This experiment uses the wet sieving method, and the water in the basin is replaced every 2-3 min until it is no longer cloudy.

4. Results and Discussion

In this section, the breakage rate function, cumulative distribution function and zero-order output characteristics are described. Each characteristic function is analyzed in detail for each of the five feed size classes: -0.600+0.425 mm, -0.425+0.300 mm, -0.300+0.212 mm, -0.212+0.150 mm and -0.150+0.106 mm, respectively.

4.1. Breakage Rate Function

The breakage rate function is a function that characterizes the breakage rate of the initial size of the mineral. If the grinding process conforms to the first-order grinding kinetics, then the breakage rate function is a constant that does not vary with time. By rearranging the terms of Equation (3) and integrating the calculation, the following equation can be obtained:
ln[m1(t)/m1(0)] =-S1t
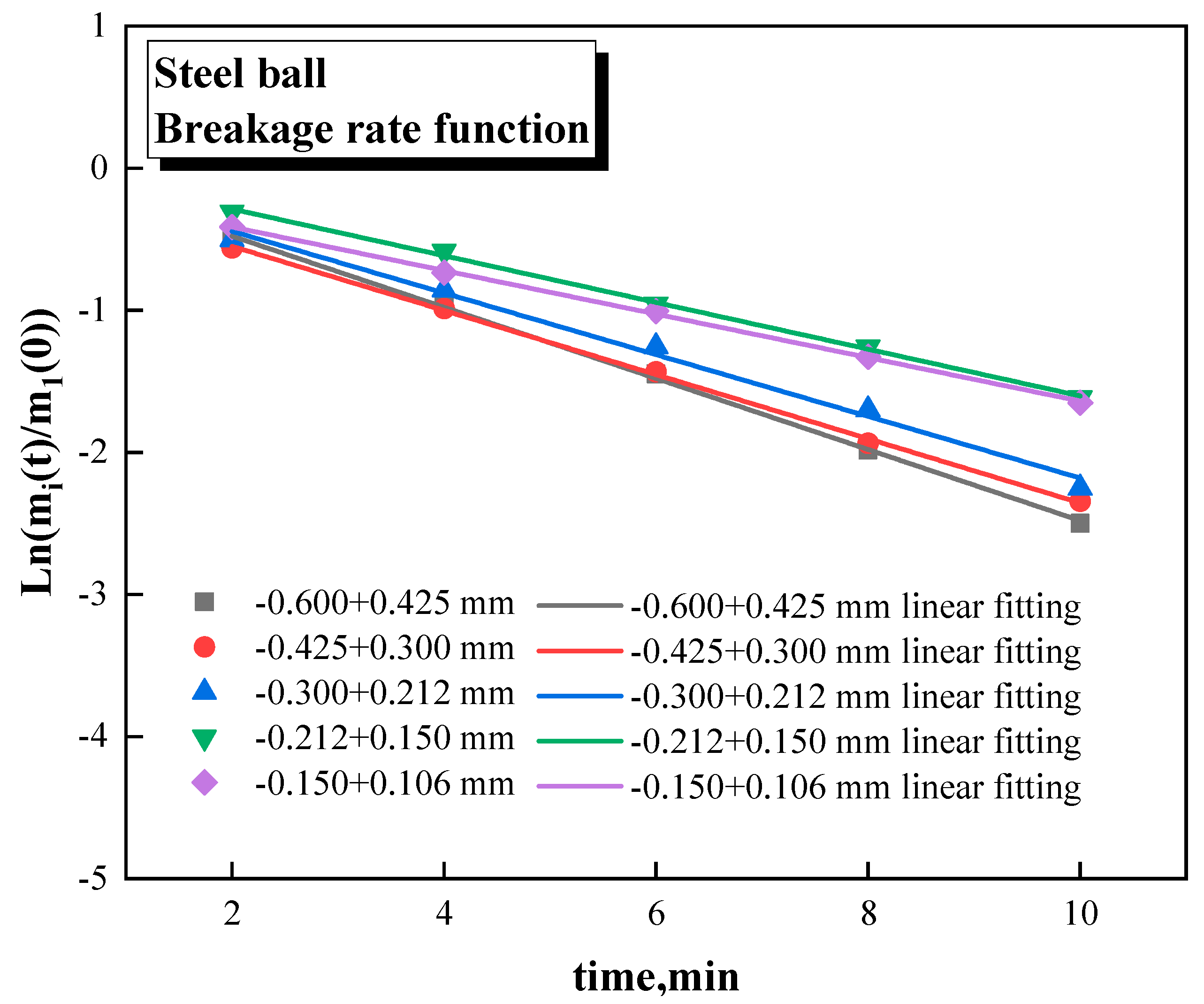
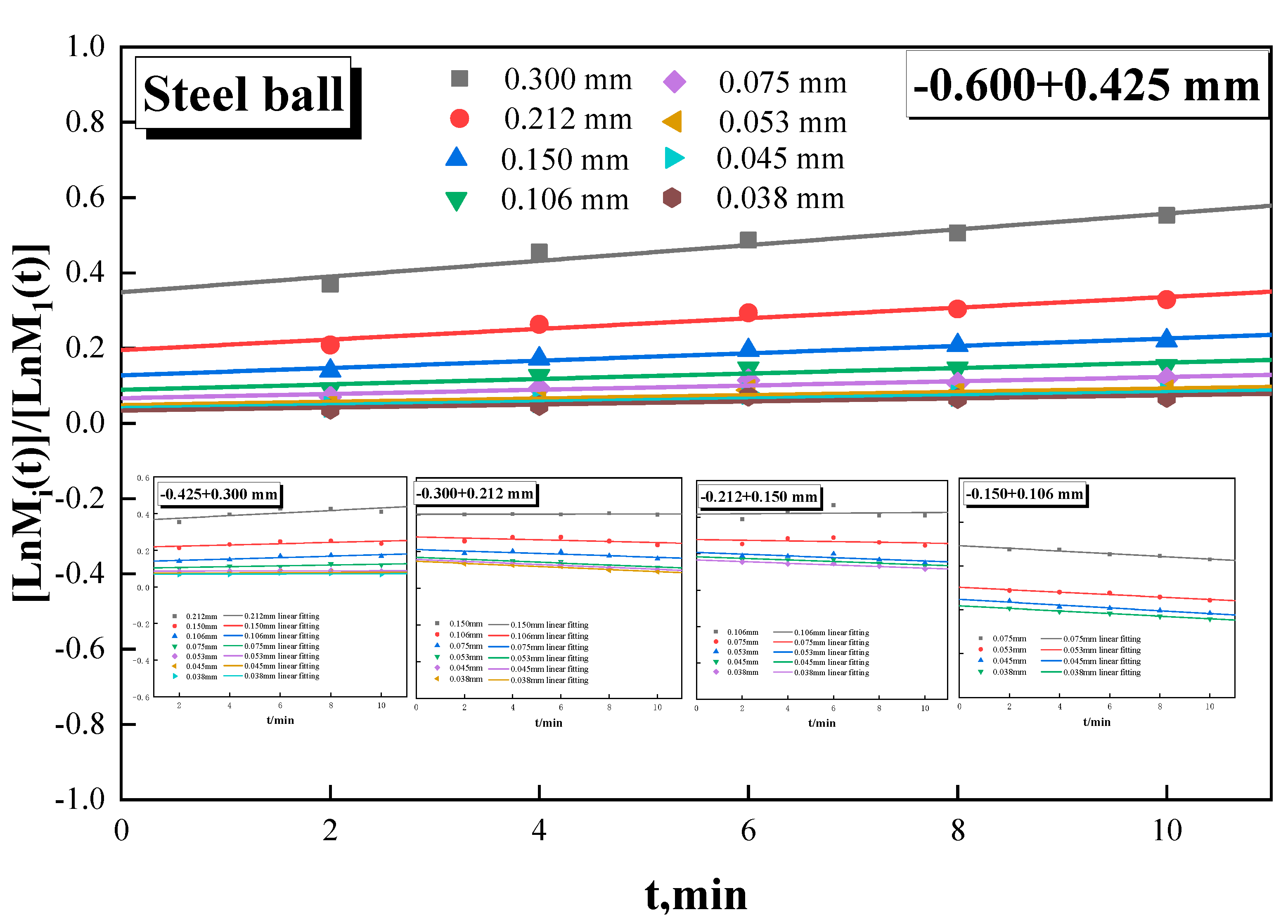
From equation (9), it can be seen that the function obtained with ln[m1(t)/m1(0)] as the vertical axis and t as the horizontal axis, with the slope of which as the breakage rate. Theoretically all the fitted lines should pass through the origin of the coordinates, but all the fitted lines are not the case according to Figure 2. This is because screening errors inevitably occur during the screening process, resulting in a small number of particles in the feed size class that are out of the size range. However, a small amount of non-conforming particles do not affect the breakage rate and do not significantly affect the experiment. Figure. 2 shows the breakage rate function of steel ball grinding, from which the breakage rate of steel ball grinding ranges from 0.15 min-1 to 0.24 min-1, with the highest value of 0.237 min-1 for -0.425 + 0.300 mm and the lowest value of 0.146 min-1 for -0.150 + 0.106 mm.
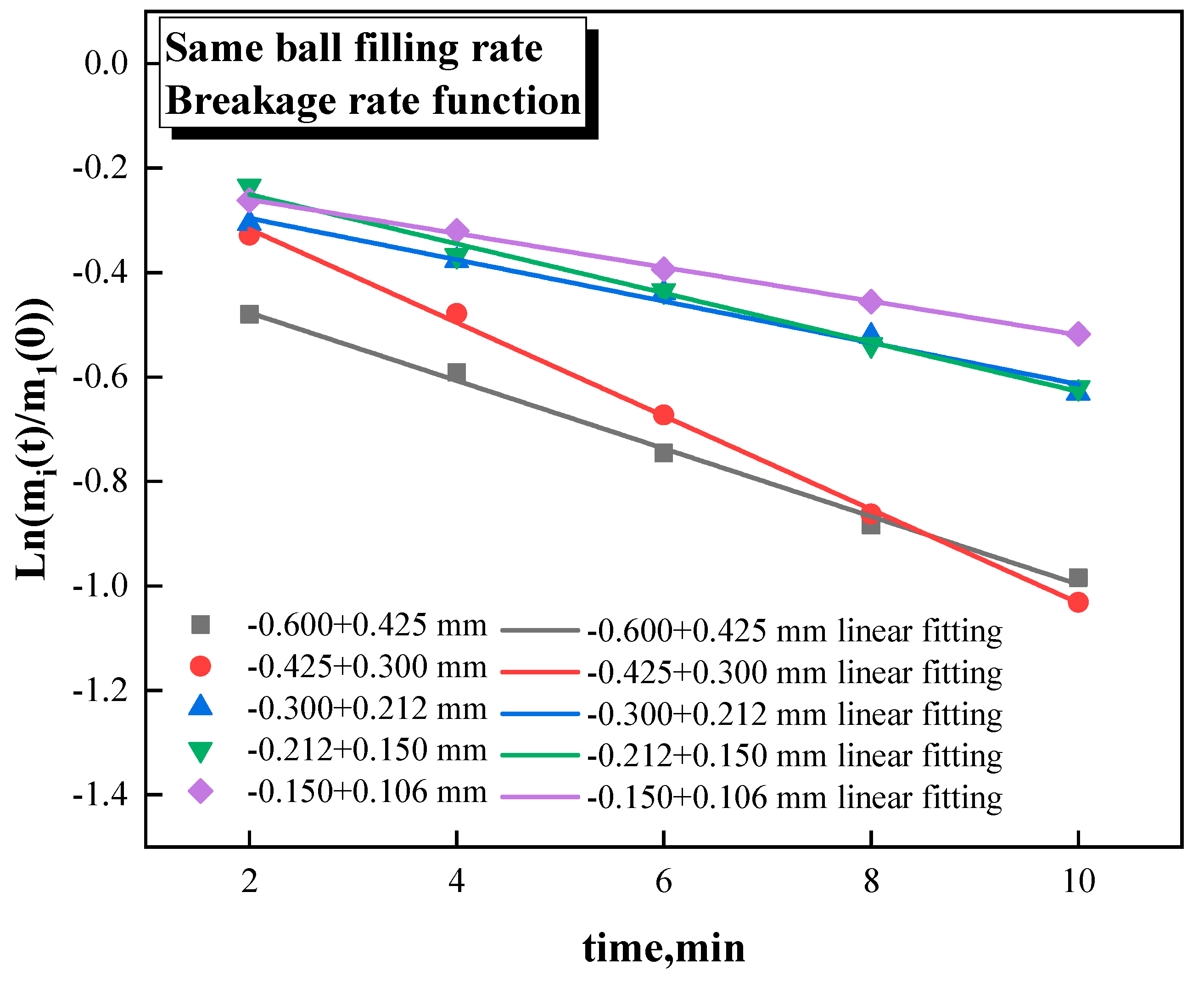
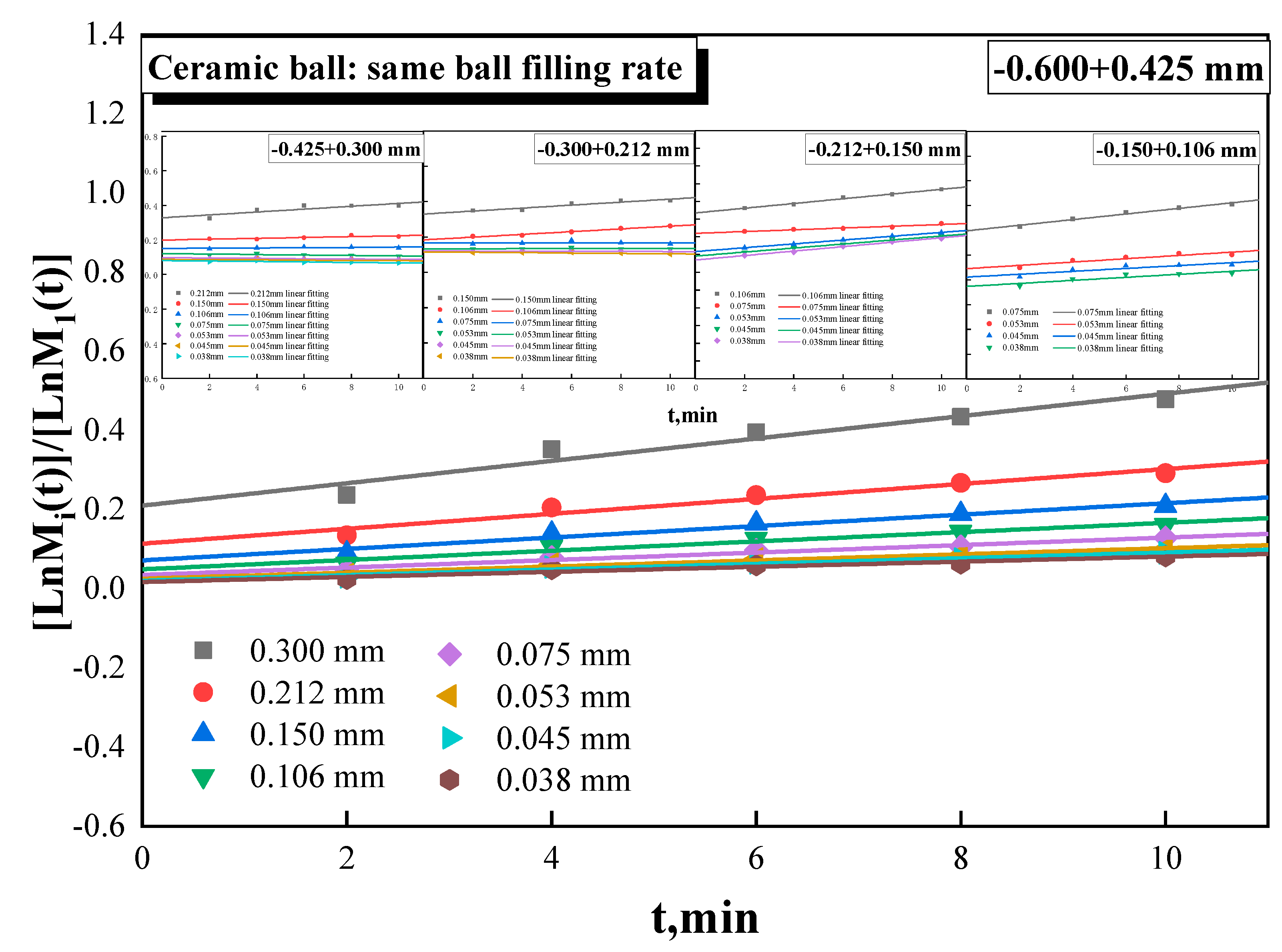
In the same case, the breakage rate function changed significantly when the grinding medium was replaced by ceramic balls instead of steel balls. Figure 3 shows the breakage rate function of ceramic ball grinding with the same filling rate: the breakage rate does not exceed 0.1 min-1, and the highest value reaches only 0.089 min-1. Moreover, the breakage rate exhibits greater variation with the change of particle size. Particularly the breakage rate of -0.425+0.300 mm is notably higher than the other size classes.
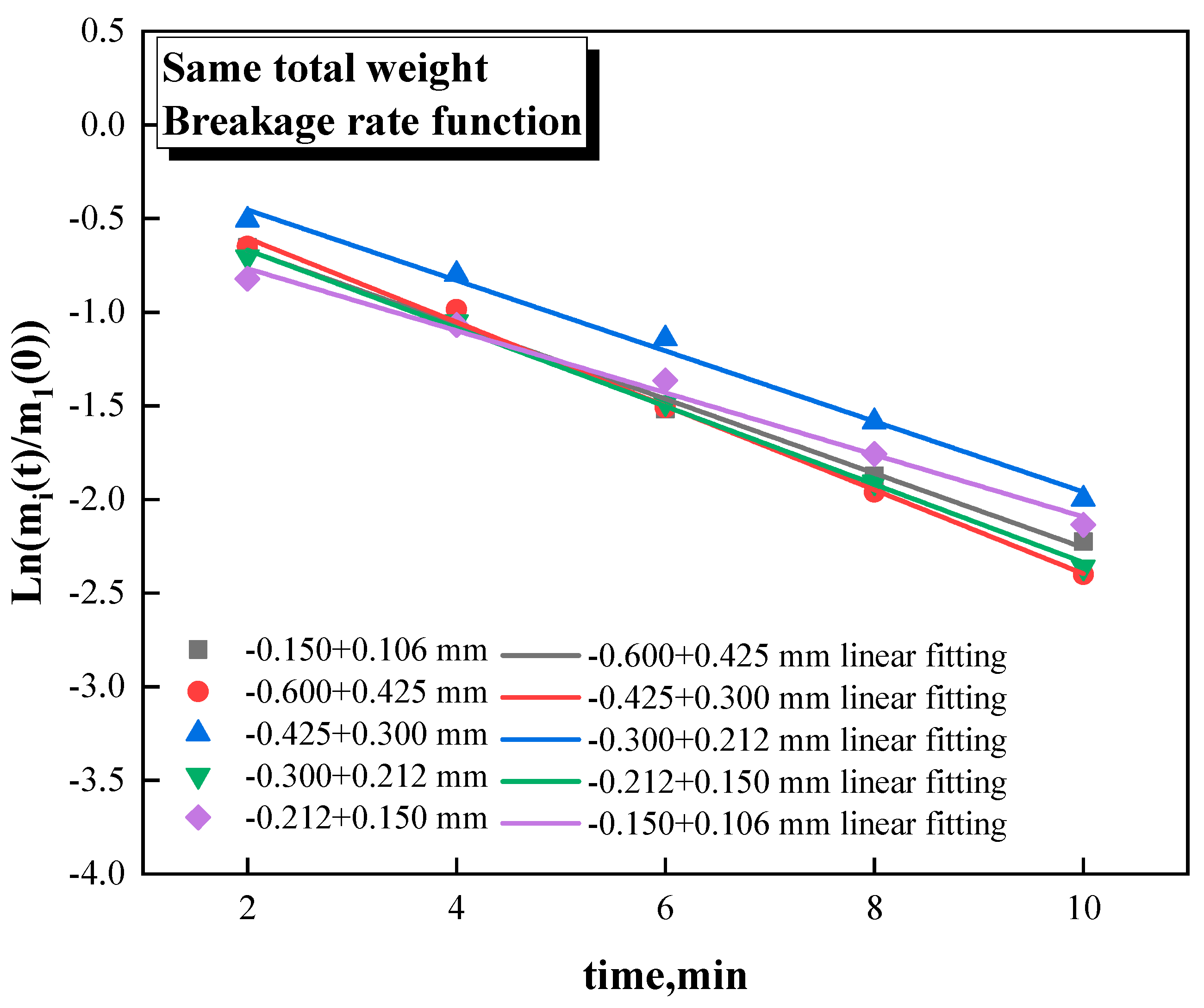
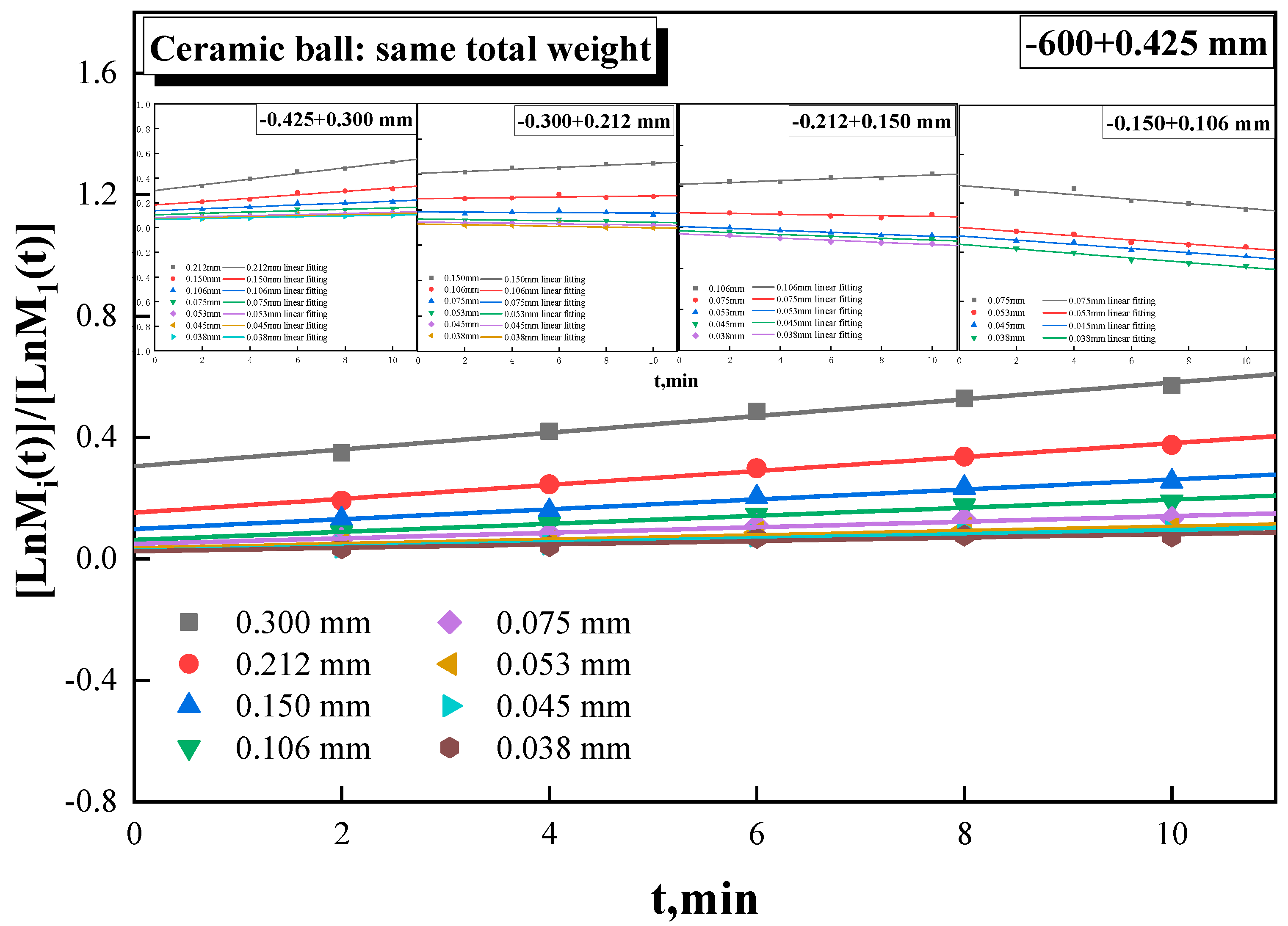
When the loading of ceramic balls was increased to the same media weight as steel ball grinding, the breakage rate of magnetite was significantly increased. As shown in Figure 4, the breakage rate fluctuated between 0.17 min-1 and 0.23 min-1 , which is in proximity to the steel ball grinding, with the highest value of 0.224 min-1 for -0.425 + 0.300 mm and the lowest value of 0.165 min-1 for -0.150 + 0.106 mm.

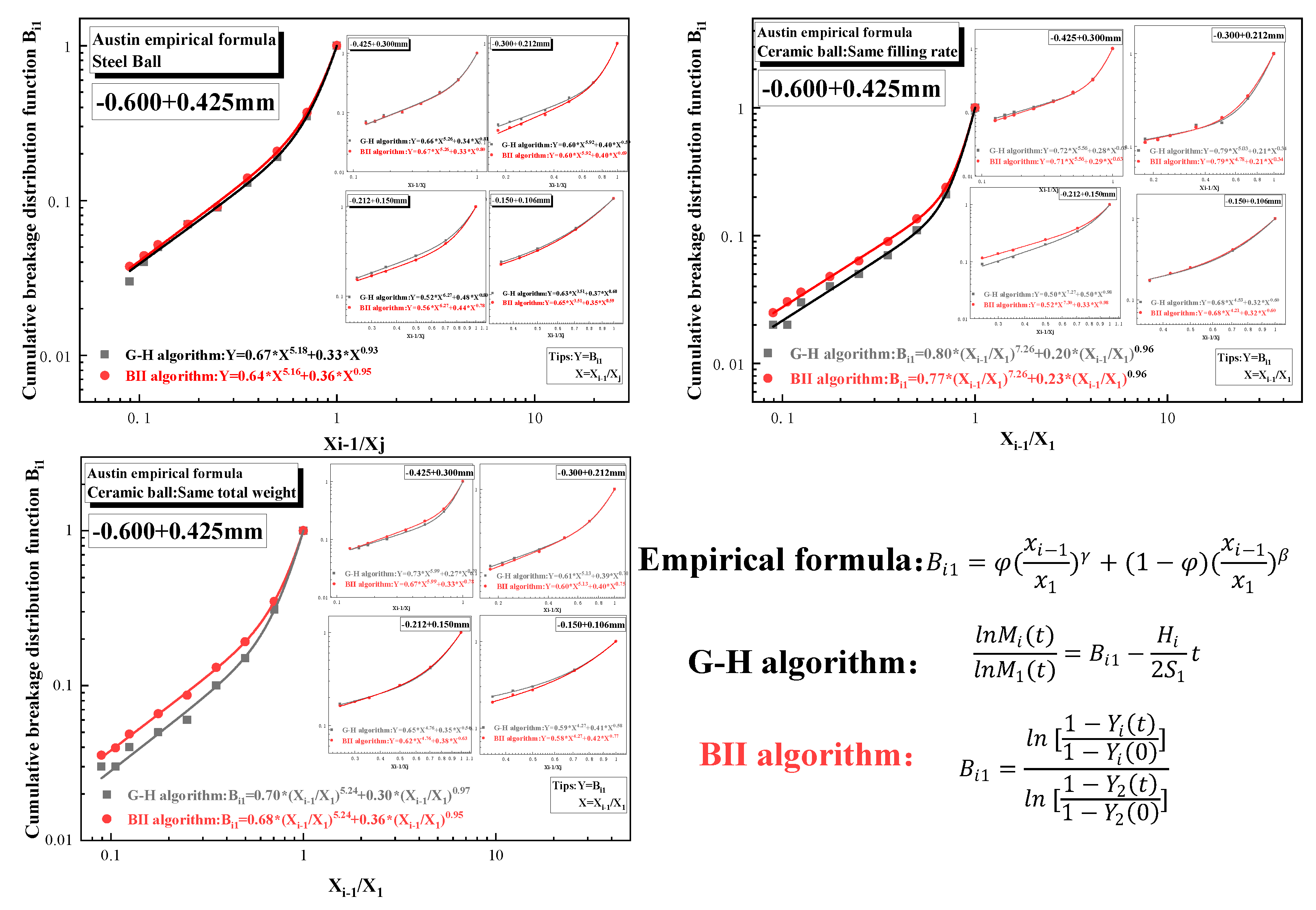
4.2. Cumulative Distribution Function

The cumulative distribution function, in addition to the breakage rate, is an essential grinding kinetic parameter that characterizes the distribution of the crushed particles after mineral breakage. In this section, the G-H algorithm is used to calculate the cumulative distribution function of each feed size under different grinding conditions. From Equation (4), it can be seen that the intercept of the line obtained by fitting with l n M i ( t ) l n M 1 ( t ) as the vertical axis and t as the horizontal axis is the cumulative distribution function Bi1. The G-H algorithm is a very close approximation to the analytical solution[12,13,32]. When the material of one size class is crushed up to 95%, the G-H algorithm can still calculate the distribution of the material in each size class accurately[33,34].
Figure 5 shows the cumulative distribution function for steel ball grinding with values fluctuating between 0 and 0.4. The maximum value is 0.35 for -0.300 + 0.212 mm and a minimum value is 0.03 for -0.045 + 0.038 mm.
Figure 6 and Figure 7 depict the cumulative distribution functions for the same filling rate and the same total weight of the medium respectively. Similar to the variation law of the breakage rate function, the value of the cumulative distribution function of the ceramic ball grinding is much smaller than that of the steel ball grinding at the same filling rate (the maximum value is 0.21). Conversely, the value is basically similar to that of the steel ball grinding at the same total media weight (The maximum value is 0.31).

4.3. Zero-Order Output Characteristics

The purpose of the grinding operation is not only to allow the minerals to facilitate sufficient monomer dissociation, but also to minimize the production of ultrafine particles, which possess a high specific surface energy and tend to adsorb on the surface of the target minerals during the separation process[35,36]. Numerous studies on the kinetic behavior of grinding have consistently shown that the mass of fine particles increases proportionally with the grinding time[37]. Through linear regression analysis, it has been observed that the yield of fines follows a linear relationship with the grinding time, indicating a zero-order output characteristic of the fines. Figure 8 shows the trend of the yield of fines over time, demonstrating a strong linear fit across all the feed size ranges of this experiment. These findings suggest that the fines magnetite exhibits a significant zero-order output characteristic.
The generation rates of each fine, obtained through linear fitting in Figure 8, are summarized in Table 3. For steel ball grinding, when the feed size class is -0.600 + 0.150 mm, the generation rate of -0.075 mm particles remains almost unchanged at an approximate value of 2.60 min-1, and there are only minor fluctuations in the other three size classes.
For the ceramic ball grinding with same filling rate, the lower breakage rate results in a relatively slow generation rate of the fines, with the highest generation rate being only 1.18 min-1. However, it is worth mentioning that the different feed size has a significant effect on the fines generation rate. As the feed size gradually decreases, the fines generation rate initially decreases and then increases, reaching its lowest value at -0.300+0.212 mm.
For the ceramic ball grinding with the same total media weight, the generation rate of fines is slightly higher than that of steel ball grinding. Unlike the previous two grinding methods, there is no clear pattern of variation in the fines generation rate with particle size. However, similar to steel ball grinding, ceramic ball grinding also exhibits a minimum generation rate of fines when the feed size is -0.300 + 0.212 mm.

5. Comparison of Grinding Characteristics

5.1. Breakage Rate Function

The occurrence of a breakage event requires both the particle collision and subsequent breakage. The probability of the particle collision is referred to as collision probability, while the probability of breakage following a collision is known as the breakage probability. For particles in a conventional ball mill, there are two opposing factors to consider. On the one hand, the smaller the particle size, the smaller the mechanical strength of the particle and the greater the probability of breakage. On the other hand, the smaller the particle size, the smaller the probability of collision. So theoretically, the crushing effect of the particles will increase and then decrease with the decrease of the feed size, reaching a maximum at a certain size.
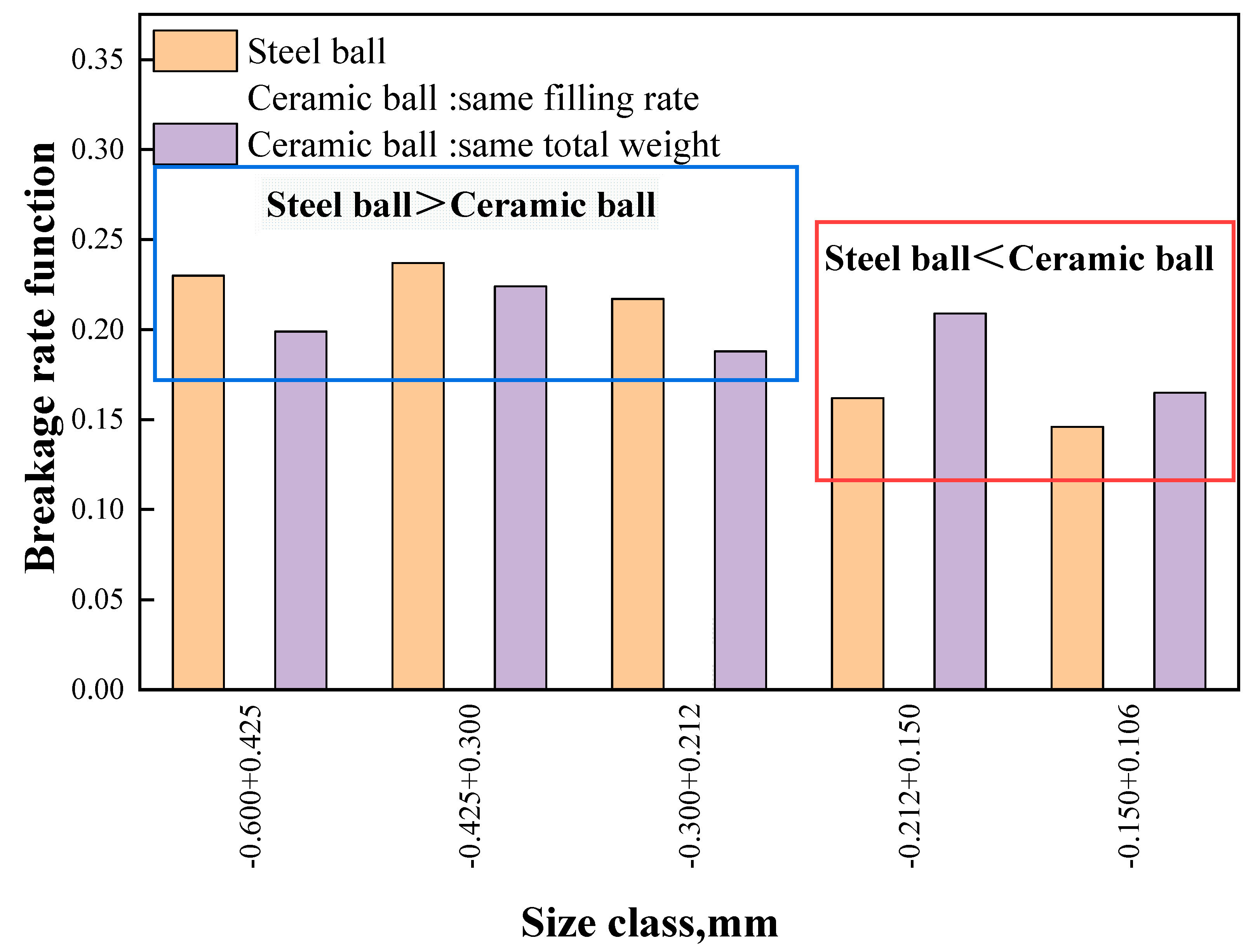
Figure 9 comparison of breakage rate functions shows the breakage rate of each feed size class under different grinding conditions. The variation of the breakage rate for steel ball grinding and ceramic ball grinding with the same filling rate is fully consistent with this theory. The breakage rate increases and then decreases as particle size decreases, reaching a maximum at -0.425+0.300 mm. The breakage rate of ceramic ball grinding with same filling rate is lower than 0.9 min-1. This is due to two reasons: On the one hand, the lower mass of the ceramic ball monomer results in insufficient stress during collision with magnetite, leading to a lower breakage probability. On the other hand, the lower filling rate reduces the low collision probability.
When comparing steel ball grinding and ceramic ball grinding with the same total weight of media, it was found that the average breakage rate of steel ball grinding was 11.93% higher than that of ceramic ball grinding when the feed size was larger than 0.212 mm. Conversely, the average breakage rate of ceramic ball grinding was 21.43% higher than that of steel ball grinding when the feed size was smaller than 0.212 mm. These findings indicated that the feed size is the decisive parameter of ceramic ball grinding. When the size is too large, the ceramic ball grinding is not as effective as the steel ball grinding. However, when the size decreases, the advantage of ceramic ball grinding gradually comes to the fore.

5.2. Cumulative Distribution Function

When it comes to the cumulative distribution function, a second calculation method called BⅡ Algorithm needs to be introduced. The BⅡ algorithm, proposed by Austin, is a method for calculating the cumulative distribution function and gained popularity after the 1980s. In this paper, both G-H algorithm and BⅡ algorithm are used to calculate the cumulative distribution function in order to verify the accuracy of the G-H algorithm. The results obtained from both algorithms are then regressed using Austin empirical formula to finally compare the variability of parameters. The Austin empirical formula is a mathematical model consisting of two power functions that share the same independent variables. This special composition of functions determines that there will be greater errors in the regression calculation process. To enhance the accuracy of the calculation, it is usually necessary to fix the value of a parameter, during the regression calculation, typically denoted as β[38]. Figure 10 shows the cumulative distribution functions obtained by different algorithms for each grain size magnetite in different grinding circumstances. It can be seen that both algorithms yield relatively accurate values of the cumulative distribution functions, indicating that the narrow size magnetite fully conforms to the first-order grinding kinetic behavior.
The individual parameters obtained from the regression calculations are summarized in Table 4. A peculiar phenomenon arises for the three parameters of the cumulative distribution function in the case of magnetite with particle sizes less than 0.600 mm, , where the values of both φ and γ are less than 1. After summarizing similar studies from other scholars[16,22,39-42], it is evident that the law applies to the cumulative distribution function of all minerals. Chimwani[40] has pointed out that the parameter γ is a quantity related to the material properties and its value is generally greater than 0.6.However, this conclusion does not apply to fine magnetite. The values of the parameters φ and 1-φ as coefficients of two power functions must be have one value greater than 0.5 and the other less than 0.5. From the results of the linear regression calculations of the 15 data sets, it can be seen that the value of the parameter φ is always less than 0.5 and the exponent of the power function corresponding to the parameter φ is γ. Combined with the analysis of the generation rate of fine magnetite, for steel ball grinding, the parameter β has the largest value when the generation rate of the finest size class -0.038 mm is the lowest, such as size class -0.212+0.150 mm. For ceramic ball grinding, the parameter β has the largest value when the generation rate of the -0.038 mm is the largest, such as the size class -0.212+0.150 mm at the same filling rate and -0.425+0.300 mm at the same total weight. Therefore, the biggest difference between steel ball grinding and ceramic ball grinding in terms of the cumulative distribution function lies in the variation characteristics of the parameter β with respect to the fines generation rate.

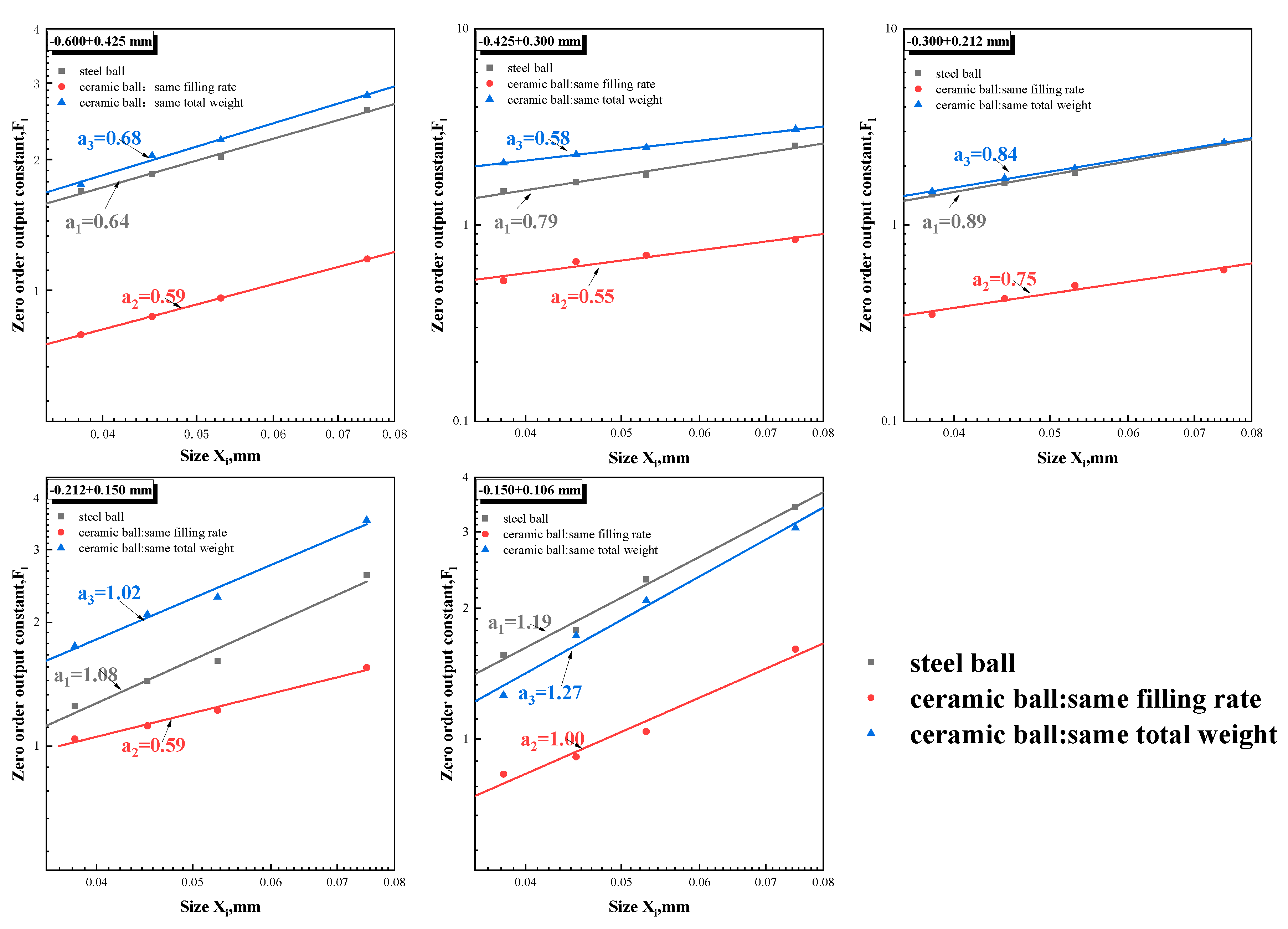
5.3. Zero-Order Output Characteristics

The Equation (10) below was concluded by taking the logarithm of both sides of Equation (8) yields:
l n F i = a l n ( x i ) + l n k
Where Fi is the generation rate of the fine particle size and xi is the corresponding particle size. As shown in Figure 11 with ln(Fi) as the vertical axis and ln(xi) as the horizontal axis, the slope of the straight line obtained by linear fitting is the zero-order output constant a. The zero-order output constant a is a parameter characterizing the relationship between the rate of production of particles smaller than a certain size It is theoretically independent of the ball mill operating condition and the physical properties of the mineral being processed. However, as can be seen in Figure 11, the variation of the value of a is significant regardless of the incoming particle size. The value of a is 0.64 for steel ball grinding, while 0.68 and 0.50 for ceramic ball grinding, taking the incoming particle size class of -0.600+0.425 mm as an example. The fragmentation mechanism during steel ball grinding primarily involves impact caused by ball and mineral collision. This mechanism is related to the compressive strength and impact resistance of minerals[43,44]. While ceramic ball grinding, ball and mineral collision instant kinetic energy is more difficult to complete the breakage of minerals, the crushing process primarily relies on tangential stress-based abrasion, which is related to the wear resistance of the minerals [45].
Figure 12(a) shows the surface morphology of -600+0.325 mm magnetite after grinding by ceramic balls for 6 min. Due to the smaller probability of impact crushing event and a greater occurrence of abrasion event during the grinding process of ceramic balls, a large proportion of fine flaky particles adsorbed on the surface of large particles in the grinding product. Figure 12(b) shows the surface morphology of -600+0.325 mm magnetite after 6 minutes’ of steel ball grinding. Impact crushing results in the formation of irregularly shaped fines, leading to a variety of shapes of fines in the steel ball grinding product.
In summary, the main crushing form of magnetite has changed from impact to abrasion in ceramic ball grinding compared to steel ball grinding, which causes a large change in the value of the zero-order output constant a.
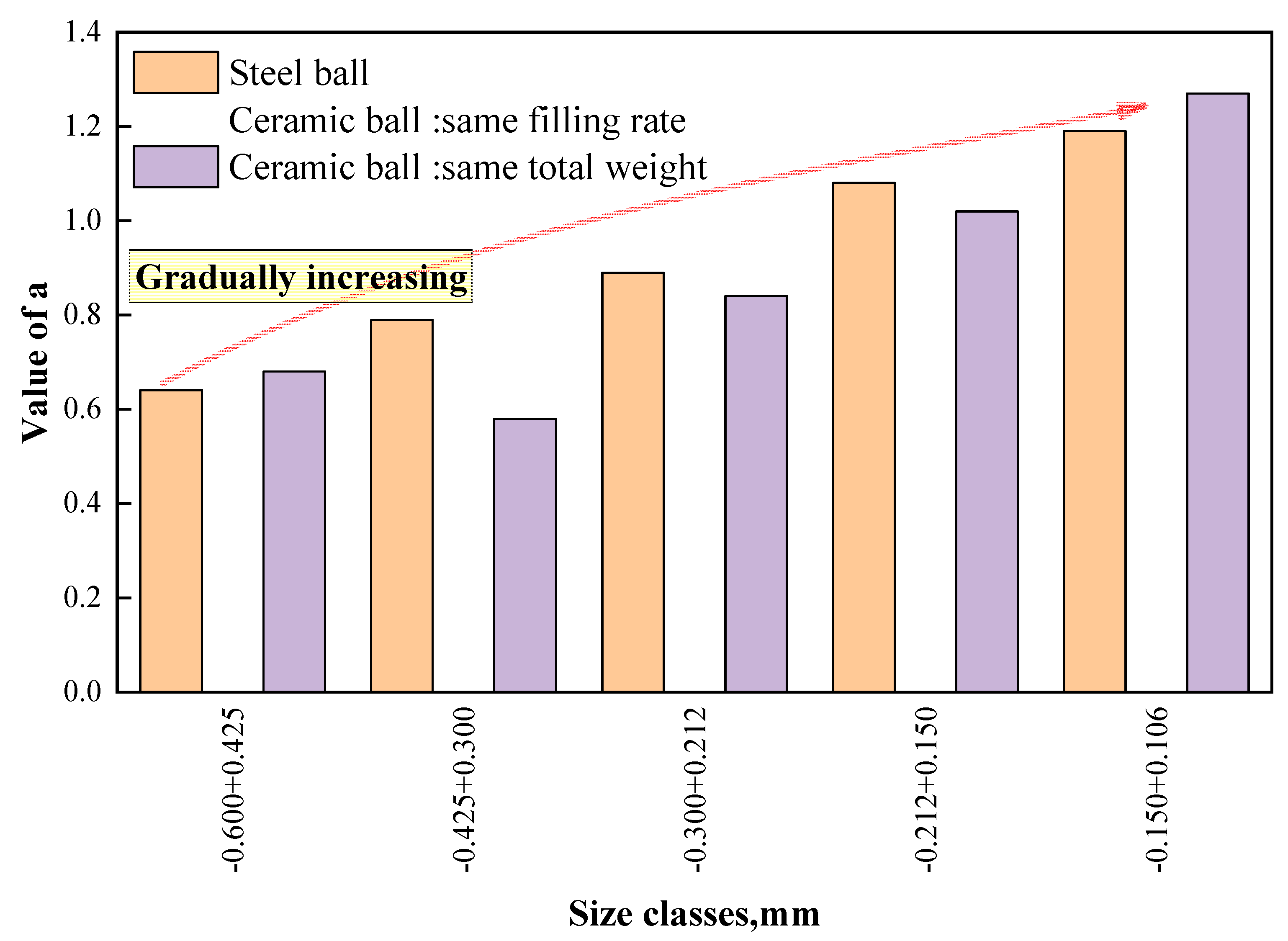
In the course of investigating the zero-order output constant, we made a novel discovery regarding a certain correlation between the value of a and the feed size. Figure 13 shows the relationship between the zero-order output constant and the feed size. It can be seen that for both ceramic and steel ball grinding, as the feed size decreases, the value of a increases. This trend is particularly significant when the breakage rate is higher. Taking steel ball grinding as an example, the value of a for -0.150+0.106 mm magnetite is approximately 1.19, which is roughly twice that of -0.600+0.425 mm magnetite. It shows that the zero-order output constant is influenced not only by the working condition of the ball mill but also by the feed size as long as these changing parameters affecting the mechanical crushing process of the minerals being ground. Therefore, the effects of ball mill media type and feed size need to be fully considered when studying the zero-order output characteristics of mineral grinding processes in the future.

6. Conclusions

In this paper, five size classes magnetite ore were studied, and the grinding kinetics of ceramic ball grinding and steel ball grinding were comparatively studied to derive the ceramic grinding characteristics of fine magnetite. In order to have a more comprehensive understanding of the characteristics of magnetite ceramic ball grinding, two types of ceramic ball grinding methods with the same filling rate and the same total weight as steel ball grinding were chosen in this paper. The comparative study focused on the breakage rate function, cumulative distribution function and zero-order output characteristics of fine magnetite. The findings of the study are as follows:
1.
When magnetite is the ceramic ball ground with the same filling rate, the breakage rate is basically below 0.10 min-1. However, when the ceramic ball ground with the same total weight, the breakage rate is basically around 0.20 min-1 which is close to that of steel ball grinding. Furthermore, the average breakage rate of ceramic ball grinding was 11.93% lower than that of steel ball grinding when the feed size was larger than 0.212 mm, while the average breakage rate of ceramic ball grinding was 21.43% higher than that of steel ball grinding when the feed size was smaller than 0.212 mm.
2.
The biggest difference between steel ball grinding and ceramic ball grinding with respect to the cumulative distribution function is the difference in the variation characteristics of the parameter β with respect to the fines generation rate. For ceramic ball grinding, the parameter β has the largest value when the generation rate of the -0.038 mm is the largest which is exactly the opposite to the trend observed in steel ball grinding.
3.
The main crushing form of magnetite has changed from impact to abrasion in ceramic ball grinding compared with steel ball grinding, leading to a significant change in the value of the zero-order output constant a.
In summary, ceramic ball grinding exhibits distinct kinetic characteristics compared with steel ball grinding, challenging the previous deterministic conclusions about steel ball grinding. The study revealed that the main crushing form of magnetite changed from impact to abrasion in ceramic ball grinding compared with steel ball grinding, which significantly affected the value of the zero-order output constant a. From the above-mentioned analysis, Ceramic ball grinding deserves more attention as an energy-saving grinding method with unique features.

Acknowledgments

The authors gratefully acknowledge the financial support from the National Natural Science Foundation of China (No. 51764015).

References

  1. Austin, L.; Luckie, P. Methods for determination of breakage distribution parameters. Powder Technol. 1972, 5, 215–222. [Google Scholar] [CrossRef]
  2. Austin, L.; Luckie, P. Note on influence of interval size on the first-order hypothesis of grinding. Powder Technol. 1971, 4, 109–110. [Google Scholar] [CrossRef]
  3. Austin, L. G. (1971c). A Review: Introduction to the MathmaticaI Description of Grinding as a Rate Process Powder Technology, 5, 1-17. [CrossRef]
  4. Austin, L. G. (1981). An analysis of fine grinding in ball mill Powder Technology, 28, 83-90.
  5. Austin, L. G. (1999). A discussion of equations for the analysis of batch grinding data Powder Technology, 106, 71-77. [CrossRef]
  6. Bilgili, E.; Yepes, J.; Scarlett, B. Formulation of a non-linear framework for population balance modeling of batch grinding: Beyond first-order kinetics. Chem. Eng. Sci. 2006, 61, 33–44. [Google Scholar] [CrossRef]
  7. Capece, M.; Bilgili, E.; Dave, R. Identification of the breakage rate and distribution parameters in a non-linear population balance model for batch milling. Powder Technol. 2011, 208, 195–204. [Google Scholar] [CrossRef]
  8. Chimwani, N.; Glasser, D.; Hildebrandt, D.; Metzger, M.J.; Mulenga, F.K. Determination of the milling parameters of a platinum group minerals ore to optimize product size distribution for flotation purposes. Miner. Eng. 2013, 43-44, 67–78. [Google Scholar] [CrossRef]
  9. Epstein, B. Logarithmico-Normal Distribution in Breakage of Solids. Ind. Eng. Chem. 1948, 40, 2289–2291. [Google Scholar] [CrossRef]
  10. Fang, X.; Wu, C.; Liao, N.; Yuan, C.; Xie, B.; Tong, J. The first attempt of applying ceramic balls in industrial tumbling mill: A case study. Miner. Eng. 2022, 180, 107504. [Google Scholar] [CrossRef]
  11. Fang, X.; Wu, C.; Yuan, C.; Liao, N.; Chen, Z.; Li, Y.; Lai, J.; Zhang, Z. Can ceramic balls and steel balls be combined in an industrial tumbling mill? Powder Technol. 2022, 412. [Google Scholar] [CrossRef]
  12. Fuerstenau, D.; Phatak, P.; Kapur, P.; Abouzeid, A.-Z. Simulation of the grinding of coarse/fine (heterogeneous) systems in a ball mill. Int. J. Miner. Process. 2011, 99, 32–38. [Google Scholar] [CrossRef]
  13. Genç. ; Ergün,.; Benzer, A. The dependence of specific discharge and breakage rate functions on feed size distributions, operational and design parameters of industrial scale multi-compartment cement ball mills. Powder Technol. 2013, 239, 137–146. [Google Scholar] [CrossRef]
  14. Gupta, V. Validation of an energy–size relationship obtained from a similarity solution to the batch grinding equation. Powder Technol. 2013, 249, 396–402. [Google Scholar] [CrossRef]
  15. Gupta, V.K. Understanding the drawbacks of the currently popular approach to determining the breakage rate parameters for process analysis and mill scale-up design. Part. Sci. Technol. 2019, 38, 821–826. [Google Scholar] [CrossRef]
  16. Gupta, V. Effect of particulate environment on the grinding kinetics of mixtures of minerals in ball mills. Powder Technol. 2020, 375, 549–558. [Google Scholar] [CrossRef]
  17. Gupta, V. Population balance modeling approach to determining the mill diameter scale-up factor: Consideration of size distributions of the ball and particulate contents of the mill. Powder Technol. 2021, 395, 412–423. [Google Scholar] [CrossRef]
  18. Hennart, S.; Wildeboer, W.; van Hee, P.; Meesters, G. Identification of the grinding mechanisms and their origin in a stirred ball mill using population balances. Chem. Eng. Sci. 2009, 64, 4123–4130. [Google Scholar] [CrossRef]
  19. Herbst, J.; Fuerstenau, D. Scale-up procedure for continuous grinding mill design using population balance models. Int. J. Miner. Process. 1980, 7, 1–31. [Google Scholar] [CrossRef]
  20. Hornung, U. (1990). Diffusion Models for Fractured Media. Journal of Mathematic Analysis and Application, 147, 69-80. [CrossRef]
  21. J. Dodds. ( 13, 113–124.
  22. Koleini, S.M.J.; Barani, K.; Rezaei, B. The Effect of Microwave Treatment on Dry Grinding Kinetics of Iron Ore. Miner. Process. Extr. Met. Rev. 2012, 33, 159–169. [Google Scholar] [CrossRef]
  23. Kapur, P. C. (1970). Appropriate solutions to the discretized batch grinding equation Chemistry Engineering Science, 25, 1111-1113.
  24. Kapur, P. An improved method for estimating the feed-size breakage distribution functions. Powder Technol. 1982, 33, 269–275. [Google Scholar] [CrossRef]
  25. Larsson, S.; Pålsson, B.I.; Parian, M.; Jonsén, P. A novel approach for modelling of physical interactions between slurry, grinding media and mill structure in wet stirred media mills. Miner. Eng. 2020, 148. [Google Scholar] [CrossRef]
  26. Li, C.; Gao, Z. Effect of grinding media on the surface property and flotation behavior of scheelite particles. Powder Technol. 2017, 322, 386–392. [Google Scholar] [CrossRef]
  27. Li, P.; Cao, Z.; Zhao, R.; Li, G.; Yu, M.; Zhang, S. The kinetics and efficiency of batch ball grinding with cemented tungsten carbide balls. Adv. Powder Technol. 2020, 31, 2412–2420. [Google Scholar] [CrossRef]
  28. Liao, N.; Wu, C.; Xu, J.; Feng, B.; Wu, J.; Gong, Y. Effect of Grinding Media on Grinding-Flotation Behavior of Chalcopyrite and Pyrite. Front. Mater. 2020, 7. [Google Scholar] [CrossRef]
  29. Norgate, T.; Haque, N. Energy and greenhouse gas impacts of mining and mineral processing operations. J. Clean. Prod. 2010, 18, 266–274. [Google Scholar] [CrossRef]
  30. Ozkan, A.; Yekeler, M.; Calkaya, M. Kinetics of fine wet grinding of zeolite in a steel ball mill in comparison to dry grinding. Int. J. Miner. Process. 2009, 90, 67–73. [Google Scholar] [CrossRef]
  31. Palaniandy, S.; Halomoan, R.; Ishikawa, H. TowerMill circuit performance in the magnetite grinding circuit – The multi-component approach. Miner. Eng. 2018, 133, 10–18. [Google Scholar] [CrossRef]
  32. Petrakis, E.; Stamboliadis, E.; Komnitsas, K. Identification of Optimal Mill Operating Parameters during Grinding of Quartz with the Use of Population Balance Modeling. KONA Powder Part. J. 2017, 34, 213–223. [Google Scholar] [CrossRef]
  33. Purker, P.; Agrawal, R.; Kapur, P. A G-H scheme for back-calculation of breakage rate functions from batch grinding data. Powder Technol. 1986, 45, 281–286. [Google Scholar] [CrossRef]
  34. Qian, H.; Kong, Q.; Zhang, B. The effects of grinding media shapes on the grinding kinetics of cement clinker in ball mill. Powder Technol. 2013, 235, 422–425. [Google Scholar] [CrossRef]
  35. Reichert, M.; Gerold, C.; Fredriksson, A.; Adolfsson, G.; Lieberwirth, H. Research of iron ore grinding in a vertical-roller-mill. Miner. Eng. 2015, 73, 109–115. [Google Scholar] [CrossRef]
  36. Reid, K. J. (1965). A solution to the batch grinding equation Chemistry Engineering Science, 20, 953-963. [CrossRef]
  37. Sedlatschek. ( 6, 148–153.
  38. V.K.Gupta. (1981). The Estimation of Bate and Breakage Distribution P ammeters from Batch Grinding Data for a Complex Pyritic Ore Using a Back-Calculation Method. Powder Technology, 28, 97-106. [CrossRef]
  39. Venkataraman, K.; Fuerstenau, D. Application of the population balance model to the grinding of mixtures of minerals. Powder Technol. 1984, 39, 133–142. [Google Scholar] [CrossRef]
  40. Verma, R.; Rajamani, R.K. Environment-dependent breakage rates in ball milling. Powder Technol. 1995, 84, 127–137. [Google Scholar] [CrossRef]
  41. Yuan, C.; Wu, C.; Fang, X.; Liao, N.; Tong, J.; Yu, C. Effect of Slurry Concentration on the Ceramic Ball Grinding Characteristics of Magnetite. Minerals 2022, 12, 1569. [Google Scholar] [CrossRef]
  42. Yuan, C.; Wu, C.; Ling, L.; Li, Z.; Xie, F.; Yao, X.; Wang, Y. Effect of Intensive Abrasion Breakage on Secondary Ball Mills for Magnetite. Minerals 2023, 13, 713. [Google Scholar] [CrossRef]
  43. Zhang, X.; Han, Y.; Gao, P.; Li, Y. Effects of grinding media on grinding products and flotation performance of chalcopyrite. Miner. Eng. 2019, 145, 106070. [Google Scholar] [CrossRef]
  44. Zhang, X.; Qin, Y.; Jin, J.; Li, Y.; Gao, P. High-efficiency and energy-conservation grinding technology using a special ceramic-medium stirred mill: A pilot-scale study. Powder Technol. 2021, 396, 354–365. [Google Scholar] [CrossRef]
  45. Zhao, R.; Han, Y.; He, M.; Li, Y. Grinding kinetics of quartz and chlorite in wet ball milling. Powder Technol. 2017, 305, 418–425. [Google Scholar] [CrossRef]
Preprints 81819 g001
Figure 1. Experimental protocol and equipment.
Figure 1. Experimental protocol and equipment.
Preprints 81819 g001
Preprints 81819 g002
Figure 2. Breakage rate function of steel ball grinding.
Figure 2. Breakage rate function of steel ball grinding.
Preprints 81819 g002
Preprints 81819 g003
Figure 3. Breakage rate function of ceramic ball grinding with the same filling rate.
Figure 3. Breakage rate function of ceramic ball grinding with the same filling rate.
Preprints 81819 g003
Preprints 81819 g004
Figure 4. Breakage rate function of ceramic ball grinding with the same total media weight.
Figure 4. Breakage rate function of ceramic ball grinding with the same total media weight.
Preprints 81819 g004
Preprints 81819 g005
Figure 5. Cumulative distribution function of steel ball grinding.
Figure 5. Cumulative distribution function of steel ball grinding.
Preprints 81819 g005
Preprints 81819 g006
Figure 6. Cumulative distribution function of ceramic ball grinding with same filling rate.
Figure 6. Cumulative distribution function of ceramic ball grinding with same filling rate.
Preprints 81819 g006
Preprints 81819 g007
Figure 7. Cumulative distribution function of ceramic ball grinding with the same total weight.
Figure 7. Cumulative distribution function of ceramic ball grinding with the same total weight.
Preprints 81819 g007
Preprints 81819 g008
Figure 8. The case of zero-order output characteristics.
Figure 8. The case of zero-order output characteristics.
Preprints 81819 g008
Preprints 81819 g009
Figure 9. Comparison of breakage rate functions.
Figure 9. Comparison of breakage rate functions.
Preprints 81819 g009
Preprints 81819 g010
Figure 10. Regression calculation and comparison of cumulative distribution functions.
Figure 10. Regression calculation and comparison of cumulative distribution functions.
Preprints 81819 g010
Preprints 81819 g011
Figure 11. Comparison of zero-order output constants.
Figure 11. Comparison of zero-order output constants.
Preprints 81819 g011
Preprints 81819 g012
Figure 12. Surface morphology of particles after grinding for 6 min through different grinding.
Figure 12. Surface morphology of particles after grinding for 6 min through different grinding.
Preprints 81819 g012
Preprints 81819 g013
Figure 13. Comparison of the values of the zero-order output characteristics parameter a.
Figure 13. Comparison of the values of the zero-order output characteristics parameter a.
Preprints 81819 g013
Table 1. Compound composition of the magnetite used in the experiment.
Table 1. Compound composition of the magnetite used in the experiment.
Compound Fe3O4 SiO2 SO3 CaO Al2O3 MgO TiO2
Wt/ % 93.64 5.35 2.65 2.08 2.00 1.23 0.852
Table 2. Comparison of physical parameters of grinding media.
Table 2. Comparison of physical parameters of grinding media.
Category Steel Ball Ceramic Ball
Elements Fe, Cr, C Al, Si
Trace elements Si, Mn, P, Mo, Al Ca, Mg
True density / ( t ∙ m − 3 ) 7.3~7.8 3.7
Bulk density / ( t ∙ m − 3 ) 4.85 2.3
Mohs hardness 6.8 9.0
Self-wear / ( g ∙ ( k g ∙ h ) − 1 ) 60 5
Table 3. Generation rate of fine magnetite.
Table 3. Generation rate of fine magnetite.
Feed size classes/ mm size/ mm Generation rate/ min-1
steel grinding same filling rate same total weight
-0.600+0.425 0.075 2.60 1.18 2.82
0.053 2.02 0.96 2.22
0.045 1.85 0.88 2.04
0.038 1.69 0.97 1.75
-0.425+0.300 0.075 2.53 0.84 3.06
0.053 1.79 0.70 2.48
0.045 1.65 0.64 2.30
0.038 1.48 0.52 2.07
-0.300+0.212 0.075 2.60 0.59 2.63
0.053 1.84 0.49 1.94
0.045 1.63 0.43 1.73
0.038 1.43 0.36 1.49
-0.212+0.150 0.075 2.60 1.26 3.54
0.053 1.61 1.22 2.30
0.045 1.44 1.15 2.09
0.038 1.25 1.14 1.75
-0.150+0.106 0.075 3.42 1.61 3.06
0.053 2.34 1.04 2.08
0.045 1.78 0.91 1.73
0.038 1.56 0.82 1.26
Table 4. Parameters of the cumulative distribution function for different size classes.
Table 4. Parameters of the cumulative distribution function for different size classes.
Bi1 -0.600+0.425 mm -0.425+0.300 mm -0.300+0.212 mm -0.212+0.150 mm -0.150+0.106 mm
φ β γ φ β γ φ β γ φ β γ φ β γ
Steel ball 0.34 5.18 0.93 0.34 5.26 0.81 0.40 5.92 0.59 0.48 6.27 0.80 0.35 3.51 0.59
Ceramic ball
(same filling rate)		 0.20 7.26 0.96 0.28 5.56 0.60 0.21 4.78 0.34 0.48 7.30 0.98 0.32 4.53 0.60
Ceramic ball
(same total weight)		 0.30 5.24 0.97 0.27 5.99 0.79 0.40 5.13 0.75 0.38 4.76 0.63 0.42 4.27 0.58
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated